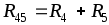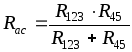Что такое электрическая схема, ветвь, узел, контур.

Электрическая схема представляет собой графическое изображение электрической цепи. Она показывает, как осуществляется соединение элементов в рассматриваемой электрической цепи.

Простым языком электрическая схема это упрощенное изображение электрической цепи.

Для отображение электрических компонентов (конденсаторов, резисторов, микросхем и т. д.) в электрических схемах используются их условно графические обозначения.  

Для отображения электрических соединений (дорожек, проводов, соединения между радиоэлементами) применяют простую линию соединяющие два условно графических обозначения. Причём все ненужные изгибы дорожек удаляют.

В состав электрической схемы входят: ветвь и условно графические обозначение электрических элементов так же могут входить контур и узел.

 

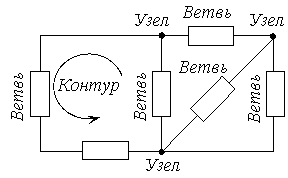
  Ветвь – участок цепи состоящий из одного или нескольких элементов вдоль которого ток один и тот же.

Ветви присоединённые к одной паре узлов называются параллельными.

Любой замкнутый путь, проходящий по нескольким ветвям называется контуром. На верхнем рисунке, контурами можно считать ABD; BCD; ABC.

Узел – место соединения трёх и 

более ветвей. 

• Узел A
• Узел B
• Узел C
• Узел D

Точки К и Е не являются узлами.

Электрическая цепь — Википедия

Материал из Википедии — свободной энциклопедии

Электрическая цепь
Условное обозначение электрической цепи
Изучается в	Теория электрических цепей[d]
Альтернативное имя	гальваническая цепь
Медиафайлы на Викискладе

Электри́ческая цепь (гальвани́ческая цепь) — совокупность устройств, элементов, предназначенных для протекания электрического тока, электромагнитные процессы в которых могут быть описаны с помощью понятий сила тока и напряжение.

Изображение электрической цепи с помощью условных знаков называют электрической схемой (рисунок 1).

Неразветвленные и разветвленные электрические цепи[править | править код]

Рисунок 1 — Разветвленная цепь

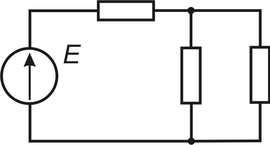
Электрические цепи подразделяют на неразветвленные и разветвленные. Во всех её элементах неразветвленной цепи течёт один и тот же ток. Простейшая разветвленная цепь изображена на рисунке 1. В ней имеются три ветви и два узла. В каждой ветви течёт свой ток. Ветвь можно определить как участок цепи, образованный последовательно соединенными элементами (через которые течёт одинаковый ток) и заключённый между двумя узлами. В свою очередь, узел есть точка цепи, в которой сходятся не менее трёх ветвей. Если в месте пересечения двух линий на электрической схеме поставлена точка (рисунок 1), то в этом месте есть электрическое соединение двух линий, в противном случае его нет. Узел, в котором сходятся две ветви, одна из которых является продолжением другой, называют устранимым или вырожденным узлом.

Линейные и нелинейные электрические цепи[править | править код]

Линейной электрической цепью называют такую цепь, все компоненты которой линейные. К линейным компонентам относятся зависимые и независимые идеализированные источники токов и напряжений, резисторы (подчиняющиеся закону Ома), и любые другие компоненты, описываемые линейными дифференциальными уравнениями, наиболее известны электрические конденсаторы и катушки индуктивности. Если цепь содержит отличные от перечисленных компоненты, то она называется нелинейной.

Изображение электрической цепи с помощью условных обозначений называют электрической схемой. Функция зависимости тока, протекающего по двухполюсному компоненту, от напряжения на этом компоненте называется вольт-амперной характеристикой (ВАХ). Часто ВАХ изображают графически в декартовых координатах. При этом по оси абсцисс на графике обычно откладывают напряжение, а по оси ординат — ток.

В частности, омические резисторы, ВАХ которых описывается линейной функцией и на графике ВАХ являются прямыми линиями, называют линейными.

Примерами линейных (как правило, в очень хорошем приближении) цепей являются цепи, содержащие только резисторы, конденсаторы и катушки индуктивности без ферромагнитных сердечников.

Некоторые нелинейные цепи можно приближенно описывать как линейные, если изменение приращений токов или напряжений на компоненте мало, при этом нелинейная ВАХ такого компонента заменяется линейной (касательной к ВАХ в рабочей точке). Этот подход называют «линеаризацией». При этом к цепи может быть применён мощный математический аппарат анализа линейных цепей. Примерами таких нелинейных цепей, анализируемых как линейные, являются практически любые электронные устройства, работающие в линейном режиме и содержащие нелинейные активные и пассивные компоненты (усилители, генераторы и др.).

Законы, действующие в электрических цепях[править | править код]

• Электротехника: Учеб. для вузов/А. С. Касаткин, М. В. Немцов. — 7-е изд., стер.— М.: Высш. шк., 2003.— 542 с.: ил. ISBN 5-06-003595-6
• Бессонов Л. А. Теоретические основы электротехники. Электрические цепи. — М.: Гардарики, 2002. — 638 с. — ISBN 5-8297-0026-3.

8.Электрическая схема, её ветви, узлы, контуры.

Электрическая схема представляет собой графическое изображение электрической цепи. Она показывает, как осуществляется соединение элементов рассматриваемой электрической цепи

Ветвь образуется одним или несколькими последовательно соединенными элементами цепи.

Узел — место соединения трех или большего числа ветвей.

Любой замкнутый путь, проходящий по нескольким ветвям, называется контуром

9.Последовательное и параллельное соединение элементов. Устранимый узел.

Под последовательным сопротивлением понимают такое соединение, при котором через все элементы проходит один и тот же ток.

Ветви, присоединенные к 1-ой паре узлов – параллельные ветви. Напряжение на всех параллельных ветвях одинаково.

Узел – место соединения 3-ех и большего числа ветвей.

Устранимый узел – место соединения 2-ух ветвей.

10.Закон Ома для пассивного и активного участка электрической цепи. Применение закона Ома

Закон Ома для пассивного участка электрической цепи.

При протекании электрического тока через сопротивление R, напряжение U и ток I на этом участке связаны между собою согласно закону Ома: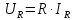

Сопротивление R — это коэффициент пропорциональности между током и напряжением.

Закон Ома можно записать через разность потенциалов:

Закон Ома для активного участка цепи между точками а и в имеет вид:

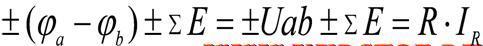
Напряжение на участке электрической цепи Uab и ЭДС берутся со знаком «плюс», если их направление совпадает с направление протекания тока. Напряжение (разность потенциалов) и источник электродвижущей силы берутся со знаком «минус», если их направление не совпадает с направлением протекания тока.

Пример составления уравнения по закону Ома

Рассмотрим пример решения задачи на составления уравнения по закону Ома для участка линейной электрической цепи с двумя источниками ЭДС.

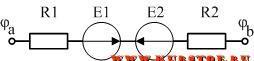
Пусть в данной электрической цепи направление тока будет из точки «a» в точку «b». Напряжение Uab Направляется всегда из первой буквы («a») к последней («b»).

Согласно правилу составления уравнения по закону Ома источник ЭДС E1 берем со знаком «плюс», т.к. его направление (направление стрелочки) совпадает с направлением протекающего тока.

Источник ЭДС E2 берем со знаком «минус», т.к. его направление (направление стрелочки) не совпадает с направлением протекающего тока.

Напряжение Uab или разность потенциалов φa — φb берем со знаком «плюс», т.к. его направление совпадает с направление протекающего тока.

Сопротивление R1 и R1 соединены последовательно. При последовательном соединении сопротивлений их эквивалентное значение равно сумме.

В результате составленное уравнение по закону Ома будет иметь вид:

Пусть потенциал в данной задаче потенциал точки «а» равен 10 вольт, потенциал точки «b» = 7 вольт, E1=25 В, E2=17 В, R1=5 Ом, R2=10 Ом. Рассчитаем величину тока:

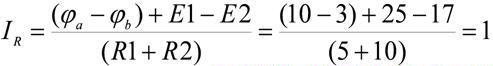
Полученный ток равен 1 Ампер.

11. Потенциальная диаграмма и ее построение

Под потенциальной диаграм­мой понимают график распределения потенциала вдоль какого-ли­бо участка цепи или замкнутого контура. По оси абсцисс на нем откладывают сопротивления вдоль контура, начиная с какой-либо произвольной точки, по оси ординат — потенциалы. Каждой точке участка цепи или замкнутого контура соответствует своя точка на потенциальной диаграмме.

Потенциальная диаграмма построена, начиная с точки a, которая условно принята за начало отсчета. Потенциал _aпринят равным нулю.

Точка цепи, потенциал которой условно принимается равным нулю, называется базисной.

Если в условии задачи не оговорено, какая точка является базисной, то можно потенциал любой точки условно приравнивать к нулю. Тогда потенциалы всех остальных точек будут определяться относительно выбранного базиса.

3.Топологические элементы электрической цепи (ветвь, узел, контур). Положительные направления тока, напряжения и эдс.

Ветвь – это участок электрической цепи от одного узла до другого узла. Ветвь обычно содержит один или несколько последовательно соединенных элементов цепи: сопротивления, источники ЭДС или источники тока.

Узел – это участок электрической цепи, содержащий соединения трех или более числа ветвей. Ветви, которые подключены к одной паре узлов называются 

параллельными. Параллельные ветви или параллельное соединение ветвей всегда находится под общим (одинаковым по величине) напряжением.

Контур — это замкнутый участок электрической цепи. Любой замкнутый путь, проложенный через ветви цепи и есть замкнутый контур

За положительные направления ЭДС источника принимают направления от концов фаз к их началам. Как это обычно делается для источников, фазные токи направляют согласно с ЭДС, а фазные напряжения — в противоположную сторону.

Линейные напряжения направляют следующим образом: напряжение U_ab — от а к b, U_bc — отb к с, U_ca — от с к а. Линейные токи во всех линейных проводах направляют к приемникам.

Фазные напряжения и токи приемников направляют в одну и ту же сторону, как это обычно делается для приемников. Ток нейтрального провода IN направляют от приемника к источнику

4. Закон Ома.

Зако́н О́ма — физический закон, определяющий связь электродвижущей силы источника или электрического напряжения с силой тока и сопротивлением проводника.

Закон Ома для полной цепи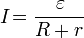

Другая запись формулы

Формулировка: Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи

5.Законы Кирхгофа

Первое правило Кирхгофа:

 Алгебраическая сумма токов в каждом узле любой цепи равна нулю. При этом втекающий в узел ток принято считать положительным, а вытекающий — отрицательным:

Второе правило Кирхгофа:

Алгебраическая сумма падений напряжений на всех ветвях, принадлежащих любому замкнутому контуру цепи, равна алгебраической сумме ЭДС ветвей этого контура. Если в контуре нет источников ЭДС, то суммарное падение напряжений равно нулю:

для постоянных напряжений:

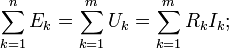
для переменных напряжений: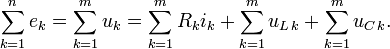

6.Свойства последовательного и параллельного соединения

Свойства последовательного соединения

А)При последовательном соединении проводников сила тока в них одинакова

Б) Напряжение на участке, состоящем из последовательно соединённых проводников, равно сумме напряжений на каждом проводнике

В) Сопротивление участка, состоящего из последовательно соединённых проводников, равно сумме сопротивлений каждого проводника

Свойства параллельного соединения

А) Напряжение на каждой ветви одинаково и равно напряжению на неразветвлённой части цепи.

Б) Сила тока в неразветвлённой части цепи равна сумме сил токов в каждой ветви

В) Величина, обратная сопротивлению участка параллельного соединения, равна сумме величин, обратных сопротивлениям ветвей

7.Расчет цепи постоянного тока с единственным источником

8.Метод контурных токов

Метод контурных токов — метод сокращения размерности системы уравнений, описывающей электрическую цепь

Идея метода контурных токов: уравнения составляются только по второму закону Кирхгофа, но не для действительных, а для воображаемых токов, циркулирующих по замкнутым контурам, т.е. в случае выбора главных контуров равных токам ветвей связи. Число уравнений равно числу независимых контуров, т.е. числу ветвей связи графа . Первый закон Кирхгофа выполняется автоматически. Контуры можно выбирать произвольно, лишь бы их число было равно  и чтобы каждый новый контур содержал хотя бы одну ветвь, не входящую в предыдущие. Такие контуры называются независимыми.

Направления истинных и контурных токов выбираются произвольно. Выбор положительных направлений перед началом расчета может не определять действительные направления токов в цепи. Если в результате расчета какой-либо из токов, как и при использовании уравнений по законам Кирхгофа, получится со знаком “-”, это означает, что его истинное направление противоположно.

При составлении уравнений необходимо помнить следующее:

 — сумма сопротивлений, входящих в i-й контур;

 — сумма сопротивлений, общих для i-го и k-го контуров, причем    ;

-члены на главной диагонали всегда пишутся со знаком “+”;

-знак “+” перед остальными членами ставится в случае, если через общее сопротивление  i-й и k- й контурные токи проходят в одном направлении, в противном случае ставится знак “-”;

-если i-й и k- й контуры не имеют общих сопротивлений, то ;

-в правой части уравнений записывается алгебраическая сумма ЭДС, входящих в контур: со знаком “+”, если направление ЭДС совпадает с выбранным направлением контурного тока, и “-”, если не совпадает

3.Раскройте понятия схема электрической цепи, узел, ветвь, контур. Приведите пример. Укажите количество узлов, ветвей и независимых контуров в электрической цепи (рисунок 1)

Графическое изображение электрической цепи, содержащее условные обозначения ее элементов, называется схемой электри­ческой цепи.

Участок, вдоль которого ток один и тот же, называется ветвью электрической цепи.

Место соединения ветвей называется узлом электрической цепи.

Узел образуется при соединении в одной точке не менее трех ветвей, например на схеме рис. 3.16 к узлу 6 подключены четыре ветви.Всего узлов четыре 1,3,4,6.

Ветви, не содержащие источников электрической энергии, называются пассивными, а ветви, в которые входят ис­точники,—активными.

Любой замкнутый путь, проходящий по нескольким ветвям, называется контуром электрической цепи. Контур не включающий в себя остальные называется назависимым контуром электрической цепи.

На рис. 3.16 таких контуров четыре:1-2-3-1; 1-3-6-1; 3-4-6-3, 4-5-6-4.

На схемах стрелками отмечаются положительные направления ЭДС напряжений и токов. Направление ЭДС может быть указано обозначением полярности зажимов источника: внутри источника ЭДС направлена от отрицательного зажима к положи­тельному (так же как и ток).

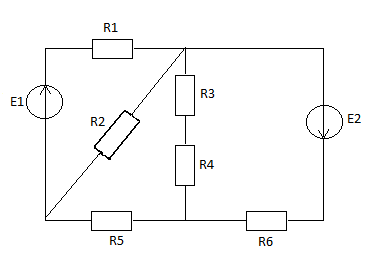
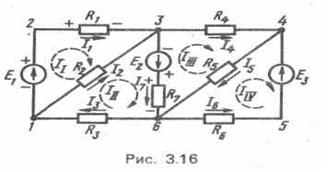
Рисунок 1-Схема электрической цепи

В предложенной схеме (рисунок 1)

количество узлов 3

количество ветвей 5

количество независимых контуров3

4.Сформулируйте первый и второй законы Кирхгофа. Приведите примеры в общем виде.

Первый закон Кирхгофа

Первый закон Кирхгофа применяется к узлу электрической цепи: алгебраическая сумма токов в ветвях соединённых в один узел равна нулю:

∑ I  = 0 , (1)

где I – ток в ветви,А.

В эту сумму токи входят с разными знаками, в зависимости от направления их по отношению к узлу. На основании первого закона Кирхгофа для каждого узла можно составить уравнение токов. Например для схемы 1 уравнения имеют вид:

Узел 1: — I1 – I2 + I3 =0

Узел 3: I1 + I2 – I7 – I4 = 0

Узел 4: I4 – I5 + I6 = 0

Узел 6: — I3 + I7 + I5 – I6 = 0

Этот закон следует из принципа непрерывности тока. Если допустить преобладание в узле токов одного направления, то заряд одного знака должен накапливаться, а потенциал узловой точки непрерывно изменяться, что в реальных цепях не наблюдается.

Пример:

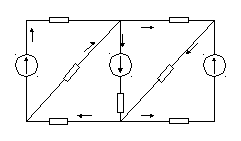
2 R1 3 R4 4

I1 I7 I4

I2 I5

E1 R2 E2 R5 E3

R3 I3 R7 I6 R6

1 6 5

Рисунок 1-Схема электрической цепи

Второй закон Кирхгофа

Второй закон Кирхгофа применяется к контурам электрических цепей: в контуре электрической цепи алгебраическая сумма ЭДС , входящих в контур,равна алгебраической сумме падений напряжений на пассивных элементах этого контура:

∑ E = ∑IR, (2)

где I – ток в ветви,А;

Е-ЭДС,В;

R-сопротивление, Ом.

При этом положительными считаются токи и ЭДС, направление которых совпадает с направлением обхода.

Согласно этому правилу, запишем уравнения для двух других контуров схемы, представленной на схеме 1:

для 1-2-3-1

I1R1 – I2R2 = E1

для 3-4-6-3

I4R4 + I5R5 – I7R7 = -E2

для 1-3-6-1

I7R7 + I2R2 + I3R3 = E2

для 6-5-4-6

I6R6 + I5R5 = E3

Структура электрической цепи

К структурным или топологическим свойствам цепи относятся такие ее особенности, которые не связаны с характеристиками входящих в нее активных и пассивных элементов. К ним относятся следующие понятия: ветвь, узел, контур.

Ветвью электрической цепи называют участок, элементы которого включены последовательно друг за другом и обтекаются одним и тем же током.

Узлом электрической цепи называют место соединения нескольких ветвей. Узел связывает не менее трех ветвей и является точкой разветвления.

Ветви считаются соединенными последовательно, если они обтекаются одним и тем же током. Ветви считаются соединенными параллельно, если они присоединены к одной и той же паре узлов. Таким образом, при последовательном соединении элементов общим параметром для них является ток, при параллельном – напряжение между узлами.

Контуром электрической цепи называется совокупность следующих друг за другом ветвей. Узлы, в которых эти ветви соединяются, являются точками разветвления. При обходе замкнутого контура начальная и конечная точки совпадают. В дальнейшем под контуром понимается замкнутый контур.

Цепь, в которой отсутствуют разветвления, называют одноконтурной, при наличии разветвлений – многоконтурной. Многоконтурная цепь характеризуется числом независимых контуров. Совокупность независимых контуров определяется тем, что каждый из последующих контуров, начиная от элементарного, отличается по меньшей мере одной новой ветвью. Число независимых контуров может быть определено по формуле Эйлера:

(1.8)

где m – количество ветвей,

n – количество узлов, причем m > n всегда.

Пример.

В цепи на рис. 1.10. четыре узла: a, b, c, d; шесть ветвей: ab, bd, bc, ad, dc, ac. Т.о., количество независимых контуров по формуле Эйлера определится следующим образом:

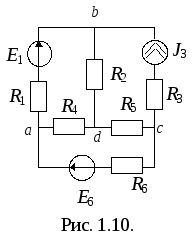
p = 6 — 4 + 1 = 3.

Это могут быть следующие контуры: abcd, dbc, adc или abd, dbca, adc и другие.

3. Законы Кирхгофа

Законы Кирхгофа являются основой теории линейных цепей и представляют собой так же, как и закон Ома, обобщение опытных данных.

I закон Кирхгофа (для токов): алгебраическая сумма токов в узле равна нулю, или сумма притекающих и сумма истекающих токов одинаковы. Как правило, при суммировании притекающие токи берутся со знаком «+», а истекающие – со знаком «–».

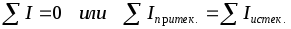(1.8)

II закон Кирхгофа (для напряжений): алгебраическая сумма ЭДС всех источников, встречающихся при обходе контура, равна алгебраической сумме напряжений на всех потребителях. В алгебраической форме

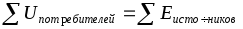. (1.8)

В сумму со знаком «+» входят ЭДС содействующих источников (т.е. тех источников, которые действуют в направлении, согласном с обходом контура) и со знаком «–» ЭДС противодействующих источников. При суммировании напряжений потребителей со знаком «+» берутся напряжения на всех потребителях, токи которых направлены согласно с обходом контура, и со знаком «–» берутся напряжения всех остальных потребителей. Направление обхода контура выбирается произвольно.

4. Преобразование линейных пассивных электрических цепей

Эквивалентное преобразование части пассивной электрической цепи состоит в такой ее замене другой пассивной цепью, при которой остаются неизменными токи и напряжения остальной цепи, не подвергшейся преобразованию. К простейшим преобразованиям относятся замена последовательно и параллельно соединенных потребителей эквивалентным потребителем.

При последовательном соединении роль эквивалентного сопротивления (или сопротивления эквивалентного потребителя) играет сумма сопротивлений всех потребителей (рис. 1.11.).

(1.10) Это следует из II закона Кирхгофа: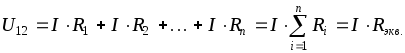

(1.11)

При двух последовательно соединенных потребителях:

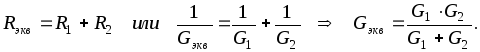(1.12)

При параллельном соединении роль эквивалентной проводимости (или проводимости эквивалентного потребителя) играет сумма проводимостей всех потребителей (рис. 1.12.).

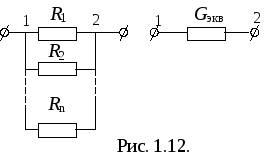
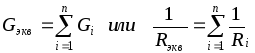. (1.13)

Это следует из I закона Кирхгофа:

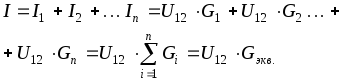При двух параллельно соединенных потребителях:

(1.14)

Таким образом, для расчета цепей с последовательно включенными потребителями целесообразно их свойства выражать значениями сопротивлений, а для параллельно включенных – значениями проводимостей.

Определение эквивалентного сопротивления при смешанном соединении потребителей выполняется путем постепенного упрощения (сворачивания) исходной цепи.

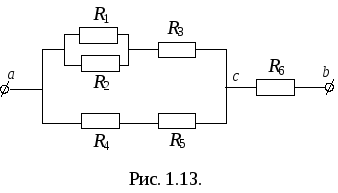
Пример.

1. 

   Параллельное соединение R₁ и R₂:

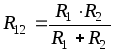
2. Последовательное соединение R₁₂ и R₃:

3. Последовательное соединение R₄ и R₅:

4. Параллельное соединение R₁₂₃ и R₄₅:

5. Последовательное соединение R_ас и R_6:

Таким образом, эквивалентное сопротивление

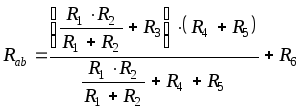
Более сложными являются взаимные преобразования потребителей, соединенных звездой или треугольником. К таким преобразованиям следует обращаться в тех случаях, когда в цепи, подлежащей упрощению, нельзя выделить параллельное или последовательное соединения потребителей.

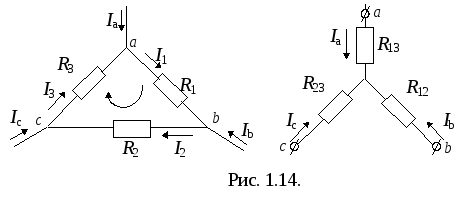
В узлах a, b, c и треугольник , и звезда на рис. 1.14. соединяются с остальной частью схемы. Преобразование треугольника в звезду должно быть таковым, чтобы при одинаковых значениях потенциалов одноименных точек треугольника и звезды притекающие к этим точкам токи были одинаковы, тогда вся внешняя схема «не заметит» произведенной замены.

Выразим U_ab треугольника через параметры потребителей и притекающие к этим узлам токи. Запишем уравнения Кирхгофа для контура и узлов a и b.

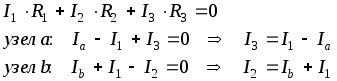
Заменим в первом уравнении токи I₃ и I₂ на соответствующие выражения:

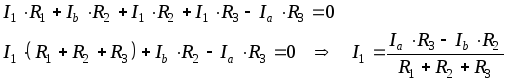
По закону Ома напряжение U_ab для соединения потребителей треугольником:

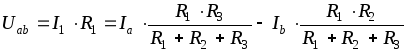(1.15)

Теперь получим выражение для этого же напряжения при соединении потребителей звездой:

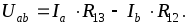(1.16)

Для эквивалентности данных цепей при произвольных значениях токов I_a и I_b необходимо равенство напряжений U_ab для соединения потребителей треугольником и звездой. Это возможно только при одинаковых коэффициентах уравнений (1.15) и (1.16), т.е.

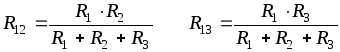(1.17)

Аналогично можно получить выражения для определения :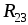

(1.18)

Таким образом, сопротивление луча звезды равно произведению сопротивлений прилегающих сторон треугольника, деленному на сумму сопротивлений трех сторон треугольника.

Формулы обратного преобразования можно вывести независимо, либо как следствие соотношений (1.17) и (1.18) через проводимости:

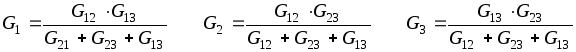(1.19)

или через сопротивления:

(1.20)

Следовательно, сопротивление стороны треугольника равно сумме сопротивлений прилегающих лучей звезды и произведения их, деленного на сопротивление третьего луча.

Ветвь электрической цепи — это… Что такое Ветвь электрической цепи?



Строительный словарь.

• Вероятность восстановления
• Взрывобезопасное электротехническое изделие (электротехническое устройство, электрооборудование)

Смотреть что такое «Ветвь электрической цепи» в других словарях:

• Ветвь электрической цепи — участок электрической цепи, вдоль которого протекает один и тот же электрический ток… Источник: ЭЛЕКТРОТЕХНИКА . ТЕРМИНЫ И ОПРЕДЕЛЕНИЯ ОСНОВНЫХ ПОНЯТИЙ. ГОСТ Р 52002 2003 (утв. Постановлением Госстандарта РФ от 09.01.2003 N 3 ст) …   Официальная терминология

• ветвь электрической цепи — Участок электрической цепи, вдоль которого протекает один и тот же ток [ГОСТ 19880 74] [ОАО РАО «ЕЭС России» СТО 17330282.27.010.001 2008] Тематики электротехника, основные понятия EN circuit branchelectric circuit branch …   Справочник технического переводчика

• ветвь (электрической цепи) — 102 ветвь (электрической цепи) Участок электрической цепи, вдоль которого протекает один и тот же электрический ток Источник: ГОСТ Р 52002 2003: Электротехника. Термины и определения основных понятий оригинал документа …   Словарь-справочник терминов нормативно-технической документации

• Ветвь электрической цепи — 93. Ветвь электрической цепи Участок электрической цепи, вдоль которого протекает один и тот же ток Источник: ГОСТ 19880 74: Электротехника. Основные понятия. Термины и определения оригинал документа …   Словарь-справочник терминов нормативно-технической документации

• Ветвь (электрической цепи) — 1. Участок электрической цепи, вдоль которого протекает один и тот же электрический ток Употребляется в документе: ГОСТ Р 52002 2003 Электротехника. Термины и определения основных понятий …   Телекоммуникационный словарь

• ветвь электрической цепи — Весь участок электрической цепи, вдоль которого в любой момент времени ток имеет одно и то же значение …   Политехнический терминологический толковый словарь

• путь графа (электрической цепи) — 208 путь графа (электрической цепи) Непрерывная последовательность ветвей графа электрической цепи, в которой любая ветвь и любой узел встречаются только один раз Источник: ГОСТ Р 52002 2003: Электротехника. Термины и определения основных понятий …   Словарь-справочник терминов нормативно-технической документации

• связь графа (электрической цепи) — 206 связь графа (электрической цепи) Ветвь графа электрической цепи, не принадлежащая его дереву Источник: ГОСТ Р 52002 2003: Электротехника. Термины и определения основных понятий оригинал документа …   Словарь-справочник терминов нормативно-технической документации

• Путь графа (электрической цепи) — 1. Непрерывная последовательность ветвей графа электрической цепи, в которой любая ветвь и любой узел встречаются только один раз Употребляется в документе: ГОСТ Р 52002 2003 Электротехника. Термины и определения основных понятий …   Телекоммуникационный словарь

• Связь графа (электрической цепи) — 1. Ветвь графа электрической цепи, не принадлежащая его дереву Употребляется в документе: ГОСТ Р 52002 2003 Электротехника. Термины и определения основных понятий …   Телекоммуникационный словарь