Векторная диаграмма токов и напряжений: график, обозначения, виды
Использование векторных диаграмм при анализе, расчете цепей переменного тока делает возможным рассмотреть более доступно и наглядно происходящие процессы, а также в некоторых случаях значительно упростить выполняемые расчеты.
Векторной диаграммой принято называть геометрическое представление изменяющихся по синусоидальному (либо косинусоидальному) закону направленных отрезков — векторов, отображающих параметры и величины действующих синусоидальных токов, напряжений либо их амплитудных величин.
Широкое применение векторные диаграммы нашли в электротехнике, теории колебаний, акустике, оптике и т.д.
Различают 2-х вида векторных диаграмм:
- точные;
- качественные.
Интересное видео о векторных диаграммах смотрите ниже:
Точные изображаются по результатам численных расчетов при условии соответствия масштабов действующих значений.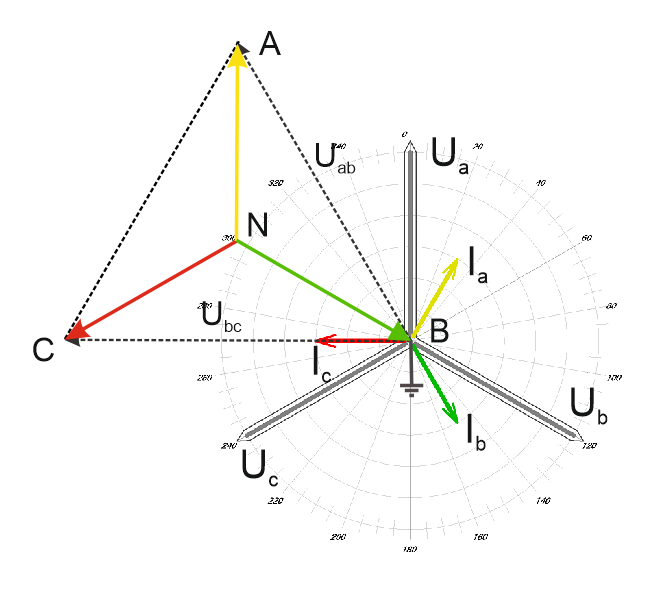
При их построении можно геометрически определить фазы и амплитудные значения искомых величин.
Васильев Дмитрий Петрович
Профессор электротехники СПбГПУ
Качественные диаграммы изображаются с учетом взаимных соотношений между электрическими величинами, без указания численных характеристик.
Они являются одним из основных средств анализа электрических цепей, позволяя наглядно иллюстрировать и качественно контролировать ход решения задачи и легко установить квадрант, в котором располагается искомый вектор.
Для удобства при построении диаграмм анализируют неподвижные векторы для определенного момента времени, который выбирается таким образом, чтобы диаграмма имела удобный для понимания вид. Ось OХ соответствует величинам действительных чисел, ось OY — оси мнимых чисел (мнимая единица). Синусоида отображает движение конца проекции на ось OY. Каждому напряжению и току соответствует собственный вектор на плоскости в полярных координатах. Его длина отображает амплитудное значение величины тока, при этом угол равен фазе.
Векторы, изображаемые на такой диаграмме, характеризуются равновеликой угловой частотой ω. В виду чего при вращении их взаимное расположение не изменяется.
Ещё одно полезное видео о векторных диаграммах:
Поэтому при изображении векторных диаграмм один вектор можно направить произвольным образом (например, по оси ОХ).
А остальные — изображать по отношению к исходному под различными углами, соответственно равными углам сдвига фаз.
Таким образом, векторная диаграмма дает отчетливое представление об опережении либо отставании различных электрических величин.
Допустим у нас есть ток, величина которого изменяется по некоторому закону:
i = Im sin (ω t + φ).
С начала координат 0 под углом φ проведем вектор Im, величина которого соответствует Im. Его направление выбирается так, чтобы с положительным направлением оси OX вектор составлял угол — соответствующий фазе φ.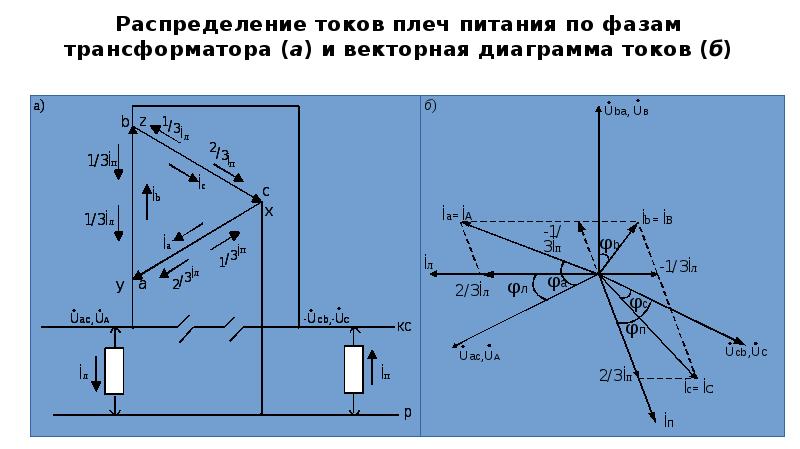
Абрамян Евгений Павлович
Доцент кафедры электротехники СПбГПУ
Проекция вектора на вертикальную ось и определяет значение мгновенного тока в начальный момент времени.
В основном векторные диаграммы изображают для действующих значений, а не амплитудных. Векторы действующих значений количественно отличаются от амплитудных значений — масштабом, поскольку:
I = Im /√2.
Основным преимуществом векторных диаграмм называют возможность простого и быстрого сложения и вычитания 2-х параметров при расчете электроцепей.
Построение векторных диаграмм
Наверняка при решении задач по электротехнике многие сталкивались с некоторыми сложностями в построении векторных диаграмм. Начнем с определения векторной диаграммы.
Векторная диаграмма — это изображение синусоидально изменяющихся величин в виде векторов на плоскости.
Векторные диаграммы применяют потому, что сложение и вычитание синусоидальных величин, неизбежные при расчете цепей переменного тока, наиболее просто выполняются в векторной форме.
Кроме того векторные диаграммы отличаются простотой и наглядностью.
Построение векторной диаграммы выполняется в прямоугольной плоскости. Чтобы построить диаграмму нужно провести вектор длиною равный амплитудному значению искомой величины, под углом сдвига относительно другой величины. Возможно, вы не сразу поймете смысл сказанного, для этого нужно изучить пример.
В качестве примера рассмотрим построение векторной диаграммы для цепи, состоящей из последовательно подключенных конденсатора, резистора и катушки. Напряжение на катушке UL=15 В, напряжение на конденсаторе UC=20 В, напряжение на резисторе UR=10 В, ток в цепи I=3 А. Требуется найти общее напряжение.
Катушка носит индуктивный характер, а значит, в ней напряжение опережает ток по фазе на 90°.
Конденсатор носит емкостной характер, значит, ток в нем опережает по фазе напряжение на 90°.
Резистор обладает только активным сопротивлением, и напряжение в нем совпадает по фазе с током.
Итак, для начала отложим вектор тока в масштабе. Масштаб для тока у нас будет 1 А/см.
Теперь отложим вектор напряжения на катушке, масштаб для напряжения возьмем 5 В/см, получается, что нужно отложить шесть клеток вверх, так как напряжение в катушке опережает ток. Для наглядности обозначим синим цветом.
Далее мы будем откладывать вектор активного сопротивления, так как напряжение в одной фазе с током, то мы его откладываем из конца вектора UL
Следующим шагом отложим вектор напряжения на конденсаторе, так как оно запаздывает на 90°, мы его отложим вертикально вниз, из конца вектора UR.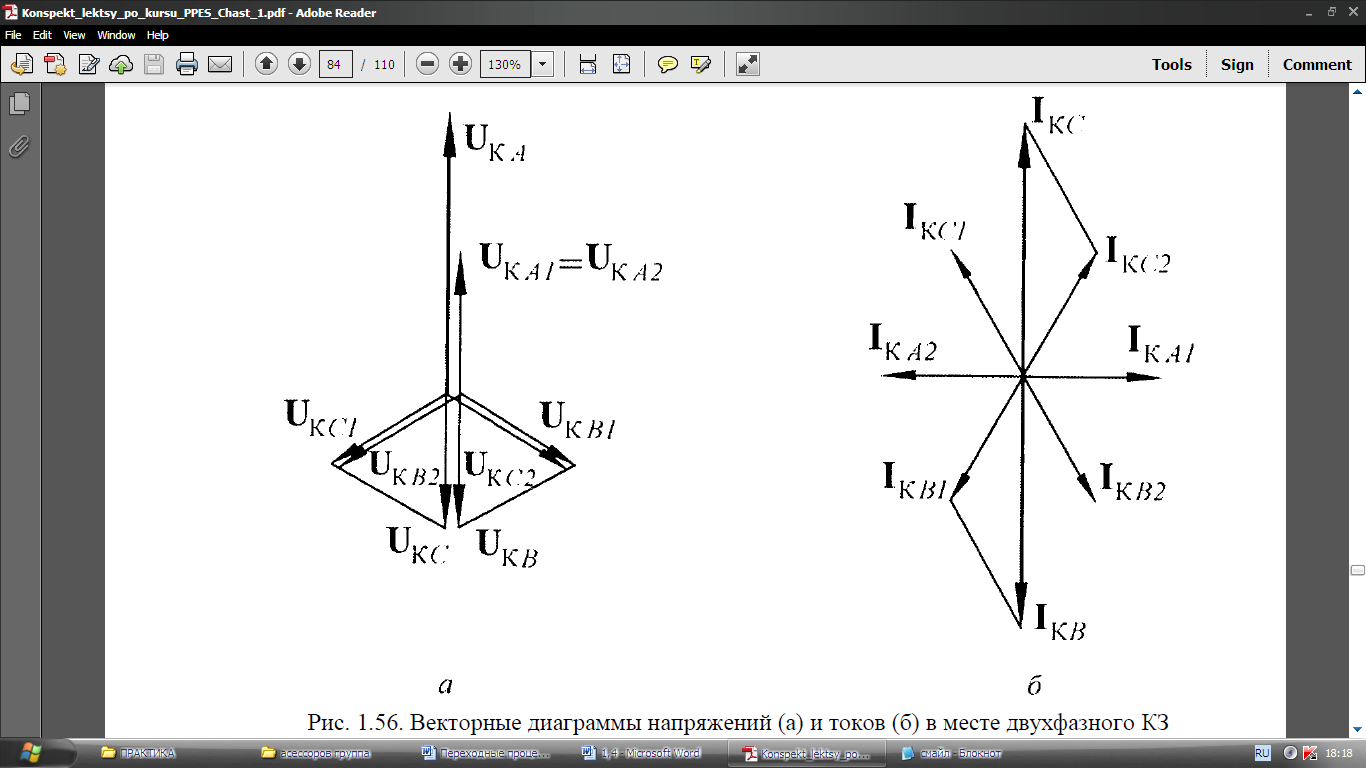
Обозначим желтым цветом.
И последним этапом мы отложим вектор общего напряжения, из начала координат в конец вектора UC и обозначим его зеленым цветом.
Общее напряжение получилось равным 2,23 В, причем
Аналогичным образом выполняется построение векторной диаграммы токов.
Читайте также последовательная RLС-цепь
правила построения диаграмм, онлайн построение
Цифровое представление динамических процессов затрудняет восприятие, усложняет расчет выходных параметров после изменения условий на входе или в результате выполненной обработки. Векторная диаграмма токов и напряжений помогает успешно решать обозначенные задачи. Ознакомление с теорией и практическими примерами поможет освоить данную технологию.
Диаграмма, поясняющая процесс короткого замыкания в трехфазной цепи счетчика электроэнергии
Для корректного отображения переменных величин, которые определяют функциональность радиотехнических устройств, хорошо подходит векторная графика.
Подразумевается соответствующее изменение основных параметров сигнала по стандартной синусоидальной (косинусоидальной) кривой. Для наглядного представления процесса гармоническое колебание представляют, как проекцию вектора на координатную ось.
С применением типовых формул несложно рассчитать длину, которая получится равной амплитуде в определенный момент времени. Угол наклона будет показывать фазу. Суммарные влияния и соответствующие изменения векторов подчиняются обычным правилам геометрии.
Различают качественные и точные диаграммы. Первые применяют для учета взаимных связей. Они помогают сделать предварительную оценку либо используются для полноценной замены вычислений. Другие создают с учетом полученных результатов, которые определяют размеры и направленность отдельных векторов.
Круговая диаграмма
Допустим, что надо изучить изменение параметров тока в цепи при разных значениях сопротивления резистора в диапазоне от нуля до бесконечности. В этой схеме напряжение на выходе (U) будет равно сумме значений (UR и UL) на каждом из элементов.
Линейная диаграмма
Здесь изображен двухполюсный элемент с активной и реактивной составляющими проводимости (G и jB, соответственно). Аналогичными параметрами обладает классический колебательный контур, созданный с применением параллельной схемы. Отмеченные выше параметры можно изобразить векторами, которые расположены постоянно под углом 90°. Изменение реактивной компоненты сопровождается перемещением вектора тока (I1…I3). Образованная линия располагается перпендикулярно U и на расстоянии Ia от нулевой точки оси координат.
Такой инструментарий помогает строить наглядные графические схемы колебательных процессов.
Аналогичный результат обеспечивает применение комплексных числовых выражений. В этом варианте, кроме оси с действительными, применяют дополнительный координатный отрезок с мнимыми значениями. Для представления вектора пользуются формулой
- А – длина;
- W – угловая скорость;
- f0 – начальный угол.
Значение действительной части равно A*cos*(w*t+f0). Это выражение описывает типичное гармоническое колебание с базовыми характеристиками.
Примеры примененияВ следующих разделах приведены описания задач, которые решают с помощью представленной методики. Следует подчеркнуть, что применение комплексных чисел пригодно для сложных расчетов с высокой точностью. Однако на практике достаточно часто сравнительно простой векторной графики с наглядным отображением исходной информации на одном рисунке.
Таким термином обозначают устройство, которое можно вывести из равновесного состояния. После этого система возвращается в сторону исходного положения, причем сила (F) соответствующего воздействия зависит от дальности первичного перемещения (d) прямо пропорционально. Величину ее можно уточнить с помощью постоянного корректирующего коэффициента (k). Отмеченные определения связаны формулой F=-d*k
Формулы для расчета основных параметров гармонического осциллятора
Продолжая изучение темы на примерах механических процессов, можно отметить возможность построения двухмерной схемы.
Скорость в этом случае на оси Х отображается так же, как и в одномерном варианте. Однако здесь можно учесть дополнительно фактор ускорения, которое направляют под углом 90° к предыдущему вектору.
В этом случае также можно воспользоваться для изучения взаимного влияния дополнительных факторов векторной графикой. Как и в предыдущем примере, скорость и другие величины представляют в двухмерном виде. Чтобы правильно моделировать процесс, проверяют суммарное воздействие внешних сил. Его направляют к центру системы (точке равновесия). С применением геометрических формул вычисляют амплитуду механических колебаний после начального воздействия с учетом коэффициента затухания и других значимых факторов.
Векторную графику применяют для сравнительно несложных цепей, которые созданы из набора элементов линейной категории: конденсаторы, резисторы, катушки индуктивности.
Векторная диаграмма для схемы соединений без нейтрального провода – звезда
Векторная диаграмма в данном случае выполняет функцию вспомогательного чертежа, который упрощает решение геометрических задач. Для катушек и конденсаторов, чтобы не пользоваться комплексным исчислением, вводят специальный термин – реактивное сопротивление. При синусоидальном токе изменение напряжения на индуктивном элементе описывается формулой U=-L*w*I0sin(w*t+f0).
Несложно увидеть подобие с классическим законом Ома. Однако в данном примере изменяется фаза. По этому параметру на конденсаторе напряжение отстает от тока на 90°. В индуктивности – обратное распределение. Эти особенности учитывают при размещении векторов на рисунке. В формуле учитывается частота, которая оказывает влияние на величину этого элемента.
Схемы и векторные диаграммы для идеального элемента и диэлектрика с потерями
Преобразование ФурьеВекторные технологии применяют для анализа спектров радиосигналов в определенном диапазоне.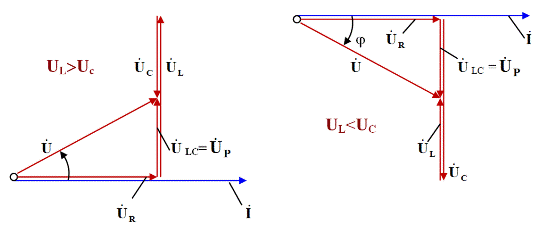
Несмотря на простоту методики, она вполне подходит для получения достаточно точных результатов.
В ходе изучения таких источников сигналов рекомендуется работать со сравнительно небольшой разницей частот. Это поможет создать график в удобном для пользователя масштабе.
Фурье-образ прямоугольного сигналаВ этом примере оперируют суммой синусоидальных сигналов. Последовательное сложение векторов образует многоугольник, вращающийся вокруг единой точки. Для правильных расчетов следует учитывать отличия непрерывного и дискретного распределения спектра.
ДифракцияДля этого случая пользуются тем же отображением отдельных синусоид в виде векторов, как и в предыдущем примере. Суммарное значение также вписывается в окружность.
Построение векторной диаграммы напряжений и токовДля изучения технологии выберем однофазный источник синусоидального напряжения (U).
Ток изменяется по формуле I=Im*cos w*t. Подключенная цепь содержит последовательно подключенные компоненты со следующими значениями:
- резистор: Ur=Im*R*cos w*t;
- конденсатор: Uc=Im*Rc*cos (w*t-π/2), Rc=1/w*C;
- катушка: UL= Im*RL*cos(w*t+π/2), RL=w*L.
При прохождении по цепи переменного тока на реактивных элементах будет соответствующий сдвиг фаз. Чтобы построить вектора правильно, рассчитывают амплитуды и учитывают изменение направлений. Ниже приведена последовательность создания графики вручную.
Диаграмма напряжений и токов на отдельных элементах
Далее с применением элементарных правил геометрии проверяют взаимное влияние векторов.
Решение векторного уравнения
На первом рисунке приведен результат сложения двух векторов при условии, когда Uc меньше UL. Добавив значение на сопротивление, получим результирующее напряжение Um. На третьей иллюстрации отмечен общий фазовый сдвиг.
Векторное отображение процессов в параллельном колебательном контуре, резонанс напряжений
В топографической диаграмме начало координат совмещают с так называемой точкой «нулевого потенциала».
Такое решение упрощает изучение отдельных участков сложных схем.
Специализированный редактор онлайн
В интернете можно найти программу для построения векторных диаграмм в режиме online.
Видеоправила построения диаграмм, онлайн построение
Векторные диаграммы и комплексное представление
Векторные диаграммы можно считать вариантом (и иллюстрацией) представления колебаний в виде комплексных чисел. При таком сопоставлении ось Ox соответствует оси действительных чисел, а ось Oy — оси чисто мнимых чисел (положительный единичный вектор вдоль которой есть мнимая единица).
Тогда вектор длиной A, вращающийся в комплексной плоскости с постоянной угловой скоростью ω с начальным углом φ, запишется как комплексное число
- Aei(ωt+φ),{\displaystyle Ae^{i(\omega t+\varphi _{0})},}
а его действительная часть
- Re(Aei(ωt+φ))=Acos(ωt+φ),{\displaystyle \mathrm {Re} {\big (}Ae^{i(\omega t+\varphi _{0})}{\big )}=A\mathrm {cos} {\big (}\omega t+\varphi _{0}{\big )},}
-есть гармоническое колебание с циклической частотой ω и начальной фазой φ.
Хотя, как видно уже из вышесказанного, векторные диаграммы и комплексное представление колебаний теснейшим образом связаны и по сути представляют собой варианты или разные стороны одного и того же метода, они, тем не менее, обладают своими особенностями и могут применяться и по отдельности.
- Метод векторных диаграмм может излагаться отдельно в курсах электротехники или элементарной физики, если по тем или иным причинам (обычно связанным с умеренным уровнем математической подготовки учащихся и недостатком времени) надо избежать использования комплексных чисел (в явном виде) вообще.
- Метод комплексного представления (который при необходимости или желании может включать и графическое представление, что, правда, совершенно не обязательно и иногда излишне) вообще говоря более мощен, так как естественно включает в себя, например, составление и решение систем уравнений любой сложности, в то время как метод векторных диаграмм в чистом виде всё же ограничен задачами, подразумевающим суммирование, которое можно изобразить на одном чертеже.
- Однако метод векторных диаграмм (в чистом виде или в качестве графической составляющей метода комплексного представления) — более нагляден, а значит в некоторых случаях потенциально более надежен (позволяет до некоторой степени избежать грубых случайных ошибок, которые могут встречаться при абстрактных алгебраических вычислениях) и позволяет в некоторых случаях достичь в каком-то смысле более глубокого понимания задачи.
Построение векторной диаграммы напряжений.
4.1 На комплексной плоскости строятся векторы фазных напряжений питающей сети А, В, С; соединив их концы, получают векторы линейных напряжений АВ, ВС, СА. Затем строятся векторы фазных напряжений нагрузки А нагр., В нагр., С нагр. Для их построения можно использовать обе формы записи комплексов токов и напряжений.
Например, вектор А нагр. строится по показательной форме следующим образом: от оси +1 под углом 6 10 , т.е. против часовой стрелки, откладывается отрезок длиной 6,96 см; по алгебраической форме его можно построить, отложив по оси +1 отрезок длиной 6,81 см, а по оси + j отрезок длиной 0,76 см, концы этих отрезков являются координатами конца вектора А нагр.
4.2 Т.к. линейные напряжения нагрузки заданы питающей сетью, для определения положения нейтрали нагрузки необходимо выполнить параллельный перенос векторов фазных напряжений нагрузки А нагр., В нагр., С нагр. так, чтобы их концы совпали с концами фазных напряжений питающей сети.
Точка 0, в которой окажутся их начала, есть нейтраль нагрузки. В этой точке находится конец вектора напряжения смещения нейтрали 0, его начало расположено в точке 0. Этот вектор можно также построить, используя данные таблицы 9.
Векторная диаграмма для первой ветви
Рис. 2
Спроецируем вектор тока I1 на оси координат. Горизонтальная составляющая тока будет представлять собой активную составляющую I1R, а вертикальная — I1L. Количественные значения этих составляющих будут равны:
Во вторую ветвь включен конденсатор. Его сопротивление
Этот ток опережает по фазе напряжение на 90°. Для определения тока I в неразветвленной части цепи воспользуемся формулой:
Его значение можно получить и графическим путем, сложив векторы I1 и I2 (рис.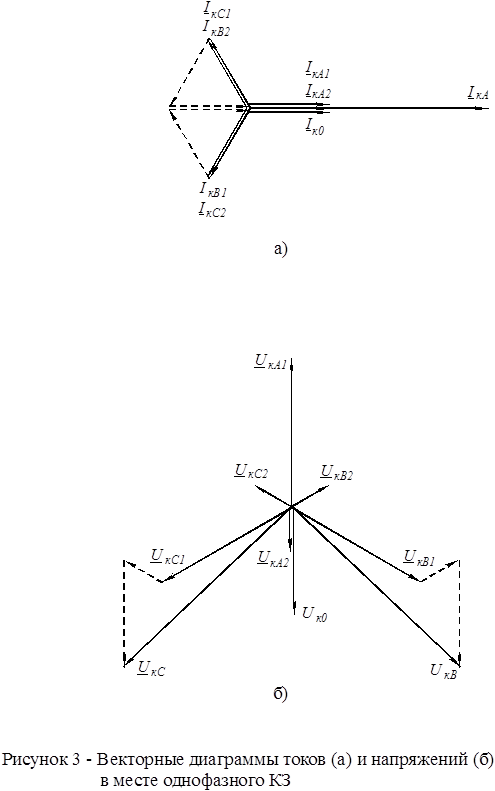
3). Угол сдвига между током и напряжением обозначим буквой φ. Здесь возможны различные режимы в работе цепи. При φ = +90° преобладающим будет емкостный ток, при φ = -90° — индуктивный.
Вы здесь
Онлайн калькулятор — Учеба и наука — Математика — Аналитическая геометрия — Векторы
Векторы
Векторы представляют собой особый раздел аналитической геометрии, который в том числе оказал значительное влияние на развитие физики. Сам по себе вектор выглядит как отрезок, который имеет начало и имеет конец, определен заданной конечными точками длиной этого отрезка. Но внутри вектора кроется множество других скрытых функций, за счет того что вектор задает направление. Поэтому если для отрезка не имеет значения какая точка названа началом, а какая концом, и чаще просто применяется принцип чтения «слева направо», то для векторов AB и BA – это диаметрально противоположные понятия.
Итак, в векторе присутствует две важных составляющих – это его длина и направление. Тем не менее, координатами вектора задается не его фактическая длина, а местоположение на плоскости или в пространстве. Поэтому длина вектора, иначе называемая модуль вектора, вычисляется, используя прямоугольный треугольник с осями координат. Дальнейшие действия с вектором также чаще используют именно его координаты, нежели фактическую длину
Работе с векторами можно провести аналогию с целыми числами, — как только появляются отрицательные числа на числовой оси, приходится не только считать значение примера, но и все время обращать внимание на знаки. Так и с векторами, во всех действиях – будь то сложение, вычитание, умножение скалярное или векторное и другие действия, приходится не только учитывать реальные масштабы вектора – координаты, длина или угол, но и принимать в расчет его направление
К слову, направления векторов также находят отражение в знаках – обратный изначальному вектор всегда будет со знаком «минус».
В данном разделе разложены все основные действия с векторами, такие как нахождение длины вектора, координат вектора, сложение векторов, вычитание векторов, скалярное произведение векторов, векторное произведение векторов, смешанное произведение трех векторов, вычисление угла между векторами и другие. Все расчет можно произвести для векторов на плоскости или для векторов в пространстве. Также доступен векторный калькулятор, который вычисляет все возможные параметры одного и более векторов, с заданными координатами точек вектора.
Векторный калькулятор | Координаты вектора по двум точкам | Направляющие косинусы вектора |
Длина вектора, модуль вектора | Сложение векторов | Вычитание векторов |
Умножение вектора на число | Скалярное произведение векторов | Угол между векторами |
Проекция вектора на вектор | Векторное произведение векторов | Смешанное произведение векторов |
Коллинеарность и ортогональность векторов | Компланарность векторов |
Векторная диаграмма в режиме резонанса токов
Рис. 4
Рассмотренный выше случай параллельного соединения R, L и C может быть также проанализирован с точки зрения повышения cosφ для электроустановок. Известно, что cosφ является технико-экономическим параметром в работе электроустановок. Определяется он по формуле:
cosφ = P / S, где
Р — активная мощность электроустановок, кВт;
S — полная мощность электроустановок, кВт.
На практике cosφ определяют снятием со счетчиков показаний активной и реактивной энергии и, разделив одно показание на другое, получают tgφ. Далее по таблицам находят и cosφ.
Чем больше cosφ, тем экономичнее работает энергосистема, так как при одних и тех же значениях тока и напряжения (на которые рассчитан генератор) от него можно получить большую активную мощность.
Снижение cosφ приводит к неполному использованию оборудования и при этом уменьшается КПД установки. Тарифы на электроэнергию предусматривают меньшую стоимость 1 киловатт-часа при высоком cosφ, в сравнении с низким.
Мероприятия по повышению cosφ:
- недопущение холостых ходов электрооборудования;
- полная загрузка электродвигателей, трансформаторов и т.д.
Кроме этого, на cosφ положительно сказывается подключение к сети статических конденсаторов.
Векторная графика
В отличие от растровых, векторные изображения состоят уже не из пикселей, а из множества опорных точек и соединяющих их кривых. Векторное изображение описывается математическими формулами и, соответственно, не требует наличия информации о каждом пикселе. Сколько ни увеличивай масштаб векторного изображения, вы никогда не увидите пикселей.
Самые популярные векторные форматы: SVG, AI.
Векторное изображение и его увеличенный фрагмент
Применение
Векторная графика используется для иллюстраций, иконок, логотипов и технических чертежей, но сложна для воспроизведения фотореалистичных изображений. Самый популярный редактор векторной графики — Adobe Illustrator.
Пример использования векторной графики: социальные иконки (источник изображения: MacKenzie www.freevector.com/social-websites-icons)
Пример использования векторной графики: иллюстрация (автор изображения: Катя Климович)
Преимущества
- Малый объём занимаемой памяти — векторные изображения имеют меньший размер, так как содержат в себе малое количество информации.
- Векторные изображения отлично масштабируются — можно бесконечно изменять размер изображения без потерь качества.
Недостатки
- Чтобы отобразить векторное изображение требуется произвести ряд вычислений, соответственно, сложные изображения могут требовать повышенных вычислительных мощностей.
- Не каждая графическая сцена может быть представлена в векторном виде: для сложного изображения с широкой цветовой гаммой может потребоваться огромное количество точек и кривых, что сведёт «на нет» все преимущества векторной графики.
- Процесс создания и редактирования векторной графики отличается от привычной многим модели — для работы с вектором потребуются дополнительные знания.
Опыт холостого хода
После изготовления трансформатора необходимо провести ряд испытаний, одним из которых является опытом холостого хода. Данное испытание трансформатора проводится при разомкнутой вторичной обмотке и подачей номинального напряжения на первичную обмотку. По результатам проведения опыта холостого хода определяют коэффициент трансформации и мощность потерь в магнитопроводе.
Для проведения опыта холостого хода собирают схему изображенную ниже
Как видно на схеме к первичной обмотке трансформатора необходимо подключить вольтметр PV1, амперметр РА1 и ваттметр PW1, а к вторичной обмотке – вольтметр PV2.
Для снятия характеристик холостого хода трансформатора на его первичную обмотку подают номинальное напряжение = UH, которое можно изменять при необходимости снятия динамических характеристик примерно от 30% до 110% UH. После подачи напряжения в первичную обмотку снимают показания по приборам: ток холостого хода IХХ, мощность холостого хода РХХ, напряжение на вторичной обмотке U2 трансформатора.
По результатам проведения опыта холостого хода можно определить следующие параметры:
— процентное отношение тока холостого тока IXX%
где IH – номинальное значение тока в первичной обмотке трансформатора.
— коэффициент трансформации трансформатора k
где U1 и U2 – напряжения, снимаемые с вольтметров PV1 и PV2, соответственно.
— активное сопротивление намагничивающего контура RC
где РХХ – мощность, снимаемая с ваттметра PW1.
— полное сопротивление намагничивающего контура ZC
— реактивное сопротивление намагничивающего контура ХС
— коэффициент мощности холостого хода cos φXX
При проведении опыта холостого хода следует отметить, что в начальный момент подачи напряжения возникает недопустимо большой ток в разы превышающий номинальный, а так как ток холостого хода составляет 3 – 10 % от номинального тока, то пусковой ток превышает ток холостого тока в десятки раз. Поэтому в начальный момент необходимо замкнуть выводы амперметра РА1.
Кроме опыта холостого хода для испытания трансформатора проводят опыт короткого замыкания, о котором я расскажу в следующей статье.
Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.
Заказать решение ТОЭ
- Метрология Электрические измерения
- Пигарев А.Ю. РГЗ по электротехнике и электронике в Multisim
- Теория линейных электрических цепей ТЛЭЦ
- —
Теория линейных электрических цепей железнодорожной автоматики, телемеханики и связи: задание на контрольные работы № 1 и 2 с методическими указаниями для студентов IV курса специальности Автоматика, телемеханика и связь на железнодорожном транспорте- —
Контрольная работа №1 - —
Контрольная работа №2
- —
- —
- Электротехника и основы электроники
- —
Электротехника и основы электроники: Методические указания и контрольные задания для студентов-заочников инженерно-технических специальностей высших учебных заведений / Соколов Б.П., Соколов В.Б. – М.: Высш. шк., 1985. – 128 с, ил- —
Контрольная работа № 1 Электрические цепи - —
Контрольная работа № 2 Трансформаторы и электрические машины - —
Контрольная работа № 3 Основы электроники
- —
- —
- Теоретические основы электротехники ТОЭ
- —
Артеменко Ю.П., Сапожникова Н.М. Теоретические основы электротехники: Пособие по выполнению курсовой работы МГТУ ГА 2009 - —
Переходные процессы Переходные процессы в электрических цепях - —
Теоретические основы электротехники Методические указания и контрольные задания для студентов технических специальностей вузов- —
Задание 1 Линейные электрические цепи постоянного и синусоидального тока- —
Задача 1.1 Линейные электрические цепи постоянного тока - —
Задача 1.2 Линейные электрические цепи синусоидального тока
- —
- —
Задание 2 Четырехполюсники, трехфазные цепи, периодические несинусоидальные токи, электрические фильтры, цепи с управляемыми источниками
- —
- —
Теоретические основы электротехники сб. заданий Р.Я. Сулейманов Т.А. Никитина Екатеринбург УрГУПС 2010 - —
Трехфазные цепи. Расчет трехфазных цепей - —
УГТУ-УПИ Решение ТОЭ Билеты по ТОЭ - —
Электромагнитное поле Электростатическое поле Электростатическое поле постоянного тока в проводящей среде Магнитное поле постоянного тока
- —
Заказать решение ТОЭ
- Метрология Электрические измерения
- Пигарев А.Ю. РГЗ по электротехнике и электронике в Multisim
- Теория линейных электрических цепей ТЛЭЦ
- —
Теория линейных электрических цепей железнодорожной автоматики, телемеханики и связи: задание на контрольные работы № 1 и 2 с методическими указаниями для студентов IV курса специальности Автоматика, телемеханика и связь на железнодорожном транспорте- —
Контрольная работа №1 - —
Контрольная работа №2
- —
- —
- Электротехника и основы электроники
- —
Электротехника и основы электроники: Методические указания и контрольные задания для студентов-заочников инженерно-технических специальностей высших учебных заведений / Соколов Б.П., Соколов В.Б. – М.: Высш. шк., 1985. – 128 с, ил- —
Контрольная работа № 1 Электрические цепи - —
Контрольная работа № 2 Трансформаторы и электрические машины - —
Контрольная работа № 3 Основы электроники
- —
- —
- Теоретические основы электротехники ТОЭ
- —
Артеменко Ю.П., Сапожникова Н.М. Теоретические основы электротехники: Пособие по выполнению курсовой работы МГТУ ГА 2009 - —
Переходные процессы Переходные процессы в электрических цепях - —
Теоретические основы электротехники Методические указания и контрольные задания для студентов технических специальностей вузов- —
Задание 1 Линейные электрические цепи постоянного и синусоидального тока- —
Задача 1.1 Линейные электрические цепи постоянного тока - —
Задача 1.2 Линейные электрические цепи синусоидального тока
- —
- —
Задание 2 Четырехполюсники, трехфазные цепи, периодические несинусоидальные токи, электрические фильтры, цепи с управляемыми источниками
- —
- —
Теоретические основы электротехники сб. заданий Р.Я. Сулейманов Т.А. Никитина Екатеринбург УрГУПС 2010 - —
Трехфазные цепи. Расчет трехфазных цепей - —
УГТУ-УПИ Решение ТОЭ Билеты по ТОЭ - —
Электромагнитное поле Электростатическое поле Электростатическое поле постоянного тока в проводящей среде Магнитное поле постоянного тока
- —
правила построения диаграмм, онлайн построение
В целом, для лучшего понимания процедур, происходящих в радиотехнических цепях, их взаимосвязи между собой, бывает недостаточно оперировать характеристиками и параметрами данной цепи, имеющими цифровое отображение. В связи с тем, что основная масса цепей характеризуется переменными значениями приложенного напряжения и протекающего тока, являющимися синусоидальными функциями времени, то исчерпывающий ответ по состоянию цепи может дать ее графическая презентация посредством векторной гистограммы.
Векторная диаграмма напряжений и токов
Разновидности векторных диаграмм
Любую характеристику электротехнической цепи, изменяющуюся по синусоидальному или косинусоидальному принципу, можно отобразить посредством точки на поверхности, в соответствующей системе величин. В качестве размерности по оси Х выступает действительный компонент параметра, по оси Y размещается воображаемая составляющая. Именно такие составляющие входят в алгебраическую модель записи комплексной величины. Последующее соединение точки на поверхности и нулевой точки системы координат позволит рассматривать эту прямую и ее угол с действительной осью как изображение комплексного числа. На практике положительно направленный отрезок принято называть вектором.
Векторной диаграммой принято называть множество положительно направленных отрезков на комплексной поверхности, которая соответствует комплексным значениям и параметрам гальванической цепи и их взаимосвязям. По своему характеру векторные диаграммы подразделяются на:
- Точные гистограммы;
- Качественные гистограммы.
Особенностями достоверных гистограмм является соблюдение пропорций всех характеристик и параметров, полученных путем вычислений. Данные диаграммы находят свое применение в проверке ранее проведенных расчетов. В основе использования качественных гистограмм лежит учет взаимного влияния характеристик друг на друга, и в основном они предшествуют расчетам либо заменяют их.
Векторные диаграммы токов и напряжений визуально отображают процесс достижения цели по расчету электротехнической цепи. При соблюдении всех правил по построению векторных отрезков можно просто из гистограммы установить фазы и амплитуды вещественных характеристик. Построение качественных гистограмм поможет контролировать правильный процесс решения задачи и с легкостью определить сектор с определяемыми векторами. В зависимости от особенностей построения, графические диаграммы делятся на такие типы:
- Круговая диаграмма, представляющая собой графическую гистограмму, образованную вектором, описывающим своим концом круг или полукруг, при любых изменениях характеристик цепи;
- Линейная диаграмма, представляющая собой графический рисунок в виде прямой линии, образованной вектором, посредством изменения характеристик цепи.
Построение векторной диаграммы напряжений и токов
Для лучшего понимания того, как построить векторную диаграмму токов и напряжений, следует рассматривать RLC цепь, состоящую из пассивного элемента в виде резистора и реактивных элементов в виде катушки индуктивности и конденсатора.
Схема цепи с последовательным соединением элементов
Перед тем, как построить векторную диаграмму токов и напряжений, необходимо охарактеризовать все известные параметры цепи. Согласно схемы цепи, изображенной на картинке а:
- U – величина переменного напряжения в текущий момент времени;
- I – мощность тока в заданный момент времени;
- UА – напряжение, падающее на активном сопротивлении;
- UC – напряжение, падающее на емкостной нагрузке;
- UL – напряжение, падающее на индуктивной нагрузке.
Поскольку входное напряжение U изменяется по колебательному закону, то сила тока характеризуется уравнением:
I=Im*cosωt, где:
- Im – максимальная амплитуда тока;
- ω – частота тока;
- t – время.
Суммарное входное напряжение, в соответствии со вторым законом Кирхгофа, равно общей величине напряжений на всех элементах цепи:
U=UC+UL+UA.
В соответствии с законом Ома, падение напряжения на резистивном компоненте равняется:
UA= Im*R*cosωt.
Противодействие току активного элемента зависит сугубо от свойства проводника и не обуславливается ни характеристиками тока, ни аспектом времени и, соответственно, имеет идентичный с напряжением фазовый сдвиг.
Поскольку конденсатору в цепи с электротоком, изменяющимся по синусоиде, свойственно наличие реактивного емкостного сопротивления, и ввиду того, что напряжение на нем постоянно имеет фазовое отставание от протекающего тока на π/2, то уместно выражение:
- RC=XC=1/ωC;
- UC=Im*RС*cos(ωt-π/2), где:
- RC – сопротивление конденсатора;
- XC – реактивный импеданс конденсатора;
- C – емкость конденсатора.
Реактивное индуктивное сопротивление катушки индуктивности обуславливается наличием изменяющегося по синусоидальному закону электротока, и поскольку напряжение на любом отрезке времени имеет фазовое опережение по отношению к электротоку на π/2, то формула, описывающая колебательный процесс на элементе, выглядит как:
- RL=XL=ωL;
- UL=Im*RL*cos(ωt+π/2), где:
- RL – сопротивление катушки индуктивности;
- XL – реактивный импеданс катушки индуктивности;
- L – индуктивность катушки.
Следовательно, общее напряжение, подведенное к цепи, выглядит:
U=Um*cos(ωt±φ), где:
- Um – максимальная величина напряжения;
- φ – фазовый сдвиг.
Ввиду того, что напряжение и электроток изменяются по синусоидальному закону, и их фиксированные показатели отличаются лишь фазовым сдвигом, то данные величины строятся как вектора.
В соответствии с законом сохранения электрического заряда, в любой момент времени сила протекающего тока одинакова, то целесообразно сформировать векторную гистограмму токов.
Векторная диаграмма токов и напряжений RLC цепочке
Пусть по оси Х отображается амплитудное значение электротока в цепочке. Поскольку напряжение и электроток на резисторе имеют одинаковый фазовый сдвиг, то вектора данных характеристик будут ориентированы в одну сторону, согласно картинке а.
Напряжение на емкостной нагрузке отстает от электрического тока на π/2, и его вектор будет направлен под прямым углом вниз, перпендикулярно напряжению активного сопротивления, согласно картинке в.
Напряжение на индуктивной нагрузке опережает электрический ток на π/2, и ее вектор будет ориентирован под прямым углом вверх, перпендикулярно напряжению на активном сопротивлении, согласно картинке б.
Для наглядности векторных преобразований пусть UL>UС. Сложив вектора напряжений на реактивных компонентах, получаем, что вектор UL-UС будет направлен перпендикулярно вверх. Суммировав вектора разности напряжений на реактивных компонентах и напряжения на сопротивлении получаем вектор, характеризующий дисперсное значение общего напряжения, согласно картинке 2(б).
Аналогично электрическому току, изменяющемуся по синусоидальному закону, напряжение меняется по такому же закону, однако с некоторым фазовым сдвигом. Наблюдается постоянный фазовый сдвиг между напряжением и током.
После простых преобразований по постулату Ома, уравнение полного импеданса заданной электрической цепи выглядит как:
Z=√R2+(1/ωC- ωL)2.
Векторная гистограмма общего и реактивных сопротивлений изображена на картинке 2в.
Построение векторных диаграмм токов и напряжений может значительно упростить процесс расчета характеристик контура. Вместе с тем сама процедура позволит наглядно видеть поведение исследуемых характеристик, в зависимости от входных величин. При большом объеме вычислительных операций целесообразно воспользоваться одной из онлайн программ по построению векторных графиков.
Видео
Оцените статью:Векторные диаграммы синусоидальных функций Электротехника, Схемотехника, Аналоговые…
Привет, мой друг, тебе интересно узнать все про векторные диаграммы синусоидальных функций, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое векторные диаграммы синусоидальных функций , настоятельно рекомендую прочитать все из категории Электротехника, Схемотехника, Аналоговые устройства
Геометрический образ комплексных величин синусоидальных функций на комплексной плоскости называют векторной диаграммой. Векторные диаграммы широко используют для анализа электрических цепей.
Рассмотрим пример:
Дано:
Построим векторную диаграмму на комплексной плоскости:
Анализируя векторную диаграмму можно сделать вывод, что функция тока опережает функцию напряжения на угол 90°.
Точно так же будет выглядеть векторная диаграмма действующих значений
Только размеры векторов уменьшаться в раз.
Рассмотрим второй пример:
На рис.3 показан узел электрической цепи и приведена векторная диаграмма токов . Об этом говорит сайт https://intellect.icu . Необходимо определить ток I0 и построить векторную диаграмму токов.
Рис.3
Ток 0 по известным токам 1 и 2 на векторной диаграмме определяется в соответствии с первым законом Кирхгофа по правилу параллелограмма.
Сопоставление диаграмм доказывает важность фазовых соотношений в цепях переменного тока, потому что, при неизмененных амплитудах (действующих значениях) суммируемых токов или напряжений результирующие величины этих токов и напряжений существенно отличаются по амплитудам за счет различия в фазовых соотношениях
Как ты считаеешь, будет ли теория про векторные диаграммы синусоидальных функций улучшена в обозримом будующем? Надеюсь, что теперь ты понял что такое векторные диаграммы синусоидальных функций и для чего все это нужно, а если не понял, или есть замечания, то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Электротехника, Схемотехника, Аналоговые устройства
Построение векторной диаграммы напряжений. Катушка. Конденсатор. Сопротивление. Сдвиг фаз.
Достаточно сложным и чаще всего не изучаемым аспектом темы переменный ток является метод построения векторных диаграмм. Анализируя вынужденные электромагнитные колебания, мы уже обсудили сдвиг тока и напряжения на реактивных сопротивлениях (катушка индуктивности и конденсатор) по сравнению с активным сопротивлением (резистор). Тогда одним из задаваемых вопросов задачи является вопрос о направлении суммарного тока или напряжения в данный конкретный момент времени. Для ответа на этот вопрос и используется метод построения векторных диаграмм.
Векторная диаграмма — это изображение гармонически изменяющихся величин (текущего тока и напряжения) в виде векторов на плоскости.
Рис. 1. Векторная диаграмма
Построение векторных диаграмм происходит в прямоугольной декартовой системе координат. Построение начинается с проведения вектора, численно равного амплитудному значению тока в цепи. Данный вектор сонаправим в осью ОХ (рис. 1.1).
Т.к. напряжение на активном сопротивлении находится в одной фазе с током, то вектор амплитуды напряжения сонаправлен с вектором тока (рис. 1.2. красный).
На катушке напряжение опережает ток, поэтому отложим вектор амплитуды напряжения на катушке (
) вверх под углом относительно вектора тока (рис. 1.2. синий).На конденсаторе напряжение отстаёт от тока, поэтому отложим вектор амплитуды напряжения на конденсаторе (
) вниз под углом относительно вектора тока (рис. 1.2. зелёный).Угол
, используемый в логике построений, используется в случае идеальности контура и катушки.Для построения общего вектора напряжения достаточно векторно сложить напряжения:
(1)Проще всего сначала найти вектор-сумму
(т.к. они расположены вдоль одной прямой). В нашем случае, эти вектора разнонаправлены, найдём (рис. 1.3. жёлтый).И последнее, осталось сложить получившийся вектор с вектором
для получения значения полного напряжения в цепи (рис. 1.4. оранжевый). Для получения модуля вектора воспользуемся теоремой Пифагора, т.к. вектора находятся под прямым углом. Тогда: (2)Угол
— угол между вектором силы тока и полного напряжения называется сдвигом фаз между колебаниями силы тока и напряжения. Данный параметр можно найти и исходя из параметров системы: (3)Вывод: задачи на данную тематику касаются поиска сдвига фаз между колебаниями силы тока и напряжения через график (рис. 1.4) или через соотношение (3), а также поиска полного напряжения в цепи также через график (рис. 1.4) или через соотношение (2).
Поделиться ссылкой:
векторных диаграмм | Powermetrix | Оборудование для проверки электрических счетчиков
Ключ к пониманию векторных диаграмм и условных обозначений на основе углов
Патч микропрограммы1.1.0.8 вносит незначительные изменения в способ, которым PowerMaster смотрит и отображает мощность и фазовые углы, что упрощает понимание векторных диаграмм. Изменение было основано на желании быть более стандартизированным на основе последней версии справочника метролога.
Рисунок 1: Векторная диаграмма Unity
При взгляде на типичную векторную диаграмму на измерителе предполагается, что векторы тока вращаются против часовой стрелки, а векторы напряжения неподвижны в их заранее определенных положениях.В демонстрационных целях на Рисунке 1 изображена 4-проводная система с конфигурацией «звезда» с вращением ABC. Напряжение фазы A, или Va, лежит на первичной оси «x» при фазовом сдвиге 0 °. Ia также лежит поверх вектора напряжения под углом 0 °, что указывает на коэффициент мощности, равный единице, или коэффициент мощности, равный 1. Пары напряжения и тока фаз B и C разделены на 120 градусов.
Когда происходит фазовый сдвиг между напряжением и током, это происходит из-за реактивного сопротивления нагрузки, обычно в форме индуктивности. Это создает запаздывающий коэффициент мощности.Когда что-то упоминается как опережающее или запаздывающее, это средство соотнесения фазового отношения формы волны тока с формой волны напряжения, и всегда со ссылкой на то, что делает ток. Вспомнив следующую фразу, «ЭЛИ, ледяной человек» описывает следующее:
- E — Электродвижущая сила, напряжение
- I — текущий
- C — емкость
- L — Индуктивность
ELI означает, что в индуктивной цепи ток отстает от напряжения.ICE выдает ток, опережающий напряжение в емкостной цепи. На рисунке 2 представлена типичная векторная диаграмма с фазовым сдвигом 60 ° (PF = 0,5), показывающая ток, опережающий напряжение, и ток, отстающий от напряжения.
Рис. 2a: ток запаздывания 60 °
Рис. 2b: Ведущий ток 60 °
При просмотре векторной диаграммы понимание контрольной точки и направления обязательно для понимания того, какое измерение мощности представляют векторы.Зная это, легко с первого взгляда определить необходимое количество, которое представляет каждый вектор. В электрических системах мощность может быть выражена тремя разными величинами, иногда с разными названиями. Ниже приведены три формы власти, а также различные способы их определения.
- Вт: Фактическое количество мощности, рассеиваемой в цепи. Также называется:
- Реальная мощность
- Истинная сила
- -P
- Может быть положительным или отрицательным
- Вольт-Ампер: произведение напряжения и тока цепи без привязки к фазовому углу.Также называется:
- Полная мощность
- S
- Всегда беззнаковое значение, ни положительное, ни отрицательное
- Вольт-ампер, реактивная: мощность, потребляемая и возвращаемая нагрузками за счет реактивной мощности. Также называется:
- Варс
- Реактивная мощность
- Q
- Может быть положительным или отрицательным.
Как показано, может быть сложно отслеживать различные мощности, но использование векторной диаграммы может помочь упростить процесс.Глядя на вектор, можно определить большой объем информации о нагрузке и правильности работы системы. Взаимосвязь между приведенными выше значениями определяется коэффициентом мощности (PF), который представляет собой отношение реальной мощности к полной мощности, и его можно рассматривать как значения от -1 до 1. Его можно рассчитать по следующей формуле:
pf = \ frac {Ватт} {VA}Где Pf = коэффициент мощности и = разность фаз между напряжением и током. Другой способ расчета коэффициента мощности:
pf = \ cos \ thetaПонимание этой взаимосвязи может помочь понять различные векторные диаграммы.Одна из причин заключается в том, что векторная диаграмма может быть разбита на 4 части, иногда называемые квадрантами. Приведенная ниже диаграмма составлена со ссылкой на рисунок 3.
Рис. 3: Условные обозначения на основе углов векторной диаграммы
| Вт | ВАР | ПФ | |
| 0-90 ° | Положительно | Положительно | Положительно |
| 90 — 180 ° | Отрицательный | Положительно | Отрицательный |
| 180 — 270 ° | Отрицательный | Отрицательный | Отрицательный |
| 270 — 360 ° | Положительно | Отрицательный | Положительно |
Таблица 1: Условные обозначения на основе углов векторной диаграммы
При 0 ° и 180 ° коэффициент мощности равен 1 и -1 соответственно, а при 90 ° и 270 ° он равен 0.Это углы, при которых знаки будут менять значения. Обратите внимание, знаки основаны на ссылке между Va и Ia соответственно. Например, если Va находится на 0, а Ia на 200 °, тогда ватты, переменные и коэффициент мощности будут отрицательными.
На основе знака и местоположения вектора можно определить, получена или передана мощность. Предоставляемая мощность — это мощность, потребляемая нагрузкой, или оплачиваемая мощность. Полученная мощность — это мощность, которая вырабатывается и возвращается в сеть или перед точкой измерения.Во многих случаях это обнаруживается в местах, где солнечные панели или генераторы используются в сценариях снижения пиковой нагрузки или распределения нагрузки. Например, когда солнце не светит и нагрузка низкая, солнечная панель будет отправлять дополнительную мощность обратно в сеть, иногда для оплаты счетов. Когда солнце садится или нагрузка выше, чем может обеспечить солнечная панель, энергия перетекает в сторону нагрузки и оплачивается. С появлением солнечных панелей и распределенной генерации первостепенным приоритетом является то, чтобы любой счетчик в ситуации, когда мощность является двунаправленной (может течь в любом направлении), чтобы счетчик испытывал мощность, протекающую в обоих направлениях.
Таблица 2 показывает, чего ожидать, исходя из фазовых углов векторной диаграммы.
| Вт | ВАР | |
| 0-90 ° | Поставка | Поставка |
| 90 — 180 ° | Поступило | Поставка |
| 180 — 270 ° | Поступило | Поступило |
| 270 — 360 ° | Поставка | Поступило |
Таблица 2: Полученная и отданная мощность
При выполнении теста быстрый взгляд на векторную диаграмму, наряду с вышеуказанными знаниями, может помочь диагностировать установку счетчика за короткий период времени.
ПОДРОБНЕЕ
Если вы чувствовали, что вам нужно вернуться в старшую школу, чтобы разобраться в этом, вот несколько ссылок, которые помогут вам снова сесть в седло:
Класс физики: векторные диаграммыYouTube
Пожалуйста, задавайте вопросы и комментарии ниже или свяжитесь с нами здесь.
Какой электрический элемент соответствует векторной диаграмме.Построение векторных диаграмм токов и напряжений
а) Понятие векторов
На рис. 1-4 показана кривая изменения переменного тока во времени. Ток сначала увеличивается от нуля (при = 0 °) до максимального положительного значения + IM (при = 90 °), затем уменьшается, проходит через ноль (при = 180 °), достигает максимального отрицательного значения — IM (при = 270 °). °) и, наконец, возвращается к нулю (при = 360 °). После этого повторяется весь цикл текущего изменения.
Кривая изменения переменного тока во времени, построенная на рис.1-4, называется синусоидой. Время T, в течение которого происходит полный цикл изменения тока, соответствующий изменению угла до 360 °, называется периодом переменного тока. Количество периодов в 1 с называется частотой переменного тока. В промышленных установках и в быту в СССР и других странах Европы в основном используется переменный ток частотой 50 Гц. Этот ток проходит 50 раз в секунду в положительном и отрицательном направлении.
Изменение переменного тока с течением времени можно записать как:
, где i — мгновенное значение тока, i.е. текущее значение в каждый момент времени; I м — максимальное значение тока; — угловая частота переменного тока, f = 50 Гц, = 314; — начальный угол, соответствующий моменту времени, с которого начинается время (при t = 0).
Для частного случая, показанного на рис. 1-4,
Анализируя действие устройств релейной защиты и автоматики, необходимо сравнить токи и напряжения, сложить или вычесть их, определить углы между ними и выполнить другие операции. Для использования кривых, аналогичных показанным на рис.1-4, неудобно, так как построение синусоид тока и напряжения занимает много времени и не дает простого и наглядного результата. Поэтому для упрощения принято изображать токи и напряжения в виде отрезков прямых линий, имеющих определенную длину и направление, так называемых векторов (ОА на рис. 1-4). Один конец вектора фиксируется в точке O — начале координат, а другой вращается против часовой стрелки.
Мгновенное значение тока или напряжения в каждый момент времени определяется проекцией на вертикальную ось вектора, длина которого равна максимальному значению электрической величины тока или напряжения.Эта проекция станет либо положительной, либо отрицательной, принимая максимальные значения при вертикальном расположении вектора.
За время T, равное периоду переменного тока, вектор совершит полный оборот по окружности (360 °), занимая последовательные позиции и т. Д. При частоте переменного тока 50 Гц вектор выполнит 50 оборотов в секунду.
Таким образом, вектор тока или напряжения представляет собой отрезок прямой, равный по величине максимальному значению тока или напряжения, вращающийся относительно точки O против часовой стрелки, движущийся по часовой стрелке со скоростью, определяемой частотой переменного тока.Зная положение вектора в каждый момент времени, вы можете определить мгновенное значение тока или напряжения в данный момент. Так, для положения текущего вектора OA, показанного на рис. 1-5, его мгновенное значение определяется проекцией на вертикальную ось, т.е.
На основе рис. 1-5, можно также сказать, что ток в данный момент времени имеет положительное значение. Однако это не дает полной картины процесса в цепи переменного тока, поскольку неизвестно, что означает положительный или отрицательный ток, положительное или отрицательное напряжение.
Чтобы векторные диаграммы токов и напряжений давали полную картину, они должны быть связаны с фактическим потоком процесса в цепи переменного тока, т. Е. Условные положительные направления токов и напряжений должны быть приняты в цепи в вопрос.
Без выполнения этого условия, если не заданы положительные направления токов и напряжений, любая векторная диаграмма не имеет смысла.
Рассмотрим простую однофазную цепь переменного тока, показанную на рис.1-6, и. От однофазного генератора энергия передается на активную резистивную нагрузку R. Зададим положительные направления токов и напряжений в рассматриваемой цепи.
Для условного положительного направления напряжения и эд. мы принимаем направление, когда потенциал выхода генератора или нагрузки, подключенной к линии, выше, чем потенциал выхода, подключенного к земле. В соответствии с правилами, принятыми в электротехнике, положительное направление для эл.d. он обозначен стрелкой, направленной в сторону более высокого потенциала (от земли к линейному выходу), а для напряжения — стрелкой, направленной в сторону более низкого потенциала (от линейного выхода к земле).
Построить векторы e. d. и ток, характеризующий работу рассматриваемой схемы (рис. 1-6, б). Вектор е. d. произвольно обозначьте вертикальную линию стрелкой вверх. Для построения вектора тока запишем уравнение схемы по второму закону Кирхгофа:
Так как знаки текущих векторов и эл.d. в выражении (1-7) совпадают, текущий вектор будет совпадать с вектором e. d. и рис. 1-6, стр.
Здесь и в дальнейшем при построении векторов мы будем откладывать их по величине, равной действующим значениям тока и напряжения, что удобно для выполнения различных математических операций с векторами. Как известно, действующие значения тока и напряжения меньше соответствующих максимальных (амплитудных) значений.
Для заданных положительных направлений тока и напряжения знак мощности также определяется однозначно.В этом случае мощность от шин генератора до линии будет считаться положительной:
как текущие векторы и e. d. на рис. 1-6, б такие же.
Аналогичные соображения можно сделать для трехфазной цепи переменного тока, показанной на рис. 1-7, и.
В этом случае во всех фазах берутся одинаковые положительные направления, что соответствует симметричной диаграмме токов и напряжений, показанной на рис. 1-7, стр. Обратите внимание, что это называется симметричными векторами трехфазной системы, когда все три вектора равны по величине и сдвинуты относительно друг друга на угол 120 °.
Вообще говоря, вовсе не обязательно следовать одним и тем же положительным направлениям на всех фазах. Однако неудобно брать разные положительные направления в разных фазах, так как вам придется изобразить асимметричные системные векторы при работе электрической цепи в нормальном симметричном режиме, когда все три фазы находятся в одинаковых условиях.
б) Векторные операции
Когда мы рассматриваем только одну кривую тока или напряжения, начальное значение угла, с которого начинается отсчет, или, другими словами, положение вектора на диаграмме, соответствующее начальному моменту времени, может быть принято произвольным.Если одновременно рассматриваются два и более тока и напряжения, то, задав начальное положение на схеме одного из векторов, мы тем самым определяем положение всех остальных векторов.
Все три вектора фазных напряжений, показанные на рис. 1-7, б, вращаются против часовой стрелки с одинаковой скоростью, определяемой частотой переменного тока. При этом они пересекают вертикальную ось, которая совпадает с направлением вектора на рис. 1-7, б, попеременно с определенной последовательностью, а именно, которая называется чередованием фаз напряжения (или тока).
Для определения относительного положения двух векторов обычно говорят, что один из них находится впереди или позади другого. В этом случае ведущим вектором считается тот, который при повороте против часовой стрелки пересекает вертикальную ось раньше. Так, например, можно сказать, что вектор напряжения на рис. 1-7, b на 120 ° впереди угла, или, с другой стороны, вектор на 120 ° позади вектора. Как видно из рис. 1-7 выражение «вектор отстает на угол 120 °» эквивалентно выражению «вектор опережает угол 240 °».
При анализе различных электрических цепей необходимо складывать или вычитать векторы тока и напряжения. Сложение векторов производится геометрическим суммированием по правилу параллелограмма, как показано на рис. 1-8, а, на котором строится сумма токов
Поскольку вычитание является обратным сложению, очевидно, что для определения разности токов (например, достаточно прибавить к току вектор
При этом на рис.1-8, и показано, что вектор разности токов можно построить проще, соединив концы векторов линией. Стрелка вектора разности токов направлена в сторону первого вектора, т.е.
Полностью аналогичным образом строится векторная диаграмма межфазных напряжений, например (рис. 1-8, б).
Очевидно, положение вектора на плоскости определяется его проекциями на любые две оси.Например, чтобы определить положение вектора OA (рис. 1-9), достаточно знать его проекции на взаимно перпендикулярные оси.
Нанесите проекции вектора на оси координат и восстановите перпендикуляры к осям по точкам. Точкой пересечения этих перпендикуляров является точка A — один конец вектора, второй конец которого — точка O — начало координат.
c) Назначение векторных диаграмм
Работникам, занимающимся проектированием и эксплуатацией релейной защиты, очень часто приходится использовать в своей работе так называемые векторные диаграммы — векторы токов и напряжений, построенные на плоскости в определенной комбинации, соответствующей электрическим процессам, происходящим в Рассматриваемая схема.
Векторные диаграммы токов и напряжений строятся при расчете коротких замыканий, при анализе распределения тока в нормальном режиме.
|
Анализ векторных диаграмм токов и напряжений является одним из основных, а в некоторых случаях единственным способом проверки правильности подключения цепей тока и напряжения и включения реле в схемах дифференциальной и направленной защиты.
На самом деле построение векторной диаграммы целесообразно во всех случаях, когда на рассматриваемое реле подаются два и более. электрические величины: разница токов в максимальной токовой или дифференциальной защите, ток и напряжение в реле направления мощности или реле направленного сопротивления. Векторная диаграмма позволяет сделать вывод о том, как сработает защита при коротком замыкании, то есть оценить правильность ее включения. Взаимное расположение векторов токов и напряжений на схеме определяется характеристикой рассматриваемой цепи, а также условно принятыми положительными направлениями токов и напряжений.
Например, рассмотрим две векторные диаграммы.
На рис. 1-10, и показана однофазная цепь переменного тока, состоящая из генератора и последовательно соединенных емкостного активного и индуктивного сопротивлений (предположим, что индуктивное сопротивление больше емкостного x L> x C). Положительные направления токов и напряжений, а также в рассмотренных выше случаях указаны на рис. 1-10 и стрелки. Построение векторной диаграммы начнем с вектора e.D. s, который расположен на рис. 1-10, б вертикально. Величина протекающего в рассматриваемой цепи тока определяется из следующего выражения:
Поскольку в рассматриваемой цепочке есть активное и реактивное сопротивления, при x L> x C вектор тока отстает от вектора напряжения на угол:
На рис. 1-10, б построен вектор, отстающий от вектора на угол 90 °. Напряжение в точке n определяется разностью векторов.Аналогично определяется напряжение в точке м:
|
г) Векторные диаграммы при наличии трансформации
Если в электрической цепи присутствуют трансформаторы, необходимо ввести дополнительные условия, чтобы сравнить векторные диаграммы токов и напряжений на разных сторонах трансформатора. Положительные направления токов следует устанавливать с учетом полярности обмоток трансформатора.
В зависимости от направления намотки обмоток трансформатора меняется взаимное направление токов в них. Для того чтобы определить направление токов в обмотках силового трансформатора и сравнить их между собой, обмоткам трансформатора нанесены обозначения «начало и конец».
Нарисуем схему, показанную на рис. 1-6, только между источником e. d. и нагрузка включит трансформатор (рис. 1-12, а). Обозначим начало обмоток силового трансформатора буквами А и а, концы — Х и х.При этом следует учитывать, что «начало» одной из обмоток берется произвольно, а вторая определяется исходя из условных положительных направлений токов, заданных для обеих обмоток трансформатора. 1-12, а положительные направления токов в обмотках силовых трансформаторов указаны. В первичной обмотке направление тока от «начала» к «концу» считается положительным, а во вторичной обмотке — от «конца» к «началу».
В результате при таких положительных направлениях направление тока в сопротивлении нагрузки остается таким же, как до включения трансформатора (см. Рис. 1-6 и 1-12).
где — магнитные потоки в магнитных сердечниках трансформатора, а — силы намагничивания, создающие эти потоки (nc).
Из последнего уравнения
Согласно равенству (1-11) векторы имеют одинаковые знаки и, следовательно, будут совпадать по направлению (рис.1-12, б).
Принятые положительные направления токов в обмотках трансформатора удобны тем, что первичный и
вторичный токи на векторной диаграмме совпадают по направлению (рисунок 1-12, б). Для напряжений также удобно принимать такие положительные направления, чтобы векторы вторичного и первичного напряжений совпадали, как показано на рис. 1-12.
В данном случае происходит подключение трансформатора по схеме 1 / 1-12. Соответственно, для трехфазного трансформатора схема подключения и векторная диаграмма токов и напряжений показаны на рис.1-14.
На рис. 1-15 б используются для построения векторных диаграмм напряжений, соответствующих схеме подключения трансформатора
.На стороне более высокого напряжения, где обмотки соединены звездой, межфазные напряжения в несколько раз превышают фазные напряжения. На стороне низкого напряжения, где обмотки соединены треугольником, междуфазное напряжение и фазное напряжение равны. Межфазные напряжения на стороне низкого напряжения на 30 ° отстают от тех же межфазных напряжений стороны высокого напряжения, что соответствует схеме подключения
Для рассматриваемой схемы соединения обмоток трансформатора можно построить векторные диаграммы токов, идущих от обе его стороны.При этом следует учитывать, что исходя из принятых нами условий определяются только положительные направления токов в обмотках трансформатора. Положительные направления токов в линейных проводах, соединяющих выводы обмоток низкого напряжения трансформатора с шинами, могут быть приняты произвольно, независимо от положительного направления токов, проходящих в треугольнике.
Так, например, если мы возьмем положительное направление токов в фазах на стороне низкого напряжения от соединенных треугольником клемм к шинам (рисунок 1-15, а), мы можем записать следующие равенства:
Соответствующая векторная диаграмма токов представлена на рис.1-15, в.
|
Аналогичным образом можно построить векторную диаграмму токов для случая, когда положительные направления токов снимаются с шин на выходы треугольника (рис. 1-16, а). Этому случаю соответствуют следующие равенства:
и векторные диаграммы, показанные на рис. 1-16 б. Сравнивая текущие графики, представленные на рис. 1-15, в и 1-16, б, можно сделать вывод, что векторы фазных токов, проходящих в проводах, соединяющих концы обмоток низкого напряжения
, напряжения трансформатора и шины находятся в тивофазе.Конечно, и те, и другие диаграммы верны.
Таким образом, при наличии в цепи обмоток, соединенных треугольником, необходимо указать положительные направления токов как в самих обмотках, так и в линейных проводах, соединяющих треугольник с шинами.
В этом случае при определении группы подключений силового трансформатора удобно брать положительные направления от выводов низкого напряжения к шинам, так как векторные диаграммы тока совпадают с принятым обозначением групп подключения силовых трансформаторов ( сравните рис.1-15, б и в). Аналогичным образом можно построить векторные диаграммы тока для других групп соединений силовых трансформаторов. Сформулированные выше правила построения векторных диаграмм токов и напряжений в цепях с трансформаторами справедливы и для измерительных трансформаторов тока и напряжения.
Рисунок 25 — Векторная диаграмма токов в точке короткого замыкания
Рисунок 26 — Векторная диаграмма токов в сечении AA
Рисунок 27- Векторная диаграмма напряжений в сечении AA
Рисунок 28 — Векторная диаграмма токов в сечении bb
Рисунок 29 — Векторная диаграмма напряжений поперечного сечения bb
Расчет периодической составляющей тока короткого замыкания методом типовых кривых.
Задача III. Расчет периодической составляющей тока трехфазного КЗ
Метод типовых кривых.
При определении периодического тока трехфазного короткого замыкания составляется диаграмма прямой последовательности для начального момента времени, в который генераторы представлены параметрами переходных процессов; нагрузки не учитываются (рисунок 2). Общая методика расчета описана в разделе После эквивалента была получена промежуточная схема (Рисунок 30), которая преобразована в радиальный вид относительно точки короткого замыкания (Рисунок 31).В этом случае используются коэффициенты распределения тока.
В процессе упрощения схемы замещения были получены следующие сопротивления: X 15 = X 1 + X 2/2 = 0 + 0,975425 / 2 = 0,4877125 о.е.
X 16 = X 4 + X 5 = 0,84 + 1,53 = 2,37 о.е.
Рисунок 30- Промежуточная схема Рисунок 31- Расчетная схема
Х 17 = Х 6 + Х 7 = 0,88 + 0 = 0,88 о.е.
X 18 = X 11 + X 9/2 = 0 + 1,240076 / 2 = 0,620038 о.е.
Х 19 = Х 12 + Х 13 = 2.117202 + 0,192308 = 2,30951 о.е.
X EC = X 18 * X 19 / (X 18 + X 19) = 0,620038 * 2,30951 / (0,620038 + 2,30951) = 0,488807 о.е.
C 1 = X EC / X 18 = 0,488807 / 0,620038 = 0,78835.
C 2 = X EC / X 19 = 0,488807 / 2,30951 = 0,21165.
X 20 = (X экв + X 17) / C 1 = 1,736294 о.е.
X 21 = (X экв + X 17) / C 2 = 6,467324 п.э.
Получается схема, показанная на рисунке 31. Затем начальные периодические токи локализуются в месте повреждения.
I «G = E 2 / X 16 * I B = 1,13 / 2,27 * 2,5 · 102 = 1,196846 кА.
I «C1 = E 1 / X 15 * I B = 1 / 0,4877125 * 2,5102 = 5,146885 кА.
I «C2 = E 3 / X 20 * I B = 1 / 1,736294 * 2,5102 = 1,445723 кА.
I «C3 = E 4 / X 21 * I B = 1 / 6,467324 * 2,5102 = 0,388136 кА.
Ток в системах постоянный. Периодический ток по стандартным кривым определяется для синхронного генератора с тиристорной или высокочастотной системой возбуждения.В соответствии с методикой рассчитывается номинальный ток синхронного генератора и далее определяется номер кривой типа.
I GN = S GN / * U B = 100 / (* 0,85 * 230) = 0,295320 кА;
I * PO = I G2 «/ I GN = 1,196846 / 0,295320 = 4,05» 4.
Так как отношение I G2 «/ I GN» 4, то выбирается 4 типичных кривых:
I KZPOST = I «C2 + I» C3 + I «C1 = 5,1468885 + 1,445723 + 0,388136 = 6,980748 кА
| т, сек | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | |
| I G t / I ”G, о.е | 0,85 | 0,78 | 0,755 | 0,75 | 0,745 | |
| I G t, кА | 1,1968 | 1 017 | 0,933 | 0,903 | 0,897 | 0,891 |
| Итого I K t, кА | 8,1775 | 7,9977 | 7,9137 | 7,8837 | 7 8777 | 7 872 |
В качестве примера рассмотрим поиск периодического тока для момента времени, равного 0.1 секунда. Кривая 4 для этого момента времени определяет отношение In, t, g / Inog = 0,85.
Определяется по фактическому значению периодической составляющей тока короткого замыкания от генератора: In, t, g = 0,85 * In * I NOM = 0,85 * 4,05 * 0,2953 = 1,017 кА.
Полный периодический ток в точке K (3) в узле K с учетом типичных кривых показан на рисунке 32.
Рисунок 32- График зависимости полного периодического тока от времени повреждения Ikt = f (t)
Задача IV.Расчет периодической составляющей тока несимметричного короткого замыкания методом типовых кривых.
Для определения периодических токов короткого замыкания при К (1.1) методом типовых кривых составляется схема замены обратной последовательности без учета нагрузок (рисунок 33). Далее идет упрощение эквивалентной схемы и получение эквивалентного сопротивления обратной последовательности. Последовательность упрощений показана ниже и на рисунках 34-37.
X 15 = X 1 + X 2/2 = 0 + 0,975425 / 2 = 0,487713 о.е. X 16 = X 4 + X 5 = 0,84 + 1,87 = 2,71 о.е.
X 17 = X 6 + X 7 = 0 + 0,88 = 0,88 о.е. X 18 = X 11 + X 9/2 = 0 + 1,240076 / 2 = 0,620038 о.е.
X 19 = X 12 + X 13 = 2,117202 + 0,230769 = 2,347971 о.е.
X 20 = X 15 * X 16 / (X 15 + X 16) = 0,487713 * 2,71 / (0,487713 + 2,71) = 0,413327 о.е.
X 22 = X 17 + X 21 = 0,88 + 0,4
= 1,370508 о.е. X EC2 = X 20 * X 22 / (X 20 + X 22) = 0,413327 * 1.370508 / / (0,413327 + 1,370508) = 0,317556 о.е.
Рисунок 33 — Обратная последовательность
Рисунок 34- Схема упрощения №1
Рисунок 35- Схема упрощения №2
Рисунок 36- Схема упрощения № 3
Рисунок 37- Замена эквивалентной схемы реверс
Последовательности
Аналогично составляем схему замены нулевой последовательности (рисунок 38).Процедура упрощения схемы замены показана ниже на Рисунках 39-42.
Рисунок 38 — Схема замены расчетной нулевой последовательности
X 13 = X 1 + X 2/2 = 0 + 4,585 / 2 = 2,292 п.ф. X 14 = X 10 + X 9/2 = 0 + 6,82 / 2 = 3,41 о.е.
X 15 = X 11 + X 12 = 7,41 + 0,769 = 8,18 о.е. X 16 = X 13 * X 4 / (X 13 + X 4) = 2,29225 * 0,84 / (2,29 + 0,84) = 0,615 о.е.
X 18 = X 6 + X 17 = 0,88 + 1,338581 = 2,219 о.е.
Х 17 = 1 / (1 / Х 7 + 1 / Х 15 + 1 / Х 14) = 1 / (1 / 3,016 + 1 / 8,18 + 1 / 3,41) = 1.34 в. У.
Рисунок 39- Схема упрощения №1
Рисунок 40- Номер схемы упрощения 2
Рисунок 41 — Схема упрощения № 3
Рисунок 42 — Эквивалентная схема замещения нуля
Последовательности
Для решения проблемы мы используем эквивалентные данные в прямой последовательности из предыдущей задачи.Учитывая особенности K (1.1), получаем схему, представленную на рисунке 43. Эта схема приведена к виду, показанному на рисунке 44.
Рассмотрено для случая исправного нулевого провода. Векторные диаграммы напряжений и токов приведены на рисунках 15 и 16; На рисунке 17 показана комбинированная диаграмма тока и напряжения.
1. Построены оси комплексной плоскости: действительные значения (+1) — по горизонтали, мнимые значения (j) — по вертикали.
2. На основании значений модулей тока и напряжения и размеров полей листов, зарезервированных для построения схем, выбираются шкалы тока mI и напряжения mU.При использовании формата А4 (размеры 210х297 мм) с самыми большими модулями (см. Таблицу 8) на ток 54 А и напряжение 433 В шкалы принимаются: mI = 5 А / см, mU = 50 В / см.
3. С учетом принятых масштабов mI и mU определяется длина каждого вектора, если диаграмма построена с использованием экспоненциальной формы его записи; с помощью алгебраической формы находятся длины проекций векторов на оси действительных и мнимых величин, т.е.длины действительной и мнимой частей комплекса.
Например, для фазы A:
Длина вектора тока / ф.А / = 34,8 А / 5 А / см = 6,96 см; длина его реальной части
I f.A = 30 A / 5 A / см = 6 см,
длина его мнимой части
I f.A = -17,8 А / 5 А / см = — 3,56 см;
Длина вектора напряжения / А нагрузки / = 348 В / 50 В / см = 6,96 см; длина его реальной части
U Нагрузка. = 340,5 В / 50 В / см = 6,8 см;
длина его мнимой части
У Анагр.= 37,75 В / 50 В / см = 0,76 см.
Результаты определения длин векторов, их действительной и мнимой частей отражены в таблице 9.
Таблица 9 — Длины векторов тока и напряжения, их действительная и мнимая части для случая исправного нулевого провода.
| Величина | Масштаб, 1 / см | Длина вектора, см | Длина реальной части, см | Длина воображаемой части, см | |
| Напряжение фазы сети | U A | 50 В / см | 7,6 | 7,6 | |
| УБ | 7,6 | — 3,8 | — 6,56 | ||
| UC | 7,6 | — 3,8 | 6,56 | ||
| Напряжение фазной нагрузки | У Анагр. | 50 В / см | 6,96 | 6,8 | 0,76 |
| УФ-загрузка | 7,4 | — 4,59 | — 5,8 | ||
| Нагрузка США | 8,66 | -4,59 | 7,32 | ||
| U0 | 1,08 | 0,79 | — 0,76 |
Продолжение таблицы 9
| Фазные токи нагрузки | I ф.А. | 5 А / см | 6,96 | 6,0 | — 3,56 |
| I f.V | 7,4 | 1,87 | — 7,14 | ||
| I f.C | 3,13 | 0,1 | 3,12 | ||
| I 0 | 10,8 | 7,9 | — 7,6 |
4.1 На комплексной плоскости построены векторы фазных напряжений питающей сети A, B, C; соединив их концы, получают векторы линейного напряжения АВ, ВС, СА.Затем строятся векторы фазных напряжений нагрузки А., В нагрузке., С нагрузкой. Для их построения можно использовать обе формы регистрации комплексов токов и напряжений.
Например, загрузка вектора А. Строится по экспоненциальной форме следующим образом: от оси +1 под углом 6 10, т.е. против часовой стрелки откладывается длина 6,96 см; в алгебраической форме его можно построить, положив на ось +1 длину 6,81 см и на ось + j длиной 0,76 см, концы этих отрезков являются координатами конца вектора нагрузки А.
4.2. Поскольку сетевое напряжение, нагрузки устанавливаются сетью; Для определения положения нейтрали нагрузки необходимо выполнить параллельную передачу вектора фазовых напряжений нагрузки A, B, C. так, чтобы их концы совпадали с концами фазных напряжений питающей сети.
Точка 0, которая будет их началом, есть нейтральная нагрузка. В этой точке находится конец вектора напряжения смещения нейтрали 0, его начало находится в точке 0.Этот вектор также можно построить, используя данные в таблице 9.
5. Построение векторной токовой диаграммы.5.1 Построение векторов фазных токов нагрузки f.A, f.V, f.C аналогично построению векторов фазных напряжений.
5.2 Путем сложения векторов фазного тока получается вектор тока в нейтральном проводе 0; его длина и длина выступов на оси должны совпадать с указанными в таблице 8.
Векторные диаграммы токов и напряжений для случая обрыва нулевого провода строятся аналогично.
Необходимо проанализировать результаты расчета и построения векторных диаграмм и сделать выводы о влиянии асимметрии нагрузки на величину ее фазных напряжений и на напряжение нейтрали; Особое внимание следует обратить на последствия разрыва сети нулевого провода при несимметричной нагрузке.
Примечание . Допускается совмещение диаграмм токов и напряжений при условии, что они выполнены в разных цветах.
Рисунок 15.Векторная диаграмма напряжений
Рисунок 16. Векторная диаграмма тока.
Рисунок 17. Совмещенная векторная диаграмма напряжений и токов.
Порядок построения векторных диаграмм напряжений и токов. Построение векторных диаграмм
Задача 6.1. В схеме, показанной на рисунке 6.1, были измерены напряжения на активном сопротивлении. U R и на зажимах катушки U K, а также угол φ между напряжением Ū К и ток Я .
Измерения дали следующие результаты: U R = 100 В U К = 120, φ = 75º.
Требуется для определения значения входного напряжения U .
Строим векторную диаграмму заданной цепочки (рис. 6.2).
Так как схема неразветвленная, начинаем построение с вектора тока Ī .Рисуем по нему вектор. Ū R и прибавляем к нему вектор Ū K, угол опережения тока φ . Сумма векторов Ū R и Ū K дает вектор входного напряжения Ū , длину которого, определяющую величину входного напряжения, находим по теореме косинусов:
Задача 6.2. В схеме на рис. 6.3 резонанс.
Найти текущее значение I 3 если U = 80 В, I 2 = 4 А, R = 25 Ом.
Задача легко решается с помощью векторной диаграммы. Поскольку резонанс в контуре, напряжение и ток на входе контура совпадают по фазе, векторы Ū и Ī 1 направлены в одну сторону (рис.6.4). Напряжение в первой секции отстает от тока. Ī 1 под углом 90º. Вектор Ū 1 прямой перпендикуляр вниз. Вектор Ū 2 начертить от конца вектора Ū 1 до конца вектора Ū — чтобы было равенство: Ū 1 + Ū 2 = Ū . Текущий Ī 2 находится в фазе с напряжением 2 и Ī 3 позади него под углом 90 °.В сумме дают ток Я 1.
По закону Ома для второй ветви:
Из треугольника ade :
По подобию треугольников abc и ade следует:
Вычислить:
Задача 6.3. К катушке с параметрами R и L подключены параллельно емкость C (рис.6.5, а). Известно, что даны резонанс в цепи и значения двух токов: I От до = 5 А и I = 3 А. Какая емкость конденсатора, если значение питающего напряжения U = 220 В, а его частота f = 50 Гц?
Векторная диаграмма быстро приводит к результату (рис. 6.5, б).
Текущий Я отстает от напряжения Ū под некоторым углом, текущий Ī с опережает напряжение на 90º.В сумме эти два тока дают общий ток: Ом. = Я С до + Я с. Поскольку в цепи резонанс, вектор полного тока направлен по вектору напряжения.
Текущая диаграмма представляет собой прямоугольный треугольник, из которого следует:
Емкость
и емкость конденсатора
ЗАКЛЮЧЕНИЕ
Векторная диаграмма дает полную информацию об электрической цепи.Можно даже сказать, что это один из способов изображения электрической цепи — его конфигурация позволяет определить структуру цепи. А если он построен в масштабе, он дает числовые значения напряжений и токов на всех элементах схемы, а также позволяет найти значения всех сопротивлений.
ТЕСТОВЫЕ ВОПРОСЫ
1. Что такое вектор? Как соотносятся векторы тока и напряжения в электрической цепи?
2. Каковы правила добавления векторов?
3.Как векторы тока и напряжения в удельном сопротивлении, индуктивности и емкости направлены относительно друг друга?
4. Какие законы электрической схемы используются при построении векторных диаграмм?
5. С какого вектора целесообразно начинать построение векторной диаграммы?
6. В какой последовательности откладывать векторы при построении диаграммы?
ЗАДАЧИ УПРАВЛЕНИЯ
В схеме, заданной учителем, обозначьте напряжения и токи на всех участках и постройте векторную диаграмму.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Теоретические основы электротехники: в 3 тоннах. Учебник для вузов. Том 1. — 4-е изд. / К.С. Демирчян, Л. Нейман, Н.В. Коровин, В.Л. Чечурин. — СПБ .: Питер, 2004, — 463 с., Илл.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Теоретические основы электротехники: в 3 т. Учебник для вузов. Том 1. — 4-е изд. / К.С. Демаркян, Л. Нейман, Н.В. Коровин, В.Л. Чечурин.- СПБ .: Питер, 2004, — 463 с., Ил.
2. Матющенко В.С. Теоретические основы электротехники. Линейные электрические цепи постоянного и однофазного синусоидального тока: учеб. пособие / В.С. Матющенко. — Хабаровск. — Хабаровск: Издательство ДВГУПС, 2002. — 112 с.
3. Матющенко В.С. Расчет сложных электрических цепей постоянного и синусоидального токов: учеб. пособие / В.С. Матющенко. — Хабаровск: Изд-во ФЕДУПС, 2004.- 69 с.
Задача 3
Сначала создается вектор тока, затем вектор напряжения.
Задача 4
Постройте качественную векторную диаграмму.
Строительство осуществляется с использованием свойств элементов.
Задача 5
Постройте качественную векторную диаграмму схемы при условии, что XL> XC.
Строительство осуществляется с использованием свойств элементов.
Задача
В последовательной цепи АТ определить показания приборов, составить и рассчитать баланс мощности, определить коэффициент мощности, построить топографическую векторную диаграмму.
R1 = 10 Ом
R2 = 20 Ом
C = 31,8 мкФ
L = 0,127 GN
f = 50 Гц
один). Определить полное комплексное сопротивление реактивных элементов
2). Переводим напряжение источника в алгебраическую форму
3). Определить сопротивление эквивалентной цепи.
Схема имеет активно-емкостной характер.
четыре). Определить ток в цепи
пять). Амперметр покажет текущее значение тока
6).Определите показание вольтметра, действующее значение напряжения на конденсаторе
7). Определить источник питания и приемники
Мощность приемника
Из расчетов видно, что весы сходятся с погрешностью менее процента.
восемь). Определить коэффициент мощности
9) построение топографической векторной диаграммы
Определить напряжения на элементах схемы
Выбор масштаба тока 2 см — 1 А; по напряжению 2см — 50 В
Правило построения векторной диаграммы, при последовательном включении элементов:
строим вектор тока
строим вектор напряжений
складываем вектор напряжений по правилу параллелограмма.
В основном векторные диаграммы строятся на комплексной плоскости и
бывает двух типов: — векторные диаграммы токов и напряжений ;
— векторные топографические диаграммы напряжений .
Все Векторные диаграммы построены с возможностью масштабирования, как для токов, так и для напряжений. На комплексной плоскости расположены оси координат. +1 и + j . Способ построения схем зависит от монтажной схемы электрической схемы.Если элементы схемы R, L, C соединены последовательно, то «эталоном» на схеме является вектор тока, общий для всех элементов. Затем векторы напряжения строятся с учетом фазового сдвига между током и напряжениями на элементах (см. Диаграмму A). Геометрическая сумма векторов напряжения должна быть равна вектору напряжения, приложенному к электрической цепи.
Диаграмма A Диаграмма B
Если элементы схемы R, L, C соединены параллельно, то «эталоном» на схеме является вектор напряжения, общий для всех элементов.Далее векторы тока строятся с учетом фазового сдвига между напряжением и токами в ветвях цепи (см. Диаграмму B). Геометрическая сумма векторов токов в ветвях должна быть равна суммарному току в электрической цепи.
Топографическая диаграмма напряжений — это диаграмма комплексных потенциалов точек электрической цепи, расположенных в определенном порядке. Потенциал одной из точек предполагается равным нулю, далее возможны два варианта: сначала рассчитываются потенциалы остальных точек относительно этого потенциала; во-вторых, с этого момента модули напряжения наносятся на элементы с соответствующими углами сдвига фаз.Порядок построения топографической диаграммы показан на простом примере (см. Диаграмму B и диаграмму B).
Схема B Схема B
Электрические цепиAT При смешанном сочетании элементов топографическая диаграмма напряжений обычно строится в несколько этапов. В этом случае схемы сначала строятся для отдельных ветвей цепи, что предполагает наличие векторной диаграммы тока для всей цепи, а затем объединяются в общую топографическую схему.
Окончание работы —
векторных диаграмм | IamTechnical.com
Временные характеристики синусоидальных переменных напряжений и токов могут быть представлены не только с помощью линейных диаграмм, которые мы видели до сих пор, но также с помощью векторных диаграмм, которые могут оказаться более подходящими в некоторых случаях. На рисунках ниже показана взаимосвязь между линейной и векторной диаграммами синусоидального переменного напряжения u с пиковым значением u 0 и частотой f .Вектор можно рассматривать как линию длиной u0, вращающуюся против часовой стрелки с частотой f или угловой частотой w = 2 · pi · f относительно начала координат.
Нулевая точка на линейной диаграмме в момент времени t = 0, где начинается синусоидальная кривая, соответствует начальному горизонтальному положению вектора, в котором стрелка направления указывает вправо. Векторная диаграмма также показывает второй вектор с фазовым углом w · t = 60 °. Перпендикулярная линия (пунктирная синяя) от вершины этого вектора к горизонтальной оси представляет мгновенное значение u напряжения при этом фазовом угле в соответствии с уравнением.
Следующая анимация иллюстрирует взаимосвязь между векторной и линейной диаграммами.
Если напряжение u 1 с пиковым значением u 10 демонстрирует колебания, опережающие напряжение u 2 (пиковое значение u 20 ) на фазовый угол j на соответствующей диаграмме показаны два вектора u 2 , смещенные относительно u 1 на угол j (см. иллюстрацию ниже).
Векторы на векторной диаграмме рисуются в начальной позиции, представляющей фазовый угол, который они принимают в момент времени t = 0, то есть своего рода снимок во время непрерывного вращения вектора. Основным преимуществом векторных диаграмм перед линейными диаграммами является то, что их можно очень легко использовать для представления синусоидальных переменных величин. Векторные диаграммы оказываются особенно практичными, если необходимо одновременно отображать несколько переменных величин с фазовым смещением, как в приведенном выше примере.Вместо пиковых значений векторные диаграммы могут также представлять среднеквадратичные значения U и I, которые отличаются просто коэффициентом √2.
Синусоидальные переменные величины идентичных частот могут быть визуализированы в векторных диаграммах, где длина вектора указывает значение напряжения или тока, а углы между векторами указывают фазовый сдвиг между соответствующими переменными величинами.
Электрические фазовые диаграммы | Electrical Academia
Вектор — это линия, которая по своей длине и направлению представляет величину и угол приложения силы, скорости или другой векторной величины.«Фазор» — это термин, используемый для описания вращающихся векторов, которые появляются в электрических расчетах. Векторы напряжения и тока представляют собой среднеквадратичное значение напряжения или тока по их длине и углу разности фаз между вектором и опорной плоскостью.
Фазорные диаграммыПеременные токи и напряжения, а также их фазовое соотношение могут быть представлены с помощью синусоидальных волн, как на рис. 1 (а), 2 (а) и 3 (а) , но это метод неудобный.Более простой метод — использовать векторы в векторной диаграмме, как на рисунках 1 (b), 2 (b) и 3 (b). Поскольку среднеквадратичные значения переменного тока очень важны, векторные диаграммы почти всегда масштабируются для представления среднеквадратичных значений и, если не указано иное.
Рисунок 1 Синфазные электрические фазоры
Рисунок 2 Электрический вектор с запаздыванием
Рисунок 3 Ведущий электрический фазор
Ссылаясь на Рисунок A , эталонный вектор всегда отображается по горизонтали и вправо, и все фазовые углы должны измеряться от опорного вектора.При выборе эталонного вектора обычно выбирают величину, которая имеет одинаковое значение во всех частях схемы.
Рисунок A Схема электрического фазора
Для цепи серии в качестве опорного вектора используется ток, поскольку ток является общим для всех частей схемы.
Для параллельной цепи напряжение используется в качестве опорного вектора, поскольку напряжение является общим для всех частей схемы.
Позже вы увидите, что трансформаторы имеют магнитный поток , который является общим для входа и выхода трансформатора, и поэтому магнитный поток становится опорным вектором.
Переменные токи возникают при приложении переменного напряжения к нагрузке. Когда кривые тока и напряжения проходят через нулевое положение одновременно и увеличиваются до своих максимальных значений в одном и том же направлении, формы волн находятся в фазе друг с другом, как показано на рис. 1 (a) .Векторная диаграмма для синфазного состояния показана на Рис. 1 (b) .
В этой книге принято различие между векторами напряжения и тока. Вектор напряжения отображается красным цветом, а вектор тока — синим.
В некоторых схемах кривые тока и напряжения не достигают своих нулевых и максимальных значений одновременно, и говорят, что они «не совпадают по фазе», а угол опережения или запаздывания называется «фазовым углом» (символ φ).
Следует отметить, что этот символ используется по соглашению для обозначения угла между двумя векторами и не является взаимозаменяемым с символом «тета» (θ), используемым для обозначения угла поворота.Второе соглашение заключается в том, что предполагается, что все векторы вращаются против часовой стрелки, начиная с положительной оси x.
Рисунок 2 (a) показывает ток, отстающий от напряжения на 60 ° и Рисунок 2 (b) показывает то же состояние с использованием векторов.
Рисунок 3 (a) показывает ток, опережающий напряжение на 60 ° и Рисунок 3 (b) показывает то же состояние с использованием векторов.
Сложение фазов графическим методомПеременные значения тока или напряжения нельзя складывать арифметически, если они не совпадают по фазе.Если два напряжения переменного тока подключены последовательно, они могут не совпадать по фазе друг с другом. Один из методов добавления векторов состоит в том, чтобы нарисовать векторы в масштабе и угле, используя значения RMS, а затем сложить их вместе, используя метод параллелограмма, как показано в Пример 1 и Рисунок 4 .
Рисунок 4 Метод параллелограмма
Пример 1
Два напряжения A и B соединены последовательно. Напряжение A составляет 150 В и опережает ток на 45 °, напряжение B составляет 100 В и отстает от тока на 30 °.Найдите полную ЭДС и фазовый угол.
Поскольку два напряжения идут последовательно, ток используется в качестве опорного вектора. Чтобы построить векторную диаграмму, выполните следующие действия: ( Рисунок 4 )
Шаг 1. Нарисуйте текущий вектор по горизонтали вправо в качестве опорного вектора.
Шаг 2. Нарисуйте векторы для VA и VB в масштабе, измеряя фазовые углы от опорного вектора с помощью транспортира.
Шаг 3. Постройте векторный параллелограмм.
Шаг 4. Изобразите результат, определите полную ЭДС по шкале и измерьте фазовый угол.
Общее напряжение = 201 В (ANS A)
Фазовый угол Φ = 17 ° вперед (ANS B)
Сложение векторов математическим методомГрафический метод полезен для оценки общего значения, и часто это все электрику нужно. Но современные калькуляторы упрощают эту задачу и делают ее намного более точной за счет использования тригонометрии, и многие из них включают функцию преобразования полярных чисел в прямоугольные, которую вы скоро увидите как полезную (даже на iPhone есть приложение.для этого!).
Расчет может быть выполнен с использованием нескольких методов, но наиболее распространенный метод использует тригонометрию в процессе преобразования векторов полярной формы в горизонтальные и вертикальные компоненты, известные как прямоугольная форма. Синфазные фазовые факторы можно напрямую складывать вместе, поэтому добавляются горизонтальные части, а также вертикальные части. Полученная в результате прямоугольная форма затем преобразуется обратно в фазор полярной формы с использованием теоремы Пифагора и функции arc – tan (tan −1 ).Этот процесс используется в , Пример 2 (а) .
Некоторые научные калькуляторы даже имеют функцию преобразования полярной формы в прямоугольную и прямоугольную в полярную и могут даже добавлять прямоугольную форму, делая весь процесс быстрым и простым, как показано в Пример 2 (b) .
Пример 2
Два напряжения A и B соединены последовательно. Напряжение A составляет 150 В и опережает ток на 45 °, напряжение B составляет 100 В и отстает от тока на 30 °.
| (a) | Найдите полную ЭДС и фазовый угол тригонометрическим методом. |
| (b) | Найдите общую ЭДС и фазовый угол, используя функции преобразования полярного сигнала в прямоугольный (P> R) и преобразования из прямоугольного в полярный (R> P) на подходящем калькуляторе. |
На рисунке 5 показана векторная диаграмма с математическими вычислениями, использованными для определения каждого. Это в конечном итоге становится довольно загроможденным, поэтому векторный эскиз обычно рисуется в верхней части расчета, а математические вычисления выполняются под диаграммой, как в примере 2 .
Рисунок 5 Тригонометрический метод
Векторная диаграмма соединения звездой и треугольником — нарушение напряжения
В этой статье звезда (звезда) и соединение треугольником обсуждается в отношении напряжений линия-линия, фаза-нейтраль. и токи. Кроме того, векторные фазовые углы между соединением треугольником и звездой также обсуждается.
Соединение WYE — Напряжение
Для соединения WYE источник нейтраль подключена к нейтрали нагрузки.Даже если нет нейтрального провод, но нейтраль источника и нейтраль нагрузки заземлены (заземлены) применимы те же обсуждения. Если нейтраль источника и нагрузки и незаземленная, напряжения будут такими же, как и при заземленной нейтрали, ЗА ИСКЛЮЧЕНИЕМ неисправности в система. Когда есть замыкание на землю на источнике с незаземленной звездой, напряжения станут несимметричными. Когда есть замыкание на землю на заземленной звездой источник, напряжения будут по большей части сбалансированы.
Напряжение соединения звездойДля этого обсуждения предположим, что напряжения источника между фазой и нейтралью следующие:
Линия к нейтрали напряжения нагрузки при подключенной звездой нагрузке будет такой же, как указано выше.
Однако линейное напряжение (фаза-фаза) на нагрузке будет иметь следующий вид:
То есть в трехфазном Система с заземлением звездой с напряжениями прямой последовательности, линейное напряжение составляет √3, умноженное на напряжение фаза-нейтраль, и выводов на 30 0 . Векторная диаграмма ниже представлена эта величина и изменение фазового угла.
Векторы напряжения соединения звездойСледует отметить следующие важные моменты:
Напряжение фаза-нейтраль: для сбалансированной системы сумма напряжение фаза-нейтраль (Van + Vbn + Vcn) равно нулю.Для несимметричного напряжения эта сумма не будет равным нулю и приведет к нулевому напряжению нейтрали и приведет к протеканию тока нейтрали, если нейтрали соединены вместе.
Линейное напряжение: для симметричной или несимметричной системы сумма линейных напряжений (Vab + Vbc + Vca) равно нулю. Это потому, что линейные векторы образуют замкнутый треугольник и даже если одна из величин напряжения уменьшается, другие напряжения корректируются до образуют замкнутый треугольник.
Соединение звездой треугольник напряженияСоединение WYE — Текущее
Для нагрузки, подключенной звездой со звездочкой подключенный источник, линейные токи уравновешены смещением 120 0 между любыми двумя фазами.Линейные токи и ток нагрузки будут равны.
Соединительные токи звездыДля нагрузки, подключенной звездой, нейтраль ток вычисляется путем добавления следующего векторно . Это означает, что амплитуда и фазовый угол должны быть считается.
Для сбалансированных трехфазных токов сумма Ia + Ib + Ic будет равна нулю. Даже если сопротивление на соединение нейтрали изменяется от 0 до ∞, ток нейтрали будет равен нулю при условии, что система сбалансирована .Если система несбалансированная нейтральная ток будет течь между нейтральными точками источника нагрузки и источника.
Соединение ТРЕУГОЛЬНИКОМ — Напряжение
Для нагрузки, подключенной по схеме треугольник, линейное напряжение источника и треугольник подключенная нагрузка линейные напряжения будут такими же, как . Хотя нет нейтраль для дельта-системы, воображаемая нейтраль в центре тяжести дельты можно предположить треугольник. Когда система уравновешена, эта воображаемая нейтральная и нейтраль источника будет на той же потенциал земли .Следовательно, когда дельта сбалансирована, линия-земля потенциал на нагрузке такой же, как напряжение между фазой и нейтралью источника. Когда есть замыкание на землю в системе треугольник (система становится несбалансированной), напряжения относительно земли не совпадают.
Напряжение соединения треугольникомСоединение DELTA — Текущее значение
На рисунке ниже изображена звезда подключенный источник, питающий сбалансированную нагрузку, подключенную по схеме треугольника. Линейные токи в этот кейс присваивается:
Для сбалансированных токов нагрузки по трем треугольникам сумма IAB + IBC + ICA будет равна нулю.Если дельта-импедансы нагрузки не сбалансированы, то фазные токи (IAB, IBC и т. Д.) Не будут сбалансированы. Однако даже в этом случае сумма линейных токов (Ia + Ib + Ic) будет равна нулю, поскольку нулевой провод отсутствует.
Векторы тока соединения треугольникомДополнительное чтение:
Подключение трансформатора: фазовый сдвиг и полярность
Соединение конденсаторов звездой и треугольником
Разбитая дельта
Калькулятор преобразования дельта-звезда
Введение в использование векторных диаграмм на осциллографах для анализа трехфазной мощности
Когда вы работаете с 3-фазными системами, наличие векторных диаграмм на вашем осциллографе может сэкономить время во время настройки и обеспечить более быстрое понимание вашей системы.
Как правило, переменные напряжения или токи представляются графически как зависимости напряжения или тока от времени. Это традиционный вид осциллографа.
Трехфазная система состоит из трех синусоидальных напряжений переменного тока и токов одинаковой частоты. Если на одной оси отложено 6 или более осциллограмм, график будет очень загруженным. Может быть трудно различить важную информацию о величинах и фазовых углах. Инженеры-электрики рано поняли это и избрали более простой способ.
Фазорные диаграммы представляют величину и соотношение направлений между двумя или более векторами. Благодаря своей способности эффективно передавать информацию об амплитуде и фазе, векторная диаграмма популярна и широко используется при анализе трехфазных энергосистем.
Наличие векторных диаграмм на вашем осциллографе дает два ключевых преимущества:
1. Он обеспечивает быстрый способ проверки вашей настройки.
2. Он быстро показывает характер нагрузок в вашей системе.
1.Проверьте свой Setup
Диаграммыпозволяют быстро убедиться, что ваши датчики ориентированы правильно. Настройка измерений в трехфазных системах может быть сложной задачей. Необходимо подключить три или более датчиков напряжения с соблюдением полярности. Также необходимо подключить три или более токовых пробника и сориентировать их стрелками в сторону нагрузки. Проблема заключается в определении правильной полярности, а не в самих токовых пробниках. Накладные датчики тока просты в эксплуатации. Просто поместите проводник в челюсть и полностью закройте челюсть.Проволоку не нужно центрировать в отверстии, и ничего страшного, если она проходит под углом.
Нагрузки двигателя индуктивные, поэтому на векторной диаграмме вектор напряжения должен опережать вектор тока. Если на векторной диаграмме отображается опережающий вектор тока, рекомендуется проверить соединения тестовой установки. Обычно это происходит из-за токовых клещей с обратной полярностью.
Датчики тока подключены в обратном направлении. Обратите внимание на векторы тока, опережающие соответствующие векторы напряжения
Путем изменения направления датчиков тока проблема с подключением решена.Обратите внимание на то, что векторы тока теперь отстают от соответствующих векторов напряжения, указывающих на правильную ориентацию датчиков тока.
2. Разберитесь в своих нагрузках
В сбалансированной трехфазной системе каждый из трех векторов напряжения номинально разнесен на 120 градусов. В сбалансированной системе с одинаковыми нагрузками на каждую фазу векторы тока также будут находиться на расстоянии 120 градусов друг от друга. В этой сбалансированной системе сумма линейных токов равна нулю в любой момент, и сумма линейных напряжений также равна нулю.
Но практические системы не ведут себя как учебные системы. Различия в импедансах нагрузки между тремя фазами приведут к дисбалансу. Они могут проявляться как разная длина в векторах и разные углы между векторами напряжения и тока.
Векторная диаграмма идеально подходит для наблюдения за эффектами индуктивных или емкостных нагрузок. Для чисто резистивных нагрузок напряжение и ток будут синфазными, что означает отсутствие запаздывания между напряжением и током. Однако, поскольку двигатели являются индуктивными по своей природе, вектор тока всегда будет отставать от соответствующего вектора напряжения.Для хорошей конструкции моторного привода этот фазовый угол между векторами напряжения и тока поддерживается на минимальном уровне.
Типичная фазовая диаграмма в виде линии-линии (слева / вверху) и ее соответствующая конфигурация с нейтральной линией (справа / снизу). На левом изображении обратите внимание на углы между векторами напряжения в верхнем левом углу (0 градусов, -120 градусов и -119,7 градусов), указывающие на почти сбалансированную нагрузку. Векторы тока отстают от соответствующих векторов напряжения, что указывает на правильность подключений.Конфигурация «линия-нейтраль» математически выводится из конфигурации «линия-линия» без изменения физического соединения.
Заключение
Фазорные диаграммы — отличные наглядные инструменты, которые помогут вам понять трехфазные системы. Они обеспечивают хорошее общее представление о ваших проектах и быстро показывают влияние изменений дизайна.
Tektronix Inverter Motor Drive Analysis Solution (5-IMDA) предлагает уникальные векторные диаграммы на основе осциллографов для быстрого анализа ваших трехфазных схем.