правила построения диаграмм, онлайн построение
Цифровое представление динамических процессов затрудняет восприятие, усложняет расчет выходных параметров после изменения условий на входе или в результате выполненной обработки. Векторная диаграмма токов и напряжений помогает успешно решать обозначенные задачи. Ознакомление с теорией и практическими примерами поможет освоить данную технологию.
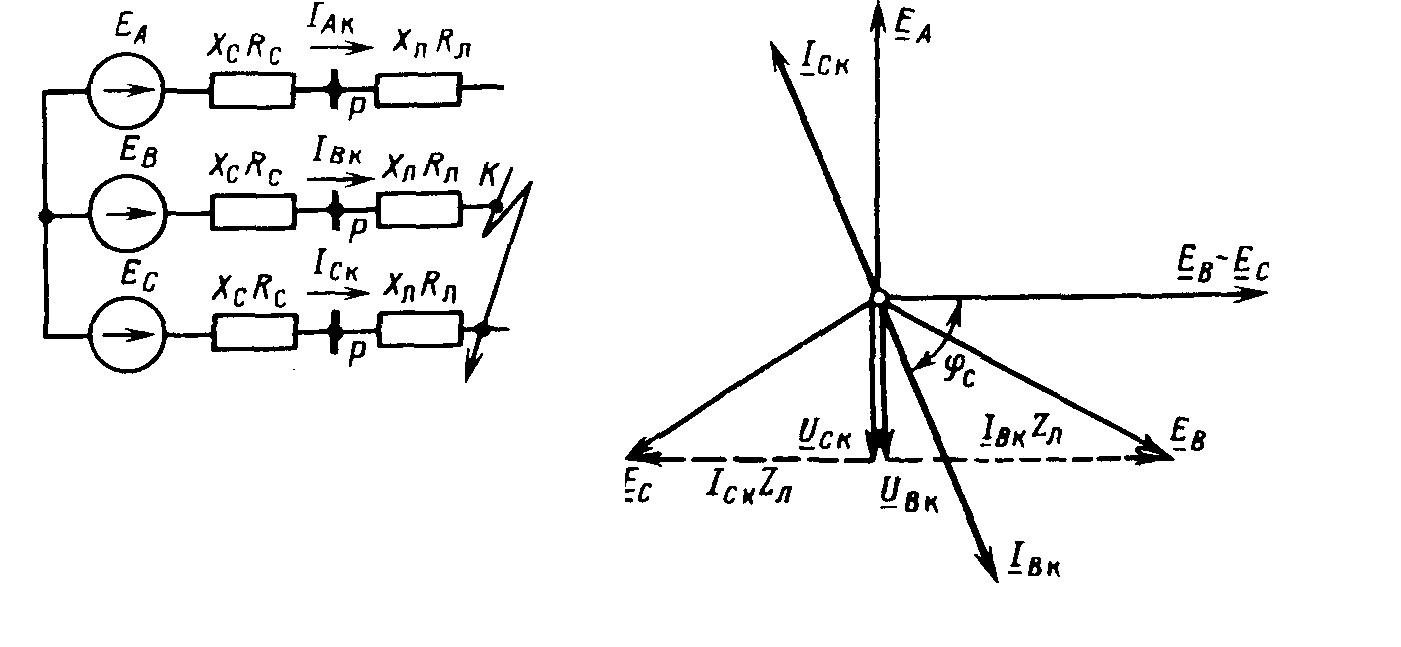
Диаграмма, поясняющая процесс короткого замыкания в трехфазной цепи счетчика электроэнергии
Разновидности векторных диаграмм
Для корректного отображения переменных величин, которые определяют функциональность радиотехнических устройств, хорошо подходит векторная графика. Подразумевается соответствующее изменение основных параметров сигнала по стандартной синусоидальной (косинусоидальной) кривой. Для наглядного представления процесса гармоническое колебание представляют, как проекцию вектора на координатную ось.
С применением типовых формул несложно рассчитать длину, которая получится равной амплитуде в определенный момент времени. Угол наклона будет показывать фазу. Суммарные влияния и соответствующие изменения векторов подчиняются обычным правилам геометрии.
Различают качественные и точные диаграммы. Первые применяют для учета взаимных связей. Они помогают сделать предварительную оценку либо используются для полноценной замены вычислений. Другие создают с учетом полученных результатов, которые определяют размеры и направленность отдельных векторов.
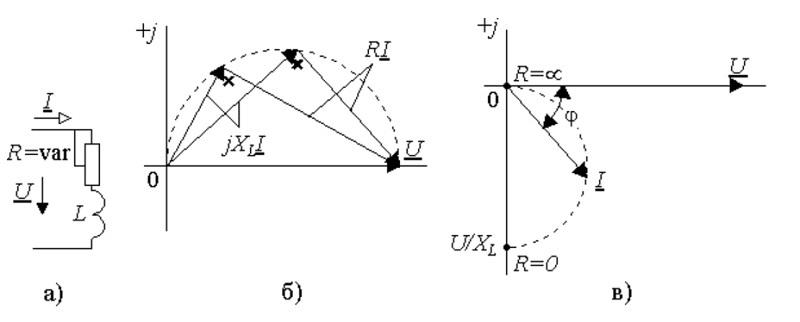
Круговая диаграмма
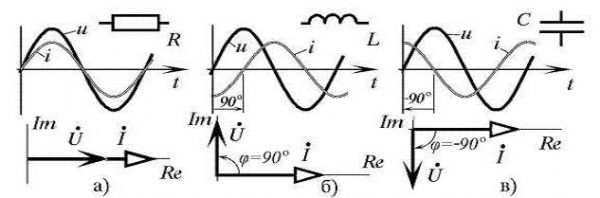
Допустим, что надо изучить изменение параметров тока в цепи при разных значениях сопротивления резистора в диапазоне от нуля до бесконечности. В этой схеме напряжение на выходе (U) будет равно сумме значений (UR и UL) на каждом из элементов. Индуктивный характер второй величины подразумевает перпендикулярное взаимное расположение, что хорошо видно на части рисунка б). Образованные треугольники отлично вписываются в сегмент окружности 180 градусов. Эта кривая соответствует всем возможным точкам, через которые проходит конец вектора UR при соответствующем изменении электрического сопротивления. Вторая диаграмма в) демонстрирует отставание тока по фазе на угол 90°.
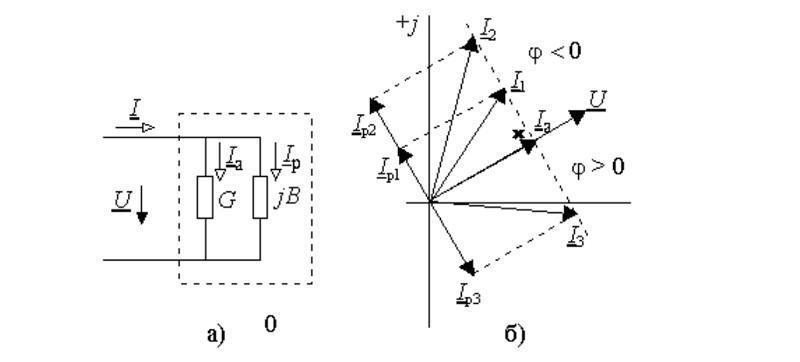
Линейная диаграмма
Здесь изображен двухполюсный элемент с активной и реактивной составляющими проводимости (G и jB, соответственно). Аналогичными параметрами обладает классический колебательный контур, созданный с применением параллельной схемы. Отмеченные выше параметры можно изобразить векторами, которые расположены постоянно под углом 90°. Изменение реактивной компоненты сопровождается перемещением вектора тока (I1…I3). Образованная линия располагается перпендикулярно U и на расстоянии Ia от нулевой точки оси координат.
Векторные диаграммы и комплексное представление
Такой инструментарий помогает строить наглядные графические схемы колебательных процессов. Аналогичный результат обеспечивает применение комплексных числовых выражений. В этом варианте, кроме оси с действительными, применяют дополнительный координатный отрезок с мнимыми значениями.
- А – длина;
- W – угловая скорость;
- f0 – начальный угол.
Значение действительной части равно A*cos*(w*t+f0). Это выражение описывает типичное гармоническое колебание с базовыми характеристиками.
Примеры применения
В следующих разделах приведены описания задач, которые решают с помощью представленной методики. Следует подчеркнуть, что применение комплексных чисел пригодно для сложных расчетов с высокой точностью. Однако на практике достаточно часто сравнительно простой векторной графики с наглядным отображением исходной информации на одном рисунке.
Механика, гармонический осциллятор
Таким термином обозначают устройство, которое можно вывести из равновесного состояния. После этого система возвращается в сторону исходного положения, причем сила (F) соответствующего воздействия зависит от дальности первичного перемещения (d) прямо пропорционально. Величину ее можно уточнить с помощью постоянного корректирующего коэффициента (k). Отмеченные определения связаны формулой F=-d*k
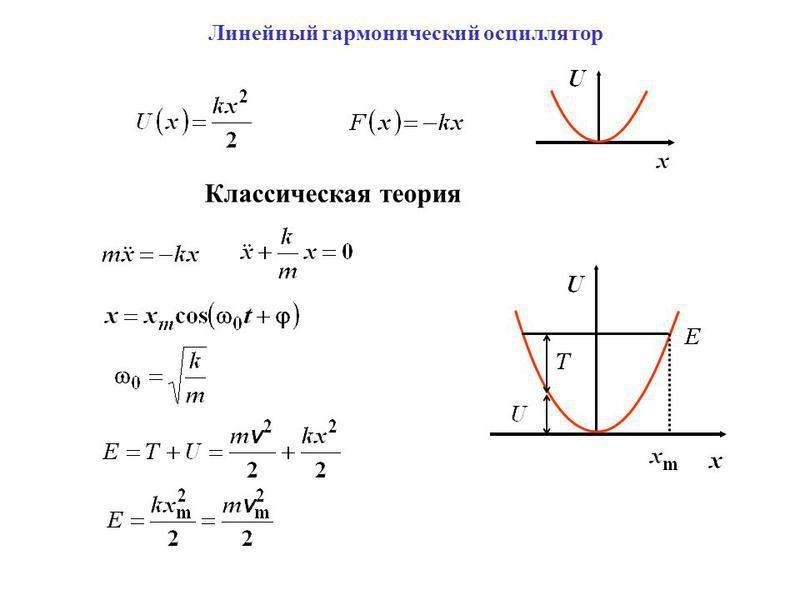
Формулы для расчета основных параметров гармонического осциллятора
К сведению. Аналогичные процессы происходят в системах иной природы. Пример – создание аналога на основе электротехнического колебательного контура (последовательного или параллельного). Формулы остаются теми же с заменой соответствующих параметров.
Свободные гармонические колебания без затухания
Продолжая изучение темы на примерах механических процессов, можно отметить возможность построения двухмерной схемы. Скорость в этом случае на оси Х отображается так же, как и в одномерном варианте. Однако здесь можно учесть дополнительно фактор ускорения, которое направляют под углом 90° к предыдущему вектору.
Гармонический осциллятор с затуханием и внешней вынуждающей силой
В этом случае также можно воспользоваться для изучения взаимного влияния дополнительных факторов векторной графикой. Как и в предыдущем примере, скорость и другие величины представляют в двухмерном виде. Чтобы правильно моделировать процесс, проверяют суммарное воздействие внешних сил. Его направляют к центру системы (точке равновесия). С применением геометрических формул вычисляют амплитуду механических колебаний после начального воздействия с учетом коэффициента затухания и других значимых факторов.
Расчет электрических цепей
Векторную графику применяют для сравнительно несложных цепей, которые созданы из набора элементов линейной категории: конденсаторы, резисторы, катушки индуктивности. Для более сложных схем пользуются методикой расчета «Комплексных амплитуд», в которой реактивные компоненты определяют с помощью импедансов.
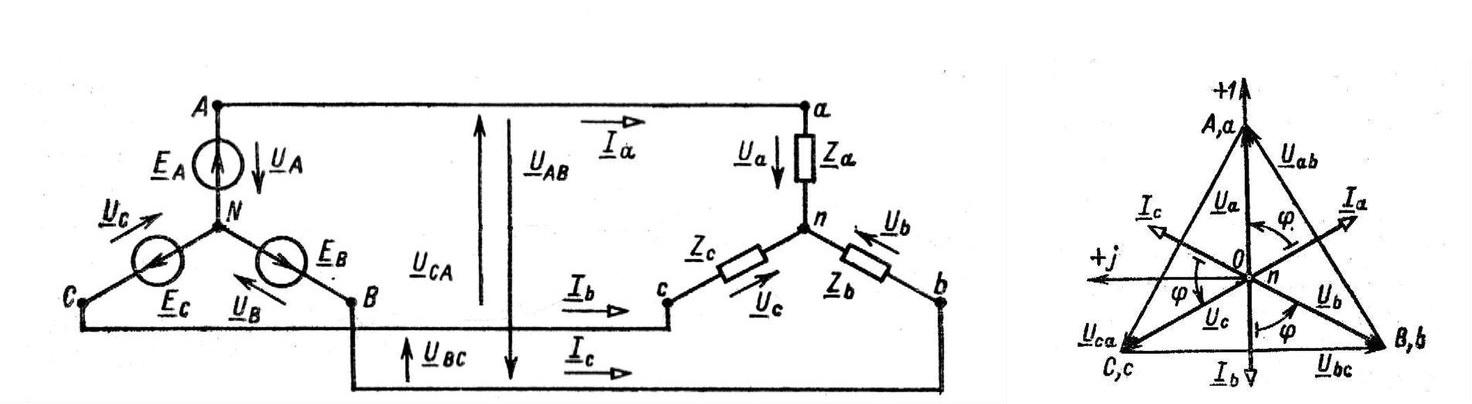
Векторная диаграмма для схемы соединений без нейтрального провода – звезда
Векторная диаграмма в данном случае выполняет функцию вспомогательного чертежа, который упрощает решение геометрических задач. Для катушек и конденсаторов, чтобы не пользоваться комплексным исчислением, вводят специальный термин – реактивное сопротивление. При синусоидальном токе изменение напряжения на индуктивном элементе описывается формулой U=-L*w*I0sin(w*t+f0).
Несложно увидеть подобие с классическим законом Ома. Однако в данном примере изменяется фаза. По этому параметру на конденсаторе напряжение отстает от тока на 90°. В индуктивности – обратное распределение. Эти особенности учитывают при размещении векторов на рисунке. В формуле учитывается частота, которая оказывает влияние на величину этого элемента.
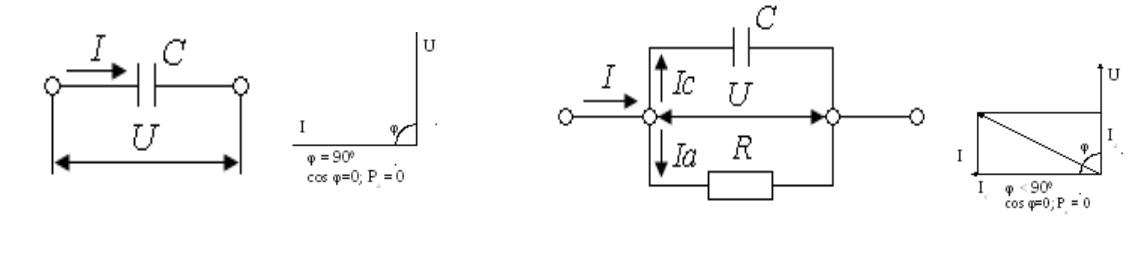
Схемы и векторные диаграммы для идеального элемента и диэлектрика с потерями
Преобразование Фурье
Векторные технологии применяют для анализа спектров радиосигналов в определенном диапазоне. Несмотря на простоту методики, она вполне подходит для получения достаточно точных результатов.
Сложение двух синусоидальных колебаний
В ходе изучения таких источников сигналов рекомендуется работать со сравнительно небольшой разницей частот. Это поможет создать график в удобном для пользователя масштабе.
Фурье-образ прямоугольного сигнала
В этом примере оперируют суммой синусоидальных сигналов. Последовательное сложение векторов образует многоугольник, вращающийся вокруг единой точки. Для правильных расчетов следует учитывать отличия непрерывного и дискретного распределения спектра.
Дифракция
Для этого случая пользуются тем же отображением отдельных синусоид в виде векторов, как и в предыдущем примере. Суммарное значение также вписывается в окружность.
Построение векторной диаграммы напряжений и токов
Для изучения технологии выберем однофазный источник синусоидального напряжения (U). Ток изменяется по формуле I=Im*cos w*t. Подключенная цепь содержит последовательно подключенные компоненты со следующими значениями:
- резистор: Ur=Im*R*cos w*t;
- конденсатор: Uc=Im*Rc*cos (w*t-π/2), Rc=1/w*C;
- катушка: UL= Im*RL*cos(w*t+π/2), RL=w*L.
При прохождении по цепи переменного тока на реактивных элементах будет соответствующий сдвиг фаз. Чтобы построить вектора правильно, рассчитывают амплитуды и учитывают изменение направлений. Ниже приведена последовательность создания графики вручную.
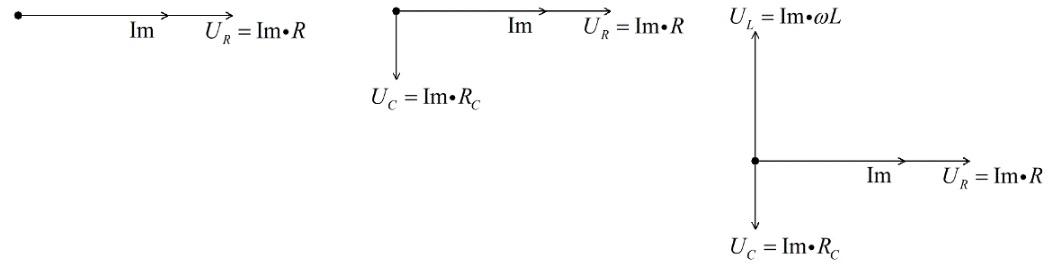
Диаграмма напряжений и токов на отдельных элементах
Далее с применением элементарных правил геометрии проверяют взаимное влияние векторов.
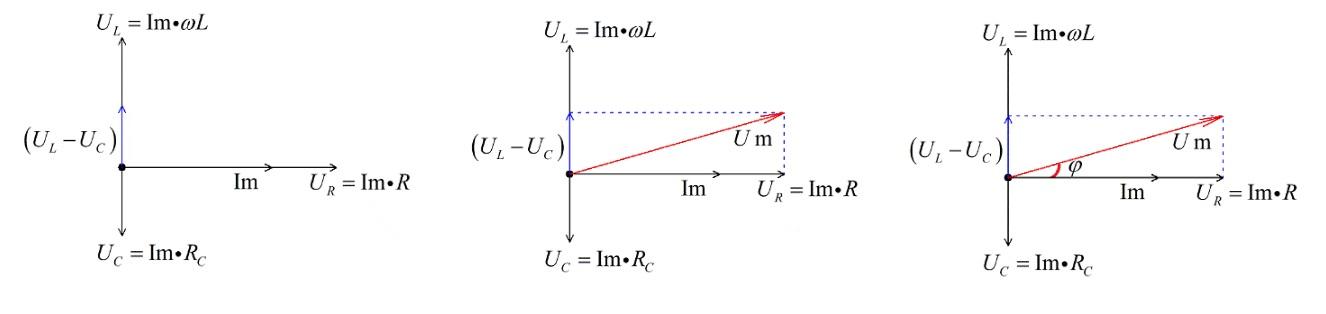
Решение векторного уравнения
На первом рисунке приведен результат сложения двух векторов при условии, когда Uc меньше UL. Добавив значение на сопротивление, получим результирующее напряжение Um. На третьей иллюстрации отмечен общий фазовый сдвиг.
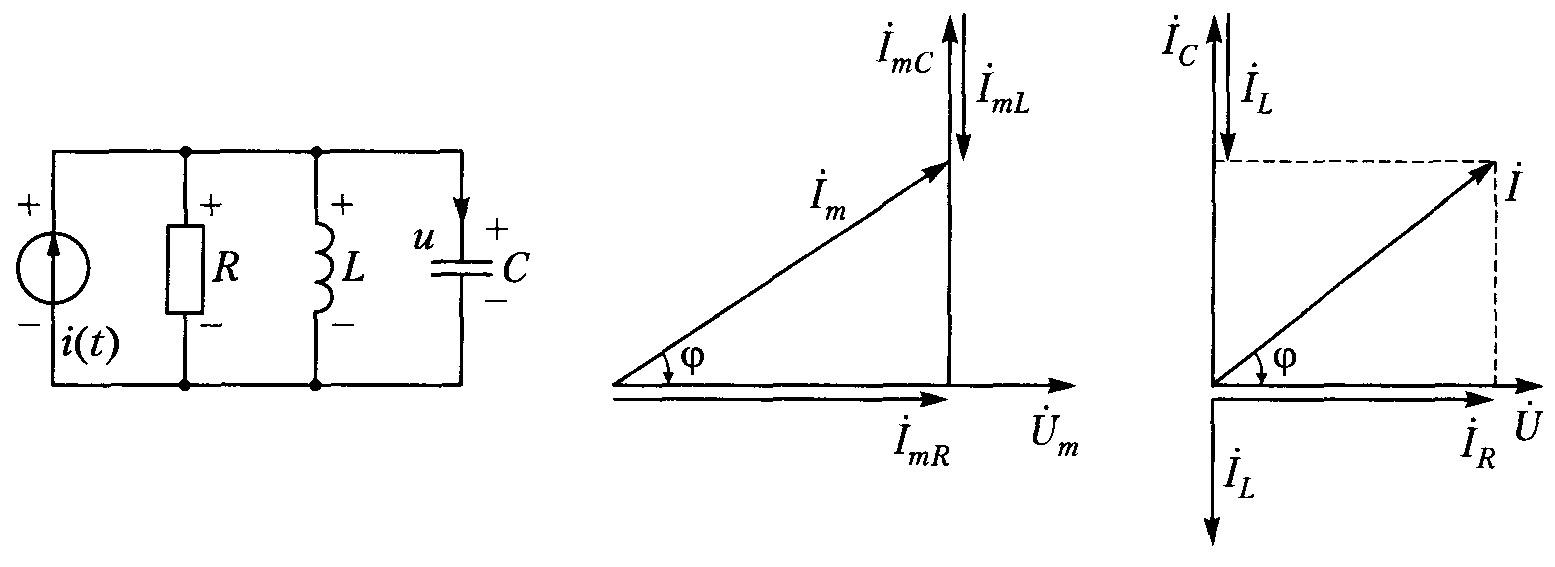
Векторное отображение процессов в параллельном колебательном контуре, резонанс напряжений
В топографической диаграмме начало координат совмещают с так называемой точкой «нулевого потенциала». Такое решение упрощает изучение отдельных участков сложных схем.
Специализированный редактор онлайн
В интернете можно найти программу для построения векторных диаграмм в режиме online.
Видео
Векторная диаграмма токов и напряжений: график, обозначения, виды
 Использование векторных диаграмм при анализе, расчете цепей переменного тока делает возможным рассмотреть более доступно и наглядно происходящие процессы, а также в некоторых случаях значительно упростить выполняемые расчеты.
Использование векторных диаграмм при анализе, расчете цепей переменного тока делает возможным рассмотреть более доступно и наглядно происходящие процессы, а также в некоторых случаях значительно упростить выполняемые расчеты.
Векторной диаграммой принято называть геометрическое представление изменяющихся по синусоидальному (либо косинусоидальному) закону направленных отрезков — векторов, отображающих параметры и величины действующих синусоидальных токов, напряжений либо их амплитудных величин.
Широкое применение векторные диаграммы нашли в электротехнике, теории колебаний, акустике, оптике и т.д.
Различают 2-х вида векторных диаграмм:
- точные;
- качественные.
Интересное видео о векторных диаграммах смотрите ниже:
Точные изображаются по результатам численных расчетов при условии соответствия масштабов действующих значений. При их построении можно геометрически определить фазы и амплитудные значения искомых величин.
Качественные диаграммы изображаются с учетом взаимных соотношений между электрическими величинами, без указания численных характеристик.
Они являются одним из основных средств анализа электрических цепей, позволяя наглядно иллюстрировать и качественно контролировать ход решения задачи и легко установить квадрант, в котором располагается искомый вектор.
 Для удобства при построении диаграмм анализируют неподвижные векторы для определенного момента времени, который выбирается таким образом, чтобы диаграмма имела удобный для понимания вид. Ось OХ соответствует величинам действительных чисел, ось OY — оси мнимых чисел (мнимая единица). Синусоида отображает движение конца проекции на ось OY. Каждому напряжению и току соответствует собственный вектор на плоскости в полярных координатах. Его длина отображает амплитудное значение величины тока, при этом угол равен фазе.
Для удобства при построении диаграмм анализируют неподвижные векторы для определенного момента времени, который выбирается таким образом, чтобы диаграмма имела удобный для понимания вид. Ось OХ соответствует величинам действительных чисел, ось OY — оси мнимых чисел (мнимая единица). Синусоида отображает движение конца проекции на ось OY. Каждому напряжению и току соответствует собственный вектор на плоскости в полярных координатах. Его длина отображает амплитудное значение величины тока, при этом угол равен фазе.
Векторы, изображаемые на такой диаграмме, характеризуются равновеликой угловой частотой ω. В виду чего при вращении их взаимное расположение не изменяется.
Ещё одно полезное видео о векторных диаграммах:
Поэтому при изображении векторных диаграмм один вектор можно направить произвольным образом (например, по оси ОХ).
А остальные — изображать по отношению к исходному под различными углами, соответственно равными углам сдвига фаз.
Таким образом, векторная диаграмма дает отчетливое представление об опережении либо отставании различных электрических величин.
Допустим у нас есть ток, величина которого изменяется по некоторому закону:
i = Im sin (ω t + φ).
С начала координат 0 под углом φ проведем вектор Im, величина которого соответствует Im. Его направление выбирается так, чтобы с положительным направлением оси OX вектор составлял угол — соответствующий фазе φ.
Проекция вектора на вертикальную ось и определяет значение мгновенного тока в начальный момент времени.
В основном векторные диаграммы изображают для действующих значений, а не амплитудных. Векторы действующих значений количественно отличаются от амплитудных значений — масштабом, поскольку:
I = Im /√2.

Основным преимуществом векторных диаграмм называют возможность простого и быстрого сложения и вычитания 2-х параметров при расчете электроцепей.
правила построения диаграмм, онлайн построение
В целом, для лучшего понимания процедур, происходящих в радиотехнических цепях, их взаимосвязи между собой, бывает недостаточно оперировать характеристиками и параметрами данной цепи, имеющими цифровое отображение. В связи с тем, что основная масса цепей характеризуется переменными значениями приложенного напряжения и протекающего тока, являющимися синусоидальными функциями времени, то исчерпывающий ответ по состоянию цепи может дать ее графическая презентация посредством векторной гистограммы.
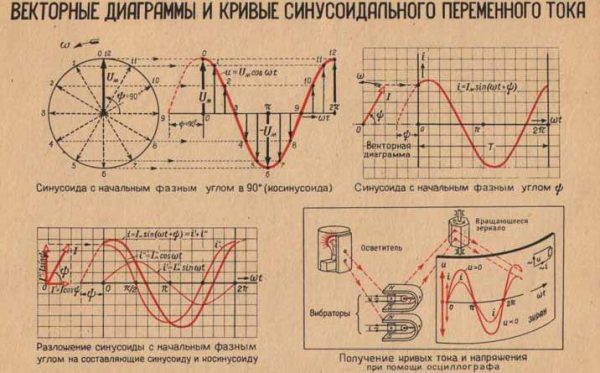
Векторная диаграмма напряжений и токов
Разновидности векторных диаграмм
Любую характеристику электротехнической цепи, изменяющуюся по синусоидальному или косинусоидальному принципу, можно отобразить посредством точки на поверхности, в соответствующей системе величин. В качестве размерности по оси Х выступает действительный компонент параметра, по оси Y размещается воображаемая составляющая. Именно такие составляющие входят в алгебраическую модель записи комплексной величины. Последующее соединение точки на поверхности и нулевой точки системы координат позволит рассматривать эту прямую и ее угол с действительной осью как изображение комплексного числа. На практике положительно направленный отрезок принято называть вектором.
Векторной диаграммой принято называть множество положительно направленных отрезков на комплексной поверхности, которая соответствует комплексным значениям и параметрам гальванической цепи и их взаимосвязям. По своему характеру векторные диаграммы подразделяются на:
- Точные гистограммы;
- Качественные гистограммы.
Особенностями достоверных гистограмм является соблюдение пропорций всех характеристик и параметров, полученных путем вычислений. Данные диаграммы находят свое применение в проверке ранее проведенных расчетов. В основе использования качественных гистограмм лежит учет взаимного влияния характеристик друг на друга, и в основном они предшествуют расчетам либо заменяют их.
Векторные диаграммы токов и напряжений визуально отображают процесс достижения цели по расчету электротехнической цепи. При соблюдении всех правил по построению векторных отрезков можно просто из гистограммы установить фазы и амплитуды вещественных характеристик. Построение качественных гистограмм поможет контролировать правильный процесс решения задачи и с легкостью определить сектор с определяемыми векторами. В зависимости от особенностей построения, графические диаграммы делятся на такие типы:
- Круговая диаграмма, представляющая собой графическую гистограмму, образованную вектором, описывающим своим концом круг или полукруг, при любых изменениях характеристик цепи;
- Линейная диаграмма, представляющая собой графический рисунок в виде прямой линии, образованной вектором, посредством изменения характеристик цепи.
Построение векторной диаграммы напряжений и токов
Для лучшего понимания того, как построить векторную диаграмму токов и напряжений, следует рассматривать RLC цепь, состоящую из пассивного элемента в виде резистора и реактивных элементов в виде катушки индуктивности и конденсатора.
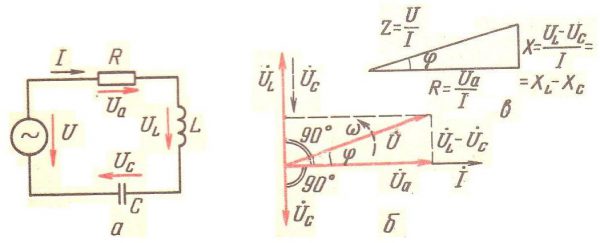
Схема цепи с последовательным соединением элементов
Перед тем, как построить векторную диаграмму токов и напряжений, необходимо охарактеризовать все известные параметры цепи. Согласно схемы цепи, изображенной на картинке а:
- U – величина переменного напряжения в текущий момент времени;
- I – мощность тока в заданный момент времени;
- UА – напряжение, падающее на активном сопротивлении;
- UC – напряжение, падающее на емкостной нагрузке;
- UL – напряжение, падающее на индуктивной нагрузке.
Поскольку входное напряжение U изменяется по колебательному закону, то сила тока характеризуется уравнением:
I=Im*cosωt, где:
- Im – максимальная амплитуда тока;
- ω – частота тока;
- t – время.
Суммарное входное напряжение, в соответствии со вторым законом Кирхгофа, равно общей величине напряжений на всех элементах цепи:
U=UC+UL+UA.
В соответствии с законом Ома, падение напряжения на резистивном компоненте равняется:
UA= Im*R*cosωt.
Противодействие току активного элемента зависит сугубо от свойства проводника и не обуславливается ни характеристиками тока, ни аспектом времени и, соответственно, имеет идентичный с напряжением фазовый сдвиг.
Поскольку конденсатору в цепи с электротоком, изменяющимся по синусоиде, свойственно наличие реактивного емкостного сопротивления, и ввиду того, что напряжение на нем постоянно имеет фазовое отставание от протекающего тока на π/2, то уместно выражение:
- RC=XC=1/ωC;
- UC=Im*RС*cos(ωt-π/2), где:
- RC – сопротивление конденсатора;
- XC – реактивный импеданс конденсатора;
- C – емкость конденсатора.
Реактивное индуктивное сопротивление катушки индуктивности обуславливается наличием изменяющегося по синусоидальному закону электротока, и поскольку напряжение на любом отрезке времени имеет фазовое опережение по отношению к электротоку на π/2, то формула, описывающая колебательный процесс на элементе, выглядит как:
- RL=XL=ωL;
- UL=Im*RL*cos(ωt+π/2), где:
- RL – сопротивление катушки индуктивности;
- XL – реактивный импеданс катушки индуктивности;
- L – индуктивность катушки.
Следовательно, общее напряжение, подведенное к цепи, выглядит:
U=Um*cos(ωt±φ), где:
- Um – максимальная величина напряжения;
- φ – фазовый сдвиг.
Ввиду того, что напряжение и электроток изменяются по синусоидальному закону, и их фиксированные показатели отличаются лишь фазовым сдвигом, то данные величины строятся как вектора.
В соответствии с законом сохранения электрического заряда, в любой момент времени сила протекающего тока одинакова, то целесообразно сформировать векторную гистограмму токов.
Векторная диаграмма токов и напряжений RLC цепочке
Пусть по оси Х отображается амплитудное значение электротока в цепочке. Поскольку напряжение и электроток на резисторе имеют одинаковый фазовый сдвиг, то вектора данных характеристик будут ориентированы в одну сторону, согласно картинке а.
Напряжение на емкостной нагрузке отстает от электрического тока на π/2, и его вектор будет направлен под прямым углом вниз, перпендикулярно напряжению активного сопротивления, согласно картинке в.
Напряжение на индуктивной нагрузке опережает электрический ток на π/2, и ее вектор будет ориентирован под прямым углом вверх, перпендикулярно напряжению на активном сопротивлении, согласно картинке б.
Для наглядности векторных преобразований пусть UL>UС. Сложив вектора напряжений на реактивных компонентах, получаем, что вектор UL-UС будет направлен перпендикулярно вверх. Суммировав вектора разности напряжений на реактивных компонентах и напряжения на сопротивлении получаем вектор, характеризующий дисперсное значение общего напряжения, согласно картинке 2(б).
Аналогично электрическому току, изменяющемуся по синусоидальному закону, напряжение меняется по такому же закону, однако с некоторым фазовым сдвигом. Наблюдается постоянный фазовый сдвиг между напряжением и током.
После простых преобразований по постулату Ома, уравнение полного импеданса заданной электрической цепи выглядит как:
Z=√R2+(1/ωC- ωL)2.
Векторная гистограмма общего и реактивных сопротивлений изображена на картинке 2в.
Построение векторных диаграмм токов и напряжений может значительно упростить процесс расчета характеристик контура. Вместе с тем сама процедура позволит наглядно видеть поведение исследуемых характеристик, в зависимости от входных величин. При большом объеме вычислительных операций целесообразно воспользоваться одной из онлайн программ по построению векторных графиков.
Видео
Оцените статью:Указания по построению векторных диаграмм
Построение векторных диаграмм
для всех пунктов программы лабораторной работы начинается
с построения симметричной трехлучевой
звезды векторов фазных напряжений
генератора  (рис. 9). Звезда векторов напряжений
строится с соблюдением выбранного
масштаба (обычно рекомендуется 1 см = 20
В). На этой же диаграмме показываются
векторы линейных напряжений генератора
(рис. 9). Звезда векторов напряжений
строится с соблюдением выбранного
масштаба (обычно рекомендуется 1 см = 20
В). На этой же диаграмме показываются
векторы линейных напряжений генератора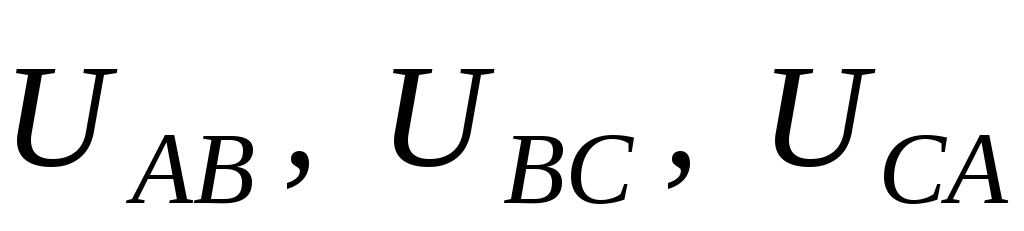 в виде сторон равностороннего треугольника,
вершинами которого являются концы
векторов фазных напряжений (рис. 6).
в виде сторон равностороннего треугольника,
вершинами которого являются концы
векторов фазных напряжений (рис. 6).
Такая векторная диаграмма генератора сохраняется для всех пунктов настоящей работы. Если ее дополнить векторной диаграммой фазных напряжений приемника (в том числе при обрыве нейтрального провода и несимметричном приемнике), то ее можно назвать «топографической».
Векторные диаграммы принято называть топографическими, если электрические потенциалы точек на диаграмме имеют те же буквенные обозначения, что и на соответствующих точках в схеме четырехпроводной звезды (рис. 4 и рис. 10а).
Покажем порядок построения такой топографической векторной диаграммы для случая симметричной нагрузки при наличии нейтрального провода (рубильник Р2 на схеме рисунка 10б замкнут).
В начале
строится звезда векторов фазных
напряжений генератора
начале
строится звезда векторов фазных
напряжений генератора с центром в точкеN (рис. 11) одним из рассмотренных ранее
методов. Длины векторов определяются
измеренным напряжением UФ питающей сети и выбранным масштабом
напряжений. Концы векторов на диаграмме
обозначаются буквами А,
В, С.
Затем строятся векторы линейных
напряжений генератора (и приемника)
с центром в точкеN (рис. 11) одним из рассмотренных ранее
методов. Длины векторов определяются
измеренным напряжением UФ питающей сети и выбранным масштабом
напряжений. Концы векторов на диаграмме
обозначаются буквами А,
В, С.
Затем строятся векторы линейных
напряжений генератора (и приемника)  ,
,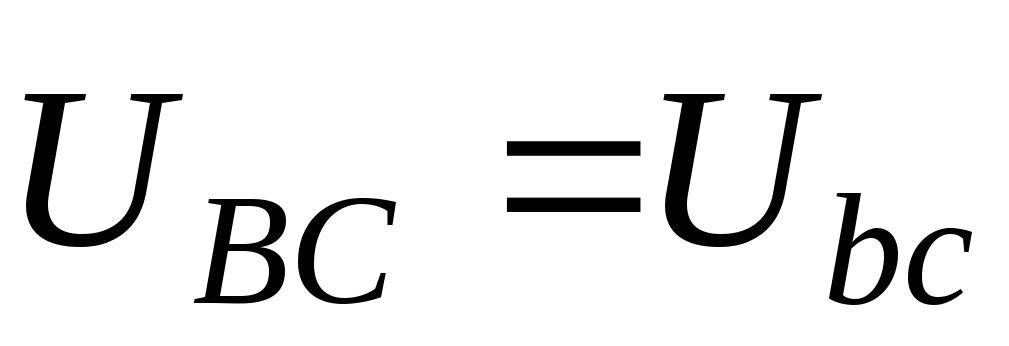 ,
,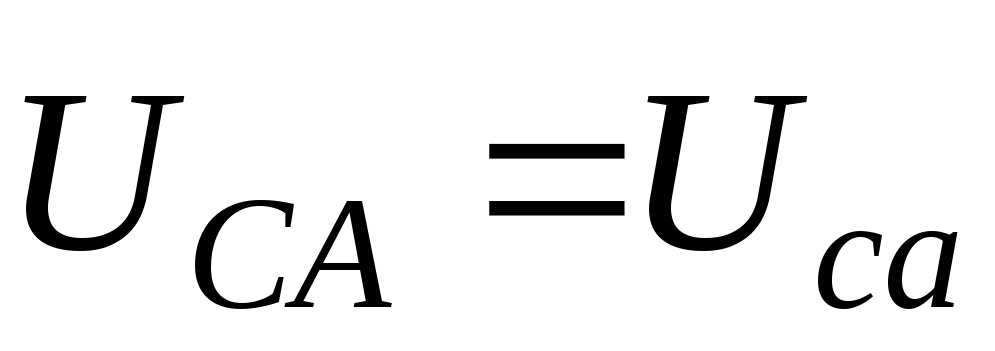 в виде сторон правильного (равностороннего)
треугольника. Очевидно при наличии
нейтрального провода потенциал
нейтральной точкиn приемника равен потенциалу нейтральной
точки N генератора, и обе точки находятся в
центре тяжести векторного треугольника (рис.
11). Является
очевидным, что длины построенных векторов
в масштабе напряжений соответствуют
напряжениям между двумя одноименными
точками на электрической схеме (рис.
10б).
в виде сторон правильного (равностороннего)
треугольника. Очевидно при наличии
нейтрального провода потенциал
нейтральной точкиn приемника равен потенциалу нейтральной
точки N генератора, и обе точки находятся в
центре тяжести векторного треугольника (рис.
11). Является
очевидным, что длины построенных векторов
в масштабе напряжений соответствуют
напряжениям между двумя одноименными
точками на электрической схеме (рис.
10б).
При
наличии нейтрального провода,
когда нейтральная точка n приемника совпадает с точкой N, фазные
напряжения приемника и генератора равны друг другу 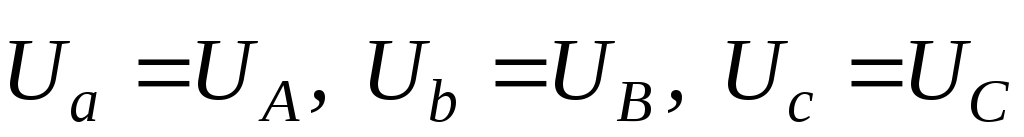 (рис. 11)независимо
от того, симметричный приемник или
несимметричный.
(рис. 11)независимо
от того, симметричный приемник или
несимметричный.
Полученная векторная
диаграмма фазных напряжений приемника 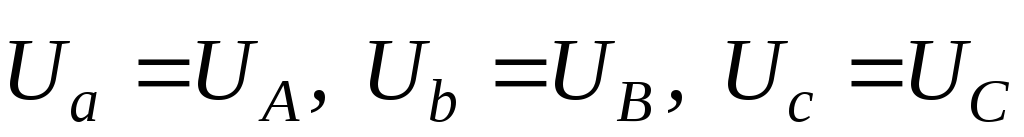 позволяет увязать с ней векторную
диаграмму токов, которая представляет
собой графическое решение первого
закона Кирхгофа для узловых точекN и n.
позволяет увязать с ней векторную
диаграмму токов, которая представляет
собой графическое решение первого
закона Кирхгофа для узловых точекN и n.
При симметричной нагрузке (по определению) фазные (линейные) токи IЛ равны друг другу по величине IA = IB = IC и сдвинуты по фазе относительно «своих» фазных напряжений Ua, Ub, Uc на один и тот же угол φ = 0, так как в фазах приемника включены резисторы (активная нагрузка).
Задавшись
масштабом для токов (рекомендуется 1 см
= 0,25 А), строят векторы токов и проводят
их графическое сложение (рис. 11) для
определения вектора в нейтральном
проводе  .
На векторной диаграмме эта операция
показана с изображением векторов
.
На векторной диаграмме эта операция
показана с изображением векторов и
и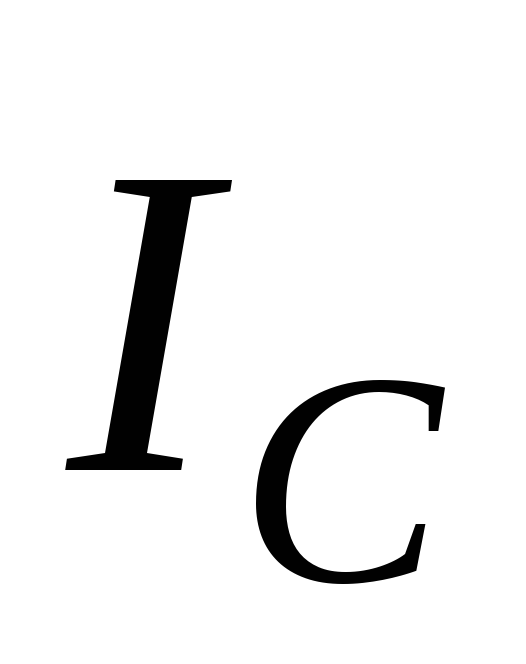 пунктиром. Как видно из диаграммы конец
третьего слагаемого
пунктиром. Как видно из диаграммы конец
третьего слагаемого совпадает с началом первого
совпадает с началом первого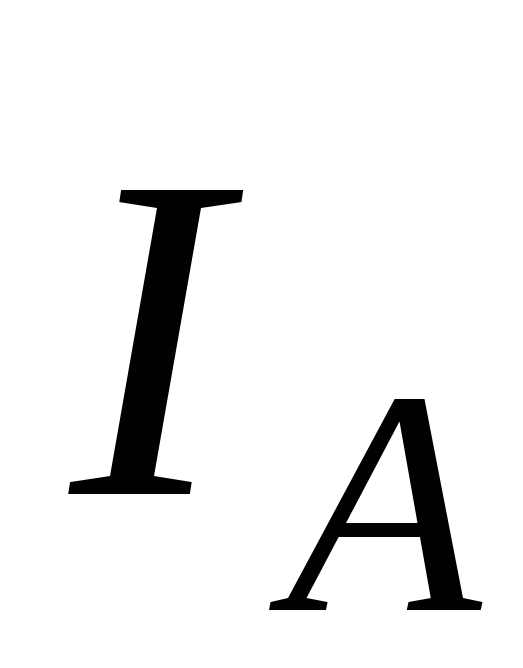 (в точкеN, n),
что означает
(в точкеN, n),
что означает  =
0, подтверждая такие же показания
амперметраAN (рис. 10б).
=
0, подтверждая такие же показания
амперметраAN (рис. 10б).
Поскольку показания приборов в схеме (рис. 10б) при выполнении второй части рассматриваемого режима (при разомкнутом рубильнике Р2) полностью идентичны с первой частью, необходимость построения второй такой же диаграммы отпадает.
Векторная диаграмма при симметричной нагрузке, показанная на рисунке 11, справедлива как для случая с нейтральным проводом, так и без него. При построении топографической диаграммы для других предусмотренных программой лабораторной работы пунктов можно не показывать в вершинах треугольника линейных напряжений начала фаз приемника a, b, c, поскольку их потенциалы всегда совпадают с потенциалами начал фаз генератора (питающей сети) A, B, C.
Векторные
диаграммы напряжений и токов,
соответствующие разгрузке одной фазы
(a–x) приемника при наличии и обрыве нейтрального
провода представлены на рисунках 12а и
12б соответственно. При
обрыве фазы a–x (ключ Ка в схеме на рисунке 10б разомкнут) и
замкнутом нейтральном проводе,
ток IA = 0. Токи IB и IC остаются равными по величине и совпадают
по фазе с напряжениями Ub и Uc (рис. 12а). Ток в нейтральном проводе
определяется в соответствии с первым
законом Кирхгофа:
.
На векторной диаграмме эта операция
проделана геометрическим сложением
векторов по правилу многоугольника
(треугольника).При
обрыве фазы a–x и обрыве нейтрального
провода векторная диаграмма принимает вид,
показанный на рисунке 12б. Построив
векторную диаграмму фазных и линейных
напряжений генератора, находят положение
(потенциал) нейтральной точки приемника n.
Для этого с помощью циркуля его растворами
(радиусами), равными фазным напряжениям
(с соблюдением масштаба) Ua, Ub, Uc,
делают засечки из вершин треугольника
линейных напряжений соответственно А, В, С.
Точка пересечения этих засечек и есть
точка n,
которая должна оказаться на середине
вектора 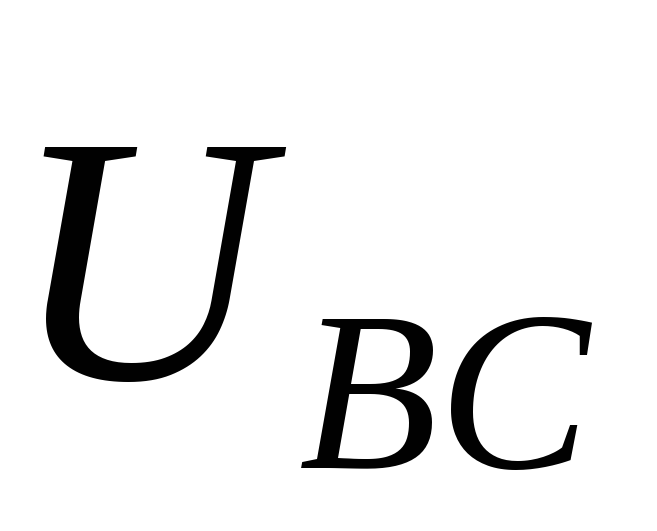 ,
так как при обрыве одной фазы и нейтрального
провода получается однофазная цепь,
подключенная к линейному напряжениюUBC.
,
так как при обрыве одной фазы и нейтрального
провода получается однофазная цепь,
подключенная к линейному напряжениюUBC.

Рис. 12
Из
точки n в вершины треугольника АВС проводятся фазные напряжения приемника 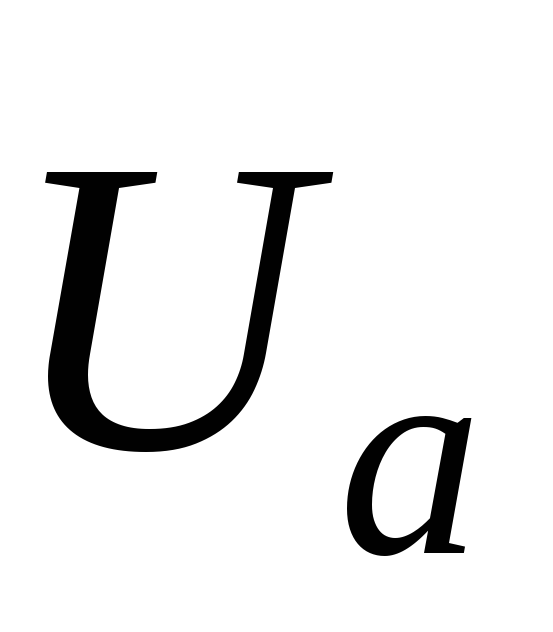 ,
, и
и .
Нетрудно показать, что
.
Нетрудно показать, что 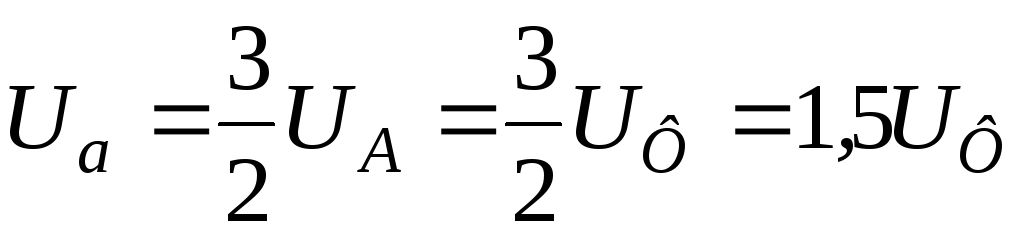 ,
,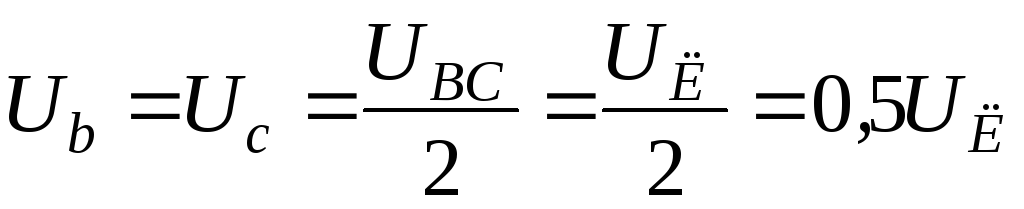 .
Соединив
точки N и n,
получают вектор
.
Соединив
точки N и n,
получают вектор 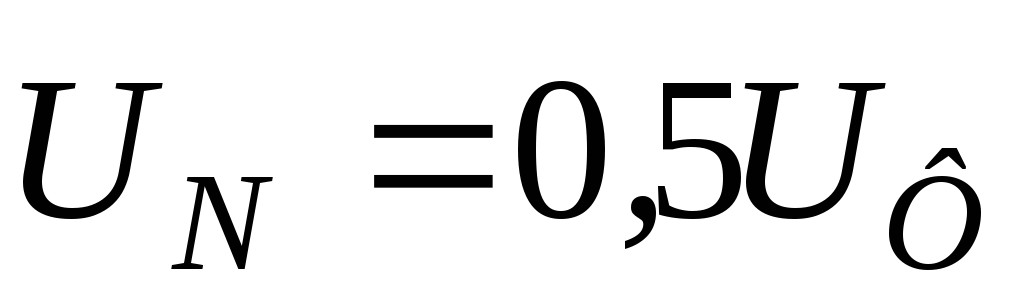 (рис. 12б). Векторы
токов
(рис. 12б). Векторы
токов 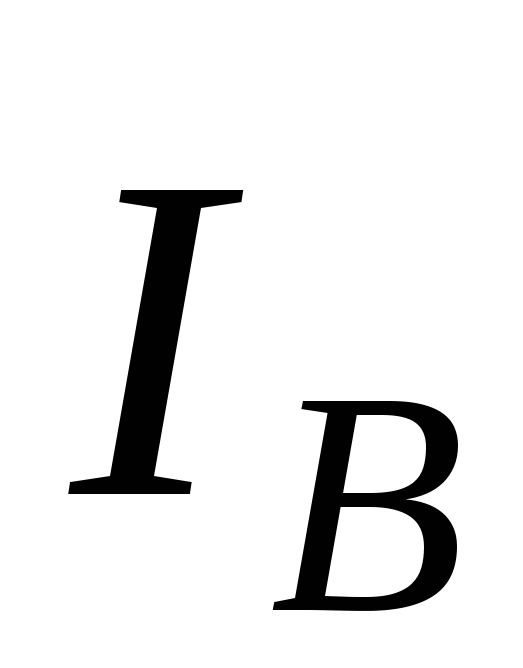 и
и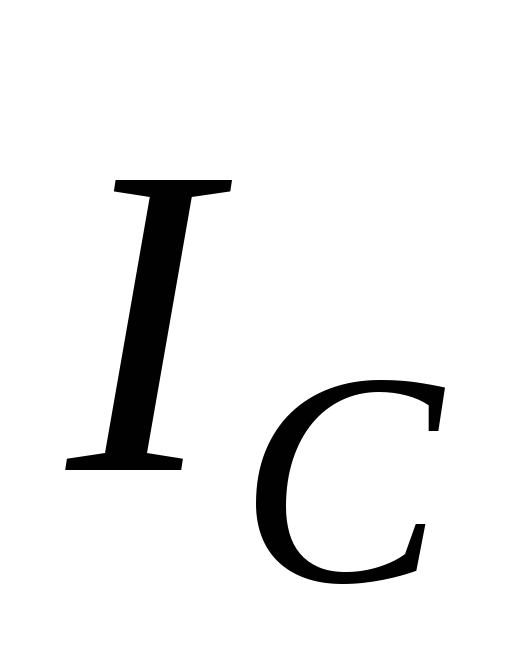 совпадают с векторами напряжений
совпадают с векторами напряжений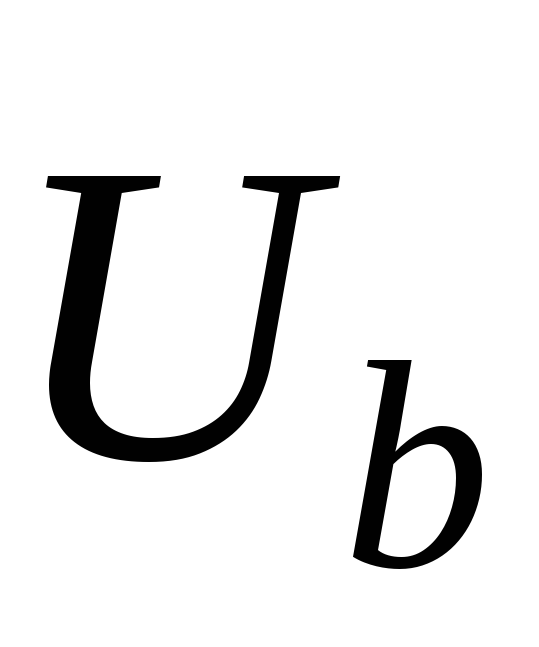 и
и ,
находятся в противофазе и дают в сумме
ноль:
,
находятся в противофазе и дают в сумме
ноль: ,
поскольку нейтральный провод отсутствует.
,
поскольку нейтральный провод отсутствует.
Векторные
диаграммы напряжений и токов,
соответствующие разгрузке двух фаз
(a–x и b–y)
приемника при наличии нейтрального провода и без
него представлены на рисунках 13а и 13б
соответственно. При
обрыве двух фаз (ключи Ка и Кb в схеме на рисунке 10б разомкнуты) и
наличии нейтрального провода (Р2 замкнут) IA = 0 и IB = 0, и существует замкнутая цепь одной
фазы c–z,
ток которой IC равен току нейтрального провода IC = IN,
фазы a–x и b–y,
а также линейные провода A–a, B–b (рис. 10б) обесточены. Векторная диаграмма
для этого случая имеет вид, показанный
на рисунке 13а. При
обрыве двух фаз и нейтрального провода (рубильник Р2 на схеме рисунка 10б разомкнут) цепь
оказывается разомкнутой, и все участки
цепи обесточены (IA = IB = IC = 0), за исключением высокоомных цепей
вольтметров, токами в которых всегда
пренебрегают ввиду их малости. Векторная
диаграмма для этого режима показана на
рисунке 13б. Токи на диаграмме отсутствуют;
по результатам измерений показаны три
вектора напряжения 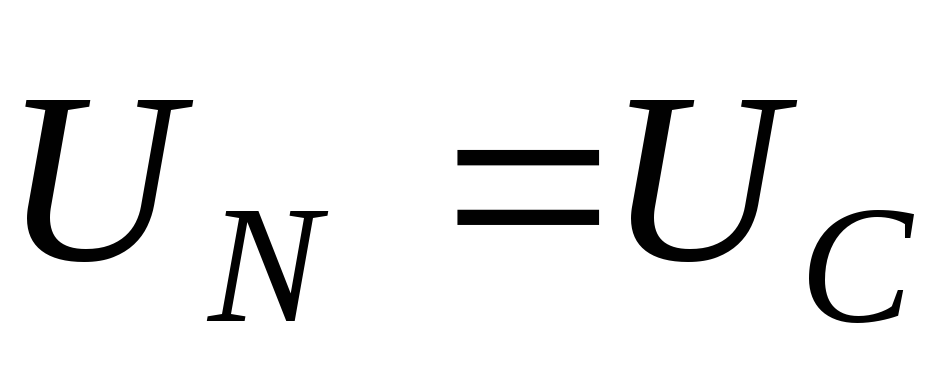 ,
,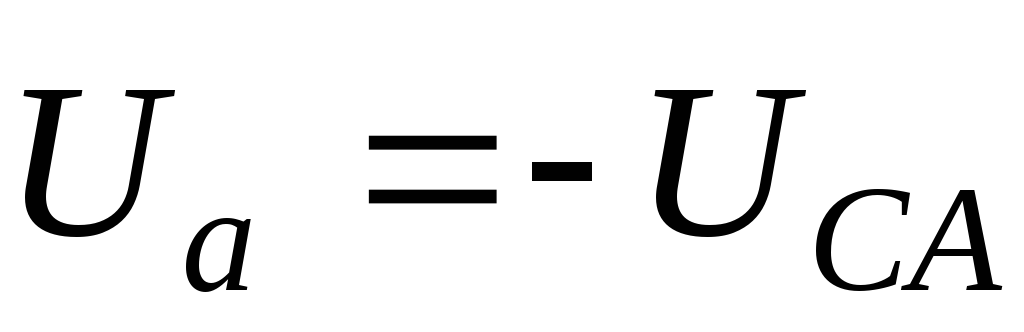 и
и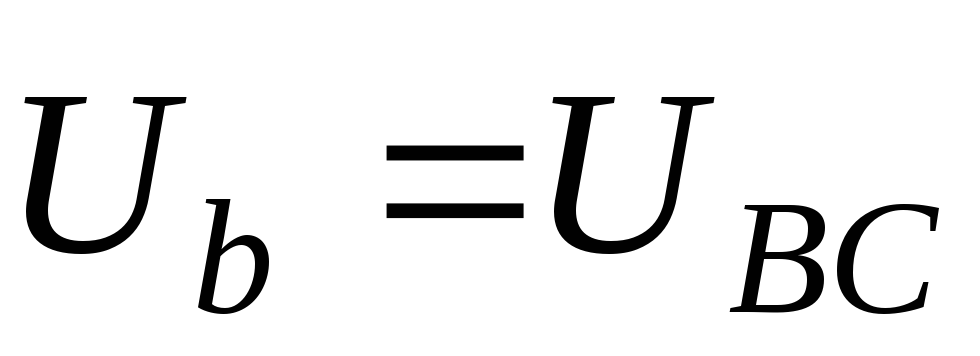 .
Их величины и направления обусловлены
тем, что потенциал нейтральной точкиn оказался в вершине С треугольника линейных напряжений.
Напряжение на фазе c–z приемника Uc = 0, поскольку падение напряжения Uc = ICzc = 0, т.к. IC = 0. Напряжение смещения нейтрали
.
Их величины и направления обусловлены
тем, что потенциал нейтральной точкиn оказался в вершине С треугольника линейных напряжений.
Напряжение на фазе c–z приемника Uc = 0, поскольку падение напряжения Uc = ICzc = 0, т.к. IC = 0. Напряжение смещения нейтрали  по величине равно фазному напряжению
генератораUN = UФ,
поскольку вольтметр VN при разомкнутом рубильнике Р2 (рис. 10а) подключен одним зажимом к
нейтральной точке N генератора, а другим через обесточенную
фазу c–z приемника подключен к линейному проводу
С–с питающей сети. Равенство фазных
напряжений разомкнутых фаз a–b и c–z соответствующим линейным напряжениям
объясняется тем, что на нейтральную
точку n приемника при разомкнутом рубильнике Р2 через цепь незамкнутой фазы c–z подается потенциал линейного провода
С–с.
по величине равно фазному напряжению
генератораUN = UФ,
поскольку вольтметр VN при разомкнутом рубильнике Р2 (рис. 10а) подключен одним зажимом к
нейтральной точке N генератора, а другим через обесточенную
фазу c–z приемника подключен к линейному проводу
С–с питающей сети. Равенство фазных
напряжений разомкнутых фаз a–b и c–z соответствующим линейным напряжениям
объясняется тем, что на нейтральную
точку n приемника при разомкнутом рубильнике Р2 через цепь незамкнутой фазы c–z подается потенциал линейного провода
С–с.

Рис. 13
Векторные
диаграммы для общего случая несимметричной
нагрузки,
когда по трем фазам приемника протекают
разные по величине токи IA IB IC,
показаны
на рисунках 14а и 14б. Как и в предыдущих
случаях вначале строятся векторные
диаграммы напряжений генератора в виде симметричной звезды и правильного
треугольника (рис. 6). Векторная
диаграмма при наличии нейтрального
провода показана
на рисунке 14а, где векторы токов 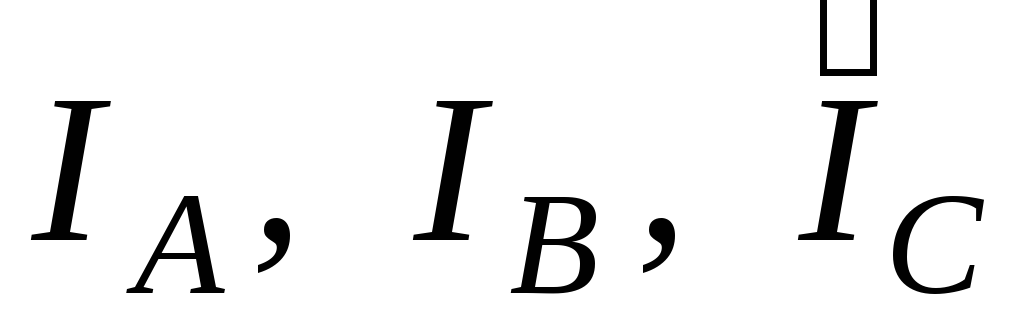 с учетом масштаба построены совпадающими
со «своими» фазными напряжениями
с учетом масштаба построены совпадающими
со «своими» фазными напряжениями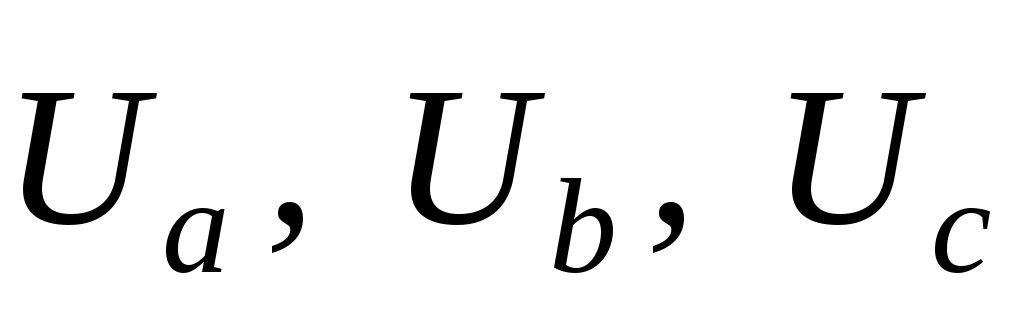 .
Вектор тока в нейтральном проводе
.
Вектор тока в нейтральном проводе строится графически сложением векторов
по правилу многоугольника (четырехугольника).
Измерив длину вектора
строится графически сложением векторов
по правилу многоугольника (четырехугольника).
Измерив длину вектора и учтя масштаб, можно сравнить результат
с величиной токаIN,
измеренного амперметром AN (рис. 10а, б), убедившись в правильности
проделанных графических построений. Векторная диаграмма при обрыве
нейтрального провода и несимметричном
приемнике приведена на рисунке 14б. Изобразив
векторную диаграмму фазных и линейных
напряжений генератора, необходимо построить
несимметричную звезду векторов фазных
напряжений приемника
и учтя масштаб, можно сравнить результат
с величиной токаIN,
измеренного амперметром AN (рис. 10а, б), убедившись в правильности
проделанных графических построений. Векторная диаграмма при обрыве
нейтрального провода и несимметричном
приемнике приведена на рисунке 14б. Изобразив
векторную диаграмму фазных и линейных
напряжений генератора, необходимо построить
несимметричную звезду векторов фазных
напряжений приемника  .
Является очевидным, что следует сначала
определить на диаграмме положение
нейтральной точкиn приемника, которая является центром
этой звезды. Для этого используется метод
засечек,
которые делаются (с
учетом масштаба напряжений)
циркулем с раствором, соответствующим
каждому из измеренных фазных напряжений
приемника. Например, первую засечку
делают при растворе циркуля, равном в
масштабе фазному напряжению Ua,
поставив ножку циркуля в вершину
треугольника А.
Затем делают две аналогичные засечки
из точек В и С.
Точка пересечения трех засечек и есть
точка n.
Соединив ее с вершинами треугольника А,
В, С,
получают звезду векторов фазных
напряжений приемника. Соединив нейтральную
точку генератора N с точкой n,
получают вектор напряжения смещения
нейтрали
.
Является очевидным, что следует сначала
определить на диаграмме положение
нейтральной точкиn приемника, которая является центром
этой звезды. Для этого используется метод
засечек,
которые делаются (с
учетом масштаба напряжений)
циркулем с раствором, соответствующим
каждому из измеренных фазных напряжений
приемника. Например, первую засечку
делают при растворе циркуля, равном в
масштабе фазному напряжению Ua,
поставив ножку циркуля в вершину
треугольника А.
Затем делают две аналогичные засечки
из точек В и С.
Точка пересечения трех засечек и есть
точка n.
Соединив ее с вершинами треугольника А,
В, С,
получают звезду векторов фазных
напряжений приемника. Соединив нейтральную
точку генератора N с точкой n,
получают вектор напряжения смещения
нейтрали 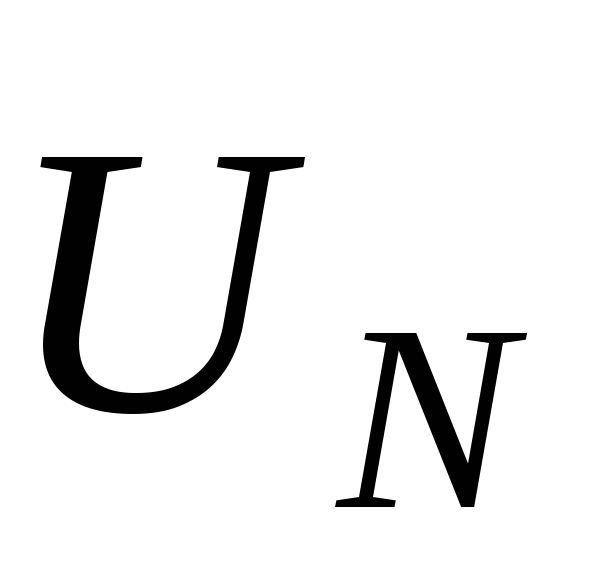 ,
длину которого можно измерить и (с учетом
масштаба) сравнить с полученными данными
измеренияUN вольтметром VN (рис. 10а, б).
,
длину которого можно измерить и (с учетом
масштаба) сравнить с полученными данными
измеренияUN вольтметром VN (рис. 10а, б).

Рис. 14
Расчетные формулы для заполнения раздела таблицы измерений и вычислений (табл. 1) «Вычисления». Поскольку все режимы исследуются применительно к активному приемнику (все фазы приемника резисторы), то следует рассчитать активные мощности приемника по результатам измерения фазных токов и напряжений с учетом того, что угол φa=φb=φc=φ= 0 и cosφ = 1.
Активные мощности приемника:
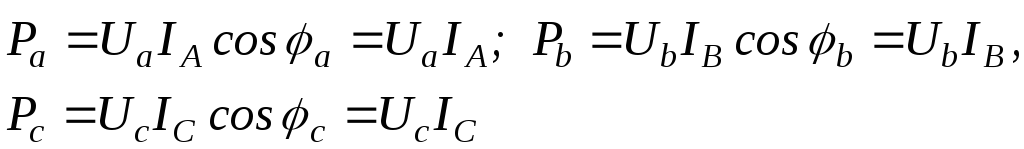
Активная мощность всей цепи равна сумме активных мощностей отдельных фаз и вычисляется по формуле:

При симметричной нагрузке активная мощность вычисляется по формуле:

Полученные расчетом данные рекомендуется сравнить с результатами измерений ваттметрами.
Контрольные вопросы
Каков принцип соединения звездой?
Что называется фазным и линейным током и напряжением?
Роль нейтрального провода.
Почему в нейтральном проводе не ставят предохранителей?
Что означает независимая работа фаз приемника?
Что такое симметричная и несимметричная нагрузка трехфазной цепи?
Как строятся топографические векторные диаграммы при соединении трехфазной цепи звездой?
РЕЛЕЙКА: Векторные диаграммы
Понятие о векторах. На рис.1.4 приведена кривая изменения переменного тока во времени. Ток сначала растет от нуля (при φ=0º) до максимального положительного значения + Imax (при φ=90о), затем убывает, переходит через нуль (при φ=180о), достигает максимального отрицательного значения – Imax (при φ=270о) и, наконец, возвращается к нулю (при φ=360о). после этого цикл изменения тока повторяется.
Кривая изменения переменного тока во времени, приведенная на рис.1.4, называется синусоидой. Время Т, в течение которого происходит полный цикл изменения тока, соответствующий изменению угла на 360о, называется периодом переменного тока. Число периодов за 1 секунду называется частотой переменного тока. В промышленных
установках и в быту в на территории бывшего СССР и в других странах Европы используется главным образом переменный ток частотой 50 Гц. Этот ток 50 раз в секунду принимает положительное и отрицательное направление. Изменение переменного тока во времени можно записать в следующем виде.Где i – мгновенное значение тока, т.е. значение тока в каждый момент времени; Imax – максимальное значение тока; ω=2πf – угловая частота переменного тока, f=50 Гц, ω=2π·50=314; α – начальный угол, соответствующий моменту времени, с которого начинается отсчет времени (при t=0). Для частного случая, показанного на рис.1.4, α=0о.
Анализируя действие устройств релейной защиты и автоматики, необходимо сопоставлять токи и напряжения, складывать или вычитать их, определять углы между ними и производить другие операции. Пользоваться при этом кривыми, подобными приведенной на рис.1.4, неудобно, поскольку построение синусоид тока и напряжения занимает много времени и не дает простого и наглядного результата. Поэтому для упрощения принято изображать токи и напряжения в виде отрезков прямых линий, имеющих определенную длину и направление, — так называемых векторов (А0 на рис.1.4). один конец вектора закреплен на точке 0 – начало координат, а второй вращается против часовой стрелки.
Мгновенное значение тока или напряжения в каждый момент времени определяется проекцией на вертикальную ось вектора, длина которого равна максимальному значению тока или напряжения. Эта проекция будет становится то положительной, то отрицательной, принимая максимальные значения при вертикальном расположении вектора. За время Т, равное периоду переменного тока, вектор совершит полный оборот по окружности (360о), занимая последовательно положения 0А’,0A”, 0A’’’ и т.д. При частоте переменного тока 50 Гц вектор будет совершать 50 об/с.
Таким образом, вектор тока или напряжения – это отрезок прямой, равный по величине максимальному значению тока или напряжения, вращающийся относительно точки 0 против движения часовой стрелки со скоростью, определяемой частотой переменного тока. Зная положение вектора в каждый момент времени, можно определить мгновенное значение тока или напряжения в данный момент. Так, для положения вектора тока 0А, показанного на рис.1.5, его мгновенное значение определяется проекцией на вертикальную ось, т.е. 0А”=0А sin φ.
На основании рис.1.5 можно также сказать, что ток в данный момент времени имеет положительное значение. Однако это ещё не дает полного представления о протекании процесса в цепи переменного тока, так как неизвестно, что значит положительный или отрицательный ток, положительное или отрицательное напряжение.
Для того чтобы векторные диаграммы токов и напряжений давали полную картину, их нужно увязать с фактическим протеканием процесса в цепи переменного тока, т.е. необходимо предварительно принять условные положительные направления токов и напряжений в рассматриваемой схеме. Без выполнения этого условия, если не заданы положительные направления токов и напряжений, любая векторная диаграмма не имеет никакого смысла.
Рассмотрим простую однофазную цепь переменного тока, приведенную на рис.1.6, а. От однофазного генератора энергия предается в активное сопротивление нагрузкиR. Зададимся положительными направлениями токов и напряжений в рассматриваемой цепи. За условное положительное направление напряжения и ЭДС примем направление, когда потенциал вывода генератора или нагрузки, связанного с линией, выше потенциала вывода, соединенного с землей. В соответствии с правилами, принятыми в электротехнике, положительное направление для ЭДС обозначено стрелкой, направленной в сторону более высокого потенциала (от земли к линейному выводу), а для напряжения – стрелкой, направленной в сторону более низкого потенциала (от линейного вывода к земле).
Переменный ток будет считать положительным, когда во внешней цепи он проходит от шин генератора к нагрузке (обозначено стрелкой). Построим векторы ЭДС и тока, характеризующие работу рассматриваемой цепи (рис.1.6, б). Вектор ЭДС произвольно обозначим вертикальной линией со стрелкой, направленной вверх. Для построения вектора тока запишем для цепи уравнение согласно второму закону Кирхгофа:
отсюда
Поскольку знаки векторов тока и ЭДС в выражении совпадают, вектор тока будет совпадать с вектором ЭДС и на рис.1.6, б.
Здесь и в дальнейшем при построении векторов будем откладывать их по величине равным эффективному значению тока и напряжения, что удобно для выполнения различных математических операций с векторами. Как известно, эффективные значения тока и напряжений в √2 раз меньше соответствующих максимальных (амплитудных).
При заданных положительных направлениях тока и напряжения однозначно определяется и знак мощности. Положительной в рассматриваемом случае будем считать мощность, направленная от шин генератора в линию:
так как векторы тока и ЭДС на рис.1.6, б совпадают.
Аналогичные соображения могут быть высказаны и для трехфазной цепи переменного тока, показанной на рис.1.7, а. В этом случае во всех фазах приняты одинаковые положительные направления, чему соответствует симметричная диаграмма токов и напряжений, приведенная на рис.1.7, б. Отметим, что симметричной называется такая трехфазная система векторов, когда все три вектора равны по величине и сдвинуты относительно друг друга на угол 120о.
Операции с векторами. Когда мы рассматриваем только одну кривую тока или напряжения, начальное значение угла, с которого начинается отсчет, или, иначе говоря, положение вектора на диаграмме, соответствующее начальному моменту времени, может быть принято произвольным. Если же одновременно рассматриваются два или несколько токов и напряжений, то, задавшись начальным положением на диаграмме одного из векторов, мы тем самым уже определяем положение всех других векторов.
Все три вектора фазных напряжений: , показанные на рис.1.7, б, вращаются против часовой стрелки с одинаковой скоростью, определяемой частотой переменного тока. При этом они пересекают вертикальную ось, совпадающую с направлением вектора на рис.1.7, б, поочередно с определенной последовательностью, а именно ,,, которая называется чередованием фаз напряжения (или тока). Для того чтобы определить взаимное расположение двух векторов, обычно говорят, что один из них опережает или отстает от другого. При этом опережающим считается вектор, который при вращении против часовой стрелки раньше пересечет вертикальную ось. Так, например, можно сказать, что вектор напряжения на рис.1.7, б опережает на угол 120о или, с другой стороны, вектор отстает от вектора на угол 120о. Как видно из рис.1.7, выражение «вектор отстает на угол 120о», равноценно выражению «вектор опережает на угол 240о». Сложение векторов производится геометрическим суммированием по правилу параллелограмма, как показано на рис.1.8, а, на котором построена сумма токов (). Так как вычитание – действие, обратное сложению, для определения разности токов (например, ) достаточно к току прибавить вектор, обратный . Вместе с тем на рис.1.8, а показано, что вектор разности токов () можно построить проще, соединив линией концы векторов и . При этом стрелка вектора разности токов направляется в сторону первого вектора, т.е. . Аналогично строится векторная диаграмма межфазных напряжений, например, (рис.1.8, б).Очевидно, что положение вектора на плоскости определяется его проекциями на две любые оси. Так, например, для того чтобы определить положение вектора 0А(рис.1.9), достаточно знать его проекции на взаимно перпендикулярные оси:
0A’= 0A cos φ;
0A’’= 0A sin φ = 0A cos (90o – φ).
Отложим на осях координат проекции векторов 0А’ и 0А’’ и восстановим из точек А’ и A’’ перпендикуляры к осям. Точка пересечения этих перпендикуляров и есть точка А – один конец вектора, вторым концов которого является точка 0 – начало координат.
Назначение векторных диаграмм. Работникам, занимающимся проектированием и эксплуатацией релейной защиты, часто приходится использовать в своей работе так называемые векторные диаграммы – векторы токов и напряжений, построенные на плоскости в определенном сочетании, соответствующем электрическим процессам, происходящим в рассматриваемой схеме.
Анализ векторных диаграмм токов и напряжений является одним из важных, а в ряде случаев единственным способом проверки правильности соединения цепей тока и напряжения и включения реле в схемах дифференциальных и направленных защит.
По сути построение векторной диаграммы целесообразно во всех случаях, когда к рассматриваемому реле подаются две или более электрические величины: разность токов в максимальной токовой или дифференциальной защите, ток и напряжение в реле направления мощности или в направленном реле сопротивления. Векторная диаграмма позволяет сделать заключение о том, как рассматриваемая защита будет работать при КЗ, т.е. оценить правильность ее включения. Взаимное расположение векторов токов и напряжений на диаграмме определяется характеристикой рассматриваемой цепи, а также условно принятыми положительными направлениями токов и напряжений. Для примера рассмотрим две векторные диаграммы.
На рис.1.10 показана однофазная цепь переменного тока, состоящая из генератора и последовательно соединенных емкостного, активного и индуктивного сопротивлений (примем при этом, что индуктивное сопротивление больше емкостного ХL > XC). Положительные направления токов и напряжений, так же как и в случаях, рассмотренных выше, обозначены на рис.1.10, а стрелками.
Построение векторной диаграммы начнем с вектора ЭДС Е, который расположим на рис.1.10, б вертикально. Ток, проходящий в рассматриваемой цепи, определится из следующего выражения:
Поскольку в рассматриваемой цепи имеются активные и реактивные сопротивления, причем ХL > XC, вектор тока отстает от вектора напряжения на угол φ:
Напряжение в точке n на рис.1.10, а определится согласно следующему выражению:
Как видно из рис.1.10, б, этот последний вектор будет равен падению напряжения в индуктивном сопротивлении .Рассмотрим другую цепь переменного тока, приведенную на рис.1.11, а, и построим векторную диаграмму, характеризирующую распределение токов в параллельных ветвях. Для построения диаграммы примем, что активное и емкостное сопротивление равны R=XC.
Построение векторной диаграммы начнем с вектора , который расположим горизонтально. Затем построим вектор падения напряжения на сопротивлениях , отстающий от вектора на угол φ, так как результирующее сопротивление имеет активно-емкостной характер. Угол φ определяется следующим выражением: В рассматриваемом случае φ=45о. Вектор тока , проходящего по активному сопротивлению, совпадает с , а опережает на 90о, как показано на рис.1.11, б.Вопросы для самопроверки:
Что такое вектор? Зачем нужны векторные диаграммы?
Что такое частота переменного тока?
Что означает, когда говорят, что один вектор «опережает» или «отстает» от другого вектора?
Как производится сложение и вычитание векторов?
Построение векторных диаграмм
Наверняка при решении задач по электротехнике многие сталкивались с некоторыми сложностями в построении векторных диаграмм. Начнем с определения векторной диаграммы.
Векторная диаграмма — это изображение синусоидально изменяющихся величин в виде векторов на плоскости.
Векторные диаграммы применяют потому, что сложение и вычитание синусоидальных величин, неизбежные при расчете цепей переменного тока, наиболее просто выполняются в векторной форме. Кроме того векторные диаграммы отличаются простотой и наглядностью.
Построение векторной диаграммы выполняется в прямоугольной плоскости. Чтобы построить диаграмму нужно провести вектор длиною равный амплитудному значению искомой величины, под углом сдвига относительно другой величины. Возможно, вы не сразу поймете смысл сказанного, для этого нужно изучить пример.
В качестве примера рассмотрим построение векторной диаграммы для цепи, состоящей из последовательно подключенных конденсатора, резистора и катушки. Напряжение на катушке UL=15 В, напряжение на конденсаторе UC=20 В, напряжение на резисторе UR=10 В, ток в цепи I=3 А. Требуется найти общее напряжение.
Катушка носит индуктивный характер, а значит, в ней напряжение опережает ток по фазе на 90°.
Конденсатор носит емкостной характер, значит, ток в нем опережает по фазе напряжение на 90°.
Резистор обладает только активным сопротивлением, и напряжение в нем совпадает по фазе с током.
Итак, для начала отложим вектор тока в масштабе. Масштаб для тока у нас будет 1 А/см.

Теперь отложим вектор напряжения на катушке, масштаб для напряжения возьмем 5 В/см, получается, что нужно отложить шесть клеток вверх, так как напряжение в катушке опережает ток. Для наглядности обозначим синим цветом.

Далее мы будем откладывать вектор активного сопротивления, так как напряжение в одной фазе с током, то мы его откладываем из конца вектора UL параллельно вектору тока I. Обозначим его красным цветом.

Следующим шагом отложим вектор напряжения на конденсаторе, так как оно запаздывает на 90°, мы его отложим вертикально вниз, из конца вектора UR. Обозначим желтым цветом.

И последним этапом мы отложим вектор общего напряжения, из начала координат в конец вектора UC и обозначим его зеленым цветом.

Общее напряжение получилось равным 2,23 В, причем характер цепи емкостной, так как напряжение отстает от тока.
Аналогичным образом выполняется построение векторной диаграммы токов.
Читайте также последовательная RLС-цепь
Векторная диаграмма напряжений и токов
Содержание:
- Основные виды и построение векторных диаграмм
- Порядок построения диаграмм
- Видео: метод векторных диаграмм
При выполнении анализа и расчета цепей переменного тока требуется доступное и наглядное отражение всех текущих процессов. С этой целью используется векторная диаграмма напряжений и токов, существенно облегчающая проведение всех необходимых расчетов. Она представляет собой направленные отрезки – векторы, изменяющиеся в соответствии с синусоидальным или косинусоидальным законом. С помощью этих геометрических представлений отображаются действующие синусоидальные токи, напряжения, а также их параметры и амплитудные величины.
Виды и построение векторных диаграмм
Векторные диаграммы широко применяются в акустике, электротехнике, оптике и других областях. Они разделяются на два основных вида – точные и качественные.

Для изображения точных векторных диаграмм применяются численные расчеты с условием, что действующие значения будут соответствовать определенным масштабам. Правильное построение дает возможность геометрического определения фаз и амплитудных значений нужных величин.
При составлении качественных диаграмм в первую очередь учитываются взаимные соотношения между электрическими параметрами, без использования каких-либо числовых данных. Они относятся к основным средствам, позволяющим анализировать электрические цепи, наглядно демонстрировать и осуществлять качественный контроль над решением той или иной задачи. С помощью диаграмм довольно просто определяется квадрант, где расположен нужный вектор.
Для того чтобы сделать построение диаграмм более удобным, необходимо проанализировать состояние неподвижных векторов на определенный момент времени, выбираемый с таким условием, чтобы сама диаграмма приобрела наиболее оптимальный внешний вид.

На оси ОХ будут откладываться действительные числа, а на оси OY – мнимые числа или единицы. С помощью синусоиды отображается движущийся конец проекции на ось OY. Каждое значение напряжения и тока отображается на плоскости в полярных координатах, в соответствии с собственным вектором. Его длина будет отображать значение амплитудной величины тока, а углы будут равны фазам. Для векторов, отображаемых на диаграмме, характерна равновеликая угловая частота, обозначаемая символом ω. Поэтому во время вращения взаимное расположение угловых частот остается неизменным. Это дает возможность при построении диаграмм направить один вектор произвольно, а остальные отобразить по отношению к нему под различными углами в соответствии со сдвигами фаз.
Порядок построения диаграмм
Таким образом, с помощью векторных диаграмм, возможно очень четко представить себе опережение или отставание, затрагивающее различные электрические величины. В качестве примера можно рассмотреть ток, у которого величина изменяется по определенному закону: i = Im sin (ω t + φ).
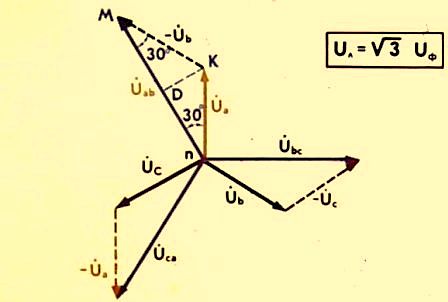
Для построения диаграммы необходимо от начальной точки координат «0» под определенным углом φ провести вектор Im. Его величина будет соответствовать такому же току. Направление вектора следует выбирать таким образом, чтобы он составлял угол с осью ОХ, равный фазе φ. Проекция вектора на вертикальной оси даст значение мгновенного тока в первоначальный период времени.
В большинстве случаев на векторных диаграммах отображаются не амплитудные, а действующие значения. Отличие действующих и амплитудных значений представляет собой пропорцию в определенном масштабе: I = Im /√2. Таким образом, векторная диаграмма напряжений и токов дает возможность быстро и просто выполнять все необходимые действия с двумя основными параметрами при расчетах электрических цепей и получать точные результаты.



