Скалярное поле. Векторное поле. Основные понятия и задачи
Теория поля является разделом математики, однако понятие поля лежит в основе многих представлений современной физики. В общем случае говорят, что в пространстве задано поле некоторой величины u, если в каждой точке пространства (или некоторой его части) определено значение этой величины. Так, например, при изучении потока газа приходится исследовать несколько полей: температурное поле (в каждой точке температура имеет определённое значение), поле давлений, поле скоростей и другие поля.
Поле величины u называется стационарным, (или установившимся), если u не зависит от времени t. В противном случае поле называется нестационарным (или неустановившимся). Таким образом, величина u есть функция точки M и времени t.
В задачах физики чаще всего приходится иметь дело со скалярными и векторными величинами. В соответствии с этим различают два вида полей: скалярные и векторные.
Пусть D — некоторая область на плоскости или в пространстве.
Определение скалярного поля. Если в области D каждой точке M(x,y,z) пространства или точке M(x,y) плоскости в каждый момент времени t по определённому закону ставится в соответствие значение скалярной величины u, то функция u(x,y,z,t) в случае пространства или u(x,y,t) в случае плоскости называется скалярным полем.
Понятия скалярного поля и функции, определённой в области
Примером скалярного поля может служить поле температур воздуха в некотором помещении, если температуру рассматривать как функцию точки. В точках, расположенных ближе к источнику тепла, температура выше, чем в точках, расположенных дальше от источника тепла. Можно привести и такие примеры, как поле освещённости, поле плотности массы и тому подобные.
Для получения более полного представления о скалярном поле используется его графическое изображение — поверхности уровня в пространстве и линии уровня на плоскости.
Линии уровня широко используются при составлении топографических и метеорологических карт. На топографических картах линия уровня — линия, в точках которой отмечена одна и та же высота над уровнем моря. На метеорологических картах строят два вида линий уровня — изотермы (линии одинаковой температуры) и изобары (линии одинакового давления).
Определение. Поверхностью уровня скалярного поля называется множество всех тех точек пространства, в которых скалярное поле постоянно.
Уравнение поверхности уровня скалярного поля u(x,y,z):
u(x,y,z) = C.
При постоянном изменении значения C поверхности уровня заполняют всю область пространства. Если поверхности уровня размещены плотно, скалярное поле изменяется быстро. Если же поверхности уровня расположены редко, скалярное поле изменяется медленно.
Определение. Линией уровня скалярного поля называется множество всех тех точек на плоскости, в которых скалярное поле постоянно.
Уравнение линии уровня скалярного поля u(x,y):
u(x,y) = C.
Пример 1. Определить поверхности уровня скалярного поля

Решение. Уравнением поверхностей уровня данного скалярного поля является
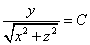
или
 .
.
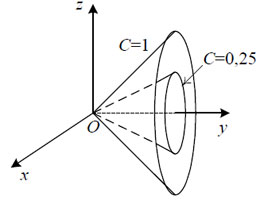
Поверхностями уровня являются конусы с вершиной в начале координат и осью вращения
Oy. Так как по области определения
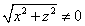
Пример 2. Определить линии уровня скалярного поля
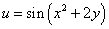 и их вид.
и их вид.
Решение. Уравнением линий уровня данного скалярного поля является
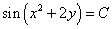 .
.
Из этого уравнения выразим «игрек»:
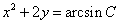
Так как arcsinC — также константа, обозначим её C1. Тогда
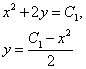
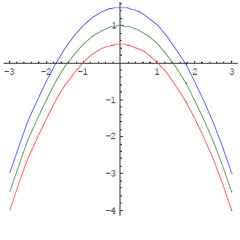
Графиками этих линий являются параболы с вершиной в точках
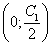 и ветвями вниз. На рисунке
изображены линии уровня в трёх случаях:
C1 = 1 — красная линия,
и ветвями вниз. На рисунке
изображены линии уровня в трёх случаях:
C1 = 1 — красная линия,
Понятие векторного поля во многом аналогично понятию скалярного поля.
Определение векторного поля. Если в некоторой области пространства
каждой точке M по определённому закону ставится в соответствие
вектор 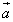 , то векторная
функция
, то векторная
функция 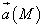 называется
полем вектора или векторным полем.
называется
полем вектора или векторным полем.
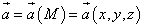
Примерами векторного поля являются поля скорости и ускорения в текущей жидкости или газе, поле силы гравитации, поле интенсивности электростатического поля и тому подобные. Вообще, примером векторного поля может служить поле сил любой природы.
Мы будем рассматривать только стационарные векторные поля, то есть поля, не зависящие от времени.
Проекции вектора 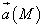
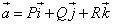 .
.
Таким образом, векторное поле можно определить тремя скалярными функциями P, Q, R. Пусть эти функции и их частные производные по переменным x,y,z являются непрерывными функциями.
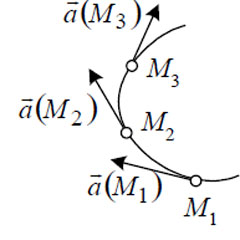
Векторные линии поля силы обычно называют линиями силы, векторные линии поля скоростей потока жидкости или газа — векторами потока. У стационарного потока жидкости линии потока совпадают с траекториями частиц жидкости.
Уравнения векторных линий можно найти, решив систему дифференциальных уравнений
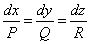

Поделиться с друзьями
2 Векторное поле. Векторные линии
Если
в каждой точке  пространственной
области
пространственной
области задан определенный вектор
задан определенный вектор
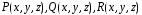 ,
являющимися проекциями вектора
,
являющимися проекциями вектора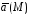 на координатные оси декартовой системы:
на координатные оси декартовой системы:  .
.
Примерами векторных полей могут служить поле электрической напряженности, силовое поле, поле скоростей текущей жидкости и др. Векторное поле тоже может быть плоским, например,
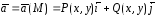 .
.
Векторной
линией поля  называется такая линия, касательная в
каждой точке которой направлена вдоль
заданного в этой точке вектора поля
(рисунок 1).
называется такая линия, касательная в
каждой точке которой направлена вдоль
заданного в этой точке вектора поля
(рисунок 1).

Рисунок 1
Всякое
векторное поле  обладает семейством векторных линий.
Уравнения этого семейства есть общее
решение дифференциальных уравнений
вида
обладает семейством векторных линий.
Уравнения этого семейства есть общее
решение дифференциальных уравнений
вида
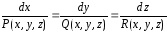 .
(4)
.
(4)
Задача
2. Для плоского
поля  найти уравнения семейства векторных
линий и векторной линии, проходящей
через точку
найти уравнения семейства векторных
линий и векторной линии, проходящей
через точку
Решение. Так как 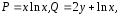 то,
согласно равенству (4), уравнение семейства
одно и определяется общим решением
дифференциального уравнения
то,
согласно равенству (4), уравнение семейства
одно и определяется общим решением
дифференциального уравнения

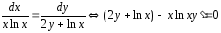 .
.
Это
уравнение линейное относительно 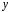 как функции от
как функции от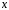 .
Решая его методом вариации произвольной
постоянной, получим общее решение в
виде
.
Решая его методом вариации произвольной
постоянной, получим общее решение в
виде
 .
.
Выделим
из этого семейства одно решение то,
которое представляет собой уравнение
векторной линии, проходящей через точку  .
Подставив в общее решение
.
Подставив в общее решение получим
получим Итак, искомая векторная линия
Итак, искомая векторная линия
3 Поток векторного поля
Пусть
в поле вектора  задана ориентированная поверхность
задана ориентированная поверхность .
Обозначим через
.
Обозначим через единичный вектор нормали к выбранной
стороне поверхности в ее произвольной
точке. Поверхностный интеграл первого
рода по поверхности
единичный вектор нормали к выбранной
стороне поверхности в ее произвольной
точке. Поверхностный интеграл первого
рода по поверхности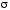 от скалярного произведения вектора
от скалярного произведения вектора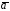 на вектор
на вектор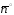
 (5)
(5)
называется потоком
векторного поля через ориентированную поверхность  и обозначается
и обозначается .
В случае замкнутой поверхности
.
В случае замкнутой поверхности поток записывается в виде
поток записывается в виде
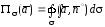 .
.
Если
ввести в рассмотрение вектор 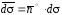 и обозначить его проекции на оси координат
и обозначить его проекции на оси координат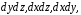 то формулу (5) можно переписать в виде
то формулу (5) можно переписать в виде
 (6)
(6)
где
вектор 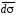 направлен по нормали к выбранной стороне
поверхности
направлен по нормали к выбранной стороне
поверхности .
Правая часть равенства (6) является
поверхностным интегралом второго рода.
.
Правая часть равенства (6) является
поверхностным интегралом второго рода.
Если,
например,  – поле скоростей текущей жидкости в
области
– поле скоростей текущей жидкости в
области и
и – незамкнутая поверхность с выбранным
направлением нормали
– незамкнутая поверхность с выбранным
направлением нормали ,
то
,
то равен количеству жидкости, проходящей
в единицу времени через поверхность
равен количеству жидкости, проходящей
в единицу времени через поверхность в направлении
в направлении .
Если
.
Если – замкнутая поверхность, ограничивающая
некоторую область
– замкнутая поверхность, ограничивающая
некоторую область с внешней нормалью
с внешней нормалью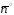 ,
то
,
то равен разности количеств втекающей в
эту область жидкости и вытекающей. Когда
равен разности количеств втекающей в
эту область жидкости и вытекающей. Когда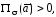 это означает, что в области
это означает, что в области имеютсяисточники (где векторные
линии порождаются), а если
имеютсяисточники (где векторные
линии порождаются), а если  то это указывает на наличие в области
то это указывает на наличие в области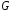 стоков (где векторные линии заканчиваются).
стоков (где векторные линии заканчиваются).
Если
ориентированная поверхность  задана явно непрерывно дифференцируемой
функцией
задана явно непрерывно дифференцируемой
функцией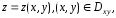 то по формуле (6) можно получить следующую
формулу, связывающую поверхностный
интеграл по поверхности
то по формуле (6) можно получить следующую
формулу, связывающую поверхностный
интеграл по поверхности с двойным интегралом по проекции
с двойным интегралом по проекции этой поверхности на плоскость
этой поверхности на плоскость :
:
 (7)
(7)
где
знак плюс берется, когда интегрирование
в левой части ведется по стороне  положительно ориентированной по
отношению к оси
положительно ориентированной по
отношению к оси — вектор нормали к ориентированной
поверхности. Запись
— вектор нормали к ориентированной
поверхности. Запись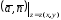 означает, что в произведении
означает, что в произведении переменную
переменную следует заменить на
следует заменить на
Если
поверхность  задана явно уравнением
задана явно уравнением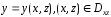 или
или то соответственно меняются роли
переменных в формуле (7).
то соответственно меняются роли
переменных в формуле (7).
Замечание. Если
поверхность 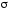 задана уравнением
задана уравнением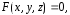 которое неоднозначно разрешается
относительно одной из переменных и,
следовательно, поверхностьнеоднозначно проецируется на
соответствующую координатную плоскость
(например
которое неоднозначно разрешается
относительно одной из переменных и,
следовательно, поверхностьнеоднозначно проецируется на
соответствующую координатную плоскость
(например — цилиндрическая поверхность неоднозначно
проецирующаяся на плоскость
— цилиндрическая поверхность неоднозначно
проецирующаяся на плоскость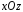 ),
ее следует разбить на части, однозначно
проецирующиеся на координатную плоскость.
),
ее следует разбить на части, однозначно
проецирующиеся на координатную плоскость.
Задача
3. Вычислить
поток вектора  через нижнюю сторону поверхности
через нижнюю сторону поверхности ,
отсеченной плоскостью
,
отсеченной плоскостью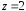 (рисунок 2).
(рисунок 2).

Рисунок 2
Решение. Учитывая, что  имеет различный знак
имеет различный знак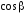 для правой и левой части поверхности
для правой и левой части поверхности ,
а
,
а – сохраняет отрицательный знак для
всей поверхности, будем иметь
– сохраняет отрицательный знак для
всей поверхности, будем иметь

где 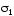 –
правая часть поверхности (нормаль к ней
составляет с
–
правая часть поверхности (нормаль к ней
составляет с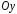 острый угол),
острый угол), –
левая часть поверхности. Первые два
слагаемых уничтожаются, так как
–
левая часть поверхности. Первые два
слагаемых уничтожаются, так как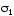 и
и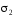 имеют одинаковую проекцию на
имеют одинаковую проекцию на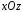 Окончательно имеем :
Окончательно имеем :
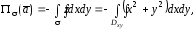
где 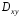 –
проекция
–
проекция на
на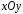 имеет форму круга с границей
имеет форму круга с границей .
Поэтому, переходя к полярным координатам,
получим
.
Поэтому, переходя к полярным координатам,
получим

Векторное поле Википедия
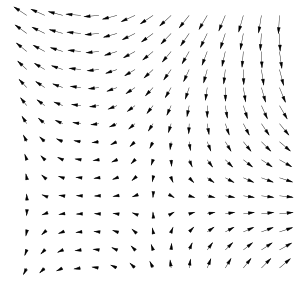
Векторное поле — это отображение, которое каждой точке рассматриваемого пространства ставит в соответствие вектор с началом в этой точке. Например, вектор скорости ветра в данный момент времени различен в разных точках и может быть описан векторным полем.
Определение и вариации[ | ]
Евклидово пространство[ | ]
Векторное поле на евклидовом (или псевдоевклидовом) пространстве[1]E{\displaystyle {\mathcal {E}}} определяется как вектор-функция точки пространства, отображающая это пространство в (на) себя[2]:
- F:E⟶E.{\displaystyle {\mathcal {F}}:{\mathcal {E}}\longrightarrow {\mathcal {E}}.}
То есть, каждой точке пространства сопоставляется некоторый вектор (значение векторного поля в данной точке пространства). В общем случае этот вектор различается для разных точек пространства, то есть в общем случае векторное поле принимает разные значения в разных точках пространства. В каждой точке пространства вектор поля имеет определенную величину и определенное (за исключением тех случаев, когда поле обращается в ноль) направление в этом пространстве[3].
- В литературе (особенно в более старой, а также в физической) применительно к векторному полю на некотором пространстве употребляется также предлог в (то есть говорят и поле на пространстве, и поле в пространстве).
Многообразие[ | ]
В более общем случае, когда исходное пространство является многообразием, векторное поле определяется как сечение касательного расслоения к данному многообразию, то есть отображение, которое каждой точке p{\displaystyle p}
2 Векторное поле. Векторные линии
Если
в каждой точке 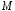 пространственной
области
пространственной
области задан определенный вектор
задан определенный вектор то говорят, что в этой области задановекторное
поле. Векторное
поле задается тремя скалярными функциями
то говорят, что в этой области задановекторное
поле. Векторное
поле задается тремя скалярными функциями 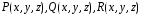 ,
являющимися проекциями вектора
,
являющимися проекциями вектора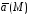 на координатные оси декартовой системы:
на координатные оси декартовой системы:
 .
.
Примерами векторных полей могут служить поле электрической напряженности, силовое поле, поле скоростей текущей жидкости и др. Векторное поле тоже может быть плоским, например,
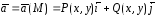 .
.
Векторной
линией поля 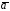 называется такая линия, касательная в
каждой точке которой направлена вдоль
заданного в этой точке вектора поля
(рисунок 1).
называется такая линия, касательная в
каждой точке которой направлена вдоль
заданного в этой точке вектора поля
(рисунок 1).

Рисунок 1
Всякое
векторное поле 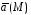 обладает семейством векторных линий.
Уравнения этого семейства есть общее
решение дифференциальных уравнений
вида
обладает семейством векторных линий.
Уравнения этого семейства есть общее
решение дифференциальных уравнений
вида
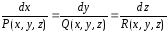 .
(4)
.
(4)
Задача
2. Для плоского
поля  найти уравнения семейства векторных
линий и векторной линии, проходящей
через точку
найти уравнения семейства векторных
линий и векторной линии, проходящей
через точку
Решение. Так как  то,
согласно равенству (4), уравнение семейства
одно и определяется общим решением
дифференциального уравнения
то,
согласно равенству (4), уравнение семейства
одно и определяется общим решением
дифференциального уравнения

 .
.
Это
уравнение линейное относительно 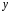 как функции от
как функции от .
Решая его методом вариации произвольной
постоянной, получим общее решение в
виде
.
Решая его методом вариации произвольной
постоянной, получим общее решение в
виде
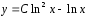 .
.
Выделим
из этого семейства одно решение то,
которое представляет собой уравнение
векторной линии, проходящей через точку  .
Подставив в общее решение
.
Подставив в общее решение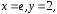 получим
получим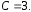 Итак, искомая векторная линия
Итак, искомая векторная линия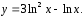
3 Поток векторного поля
Пусть
в поле вектора  задана ориентированная поверхность
задана ориентированная поверхность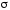 .
Обозначим через
.
Обозначим через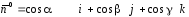 единичный вектор нормали к выбранной
стороне поверхности в ее произвольной
точке. Поверхностный интеграл первого
рода по поверхности
единичный вектор нормали к выбранной
стороне поверхности в ее произвольной
точке. Поверхностный интеграл первого
рода по поверхности от скалярного произведения вектора
от скалярного произведения вектора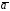 на вектор
на вектор
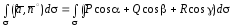 (5)
(5)
называется потоком
векторного поля через ориентированную поверхность  и обозначается
и обозначается .
В случае замкнутой поверхности
.
В случае замкнутой поверхности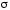 поток записывается в виде
поток записывается в виде
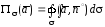 .
.
Если
ввести в рассмотрение вектор  и обозначить его проекции на оси координат
и обозначить его проекции на оси координат то формулу (5) можно переписать в виде
то формулу (5) можно переписать в виде
 (6)
(6)
где
вектор 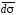 направлен по нормали к выбранной стороне
поверхности
направлен по нормали к выбранной стороне
поверхности .
Правая часть равенства (6) является
поверхностным интегралом второго рода.
.
Правая часть равенства (6) является
поверхностным интегралом второго рода.
Если,
например,
– поле скоростей текущей жидкости в
области и
и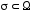 – незамкнутая поверхность с выбранным
направлением нормали
– незамкнутая поверхность с выбранным
направлением нормали ,
то
,
то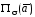 равен количеству жидкости, проходящей
в единицу времени через поверхность
равен количеству жидкости, проходящей
в единицу времени через поверхность в направлении
в направлении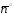 .
Если
.
Если – замкнутая поверхность, ограничивающая
некоторую область
– замкнутая поверхность, ограничивающая
некоторую область с внешней нормалью
с внешней нормалью ,
то
,
то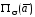 равен разности количеств втекающей в
эту область жидкости и вытекающей. Когда
равен разности количеств втекающей в
эту область жидкости и вытекающей. Когда это означает, что в области
это означает, что в области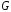 имеютсяисточники (где векторные
линии порождаются), а если
имеютсяисточники (где векторные
линии порождаются), а если 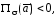 то это указывает на наличие в области
то это указывает на наличие в области стоков (где векторные линии заканчиваются).
стоков (где векторные линии заканчиваются).
Если
ориентированная поверхность 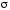 задана явно непрерывно дифференцируемой
функцией
задана явно непрерывно дифференцируемой
функцией то по формуле (6) можно получить следующую
формулу, связывающую поверхностный
интеграл по поверхности
то по формуле (6) можно получить следующую
формулу, связывающую поверхностный
интеграл по поверхности с двойным интегралом по проекции
с двойным интегралом по проекции этой поверхности на плоскость
этой поверхности на плоскость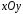 :
:
 (7)
(7)
где
знак плюс берется, когда интегрирование
в левой части ведется по стороне  положительно ориентированной по
отношению к оси
положительно ориентированной по
отношению к оси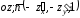 — вектор нормали к ориентированной
поверхности. Запись
— вектор нормали к ориентированной
поверхности. Запись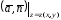 означает, что в произведении
означает, что в произведении переменную
переменную следует заменить на
следует заменить на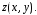
Если
поверхность 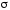 задана явно уравнением
задана явно уравнением или
или то соответственно меняются роли
переменных в формуле (7).
то соответственно меняются роли
переменных в формуле (7).
Замечание. Если
поверхность  задана уравнением
задана уравнением которое неоднозначно разрешается
относительно одной из переменных и,
следовательно, поверхность
которое неоднозначно разрешается
относительно одной из переменных и,
следовательно, поверхность неоднозначно проецируется на
соответствующую координатную плоскость
(например
неоднозначно проецируется на
соответствующую координатную плоскость
(например — цилиндрическая поверхность неоднозначно
проецирующаяся на плоскость
— цилиндрическая поверхность неоднозначно
проецирующаяся на плоскость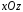 ),
ее следует разбить на части, однозначно
проецирующиеся на координатную плоскость.
),
ее следует разбить на части, однозначно
проецирующиеся на координатную плоскость.
Задача
3. Вычислить
поток вектора  через нижнюю сторону поверхности
через нижнюю сторону поверхности ,
отсеченной плоскостью
,
отсеченной плоскостью (рисунок 2).
(рисунок 2).
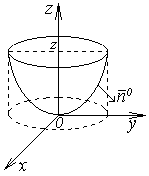
Рисунок 2
Решение. Учитывая, что 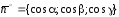 имеет различный знак
имеет различный знак для правой и левой части поверхности
для правой и левой части поверхности ,
а
,
а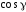 – сохраняет отрицательный знак для
всей поверхности, будем иметь
– сохраняет отрицательный знак для
всей поверхности, будем иметь
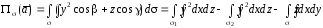
где  –
правая часть поверхности (нормаль к ней
составляет с
–
правая часть поверхности (нормаль к ней
составляет с острый угол),
острый угол),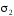 –
левая часть поверхности. Первые два
слагаемых уничтожаются, так как
–
левая часть поверхности. Первые два
слагаемых уничтожаются, так как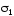 и
и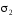 имеют одинаковую проекцию на
имеют одинаковую проекцию на Окончательно имеем :
Окончательно имеем :

где  –
проекция
–
проекция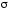 на
на имеет форму круга с границей
имеет форму круга с границей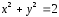 .
Поэтому, переходя к полярным координатам,
получим
.
Поэтому, переходя к полярным координатам,
получим

Потенциальное векторное поле — Википедия
Материал из Википедии — свободной энциклопедии
Потенциальное (или безвихревое) векторное поле в математике — векторное поле, которое можно представить как градиент некоторой скалярной функции координат. Необходимым условием потенциальности векторного поля в трёхмерном пространстве является равенство нулю ротора поля. Однако это условие не является достаточным — если рассматриваемая область пространства не является односвязной, то скалярный потенциал может быть многозначной функцией.
В физике, имеющей дело с силовыми полями, математическое условие потенциальности силового поля можно представить как требование равенства нулю работы при мгновенном перемещении частицы, на которую действует поле, по замкнутому контуру. Этот контур не обязан быть траекторией частицы, движущейся под действием только данных сил. В качестве потенциала поля в этом случае можно выбрать работу по мгновенному перемещению пробной частицы из некоторой произвольно выбранной исходной точки в заданную точку (по определению эта работа не зависит от пути перемещения). Например, потенциальными являются статическое электрическое поле, а также гравитационное поле в ньютоновой теории гравитации.
В некоторых источниках потенциальным полем сил считается только поле с потенциалом, не зависящим от времени. Это связано с тем, что потенциал для сил, зависящий от времени, вообще говоря, не является потенциальной энергией тела, движущегося под действием этих сил. Поскольку силы совершают работу не одномоментно, работа сил над телом будет зависеть от его траектории и от скорости прохождения по ней. В этих условиях сама потенциальная энергия не определена, так как по определению должна зависеть только от положения тела, но не от пути. Тем не менее, и для этого случая потенциал для сил может существовать, и может входить в уравнения движения так же, как и потенциальная энергия для тех случаев, когда она существует.
Пусть v→{\displaystyle {\vec {v}}} — потенциальное векторное поле; оно выражается через потенциал ϕ{\displaystyle \phi } как
- v→=∇ϕ{\displaystyle {\vec {v}}=\nabla \phi } (или в другой записи v→=gradϕ{\displaystyle {\vec {v}}=\operatorname {grad} \phi }).
Для поля сил и потенциала сил эта же формула записывается как
- F→(r→,t)=−∇U(r→,t){\displaystyle {\vec {F}}({\vec {r}},t)=-\nabla U({\vec {r}},t)},
то есть для сил потенциалом ϕ{\displaystyle \phi } является −U{\displaystyle -U}. Когда U не зависит от времени, оно является потенциальной энергией, и тогда знак «-» возникает просто по определению. В противном случае знак сохраняется ради единообразия.
Для поля ϕ{\displaystyle \phi } выполняется свойство независимости интеграла от пути P{\displaystyle P}:
- ∫Pv→⋅dr→=ϕ(B)−ϕ(A){\displaystyle \int _{P}{\vec {v}}\cdot d{\vec {r}}=\phi (B)-\phi (A)},
Это равносильно
- ∮v→⋅dr→=0{\displaystyle \oint {\vec {v}}\cdot d{\vec {r}}=0}.
Интеграл по замкнутому контуру обращается в 0, поскольку начальная и конечная точка совпадают. И наоборот, предыдущую формулу можно вывести из этой, если разбить замкнутый контур на два незамкнутых.
Необходимое условие записывается как ∇×v→=0{\displaystyle \nabla \times {\vec {v}}=0} (или в другой записи rotv→=0{\displaystyle \operatorname {rot} {\vec {v}}=0}).
На языке дифференциальных форм потенциальное поле — это точная 1-форма — то есть форма, которая является (внешним) дифференциалом 0-формы (функции). Градиенту соответствует взятие внешнего дифференциала от 0-формы (потенциала), ротору соответствует взятие внешнего дифференциала от 1-формы (поля). Необходимое условие следует из того, что второй внешний дифференциал всегда равен нулю: d2=0{\displaystyle d^{2}=0}. Интегральные формулы следуют из (обобщённой) теоремы Стокса.
Потенциальное векторное поле — это… Что такое Потенциальное векторное поле?
Потенциальное (или безвихревое) векторное поле в математике — векторное поле, которое можно представить как градиент некоторой скалярной функции координат (потенциала). Необходимым условием потенциальности векторного поля в трёхмерном пространстве является равенство нулю ротора поля. Однако это условие не является достаточным (например, в многосвязной области у безвихревого поля может не существовать скалярный потенциал).
В физике, имеющей дело с силовыми полями, математическое условие потенциальности силового поля можно представить как требование равенства нулю работы при мгновенном перемещении частицы, на которую действует поле, по замкнутому контуру. Этот контур не обязан быть траекторией частицы, движущейся под действием только данных сил. В качестве потенциала поля в этом случае можно выбрать работу по мгновенному перемещению пробной частицы из некоторой произвольно выбранной исходной точки в заданную точку (по определению эта работа не зависит от пути перемещения). Например, потенциальными являются статическое электрическое поле, а также гравитационное поле в ньютоновой теории гравитации.
В некоторых источниках потенциальным полем сил считается только поле с потенциалом, не зависящим от времени. Это связано с тем, что потенциал для сил, зависящий от времени, вообще говоря, не является потенциальной энергией тела, движущегося под действием этих сил. Поскольку силы совершают работу не одномоментно, работа сил над телом будет зависеть от его траектории и от скорости прохождения по ней. В этих условиях сама потенциальная энергия не определена, так как по определению должна зависеть только от положения тела, но не от пути. Тем не менее, и для этого случая потенциал для сил может существовать, и может входить в уравнения движения так же, как и потенциальная энергия для тех случаев, когда она существует.
Пусть — потенциальное векторное поле; оно выражается через потенциал как
- (или в другой записи ).
Для поля сил и потенциала сил эта же формула записывается как
- ,
то есть для сил потенциалом является . Когда U не зависит от времени, оно является потенциальной энергией, и тогда знак «-» возникает просто по определению. В противном случае знак сохраняется ради единообразия.
Для поля выполняется свойство независимости интеграла от пути :
- ,
Это равносильно
- .
Интеграл по замкнутому контуру обращается в 0, поскольку начальная и конечная точка совпадают. И наоборот, предыдущую формулу можно вывести из этой, если разбить замкнутый контур на два незамкнутых.
Необходимое условие записывается как (или в другой записи ).
На языке дифференциальных форм потенциальное поле — это точная 1-форма — то есть форма, которая является (внешним) дифференциалом 0-формы (функции). Градиенту соответствует взятие внешнего дифференциала от 0-формы (потенциала), ротору соответствует взятие внешнего дифференциала от 1-формы (поля). Необходимое условие следует из того, что второй внешний дифференциал всегда равен нулю: . Интегральные формулы следуют из (обобщённой) теоремы Стокса.
 |
См. также
Виды векторных полей
Определение. Векторное
поле называется соленоидальным в
области  ,
если его дивергенция равна нулю в каждой
точке этой области
,
если его дивергенция равна нулю в каждой
точке этой области . Для соленоидального поля характерно,
что в области
. Для соленоидального поля характерно,
что в области отсутствуют
источники и стоки, а поток
отсутствуют
источники и стоки, а поток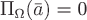 для
любой замкнутой поверхности
для
любой замкнутой поверхности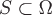 ,
т.к. по теореме Остроградского-Гаусса
,
т.к. по теореме Остроградского-Гаусса .
.
Для
соленоидальных полей имеет место закон
сохранения интенсивности векторной
трубки, состоящий в следующем. Теорема. В
соленоидальном поле поток вектора через
поперечное сечение векторной трубки
остается постоянным вдоль этой
трубки. Доказательство. Пусть 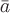 —
соленоидальное поле, т.е.
—
соленоидальное поле, т.е.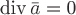 .
Рассмотрим некоторую векторную трубку,
т.е часть часть пространства ограниченную
векторными линиями, пересекающими
некоторый заданный контур. Пересечем
векторную трубку двумя поперечными
сечениями
.
Рассмотрим некоторую векторную трубку,
т.е часть часть пространства ограниченную
векторными линиями, пересекающими
некоторый заданный контур. Пересечем
векторную трубку двумя поперечными
сечениями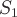 и
и .
Эти сечения вместе с боковой поверхностью
.
Эти сечения вместе с боковой поверхностью образуют
замкнутую поверхность
образуют
замкнутую поверхность .
.
Т.к.
поле соленоидально, то поток через
замкнутую поверхность  равен
нулю:
равен
нулю: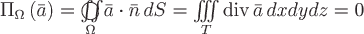 .
Поэтому получим:
.
Поэтому получим:
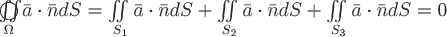 .
.
На
боковой поверхности  вектор
вектор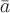 направлен
по касательной к векторной линии, т.е.
лежит в касательной плоскости. Поэтому
направлен
по касательной к векторной линии, т.е.
лежит в касательной плоскости. Поэтому перпендикулярен
вектору нормали к поверхности
перпендикулярен
вектору нормали к поверхности ,
т.е.
,
т.е.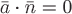 ,
откуда
,
откуда .
На
поверхностях
.
На
поверхностях и
и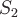 направления
нормалей берутся внешними к поверхностям.
На поверхности
направления
нормалей берутся внешними к поверхностям.
На поверхности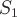 (см.
рисунок) внешняя нормаль направлена в
сторону, противоположному направлению
векторных линий. Поэтому заменив ее на
внутреннюю нормаль и, соответственно,
поменяв ориентацию
(см.
рисунок) внешняя нормаль направлена в
сторону, противоположному направлению
векторных линий. Поэтому заменив ее на
внутреннюю нормаль и, соответственно,
поменяв ориентацию ,
будем иметь:
,
будем иметь:
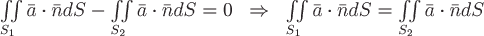 .
.
Поэтому
поток соленоидального поля через любое
поперечное сечение векторной трубки
имеет одно и тоже значение. Иногда
соленоидальное поле назвают трубчатым.
Это
согласуется с физическими моделями
соленоидальных полей, когда говорят,
что поле несжимаемо, что через поперечное
сечение трубки проходит одинаковое
количество векторных линий. Т.е. векторные
линии не возникают и не пропадают ни в
какой точке поля. Они либо уходят в
бесконечность, либо являются
замкнутыми. Пример
1. Поле напряженности  магнитного
поля, образованного электрическим
током, текущему по бесконечному
прямолинейному проводу, соленоидально
всюду, кроме точек оси
магнитного
поля, образованного электрическим
током, текущему по бесконечному
прямолинейному проводу, соленоидально
всюду, кроме точек оси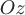 ,
т.к.
,
т.к. .Пример
2. Поле электрической напряженности
точечного заряда
.Пример
2. Поле электрической напряженности
точечного заряда  также
соленоидально всюду, за исключением
начала координат.
также
соленоидально всюду, за исключением
начала координат.
Определение. Векторное поле 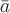 называетсябезвихревым в
области
называетсябезвихревым в
области  ,
если в каждой ее точке
,
если в каждой ее точке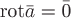 .Определение. Векторное поле
.Определение. Векторное поле  ,
заданное в области
,
заданное в области ,
называетсяпотенциальным,
если в этой области существует такая
скалярная функция
,
называетсяпотенциальным,
если в этой области существует такая
скалярная функция 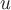 ,
что вектор
,
что вектор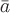 можно
представить в виде градиента этой
функции:
можно
представить в виде градиента этой
функции:
 .
.
Функция 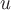 называется
потенциальной функцией или потенциалом
векторного поля
называется
потенциальной функцией или потенциалом
векторного поля . Из формулы
. Из формулы следует,
что
следует,
что
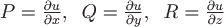 и
и 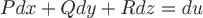 ,
,
т.
е. 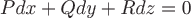 –
есть полный дифференциал потенциала
этого поля. Критерием потенциальности
векторного поля
–
есть полный дифференциал потенциала
этого поля. Критерием потенциальности
векторного поля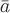 служит
равенство
служит
равенство
 .
.
Следовательно,
для того чтобы ВП было потенциальным
необходимо и достаточно, чтобы оно было
безвихревым.
Выполнение условия 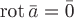 в
области
в
области приводит
не только к потенциальности ВП, но и к
следующим результатам:а) в
области
приводит
не только к потенциальности ВП, но и к
следующим результатам:а) в
области  существует
потенциал
существует
потенциал ,
который может быть определен с точностью
до постоянной по формуле
,
который может быть определен с точностью
до постоянной по формуле
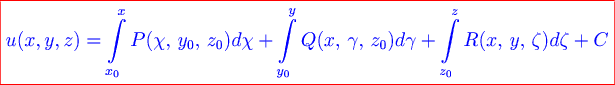
где 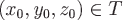 –
любая фиксированная точка;
–
любая фиксированная точка; –
переменная точка в области
–
переменная точка в области ;–
произвольная постоянная. Во втором
интеграле формулы постоянен,
а в третьем
;–
произвольная постоянная. Во втором
интеграле формулы постоянен,
а в третьем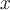 и
и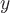 постоянные
величины;б) циркуляция векторного поля по любому
замкнутому контуру
постоянные
величины;б) циркуляция векторного поля по любому
замкнутому контуру  равна
нулю:
равна
нулю:
 .
.
Если
же хотя бы в одной точке, внутренней по
отношению к контуру  ,
поле
,
поле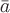 не
определено, циркуляция по этому контуру
может и не обратиться в нуль, хотя поле
потенциально;в) для любых двух точек
не
определено, циркуляция по этому контуру
может и не обратиться в нуль, хотя поле
потенциально;в) для любых двух точек  и
и областизначение
линейного интеграла векторного поля
областизначение
линейного интеграла векторного поля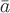

не
зависит от пути интегрирования в области 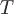 ;г) линейный
интеграл этого поля вдоль любого контура
;г) линейный
интеграл этого поля вдоль любого контура 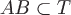 ,
соединяющего точки
,
соединяющего точки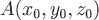 и
и равен
разности значений потенциала
равен
разности значений потенциала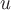 в
конечной и начальной точках контура:
в
конечной и начальной точках контура:
 .
.
Физический
смысл этого результата: если  –
силовое поле, то разность потенциалов
между точками
–
силовое поле, то разность потенциалов
между точками и
и равна
работе, которую поле совершает при
перемещении материальной точки из
равна
работе, которую поле совершает при
перемещении материальной точки из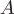 в
в .Пример
3. Доказать, что векторное поле
.Пример
3. Доказать, что векторное поле 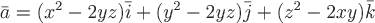 является
потенциальным. Найти его потенциал и
вычислить линейный интеграл поля от
точки
является
потенциальным. Найти его потенциал и
вычислить линейный интеграл поля от
точки до
точки
до
точки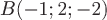 .Решение. Так
как поле определено и дифференцируемо
в любой точке пространства и
.Решение. Так
как поле определено и дифференцируемо
в любой точке пространства и 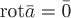 (проверьте
самостоятельно), то данное поле
потенциально. Найдем потенциал поля,
взяв в качестве точки
(проверьте
самостоятельно), то данное поле
потенциально. Найдем потенциал поля,
взяв в качестве точки начало
координат:
начало
координат: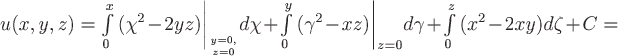
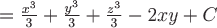 . Вычислим
линейный интеграл :
. Вычислим
линейный интеграл : .Определение. Векторное поле
.Определение. Векторное поле  называетсягармоническим,
если оно одновременно является и
потенциальным и соленоидальным, т.е.
называетсягармоническим,
если оно одновременно является и
потенциальным и соленоидальным, т.е.  и
и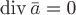 . Из
определения следует, что гармоническое
поле одновременно является полем
безвихревым и без источников и стоков.
Потенциал этого поля удовлетворяет
условию:
. Из
определения следует, что гармоническое
поле одновременно является полем
безвихревым и без источников и стоков.
Потенциал этого поля удовлетворяет
условию: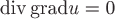 .Пример
4. Выяснить тип векторного поля
.Пример
4. Выяснить тип векторного поля  .Решение. Найдем
ротор векторного поля
.Решение. Найдем
ротор векторного поля 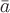 :
: . Рассчитаем
дивергенцию векторного поля
. Рассчитаем
дивергенцию векторного поля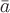 :
: Следовательно,
поле
Следовательно,
поле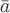 –
гармоническое.
–
гармоническое.
Существует теорема Гельмгольца о разложении произвольного поля на две компоненты — потенциальную и соленоидальную.
Теорема.
Если дивергенция и ротор векторного
поля 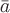 определены
в каждой точке области
определены
в каждой точке области пространства,
то всюду в
пространства,
то всюду в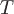 функция
может быть представлена в виде суммы
безвихревого (потенуиального) поля
функция
может быть представлена в виде суммы
безвихревого (потенуиального) поля и
соленоидального поля
и
соленоидального поля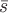 :
:
 ,
,
где  и
и для
всех точек области
для
всех точек области . Замечание. Для
описания электромагнитных полей
существуют система уравнений
Максвелла,
накопленных к середине XIX века на основе
экспериментальных результатов. 1)
. Замечание. Для
описания электромагнитных полей
существуют система уравнений
Максвелла,
накопленных к середине XIX века на основе
экспериментальных результатов. 1)  ,
т.е. электрический ток и изменение
электрической индукции порождают
вихревое магнитное поле.2)
,
т.е. электрический ток и изменение
электрической индукции порождают
вихревое магнитное поле.2)  ,
т.е. изменение магнитной индукции
порождает вихревое электрическое
поле. 3)
,
т.е. изменение магнитной индукции
порождает вихревое электрическое
поле. 3) 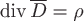 ,
т.е. электрический заряд является
источником электрической индукции.4)
,
т.е. электрический заряд является
источником электрической индукции.4)  ,
т.е. магнитных зарядов не существует.Вопрос. Поле
,
т.е. магнитных зарядов не существует.Вопрос. Поле  является
является
 Гармоническим
Гармоническим
 Недостаточно
данных для ответа
Недостаточно
данных для ответа
 Соленоидальным
Соленоидальным
 Произвольным
Произвольным
 Потенциальным
Потенциальным



