Координаты векторов. Операции с векторами.. Видеоурок. Геометрия 9 Класс
Можно встретить удачные и неудачные жилые массивы: в первых ветра практически нет, независимо от погоды, а во вторых, наоборот, есть почти всегда. Это зависит от того, были ли учтены при проектировании направление и сила ветра, который преимущественно дует в данном районе. Эту информацию нужно использовать при строительстве не только жилых районов, но и аэродромов, дорог и т. д.
Чтобы ее получить, на основании многолетних наблюдений, наносят направления ветра на так называемую розу ветров (см. рис. 1). Чем чаще дует ветер в данном направлении, тем дальше соответствующая точка от точки  (см. рис. 2).
(см. рис. 2).
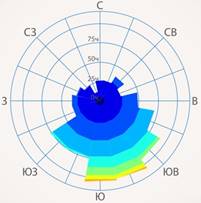
Рис. 1. Роза ветров

Рис. 2. Чем чаще дует ветер в данном направлении, тем дальше соответствующая точка от точки 
Рассмотрим декартову систему координат с центром в точке  на плоскости. Соединяя точку
на плоскости. Соединяя точку  с точкой розы ветров вдоль выбранного направления
с точкой розы ветров вдоль выбранного направления 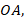

Рис. 3. Радиус-вектор 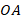
Название «радиус-вектор» понятно – как и радиус окружности, начало любого радиус-вектора зафиксировано в одной точке, центре (начале координат) (см. рис. 4).
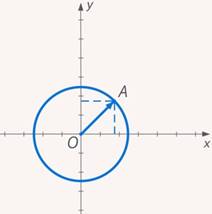
Рис. 4. Начало любого радиус-вектора зафиксировано в начале координат
Как описать этот вектор алгебраически? Любой точке на плоскости будет соответствовать ровно один радиус-вектор (см. рис. 5) (говорят, что точка  и радиус-вектор
и радиус-вектор 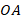 однозначно задают друг друга).
однозначно задают друг друга).
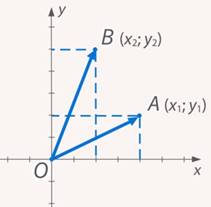
Рис. 5. Любой точке на плоскости соответствует ровно один радиус-вектор
Сама же точка однозначно задается своими координатами. Т. е. координаты 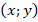 точки
точки  задают и саму точку, и радиус-вектор
задают и саму точку, и радиус-вектор 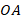 (см. рис. 6).
(см. рис. 6).
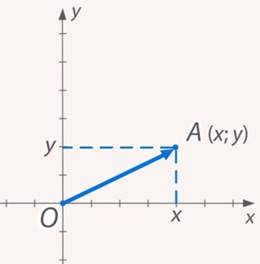
Рис. 6. Координаты 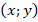 точки
точки  задают и саму точку, и радиус-вектор
задают и саму точку, и радиус-вектор 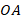
Но тогда почему бы координаты точки 
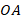 ? Именно так мы и поступим. Будем называть координатами радиус-вектора
? Именно так мы и поступим. Будем называть координатами радиус-вектора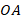 координаты
координаты 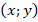 его конца
его конца  :
: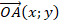
Мы говорили, что векторы равны (см. рис. 7), если у них равны длины и они сонаправлены: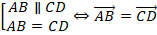
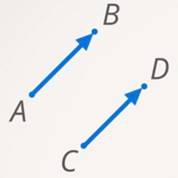
Рис. 7. Равные векторы 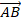 и
и 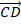
Понятно, что у равных векторов должны быть равны и координаты:

Рассмотрим произвольный вектор  (см. рис. 8).
(см. рис. 8).
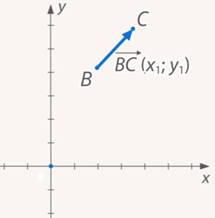
Рис. 8. Произвольный вектор 
Построим вектор 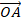
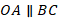

Получаем параллелограмм  (см. рис. 9) (по признаку – две противоположные стороны равны и параллельны).
(см. рис. 9) (по признаку – две противоположные стороны равны и параллельны).
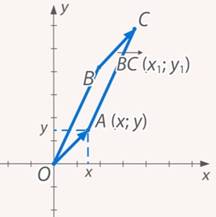
Рис. 9. Параллелограмм 
Векторы 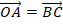 (по построению), значит, координаты вектора
(по построению), значит, координаты вектора  равны координатам радиус-вектора
равны координатам радиус-вектора 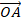 и, соответственно, равны координатам точки
и, соответственно, равны координатам точки 
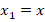
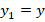
Как видим, любому вектору на плоскости можно поставить в соответствие упорядоченную пару чисел – его координаты.
Понятно, что координаты вектора должны однозначно определяться координатами его конца и начала (т. к. начало и конец задают сам вектор).Попробуем определить, как именно.
Пусть точки 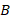
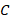 из нашего предыдущего примера имеют координаты, соответственно,
из нашего предыдущего примера имеют координаты, соответственно, 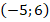 и
и 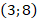 . Вычислим координаты точки
. Вычислим координаты точки 
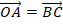 (см. рис. 10).
(см. рис. 10).
Рис. 10. Радиус-вектор 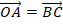 , где
, где  ,
, 
Чтобы из точки 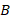 попасть в точку
попасть в точку 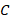 , нужно передвинуться на
, нужно передвинуться на 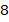 единиц вправо и на
единиц вправо и на  вверх (см. рис. 11).
вверх (см. рис. 11).
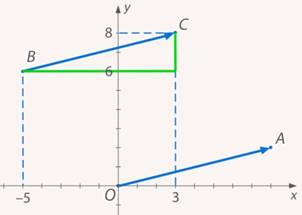
Рис. 11. Путь из точки  в точку
в точку 
Такое же перемещение из начала координат приведет нас в точку  (см. рис. 12).
(см. рис. 12).
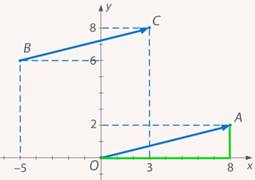
Рис. 12. Путь из точки  в точку
в точку 
Значит, координаты радиус-вектора 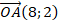 . Тогда и координаты равного ему вектора
. Тогда и координаты равного ему вектора 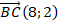 .
.
Уберем вспомогательный радиус-вектор 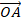 и попробуем определить координаты вектора
и попробуем определить координаты вектора  без его помощи. Чтобы переместиться их точки
без его помощи. Чтобы переместиться их точки 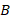 в точку
в точку 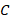 , нам нужно переместиться на
, нам нужно переместиться на 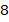 единиц вправо и на
единиц вправо и на 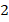 вверх – это и будут координаты вектора
вверх – это и будут координаты вектора  (см. рис. 13).
(см. рис. 13).
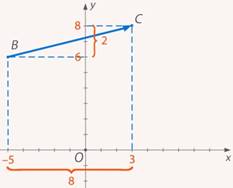
Рис. 13. Чтобы переместиться их точки 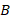 в точку
в точку 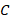 , нужно переместиться на
, нужно переместиться на 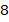 единиц вправо и на
единиц вправо и на 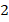 вверх
вверх
Связанные и свободные векторы
Чтобы определить координаты радиус-вектора 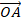 , нам было достаточно двух чисел – координат точки
, нам было достаточно двух чисел – координат точки  . Чтобы определить координаты произвольного вектора
. Чтобы определить координаты произвольного вектора  – уже четыре числа: координаты точек
– уже четыре числа: координаты точек 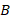 и
и 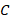 . Есть ли в этом противоречие?
. Есть ли в этом противоречие?
Конечно, нет. В определении радиус-вектора уже «спрятаны» две дополнительные координаты – его начало всегда совпадает с точкой 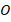 , координаты которой мы знаем –
, координаты которой мы знаем – . Если перемещение из точки
. Если перемещение из точки 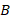 в точку
в точку 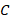 по горизонтали мы искали как ра
по горизонтали мы искали как ра
Сложение и вычитание векторов. Видеоурок. Геометрия 8 Класс
Тема: Векторы
Урок: Сложение и вычитание векторов
На предыдущем уроке мы определили понятие вектора, сказали, какие векторы называются равными, коллинеарными, сонаправленными и противонаправленными.
Теперь пусть задано два вектора – вектора 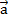 и
и 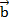 . Найдем сумму этих двух векторов
. Найдем сумму этих двух векторов  . Для этого отложим из некоторой точки А вектор
. Для этого отложим из некоторой точки А вектор 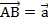 . Из точки В отложим вектор
. Из точки В отложим вектор  . Тогда вектор
. Тогда вектор  называют суммой заданных векторов:
называют суммой заданных векторов: 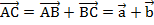 (см. Рис. 1).
(см. Рис. 1).
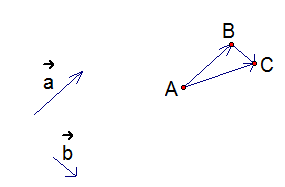
Рис. 1
Данное определение можно объяснить так: пусть был задан груз, и сначала на него подействовала сила 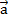 – он переместился из точки А в точку В, после этого подействовала сила
– он переместился из точки А в точку В, после этого подействовала сила 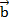 – груз переместился из точки В в точку С. Но в результате действия двух этих сил груз переместился из точки А в точку С.
– груз переместился из точки В в точку С. Но в результате действия двух этих сил груз переместился из точки А в точку С.
Таким образом, мы получили определение суммы двух векторов – правило треугольника.
Правило треугольника
Для того чтобы получить сумму двух векторов, нужно из произвольной точки отложить первый вектор, из конца полученного вектора отложить второй вектор, и построить вектор, соединяющий начало первого с концом второго – это и будет сумма двух векторов.
Можно провести аналогию с числами. Мы ввели понятие числа, научились складывать числа, определили законы сложения и так далее. Теперь мы ввели понятие вектора, научились находить равные вектора, складывать вектора. Теперь нужно определить законы сложения.
Законы сложения векторов
Для любых векторов 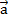 ,
, 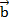 и
и 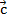 справедливы следующие равенства:
справедливы следующие равенства:
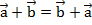 – переместительный закон.
– переместительный закон.
Доказательство: отложим из точки сначала вектор 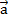 , получаем точку В, из нее откладываем вектор
, получаем точку В, из нее откладываем вектор 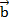 , получаем точку С и вектор
, получаем точку С и вектор 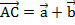 .
.
Теперь отложим из точки А сначала вектор 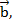 получим точку В, из нее отложим вектор
получим точку В, из нее отложим вектор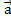 , получим точку С и вектор
, получим точку С и вектор 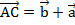 .
.
Чтобы доказать равенство полученных векторов, выполним оба построения из одной точки и получим таким образом правило параллелограмма (см. Рис. 2).
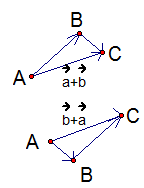
Рис. 2
Откладываем из точки А вектор 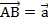 и вектор
и вектор  . Из точки В откладываем вектор
. Из точки В откладываем вектор  , вектора
, вектора 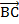 и
и 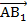 равны, а значит, стороны ВС и АВ1 четырехугольника АВСВ1 параллельны. Аналогично параллельны и стороны АВ и В1С, таким образом, мы получили параллелограмм. АС – диагональ параллелограмма.
равны, а значит, стороны ВС и АВ1 четырехугольника АВСВ1 параллельны. Аналогично параллельны и стороны АВ и В1С, таким образом, мы получили параллелограмм. АС – диагональ параллелограмма. 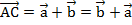 , таким образом, мы доказали переместительный
, таким образом, мы доказали переместительный
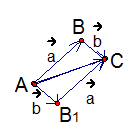
Рис. 3
закон сложения векторов и получили правило параллелограмма (см. Рис. 3).
Правило параллелограмма
Чтобы получить сумму двух векторов, нужно из произвольной точки отложить эти два вектора и построить на них параллелограмм. Диагональ параллелограмма, исходящая из начальной точки, и будет суммой заданных векторов.
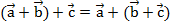 – сочетательный закон;
– сочетательный закон;
Из произвольной точки А отложим вектор 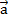 , прибавим к нему вектор
, прибавим к нему вектор 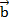 , получим их сумму
, получим их сумму  . К этой сумме прибавим вектор
. К этой сумме прибавим вектор 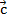 , получим результат
, получим результат 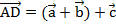 (см. Рис. 4).
(см. Рис. 4).

Рис. 4
В правой части выражения мы сначала получили сумму векторов 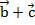 , после прибавили ее к вектору
, после прибавили ее к вектору 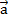 и получили результат:
и получили результат: 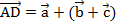 (см. Рис. 5).
(см. Рис. 5).
Таким образом, мы доказали сочетательный закон сложения векторов.

Рис. 5
Правило многоугольника
Чтобы сложить несколько векторов, нужно из произвольной точки отложить первый вектор, из его конца отложить второй вектор, из конца второго вектора отложить третий и так далее; когда все векторы отложены, соединив начальную точку с концом последнего вектора, получим сумму нескольких векторов (см. Рис. 6).

Рис. 6
По аналогии с действительными числами после того, как мы научились их складывать, нужна обратная операция – вычитание.
Пусть задано два вектора – векторы 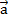 и
и 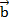 . Найдем разность этих двух векторов
. Найдем разность этих двух векторов 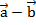 .
.
Определение
Разностью двух векторов 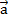 и
и 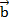 называют такой третий вектор, сумма которого с вектором
называют такой третий вектор, сумма которого с вектором 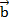 равна вектору
равна вектору 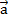 .
.
Если задан вектор 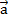 , то можно построить противоположный ему вектор
, то можно построить противоположный ему вектор  , который будет равен по длине, но противонаправлен. Сумма противоположных векторов всегда есть нулевой вектор:
, который будет равен по длине, но противонаправлен. Сумма противоположных векторов всегда есть нулевой вектор: 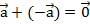 . Таким образом,
. Таким образом, 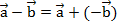 .
.
Отложим из произвольной точки вектор 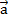 , из его конца отложим вектор
, из его конца отложим вектор 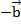 , получим в результате вектор
, получим в результате вектор 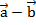 (см. Рис. 7).
(см. Рис. 7).

Рис. 7
Рассмотрим вычитание векторов на параллелограмме. Из точки А отложим векторы 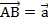 и
и 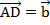 . Из точек В и D отложим векторв
. Из точек В и D отложим векторв  и
и 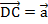 соответственно. Диагональ АС – это сумма векторов
соответственно. Диагональ АС – это сумма векторов 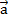 и
и 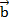 :
: 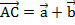 . Но в параллелограмме есть еще вторая диагональ – BD. Прибавим к вектору
. Но в параллелограмме есть еще вторая диагональ – BD. Прибавим к вектору 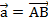 вектор
вектор 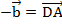 , получим вектор
, получим вектор  (см. Рис. 8).
(см. Рис. 8).
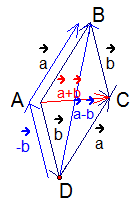
Рис. 8
Итак, на данном уроке мы вывели правила сложения и вычитания векторов при помощи треугольника и параллелограмма, сформулировали законы сложения векторов.
Список литературы
- Александров А.Д. и др. Геометрия, 8 класс. – М.: Просвещение, 2006.
- Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия, 8 класс. – М.: Просвещение, 2011.
- Мерзляк А.Г., Полонский В.Б., Якир С.М. Геометрия, 8 класс. – М.: ВЕНТАНА-ГРАФ, 2009.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Emomi.com (Источник).
- Prosto-o-slognom.ru (Источник).
- Изучение математики онлайн (Источник).
Домашнее задание
- Задание 1: дан треугольник
 , найдите сумму векторов:
, найдите сумму векторов:  и
и  ;
;  и
и  ;
;  и
и  ;
;  и
и  .
. - Задание 2: турист прошел 20 км на восток из города А в город В, а потом 30 км на восток в город С. Выбрав подходящий масштаб, начертите векторы
 и
и  Равны ли векторы
Равны ли векторы  и
и  ?
? - Задание 3: начертите попарно неколлинеарные векторы
 ,
,  и
и  и постройте векторы
и постройте векторы  ,
,  ,
,  .
.
Вектор в системе координат — урок. Геометрия, 9 класс.
Вспомним, что при умножении вектора на число k≠0 мы получаем два коллинеарных (параллельных) вектора, которые или сонаправлены, если k>0, или противоположно направлены, если k<0. Длины векторов различаются \(k\) раз.

Справедливо и обратное суждение.
Если ненулевые векторы коллинеарны, то обязательно можно найти число k≠0 так, что b→=k⋅a→.
Для неколлинеарных векторов справедливо суждение, что каждый вектор на плоскости можно представить в виде c→=k⋅a→+m⋅b→. Говорят, что вектор c→ разложен по векторам a→ и b→, а числа \(k\) и \(m\) называют коэффициентами разложения.
Это справедливо для любого вектора на плоскости, причём коэффициенты определяются единственным образом.
Выберем два не коллинеарных вектора на осях системы координат. Пусть длина каждого из них будет равна единичному отрезку в этой системе координат. Эти векторы называют координатными векторами и обозначают i→ и j→.

Если от начала координат отложить вектор a→, то его можно разложить по векторам i→ и j→ следующим образом: a→=3⋅i→+2⋅j→.
В этом разложении коэффициенты координатных векторов называют координатами вектора a→.
Это записывают как a→3;2.
Любой вектор, который равен с вектором a→, можно переместить и отложить от начала координат. Следовательно, можем сделать вывод.
Равные векторы имеют равные координаты.
Но в то же время в координатной системе можно переместить векторы i→ и j→, таким образом определить координаты векторов независимо от их места расположения в координатной системе.
Легко понять, что разница между абсциссами (координатами x) конечной и начальной точки вектора и есть абсцисса вектора, а разница между ординатами (координатами y) конечной и начальной точки вектора есть ордината вектора.
Связь между координатами противоположных векторов следует из того, что, если умножить вектор на \(-1\), результатом будет противоположный вектор.
У противоположных векторов противоположные координаты.
Важно понять ещё несколько интересных связей между координатами векторов одинаковой длины.

Векторы и операции над векторами
Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.

Прежде чем Вы узнаете всё о векторах и операциях над ними, настройтесь на решение несложной задачи. Есть вектор Вашей предприимчивости и вектор Ваших инновационных способностей. Вектор предприимчивости ведёт Вас к Цели 1, а вектор инновационных способностей — к Цели 2. Правила игры таковы, что Вы не можете двигаться сразу по направлениям двух этих векторов и достигнуть сразу двух целей. Векторы взаимодействуют, или, если говорить математическим языком, над векторами производится некоторая операция. Результатом этой операции становится вектор «Результат», который приводит Вас к Цели 3.
А теперь скажите: результатом какой операции над векторами «Предприимчивость» и «Инновационные способности» является вектор «Результат»? Если не можете сказать сразу, не унывайте. По мере изучения этого урока Вы сможете ответить на этот вопрос.
Как мы уже увидели выше, вектор обязательно идёт от некоторой точки A по прямой к некоторой точке
B. Следовательно, каждый вектор имеет не только числовое значение — длину, но также физическое и
геометрическое — направленность. Из этого выводится первое, самое простое определение вектора. Итак, вектор —
это направленный отрезок, идущий от точки A к точке B. Обозначается он так:
 .
.

А чтобы приступить к различным операциям с векторами, нам нужно познакомиться с ещё одним определением вектора.
Вектор — это вид представления точки, до которой требуется добраться из некоторой начальной точки. Например, трёхмерный вектор, как правило, записывается в виде (х, y, z). Говоря совсем просто, эти числа означают, как далеко требуется пройти в трёх различных направлениях, чтобы добраться до точки.
Пусть дан вектор. При этом x = 3 (правая рука указывает направо), y = 1 (левая рука указывает вперёд), z = 5 (под точкой стоит лестница, ведущая вверх). По этим данным вы найдёте точку, проходя 3 метра в направлении, указываемом правой рукой, затем 1 метр в направлении, указываемом левой рукой, а далее Вас ждёт лестница и, поднимаясь на 5 метров, Вы, наконец, окажетесь в конечной точке.
Все остальные термины — это уточнения представленного выше объяснения, необходимые для различных операций над векторами, то есть, решения практических задач. Пройдёмся по этим более строгим определениям, останавливаясь на типичных задачах на векторы.
Физическими примерами векторных величин могут служить смещение материальной точки, двигающейся в пространстве, скорость и ускорение этой точки, а также действующая на неё сила.
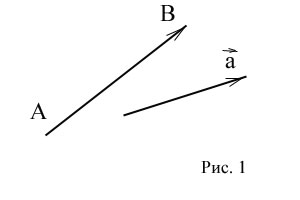
Геометрический вектор представлен в двумерном и трёхмерном пространстве в виде направленного отрезка. Это отрезок, у которого различают начало и конец.
Если A — начало вектора, а B — его конец, то вектор обозначается
символом  или одной строчной буквой
или одной строчной буквой 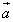 . На рисунке
конец вектора указывается стрелкой (рис. 1)
. На рисунке
конец вектора указывается стрелкой (рис. 1)
Длиной (или модулем) геометрического вектора  называется длина порождающего его отрезка
называется длина порождающего его отрезка 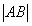
Два вектора называются равными, если они могут быть совмещены (при совпадении направлений) путём параллельного переноса, т.е. если они параллельны, направлены в одну и ту же сторону и имеют равные длины.
В физике часто рассматриваются закреплённые векторы, заданные точкой приложения, длиной и направлением. Если точка приложения вектора не имеет значения, то его можно переносить, сохраняя длину и направление в любую точку пространства. В этом случае вектор называется свободным. Мы договоримся рассматривать только свободные векторы.
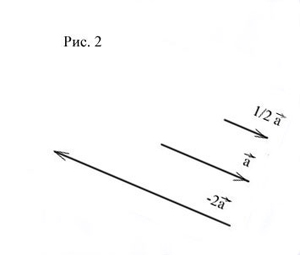
Умножение вектора на число

Сложение и вычитание векторов
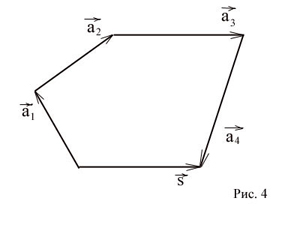
Слагаемые 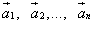 называются составляющими вектора
называются составляющими вектора 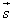 , а
сформулированное правило — правилом многоугольника. Этот многоугольник может и не быть плоским.
, а
сформулированное правило — правилом многоугольника. Этот многоугольник может и не быть плоским.
Пример 1. Упростить выражение:
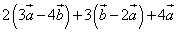 .
.
Решение:
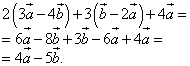 ,
,
то есть, векторы можно складывать и умножать на числа так же, как и многочлены (в частности, также задачи на упрощение выражений). Обычно необходимость упрощать линейно подобные выражения с векторами возникает перед вычислением произведений векторов.
Пример 2. Векторы 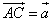 и
и
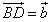 служат диагоналями параллелограмма ABCD (рис. 4а).
Выразить через
служат диагоналями параллелограмма ABCD (рис. 4а).
Выразить через 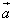 и
и 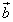 векторы
векторы 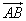 ,
,  ,
,
 и
и 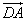 ,
являющиеся сторонами этого параллелограмма.
,
являющиеся сторонами этого параллелограмма.
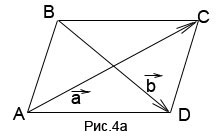
Решение. Точка пересечения диагоналей параллелограмма делит каждую диагональ пополам. Длины требуемых в условии задачи векторов находим либо как половины сумм векторов, образующих с искомыми треугольник, либо как половины разностей (в зависимости от направления вектора, служащего диагональю), либо, как в последнем случае, половины суммы, взятой со знаком минус. Результат — требуемые в условии задачи векторы:
Есть все основания полагать, что теперь Вы правильно ответили на вопрос о векторах «Предприимчивость» и «Инновационные способности» в начале этого урока. Правильный ответ: над этими векторами производится операция сложения.
Решить задачи на векторы самостоятельно, а затем посмотреть решения
Как найти длину суммы векторов?
Эта задача занимает особое место в операциях с векторами, так как предполагает использование тригонометрических свойств. Допустим, Вам попалась задача вроде следующей:
Даны длины векторов 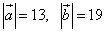 и длина суммы этих векторов
и длина суммы этих векторов 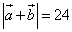 .
Найти длину разности этих векторов
.
Найти длину разности этих векторов 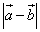 .
.
Решения этой и других подобных задач и объяснения, как их решать — в уроке «Сложение векторов: длина суммы векторов и теорема косинусов«.
А проверить решение таких задач можно на Калькуляторе онлайн «Неизвестная сторона треугольника (сложение векторов и теорема косинусов)».
А где произведения векторов?
Произведения вектора на вектор не являются линейными операциями и рассматриваются отдельно. И у нас есть уроки «Скалярное произведение векторов» и «Векторное и смешанное произведения векторов».
Проекция вектора на ось равна произведению длины проектируемого вектора на косинус угла между вектором и осью:

Как известно, проекцией точки A на прямую (плоскость) служит основание
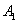 перпендикуляра
перпендикуляра 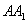 ,
опущенного из этой точки на прямую (плоскость).
,
опущенного из этой точки на прямую (плоскость).
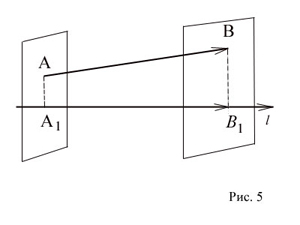
Пусть  —
произвольный вектор (Рис. 5), а
—
произвольный вектор (Рис. 5), а 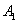 и
и 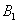 —
проекции его начала (точки A) и конца (точки B) на ось l. (Для построения проекции точки A) на прямую проводим
через точку A плоскость, перпендикулярную прямой. Пересечение прямой и плоскости определит требуемую проекцию.
—
проекции его начала (точки A) и конца (точки B) на ось l. (Для построения проекции точки A) на прямую проводим
через точку A плоскость, перпендикулярную прямой. Пересечение прямой и плоскости определит требуемую проекцию.
Составляющей вектора 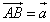 на оси l
называется такой вектор
на оси l
называется такой вектор 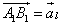 , лежащий на этой оси,
начало которого совпадает с проекцией начала, а конец — с проекцией конца вектора
, лежащий на этой оси,
начало которого совпадает с проекцией начала, а конец — с проекцией конца вектора  .
.
Проекцией вектора  на ось l
называется число
на ось l
называется число
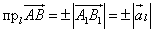 ,
,
равное длине составляющего вектора на этой оси, взятое со знаком плюс, если направление составляюшей совпадает с направлением оси l, и со знаком минус, если эти направления противоположны.
Основные свойства проекций вектора на ось:
1. Проекции равных векторов на одну и ту же ось равны между собой.
2. При умножении вектора на число его проекция умножается на это же число.
3. Проекция суммы векторов на какую-либо ось равна сумме проекций на эту же ось слагаемых векторов.
4. Проекция вектора на ось равна произведению длины проектируемого вектора на косинус угла между вектором и осью:

Пример 5. Рассчитать проекцию суммы векторов 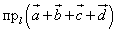 на ось l,
если
на ось l,
если  , а углы —
, а углы —
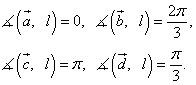 .
.
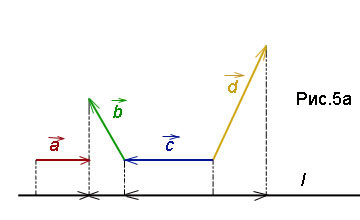
Решение. Спроектируем векторы на ось l как определено в теоретической справке выше. Из рис.5а очевидно, что проекция суммы векторов равна сумме проекций векторов. Вычисляем эти проекции:
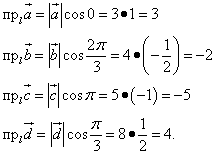
Находим окончательную проекцию суммы векторов:
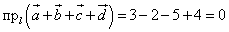 .
.
Знакомство с прямоугольной декартовой системой координат в пространстве состоялось в соответствующем уроке, желательно открыть его в новом окне.
В упорядоченной системе координатных осей 0xyz ось Ox называется осью абсцисс, ось 0y – осью ординат, и ось 0z – осью аппликат.
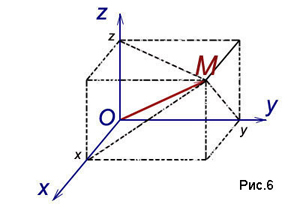
С произвольной точкой М пространства свяжем вектор
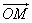 ,
,
называемый радиус-вектором точки М и спроецируем его на каждую из координатных осей. Обозначим величины соответствующих проекций:
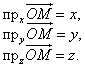
Числа x, y, z называются координатами точки М , соответственно абсциссой, ординатой и аппликатой, и записываются в виде упорядоченной точки чисел: M (x; y; z) (рис.6).
Вектор единичной длины, направление которого совпадает с направлением оси, называют единичным вектором(или ортом) оси. Обозначим через

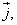

Соответственно орты координатных осей Ox, Oy, Oz

Теорема. Всякий вектор может быть разложен по ортам координатных осей:
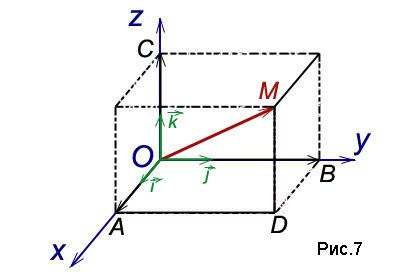
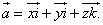 (2)
(2)
Равенство (2) называется разложением вектора по координатным осям. Коэффициентами этого разложения являются проекции вектора на координатные оси. Таким образом, коэффициентами разложения (2) вектора по координатным осям являются координаты вектора.
После выбора в пространстве определённой системы координат вектор и тройка его координат однозначно определяют друг друга, поэтому вектор может быть записан в форме
 (3)
(3)
Представления вектора в виде (2) и (3) тождественны.
Как мы уже отмечали, векторы называются коллинеарными, если они связаны отношением
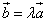 .
.
Пусть даны векторы 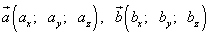 .
Эти векторы коллинеарны, если координаты векторов связаны отношением
.
Эти векторы коллинеарны, если координаты векторов связаны отношением
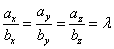 ,
,
то есть, координаты векторов пропорциональны.
Пример 6. Даны векторы 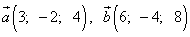 .
Коллинеарны ли эти векторы?
.
Коллинеарны ли эти векторы?
Решение. Выясним соотношение координат данных векторов:
 .
.
Координаты векторов пропорциональны, следовательно, векторы коллинеарны, или, что то же самое, параллельны.
Вследствие взаимной перпендикулярности координатных осей длина вектора
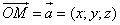
равна длине диагонали прямоугольного параллелепипеда, построенного на векторах

и выражается равенством
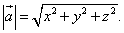 (4)
(4)
Вектор полностью определяется заданием двух точек (начала и конца), поэтому координаты вектора можно выразить через координаты этих точек.
Пусть в заданной системе координат начало вектора 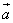 находится в точке
находится в точке
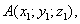
а конец – в точке
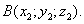
(рис.8).
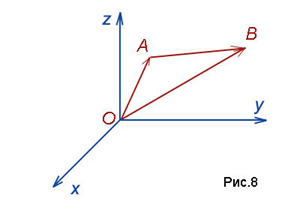
Тогда
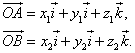
Из равенства

следует, что

Отсюда
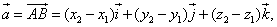
или в координатной форме
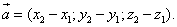 (5)
(5)
Следовательно, координаты вектора равны разностям одноимённых координат конца и начала вектора. Формула (4) в этом случае примет вид
 (6)
(6)
Направление вектора определяют направляющие косинусы. Это косинусы углов, которые вектор образует с осями Ox, Oy и Oz. Обозначим эти углы соответственно α, β и γ. Тогда косинусы этих углов можно найти по формулам
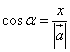 ,
,
 ,
,
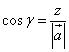 .
.
Направляющие косинусы вектора являются также координатами орта этого вектора и, таким образом, орт вектора
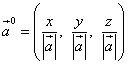
или
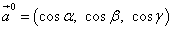 .
.
Учитывая, что длина орта вектора равна одной единице, то есть
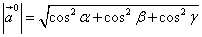 ,
,
получаем следующее равенство для направляющих косинусов:
 .
.
Пример 7. Найти длину вектора x = (3; 0; 4).
Решение. Длина вектора равна
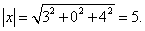
Пример 8. Даны точки:
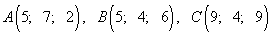
Выяснить, равнобедренный ли треугольник, построенный на этих точках.
Решение. По формуле длины вектора (6) найдём длины сторон и установим, есть ли среди них две равные:

Две равные стороны нашлись, следовательно необходимость искать длину третьей стороны отпадает, а заданный треугольник является равнобедренным.
Пример 9. Найти длину вектора 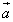 и его направляющие косинусы, если
и его направляющие косинусы, если  .
.
Решение. Координаты вектора даны:
 .
.
Длина вектора равна квадратному корню из суммы квадратов координат вектора:
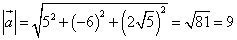 .
.
Находим направляющие косинусы:
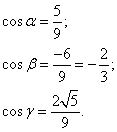
Решить задачу на векторы самостоятельно, а затем посмотреть решение
Пусть даны два вектора 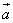 и
и 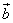 , заданные своими проекциями:
, заданные своими проекциями:
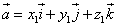
или
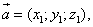
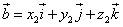
или

Укажем действия над этими векторами.
1.Сложение:
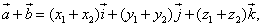
или, что то же

(при сложении двух векторов одноимённые координаты складываются).
2.Вычитание:
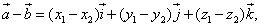
или, что то же
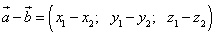 ,
,
(при вычитании двух векторов одноимённые координаты вычитаются).
3.Умножение вектора на число:
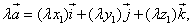
или, что то же
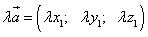 ,
,
(при умножении вектора на число все координаты умножаются на это число).
Пример 11. Даны два вектора, заданные координатами:
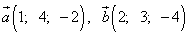 .
.
Найти заданный координатами вектор, являющийся суммой этих векторов:  .
.
Решение:
 .
.
Решить задачи на координаты векторов самостоятельно, а затем посмотреть решение
При изучении многих вопросов, в частности, экономических, оказалось удобным обобщить рассмотренные приёмы установления соответствия между числами и точками двумерного и трёхмерного пространства и рассматривать последовательности n действительных чисел как «точки» некоторого абстрактного «n-мерного пространства», а сами числа — как «координаты» этих точек. За составляющие n-мерного вектора можно принимать такие данные, как урожайность различных культур, объёмы продаж товаров, технические коэффициенты, номенклатура товаров на складах и т.д.
n-мерным вектором называется упорядоченный набор из n действительных чисел, записываемых в виде
 ,
,
где
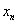 -
i – й элемент (или i – я координата) вектора x.
-
i – й элемент (или i – я координата) вектора x.
Возможна и другая запись вектора – в виде столбца координат:

Размерность вектора определяется числом его координат и является его отличительной характеристикой. Например, (2; 5) – двухмерный вектор, (2; -3; 0) – трёхмерный, (1; 3; -2; -4; 7) – пятимерный,
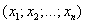 —
—
n – мерный вектор.
Нулевым вектором называется вектор, все координаты которого равны нулю:
0 = (0; 0; …; 0).
Введём операции над n-мерными векторами.
Произведением вектора
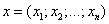
на действительное число 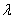 называется вектор
называется вектор
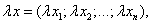
(при умножении вектора на число каждая его координата умножается на это число).
Зная вектор
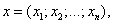
можно получить противоположный вектор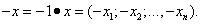
Суммой векторов
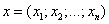
и
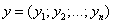
называется вектор
 ,
,
(при сложении векторов одной и той же размерности их соответствующие координаты почленно складываются).
Если в плане продаж сети торговых предприятий продажи товаров определить как положительные уровни товаров, а затраты на продажи – как отрицательные, то получим вектор затрат-продаж
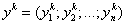 ,
,
где
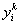 —
—
продажи (затраты) k – м предприятием товара i, а k = 1, 2, 3,…, m .
Суммарный вектор затрат-продаж y определяется суммированием векторов затрат-продаж всех m предприятий сети:
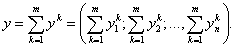
Сумма противоположных векторов даёт нулевой вектор:
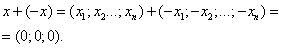
При вычитании двух векторов одной и той же размерности их соответствующие координаты почленно вычитаются:
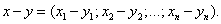
Операции над n-мерными векторами удовлетворяют следующим свойствам.
Свойство 1.
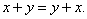
Свойство 2.
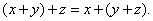
Свойство 3.
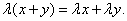
Свойство 4.

Свойство 5.

Свойство 6.

Поделиться с друзьями
Весь блок «Аналитическая геометрия»
- Векторы
- Плоскость
- Прямая на плоскости
Онлайн калькуляторы, расчеты и формулы на GELEOT.RU
Векторы представляют собой особый раздел аналитической геометрии, который в том числе оказал значительное влияние на развитие физики. Сам по себе вектор выглядит как отрезок, который имеет начало и имеет конец, определен заданной конечными точками длиной этого отрезка. Но внутри вектора кроется множество других скрытых функций, за счет того что вектор задает направление. Поэтому если для отрезка не имеет значения какая точка названа началом, а какая концом, и чаще просто применяется принцип чтения «слева направо», то для векторов AB и BA – это диаметрально противоположные понятия.
Итак, в векторе присутствует две важных составляющих – это его длина и направление. Тем не менее, координатами вектора задается не его фактическая длина, а местоположение на плоскости или в пространстве. Поэтому длина вектора, иначе называемая модуль вектора, вычисляется, используя прямоугольный треугольник с осями координат. Дальнейшие действия с вектором также чаще используют именно его координаты, нежели фактическую длину. Работе с векторами можно провести аналогию с целыми числами, — как только появляются отрицательные числа на числовой оси, приходится не только считать значение примера, но и все время обращать внимание на знаки. Так и с векторами, во всех действиях – будь то сложение, вычитание, умножение скалярное или векторное и другие действия, приходится не только учитывать реальные масштабы вектора – координаты, длина или угол, но и принимать в расчет его направление. К слову, направления векторов также находят отражение в знаках – обратный изначальному вектор всегда будет со знаком «минус».
В данном разделе разложены все основные действия с векторами, такие как нахождение длины вектора, координат вектора, сложение векторов, вычитание векторов, скалярное произведение векторов, векторное произведение векторов, смешанное произведение трех векторов, вычисление угла между векторами и другие. Все расчет можно произвести для векторов на плоскости или для векторов в пространстве. Также доступен векторный калькулятор, который вычисляет все возможные параметры одного и более векторов, с заданными координатами точек вектора.
Как построить вектор?
Вектором принято называть отрезок, который имеет заданное направление. Как начало, так и конец вектора имеют фиксированную позицию, с помощью которых и определяется направление вектора. Рассмотрим подробнее, как построить вектор по заданным координатам.
- Начертить систему координат (x, y, z) в пространстве, отметить на осях единичные отрезки.
- Отложить на двух осях нужные координаты, провести от них пунктиром линии, параллельные осям, до пересечения. Поучится точка пересечения, которую нужно соединить пунктиром с началом координат.
- Провести вектор из начала координат до полученной точки.
- Отложить на третьей оси нужное число, через данную точку провести пунктирную линию, которая будет параллельна построенному вектору.
- Из конца вектора провести пунктиром линию, параллельную третьей оси до пересечения с линией из прошлого пункта.
- В завершении соединить начало координат и полученную точку.
Иногда требуется построить вектор, который будет результатом сложения или вычитания других векторов. Поэтому сейчас мы рассмотрим операции с векторами, узнаем, как их складывать и вычитать.
Операции над вектором
Геометрические векторы можно складывать несколькими способами. Так, например, наиболее распространенным способом сложения векторов является правило треугольника. Чтобы сложить два вектора по этому правилу, необходимо расположить векторы параллельно друг другу таким образом, чтобы начало первого вектора совпадало с концом второго, при этом третья сторона полученного треугольника будет являться вектором суммы.
Также можно рассчитать сумму векторов по правилу параллелограмма. Векторы должны начинаться из одной точки, параллельно каждому вектору нужно начертить линию так, чтобы в итоге получился параллелограмм. Диагональ построенного параллелограмма будет являться суммой этих векторов.
Для вычитания двух векторов нужно сложить первый вектор и вектор, который будет противоположным второму. Для этого также используется правило треугольника, которое имеет следующую формулировку: разность векторов, которые перенесены таким образом, что их начала совпадают, является вектором, начало которого совпадает с концом вычитаемого вектора, а также с концом уменьшаемого вектора.
Векторы на координатной плоскости
Теорема
В прямоугольной системе координат расстояние между точками \(P(x_1; y_1)\) и \(Q(x_2; y_2)\) выражается формулой \(\rho(P, Q) = \sqrt{(x_1 — x_2)^2 + (y_1 — y_2)^2}\).
Доказательство
Если \(PQ\parallel Ox\), то он лежит на некоторой прямой \(y = C\), тогда \(y_1 = y_2 = C\), следовательно, \(\sqrt{(x_1 — x_2)^2 + (y_1 — y_2)^2} = |x_1 — x_2|\), что равно его длине.
Если \(PQ\parallel Oy\), то он лежит на некоторой прямой \(x = C\), тогда \(x_1 = x_2 = C\), следовательно, \(\sqrt{(x_1 — x_2)^2 + (y_1 — y_2)^2} = |y_1 — y_2|\), что равно его длине.

Если \(PQ\) не параллелен осям, то рассмотрим прямоугольный треугольник \(PQM\), в котором \(PM\parallel Ox\), \(QM\parallel Oy\). По теореме Пифагора \(PQ^2 = PM^2 + QM^2\). Так как \(PM\parallel Ox\), то \(PM\) лежит на некоторой прямой \(y = C\), откуда \(PM = |x_1 — x_2|\), аналогично \(QM = |y_1 — y_2|\), тогда \(PQ^2 = (x_1 — x_2)^2 + (y_1 — y_2)^2\), откуда получаем требуемое равенство.
Утверждение
Если в прямоугольной системе координат точка \(M\) – середина отрезка \(PQ\), где \(P(x_1;y_1), \ Q(x_2;y_2)\), то
\[M\left(\dfrac{x_1 + x_2}{2}; \dfrac{y_1 + y_2}{2}\right)\]
Доказательство
Пусть \(M(a;b)\).
1) Пусть \(PQ\parallel Oy \Rightarrow x_1=x_2=a\). Значит, \(a=\dfrac{x_1+x_2}2=\dfrac{a+a}2\) – верно.
Т.к. \(PM=MQ\), следовательно, \(|y_2-b|=|y_1-b| \Rightarrow y_2-b=y_1-b\) или \(y_2-b=b-y_1\), что равносильно \(y_2=y_1\) или \(b=\dfrac{y_1+y_2}2\). Первое равенство невозможно (т.к. тогда точки \(P\) и \(Q\) совпадают).
2) Случай \(PQ\parallel Ox \Rightarrow y_1=y_2=b\) доказывается аналогично.
3) \(x_1\ne x_2, y_1\ne y_2\).
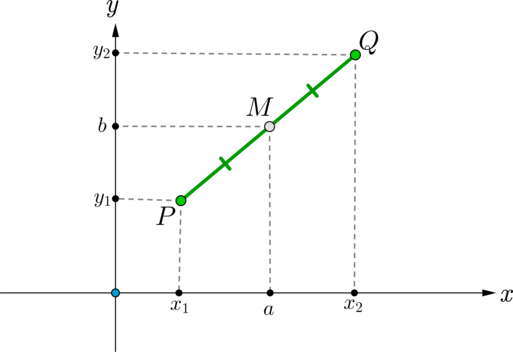
Тогда \(Ma=b\) – средняя линия трапеции \(x_1PQx_2\), следовательно, равна полусумме оснований, то есть \(b=\dfrac{y_1+y_2}2\).
Аналогично \(a=\dfrac{x_1+x_2}2\).
\[{\Large{\text{Векторы на координатной плоскости}}}\]
Лемма
Если векторы \(\overrightarrow a\) и \(\overrightarrow b\) коллинеарны, то существует такое число \(\lambda\ne 0\), что \(\overrightarrow a=\lambda\overrightarrow b\).
Доказательство
1) Если \(\overrightarrow a\uparrow \uparrow \overrightarrow b\).
Рассмотрим вектор \(\dfrac1{|\overrightarrow a|}\overrightarrow a\). Данный вектор сонавправлен с \(\overrightarrow a\), а его длина равна \(1\). Тогда вектор \(\dfrac{|\overrightarrow b|}{|\overrightarrow a|}\overrightarrow a\) также сонаправлен с \(\overrightarrow a\), но его длина равна \(|\overrightarrow b|\). То есть равен вектору \(\overrightarrow b\).
2) Если \(\overrightarrow a\uparrow \downarrow \overrightarrow b\).
Аналогично доказывается, что \(\overrightarrow b=-\dfrac{|\overrightarrow b|}{|\overrightarrow a|}\overrightarrow a\).
Определение
Если вектор \(\overrightarrow p\) представлен как линейная комбинация двух векторов: \(\overrightarrow p=\alpha\overrightarrow a+\beta \overrightarrow b\), то говорят, что вектор \(\overrightarrow p\) разложен по векторам \(\overrightarrow a\) и \(\overrightarrow b\).
\(\alpha, \beta\) – коэффициенты разложения.
Пусть векторы \(\overrightarrow i\), \(\overrightarrow j\) – векторы, длины которых равны \(1\), а направление совпадает с направлением осей \(Ox\) и \(Oy\) соответственно. Такие векторы называются единичными векторами.
Тогда если \(\overrightarrow p=a\overrightarrow i+b\overrightarrow j\), то \(\{a;b\}\) – координаты вектора \(\overrightarrow p\).

Свойства координат вектора
1. Равные векторы имеют равные координаты.
2. Координаты суммы векторов равны сумме координат каждого вектора: если \(\overrightarrow a\{x_1;y_1\}, \ \overrightarrow b\{x_2;y_2\}\), то \(\overrightarrow a+\overrightarrow b=\{x_1+x_2;y_1+y_2\}\).
3. Каждая координата произведения вектора на число равна произведению соответствующей координаты данного вектора на это число: \(\overrightarrow a\{x;y\}, \ \lambda \) – число, то \(\lambda\overrightarrow a\{\lambda x;\lambda y\}\).
Теорема
Если точки \(A(x_1;y_1), \ B(x_2;y_2)\), то \(\overrightarrow
{AB}\{x_2-x_1;y_2-y_1\}\).
То есть каждая координата вектора равна разности соответствующих координат его конца и начала.

Следствие
Если \(\overrightarrow a\{x;y\}\), то длина \(|\overrightarrow a|=\sqrt{x^2+y^2}\).
\[{\Large{\text{Скалярное произведение векторов}}}\]
Определение
Пусть от одной точки отложены два вектора \(\overrightarrow {AB}\) и \(\overrightarrow {AC}\). Тогда угол между этими векторами – это угол \(\angle BAC\), не превышающий развернутого угла.

Скалярное произведение векторов \(\overrightarrow a\) и \(\overrightarrow b\) – это число, равное произведению длин этих векторов на косинус угла между ними.
Обозначение: \(\overrightarrow a\cdot \overrightarrow b\) или \((\overrightarrow a, \overrightarrow b)\). \[(\overrightarrow a, \overrightarrow b)=|\overrightarrow a|\cdot
|\overrightarrow b|\cdot \cos\widehat{(\overrightarrow a,
\overrightarrow b)}\]
Следствия
1. Если ненулевые векторы взаимно перпендикулярны, то косинус угла между ними равен нулю, следовательно, и их скалярное произведение равно нулю.
2. Если угол между ненулевыми векторами острый, то скалярное произведение положительно.
3. Если угол между ненулевыми векторами тупой, то скалярное произведение отрицательно.
4.Скалярное произведение вектора на себя равно квадрату его длины: \(\overrightarrow a\cdot \overrightarrow a=|\overrightarrow a|^2\).
Теорема
В прямоугольной системе координат скалярное произведение векторов \(\overrightarrow a\{x_1;y_1\}\) и \(\overrightarrow b\{x_2;y_2\}\) выражается формулой:
\[\overrightarrow a\cdot \overrightarrow b=x_1x_2+y_1y_2\]
Доказательство
Рассмотрим вектор \(\overrightarrow c\):
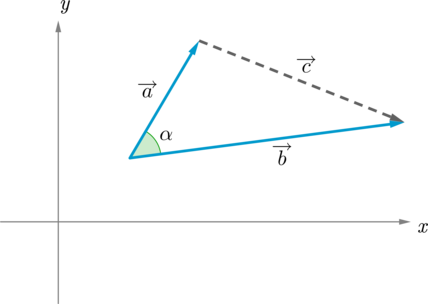
Т.к. \(\overrightarrow a+\overrightarrow c=\overrightarrow b \Rightarrow \overrightarrow c=\overrightarrow b-\overrightarrow a \Rightarrow \overrightarrow c \{x_2-x_1; y_2-y_1\}\).
По теореме косинусов: \(|c|^2=|a|^2+|b|^2-2|a||b|\cos\alpha\), но \(|a||b|\cos \alpha=\overrightarrow a\cdot \overrightarrow b\), значит: \[\overrightarrow a\cdot \overrightarrow b=\dfrac12\left(|a|^2+|b|^2-|c|^2\right) =\dfrac12\left(x_1^2+y_1^2+x_2^2+y_2^2-(x_2-x_1)^2-(y_2-y_1)^2\right)=x_1x_2+y_1y_2\]
Свойства скалярного произведения
Для любых векторов \(\overrightarrow a, \overrightarrow b, \overrightarrow c\) и любого числа \(\lambda\) справедливо:
1. Скалярное произведение вектора на себя всегда неотрицательно, причем равно нулю оно тогда и только тогда, когда вектор нулевой: \(\overrightarrow a^2\geqslant 0, \quad \overrightarrow a^2=0 \Leftrightarrow |\overrightarrow a|=0\).
2. Переместительный закон: \(\overrightarrow a\cdot \overrightarrow b=\overrightarrow b\cdot \overrightarrow a\).
3. Распределительный закон: \(\overrightarrow a \cdot (\overrightarrow b+\overrightarrow c)=\overrightarrow a\cdot \overrightarrow b+\overrightarrow a\cdot \overrightarrow c\).
4. Сочетательный закон: \((\lambda\overrightarrow a)\cdot \overrightarrow b=\lambda (\overrightarrow a\cdot \overrightarrow b)\).




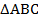 , найдите сумму векторов:
, найдите сумму векторов: 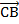 ;
;  и
и 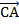 и
и 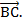 Равны ли векторы
Равны ли векторы 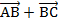 и
и  ,
,  и
и 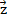 и постройте векторы
и постройте векторы  ,
, 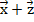 ,
, 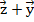 .
.