Вектор индукции магнитного поля

Определение

Силовой характеристикой магнитного поля является вектор магнитной индукции $\overrightarrow{B}$. Вектор магнитной индукции является основной характеристикой магнитного поля. Он равен пределу отношения силы, с которой магнитное поле действует на элементарный ток ($Idl$) к произведению тока $(I)$ и величины элемента проводника ($dl$):

Вектор индукции направлен перпендикулярно направлению элементарного тока (или чаще говорят элементу проводника ($\overrightarrow{dl}$)) из (1) и перпендикулярен направлению силы, которая действует со стороны магнитного поля.

Если $\overrightarrow{B}$=const, то магнитное поле называют однородным. Если магнитное поле неизменно во времени, то его называют постоянным.

Иногда модуль вектора индукции однородного магнитного поля определяют как:

где $M_{max}$ — максимальный вращающий момент, действующий на контур с током, который помещен в магнитное поле, $p_m=IS$ — магнитный момент контура ($S$- площадь контура).

За направление вектора $\overrightarrow{B}$ принимают направление, в котором устанавливается под действием поля положительная нормаль к контуру с током. Или иначе, говорят, что вектор магнитной индукции направлен в сторону поступательного перемещения правого винта, если его вращать по направлению течения тока в контуре.

Очень часто, определение для вектора магнитной индукции записывают в виде:

где $\overrightarrow{dF}$ — сила, действующая на элемент с током. В том случае, если проводник прямолинейный и магнитная индукция во всех точках постоянна, то формулу (2) можно преобразовать в выражение:

Рис. 1

Модуль вектора индукции можно определить, так же исходя из силы Лоренца ($\overrightarrow{F}$), которая действует на движущуюся, со скоростью $\overrightarrow{v}$ заряженную частицу (заряд q) в магнитном поле:

Основной единицей измерения магнитной индукции в системе СИ является тесла (Тл).

Принцип суперпозиции вектора индукции магнитного поля

Эмпирический доказано, что для магнитного поля выполняется принцип суперпозиции:

Готовые работы на аналогичную тему

Если магнитное поле порождается несколькими токами (движущимися зарядами), то оно равно векторной сумме отдельных полей:

Пример 1

Задание: Проводник имеет форму квадрата, сторона которого равна d, по нему течет ток силы I. Найдите магнитную индукцию поля в точке пересечения диагоналей квадрата.

Решение:

Допустим, что плоскость проводника совпадает с плоскостью рис.2. Зададим направление токов.

Рис. 2

В точке О магнитное поле создают четыре прямолинейные проводника с током. Напряженности всех четырех полей направлены в соответствии с правилом правого винта от нас, перпендикулярно плоскости рисунка. Следовательно, векторную сумму полей в принципе суперпозиции заменим на алгебраическую, запишем:

\[B=B_1+B_2+B_3+B_4\left(1.1\right).\]

Причем из симметрии, очевидно, что модули всех индукций равны, значит, запишем, что:

\[B=4B_1\left(1.2\right).\]

В разделе «Электромагнетизм» мы нашли, формулу для расчета модуля вектора магнитной индукции прямолинейного проводника с током. В применении к нашему случаю модуль $\overrightarrow{B}$ будет иметь вид:

\[B_1=\frac{{\mu }_0I}{4\pi b}\left(cos\alpha -cos\beta \right)\left(1. 3\right),\]

углы $\alpha $ и $\beta $ указаны на рис.1. В (1.3) $\beta =\pi -\alpha \to cos\beta ={cos \left(\pi -\alpha \right)\ }=-cos\alpha .$ Перепишем (1.3):

\[B_1=\frac{{\mu }_0I}{2\pi b}cos\alpha \left(1.4\right).\]

Так как мы имеем дело с квадратом, то заметим, что: $b=\frac{d}{2},\alpha =\frac{\pi }{4}\to cos\alpha =\frac{\sqrt{2}}{2}.$ Подставим в (1.4), то что мы получили и (1.4) подставим в (1.2), имеем:

\[B=4\cdot \frac{{\mu }_0I}{\pi d}\cdot \frac{\sqrt{2}}{2}=\frac{2\sqrt{2}}{\pi d}{\mu }_0I.\]

Ответ: $B=\frac{2\sqrt{2}}{\pi d}{\mu }_0I.$

Пример 2

Задание: Бесконечно длинный проводник с током (I) согнут под прямым углом (рис.2). Найдите магнитную индукцию поля в точке А, которая указана на рис. 3.

Рис. 3

Решение:

В точке А поле создается двумя частями проводника:

\[\overrightarrow{B}=\overrightarrow{B_{II}}+\overrightarrow{B_{\bot }}\left(2.1\right).\]

Рассмотрим горизонтальный участок, на продолжении которого лежит точка А.

3}}\left(2.2\right),\]

где $\overrightarrow{r}$ — радиус-вектор, проведенный от элемента тока $Id\overrightarrow{l}$ к точке, в которой ищется индукция магнитного поля ($\overrightarrow{B}$).

Индукция магнитного поля бесконечного прямолинейного проводника с током (I) в точке А была бы равна:

\[B’=\frac{{\mu }_0}{2\pi }\frac{I}{b}\left(2.3\right).\]

У нас полу бесконечный проводник, следовательно, из принципа суперпозиции получим, что для нашего проводника индукция равна:

\[{B=B}_{\bot }=\frac{1}{2}B’=\frac{{\mu }_0}{\pi }\frac{I}{b}.\]

Ответ: $B=\frac{{\mu }_0}{\pi }\frac{I}{b}.$

Вектор магнитной индукции, теория и примеры

Определение и общие понятия вектора магнитной индукции

Результаты экспериментов Ампера с проводниками в магнитном поле показали, что способность магнитного поля вызывать появление механической силы, которая оказывает действие на элемент с током, можно количественно описать, если задать в каждой точке поля некоторый вектор (), который назвали вектором магнитной индукции.

Сила, которая действует на элемент тока () равна:

   

где – сила Ампера. Выражение (1) можно считать определением магнитной индукции. Величина B равна пределу отношения силы (dF), с которой действует магнитное поле на элементарный проводник с током, к силе тока (I) умноженной на длину этого проводника (dl), при длине проводника стремящейся к нулю. При этом проводник имеет такое расположение в магнитном поле, что данный предел имеет максимальное значение:

   

Эмпирически легко показать, что магнитное поле, воздействуя на рамку с током, оказывает на нее ориентирующее действие, разворачивая ее определенным образом. Это связано с тем, что магнитное поле имеет направление. За направление магнитного поля в точке принимают направление положительной нормали к рассматриваемой рамке. В качестве направления магнитного поля, так же можно принимать направление силы, которая оказывает воздействие на северный полюс магнитной стрелки, если его размещают в точку поля.

Принцип суперпозиции для вектора магнитной индукции

Для магнитного поля выполняется принцип наложения (суперпозиции), который означает, что если присутствует несколько контуров с током и каждый из них создает поле с какой – то магнитной индукцией, то индукция результирующего поля равна векторной сумме отдельных индукций:

   

В частности магнитную индукцию поля, которое создано контуром с током находят как сумму индукций отдельных элементов тока, на которые разбивают рассматриваемый контур.

Закон Био-Савара-Лапласа

Этот закон дает возможность определить вектор магнитной индукции () в любой точке магнитного поля, которое создает в вакууме элемент проводника с током:

   

где I – сила тока; – вектор элемента проводника, который по модулю равен длине проводника, а направление его совпадает с направлением течения тока; – радиус-вектор, который проводят от элементарного проводника к точке, в которой ищут поле; – магнитная постоянная. Вектор является перпендикулярным к плоскости в которой расположены и , конкретное направление вектора магнитной индукции определяют при помощи правила буравчика (правого винта).

В однородном изотропном магнетике, заполняющем пространство, вектор магнитной индукции в вакууме( и в веществе (), при одинаковых условиях, связаны соотношением:

   

где – относительная магнитная проницаемость вещества.

Примеры решения задач

Магнитное поле, силовые линии, вектор магнитной индукции, принцип суперпозиции. Курсы по физике

Тестирование онлайн

• Магнитное поле. Основные понятия

• Магнитное поле. Вектор магнитной индукции

Магнитное поле

Уже в VI в. до н.э. в Китае было известно, что некоторые руды обладают способностью притягиваться друг к другу и притягивать железные предметы. Куски таких руд были найдены возле города Магнесии в Малой Азии, поэтому они получили название магнитов.

Посредством чего взаимодействуют магнит и железные предметы? Вспомним, почему притягиваются наэлектризованные тела? Потому что около электрического заряда образуется своеобразная форма материи — электрическое поле. Вокруг магнита существует подобная форма материи, но имеет другую природу происхождения (ведь руда электрически нейтральна), ее называют

магнитным полем.

Для изучения магнитного поля используют прямой или подковообразный магниты. Определенные места магнита обладают наибольшим притягивающим действием, их называют полюсами (северный и южный). Разноименные магнитные полюса притягиваются, а одноименные — отталкиваются.

Для силовой характеристики магнитного поля используют вектор индукции магнитного поля B. Магнитное поле графически изображают при помощи силовых линий (линии магнитной индукции). Линии являются замкнутыми, не имеют ни начала, ни конца. Место, из которого выходят магнитные линии — северный полюс (North), входят магнитные линии в южный полюс (South).

Магнитное поле можно сделать «видимым» с помощью железных опилок.

Магнитное поле проводника с током

А теперь о том, что обнаружили Ханс Кристиан Эрстед и Андре Мари Ампер в 1820 г. Оказывается, магнитное поле существует не только вокруг магнита, но и любого проводника с током. Любой провод, например, шнур от лампы, по которому протекает электрический ток, является магнитом! Провод с током взаимодействует с магнитом (попробуйте поднести к нему компас), два провода с током взаимодействуют друг с другом.

Силовые линии магнитного поля прямого тока — это окружности вокруг проводника.

Направление вектора магнитной индукции

Направление магнитного поля в данной точке можно определить как направление, которое указывает северный полюс стрелки компаса, помещенного в эту точку.

Направление линий магнитной индукции зависит от направления тока в проводнике.

Определяется направление вектора индукции по правилу буравчика или правилу правой руки.

Вектор магнитной индукции

Это векторная величина, характеризующая силовое действие поля.

Индукция магнитного поля бесконечного прямолинейного проводника с током на расстоянии r от него:

Индукция магнитного поля в центре тонкого кругового витка радиуса r:

Индукция магнитного поля соленоида (катушка, витки которой последовательно обходятся током в одном направлении):

Принцип суперпозиции

Если магнитное поле в данной точке пространства создается несколькими источниками поля, то магнитная индукция — векторная сумма индукций каждого из полей в отдельности

Земля является не только большим отрицательным зарядом и источником электрического поля, но в то же время магнитное поле нашей планеты подобно полю прямого магнита гигантских размеров.

Географический юг находится недалеко от магнитного севера, а географический север приближен к магнитному югу. Если компас разместить в магнитном поле Земли, то его северная стрелка ориентируется вдоль линий магнитной индукции в направлении южного магнитного полюса, то есть укажет нам, где располагается географический север.

Характерные элементы земного магнетизма весьма медленно изменяются с течением времени — вековые изменения. Однако время от времени происходят магнитные бури, когда в течение нескольких часов магнитное поле Земли сильно искажается, а затем постепенно возвращается к прежним значениям. Такое резкое изменение влияет на самочувствие людей.

Магнитное поле Земли является «щитом», прикрывающего нашу планету от частиц, проникающих из космоса («солнечного ветра»). Вблизи магнитных полюсов потоки частиц подходят гораздо ближе к поверхности Земли. При мощных солнечных вспышках магнитосфера деформируется, и эти частицы могут переходить в верхние слои атмосферы, где сталкиваются с молекулами газа, образуются полярные сияния.

Частицы диоксида железа на магнитной пленке хорошо намагничиваются в процессе записи.

Поезда на магнитной подушке скользят над поверхностью совершенно без трения. Поезд способен развивать скорость до 650 км/ч.

Работа головного мозга, пульсация сердца сопровождается электрическими импульсами. При этом в органах возникает слабое магнитное поле.

Электричество и магнетизм

В присутствии магнетика вектор магнитной индукции  равен сумме векторов магнитной индукции внешнего магнитного поля , создаваемого независимыми от магнетика токами, и магнитной индукции собственного поля магнетика  

(7.1)

Поле , создаваемое намагниченным магнетиком, разумеется, зависит от того, как намагничен магнетик, а намагничивается он суммарным полем , поэтому  само является функцией : . Исключением в этом смысле может быть постоянный магнит, намагниченность которого не зависит, или практически не зависит от наличия или отсутствия внешнего магнитного поля, в частности, такое вещество, которое может оставаться намагниченным и в отсутствие внешнего — намагничивающего — поля.  

Далее будет показано, что если магнитное поле вне магнетика параллельно его поверхности, то поле  связано с магнитной индукцией  в вакууме (то есть в отсутствие магнетика) соотношением

Безразмерная величина m называется магнитной проницаемостью. Все магнетики, в зависимости от характера влияния их собственного поля на суммарное магнитное поле, можно разделить на три группы:

 В парамагнитных телах собственное поле  увеличивает магнитный поток и, следовательно, парамагнитные тела притягиваются к магниту. В отличие от парамагнитных тел диамагнитные тела уменьшают магнитный поток. Это означает, как уже было сказано, что в диамагнитном теле под действием внешнего поля возникает собственное магнитное поле противоположное направлению внешнего магнитного поля. Следовательно, диамагнитные тела своим собственным магнитным полем отталкиваются от магнита. 

Видео 7.1. Поведение пара- и диамагнетиков в неоднородном магнитном поле.

Как показывает опыт, вектор магнитной индукции собственного поля пара- и диамагнетика пропорционален вектору магнитной индукции внешнего поля B₀

(7.2)

 

Безразмерный коэффициент пропорциональности c_m называется магнитной восприимчивостью вещества и является безразмерной величиной. У диамагнитных веществ магнитная восприимчивость является отрицательной величиной (c_m < 0), у парамагнитных положительной (c_m > 0). У ферромагнетиков магнитная восприимчивость c_m зависит от величины магнитной индукции внешнего поля B₀, поэтому в общем случае зависимость собственного поля ферромагнетика от внешнего нельзя считать линейной.  

Результирующее магнитное поле в присутствии магнетика равно:

(7. 3)

Сравнивая (7.3) с (7.1), получим

(7.4)

Отсюда находим связь собственного поля с внешним

(7.5)

аналогичную соответствующим выражениям для диэлектриков. 

Для объяснения намагничивания тел Ампер предположил, что в атомах и молекулах вещества циркулируют особые круговые токи — молекулярные токи. Каждый такой ток создает в окружающем пространстве магнитное поле. В силу хаотической ориентации магнитных моментов отдельных молекулярных токов суммарный магнитный момент тела равен нулю. Под действием внешнего магнитного поля магнитные моменты молекулярных токов приобретают преимущественную ориентацию в одном направлении, вследствие чего вещество намагничивается — его суммарный магнитный момент становится отличным от нуля, возникает дополнительное поле  (рис. 7.1).

Рис. 7.1. Молекулярные токи в магнетике

Вектор магнитной индукции. Сила Ампера

 

Направление вектора магнитной индукции \vec{B}

 

Определение: за направление вектора магнитной индукции принимают направление от южного полюса к северному свободно устанавливающейся в магнитном поле магнитной стрелки.

Это направление совпадает с направлением положительной нормали к контуру с током.

Определение: нормаль – это единичный вектор, перпендикулярный данной поверхности.

Направление положительной нормали определяется по правилу буравчика (правой руки)

 

Правило буравчика: если буравчик (правый винт, штопор) вращать так, чтобы поступательно он двигался по току, то его рукоятка будет вращаться по направлению поля.

Расположение магнитных полюсов Земли и направление магнитного поля Земли

 

Магнитные полюса Земли перепутаны: рядом с северным географическим полюсом расположен южный магнитный, а рядом с южным географическим – северный магнитный.

Направление магнитного поля постоянных магнитов

 

Модуль вектора магнитной индукции

 

Магнитное поле оказывает на рамку с током ориентирующее действие, она поворачивается под действием магнитных сил.

Если рамка перпендикулярна плоскости прямоугольника \Rightarrow действующий на нее момент сил максимален.

 

B=\frac{M}{IS}

M – максимальный момент сил, действующих на рамку со стороны поля

 

Сила Ампера

 

Сила Ампера действует со стороны магнитного поля на проводник с током.

 

B_{\parallel}=B\cos\alpha – горизонтальная составляющая вектора магнитной индукции (не оказывает влияния на проводник).

B_{\perp}=B\sin\alpha – вертикальная составляющая вектора магнитной индукции.

l – длина участка проводника.

F_{A}=IBl\sin\alpha

Правило левой руки: если левую руку расположить так, чтобы пальцы были направлены по току, а вертикальная оставляющая вектора магнитной индукции входила в ладонь, то отогнутый на 90 градусов большой палец левой руки покажет направление силы Ампера.

 

Вектор магн индукции | От урока до экзамена

При прохождении тока по проводнику вокруг него образуется магнитное поле. Векторную характеристику магнитного поля называют вектором магнитной индукции . Это поле оказывает на рамку с током, помещенную в поле, ориентирующее действие. Такое  действием магнитного поля на рамку с током или магнитную стрелку можно использовать для определения направления вектора магнитной индукции. За  принимается направление, который показывает северный полюс N магнитной стрелки. Для определения направления вектора магнитной индукции поля, созданного прямолинейным проводником с током, пользуются правилом буравчика: если направление поступательного движения буравчика совпадает с направлением тока в проводнике, то направление вращения ручки буравчика указывает направление вектора магнитной индукции.

направление вектора магнитного поля прямого проводника с током.

Если между полюсами подковообразного магнита поместить проводник с током, то он будет втягиваться или выталкиваться из поля магнита. Закон, определяющий силу, действующую на отдельный небольшой участок проводника, был установлен в 1820 г. А. Ампером. 

Сила действия однородного маг­нитного поля на проводник с током прямо пропорциональна силе тока, длине проводника, модулю вектора индукции магнитного поля, синусу угла между вектором индукции магнитного поля и проводником:

F=B^.I^.ℓ^. sin α  — закон Ампера.

• Сила Ампера максимальна, если вектор магнитной индукции перпендикулярен проводнику.
• Если вектор магнитной индукции параллелен проводнику, то магнитное поле не оказывает никакого действия на проводник с током, т.е. сила Ампера равна нулю.

Направление силы Ампера (правило левой руки) Если левую руку расположить так, чтобы перпендикулярная составляющая вектора В входила в ладонь, а четыре вытянутых пальца были направлены по направлению тока, то отогнутый на 90° большой палец покажет направление силы, действующей на проводник с током.

Макроскопическим проявлением силы Лоренца является сила Ампера. Запишем силу, действующую на одну частицу. Если заряженная частица влетает в магнитное поле со скоростью , на нее со стороны магнитного поля действует сила, которую называют силой Лоренца: ,  a – угол между векторами и . 

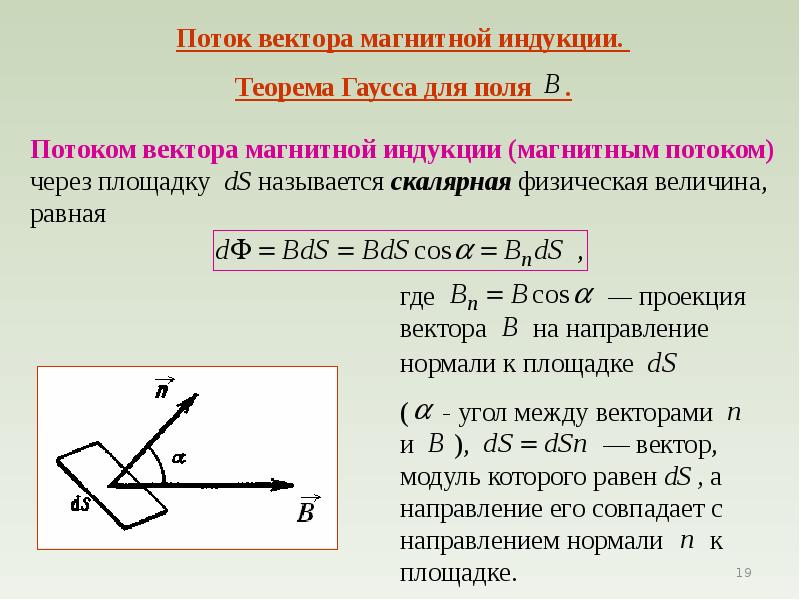
• В однородном магнитном поле, направленном перпендикулярно вектору скорости, под действием силы Лоренца заряженная частица будет равномерно двигаться по окружности постоянного радиуса r. Сила Лоренца в этом случае является центростремительной силой:
• Если заряженная частица движется в магнитном поле так, что вектор скорости   составляет с вектором магнитной индукции  угол a , то траекторией движения частицы является винтовая линия с радиусом r.

Если расположить левую руку так, чтобы  составляющая магнитной индукции  , перпендикулярная скорости заряда, входила в ладонь, а четыре вытянутых пальца были направлены по движению положительного заряда, то отогнутый на 90⁰ большой палец  укажет направление действующей на заряд силы Лоренца F_л

.

Вектор магнитной индукции — Студопедия

Вектор магнитной индукции (В) — это основная силовая характеристика магнитного поля (обозначается В). Пробный контур, помещенный в магнитное поле, испытывает со стороны магнитного поля действие вращающего момента сил М.

Бесконечно длинный ток величины I создает на расстоянии r от себя магнитное поле:

где Мо — магнитная постоянная, R — расстояние, I — сила тока в проводнике.

Магнитная индукция — это векторная физическая величина, являющаяся силовой характеристикой в данной точке магнитного поля.

Единица магнитной индукции — тесла (Тл).

Магнитная индукция — векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой магнитное поле действует на заряд , движущийся со скоростью .

В вакууме B = μ₀H.

Более конкретно, — это такой вектор, что сила Лоренца , действующая со стороны магнитного поля на заряд , движущийся со скоростью , равна

где косым крестом обозначено векторное произведение, α — угол между векторами скорости и магнитной индукции (направление вектора перпендикулярно им обоим и направлено по правилу буравчика).

Вектор магнитной индукции (В) – аналог напряженности электрического поля. Основной силовой характеристикой маг­нитного поля является вектор магнитной индукции.

Опытным путем было установлено, что для одной и той же точки магнитного поля максимальный вращающий момент М (момент сил) пропорционален произведению силы тока I в контуре на его площадь S. Величину IS называют магнитным моментом контура Pm.

Рисунок– Электрический ток (I), проходя по проводнику, создаёт магнитное поле (B) вокруг проводника.

Рисунок – Правило буравчика

Правило буравчика (винта): Если направление поступательного движения буравчика (винта) совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направлением вектора магнитной индукции поля, создаваемого этим током.

На практике удобно пользоваться следующим правилом: Если обхватить соленоид (катушку) правой рукой так, что бы четыре пальца были направлены по току, то отогнутый большой палец покажет направление магнитного поля внутри соленоида.

А) Б)

Рисунок 3.2 – А) Образование магнитного потока в соленоиде

Б) Схема полей в соленоиде при протекании по обмотке переменного тока

Единица измерения В в СИ — тесла (Тл). Единица названа в честь сербского электротехника Н. Тесла.

GMW Associates — Векторы и компоненты магнитного поля

Магнитное поле в любой точке пространства является векторной величиной. Это означает, что есть направление, связанное с полем, а также его напряженность. Рассмотрим стрелку ниже:

Направление стрелки можно рассматривать как направление магнитного поля. Длину стрелки можно представить как силу поля, то есть чем длиннее стрелка, тем сильнее поле. Назовите эту длину B.

Если я помещу набор осей на стрелку, я могу разделить поле на два компонента поля, а именно компонент x и компонент y. Назовите эти длины Bx и By.

Теперь я могу описать длину стрелки или силу магнитного поля в терминах компонентов x и y. Используя теорему Пифагора:

Теперь представьте, что существует третье направление, так что стрелка B может указывать из (или внутрь) плоскости страницы.Теперь есть третий компонент, а именно Bz, который в нашем примере представляет собой длину компонента, простирающегося от страницы к краю стрелки.

Используя ту же математику, я теперь могу описать B как:

Величина B — это сила магнитного поля. Bx, By и Bz — три составляющие, измеренные трехосевым тесламетром (гауссметром). Одноосное измерительное устройство будет изменять свои показания в зависимости от того, в какую сторону ориентирована чувствительная ось по отношению к направлению магнитного поля.Чтобы получить полное представление о магнитном поле в любой точке пространства, необходимо не только значение B, но и направление, которое может быть выражено тремя компонентами: Bx, By и Bz.

Некоторые датчики магнитного поля измеряют только одну составляющую магнитного поля (флюксгейт и приборы на эффекте Холла). Они называются одноосевыми устройствами.

Другие инструменты измеряют только полную амплитуду поля (ЯМР, СОЭ). Это количество B выше.

Можно объединить трехосевые датчики для получения трех измерений поля в одном корпусе датчика.Они называются трехкоординатными устройствами.

9.2: Магнитный векторный потенциал

Хотя мы не можем выразить магнитное поле как градиент скалярной потенциальной функции, мы определим вектор величиной \ (\ textbf {A} \), чья curl равна магнитное поле:

\ [\ textbf {B} = \ textbf {curl A} = \ nabla \ times \ textbf {A}. \ Label {9.2.1} \]

Так же, как \ (\ textbf {E} = — \ nabla V \) не определяет \ (V \) однозначно (потому что мы можем добавить к нему произвольную константу), точно так же и уравнение \ ref {9.2 \) можно записать \ (- \ nabla (1 / r) \). (Если это не очевидно, перейдите к выражению для \ (\ nabla ψ \) в сферических координатах и ​​положите \ (ψ = 1 / r \).) Закон Био-Савара принимает вид

\ [\ textbf {dB} = — \ frac {\ mu I} {4 \ pi} \ nabla (1 / r) \ times \ textbf {ds} = \ frac {\ mu I} {4 \ pi} \ textbf {ds} \ times \ nabla (1 / r). \ label {9.2.3} \]

Поскольку \ (\ textbf {ds} \) не зависит от \ (r \), наблу можно переместить влево от перекрестного произведения, чтобы получить

\ [\ textbf {dB} = \ nabla \ times \ frac {\ mu I} {4 \ pi r} \ textbf {ds}.\ label {9.2.4} \]

Таким образом, выражение \ (\ frac {\ mu I} {4 \ pi r} \ textbf {ds} \) представляет собой вклад \ (\ textbf {dA} \) в вектор магнитного потенциала от элемента схемы \ (\ textbf {ds} \). Конечно, изолированный элемент схемы не может существовать сам по себе, поэтому для векторного потенциала магнитного поля от полной цепи необходимо вычислить линейный интеграл этого элемента вокруг цепи.

Магнитный векторный потенциал — обзор

2 Историческая перспектива

Теория Рэмси для ядерного экранирования в диамагнитном ЯМР [10,11] основана на орбитальных взаимодействиях. Расширение выражения для нерелятивистской (NR) кинетической энергии π ² /2 m _e при наличии вкладов магнитного векторного потенциала (как внешнего поля, так и поля ядерного магнитного диполя) в импульс, π = p + A ₀ + A _K , приводит [29], с одной стороны, к орбитальному зеемановскому и орбитальному сверхтонкому (парамагнитному ядерному спин-электронному взаимодействию) взаимодействиям, которые линейны по магнитное поле B ₀ и ядерный магнитный момент μ _K = γ _K ħ I _K соответственно.Здесь I _K — безразмерный ядерный спин, а γ _K — гиромагнитное отношение. Как подробно описано в главе 2 этого тома, эти взаимодействия приводят к возникновению парамагнитной части тензора экранирования σ _K в выражении теории возмущений второго порядка. С другой стороны, квадратичные члены гамильтониана включают оператор, билинейный в B ₀ и I _K и, следовательно, диамагнитный вклад первого порядка (математическое ожидание) в σ _K .

ЯМР парамагнитных соединений с открытой оболочкой представлял интерес с самого начала, а контактное экранирование было сформулировано МакКоннеллом и Чеснутом в 1958 году [30] как среднее значение (в первую очередь FC) изотропного сверхтонкого взаимодействия в спиновой поляризованное зеемановское многообразие в основном электронном состоянии, так как

(1) σK, ετcon = −2πγKμBgeAKisoδετSS + 13kT

, где ετ — декартовы индексы тензора экранирования, A _K ^{изотропный Константа HFC (в единицах частоты), δ _ετ — дельта Кронекера (подчеркивая тот факт, что это изотропный вклад в тензор экранирования), g _e — свободный электрон g -фактор, μ _B — магнетон Бора, а T — абсолютная температура. Уравнение (1) можно рассматривать как сверхтонкое взаимодействие ядерного магнитного момента со средним спином электрона Кюри в присутствии магнитного поля. Аналогичным образом, усреднение диполярного сверхтонкого взаимодействия приводит к полностью анизотропному вкладу ранга 2}

(2) σK, ετdip = −2πγKμBgeAK, ετdipSS + 13kT

, который является симметричным по тензорным индексам ετ . Здесь A _K ^dip — диполярный тензор HFC. Традиционно уравнения.(1) и (2) связаны с существованием спиновой плотности на s- и p-орбиталях центра ЯМР [4].

Эти формулы до сих пор преимущественно используются при расчетах экранирования pNMR и сравнении соответствующих химических сдвигов с экспериментальными данными. В последнем случае часто используется приближение эквивалентной (изоструктурной) диамагнитной системы, где предполагается, что орбитальная (Рамсеевская) часть константы экранирования парамагнитной системы идентична таковой у близкородственной диамагнитной молекулы.

Важным компонентом в анализе сдвига pNMR была концепция псевдоконтактного сдвига (PCS) [30–32], изотропного вклада, являющегося результатом дальнодействующего диполярного взаимодействия ядерных и электронных спинов, опосредованного анизотропией Δg ˜ электронного g -тензора, который параметризует электронное зеемановское взаимодействие с B ₀ в ЭПР. В свою очередь, эта величина пропорциональна спиновой намагничиваемости молекулы. В частности, этот вклад сдвига сам по себе кодирует расстояние от неспаренного электрона (предполагаемого локализованным, т.е.g., в металлическом центре) и ядре ЯМР. Следовательно, PCS обеспечивает управление молекулярной структурой и используется для определения структуры, например, металлопротеинов. Чтобы извлечь вклад PCS из экспериментальных данных химического сдвига, необходимо исключить как орбитальный сдвиг (с помощью эквивалентного диамагнитного соединения), так и контактный сдвиг, последний часто с помощью экспериментов ЭПР или эмпирически масштабированных или скорректированных квантово-химических расчетов.

Новое развитие теории экранирования pNMR началось в 2003 году, когда Rinkevicius et al. [33] сформулировал химический сдвиг спиновой системы дублета ( S = 1/2) на пределе NR. На этом уровне теории тензор экранирования состоит из контактных и дипольных членов формул. (1) и (2), в дополнение к орбитальным членам Рамсея. Последние рассчитываются для интересующей парамагнитной системы, что позволяет отказаться от использования эквивалентной диамагнитной молекулы. Годом позже Мун и Патчковский [34] представили элегантную основу для систематического расширения теории, все еще для дублетных систем, но теперь включающих, например, PCS, путем учета отклонения тензора g от изотропного свободного электрона. значение, сбн. г — тензор сдвига Δ г = г — г _e 1 . Это отклонение возникает в первую очередь из-за спин-орбитального (SO) взаимодействия. В 2005 году Пеннанен и Ваара [35] представили последовательную реализацию теории Муна – Патчковского в единой программе квантовой химии (deMon-Master) и расширили подход, включив SO-поправки к тензору HFC. Эта структура облегчила расчеты сдвига pNMR для легких ядер в системах S = ½.Релятивистские эффекты, возникающие из-за тяжелых атомов в молекуле, могут быть включены с помощью скалярных релятивистских и SO-псевдопотенциалов на этих центрах.

Оставшейся проблемой теории на тот момент было включение спиновых взаимодействий более высокого порядка, происходящих в системах с более чем одним неспаренным электроном ( S > ½), в первую очередь ZFS-взаимодействия, которое проявляется в члене самосвязи. эффективного спина электрона в гамильтониане ЭПР [28]. Курланд и МакГарви [32] уже аналитически рассмотрели ситуацию в случае осевой симметрии.Первоначально проблема была рассмотрена квантово-химическим методом Hrobárik et al. [36], который представил апостериорную коррекцию экранирования, примененную после стандартного расчета без учета ZFS. Помимо приближенного характера, метод практически ограничен осесимметричными системами. Наконец, в 2008 г. Пеннанен и Ваара [37] работали над теорией Луны и Пачковского и сумели обобщить ее для систем общей пространственной симметрии S > ½. В этом подходе ZFS систематически учитывается с самого начала в условиях сверхтонкого экранирования электронов, зависящих от спина и температуры.Существенным элементом теории является признание того факта, что проблема неспаренных электронов в магнитном поле обязательно включает статистическое усреднение сверхтонких и зеемановских взаимодействий во множестве уровней энергии, которые в присутствии ZFS нелинейно зависят от B ₀ . В результате систематического расширения вкладов в зеемановские и сверхтонкие взаимодействия в соответствии с порядком постоянной тонкой структуры α, , в котором они появляются (порядки различных взаимодействий лучше всего оцениваются в системе атомных единиц, где комбинация μ ₀ /4 π , появляющееся в сверхтонких операторах, переходит в α ² ), сверхтонкий сдвиг может быть проанализирован в нескольких терминах контактного и диполярного типа, а также в виде PCS и анизотропных контактных вкладов. В частности, с помощью этого подхода были обобщены тензорные симметрии ранее известных членов сверхтонкого экранирования, в результате чего были введены несколько ранее неизвестных вкладов изотропного сдвига. В следующих разделах мы углубимся в формулировку этой новой теории [37].

Векторный магнитный потенциал

Магнитный векторный потенциал
следующий: Закон Био-Савара Up: Уравнения Максвелла, не зависящие от времени Предыдущая: Теорема Гельмгольца

Магнитный векторный потенциал Электрические поля, создаваемые стационарными зарядами, подчиняются

(315)

Это сразу позволяет нам писать

(316)

поскольку изгиб градиента автоматически равен нулю. Фактически, когда бы мы ни приехали через безвихревое векторное поле в физике мы всегда можем записать его как градиент некоторого скалярного поля. Это явно полезная вещь, поскольку она позволяет нам заменить векторное поле гораздо более простым скалярным полем. Величина в приведенном выше уравнении известен как электрический скалярный потенциал .

Магнитные поля, создаваемые постоянными токами (и нестационарными токами, если на то пошло) удовлетворить

(317)

Это сразу позволяет нам писать

(318)

так как расходимость завитка автоматически равна нулю.Фактически, когда бы мы ни приехали через соленоидальное векторное поле в физике мы всегда можем записать его как локон некоторых других векторное поле. Однако это не очень полезная вещь, поскольку это только позволяет нам заменять одно векторное поле другим. Тем не менее, уравнение. (318) один из наиболее полезные уравнения мы встретим в этом курсе лекций. Количество известен как магнитный векторный потенциал .

Мы знаем из теоремы Гельмгольца, что векторное поле полностью определяется его расхождение и его завиток.Ротор векторного потенциала дает нам магнитную поле через уравнение. (318). Однако расхождение не имеет физического значение. Фактически, мы полностью свободны в выборе к быть кем угодно. Обратите внимание, что согласно формуле. (318) магнитное поле инвариантен относительно преобразования

(319)

Другими словами, векторный потенциал не определен до градиента скалярной поле. Это просто еще один способ сказать, что мы свободны выбирать . Напомним, что электрический скалярный потенциал не определен до произвольная аддитивная константа, так как преобразование

(320)

оставляет электрическое поле инвариантным в уравнении. (316). Преобразования (319) и (320) являются примерами того, что математики называют калибровочными преобразованиями . Выбор конкретной функции или конкретной константы называется выбором измерять. Мы можем изменить калибр так, чтобы он был таким, какой мы нравиться.Самый разумный выбор — тот, который делает наши уравнения максимально простыми. насколько возможно. Обычная калибровка скалярного потенциала такова что на бесконечности. Обычный калибр для таково, что

(321)

Этот конкретный выбор известен как кулоновский калибр .

Очевидно, что мы всегда можем добавить константу, чтобы сделать он равен нулю на бесконечности. Но совсем не очевидно, что мы всегда можем выполнить преобразование калибра, например, чтобы сделать нуль.Предположим, что мы нашли некоторое векторное поле, ротор которого дает магнитное поле, но расходимость которого не равна нулю. Позволять

(322)

Вопрос в том, можем ли мы найти такое скалярное поле, чтобы после выполнения калибровочного преобразования (319) остается . Принимая расхождение уравнения. (319) ясно, что нам нужно найти функция, которая удовлетворяет

(323)

Но это всего лишь уравнение Пуассона.Мы знаем, что всегда можем найти единственное решение этого уравнения (см. раздел 3.11). Это доказывает, что на практике мы всегда можем установить дивергенцию равной нулю.

Рассмотрим снова бесконечный прямой провод, направленный вдоль оси -оси и проводящий ток. Магнитное поле, создаваемое такой проволокой, равно написано

(324)

Мы хотим найти векторный потенциал ротор которого равен указанному выше магнитному полю, а расходимость — нуль.Нетрудно заметить, что

(325)

отвечает всем требованиям. Обратите внимание, что векторный потенциал параллелен направлению тока. Этот можно предположить, что существует более прямая связь между векторный потенциал и ток, чем между магнитным полем и текущий. Потенциал не очень хорошо проявляется на оси, но это просто потому, что мы имеем дело с бесконечно тонким током.

Давайте возьмем ротор из уравнения. (318). Мы находим, что

(326)

где использовалось калибровочное условие Кулона (321). Мы можем объединить вышеперечисленное связь с уравнением поля (274), чтобы дать

(327)

Записав это в компонентной форме, получим

Но это всего лишь троекратное уравнение Пуассона.Мы можем сразу напишите уникальные решения вышеуказанных уравнений:

			(331)
			(332)
			(333)

Эти решения могут быть рекомбинированы для образования единого векторного решения.

(334)

Конечно, мы уже видели подобное уравнение раньше:

(335)

Уравнения (334) и (335) являются единственными решениями (при произвольном выборе калибровки) к уравнениям поля (279) — (282): они задают магнитную векторные и электрические скалярные потенциалы, порожденные набором стационарных зарядов, плотности заряда и набора постоянных токов, плотности тока .Кстати, мы можем доказать, что Уравнение (334) удовлетворяет калибровочному условию повторяя анализ уравнений. (300) — (307) (с а также ), и используя тот факт, что для установившихся токов.

---

следующий: Закон Био-Савара Up: Уравнения Максвелла, не зависящие от времени Предыдущая: Теорема Гельмгольца

Ричард Фицпатрик 2006-02-02

Самостоятельная сборка высокочувствительных трехмерных датчиков угла вектора магнитного поля

Реферат

Новые роботизированные, биоэлектронные и диагностические системы требуют разнообразных компактных и высокопроизводительных датчиков. Среди них компактные трехмерные (3D) векторные угловые энкодеры необходимы для определения пространственного положения и ориентации в трехмерной среде. Однако изготовление трехмерных векторных датчиков является сложной задачей, связанной с трудоемкой и дорогостоящей последовательной обработкой, необходимой для ориентации отдельных сенсорных элементов в трехмерном пространстве. В этой работе мы демонстрируем потенциал трехмерной самосборки для одновременной переориентации многочисленных гигантских магниторезистивных (GMR) датчиков спинового клапана для интеллектуального изготовления трехмерных магнитных угловых энкодеров.Во время процесса самосборки датчики GMR приводятся в желаемое ортогональное положение в трех декартовых плоскостях в одновременном процессе, в результате чего получаются монолитные высокопроизводительные устройства. Мы изготовили векторные угловые энкодеры с эквивалентной угловой точностью во всех направлениях 0,14 °, а также с низким уровнем шума и низким энергопотреблением при высокоскоростной работе на частотах до 1 кГц.

ВВЕДЕНИЕ

Направленные анизотропные датчики, преобразователи и исполнительные механизмы необходимы для следующего поколения электронных устройств и систем.Эти устройства основаны на материалах или структурах, у которых есть главная ось или плоскость, имеющая отношение к физическим величинам, таким как акустические, оптические, электрические и магнитные векторные поля, а также их градиенты. Для точного трехмерного (3D) зондирования они требуют точной ориентации функциональных элементов в трехмерном пространстве. Многочисленные приложения, такие как навигация ( 1 ), робототехника ( 2 , 3 ), биоэлектроника ( 4 ) и биомедицина ( 5 ), полагаются на угловые энкодеры с датчиками магнитного поля, которые обычно используются для этих задач. за счет обеспечения ключевой функции, а именно определения ориентации вектора магнитного поля, которая включает одновременную работу нескольких специально ориентированных магнитных датчиков.Широкий диапазон применения магнитных датчиков обусловлен тем, что статическое магнитное поле может проникать через наиболее распространенные препятствия, тогда как оптические, акустические и электростатические поля обычно страдают от эффектов отражения, поглощения или экранирования. Эта особенность позволяет упростить упаковку и защиту магнитосенсорных систем и магнитов, избавившись от дорогостоящих оптических окон и паразитных экранирующих эффектов. Подавляющее большинство всех магнитных датчиков, используемых в различных приложениях, основаны на эффектах Холла или магнитосопротивления (MR), которые различаются по точности и направлению измерения относительно подложки, на которой они изготовлены ( 6 ).Из-за их относительно простой конструкции по сравнению с MR-датчиками, устройства на основе эффекта Холла встречаются чаще всего, несмотря на их низкую угловую точность и необходимость в интегральной кремниевой схеме для повышения чувствительности и точности ( 7 ), что является почему эти датчики лучше всего подходят для обнаружения сильных магнитных полей. Датчики на эффекте Холла совместимы с производством полупроводников на основе Si или GaAs ( 8 ), а также с другими материалами, такими как Bi ( 9 ).Напротив, MR-датчики, такие как анизотропные MR и гигантские MR (GMR) датчики, представляют собой тонкопленочные устройства, которые демонстрируют на несколько порядков более высокую чувствительность (в диапазоне килоом / тесла) по сравнению с устройствами на эффекте Холла, что положительно влияет на угловой точность угловых датчиков MR. Эти датчики не требуют монокристаллических полупроводников, потребляют меньше энергии и могут быть настроены для ряда конкретных приложений, включая магнитное накопление и логику ( 10 ) или измерение слабого и сильного магнитного поля ( 11 ).Датчики GMR также были исследованы в новых и интересных биомедицинских и биоаналитических системах ( 12 , 13 ). Они достаточно прочные для изготовления на обычных монокристаллических пластинах ( 14 ), а также на полимерных подложках, где последняя технология привела к появлению новых классов гибких ( 15 — 18 ), растягиваемых ( 19 — ). 22 ) и печатные ( 23 — 25 ) магнитоэлектронные устройства.Их можно разделить на те, которые расположены в плоскости, например, многослойные GMR и спиновые клапаны (SV), или внеплоскостные, например, в туннельных устройствах MR (TMR) ( 10 , 11 ). Направление чувствительности для устройств SV и TMR может быть спроектировано в процессе планарного производства, который определяет реакцию сигнала, полученного по отношению к внешнему магнитному полю.

Планарные технологии микротехнологии очень эффективны, так как изготовление целых массивов устройств выполняется параллельно.Однако эта технология накладывает некоторые ограничения, так как готовые устройства имеют идентичные свойства, в частности направление их чувствительности в случае угловых энкодеров. Из-за этого ограничения остается проблемой приспособить различные пространственно ориентированные магнитные датчики во время параллельного производства. Например, это может включать вертикальное легирование датчиков на эффекте Холла ( 26, ) или процедуры изготовления на топографически структурированных поверхностях ( 27, ), которые могут привести к существенным различиям в характеристиках.В противном случае реализация различных направлений считывания может потребовать установки дорогих концентраторов потока (например, трехмерных ферритовых шариков) ( 1 ) или усовершенствованных технологий микроэлектромеханических систем ( 6 , 28 ). В качестве альтернативы, переориентация направления чувствительности для МР-устройств может быть достигнута индивидуальным локальным лазерным отжигом ( 29 — 31 ) или технологией подбора и установки ( 32 ), которая, например, была продемонстрирована для Датчики на эффекте Холла.Все эти попытки ясно демонстрируют, что пространственная перестройка, особенно в трехмерном декартовом базисе, на сегодняшний день является наиболее сложным и дорогостоящим процессом, задействованным в производстве трехмерных векторных кодировщиков магнитного поля.

Формируемые ультратонкие материалы ( 33 ) позволяют осуществлять трехмерную пространственную перестановку датчиков в масштабе пластины, что может значительно упростить производство. Преобразование формы становится жизненно важной стратегией при создании компактных и сложных трехмерных мезоскопических систем, для которых традиционные технологии оказались неадекватными ( 34 — 38 ).Благодаря совместимости с установленными технологиями микротехнологии самосгибание и сворачивание ультратонких мембран с двухмерным рисунком из различных материалов привлекло особое внимание среди ряда процессов самосборки ( 36 ) для создания роботов ( 39 ), доставки лекарств. строительные леса ( 40 ), пассивные электронные компоненты ( 41 — 43 ), датчики ( 41 , 44 — 46 ), электроника ( 47 ) и инструменты для микрохирургии ( 48 ) .При нанесении на жесткие подложки новые органические и неорганические формообразующие материалы с микрорельефом планарного типа способны к самосборке в различные трехмерные мезоскопические структуры, включая многогранные ( 49 ), цилиндрические ( 50 , 51 ) и более сложные ( 52 ) формы. Эти моделируемые платформы полагаются на параллельную обработку в масштабе пластины и уже были продемонстрированы для повышения точности, производительности и эффективности производства сложных трехмерных фотонных, сенсорных, накопительных и электромагнитных функциональных элементов, а также схем и систем ( 8 , 38 , 44 , 47 , 53 ).Кроме того, кривизна может влиять на магнитные свойства некоторых ферромагнитных (FM) структур ( 54 ), в то время как другие ( 19 ) остаются неизменными. Эти эффекты были исследованы и недавно рассмотрены ( 55 ), показав большие перспективы, например, для сверхбыстрых магнитных запоминающих устройств ( 56 ) и магнитных датчиков ( 44 ).

Здесь мы демонстрируем угловые кодеры GMR 3D путем формирования ортогональной декартовой основы с использованием специально разработанных ультратонких пленок, которые самостоятельно собираются в архитектуру «швейцарский рулон» ( 41 , 42 , 44 , 47 ).Вся конфигурация измеряет проекции вектора магнитного поля в трехмерном пространстве без неоднозначностей и с высокой угловой точностью.

В этой работе мы подготовили высокочувствительный набор слоев SV с верхними штырями, который в упрощенном виде изображен на рис. 1A. Эта структура состоит из трех FM-слоев, разделенных немагнитным проводящим разделительным слоем. Направление намагничивания верхнего FM-слоя фиксируется обменным смещением, создаваемым соседним анти-FM-слоем, и может быть определено в процессе намагничивания. Средний FM-слой служит опорным слоем и антиферромагентным обменом связан с закрепленным верхним FM-слоем, образуя синтетический антиферромагнетик (SAF) ( 57 ). В идеале нижний FM-слой может свободно вращаться в направлении внешнего магнитного поля. Это достигается за счет эффективного подавления поля рассеяния на краях FM-слоев, включенных в SAF. Анизотропия магнитной формы в плоскости регулируется путем формирования многослойной структуры в виде эллипсов с небольшими участками, соединенными Cr / Au-электродами.Небольшой размер датчиков используется специально, чтобы избежать каких-либо эффектов, связанных с кривизной, в конечном трубчатом самосборном устройстве, которое было оптимизировано экспериментально, чтобы быть максимально приближенным к синусоидальному отклику. При воздействии внешнего магнитного поля постоянного тока (DC) силой 25 мТл (работающего в пределах плато между эффективным полем анизотропии и полем обменного смещения), вращающегося в плоскости датчика, МР-отклик имеет характерную синусоидальную форму (рис. 1B) с разницей размаха сопротивления примерно в 1 Ом (сопротивление датчика составляет около 13 Ом), что соответствует отношению GMR от 7 до 8% [R (H) — RsatRsat, где R _sat — сопротивление, когда свободный слой совмещен с опорным слоем].На этом графике низкие и высокие значения сопротивления соответствуют параллельной и антипараллельной ориентациям намагниченности, соответственно, как свободного, так и опорного FM-слоя. Отклик одного датчика демонстрирует угловую неоднозначность в плоскости датчика, как показано на фиг. 1B, что требует наличия второго датчика в плоскости с направлением ортогонального обменного смещения. Некоторые другие сложные измерительные конфигурации, такие как конфигурация дифференциального моста ( 18 ), потребуют еще большего количества датчиков.Для лучшей визуализации и понимания концепции нашего 3D-датчика GMR на рис. 1C показана декартова основа. Здесь каждая из трех ортогональных декартовых плоскостей содержит два датчика, которые обеспечивают зависимости sin и cos от относительных углов (φ, θ и ρ) проекций вектора трехмерного магнитного поля. Теоретически требуются только три ортогональных датчика ( 8 ), причем два датчика находятся, например, в плоскости XY , а третий — в другой ортогональной плоскости, такой как плоскость XZ или YZ .Однако из-за потери точности при некоторых угловых экстремумах (например, магнитное поле перпендикулярно одной из декартовых плоскостей) полезно иметь шесть датчиков, чтобы обеспечить точную работу при произвольной ориентации поля. Обычно такую ​​конфигурацию магнитных датчиков довольно сложно получить с помощью обычных процессов микротехнологии; однако одновременная самоорганизация датчиков SV, которые изначально намагничены только в одном направлении, упрощает задачу.

Инжир.1 Конструкция КА и концепция самосборки.

( A ) Схема, на которой показан упрощенный набор слоев датчика магнитного поля SV. ( B ) Набор из шести SV, расположенных внутри ортогональной декартовой трехмерной базы. Каждая ортогональная плоскость содержит ортогональную пару датчиков, которые должны быть переставлены из их плоского однонаправленного состояния. ( C ) Под воздействием внешнего вращающегося магнитного поля этот датчик имеет синусоидальный отклик. ( D ) Датчики 3D SV переориентированы в конкретную трехмерную конфигурацию за счет применения технологии самосборки в свернутом виде, что приводит к синусоидальному и косинусному отклику каждой пары датчиков на каждой плоскости.( E ) Плоское состояние SV с направлением штифта, установленным под углом 45 ° к направлению прокатки.

Мы разработали макет с восемью датчиками, которые должны быть подготовлены в плоскости на верхней части полимерной моделируемой платформы, чтобы использовать традиционные технологии литографического структурирования и тонкопленочные технологии. Все датчики должны быть намагничены за один этап, чтобы вызвать желаемое направление обменного смещения, чтобы соответствовать подходу параллельного производства, как показано на рис. 1D. В этой схеме каждый набор из четырех датчиков подготовлен на одной из двух полимерных формуемых структур для самостоятельной сборки. Направление самосборки определяется специально разработанными (рис. 1С) местами крепления и отверстиями в армирующем полиимидном (PI) слое для определения направлений самосборки + 45 ° и -45 ° для каждой конструкции с учетом намагниченности КА. Такое расположение автоматически приводит к двум ортогональным трубчатым ( 8 ) архитектурам (рис. 1E), так что все датчики правильно выровнены в трехмерном пространстве. Это означает, что наклонная ориентация трубчатых осей 45 ° относительно начального направления намагничивания обеспечивает два ортогональных датчика на декартову плоскость (рис.1С). Эта перегруппировка может быть достигнута без какой-либо дополнительной обработки, которая в противном случае потребовалась бы в обычном процессе изготовления. Из восьми подготовленных датчиков фактически необходимы только шесть, а два дополнительных датчика (рис. 1D) используются в качестве резервных. Здесь датчики от S1 до S6 обозначены цветами, соответствующими конкретным датчикам на фиг.1 (от C до E) для лучшего визуального восприятия их фактического положения в трехмерном пространстве до и после процесса самосборки.

РЕЗУЛЬТАТЫ

Изготовление пластин в масштабе и характеристика планарного состояния

Чтобы подтвердить эту концепцию, мы подготовили ряд трехмерных угловых энкодеров (рис.2A) на квадратных подложках с размерами 50 мм на 50 мм в параллельном, плоском процессе микротехнологии с последующей самосборкой в ​​трубчатую архитектуру швейцарского рулона (рис. 2B). Изготовление моделируемой платформы начинается с полимерных ультратонких пленок (рис. 2C), сформированных путем центрифугирования и прямого литографического рисунка жертвенного (SL) слоя (700 нм), набухающего слоя гидрогеля трапециевидной формы (HG) (350 нм), и жесткий слой PI (800 нм). После этого мы подготовили магнитные датчики путем напыления и формирования рисунка отрыва.Подробный оптимизированный набор слоев состоит из Ta ^{0,5 нм} / Ni ₈₀ Fe ₂₀ ^{2,0 нм} / Co ₉₀ Fe ₁₀ ^{0,6 нм} / Cu ^{1,6 нм} / Co ₉₀ Fe ₁₀ ^{0,6 нм} / Ni ₈₀ Fe ₂₀ ^{1,0 нм} / Ru ^{0,8 нм} / Co ₉₀ Fe ₁₀ ^{1,0 нм} / Ni ₈₀ Fe ₂₀ ^{1,0 нм} / Ir ₁₉ Mn ₈₁ ^{8. 0 нм} / Ta ^{0,2 ​​нм} , что показано на рис. 2D. Изготовление планарной поверхности выполняется (рис. 2E) путем нанесения и формирования рисунка электродов Cr ^{5 нм} / Au ^{50 нм} и заключительного инкапсулирующего слоя PI (250 нм). Весь пакет схематически показан на фиг. 2E. Из-за ограничений по размеру нашей установки намагничивания (что не относится к промышленным системам), подложка была нарезана кубиками перед скатыванием в матрицу 4 на 4 с датчиками 10 мм на 8 мм, а затем намагничена в специально созданном вакууме. печь отжига с наложенным магнитным полем, создаваемым электромагнитом, как показано на схеме на рис.2F. Поле прикладывалось вдоль короткой оси эллипсов SV и ориентировано под 45 ° по отношению к направлению самосборки (рис. 1C). Отжиг проводился при 300 ° C в течение 1 часа в поле ~ 700 мТл, достаточном для рекристаллизации анти-FM слоев IrMn и Ru для достижения сильной связи в SAF.

Рис. 2 Изготовление трехмерного энкодера векторного поля в масштабе пластины, изготовленного на квадратных стеклянных подложках размером 50 мм на 50 мм, и их магнитоэлектрические характеристики в плоском состоянии.

( A ) Исходные планарные устройства. ( B ) Самособирающиеся устройства в масштабе пластины. ( C ) Изготовленная плоская формуемая полимерная стопка. ( D ) Схема, на которой показан точный стек SV. ( E ) Упрощенная схема полного набора слоев, включающая формуемую полимерную платформу, сенсорные элементы, контактную металлизацию и герметизирующий слой. Эллипсы SV имеют рисунок, а затем электрически соединяются с электродами Cr / Au и защищены тонким слоем PI.( F ) Схема, на которой изображена установка намагничивания вакуумной печи, намагничивающая SV при 300 ° C в течение 1 часа с наложенным магнитным полем ~ 700 мТл, создаваемым электромагнитом. Фото: Даниил Карнаушенко, Институт интегративных нанонаук, Лейбниц IFW в Дрездене.

Мы охарактеризовали эти плоские КА в качающемся и вращающемся магнитных полях после завершения намагничивания. Характеристика качающегося поля (вперед и назад) (рис. 3A) показывает резкое переключение намагниченности около 0 мТл с небольшим гистерезисом около 0.1 мТл и крутизна чувствительности около 120 В / (В). Кривые крутизны как для слабого, так и для сильного поля могут использоваться для измерения значения поля, указывающего, например, неправильное рабочее расстояние до магнита. Мы смогли достичь высоких отношений GMR (от 7 до 8%) и больших плато обменных смещений примерно до 100 мТл. Постоянное сопротивление плато определяет рабочий диапазон для SV, который нечувствителен к изменениям внешнего поля, как это может иметь место, когда источник поля движется к датчику или от него.Это важная особенность, когда для восстановления векторного поля используются массивы датчиков ( 27 ). При таком большом плато каждый элемент чувствителен к направлению поля, но не к его силе. Это поведение можно увидеть в отклике вращающегося магнитного поля SV (S4) на фиг. 3B, где мы изменяем расстояние между магнитом и датчиком, тем самым влияя на напряженность магнитного поля. Оптимальный рабочий диапазон составляет от 5 до 50 мТл, где отклонение от синусоидальной кривой отклика не является критическим.Итак, в нашей конфигурации и для дальнейших целей определения направления мы установили поле на постоянное значение 25 мТл в пределах диапазона плато в плоскости датчиков и выполнили измерения вращающегося поля. Характеристики, связанные с вращающимся вектором поля в общей плоскости с датчиками SV до самосборки, показаны на фиг. 3C, где видны эквивалентные перекрывающиеся cos-образные отклики. Соответствующие измерения для вращающегося поля в ортогональной плоскости показаны на рис.3D. Обратите внимание, что в исходной плоской форме смещения кривых не наблюдалось. Все характеристики, как и ожидалось, перекрываются и имеют наибольшее сопротивление вдоль оси намагничивания, демонстрируя желаемую однонаправленную ориентацию намагниченности датчиков в результате процесса полевого отжига. Для работы в 3D важно знать реакцию датчиков на наклон плоскости магнитного поля.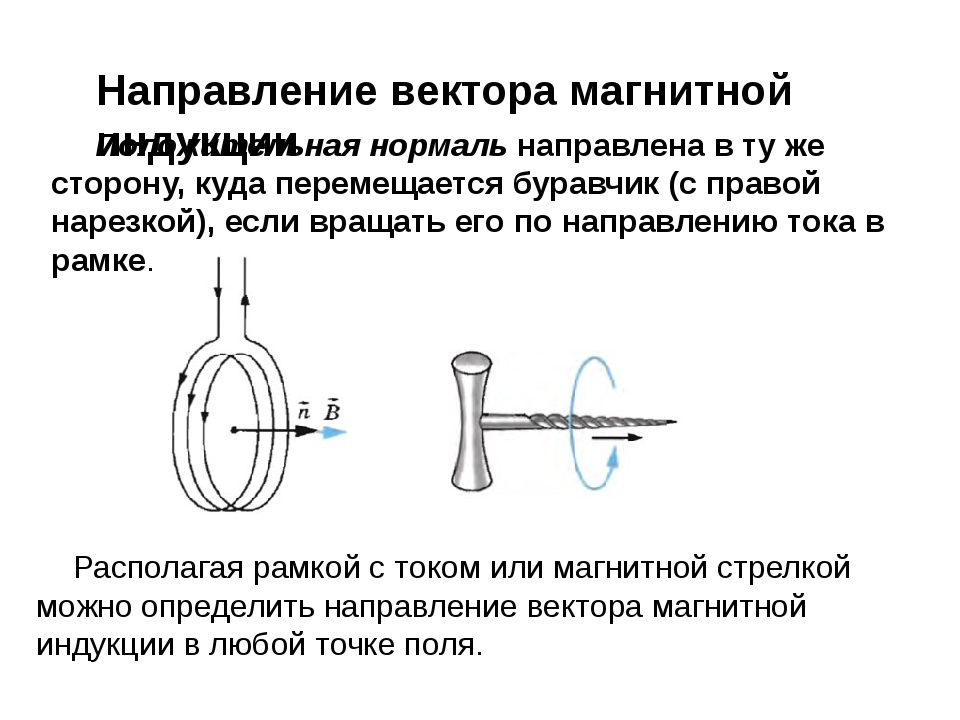 Поэтому мы провели еще одну характеристику, наклонив вращающуюся плоскость поля (рис.3E) и запись откликов датчика SV. Эти ответы имеют синусоидальную форму до угла наклона 45 °. Это важный результат, поскольку углы, превышающие 45 °, затем могут быть измерены другим набором SV-датчиков, расположенных в другой ортогональной главной плоскости.

Рис. 3 Планарное устройство с шестью элементами SV, характеризующееся качающимся и вращающимся магнитным полем.

( A ) МР-характеристика качающегося поля одного из КА, измеренная в направлении намагничивания.( B ) Характеристика вращающегося поля одного из КА (S4) в зависимости от напряженности поля (расстояния до магнита). ( C ) Характеристика вращающегося поля шести SV в их исходном плоском состоянии непосредственно после намагничивания. ( D ) Характеристика вращающегося поля шести SV, измеренная в ортогональной плоскости по отношению к плоскости вращающегося магнитного поля, выявляющая эквивалентную характеристику переключения для всех датчиков. ( E ) Конфигурация, которая использовалась для измерения откликов КА относительно вращающейся плоскости поля, выявляя синусоидальную форму с наклоном до 45 °, что достаточно для работы в 3D, так как за пределами этого угла другой набор датчиков расположен в ортогональная главная плоскость возьмет верх, таким образом избегая любых слепых секторов.

Самособирающиеся 3D угловые энкодеры GMR и 3D-характеристика

Самосборка плоских структур (рис. 4A) начинается с изотропного травления SL в водном растворе неорганических кислот и органического основания. После травления подложку переводили в щелочной раствор, набухающий ГГ. Усиленный слоем PI, HG снимает напряжение, скручивая структуры в рулоны (рис.4, B и C) из 36 трубчатых структур только с одной дефектной трубкой (рис.2B), в результате чего выход превышает 97%. На рис. 5 дополнительно показаны однотрубные устройства, которые были изготовлены во время оптимизации условий прокатки, демонстрирующие аналогичный выход продукции и отклонение диаметров примерно на 15 мкм в успешно собранных устройствах на пластине (рис. 5D). Каждый швейцарский рулет оснащен четырьмя магнитными датчиками SV, перенастроенными в трехмерное пространство. Толщина слоев HG и PI регулируется для настройки диаметра на 250 мкм для размещения датчиков на поверхности трубки с азимутальным расстоянием 90 ° (рис.1D, 2B и 4C).

Рис. 4 Самостоятельная сборка устройств Diced в трехмерные магнитные датчики и их характеристики.

( А ) Планарное устройство с набором намагниченных и электрически связанных КА перед самостоятельной сборкой. ( B ) Приборы после самосборки выявили две ортогональные трубки диаметром 250 мкм и длиной 2,3 мм. Длина прокатки 1,58 мм. ( C ) Увеличение двух трубок, показывающее один из восьми SV. ( D ) Трехмерный датчик характеризовался вращением магнитного поля постоянного радиально намагниченного магнита.Положение магнита можно регулировать, наклоняя магнит вокруг датчика и настраивая расстояние между магнитом и датчиком. Сам датчик можно поворачивать в горизонтальной плоскости. Это позволяет установить вращающуюся плоскость магнитного поля в любую произвольную ориентацию по отношению к датчику. ( E ) Схема, изображающая последовательное электрическое соединение датчиков, их питание и получение сигнала. ( F ) Поведение пары XY (S2 и S4) ортогональных магнитных датчиков, сформированных на противоположных сторонах соответствующей трубки, и эскиз, показывающий ориентацию вращающегося магнита по отношению к датчикам.( G ) Поведение пары XZ (S5 и S6) ортогональных магнитных датчиков, сформированных на противоположных сторонах соответствующей трубки, и эскиз, показывающий ориентацию вращающегося магнита по отношению к датчикам. ( H ) Поведение пары YZ (S1 и S3) ортогональных магнитных датчиков, сформированных на противоположных сторонах соответствующей трубки, и эскиз, показывающий ориентацию вращающегося магнита по отношению к датчикам. Фото: Даниил Карнаушенко, Институт интегративных нанонаук, Лейбниц IFW в Дрездене.

Рис. 5 Структуры, использованные на этапе оптимизации.

( A ) Изготавливается из плоских стеклянных квадратов 100 мм на 100 мм; устройства были нарезаны кубиками (удалены края). ( B ) Самособирающиеся устройства в виде массива трубок. Из 180 структур 168 были собраны самостоятельно, чтобы показать выход производства более 93% в параллельном процессе в масштабе пластины. ( C ) Демонстрация качества самостоятельной сборки в увеличенном виде трубчатой ​​конструкции, несущей датчики магнитного поля и электроды.( D ) Статистическое распределение диаметров 168 собранных устройств на пластине. ( E — G ) Единая основная плоскость-13 отклик датчиков, размещенных на трубке диаметром 230 мкм (E), 260 мкм (F) и 280 мкм (G) после амплитуды, смещения и фазы компенсация. ( H ) Схемы, поясняющие разориентацию КА и главных плоскостей из-за изменений диаметра трубы. ( I ) Расчет азимутальной и проекционной разориентации КА, принадлежащих одной главной плоскости.( J ) Расчет разориентации главных плоскостей. Фото: Даниил Карнаушенко, Институт интегративных нанонаук, Лейбниц IFW в Дрездене.

В этой конфигурации каждый из пары датчиков, разнесенных на 180 °, образует декартовы главные плоскости, ортогональные друг другу. Как обсуждалось ранее, одиночная трубка позволяет сформировать полуортогональный базис, содержащий две ортогональные плоскости. Две ортогональные трубки образуют ортогональную декартову основу с двумя дополнительными датчиками из восьми подготовленных датчиков.Для характеризации мы использовали постоянный магнит NdFeB (10 мм на 5 мм), намагниченный в радиальном направлении и создающий поле примерно 400 мТл на поверхности. Магнит был прикреплен к оси шагового двигателя, который был установлен на моторизованной механической платформе. Установка имела четыре степени свободы: (i) ось вращения магнита, (ii) ось наклона магнита вокруг датчика, (iii) переменное расстояние магнита относительно датчика и (iv) горизонтальная ориентация магнита. датчик по отношению к трем другим осям.Эта установка позволяла определять любую ориентацию вращающейся плоскости поля по отношению к датчику. Кроме того, регулируемое расстояние между магнитом и датчиком позволяло регулировать напряженность магнитного поля. Самостоятельно собранный 3D-датчик был прикреплен к печатной плате (PCB) и соединен проводом для электромагнитных характеристик (рис. 4D). Все эллиптические SV были подключены последовательно и снабжены током 1 мА (рис. 4E). Каждый из элементов SV был оборудован собственными электродами напряжения, что позволяло параллельный сбор всех сигналов датчиков в конфигурации с четырьмя датчиками.Определение характеристик 3D-сенсора осуществлялось с помощью собственной электронной схемы, оснащенной восемью дифференциальными каналами одновременного сбора данных с 24-битным разрешением. Мы охарактеризовали готовые устройства вращением магнитного поля во всех его основных плоскостях, а именно XY , XZ и YZ . Характеристики датчиков в соответствующих плоскостях показаны на рис. 4 (с F по H) с поясняющими рисунками ниже. Видно, что отклик самосборного устройства изменился по сравнению с его планарным состоянием (рис.3, Б и В). Датчики демонстрируют характерный отклик cos и sin, как и ожидалось из описанной концепции. Это указывает на то, что правильная ориентация датчиков в трехмерном пространстве была достигнута в полностью параллельном процессе масштабирования пластины за счет применения метода самосборки и свертывания, обеспечиваемого платформой из формуемого материала. Все отклики измерялись на расстоянии 14 мм между поверхностью магнита и датчиком. Отклики других датчиков на эти ориентации вращающейся плоскости поля показаны на рис.От S1 до S3. Однако внимательный анализ кривых (рис. 4, F — H) выявил отклонение от идеального синусоидального и косинусного отклика, а также небольшой сдвиг в желаемом фазовом сдвиге на 90 °.

ОБСУЖДЕНИЕ

Эта проблема связана с небольшим изменением диаметра трубы и несоосностью датчиков в трехмерном пространстве, что можно улучшить с помощью более точной настройки толщины полимера и контроля самосборки, включая химические условия, такие как pH раствора.Чтобы лучше понять этот вопрос, мы измерили датчики, сформированные на трубках трех разных диаметров (рис. 5, от E до G), что соответствует экспериментальному распределению диаметров, приведенному на рис. 5D. Никаких существенных изменений в отклике датчиков и отклонений от синусоидальной формы не обнаружено. Мы смоделировали влияние отклонения диаметра на ориентацию датчиков. Ориентация двух датчиков в одной основной плоскости изменяется в зависимости от диаметра трубки, как показано на рис.5I (черная кривая). Моделирование показывает, что относительная ориентация двух обращенных друг к другу датчиков ρ значительно изменяется, если диаметр трубки имеет разброс ± 25 мкм от идеального значения (250–260 мкм), что соответствует разбросу диаметров, который мы наблюдали на одной пластине. ρ имеет почти линейную зависимость от угла разориентации и достигает 21 °. Однако влияние отклонения на относительную ориентацию двух проекций датчика (α, который в идеале составляет 90 °) на главную плоскость очень мало (<2 °) даже для самого большого разброса диаметров (см.рис.5I, синяя кривая). Это отражено в экспериментальных данных для каждой главной плоскости (рис. 5, от E до G). Кроме того, каждая главная плоскость также разориентирована (рис. 5H). Различия в диаметре трубки приводят к разориентации двух основных плоскостей (θ), которые определяются четырьмя SV, переносимыми трубкой (два датчика на плоскость). Обратите внимание, что третья главная плоскость имеет аналогичную разориентацию, поскольку она определяется относительной ориентацией двух трубок. На рис. 5Н показано, как угол между двумя основными плоскостями (31 и 42), включенными в одну трубку, изменяется при изменении диаметра.Ориентация одной главной плоскости определяется в середине азимутального расстояния между двумя соответствующими датчиками (например, S1 и S3). Оказывается, что главные плоскости приобретают максимальное отклонение всего на ± 10 ° от идеальной ортогональной ориентации (рис. 5J). Это, в свою очередь, означает, что наблюдаемое изменение диаметра трубки не оказывает значительного влияния на точность окончательного кодирования угла и достаточно мало, чтобы хорошо откалибровать датчик и удалить соответствующие ошибки из его отклика.В процедуре калибровки должны быть измерены отклики всех датчиков и должны быть получены преобразования Фурье для каждого отклика, обеспечивающие относительные фазы. Это должно быть сделано для трех строго ортогональных плоскостей, где одна плоскость, например, параллельна подложке. Затем вращающееся магнитное поле прикладывается в каждой плоскости с помощью трехосного набора катушек Гельмгольца, электромагнита или вращающегося постоянного магнита.

Мы охарактеризовали угловую точность датчиков путем измерения определенного углового шага (−4.От 5 ° до + 4,5 °) чувствительности датчика (S4) в районе его максимальной угловой чувствительности. Мы измерили этот отклик при трех разных токах смещения (0,5, 1,0 и 1,5 мА), чтобы выяснить изменение амплитуды сигнала (рис. 6A). Несмотря на различия в токе смещения, шум остается постоянным со среднеквадратичным значением 1,86 мкВ (рис. 6B), что всего в семь раз выше разрешения (250 нВ) используемого 24-битного аналогового сигнала. в цифровой преобразователь (АЦП). Характеристики датчика с низким уровнем шума показаны в виде спектральной плотности мощности на рис.6D, демонстрирующий минимальный уровень шума лучше, чем -130 дБ (V ² ) / Гц для данных, полученных при частоте дискретизации 1 кГц в течение нескольких секунд с использованием того же АЦП. Максимально возможная угловая точность датчика напрямую зависит от тока смещения и уровня шума и достигает максимальной точности 0,14 ° при значении тока смещения 1,5 мА (рис. 6C). Мы также охарактеризовали угловую точность всей сборки 3D-датчика, сориентировав плоскость вращающегося магнита на 45 ° по отношению к основным плоскостям и выполнив те же измерения с шагом 9 ° (рис.6E). Отклик датчиков показывает эквивалентную точность среди всех датчиков в сборке, демонстрируя полную и точную работу набора датчиков в трехмерном пространстве (рис. 6F). Насколько нам известно, это самая высокая угловая точность по сравнению с ранее заявленными датчиками углового магнитного поля ( 18 , 58 ) или даже коммерческими устройствами TMR (например, TLE5501 Infineon Technologies AG) и сопоставима с коммерческими кремниевыми датчиками. компоненты на основе (например, MLX Melexis NV), которые, однако, используют интегральные схемы, предусилители и т. д.Предел точности наших 3D-датчиков можно еще больше повысить за счет увеличения тока смещения. Однако был выбран малый уровень тока возбуждения (в диапазоне микроампер), чтобы избежать резистивного перегрева из-за низкой теплоемкости и рассеиваемой мощности на поверхности тонких (~ 1 мкм) стопок полимерных слоев. Мы решили эту проблему, измерив тепловое разрушение датчиков для двух случаев: в виде изготовленных датчиков и герметизированных датчиков (рис. S4, A и B, соответственно). Во втором случае наблюдается явное увеличение тока пробоя и напряжения, вызванное повышенным тепловыделением через герметизирующий материал.Инкапсуляция также увеличивает механическую стабильность конструкции, тем самым решая одну из основных проблем в трехмерной самосборной электронике в целом ( 33 ). После инкапсуляции с конечными устройствами можно легко обращаться и даже нагружать их пальцем или с определенной массой, создающей силу 5,5 Н, без риска повреждения датчика или деформации трубок (рис. S5, A и B). Это демонстрирует потребность в новых решениях по управлению теплом для трехмерной самосборной электроники, которые потребуются в будущем.Эти решения могут включать в себя пассивные радиаторы, оптимизированную геометрию, интегрированные в трубы жидкостные системы ( 59 ) и / или радиальные самособирающиеся элементы Пельтье ( 60 ), и это лишь некоторые из них.

Рис. 6 Характеристики высокопроизводительного КА (S4) после самостоятельной сборки.

( A ) Отклик по напряжению датчика, измеренный вблизи cos (φ), где φ = 90 °, выявляющий скачок напряжения в ответ на изменение направления поля от -4,5 ° до + 4,5 ° для различных значений смещения Текущий.( B ) Уровень шума не зависит от тока смещения со среднеквадратичным значением 1,86 мкВ. ( C ) Шум имеет плоскую спектральную плотность мощности с нижним пределом лучше -130 дБ (V ² ) / Гц. ( D ) Стандартные отклонения измеренных углов соответствуют 0,14 °, 0,21 ° и 0,43 ° в зависимости от токов смещения 1,5, 1,0 и 0,5 мА соответственно. ( E ) Трехмерная угловая точность отклика датчиков была измерена с использованием ориентации плоскости вращающегося магнита под углом 45 ° ко всем основным плоскостям, в которых выполнялся шаг 9 °.( F ) Отклик датчиков с эквивалентной угловой точностью во всех направлениях для всех датчиков (временная ось для ступенчатого отклика скорректирована для лучшего визуального восприятия).

Мы продемонстрировали высокопроизводительные трехмерные датчики угла магнитного поля, использующие самосборку из формованных материалов. Все этапы изготовления, включая процедуру самостоятельной сборки, параллельны по своей природе и совместимы с производством пластин в масштабе, что обеспечивает небольшие отклонения в конечной геометрии.Наши самосборные датчики GMR обладают низким уровнем шума и способны определять с точностью до 0,14 ° эквивалентно во всех трех измерениях без необходимости дополнительной последовательной обработки. Кроме того, мы достигли исключительно высокого рабочего диапазона (от 5 до 100 мТл), низкого энергопотребления (всего 30 мкВт на чувствительный элемент) и высокой скорости работы до 1 кГц. Наша работа не только демонстрирует новые высокопроизводительные 3D-энкодеры магнитного поля, но также открывает альтернативные технологические пути в производстве 3D-электроники, которые могут привести к полностью параллельным массовым устройствам, работающим со статическими, низкочастотными и высокочастотными полями, их градиентами, и векторы Пойнтинга.

МАТЕРИАЛЫ И МЕТОДЫ

Обработка подложек

В качестве подложек использовались стекла квадратной формы размером 50 мм на 50 мм на 1 мм (экостекло D263T, SCHOTT AG, Майнц, Германия). Первоначально все подложки были промыты в профессиональной моечной машине DS 500 (STEELCO S.p.A., Riese Pio, Италия) для удаления всех органических и неорганических загрязнений, присутствующих в виде пыли или пленок. Затем поверхность активировали кислородной плазмой в GIGAbatch 310M (PVA Metrology & Plasma Solutions GmbH, Веттенберг, Германия).Это дополнительно обеспечивает химическую модификацию поверхности монослоем 3- (триметоксисилил) пропилметакрилата (TMSPM). Для этого стаканы помещали в вакуумную печь при 150 ° C на 2 часа вместе с 250 мкл TMSPM.

Полимерная платформа

Трехмерная перестройка датчиков GMR была основана на полимерной платформе, подробно описанной в наших предыдущих работах ( 41 , 42 , 44 , 47 ). Сначала на подложку толщиной 700 нм был нанесен металлоорганический фототекстовый комплекс на основе лантана и акриловой кислоты, на который с помощью оптической литографии был нанесен узор с помощью выравнивателя маски MA6 (SÜSS MicroTec SE, Гархинг, Германия) для формирования слоя SL.Двухслойная система, состоящая из фотошаблонов HG и PI, позволяет получить желаемую трубчатую геометрию. После высвобождения из подложки HG набухал в растворе щелочи, что приводило к механическому напряжению на границе раздела HG / PI, что приводило к процессу прокатки. Подобно SL, HG был нанесен методом центрифугирования сверху при 6000 оборотах в минуту (об / мин), что привело к толщине 350 нм, а затем был нанесен узор с помощью оптической литографии. Трапецеидальная форма слоя HG предотвращает скатывание конструкции по бокам во время травления SL.Затем армирующий PI был нанесен методом центрифугирования со скоростью 3000 об / мин, в результате чего был получен слой толщиной 800 нм, на который также был нанесен рисунок с помощью оптической литографии.

Спиновые клапаны

В данной работе сенсорные элементы GMR состояли из SV с верхними штырями со следующей последовательностью слоев: Ta ^{0,5 нм} / Ni ₈₀ Fe ₂₀ ^{2,0 нм} / Co ₉₀ Fe ₁₀ ^{0,6 нм} / Cu ^{1,6 нм} / Co ₉₀ Fe ₁₀ ^{0,6 нм} / Ni ₈₀ Fe ₂₀ ^{1.0 нм} / Ru ^{0,8 нм} / Co ₉₀ Fe ₁₀ ^{1,0 нм} / Ni ₈₀ Fe ₂₀ ^{1,0 нм} / Ir ₁₉ Mn ₈₁ ^{8,0 нм} / Ta ^{0,2 ​​нм} . Структурирование эллипсов SV (85 мкм для его большой оси и 55 мкм для его малой оси) было выполнено методом снятия с использованием слоя фоторезиста (AZ5214E ​​Microchemicals GmbH, Ульм, Германия) перед нанесением пакета слоев, который был сформирован с помощью оптической литографии. . Пакет SV был изготовлен методом магнетронного распыления с базовым давлением 2.4 × 10 ^–6 и 1,4 × 10 ^–3 –мбар атмосферы Ar во время осаждения с использованием мишеней диаметром 100 мм и мощностью 100 Вт для каждого материала. Толщина регулировалась точным временем последовательности нанесения, которая выполнялась при комнатной температуре непосредственно на верхнюю часть пакета полимерных слоев. Позже фоторезист растворили в ацетоне, обнажив эллипсоидальные элементы SV на слое PI.

Намагничивание датчиков

Намагничивание датчиков осуществляли отжигом в магнитном поле с помощью вакуумной печи собственного производства, помещенной между полюсными наконечниками электромагнита.Намагничивание осуществляли путем фиксации устройств 4 x 4, вырезанных из подложки размером 50 на 50 мм, а затем откачивания до давления лучше 2 × 10 ^-5 мбар с помощью турбонасоса. Отжиг был запрограммирован на постепенное увеличение от комнатной температуры до 300 ° C в течение 30 минут, выдерживался в течение 1 часа при этой температуре, а затем снова снижался до комнатной температуры в течение следующих 30 минут. Во время этой процедуры было приложено магнитное поле 700 мТл, в результате чего намагниченные КА.

Самосборка трубки

Из-за избирательного травления SL в растворе гипофосфорной кислоты, хлорной кислоты и бензотриазола (все химические вещества получены от Sigma-Aldrich Co.LLC, Германия) двухслойную систему HG / PI высвобождали с подложки. На основе рисунка всех трех полимерных слоев SL присутствовал только в областях с HG наверху, так что PI был постоянно прикреплен к стеклянной подложке. После высвобождения бислоя HG / PI HG набухали щелочным раствором гидроксида натрия и гидроксида тетраметиламмония. Оптимальное значение pH 8,0 устанавливали уксусной кислотой.

Магнитоэлектрические характеристики

Для проверки отклика конечного устройства на внешние магнитные поля, круглый постоянный магнит NdFeB с радиальным намагничиванием был присоединен к шаговому двигателю.При вращении постоянного магнита в непосредственной близости от магнита создавалось вращающееся магнитное поле. Шаговый двигатель был прикреплен к поступательной ступени, с помощью которой расстояние от магнита до датчика позволяло регулировать напряженность магнитного поля. Кроме того, трансляционный столик был прикреплен к вращающемуся столику, так что плоскость магнитного поля могла изменяться путем наклона постоянного магнита. Датчик был приклеен, а электроды прикреплены к обычной печатной плате, помещенной на вращающийся столик, что позволяет регулировать горизонтальную ориентацию датчика.Сбор электрического сигнала производился с помощью внутренней электронной схемы, содержащей дифференциальный 24-разрядный АЦП с дискретизацией 1 кГц, подключенный к компьютеру через интерфейс USB. Эта установка позволяла генерировать вращающееся магнитное поле в любой произвольной плоскости в трехмерном пространстве. Магнитное поле измеряли с помощью калиброванного магнитометра HG-09 gaussmeter (Goudsmit Magnetic Systems).

Инкапсуляция

Для защиты сенсоров и улучшения рассеивания тепла мы нанесли на сенсоры раствор мономеров, содержащий 1: 1: 0.03 молярное соотношение триаллил-1,3,5-триазин-2,4,6 (1 H , 3 H , 5 H ) -триона (TATATO, полученный от Sigma-Aldrich Co. LLC, Германия) , трис [2- (3-меркаптопропионилокси) этил] изоцианурат (THIOCURE TEMPIC) (предоставленный Bruno Bock Chemische Fabrik GmbH & Co. KG) и радикальный фотоинициатор Irgacure 365 (полученный от Sigma-Aldrich Co. LLC, Германия). Затем мы фотополимеризовали этот раствор, используя источник ультрафиолетового светодиода с длиной волны 365 нм, в результате чего была получена прочная капсула, которая защищает от любого внешнего механического воздействия, а также служит хорошим радиатором для датчиков во время электрических испытаний.

ДОПОЛНИТЕЛЬНЫЕ МАТЕРИАЛЫ

Дополнительные материалы к этой статье доступны по адресу http://advances.sciencemag.org/cgi/content/full/5/12/eaay7459/DC1

Рис. S1. Характеристика пар ZY и XZ (S1 и S3 и S5 и S6, соответственно) ортогональных магнитных датчиков, сформированных на противоположных сторонах соответствующей трубки с полем, вращающимся в плоскости XY .

Рис. S2. Характеристика пар XY, и XZ (S2 и S4 и S5 и S6, соответственно) ортогональных магнитных датчиков, сформированных на противоположных сторонах соответствующей трубки с полем, вращающимся в плоскости ZY .

Рис. S3. Характеристика пар XY, и ZY (S2 и S4 и S1 и S3, соответственно) ортогональных магнитных датчиков, сформированных на противоположных сторонах соответствующей трубки с полем, вращающимся в плоскости XZ .

Рис. S4. Электрический пробой датчиков из-за перегрева под действием электрического напряжения.

Рис. S5. Проверка механической надежности герметизированных устройств.

Это статья в открытом доступе, распространяемая в соответствии с условиями некоммерческой лицензии Creative Commons Attribution, которая разрешает использование, распространение и воспроизведение на любом носителе, при условии, что конечное использование будет , а не для коммерческих целей и при условии, что оригинальная работа правильно процитирована.

ССЫЛКИ И ПРИМЕЧАНИЯ

1. ↵
2. ↵

   Shaohui Foong, Kok-Meng Lee, Kun Bai, Международная конференция IEEE по робототехнике и автоматизации, 2010 г. (IEEE, 2010), стр. 5447–5452.

3. ↵

   Б. Г. А. Ламбрехт, Х. Казеруни, 2009 Международная конференция IEEE по робототехнике и автоматизации (IEEE, 2009), стр. 639–645.

4. ↵

   M. C. Carrozza, P. Dario, F. Vecchi, S. Roccella, M. Zecca, F. Sebastiani, Proceedings 2003 IEEE / RSJ International Conference on Intelligent Robots and Systems (IROS 2003) (Cat.No 03Ч47453) (IEEE, 2004), т. 3. С. 2642–2647.

5. ↵
6. ↵
7. ↵
8. ↵
9. ↵
10. ↵
11. ↵

    C. Reig, S. Cardoso, SC Mukhopadhyay, Гигантские датчики магнитосопротивления (GMR) 30 Smart , в Instrumentation (Springer Berlin Heidelberg, Berlin, Heidelberg, 2013), т. 6.

12. ↵
13. ↵
14. ↵
15. ↵
18. ↵
19. ↵
22. ↵
23. ↵
25. ↵
↵
26. ↵
27. ↵
28. ↵
30. ↵
32. ↵
33. ↵
34. ↵
35. ↵
36. ↵
37. ↵
38. 99
90 38
39. ↵
40. ↵
41. ↵
42. ↵
43. ↵
44. ↵
45. ↵
46. ↵
47. ↵
48. ↵
49. 33 ↵

Благодарности C. C. Krien и I. Fiering (Leibniz IFW Dresden) за нанесение металлических тонких пленок, а также L. Schröder за помощь в чистой комнате. Мы высоко ценим поддержку в разработке экспериментальных установок со стороны отдела исследовательских технологий Лейбницкого IFW в Дрездене и команды чистых помещений во главе с Р. Энгельхардом (Leibniz IFW Dresden). Финансирование: Эта работа была поддержана Немецким исследовательским фондом DFG (Премия Готфрида Вильгельма Лейбница присуждена в 2018 г., HO 1483/64 и KA5051 / 1-1). Вклад авторов: C.B. and D.K. внес равный вклад в эту работу. Д.К. и O.G.S. задумал идею. C.B., D.K. и D.D.K. разработал эксперимент. C.B., D.K., D.D.K., A.M. и M.F. проводил эксперименты. C.B., D.K. и T.K. проанализировали данные. D.K., C.B. и T.K. написал рукопись при участии всех авторов. Д.К. и O.G.S. руководил работой. В обсуждениях участвовали все авторы. Конкурирующие интересы: D.K., D.D.K. и O.G.S. являются изобретателями по заявке на патент, связанной с этой работой, поданной Leibniz IFW Dresden (no.PCT / EP2017 / 075200, подана 4 октября 2017 г.). Авторы заявляют, что у них нет других конкурирующих интересов. Доступность данных и материалов: Все данные, необходимые для оценки выводов в статье, представлены в документе и / или дополнительных материалах. Дополнительные данные, относящиеся к этой статье, могут быть запрошены у авторов.

• Copyright © 2019 Авторы, некоторые права защищены; эксклюзивный лицензиат Американской ассоциации содействия развитию науки. Никаких претензий к оригинальному U.С. Правительственные работы. Распространяется по некоммерческой лицензии Creative Commons Attribution 4.0 (CC BY-NC).

Первые результаты на орбите результатов измерения векторного магнитного поля с помощью высокоточного магнитометра на борту китайского сейсмо-электромагнитного спутника | Земля, планеты и космос

Спутниковые помехи измерениям HPM

Помехи от магнитного крутящего момента

Магнитный крутящий момент спутника разработан для работы на широтах ± 65 ° или выше.После работы он будет создавать помехи около 100 нТл на датчиках HPM. Магнитный момент практически не работает в пределах ± 65 ° широты. Однако, чтобы лучше контролировать остаточную намагниченность спутника, когда любой компонент геомагнитного поля становится равным нулю, магнитный момент начинает работать в соответствии с будущим направлением поля, чтобы намагнитить его внутреннее ядро ​​на 2 с. Нулевой компонент магнитного поля основан на расчетах спутником по модели геомагнитного поля.На рисунке 14 показано глобальное функционирование магнитного момента 24 августа 2018 года.

Рис. 14

Глобальное распределение работы магнитного момента 24 августа 2018 года. Когда любой компонент геомагнитного поля становится нулевым, магнитный момент намагничивает его. внутреннее ядро ​​на 2 с

Данные с высокой частотой дискретизации, передаваемые по каналу SPI, редко подвергаются влиянию магнитного момента. В то время как данные телеметрии глобального покрытия, передаваемые по шине CAN, загрязняются магнитным моментом на широте 65 ° или выше.В настоящее время помехи магнитного момента не удаляются из данных, и пользователь данных может судить о состоянии магнитного момента в соответствии с флагом качества данных. Последующий анализ данных в этой статье использует данные с высокой частотой дискретизации, передаваемые по каналу SPI.

Магнитный крутящий момент использует режим широтно-импульсной модуляции, поэтому уровни помех хорошо совпадают каждый раз, когда он работает. На рисунке 15 показана z-компонента FGM, когда магнитный крутящий момент работает в экваториальной области в течение 2 с.На рис. 15а фоновое магнитное поле было усреднено и вычтено из данных FGM, чтобы показать интерференцию магнитного поля магнитного момента. Из-за проницаемости магнитомягкого материала внутри магнитного крутящего момента магнитное поле, создаваемое магнитным крутящим моментом, имеет очевидный гистерезис. До и после срабатывания магнитного крутящего момента фоновые невязки изменяются при разных направлениях намагничивания на рис. 15b, что согласуется с результатами наземных магнитных испытаний спутника.Это влияние можно точно устранить с помощью данных наземной калибровки.

Рис. 15

Возмущения магнитного поля при измерениях FGM. a Возмущения магнитного поля на z-компоненте FGM2 при действии магнитного момента. Показаны девять рядов данных. Магнитный крутящий момент использует режим широтно-импульсной модуляции, поэтому уровни помех хорошо совпадают каждый раз, когда он работает. b Остатки при разных направлениях намагничивания различаются.С помощью данных наземной калибровки эту разницу можно точно устранить

Помехи от трехдиапазонного радиомаяка

Трехдиапазонный радиомаяк (TBB) — это трехчастотный радиомаяк, разработанный для обеспечения передачи на очень высоких частотах (VHF), сверхвысоких частотах (UHF) и L-диапазоне. (150/400/1067 МГц) (Chen et al.2018). Антенна TBB и штанга для датчиков HPM развернуты в плоскости + z спутника. Когда TBB передает сигналы на землю, сигналы могут попадать в кабели жгута датчика HPM и появляться как помехи при измерениях FGM.На рисунке 16 показано сравнение магнитного поля, измеренного HPM и моделью IGRF, когда TBB работает. Можно видеть, что TBB имеет разные помехи для трех компонентов FGM. Передача сигнала датчика CDSM осуществляется по оптоволокну, поэтому TBB не влияет на CDSM.

Рис. 16

Помехи, вызванные TBB. Когда трехдиапазонный маяк передает сигналы на землю, измерения FGM нарушаются

Проверяя скалярную разницу между FGM и CDSM, можно четко идентифицировать помехи, создаваемые TBB.TBB работает только тогда, когда его сигналы могут быть приняты взаимодействующими наземными станциями в материковом Китае, что означает, что помехи измерениям FGM очень ограничены. В данных HPM помехи от TBB не удаляются, и данные помечаются флагом качества, когда им мешает TBB.

Помехи от вращения солнечного крыла

В настоящее время CSES всегда вращает свое солнечное крыло на орбите. Во время вращения солнечного крыла некоторые микровибрации передаются на датчики FGM через платформу спутника и стрелу.На рисунке 17 сравнивается спектр данных FGM, когда солнечное крыло вращается, с данными, когда оно не вращается. Видно, что когда солнечное крыло неподвижно, спектр FGM очень чистый. Во время вращения солнечного крыла можно обнаружить помехи на нескольких определенных частотах, как показано стрелками на правой панели. На рисунке 18 показана спектральная плотность мощности (PSD) данных FGM после высокочастотной фильтрации с частотой отсечки 0,1 Гц и не вращающимся крылом солнечного света. Это можно интерпретировать как уровень шума FGM.Благодаря долгосрочному анализу и статистике, уровень шума каждого компонента датчика FGM может быть выше 18 \ ({\ text {pT}} / \ sqrt {\ text {Hz}} \) @ 1 Гц. В этом случае неестественные помехи иногда возникают примерно на 0,7 Гц в дневное время. Когда солнечное крыло вращается, шум FGM не изменяется, но помехи возникают на нескольких частотах ниже 1,25 Гц, и их появление имеет определенную корреляцию с орбитальным положением. Подробный механизм все еще исследуется.Предупреждаем пользователей об анализе геомагнитных пульсаций на этих частотах.

Рис. 17

Влияние вращения солнечного крыла. Две орбиты повторного посещения в спокойных геомагнитных условиях были выбраны для сравнения влияния вращения солнечного крыла. На левой панели показан спектр компонентов FGM, когда солнечное крыло не вращается 2 мая 2018 года, а на правой панели показан спектр, когда солнечное крыло вращается 11 июня 2018 года. Когда солнечное крыло может быть идентифицировано несколько конкретных частотных интерференций вращается

Фиг.18

Спектральная плотность мощности шума на орбите (PSD) FGM1 и FGM2. Данные проходят через фильтр верхних частот с частотой среза 0,1 Гц, и солнечное крыло не вращается

Сравнение скалярных данных FGM и скалярных данных CDSM

Разница между данными скалярного магнитного поля из CDSM и вычисленными FGM превышает 100 нТл до линейной калибровки FGM. Отклонение между двумя значениями скалярного магнитного поля может быть меньше 0,5 нТл или даже достигнуть нуля, если параметры FGM должным образом скорректированы.На рисунке 19 показано скалярное отклонение между FGM1, FGM2 и CDSM, когда данные, на которые влияют TBB и магнитный момент, удалены. Средние значения скалярного отклонения любого из двух датчиков ниже 0,1 нТл, скалярная дисперсия FGM1 и CDSM составляет 0,61 нТл, скалярная дисперсия FGM2 и CDSM составляет 0,43 нТл, а скалярная дисперсия FGM1 и FGM2 составляет 0,5 нТл. Результаты показывают хорошую согласованность результатов трех датчиков после линейной коррекции на орбите.

Фиг.19

Скалярные отклонения между данными FGM 1, FGM 2 и CDSM относятся к августу 2018 г .; помехи от TBB и магнитного момента удаляются перед расчетом отклонений

Сравнение с данными спутника SWARM

Можно сравнить данные магнитного поля спутников CSES и SWARM. Однако высота CSES и трех спутников SWARM различна. Кроме того, различаются моменты времени, когда спутники пролетают над одними и теми же пересечениями широты и долготы, и прямое сравнение приведет к относительно большим различиям.

Модель CHAOS — это геомагнитная модель, разработанная с использованием спутниковых данных и данных наземных наблюдений. Также учитывается влияние кольцевого тока (Olsen et al. 2006). Используя модель CHAOS в качестве справки:

$$ \ begin {align} \ Delta B & = B _ {\ text {CSES}} — B _ {\ text {SWARM}} — \ left ({B _ {\ text {CHAOS }} \ left ({t _ {\ text {CSES}}, h _ {\ text {CSES}}} \ right)} \ right. \\ & \ quad \ left. {- B _ {\ text {CHAOS}} \ left ({t _ {\ text {SWARM}}, h _ {\ text {SWARM}}} \ right)} \ right), \ end {align} $$

отклонение, вызванное разницей во времени и высоте орбиты, может быть уменьшенным.

На рисунке 20 показаны индексы Dst и Kp с 30 августа по 3 сентября 2018 г., предоставленные Мировым центром данных по геомагнетизму, Киото. Видно, что геомагнитное поле в этот период относительно спокойное, и сравниваются данные CSES и SWARM за этот период времени. Результаты и статистика показаны на рис. 21 и в таблице 3. Сравнение показывает, что как векторные, так и скалярные различия достаточно согласованы. Отклонение векторных данных зависит от широты.Изменения солнечной освещенности на спутнике вызывают деформацию штанги HPM и конструкции спутника. Соотношение ориентации между векторными датчиками магнитного поля и звездными датчиками изменяется.

Рис.20

Индекс Dst и Kp с 30 августа по 3 сентября 2018 г.

Рис.21

Сравнение данных магнитного поля CSES и SWARM B с 30 августа по 3 сентября 2018 г.

Таблица 3 Статистика спутниковых данных CSES и SWARM A, B и C с 30 августа по 3 сентября 2018 г.

Неопределенность данных векторного магнитного поля отражает неопределенность юстировки датчика.По результатам сравнения, погрешность юстировки датчика составляет порядка 0,01–0,05 ° в зависимости от широты.

Что означает вектор магнитного поля?

Зачем нужны векторы?

Векторы представляют собой набор физических величин, для полного описания которых требуется как величина (или длина), так и направление (пространственная ориентация). Возьмем, к примеру, реальную жизненную ситуацию. Вы спрашиваете меня, сколько шариков у меня в сумке. Я говорю, что это 10.Для ответа достаточно «10». А теперь задам другой вопрос. Как далеко отсюда твой дом? Вы, наверное, сказали бы около 20 км; не только 20. Необходимо включить дополнительные «км», чтобы полностью определить решение. Теперь мы спрашиваем, как добраться до вашего дома? Конечно, вам нужна помощь в направлениях на север, юг, восток, запад.

Аналогично некоторым физическим величинам. Упоминание только их количества кажется бессмысленным. Мы называем эти величины векторами. Эти величины требуют направления (представленного стрелками) вдоль каждой координаты плюс значение, принятое в некоторой точке, представленное точкой пробела.

Магнитное поле — вектор?

Ответ — нет. На самом деле это псевдовектор. Рассмотрим прямой длинный провод с током и постоянный ток, протекающий по нему. Это создаст магнитное поле, при этом силовые линии образуют замкнутые контуры или концентрические кольца вокруг провода. Как указать направление замкнутого контура. На самом деле силовые линии даже не циркулируют. Тогда как мы узнаем, что силовые линии имеют изгиб?

Как магнитное поле стало вектором?

Проделайте такой же эксперимент, как указано выше.Сначала заставьте ток течь вверх по проводу. Он будет генерировать магнитное поле в некоторой точке рядом с проводом, направление которого можно измерить с помощью компаса. Сохраняйте положение компаса фиксированным (т. Е. Расстояние между проводом и компасом). Стрелка компаса отклоняется в направлении линии поля в этой точке (которую мы представляем, проводя касательную к петле в этой точке). Теперь поменяйте направление тока. Удивительно, но вы видите, что стрелка компаса отклоняется в противоположном направлении.Что это значит? Это означает, что даже если силовые линии не циркулируют, их направление должно быть указано, чтобы указывать направление потока тока и, таким образом, силу, действующую на движущийся заряд.