Глава 15. Магнитное поле
§ 15.1 Вектор магнитной индукции. Закон Био-Савара-Лапласа и его применение
Все электрические и магнитные явления взаимосвязаны и взаимозависимы, так как являются различными формами проявления единого электромагнитного поля.
Источниками магнитного поля являются движущиеся электрические заряды (токи). Магнитное поле возникает в пространстве, окружающем проводники с током, подобно тому, как в пространстве, окружающем неподвижные электрические заряды, возникает электрическое поле. Магнитное поле постоянных магнитов также создается электрическими микротоками, циркулирующими внутри молекул вещества (гипотеза Ампера).
Магнитным полем называется вид материи, через которую передаётся силовое воздействие на движущиеся электрические заряды и тела, обладающие магнитным моментом.
Пробным элементом для изучения магнитного поля является бесконечно маленькая магнитная стрелка или контур с током, которые своим магнитным полем не искажают исследованное поле. Основным свойством неизменного во времени магнитного поля служит силовое воздействие его как на движущиеся в нем заряженные тела, так и на проводники с электрическим током (неподвижный электрический заряд, находящийся в магнитном поле, не испытывает никакого воздействия с его стороны).
Силовой
характеристикой магнитного поля является вектор
магнитной индукции  .
.
❖ Единица магнитной индукции — тесла (Тл).
Магнитное поле может быть описано полностью, если в каждой его точке найдены модуль и направление магнитной индукции
 .
.Подобно тому, как электрические поля графически изображают с помощью линий напряжённости (силовых линий), магнитные поля изображают с помощью линий магнитной индукции (силовых линий).
Л инии
магнитной индукции – линии, касательные к которым в данной
точке совпадают по направлению с вектором
инии
магнитной индукции – линии, касательные к которым в данной
точке совпадают по направлению с вектором 
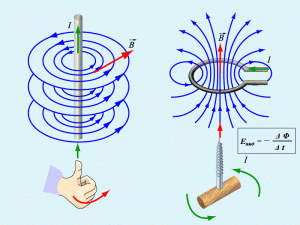
Направление В можно определить по правилу буравчика (рис.15.1): если буравчик с правой резьбой ввинчивать по направлению тока в проводнике, то направление вращения рукоятки буравчика совпадает с направлением вектора магнитной индукции магнитного поля, создаваемого этим током.
а
б
Есть и другое правило для определения направления – правило
обхвата правой рукой: если
обхватить проводник правой рукой,
направив отставленный большой палец
вдоль тока, то остальные пальцы этой
руки укажут направление вектора магнитной
индукции магнитного поля данного тока.
– правило
обхвата правой рукой: если
обхватить проводник правой рукой,
направив отставленный большой палец
вдоль тока, то остальные пальцы этой
руки укажут направление вектора магнитной
индукции магнитного поля данного тока.Силовые линии магнитного поля прямолинейного провода с током представляют собой концентрические окружности, охватывающие проводник и лежащие в плоскости перпендикулярной току. Центр этих окружностей находится на оси проводника.
Силовые линии магнитного поля не имеют ни начала, ни конца, они либо замкнуты, либо выходят из бесконечности и уходят снова в бесконечность. Это отличает их от линий напряжённости электрического поля. Замкнутость силовых линий магнитной индукции говорит о том, что в магнитном поле не существует источников и стоков, или в природе не существует магнитных зарядов, на которых они начинались или кончались. Такие поля называют вихревыми.
Магнитное поле является вихревым.
Циркуляция вектора магнитной индукции по любому замкнутому контуру не равна нулю:
 (15.1)
(15.1)
В
отличии от потенциального, каким является
электростатическое поле 
Магнитное поле называют однородным, если векторы магнитной индукции во всех его точках одинаковы:
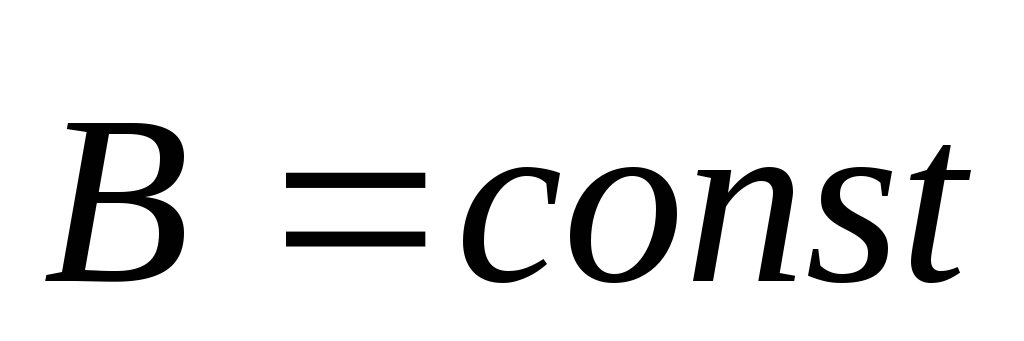 (15.2)
(15.2)
Линии
магнитной индукции однородного поля
параллельны, и их густота везде одинакова.
Плотностью линий магнитной индукции
можно характеризовать магнитную индукцию  .
.
Обобщая экспериментальные данные французских физиков Био и Савара, Лаплас (французский математик) предложил формулу, по которой можно вычислить индукцию магнитного поля, создаваемого элементом тока в точке М, расположенной от этого элемента на расстоянии r (рис. 15.2)
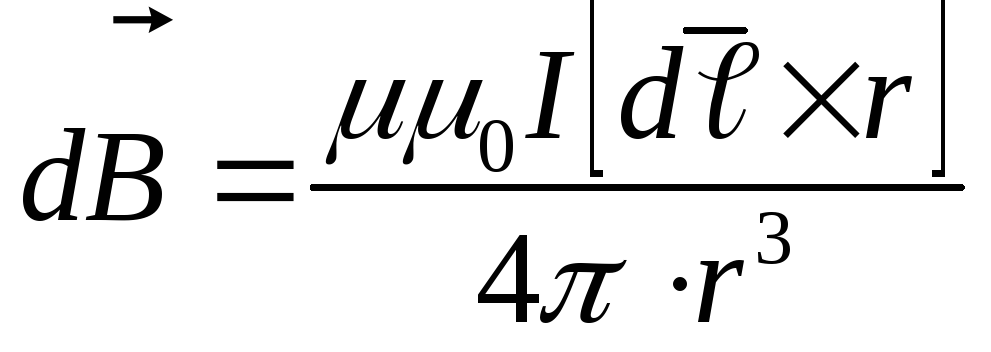 или
или
 (15.3)
(15.3)
По формуле (15.3) определяем индукцию поля, создаваемого участком проводника, по которому течёт ток I. Чтобы найти индукцию магнитного поля, создаваемого всем проводником, нужно применить принцип суперпозиции, или наложения полей.
Определим напряжённость поля, создаваемого прямолинейным бесконечно длинным проводником с током в точке М, находящейся на расстоянии r0 от проводника. Выделим на проводнике элемент тока Idℓ (рис. 15.2) и проведем радиус-вектор г в точку
 (15.4)
(15.4)
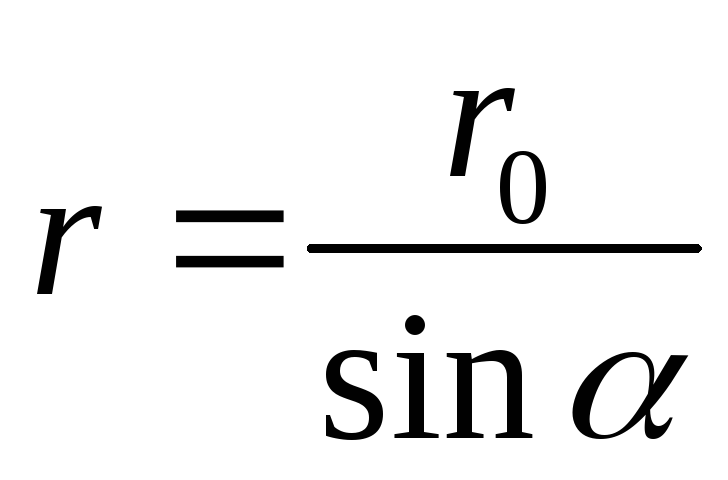 (15.5)
(15.5)
Подставляя эти выражения в (15.3), находим, что магнитная индукция поля, создаваемая элементом тока d
 (15.6)
(15.6)
Чтобы определить магнитную индукцию, создаваемого бесконечно длинным прямолинейным проводником с током, нужно проинтегрировать выражение (15.6) в пределах от α1 до α2
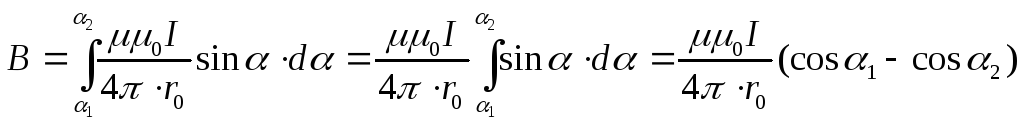

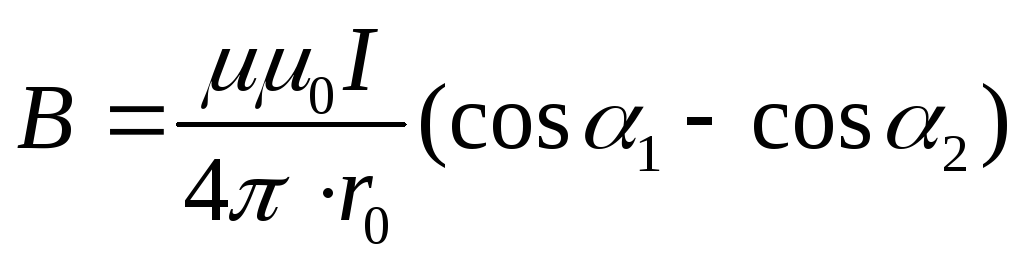
Используя формулу (15.7) можно определить магнитную индукцию поля, создаваемого проводником конечной длины (рис.15.3).
Для бесконечно длинного проводника: α1→0; cos 0=1.
α1→π; cos π =-1
Подставим в (15.7), получим
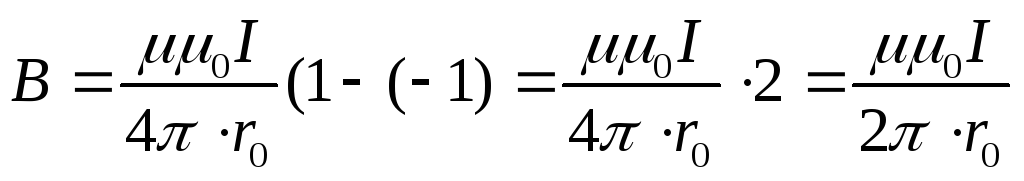 (15.8)
(15.8)
Магнитная индукция поля, создаваемого бесконечно длинным проводником, равна

Я = —
П усть
ток протекает по окружности (рис. 15.4). В
этом случае все элементы проводника
перпендикулярны радиус-векторуr
и sinα=1.
Расстояние всех элементов проводника
до центра одинаково и равно r.
усть
ток протекает по окружности (рис. 15.4). В
этом случае все элементы проводника
перпендикулярны радиус-векторуr
и sinα=1.
Расстояние всех элементов проводника
до центра одинаково и равно r. 
Магнитная индукция в центре кругового тока равна

Принцип суперпозиции позволяет описать поле, создаваемое любой системой проводников. В общем случае принцип суперпозиции для магнитных полей формулируется так: магнитная индукция поля, создаваемого несколькими проводниками с током, равна векторной сумме магнитных индукций, создаваемых каждым из проводников в отдельности.
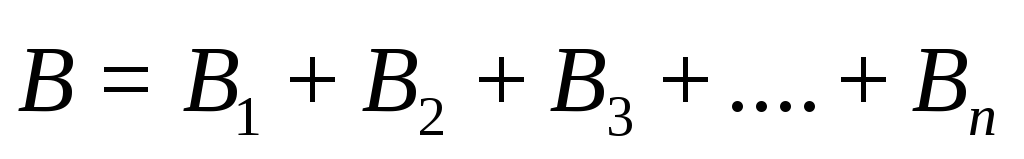 или
или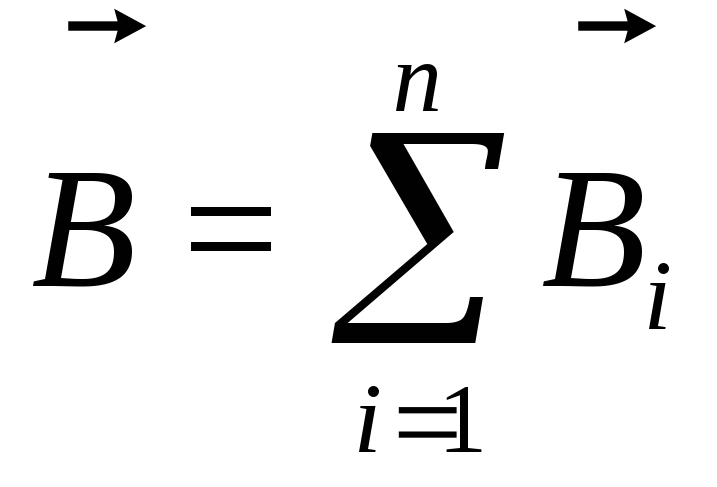 (15.11)
(15.11)
Из принципа суперпозиции полей следует, что при наложении полей они не оказывают никакого влияния друг на друга.
Магнитное поле в вакууме принято характеризовать не индукцией В, а напряжённостью Н магнитного поля. Эти величины связаны между собой:
 (15.12)
(15.12)
Векторы  и
и  совпадают
по направлению.
совпадают
по направлению.
Вектор магн индукции | От урока до экзамена
При прохождении тока по проводнику вокруг него образуется магнитное поле. Векторную характеристику магнитного поля называют вектором магнитной индукции . Это поле оказывает на рамку с током, помещенную в поле, ориентирующее действие. Такое действием магнитного поля на рамку с током или магнитную стрелку можно использовать для определения направления вектора магнитной индукции. За принимается направление, который показывает северный полюс N магнитной стрелки. Для определения направления вектора магнитной индукции поля, созданного прямолинейным проводником с током, пользуются правилом буравчика: если направление поступательного движения буравчика совпадает с направлением тока в проводнике, то направление вращения ручки буравчика указывает направление вектора магнитной индукции.
направление вектора магнитного поля прямого проводника с током.Если между полюсами подковообразного магнита поместить проводник с током, то он будет втягиваться или выталкиваться из поля магнита. Закон, определяющий силу, действующую на отдельный небольшой участок проводника, был установлен в 1820 г. А. Ампером.
Сила действия однородного магнитного поля на проводник с током прямо пропорциональна силе тока, длине проводника, модулю вектора индукции магнитного поля, синусу угла между вектором индукции магнитного поля и проводником:
F=B.I.ℓ. sin α — закон Ампера.
- Сила Ампера максимальна, если вектор магнитной индукции перпендикулярен проводнику.
- Если вектор магнитной индукции параллелен проводнику, то магнитное поле не оказывает никакого действия на проводник с током, т.е. сила Ампера равна нулю.
Направление силы Ампера (правило левой руки) Если левую руку расположить так, чтобы перпендикулярная составляющая вектора В входила в ладонь, а четыре вытянутых пальца были направлены по направлению тока, то отогнутый на 90° большой палец покажет направление силы, действующей на проводник с током.
Макроскопическим проявлением силы Лоренца является сила Ампера. Запишем силу, действующую на одну частицу. Если заряженная частица влетает в магнитное поле со скоростью , на нее со стороны магнитного поля действует сила, которую называют силой Лоренца: , a – угол между векторами и .
- В однородном магнитном поле, направленном перпендикулярно вектору скорости, под действием силы Лоренца заряженная частица будет равномерно двигаться по окружности постоянного радиуса r. Сила Лоренца в этом случае является центростремительной силой:
- Если заряженная частица движется в магнитном поле так, что вектор скорости составляет с вектором магнитной индукции угол a , то траекторией движения частицы является винтовая линия с радиусом r.
Если расположить левую руку так, чтобы составляющая магнитной индукции , перпендикулярная скорости заряда, входила в ладонь, а четыре вытянутых пальца были направлены по движению положительного заряда, то отогнутый на 900 большой палец укажет направление действующей на заряд силы Лоренца Fл
.
16. Вектор магнитной индукции
это основная силовая характеристика магнитного поля (обозначается В). Пробный контур, помещенный в магнитное поле, испытывает со стороны магнитного поля действие вращающего момента сил М.
Опытным путем было установлено, что для одной и той же точки магнитного поля максимальный вращающий момент М (момент сил) пропорционален произведению силы тока I в контуре на его площадь S. Величину IS называют магнитным моментом контура Pm.

Закон Био Савара Лапласа — Магнитное поле любого тока может быть вычислено как векторная сумма полей, создаваемая отдельными участками токов.
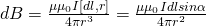
Закон Ампера
сила, действующая на проводник с током, помещенный в однородное магнитное поле, пропорциональна длине проводника, вектору магнитной индукции, силе тока и синусу угла между вектором магнитной индукции и проводником.

Если размер проводника произволен, а поле неоднородно, то формула выглядит следующим образом:
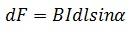
Направление силы Ампера определяется по правилу левой руки.
Сила Лоренца
Так как электрический ток представляет собой упорядоченное движение зарядов, то действие магнитного поля на проводник с током есть результат его действия на отдельные движущиеся заряды.
Силу, действующую со стороны магнитного поля на движущиеся в нем заряды, называют силой Лоренца.
Сила Лоренца определяется соотношением:
Fл = q·V·B·sin
где q — величина движущегося заряда; V — модуль его скорости; B — модуль вектора индукции магнитного поля; — угол между вектором скорости заряда и вектором магнитной индукции.
17. Закон индукции Фарадея — Изменение потока магнитной индукции, проходящего через незамкнутую поверхность S, взятое с обратным знаком, пропорционально циркуляции электрического поля на замкнутом контуре , l который является границей поверхности S.
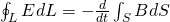
Другими словами :
Закон Фарадея для электромагнитной индукции — Для любого замкнутого контура индуцированная электродвижущая сила (ЭДС) равна скорости изменения магнитного потока, проходящего через этот контур
В формуле мы использовали :
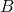 —Поток магнитной
индукции
—Поток магнитной
индукции
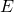 —Электрическое поле
—Электрическое поле
 —Бесконечно малый
элемент контура
—Бесконечно малый
элемент контура
—Бесконечно малый элемент вектора поверхности
18. Электромагнитная природа света. Т.к.
свет представляет собой электромагнитные
волны, то в основе волновой оптики лежат
уравнения Максвелла и вытекающие из
них соотношения для электромагнитных
волн. Согласно электромагнитной теории
Максвелла  ,
где с и v соответственно скорости
распространения света в среде с
диэлектрической проницаемостью
,
где с и v соответственно скорости
распространения света в среде с
диэлектрической проницаемостью 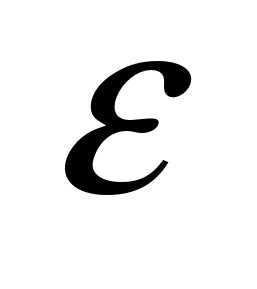 и
магнитной проницаемостью
и
магнитной проницаемостью и
в вакууме. Это соотношение связывает
оптические, электрические и магнитные
постоянные вещ-ва. По Максвеллу,
и
в вакууме. Это соотношение связывает
оптические, электрические и магнитные
постоянные вещ-ва. По Максвеллу,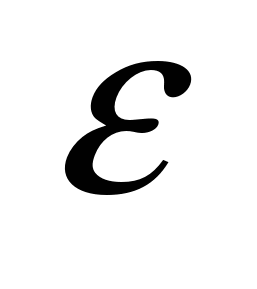 и
и —
величины, не зависящие от длины волны
света, поэтому электромагнитная теория
не могла объяснить явление дисперсии
(зависимость показателя преломления
от длины волны). Значения показателя
преломления характеризуют оптическую
плотность среды (оптически более и менее
плотные среды). Длина световой волны в
среде с показателем n связана с длиной
волны в вакууме:
—
величины, не зависящие от длины волны
света, поэтому электромагнитная теория
не могла объяснить явление дисперсии
(зависимость показателя преломления
от длины волны). Значения показателя
преломления характеризуют оптическую
плотность среды (оптически более и менее
плотные среды). Длина световой волны в
среде с показателем n связана с длиной
волны в вакууме: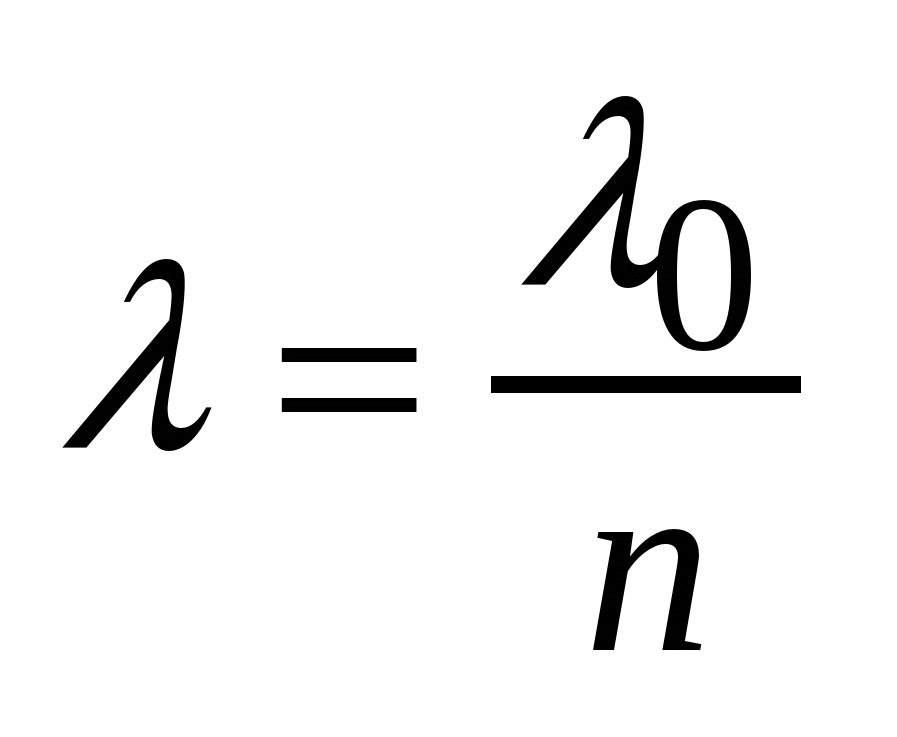 .
.
Вектор индукции магнитного поля
Определение
Силовой характеристикой магнитного поля является вектор магнитной индукции $\overrightarrow{B}$. Вектор магнитной индукции является основной характеристикой магнитного поля. Он равен пределу отношения силы, с которой магнитное поле действует на элементарный ток ($Idl$) к произведению тока $(I)$ и величины элемента проводника ($dl$):
Вектор индукции направлен перпендикулярно направлению элементарного тока (или чаще говорят элементу проводника ($\overrightarrow{dl}$)) из (1) и перпендикулярен направлению силы, которая действует со стороны магнитного поля.
Если $\overrightarrow{B}$=const, то магнитное поле называют однородным. Если магнитное поле неизменно во времени, то его называют постоянным.
Иногда модуль вектора индукции однородного магнитного поля определяют как:
где $M_{max}$ — максимальный вращающий момент, действующий на контур с током, который помещен в магнитное поле, $p_m=IS$ — магнитный момент контура ($S$- площадь контура). За направление вектора $\overrightarrow{B}$ принимают направление, в котором устанавливается под действием поля положительная нормаль к контуру с током. Или иначе, говорят, что вектор магнитной индукции направлен в сторону поступательного перемещения правого винта, если его вращать по направлению течения тока в контуре.
Очень часто, определение для вектора магнитной индукции записывают в виде:
где $\overrightarrow{dF}$ — сила, действующая на элемент с током. В том случае, если проводник прямолинейный и магнитная индукция во всех точках постоянна, то формулу (2) можно преобразовать в выражение:

Рис. 1
Модуль вектора индукции можно определить, так же исходя из силы Лоренца ($\overrightarrow{F}$), которая действует на движущуюся, со скоростью $\overrightarrow{v}$ заряженную частицу (заряд q) в магнитном поле:
Основной единицей измерения магнитной индукции в системе СИ является тесла (Тл).
Принцип суперпозиции вектора индукции магнитного поля
Эмпирический доказано, что для магнитного поля выполняется принцип суперпозиции:
Если магнитное поле порождается несколькими токами (движущимися зарядами), то оно равно векторной сумме отдельных полей:
Пример 1
Задание: Проводник имеет форму квадрата, сторона которого равна d, по нему течет ток силы I. Найдите магнитную индукцию поля в точке пересечения диагоналей квадрата.
Решение:
Допустим, что плоскость проводника совпадает с плоскостью рис.2. Зададим направление токов.

Рис. 2
В точке О магнитное поле создают четыре прямолинейные проводника с током. Напряженности всех четырех полей направлены в соответствии с правилом правого винта от нас, перпендикулярно плоскости рисунка. Следовательно, векторную сумму полей в принципе суперпозиции заменим на алгебраическую, запишем:
\[B=B_1+B_2+B_3+B_4\left(1.1\right).\]Причем из симметрии, очевидно, что модули всех индукций равны, значит, запишем, что:
\[B=4B_1\left(1.2\right).\]В разделе «Электромагнетизм» мы нашли, формулу для расчета модуля вектора магнитной индукции прямолинейного проводника с током. В применении к нашему случаю модуль $\overrightarrow{B}$ будет иметь вид:
\[B_1=\frac{{\mu }_0I}{4\pi b}\left(cos\alpha -cos\beta \right)\left(1.3\right),\]углы $\alpha $ и $\beta $ указаны на рис.1. В (1.3) $\beta =\pi -\alpha \to cos\beta ={cos \left(\pi -\alpha \right)\ }=-cos\alpha .$ Перепишем (1.3):
\[B_1=\frac{{\mu }_0I}{2\pi b}cos\alpha \left(1.4\right).\]Так как мы имеем дело с квадратом, то заметим, что: $b=\frac{d}{2},\alpha =\frac{\pi }{4}\to cos\alpha =\frac{\sqrt{2}}{2}.$ Подставим в (1.4), то что мы получили и (1.4) подставим в (1.2), имеем:
\[B=4\cdot \frac{{\mu }_0I}{\pi d}\cdot \frac{\sqrt{2}}{2}=\frac{2\sqrt{2}}{\pi d}{\mu }_0I.\]Ответ: $B=\frac{2\sqrt{2}}{\pi d}{\mu }_0I.$
Пример 2
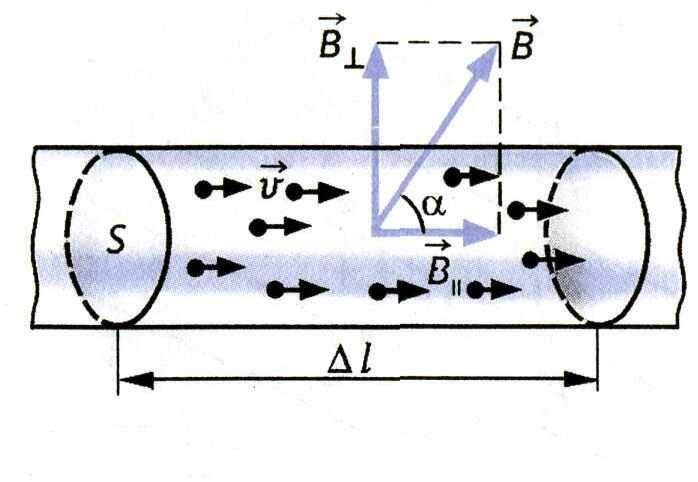
Задание: Бесконечно длинный проводник с током (I) согнут под прямым углом (рис.2). Найдите магнитную индукцию поля в точке А, которая указана на рис. 3.
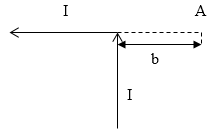
Рис. 3
Решение:
В точке А поле создается двумя частями проводника:
\[\overrightarrow{B}=\overrightarrow{B_{II}}+\overrightarrow{B_{\bot }}\left(2.1\right).\]Рассмотрим горизонтальный участок, на продолжении которого лежит точка А. Этот участок проводника с током создает поле в точке А индукция $(\overrightarrow{B_{II}})$которого, равна нулю, так как в точке А углы между всеми элементами с током и радиус-векторами будут равны $\pi .\ $Следовательно, векторное произведение ($\left[d\overrightarrow{l}\overrightarrow{r}\right]$), в законе Био — Савара — Лапласа равно нулю:
\[\overrightarrow{B}=\frac{{\mu }_0}{4\pi }\oint{\frac{I\left[d\overrightarrow{l}\overrightarrow{r}\right]}{r^3}}\left(2.2\right),\]где $\overrightarrow{r}$ — радиус-вектор, проведенный от элемента тока $Id\overrightarrow{l}$ к точке, в которой ищется индукция магнитного поля ($\overrightarrow{B}$).
Индукция магнитного поля бесконечного прямолинейного проводника с током (I) в точке А была бы равна:
\[B’=\frac{{\mu }_0}{2\pi }\frac{I}{b}\left(2.3\right).\]У нас полу бесконечный проводник, следовательно, из принципа суперпозиции получим, что для нашего проводника индукция равна:
\[{B=B}_{\bot }=\frac{1}{2}B’=\frac{{\mu }_0}{\pi }\frac{I}{b}.\]Ответ: $B=\frac{{\mu }_0}{\pi }\frac{I}{b}.$
Вектор магнитной индукции, теория и примеры
Определение и общие понятия вектора магнитной индукции
Результаты экспериментов Ампера с проводниками в магнитном поле показали, что способность магнитного поля вызывать появление механической силы, которая оказывает действие на элемент с током, можно количественно описать, если задать в каждой точке поля некоторый вектор (), который назвали вектором магнитной индукции. Сила, которая действует на элемент тока () равна:
где – сила Ампера. Выражение (1) можно считать определением магнитной индукции. Величина B равна пределу отношения силы (dF), с которой действует магнитное поле на элементарный проводник с током, к силе тока (I) умноженной на длину этого проводника (dl), при длине проводника стремящейся к нулю. При этом проводник имеет такое расположение в магнитном поле, что данный предел имеет максимальное значение:
Эмпирически легко показать, что магнитное поле, воздействуя на рамку с током, оказывает на нее ориентирующее действие, разворачивая ее определенным образом. Это связано с тем, что магнитное поле имеет направление. За направление магнитного поля в точке принимают направление положительной нормали к рассматриваемой рамке. В качестве направления магнитного поля, так же можно принимать направление силы, которая оказывает воздействие на северный полюс магнитной стрелки, если его размещают в точку поля.
Принцип суперпозиции для вектора магнитной индукции
Для магнитного поля выполняется принцип наложения (суперпозиции), который означает, что если присутствует несколько контуров с током и каждый из них создает поле с какой – то магнитной индукцией, то индукция результирующего поля равна векторной сумме отдельных индукций:
В частности магнитную индукцию поля, которое создано контуром с током находят как сумму индукций отдельных элементов тока, на которые разбивают рассматриваемый контур.
Закон Био-Савара-Лапласа
Этот закон дает возможность определить вектор магнитной индукции () в любой точке магнитного поля, которое создает в вакууме элемент проводника с током:
где I – сила тока; – вектор элемента проводника, который по модулю равен длине проводника, а направление его совпадает с направлением течения тока; – радиус-вектор, который проводят от элементарного проводника к точке, в которой ищут поле; – магнитная постоянная. Вектор является перпендикулярным к плоскости в которой расположены и , конкретное направление вектора магнитной индукции определяют при помощи правила буравчика (правого винта).
В однородном изотропном магнетике, заполняющем пространство, вектор магнитной индукции в вакууме( и в веществе (), при одинаковых условиях, связаны соотношением:
где – относительная магнитная проницаемость вещества.
Примеры решения задач
Вектор напряженности магнитного поля
Вектор напряжённости магнитного поля как вспомогательный вектор для описания поля в магнетиках
Когда мы рассматриваем магнитное поле в вакууме при отсутствии магнетиков, магнитное поле порождается токами проводимости и выполняется равенство:
где $\overrightarrow{j}$ — вектор плотности токов проводимости.
В магнетиках поле возникает благодаря токам проводимости и молекулярным токам ($\overrightarrow{j_m}$), что необходимо учитывать. Для молекулярных токов имеет место векторное равенство:
где $\overrightarrow{j_m}$ — объемная плотность молекулярных токов, $\overrightarrow{J\ }$ — вектор намагниченности. Так, при наличии магнетиков выражение (1) с учетом равенства (2) примет вид:
Выразим ток проводимости из уравнения (3), получим:
Определение вектора напряженности магнитного поля
Вектором напряженности магнитного поля называют вектор, равный:
Напряженность магнитного поля не является чисто полевой величиной, так как включает вектор $\overrightarrow{J\ },\ $который является характеристикой намагниченности среды. По своему значению $\overrightarrow{H}$ является вспомогательным вектором и играет роль подобную вектору электрического смещения $\overrightarrow{D\ }\ $в электричестве.
Основные уравнения для вектора напряженности
Из определения вектора $\overrightarrow{H}$ и уравнения (4), следует весьма удобное уравнение для вычисления поля в магнетиках:
Закон полного тока при наличии магнетиков имеет вид:
Формула (7) выражает теорему о циркуляции вектора напряженности магнитного поля, которая гласит:
Теорема
«Циркуляция вектора напряженности магнитного поля по некоторому контуру равна алгебраической сумме макроскопических токов, которые охвачены заданным контуром».
В вакууме $\overrightarrow{J\ }=0$, тогда:
\[\overrightarrow{H}=\frac{\overrightarrow{B}}{{\mu }_0}\left(8\right).\]Напряженность поля прямолинейного бесконечного проводника в вакууме определяется формулой:
\[H=\frac{1}{2\pi }\frac{I}{b}\left(9\right),\]где $b$ — расстояние от проводника до точки, где рассматривается поле. Из формулы (9) определяется размерность напряженности магнитного поля. Основная единица напряженности в системе СИ — ампер деленный на метр ($\frac{А}{м}$).
Связь и вектора напряженности магнитного поля с намагниченностью и вектором магнитной индукции
Обычно вектор намагниченности ($\overrightarrow{J}$) связывают с вектором напряженности в каждой точке магнетика:
\[\overrightarrow{J}=\varkappa \overrightarrow{H}\left(10\right),\]где $\varkappa $ — магнитная восприимчивость, безразмерная величина. Для неферромагнитных веществ и в не больших полях $\varkappa $ не зависит от напряженности. В анизотропных средах $\varkappa $ является тензором и направления $\overrightarrow{J}$ и $\overrightarrow{H}$ не совпадают.
Помимо магнитной восприимчивости в магнетиках используют другую безразмерную физическую величину, которая характеризует магнитные свойства вещества — это относительная магнитная проницаемость (или просто магнитная проницаемость ($\mu $)) вещества. Причем:
\[\mu =1+\varkappa \ \left(11\right).\]Тогда между индукцией магнитного поля в магнетике и напряженностью магнитного поля существует следующая связь:
\[\overrightarrow{B}=\mu {\mu }_0\overrightarrow{H}\left(12\right).\]Формула (12) показывает, что в изотропных средах векторы $\overrightarrow{B}$ и $\overrightarrow{H}$ имею одинаковое направление, однако по модулю напряженность поля в $\mu {\mu }_0$ раз меньше.
Пример 1
Задание: По оси бесконечного прямого круглого цилиндра радиуса R течет ток силы I. Магнитная проницаемость вещества цилиндра равна $\mu $. Вне цилиндра вакуум (${\mu }_v=1$). Найдите формулу для вычисления напряженности во всех точках пространства.
Решение:
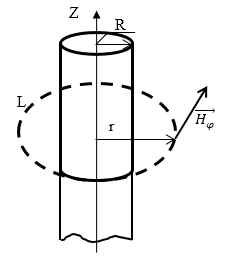
Рис. 1
Пусть ток течет в направлении оси Z. Линиями напряженности такого цилиндра являются концентрические окружности с центрами, которые лежат на оси цилиндра.
В качестве контура интегрирования (L) возьмем окружность радиусом r, центр окружности лежит на оси цилиндра, плоскость окружности перпендикулярна току. По закону полного тока для напряженности магнитного поля имеем:
\[\oint\limits_L{\overrightarrow{H\ }\overrightarrow{dl}}=H_{\varphi }2\pi r=I\left(1.1\right).\]Из (1.1) выразим напряженность поле, получим:
\[H_{\varphi }=\frac{I}{2\pi r}\left(1.2\right),\]где $H_{\varphi }$ — напряжённость магнитного поля, касательная к окружности. В таком случае индукция магнитного поля равна:
\[B_{\varphi }=\left\{ \begin{array}{c} \mu {\mu }_0H_{\varphi }=\mu {\mu }_0\frac{I}{2\pi r}\ (при\ 0\le r\le R) \\ {\mu }_0H_{\varphi }={\mu }_0\frac{I}{2\pi r}\left(при\ r\ge R\right). \end{array} \right.\]На границе цилиндра индукция магнитного поля терпит разрыв.
Ответ: $B_{\varphi }=\left\{ \begin{array}{c} \mu {\mu }_0H_{\varphi }=\mu {\mu }_0\frac{I}{2\pi r}\ (при\ 0\le r\le R) \\ {\mu }_0H_{\varphi }={\mu }_0\frac{I}{2\pi r}\left(при\ r\ge R\right). \end{array} \right.$.Пример 2
Задание: Найдите намагниченность меди и магнитную индукцию поля, если удельная магнитная восприимчивость вещества ${\varkappa }_u=-1,1\cdot {10}^{-9}\frac{м^3}{кг}.$ Напряженность магнитного поля равна ${10}^6\frac{А}{м}$.
Решение:
Магнитная восприимчивость ($\varkappa $) связана с удельной магнитной восприимчивостью (${\varkappa }_u$) соотношением:
\[\varkappa =\rho {\varkappa }_u\left(2.1\right),\]где $\rho =8930\frac{кг}{м^3}$ — массовая плотность меди.
Намагниченность имеет связь с напряженностью магнитного поля, которая имеет вид (считаем медь изотропной):
\[J=\varkappa H=\rho {\varkappa }_uH\ \left(2.2\right).\]Индукция магнитного поля, также связана с напряженностью:
\[B=\mu {\mu }_0H={\mu }_0(H+J)\left(2.3\right).\]Так как все величины даны в СИ, проведем вычисления:
\[J=8930\cdot \left(-1,1\cdot {10}^{-9}\right){10}^6=-9,823\left(\frac{А}{м}\right).\] \[B=4\pi \cdot {10}^{-7}\left(9,823+{10}^6\right)=1,26\ \left(Тл\right).\]Ответ: $J=-9,823\frac{А}{м},\ B=1,26\ Тл.$
магнитный вектор — это… Что такое магнитный вектор?
- магнитный вектор
- magnetischer Vektor
магнитный вектор
Вектор напряженности магнитного поля световой волны.
[Сборник рекомендуемых терминов. Выпуск 79. Физическая оптика. Академия наук СССР. Комитет научно-технической терминологии. 1970 г.]Тематики
- физическая оптика
Обобщающие термины
- основные свойства оптического излучения
- световые волны
EN
DE
Русско-немецкий словарь нормативно-технической терминологии. academic.ru. 2015.
- магнитный
- магнитный вектор излучения
Смотреть что такое «магнитный вектор» в других словарях:
магнитный вектор — Вектор напряженности магнитного поля световой волны. [Сборник рекомендуемых терминов. Выпуск 79. Физическая оптика. Академия наук СССР. Комитет научно технической терминологии. 1970 г.] Тематики физическая оптика Обобщающие термины основные… … Справочник технического переводчика
магнитный вектор — magnetinis vektorius statusas T sritis fizika atitikmenys: angl. magnetic vector vok. magnetischer Vektor, m rus. магнитный вектор, m pranc. vecteur magnétique, m … Fizikos terminų žodynas
магнитный вектор излучения — ( ) Вектор напряженности магнитного излучения. [ГОСТ 7601 78] Тематики оптика, оптические приборы и измерения Обобщающие термины величины оптического излучения EN magnetic vector of radiation DE magnetischer Vektor der Strahlung FR vecteur… … Справочник технического переводчика
МАГНИТНЫЙ МОМЕНТ — основная величина, характеризующая магн. свойства в ва. Источником магнетизма (М. м.), согласно классич. теории эл. магн. явлений, явл. макро и микро(атомные) электрич. токи. Элем. источником магнетизма считают замкнутый ток. Из опыта и классич.… … Физическая энциклопедия
Магнитный момент — Размерность L2I Единицы измерения СИ А⋅м2 … Википедия
МАГНИТНЫЙ ПОТОК — (поток магнитной индукции), поток Ф вектора магн. индукции В через к. л. поверхность. М. п. dФ через малую площадку dS, в пределах к рой вектор В можно считать неизменным, выражается произведением величины площадки и проекции Bn вектора на… … Физическая энциклопедия
МАГНИТНЫЙ МОНОПОЛБ — гипотетич. частица, обладающая положит. или отрицат. магн. зарядом точечным источником радиального магн. поля. М. м. можно представлять как отдельно взятый полюс длинного и тонкого пост. магнита. Магн. заряд определяет напряжённость магн. поля… … Физическая энциклопедия
МАГНИТНЫЙ ПОТОК — поток вектора магнитной индукции В через какую либо поверхность. Магнитный поток через малую площадку dS, в пределах которой вектор В неизменен, равен dФ = ВndS, где Bn проекция вектора на нормаль к площадке dS. Магнитный поток Ф через конечную… … Большой Энциклопедический словарь
Вектор намагничивания — магнитный момент элементарного объёма, используемый для описания магнитного состояния вещества. По отношению к направлению вектора магнитного поля различают продольную намагниченность и поперечную намагниченность. Поперечная намагниченность… … Википедия
Магнитный диполь — Классическая электродинамика Магнитное поле соленоида Электричество · Магнетизм Электростатика Закон Кулона … Википедия
Магнитный монополь — Магнитный монополь гипотетическая элементарная частица, обладающая ненулевым магнитным зарядом точечный источник радиального магнитного поля. Магнитный заряд является источником статического магнитного поля совершенно так же, как… … Википедия



