Единица измерения энергии, теория и онлайн калькуляторы

Определение

Энергия — это физическая величина служащая мерой разных форм движения и взаимодействия материи, мерой перехода разных форм материи.

Энергия отображает способность физической системы к совершению работы, при этом работа является мерой изменения энергии. Из этого следует, что работа и энергия имеют одинаковые единицы измерения.

Единицы измерения энергии в Международной системе единиц

В международной системе единиц (СИ) джоуль (Дж) — единица измерения энергии и работы. Исходя из механического определения работы:

\[A=\overline{F}\cdot \overline{s}(1)\]

один джоуль — это работа ($A$), которую совершает сила ($\overline{F}$) в один ньютон при перемещении ($\overline{s}$) точки приложения силы в один метр:

\[1\ Дж=1\ Н\cdot 1\ м.\]

Джоуль не является основной единицей системы СИ. Через основные единицы джоуль легко выразить, используя механическое определение работы и единицы измерения соответствующих величин:

\[\left[A\right]=\left[F\right]\left[s\right]=Н\cdot м=\frac{кг\cdot м}{с^2}\cdot м=\frac{кг\cdot м^2}{с^2}.\]

Такую же размерность можно получить, если использовать определение энергии вида:

\[E=mc^2\left(2\right),\]

где $c$ — скорость света; $m$ — масса тела. Исходя из выражения (2), имеем:

\[\left[A\right]=\left[E\right]=кг\cdot {\left(\frac{м}{с}\right)}^2=\frac{кг\cdot м^2}{с^2}.\]

И так, мы убедились, что джоуль — единица измерения энергии. Насколько велик джоуль можно понять, если решить простую задачу: тело массой 2 кг движется со скоростью 1$\frac{м}{с}$ , какова его кинетическая энергия? Вычислим кинетическую энергию ($E_k$) нашего тела используя ее определение:

\[E_k=\frac{mv^2}{2}\left(3\right),\]

получаем:

\[E_k=\frac{2\cdot 1^2}{2}=1\ \left({\rm Дж}\right).\]

Единицы измерения энергии в других системах единиц

В системе СГС (сантиметр, грамм, секунда) энергия (и работа) измеряются в эргах (эрг). При этом одни эрг равен:

\[1\ эрг=1\ дин\cdot 1\ см.\]

Зная, что:

\[1\ Н={10}^5{\rm дин};;1\ {\rm м}=100\ см,\]

получаем:

\[1\ Дж={10}^7эрг.\]

В технических расчетах встречается такая единица измерения энергии как килограммометр (кгм) или килограмм силы (кгс) на метр (м): (кгсм). При этом считают, что:

\[1кгсм=1\ кгс\cdot 1\ м=9,81\ Дж.\]

При расчетах тепла часто в качестве единицы измерения энергии используют калорию. Калорию определяют как:

\[1\ кал=4,1868\ Дж.\]

Гигакалорию (Гкал) применяют в теплоэнергетике, коммунальных хозяйствах, система отопления.

Энергию можно выражать в киловатт часах:

\[1\ кВт\cdot ч=3,6\cdot {10}^5Дж.\]

В основном данную единицу измерения используют в электроэнергетике.

В атомной и квантовой физике применяют такую единицу измерения энергии как электрон-вольт (эВ). При этом полагают, что:

\[1\ эВ=1,6\cdot {10}^{-19}Дж.\]

Электрон — вольт — это энергия, которую приобретает частица, имеющая элементарный заряд (з

Единицы теплоты

 

“…- Сколько попугаев в тебе поместится, такой у тебя рост.
– Очень надо! Я не стану глотать столько попугаев!…”

Из м/ф “38 попугаев”

В соответствии с международными правилами СИ (международная система единиц измерения) количество тепловой энергии или количество тепла измеряется в Джоулях [Дж], также существуют кратные единицы килоДжоуль [кДж] = 1000 Дж., МегаДжоуль [МДж] = 1 000 000 Дж, ГигаДжоуль [ГДж] = 1 000 000 000 Дж. и пр. Эта единица измерения тепловой энергии является основной международной единицей и наиболее часто используется при проведении научных и научно-технических расчётов.

Однако, все из нас знают или хотя бы раз слышали и другую единицу измерения количества теплоты (или просто тепла) это калория, а также килокалория, Мегакалория и Гигакалория, что означают приставки кило, Гига и Мега, смотреть пример с Джоулями выше. В нашей стране исторически сложилось так, что при расчёте тарифов за отопление,  будь то отопление электроэнергией, газовыми или пеллетными котлами принято считать стоимость именно одной Гигакалории тепловой энергии.

Так что же такое Гигакалория, килоВатт, килоВатт*час или килоВатт/час и Джоули и как они связаны между собой?, вы узнаете в этой статье.

Итак, основная единица тепловой энергии это, как уже было сказано, Джоуль. Но прежде чем говорить об единицах измерения необходимо в принципе на бытовом уровне разъяснить что такое тепловая энергия и как и для чего её измерять.

Всем нам с детства известно, чтобы согреться (получить тепловую энергию) нужно что-то поджечь, поэтому все мы жгли костры, традиционное топливо для костра – это дрова.  Таким образом, очевидно, при горении топлива (любого: дрова, уголь, пеллеты, природный газ, солярка) выделяется тепловая энергия (тепло).  Но, чтобы нагреть, к примеру, различные объёмы воды требуется разное количество дров (или иного топлива). Ясно, что для нагрева двух литров воды достаточно нескольких пален в костре, а чтобы приготовить полведра супа на весь лагерь, нужно запастись несколькими вязанками дров. Чтобы не измерять такие строгие технические величины, как количество теплоты и теплота сгорания топлива вязанками дров и вёдрами с супом, теплотехники решили внести ясность и порядок и договорились выдумать единицу количества теплоты. Чтобы эта единица была везде одинаковая её определили так: для нагрева одного килограмма воды на один градус при нормальных условиях (атмосферном давлении) требуется 4 190 калорий, или 4,19 килокалории, следовательно, чтобы нагреть один грамм воды будет достаточно в тысячу раз меньше теплоты – 4,19 калории.

Калория связана с международной единицей тепловой энергии – Джоулем следующим соотношением:

1 калория = 4,19 Джоуля.

Таким образом, для нагрева 1 грамма воды на один градус потребуется 4,19 Джоуля тепловой энергии, а для нагрева одного килограмма воды 4 190 Джоулей тепла.

В технике, наряду с единицей измерения тепловой (и всякой другой) энергии существует единица мощности и, в соответствии с международной системой (СИ) это Ватт. Понятие мощности также применимо и к нагревательным приборам. Если нагревательный прибор способен отдать за 1 секунду 1 Джоуль тепловой энергии, то его мощность равна 1 Ватт.  Мощность, это способность прибора производить (создавать) определённое количество энергии (в нашем случае тепловой энергии) в единицу времени. Вернёмся к нашему примеру с водой, чтобы нагреть один килограмм (или один литр, в случае с водой килограмм равен литру) воды на один градус Цельсия (или Кельвина, без разницы) нам потребуется мощность  1 килокалория или 4 190 Дж. тепловой энергии. Чтобы нагреть один килограмм воды за 1 секунду времени на 1 грдус нам нужен прибор следующей мощности:

4190 Дж./1 с. = 4 190 Вт. или 4,19 кВт.

Если мы хотим нагреть наш килограмм воды на 25 градусов за ту же секунду, то нам потребуется мощность в двадцать пять раз больше т.е.

4,19*25 =104,75 кВт.

Таким образом, можно сделать вывод, что пеллетный котёл мощностью 104,75 кВт. нагревает 1 литр воды на 25 градусов за одну секунду.

Раз мы добрались до Ватт и килоВатт, следует и о них словечко замолвить. Как уже было сказано Ватт – это единица мощности, в том числе и тепловой мощности котла, но ведь кроме пеллетных котлов и газовых котлов человечеству знакомы и электрокотлы, мощность которых измеряется, разумеется, в тех же килоВаттах и потребляют они не пеллеты и не газ, а электроэнергию,  количество которой измеряется в килоВатт часах. Правильное написание единицы энергии килоВатт*час (именно, килоВатт умножить на час, а не разделить), запись кВт/час – является ошибкой!

В электрокотлах электрическая энергия преобразуется в тепловую (так называемое, Джоулево тепло), и , если котёл потребил 1 кВт*час электроэнергии, то сколько же он выработал тепла? Чтобы ответить на это простой вопрос, нужно выполнить простой расчёт.

Преобразуем килоВатты  в  килоДжоули/секунды (килоДжоуль в секунду), а часы в секунды: в одном часе 3 600 секунд, получим:

1 кВт*час =[ 1 кДж/с]*3600 c.=1 000 Дж *3600 с = 3 600 000 Джоулей или 3,6 МДж.

Итак,

1 кВт*час = 3,6 МДж.

В свою очередь, 3,6 МДж/4,19 = 0,859 Мкал = 859 ккал = 859 000 кал. Энергии (тепловой).

Теперь перейдём к Гигакалории, цену которой на различных видах топлива любят считать теплотехники.

1 Гкал = 1 000 000 000 кал.

1 000 000 000 кал. = 4,19*1 000 000 000 = 4 190 000 000 Дж.= 4 190 МДж. = 4,19 ГДж.

Или зная, что 1 кВт*час = 3,6 МДж пересчитаем 1 Гигакалорию на килоВатт*часы:

1 Гкал =  4190 МДж/3,6 МДж = 1 163 кВт*часов!

 

Если прочитав данную статью вы решили, проконсультироваться со специалистом нашей компании по любому вопросу, связанному с теплоснабжением, то вам Сюда!

 

 

 

 

В чем измеряется энергия 🚩 единица измерения электрической энергии 🚩 Естественные науки

Джеймс Джоуль развил и доработал законы Ньютона, что сыграло важную роль в определении видов механической энергии. В частности, он показал, что теплота – это разновидность энергии.

Связь между силой и энергией

Чтобы понять, что такое джоуль, нужно сперва обратиться к определению понятия единицы силы – ньютона. Ньютон – это сила, которая может ускорить 1 кг массы со скоростью 1 метр в секунду. Джоуль – это количество израсходованной энергии или работы. Так, 1 джоуль равен израсходованной силе в 1 ньютон.

Мощность и энергия

Когда речь заходит о приборах, которыми люди пользуются дома, то обычно никого не интересует, сколько устройство расходует энергии в секунду. Важнее то, с какой скоростью прибор забирает энергию за единицу времени. Такая величина называется «мощность». Ее можно представить формулой:

Мощность = энергия/время

В частности, разновидностью мощности является электроэнергия. Ее измеряют в ваттах. Ватт – это единица измерения мощности, названная в честь ученого Джеймса Уатта. Соотношение ватта и джоуля можно выразить формулой:

1 ватт = 1 джоуль/1 секунда

Хотя энергия и мощность тесно связаны, их не следует путать. Важно понимать, что мощность – это скорость поглощаемой энергии, а не само количество энергии. Прибегнув к помощи алгебры, можно выразить энергию простым уравнением:

Энергия = сила *время

Опираясь на вышесказанное, можно утверждать, что электрическая лампочка мощностью в 100 ватт – это прибор, который превращает 100 джоулей электрической энергии в 100 джоулей электромагнитного излучения (или света) каждую секунду. Если не погашать такую лампу в течение часа, то энергия, которую она поглотит, будет равна 360000 джоулей. Это можно показать в уравнении:

Энергия = сила*время= 100 дж./сек. * 3600 секунд = 360000 джоулей

Ватты – это удобная единица измерения, когда речь заходит об электроприборах. Например, с их помощью можно определить мощность ламп. Но бывают ситуации, когда важно знать расход энергии в целом. Например, вам нужно посчитать, сколько придется заплатить за электроэнергию по квитанции. На практике для подсчета энергопотребления пользоваться джоулями в качестве единицы измерения не очень удобно. Тогда используется другая единица – киловатт в час. 1 киловатт в час энергии равен 1000 ваттам мощности, поглощаемой за 60 минут. Примерно столько энергии уходит на работу обычного фена для волос в течение одного часа.

В измерении электроэнергии также применяют амперы и вольты. Вольт – это единица измерения определенного заряда энергии. С помощью амперов измеряют электрический ток.

Калории и джоули

Энергия также может измеряться в калориях. Калории, как правило, связаны с едой. Но их можно использовать для измерения и других видов энергии. 1 калория равна 4, 184 джоуля.

Чтобы израсходовать 1 литр бензина, потребуется 7 750 000 калорий.

Калории, которые вы видите на упаковках с пищевыми продуктами, — это, на самом деле, килокалории. В одной килокалории содержится 1000 калорий.

В каких единицах измеряются энергия, работа и мощность? Как эти величины связаны между собой и что они характеризуют? Что такое механический эквивалент теплоты?

Министерство образований Российской Федерации

Томский межвузовский центр

дистанционного образования

Томский государственный университет

систем управления и радиоэлектроники

(ТУСУР)

ОТЧЕТ

По контрольной работе № — 1

по дисциплине «Концепции современного естествознания»

Студент ТМЦДО гр.: з-836-а

специальность: 80505

Лариса Васильевна Книженцева

31 октября 2009 год.

Риддер

2009г.

1. Что понимается под понятием «закон природы»? Чем отличается закон природы от закона, установленного государством? Как формировалась система доказательств в науке и обществе? Определите понятия «научная революция» и приведите примеры.

Закон природы — для человека нового времени самый значительный и (в области неорганического) самый непреложный закон, понятие которого установилось окончательно только в 17 — 18 вв. как результат прогресса точных наук; иногда под законом природы понимается математическое выражение какого-либо природного явления, которое совершается при известных обстоятельствах всегда и всюду с одинаковой необходимостью.

Естественные законы, сопряжены с разумом, то гражданские —  опираются на силу. Однако по своему содержанию они одинаковы. Всякие произвольные выдумки законодателей не могут быть гражданскими законами, ибо последние суть те же естественные законы, но только подкрепленные авторитетом и мощью государства. Их нельзя ни отменять, ни изменять простым  волеизъявлением государства.

2. Сформулируйте основные законы классической механики материальной точки. Как моделируется система, состоящая из двух и более материальных точек? Приведите примеры задач, в которых можно считать Землю материальной точкой и примеры в которых нельзя.

МАТЕРИАЛЬНАЯ ТОЧКА – модельное понятие (абстракция) классической механики, обозначающее тело исчезающие малых размеров, но обладающее некоторой массой.

С одной стороны, материальная точка – простейший объект механики, так как его положение в пространстве определяется всего тремя числами. Например, тремя декартовыми координатами той точки пространства, в которой находится наша материальная точка. С другой стороны, материальная точка – основной опорный объект механики, так как именно для нее сформулированы основные законы механики. Все другие объекты механики – материальные тела и среды – могут быть представлены в виде той или иной совокупности материальных точек. Например, любое тело можно «разрезать» на малые части и каждую из них принять в качестве материальной точки с соответствующей массой. Когда можно «заменить» реальное тело материальной точкой при постановке задачи о движении тела, зависит от тех вопросов, на которые должно ответить решение формулируемой задачи.

Возможны различные подходы к вопросу об использовании модели материальной точки. Один из них носит эмпирический характер. Считают, что модель материальной точки применима тогда, когда размеры движущихся тел пренебрежимо малы по сравнению с величиной относительных перемещений этих тел. В качестве иллюстрации можно привести Солнечную систему. Если считать, что Солнце – неподвижная материальная точка и считать оно действует на другую материальную точку-планету по закону всемирного тяготения, то задача о движении точки-планеты имеет известное решение. Среди возможных траекторий движения точки есть и такие, на которых выполняются законы Кеплера, эмпирически установленные для планет солнечной системы. Таким образом, при описании орбитальных движений планет модель материальной точки вполне удовлетворительна. (Однако построение математической модели таких явлений как солнечные и лунные затмения требует учета реальных размеров Солнца, Земли и Луны, хотя эти явления, очевидно, связаны с орбитальными движениями.)

Отношение диаметра Солнца к диаметру орбиты ближайшей планеты – Меркурию – составляет величину ~ 1·10^–2, а отношения диаметров ближних к Солнцу планет к диаметрам их орбит – величины ~ 1 ÷ 2·10^–4. Могут ли эти числа служить формальным критерием для пренебрежения размерами тела в других задачах и, следовательно, для приемлемости модели материальной точки? Практика показывает, что нет.

Например, маленькая пуля размером l = 1 ÷ 2 см пролетает расстояние L = 1 ÷ 2 км, т.е. отношение

, однако траектория полета (да и дальность) существенно зависит не только от массы пули, но и от ее формы, и от того, вращается ли она. Поэтому даже маленькую пулю, строго говоря, нельзя считать материальной точкой. Если в задачах внешней баллистики метаемое тело часто считают материальной точкой, то это сопровождается оговорками ряда дополнительных условий, как правило, эмпирически учитывающих реальные характеристики тела. Если обратиться к космонавтике, то когда космический аппарат (КА) выведен на рабочую орбиту, при дальнейших расчетах траектории его полета он считается материальной точкой, так как никакие изменения формы КА не оказывают сколько-нибудь заметного влияния на траекторию. Лишь иногда, при коррекциях траектории возникает необходимость обеспечения точной ориентации реактивных двигателей в пространстве. Когда же спускаемый отсек приблизится к поверхности Земли на расстояние ~100 км, он сразу «превращается» в тело, поскольку от того, каким «боком» он входит в плотные слои атмосферы, зависит, доставит ли отсек в нужную точку Земли космонавтов и возвращаемые материалы. Модель материальной точки оказалась практически неприемлемой для описания движений таких физических объектов микромира, как элементарные частицы, атомные ядра, электрон и т.п.

Другой подход к вопросу об использовании модели материальной точки носит рациональный характер. По закону изменения количества движения системы, примененному к отдельному телу, центр масс С тела имеет такое же ускорение, как и некоторая (назовем ее эквивалентной) материальная точка, на которую действуют те же силы, что и на тело, т.е.

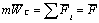
Вообще говоря, результирующая сила может быть представлена в виде суммы , где зависит только от

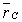
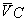и (радиус-вектор и скорость точки С), а 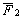– и от угловой скорости тела и его ориентации.

Если F₂ = 0, то приведенное выше соотношение превращается в уравнение движения эквивалентной материальной точки.

В этом случае говорят, что движение центра масс тела не зависит от вращательного движения тела. Таким образом, возможность использования модели материальной точки получает математическое строгое (а не только эмпирическое) обоснование. Естественно, что на практике условие F

2 = 0 выполняется редко и обычно F₂ № 0, однако может оказаться, что F₂ в каком-то смысле мало по сравнению с F₁. Тогда можно говорить, что модель эквивалентной материальной точки является некоторым приближением при описании движения тела. Оценка точности такого приближения может быть получена математически и если эта оценка окажется приемлемой для «потребителя», то замена тела на эквивалентную материальную точку допустима, в противном случае такая замена приведет к значительным ошибкам.

Это может иметь место и тогда, когда тело движется поступательно и с точки зрения кинематики его можно «заменить» на некоторую эквивалентную точку.

Единица измерения энергии и работы в международной системе (СИ) — Джоуль.   В системе СИ мощность измеряется в Ваттах, или в Джоулях в секунду.

Физическая величина, равная произведению модуля силы на модуль перемещения и косинус угла между ними, называется механической работой: А = Fs cos а. Работа — величина скалярная. Единица работы — джоуль (Дж). Дж — это работа, совершаемая силой в 1 Н при перемещении на 1 м.

В зависимости от направлений векторов силы и перемещения механическая работа может быть положительной, отрицательной или равной нулю. Например, если векторы F и s сонаправлены, то cos 0° = 1 и А > 0 . Если векторы F и s направлены в противоположные стороны, то cos 180° = -1 и А < 0. Если же F и s перпендикулярны, то cos 90° = 0 и А = 0.

Энергией называется физическая величина, измеряемая работой, которую может совершить тело или система тел. Энергия, как и работа, измеряется в джоулях.   К механической энергии относятся: потенциальная энергия тяготения , потенциальная энергия деформированных тел 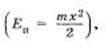 кинетическая энергия движущихся тел 

Переход механической энергии из одного вида в другой подчиняется закону сохранения механической энергии: в изолированной системе тел, между которыми действуют лишь силы тяготения и упругости, механическая энергия остается неизменной. Поэтому механическая энергия тела в процессе его движения не меняется. По мере падения тела его потенциальная энергия будет уменьшаться, но зато будет возрастать кинетическая энергия.

Механический эквивалент теплоты, количество работы, эквивалентное единице количества переданной в процессе теплообмена теплоты (калории или килокалории). Понятие механический эквивалент теплоты возникло в связи с тем, что исторически механическую работу и количество теплоты измеряли в разных единицах. С установлением эквивалентности механической работы и теплоты были осуществлены тщательные измерения механического эквивалента теплоты. Результаты измерений показали, что 1 ккал = 426,9 кгс×м. В Международной системе единиц (СИ) нет необходимости пользоваться понятием механический эквивалент теплоты, в этой системе принята одна единица для измерения как работы, так и количества переданной теплоты — джоуль. 1 дж = 0,239 кал = 0,102 кгс×м.

4. Как определяют расстояния до звезд? Что такое «параллакс» и «звездная величина»?

Для измерения расстояний внутри Солнечной системы используется астрономическая единица, равная среднему расстоянию Земли от Солнца. 1 астрономическая единица (а. е.) = 149 600 000 000 м. Но все звезды так далеки от нас, что расстояние до каждой из них, кроме Солнца, во много раз превышает расстояние от Земли до любой из планет Солнечной системы. Чтобы избежать использования громоздких чисел, потребовалось ввести новые единицы измерения. Для измерения расстояний до ближайших звезд астрономы ввели единицу длины, называемую парсеком. Она напрямую связана с эффектом параллакса — кажущимся смещением объекта по отношению к более далеким объектам при движении наблюдателя. Основной трудностью при таком способе измерений являются громадные расстояния до звезд и крайне малые величины углов их параллактических смещений. Один парсек — это такое расстояние, с которого средний радиус земной орбиты (равный 1 а. е.), перпендикулярный лучу зрения, виден под углом 1″. Иначе говоря, один парсек равен расстоянию до объекта, годичный параллакс которого (годовое смещение на небе, обязанное движению Земли вокруг Солнца) составляет 1″ (одну дуговую секунду). (Слово парсек образовано из слов параллакс и секунда.) 1 парсек (пс) = 31 * 1015 м (31 o КР означает 31 с 15 нулями).

В качестве единицы длины в астрономии применяется также световой год. Это расстояние, которое свет проходит за один год, распространяясь со скоростью 300000 км/с.

1 световой год = 0,3066 пс = 63 240 а. е. = = 9,5 o 10*5 м. Для измерения еще больших расстояний применяются единицы:

1 килопарсек (кпс) — 1000 пс;

1 мегапарсек (Мпс) = 1 000 000 пс.

Астрономы измеряют расстояния почти исключительно в парсеках, килопарсеках и мегапарсеках. Световой год используется редко. Если расстояние до звезд составляет сотни и более парсек, их параллактическое смещение становится незаметным. Метод параллакса не выводит нас даже за пределы собственной Галактики. Тогда для определения расстояний до звезд используют другие, косвенные методы. Один из таких методов состоит в сопоставлении видимого блеска звезд. Некоторые звезды кажутся нам более яркими, другие — более слабыми. Однако это еще не говорит об истинной мощности излучения звезд, поскольку все они находятся на разных расстояниях. Истинной характеристикой звезды служит ее абсолютный блеск (или светимость), то есть количество световой энергии, ежесекундно выделяемое звездой. Чаще всего светимость выражают в единицах светимости Солнца. Эта величина равна 3,8 o 1026 Вт. Таким образом, если известно, что абсолютный блеск (или светимость) двух звезд одинаков, то можно заключить, что звезда, которая кажется во много раз более слабой, чем другая, находится значительно дальше. Трудность состоит в том, что абсолютный блеск (светимость) звезд различен. Однако благодаря многолетним исследованиям астрономы научились распознавать звезды с одинаковой светимостью независимо от расстояния до них.

Другой косвенный метод определения расстояния до звезд требует анализа звездных спектров. По спектрам звезд изучаются их состав и строение, физические процессы, протекающие в них, определяются расстояния до звезд и исследуется их движение в пространстве.

Кроме этих двух косвенных методов определения расстояний до звезд, существует еще один — по переменным звездам типа 8 Цефея. Причем этот метод пригоден как для отдельных звезд, так и для звездных скоплений и даже галактик. Цефеиды — это пульсирующие переменные звезды, блеск которых регулярно меняется. Название происходит от звезды дельта (6) Цефея — одной из наиболее типичных для данного класса.

Правда, случается, что цефеиды прийти на помощь астрономам не могут по той простой причине, что в исследуемом районе их попросту нет. Тогда при измерении расстояния до далекой галактики астрономы опираются на допущение, что блеск самой яркой звезды этой галактики (голубого гиганта) совпадает с блеском самого яркого голубого гиганта нашей Галактики. Если же дело доходит до измерения расстояний до столь отдаленных галактик, в которых отдельные звезды неразличимы, то тогда делается допущение, что светимость самой яркой галактики в скоплении галактик равна светимости самой яркой галактики в более близком к нам скоплении галактик, расстояние до которого известно.

Параллакс (параллактическое смещение) в астрономии, видимое перемещение светил на небесной сфере, обусловленное перемещением наблюдателя в пространстве вследствие вращения Земли (суточный Параллакс), обращения Земли вокруг Солнца (годичный Параллакс) и движения Солнечной системы в Галактике (вековой Параллакс). Точно измеренные Параллакс небесных светил и групп светил позволяют определять расстояния до них.

Звездная величина – мера блеска небесного светила, изменение ее на 1 соответствует изменению блеска в 2,5 раза.

В каких единицах измеряют работу и энергию. Движение. Теплота

В каких единицах измеряют работу и энергию

Так как работа равна изменению энергии, то работа и энергия – разумеется, как потенциальная, так и кинетическая – измеряются в одних и тех же единицах. Работа равна произведению силы на путь. Работу силы в одну дину на пути в один сантиметр называют эргом:

1 эрг = 1 дина·1 см.

Это очень небольшая работа. Такую работу против силы тяжести совершит комар, чтобы перелететь с большого пальца руки на указательный. Более крупная единица работы и энергии, употребляющаяся в физике, – джоуль. Он в 10 миллионов раз больше эрга:

1 джоуль = 10 млн. эргов.

Довольно часто используется единица работы 1 килограммометр (1 кГм) – это работа, которая совершается силой в 1 кГ на пути в 1 м. Примерно такая работа совершается килограммовой гирей, упавшей на пол со стола.

Как нам известно, сила в 1 кГ равна 981 000 дин, 1 м равен 100 см. Значит, 1 кГм работы равен 98 100 000 эргов или 9,81 джоулей. Наоборот, 1 джоуль равен 0,102 кГм.

Новая система единиц (СИ), о которой мы уже упоминали и еще будем упоминать, предлагает в качестве единицы работы и энергии использовать джоуль и определяет его как работу силы в 1 ньютон (см. стр. 44) на пути в 1 метр. Зная, как просто определяется в данном случае сила, нетрудно понять, в чем заключаются преимущества новой системы единиц.

Поделитесь на страничке

Следующая глава >

Эквивалентность массы и энергии — Википедия

Эта статья включает описание термина «энергия покоя»

Эта статья включает описание термина «E=mc²»; см. также другие значения.

Эквивале́нтность ма́ссы и эне́ргии — физическая концепция теории относительности, согласно которой полная энергия физического объекта (физической системы, тела) равна его (её) массе, умноженной на размерный множитель квадрата скорости света в вакууме:

E=mc2{\displaystyle \ E=mc^{2}},

(1)

где E{\displaystyle E} — энергия объекта, m{\displaystyle m} — его масса, c{\displaystyle c} — скорость света в вакууме, равная 299 792 458 м/с.

В зависимости от того, что понимается под терминами «масса» и «энергия», данная концепция может быть интерпретирована двояко:

1) с одной стороны, концепция означает, что масса тела (инвариантная масса, называемая также массой покоя)^[1] равна (с точностью до постоянного множителя c²)^[2] энергии, «заключённой в нём», то есть его энергии, измеренной или вычисленной в сопутствующей системе отсчёта (системе отсчёта покоя), так называемой энергии покоя, или в широком смысле внутренней энергии этого тела^[3],

E0=mc2{\displaystyle E_{0}=mc^{2}},

(2)

где E0{\displaystyle E_{0}} — энергия покоя тела, m{\displaystyle m} — его масса покоя;

2) с другой стороны, можно утверждать, что любому виду энергии (не обязательно внутренней) физического объекта (не обязательно тела) соответствует некая масса; например, для любого движущегося объекта было введено понятие релятивистской массы, равной (с точностью до множителя c²) полной энергии этого объекта (включая кинетическую)^[4],

mrelc2=E{\displaystyle \ m_{rel}c^{2}=E},

(3)

где E{\displaystyle E} — полная энергия объекта, mrel{\displaystyle m_{rel}} — его релятивистская масса.

Формула на небоскрёбе Тайбэй 101 во время одного из мероприятий Всемирного года физики (2005)

Первая интерпретация не является лишь частным случаем второй. Хотя энергия покоя является частным случаем энергии, а m{\displaystyle m} практически равна mrel{\displaystyle m_{rel}} в случае нулевой или малой скорости движения тела, но m{\displaystyle m} имеет выходящее за рамки второй интерпретации физическое содержание: эта величина является скалярным (то есть выражаемым одним числом) инвариантным (неизменным при смене системы отсчёта) множителем в определении 4-вектора энергии-импульса, аналогичным ньютоновской массе и являющимся её прямым обобщением^[5], и к тому же m{\displaystyle m} является модулем 4-импульса. Дополнительно, именно m{\displaystyle m} (а не mrel{\displaystyle m_{rel}}) является единственным скаляром, который не только характеризует инертные свойства тела при малых скоростях, но и через который эти свойства могут быть достаточно просто записаны для любой скорости движения тела^[6].

Таким образом, m{\displaystyle m} — инвариантная масса — физическая величина, имеющая самостоятельное и во многом более фундаментальное значение^[7].

В современной теоретической физике концепция эквивалентности массы и энергии используется в первом смысле^[8]. Главной причиной, почему приписывание массы любому виду энергии считается чисто терминологически неудачным и поэтому практически вышло из употребления в стандартной научной терминологии, является следующая из этого полная синонимичность понятий массы и энергии. Кроме того, неаккуратное использование такого подхода может запутывать^[9] и в конечном итоге оказывается неоправданным. Таким образом, в настоящее время термин «релятивистская масса» в профессиональной литературе практически не встречается, а когда говорится о массе, имеется в виду инвариантная масса. В то же время термин «релятивистская масса» используется для качественных рассуждений в прикладных вопросах, а также в образовательном процессе и в научно-популярной литературе. Этот термин подчёркивает увеличение инертных свойств движущегося тела вместе с его энергией, что само по себе вполне содержательно^[10].

В наиболее универсальной форме принцип был сформулирован впервые Альбертом Эйнштейном в 1905 году, однако представления о связи энергии и инертных свойств тела развивались и в более ранних работах других исследователей.

В современной культуре формула E=mc2{\displaystyle E=mc^{2}} является едва ли не самой известной из всех физических формул, что обусловливается её связью с устрашающей мощью атомного оружия. Кроме того, именно эта формула является символом теории относительности и широко используется популяризаторами науки^[11].

Эквивалентность инвариантной массы и энергии покоя[править | править код]

Исторически принцип эквивалентности массы и энергии был впервые сформулирован в своей окончательной форме при построении специальной теории относительности Альбертом Эйнштейном. Им было показано, что для свободно движущейся частицы, а также свободного тела и вообще любой замкнутой системы частиц, выполняются следующие соотношения^[12]:

E2−p→2c2=m2c4p→=Ev→c2{\displaystyle \ E^{2}-{\vec {p}}^{\,2}c^{2}=m^{2}c^{4}\qquad {\vec {p}}={\frac {E{\vec {v}}}{c^{2}}}},

(1.1)

где E{\displaystyle E}, p→{\displaystyle {\vec {p}}}, v→{\displaystyle {\vec {v}}}, m{\displaystyle m} — энергия, импульс, скорость и инвариантная масса системы или частицы, соответственно, c{\displaystyle c} — скорость света в вакууме. Из этих выражений видно, что в релятивистской механике, даже когда в нуль обращаются скорость и импульс тела (массивного объекта), его энергия в нуль не обращается^[13], оставаясь равной некоторой величине, определяемой массой тела:

E0=mc2{\displaystyle E_{0}=mc^{2}}.

(1.2)

Эта величина носит название энергии покоя,^[14] и данное выражение устанавливает эквивалентность массы тела этой энергии. На основании этого факта Эйнштейном был сделан вывод, что масса тела является одной из форм энергии^[3] и что тем самым законы сохранения массы и энергии объединены в один закон сохранения^[15].

Энергия и импульс тела являются компонентами 4-вектора энергии-импульса (четырёхимпульса)^[16] (энергия — временной, импульс — пространственными) и соответствующим образом преобразуются при переходе из одной системы отсчёта в другую, а масса тела является лоренц-инвариантом, оставаясь при переходе в другие системы отсчёта постоянной, и имея смысл модуля вектора четырёхимпульса.

Следует также отметить, что несмотря на то, что энергия и импульс частиц аддитивны^[17], то есть для системы частиц имеем:

E=∑iEip→=∑ip→i{\displaystyle \ E=\sum _{i}E_{i}\qquad {\vec {p}}=\sum _{i}{\vec {p}}_{i}}

(1.3)

масса частиц аддитивной не является,^[12] то есть масса системы частиц, в общем случае, не равна сумме масс составляющих её частиц.

Таким образом, энергия (неинвариантная, аддитивная, временная компонента четырёхимпульса) и масса (инвариантный, неаддитивный модуль четырёхимпульса) — это две разные физические величины.^[7]

Эквивалентность инвариантной массы и энергии покоя означает, что в сопутствующей системе отсчёта, в которой свободное тело покоится, его энергия (с точностью до множителя c2{\displaystyle c^{2}}) равна его инвариантной массе^[7][18].

Четырёхимпульс равен произведению инвариантной массы на четырёхскорость тела.

pμ=mUμ{\displaystyle p^{\mu }=m\,U^{\mu }\!},

(1.4)

Это соотношение следует считать аналогом в специальной теории относительности классического определения импульса через массу и скорость.

После того, как Эйнштейн предложил принцип эквивалентности массы и энергии, стало очевидно, что понятие массы может интерпретироваться двояко. С одной стороны, это инвариантная масса, которая — именно в силу инвариантности — совпадает с той массой, что фигурирует в классической физике, с другой — можно ввести так называемую релятивистскую массу, эквивалентную полной (включая кинетическую) энергии физического объекта^[4]:

mrel=Ec2,{\displaystyle m_{\mathrm {rel} }={\frac {E}{c^{2}}},}

где mrel{\displaystyle m_{\mathrm {rel} }} — релятивистская масса, E{\displaystyle E} — полная энергия объекта.

Для массивного объекта (тела) эти две массы связаны между собой соотношением:

mrel=m1−v2c2,{\displaystyle m_{\mathrm {rel} }={\frac {m}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}},}

где m{\displaystyle m} — инвариантная («классическая») масса, v{\displaystyle v} — скорость тела.

Соответственно,

E=mrelc2=mc21−v2c2.{\displaystyle E=m_{\mathrm {rel} }{c^{2}}={\frac {mc^{2}}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}.}

Энергия и релятивистская масса — это одна и та же физическая величина (неинвариантная, аддитивная, временная компонента четырёхимпульса).^[7]

Эквивалентность релятивистской массы и энергии означает, что во всех системах отсчёта энергия физического объекта (с точностью до множителя c2{\displaystyle c^{2}}) равна его релятивистской массе^[7][19].

Введённая таким образом релятивистская масса является коэффициентом пропорциональности между трёхмерным («классическим») импульсом и скоростью тела^[4]:

p→=mrelv→.{\displaystyle {\vec {p}}=m_{\mathrm {rel} }{\vec {v}}.}

Аналогичное соотношение выполняется в классической физике для инвариантной массы, что также приводится как аргумент в пользу введения понятия релятивистской массы. Это в дальнейшем привело к тезису, что масса тела зависит от скорости его движения^[20].

В процессе создания теории относительности обсуждались понятия продольной и поперечной массы массивной частицы (тела). Пусть сила, действующая на тело, равна скорости изменения релятивистского импульса. Тогда связь силы F→{\displaystyle {\vec {F}}} и ускорения a→=dv→/dt{\displaystyle {\vec {a}}=d{\vec {v}}/dt} существенно изменяется по сравнению с классической механикой:

F→=dp→dt=ma→1−v2/c2+mv→⋅(v→a→)/c2(1−v2/c2)3/2.{\displaystyle {\vec {F}}={\frac {d{\vec {p}}}{dt}}={\frac {m{\vec {a}}}{\sqrt {1-v^{2}/c^{2}}}}+{\frac {m{\vec {v}}\cdot ({\vec {v}}{\vec {a}})/c^{2}}{(1-v^{2}/c^{2})^{3/2}}}.}

Если скорость перпендикулярна силе, то F→=mγa→,{\displaystyle {\vec {F}}=m\gamma {\vec {a}},} а если параллельна, то F→=mγ3a→,{\displaystyle {\vec {F}}=m\gamma ^{3}{\vec {a}},} где γ=1/1−v2/c2{\displaystyle \gamma =1/{\sqrt {1-v^{2}/c^{2}}}} — релятивистский фактор. Поэтому mγ=mrel{\displaystyle m\gamma =m_{\mathrm {rel} }} называют поперечной массой, а mγ3{\displaystyle m\gamma ^{3}} — продольной.

Утверждение о том, что масса зависит от скорости, вошло во многие учебные курсы и в силу своей парадоксальности приобрело широкую известность среди неспециалистов. Однако в современной физике избегают использовать термин «релятивистская масса», используя вместо него понятие энергии, а под термином «масса» понимая инвариантную массу (покоя). В частности, выделяются следующие недостатки введения термина «релятивистская масса»^[8]:

• неинвариантность релятивистской массы относительно преобразований Лоренца;
• синонимичность понятий энергия и релятивистская масса, и, как следствие, избыточность введения нового термина;
• наличие различных по величине продольной и поперечной релятивистских масс и невозможность единообразной записи аналога второго закона Ньютона в виде

mreldv→dt=F→;{\displaystyle m_{\mathrm {rel} }{\frac {d{\vec {v}}}{dt}}={\vec {F}};}

• методологические сложности преподавания специальной теории относительности, наличие специальных правил, когда и как следует пользоваться понятием «релятивистская масса» во избежание ошибок;
• путаница в терминах «масса», «масса покоя» и «релятивистская масса»: часть источников просто массой называют одно, часть — другое.

Несмотря на указанные недостатки, понятие релятивистской массы используется и в учебной,^[21] и в научной литературе. Следует, правда, отметить, что в научных статьях понятие релятивистской массы используется по большей части только при качественных рассуждениях как синоним увеличения инертности частицы, движущейся с околосветовой скоростью.

В классической физике гравитационное взаимодействие описывается законом всемирного тяготения Ньютона, и его величина определяется гравитационной массой тела^[22], которая с высокой степенью точности равна по величине инертной массе, о которой шла речь выше, что позволяет говорить о просто массе тела^[23].

В релятивистской физике гравитация подчиняется законам общей теории относительности, в основе которой лежит принцип эквивалентности, заключающийся в неотличимости явлений, происходящих локально в гравитационном поле, от аналогичных явлений в неинерциальной системе отсчёта, движущейся с ускорением, равным ускорению свободного падения в гравитационном поле. Можно показать, что данный принцип эквивалентен утверждению о равенстве инертной и гравитационной масс^[24].

В общей теории относительности энергия играет ту же роль, что и гравитационная масса в классической теории. Действительно, величина гравитационного взаимодействия в этой теории определяется так называемым тензором энергии-импульса, являющимся обобщением понятия энергии^[25].

В простейшем случае точечной частицы в центрально-симметричном гравитационном поле объекта, масса которого много больше массы частицы, сила, действующая на частицу, определяется выражением^[8]:

F→=−GMEc2(1+β2)r→−(r→β→)β→r3,{\displaystyle {\vec {F}}=-GM{\frac {E}{c^{2}}}{\frac {(1+\beta ^{2}){\vec {r}}-({\vec {r}}{\vec {\beta }}){\vec {\beta }}}{r^{3}}},}

где G — гравитационная постоянная, M — масса тяжёлого объекта, E — полная энергия частицы, β=v/c,{\displaystyle \beta =v/c,} v — скорость частицы, r→{\displaystyle {\vec {r}}} — радиус-вектор, проведённый из центра тяжёлого объекта в точку нахождения частицы. Из этого выражения видна главная особенность гравитационного взаимодействия в релятивистском случае по сравнению с классической физикой: оно зависит не только от массы частицы, но и от величины и направления её скорости. Последнее обстоятельство, в частности, не позволяет ввести однозначным образом некую эффективную гравитационную релятивистскую массу, сводившую бы закон тяготения к классическому виду^[8].

Предельный случай безмассовой частицы[править | править код]

Важным предельным случаем является случай частицы, масса которой равна нулю. Примером такой частицы является фотон — частица-переносчик электромагнитного взаимодействия^[26]. Из приведённых выше формул следует, что для такой частицы справедливы следующие соотношения:

E=pc,v=c.{\displaystyle E=pc,\qquad v=c.}

Таким образом, частица с нулевой массой вне зависимости от своей энергии всегда движется со скоростью света. Для безмассовых частиц введение понятия «релятивистской массы» в особой степени не имеет смысла, поскольку, например, при наличии силы в продольном направлении скорость частицы постоянна, а ускорение, следовательно, равно нулю, что требует бесконечной по величине эффективной массы тела. В то же время, наличие поперечной силы приводит к изменению направления скорости, и, следовательно, «поперечная масса» фотона имеет конечную величину.

Аналогично бессмысленно для фотона вводить эффективную гравитационную массу. В случае центрально-симметричного поля, рассмотренного выше, для фотона, падающего вертикально вниз, она будет равна E/c2{\displaystyle E/c^{2}}, а для фотона, летящего перпендикулярно направлению на гравитационный центр, — 2E/c2{\displaystyle 2E/c^{2}}^[8].

Полученная А. Эйнштейном эквивалентность массы тела запасённой в теле энергии стала одним из главных практически важных результатов специальной теории относительности. Соотношение E0=mc2{\displaystyle E_{0}=mc^{2}} показало, что в веществе заложены огромные (благодаря квадрату скорости света) запасы энергии, которые могут быть использованы в энергетике и военных технологиях^[28].

Количественные соотношения между массой и энергией[править | править код]

В международной системе единиц СИ отношение энергии и массы E/m{\displaystyle E/m} выражается в джоулях на килограмм, и оно численно равно квадрату значения скорости света c{\displaystyle c} в метрах в секунду:

Em=c2=(299 792 458 m/s)2{\displaystyle {\frac {E}{m}}=c^{2}=({\text{299 792 458 m/s}})^{2}} = 89 875 517 873 681 764 Дж/кг (≈9,0⋅10¹⁶ джоулей на килограмм).

Таким образом, 1 грамм массы эквивалентен следующим значениям энергии:

В ядерной физике часто применяется значение отношения энергии и массы, выраженное в мегаэлектронвольтах на атомную единицу массы — ≈931,494 МэВ/а.е.м.

Примеры взаимопревращения энергии покоя и кинетической энергии[править | править код]

Энергия покоя способна переходить в кинетическую энергию частиц в результате ядерных и химических реакций, если в них масса вещества, вступившего в реакцию, больше массы вещества, получившегося в результате. Примерами таких реакций являются^[8]:

e−+e+→2γ.{\displaystyle e^{-}+e^{+}\rightarrow 2\gamma .}

2e−+4p+→24He+2νe+Ekin.{\displaystyle 2e^{-}+4p^{+}\rightarrow {}_{2}^{4}\mathrm {He} +2\nu _{e}+E_{\mathrm {kin} }.}

92235U+01n→3693Kr+56140Ba+3 01n.{\displaystyle {}_{92}^{235}\mathrm {U} +{}_{0}^{1}n\rightarrow {}_{36}^{93}\mathrm {Kr} +{}_{56}^{140}\mathrm {Ba} +3~{}_{0}^{1}n.}

Ch5+2O2→CO2+2h3O.{\displaystyle \mathrm {CH} _{4}+2\mathrm {O} _{2}\rightarrow \mathrm {CO} _{2}+2\mathrm {H} _{2}\mathrm {O} .}

В этой реакции выделяется порядка 35,6 МДж тепловой энергии на кубический метр метана, что составляет порядка 10⁻¹⁰ от его энергии покоя. Таким образом, в химических реакциях преобразование энергии покоя в кинетическую энергию значительно ниже, чем в ядерных. На практике этим вкладом в изменение массы прореагировавших веществ в большинстве случаев можно пренебречь, так как оно обычно лежит вне пределов возможности измерений.

Важно отметить, что в практических применениях превращение энергии покоя в энергию излучения редко происходит со стопроцентной эффективностью. Теоретически совершенным превращением было бы столкновение материи с антиматерией, однако в большинстве случаев вместо излучения возникают побочные продукты и вследствие этого только очень малое количество энергии покоя превращается в энергию излучения.

Существуют также обратные процессы, увеличивающие энергию покоя, а следовательно и массу. Например, при нагревании тела увеличивается его внутренняя энергия, в результате чего возрастает масса тела^[29]. Другой пример — столкновение частиц. В подобных реакциях могут рождаться новые частицы, массы которых существенно больше, чем у исходных. «Источником» массы таких частиц является кинетическая энергия столкновения.

История и вопросы приоритета