ТРЕХФАЗНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ
Типовые задачи с решениями
1. К источнику трехфазной сети с линейным напряжением Uл = 380 В и частотой f = 50 Гц подключена равномерная нагрузка, соединенная по схеме «звезда», с полным сопротивлением в фазе Z = 90 Ом и индуктивностью L = 180 мГн. Определить активную, реактивную и полную мощности, коэффициент мощности, действующие значения линейного тока и напряжения. построить векторную диаграмму токов и напряжений.
Решение. Фазное напряжение
Фазный ток
Линейный ток
Реактивное сопротивление в фазе
Активное сопротивление в фазе
Коэффициент мощности катушки
Мощности, потребляемые нагрузкой:
активная
или
реактивная
полная
2. К четырехпроводной трехфазной сети с действующим значением линейного напряжения 220 В подключена неравномерная активная нагрузка с потребляемой мощностью в фазах
Решение. Напряжение в каждой фазе Токи в фазах Ток в нейтральном проводе определяем из векторной диаграммы как сумму векторов фазных токов: Ответ:
3. К трехфазной четырехпроводной сети с действующим значением линейного напряжения Uл = 380 В и частотой f = 50 Гц подключен приемник энергии, соединенный по схеме «звезда». В фазу А включена катушка с индуктивностью L = 0,18 Гн и активным сопротивлением RA = 80 Ом, в фазу
Решение. Фазное напряжение
Полное сопротивление: в фазе А — в фазе В — в фазе С —
Фазные токи
Активная мощность:
в фазе А— в фазе В— в фазе С—
Реактивная мощность:
в фазе А— в фазе В— в фазе
Полная мощность нагрузки
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Схема соединения «звезда»
1. Три резистора, каждый сопротивлением R = 125 Ом, соединены по схеме «звезда» и включены в трехфазную четырехпроводную сеть. Ток каждой фазы I = 880 мА. Определить действующие значения фазного и линейного напряжений, линейного тока, полную потребляемую мощность нагрузки, построить векторную диаграмму токов и напряжений.
2. Определить действующие значения токов в каждой фазе, если в фазе А (из задачи1) сопротивление нагрузки увеличить в двое; линейное напряжение при этом остается прежним.
3. Потребитель, соединенный по схеме «звезда» (нагрузка равномерная), включен в трехфазную сеть переменного тока с действующим значением линейного напряжения Uл = 380 В. Коэффициент мощности нагрузки cosφ = 0,5 ток в фазе Iф = 22 А. Определить полное, активное и реактивное сопротивления потребителя в фазе, а также полную, активную и реактивную мощности нагрузки.
4. Три индуктивные катушки с активным сопротивлением R = 34,2 Ом и индуктивным сопротивлением ХL = 23,5 Ом соединены по схеме «звезда» и подключены к источнику трехфазного напряжения. Активная мощность в фазе Р
5. К источнику трехфазного напряжения с действующим значением линейного напряжения Uл = 380 В и частотой f = 50 Гц подключена равномерная индуктивная нагрузка, соединенная по схеме «звезда». Действующее значение тока в фазе Iф = 1,25 А, коэффициент мощности нагрузки cosφ = 0,456. Определить полное и активное сопротивления нагрузки, ее индуктивность, полную потребляемую мощность. Построить векторную диаграмму токов и напряжений.
6. В трехфазную сеть с действующим значением линейного напряжения Uл = 220 В включена равномерная активная нагрузка по схеме «звезда» с сопротивлением в каждой фазе
7. В трехфазную сеть с действующим значением линейного напряжения Uл = 380 В включена активная нагрузка, соединенная по схеме «звезда». Сопротивления резисторов в фазах А, В и С соответственно равны 15, 15 и 35 Ом. Определить действующие значения напряжений в фазах, если в фазе А произошел разрыв цепи. Построить векторную диаграмму токов и напряжений.
8. Полная мощность S, потребляемая равномерной нагрузкой, соединенной по схеме «звезда», состоящей из конденсатора емкостью
9. В сеть трехфазного тока включена равномерная нагрузка с активным сопротивлением в каждой фазе R = 8 Ом и индуктивным сопротивлением XL = 14 Ом, соединенная по схеме «звезда». Определить напряжение в начале линии, имеющей активное сопротивление Rл = 0,6 Ом, если напряжение на нагрузке
10. К трехфазному генератору с ЭДС в фазе Еф = 309 В, обмотки которого соединены по схеме «звезда» и имеют активное и индуктивное сопротивления в фазе R = 0,5 Ом и XL = 1,5 Ом, подключена равномерная нагрузка, соединенная по схеме «звезда» с активным и индуктивным сопротивлениями в фазе 10 и 12 Ом. Определить действующие значения линейного напряжения генератора и нагрузки, ток в линии и потери напряжения в линии, если Rл = Хл = 2,5 Ом.
11. В сеть с действующим значением линейного напряжения
12. Три одинаковые группы ламп накаливания, соединены по схеме «звезда», включены в трехфазную четырехпроводную сеть с действующим значением линейного напряжения Uл = 380 В. Определить полную мощность, потребляемую нагрузкой, если линейный ток Iл = 16,5 А.
4. В трехфазную сеть с действующим значением линейного напряжения 220 В и частотой 50 Гц включен потребитель, соединенный по схеме «треугольник» и имеющий равномерную нагрузку, состоящую из катушки с индуктивностью
Решение. Фазное напряжение
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
1.3.2 Решение типовых задач1
Примеры решения типовых задач
Задача 1.3.1 Трехфазный асинхронный двигатель включен в сеть 380 В по схеме «звезда». Параметры обмоток следующие: Rф = 2 Ом, Хф = 8 Ом.
Требуется: изобразить схему включения двигателя в сеть; определить фазные и линейные токи; определить потребляемую активную мощность; построить векторную диаграмму токов и напряжений; рассмотреть два аварийных режима – обрыв и короткое замыкание фазы А.
Решение:
Т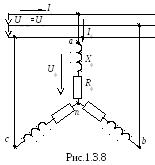 рехфазный
асинхронный двигатель является
рехфазный
асинхронный двигатель является
Номинальное
напряжение сети является линейным
напряжением, т. е.  ,
тогда фазное напряжение
,
тогда фазное напряжение
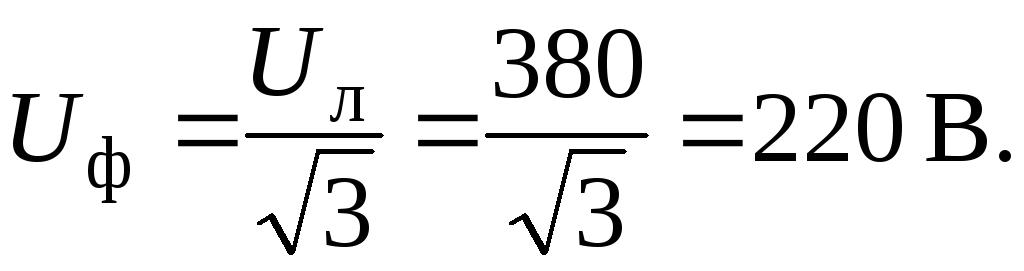 Поскольку
нагрузка симметричная, то расчет можно
проводить для одной фазы.
Поскольку
нагрузка симметричная, то расчет можно
проводить для одной фазы.
Полное сопротивление фазы
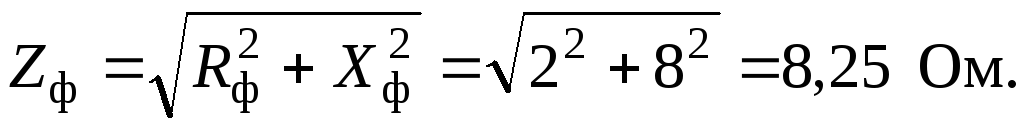
Ф
А(а)
азный ток 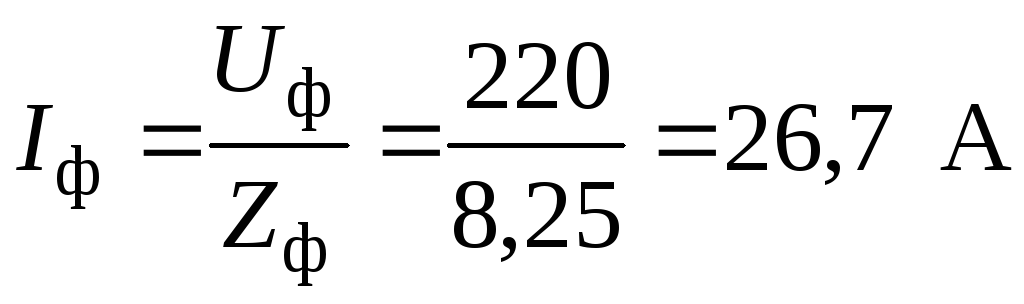 .
.
Для
схемы «звезда» линейный ток 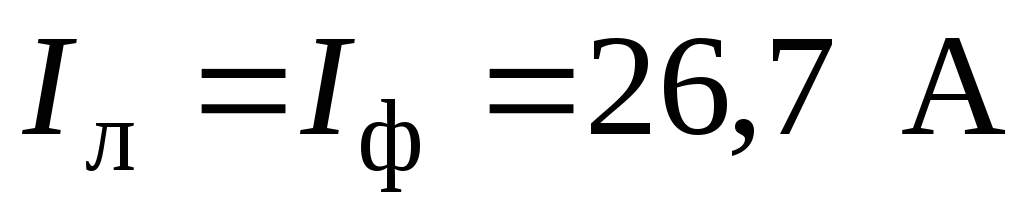 .
Потребляемая активная мощность
.
Потребляемая активная мощность
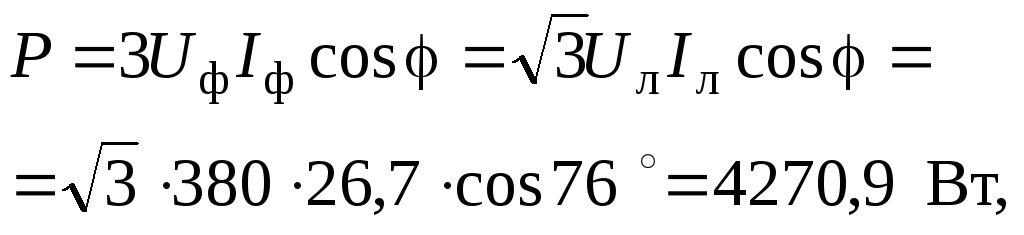
г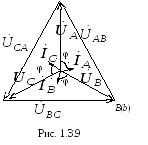 де
— фазовый угол,
де
— фазовый угол,
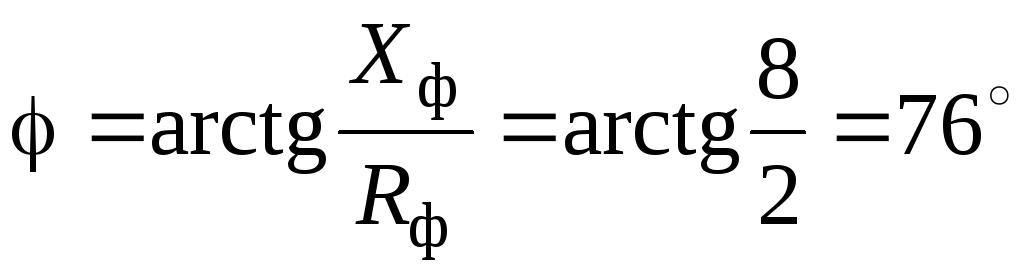 .
.
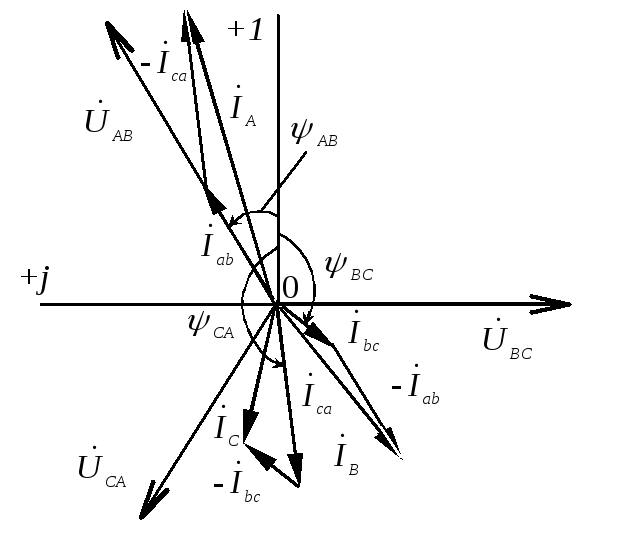
Векторная диаграмма
токов и напряжений показана на рис.
1.3.9. Для построения векторной диаграммы
необходимо выбрать масштабы напряжений 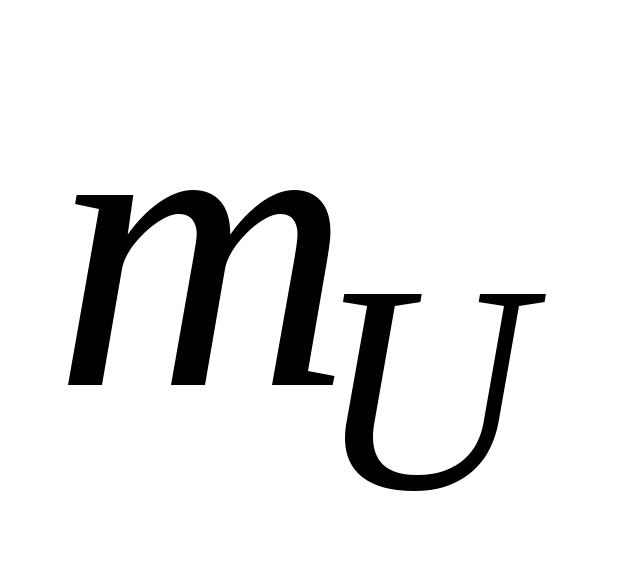 и токов
и токов  .
.
Рассмотрим аварийный режим работы– обрыв фазы А (рис.1.3.10).
В этом случае
трехфазная цепь превращается в однофазную 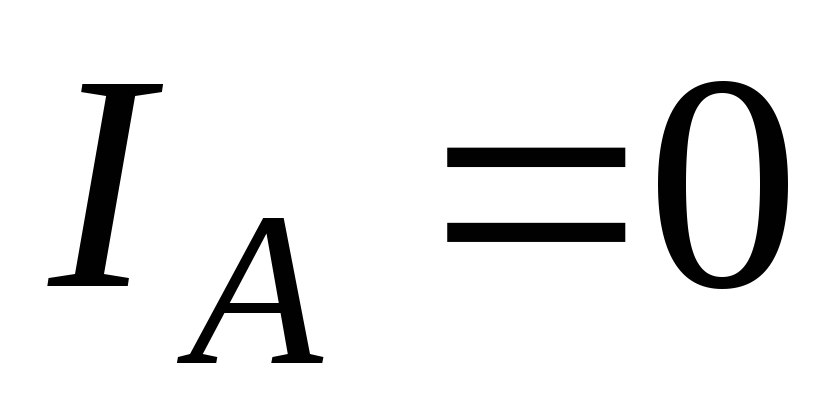 ,
причем фазы b и с оказываются включенными последовательно
на линейное напряжение
,
причем фазы b и с оказываются включенными последовательно
на линейное напряжение 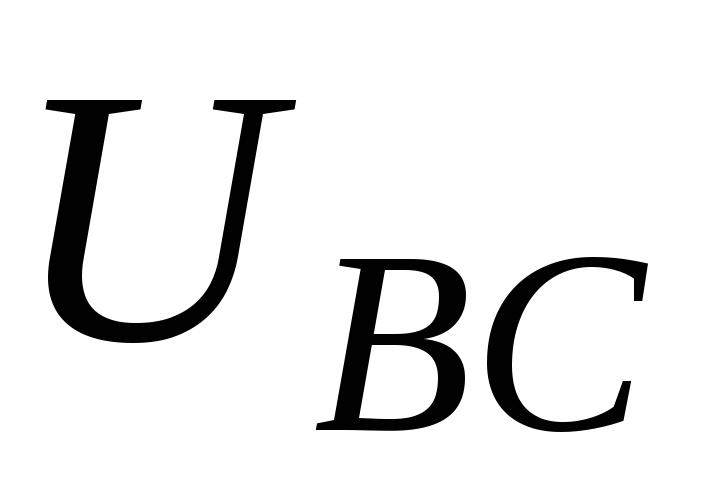 ,
т. е. на каждую из этих фаз падает
напряжение
,
т. е. на каждую из этих фаз падает
напряжение 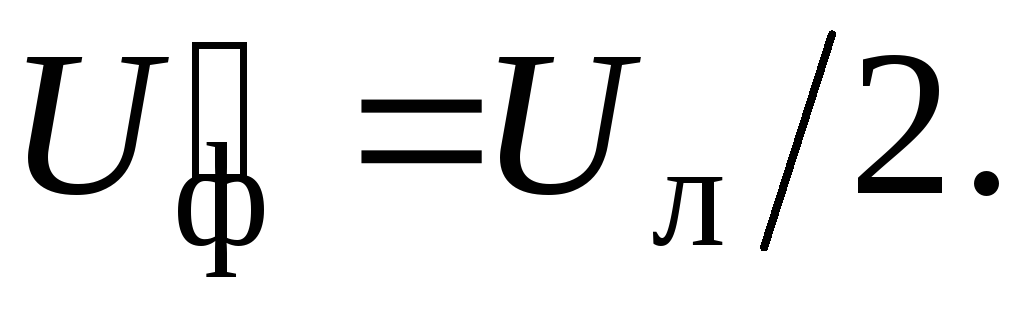
Фазные и линейные токи
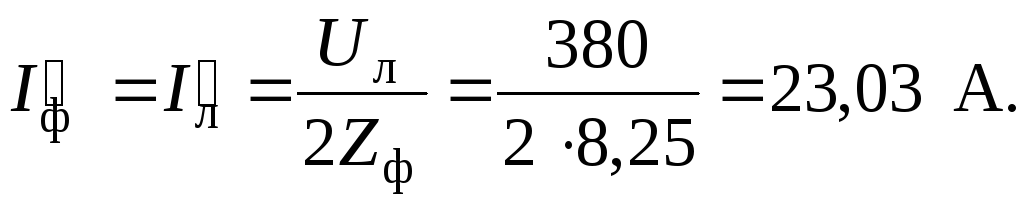
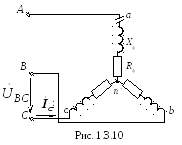 .
.
Потребляемая мощность
Рис. 1.3.11 Как видно из расчета, потребляемая мощность снизилась почти в два раза. Если обрыв фазы
произошел внутри самого двигателя
(обрыв обмотки), то эта обмотка
оказывается под повышенным напряжением | |
Рассмотрим аварийный режим работы – короткое замыкание фазы «а» (рис. 1.3.12, а, б).
При коротком
замыкании фазы нейтральная точка
оказывается связана с питающей точкой А,
значит, неповрежденные фазы b и с окажутся включенными на линейное
напряжение 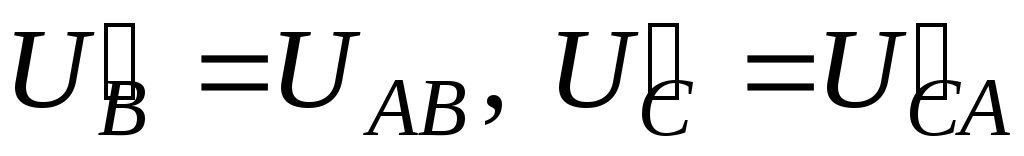 ,
что видно из векторной диаграммы.
,
что видно из векторной диаграммы.
Токи в неповрежденных фазах
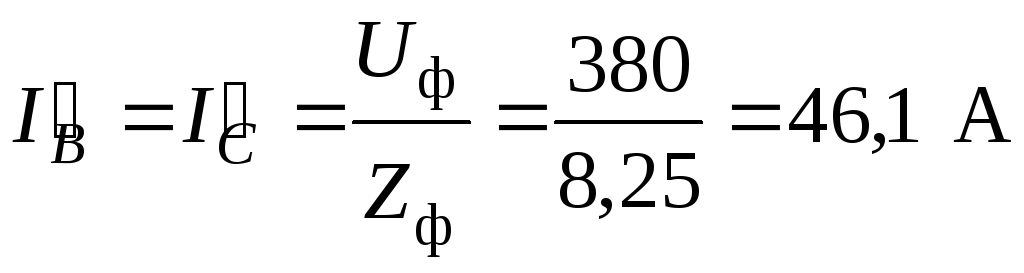 .
.
а | б |
Рис. 1.3.12
Ток в фазе а равен геометрической сумме токов 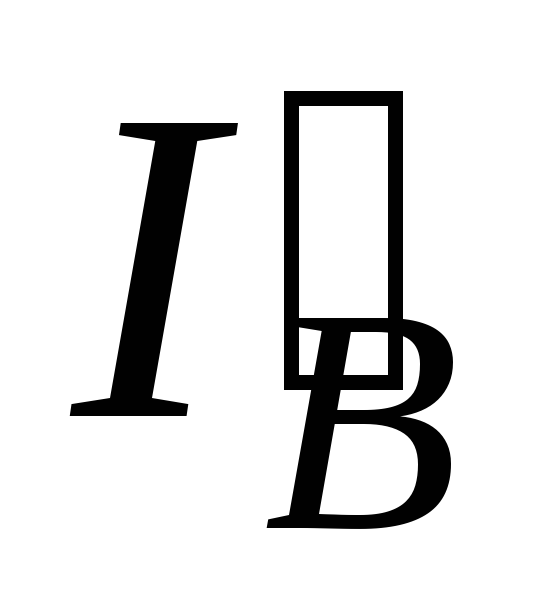 и
и  ( по векторной диаграмме составляет
примерно 69 А).
( по векторной диаграмме составляет
примерно 69 А).
Задача 1.3.2. Три однофазных приемника включены в
трехфазную сеть с напряжением 380 В по
схеме “звезда с нейтральным проводом”.
Сопротивления приемников: 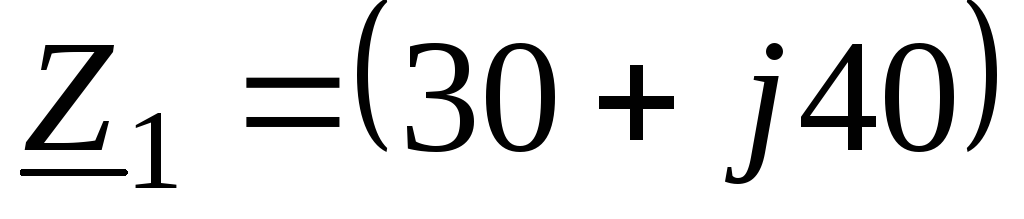 Ом;
Ом; 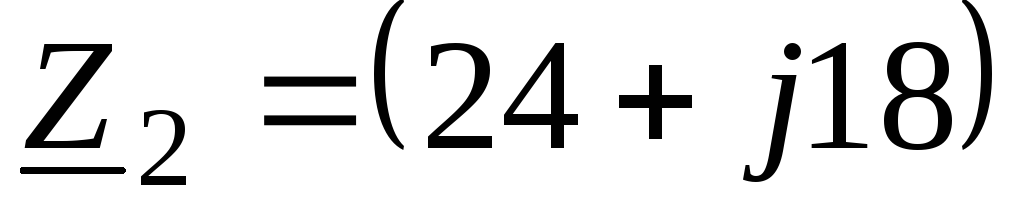 Ом;
Ом; 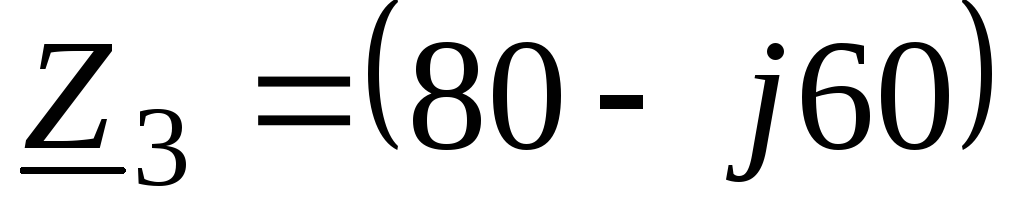 Ом.
Ом.
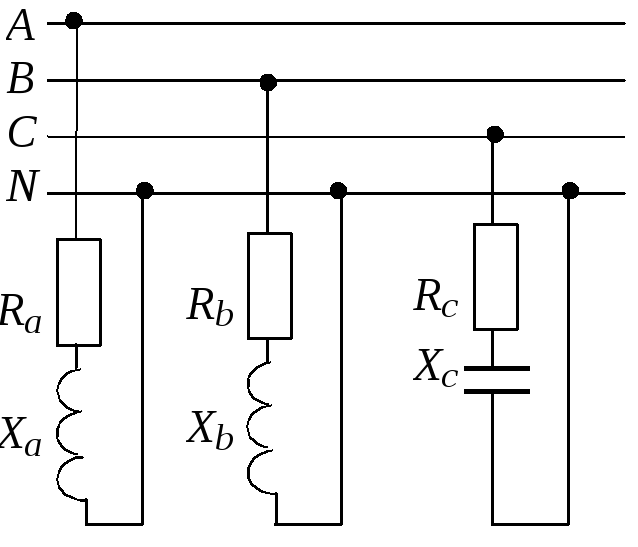
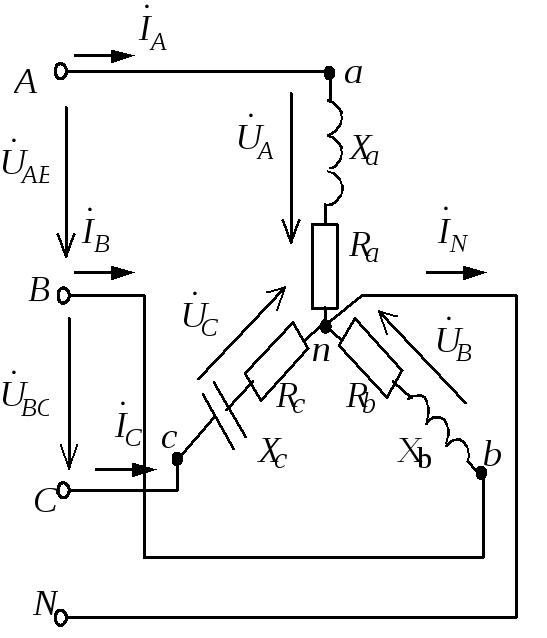
Требуется изобразить схему включения приемников; определить токи в проводах сети; построить векторную диаграмму токов и напряжений; вычислить активную, реактивную и полную (кажущуюся) мощности.
Решение:
Схема включения приемников принципиальная и расчетная представлены на рис. 1.3.13, а,б.
а | б |
Рис. 1.3.13 | |
Наличие нейтрального провода обеспечивает симметричную систему фазных напряжений на приемниках. Напряжение сети – линейное напряжение
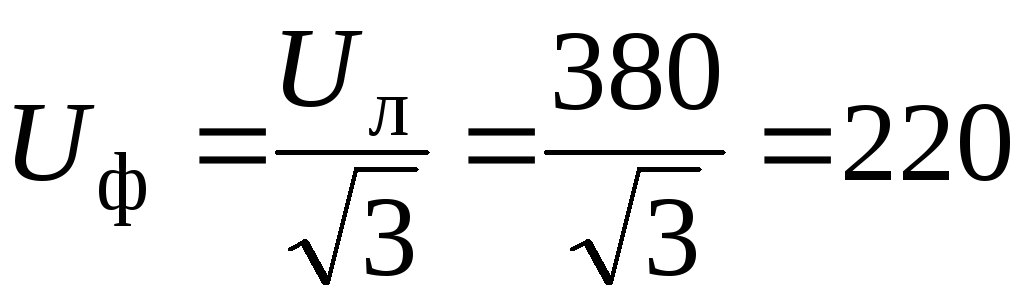 В.
В.
Система фазных напряжений в комплексной форме

Сопротивления фаз

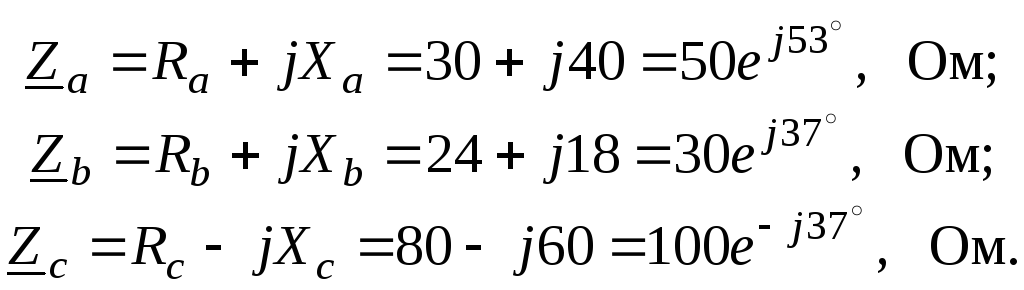
Для схемы “звезда“ фазные и линейные токи равны между собой и составляют

Ток в нейтральном проводе

При построении
векторных диаграмм фазные и линейные
напряжения и токи строятся относительно
комплексных осей откладываются с
учетом начальных фаз. Ток в нейтральном
проводе – это результат геометрического
сложения векторов фазных токов, и его
расположение и длина должны
соответствовать расчетному значению | Рис. 1.3.13 |
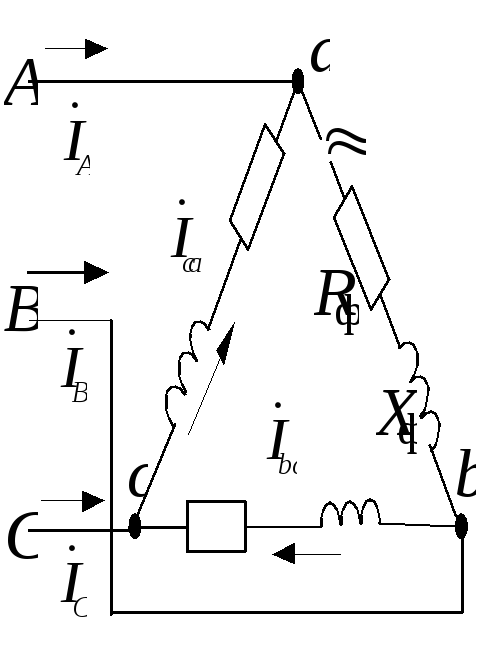
Задача 1.3.3. К трехфазной системе напряжением 380 В подключены три одинаковых приемника (RФ = 3 Ом, XLФ = 4 Ом), соединенные по схеме “треугольник“ (рис.1.3.14). Определить токи в фазных и линейных проводах и потребляемую мощность (активную, реактивную, полную). Построить векторную диаграмму токов и напряжений.
Рассмотреть аварийные режимы – обрывы фазного и линейных проводов.
Решение:
Нагрузка фаз одинакова, поэтому расчет проводится для одной фазы. Напряжение сети — это линейное напряжение, в схеме “треугольник “ Uф = Uл = 380 В. Комплексное сопротивление фазы: где | Рис. 1.3.14 |
Фазные токи:
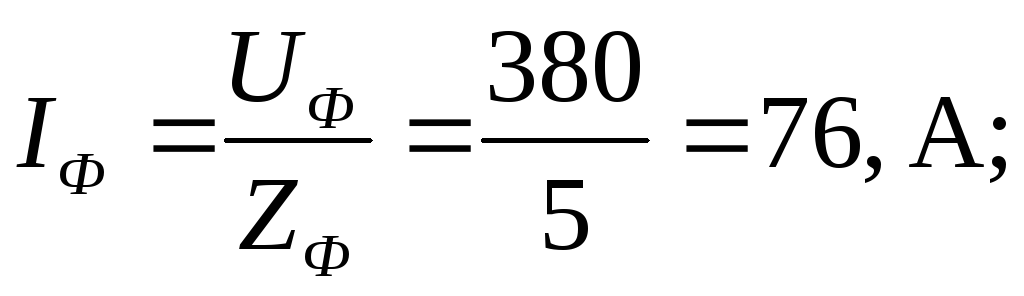
линейные токи (только для симметричной нагрузки):
Активная мощность, потребляемая нагрузкой:
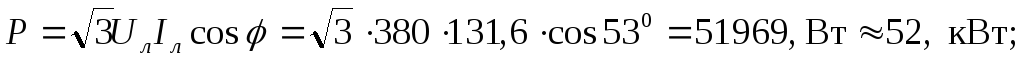
реактивная мощность:

полная мощность:
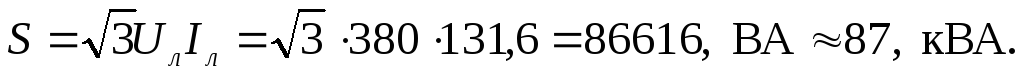
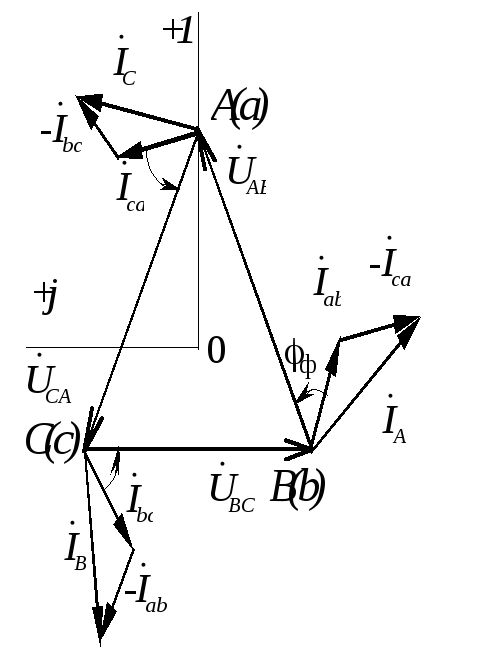
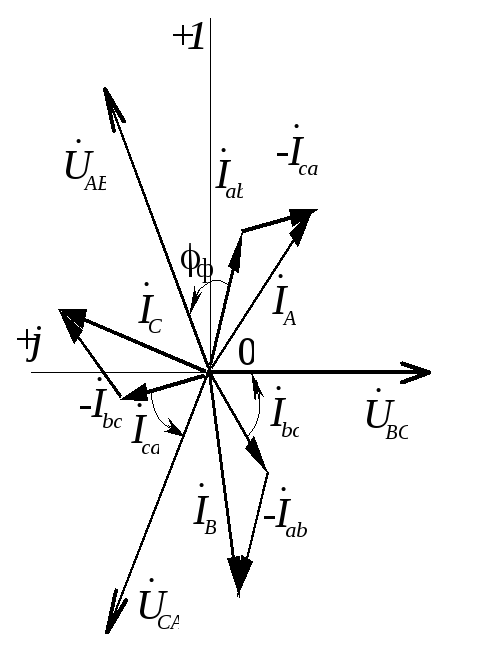
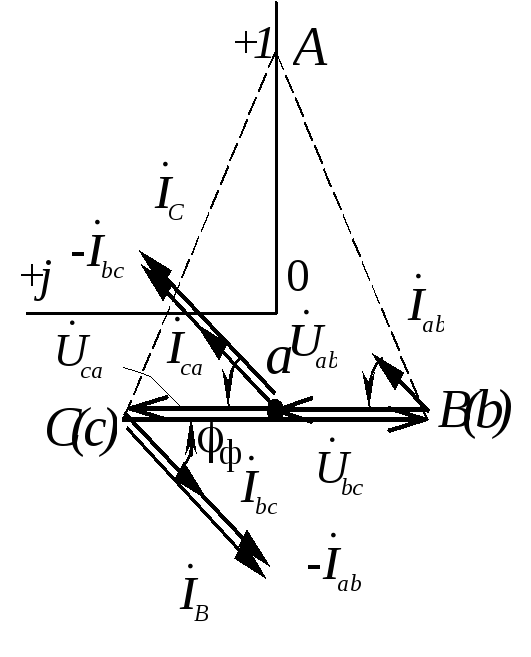
Векторная диаграмма может быть построена в двух вариантах в зависимости от изображения системы напряжений (рис.1.3.15 ). Предварительно выбирают масштабы тока и напряжения.
| |
Рис. 1.3.15 | |
Фазные токи отстают от соответствующих напряжений на угол Ф = 53. Линейные токи находятся из соотношений:
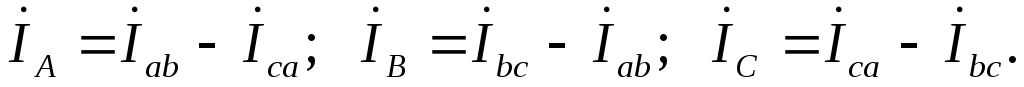
Рассмотрим обрыв фазы “аb” (рис.1.3.16,а). Определим токи в неповрежденных фазах и в линии, построим векторную диаграмму токов и напряжений.
а) | б) |
Рис. 1.3.16 | |
Токи в неповрежденных фазах не изменяются, так как не изменяются напряжения:
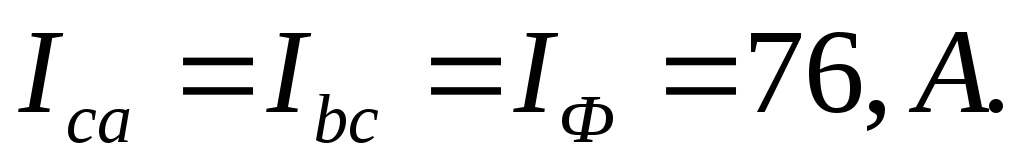
Линейные токи по
первому закону Кирхгофа (с учетом 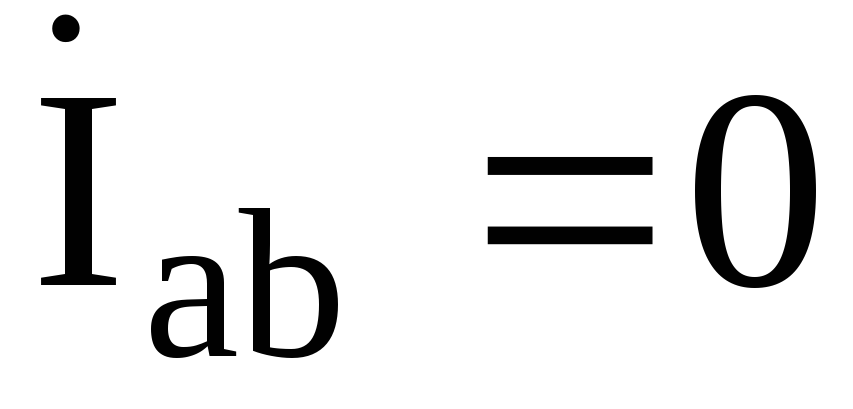 ):
):
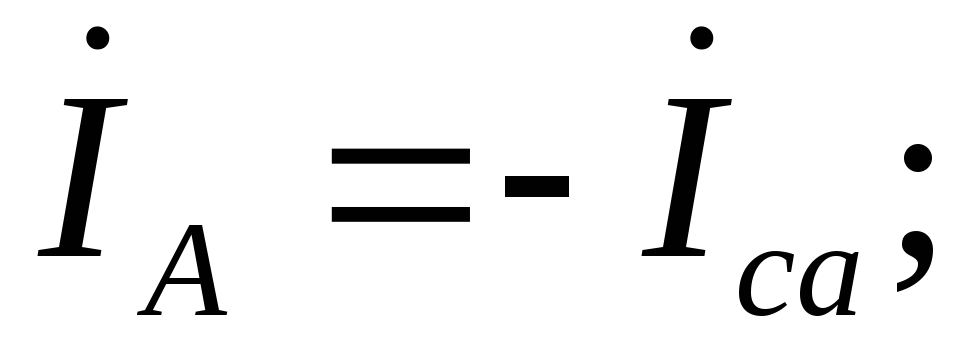
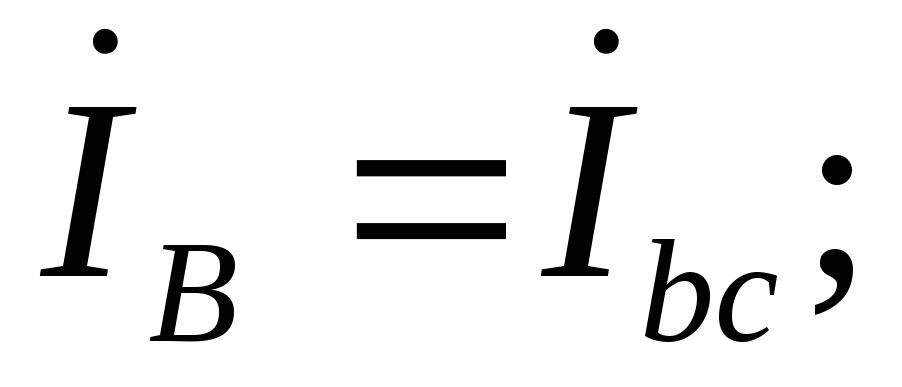
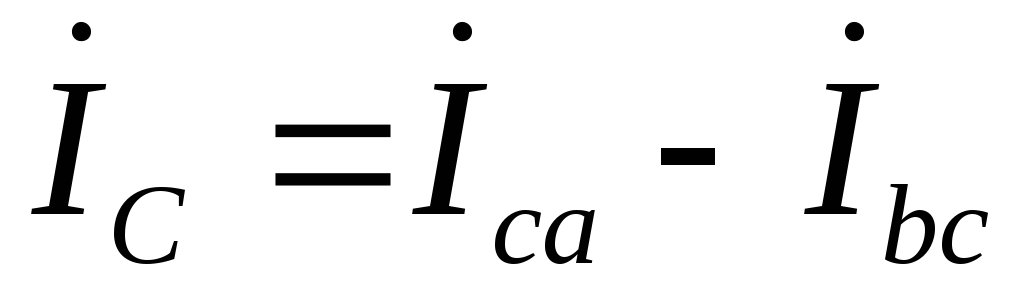 .
.
Из этих уравнений
следует, что действующие значения
линейных токов 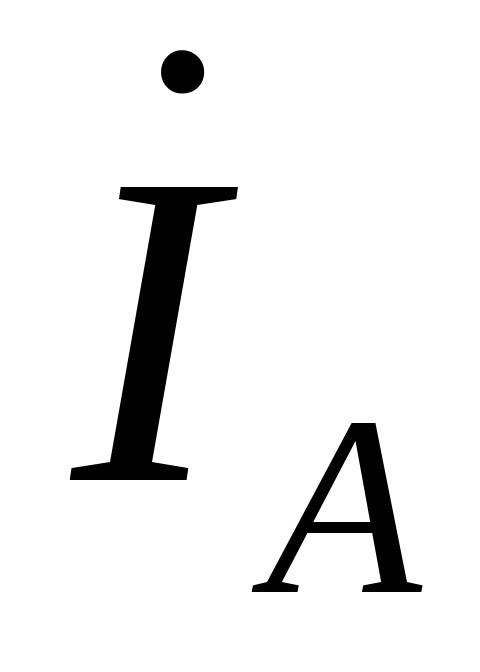 и
и  равны действующим значениям фазных
токов
равны действующим значениям фазных
токов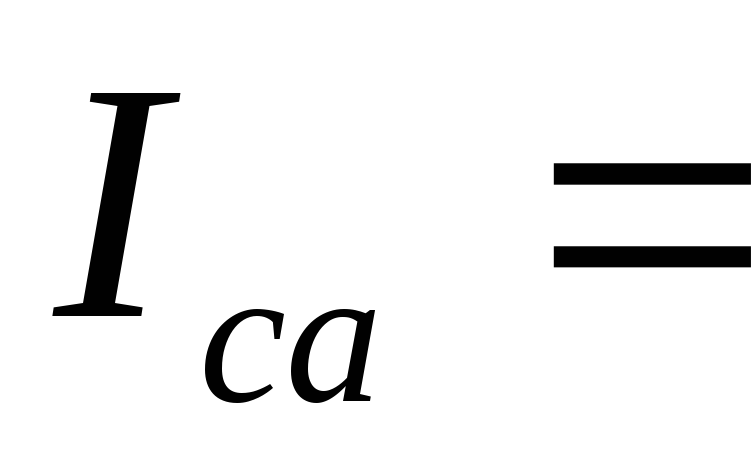
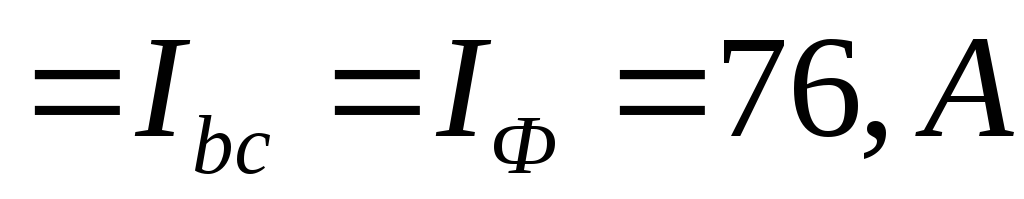 ,
а у линейного тока действующее значение
не изменяется
,
а у линейного тока действующее значение
не изменяется 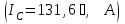
Векторная диаграмма токов и напряжений строится аналогично симметричному режиму и приведена на рис.1.3.16,б.
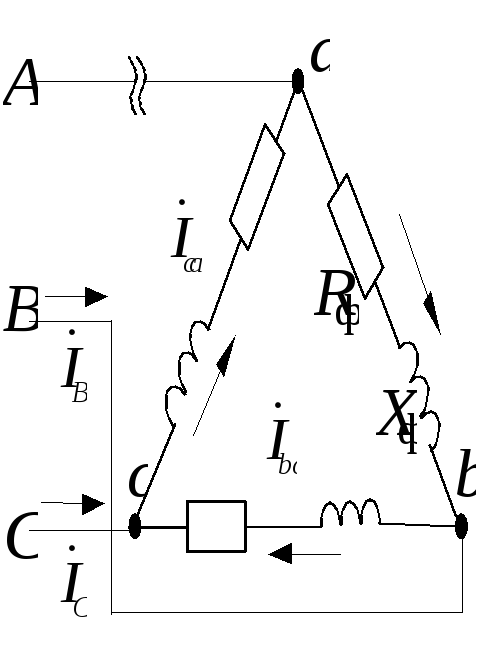
Рассмотрим обрыв линейного провода А (рис.1.3.17,а). Определим фазные и линейные токи и построим векторную диаграмму токов и напряжений.
К приемнику подводится только напряжение
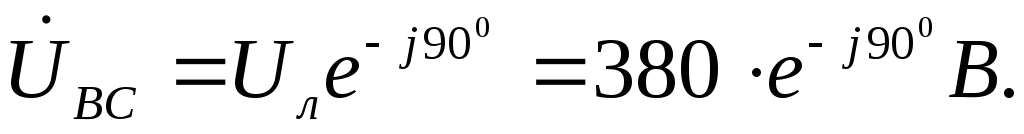
Сопротивление
фазы “bс”
включено на полное напряжение  ,
а равные сопротивления фаз “аb”
и ”са”
включены последовательно друг с другом,
причем к каждому из них подведена
половина напряжения
,
а равные сопротивления фаз “аb”
и ”са”
включены последовательно друг с другом,
причем к каждому из них подведена
половина напряжения 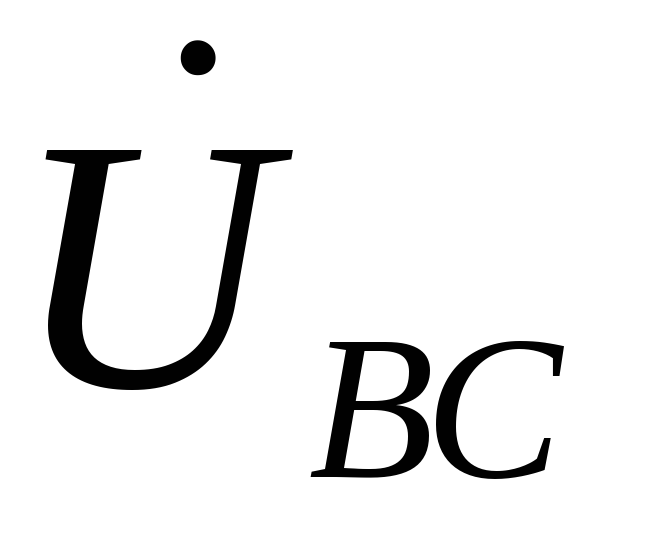 .
.
а) б) Рис.1.3.17 |
Сеть становится аналогичной однофазной с двумя параллельными ветвями:
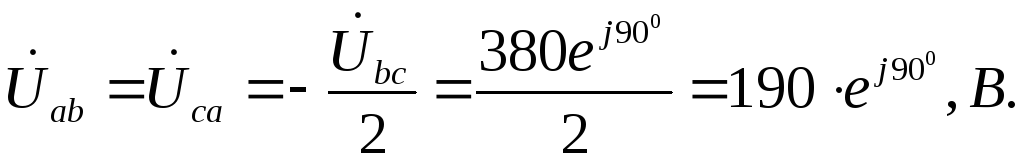
Ток фазы “bс” не изменяется:
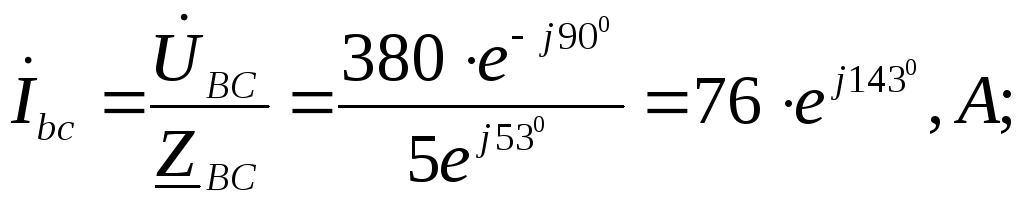
токи других фаз :
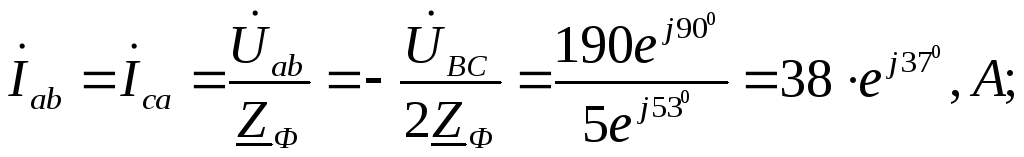
линейные токи (
при  )
:
)
:

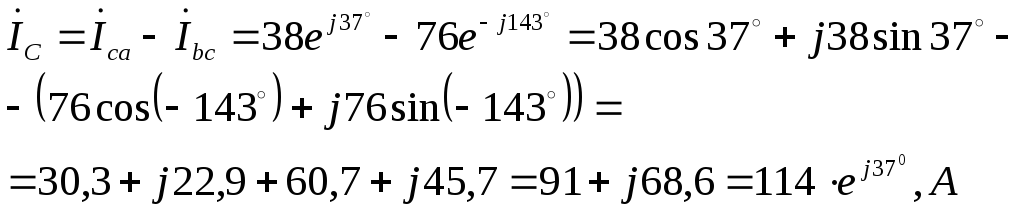
Векторная диаграмма токов и напряжений представлена на рис. 1.3.17,б.
Задача 1.3.4 В трехфазную сеть напряжением 380 В, частотой f = 50 Гц включен трехфазный асинхронный двигатель по схеме “треугольник“. Потребляемая активная мощность P = 1,44 кВт, коэффициент мощности cos = 0,85. Определить потребляемый двигателем ток, токи в обмотках двигателя, активное и индуктивное сопротивления, индуктивность катушек, полную и реактивную потребляемые мощности.
Решение:
Двигатель является симметричной нагрузкой, поэтому расчет ведем на фазу.
Сеть маркируется линейным напряжением, поэтому UЛ = 380 В.
При соединении по схеме “треугольник“ UЛ = UФ= 380 В.
Активная мощность, потребляемая нагрузкой,

отсюда фазный ток, протекающий в обмотках двигателя:
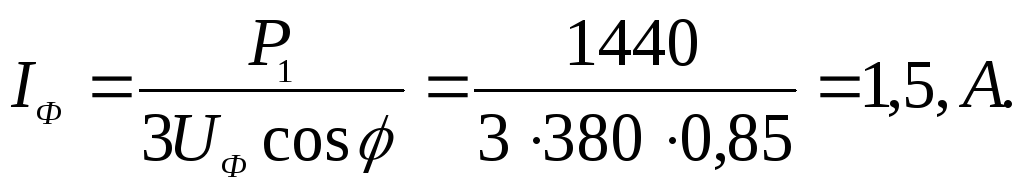
Потребляемые двигателем токи — линейные токи:
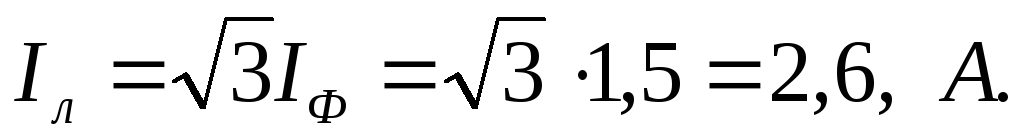
Полное сопротивление фазы обмотки двигателя:
 Ом,
Ом,
активное сопротивление
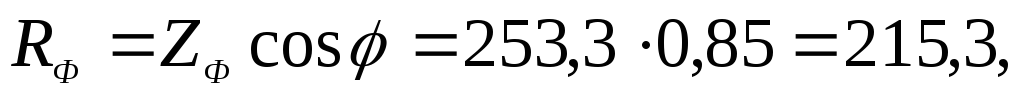 Ом,
Ом,
индуктивное сопротивление
 Ом.
Ом.
Индуктивность обмотки определяется из выражения
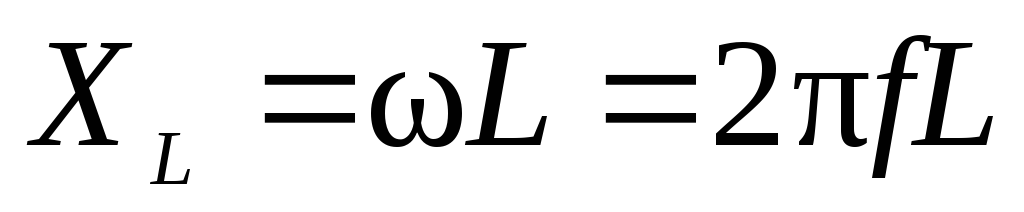 ,
,
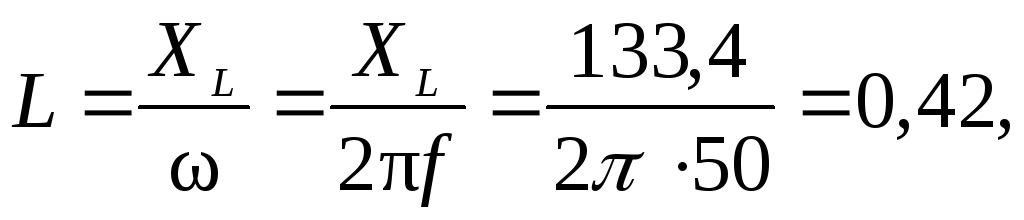 Гн.
Гн.
Полная потребляемая мощность:
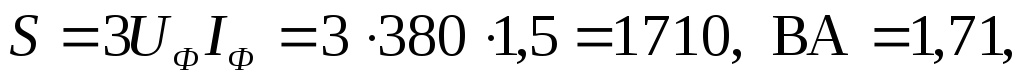 кВА;
кВА;
реактивная мощность:
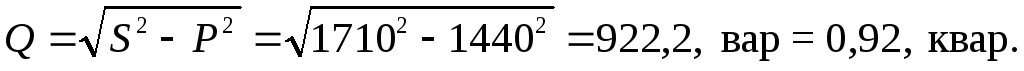
Задача 7.3 К трехпроводной трехфазной линии с напряжением 380 В подключены три однофазных приемника с параметрами: R1= 5 Ом, R2= 6 Ом, XL2= 8 Ом, R3=4 Ом, XC3= 3 Ом. Определить токи в фазах и линейных проводах, активную, реактивную и полную мощности и построить векторную диаграмму токов и напряжений.
Решение:
| Однофазные приемники к трехпроводной сети подключаются по схеме “треугольник“ (рис.1.3.18). Нагрузка несимметричная, ток каждой фазы нужно считать отдельно. Исходная система напряжений: Комплексные сопротивления фаз: |
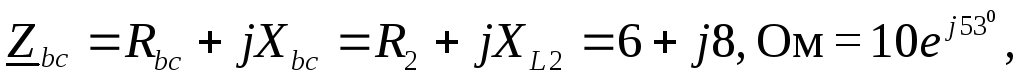 Ом;
Ом;
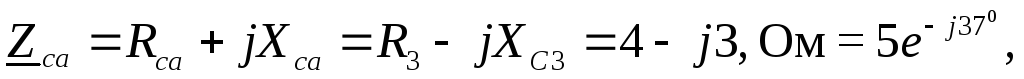 Ом;
Ом;
Фазные токи:
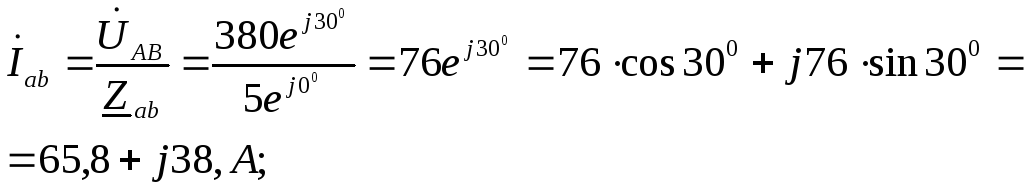
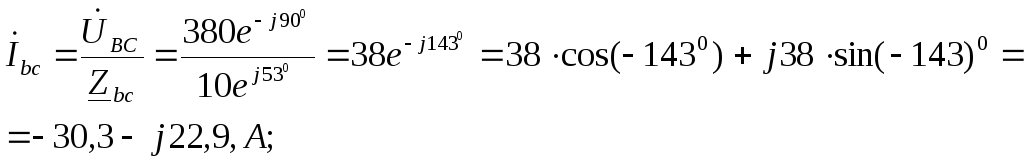
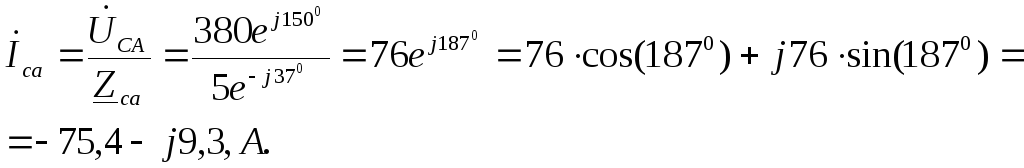
Линейные токи:
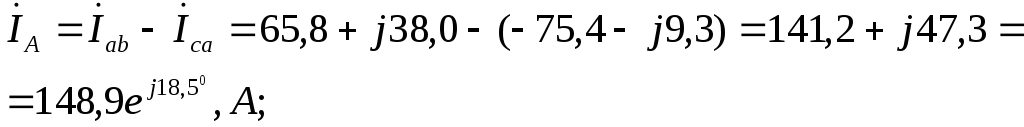
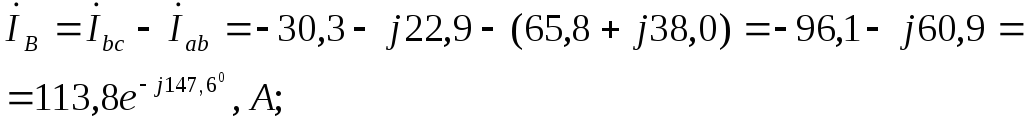
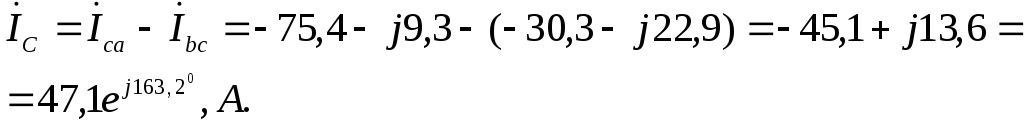
Сумма линейных токов должна равняться нулю, и действительно,

Активная мощность:
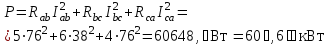
Реактивная мощность:
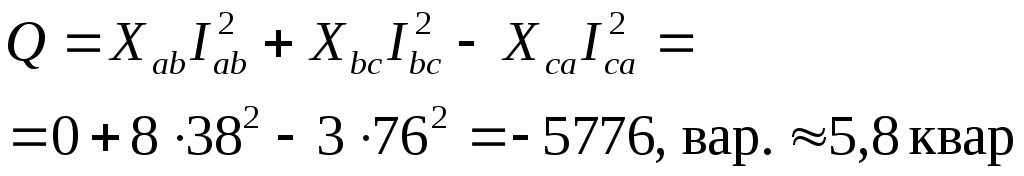
здесь знак “минус” показывает, что преобладает емкостная нагрузка.
Полная мощность:
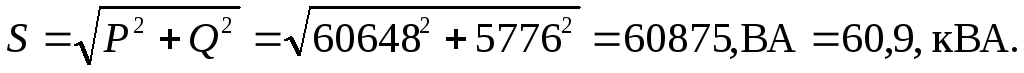
Векторные диаграммы токов и напряжений в двух вариантах (для разного представления исходной системы напряжений) приведены на рис.1.3.19.
Предварительно
выбирают масштабы тока и напряжения.
Векторы фазных токов 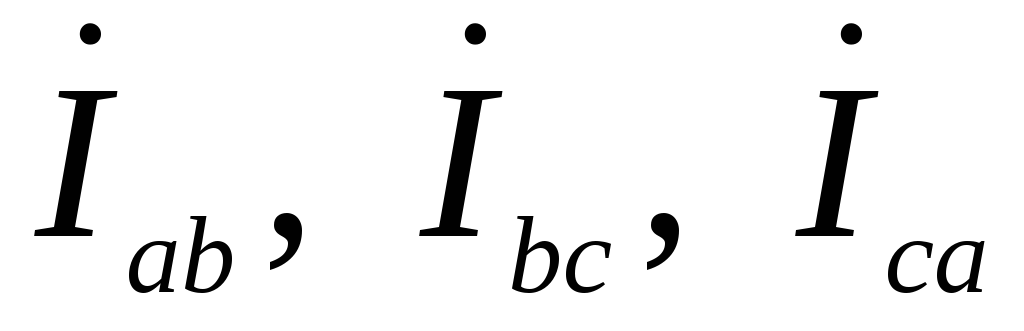 откладывают относительно векторов
соответствующих напряжений под углами
откладывают относительно векторов
соответствующих напряжений под углами 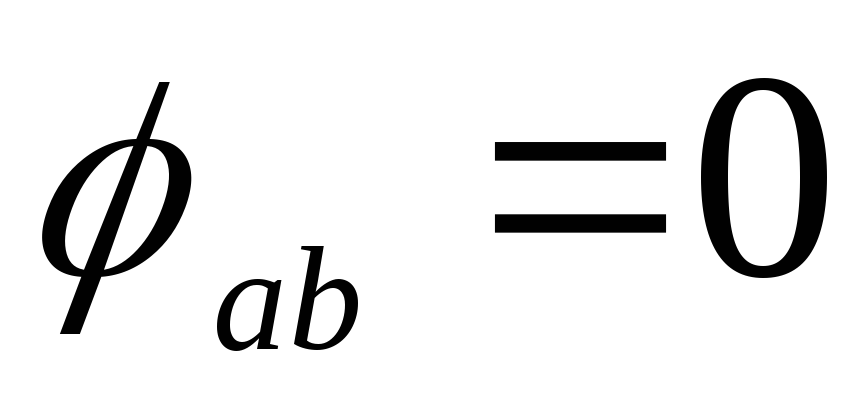 ,
, 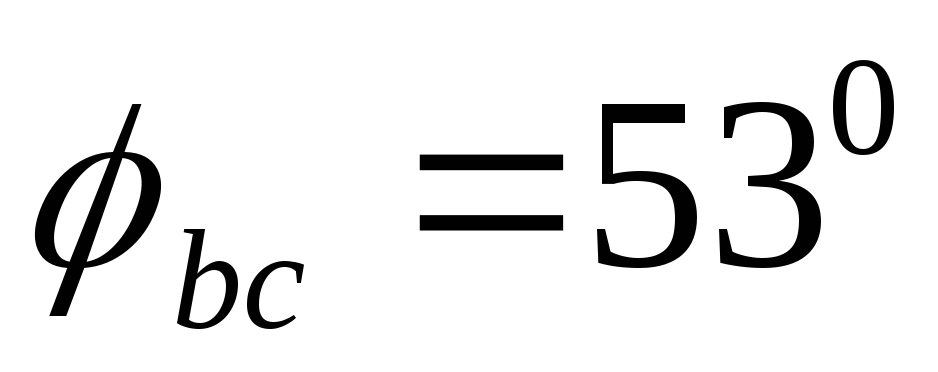 ,
, 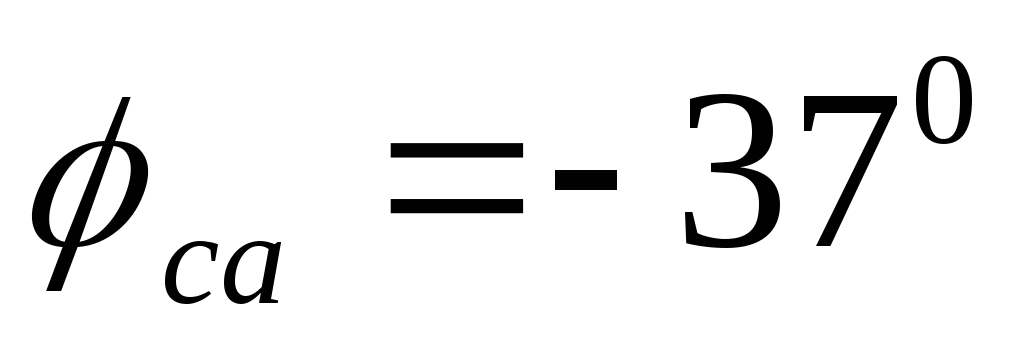 или в соответствии с полученными их
начальными фазами
или в соответствии с полученными их
начальными фазами 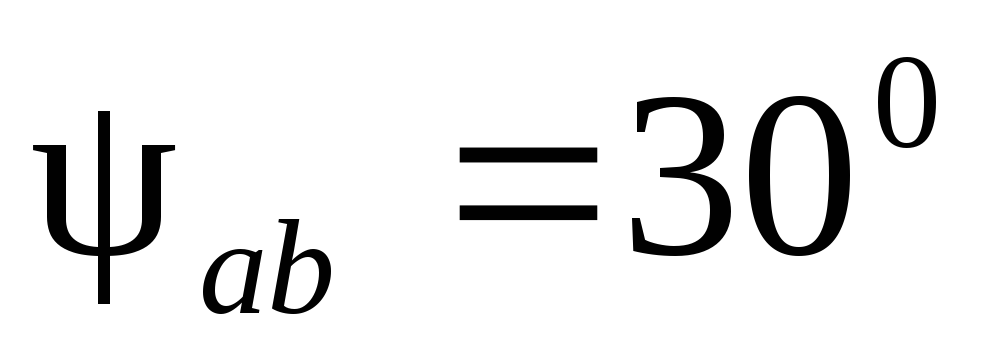 ;
; 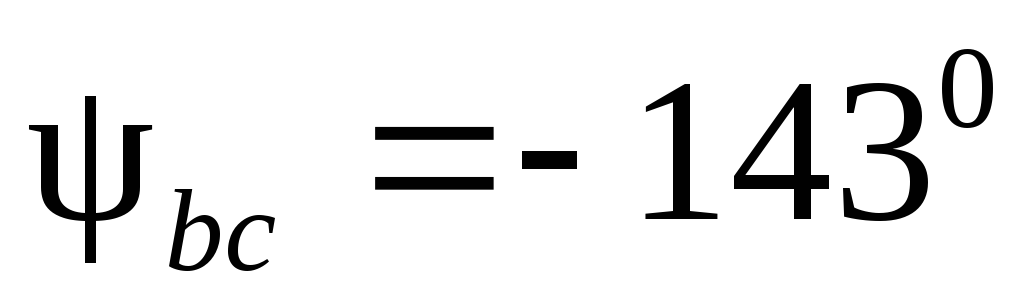 ;
; 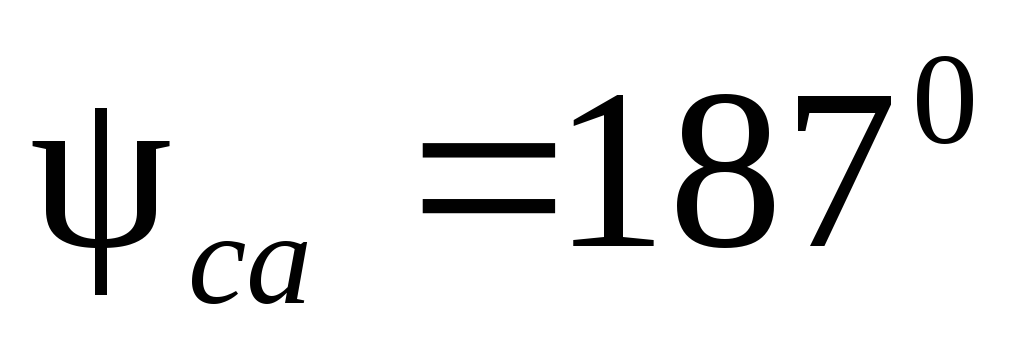 .
Затем по первому закону Кирхгофа строят
векторы линейных токов
.
Затем по первому закону Кирхгофа строят
векторы линейных токов 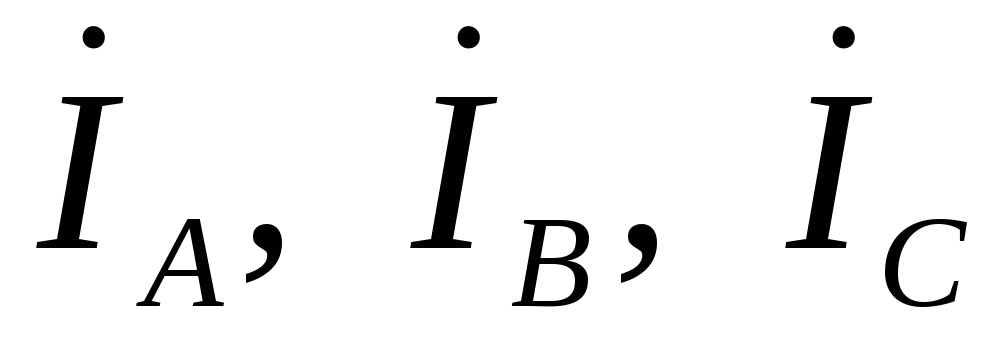 ,
длина и направление которых должны
соответствовать расчетным данным.
,
длина и направление которых должны
соответствовать расчетным данным.
| |
Рис.1.3.19 Векторные диаграммы токов и напряжений несимметричной нагрузки | |
3.2. Соединение звездой. Четырехпроводная система трехфазного тока
Если объединить между собой три конца обмоток генератора х, у, z и три вывода сопротивлений нагрузки ZA, ZB, ZC в общие точки N и n, а свободные начала обмоток генератора А, В, С и выводы сопротивлений нагрузки, соединить соответственно между собой, то получится соединение звездой.
Если общие точки N и n также соединить между собой, то получится четырехпроводная трехфазная система переменного тока (рис. 3.4), называемая также соединение звездой с нулевым проводом. Обмотки генератора NА, NВ и NС называются фазами генератора, а сопротивления ZA, ZB, ZC– фазами нагрузки.
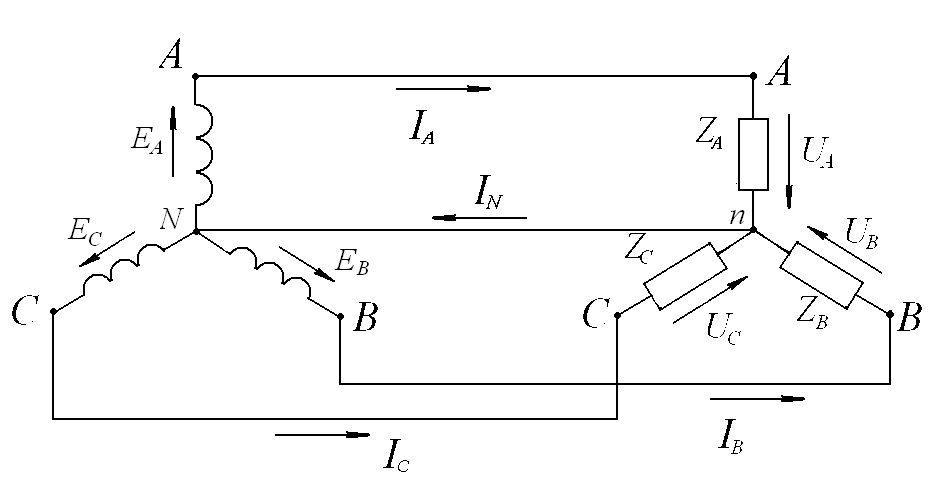
Рис. 3.4. Четырехпроводная система трехфазного тока.
Точки N и n называются соответственно нулевой точкой генератора и нулевой точкой нагрузки, а провод Nn называется нулевым или нейтральным проводом.
Провода АА, ВВ и СС называются линейными проводами.
Напряжение между линейным и нулевым проводами называют фазным напряжением и обозначают через UA, UBи UC. Напряжение между двумя линейными проводами называют линейным напряжением и обозначают через UAB, UBCи UCA.
Как видно на рис. 3.4 к сопротивлениям нагрузки ZA, ZBи ZC подведены фазные напряжения, положительные направления которых показаны стрелками. В трехфазных цепях переменного тока различают линейные Iл и фазные Iф токи. Линейными называют токи IА IВ и IС, проходящие по линейным проводам. Токи, проходящие по обмоткам генератора или по сопротивлениям нагрузки – называются фазными токами.
При соединении звездой каждая фаза генератора, линейный провод и фаза нагрузки, соединены между собой последовательно, и через них проходит один и тот же ток. Следовательно, при соединении звездой линейный ток равен фазному, т.е. Iл = Iф.
В трехфазных цепях при соединении звездой фазные токи вызываются только фазными напряжениями и между ними существуют соотношения, определяемые законом Ома:
IА = 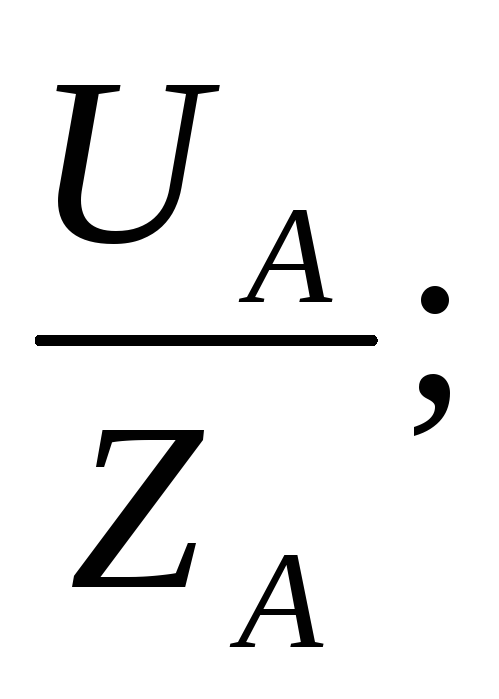 IВ =
IВ = 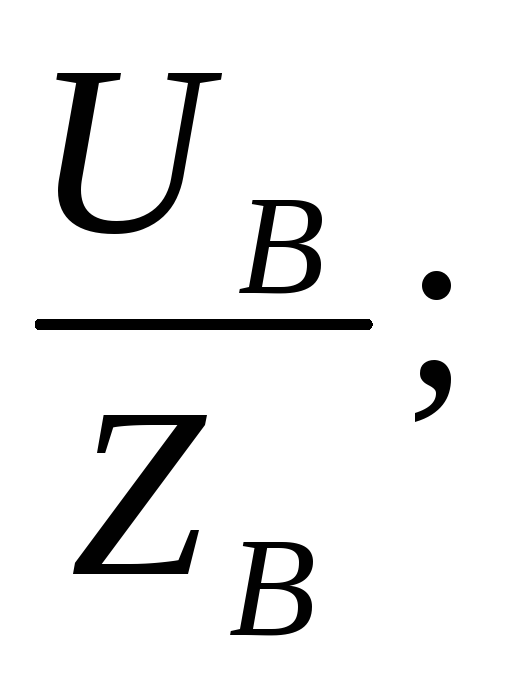 IС =
IС = 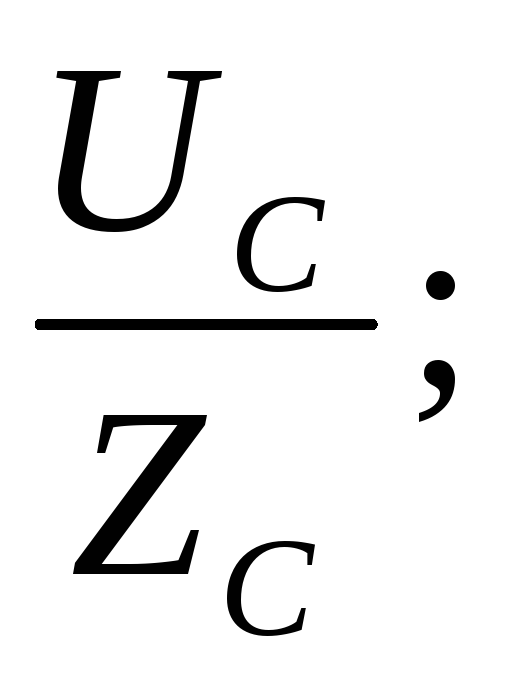
Сдвиг по фазе между фазным током и фазным напряжениям определяется по формулам:
сos
φА=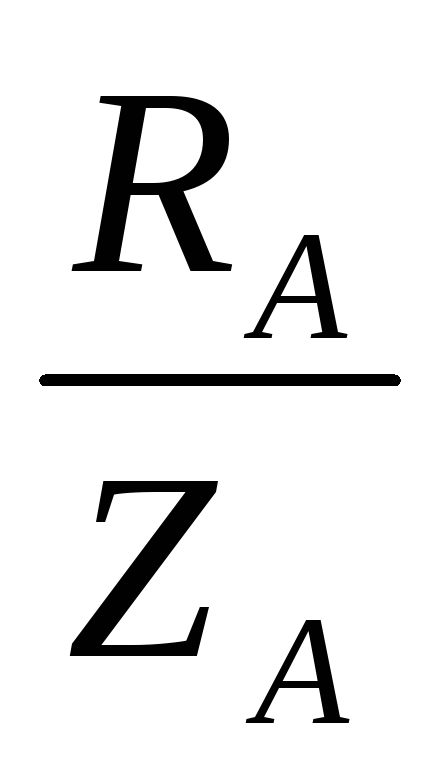 ;
сos
φВ=
;
сos
φВ=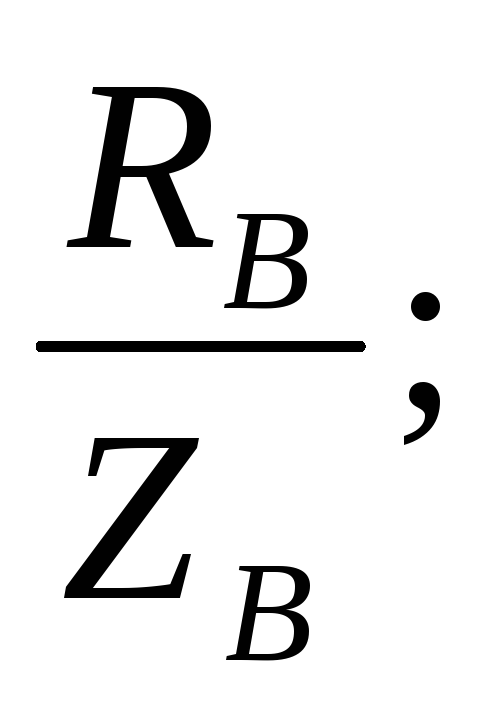 сos С=
сos С=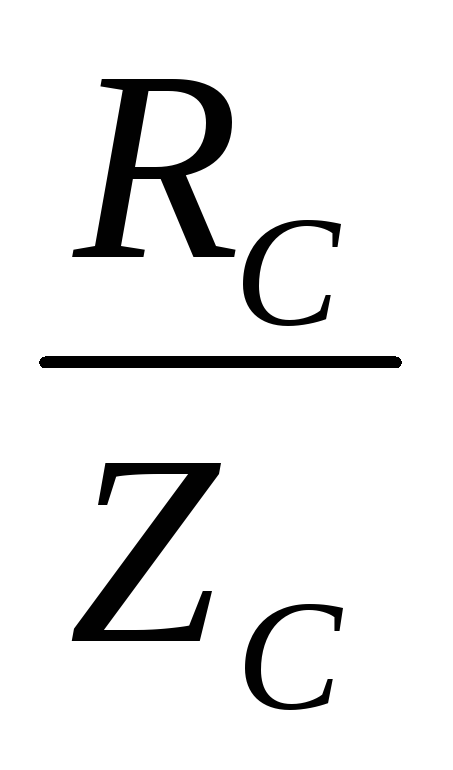
Величину тока, протекающего по нулевому проводу, определяют как геометрическую сумму фазных токов:
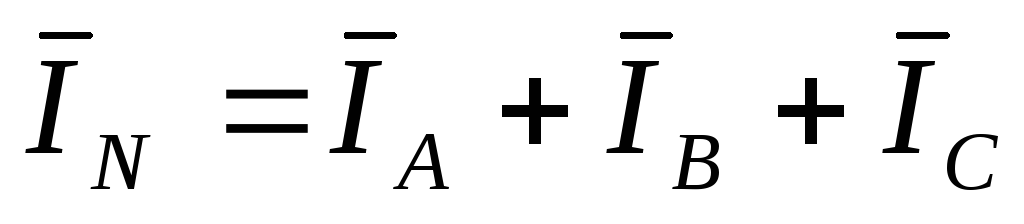
В трехфазных цепях различают симметричные и несимметричные нагрузки. Нагрузка называется симметричной, если сопротивления и углы сдвига между током и напряжением всех фаз нагрузки одинаковы, т.е.
ZA = ZB = ZC; φA= φB= φC . (3.1)
Еслихотя бы одно из условий (3.1) не выполняется, нагрузка трехфазной системы называется несимметричной.
Составим систему уравнений для определения мгновенных значений линейных напряжений:
uAB=uA + (-uB)
uBC=uB + (-uC) (3.2)
uCA=uC + (-uA)
В действующих значениях напряжений система (3.2) будет справедлива в векторной форме
 AB=
AB= A —
A —  B
B
 BC=
BC= B —
B —  C (3.3)
C (3.3)
 CA=
CA= C —
C — A
A
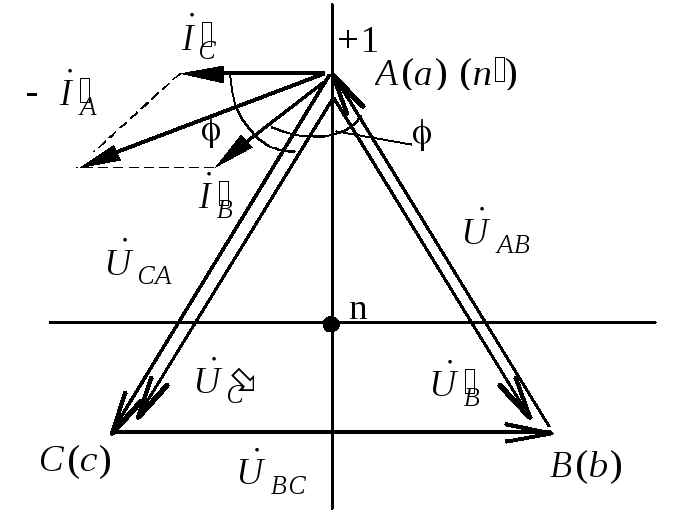
На основе уравнений (3.3) построим полярную векторную диаграмму фазных и линейных напряжений (рис. 3.5). Векторная диаграмма называется полярной, если все вектора начинаются из одной и той же точки, называемой полюсом.
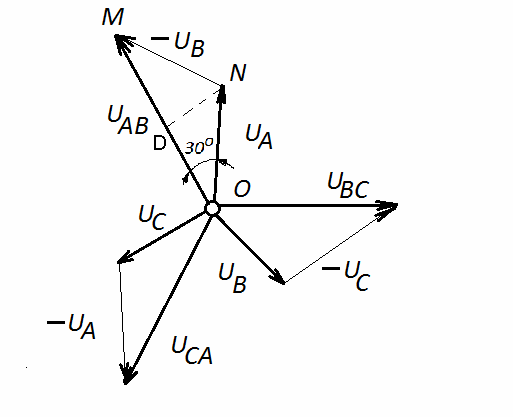
Рис. 3.5 Полярная векторная диаграмма напряжений четырехпроводной трехфазной системы «звезда».
Из диаграммы видно, что все три линейных напряжения равны между собой и смещены друг от друга на 120о.
Из равнобедренного треугольника OMN находим:
OM
= 2OD
= 2ON
cos30o = 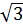 ON
ON
Так как Uл =UAB=OM,
Uф=UA=ON,
то окончательно получаем Uл = 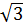 Uф.
Uф.
Таким образом, в
четырехпроводной системе «звезда»
линейное напряжение в 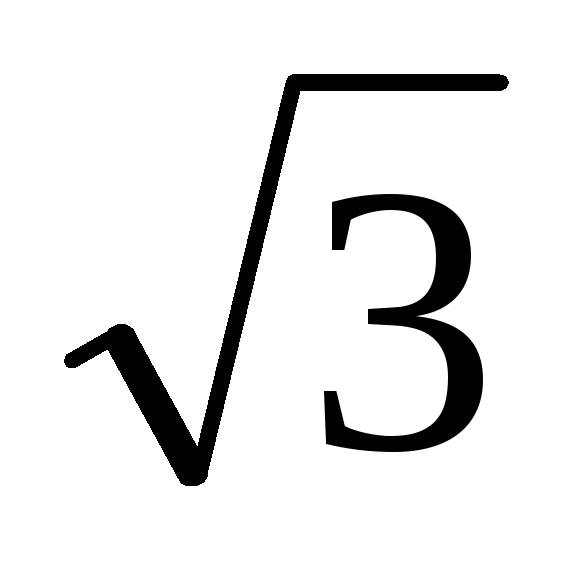 раз
больше фазного напряжения.
раз
больше фазного напряжения.
Четырехпроводная система трехфазного тока «звезда» применяется для питания несимметричной нагрузки, например, осветительной, где симметричность нагрузки нарушается при отключении ламп накаливания, включаемых в одну из фаз.
Осветительная нагрузка, представляющая собой определенное число ламп накаливания, включенных в каждую из фаз параллельно друг другу, является чисто активной нагрузкой.
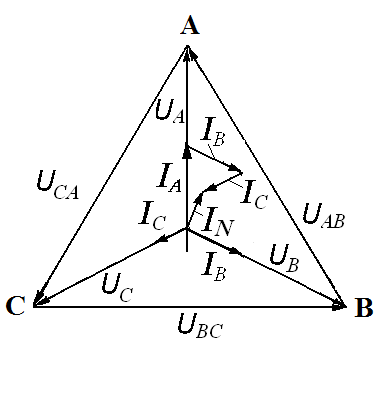
Проанализируем работу четырехпроводной трехфазной системы «звезда» для симметричной и несимметричной активной нагрузки для чего построим топологические векторные диаграммы напряжений и токов (рис.3.6). Заметим, что при активной нагрузке вектора токов будут совпадать по фазе с векторами соответствующих напряжений, что облегчает анализ.
а) б)
Рис.3.6. Топографическая векторная диаграмма четырехпроводной трехфазной системы «звезда» при активной нагрузке: а) симметричная нагрузка; б) несимметричная нагрузка
Для симметричной активной нагрузки
ZA = ZB = ZC = RA = RB = RC
IA = IB = IC = IФ = 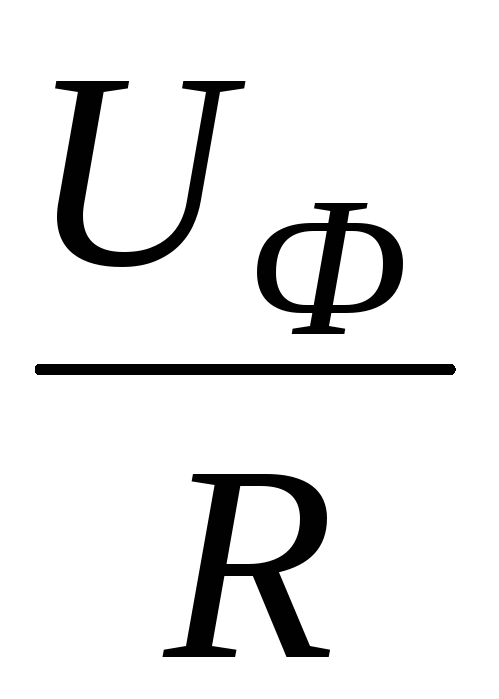 =
=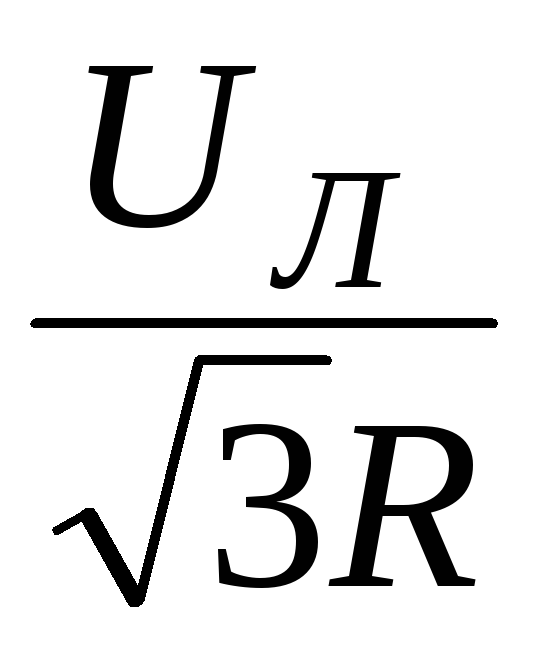
Из (рис. 3.6 а) получаем 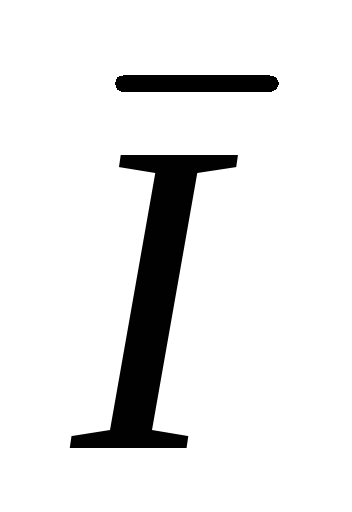 A +
A + 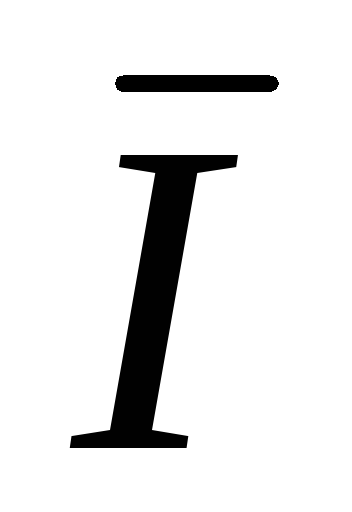 B +
B + 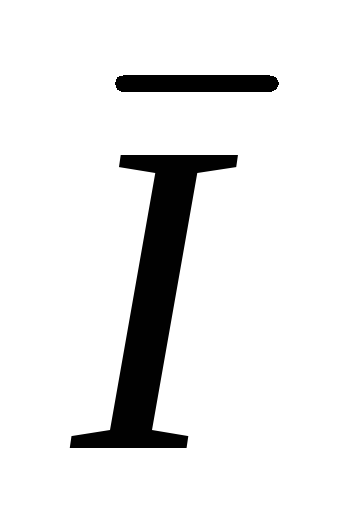 C = 0.
C = 0.
Для несимметричной активной нагрузки ZA = RA ; ZB = RB ; ZC = RC ; RA ≠ RB ≠ RC ; IA ≠ IB ≠ IC.
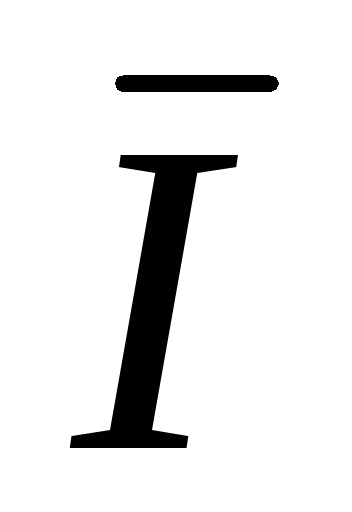 N =
N =  A +
A + 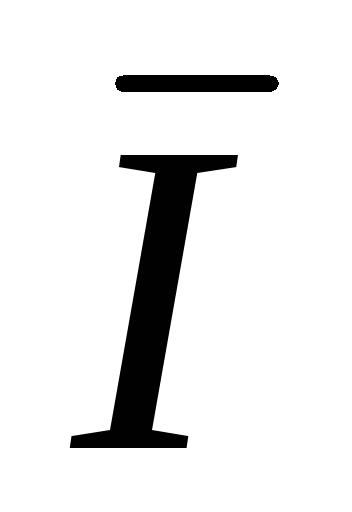 B +
B + 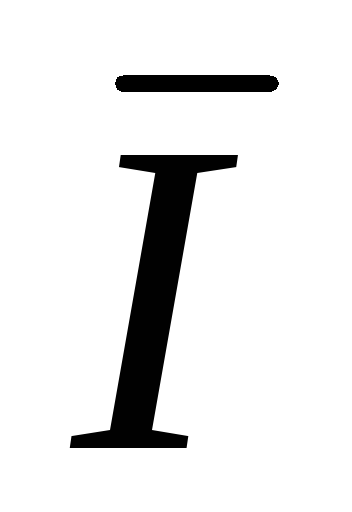 C .
C .
Анализ работы четырехпроводной системы трехфазного тока, включенной по схеме звезда, позволяет сделать следующие выводы:
1. Линейные токи равны фазным.
2. Все линейные напряжения равны между собой и смещены друг от друга на 120о.
3. Все фазные
напряжения равны между собой и в 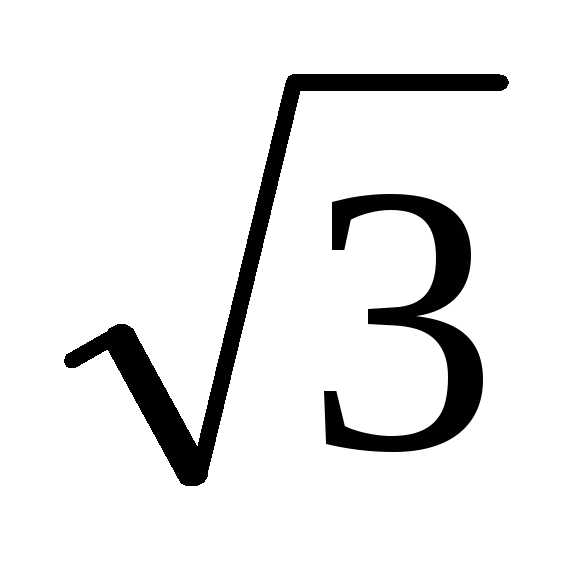 раз меньше линейных напряжений, независимо
от симметричности нагрузки.
раз меньше линейных напряжений, независимо
от симметричности нагрузки.
4. При несимметричной
нагрузке ток в нулевом проводе определяется
как геометрическая сумма фазных токов
(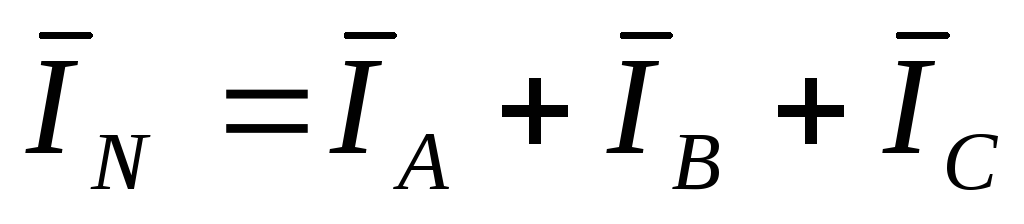 ),
при симметричной нагрузке ток в нулевом
проводе равен нулю (
),
при симметричной нагрузке ток в нулевом
проводе равен нулю (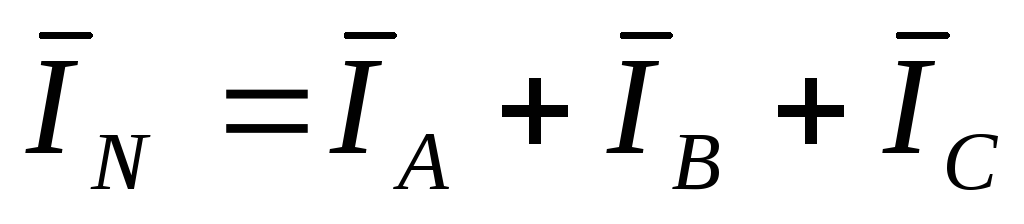 =0).
=0).
Методические указания по теме «Трехфазные электрические цепи» — Мегаобучалка
В трехфазных цепях потребители соединяют по схемам «звезда»» или «треугольник».
При соединении приемников энергии звездой линейные напряжения обозначаются UАВ, UВС, UСА.В общем виде UЛ. Фазные напряжения обозначаются UА, UВ, UС, в общем виде UФ.
Токи обозначаются IА, IВ, IС, причем, линейный ток равен фазному: I Л= IФ.
При наличии нулевого провода при любой нагрузке, а при равномерной нагрузке и без нулевого провода UЛ = √3 UФ (линейное напряжение больше фазного в √3 раз). При равномерной нагрузке фаз активная мощность всей цепи Р = √3 UЛ IЛ cos φФ или Р = 3 UФ IФ cos φФ
При неравномерной нагрузке мощность всей цепи
Р = РФ1 + Рф2 + Рфз, гдеРФ = UФ IФ cos φФ
При соединении потребителей треугольником фазное напряжение равно линейному: U Л=UФ. обозначаются напряжения UАВ, UВС, UСА.
Фазные токи обозначаются IАВ, IВС, IСА
Линейные токи обозначаются IА, IВ, IС, в общем виде IЛ.
При равномерной нагрузке фаз IЛ = √3 IФ.
При неравномерной нагрузке фаз линейные токи определяются на основании первого закона Кирхгофа из векторной диаграммы, как геометрическая разность фазных токов.
При соединении приемников энергии звездой сеть может быть четырехпроводной — при наличии нулевого провода, или трехпроводной — без нулевого провода.
При соединении приемников энергии треугольником сеть может быть толькотрехпроводной.
4.2. Пример решения задачи по схеме «звезда»
В четырехпроводную сеть (см. рис.)трехфазного тока с линейным напряжением UЛ = 380 В включены по схеме «звезда» три группы электрических ламп накаливания одинаковой мощности. В каждой группе лампы соединены параллельно. В среднем сопротивление одной лампы составляет R лампы = 484 Ом.
Первая группа ламп включена в фазу А, число ламп в ней nА = 88 шт.
Вторая группа ламп включена б фазу В, число ламп в ней nВ =33 шт.
Третья группа ламп включена в фазу С, числе ламп в ней nс = 55 шт.
Определить ток ламп I , напряжение U ламп, мощность Р ламп, на которые рассчитана лампа; Токи IА, IВ, IС,, протекающие в фазах и линейных проводах; мощности РА , PВ, PС, P, потребляемые фазами и всей цепью. Построить в масштабе векторную диаграмму напряжений и токов и из неё графически определить величину тока в нулевом проводе I0 .
Дано. Uл = 380 В Rламп = 484 ОМ
n A= 88 шт. n B = 33 шт. n C= 55 шт.
Определить: Токи и напряжения на лампах., токи IА, IВ, IС, графически из векторной диаграммы РА , PВ, PС, P. Построить в масштабе векторную диаграмму напряжений и токов.
Решение I. Запишем линейные напряжения. По условию задачи UАВ = UВС = UСА = 380В.
Тогда фазные напряжения UА, UВ, UС в общем виде будут UФ = UЛ /√3 = 380 В / √3 =220 В.
таким образом, UА = UВ = UС = 220 В
2. Все лампы цепи включены на фазные напряжения, поэтому Uламп= UФ= 220 В.
3. Ток ламп по закону Ома Iламп = Uламп / Rламп = 220 В / 484 Ом = 0, 455 А.
(Если не дано сопротивление Rламп, а дана мощностьРламп , то из формулы Рламп= Uламп ∙ Iламп можно найти ток Iламп , а затем найти сопротивление Rламп.)
4. Мощность лампы Рламп= Uламп ∙ Iламп = 220 В ∙0,455 А = 100 Вт
Мощность лампы можно также найти по формулам
Рламп = U2ламп / Rамп или Р ламп = I2ламп• Rламп
5. Сопротивления фаз (они активные):
RА = Rламп / n A = 484 Ом / 88 = 5,5 Ом
RВ = Rламп / n В = 484 Ом / 33 = 14,6 Ом,
RС = Rламп / n С = 484 Ом / 55= 8,8 Ом .
6. Токи фаз по закону Ома
IА = UA/ RА = 220 В / 5,5 Ом= 40 А,
IВ =UВ / RВ =220 В / 14,6 Ом = 15 А,
IС = Uc /RС= 220 В / 8,8 Ом = 25 А.
(Если не даны количества ламп nA, nВ, nС на каждой фазе, а даны фазные токи IА, IВ, IС, то из формул
IА = Iламп∙n А,IВ = Iламп∙n В,IС = Iламп∙n Снаходим количество ламп, а затем сопротивления фаз).
Фазные токи ламп можно было найти по значению тока лампы и количеству лампв фазе
IА = Iламп∙n АIВ = Iламп∙n ВIС = Iламп∙n С
7. Мощности, потребляемые фазами (они активные)
РA = UA ∙ IА = 220 В ∙ 40 А = 8800 Вт
РВ = UВ ∙ IВ = 220 В ∙ 15 А = 3300 Вт.
РС = UС ∙ IС = 220 В ∙25 А = 5500 Вт
Другие способы определения мощностей фаз:
РА = U2A / RА РВ = U2В / RВ РС = U2С / RС
РА = I2A ∙ RА РВ = I 2В ∙ RВ РС = I 2С ∙ RС
РА = Рламп ∙ n АРВ = Рламп ∙ n ВРС = Рламп ∙ n С
8. Мощность, потребляемая цепью, Р = РА + РВ + РС = 8800 Вт + ЗЗ00 Вт + 5500 Вт = 17600 Вт
9. Построить векторную диаграмму напряжений и токов.
Порядок построения векторной диаграммы(см.рис.)
1. Построение векторной диаграммы начинаем с вывода масштаба для напряжения и тока (в контрольной работе эти масштабы вам будут заданы).
Пусть m U = 44 В / см , m I= 10 А / см
2. Из точки 0 проводил три вектора фазных напряжений UА, UВ, UС, углы между которыми составляют 120° (эти углы строят с максимально возможной точностью, используя циркуль или транспортир). В выбранном масштабе их длина будет LUФ =UФ / m U =220 В / 44(В / см)=5 см
3. Соединив концы векторов фазных напряжений, получим треугольник линейных напряжений UАВ, Ubc , Uca
Направление этих векторов совпадает с обходом против часовой стрелки. Возможны и другие способы изображения линейных напряжений (см. их в учебной литературе).
Измеряя векторы линейных напряжений, убедимся, что с учетом масштаба их длина будет равна LUисоответствовать напряжению U = LU ∙ m U=380 В.
3. Нагрузка фаз активная (электрические лампы накаливания обладают активным сопротивлением), поэтому токи IА, IВ, IСбудут совпадать по фазе с соответствующими фазными напряжениями. В выбранном масштабе их длина будет
LIA =IА / m I =40 А / 10 (A / см) = 4 см
LIВ =IВ / m I =15 А / 10 (A / см) = 1,5 см
LIС =IС / m I =25 А / 10 (A / см) = 2,5 см
4. Геометрически складываем токи IА, IВ, IСи получаем ток в нулевом проводе: I0 = IА + IВ + IС
При этом векторы токов можно складывать в любой последовательности. Так, на диаграмме к концу вектора IСпутем параллельного переноса пристроен вектор IА, к концу вектора IА пристроен путем параллельного переноса вектор IВ. Точка 0 соединена с концом вектора IВ – это и есть ток в нулевом проводе I0 . Величина токов в нулевом проводе I0 = LI0 ∙ m I= 2,2 см ∙ 10 А/см = 22 А
Т.е. ток в кулевом проводе определен графически, его величина I0 = 22 А.
Задача 9. Расчёт трёхфазной четырёхпроводной цепи, соединенной звездой.
Комплексные сопротивления фаз приёмника
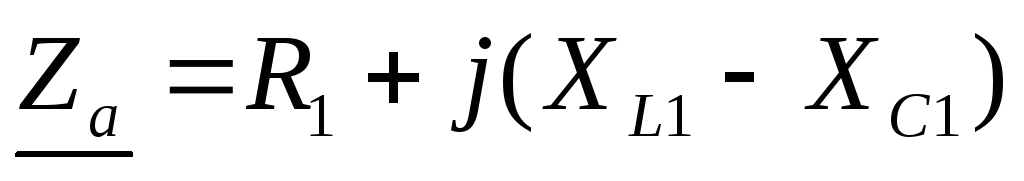 ;
; ;
;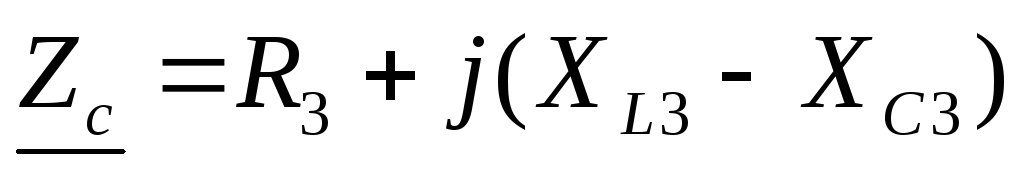 .
.
Числовые значения R1,XL1, … ,XC3даны в табл. 16. Значение линейного напряженияUЛсети, к которой подключен приемник, приведено в табл. 17. Сопротивление нейтрального провода принимается равным нулю.
Начертить схему цепи и показать на ней условно положительные направления линейных и фазных напряжений, линейных токов и тока в нейтральном проводе. (Элементы цепи, сопротивления которых равны нулю, на схеме не показывать.)
Определить: линейные токи Ia,Ib,Icи ток в нейтральном проводеIN;
комплексные мощности фаз приемника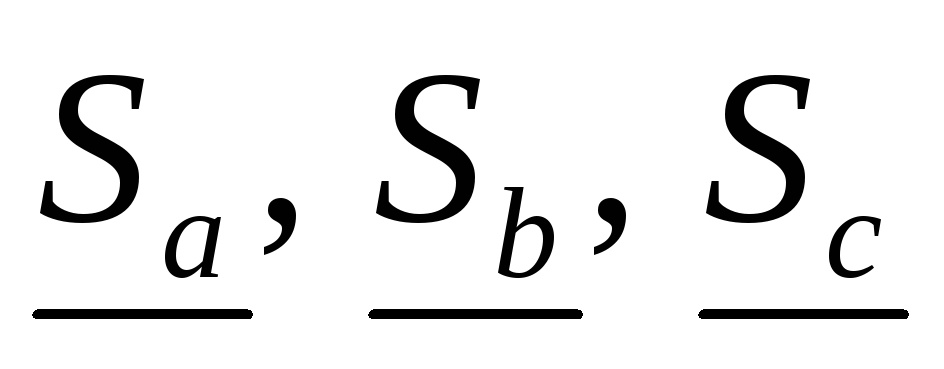 и всех трех фаз
и всех трех фаз ;
углы сдвига между фазными напряжениями
и токами φa, φb,
φc.
;
углы сдвига между фазными напряжениями
и токами φa, φb,
φc.
Построить векторную диаграмму напряжений и токов.
Таблица 16
Номер личного варианта | Сопротивления, Ом | ||||||||
R1 | XL1 | XC1 | R2 | XL2 | XC2 | R3 | XL3 | XC3 | |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
1 | 3 | 8 | 4 | 4 | 3 | 4 | 0 | 18 | 6 |
2 | 4 | 7 | 4 | 4 | 3 | 0 | 10 | 6 | 6 |
3 | 3 | 8 | 4 | 3 | 4 | 0 | 0 | 12 | 2 |
4 | 4 | 7 | 4 | 4 | 3 | 0 | 0 | 5 | 15 |
5 | 6 | 4 | 12 | 6 | 0 | 8 | 9 | 12 | 0 |
6 | 8 | 4 | 10 | 8 | 0 | 6 | 15 | 8 | 8 |
7 | 6 | 4 | 12 | 6 | 0 | 8 | 0 | 25 | 10 |
8 | 8 | 4 | 10 | 8 | 0 | 6 | 10 | 10 | 25 |
9 | 4 | 6 | 9 | 4 | 7 | 4 | 12 | 0 | 16 |
10 | 4 | 9 | 12 | 4 | 4 | 7 | 20 | 25 | 5 |
11 | 4 | 12 | 9 | 4 | 7 | 4 | 0 | 28 | 8 |
12 | 4 | 9 | 12 | 4 | 4 | 7 | 10 | 10 | 20 |
13 | 9 | 17 | 5 | 9 | 12 | 0 | 8 | 10 | 16 |
14 | 12 | 14 | 5 | 12 | 9 | 0 | 10 | 10 | 10 |
15 | 9 | 17 | 5 | 9 | 12 | 0 | 0 | 15 | 5 |
16 | 12 | 14 | 5 | 12 | 9 | 0 | 0 | 6 | 16 |
17 | 12 | 6 | 12 | 10 | 26 | 16 | 16 | 12 | 0 |
18 | 16 | 6 | 6 | 18 | 16 | 10 | 22 | 20 | 8 |
19 | 12 | 6 | 22 | 12 | 10 | 26 | 0 | 28 | 8 |
20 | 16 | 6 | 18 | 16 | 10 | 22 | 0 | 12 | 32 |
21 | 15 | 25 | 5 | 15 | 20 | 0 | 21 | 10 | 28 |
22 | 20 | 20 | 15 | 20 | 15 | 0 | 35 | 10 | 10 |
23 | 15 | 25 | 5 | 15 | 20 | 0 | 0 | 45 | 10 |
24 | 20 | 20 | 15 | 20 | 15 | 0 | 0 | 10 | 45 |
25 | 18 | 4 | 28 | 18 | 0 | 24 | 24 | 32 | 0 |
Таблица 17
Номер группового варианта | 1 | 2 | 3 | 4 | 5 |
Линейное напряжение сети, В | 660 | 380 | 220 | 690 | 400 |
Методические указания и пример расчета
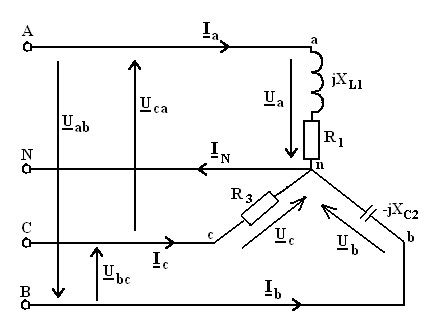
Рисунок 29
Решение данной задачи рассматривается при следующих исходных данных: UЛ= 380 В;R1= 11,XL1= 19,XC2= 44,R3= 22 Ом; сопротивленияXC1,R2,XL2,XC3равны нулю. Это решение осуществляется в следующем порядке.
Составляется подлежащая расчету схема цепи с учетом исходных данных.
Определяется действующее значение
фазного напряжения приемника: 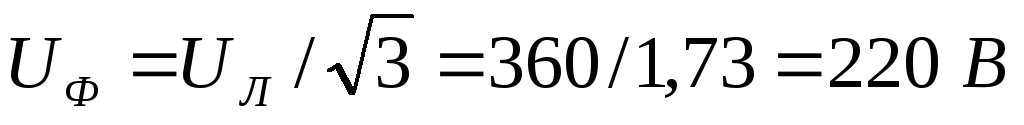 .
.
Составляется симметричная система фазовых комплексных напряжений приемника:
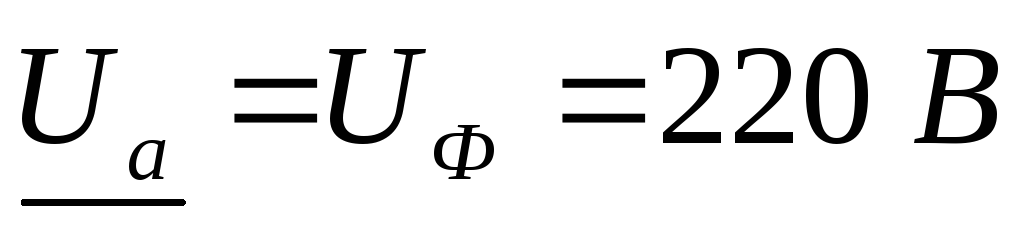 ;
;
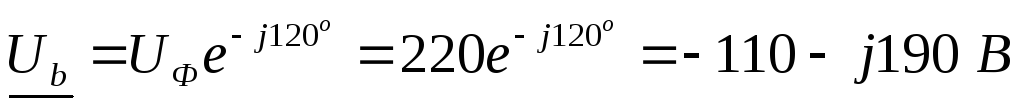 ;
;
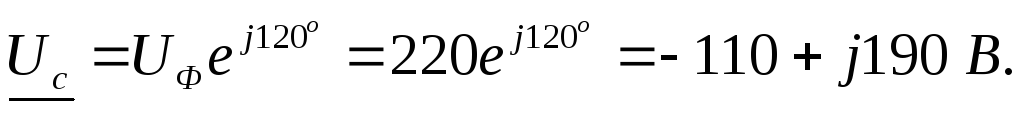
Составляются комплексные сопротивления
фаз приемника: 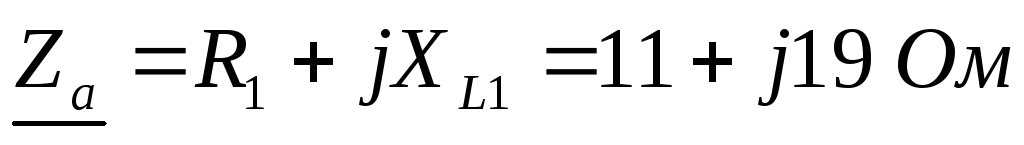 ;
;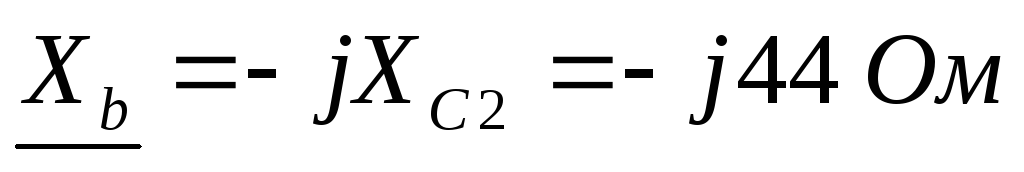 ;
;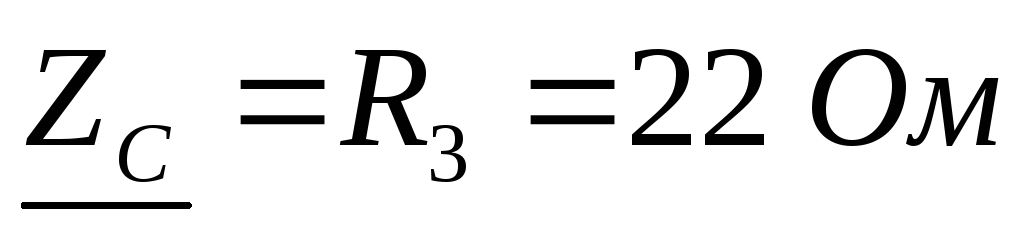 .
.
Определяются комплексные и действующие значения линейных токов и тока в нейтральном проводе:
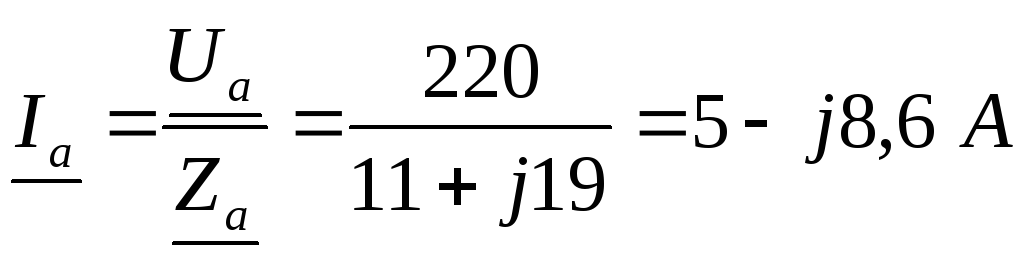 ;
; 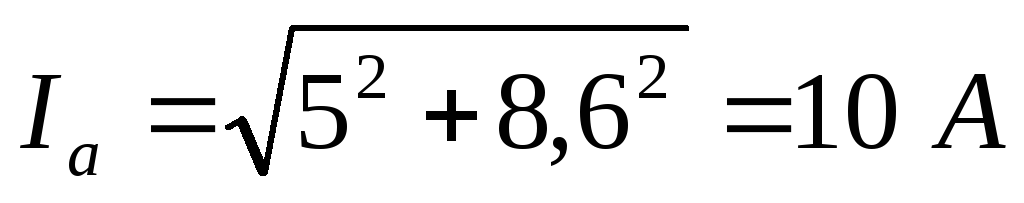 ;
;
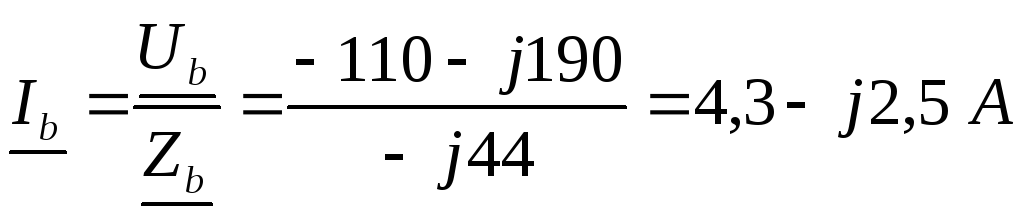 ;
; 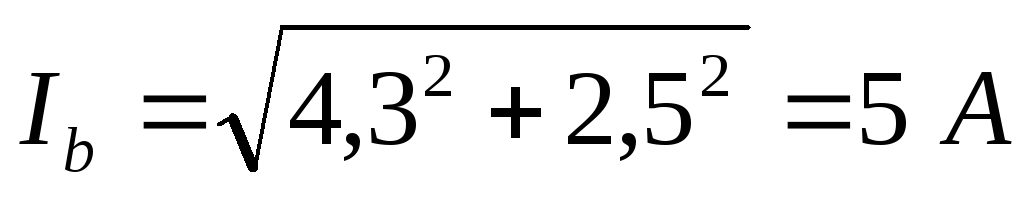 ;
;
 ;
; 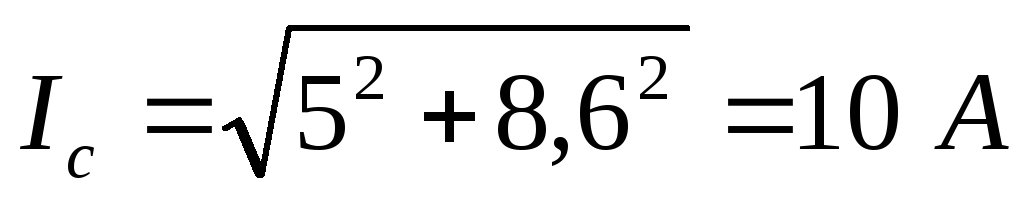 ;
;
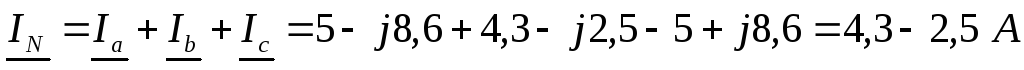 ;
;
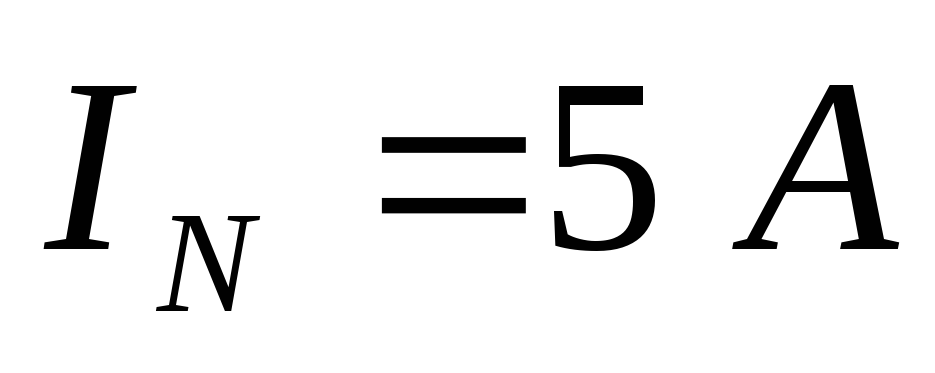 .
(В данной цепи ток
.
(В данной цепи ток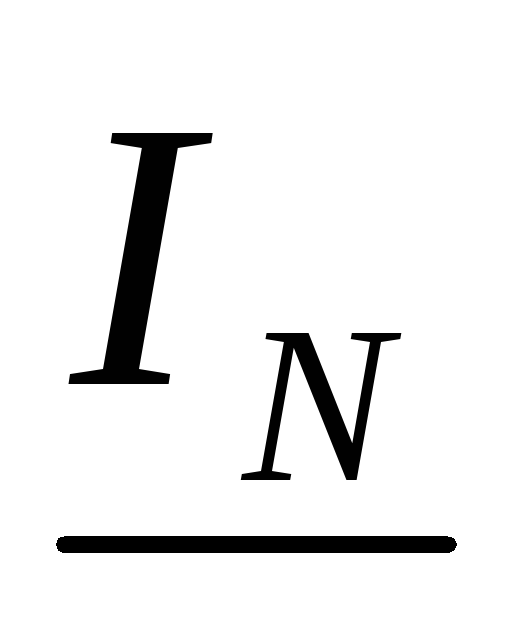 случайно оказался равным току
случайно оказался равным току .)
.)
Определяются углы сдвига фаз между
фазными напряжениями и токами: 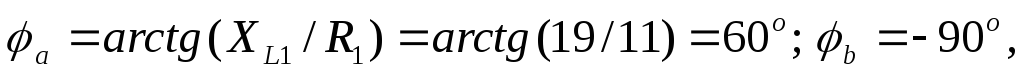 так как приемник фазыbемкостный,
так как приемник фазыbемкостный,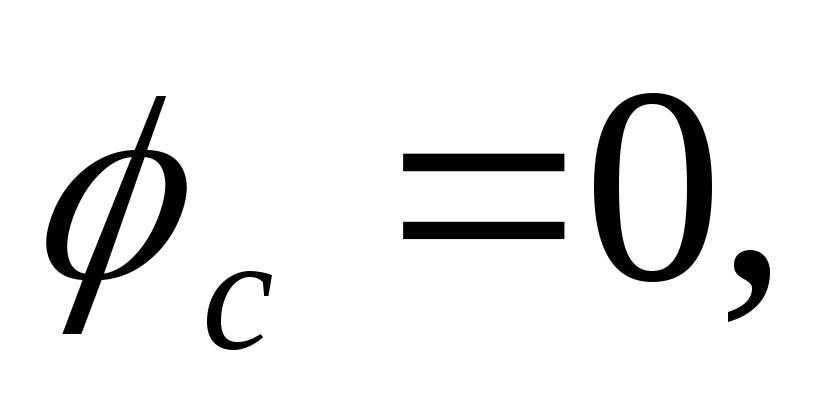 так как приёмник фазы с – резистивный.
так как приёмник фазы с – резистивный.
Определяются комплексные мощности фаз и всей цепи:
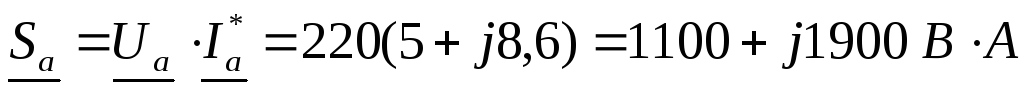 ;
;
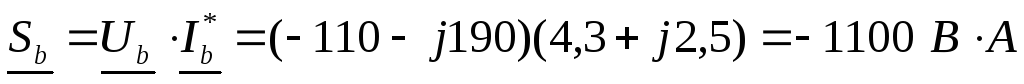 ;
;
 ;
;
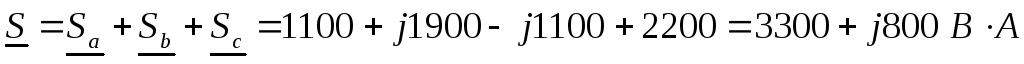 .
.
Строится векторная диаграмма напряжений и токов (рис. 30).
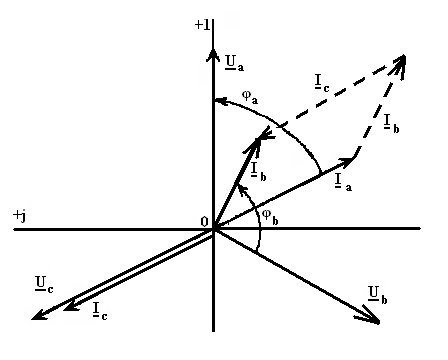
Рисунок 30
3. Трехфазные цепи
1. Трехфазные электрические сети в зависимости от числа проводов, соединяющих источник и приемник, бывают четырехпроводными и трехпроводными.
2. Все величины, относящиеся к источникам, записываются с индексами, обозначенными прописными буквами (A, B, C, N), а величины, относящиеся к приемникам, – с индексами, обозначенными строчными буквами (a, b, c, n для схемы “звезда” и ab, bc, ca для схемы “треугольник”).
3.
В четырехпроводных сетях к приемникам
подводятся два напряжения: линейное 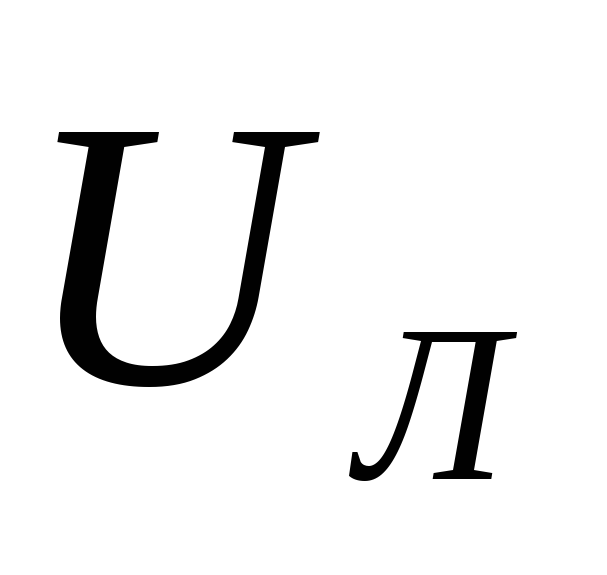 (напряжение между линейными проводами)
и фазное
(напряжение между линейными проводами)
и фазное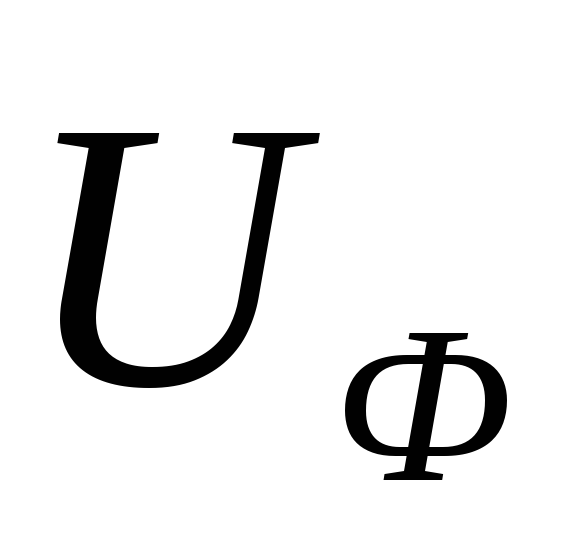 (напряжение между линейными и нейтральным
проводом), которые связанны между собой
соотношением
(напряжение между линейными и нейтральным
проводом), которые связанны между собой
соотношением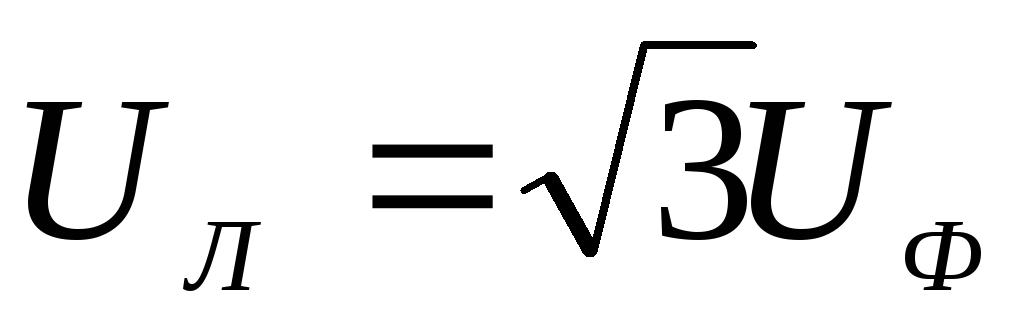 .
.
В комплексной форме фазные напряжения выражаются формулами
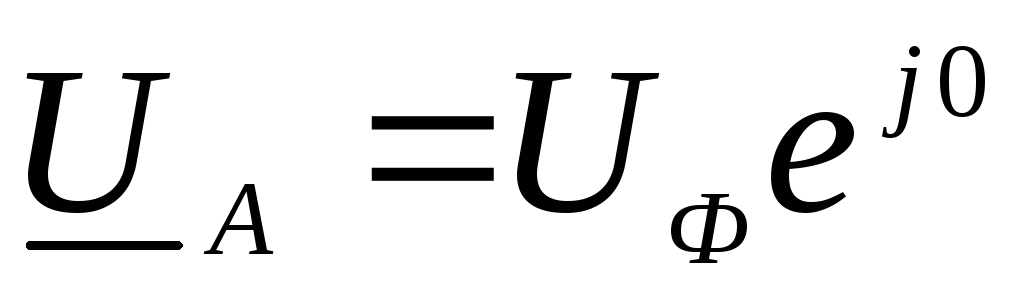 ,
, 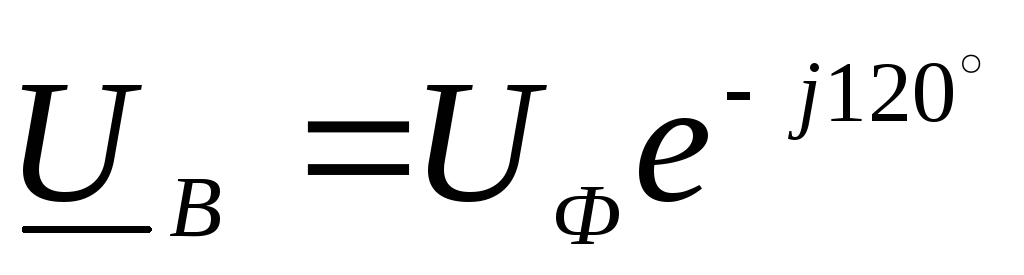 ,
,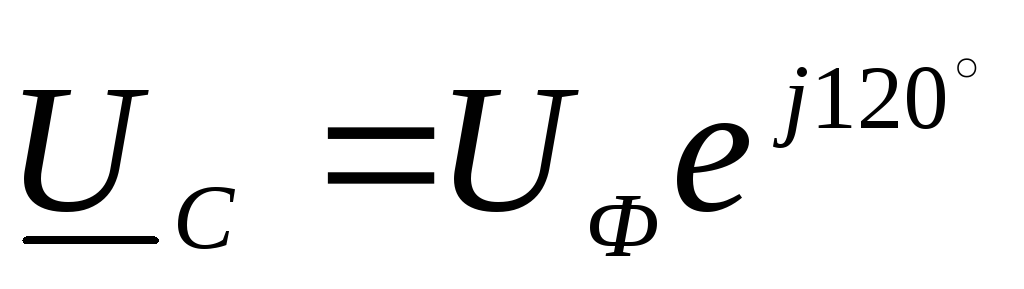 .
.
(здесь
начальная фаза напряжения  принята равной нулю).
принята равной нулю).
Комплексные линейные напряжения
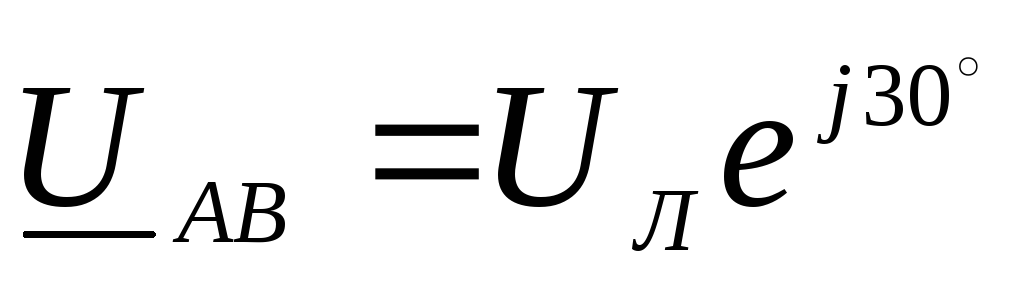 ,
, 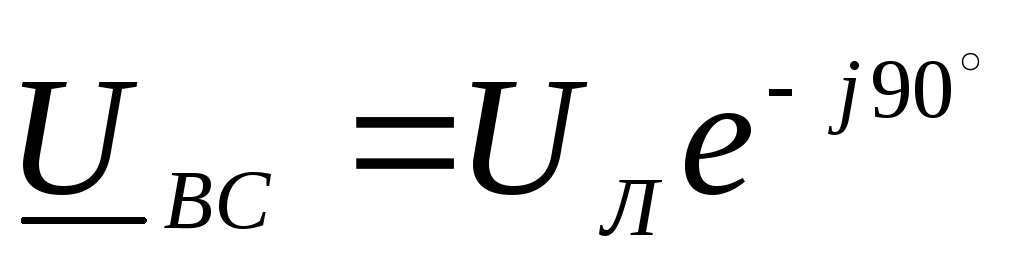 ,
,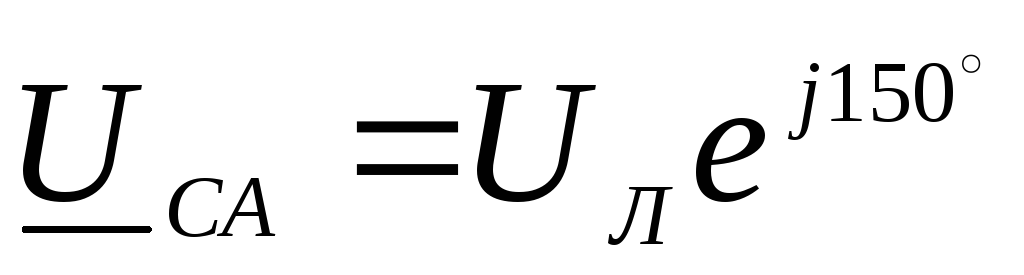 .
.
Топографическая диаграмма линейных и фазных напряжений изображена на
рис.
117, а.
Для токов в четырехпроводной системе
справедливо уравнение первого закона
Кирхгофа: 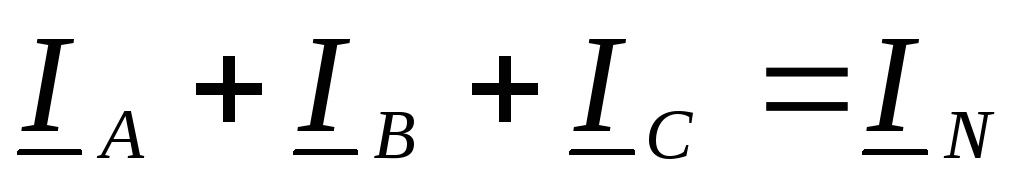 .
.
4.
В трехпроводных сетях к приемникам
подводятся только линейные напряжения 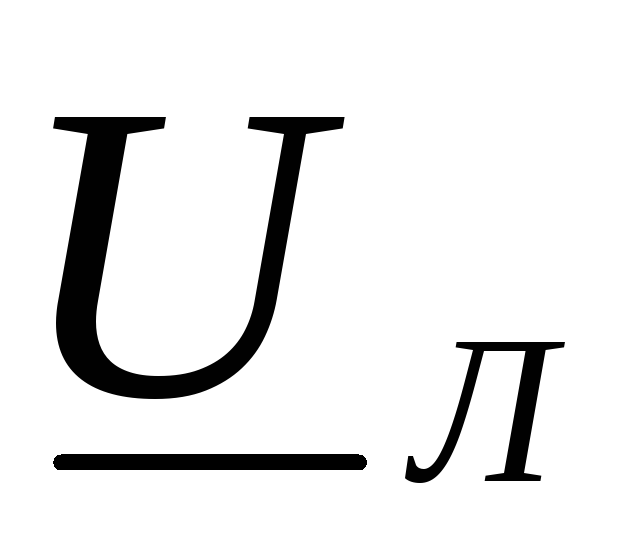 :
: ,
,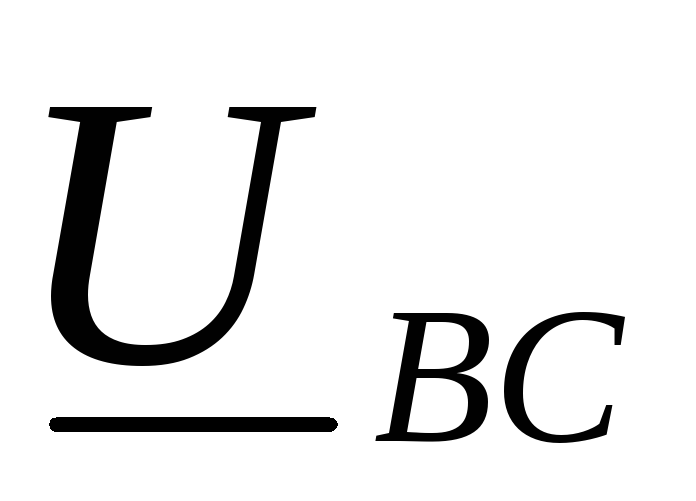 ,
, .
Их топографическая диаграмма изображена
на рис. 117,б.
.
Их топографическая диаграмма изображена
на рис. 117,б.
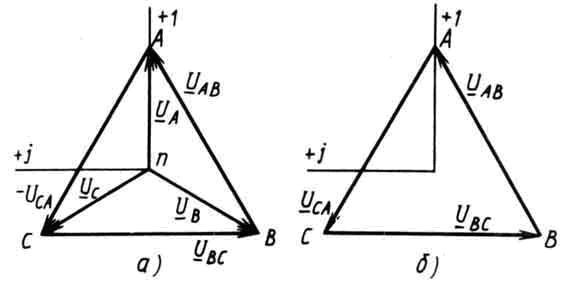
Рис. 117
Токи
в трехпроводной системе связаны
уравнением первого закона Кирхгофа: 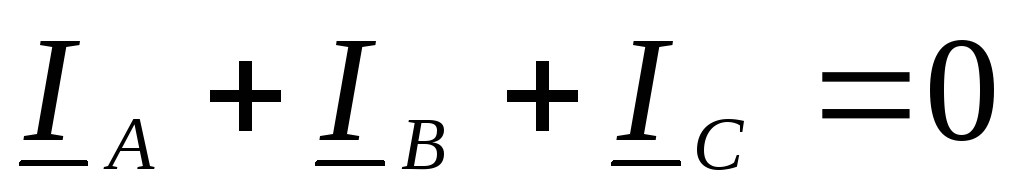 .
.
5.
Положительные напряжения токов 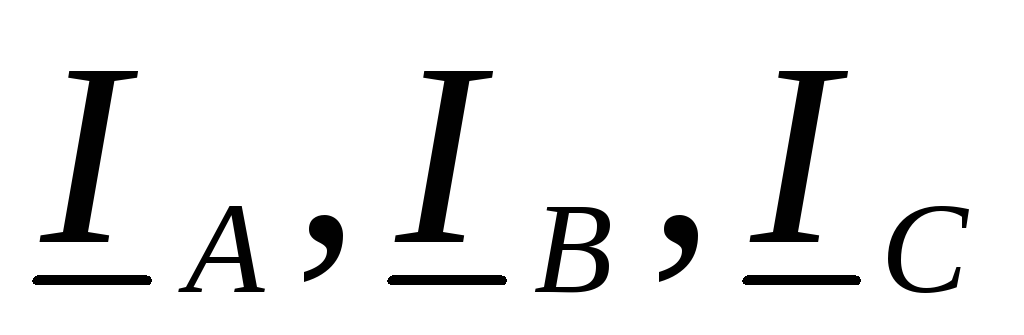 в линейных проводах приняты от источников
к приемнику, а в нейтральном проводе
в линейных проводах приняты от источников
к приемнику, а в нейтральном проводе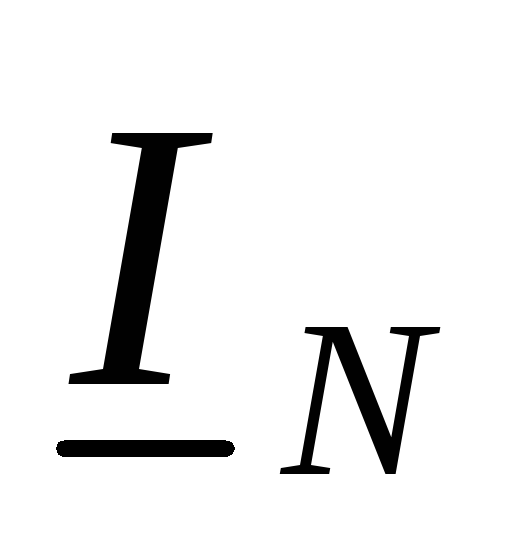 – от приемника к источнику.
– от приемника к источнику.
В
схеме “звезда” фазные токи 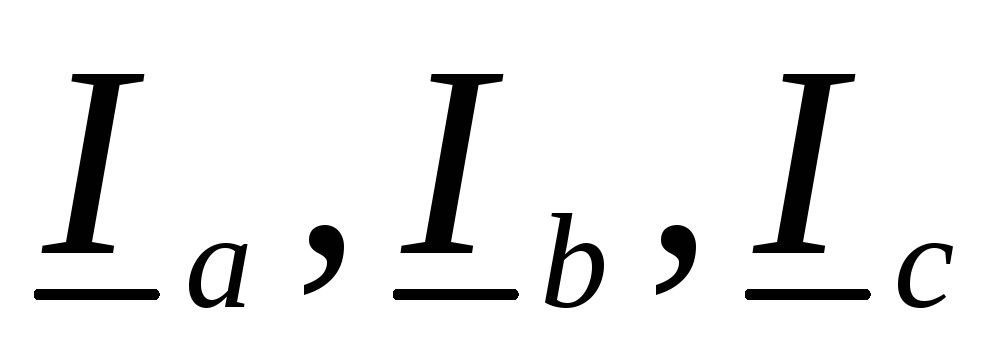 совпадают по направлению с линейными,
а в схеме “треугольник” токи
совпадают по направлению с линейными,
а в схеме “треугольник” токи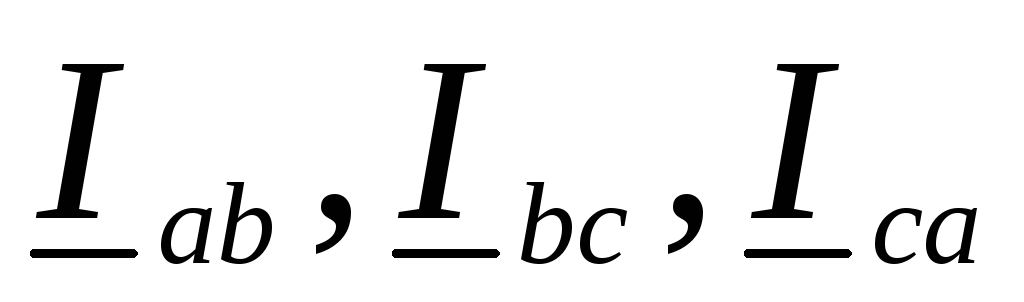 приняты направленными по часовой
стрелке.
приняты направленными по часовой
стрелке.
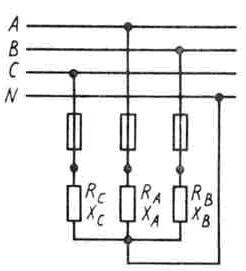
Рис. 118
6. Приемники электрической энергии могут быть соединены по схемам “звезда” с нейтральным проводом, “звезда” без нейтрального провода и “треугольник”. В каждой схеме соединений различают симметричный и несимметричный режимы.
При симметричном режиме комплексные соединения всех фаз одинаковы, при несимметричном – разные.
7. При решении задач необходимо прежде всего установить схему соединений приемников и выяснить, симметрична или несимметрична нагрузка.
8.
Расчет трехфазной цепи в симметричном
режиме сводится к расчету одной фазы и
выполняется аналогично расчету цепи
однофазного синусоидального тока. Так,
ток в фазе при соединении приемника
звездой или звездой с нейтральным
проводом, например, в фазе а,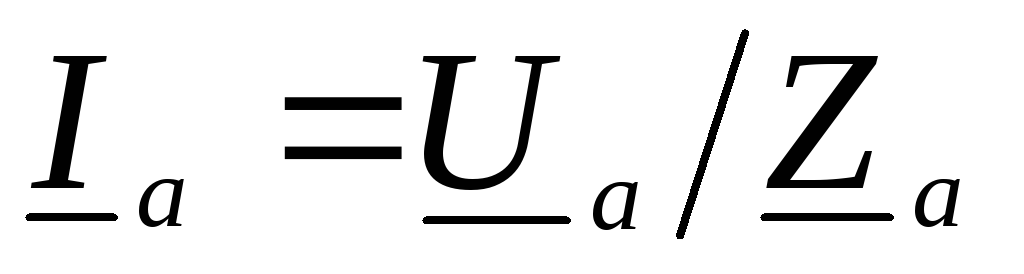 ,
а при соединении приемника треугольником,
например, в фазеab,
,
а при соединении приемника треугольником,
например, в фазеab, 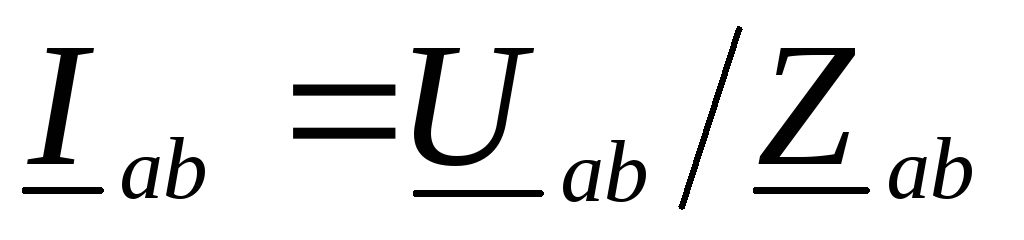 .
В остальных фазах значения токов (их
модули) те же, а начальные фазы сдвинуты
на
.
В остальных фазах значения токов (их
модули) те же, а начальные фазы сдвинуты
на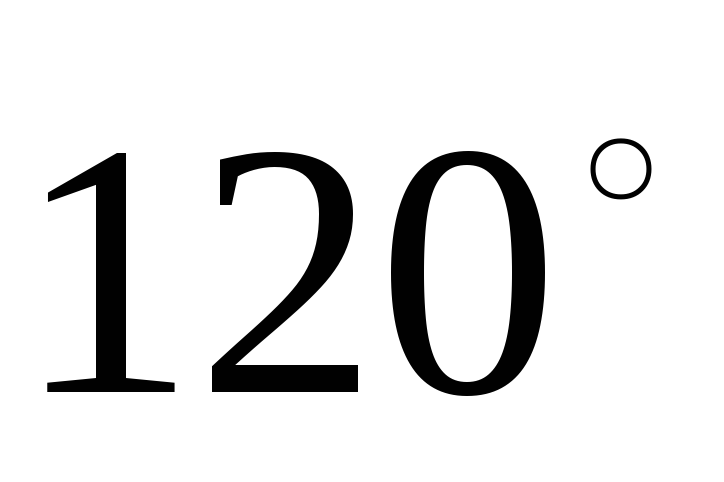 .
.
Пример. К трехфазной
линии с линейным напряжением 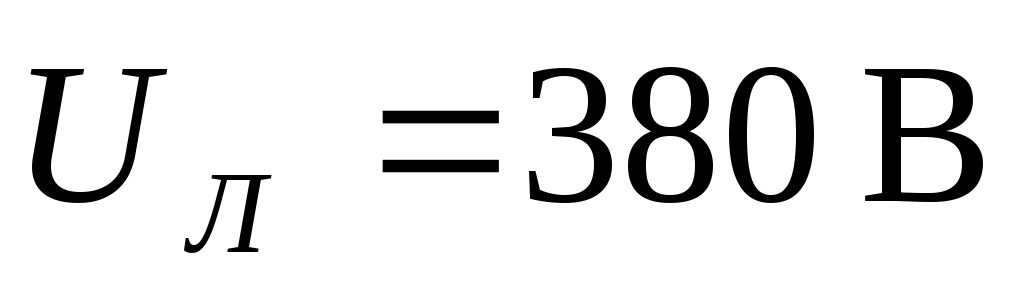 подключены три одинаковых приемника,
соединенные по схеме “звезда” с
нейтральным проводом (рис. 118). Активное
и реактивное сопротивление каждого
приемника соответственно равны
подключены три одинаковых приемника,
соединенные по схеме “звезда” с
нейтральным проводом (рис. 118). Активное
и реактивное сопротивление каждого
приемника соответственно равны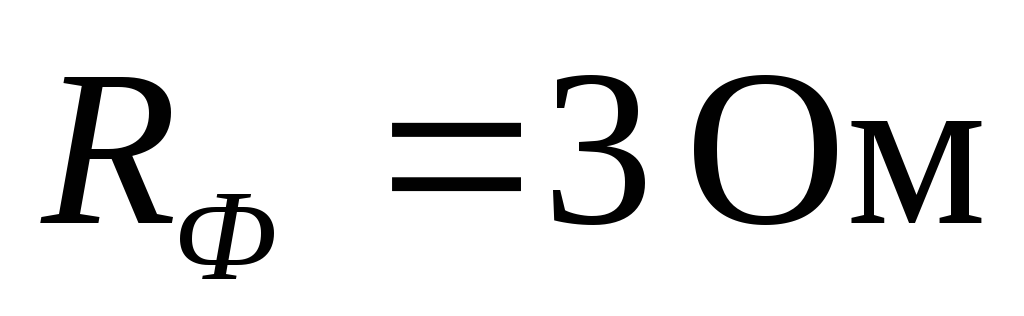 ,
,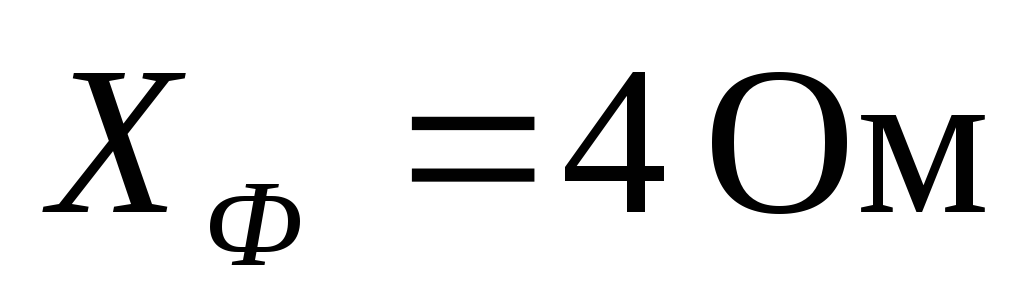 .
Определить токи в фазах и нейтральном
проводе, построить совмещенную
топографическую диаграмму напряжений
и векторную диаграмму токов.
.
Определить токи в фазах и нейтральном
проводе, построить совмещенную
топографическую диаграмму напряжений
и векторную диаграмму токов.
В трехфазном режиме нагрузка всех фаз одинакова, поэтому расчет проводят для одной фазы.
Напряжение фазы 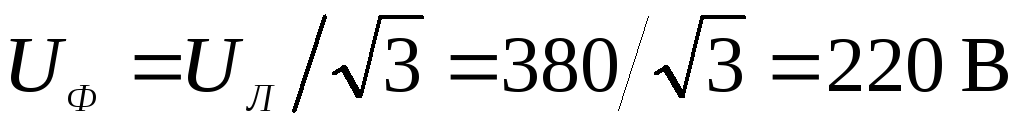 или в комплексной форме, принимая
начальную фазу,
или в комплексной форме, принимая
начальную фазу,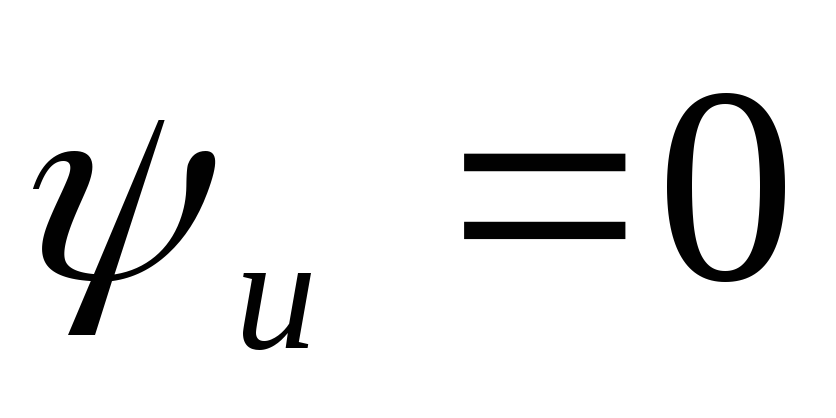 ,
, .
.
Комплексное
сопротивление фазы 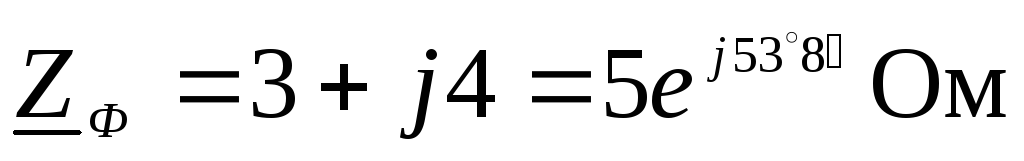 .
.
Ток
фазы 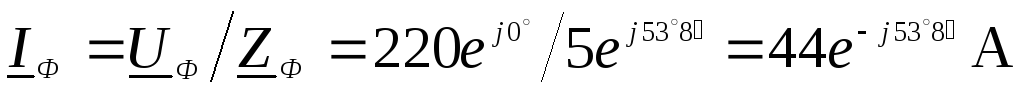 .
.
Ток
в нейтральном проводе 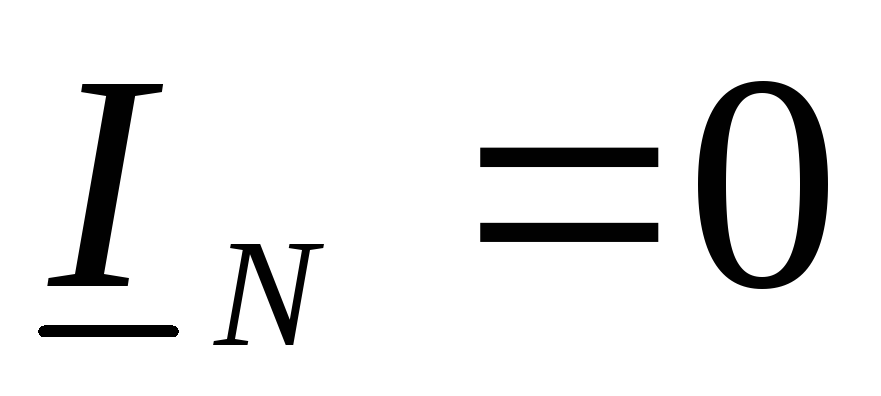 ,
так как нагрузка симметричная .
,
так как нагрузка симметричная .
Для построения совмещенной топографической диаграммы напряжений и векторной диаграммы токов (рис. 119) выбираем масштаб напряжений и токов.
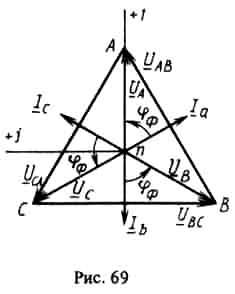
Рис. 119
Строим
топографическую диаграмму напряжений
и откладываем векторы тока под углом 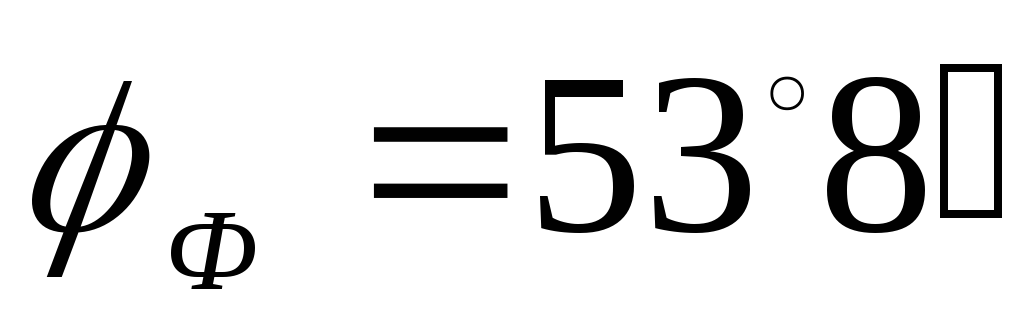 к векторам фазных напряжений.
к векторам фазных напряжений.
9.
В схеме “звезда” c
нейтральным проводом при несимметричной
нагрузке режим работы каждой фазы
независим от работы других фаз и потенциал
нейтральной точки приемника при любой
нагрузке равен нулю  ,
поэтому токи в фазах
,
поэтому токи в фазах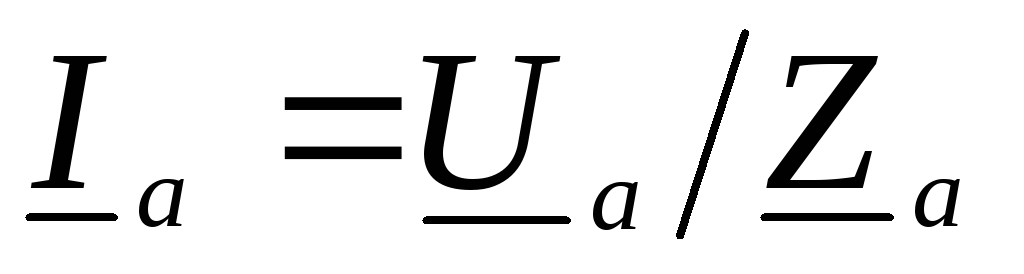 ,
,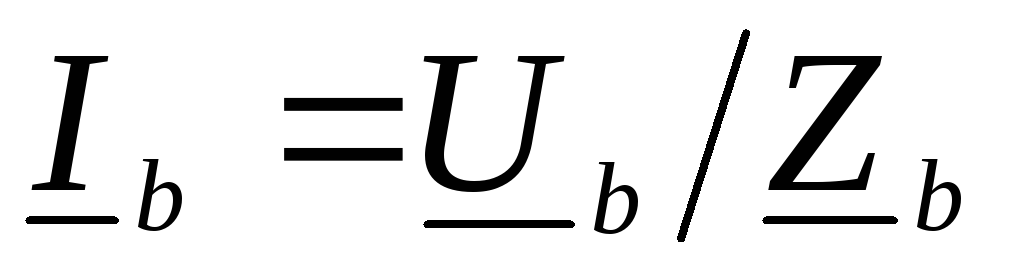 ,
,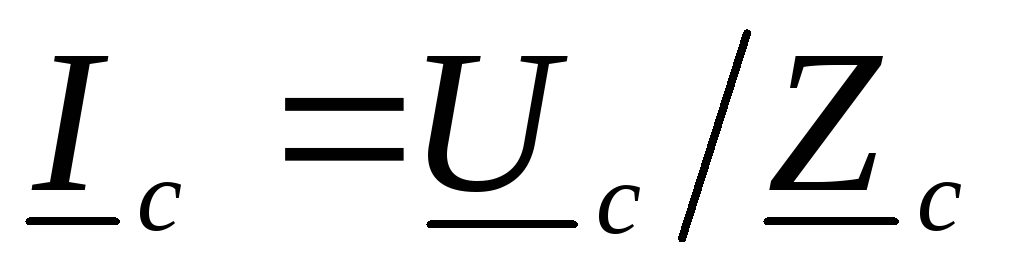 .
.
Ток
в нейтральном проводе 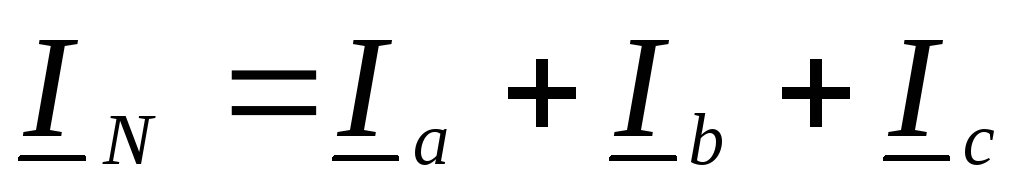 .
Он также может быть найден из векторной
диаграммы.
.
Он также может быть найден из векторной
диаграммы.
Пример. К трехфазной линии с линейным напряжением
подключен несимметричный приемник,
соединенный по схеме “звезда” с
нейтральным проводом (см. рис. 118). Активные
и реактивные сопротивления фаз приемника
соответственно равны: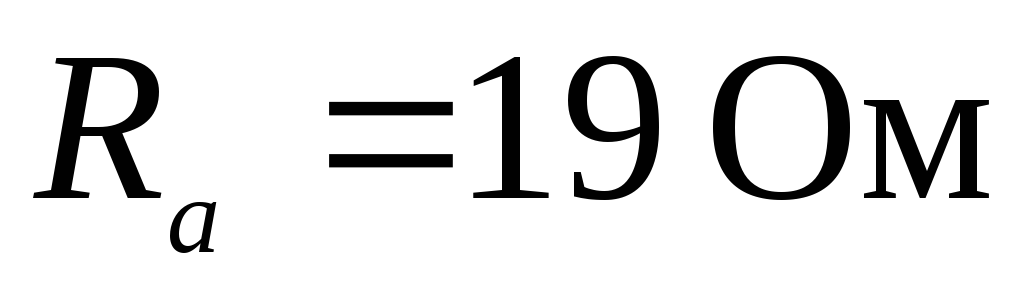 ,
,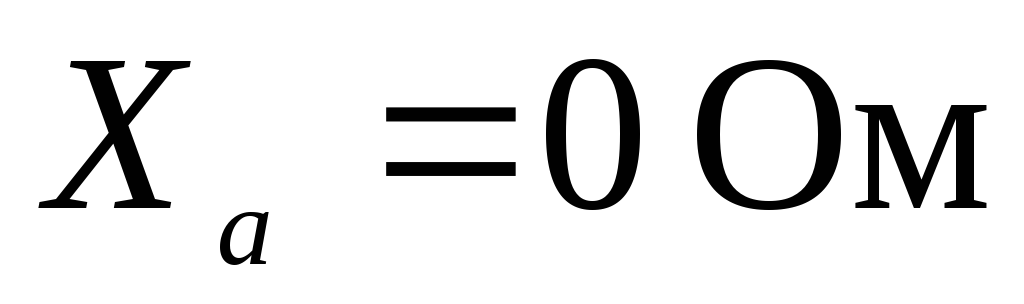 ,
,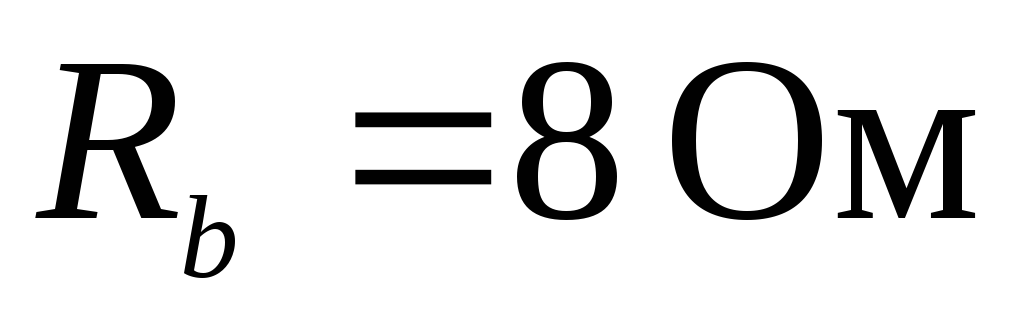 ,
,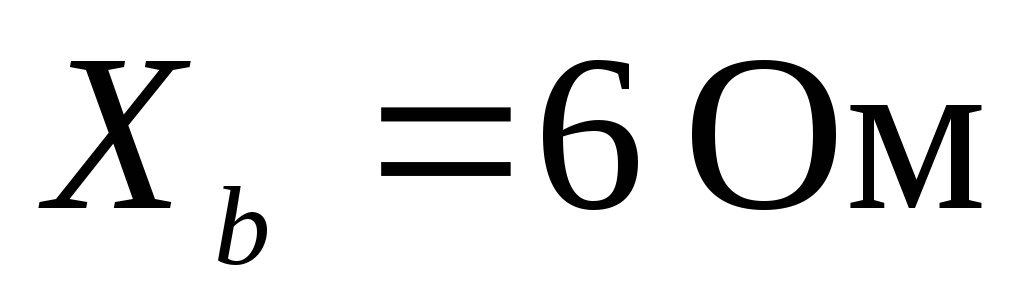 ,
,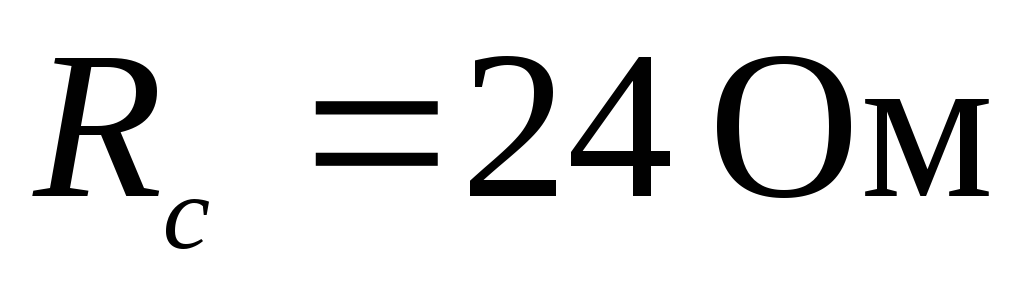 ,
,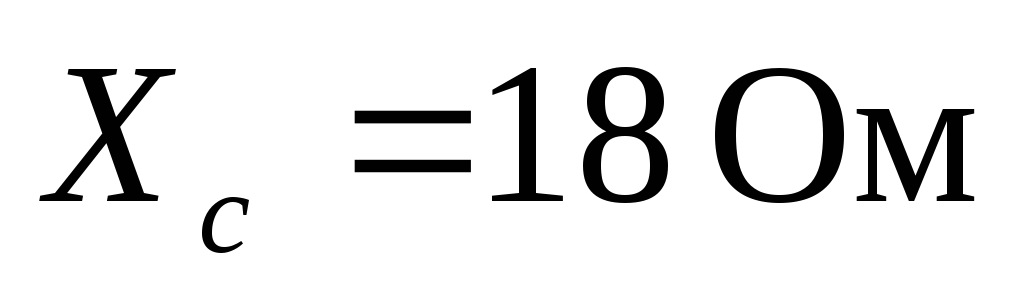 .
Сопротивлением нейтрального провода
можно пренебречь. Определить токи в
фазах приемника, в линейных проводах и
нейтральном проводе.
.
Сопротивлением нейтрального провода
можно пренебречь. Определить токи в
фазах приемника, в линейных проводах и
нейтральном проводе.
Токи
в линейных проводах и фазах приемника
одинаковы и рассчитываются по закону
Ома: 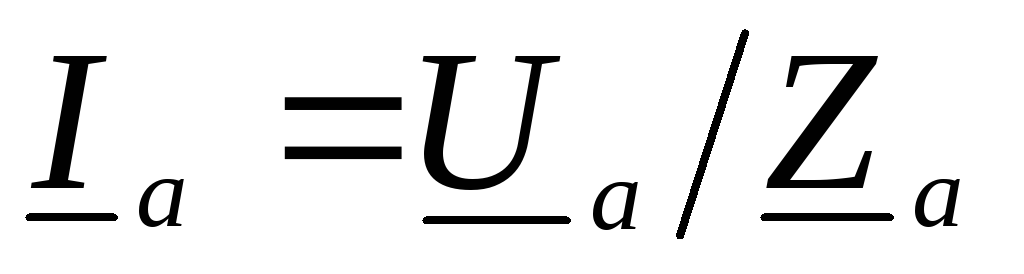 ,
,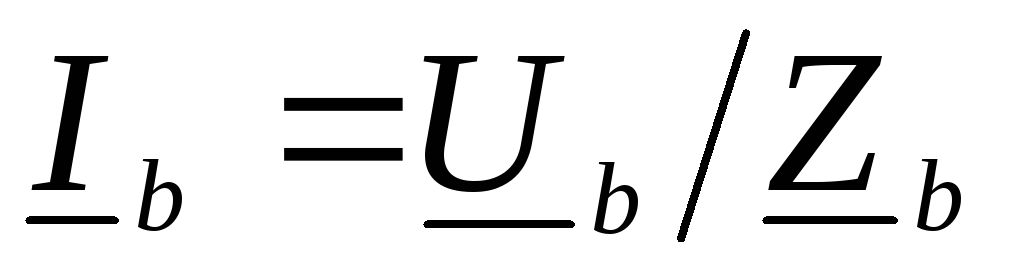 ,
,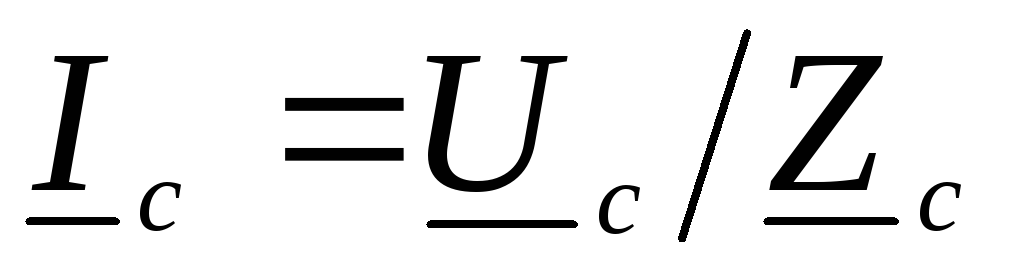 .
.
Фазное
напряжение  .
.
Комплексные фазные напряжения
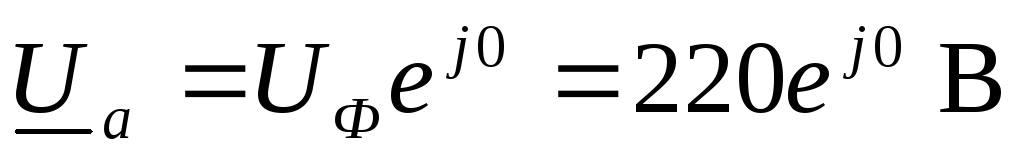 ,
, 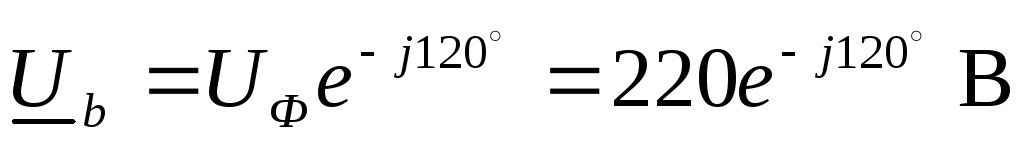 ,
,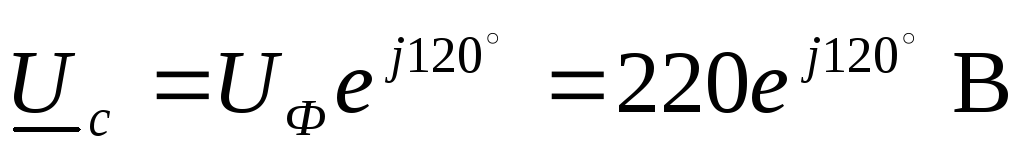 .
.
Комплексные сопротивления фаз и токи в фазах и линиях:
 ,
, 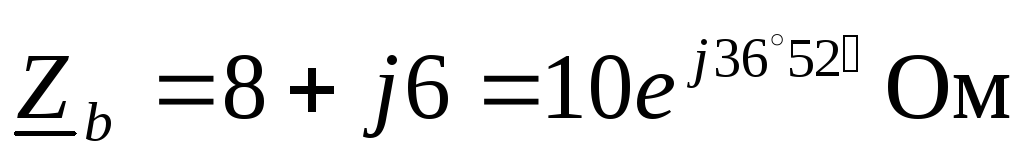 ,
,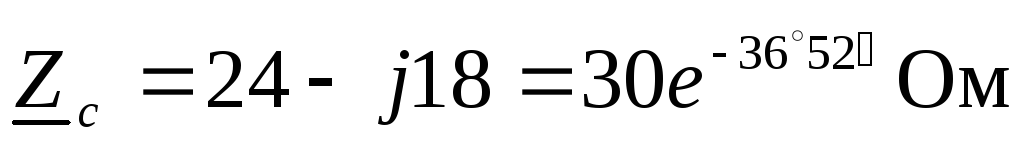 ,
,
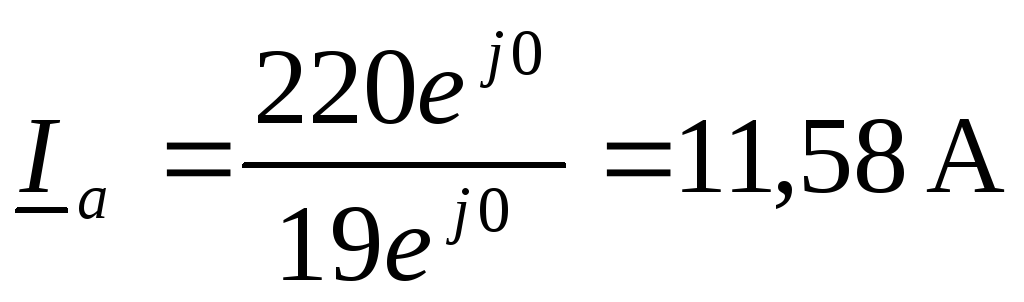 ,
,  ,
,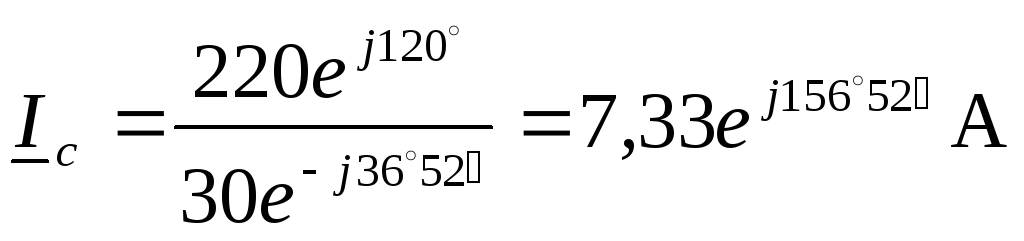 .
.
Ток в нейтральном проводе
 .
.
Для
построения топографической диаграммы
напряжений выбираем масштабы напряжения 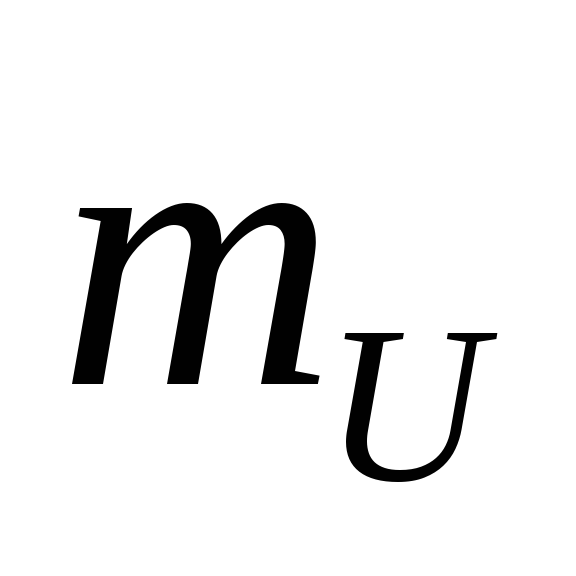 и тока
и тока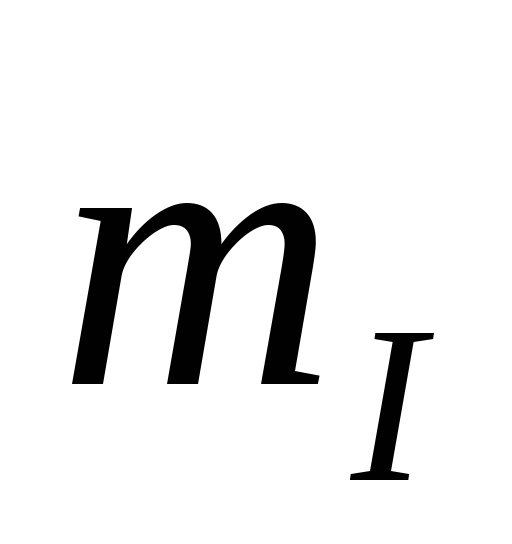 .
В выбранном масштабе строим топографическую
диаграмму напряжений, аналогичную рис.
117. При построении векторной диаграммы
токов учитываем, что векторы токов в
фазах сдвинуты относительно векторов
фазных напряжений: в фазеа на угол
.
В выбранном масштабе строим топографическую
диаграмму напряжений, аналогичную рис.
117. При построении векторной диаграммы
токов учитываем, что векторы токов в
фазах сдвинуты относительно векторов
фазных напряжений: в фазеа на угол 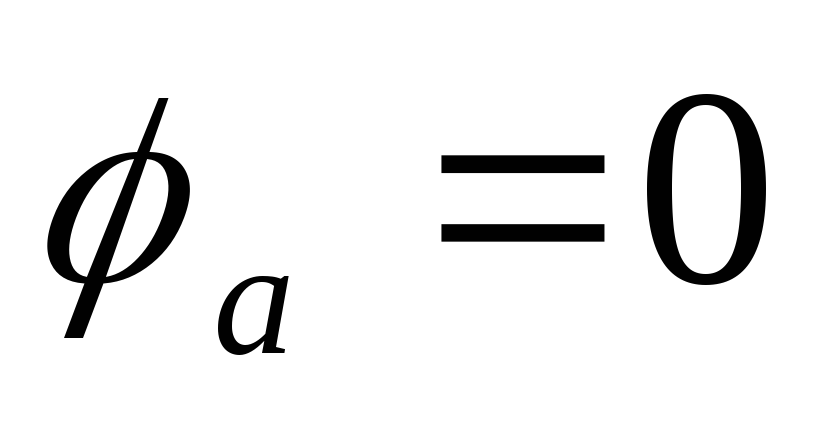 – нагрузка чисто активная
– нагрузка чисто активная
(Х = 0), в фазе b на угол 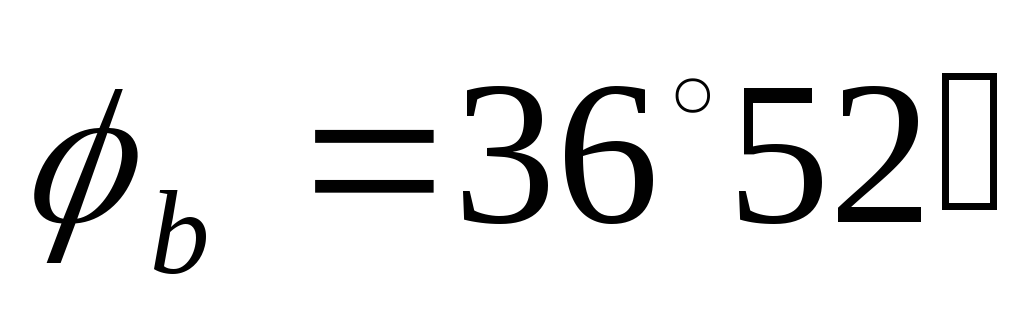 –
нагрузка активно – индуктивная и в
фазес на угол
–
нагрузка активно – индуктивная и в
фазес на угол 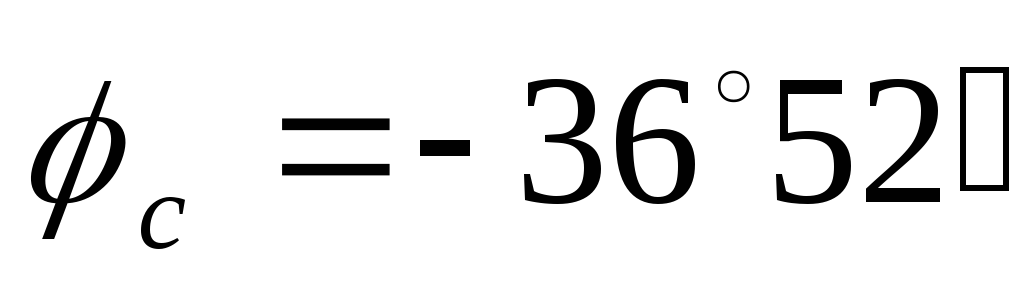 — нагрузка активно – емкостная (Х = -18 Ом).
— нагрузка активно – емкостная (Х = -18 Ом).
Ток
в нейтральном проводе по модулю равен
20,91 А, а его начальная фаза 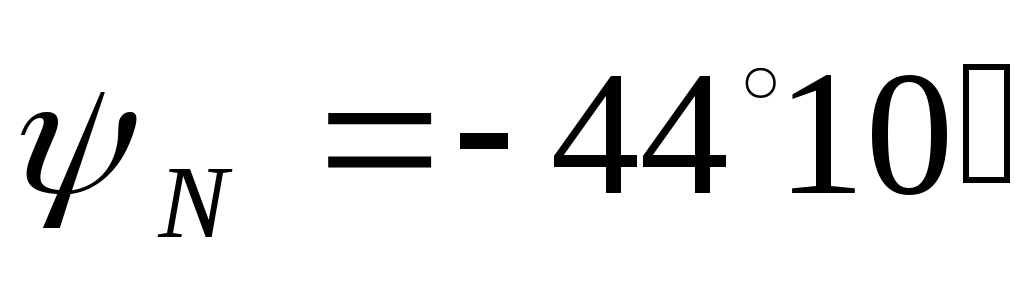 .
На диаграмме рис. 120 откладываем
рассчитанные значения токов с учетом
угла сдвига фаз относительно фазного
напряжения. Вектор тока в нейтральном
проводе можно построить двумя способами:
суммируя векторы или
.
На диаграмме рис. 120 откладываем
рассчитанные значения токов с учетом
угла сдвига фаз относительно фазного
напряжения. Вектор тока в нейтральном
проводе можно построить двумя способами:
суммируя векторы или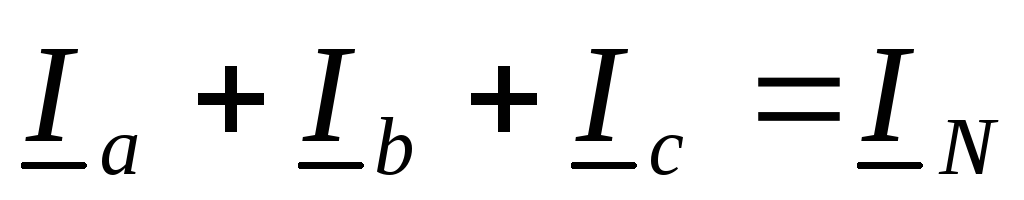 откладывая
векторв соответствии с расчетными данными.
откладывая
векторв соответствии с расчетными данными.
10.
В схеме “звезда” без нейтрального
провода (рис. 121) при несимметричной
нагрузке потенциал нейтральной точки
не равен нулю (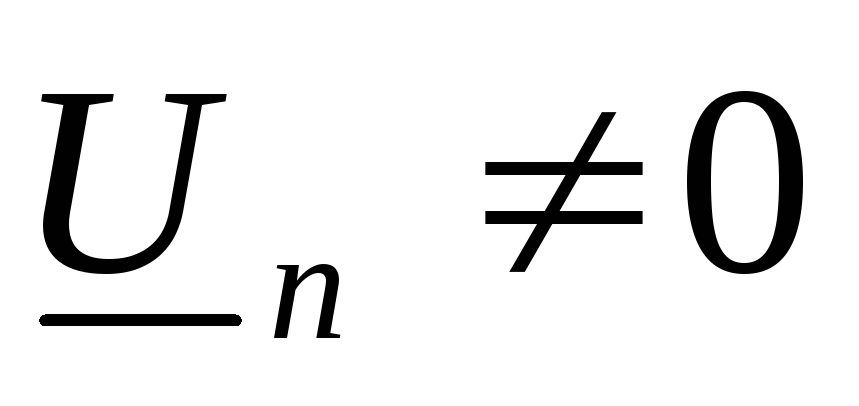 –
нейтраль смещается). Если пренебречь
сопротивлением нейтрального провода,
то
–
нейтраль смещается). Если пренебречь
сопротивлением нейтрального провода,
то
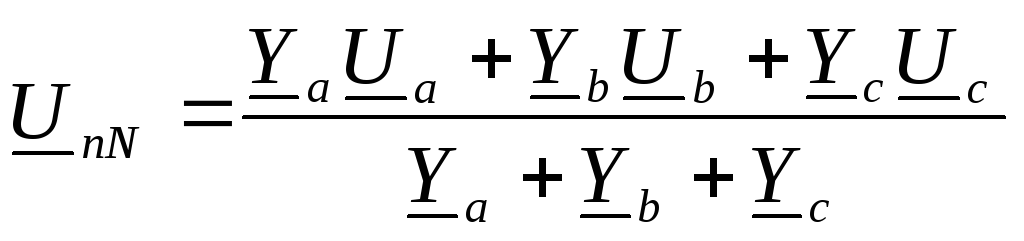 ,
,
где 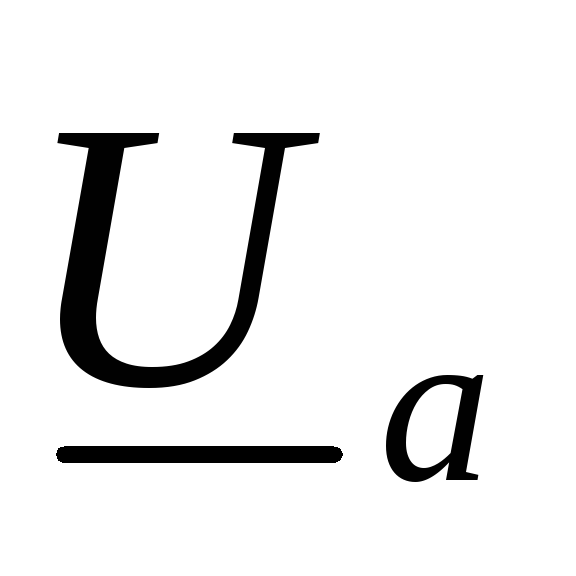 ,
,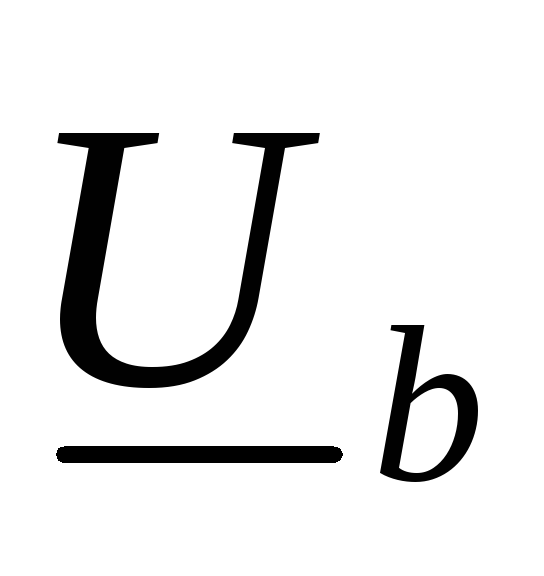 ,
,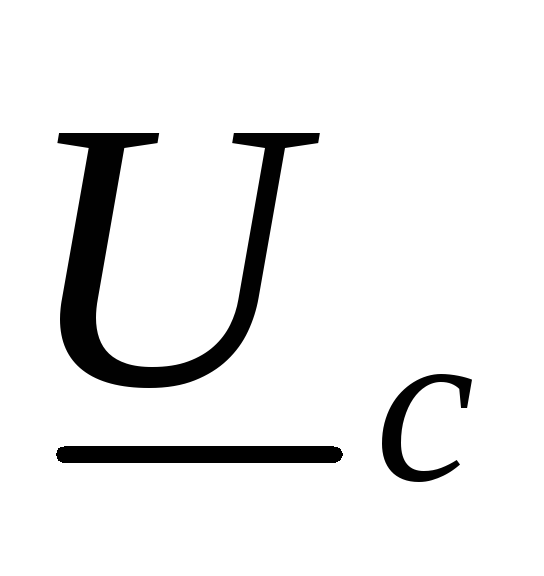 –
комплексные фазные напряжения источника
питания;
–
комплексные фазные напряжения источника
питания; 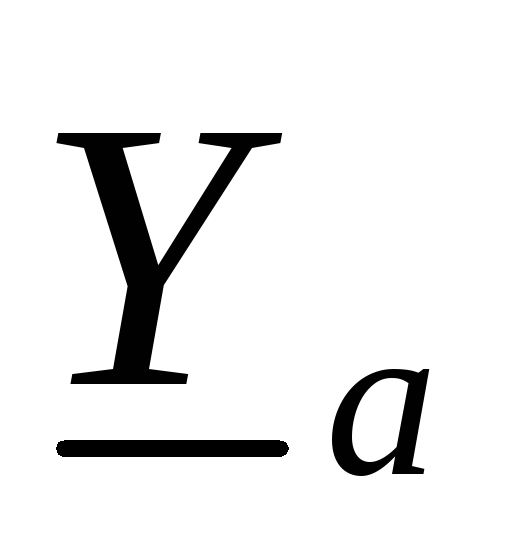 ,
,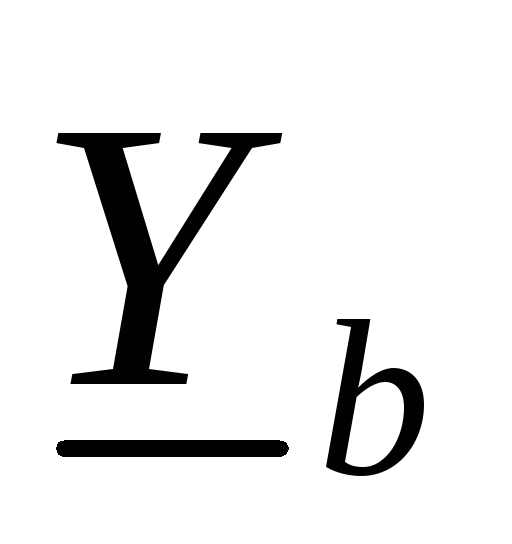 ,
,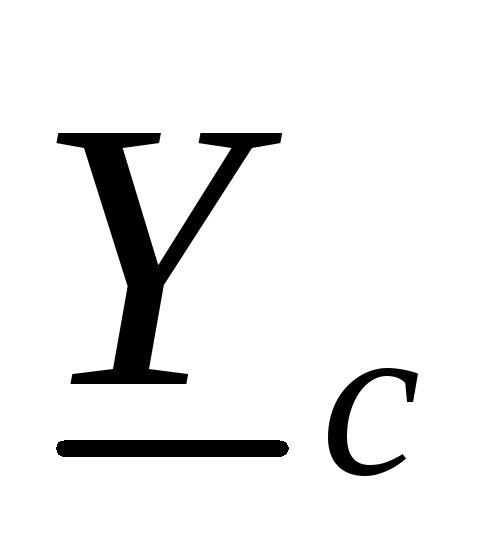 – комплексные проводимости фаз
(ветвей).
– комплексные проводимости фаз
(ветвей).
Так
как 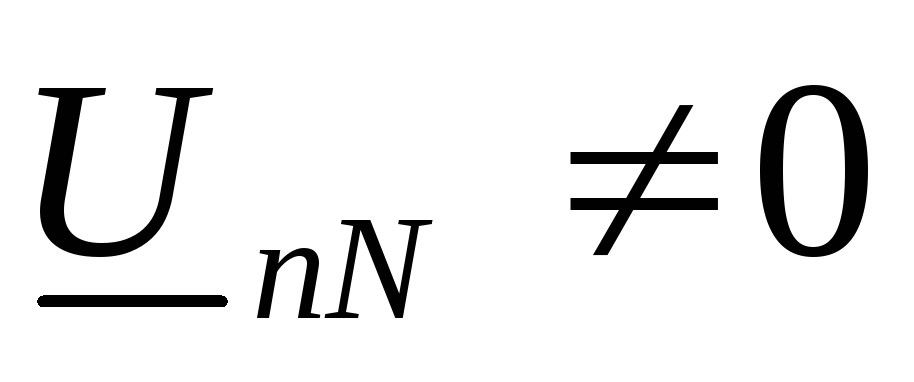 ,
то напряжение фаз приемника не одинаковы
и определяются по формулам
,
то напряжение фаз приемника не одинаковы
и определяются по формулам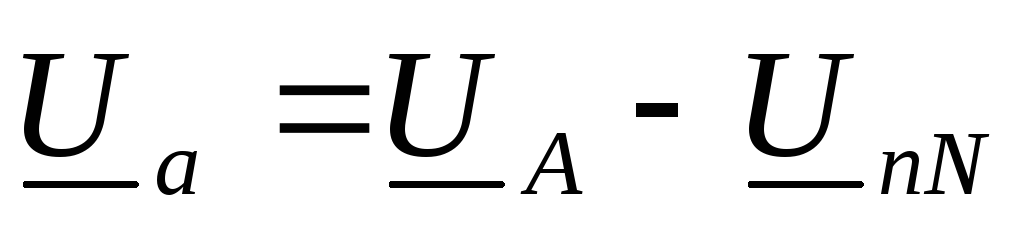 ,
,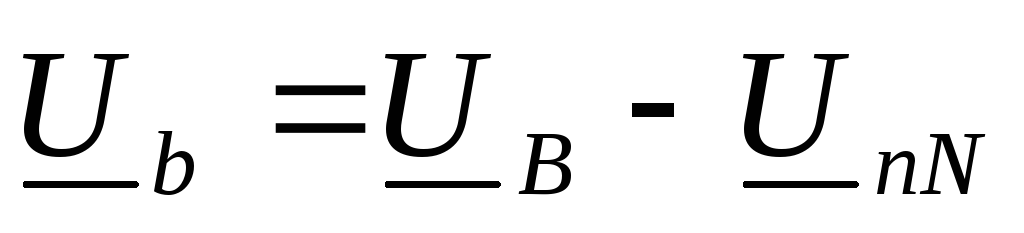 ,
,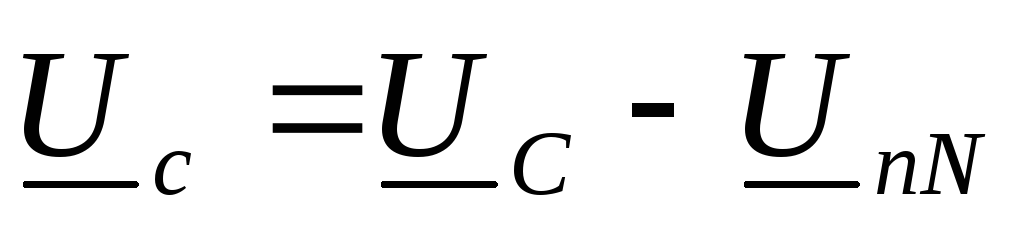 .
Токи в фазах
.
Токи в фазах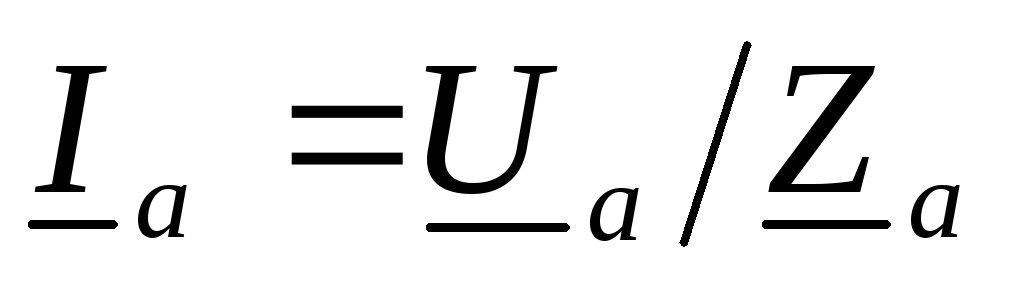 ,
,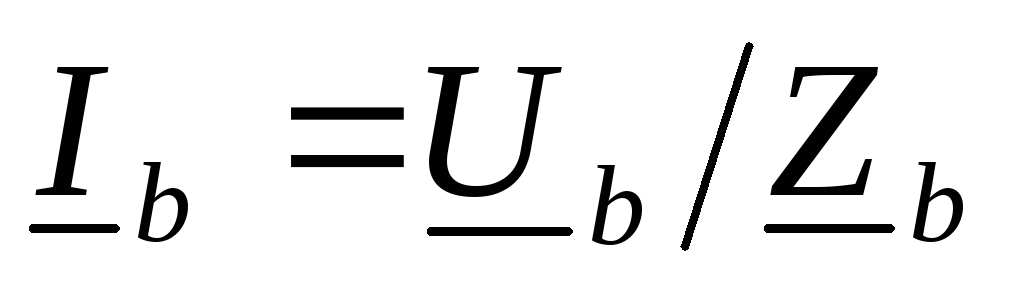 ,
,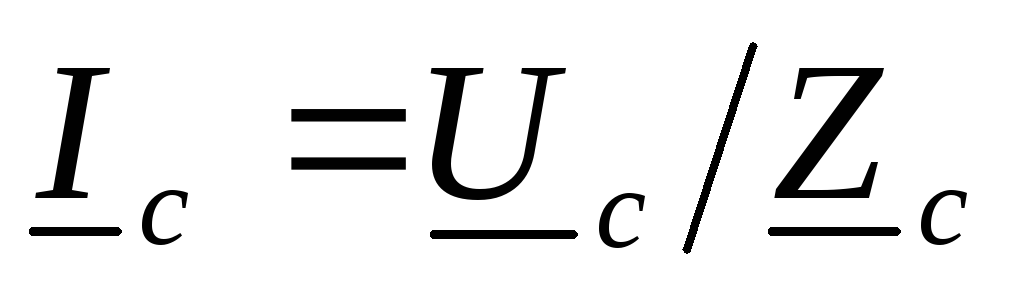 .
.
Пример. К трехпроводной сети с линейным
напряжением 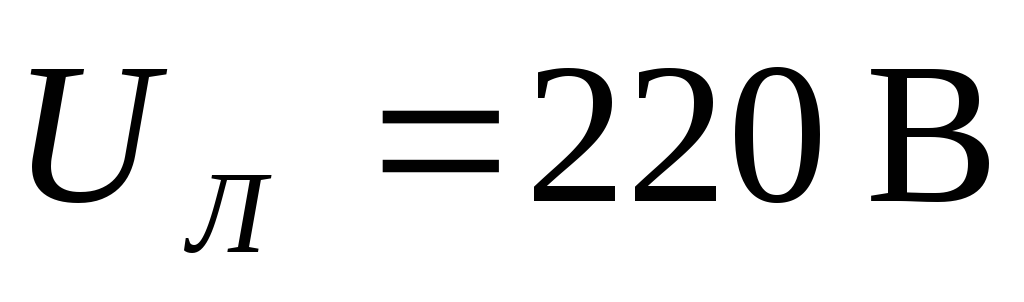 подключена
нагрузка, соединенная звездой (см. рис.
121):
подключена
нагрузка, соединенная звездой (см. рис.
121):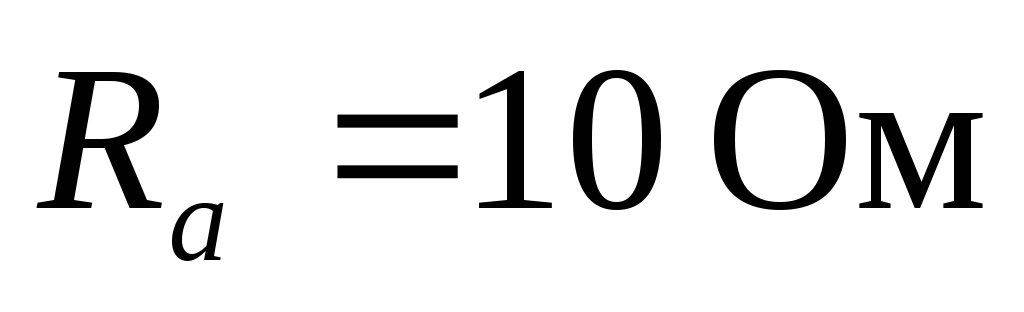 ,
,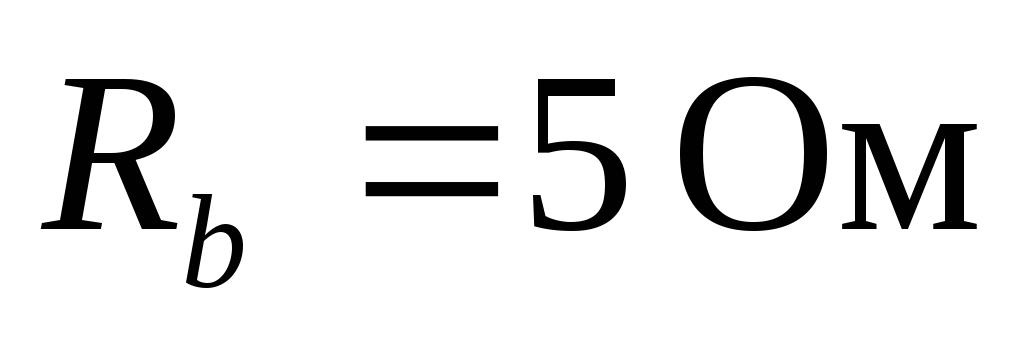 ,
,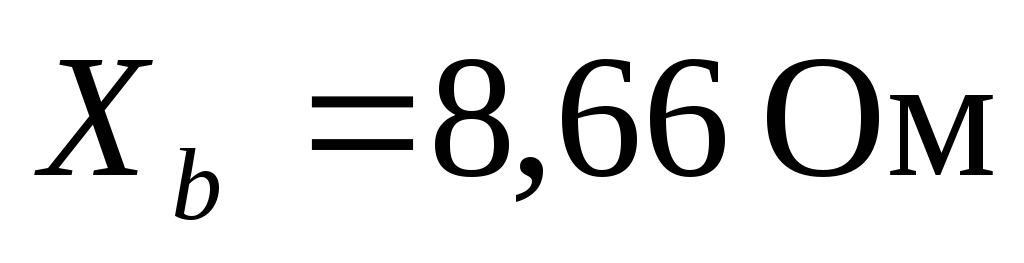 ,
,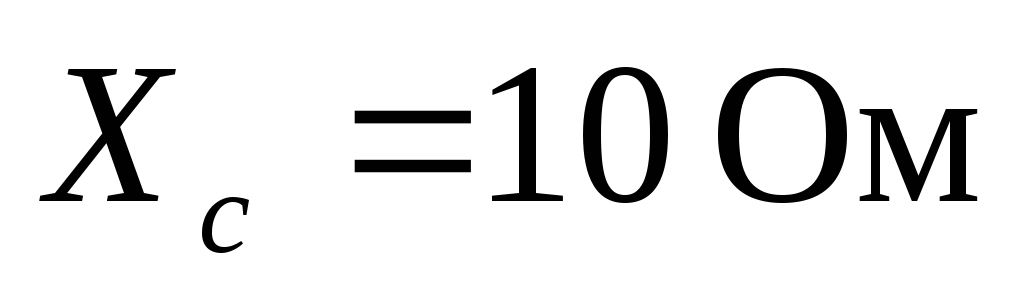 .
Определить токи в ветвях, построить
совмещенную топографическую диаграмму
напряжений и векторную диаграмму токов.
.
Определить токи в ветвях, построить
совмещенную топографическую диаграмму
напряжений и векторную диаграмму токов.
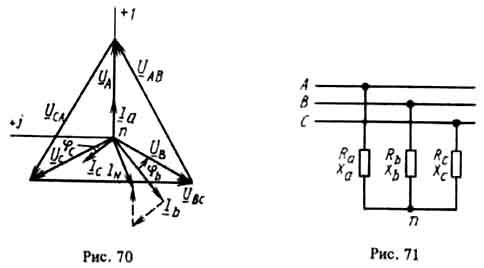
Рис. 120 Рис.121
Фазное
напряжение источника, т. е. потенциалы
входных выводов нагрузки, 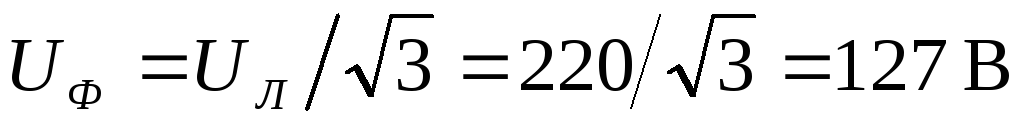 ,
или в комплексной форме
,
или в комплексной форме
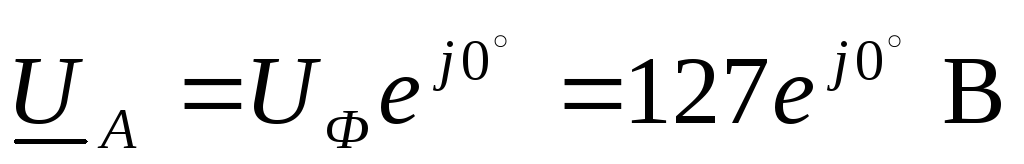 ,
, 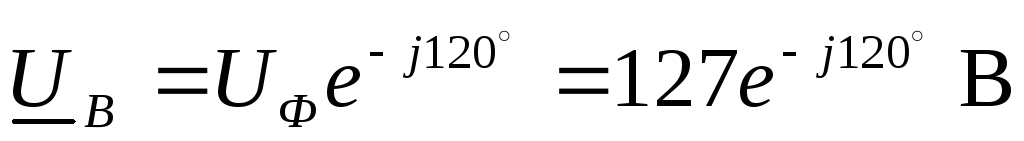 ,
,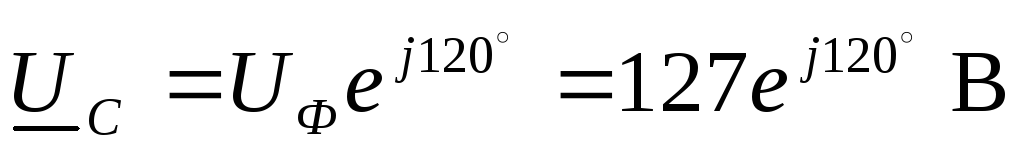 .
.
Сопротивление нагрузки
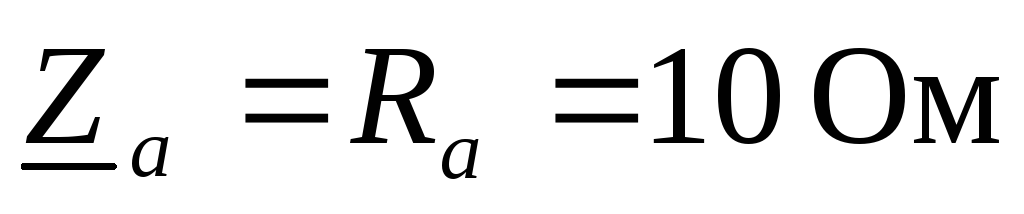 ,
,
,
,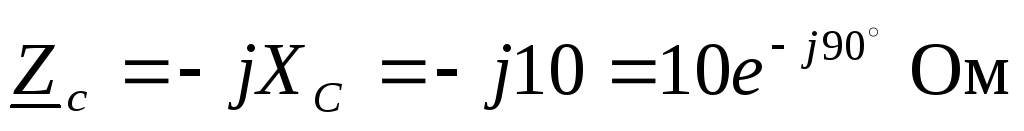 .
.
Проводимости нагрузки
 ,
, 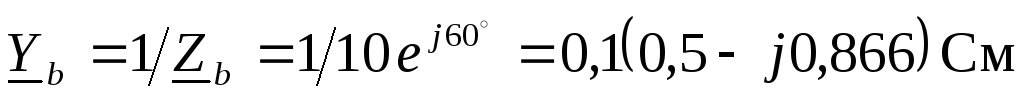 ,
,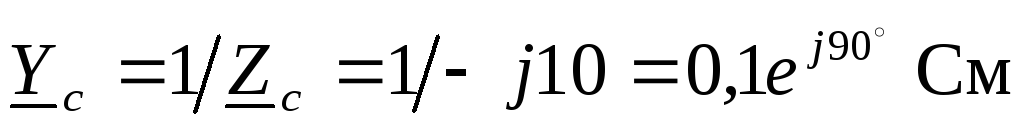 .
.
Потенциал нейтральной точки приемника
 .
.
Комплексные фазные напряжения приемника:
 ,
,
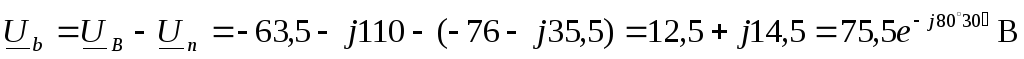 ,
,
 .
.
Токи в фазах нагрузки и линии:
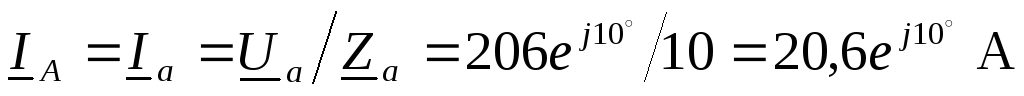 ,
,
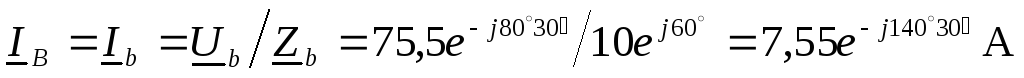 ,
,
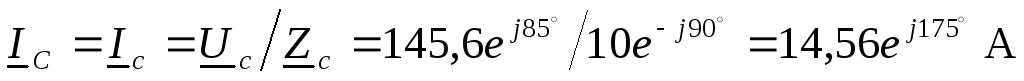 .
.
Для
построения векторных диаграмм выбираем
масштабы напряжения 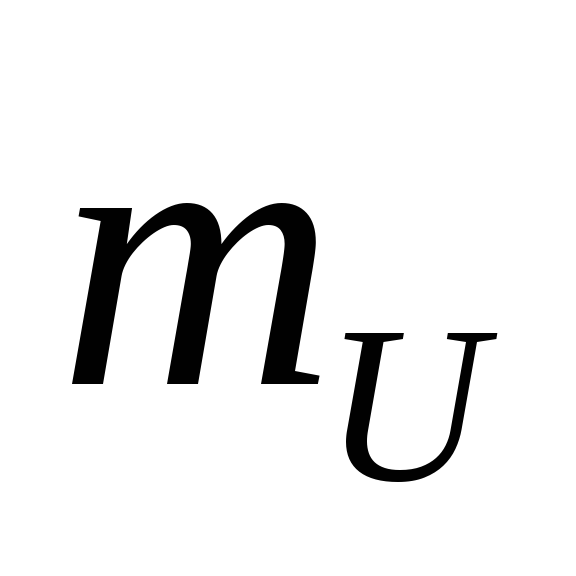 и
и
тока 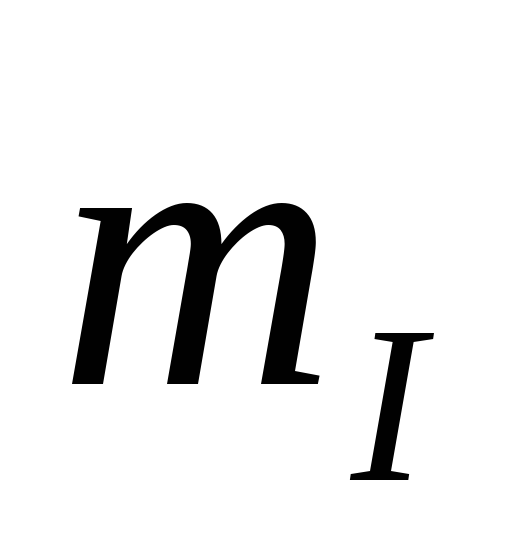 .
Строим топографическую диаграмму
напряжений источника и откладываем на
ней потенциал нейтральной точки приемника
.
Строим топографическую диаграмму
напряжений источника и откладываем на
ней потенциал нейтральной точки приемника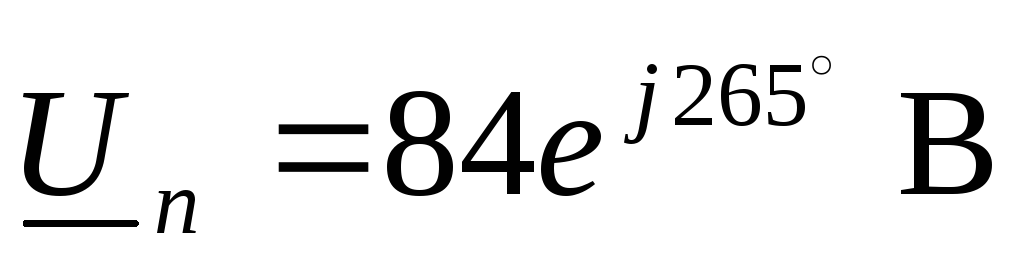 (рис. 122). Векторы, соединяющие точкиn и A, B, C,
соответственно будут векторами фазных
напряжений приемников
(рис. 122). Векторы, соединяющие точкиn и A, B, C,
соответственно будут векторами фазных
напряжений приемников 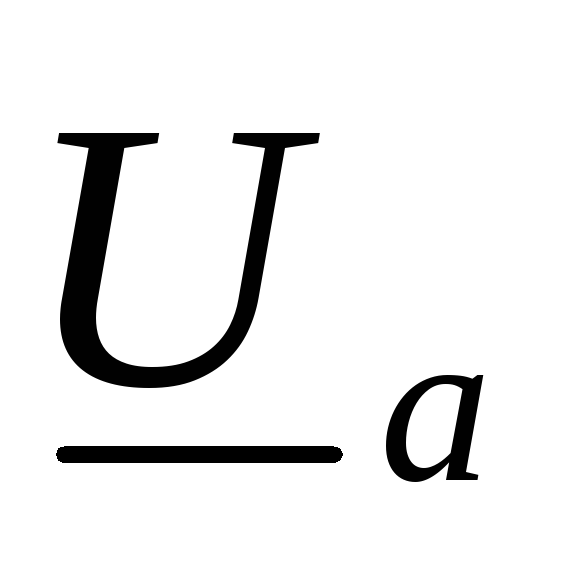 ,
,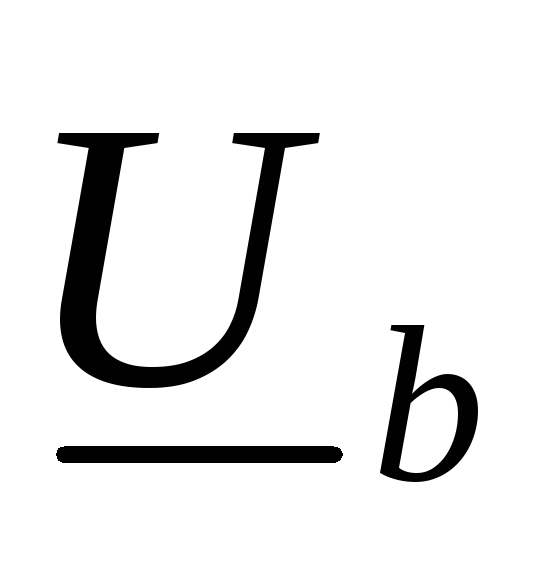 ,
,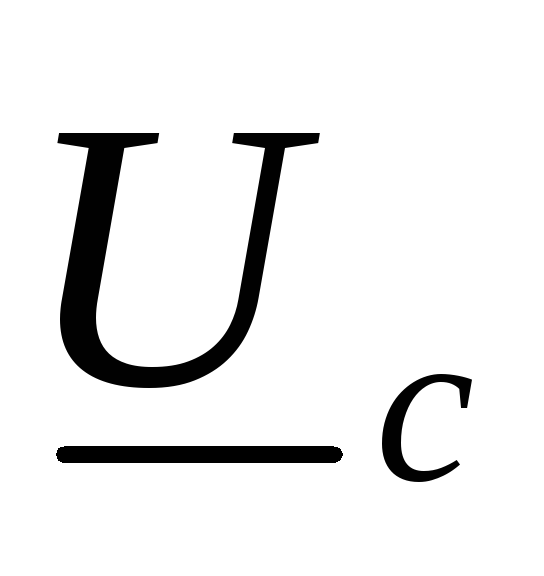 .
.
Относительно этих
векторов с учетом фазных углов сдвига
фаз в нагрузке  ,
, ,
,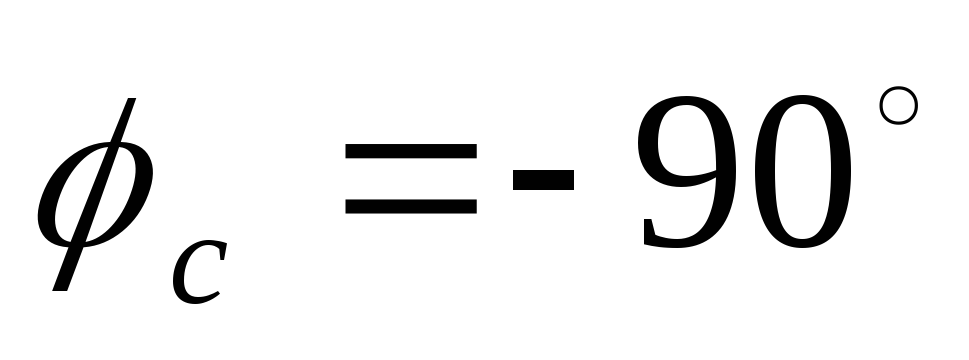 откладываем векторы токов
откладываем векторы токов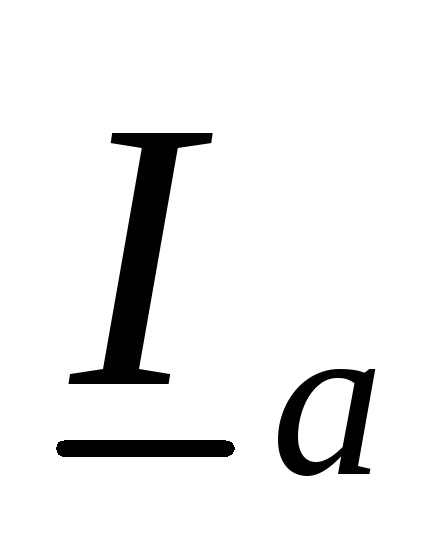 ,
,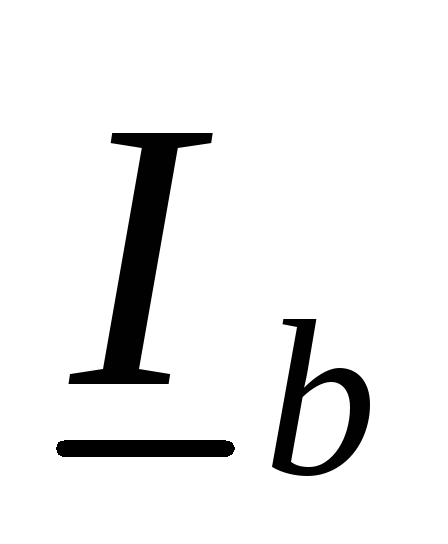 ,
,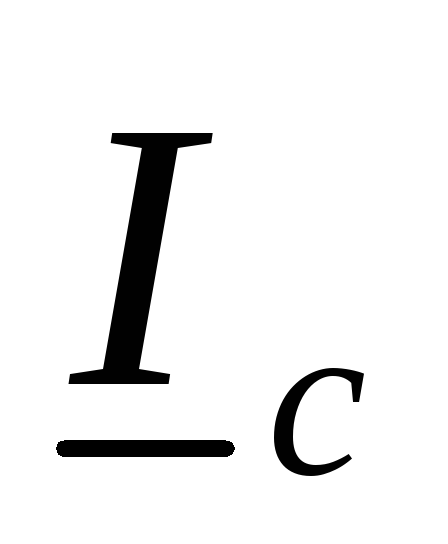 .
.
Топографическая
диаграмма напряжений показывает, что
вследствие смещения потенциала
нейтральной точки приемника из нуля
симметрия фазных напряжений приемника
нарушается: напряжение 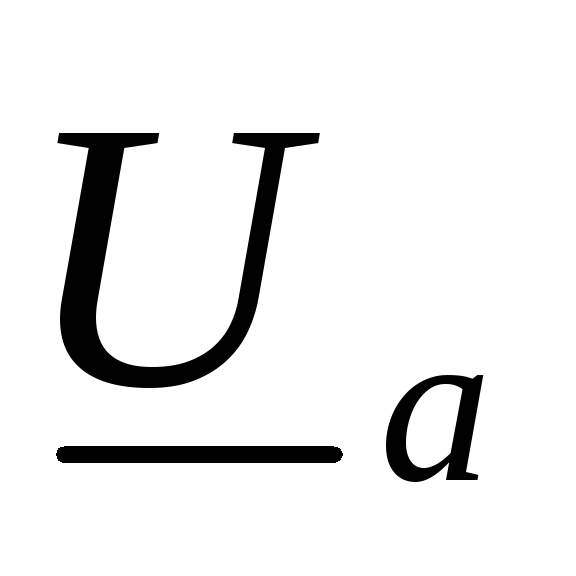 фазыа с127 В возрастает до 206 В, напряжение
фазыа с127 В возрастает до 206 В, напряжение 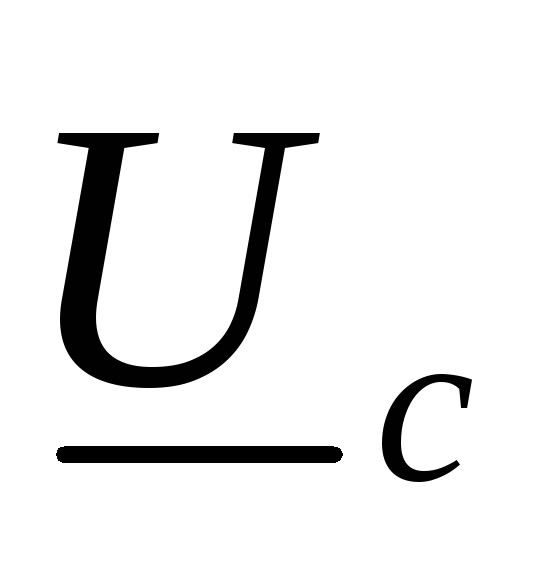 фазыс – до 145,6 В, а напряжение
фазыс – до 145,6 В, а напряжение 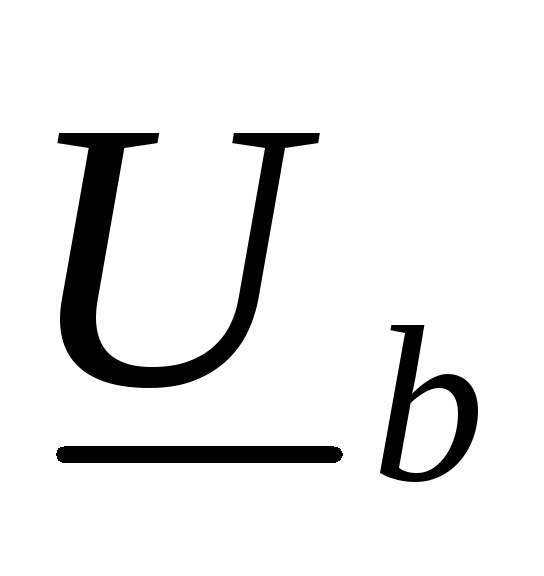 фазыb падает до 75,5 В.
фазыb падает до 75,5 В.
11.
В схеме “треугольник” (рис. 123) режим
работы каждой фазы независим от режима
работы двух других фаз, поэтому токи в
фазах равны: 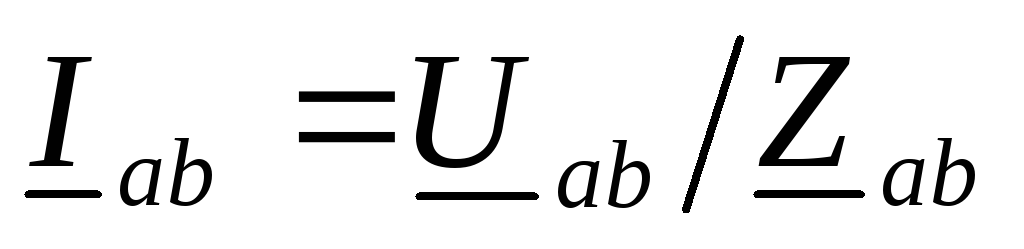 ,
,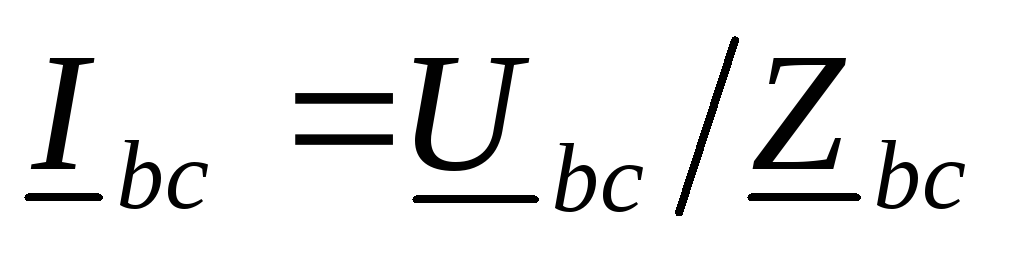 ,
, .
.
Токи в линейных проводах определяются по первому закону Кирхгофа для узловых точек a, b, c:
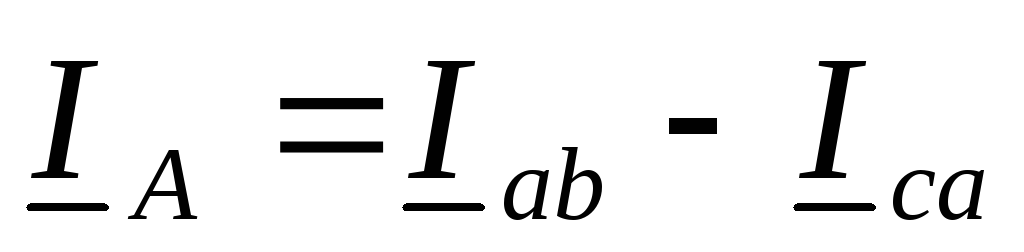 ,
, 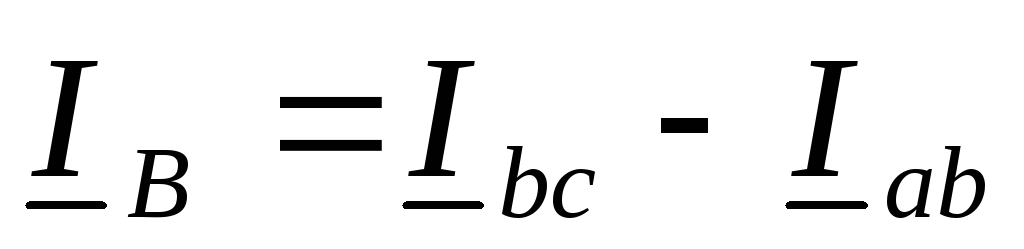 ,
,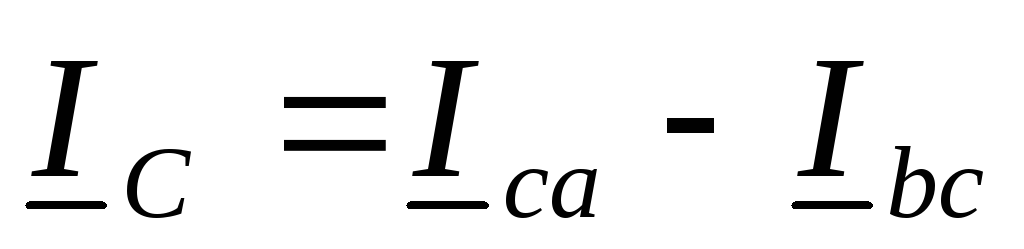 .
.
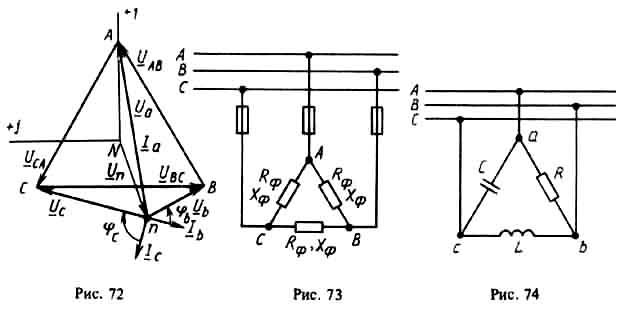
Рис. 122 Рис. 123 Рис. 124
Линейные токи 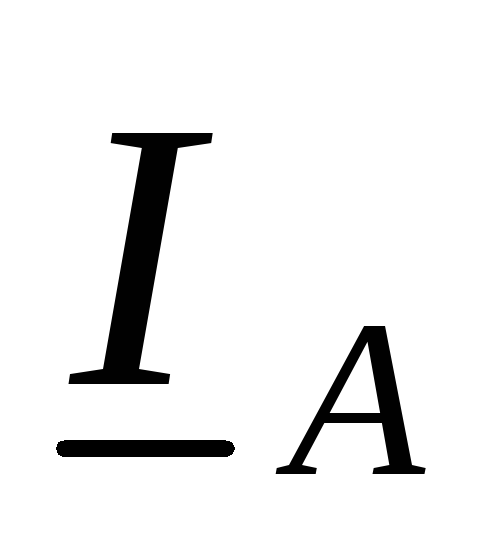 ,
,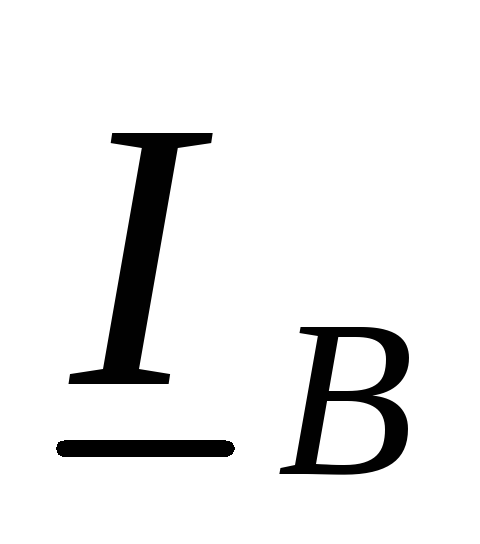 ,
,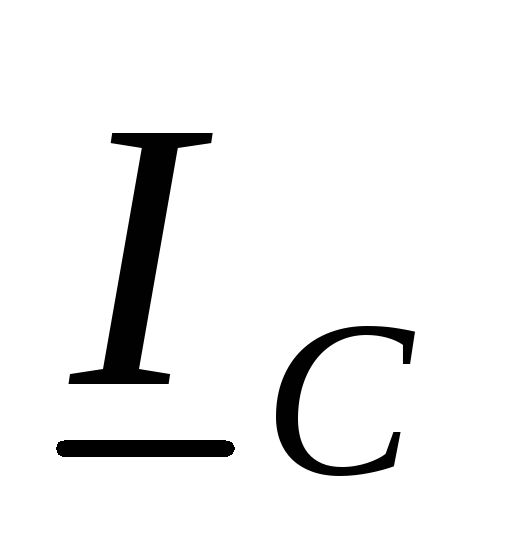 могут быть найдены графически при
построении векторной диаграммы.
могут быть найдены графически при
построении векторной диаграммы.
Пример. К трехпроводной трехфазной линии с
линейным напряжением 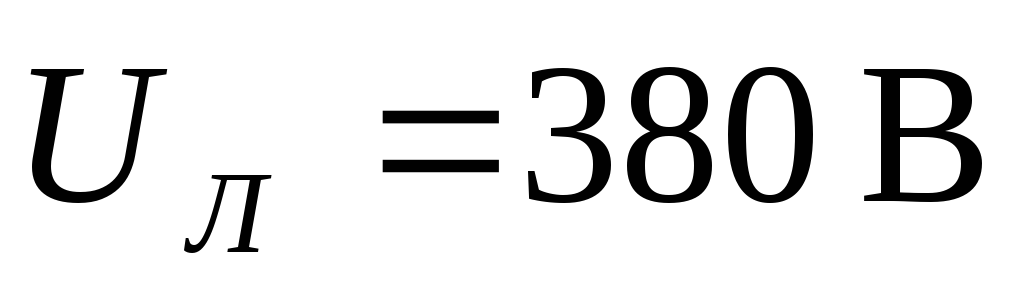 подключен
трехфазный приемник, соединенный
треугольником:
подключен
трехфазный приемник, соединенный
треугольником: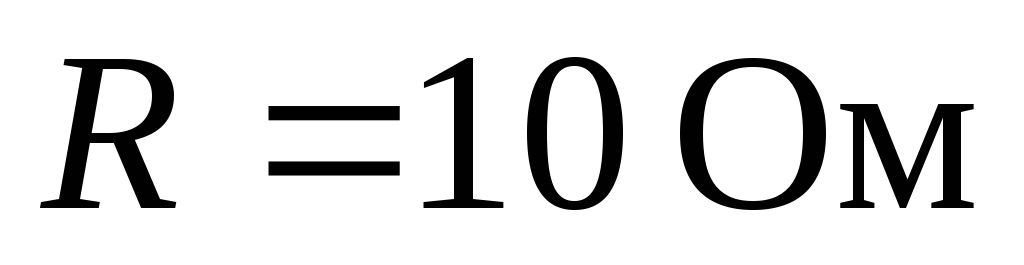 ,
,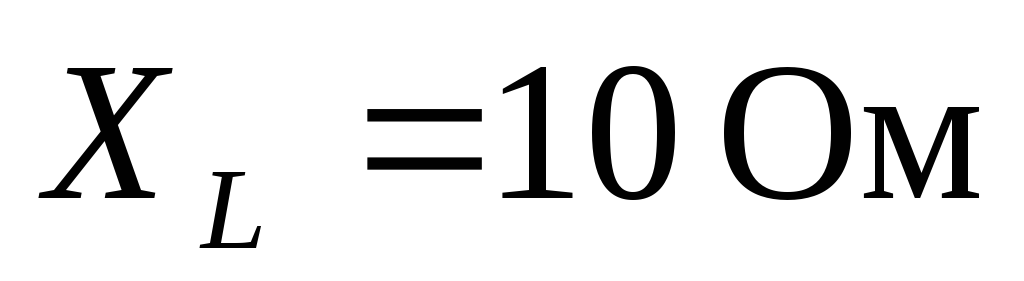 ,
,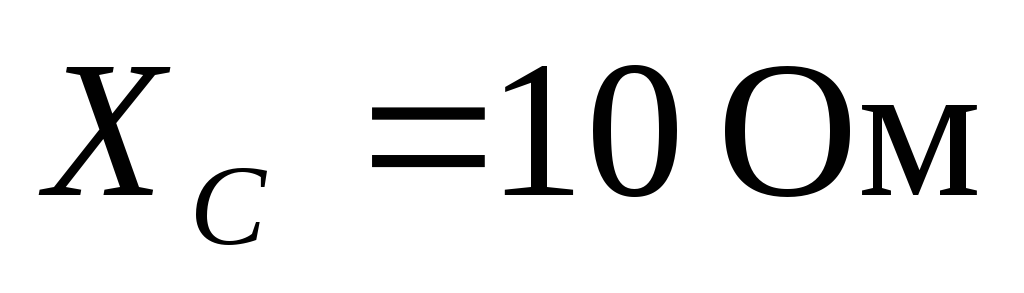 (рис. 124). Рассчитать токи в фазах и в
линии, построить совместную топографическую
диаграмму напряжений и векторную
диаграмму токов.
(рис. 124). Рассчитать токи в фазах и в
линии, построить совместную топографическую
диаграмму напряжений и векторную
диаграмму токов.
Сопротивление фаз по модулю одинаковы, но по фазному углу – разные, следовательно, нагрузка не симметричная и ток каждой фазы необходимо рассчитывать отдельно.
Комплексные сопротивления фаз
 ,
, 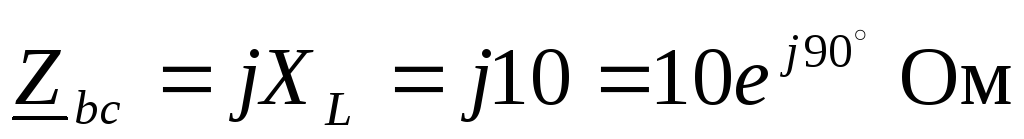 ,
,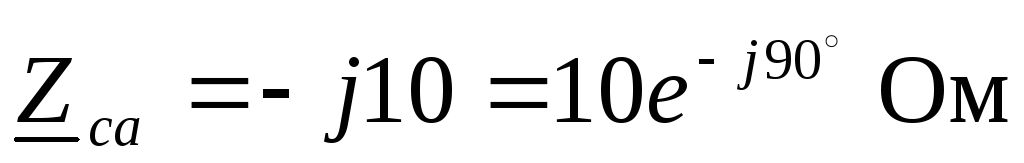 .
.
Комплексные линейные напряжения
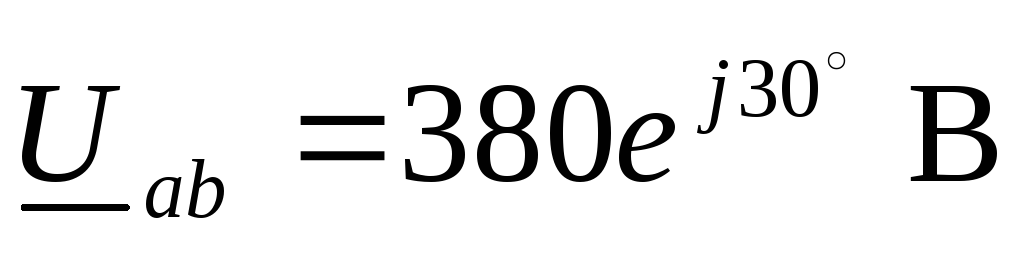
 ,
,  ,
,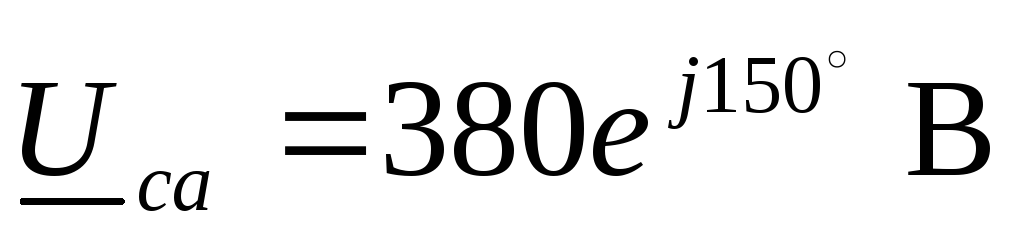 .
.
Рис. 125
Фазные токи
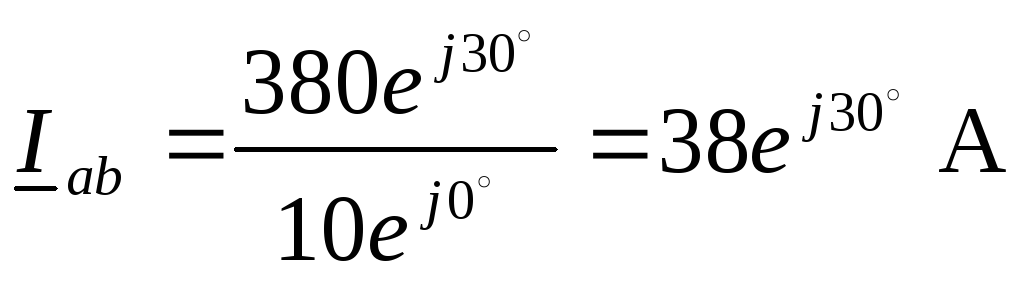 ,
, 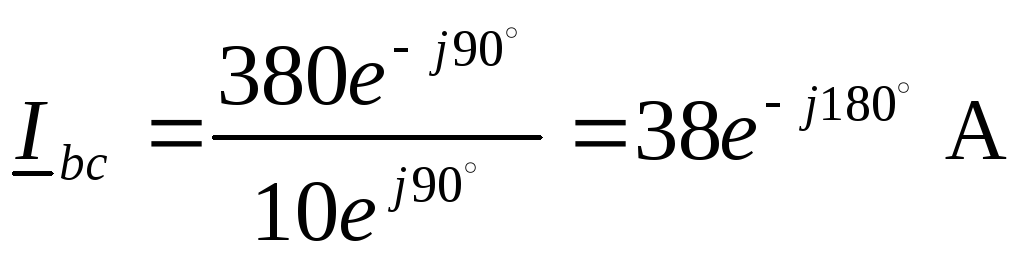 ,
,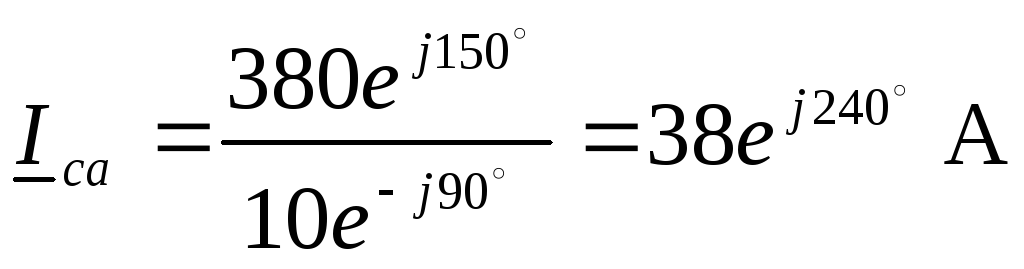 .
.
Линейные токи
 ,
,
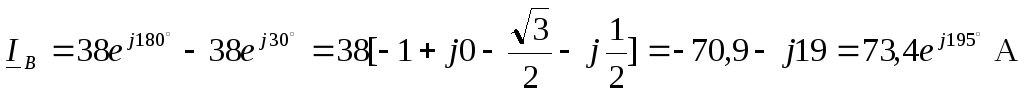 ,
,
 .
.
Для
построения векторных диаграмм выбираем
масштабы напряжения 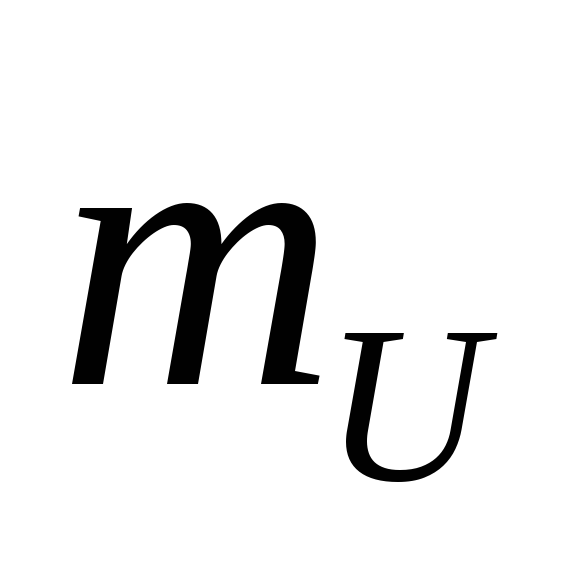 и
и
тока 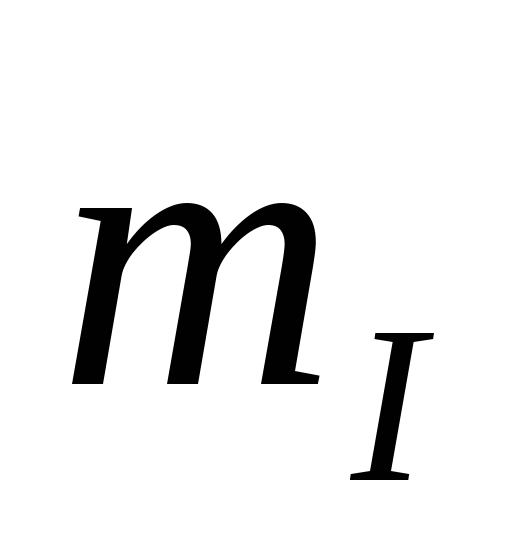 .
Далее строим топографическую диаграмму
напряжений, аналогичную рис. 137,б.
Векторы фазных токов
.
Далее строим топографическую диаграмму
напряжений, аналогичную рис. 137,б.
Векторы фазных токов 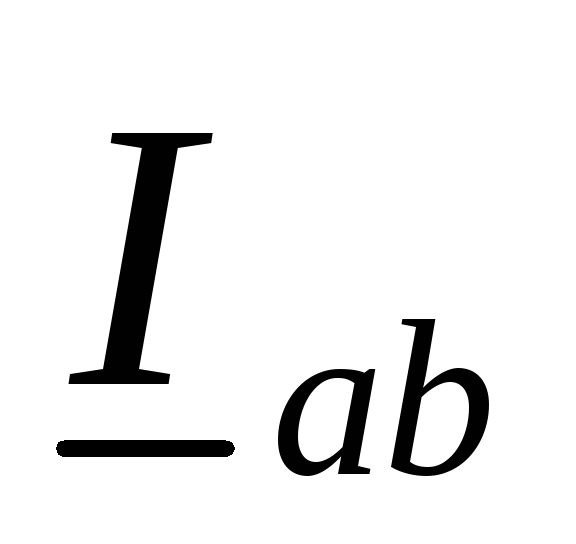 ,
,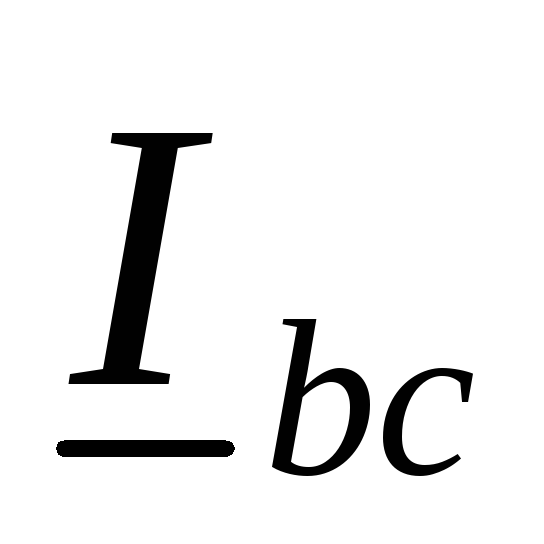 ,
,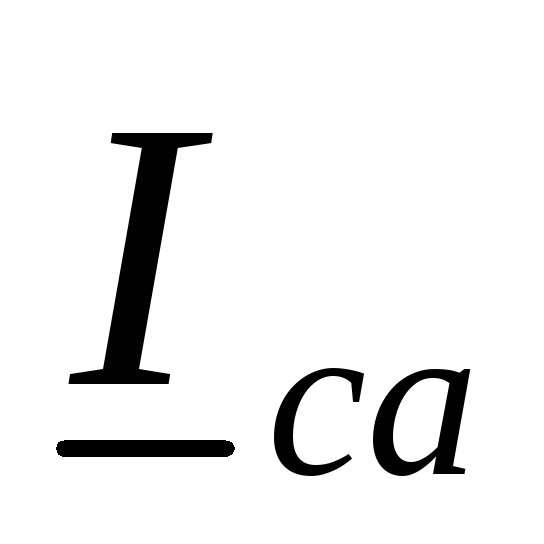 с учетом масштаба откладываем
соответственно относительно векторов
линейных напряжений
с учетом масштаба откладываем
соответственно относительно векторов
линейных напряжений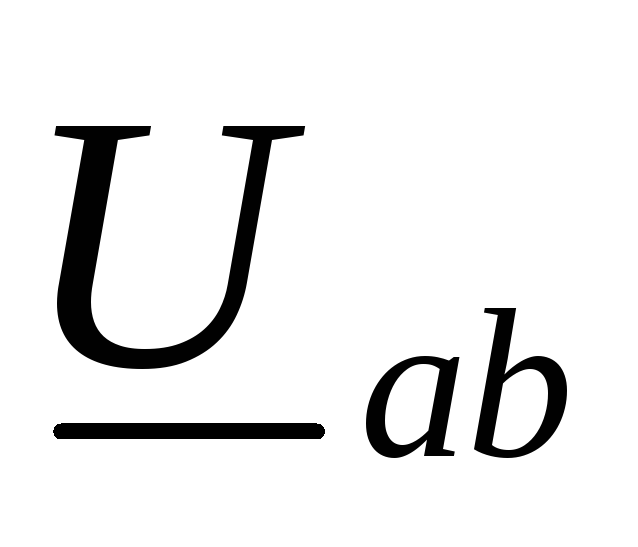 ,
,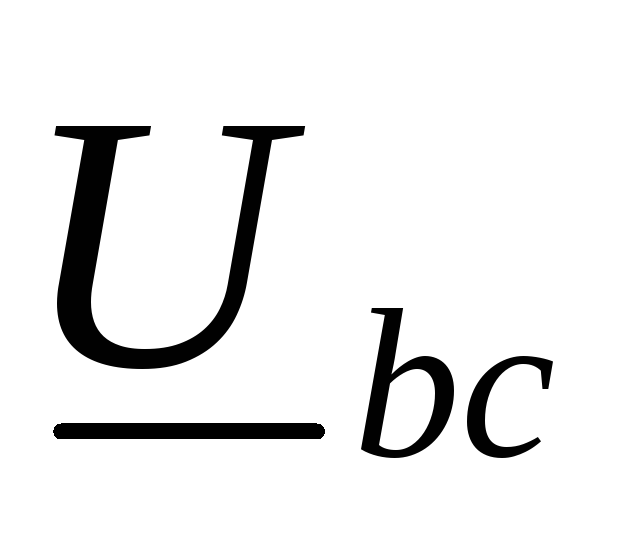 ,
,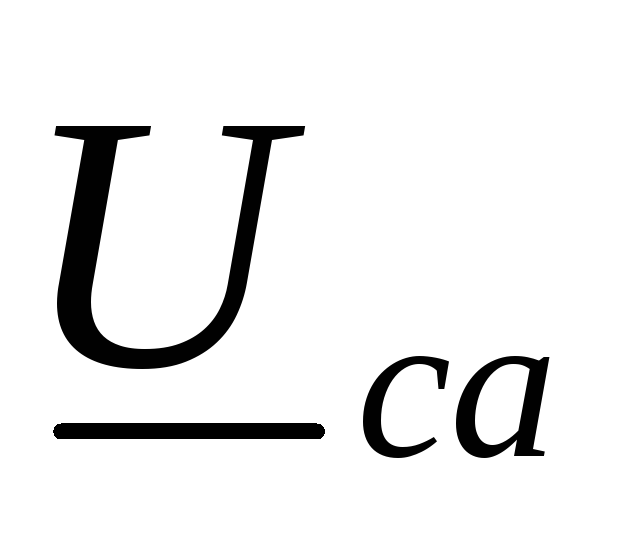 под углами
под углами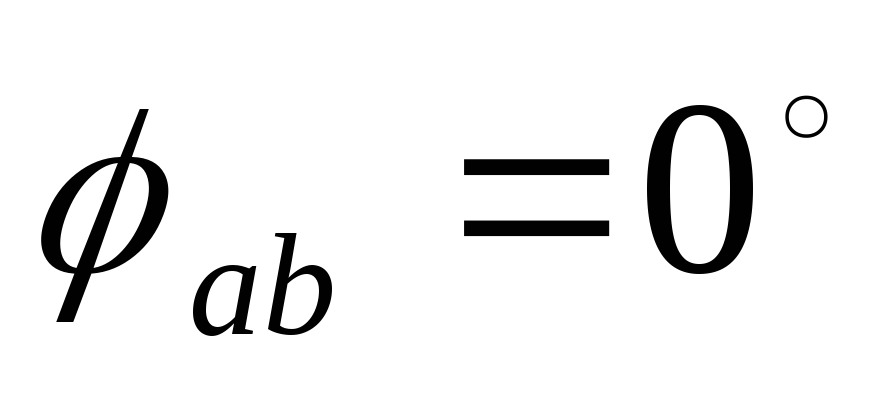 ,
,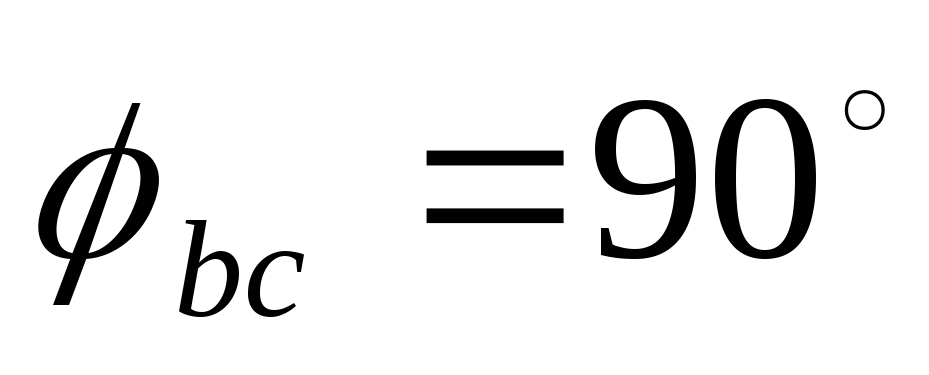 ,
,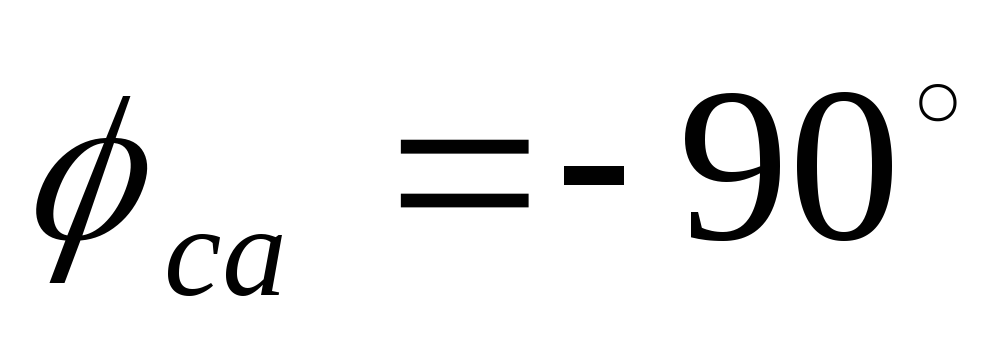 (рис. 125). Затем по уравнениям строим
векторы
(рис. 125). Затем по уравнениям строим
векторы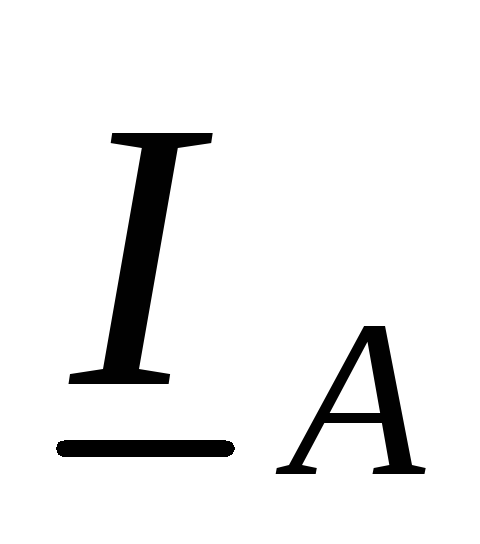 ,
,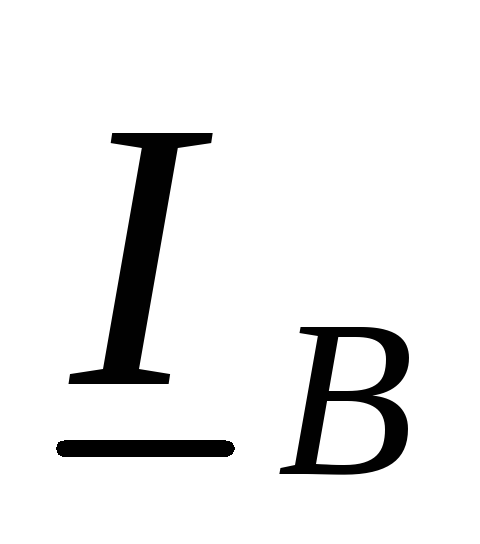 ,
,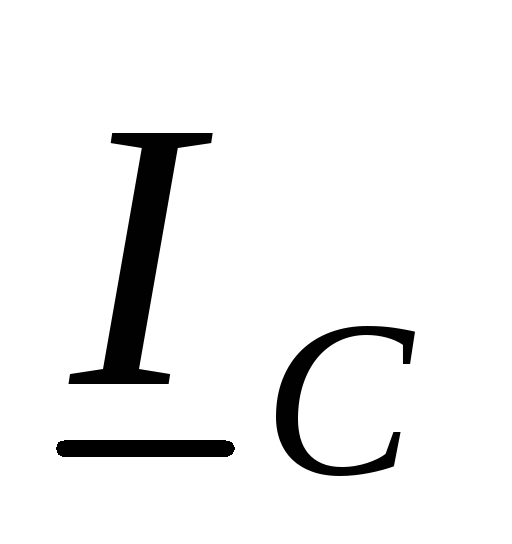 ,
значения и направления которых должны
соответствовать расчетным данным.
,
значения и направления которых должны
соответствовать расчетным данным.
12. При построении векторных диаграмм рекомендуется строить совмещенные векторные диаграммы: топографическую диаграмму напряжений и векторную диаграмму токов. Их построения проводят в следующем порядке: выбирают масштабы напряжений и токов; строят векторы линейных напряжений; для схем “звезда” определяют положение нейтральной точки и откладывают векторы фазных напряжений; векторы фазных токов откладывают с учетом сдвига фаз относительно векторов соответствующих фазных напряжений в каждом приемнике; векторы линейных токов для схемы “треугольник” строят по уравнениям первого закона Кирхгофа.
12. Мощности трехфазной системы рассчитывают по следующим формулам:
а) при симметричной нагрузке и любой схеме соединения приемника:
активная
мощность:  ;
;
реактивная
мощность: 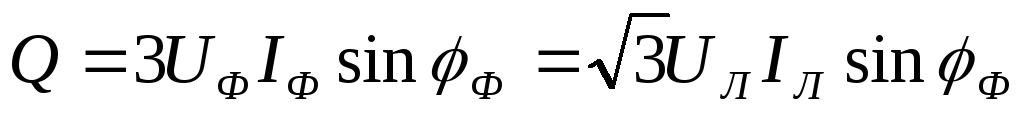 ;
;
полная
мощность:  и
и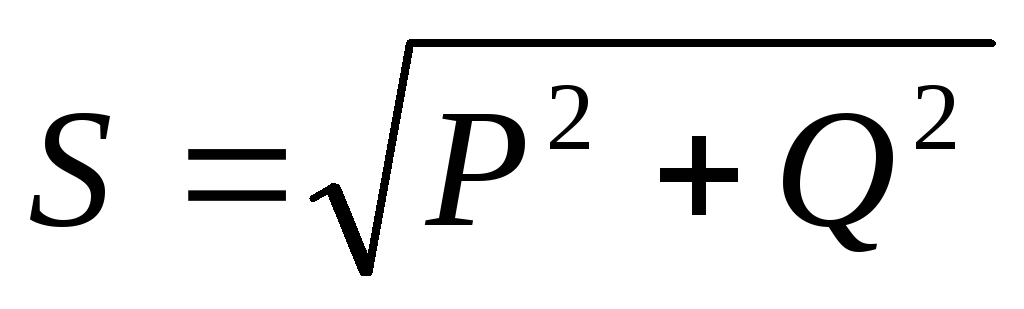 .
.
б) при несимметричной нагрузке:
активная
мощность: 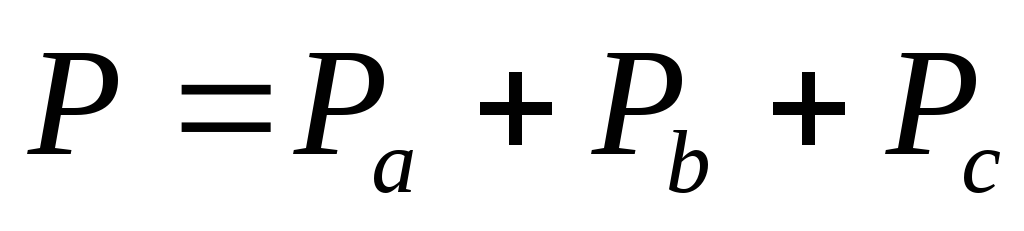 – для схемы “звезда” и
– для схемы “звезда” и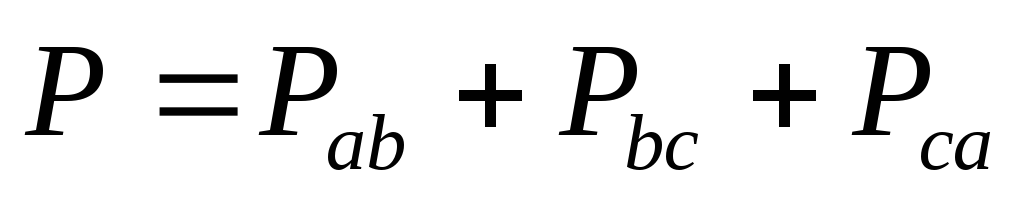 – для схемы “треугольник”;
– для схемы “треугольник”;
реактивная
мощность: 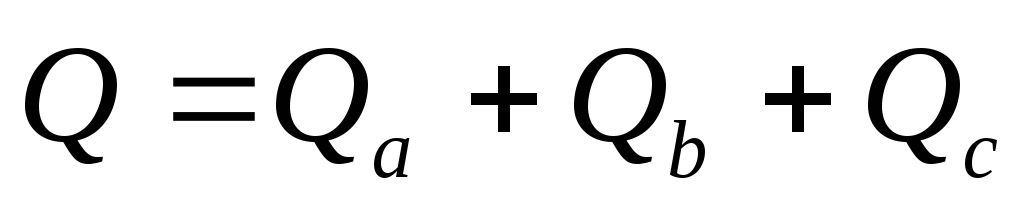 – для схемы “звезда” и
– для схемы “звезда” и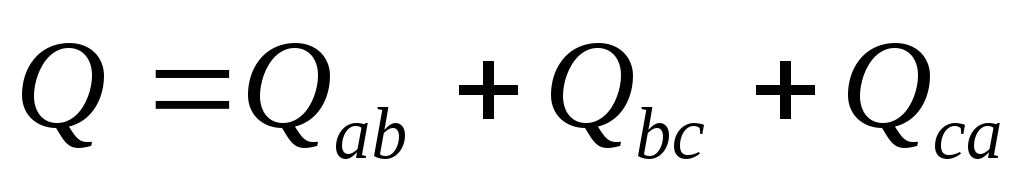 – для схемы “треугольник”;
– для схемы “треугольник”;
полная
мощность: 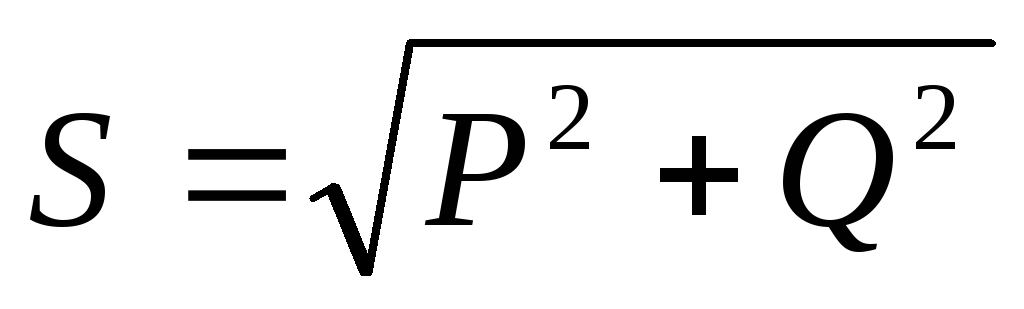 ,
но
,
но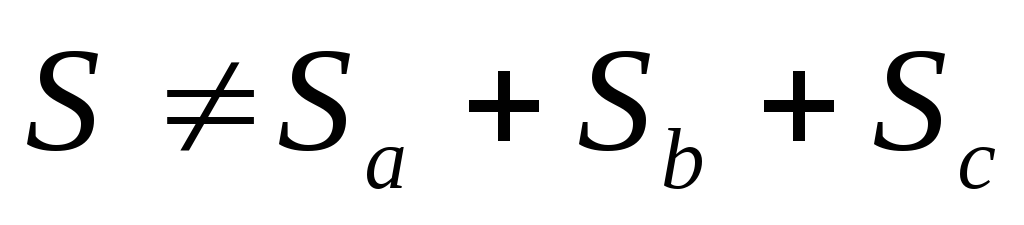 ,
или
,
или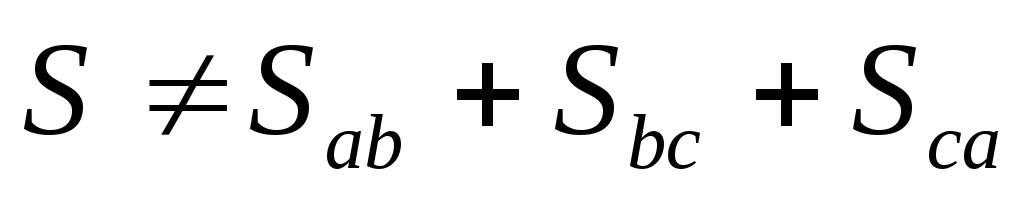 ;
;
комплексная
мощность: 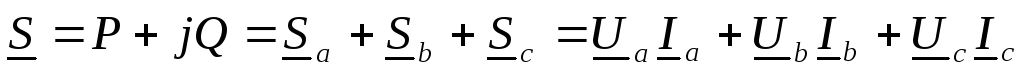 ,
или
,
или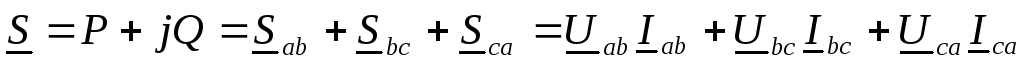 .
.
Контрольная Задача 1 📝 В трёхфазную четырёхпроводную сеть с линейным нап
Задача 1 В трёхфазную четырёхпроводную сеть с линейным напряжением…
Электротехника
Заказ выполнен
Задача 1 В трёхфазную четырёхпроводную сеть с линейным напряжением Uном, В включи-ли звездой разные по характеру сопротивления. Определить: 1. Фазные токи. 2. Ток в нулевом проводе. 3. Полную, активную и реактивную мощность. 4. Переключить данную нагрузку со звезды на треугольник и рассчитать линей-ные токи. Задачу решить двумя методами: графоаналитическим и символическим. U ном 220В Задача 2 В электрической цепи, состоящей из последовательно соединённых активного сопротивления R, индуктивности L и ёмкости С, несинусоидальное напряжение изменяется по следующему закону: Определить действующие значения несинусоидальных напряжений и тока, активную мощность цепи, коэффициент мощности, если частота основной гармоники f . Написать уравнение мгновенного значения тока цепи, мгновенные падения напряжений на каждом участке R, 30 Ом L, 63.8 мГн C, 53 мкФ f, 50 Гц Um1 423 В Um3, 282 В Um5, 70.5В Задача 3 Для катушки, намотанной на сердечник из электротехнической стали, разветвлен-ная схема замещения которой представлена на рисунке 9, определить величину тока I в ка-тушке, подаваемое напряжение U, мощность потерь в обмотке катушки Pмеди и в сердечни-ке Pстали. В масштабе постройте полную векторную диаграмму катушки и начертите её неразветвленную схему замещения. Rкат, 2 Ом . Xрасс, 1.8 Ом . Go,0.021 См . Bo,0.21 См . UI,120 В
Это место для переписки тет-а-тет между заказчиком и исполнителем.Войдите в личный кабинет (авторизуйтесь на сайте) или зарегистрируйтесь, чтобы
получить доступ ко всем возможностям сайта.




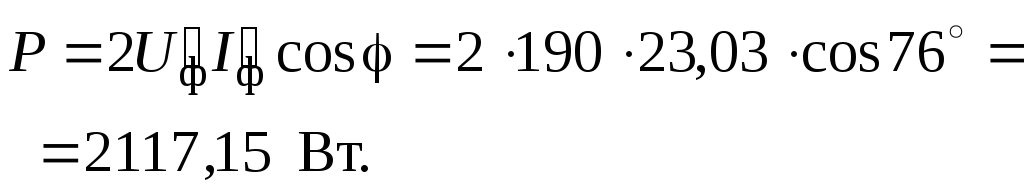
 ,
что видно из векторной диаграммы
(рис.1.3.11). Неповрежденные обмотки
находятся под пониженным напряжением,
что не опасно для них.
,
что видно из векторной диаграммы
(рис.1.3.11). Неповрежденные обмотки
находятся под пониженным напряжением,
что не опасно для них.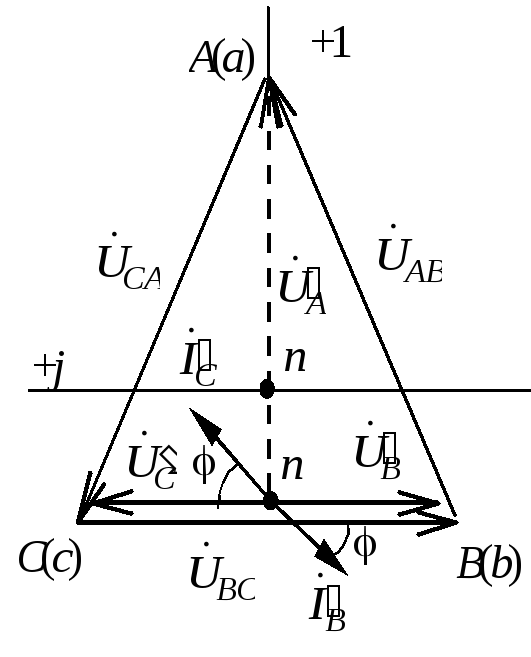
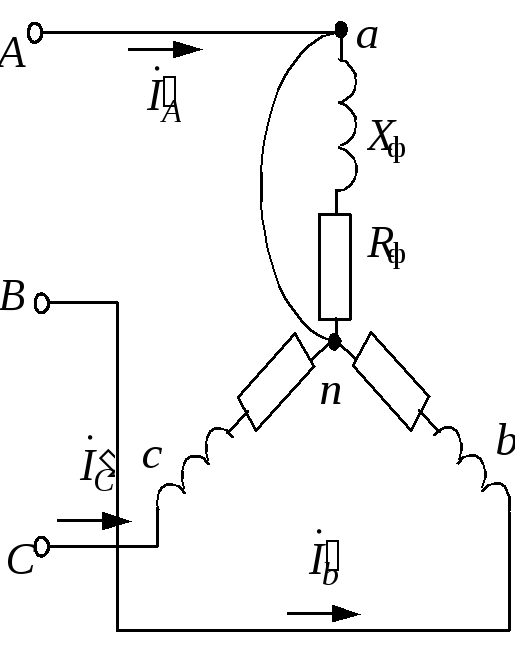
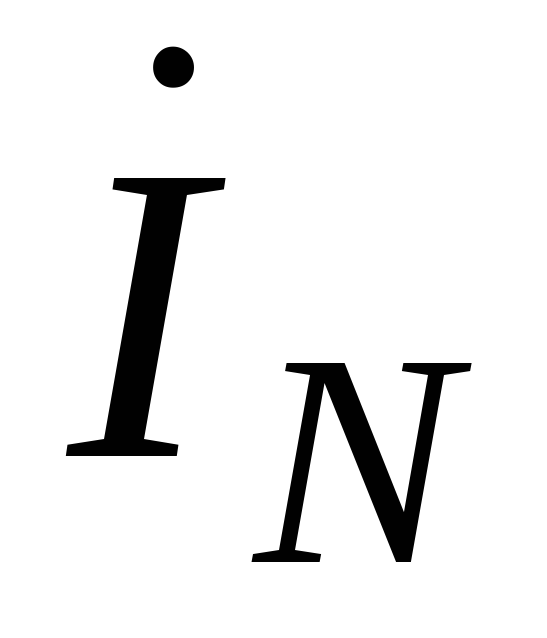 (рис. 1.3.13).
(рис. 1.3.13).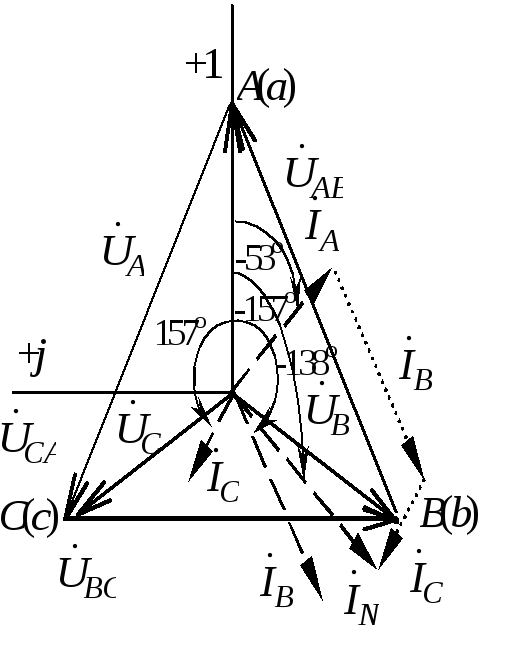
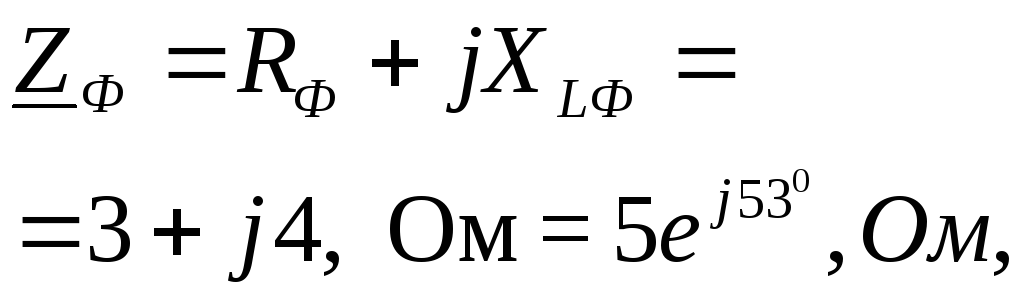

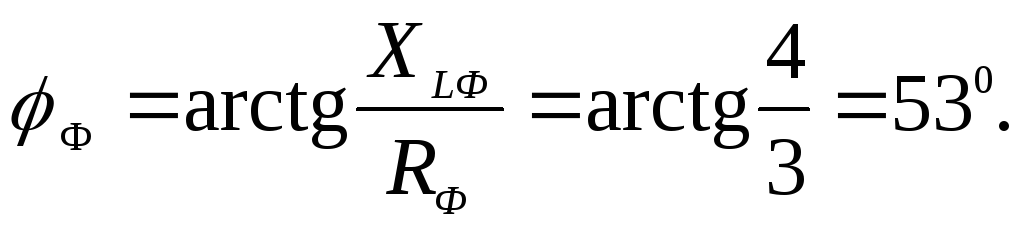



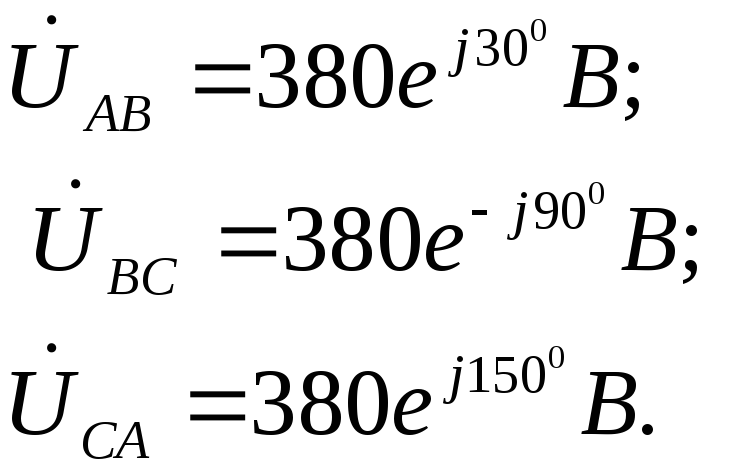
 Ом;
Ом;