Методические указания к решению задач 4
Решение задач, этой группы требует знания учебного материала по теме 1.6, отчетливого представления об особенностях соединения фаз источников и потребителей в «звезду» и «треугольник», соотношениях между линейными и фазными величинами при таких соединениях, а также умения строить векторные диаграммы при симметричной и несимметричной нагрузках. Содержание задач и схемы цепей приведены в условиях задач, а данные к ним — в соответствующих таблицах. Для пояснения общей методики решения задач на трехфазные цепи, включая построение векторных диаграмм, рассмотрены типовые примеры 5 — 10.
Пример 5. В трехфазную четырехпроводную сеть включены звездой лампы накаливания мощностью Р=300 Вт каждая. В фазуАвключили 30 ламп, в фазу В —50 ламп и в фазу С —20 ламп. Линейное напряжение сети
Uном=380В (рис. 5, а). Определить токи в фазах и начертить векторную диаграмму цепи, из которой найти числовое значение тока в нулевом проводе.
Решение. 1. Определяем фазные напряжения установки:
2. Находим фазные токи:
3. Для построения векторной диаграммы выбираем масштабы по току: 1 см- 20 А и по напряжению: 1 см-44 В. Построение диаграммы начинаем с векторов фазных напряжений (рис. 5, б), располагая их под углом 120° друг относительно друг друга. Чередование фаз обычное: за фазойА-фаза В, за фазой В — фаза С. Лампы накаливания являются активной нагрузкой, поэтому ток в каждой фазе совпадает с соответствующим фазным напряжением. В фазе «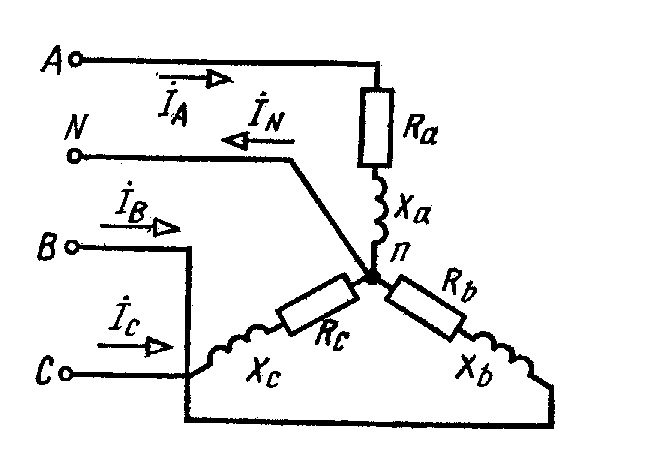 Векторы линейных напряжений на диаграмме не показаны, чтобы не усложнять чертеж.
Векторы линейных напряжений на диаграмме не показаны, чтобы не усложнять чертеж.
Пример 6. В трехфазную четырехпроводную сеть включили звездой несимметричную нагрузку: в фазу
Решение. 1. Определяем фазные напряжения установки:
2. Находим фазные токи
Здесь
Для построения векторной диаграммы выбираем масштаб по току: 1см — 10 А и по напряжению: 1 см — 100 В. Построение диаграммы начинаем с векторов фазных напряжений , и , располагая их под углом 120° друг относительно друга (рис.
Ток совпадает с напряжением . Ток в нулевом проводе равен геометрической сумме трех фазных токов. Измеряя длину вектора тока , которая оказалась равной 6,8 см, находим ток =68 А.
Пример 7. По заданной векторной диаграмме для трехфазной цепи (рис. 7, а) определить характер нагрузки каждой фазы и вычислить ее сопротивление. Начертить соответствующую схему цепи. Нагрузка соединена в звезду. Определить активную и реактивную мощности, потребляемые цепью. Значения напряжений, токов и фазных углов приведены на диаграмме. Векторы линейных напряжений не показаны.
Решение. 1. Рассматривая векторную диаграмму, можно заметить, что ток в фазе Ее активное и индуктивное сопротивления вычисляем по формулам
Ее активное и индуктивное сопротивления вычисляем по формулам
В фазе В ток совпадает с напряжением , значит в фазу В включено активное сопротивление
.
В фазе С ток IC отстаёт от напряжения на угол , значит в фазу С включены конденсатор и активное сопротивление. Полное сопротивление фазы
Определим активное и емкостное сопротивления:
Схема цепи приведена на рис. 7, б.
2.Определяем мощности, потребляемые цепью. Активная мощность
Реактивная мощность
.
Знак минус показывает, что в цепи преобладает емкость.
Пример 8. В трехфазную сеть включили треугольником несимметричную нагрузку (рис. 8, а): в фазу «АВ» — конденсатор с емкостным сопротивлением =10 Ом; в фазу «ВС» — катушку с активным сопротивлением = 4 Ом и индуктивным 3 Ом; в фазу «CA» — активное сопротивление = 10Ом. Линейное напряжение сети = 220 В. Определить фазные токи, углы сдвига фаз и начертить в масштабе векторную диаграмму цепи. По векторной диаграмме определить числовые значения линейных токов.
Линейное напряжение сети = 220 В. Определить фазные токи, углы сдвига фаз и начертить в масштабе векторную диаграмму цепи. По векторной диаграмме определить числовые значения линейных токов.
Решение.1. Определяем фазные токи и углы сдвига фаз:
, где Ом
Отсюда угол =36°50′.
;
Для построения векторной диаграммы выбираем масштаб по току: 1 см- 10 А, по напряжению: 1 см- 80 В. Затем в принятом масштабе откладываем векторы фазных (они же линейные) напряжений под углом 120° друг относительно друга (рис. 8, б). Под углом = —90° к вектору напряжения откладываем вектор тока ; в фазе ВС вектор тока должен отставать от вектора напряжения на угол = 36°50′, а в фазе «СA» вектор тока совпадает с вектором напряжения . Затемстроим векторы линейных токов на основании известных уравнении
; ;
Измеряя длины векторов линейных токов и пользуясь принятым масштабом, находим значения линейных токов:
Пример 9.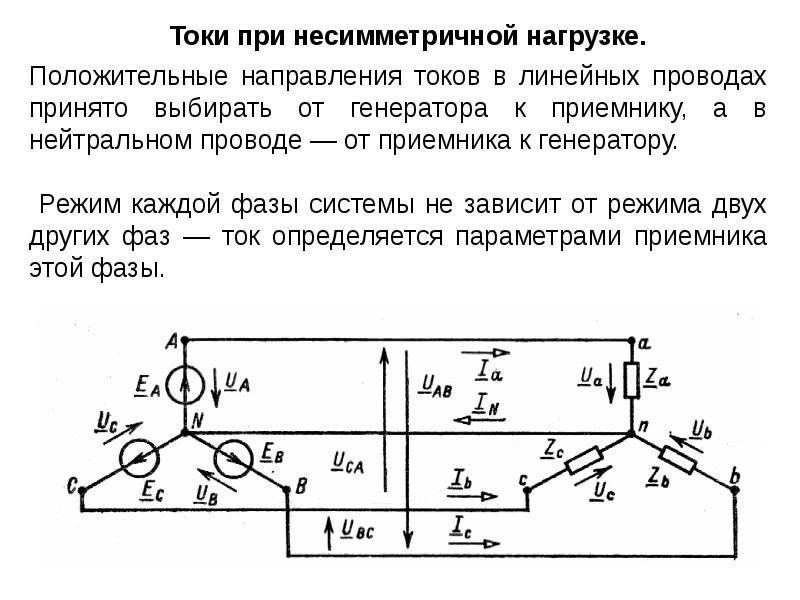 По векторной диаграммы для трехфазной цепи (рис. 9, а) определить характер нагрузки в каждой фазе, вычислить ее сопротивление и начертить схему включения. Нагрузка несимметричная, соединена в треугольник. Значения напряжений, фазных токов и углов сдвига фаз указаны на диаграмме.
По векторной диаграммы для трехфазной цепи (рис. 9, а) определить характер нагрузки в каждой фазе, вычислить ее сопротивление и начертить схему включения. Нагрузка несимметричная, соединена в треугольник. Значения напряжений, фазных токов и углов сдвига фаз указаны на диаграмме.
Решение. 1. Рассматривая векторную диаграмму, можно заключить, что
ток в фазе «AB» совпадает с напряжением , значит в фазу «АВ» включено активное сопротивление
Ом
В фазе «ВС» ток опережает напряжение на угол 90°, значит в фазе «ВС» включено емкостное сопротивление
Ом
В фазе «СА» ток отстает от напряжения на угол , значит в фазу «СА» включено активно-индуктивное сопротивление
Ом
Очевидно,
Ом
Ом
2. На основании вычислений чертим схему цепи (рис. 9, б).
Пример 10. В трехфазную четырехпроводную сеть включены печь сопротивления, представляющая собой симметричную нагрузку, соединенную треугольником, и несимметричная осветительная нагрузка в виде ламп накаливания, соединенных звездой (рис.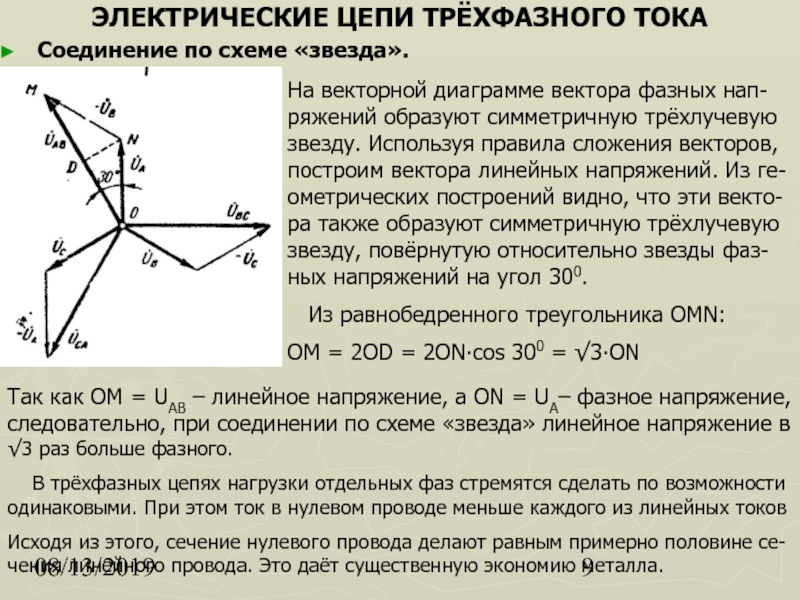
Решение. 1. Находим фазные токи, потребляемые печью:
Таким образом, амперметр А1 покажет силу тока 26,3 А.
2. Линейные токи, потребляемые симметричной нагрузкой, превышают фазные в раза, т. е. . Это значение покажет амперметр А2.
3. Определяем фазные токи, потребляемые лампами. Лампы соединены звездой и включены на фазные напряжения .
Это напряжение покажет вольтметр Vл., поэтому фазные токи:
показание амперметра А3:
показание амперметра А4:
Показание амперметра А5:
Амперметры А3, А4, А5, включенные в линейные провода, соответственно покажут эти токи.
4. Для определения тока в нулевом проводе I0 начертим в масштабе векторную диаграмму цепи, где включены лампы.
Выбираем масштабдля напряжений и токов: 1 см — 100 В; 1 см — 10 А. Затем в принятом масштабе откладываем векторы фазных напряжении располагая их под углом 120º друг относительно друга (рис. 10, б). Чередование фаз обычное: за фазой А – фаза В, за фазой В – фаза С. Лампы накаливания являются активной нагрузкой, поэтому ток в каждой фазе совпадает с соответствующим фазным напряжением. В фазе А ток =45,4 А, поэтому на диаграмме он выразится вектором, длина которого равна 45,4:10=4,54 см; длина вектора фазного напряжения составит: 220:100=2,2 см. Аналогично строим векторы токов и напряжений в остальных фазах. Ток Iо в нулевом проводе определяется геометрическом суммой всех трех фазных токов . Измеряя длину вектора тока Iо, которая оказалась равной 1,5 см, получим значение тока в нулевом проводе Векторы линейных напряжений на диаграмме не показаны, чтобы не усложнять чертеж.
Задача№ 4 (варианты с 1, 11, 21)
Для освещения трех одинаковых участков производственного помещения установили люминесцентные лампы мощностью РЛ=40 Вт каждая. Общее число ламп в помещении n распределено поровну между участками. Лампы рассчитаны на напряжение UЛ; линейное напряжение трехфазной сети равноUH0М.Каждый участок получает питание от одной фазы сети при соединении ламп звездой либо от двух соответствующих фаз при соединении ламп треугольником. Для работы ламп использованы специальные пускорегулирующие аппараты, содержащие катушки со стальными магнитопроводами, поэтому коэффициент мощности ламп меньше единицы; cos φ = 0,95.
Общее число ламп в помещении n распределено поровну между участками. Лампы рассчитаны на напряжение UЛ; линейное напряжение трехфазной сети равноUH0М.Каждый участок получает питание от одной фазы сети при соединении ламп звездой либо от двух соответствующих фаз при соединении ламп треугольником. Для работы ламп использованы специальные пускорегулирующие аппараты, содержащие катушки со стальными магнитопроводами, поэтому коэффициент мощности ламп меньше единицы; cos φ = 0,95.
Выбрать необходимую схему присоединения ламп к трехфазной сети (звездой или треугольником) и начертить ее. Определить линейные токи IЛ в проводниках сети, питающей лампы при равномерной нагрузке фаз. Начертить в масштабе векторную диаграмму цепи и пояснить ее построение. Какая активная энергия будет израсходована всеми лампами за 8 ч работы?
Указания: 1. Ток (в А), потребляемый лампами участка:
2. При равенстве напряжений ламп и сети лампы следует включить треугольником. Если напряжение сети превышает напряжение ламп в √3 раза, лампы включают звездой.
При равенстве напряжений ламп и сети лампы следует включить треугольником. Если напряжение сети превышает напряжение ламп в √3 раза, лампы включают звездой.
3. При включении ламп звездой линейный ток IЛ равен току I. При включении ламп треугольником линейный ток IЛ = √3I.
4. Потребляемую лампами энергию (в кВт*ч) за время t определяем по формуле:
Данные для своего варианта взять из табл. 6.
Таблица 6
| Номер варианта | п, шт. | UЛ В | UНОМ В |
Задача №5 (варианты 2,12, 22)
Каждая фаза трехфазного симметричного потребителя (электродвигатель переменного тока) рассчитана на фазное напряжение Uф и имеет активное Rф и индуктивное хф сопротивления.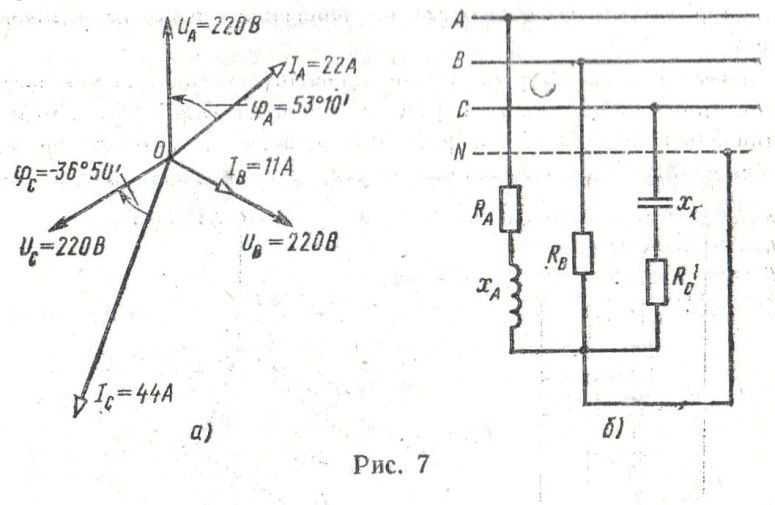 Номинальное напряжение сети Uном1. Выбрать схему соединения потребителя в зависимости от номинального напряжения сети Uном1 (звездой или треугольником) и начертить ее. Определить активную Р, реактивную Q и полную S мощности, расходуемые потребителем. Вычислить потребляемый линейный ток.
Номинальное напряжение сети Uном1. Выбрать схему соединения потребителя в зависимости от номинального напряжения сети Uном1 (звездой или треугольником) и начертить ее. Определить активную Р, реактивную Q и полную S мощности, расходуемые потребителем. Вычислить потребляемый линейный ток.
Как нужно соединить фазы потребителя (звездой или треугольником) для включения его в сеть с номинальным напряжением Uном2? Вычислить линейные токи в проводах при таком включении. Данные для своего варианта взять из табл. 7.
На основании вычисленных линейных токов при напряжениях Uном1 и Uном2 сделать заключение о необходимых сечениях проводников для присоединения потребителя к сети.
Указание. 1. Фазный ток потребителя определяем по формуле
, где .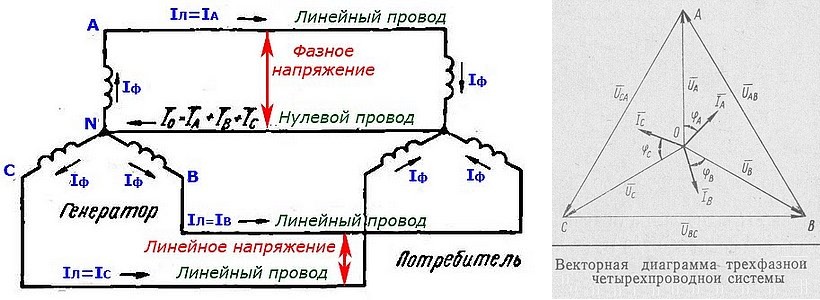
2. Активная, реактивная и полная мощности потребителя вычисляем соответственно по формулам
; ; .
Здесь Iл — линейный ток, при соединении звездой Iл= Iф, при соединении треугольником ; коэффициент мощности находим по формуле . Значение определяем по таблице Брадиса, зная .
Таблица 7
| Номер варианта | UФ В | RФ Ом | хФ Ом | UНОМ1 В | UНОМ2 В |
| 8,5 | 5,25 | ||||
| 10,5 | |||||
Задача № 6(варианты 3, 13, 23)
В трехфазную четырехпроводную сеть с линейным напряжением UH0М включили звездой разные по характеру сопротивления (см. рис. 46—55). Определить линейные токи и начертить в масштабе векторную диаграмму цепи. По векторной диаграмме определить числовое значение тока в нулевом проводе. Данные для своего варианта взять из табл. 8.
рис. 46—55). Определить линейные токи и начертить в масштабе векторную диаграмму цепи. По векторной диаграмме определить числовое значение тока в нулевом проводе. Данные для своего варианта взять из табл. 8.
Какие сопротивления надо включить в фазы В и С приведенной схемы, чтобы ток в нулевом проводе стал равен нулю при неизменных значениях сопротивлений в фазе А?
Указание. См. решение типового примера 6.
Таблица 8
| Номер варианта | Номер рисунка | UНОМ В |
Схемы к задаче №6
| Рис. 46 | Рис. 47 |
| Рис. 48 |
Задача №7(варианты 4, 14, 24)
В трехфазную четырехпроводную сеть включили трехфазную сушильную печь, представляющую собой симметричную активно — индуктивную нагрузку с сопротивлениямиRП и хП, и лампы накаливания мощностью РЛ каждая. Обмотки печи соединены треугольником, лампы накаливания — звездой. Количество ламп в каждой фазе nА, nВ и nС задано. Номинальное напряжение сети UНОМ. Схема сети приведена на рис. 56. Определить показания амперметров А1, А2, A3, А4, A5и вольтметра VЛ. Начертить в масштабе векторную диаграмму цепи для соединения ламп накаливания, из которой найти числовое значение тока в нулевом проводе I0 (показание амперметра А0). Данные для своего варианта взять из табл. 9.
Обмотки печи соединены треугольником, лампы накаливания — звездой. Количество ламп в каждой фазе nА, nВ и nС задано. Номинальное напряжение сети UНОМ. Схема сети приведена на рис. 56. Определить показания амперметров А1, А2, A3, А4, A5и вольтметра VЛ. Начертить в масштабе векторную диаграмму цепи для соединения ламп накаливания, из которой найти числовое значение тока в нулевом проводе I0 (показание амперметра А0). Данные для своего варианта взять из табл. 9.
Указание. См. решение типового примера 10.
Таблица 9
| Номер варианта | RП Ом | хП Ом | РЛ Вт | nА шт. | nВ шт. | nС шт. | UНОМ В |
Задача №8(варианты 5, 15, 25)
Три одинаковых резистора с сопротивлениями R каждый соединили звездой, включили в трехфазную сеть с линейным напряжениемUНОМ1 и измерили потребляемые токи IНОМ1.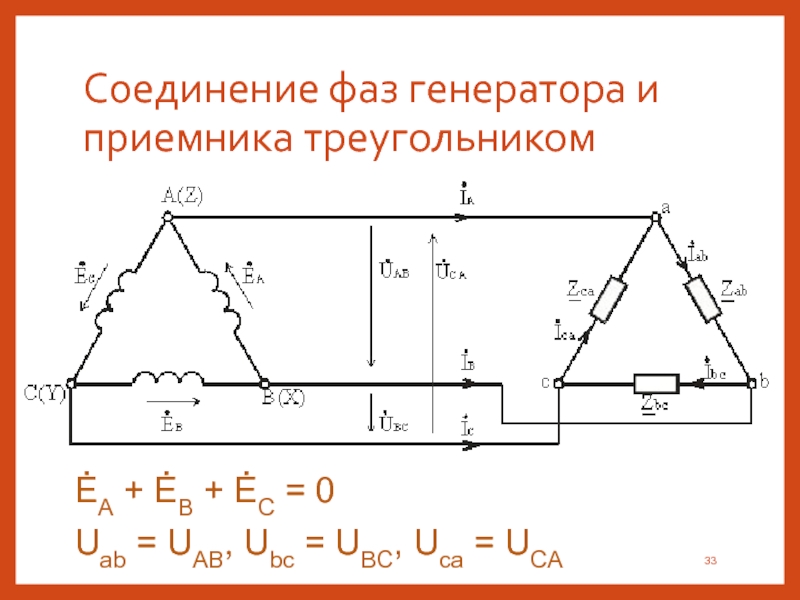 Затем резисторы соединили треугольником, включили в ту же сеть и измерили фазные IФ2 и линейные IНОМ2 токи. Определить, во сколько раз при таком переключении изменились фазные и линейные токи и потребляемые цепью активные мощности, т.е. найти отношения IФ2/IНОМ1, IНОМ2/IНОМ1 и Р2/Р1. Начертить в масштабе векторную диаграмму цепи при соединении резисторов треугольником. Данные для своего варианта взять из табл. 10.
Затем резисторы соединили треугольником, включили в ту же сеть и измерили фазные IФ2 и линейные IНОМ2 токи. Определить, во сколько раз при таком переключении изменились фазные и линейные токи и потребляемые цепью активные мощности, т.е. найти отношения IФ2/IНОМ1, IНОМ2/IНОМ1 и Р2/Р1. Начертить в масштабе векторную диаграмму цепи при соединении резисторов треугольником. Данные для своего варианта взять из табл. 10.
Указание. Активная мощность цепи Р = 3РФ = 3UФIФ.
Таблица 10
| Номер варианта | R Ом | UНОМ1 В |
Задача №9(варианты 6, 16, 26)
По заданной векторной диаграмме для трехфазной цепи определить характер сопротивлений в каждой фазе (активное, индуктивное емкостное, смешанное), вычислить значение каждого сопротивления н начертить схему присоединения сопротивлений к сети. Сопротивления соединены звездой с нулевым проводом. Пользуясь векторной диаграммой, построенной в масштабе, определить графически ток в нулевом проводе. Данные для своего варианта взять из табл. 11. Пояснить с помощью логических рассуждений, как изменится ток в нулевом проводе при уменьшении частоты тока в два раза.
Сопротивления соединены звездой с нулевым проводом. Пользуясь векторной диаграммой, построенной в масштабе, определить графически ток в нулевом проводе. Данные для своего варианта взять из табл. 11. Пояснить с помощью логических рассуждений, как изменится ток в нулевом проводе при уменьшении частоты тока в два раза.
Указание. См. решение типового примера 7.
Таблица 11
| Номер варианта | Номер рисунка |
Задача №10(варианты 7, 17, 27)
Трехфазная нагревательная печь состоит из трех одинаковых резисторов сопротивлением R? каждый, соединенных звездой. Печь включена в сеть с линейным напряжением UНОМ. Как следует изменить сопротивления резисторов, чтобы при их соединении треугольником и включении в ту же сеть линейные токи и потребляемые активные мощности остались прежними? Для случая соединения резисторов треугольником начертить в масштабе векторную диаграмму цепи.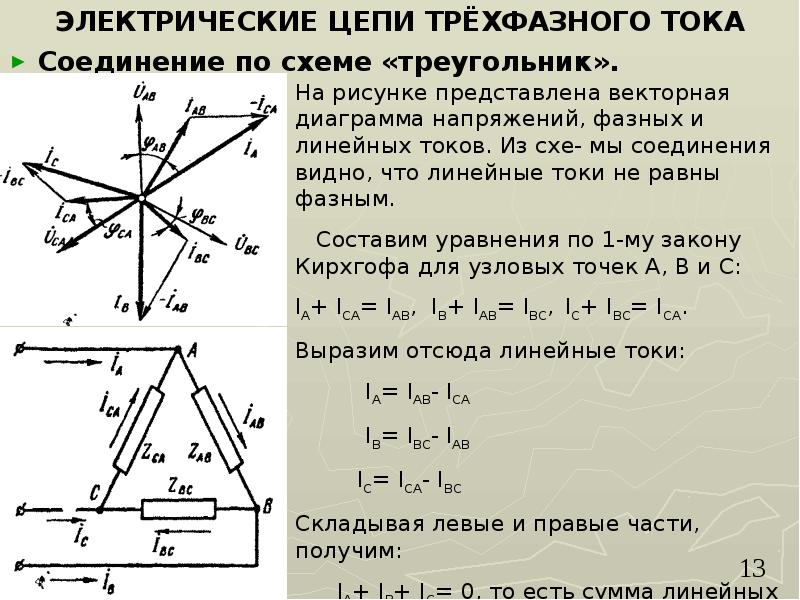 Данные для своего варианта взять из табл. 12.
Данные для своего варианта взять из табл. 12.
Указание. При соединении треугольником линейный ток IНОМ = √3IФ, где фазный ток IФ = UНОМ/R?. При соединении звездой для сохранения постоянства линейного тока должно соблюдаться равенство
Отсюда определяется величинаRY .
Таблица 12
| Номер варианта | R? Ом | UНОМ В |
Задача №11(варианты 8, 18, 28)
По заданной векторной диаграмме для трехфазной цени определить характер сопротивлений во всех фазах (активное, индуктивное, емкостное, смешанное), вычислить значения каждого сопротивления н начертить схему присоединения сопротивлений к сети.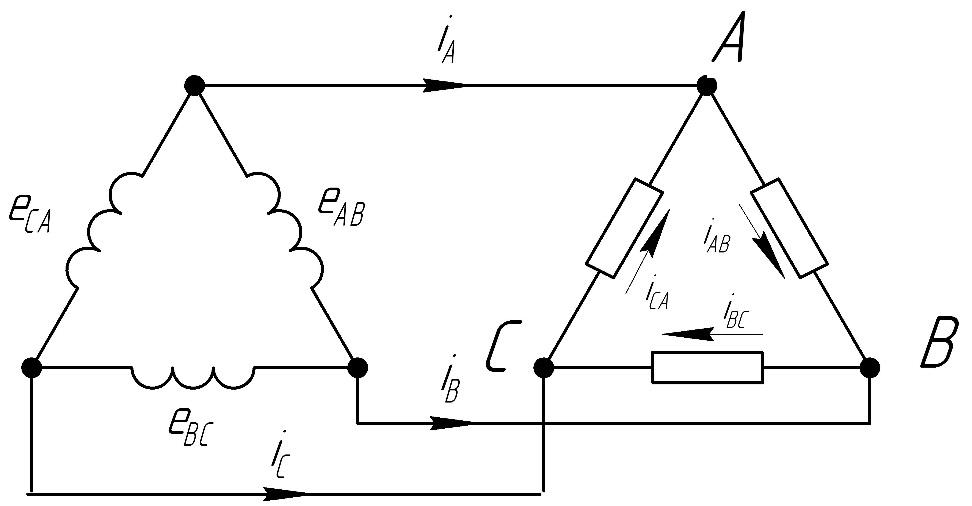 Сопротивлении соединены треугольником. Закончить построение векторной диаграммы, показав на ней векторы линейных токов IА IВ и IС. Данные для своего варианта взять из табл. 13.
Сопротивлении соединены треугольником. Закончить построение векторной диаграммы, показав на ней векторы линейных токов IА IВ и IС. Данные для своего варианта взять из табл. 13.
Указание. См. решение типового примера 9.
Таблица 13
| Номер варианта | Номер рисунка |
Задача №12(варианты 9, 19, 29)
С помощью элементов, приведенных на рис. 77, составить принципиальную схему включения двух трехфазных электродвигателей Д1 и Д2 и двух групп ламп накаливанияJI1 иJI2 в трехфазную четырехпроводную сеть. Электродвигатели и лампы включаются в сеть через автоматические выключателиAД1 иAД2 и АЛ1 и АЛ2. Выключатели служат для включения и отключения потребителей и защиты электрической сети от токов короткого замыкания и токов перегрузки. Номинальное напряжение сети UНОМ. Обмотка каждой фазы электродвигателя рассчитана на напряжение UД; номинальное напряжение ламп UЛ. Эти величины заданы в таблице вариантов. В задаче необходимо выполнить следующее:
Выключатели служат для включения и отключения потребителей и защиты электрической сети от токов короткого замыкания и токов перегрузки. Номинальное напряжение сети UНОМ. Обмотка каждой фазы электродвигателя рассчитана на напряжение UД; номинальное напряжение ламп UЛ. Эти величины заданы в таблице вариантов. В задаче необходимо выполнить следующее:
1) в зависимости от напряжения сети соответствующим образом соединить между собой обмотки каждого электродвигателя (в звезду или треугольник), показанные на рисунке в его корпусе, и присоединить их к сети;
2) соединить лампы в каждой группе с учетом их напряжений (в звезду или треугольник) и присоединить их к сети;
3) принимая мощность лампы равной РЛ, определить потребляемый лампой ток и начертить в масштабе векторную диаграмму для участка цепи, содержащего лампы. Данные для своего варианта взять из табл. 14.
Указание. См. решение типового примера 5.
решение типового примера 5.
Таблица 14
| Номер варианта | UНОМ В | UД В | UЛ В | РЛ Вт |
Задача №13(варианты 10, 20, 30)
В трехфазную трехпроводную сеть с линейным напряжением UНОМ включили треугольником разные по характеру сопротивления (рис. 78—80). Определить фазные токи и начертить в масштабе векторную диаграмму цепи. Из векторной диаграммы определить числовые значения линейных токов. Данные для своего варианта взять из табл. 15.
Как изменятся значения фазных и линейных токов и взаимное расположение векторов токов и напряжений при увеличении частоты тока в сети в два раза?
Указание. См. решение типового примера 8.
См. решение типового примера 8.
Таблица 15
| Номер варианта | Номер рисунка | UНОМ В |
1.3.2 Решение типовых задач1
Примеры решения типовых задач
Задача 1.3.1 Трехфазный асинхронный двигатель включен в сеть 380 В по схеме «звезда». Параметры обмоток следующие: Rф = 2 Ом, Хф = 8 Ом.
Требуется:
изобразить схему включения двигателя
в сеть; определить фазные и линейные
токи; определить потребляемую активную
мощность; построить векторную диаграмму
токов и напряжений; рассмотреть два
аварийных режима – обрыв и короткое
замыкание фазы А.
Решение:
Трехфазный асинхронный двигатель является симметричной активно-индуктивной нагрузкой, поэтому включается в сеть по схеме «звезда» без нейтрального провода. Его схема замещения представлена на рис. 1.3.8
Номинальное напряжение сети является линейным напряжением, т. е. , тогда фазное напряжение
Поскольку нагрузка симметричная, то расчет можно проводить для одной фазы.
Полное сопротивление фазы
Ф
А(а)
азный ток.
Для схемы «звезда» линейный ток . Потребляемая активная мощность
где — фазовый угол,
.
Векторная диаграмма
токов и напряжений показана на рис.
1.3.9. Для построения векторной диаграммы
необходимо выбрать масштабы напряжений и токов
.
Рассмотрим аварийный режим работы– обрыв фазы А (рис.1.3.10).
В этом случае трехфазная цепь превращается в однофазную , причем фазы b и с оказываются включенными последовательно на линейное напряжение , т. е. на каждую из этих фаз падает напряжение
Фазные и линейные токи
.
Потребляемая мощность Рис. 1.3.11 Как видно из расчета, потребляемая мощность снизилась почти в два раза.Если обрыв фазы произошел внутри самого двигателя (обрыв обмотки), то эта обмотка оказывается под повышенным напряжением , что видно из векторной диаграммы (рис.1.3.11). Неповрежденные обмотки находятся под пониженным напряжением, что не опасно для них. |
Рассмотрим аварийный
режим работы – короткое замыкание фазы
«а» (рис. 1.3.12, а, б).
1.3.12, а, б).
При коротком замыкании фазы нейтральная точка оказывается связана с питающей точкой А, значит, неповрежденные фазы b и с окажутся включенными на линейное напряжение , что видно из векторной диаграммы.
Токи в неповрежденных фазах
.
а | б |
Рис. 1.3.12
Ток в фазе а равен геометрической сумме токов и ( по векторной диаграмме составляет примерно 69 А).
Задача 1.3.2. Три однофазных приемника включены в трехфазную сеть с напряжением 380 В по схеме “звезда с нейтральным проводом”. Сопротивления приемников: Ом; Ом; Ом.
Требуется
изобразить схему включения приемников;
определить токи в проводах сети; построить
векторную диаграмму токов и напряжений;
вычислить активную, реактивную и полную
(кажущуюся) мощности.
Решение:
Схема включения приемников принципиальная и расчетная представлены на рис. 1.3.13, а,б.
а | б |
Рис. 1.3.13 | |
Наличие нейтрального провода обеспечивает симметричную систему фазных напряжений на приемниках. Напряжение сети – линейное напряжение
В.
Система фазных напряжений в комплексной форме
Сопротивления фаз
Для схемы “звезда“ фазные и линейные токи равны между собой и составляют
Ток в нейтральном проводе
При построении векторных диаграмм фазные и линейные напряжения и токи строятся относительно комплексных осей откладываются с учетом начальных фаз. Ток в нейтральном проводе – это результат геометрического сложения векторов фазных токов, и его расположение и длина должны соответствовать расчетному значению (рис. 1.3.13). | Рис. 1.3.13 |
Задача 1.3.3. К трехфазной системе напряжением 380 В подключены три одинаковых приемника (RФ = 3 Ом, XLФ = 4 Ом), соединенные по схеме “треугольник“ (рис.1.3.14). Определить токи в фазных и линейных проводах и потребляемую мощность (активную, реактивную, полную). Построить векторную диаграмму токов и напряжений.
Рассмотреть аварийные режимы – обрывы фазного и линейных проводов.
Решение:
Нагрузка фаз одинакова, поэтому расчет проводится для одной фазы. Напряжение сети — это линейное напряжение, в схеме “треугольник “ Uф = Uл = 380 В. Комплексное сопротивление фазы: где | Рис. 1.3.14 |
Фазные токи:
линейные токи (только для симметричной нагрузки):
Активная мощность, потребляемая нагрузкой:
реактивная мощность:
полная мощность:
Векторная диаграмма может быть построена в двух вариантах в зависимости от изображения системы напряжений (рис.1.3.15 ). Предварительно выбирают масштабы тока и напряжения.
Рис. 1.3.15 | |
Фазные токи отстают от соответствующих напряжений на угол Ф = 53. Линейные токи находятся из соотношений:
Рассмотрим обрыв фазы “аb” (рис.1.3.16,а). Определим токи в неповрежденных фазах и в линии, построим векторную диаграмму токов и напряжений.
а) | б) |
Рис. 1.3.16 | |
Токи в неповрежденных фазах не изменяются, так как не изменяются напряжения:
Линейные токи по первому закону Кирхгофа (с учетом ):
.
Из этих уравнений следует, что действующие значения линейных токов и равны действующим значениям фазных токов, а у линейного тока действующее значение не изменяется
Векторная диаграмма токов и напряжений строится аналогично симметричному режиму и приведена на рис.1.3.16,б.
Рассмотрим обрыв линейного провода А (рис.1.3.17,а). Определим фазные и линейные токи и построим векторную диаграмму токов и напряжений.
К приемнику подводится только напряжение
Сопротивление фазы “bс” включено на полное напряжение , а равные сопротивления фаз “аb” и ”са” включены последовательно друг с другом, причем к каждому из них подведена половина напряжения .
а) б) Рис.1.3.17 |
Сеть становится аналогичной однофазной с двумя параллельными ветвями:
Ток фазы “bс” не изменяется:
токи других фаз :
линейные токи ( при ) :
Векторная диаграмма токов и напряжений представлена на рис. 1.3.17,б.
Задача 1.3.4 В трехфазную сеть напряжением 380 В, частотой f = 50 Гц включен трехфазный асинхронный двигатель по схеме “треугольник“. Потребляемая активная мощность P = 1,44 кВт, коэффициент мощности cos = 0,85. Определить потребляемый двигателем ток, токи в обмотках двигателя, активное и индуктивное сопротивления, индуктивность катушек, полную и реактивную потребляемые мощности.
Решение:
Двигатель является симметричной нагрузкой, поэтому расчет ведем на фазу.
Сеть маркируется линейным напряжением, поэтому UЛ = 380 В.
При соединении по схеме “треугольник“ UЛ = UФ= 380 В.
Активная мощность, потребляемая нагрузкой,
отсюда фазный ток, протекающий в обмотках двигателя:
Потребляемые двигателем токи — линейные токи:
Полное сопротивление фазы обмотки двигателя:
Ом,
активное сопротивление
Ом,
индуктивное сопротивление
Ом.
Индуктивность обмотки определяется из выражения
,
Гн.
Полная потребляемая мощность:
кВА;
реактивная мощность:
Задача 7.3 К трехпроводной трехфазной линии с напряжением 380 В подключены три однофазных приемника с параметрами: R1= 5 Ом, R2= 6 Ом, XL2= 8 Ом, R3=4 Ом, XC3= 3 Ом. Определить токи в фазах и линейных проводах, активную, реактивную и полную мощности и построить векторную диаграмму токов и напряжений.
Решение:
Однофазные приемники к трехпроводной сети подключаются по схеме “треугольник“ (рис.1.3.18). Нагрузка несимметричная, ток каждой фазы нужно считать отдельно. Исходная система напряжений: Комплексные сопротивления фаз: Ом; | |
Ом;
Ом;
Фазные токи:
Линейные токи:
Сумма линейных токов должна равняться нулю, и действительно,
Активная мощность:
Реактивная мощность:
здесь знак “минус” показывает, что преобладает емкостная нагрузка.
Полная мощность:
Векторные диаграммы токов и напряжений в двух вариантах (для разного представления исходной системы напряжений) приведены на рис.1.3.19.
Предварительно выбирают масштабы тока и напряжения. Векторы фазных токов откладывают относительно векторов соответствующих напряжений под углами , , или в соответствии с полученными их начальными фазами ; ; . Затем по первому закону Кирхгофа строят векторы линейных токов , длина и направление которых должны соответствовать расчетным данным.
Рис.1.3.19 Векторные диаграммы токов и напряжений несимметричной нагрузки | |
Методические указания по выполнению контрольной работы № 2 — Студопедия.Нет
Задачи 1 – 40 посвящены теме «Трехфазные цепи». В трехфазных цепях потребители соединяются по схеме звезда или треугольник.
При соединении приемников звездой линейные напряжения обозначаются UAB, UBC, UCA в общем виде – Uл; фазные обозначаются UA, UB, UC; в общем виде Uф.
Токи – IA, IB, IC; причем токи линейные равны соответствующим фазным
токам:
При наличии нейтрального провода при любой нагрузке, а при равномерной нагрузке и без нейтрального провода:
При соединении потребителей энергии треугольником фазное напряжение равно линейному: . Обозначаются напряжения: UAB, UBC, UCA.
Фазные токи обозначаются IAB, IBC, ICA в общем виде – Iл . При неравномерной нагрузке фаз линейные токи определяются из векторной диаграммы как геометрическая разность фазных токов.
При присоединении приемников энергии звездой сеть может быть четырехпроводной (при наличии нейтрального провода) или трехпроводной (без нейтрального провода). При соединении треугольником — только трехпроводной.
Задания 1 – 20
Пример 1
В трехфазную четырехпроводную сеть включили звездой несимметричную нагрузку: в фазу А – конденсатор с емкостным сопротивлением хA = 10 Ом; в фазу В – активное сопротивление RB = 8 Ом и индуктивное xB = 6 Ом, в фазу С – активное сопротивление RС = 5 Ом. Линейное напряжение сети Uном = 380 В.
Определить фазные токи, начертить в масштабе векторную диаграмму цепи и найти графически ток в нулевом проводе. Схема цепи дана на рис. 13, а.
Рис. 13
Решение.
1. Определяем фазные напряжения установки
2. Находим фазные токи
Для построения векторной диаграммы выбираем масштабы по току: 1 см — 10 А и по напряжению: 1 см — 100 В. Построение диаграммы начинаем с векторов фазных напряжений UА, UBи UC, располагая их под углом 120° друг относительно друга (рис. 13, б). Ток IA опережает напряжение UA на угол 90°; ток IB отстает от напряжения UB на угол φB, который определяется из выражения
Ток IC совпадает с напряжением UC. Ток в нулевом проводе равен геометрической сумме трех фазных токов. Измеряя длину вектора тока I0 которая оказалась равной 6,8 см, находим ток I0 = 68 А,
Пример 2
По заданной векторной диаграмме для трехфазной цепи (рис. 14, а) определить характер нагрузки каждой фазы и вычислить ее сопротивление. Начертить соответствующую схему цепи. Нагрузка включена в звезду.
Определить активную и реактивную мощности, потребляемые цепью. Значения напряжений, токов и фазных углов приведены на диаграмме. Векторы линейных напряжений не показаны.
Рис. 14
Решение.
1. Рассматривая векторную диаграмму, можно заметить, что ток в фазе А отстает от фазного напряжения UA на угол φA = 53°10′, значит в фазу А включена катушка с полным сопротивлением zA = UA / IA = 220/22 = 10 Ом. Ее активное и индуктивное сопротивления вычисляем по формулам
В фазе В ток IB совпадает с напряжением UB, значит в фазу В включено активное сопротивление
В фазе С ток IС опережает напряжение UCна угол φC = 36°50′, значит в фазу С включены конденсатор и активное сопротивление. Полное сопротивление фазы
Определим активное и емкостное сопротивления
Схема цепи приведена на Рис. 14, б.
2. Определяем мощности, потребляемые цепью. Активная мощность
Реактивная мощность
Знак минус показывает, что в цепи преобладает емкость.
Задания 21 – 40
Пример 3
По векторной диаграмме для трехфазной цепи (рис. 15, а) определить характер нагрузки в каждой фазе, вычислить ее сопротивление и начертить схему включения. Нагрузка несимметричная, соединена в треугольник. Значения напряжений, фазных токов и углов сдвига фаз указаны на диаграмме.
Рис. 15
Решение.
1. Рассматривая векторную диаграмму, можно заключить, что ток IAB в фазе АВ совпадает с напряжением UAB, значит в фазу АВ включено активное сопротивление
В фазе ВС ток IBC опережает напряжение на угол φВС = – 90о, значит в фазу ВС включено емкостное сопротивление
В фазе СА ток ICA отстает от напряжения UCA на угол φСА = 36о50′, значит в фазу СА включено активно-индуктивное сопротивление
Очевидно,
2. На основании вычислений чертим схему цепи (рис 15. б)
Пример 4
В трехфазную сеть включили треугольником несимметричную нагрузку (рис. 16, а): в фазу АВ – конденсатор с емкостным сопротивлением хAB = 10 Ом; в фазу ВС – катушку с активным сопротивлением RBC = 4 Ом и индуктивным хBC= 3 Ом; в фазу СА – активное сопротивление RCA = 10 Ом. Линейное напряжение сети Uном = 220 В.
Определить фазные токи, углы сдвига фаз и начертить в масштабе векторную диаграмму цепи. По векторной диаграмме определить числовые значения линейных токов.
Рис. 16
Решение
1. Определяем фазные токи и углы сдвига фаз;
Отсюда угол φBC = 36o50’.
Для построения векторной диаграммы выбираем масштаб по току: 1 см — 10 А, по напряжению: 1 см — 80 В. Затем в принятом масштабе откладываем векторы фазных (они же линейные) напряжений UAB, UBC, UCA углом 120° друг относительно друга (рис. 16, б). Под углом φAB = 90° к вектору напряжения UABоткладываем вектор тока IAB; в фазе ВС вектор тока IBCдолжен отставать от вектора напряжения UBC на угол φBC = 36°50′, а в фазе СА вектор тока ICA совпадает с вектором напряжения UCA. Затем строим векторы линейных токов на основании известных уравнений
Измеряя длины векторов линейных токов и пользуясь принятым масштабом, находим значения линейных токов:
Трехфазный ток — Технарь
Пример
В каждую фазу трехфазной четырехпроводной цепи нейтральным проводом включены сопротивления, как показано на рис. 61, а (соединение звездой). Сопротивления во всех фазах одинаковы и равны: активные 8,0 Ом, индуктивные 12 Ом, емкостные 6,0 Ом. Линейное напряжение сети 220 В. Для каждой фазы нагрузки определить: 1) полное сопротивление, коэффициент мощности, сдвиг фаз между током и напряжением, фазные токи; активную, реактивную и полную мощности каждой фазы; 2) линейные токи, ток в нейтральном проводе; активную, реактивную и полную мощности потребителя. Построить векторную диаграмму.
Дано: r1=r2= r3=Rф=8,0 Ом — активные сопротивления фаз; XL1=XL2=XL3=XLф =12 Ом — индуктивные сопротивления фаз; XC1=XC2=XC3=XCф=6,0 Ом — емкостные сопротивления фаз; Uл=220 В — линейное напряжение.
Найти: 1) Zф— полное сопротивление каждой фазы; cos φф— коэффициент мощности; φф— сдвиг фаз между током и напряжением; Iф—фазные токи; Рф, Qф, Sф — соответственно активную, реактивную, полную мощности; 2) Iл — линейные токи, I0— ток в нейтральном проводе; P,Q,S— активную, реактивную, полную мощности нагрузки.
Решение. 1) Так как в данной задаче соответствующие сопротивления всех фаз одинаковы (симметричная нагрузка), достаточно произвести вычисления для одной фазы. Полное сопротивление фазы найдем по формуле:
Вычисляем полное сопротивление фазы:
Коэффициент мощности фазы определим по формуле:
затем найдем сдвиг фазы φф между током и напряжением. Для определения направления сдвига фаз определим sin φф:
Если sin φф>0 (нагрузка преимущественно индуктивная), ток отстает от напряжения на угол φф; если sin φф<0 (нагрузка преимущественно емкостная), ток опережает напряжение по фазе.
Находим коэффициент мощности фазы:
так как sin φф >0, то ток отстает по фазе от напряжения, и на векторной диаграмме вектор тока сдвинут на 36°52′ в сторону отставания (по часовой стрелке) от вектора напряжения. При симметричной нагрузке коэффициент мощности всей нагрузки равен коэффициенту мощности фазы: cosφ=cos φф=0,80.
Фазные токи найдем по закону Ома:
При соединении звездой с нейтральным проводом напряжение на каждой фазе, независимо от вида и сопротивления фазы, всегда одинаково и равно Uф =Uл /√(3), тогда Iф = Uл/√(3)Zф. При соединении звездой линейные токи равны фазным:
Находим фазные и линейные токи:
Активную, реактивную и полную мощности фаз определяем из формул:
Подставляя числовые значения, находим активную, реактивную и полную мощности фазы:
2) Ток в нейтральном проводе определяется по векторной диаграмме:
При симметричной нагрузке ток в нейтральном проводе I0=0.
Активная мощность всей нагрузки равна сумме активных мощностей фаз:
Для симметричной нагрузки Р = ЗРф =√(3), IлUл cos φф
Реактивная мощность нагрузки равна алгебраической сумме реактивных мощностей фаз:
(Знак «+» при преобладании индуктивной нагрузки, «—» — емкостной.) В данной задаче:
Определим полную мощность нагрузки как:
В данной задаче S=3Sф
Находим активную, реактивную и полную мощности нагрузки:
Строим векторную диаграмму (см. рис. 61, б). Построение начинаем с фазных напряжений, располагая их под углом 120° друг к другу. Под углами φА, φБ, φС (в данной задаче 36°52′) к соответствующим векторам фазных напряжений строим векторы фазных токов; Iф=12,7 А, Uф=127 В.
Ответ. 1) Полное сопротивление фазы 10 Ом; коэффициент мощности 0,80; сдвиг фаз между током и напряжением 36°52′; фазные и линейные токи 12,7 А; мощности фазы: активная 1,29 кВт, реактивная 0,968 вар, полная 1,61 кВ*А; 2) ток в нейтральном проводе равен нулю; мощность нагрузки: активная 3,87 кВт, реактивная 2,90 квар, полная 4,84 кВ*А.
ПримерПотребитель, представляющий собой симметричную нагрузку, фазы которой соединены треугольником, включен в сеть трехфазного тока с линейным напряжением 220 В (рис. 62). Соответствующие сопротивления во всех фазах одинаковы и равны: активные 6,0 Ом, индуктивные 4,0 Ом, емкостные 12 Ом. Определить: полное сопротивление каждой фазы, коэффициент мощности фазы, фазные и линейные токи; активную, реактивную, полную фазные мощности; активную, реактивную и полную мощности нагрузки.
Дано: Uл—220 В — линейное напряжение цепи; r1=r2=r3 =R=6,0 Ом — активные сопротивления фаз; XL1=XL2=XL3=XL= 4,0 Ом — индуктивные сопротивления XC1=XC2=XC3=XC = 12 Ом — емкостные сопротивления фаз.
Найти: Zф— полное сопротивление каждой фазы, cos φф— коэффициент мощности фазы, Iф, Iл — фазные и линиейные токи; ; Рф, Qф , Sф — активную, реактивную, полную мощности фаз; Р,Q, S — активную, реактивную и полную мощности нагрузки.
Решение. При симметричной нагрузке достаточно определить все необходимые величины для одной фазы.
Полное сопротивление фазы найдём по формуле:
Коэффициент мощности фазы:
в данной задаче коэффициент мощности всей нагрузки:
Фазный ток находим по закону Ома для участка цепи:
При соединении треугольником фазное напряжение равно линейному, Uф =Uл, поэтому IФ=Uл/Zф.
Для нахождения линейного тока учитываем, что при симметричной нагрузке:
Подставляя числовые значения, получаем:
Соответствующие мощности фаз определяем по формулам:
Активную мощность нагрузки определим по формуле:
Находим реактивную мощность нагрузки:
Определяем полную мощность нагрузки:
Ответ. Полное сопротивление фазы 10 Ом, коэффициент мощности фазы 0,60, фазные токи 22 А, линейные токи 38,1 А; мощности фаз: активная 2,9 кВт, реактивная 3,87 квар, полная 4,84 кВ*А; мощности нагрузки: активная 8,7 кВт, реактивная —11,6 квар; полная 14,5 кв*А.
Методические указания к решению задачи 2 — FINDOUT.SU
Решение задач этой группы требует знаний учебного материала
темы 1 5, умения решать однофазные неразветвленные цепи, знать в трехфазных цепях соотношения между линейными и фазными напряжениями и токами при соединении потребителей «звездой» и «треугольником» и строить векторные диаграммы.
Пример 2. В трехфазную четырехпроводную сеть включили звездой несимметричную нагрузку: в фазу А — индуктивный элемент с индуктивностью L A=31,8 мГн, в фазу В — резистор с сопротивлением R B=30 Ом и ёмкостный элемент с ёмкостью C B=795 мкф, в фазу C – резистор с сопротивлением R С = 10 Ом. Линейное напряжение сети Uном=380В
Определить фазные токи I A , I B , I C, активную мощность
цепи Р , реактивную мощность Q и полную мощность S, частота сети f=50Гц
Построить векторную диаграмму и по ней определить ток в нейтральном проводе.
Схема цепи дана на рис. 2.
Решение
Дано:
Определить: I A, I B, I C, P, Q, S, I N.
1. Определяем фазные напряжения:
В четырехпроводной цепи при любой нагрузке фаз выполняется соотношение:
2. Определяем сопротивление индуктивного элемента L A:
З. Определяем сопротивление емкостного элемента в фазе В:
4. Определяем полное сопротивление в фазе В:
5. Находим фазные токи, применяя закон Ома для участка цепи:
6. Определяем активную мощность фазы А:
7. Определяем активную мощность фазы В:
8. Определяем активную мощность фазы С:
9. Активная мощность трехфазной цепи равна:
10. Определяем реактивную мощность фазы А:
11. Определяем реактивную мощность фазы В:
12. Определяем реактивную мощность фазы С:
13. Реактивная мощность цепи:
14. Полная мощность трехфазной цепи равна:
Для построения векторных диаграмм выбираем масштабы по току и напряжению:
Определяем длины векторов токов I A , I B , I C и фазных напряжений U A, U B , U C:
Определяем угол сдвига фаз меж током I A и фазным напряжением U A:
Вектор тока I A отстаёт от напряжения на 90o, так как в фазе А включен индуктивный элемент.
Определяем угол сдвига фаз между током I B и напряжением U B:
Вектор тока опережает напряжение на 53о10 так как в фазе включена активно — емкостная нагрузка.
Определяем угол сдвига фаз между током I C и напряжением U C :
Вектор тока I Cсовпадает по фазе с напряжением UC, в фазе С включена активная нагрузка, на угол сдвига фаз равен
Строим векторы фазных напряжений U A , U B , UCпод углом 120о друг относительно друга и векторы фазных токов I A , I B , I C, учитывая углы сдвига фаз
На основании уравнения, составленного по 1-му закону Кирхгофа, строим вектор тока в нейтральном проводе
Рис. 3
Измеряя длину вектора IN получаем: lIN = 4,4 см, отсюда IN = lIN *MI=4,4*10=44А.
Ответ: I A =22А, I B=44А, I C =22А, I N =44А, Р=10,65 кВт, Q =2,9 кВАр, S = 10,6 кВА.
Пример 3. В трехфазную сеть включили треугольником несимметричную нагрузку. В фазу AB – емкостный элемент CAB=318 мкф, в фазу BC – индуктивный элемент с активным сопротивлением RBC= 4 Ом и индуктивностью LBC = 9,6 мГн, в фазу CA – резистор с сопротивлением RCA = 10 Ом. Линейное напряжение UHOM = 220 В. Определить фазные токи, активную мощность P, реактивную мощность Q и полную мощность трехфазной цепи S. Частота цепи f = 50 Гц. Построить векторную диаграмму напряжений и токов и по ней определить линейные токи IA , IB , IC . Схема цепи дана на рис. 4.
Решение
Дано:
Определить:
1. При соединении потребителей треугольником выполняется соотношение:
2. Определяем сопротивление емкостного элемента в фазе АВ:
З. Определяем сопротивление индуктивного элемента в фазе ВС:
4. Определяем полное сопротивление фазы ВС:
5. Определяем фазные токи:
6. Определяем активную мощность Р АВ:
7. Определяем активную мощность Р ВС:
8. Определяем активную мощность фазы СА:
9. Определяем реактивную мощность фазы Q АВ:
10. Определяем реактивную мощность Q ВС :
11. Определяем реактивную мощность Q СА :
12. Определяем активную мощность трехфазной цепи:
13. Определяем реактивную мощность всей цепи:
14. Определяем полную мощность трехфазной цепи:
Для построения векторной диаграммы выбираем масштабы по току MU= 10 А/см и по напряжению MU = 50 В/см.
Определяем длины векторов фазных токов и фазных (они же линейные) напряжений:
Определяем угол сдвига фаз между током I АВ и напряжением UAB:
Вектор тока I АВ опережает вектор напряжения UA на 90о так как а фазе АВ включен емкостный элемент.
Определяем угол сдвига фаз между током I ВС и напряжением UBС :
Вектор тока I ВС отстает от вектора напряжения UBС на угол , так как в фазе ВС включена активно — индуктивная нагрузка.
Определяем угол сдвига фаз между током I СА и напряжением U СА :
Вектор тока I СА совпадает по фазе с вектором напряжения U СА, так как нагрузка в фазе СА чисто активная,
Строим векторы фазных напряжений U АВ , U ВС , U СА под углом 120° друг относительно друга и векторы фазных токов I АВ , I ВС , I СА с учётом углов сдвига фаз
Затем строим векторы линейных токов на основании уравнений, составленных по 1-му закону Кирхгофа.
Измеряя длину векторов линейных токов IA, IB, IC, получаем:
Ответ: I АВ =22 А, I ВC =44 А, ICA = 22 А, Р = 12,6 кВт, Q = 0,97 кВАр,
S= 12,64 кВА, I А = 10 А, IB= 55А, IC =46 А.
Трехфазные цепи (страница 1)
1. Линейное напряжение трехфазного генератора, соединенного звездой, равно 10500 В.
Определить напряжение между зажимами каждой фазы генератора. Какое напряжение было бы между зажимами генератора при соединении его обмоток треугольником?
Решение:
Фазное напряжение трехфазного генератора при схеме соединения звездой в раз меньше линейного напряжения:
В схеме соединения треугольником провода линии присоединяются к общим зажимам двух обмоток, и линейное напряжение между двумя проводами равно напряжению фазной обмотки:
2. Действующее значение э. д. с. в каждой обмотке симметричного трехфазного генератора равно 230 В.
Определить линейные напряжения при соединении обмоток неправильной звездой («веером») в режиме холостого хода.
Решение:
Неправильное присоединение одной из обмоток генератора к двум остальным при соединении звездой приводит к повороту вектора э. д. с. на 180° (рис. 35) по сравнению с нормальным расположением. Вместо симметричной трехлучевой звезды векторов получается так называемый веер векторов с углами по 60° между ними. Как видно из векторной диаграммы, напряжение
Следовательно, неправильное соединение обмоток звездой можно обнаружить путем измерения. При правильном соединении все линейные напряжения равны .
3. В каждой обмотке трехфазного генератора индуктируется э. д. с, равная 132 В.
Определить линейное напряжение генератора при холостом ходе в случае соединения обмоток треугольником.
Решение:
При правильном соединении обмоток трехфазного генератора треугольником результирующая э. д. с. в контуре обмоток равна нулю, так как сумма э. д. с. симметричной трехфазной системы равна нулю. Следовательно, при холостом ходе в контуре треугольника обмоток ток отсутствует и напряжение между концом и началом обмотки равно э. д. с. Это так называемое фазное напряжение. В схеме соединения генератора треугольником провода трехфазной линии присоединяют к точкам соединения обмоток. Каждый провод при этом присоединен к зажимам двух обмоток, а каждая пара проводов линии — к зажимам одной из трех обмоток. Поэтому линейное напряжение генератора, т. е. напряжение между двумя линейными проводами, оказывается равным при схеме соединения треугольником фазному напряжению, а при холостом ходе генератора — фазной э. д. с. генератора (132 В).
4. Фазная э, д. с. трехфазного генератора Е=247 В, частота сети f=50 Гц, активное сопротивление обмотки r=1,1 Ом, индуктивное сопротивление .
Определить величину тока в контуре треугольника при неправильном соединении обмоток генератора в режиме холостого хода.
Решение:
Переключение начала и конца обмотки трехфазного генератора поворачивает вектор э. д. с. этой обмотки на диаграмме на 180°. Дело в том, что после переключения положительное направление э. д. с. этой обмотки будет относительно зажимов остальных обмоток таким, каким было отрицательное направление э. д. с. в первоначальной схеме. Таким образом, при неправильном соединении, например, фазы В по отношению к остальным фазам получим векторную диаграмму, показанную на рис. 36.
Результирующая э. д. с. в контуре равна удвоенному значению фазной э. д. с, т. е. 494 В. Эта э. д. с. обусловливает ток в контуре, величина которого определяется по закону Ома:
где z — полное сопротивление фазной обмотки:
Следовательно,
Если оставить включенной схему неправильного соединения обмоток треугольником, то даже при холостом ходе генератора в контуре обмоток будет непроизводительно расходоваться энергия, переходящая в тепло. В рассматриваемой задаче потери мощности в контуре
Поэтому, прежде чем замыкать контур треугольника обмоток, следует проверить равнопотенциальность соединяемых точек при помощи вольтметра (рис. 37). При правильном соединении обмоток треугольником подвижная часть вольтметра не отклоняется.
5. К четырехпроводной трехфазной линии поочередно присоединяют три электрические лампы мощностью по 60 Вт каждая между линейным (соответственно А, В и С) и нейтральным проводами.
Определить изменение токов в проводах линии в каждом случае присоединения к ней ламп, если напряжение между каждым линейным проводом и нейтральным проводом 120 В.
Решение:
Пусть до присоединения к четырехпроводной трехфазной линии ламп в ее проводах не было токов. Тогда присоединение электрической лампы между линейным А и нейтральным N проводами вызовет ток в этих проводах, равный
Благодаря нейтральному проводу поддерживаются равными три фазных напряжения: и на векторной диаграмме узловой точке n цепи (рис. 38) соответствует точка того же наименования, расположенная в центре тяжести треугольника векторов линейных напряжений (рис. 39).
Электрическая лампа является однофазным приемником энергии, не вызывающим сдвига фаз тока относительно напряжения . Следовательно, вектор тока совпадает по фазе с вектором напряжения . Согласно первому закону Кирхгофа, примененному к точке n цепи (рис. 39), ток в нейтральном проводе изображается тем же вектором, что и ток в проводе А. Из этого рисунка видно, что при отсутствии нейтрального провода лампу нельзя было бы включить на фазное напряжение .
Представим себе, что в дополнение к уже включенной лампе (см. рис. 38) присоединена вторая такая же лампа между линейным В и нейтральным N проводами (рис. 40).
Ток в проводе А при этом не изменился, но появился ток в проводе В. В нейтральном проводе N стал проходить ток , равный геометрической сумме токов .
Ток в линейном проводе В
Он совпадает по фазе с напряжением и тем самым отстает по фазе от тока на 1/3 периода (120°) (см. рис. 40).
Так как , то при определении тока в нейтральном проводе путем сложения векторов этих линейных токов получим ромб с углом в 120°. Диагональ ромба делит этот угол пополам, поэтому длина диагонали ромба равна его стороне, т. е.
Таким образом, величина тока в нейтральном проводе осталась той же, что и при одной лампе в проводе А, только вектор этого тока на диаграмме повернулся на 60° по ходу часовой стрелки.
Наконец, допустим, что присоединена третья лампа (в дополнение к прежним двум) между линейным С и нейтральным N проводами (рис. 41). В этом случае ток
стал проходить в проводе С, причем ввиду отсутствия сдвига фаз этого тока относительно напряжения вектор тока на диаграмме начал совпадать по фазе с вектором напряжения .
Получилась симметричная трехлучевая звезда векторов токов. Геометрическое сложение этих векторов дает нуль: . Следовательно, при симметричном режиме нагрузки ток в нейтральном проводе равен нулю.
Таким образом, отсутствие тока в нейтральном проводе при однородной (например, активной) нагрузке свидетельствует о симметрии режима в трехфазной цепи.
6. Трехфазный асинхронный электродвигатель типа МАД-126/8 в схеме соединения обмоток статора звездой при номинальной нагрузке и номинальном напряжении 500 В имеет токи в обмотках статора по 220 А и развивает номинальную мощность на валу 130 кВт.
Определить и мощность на входе, если к. п. д. при номинальной нагрузке . Построить в масштабе векторную диаграмму.
Решение:
К. п. д. , откуда
Трехфазный электродвигатель — это симметричный приемник энергии, поэтому коэффициент мощности
Этому значению коэффициента мощности соответствует угол .
Строим векторную диаграмму в масштабе: (рис. 42). Так как трехфазный электродвигатель представляет собой симметричный приемник энергии, то геометрическая сумма его токов равна нулю и нейтральный провод становится Лишним. Поэтому при любой схеме соединения обмоток трехфазного двигателя к нему подводят только три провода.
7. Три одинаковые катушки включены звездой и присоединены к трехпроводной трехфазной цепи с линейным напряжением 220 В. Начало и конец одной из катушек (фаза А) замкнуты накоротко медной пластиной.
Определить токи при коротком замыкании в фазе А. Построить в масштабе векторную диаграмму.
Решение:
Замыкание накоротко точек A и n (рис. 43) делает потенциал точки n равным потенциалу точки А.
Катушки фаз В и С оказываются включенными на линейное напряжение. Токи в них равны по величине:
Они отстают по фазе соответственно от напряжений на угол, тангенс которого
Из таблиц тригонометрических величин . Ток в замкнутой накоротко фазе А определяют в этом случае по первому закону Кирхгофа:
Следовательно, вектор тока противоположен по направлению вектору, представляющему собой сумму векторов . Строим векторную диаграмму масштаба: .
Непосредственное измерение дает для величины тока замкнутой накоротко фазы А значение .
При нормальных условиях токи во всех линейных проводах были бы равны:
Поэтому в замкнутой накоротко фазе схемы «симметричная звезда» ток больше, чем при нормальной работе, в 3 раза, при этом в двух других фазах ток увеличивается в раз.
Ток замыкается через пластину, замкнувшую зажимы катушки. В этой катушке не может быть пробоя междувитковой изоляции, так как напряжение между зажимами катушки равно нулю. Опаснее для изоляции катушки внезапное прекращение тока, так как при этом в катушке индуктируется очень большая э. д. с. самоиндукции.
8. К трехпроводной трехфазной линии напряжением 122 В и частотой 50 Гц присоединены включенные звездой катушки . В проводе С линии расплавилась плавкая вставка предохранителя (рис. 44).
Определить токи. Построить в масштабе векторную диаграмму.
Решение:
Вследствие расплавления плавкой вставки предохранителя ток в линейном проводе С прекратился. Потенциалы точек и n стали равными.
В схеме под действием линейного напряжения продолжается прохождение тока в катушках фаз А и В, включенных теперь последовательно.
Так как катушки одинаковы, то напряжение делится между ними поровну.
Это означает, что точка n диаграммы находится посередине вектора линейного напряжения . Отрезок An означает напряжение , а отрезок Вn — напряжение .
Симметричная трехлучевая звезда векторов фазных напряжений, которая характеризовала симметричный режим при всех исправных предохранителях, искажается ввиду смещения точки n из центра тяжести треугольника линейных напряжений на середину стороны АВ (см. рис. 44). Токи равны по величине:
Они отстают по фазе соответственно от напряжений на угол, тангенс которого
Из таблиц тригонометрических величин .
Строим векторную диаграмму в масштабе: . Так как потенциал точки равен потенциалу точки n (в фазе С тока нет), то разность потенциалов между точками С и n такая же, как и между точками т.е. как между концами провода. Из векторной диаграммы следует, что это напряжение в 1,5 раза превышает номинальное фазное напряжение установки:
Если бы электромонтер стал сращивать концы провода (без отключения установки), он подвергся бы действию указанного напряжения.
9. Три активных сопротивления: — соединены звездой и присоединены к трехпроводной трехфазной линии с линейными напряжениями 120 В.
Определить напряжения на отдельных сопротивлениях и токи в них.
Решение:
Нагрузка фаз по условию задачи однородная (активная): . Однако симметричный режим в цепи невозможен, так как . В случае отсутствия нейтрального провода также невозможно обеспечить равенство напряжений на отдельных фазах при такой нагрузке.
Изменение фазных напряжений при изменении нагрузки в одной фазе можно связать со смещением точки n на векторной диаграмме. При симметричном режиме в цепи точка n находится в центре тяжести треугольника линейных напряжений.
Допустим, что в линейном проводе С произошел разрыв, прекративший ток в этой фазе . В других фазах проходит ток при действии линейного напряжения в неразветвленной цепи, состоящей из сопротивлений (рис. 45). Этот ток определяется по закону Ома:
При этом напряжение на сопротивлении
а напряжение на сопротивлении
Оба эти напряжения совпадают по фазе с током и, следовательно, с напряжением (так как ).
Напряжения являются частями напряжения , причем
Точка n, обозначенная в виде , в случае обрыва фазы С находится на стороне АВ треугольника векторов линейных напряжений и делит ее в отношении 1:2 (рис. 48). Этот треугольник построен в масштабе . Точку , нанесенную на стороне AB, соединяем отрезком прямой с вершиной С, в которой располагается точка n при коротком замыкании фазы С , когда потенциалы точек n и С равны.
Допустим, что разрыв произошел в линейном проводе В (рис. 47). В этом случае ток , а в фазах С и А проходит один и тот же ток, равный, по закону Ома,
Напряжения на участках неразветвленной цепи относятся, как сопротивления этих участков: ; кроме того, соблюдается равенство . Следовательно, сторону СА следует разбить на части, относящиеся друг к другу как 3:1 (точка на рис. 48).
Соединяем отрезком прямой точку с точкой В, в которой располагается точка n при коротком замыкании фазы В. Прямые, проведенные внутри треугольника АВС, пересекаются в точке n; она соответствует узловой точке n электрической схемы для случая всех трех исправных проводов, так как точка пересечения этих прямых удовлетворяет обоим условиям, положенным в основу проведения прямых, т. е.
Именно в таком соотношении находятся сопротивления фаз по условию задачи.
Теперь рассмотрим отрезки прямых, соединяющих точку n с точками А, В и С. На векторной диаграмме эти точки соответствуют потенциалам одноименных точек схемы, а отрезки прямых — напряжениям схемы. Отрезок An означает напряжение , отрезок Вn — соответственно напряжение , отрезок Сn — напряжение (в масштабе, принятом в начале построения ).
Путем измерения этих отрезков и применения масштаба устанавливаем, что .
Далее, зная сопротивления , определяем по закону Ома токи:
Эти токи совпадают по фазе соответственно с напряжениями , так как нагрузка активная.
Построим векторы токов в масштабе , направляя векторы токов вдоль векторов соответствующих напряжений. Сумма построенных векторов токов должна равняться нулю:
Несмотря на то что меньшее напряжение оказалось в фазе с меньшим сопротивлением (фаза А), ток в ней по сравнению с токами других фаз наибольший.
Линейное и фазное напряжение: трехфазные цепи
Линейное и фазное напряжение – отличие и соотношение
В этой краткой статье, не вдаваясь в историю сетей переменного тока, разберемся в соотношениях между фазными и линейными напряжениями. Ответим на вопросы о том, что такое фазное напряжение и что такое линейное напряжение, как они соотносятся между собой и почему эти соотношения именно таковы.
Ни для кого не секрет, что сегодня электроэнергия от генерирующих электростанций подается к потребителям по высоковольтным линиям электропередач с частотой 50 Гц. На трансформаторных подстанциях высокое синусоидальное напряжение понижается, и распределяется по потребителям на уровне 220 или 380 вольт. Где-то сеть однофазная, где-то трехфазная, однако давайте разбираться.
Действующее значение и амплитудное значение напряжения
Прежде всего отметим, что когда говорят 220 или 380 вольт, то имеют ввиду действующие значения напряжений, выражаясь математическим языком – среднеквадратичные значения напряжений . Что это значит?
Это значит, что на самом деле амплитуда Um (максимум) синусоидального напряжения, фазного Umф или линейного Umл, всегда больше этого действующего значения. Для синусоидального напряжения его амплитуда больше действующего значения в корень из 2 раз, то есть в 1,414 раза.
Так что для фазного напряжения в 220 вольт амплитуда равна 310 вольт, а для линейного напряжения в 380 вольт амплитуда окажется равной 537 вольт. А если учесть, что напряжение в сети никогда не бывает стабильным, то эти значения могут быть как ниже, так и выше. Данное обстоятельство всегда следует учитывать, например выбирая конденсаторы для трехфазного асинхронного электродвигателя.
Фазное сетевой напряжение
Обмотки генератора соединены по схеме «звезда», и объединены концами X, Y и Z в одной точке (в центре звезды), которая называется нейтралью или нулевой точкой генератора. Это четырехпроводная трехфазная схема. К выводам обмоток A, B и C присоединяются линейные провода L1, L2 и L3, а к нулевой точке — нейтральный провод N.
Напряжения между выводом A и нулевой точкой, B и нулевой точкой, С и нулевой точкой, – называются фазными напряжениями, их обозначают Ua, Ub и Uc, ну а поскольку сеть симметрична, то можно просто написать Uф — фазное напряжение.
В трехфазных сетях переменного тока большинства стран стандартное фазное напряжение равно приблизительно 220 вольт — напряжение между фазным проводом и нейтральной точкой, которая обычно заземляется, и ее потенциал принимается равным нулю, потому она и называется еще нулевой точкой .
Линейное напряжение трехфазной сети
Напряжения между выводом A и выводом B, между выводом B и выводом C, между выводом C и выводом A, – называются линейными напряжениями, то есть это напряжения между линейными проводниками трехфазной сети. Их обозначают Uab, Ubc, Uca, или можно просто написать Uл.
Стандартное линейное напряжение в большинстве стран равно приблизительно 380 вольт. Легко заметить в данном случае, что 380 больше 220 в 1,727 раза, и, пренебрегая потерями, ясно, что это квадратный корень из 3, то есть 1,732. Безусловно, напряжение в сети все время в ту или другую сторону колеблется в зависимости от текущей загруженности сети, но соотношение между линейными и фазными напряжениями именно таково.
Откуда взялся корень из 3
В электротехнике часто применяют векторный метод изображения синусоидально изменяющихся во времени величин напряжений и токов.
График зависимости величины проекции от времени есть синусоида. И если амплитуда напряжения — это длина вектора U, то проекция, которая меняется со временем — это текущее значение напряжения, а синусоида отражает динамику напряжения.
Так вот, если теперь изобразить векторную диаграмму трехфазных напряжений, то получится, что между векторами трех фаз одинаковые углы по 120°, и тогда если длины векторов — это действующие значения фазных напряжений Uф, то чтобы найти линейные напряжения Uл, необходимо вычислить РАЗНОСТЬ любой пары векторов двух фазных напряжений. Например Ua – Ub.
Выполнив построение методом параллелограмма, увидим, что вектор Uл = Uа + (-Ub), и в результате Uл = 1,732Uф. Отсюда и получается, что если стандартные фазные напряжения равны 220 вольт, то соответствующие линейные будут равны 380 вольт.
Особенности линейного напряжения
Электрические цепи характеризуются наличием различных типов напряжения. Линейное напряжение (ЛН) возникает между фазовыми проводами трёхфазной цепи. У всех частей (фаз) многофазной цепи характеристика тока идентична. Название цепей (шести-, трёх- или 2-фазные) обуславливаются числом фаз. Наибольшее распространение получили трёхфазные электроцепи, так как являются наиболее экономичными в сравнении с многофазными или 2-фазными. А также позволяют на одном агрегате получить ЛН и фазное напряжение (ФН).
Какое напряжение называется линейным, а какое фазным
Линейным называется напряженье между 2-мя фазами линии или когда определяется величина между 2-мя проводами различных фаз.
Напряжение между любой фазой и нулём — фазное. Оно меряется между начальной и конечной стадией фазы. Практически ФН от ЛН отличается на 58-60 процентов. То есть, величины ЛН в 1,73 раза больше величин ФН.
Трёхфазные цепи имеют 380В ЛН, что позволяет получить 220В фазного.
Отличия
Специфика ЛН — это показатель, по которому производится расчёт токов и остальных величин трёхфазной цепи. Подобная схема позволяет подключать одно- и трёхфазные контакты. Номинальное равно 380В и меняется при изменениях в ограниченной сети, к примеру, вследствие скачков.
Популярнейшей является цепь с нейтралью и заземлением. Подключение в такой системе производится по схеме:
- к фазным проводам подсоединяются однофазные провода;
- к 3-фазным — 3-фазные.
Широта применения ЛН обуславливается его безопасностью и комфортностью разветвления цепи. Оборудование в таком случае подключается к фазному выводу, и лишь он не безопасен.
Расчёт системы несложен, при этом действуют стандартные физические формулы. Параметры ЛН сети замеряются мультиметром, а ФН — спецустройствами, например, вольтметром, датчиком тока, тестером.
- Разводка подобной проводки не нуждается в применении профессионального оборудования. Достаточно отвёрток, которые имеют индикаторы.
- Вероятность удара током очень мала. Подобное объясняется присутствующей в цепи свободной нейтралью. Соединение проводников не требует подключения 0-вого вывода.
- Схема подходит для всех видов тока.
Важно! К 3-фазной цепи можно подключить 1-фазную. Наоборот сделать нельзя.
- Подобная схема подключения пригодна для многих устройств, которым необходима высокая мощность, чтобы работать. ЛН позволяет увеличить КПД двигателя на33%.
При переключении обмоток генератора к треугольнику со звезды обуславливает увеличение в 1,73 раза величины ЛН.
Важно! Сложность обнаружения повреждений в линейном соединении является немаловажным недостатком цепи, так как вследствие этого может случиться пожар.
Отличие между ЛН и ФН состоит в различии соединяемых проводов обмоток. Чтобы проконтролировать параметры ЛН и ФН потребуется импульсный стабилизатор, по-другому — линейный стабилизатор. Этот прибор даёт возможность, сохраняя показатель на одном уровне, приводить в норму напряжение, если оно резко выросло. Прибор можно подключить к контактам электорооборудования, обычной розетке.
Соотношения фазного и линейного напряжения
Соотношение между напряжением линейным и фазным составляет 1,73. То есть при ста процентах мощности ЛН, напряжение фазы будет 58%. То есть, ЛН превышает ФН в 1,73 раза и при этом стабильно.
Напряжение в трёхфазной цепи оценивается по параметрам линейной составляющей. Обычно оно 380 вольт и тождественно 220 вольтам фазной компоненты сети трёхфазного электротока. В электрических сетях, где имеется четыре провода, напряжение 3-фазного тока обозначается 380/220В. Это позволяет подключить к подобной сети оборудование с 1-фазным потреблением электричества 220В и мощных приборов, которые могут работать от 380В.
Универсальной и приемлемой в большинстве случаев является трёхфазная цепь 380/220В 0-вым проводом. Электроприборы, которые функционируют от однофазного напряженья 220В, могут при подсоединении к паре проводов ФН питаться от ЛН.
Электрооборудование, которое запитывается от трёхфазной сети может работать, только если имеется подсоединение одновременно к 3-м выводам различных фаз. Тогда заземление не обязательно, но если изоляционный материал провода будет повреждён, то отсутствие 0-ого значительно увеличивает опасность удара электрическим током.
Важно! При понижении ЛН меняются величины ФН. При уже выясненном значении междуфазного напряжения определить величину ФН труда не составит.
Чему равно линейное напряжение
В большей части стран мира стандартное ЛН составляет примерно 380В.
В трёхфазных цепях фазное и линейное напряжение находятся в соотношении 220В/380В соответственно.
В чем измеряется
Согласно ГОСТ 13109 норма напряжения в электрической сети варьирует в диапазоне от 198В до 242В (то есть 220В плюс или минус 10 процентов). При частой поломке бытовой техники, ламп или их мигании потребуется измерение напряжения в электрической проводке. Подобная проверка делается мультиметром или вольтметром. Ночью, когда электроприборы используются по минимуму, полученные значения будут максимальными.
Мультиметром измеряется напряжение в трёхфазной сети так:
- Между рабочим 0 и каждой из фаз: А-N, В-N, С-N.
- Линейные напряжения: А-В, А-С, В-С.
Всего должно получиться шесть измерений. Иногда делается ещё один замер — между заземляющим и нулевым рабочим проводником: N-PE.
Как измерить
Измерить подобную систему можно мультиметром или применив физические формулы.
ЛН рассчитывается по формуле Кирхгофа: ∑ Ik = 0. Здесь сила тока равняется нулю во всех частях электроцепи, то есть к=1. Используется также закон Ома: I=U/R. Применив обе формулы можно высчитать параметры клейма или электросети.
В системе из несколько линий, потребуется найти напряжение между 0 и фазой IL = IF. Значения IL и IF непостоянные и меняются при разных вариациях подключения. Потому линейные параметры точно такие же, как и фазные.
Фазное
Для того чтобы получить показания подключения фазного вида, потребуется специальное оборудование, например, мультиметр, вольтметр. Для того чтобы измерить токи и напряжения в трёхфазных цепях обычно достаточно знать данные одного линейного тока и одного ЛН.
ФН измеряется при проседании (падении) линейного. Из линейных величин извлекается Квадратный корень из трёх. Полученный показатель и есть параметры ФН.
Линейное
Для расчёта соотношения линейного проводника и фазы применяется формула: Uл=Uф∙√3, Uф — фазовое, Uл — линейное.
Важно! Формула справедлива, только если IL = IF. Когда в цепь добавлены другие отводящие элементы, то для них потребуется сделать персональный расчёт фазового напряжения. Тогда Uф нужно заменить цифровыми величинами самостоятельного клейма.
Реактивная трёхфазная мощность рассчитывается по формуле: Q = Qа + Qb + Qс. Значение активной мощности можно найти, используя аналогичную формулу: P = Pа + Pb + Pс. Необходимость в подобных расчётах возникает, если к электрической сети подключается промышленная система.
Распространённость сетей с линейным током объясняется их относительной безопасностью и несложностью разведения электропроводки. Электрооборудование присоединено исключительно к одному фазному проводу (по нему проходит ток) и только он может быть опасен, второй — это заземление. ЛН возникает в трёхфазной цепи и даёт увеличение приблизительно на 73%.
Фазное и линейное напряжение
Одним из вариантов систем многофазных электрических цепей является трехфазная цепь. В многофазных электрических цепях происходит действие синусоидальных электродвижущих сил с одинаковой частотой. Они отличаются друг от друга по фазе и создаются от общего источника энергии. В трехфазных цепях важными параметрами являются фазное и линейное напряжение, отличающиеся своими электрическими характеристиками.
Что такое фаза
Каждая часть многофазной системы, имеющая одинаковую характеристику тока, называется фазой. Поэтому определение фазы имеет двоякое значение в электротехнике. Во-первых, как величина, изменяющаяся синусоидально, а во-вторых, как отдельная часть в системе многофазных электрических цепей. Количество фаз определяет наименование цепей: двухфазные, трехфазные, шестифазные и т.д.
Самыми распространенными цепями в современной энергетике являются трехфазные. Они имеют ряд преимуществ перед другими видами цепей, как однофазными, так и многофазными. Они более экономичны при производстве и передаче электроэнергии. Трехфазное напряжение возникает в результате вращения магнита внутри катушки. С его помощью достаточно просто образуется вращающееся круговое магнитное поле, обеспечивающее работу асинхронных двигателей. Данное явление известно, как ЭДС или по-другому, электродвижущая сила индукции.
Вращающийся магнит называется ротором, а катушки, расположенные вокруг него, образуют статор. Переменное напряжение получается путем преобразования постоянного напряжения, когда прямая линия принимает синусоидальную конфигурацию с изменяющимися положительными и отрицательными значениями.
Изменение магнитного потока происходит за счет вращения ротора, что и приводит к образованию переменного напряжения. В статоре имеется три катушки, в каждой из которых присутствует собственная отдельная электрическая цепь. Каждая катушка сдвинута относительно друг друга на 120 градусов по окружности. Под действием вращающегося магнита во всех катушках возникает одинаковое переменное напряжение между фазами в трехфазной сети.
Трехфазные цепи дают возможность получать два эксплуатационных напряжения на одной установке – фазное и линейное.
Фазное и линейное напряжение в трехфазных цепях
Фазное напряжение – возникает между началом и концом какой-либо фазы. По другому его еще определяют, как напряжение между одним из фазных проводов и нулевым проводом.
Линейное – определяется как межфазное или между фазное – возникающее между двумя проводами или одинаковыми выводами разных фаз.
Рассматривая фазные и линейные напряжения и токи, следует отметить, что показатель фазного напряжения составляет примерно 58% от параметров линейного. Таким образом, при нормальных условиях эксплуатации показатели линейных одинаковы и превышают фазные в 1,73 раза. То есть, если линейное напряжение 380, чему равно фазное можно определить с помощью этого коэффициента.
В трехфазной сети напряжение, как правило, оценивают по данным линейного напряжения. Для трехфазных линий, которые отходят от подстанции, устанавливается линейное напряжение номиналом 380 вольт. Это соответствует фазному в 220 вольт. В трехфазных четырех проводных сетях номинальное напряжение указывается с обозначением обеих величин – 380/220 В. Это означает, что в такую сеть подключаются как приборы с 380 вольт, так и однофазные – на 220 вольт.
Наибольшее распространение получила трехфазная система 380/220 вольт с заземленным нулевым проводом. Однофазные электроприборы на 220 вольт подключаются к линейному напряжению между любой парой фазных проводов. Трехфазные электроприборы подключаются к трем различным проводам фаз. В последнем случае не требуется использование нулевого провода, при этом отсутствие заземления повышает риск поражения током, когда нарушена изоляция.
Отличие линейного напряжения от фазного
Прежде чем рассматривать практическое значение этих параметров, необходимо точно знать, чем различаются между собой линейное и фазное напряжения. Определенное межфазное напряжение в трехфазной цепи может возникнуть либо между двумя фазами, либо между одной из фаз и нулевым проводом. Подобное взаимодействие становится возможным из-за использования в схеме четырехпроводной трехфазной цепи. Ее основными характеристиками являются напряжение и частота.
Напряжение, возникающее между двумя фазными проводниками, считается линейным, а между фазным и нулевым возникает фазное. Линейное напряжение используется для расчета токов и других параметров трехфазной цепи. К таким схемам возможно подключение не только трехфазных контактов, но и однофазных, например, различных бытовых приборов. Номинальное значение линейного напряжения составляет 380 В. Иногда оно изменяется под действием различных факторов, появляющихся в локальной сети. Таким образом, все основные различия между обоими видами напряжений заключаются в способах соединения обмоток.
Наибольшее распространение получило линейное напряжение, из-за безопасного использования и удобного распределения сетей. Для его замеров достаточно мультиметра, тогда как определение характеристик фазного напряжения требует использования вольтметров, датчиков тока и других специальных приборов.
Контроль и выравнивание данного параметра осуществляется с помощью линейного стабилизатора напряжения. Этот прибор обеспечивает поддержание этого показателя на нормативном уровне, в том числе он нормализует и повышенное напряжение.
Использование линейного и фазного напряжения
Классическим примером использования линейного и фазного напряжения считаются соединения, используемые при запуске трехфазного генератора. В его конструкцию входят первичные и вторичные обмотки, которые могут соединяться звездой или треугольником.
Схема «треугольник» предполагает соединение конца первой фазы с началом второй. Кроме того, каждый фазный проводник соединяется с линейными проводами источника тока. В результате, происходит выравнивание токов, а фазное напряжение становится равным линейному. По такой же схеме подключаются электродвигатели и трансформаторы.
Другим вариантом является схема «звезда». В этом случае начала всех обмоток подключаются к одной сети при помощи перемычек. Таким образом, в обмотки будет поступать ток с характеристиками этой сети, а межфазное напряжение вступит во взаимодействие со всеми активными контактами.
В чем главные отличия линейного и фазного напряжения?
Одним из видов систем с множеством фаз, представлены цепи, состоящие из трех фаз. В них действуют электродвижущие силы синусоидального типа, возникающие с синхронной частотой, от единого генератора энергии, и имеют разницу в фазе.
Электрическое напряжение трехфазных сетей
Под фазой, понимаются самостоятельные блоки системы с множеством фаз, имеющие идентичные друг другу параметры тока. Поэтому, в электротехнической области, определение фазы имеет двойное толкование.
Во-первых, как значение, имеющее синусоидальное колебание, а во-вторых, как самостоятельный элемент в электросети с множеством фаз. В соответствии с их количеством и маркируется конкретная цепь: двухфазная, трехфазная, шестифазная и т.д.
Сегодня в электроэнергетике, наиболее популярными являются цепи с трехфазным током. Они обладают целым перечнем достоинств, выделяющих их среди своих однофазных и многофазных аналогов, так как, во-первых, более дешевы по технологии монтажа и транспортировки электроэнергии с наименьшими потерями и затратами.
Во-вторых, они имеют свойство легко образовывать движущееся по кругу магнитное поле, которое является движущей силой для асинхронных двигателей, которые используются не только на предприятиях, но и в быту, например, в подъемном механизме высотных лифтов и т.д.
Электрические цепи, имеющие три фазы, позволяют одновременно пользоваться двумя видами напряжения от одного источника электроэнергии – линейным и фазным.
Виды напряжения
Знание их особенностей и характеристик эксплуатации, крайне необходимо для манипуляций в электрощитах и при работе с устройствами, питаемыми от 380 вольт:
- Линейное. Его обозначают как межфазный ток, то есть проходящий между парой контактов или идентичными клеймами разных фаз. Оно определяется разностью потенциалов пары фазных контактов.
- Фазное. Оно появляется при замыкании начального и конечного выводов фазы. Также, его обозначают как ток, возникающий при замыкании одного из контактов фазы с нулевым выводом. Его величина определяется абсолютным значением разности выводов от фазы и Земли.
Отличия
В обычной квартире, или частном доме, как правило, существует только однофазный тип сети 220 вольт, поэтому, к их щиту электропитания, подведены в основном два провода – фаза и ноль, реже к ним добавляется третий – заземление.
К высотным многоквартирным зданиям с офисами, гостиницами или торговыми центрами, подводится сразу 4 или 5 кабелей электропитания, обеспечивающих три фазы сети 380 вольт.
Почему такое жесткое разделение? Дело в том, что трехфазное напряжение, во-первых, само отличается повышенной мощностью, а во-вторых, оно специфически подходит для питания особых сверхмощных электродвигателей трехфазного типа, которые используются на заводах, в электролебедках лифтов, эскалаторных подъемниках и т.д.
Такие двигатели при включении в трехфазную сеть вырабатывают в разы большее усилие, чем их однофазные аналоги тех же габаритов и веса.
Соединяя проводники не нужно монтировать нулевой контакт, ведь вероятность пробоя очень мала, благодаря не занятой нейтрали.
Но такая схема сети имеет и свое слабое место, так как в линейной схеме монтажа крайне сложно найти место повреждения проводника в случае аварии или поломки, что может повысить риск возникновения пожара.
Таким образом, главным отличием между фазным и линейным типами являются разные схемы подключения проводов обмоток источника и потребителя электроэнергии.
Соотношение
Значение напряжения фазы равняется около 58% от мощности линейного аналога. То есть, при обычных эксплуатационных параметрах, линейное значение стабильно и превосходит фазное в 1,73 раза.
Оценка напряжения в сети трехфазного электрического тока, в основном производится по показателям его линейной составляющей. Для линий тока этого типа, подающегося с подстанций, оно, как правило, равняется 380 вольтам, и идентично фазному аналогу в 220 В.
В электросетях с четырьмя проводами, напряжение трехфазного тока маркируется обоими значениями – 380/220 В. Это обеспечивает возможность питания от такой сети устройств, как с однофазным потреблением электроэнергии 220 вольт, так и более мощных агрегатов, рассчитанных на ток 380 В.
Самой доступной и универсальной стала система трехфазного типа 380/220 В, имеющая нулевой провод, так называемое заземление. Электрические агрегаты, работающие на одной фазе 220 В., могут быть запитаны от линейного напряжения при подключении к любой паре фазных выводов.
В этом случае, применение нулевого вывода в качестве заземления, не является обязательным, хотя в случае повреждения изоляции проводов, его отсутствие серьезно повышает вероятность удара током.
Схема
Агрегаты трехфазного тока имеют две схемы подключения в сеть: первая – «звезда», вторая – «треугольником». В первом варианте, начальные контакты всех трех обмоток генератора замыкаются вместе по параллельной схеме, что, как и в случае с обычными щелочными батарейками не даст прироста мощности.
Вторая, последовательная схема подключения обмоток источника тока, где каждый начальный вывод подключается к конечному контакту предыдущей обмотки, дает трехкратный прирост напряжения за счет эффекта суммирования напряжений при последовательном подключении.
Кроме того, такие же схемы подключения имеют и нагрузку в виде электродвигателя, только устройство, подключенное в трехфазную сеть по схеме «звезда», при токе в 2,2 А будет выдавать мощность 2190Вт, а тот же агрегат, подключенный «треугольником», способен выдать в три раза большую мощность – 5570, за счет того, что благодаря последовательному подключению катушек и внутри двигателя, сила тока суммируется и доходит до 10 А.
Расчет линейного и фазного напряжения
Сети с линейным током нашли широкое применение за счет своих характеристик меньшей травмоопасности и легкости разведения такой электропроводки. Все электрические устройства в этом случае соединены только с одним фазным проводом, по которому и идет ток, и только он один и представляет опасность, а второй – это земля.
Рассчитать такую систему несложно, можно руководствоваться обычными формулами из школьного курса физики. Кроме того, для измерения этого параметра сети, достаточно использовать обычный мультиметр, в то время как для снятия показаний подключения фазного типа, придется задействовать целую систему оборудования.
Для подсчета напряжения линейного тока, применяют формулу Кирхгофа:
Уравнение которой гласит, что каждой из частей электрической цепи, сила тока равна нулю – k=1.
И закон Ома:
Используя их, можно без труда произвести расчеты каждой характеристики конкретного клейма или электросети.
В случае разделения системы на несколько линий, может появиться необходимость рассчитать напряжение между фазой и нулем:
Эти значения являются переменными, и меняются при разных вариантах подключения. Поэтому, линейные характеристики идентичны фазовым.
Однако, в некоторых случаях, требуется вычислить чему равно соотношение фазы и линейного проводника.
Для этого, применяют формулу:
Uл – линейное, Uф – фазовое. Формула справедлива, только если – IL = IF.
При добавлении в электросистему дополнительных отводящих элементов, необходимо и персонально для них рассчитывать фазовое напряжение. В этом случае, значение Uф заменяется на цифровые данные самостоятельного клейма.
При подключении промышленных систем к электросети, может появиться необходимость в расчете значения реактивной трехфазной мощности, которое вычисляется по следующей формуле:
Идентичная структура формулы активной мощности:
Примеры расчета:
Например, катушки трехфазного источника тока подключены по схеме «звезда», их электродвижущая сила 220В. Необходимо вычислить линейное напряжение в схеме.
Линейные напряжения в этом подключении будут одинаковы и определяются как:
Что такое линейное и фазное напряжение, каково их соотношение?
Переменное напряжение и его величины
Напряжение различают по роду тока: переменное и постоянное. Переменное может быть разной формы, основная суть в том, что с течением времени изменяется его знак и величина. У постоянного знак всегда одной полярности, а величина может быть стабилизированной или нестабилизированной.
В наших розетках напряжение переменное синусоидальной формы. Выделяют разные его значения, чаще всего используются понятия мгновенное, амплитудное и действующее. Как понятно из названия, мгновенное напряжение — это количество вольт в конкретный момент времени. Амплитудное – это размах синусоиды относительно нуля в вольтах, действующее — это интеграл от функции напряжения по времени, соотношение между ними такое: действующее в √2 или 1,41 раз меньше амплитудного. Вот как это выглядит на графике:
Напряжение в трехфазных цепях
В трёхфазных цепях выделяют два вида напряжения – линейное и фазное. Чтобы разобрать их отличия нужно взглянуть на векторную диаграмму и график. Ниже вы видите три вектора Ua, Ub, Uc – это вектора напряжений или фаз. Угол между ними 120°, иногда говорят 120 электрических градусов. Этот угол соответствует таковому в простейших электрических машинах между обмотками (полюсами).
Если отразить вектор Ub так, чтобы сохранился его угол наклона, но начало и конец поменялись местами, его знак изменится на противоположный. Тогда установим начала вектора –Ub в конец вектора Ua, расстояние между началом Ua и концом –Ub будет соответствовать вектору линейного напряжения Uл.
Простыми словами мы видим, что величина линейного напряжения больше чем фазного. Давайте разберем график напряжений в трёхфазной сети.
Красной вертикальной линией выделено линейное напряжение межу фазой 1 и фазой 2, а желтой линией выделено фазное амплитудное фазы 2.
КРАТКО: Линейное напряжение измеряется между фазой и фазой, а фазное между фазой и нулём.
С точки зрения расчетов, разница между напряжениями обуславливается решением этой формулы:
Линейное напряжение больше фазного в √3 или в 1,73 раза.
Нагрузка к трёхфазной сети может быть подключена по трём или четырем проводам. Четвертый проводник – нулевой (нейтральный). В зависимости от типа сеть может быть с изолированной нейтралью и глухозаземленной. Вообще при равномерной нагрузке три фазы можно подать и без нулевого провода. Он нужен для того, чтобы напряжения и токи распределялись равномерно и не было перекоса фаз, а также в качестве защитного. В глухозаземленных сетях, при пробое на корпус выбьет автоматический разъединитель или перегорит предохранитель в щите, так вы избежите опасности поражения электрическим током.
Отлично то, что в такой сети у нас одновременно есть два напряжения, которые можно использовать исходя из требований нагрузки.
Для примера: обратите внимание на электрический щиток в подъезде вашего дома. К вам приходит три фазы, а в квартиру заведена одна из них и ноль. Таким образом, вы получаете в розетках 220В (фазное), а между фазами в подъезде 380В (линейное).
Схемы подключения потребителей к трём фазам
Все двигателя, мощные нагреватели и прочая трёхфазная нагрузка может быть подключена по схеме звезды или треугольника. При этом большинство электродвигателей в борно имеют набор перемычек, которые в зависимости от их положения формируют звезду или треугольник из обмоток, но об этом позже. Что такое соединение звездой?
Соединение звездой предполагает соединение обмоток генератора таким образом, когда концы обмоток соединяются в одну точку, а к началам обмоток подключается нагрузка. Звездой же соединяются и обмотки двигателя и мощных нагревателей, только вместо обмоток в них выступают ТЭНы.
Давайте рассуждать на примере электродвигателя. При соединении его обмоток звездой линейное напряжение 380 В приложено к двум обмоткам, и так с каждой парой фаз.
На рисунке A, B, C – начала обмоток, а X, Y, Z – концы, соединенные в одну точку и эта точка заземлена. Здесь вы видите сеть с глухозаземленной нейтралью (провод N). На практике это выглядит так, как на фото борно электродвигателя:
Красным квадратом выделены концы обмоток, они соединены между собой перемычками, такое расположение перемычек (в линию) говорит о том, что они соединены по звезде. Синим цветом – питающие три фазы.
На этом фото промаркированы начала (W1, V1, U1) и концы (W2, V2, U2), обратите внимание на то, что они сдвинуты относительно начал, это нужно для удобного соединения в треугольник:
При соединении в треугольник к каждой обмотке приложено линейное напряжение, это приводит к тому, что протекают большие токи. Обмотка должна быть рассчитана на такое подключение.
У каждого из способов включения есть свои достоинства и недостатки, некоторые двигателя вообще в процессе пуска переключаются со звезды на треугольник.
Нюансы
В продолжение разговора о двигателях нельзя оставить без внимания вопрос выбора схемы включения. Дело в том, что обычно двигателя на своем шильдике содержат маркировку:
В первой строке вы видите условные обозначения треугольника и звезды, обратите внимание, треугольник идет первым. Далее 220/380В – это напряжение на треугольнике и звезде, значит, что при соединении треугольником нужно, чтобы линейное напряжение было равно 220В. Если в вашей сети напряжение равно 380 – значит нужно подключать двигатель в звезду. В то время как фазное всегда на 1,73 меньше, не зависимо от величины линейного.
Отличным примером является следующий двигатель:
Здесь номинальные напряжения уже 380/660, это значит, что его для линейного 380 нужно подключать треугольником, а звезда предназначена для питания от трёх фаз 660В.
Если в мощных нагрузках чаще оперируют с величинами межфазного напряжения, то в осветительных цепях в 99% % случаев используют фазное напряжение (между фазой и нулем). Исключением являются электрокраны и подобное, где может использоваться трансформатор с вторичными обмотками с линейным 220 В. Но это скорее тонкости и специфика конкретных устройств. Новичкам запомнить проще так: фазное напряжение – это то, которое в розетке между фазой и нулем, линейное – в линии.
Линейное и фазное напряжение: трехфазные цепи
Трехфазная цепь является частным случаем многофазных электрических систем, представляющих собой совокупность электрических цепей, в которых действуют ЭДС одинаковой частоты, сдвинутые по фазе относительно друг друга на определенный угол. Отметим, что обычно эти ЭДС, в первую очередь в силовой энергетике, синусоидальны. Однако, в современных электромеханических системах, где для управления исполнительными двигателями используются преобразователи частоты, система напряжений в общем случае является несинусоидальной. Каждую из частей многофазной системы, характеризующуюся одинаковым током, называют фазой, т.е. фаза – это участок цепи, относящийся к соответствующей обмотке генератора или трансформатора, линии и нагрузке.
Таким образом, понятие «фаза» имеет в электротехнике два различных значения:
- фаза как аргумент синусоидально изменяющейся величины;
- фаза как составная часть многофазной электрической системы.
Разработка многофазных систем была обусловлена исторически. Исследования в данной области были вызваны требованиями развивающегося производства, а успехам в развитии многофазных систем способствовали открытия в физике электрических и магнитных явлений.
Важнейшей предпосылкой разработки многофазных электрических систем явилось открытие явления вращающегося магнитного поля (Г.Феррарис и Н.Тесла, 1888 г.). Первые электрические двигатели были двухфазными, но они имели невысокие рабочие характеристики. Наиболее рациональной и перспективной оказалась трехфазная система, основные преимущества которой будут рассмотрены далее. Большой вклад в разработку трехфазных систем внес выдающийся русский ученый-электротехник М.О.Доливо-Добровольский, создавший трехфазные асинхронные двигатели, трансформаторы, предложивший трех- и четырехпроводные цепи, в связи с чем по праву считающийся основоположником трехфазных систем.
Источником трехфазного напряжения является трехфазный генератор, на статоре которого (см. рис. 1) размещена трехфазная обмотка. Фазы этой обмотки располагаются таким образом, чтобы их магнитные оси были сдвинуты в пространстве друг относительно друга на эл. рад. На рис. 1 каждая фаза статора условно показана в виде одного витка. Начала обмоток принято обозначать заглавными буквами А,В,С, а концы- соответственно прописными x,y,z. ЭДС в неподвижных обмотках статора индуцируются в результате пересечения их витков магнитным полем, создаваемым током обмотки возбуждения вращающегося ротора (на рис. 1 ротор условно изображен в виде постоянного магнита, что используется на практике при относительно небольших мощностях). При вращении ротора с равномерной скоростью в обмотках фаз статора индуцируются периодически изменяющиеся синусоидальные ЭДС одинаковой частоты и амплитуды, но отличающиеся вследствие пространственного сдвига друг от друга по фазе на рад. (см. рис. 2).
Трехфазные системы в настоящее время получили наибольшее распространение. На трехфазном токе работают все крупные электростанции и потребители, что связано с рядом преимуществ трехфазных цепей перед однофазными, важнейшими из которых являются:
– экономичность передачи электроэнергии на большие расстояния;
– самым надежным и экономичным, удовлетворяющим требованиям промышленного электропривода является асинхронный двигатель с короткозамкнутым ротором;
– возможность получения с помощью неподвижных обмоток вращающегося магнитного поля, на чем основана работа синхронного и асинхронного двигателей, а также ряда других электротехнических устройств;
– уравновешенность симметричных трехфазных систем.
Для рассмотрения важнейшего свойства уравновешенности трехфазной системы, которое будет доказано далее, введем понятие симметрии многофазной системы.
Система ЭДС (напряжений, токов и т.д.) называется симметричной, если она состоит из m одинаковых по модулю векторов ЭДС (напряжений, токов и т.д.), сдвинутых по фазе друг относительно друга на одинаковый угол . В частности векторная диаграмма для симметричной системы ЭДС, соответствующей трехфазной системе синусоид на рис. 2, представлена на рис. 3.
| Рис.3 | Рис.4 |
Из несимметричных систем наибольший практический интерес представляет двухфазная система с 90-градусным сдвигом фаз (см. рис. 4).
Все симметричные трех- и m-фазные (m>3) системы, а также двухфазная система являются уравновешенными. Это означает, что хотя в отдельных фазах мгновенная мощность пульсирует (см. рис. 5,а), изменяя за время одного периода не только величину, но в общем случае и знак, суммарная мгновенная мощность всех фаз остается величиной постоянной в течение всего периода синусоидальной ЭДС (см. рис. 5,б).
Уравновешенность имеет важнейшее практическое значение. Если бы суммарная мгновенная мощность пульсировала, то на валу между турбиной и генератором действовал бы пульсирующий момент. Такая переменная механическая нагрузка вредно отражалась бы на энергогенерирующей установке, сокращая срок ее службы. Эти же соображения относятся и к многофазным электродвигателям.
Если симметрия нарушается (двухфазная система Тесла в силу своей специфики в расчет не принимается), то нарушается и уравновешенность. Поэтому в энергетике строго следят за тем, чтобы нагрузка генератора оставалась симметричной.
Схемы соединения трехфазных систем
Трехфазный генератор (трансформатор) имеет три выходные обмотки, одинаковые по числу витков, но развивающие ЭДС, сдвинутые по фазе на 120°. Можно было бы использовать систему, в которой фазы обмотки генератора не были бы гальванически соединены друг с другом. Это так называемая несвязная система. В этом случае каждую фазу генератора необходимо соединять с приемником двумя проводами, т.е. будет иметь место шестипроводная линия, что неэкономично. В этой связи подобные системы не получили широкого применения на практике.
Для уменьшения количества проводов в линии фазы генератора гальванически связывают между собой. Различают два вида соединений: в звезду и в треугольник. В свою очередь при соединении в звезду система может быть трех- и четырехпроводной.
Соединение в звезду
На рис. 6 приведена трехфазная система при соединении фаз генератора и нагрузки в звезду. Здесь провода АА’, ВВ’ и СС’ – линейные провода.
Линейным называется провод, соединяющий начала фаз обмотки генератора и приемника. Точка, в которой концы фаз соединяются в общий узел, называется нейтральной (на рис. 6 N и N’ – соответственно нейтральные точки генератора и нагрузки).
Провод, соединяющий нейтральные точки генератора и приемника, называется нейтральным (на рис. 6 показан пунктиром). Трехфазная система при соединении в звезду без нейтрального провода называется трехпроводной, с нейтральным проводом – четырехпроводной.
Все величины, относящиеся к фазам, носят название фазных переменных, к линии – линейных. Как видно из схемы на рис. 6, при соединении в звезду линейные токи и равны соответствующим фазным токам. При наличии нейтрального провода ток в нейтральном проводе . Если система фазных токов симметрична, то . Следовательно, если бы симметрия токов была гарантирована, то нейтральный провод был бы не нужен. Как будет показано далее, нейтральный провод обеспечивает поддержание симметрии напряжений на нагрузке при несимметрии самой нагрузки.
Поскольку напряжение на источнике противоположно направлению его ЭДС, фазные напряжения генератора (см. рис. 6) действуют от точек А,В и С к нейтральной точке N; – фазные напряжения нагрузки.
Линейные напряжения действуют между линейными проводами. В соответствии со вторым законом Кирхгофа для линейных напряжений можно записать
| ; | (1) |
| ; | (2) |
| . | (3) |
Отметим, что всегда – как сумма напряжений по замкнутому контуру.
На рис. 7 представлена векторная диаграмма для симметричной системы напряжений. Как показывает ее анализ (лучи фазных напряжений образуют стороны равнобедренных треугольников с углами при основании, равными 300), в этом случае
| (4) |
Обычно при расчетах принимается . Тогда для случая прямого чередования фаз , (при обратном чередовании фаз фазовые сдвиги у и меняются местами). С учетом этого на основании соотношений (1) …(3) могут быть определены комплексы линейных напряжений. Однако при симметрии напряжений эти величины легко определяются непосредственно из векторной диаграммы на рис. 7. Направляя вещественную ось системы координат по вектору (его начальная фаза равна нулю), отсчитываем фазовые сдвиги линейных напряжений по отношению к этой оси, а их модули определяем в соответствии с (4). Так для линейных напряжений и получаем: ; .
Соединение в треугольник
В связи с тем, что значительная часть приемников, включаемых в трехфазные цепи, бывает несимметричной, очень важно на практике, например, в схемах с осветительными приборами, обеспечивать независимость режимов работы отдельных фаз. Кроме четырехпроводной, подобными свойствами обладают и трехпроводные цепи при соединении фаз приемника в треугольник. Но в треугольник также можно соединить и фазы генератора (см. рис. 8).
Для симметричной системы ЭДС имеем
.
Таким образом, при отсутствии нагрузки в фазах генератора в схеме на рис. 8 токи будут равны нулю. Однако, если поменять местами начало и конец любой из фаз, то и в треугольнике будет протекать ток короткого замыкания. Следовательно, для треугольника нужно строго соблюдать порядок соединения фаз: начало одной фазы соединяется с концом другой.
Схема соединения фаз генератора и приемника в треугольник представлена на рис. 9.
Очевидно, что при соединении в треугольник линейные напряжения равны соответствующим фазным. По первому закону Кирхгофа связь между линейными и фазными токами приемника определяется соотношениями
Аналогично можно выразить линейные токи через фазные токи генератора.
На рис. 10 представлена векторная диаграмма симметричной системы линейных и фазных токов. Ее анализ показывает, что при симметрии токов
| . | (5) |
В заключение отметим, что помимо рассмотренных соединений «звезда – звезда» и «треугольник – треугольник» на практике также применяются схемы «звезда – треугольник» и «треугольник – звезда».
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Контрольные вопросы и задачи
- Какой принцип действия у трехфазного генератора?
- В чем заключаются основные преимущества трехфазных систем?
- Какие системы обладают свойством уравновешенности, в чем оно выражается?
- Какие существуют схемы соединения в трехфазных цепях?
- Какие соотношения между фазными и линейными величинами имеют место при соединении в звезду и в треугольник?
- Что будет, если поменять местами начало и конец одной из фаз генератора при соединении в треугольник, и почему?
- Определите комплексы линейных напряжений, если при соединении фаз генератора в звезду начало и конец обмотки фазы С поменяли местами.
- На диаграмме на рис. 10 (трехфазная система токов симметрична) . Определить комплексы остальных фазных и линейных токов.
- Какие схемы соединения обеспечивают автономность работы фаз нагрузки?
Четырехпроводные схемы треугольника — Continental Control Systems, LLC
Четырехпроводная схема подключения по схеме «треугольник» (4WD) — это подключение по схеме «трехфазный треугольник» с центральным ответвлением на одной из обмоток трансформатора для создания нейтрали для однофазных нагрузок. Нагрузки двигателей обычно подключаются к фазам A, B и C, а однофазные нагрузки подключаются к фазе A или C и к нейтрали. Фаза B, «высокая» ветвь, не используется для однофазных нагрузок.
Этот тип обслуживания, который также известен как услуга «высокая нога», «дикая нога», «стингер-нога» или «дикая фаза», распространен на старых производственных предприятиях с в основном трехфазными двигателями и около 120 вольт однофазного освещения и розеток.
Загрузить: Four Wire Delta Service (AN-113) (PDF, 1 страница)
120/208/240 Вольт Сервис
| Совместимые модели WattNode |
|---|
| Любая дельта 240 вольт (3D) модель |
Это наиболее распространенная четырехпроводная трехфазная схема подключения по схеме «треугольник» и, по сути, представляет собой трехфазную трехпроводную схему подключения по схеме «треугольник» с напряжением 240 В, при этом одна из центральных обмоток трансформатора на 240 вольт отводится для обеспечения двух цепей 120 В переменного тока, которые на 180 градусов не совпадают по фазе друг с другом.Напряжение, измеренное от этой центральной отводной нейтрали до третьей «дикой» ветви, составляет 208 В пер.
Эта услуга почти всегда имеет нейтральное соединение, но в некоторых редких случаях нейтральный провод недоступен. Обычно он находится у служебного входа, но может не доходить до панели или нагрузки. Теоретически четырехпроводный треугольник без нейтрали — это просто трехфазный треугольник, но есть одно отличие. В нормальном трехфазном треугольнике заземление будет либо центральным напряжением, либо одной ветвью, но трехфазная дельта, полученная от четырехпроводного дельта-трансформатора, будет иметь заземление на полпути между двумя ветвями.Измерители WattNode модели Delta — лучший выбор, так как они будут работать с нейтральным подключением или без него.
240/415/480 Вольт Сервис
| Совместимые модели WattNode |
|---|
| Любая дельта 480 вольт (3D) модель |
Это встречается гораздо реже, но иногда мы получаем запросы на измерение этого типа услуги, которая по сути идентична услуге 120/208/240, но с удвоением всех напряжений.
Общие примечания
- Высоковольтная ветвь или фаза с более высоким напряжением, измеренным относительно нейтрали, традиционно называлась «фазой B». Изменение NEC 2008 года теперь позволяет обозначать верхнюю ветвь четырехпроводной трехфазной сети, связанной с дельтой, как фазу «C», а не фазу «B».
- Кодекс NEC требует, чтобы верхняя часть ноги была обозначена оранжевым цветом (ее часто называли дельтой красной ноги) или другими эффективными средствами, и обычно это фаза «B».Однако, чтобы приспособиться к конфигурациям счетчиков коммунальных услуг, разрешается использовать верхнюю опору в фазе «C», когда счетчики являются частью распределительного щита или щитовой панели. Для изменения кода в этом разделе требуется четкая, постоянная маркировка полей на распределительном щите или щите управления.
- На этикетке коробки CAT III на текущих производимых счетчиках WattNode указано « Ø-N 140 В ~ » (или « Ø-N 277 В ~ »), но напряжение между фазой и нейтралью на высокой ветви будет 208 В пер. (или 416 В переменного тока). Это нормально и не повредит глюкометру.
- Фазовые углы (относительно нейтрали) будут A = 0 градусов, B = 90 градусов, C = 180 градусов. Это отличается от обычной схемы 3Y-208 или 3D-208, где фазовые углы составляют 0, 120, 240 градусов.
- Для точных измерений межфазного (или межфазного) напряжения настройте параметр PhaseOffset следующим образом:
- Для моделей BACnet установите для объекта PhaseOffset значение 3 .
- Для прошивки Modbus версии 16 или более поздней установите регистр PhaseOffset (1619) на 90 .
- В версиях прошивки Modbus до версии 16 измерения межфазного напряжения неточны, но другие измерения будут работать нормально.
- Из-за необычных фазовых углов при измерении цепи 4WD с резистивной нагрузкой коэффициенты мощности будут равны 1,0, 0,87, 0,87. При нагрузке двигателя вы можете получить такие коэффициенты мощности, как 0.9, 0,5, 0,0 (или даже отрицательный на одной фазе). Следует ожидать очень несбалансированных показаний мощности (кВт) и изменения реактивной мощности от фазы к фазе. Но, если все подключено правильно, фазные токи должны почти совпадать.
- Средний измеренный коэффициент мощности может быть неточным для четырехпроводных схем, связанных треугольником.
См. Также
Трехфазная четырехпроводная система— обзор
Первый член суммы в скобках представляет показание ваттметра с i 1 в его токовой цепи и v 1 — v м через его цепь напряжения, т.е.е. подключен между клеммами 1 и M. Отсюда следует, что три ваттметра могут измерять мощность в трехфазной четырехпроводной системе, а два — в трехфазной трехпроводной системе. Некоторые из распространенных случаев перечислены ниже.
Трехфазный, четырехпроводной, несимметричная нагрузка -Подключения показаны на Рисунок 3.23 (a) . Ваттметры W 1 , W 2 и W 3 измеряют фазные мощности по отдельности. Суммарная мощность складывается из показаний:
Рисунок 3.23. Измерение трехфазной мощности
P = P1 + P2 + P3
Трехфазное, четырехпроводное, со сбалансированной нагрузкой — с подключениями, показанными на Рисунок 3.23 (a) , все счетчики читают одинаково. Два ваттметра можно не устанавливать, а показания оставшегося прибора умножать на 3.
Трехфазный, трехпроводной, несимметричная нагрузка — два ваттметра соединены своими токовыми цепями в любом пара линий, как в Рисунок 3.23 (б) . Полная мощность — это алгебраическая сумма показаний, независимо от формы сигнала. Двухэлементный ваттметр автоматически суммирует мощность; с отдельными инструментами, при определенных условиях, описанных ниже, можно будет читать наоборот.
Трехфазный, трехпроводной, со сбалансированной нагрузкой — с синусоидальным напряжением и током в условиях , рис. 3.23 (c) . Ваттметры W 1 и W 2 показывают мощность P 1 и P 2 , где
P1 = VabIacos (30∘ + ϕ) = V1I1cos (30∘ + ϕ) P2 = VcbIccos (30 ∘ + ϕ) = V1I1cos (30∘ − ϕ)
Полная активная мощность P = P 1 + P 2 , следовательно,
P = V1I1 [cos (30∘ + ϕ) + cos (30∘ − ϕ)] = √3V1I1cosϕ
, где cos ϕ — коэффициент мощности фазы .Алгебраическая разность равна P 1 — P 2 = V 1 I 1 sin ϕ, откуда реактивная мощность определяется как
Q = √3V1 √1sin ( P1-P2)
, а фазовый угол можно получить из ϕ = arctan ( Q / P ). При ϕ = 0 (единичный коэффициент мощности) оба ваттметра показывают одинаковые значения; для ϕ = 60 ° (коэффициент мощности 0,5 с запаздыванием) W 1 считывает ноль; а для более низких коэффициентов мощности запаздывания W 1 имеет тенденцию считываться в обратном направлении.
Границы | Трехфазное четырехпроводное совместное управление фотоэлектрическим инвертором и ESS для низковольтных распределительных сетей с высокой долей фотоэлектрических модулей на базе OPF
Введение
В последние годы, с быстрым развитием экономики, загрязнение окружающей среды и энергетический кризис становится все более заметным. Для достижения устойчивого развития энергетики активно продвигается производство фотоэлектрических и других возобновляемых источников энергии (Zehar and Sayah, 2008).Однако крупномасштабная бытовая интеграция фотоэлектрических элементов повлияет на узловое напряжение и сетевые потери трехфазной четырехпроводной структуры низковольтной распределительной сети. Несоответствие между бытовой фотоэлектрической генерацией и бытовой нагрузкой приводит к нарушению верхнего предела напряжения в течение дня и нижнего предела в вечернее время (Aziz and Ketjoy, 2017). Кроме того, трехфазная четырехпроводная структура низковольтной распределительной сети приведет к трехфазной несбалансированности при наличии трехфазных нагрузок и асимметричных параметров линии (Pansakul and Hongesombut, 2014).Поэтому важно провести исследования по использованию фотоэлектрических элементов для трехфазной четырехпроводной системы низковольтной распределительной сети.
В настоящее время существует большое количество литературы по использованию фотоэлектрических систем в распределительных сетях. Регулирование напряжения может выполняться путем регулировки положения РПН под нагрузкой (Liu et al., 2012). Однако в результате ограничения положения ответвления величина регулирования напряжения не является непрерывной. Также частое регулирование ответвлений приводит к сокращению срока службы трансформаторов.Другой метод — уменьшить активную мощность фотоэлектрических элементов (Tonkoski, 2009; Reinaldo et al., 2011), чтобы подавить возникновение перенапряжения, однако это снизит доход владельцев фотоэлектрических устройств. Кроме того, этот метод выполняет только регулировку напряжения и не улучшит использование фотоэлектрических элементов в распределительной сети. Возможность регулирования реактивной мощности фотоэлектрического инвертора (Qian et al., 2018) может быть использована для достижения фотоэлектрического использования. По сравнению с двумя предыдущими методами, этот метод имеет более плавный контролируемый объем и не потребует дополнительных инвестиций или потери доходов от генерации.Однако могут быть недостатки в виде недостаточной реактивной мощности, приводящие к неудовлетворительному регулированию напряжения. В настоящее время оборудование для хранения энергии также широко используется для регулирования напряжения после подключения низковольтной распределительной сети к фотоэлектрической. В частности, в большом количестве литературы изучается метод согласованного управления накопителем энергии и инвертором реактивной мощности (Zhang et al., 2020). Эта стратегия может эффективно подавить превышение предела напряжения, полностью использовать возможности оборудования за счет координации оборудования, значительно снизить затраты на регулирование напряжения и потери в сети.Хотя в трехфазной четырехпроводной системе на одну нейтральную линию больше, чем в трехфазной четырехпроводной системе, стратегия управления, принятая в трехфазной трехпроводной системе, по-прежнему применима к трехфазной четырехпроводной системе. Следовательно, если учесть инвестиционные затраты, для трехфазной трехпроводной низковольтной распределительной сети и трехфазной четырехпроводной низковольтной распределительной сети с одинаковой нагрузкой и управляющим оборудованием имеется только промежуток нейтральной линии. в их инвестиционных затратах.
Проблема OPF распределительной сети требует рассмотрения осуществимости модели и решения. С точки зрения модели, задача OPF состоит в том, чтобы найти оптимальное состояние регулируемой переменной энергосистемы, чтобы целевые функции, такие как потери в сети и эксплуатационные расходы распределительной сети, достигли оптимизации. Литература (Gill et al., 2014) основана на предпосылке обеспечения безопасной работы энергосистемы и направлена на максимизацию производства фотоэлектрической энергии и ее преимуществ для создания динамической модели оптимального потока мощности активной распределительной сети.Литература (Alsenani and Paudyal, 2018) направлена на минимизацию потерь в сети, предлагая модель OPF для устранения трехфазного дисбаланса в распределительной сети. Однако в приведенной выше литературе не учитывается, что низковольтная распределительная сеть на самом деле представляет собой трехфазную четырехпроводную систему. Нейтральный провод делает трехфазную трехпроводную систему и трехфазную четырехпроводную систему существенно разными по методам расчета и другим аспектам (Bozchalui and Sharma, 2014). Напряжение и ток нейтральной линии, а также напряжение и ток фазной линии должны соответствовать закону Кирхгофа, который нельзя получить напрямую с помощью методов, аналогичных симметричным компонентам в трехфазной трехпроводной системе.Трехфазная трехпроводная модель не может точно отразить трехфазный дисбаланс. Однако исследований по модели трехфазной четырехпроводной системы на ОБТК сравнительно мало.
Для решения OPF ученые установили модель OPF как модель линейного или нелинейного программирования и непосредственно решили ее на основе алгоритмов искусственного интеллекта, таких как генетический алгоритм (Martins and Carmenlt, 2011), алгоритм роя частиц (Niknam et al. ., 2012) и т. Д. Однако скорость решения невысока и может легко попасть в локальную оптимизацию вместо глобальной.Другие ученые использовали выпуклую модель релаксации выпуклости, которая сначала исключала фазовый угол напряжения и тока, а затем использовала конусную релаксацию второго порядка для выпуклости исходной модели (Bose et al., 2016; Tian et al., 2016; Ju et al., 2017; Zafar et al., 2020). Однако, поскольку решения OPF, такие как конусы второго порядка, должны устранять фазовый угол между напряжением и током, этот метод не может рассчитать напряжение и ток на нейтральной линии. Следовательно, его нельзя применять к трехфазной четырехпроводной системе.В настоящее время исследование направлено только на решение некоторых конкретных проблем, таких как минимизация потерь в сети, трехфазного дисбаланса и т. Д. Немного Практически не уделяется внимания реальной модели трехфазной четырехпроводной системы распределения низкого напряжения. сети. Для трехфазной четырехпроводной модели ОБТК не предложено никакого эффективного метода решения. Следовательно, необходимо предложить метод расчета для ОБТК трехфазной четырехпроводной распределительной сети.
Основные вклады в этот документ резюмируются следующим образом.
(1) Из-за отсутствия исследований трехфазной четырехпроводной модели OPF СИСТЕМЫ в существующих литературных исследованиях, в этой статье устанавливается модель OPF, основанная на оптимальном скоординированном управлении генерированием фотоэлектрической энергии и накоплением энергии для трехфазной четырехпроводной сети. -проводная низковольтная распределительная сеть, нацеленная на потерю сети, трехфазный дисбаланс и отклонение напряжения, и принимая в качестве ограничений напряжение нейтральной линии, фотоэлектрические элементы и накопление энергии.
(2) Поскольку обсуждается, что метод решения OPF в настоящем исследовании не применим к модели в этой статье, предлагается решение выпуклого процесса оптимальной модели потока мощности, основанное на использовании фотоэлектрических элементов в низковольтной распределительной сети.На основе установленной модели оптимального потока мощности трехфазной четырехпроводной низковольтной распределительной сети все вогнутые функции в модели преобразуются в выпуклые функции. После этого может быть эффективно решена трехфазная четырехпроводная модель OPF.
Остающийся документ имеет следующую структуру. В разделе 2 представлены математические формулировки топологии трехфазной четырехпроводной низковольтной распределительной сети и низковольтных компонентов, содержащих фотоэлектрические элементы и аккумуляторы энергии.Раздел 3 устанавливает модель координированного управления фотоэлектрическими элементами и накопителями энергии в трехфазной четырехпроводной системе низковольтной распределительной сети. В разделе 4 предлагается метод решения, основанный на трехфазном четырехпроводном оптимальном потоке мощности. Раздел 5 показывает эффективность предложенного метода оптимизации посредством моделирования. Раздел 6 завершает исследование.
Уравнение трехфазной четырехпроводной низковольтной распределительной сети с фотоэлектрическими и накопителями энергии Заголовки
Сетевые уравнения, содержащие фотоэлектрические и накопление энергии в трехфазной четырехпроводной распределительной сети низкого напряжения
Топология сети трехфазной четверки -Wire Низковольтная распределительная сеть
Низковольтная распределительная сеть (LVDN) в Китае имеет трехфазную четырехпроводную структуру.Модель распределительной сети между двумя шинами (m-1) и m показана на рисунке 1. Эта модель имеет только один опорный узел, который является нейтральным узлом в начале линии. Все остальные узлы принимают это за точку отсчета. Модель содержит две шины (m-1) и m. Каждая шина состоит из четырех узлов: (4i-3), (4i-2), (4i-1), (4i) и (4j-3), (4j-2), (4j-1), и (4j), представляющие три фазы a, b и c на сборных шинах (m-1) и m соответственно, и нейтральную линию n. Каждая фазовая линия имеет свой собственный импеданс, а связь между каждой фазовой линией выражается взаимным импедансом.Линии фаз a, b и c подключены к нейтральной линии через нагрузку, образуя замкнутый контур.
РИСУНОК 1 . Модель трехфазной четырехпроводной распределительной сети низкого напряжения.
Модель ответвления
В соответствии с топологией LVDN трехфазная четырехпроводная система между любыми двумя шинами (m-1) и m может быть представлена последовательной матрицей импеданса 4 × 4.
Zl, m = [ZaaZabZacZanZbaZbbZbcZbnZcaZcbZccZcnZnaZnbZncZnn] (1)где Z gg — это диагональный элемент матрицы последовательного импеданса, а также трехфазного импеданса, который представляет собой нейтральная линия n; Z gh — это недиагональный элемент матрицы последовательного импеданса (g ≠ h), который представляет собой взаимный импеданс между трехфазным a, b, c и нейтральной линией n.
Чтобы получить общую модель LVDN, все формулы расчета представлены в матрице. Следовательно, матрица проводимости Y узла LVDN с m шинами может быть выражена как:
Yl = [Zl, 1−1 + ∑k∈c (1) Zl, k − 1 ⋯ — (Zl, m − 1 + ∑ k∈c (m) Zl, k − 1) ⋮ ⋱ ⋮ — (Zl, m − 1 + ∑k∈c (m) Zl, k − 1) ⋯ Zl, m − 1 + ∑k∈c (m) Zl, k − 1] (2)где c (m) представляет собой набор шин, соединенных с шиной m; Zl, m − 1 — обратная матрица матрицы последовательного импеданса, подключенного между шинами (m-1) и m; ∑k∈c (m) Zl, k − 1 — это сумма обратных матриц всей матрицы последовательного импеданса, подключенной к шине m.
Подставляя уравнение 1 в уравнение 2, можно получить общую матрицу проводимости узла LVDN.
Y = [Yl11Yl12 ⋯ Yl12 ⋯ Yl1NYl21Yl22 ⋯ Yl2i ⋯ Yl2N ⋮⋮ ⋱ ⋮ ⋱ ⋮ Yli1Yli2 ⋯ Ylii ⋯ YliN ⋮⋮ ⋱ ⋮ ⋮ YlN1YlN2 ⋯ YlNN10 (36) — число N000 узлов в N1NN10 (36), где 907 YlN представляет собой число узлов 9 NNN10 (36). LVDN.Подключение нагрузки в низковольтной распределительной сети
Фотоэлектрическое накопление энергии в низковольтной распределительной сети очень распространено, эффективное использование экологически чистой энергии и контроль напряжения распределительной сети имеют очень очевидный эффект.
Как показано на рисунке 2, на примере фазы b. Фотоэлектрическая система, нагрузка и накопитель энергии подключены к однофазной сети распределительной сети. Фаза b и нейтраль n соединены в замкнутый контур.
РИСУНОК 2 . Иллюстрация подключения PV, НАГРУЗКИ и ESS на фазе b.
Фотоэлектрические системы, нагрузка и накопители энергии используют модель постоянной мощности для получения тока инжекции в узле i.
Ii (t) = (PPV, i (t) + PESS, i (t) −PLOAD, i (t)) — j (QPV, i (t) −QLOAD, i (t)) Uφ, i ∗ ( 4), где PPV, i (t), QPV, i (t) представляют собой фотоэлектрическую активную мощность и реактивную мощность узла i в момент времени t; PLOAD, i (t), QLOAD, i (t) представляют активную и реактивную мощность нагрузки в узле i в момент времени t; PESS, i (t) представляет активную мощность накопителя энергии в узле i в момент времени t.Если накопитель энергии не подключен, значение равно 0.
Накопитель Модель
Регулирование мощности заряда и разряда накопителя энергии является эффективным способом управления напряжением. Когда в течение дня вырабатывается большое количество фотоэлектрической энергии и она не может быть полностью поглощена электросетью, чрезмерная энергия может быть поглощена за счет накопления энергии. Накопитель энергии высвобождает активную мощность, чтобы компенсировать нехватку электроэнергии в сети вечером, когда фотоэлектрическая энергия не вырабатывает и потребность в энергии высока.Состояние заряда (SOC) накопителя энергии является важным показателем для измерения емкости заряда и разряда накопителя энергии. Он представляет собой отношение оставшейся емкости заряда и разряда системы накопления энергии к ее полной емкости. Выражается в процентах. Диапазон значений [0,1]. SOC на следующем временном шаге тесно связан с SOC на текущем временном шаге. SOC накопления энергии может быть выражено как:
SOCESS, i (t + Δt) = SOCESS, i (t) −Pcharge, i (t) ηchargeΔtEN + Pdischarge, i (t) ΔtηdischargeEN (5)где SOCESS, i ( t) представляет SOC накопителя энергии узла i в момент времени t; SOCESS, i (t + Δt) представляет SOC накопления энергии узла i на следующем временном шаге; Δ t — временной интервал; E N — емкость накопителя энергии; ηcharge, ηdischarge — эффективность зарядки и разрядка накопителя энергии; В момент времени t Pcharge, i (t), Pdischarge, i (t) представляет мощность зарядки накопителя и мощность разрядки узла i.
Фотоэлектрический инвертор Модель
Модель полностью использует реактивную мощность фотоэлектрических инверторов для регулирования напряжения. Фотогальваника поглощает реактивную мощность для снижения перенапряжения и генерирует реактивную мощность для повышения пониженного напряжения. Соотношение между регулируемой реактивной мощностью и инвертором составляет
QPV, φmax = ± SPV, φ2 − PPV, φ2, φ∈abc (6)где QPV, φmax — максимальная выходная реактивная мощность инвертора, установленного в фаза φ (узел i). S pv, φ — номинальная мощность фотоэлектрического инвертора, установленного в фазе φ , что в 1,1 раза превышает номинальную активную мощность. P pv, φ — активная фотоэлектрическая мощность, установленная в фазе φ .
Матрица трехфазного четырехпроводного алгоритма потока мощности для низковольтной распределительной сети
Согласно теории схем, напряжение и ток узла должны удовлетворять уравнению напряжения узла.В трехфазной четырехпроводной системе уравнение узлового напряжения LVDN может быть получено через матрицу узловой проводимости.
где [V (t)] представляет собой матрицу, содержащую напряжение каждого узла в момент времени t, ее размер равен N × 1; [Iin (t)] представляет собой матрицу, составленную из тока, подаваемого каждым узлом в момент времени t, и ее размер составляет N × 1. Каждый элемент Ii (t) матрицы [Iin (t)] может быть получен с помощью уравнения 4 .
Чтобы получить напряжение каждого узла, уравнение 7 может быть изменено
[V (t)] = [Y] -1 [Iin (t)] (8)Решив уравнение 8, напряжение каждого узел можно получить.
[V1 (t) V2 (t) ⋮ Vi (t) ⋮ VN (t)] = [Yl11Yl12 ⋯ Yl1i ⋯ Yl1NYl21Yl22 ⋯ Yl2i ⋯ Yl2N ⋮⋮ ⋱ ⋮ ⋱ ⋮ Yli1Yli2 ⋯ Ylii ⋯ YlN ⋱ ⋯ YlNi ⋯ YlNN] −1 [I1 (t) I2 (t) ⋮ Ii (t) ⋮ IN (t)] (9)Однако матрица проводимости узлов [Y] является сингулярной матрицей, которая не может быть обратной. Следовательно, необходимо улучшить матрицу проводимости узлов [Y].
Y ‘= [E0 ⋯ 0 ⋯ 0Yl51Yl52 ⋯ Yl5i ⋯ Yl5N ⋮⋮ ⋱ ⋮ ⋱ Yli1Yli2 ⋯ Ylii ⋯ YliN ⋮⋮ ⋱ ⋮ ⋱ ⋮ YlN1YlN2 ⋯ YlNi ⋯ YlNN10] ( — тождественная матрица с матрицей a . размер 4 × 4.Модель скоординированного управления фотоэлектрическими элементами и накопителями энергии в трехфазных четырехпроводных низковольтных распределительных сетях
Метод скоординированного управления фотоэлектрическими элементами и накопителями энергии для трехфазных четырехпроводных низковольтных распределительных сетей. Сеть распределения напряжения, предложенная в этой статье, относится к идее управления, предложенной в (Zhang et al., 2020), которая представляет собой двухэтапную стратегию распределенного управления инвертором и накопителем энергии. Он сначала регулирует реактивную мощность инвертора, а затем регулирует активную мощность накопителя энергии во время управления напряжением.
Цель Функция
Управление оптимизацией LVDN включает несколько целей оптимизации. В этой статье целью является минимизация потерь в сети, трехфазного дисбаланса и отклонения напряжения. Установлена трехфазная четырехпроводная система модели ОБТК.Переменными оптимизации являются фотоэлектрическая реактивная мощность и активная мощность накопителя энергии. Проблема с несколькими целями преобразуется в проблему с одной целью путем взвешивания. Общая целевая функция может быть выражена как
minF = ω1F / F1ref1 + ω2F2 / F2ref + ω3F3 / F3ref (11), где F — значение целевой функции; F 1 , F 2 , F 3 — значение целевой функции потерь в сети, трехфазного дисбаланса и отклонения напряжения; F 1 ref , F 2 ref и F 3 ref — эталонные значения каждой целевой функции, которые используются в качестве эталона для стандартизации каждой целевой функции. на единицу.В этой статье потери в сети, трехфазный дисбаланс и отклонение напряжения без контроля используются в качестве опорных значений. ω 1 , ω 2 и ω 3 — весовые значения каждой целевой функции и должны удовлетворять ω1 + ω2 + ω3 = 1 и ω1≥0, ω2≥0, ω3 ≥0.
(1) Потери в сети
Потери в сети — важный показатель для измерения экономичности LVDN. Целевая функция для расчета сетевых потерь LVDN:
F1 = ∑t = 1TPloss (t) ⋅Δt = ∑t = 1T [[Iline (t)] ∗ ⊗ [Iline (t)]] T⋅ [R ] ⋅Δt (12)где [Iline (t)] = [Iline, 1abc (t) Iline, 1n (t) ⋯ Iline, (m − 1) abc (t) Iline, (m − 1) abc (t )] T; [R] = [R1abcR1n R (m − 1) abcR (m − 1) n] T; [Iline (t)] представляет собой комплексную матрицу, содержащую амплитуду и фазовый угол тока ответвления в момент времени t, с размером l × 1, где l представляет количество ответвлений в распределительной сети; [Iline, mabc (t)] представляет токи трех фаз a, b и c на линии m-сегмента в момент времени t, с размером 3 × 1; [Iline, mn (t)] представляет ток нейтральной линии n на m-сегментной линии в момент времени t с размером l × 1; R — сопротивление ветви размером l × 1; Rmabc включает значение сопротивления трех фаз a, b и c на линии m-сегмента с размером 3 × 1; Rmn представляет собой значение сопротивления нейтральной линии n на линии m-сегмента с размером l × 1.Определяется новый символ операции ⊗, который представляет собой умножение соответствующих элементов двух матриц.
(2) Коэффициент трехфазной несимметрии
Коэффициент несимметрии напряжения (VUF) также является важным показателем в LVDN. Определение может быть отношением фундаментальной составляющей отрицательной последовательности к фундаментальной составляющей положительной последовательности.
УВУФ, m (t) = | V-, m (t) V +, m (t) | = | Va, m (t) + αVb, m (t) + α2Vc, sm (t) Va, m (t ) + α2Vb, m (t) + αVc, m (t) | (13)где Va, m (t), Vb, m (t), Vc, m (t) представляют собой напряжение каждой фазы на шине m ; V-, m (t) представляет собой напряжение обратной последовательности; V +, m (t) представляет собой напряжение прямой последовательности; α = 1∠120∘.
В качестве целевой функции возьмем минимизацию трехфазного дисбаланса каждой шины в распределительной сети:
F2 = ∑t = 1T∑i = 1lUVUF, m (t) (14), где l представляет количество ветвей в LVDN.
(3) Отклонение напряжения
Разница между фактическим напряжением каждой точки и номинальным напряжением системы называется отклонением напряжения. Целевая функция для расчета отклонения напряжения LVDN:
ΔUφ = (Uφ, m (t) −UNUN) 2 (15) F3 = ∑t = 1T∑m∑φ∈abcΔUφ (16)где ΔUφ представляет собой отклонение напряжения определенной фазы в определенном узле в определенное время; U N представляет стандартное напряжение системы.
При выборе целевого веса в основном учитывается важность различных показателей в модели оптимизации. Поскольку сетевые потери тесно связаны с эксплуатационными расходами распределительной сети, чем меньше значение, тем лучше результаты. Трехфазный дисбаланс соответствует требованиям GB / T 12,325–2008 «Несимметрия трехфазных напряжений качества электроэнергии». Допустимое значение неуравновешенности напряжений в общедоступной точке подключения энергосистемы при нормальной работе электросети составляет 2%, а за короткое время оно не должно превышать 4%.То есть VUF менее 2% может соответствовать требованиям. Следовательно, экономика (сетевые потери) является основной задачей оптимизационной модели в этой статье, и ее вес должен быть больше веса трехфазного дисбаланса. В этой статье сначала используются веса двух целевых функций 0,85 и 0,15. Влияние различных весов на эффект контроля будет более подробно проанализировано в разделе тематического исследования.
Ограничения
(1) Ограничения по току ветви
где Iij (t) представляет ток ветви ij, которая соединяет узел i и узел j; Iij, max представляет собой максимально допустимое значение тока ветви.В этой бумаге используется 100А.
(2) Ограничения по напряжению
Для амплитуды напряжения каждого узла в фазах a, b и c в соответствии с национальными стандартами должен быть максимальный и минимальный предел для обеспечения безопасной работы электросети.
Vi, min≤ | Vi (t) | ≤Vi, max (18)где | Vi (t) | представляет амплитуду напряжения узла i в момент времени t; Vi, min представляет собой минимально допустимое напряжение в узле i, Vi, max представляет собой максимально допустимое напряжение. Согласно GB / T 12,325–2008 «Допустимый диапазон напряжения качества электроэнергии», отклонение однофазного напряжения питания 220 В составляет –10% –7% от номинального напряжения.
(3) Ограничения напряжения нейтральной линии
| Vi, нейтраль (t) | ≤Vneutral, max, i∈n (19)где | vi, нейтраль (t) | представляет амплитуду напряжения узла i на нейтральной линии в момент времени t; Vneutral, max представляет собой максимально допустимое значение напряжения нейтральной линии. Согласно DL / T 620–1997 «Координация защиты от перенапряжения и изоляции для электрических установок переменного тока» скорость смещения напряжения нейтральной точки должна быть менее 15% от фазного напряжения.
(4) Ограничения мощности фотоэлектрических инверторов
Реактивная мощность фотоэлектрических инверторов не безгранична, а активная мощность и мощность фотоэлектрических инверторов должны соответствовать определенным ограничениям.
Pφ2 + Qφ2≤Sφ2, φ∈abc (20)где P φ указывает активную мощность фотоэлектрического инвертора, подключенного к фазе φ ; Q φ указывает реактивную мощность фотоэлектрического инвертора, подключенного к фазе φ ; S φ указывает мощность фотоэлектрического инвертора, подключенного к фазе φ .
(5) Ограничения накопления энергии
Пределы SOCESS в момент времени t:
SOCESS, min≤SOCESS, i (t) ≤SOCESS, max (21)где SOCESS, min, SOCESS, max представляют минимум и максимум допустимый SOC накопителя энергии. Эта статья занимает 20 и 80%.
Возьмем один день как цикл зарядки и разрядки накопителя энергии, начальное состояние каждого цикла должно быть одинаковым.
SOCESS, i (t0) = SOCESS, i (tn) (22)где SOCESS, i (t0) представляет начальный SOC дня, SOCESS, i (tn) представляет SOC в конце дня.
Кроме того, накопитель энергии должен соответствовать ограничениям по мощности зарядки и разрядки.
{Pcharge, i, minDischarge, i (t) ≤Pcharge, i (t) ≤Pcharge, i, maxDcharge, i (t) Pdischarge, i, minDdischarge, i (t) ≤Pdischarge, i (t) ≤Pdischarge, i, maxDdischarge, i (t) Dcharge, i (t) + Ddischarge, i (t) ≤1 (23), где Pcharge, i, min, Pcharge, i, max представляют минимальное и максимальное значения мощности заряда накопителя энергии ; Pdischarge, i, min, Pdischarge, i, max представляют минимальное и максимальное значения разрядной мощности накопителя энергии; Dcharge, i (t), Ddischarge, i (t) — двоичные переменные.
(6) Ограничения мощности на межкоммутаторной линии
После того, как большая часть фотоэлектрических элементов будет интегрирована, возникнет явление перетока мощности от LVDN к электросети верхнего уровня. Чтобы обеспечить нормальную работу каждого устройства, соединительная линия между зоной низковольтной станции и электросетью верхнего уровня должна соответствовать пределу мощности.
Pcon, min≤Pcon (t) ≤Pcon, max (24)где Pcon, min, Pcon, max представляют верхний и нижний предел связующей линии. Значение не должно быть больше номинала распределительного трансформатора.Pcon (t) представляет собой фактическую мощность соединительной линии в момент времени t.
Метод решения, основанный на модели оптимального потока мощности в трехфазной четырехпроводной системе
В этой статье используется комплексная форма для представления как величины, так и фазового угла переменных, а модель оптимизации содержит невыпуклые нелинейные ограничения. Следовательно, проблема OPF — это проблема невыпуклого программирования. Получить глобальное оптимальное решение сложно. Для решения задачи все переменные разбиты на действительную и мнимую части.Для уравнения 8 это можно упростить следующей формулой.
[В] = [Vre + jVre] = [Re (Y) + Im (Y)] — 1⋅ [Iin, re + jIin, im] (25)Следовательно, действительная и мнимая части напряжения каждого узла могут быть представленным:
[Vre] = [Re (Y)] — 1⋅ [Iin, re] — [Im (Y)] — 1⋅ [Iin, im] (26) [Vim] = [Im (Y)] −1⋅ [Iin, re] + [Re (Y)] — 1⋅ [Iin, im] (27)(1) Верхнее ограничение напряжения
Напряжение делится на действительную и мнимую части. Суть ограничения верхнего напряжения заключается в том, что длина модуля комплексного числа меньше указанного значения.
Vi, re2 (t) + Vi, im2 (t) ≤Vi, max2 (28)где Vi, re (t) представляет собой действительную часть напряжения узла i в момент времени t; Vi, re (t) представляет мнимую часть напряжения узла i в момент времени t; Vi, max представляет собой максимально допустимое значение напряжения узла i.
(2) Ограничение по нижнему напряжению
Ограничение по нижнему напряжению — это вогнутая функция, которую трудно решить, и трудно поддерживать оптимальность решения. Следовательно, это ограничение можно линеаризовать, чтобы обеспечить оптимизацию выпуклой функции.
−D1a [Vi, re (t)] — D2a [Vi, im (t)] ≤ − Vi, min, i∈a (29) −D1b [Vi, re (t)] — D2b [Vi, im ( t)] ≤ − Vi, min, i∈b (30) −D1c [Vi, re (t)] — D2c [Vi, im (t)] ≤ − Vi, min, i∈c (31), где D 1 a, D 2 b , D 1 a , D 2 b , D 1 D 2 b представляет коэффициенты ограничения нижнего напряжения фазы a, b и c, результаты метода решения равны 1.001, 0, -0,5005, -0,8668, -0,5005 и 0,8668 соответственно. Vi, min — минимально допустимое напряжение.
(3) Трехфазный дисбаланс
Хотя отрицательная и положительная составляющие тока являются выпуклыми функциями, их соотношение является вогнутой функцией. Следовательно, ограничение трехфазного дисбаланса должно быть выпуклым. В реальной распределительной сети текущее значение прямой последовательности тока ответвления намного больше, чем текущее значение обратной последовательности. Длина модуля могла быть примерно равна среднему току ветви.Следовательно, формула трехфазного дисбаланса может быть аппроксимирована следующим образом:
UVUF, m (t) = | V−, m (t) V +, m (t) | ≅ | Vφ (t) Va, m (t) + α2Vb , m (t) + αVc, m (t) | (32)где Vφ (t) обозначает номинальное напряжение фазы φ .
Следовательно, ограничение дисбаланса может быть представлено следующим образом:
VUFbus2 (t) ≤VUFbus, max2 (33)(4) Ограничение напряжения нейтральной линии
Напряжение нейтральной линии разделено на действительную и мнимую части.
Vi, re2 (t) + Vi, im2 (t) ≤Vneutral, max2, i∈N (34)где Vneutral, max представляет собой максимально допустимое значение напряжения нейтральной линии.
(5) Ограничения по току ветви
Значение тока ветви ограничено:
, где Iij (t) представляет ток ветви ij, соединяющей узел i и узел j в момент времени t; Iij, max представляет собой максимально допустимое значение тока ветви.
Используйте форму множественного числа при решении Iij.
Iij = YijVij = Yij (Vi − Vj) (36)Левая часть уравнения. 35 может быть:
| Iij | = | Yij || Vij | = (Gij2 + Bij2) ⋅ (Vi, re − Vj, re) 2+ (Vi, im − Vj, im) 2 (37)Удалите радикал и далее выпукло формулу расчета:
| Iij | 2 = | Yij | 2⋅ | Vij | 2 = (Gij2 + Bij2) ⋅ [(Vi, re − Vj, re) 2+ (Vi, im − Vj, im) 2] (38)Следовательно, ограничение по току ветви может быть:
Благодаря выпуклой обработке модели исходная невыпуклая нелинейная задача преобразуется в легко решаемую задачу выпуклого программирования.Исходная задача имеет глобальную оптимальность. Она решается с помощью метода ветвей и границ и метода секущей плоскости, включенного в зрелый пакет алгоритмов CPLEX. В этой статье платформа YALMIP используется для разработки программы координированного управления фотоэлектрическими накопителями на основе OPF в операционной среде MATLAB, которая вызывает профессиональный пакет алгоритмов CPLEX и напрямую вычисляет глобальное оптимальное решение исходной задачи оптимального управления.
Настройки моделирования
Трехфазная четырехпроводная распределительная сеть низкого напряжения с 21 шиной использовалась для исследований моделирования, см. Рисунок 3.Длина всех линий \ 50 м. Номинальное напряжение 380 В. Собственное сопротивление линии Zii = 0,650 + j0,412 Ом / км, взаимное сопротивление Zij = (0,01 × Zii) Ом / км. Каждая шина может быть подключена к однофазной или трехфазной фотоэлектрической системе, а трехфазная может регулироваться независимо. Номинальная мощность однофазной фотоэлектрической генерации составляет 5 кВт, а мощность инвертора в 1,1 раза превышает номинальную активную мощность. Накопитель энергии подключен к шине 4 и шине 13 через трехфазное соединение и может регулироваться независимо.Номинальная энергоемкость накопителя энергии — 20 кВтч. Эффективность зарядки и разрядки составляет 0,94. Верхний предел мощности накопления энергии каждой фазы составляет 4 кВт. Весовые коэффициенты равны ω1 = 0,7, ω2 = 0,2 и ω2 = 0,1.
РИСУНОК 3 . Распределительная сеть низкого напряжения с 21 автобусом.
Кривая мощности фотоэлектрической панели показана на Рисунке 4A. Это значение на единицу, при этом пиковое значение является базовым. Поскольку фактическое расстояние передачи электроэнергии в низковольтной распределительной сети невелико, такие условия, как температура и свет, не будут сильно отличаться.Таким образом, типичные дневные кривые фотоэлектрической мощности, подключенные к каждому узлу, аналогичны. Типичная суточная кривая нагрузки показана на рисунке 4B, которая также рассчитана на единицу стоимости. Значения на единицу типичных кривых нагрузки на каждой шине аналогичны. Для получения подробной информации о PV и базовых данных нагрузки каждого узла.
РИСУНОК 4 . Типичные дневные кривые мощности. (A) Кривая выходной мощности PV. (B) Кривая нагрузки.
Повышение уровня нарушения напряжения, потери сети и трехфазного дисбаланса
Эффективность метода управления в этой статье проверяется путем сравнения результатов расчета различных показателей распределительной сети с «без контроля» и «под контролем».
(1) Сравнение напряжений
Поскольку нагрузка на фазе b выше, чем на других двух фазах, а интеграция фотоэлектрических модулей на фазе b является максимальной, фаза b берется в качестве примера для сравнения напряжения с управлением и без него. См. Рисунок 5 с результатами моделирования. Синяя полоса показывает напряжение перед управлением. Когда выработка фотоэлектрической энергии высока в течение дня, нагрузки находятся в периоде низкого потребления, а напряжение превышает верхний предел. Это приведет к обратному потоку мощности и трехфазному дисбалансу.Вечером фотоэлектрические батареи не выходят из строя, и нагрузки находятся в периоде пикового потребления. Напряжение ниже нижнего предела. Несоответствие времени между фотоэлектрическими элементами и нагрузками приводит к более высокому напряжению днем и более низкому напряжению вечером. Красная полоса указывает на предложенную схему управления, и видно, что нарушение напряжения может быть эффективно подавлено. Когда дневное напряжение превышает верхний предел, фотоэлектрический инвертор поглощает реактивную мощность и подавляет нарушение напряжения.Когда реактивной мощности инвертора недостаточно, накопитель энергии заряжается, а напряжение поддерживается за счет скоординированного управления фотоэлектрическим инвертором и накопителем энергии. Напряжение регулируется в пределах 1,07 о.е. Это может не только компенсировать недостатки превышения запаса реактивной мощности инвертора, когда напряжение превышает предел, но также и недостаток, когда SOC достигает предела и не может далее заряжаться или разряжаться. Совместное управление этими двумя устройствами позволяет регулировать напряжение оптимальным образом.Вечером, когда электроснабжения недостаточно, энергия, накопленная в накопителе энергии в течение дня, полностью используется для поддержания напряжения в электросети выше 0,9 о.е.
(2) Сравнение трехфазного дисбаланса
РИСУНОК 5 . Метод контроля узлового напряжения. Узловое напряжение под контролем. (A) напряжение фазы a (B) напряжение фазы b (C) напряжение фазы c. Узловое напряжение под контролем. (A) напряжение фазы a (B) напряжение фазы b (C) напряжение фазы c.
Без управления, поскольку нагрузка подключена несимметрично, а фотоэлектрические элементы подключены через однофазное соединение, это приводит к серьезной трехфазной несимметрии. Дисбаланс может достигать 10,8%. С контролем, предложенным в этой статье, весь дисбаланс ограничен в пределах 2%. Максимальное значение составляет 0,59% в 12:00. Это связано с тем, что выработка фотоэлектрической энергии достаточна, а нагрузка мала, крупномасштабное однофазное фотоэлектрическое соединение приводит к максимальному трехфазному дисбалансу. Однако дисбаланс все равно меньше требуемых 2%.Таким образом, предложенный метод управления эффективно снижает трехфазный дисбаланс.
(3) Сравнение потерь в сети
Суммарные потери в распределительной сети без контроля составляют 83,21 кВтч. При достижении верхнего предела напряжения в течение дня или при нижнем пределе напряжения в ночное время потери в сети являются наибольшими в течение дня. Это связано с тем, что обратный поток мощности, который возникает, когда фотоэлектрическая мощность велика в течение дня, создает дополнительные сетевые потери в сети, а большая нагрузка увеличивает потери в сети вечером.Кроме того, трехфазный дисбаланс, вызванный асимметричным подключением фотоэлектрических элементов и нагрузок, заставляет нейтральную линию генерировать ток, что еще больше увеличивает потери в сети. Согласно схеме управления, общие потери в сети составляют 65,87 кВтч, и потери в сети велики, когда фотоэлектрическая мощность велика в течение дня. В то же время улучшается трехфазный дисбаланс, что снижает ток нейтрали до нуля и дополнительно снижает потери в сети. Таким образом, метод, предложенный в этой статье, эффективно снижает потери в сети.
(4) Изменения SOC фотоэлектрических модулей и аккумуляторов при предложенном управлении
Реактивная мощность фотоэлектрических модулей на шине 16 приведена на рисунке 7. Поскольку шина расположена в конце линии, наиболее вероятно возникновение нарушения напряжения. . С помощью предложенной схемы фотоэлектрическая реактивная мощность регулируется для улучшения превышения предела напряжения и трехфазного дисбаланса. Видно, что когда верхняя граница напряжения днем очевидна. Фотогальваника поглощает реактивную мощность и смягчает нарушение верхнего предела напряжения.
РИСУНОК 6 . Сравнение трехфазных дисбалансов. ВУФ без контроля. VUF под контролем.
РИСУНОК 7 . Реактивная мощность PV под контролем.
На рисунке 8 показана мощность зарядки и разрядки накопителя энергии на шине 13. Поскольку шина расположена в конце линии, это также точка, где наиболее вероятно возникновение нарушения напряжения. В дневное время избыточная энергия используется для зарядки накопителей энергии. Вечером, когда спрос на электроэнергию высок, накопитель энергии разряжается, чтобы удовлетворить спрос.
РИСУНОК 8 . Активная мощность СЭ под контролем.
На рисунке 9 показаны изменения SOC накопителя энергии на шине 13. Около 10:00 выработка фотоэлектрической энергии продолжает расти с увеличением интенсивности света. В это время нагрузка составляет минимальное значение в течение дня. Накопитель энергии начинает переходить в состояние зарядки, а SOC продолжает увеличиваться с 20%. Примерно в 15:00 накопитель энергии достигает максимального предела энергии на уровне 80%. Во время заката, вслед за уменьшением интенсивности света, мощность фотоэлектрического инвертора непрерывно уменьшается, в то время как нагрузка начинает увеличиваться до периода пикового потребления.Накопитель энергии начинает разряжаться для питания нагрузки. SOC начинает падать до достижения нижнего предела энергии на уровне 20%. Это не повлияет на действие накопителя энергии в следующем цикле.
РИСУНОК 9 . SOC СЭ под контролем.
Сравнение результатов различных методов управления
Целевой вес указывает на важность каждого показателя в целевой функции. Следовательно, эффективность управления связана со значением веса. Среди трех целевых функций модели наиболее важными являются потери в сети и коэффициент трехфазного дисбаланса.В этом разделе вес отклонения напряжения всегда поддерживается равным 0. Анализируется эффективность управления с различными весами сетевых потерь и коэффициентом трехфазного дисбаланса. На рисунке 9 показаны результаты контроля различных схем взвешивания.
Из результатов видно, что изменение отклонения напряжения в целевой функции очень мало влияет на результаты, почти не меняется, поэтому здесь можно пренебречь весом отклонения напряжения и влиянием потери в сети и влияние трехфазного дисбаланса на результаты могут быть проанализированы.Сделаны следующие выводы.
(1) Учитывается только индекс трехфазного дисбаланса. В настоящее время эффект контроля трехфазного дисбаланса распределительной сети является оптимальным, достигая минимального значения 0,52%. Однако потери в сети значительно ухудшаются, достигая максимального значения 78,31 кВтч.
(2) Когда вес потери сети составляет 0,05, а вес трехфазного дисбаланса равен 0,9, вес корректируется лишь незначительно. Индекс сетевых потерь резко меняется.Хотя потери в сети намного меньше, трехфазный дисбаланс по-прежнему составляет 0,52%.
(3) Вес потерь в сети еще больше увеличивается, а вес трехфазного дисбаланса еще меньше. Потери в сети немного уменьшены, но не очевидны, а трехфазный дисбаланс составляет 0,52%. Когда вес трехфазного дисбаланса уменьшается до 0,1, можно увидеть только незначительные изменения, но все еще в пределах национального стандарта (2%).
(4) Учитывайте только индекс сетевых потерь. Хотя потери в сети могут достигать минимального значения 45.77 кВтч, влияние управления на трехфазную несимметрию сети неочевидно. В это время трехфазный дисбаланс составляет 9,48%, что намного превышает указанные 2%.
Таким образом, исходя из предположения, что потери в сети и трехфазный дисбаланс находятся в пределах национального стандартного диапазона, разумное значение веса определяется на основе принципа, согласно которому трехфазный дисбаланс и потери в сети существенно не увеличиваются. Это может обеспечить безопасность работы энергосистемы, а также снизить ее эксплуатационные расходы.Следовательно, индекс трехфазного дисбаланса имеет меньший вес.
Сравнение моделирования трехфазной трехпроводной и трехфазной четырехпроводной системы
Чтобы проверить превосходство метода управления, предложенного в этой статье, трехфазная трехпроводная система с использованием конуса второго порядка Сравнивается и анализируется релаксационное решение и трехфазная четырехпроводная система на базе OPF, предложенная в данной статье. Поскольку модель оптимизации конуса второго порядка не может рассчитать трехфазный дисбаланс, результаты этого метода сравниваются с результатами модели конуса второго порядка, основанной на трехфазной трехпроводной системе.
Как видно из таблицы 2, по сравнению с трехфазной трехпроводной системой и трехфазной четырехпроводной системой общие потери в сети отличаются на 3,41 кВтч, а потери в трехфазной четырехпроводной нейтрали составляют 4,07 кВтч. При одинаковых условиях моделирования разница между полными потерями в двух типах распределительных сетей приблизительно равна потерям в нейтральной линии. Кроме того, потери каждой фазы у двух моделей совершенно разные. Например, потеря фазы трехфазной трехпроводной системы составляет 15.84 кВтч, а потеря фазы трехфазной четырехпроводной системы составляет 18,79 кВтч. В это время потери в сети и отклонение напряжения трехфазной трехпроводной системы имеют высокие погрешности. Следовательно, в трехфазной симметричной низковольтной распределительной сети нейтраль не имеет тока. Эти два типа распределительных сетей могут быть приблизительно эквивалентными. Для трехфазной несимметричной низковольтной распределительной сети расчет трехфазной трехпроводной системы приведет к ошибкам.
ТАБЛИЦА 1 .Результат при разных стратегиях.
ТАБЛИЦА 2 . Результат при другой строчной структуре.
Заключение
В данной статье были изучены проблемы подключения крупномасштабной бытовой фотоэлектрической системы к трехфазной четырехпроводной низковольтной распределительной сети, включая нарушение напряжения и трехфазную несимметрию. Предлагается низковольтный фотоэлектрический накопитель энергии на основе метода кооперативного управления трехфазной четырехпроводной сетью OPF.
(1) Для низковольтной распределительной сети с высокой долей фотоэлектрических элементов предложенный метод совместного управления фотоэлектрическим накопителем энергии может полностью улучшить технические показатели энергосистемы.Напряжение узла можно регулировать в диапазоне 0,9–1,07 о.е., а также эффективно снижать трехфазный дисбаланс и потери в сети.
(2) Предлагаемый трехфазный четырехпроводной алгоритм оптимального потока мощности преодолевает недостатки существующего метода, который не может точно рассчитать напряжение и ток нейтральной линии. Это обеспечивает правильность результатов расчета оптимизации сети в случае трехфазной неуравновешенности. Имеет хорошую адаптируемость к низковольтной распределительной сети.
(3) В целевой функции потери в сети, трехфазный дисбаланс и вес отклонения напряжения по-разному влияют на результаты контроля. Вес потерь в сети более чувствителен к целевой функции, чем трехфазный дисбаланс и отклонение напряжения. Эффект управления лучше, когда вес потери сети установлен в диапазоне 0,7–0,9.
Заявление о доступности данных
Исходные материалы, представленные в исследовании, включены в статью / дополнительные материалы, дальнейшие запросы можно направить соответствующему автору.
Вклад авторов
Работа является совместной работой авторов. JF разработала модель координированного управления, TL внесла свой вклад в введение, SG и YW внесли свой вклад в модели активной мощности REG с несколькими состояниями с учетом ошибок прогноза, KT и YD участвовали в тематическом исследовании.
Финансирование
Это исследование финансировалось Пекинской ключевой лабораторией энергосберегающих технологий распределительных трансформаторов (Китайский научно-исследовательский институт электроэнергетики), грант № 51201
Конфликт интересов
Авторы заявляют, что исследование проводилось в отсутствие каких-либо коммерческих или финансовых отношений, которые могли бы быть истолкованы как потенциальный конфликт интересов.
Приложение
ТАБЛИЦА A1 . Трехфазная четырехпроводная испытательная система с 21 шиной.
Источники
Алсенани Т. Р. и Паудьял С. (2018). «Распределенный подход для решения задач оптимального потока мощности в трехфазных несбалансированных распределительных сетях», на конференции по энергетике австралийских университетов (AUPEC) 2018 г., Окленд, Новая Зеландия, 29–30 ноября 2018 г. (IEEE), 1–6.
Google Scholar
Азиз, Т., и Кетджой, Н. (2017). Пределы проникновения фотоэлектрических модулей в сети низкого напряжения и колебания напряжения. IEEE Access 5 (99), 1. doi: 10.1109 / ACCESS.2017.2747086
CrossRef Полный текст | Google Scholar
Bose, A., Tian, Z., Wu, W., and Zhang, B. (2016). Смешанная целочисленная модель конусного программирования второго порядка для оптимизации VAR и реконфигурации сети в активных распределительных сетях. IET Gener. Трансм. Дистриб. 10 (8), 1938–1946.doi: 10.1049 / iet-gtd.2015.1228
CrossRef Полный текст | Google Scholar
Bozchalui, M., and Sharma, R. (2014). Оптимальная работа накопителей энергии в системах распределения с возобновляемыми энергоресурсами . 2014 г. Конференция по энергетическим системам университета Клемсона, Клемсон, Южная Каролина, 11–14 марта 2014 г. (IEEE).
CrossRef Полный текст | Google Scholar
Gill, S., Kockar, I., and Ault, G. (2014). Оптимальный динамический поток мощности для активных распределительных сетей. IEEE Trans.Power Syst. 29 (1), 121–131. doi: 10.1109 / TPWRS.2013.2279263
CrossRef Полный текст | Google Scholar
Ju, Y., Wu, W., Lin, Y., Ye, L., and Ge, F. (2017). Трехфазная модель оптимального потока нагрузки и алгоритм для активных распределительных сетей . 2017 Общее собрание IEEE Power and Energy Society, Чикагол, Иллинойс, 16–20 июля 2017 г. (IEEE), 1–5.
Google Scholar
Лю X., Айчхорн А., Лю Дж. И Ли Х. (2012). Скоординированное управление распределенной системой накопления энергии с трансформаторами РПН для снижения повышения напряжения при высоком проникновении фотоэлектрических элементов. IEEE Trans. Smart Grid 3 (2), 897–906. doi: 10.1109 / TSG.2011.2177501
CrossRef Полный текст | Google Scholar
Мартинс, В. Ф., и Карменлт, Л. Т. Б. (2011). Интегрированное планирование активной распределительной сети с учетом неопределенностей распределенной генерации и реакции на нагрузку. IEEE Trans. Power Syst. 26 (4), 2164–2172. doi: 10.1109 / TPWRS.2011.2122347
CrossRef Полный текст | Google Scholar
Niknam, T., Narimani, M. R., Aghaei, J., and Azizipanah-Abarghooee, R.(2012). Улучшенная оптимизация роя частиц для многоцелевого оптимального потока мощности с учетом стоимости, потерь, выбросов и индекса стабильности напряжения. IET Gener. Трансм. Дистриб. 6 (6), 515–527. doi: 10.1049 / iet-gtd.2011.0851
CrossRef Полный текст | Google Scholar
О’Нил, Р. П., Кастильо, А., и Каин, М. (2012). Формулировка IV и линейные приближения задачи оптимального потока мощности переменного тока . Вашингтон, округ Колумбия: Технический персонал Федеральной комиссии по регулированию энергетики.Бумага.
Google Scholar
Пансакул, К., и Хонгесомбут, К. (2014). Анализ дисбаланса напряжения из-за солнечных фотоэлектрических систем в низковольтных жилых распределительных сетях . 2014 Международный конгресс по электротехнике (iEECON), Чонбури, Таиланд, 19–21 марта 2014 г. (IEEE).
CrossRef Полный текст | Google Scholar
Qian, M., Qin, H., Zhao, D., Chen, N., Jiang, J., Wang, B., et al. (2018). Многоуровневая стратегия управления реактивной мощностью для фотоэлектрической электростанции на основе анализа чувствительности .2018 Китайская международная конференция по распределению электроэнергии (CICED), Тяньцзинь, Китай, 17–19 сентября 2018 г. (IEEE), 1838–1842 гг.
Google Scholar
Рейнальдо Т., Лопес Л. и Тарехм Х. М. Э.-Ф. (2011). Скоординированное ограничение активной мощности фотоэлектрических инверторов, подключенных к сети, для предотвращения перенапряжения. IEEE Trans. Поддерживать. Энергия 2 (2), 139–147. doi: 10.1109 / TSTE.2010.2098483
CrossRef Полный текст | Google Scholar
Tian, Z., Wu, W., Zhang, B., и Бозе, А. (2016). Смешанная целочисленная модель конусного программирования второго порядка для оптимизации VAR и реконфигурации сети в активных распределительных сетях. IET Gener. Трансм. Дистриб. 10 (8), 1938–1946. doi: 10.1049 / iet-gtd.2015.1228
CrossRef Полный текст | Google Scholar
Тонкоски, Л. (2009). Регулировка напряжения в радиальных распределительных фидерах с высоким проникновением фотоэлектрических элементов . 2009 Конференция IEEE Energy 2030, Атланта, Джорджия, 1–7 сентября 2009 г. (IEEE).
Google Scholar
Зафар Р., Равишанкар Дж., Флетчер Дж. Э. и Пота Х. Р. (2020). Оптимальная диспетчеризация аккумуляторной системы хранения энергии с использованием выпуклых релаксаций в несбалансированных распределительных сетях. IEEE Trans. Indust. Поставить в известность. 16 (1), 97–108. doi: 10.1109 / TII.2019.2912925
CrossRef Полный текст | Google Scholar
Zehar, K., and Sayah, S. (2008). Оптимальный поток энергии с ограничениями окружающей среды с использованием алгоритма быстрого последовательного линейного программирования: приложение к алжирской энергосистеме. Energy Convers. Manag. 49 (11), 3362–3366. doi: 10.1016 / j.enconman.2007.10.033
CrossRef Полный текст | Google Scholar
Zhang, B., Tang, W., Cai, Y., Wang, Z., Li, T., and Zhang, H. (2020). Стратегия распределенного управления бытовым фотоэлектрическим инвертором и накопителем энергии на основе консенсусного алгоритма. Авто. Избрать. Power Syst. 44 (02), 86–96. doi: 10.7500 / AEPS201
005
CrossRef Полный текст | Google Scholar
Типы систем распределения питания переменного тока
Как мы все знаем, электроэнергия почти исключительно генерируется, передается и распределяется в форме переменного тока.Распределительная система обычно начинается с подстанции, где мощность доставляется по сети передачи. В некоторых случаях система распределения может начинаться с самой генерирующей станции, например, когда потребители находятся рядом с генерирующей станцией. Для больших территорий или промышленных зон также можно использовать первичное и вторичное распределение.Типы систем распределения питания переменного тока
В зависимости от фаз и проводов распределительную систему переменного тока можно классифицировать как —- Однофазная 2-проводная система
- Однофазная, 3-проводная система
- Двухфазная, 3-проводная система
- Двухфазная, 4-проводная система
- Трехфазная, трехпроводная система
- Трехфазная, 4-проводная система
Однофазное, 2-проводное распределение
Эта система может использоваться на очень коротких расстояниях.На следующем рисунке показана однофазная двухпроводная система с заземленным — рис. (A) одним из двух проводов и рис. (б) средняя точка фазной обмотки заземлена.Однофазная, 3-проводная система
Эта система в принципе идентична 3-проводной системе распределения постоянного тока. Нейтральный провод отводится от вторичной обмотки трансформатора и заземляется. Эта система также называется двухфазной системой распределения электроэнергии . Он обычно используется в Северной Америке для бытового питания.Двухфазная, 3-проводная система
В этой системе нейтральный провод отводится от места соединения двух фазных обмоток, напряжения которых находятся в квадратуре друг с другом. Напряжение между нулевым проводом и любым из внешних фазных проводов составляет V. В то время как напряжение между внешними фазными проводами составляет √2V. По сравнению с двухфазной 4-проводной системой эта система страдает дисбалансом напряжений из-за несимметричного напряжения в нейтрали.Двухфазная, 4-проводная система
В этой системе 4 провода отводятся от двух фазных обмоток, напряжения которых находятся в квадратуре друг с другом.Середины обеих фазных обмоток соединены вместе. Если напряжение между двумя проводами одной фазы равно В, то напряжение между двумя проводами разной фазы будет 0,707 В.Трехфазная, 3-проводная система распределения
Трехфазные системы очень широко используются для распределения питания переменного тока . Три фазы могут быть соединены треугольником или звездой с заземлением нейтрали. Напряжение между двумя фазами или линиями для соединения треугольником равно V, где V — напряжение на фазной обмотке.При соединении звездой напряжение между двумя фазами составляет √3V.Трехфазная, 4-проводная система распределения
В этой системе используются фазные обмотки, соединенные звездой, а четвертый провод или нейтральный провод отводится от звезды. Если напряжение каждой обмотки равно V, то линейное напряжение (линейное напряжение) равно √3V, а линейное напряжение (фазное напряжение) равно V. Этот тип распределительной системы широко используется в Индия и многие другие страны. В этих странах стандартное фазное напряжение составляет 230 вольт, а линейное напряжение √3×230 = 400 вольт.Однофазные бытовые нагрузки, однофазные двигатели, работающие от 230 В и т. Д., Подключаются между любой одной фазой и нейтралью. Трехфазные нагрузки, такие как трехфазные асинхронные двигатели, подключены ко всем трем фазам и нейтрали.Классификация по схеме подключения
Распределительную систему можно классифицировать по схеме подключения или топологии следующим образом —- Радиальная система
- Кольцевая основная система
- Объединенная система
Трехфазное питание: объяснение треугольника и звезды
Электричество используется для питания множества устройств, которые предназначены для удобства и необходимости людей и процессов по всему миру. Трехфазное питание играет ключевую роль в проектировании электрических систем, а трехфазные фильтры электромагнитных помех являются важной частью электрических устройств на различных рынках, в первую очередь в тяжелых промышленных приложениях. Большинству устройств в промышленных приложениях требуется большая мощность для обеспечения достаточного количества электроэнергии для поддержки больших двигателей, систем обогрева, инверторов, выпрямителей, источника питания и индукционных цепей.Из-за этого высокомощное оборудование обычно проектируется для трехфазного или многофазного переменного тока, в котором общая потребляемая мощность делится между многими фазами, оптимизируя систему энергоснабжения (генерацию и распределение) и конструкцию оборудования.
В трехфазной системе есть три проводника, по которым протекает переменный ток. Они называются фазами и обычно обозначаются как A, B и C. Каждая фаза настроена на одну и ту же частоту и амплитуду напряжения, но сдвинута по фазе на 120 °, обеспечивая постоянную передачу мощности во время электрических циклов.
Конфигурации с трехфазным питанием особенно важны, поскольку они могут поддерживать в три раза больше мощности, используя всего в 1 ½ — 2 раза больше проводов, чем конфигурация с однофазным питанием. Это может помочь снизить стоимость и количество материалов, необходимых для проектирования системы. Это также может упростить конструкцию двигателя, исключив необходимость в пусковых конденсаторах.
Однако преобразование большой мощности (инвертирование, выпрямление) генерирует шум с чрезмерно высокими частотами (EMI), который обычно представляет собой высшие гармоники различных частот переключения.
По этой причине 3-фазные фильтры электромагнитных помех становятся особенно важными в трехфазных приложениях, поскольку они уменьшают количество электромагнитных помех, предотвращают нарушения в работе оборудования и помогают компаниям соблюдать правила электромагнитной совместимости.
Различия между Delta и WYE
Трехфазные системы могут быть сконфигурированы двумя различными способами для поддержания равных нагрузок; они известны как конфигурации Delta и WYE. Названия «Дельта» и «WYE» представляют собой специфические индикаторы форм, на которые напоминают провода после соединения друг с другом.«Дельта» происходит от греческого символа «Δ», а «WYE» напоминает букву «Y» и также известна как «звездная» цепь. Обе конфигурации, Delta и WYE, обладают гибкостью для подачи питания по трем проводам, но основные различия между ними основаны на количестве проводов, доступных в каждой конфигурации, и потоке тока. Конфигурация WYE приобрела популярность в последние годы, поскольку она имеет нейтральный провод, который позволяет подключать как фазу к нейтрали (однофазное), так и линейное (2/3 фазы).
Что такое фильтры трехфазной сети?
Трехфазные фильтры электромагнитных помехразработаны в соответствии со строгими требованиями норм электромагнитной совместимости для промышленных приложений. Правила определяют максимально допустимые уровни шума (в дБ), допустимые на линиях электропередач. Общие требования к конструкции 3-фазного фильтра электромагнитных помех включают входные токи, линейное напряжение, ограничение размера и требуемые вносимые потери. В дополнение к этому, конфигурация 3-фазного фильтра электромагнитных помех играет важную роль в конструкции.
Дельта-трехфазный фильтр электромагнитных помех
3-фазные фильтры электромагнитных помехDelta предназначены для уменьшения электромагнитных помех в устройствах, подключенных к трехфазному питанию, подключенному по схеме «треугольник». Конфигурация Delta состоит из четырех проводов; три токоведущих и один заземляющий провод. Фазовые нагрузки (например, обмотки двигателя) соединены друг с другом в форме треугольника, где соединение выполняется от одного конца обмотки к начальному концу другого, образуя замкнутую цепь.
В этой конфигурации нет нейтрального провода, но он может питаться от трехфазной сети WYE, если нейтральная линия не подключена / заземлена.Дельта-система используется для передачи энергии из-за более низкой стоимости из-за отсутствия нейтрального кабеля. Он также используется в приложениях, требующих высокого пускового момента.
Из-за отсутствия нейтрального провода конденсаторы, используемые в трехфазных фильтрах электромагнитных помех Delta, должны быть рассчитаны на линейное (междуфазное) напряжение, что может увеличить размер, вес и стоимость. Однако отсутствие нейтрального провода позволяет получить более высокие номинальные токи, чем WYE, и лучшую производительность при том же заданном кубическом объеме.
Проектирование и трехфазный дельта-фильтр электромагнитных помех
- Определите максимальную мощность, требуемую нагрузкой.
- Разделите максимальную мощность, требуемую нагрузкой, на 3, чтобы получить мощность на каждую фазу.
- Разделите ответ на линейное напряжение.
- Умножьте предыдущий ответ на квадратный корень из 3.
Преимущества дельта-конфигурации
- Дельта-конфигурации обычно могут быть разработаны для работы с более высоким током и более эффективны.
- Защита для дельта-конфигураций может быть простой. Конфигурации
- Delta обычно настраиваются для тяжелых условий эксплуатации и предпочтительны для выработки и передачи электроэнергии.
WYE 3-фазный фильтр для защиты от электромагнитных помех
Фильтры EMIWYE предназначены для фильтрации типичных устройств преобразования мощности в режиме переключения и других приложений, требующих нейтрального подключения. Эта конфигурация состоит из пяти проводов; три провода под напряжением, нейтраль и земля.В конфигурации WYE фазные нагрузки подключаются в единственной (нейтральной) точке, к которой подключается нейтральный провод.
Когда нагрузки WYE-конфигурации полностью сбалансированы, через нейтральный провод ток не течет. Когда нагрузки неуравновешены, через нейтральный провод проходит ток. Эта конфигурация позволяет использовать в фильтре конденсаторы более низкого напряжения (120 В переменного тока в системе 208 В переменного тока и 277 В переменного тока в системе 480 В переменного тока), что может привести к экономии затрат, веса и объема.
Во многих случаях нейтральный провод можно оставить плавающим.Однако, как упоминалось ранее, конфигурация WYE обеспечивает гибкость для подключения нагрузок в цепи между фазой и нейтралью или между фазами. В отличие от Delta, эта конфигурация может использоваться как четырехпроводная схема или пятипроводная схема. Конфигурации WYE обычно используются в сетях распределения электроэнергии. Это в первую очередь требуется в приложениях, требующих меньшего пускового тока и перемещаемых на большие расстояния.
Проектирование и трехфазный фильтр электромагнитных помех WYE
- Определите максимальную мощность, требуемую нагрузкой.
- Разделите максимальную мощность, требуемую нагрузкой, на 3, чтобы получить мощность на каждую фазу.
- Разделите ответ на напряжение между фазой и нейтралью / землей.
Преимущества конфигураций WYE
- Предпочтительно для распределения электроэнергии, поскольку он может поддерживать однофазные (фаза-нейтраль), 2-фазные (междуфазные) и трехфазные нагрузки.
- Точка звезды обычно заземлена, что отлично подходит для несимметричных нагрузок.
- Для такой же поддержки напряжения требуется меньшая изоляция.
Стоимость трехфазных фильтров линии питания Delta по сравнению с WYE
Конфигурация трехфазного дельта-фильтра электромагнитных помех может быть технически более рентабельной, чем конфигурации WYE, поскольку для нее требуется только трехжильный кабель вместо четырех, что снижает стоимость материалов для изготовления блоков. Однако некоторые из этих рентабельности могут быть компенсированы необходимостью в компонентах, рассчитанных на высокое напряжение.
Конфигурации трехфазного фильтра электромагнитных помех Astrodyne TDI с дельта- и WYE-конфигурациями
Astrodyne TDI предлагает 3-фазные фильтры электромагнитных помех в конфигурациях Delta и WYE, чтобы помочь уменьшить электромагнитные помехи в различных приложениях и обеспечить соответствие международным стандартам излучения.Наши трехфазные фильтры электромагнитных помех находятся в диапазоне от 480 В / 520 В до 600 В переменного тока с номинальным током до 2500 А. Сетевые фильтры предлагаются в одно-, двух- и многоступенчатом исполнении, с более высокими значениями тока и напряжения, доступными по запросу.
Благодаря нашему обширному ассортименту фильтров и сильным конструктивным возможностям наша команда инженеров может гарантировать, что найдет наиболее эффективное решение для трехфазного фильтра электромагнитных помех, соответствующее любой спецификации и самым сложным приложениям.
Просмотрите нашу подборку трехфазных фильтров электромагнитных помех или свяжитесь с нашей командой, чтобы узнать больше о продукте, который поможет удовлетворить ваши требования.
Трехфазная несимметричная нагрузка | Четырехпроводная несимметричная нагрузка с соединением звездой
Трехфазная несимметричная нагрузка:Трехфазные нагрузки с одинаковым импедансом и коэффициентом мощности в каждой фазе называются сбалансированными нагрузками. Проблемы со сбалансированными нагрузками можно решить, рассматривая только одну фазу; условия на двух других фазах аналогичны. Однако мы можем столкнуться с ситуацией, когда нагрузки неуравновешены, т.е. каждая фаза нагрузки имеет разный импеданс и / или коэффициент мощности.В этом случае ток и мощность в каждой фазе будут разными. На практике мы можем встретить следующую трехфазную несимметричную нагрузку:
- Четырехпроводная несимметричная нагрузка с подключением звездой
- Несимметричная Δ подключенная нагрузка
- Несимметричная 3-проводная нагрузка, подключенная по схеме Y
Широко используется 3-фазная 4-проводная система, которая подключается между любой линией и нулевым проводом, а 3-фазная нагрузка подключается к трем линиям.Трехфазная 4-проводная система неизменно несет несимметричные нагрузки. В этой главе мы обсудим только этот тип трехфазной несимметричной нагрузки.
Несбалансированные нагрузки с четырехпроводным соединением звездой:Мы можем получить этот тип нагрузки двумя способами. Во-первых, мы можем подключить 3-фазную 4-проводную несимметричную нагрузку к 3-фазному 4-проводному источнику питания, как показано на рис. 14.10. Обратите внимание, что точка звезды N источника питания соединена с точкой звезды N ‘нагрузки. Во-вторых, мы можем подключать однофазные нагрузки между любой линией и нулевым проводом, как показано на рис.14.11. Это также приведет к 3-фазной, 4-проводной несимметричной нагрузке, потому что редко возможно, чтобы однофазные нагрузки на всех трех фазах имели одинаковую величину и коэффициент мощности. Поскольку нагрузка неуравновешена, линейные токи будут разными по величине и смещены друг от друга на разные углы. Ток в нейтральном проводе будет векторной суммой трех линейных токов, т.е.
Ток в нейтральном проводе,
Следует внимательно отметить следующие моменты
1.Поскольку нейтральный провод имеет незначительное сопротивление, нейтраль питания N и нейтраль нагрузки N ’будут иметь одинаковый потенциал. Это означает, что напряжение на каждом импедансе равно фазному напряжению источника питания. Однако ток в каждой фазе (или линии) будет отличаться из-за неравных сопротивлений.
2. Величина тока, протекающего в нейтральном проводе, будет зависеть от величин линейных токов и их векторных соотношений. В большинстве схем, встречающихся на практике, ток нейтрали равен или меньше одного из линейных токов.Исключение составляют цепи с серьезным дисбалансом.
Common Electrical Services — PVeducation.com
По мере того, как вы узнаете о проектировании и установке солнечной системы, вы также должны узнать об электрических услугах. Вот краткое изложение некоторых из распространенных электрических служб, имеющихся в Соединенных Штатах. Думайте об услугах электроснабжения либо как об основных услугах, предоставляемых коммунальным предприятием, либо как об услугах, созданных с помощью трансформатора, расположенного внутри коммерческого объекта.
Однофазный трехпроводной
Это наиболее распространенная электрическая услуга в США, поскольку она используется в типичном жилом доме. Линия 1 и Линия 2 считаются горячими проводами в сервисе. Нейтраль соединена с землей. Напряжение между линией 1 и линией 2 составляет 240 В, и оно используется для больших нагрузок в доме, таких как электрический водонагреватель или кондиционер. Если вы посмотрите на электрическую панель своего дома, это будут более крупные двухполюсные выключатели. Напряжение от линии 1 или линии 2 до нейтрали составляет 120 В и используется для небольших нагрузок, таких как освещение и розетки.
Трехфазный четырехпроводной 208Y120V Звезда
Эта электрическая служба — самая распространенная электрическая служба в США для коммерческих объектов. Трехфазная сеть на 208 В используется для питания больших нагрузок, а для розеток доступно стандартное напряжение 120 В. Название этой услуги немного избыточно, так как эту услугу часто называют трехфазной 208Y120. Уай произносится как «Y» и означает, что в службе присутствует нейтральный.
Трехфазный четырехпроводной 480Y277V Звезда
Эта электрическая служба используется в крупных коммерческих и промышленных объектах.Трехфазное напряжение 480 В используется для питания больших нагрузок, например двигателей. 277V часто используется для цепей освещения и небольших нагрузок. Когда это основное обслуживание объекта, вы, как правило, найдете трансформатор на 480 В Delta \ 208Y120V, который питает вспомогательную панель, обеспечивая стандартные 120 В для розеток и небольших нагрузок.
Трехфазный трехпроводной треугольник
Внутри коммерческих и промышленных объектов моторные нагрузки обычно работают по схеме треугольника.Как видно из вышеизложенного, в дельта-сервисе нет нейтралов. Я использовал 480 В в качестве напряжения выше, но это может быть любое напряжение, 240 В, 400 В, 480 и 600 В — обычные напряжения трансформатора.
Трехфазный, четырехпроводной, треугольник с высокой ветвью
К счастью, эта услуга менее распространена, чем все остальные, представленные выше. Эта услуга распространена в старых объектах, которые имеют только небольшие трехфазные нагрузки. Это обходится коммунальному предприятию дешевле, потому что на опоре электросети требуется только 2 трансформатора.
Если вы столкнетесь с подобным сервисом, вы должны быть очень осторожны с дизайном вашей солнечной системы. Инверторы, подключенные к солнечной сети, нередко требуют подключения нейтрали на их выходе. В этом случае инвертор будет проверять напряжения не только между фазой, но и между фазой и нейтралью. Согласно UL разрешены жесткие допуски по напряжению, поэтому высокая ножка предотвратит запуск инвертора. Некоторые трехфазные инверторы имеют конструкцию, не требующую подключения нейтрали, и их можно использовать.Другое решение для небольших солнечных систем — использовать однофазный инвертор, подключенный к фазе A и фазе C, это позволяет избежать высокого напряжения и до тех пор, пока он не заработает. Если система больше, лучше всего использовать 3-фазный инвертор, обычно эти инверторы начинаются с мощности 15 кВт, поэтому, если вы можете найти тот, который будет работать с трехфазным треугольником 240 В, это может сработать. Я намеренно говорю, что может, потому что вам нужно проверить с помощью утилиты. Если вы можете разместить трансформаторы на опоре электросети, вы увидите, что один из них меньше другого и в зависимости от номинальной мощности усилителя при условии, что это может быть ограничивающим фактором для максимального размера солнечной системы.В некоторых случаях коммунальное предприятие может принудительно установить третий полюсный переходник, чтобы превратить его в более стандартный трехфазный тип обслуживания. Если это так, то обычно это связано с тем, что коммунальное предприятие заботится о балансировании выходной мощности солнечной системы в своей сети.
При выполнении оценки места, прежде чем вы войдете в собственность, попытайтесь найти электрическую службу и найти трансформаторы на столбах. Если вы видите только два, это значит, что у них высокая ножка. Также посчитайте электрические провода над головой, их три наверху столба? В некоторых сельских районах коммунальное предприятие может протянуть только один или два провода на вершине столба.Если есть один, обслуживание, скорее всего, будет однофазным, а если два, скорее всего, это высокий этап. Еще один индикатор — панель автоматического выключателя, поскольку на ней должно быть указано, что внутри высокая ножка. Если нет маркировки, но вы видите, что однофазные выключатели пропускаются, и есть много пропущенных неиспользуемых мест, есть большая вероятность, что это высокая ветка.
.



