МЦКО
В Москве растет число выпускников, набравших больше 81 балла на экзамене по физике. В прошлом году они составляли 23% от всех участников. Как стать высокобалльником, на какие задания обратить внимание при подготовке и как избежать ошибок? На эти и другие вопросы отвечают председатель предметной комиссии ЕГЭ по физике города Москвы Татьяна Мельникова и ответственный секретарь предметной комиссии Лариса Капустина.
Много ли выпускников сдают физику в качестве предмета по выбору?
В Москве процент выпускников, которые сдают физику в качестве предмета по выбору, год от года остается примерно на одном и том же уровне — около 18% (это от 10,5 до 11,5 тысячи человек). В основном ее выбирают мальчики, они составляют около 80% сдающих. А в целом по стране физике отдают предпочтение примерно 23–25% выпускников.
Чем ЕГЭ по физике будет отличаться от экзамена прошлого года?
В этом году изменения в экзамене небольшие. Во-первых, в вопросе 24 по астрономии не будет указываться, сколько именно правильных утверждений из пяти представленных надо выбрать.
Во-вторых, появилась ещё одна задача с развёрнутым ответом по механике. Она, в отличие от задачи по механике в задании 29, повышенного, а не высокого уровня сложности, и оценивается максимум в два балла. Остальные задания с развёрнутым ответом по-прежнему оцениваются максимум в три балла.
Как эффективнее всего готовиться к экзамену?
Мы рекомендуем обратить внимание на задания из открытого банка ЕГЭ, представленные на сайте ФИПИ. Также при подготовке обязательно обратитесь к кодификатору ЕГЭ по физике. В нем приведены не только все элементы содержания, которые проверяются в экзаменационной работе, но и все формулы, которые понадобятся при выполнении задач.
Помните, что для всех заданий первой части ответом будет целое число или конечная десятичная дробь. Ответ записывайте в бланк ответов № 1 в тех единицах измерения, которые указаны в условии задачи.
При решении не забывайте пользоваться справочными материалами, указанными в начале контрольных измерительных материалов.
В задачах № 26 и № 27 иногда возникает необходимость в округлении результата. В этом случае в тексте задания указывается необходимая точность (например, «ответ округлите до десятых»).
В первой части есть задания повышенного уровня сложности на множественный выбор (задания № 5 по механике, № 11 по молекулярной физике и термодинамике и № 16 по электродинамике). В них из пяти утверждений, описывающий физически процесс или опыт, необходимо выбрать два верных. Не спешите с выбором, внимательно проанализируйте каждое из утверждений, для проверки некоторых из них воспользуйтесь формулами. Одно из утверждений обычно найти несложно, оно лежит на поверхности и описывает простые свойства физического процесса. Поиск второго требует более детального анализа и осмысления, а иногда и некоторых расчетов.
Мы рекомендуем проверять свои знания в онлайн-сервисе «Мои достижения» Московского центра качества образования. Задачи с развернутым ответом проверяют эксперты, которые могут провести видеоконсультацию и объяснить, какие ошибки были допущены.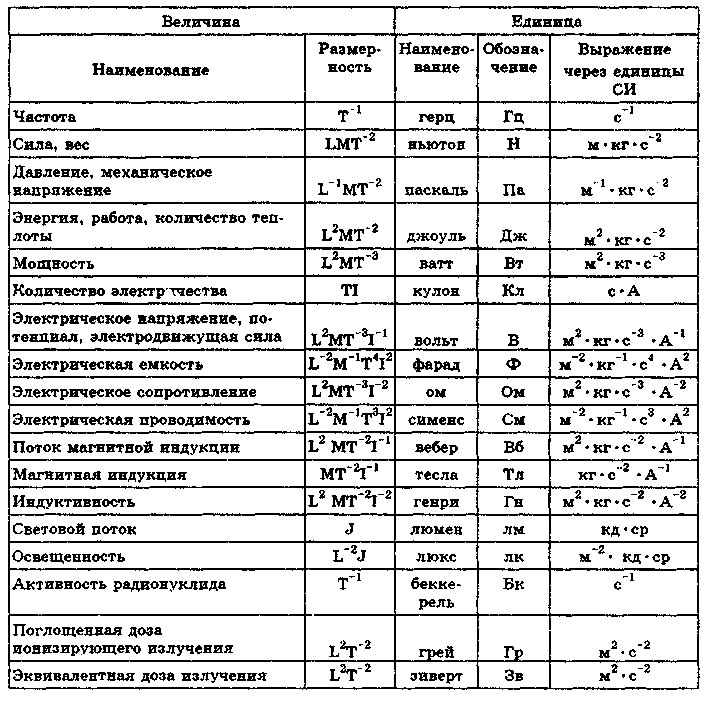
Насколько сложно получить высокие баллы на ЕГЭ по физике?
Для получения максимального балла на ЕГЭ нужно научиться выполнять задания с развернутым ответом (в этом году в экзаменационной работе их будет шесть). Всего за их правильное выполнение можно получить 17 баллов. Критерии оценивания можно найти в демонстрационном варианте.
При решении задачи № 27 необходимо записать рассуждения, указать физические явления и законы, а главное, четко сформулировать полный ответ. Как правило, цепочка логических рассуждений, необходимая для объяснения, содержит не менее трех звеньев. Стоит отметить, что, согласно критериям оценивания, при неверном ответе, даже при полностью верных рассуждениях, максимальная оценка за такое решение не превысит одного балла.
Для того чтобы получить максимально возможные три балла в задачах 29–32, вам необходимо:
- записать необходимые для решения формулы и физические законы;
- описать все буквенные обозначения физических величин, используемых в решении, за исключением констант и физических величин из условия задачи;
- сделать рисунок с указанием сил, действующих на тело, если это указано в условии;
- провести необходимые преобразования и расчеты, при этом допускается решение «по частям»;
- представить правильный ответ с указанием единиц измерения нужной величины.

Согласно критериям оценивания расчетных задач, отсутствие любого пункта из этого списка (рисунок, обозначения физических величин, математические преобразования и расчеты или ошибки в преобразованиях или расчетах, а также в указании единиц измерения) даже при правильном ответе снижает оценку на один балл.
Если же в решении всего одна ошибка в написании или применении физических формул или законов, оно не может быть оценено более чем в один балл.
Имейте в виду, что «авторское решение» не означает «единственно правильное». Ваше решение может быть принципиально другим
Например, очень часто задачу по механике можно решать из динамических и кинематических представлений, а можно — через законы сохранения энергии. Главное, чтобы решение соответствовало описанной в задаче ситуации и было доведено до конца без ошибок.
Какие ошибки чаще всего допускают ученики?
Всех участников ЕГЭ по физике условно можно разделить на четыре группы по уровню подготовки.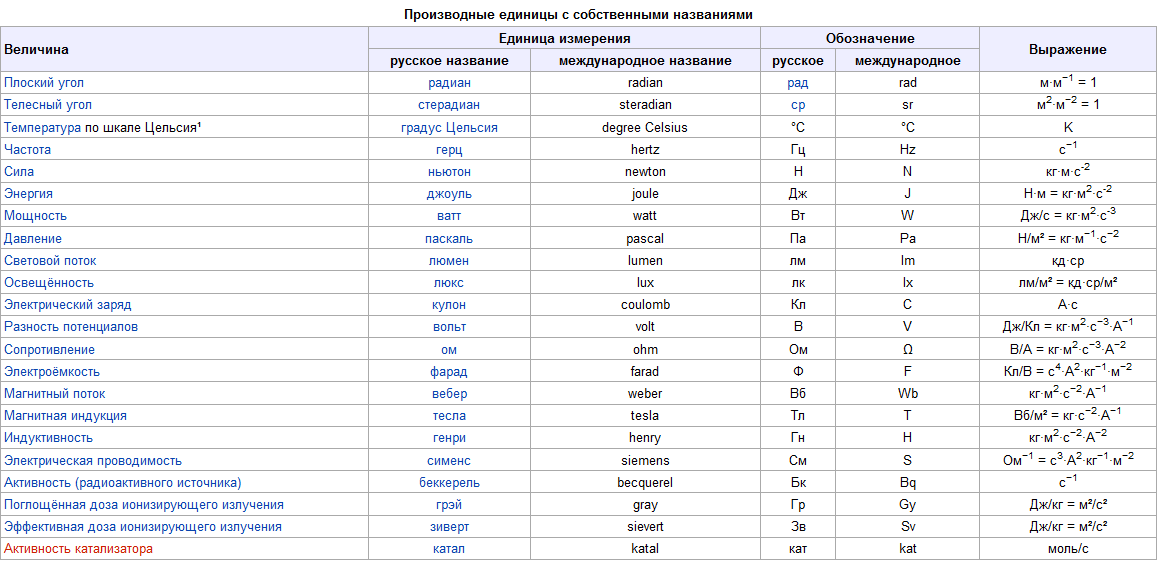
Первая — это выпускники с самым низким уровнем подготовки, то есть те, кто не достигает минимального балла (36). Они демонстрируют разрозненные знания и справляются лишь с некоторыми заданиями базового уровня, как правило, по механике и молекулярной физике. Таких в Москве в прошлом году было всего 3%.
Вторая группа, самая многочисленная, — это выпускники, набравшие от 36 до 60 итоговых баллов. В 2019 году в нее вошли 47% от всех сдающих экзамен. Эти выпускники справляются в основном с заданиями первой части, но не приступают ко второй. А если и приступают, то больше одной-двух формул не могут написать.
Для первой и второй групп типичная ошибка — слабое знание курса физики.
В третью группу входят выпускники, набравшие от 61 до 80 итоговых баллов. Это те, кого с удовольствием примут учиться на технические специальности. Таких выпускников в прошлом году было около 26%. Они весьма успешно выполняют задания первой части по всем разделам курса физики. Камнем преткновения для них, как правило, становятся графические задания на изменение физических величин в различных процессах по механике и электродинамике. И в решении задач высокого уровня второй части они также не очень успешны. К решению некоторых они не приступают вовсе либо не доводят его до конца, споткнувшись о математику.
Камнем преткновения для них, как правило, становятся графические задания на изменение физических величин в различных процессах по механике и электродинамике. И в решении задач высокого уровня второй части они также не очень успешны. К решению некоторых они не приступают вовсе либо не доводят его до конца, споткнувшись о математику.
Четвертая группа — это высокобалльники, выпускники, набравшие от 81 до 100 баллов. Их с нетерпением ждут в лучших вузах Москвы. В прошлом году они составляли 23% от всех сдающих физику. Можно похвалить столицу: больше нигде нет такого большого процента высокобалльников! И самое главное — доля таких участников у нас год от года увеличивается. Ошибок они допускают крайне мало, в основном по невнимательности: в первой части не в тех единицах могут представить ответ, во второй части из-за кажущейся очевидности пропускают логически важные моменты преобразований или вычислений, могут забыть подставить единицы измерения, использовать не начальную формулу или закон, а сразу то, что получается в результате преобразований.
С чем чаще всего у выпускников возникают сложности?
Три года назад в школу вернули преподавание астрономии, и в контрольных измерительных материалах по физике появился вопрос, на который, как показывает статистика, далеко не все выпускники могут дать правильный ответ.
Астрономии посвящён всего один вопрос во всей работе ЕГЭ, но за его верное выполнение можно получить два первичных балла, а это означает, что итоговых баллов может быть даже четыре
Чтобы успешно справиться с этим заданием, нужно посмотреть в кодификаторе раздел «Элементы астрофизики» и «Механика», где есть необходимые для астрономических вычислений формулы первой и второй космических скоростей. Некоторые сведения можно почерпнуть из справочных материалов.
Обратите внимание, что упор в астрономических заданиях делается не на проверку знания огромного количества данных, а на умение анализировать представленный в виде таблицы материал.
Какие рекомендации вы можете дать учителям?
В период подготовки к экзамену очень важно не оставлять учеников, стараться систематическими занятиями поддерживать набранную форму, решать различные задачи. При этом важно не только оценивать «правильно — неправильно», но и разбирать ошибки, повторяя наиболее западающие темы курса физики. Начиная с седьмого класса, когда идет изучение физики явлений, нужно чаще обращать внимание детей на мир вокруг нас и на место физических законов в нем.
А родителям выпускников?
Для выпускника в период подготовки к экзамену важно соблюдать распорядок дня, хорошо питаться, сочетать умственную и физическую нагрузку. Родители могут обеспечить ему все условия для этого.
Чтобы успешно сдать экзамен, нужно иметь не только хорошие знания, но и терпение, поэтому подготовка должна проходить в доброжелательной, спокойной атмосфере. Создать ее для ребенка — задача родителей.
Создать ее для ребенка — задача родителей.
https://mel.fm/ekzameny/9218743-ege_physics_guide
Прощай, килограмм! Почему наша единица массы безнадежно устарела
- Николай Воронин
- Корреспондент по вопросам науки и технологий
Автор фото, Getty Images
Подпись к фото,Эталоны килограмма немного тяжелеют по мере загрязнения поверхности и теряют вес в процессе очистки, так что их массу нельзя считать постоянной
В понедельник, 20 мая — во Всемирный день метрологии — вступает в силу новое определение килограмма, стандартной единицы массы, используемой по всему миру.
И хотя это никак не отразится на нашей повседневной жизни, значение этого шага для научного мира и промышленности, где требуются предельно точные измерения, трудно переоценить.
Килограмм — одна из семи основных единиц международной системы измерений (СИ).
Определения четырех из них — самого килограмма, а также ампера (измеряет силу тока), кельвина (температуру) и моля (количество вещества) — были пересмотрены на Всеобщей конференции мер и весов, которая прошла в конце прошлого года под Парижем, в Версале.
Автор фото, Getty Images
Подпись к фото,Все килограммовые гири мира сделаны по образцу оригинального эталона, хранящегося во Франции
Оригинальный килограмм
Килограмм — последняя из единиц СИ, в основе которой лежал реальный физический объект. Принятое еще в 1901 году официальное определение ровно так и звучало: «Килограмм — это единица массы, равная массе международного прототипа килограмма».
Международный прототип — это 4-сантиметровый цилиндр, состоящий на 90% из платины и на 10% из иридия. Он был произведен в Лондоне и с 1889 года хранится в Международном бюро мер и весов в городе Севре под Парижем.
Но физические объекты могут терять атомы (фактически испаряться) или, напротив, впитывать молекулы из окружающего воздуха, так что за прошедшее столетие масса эталона изменилась на несколько десятков микрограммов.
А это значит, что все остальные прототипы килограмма, по которым калибруют весы по всему миру, строго говоря, были не идеально точны.
Автор фото, Getty Images
Подпись к фото,В повседневной жизни отклонения на тысячные доли грамма заметить невозможно
Столь незначительные отклонения не имеют никакого значения в привычной нам жизни, однако представляют огромную проблему для точных научных вычислений.
«Если когда-нибудь инопланетяне прилетят на Землю, о чем нам еще с ними разговаривать, если не о физике? Но чтобы говорить о физике, нужно будет договориться и об общих единицах измерений. И если мы скажем, что в основе нашей единицы массы лежит металлическая гиря из Парижа, над нами будет смеяться вся Вселенная», — заявил накануне голосования представитель Национального института стандартов и технологий США Стивен Шламмингер.
Новый килограмм
По большому счету, голосование на Всеобщей конференции мер и весов в ноябре прошлого года было формальным: напряженные дебаты уже прошли, (несколько стран предлагали свои, альтернативные определения), решение было согласовано заранее.
Теперь килограмм предполагается измерять при помощи так называемых весов Ватта (или баланса Киббла) — этот прибор определяет массу через постоянную Планка, основную константу квантовой теории.
Проще говоря, определение килограмма увязано с количеством электромагнитной энергии, необходимой для того, чтобы уравновесить объект соответствующей массы. Эталонную гирю заменят электрический ток и напряжение.
Эти величины, в отличие от самого физического объекта, не могут измениться или пропасть. А кроме того, точно отмерять килограмм теперь смогут любые ученые по всему миру, а не только те, у кого есть доступ к оригинальной парижской гире или ее копии.
По словам главы британской Национальной физической лаборатории Теодора Йанссена, отвечающего за стандарты измерения, пятничное голосование — поворотный момент в истории физики.
«Теперь все единицы системы СИ будут основаны на фундаментальных константах природы — вечных, неизменных величинах, — объясняет он. — Это позволит проводить куда более точные измерения и укрепит основы науки в целом».
Автор фото, EPA
Подпись к фото,Так выглядят весы Ватта
Наука — Физико-технический институт
Нанотехнологии – развивающееся научное направление в университете в тесном сотрудничестве с Научно-образовательным центром «Нанотехнологии» под руководством доктора наук Удовиченко Сергея Юрьевича. располагая богатым материально-техническим оснащением для проведения научных исследований студенты и аспиранты достигают значительных успехов. Аспирант кафедры экспериментальной физики и нанотехнологий Бобылев Андрей Николаевич под научным руководством профессора С.Ю. Удовиченко им опубликовал 5 научных работ в журналах, индексируемых в международных системах цитирования («Web of Science», «Scopus»), 3 публикации в журналах «списка ВАК» и подал заявку на изобретение.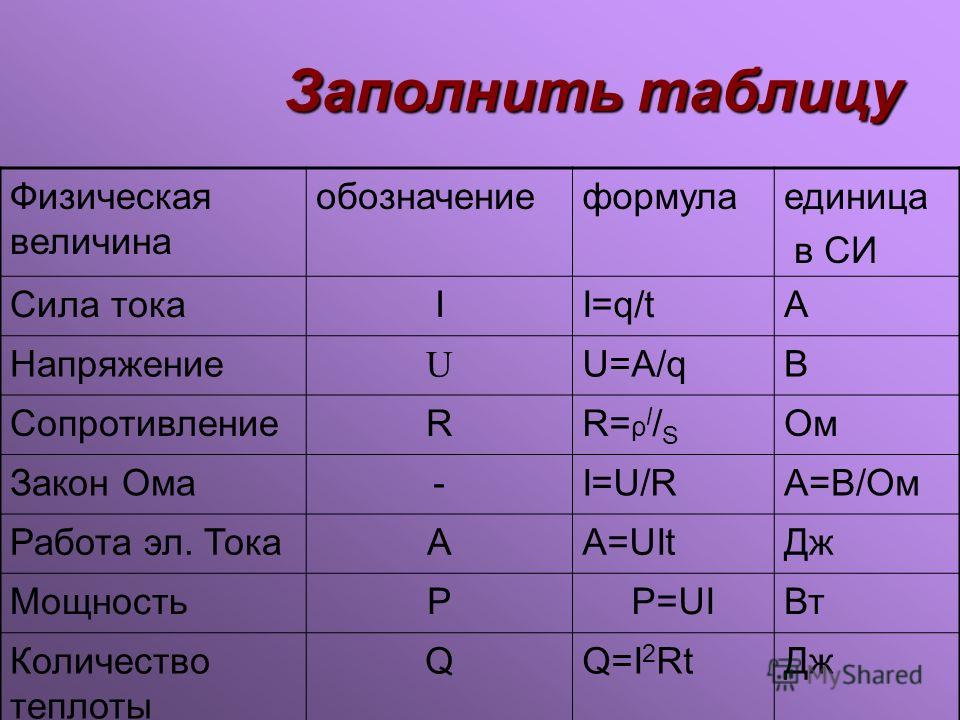 помимо это Андрей Николаевич является победителем регионального конкурса для получения гранта на выполнение научно-исследовательского проекта УМНИК — 2017 по теме «Разработка и исследование тонкоплёночных электронных устройств на основе смешанных оксидов металлов». В феврале 2018 года Ректор ТюмГУ Валерий Фальков за выдающиеся успехи в учебе и научно-исследовательской деятельности назначил А.Н. Бобылеву именную стипендию.
помимо это Андрей Николаевич является победителем регионального конкурса для получения гранта на выполнение научно-исследовательского проекта УМНИК — 2017 по теме «Разработка и исследование тонкоплёночных электронных устройств на основе смешанных оксидов металлов». В феврале 2018 года Ректор ТюмГУ Валерий Фальков за выдающиеся успехи в учебе и научно-исследовательской деятельности назначил А.Н. Бобылеву именную стипендию.
Аспирант 1 — го года очного обучения кафедры ЭФиНТ Бусыгин Александр Николаевич в феврале 2018 года стал победителем Федерального конкурса для получения гранта на выполнение научно-исследовательского проекта УМНИК в Сколтехе — 2017 «Разработка нейроморфного сопроцессора на базе мемристоров и КМОП логики».
Будучи магистрантом в апреле 2017 года Бусыгин А.Н. принял участие во Всероссийской студенческой олимпиаде по радиофизике, проходившей в Национальном исследовательском Томском государственном университете, занял третье призовое место и получил звание «Лауреата премии Президента РФ для талантливой молодежи».
Под руководством научного руководителя д-ра физ.-мат. наук, профессора С.Ю. Удовиченко им опубликовано 2 статьи в журнале из из коллекции «Web of Science» и 2 статьи в журналах из «списка ВАК», получил патент на изобретение и зарегистрировал 3 заявки на изобретение.
С сентября 2017 года А.Н. Бусыгин является именным стипендиатом Ректора ТюмГУ Валерия Фалькова.
Многофазная расходометрия – направление, развивающееся при поддержке и активном участии завода ГМС Нефтемаш и сотрудников базовой кафедры расходометрии нефти и газа. Успешные идеи и разработки сотрудников, аспирантов и студентов кафедры были удостоены грантовой поддержки и призовых мест на конкурсах и конференциях. Среди победителей грантового конкурса УМНИК Григорьев Борис с темой «Разработка поточного вискозиметра, способного измерять изменяющуюся вязкость жидкого гомогенного флюида», посредством байпасирования части потока через измерительное устройство. Зайцев Евгений с темой «Разработка матричной ячейки широкодиапазонного поточного влагомера нефти и нефтепродуктов». Проект направлен на разработку измерительной ячейки поточного влагомера, способного производить измерения обводненности в диапазоне содержания воды от 0 до 100% и содержания газа от 0 до 75 % в негомогенном потоке. В основе принципа действия лежит абсорбционная спектроскопия в ближней области инфракрасного спектра. Для получения информации об обводненности по всему сечению потока будет использоваться матричный приемник инфракрасного излучения.
Проект направлен на разработку измерительной ячейки поточного влагомера, способного производить измерения обводненности в диапазоне содержания воды от 0 до 100% и содержания газа от 0 до 75 % в негомогенном потоке. В основе принципа действия лежит абсорбционная спектроскопия в ближней области инфракрасного спектра. Для получения информации об обводненности по всему сечению потока будет использоваться матричный приемник инфракрасного излучения.
Бессараб Алексей, выполняющий исследования в интересах завода с проектом «Разработка поточного ультразвукового многоканального анализатора количественного содержания газовой фазы в газожидкостном потоке».
Осенью 2017 года Екатерина Хлопотова выиграла грант УМНИК с финансированием 500 000руб по теме «Разработка оптического интерференционного расходомера». Для её подготовки к выступлению и выполнения самого проекта продела большая работа: в успешном выполнении проекта удалось заинтересовать завод нефтегазового оборудования ГМС Нефтемаш, получено письмо поддержки и подана совместная заявка на патент. Екатерина — победитель конкурса «Open Innovations Startup Tour’18» («Сколково») в номинации «Женский трек» за лучший проект, представленный женщиной.
Екатерина — победитель конкурса «Open Innovations Startup Tour’18» («Сколково») в номинации «Женский трек» за лучший проект, представленный женщиной.
Фотоника и микрофлюидика — направление, руководителем и идейным лидером в которм выступает Наталья Анатольевна Иванова. Она без преувеличения один из столпов науки университета. ее тематика исследований это фронтир мировой повестки. В числе ее достижений зарубежные и российские гранты, множество публикаций в самых рейтинговых журналах квартиля Q1 и Q2. В ее команде 5 аспирантов кафедры ЭФиНТ которые уже отметились достижениями в науке:
Кубочкин Николай и Клюев Денис представили свои доклады на международной конференции Bubble & Drop: Scientific convention – 2017, Франция, Лион. Александр Малюк выступил в Мюнхене на международной конференции EOS on Optofluidics. Помимо перечисленного Кубочкин Николай уже в 2018г выиграл грант Российского фонда фундаментальных исследований. Аспиранты Натальи Анатольевны это в первую очередь исследователи, публикующие свои достижения в ведущих мировых научных изданиях. В 2017г на под впечатлением научной деятельности коллектива научно-исследовательской лаборатории фотоники и микрофлюидики в аспирантуру Тюменского госудорственного университета поступил гражданин Йемена Аль-Музайкер Мохаммед Али Яхья Али, который за год проявил разносторонние качества исследователя и организатора. Студенты, которым удается попасть в коллектив лаборатории уже через несколько месяцев демонстрируют исследования уровня магистерской диссертации.
В 2017г на под впечатлением научной деятельности коллектива научно-исследовательской лаборатории фотоники и микрофлюидики в аспирантуру Тюменского госудорственного университета поступил гражданин Йемена Аль-Музайкер Мохаммед Али Яхья Али, который за год проявил разносторонние качества исследователя и организатора. Студенты, которым удается попасть в коллектив лаборатории уже через несколько месяцев демонстрируют исследования уровня магистерской диссертации.
Материально-техническая база лаборатории оснащена новейшим оборудованием, что позволяет делать научные открытия мирового уровня.
Исследования горных пород и пластовых флюидов – направление, базирующееся на лаборатории керновых исследований и ее коллективе. Тюмень — нефтегазовая столица России, поэтому было бы странным отсутствие лаборатории, с оборудованием для исследования горных пород – керна, извлеченного из скважин пробуренных в нефтегазоносных пластах и пластовых флюидов: воды и нефти. В лаборатории работают над выполнением диссертации Кузина Ольга Александровна, на счету которой 2 статьи в журналах Нефтегазовое дело и Вестник Тюменского государственного университета и большой объём еще не опубликованных результатов экспериментальных исследований. Поточняк Игорь – магистрант, под руководством Григорьева Б.В. подготовил публикацию в журнал ВАК и занял III место в секции «Энергетика. Электроника. Теплотехника» на Региональном конкурсе студенческих научных работ – 2017 в г. Ишим.
Поточняк Игорь – магистрант, под руководством Григорьева Б.В. подготовил публикацию в журнал ВАК и занял III место в секции «Энергетика. Электроника. Теплотехника» на Региональном конкурсе студенческих научных работ – 2017 в г. Ишим.
Воробьев Владимир Викторович за 2017 год получил 4 патента на изобретения и полезные модели. Ряд инновационных решений, которых применены в лаборатории керновых исследований и разработке прототипов устройств по теме научных и грантовых тем выполняемых в лаборатории.
Лаборатория регулярно участвует в реализации проектов университета по постановлению Правительства РФ № 218: «Создание технологии и комплекса оборудования для термохимического воздействия на нефтегазоносные пласты с целью увеличения добычи углеводородного сырья и восстановления экологической обстановки на месторождениях взамен импортной технологии гидравлического разрыва пласта «проппант – гелевыми составами». В этом масштабном проекте в лаборатории выполянются исследования фильтрационно-емкостных свойств образцов нефтегазоносных пород и пластовых флюидов.
Методы увеличения нефтеотдачи – направление, которое берет свое начало из проекта университета по постановлению Правительства РФ № 218: «Создание технологии и комплекса оборудования для термохимического воздействия на нефтегазоносные пласты с целью увеличения добычи углеводородного сырья и восстановления экологической обстановки на месторождениях взамен импортной технологии гидравлического разрыва пласта «проппант – гелевыми составами». Главным исполнителем по проекту выступает Вершинин Владимир Евгеньевич, старший преподаватель кафедры Моделирования физических процессов и систем, который тесно работает с Технопарком Тюменского государственного университета и Сибнефтемашем — компанией группы ГМС. со своей научной группой, в составе аспиранта Артема Варравы, и студентов кафедры разрабатывают принципиально новый метод повышения нефтеотдачи, а именно термобарохимического воздействия на пласт при обработке скважин водными растворами бинарных смесей. Результатов которого ждут нефтяники. Внедрение позволит снизить экономические издержки и повысить процент извлечения нефти.
Внедрение позволит снизить экономические издержки и повысить процент извлечения нефти.
Подземная гидродинамика – направление, развитию которого способствует сотрудничество физико-технического института с Институтом теоретической и прикладной механики СО РАН, где работают выдающие ученые Губайдуллин Амир Анварович, Мусакаев Наиль Габсалямович, Родионов Сергей Павлович и молодые кандидаты наук, выпускники ФТИ и аспиранты института. Их научная деятельность охватывает широкий круг задач, таких как оптимальное управление системой скважин, моделирование процесса двухфазной фильтрации с учетом различных факторов, теоретическое исследование процесса добычи газа динамика образования и разложения гидратов в системах добычи, транспортировки и хранения газа, решения обратной задачи восстановления гидропроводности нефтяного месторождения, методика экспресс оценки состояния нефтяного месторождения и многих других актуальных тем нефтегазовой тематики. Все, вовлеченные в это направление имеют высокие показатели публикационной активности, в чем несложно убедиться, открыв наукометрическую базу данных. Студенты и выпускники ФТИ, продолжающие свою деятельность в ИТПМ удостаиваются грантовой поддержки молодым ученым, в 2017 году таковыми стали Пятков Александр и Дмитрий Легостаев – победители конкурса УМНИК.
Студенты и выпускники ФТИ, продолжающие свою деятельность в ИТПМ удостаиваются грантовой поддержки молодым ученым, в 2017 году таковыми стали Пятков Александр и Дмитрий Легостаев – победители конкурса УМНИК.
Инновационные подходы в теории и методике обучения физике. Подготовка школьного учителя физики – ответственная задача, которая в Тюменском государственном университете возложена на плечи доцента кафедры моделирования физических процессов и систем, кандидата педагогических наук Дружининой Ольги Михайловны. Дружинина О.М. курирует направление подготовки прикладного бакалавриата «Педагогическое образование», профиль подготовки «Физическое образование». Ее студенты не ограничиваются посещением лекций и практик, ежегодно выезжают на конференции и олимпиады. Например, ежегодная Всероссийская студенческая олимпиада по теории и методике обучения физике им. А.В. Усовой.( г. Челябинск),где практически всегда занимают призовые места. Осенью и зимой студенты проходят практику в школах города, получают опыт работы со школьниками разных классов, применяют новые подходы к образовательной деятельности, которым их обучают Ольга Михайловна и доктор педагогических наук Игнатова Валентина Александровна.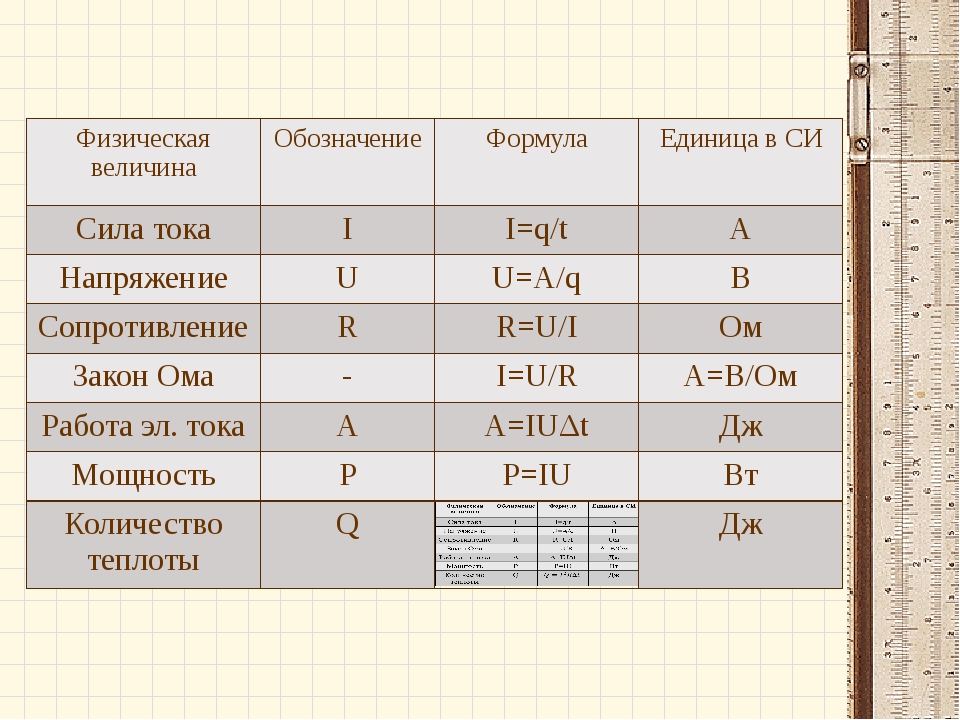 Направления научно-исследовательских работ студентов: методика преподавания физики в учебных заведениях различного профиля, внешняя и внутренняя дифференциация процесса обучения физике, организация работы с одарёнными школьниками, проектная деятельность в учебно-воспитательном процессе школы и вуза, преемственность(школа-вуз) в преподавании курса физики и астрономии, индивидуализация процесса обучения физике, современные формы и методы работы со школьниками, разработка содержания и дидактического обеспечения курса физики в свете дифференциации современной системы образования, проблемы экологического и политехнического образования.
Направления научно-исследовательских работ студентов: методика преподавания физики в учебных заведениях различного профиля, внешняя и внутренняя дифференциация процесса обучения физике, организация работы с одарёнными школьниками, проектная деятельность в учебно-воспитательном процессе школы и вуза, преемственность(школа-вуз) в преподавании курса физики и астрономии, индивидуализация процесса обучения физике, современные формы и методы работы со школьниками, разработка содержания и дидактического обеспечения курса физики в свете дифференциации современной системы образования, проблемы экологического и политехнического образования.
Лазерная спектроскопия — недооцененное направление с высоким потенциалом. Результаты научных исследований в этой области находят прикладное применение: доценты кафедры экспериментальной физики и нанотехнологий Монтанари С.Г., Михеев В.А. и Гармонов А.А. разработали для ООО «Газпром трансгаз Югорск», систему диагностики утечек газа «Аэропоиск-3М»и ежегодно на договорной основе проводят ее техническое обслуживание. В 2018 году ими была подготовлена статья в журнал, индексируемый базой данных RSCI, описывающая разработанный авторами блок питания для импульсных лазеров без емкостного накопителя. Сергей Георгиевич вместе со студентами Горбуновой Е. и Шмелевой Д. разработал лабораторный стенд для тестирования и измерения параметров ИК фотоприемников.
В 2018 году ими была подготовлена статья в журнал, индексируемый базой данных RSCI, описывающая разработанный авторами блок питания для импульсных лазеров без емкостного накопителя. Сергей Георгиевич вместе со студентами Горбуновой Е. и Шмелевой Д. разработал лабораторный стенд для тестирования и измерения параметров ИК фотоприемников.
Кафедра «Физика» | О кафедре
Кафедра физики ведет свою историю с 1931 г., когда в соответствии с Постановлением СНК СССР от 13 декабря 1930 г. был образован МАДИ. В апреле 1931 г. в МАДИ был принят в должности заведующего физической лабораторией Петр Петрович Кандидов (родился в 1885 г.), он являлся выпускником физического факультета МГУ (1910 г.) и имел звание профессора. Будучи студентом МГУ, П.П. Кандидов под руководством Петра Петровича Лазарева, выдающегося ученого и организатора первого советского научно-исследовательского института по физике, ныне Физического института имени П.Н. Лебедева РАН, изучал влияние электрического заряда на поверхностное натяжение на границе между эфиром и водой. Эта работа из области молекулярной физики и физической химии выполнялась в лаборатории Петра Николаевича Лебедева [Успехи физических наук, 1945, т.27, в.1, с. 3].П.Н. Лебедев являлся учителем и другом Лазарева. Полученные Кандидовым результаты впоследствии были использованы Лазаревым в его ионной теории возбуждения. П.П. Кандидов являлся первым заведующим кафедрой «Физика» в Московском институте механизации и электрификации сельского хозяйства (МИМЭСХ), которая была организована в 1930 г. при его непосредственном участии. С 1 сентября 1933 г. П.П. Кандидов был назначен в должности профессора и заведующего кафедрой физики МАДИ, совмещая заведование одноименной кафедрой в МИМЭСХ. Заведующим кафедрой физики в МАДИ П.П. Кандидов проработал до конца 1952 г., до ухода на пенсию по инвалидности.
Эта работа из области молекулярной физики и физической химии выполнялась в лаборатории Петра Николаевича Лебедева [Успехи физических наук, 1945, т.27, в.1, с. 3].П.Н. Лебедев являлся учителем и другом Лазарева. Полученные Кандидовым результаты впоследствии были использованы Лазаревым в его ионной теории возбуждения. П.П. Кандидов являлся первым заведующим кафедрой «Физика» в Московском институте механизации и электрификации сельского хозяйства (МИМЭСХ), которая была организована в 1930 г. при его непосредственном участии. С 1 сентября 1933 г. П.П. Кандидов был назначен в должности профессора и заведующего кафедрой физики МАДИ, совмещая заведование одноименной кафедрой в МИМЭСХ. Заведующим кафедрой физики в МАДИ П.П. Кандидов проработал до конца 1952 г., до ухода на пенсию по инвалидности.
Преподаватели кафедры , 1932год
В составе кафедры физики в 1946 г. были всего 5 преподавателей:
- Кандидов Петр Петрович, профессор
- Велецкая Ольга Ивановна, кандидат физ.
 -мат. наук, доцент
-мат. наук, доцент - Преображенский Николай Иванович, кандидат физ.-мат. наук, доцент
- Рубенштейн Борис Евсеевич, доцент
- Кондорский Сергей Михайлович, ассистент.
Н.И. Преображенский работал в МАДИ по совместительству, с 1936 по 1974 г. он заведовал кафедрой физики в Московском институте механизации и электрификации сельского хозяйства, был известным специалистом в области физики полупроводников.
В планах научных исследований, проводимых на кафедре «Физика» в МАДИ в 1940-е гг. значились проблемные темы: «Измерения деформации при статических и динамических нагрузках» (руководитель и исполнитель О.И. Велецкая), «Исследования физико-механических свойств асфальта в зависимости от природы и концентрации асфальтирующих добавок» (руководитель П.П. Кандидов), а также бюджетные темы: «Вопросы теории аморфного состояния вещества» (руководитель П.П. Кандидов), «Влияние вязкости на магнитную проницаемость» (руководитель О. И. Велецкая).
И. Велецкая).
В разные годы кафедрой заведовали: Кандидов П.П., Поройков И.В., Корнеев Ю.В., Котов Б.И., Панасюк В.С., Рудой Ю.Г., Сапогин Л.Г. В 2012 г. в должности заведующего избрана А.Ф.Смык, кандидат физ.-мат. наук, доцент. Она является автором более 80 научных и учебно-методических работ.
В истории кафедры можно выделить два периода, характерные по своим достижениям. Первый можно условно назвать «новой историей», он начался в конце 1950-х годов и во многом связан с деятельностью ректора МАДИ Леонида Леонидовича Афанасьева. Кафедру физики в эти годы возглавлял Иван Васильевич Поройков. Он был специалистом в области рентгеноструктурного анализа. Это был очень порядочный и строгий руководитель. Стоило кому-нибудь из сотрудников нарушить дисциплину
(например, опоздать на занятие) как он немедленно писал докладную в учебную часть, а виновный получал выговор. Несмотря на это И.В. Поройков пользовался уважением преподавателей и сотрудников кафедры. Помимо традиционных лабораторных работ по механике, молекулярной физике и электричеству на кафедре выполнялись лабораторные работы в радиационной лаборатории с использованием рентгеновской установки, измеряющей интенсивность рентгеновского излучения по плотности почернения фотопластинки.
Следующим после И.В. Поройкова заведующим был проф. Ю.В. Корнев.
Конец 1960-х гг. связан с началом деятельности нового заведующего Б.И. Котова. Этот период характеризуется началом развития хоздоговорных исследований, пик которых приходится на конец 60-х – начало 70-х. Тогда начинается «новейшая история» кафедры. В 1968 г. кафедру возглавил д.т.н., профессор Вадим Семенович Панасюк, вместе с ним пришел работать доцент Юрий Григорьевич Рудой – к тому времени к.ф.-м.н. (защита в мае 1967 г. на физфаке МГУ, тема – квантовая теория магнетизма, научный руководитель – акад. Н.Н. Боголюбов). В.С. Панасюк приехал из Новосибирска, где он работал под руководством акад. Г.И. Будкера в институте ядерной физики СО АН СССР, стал дважды лауреатом Ленинской и Государственной премий за работы в области электронных ускорителей на встречных пучках (в США до сих пор не достигли этого результата). Основным местом работы В.С. Панасюка был (и оставался до конца его жизни) ВНИИ оптико-физических измерений ГК СССР по стандартам; научные работы В. С. велись по оборонной тематике в области пучкового оружия и т.п. В качестве заведующего на кафедре физики МАДИ В.С. Панасюк проработал до 1979 г., далее до конца жизни – в качестве профессора.
С. велись по оборонной тематике в области пучкового оружия и т.п. В качестве заведующего на кафедре физики МАДИ В.С. Панасюк проработал до 1979 г., далее до конца жизни – в качестве профессора.
Столь сильный состав кафедры физики МАДИ привел к двум серьезным достижениям – как в области научно-методической работы, так и научной – прежде всего хоздоговорной – работы.
На кафедре была разработана новая учебная программа курса общей физики для технических вузов, которая с трудом пробивала себе дорогу, однако спустя ряд лет была принята за основу действующей и поныне официальной программы Минобрнауки. Признанием заслуг кафедры в этой области явилось назначение трех преподавателей кафедры (доц. В.Б. Зернов, доц. Ю.Г. Рудой, асс. З.С. Сазонова) в состав Научно-методического совета при Минобразовании СССР, причем доц. В.Б. Зернов – в качестве зам. председателя НМС.
Инициатором создания программы выступил доц. В.Б. Зернов, активное участие в разработке и издании лекционного курса приняли доц. Ю.Г. Рудой, ст. преп. Е.Н. Фигуровская, а позднее доц. И.В. Карпенко, доц. В.Г. Захаров, доц. М.Я. Юшина,. Методическое обеспечение практических занятий было разработано в основном ст. преп. Т.А. Тимофеевой и ст. преп. И.Л. Скворцовой; обновлением лабораторного практикума руководил лично проф. В.С. Панасюк и доц. К.Н. Сачков, а в разработке методических материалов для практикума принимали участие практически все преподаватели кафедры. Демонстрационный кабинет был модернизирован усилиями доц. Тимофеева А.И. и доц. Захарова В.Г.
Ю.Г. Рудой, ст. преп. Е.Н. Фигуровская, а позднее доц. И.В. Карпенко, доц. В.Г. Захаров, доц. М.Я. Юшина,. Методическое обеспечение практических занятий было разработано в основном ст. преп. Т.А. Тимофеевой и ст. преп. И.Л. Скворцовой; обновлением лабораторного практикума руководил лично проф. В.С. Панасюк и доц. К.Н. Сачков, а в разработке методических материалов для практикума принимали участие практически все преподаватели кафедры. Демонстрационный кабинет был модернизирован усилиями доц. Тимофеева А.И. и доц. Захарова В.Г.
Была обновлена научная база кафедры, поскольку В.С. Панасюк совершенно справедливо полагал, что только преподавать физику без занятий ею как наукой – прежде всего экспериментальной – недостаточно. Работы были практически полностью хоздоговорные, поскольку бюджетное финансирование для общенаучных кафедр не предусматривалось. Тематика работ в основном диктовалась интересами автомобильно-дорожной отрасли, прежде всего к ее экологическим аспектам. К основным достижениям следует отнести лазерный анализ вредных примесей (доц. В.И. Черненький, доц. З.С. Сазонова), причем соответствующий мобильный прибор типа лидара был удостоен диплома и серебряной медали ВДНХ. З. С. Сазонова активно в течение многих лет занималась научной деятельностью в содружестве с кафедрой металловедения по тематике «Лазерные модификации физических и технологических свойств поверхности металлов и сплавов» и с кафедрой технологии конструкционных материалов по тематике «Ультразвуковые методы разборки и очистки поверхностей прецизионных деталей».
В.И. Черненький, доц. З.С. Сазонова), причем соответствующий мобильный прибор типа лидара был удостоен диплома и серебряной медали ВДНХ. З. С. Сазонова активно в течение многих лет занималась научной деятельностью в содружестве с кафедрой металловедения по тематике «Лазерные модификации физических и технологических свойств поверхности металлов и сплавов» и с кафедрой технологии конструкционных материалов по тематике «Ультразвуковые методы разборки и очистки поверхностей прецизионных деталей».
Позднее (в начале 80-ых годов) возникло новое направление теоретических исследований в интересах института проблем управления АН СССР (рук. – проф. Л.Г. Сапогин, исполнители – проф. Ю.Г. Рудой, доц. В.Н. Каданцев, доц. М.Я. Юшина). Кроме того, на кафедре много лет существовало направление госбюджетных научных исследований в области квантовой теории магнетизма, проводимое совместно с математическим институтом им. В.А. Стеклова АН СССР (рук. – проф. Ю.Г. Рудой, доц. В.И. Лымарь).
В рамках этой тематики были защищены две диссертации – кандидатская (В. И. Лымарь, 1979, физфак МГУ) и докторская (Ю.Г. Рудой, 1980, математический институт им. Стеклова) и опубликовано несколько десятков статей – в основном в журнале «Теоретическая и математическая физика», а также имелось участие в коллективных научных монографиях.
И. Лымарь, 1979, физфак МГУ) и докторская (Ю.Г. Рудой, 1980, математический институт им. Стеклова) и опубликовано несколько десятков статей – в основном в журнале «Теоретическая и математическая физика», а также имелось участие в коллективных научных монографиях.
Направления научной работы кафедры « Физика» в 1991-е гг.
Середина 80-х характеризуется началом внедрения компьютеров в учебный процесс. В это время усилиями проф. Ю.Г. Рудого, доц. В.Г. Захарова и доц. И.А. Авенариус был создан новый компьютерный класс. За создание компьютерной программы «Индивидуальные домашние задания для студентов» и её внедрение доц. Захаров В.Г., представивший программу на всесоюзный конкурс, получил грамоту и премию Минвуза СССР.
Доценты Черненький В.И., Максименков П.П. и Сачков К.Н. исследовали возможность оценки лазерным методом наличие в атмосфере вредных примесей. Методика лазерной спектроскопии нашла практическое применение при оценке загрязнения атмосферы в Москве, что было отмечено премией Минвуза СССР и серебряной медалью ВДНХ.
К большим научным достижениям кафедры можно отнести разработку новой унитарной квантовой теории, автором которой явился профессор, д.т.н. Лев Георгиевич Сапогин. Л.Г. Сапогин в 1 г. стал новым заведующим кафедрой физики. Кроме этого он возглавил научный коллектив в составе: профессора Ю.А. Рябова, генерал – майора, космонавта В.А. Джанибекова, В.А. Бойченко, профессора В.И. Участкина, ст. преподавателя Б.Л. Афанасьева. В 2008 г. была издана книга «Унитарная квантовая теория и новые источники энергии» (авторы – Л.Г. Сапогин, Ю.А. Рябов, В.А. Бойченко) на русском и английском языках, в которой изложена новая унитарная квантовая теория Сапогина.
На кафедре физики ряд преподавателей поддерживали на протяжении многих конференциях – доценты З.С. Сазонова, Г.К. Ипполитова, И.А. Авенариус, В.Г. Захаров, Т.М. Ткачева. Преподавание в зарубежных университетах в разное время осуществляли доценты П.П. Максименков, А.И. Тимофеев лет международные контакты с другими ВУЗами, участвовали в международных, И. А. Авенариус, В.Г. Захаров, С.П. Меркурова.
А. Авенариус, В.Г. Захаров, С.П. Меркурова.
Доц. В.Г. Захаров, доц. Г.К. Ипполитова, проф. З.С. Сазонова имеют звание «Международный преподаватель инженерного ВУЗА».
Постановлением Коллегии ГОСКОМ СССР по народному образованию от 21.06. 1991-го года Сазоновой З.С. присуждена II-я премия за значительные успехи в перестройке содержания учебно-воспитательного процесса, его обновления в свете современных достижений и перспектив развития науки, техники и культуры, создание спецкурсов по направлениям Сазоновой З.С. выдано Удостоверение в том, что она за заслуги в области высшего образования СССР награждена нагрудным значком «За отличные успехи в работе» Документ подписан Г.А. Ягодиным.
В соответствии с Приказом Министерства образования РФ за заслуги в области образования РФ проф. З.С. Сазонова, доц. Г. К. Ипполитова награждены нагрудным знаком «Почетный работник ВПО РФ»; В соответствии с Указом Президента РФ От 28.11.2011 года Сазонова З.С. награждена медалью ордена «За заслуги перед Отечеством» II-й степени
Проф. З. С. Сазонова начиная с 2001-года – профессор кафедры инженерной педагогики МАДИ и зам. зав. этой кафедры, совмещала эту работу с работой профессора по кафедре физики МАДИ вплоть до 2008-го года. С 2008 года – профессор и зам. зав. каф. инж. педагогики, директор ЦИП МАДИ и декан ФПКП, но непрерывно взаимодействует с кафедрой физики, ежегодно проводит совместные научно-методические конференции.
З. С. Сазонова начиная с 2001-года – профессор кафедры инженерной педагогики МАДИ и зам. зав. этой кафедры, совмещала эту работу с работой профессора по кафедре физики МАДИ вплоть до 2008-го года. С 2008 года – профессор и зам. зав. каф. инж. педагогики, директор ЦИП МАДИ и декан ФПКП, но непрерывно взаимодействует с кафедрой физики, ежегодно проводит совместные научно-методические конференции.
Доц. Ипполитова Г.К. принимала активное участие в работе международного общества по инженерной педагогике (IGIP). С 1997 года являлась референтом Российского мониторингового комитета IGIP, при ее участии более 200 преподавателей российских вузов получили звание «Европейский/Международный преподаватель инженерного вуза». Принимала участие в 8 Международных Симпозиумах по инженерной педагогике, проводила организационную работу по подготовке Российской делегации на Симпозиумы и сама выступала с докладами. При проведении Симпозиумов IGIP в МАДИ являлась членом оргкомитета, отвечала за культурную программу Симпозиума. Ее статья « Международная деятельность России в области инженерной педагогики: результаты и перспективы» опубликована в трудах IGIP (№ 34)
Ее статья « Международная деятельность России в области инженерной педагогики: результаты и перспективы» опубликована в трудах IGIP (№ 34)
Ипполитова Г.К. регулярно публикует статьи в сборниках МАДИ «Инженерная педагогика» и в отчетах МАДИ, подготовила методическое пособие «Методические аспекты признания квалификации ”Международный преподаватель инженерного вуза”
Новым заведующим кафедрой в 2013 г. избрана А.Ф. Смык. С 1982 по 1992 г. Она работала в Институте физики им. Л.В. Киренского Сибирского отделения Академии наук СССР, где защитила кандидатскую диссертацию по специальности «Физика магнитных явлений». С 1992 г. началась ее преподавательская деятельность, сначала в должности старшего преподавателя, затем доцента на кафедре физики в технических вузах, приобретен большой опыт преподавания курса физики для различных технических направлений подготовки.
А.Ф.Смык является автором более 50 научных статей в центральной печати, 2 авторских свидетельств на изобретения, различных учебных и методических пособий для изучения курса физики. Под руководством А.Ф.Смык на кафедре физики разработана и сертифицирована компьютерная программа «Информационная система МАДИ для обучения студентов («ИС МАДИ»). В настоящее время область ее научных интересов – история науки и техники, основные работы посвящены вопросам истории квантовой механики, истории высшего технического образования в России, истории отечественного двигателестроения. В 2013 г. А.Ф. Смык защитила диссертацию на соискание ученой степени доктора физ.-мат. наук.
Кафедра «Физика», сентябрь 2015 г.
Слева направо: 1-ряд — Ткачева Т.М., Авенариус И.А., Сазонова З.С. (кафедра инженерной педагогики), Тимофеева Т.А., Смык А.Ф., Ипполитова Г.К., Тимофеева Г.Ю.
2-ряд — Гусева Е.А., Михайлишин В.И., Белкова Ю.А., Спиридонова Л.В., Симонова Н.А., Ширина Т.А., Бахтина Е.Ю., Максименков П.П., Портнов Ю.А.
Кафедра «Физика», сентябрь 2016 г.
Слева направо: 1-ряд — Гусева Е.А., Авенариус И.А., Симонова Н.А., Смык А.Ф., Тимофеева Г.Ю., Бахтина Е.Ю., Михайлишина Г.Ф.
2-ряд – Хайруллин Д.Ф., Михайлишин В.И., Никеров В.А., Ширина Т.А., Ткачева Т.М., Спиридонова Л.В., Воротынцева И.И., Белкова Ю.А., Максименков П.П., Портнов Ю.А.
Кафедра «Физика», сентябрь 2019г.
Слева направо: 1-ряд — Смык А.Ф., Ткачева Т.М., Кузьмина Н.Б., Ширина Т.А., Симонова Н.А.
2-ряд — Филоненко Е.А., Тимофеева Г.Ю., Салагубов А.И., Кушко А.Н., Форш Е.А., Гусева Е.А., Белкова Ю.А., Спиридонова Л.В., Шипулин И.А., Томилин К.А., Сорокина М.В., Портнов Ю.А.
Измерения на грани фантастики. Нобелевская премия по физике 2017 года ушла за детекцию гравитационных волн
Как и многие другие истории в физике, о гравитационных волнах начинают рассказывать с Альберта Эйнштейна. Именно он предсказал (хотя поначалу собирался утверждать совершенно обратное!), что массивные, движущиеся с ускорением тела так возмущают ткань пространства-времени вокруг себя, что запускают гравитационные волны, то есть пространство вокруг этих объектов физически сжимается и разжимается, а со временем эти колебания разбегаются по всей Вселенной, как разбегаются круги по воде от брошенного камня.
Как поймать гравитационную волну?
За десятки лет измерений поймать, то есть достоверно зафиксировать гравитационные волны пытались многие физики, но впервые это получилось только 14 сентября 2015 года. Это было измерение на пределе доступной человечеству точности, возможно, самый тонкий эксперимент современной науки. Гравитационная волна, запущенная слиянием двух черных дыр в миллиарде с лишним световых лет от нас привела к тому, что четырехкилометровые плечи гравитационных телескопов коллаборации LIGO (Laser Interferometer Gravitational-Wave Observatory, или лазерно-интерферометрическая гравитационно-волновая обсерватория) сжимались и разжимались на какие-то исчезающие доли от характерных размеров атомов, что было зафиксировано с помощью сверхточной оптики. Событие абсолютно циклопических, вселенских масштабов вызвало на Земле крошечный, еле заметный отзвук.
Так выглядела первая «пойманная» детекторами LIGO гравитационная волна / Иллюстрация: Johan Jarnestad/The Royal Swedish Academy of Sciences«То, что используется для детектирования гравитационных волн сейчас, — это самые последние достижения в сфере лазерной физики и вакуумных технологий и новейшие средства для обработки и расшифровки информации. Действительно, без такого уровня технологий, которые есть сейчас, помыслить два-три десятка лет назад о том, что мы можем детектировать гравитационные волны, было нельзя», — отметил в беседе с корреспондентом портала «Чердак» президент Российской академии наук Александр Сергеев. Его научная группа из Института прикладной физики РАН — одна из участников коллаборации LIGO (вторая российская группа возглавляется Валерием Митрофановым из МГУ).
Неудивительно, что после этого физики из LIGO взяли несколько месяцев на проверку результатов и только 11 февраля 2016 года рассказали миру о своем открытии — почти вековая охота за гравитационными волнами наконец закончилась удачей.
После этого LIGO детектировал еще несколько гравитационных событий. Некоторые из них были отсеяны за недостаточной достоверностью (то есть плечи интерферометров снова начинали колебаться, но такое же поведение в этих случаях можно было объяснить и фоновыми процессами), но в копилку физиков все-таки упало еще целых три события. Гравитационные волны от слияния других черных дыр приходили на Землю еще 25 декабря 2015 года, 4 января 2017 года и 14 августа 2017 года.
О последнем из них сообщили совсем недавно, меньше недели назад. В этот раз гравитационный сигнал был зафиксирован уже с помощью трех установок: вместе с американскими LIGO начал работать гравитационный телескоп европейской коллаборации VIRGO. Гравитационная волна по очереди прошла через каждую из установок, что позволило значительно увеличить точность определения места ее рождения.
Сотрудник LIGO в трубе детектора / Фото: Caltech/MIT/LIGO LabПочему это важно?
Здесь есть два главных аспекта. Первый — фундаментальный. Предсказания гравитационных волн — это важная часть общей теории относительности (ОТО), а потому их экспериментальное обнаружение еще раз подтверждает ОТО.
«Регистрация [гравитационных волн] — это мощнейшее подтверждение фундамента, на котором стоит наука. Люди уверены в общей теории относительности и уверенно с ней работают… Это фундаментальнейшая вещь. Конечно, деваться было некуда, надо было давать премию», — сказал корреспонденту «Чердака» ведущий научный сотрудник Института ядерных исследований РАН и Астрокосмического центра ФИАН Борис Штерн.
Кроме этого, успех с гравитационными волнами косвенно подтверждает многие астрофизические модели. Ведь физики сначала рассчитали, как должны выглядеть гипотетические сигналы от различных гравитационных событий, например того же слияния черных дыр, и только потом получили точно такие же сигналы в наблюдении.
Схематичная демонстрация того, как Солнце и Земля искажают пространство-время (зеленая сетка) / Изображение: T. Pyle/Caltech/MIT/LIGO LabВторой аспект с важностью гравитационных волн чуть менее фундаментальный — он скорей про расширение возможностей человечества. Четыре события за два года — это уже тенденция. По обещаниям физиков, точность гравитационных телескопов дальше будет только повышаться, событий будет фиксироваться только больше, и так мы разглядим наш мир с еще одного, необычного ракурса. К оптическим, рентгеновским, радио- и многим другим телескопам теперь добавляются гравитационные.
С их помощью можно «разглядеть» многие буквально невидимые вещи. Например, слияние тех же самых черных дыр скорей всего не оставляет никаких следов в любых диапазонах электромагнитных волн, и, соответственно, может быть зафиксировано только с помощью гравитационных телескопов.
Что будет дальше?
Тут есть разные прогнозы. Одни рассуждают о новой физике, другие ждут обнаружения реликтовых гравитационных волн, гуляющих по Вселенной с первых моментов ее создания.
«Это только первые гравитационные волны от астрофизических, хотя и очень необычных объектов — черных дыр. А вот теперь все астрофизики будут ждать открытия из тех эпох, когда рождалась наша Вселенная. Кроме гравитационных волн никакие сигналы оттуда не доходят. И то, что мы научились их ловить, — мы открыли канал, которые позволит заглянуть в то время, когда рождалась Вселенная, а может быть, еще и до этого», — рассказал корреспонденту «Чердака» заведующий лабораторией космического мониторинга ГАИШ МГУ Владимир Липунов.
Но самый реалистичный сценарий — это одновременное детектирование гравитационных событий с помощью других телескопов.
Сейчас LIGO и VIRGO уже скидывают координаты событий другим телескопам (например, автоматическим телескопам системы МАСТЕР, которой руководит Липунов), но те пока ни разу не видели никаких «отпечатков» волн в других диапазонах. Поэтому все эти гравитационные события пока остаются в некой степени анонимными — мы знаем, на каком примерно расстоянии от Земли встретились две черные дыры и какова была их масса, но где точно это произошло или что, например, было на месте черных дыр до этого, сказать не можем.
Поэтому физики очень ждут регистрации гравитационных волн от какого-нибудь другого события, например столкновения двух нейтронных звезд, которое должно быть видно и в других диапазонах. По слухам, в конце августа физики даже уже зарегистрировали такой сигнал от двух нейтронных звезд в галактике NGC 4993 в 130 миллионах световых лет от Земли, но пока официального подтверждения этому нет. Но и того, что есть, уже вполне достаточно для одного из самых быстрых вручений Нобелевской премии — после открытия ученые прождали ее меньше двух лет.
И это, кажется, только начало большой научной истории. «Эти три телескопа (имеются в виду два телескопа LIGO и один VIRGO — прим. „Чердака“) сделали еще одно величайшее открытие — вот тут мы уже поучаствовали. Но об этом я сейчас не могу говорить. 16 октября будет пресс-конференция у нас в МГУ и прямая трансляция из Америки», — сказал Липунов (выделение наше — прим. «Чердака»).
Так что — задержите дыхание, пристегните ремни. Кажется, на вручении Нобелевской премии история с охотой на гравитационные волны еще не заканчивается.
Михаил Петров
Что такое «сигма»? • Физика элементарных частиц • LHC на «Элементах»
Сигмой (σ) в статистическом анализе обозначают стандартное отклонение. Опуская тонкости, которые будут обсуждены ниже, можно сказать, что стандартное отклонение — это та погрешность, то «± сколько-то», которым обязательно сопровождают измерение величины. Если вы измерили массу предмета и получили результат 100 ± 5 грамм, то величина «110 грамм» отличается от измеренного результата на два стандартных отклонения (то есть на 2 сигмы), величина «50 грамм» отличается на 10 стандартных отклонений (на 10 сигм).
Зачем всё это нужно: сигмы и вероятности
При обсуждении погрешностей мы уже говорили, что фраза «измеренная масса равна 100 ± 5 грамм» вовсе не означает, что истинная масса гарантированно лежит в интервале от 95 до 105 грамм. Она может оказаться и за пределами этого интервала «± 1σ», но, как правило, недалеко. В небольшом проценте случаев может даже случиться, что она выходит за пределы интервала «± 2σ», и уж совсем редко она оказывается за пределами «± 3σ». В общем, тенденция ясна: количество сигм связано с вероятностью того, что истинное значение будет настолько отличаться от измеренного.
Пропустим все математические подробности и покажем результат для самого простого и распространенного случая, который называется «нормальное распределение» (см. рисунок). Вероятность попасть в интервал ± 1σ — примерно 68%, в интервал ± 2σ — примерно 95%, в интервал ± 3σ — примерно 99,8%, и т. д. Итак, можно сформулировать некую договоренность:
Договоренность: выражение какого-то отличия в количестве сигм — это сообщение о том, какова вероятность, что такое или еще более сильное отличие могло произойти за счет случайного стечения обстоятельств при измерении.
Использовать эту договоренность можно разными способами. Если вы просто сообщаете результат измерения (100 ± 5 грамм) и уверены в том, что нормальное распределение применимо, то вы можете сказать, что истинное значение массы с вероятностью 68% лежит в этом интервале, с вероятностью 95% лежит в интервале от 90 до 110 грамм, и т. д.
Вы можете также сравнивать результат вашего измерения с чужим измерением той же самой величины или с теоретическими расчетами. Вы видите, что числа отличаются, и хотите понять, имеете ли вы право утверждать, что между двумя результатами есть статистически значимое расхождение — то есть несогласие, которое нельзя списать на случайную статистическую флуктуацию в данных. Тогда утверждения звучат так:
- Если отличие составляет меньше 1σ, то вероятность того, что два числа согласуются друг с другом, больше 32%. В таком случае просто говорят, что два результата совпадают в пределах погрешностей.
- Если отличие составляет меньше 3σ, то вероятность того, что два числа согласуются друг с другом, больше 0,2%. В физике элементарных частиц такой вероятности недостаточно для каких-либо серьезных выводов, и принято говорить: различие между двумя результатами не является статистически значимым.
- Если отличие от 3σ до 5σ, то это повод подозревать что-то серьезное. Впрочем, даже в этом случае физики говорят осторожно: данные указывают на существование различия между двумя результатами.
- И только если два результата отличаются на 5σ или больше, физики четко заявляют: два результата отличаются друг от друга.
Эти выражения особенно стандартны, когда речь идет о поиске новой частицы. Вы сравниваете экспериментальные данные с теоретическим предсказанием, сделанным без новой частицы, и, если видите отличие от 3 до 5 сигм, вы говорите: получено указание на существование новой частицы (по-английски, evidence). Если же отличие превышает 5 сигм, вы говорите: мы открыли новую частицу (discovery).
«Уверенность» против «статистической значимости»
Заметьте, что в приведенных выше примерах нас интересовали вопросы, на которые можно ответить «да» или «нет». Проступает ли в полученных данных какая-то новая частица? Согласуется ли распределение по импульсу с теоретическими расчетами? Зависит ли сечение процесса от энергии столкновений? Совпадает ли масса у частицы и ее античастицы? Попытка ответить на эти вопросы с помощью данных называется на научном языке проверкой гипотез. Вопросы, которые требуют развернутого ответа (подсчитать что-то, объяснить что-то и т. п.), гипотезами не называются.
В простейшем приближении результат экспериментальной проверки гипотезы выглядит так: ответ «да» с вероятностью p и ответ «нет» с вероятностью 1 – p. Эти вероятности очень важны для сообщения результата; физики обычно избегают абсолютных утверждений («мы открыли» или «мы опровергли») без указания вероятностей.
Но тут сразу же надо сделать важное уточнение. Если его четко осознать, то станет понятным, почему такие стандартные для научно-популярных новостей фразы, как «Ученые на 99% уверены, что открыли что-то новое», — обманчивы.
Точная формулировка, которую обычно используют ученые, такова:
При проверке гипотезы получен ответ «да» на уровне статистической значимости p.
При этом величина p часто выражается в виде количества сигм. В англоязычной литературе используется словосочетание confidence level, CL (доверительный уровень). В русскоязычной еще иногда говорят «статистическая достоверность», но такое выражение может привести к путанице в понимании.
Отличие «популярной» фразы от истинного утверждения вот в чём. Во всяком измерении есть не только статистические, но и систематические погрешности. Описанные выше правила связи вероятностей и количества сигм работают только для статистических погрешностей — и то если к ним применимо нормальное распределение. Если статистические погрешности всегда можно обсчитать аккуратно, то систематические погрешности — это немножко искусство. Более того, из многолетнего опыта известно, что сильные систематические отклонения уж точно не описываются нормальным распределением, и потому для них эти правила пересчета не справедливы. Так что даже если экспериментаторы всё перепроверили много раз и указали систематическую погрешность, всегда остается риск, что они что-то упустили из виду. Корректно оценить этот риск невозможно, поэтому вы на самом деле не знаете, с какой истинной вероятностью ваш ответ верен.
Конечно, по умолчанию систематическим погрешностям стоит доверять, особенно если они исходят от опытных экспериментальных групп. Но вековой опыт изучения элементарных частиц показывает, что несмотря на все предосторожности регулярно случаются проколы. Бывает, что коллаборация получает результат, сильно противоречащий какой-то гипотезе, перепроверяет анализ много раз и никаких ошибок у себя не находит. Однако этот результат затем не подтверждается другими — порой намного более точными! — экспериментами. Почему первый эксперимент дал такой странный результат, что в нём было не то, где там ошибка или неучтенная погрешность — всё это зачастую так и остается непонятым (впрочем, иногда источник ошибки быстро вскрывается, как это случилось со «сверхсветовыми» нейтрино в эксперименте OPERA).
Физики к таким оборотам событий уже привыкли, поэтому каждый экспериментальный результат, сильно отличающийся от всей сложившейся к тому времени картины, вызывает оправданный скепсис. Физики так консервативны в своем отношении вовсе не потому, что они ретрограды и намертво уверовали в какую-то одну теорию, как это хотят представить опровергатели физики. Они просто научены всем предыдущим опытом в физике частиц и знают, чем это обычно кончается. Поэтому без независимого подтверждения другими экспериментами подобные сенсации они не поддерживают.
ФЭЧ в сравнении с другими науками
Надо сказать, что сформулированные выше жесткие критерии статистической достоверности характерны именно для физики элементарных частиц и некоторых смежных разделов. Во многих других разделах физики, а тем более в других дисциплинах (в особенности, в биомедицинских науках) критерии намного слабее.
Предположим, вы измерили некие данные и хотите узнать, какова вероятность того, что они «вписываются в норму». Вы проводите статистический тест, который дает вам вероятность того, что «нормальная ситуация» без какого-либо реального отклонения только за счет статистической флуктуации даст вот такое или еще более сильное отклонение. Эта вероятность называется p-значение. В биологии пороговое p-значение, ниже которого уже уверенно говорят про реальное отличие, составляет один или даже несколько процентов. В физике элементарных частиц такое отличие вообще не считают значимым, тут нет даже «указания на существование» какого-то отличия! Ответственное заявление об отличии звучит в ФЭЧ только для p-значений меньше одной двухмиллионной (то есть отклонение больше 5σ). Такой жесткий подход к достоверности утверждений выработался в ФЭЧ примерно полвека назад, в эпоху, когда экспериментаторы видели много отклонений со значимостью в районе 3σ и смело заявляли об открытии новых частиц, хотя потом эти «открытия» не подтверждались. Подробный рассказ об истоках этого критерия см. в постах Tommaso Dorigo (часть 1, часть 2).
Обзор учебника по физике 7 класс Перышкина И.М.
Об авторах
Это пособие написали четыре автора: И.М. Пёрышкин, А.И. Иванов, Е.М. Гутник и М.А. Петрова. Они взяли за основу классическую «Физику» А.В. Пёрышкина и Е.М. Гутника, но дополнили заданиями к ОГЭ и ВПР, новой информацией о достижениях физики, материалами для дополнительного чтения и задачами для коллективной работы и развития функциональной грамотности. Коллектив авторов новый, но редакторы прежние.
Обзор тем
В 7 классе дети знакомятся с:
- методом научного познания;
- явлениями физики;
- основными понятиями;
- измерением величины;
- лабораторными экспериментами.
В учебнике отдельные явления и законы рассматриваются в общей системе науки. Например, информация о строении вещества в седьмом классе помогает изучать массу, плотность, давление газа, закон Паскаля и изменения атмосферного давления.
Главы учебника и их основное содержание
- Введение: роль физики в познании окружающего мира, экскурс в историю развития наук о природе.
- Первоначальные сведения о строении вещества: молекула, диффузия, опыты.
- Взаимодействие тел: механическое движение, скорость, векторы, ускорение, инерция, зависимость силы тяжести от массы тела, динамометр.
- Давление твёрдых тел, жидкостей и газов: формулы, единицы измерения, причины возникновения, различие между телами, атмосферное давление, манометр.
- Работа и мощность. Энергия: механическая работа, мощность, единицы измерения, рычаг, наклонная плоскость, момент силы, центр тяжести, «золотое правило» механики, потенциальная энергия.
В учебнике два вида текстов: основной и дополнительный. Оба помогают ребёнку понять суть явлений и проследить взаимосвязь с другими науками. Задания в конце каждого параграфа предлагается либо осмыслить самостоятельно, либо обсудить в группах. Также есть раздел «Это любопытно», который знакомит с интересными фактами.
Преимущества и недостатки
Плюсы:
- Текст легко читается, материал изложен доступно.
- Законы физики и механизм работы разных явлений объясняются с помощью аналогий.
- Есть много примеров и вариантов применения законов физики в окружающем мире, описания опытов с рисунками и информации об исторических открытиях.
- В учебнике есть не только текст, но и графики и таблицы.
- Вопросы вида «Обсудим?», которые часто встречаются в контрольных и ОГЭ.
- После каждого параграфа есть примеры решения задач с оформлением и подробными рассуждениями.
- В конце учебника находится сборник задач.
- Уделено особое внимание работе с измерениями физических величин.
- Лабораторные работы даются с подробной инструкцией. Можно записывать результаты измерений с погрешностью.
- В перспективе ОГЭ по физике будет включать задания на самостоятельное планирование эксперимента. Это принципиально новое задание. В учебнике вместе с базовыми лабораторными работами введены те, что помогут сформировать этот навык.
Минусы:
- В конце параграфа не подводятся итоги: ребёнку самостоятельно придётся работать с текстом, в котором не всегда выделены важные моменты.
- Учебник перегружен информацией.
- Нужна помощь взрослого, чтобы понять текст.
Спорный момент: у учебника нет решебника. С одной стороны, это помогает самостоятельно и системно подходить к изучению физики, но с другой — невозможно проверить решение.
Обзор программы ЭДШ по физике в 7 классе
В домашней школе «Фоксфорда» физику в седьмом классе изучают по учебнику И. М. Пёрышкина. Курс даёт расширенные знания о строении веществ, взаимодействии тел, гидростатики и энергии. Формирует умение работать с данными исследований и измерений, знакомит с достижениями и дальнейшим развитием физики.
Что такое измерение в физике
Что такое измерение в физикеИзмерение — это процесс определения длины, размера или количества вещества. С давних времен люди использовали несколько способов измерения длины. Физическая величина (например, длина) должна измеряться относительно некоторой фиксированной величины. Фиксированная величина, относительно которой измеряется физическая величина, называется единицей. Единица используется как эталон измерения.Раньше люди использовали разные части тела, такие как размах рук, локоть и сажень, для измерения длины.
Фут, темп и ярд — это некоторые другие единицы длины, основанные на частях тела. Однако эти устройства ненадежны, поскольку длина частей тела варьируется от человека к человеку. Таким образом, люди осознали необходимость
Стандартные единицы измеренияСтандартные единицы измерения Единицы, которые имеют фиксированное количество и не меняются от человека к человеку и от места к месту, называются стандартными единицами.Например, метрическая система, созданная французами в 1790 году, представляет собой стандартный набор единиц.
Принятие стандартных единиц измерения не решает проблемы. Люди в разных странах могут использовать разные наборы стандартных единиц измерения. Ради единообразия ученые всего мира приняли единый набор единиц. Эта система называется Международной системой единиц или единицей СИ. Принятие единиц СИ в 1960 году облегчило ученым из разных стран обмен друг с другом своими результатами.
Единица измерения длины в системе СИ — метр. Некоторые общепринятые стандартные единицы длины — это дюйм, миллиметр, сантиметр и километр.
В зависимости от размера объекта, который нам нужно измерить, мы должны выбрать подходящую единицу измерения. Например, мы используем метры для измерения длины куска ткани, километры для измерения расстояния от одного места до другого, миллиметры для измерения толщины волос и так далее. Сантиметр (см) и миллиметр (мм) используются для измерения более коротких расстояний, а километры (км) используются для измерения более длинных расстояний.
Один километр делится на 1000 равных участков, каждое из которых называется метром. Один метр делится на 100 равных частей, каждая из которых называется сантиметром, который снова делится на равные части. Каждое деление называется миллиметром.
Обычно используемые единицы длины:
10 миллиметров = 1 сантиметр (см)
100 сантиметров = 1 метр (м)
1000 метров = 1 километр (км)
Единицу измерения можно преобразовать в другую. Вот пример.
Пример 1: Раджу и его друг Ахил живут на расстоянии 2000 м друг от друга.Выразите расстояние между домами в километрах (км).
Решение: Мы знаем, что 1000 м = 1 км
Следовательно, 2000 м = 2 км
Следовательно, расстояние между двумя домами составляет 2 км.
Физические измерения и единицы измерения СИ
HelpYouBetter »Физика» Единицы и измерения »Физические измерения и единицы измерения СИПожалуйста, прочтите эту статью, которая даст вам более простое описание необходимости измерения, основных величин и производные величины, система единиц, единицы измерения СИ, преимущества и определения единиц СИ и т. д.подробно.
Важность измерения в физике:
Столкнувшись с такими вопросами, как расстояние от Солнца до Земли, какова скорость света, какова масса электрона, каждый понимает важность измерения. С самых древних времен человек начал измерять различные физические величины общепринятыми методами. Его шаги использовались для измерения длины, а тень от солнца — для измерения времени. Но по мере развития науки эти типы измерений становились неадекватными.Он ввел точные и четко определенные методы измерения различных физических величин, благодаря которым он достиг совершенства в измерениях.
Измерение означает, что действие по измерению чего-либо или измерение определяется как процесс определения значения неизвестной величины путем сравнения ее с некоторым заранее определенным стандартом.
Что такое единица в физике?
Любая величина, которую можно измерить, называется физической величиной. Измерение физической величины всегда включает сравнение измеряемой величины с эталоном того же типа.Этот эталонный стандарт, используемый для сравнения, называется единицей физической величины.
Стандартная единица измерения измерения определяется как единица измерения, имеющая фиксированное значение, которое не меняется от человека к человеку или от места к месту. Например, «секунда» — это стандартная единица измерения времени. Независимо от того, используется ли секунда тем или иным человеком, используется ли вторая в той или иной стране, она всегда представляет собой «одинаковую продолжительность времени».Продолжительность секунды не меняется от человека к человеку или от места к месту. Фактически, куда бы мы ни пошли в мире, секунда имеет фиксированную продолжительность времени, которая никогда не меняется. Таким образом, «секунда» означает «одинаковую продолжительность» для всех. Итак, секунда — это стандартная единица измерения времени. Для единообразия измерений необходимо иметь стандартные единицы измерения.
Характеристики стандартной единицы
Желательные характеристики стандартной единицы:
- Единица должна быть четко определена.
- Он должен быть очень точным.
- Он должен легко воспроизводиться.
- Устройство должно оставаться неизменным независимо от места, времени и физических условий.
- Он должен быть легко сопоставим с другими аналогичными устройствами.
Разница между фундаментальными и производными величинами
Существуют определенные физические величины, которые нельзя объяснить в терминах других физических величин. Они называются фундаментальными величинами . Это длина, масса, время, электрический ток, температура, сила света и количество вещества.Единицы, используемые для измерения основных величин, называются основных единиц или основных единиц ; то есть основными единицами измерения являются единицы длины, массы, времени, электрического тока, температуры, силы света и количества вещества.
Количества, производные от основных величин, называются производными величинами . например объем, скорость и т. Д. Единицы производных величин называются производными единицами и вычитаются из основных единиц.например единицы плотности, скорости, силы, работы и т.д. производная единица.
Итак, вкратце, мы можем записать разницу между фундаментальными и производными величинами как:
- Фундаментальные величины — это базовые величины системы единиц, которые не зависят от других физических величин.
- Производные количества — это количества, производные от основных величин.
Другая система единиц
Система единиц — это набор связанных единиц, включая как основные, так и производные единицы, которые используются для вычислений. Некоторые единицы существуют более чем в одной системе единиц.
Для измерения физических величин используются следующие системы единиц:
C.G.S Unit
C.Система единиц G.S. (Сантиметр, Грамм, Вторая система) — французская система. Эта система имеет дело только с тремя основными единицами измерения — сантиметром, граммом и секундой для длины, массы и времени соответственно.
F.P.S Unit
F.P.S. Система единиц (фут, фунт, секунда) — британская система. Эта система имеет дело только с тремя основными единицами измерения длины, массы и времени — футом, фунтом и секундами.
M.K.S Единицы
M.К.С. Система единиц (Метр, Килограмм, Вторая система) была создана во Франции. Эта система также имеет дело с тремя основными единицами измерения — метр, килограмм и секунда для длины, массы и времени соответственно. Эта система также называется метрической системой единиц и тесно связана с системой единиц C.G.S.
Единицы измерения СИ
Система измерения, принятая в настоящее время на международном уровне, — это система, предложенная Одиннадцатой Генеральной конференцией мер и весов, состоявшейся в 1960 году во Франции, и известная как Международная система объединений или Международная система мер. Единицы сокращенно обозначаются как единицы измерения СИ.
Согласно этой системе существует семь основных или основных единиц и три дополнительных единицы. Основные единицы:- метр (м) для длины,
- килограмм (кг) для массы,
- секунды (с) для времени,
- Кельвина (K) для температуры,
- ампер (А) для электрического тока,
- кандела (кд) для силы света и
- моль (моль) для количества вещества.
Дополнительные единицы:
- радиан (рад) для угла,
- стерадиан (ср) для телесного угла,
- беккерель (Бк) для радиоактивности.
Список единиц СИ
Список единиц СИ для основных и дополнительных величин и символы, используемые для их представления, упомянуты в таблице ниже.
| Sl. Номер | Физическое количество | Единица | Обозначение единицы | ||||
| 1. | Длина | Метр | м | ||||
| 2. | Масса | Килограмм | кг | ||||
| 3. | Время | Секунда | с | ||||
| 4. | Температура | Кельвин | K | Ампер | A | ||
| 6. | Сила света | Кандела | кд | ||||
| 7. | Количество вещества | Моль | моль | Основные величины и их единицы в системе СИ||||
| Sl.Номер | Физическая величина | Единица | Символ для агрегата |
| 1. | Угол | Радиан | рад | сплошной | sr |
| 3. | Радиоактивность | Беккерель | Бк |
Список единиц СИ 2: Дополнительные величины и их единицы СИ
Список единиц СИ для некоторых производных величин и символов, используемых для представляют их приведены ниже.
| Sl. Номер | Физическая величина | Единица | Символ для единицы | ||||
| 1. | Площадь | Квадратный метр | м 2 | Объем | Кубический метр | м 3 | |
| 3. | Плотность | килограмм на кубический метр | кг / м 3 | ||||
| 4. | Скорость | метров в секунду | м / с | ||||
| 5. | Ускорение | метров в секунду в квадрате | м / с 2 | ||||
| 6. | N | ||||||
| 7. | Работа, энергия | Джоуль | Дж | ||||
| 8. | Мощность | Вт | Вт | ||||
| 9. | Давление | Н / м 2 | |||||
| 10. | Поверхностное натяжение | Ньютон на метр | Н / м | ||||
| 11. | Крутящий момент | Ньютон-метр | Нм | ||||
| 12. | Электрический заряд | Coulomb 13. | Электрический потенциал | Вольт | В | ||
| 14. | Электрическое сопротивление | Ом | Ом | ||||
| 15. | Магнитная индукция | Tesla | Световой поток | Люмен | лм |
Список единиц СИ 3: Некоторые производные единицы СИ
Единицы СИ и размерные формулы для более чем 100 физических величин написаны в моей предыдущей статье о размерах и размерный анализ физических величин.
Преимущества единиц СИ
Система единиц СИ имеет несколько явных преимуществ перед всеми другими используемыми системами. Основные преимущества единиц СИ:
- единиц СИ проще, чем все остальные системы единиц.
- Система единиц СИ является всеобъемлющей. , то есть , семь базовых единиц системы СИ охватывают все отрасли науки, техники и технологий.
- СИ — рациональная система единиц. , то есть , эта система использует одну единицу для одной физической величины.
- Система единиц СИ согласована. , то есть Все производные единицы могут быть легко получены из основных и дополнительных единиц путем их умножения или деления.
- Основные единицы СИ удовлетворяют всем характеристикам, которыми должна обладать единица.
- Система единиц СИ — это метрическая система. , т. Е. кратные и подкратные единицы могут быть легко выражены как степени 10.
- единиц СИ являются международно признанными.
Определения единиц СИ
Определения основных единиц СИ приведены ниже:
Определение метра
Метр (м) — это единица длины. Счетчик определяется как длина, равная 1 650 763,73 длин волн оранжево-красного света, излучаемого атомом Криптона-86 в электрическом разряде.С 1983 года стандартный метр определяется как длина пути, пройденного светом в вакууме за секунду.
Определение килограмма
Килограмм (кг) — это единица измерения массы. Килограмм определяется как масса платино-иридиевого цилиндра, хранящегося в Международном бюро мер и весов в Севре во Франции.
Секунда определения
Секунда (с) — единица времени. Второй определяется как время, необходимое для 9 192 631 770 циклов излучения, которое вызывает переход атомов цезия – 133 между двумя указанными более низкими энергетическими полосами.
Определение Кельвина
Кельвин (К) — единица измерения температуры. Кельвин определяется как термодинамическая температура тройной точки воды (тройная точка — это температура, при которой сосуществуют три состояния воды, то есть лед, вода и водяной пар).
Определение ампер
Ампер (А) — это единица измерения электрического тока. Ампер — это тот постоянный ток, который, если его поддерживать в двух прямых параллельных проводниках бесконечной длины и с ничтожно малой площадью поперечного сечения и помещать на расстоянии одного метра в вакууме, создавал бы силу 2 x 10 -7 Ньютон / метр между ними. .
Определение канделы
Кандела (кд) — единица силы света. Кандела определяется как сила света в направлении, перпендикулярном поверхности квадратного метра площади черного тела, сохраняемой при температуре замерзания платины под давлением 101,325 Н / м 2 .
Определение моля
Моль (моль) — это единица измерения количества вещества. Моль — это количество вещества, которое содержит столько элементарных единиц, сколько атомов углерода ровно в 0.012 кг углерода-12.
Определения дополнительных единиц СИ приведены ниже:
Определение беккереля
Беккерель (Бк) — это единица измерения радиоактивности. Беккерель определяется как количество радиоактивного вещества, которое разрушается один раз в секунду. Ранее единицей радиоактивности была кюри.
Итак, позвольте мне завершить эту тему, задав один вопрос;
Зачем нужны стандартные единицы измерения?
Стандартные единицы измерения необходимы, потому что отсутствие стандартной единицы измерения приведет к путанице и потере времени при постоянном преобразовании одной единицы в другую.Итак, ради единообразия, ученые со всего мира приняли систему единиц измерения СИ в качестве стандартной системы единиц измерения, и теперь СИ используется в качестве официальной системы измерения почти во всех странах мира, кроме США. Штаты, Мьянма и Либерия.
Итак, это все об основах измерения в физике и единицах измерения СИ. Если вы хотите узнать больше об измерениях, подумайте о прочтении других моих статей по теме о различных ошибках, возникающих при измерениях, размерах, размерных формулах и размерном анализе физических величин, различных диаграммах, используемых для измерения и т. Д.
Надеюсь, вам понравилось читать эту статью об измерениях в физике, и если вы считаете, что я что-то упустил или у вас есть какие-либо предложения, дайте мне знать в комментариях.
Также, если вы найдете эту статью полезной, не забудьте поделиться ею на Facebook.
1: Единицы и измерения — Physics LibreTexts
- Последнее обновление
- Сохранить как PDF
- Авторы и авторства
На эскизе изображена галактика Водоворот, которую мы исследуем в первом разделе этой главы.Галактики столь же огромны, как атомы малы, но одни и те же законы физики описывают и то, и другое вместе со всей остальной природой, что свидетельствует о единстве, лежащем в основе Вселенной. Законов физики на удивление мало, что подразумевает лежащую в основе простоту кажущуюся сложность природы. Из этого текста вы узнаете о законах физики. Может показаться, что галактики и атомы далеки от вашей повседневной жизни, но когда вы начнете исследовать этот обширный предмет, вы скоро поймете, что физика играет в вашей жизни гораздо большую роль, чем вы думали вначале, независимо от ваших жизненных целей. или выбор карьеры.
- 1.1: Введение в единицы измерения и измерения
- Законов физики на удивление мало, что подразумевает лежащую в основе простоту кажущуюся сложность природы. Из этого текста вы узнаете о законах физики. Может показаться, что галактики и атомы далеки от вашей повседневной жизни, но когда вы начнете исследовать этот обширный предмет, вы скоро поймете, что физика играет в вашей жизни гораздо большую роль, чем вы думали вначале, независимо от ваших жизненных целей. или выбор карьеры.
- 1.2: Объем и масштаб физики
- Физика — это попытка найти простые законы, описывающие все природные явления. Он работает в широком диапазоне масштабов, включая длину, массу и время. Ученые пытаются описать мир, формулируя модели, теории и законы. Они используют порядки величин для отслеживания и сравнения явлений, происходящих в определенных масштабах.
- 1.3: Единицы и стандарты
- Системы единиц состоят из небольшого числа основных единиц, которые определяются путем точных и точных измерений традиционно выбранных основных величин.Две обычно используемые системы единиц — это английские единицы и единицы СИ. Единицы СИ — это метрическая система единиц, то есть значения могут быть рассчитаны с коэффициентом 10. Базовыми единицами измерения длины, массы и времени СИ являются метр (м), килограмм (кг) и секунда (с), соответственно.
- 1.4: Преобразование единиц
- Умножение на коэффициенты преобразования позволяет количествам изменять единицы. Операция должна быть выполнена таким образом, чтобы единицы, от которых вы хотите избавиться, были отменены, а единицы, которые вы хотите получить, остались.Единицы подчиняются правилам алгебры, поэтому, например, если единица возведена в квадрат, необходимы два множителя, чтобы отменить ее.
- 1.5: Анализ измерений
- Размерность физической величины — это просто выражение основных величин, из которых она получена. Все уравнения, выражающие физические законы или принципы, должны быть согласованными по размерам. Этот факт можно использовать как помощь в запоминании физических законов, как способ проверить, возможны ли заявленные отношения между физическими величинами, и даже вывести новые физические законы.
- 1.6: Оценки и расчеты Ферми
- Оценка — это приблизительное обоснованное предположение о значении физической величины, основанное на предыдущем опыте и здравых физических соображениях. Вот некоторые стратегии, которые могут помочь при оценке: 1) Получите большую длину из меньшей длины. 2) Получите площади и объемы из длин. 3) Получите массы из объемов и плотностей. 4) Если ничего не помогает, свяжите его. Один «сиг. Инжир.» Это хорошо. 5) Спросите себя: есть ли в этом смысл?
- 1.7: Значимые цифры
- Точность измеренного значения означает, насколько близко результат измерения к принятому эталонному значению. Точность измеренных значений означает, насколько близко согласие между повторными измерениями. Значительные цифры выражают точность измерительного инструмента. При выполнении математических операций с измеренными значениями существуют правила стандартизации точности окончательного ответа.
- 1.8: Решение задач в физике
- Три этапа процесса решения физических задач, используемых в этой текстовой карте, следующие: 1) Стратегия: определение задействованных физических принципов и разработка стратегии их использования для их решения. решать проблему.2) Решение: выполните математические вычисления, необходимые для получения численного решения с правильными единицами измерения. 3) Значимость: проверьте решение, чтобы убедиться, что оно имеет смысл, и оцените его значимость.
- 1.A: Единицы и измерения (ответы)
- 1.E: Единицы измерения (упражнения)
- 1.S: Единицы и измерения (Сводка)
Миниатюра. На этом изображении может отображаться любое количество объектов.Это может быть водоворот в резервуаре с водой или коллаж из красок и блестящих бусинок, сделанный для художественного класса. Не зная размера объекта в единицах, которые мы все узнаем, таких как метры или дюймы, трудно понять, на что мы смотрим. Фактически, это изображение показывает галактику Водоворот (и сопутствующую ей галактику), диаметр которой составляет около 60 000 световых лет (около 6 × 10 17 км в поперечнике). (Источник: С. Беквит (STScI) Группа наследия Хаббла, (STScI / AURA), ЕКА, НАСА)
Авторы и авторство
Сэмюэл Дж.Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами. Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
Измерение в науке (Стэнфордская энциклопедия философии)
Современные философские дискуссии об измерении — начиная с с конца девятнадцатого века до наших дней — можно разделить по нескольким направлениям обучения.Эти пряди отражают разные взгляды на природу измерения и условия, которые делают измерение возможно и надежно. Основные нити математические теории измерения, операционализм, конвенционализм, реализм, теоретико-информационные счета и счета на основе моделей. Эти пряди стипендий, по большей части, не составляют непосредственно конкурирующие взгляды. Вместо этого их лучше всего понимать как выделение различные и дополнительные аспекты измерения. Ниже приводится очень приблизительный обзор этих перспектив:
- Математические теории измерение рассматривать измерение как отображение качественного эмпирические отношения к отношениям между числами (или другими математическими сущностей).
- Операционалисты и конвенционалисты просмотр измерение как набор операций, формирующих смысл и / или регулировать использование количественного термина.
- Реалисты рассматривают измерение как оценку независимые от разума свойства и / или отношения.
- Теоретико-информационные счета Просмотр измерений как сбор и интерпретация информации о система.
- Счета на основе моделей рассматривают измерения как согласованное присвоение значений параметрам в теоретической и / или статистическая модель процесса.
Эти точки зрения в принципе согласуются друг с другом. В то время как математические теории измерения имеют дело с математическими основы измерительных шкал, операционализм и конвенционализм в первую очередь связаны с семантикой количественных терминов, реализмом занимается метафизическим статусом измеримых величин, теоретико-информационные и модельные счета связаны с эпистемологические аспекты измерения. Тем не менее, предмет домен не так аккуратно разделен, как предполагает приведенный выше список.Проблемы по метафизике, эпистемологии, семантике и математике основы измерения взаимосвязаны и часто опираются на одну Другая. Отсюда, например, операционалисты и конвенционалисты часто придерживался антиреалистических взглядов, а сторонники модельного счета выступили против преобладающей эмпирической интерпретации математических теорий измерения. Эти тонкости станут ясно в следующем обсуждении.
Список направлений стипендии не является исчерпывающим и неисключительным. исчерпывающий.Он отражает историческую траекторию философского обсуждение до сих пор, а не какое-либо принципиальное различие между разные уровни анализа измерений. Некоторые философские труды по замерам относятся к более чем одной нити, в то время как многие другие работы тоже не подходят прямо. Это особенно актуально, поскольку начале 2000-х, когда измерение вернулось на первый план философская дискуссия после нескольких десятилетий относительного пренебрежения. Эту недавнюю стипендию иногда называют « эпистемология измерения », и включает в себя богатый набор работ которые еще нельзя разделить на отдельные школы мысли.В последний раздел этой записи будет посвящен обзору некоторых из эти события.
Хотя философия измерения сформировалась как отдельная область исследование только во второй половине девятнадцатого века, фундаментальные концепции измерения, такие как величина и количество обсуждаются с древних времен. Согласно Евклиду Элементы , величина — например, линия, поверхность или твердый — измеряет другое, когда последнее является целым кратным первое (Книга V, опр.1 и 2). Две величины имеют общую измерять, когда они оба целые кратные некоторой величины, и несоизмеримым в противном случае (Книга X, определение 1). Открытие несоизмеримые величины позволили Евклиду и его современникам развивать понятие отношения величин. Соотношения могут быть либо рациональным, либо иррациональным, поэтому понятие отношения более общий, чем мера (Michell 2003, 2004a; Grattan-Guinness 1996).
Аристотель различал количество и качество.Примеры количества — это числа, линии, поверхности, тела, время и место, а примерами качеств являются справедливость, здоровье, горячность и бледность ( Категории §6 и §8). В соответствии с Аристотеля, количества допускают равенство и неравенство, но не допускают градусов, так как «одна вещь не более четырех футов, чем другая» (Там же 6.6a19). Качества, наоборот, не допускают равенства или неравенство, но допускают степени, «потому что одно называется более бледный или менее бледный, чем другой »(там же 8.10b26).Аристотель не уточняет, являются ли степени таких качеств, как бледность соответствуют различным качествам или одинаковому качеству, бледность, была способна к разной интенсивности. Эта тема была на центр продолжающихся дебатов в тринадцатом и четырнадцатом веках (Юнг 2011). Дунс Скот поддержал «теорию сложения», согласно которому изменение степени качества может быть объясняется сложением или вычитанием меньших степеней этого качество (2011: 553). Позднее эта теория была уточнена Николь Орем, которые использовали геометрические фигуры для представления изменений интенсивности такие качества, как скорость (Clagett 1968; Sylla 1971).Oresme’s геометрические представления установили подмножество качеств, которые поддаются количественной обработке, что ставит под сомнение строгая аристотелевская дихотомия количества и качества. Эти развития сделали возможным формулировку количественных законов движение в течение шестнадцатого и семнадцатого веков (Грант 1996).
Концепция качественной интенсивности была развита Лейбницем. и Канта. «Принцип непрерывности» Лейбница заявил что все естественные изменения происходят постепенно.Лейбниц утверждал, что этот принцип применим не только к изменениям в расширенных величинах, таких как длины и продолжительности, но также и интенсивности репрезентативных состояния сознания, такие как звуки (Jorgensen 2009; Diehl 2012). Считается, что Кант опирался на принцип Лейбница преемственности, чтобы сформулировать его различие между экстенсивным и интенсивные величины. Согласно Канту, экстенсивные величины те, «в которых представление частей делает возможным представление целого »(1787: A162 / B203).Пример это длина: линия может быть мысленно представлена только последовательным синтез, в котором части линии соединяются, образуя целое. Для Канта возможность такого синтеза обосновывалась в формах интуиция, а именно пространство и время. Интенсивные величины, такие как тепло или цвета, также бывают в непрерывной степени, но их восприятие требует место в мгновение ока, а не через последовательный синтез части. Степени интенсивных величин «могут быть только представлен через приближение к отрицанию »(1787: A 168 / B210), то есть представляя их постепенное уменьшение до тех пор, пока полное отсутствие.
Научные разработки девятнадцатого века бросили вызов различие между экстенсивными и интенсивными величинами. Термодинамика и волновая оптика показала, что разница в температуре и оттенке соответствовали различиям в пространственно-временных величинах, таких как скорость и длина волны. Электрические величины, такие как сопротивление и было показано, что проводимость может складываться и делиться, несмотря на не является обширным в кантовском смысле, т.е. не синтезируется из пространственные или временные части.Более того, ранние эксперименты в психофизики предположили, что интенсивности ощущений, такие как яркость и громкость можно представить как сумму «всего заметные различия »между стимулами и, следовательно, могут быть мыслится как состоящие из частей (см. Раздел 3.3). Эти результаты, наряду с достижениями в аксиоматизации ветвей математики, мотивировала некоторых из ведущих ученых конца девятнадцатого века, чтобы попытаться прояснить математические основы измерения (Максвелл 1873; фон Крис 1882; Гельмгольц 1887; Мах 1896; Poincaré 1898; Hölder 1901; для исторических обзоров см. Darrigol 2003; Michell 1993, 2003; Канту и Шлаудт 2013; Бьяджоли 2016: гл.4, 2018). Эти работы сегодня рассматриваются как предшественники научной стипендии, известной как «измерение теория ».
Математические теории измерения (часто называемые собирательно как «теория измерения») относятся к условиям при какие отношения между числами (и другими математическими объектами) могут быть используется для выражения отношений между объекты. [2] Чтобы понять необходимость математических теорий измерения, примите во внимание тот факт, что отношения, выставленные числа, такие как равенство, сумма, разница и соотношение, не всегда соответствуют отношениям между объектами, измеряемыми этими числа.Например, 60 — это дважды 30, но можно ошибиться в думая, что объект, измеренный при 60 градусах Цельсия, в два раза горячее как объект при 30 градусах Цельсия. Это потому, что нулевая точка шкала Цельсия произвольна и не соответствует отсутствию из температура. [3] Точно так же числовые интервалы не всегда несут эмпирические данные. Информация. Когда испытуемых просят оценить по шкале от 1 до 7 насколько сильно они согласны с данным утверждением, прима нет facie причина думать, что интервалы между 5 и 6 и от 6 до 7 соответствует равному приросту силы мнения.В качестве третьего примера: равенство чисел транзитивно [если (a = b & b = c), затем a = c], но эмпирические сравнения физических величины обнаруживают лишь приблизительное равенство, которое не является переходным связь. Эти примеры показывают, что не все математические отношения между числами, используемыми в измерениях, эмпирически значительный, и что различные виды шкалы измерения передают различные виды эмпирически значимой информации.
Изучение шкал измерений и эмпирической информации в них Передача — это основная задача математических теорий измерения.В его основополагающее эссе 1887 года «Подсчет и измерение», Германн фон Гельмгольц сформулировал ключевой вопрос теории измерений как следует:
[W] hat — это объективный смысл выражения через деноминацию нумерует отношения реальных объектов как величины, а под каким условия мы можем это сделать? (1887: 4)
Вообще говоря, теория измерений направлена на: (i) выявление предположения, лежащие в основе использования различных математических структур для описывать аспекты эмпирического мира и (ii) извлекать уроки из адекватность и пределы использования этих математических структур для описание аспектов эмпирического мира.По следам Отто Гёльдера (1901), теоретики измерения часто достигают этих целей через формальные доказательства, с предположениями в (i), служащими аксиомами и уроками в (ii) следующее как теоремы. Ключевое понимание теории измерений: что эмпирически значимые аспекты данной математической структура — это те, которые отражают соответствующие отношения между объекты измерения. Например, отношение «больше чем »среди чисел является эмпирически значимым для измерения длина, поскольку она отражает отношение «длиннее, чем» среди объектов.Это отражение или отображение отношений между объекты и математические объекты составляют шкалу измерения. В качестве будет пояснено ниже, шкалы измерений обычно понимаются как изоморфизмы или гомоморфизмы между объектами и математическими сущности.
Помимо этих общих целей и заявлений, теория измерений — это весьма неоднородный корпус ученых. В него входят произведения, охватывающие с конца девятнадцатого века до наших дней и поддерживают широкую множество взглядов на онтологию, эпистемологию и семантику измерение.Два основных различия между математическими теориями Особого упоминания заслуживают измерения. Первый касается природа relata , или «объекты», чьи номера отношений должны быть зеркальными. Эти relata могут быть понимается как минимум четырьмя разными способами: как конкретный человек объекты, как качественные наблюдения за конкретными отдельными объектами, как абстрактные представления отдельных объектов или как универсальные свойства объектов. Какая интерпретация будет принята, зависит от большая часть авторского метафизического и эпистемологического обязательства.Этот вопрос будет особенно актуален для обсуждения. реалистичных счетов измерения (Раздел 5). Во-вторых, разные теоретики измерения занимают разные позиции. на вид эмпирических данных, необходимых для установления сопоставления между объектами и числами. В результате измерения теоретики пришли к разному мнению о необходимых условиях для установление измеримости атрибутов, в частности, о измеримы ли психологические атрибуты. Споры о измеримость оказались очень плодотворными для развития теории измерений, и в следующих подразделах будут представлены некоторые этих дебатов и разработанных в них центральных концепций.
3.1 Основные и производные измерения
В конце девятнадцатого и начале двадцатого веков несколько Были предприняты попытки дать универсальное определение измерения. Хотя мнения об измерениях различались, единодушное мнение заключалось в том, что Измерение — это метод присвоения чисел звездной величине. Например, Гельмгольц (1887: 17) определил измерение как процедуру по которому можно найти номинальное число, которое выражает значение величина, где «номинальное число» — это число вместе с агрегатом, эл.г., 5 метров, а величина — качество объекты, которые можно упорядочить от меньшего к большему, например, длина. Бертран Рассел аналогичным образом заявил, что размер равен
.любой метод, с помощью которого уникальная и взаимная корреспонденция установленный между всеми или некоторыми величинами вида и всеми или некоторые числа, целые, рациональные или действительные. (1903: 176)
Норман Кэмпбелл определил измерение просто как «процесс присвоение чисел для представления качеств », где качество — это свойство, допускающее непроизвольный порядок (1920: 267).
Определение измерения как числового задания поднимает вопрос: какие задания подходят и при каких условиях? Рано теоретики измерения, такие как Гельмгольц (1887 г.), Гельдер (1901 г.) и Кэмпбелл (1920) утверждал, что числа подходят для выражения величины, поскольку алгебраические операции между числами отражают эмпирические отношения между величинами. Например, качественный отношение «длиннее чем» среди жестких стержней (примерно) переходные и асимметричные, и в этом отношении разделяет структурные функции с отношением «больше чем» среди чисел.Кроме того, сквозное соединение жестких стержней разделяет конструктивные особенности. функции, такие как ассоциативность и коммутативность, с математическая операция сложения. Аналогичная ситуация имеет место для измерение веса с помощью равноблочных весов. Здесь отклонение оружие обеспечивает упорядочивание весов и наложение гирь на одна кастрюля представляет собой соединение.
Ранние теоретики измерения сформулировали аксиомы, описывающие эти качественных эмпирических структур и использовал эти аксиомы для доказательства теоремы об адекватности приписывания чисел величинам, которые выставлять такие конструкции.В частности, они доказали, что заказывая и конкатенации вместе достаточно для построения аддитивное числовое представление соответствующих величин. Аддитивное представление — это такое представление, в котором сложение эмпирически осмысленное, а значит, и умножение, деление и т. д. Кэмпбелл так называемые процедуры измерения, которые удовлетворяют условиям аддитивность «фундаментальная», потому что они не включают измерение любой другой величины (1920: 277). Виды величин для которого была применена фундаментальная процедура измерения. найдено — например, длина, площадь, объем, продолжительность, вес и электрическое сопротивление — Кэмпбелл назвал «фундаментальным величины ».Отличительной чертой таких масштабов является то, что это их можно сгенерировать, объединив стандартную последовательность равные единицы, как в примере с серией одинаковых отметок на линейка.
Хотя они считали аддитивность отличительной чертой измерения, большинство ранние теоретики измерения признали, что аддитивность не необходимо для измерения. Существуют и другие величины, допускающие упорядочение. от меньшего к большему, но чьи соотношения и / или различия не могут в настоящее время быть определенными, кроме как через их отношения с другими, фундаментально измеримые величины.Примеры: температура, которая может быть измерен путем определения объема ртутного столба, и плотность, которая может быть измерена как отношение массы к объему. Такой косвенное определение стало называться «производным» измерения и соответствующие величины «получены величины »(Кэмпбелл 1920: 275–77).
На первый взгляд, различие между фундаментальным и производным измерение может показаться напоминанием о различии между обширными и интенсивные величины, и действительно фундаментальное измерение иногда называют «обширным».Тем не менее важно отметить, что эти два различия основаны на существенно разных критерии измеримости. Как обсуждалось в Раздел 2, экстенсивно-интенсивное различие сосредоточено на внутреннем структура рассматриваемой величины, т. е. является ли она состоит из пространственно-временных частей. Основополагающий различие, напротив, сосредотачивается на свойствах измерения операций . Принципиально измеримая величина — это величина в котором была найдена фундаментальная измерительная операция.Следовательно, фундаментальность не является внутренним свойством величина: полученная величина может стать фундаментальной с открытие новых операций по его измерению. Более того, в фундаментальное измерение, числовое присвоение не должно отражать структура пространственно-временной части. Электрическое сопротивление, для Например, можно принципиально измерить, подключив резисторы в серия (Кэмпбелл 1920: 293). Это считается фундаментальным операция измерения, потому что она имеет общую структуру с числовым кроме того, даже если объекты с одинаковым сопротивлением обычно не равные по размеру.
Различие между фундаментальным и производным измерением было отредактировано последующими авторами. Брайан Эллис (1966: гл. 5–8) различают три типа измерения: фундаментальный, ассоциативное и производное. Фундаментальные измерения требуют заказа и операции конкатенации, удовлетворяющие тем же условиям, указанным в Кэмпбелл. Процедуры ассоциативных измерений основаны на корреляция двух отношений порядка, например, корреляция между объемом ртутного столба и его температурой.Полученный процедуры измерения заключаются в определении значения константа в физическом законе. Константа может быть локальной, как в определение удельной плотности воды по массе и объему, или универсальный, как в определении ньютоновского гравитационного постоянная от силы, массы и расстояния. Генри Кибург (1984: гл. 5–7) предложил несколько иное тройное различие между прямое, косвенное и систематическое измерение, которое не полностью перекрываются с тем из Эллис. [4] Более радикальный пересмотр различия между фундаментальным и производное измерение было предложено Р. Дунканом Люсом и Джоном Тьюки. (1964) в своей работе по совместному измерению, которая будет обсуждаться в Раздел 3.4.
3.2 Классификация весов
В предыдущем подразделе обсуждалась аксиоматизация эмпирических структуры, линия расследования, которая восходит к ранним дням теория измерений. Дополнительная информация в рамках измерения Теория касается классификации шкал измерений.В психофизик С.С.Стивенс (1946, 1951) выделил четыре виды шкал: именные, порядковые, интервальные и передаточные. Номинальные шкалы представлять объекты как принадлежащие к классам, не имеющим особого порядок, например, мужской и женский. Порядковые шкалы представляют порядок, но не дальнейшая алгебраическая структура. Например, минеральная шкала Мооса твердость представляет собой минералы с номерами от 1 (самый мягкий) до 10 (самый сложный), но нет никакого эмпирического значения равенства между интервалы или отношения тех числа. [5] Цельсия и Фаренгейта являются примерами интервальных шкал: они представляют равенство или неравенство между интервалами температуры, но не отношения температур, потому что их нулевые точки произвольны. Шкала Кельвина, напротив, представляет собой шкалу отношений, как и знакомые шкалы, отображающие массу в килограммах, длину в метрах и продолжительность в секундах. Позже Стивенс уточнил эту классификацию и различают линейные и логарифмические интервальные шкалы (1959: 31–34) и между шкалами отношений с натуральной единицей и без нее. (1959: 34).Шкалы соотношений с натуральными единицами измерения, например, используемые для подсчета дискретных объектов и представления вероятностей, были названы «абсолютными» шкалами.
Как отмечает Стивенс, типы шкал индивидуализируются по семействам трансформации, которые они могут претерпеть без потери эмпирических Информация. Эмпирические зависимости, представленные на шкалах отношений, для например, инвариантны относительно умножения на положительное число, например, умножение на 2,54 преобразует дюймы в сантиметры. Линейные интервальные шкалы допускают как умножение на положительное число и постоянный сдвиг, e.g., преобразование из Цельсия в Фаренгейт в соответствии с формулой ° C × 9/5 + 32 = ° F. Порядковые шкалы допускают любую функцию преобразования, пока она монотонно-возрастающие, а номинальные шкалы допускают любые взаимно однозначные подмена. Абсолютные шкалы не допускают никаких преобразований, кроме личность. Классификация весов Стивенса была позже обобщено Луи Наренсом (1981, 1985: гл. 2) и Люс и др. (1990: Гл. 20) с точки зрения однородности и уникальности соответствующих группы трансформации.
В то время как классификация шкал Стивенса встретила общие одобрение в научных и философских кругах, его шире последствия для теории измерений стали темой значительных дебаты. Особо оспаривались два вопроса. Во-первых, было ли операции классификации и упорядочивания заслуживают того, чтобы называться «Измерительные» операции и, соответственно, представление величин на номинальной и порядковой шкалах должно считать как измерение. Несколько физиков, в том числе Кэмпбелл, утверждали, что что операции классификации и упорядочивания не обеспечили достаточно богатая структура, чтобы гарантировать использование чисел, и, следовательно, не должны считаться измерительными операциями.Второй оспариваемый вопрос нужно ли было найти операцию конкатенации для величины прежде, чем это можно было фундаментально измерить по шкале отношений. Обсуждение стал особенно горячим, когда снова разгорелся более длительный спор окружающая измеримость интенсивности ощущений. Это чтобы мы переходим к этой дискуссии.
3.3 Измеримость ощущений
Один из главных катализаторов развития математических теорий. измерения были продолжающимися дебатами об измеримости в психология.Эти дебаты часто восходят к работе Густава Фехнера. (1860) Элементы психофизики , в котором он описал метод измерения интенсивности ощущений. Метод Фехнера был основан на записи «едва заметных различия »между ощущениями, связанными с парами стимулы, например, два звука разной интенсивности. Эти различия были приняты равные приращения интенсивности ощущения. В качестве Фехнер показал, что при этом предположении устойчивая линейная зависимость между интенсивностью ощущений и логарифмом интенсивность стимула, отношение, которое стало известно как «Закон Фехнера» (Heidelberger 1993a: 203; Luce and Suppes 2004: 11–2).Этот закон, в свою очередь, предоставляет метод для косвенно измеряя интенсивность ощущений путем измерения интенсивность стимула и, следовательно, утверждал Фехнер, обеспечивает обоснование измерения интенсивности ощущений на реальном числа.
Утверждения Фехнера об измеримости ощущений стал предметом серии дебатов, которые длились почти столетие и оказался чрезвычайно плодотворным для философии измерения, с участием таких ключевых фигур, как Мах, Гельмгольц, Кэмпбелл и Стивенс (Heidelberger 1993a: Ch.6 и 1993b; Мичелл 1999: гл. 6). Те возражая против измеримости ощущений, например, Кэмпбелл, подчеркнул необходимость эмпирической операции конкатенации для фундаментальное измерение. Поскольку интенсивности ощущений не могут быть соединены друг с другом способом, обеспечиваемым длинами и веса, фундаментального измерения ощущений быть не может. интенсивность. Более того, Кэмпбелл утверждал, что ни одно из психофизических обнаруженные к настоящему времени закономерности достаточно универсальны, чтобы их можно было считать как законы в том смысле, который требуется для производных измерений (Кэмпбелл в Ferguson et al.1940: 347). Все, что показали психофизики, что интенсивности ощущений можно последовательно упорядочить, но упорядочить сам по себе еще не гарантирует использование числовых соотношений, таких как суммы и соотношения для выражения эмпирических результатов.
Центральным оппонентом Кэмпбелла в этой дискуссии был Стивенс, чей Различие между типами шкалы измерений обсуждалось выше. Стивенс определил измерение как «присвоение цифр объекты или события в соответствии с правилами »(1951: 1) и утверждал, что любое последовательное и неслучайное назначение считается измерением в в широком смысле (1975: 47).В полезных случаях научного исследования Стивенс заявлено, измерение может быть истолковано несколько более узко как числовое присвоение, основанное на результатах сопоставления операции, такие как связь температуры с объемом ртути или соответствие ощущений друг другу. Стивенс выступал против считают, что отношения между числами должны отражать качественные эмпирические структур, утверждая вместо этого, что шкалы измерений должны быть рассматриваются как произвольные формальные схемы и принимаются в соответствии с их полезность для описания эмпирических данных.Например, приняв шкала соотношения для измерения ощущений громкости, громкости и плотность звуков приводит к формулировке простого линейного соотношения среди отчетов подопытных: громкость = громкость × плотность (1975: 57–8). Такое присвоение чисел ощущениям считается измерением, потому что оно непротиворечиво и неслучайно, потому что он основан на операциях согласования, выполняемых экспериментальными субъектов, и потому что он фиксирует закономерности в экспериментальной полученные результаты. По словам Стивенса, эти условия совпадают. достаточно, чтобы оправдать использование шкалы отношений для измерения ощущения, несмотря на то, что «ощущения не могут быть разделены на составные части или уложены встык, как измерения палки »(1975: 38; см. также Hempel 1952: 68–9).
3.4 Репрезентативная теория измерения
В середине двадцатого века два основных направления исследований в теория измерения, посвященная эмпирическим условиям количественная оценка и классификация шкал, сошлись в работах Патрика Суппеса (1951; Скотт и Суппс, 1958); для исторических обзоров см. Savage and Ehrlich 1992; Diez 1997a, b). Работа Суппеса заложила основу репрезентативной теории Измерение (RTM), которое остается наиболее влиятельным математическим теория измерений на сегодняшний день (Krantz et al.1971; Suppes et al. 1989; Luce et al. 1990). RTM определяет измерение как построение отображения эмпирических реляционных структур в числовые реляционные структуры (Krantz et al. 1971: 9). Эмпирический реляционный конструкция состоит из набора эмпирических объектов (например, жестких стержней) наряду с определенными качественными отношениями между ними (например, упорядочивание, конкатенация), а числовая реляционная структура состоит из набор чисел (например, действительные числа) и конкретные математические отношения между ними (e.g., «равно или больше», добавление). Проще говоря, шкала измерения — это соотношение «многие к одному». отображение — гомоморфизм — от эмпирического к числовому реляционная структура, а измерение — это построение Весы. [6] RTM очень подробно описывает предположения, лежащие в основе построение различных типов измерительных шкал. Каждый тип масштаба связана с набором предположений о качественном отношения, возникающие между объектами, представленными на этом типе шкалы.Из этих допущений или аксиом авторы RTM выводят репрезентативная адекватность каждого типа шкалы, а также семейства допустимые преобразования, делающие этот тип шкалы уникальным. В этом способ RTM обеспечивает концептуальную связь между эмпирической базой измерение и типология Весы. [7]
Что касается измеримости, Репрезентативная теория принимает средний путь между либеральным подходом Стивенса и Строгий упор на операции конкатенации, поддерживаемый Кэмпбеллом.Нравиться Кэмпбелл, RTM признает, что правила количественной оценки должны быть основаны на известные эмпирические структуры и не должны выбираться произвольно, чтобы соответствовать данные. Однако RTM отвергает идею о том, что аддитивные шкалы адекватно только тогда, когда доступны операции конкатенации (Luce и Суппес 2004: 15). Вместо этого RTM отстаивает существование фундаментальных операции измерения, не связанные с конкатенацией. Центральный пример этого типа операции известен как «аддитивный конджойнт измерение »(Люс и Тьюки, 1964; Кранц и др.1971: 17–21 и гл. 6–7). Здесь измерения двух и более различные типы атрибутов, такие как температура и давление газа, получаются путем наблюдения за их совместным действием, таким как объем газа. Люси и Тьюки показали это, установив определенные качественные отношения между объемами при изменении температуры и давления, можно построить аддитивные представления температуры и давления, без использования каких-либо предшествующих методов объем измерения. Подобная процедура может быть обобщена на любой случай. соответствующим образом связанный триплет атрибутов, таких как громкость, интенсивность и частота чистых тонов или предпочтение награды, размер и задержка в получении (Люс и Суппес 2004: 17).В открытие аддитивного совместного измерения привело авторов RTM к разделить фундаментальные измерения на два вида: традиционные измерения процедуры, основанные на операциях конкатенации, которые они назвали «Обширное измерение», а также совместное или «Неэкстенсивное» фундаментальное измерение. Под этим новым концепция фундаментальности, все традиционные физические атрибуты можно измерить фундаментально, как и многие психологические атрибуты (Кранц и др. 1971: 502–3).
Выше мы видели, что математические теории измерения в первую очередь связаны с математическими свойствами измерительных шкал и условия их применения.Родственная, но отличная нить стипендия касается значения и использования количественных терминов. Научный теории и модели обычно выражаются в терминах количественных отношения между параметрами, имеющими имена, такие как «Продолжительность», «уровень безработицы» и «Интроверсия». Реалист по поводу одного из этих терминов мог бы утверждают, что это относится к набору свойств или отношений, которые существуют независимо от измерения. Операционалист или конвенционалист будет утверждать, что способ применения таких количественных терминов к бетону детали зависят от нетривиального выбора, сделанного людьми, и конкретно о вариантах выбора, которые связаны с тем, как соответствующие количество измеряется.Обратите внимание, что в соответствии с этой широкой концепцией реализм совместим с операционализмом и конвенционализмом. То есть это возможно, что выбор метода измерения регулирует использование количество-член и что, учитывая правильный выбор , этот термин преуспевает в ссылке на независимое от разума свойство или отношение. Тем не менее многие операционалисты и конвенционалисты приняли более сильные взгляды, согласно которым нет фактов по делу как какая из нескольких и нетривиально разных операций верна для применения данного количественного термина.Эти более сильные варианты несовместим с реализмом об измерениях. Этот раздел будет посвященный операционализму и конвенционализму, а следующий реализм об измерении.
Операционализм (или «операционизм») в отношении измерения — это точка зрения, что значение количественных понятий определяется набор операций, используемых для их измерения. Самое сильное выражение операционализма появляется в ранних работах Перси Бриджмена (1927), кто утверждал, что
под любым понятием мы понимаем не что иное, как набор операций; в понятие является синонимом соответствующего набора операций.(1927: 5)
Например, длина будет определяться как результат операции сцепления жестких стержней. Согласно этой крайней версии операционализм, разные операции измеряют разные величины. Длина измеряется линейками и синхронизацией электромагнитных импульсов. следует, строго говоря, различать два различных количественные понятия, помеченные как «длина-1» и «Длина-2» соответственно. Этот вывод привел Бриджмена к утверждают, что принятые в настоящее время количественные концепции имеют «Суставы», в которых различные операции пересекаются в своих область применения.Он предостерег от догматической веры в единство количественных концепций в этих «суставах», вместо этого это единство проверяется экспериментами всякий раз, когда применение количественное понятие должно быть расширено в новую область. Тем не менее, Бриджмен признал, что до тех пор, пока результаты различных операций согласен в пределах экспериментальной ошибки, прагматически оправдано маркировать соответствующие величины с таким же названием (1927: 16). [8]
Операционализм стал влиятельным в психологии, где он был хорошо принят бихевиористами, такими как Эдвин Боринг (1945) и Б.Ф. Скиннер (1945). В самом деле, Скиннер утверждал, что бихевиоризм «Не более чем тщательный оперативный анализ традиционные менталистские концепции »(1945: 271). Стивенс, который был Ученик Скуки был одним из главных пропагандистов операционализма в психологии, и утверждал, что психологические концепции имеют эмпирические имея в виду, только если они означают определенные и конкретные операции (1935: 517; см. также Isaac 2017). Идея о том, что концепции определяются операции измерения согласуются с либеральными взглядами Стивенса по измеримости, о которых говорилось выше (Раздел 3.3). Поскольку присвоение номеров объектам выполняется в в соответствии с конкретными и последовательными правилами, Стивенс утверждал, что такое присвоение имеет эмпирическое значение и не должно удовлетворять никаким дополнительные ограничения. Тем не менее Стивенс, вероятно, не принял антиреалистический взгляд на психологические атрибуты. Вместо этого там веские причины думать, что он понимал операционализм как методологический подход, который был ценен в той мере, в какой он позволили психологам обосновать выводы, которые они сделали из эксперименты (Feest 2005).Например, Стивенс не лечил операционные определения как априори , но как поддающиеся улучшение в свете эмпирических открытий, подразумевая, что он взял психологические атрибуты существуют независимо от таких определений (Стивенс 1935: 527). Это говорит о том, что операционализм Стивенса было более умеренным разнообразием, чем то, что было обнаружено в ранних произведениях из Бриджмен. [9]
Операционализм с первоначальным энтузиазмом встретил логические позитивисты, которые рассматривал это как сродни верификации.Тем не менее, это было скоро показали, что любая попытка основать теорию значения на операционалистские принципы были полны проблем. Среди таких проблемы заключались в том, что автоматическая надежность операционализма приписывала измерения, неясности, связанные с понятием эксплуатации, чрезмерно ограничительный эксплуатационный критерий осмысленность и тот факт, что многие полезные теоретические концепции не хватает четких операционных определений (Чанг 2009 г.). [10] В частности, Карл Хемпель (1956, 1966) критиковал операционалистов. за неспособность дать определение диспозиционных терминов, таких как «Растворимость в воде», и для умножения количества научные концепции в манере, которая противоречит необходимости систематические и простые теории.Соответственно, большинство авторов семантика количественных терминов избегает поддержки операционного анализ. [11]
Более широко пропагандируемый подход допускал традиционный элемент в использование количественных терминов, сопротивляясь попыткам уменьшить значение количественных терминов в операциях измерения. Эти аккаунты классифицируются под общей рубрикой «Конвенционализм», хотя они различаются аспекты измерения, которые они считают общепринятыми, и в степени произвол они приписывают таким условности. [12] Первым предшественником конвенционализма был Эрнст Мах, исследовавший понятие равенства температурных интервалов (1896: 52). Мах отметил, что разные типы термометрической жидкости расширяются при разных (и нелинейно связанные) скорости при нагревании, в связи с чем возникает вопрос: какая жидкость расширяется наиболее равномерно с температурой? В соответствии с Мах, неважно, какая жидкость расширяется больше. равномерно, поскольку само понятие равенства температур интервалы не имеют определенного применения до обычного выбор стандартной термометрической жидкости.Мах придумал термин «Принцип согласованности» для такого рода условно выбранный принцип применения количества концепция. Понятия однородности времени и пространства получили аналогичные обработки Анри Пуанкаре (1898, 1902: Часть 2). Пуанкаре утверждал, что процедуры, используемые для определения равенства среди длительностей проистекает из бессознательного предпочтения ученых описательная простота, а не из каких-либо фактов о природе. Точно так же выбор ученых представить пространство либо Евклидова или неевклидова геометрия не определяется опытом но по соображениям удобства.
Конвенционализм в отношении измерения достиг своего максимума. сложное выражение в логическом позитивизме. Логические позитивисты как Ганс Райхенбах и Рудольф Карнап предложили «координационный определения »или« правила соответствия »в качестве семантическая связь между теоретическими и наблюдательными терминами. Эти a априори , утверждения, подобные определениям, предназначались для регулирования использование теоретических терминов, связав их с эмпирическими процедурами (Reichenbach 1927: 14–19; Carnap 1966: Ch.24). Пример координирующим определением является утверждение: «мерный стержень сохраняет свою длину при транспортировке ». По словам Райхенбаха, это утверждение не может быть проверено эмпирически, потому что универсальный и могла существовать экспериментально необнаруживаемая сила, которая в равной степени искажает длина каждого объекта при транспортировке. В соответствии с верификационизм, утверждения, которые не поддаются проверке, не являются ни правдой, ни ложный. Вместо этого Райхенбах использовал это заявление, чтобы выразить произвольное правило, регулирующее использование понятия равенства length, а именно для определения того, являются ли конкретные экземпляры length равны (Reichenbach 1927: 16).В то же время координационные определения не рассматривались как замена, а скорее как необходимые дополнения к знакомому типу теоретических определений понятий с точки зрения других концепций (1927: 14). Под условным точки зрения, то спецификация измерительных операций не исчерпать значение таких понятий, как длина или равенство длины, тем самым избегая многих проблем, связанных с операционализм. [13]
Реалисты в области измерения утверждают, что измерение лучше всего понимается как эмпирическая оценка объективного свойства или связь.Сделаем несколько пояснительных замечаний в отношении это характеристика измерения. Во-первых, термин «Объективный» не предназначен для исключения ментальных свойств или отношения, которые являются объектами психологического измерения. Скорее, измеримые свойства или отношения считаются объективными, поскольку поскольку они не зависят от верований и обычаев людей выполнение измерения и методы, используемые для измерения. Для Например, реалист будет утверждать, что отношение длины данного сплошная штанга к стандартному счетчику имеет объективное значение независимо от измеряется ли и как.Во-вторых, срок «Оценка» используется реалистами, чтобы подчеркнуть факт что результаты измерений представляют собой всего лишь приближений истинных ценности (Trout 1998: 46). В-третьих, по мнению реалистов, измерение направленных на получение знаний о свойствах и отношениях, скорее чем при присвоении значений непосредственно отдельным объектам. Это значимы, потому что наблюдаемые объекты (например, рычаги, химические решения, люди) часто определяют измеримые свойства и отношения, которые не наблюдаются напрямую (например,г., количество механических работа, кислая, интеллект). Заявления о знаниях о таких свойства и отношения должны предполагать некоторую фоновую теорию. К перенос акцента с объектов на свойства и отношения, реалисты подчеркивают теоретический характер измерений.
Реализм в отношении измерения не следует путать с реализмом в отношении сущности (например, электроны). Реализм в измерении обязательно влечет за собой реализм в отношении свойств (например, температуры), поскольку в принципе можно было принять только реальность отношений (напр.грамм., соотношения между количествами), не принимая во внимание реальность лежащих в основе характеристики. Тем не менее, большинство философов, защищавших реализм, об измерении сделали это, аргументируя это тем, что придерживаются некоторой формы реализма о собственности (Байерли и Лазара 1973; Свойер 1987; Манди 1987; Форель 1998, 2000). Эти реалисты утверждают, что по крайней мере некоторые измеримые свойства существуют независимо от убеждений и соглашений люди, которые их измеряют, и что существование и структура этих properties наилучшим образом объясняет ключевые особенности измерения, включая полезность чисел при выражении результаты измерений и надежность средств измерений.
Например, типичный реалист по поводу измерения длины будет утверждать, что что эмпирические закономерности, отображаемые отдельными объектами » длины, когда они упорядочены и объединены, лучше всего объясняются предполагая, что длина является объективным свойством, имеющим обширную структура (Swoyer 1987: 271–27). То есть отношения между длинами такие как «дольше чем» и «сумма» существуют независимо от того, заказываются ли какие-либо объекты и соединены людьми, и действительно независимо от того, являются ли объекты какая-то конкретная длина вообще существует.Существование обширная структура собственности означает, что длины разделяют большую часть их структура с положительными действительными числами, и это объясняет полезность положительных вещественных чисел в представлении длин. Более того, если измеримые свойства анализируются с точки зрения диспозиции, становится Легко объяснить, почему некоторые измерительные приборы надежны. Для Например, если предположить, что определенное количество электрического тока в проволока влечет за собой склонность отклонять стрелку амперметра определенным угла, следует, что показания амперметра контрфактически зависят от количества электрического тока в проводе, следовательно, амперметр надежен (Trout 1998: 65).
Другой аргумент в пользу реализма в отношении измерения принадлежит Джоэлю. Мичелл (1994, 2005), который предлагает реалистичную теорию чисел, основанную на евклидова концепция соотношения. По словам Мичелла, цифры соотношения между величинами и, следовательно, существуют в пространстве и времени. В частности, реальных чисел — это отношения между парами бесконечные стандартные последовательности, например, последовательность длин обычно обозначается «1 метр», «2 метра» и т. д., а последовательность целых кратных длины, которую мы пытаемся измерить.Измерение — это открытие и оценка таких соотношений. An Интересным следствием этого эмпирического реализма в отношении чисел является это измерение — не репрезентативная деятельность, а скорее деятельность по приближению независимых от разума чисел (Michell 1994: 400).
Реалистические представления об измерениях в основном формулируются противоположно к сильным версиям операционализма и конвенционализма, которые доминировали философские дискуссии об измерениях с 1930-х годов до 1960-х гг.Помимо недостатков операционализма уже обсуждалось в предыдущем разделе, реалисты отмечают, что антиреализм в отношении измеримых величин не может понять научная практика. Если бы количества не имели реальных значений независимо от выбор методики измерения, было бы трудно объясните, что ученые подразумевают под «точностью измерения» и «Ошибка измерения» и почему они пытаются повысить точность и уменьшить ошибку. Напротив, реалисты могут легко понять смысл понятия точности и ошибки с точки зрения расстояния между реальными и измеренные значения (Byerly and Lazara 1973: 17–8; Swoyer 1987: 239; Форель 1998: 57).С этим тесно связан тот факт, что более новые процедуры измерения имеют тенденцию к повышению точности по сравнению с более старыми. Если бы выбор процедуры измерения был просто обычным, он бы трудно разобраться в таком прогрессе. Кроме того, реализм дает интуитивно понятное объяснение того, почему разные измерения процедуры часто дают аналогичные результаты, а именно потому, что они чувствительны к тем же фактам (Swoyer 1987: 239; Trout 1998: 56). Наконец, реалисты отмечают, что конструкция измерительной аппаратуры и при анализе результатов измерений руководствуемся теоретическими предположения о причинно-следственных связях между величинами.В способность таких причинно-следственных предположений направлять измерения предполагает, что количества онтологически предшествуют процедурам измерения их. [14]
Хотя их позиция по отношению к операционализму и конвенционализму остается неизменной. в значительной степени критичны, реалисты более снисходительны в своих оценках математические теории измерения. Брент Манди (1987) и Крис Swoyer (1987) оба принимают аксиоматическую трактовку измерения. шкалы, но возражают против эмпирической интерпретации, данной аксиомы выдающихся теоретиков измерений, таких как Кэмпбелл (1920) и Эрнест Нагель (1931; Коэн и Нагель 1934: гл.15). Скорее, чем интерпретация аксиом как относящихся к конкретным объектам или к наблюдаемые отношения между такими объектами, Манди и Свойер переосмысливают аксиомы, относящиеся к универсальным величинам, например, к универсальное свойство быть длиной 5 метров, а не бетоном экземпляры этого свойства. Эта конструкция сохраняет интуиция, что утверждения типа «размер x вдвое больше размером y ”- это в первую очередь около двух размеров , и только производно об объектах x и и сами (Манди 1987: 34). [15] Манди и Свойер утверждают, что их интерпретация является более общей, потому что это логически влечет за собой все последствия первого порядка эмпирическая интерпретация наряду с дополнительными утверждениями второго порядка о всемирных величинах. Более того, согласно их интерпретации теория измерения становится подлинной научной теорией с объяснительные гипотезы и проверяемые прогнозы. Основываясь на этом работы, Джо Вольф (2020a) недавно предложила новую реалистичную версию величин, которая опирается на репрезентативную теорию Измерение.Согласно структуралистской теории Вольфа количество, количественные атрибуты — это реляционные структуры. В частности, атрибут является количественным, если его структура имеет переводы, образующие архимедову упорядоченную группу. Вольфа сосредоточиться на переводах, а не на конкретных отношениях, таких как конкатенация и упорядочение, означает, что количественность может быть реализуется несколькими способами и не ограничивается обширными конструкции. Это также означает, что быть количеством ничего не значит. специально для чисел, как числовых, так и нечисловых структуры могут быть количественными.
Теоретико-информационные отчеты об измерениях основаны на аналогии между измерительными системами и системами связи. В простом система связи, сообщение (вход) кодируется в сигнал на конец передатчика, отправленный на конец приемника, и затем декодируется обратно (вывод). Точность передачи зависит от об особенностях системы связи, а также об особенностях окружающая среда, т. е. уровень фонового шума. Аналогичным образом, измеряя инструменты можно рассматривать как «информационные машины» (Финкельштейн 1977), которые взаимодействуют с объектом в данном состоянии (ввод), кодируйте это состояние во внутренний сигнал и преобразуйте это сигнал в считывание (вывод).Точность измерения аналогично зависит от инструмента, а также от уровня шума в его среде. Задуманный как особый вид информации передачи, измерение становится анализируемым с точки зрения концептуальный аппарат теории информации (Hartley 1928; Shannon 1948; Шеннон и Уивер 1949). Например, информация о том, что чтение \ (y_i \) сообщает о возникновении состояния \ (x_k \) объект можно количественно оценить как \ (\ log \ left [\ frac {p (x_k \ mid y_i)} {p (x_k)} \ right] \), а именно как функция уменьшения неопределенность в отношении состояния объекта (Finkelstein 1975: 222; для альтернативные формулировки см. Brillouin 1962: Ch.15; Кирпатовский 1974; и Мари 1999: 185).
Людвик Финкельштейн (1975, 1977) и Лука Мари (1999) предложили возможность синтеза теории информации Шеннона-Уивера и теория измерений. По их мнению, обе теории апеллируют к центру. к идее отображения: теория информации касается отображения между символами во входных и выходных сообщениях, при измерении теория касается отображения между объектами и числами. Если измерение аналогично манипулированию символами, тогда Теория Шеннона-Уивера могла бы обеспечить формализацию синтаксиса измерения, в то время как теория измерений могла бы обеспечить формализацию его семантика.Тем не менее, Мари (1999: 185) также предупреждает, что аналогия между системами связи и измерения ограничена. В то время как сообщение отправителя может быть известно с произвольной точностью. независимо от его передачи состояние объекта не может быть известно с произвольной точностью независимо от его измерения.
Изначально теоретико-информационные отчеты об измерениях были разработаны метрологами — специалистами в области физических измерений и стандартизация — с небольшим участием философов.Независимо от достижений в метрологии, Бас ван Фраассен (2008: 141–185) недавно предложил концепцию измерения в какая информация играет ключевую роль. Он считает измерение составленным двух уровней: на физическом уровне измерительная аппаратура взаимодействует с объектом и производит чтение, например, указатель позиция. [16] На абстрактном уровне фоновая теория представляет собой возможные состояния объекта в пространстве параметров. Измерение находит объект в подобласти этого абстрактного пространства параметров, тем самым сокращая диапазон возможных состояний (2008: 164 и 172).Это сокращение возможностей сводится к сбору информация об измеряемом объекте. Анализ Ван Фраассена измерения отличается от теоретико-информационных счетов, разработанных в метрологии в ее явном обращении к фоновой теории, и в тот факт, что он не ссылается на символическую концепцию информации разработан Шеннон и Уивер.
С начала 2000-х годов нахлынула новая волна философских исследований. появилось, что подчеркивает взаимосвязь между измерением и теоретическое и статистическое моделирование (Morgan 2001; Boumans 2005a, 2015; Mari 2005b; Мари и Джордани 2013; Таль 2016, 2017; Паркер 2017; Мияке 2017).Согласно расчетам, основанным на модели, измерение состоит из двух уровней: (i) конкретный процесс, включающий взаимодействие между интересующий объект, инструмент и окружение; и (ii) a теоретическая и / или статистическая модель этого процесса, где «Модель» означает абстрактное и локальное представление построены на основе упрощающих предположений. Центральная цель измерение в соответствии с этой точкой зрения заключается в присвоении значений одному или нескольким интересующих параметров модели таким образом, чтобы eptemic desiderata, в частности последовательность и последовательность.
Счета на основе моделей были разработаны на основе изучения измерений практики в науке, и особенно в метрологии. Метрология, официально определяется как «наука об измерениях и ее приложение »(JCGM 2012: 2.2), является предметом изучения с разработкой, обслуживанием и усовершенствованием средств измерений в естественных и технических науках. Метрологи обычно работают в бюро стандартизации или в специализированных лабораториях, ответственный за калибровку измерительного оборудования, сравнение стандартов и оценка измерений неопределенности, среди других задач.Только недавно философы начали заниматься богатыми концептуальными проблемами лежащей в основе метрологической практики, и особенно с выводами участвует в оценке и повышении точности измерений стандарты (Chang 2004; Boumans 2005a: Chap. 5, 2005b, 2007a; Frigerio и другие. 2010; Teller 2013, 2018; Риордан 2015; Шлаудт и Хубер 2015; Tal 2016a, 2018; Mitchell et al. 2017; Месснер и Нордманн 2017; de Courtenay et al. 2019).
Основной мотивацией для разработки модельных счетов является попытка прояснить эпистемологические принципы, лежащие в основе аспекты измерительной практики.Например, метрологи используют разнообразие методов калибровки средств измерений, стандартизация и отслеживание единиц и оценка неопределенности (обсуждение метрологии см. в предыдущем раздел). Традиционные философские учения, такие как математические теории измерения не основываются на предположениях, умозаключениях закономерности, доказательственные основания или критерии успеха, связанные с такими методы. Как отмечает Frigerio et al. (2010) утверждают, что теория измерений плохо подходит для разъяснения этих аспектов измерения, потому что он абстрагируется от процесса измерения и сосредотачивается исключительно на математические свойства весов.Напротив, модельные бухгалтеры считают построение шкалы лишь одной из нескольких задач участвует в измерении, наряду с определением измеряемого параметры, конструкция и калибровка прибора, отбор образцов и подготовка, обнаружение ошибок и оценка неопределенности, среди прочего (2010: 145–7).
7.1 Роль моделей в измерении
Согласно модельным расчетам, измерение предполагает взаимодействие между интересующим объектом («система под измерение »), инструмент (« измерение система ») и среду, которая включает в себя измерения предметы.Другие, вторичные взаимодействия также могут иметь отношение к определение результата измерения, например, взаимодействие между измерительным прибором и эталонами, используемыми для его калибровка и цепочка сравнений, которые отслеживают эталон эталон обратно к первичным эталонам (Mari 2003: 25). Измерение продолжается путем представления этих взаимодействий с набором параметры и присвоение значений подмножеству этих параметров (известные как «измеряемые величины») на основе результатов взаимодействия.Когда измеряемые параметры являются числовыми, они называются «Количества». Хотя измеряемые величины не обязательно должны быть количествами, будет предложен сценарий количественного измерения, в котором следует.
Два вида результатов измерений различаются по моделям. счета [JCGM 2012: 2.9 и 4.1; Джордани и Мари 2012: 2146; Таль 2013]:
- Показания прибора (или «Показания»): это свойства измерительного прибор в конечном состоянии после того, как процесс измерения полный.Примеры: цифры на дисплее, отметки при множественном выборе. анкета и биты, хранящиеся в памяти устройства. Показания могут быть представлены числами, но такие числа описывают состояния инструмент, и его не следует путать с результатами измерения, которые касаются состояний измеряемого объекта.
- Результаты измерения (или «результаты»): это заявления о знании значений одной или нескольких величин приписываются измеряемому объекту и обычно сопровождаются указанием единицы измерения и шкалы и сметы неопределенности измерения.Например, результат измерения может быть следующим: выражается предложением «масса объекта a составляет 20 ± 1 грамм с вероятностью 68% ».
Сторонники теории, основанной на моделях, подчеркивают, что выводы из показания приборов к результатам измерений нетривиальны и зависят от множества теоретических и статистических предположений о объект измерения, прибор, окружающая среда и процесс калибровки. Результаты измерений часто достигаются через статистический анализ нескольких показаний, включая предположения о форме распределения показаний и случайность воздействия окружающей среды (Боген и Вудворд 1988: 307–310).Результаты измерений также включают поправки на систематические эффекты, и такие поправки основаны на теоретических предположения относительно работы прибора и его взаимодействия с объектом и окружающей средой. Например, длина измерения должны быть скорректированы для изменения измерения длина стержня с температурой, поправка, которая выводится из теоретического уравнения теплового расширения. Систематический исправления связаны с собственными неопределенностями, например, в определение значений констант, и эти неопределенности оценивается посредством вторичных экспериментов, включающих дальнейшие теоретические и статистические допущения.Более того, неопределенность, связанная с результат измерения зависит от методов, используемых для калибровка прибора. Калибровка включает дополнительные предположения о приборе, калибрующем аппарате, измеряемая величина и свойства эталонов (Ротбарт и Слейден 1994; Франклин 1997; Бэрд 2004: Глава 4; Солер и др. al. 2013). Еще один компонент неопределенности проистекает из неопределенности. в определении измеряемой величины и известен как «Неопределенность определений» (Мари и Джордани, 2013; Grégis 2015).Наконец, измерение включает в себя фон предположения о типе весов и системе единиц измерения, и эти предположения часто связаны с более широкими теоретическими и технологическими соображения, касающиеся определения и реализации весов и единицы.
Эти различные теоретические и статистические предположения составляют основу для построения одной или нескольких моделей измерительного процесса. В отличие от математических теорий измерения, где термин «Модель» обозначает теоретико-множественную структуру, которая интерпретирует формальный язык, здесь термин «модель» обозначает абстрактное и локальное представление целевой системы, которая построен на упрощении предположения. [17] Соответствующей целевой системой в этом случае является процесс измерения, то есть система, состоящая из измерительного прибора, объектов или события, подлежащие измерению, окружающая среда (включая людей-операторов), вторичные инструменты и эталоны, эволюция во времени эти компоненты и их различные взаимодействия друг с другом. Измерение рассматривается как набор процедур, цель которых — согласованно присваивать значения параметрам модели на основе прибора показания. Поэтому модели рассматриваются как необходимые предварительные условия для возможность вывода результатов измерений из прибора показания, и как решающее значение для определения содержания измерения результаты.Как подчеркивают сторонники модельных расчетов, показания, полученные с помощью одного и того же процесса измерения, могут использоваться для установить разные результаты измерения в зависимости от того, как процесс измерения моделируется, например, в зависимости от того, в какой среде учитываются влияния, статистические допущения используется для анализа шума, и какие приближения используются при применении фоновая теория. Как выразился Лука Мари,
любой результат измерения содержит информацию, имеющую значение только в контекст метрологической модели, такая модель требуется для включить спецификацию для всех сущностей, которые явно или неявно фигурируют в выражении результата измерения.(2003: 25)
Точно так же говорят, что модели обеспечивают необходимый контекст для оценка различных аспектов качества результатов измерений, включая точность, прецизионность, погрешность и неопределенность (Boumans 2006, 2007a, 2009, 2012b; Мари 2005b).
Основанные на моделях описания расходятся с эмпирическими интерпретациями теории измерений в том, что они не требуют отношений между результаты измерения должны быть изоморфны или гомоморфны наблюдаемым отношения между объектами измерения (Mari 2000).Действительно, согласно модельным расчетам отношения между измеряемыми объектами вовсе не обязательно быть наблюдаемыми до их измерения (Frigerio et al. al. 2010: 125). Вместо этого ключевое нормативное требование основанной на моделях счетов заключается в том, что значения присваиваются параметрам модели в согласованном манера. Критерий согласованности можно рассматривать как сочетание двух подкритерии: (i) согласованность допущений модели с соответствующими фоновые теории или другие существенные предположения о измеряемая величина; и (ii) объективность, i.е. взаимное согласованность результатов измерений по разным измерениям инструменты, окружающая среда и модели [18] (Frigerio et al.2010; Tal 2017a; Teller 2018). Первое Подкритерий предназначен для обеспечения того, чтобы предполагаемое количество измеряется, в то время как второй подкритерий предназначен для обеспечения что результаты измерения могут быть разумно отнесены к измеряемым объект , а не какой-то артефакт измерения инструмент, среда или модель.Взятые вместе, эти двое требования гарантируют, что результаты измерений остаются действительными независимо от конкретных допущений, связанных с их производства, и, следовательно, контекстная зависимость измерения результаты не угрожают их общей применимости.
7.2 Модели и измерения в экономике
Помимо их применимости к физическим измерениям, основанные на моделях Анализ также проливает свет на измерения в экономике. Как физический количества, значения экономических переменных часто невозможно наблюдать непосредственно и должны выводиться из наблюдений, основанных на абстрактных и идеализированные модели.Экономист девятнадцатого века Уильям Джевонс за Например, измерять изменения в стоимости золота, постулируя определенные причинно-следственные связи между стоимостью золота, предложением золота и общий уровень цен (Hoover and Dowell 2001: 155–159; Morgan 2001: 239). Как показывает Джулиан Рейсс (2001), Джевонс измерения стали возможны благодаря использованию двух моделей: причинно-теоретическая модель экономики, в основе которой предположение, что количество золота может увеличиваться или низкие цены; и статистическая модель данных, основанная на предположение, что местные колебания цен взаимно независимы и поэтому компенсируют друг друга при усреднении.Взятый вместе эти модели позволили Джевонсу сделать вывод об изменении значения золота из данных об исторических ценах различных товары. [19]
Способы, которыми модели функционируют в экономических измерениях, привели к некоторые философы считают определенные экономические модели инструменты сами по себе, по аналогии с линейками и весами (Boumans 1999, 2005c, 2006, 2007a, 2009, 2012a, 2015; Morgan 2001). Марсель Буманс объясняет, как макроэкономисты могут изолировать переменная, представляющая интерес от внешних воздействий, путем настройки параметров в модель макроэкономической системы.Этот метод освобождает экономистов от невозможной задачи управления реальной системой. Как Боуман утверждает, что макроэкономические модели функционируют как инструменты измерения, поскольку поскольку они создают инвариантные отношения между входами (показаниями) и выходов (результатов), и насколько эта инвариантность может быть проверена с помощью калибровка по известным и стабильным фактам. Когда такие модельные процедуры сочетаются с экспертной оценкой, они могут производить надежные измерения экономических явлений даже вне контроля лабораторные настройки (Boumans 2015: гл.5).
7.3 Психометрические модели и конструктивная валидность
Еще одна область, в которой модели играют центральную роль в измерениях, — это психология. Измерение большинства психологических атрибутов, таких как интеллект, тревога и депрессия, не полагаются на гомоморфные отображения типа, поддерживаемого Репрезентативной теорией Измерение (Уилсон 2013: 3766). Вместо этого психометрическая теория полагается преимущественно на разработке абстрактных моделей, предназначенных для прогнозировать производительность испытуемых в определенных задачах.Эти модели построены на основе существенных и статистических предположений о измеряемый психологический атрибут и его отношение к каждому задача измерения. Например, Теория отклика предмета, популярная подход к психологическому измерению, использует различные модели для оценить надежность и валидность анкет. Рассмотрим анкета, предназначенная для оценки понимания английского языка («способность»), предлагая испытуемым серию да / нет вопросы («предметы»).Одна из самых простых моделей Для калибровки таких вопросников используется модель Раша (Rasch 1960). Эта модель предполагает простое алгебраическое соотношение — известное как «журнал шансов» — между вероятностями что испытуемый ответит на заданный вопрос правильно, сложность этот конкретный предмет и способности субъекта. Новый анкеты калибруются путем проверки соответствия между их указания и прогнозы модели Раша и назначение уровни сложности для каждого элемента соответственно.Затем модель используется в в сочетании с анкетой для определения уровня владения английским языком понимание (результаты) из исходных баллов анкеты (показания) (Уилсон 2013; Мари и Уилсон 2014).
Своего рода статистическая калибровка (или «масштабирование») модели Раша дает повторяемые результаты, но часто только первый шаг к полноценному психологическому измерению. Психологов обычно интересуют результаты какой-либо меры. ради самого себя, но ради оценки некоторых основных и латентный психологический признак, e.г., понимание английского языка. Хорошего соответствия между ответами на вопросы и статистической моделью пока нет. определить, что измеряет анкета. Процесс установление того, что процедура измеряет предполагаемый психологический атрибут известен как «проверка». Один из способов проверки психометрический инструмент предназначен для проверки того, могут ли различные процедуры, предназначены для измерения одного и того же скрытого атрибута. полученные результаты. Такое тестирование относится к семейству методов валидации. известная как «проверка конструкции».Конструкция — это абстрактное представление скрытого атрибута, предназначенного для измерено, а
отражает гипотезу […] о том, что различные виды поведения коррелируют друг с другом в исследованиях индивидуальных различий и / или аналогично будут затронуты экспериментальные манипуляции. (Nunnally И Бернштейн 1994: 85)
Конструкции обозначаются переменными в модели, которая предсказывает, какие корреляции будут наблюдаться между показаниями различных меры, если они действительно являются показателями одного и того же атрибута.Такой модели включают существенные предположения об атрибуте, в том числе его внутренняя структура и его отношения с другими атрибутами, и статистические допущения о корреляции между различными показателями (Campbell & Fiske 1959; Nunnally & Bernstein 1994: Ch. 3; Angner 2008).
В последние годы философы науки все больше становятся интересуется психометрикой и концепцией валидности. Одна дискуссия касается онтологического статуса скрытых психологических атрибутов.Денни Борсбум выступил против операционализма по поводу латентного атрибуты, и в пользу определения действительности таким образом, чтобы охватывает реализм: «тест действителен для измерения атрибута, если и только если а) атрибут существует, и б) вариации в атрибута причинно порождают вариации в результатах методика измерения »(2005: 150; см. также Hood 2009, 2013; Праздник 2020). Элина Вессонен защищала умеренную форму операционализм о психологических атрибутах и утверждал, что умеренный операционализм совместим с осторожным реализмом (2019).Еще одна недавняя дискуссия посвящена обоснованию разработать процедуры проверки. По словам Анны Александровой, проверка конструкции в принципе является оправданной методологией, поскольку поскольку он устанавливает согласованность с теоретическими предположениями и фоновые знания о скрытом атрибуте. Однако Александрова отмечает, что на практике врачи-психометристы, намеревающиеся измерить счастье и благополучие часто избегают теоретических рассуждений об этих конструирует, а вместо этого апеллирует к народным верованиям респондентов.Это сводит на нет цель проверки конструкции и превращает ее в узкое, техническое упражнение (Александрова, Хайброн, 2016; Александрова 2017; см. также McClimans et al. 2017).
Более фундаментальная критика психометрии заключается в том, что она догматически предполагает, что психологические атрибуты могут быть количественно. Мичелл (2000, 2004b) утверждает, что психометристы не предпринимали серьезных попыток проверить, являются ли атрибуты, которые они подразумевают для измерения имеют количественную структуру, а вместо этого расплывчатое представление об измерении, которое маскирует это пренебрежение.В ответ, Борсбум и Мелленберг (2004) утверждают, что ответ на предмет Теория обеспечивает вероятностные тесты количественной оценки атрибуты. Психометристы, строящие статистическую модель сначала предположить, что атрибут является количественным, а затем подвергнуть модель эмпирическим испытаниям. В случае успеха такие испытания обеспечивают косвенное подтверждение исходной гипотезы, например к показывая, что атрибут имеет аддитивную объединенную структуру (см. также Vessonen 2020).
Несколько ученых указали на сходство способов моделирования используются для стандартизации измеряемых величин в натуральных и социальные науки.Например, Марк Уилсон (2013) утверждает, что психометрические модели можно рассматривать как инструменты для построения эталоны в том же смысле слова «измерение эталон », применяемый метрологами. Другие вызвали сомнения по поводу целесообразность и желательность принятия примера естественные науки при стандартизации конструкций в социальных науках. Нэнси Картрайт и Роза Рунхардт (2014) обсуждают «Баллунг» — термин, заимствованный у Отто Нейрата. для обозначения концепций с нечеткой и контекстно-зависимой областью действия.Примеры понятий Баллунга — это раса, бедность, социальная изоляция и качество программ докторантуры. Такие концепции слишком многогранны, чтобы их измеряется по одной метрике без потери смысла и должен быть представлен либо матрицей индексов, либо несколькими разными меры в зависимости от целей и ценностей (см. также Брэдберн, Картрайт и Фуллер, 2016 г., Другие Интернет-ресурсы). Александрова (2008) отмечает, что этические соображения влияют на вопросы об обоснованности мер благосостояния не менее соображения воспроизводимости.Такие этические соображения контекстно-зависимый и может применяться только по частям. В аналогичном vein, Лия МакКлиманс (2010) утверждает, что единообразие не всегда подходящая цель для разработки анкет, поскольку открытость вопросов часто неизбежны и желательны для получения соответствующая информация от предметы. [20] Переплетение этических и эпистемологических соображений особенно наглядно, когда психометрические анкеты используются в медицинских контексты для оценки благополучия и психического здоровья пациентов.В таком случаи, небольшие изменения в дизайне анкеты или анализа его результатов могут нанести значительный вред пациентам или принести им пользу. (McClimans 2017; Stegenga 2018, глава 8). Эти идеи подчеркивают ценностный и контекстуальный характер измерения умственных и социальные явления.
Разработка модельных счетов обсуждалась в предыдущем раздел является частью более крупного «эпистемологического поворота» в философия измерения, возникшая в начале 2000-х гг.Скорее чем упор на математические основы, метафизику или семантика измерения, философские работы последних лет имеют тенденцию к сосредоточиться на предпосылках и шаблонах вывода, участвующих в конкретные практики измерения, а также исторические, социальные и материальные размеры измерения. Философское изучение этих темы называют «эпистемологией измерение »(Mari 2003, 2005a; Leplège 2003; Tal 2017a). В самом широком смысле эпистемология измерения — это изучение отношения между измерением и знанием.Центральные темы которые подпадают под сферу эпистемологии измерения, включают условия, при которых измерение производит знание; в содержание, объем, обоснование и пределы таких знаний; в причины, по которым определенные методики измерения и стандартизация успешна или не поддерживает определенные знания претензии и отношения между измерениями и другими познавательная деятельность, такая как наблюдение, теоретизирование, экспериментирование, моделирование и расчет.Следуя этим цели, философы опираются на работы историков и социологи науки, занимающиеся измерением практики в течение более длительного периода (Wise and Smith 1986; Latour 1987: Ch. 6; Schaffer 1992; Портер 1995, 2007; Wise 1995; Ольха 2002; Галисон 2003; Gooday 2004; Crease 2011), а также по истории и философия научных экспериментов (Harré 1981; Hacking 1983; Франклин 1986; Картрайт 1999). Следующие подразделы изучите некоторые из тем, обсуждаемых в этом быстрорастущем корпусе литература.
8.1 Стандартизация и научный прогресс
Тема, которая привлекла значительное внимание философов в последние годы — это выбор и совершенствование измерений стандарты. Вообще говоря, стандартизация количественной концепции означает: предписать определенный способ применения этой концепции к конкретный подробности. [21] Стандартизация измерительного прибора означает оценку того, насколько хорошо результаты измерений этим прибором соответствуют предписанному режиму применение соответствующей концепции. [22] Соответственно, термин «эталон» имеет не менее два значения: с одной стороны, он обычно используется для обозначения абстрактные правила и определения, регулирующие использование количества понятия, такие как определение счетчика. С другой стороны, термин «эталон» также обычно используется для обозначения к конкретным артефактам и процедурам, которые считаются образцовыми применение количественной концепции, такой как металлический стержень, который служил эталонным счетчиком до 1960 г.Эта двойственность смысла отражает двойственную природу стандартизации, которая включает в себя как абстрактные и конкретные аспекты.
В Раздел 4 было отмечено, что стандартизация предполагает выбор среди нетривиальных альтернативы, такие как выбор между различными термометрическими жидкостями или среди разных способов обозначения одинаковой продолжительности. Эти варианты нетривиальны в том смысле, что они влияют на то, температурные (или временные) интервалы считаются равными и, следовательно, влияют на содержат ли утверждения естественного права термин «Температура» (или «время») оказываются верными.Обращение к теории, чтобы решить, какой стандарт более точен, было бы круговой, поскольку теория не может быть однозначно применена к подробные сведения перед выбором эталона. Этот округлость по-разному называли «проблемой координации »(van Fraassen 2008: Ch. 5) и« проблема номических измерений »(Chang 2004: Ch. 2). Как уже упоминалось, конвенционалисты попытались уйти от округлости, постулируя как априори утверждений, известных как «координационные определения », которые должны были связать количественные термины с специфические измерительные операции.Недостатком этого решения является то, что предполагается, что выбор эталона произвольный и статичны, тогда как на практике эталоны обычно выбираются на основе эмпирических соображений и в конечном итоге улучшаются или заменены стандартами, которые считаются более точными.
Новое направление работ по проблеме координации появилось в последние годы, в первую очередь из произведений Хасока Чанга (2001, 2004, 2007; Барвич и Чанг, 2015) и Бас ван Фраассен (2008: Гл.5; 2009, 2012; см. также Padovani 2015, 2017; Мишель 2019). Эти Работы используют исторический и последовательный подход к проблеме. Вместо того, чтобы пытаться полностью избежать проблемы округлости, как и их предшественники, они намеревались показать, что округлость не порочный. Чанг утверждает, что построение количественной концепции и Стандартизация его измерения — это взаимозависимые и повторяющиеся задачи. Каждая «эпистемическая итерация» в истории стандартизация уважает существующие традиции и в то же время исправляя их (Chang 2004: Ch.5). Донаучная концепция температура, например, была связана с грубым и неоднозначным методы упорядочивания предметов от горячего к холодному. Термоскопы и в конечном итоге термометры помогли изменить первоначальную концепцию и сделали это точнее. С каждой такой итерацией количественное понятие было пересмотрены на более стабильный набор стандартов, которые, в свою очередь, позволил более точно проверить теоретические предсказания, облегчение последующего развития теории и построения более стабильных стандартов и так далее.
Как этот процесс избегает порочной замкнутости, становится ясно, когда мы посмотрим. при этом либо «сверху», т. е. в ретроспективе с учетом наших текущие научные знания, или «изнутри», глядя в исторических событиях в их первоначальном контексте (ван Фраассен 2008: 122). С любой точки зрения координация успешна, потому что это увеличивает согласованность между элементами теории и инструментария. На вопросы «что считать количественным измерением?» X ? » и «какое количество X ?», хотя и не имеют ответа независимо друг от друга, адресованы вместе в процессе взаимного уточнения.Только когда человек принимает фундаменталистской точки зрения и пытается найти отправную точку для координация, свободная от предположений, что этот исторический процесс ошибочно, кажется, не имеет эпистемического обоснования (2008: 137).
В новой литературе по координации смещается акцент обсуждение от определений количественных терминов к реализаций этих определений. На метрологическом жаргоне «Реализация» — это физический инструмент или процедура, приблизительно удовлетворяет данному определению (ср.JCGM 2012: 5.1). Примеры метрологических реализаций — официальные прототипы килограмм и часы с цезиевым фонтаном, используемые для стандартизации второй. Недавние исследования показывают, что методы, используемые для проектирования, поддерживать и сравнивать реализации имеют прямое отношение к практическое применение понятий количества, единицы и масштаба, не менее чем определения этих понятий (Riordan 2015; Tal 2016). В связь между определением и реализацией единицы становится особенно сложно, когда определение сформулировано в теоретических терминах.Некоторые из основных единиц Международной системы (СИ) — включая метр, килограмм, ампер, кельвин и моль — нет больше определяется ссылкой на какой-либо конкретный вид физической системы, но фиксируя численное значение фундаментальной физической постоянной. Килограмм, например, был переопределен в 2019 году как единица массы. такое, что числовое значение постоянной Планка точно равно 6,62607015 × 10 -34 кг м 2 с -1 (BIPM 2019: 131). Понимание килограмма под этим определением — это в высшей степени теоретическая задача.Изучение практической реализации такие подразделения пролили новый свет на развивающиеся отношения между измерения и теория (Tal 2018; de Courtenay et al 2019; Wolff 2020b).
8.2 Теоретическая основа измерения
Как уже обсуждалось выше (разделы 7 а также 8.1), теория и измерение взаимозависимы как исторически, так и концептуально. С исторической стороны развитие теории и измерение происходит через итерационные и взаимные уточнения. На концептуальная сторона, спецификация форм методик измерения эмпирическое содержание теоретических концепций, а теория дает систематическая интерпретация показаний измерения инструменты.Эта взаимозависимость измерения и теории может показаться как угроза доказательной роли, которую измерение должно играть в научном предприятии. В конце концов, результаты измерений думал, что может проверить теоретические гипотезы, и это, кажется, требуют некоторой степени независимости измерения от теории. Этот угроза особенно очевидна, когда теоретическая гипотеза испытанный уже предполагается как часть модели измерения инструмент. Чтобы процитировать пример из работы Франклина и др.(1989: 230):
На первый взгляд может показаться замкнутым кругом, если кто-то должны были использовать ртутный термометр для измерения температуры объекты как часть эксперимента, чтобы проверить, расширяются ли объекты по мере повышения их температуры.
Тем не менее Франклин и др. сделать вывод, что округлость не беспощадный. Ртутный термометр можно откалибровать по другому термометр, принцип действия которого не предполагает закона теплового расширения, например, газовый термометр постоянного объема, тем самым подтверждая надежность ртутного термометра на независимые основания.Говоря шире, в контексте локальной проверки гипотез угроза замкнутости обычно может быть избегать обращения к другим видам инструментов и другим частям теория.
Другой вид беспокойства по поводу доказательной функции измерения возникает в глобальном масштабе, когда проводится проверка всех теорий. обеспокоенный. Как утверждает Томас Кун (1961), научные теории обычно принимаются задолго до количественных методов их тестирования становятся доступными. Надежность недавно введенного измерения методы обычно проверяются на соответствие предсказаниям теории а не наоборот.По словам Куна, « путь от научного закона к научному измерению редко бывает ехал в обратном направлении »(1961: 189). Например, Закон Дальтона, который гласит, что веса элементов в химические соединения связаны друг с другом целиком пропорции, изначально противоречащие некоторым из наиболее известных мерки таких пропорций. Только предполагая Закон Дальтона, который последующие химики-экспериментаторы смогли исправить и улучшить свои методы измерения (1961: 173).Следовательно, Кун утверждает, что функция измерения в физических науках не для проверки теории, а для ее применения во все большем объеме и точность, и, в конечном итоге, позволить стойким аномалиям выйти на поверхность это ускорит следующий кризис и научную революцию. Примечание что Кун не утверждает, что измерение не имеет доказательной роли для играть в науку. Вместо этого он утверждает, что измерения не могут проверить теория изолирована, но только в сравнении с альтернативной теорией это предлагается в попытке объяснить обнаруженные аномалии за счет все более точных измерений (для яркого обсуждения о диссертации Куна см. Hacking 1983: 243–5).
Традиционные дискуссии о теоретической нагруженности, как и у Куна, были проводится на фоне логических позитивистов различие между теоретическим и наблюдательным языком. В теоретическая нагруженность измерения правильно воспринималась как угроза возможность четкого разграничения между двумя языками. Современные дискуссии, напротив, больше не ведутся. теоретическая нагруженность как эпистемологическая угроза, но воспринимается как должное что некоторый уровень теоретической нагруженности является предпосылкой для измерений иметь какую-либо доказательную силу.Без какого-то минимального существенного предположения об измеряемой величине, например о ее приемлемости манипулированию и его отношениям к другим величинам, это было бы невозможно интерпретировать показания средств измерений и следовательно, невозможно установить доказательную релевантность этих показания. Об этом уже говорил Пьер Дюгем (1906: 153–6; см. также Carrier 1994: 9–19). Кроме того, современные авторы подчеркивают, что теоретические предположения играют важные роли в исправлении ошибок измерения и оценке неопределенности измерения.Действительно, физические процедуры измерения становятся на более точными на , когда лежащая в их основе модель деидеализованный, процесс, который включает в себя увеличение теоретических богатство модели (Tal 2011).
Признание того, что теория имеет решающее значение для гарантии Доказательная надежность измерений обращает внимание на «Проблема обоснования наблюдений», которая является обратной вызов традиционной угрозе теоретической нагруженности (Tal 2016b). Задача состоит в том, чтобы указать, какую роль наблюдение играет в измерение, и особенно какая связь с наблюдением необходимо и / или достаточно для того, чтобы измерения могли сыграть доказательная роль в науках.Эта проблема особенно очевидна, когда одна попытка объяснить растущее использование вычислительных методы выполнения задач, которые традиционно решались измерительные приборы. В роли Маргарет Моррисон (2009) и Венди Паркер (2017) утверждают, есть случаи, когда достоверная количественная информация собирается о целевой системе с помощью компьютера моделирование, но таким образом, чтобы удовлетворить некоторые из основных Desiderata для измерения, например, эмпирическое обоснование и ретроспективный (см. также Lusk 2016).На такую информацию не полагается по сигналам, передаваемым от конкретного объекта, представляющего интерес, к инструмента, но на использовании теоретических и статистических моделей для обрабатывать эмпирические данные о связанных объектах. Например, данные методы ассимиляции обычно используются для оценки прошлых атмосферных температуры в регионах, где нет показаний термометра. Некоторые методы делают это путем подбора вычислительной модели поведение атмосферы на комбинацию доступных данных из близлежащие регионы и модельный прогноз условий на момент наблюдение (Parker 2017).Эти оценки затем используются в различных способов, в том числе в качестве данных для оценки перспективных климатических моделей. Независимо от того, называют ли эти оценки «Измерения», они ставят под сомнение идею о том, что производство надежные количественные данные о состоянии объекта требуют наблюдая за этим объектом, как бы слабо он ни понимал термин «Наблюдение». [23]
8,3 Точность и прецизионность
Два ключевых аспекта надежности результатов измерений: тщательность и точность.Рассмотрим серию повторяющихся весов измерения, выполненные на конкретном объекте с равными руками остаток средств. С реалистической, «ошибочной» точки зрения, результаты этих измерений точны , если они близки истинному значению измеряемой величины — в нашем случае истинное соотношение веса объекта к выбранному unit — и — точный , если они расположены близко друг к другу. An аналогия, которую часто цитируют, чтобы прояснить основанное на ошибках различие, заключается в том, что стрелы стреляют в цель с точностью, аналогичной близости попадания в яблочко и точность, аналогичная плотности распространения хитов (ср.JCGM 2012: 2.13 и 2.15, Teller 2013: 192). Хотя интуитивно понятный, основанный на ошибках способ выделения различий вызывает эпистемологическую трудность. Принято считать, что точные истинные значения большинства величин, представляющих интерес для науки, непознаваемым, по крайней мере, когда эти количества измеряются в непрерывном Весы. Если это предположение выполнено, то точность, с которой измеряемые величины не могут быть известны с точностью, а только оценивается путем сравнения неточных измерений друг с другом.И все еще неясно, почему сходимость между неточными измерениями должна быть воспринимается как указание на истину. Ведь измерения могли быть страдают от общей предвзятости, которая предотвращает их индивидуальные неточности от взаимного нейтрализации при усреднении. В отсутствие когнитивный доступ к истинным ценностям, как оценивается измерение точность возможна?
Отвечая на этот вопрос, философы извлекли пользу из изучения различные значения термина «точность измерения» как используется практикующими учеными.По крайней мере, пять разных чувств определены: метафизические, эпистемологические, операционные, сравнительные и прагматичный (Tal 2011: 1084–5). В частности, эпистемологические или «Основанный на неопределенности» смысл этого термина метафизически нейтрален и не предполагает существования истинных ценностей. Вместо, за точность результата измерения принимается близость согласие между ценностями, разумно отнесенными к данному количеству доступные эмпирические данные и базовые знания (см. JCGM 2012: 2.13 Заметка 3; Джордани и Мари 2012; де Куртенэ и Грежис 2017).Таким образом, точность измерения может быть оценена следующим образом: установление устойчивости среди последствий моделей, представляющих различные измерительные процессы (Basso 2017; Tal 2017b; Bokulich 2020; Стейли 2020).
Согласно концепции, основанной на неопределенности, неточность — это особый вид. неточности. Например, неточность измерения веса составляет широта разброса ценностей, которые обоснованно приписываются вес объекта с учетом показаний весов и доступные базовые знания о том, как работает баланс, и стандартные веса использовались.Неточность этих измерений заключается в компонент неточности, возникающий из-за неконтролируемых изменений показания баланса при повторных испытаниях. Другие источники неточности, помимо неточности, включают несовершенные исправления систематические ошибки, неточно известные физические константы и неопределенные определения измеряемых величин, среди прочего (см. Раздел 7.1).
Пол Теллер (2018) выдвигает другое возражение против ошибочного понятие точности измерения. Он возражает против предположения, что он называет «реализмом точности измерений», согласно которому в действительности измеримые величины имеют определенные значения.Теллер утверждает что это предположение неверно в том, что касается величин обычно измеряется в физике, потому что любое уточнение определенного значения (или диапазоны значений) для таких величин предполагает идеализацию и следовательно, не может относиться ни к чему в действительности. Например, концепция обычно понимается под фразой «скорость звука в воздух »включает в себя множество неявных идеализаций, касающихся однородность химического состава воздуха, температуры и давление, а также стабильность единиц измерения.Удаление эти идеализации полностью потребуют добавления бесконечного количества детали к каждой спецификации. Как утверждает Теллер, точность измерения следует понимать как полезную идеализацию, а именно как концепция, которая позволяет ученым оценивать согласованность и согласованность среди результатов измерения как будто лингвистическое выражение эти результаты зацепились за все в мире. Точность аналогично идеализированная концепция, основанная на неограниченном и неопределенное определение того, что считается повторением измерения при «тех же» обстоятельствах (Teller 2013: 194).
Введение в измеренияВведение в измерения
[Лаборатория Показатель]
Физика и измерения
«Путем сравнения результатов точных измерений с численными предсказаниями теории, мы можем приобретаем значительную уверенность в правильности теории, и мы может определить, в каких аспектах его необходимо изменить. это часто можно объяснить явление в нескольких грубых качественные способы, и если мы довольны этим, это может быть невозможно решить, какая теория верна.Но если теория может быть предоставленным, который правильно предсказывает результаты измерений четыре или пять (или даже две или три) значащих цифры, теория вряд ли может быть очень ошибочной. Грубое соглашение может быть совпадение, но близкого согласия вряд ли будет. Более того, в истории науки было много случаев, когда малые но значительные расхождения между теорией и точными измерения привели к разработке новых и более далеко идущие теории.Такие незначительные несоответствия даже не были бы обнаружены, если бы мы довольствовались простым качественное объяснение явлений ». — Кейт Р. Саймон, Механика, второе издание , 1964
Ученые делают прогнозы. — прогнозы, основанные на их гипотезах, законы и теории. Проверка предсказания заключается в том, работает ли оно в «реальном мире» — сделайте результаты экспериментов совпадают с теоретическим предсказанием? Если результаты не совпадают (и эти результаты подтверждены другими компетентными учеными) то гипотеза, на основании которой был сделан прогноз, должна быть изменена или заброшенный.Высшим авторитетом в науке является природа, а не то, что она говорится в книге «.
Вы, возможно, не думали об этом, но когда вы решаете «физику проблема «в учебнике вы делаете теоретический прогноз. Когда вы рассчитываете, что в какой-то ситуации автомобиль должен занести 20 метров, Настоящая проверка правильности вашего результата — это настоящая машина действительно занесет 20 метров в этой ситуации — не то, что книга говорит «в» разделе ответов.«
Физика — это количественная наука. Физики занимаются числа — но , а не , просто числа математика. Этот — важный момент, который часто упускают из виду начинающие физики. Числа физиков часто (или могут быть) измерений , а не чистые числа математик.
Следовательно, физики измеряют вещи. Измерение очень важно в физике — физики серьезно относятся к измерениям.Один из основных вкладов физики в другие науки и общество многие измерительные приборы и методы, которыми располагает физика развитый. В «повседневной жизни» берем линейку и измеряем что-то, не задумываясь об этом. Физики думают о их измерения, и нужно иметь гораздо более сложные понимание процесса измерения, чем у «нормальных» людей.
Начинающие физики часто имеют очень искаженное представление обо всем это.Вы, возможно, помните, как проводили эксперимент, например, определяли ускорение свободного падения. Ускорение свободного падения «должно быть «9,8 м / с 2 — это все знают. Ваш» ответ «пришел 10,3 м / с 2 , значит, ваш эксперимент «не сработал» — вы «по ошибке» — возможно, вы даже вычислили свой «процент ошибки». Многих начинающих физиков обременяют следующие заблуждения (которые мы постараемся исправить в страницы):
- Размеры — числа, и…
- Существуют точные значения физических величин (например, ускорение свободного падения), и …
- Кто-нибудь (возможно, известный физик) знает, что это за точные значения, и …
- Мои значения всегда неверны, так что …
- Физические эксперименты «не работают».
Итак, этот блок начинается с краткого знакомства с четырьмя типами чисел, с которыми должен иметь дело физик-экспериментатор, с последующим подробным обсуждением процесса измерения — что точность в том, почему это вызывает беспокойство и как с этим бороться в замеры и расчеты.Затем идет обсуждение точность и, наконец, прямые ответы на вопрос: «Хорошо, а как я вообще-то анализирую этот эксперимент? »
Содержание единицы измерения
Литература и ссылки:
- Робертс, Дана, «Ошибки, неточности и характер физика », Учитель физики, март 1983 г. — очень полезный вступление; ссылка, которую я использовал в течение многих лет.
- Тейлор, Джон Р. «Введение в анализ ошибок — Исследование неопределенностей физических измерений, во-вторых. Издание «, University Science Books — Это действительно фантастическая ссылка! К сожалению, я нашел его после того, как написал первый черновик этого блока … (но теперь я замечаю, что это упоминается и Робертсом …)
- Ошибка Анализ — пишется на уровне первокурсника колледжа (без расчетов) проф.Дональд Э. Симанек из Университета Лок-Хейвен. (добавлено в марте 4, 1999)
- NIST Физика Лаборатория — много полезной информации из Национального Институт науки и технологий
- NIST Ссылка на константы, единицы измерения и неопределенность — очень информативно и интересно — возможно немного технического
- Точность и Точность — составлено профессиональным геодезистом
- Точность, Точность и неопределенность измерения — краткое руководство с точки зрения химии
- Наука измерения — точность vs.Точность — от Гавайи
- Точность против точности и ошибки против неопределенности — учебное пособие с практическая викторина
- Ошибка, Точность и прецизионность — от Университета Колорадо
- Точность и точность — еще одна перспектива химии
- Точность и точность — хорошее обсуждение
[Лаборатория Показатель]
последнее обновление 13 октября 2008 г., автор: JL Stanbrough
Определение измерений в науке
В науке измерение — это набор количественных или числовых данных, описывающих свойство объекта или события.Измерение производится путем сравнения количества со стандартной единицей измерения. Поскольку это сравнение не может быть идеальным, измерения по своей сути включают ошибку, то есть насколько измеренное значение отклоняется от истинного значения. Изучение измерений называется метрологией.
Существует множество систем измерения, которые использовались на протяжении всей истории и во всем мире, но с 18 века был достигнут прогресс в установлении международного стандарта. В современной Международной системе единиц (СИ) все типы физических измерений основаны на семи основных единицах.
Методы измерения
- Длину веревки можно измерить, сравнив ее с метровой палкой.
- Объем капли воды можно измерить с помощью градуированного цилиндра.
- Масса образца может быть измерена с помощью весов или весов.
- Температуру пожара можно измерить с помощью термопары.
Сравнение измерений
Измерение объема стакана воды с помощью колбы Эрленмейера даст вам лучшее измерение, чем попытки измерить его объем, поместив его в ведро, даже если оба измерения указаны с использованием одной и той же единицы (например.г., миллилитры). Точность имеет значение, поэтому есть критерии, которые ученые используют для сравнения измерений: тип, величина, единица измерения и погрешность.
Уровень или тип — это методика, используемая для измерения. Величина — это фактическое числовое значение измерения (например, 45 или 0,237). Единица измерения — это отношение числа к стандарту количества (например, грамм, кандела, микрометр). Неопределенность отражает систематические и случайные ошибки измерения. Неопределенность — это описание уверенности в точности и точности измерения, которое обычно выражается как ошибка.
Измерительные системы
Измерения калибруются, то есть сравниваются с набором стандартов в системе, чтобы измерительное устройство могло выдать значение, которое соответствует тому, что другой человек получил бы, если бы измерение было повторено. Вы можете встретить несколько распространенных стандартных систем:
- Международная система единиц (SI) : SI происходит от французского названия Système International d’Unités. Это наиболее часто используемая метрическая система.
- Метрическая система : СИ — это особая метрическая система, которая представляет собой десятичную систему измерения. Примерами двух распространенных форм метрической системы являются система MKS (метр, килограмм, секунда в качестве основных единиц) и система CGS (сантиметр, грамм и секунда в качестве основных единиц). В системе СИ и других формах метрической системы существует множество единиц, построенных на комбинации основных единиц. Они называются производными единицами.
- Английская система : Британская или имперская система измерений была распространена до того, как единицы СИ были приняты на международном уровне.Хотя Великобритания в основном приняла систему СИ, Соединенные Штаты и некоторые страны Карибского бассейна по-прежнему используют английскую систему в ненаучных целях. Эта система основана на единицах фут-фунт-секунда для единиц длины, массы и времени.
Ознакомьтесь с семью константами, определяющими СИ. Следующие семь определений базовых единиц СИ основаны на брошюре BIPM SI (9-е издание). Определения основных единиц СИ Моль (символ моль) — это единица измерения количества вещества в системе СИ. Один моль содержит ровно 6,022 140 76 x 10 23 элементарных объекта. Это число представляет собой фиксированное числовое значение постоянной Авогадро, N A , выраженное в единицах моль -1 , и называется числом Авогадро.Количество вещества, символ n , в системе является мерой количества определенных элементарных объектов. Элементарным объектом может быть атом, молекула, ион, электрон, любая другая частица или определенная группа частиц. | ||




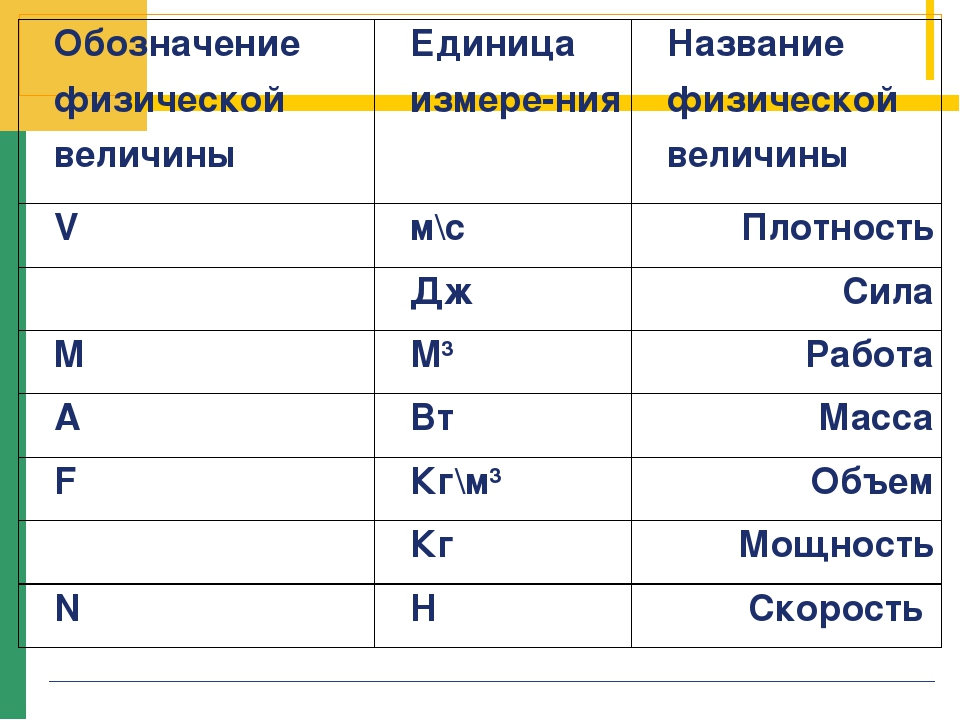
 -мат. наук, доцент
-мат. наук, доцент