Постоянная Планка — это… Что такое Постоянная Планка?
Постоя́нная Пла́нка (квант действия) — основная константа квантовой теории, коэффициент, связывающий величину энергии кванта электромагнитного излучения с его частотой так же, как и вообще величину кванта энергии любой линейной колебательной физической системы с её частотой. Связывает энергию и импульс с частотой и пространственной частотой, действия с фазой. Является квантом момента импульса. Впервые упомянута Планком в работе, посвящённой тепловому излучению, и потому названа в его честь. Обычное обозначение — латинское .
- Дж·c[1]
- эрг·c.
- эВ·c[1].
Часто применяется величина :
- Дж·c[1],
- эрг·c,
- эВ·c[1],
называемая редуцированной (иногда рационализированной или приведённой) постоянной Планка или постоянной Дирака.
На 24-й Генеральной конференции по мерам и весам 17—21 октября 2011 года была единогласно принята резолюция[2]
Физический смысл
В квантовой механике импульс имеет физический смысл волнового вектора, энергия — частоты, а действие — фазы волны, однако традиционно (исторически) механические величины измеряются в других единицах(кг·м/с, Дж, Дж·с), чем соответствующие волновые (м
- (импульс)
- (энергия)
- (действие)
Если бы система физических единиц формировалась уже после возникновения квантовой механики и приспосабливалась для упрощения основных теоретических формул, константа Планка вероятно просто была бы сделана равной единице, или, во всяком случае, более круглому числу. В теоретической физике очень часто для упрощения формул используется система единиц с , в ней
- .
Постоянная Планка имеет и простую оценочную роль в разграничении областей применимости классической и квантовой физики: она в сравнении с величиной характерных для рассматриваемой системы величин действия или момента импульса, или произведений характерного импульса на характерный размер, или характерной энергии на характерное время, показывает, насколько применима к данной физической системе классическая механика. А именно, если — действие системы, а — её момент импульса, то при или поведение системы с хорошей точностью описывается классической механикой. Эти оценки достаточно прямо связаны с соотношениями неопределенностей Гейзенберга.
История открытия
Формула Планка для теплового излучения
Формула Планка — выражение для спектральной плотности мощности излучения абсолютно чёрного тела, которое было получено Максом Планком для равновесной плотности излучения . Формула Планка была получена после того, как стало ясно, что формула Рэлея — Джинса удовлетворительно описывает излучение только в области длинных волн. В 1900 году Планк предложил формулу с постоянной (впоследствии названной постоянной Планка), которая хорошо согласовывалась с экспериментальными данными. При этом Планк полагал, что данная формула является всего лишь удачным математическим трюком, но не имеет физического смысла. То есть Планк не предполагал, что электромагнитное излучение испускается в виде отдельных порций энергии (квантов), величина которых связана с частотой излучения выражением:
Коэффициент пропорциональности впоследствии назвали постоянной Планка, = 1.054·10−34 Дж·с.
Фотоэффект
Фотоэффект — это испускание электронов веществом под действием света (и, вообще говоря, любого электромагнитного излучения). В конденсированных веществах (твёрдых и жидких) выделяют внешний и внутренний фотоэффект.
Фотоэффект был объяснён в 1905 году Альбертом Эйнштейном (за что в 1921 году он, благодаря номинации шведского физика Озеена, получил Нобелевскую премию) на основе гипотезы Планка о квантовой природе света. В работе Эйнштейна содержалась важная новая гипотеза — если Планк предположил, что свет
где — т. н. работа выхода (минимальная энергия, необходимая для удаления электрона из вещества), — кинетическая энергия вылетающего электрона, — частота падающего фотона с энергией , — постоянная Планка. Из этой формулы следует существование красной границы фотоэффекта, то есть существование наименьшей частоты, ниже которой энергии фотона уже не достаточно для того, чтобы «выбить» электрон из тела. Суть формулы заключается в том, что энергия фотона расходуется на ионизацию атома вещества и на работу, необходимую для «вырывания» электрона, а остаток переходит в кинетическую энергию электрона.
Эффект Комптона
Методы измерения
Использование законов фотоэффекта
При данном способе измерения постоянной Планка используется закон Эйнштейна для фотоэффекта:
где — максимальная кинетическая энергия вылетевших с катода фотоэлектронов,
- — частота падающего света,
- — т. н. работа выхода электрона.
Измерение проводится так. Сначала катод фотоэлемента облучают монохроматическим светом с частотой , при этом на фотоэлемент подают запирающее напряжение, так, чтобы ток через фотоэлемент прекратился. При этом имеет место следующее соотношение, непосредственно вытекающее из закона Эйнштейна:
где — заряд электрона.
Затем тот же фотоэлемент облучают монохроматическим светом с частотой и точно также запирают его с помощью напряжения
Почленно вычитая второе выражение из первого, получаем
откуда следует
Анализ спектра тормозного рентгеновского излучения
Этот способ считается самым точным из существующих. Используется тот факт, что частотный спектр тормозного рентгеновского излучения имеет точную верхнюю границу, называемую фиолетовой границей. Её существование вытекает из квантовых свойств электромагнитного излучения и закона сохранения энергии. Действительно,
где — скорость света,
- — длина волны рентгеновского излучения,
- — заряд электрона,
- — ускоряющее напряжение между электродами рентгеновской трубки.
Тогда постоянная Планка равна
Примечания
Литература
- John D. Barrow. The Constants of Nature; From Alpha to Omega — The Numbers that Encode the Deepest Secrets of the Universe. — Pantheon Books, 2002. — ISBN 0-37-542221-8
Ссылки
Постоянная Планка — Википедия. Что такое Постоянная Планка
Постоя́нная Пла́нка (квант действия) — основная константа квантовой теории, коэффициент, связывающий величину энергии кванта электромагнитного излучения с его частотой, так же как и вообще величину кванта энергии любой линейной колебательной физической системы с её частотой. Связывает энергию и импульс с частотой и пространственной частотой, действие с фазой. Является квантом момента импульса. Впервые упомянута Планком в работе, посвящённой тепловому излучению, и потому названа в его честь. Обычное обозначение — латинское h{\displaystyle h}.
- h = 6,626 070 040(81) × 10−34Дж·c[1];
- h = 6,626 070 040(81) × 10−27эрг·c;
- h = 4,135 667 662(25) × 10−15эВ·c[1].
Часто применяется величина ℏ≡h3π{\displaystyle \hbar \equiv {\frac {h}{2\pi }}}:
- ħ = 1,054 571 800(13) × 10−34Дж·c[1];
- ħ = 1,054 571 800(13) × 10−27эрг·c;
- ħ = 6,582 119 514(40) × 10−16эВ·c[1],
называемая редуцированной (иногда рационализированной или приведённой) постоянной Планка или постоянной Дирака. Применение этого обозначения упрощает многие формулы квантовой механики, так как в эти формулы традиционная постоянная Планка входит в виде деленной на константу 2π{\displaystyle {2\pi }}.
В ряде естественных систем единиц является единицей измерения действия[2]. В планковской системе единиц, также относящейся к естественным системам, служит в качестве одной из основных единиц системы.
На XXIV Генеральной конференции по мерам и весам (ГКМВ) 17—21 октября 2011 года была единогласно принята резолюция[3], в которой, в частности, предложено в будущей ревизии Международной системы единиц (СИ) переопределить единицы измерений СИ таким образом, чтобы постоянная Планка была равной точно 6,62606X·10−34 Дж·с, где Х заменяет одну или более значащих цифр, которые будут определены в дальнейшем на основании наиболее точных рекомендаций CODATA[4]. В этой же резолюции предложено таким же образом определить как точные значения постоянную Авогадро, элементарный заряд и постоянную Больцмана. XXV ГКМВ, состоявшаяся в 2014 году, приняла решение продолжить работу по подготовке новой ревизии СИ, включающей привязку основных единиц СИ к
Физический смысл
В квантовой механике импульс имеет физический смысл волнового вектора[источник не указан 240 дней], энергия — частоты, а действие — фазы волны, однако традиционно (исторически) механические величины измеряются в других единицах (кг·м/с, Дж, Дж·с), чем соответствующие волновые (м−1, с−1, безразмерные единицы фазы). Постоянная Планка играет роль переводного коэффициента (всегда одного и того же), связывающего эти две системы единиц — квантовую и традиционную:
- p=ℏk(|p|=2πℏ/λ){\displaystyle \mathbf {p} =\hbar \mathbf {k} \,\,\,(|\mathbf {p} |=2\pi \hbar /\lambda )} (импульс),
- E=ℏω{\displaystyle E=\hbar \omega } (энергия),
- S=ℏϕ{\displaystyle S=\hbar \phi } (действие).
Если бы система физических единиц формировалась уже после возникновения квантовой механики и приспосабливалась для упрощения основных теоретических формул, константа Планка вероятно просто была бы сделана равной единице, или, во всяком случае, более круглому числу. В теоретической физике очень часто для упрощения формул используется система единиц с ℏ=1{\displaystyle \hbar =1}, в ней
- p=k(|p|=2π/λ),{\displaystyle \mathbf {p} =\mathbf {k} \,\,\,(|\mathbf {p} |=2\pi /\lambda ),}
- E=ω,{\displaystyle E=\omega ,}
- S=ϕ,{\displaystyle S=\phi ,}
- (ℏ=1).{\displaystyle (\hbar =1).}
Постоянная Планка имеет и простую оценочную роль в разграничении областей применимости классической и квантовой физики: она в сравнении с величиной характерных для рассматриваемой системы величин действия или момента импульса, или произведений характерного импульса на характерный размер, или характерной энергии на характерное время, показывает, насколько применима к данной физической системе классическая механика. А именно, если S{\displaystyle S} — действие системы, а M{\displaystyle M} — её момент импульса, то при Sℏ≫1{\displaystyle {\frac {S}{\hbar }}\gg 1} или Mℏ≫1{\displaystyle {\frac {M}{\hbar }}\gg 1} поведение системы с хорошей точностью описывается классической механикой. Эти оценки достаточно прямо связаны с соотношениями неопределённостей Гейзенберга.
История открытия
Формула Планка для теплового излучения
Формула Планка — выражение для спектральной плотности мощности излучения абсолютно чёрного тела, которое было получено Максом Планком для равновесной плотности излучения u(ω,T){\displaystyle u(\omega ,T)}. Формула Планка была получена после того, как стало ясно, что формула Рэлея — Джинса удовлетворительно описывает излучение только в области длинных волн. В 1900 году Планк предложил формулу с постоянной (впоследствии названной постоянной Планка), которая хорошо согласовывалась с экспериментальными данными. При этом Планк полагал, что данная формула является всего лишь удачным математическим трюком, но не имеет физического смысла. То есть Планк не предполагал, что электромагнитное излучение испускается в виде отдельных порций энергии (квантов), величина которых связана с циклической частотой излучения выражением:
- ε=ℏω.{\displaystyle \varepsilon =\hbar \omega .}
Коэффициент пропорциональности ħ впоследствии назвали постоянной Планка, ħ ≈ 1,054·10−34 Дж·с.
Фотоэффект
Фотоэффект — это испускание электронов веществом под действием света (и, вообще говоря, любого электромагнитного излучения). В конденсированных веществах (твёрдых и жидких) выделяют внешний и внутренний фотоэффект.
Фотоэффект был объяснён в 1905 году Альбертом Эйнштейном (за что в 1921 году он, благодаря номинации шведского физика Озеена, получил Нобелевскую премию) на основе гипотезы Планка о квантовой природе света. В работе Эйнштейна содержалась важная новая гипотеза — если Планк предположил, что свет излучается только квантованными порциями, то Эйнштейн уже считал, что свет и существует только в виде квантованных порций. Из закона сохранения энергии, при представлении света в виде частиц (фотонов), следует формула Эйнштейна для фотоэффекта:
- ℏω=Aout+mv22,{\displaystyle \hbar \omega =A_{out}+{\frac {mv^{2}}{2}},}
где Aout{\displaystyle A_{out}} — т. н. работа выхода (минимальная энергия, необходимая для удаления электрона из вещества), mv22{\displaystyle {\frac {mv^{2}}{2}}} — кинетическая энергия вылетающего электрона, ω{\displaystyle \omega } — частота падающего фотона с энергией ℏω,{\displaystyle \hbar \omega ,} ℏ{\displaystyle \hbar } — постоянная Планка. Из этой формулы следует существование красной границы фотоэффекта, то есть существование наименьшей частоты, ниже которой энергии фотона уже недостаточно для того, чтобы «выбить» электрон из тела. Суть формулы заключается в том, что энергия фотона расходуется на ионизацию атома вещества, то есть на работу, необходимую для «вырывания» электрона, а остаток переходит в кинетическую энергию электрона.
Эффект Комптона
Методы измерения
Использование законов фотоэффекта
При данном способе измерения постоянной Планка используется закон Эйнштейна для фотоэффекта:
- Kmax=hν−A,{\displaystyle K_{max}=h\nu -A,}
где Kmax{\displaystyle K_{max}} — максимальная кинетическая энергия вылетевших с катода фотоэлектронов,
- ν{\displaystyle \nu } — частота падающего света,
- A{\displaystyle A} — т. н. работа выхода электрона.
Измерение проводится так. Сначала катод фотоэлемента облучают монохроматическим светом с частотой ν1{\displaystyle \nu _{1}}, при этом на фотоэлемент подают запирающее напряжение, так, чтобы ток через фотоэлемент прекратился. При этом имеет место следующее соотношение, непосредственно вытекающее из закона Эйнштейна:
- hν1=A+eU1,{\displaystyle h\nu _{1}=A+eU_{1},}
где e{\displaystyle e} — заряд электрона.
Затем тот же фотоэлемент облучают монохроматическим светом с частотой ν2{\displaystyle \nu _{2}} и точно так же запирают его с помощью напряжения U2:{\displaystyle U_{2}:}
- hν2=A+eU2.{\displaystyle h\nu _{2}=A+eU_{2}.}
Почленно вычитая второе выражение из первого, получаем
- h(ν1−ν2)=e(U1−U2),{\displaystyle h(\nu _{1}-\nu _{2})=e(U_{1}-U_{2}),}
откуда следует
- h=e(U1−U2)(ν1−ν2).{\displaystyle h={\frac {e(U_{1}-U_{2})}{(\nu _{1}-\nu _{2})}}.}
Анализ спектра тормозного рентгеновского излучения
Этот способ считается самым точным из существующих. Используется тот факт, что частотный спектр тормозного рентгеновского излучения имеет точную верхнюю границу, называемую фиолетовой границей. Её существование вытекает из квантовых свойств электромагнитного излучения и закона сохранения энергии. Действительно,
- hcλ=eU,{\displaystyle h{\frac {c}{\lambda }}=eU,}
где c{\displaystyle c} — скорость света,
- λ{\displaystyle \lambda } — длина волны рентгеновского излучения,
- e{\displaystyle e} — заряд электрона,
- U{\displaystyle U} — ускоряющее напряжение между электродами рентгеновской трубки.
Тогда постоянная Планка равна
- h=λUec.{\displaystyle h={\frac {{\lambda }{Ue}}{c}}.}
См. также
Примечания
Литература
Ссылки
Постоянная Планка — Википедия
Постоя́нная Пла́нка (квант действия) — основная константа квантовой теории, коэффициент, связывающий величину энергии кванта электромагнитного излучения с его частотой, так же как и вообще величину кванта энергии любой линейной колебательной физической системы с её частотой. Связывает энергию и импульс с частотой и пространственной частотой, действие с фазой. Является квантом момента импульса. Впервые упомянута Планком в работе, посвящённой тепловому излучению, и потому названа в его честь. Обычное обозначение — латинское h{\displaystyle h}.
- h = 6,626 070 040(81) × 10−34Дж·c[1];
- h = 6,626 070 040(81) × 10−27эрг·c;
- h = 4,135 667 662(25) × 10−15эВ·c[1].
Часто применяется величина ℏ≡h3π{\displaystyle \hbar \equiv {\frac {h}{2\pi }}}:
- ħ = 1,054 571 800(13) × 10−34Дж·c[1];
- ħ = 1,054 571 800(13) × 10−27эрг·c;
- ħ = 6,582 119 514(40) × 10−16эВ·c[1],
называемая редуцированной (иногда рационализированной или приведённой) постоянной Планка или постоянной Дирака. Применение этого обозначения упрощает многие формулы квантовой механики, так как в эти формулы традиционная постоянная Планка входит в виде деленной на константу 2π{\displaystyle {2\pi }}.
В ряде естественных систем единиц является единицей измерения действия[2]. В планковской системе единиц, также относящейся к естественным системам, служит в качестве одной из основных единиц системы.
На XXIV Генеральной конференции по мерам и весам (ГКМВ) 17—21 октября 2011 года была единогласно принята резолюция[3], в которой, в частности, предложено в будущей ревизии Международной системы единиц (СИ) переопределить единицы измерений СИ таким образом, чтобы постоянная Планка была равной точно 6,62606X·10−34 Дж·с, где Х заменяет одну или более значащих цифр, которые будут определены в дальнейшем на основании наиболее точных рекомендаций CODATA[4]. В этой же резолюции предложено таким же образом определить как точные значения постоянную Авогадро, элементарный заряд и постоянную Больцмана. XXV ГКМВ, состоявшаяся в 2014 году, приняла решение продолжить работу по подготовке новой ревизии СИ, включающей привязку основных единиц СИ к точному значению постоянной Планка, и предварительно наметила закончить эту работу к 2018 году с тем, чтобы заменить существующую СИ обновлённым вариантом на XXVI ГКМВ[5].
Физический смысл
В квантовой механике импульс имеет физический смысл волнового вектора[источник не указан 240 дней], энергия — частоты, а действие — фазы волны, однако традиционно (исторически) механические величины измеряются в других единицах (кг·м/с, Дж, Дж·с), чем соответствующие волновые (м−1, с−1, безразмерные единицы фазы). Постоянная Планка играет роль переводного коэффициента (всегда одного и того же), связывающего эти две системы единиц — квантовую и традиционную:
- p=ℏk(|p|=2πℏ/λ){\displaystyle \mathbf {p} =\hbar \mathbf {k} \,\,\,(|\mathbf {p} |=2\pi \hbar /\lambda )} (импульс),
- E=ℏω{\displaystyle E=\hbar \omega } (энергия),
- S=ℏϕ{\displaystyle S=\hbar \phi } (действие).
Если бы система физических единиц формировалась уже после возникновения квантовой механики и приспосабливалась для упрощения основных теоретических формул, константа Планка вероятно просто была бы сделана равной единице, или, во всяком случае, более круглому числу. В теоретической физике очень часто для упрощения формул используется система единиц с ℏ=1{\displaystyle \hbar =1}, в ней
- p=k(|p|=2π/λ),{\displaystyle \mathbf {p} =\mathbf {k} \,\,\,(|\mathbf {p} |=2\pi /\lambda ),}
- E=ω,{\displaystyle E=\omega ,}
- S=ϕ,{\displaystyle S=\phi ,}
- (ℏ=1).{\displaystyle (\hbar =1).}
Постоянная Планка имеет и простую оценочную роль в разграничении областей применимости классической и квантовой физики: она в сравнении с величиной характерных для рассматриваемой системы величин действия или момента импульса, или произведений характерного импульса на характерный размер, или характерной энергии на характерное время, показывает, насколько применима к данной физической системе классическая механика. А именно, если S{\displaystyle S} — действие системы, а M{\displaystyle M} — её момент импульса, то при Sℏ≫1{\displaystyle {\frac {S}{\hbar }}\gg 1} или Mℏ≫1{\displaystyle {\frac {M}{\hbar }}\gg 1} поведение системы с хорошей точностью описывается классической механикой. Эти оценки достаточно прямо связаны с соотношениями неопределённостей Гейзенберга.
История открытия
Формула Планка для теплового излучения
Формула Планка — выражение для спектральной плотности мощности излучения абсолютно чёрного тела, которое было получено Максом Планком для равновесной плотности излучения u(ω,T){\displaystyle u(\omega ,T)}. Формула Планка была получена после того, как стало ясно, что формула Рэлея — Джинса удовлетворительно описывает излучение только в области длинных волн. В 1900 году Планк предложил формулу с постоянной (впоследствии названной постоянной Планка), которая хорошо согласовывалась с экспериментальными данными. При этом Планк полагал, что данная формула является всего лишь удачным математическим трюком, но не имеет физического смысла. То есть Планк не предполагал, что электромагнитное излучение испускается в виде отдельных порций энергии (квантов), величина которых связана с циклической частотой излучения выражением:
- ε=ℏω.{\displaystyle \varepsilon =\hbar \omega .}
Коэффициент пропорциональности ħ впоследствии назвали постоянной Планка, ħ ≈ 1,054·10−34 Дж·с.
Фотоэффект
Фотоэффект — это испускание электронов веществом под действием света (и, вообще говоря, любого электромагнитного излучения). В конденсированных веществах (твёрдых и жидких) выделяют внешний и внутренний фотоэффект.
Фотоэффект был объяснён в 1905 году Альбертом Эйнштейном (за что в 1921 году он, благодаря номинации шведского физика Озеена, получил Нобелевскую премию) на основе гипотезы Планка о квантовой природе света. В работе Эйнштейна содержалась важная новая гипотеза — если Планк предположил, что свет излучается только квантованными порциями, то Эйнштейн уже считал, что свет и существует только в виде квантованных порций. Из закона сохранения энергии, при представлении света в виде частиц (фотонов), следует формула Эйнштейна для фотоэффекта:
- ℏω=Aout+mv22,{\displaystyle \hbar \omega =A_{out}+{\frac {mv^{2}}{2}},}
где Aout{\displaystyle A_{out}} — т. н. работа выхода (минимальная энергия, необходимая для удаления электрона из вещества), mv22{\displaystyle {\frac {mv^{2}}{2}}} — кинетическая энергия вылетающего электрона, ω{\displaystyle \omega } — частота падающего фотона с энергией ℏω,{\displaystyle \hbar \omega ,} ℏ{\displaystyle \hbar } — постоянная Планка. Из этой формулы следует существование красной границы фотоэффекта, то есть существование наименьшей частоты, ниже которой энергии фотона уже недостаточно для того, чтобы «выбить» электрон из тела. Суть формулы заключается в том, что энергия фотона расходуется на ионизацию атома вещества, то есть на работу, необходимую для «вырывания» электрона, а остаток переходит в кинетическую энергию электрона.
Эффект Комптона
Методы измерения
Использование законов фотоэффекта
При данном способе измерения постоянной Планка используется закон Эйнштейна для фотоэффекта:
- Kmax=hν−A,{\displaystyle K_{max}=h\nu -A,}
где Kmax{\displaystyle K_{max}} — максимальная кинетическая энергия вылетевших с катода фотоэлектронов,
- ν{\displaystyle \nu } — частота падающего света,
- A{\displaystyle A} — т. н. работа выхода электрона.
Измерение проводится так. Сначала катод фотоэлемента облучают монохроматическим светом с частотой ν1{\displaystyle \nu _{1}}, при этом на фотоэлемент подают запирающее напряжение, так, чтобы ток через фотоэлемент прекратился. При этом имеет место следующее соотношение, непосредственно вытекающее из закона Эйнштейна:
- hν1=A+eU1,{\displaystyle h\nu _{1}=A+eU_{1},}
где e{\displaystyle e} — заряд электрона.
Затем тот же фотоэлемент облучают монохроматическим светом с частотой ν2{\displaystyle \nu _{2}} и точно так же запирают его с помощью напряжения U2:{\displaystyle U_{2}:}
- hν2=A+eU2.{\displaystyle h\nu _{2}=A+eU_{2}.}
Почленно вычитая второе выражение из первого, получаем
- h(ν1−ν2)=e(U1−U2),{\displaystyle h(\nu _{1}-\nu _{2})=e(U_{1}-U_{2}),}
откуда следует
- h=e(U1−U2)(ν1−ν2).{\displaystyle h={\frac {e(U_{1}-U_{2})}{(\nu _{1}-\nu _{2})}}.}
Анализ спектра тормозного рентгеновского излучения
Этот способ считается самым точным из существующих. Используется тот факт, что частотный спектр тормозного рентгеновского излучения имеет точную верхнюю границу, называемую фиолетовой границей. Её существование вытекает из квантовых свойств электромагнитного излучения и закона сохранения энергии. Действительно,
- hcλ=eU,{\displaystyle h{\frac {c}{\lambda }}=eU,}
где c{\displaystyle c} — скорость света,
- λ{\displaystyle \lambda } — длина волны рентгеновского излучения,
- e{\displaystyle e} — заряд электрона,
- U{\displaystyle U} — ускоряющее напряжение между электродами рентгеновской трубки.
Тогда постоянная Планка равна
- h=λUec.{\displaystyle h={\frac {{\lambda }{Ue}}{c}}.}
См. также
Примечания
Литература
Ссылки
Физики уточнили значение постоянной Планка
Американские физики получили наиболее точное на сегодняшний день значение постоянной Планка со стандартным отклонением 13 частей на миллиард.
Постоянная Планка (h) — коэффициент, который связывает величину энергии кванта любой линейной колебательной физической системы с ее частотой. Первоначально константа применялась к закономерностям, характерным для электромагнитного излучения, и сейчас широко используется в квантовой механике, например при оценке момента импульса и фазы колебаний, а также в определении планковских единиц, включая метр и секунду. В 2011 году участники Генеральной конференции по мерам и весам приняли резолюцию о ревизии Международной системы единиц СИ с помощью уточнения постоянной Планка. Согласно проекту, к 2018 году ученые должны представить наиболее достоверные результаты измерений контанты.
Инициатива предполагает новое определение четырех единиц: килограмма, ампера, кельвина и моль. Самое точное значение числа Авогадро, необходимое для работы с последним, было получено в 2015 году. Оценка постоянной Планка, в свою очередь, важна для переосмысления килограмма. Сейчас эта единица массы определяется через платиново-иридиевый эталон — цилиндр, который был изготовлен в 1879 году и хранится в Международном бюро мер и весов. Чтобы детализировать константу и уменьшить ее зависимость от прототипа, специалисты из Национального института стандартов и технологий (NIST) США, Национальной физической лаборатории (NPL) Великобритании и других стран проводят эксперименты с ватт-весами.

Конструкция ватт-весов NIST-4 / ©L. S. Chao et al., CPEM, 2014
Технология ватт-весов была предложена британским физиком Брайаном Кибблом (Bryan Kibble) в 1975 году. Установка работает так. Через токопроводящую катушку, расположенную между двумя постоянными магнитами, пропускают электричество, в результате чего возникает магнитное поле, взаимодействующее с постоянным полем магнитов. Затем с поправкой на гравитационное ускорение рассчитывается электромагнитная энергия, необходимая для уравновешивания груза массой, кратной стандартному килограмму. Постоянная Планка пропорциональна количеству этой энергии. Варьируя напряжение, ученые также могут проследить динамику величины исходя из скорости вращения колебательного контура.
В 2016 году американские исследователи с помощью ватт-весов NIST-4 получили постоянную Планка с относительным стандартным отклонением не более 34 частей на миллиард (34×10-9): 6,62 606 983×10-34 джоуль-секунды. В новой статье авторы обобщили итоги более чем 10 тысяч экспериментов, проведенных с 2015 по 2017 годы, сократив стандартное отклонение до 13 частей на миллиард (13×10-9). Уточненное значение постоянной Планка составило 6,626 069 934 (89)×10-34 джоуль-секунды. Помимо накопления большого объема статистических данных, увеличить достоверность измерений позволили грузы разной массы (0,5–2 килограмма), а также изменения скорости катушки (0,5–2 миллиметра в секунду).
По словам ученых, показатели, полученные с помощью разных режимов работы ватт-весов, неидентичны, но хорошо согласуются между собой, относительное стандартное отклонение соответствует рекомендациям Комитета по данным для науки и техники (CODATA) — не более 20 частей на миллиард (20×10-9). Переопределить единицы СИ с учетом уточненной постоянной Планка планируется в ноябре следующего года. Расчетная величина килограмма будет сравниваться с новым физическим эталоном — сферой из высокочистого кремния-28.
Подробности работы представлены в журнале Metrologia.
О других физических константах читайте в нашем материале.
Нашли опечатку? Выделите фрагмент и нажмите Ctrl + Enter.
Скопировать ссылку
Планковские единицы — Википедия
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 15 февраля 2019; проверки требует 1 правка. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 15 февраля 2019; проверки требует 1 правка.Пла́нковские едини́цы — система единиц измерения, одна из естественных систем единиц. Предложена в 1901 году немецким физиком Максом Планком и названа в его честь[1].
Система планковских единиц не имеет широкого распространения не только потому, что величины входящих в неё единиц очень далеки от практики, но и, главным образом, потому что в этой системе уравнения теоретической физики не получают упрощения[2].
Ныне под планковской системой понимается система единиц, в которой в качестве основных единиц выбраны следующие фундаментальные физические постоянные[3]:
При этом значение коэффициента пропорциональности в законе Кулона выбрано равным единице[4].
Обычно, говоря о планковской системе, указывают, что в этом случае выполняется c=1,{\displaystyle c=1,} ℏ=1,{\displaystyle \hbar =1,} k=1{\displaystyle k=1} и G=1.{\displaystyle G=1.} Однако в действительности такая форма записи не точна. Она отражает лишь то, что соответствующая постоянная выбрана в качестве меры. Следует иметь в виду, что в планковской системе размерности отнюдь не исчезают, скорее наоборот, они приобретают фундаментальный характер, поскольку составляются из фундаментальных постоянных[4].
Из основных планковских единиц выводятся все остальные (производные) единицы системы, часть из которых приведена ниже. Значения c,G,ℏ{\displaystyle c,\,G,\,\hbar } и k{\displaystyle k} в единицах Международной системы единиц (СИ), использованные в расчётах, рекомендованы CODATA[5].
- Планковская масса mP=ℏcG≈2,176434(24)×10−8{\displaystyle m_{\text{P}}={\sqrt {\frac {\hbar c}{G}}}\approx 2{,}176434(24)\times 10^{-8}} кг.
- Планковская длина lP=ℏmPc=ℏGc3≈1,616255(18)×10−35{\displaystyle l_{\text{P}}={\frac {\hbar }{m_{\text{P}}c}}={\sqrt {\frac {\hbar G}{c^{3}}}}\approx 1{,}616255(18)\times 10^{-35}} м.
- Планковское время tP=lPc=ℏGc5≈5,391247(60)×10−44{\displaystyle t_{\text{P}}={\frac {l_{\text{P}}}{c}}={\sqrt {\frac {\hbar G}{c^{5}}}}\approx 5{,}391247(60)\times 10^{-44}} с.
- Планковское ускорение aP=lPtP2=ctP≈5,561×1051{\displaystyle a_{\text{P}}={\frac {l_{\text{P}}}{t_{\text{P}}^{2}}}={\frac {c}{t_{\text{P}}}}\approx 5{,}561\times 10^{51}} м/с2.
- Планковская энергия EP=mPc2=ℏtP=ℏc5G≈1,9561×109{\displaystyle E_{\text{P}}=m_{\text{P}}c^{2}={\frac {\hbar }{t_{\text{P}}}}={\sqrt {\frac {\hbar c^{5}}{G}}}\approx 1{,}9561\times 10^{9}} Дж.
- Планковская температура TP=EPk=ℏc5k2G≈1,416784(16)×1032{\displaystyle T_{\text{P}}={\frac {E_{\text{P}}}{k}}={\sqrt {\frac {\hbar c^{5}}{k^{2}G}}}\approx 1{,}416784(16)\times 10^{32}} К.
- Планковский заряд qP=4πε0ℏc=2chε0=eα≈1,8755459×10−18{\displaystyle q_{\text{P}}={\sqrt {4\pi \varepsilon _{0}\hbar c}}={\sqrt {2ch\varepsilon _{0}}}={\frac {e}{\sqrt {\alpha }}}\approx 1{,}8755459\times 10^{-18}} Кл, где e{\displaystyle e} — элементарный электрический заряд, α{\displaystyle \alpha } — постоянная тонкой структуры, h{\displaystyle h} — постоянная Планка. Соответственно, постоянная тонкой структуры — это квадрат заряда электрона, выраженного в планковских зарядах.
- Планковский ток IP=qP/tP=c64πε0/G=2c3πε0/G≈3,4789×1025{\displaystyle I_{\text{P}}=q_{\text{P}}/t_{\text{P}}={\sqrt {c^{6}4\pi \varepsilon _{0}/G}}=2c^{3}{\sqrt {\pi \varepsilon _{0}/G}}\approx 3{,}4789\times 10^{25}} А.
- Планковская сила FP=mPctP=c4G=1,21027×1044{\displaystyle F_{\text{P}}={\frac {m_{\text{P}}c}{t_{\text{P}}}}={\frac {c^{4}}{G}}=1{,}21027\times 10^{44}} Н.
- Планковское давление
- Планковская угловая частота ωP=1tP=c5ℏG≈1,85487×1043{\displaystyle \omega _{\text{P}}={\frac {1}{t_{\text{P}}}}={\sqrt {\frac {c^{5}}{\hbar G}}}\approx 1{,}85487\times 10^{43}} c−1.
- Планковская мощность (или светимость) LP=mPc2tP=c5G≈3,62831⋅1052{\displaystyle L_{\mathrm {P} }={\frac {m_{\text{P}}c^{2}}{t_{\text{P}}}}={\frac {c^{5}}{G}}\approx 3{,}62831\cdot 10^{52}} Вт.
Система планковских единиц впервые предложена в 1899 году Максом Планком на основе скорости света c{\displaystyle c}, гравитационной постоянной G{\displaystyle G} и двух ввёденных им новых постоянных теории теплового излучения a{\displaystyle a} и b{\displaystyle b} (они отличаются от современных постоянных hk{\displaystyle {\frac {h}{k}}} и h{\displaystyle h} на безразмерные множители)[6]. Первоначально планковские единицы были введены в докладе, сделанном 18 мая 1899 года на заседании Академии наук в Берлине и посвящённом обзору теории явлений теплового излучения, рассматриваемых с точки зрения электромагнитной теории света, и значению второго начала термодинамики в ней.
Все до сих пор используемые системы единиц, в том числе так называемая абсолютная СГС-система, обязаны своим происхождением пока что случайному стечению обстоятельств, поскольку выбор единиц, лежащих в основе каждой системы, сделан не исходя из общей точки зрения, обязательно приемлемой для всех мест и времен, но исключительно исходя из потребностей нашей земной культуры… В связи с этим представляло бы интерес заметить, что, используя обе постоянные a{\displaystyle a} и b{\displaystyle b}… мы получаем возможность установить единицы длины, массы, времени и температуры, которые не зависели бы от выбора каких-либо тел или веществ и обязательно сохраняли бы своё значение для всех времен и для всех культур, в том числе и внеземных и нечеловеческих, и которые поэтому можно было бы ввести в качестве «естественных единиц измерений».
— Планк М. Избранные труды. М.: Наука, 1975. С. 232.
В 1900 году Макс Планк предложил новый закон излучения (закон Планка), в котором фигурировали две новые постоянные h{\displaystyle h} и k.{\displaystyle k.} В 1901 году Планком была предложена система на основе постоянных c,{\displaystyle c,} G,{\displaystyle G,} h{\displaystyle h} и k{\displaystyle k}[1].
ПЛАНКА ПОСТОЯННАЯ | Энциклопедия Кругосвет
ПЛАНКА ПОСТОЯННАЯ h, одна из универсальных числовых констант природы, входящая во многие формулы и физические законы, описывающие поведение материи и энергии в масштабах микромира. Существование этой константы было установлено в 1900 профессором физики Берлинского университета М.Планком в работе, заложившей основы квантовой теории. Им же была дана предварительная оценка ее величины. Принятое в настоящее время значение постоянной Планка равно (6,6260755 ± 0,00023)Ч10–34 ДжЧс.
Планк сделал это открытие, пытаясь найти теоретическое объяснение спектра излучения, испускаемого нагретыми телами. Такое излучение испускают все тела, состоящие из большого числа атомов, при любой температуре выше абсолютного нуля, однако оно становится заметным лишь при температурах, близких к температуре кипения воды 100° С и выше нее. Кроме того, оно охватывает весь спектр частот от радиочастотного диапазона до инфракрасной, видимой и ультрафиолетовой областей. В области видимого света излучение становится достаточно ярким лишь примерно при 550° С. Зависимость интенсивности излучения за единицу времени от частоты характеризуется спектральными распределениями, представленными на рис. 1 для нескольких значений температуры. Интенсивность излучения при данном значении частоты есть количество энергии, излучаемой в узкой полосе частот в окрестности данной частоты. Площадь кривой пропорциональна полной энергии, излучаемой на всех частотах. Как нетрудно видеть, эта площадь быстро увеличивается с повышением температуры.
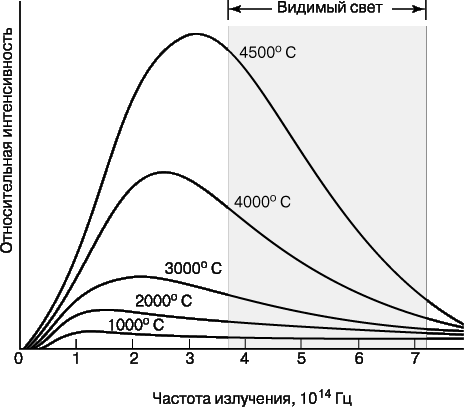
Планк хотел вывести теоретически функцию спектрального распределения и найти объяснение двух простых установленных экспериментально закономерностей: частота, отвечающая наиболее яркому свечению нагретого тела, пропорциональна абсолютной температуре, а полная энергия, излучаемая за 1 с единичной площадкой поверхности абсолютно черного тела, – четвертой степени его абсолютной температуры.
Первую закономерность можно выразить формулой

где nm – частота, соответствующая максимальной интенсивности излучения, Т – абсолютная температура тела, а a – постоянная, зависящая от свойств излучающего объекта. Вторая закономерность выражается формулой

где Е – полная энергия, излучаемая единичной площадкой поверхности за 1 с, s – постоянная, характеризующая излучающий объект, а Т – абсолютная температура тела. Первая формула называется законом смещения Вина, а вторая – законом Стефана – Больцмана. Планк стремился на основании этих законов вывести точное выражение для спектрального распределения излучаемой энергии при любой температуре.
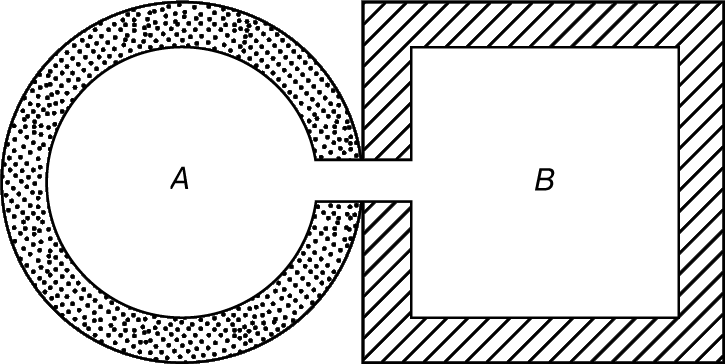
Универсальный характер явления можно было объяснить с позиций второго начала термодинамики, согласно которому тепловые процессы, протекающие самопроизвольно в физической системе, всегда идут в направлении установления в системе теплового равновесия. Представим себе, что два полых тела А и В разной формы, разного размера и из разного материала с одной температурой обращены друг к другу, как показано на рис. 2. Если предположить, что из А в В приходит больше излучения, чем из В в А, то тело В неизбежно становилось бы более теплым за счет А и равновесие самопроизвольно нарушалось бы. Такая возможность исключается вторым началом термодинамики, а следовательно, оба тела должны излучать одинаковое количество энергии, и, стало быть, величина s в формуле (2) не зависит от размера и материала излучающей поверхности, при условии, что последняя представляет собой некую полость. Если полости разделить цветным экраном, который фильтровал бы и отражал обратно все излучение, кроме излучения с какой-либо одной частотой, то все сказанное осталось бы справедливым. Это означает, что количество излучения, испускаемого каждой полостью в каждом участке спектра, одно и то же, и функция спектрального распределения для полости носит характер универсального закона природы, причем величина a в формуле (1), подобно величине s, является универсальной физической константой.
Планк, хорошо владевший термодинамикой, предпочел именно такое решение проблемы и, действуя методом проб и ошибок, нашел термодинамическую формулу, которая позволяла вычислять функцию спектрального распределения. Полученная формула согласовалась со всеми имевшимися экспериментальными данными и, в частности, с эмпирическими формулами (1) и (2). Чтобы объяснить это, Планк воспользовался хитроумной уловкой, подсказанной вторым началом термодинамики. Справедливо полагая, что термодинамика вещества лучше изучена, нежели термодинамика излучения, он сосредоточил свое внимание преимущественно на веществе стенок полости, а не на излучении внутри нее. Поскольку постоянные, входящие в законы Вина и Стефана – Больцмана, не зависят от природы вещества, Планк был вправе делать любые предположения относительно материала стенок. Он выбрал модель, в которой стенки состоят из огромного числа крошечных электрически заряженных осцилляторов, каждый со своей частотой. Осцилляторы под действием падающего на них излучения могут колебаться, излучая при этом энергию. Весь процесс можно было исследовать исходя из хорошо известных законов электродинамики, т.е. функцию спектрального распределения можно было найти, вычислив среднюю энергию осцилляторов с разными частотами. Обратив последовательность рассуждений, Планк, исходя из угаданной им правильной функции спектрального распределения, нашел формулу для средней энергии U осциллятора с частотой n в полости, находящейся в равновесии при абсолютной температуре Т:

где b – величина, определяемая экспериментально, а k – постоянная (называемая постоянной Больцмана, хотя впервые была введена Планком), которая фигурирует в термодинамике и кинетической теории газов. Поскольку эта постоянная обычно входит с множителем Т, удобно ввести новую постоянную h = bk. Тогда b = h/k и формулу (3) можно переписать в виде

Новая постоянная h и представляет собой постоянную Планка; вычисленное Планком ее значение составило 6,55Ч10–34 ДжЧс, что всего лишь примерно на 1% отличается от современного значения. Теория Планка позволила выразить величину s в формуле (2) через h, k и скорость света с:
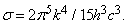
Это выражение согласовалось с экспериментом в пределах той точности, с которой были известны константы; позднее более точные измерения не обнаружили расхождений.
Таким образом, проблема объяснения функции спектрального распределения свелась к более «простой» задаче. Нужно было объяснить, каков физический смысл постоянной h или, вернее, произведения hn. Открытие Планка состояло в том, что объяснить ее физический смысл можно, лишь введя в механику совершенно новое понятие «кванта энергии». 14 декабря 1900 на заседании Немецкого физического общества Планк в своем докладе показал, что формулу (4), а тем самым и остальные формулы можно объяснить, если предположить, что осциллятор с частотой n обменивается энергией с электромагнитным полем не непрерывно, а как бы ступенями, приобретая и теряя свою энергию дискретными порциями, квантами, каждый из которых равен hn. См. также ЭЛЕКТРОМАГНИТНОЕ ИЗЛУЧЕНИЕ; ТЕПЛОТА; ТЕРМОДИНАМИКА. Следствия из сделанного Планком открытия изложены в статьях ФОТОЭЛЕКТРИЧЕСКИЙ ЭФФЕКТ; КОМПТОНА ЭФФЕКТ; АТОМ; АТОМА СТРОЕНИЕ; КВАНТОВАЯ МЕХАНИКА.
Квантовая механика представляет собой общую теорию явлений в масштабе микромира. Открытие Планка выступает ныне как вытекающее из уравнений этой теории важное следствие особого характера. В частности, оказалось, что оно имеет силу для всех процессов обмена энергией, которые происходят при колебательном движении, например в акустике и в электромагнитных явлениях. Им объясняется высокая проникающая способность рентгеновского излучения, частоты которого в 100–10 000 раз превышают частоты, характерные для видимого света, и кванты которого имеют соответственно более высокую энергию. Открытие Планка служит основой всей волновой теории материи, имеющей дело с волновыми свойствами элементарных частиц и их комбинаций.
Из теории Максвелла известно, что пучок света с энергией Е несет импульс р, равный

где с – скорость света. Если кванты света рассматривать как частицы, каждая из которых имеет энергию hn, то естественно предположить наличие у каждой из них импульса p, равного hn/c. Фундаментальное соотношение, связывающее длину волны l с частотой n и скоростью света с, имеет вид

так что выражение для импульса можно записать в виде h/l. В 1923 аспирант Л.де Бройль высказал предположение, что не только свету, но и всем формам материи свойствен корпускулярно-волновой дуализм, выражающийся в соотношениях

между характеристиками волны и частицы. Эта гипотеза подтвердилась, что сделало постоянную Планка универсальной физической константой. Ее роль оказалась гораздо более значительной, чем можно было бы предполагать с самого начала.
| Адроны | msimagelist>|
| Альфа-распад | msimagelist>|
| Альфа-частица | msimagelist>|
| Аннигиляция | msimagelist>|
| Антивещество | msimagelist>|
| Антинейтрон | msimagelist>|
| Антипротон | msimagelist>|
| Античастицы | msimagelist>|
| Атом | msimagelist>|
| Атомная единица массы | msimagelist>|
| Атомная электростанция | msimagelist>|
| Барионное число | msimagelist>|
| Барионы | msimagelist>|
| Бета-распад | msimagelist>|
| Бетатрон | msimagelist>|
| Бета-частицы | msimagelist>|
| Бозе – Эйнштейна статистика | msimagelist>|
| Бозоны | msimagelist>|
| Большой адронный коллайдер | msimagelist>|
| Большой Взрыв | msimagelist>|
| Боттом. Боттомоний | msimagelist>|
| Брейта-Вигнера формула | msimagelist>|
| Быстрота | msimagelist>|
| Векторная доминантность | msimagelist>|
| Великое объединение | msimagelist>|
| Взаимодействие частиц | msimagelist>|
| Вильсона камера | msimagelist>|
| Виртуальные частицы | msimagelist>|
| Водорода атом | msimagelist>|
| Возбуждённые состояния ядер | msimagelist>|
| Волновая функция | msimagelist>|
| Волновое уравнение | msimagelist>|
| Волны де Бройля | msimagelist>|
| Встречные пучки | msimagelist>|
| Гамильтониан | msimagelist>|
| Гамма-излучение | msimagelist>|
| Гамма-квант | msimagelist>|
| Гамма-спектрометр | msimagelist>|
| Гамма-спектроскопия | msimagelist>|
| Гаусса распределение | msimagelist>|
| Гейгера счётчик | msimagelist>|
| Гигантский дипольный резонанс | msimagelist>|
| Гиперядра | msimagelist>|
| Глюоны | msimagelist>|
| Годоскоп | msimagelist>|
| Гравитационное взаимодействие | msimagelist>|
| Дейтрон | msimagelist>|
| Деление атомных ядер | msimagelist>|
| Детекторы частиц | msimagelist>|
| Дирака уравнение | msimagelist>|
| Дифракция частиц | msimagelist>|
| Доза излучения | msimagelist>|
| Дозиметр | msimagelist>|
| Доплера эффект | msimagelist>|
| Единая теория поля | msimagelist>|
| Зарядовое сопряжение | msimagelist>|
| Зеркальные ядра | msimagelist>|
| Избыток массы (дефект массы) | msimagelist>|
| Изобары | msimagelist>|
| Изомерия ядерная | msimagelist>|
| Изоспин | msimagelist>|
| Изоспиновый мультиплет | msimagelist>|
| Изотопов разделение | msimagelist>|
| Изотопы | msimagelist>|
| Ионизирующее излучение | msimagelist>|
| Искровая камера | msimagelist>|
| Квантовая механика | msimagelist>|
| Квантовая теория поля | msimagelist>|
| Квантовые операторы | msimagelist>|
| Квантовые числа | msimagelist>|
| Квантовый переход | msimagelist>|
| Квант света | msimagelist>|
| Кварк-глюонная плазма | msimagelist>|
| Кварки | msimagelist>|
| Коллайдер | msimagelist>|
| Комбинированная инверсия | msimagelist>|
| Комптона эффект | msimagelist>|
| Комптоновская длина волны | msimagelist>|
| Конверсия внутренняя | msimagelist>|
| Константы связи | msimagelist>|
| Конфайнмент | msimagelist>|
| Корпускулярно волновой дуализм | msimagelist>|
| Космические лучи | msimagelist>|
| Критическая масса | msimagelist>|
| Лептоны | msimagelist>|
| Линейные ускорители | msimagelist>|
| Лоренца преобразования | msimagelist>|
| Лоренца сила | msimagelist>|
| Магические ядра | msimagelist>|
| Магнитный дипольный момент ядра | msimagelist>|
| Магнитный спектрометр | msimagelist>|
| Максвелла уравнения | msimagelist>|
| Масса частицы | msimagelist>|
| Масс-спектрометр | msimagelist>|
| Массовое число | msimagelist>|
| Масштабная инвариантность | msimagelist>|
| Мезоны | msimagelist>|
| Мессбауэра эффект | msimagelist>|
| Меченые атомы | msimagelist>|
| Микротрон | msimagelist>|
| Нейтрино | msimagelist>|
| Нейтрон | msimagelist>|
| Нейтронная звезда | msimagelist>|
| Нейтронная физика | msimagelist>|
| Неопределённостей соотношения | msimagelist>|
| Нормы радиационной безопасности | msimagelist>|
| Нуклеосинтез | msimagelist>|
| Нуклид | msimagelist>|
| Нуклон | msimagelist>|
| Обращение времени | msimagelist>|
| Орбитальный момент | msimagelist>|
| Осциллятор | msimagelist>|
| Отбора правила | msimagelist>|
| Пар образование | msimagelist>|
| Период полураспада | msimagelist>|
| Планка постоянная | msimagelist>|
| Планка формула | msimagelist>|
| Позитрон | msimagelist>|
| Поляризация | msimagelist>|
| Поляризация вакуума | msimagelist>|
| Потенциальная яма | msimagelist>|
| Потенциальный барьер | msimagelist>|
| Принцип Паули | msimagelist>|
| Принцип суперпозиции | msimagelist>|
| Промежуточные W-, Z-бозоны | msimagelist>|
| Пропагатор | msimagelist>|
| Пропорциональный счётчик | msimagelist>|
| Пространственная инверсия | msimagelist>|
| Пространственная четность | msimagelist>|
| Протон | msimagelist>|
| Пуассона распределение | msimagelist>|
| Пузырьковая камера | msimagelist>|
| Радиационный фон | msimagelist>|
| Радиоактивность | msimagelist>|
| Радиоактивные семейства | msimagelist>|
| Радиометрия | msimagelist>|
| Расходимости | msimagelist>|
| Резерфорда опыт | msimagelist>|
| Резонансы (резонансные частицы) | msimagelist>|
| Реликтовое микроволновое излучение | msimagelist>|
| Светимость ускорителя | msimagelist>|
| Сечение эффективное | msimagelist>|
| Сильное взаимодействие | msimagelist>|
| Синтеза реакции | msimagelist>|
| Синхротрон | msimagelist>|
| Синхрофазотрон | msimagelist>|
| Синхроциклотрон | msimagelist>|
| Система единиц измерений | msimagelist>|
| Слабое взаимодействие | msimagelist>|
| Солнечные нейтрино | msimagelist>|
| Сохранения законы | msimagelist>|
| Спаривания эффект | msimagelist>|
| Спин | msimagelist>|
| Спин-орбитальное взаимодействие | msimagelist>|
| Спиральность | msimagelist>|
| Стандартная модель | msimagelist>|
| Статистика | msimagelist>|
| Странные частицы | msimagelist>|
| Струи адронные | msimagelist>|
| Субатомные частицы | msimagelist>|
| Суперсимметрия | msimagelist>|
| Сферическая система координат | msimagelist>|
| Тёмная материя | msimagelist>|
| Термоядерные реакции | msimagelist>|
| Термоядерный реактор | msimagelist>|
| Тормозное излучение | msimagelist>|
| Трансурановые элементы | msimagelist>|
| Трек | msimagelist>|
| Туннельный эффект | msimagelist>|
| Ускорители заряженных частиц | msimagelist>|
| Фазотрон | msimagelist>|
| Фейнмана диаграммы | msimagelist>|
| Фермионы | msimagelist>|
| Формфактор | msimagelist>|
| Фотон | msimagelist>|
| Фотоэффект | msimagelist>|
| Фундаментальная длина | msimagelist>|
| Хиггса бозон | msimagelist>|
| Цвет | msimagelist>|
| Цепные ядерные реакции | msimagelist>|
| Цикл CNO | msimagelist>|
| Циклические ускорители | msimagelist>|
| Циклотрон | msimagelist>|
| Чарм. Чармоний | msimagelist>|
| Черенковский счётчик | msimagelist>|
| Черенковсое излучение | msimagelist>|
| Черные дыры | msimagelist>|
| Шредингера уравнение | msimagelist>|
| Электрический квадрупольный момент ядра | msimagelist>|
| Электромагнитное взаимодействие | msimagelist>|
| Электрон | msimagelist>|
| Электрослабое взаимодействие | msimagelist>|
| Элементарные частицы | msimagelist>|
| Ядерная физика | msimagelist>|
| Ядерная энергия | msimagelist>|
| Ядерные модели | msimagelist>|
| Ядерные реакции | msimagelist>|
| Ядерный взрыв | msimagelist>|
| Ядерный реактор | msimagelist>|
| Ядра энергия связи | msimagelist>|
| Ядро атомное | msimagelist>|
| Ядерный магнитный резонанс (ЯМР) | msimagelist>



