конденсатора в цепи переменного тока, формула

Электросопротивление — это параметр в электротехнике, характеризующий возможность вещества препятствовать прохождению электричества. В зависимости от качеств материала, электросопротивляемость может уменьшаться до крайне маленьких величин (микро\милиОмы — у проводников, металлов) или повышаться до огромных значений (ГигаОмы — изоляторов, диэлектриков). Величина противоположная сопротивлению — проводимость.

Что такое

Цепь, по которой протекает непостоянный ток, обладает полным сопротивлением. Вычисляется оно по сумме активного и реактивного сопротивлений, возведенных в квадрат.

Формула вычисления

Графическое изображение этой формулы представляет собой треугольник. Его катеты представлены активным и реактивным сопротивлениями, а гипотенуза полным электросопротивлением.

Графическое отображение формулы

Емкостное электросопротивление (Xc) является одним из видов реактивного сопротивления. Этот показатель характеризует противодействие электроемкости в цепи электротоку с переменными параметрами.

Преобразование электроэнергии в тепловую в момент протекания электричества сквозь емкость не возникает (свойство реактивного сопротивления). Вместо этого осуществляется передача энергии электрического тока электрическому полю и обратно. Потерь энергии при таком обмене не происходит.

Емкостное сопротивление конденсатора можно сравнить с кастрюлей, наполняемой жидкостью, при полном заполнении ее объема она переворачивается, выливая содержимое, а затем наполняется заново. После достижения максимального заряда конденсатора происходит разрядка, затем он заряжается вновь.

Дополнительная информация:

 Конденсатор цепи способен накопить лишь ограниченную величину заряда до перемены полярности напряжения. По данной причине непостоянный ток не падает до нуля, важное отличие от постоянного электричества. Низкие значения частоты тока соответствуют низким показателям заряда, накопленного конденсатором, низким значениям противодействия электричеству, что придает реактивные свойства.

По сути, Xc — это противостояние электродвижущей силы конденсатора, уровню его заряда.

От чего зависит сопротивление конденсаторов цепей переменного тока

Показатели его, зависят не только от емкостных характеристик последнего, но и от частотной характеристики электротока, протекающего по цепи. Когда речь идет о сопротивлении резистора, то говорится о параметрах самого резистора, например, материале, форме, но полностью отсутствует взаимосвязь сопротивления его и показателей частоты электричества цепи (речь идет об идеальном резисторе, паразитные параметры которому не характерны). Когда речь идет об устройстве накопления энергии и заряда электрического поля — все иначе. Конденсатор одной и той же емкости при разных частотах тока обладает неодинаковым уровнем сопротивления. Амплитуда протекающего через него электричества при постоянной амплитуде напряжения обладает разной величиной.

Вычисление Xc

Рассматривая эту формулу сопротивления конденсатора в цепи переменного тока, к каким выводам можно прийти? При повышении частотных показателей сигнала, электросопротивляемость конденсатора снижается.

При повышении емкостных характеристик устройства для накопления заряда и энергии электрического поля Xc переменного электричества, проходящего сквозь него, будет стремиться вниз.

График, отображающий эту величину конденсатора при непостоянном токе цепи, имеет форму гиперболы

Момент приближения значений частоты к нулевым отметкам на оси (когда переменный электроток становится похож своими параметрами на постоянный), сопровождается возрастанием Xc конденсатора до беспредельных величин. Это действительно так: известно, что конденсатор сети постоянного тока является фактически разрывом цепи. Реальная электросопротивляемость, естественно, не бесконечна, ее ограничивает уровень конденсаторной утечки. Но величины его остаются на высоком уровне, который невозможно не учитывать.

При возрастании цифр частоты до уровня бесконечных значений, емкостное сопротивление электроконденсатора стремится к нулевым отметкам. Такое характеризует идеальные модели. В реальных условиях конденсатор имеет неприятные характеристики (такие как индуктивность и сопротивления утечек), поэтому снижение емкостного сопротивления происходит до определенных значений, после которых оно возрастает.

Обратите внимание! При подключении конденсатора к цепочке электричества с переменными параметрами, его мощность не тратится, потому что фазовые характеристики напряжения и силы тока сдвинуты на 90° в отношении друг друга. В одну четверть периода происходит зарядка электроконденсатора (энергия запасается в его электрополе), в следующее время происходит его разрядка, энергия поступает обратно в цепочку. Его электросопротивляемость является безваттной, реактивной.

Причины ёмкостного сопротивления

Причиной возникновения сопротивления емкостного считается уровень напряжения, возникающий на конденсаторе в процессе его заряда. Вектор его действия встречен вектору напряжения источника электричества, потому создает помеху воспроизведению электротока этим источником.

Как рассчитать Xc

Сила тока цепи с постоянными показателями напряжения в момент работы электроконденсатора равно 0. Ее значения в цепи с переменным напряжением после подключения конденсатора I ? 0. В итоге, цепочке с непостоянным напряжением конденсатор придает Xc меньшее, чем цепочке с неизменным показателем напряжения.

Формула вычисления показателя напряжения за одну секунду

 

Формула расчета величины силы электротока за мгновение

Получается, что изменения напряжения отличаются по фазе от изменений тока на π/2.

По закону, сформулированному Омом, показатели силы электротока находятся в прямой пропорциональной зависимости от величины напряжения цепи. Формула вычисления наибольших величин напряженности и силы тока:

Наибольшие величины напряженности и силы тока можно рассчитывать по формулеОкончательная формула расчета емкостного сопротивления в цепи переменного тока

ω = 2πf.

f — показатель частоты непостоянного тока, измеряется в герцах;

ω — показатель угловой частоты тока;

С — размер конденсатора в фарадах.

Важно! Xc не выступает параметром проводника, оно находится в зависимости от такой характеристики электроцепи, как частота электротока.

Повышение значений данной величины вызывает рост пропускающей способности конденсатора (предел его сопротивления току непостоянному понижается).

Представим, к цепи подключен конденсатор, емкостью 1 мкФ. Необходимо вычислить, уровень емкостного сопротивления при величине частоты 50 Гц и как изменится емкостное сопротивление цепи переменного тока при частоте 1 кГц. Амплитуда напряжения, подведенного к конденсатору, составляет 50 В.

После введения данных в формулу, определяющую Xc, и получаются значения:

Результат для частоты 50 ГцРезультат для 1 кГц

Емкостное сопротивление приравнивается к соотношению отклонений колебаний напряжения зажимов электрической цепочки с емкостными параметрами (с небольшими индуктивным и активным сопротивлениями) к колебаниям электротока цепочки. Она равнозначна электроконденсатору.

В чем измеряется емкостное электросопротивление

R представлено отношением напряжения к силе тока замкнутой электрической цепи, по закону Ома.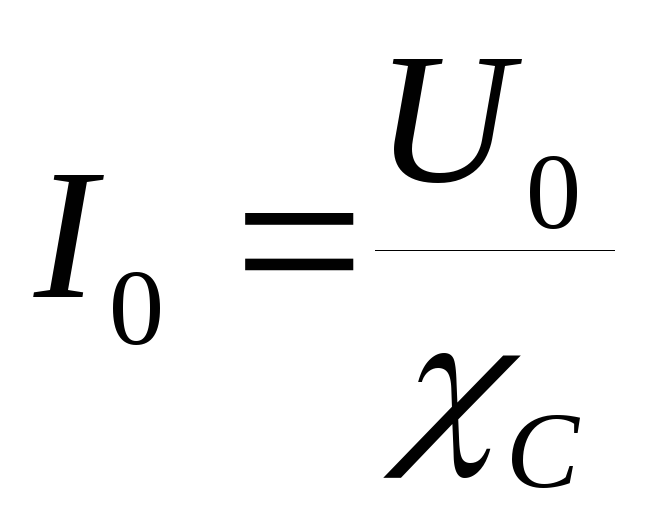 Единицы измерения — Ом. Xc, как его разновидность, тоже измеряется в Омах.

Конденсаторы применяются при изготовлении фильтров. При параллельном присоединении к цепи, он способен задерживать высокие частоты, при последовательном удаляет низкие. Также они используются с целью отсечения переменной части от постоянной. Он незаменим в радиотехнике, при производстве датчиков приближения, для контроля процессов производства. Технологии, обладающие выше описанными свойствами, используются во всех областях промышленности.

Емкостное сопротивление

Deprecated: Non-static method Date_TimeZone::getDefault() should not be called statically, assuming $this from incompatible context in /home/carkey/hitech/hardtech/kernel/pear/date/Date.php on line

201

Deprecated: Non-static method Date_TimeZone::isValidID() should not be called statically, assuming $this from incompatible context in /home/carkey/hitech/hardtech/kernel/pear/date/Date. php on line 576

Notice: Undefined offset: 1 in /home/carkey/hitech/hardtech/kernel/common/common/common.class.php on line 343

Notice: Undefined offset: 1 in /home/carkey/hitech/hardtech/kernel/common/common/common.class.php on line 343

Deprecated: mysql_escape_string(): This function is deprecated; use mysql_real_escape_string() instead. in

/home/carkey/hitech/hardtech/kernel/common/db/mysql.class.php on line 135

Deprecated: mysql_escape_string(): This function is deprecated; use mysql_real_escape_string() instead. in /home/carkey/hitech/hardtech/kernel/common/db/mysql.class.php on line 135

Deprecated: mysql_escape_string(): This function is deprecated; use mysql_real_escape_string() instead. in /home/carkey/hitech/hardtech/kernel/common/db/mysql.class.php on line 135

Deprecated: mysql_escape_string(): This function is deprecated; use mysql_real_escape_string() instead. in /home/carkey/hitech/hardtech/kernel/common/db/mysql.class.php on line 135

Емкостное сопротивление
­Обратим внимание на то, что включение конденсатора в цепь последовательно с электрической лампой уменьшает величину тока в цепи. Следовательно, конденсатор представляет собой для переменного тока некоторое сопротивление. Сопротивление конденсатора переменному току называется емкостным сопротивлением. Емкостное сопротивление измеряется в омах, килоомах, мегомах, как и обычное сопротивление. Его принято обозначать Хс (икс це). Причиной емкостного сопротивления является напряжение, которое появляется на конденсаторе при его заряде. Это напряжение действует встречно с напряжением источника тока и потому препятствует источнику тока создавать ток.

Емкостное сопротивление обратно пропорционально емкости конденсатора и частоте переменного тока. Иными словами, емкостное сопротивление тем меньше, чем больше емкость конденсатора и чем выше частота. Действительно, чем больше емкость конденсатора, тем большее количества электричества накапливается на его пластинах, когда он заряжается до амплитуды напряжения источника. Следовательно, в течение каждой четверти периода по цепи проходит большое количество электричества и ток в цепи больше. А это и означает, что емкостное сопротивление с увеличением емкости уменьшается. Если увеличить частоту приложенного напряжения, длительность каждой четверти периода уменьшится; следовательно, заряд и разряд конденсатора, будут происходить быстрее и ток в цепи увеличится. Следовательно, емкостное сопротивление с повышением частоты уменьшается.

Это интересно: еще относительно недавно никто и не предполагал, что знакомые лишь по футуристическим шпионским фильмам цифровые видеорегистраторы станут столь широко распространены и доступны, а главное — полезны. ­

Наша продукция

…

Warning: Unknown: write failed: Disk quota exceeded (122) in Unknown on line 0

Warning: Unknown: Failed to write session data (files). Please verify that the current setting of session. save_path is correct (/opt/alt/php56/var/lib/php/session) in Unknown on line 0

Глава 17. Резонансные цепи . Введение в электронику

ЦЕЛИ

После изучения этой главы студент должен быть в состоянии:

• Написать формулы для определения емкостного и индуктивного сопротивления.

• Описать, как реагируют на переменный ток и напряжение конденсаторы и катушки индуктивности.

• Дать определение реактивного сопротивления последовательной цепи и уметь определить характер цепи (индуктивный или емкостный).

• Дать определение термина импеданс.

• Уметь вычислять импеданс, который содержит как резистивную, так и емкостную или индуктивную составляющие.

• Объяснить, как должен быть модифицирован закон Ома перед использованием его для цепей переменного тока.

• Уметь вычислять Х_с, X_L, X, Z и I_т в последовательных RLC цепях.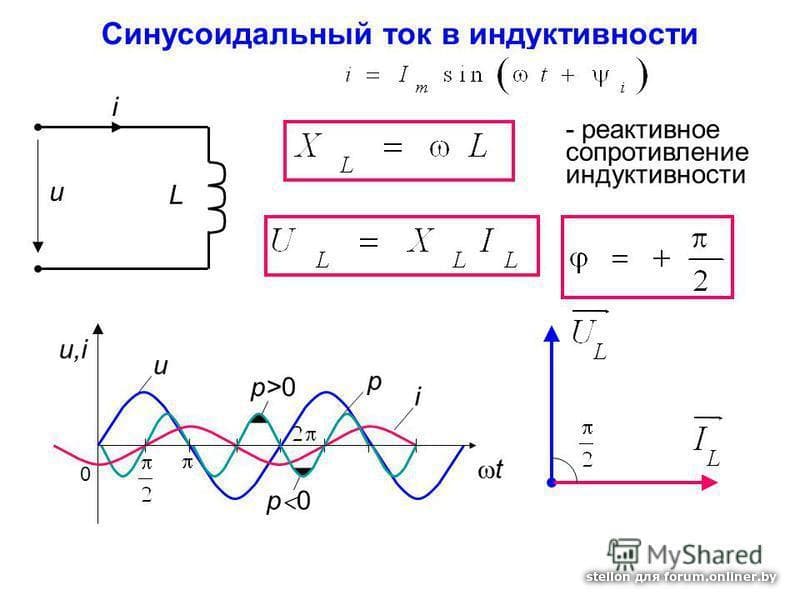

• Уметь вычислять I_c, I_L, I_x, I_R и I_z в параллельных RLC цепях.

В предыдущих главах сопротивление, емкость и индуктивность в цепях переменного тока рассматривались по отдельности. В этой главе исследуется комбинация сопротивления, емкости и индуктивности в цепи переменного тока. Рассматриваемые вопросы не являются новым материалом, но применяют все изложенные ранее принципы.

Когда реактивное сопротивление катушки индуктивности равно реактивному сопротивлению конденсатора в цепи, возникает резонанс. Резонансные цепи широко используются в электронике.

17-1. РЕАКТИВНОЕ СОПРОТИВЛЕНИЕ

Емкостное реактивное сопротивление — это противодействие, которое конденсатор оказывает переменному току. Оно измеряется в омах и обозначается символом Х_с. Емкостное реактивное сопротивление вычисляется по формуле:

Х_с = 1/2πfC

Заметим, что при использовании этой формулы емкость должна быть выражена в фарадах (а не в долях фарады).

Индуктивное реактивное сопротивление — это противодействие, которое катушка индуктивности оказывает переменному току. Оно измеряется в омах и обозначается символом X_L. Индуктивное реактивное сопротивление вычисляется по формуле:

X_L = 2πfL.

Заметим, что при использовании этой формулы индуктивность должна быть выражена в генри (а не в долях генри).

Емкостное реактивное сопротивление служит причиной того, что ток опережает по фазе напряжение. Индуктивное реактивное сопротивление служит причиной того, что ток отстает по фазе от напряжения. Емкостное и индуктивное реактивные сопротивления прямо противоположны по создаваемым эффектам и, следовательно, когда в цепи присутствуют и индуктивность и емкость, общий эффект определяется разностью их значений. Эта разность называется реактивным сопротивлением и обозначается символом X. Реактивное сопротивление может быть выражено следующими формулами:

X = Х_с — X_L или X = X_L — Х_с.

_{ПРИМЕР: Чему равно реактивное сопротивление цепи, содержащей конденсатор емкостью 1 мкФ, соединенный последовательно с индуктивностью 10 генри (рис. 17-1), работающей на частоте 60 герц?}

_{Рис. 17-1}

_Дано:

_{f = 60 Гц; L = 10 Гн; С = 1 мкФ}

_{Х =?}

_{Решение:} 

_{Хс = 1/2πfC} 

_{Хс =1/(6,28)(60)(0,000001)}

_{Хс =2654 Ом}

_{XL = 2πfL}

_{XL = (6,28)(60)(10)}

_{XL = 3768 Ом}

_{X = XL- XC = 3768–2654}

_{X = 1114 Ом (индуктивное).}

_{ПРИМЕР: Чему равно реактивное сопротивление цепи, содержащей конденсатор емкостью 1 мкФ, соединенный последовательно с индуктивностью 1 генри (рис. 17-2), работающей на частоте 60 герц?}

_{Рис. 17-2} 

 _Дано:

_{f = 60 Гц; L = 1 Гн; С = 1 мкФ}

_{Х =?}

_{Решение:} 

_{Хс = 1/2πfC} 

_{Хс = 1/(6,28)(60)(0,000001)}

_{Хс =2654 Ом}

_{XL = 2πfL}

_{XL = (6,28)(60)(1)}

_{XL = 376,8 Ом}

_{X = XC — XL = 2654 — 376,8}

_{X = 2277,2 Ом (емкостное).}

Эти примеры иллюстрируют важный момент. Когда емкостное и индуктивное реактивные сопротивления соединены последовательно, меньшее значение всегда вычитается из большего. Получающееся в результате реактивное сопротивление характеризуется большим значением.

17-1. Вопросы

1. Каково фазовое соотношение между током и напряжением на конденсаторе?

2. Каково фазовое соотношение между током и напряжением на катушке индуктивности?

3. По какой формуле определяется полное реактивное сопротивление последовательной цепи, когда известны значения Х_с и X_L?

4. Какова величина полного реактивного сопротивления (X) последовательной цепи, содержащей Х_с = 50 ом и X_L = 20 ом? Укажите, является X емкостным или индуктивным.

17-2. ИМПЕДАНС

Реактивное сопротивление, как емкостное, так и индуктивное, противодействует протеканию тока в цепях переменного тока. Активное сопротивление также препятствует протеканию тока в цепи. Комбинированное противодействие реактивного и активного сопротивлений называется импедансом и обозначается символом Z.

И активное, и реактивное сопротивления измеряются в омах. Следовательно, кажется логичным сложить эти сопротивления для того, чтобы получить импеданс. Однако этого делать нельзя, поскольку активное и реактивное сопротивления — величины векторные. В цепях переменного тока, содержащих только активное сопротивление, ток и напряжение находятся в фазе. И ток, и напряжение достигают своих максимальных значений одновременно.

Как упоминалось ранее, в цепях переменного тока, содержащих только реактивные сопротивления, ток будет либо опережать, либо отставать от напряжения на 90 градусов. Следовательно, напряжение в чисто реактивной цепи будет отличаться по фазе на 90 градусов от напряжения в чисто резистивной цепи.

Когда цепь содержит и активное, и реактивное сопротивление, импеданс будет больше любого их них. Кроме того, ток в такой цепи будет не в фазе с напряжением. Сдвиг по фазе будет в пределах от нуля до 90 градусов.

Для того чтобы найти импеданс, используется векторная диаграмма — прямоугольный треугольник сопротивлений. Это может быть сделано потому, что ток через резистор находится в фазе с напряжением на нем, а ток через реактивную нагрузку сдвинут по фазе на 90 градусов относительно напряжения на ней. Они находятся под прямым углом друг к другу.

ПРИМЕР: Чему равен импеданс последовательно соединенных резистора сопротивлением 150 ом и индуктивного реактивного сопротивления 100 ом?

В качестве первого шага нарисуем основание треугольника, представляющее резистор 150 ом. Далее нарисуем линию под углом 90 градусов к основанию, представляющую индуктивное сопротивление 100 ом. После этого соединим концы линий, образуя гипотенузу треугольника. Гипотенуза представляет импеданс цепи (рис. 17-3).

Рис.  17-3. Векторная диаграмма.

Теорема Пифагора утверждает:

с² = а² + Ь²,

где с — гипотенуза, а и b — катеты.

Графически это представлено на рис. 17-4.

Рис. 17-4. Векторная диаграмма, показывающая связь активного сопротивления, реактивного индуктивного сопротивления и импеданса в последовательной цепи.

Если импеданс, активное и реактивное сопротивления заменить соответствующими символами, то формула будет выглядеть следующим образом:

Z² = R² + X².

Вернемся к определению импеданса последовательной комбинации резистора 150 ом и индуктивного сопротивления 100 ом.

Дано:

R = 150 Ом; X_L = 100 Ом.

Решение:

Z² = R² + X²

Z² =(150)² + (100)² = 32500

Z = √(32500) = 180,28 Ом.

Если вместо индуктивного в цепи находится емкостное сопротивление, то линию, представляющую емкостное сопротивление, обычно рисуют направленной вниз. Это показывает, что оно действует в направлении противоположном индуктивному сопротивлению, которое рисуют направленным вверх.

В последовательной цепи с емкостным реактивным сопротивлением формула для вычисления импеданса будет выглядеть следующим образом:

Z² = R² + Х²_С.

_{ПРИМЕР: Чему равен импеданс цепи, содержащей резистор сопротивлением 220 ом, соединенный последовательно с конденсатором, имеющим емкостное реактивное сопротивление 270 ом?}

_Дано:

_{R = 220 Ом; Xc = 270 Ом.}

_{Решение:}

_{Z² = R² + X²c}

_{Z² = (220)² + (270)² = 121300}

_{Z = √(121300) = 348,28 Oм.}

_{Z = 348,28 Ом.}

_{Если последовательная цепь содержит индуктивное и емкостное реактивные сопротивления, а также активное сопротивление, необходимо найти полное реактивное сопротивление (X). Реактивное сопротивление может быть либо индуктивным, либо емкостным. Следовательно, может быть использована одна из следующих формул:} 

_{Z² = R² + X²L;}

_{Z² = R² + Х²с.}

17-2. Вопросы

1. Как называется полное противодействие в цепи переменного тока?

2. Какая формула используется для вычисления величины полного противодействия в последовательной цепи?

3. Чему равно значение Z в последовательной цепи переменного тока, где Х_с = 3 Ом, X_L = 6 Ом, a R = 4 Ом?

17-3 ЗАКОН ОМА

Закон Ома не может быть применен в цепях переменного тока потому, что он не учитывает реактивное сопротивление. Модифицируя закон Ома путем учета импеданса, можно получить общий закон, который применим к цепям переменного тока.

I = E/R преобразуется в I = E/Z

Эта формула применима к переменному току, текущему в любой цепи.

_{ПРИМЕР: Последовательная цепь содержит резистор сопротивлением 510 ом, индуктивное сопротивление 250 ом и емкостное сопротивление 150 ом. Какой ток течет по цепи, если к ней приложено напряжение 120 вольт?}

_Дано:

_{R = 510 Ом; XL = 250 Ом; Xc = 150 Ом; E = 120 В}

_{Решение:}

_{X = ХL + Хc = 250–150}

_{X = 100 Ом (индуктивное)}

_{Z² = R² + X²}

_{Z² =(510)² +(100)²}

_{Z = √(270100)}

_{Z = 519,71 Ом}

_{I = E/Z = 120/519,71}

_{I = 0,23 А или 230 мА.}

17-3. Вопросы

1. Каким образом модифицируется закон Ома, чтобы его можно было применить к цепям переменного тока для определения напряжения и тока?

2. Последовательная цепь содержит резистор сопротивлением 510 ом, индуктивное сопротивление 300 ом и емкостное сопротивление 375 ом. Какой ток течет по цепи, если к ней приложено напряжение 120 вольт?

17-4. ЦЕПИ RLC

Материал, изложенный до сих пор, применим ко всем цепям переменного тока. В приведенных примерах рассматривались последовательные цепи. Понятия, рассмотренные в этом параграфе, не содержат нового материала, но используют все принципы, изложенные ранее.

_{ПРИМЕР: На рис. 17-5 показана последовательная RLC цепь. Необходимо вычислить Хс, XL, X, Z и IT.}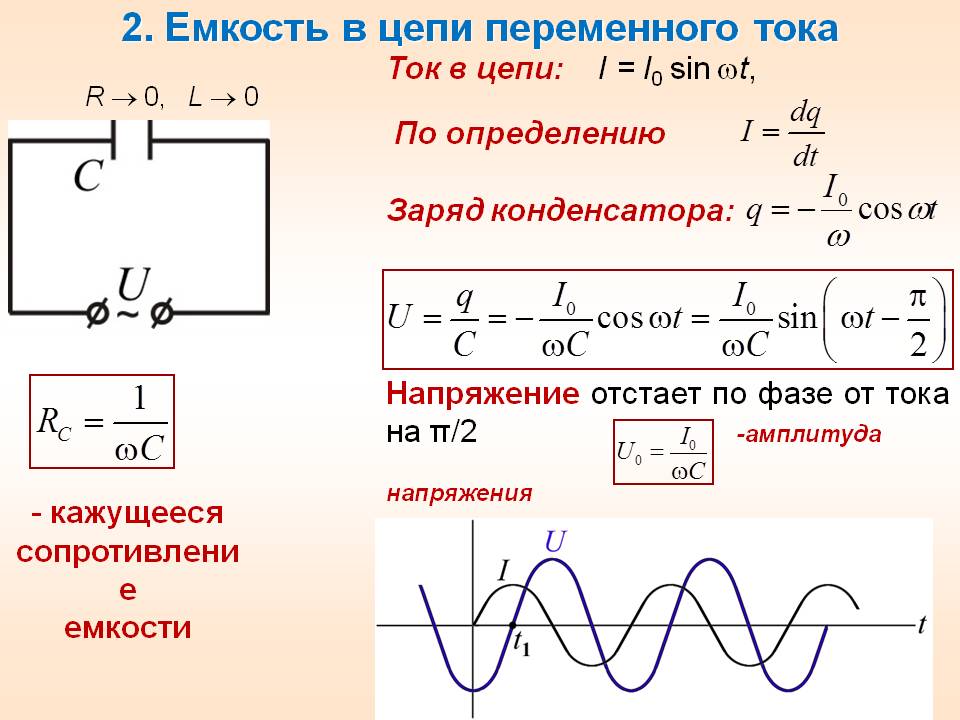

_{Рис. 17-5. Последовательная цепь RLC.}

_{Сначала вычислим Хс, XL и X.}

 _Дано:

_{f = 60 Гц; С = 470 мкФ; L = 27 мГн.}

_{Решение:}

_{Xc = 1/2πfC}

_{Xc = 1/(6,28)(60)(0,000470)}

_{XC = 5,65 Ом}

_{XL = 2πfL}

_{XL = (6,28)(60)(0,027)}

_{XL = 10,17 Ом}

_{X = XL — Xc = 10,17 — 5,65}

_{X = 4,52 Ом (индуктивное).}

_{Используем значение X для вычисления Z.}

 _Дано:

_{X = 4,52 Ом; R = 10 Ом.}

_{Решение:}

_{Z² = R² + X²}

_{Z² = (10)² + (4,52)² = 120,43}

_{Z = √(120,43) = 10,97 Ом.}

_{Это значение Z может быть использовано для вычисления полного тока (IT).}

_Дано:

_{Z = 10,97 Ом; E = 120 В.}

_{Решение:}

_{IT = E/Z = 120/10,97}

_{IT = 10,94 A.} 

Помните, что во всех частях последовательной цепи течет один и тот же ток.

Если элементы в цепях соединены параллельно, то следует учесть одно главное различие между последовательными и параллельными цепями. При последовательном соединении по всей цепи течет один и тот же ток, а в параллельной цепи к каждой ветви приложено одинаковое напряжение. Вследствие этой разницы полный импеданс параллельной цепи должен вычисляться на основе тока в цепи.

В последовательной цепи RLC для вычисления реактивного сопротивления и импеданса используются следующие формулы:

X = Х_с — X_L или X = X_L — Х_с, Z² = R² + X².

В случае параллельных цепей должны использоваться следующие формулы:

I_X = I_с — I_L или I_X = I_L — I_X; I²_Z = (I_R)² + (I_X)²

Импеданс параллельной цепи находится с помощью формулы:

I_Z = E/Z

Замечание: Если неизвестно напряжение (Е), приложенное к цепи, то для вычисления I_c, I_L, I_x, I_R и I_Z можно использовать любое значение Е. То же значение напряжения должно использоваться для вычисления импеданса.

_{ПРИМЕР: Найти значение Z для цепи, показанной на рис. 17-6.}

_{Рис. 17-6. Параллельная цепь RLC.}

_Дано:

_{Е = 120 В; R = 60 Ом; Хс = 75 Ом; XL = 50 Ом.}

_{Решение:}

_{Первым шагом в вычислении Z является вычисление токов отдельных ветвей.}

_{IR = E/R = 120/60 = 2 A} 

_{Ix = E/Xc = 120/75 = 1,6 A}

_{IL = E/XL = 120/50 = 2,4 A}

_{Используя значения IR, Ic, IL, вычислим Ix и Iz}

_{IX = IL — Ic = 2,4 – 1,6}

_{Ix = 0,8 А (индуктивный)}

_{I²z = (IR)^{2 +} (Ix)²}

_{I²z = (2)² + (0,8)² = 4,64}

_{Iz = √(4,64) = 2,15 A.}

_{Используя значение Iz, вычислим Z.}

_{Iz = E/Z}

_{2,15 = 120/Z} 

_{Z = 120/2,15 = 55,8 Ом}

В завершение этой главы отметим, что мы рассмотрели все блоки, из которых строятся электрические цепи. При изложении материала использовались ранее изученные понятия и соотношения.

17-4. Вопрос

1. Чем отличаются вычисления импеданса для последовательной цепи переменного тока и для параллельной цепи?

РЕЗЮМЕ

• Конденсатор в цепи переменного тока оказывает противодействие любому изменению напряжения, так же как он это делает в цепи постоянного тока.

• Ток опережает по фазе напряжение на конденсаторе на 90 градусов.

• Противодействие, оказываемое конденсатором переменному току, называется емкостным реактивным сопротивлением. Оно обозначается Х_с и вычисляется по формуле:

X_C = 1/2πfC

• Катушка индуктивности в цепи переменного тока противодействует любому изменению тока, так же как она это делает в цепи постоянного тока.

• На катушке индуктивности ток отстает по фазе от напряжения на 90 градусов.

• Противодействие, оказываемое катушкой индуктивности переменному току, называется индуктивным реактивным сопротивлением. Оно обозначается X_L и вычисляется по формуле

X_L = 2πfL.

• Полное реактивное сопротивление последовательной цепи переменного тока определяется формулами X = X_C — X_L или X = X_L — X_C.

• Полное реактивное сопротивление последовательной цепи переменного тока является либо емкостным, либо индуктивным, в зависимости от того, какая величина больше, Х_C или X_L.

• В параллельной цепи реактивное сопротивление определяется с помощью формул

I_Z = E/Z

где I_z определяется формулой I_z² = (I_R)² + (I_X)², а I_х вычисляется по формуле I_X = I_C — I_L или I_X = I_L — I_C.

• Реактивное сопротивление параллельной цепи также может быть емкостным или индуктивным, в зависимости то того, какая величина больше I_C или I_L.

• Полное сопротивление цепи переменного тока называется импедансом. Он обозначается символом Z. В последовательной цепи Z² = R² + X². В параллельной цепи I²_Z = (I_R)² + (I_X)² и

I_Z = E/Z

• Получена формула для закона Ома, который можно применять для пеней переменного тока:

I = E/Z

Глава 17. САМОПРОВЕРКА

1. Чему равны значения Х_С, X_L, X, Z и I_T для цепи, изображенной на рис. 17-7?

Рис. 17-7. Последовательная цепь RLC.

2.  Чему равны значения I_C, I_L, I_X, I_R и I_Z для цепи, изображенной на рис. 17-8?

Рис. 17-8. Параллельная цепь RLC.

Сопротивление конденсатора, теория и примеры

Сопротивление конденсатора постоянному току

Конденсатор характеризуют при помощи ряда параметров (емкость, рабочее напряжение и т. д), одной из таких характеристик является сопротивление. Конденсатор практически не пропускает постоянный электрический ток. То есть сопротивление конденсатора является бесконечно большим для постоянного тока, но это идеальный случай. Через реальный диэлектрик очень малый ток протекать может. Этот ток называют током утечки. Ток утечки является показателем качества диэлектрика, который применяется при изготовлении конденсатора. У современных конденсаторов ток утечки составляет некоторые доли микроампера. Сопротивление конденсатора в таком случае можно вычислить, используя закон Ома для участка цепи, зная величину напряжения, до которой заряжен конденсатор и ток утечки. Но обычно при решении учебных задач сопротивление конденсатора постоянному току считают бесконечно большим.

Сопротивление конденсатора переменному напряжению

При включении конденсатора в цепь с переменным током, ток свободно проходит через конденсатор. Это объясняется очень просто: происходит процесс постоянной зарядки и разрядки конденсатора. При этом говорят, что в цепи присутствует емкостное сопротивление конденсатора, помимо активного сопротивления.

И так, конденсатор, который включен в цепь переменного тока, ведет себя как сопротивление, то есть оказывает влияние на силу тока, текущую в цепи. Величину емкостного сопротивления обозначим как , его величина связана с частотой тока и определена формулой:

   

где – частота переменного тока; – угловая частота тока; C – емкость конденсатора.

Если конденсатор включен в цепь переменного тока, то в нем не затрачивается мощность, потому что фаза тока сдвинута по отношению к напряжению на . Если рассмотреть один период колебания тока в цепи (T), то происходит следующее: при заряде конденсатора (это составляет ) энергия в поле конденсатора запасается; на следующем отрезке времени () конденсатор разряжается и отдает энергию в цепь. Поэтому ёмкостное сопротивление называют реактивным (безваттным).

Следует заметить, что в каждом реальном конденсаторе реальная мощность (мощность потерь) все же тратится, при течении через него переменного тока. Это вызвано тем, что происходят изменения в состоянии диэлектрика конденсатора. Помимо этого существует некоторая утечка в изоляции обкладок конденсатора, поэтому появляется небольшое активное сопротивление, которое как бы включено параллельно конденсатору.

Примеры решения задач

Цепь переменного тока с емкостным сопротивлением.

Емкость в цепи переменного тока

Рассмотрим теперь цепь переменного тока (рис. 58, а), в которую включена электрическая емкость (конденсатор). Активным сопротивлением этой цепи пренебрегаем (r = 0). Полярность зажимов генератора переменного тока, включенного в цепь с емкостью, меняется с частотой ω = 2πf.
В первую четверть периода (рис. 58, в) конденсатор заряжается и на его пластинах появляются противоположные по знаку электрические заряды (на левой пластине плюс, на правой — минус).
При заряде конденсатора по проводам, соединяющим генератор с пластинами, перемещаются электрические заряды, следовательно, протекает зарядный ток, измеряемый миллиамперметром. Через диэлектрик конденсатора ток не проходит. Как видно на волновой диаграмме, в первую четверть периода во время заряда конденсатора напряжение на пластинах конденсатора возрастает от нуля до максимального значения, сила тока, наоборот, в начале заряда будет максимальной, а в конце заряда, когда напряжение на конденсаторе (U_c) окажется равным напряжению генератора (U_г), она станет равной нулю.
За вторую четверть периода напряжение генератора постепенно убывает и становится равным нулю. В это время конденсатор разряжается. При этом разрядный ток, протекающий по проводам, имеет направление, противоположное направлению тока заряда.
За третью четверть периода полярность на зажимах генератора изменится и напряжение возрастет от нуля до наибольшего значения. В это время конденсатор вновь зарядится, но полярность на его пластинах изменится. На левой пластине будет отрицательный заряд, на правой пластине — положительный заряд. По проводам пройдет зарядный ток, сила которого к концу заряда конденсатора, когда U_c = U_г, станет равной нулю.
В четвертую часть периода напряжение генератора убывает и становится равным нулю. Конденсатор в это время вторично разряжается, и по проводам, соединяющим генератор с пластинами конденсатора, вновь протекает разрядный ток.
Из сказанного следует, что за один период изменения переменного напряжения дважды происходит процесс заряда и разряда конденсатора и при этом в его цепи протекает переменный ток. Кроме того, при заряде и разряде конденсатора ток в цепи и напряжение не совпадают по фазе. Ток опережает по фазе напряжение на четверть периода, т. е. на 90°.
Построим векторную диаграмму для цепи переменного тока с емкостью (рис. 58, б). Для этого отложим вектор тока I в выбранном масштабе по горизонтали. Чтобы на векторной диаграмме показать, что напряжение отстает от тока на угол φ = 90°, откладываем вектор напряжения U_c вниз под углом 90°.
Выясним, от чего зависит сила тока в цепи с емкостью. Обозначим сопротивление цепи X_c и назовем его емкостным сопротивлением. Тогда закон Ома для цепи с емкостью можно выразить так: где U — напряжение генератора, в;
X_c — емкостное сопротивление, ом;
I — сила тока, а. Известно, что сила тока в цепи определяется количеством электрических зарядов, проходящих через поперечное сечение проводника в единицу времени: Если в единицу времени по проводам протекает большое количество зарядов, то сила тока будет большой, и наоборот, когда по проводам в каждую секунду протекает малое количество зарядов, то сила тока оказывается незначительной.
Допустим, что частота переменного тока, вырабатываемого генератором, большая. В этом случае в каждую секунду конденсатор много раз (часто) заряжается и разряжается. В проводах, идущих от генератора к пластинам конденсатора, будет перемещаться в каждую секунду большое количество электрических зарядов. Поэтому можно сказать, что в рассматриваемой цепи возникает большая сила тока и в данном случае, согласно закону Ома, емкостное сопротивление цепи X_c оказывается малой величиной.
Если же частота переменного тока генератора будет мала, то конденсатор в каждую секунду зарядится и разрядится меньшее количество раз. В связи с этим по проводам цепи в каждую секунду пройдет незначительное количество зарядов и сила тока будет мала, а следовательно, емкостное сопротивление цепи, наоборот, будет большим.
Из сказанного можно сделать вывод, что емкостное сопротивление обратно пропорционально частоте переменного тока.
Емкостное сопротивление зависит не только от частоты переменного тока, но и от величины емкости, включенной в цепь.
Допустим, что в цепь включен конденсатор большой емкости. Количество электричества, которое накапливает конденсатор при заряде и отдает при разряде, прямо пропорционально его емкости:

q = C U.

Чем больше емкость конденсатора, включенного в цепь переменного тока, тем большее количество электричества переместится при заряде и разряде по проводам, идущим от генератора к его пластинам. Поэтому в проводах возникает ток большой силы и в данном случае, согласно закону Ома, емкостное сопротивление цепи X_c будет мало.
Если же включенная в цепь емкость мала, то при заряде и разряде по проводам пройдет меньшее количество электрических зарядов и сила тока будет незначительной, следовательно, емкостное сопротивление цепи, наоборот, будет большим.
Из сказанного можно сделать вывод, что емкостное сопротивление обратно пропорционально емкости.
Таким образом, емкостное сопротивление: где X_c — емкостное сопротивление, ом;
ω — угловая частота переменного тока, рад/сек;
С — емкость, ф.
Известно, что угловая частота ω = 2πf.
Поэтому емкостное сопротивление можно определить так: где f — частота переменного тока, гц.
Если включенная емкость измеряется в микрофарадах, то емкостное сопротивление Если емкость измеряется в пикофарадах, то Следует подчеркнуть, что имеется существенное различие между емкостным и активным сопротивлениями. Как известно, активная нагрузка безвозвратно потребляет энергию генератора переменного тока.
Если же к источнику переменного тока присоединена емкость, то, как было рассмотрено выше, энергия генератора расходуется при заряде конденсатора на создание электрического поля между пластинами и возвращается обратно генератору при разряде конденсатора.
Следовательно, емкостная нагрузка не потребляет энергию генератора, а в цепи с емкостью происходит «перекачивание» энергии из генератора в конденсатор и обратно. По этой причине емкостное сопротивление, как и индуктивное, называется реактивным. Пример.  Конденсатор емкостью С = 2 мкф включен в цепь переменного тока, частота которого 50 гц. Определить:
1) его емкостное сопротивление при частоте f = 50 гц;
2) емкостное сопротивление этого конденсатора переменному току, частота которого 500 гц.
Решение. Емкостное сопротивление конденсатора переменному току при частоте f = 50 гц При частоте f = 500 гц Из приведенного примера видно, что емкостное сопротивление конденсатора уменьшается с повышением частоты, а с уменьшением частоты переменного тока емкостное сопротивление возрастает. Для постоянного тока, когда напряжение на зажимах цепи не изменяется, конденсатор практически обладает бесконечно большим сопротивлением и поэтому он постоянного тока не пропускает.

Реактивное сопротивление

Итак, катушки индуктивности и конденсаторы препятствуют протеканию переменного тока. Такое сопротивление по переменному току носит название реактивного сопротивления Х и измеряется в омах. Реактивное сопротивление зависит как от величины индуктивности и емкости, так и от частоты сигнала.

Катушка индуктивности имеет индуктивное реактивное сопротивление VL равное

где f — частота в герцах, a L — индуктивность в генри.
Так как ω = 2πf, то можно записать XL = ωL. Например, реактивное сопротивление катушки с индуктивностью 10 мГн, на которую подается сигнал частотой 1 кГц, равно

XL = 2π*1*103*10 *10-3 = 62,8 Ом.

Реактивное сопротивление катушки индуктивности возрастает с увеличением частоты сигнала (рис. 4.26).
Конденсатор имеет емкостное сопротивление XC равное

где С — емкость в фарадах. Например, реактивное сопротивление конденсатора емкостью 1 мкФ, на который подается сигнал частотой 10 кГц, равно

   

Рис. 4.26. Зависимость индуктивного                                            Рис. 4.27.
сопротивления от частоты.

Рис. 4.28. Векторная сумма емкостного (XC)

и индуктивного (XL) сопротивлений.

                                                                                                                                         Рис. 4.29.
(а) Катушка индуктивности, соединенная последовательно с резистором R.
(б) Векторное представление R, XL и их векторной суммы Z

Реактивное сопротивление конденсатора уменьшается с увеличением частоты сигнала (рис. 4.27).
Результирующее сопротивление цепи, включающей в себя емкостное сопротивление XC и индуктивное сопротивление XL, равно векторной сумме XC и XL. Векторы XC и XL, как видно из рис. 4.28(б), находятся в противофазе, т. е. разность фаз между ними равна 1800. Поэтому результирующее сопротивление просто равно разности между XC и XL. Например, пусть XL = 100 Ом, а XC = 70 Ом. Тогда результирующее реактивное сопротивление Х = 100 – 70 = 30 Ом и является индуктивным так как XL больше, чем XС.

 

Импеданс
Результирующее сопротивление цепи, содержащей как активное, так и реактивное (индуктивное либо емкостное) сопротивление, носит название импеданса или полного сопротивления цепи.
Импеданс Z является векторной суммой реактивного сопротивления Х и активного сопротивления R.
Рассмотрим, например, схему, изображенную на рис. 4.29. Она включает в себя индуктивное сопротивление XL соединенное последовательно с резистором R. Как видно из рис. 4.29(б), вектор XL опережает вектор R на 90°. Импеданс равен

Если XL = 400 Ом и R = 300 Ом, то Z = 500 Ом.

Добавить комментарий

АКТИВНОЕ ЕМКОСТНОЕ ИНДУКТИВНОЕ СОПРОТИВЛЕНИЕ В ЭЛЕКТРИЧЕСКОЙ ЦЕПИ ПЕРЕМЕННОГО

АКТИВНОЕ, ЕМКОСТНОЕ, ИНДУКТИВНОЕ СОПРОТИВЛЕНИЕ В ЭЛЕКТРИЧЕСКОЙ ЦЕПИ ПЕРЕМЕННОГО ТОКА Мясникова А. 11 Д

Сопротивление, включенное в цепь переменного тока, в котором происходит превращение электрической энергии в полезную работу или в тепловую энергию, называется активным сопротивлением. Активным сопротивлением обладают все проводники. Сопротивление активное — величина, характеризующая сопротивление электрической цепи (её участка) переменному току, обусловленное необратимым превращением электрической энергии в другие формы энергии например, в механическую энергию (в электродвигателях), в химическую энергию (при электролизе, заряде аккумуляторов), в тепловую энергию (нагрев проводников, диэлектриков). Выражается отношением активной мощности, поглощаемой на участке цепи, к квадрату действующего значения тока на этом участке, измеряется в омах.

АКТИВНОЕ СОПРОТИВЛЕНИЕ ПРОВОДНИКА ЭЛЕКТРИЧЕСКОМУ ТОКУ РАССЧИТЫВАЕТСЯ ПО ФОРМУЛЕ: R — сопротивление (Ом) U — разность электрических потенциалов на концах проводника (В) I — ток, протекающий между концами проводника под действием разности потенциалов (А)

Сопротивление однородного проводника постоянного сечения зависит от свойств вещества проводника, его длины, сечения и вычисляется по формуле: R — сопротивление проводника (Ом) ρ — удельное сопротивление проводника (Ом м) l — длина проводника (м) S — площадь сечения проводника (м 2)

Сопротивление характеризующая индуктивное — сопротивление, величина, оказываемое переменному току индуктивностью цепи (её участка). Элементы, связанные с наличием только магнитного поля, называются индуктивностями. Индуктивностью обладают катушки реле, обмотки электродвигателей и трансформаторов. Измеряется в Омах.

ИНДУКТИВНОЕ СОПРОТИВЛЕНИЕ ПРОВОДНИКА ЭЛЕКТРИЧЕСКОМУ ТОКУ РАССЧИТЫВАЕТСЯ ПО ФОРМУЛЕ: XL — индуктивное сопротивление (Ом) ω — циклическая частота переменного тока (рад/с) L — индуктивность (Гн)

Ёмкостное сопротивление — это сопротивление переменному току, которое оказывает проводник, включенный в цепь переменного тока и не имеющий заметного сопротивления и индуктивности, но имеющий заметную емкость С. Элементы, связанные с наличием электрического поля, называются емкостями. Емкостью обладают конденсаторы, длинные линии электропередачи и т. д. Ток в цепи с емкостью опережает напряжение по фазе на 90 градусов. Емкостное сопротивление является реактивным, то есть потерь энергии в нем не происходит как, например, в активном сопротивлении. Емкостное сопротивление обратно пропорционально частоте переменного тока. Измеряется в Омах.

ЭКСПЕРИМЕНТ Оборудование: конденсатор, лампа накаливания и два источника напряжения — один постоянного тока, другой переменного. Для начала построим цепь, состоящую из источника постоянного напряжения, лампы и конденсатора. Все это включено последовательно. При включении тока лампа вспыхнет на короткое время, а потом погаснет, так как для постоянного тока конденсатор имеет большое электрическое сопротивление, ведь между обкладками конденсатора находится диэлектрик, через который постоянный ток не способен пройти. Вспыхнет лампа потому, что в момент включения источника постоянного напряжения идет кратковременный импульс тока, заряжающий конденсатор. А раз ток идет значит и лампа светится.

Заменим в этой цепи источник постоянного напряжения на генератор переменного. При включении такой цепи обнаружим, что лампа будет светится непрерывно. Происходит это потому, что конденсатор в цепи переменного тока заряжается за четверть периода. Когда напряжение на нем достигнет амплитудного значения, оно начинает уменьшаться, и конденсатор будет разряжаться следующие четверть периода. В следующие полпериода процесс повторится снова, но напряжение в этот раз уже будет отрицательным. Таким образом, в цепи непрерывно течет ток, хотя он и меняет при этом свое направление дважды за период. Но через диэлектрик конденсатора заряды не проходят. Как же это происходит? Представим себе конденсатор, подключаемый к источнику постоянного напряжения. При включении, источник убирает электроны с одной обкладки, тем самым создавая на ней положительный заряд. А на второй обкладке добавляет электронов, создавая тем самым равный по величине, но противоположный по знаку отрицательный заряд. В момент перераспределения зарядов в цепи протекает ток заряда конденсатора. Хотя электроны при этом не движутся через диэлектрик конденсатора.

Если теперь из цепи исключить конденсатор, то лампа будет светить ярче. Это говорит о том, что емкость создает сопротивление, току ограничивая его величину. Происходит это из-за того что при заданной частоте тока значение ёмкости мало и она не успевает накопить достаточно энергии в виде зарядов на своих обкладках. И при разряде будет протекать ток меньше чем способен развить источник тока. Отсюда следует, что емкостное сопротивление зависит как от частоты, так и от величины емкости конденсатора.

ЁМКОСТНОЕ СОПРОТИВЛЕНИЕ ПРОВОДНИКА ЭЛЕКТРИЧЕСКОМУ ТОКУ РАССЧИТЫВАЕТСЯ ПО ФОРМУЛЕ: XС — емкостное сопротивление проводника переменному току (Ом) ω — циклическая частота переменного тока (рад/с) С — емкость проводника (Ф)

В чем разница между сопротивлением и импедансом?

Спросил: Венудхар

Ответ

Сопротивление — это понятие, используемое для постоянного тока (постоянного тока), тогда как полное сопротивление — это эквивалент переменного тока (переменного тока).

Сопротивление возникает из-за столкновения электронов в проводнике с ионной решеткой проводника, что означает преобразование электрической энергии в тепло. У разных материалов разное удельное сопротивление (свойство, определяющее, насколько резистивным будет материал заданных размеров).

Однако, рассматривая переменный ток, вы должны помнить, что он колеблется как синусоида, поэтому знак всегда меняется. Это означает, что необходимо учитывать другие эффекты, а именно индуктивность и емкость.

Индуктивность наиболее очевидна в витой проволоке. Когда через провод течет ток, вокруг него создается круговое магнитное поле. Если вы скручиваете провод в соленоид, поля вокруг провода суммируются, и вы получаете магнитное поле, подобное магнитному стержню снаружи, но вы получаете однородное магнитное поле внутри.С переменным током, поскольку знак всегда меняется, направление поля в проводах всегда меняется — поэтому магнитное поле соленоида также постоянно меняется. Теперь, когда силовые линии пересекают проводник, ЭДС создается таким образом, чтобы уменьшить создавшие его эффекты (это комбинация законов Ленца и Фарадея, которые математически утверждают, что E = N * d (thi) / dt, где thi магнитный поток). Это означает, что при протекании переменного тока через проводник индуцируется небольшая обратная ЭДС или обратный ток, уменьшая общий ток.

Емкость — это свойство, лучше всего иллюстрируемое двумя металлическими пластинами, разделенными изолятором (который мы называем конденсатором). Когда ток течет, электроны накапливаются на отрицательной пластине. Электрическое поле распространяется и отталкивает электроны на противоположной пластине, делая ее положительно заряженной. Из-за накопления электронов на отрицательной пластине входящие электроны также отталкиваются, поэтому общий ток в конечном итоге падает до нуля в результате экспоненциального затухания. Емкость определяется как заряд, накопленный / перемещаемый через конденсатор, деленный на разность потенциалов на нем, а также может быть рассчитан по размеру пластин и примитивности изолятора.

Итак, просто сопротивление и импеданс имеют разное фундаментальное происхождение, даже если расчет их значений одинаков:

R = V / I
Ответил: Мартин Арчер, студент-физик, Имперский колледж Лондона, Великобритания

Импеданс — это более общий термин для обозначения сопротивления, который также включает реактивное сопротивление.

Другими словами, сопротивление — это противодействие постоянному электрическому току. Чистое сопротивление не меняется с частотой, и обычно единственное сопротивление рассматривается только при постоянном токе (постоянный ток — не меняется) электричестве.

Реактивное сопротивление, однако, является мерой сопротивления электричеству переменного тока из-за емкости или индуктивности. Это противодействие меняется с частотой. Например, конденсатор пропускает постоянный ток только короткое время, пока он не зарядится; в этот момент ток перестанет течь, и он будет выглядеть как открытое. Однако, если на этот конденсатор подается очень высокая частота (сигнал с напряжением, которое очень быстро меняется взад и вперед), конденсатор будет выглядеть как короткое замыкание.Конденсатор имеет реактивное сопротивление, обратно пропорциональное частоте. Катушка индуктивности имеет реактивное сопротивление, которое прямо пропорционально частоте — постоянный ток легко протекает, в то время как высокочастотный переменный ток прекращается.

Импеданс — это суммарный вклад как сопротивления, так и реактивного сопротивления. Это важно для анализа и проектирования переменного тока. При постоянном токе реактивные элементы могут быть заменены их стационарной моделью (конденсатор -> разомкнут, индуктор -> короткое замыкание) и может быть учтено сопротивление. (это неверно для анализа переходных процессов)

Важно отметить, что хотя энергия поступает в оба, она «сгорает» только из-за сопротивления.Мощность должна быть выражена в виде активной и реактивной мощности. Резистивная мощность фактически сжигает энергию в тепло, в то время как реактивная мощность просто накапливает энергию в E-полях и B-полях.

Часто вы слышите об «импедансе» линий передачи, таких как кабели, которые проходят между компонентами вашей стереосистемы, и об импедансе таких вещей, как динамики. Вы также услышите, что важно совместить их, иначе вы получите отражение.

Это гораздо более сложный предмет, который несколько ответов прокомментировали в недавних вопросах о свете и его скорости.

Однако я хочу упомянуть, что когда вы слышите об импедансе линии передачи, такой как кабель динамика, антенна, коаксиальный кабель или что-то еще, это не означает энергию, которая «сжигается» в кабеле. Это связано с тем, как энергия накапливается в кабеле при распространении по нему. Кабель не нагревается (ну, на самом деле это так, но для простоты предполагается случай без потерь) нагревается по мере прохождения сигнала по нему. Неправильно думать о 75-омном кабеле как о 75-омном резисторе.«Эти 75 Ом — это чисто реактивное сопротивление (в идеале, хотя в реальных кабелях действительно есть затухание).

Обратите внимание, что импеданс и реактивное сопротивление даны в единицах «Ом», как и сопротивление. Емкость измеряется в Фарадах, а индуктивность — в Генри, и они относятся к импедансу, но не являются мерой импеданса. Как я уже сказал, импеданс конденсатора обратно пропорционален его емкости, а импеданс катушки индуктивности прямо пропорционален его индуктивности.

Это может показаться немного абстрактным. Импеданс на самом деле представляет собой абстракцию гораздо более сложных вещей (таких как постоянные времени и время нарастания), которые инженеры-электрики должны постоянно учитывать. Идея «импеданса» позволяет объединить многие из этих вещей в одну тему, чтобы их было легче передать.

Короткий ответ — импеданс включает реактивное сопротивление, а реактивное сопротивление включает эффекты, которые зависят от частоты из-за индуктивности и емкости.
Ответил: Тед Павлик, студент-электротехник, Ohio St.

Узнайте о емкостном реактивном сопротивлении | Chegg.com

Емкостное реактивное сопротивление почти такое же, как сопротивление любого проводника. Однако это считается, когда источником является переменный ток. Он обозначается как XC \ mathop {X} _ {C} XC Емкостное реактивное сопротивление обратно пропорционально частоте сигнала и емкости элемента схемы. Математическая зависимость, представляющая пропорциональность емкостного реактивного сопротивления и частоты источника, задается следующим образом:

XC = −12πfC \ mathop {X} _ {C} = — \ frac {1} {2 \ pi fC} XC = — 2πfC1

Используя указанное выше соотношение, можно рассчитать емкость элемента схемы. {2}} } Z = R2 + (XL −XC) 2

Где Z импеданс цепи LCR, R Сопротивление цепи LCR, XL {{X} _ {L}} XL Емкостное реактивное сопротивление LCR цепи, и XL {{X} _ {L}} XL Индуктивное реактивное сопротивление цепи LCR.

Пример проблемы:

Каким будет значение конденсатора в фарадах, если его емкостное реактивное сопротивление составляет 200 Ом и он подключен к источнику питания с частотой 50 Гц?

Решение: Дано: Емкостное реактивное сопротивление = 200 Ом

Частота входного сигнала переменного тока f = 50 Гц

Емкость (C) =?

Емкость данного элемента схемы рассчитывается как:

C = 12πfXCC = \ frac {1} {2 \ pi f \ mathop {X} _ {C}} C = 2πfXC 1

C = 12 × 3,14 × 50 × 200C = \ frac {1} {2 \ times 3.14 \ times 50 \ times 200} C = 2 × 3,14 × 50 × 2001
C = 1314 × 200C = \ frac {1} {314 \ times 200} C = 314 × 2001

Следовательно, емкость данная схема в фарадах = 15,92 мкФ.

Аналогичным образом можно вычислить частоту входного сигнала для заданного емкостного сопротивления и емкости элемента схемы. Мы также можем вычислить угловую частоту входного источника как ω = 2πf \ omega = 2 \ pi fω = 2πf.

Емкостное реактивное сопротивление — Как найти последовательные и параллельные конденсаторы

Найдите емкостное реактивное сопротивление цепи с последовательными или параллельными конденсаторами, используя этот простой двухэтапный процесс.

Шаг 1: Найдите общую емкость цепи

Предположим, у нас есть три конденсатора, 12 Ф, 20 Ф и 30 Ф, подключенных к источнику с частотой 60 Гц. Каково полное емкостное реактивное сопротивление (X _C ) при последовательном или параллельном подключении?

1А. Для конденсаторов серии

Когда конденсаторы соединены последовательно, общая емкость меньше, чем любая из отдельных емкостей последовательных конденсаторов. Если два или более конденсатора соединены последовательно, общий эффект будет таким, как у одного (эквивалентного) конденсатора, имеющего суммарное расстояние между пластинами отдельных конденсаторов.

Конденсаторы серии Пример:

1/12 = 0,083, 1/20 = 0,050, 1/30 = 0,033

0,083 + 0,050 + 0,033 = 0,166

1 / 0,163 = 6,02 мкФ

Примечание: математика упрощена для целей иллюстрации. Для более точных чисел воспользуйтесь калькулятором.

1Б. Для параллельных конденсаторов

При параллельном подключении конденсаторов общая емкость складывается из емкостей отдельных конденсаторов. Если два или более конденсатора соединены параллельно, общий эффект будет таким, как у одного эквивалентного конденсатора, имеющего сумму площадей пластин отдельных конденсаторов.

Параллельные конденсаторы Пример:

12 + 20 + 30 = 62 мкФ

---

Шаг 2: Найдите емкостное реактивное сопротивление

Как и сопротивление, реактивное сопротивление измеряется в Ом, но ему присваивается символ X, чтобы отличить его от чисто резистивного значения R, и поскольку рассматриваемый компонент является конденсатором, реактивное сопротивление конденсатора называется емкостным реактивным сопротивлением (X _C ) который измеряется в Ом.

Поскольку конденсаторы заряжаются и разряжаются пропорционально скорости изменения напряжения на них, чем быстрее изменяется напряжение, тем больше тока течет. Точно так же, чем медленнее изменяется напряжение, тем меньше будет протекать ток. Это означает, что реактивное сопротивление конденсатора переменного тока «обратно пропорционально» частоте источника питания.

X _C — емкостное реактивное сопротивление в омах, f — частота в герцах, а C — емкость переменного тока в фарадах. Очень важно преобразовать наш пример из микрофарад в фарады, чтобы получить правильный результат!

1 мкФ = 0,000001 F

Серия 60 Гц Пример:

6,02 мкФ = 0,000006 Ф (упрощенно)
2 х 3,14 х 60 х 0,000006 = 0,0022608
1 / 0,0022608 = 442,32 Ом

60 Гц Параллельный Пример:

62 мкФ = 0,000062 F
2 х 3. 14 х 60 х 0,000062 = 0,0233616
1 / 0,0233616 = 42,805 Ом

Теперь посмотрим, что произойдет при изменении частоты на 400 Гц :

Серия 400 Гц Пример:

2 х 3,14 х 400 х 0,000006 = 0,015072
1 / 0,015072 = 66,34 Ом

Параллельный 400 Гц Пример:

2 х 3,14 х 400 х 0,000062 = 0,155744
1 / 0,155744 = 6,42 Ом

---

Полезные ссылки

на комментарий.

Capacitive Reactance Xc — Engineer-Educators.com

Эффективность конденсатора в пропускании потока переменного тока зависит от емкости цепи и применяемой частоты. В какой степени конденсатор пропускает поток переменного тока, во многом зависит от величины емкости конденсатора, выраженной в фарадах (f). Чем больше емкость конденсатора, тем большее количество электронов, измеряемое в кулонах, необходимо для приведения конденсатора в полностью заряженное состояние. Как только конденсатор приближается или фактически достигает полностью заряженного состояния, полярность конденсатора будет противоположной полярности приложенного напряжения, по существу действуя в этом случае как разомкнутая цепь. Чтобы дополнительно проиллюстрировать эту характеристику и то, как она проявляется в цепи переменного тока, рассмотрим следующее. Если конденсатор имеет большую емкость, что означает, что ему требуется относительно большое количество электронов, чтобы привести его в полностью заряженное состояние, тогда через конденсатор может проходить ток довольно высокой частоты, при этом конденсатор никогда не достигает полного заряда.В этом случае, если частота достаточно высока, а емкость достаточно велика, чтобы конденсатору никогда не хватило времени, чтобы когда-либо достичь полного заряда, возможно, что конденсатор может оказывать очень маленькое сопротивление току или совсем его не иметь. Однако чем меньше емкость, тем меньше электронов требуется, чтобы довести его до полного заряда, и более вероятно, что конденсатор накопит достаточно противоположного заряда, чтобы он мог оказывать большое сопротивление току, если не вплоть до разомкнутой цепи. Между этими двумя крайними условиями лежит целый ряд возможностей противодействия току в зависимости от комбинации приложенной частоты и выбранной емкости. Ток в цепи переменного тока можно контролировать, изменяя емкость цепи аналогично тому, как сопротивление может управлять током. Фактическое реактивное сопротивление переменного тока Xc, которое, как и сопротивление, измеряется в омах (Ом). Емкостное реактивное сопротивление Xc определяется следующим образом:

Пример задачи:
Предполагается последовательная цепь, в которой подаваемое напряжение составляет 110 вольт при 60 гц, а емкость конденсатора составляет 80 Mf.Найдите емкостное реактивное сопротивление и ток.

Решение:
Для определения емкостного реактивного сопротивления используется уравнение Xc = 1 / (2 p f C). Во-первых, емкость 80 МФ заменяется на фарады путем деления 80 на 1000000, поскольку 1 миллион микрофарад равен 1 фараду. Это частное равно 0,000080 фарада. Это подставляется в уравнение и

После определения реактивного сопротивления закон Ома может быть использован таким же образом, как он используется в цепях постоянного тока для определения тока.

(a) Емкостная измерительная установка для измерения удельного сопротивления высокого …

Контекст 1

… μ ω — подвижность электронов на переменном токе, μ n — подвижность электронов на постоянном токе, а τ — время релаксации электронов. Для металлов и большинства полупроводников ωτ 1 вплоть до микроволновых частот, поэтому переменную и микроволновую подвижности можно считать такими же, как подвижность на постоянном токе. Концентрацию и подвижность носителей заряда труднее определить бесконтактными методами переменного и микроволнового излучения, чем методами постоянного тока, потому что в большинстве из них напряжение Холла невозможно напрямую измерить, поэтому коэффициент Холла обычно определяется на основе измерений проводимости. компоненты тензора. Наиболее часто используемые методы бесконтактного измерения удельного сопротивления высокоомных (HR) полупроводников — это емкостные методы, основанные на выборке в частотной области. В нашем эксперименте наилучшее соответствие данным измерений было получено для значения удельного сопротивления ρ = 1,43 · 10 8 см. Типичный диапазон измерения удельного сопротивления с использованием метода измерения импеданса в частотной области составляет от 10 4 до 10 9 см, а погрешности измерения не превышают нескольких процентов. Коаксиальный конденсаторный зонд без нижнего электрода, показанный на рисунке 3 (c), также можно использовать для бесконтактных измерений удельного сопротивления полупроводниковых пластин.При малых воздушных зазорах между образцом и электродами силовые линии электрического поля параллельны границе раздела воздух – полупроводник. В результате воздушная часть конденсатора параллельна полупроводниковой части двухслойного конденсатора. Если размер воздушного зазора намного меньше толщины полупроводникового образца, то общая емкость примерно равна емкости полупроводника. Его эквивалентная схема — это просто параллельное соединение R sem и C sem.На определенной частоте реактивное сопротивление этого конденсатора равно его сопротивлению. Эта частота называется частотой среза f c. Зная диэлектрическую проницаемость полупроводника и частоту отсечки, удельное сопротивление образца можно найти как ρ = 1 / (ω c ε r), где ω c = 2 π f c обозначает угловую частоту отсечки. Такой метод используется в одном из коммерческих инструментов, предназначенных для бесконтактного картирования удельного сопротивления полупроводников HR. Альтернативный метод определения удельного сопротивления основан на измерениях заряда во временной области (TDCM) емкостной ячейки, как показано на рисунке 3 (a).Временной отклик эквивалентной схемы, показанной на рисунке 3 (b), можно легко проанализировать, решив систему двух обыкновенных дифференциальных уравнений. Система имеет аналитические решения, но численные решения могут быть легко получены с помощью решателя жестких дифференциальных уравнений, например в среде MATLAB. Предположим, что в момент времени t = 0 импульсное ступенчатое напряжение величиной 10 В было приложено к схеме, показанной на рисунке 3 (b). Результаты расчета зависящих от времени напряжений на конденсаторе C sem (U S) и на конденсаторе C a (U) показаны на рисунке 5 (a) (для ясности используется логарифмическая шкала времени).Предполагалось, что все параметры измерительной ячейки и образца такие же, как те, что указаны в описании рисунка 4. При приложении ступенчатого напряжения конденсаторы C sem и C a заряжаются почти мгновенно (постоянная времени зарядки зависит от значение резистора R c) и распределение напряжения между емкостями C sem и C a зависит от их значений реактивного сопротивления. Через некоторое время конденсатор C sem разряжается через сопротивление R sem с постоянной времени τ = R sem (C a + C sem).Из измерений постоянной времени τ (предполагая, что емкости C sem и C a известны), мы можем определить R sem, а затем удельное сопротивление (проводимость) испытуемого образца. Диапазон измерения удельного сопротивления для имеющихся в продаже емкостных систем измерения во временной области составляет от 10 5 до 10 12 см. Минимальная измеряемая площадь на образцах с помощью этого метода очень мала (в диапазоне 1–5 мм 2), что очень полезно для инструментов для картирования удельного сопротивления. Подвижность и концентрация носителей заряда в методе TDCM определяются из измерений проводимости σ 0 без какого-либо магнитного поля с использованием емкостной ячейки, показанной на рисунке 3 (a), а затем путем измерения проводимости σ xx в присутствии статическое магнитное поле, параллельное пластине [15].Если значение магнитного поля B z известно, то мы можем легко найти подвижность носителей заряда μ n (или μ p) из уравнения (18). Однако следует отметить, что для получения измеримой разницы между значениями проводимости в отсутствие и в присутствии магнитного поля (например, 1%) произведение μ B z должно быть порядка 0,1. Это ограничивает минимальную измеряемую подвижность примерно до 600 см 2 В — 1 с — 1, если в системе измерения используется электромагнит, обеспечивающий магнитную индукцию 1,6 Тл.Также было замечено, что определение подвижности из измерений магнитной проводимости методом TDCM может привести к результатам, отличным от результатов, полученных из измерений постоянного тока, основанных на эффекте Холла [15]. Одна из причин такого различия заключается в том, что модель Друде дает только приближенные выражения для тензора проводимости, особенно для полярных полупроводников, таких как InSb. Более продвинутые модели проводимости были изучены в литературе [16], и было доказано, что рассчитанные значения проводимости, полученные с помощью продвинутых моделей, заметно отличаются от тех, которые получены с применением теории Друде.Тем не менее, преимуществ метода TDCM и точности простой модели Друде достаточно для практического применения метода магнитопроводимости для определения подвижности пластин GaAs и GaN с высоким удельным сопротивлением и высокой подвижностью, производимых промышленностью. Метод измерения вихревых токов долгое время использовался для неразрушающего контроля металлов (см., Например, [17]), а позже, в 1976 году, Миллер и др. Из Bell. Лаборатории [18].В настоящее время этот метод рекомендуется в качестве стандартного …

Контекст 2

… μ ω — подвижность электронов на переменном токе, μ n — подвижность электронов на постоянном токе, а τ — время релаксации. электронов. Для металлов и большинства полупроводников ωτ 1 вплоть до микроволновых частот, поэтому переменную и микроволновую подвижности можно считать такими же, как подвижность на постоянном токе. Концентрацию и подвижность носителей заряда труднее определить бесконтактными методами переменного и микроволнового излучения, чем методами постоянного тока, потому что в большинстве из них напряжение Холла невозможно напрямую измерить, поэтому коэффициент Холла обычно определяется на основе измерений проводимости. компоненты тензора.Наиболее часто используемые методы бесконтактного измерения удельного сопротивления высокоомных (HR) полупроводников — это емкостные методы, основанные на выборке в частотной области. В нашем эксперименте наилучшее соответствие данным измерений было получено для значения удельного сопротивления ρ = 1,43 · 10 8 см. Типичный диапазон измерения удельного сопротивления с использованием метода измерения импеданса в частотной области составляет от 10 4 до 10 9 см, а погрешности измерения не превышают нескольких процентов. Коаксиальный конденсаторный зонд без нижнего электрода, показанный на рисунке 3 (c), также можно использовать для бесконтактных измерений удельного сопротивления полупроводниковых пластин.При малых воздушных зазорах между образцом и электродами силовые линии электрического поля параллельны границе раздела воздух – полупроводник. В результате воздушная часть конденсатора параллельна полупроводниковой части двухслойного конденсатора. Если размер воздушного зазора намного меньше толщины полупроводникового образца, то общая емкость примерно равна емкости полупроводника. Его эквивалентная схема — это просто параллельное соединение R sem и C sem.На определенной частоте реактивное сопротивление этого конденсатора равно его сопротивлению. Эта частота называется частотой среза f c. Зная диэлектрическую проницаемость полупроводника и частоту отсечки, удельное сопротивление образца можно найти как ρ = 1 / (ω c ε r), где ω c = 2 π f c обозначает угловую частоту отсечки. Такой метод используется в одном из коммерческих инструментов, предназначенных для бесконтактного картирования удельного сопротивления полупроводников HR. Альтернативный метод определения удельного сопротивления основан на измерениях заряда во временной области (TDCM) емкостной ячейки, как показано на рисунке 3 (a).Временной отклик эквивалентной схемы, показанной на рисунке 3 (b), можно легко проанализировать, решив систему двух обыкновенных дифференциальных уравнений. Система имеет аналитические решения, но численные решения могут быть легко получены с помощью решателя жестких дифференциальных уравнений, например в среде MATLAB. Предположим, что в момент времени t = 0 импульсное ступенчатое напряжение величиной 10 В было приложено к схеме, показанной на рисунке 3 (b). Результаты расчета зависящих от времени напряжений на конденсаторе C sem (U S) и на конденсаторе C a (U) показаны на рисунке 5 (a) (для ясности используется логарифмическая шкала времени).Предполагалось, что все параметры измерительной ячейки и образца такие же, как те, что указаны в описании рисунка 4. При приложении ступенчатого напряжения конденсаторы C sem и C a заряжаются почти мгновенно (постоянная времени зарядки зависит от значение резистора R c) и распределение напряжения между емкостями C sem и C a зависит от их значений реактивного сопротивления. Через некоторое время конденсатор C sem разряжается через сопротивление R sem с постоянной времени τ = R sem (C a + C sem).Из измерений постоянной времени τ (предполагая, что емкости C sem и C a известны), мы можем определить R sem, а затем удельное сопротивление (проводимость) испытуемого образца. Диапазон измерения удельного сопротивления для имеющихся в продаже емкостных систем измерения во временной области составляет от 10 5 до 10 12 см. Минимальная измеряемая площадь на образцах с помощью этого метода очень мала (в диапазоне 1–5 мм 2), что очень полезно для инструментов для картирования удельного сопротивления. Подвижность и концентрация носителей заряда в методе TDCM определяются из измерений проводимости σ 0 без какого-либо магнитного поля с использованием емкостной ячейки, показанной на рисунке 3 (a), а затем путем измерения проводимости σ xx в присутствии статическое магнитное поле, параллельное пластине [15].Если значение магнитного поля B z известно, то мы можем легко найти подвижность носителей заряда μ n (или μ p) из уравнения (18). Однако следует отметить, что для получения измеримой разницы между значениями проводимости в отсутствие и в присутствии магнитного поля (например, 1%) произведение μ B z должно быть порядка 0,1. Это ограничивает минимальную измеряемую подвижность примерно до 600 см 2 В — 1 с — 1, если в системе измерения используется электромагнит, обеспечивающий магнитную индукцию 1,6 Тл.Также было замечено, что определение подвижности из измерений магнитной проводимости методом TDCM может привести к результатам, отличным от результатов, полученных из измерений постоянного тока, основанных на эффекте Холла [15]. Одна из причин такого различия заключается в том, что модель Друде дает только приближенные выражения для тензора проводимости, особенно для полярных полупроводников, таких как InSb. Более продвинутые модели проводимости были изучены в литературе [16], и было доказано, что рассчитанные значения проводимости, полученные с помощью продвинутых моделей, заметно отличаются от тех, которые получены с применением теории Друде.Тем не менее, преимуществ метода TDCM и точности простой модели Друде достаточно для практического применения метода магнитопроводимости для определения подвижности пластин GaAs и GaN с высоким удельным сопротивлением и высокой подвижностью, производимых промышленностью. Метод измерения вихревых токов долгое время использовался для неразрушающего контроля металлов (см., Например, [17]), а позже, в 1976 году, Миллер и др. Из Bell. Лаборатории [18].В настоящее время этот метод рекомендуется в качестве стандартного метода для бесконтактного измерения удельного сопротивления полупроводников, и он реализован в имеющихся в продаже приборах для картирования удельного сопротивления. Вихретоковый зонд состоит из РЧ-катушки, намотанной вокруг ферритового сердечника, который физически разделен, чтобы обеспечить зазор для введения образца, как показано на рисунке 6. Цепь колеблющегося резервуара (РЧ-катушка и конденсатор, включенные параллельно) индуцируют вихревые токи в образце, которые рассеивают электромагнитную энергию, подаваемую генератором ВЧ тока.Мощность, потребляемая в этом процессе, при условии отсутствия утечки магнитного потока и незначительных явлений скин-эффекта, пропорциональна проводимости листа (обратной сопротивлению листа) образца. В электронной системе, показанной на рисунке 6, ВЧ-напряжение поддерживается постоянным, так что ток, подаваемый из ВЧ-генератора, пропорционален проводимости листа образца. Чтобы получить абсолютное значение проводимости листа испытуемого образца, систему сначала калибруют с использованием прослеживаемых стандартных эталонных материалов.Вихретоковые датчики отлично подходят для измерения удельного сопротивления полупроводниковых пластин и сопротивления проводящих слоев на непроводящих подложках. Типичные диапазоны измерений, указанные в …

Контекст 3

… μ ω — подвижность электронов на переменном токе, μ n — подвижность электронов на постоянном токе, а τ — время релаксации электроны. Для металлов и большинства полупроводников ωτ 1 вплоть до микроволновых частот, поэтому переменную и микроволновую подвижности можно считать такими же, как подвижность на постоянном токе.Концентрацию и подвижность носителей заряда труднее определить бесконтактными методами переменного и микроволнового излучения, чем методами постоянного тока, потому что в большинстве из них напряжение Холла невозможно напрямую измерить, поэтому коэффициент Холла обычно определяется на основе измерений проводимости. компоненты тензора. Наиболее часто используемые методы бесконтактного измерения удельного сопротивления высокоомных (HR) полупроводников — это емкостные методы, основанные на выборке в частотной области.В нашем эксперименте наилучшее соответствие данным измерений было получено для значения удельного сопротивления ρ = 1,43 · 10 8 см. Типичный диапазон измерения удельного сопротивления с использованием метода измерения импеданса в частотной области составляет от 10 4 до 10 9 см, а погрешности измерения не превышают нескольких процентов. Коаксиальный конденсаторный зонд без нижнего электрода, показанный на рисунке 3 (c), также можно использовать для бесконтактных измерений удельного сопротивления полупроводниковых пластин. При малых воздушных зазорах между образцом и электродами силовые линии электрического поля параллельны границе раздела воздух – полупроводник.В результате воздушная часть конденсатора параллельна полупроводниковой части двухслойного конденсатора. Если размер воздушного зазора намного меньше толщины полупроводникового образца, то общая емкость примерно равна емкости полупроводника. Его эквивалентная схема — это просто параллельное соединение R sem и C sem. На определенной частоте реактивное сопротивление этого конденсатора равно его сопротивлению. Эта частота называется частотой среза f c.Зная диэлектрическую проницаемость полупроводника и частоту отсечки, удельное сопротивление образца можно найти как ρ = 1 / (ω c ε r), где ω c = 2 π f c обозначает угловую частоту отсечки. Такой метод используется в одном из коммерческих инструментов, предназначенных для бесконтактного картирования удельного сопротивления полупроводников HR. Альтернативный метод определения удельного сопротивления основан на измерениях заряда во временной области (TDCM) емкостной ячейки, как показано на рисунке 3 (a). Временной отклик эквивалентной схемы, показанной на рисунке 3 (b), можно легко проанализировать, решив систему двух обыкновенных дифференциальных уравнений.Система имеет аналитические решения, но численные решения могут быть легко получены с помощью решателя жестких дифференциальных уравнений, например в среде MATLAB. Предположим, что в момент времени t = 0 импульсное ступенчатое напряжение величиной 10 В было приложено к схеме, показанной на рисунке 3 (b). Результаты расчета зависящих от времени напряжений на конденсаторе C sem (U S) и на конденсаторе C a (U) показаны на рисунке 5 (a) (для ясности используется логарифмическая шкала времени). Предполагалось, что все параметры измерительной ячейки и образца такие же, как те, которые указаны в описании рисунка 4.При подаче ступенчатого напряжения конденсаторы C sem и C a заряжаются почти мгновенно (постоянная времени зарядки зависит от номинала резистора R c), а распределение напряжения между емкостями C sem и C a зависит от их значений реактивного сопротивления. Через некоторое время конденсатор C sem разряжается через сопротивление R sem с постоянной времени τ = R sem (C a + C sem). Из измерений постоянной времени τ (предполагая, что емкости C sem и C a известны), мы можем определить R sem, а затем удельное сопротивление (проводимость) испытуемого образца.Диапазон измерения удельного сопротивления для имеющихся в продаже емкостных систем измерения во временной области составляет от 10 5 до 10 12 см. Минимальная измеряемая площадь на образцах с помощью этого метода очень мала (в диапазоне 1–5 мм 2), что очень полезно для инструментов для картирования удельного сопротивления. Подвижность и концентрация носителей заряда в методе TDCM определяются из измерений проводимости σ 0 без какого-либо магнитного поля с использованием емкостной ячейки, показанной на рисунке 3 (a), а затем путем измерения проводимости σ xx в присутствии статическое магнитное поле, параллельное пластине [15].Если значение магнитного поля B z известно, то мы можем легко найти подвижность носителей заряда μ n (или μ p) из уравнения (18). Однако следует отметить, что для получения измеримой разницы между значениями проводимости в отсутствие и в присутствии магнитного поля (например, 1%) произведение μ B z должно быть порядка 0,1. Это ограничивает минимальную измеряемую подвижность примерно до 600 см 2 В — 1 с — 1, если в системе измерения используется электромагнит, обеспечивающий магнитную индукцию 1,6 Тл.Также было замечено, что определение подвижности из измерений магнитной проводимости методом TDCM может привести к результатам, отличным от результатов, полученных из измерений постоянного тока, основанных на эффекте Холла [15]. Одна из причин такого различия заключается в том, что модель Друде дает только приближенные выражения для тензора проводимости, особенно для полярных полупроводников, таких как InSb. Более продвинутые модели проводимости были изучены в литературе [16], и было доказано, что рассчитанные значения проводимости, полученные с помощью продвинутых моделей, заметно отличаются от тех, которые получены с применением теории Друде.Тем не менее, преимуществ метода TDCM и точности простой модели Друде достаточно для практического применения метода магнитопроводимости для определения подвижности пластин GaAs и GaN с высоким удельным сопротивлением и высокой подвижностью, производимых промышленностью. Метод измерения вихревых токов долгое время использовался для неразрушающего контроля металлов (см., Например, [17]), а позже, в 1976 году, Миллер и др. Из Bell. Лаборатории [18].В настоящее время этот метод рекомендуется в качестве стандартного метода для бесконтактного измерения удельного сопротивления полупроводников, и он реализован в имеющихся в продаже приборах для картирования удельного сопротивления. Вихретоковый зонд состоит из РЧ-катушки, намотанной вокруг ферритового сердечника, который физически разделен, чтобы обеспечить зазор для введения образца, как показано на рисунке 6. Цепь колеблющегося резервуара (РЧ-катушка и конденсатор, включенные параллельно) индуцируют вихревые токи в образце, которые рассеивают электромагнитную энергию, подаваемую генератором ВЧ тока.Мощность, потребляемая в этом процессе, при условии отсутствия утечки магнитного потока и незначительных явлений скин-эффекта, пропорциональна проводимости листа (обратной сопротивлению листа) образца. В электронной системе, показанной на рисунке 6, ВЧ-напряжение поддерживается постоянным, так что ток, подаваемый из ВЧ-генератора, пропорционален проводимости листа образца. Чтобы получить абсолютное значение проводимости листа испытуемого образца, систему сначала калибруют с использованием прослеживаемых стандартных эталонных материалов.Вихретоковые датчики отлично подходят для измерения удельного сопротивления полупроводниковых пластин и сопротивления проводящих слоев на непроводящих …

Контекст 4

… μ ω — подвижность электронов на переменном токе, μ n — подвижность электронов на постоянном токе, а τ — время релаксации электронов. Для металлов и большинства полупроводников ωτ 1 вплоть до микроволновых частот, поэтому переменную и микроволновую подвижности можно считать такими же, как подвижность на постоянном токе.Концентрацию и подвижность носителей заряда труднее определить бесконтактными методами переменного и микроволнового излучения, чем методами постоянного тока, потому что в большинстве из них напряжение Холла невозможно напрямую измерить, поэтому коэффициент Холла обычно определяется на основе измерений проводимости. компоненты тензора. Наиболее часто используемые методы бесконтактного измерения удельного сопротивления высокоомных (HR) полупроводников — это емкостные методы, основанные на выборке в частотной области.В нашем эксперименте наилучшее соответствие данным измерений было получено для значения удельного сопротивления ρ = 1,43 · 10 8 см. Типичный диапазон измерения удельного сопротивления с использованием метода измерения импеданса в частотной области составляет от 10 4 до 10 9 см, а погрешности измерения не превышают нескольких процентов. Коаксиальный конденсаторный зонд без нижнего электрода, показанный на рисунке 3 (c), также можно использовать для бесконтактных измерений удельного сопротивления полупроводниковых пластин. При малых воздушных зазорах между образцом и электродами силовые линии электрического поля параллельны границе раздела воздух – полупроводник.В результате воздушная часть конденсатора параллельна полупроводниковой части двухслойного конденсатора. Если размер воздушного зазора намного меньше толщины полупроводникового образца, то общая емкость примерно равна емкости полупроводника. Его эквивалентная схема — это просто параллельное соединение R sem и C sem. На определенной частоте реактивное сопротивление этого конденсатора равно его сопротивлению. Эта частота называется частотой среза f c.Зная диэлектрическую проницаемость полупроводника и частоту отсечки, удельное сопротивление образца можно найти как ρ = 1 / (ω c ε r), где ω c = 2 π f c обозначает угловую частоту отсечки. Такой метод используется в одном из коммерческих инструментов, предназначенных для бесконтактного картирования удельного сопротивления полупроводников HR. Альтернативный метод определения удельного сопротивления основан на измерениях заряда во временной области (TDCM) емкостной ячейки, как показано на рисунке 3 (a). Временной отклик эквивалентной схемы, показанной на рисунке 3 (b), можно легко проанализировать, решив систему двух обыкновенных дифференциальных уравнений.Система имеет аналитические решения, но численные решения могут быть легко получены с помощью решателя жестких дифференциальных уравнений, например в среде MATLAB. Предположим, что в момент времени t = 0 импульсное ступенчатое напряжение величиной 10 В было приложено к схеме, показанной на рисунке 3 (b). Результаты расчета зависящих от времени напряжений на конденсаторе C sem (U S) и на конденсаторе C a (U) показаны на рисунке 5 (a) (для ясности используется логарифмическая шкала времени). Предполагалось, что все параметры измерительной ячейки и образца такие же, как те, которые указаны в описании рисунка 4.При подаче ступенчатого напряжения конденсаторы C sem и C a заряжаются почти мгновенно (постоянная времени зарядки зависит от номинала резистора R c), а распределение напряжения между емкостями C sem и C a зависит от их значений реактивного сопротивления. Через некоторое время конденсатор C sem разряжается через сопротивление R sem с постоянной времени τ = R sem (C a + C sem). Из измерений постоянной времени τ (предполагая, что емкости C sem и C a известны), мы можем определить R sem, а затем удельное сопротивление (проводимость) испытуемого образца.Диапазон измерения удельного сопротивления для имеющихся в продаже емкостных систем измерения во временной области составляет от 10 5 до 10 12 см. Минимальная измеряемая площадь на образцах с помощью этого метода очень мала (в диапазоне 1–5 мм 2), что очень полезно для инструментов для картирования удельного сопротивления. Подвижность и концентрация носителей заряда в методе TDCM определяются из измерений проводимости σ 0 без какого-либо магнитного поля с использованием емкостной ячейки, показанной на рисунке 3 (a), а затем путем измерения проводимости σ xx в присутствии статическое магнитное поле, параллельное пластине [15].Если значение магнитного поля B z известно, то мы можем легко найти подвижность носителей заряда μ n (или μ p) из уравнения (18). Однако следует отметить, что для получения измеримой разницы между значениями проводимости в отсутствие и в присутствии магнитного поля (например, 1%) произведение μ B z должно быть порядка 0,1. Это ограничивает минимальную измеряемую подвижность примерно до 600 см 2 В — 1 с — 1, если в системе измерения используется электромагнит, обеспечивающий магнитную индукцию 1,6 Тл.Также было замечено, что определение подвижности из измерений магнитной проводимости методом TDCM может привести к результатам, отличным от результатов, полученных из измерений постоянного тока, основанных на эффекте Холла [15]. Одна из причин такого различия заключается в том, что модель Друде дает только приближенные выражения для тензора проводимости, особенно для полярных полупроводников, таких как InSb. Более продвинутые модели проводимости были изучены в литературе [16], и было доказано, что рассчитанные значения проводимости, полученные с помощью продвинутых моделей, заметно отличаются от тех, которые получены с применением теории Друде.Тем не менее, преимуществ метода TDCM и точности простой модели Друде достаточно для практического применения метода магнитопроводимости для определения подвижности пластин GaAs и GaN с высоким удельным сопротивлением и высокой подвижностью, производимых промышленностью. Метод измерения вихревых токов долгое время использовался для неразрушающего контроля металлов (см., Например, [17]), а позже, в 1976 году, Миллер и др. Из Bell. Лаборатории [18].В настоящее время этот метод рекомендуется в качестве стандартного метода для бесконтактного измерения удельного сопротивления полупроводников, и он реализован в имеющихся в продаже приборах для картирования удельного сопротивления. Вихретоковый зонд состоит из РЧ-катушки, намотанной вокруг ферритового сердечника, который физически разделен, чтобы обеспечить зазор для введения образца, как показано на рисунке 6. Цепь колеблющегося резервуара (РЧ-катушка и конденсатор, включенные параллельно) индуцируют вихревые токи в образце, которые рассеивают электромагнитную энергию, подаваемую генератором ВЧ тока.Мощность, потребляемая в этом процессе, при условии отсутствия утечки магнитного потока и незначительных явлений скин-эффекта, пропорциональна проводимости листа (обратной сопротивлению листа) образца. В электронной системе, показанной на рисунке 6, ВЧ-напряжение поддерживается постоянным, так что ток, подаваемый из ВЧ-генератора, пропорционален проводимости листа образца. Чтобы получить абсолютное значение проводимости листа испытуемого образца, систему сначала калибруют с использованием прослеживаемых стандартных эталонных материалов.Вихретоковые датчики отлично подходят для измерения удельного сопротивления полупроводниковых пластин и сопротивления проводящих слоев на непроводящих подложках. Типичные диапазоны измерения, указанные производителями вихретоковых систем измерения, составляют от 0,1 до 100 кОм для сопротивления листа и от 10–3 см до 10 4 см для удельного сопротивления. Для имеющихся в продаже приборов для картирования вихретокового сопротивления минимальная измеряемая площадь на образцах составляет приблизительно 140 мм 2.Модификация вихретокового метода с использованием импульсного напряжения вместо временной гармоники RF …

Контекст 5

… μ ω — подвижность электронов на переменном токе, μ n — подвижность электронов на постоянном токе, а τ — время релаксации электронов. Для металлов и большинства полупроводников ωτ 1 вплоть до микроволновых частот, поэтому переменную и микроволновую подвижности можно считать такими же, как подвижность на постоянном токе. Концентрацию и подвижность носителей заряда труднее определить бесконтактными методами переменного и микроволнового излучения, чем методами постоянного тока, потому что в большинстве из них напряжение Холла невозможно напрямую измерить, поэтому коэффициент Холла обычно определяется на основе измерений проводимости. компоненты тензора.Наиболее часто используемые методы бесконтактного измерения удельного сопротивления высокоомных (HR) полупроводников — это емкостные методы, основанные на выборке в частотной области. В нашем эксперименте наилучшее соответствие данным измерений было получено для значения удельного сопротивления ρ = 1,43 · 10 8 см. Типичный диапазон измерения удельного сопротивления с использованием метода измерения импеданса в частотной области составляет от 10 4 до 10 9 см, а погрешности измерения не превышают нескольких процентов. Коаксиальный конденсаторный зонд без нижнего электрода, показанный на рисунке 3 (c), также можно использовать для бесконтактных измерений удельного сопротивления полупроводниковых пластин.При малых воздушных зазорах между образцом и электродами силовые линии электрического поля параллельны границе раздела воздух – полупроводник. В результате воздушная часть конденсатора параллельна полупроводниковой части двухслойного конденсатора. Если размер воздушного зазора намного меньше толщины полупроводникового образца, то общая емкость примерно равна емкости полупроводника. Его эквивалентная схема — это просто параллельное соединение R sem и C sem.На определенной частоте реактивное сопротивление этого конденсатора равно его сопротивлению. Эта частота называется частотой среза f c. Зная диэлектрическую проницаемость полупроводника и частоту отсечки, удельное сопротивление образца можно найти как ρ = 1 / (ω c ε r), где ω c = 2 π f c обозначает угловую частоту отсечки. Такой метод используется в одном из коммерческих инструментов, предназначенных для бесконтактного картирования удельного сопротивления полупроводников HR. Альтернативный метод определения удельного сопротивления основан на измерениях заряда во временной области (TDCM) емкостной ячейки, как показано на рисунке 3 (a).Временной отклик эквивалентной схемы, показанной на рисунке 3 (b), можно легко проанализировать, решив систему двух обыкновенных дифференциальных уравнений. Система имеет аналитические решения, но численные решения могут быть легко получены с помощью решателя жестких дифференциальных уравнений, например в среде MATLAB. Предположим, что в момент времени t = 0 импульсное ступенчатое напряжение величиной 10 В было приложено к схеме, показанной на рисунке 3 (b). Результаты расчета зависящих от времени напряжений на конденсаторе C sem (U S) и на конденсаторе C a (U) показаны на рисунке 5 (a) (для ясности используется логарифмическая шкала времени).Предполагалось, что все параметры измерительной ячейки и образца такие же, как те, что указаны в описании рисунка 4. При приложении ступенчатого напряжения конденсаторы C sem и C a заряжаются почти мгновенно (постоянная времени зарядки зависит от значение резистора R c) и распределение напряжения между емкостями C sem и C a зависит от их значений реактивного сопротивления. Через некоторое время конденсатор C sem разряжается через сопротивление R sem с постоянной времени τ = R sem (C a + C sem).Из измерений постоянной времени τ (предполагая, что емкости C sem и C a известны), мы можем определить R sem, а затем удельное сопротивление (проводимость) испытуемого образца. Диапазон измерения удельного сопротивления для имеющихся в продаже емкостных систем измерения во временной области составляет от 10 5 до 10 12 см. Минимальная измеряемая площадь на образцах с помощью этого метода очень мала (в диапазоне 1–5 мм 2), что очень полезно для инструментов для картирования удельного сопротивления. Подвижность и концентрация носителей заряда в методе TDCM определяются из измерений проводимости σ 0 без какого-либо магнитного поля с использованием емкостной ячейки, показанной на рисунке 3 (a), а затем путем измерения проводимости σ xx в присутствии статическое магнитное поле, параллельное пластине [15].Если значение магнитного поля B z известно, то мы можем легко найти подвижность носителей заряда μ n (или μ p) из уравнения (18). Однако следует отметить, что для получения измеримой разницы между значениями проводимости в отсутствие и в присутствии магнитного поля (например, 1%) произведение μ B z должно быть порядка 0,1. Это ограничивает минимальную измеряемую подвижность примерно до 600 см 2 В — 1 с — 1, если в системе измерения используется электромагнит, обеспечивающий магнитную индукцию 1,6 Тл.Также было замечено, что определение подвижности из измерений магнитной проводимости методом TDCM может привести к результатам, отличным от результатов, полученных из измерений постоянного тока, основанных на эффекте Холла [15]. Одна из причин такого различия заключается в том, что модель Друде дает только приближенные выражения для тензора проводимости, особенно для полярных полупроводников, таких как InSb. Более продвинутые модели проводимости были изучены в литературе [16], и было доказано, что рассчитанные значения проводимости, полученные с помощью продвинутых моделей, заметно отличаются от тех, которые получены с применением теории Друде.Тем не менее, преимуществ метода TDCM и точности простой модели Друде достаточно для практического применения метода магнитопроводимости для определения подвижности пластин GaAs и GaN с высоким удельным сопротивлением и высокой подвижностью, производимых промышленностью. Метод измерения вихревых токов долгое время использовался для неразрушающего контроля металлов (см., Например, [17]), а позже, в 1976 году, Миллер и др. Из Bell. Лаборатории [18].В настоящее время этот метод рекомендуется в качестве стандартного метода для бесконтактного измерения удельного сопротивления полупроводников, и он реализован в имеющихся в продаже приборах для картирования удельного сопротивления. Вихретоковый зонд состоит из РЧ-катушки, намотанной вокруг ферритового сердечника, который физически разделен, чтобы обеспечить зазор для введения образца, как показано на рисунке 6. Цепь колеблющегося резервуара (РЧ-катушка и конденсатор, включенные параллельно) индуцируют вихревые токи в образце, которые рассеивают электромагнитную энергию, подаваемую генератором ВЧ тока.Мощность, потребляемая в этом процессе, при условии отсутствия утечки магнитного потока и незначительных явлений скин-эффекта, пропорциональна проводимости листа (обратной сопротивлению листа) образца. В электронной системе, показанной на рисунке 6, ВЧ-напряжение поддерживается постоянным, так что ток, подаваемый из ВЧ-генератора, пропорционален проводимости листа образца. Чтобы получить абсолютное значение проводимости листа испытуемого образца, систему сначала калибруют с использованием прослеживаемых стандартных эталонных материалов.Вихретоковые датчики отлично подходят для измерения удельного сопротивления полупроводниковых пластин и сопротивления проводящих слоев на непроводящих подложках. Типичные диапазоны измерения, указанные производителями вихретоковых систем измерения, составляют от 0,1 до 100 кОм для сопротивления листа и от 10–3 см до 10 4 см для удельного сопротивления. Для имеющихся в продаже приборов для картирования вихретокового сопротивления минимальная измеряемая площадь на образцах составляет приблизительно 140 мм 2.Также была реализована модификация метода вихревых токов с использованием импульсного напряжения вместо источника ВЧ-тока с гармонической временной гармоникой [19]. Первые микроволновые методы были использованы для измерения проводимости полупроводников более 50 лет назад [20, 21]. В то время большинство исследователей использовали для этой цели резонансные резонаторы [20, 21], хотя другие использовали методы пропускания / отражения [22, 23]. У микроволновых методов есть два преимущества: устранение необходимости физического контакта с образцами и возможность работать при низких уровнях сигнала, чтобы избежать эффектов нагрева электронов.Быстро стало понятно, что только некоторые микроволновые методы позволяют проводить действительно бесконтактные измерения [22]. Это в том случае, когда электрические токи не протекают через границы полупроводник – металл. Это происходит, когда испытуемый образец отделен от металлических частей резонансной полости или линии передачи, или если микроволновые токи, протекающие в образце, не имеют компонентов, перпендикулярных поверхности образца. Конкретными модами, которые позволяют проводить бесконтактные измерения на дисковых образцах, являются моды TE 0m в цилиндрических волноводах [23] и моды TE 0mn в цилиндрических резонаторах [24].Последний метод очень полезен для измерения температуры массивных полупроводниковых образцов со средним и высоким удельным сопротивлением [25]. Типичными резонаторами, используемыми для измерения образцов в форме диска или стержня, где используются моды TE 0mn, являются …

Контекст 6

… появляется тензор проводимости). Определение эффекта Холла основано на измерении отношения мощности микроволн (P / P) в зависимости от смещения статического магнитного поля, где P — мощность микроволн, падающая на резонатор, используемый для возбуждения одной из вырожденных мод, т.е.грамм. режим TE 011, а P 2 — это микроволновая мощность, измеренная во втором режиме, например режим TE 101. Измерения подвижности в двухмодовых резонаторах высокочувствительны, и с их помощью можно определить низкие подвижности вплоть до 0,1 см 2 В — 1 с — 1 [33]; однако эти полости можно использовать только в лабораторных экспериментах на специально подготовленных образцах. Эти измерения занимают много времени и требуют точного позиционирования образца и начальной настройки резонатора. Сравнивая определение подвижности по измерениям магнитопроводимости с измерением эффекта Фарадея (который пропорционален отношению σ xy / σ xy), мы можем сделать вывод, что второй подход позволяет определять гораздо меньшие значения подвижности для данного магнитного поля. напряженность поля.Это связано с тем, что σ xy / σ xx = μ n B z (это можно вывести из уравнений (18) и (19)), в то время как магнитопроводимость обратно пропорциональна 1 + (μ n B z) 2. По этой причине в коммерчески доступных микроволновых системах измерения подвижности используются круглые волноводы, переносящие ТЕ-моду. Как упоминалось ранее, сверхпроводники можно охарактеризовать на микроволновых частотах по большой мнимой части их проводимости или большой отрицательной диэлектрической проницаемости, поэтому электромагнитные поля очень быстро затухают в направлении, перпендикулярном поверхности образца сверхпроводника.В результате только тонкий слой образца с толщиной порядка лондонской глубины проникновения эффективно взаимодействует с электромагнитным полем в измерительной ячейке. Также мнимая часть проводимости не вносит никаких потерь. СВЧ сверхпроводящие резонаторы из ниобия могут иметь добротность порядка сотен миллионов. По этой причине в большинстве методов, предназначенных для определения свойств материалов сверхпроводников на микроволновых частотах, используются резонаторы с очень высокой добротностью, поскольку они могут обеспечить достаточно высокую чувствительность измерения.Поскольку потери в проводнике в сверхпроводниках очень малы, идеальный резонатор для этой цели должен иметь паразитные потери, которые меньше или сопоставимы с потерями в образце. Одним из наиболее удобных резонаторов, предназначенных для измерения поверхностного волнового сопротивления (реальной части волнового сопротивления) высокотемпературного сверхпроводника (ВТСП) в сверхпроводящем состоянии, является стержневой сапфировый диэлектрический резонатор с двумя концевыми пластинами из сверхпроводящих образцов. Сапфировые диэлектрические резонаторы были независимо представлены несколькими исследовательскими группами [37–39], и в настоящее время они обычно используются для определения характеристик ВТСП во многих исследовательских и промышленных лабораториях.Метод стержневого сапфирового резонатора прост и имеет почти незначительные паразитные потери из-за чрезвычайно низких диэлектрических потерь сапфира. При температуре 4 К и частоте 10 ГГц сапфир показывает тангенс угла диэлектрических потерь <10 - 9. Другими полезными ячейками для микроволнового анализа сверхпроводящих материалов являются полости из ниобия, которые хранятся в ваннах с жидким гелием. В качестве держателя образца используется сапфировый горячий палец, позволяющий измерять переменную температуру и расположенный в центре такой полости [40, 41].В принципе, методы микроволнового резонатора позволяют измерять температуру обоих компонентов комплексной проводимости. Однако в большинстве случаев возможны только относительные измерения. Абсолютные измерения требуют знания лондонской глубины проникновения (или мнимой части проводимости) при температуре 0 К. Абсолютное значение лондонской глубины проникновения можно определить только с разумной точностью из данных измерений в микроволновом резонаторе для очень тонкие сверхпроводящие пленки толщиной порядка 10–50 нм.Большую часть информации по этой теме можно найти в [42]. В настоящее время доступно несколько методов, позволяющих бесконтактно измерять проводимость и сопротивление слоев различных материалов, включая полупроводники, металлы и сверхпроводники. Для плоских образцов бесконтактные измерения можно проводить до толщины одного атомного слоя (например, в графене). Диапазоны измерения удельного сопротивления для различных методов измерения суммированы на рисунке 13. Можно видеть, что образцы с самым высоким удельным сопротивлением могут быть измерены только с помощью емкостных методов.Среди методов, которые обсуждались до сих пор, емкостные методы обеспечивают самое высокое пространственное разрешение при картировании удельного сопротивления. Одним из основных недостатков емкостных методов является сложность измерения сопротивления листа тонких пленок, нанесенных на изолирующие или полуизолирующие подложки, особенно для типичных ячеек (рис. 3 (а)), где электрическое поле перпендикулярно образцу. Микроволновые методы позволяют проводить измерения в самом широком диапазоне удельного сопротивления от 10 - 9 до 10 5 см. Они также позволяют проводить измерения тонких пленок, имеющих большие значения сопротивления листа до 10 М / квадрат.Вихретоковый метод можно использовать в промежуточных диапазонах для измерения как сопротивления листа, так и проводимости. Большинство обсуждаемых методов позволяют картировать удельное сопротивление, хотя и с различным пространственным разрешением. Бесконтактные измерения подвижности и концентрации носителей заряда, которые до сих пор находили коммерческое применение, основаны на микроволновых измерениях фарадеевского вращения или эффектов магнитосопротивления. Как уже упоминалось в разделе 6 настоящего обзора, на рынке доступны системы бесконтактного картирования подвижности, основанные на измерениях фарадеевского вращения или эффекта магнитопроводимости.Главное преимущество бесконтактных методов в том, что они неразрушающие. Они также позволяют быстро контролировать качество любых материалов, в том числе тех, для которых метод четырехточечного зонда не работает, таких как GaN, SiC или графен. Дальнейшая работа над бесконтактными методами измерения проводимости и сопротивления листов материалов, вероятно, будет осуществляться в двух направлениях. Первое направление будет направлено на совершенствование существующих методов в части их точности, пространственного разрешения и автоматизации измерений.Второй будет сосредоточен на локальных наноразмерных измерениях в горизонтальных измерениях. За последние два десятилетия была развита техника микроволнового микроскопа [43, 44]. Они уже нашли применение в качестве инструмента количественного измерения сопротивления и проводимости тонких пленок [45, 46], а также для измерения сигналов локального эффекта Холла [47]. Пока точность измерения сопротивления листа для методов микроволнового микроскопа не так высока, как для других бесконтактных методов, но в будущем она, безусловно, будет улучшена.Следует также отметить, что пластовое сопротивление тонких хорошо проводящих материалов можно измерить в терагерцовом диапазоне частот [48]. Эксперименты на таких высоких частотах (инфракрасном) потенциально предлагают очень малый масштаб измерений. Скорее всего, измерения проводимости и сопротивления листа на проводящих / полупроводниковых поверхностях большой площади, таких как полупроводниковые пластины или тонкие проводящие пленки, будут выполняться чаще, чем в настоящее время с помощью бесконтактных методов. Это особенно верно для полупроводников с большой запрещенной зоной энергии, таких как GaN или SiC.С другой стороны, методы, в которых используется метод микроскопического четырехточечного зонда, будут широко использоваться для измерений всех материалов, обеспечивающих хорошие линейные электрические контакты с зондами. Несомненно, что метод M4PP будет чаще использоваться для микромасштабных измерений на различных этапах технологических процессов в кремниевой технологии из-за его исключительного пространственного разрешения. Этот обзор посвящен моей недавно скончавшейся жене Барбаре, которая вдохновила меня на эту работу.Работа частично поддержана проектами N R02 004210 и ...

Количественное определение проводящих волокон с помощью емкостной связи

Данная работа представляет собой исследование бесконтактного детектора проводимости с емкостной связью (C4D) для волоконных световодов микронных размеров. Следуя предыдущему отчету о качественном применении C4D для волокон, настоящее исследование обеспечивает тщательный анализ реакции сигнала на проводимость волокна. Используя волокна из восстановленного оксида графена (RGO), были исследованы характеристики детектора в зависимости от длины волокна, площади поперечного сечения и сопротивления.Для изучения влияния изоляционных покрытий были исследованы также волокна RGO с париленовым покрытием. Кроме того, измерения проводились в различных средах связи, таких как капиллярная трубка или воздух. Анализ данных измерений позволил определить C4D-проводимость различных волокон RGO и определить корреляцию с контактными методами посредством эмпирических соотношений. Было обнаружено, что предел обнаружения и чувствительность измерения сопротивления в основном зависят от конструкции датчика, а также от свойств волокна.Порог обнаружения можно определить как отношение импеданса связи к сопротивлению волокна. В нашем случае предел обнаружения был найден для отношений импедансов, равных 14. Этот предел устанавливает режим работы в C4D для волокон, которые могут использоваться в качестве детектора площади или сопротивления для отношения импедансов выше или ниже порога обнаружения. Полулогарифмический линейный отклик сопротивления волокна на выходное напряжение был обнаружен для соотношений импедансов от 2,66 до 0,63. Эти соотношения импедансов могут служить эталоном для проектирования C4D, в зависимости от испытуемых волокон и необходимой аналитической информации.Таким образом, мы предполагаем, что C4D может стать новым инструментом для определения характеристик волокон микронного размера благодаря его применимости к любому проводящему материалу, простоте использования и бесконтактному характеру измерения.

У вас есть доступ к этой статье

Подождите, пока мы загрузим ваш контент… Что-то пошло не так. Попробуйте снова?

Измерение ESR и индуктивности конденсатора

Измерение ESR и индуктивности конденсатора Высокочастотные измерения Страница в Интернете
Дуглас К.Смит

Адрес: P.O. Box 1457, Los Gatos, CA 95031
ТЕЛ: 800-323-3956 / 408-356-4186
ФАКС: 408-358-3799
Мобильный: 408-858-4528
URL: www.dsmith.org
Электронная почта: [email protected]

---

Измерительный конденсатор Самоиндуктивность и ESR

Рис. 1. Контрольная схема для измерения самоиндукции конденсатора и ESR

Техническая информация

Паразитные параметры конденсатора, то есть его эквивалента серии сопротивление (ESR) и его индуктивность влияют на работу конденсатора в цепях.Некоторые приложения очень чувствительны к этим параметрам. Например, байпасный конденсатор, используемый между питанием и землей в цифровой цепи, должен иметь возможность быстро подавать ток на близлежащие активные устройства. Если это тоже большой индуктивности он не сможет этого сделать. Точно так же переходный реакция конденсатора, используемого для отвода импульса тока из-за электростатического Разряд очень важен для способности конденсатора выполнять свою работу.

Итак, как можно измерить паразитные параметры конденсатора? Один конечно, можно было бы подключить конденсатор к анализатору цепей и получить очень хорошая характеристика.Однако такой инструмент может быть довольно дорогим. Даже менее дорогие приборы для измерения емкости могут быть недоступны. при необходимости. Оба инструмента не могут предоставить информацию в удобной форме. полезная форма. Если у вас есть генератор импульсов (желательно с выходом 50 Ом импеданс) и осциллографом, вы можете легко измерить переходную характеристику конденсатора. Исходя из этих данных, ESR и индуктивность конденсатора можно определить.

Сначала постройте простую сеть, показанную на Рисунке 1 в конце коаксиальный кабель 50 Ом, питаемый от генератора импульсов 50 Ом.Резистор 50 Ом используется на рисунке 1 для отключения коаксиального кабеля во время нарастающего фронта и обеспечения полное сопротивление источника 100 Ом. Показанный резистор — 51 Ом. Резистор из углеродного состава на 1/2 Вт с одним обрезанным выводом, резистор просто устанавливается с обрезанным проводом, полностью вставленным в разъем BNC. Возможно, потребуется немного припаять вывод резистора. так, чтобы он оставался надежно в разъеме BNC. Конденсатор, подлежащий испытанию подключается между концом резистора и корпусом разъема BNC.Осциллограф подключается непосредственно к конденсатору с помощью проводов. как можно короче, чтобы подключить зонд. Пробники с резистивным входом Рекомендуется импеданс от 500 до 1000 Ом. Стандартные пробники 10X «Hi-Z» часто имеют эффекты нарастающего фронта, которые искажают часть формы волны используется для расчетов.

Для длительности импульса, большой по отношению к постоянной времени RC, можно увидеть экспоненциальный рост напряжения холостого хода импульса источник. Для целей этого обсуждения мы рассмотрим первые пару сотен милливольт экспоненциального нарастания на 5 вольт.Пример это показано на рисунке 2.

Рисунок 2. Начальный подъем

На рисунке 2 показано начало экспоненциального роста напряжения на конденсатор при запуске генератора импульсов. Вертикальный масштаб около 200 мВ, а горизонтальное время составляет небольшую часть постоянной времени RC. 100 Ом и измеряемый конденсатор. Поскольку напряжение на конденсаторе все еще очень мало по сравнению с выходом холостого хода генератора 5 В, ток через конденсатор можно считать постоянным и равным к напряжению холостого хода генератора, деленному на 100 Ом, 50 мА в этом кейс.

Время нарастания тока будет таким же, как и напряжение генератора. Если подъем представляет собой наклон с постоянным наклоном и конденсатор не имеет индуктивности, начальный подъем, показанный на рисунке 2, будет следовать пунктирной линии, а затем наклон изменится на начальный наклон экспоненциального роста, определенного к:

1) dv / dt = i / C = 50 мА / C
где C — значение конденсатора при этом низком напряжении.
и время нарастания текущего << RC.

Смещение между базовой линией и началом экспоненты подъем — это просто напряжение, которое развивает ток, в данном случае 50 мА. через ESR конденсатора. ESR можно легко оценить в этом в случае деления смещения напряжения (обозначенного ESR на рисунке 2) на 50 мА.

Паразитная индуктивность в конденсаторе вызовет всплеск формы волны показано на рисунке 2, превышающее значение пунктирной линии по ее длине. Если бы подъем тока на самом деле был пандусом с постоянным уклоном и очень крутым углы (high di ² / dt), то пик будет прямоугольным импульсом ценности:

2) E = L * di / dt
где L — паразитная индуктивность конденсатора.

Повышение тока от генератора, используемого для данных в этой статье. не был пандус с очень острыми углами и постоянным уклоном (случай для большинство генераторов, которые я использовал). Эта характеристика генератора в сочетании с зондовыми эффектами привело к образованию пика спайка Ldi / dt, так как показано на рисунке 2. Используя уравнение 2, индуктивность конденсатора может рассчитываться. Часто нет необходимости рассчитывать индуктивность или ESR, но просто выберите конденсатор из нескольких доступных, который имеет самая низкая индуктивность и / или ESR.

Припаивание компонентов к разъему BNC, как показано на рисунке 1, работает. до 300 МГц. Я оцениваю индуктивное сопротивление петли, образованной конденсатор и резистор должны быть около 20 Ом на частоте 300 МГц (оценка индуктивность при 10 нГн). Это достаточно мало по сравнению с 100 Ом. сопротивление в цепи, чтобы существенно не влиять на начальный ток очень. Для этого диапазона частот генератор с временем нарастания 1 до двух наносекунд хватит.

Если вам нужно проверить конденсатор, используя более быстрое время нарастания, он Лучше всего построить испытательную установку на небольшой печатной плате с заземлением. плоские и контролируемые импедансы.В этот момент паразитная емкость резистора 50 Ом также будет проблемой, которую следует принять во внимание. К счастью, такая точность часто не нужна. Особенно, если просто сравнение относительной производительности нескольких конденсаторов.

Данные

На рисунке 3 ниже показан начальный подъем от генератора. Черный квадрат указывает вертикальную шкалу напряжения и горизонтальную шкалу времени. Открыто напряжение в цепи было немногим более 4 В с временем нарастания около 5 наносекунд.Данные на рисунках с 3 по 6 были получены с помощью аналогового осциллографа несколько лет назад. назад. На рисунках с 4 по 6 показаны данные, полученные от нескольких выводных конденсаторов. (в отличие от поверхностного монтажа). Для каждого конденсатора было снято по две трассы. Нижняя кривая была измерена на корпусе конденсатора, где выводы входят в а верхний след включал минимальное количество свинца, чтобы практически подключить конденсатор к печатной монтажной плате. Верхний след не требуется для современных конденсаторов для поверхностного монтажа, если только кто-то не хочет смоделировать индуктивность подключения конденсатора к интересующей точке на печатной монтажной плате.

Рисунок 3. Вход от генератора импульсов

На рис. 4 показаны данные для электролитического конденсатора емкостью 4 мкФ. Смещение ESR составляет около 50 мВ, что дает оценку ESR чуть более одного Ом. Уведомление что, по-видимому, есть некоторые колебания на участке 1 / C наклона. Это может быть резонанс зонда осциллографа или резонанс в конденсаторе. В данные были получены с помощью стандартного зонда 10X Hi-Z, поэтому зонд является подозрительным. Я видел конденсаторы с ярко выраженными колебаниями от внутреннего резонанса.Если вы планируете поставить большой конденсатор параллельно меньшему один, особенно если они построены по разным технологиям, это было бы неплохо проверить импульсную характеристику комбинации используя этот метод. Возможно, что меньший конденсатор резонирует с индуктивностью большего, вызывая неожиданный результат.

Рис. 4. Конденсатор 4 мкФ

На рисунке 5 показан результат для конденсатора 1 мкФ той же конструкции. как конденсатор емкостью 4 мкФ, испытанный на Рисунке 4.Обратите внимание, что индуктивность аналогична к конденсатору 4 мкФ, но ESR немного ниже. Поскольку аналоговый прицел использовался, форма волны повторялась, а небольшой наклон слева половина формы волны была концом экспоненциального спада с 5 вольт. Если на цифровом осциллографе использовался одиночный импульс, наклон слева от пик Ldi / dt будет равен нулю.

Рисунок 5. Конденсатор 1 мкФ

На рисунке 6 показан результат для радиального керамического конденсатора емкостью 1 мкФ (квадратный кейс).Обратите внимание на низкую индуктивность и неопределяемое ESR. Отметим также, что наклон экспоненциального нарастания 1 / C более пологий, что указывает на большую емкость чем конденсатор 1 мкФ на Рисунке 5. Это может быть связано с тем, что электролитический конденсатор, используемый на Рисунке 5, может иметь меньшую емкость вблизи нулевое напряжение, чем при его рабочем напряжении, тогда как керамический конденсатор имеет более постоянную емкость с напряжением. Индуктивность, соответствующая к нижнему следу оценивается в 4,4 нГн.

Рисунок 6. Керамический конденсатор 1 мкФ

Интересно отметить, что керамический конденсатор 0,1 мкФ в том же размер пакета, поскольку 1 мкФ на Рисунке 6 показал немного больше индуктивность в этой испытательной установке. Я считаю, что это произошло из-за того, что меньший конденсатор не заполнял корпус и внутреннюю индуктивность вывода вызвал эффект. В этом случае конденсатор емкостью 1 мкФ был лучшим выбором, чем 0,1 мкФ!

Одним из преимуществ этого теста является то, что выходной сигнал переходная характеристика конденсатора.Напряжения, возникающие в конденсатор в этом тесте напрямую связан с тем, что будет происходить в реальной цепи, если время нарастания тока от генератора такое же, как конденсатор увидим по назначению.

Начало страницы
Дом

---

Вопросы или предложения? Свяжитесь со мной по адресу [email protected]

Авторские права © 2000 Дуглас С. Смит .