2.9. Последовательный колебательный контур. Резонанс напряжений

Последовательным колебательным контуром называют такую цепь, в которой катушка и конденсатор соединены последовательно отно­сительно входных зажимов (рис. 2.14). В такой цепи можно наблюдать резонанс напряжений. При резонансе напряжений индуктивное и ем­костное сопротивления взаимно компенсируются и в результате этого реактивные сопротивление и мощность цепи равны нулю.

При резонансе напряжений, возни­кающем в цепи с последовательным соединением индуктивных и емкостных элементов, ток и напряжение цепи совпа­дают по фазе. В этом случае угол сдвига фаз между током и напряжением равен нулюи полное сопротивлениецепи равно ее активному сопротивле­нию. Если

то уголпри

Следовательно, при резонансе

илиоткуда угловая частота при резонансе

и резонансная частота

Таким образом, основным условием возникновения резонанса напря­жений в цепи является равенство реактивных сопротивлений так как в этом случае частота колебательного контураравна частоте сети ω, питающей данную цепь.

Итак, индуктивное и емкостное сопротивления при резонансе равны, т. е.

(2.59)

так как

Величину ρ называют характеристическим сопротивлением контура.

Отношение напряжения на индуктивности или на емкости к напря­жению, приложенному к цепи при резонансе, называют добротностью контура или коэффициентом резонанса:

(2.60)

откуда

Коэффициент резонанса показывает во сколько раз напряжение на индуктивных или емкостных элементах при резонансе больше, чем напряжение, приложенное к цепи. Добротностью контура называют также отношение характеристического сопротивления контурак его активному сопротивлениюr. Так как характеристическое сопротивле­ние обычно составляет в среднем сотни Ом, а сопротивление r — несколько Ом, то добротность колебательных контуров, состоя­щих из индуктивных катушек и конденсаторов, находится в пределах 200-500.

Величину, обратную добротности, называют затуханием контура:

(2.61)

Сопротивление r в радиотехнических контурах является, как правило, собственным сопротивлением катушек и конденсаторов. Его иногда называют сопротивлением потерь контура.

Понятие «затухание контура» связано с тем, что при отключении колебательного контура от источника питания, когда контур накоротко замкнут, колебательный процесс затухает тем быстрее, чем больше коэффициент d.

Рассмотрим схему рис. 2.14 без нагрузки (U_{C =} U_Cхх). Тогда

а ток при резонансе напряжений (2.62)

Ток при резонансе напряжений значительно больше тока цепи в отсутствие резонанса, так как при резонансе его значение ограни­чено только сопротивлением r. При резонансе напряжение на индуктив­ности и емкости при больших по сравнению с r значениях может быть во много раз больше напряжения сети:

Напряжение на активном сопротивлении при резонансе равно напряжению, приложенному к цепи:

На рис. 2.15 представлена векторная диаграмма напряжений цепи рис. 2.14 при резонансе напряжений. Так как при резонансето в этом случае и

Рассмотрим энергетические процессы, наблюдаемые в данной цепи при резонансе напряжений. Для этого определим сумму мгновенных значений энергий магнитного и электрического полей цепи, т. е.

Если принять при резонансе ток в контурето напряжение на емкости

Тогда суммарная энергия

(2.63)

Следовательно, при резонансе напряжений суммарная энергия магнитного и электрического полей остается постоянной, при этом непрерывно происходит перераспределение энергии магнитного и электрического полей, т. е. увеличение энергии магнитного поля сопро­вождается уменьшением энергии электрического поля и наоборот.

Таким образом, энергия, первоначально запасенная в контуре от источника (сети), колеблется при резонансе между индуктивностью и емкостью, причем без участия в этом процессе источника. Поэтому такой контур называют колебательным.

Итак, при резонансе на долю источника остается лишь покрытие расхода энергии в активном сопротивлении; следовательно, полная мощ­ность равна активной мощности

так как реактивная мощность при резонансе равна нулю:

где

Коэффициент мощности при резонансе

toe / LECT / rezonans

ЯВЛЕНИЯ РЕЗОНАНСА

РЕЗОНАНС НАПРЯЖЕНИЙ

Рассмотрим контур, состоящий из последовательно соединенных сопротивления, индуктивности и емкости (рис. 1)

Рис. 1. Последовательный контур.

Напомним принятые обозначения:

1. строчными буквами обозначаются мгновенные значения: u, i, u_L, u_C;

2. заглавными буквами обозначаются действующие значения:

U, I, U_L, U_C;

3. подчеркнутыми заглавными буквами — комплексные действующие значения: U, I, U_L, U_C.

Входное сопротивление контура:

.

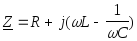Комплексное действующее значение тока контура имеет вид:

,

отсюда получается действующее значение тока

.

Аналогичным образом получаются выражения для действующих значений напряжений на индуктивности (U_L, U_L) и на емкости (U_C, U_C).

;

.

Условием наступления резонанса напряжений является равенство нулю реактивной составляющей входного сопротивления контура:

.

При резонансе реактивные сопротивления индуктивности и емкости равны:

,

эта величина называется характеристическим сопротивлением контура.

Отношение характеристического сопротивления контура к его омическому сопротивлению называется добротностью контура:

.

Заметим, что при =₀ отношение действующих значений напряжений на индуктивности и на емкости к действующему значению входного напряжения равно добротности:

.

Преобразуем выражение для действующего значения тока контура, вынеся активное сопротивление R за знак радикала а характеристическое сопротивление =₀L за скобки и учитывая определение Q:

.

Аналогичным образом получаем выражения для действующих значений напряжений на индуктивности и на емкости:

.

Введя относительную частоту _*=/₀, преобразуем полученные формулы к следующему виду:

Найдем точки максимумов этих трех кривых.

Очевидно, что при резонансной частоте полное входное сопротивление контура (z=Z) минимально и равно активному сопротивлению, тогда действующее значение тока максимально и равно:

Чтобы найти точки максимумов кривых U_L() и U_C() необходимо продифференцировать их по частоте, например:

приравняв к нулю числитель полученной дроби, уравнение для частоты максимума для действующего значения напряжения на индуктивности:

,

таким образом, частота максимума действующего значения напряжения на индуктивности равна:

.

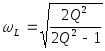Аналогично, частота максимума действующего значения напряжения на емкости равна:

.

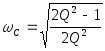Отметим, что: _L>₀, _C<₀, _L_C=₀². Если Q<1/2, то _L и _C — мнимые, т.е. кривые U_L() и U_C() не имеют максимумов.

Рассмотрим зависимость I() (рис. 2). Полосой пропускания называется частотный диапазон ₁₂, в котором выполняется условие:

.

Уравнение для границ полосы пропускания имеет вид:

.

Это — уравнение четвертого порядка, два корня которого являются границами полосы пропускания и имеют вид (два других корня — отрицательные и не имеют физического смысла):

.

Легко видеть, что: ₁₂=₀².

Рис. 2.

На рис. 2 представлены зависимости от нормированной частоты действующих значений (амплитуд): тока — сплошная линия, напряжения на емкости — штриховая линия, напряжения на индуктивности — пунктирная линия, а также разности фаз входного напряжения и тока (=_u-_i) — штрих-пунктирная линия при добротности Q=2.

На рис. 3 представлены зависимости от нормированной частоты отношений действующих значений (амплитуд) тока к действующему значению (амплитуде) тока на резонансной частоте для различных значений добротности: при Q=0.5 — сплошная линия, при Q=1 — пунктирная линия, при Q=10 — штриховая линия. Из рисунка видно, что чем больше добротность, тем лучше избирательные свойства цепи: т.е. цепь лучше выделяет сигнал определенной частоты из суммы сигналов различных частот.

Рис. 3.

РЕЗОНАНС ТОКОВ

Рассмотрим параллельный контур (рис. 4).

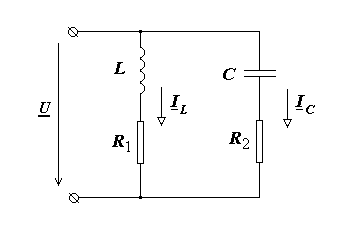
Рис. 4

Вычислим входную проводимость схемы:

Резонанс наступает, когда реактивная часть входной проводимости становится равной нулю:

Вводя обозначения:

,

получим:

.

Резонанс возможен, если одновременно R₁> и R₂> или R₁< и R₂<, если R₁<, а R₂> или наоборот, то резонансная частота — мнимая, т.е. резонанс не наступает, если же R₁=R₂=, то _Р=0/0, т.е. резонанс наступает при любой частоте. Рассмотрим входное сопротивление контура в этом случае:

Т.о. входное сопротивление контура равно  и от  не зависит.

На рис. 5, а, б показаны векторные диаграммы резонанса в идеальном (R₁=R₂=0) и реальном контурах. Если R₁=R₂=0, то активная входная проводимость равна нулю, резонансная частота _Р=₀, токи индуктивности и емкости равны и противоположны по фазе, входной ток равен нулю.

а) идеальный контур	б) реальный контур

Рис. 5.

ПОНЯТИЕ О РЕЗОНАНСЕ В СЛОЖНЫХ ЦЕПЯХ

Условие резонанса b=0 или x=0 в разветвленной цепи с несколькими индуктивностями и емкостями дают для частоты  уравнения, которые могут иметь несколько действительных корней, т.е. у разветвленной цепи может быть несколько резонансных частот.

Пример.

Найдем входное сопротивление цепи, изображенной на рис. 6.

Рис. 6.

Если Z=0, наступает резонанс напряжений:

Входная проводимость этой цепи равна:

При Y=0 наступает резонанс токов:

.

Задача (4.88, Поливанов).

Для схемы рис. 7 даны L,C. При каком R входное сопротивление чисто активное на любой частоте?

Рис. 7.

Входное сопротивление равно:

Найдем величину R из условия равенства нулю мнимой части:

Т.о. получаем, что если активное сопротивление равно характеристическому, резонанс наступает на любой частоте.

Задача.

Найти L₀, при котором фазы u и i совпадают. R=2 Ом, L=2 мГн, C=250 мкФ, =210³ с^-1.

Рис. 8.

Входное сопротивление равно:

.

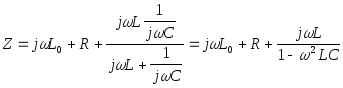Чтобы фазы входного напряжения u и входного тока i совпадали, необходимо, чтобы реактивная составляющая входного сопротивления была равна нулю:

.

Резонанс токов наступает, если реактивная составляющая входной проводимости равна нулю:

,

отсюда:

.

46)Обобщенная резонансная характеристика, полоса пропускания.

Из приведенных характеристик следует, что RLC — контур обладает избирательными свойствами. Самое большое значение тока имеет место в режиме резонанса ( = ₀). Для оценки избирательных свойств контура вводят понятие полосы пропускания контура. Она равна разности частот, которым соответствует отношение до и после резонанса, равное. Параметры цепи оказывают большое влияние на избирательность. Чем больше добротность контура, тем выше его избирательность. В этом можно убедиться при рассмотрении кривых на рис. 4.7

(– отношение тока текущей

частоты к току резонансной частоты; – отношение текущей частоты к резонансной. Чем больше добротность контура, тем лучше его избирательные свойства и тем меньше полоса пропускания.

47) Частотные характеристики и резонансные кривые параллельного резонансного контура.

В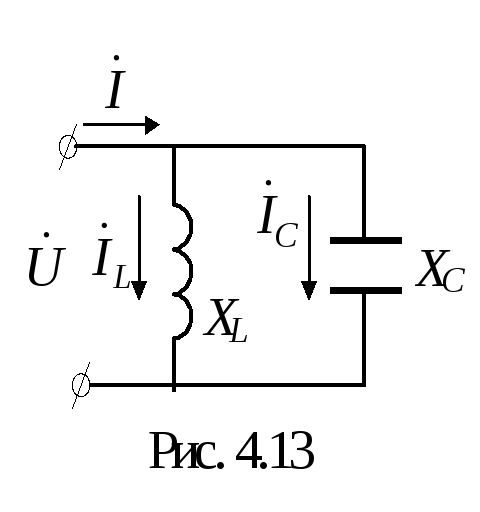качестве частотных характеристик в контуре на рис. 4.13 выступают зависимости, значения которых при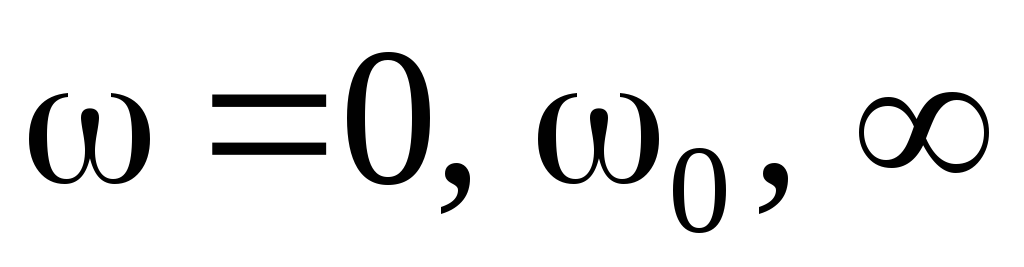приведены в табл. 4.3.

Характер изменения зависимостей приведен на рис. 4.14.

Таблица 4.3


0		0	
0			0
	0		

Учитывая, что , характер резонансных кривыхполностью совпадает с соответствующими частотными зависимостями. Притакой контур выполняет роль фильтра – пробки, проводимость его, а следовательно, и токобщей ветви, равны нулю, а сопротивление – бесконечности.

48)Резонанс напряжений в разветвленных электрических цепях. 49)Резонанс токов в разветвленных электрических ветвях

Всложных схемах, в которых имеет место одновременно и последовательное, и параллельное соединение ветвей с индуктивностью и емкостью, может наблюдаться резонанс напряжения и токов. Покажем это на примере схемы, приведенной на рис. 4.15. Входное сопротивление

В этой схеме резонанс напряжений возможен при условии , при этом резонансная частота

.Входная проводимость этой схемы

. (4.17)

При резонансе токов В = 0. При этом резонансная частота

.

Численные значения частот в режиме резонанса токов и напряжений различны для одной и той же схемы.

Таким образом, цепь с несколькими RLC — контурами, которые могут быть соединены произвольно, может давать несколько резонансов токов и напряжений. Анализ осуществляется путем расчета цепи. Рассматривается, которая представляет собой дробь. Известно, что условие резонанса напряженийX=0, т.е. . Следовательно, равенство нулю числителядает резонансную частоту для резонанса напряжений. Условие резонанса токовB = 0 или , т.е.. Следовательно, равенство нулю знаменателядает резонансную частоту для резонанса токов. Таким образом, задача сводится к определению нулей и полюсов.

2.5. Резонанс в сложных контурах

В двухполюсниках, содержащих более двух реактивных элементов (рис. 2.11), входной ток может принимать различные экстремальные значения при нескольких частотах. Это связано с возникновением резонанса на отдельных участках схемы при изменении частоты питающего напряжения или при изменении параметров реактивных элементов. При резонансе сопротивление всей цепи отлично от нуля или принимает конечное значение, если в цепи есть ветви с активным сопротивлением. Рассмотрим в качестве примера цепь с идеальными реактивными элементами (рис. 2.11.а.)

Рис. 2.11.

Полное сопротивление цепи равно:

.

При равенстве проводимостей параллельных ветвей

,

где ,

в цепи возникает резонанс токов. При этом входная Yпроводимость и ток на входе цепи равны нулю, а резонансная частота определяется как.

Другой резонанс имеет место, когда .

Последние условие выполняется при частоте .

В этом случае нулю равно полное сопротивление цепи, а входной ток стремится к бесконечности.

Резонансная характеристика входного тока для подобных схем имеет характерный вид и построена для конкретной схемы (рис.2.11.а) в программе rezon_ui.mcd приложения. В этих схемах при частоте, близкой к нулю, ток стремится к бесконечности, по мере роста частоты величина тока убывает, и резонанс токов в параллельных ветвях всегда наступает раньше, чем резонанс на входе схемы.

В той же программе приводится алгоритм построения резонансной кривой для трехэлементной схемы, рис. 2.11.б. При нулевой частоте ток схемы равен нулю по причине нулевой проводимости конденсатора. По мере роста частоты ток возрастает, входное сопротивление падает, и при некоторой частоте наступает резонанс напряжений (входное сопротивление схемы становится равным нулю). Резонанс токов в такой схеме наступает при более высокой частоте.

Сравнивая резонансные кривые рассмотренных контуров, можно заметить их определенное «зеркальное» подобие.

При изучении этого раздела рекомендуется более подробно рассмотреть резонансные явления в контурах с реальными элементами, например, дополнив схему на рис. 2.11.а активным сопротивлением, включенным последовательно индуктивности L₁. В этом случае условием резонанса будет равенство нулю реактивной составляющей входной проводимости. В схеме рис. 2.11.с при условии , что

,

можно получить интересный эффект сохранения резонанса при любой частоте, так как входная проводимость остается всегда активной.

2.6. Вопросы

Для более глубокого понимания математических и энергетических соотношений при резонансах в электрических цепях рекомендуется провести численные эксперименты на основе приведенных в приложении программных файлов и ответить на следующие вопросы.

1. При каких условиях частота резонанса тока совпадает с частотой резонанса напряжений?

2. Для схемы рис.2.11.с:

-запишите условие резонанса и аналитическое выражение резонансной частоты через параметры схемы ;

-проанализируйте последнее выражение для условия R₁ =R₂ ==и приусловииR₁ =R₂= 0 ;

-определите, возможен ли в схеме резонанс при условии и;

— выведите формулу для вычисления добротности схемы через ее резонансную частоту и параметры .

Резонанс напряжений в цепи переменного тока. Условия возникновения и практическое значение

Резонансом в электрических цепях называется режим участка электрической цепи, содержащей индуктивный (Х_L) и емкостной (Х_С) элементы, при котором угол сдвига фаз j между напряжением и током равен нулю (j=0).

Резонанс напряжений возникает на участке с последовательным соединением R,L,C. При этом индуктивное сопротивление равно емкостному, то есть .

Угол сдвига фаз j определяется по формуле:

.При j=0 или можно записать

Из последнего соотношения следует, что резонанс напряжения в цепи можно достигнуть следующими способами:

изменением индуктивности L катушки;

изменением электрической емкости С конденсатора;

изменением частоты тока f питающей сети.

Характерные особенности резонанса напряжений:

1. Полное сопротивление Z цепи при резонансе равно активному сопротивлению

.

2. Результирующий ток в цепи имеет максимальное значение

.

Зависимость тока I от частоты f имеет вид:

3. Напряжение на участке с активным сопротивлением R равно напряжению питания U и совпадает с ним по фазе .

4. Активная мощность при резонансе имеет максимальное значение

.

Можно предположить, что в цепи существует следующее соотношение между активным (R) и реактивными сопротивлениями ( и X_C)

,

тогда можно записать

.

То есть напряжения на участках с реактивными элементами (U_Lи U_C) будут больше напряжения питания U.

Свойство усиления напряжения на реактивных элементах при резонансе напряжения используется в технике.

Коэффициент усиления напряжения равен добротности Q контура

.

Однако повышенное напряжение на реактивных элементах может привести к пробою электрической изоляции проводов и представлять опасность для обслуживающего персонала.

Векторная диаграмма при резонансе напряжений строится с учетом особенностей режима резонанса

 

j=0, ,

Расчет цепи переменного тока с использованием комплексных чисел.

Алгебраическая форма записи комплексного числа:

,

Тригонометрическая:

,

Показательная:

,

модуль комплексного числа:

аргумент

Свойства цепей с параллельным соединением элементов. Резонанс токов. Условия возникновения. Векторные диаграммы

Рис. 2.13

Схему нарисую быстро. Скажи прсото резонанс токов.

 

Мощности в цепи переменного тока (активная, реактивная и полная). Треугольник мощностей. Коэффициент мощности и его экономическое значение.

В цепи переменного тока различают три вида мощности.

1. Активная мощность Р, обусловленная наличием в цепи активного сопротивления R. В активном сопротивлении происходит необратимое преобразование электрической энергии в другие виды, например, в резисторе происходит преобразование электрической энергии в тепловую энергию

.

Единица измерения активной мощности – ВАТТ.

2. Реактивная мощность Q, обусловленная наличием реактивных элементов (катушек и конденсаторов)

.

Единица измерения ВА_р – ВОЛЬТ-АМПЕР реактивный.

На реактивных сопротивлениях Х_L и Х_C имеет место процесс колебания энергии от катушки индуктивности к конденсатору и наоборот, необратимых преобразований нет.

Для индуктивного элемента Q_L> 0, для емкостного элемента Q_C< 0.

При последовательном соединении L и C суммарная реактивная мощность

.

3. Кроме активной и реактивной мощностей цепь синусоидального тока характеризируется полной мощностью S. Единица измерения ВА (ВОЛЬТ – АМПЕР).

.

Треугольник мощностей

cosj = .

Он показывает, какая часть электрической энергии, потребляемой из сети используется на выполнение полезной работы. При низком коэффициенте мощности машины переменного тока и трансформаторы, проектируемые на заданную полную мощность, оказываются недоиспользованными по активной мощности, что приводит к непроизводительным капитальным затратам. Улучшение коэффициента мощности приемников электрической энергии способствует уменьшению потерь энергии в электрических сетях, обмотках трансформаторов и электрических генераторов. Для повышения экономичности систем электроснабжения предприятий в настоящее время устанавливается допустимое значение реактивной мощности и нормируется значение .

Этот показатель определяется по показаниям счетчиков активной и реактивной энергии.

Трехфазные цепи. Соединение приемников электрической энергии звездой и треугольником. Мгновенные и действующие значения ЭДС. Соотношения между линейными и фазными значениями токов и напряжений. Векторная диаграмма.

Трехфазная система представляет собой совокупность трех электрических цепей, в которых действуют ЭДС с одинаковыми частотами и амплитудами и сдвинутые по фазе относительно друг друга на 120°

 

 

I_л — линейный ток — это ток протекающий по линейному проводу;
U_л — линейное напряжение — это напряжение между линейными проводами;
I_ф — фазный ток — это ток, протекающий от начала к концу фазной обмотки или приемника энергии (или наоборот: от конца — к началу).
U_ф — фазное напряжение — это напряжение между началом и концом фазной обмотки или приемника

 

соединение звездой

мгновенные значения ЭДС трехфазной системы:

В комплексной форме действующие значения ЭДС могут быть представлены в виде:

.

для звезды выполняются следующие соотношения:

линейный ток равен фазному : .

линейное напряжение больше фазного в  раз

.

Для треугольника