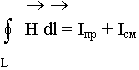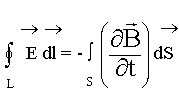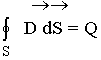Уравнения Максвелла | Все Формулы
![Rendered by QuickLaTeX.com \[ \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-9b26b31cc88858c6b01bc73f6d36171f_l3.png)
Система уравнений Максвелла является обобщением основных законов об электрических и электромагнитных явлениях. Она описывает абсолютно все электромагнитные явления. Являясь основой теории электромагнитного поля, эта система уравнений позволяет решать задачи, связанные с отысканием электрических и магнитных полей, создаваемых заданным распределением электрических зарядов и токов. Уравнения Максвелла были отправной точкой для создания общей теории относительности Эйнштейна. В теории Максвелла раскрывается электромагнитная природа света. Уравнения сформулированы Дж. Максвеллом в шестидесятых годах 19 века на основе обобщения эмпирических законов и развития идей ученых, исследовавших электромагнитные явления до него (Законы Кулона, Био – Савара, Ампера и, в особенности, исследования Фарадея). Сам Максвелл записал 20 уравнений с 20 неизвестными в дифференциальной форме, которые позднее были преобразованы. Современная форма Максвелла дана немецким физиком Г. Герцем и английским физиком О. Хевисайдом. Запишем уравнения используя систему единиц Гаусса.
В состав системы уравнений Максвелла входят четыре уравнения.
Первое уравнение:
![Rendered by QuickLaTeX.com \[ \[rot\overline{E}=-\frac{1}{c}\frac{\partial \overline{B}}{\partial t}\qquad (1.1)\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-9d63549643d28adf4424ab5d86fdef42_l3.png)
\]
Это Закон Фарадея (Закон электромагнитной индукции).
где
![Rendered by QuickLaTeX.com \[\overline{E}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-feee400f68db6bf5b9add5dac385c317_l3.png)
-напряженность электрического поля,
![Rendered by QuickLaTeX.com \[\overline{B}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-8000563a9026417a8f93a845b7a41990_l3.png)
-вектор магнитной индукции, c – скорость света в вакууме.
Это уравнение говорит, о том, что ротор напряженности электрического поля
![Rendered by QuickLaTeX.com \[\overline{E}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-feee400f68db6bf5b9add5dac385c317_l3.png)
равен потоку (т.е. скорости изменения во времени) вектора магнитной индукции
![Rendered by QuickLaTeX.com \[ \overline{B}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-1460acd8acfd006d69a08084bc3bc885_l3.png)
сквозь этот контур.Уравнение (1.1) представляет собой первое уравнение Максвелла в дифференциальной форме.
Это же уравнение можно записать в интегральной форме, тогда оно примет следующий вид:
![Rendered by QuickLaTeX.com \[ \[\oint_L{\overline{E}\cdot \overline{dl}=-\frac{1}{c}\frac{\partial \Phi_m}{\partial t}}\ (1.2.)\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-a21c928cf72bec3b2bc5d646871b78bb_l3.png)
или
![Rendered by QuickLaTeX.com \[ \[\oint_L{\overline{E}\cdot \overline{dl}=-\frac{1}{c}\int_S{\frac{\partial B_n}{\partial t}}}dS\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-e8f3e66ca0bde69c9818c8b83aa2fc29_l3.png)
где
![Rendered by QuickLaTeX.com \[ B_n\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-93833dc0fb3b69e2324b2fd69c8f2a43_l3.png)
– проекция на нормаль к площадке dS вектора магнитной индукции,
![Rendered by QuickLaTeX.com \[\Phi_m\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-d7308b4bd6348f9e417ddc9989510a0c_l3.png)
– магнитный поток.
Уравнения Максвелла в интегральной формерис. 2.
Циркуляция вектора напряженности электрического поля вдоль замкнутого контура L (ЭДС индукции) определяется скоростью изменения потока вектора магнитной индукции через поверхность, ограниченную данным контуром. Знак минус по правилу Ленца означает направление индукционного тока.
Согласно Максвеллу закон электромагнитной индукции (а это именно он), справедлив для любого замкнутого контура, произвольно выбранного в переменном магнитном поле.
Смысл этого уравнения: Переменное магнитное поле в любой точке пространства создает вихревое электрическое поле.
Второе уравнение Максвелла:
![Rendered by QuickLaTeX.com \[ \[rot\overline{H}=\frac{4\pi}{c}\overline{j}+\frac{1}{c}\frac{\partial \overline{D}}{\partial t}\qquad (2.1)\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-a4b732ebcf9c577dae0c8f70ee14f421_l3.png)
где
![Rendered by QuickLaTeX.com \[ \overline{H}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-785dac0f0eca31c703d823bdc44c20d1_l3.png)
-вектор магнитной напряженности,
![Rendered by QuickLaTeX.com \[ \overline{j}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-0d5407865818e9e6dd7f1f1ed0f04b54_l3.png)
— плотность электрического тока,
![Rendered by QuickLaTeX.com \[ \overline{D}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-a27bc6aede55a57e22ebae62d4e69258_l3.png)
— вектор электрического смещения.
Данное уравнение Максвелла является обобщением эмпирического закона Био-Савара о том, что магнитные поля возбуждаются электрическими токами. Смысл второго уравнения в том, что источником возникновения вихревого магнитного поля является также переменное электрическое поле, магнитное действие которого характеризуется током смещения. ( \frac{\partial \overline{D}}{\partial t}-плотность тока смещения).
В интегральном виде второе уравнение Максвелла (Теорема о циркуляции магнитного поля) представлено следующим образом:
![Rendered by QuickLaTeX.com \[ \[\oint_L{\overline{H}\cdot \overline{dl}} = \frac{4\pi}{c}\int_S{(j_n+\frac{1}{4\pi}\frac{\partial D_n}{\partial t})}ds\qquad (2.2)\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-1e99766fe4134648b2f4a317f4b36816_l3.png)
или
![Rendered by QuickLaTeX.com \[ \[\oint_L{\overline{H}\cdot \overline{dl}}=\sum^n_{k=1}{I_k+I_{shift}}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-b6e3705a57a0f2d3322ca109df8296e8_l3.png)
Циркуляция вектора напряжённости магнитного поля по произвольному контуру равна алгебраической сумме токов проводимости и тока смещения, сцепленных с контуром.
Когда Максвелл вводил уравнения (более ста лет тому назад!), природа электромагнитного поля была не понятна. В настоящее время природа поля выяснена, и стало ясно, что I_{shift} может быть названo «током» лишь формально. По pяду расчетных соображений такое название, не придавая ему прямого физического смысла, целесообразно сохранить, что в электротехнике и делается. По этой же причине вектор D, входящий в выражение для тока смещения, называют вектором электрического смещения.
Помимо первых двух уравнений в систему уравнений Максвелла входит теорема Гаусса-Остроградского для электрического и магнитного полей:
![Rendered by QuickLaTeX.com \[ \[div\overline{D}=4\pi \rho \qquad (3.1)\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-0583dfdf72c883c6a4344d07a7bba416_l3.png)
и
![Rendered by QuickLaTeX.com \[ \[div\overline{B}=0\qquad (4.1)\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-7951b58746ad17b823862e3fe6a72296_l3.png)
где
![Rendered by QuickLaTeX.com \[\rho —плотность электрического заряда. Что в интегральном виде представляет собой следующее: \[ \[\Phi_e=\oint_S{D_ndS}=4\pi q\qquad (3.2)\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-4eda9e7afd93f0d219105504ba5417a3_l3.png)
и
![Rendered by QuickLaTeX.com \[ \[\Phi_m=\oint_S{B_ndS}=0\qquad (4.2)\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-d397cf33409d0d86dcfe38ec0ff5ff8c_l3.png)
где
![Rendered by QuickLaTeX.com \[\Phi_e-поток электрического смещения \[\overline{D},\ \Phi_m\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-b0b637b8850a0ddb7f4c9f7b729cfade_l3.png)
— поток магнитной индукции
![Rendered by QuickLaTeX.com \[\overline{B}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-8000563a9026417a8f93a845b7a41990_l3.png)
сквозь замкнутую поверхность, охватывающую свободный заряд q.
Смысл уравнения 3.2. Электрический заряд – источник электрической индукции.
Уравнение 4.2 выражает факт отсутствия свободных магнитных зарядов.
Полная система уравнений Максвелла в дифференциальном виде (характеризует поле в каждой точке пространства):
![Rendered by QuickLaTeX.com \[ \[rot\overline{E}=-\frac{1}{c}\frac{\partial \overline{B}}{\partial t}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-398725d6b64d766341dbe99024bcae21_l3.png)
![Rendered by QuickLaTeX.com \[ \[rot\overline{H}=\frac{4\pi}{c}\overline{j}+\frac{1}{c}\frac{\partial \overline{D}}{\partial t}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-37a88186f81270e23ee736bb1f25a722_l3.png)
![Rendered by QuickLaTeX.com \[ \[div\overline{D}=4\pi \rho \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-41f289a1b91f76664fff095def5514ea_l3.png)
![Rendered by QuickLaTeX.com \[ \[div\overline{B}=0\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-39ddece54c5fd5589ce9b8db34fc3630_l3.png)
Полная система уравнений Максвелла в интегральном виде
Полная система уравнений Максвелла в интегральном виде (интегральная форма записи уравнений облегчает их физическую интерпретацию так ка делает их визуально ближе к известным эмпирическим законам):
![Rendered by QuickLaTeX.com \[ \[\oint_L{\overline{E}\cdot \overline{dl}=-\frac{1}{c}\int_S{\frac{\partial B_n}{\partial t}}}dS\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-f432c4f234fca38f37fd62cb3370852e_l3.png)
![Rendered by QuickLaTeX.com \[ \[\oint_L{\overline{H}\cdot \overline{dl}}=\sum^n_{k=1}{I_k+I_{shift}}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-b6e3705a57a0f2d3322ca109df8296e8_l3.png)
![Rendered by QuickLaTeX.com \[ \[\Phi_e=\oint_S{D_ndS}=4\pi q\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-6d28861433043913bfefe70393048096_l3.png)
![Rendered by QuickLaTeX.com \[ \[\Phi_m=\oint_S{B_ndS}=0\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-83a7b3ea01df3da9d361db3a9cace0ff_l3.png)
Систему уравнений Максвелла дополняют «материальными уравнениями», связывающими векторы
![Rendered by QuickLaTeX.com \[ \overline{E,\ } \overline{D,\ }\overline{B,\ } \overline{H\ } c величинами, описывающими электрические и магнитные свойства среды. \[ \[\overline{D}=\varepsilon {\varepsilon}_0\overline{E}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-554b05247f1dc8118734626e94f4e413_l3.png)
![Rendered by QuickLaTeX.com \[ \[\overline{B}=\mu {\mu}_0\overline{H}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-ca50fa6a86b6f32814919a79a5229091_l3.png)
![Rendered by QuickLaTeX.com \[ \[\overline{j}=\gamma \overline{E}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-47482a7dc8c3887d797b320932deba3d_l3.png)
где
![Rendered by QuickLaTeX.com \[\varepsilon - относительная диэлектрическая проницаемость, \mu - относительная магнитная проницаемость, \[\gamma\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-62d88edff65785387da798a48c7dfde0_l3.png)
-удельная электропроводность,
![Rendered by QuickLaTeX.com \[{\varepsilon}_0 - электрическая постоянная, \[{\mu}_0\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-aae73eb2dd53903f8dd5355807193787_l3.png)
– магнитная постоянная. Среда предполагается изотропной, неферрромагнитной, несегнетоэлектрической.
На границе раздела двух сред выполняются граничные условия:
![Rendered by QuickLaTeX.com \[ \[D_{1n}-D_{2n}=\sigma,\ B_{1n}=B_{2n}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-ac4c1ea49fc12503cae9b850da90acf2_l3.png)
![Rendered by QuickLaTeX.com \[ \[H_{1\tau}-H_{2\tau}=j_{pov},\ E_{1\tau}=E_{2\tau}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-0d4393f0c5c451165d93165c79e35c3c_l3.png)
где \sigma— поверхностная плотность свободных зарядов, n- единичный вектор нормали к границе раздела, проведенный из среды 2 в 1, \[\tau – единичный вектор, касательный к границе, \[j_{pov}— проекция вектора плотности поверхностных токов проводимости на единичный вектор.
Данные уравнения выражают непрерывность нормальных составляющих вектора магнитной индукции и скачок нормальных составляющих вектора смещения. Непрерывность касательных составляющих вектора напряженностей электрического поля на границе раздела и скачок этих составляющих для напряженности магнитного поля.
3. Уравнения Максвелла. Дифференциальные уравнения электромагнитного поля. Электромагнитные поля и волны
3.1. Первое уравнение Максвелла
3.2. Второе уравнение Максвелла
3.3. Третье уравнение Максвелла
3.4. Четвертое уравнение Максвелла
3.5. Закон сохранения заряда в дифференциальной форме
3.6. Таблица уравнений ЭМП
Интегральные уравнения не позволяют получать информацию об электромагнитных процессах в каждой точке пространства. Они дают усредненные решения полей в пространстве.
Хорошо развитый аппарат математических решений позволят переходить от интегральной формы к дифференциальным решениям.
Впервые переход от интегральных уравнений к дифференциальным сделал Максвелл.
3.1. Первое уравнение Максвелла
Первое уравнение Максвелла является дифференциальной формулировкой закона полного тока:
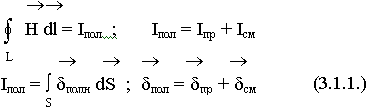
S — опирается на контур L.

Используем теорему Стокса:
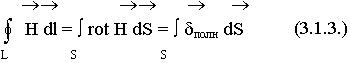
Равенство сохраняет силу по любой поверхности, опирающейся на контур L, отсюда следует, что подинтегральные функции равны.
 — дифференциальная форма закона Ома.
— дифференциальная форма закона Ома.
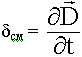

Физический смысл 1-го уравнения Максвелла.
Источниками вихревых магнитных полей являются токи проводимости и токи смещения.
3.2. Второе уравнение Максвелла
Второе уравнение Максвелла является дифференциальной формулировкой закона электромагнитной индукции:

Физический смысл. Вихревое электрическое поле создается переменным магнитным полем.
3.3. Третье уравнение Максвелла
Третье уравнение Максвелла является дифференциальной формулировкой теоремы Гаусса для электрических полей.

Воспользуемся теоремой Остроградского-Гаусса, которая позволяет осуществить переход от
поверхностного интеграла П (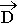 ) к объемному интегралу от (div D):
) к объемному интегралу от (div D):

Запишем правую часть уравнения (3.3.1.) для объемного заряда. Объединим два выражения:
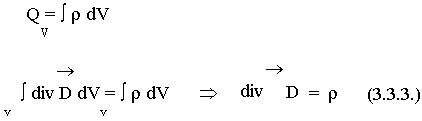
— третье уравнение Максвелла. (3.3.3.)
Физический смысл. Источниками электрического поля (векторов Е и D) являются заряды с плотностью r .
3.4. Четвертое уравнение Максвелла
Четвертое уравнение Максвелла является дифференциальной формулировкой теоремы Гаусса для магнитных полей:

Физический смысл. Дивергенция вектора  любой точке пространства равняется нулю, т.е. — источников нет (магнитные заряды в природе отсутствуют). Нет ни стоков, ни источников.
любой точке пространства равняется нулю, т.е. — источников нет (магнитные заряды в природе отсутствуют). Нет ни стоков, ни источников.
3.5. Закон сохранения заряда в дифференциальной форме
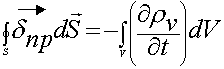
Используем теорему Остроградского-Гаусса:

— это уравнение является следствием из предыдущих уравнений
3.6. Таблица интегральных и дифференциальных уравнений электромагнитного поля
Материальные уравнения среды.
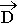 =
= 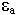

Все эти уравнения являются обобщением в математической форме опытов всего человечества об электромагнитных явлениях. Они не доказываются и не выводятся — это результат опытов.
 =
= 

 =
= 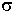

 =
= 
|
Интегральные уравнения электромагнитного поля |
Дифференциальные уравнения электромагнитного поля. Уравнения Максвелла |
|
1. Закон полного тока:
2. Закон электромагнитной индукции:
3. Теорема Гаусса для электрических полей:
4. Теорема Гаусса для магнитных полей:
5. Закон сохранения заряда
|
|
Уравнения Максвелла | Все формулы
Система уравнений Максвелла является обобщением основных законов об электрических и электромагнитных явлениях. Она описывает абсолютно все электромагнитные явления. Являясь основой теории электромагнитного поля, эта система уравнений позволяет решать задачи, связанные с отысканием электрических и магнитных полей, создаваемых заданным распределением электрических зарядов и токов. Уравнения Максвелла были отправной точкой для создания общей теории относительности Эйнштейна. В теории Максвелла раскрывается электромагнитная природа света. Уравнения сформулированы Дж. Максвеллом в шестидесятых годах 19 века на основе обобщения эмпирических законов и развития идей ученых, исследовавших электромагнитные явления до него (Законы Кулона, Био – Савара, Ампера и, в особенности, исследования Фарадея). Сам Максвелл записал 20 уравнений с 20 неизвестными в дифференциальной форме, которые позднее были преобразованы. Современная форма Максвелла дана немецким физиком Г. Герцем и английским физиком О. Хевисайдом. Запишем уравнения используя систему единиц Гаусса.
Система уравнений Максвелла
В состав системы уравнений Максвелла входят четыре уравнения.
Первое уравнение:
Это Закон Фарадея (Закон электромагнитной индукции).
где -напряженность электрического поля, -вектор магнитной индукции, c – скорость света в вакууме.
Это уравнение говорит, о том, что ротор напряженности электрического поля равен потоку (т.е. скорости изменения во времени) вектора магнитной индукции сквозь этот контур.Уравнение (1.1) представляет собой первое уравнение Максвелла в дифференциальной форме.
Это же уравнение можно записать в интегральной форме, тогда оно примет следующий вид:
или
где – проекция на нормаль к площадке dS вектора магнитной индукции,
– магнитный поток.
рис. 2.
Циркуляция вектора напряженности электрического поля вдоль замкнутого контура L (ЭДС индукции) определяется скоростью изменения потока вектора магнитной индукции через поверхность, ограниченную данным контуром. Знак минус по правилу Ленца означает направление индукционного тока.
Согласно Максвеллу закон электромагнитной индукции (а это именно он), справедлив для любого замкнутого контура, произвольно выбранного в переменном магнитном поле.
Смысл этого уравнения: Переменное магнитное поле в любой точке пространства создает вихревое электрическое поле.
Второе уравнение Максвелла:
где -вектор магнитной напряженности, — плотность электрического тока, — вектор электрического смещения.
Данное уравнение Максвелла является обобщением эмпирического закона Био-Савара о том, что магнитные поля возбуждаются электрическими токами. Смысл второго уравнения в том, что источником возникновения вихревого магнитного поля является также переменное электрическое поле, магнитное действие которого характеризуется током смещения. ( -плотность тока смещения).
В интегральном виде второе уравнение Максвелла (Теорема о циркуляции магнитного поля) представлено следующим образом:
или
Циркуляция вектора напряжённости магнитного поля по произвольному контуру равна алгебраической сумме токов проводимости и тока смещения, сцепленных с контуром.
Когда Максвелл вводил уравнения (более ста лет тому назад!), природа электромагнитного поля была не понятна. В настоящее время природа поля выяснена, и стало ясно, что может быть названo «током» лишь формально. По pяду расчетных соображений такое название, не придавая ему прямого физического смысла, целесообразно сохранить, что в электротехнике и делается. По этой же причине вектор D, входящий в выражение для тока смещения, называют вектором электрического смещения.
Помимо первых двух уравнений в систему уравнений Максвелла входит теорема Гаусса-Остроградского для электрического и магнитного полей:
и
где —плотность электрического заряда.
Что в интегральном виде представляет собой следующее:
и
где -поток электрического смещения — поток магнитной индукции сквозь замкнутую поверхность, охватывающую свободный заряд q.
Смысл уравнения 3.2. Электрический заряд – источник электрической индукции.
Уравнение 4.2 выражает факт отсутствия свободных магнитных зарядов.
Полная система уравнений Максвелла в дифференциальном виде (характеризует поле в каждой точке пространства):
Полная система уравнений Максвелла в интегральном виде
Полная система уравнений Максвелла в интегральном виде (интегральная форма записи уравнений облегчает их физическую интерпретацию так ка делает их визуально ближе к известным эмпирическим законам):
Систему уравнений Максвелла дополняют «материальными уравнениями», связывающими векторы c величинами, описывающими электрические и магнитные свойства среды.
где – относительная диэлектрическая проницаемость, – относительная магнитная проницаемость, -удельная электропроводность, – электрическая постоянная, – магнитная постоянная. Среда предполагается изотропной, неферрромагнитной, несегнетоэлектрической.
На границе раздела двух сред выполняются граничные условия:
где — поверхностная плотность свободных зарядов, n- единичный вектор нормали к границе раздела, проведенный из среды 2 в 1, единичный вектор, касательный к границе, — проекция вектора плотности поверхностных токов проводимости на единичный вектор.
Данные уравнения выражают непрерывность нормальных составляющих вектора магнитной индукции и скачок нормальных составляющих вектора смещения. Непрерывность касательных составляющих вектора напряженностей электрического поля на границе раздела и скачок этих составляющих для напряженности магнитного поля.
Примеры решения задач
Единая теория электрических и магнитных явлений. Система уравнений Максвелла
Итак, переменное магнитное поле вызывает появление вихревого электрического поля. Переменное электрическое поле вызывает появление магнитного поля. Взаимно порождаясь, они могут существовать независимо от источников заряда или токов, которые первоначально создали одно из них. В сумме это есть электромагнитное поле (ЭМП). Превращение одного поля в другое и распространение в пространстве есть способ существования ЭМП. Конкретные проявления ЭМП – радиоволны, свет, гамма-лучи и т.д.
В 1860 г. знаменитый английский физик Джеймс Клерк Максвелл создал единую теорию электрических и магнитных явлений, в которой он использовал понятие ток смещения, дал определение ЭМП и предсказал существование в свободном пространстве электромагнитного излучения, которое распространяется со скоростью света.
Теорию ЭМП Максвелл сформулировал в виде системы нескольких уравнений. В учении об электромагнетизме эти уравнения Максвелла играют такую же роль, как уравнения (или законы) Ньютона в механике.
1) Мы знаем теорему о циркуляции вектора напряжённости магнитного поля:
,
но: ; т.е. , тогда
| , | (7.3.1) |
Это уравнение является обобщением закона Био–Савара–Лапласа и показывает, что циркуляция вектора по произвольному замкнутому контуру L равна сумме токов проводимости и токов смещения сквозь поверхность, натянутую на этот контур. Или другими словами, показывает связь между полным током и порождаемым им магнитным полем.
В дифференциальной форме это уравнение Максвелла выглядит так:
где2) Рассматривая явление электромагнитной индукции, мы сделали вывод, что ЭДС индукции . Перейдем от вихревого электрического поля к магнитному:
| , | (7.3.2) |
Это уравнение описывает явление электромагнитной индукции (закон Фарадея) и устанавливает количественную связь между электрическими и магнитными полями: переменное электрическое поле порождает переменное магнитное поле. В этом физический смысл уравнения.
В дифференциальной форме это уравнение выглядит так:
Различие в знаках этого уравнения Максвелла соответствует закону сохранения энергии и правилу Ленца. Если бы знаки при и были одинаковы, то бесконечно малое увеличение одного из полей вызвало бы неограниченное увеличение обоих полей, а бесконечно малое уменьшение одного из полей, приводило бы к полному исчезновению обоих полей. То есть различие в знаках является необходимым условием существования устойчивого ЭМП.3) Ещё два уравнения выражают теорему Остроградского–Гаусса для электрического и магнитного полей (статических полей)
| , | (7.3.3) |
Поток вектора электрического смещения через замкнутую поверхность S равен сумме зарядов внутри этой поверхности. Это уравнение показывает также, что силовые линии вектора и начинаются и заканчиваются на зарядах.
В дифференциальной форме
где
4) И для магнитного поля
| , | (7.3.4) |
Это уравнение выражает то свойство магнитного поля, что линии вектора магнитной индукции всегда замкнуты и что магнитных зарядов нет.
В дифференциальной форме
| , | (7.3.5) |
5, 6, 7) Наконец надо помнить, что величины, входящие в эти четыре уравнения не независимы, и между ними существует связь:
| , | (7.3.6) |
| , | (7.3.7) |
| , | (7.3.8) |
здесь σ – удельная проводимость, – плотность сторонних токов.
Эти уравнения называются уравнениями состояния или материальными уравнениями. Вид этих уравнений определяется электрическими и магнитными свойствами среды. В общем случае уравнения состояния очень сложны и нелинейны.
Уравнения (7.3.1 – 7.3.8) составляют полную систему уравнений Максвелла. Они являются наиболее общими для электрических и магнитных полей в покоящихся средах. Уравнения Максвелла – инвариантны относительно преобразований Лоренца. Физический смысл уравнений Максвелла в дифференциальной и интегральной формах полностью эквивалентен.
Таким образом, полная система уравнений Максвелла в дифференциальной и интегральной формах имеет вид:
;
– обобщенный закон Био–Савара–Лапласа;
; – закон Фарадея;
; – теорема Гаусса; – отсутствие магнитных зарядов;
, ,
Аудио-видео демонстрации по теме или смежным темам: 1. Солнечная корона. 2. Солнечная плазма.Соотношения Максвелла (термодинамика) — Википедия
 Соотношения Максвелла (1871)
Эта статья о термодинамических уравнениях Максвелла; об электродинамических уравнениях Максвелла см. Уравнения Максвелла.
Соотношения Максвелла (1871)
Эта статья о термодинамических уравнениях Максвелла; об электродинамических уравнениях Максвелла см. Уравнения Максвелла.Соотношения Максвелла (термодинамические уравнения Максвелла) — тождественные соотношения между производными термодинамических величин[1]. Являются следствием математического тождества — равенства смешанных производных термодинамического потенциала.
Соотношения используются при выполнении математических выкладок с целью преобразования термодинамических формул. Они существенно расширяют аппарат термодинамики, так как позволяют выразить трудноизмеримые или вообще не допускающие прямое измерение термодинамические величины (как, например, энтропия или химический потенциал) через экспериментально измеримые.
Введены в термодинамику в 1871 году Джеймсом Клерком Максвеллом[2][3] и носят его имя.
Первая публикация соотношений МаксвеллаДо поступления на работу в Кавендишскую лабораторию в 1871 году Максвелл уделял много внимания написанию монографий по кинетической теории газов и по электричеству. В частности, он закончил свой учебник «Теория теплоты» (Theory of Heat)[4], изданный в 1871 году и несколько раз переиздававшийся ещё при жизни автора. Большая часть этой книги была посвящена феноменологическому рассмотрению тепловых явлений[5]. В главе 7 этой книги Максвелл рассмотрел элементарный цикл Карно и, вычисляя из геометрических соображений его площадь на термодинамической диаграмме, получил четыре соотношения между термодинамическими величинами[2], называемые соотношениями Максвелла[6].
В последние годы жизни Максвелл уделял много внимания работам Дж. Уилларда Гиббса и взял на вооружение его методы при подготовке переизданий «Теории теплоты», а также всячески пропагандировал их в статьях и выступлениях. На их основе он уточнил используемое им в книге определение энтропии[6], понятие которой при первой публикации соотношений Максвелла даже не использовалось при их формулировании[K 1].
Соотношения Максвелла выводятся из равенства смешанных производных от термодинамических потенциалов. Для любого термодинамического потенциала f{\displaystyle f}, рассматриваемого как функция независимых переменных x{\displaystyle x} и y,{\displaystyle y,} справедливо соотношение:
- ∂∂y(∂f∂x)y=∂∂x(∂f∂y)x.(∗){\displaystyle {\frac {\partial }{\partial y}}\left({\frac {\partial f}{\partial x}}\right)_{y}={\frac {\partial }{\partial x}}\left({\frac {\partial f}{\partial y}}\right)_{x}.\qquad \qquad (*)}
Внизу справа у частных производных, как это принято в термодинамике, указаны переменные, которые при вычислении производной считают постоянными. Причиной введения такого обозначения является то, что в термодинамике для одной и той же функции используют различные наборы независимых переменных, которые, во избежание неопределённости, приходится перечислять.
Примером термодинамического потенциала может служить внутренняя энергия U{\displaystyle U}. Запишем выражение для её дифференциала[7]: dU=TdS−PdV,{\displaystyle dU=TdS-PdV,} где T{\displaystyle T} — термодинамическая температура, S{\displaystyle S} — энтропия, P{\displaystyle P} — давление и V{\displaystyle V} — объём. Выражение является полным дифференциалом относительно независимых переменных S,V:{\displaystyle S,\,V:}
- dU=(∂U∂S)VdS+(∂U∂V)SdV,{\displaystyle dU=\left({\frac {\partial U}{\partial S}}\right)_{V}dS+\left({\frac {\partial U}{\partial V}}\right)_{S}dV,}
что позволяет получить производные внутренней энергии[8]:
- (∂U∂S)V=T,(∂U∂V)S=−P.{\displaystyle \left({\frac {\partial U}{\partial S}}\right)_{V}=T,\qquad \left({\frac {\partial U}{\partial V}}\right)_{S}=-P.}
Из уравнения (*) при f=U,x=S,y=V{\displaystyle f=U,\,x=S,\,y=V}:
- ∂∂V(∂U∂S)V=∂∂S(∂U∂V)S{\displaystyle {\frac {\partial }{\partial V}}\left({\frac {\partial U}{\partial S}}\right)_{V}={\frac {\partial }{\partial S}}\left({\frac {\partial U}{\partial V}}\right)_{S}}
следует первое соотношение Максвелла[9][10] для смешанных производных внутренней энергии:
- (∂T∂V)S=−(∂P∂S)V.{\displaystyle \left({\frac {\partial T}{\partial V}}\right)_{S}=-\left({\frac {\partial P}{\partial S}}\right)_{V}.}
Используя выражение для производной обратной функции,
- (∂y∂x)z=1/(∂x∂y)z,{\displaystyle \left({\frac {\partial y}{\partial x}}\right)_{z}=1\left/\left({\frac {\partial x}{\partial y}}\right)_{z}\right.,}
первое соотношение Максвелла можно привести к следующему виду:
- (∂V∂T)S=−(∂S∂P)V.{\displaystyle \left({\frac {\partial V}{\partial T}}\right)_{S}=-\left({\frac {\partial S}{\partial P}}\right)_{V}.}
Далее из выражения dF=−SdT−PdV{\displaystyle dF=-SdT-PdV} для дифференциала свободной энергии Гельмгольца F=U−TS{\displaystyle F=U-TS} следуют выражения для её производных первого порядка[11]:
- (∂F∂T)V=−S,(∂F∂V)T=−P(F1){\displaystyle \left({\frac {\partial F}{\partial T}}\right)_{V}=-S,\qquad \left({\frac {\partial F}{\partial V}}\right)_{T}=-P\qquad \qquad (F1)}
и второе соотношение Максвелла[12][13][14] для смешанных производных свободной энергии:
- (∂S∂V)T=(∂P∂T)V,(∂V∂S)T=(∂T∂P)V.(F2){\displaystyle \left({\frac {\partial S}{\partial V}}\right)_{T}=\left({\frac {\partial P}{\partial T}}\right)_{V},\qquad \left({\frac {\partial V}{\partial S}}\right)_{T}=\left({\frac {\partial T}{\partial P}}\right)_{V}.\qquad \qquad (F2)}
Аналогичным образом из выражения dH=TdS+VdP{\displaystyle dH=TdS+VdP} для дифференциала энтальпии H=U+PV{\displaystyle H=U+PV} могут быть получены производные энтальпии[15]:
- (∂H∂S)P=T,(∂H∂P)S=V{\displaystyle \left({\frac {\partial H}{\partial S}}\right)_{P}=T,\qquad \left({\frac {\partial H}{\partial P}}\right)_{S}=V}
и третье соотношение Максвелла[16][17] для смешанных производных энтальпии:
- (∂T∂P)S=(∂V∂S)P,(∂P∂T)S=(∂S∂V)P.{\displaystyle \left({\frac {\partial T}{\partial P}}\right)_{S}=\left({\frac {\partial V}{\partial S}}\right)_{P},\qquad \left({\frac {\partial P}{\partial T}}\right)_{S}=\left({\frac {\partial S}{\partial V}}\right)_{P}.}
Наконец, из выражения dG=−SdT+VdP{\displaystyle dG=-SdT+VdP} для дифференциала энергии Гиббса G=U−TS+PV{\displaystyle G=U-TS+PV} выводятся производные энергии Гиббса[18]:
- (∂G∂T)P=−S,(∂G∂P)T=V(G1){\displaystyle \left({\frac {\partial G}{\partial T}}\right)_{P}=-S,\qquad \left({\frac {\partial G}{\partial P}}\right)_{T}=V\qquad \qquad (G1)}
и четвёртое соотношение Максвелла[19][20][21] для смешанных производных энергии Гиббса:
- (∂S∂P)T=−(∂V∂T)P,(∂P∂S)T=−(∂T∂V)P.(G2){\displaystyle \left({\frac {\partial S}{\partial P}}\right)_{T}=-\left({\frac {\partial V}{\partial T}}\right)_{P},\qquad \left({\frac {\partial P}{\partial S}}\right)_{T}=-\left({\frac {\partial T}{\partial V}}\right)_{P}.\qquad \qquad (G2)}
Ещё два соотношения, хотя и отсутствуют в книге Максвелла[4], в современной литературе могут называться соотношениями Максвелла[22]:
- (∂T∂P)V(∂S∂V)P{\displaystyle \left({\frac {\partial T}{\partial P}}\right)_{V}\left({\frac {\partial S}{\partial V}}\right)_{P}}−(∂T∂V)P(∂S∂P)V=1,(M5){\displaystyle -\left({\frac {\partial T}{\partial V}}\right)_{P}\left({\frac {\partial S}{\partial P}}\right)_{V}=1,\qquad \qquad (M5)}
- (∂P∂T)S(∂V∂S)T−(∂P∂S)T(∂V∂T)S=1.(M6){\displaystyle \left({\frac {\partial P}{\partial T}}\right)_{S}\left({\frac {\partial V}{\partial S}}\right)_{T}-\left({\frac {\partial P}{\partial S}}\right)_{T}\left({\frac {\partial V}{\partial T}}\right)_{S}=1.\qquad \qquad (M6)}
Запись через якобианы и вывод соотношений (M5—6)[править | править код]
Уравнения Максвелла из книги[22].Для краткой и элегантной записи термодинамических формул, в том числе соотношений Максвелла, используют якобианы. Вот как выглядит первое соотношение Максвелла, выраженное через якобианы[23]:
- D(T,S)D(V,S)=D(P,V)D(V,S)(J){\displaystyle {\frac {D(T,S)}{D(V,S)}}={\frac {D(P,V)}{D(V,S)}}\qquad \qquad (J)}
Если умножить обе части уравнения (J) на D(V,S)D(P,V){\displaystyle {\frac {D(V,S)}{D(P,V)}}} и использовать правила преобразования якобианов, получается тождество:
- D(T,S)D(P,V)=1,{\displaystyle {\frac {D(T,S)}{D(P,V)}}=1,}
которое представляет собой соотношение Максвелла (M5), записанное через якобианы[23][22]. Если же домножить обе части уравнения (J) на D(V,S)D(T,S){\displaystyle {\frac {D(V,S)}{D(T,S)}}}, получается тождество:
- D(P,V)D(T,S)=1,{\displaystyle {\frac {D(P,V)}{D(T,S)}}=1,}
которое представляет собой соотношение Максвелла (M6)[22].
Примеры использования соотношений Максвелла[править | править код]
С помощью соотношений Максвелла выводятся практически важные уравнения, интегрированием которых можно вычислить энтропию любого состояния по экспериментальным данным[24]. Они получаются из выражений для полного дифференциала энтропии как функции независимых переменных T,V{\displaystyle T,\,V} или T,P{\displaystyle T,\,P}:
- dS=(∂S∂T)VdT+(∂S∂V)TdV,dS=(∂S∂T)PdT+(∂S∂P)TdP.{\displaystyle dS=\left({\frac {\partial S}{\partial T}}\right)_{V}dT+\left({\frac {\partial S}{\partial V}}\right)_{T}dV,\qquad \qquad dS=\left({\frac {\partial S}{\partial T}}\right)_{P}dT+\left({\frac {\partial S}{\partial P}}\right)_{T}dP.}
Температурная производная энтропии выражается через (измеримую) теплоёмкость при постоянном объёме CV≡(∂U∂T)V=T(∂S∂T)V{\displaystyle C_{V}\equiv \left({\frac {\partial U}{\partial T}}\right)_{V}=T\left({\frac {\partial S}{\partial T}}\right)_{V}} или при постоянном давлении CP≡(∂H∂T)P=T(∂S∂T)P{\displaystyle C_{P}\equiv \left({\frac {\partial H}{\partial T}}\right)_{P}=T\left({\frac {\partial S}{\partial T}}\right)_{P}}. Производная энтропии по объёму выражается с помощью второго соотношения Максвелла (F2), а производная по давлению — с помощью четвёртого соотношения Максвелла (G2), что даёт искомые уравнения для определения энтропии:
- dS=CVTdT+(∂P∂T)VdV,dS=CPTdT−(∂V∂T)PdP.{\displaystyle dS={\frac {C_{V}}{T}}dT+\left({\frac {\partial P}{\partial T}}\right)_{V}dV,\qquad \qquad dS={\frac {C_{P}}{T}}dT-\left({\frac {\partial V}{\partial T}}\right)_{P}dP.}
Подстановка первого из этих уравнений в выражение для дифференциала внутренней энергии позволяет определить зависимость последней от температуры и объёма[21]:
- dU=CVdT+(∂U∂V)TdV,{\displaystyle dU=C_{V}dT+\left({\frac {\partial U}{\partial V}}\right)_{T}dV,\quad } где (∂U∂V)T=T(∂P∂T)V−P,{\displaystyle \quad \left({\frac {\partial U}{\partial V}}\right)_{T}=T\left({\frac {\partial P}{\partial T}}\right)_{V}-P,}
Для идеального газа при постоянном объёме давление пропорционально температуре (закон Шарля), так что (∂P/∂T)V=P/T{\displaystyle \left({\partial P}/{\partial T}\right)_{V}={P}/T}, и полученное выражение для (∂U/∂V)T{\displaystyle (\partial U/\partial V)_{T}} обращается в ноль. Отсюда вытекает закон Джоуля — независимость внутренней энергии газа от объёма, а также связь между теплоёмкостями CV{\displaystyle C_{V}} и CP{\displaystyle C_{P}}:
Выражение для разности CP−CV{\displaystyle C_{P}-C_{V}} (вывод)Уравнения Максвелла • Джеймс Трефил, энциклопедия «Двести законов мироздания»
Шотландский физик, один из самых выдающихся теоретиков XIX столетия. Родился в Эдинбурге, происходит из старинного дворянского рода. Учился в Эдинбургском и Кембриджском университетах. Первую научную статью (о методе начертания идеального овала) опубликовал в возрасте 14 лет. Максвелл занимал должность профессора кафедры экспериментальной физики Кембриджского университета, когда в 48 лет безвременно скончался от рака.
Первым большим теоретическим исследованием Клерка Максвелла, как его часто именуют, стала работа по теории цвета и цветного зрения. Он первым показал, что вся гамма видимых цветов может быть получена путем смешения трех основных цветов — красного, желтого и синего; объяснил природу дальтонизма (дефекта зрения, приводящего к нарушению восприятия цветовой гаммы) врожденным или приобретенным дефектом рецепторов сетчатки глаза. Он первым изобрел реально работающий цветной фотоаппарат (с использованием тартановой ленты в качестве светочувствительного материала) и продемонстрировал его работу на собрании Лондонского королевского общества в 1861 году. Как бы между делом тщательно рассчитал возможную структуру колец Сатурна и доказал, что они не могут быть жидкими, как ранее считалось, а должны состоять из твердых частиц.
Максвелл внес важный вклад в развитие многих отраслей естествознания. Но, пожалуй, наиважнейшее его достижение состоит в развитии теории электромагнетизма и постановке ее на прочную математическую основу. Заниматься этим вопросом Максвелл начал в середине 1850-х годов. По иронии судьбы Максвелл твердо верил в существование светоносного эфира, и все свои уравнения выводил исходя из того, что эфир существует, и в нем возбуждаются электромагнитные волны, имеющие, как следствие, конечную скорость распространения. До результатов опыта Майкельсона—Морли, опровергающих теорию существования эфира, Максвелл не дожил. (Как не дожил он и до безоговорочного признания своей теории. Окончательно волновая природа света и правильность уравнений Максвелла были подтверждены опытами Герца лишь в 1888 году, а до того времени большинство физиков, включая самого Герца, с недоверием относились к столь смелой теории. — Примечание переводчика.) К счастью для него и для нас, теорию Максвелла этот опыт не отменил, поскольку уравнения Максвелла выполняются независимо от наличия или отсутствия эфира.
Наконец, Максвелл внес огромный вклад в становление статистической механики, найдя распределение молекул газа по скоростям, ставшее краеугольным камнем молекулярно-кинетической теории. Наконец, сам же Максвелл и подметил несовершенство этой теории, сформулировав парадокс, позже получивший название демона Максвелла.
Уравнения Максвелла
Значение уравнений Максвелла
Уравнения Дж. Максвелла создают основу для предложенной им теории электромагнитных явлений, которая объяснила все известные в то время эмпирические факты, некоторые эффекты предсказала. Главным выводом теории Максвелла стало положение о существовании электромагнитных волн, которые распространяются со скоростью света.
Замечание
Уравнения, предложенные Максвеллом, в электромагнетизме играют роль подобную роли законов Ньютона в классической механике. Они явились обобщением экспериментальных законов и продолжением идей ученых (Кулона, Ампера, Фарадея и др.) изучавших электромагнетизм до Максвелла.
Замечание 1
Сам Максвелл предложил двадцать уравнений в дифференциальной форме с двадцатью неизвестными величинами. В современном виде мы имеем систему уравнений Максвелла благодаря немецкому физику Г. Герцу и англичанину О. Хэвисайду. С помощью этих уравнений можно описать все электромагнитные явления.
Система уравнений Максвелла
Определение 1
Систему уравнений Максвелла составляют:
\[rot\overrightarrow{H}=\overrightarrow{j}+\frac{\partial \overrightarrow{D}}{\partial t}\left(1\right),\] \[rot\overrightarrow{E}=-\frac{\partial \overrightarrow{B}}{\partial t}\left(2\right),\] \[div\overrightarrow{B}=0\left(3\right),\] \[div\overrightarrow{D}=\rho \left(4\right).\]Выражения (1)-(4) называют полевыми уравнениями, они применимы для описания всех макроскопических электромагнитных явлений. Иногда уравнения системы Максвелла группируют в пары, первую пару составляют из второго и третьего уравнения, вторую пару — из первого и четвертого уравнений. При этом говорят, что в первую пару уравнений входят только основные характеристики поля ($\overrightarrow{E}\ и\ \overrightarrow{B}$), а во вторую пару — вспомогательные ($\overrightarrow{D}\ и\ \overrightarrow{H}$).
Каждое из векторных уравнений (1) и (2) эквивалентно трем скалярным уравнениям. Эти уравнения связывают компоненты векторов, которые находятся в левой и правой частях выражений. Так, в скалярном виде уравнение (1) представляется как:
В скалярном виде уравнение (2) запишем как:
Третье уравнение из системы Максвелла в скалярном виде:
Четвертое уравнение в скалярной форме примет следующий вид:
Для того чтобы рассмотреть конкретную ситуацию, систему уравнений (1)-(4) дополняют следующими материальными уравнениями, которые учитывают электромагнитные свойства среды:
Замечание 2
Необходимо отметить, что существует целый ряд явлений, в которых материальные уравнения существенно отличны от уравнений (5), например, если речь идет о нелинейных явлениях. В таких случаях получение материальных уравнений составляет отдельную научную задачу.
Физический смысл уравнений Максвелла
Уравнение (1) системы указывает на то, что двумя возможными источниками магнитного поля являются токи проводимости ($\overrightarrow{j}$) и токи смещения ($\frac{\partial \overrightarrow{D}}{\partial t}$).
Уравнение (2) является законом электромагнитной индукции и отображает тот факт, что переменное магнитное поле — один из источников возникновения электрического поля.
Следующим источником электрического поля служат электрические заряды, что и отображает уравнение (4), которое является, по сути, законом Кулона.
Уравнение (3) означает, что линии магнитной индукции не имеют источников (они либо замкнуты, либо уходят в бесконечность), что приводит к выводу об отсутствии магнитных зарядов, которые создают магнитное поле.
Материальные уравнения (5) — это соотношения между векторами поля и токами. Диэлектрические свойства среды заключены в диэлектрической проницаемости ($\varepsilon $). Магнитные свойства, которые описывает намагниченность, учтены в магнитной проницаемости ($\mu $). Проводящие свойства среды сосредоточены в удельной проводимости ($\sigma $).
Уравнения поля линейны и учитывают принцип суперпозиции.
Границы применимости уравнений Максвелла
Система уравнений Максвелла ограничена следующими условиями:
Материальные тела должны быть неподвижны в поле.
Постоянные $\varepsilon ,\ \mu ,\sigma $ могут зависеть от координат, но не должны зависеть от времени и векторов поля.
В поле не должно находиться постоянных магнитов и ферромагнитных тел.
Если существует необходимость учета движения среды, то уравнения системы Максвелла оставляют неизменными, а движение учитывается в материальных уравнениях, которые становятся зависимыми от скорости среды и существенно усложняются. Кроме прочего материальные уравнения перестают быть соотношениями между парами величин, как в (5). Например, плотность тока проводимости становится зависимой от индукции магнитного поля, а не только от напряженности электрического поля.
Замечание 3
Магнитное поле постоянных магнитов, например, можно описать, используя систему Максвелла, если известна намагниченность. Но, если заданы токи, то в присутствии ферромагнетиков описать поле при помощи данных уравнений не получится.
Пример 1
Задание: Докажите, что из уравнений Максвелла следует закон сохранения заряда.
Решение:
В качестве основания для решения задачи используем из системы Максвелла уравнение:
\[rot\overrightarrow{H}=\overrightarrow{j}+\frac{\partial \overrightarrow{D}}{\partial t}\left(1.1\right).\]Проведем операцию дивергирования в обеих частях выражения (1.1):
\[div\left(rot\overrightarrow{H}\right)=div\left(\overrightarrow{j}+\frac{\partial \overrightarrow{D}}{\partial t}\right)\left(1.2\right).\]Для выражения (1.2) в соответствии с теоремой равенстве нулю дивергенции ротора имеем:
\[div\left(rot\overrightarrow{H}\right)=0\ \left(1.3\right).\]Следовательно, получаем:
\[0=div\left(\overrightarrow{j}\right)+div\left(\frac{\partial \overrightarrow{D}}{\partial t}\right)\left(1.4\right).\]Рассмотрим второе слагаемое в правой части. Мы можем поменять порядок дифференцирования, так как время и пространственные координаты независимы, то есть записать:
\[div\left(\frac{\partial \overrightarrow{D}}{\partial t}\right)=\frac{\partial div(\overrightarrow{D)}}{\partial t}\left(1.5\right).\]В соответствии с системой Максвелла мы знаем, что источниками электрических полей служат заряды или:
\[div\overrightarrow{D}=\rho \left(1.6\right).\]Что позволяет нам записать уравнение (1.4) в виде:
\[0=div\left(\overrightarrow{j}\right)+\left(\frac{\partial \rho }{\partial t}\right)\left(1.7\right).\]Что дает нам закон сохранения заряда, который записан в виде:
\[div\left(\overrightarrow{j}\right)=-\frac{\partial \rho }{\partial t}(1.8).\]Данное уравнение называют уравнением непрерывности тока, оно содержит в себе закон сохранения заряда, что совершенно очевидно, если выражение (1.8), записать в интегральной форме:
\[\oint\limits_S{\overrightarrow{j}}d\overrightarrow{S}=-\frac{\partial }{\partial t}\int{\rho dV}(1.9).\]тогда если области замкнуты и изолированы получаем:
\[\oint\limits_S{\overrightarrow{j}}d\overrightarrow{S}=0\to \int{\rho dV}=const.\]Что требовалось доказать.
Пример 2
Задание: Покажите, что уравнения $rot\overrightarrow{E}=-\frac{\partial \overrightarrow{B}}{\partial t}$ и $div\overrightarrow{B}=0$ , входящие в систему Максвелла не противоречат друг другу.
Решение:
За основу решения примем уравнение:
\[rot\overrightarrow{E}=-\frac{\partial \overrightarrow{B}}{\partial t}\left(2.1\right).\]Возьмём дивергенцию от обеих частей уравнения:
\[div(rot\overrightarrow{E)}=-div(\frac{\partial \overrightarrow{B}}{\partial t})\left(2.2\right).\]В соответствии с теоремой равенстве нулю дивергенции ротора имеем:
\[div(rot\overrightarrow{E)}=0.\]Соответственно, получаем, что
\[div\left(\frac{\partial \overrightarrow{B}}{\partial t}\right)=\frac{\partial div\overrightarrow{B}}{\partial t}=0\to div\overrightarrow{B}=const.\]Выражение $div\overrightarrow{B}=const$ не противоречит тому, что $div\overrightarrow{B}=0$.
Мы получили, что уравнения $rot\overrightarrow{E}=-\frac{\partial \overrightarrow{B}}{\partial t}$ и $div\overrightarrow{B}=0$ совместны, что требовалось показать.