1.6. Теплоёмкость. Уравнение кирхгофа.
Теплоёмкость – то количество теплоты, которое необходимо сообщить или отнять телу или системе, чтобы их температура изменилась на 1 градус. Теплоёмкость — величина экстенсивная, так как зависит от размера системы. Теплоёмкость, рассчитанная на 1 моль вещества, называется мольной, а на единицу массы – удельной.
Различают:
— истинную
теплоёмкость:  [
[ ]. (1.25)
]. (1.25)
— среднюю
теплоёмкость:  . (1.26)
. (1.26)
Наиболее часто используются следующие теплоемкости:
1. Изохорная теплоемкость. При нагреве или охлаждении вещества при постоянном объеме справедливо:
.  . (1.27)
. (1.27)
2. Изобарная теплоемкость. При нагреве или охлаждении вещества при постоянном давлении справедливо:
.  . (1.28)
. (1.28)
Следует знать, что теплоёмкость при постоянном давлении Ср больше, чем теплоёмкость при постоянном объёме СV, так как нагревание вещества при постоянном давлении сопровождается работой расширения, т.е.

Для идеальных газов справедливо уравнение Майера:
 . (1.30)
. (1.30)
Величина R (универсальная газовая постоянная) равна работе расширения 1 моля идеального газа (при р = const) при увеличении его температуры на 1 градус.
Отношение 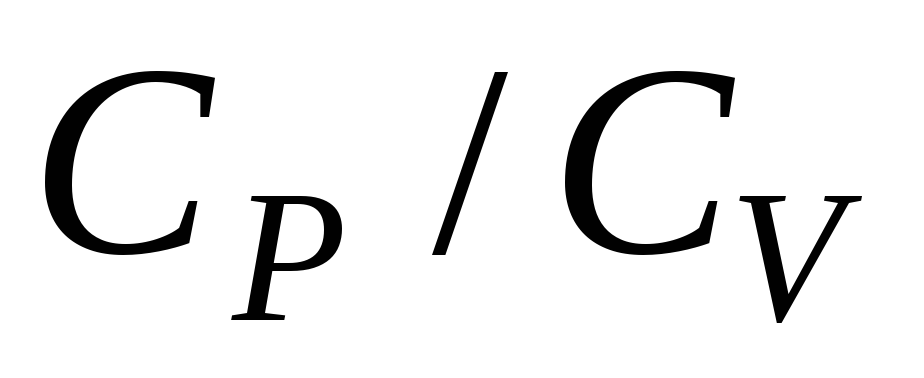 обозначается символом
обозначается символом (адиабатический
коэффициент),
который всегда больше нуля (
(адиабатический
коэффициент),
который всегда больше нуля (
Зависимость теплоёмкости веществ в области не очень низких температур (Т ≥ 298 К) обычно выражается в виде следующих полиномов:
 . (1.31)
. (1.31)
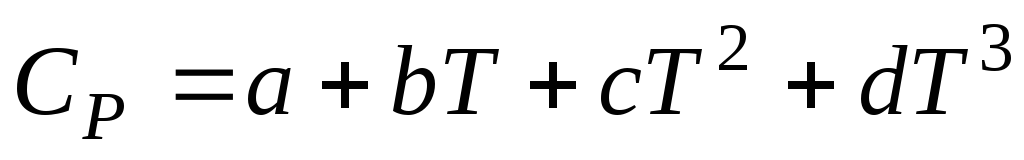 . (1.32)
. (1.32)
Значения a, b, c, c´, d приведены в справочниках физико-химических и термодинамических величин.
Рассмотрим уравнение Кирхгоффа, описывающее зависимость энтальпии реакции от температуры:
 , (1.33)
, (1.33)
где
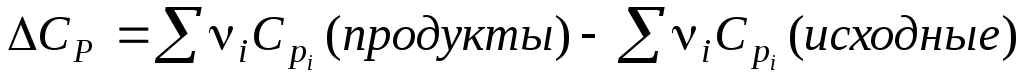 ,
,
т. е. разность между суммой теплоёмкостей продуктов реакции и исходных веществ с учётом стехиометрических коэффициентов.
Для вычисления интеграла необходимо знать зависимость теплоёмкости от температуры для всех веществ, что не всегда возможно. Поэтому уравнение Кирхгоффа применяют в трёх приближениях.
При наиболее грубом приближении полагают, что Сp = 0, т.е. считают равными суммарные теплоёмкости продуктов и исходных веществ. Тогда

т.е. тепловой эффект считается не зависящим от температуры. Этим приближением пользуются, если теплоемкости некоторых участников реакции неизвестны.
Во втором приближении считают разность теплоёмкостей постоянной величиной СР = const. Тогда
 . (1.34)
. (1.34)
Это уравнение применяют только для небольшого интервала температур Т2 – Т1, в котором известны величины теплоёмкостей.
В наиболее точном приближении используют зависимость всех СРi от температуры. Если теплоемкости веществ даны в виде полиномов, например (1.34), то уравнение Кирхгоффа можно проинтегрировать, после чего оно будет иметь следующий вид:
 . (1.35)
. (1.35)
Последнее уравнение можно использовать только в том интервале температур Т2 – Т1, для которого определены коэффициенты ai, bi, ci температурной зависимости теплоёмкостей веществ.
Лекция 2
Второй закон термодинамики. Энтропия. Вычисление изменения энтропии для различных процессов. Постулат Планка. Энергия Гиббса и энергия Гельмгольца. Уравнение Гиббса-Гельмгольца. Самопроизвольное протекание химических реакций. Расчет изменения энергии Гиббса в химических реакциях. Химический потенциал. Активность и летучесть.
Правила Кирхгофа — Википедия
Пра́вила Кирхго́фа (часто в технической литературе ошибочно называются Зако́нами Кирхго́фа) — соотношения, которые выполняются между токами и напряжениями на участках любой электрической цепи.
Решения систем линейных уравнений, составленных на основе правил Кирхгофа, позволяют найти все токи и напряжения в электрических цепях постоянного, переменного и квазистационарного тока
Имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения многих задач в теории электрических цепей и практических расчётов сложных электрических цепей.
Применение правил Кирхгофа к линейной электрической цепи позволяет получить систему линейных уравнений относительно токов или напряжений и, соответственно, при решении этой системы найти значения токов на всех ветвях цепи и все межузловые напряжения.
Сформулированы Густавом Кирхгофом в 1845 году[2].
Название «Правила» корректнее потому, что эти правила не являются фундаментальными законами природы, а вытекают из фундаментальных законов сохранения заряда и безвихревости электростатического поля (третье уравнение Максвелла при неизменном магнитном поле). Эти правила не следует путать с ещё двумя законами Кирхгофа в химии и физике.
Формулировка правил
Определения
Для формулировки правил Кирхгофа вводятся понятия узел, ветвь и контур электрической цепи. Ветвью называют участок электрической цепи с одним и тем же током, например, на рис. отрезок, обозначенный R1, I1 есть ветвь. Узлом называют точку соединения трех и более ветвей (на рис. обозначены жирными точками). Контур — замкнутый путь, проходящий через несколько ветвей и узлов разветвлённой электрической цепи. Термин
В терминах данных определений правила Кирхгофа формулируются следующим образом.
Первое правило
Сколько тока втекает в узел, столько из него и вытекает.i2 + i3 = i1 + i4
Первое правило Кирхгофа гласит, что алгебраическая сумма токов ветвей, сходящихся в каждом узле любой цепи, равна нулю. При этом направленный к узлу ток принято считать положительным, а направленный от узла — отрицательным: Алгебраическая сумма токов, направленных к узлу, равна сумме направленных от узла.
- ∑j=1nIj=0.{\displaystyle \sum \limits _{j=1}^{n}I_{j}=0.}
Иными словами, сколько тока втекает в узел, столько из него и вытекает. Это правило следует из фундаментального закона сохранения заряда.
Второе правило
Второе правило Кирхгофа (правило напряжений Кирхгофа) гласит, что алгебраическая сумма напряжений на резистивных элементах замкнутого контура равна алгебраической сумме ЭДС, входящих в этот контур. Если в контуре нет источников ЭДС (идеализированных генераторов напряжения), то суммарное падение напряжений равно нулю:
- для постоянных напряжений ∑k=1nEk=∑k=1mUk=∑k=1mRkIk;{\displaystyle \sum _{k=1}^{n}E_{k}=\sum _{k=1}^{m}U_{k}=\sum _{k=1}^{m}R_{k}I_{k};}
- для переменных напряжений ∑k=1nek=∑k=1muk=∑k=1mRkik+∑k=1muLk+∑k=1muCk.{\displaystyle \sum _{k=1}^{n}e_{k}=\sum _{k=1}^{m}u_{k}=\sum _{k=1}^{m}R_{k}i_{k}+\sum _{k=1}^{m}u_{L\,k}+\sum _{k=1}^{m}u_{C\,k}.}
Это правило вытекает из 3-го уравнения Максвелла, в частном случае стационарного магнитного поля.
Иными словами, при полном обходе контура потенциал, изменяясь, возвращается к исходному значению. Частным случаем второго правила для цепи, состоящей из одного контура, является закон Ома для этой цепи. При составлении уравнения напряжений для контура нужно выбрать положительное направление обхода контура. При этом падение напряжения на ветви считают положительным, если направление обхода данной ветви совпадает с ранее выбранным направлением тока ветви, и отрицательным — в противном случае (см. далее).
Правила Кирхгофа справедливы для линейных и нелинейных линеаризованных цепей при любом характере изменения во времени токов и напряжений.
Особенности составления уравнений для расчёта токов и напряжений
Если цепь содержит p{\displaystyle p} узлов, то она описывается p−1{\displaystyle p-1} уравнениями токов. Это правило может применяться и для других физических явлений (к примеру, система трубопроводов жидкости или газа с насосами), где выполняется закон сохранения частиц среды и потока этих частиц.
Если цепь содержит m{\displaystyle m} ветвей, из которых содержат источники тока ветви в количестве mi{\displaystyle m_{i}}, то она описывается m−mi−(p−1){\displaystyle m-m_{i}-(p-1)} уравнениями напряжений.
- Правила Кирхгофа, записанные для p−1{\displaystyle p-1} узлов или m−(p−1){\displaystyle m-(p-1)} контуров цепи, дают полную систему линейных уравнений, которая позволяет найти все токи и все напряжения.
- Перед тем, как составить уравнения, нужно произвольно выбрать:
- положительные направления токов в ветвях и обозначить их на схеме, при этом не обязательно следить, чтобы в узле направления токов были и втекающими, и вытекающими, окончательное решение системы уравнений всё равно даст правильные знаки токов узла;
- положительные направления обхода контуров для составления уравнений по второму закону, с целью единообразия рекомендуется для всех контуров положительные направления обхода выбирать одинаковыми (напр.: по часовой стрелке).
- Если направление тока совпадает с направлением обхода контура (которое выбирается произвольно), падение напряжения считается положительным, в противном случае — отрицательным.
- При записи линейно независимых уравнений по второму правилу Кирхгофа стремятся, чтобы в каждый новый контур, для которого составляют уравнение, входила хотя бы одна новая ветвь, не вошедшая в предыдущие контуры, для которых уже записаны уравнения по второму закону (достаточное, но не необходимое условие).
- В сложных непланарных графах электрических цепей человеку трудно увидеть независимые контуры и узлы, каждый независимый контур (узел) при составлении системы уравнений порождает ещё 1 линейное уравнение в определяющей задачу системе линейных уравнений. Подсчёт количества независимых контуров и их явное указание в конкретном графе развит в теории графов.
Пример
На этом рисунке для каждой ветви обозначен протекающий по ней ток (буквой «I») и напряжение между соединяемыми ею узлами (буквой «U»)Количество узлов: 3.
p−1=2{\displaystyle p-1=2}
Количество ветвей (в замкнутых контурах): 4. Количество ветвей, содержащих источник тока: 0.
m−mi−(p−1)=2{\displaystyle m-m_{i}-(p-1)=2}
Количество контуров: 2.
Для приведённой на рисунке цепи, в соответствии с первым правилом, выполняются следующие соотношения:
- {I1−I2−I6=0I2−I4−I3=0{\displaystyle {\begin{cases}I_{1}-I_{2}-I_{6}=0\\I_{2}-I_{4}-I_{3}=0\end{cases}}}
Обратите внимание, что для каждого узла должно быть выбрано положительное направление, например, здесь токи, втекающие в узел, считаются положительными, а вытекающие — отрицательными.
Решение полученной линейной системы алгебраических уравнений позволяет определить все токи узлов и ветвей, такой подход к анализу цепи принято называть методом контурных токов.
В соответствии со вторым правилом, справедливы соотношения:
- {U2+U4−U6=0U3+U5−U4=0{\displaystyle {\begin{cases}U_{2}+U_{4}-U_{6}=0\\U_{3}+U_{5}-U_{4}=0\end{cases}}}
Полученные системы уравнений полностью описывают анализируемую цепь, и их решения определяют все токи и все напряжения ветвей. Такой подход к анализу цепи принято называть методом узловых потенциалов.
О значении для электротехники
Правила Кирхгофа имеют прикладной характер и позволяют наряду и в сочетании с другими приёмами и способами (метод эквивалентного генератора, принцип суперпозиции, способ составления потенциальной диаграммы) решать задачи электротехники. Правила Кирхгофа нашли широкое применение благодаря простоте формулировки уравнений и возможности их решения стандартными способами линейной алгебры (методом Крамера, методом Гаусса и др.).
Значение в математике
Первое правило Кирхгофа может быть сформулировано в матричном виде. Именно, пусть электрическая цепь состоит из n{\displaystyle n} узлов. Составим матрицу A={aij}i,j=1n{\displaystyle A=\{a_{ij}\}_{i,j=1}^{n}}, где aij{\displaystyle a_{ij}} при i≠j{\displaystyle i\neq j} есть проводимость ветви, соединяющеей узлы с номерами i{\displaystyle i} и j{\displaystyle j} (если они не соединены, можно мысленно соединить их ветвью нулевой проводимости). Величины aii{\displaystyle a_{ii}} положим равными ∑i=1, i≠jn(−aij){\displaystyle \sum _{i=1,~i\neq j}^{n}(-a_{ij})}. Пусть U{\displaystyle U} — потенциал, который мы рассматриваем как функцию, определённую на множестве узлов (или, что то же самое, вектор u=(U1,U2,…,Un){\displaystyle \mathbf {u} =(U_{1},U_{2},\dots ,U_{n})} в n{\displaystyle n}-мерном пространстве Rn{\displaystyle \mathbb {R} ^{n}}). Тогда по определению проводимости имеем Iij=aij(Uj−Ui){\displaystyle I_{ij}=a_{ij}(U_{j}-U_{i})}, где Iij{\displaystyle I_{ij}} — ток в ветви, идущей из вершины i{\displaystyle i} в вершину j{\displaystyle j}. Стало быть, первое правило Кирхгофа для j{\displaystyle j}-того узла можно записать как ∑i=1, i≠jnIij=∑i=1, i≠jnaij(Uj−Ui)=0{\displaystyle \sum _{i=1,~i\neq j}^{n}I_{ij}=\sum _{i=1,~i\neq j}^{n}a_{ij}(U_{j}-U_{i})=0}, или же ∑i=1, i≠jnaijUj+(∑i=1, i≠jn(−aij))Ui=0{\displaystyle \sum _{i=1,~i\neq j}^{n}a_{ij}U_{j}+\left(\sum _{i=1,~i\neq j}^{n}(-a_{ij})\right)U_{i}=0}, или же, учитывая определение диагональных элементов матрицы, как ∑i=1naijUj=0{\displaystyle \sum _{i=1}^{n}a_{ij}U_{j}=0}. В левой части равенства легко узнать координату произведения матрицы A{\displaystyle A} на вектор-столбец u{\displaystyle \mathbf {u} }. Итак, первое правило Кирхгофа в матричном виде гласит: Au=0{\displaystyle A\mathbf {u} =0}.
В таком виде оно допускает обобщение на проводящие поверхности. У криволинейной поверхности проводимость зависит не только от точки, но и от направления. Иными словами, проводимость является функцией на касательных векторах к поверхности. Если считать, что на касательных пространствах она хорошо приближается положительно определённой квадратичной формой, можно говорить о ней как о римановой метрике g{\displaystyle g} (отличающейся от расстояния на поверхности как геометрической форме, учитывающей неизотропность её электрических свойств). Каждая точка поверхности может служить узлом, и потому потенциал будет уже не вектором, а функцией u{\displaystyle u} на поверхности. Аналогом же матрицы проводимостей будет оператор Лапласа — Бельтрами Δg{\displaystyle \Delta _{g}} метрики-проводимости, который действует на пространстве гладких функций. Первое правило Кирхгофа для поверхности гласит ровно то же: Δgu=0{\displaystyle \Delta _{g}u=0}. Иначе говоря, потенциал есть гармоническая функция.
В связи с этим матрицу A{\displaystyle A}, сопоставляемую произвольному взвешенному графу, за исключением диагонали равную матрице смежности, иногда называют дискретным лапласианом. Аналоги теорем о гармонических функциях, такие как существование гармонической функции в области с краем при заданных значениях на крае, получающейся свёрткой с некоторым ядром, имеют место и для дискретных гармонических функций. Обратно, проводящая поверхность может быть приближена сеткой сопротивлений, и дискретные гармонические функции на этой сетке приближают гармонические функции на соответствующей поверхности. На этом обстоятельстве основан интегратор Гершгорина, аналоговая вычислительая машина, использовавшаяся для решения уравнения Лапласа в 30-х — 70-х годах XX века.
В случае проводящей поверхности вместо разности потенциалов имеет смысл говорить об 1-форме du{\displaystyle du}. Связанное с ней при помощи метрики-проводимости векторное поле gradg(u){\displaystyle \mathrm {grad} _{g}(u)} — и есть электрический ток на этой поверхности. Согласно первому правилу Кирхгофа, эта 1-форма тоже гармонична (то есть лежит в ядре ходжева лапласиана, определённого на дифференциальных формах). Это даёт ключ к тому, как правильно формулировать закон Кирхгофа для случая, когда поле не потенциально: именно, 1-форма, получающаяся из тока, рассматриваемого как векторное поле, при помощи проводимости, рассматриваемой как риманова метрика, должна быть гармонична. Зная электродвижущую силу вокруг каждого топологически нетривиального контура на поверхности, можно восстановить силу и направление тока в каждой точке, притом единственным способом. В частности, размерность пространства всевозможных токов равна размерности пространства топологически нетривиальных контуров. Этот факт был одним из оснований для открытия двойственности Пуанкаре; то обстоятельство, что электродвижущие силы определяют однозначно ток (гармоническую 1-форму), является частным случаем теории Ходжа для 1-форм (теория Ходжа утверждает, что на римановом многообразии всякий класс когомологий де Рама представляется гармонической формой, притом только одной).
Закон излучения Кирхгофа
Закон излучения Кирхгофа гласит — отношение излучательной способности любого тела к его поглощательной способности одинаково для всех тел при данной температуре для данной частоты для равновесного излучения и не зависит от их формы, химического состава и проч.
Закон Кирхгофа в химии
Закон Кирхгофа гласит — температурный коэффициент теплового эффекта химической реакции равен изменению теплоёмкости системы в ходе реакции.
Примечания
Литература
- Матвеев А. Н. Электричество и магнетизм : учебное пособие. — М.: Высшая школа, 1983. — 463 с.
- Калашников С. Г. Электричество : учебное пособие. — М.: Физматлит, 2003. — 625 с.
- Бессонов Л. А. Теоретические основы электротехники. Электрические цепи. — 11-е издание. — М.: Гардарики, 2007.
- Герасимов В. Г., Кузнецов Э. В., Николаева О. В. Электротехника и электроника. Кн. 1. Электрические и магнитные цепи. — М.: Энергоатомиздат, 1996. — 288 с. — ISBN 5-283-05005-X.
2.14. Зависимость теплового эффекта от температуры. Уравнение Кирхгофа
Химические превращения далеко не всегда осуществляются при 298 К. Поэтому необходимо знать процедуру пересчета данных о тепловом эффекте процесса от базисной температуры к той, при которой реально происходит реакция.
Чтобы вывести соответствующее уравнение проведем дифференцирование по температуре выражения для энтальпии реакции:

и в результате получим:

Учитывая определительное уравнение для теплоемкости, можем записать:

Таким образом, температурный коэффициент теплового эффекта химической реакции, осуществляемой в условиях постоянства давления, равен разности сумм изобарных тетоёмкостей продуктов и исходных веществ с учетом стехиометрическш коэффициентов в уравнении химической реакции.
Это выражение называют уравнением Кирхгофа в дифференциальной форме. Применительно к процессам, протекающим при постоянном объеме, уравнение приобретает вид:
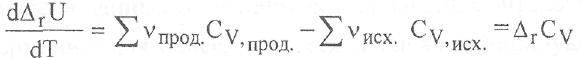
Из уравнения Кирхгофа следует, что масштаб и знак изменения энтальпии реакции с температурой определяется знаком и величиной изменения теплоемкости в ходе процесса.
Здесь можно представить несколько ситуаций, показанных на рис.9.
56
[p# 59]

Рис. 9. Схематическое представление зависимостей 2^Ср,1 и ^г^ от
Температуры:
а) ЛгСр > 0; б) ДгСр < 0; в,г) изменение знака АгСр.
При анализе приведенных зависимостей обратите внимание, что суммы теплоемкостей продуктов и исходных веществ всегда возрастают с температурой, а наклон зависимости энтальпии реакции при каждой температуре равен ДгСр,
2, Энергетика
57
[p# 60]
Таким образом:
если АГС°>0, то энтальпия реакции возрастает с повышением температуры и тем сильнее, чем больше ДгСр;
если ДгСр <0, то энтальпия реакции уменьшается с повышением
температуры;
• энтальпия реакции проходит через максимум, если в области низких температур {Ху!ср,})прод. > (Z!vicp,i)m;x.» тогда как при высоких температурах
(ZviCp,i)np<w. <(ZviCP,iW
• энтальпия реакции проходит через минимум в случае, если поведение веществ противоположно охарактеризованному в предыдущем пункте.
Изложенное выше характеризует влияние температуры на энтальпию химического процесса в качественной форме. Чтобы дать аналитическое описание зависимости энтальпии реакции от температуры, необходимо перейти к интегральной форме уравнения Кирхгофа с учётом температурной зависимости АГС°
г
2.15. Интегрирование уравнения Кирхгофа
Интегрирование уравнения Кирхгофа осуществляют от базисной до требуемой температуры. Поскольку основной массив справочных данных отнесен к 298,15 К, то обычно эту температуру и выбирают в качестве
*\
базисной ‘
Если в интервале температур 298 + Т фазовое состояние веществ, принимающих участие в реакции, остается неизменным, то процедура расчета теплового эффекта сводится к нахождению интеграла:

Интегрирование уравнения предполагает наличие данных о температурной зависимости теплоемкости. Учитывая, что в реакции могут
** В случае реакций с участием идеальных газов в качестве базисной температуры принимают абсолютный нуль. Это связано с тем, что термодинамические свойства веществ, находящихся в идеально-газовом состоянии, рассчитывают из данных о значениях молекулярных
постоянных методами статистической термодинамики, выбрав абсолютный нуль в качестве начальной температуры .
[p# 61]
58
[p# 62]
одновременно принимать участие вещества органические и неорганические, подынтегральное выражение представляют в виде:
 5
5
которое объединяет оба упоминавшихся ранее полиномиальных уравнения для температурной зависимости теплоемкости.
После интегрирования получают:
В этом выражении слагаемое, связанное с коэффициентами «а» и всеми остальными, находят из однотипных уравнений вида:


Объединяя все независящие от температуры члены, приходят к уравнению:

Константа А при этом не имеет смысла АГН298 • ^на также не имеет смысла энтальпии процесса при абсолютном нуле температуры (ДГН0) по той причине,
что уравнения температурной зависимости теплоемкости, представленные в виде рядов по температуре, справедливы только при Т>298 К,
Для некоторых реакций в справочных руководствах можно найти информацию о температурной зависимости теплового эффекта в записанной выше форме с указанием значений всех констант. Однако в большинстве случаев расчет энтальпии процесса приходится выполнять самостоятельно с помощью процедуры интегрирования, основанного на данных о величинах Лга,АгЬ,Дгс, Дгс’.
Значительно удобнее использовать информацию о высокотемпературных составляющих энтальпии для индивидуальных веществ, т.е. данные о величинах Нт — H^g.is • ^ этомслУчае операция интегрирования уже выполнена составителями справочника и расчет сводится к подстановке значений Hj -H^g 15 в уравнение:
[p# 63]
2, Энергетика 5—
[p# 64]

Для реакций, происходящих с участием идеальных газов, это уравнение принимает вид:

Процедура интегрирования с учетом всех слагаемых подынтегрального выражения оказывается излишней при отсутствии сведений о температурной зависимости теплоемкости для одного или нескольких участников процесса. В этом случае принимают

что приводит к
АГН° £ АГН°98Л5 + АгСр5298(Т-298)
Наконец, при полном отсутствии данных о теплоемкости полагают АГС° =0, и,следовательно,
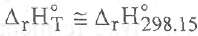
Оба приближения вполне приемлемы для процессов, которые сопровождаются большим выделением или поглощением теплоты, т.е. в случаях, когда величина слагаемого, учитывающего изменение теплоемкости с температурой, вносит малый вклад в величину энтальпии реакции. .
Вычислительная процедура становится достаточно трудоемкой в случае, когда внутри рассматриваемого температурного интервала происходит один или несколько фазовых переходов. В этой ситуации для нахождения энтальпии реакции используют уравнение:

60
[p# 65]
которое включает сумму трех слагаемых, второе из которых учитывает изменение энтальпии за счет теплоёмкостной составляющей, а третье связано с наличием фазовых переходов I рода. После каждого фазового превращения зависимость ArHx=f(T) претерпевает скачок, а зависимость ArC°=f(T)-
полное изменение в отношении характеризующего ее набора констант Дга, ДГЬ, Дгс’ и Дгс.
|
|
КИРХГОФА УРАВНЕНИЕ, термодинамич. соотношение, определяющее зависимость теплового эффекта р-ции от т-ры Т. Для р-ции при постоянном давлении р Кирхгофа уравнение имеет вид: где DH=Qp — тепловой эффект, равный изменению энтальпии системы вследствие р-ции, DСр — изменение теплоемкости системы. Если р-цию записать в форме где vi — стехиометрия, коэф. в-ва Ai (vi>0 для продуктов р-ции, vi<0 для исходных в-в), то DH и DСр рассчитывают по ф-лам: где Hi — парциальная молярная энтальпия в-ва Аi, Срi — его парциальная молярная теплоемкость; тепловой эффект относят к одному пробегу р-ции, при к-ром число молей i-го в-ва изменяется на величину vi. Значение DH (DСр) представляет разность между энтальпиями (теплоемкостями) продуктов р-ции и исходных в-в, взятых в стехиометрич. соотношении. При расчетах Hi и Срi приравнивают обычно соответствующим значениям для чистого в-ва Аi. Для р-ции при постоянном объеме Кирхгофа уравнение имеет вид: где DU=Qv — тепловой эффект, равный изменению внутр. энергии системы при одном пробеге р-ции; разность теплоемкостей СV продуктов р-ции и исходных в-в. Кирхгофа уравнение позволяет рассчитать тепловой эффект р-ции при любой т-ре Т2, если известен тепловой эффект для к.-л. одной т-ры T1 и имеются данные о зависимости теплоемкостей участвующих в р-ции в-в от т-ры в интервале между Т1 и Т2. Интегрируя ур-ние (1), получим: где DHT1 и DHT2 тепловые эффекты р-ции при т-рах Т1 и Т2. В частности, широко применяется след, форма ур-ния (4): Здесь DH0 — гипотетич. тепловой эффект, к-рый бы наблюдался, если бы принимаемые в расчетах температурные зависимости теплоемкости были справедливы вплоть до абс. нуля т-р. Ур-ние (1) применяют для приближенного определения зависимости теплот испарения и сублимации от т-ры. В этих случаях DСр=Спарр-С*p (или Српар-Сртв). Однако при точных вычислениях следует учитывать, что с изменением т-ры равновесное давление двухфазной системы изменяется. Ур-ния (1) и (2) выведены Г. Р. Кирхгофом в 1858. Н А Смирнова
Страница «КИРХГОФА УРАВНЕНИЕ» подготовлена по материалам химической энциклопедии. |
Тепловой эффект. Уравнение Кирхгофа
Так, получаем:
\[E=Q’+\tilde{A}\ \left(2\right).\]Можно записать, что $E=-Q$, где $Q$ — количество теплоты, подведенное к системе, тогда в соответствии с первым началом термодинамики, получим:
\[E=-\triangle U-\int\limits^2_1{pdV\left(3\right),}\]где $\triangle U=U_2-U_1$ — изменение внутренней энергии системы, $p$ — давление, $V$ — объем.
Понятие теплового эффекта часто применяется в термохимии. Тепловым эффектом химической реакции является количество тепла, которое выделяется в ходе этой реакции. Если тепло выделяется, то реакция называется экзотермической, если поглощается — эндотермической. Принято считать, что в экзотермической реакции $E>0$, в эндотермической — $E
Предположим, что химическая реакция протекает при $V=const$. В таком случае тепловой эффект реакции $E_V$ рассчитывается как:
\[E_V=U_1-U_2\left(4\right).\]В том случае, если реакция проходит при постоянном давлении, то выражение для теплового эффекта (3) удобнее записать, используя тепловую функцию (энтальпию — H):
Так как:
\[H=U+pV\left(5\right),\] \[E=H_1-H_2+\int\limits^2_1{Vdp\left(6\right).}\]В таком случае тепловой эффект реакции при $p=const$ равен:
\[E_p=H_1-H_2\left(7\right).\]Уравнения (4) и (5) показывают нам, что тепловой эффект реакции при изохорном и изобарном процессах не зависит от хода (промежуточных стадий) реакции, а определяется начальным и конечным состояниями системы. Это формулировка закона Гесса — первый закон термохимии. Если начальные и конечные продукты реакции — твердые или жидкие, то $E_p$ и $E_V$ почти не отличаются друг от друга. Это происходит из-за неизменности объема системы. В реакциях с газообразными составляющими в виду существенной переменности объема тепловые эффекты $E_p$ и $E_V$ существенно отличаются, чаще всего рассматривают тепловой эффект при постоянном давлении. При заданной температуре тепловой эффект реакции $E_p$ практически (а в идеальном газе совсем) не зависит от внешнего давления (которое поддерживают постоянным). Тепловой эффект определённый при t=250C и p=760 мм рт.ст. считается стандартным.
Из закона Гесса вытекают следствия, которые упрощают расчет химических реакций, в системе при $p=const$ или $V=const$:
- тепловой эффект реакции разложения химического соединения численно равен и противоположен по знаку тепловому эффекту реакции синтеза этого соединения из продуктов разложения;
- разность тепловых эффектов двух реакций, приводящих из разных состояний к одинаковым конечным состояниям, равна тепловому эффекту реакции перехода из одного начального состояния в другое;
- разность тепловых эффектов двух реакций, приводящих из одного исходного состояния к разным конечным состояниям, равна тепловому эффекту реакции перехода из одного конечного состояния в другое.
Закон Гесса позволяет оперировать термохимическими уравнениями, как алгебраическими. Зависимость количества теплоты, выделяющейся в реакции (E) от теплового эффекта реакции (Eo) и количества вещества (nb) одного из участников реакции (вещества b — исходного вещества или продукта реакции), выражается уравнением:
\[E=\frac{n_b}{{\nu }_b}E_0,(8)\]Здесь $\ {\nu }_b$— количество вещества b, задаваемое коэффициентом перед формулой вещества b в термохимическом уравнении.
Уравнение Кирхгофа
Большинство термохимических данных в справочниках приведено при температуре 298К. Для расчета тепловых эффектов при других температурах используют уравнения Кирхгофа. Уравнения Кирхгофа записываются для изохорного $(E_V)$ и изобарного ${(E}_p)$ тепловых эффектов. В дифференциальной форме они имеют вид:
\[{\left(\frac{\partial E_V}{\partial T}\right)}_V={\left(\frac{\partial U_1}{\partial T}\right)}_V-{\left(\frac{\partial U_2}{\partial T}\right)}_V=C_{V_1}-C_{V_2}=-\triangle C_V\left(9\right),\] \[{\left(\frac{\partial E_p}{\partial T}\right)}_p={\left(\frac{\partial H_1}{\partial T}\right)}_p-{\left(\frac{\partial H_2}{\partial T}\right)}_p=C_{p_1}-C_{p_2}=-\triangle C_p\left(10\right),\]В уравнениях (10) и (9) $C_V$, $C_p$- теплоемкости вещества при соответствующих процессах (изобарном и изохорном).
В интегральной форме уравнение Кирхгофа для энтальпии имеет вид:
\[H_{T_2}=H_{T_1}+\int\limits^{T_2}_{T_1}{\triangle C_p\left(T\right)dT}\left(11\right),\]где $\triangle C_p=\sum\limits_j{{\nu }_jC_p(B_j})-\sum\limits_i{{\nu }_iC_p(A_i})$ — разность изобарных теплоемкостей продуктов реакции и исходных веществ. Уравнением (11) в химии пользуются чаще всего.
Пример 2
Задание: По приведенным ниже химическим уравнениям вычислите тепловой эффект реакции (E) образования 1 моль ${Fe}_2O_{3\ }$при стандартных условиях из $Fe$ и $O_2$.
- $2Fe+O_2=2FeO,\ H\left(298K,\ 1\right)=-529,6\ кДж$
- $4FeO+O_2=2{Fe}_2O_3,\ H\left(298K,\ 2\right)=-585,2\ кДж$
Решение:
Таким образом, необходимо рассчитать тепловой эффект образования 1 моль оксида железа (${Fe}_2O_3$) в реакции:
- $2Fe+{1,5O}_2={Fe}_2O_3\ \left(2.1\right)$.
Получается, что из двух реакций, приведенных в условиях задачи, необходимо сформировать реакцию (2.1). Для этого разделим коэффициенты в реакции (2) на 2 и сложим с химическим уравнением (1), таким образом, получим:
\[2Fe+O_2+2FeO+{0,5O}_2=2FeO+{Fe}_2O_3\ \left(2.2\right).\]Проведем сокращения, получим уравнение реакции:
\[2Fe+1,5O_2={Fe}_2O_3\ \]Мы получили уравнение (2.1)
Так как приведенная выше последовательность манипуляций с химическими уравнениями 1 и 2 из условий задачи привела нас к требуемому уравнению (2.1), то проведя аналогичную схему действий с тепловыми эффектами, мы получим тепловой эффект реакции (2.1). Мы помним, что все процессы протекают в стандартных условиях, то есть при T=298K. Таким образом, получаем:
\[E\left(3\right)=H\left(1\right)+0,5H\left(2\right)\left(2.3\right),\]где цифры в скобках обозначают номер химической реакции. Проведем расчет:
\[E\left(3\right)=-529,6+0,5\cdot \left(-585,2\right)=-822,2\ \left(кДж\right).\]Ответ: Тепловой эффект реакции -822, 2 кДж.
Правила Кирхгофа — это… Что такое Правила Кирхгофа?
Правила Кирхгофа (часто, в литературе, называются не совсем корректно Зако́ны Кирхго́фа) — соотношения, которые выполняются между токами и напряжениями на участках любой электрической цепи. Правила Кирхгофа позволяют рассчитывать любые электрические цепи постоянного, переменного и квазистационарного тока.[1] Имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения многих задач в теории электрических цепей и практических расчётов сложных электрических цепей. Применение правил Кирхгофа к линейной электрической цепи позволяет получить систему линейных уравнений относительно токов или напряжений, и соответственно, найти значение токов на всех ветвях цепи и все межузловые напряжения. Сформулированы Густавом Кирхгофом в 1845 году. Название «Правила» корректнее потому, что эти правила не являются фундаментальными законами Природы, а вытекают из фундаментальных законов сохранения заряда и безвихревости электростатического поля (3-е уравнение Максвелла при неизменном магнитном поле). Эти правила не следует путать с ещё двумя законами Кирхгофа в химии и физике.
Формулировка правил
Определения
Для формулировки правил Кирхгофа, вводятся понятия узел, ветвь и контур электрической цепи. Ветвью называют любой двухполюсник, входящий в цепь, например, на рис. отрезок, обозначенный U1, I1 есть ветвь. Узлом называют точку соединения двух и более ветвей (на рис. обозначены жирными точками). Контур — замкнутые циклы из ветвей. Термин замкнутый цикл означает, что начав с некоторого узла цепи и пройдя по нескольким ветвям и узлам однократно можно вернуться в исходный узел. Ветви и узлы, проходимые при таком обходе, принято называть принадлежащими данному контуру. При этом нужно иметь в виду, что каждая ветвь и узел может одновременно принадлежать нескольким контурам.
В терминах данных определений правила Кирхгофа формулируются следующим образом.
Первое правило
Сколько тока втекает в узел, столько из него и вытекает. i2 + i3 = i1 + i4Первое правило Кирхгофа (правило токов Кирхгофа) гласит, что алгебраическая сумма токов в каждом узле любой цепи равна нулю. При этом втекающий в узел ток принято считать положительным, а вытекающий — отрицательным:
Иными словами, сколько тока втекает в узел, столько из него и вытекает. Это правило следует из фундаментального закона сохранения заряда.
Второе правило
Второе правило Кирхгофа (правило напряжений Кирхгофа) гласит, что алгебраическая сумма падений напряжений на всех ветвях, принадлежащих любому замкнутому контуру цепи, равна алгебраической сумме ЭДС ветвей этого контура. Если в контуре нет источников ЭДС (идеализированных генераторов напряжения), то суммарное падение напряжений равно нулю:
- для постоянных напряжений
- для переменных напряжений
Это правило вытекает из 3-го уравнения Максвелла, в частном случае стационарного магнитного поля.
Иными словами, при полном обходе контура потенциал, изменяясь, возвращается к исходному значению. Частным случаем второго правила для цепи, состоящей из одного контура, является закон Ома для этой цепи. При составлении уравнения напряжений для контура нужно выбрать положительное направление обхода контура. При этом падение напряжения на ветви считают положительным, если направление обхода данной ветви совпадает с ранее выбранным направлением тока ветви, и отрицательным — в противном случае (см. далее).
Правила Кирхгофа справедливы для линейных и нелинейных линеаризованных цепей при любом характере изменения во времени токов и напряжений.
- Пример
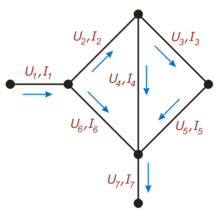 На этом рисунке для каждого проводника обозначен протекающий по нему ток (буквой «I») и напряжение между соединяемыми им узлами (буквой «U»)
На этом рисунке для каждого проводника обозначен протекающий по нему ток (буквой «I») и напряжение между соединяемыми им узлами (буквой «U»)Например, для приведённой на рисунке цепи, в соответствии с первым правилом выполняются следующие соотношения:
Обратите внимание, что для каждого узла должно быть выбрано положительное направление, например здесь, токи, втекающие в узел, считаются положительными, а вытекающие — отрицательными.
Решение полученной линейной системы алгебраических уравнений позволяет определить все токи узлов и ветвей, такой подход к анализу цепи принято называть методом контурных токов.
В соответствии со вторым правилом, справедливы соотношения:
Снова, полученная система уравнений, полностью описывает анализируемую цепь и её решение определяет все токи и все напряжения ветвей, такой подход к анализу цепи принято называть методом узловых потенциалов.
Особенности составления уравнений для расчёта токов и напряжений
Если цепь содержит узлов, то она описывается уравнениями токов. Это правило может применяться и для других физических явлений (к примеру, система трубопроводов жидкости или газа с насосами), где выполняется закон сохранения частиц среды и потока этих частиц.
Если цепь содержит ветвей, из которых содержат источники тока ветви в количестве , то она описывается уравнениями напряжений.
- Правила Кирхгофа, записанные для узлов или контуров цепи, дают полную систему линейных уравнений, которая позволяет найти все токи и все напряжения.
- Перед тем, как составить уравнения, нужно произвольно выбрать:
- положительные направления токов в ветвях и обозначить их на схеме, при этом не обязательно следить, чтобы в узле направления токов были и втекающими и вытекающими, окончательное решение системы уравнений всё равно даст правильные знаки токов узла;
- положительные направления обхода контуров для составления уравнений по второму закону, с целью единообразия рекомендуется для всех контуров положительные направления обхода выбирать одинаковыми (напр.: по часовой стрелке).
- Если направление тока совпадает с направлением обхода контура (которое выбирается произвольно), падение напряжения считается положительным, в противном случае — отрицательным.
- При записи линейно независимых уравнений по второму правилу Кирхгофа, стремятся, чтобы в каждый новый контур, для которого составляют уравнение, входила хотя бы одна новая ветвь, не вошедшая в предыдущие контуры, для которых уже записаны уравнения по второму закону (достаточное, но не необходимое условие).
- В сложных непланарных графах электрических цепей человеку трудно увидеть независимые контуры и узлы, каждый независимый контур (узел) при составлении системы уравнений порождает ещё 1 линейное уравнение, в определяющей задачу системе линейных уравнений. Подсчёт количества независимых контуров и их явное указание в конкретном графе развит в теории графов.
О значении для электротехники
Правила Кирхгофа имеют прикладной характер и позволяют наряду и в сочетании с другими приёмами и способами (метод эквивалентного генератора, принцип суперпозиции, способ составления потенциальной диаграммы) решать задачи электротехники. Правила Кирхгофа нашли широкое применение благодаря простоте формулировки уравнений и возможности их решения стандартными способами линейной алгебры (методом Крамера, методом Гаусса и др.).
Закон излучения Кирхгофа
Закон излучения Кирхгофа гласит — отношение излучательной способности любого тела к его поглощательной способности одинаково для всех тел при данной температуре для данной частоты для равновесного излучения и не зависит от их формы, химического состава и проч.
Закон Кирхгофа в химии
Закон Кирхгофа гласит — температурный коэффициент теплового эффекта химической реакции равен изменению теплоёмкости системы в ходе реакции.
Примечания
Литература
- Матвеев А. Н. Электричество и магнетизм. — Учебное пособие. — М.: Высшая школа, 1983. — 463 с.
- Калашников С. Г. Электричество. — Учебное пособие. — М.: Физматлит, 2003. — 625 с.
- Бессонов Л. А. Теоретические основы электротехники. Электрические цепи. — 11-е издание. — М.: Гардарики, 2007.
Правила Кирхгофа — это… Что такое Правила Кирхгофа?
Правила Кирхгофа (часто, в литературе, называются не совсем корректно Зако́ны Кирхго́фа) — соотношения, которые выполняются между токами и напряжениями на участках любой электрической цепи. Правила Кирхгофа позволяют рассчитывать любые электрические цепи постоянного, переменного и квазистационарного тока.[1] Имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения многих задач в теории электрических цепей и практических расчётов сложных электрических цепей. Применение правил Кирхгофа к линейной электрической цепи позволяет получить систему линейных уравнений относительно токов или напряжений, и соответственно, найти значение токов на всех ветвях цепи и все межузловые напряжения. Сформулированы Густавом Кирхгофом в 1845 году. Название «Правила» корректнее потому, что эти правила не являются фундаментальными законами Природы, а вытекают из фундаментальных законов сохранения заряда и безвихревости электростатического поля (3-е уравнение Максвелла при неизменном магнитном поле). Эти правила не следует путать с ещё двумя законами Кирхгофа в химии и физике.
Формулировка правил
Определения
Для формулировки правил Кирхгофа, вводятся понятия узел, ветвь и контур электрической цепи. Ветвью называют любой двухполюсник, входящий в цепь, например, на рис. отрезок, обозначенный U1, I1 есть ветвь. Узлом называют точку соединения двух и более ветвей (на рис. обозначены жирными точками). Контур — замкнутые циклы из ветвей. Термин замкнутый цикл означает, что начав с некоторого узла цепи и пройдя по нескольким ветвям и узлам однократно можно вернуться в исходный узел. Ветви и узлы, проходимые при таком обходе, принято называть принадлежащими данному контуру. При этом нужно иметь в виду, что каждая ветвь и узел может одновременно принадлежать нескольким контурам.
В терминах данных определений правила Кирхгофа формулируются следующим образом.
Первое правило
Сколько тока втекает в узел, столько из него и вытекает. i2 + i3 = i1 + i4Первое правило Кирхгофа (правило токов Кирхгофа) гласит, что алгебраическая сумма токов в каждом узле любой цепи равна нулю. При этом втекающий в узел ток принято считать положительным, а вытекающий — отрицательным:
Иными словами, сколько тока втекает в узел, столько из него и вытекает. Это правило следует из фундаментального закона сохранения заряда.
Второе правило
Второе правило Кирхгофа (правило напряжений Кирхгофа) гласит, что алгебраическая сумма падений напряжений на всех ветвях, принадлежащих любому замкнутому контуру цепи, равна алгебраической сумме ЭДС ветвей этого контура. Если в контуре нет источников ЭДС (идеализированных генераторов напряжения), то суммарное падение напряжений равно нулю:
- для постоянных напряжений
- для переменных напряжений
Это правило вытекает из 3-го уравнения Максвелла, в частном случае стационарного магнитного поля.
Иными словами, при полном обходе контура потенциал, изменяясь, возвращается к исходному значению. Частным случаем второго правила для цепи, состоящей из одного контура, является закон Ома для этой цепи. При составлении уравнения напряжений для контура нужно выбрать положительное направление обхода контура. При этом падение напряжения на ветви считают положительным, если направление обхода данной ветви совпадает с ранее выбранным направлением тока ветви, и отрицательным — в противном случае (см. далее).
Правила Кирхгофа справедливы для линейных и нелинейных линеаризованных цепей при любом характере изменения во времени токов и напряжений.
- Пример
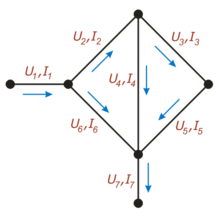 На этом рисунке для каждого проводника обозначен протекающий по нему ток (буквой «I») и напряжение между соединяемыми им узлами (буквой «U»)
На этом рисунке для каждого проводника обозначен протекающий по нему ток (буквой «I») и напряжение между соединяемыми им узлами (буквой «U»)Например, для приведённой на рисунке цепи, в соответствии с первым правилом выполняются следующие соотношения:
Обратите внимание, что для каждого узла должно быть выбрано положительное направление, например здесь, токи, втекающие в узел, считаются положительными, а вытекающие — отрицательными.
Решение полученной линейной системы алгебраических уравнений позволяет определить все токи узлов и ветвей, такой подход к анализу цепи принято называть методом контурных токов.
В соответствии со вторым правилом, справедливы соотношения:
Снова, полученная система уравнений, полностью описывает анализируемую цепь и её решение определяет все токи и все напряжения ветвей, такой подход к анализу цепи принято называть методом узловых потенциалов.
Особенности составления уравнений для расчёта токов и напряжений
Если цепь содержит узлов, то она описывается уравнениями токов. Это правило может применяться и для других физических явлений (к примеру, система трубопроводов жидкости или газа с насосами), где выполняется закон сохранения частиц среды и потока этих частиц.
Если цепь содержит ветвей, из которых содержат источники тока ветви в количестве , то она описывается уравнениями напряжений.
- Правила Кирхгофа, записанные для узлов или контуров цепи, дают полную систему линейных уравнений, которая позволяет найти все токи и все напряжения.
- Перед тем, как составить уравнения, нужно произвольно выбрать:
- положительные направления токов в ветвях и обозначить их на схеме, при этом не обязательно следить, чтобы в узле направления токов были и втекающими и вытекающими, окончательное решение системы уравнений всё равно даст правильные знаки токов узла;
- положительные направления обхода контуров для составления уравнений по второму закону, с целью единообразия рекомендуется для всех контуров положительные направления обхода выбирать одинаковыми (напр.: по часовой стрелке).
- Если направление тока совпадает с направлением обхода контура (которое выбирается произвольно), падение напряжения считается положительным, в противном случае — отрицательным.
- При записи линейно независимых уравнений по второму правилу Кирхгофа, стремятся, чтобы в каждый новый контур, для которого составляют уравнение, входила хотя бы одна новая ветвь, не вошедшая в предыдущие контуры, для которых уже записаны уравнения по второму закону (достаточное, но не необходимое условие).
- В сложных непланарных графах электрических цепей человеку трудно увидеть независимые контуры и узлы, каждый независимый контур (узел) при составлении системы уравнений порождает ещё 1 линейное уравнение, в определяющей задачу системе линейных уравнений. Подсчёт количества независимых контуров и их явное указание в конкретном графе развит в теории графов.
О значении для электротехники
Правила Кирхгофа имеют прикладной характер и позволяют наряду и в сочетании с другими приёмами и способами (метод эквивалентного генератора, принцип суперпозиции, способ составления потенциальной диаграммы) решать задачи электротехники. Правила Кирхгофа нашли широкое применение благодаря простоте формулировки уравнений и возможности их решения стандартными способами линейной алгебры (методом Крамера, методом Гаусса и др.).
Закон излучения Кирхгофа
Закон излучения Кирхгофа гласит — отношение излучательной способности любого тела к его поглощательной способности одинаково для всех тел при данной температуре для данной частоты для равновесного излучения и не зависит от их формы, химического состава и проч.
Закон Кирхгофа в химии
Закон Кирхгофа гласит — температурный коэффициент теплового эффекта химической реакции равен изменению теплоёмкости системы в ходе реакции.
Примечания
Литература
- Матвеев А. Н. Электричество и магнетизм. — Учебное пособие. — М.: Высшая школа, 1983. — 463 с.
- Калашников С. Г. Электричество. — Учебное пособие. — М.: Физматлит, 2003. — 625 с.
- Бессонов Л. А. Теоретические основы электротехники. Электрические цепи. — 11-е издание. — М.: Гардарики, 2007.




