Угловая скорость и угловое ускорение
Рассмотрим понятия угловой скорости и углового ускорения при вращении твердого тела:
Угловая скорость
Угловой скоростью называют скорость вращения тела, определяющаяся приращением угла поворота тела за промежуток времени.
Обозначение: ω (омега).
Формулы угловой скорости
Формула для расчета угловой скорости в зависимости от заданных параметров вращения может иметь вид:
- если известно количество оборотов n за единицу времени t:
- если задан угол поворота φ за единицу времени:
Размерности:
- Количество оборотов за единицу времени [об/мин], [c-1].
- Угол поворота за единицу времени [рад/с].
Быстрота изменения угла φ (перемещения из положения П1 в положение П2) – это и есть угловая скорость:
ω=dφ/dt=φ’, рад/с; с-1 (2.
Например, тело совершающее 1,5 оборота за одну секунду имеет угловую скорость
ω=1,5 с-1=9,42 рад/с.
Приняв k как единичный орт положительного направления оси, получим:
Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.
Угловое ускорение
Угловое ускорение характеризует величину изменения угловой скорости при вращении твердого тела:
Единицы измерения углового ускорения: [рад/с2], [с-2]
Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном — противоположны.
Другими словами, при положительном ускорении угловая скорость нарастает, а при отрицательном вращение замедляется.
Для некоторых частных случаев вращательного движения твердого тела могут быть использованы формулы:
В технике угловая скорость часто задается в оборотах в минуту n [об/мин]. Один оборот – это 2π
ω=n2π/60=nπ/30 рад/с; с-1.
Физика — 10
Это означает, что во сколько раз уменьшится частота обращения, во столько же раз увеличится период обращения, и наоборот.
Угол поворота — это угол, на который поворачивается радиус-вектор при движении материальной точки по окружности. Угол поворота измеряется отношением длины дуги окружности между начальным и конечным радиус-векторами к радиусу окружности (b):
φ = l
R .
Где φ — угол поворота, l — длина дуги, соответствующая углу поворота, R — радиус окружности.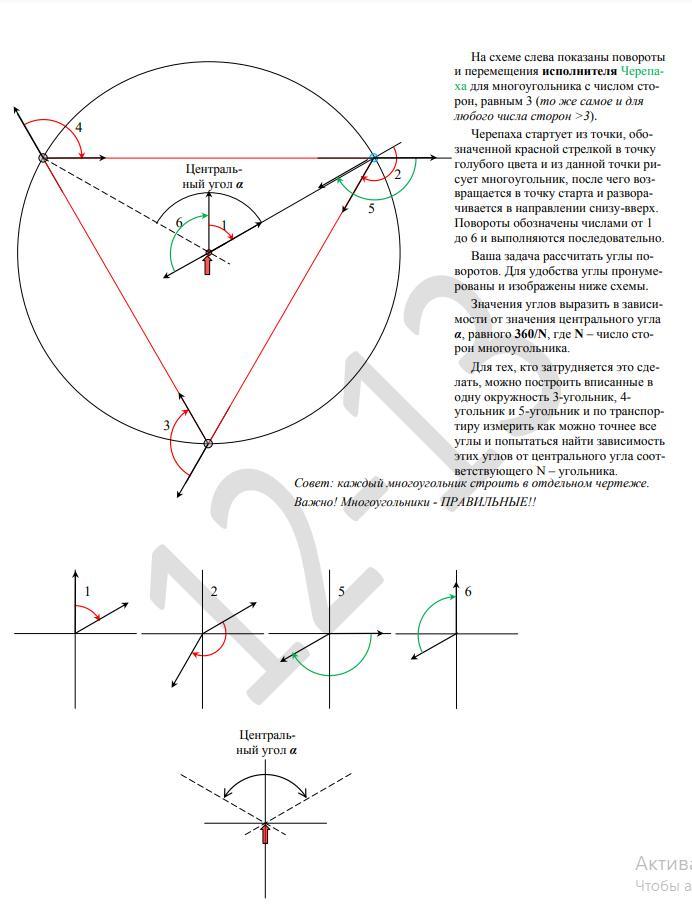 Углы поворота радиус-вектора материальной точки, движущейся равномерно по окружности, за равные промежутки времени одинаковы.
Углы поворота радиус-вектора материальной точки, движущейся равномерно по окружности, за равные промежутки времени одинаковы.
Угол поворота является скалярной величиной, единица его измерения в СИ — радиан: [φ] = 1 рад
Угловая скорость — это физическая величина, измеряемая отношением угла поворота к промежутку времени, за которое этот поворот совершен:
ω = φ
t.
Угловая скорость материальной точки, равномерно движущейся по окружности, с течением времени остается неизменной (ω = const). Единица угловой скорости в СИ — радиан в секунду:
[ω] = 1рад
с .
Материальная точка, движущаяся равномерно по окружности, за время, равное периоду обращения (t = T ), совершает один полный оборот, за это время радиус-вектор поворачивается на угол φ = 2π. Поэтому при равномерном движении по окружности между угловой скоростью и периодом обращения (частотой обращения) имеется связь:
ω = 2π
T = 2πv.
Линейная скорость. Скорость движения материальной точки по окружности называется линейной скоростью. Линейная скорость материальной точки, равномерно движущейся по окружности, оставаясь постоянной по модулю (v = const), непрерывно изменяется по направлению и в любой точке направлена по касательной к траектории (c).
Кинематика абсолютно твёрдого тела. Угловая скорость. Связь между линейной и угловой скоростями
Кинематика абсолютно твёрдого тела. Угловая скорость. Связь между линейной и угловой скоростями
- Подробности
- Просмотров: 630
«Физика — 10 класс»
Угловая скорость.
Каждая точка тела, вращающегося вокруг неподвижной оси, проходящей через точку О, движется по окружности, и различные точки проходят за время Δt разные пути. Так, АА1 > ВВ1 (рис. 1.62), поэтому модуль скорости точки А больше, чем модуль скорости точки В. Но радиус-векторы, определяющие положение точек А и В, поворачиваются за время Δt на один и тот же угол Δφ.
Угол φ — угол между осью ОХ и радиус-вектором определяющим положение точки А (см. рис. 1.62).
Пусть тело вращается равномерно, т. е. за любые равные промежутки времени радиус-векторы поворачиваются на одинаковые углы.
Чем больше угол поворота радиус-вектора, определяющего положение какой-то точки твёрдого тела, за определённый промежуток времени, тем быстрее вращается тело и тем больше его угловая скорость.
Угловой скоростью тела при равномерном вращении называется величина, равная отношению угла поворота тела υφ к промежутку времени υt, за который этот поворот произошёл.
Будем обозначать угловую скорость греческой буквой ω (омега). Тогда по определению
Угловая скорость в СИ выражается в радианах в секунду (рад/с). Например, угловая скорость вращения Земли вокруг оси 0,0000727 рад/с, а точильного диска — около 140 рад/с.
Угловую скорость можно связать с частотой вращения.
Частота вращения — число полных оборотов за единицу времени (в СИ за 1 с).
Если тело совершает ν (греческая буква «ню») оборотов за 1 с, то время одного оборота равно 1/ν секунд.
Время, за которое тело совершает один полный оборот, называют периодом вращения и обозначают буквой Т.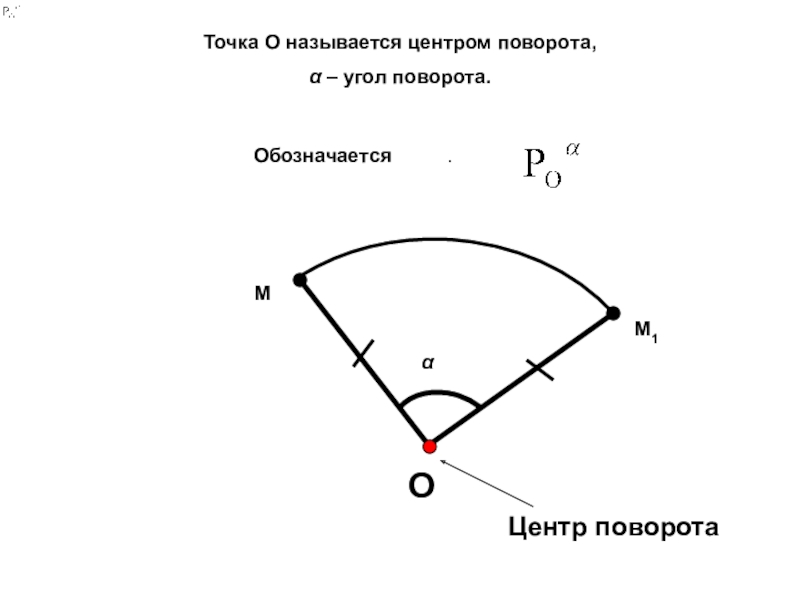
Таким образом, связь между частотой и периодом вращения можно представить в виде
Полному обороту тела соответствует угол Δφ = 2π. Поэтому согласно формуле (1.26)
Если при равномерном вращении угловая скорость известна и в начальный момент времени t0 = 0 угол φ0 = 0, то угол поворота радиус-вектора за время t согласно уравнению (1.26)
φ = ωt.
Если φ0 ≠ 0, то φ — φ0 = ωt, или φ = φ0 ± ωt.
Радиан равен центральному углу, опирающемуся на дугу, длина которой равна радиусу окружности, 1 рад = 57°17’48». В радианной мере угол равен отношению длины дуги окружности к её радиусу: φ = l/R.
Угловая скорость принимает положительные значения, если угол между радиус-вектором, определяющим положение одной из точек твёрдого тела, и осью ОХ увеличивается (рис. 1.63, а), и отрицательные, когда он уменьшается (рис. 1.63, б).
Тем самым мы можем найти положение точек вращающегося тела в любой момент времени.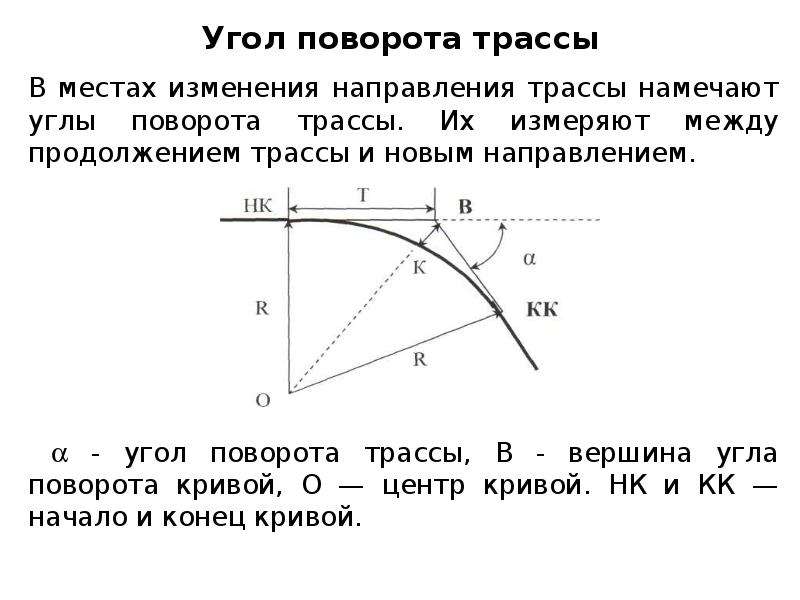
Связь между линейной и угловой скоростями.
Скорость точки, движущейся по окружности, часто называют линейной скоростью, чтобы подчеркнуть её отличие от угловой скорости.
Мы уже отмечали, что при вращении абсолютно твёрдого тела разные его точки имеют неодинаковые линейные скорости, но угловая скорость для всех точек одинакова.
Установим связь между линейной скоростью любой точки вращающегося тела и его угловой скоростью. Точка, лежащая на окружности радиусом R, за один оборот пройдёт путь 2πR. Поскольку время одного оборота тела есть период Т, то модуль линейной скорости точки можно найти так:
Так как ω = 2πν, то
Из этой формулы видно, что, чем дальше расположена точка тела от оси вращения, тем больше её линейная скорость. Для точек земного экватора υ = 463 м/с, а для точек на широте Санкт-Петербурга υ = 233 м/с. На полюсах Земли υ = 0.
Модуль центростремительного ускорения точки тела, движущейся равномерно по окружности, можно выразить через угловую скорость тела и радиус окружности:
Следовательно,
ацс = ω2R.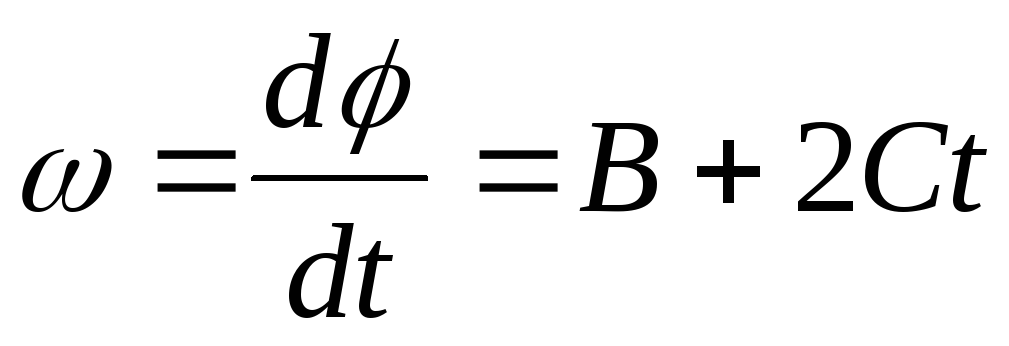
Запишем все возможные расчётные формулы для центростремительного ускорения:
Мы рассмотрели два простейших движения абсолютно твёрдого тела — поступательное и вращательное. Однако любое сложное движение абсолютно твёрдого тела можно представить как сумму двух независимых движений: поступательного и вращательного.
На основании закона независимости движений можно описать сложное движение абсолютно твёрдого тела.
Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Кинематика — Физика, учебник для 10 класса — Класс!ная физика
Физика и познание мира —
Что такое механика —
Механическое движение. Система отсчёта —
Способы описания движения —
Траектория. Путь. Перемещение —
Равномерное прямолинейное движение. Скорость. Уравнение движения —
Примеры решения задач по теме «Равномерное прямолинейное движение» —
Сложение скоростей —
Примеры решения задач по теме «Сложение скоростей» —
Мгновенная и средняя скорости —
Ускорение —
Движение с постоянным ускорением —
Определение кинематических характеристик движения с помощью графиков —
Примеры решения задач по теме «Движение с постоянным ускорением» —
Движение с постоянным ускорением свободного падения —
Примеры решения задач по теме «Движение с постоянным ускорением свободного падения» —
Равномерное движение точки по окружности —
Кинематика абсолютно твёрдого тела. Поступательное и вращательное движение —
Кинематика абсолютно твёрдого тела. Угловая скорость. Связь между линейной и угловой скоростями —
Примеры решения задач по теме «Кинематика твёрдого тела»
Поступательное и вращательное движение —
Кинематика абсолютно твёрдого тела. Угловая скорость. Связь между линейной и угловой скоростями —
Примеры решения задач по теме «Кинематика твёрдого тела»
Угловое ускорение
Система понятий кинематики включает в себя также такую величину как угловое ускорение тела. Дадим ей определение, рассмотрим основные аспекты с использованием примеров.
Основные понятия
Определение 1Угловое ускорение – величина, характеризующая изменение скорости с течением времени.
Пусть рассматриваемый промежуток времени это: Δt=t1-t, а изменение угловой скорости составит Δω=ω1-ω, тогда числовое значение среднего углового ускорения за тот же интервал времени: ε=∆ω∆t=ε. Перейдем к пределу, когда Δt>0, тогда формула углового ускорения будет иметь вид: ε=lim∆t→0∆ω∆t=dωdt=d2φdt=ω˙=φ¨.
Определение 2Числовое значение ускорения в заданный момент времени есть первая производная от угловой скорости или вторая производная от угла поворота по времени.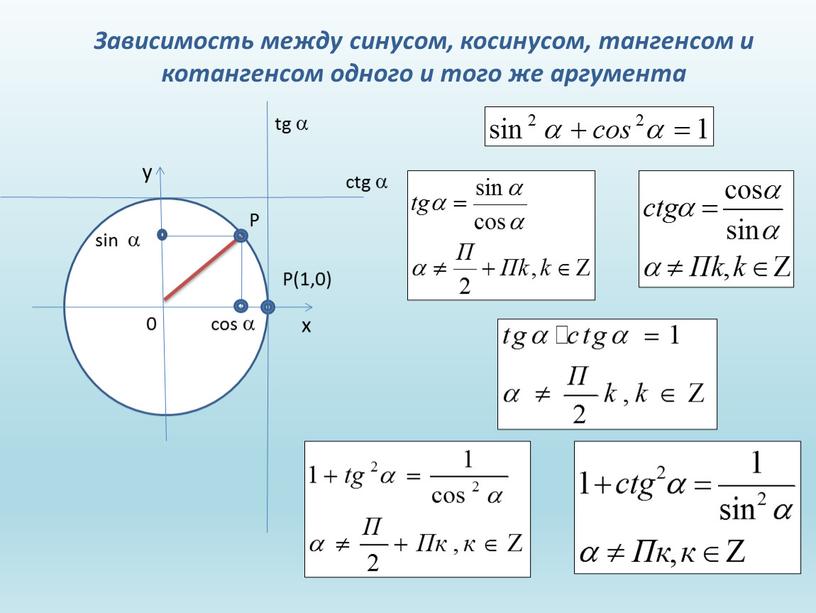
Размерность углового ускорения 1T2 (т.е. 1время2). Укажем также, в чем измеряется угловое ускорение: за единицу измерения стандартно принимается рад/с2 или иначе: 1с2(с-2).
Определение 3Ускоренное вращение тела – это вращение, при котором угловая скорость (ее модуль) возрастает с течением времени.
Определение 4Замедленное вращение тела – это вращение, при котором угловая скорость (ее модуль) убывает с течением времени.
В общем, довольно просто заметить, что, если ω и ε имеют одинаковые знаки, наблюдается ускоренное вращение, а, когда противоположные знаки – замедленное.
Рисунок 1. Вектор углового ускорения
Если мы представим угловое ускорение как вектор ε→=dω→dt, имеющий направление вдоль оси вращения, то в случае ускоренного вращения ε→ и ω→ совпадут по направлениям (левая часть
рисунка 1) и будут противоположны по направлениям в случае замедленного вращения (правая часть
рисунка 1).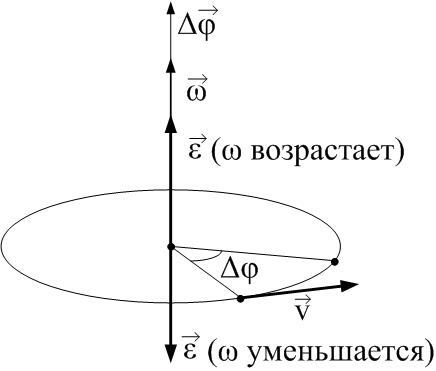
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать заданиеЗакон равнопеременного вращения
Определение 5Равнопеременное вращение – вращение, при котором угловое ускорение во все время движения является постоянным (ε=const).
Выведем формульно закон равнопеременного вращения. Пусть в начальный момент времени t0 угол вращения равен ϕ=ϕ0; угловая скорость — ω=ω0 (т.е. ω0 является начальной угловой скоростью).
Выражение ε=dωdt=ω˙=φ¨ дает нам возможность сделать запись: dω=εdt. Проинтегрируем левую часть крайней записи в пределах от ω0 до ω, а правую – в пределах от 0 до t, тогда:
ω=ω0+εt, dφ=ω0dt+εtdt.
Проинтегрируем вторично и получим формулу, выражающую закон равнопеременного вращения:
Определение 6Закон равнопеременного вращения: φ=φ0+ωt+εt22.
Вращение является равноускоренным, когда ω и ε имеют одинаковые знаки.
Вращение является равнозамедленным, когда ω и ε противоположны по знаку.
Угловое ускорение имеет связь с полным и тангенциальным ускорениями. Пусть некоторая точка вращается неравномерно по окружности с радиусом R, тогда: αr=εR. Нормальное ускорение имеет также связь с угловым: an=ω2R. Учтем это выражение и для полного ускорения получим: a=ar2+an2=Rε2+ω4 Для равнопеременного движения: ω=εt; an=ω2R=ε2t2R и a=Rε2+ε4t4=Rε1+ε2t4.
Практические примеры
Пример 1На рисунке 2 заданы различные типы вращения гироскопа (волчка). С учетом соответствующих подписей необходимо указать, какой рисунок верно демонстрирует направление углового ускорения.
Рисунок 2
Решение
Правило буравчика (правого винта) связывает направление вращения и псевдовектор угловой скорости. Рисунки 2.1. и 2.3. показывают направление псевдовектора вверх, а рисунки 2.2. и 2.4. – вниз.
Когда угловая скорость возрастает, ее приращение и вектор ускорения совпадут с вектором угловой скорости (рисунки 2. 1. и 2.4.). Когда угловая скорость будет уменьшаться, ее приращение и вектор ускорения окажутся противоположно направлены вектору угловой скорости (рисунки 2.2. и 2.3.). Таким образом, все рисунки демонстрируют верное направление углового ускорения.
1. и 2.4.). Когда угловая скорость будет уменьшаться, ее приращение и вектор ускорения окажутся противоположно направлены вектору угловой скорости (рисунки 2.2. и 2.3.). Таким образом, все рисунки демонстрируют верное направление углового ускорения.
Пусть задана некоторая материальная точка, совершающая движение по окружности с радиусом R. При этом выражение ϕ=αt3 отражает зависимость угла поворота от времени. Необходимо найти полное ускорение заданной точки как функцию времени.
Решение
Запишем выражения для угловой скорости и углового ускорения заданной точки:
ω=dφdt=3αt2; ε=6αt.
Полное ускорение запишем как:
a=ar2+an2=Rε2+ω4=R36a2t2+81a4t8=3atR4+9a2t6.
Равномерное движение по окружности в физике
Равномерное движение по окружности:
На предыдущих уроках вы ознакомились с различными видами прямолинейного движения, с величинами, характеризующими эти движения, и определили, как изменяются эти величины со временем.
Наиболее простой вид криволинейного движения — это широко распространенное в природе и технике движение по окружности. Вращение точек поверхности Земли вокруг своей оси, точек часовых стрелок, точек автомобильных колес и др. является движением по окружности. Теоретическая и практическая важность изучения движения по окружности заключается в том, что произвольную криволинейную траекторию можно представить как сумму дуг окружностей разных радиусов (а). Самый простой вид движения по окружности — это равномерное движение.
• Равномерное движение по окружности — это движение, при котором модуль скорости материальной точки в каждой точке этой окружности остается неизменным. Такое движение характеризуется следующими величинами:
Период обращения — это время, затраченное на один полный оборот материальной точки по окружности:
Где — период обращения, — число полных оборотов материальной точки за время За единицу периода обращения в СИ принята секунда:
Частота обращения — это число оборотов материальной точки по окружности, совершаемых за единицу времени:
Где — частота обращения (иногда обозначается буквой За единицу частоты обращения в СИ принят 1 герц — частота такого обращения, когда тело за секунду совершает один полный оборот:
Период и частота обращения обратно пропорциональны друг другу:
Это означает, что во сколько раз уменьшится частота обращения, во столько же раз увеличится период обращения, и наоборот.
Угол поворота — это угол, на который поворачивается радиус-вектор при движении материальной точки по окружности. Угол поворота измеряется отношением длины дуги окружности между начальным и конечным радиус-векторами к радиусу окружности (b):
Где — угол поворота, — длина дуги, соответствующая углу поворота, — радиус окружности. Углы поворота радиус-вектора материальной точки, движущейся равномерно по окружности, за равные промежутки времени одинаковы.
Угол поворота является скалярной величиной, единица его измерения в СИ — радиан:
• 1 рад — это угол поворота радиус-вектора, соответствующий дуге, длина которой равна радиусу окружности
Угловая скорость — это физическая величина, измеряемая отношением угла поворота к промежутку времени, за которое этот поворот совершен:
Угловая скорость материальной точки, равномерно движущейся по окружности, с течением времени остается неизменной Единица угловой скорости в СИ — радиан в секунду:
За единицу угловой скорости принята угловая скорость такого равномерного движения по окружности, при котором за 1 секунду радиус-вектор материальной точки поворачивается на угол в 1 радиан.
Материальная точка, движущаяся равномерно по окружности, за время, равное периоду обращения совершает один полный оборот, за это время радиус-вектор поворачивается на угол Поэтому при равномерном движении по окружности между угловой скоростью и периодом обращения (частотой обращения) имеется связь:
Линейная скорость. Скорость движения материальной точки по окружности называется линейной скоростью. Линейная скорость материальной точки, равномерно движущейся по окружности, оставаясь постоянной по модулю непрерывно изменяется по направлению и в любой точке направлена по касательной к траектории (с).
Численное значение линейной скорости при равномерном движении по окружности равно отношению пройденного пути ко времени, затраченному на его прохождение:
Материальная точка, двигаясь равномерно по окружности, за время, равное периоду обращения проходит путь, равный длине круга: Приняв это во внимание в формуле линейной скорости, получим выражение, связывающее линейную скорость с угловой скоростью:
Центростремительное ускорение:
Быстрота изменения направления линейной скорости при равномерном движении по окружности характеризуется физической величиной называемой центростремительным, или нормальным, ускорением. Вектор центростремительного, или нормального, ускорения в любой точке траектории направлен по радиусу к центру окружности (см.: с). Модуль центростремительного ускорения материальной точки при равномерном движении по окружности равен отношению квадрата линейной скорости к радиусу окружности:
Вектор центростремительного, или нормального, ускорения в любой точке траектории направлен по радиусу к центру окружности (см.: с). Модуль центростремительного ускорения материальной точки при равномерном движении по окружности равен отношению квадрата линейной скорости к радиусу окружности:
Новосибирские ученые создали инновационные датчики для приборостроительной отрасли
Точное определение угла поворота – одна из главных задач, которая стоит перед инженерами, создающими станки, авиационную и космическую технику. Команда Smart-encoder, победившая в весеннем бизнес-ускорителе А:СТАРТ, разработала датчик нового поколения, который определяет угол поворота с точностью ±2,5 угловые секунды и самостоятельно поддерживает свою точность в режиме реального времени.
Оптикоэлектронные датчики угла поворота (ОЭДУ) – важнейший элемент высокоточных систем управления в приборостроении. Сюда относится ракетно-космическая отрасль, авиационная техника, а также различные робототехнические системы в электронной промышленности и станкостроении.
Проект Smart-encoder направлен на разработку и создание отечественных ОЭДУ нового поколения с режимами метрологического самоконтроля и кратного резервирования. Разработка позволит повысить динамические, метрологические и эксплуатационные характеристики, а также уменьшить массогабаритные показатели изделий, в которых она используется.
Уникальность решения в том, что помимо самих угловых измерений введен режим линейных измерений. Они позволяют отслеживать температурные расширения и износ деталей датчика в реальном времени и вводить соответствующие поправки. Применение запатентованного учеными метода метрологического самоконтроля позволяет датчику работать в широком диапазоне температур без потери точности.
Основной метрологический элемент датчика – высокоточный измерительный растр был изготовлен специалистами АО «НПП «Геофизика-Космос» (Москва) на уникальном оборудовании, созданном учеными ИАиЭ СО РАН. Одним из основных его разработчиков является д.т.н., ведущий научный сотрудник ИАиЭ СО РАН Валерий Кирьянов.
«Наш датчик угла поворота условно можно назвать “электронным транспортиром”, который измеряет угол поворота объекта с точностью до ±2,5 угловых секунд. С его помощью можно создать, например, микросхему или деталь для автомобиля, самолета, или самого космического корабля», – добавила Анна Кирьянова, руководитель проекта.
Прототип датчика был создан в рамках программы «Старт-1» Фонда содействия инновациям. Испытания ОЭДУ успешно прошли в лабораторных условиях и показали точность ±2,5 угловые секунды. На сегодняшний день подобным результатом могут похвастаться такие зарубежные компании как Heidenhain (Германия), Renishaw (Великобритания), Fagor (Испания), Precizika Metrology (Литва/США), Koshibu Precision (Япония), которые выпускают высокоточные (погрешность преобразования от ±1,0″ до ±5″) и особо высокоточные (погрешность преобразования до ±1,0″) ОЭДУ.
«Из-за введенных санкций многие предприятия имеют серьезные проблемы с доступом к продукции зарубежных производителей ОЭДУ, поэтому у нас есть шанс решить проблему импортозамещения», – подчеркнула Анна Кирьянова.
Сейчас команда планирует осуществить первые продажи ОЭДУ, изготовленные на основе первого прототипа модели. Также ученые работают над заявкой на конкурс «Старт-2» Фонда содействия инновациям, чтобы начать разработку усовершенствованной модели ОЭДУ, которая оказалась самой востребованной по результатам проведенного CastDev клиентов в рамках бизнес-ускорителя А:СТАРТ.
«Надо понимать, что инновационный приборостроительный проект не делается “на коленке” за пару месяцев. До прототипа была создана большая научно-технологическая база, которая подкреплялась лабораторными испытаниями и созданием образцов.
Но только научных компетенций было недостаточно, поэтому мы решили пройти акселерационную программу в Академпарке. За два месяца по коммерциализации проекта мы сделали больше, чем за последние 10 лет. Мы пообщались с огромным количество заводов по всей России, получили обратную связь и теперь четко понимаем, какие модели датчиков могут быть наиболее востребованы в стране. А:СТАРТ стал для нас хорошим ускорителем и катализатором дальнейшего развития стартапа теперь уже в стенах Академпарка на правах резидентов», – отметила Анна Кирьянова.
6.1 Угол вращения и угловая скорость — College Physics chapters 1-17
Сводка
- Определите длину дуги, угол поворота, радиус кривизны и угловую скорость.
- Вычислить угловую скорость вращения колеса автомобиля.
В главе 2 «Кинематика» мы изучали движение по прямой и вводили такие понятия, как смещение, скорость и ускорение. В главе 3 «Двумерная кинематика» рассматривается движение в двух измерениях.Движение снаряда — это частный случай двумерной кинематики, в которой объект проецируется в воздух, находясь под действием силы тяжести, и приземляется на некотором расстоянии. В этой главе мы рассматриваем ситуации, когда объект не приземляется, а движется по кривой. Мы начинаем изучение равномерного кругового движения с определения двух угловых величин, необходимых для описания вращательного движения.
Когда объекты вращаются вокруг некоторой оси — например, когда компакт-диск (компакт-диск) на рисунке 1 вращается вокруг своего центра — каждая точка в объекте движется по дуге окружности.Рассмотрим линию от центра компакт-диска до его края. Каждая яма, используемая для записи звука вдоль этой линии, перемещается под одним и тем же углом за одно и то же время. Угол поворота — это величина поворота, аналогичная линейному расстоянию. Мы определяем угол поворота [latex] \ boldsymbol {\ Delta \ theta} [/ latex] как отношение длины дуги к радиусу кривизны:
[латекс] \ boldsymbol {\ Delta \ theta \: =} [/ latex] [латекс] \ boldsymbol {\ frac {\ Delta {s}} {r}}. [/ Latex]
Рисунок 1. Все точки на компакт-диске движутся по дугам окружности. Ямки вдоль линии от центра к краю все перемещаются на один и тот же угол Δ θ за время Δ t . Рисунок 2. Радиус круга повернут на угол Δ θ . Длина дуги Δ s описана по окружности.Длина дуги [latex] \ boldsymbol {\ Delta {s}} [/ latex] — это расстояние, пройденное по круговой траектории, как показано на рисунке 2. Обратите внимание, что [latex] \ boldsymbol {r} [/ latex] — это радиус кривизны круговой траектории.
Мы знаем, что за один полный оборот длина дуги равна окружности окружности с радиусом [латекс] \ boldsymbol {r}. [/ Latex] Окружность круга равна [латексу] \ boldsymbol {2 \ pi {r }}. [/ latex] Таким образом, за один полный оборот угол поворота составляет
[латекс] \ boldsymbol {\ Delta \ theta \: =} [/ latex] [латекс] \ boldsymbol {\ frac {2 \ pi {r}} {r}} [/ latex] [латекс] \ boldsymbol {= \: 2 \ pi}. [/ Latex]
Этот результат является основой для определения единиц, используемых для измерения углов поворота, [latex] \ boldsymbol {\ Delta \ theta} [/ latex] равными радианам (рад), таким образом, что
[латекс] \ boldsymbol {2 \ pi \ textbf {rad} = 1 \ textbf {революция}.0} [/ latex]
Если [latex] \ boldsymbol {\ Delta \ theta = 2 \ pi \ textbf {rad}}, [/ latex], то компакт-диск сделал один полный оборот, и каждая точка на компакт-диске вернулась в исходное положение.0}. [/ Latex]
Насколько быстро вращается объект? Мы определяем угловую скорость [латекс] \ boldsymbol {\ omega} [/ latex] как скорость изменения угла. В символах это
[латекс] \ boldsymbol {\ omega \: =} [/ latex] [латекс] \ boldsymbol {\ frac {\ Delta \ theta} {\ Delta {t}}}, [/ латекс]
, где угловой поворот [латекс] \ boldsymbol {\ Delta \ theta} [/ latex] происходит за время [latex] \ boldsymbol {\ Delta {t}}. [/ Latex] Чем больше угол поворота в данном количество времени, тем больше угловая скорость.Единицы измерения угловой скорости — радианы в секунду (рад / с).
Угловая скорость [латекс] \ boldsymbol {\ omega} [/ latex] аналогична линейной скорости [латекс] \ boldsymbol {v}. [/ Latex] Чтобы получить точное соотношение между угловой и линейной скоростью, мы снова рассмотрим яму на вращающемся компакт-диске. Эта яма перемещает длину дуги [латекс] \ boldsymbol {\ Delta {s}} [/ latex] за время [латекс] \ boldsymbol {\ Delta {t}}, [/ latex] и поэтому имеет линейную скорость
[латекс] \ boldsymbol {v \: =} [/ latex] [латекс] \ boldsymbol {\ frac {\ Delta {s}} {\ Delta {t}}}.[/ латекс]
Из [latex] \ boldsymbol {\ Delta \ theta = \ frac {\ Delta {s}} {r}} [/ latex] мы видим, что [latex] \ boldsymbol {\ Delta {s} = r \ Delta \ theta }. [/ latex] Подставляя это в выражение для [latex] \ boldsymbol {v} [/ latex], получаем
[латекс] \ boldsymbol {v \: =} [/ latex] [латекс] \ boldsymbol {\ frac {r \ Delta \ theta} {\ Delta {t}}} [/ latex] [латекс] \ boldsymbol {= \: r \ omega}. [/ latex]
Мы записываем эти отношения двумя разными способами и получаем два разных вывода:
[латекс] \ boldsymbol {v = r \ omega \ textbf {или} \ omega \: =} [/ latex] [латекс] \ boldsymbol {\ frac {v} {r}}.[/ латекс]
Первое соотношение в [латекс] \ boldsymbol {v = r \ omega \ textbf {or} \ omega \: = \ frac {v} {r}} [/ latex] утверждает, что линейная скорость [латекс] \ boldsymbol { v} [/ latex] пропорционален расстоянию от центра вращения, таким образом, он является наибольшим для точки на ободе (самый большой [латекс] \ boldsymbol {r} [/ latex]), как и следовало ожидать. Мы также можем назвать эту линейную скорость [латекс] \ boldsymbol {v} [/ latex] точки на ободе тангенциальной скоростью . Вторую взаимосвязь в [latex] \ boldsymbol {v = r \ omega \ textbf {или} \ omega \: = \ frac {v} {r}} [/ latex] можно проиллюстрировать на примере шины движущегося автомобиля.Обратите внимание, что скорость точки на ободе шины такая же, как скорость [latex] \ boldsymbol {v} [/ latex] автомобиля. См. Рис. 4. Таким образом, чем быстрее движется машина, тем быстрее вращается шина — большой [латекс] \ boldsymbol {v} [/ latex] означает большой [латекс] \ boldsymbol {\ omega}, [/ latex], потому что [латекс ] \ boldsymbol {v = r \ omega}. [/ latex] Аналогичным образом, шина большего радиуса, вращающаяся с той же угловой скоростью ([latex] \ boldsymbol {\ omega} [/ latex]), будет иметь большую линейную скорость ( [латекс] \ boldsymbol {v} [/ латекс]) для автомобиля.
Рис. 4. Автомобиль, движущийся вправо со скоростью v , имеет шину, вращающуюся с угловой скоростью ω . Скорость протектора шины относительно оси v , такая же, как если бы автомобиль был поднят домкратом. Таким образом, автомобиль движется вперед с линейной скоростью v = r ω , где r — радиус шины. Чем больше угловая скорость шины, тем больше скорость автомобиля.Пример 1: Как быстро вращается автомобильная шина?
Рассчитайте угловую скорость автомобильной шины радиусом 0,300 м, когда автомобиль движется со скоростью [латекс] \ boldsymbol {15.0 \ textbf {m / s}} [/ latex] (примерно [латекс] \ boldsymbol {54 \ textbf {км / h}} [/ latex]). См. Рисунок 4.
Стратегия
Поскольку линейная скорость обода шины такая же, как и скорость автомобиля, мы имеем [latex] \ boldsymbol {v = 15.0 \ textbf {m / s}}. [/ Latex] Дан радиус шины быть [латексом] \ boldsymbol {r = 0.300 \ textbf {m}}. [/ Latex] Зная [латекс] \ boldsymbol {v} [/ latex] и [latex] \ boldsymbol {r}, [/ latex], мы можем использовать второе соотношение в [latex] \ жирный символ {v = r \ omega, \: \ omega = \ frac {v} {r}} [/ latex] для вычисления угловой скорости.
Решение
Для вычисления угловой скорости воспользуемся следующим соотношением:
[латекс] \ boldsymbol {\ omega \: =} [/ latex] [латекс] \ boldsymbol {\ frac {v} {r}}. [/ Latex]
Замена известных,
[латекс] \ boldsymbol {\ omega \: =} [/ латекс] [латекс] \ boldsymbol {\ frac {15.0 \ textbf {m / s}} {0.300 \ textbf {m}}} [/ latex] [latex] \ boldsymbol {= \: 50.0 \ textbf {rad / s}}. [/ Latex]
Обсуждение
Когда мы отменяем единицы в приведенном выше вычислении, мы получаем 50,0 / с. Но угловая скорость должна иметь единицы рад / с. Поскольку радианы на самом деле безразмерны (радианы определяются как отношение расстояний), мы можем просто вставить их в ответ для угловой скорости. Также обратите внимание, что если бы землерой с гораздо большими шинами, скажем, радиусом 1,20 м, двигался с той же скоростью 15.0 м / с, его колеса будут вращаться медленнее. У них была бы угловая скорость
[латекс] \ boldsymbol {\ omega = (15.0 \ textbf {m / s}) / (1.20 \ textbf {m}) = 12.5 \ textbf {rad / s}}. [/ Latex]
Оба [latex] \ boldsymbol {\ omega} [/ latex] и [latex] \ boldsymbol {v} [/ latex] имеют направления (следовательно, они имеют угловую и линейную скорости соответственно). Угловая скорость имеет только два направления относительно оси вращения — либо по часовой стрелке, либо против часовой стрелки. Линейная скорость касается пути, как показано на рисунке 5.
ЭКСПЕРИМЕНТ НА ДОМУ
Привяжите какой-либо предмет к концу веревки и поверните его по горизонтальному кругу над головой (взмахнув запястьем). Поддерживайте равномерную скорость при качании объекта и измеряйте угловую скорость движения. Какая примерная скорость объекта? Определите точку рядом с вашей рукой и выполните соответствующие измерения, чтобы рассчитать линейную скорость в этой точке. Определите другие круговые движения и измерьте их угловые скорости.
Рисунок 5. Когда объект движется по кругу, здесь муха на краю старомодной виниловой пластинки, его мгновенная скорость всегда касается круга. Направление угловой скорости в этом случае — по часовой стрелке.PHET EXPLORATIONS: LADYBUG REVOLUTION
Рисунок 6. Ladybug RevolutionПрисоединяйтесь к божьей коровке и исследуйте вращательное движение. Вращайте карусель, чтобы изменить ее угол, или выберите постоянную угловую скорость или угловое ускорение. Изучите, как круговое движение связано с координатами x, y, скоростью и ускорением жука, используя векторы или графики.
- Равномерное круговое движение — это движение по окружности с постоянной скоростью. Угол поворота [латекс] \ boldsymbol {\ Delta \ theta} [/ latex] определяется как отношение длины дуги к радиусу кривизны:
[латекс] \ boldsymbol {\ Delta \ theta \: =} [/ latex] [латекс] \ boldsymbol {\ frac {\ Delta {s}} {r}}, [/ latex]
где длина дуги [latex] \ boldsymbol {\ Delta {s}} [/ latex] — это расстояние, пройденное по круговой траектории, а [latex] \ boldsymbol {r} [/ latex] — это радиус кривизны круговой траектории.0}. [/ Latex]
- Угловая скорость [латекс] \ boldsymbol {\ omega} [/ latex] — это скорость изменения угла,
[латекс] \ boldsymbol {\ omega \: =} [/ latex] [латекс] \ boldsymbol {\ frac {\ Delta \ theta} {\ Delta {t}}}, [/ латекс]
, где вращение [латекс] \ boldsymbol {\ Delta \ theta} [/ latex] происходит за время [latex] \ boldsymbol {\ Delta {t}}. [/ Latex] Единицы угловой скорости — радианы в секунду (рад / с). Линейная скорость [латекс] \ boldsymbol {v} [/ latex] и угловая скорость [латекс] \ boldsymbol {\ omega} [/ latex] связаны соотношением
[латекс] \ boldsymbol {v = r \ omega \ textbf {или} \ omega \: =} [/ latex] [латекс] \ boldsymbol {\ frac {v} {r}}.[/ латекс]
Концептуальные вопросы
1: Существует аналогия между вращательными и линейными физическими величинами. Какие вращательные величины аналогичны расстоянию и скорости?
Задачи и упражнения
1: Грузовики с полуприцепом имеют одометр на одной ступице колеса прицепа. Ступица утяжеляется так, что она не вращается, но в ней есть шестерни для подсчета количества оборотов колеса — затем она вычисляет пройденное расстояние.Если колесо имеет диаметр 1,15 м и совершает 200 000 оборотов, сколько километров должен показывать одометр?
2: Микроволновые печи вращаются со скоростью около 6 об / мин. Что это в оборотах в секунду? Какова угловая скорость в радианах в секунду?
3: Автомобиль с шинами радиусом 0,260 м проезжает 80 000 км, прежде чем износится. Сколько оборотов делают шины без учета поддержки и изменения радиуса из-за износа?
4: а) Каков период вращения Земли в секундах? б) Какова угловая скорость Земли? (c) Учитывая, что Земля имеет радиус [латекс] \ boldsymbol {6.6 \ textbf {m}} [/ latex] на его экваторе, какова линейная скорость у поверхности Земли?
5: Бейсбольный питчер выносит руку вперед во время подачи, поворачивая предплечье вокруг локтя. Если скорость мяча в руке питчера составляет 35,0 м / с, а мяч находится на расстоянии 0,300 м от локтевого сустава, какова угловая скорость предплечья?
6: В лакроссе мяч выбрасывается из сетки на конец клюшки путем вращения клюшки и предплечья вокруг локтя.Если угловая скорость мяча относительно локтевого сустава составляет 30,0 рад / с, а мяч находится на 1,30 м от локтевого сустава, какова скорость мяча?
7: Грузовик с шинами радиусом 0,420 м движется со скоростью 32,0 м / с. Какова угловая скорость вращающихся шин в радианах в секунду? Что это в об / мин?
8: Комплексные концепции
При ударе по футбольному мячу игрок, выполняющий удар, вращает ногой вокруг тазобедренного сустава.
(a) Если скорость носка ботинка кикера равна 35.0 м / с, а тазобедренный сустав находится на расстоянии 1,05 м от кончика обуви, какова угловая скорость кончика обуви?
(b) Башмак находится в контакте с первоначально неподвижным футбольным мячом весом 0,500 кг в течение 20,0 мс. Какая средняя сила прилагается к футбольному мячу, чтобы придать ему скорость 20,0 м / с?
(c) Найдите максимальную дальность полета футбольного мяча, не обращая внимания на сопротивление воздуха.
9: Создайте свою проблему
Рассмотрим аттракцион в парке развлечений, в котором участники вращаются вокруг вертикальной оси в цилиндре с вертикальными стенками.Как только угловая скорость достигает своего полного значения, пол опускается, и трение между стенами и пассажирами препятствует их скольжению. Постройте задачу, в которой вы вычисляете необходимую угловую скорость, которая гарантирует, что всадники не соскользнут со стены. Включите свободную схему тела одного всадника. Среди переменных, которые следует учитывать, — радиус цилиндра и коэффициенты трения между одеждой гонщика и стеной.
Глоссарий
- длина дуги
- [latex] \ boldsymbol {\ Delta {s}}, [/ latex] расстояние, пройденное объектом по круговой траектории
- приямок
- крошечная выемка на спиральной дорожке, отформованной в верхней части слоя поликарбоната CD
- угол поворота
- отношение длины дуги к радиусу кривизны на круговой траектории:
[латекс] \ boldsymbol {\ Delta \ theta \: =} [/ latex] [латекс] \ boldsymbol {\ frac {\ Delta {s}} {r}} [/ латекс]
- радиус кривизны
- радиус круговой траектории
- радиан
- единица измерения углов
- угловая скорость
- [latex] \ boldsymbol {\ omega}, [/ latex] скорость изменения угла, под которым объект движется по круговой траектории
Решения
Задачи и упражнения
1:
723 км
3:
[латекс] \ boldsymbol {5 \ times10 ^ 7 \ textbf {rotations}} [/ латекс]
5:
117 рад / с
7:
8:
(а) 33.3 рад / с
(б) 500 Н
(в) 40,8 м
Определение вращения в физике.
Примеры ротации в следующих темах:
Кинетическая энергия вращения: работа, энергия и сила
- Кинетическая энергия вращения — это кинетическая энергия из-за вращения объекта и является частью его общей кинетической энергии.
- Кинетическая энергия вращения — это кинетическая энергия из-за вращения объекта , которая является частью его общей кинетической энергии.
- Рассмотрение энергии вращения отдельно вокруг оси вращения объекта дает следующую зависимость от момента инерции объекта:
- Механическая работа, прикладываемая во время поворота на , равна крутящему моменту ($ \ tau $), умноженному на угол поворота ($ \ theta $): $ W = \ tau \ theta $.
- Вращение Земли на является ярким примером кинетической энергии вращения .
Угол вращения и угловая скорость
- Угол поворота является мерой того, как далеко объект поворачивается на , а угловая скорость измеряет, насколько быстро он вращается на .
- Величина, на которую объект поворачивается на , называется углом поворота и может измеряться либо в градусах, либо в радианах.
- Скорость, с которой объект вращается , задается угловой скоростью, которая представляет собой скорость изменения угла поворота во времени.
- Радиус круга равен , повернутому на на угол $ \ Delta \ theta $.
- Угловая скорость описывает скорость вращения и ориентацию мгновенной оси, вокруг которой происходит вращение .
Сохранение энергии при вращательном движении
- Энергия сохраняется при вращательном движении так же, как и при поступательном движении.
- Простейшая ситуация вращения — это ситуация, в которой результирующая сила действует перпендикулярно радиусу диска и остается перпендикулярной, когда диск начинает вращаться на .
- Кинетическая энергия (K.E.) в вращательном движении связана с моментом вращательной инерции (I) и угловой скоростью (ω):
- Конечная кинетическая энергия вращения равна работе, совершаемой крутящим моментом:
- Это подтверждает, что проделанная работа ушла в вращательную кинетическую энергию .
Угловое положение, Theta
- Угол поворота на — это величина (угол), на которую фигура повернута на вокруг фиксированной точки — часто в центре круга.
- Когда объекты вращаются на вокруг некоторой оси — например, когда CD (компакт-диск) вращается на вокруг своего центра — каждая точка в объекте следует по дуге окружности.
- Угол поворота равен величине поворота и аналогичен линейному расстоянию.
- Таким образом, за один полный оборот угол поворота составляет:
- Радиус круга равен , повернутому на на угол Δ.
Инерция вращения
- Инерция вращения — это тенденция объекта, вращающегося на , оставаться на при вращении , если к нему не приложен крутящий момент.
- На самом деле существуют точные аналоги вращения как по силе, так и по массе.
- Вращательная инерция , как показано на, — это сопротивление объектов изменениям в их вращении .
- Другими словами, вращающийся объект останется вращающимся , а не вращающийся объект останется не вращающимся , если на него не будет действовать крутящий момент.
- Величина mr2 называется вращательной инерцией или моментом инерции точечной массы m на расстоянии r от центра вращения .
Крутящий момент
- Крутящий момент — это сила, которая заставляет объекты поворачиваться или вращаться (т.е.е., стремление силы к вращению объекта вокруг оси).
- Вращение — это особый случай углового перемещения.
- В случае вращения крутящий момент определяется относительно оси таким образом, что вектор «r» ограничивается как перпендикулярно оси вращения .
- Другими словами, плоскость движения перпендикулярна оси вращения .
- Ясно, что крутящий момент при вращении соответствует силе поступательного движения.
Взаимосвязь между крутящим моментом и угловым ускорением
- Фактически, это уравнение является вторым законом Ньютона, применяемым к системе частиц, вращающихся на и вокруг заданной оси.
- Не делает никаких предположений о постоянной скорости вращения .
- Чистый крутящий момент вокруг оси вращения равен произведению инерции вращения вокруг этой оси и углового ускорения, как показано на рисунке 1.
- С вращающимися объектами , мы можем сказать, что, если не будет приложен внешний крутящий момент, вращающийся на объект будет оставаться вращающимся , а неподвижный объект не начнет вращаться .
- Из этого мы можем заключить, что только потому, что вращающийся на объект находится в поступательном равновесии, он не обязательно находится в вращательном равновесии .
The Coriolois Force
- В системе отсчета с поворотом по часовой стрелке на отклонение происходит влево от движения объекта; в одном с поворотом против часовой стрелки отклонение вправо.
- Сила Кориолиса действует в направлении, перпендикулярном оси вращения и скорости тела во вращающейся раме .
- Пропорционально скорости объекта в кадре , вращающемся .
- Они позволяют применять законы Ньютона к вращающейся на системе .
- Этот эффект отвечает за вращение больших циклонов.
Постоянное угловое ускорение
- Постоянное угловое ускорение описывает отношения между угловой скоростью, углом поворота и временем.
- Просто используя нашу интуицию, мы можем начать видеть взаимосвязь между вращающимися величинами , такими как θ (угол поворота ), ω (угловая скорость) и α (угловое ускорение).
- Точно так же кинематика вращения , движения описывает отношения между углом поворота , углом , угловой скоростью, угловым ускорением и временем.
- Используя соотношения a = rα, v = rω и x = rθ, мы выводим все остальные кинематические уравнения для вращательного движения при постоянном ускорении:
- Связать угол поворота , угловую скорость и угловое ускорение с их эквивалентами в линейной кинематике
Угловые величины как векторы
- Направление этих величин по своей природе трудно отследить — точка на вращающемся колесе постоянно вращается на и меняет направление.
- Ось вращения колеса вращения — единственное место, которое имеет фиксированное направление.
- Представьте себе ось вращения как полюс, проходящий через центр колеса.
- Эта зависимость от перспективы несколько затрудняет определение угла поворота .
- На рисунке (а) показан диск , вращающийся на против часовой стрелки, если смотреть сверху.
Honors Rotational Kinematics
Крутящий момент
Крутящий момент (τ) — это сила, заставляющая объект поворачиваться.Если вы думаете об использовании гаечного ключа для затягивания болта, то чем ближе к болту вы прикладываете усилие, тем труднее повернуть ключ, а чем дальше от болта вы прикладываете усилие, тем легче поворачивать гаечный ключ. . Это потому, что вы создаете больший крутящий момент, когда прикладываете силу на большем расстоянии от оси вращения.
Давайте посмотрим на пример гаечного ключа, поворачивающего болт. На расстоянии от оси вращения приложена сила.Назовите это расстояние r. Когда вы прикладываете силы под углом 90 градусов к воображаемой линии, ведущей от оси вращения к точке приложения силы (известной как линия действия), вы получаете максимальный крутящий момент. По мере уменьшения угла, под которым прилагаемая сила (θ), уменьшается и крутящий момент, заставляющий болт поворачиваться. Следовательно, вы можете рассчитать прилагаемый крутящий момент как:
В некоторых случаях физики будут называть rsinθ плечом рычага или плечом момента системы.Плечо рычага — это перпендикулярное расстояние от оси вращения до точки приложения силы. С другой стороны, вы можете думать о крутящем моменте как о составляющей силы, перпендикулярной рычагу, умноженной на расстояние r. Единицы крутящего момента — это единицы силы × расстояние или Ньютон-метры (Н · м).
Вопрос: Капитан пиратов берет штурвал и вращает штурвал своего корабля, прикладывая силу в 20 Ньютонов к спице колеса.Если он прикладывает силу в радиусе 0,2 метра от оси вращения под углом 80 ° к линии действия, какой крутящий момент он прикладывает к колесу?
Ответ:
Вопрос: Механик затягивает проушины на шине, прикладывая крутящий момент 110 Н · м под углом 90 ° к линии воздействия. Какая сила прилагается, если гаечный ключ равен 0.4 метра в длину?
Ответ:
Вопрос: Какой длины должен быть гаечный ключ, если механик может приложить усилие только в 200 Н?
Ответ:
Объекты, которые не имеют ускорения вращения или нулевого крутящего момента, считаются находящимися в состоянии равновесия вращения. Это означает, что любой чистый положительный (против часовой стрелки) крутящий момент уравновешивается равным результирующим отрицательным (по часовой стрелке) крутящим моментом.
Момент инерции
Ранее инерционная масса объекта (его поступательная инерция) определялась как способность этого объекта сопротивляться линейному ускорению. Точно так же инерция вращения объекта или момент инерции описывает сопротивление объекта ускорению вращения. Обозначение момента инерции объекта — I.
Объекты, большая часть массы которых находится вблизи оси вращения, имеют небольшую инерцию вращения, в то время как объекты с большей массой, расположенные дальше от оси вращения, имеют большую инерцию вращения.
Для обычных объектов вы можете найти формулу их момента инерции. Для более сложных объектов момент инерции может быть вычислен путем умножения суммы всех отдельных частиц массы, составляющих объект, на квадрат их радиуса от оси вращения. Это может быть довольно громоздким при использовании алгебры, и поэтому, как правило, оставляется на усмотрение курсов, основанных на исчислении, или численного приближения с использованием вычислительных систем.
Вопрос: Рассчитайте момент инерции твердой сферы массой 10 кг и радиусом 0.2 мес.
Ответ:
Вопрос: Рассчитайте момент инерции для полой сферы массой 10 кг и радиусом 0,2 м.
Ответ:
Второй закон Ньютона для вращения
В главе о динамике вы узнали о силах, заставляющих объекты ускоряться. Чем больше результирующая сила, тем больше линейное (или поступательное) ускорение, и чем больше масса объекта, тем меньше поступательное ускорение.
Вращательный эквивалент этого закона, 2-й закон Ньютона для вращения, связывает крутящий момент на объекте с его результирующим угловым ускорением. Чем больше чистый крутящий момент, тем больше ускорение вращения, и чем больше инерция вращения, тем меньше ускорение вращения:
Вопрос: Какое угловое ускорение испытывает однородный твердый диск массой 2 кг и радиусом 0?1 м при приложении крутящего момента 10 Н · м? Предположим, диск вращается вокруг своего центра.
Ответ:
Вопрос: Раунд-А-бой на игровой площадке с моментом инерции 100 кг · м 2 начинается в состоянии покоя и ускоряется силой 150 Н в радиусе 1 м от центра. Если эта сила приложена под углом 90 ° от линии действия в течение времени 0.5 секунд, какова конечная скорость вращения раунда?
Ответ: Начнем с создания нашего вращательного кинематического стола:
Поскольку вы знаете только два элемента в таблице, вы должны найти третий, прежде чем решать его с помощью кинематических уравнений вращения. Поскольку вам дан момент инерции кругового движения, а также приложенная сила, вы можете вычислить угловое ускорение, используя 2-й закон Ньютона для вращательного движения.
Теперь используйте вашу кинематику вращения, чтобы найти окончательную угловую скорость кругового удара.
Предсказать угол поворота для приложенного крутящего момента?
Это самая сложная проблема, с которой вы можете столкнуться, когда дело касается физики твердого тела. Вращательный момент довольно сложен. Обратите внимание, что масса не имеет значения для вращения.Тензор интерции является массовым эквивалентом вращений. Однако для вращений важно, как распределяется масса. Так что это зависит от формы объекта. Unity рассчитывает тензор интерции для всех объемов коллайдера и заданной массы.
Тензор взаимодействия 3×3 в Unity хранится как диагональная матрица (intertiaTensor) в сочетании с вращением (inertiaRotation). Диагональная матрица представляет собой инерцию вокруг каждой главной оси. Таким образом, расчет углового ускорения на основе крутящего момента уже довольно сложен.Вдобавок к этому способ применения перетаскивания в Unity не основан на физике реального мира, а представляет собой просто процентное снижение угловой скорости.
Изменение угла за кадр — это угловая скорость объекта. Конечная угловая скорость зависит от нескольких факторов. Прежде всего, Unity имеет относительно низкую настройку максимальной угловой скорости, чтобы гарантировать, что физика не выйдет из-под контроля. Это также необходимо учитывать, иначе вам придется увеличить этот предел в настройках физики.В остальном конечная скорость — это баланс между ускорением, вызванным приложенным постоянным крутящим моментом, и противодействующим сопротивлением.
Я никогда не пробовал это для вращения, но вспомогательные методы здесь должны работать одинаково для вращений, учитывая правильные значения.
Обратите внимание: если объект, который вы вращаете, не имеет однородного интервала вокруг всей оси, и вы прикладываете крутящий момент вокруг нелокальной оси, поэтому ось относительно объекта действительно изменяется, невозможно рассчитать правильное значение в качестве углового ускорения. довольно сильно отличается в зависимости от применяемой оси.. Обратите внимание, что трехмерный физический движок Unity сохраняет не угловой момент, а угловую скорость. Это упрощение, но предотвращает некоторые явления реального мира, такие как теорема о промежуточной оси, которая ответственна за кувырок, замеченный в этом видео в конце. Так что в Unity вы никогда не получите такого кувырка. Как только вы прекращаете приложение крутящего момента, ось вращения не меняется, потому что Unity сохраняет угловую скорость вместо углового момента.
Здесь я уже пытался объяснить некоторые последствия.Вот вопрос разработчика игры на ту же тему.
В настоящее время у меня нет Unity (или среды программирования в целом), поэтому я не могу проводить какие-либо тесты или предоставлять какие-либо конкретные примеры кода.
Угол поворота — обзор
2.1 Представления и операторы сплетения
В оставшейся части этой статьи мы сконцентрируемся на группах диэдра D ( n ), которые определены как группа сохраняющих геометрию отображений плоскости. которые отображают правильный n-сторонний многоугольник на себя.Набор X представляет собой набор узлов сетки на плоскости, инвариантных относительно группы диэдра. Часто X будет набором пикселей в квадратном окне.
Наиболее важные свойства диэдральных групп резюмированы в следующей теореме:
Теорема 1
- (1)
Диэдральная группа D ( n ) состоит из n вращений с углами поворота. 2πkn, k = 0… n − 1 и произведения этих углов 2πk / n, k = 0… n − 1 и произведения этих вращений с отражениями относительно любой из осей симметрии многоугольника .
- (2)
D ( n ) имеет 2n элементов .
- (3)
Элементы D ( n ) можно записать в виде пар ( ρ k , σ l ) где p — поворот на угол 2πn, σ — фиксированное отражение, а l равно нулю или единице . Умножение между элементами в D ( n ) дается формулой :
ρkσlρmσn = ρk + mσl + nifl = 0ρk − mσl + nifl = 1
Это показывает, что группы диэдра полукруглые. — прямые произведения двух циклических групп с двумя и n элементами . Другой пример прямого произведения полу — — это полу — прямое произведение группы вращения и группы перемещений . Подробнее см. [15].
Теперь предположим, что X — конечное множество, а G — группа, работающая на X . Предположим далее, что f — это функция от X до комплексных чисел. Для элемента группы g ∈ G мы определяем новую функцию f g на X как: fgx = fg − 1x.Если набор X состоит из N элементов , тогда мы можем идентифицировать пространство всех комплексных функций на X с N -мерным пространством ℂ N , и отображение f↦fg определяет линейное отображение ℂN → ℂN. Выбирая фиксированный базис в ℂ N , мы получаем, таким образом, для каждого г ∈ G и N × N матрицу T ( г ), такую, что f г = T ( г ) f .Это отображение g↦Tg, кроме того, обладает тем свойством, что Tg1g2 = Tg1Tg2 для всех g 1 g 2 ∈ G . При изменении базы в ℂ N с помощью матрицы B матрицы T ( g ) отображаются в BT ( g ) B — 1 . Это приводит к следующему определению. пространство комплексных матриц N × N , такое что T ( г 1 г 2 ) = T ( г 1 ) T ( г 2 ) для всех g 1 , g 2 ∈ G .
Два представления матрицы T 1 , T 2 эквивалентны, если существует матрица B , такая что : T 1 ( г ) = BT 2 ( г ) B — 1 для всех g ∈ G .
Уравнение T 1 ( г ) = BT 2 ( г ) B — л эквивалентно T 1 ( г ) B = BT 2 ( г ) , что также имеет значение, когда B необратимо . Мы говорим, что матрица B является матрицей переплетения для представления T, если T ( g ) B = BT ( g ) выполняется для всех g ∈ G .
Поскольку эквивалентные матричные представления описывают один и тот же объект в разных системах координат, мы можем попытаться найти систему, в которой данное представление имеет простейшее описание. Это приводит к следующему определению:
Определение 2
- (1)
Матричное представление T сводимо, если существует матрица B такая, что все матрицы BT ( g ) B — 1 имеют вид T1gT12g0T2g с квадратными матрицами T 1 ( г ) и T 2 ( г ).
- (2)
Матричное представление T неприводимо, если оно не сводится .
- (3)
Матричное представление T полностью сокращается, если существует такая матрица B, что все матрицы BT ( g ) B — l имеют вид
T1g0… 00T2g… 000 ⋯ 000… TKg
с несократимыми компонентами T k .
Для конечных групп теория представлений довольно проста: существует только конечное число различных неприводимых представлений, и все представления полностью приводимы.Более того, можно показать, что все неприводимые представления конечных групп конечномерны. Для групп диэдра этот результат резюмируется в следующей теореме:
Теорема 2
Обозначим через p поворот с углом поворота 2πn и через σ отражение от оси симметрии, как и раньше . Все элементы в D ( n ) тогда имеют форму σ l ρ k с ( l = 0,1; k = 0,… n — 1) и , если мы положим ω = e2πi / n , тогда неприводимые представления D ( n ) даются следующим образом: :
- (1)
Если n четное, то существует четыре неприводимых по размерам представления :
T11σlρk = 1T21σlρk = −1lT31σlρk = −1kT41σlρk = −1k + l
и есть n2−1 два — размерных неприводимых представлений :
ρ00 jTjk2 0ωjkω − jk0с j = 1,… n2−1
Если n нечетное, то существует два одноразмерных неприводимых представления — :
T11σlρk = 1T21σlρk = −1l
и есть n − 12 два — размерных неприводимые представления :
Tj2ρk = ωjk00ω − jkTj2σρk = 0ωjkω − jk0
с j = 1,… n − 12.
В нашем исследовании сингулярных разложений G -симметричных процессов мы в основном будем использовать следующую теорему, которая описывает структуру сплетающих операторов неприводимых представлений. Эта теорема известна как лемма Шура:
Теорема 3
- (1)
Предположим, что T — неприводимое представление, а A — сплетающий оператор. Тогда A = c ∙ id, где c — константа, а id — оператор идентичности .
- (2)
Неприводимые представления коммутативных групп одномерны .
Это можно обобщить до операторов переплетения A двух неприводимых представлений S , T одной и той же группы в двух разных пространствах, для которых AT ( g ) = S ( g ) A для всех g . Тогда можно показать, что A либо 0, либо изоморфизм.
Мы знаем, что конечные представления групп диэдра полностью приводимы, и поэтому можем предположить, что у нас есть система координат, в которой матрицы T ( g ) имеют блочно-диагональную форму
Tg = T1g0… 00T2g… 000… 000… TMg
, где T m являются несократимыми представлениями D ( n ). Теперь рассмотрим оператор переплетения C и запишем C в соответствующей блочно-диагональной форме:
C = C11C12… C1MC21C22… C2M⋅⋅… ⋅CM1CM2… CMM.
Подставляя это в уравнение переплетения CT ( г ) = T ( г ) C дает:
TgC = T1gC11T1gC12… T1gC1MT2gC21T2gC22… T2gC2M⋅⋅12TM… ⋅TMgMC1… … C2MTMg⋅⋅… ⋅CM1T1gCM2T2g… CMMTMg = CTg
Для C i , j это дает матричное уравнение T i ( g ) C ij = T j ( g ) C ij и C ij , таким образом, является оператором переплетения для несократимых представлений T i и T j .Из леммы Шура следует, что матрицы C ij либо кратны единице, либо равны нулю:
C = α11Eα12E… 0α21Eα22E… 0⋅⋅… ⋅00… αMME
(где матрицы E являются единичными матрицами разных размеров).
Переставляя базовые элементы, мы обнаруживаем, что все операторы переплетения C имеют блочно-диагональную форму:
C = C1g0… 00C2g ⋯ 000 ⋯ 000… CMg.
Вращение — основы вращательного движения
Основы вращательного движения
По сути, вращательное движение похоже на поступательное движение.Понятно? Хорошо, следующая глава.
Ну да ладно, есть тонкости. Но главное помнить, что все время и энергия, которые вы вкладываете в изучение того, как вещи скользят по столам или стреляют из пушек, по-прежнему полностью актуальны — с одной изюминкой. (Понять? Повернуть? Потому что это вращение? Э? Прекрасно, неважно.)
Вместо положения вращательное движение имеет дело с изменениями угла , (θ). Объект всегда будет на вращаться на — то есть вращаться или двигаться по кругу — вокруг оси вращения .Земля вращается вокруг оси, проходящей от Северного полюса до Южного полюса, создавая день и ночь; фигуристы крутятся вокруг оси от головы до ног, создавая головокружительные золотые медали; Star Fox вращается по оси от носа к корме своего космического корабля, создавая кувырки DO A BARREL ROLL.
Ось вращения, однако, также может находиться за пределами вращающегося объекта. Солнце, например, находится на оси, вокруг которой вращается Земля по своей орбите.
Угол — это просто способ измерить, насколько точно объект повернулся или как далеко он ушел по кругу.Конечно, мы могли бы также измерить расстояние вокруг круга с точки зрения положения (скажем, по окружности), но угол — очень удобное сокращение, и оно пригодится, если нас больше беспокоят детали вращения, чем перевод. Подсказка: в этой главе мы больше озабочены вращением, чем переводом.
Поскольку угол и положение дают нам одинаковую информацию, мы можем преобразовать их, если знаем радиус окружности. Объект, который вращается на угол θ, будет двигаться по дуге длиной:
s = rθ
Здесь r — это радиус круга, по которому движется объект.И s , и r измеряются в метрах, поэтому угол технически безразмерен. В качестве бухгалтерского инструмента мы измеряем угол в радиан, . Это похоже на градусы, с которыми вы, вероятно, знакомы: 90 ° — это прямой угол или четверть круга, 180 ° — это изменение направления или полукруг и т. Д., Но в другом масштабе. В то время как 1 ° равен кругу (поскольку полный поворот равен 360 °), 1 рад равен кругу: радианы разбивают круг на 2π части вместо 360.К сожалению, у «2π heelflip» нет такого же кольца, как у «360 heelflip», но мы решим эту проблему, как только физик выиграет медаль X-Games.
Вот радиан, эквивалентный некоторым распространенным углам:
Радианы можно переводить в градусы умножением на, но со временем вы научитесь любить радианы так же сильно, как мы. * К тому же у вас нет выбора. , поскольку мы будем использовать его в этой главе, поэтому Стокгольмский синдром нам очень поможет.
Угловая скорость
Итак, если мы измеряем угол вместо положения при вращательном движении, нам нужно знать, как угол изменяется при перемещении объектов.Введите угловую скорость (ω) и угловое ускорение (α). Угловая скорость измеряется в рад / с, точно так же поступательная скорость измеряется в м / с и представляет собой изменение угла за данный момент времени. Автомобиль может двигаться со скоростью 30 м / с, но его колеса вращаются со скоростью 130 рад / с.
Угловое ускорение — это скорость изменения угловой скорости, измеряемая в рад / с 2 , так же как поступательное ускорение измеряется в м / с 2 .По мере того, как машина набирает скорость, колеса крутятся быстрее.
Угловая скорость и угловое ускорение могут быть связаны с их поступательными аналогами точно так же, как угол связан с расстоянием дуги:
v t = rω
a t = rα
Примечание. что эти формулы дают ответы для вращательного движения в радианах. Индекс t здесь потому, что эти скорости и углы тангенциальные, — они направлены по касательной к окружности в точке, где в настоящее время находится наш объект.
Это означает, что v t и a t всегда меняют направление , если объект вращается. (Меняются ли они также по величине, зависит от α.) Это также означает, что у вращающегося объекта — например, записи — внешняя сторона движется быстрее, чем внутренняя, даже если они вращаются с той же угловой скоростью. Ого.
Это действительно ключевое различие между вращательным и поступательным движением. Объект может двигаться с постоянной скоростью, но изменять скорость вращения — например, фигурист, выполняющий лутц.Другой способ сформулировать это — принцип копейки: когда велосипед за пенни-фартинг движется, его колеса должны вращаться с совершенно разными скоростями, потому что радиусы двух колес очень разные, но их поступательные скорости идентичны (в противном случае колеса будет отделяться от рамы, и ваш, по иронии судьбы, старомодный велосипед — это не столько забавный способ передвижения, сколько отвратительный инструмент для создания дорожной сыпи).
Мы можем связать θ , ω и α друг с другом так же, как мы обрабатывали x , v и a в поступательном движении.Краткое описание некоторых ключевых идей и формул кинематики ниже.
- Объект, движущийся с постоянной скоростью v в течение t секунд, будет перемещаться x метра:
x = vt
- Объект, который движется с начальной скоростью v 0 до конечной скорости v за t секунд имеет ускорение a :
- Объект, который начинается в позиции x 0 с начальной скоростью v 0 и ускоряется со скоростью объект окажется в положении x за t секунд:
- Квадрат текущей скорости объекта v равен квадрату его начальной скорости v 0 плюс двукратное произведение его текущего положения x и ускорения a :
v 2 = v 0 2 9 0848 +2 ax
Теперь, если вы добавите слово «угловой» несколько раз в этот список, вы получите довольно полную формулировку кинематики вращения.Угловая скорость — это изменение угла, угловое ускорение — это изменение угловой скорости, а voila — вращательное движение.
- Объект, движущийся с постоянной угловой скоростью ω в течение t секунд, повернется на θ радиан:
θ = ωt
- Объект, который движется с начальной угловой скоростью ω 0 до конечной угловой скорости ω за т секунд имеет угловое ускорение α :
- Объект, начинающийся под углом θ 0 с начальной угловой скоростью ω 0 и ускоряется со скоростью α окажется под углом θ за t секунды:
- Квадрат текущей угловой скорости объекта ω равен квадрату его начальной угловой скорости ω 0 плюс двойное произведение его текущего угла θ и углового ускорения α :
ω 2 = ω 0 2 90 848 + 2αθ
Круговое движение
Если объект вынужден вращаться по кругу — скажем, американские горки, объезжающие петлю, или шар на веревке, вращающийся над вашей головой — мы можем еще больше сказать о его движении .Сила, которая удерживает наш движущийся объект по кругу, будь то сила реакции дорожки американских горок или натяжение струны, называется центростремительной силой .
Центростремительная сила всегда направлена к центру круга. ** Второй закон Ньютона гласит, что центростремительная сила должна иметь соответствующее ускорение, называемое (творчески) центростремительное ускорение :
F c = ma c
Центростремительное ускорение также указывает на центр круга.Из-за этого он находится на расстоянии 90 ° (кхм, рад) от тангенциальной скорости вращающегося объекта, и поэтому никак не влияет на скорость объекта — только на его направление.
Размер a c — и, следовательно, F c — напрямую связан с тангенциальной скоростью объекта, v t , и радиусом круга, по которому он движется, r :
Чем быстрее движется объект или чем меньший поворот он пытается сделать, тем большее усилие требуется, чтобы заставить его двигаться по кругу.
Это теория, лежащая в основе разворота самолета по крену — когда-либо был в самолете, который взлетает в направлении, противоположном его запланированной траектории полета? Самолет должен развернуться, и он делает это с помощью , крена : наклоняя крылья в поворот. Подъемная сила на плоскости, обычно направленная вертикально, затем наклоняется внутрь.
Чем больше угол крена, тем больше становится горизонтальная составляющая подъемной силы и тем большую центростремительную силу может создать самолет, позволяя ему разворачиваться.
Распространенные ошибки
Радианы, радианы, радианы. Используйте их, знайте их, любите их. За один оборот приходится 2π рад.
Brain Snack
Узнайте о серьезных банковских действиях «Голубых ангелов».
* Радианы — это очень элегантный способ измерения углов — по сути, это длина дуги окружности с радиусом 1. И они делают триггерные функции, такие как синус и косинус, более красивыми в классе исчисления. И они заставляют вас походить на ученого.Поверьте, они классные. Даже Рад.
** Это не то же самое, что центробежная сила , которую большинство энтузиастов парков развлечений используют для описания ощущения прижатия к креслу на петле американских горок. Многие люди попытаются сказать вам, что они неправы, что центробежной силы не существует — это неправда. Однако центробежная сила — это то, что физики называют фиктивной силой: сила, которая таинственным образом появляется из глубин озера Лох-Несс ночами, когда полная луна находится низко в небе и ощущается особенно неинерциальное ощущение в воздухе.Как фиктивная сила, центробежная сила не подчиняется типичным законам действия-противодействия, а вместо этого является просто результатом инерции, стремящейся нести объект по прямой. Попробуйте по-настоящему быстро повернуть в машине, посмотрите, как движутся пассажиры, а затем спросите их, не существует ли центробежной силы.
Угол поворота
А вращение это трансформация в плоскости, которая поворачивает каждую точку фигуры на определенный угол и направление относительно фиксированной точки.
Неподвижная точка называется центр вращения .
Величина поворота называется углом поворота и измеряется в градусах.
Вы можете использовать транспортир для измерения указанного угла против часовой стрелки.
Рассмотрим рисунок ниже.
Здесь, Δ А ‘ B ‘ О получается вращением Δ А B О к 180 ° о происхождении.Обратите внимание, что оба А О А ‘ а также B О B ‘ прямые.
Так, м ∠ А О А ‘ знак равно 180 ° знак равно м ∠ B О B ‘ .
Пример:
Сколько степеней имеет Δ Икс Y Z был повернут против часовой стрелки, чтобы получить Δ Икс ‘ Y ‘ Z ‘ ?
А . 90 ° B . 180 ° C . 270 ° D . 360 °
Определите соответствующие вершины вращения.
Икс ( — 6 , 2 ) → Икс ‘ ( 2 , 6 ) Y ( — 2 , 4 ) → Y ‘ ( 4 , 2 ) Z ( — 4 , 5 ) → Z ‘ ( 5 , 4 )
Точка вращения — это начало координат, нарисуйте линии, соединяющие одну из точек, скажем Икс и это изображение к источнику.
Вы можете видеть, что линии образуют угол 270 ° , против часовой стрелки.
Следовательно, Δ Икс ‘ Y ‘ Z ‘ получается вращением Δ Икс Y Z против часовой стрелки на 270 ° о происхождении.
Итак, правильный выбор — C .
Также обратите внимание, что связь между соответствующими вершинами есть
(
Икс
,
у
)
→
(
—
у
,
Икс
)
который показывает вращение против часовой стрелки
270
°
о происхождении.



