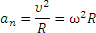Поворот — Википедия

Поворот фигуры в плоскости относительно точки O против часовой стрелки на угол α

Поворо́т (враще́ние) — движение, при котором, по крайней мере, одна точка плоскости (пространства) остаётся неподвижной.

Вращение плоскости (пространства) называется собственным (вращение первого рода) или несобственным (вращение второго рода) в зависимости от того, сохраняет оно или нет ориентацию плоскости (пространства). Часто под термином вращение понимают собственное вращение.

Для двумерной плоскости можно дать другое, эквивалентное, определение вращения: вращение плоскости это движение, при котором каждый луч, исходящий из данной точки поворачивается на один и тот же угол в одном и том же направлении.

Неподвижная точка называется центром вращения

, неподвижная прямая называется осью вращения и т. д.

Несобственное вращение (т.е. вращение, которое не сохраняет ориентацию) нельзя сделать малым (в смысле расстояния между каждой точкой и её образом), собственное — можно сделать сколь угодно малым для любой ограниченной области пространства (то есть можно подобрать для ограниченной области сколь угодно малое собственное вращение). Несобственное вращение является композицией некоторого зеркального отражения (на плоскости — осевой симметрии, в пространстве нечётной размерности — центральной) и собственного вращения.

В аналитической геометрии на плоскости собственное вращение в прямоугольных декартовых координатах выражается формулами:

x′=xcos⁡φ−ysin⁡φ,{\displaystyle x’=x\cos \varphi -y\sin \varphi ,}

y′=xsin⁡φ+ycos⁡φ,{\displaystyle y’=x\sin \varphi +y\cos \varphi ,}

где φ{\displaystyle \varphi } — угол поворота, а центр вращения выбран в начале координат.
При тех же условиях несобственное вращение плоскости выражается формулой

x′=xcos⁡φ+ysin⁡φ,{\displaystyle x’=x\cos \varphi +y\sin \varphi ,}

y′=xsin⁡φ−ycos⁡φ.{\displaystyle y’=x\sin \varphi -y\cos \varphi .}

В планиметрии поворот около точки [центра] O{\displaystyle O} на угол поворота α{\displaystyle \alpha } обозначается также ROα{\displaystyle R_{O}^{\alpha }}, где α∈(−π;π].{\displaystyle \alpha \in (-\pi ;\pi ].}
Поворот на угол β′=α+2π⋅n,{\displaystyle \beta ‘=\alpha +2\pi \cdot n,} где n∈Z{\displaystyle n\in \mathbb {Z} } и α∈(−π;π]{\displaystyle \alpha \in (-\pi ;\pi ]} отождествляется с поворотом ROα{\displaystyle R_{O}^{\alpha }} (угол поворота на полный угол 2π (360∘){\displaystyle 2\pi ~(360^{\circ })} зачастую также называется оборотом).
Если углы поворотов α,β{\displaystyle \alpha ,\beta } и их сумма α+β{\displaystyle \alpha +\beta } заключены в пределах от −π{\displaystyle -\pi } до π,{\displaystyle \pi ,} то при последовательном выполнении (композиции) поворотов их углы складываются (см. также #Композиция поворотов на плоскости (комплексный вид)):

ROβ∘ROα=ROα+β,{\displaystyle R_{O}^{\beta }\circ R_{O}^{\alpha }=R_{O}^{\alpha +\beta },}

причём композиция двух поворотов обладает свойством коммутативности:

ROβ∘ROα=ROα∘ROβ.{\displaystyle R_{O}^{\beta }\circ R_{O}^{\alpha }=R_{O}^{\alpha }\circ R_{O}^{\beta }.}

См. также Изометрия (математика)

Матричный вид[править | править код]

При использовании матричного подхода точку (x,y){\displaystyle (x,y)} записывают в виде вектора, затем умножают на матрицу:

[x′y′]=[cos⁡θ−sin⁡θsin⁡θcos⁡θ][xy]{\displaystyle {\begin{bmatrix}x’\\y’\end{bmatrix}}={\begin{bmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \end{bmatrix}}{\begin{bmatrix}x\\y\end{bmatrix}}}.

(x′,y′){\displaystyle (x’,y’)} координаты точки, полученные вращением точки (x,y){\displaystyle (x,y)}.

Векторы [xy]{\displaystyle {\begin{bmatrix}x\\y\end{bmatrix}}} и [x′y′]{\displaystyle {\begin{bmatrix}x’\\y’\end{bmatrix}}} имеют одинаковую размерность.

Комплексный вид[править | править код]

Точку можно вращать с помощью комплексных чисел. Множество всех этих чисел геометрически представляет собой двумерную плоскость. Точка (x,y){\displaystyle (x,y)} на плоскости представлена комплексным числом z=x+iy{\displaystyle z=x+iy}.

Вращение точки на угол θ{\displaystyle \theta } можно осуществить умножением eiθ{\displaystyle e^{i\theta }}, используя формулу Эйлера

eiθz=(cos⁡θ+isin⁡θ)(x+iy)=(xcos⁡θ+iycos⁡θ+ixsin⁡θ−ysin⁡θ)=(xcos⁡θ−ysin⁡θ)+i(xsin⁡θ+ycos⁡θ)=x′+iy′,{\displaystyle {\begin{aligned}e^{i\theta }z&=(\cos \theta +i\sin \theta )(x+iy)\\&=(x\cos \theta +iy\cos \theta +ix\sin \theta -y\sin \theta )\\&=(x\cos \theta -y\sin \theta )+i(x\sin \theta +y\cos \theta )\\&=x’+iy’,\end{aligned}}}

что дает такой же результат,

x′=xcos⁡θ−ysin⁡θy′=xsin⁡θ+ycos⁡θ.{\displaystyle {\begin{aligned}x’&=x\cos \theta -y\sin \theta \\y’&=x\sin \theta +y\cos \theta .\end{aligned}}}

Композиция поворотов на плоскости (комплексный вид)[править | править код]

Пусть совершается вначале поворот вокруг точки a{\displaystyle a} на угол α{\displaystyle \alpha }, затем поворот вокруг точки b{\displaystyle b} на угол β{\displaystyle \beta }. И пусть точки a{\displaystyle a} и b{\displaystyle b} представлены в виде комплексных чисел вида x+iy{\displaystyle x+iy}. Положительным считается поворот против часовой стрелки. Такая композиция поворотов эквивалентна повороту на угол γ =α+β{\displaystyle \gamma ~=\alpha +\beta } вокруг точки c{\displaystyle c}, которая вычисляется по формуле c=a+(b−a)eiα′sin⁡α′sin⁡γ′{\displaystyle c=a+(b-a)e^{i{\alpha ‘}}{\frac {\sin \alpha ‘}{\sin \gamma ‘}}},

где α′=α2{\displaystyle \alpha ‘={\frac {\alpha }{2}}}, а γ′=γ2{\displaystyle \gamma ‘={\frac {\gamma }{2}}}

Если α+β=0{\displaystyle \alpha +\beta =0}, то композиция поворотов эквивалентна параллельному сдвигу плоскости на вектор r=(b−a)(eiα−1){\displaystyle r=(b-a)(e^{i\alpha }-1)}

Кинематика вращательного движения

Лекция

Кинематика вращательного движения

План

1. Тангенциальное и нормальное ускорение

2. Радиус кривизны траектории

3. Угловая скорость, вектор угла поворота, угловое ускорение

4. Связь линейной и угловой скорости

5. Связь линейных и угловых характеристик

1. Тангенциальное и нормальное ускорение

Две составляющие ускорения: тангенциальное ускорение и нормальное ускорение.

Тангенциальное ускорение направлено по касательной к траектории

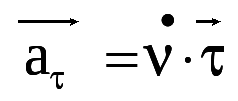
Нормальное ускорение направлено по нормали к траектории

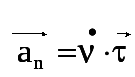
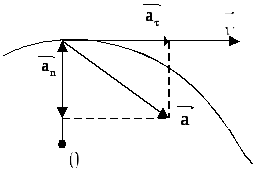
Тангенциальное ускорение характеризует изменение скорости по величине. Если скорость по величине не изменяется, то тангенциальная составляющая равна нулю, а нормальная составляющая ускорения равна полному ускорению.

Нормальное ускорение характеризует изменение скорости по направлению. Если направление скорости не изменяется, движение происходит по прямолинейной траектории.

В общем случае полное ускорение:

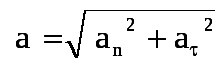
Итак, нормальная составляющая вектора ускорения

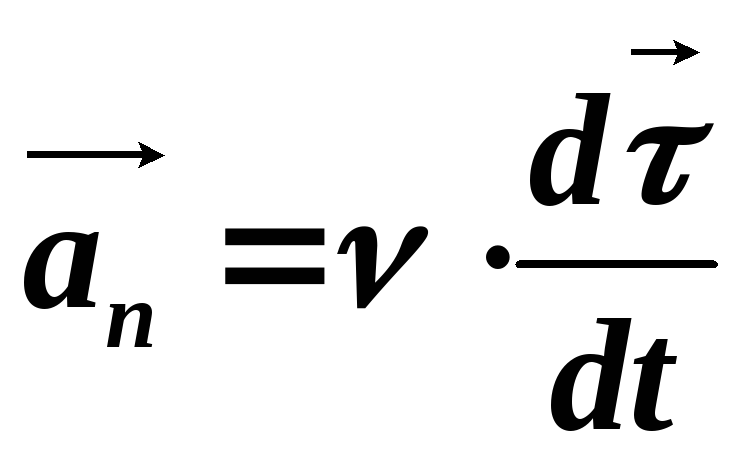
Чтобы выяснить свойства нормального ускорения, надо установить, чем определяется , т.е быстрота изменения со временем направления касательной к траектории. Она тем больше (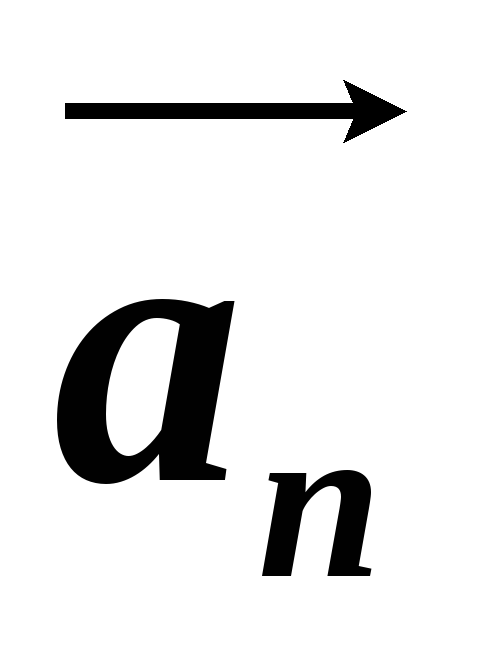), чем больше искривлена траектория и чем быстрее перемещается частица по траектории.

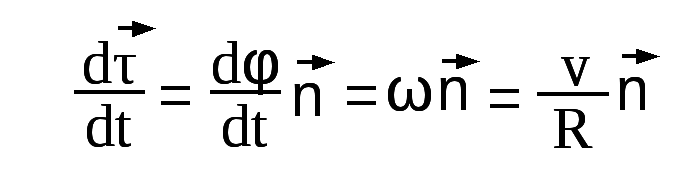
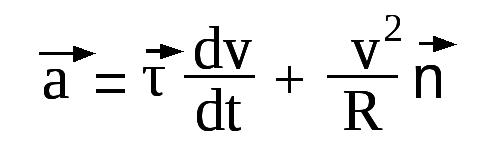
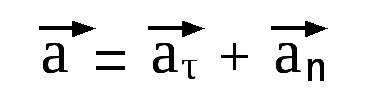
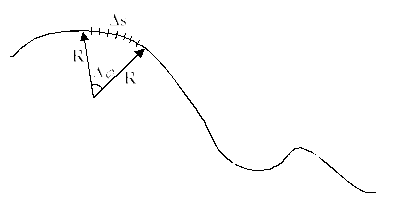
2. Радиус кривизны траектории

Радиус кривизны – это радиус окружности, которая сливается в данном месте с кривой на бесконечно малом её участке.

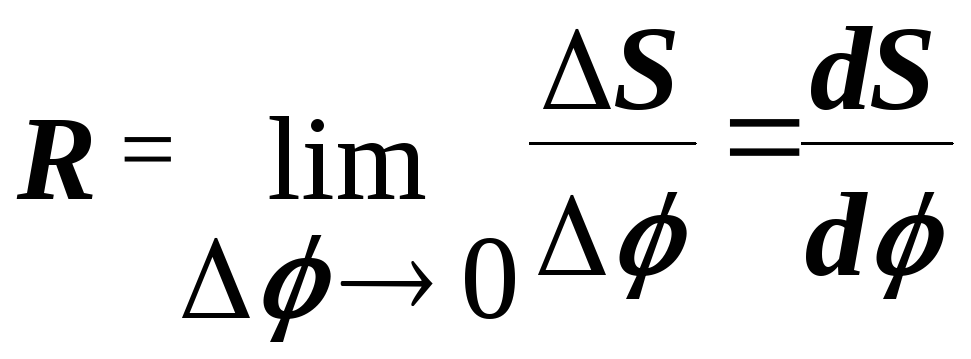
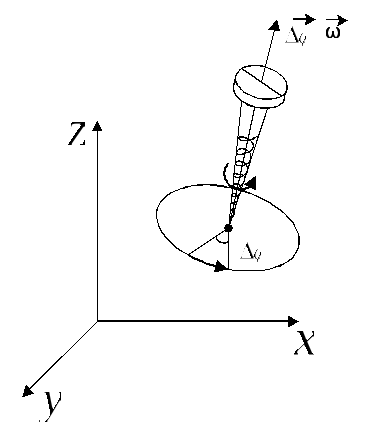
3. Угловая скорость, вектор угла поворота, угловое ускорение.

Любой поворот полностью определяется указанием оси вращения и угла поворота Δφ относительно этой оси. Если поворот осуществляется на малый угол Δφ << 2π, то можно ввести понятие вектор угла поворота.

Вектор 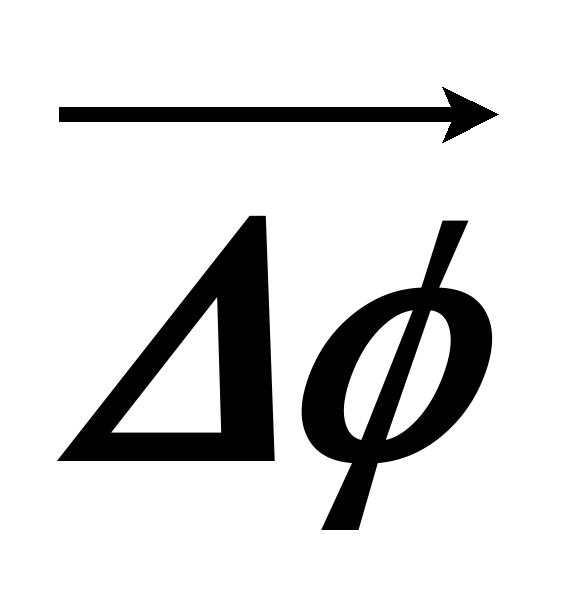направлен вдоль оси вращения, т.е. перпендикулярно плоскости, в которой происходит вращение.

Ориентация этого вектора определяется правилом буравчика.

Абсолютное значение вектора равно углу поворота Δφ.

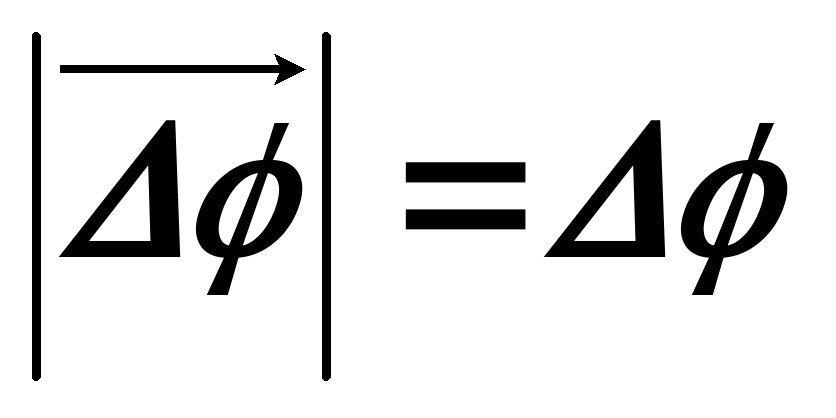
Для того, чтобы величин была вектором, она должна не только направление и абсолютное значение, но и удовлетворять правилу сложения векторов. Это можно показать, что при векторном сложении двух углов поворота правило параллелограмма не выполняется. Оно будет справедливо лишь для малого

Δφ << 2π

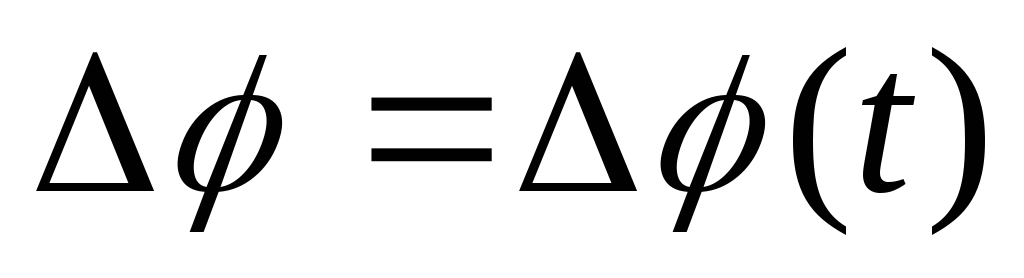
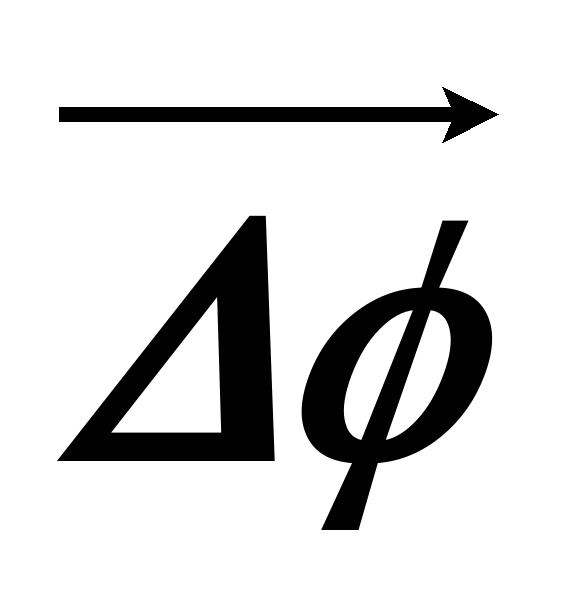— неполный вектор.

Угловой скоростью называется вектор , направление которого: определяет ориентацию плоскости вращения и по правилу буравчика направление вращения.

Модуль вектора равен производной от угла поворота по времени:

Угловая скорость, в отличие от угла поворота, является полным вектором.

Вектор 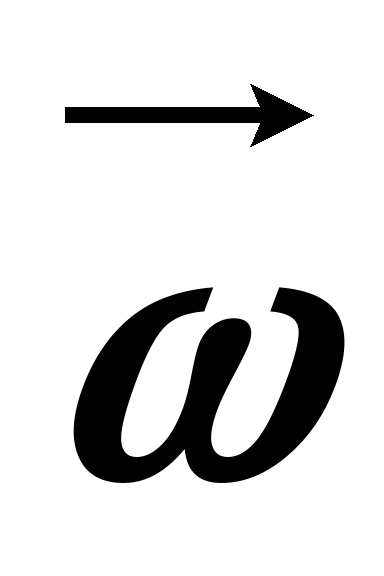может изменяться как за счёт изменения скорости вращения тела вокруг оси (по величине), так и за счёт поворота оси вращения в пространстве (по направлению).

Пусть за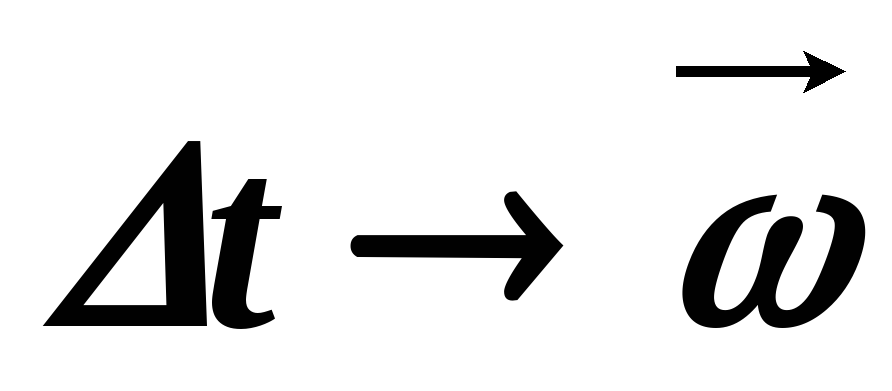

Изменение вектора угловой скорости со временем характеризуется величиной угловое ускорение:

Ускоренное

Замедленное

Модуль углового ускорения измеряется в

Угловое ускорение также как и угловая скорость – псевдовектор.

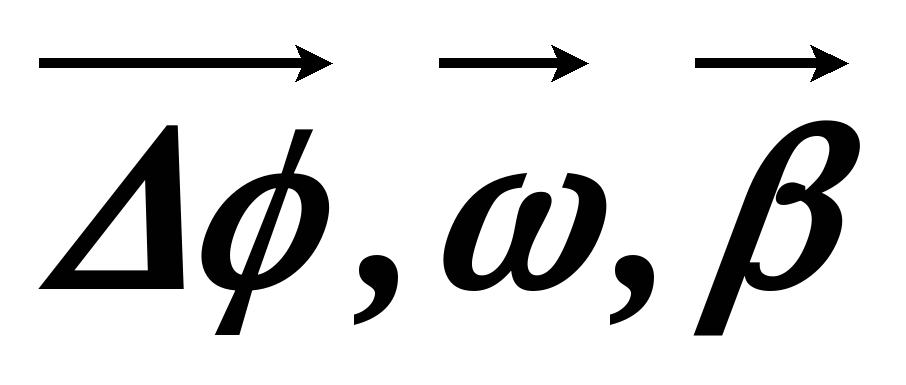— псевдовектора, т.к. направление вектора поворота

связывается с направлением вращения тела.

4. Связь линейной и угловой скорости

Пусть за малый Δt тело повернулось на Δφ. Пусть точки за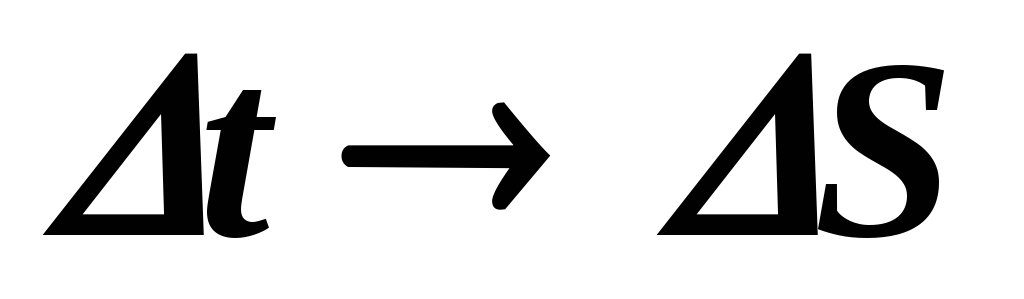

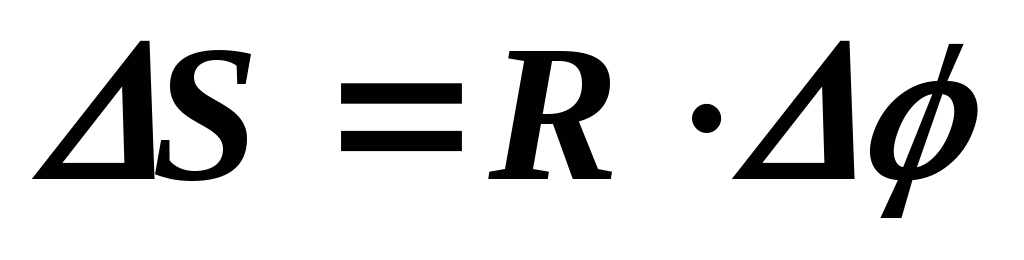
Модуль линейной скорости

Связь векторов линейной и угловой скоростей: положение точки определяется радиусом-вектором , вектор 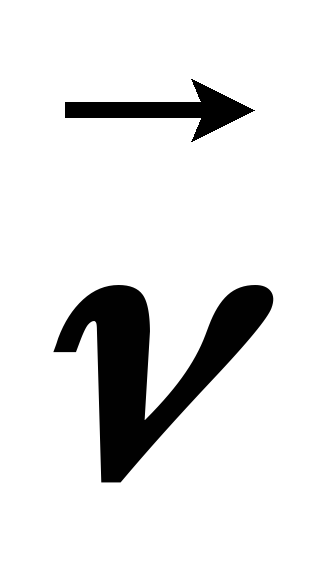из рисунка определяется как векторное произведение 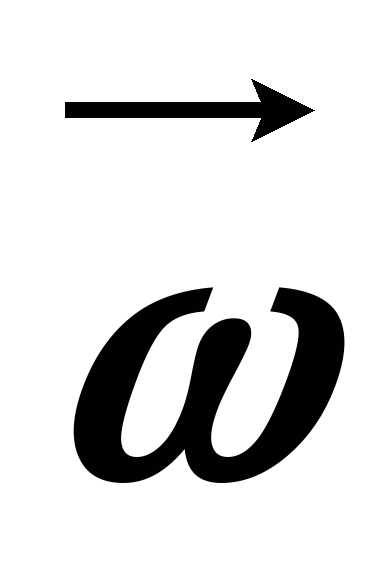и

.

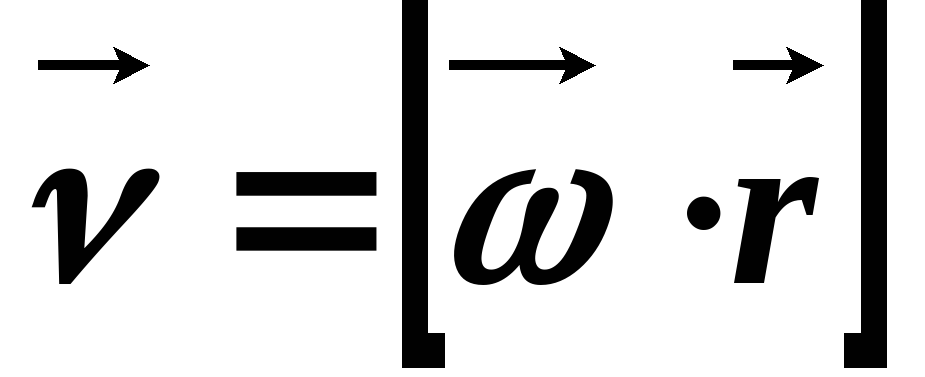
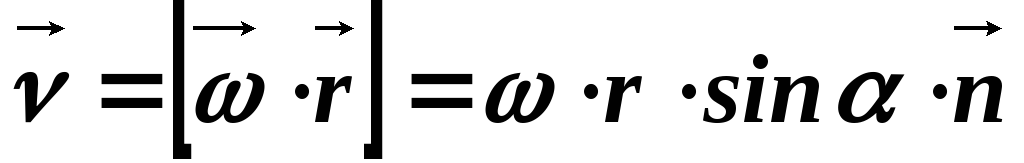
Изменение радиуса-вектора со временем только по направлению называется прецессией.

5. Связь линейных и угловых характеристик

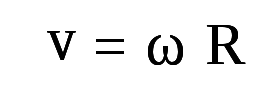
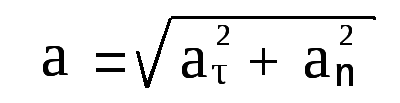
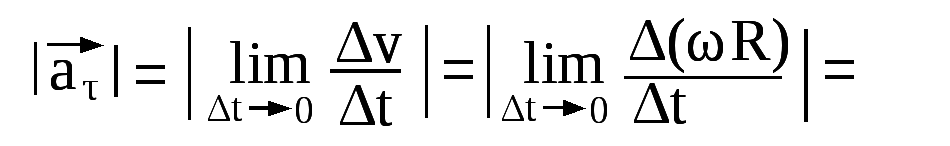
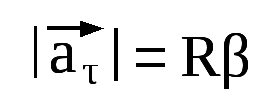
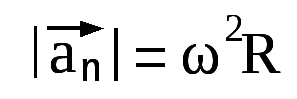
угол поворота — это… Что такое угол поворота?

3.5 угол поворота (steering angle): Общий угол полного отклонения, измеряемый между передними и задними колесами при их перемещении относительно одной или более вертикальной оси из положения обычного прямолинейного движения в положение поворота.

Примечания

1 Угол поворота для многоосных машин определяют между колесами первого переднего и последнего заднего мостов

2 Для рулевого управления с поворотными кулаками и трапецией характерно, что угол поворота колес, расположенных с внутренней стороны поворота, превышает угол поворота колес, расположенных с внешней стороны поворота, следовательно, при использовании такого рулевого управления должно быть также указано место измерения угла поворота.

Для определения угла поворота, полученного в случае комбинированного применения кинематических схем, включая систему управления с поворотными кулаками и трапецией, также необходимо указать место измерения угла поворота.

3.5 угол поворота (steering angle): Общий угол полного отклонения, измеряемый между передними и задними колесами при их перемещении относительно одной или более вертикальных осей из положения обычного прямолинейного движения в положение поворота.

Примечания

1. Угол поворота для многоосных машин определяют между колесами первого переднего и последнего заднего мостов.

2. Для системы рулевого управления Аккерманн (с поворотными кулаками, рычагами и трапецией) характерно, что угол поворота колес, расположенных с внутренней стороны поворота, превышает угол поворота колес, расположенных с внешней стороны поворота. Следовательно, при использовании такого рулевого управления должно быть также указано место измерения угла поворота.

Для определения угла поворота, полученного в случае комбинированного применения кинематических схем, включая систему Аккерманн, также необходимо указать место измерения угла поворота.

4.14. Угол поворота — общий угол отклонения, измеряемый между передними и задними колесами при их перемещении относительно одной или более вертикальных осей из положения обычного прямолинейного движения в положение поворота.

4.14.1. Угол поворота для многоосных машин определяют между колесами первого переднего и последнего заднего мостов.

4.14.2. Для ручного управления с поворотными кулаками и трапецией характерно, что угол поворота колес, расположенных с внутренней стороны поворота, превышает угол поворота колес, расположенных с внешней стороны поворота. Следовательно, для этой системы должно быть также указано место измерения угла поворота.

4.14.3. Угол поворота, полученный в случае комбинированного применения кинематических схем, включая систему управления с поворотными кулаками и трапецией, определяют по п. 4.14, при этом должно быть указано место измерения в соответствии с требованиями п. 4.14.2.

2.4.3 угол поворота: Угол между проекцией продольной оси транспортного средства и линией пересечения плоскости колеса, которая представляет собой центральную плоскость шины, перпендикулярную к оси вращения колеса, и поверхности дороги.

6.19 угол поворота: Угловое перемещение запирающего или регулирующего элемента, исчисленное от закрытого положения затвора.

6.19 угол поворота

Величина углового перемещения запирающего или регулирующего элемента, исчисленная от закрытого положения затвора.

Смотри также родственные термины:

2.3.8 угол поворота ( e): Угол, указывающий расположение светоотражающего материала при помощи соответствующего обозначения с учетом поворота вокруг исходной оси.

6.20 угол поворота номинальный

Величина полного угла поворота без учета допусков.

6.22 угол поворота относительный

Отношение значения текущего угла поворота к номинальному углу поворота.

192 угол поворота рабочего оборудования a

Максимальный угол поворота рабочего оборудования от одного крайнего положения до другого

—

Угол поворота сварного шва b

Угол, который образует поперечная ось шва со своим нулевым положением (см. черт. 3).

6.21 угол поворота текущий

Угол поворота в промежутке от закрытого до полностью открытого положения затвора.

Словарь-справочник терминов нормативно-технической документации. academic.ru. 2015.

7.2. Вращательное движение. Угловая скорость, угловое ускорение

Движение твердого тела, при котором все его точки перемещаются по окружности, центры которой расположены на перпендикулярной этим окружностям неподвижной прямой, называется вращательным. Неподвижная прямая, на которой лежат центры круговых траекторий то­чек тела, называется его осью вращения. Для образования оси вра­щения достаточно закрепить какие-либо две точки тела. В качестве примеров вращательного движения тел можно привести движение две­рей или створок окон при их открывании или закрывании.

Представим себе тело в виде цилиндра, ось AB которого лежит в подшипниках (рис. 7.3).

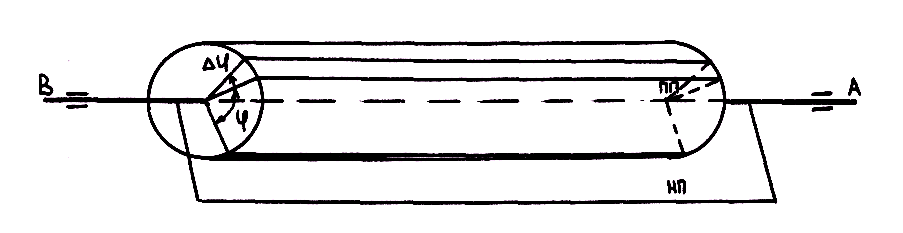
Рис. 7.3. К анализу вращательного движения твердого тела

Движением одной какой-либо точки однозначно определить вращательное движение тела нельзя.

Для установления закона вращательного движения тела, по кото­рому можно определять его положение в данный момент, проведем через ось вращения тела связанную только с нею неподвижную полуплоскость НП, а внутри тела отметим подвижную полуплоскость, ко­торая вращается около оси вместе с телом, теперь угол φ, образуемый в каждый данный момент времени полуплоскостями НП и ПП, точно определяет положение тела в пространстве (см. рис. 7.3). Угол φ называется углом поворота и выражается в радианах. Чтобы определять положение тела в пространстве в любой момент времени, необходимо знать зависимость между углом поворота φ и временем t, т. е. знать закон вращательного движения тела:

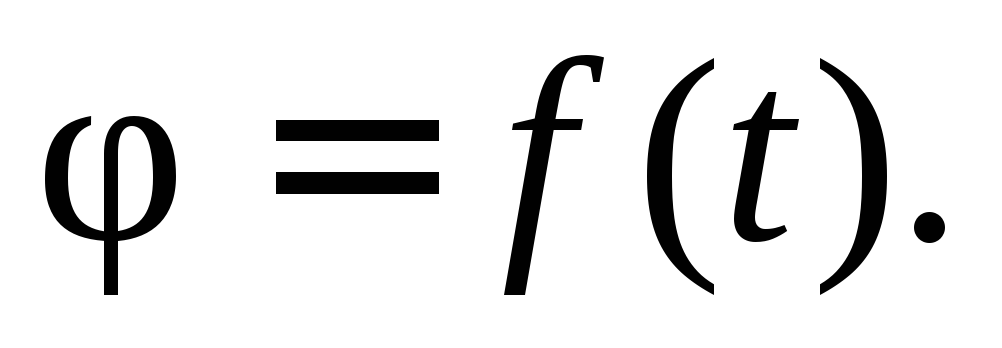
Быстрота изменения угла поворота во времени характеризуется величиной, которая называется угловой скоростью.

Представим, что в некоторый момент времени t положение вращающегося тела определяется углом поворота φ, а в момент t + Δt – углом поворота φ + Δ φ. Следовательно, за время Δt тело повернулось на угол Δ φ, и величина

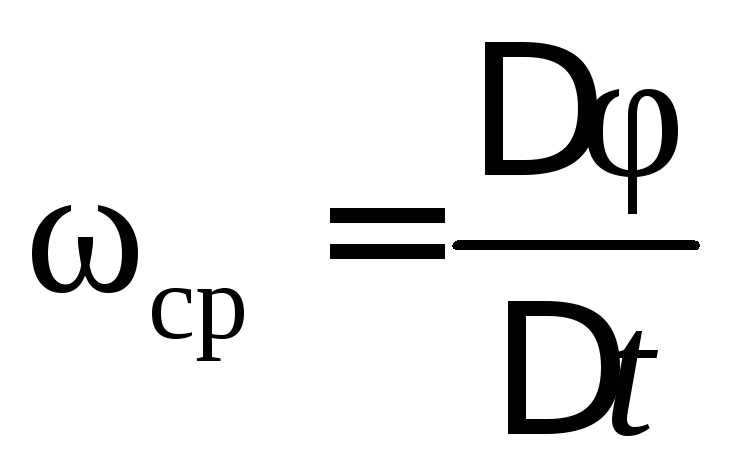
называется средней угловой скоростью.

Единицей угловой скорости является 1 рад/с. Характеристикой быстроты изменения угловой скорости служит угловое ускорение, обозначаемое . Среднее ускорение ;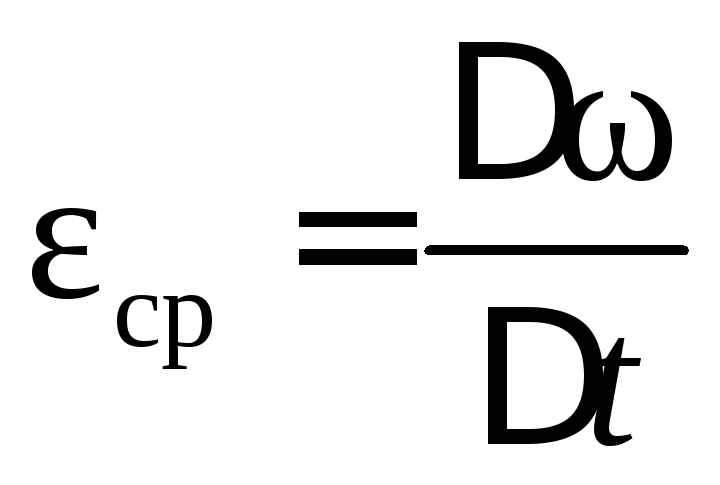

.

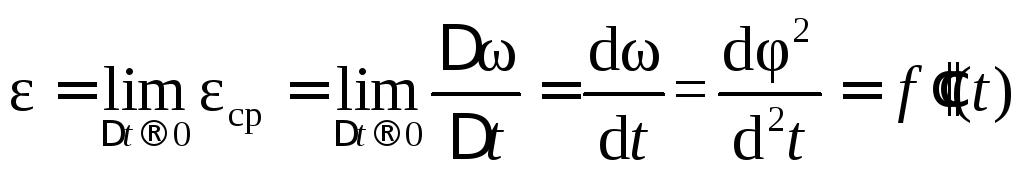Единица углового ускорения 1 рад/с².

Условимся угол поворота, отсчитываемый против хода часовой стрелки, считать положительным, а отсчитываемый по ходу часовой стрелки – отрицательным.

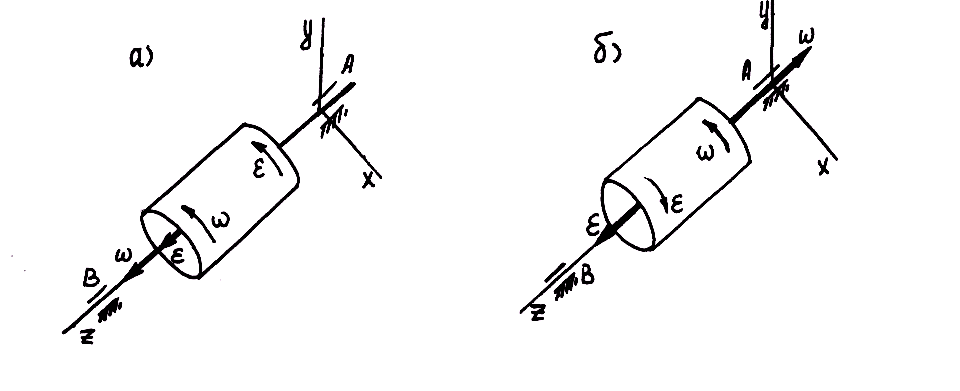
б

а

Рис. 7.4. К определению вида вращательного движения

Векторы и – это скользящие векторы, которые направлены по оси вращения, чтобы, глядя из конца вектора (или ), видеть вращение, происходящее против часовой стрелки.

Если векторы и направлены в одну сторону (рис. 7.4, а), то вращательное движение тела ускоренное – угловая скорость возрастает. Если векторы и направлены в противоположные стороны, то вращение тела замедленное – угловая скорость уменьшается (рис. 7.4, б).

7.3. Частные случаи вращательного движения

1. Равномерное вращательное движение. Если угловое ускорение 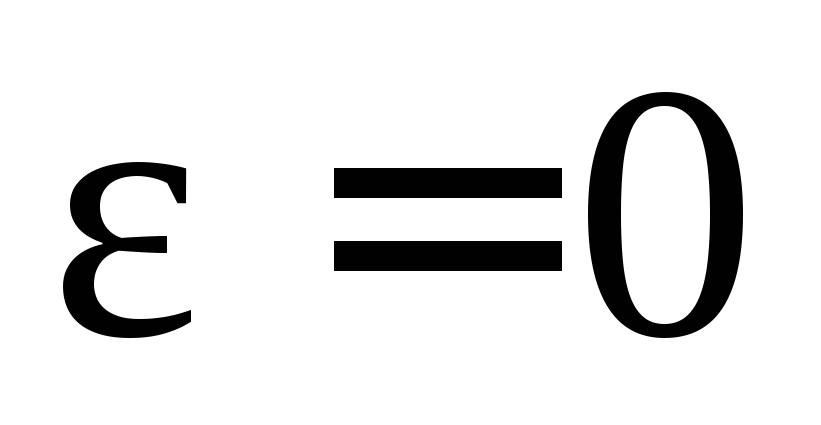и, следовательно, угловая скорость

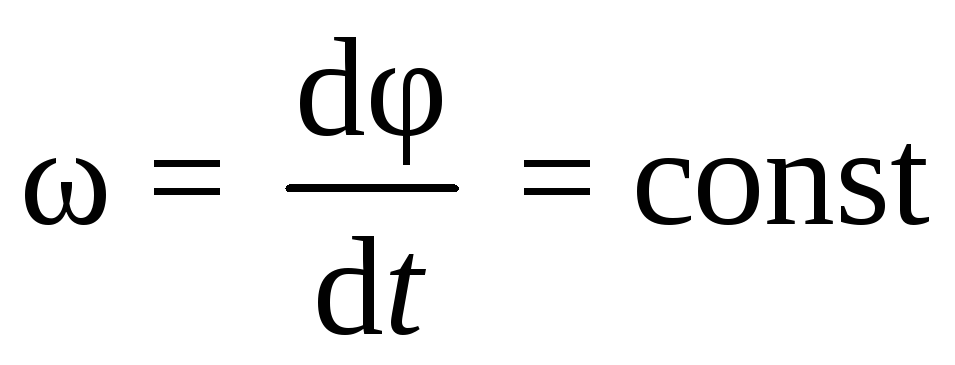, (7.1)

то вращательное движение называется равномерным. Из выражения (7.1) после разделения переменных получим

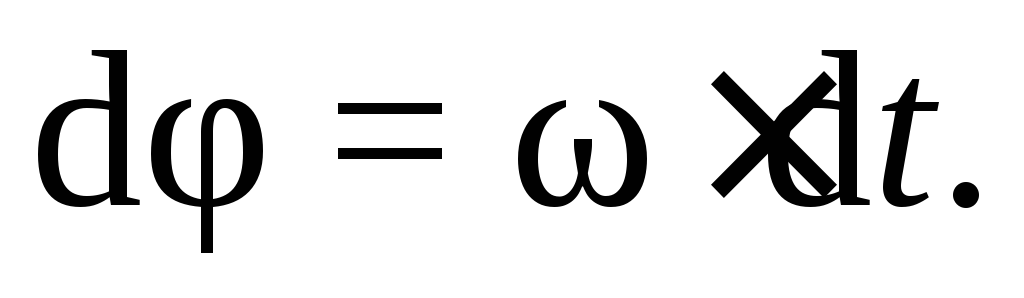
Если при изменении времени от 0 до t угол поворота изменялся от φ₀ (начальный угол поворота) до φ, то, интегрируя уравнение в этих пределах:

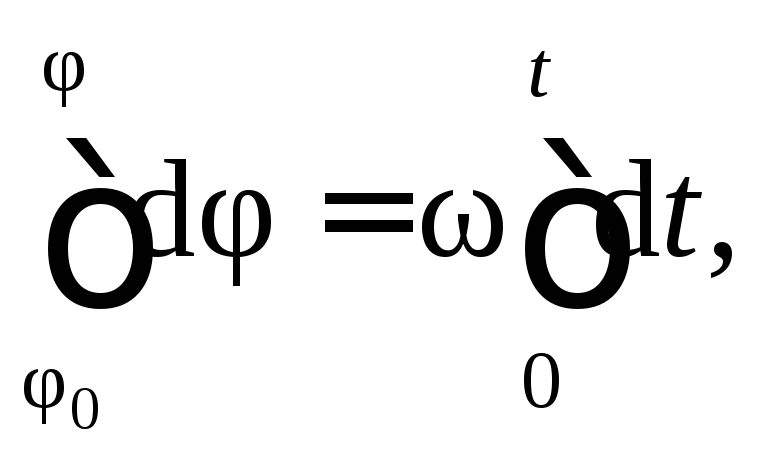
получаем уравнение равномерного вращательного движения

,

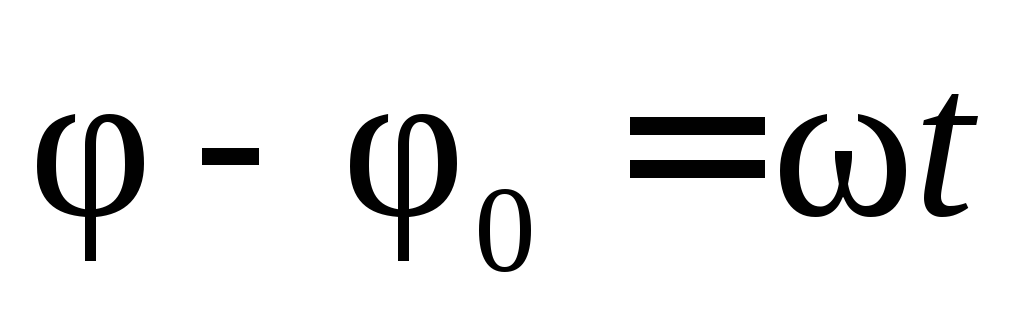которое в окончательном виде записывается так:

.

Если , то

.

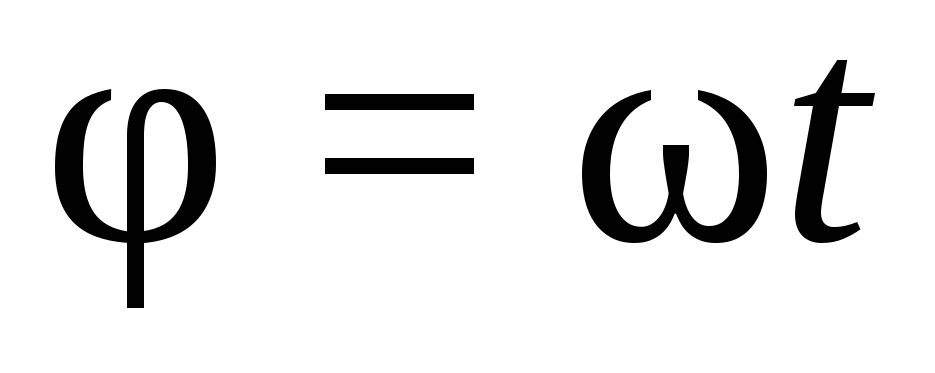Таким образом, при равномерном вращательном движении угловая скорость

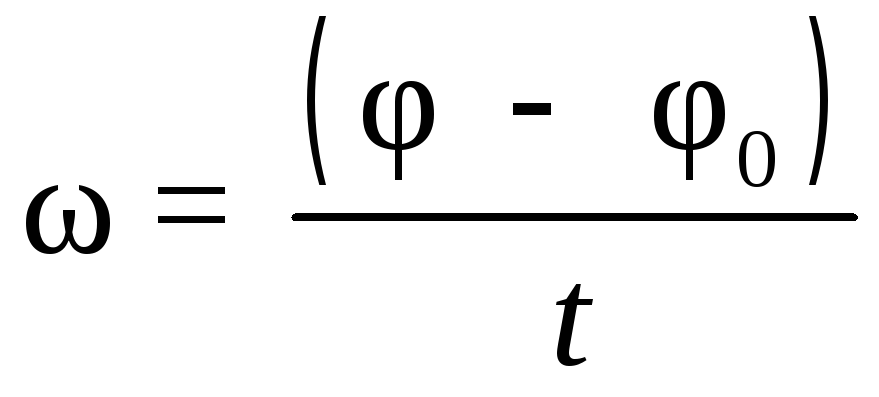или при .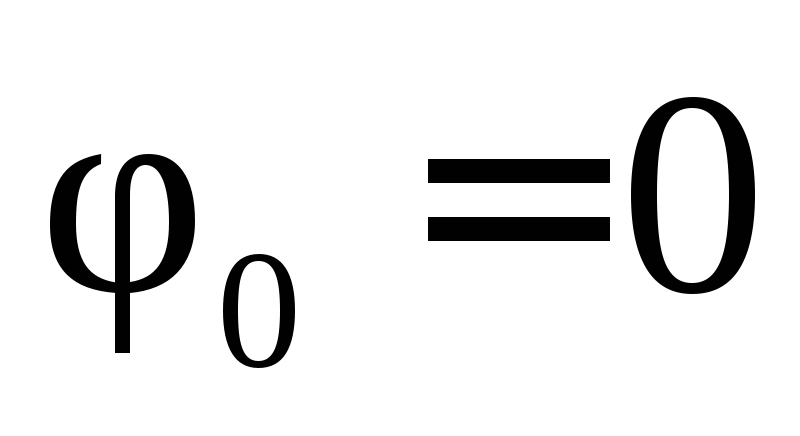

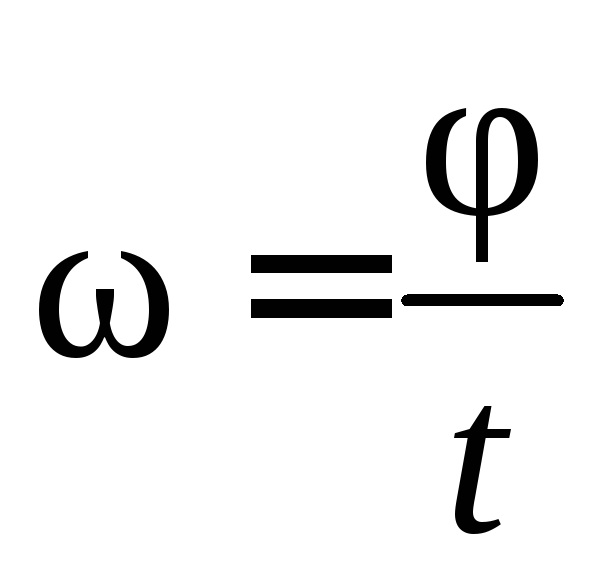2. Равнопеременное вращательное движение. Если угловое ускорение

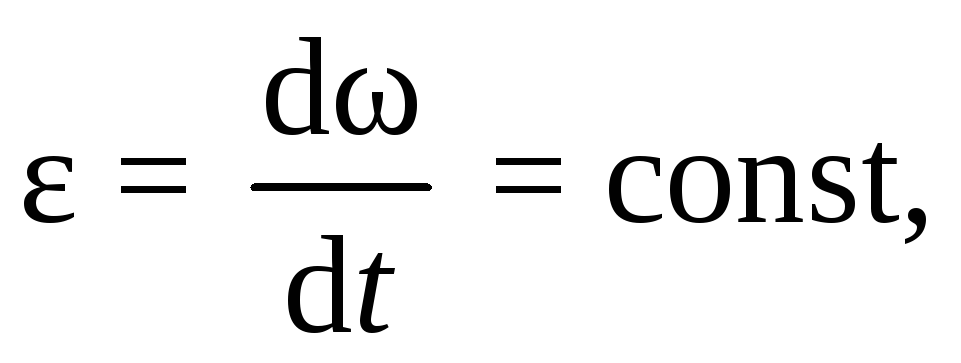(7.2)

то вращательное движение называется равнопеременным. Производя разделение переменных в выражении (7.2):

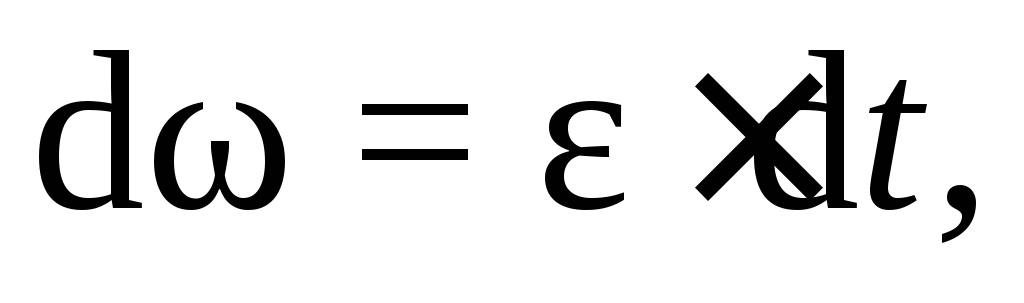
и приняв, что при изменении времени от 0 до t угловая скорость изменилась от 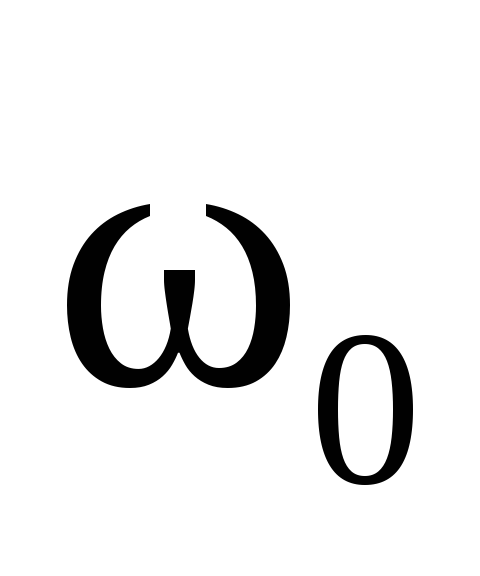(начальная угловая скорость) до , проинтегрируем уравнение в этих пределах:

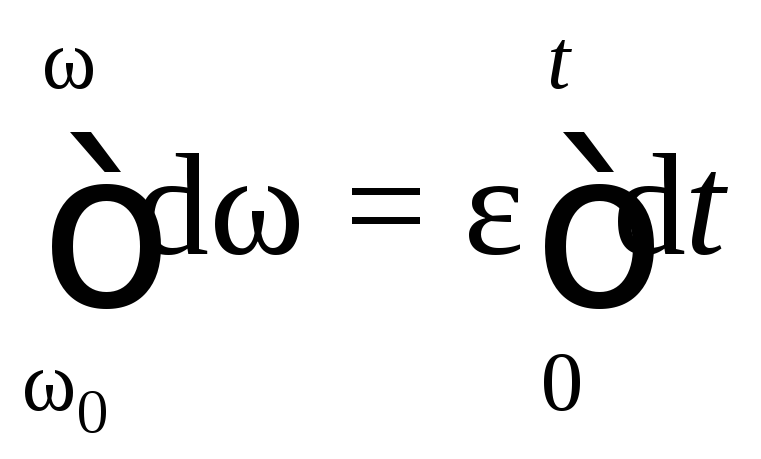или ,

т. е. получим уравнение

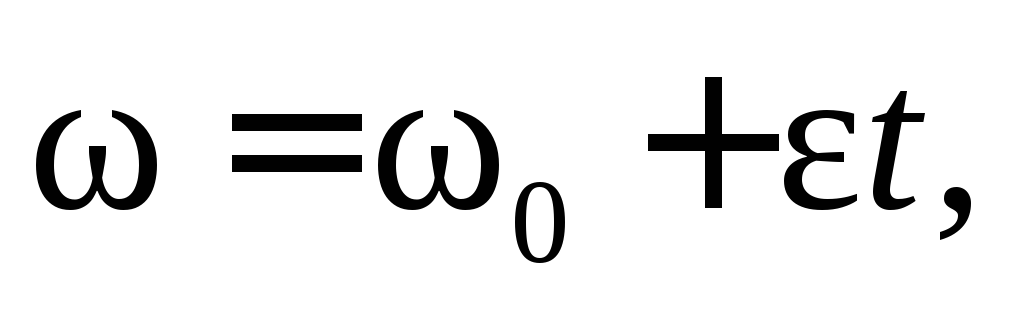(7.3)

выражающее значение угловой скорости в любой момент времени.

Закон равнопеременного вращательного движения 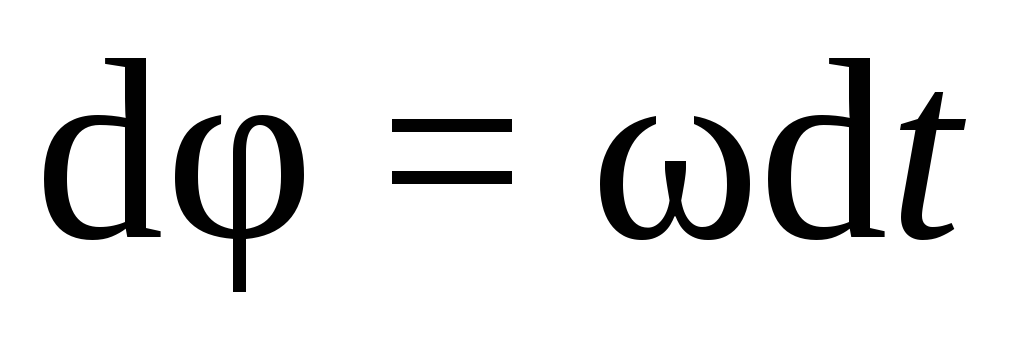или, с учетом уравнения (7.3):

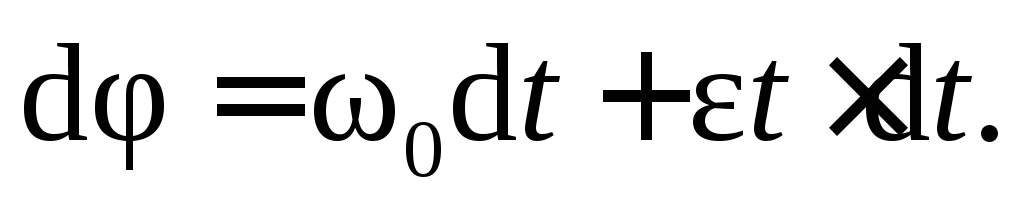
Полагая, что в течение времени от 0 до t угол поворота изменялся от до, проинтегрируем уравнение в этих пределах:

или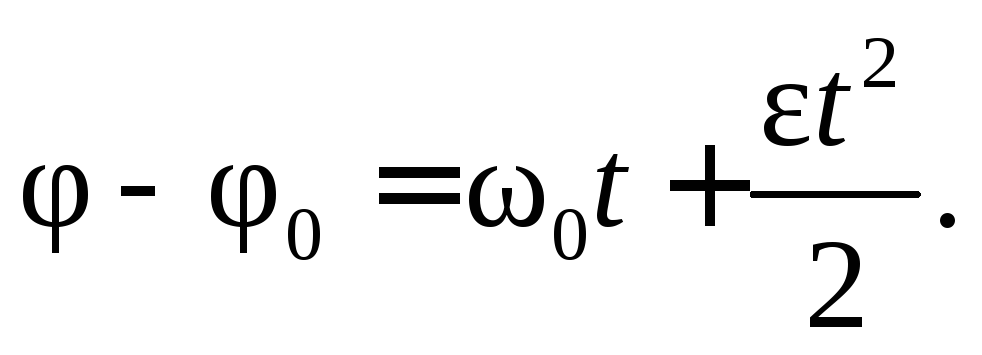

Уравнение равнопеременного вращательного движения в оконча­тельном виде

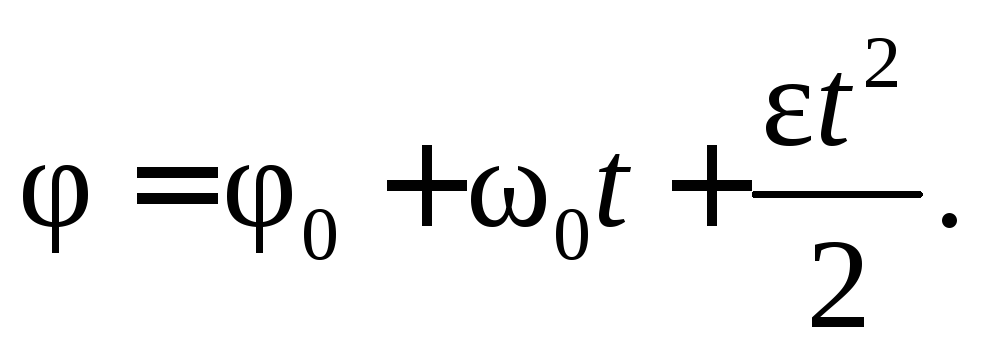(7.4)

Первую вспомогательную формулу получим, исключив из формул (7.3) и (7.4) время:

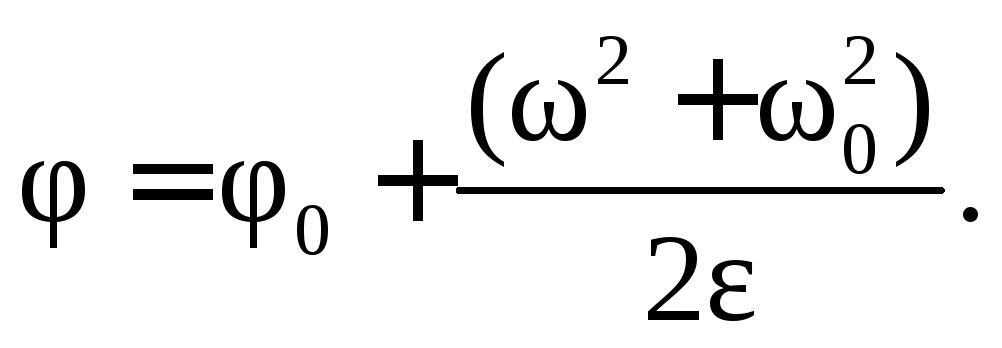(7.5)

Исключив из тех же формул угловое ускорение , получим вторую вспомогательную формулу:

(7.6)

где – средняя угловая скорость при равнопере­менном вращательном движении.

Когда 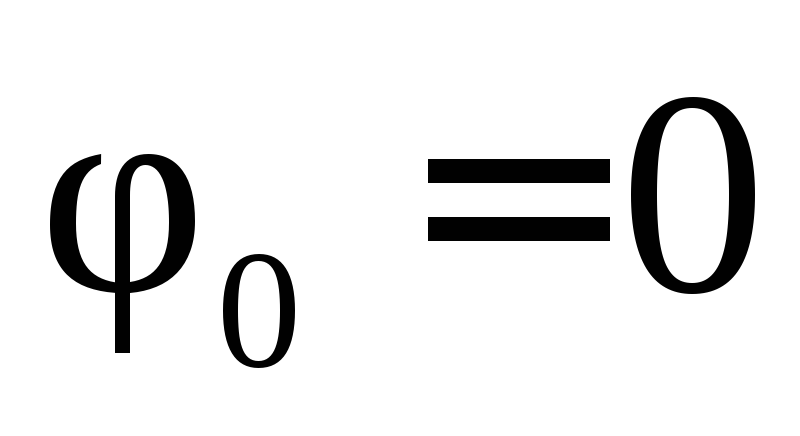и 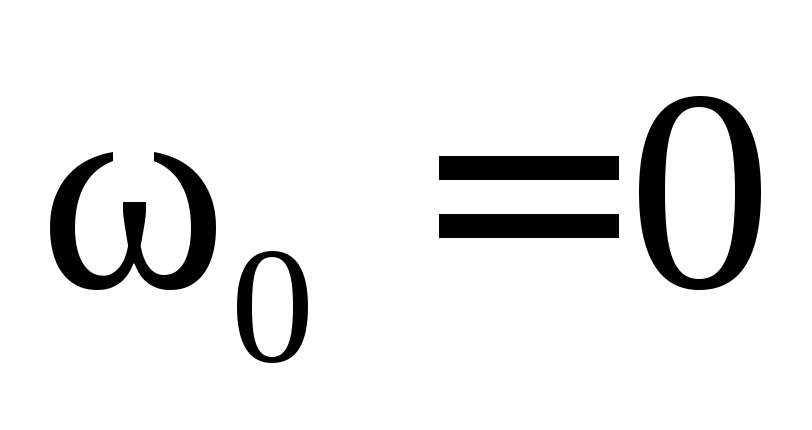, формулы (7.3)–(7.6) приобретают более простой вид:

В процессе конструирования угловое перемещение выражают не в радианах, а просто в оборотах.

Угловая скорость, выражаемая количеством оборотов в минуту, называется частотой вращения и обозначается n. Установим зависимость между (с^–1) и n (мин^–1). Так как 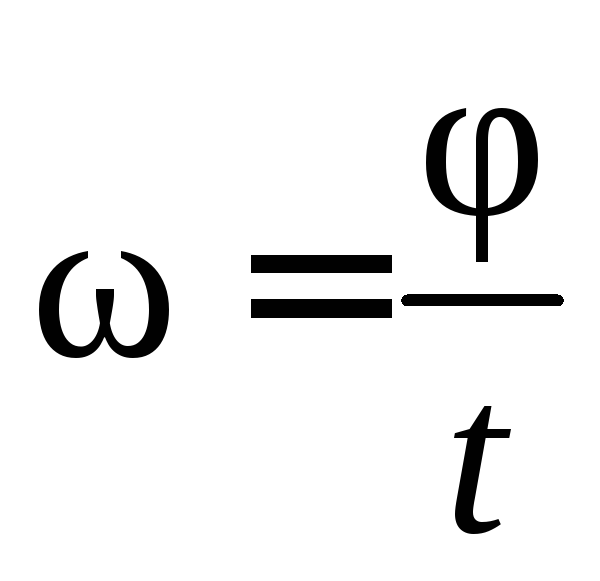, то при n (мин^–1) за t = 1 мин = 60 с угол поворота . Следовательно:

.

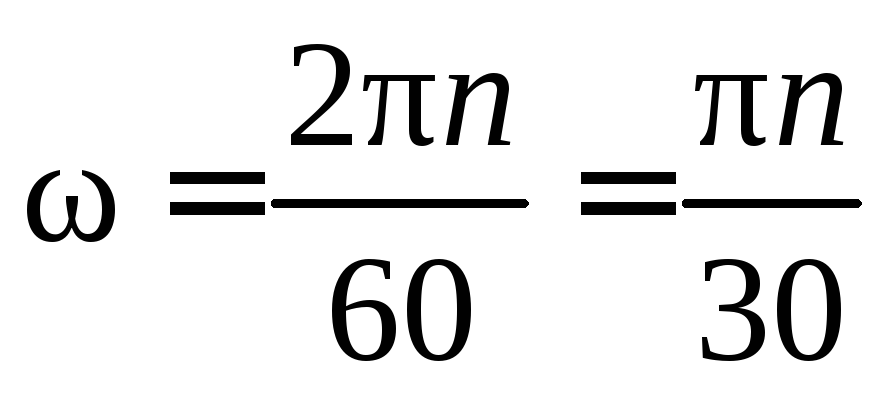При переходе от угловой скорости (с^–1) к частоте вращения n (мин^–1) имеем

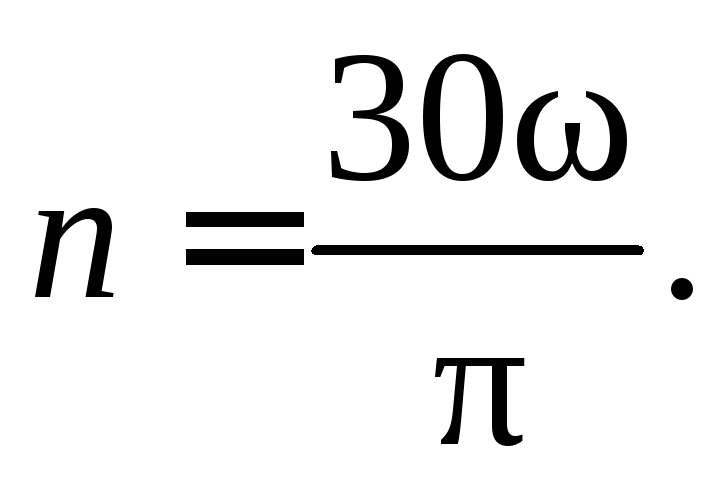
Угловая скорость при вращении тела вокруг неподвижной точки

Угловой скоростью называют векторную величину, характеризующую быстроту вращения твердого тела, определяемую как приращение угла поворота тела за промежуток времени.

Рассмотрим бесконечно малый промежуток времени Δt → 0, за который твердое тело совершает поворот на бесконечно малый угол  Δα вокруг мгновенной оси Ω (рисунок 3.2). 

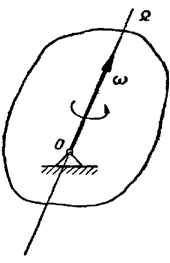
Рис. 3.2 

Предел, к которому стремится отношение  Δα / Δt, называется угловой скоростью твердого тела в рассматриваемый момент времени

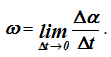
Угловая скорость является векторной величиной. Вектор угловой скорости ω может быть приложен к любой точке мгновенной оси и направлен в каждый момент времени по мгновенной оси Ω, так, чтобы, смотря навстречу этому вектору, видеть вращение тела происходящим против движения часовой стрелки.

Угловое ускорение при вращении тела

Угловым ускорением называют степень изменения угловой скорости.

За вектор углового ускорения ε при вращении тела вокруг неподвижной точки принимают вектор, который характеризует изменение угловой скорости ω в данный момент как по числовой величине, так и по направлению. Такой характеристикой является производная по времени от вектора угловой скорости ω. Таким образом, угловое ускорение определяется так:

     

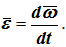
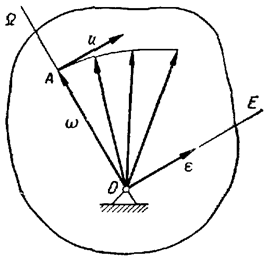
Рис. 3.3

В общем случае угловое ускорение не направлено по мгновенной оси, а, как производная по времени от вектора ω, параллельно касательной к годографу этого вектора. Условимся угловое ускорениеε изображать в любой точке прямой, параллельной этой касательной годографа угловой скорости u, но проходящей через неподвижную точку тела (рисунок 3.3). Прямая, по которой направлен вектор углового ускорения, называется осью углового ускорения и обозначается E.

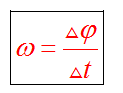
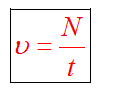
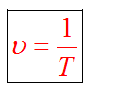
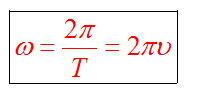
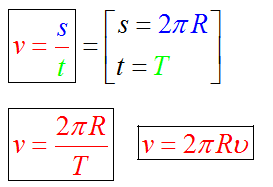
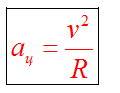
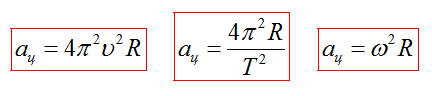
7

2 Кинематика твердого тела

     В кинематике твердого тела определяются: закон движения и кинематические характеристики тела, а также кинематические характеристики точек тела.

   В данном методическом пособии рассмотрены следующие виды движения твердого тела:

    — поступательное;

    — вращательное;

    — плоскопараллельное.

2.1 Поступательное движение

     Поступательное движение – это движение, при котором любая прямая, связанная с телом, перемещается параллельно самой себе.

     На рисунках 2.1,а и 2.1,б приведены примеры поступательного движения: движение прямоугольника в плоскости чертежа, движение каждой кабины колеса обозрения.

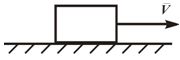
а                                  б

Рисунок 2.1

 

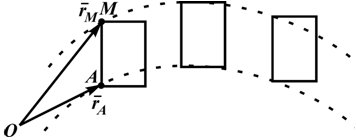
Рисунок 2.2

    Исходя из определения поступательного движения, движение твердого тела может быть задано в векторном виде формулой (рисунок 2.2):   

                                                  r_M=r_A ⊕ AM.

   В этой формуле AM —  вектор постоянный по величине и направлению, поэтому производная от него равна нулю. Для скорости и ускорения произвольной точки M  получим:

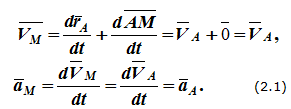
    То есть скорости и ускорения точек твердого тела при  поступательном движении равны и одинаково направлены, а траектории при наложении совпадают. 

    Для определения кинематических характеристик точек тела достаточно знать закон движения одной из них.

8

 Движение твердого тела, при котором две его точки О и О‘ остаются неподвижными, называется вращательным движением вокруг неподвижной оси, а неподвижную прямую ОО‘ называют осью вращения.         Пусть абсолютно твердое тело вращается вокруг неподвижной оси ОО‘ (рис. 2.12).

Рис. 2.12

       Проследим за некоторой точкой М этого твердого тела. За время  dt  точка М совершает элементарное перемещение  dr.         При том же самом угле поворота  dφ, другая точка, отстоящая от оси на большее или меньшее расстояние, совершает другое перемещение. Следовательно, ни само перемещение некоторой точки твердого тела, ни первая произ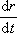водная , ни вторая производная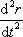не могут служить характеристикой движения всего твердого тела.        За это же время dt радиус-вектор , проведенный из точки0‘ в точку М, повернется на угол  dφ. На такой же угол повернется радиус-вектор любой другой точки (т.к. тело абсолютно твердое, в противном случае расстояние между точками должно измениться).         Угол поворота  dφ  характеризует перемещение всего тела за время dt.         Удобно ввести – вектор элементарного поворота тела, численно равныйdφ  и направленный вдоль оси вращения ОО‘ так, чтобы, глядя вдоль вектора, мы видели вращение по часовой стрелке (направление вектора 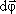и направление вращения связаны «правилом буравчика»).        Элементарные повороты удовлетворяют обычному правилу сложения векторов:

       Угловой скоростью называется вектор , численно равный первой производной от угла поворота по времени и направленный вдоль оси вращения в направлени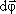и(ивсегда направлены в одну сторону).

.

(2.4.1)

       Если  ω – const, то имеет место равномерное вращение тела вокруг неподвижной оси.  Пусть  v  – линейная скорость точки М. За промежуток времени dt точка М проходит путь dr = vdt. В то же время  dr = Rdφ  (dφ — центральный угол). Тогда, можно получить связь линейной скорости и угловой:

.

(2.4.2)

       В векторной форме 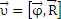.        Вектор 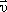ортогонален к векторамии направлен в ту же сторону, что и векторное произведение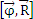.        Наряду с угловой скоростью вращения используют понятия периода и частоты вращения.         Период Т – промежуток времени, в течение которого тело совершает полный оборот (т.е. поворот на угол φ = 2π).         Частота ν – число оборотов тела за 1 секунду.         При вращении с угловой скоростью ω имеем:

,         ,.

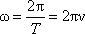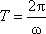       Введем вектор углового ускорения для характеристики неравномерного вращения тела:

.

(2.4.3)

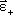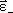       Вектор направлен в ту же сторону, что ипри ускоренном вращении, анаправлен в противоположную сторону при замедленном вращении(рис. 2.13).

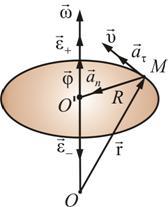Рис. 2.13

       Как и любая точка твердого тела, точка М имеет нормальную и тангенциальную составляющие ускорения. Выразим нормальное и тангенциальное ускорение точки М через угловую скорость и угловое ускорение:

	aτ = Rε;	(2.4.4)
		(2.4 5)

       Обратите внимание. Все кинематические параметры, характеризующие вращательное движение (угловое ускорение, угловая скорость и угол поворота), направлены вдоль оси вращения.         Формулы простейших случаев вращения тела вокруг неподвижной оси:

     равномерное вращение ε = 0;       ω = const;       φ = φ₀ ± ωt,

     равнопеременное вращение .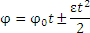

9

 Плоскопараллельным (плоским) движением (ППД) твердого тела называется такое движение, при котором все точки тела перемещаются в плоскостях параллельных некоторой неподвижной плоскости (рисунок 2.11). 

    При таком движении точки, лежащие в разных плоскостях на одном отрезке, перпендикулярном неподвижной плоскости (например M₁M₂ ) совершают одинаковые движения.

                                    

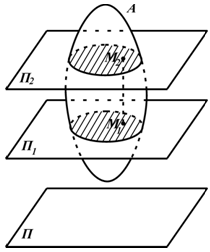
Рисунок 2.11

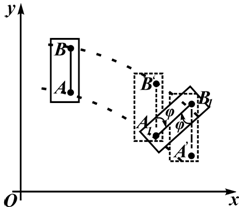
Рисунок 2.12

    Отрезок M₁M₂  движется поступательно. Поэтому изучение плоскопараллельного движения сводится к изучению движения плоской фигуры в какой-то плоскости.

    На рисунке 2.12 показано перемещение пластинки в плоской системе отсчета xOy  из одного положения в другое. Такое перемещение можно осуществить двигая пластину поступательно с траекторией точки A  с последующим поворотом на угол φ  вокруг точки A₁. Это же перемещение можно выполнить иначе. 

    Например, перемещая пластинку поступательно с траекторией точки B , с последующим поворотом вокруг B₁  на угол φ. Траектории точек A  и B различны, а угол поворота в обоих случаях  одинаков. 

     Положение пластинки вполне определяется положением скрепленного с ней отрезка (например AB), закон движения которого можно задать в виде:

                                 x_A=x_A(t),  y_A=y_A(t),  φ=φ(t).

    Точка A  в этом случае называется полюсом. Если принять за полюс точку B , то получим уравнения:

                                x_B=xB(t),  y_B=yB(t),  φ=φ(t)

    За полюс выбирается точка, закон движения которой известен.

10

ИНЕРЦИАЛЬНАЯ система ОТСЧЕТА — система отсчета, в которой справедлив закон инерции: материальная точка, на которую не действуют никакие силы, находится в состоянии покоя или равномерного прямолинейного движения. Любая система отсчета, движущаяся относительно инерциальной системы отсчета поступательно, равномерно и прямолинейно, также является инерциальной системой отсчета. Все инерциальные системы отсчета равноправны, т. е. во всех таких системах законы физики одинаковы.

Преобразования Галилея. Рассмотрим две системы отсчета движущиеся друг относительно друга и с постоянной скоростью v₀.Одну из этих систем обозначим буквой K. Будем считать неподвижной. Тогда вторая система K будет двигаться прямолинейно и равномерно. Выберем координатные оси x,y,z системы K и x’,y’,z’ системы K’ так что оси x и x’ совпадали, а оси y и y’ , z и z’, были параллельны друг другу. Найдем связь между координатами x,y,z некоторой точки P в системе K и координатами x’,y’,z’ той же точки в системе K’. Если начать отсчёт времени с того момента, когда начало координат системы, совпадали, то x=x’+v₀, кроме того, очевидно, что y=y’, z=z’. Добавим к этим соотношениям принятое в классической механике предположение, что время в обеих системах течёт одинаковым образом, то есть t=t’. Получим совокупность четырёх уравнений : x=x’+v₀t;y=y’;z=z’;t=t’, названных преобразованиями Галилея

Инвариантами преобразования Галилея являются длина тел и промежуток времени между событиями. Именно поэтому понятия длины и промежутка времени играют такую большую роль в классической физике. [4]

Дифференциал dr является инвариантом преобразований Лоренца, т.е. интервалом времени, не зависящим от ситуации — подвижной или неподвижной является исходная система отсчета. Ньютона о существовании некоего универсального, абсолютного времени. [13]

скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно движущейся системы и скорости самой движущейся системы относительно неподвижной

 

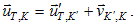
В классической механике справедлив механический принцип относительности: законы динамики одинаковы во всех инерциальных системах отсчета.

Рассмотрим две системы отсчета: инерциальную систему К (с координатами x, y, z), условно будем считать неподвижной, и систему К’ (с координатами x’, y’, z’), движущуюся относительно К равномерно и прямолинейно со скоростью υ₀ (υ₀=const)

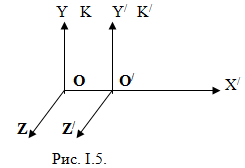
Координата точки А по отношению к системе К: х = х’ + 00′, за промежуток времени t от начала отсчета будет:

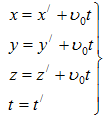(3.19)

Уравнения (3.19) носят название преобразования координат и времени Галилея. Отсчет времени начат с момента, когда начало координат обеих систем совпадают. Продифференцировав по времени t, получим выражение правила сложения скоростей в классической механике: υ=υ’+υ₀ (3.20)

Ускорения в обеих системах отсчета одинаковы, а это означает, что поведение тел в обеих системах одинаково: a=a’ (3.21), т.е. из соотношения (3.21) вытекает подтверждение механического принципа относительности: уравнения динамики при переходе от одной инерциальной системы отсчета к другой не изменяются, т.е. являются инвариантными по отношению к преобразованиям Галилея. Механический принцип относительности можно сформулировать еще следующим образом: никакими механическими опытами, проведенными в данной инерциальной системе отсчета, нельзя установить, покоится ли она или движется равномерно и прямолинейно. Например, сидя в каюте корабля, движущегося равномерно и прямолинейно, мы не можем определить, покоится корабль или движется, не выглянув в окно.

11.

2.1. Угол поворота твердого тела

При вращательном движении, в отличие от поступательного, скорости разных точек тела неодинаковы. Поэтому скорость какой-либо точки вращающегося тела не может служить характеристикойдвижения всего тела.

Пусть т. О — центр вращения тела, а — неподвижная (или мгновенная) ось вращения (рис.2.2).

Положение произвольной т. М тела будем задавать с помощью радиус-вектора , проведенного из центра О. Из рисунка видно, что:

,

где— радиус-вектор, проведенный в точку дуги окружности, по которой движется т. М. За малое время вектор поворачивается в плоскости перпендикулярной , на малыйугол . На такой же угол поворачивается за время радиус-вектор любой другой точки тела, т.к в противном случае расстояние между этими точками должны были измениться. Таким образом, угол поворота характеризует перемещение всего вращающегося тела за малый промежуток времени. Удобно ввести вектор элементарного (малого) поворота тела, численно равный и направленный вдоль мгновенной оси так, чтобы из его конца поворот тела был виден происходящим против часовой стрелки.

угол поворота, угловые скорость и ускорение. Их связь с линейной скоростью и линейным ускорением

Рис.2.4

Вращательным движением твердого тела вокруг неподвижной оси вращения называют такое движение, при котором какие-либо две его точки остаются неподвижными в процессе движения. Прямая, проходящая через эти точки, называется осью вращения; все остальные точки твердого тела при вращательном движении описывают окружности в плоскостях, перпендикулярных к оси вращения, центры которых лежат на этой оси (рис.2.4).

Основными кинематическими характеристиками вращательного движения являются: угол поворота, угловая скорость и угловое ускорение.

Угол поворота  — угол между проведенными через ось вращения неподвижной полуплоскостью (плоскостью отсчета) и полуплоскостью, жестко связанной с телом и вращающейся вместе с ним. Угол поворота — псевдовектор — вектор, численно равный углу между двумя положениями радиуса R, направленный вдоль оси вращения и связанный с направлением вращения правилом векторного произведения (правилом правого винта).

С определенной степенью точности, под углом поворота можно подразумевать псевдовектор, численно равный углу, отсчитанному между двумя последовательными положениями радиус-вектора r, и связанный с направлением вращения правилом правого винта.

Угловая скорость  — векторная физическая величина, показывающая, как изменяется угол поворота  в единицу времени, численно равная первой производной от угла поворота по времени:

. (2.16)

Вектор угловой скорости направлен вдоль оси вращения в сторону, определяемую правилом правого винта (векторного умножения).

При равномерном вращении ω = const, ω = φ/t. Равномерное вращательное движение характеризуется периодом, частотой вращения и циклической или круговой частотой.

Период (T) — время, в течение которого тело сделает один полный оборот.

Частота (n) — число оборотов, совершаемых в единицу времени.

Круговая (циклическая) частота ω — число оборотов, совершаемых за время, равное 2π. Между периодом, частотой и круговой частотой имеется связь:

ω = 2πn = 2π/T; n = 1/T. (2.17)

Угловая скорость может изменяться как по величине, так и по направлению. Векторная физическая величина, характеризующая изменению угловой скорости в единицу времени, численно равная первой производной от угловой скорости по времени или второй производной от угла поворота по времени, называется угловым ускорением

. (2.18)

Направление вектора углового ускорения совпадает с направлением вектора угловой скорости в случае ускоренного вращения и противоположно — в случае замедленного.

Отдельные точки вращающегося тела имеют различные линейные скорости, которые непрерывно изменяют свое направление и зависят от угловой скорости  и расстояния соответствующей точки до оси вращения r.

Точка, находящаяся на расстоянии r от оси вращения, двигаясь по траектории (окружности), проходит путь (рис.2.5):

Рис.2.5

S = r. (2.19)

Поделив обе части данного равенства на t; при t0 получим некоторые пределы от левой и правой частей:

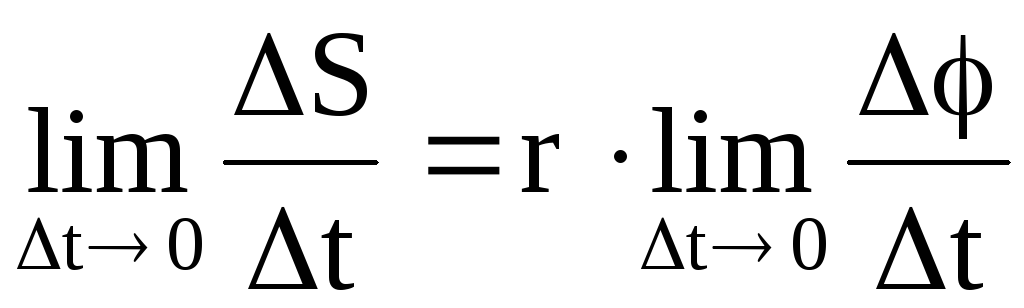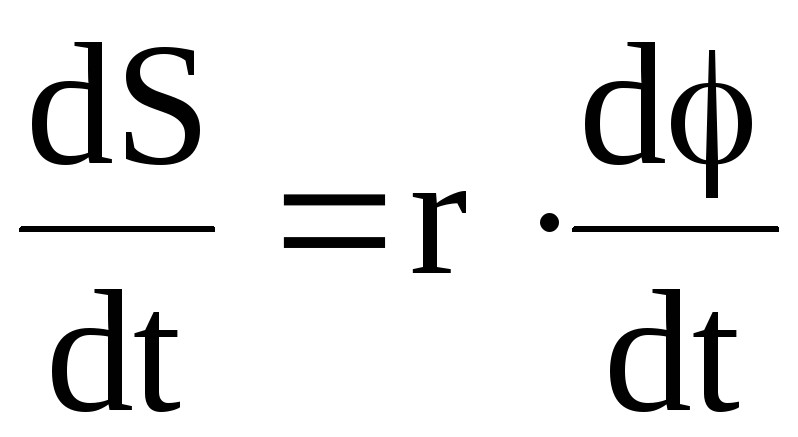или . (2.20)

Так как dS/dt = v, а dφ/dt = ω, то

v = rω. (2.21)

Полученная формула устанавливает связь между численными значениями линейной и угловой скорости, а также радиус-вектором r. Из нее видно, чем дальше отстоит точка от оси вращения, тем больше ее линейная скорость. Векторы v, ω и r перпендикулярны друг другу, следовательно, можно записать:

v = rω sinα или v = [ωr]. (2.22)

Известно, что a² = a_t² + a_n², где a_t = dv/dt, a_n = v²/r. Следовательно, связь между полным линейным ускорением, тангенциальным и нормальным ускорениями имеет вид:

(2.23)

Из написанных формул видно, что тангенциальное, нормальное и полное ускорения растут с увеличением расстояния от этих точек до оси вращения.

Можно показать, что любое сложное движение можно представить в виде поступательного и вращательного движений.

Надо отметить, что к вращательному движению применимы все формулы кинематики материальной точки, с заменой в них линейных величин соответствующими угловыми величинами. Например:

S = v₀t + at²/2; φ = ω₀t + εt² /2. (2.24)

Уравнением вращательного движения в кинематике называют выражение, которое отображает функциональную зависимость угла поворота от времени:

 = f(t).

В физике в качестве основной угловой меры принят радиан. Угол в радианах получается как отношение пройденного материальной точкой пути S к радиусу соответствующей окружности (см. рис.2.5):

.
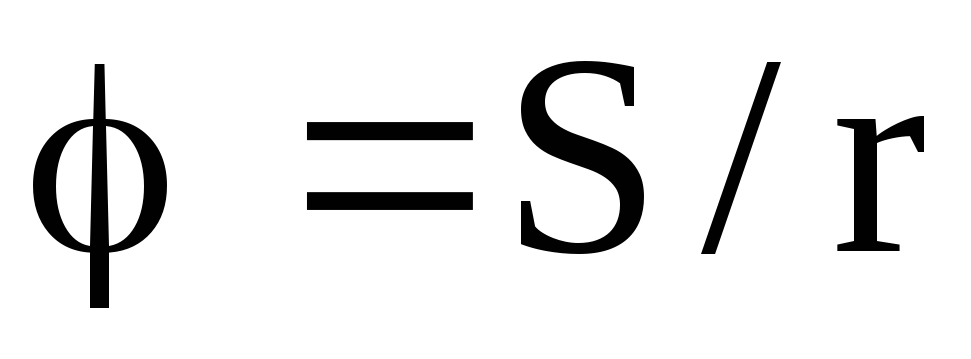
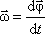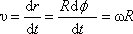