Угловая скорость при движении по окружности – Средняя угловая скорость равномерно ускоренного движения по окружности | Формулы и расчеты онлайн — groupnk.ru — Группа НК — комплексные поставки электрооборудования в Москве и регионах

Содержание

Репетитор-онлайн — подготовка к ЦТ

Пример 17. Найти линейную скорость и центростремительное ускорение точек земной поверхности на экваторе и на широте 45°. Радиус Земли считать равным 6,4 ⋅ 10⁶ м.

Решение. 1) Точка экватора движется по окружности радиусом R и совершает один оборот за время, равное периоду обращения Земли вокруг своей оси (сутки):

T=2πRv1,

где R = 6,4 ⋅ 10⁶ м — радиус Земли; v₁ — модуль линейной скорости точки (искомая величина). Рисунок иллюстрирует данную ситуацию.

Из приведенной формулы следует, что модуль линейной скорости точки

v1=2πRT=2π⋅6,4⋅10624⋅3600=465 м/с.

2) Точка, находящаяся на широте 45°, движется по окружности радиусом r и совершает один оборот за время равное, как и в предыдущем случае, периоду обращения Земли вокруг своей оси (сутки):

T=2πrv2,

где r = R cos 45° — радиус окружности для точки, находящейся на указанной широте; R — радиус Земли; v₂ — модуль линейной скорости точки, находящейся на указанной широте (искомая величина). Рисунок иллюстрирует данную ситуацию.

Из приведенной формулы следует, что модуль линейной скорости точки

v2=2πrT=2πRcos45°T2=2π⋅6,4⋅106⋅0,5224⋅3600=328 м/с.

3) Центростремительное ускорение точки, находящейся на экваторе, определяется квадратом ее линейной скорости v₁ и радиусом окружности R, по которой она движется:

aц.с1=v12R.

Центростремительное ускорение точки, находящейся на широте 45°, определяется квадратом ее линейной скорости v₂ и радиусом окружности r=Rcos45°, по которой она движется:

aц.с2=v22r=v22Rcos45°.

Для вычисления модулей центростремительных ускорений воспользуемся полученными выше значениями линейных скоростей:

aц.с1=(465)26,4⋅106≈3,4⋅10−2 м/с2=3,4 см/с2;

aц.с2=(328)26,4⋅106⋅0,52≈2,4⋅10−2 м/с2=2,4 см/с2.

Движение тела по окружности в физике » Nikulux

Движение по окружности — это вращательное движение определённой материальной точки или тела, ось вращения в выбранной системе отсчёта неподвижна и не проходит через центр тела.

Такое движение может быть :

Равномерное движение (с постоянной угловой скоростью):
Формула угловой скорости: ;
Формула скорости движения: ;
Формула угла поворота: ;
Формула ускорения: ;
Неравномерное движение (с переменной угловой скоростью):
Формула тангенциального ускорения: ;
Формула центростремительного ускорения: ;

— период вращения;
— время;
— угловая скорость;
— радиус;
— тангенциальное ускорение;
— центростремительное (полное) ускорение;

Таким не хитрым образом мы познакомились с «движение тела по окружности в физике»!

Движение по окружности — задачи

Задача 1. За промежуток времени $\Delta t=10$ с тело прошло половину окружности радиусом 100 см. Найти среднюю путевую скорость $\upsilon$

и модуль средней скорости $\left$ .

Решение: средней путевой скоростью называется средняя скорость прохождения пути, которую мы с вами вычисляем, деля весь путь (длину траектории) на все время. Модуль средней скорости еще называют средней скоростью по перемещению. Ее можно определить, разделив перемещение на время. Тогда длина пути – это длина половины окружности, а перемещение – длина диаметра.

$\upsilon=\frac{2\pi R}{2t}=\frac{\pi R}{\Delta t }=\frac{3,14}{10}=0,314$

$\[\left$

Ответ: средняя путевая скорость – 0,314 м/с, средняя скорость по перемещению – 0,2 м/с

Задача 2. Однородный диск радиусом 0,5 м катится без проскальзывания со скоростью 2 м/с. Найти скорость точек диска

. Найти геометрическое место всех точек диска, скорость которых 2 м/с. Угол $\alpha=60^{\circ}$ .

Скорость точек окружности

Решение:

Точка A – центр вращения. Поэтому ее скорость относительно поверхности, по которой катится диск, равна 0. Поскольку в условии сказано, что диск катится со скоростью 2 м/с, то это означает, что с такой скоростью относительно поверхности будет передвигаться его центр: $\vec{\upsilon_O}=2$ м/с. Поэтому точка А относительно центра будет передвигаться с точно такой же скоростью – со скоростью 2 м/с, и это и будет линейная скорость вращения диска, то есть скорость всех точек, лежащих на его краю, относительно центра $\vec{\upsilon}=2$ м/с. Линейные скорости показаны для точек оранжевыми стрелками. Эти стрелки показывают, какой была бы скорость данной точки, если бы диск не катился, а вращался бы, например, на оси, проходящей через его центр. Но наш диск катится. Поэтому к линейной скорости вращения каждой точки необходимо еще прибавить скорость движения диска относительно опоры. То есть к каждой рыжей стрелке прибавим (векторно) скорость точки О – центра диска – черную стрелку. Тогда-то и становится понятным, почему у точки скорость равна 0 – линейная скорость вращения направлена влево, а скорость качения – вправо, и поскольку они равны, то гасят друг друга: $\upsilon_A=\vec{\upsilon}+\vec{\upsilon_O}=0$ . В точке C скорости, напротив, сложатся, поскольку они сонаправлены: $\upsilon_C=\vec{\upsilon}+\vec{\upsilon_O}=4$ м/с.

Определим теперь скорости точек и . Понятно, что они будут равны численно, но направлены в разные стороны.

$\upsilon_B=\vec{\upsilon}+\vec{\upsilon_O}$

$\upsilon_B=\sqrt{2^2+2^2}=2\sqrt{2}$

Осталось разобраться с точкой . Сделаем еще один рисунок. Линейная скорость вращения всегда направлена по касательной, то есть перпендикулярно радиусу . Углы, которые образуются между векторами, показаны на рисунке, в том числе угол $\angle KEM=120^{\circ}$ . Тогда в параллелограмме EKNM угол $\angle EKN=60^{\circ}$ , а так как

$\upsilon=\upsilon_O$ , то все углы в треугольнике равны $60^{\circ}$ и он равносторонний, то есть $\upsilon_E=2$ м/с. Также можно было найти длину этого вектора скорости по теореме косинусов или складывая проекции векторов. Можно догадаться, что точка, симметричная точке E относительно A также имеет скорость, равную 2 м/с. Вообще точки, лежащие на одном и том же расстоянии от центра вращения A будут иметь равные скорости, линии равных скоростей (геометрические места точек с равными скоростями) показаны на рисунке различного цвета дугами: единственная точка (точка C) будет иметь скорость 4 м/с, точки, лежащие на рыжей дуне, будут иметь скорости, равные $\upsilon_B=2\sqrt{2}$ , точки, лежащие на синей дуге, будут иметь скорости, равные 2 м/с, как у точки E.

Пробуксовывание

Задача 3. Колесо, пробуксовывая, катится по ровной, горизонтальной дороге. Найти скорость центра колеса $\upsilon$ , если известно, что скорость нижней точки $\upsilon_1=2$ м/c, а верхней – $\upsilon_2=10$ м/c.

Решение:

Если колесо пробуксовывает, то это означает, что скорость его нижней точки не равна нулю, то есть его центр вращения – не точка касания поверхности, центр вращения будет расположен выше. Но центр вращения находится и не в центре колеса. Найти его можно, если провести вертикальный диаметр, построить вектора скоростей в масштабе, а затем, соединив концы векторов скоростей прямой линией, отметить точку пересечения этой линии с диаметром. У нас на рисунке это точка О. Точка К – центр колеса, его скорость нам и нужно найти. Из подобия треугольников ABO и DCO запишем отношения сходственных сторон:

$\frac{\upsilon_2}{AO}=\frac{\upsilon_1}{2R-AO}$

Тогда

$\frac{10}{AO}=\frac{2}{2R-AO}$

$2AO=20R-10AO$

$12AO=20R$

$AO=\frac{5}{3}R$

Тогда $OC=2R-AO=2R-\frac{5}{3}R=\frac{1}{3}R$

$OK=R-OC=R-\frac{1}{3}R=\frac{2}{3}R$

Теперь обратимся к подобным треугольникам DCO и KOL . Для них отношение сходственных сторон равно:

$\frac{OK}{OC}=\frac{\upsilon}{\upsilon_1}$

$\frac{\frac{2}{3}R }{\frac{1}{3}R }=\frac{\upsilon}{2}$

$\frac{2}{1}=\frac{\upsilon}{2}$

Откуда $\upsilon=4$ м/с.

Ну а более простым решение было бы, если бы мы просто нашли среднее арифметическое скоростей, ведь точка, про которую нас спрашивают, лежит по центру между точками приложения векторов скоростей $\upsilon_1$ и $\upsilon_2$ , при этом не забываем о векторном сложении скоростей, берем скорость $\upsilon_1$ со знаком «минус»:

$\frac{\vec{\upsilon_2}+\vec{\upsilon_1}}{2}=\frac{10-2}{2}=4$

м/с.

Ответ: 4 м/с.

Проскальзывание

Задача 4. Обруч, проскальзывая, катится по горизонтальной ровной поверхности. В некоторый момент скорость верхней точки А $\upsilon_A=6$

м/с, а нижней точки B $\upsilon_В=2$ м/с. Определить скорость концов диаметра

, перпендикулярного к

, для того же момента времени. Под какими углами они направлены к горизонту?

Решение:

Проскальзывание – это ситуация, когда скорость нижней точки (точки касания обручем земли) не нулевая, но направлена она в сторону качения. В этом случае центр вращения, так же, как и в случае пробуксовки, не совпадает с центром колеса. Более того, центр вращения даже не внутри колеса – он снаружи (точка О). Как и в предыдущей задаче, можно найти его таким же способом – проведя линию через концы скоростей и найдя ее пересечение с продолжением вертикального диаметра. И, точно так же, как в предыдущей задаче, можно определить скорость центра колеса как среднее арифметическое, только обе скорости направлены у нас теперь в одну сторону, поэтому ставим знак «плюс» перед обеими:

$\upsilon=\frac{\vec{\upsilon_A}+\vec{\upsilon_B}}{2}=\frac{6+2}{2}=4$

м/с.

Так как скорость точки есть результат векторного сложения линейной скорости вращения колеса

и скорости поступательного движения центра колеса $\upsilon$ , то можем из этого сделать вывод, что линейная скорость вращения равна 2 м/с – ровно на столько скорость центра колеса, найденная нами, отличается от скорости точки

, данной в условии задачи. Линейную скорость на рисунке не показывала, или показывала не везде. Скорости точек

равны численно, но направлены по-разному. Их скорости – также результат векторного сложения линейной скорости вращения колеса и скорости поступательного движения центра, а, так как эти две скорости перпендикулярны друг другу, то результат их сложения может быть найден по Пифагору:

$\upsilon_C=\upsilon_D=\sqrt{\upsilon^2+u^2}=\sqrt{2^2+4^2}=\sqrt{20}=4,47$

Понятно, что раз скорости перпендикулярны друг другу, то являются катетами некоторого прямоугольного треугольника, и связывает их между собой функция тангенса, поэтому угол наклона к горизонту скорости точки можно найти как

$\alpha=\operatorname {arctg}\frac{u}{\upsilon}=\operatorname {arctg}{\frac{2}{4}}=27^{\circ}$

Ответ: $\upsilon_C=\upsilon_D=4,47$ , $\alpha=27^{\circ}$

Шарик катится по двум линейкам

Задача 5. Шарик радиусом R=5 см катится равномерно и без проскальзывания по двум параллельным линейкам, расстояние между которыми равно d=6 см, и за время t=2 с проходит l=120 см. С какими скоростями движутся верхняя и нижняя точки шарика?

На рисунке изображено, как двигается шарик, при этом для удобства показан как вид спереди, так и вид сбоку. Поскольку скорость шарика равна $\upsilon=\frac{l}{t}=\frac{1,2}{2}=0,6$ м/с, то эта скорость – скорость поступательного движения его центра масс – точки А. Центр вращения шарика находится в точке О – на уровне края линеек. Определим положение точки О – определим длину отрезка . Это легко сделать, зная радиус шарика и рассмотрев рисунок, из треугольника AOB . Центр вращения в данный момент неподвижен, а точка А двигается относительно него со скоростью 0,6 м/с. Поэтому скорость нижней точки $\upsilon_1$ будет

$\frac{\upsilon}{\upsilon_1}=\frac{AO}{R-AO}$

$\upsilon_1=\frac{\upsilon (R-AO)}{AO}=\frac{0,6}{4}=0,15$

Таким же способом определяем скорость верхней точки $\upsilon_2$ :

$\frac{\upsilon}{\upsilon_2}=\frac{AO}{R+AO}$

$\upsilon_2=\frac{\upsilon (R+AO)}{AO}=\frac{0,6\cdot 0,09}{0,04}=1,35$

Ответ: скорость нижней точки 0,15 м/c, скорость верхней 1,35 м/c.

Задача 6. Автомобиль движется по закругленному шоссе, имеющему радиус кривизны R=40 м. Закон движения автомобиля имеет вид: , где A=5 м, B=12 м/с, C=-0,5 м/с. Найти скорость автомобиля $\upsilon$ , его тангенциальное $a_{\tau}$ , нормальное a_n и полное ускорения в момент времени t=4 с.

Решение.

Путь:

$s=5+12t-0,5t^2$

Производная пути – линейная скорость:

$\[s$

Вторая производная – тангенциальное ускорение:

$\[s$

Нормальное ускорение:

$a_{n}=\frac{\upsilon^2 }{R}=\frac{8^2}{40}=1,6$

Полное ускорение:

$a=\sqrt{ {a_{\tau}}^2+ {a_{n}}^2}=\sqrt{1,6^2+(-1)^2}=\sqrt{3,56}=1,9$

Задача7. Угол поворота диска радиусом R=10 см изменяется со временем по закону $\varphi=4+2t-t^3$ . Определить зависимости от времени угловой скорости, углового ускорения и линейной скорости точек диска.

Решение: угловая скорость – производная угла:

$\[\omega=\varphi$

Угловое ускорение – производная угловой скорости:

$\[\varepsilon=\varphi$

Линейная скорость:

$\upsilon=\omega R=0,2-0,3t^2$

Задача 8. Точка движется по окружности с постоянным угловым ускорением $\varepsilon=1$ рад/ c^2 . Найти угол между скоростью и ускорением через 1 с после начала движения. Начальная скорость точки равна 0.

Решение: так как тангенциальное ускорение и линейная скорость совпадают по направлению, то определим обе составляющие ускорения: как нормальную, так и тангенциальную. Угол между полным ускорением и его тангенциальной составляющей можно тогда будет найти через функцию тангенса.

Известно, что нормальное ускорение $a_n=\frac{\omega^2 }{R}$ , тангенциальное ускорение $a_{\tau}=\varepsilon R$ . При этом $\varepsilon=\omega$ , или $\omega=\varepsilon t$ . Тогда $a_n=\frac{\omega^2 }{R}=\frac{(\varepsilon t )^2}{R}$

Искомый угол:

$\alpha=\operatorname {arctg}{\frac{ a_n }{ a_{\tau}}}=\operatorname {arctg}{\frac{ \frac{\varepsilon^2 t ^2}{R}}{ \varepsilon R }}=\operatorname {arctg}{\varepsilon t^2}=\operatorname {arctg}{1}=45^{\circ}$

Ответ: $45^{\circ}$

Два концентрических колеса

Задача 9. Два концентрических колеса радиусами R=50 см и r=25 см вращаются с угловыми скоростями $\omega_1=5$ рад/c и $\omega_2=10$ рад/с соответственно. Между ними зажато третье колесо так, как показано на рисунке. Какова угловая скорость этого колеса вокруг собственной оси? Проскальзывания нет.

Решение: определим радиус маленького (третьего) колеса, м:

$r_3=\frac{R-r}{2}=\frac{0,5-0,25}{2}=0,125$

Определим линейную скорость точек первого колеса:

$\upsilon_1=\omega_1 R=2,5$

Определим линейную скорость точек второго колеса:

$\upsilon_2=\omega_2 r=2,5$

Найдем угловую скорость маленького колеса, зная, что линейная скорость его точек равна линейной скорости больших колес, так как проскальзывания нет:

$\omega=\frac{\upsilon_2}{ r_3}=\frac{2,5}{0,125}=20$

Ответ: 20 рад/с

Задача 10. Гайку закручивают на болт за время $\tau$ . Длина болта , резьба составляет угол $\alpha$ с плоскостью гайки. Найдите угловую скорость гайки, если радиус болта равен .

Скорость вращения гайки по ходу завинчивания на болт

Решение: при закручивании гайка не только вращается, но и движется вдоль болта поступательно, например, спускается вниз. Поэтому точка, взятая на ребре гайки, будет обладать двумя составляющими скорости: скорость, с которой она будет двигаться вниз вдоль болта (назовем ее $\upsilon_l$ ) и скорость, с которой эта точка вращается – это уже знакомая нам линейная скорость ( $\upsilon$ ). Тогда $\omega=\frac{\upsilon }{R}$ .

Из рисунка видно, что

$\upsilon=u \cos{\alpha}$

$\upsilon_l=u \sin{\alpha}$

С другой стороны, так как длина болта , а гайка спускается по нему за время $\tau$ , то

$\upsilon_l=\frac{l}{\tau}$

Тогда

$u \sin{\alpha}=\frac{l}{\tau}$

И можно определить :

$u=\frac{l}{\tau \sin{\alpha}}$

Тогда

$\omega=\frac{\upsilon }{R}=\frac{u \cos{\alpha}}{R}= \frac{l \cos{\alpha}}{R\tau \sin{\alpha}}$

Ответ: $\omega= \frac{l \cos{\alpha}}{R\tau \sin{\alpha}}$

Т. Движение по окружности — PhysBook

Движение тела по окружности с постоянной по модулю скоростью

Движение тела по окружности с постоянной по модулю скоростью — это движение, при котором тело за любые равные промежутки времени описывает одинаковые дуги.

Положение тела на окружности определяется радиусом-вектором $~\vec r$, проведенным из центра окружности. Модуль радиуса-вектора равен радиусу окружности R (рис. 1).

Рис. 1

За время Δt тело, двигаясь из точки А в точку В, совершает перемещение $~\Delta \vec r$, равное хорде АВ, и проходит путь, равный длине дуги l.

Радиус-вектор поворачивается на угол Δφ. Угол выражают в радианах.

Скорость $~\vec \upsilon$ движения тела по траектории (окружности) направлена по касательной к траектории. Она называется линейной скоростью. Модуль линейной скорости равен отношению длины дуги окружности l к промежутку времени Δt за который эта дуга пройдена:

$~\upsilon = \frac{l}{\Delta t}.$

Скалярная физическая величина, численно равная отношению угла поворота радиуса-вектора к промежутку времени, за который этот поворот произошел, называется угловой скоростью:

$~\omega = \frac{\Delta \varphi}{\Delta t}.$

В СИ единицей угловой скорости является радиан в секунду (рад/с).

При равномерном движении по окружности угловая скорость и модуль линейной скорости — величины постоянные: ω = const; υ = const.

Положение тела можно определить, если известен модуль радиуса-вектора $~\vec r$ и угол φ, который он составляет с осью Ox (угловая координата). Если в начальный момент времени t₀ = 0 угловая координата равна φ₀, а в момент времени t она равна φ, то угол поворота Δφ радиуса-вектора за время $~\Delta t = t — t_0 = t$ равен $~\Delta \varphi = \varphi — \varphi_0$. Тогда из последней формулы можно получить кинематическое уравнение движения материальной точки по окружности:

$~\varphi = \varphi_0 + \omega t.$

Оно позволяет определить положение тела в любой момент времени t. Учитывая, что $~\Delta \varphi = \frac{l}{R}$, получаем\[~\omega = \frac{l}{R \Delta t} = \frac{\upsilon}{R} \Rightarrow\]

$~\upsilon = \omega R$ — формула связи между линейной и угловой скоростью.

Промежуток времени Τ, в течение которого тело совершает один полный оборот, называется периодом вращения:

$~T = \frac{\Delta t}{N},$

где N — число оборотов, совершенных телом за время Δt.

За время Δt = Τ тело проходит путь $~l = 2 \pi R$. Следовательно,

$~\upsilon = \frac{2 \pi R}{T}; \ \omega = \frac{2 \pi}{T} .$

Величина ν, обратная периоду, показывающая, сколько оборотов совершает тело за единицу времени, называется частотой вращения:

$~\nu = \frac{1}{T} = \frac{N}{\Delta t}.$

Следовательно,

$~\upsilon = 2 \pi \nu R; \ \omega = 2 \pi \nu .$

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 18-19.

Презентация «Движение тела по окружности».

Автор: Александрова Зинаида Васильевна, учитель физики и информатики

Образовательное учреждение: МБОУ СОШ №5 п. Печенга, Мурманская обл.

Предмет: физика

Класс: 9 класс

Тема урока: Движение тела по окружности с постоянной по модулю скоростью

Цель урока:

дать представление о криволинейном движении, ввести понятия частоты, периода, угловой скорости, центростремительного ускорения и центростремительной силы.

Задачи урока:

Образовательные:

Повторить виды механического движения, познакомить с новыми понятиями: движение по окружности, центростремительное ускорение, период, частота;
Выявить на практике связь периода, частоты и центростремительного ускорения с радиусом обращения;
Использовать учебное лабораторное оборудование для решения практических задач.

Развивающие:

Развивать умения применять теоретические знания для решения конкретных задач;
Развивать культуру логического мышления;
Развивать интерес к предмету; познавательную деятельность при постановке и проведении эксперимента.

Воспитательные:

Формировать мировоззрение в процессе изучения физики и аргументировать свои выводы, воспитывать самостоятельность, аккуратность;
Воспитывать коммуникативную и информационную культуру учащихся

Оснащение урока:

компьютер, проектор, экран, презентация к уроку «Движение тела по окружности», распечатка карточек с заданиями;
теннисный шар, волан для бадминтона, игрушечный автомобиль, шарик на нити, штатив;
наборы для эксперимента: секундомер, штатив с муфтой и лапкой, шарик на нити, линейка.

Форма организации обучения: фронтальная, индивидуальная, групповая.

Тип урока: изучение и первичное закрепление знаний.

Учебно-методическое обеспечение: Физика. 9 класс. Учебник. Перышкин А.В., Гутник Е.М. 14-е изд., стер. — М.: Дрофа, 2012 г.

Время реализации урока: 45 минут

Авторский мультимедиа ресурс:

1. Редактор, в котором выполнен мультимедиа ресурс: MS PowerPoint

2. Вид мультимедиа ресурса: наглядная презентация учебного материала с использованием триггеров, встроенного видео и интерактивного теста.

План проведения урока

Организационный момент. Мотивация к учебной деятельности.
Актуализация опорных знаний.
Изучение нового материала.
Закрепление нового материала. Применение знаний и умений в новой ситуации.

Беседа по вопросам;
Решение задач;
Выполнение исследовательской практической работы.
Фронтальная работа с интерактивным тестом.

Подведение итогов урока.

Ход урока

Этапы урока

Временная реализация

Организационный момент. Мотивация к учебной деятельности.

Слайд 1. (Проверка готовности к уроку, объявление темы и целей урока.)

Учитель. Сегодня на уроке вы узнаете, что такое ускорение при равномерном движении тела по окружности и как его определить.

2 мин

Актуализация опорных знаний.

Слайд 2.

Физический диктант:

Изменение положения тела в пространстве с течением времени. (Движение)
Физическая величина, измеряемая в метрах. (Перемещение)
Физическая векторная величина, характеризующая быстроту движения. (Скорость)
Основная единица измерения длины в физике. (Метр)
Физическая величина, единицами измерения которой служат год, сутки, час. (Время)
Физическая векторная величина, которую можно измерить с помощью прибора акселерометра. (Ускорение)
Длина траектории. (Путь)
Единицы измерения ускорения (м/с²).

(Проведение диктанта с последующей проверкой, самооценка работ учениками)

$C:\Users\Aida\Desktop\Dvizhenie tela po okruzhnosti1\2\Dvizhenie tela po okruzhnosti Александрова З.В\Слайд2.JPG$

5 мин

Изучение нового материала.

Слайд 3.

Учитель. Мы достаточно часто наблюдаем такое движение тела, при котором его траекторией является окружность. По окружности движется, например, точка обода колеса при его вращении, точки вращающихся деталей станков, конец стрелки часов.

$C:\Users\Aida\Desktop\Dvizhenie tela po okruzhnosti1\2\Dvizhenie tela po okruzhnosti Александрова З.В\Слайд3.JPG$

Демонстрации опытов 1. Падение теннисного шара, полёт волана для бадминтона, перемещение игрушечного автомобиля, колебания шарика на нити, закреплённого в штативе. Что общего и чем отличаются эти движения по виду? (Ответы учеников)

Учитель. Прямолинейное движение – это движение, траектория которого — прямая линия, криволинейное – кривая. Приведите примеры прямолинейного и криволинейного движения, с которыми вы встречались в жизни. (Ответы учеников)

Движение тела по окружности является частным случаем криволинейного движения.

Любую кривую можно представить, как сумму дуг окружностей разного (или одинакового) радиуса.

Криволинейным движением называют такое движение, которое совершается по дугам окружностей.

Введём некоторые характеристики криволинейного движения.

Слайд 4. (просмотр видео «скорость.avi» по ссылке на слайде)

Криволинейное движение с постоянной по модулю скоростью. Движение с ускорением, т.к. скорость меняет направление.

$C:\Users\Aida\Desktop\Dvizhenie tela po okruzhnosti1\2\Dvizhenie tela po okruzhnosti Александрова З.В\Слайд4.JPG$

Слайд 5. (просмотр видео «Зависимость центростремительного ускорения от радиуса и скорости. аvi» по ссылке на слайде)

$C:\Users\Aida\Desktop\Dvizhenie tela po okruzhnosti1\2\Dvizhenie tela po okruzhnosti Александрова З.В\Слайд5.JPG$

Слайд 6. Направление векторов скорости и ускорения.

(работа с материалами слайда и анализ рисунков, рациональное использование эффектов анимации, заложенных в элементы рисунков, рис 1.)

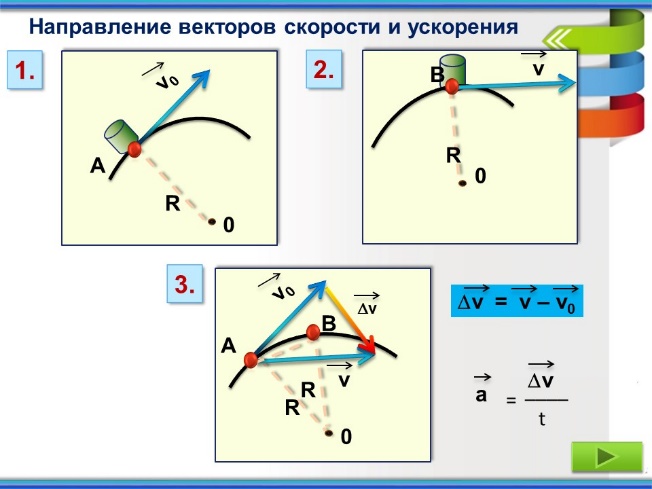
$C:\Users\Aida\Desktop\Dvizhenie tela po okruzhnosti1\2\Dvizhenie tela po okruzhnosti Александрова З.В\Слайд6.JPG$

Рис.1.

Слайд 7.

При равномерном движении тела по окружности вектор ускорения всё время перпендикулярен вектору скорости, который направлен по касательной к окружности.

Тело движется по окружности при условии, что вектор линейной скорости перпендикулярен вектору центростремительного ускорения.

Слайд 8. (работа с иллюстрациями и материалами слайда)

Центростремительное ускорение — ускорение, с которым тело движется по окружности с постоянной по модулю скоростью, всегда направлено вдоль радиуса окружности к центру.

a_ц=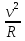

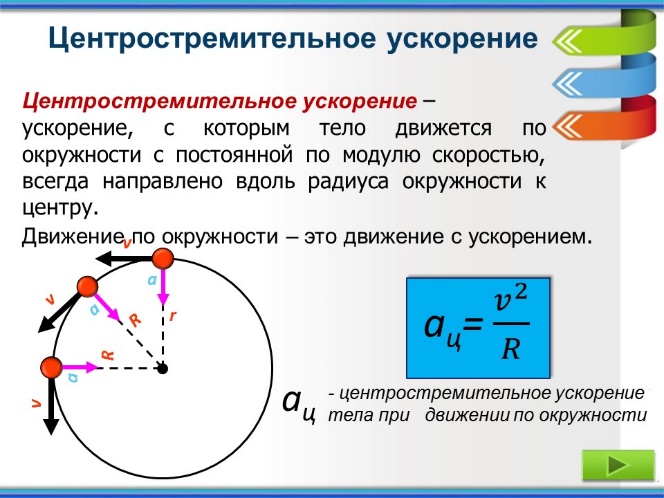
$C:\Users\Aida\Desktop\Dvizhenie tela po okruzhnosti1\2\Dvizhenie tela po okruzhnosti Александрова З.В\Слайд8.JPG$

Слайд 9.

При движении по окружности тело через определённый промежуток времени вернётся в первоначальную точку. Движение по окружности – периодическое.

Период обращения – это промежуток времени Т, в течение которого тело (точка) совершает один оборот по окружности.

Единица измерения периода — секунда

Частота вращения  – число полных оборотов в единицу времени.

[ ] = с^-1 = Гц

Единица измерения частоты

Сообщение ученика 1. Период — это величина, которая часто встречается в природе, науке и технике. Земля вращается вокруг своей оси, средний период этого вращения составляет 24 часа; полный оборот Земли вокруг Солнца происходит примерно за 365,26 суток; винт вертолёта имеет средний период вращения от 0,15 до 0,3 с; период кровообращения у человека равен примерно 21 — 22 с.

Сообщение ученика 2. Частоту измеряют специальными приборами – тахометрами.

Частота вращения технических устройств: ротор газовой турбины вращается с частотой от 200 до 300 1/с; пуля, вылетевшая из автомата Калашникова, вращается с частотой 3000 1/с.

Слайд 10. Связь периода с частотой:

Если за время t тело совершило N полных оборотов, то период обращения равен:

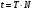
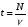
Период и частота – это взаимообратные величины: частота обратно пропорциональна периоду, а период обратно пропорционален частоте

$C:\Users\Aida\Desktop\Dvizhenie tela po okruzhnosti1\2\Dvizhenie tela po okruzhnosti Александрова З.В\Слайд10.JPG$

Слайд 11. Быстроту обращения тела характеризуют угловой скоростью.

Угловая скорость (циклическая частота)- число оборотов за единицу времени, выраженное в радианах.

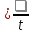
Угловая скорость – угол поворота, на который поворачивается точка за время t.

Угловая скорость измеряется в рад/с.

$C:\Users\Aida\Desktop\Dvizhenie tela po okruzhnosti1\2\Dvizhenie tela po okruzhnosti Александрова З.В\Слайд11.JPG$

Слайд 12. (просмотр видео «Путь и перемещение при криволинейном движении.avi» по ссылке на слайде)

$C:\Users\Aida\Desktop\Dvizhenie tela po okruzhnosti1\2\Dvizhenie tela po okruzhnosti Александрова З.В\Слайд12.JPG$

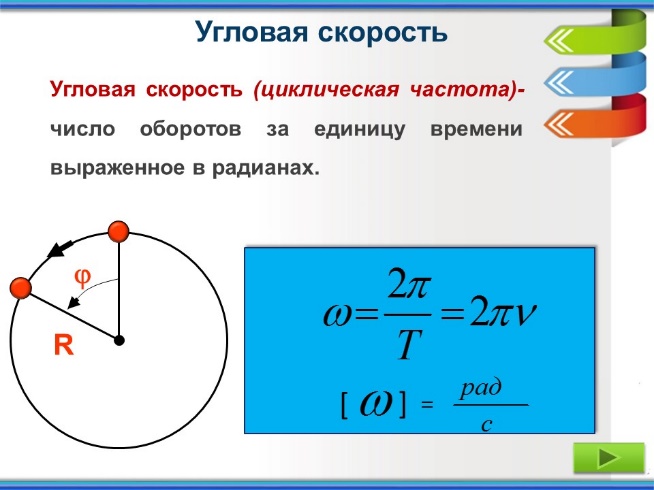
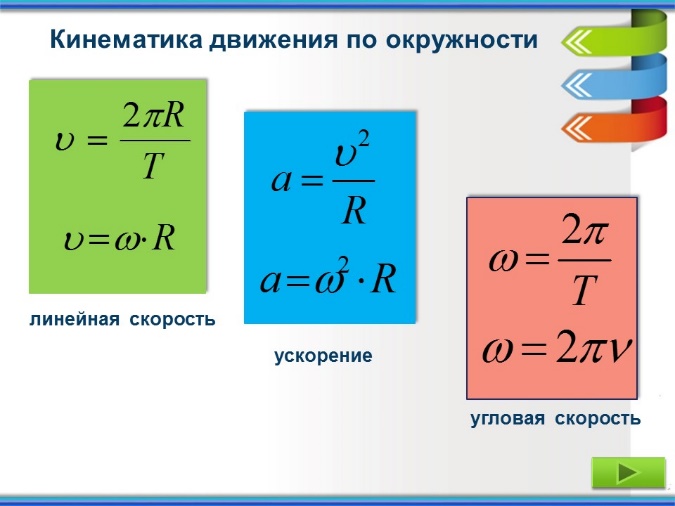
Слайд 13. Кинематика движения по окружности.

Учитель. При равномерном движении по окружности модуль его скорости не изменяется. Но скорость — векторная величина, и она характеризуется не только числовым значением, но и направлением. При равномерном движении по окружности всё время изменяется направление вектора скорости. Поэтому такое равномерное движение является ускоренным.

Линейная скорость: ;

Линейная и угловая скорости связаны соотношением:

Центростремительное ускорение: ;

Угловая скорость: ;

$C:\Users\Aida\Desktop\Dvizhenie tela po okruzhnosti1\2\Dvizhenie tela po okruzhnosti Александрова З.В\Слайд13.JPG$

Слайд 14. (работа с иллюстрациями на слайде)

Направление вектора скорости. Линейная (мгновенная скорость) всегда направлена по касательной к траектории, проведенной к той ее точке, где в данный момент находится рассматриваемое физическое тело.

Вектор скорости направлен по касательной к описываемой окружности.

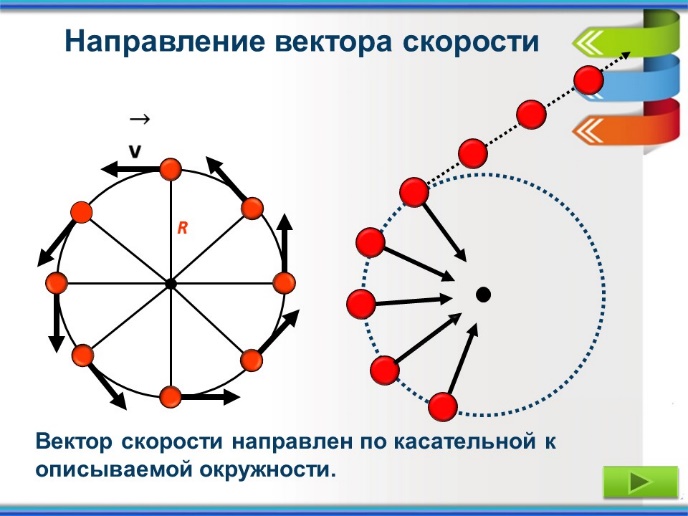
$C:\Users\Aida\Desktop\Dvizhenie tela po okruzhnosti1\2\Dvizhenie tela po okruzhnosti Александрова З.В\Слайд14.JPG$

Равномерное движение тела по окружности является движением с ускорением. При равномерном движении тела по окружности величины υ и ω остаются неизменными. В этом случае при движении изменяется только направление вектора.

Слайд 15. Центростремительная сила.

Сила, удерживающая вращающееся тело на окружности и направленная к центру вращения, называется центростремительной силой.

Чтобы получить формулу для расчёта величины центростремительной силы, надо воспользоваться вторым законом Ньютона, который применим и к любому криволинейному движению.

Подставляя в формулу 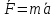значение центростремительного ускорения a_ц= 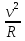, получим формулу центростремительной силы:

F =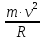

Из первой формулы видно, что при одной и той же скорости чем меньше радиус окружности, тем больше центростремительная сила. Так, на поворотах дороги на движущееся тело (поезд, автомобиль, велосипед) должна действовать по направлению к центру закругления тем большая сила, чем круче поворот, т. е. чем меньше радиус закругления.

Центростремительная сила зависит от линейной скорости: с увеличением скорости она увеличивается. Это хорошо известно всем конькобежцам, лыжникам и велосипедистам: чем с большей скоростью движешься, тем труднее сделать поворот. Шофёры очень хорошо знают, как опасно круто поворачивать автомобиль на большой скорости.

$C:\Users\Aida\Desktop\Dvizhenie tela po okruzhnosti1\2\Dvizhenie tela po okruzhnosti Александрова З.В\Слайд15.JPG$

Слайд 16.

Сводная таблица физических величин, характеризующих криволинейное движение (анализ зависимостей между величинами и формулами)

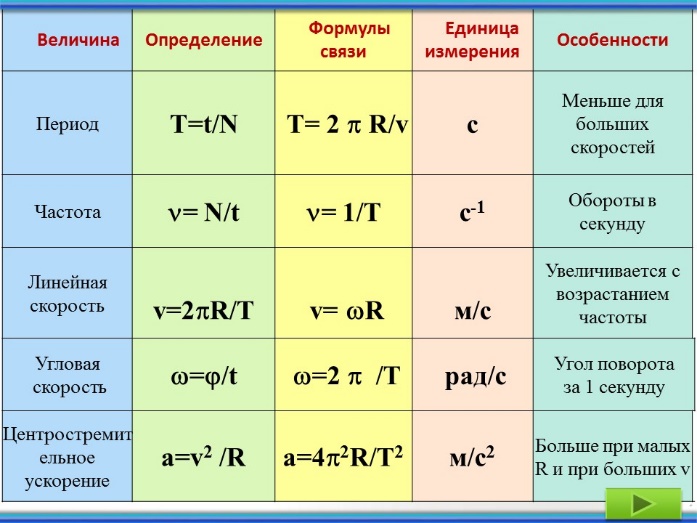
$C:\Users\Aida\Desktop\Dvizhenie tela po okruzhnosti1\2\Dvizhenie tela po okruzhnosti Александрова З.В\Слайд16.JPG$

Слайды 17, 18, 19. Примеры движение по окружности.

Круговое движение на дорогах. Движение спутников вокруг Земли.

Слайд 20. Аттракционы, карусели.

Сообщение ученика 3. В Средние века каруселями (слово тогда имело мужской род) называли рыцарские турниры. Позднее, в XVIII веке, для подготовки к турнирам, вместо схваток с реальными соперниками, стали использовать вращающуюся платформу, прообраз современной развлекательной карусели, которая тогда же появилась на городских ярмарках.

В России первый карусель был построен 16 июня 1766 года перед Зимним дворцом. Карусель состоял из четырёх кадрилей: Славянской, Римской, Индийской, Турецкой. Второй раз карусель была построена на том же месте, в том же году 11 июля. Подробное описание этих каруселей приводятся в газете Санкт-Петербургские ведомости 1766 года.

Карусель, распространённая во дворах в советское время. Карусель может приводиться в движение как двигателем (обычно электрическим), так и силами самих крутящихся, которые перед тем как сесть на карусель, раскручивают её. Такие карусели, которые нужно раскручивать самим катающимся, часто устанавливают на детских игровых площадках.

Кроме аттракционов, каруселями часто называют другие механизмы, имеющие сходное поведение — например, в автоматизированных линиях по разливу напитков, упаковке сыпучих веществ или производству печатной продукции.

В переносном смысле каруселью называют череду быстро сменяющихся предметов или событий.

18 мин

Закрепление нового материала. Применение знаний и умений в новой ситуации.

Учитель. Сегодня на этом уроке мы познакомились с описанием криволинейного движения, с новыми понятиями и новыми физическими величинами.

Беседа по вопросам:

Что такое период? Что такое частота? Как связаны между собой эти величины? В каких единицах измеряются? Как их можно определить?
Что такое угловая скорость? В каких единицах она измеряется? Как можно её рассчитать?
Что называют угловой скоростью? Что является единицей угловой скорости?
Как связаны угловая и линейная скорости движения тела?
Как направлено центростремительное ускорение? По какой формуле оно рассчитывается?

Слайд 21.

Задание 1. Заполните таблицу, решив задачи по исходным данным (Рис.2), затем мы сверим ответы. (Ученики работают самостоятельно с таблицей, необходимо заранее приготовить распечатку таблицы для каждого ученика)

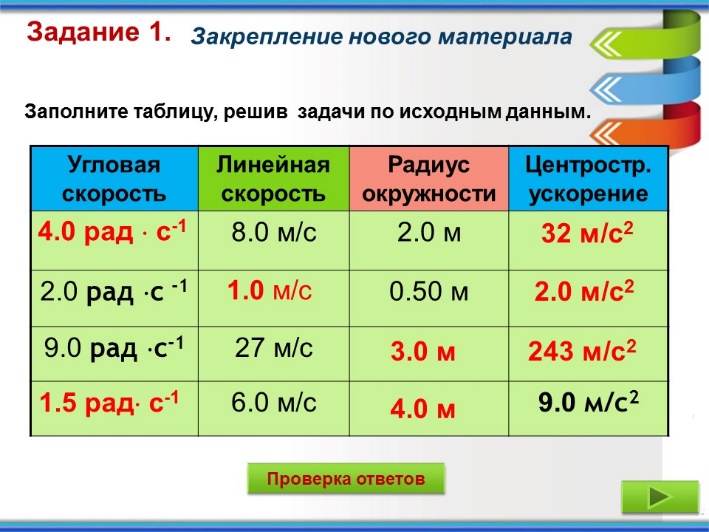
$C:\Users\Aida\Desktop\Dvizhenie tela po okruzhnosti1\2\Dvizhenie tela po okruzhnosti Александрова З.В\Слайд21.JPG$

Рис.2

Слайд 22. Задание 2. (устно)

Обратите внимание на анимационные эффекты рисунка. Сравните характеристики равномерного движения синего и красного шара. (Работа с иллюстрацией на слайде).

Слайд 23. Задание 3. (устно)

Колёса представленных видов транспорта за одно и то же время совершают равное количество оборотов. Сравните их центростремительные ускорения. (Работа с материалами слайда)

(Работа в группе, проведение эксперимента, распечатка инструкции для проведения эксперимента есть на каждом столе)

Оборудование: секундомер, линейка, шарик, закреплённый на нити, штатив с муфтой и лапкой.

Цель: исследовать зависимость периода, частоты и ускорения от радиуса вращения.

План работы

Измерьте время t 10 полных оборотов вращательного движения и радиус R вращения, шарика, закреплённого на нити в штативе.
Вычислите период Т и частоту, скорость вращения, центростремительное ускорение Результаты оформите в виде задачи.
Измените радиус вращения (длину нити), повторите опыт ещё 1 раза, стараясь сохранить прежней скорость, прикладывая прежнее усилие.
Сделайте вывод о зависимости периода, частоты и ускорения от радиуса вращения (чем меньше радиус вращения, тем меньше период обращения и больше значение частоты).

Слайды 24 -29.

Фронтальная работа с интерактивным тестом.

Необходимо выбрать один ответ из трёх возможных, если был выбран правильный ответ, то он остаётся на слайде, и начинает мигать зелёный индикатор, неверные ответы исчезают.

Тело движется по окружности с постоянной по модулю скоростью. Как изменится его центростремительное ускорение при уменьшении радиуса окружности в 3 раза?
В центрифуге стиральной машины белье при отжиме движется по окружности с постоянной по модулю скоростью в горизонтальной плоскости. Как при этом направлен вектор его ускорения?
Конькобежец движется со скоростью 10 м/с по окружности радиусом 20 м. Определите его центростремительное ускорение.
Куда направлено ускорение тела при его движении по окружности с постоянной по модулю скоростью?
Материальная точка движется по окружности с постоянной по модулю скоростью. Как изменится модуль ее центростремительного ускорения, если скорость точки увеличить втрое?
Колесо машины делает 20 оборотов за 10 с. Определите период обращения колеса?

$C:\Users\Aida\Desktop\Dvizhenie tela po okruzhnosti1\2\Dvizhenie tela po okruzhnosti Александрова З.В\Слайд24.JPG$ $C:\Users\Aida\Desktop\Dvizhenie tela po okruzhnosti1\2\Dvizhenie tela po okruzhnosti Александрова З.В\Слайд25.JPG$

Слайд 30. Решение задач (самостоятельная работа при наличии времени на уроке)

Вариант 1.

С каким периодом должна вращаться карусель радиусом 6,4 м для того, чтобы центростремительное ускорение человека на карусели было равно 10 м/с²?

На арене цирка лошадь скачет с такой скоростью, что за 1 минуту обегает 2 круга. Радиус арены равен 6,5 м. Определите период и частоту вращения, скорость и центростремительное ускорение.

Вариант 2.

Частота обращения карусели 0,05 с^-1. Человек, вращающийся на карусели, находится на расстоянии 4 м от оси вращения. Определите центростремительное ускорение человека, период обращения и угловую скорость карусели.

Точка обода колеса велосипеда совершает один оборот за 2 с. Радиус колеса 35 см. Чему равно центростремительное ускорение точки обода колеса?

$C:\Users\Aida\Desktop\Dvizhenie tela po okruzhnosti1\2\Dvizhenie tela po okruzhnosti Александрова З.В\Слайд30.JPG$

18 мин

Подведение итогов урока.

Выставление оценок. Рефлексия.

Слайд 31.

Д/з: п. 18-19, Упр.18 (2,4).

Слайд 32. Список использованных интернет – ресурсов.

2 мин

Литература:

Физика. 9 класс. Учебник. Перышкин А.В., Гутник Е.М. 14-е изд., стер. — М.: Дрофа,2012 г.

Сборник задач по физике для 7-9 классов. Перышкин А.В., 2010 г.

Л С. А. Тихомирова. Дидактический материал по физике. Физика в художественной литературе. 7 – 11 классы. – М.: Просвещение. 1996 г.

Использованные интернет — ресурсы:

http://www.livegif.ru/Gallery/TECHNIKS/SAMOLET/6T5.GIF

http://3.bp.blogspot.com/-_6Gqe59sqcI/T8ZkrXqP3GI/AAAAAAAAAjw/KuI3dGZO-7I/s1600/image003.jpg

http://www.ux1.eiu.edu/~cfadd/1150/05UCMGrav/Images/curve2.gif

http://www.ux1.eiu.edu/~cfadd/1150/05UCMGrav/Images/curve1.gif

http://imagine.gsfc.nasa.gov/YBA/cyg-X1-mass/images/ucm.gif

http://cvuweb.cvuhs.org/faculty/phil/moodle%20files/images/loop.jpg

http://www.stmary.ws/highschool/physics/home/notes/motionplane/circleRock.gif

http://www.stmary.ws/highschool/physics/home/notes/motionplane/man_rc_car_circling_lg_wht[1].gif

http://www.stmary.ws/highschool/physics/home/notes/motionplane/figure_skater_couple_death_spiral_hg_wht.gif

http://www.stmary.ws/highschool/physics/home/notes/motionplane/4952638_7498.gif

http://www

Равномерное движение точки по окружности

Движение тела по окружности довольно часто встречается в повседневной жизни. Взять хотя бы движение Земли вокруг своей оси или вокруг Солнца.

Кроме этого существуют ещё сотни примеров: вращение колеса автомобиля, вращение электронов вокруг ядра атома, движение стрелок часов и многое другое.

В первую очередь, давайте условимся, что называется равномерным движением по окружности? При прямолинейном движении мы говорили о том, что тело совершает одинаковые перемещения за равные промежутки времени. В случае с движением тела по окружности, равномерным движением называется такое движение, при котором тело поворачивается на одинаковые углы за равные промежутки времени.

Мы уже говорили о том, что мгновенная скорость направлена по касательной к траектории движения. Значит, при движении тела по окружности, его скорость будет направлена по касательной к этой окружности в данной точке. При этом, модуль скорости, так же, как и модуль ускорения остаётся постоянным, в то время как их направления постоянно меняются.

Из этого можно сделать вывод, что любое криволинейное движение является ускоренным, даже если модуль скорости остаётся постоянным.

Давайте рассмотрим ускорение при движении тела по кривой. Поскольку направление ускорения постоянно меняется, имеет смысл рассматривать мгновенное ускорение. Точно так же, как и в случае с мгновенной скоростью, мы будем брать все меньшие и меньшие промежутки времени.

Тогда, можем записать, что мгновенное ускорение — отношение изменения скорости к промежутку времени, за который это изменение произошло, при

Возьмём две произвольные точки А и В, принадлежащие окружности. В обеих точках скорость будет направлена по касательной, а модуль скорости в точке A будет равен модулю скорости в точке B.

Воспользуемся теперь сложением скоростей, чтобы найти вектор показывающий направление изменения скорости. Рассмотрим два треугольника, показанные на рисунке. Один из этих треугольников образован двумя радиусами и вектором перемещения, а второй — двумя модулями скорости и вектором изменения скорости. Эти треугольники подобны, т.к. являются равнобедренными и имеют одинаковый угол при вершине. Напомним, что мы рассматриваем промежуток времени, стремящийся к нулю. В этом случае, угол поворота будет стремиться к нулю, а значит и угол между скоростью в точке A и скоростью в точке B — тоже будет стремиться к нулю.

Поскольку сумма углов треугольника равна 180^o, и в равнобедренном треугольнике углы при основании равны, мы можем сделать вывод, что угол между вектором скорости и вектором изменения скорости составляет 90^o. Это очень важный вывод, т.к. вектор изменения скорости указывает направление ускорения. Поскольку радиус всегда перпендикулярен касательной, ускорение направлено по радиусу, то есть, стремиться к центру. Именно поэтому, ускорение при криволинейном движении называется центростремительным.

Теперь разберёмся с модулем ускорения. Мы снова используем те же два треугольника. Поскольку треугольники подобны, мы можем записать, что

Перемещение мы можем записать как произведение скорости и времени:

Теперь преобразуем выражение:

Это, как раз, и будет модулем ускорения:

Таким образом, мы выяснили, что ускорение при движении по окружности направлено к центру и численно равно отношению квадрата скорости к радиусу окружности.

В завершении темы, вспомним несколько важных физических величин, описывающих криволинейное движение. В первую очередь, это, конечно, период обращения. Периодом обращения называется время, за которое тело совершает полный оборот.

Например, период обращения Земли вокруг Солнца равен одному году.

Существует также величина, обратная периоду, которая называется частотой. Эта величина равна числу оборотов в единицу времени. Очевидно, что период обращения и частота обратно пропорциональны:

К примеру, чем быстрее вращаются лопасти вентилятора, тем больше он оборотов совершит в единицу времени и тем меньше период обращения.

Еще одной важной характеристикой движения по окружности является угловая скорость. Скорость, о которой мы говорили до этого — это фактическая скорость движения, которая называется линейной.

Угловая скорость характеризует скорость поворота, то есть изменение угла поворота в единицу времени.

Таким образом, угловая скорость измеряется в радианах в секунду:

Напомним, что радиан — это угол между двумя радиусами окружности, вырезающими на окружности дугу, длина которой равна радиусу окружности. Применительно к физике, мы можем сказать, что радиан — это такой угол, при повороте на который, точка проходит путь, равный радиусу окружности.

Мы знаем, что полный оборот — это поворот на угол, равный . Тогда, угловая скорость будет равна:

Линейная скорость будет определяться:

Также можно записать, что линейная скорость равна произведению угловой скорости и радиуса окружности:

Это вполне логично: чем дальше точка находится от центра, вокруг которого она вращается, тем больше должна быть её линейная скорость, чтобы за одинаковое время совершить поворот на одинаковый угол.

Мы рассмотрели частный случай: когда точка совершает полный оборот по окружности. В более общем случае, угловая скорость будет определяться как отношение угла поворота ко времени, за который этот поворот был совершён:

Аналогично, линейная скорость определяется как отношение длины пройденной дуги ко времени:

Для примера рассмотрим, так называемый, геостационарный спутник. Это искусственный спутник Земли, который постоянно находится над одной и той же точкой поверхности Земли (с помощью таких спутников работает спутниковое телевидение, к примеру). Для выполнения этого условия необходимо, чтобы спутник вращался с той же угловой скоростью, что и Земля.

Пример решения задачи.

Задача. Спидометр автомобиля показывает 90 км/ч, а тахометр — 2400 об/мин. Чему равен радиус колеса в таком случае?

Угловая скорость при движении по окружности – Средняя угловая скорость равномерно ускоренного движения по окружности | Формулы и расчеты онлайн

Репетитор-онлайн — подготовка к ЦТ

Движение тела по окружности в физике » Nikulux

Движение по окружности — задачи

Т. Движение по окружности — PhysBook

Движение тела по окружности с постоянной по модулю скоростью

Литература

Презентация «Движение тела по окружности».

Равномерное движение точки по окружности

Добавить комментарий Отменить ответ