Движение по окружности
Движение по окружности — простейший случай криволинейного движения тела. Когда тело движется вокруг некоторой точки, наряду с вектором перемещения удобно ввести угловое перемещение ∆φ (угол поворота относительно центра окружности), измеряемое в радианах.
Зная угловое перемещение, можно вычислить длину дуги окружности (путь), которую прошло тело.
∆l=R∆φ
Если угол поворота мал, то ∆l≈∆s.
Проиллюстрируем сказанное:
Угловая скорость
При криволинейном движении вводится понятие угловой скорости ω, то есть скорости изменения угла поворота.
Определение. Угловая скоростьУгловая скорость в данной точке траектории — предел отношения углового перемещения ∆φ к промежутку времени ∆t, за которое оно произошло. ∆t→0.
ω=∆φ∆t, ∆t→0.
Единица измерения угловой скорости — радиан в секунду (радс).
Существует связь между угловой и линейной скоростями тела при движении по окружности.
ω=vR
Нормальное ускорение
При равномерном движении по окружности, скорости v и ω остаются неизменными. Меняется только направление вектора линейной скорости.
При этом равномерное движение по окружности на тело действует центростремительное, или нормальное ускорение, направленное по радиусу окружности к ее центру.
an=∆v→∆t, ∆t→0
Модуль центростремительного ускорения можно вычислить по формуле:
an=v2R=ω2R
Докажем эти соотношения.
Рассмотрим, как изменяется вектор v→ за малый промежуток времени ∆t. ∆v→=vB→-vA→.
В точках А и В вектор скорости направлен по касательной к окружности, при этом модули скоростей в обеих точках одинаковы.
По определению ускорения:
a→=∆v→∆t, ∆t→0
Взглянем на рисунок:
Треугольники OAB и BCD подобны. Из этого следует, что OAAB=BCCD.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать заданиеЕсли значение угла ∆φ мало, расстояние AB=∆s≈v·∆t.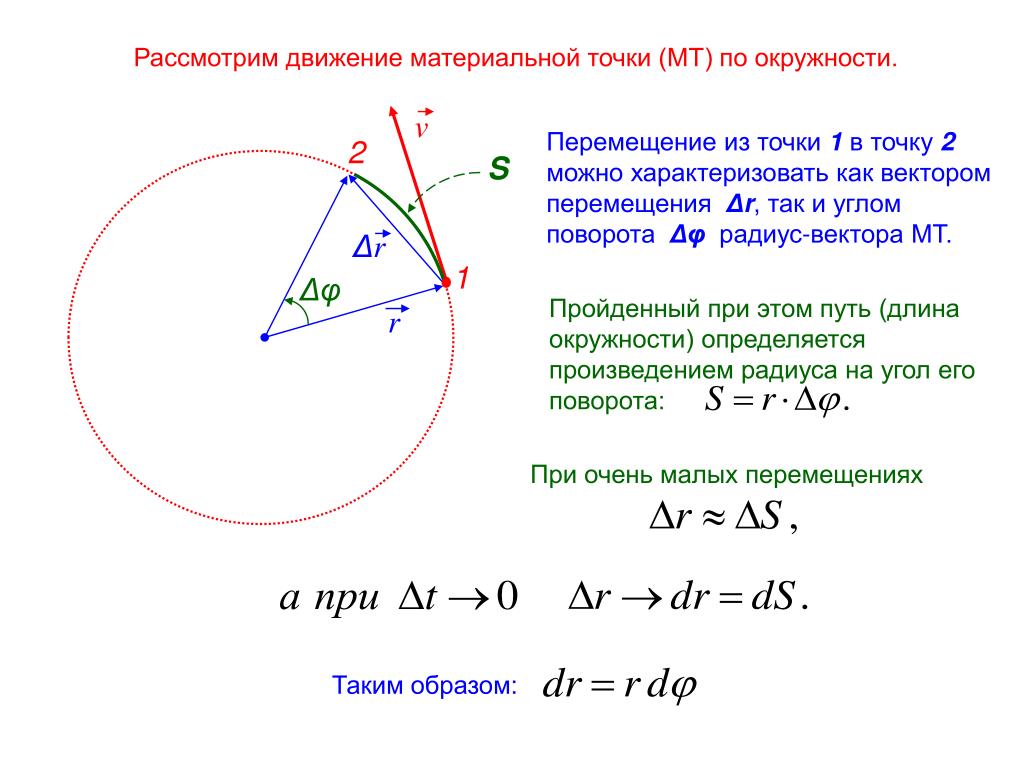
Принимая во внимание, что OA=R и CD=∆v для рассмотренных выше подобных треугольников получим:
Rv∆t=v∆v или ∆v∆t=v2R
При ∆φ→0, направление вектора ∆v→=vB→-vA→ приближается к направлению на центр окружности. Принимая, что ∆t→0, получаем:
a→=an→=∆v→∆t; ∆t→0; an→=v2R.
При равномерном движении по окружности модуль ускорения остается постоянным, а направление вектора изменяется со временем, сохраняя ориентацию на центр окружности. Именно поэтому это ускорение называется центростремительным: вектор в любой момент времени направлен к центру окружности.
Запись центростремительного ускорения в векторной форме выглядит следующим образом:
an→=-ω2R→.
Здесь R→ — радиус вектор точки на окружности с началом в ее центре.
Тангенциальное ускорение
В общем случае ускорение при движении по окружности состоит из двух компонентов — нормальное, и тангенциальное.
Рассмотрим случай, когда тело движется по окружности неравномерно. Введем понятие тангенциального (касательного) ускорения.
Его направление совпадает с направлением линейной скорости тела и в каждой точке окружности направлено по касательной к ней.
aτ=∆vτ∆t; ∆t→0
Здесь ∆vτ=v2-v1 — изменение модуля скорости за промежуток ∆t
Направление полного ускорения определяется векторной суммой нормального и тангенциального ускорений.
Движение по окружности в плоскости можно описывать при помощи двух координат: x и y. В каждый момент времени скорость тела можно разложить на составляющие vx и vy.
Если движение равномерное, величины vx и vy а также соответствующие координаты будут изменяться во времени по гармоническому закону с периодом T=2πRv=2πω
| | Адрес этой страницы (вложенность) в справочнике dpva. ru: главная страница / / Техническая информация /Поделиться:
| |||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. Вложите в письмо ссылку на страницу с ошибкой, пожалуйста. | ||||||
| Коды баннеров проекта DPVA.ru Начинка: KJR Publisiers Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator | |||||
Движение по окружности-Теория.Скорость в физике
На главную Теория Задачи Учёные Интересные статьи Шкала скоростейKинематика равномерного вращения по окружности
При движении по окружности с
постоянной по величине линейной
скоростью v тело испытывает
направленное к центру окружности
постоянное центростремительное
ускорение
aц = v2/R,
где R — радиус окружности.
Вывод формулы для центростремительного ускорения
По определению
На рисунке треугольники,
образованные векторами перемещений
и скоростей, подобны. Учитывая, что
|r1| = |r2| = R и |v1| = |v2| = v, из
подобия треугольников находим:
откуда
Поместим начало координат в
центр окружности и выберем
плоскость, в которой лежит
окружность, за плоскость (x, y).
Положение точки на окружности в
любой момент времени однозначно
определяется полярным углом j,
измеряемым в радианах (рад), причем
где j0 определяет начальную фазу (начальное положение точки на окружности в нулевой момент времени).
В случае равномерного вращения
угол j, измеряемый в радианах,
линейно растет со временем:
j = wt,
где w называется циклической
(круговой) частотой.
Размерность
циклической частоты: [w] = c-1 = Гц.
Циклическая частота равна величине угла поворота (измеренном в рад) за единицу времени, так что иначе ее называют угловой скоростью.
Зависимость координат точки на
окружности от времени в случае
равномерного вращения с заданной
частотой можно записать в виде:
x = R cos(wt + j0),
y = R sin(wt + j0).
Время, за которое совершается один оборот, называется периодом T.
Частота
n = 1/T.
Размерность частоты: [n] = с-1 = Гц.
Связь циклической частоты с
периодом и частотой: 2p = wT, откуда
w = 2p/T = 2pn.
Связь линейной скорости и угловой
скорости находится из равенства:
2pR = vT, откуда
v = 2pR/T = wR.
Выражение для
центростремительного ускорения
можно записать разными способами,
используя связи между скоростью,
частотой и периодом:
aц = v2/R = w2R = 4p2n2R = 4p2R/T2.
Связь поступательного и вращательного движений
Основные кинематические
характеристики движения по прямой с
постоянным ускорением: перемещение
s, скорость v и ускорение a.
Соответствующие характеристики при
движении по окружности радиусом R:
угловое перемещение j, угловая
скорость w и угловое ускорение a (в
случае, если тело вращается с
переменной скоростью). Из
геометрических соображений
вытекают следующие связи между
этими характеристиками:
перемещение sугловое перемещение j = s/R;
скорость vугловая скорость w = v/R;
ускорение aугловое ускорение a = a/R.
Все формулы кинематики
равноускоренного движения по прямой
могут быть превращены в формулы
кинематики вращения по окружности,
если сделать указанные замены.
Например:
s = vtj = wt,
v = v0 + atw = w0 + at.
Связь между линейной и угловой
скоростями точки при вращении по
окружности можно записать в
векторной форме. Действительно,
пусть окружность с центром в начале
координат расположена в плоскости
(x, y). В любой момент времени вектор
R, проведенный из начала координат в
точку на окружности, где находится
тело, перпендикулярен вектору
скорости тела v, направленному по
касательной к окружности в этой
точке. Определим вектор w, который
по модулю равен угловой скорости w и
направлен вдоль оси вращения в
сторону, которая определяется
правилом правого винта: если
завинчивать винт так, чтобы
направление его вращения совпадало с
направлением вращения точки по
окружности, то направление движения
винта показывает направление
вектора w.
Тогда связь трех взаимно
перпендикулярных векторов R, v и w
можно записать с помощью векторного
произведения векторов:
v = wR.Задачи на эту тему
| 1. | Задача на проверку теории | 1 вид — рецептивный | лёгкое | 2 Б. |
Задание направлено на проверку основных понятий по теме «Равномерное движение по окружности».
|
| 2. | Задача на определение модуля центростремительного ускорения | 1 вид — рецептивный | лёгкое | 1 Б. | Задача направлена на формирование умения определять модуль центростремительного ускорения. |
| 3. | Задача на определение характеристик движения по окружности | 1 вид — рецептивный | лёгкое |
2 Б.
|
Задача направлена на формирование умения определять характеристики движения по окружности: период обращения, частота обращения, модуль линейной скорости, модуль центростремительного ускорения и угловую скорость. |
| 4. | Задача на определение отношения частот через угловую скорость | 1 вид — рецептивный | лёгкое | 1 Б. |
Задача направлена на формирование умения определять соотношения частот тел, движущихся по окружности, через угловую скорость.
|
| 5. | Задача на определение модуля центростремительного ускорения | 2 вид — интерпретация | среднее | 2 Б. | Задача направлена на формирование умения определять центростремительное ускорение через радиус окружности и период движения тела. |
| 6. | Задача на определение частоты при движении по окружности | 2 вид — интерпретация | среднее |
2 Б.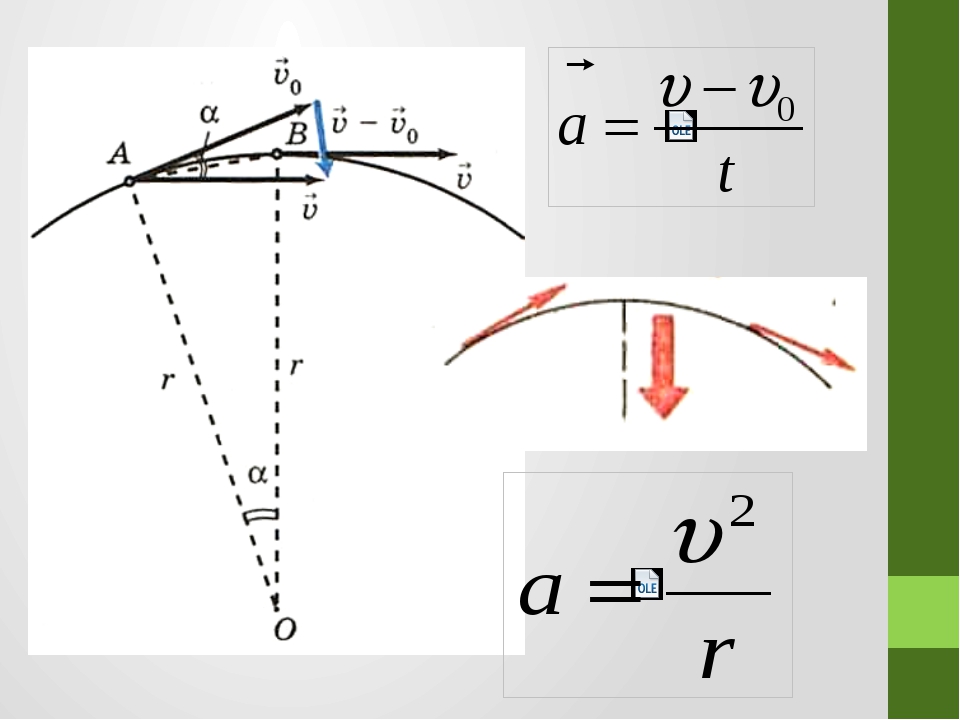
|
Задача направлена на формирование умения определять частоту движения одного тела через частоту движения другого тела, находящихся на одной прямой. |
| 7. | Задача на определение вектора перемещения тела | 2 вид — интерпретация | среднее | 1 Б. |
Задача направлена на формирование умения определять модуль перемещения тела, движущегося по окружности.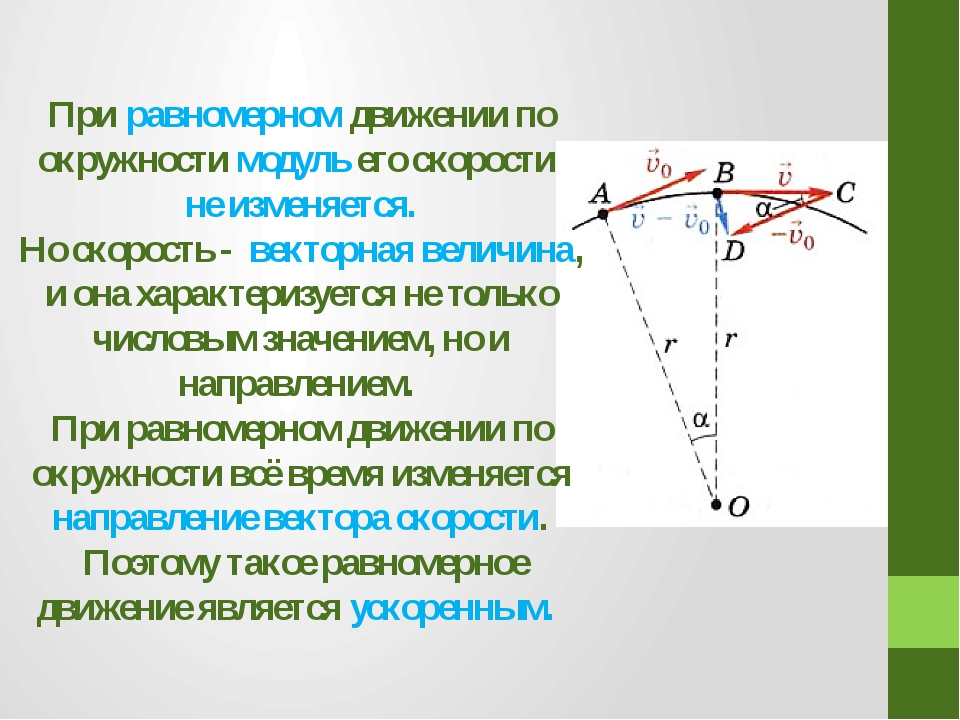
|
| 8. | Задача на определение тангенциального, нормального и полного ускорения в разных видах движения | 2 вид — интерпретация | среднее | 3 Б. | Задача направлена на формирование умения определять тангенциальное, нормальное и полное ускорения в разных видах движения. |
9.
|
Задача на определение периода обращения тела | 2 вид — интерпретация | среднее | 2 Б. | Задача направлена на формирование умения определять период обращения тела через соотношение линейных скоростей. |
| 10. | Задача на определение линейной скорости тела и пройденного пути | 2 вид — интерпретация | среднее |
3 Б.
|
Задача направлена на формирование умения определять линейную скорость и путь тела, движущегося по окружности. |
| 11. | Задача на определение ускорения при равномерном движении тела по окружности | 3 вид — анализ | сложное | 3 Б. | Задача направлена на формирование умения определять ускорение при движении по окружности. |
12.
|
Задача на определение количества оборотов колеса | 3 вид — анализ | сложное | 3 Б. | Задача направлена на формирование умения определять количество обротов тела, движущегося по окружности. |
| 13. | Задача на определение отношений ускорений | 3 вид — анализ | сложное |
4 Б.
|
Задача направлена на формирование умения определять соотношение ускорений тел: одно тело движется по окружности, другое прямолинейно и равноускоренно. |
| 14. | Задача на определение модуля линейной скорости тела | 3 вид — анализ | сложное | 3 Б. |
Задача направлена на формирование умения определять линейную скорость тела при движении по окружности при обгоне его другим телом.
|
Движение по окружности | fizmatuski.narod.ru
Движение по окружности
Движение по окружности – частный случай криволинейного движения.
При движении по окружности движение может быть:
- С постоянной по величине скоростью V=const
- С одинаково изменяющейся по величине скоростью Δ V= const
- С неодинаково изменяющейся по величине скоростью, ΔV разное, изменяется не одинаково.
!!! Но при этом во всех 3-х случаях V изменяется по направлению (всегда). Движение по окружности – это периодически повторяющееся движение.
Основными характеристиками такого движения являются:
— период – это время 1 полного оборота (t – все время, N – число оборотов за время t)
— частота – число оборотов за 1с.(Гц)
l = 2πR – путь за 1 поворот (длина окружности) (м)
L = 2πRN – путь за N оборотов (м).
1.Рассмотрим движение с постоянной по величине скоростью. По определению, скорость это путь, пройденнфй телом за единицу времени:
— это путевая скорость движения тела по окружности. Зная значения величин, входящих в эту формулу, получим формулы скорости, которые выражают зависимость от основных характеристик движения по окружности:
ω = 2πn – циклическая частота или угловая скорость (число оборотов за 2π секунды), измеряется в (Гц = рад/с).
(Гц)
Аналогия: тело со V тело проходит путь L, со скоростью ω проходит угловой путь φ (поворачивается на угол).
Угловое расстояние: φ = ωt или φ = 2πN
— ускорение, которое показываем изменение направления скорости ( но не величины) т.к. всегда перпендикулярна и направлена к центру окружности, то это ускорение называется центростремительным:
— формула, определяющая центростремительное ускорение. Подставляя вместо скорости её формулы, получим расчётные формулы для центростремительного ускорения:
— формулы для вычисления центростремительного ускорения через основные характеристики.
Рассмотрим частные случаи движения тел по окружности:
1. Движение по одному кругу, но по окружностям разного радиуса:
Если т.А и т.В двигаются синхронно то они вместе совершают 1 оборот, значит Т1 = Т2 (периоды их оборотов одинаковы), а из этого следует
ременная связь или зубчатая связь
=> n1 = n2 => ω1 = ω2, Зная связь между линейной и угловой скоростями, между ускорением и угловой скоростью, получим выражения:
2. Рассмотрим случай, когда два тела совершают круговые движения, но связаны ременной или зубчатой передачей
В этом случае скорости движения двух тел равны (нет провисания ремня ): V1 = V2
Зная формулы, связывающие линейную скорость с периодом вращения и с ускорением, получим:
2. Более сложный случай, когда скорость изменяется по величине.
— это средняя путевая скорость движения тела по окружности, где её изменение по величине характеризуется тангенциальным ускорением: ат , изменение скорости по направлению характеризуется центростремительным ускорением ац , которое в каждой точке разное, так как разной будет скорость движения по величине: . Эти два ускорения взаимно перпендикулярны т.к. ац направлено к центру окружности, а ат — по касательной ( если разгон, то по направлению скорости, если торможение, то в противоположную сторону).Так как тангенциальное ускорение не изменяется, а центростремительное изменяется, то будет изменяться и общее ускорение
Изменение скорости приведёт к изменению связанных с ним характеристик: периода, частоты и угловой скорости вращения.
(Гц)Вернуться к конспектам урока
1.6. Движение по окружностиДвижение тела по окружности является частным случаем криволинейного движения. Наряду с вектором перемещения удобно рассматривать угловое перемещение Δφ (или угол поворота), измеряемое в радианах (рис. 1.6.1). Длина дуги связана с углом поворота соотношениемПри малых углах поворота Δl ≈ Δs.
При равномерном движении тела по окружности величины υ и ω остаются неизменными. В этом случае при движении изменяется только направление вектора Равномерное движение тела по окружности является движением с ускорением. Ускорение
|
Движение по окружности: формулы и расчеты
Перемещение тел по окружности достаточно распространено в нашей жизни и в природе. Яркими примерами этого типа перемещения являются вращения ветровых мельниц, планет вокруг своих звезд и колес транспортных средств. В данной статье рассмотрим, какими формулами движение по окружности тел описывается.
Перемещение по окружности и по прямой линии в физике
В физике вопросами движения занимается кинематика. Она устанавливает связь между величинами, описывающими этот процесс. В динамике также уделяется внимание движению, однако она ориентирована на описание причин его возникновения. Другими словами, если для кинематики главными физическими величинами являются путь и скорость, то для динамики — это действующие на тела силы.
В физике принято выделять два идеальных типа траекторий движения:
- прямая линия;
- окружность.
Математический аппарат для описания движения по обоим типам траекторий развит настолько хорошо, что понимание формул, например для прямолинейного движения, автоматически приводит к пониманию выражений для движения по окружности. Единственная принципиальная разница между формулами указанных типов перемещения заключается в том, что для движения по окружности удобно использовать угловые характеристики, а не линейные.
Далее в статье будем рассматривать исключительно кинематические формулы движения по окружности тел, не вдаваясь в подробности динамики.
Угловые характеристики движения: угол поворота
Прежде чем записывать формулы движения по окружности в физике, следует ввести величины, которые будут фигурировать в этих формулах.
Начнем с угла поворота. Будем обозначать его греческой буквой θ (тета). Поскольку вращение предполагает движение точки вдоль одной и той же окружности, то значение угла поворота θ за определенный промежуток времени можно использовать для определения количества оборотов, которое сделала эта точка. Напомним, что вся окружность равна 2*pi радиан, или 360o. Тогда формула для числа оборотов n через угол θ примет вид:
n = θ/(2*pi)
Здесь и далее во всех формулах угол выражается в радианах.
Пользуясь известным углом θ, также можно определить линейное расстояние, которое точка прошла вдоль окружности. Это расстояние будет равно:
L = θ*r
Здесь r — радиус рассматриваемой окружности.
Угловая скорость и ускорение
Кинематические формулы движения по окружности точки предполагают также использование понятий угловой скорости и углового ускорения. Обозначим первую буквой ω (омега), а вторую буквой α (альфа).
Физический смысл угловой скорости ω прост: эта величина показывает, на какой угол в радианах поворачивается точка за каждую секунду времени. Данное определение имеет следующее математическое представление:
ω = dθ/dt
Эта формула скорости движения по окружности записана в дифференциальной форме. Полученная с ее помощью величина ω называется мгновенной скоростью. Ее удобно использовать, если движение не является равномерным, то есть происходит с переменной скоростью.
Угловое ускорение α — это величина, которая описывает быстроту изменения скорости ω, то есть:
α = dω/dt
Угловое ускорение измеряется в радианах в секунду квадратную (рад/с2). Так, 1 рад/с2 означает, что тело увеличивает за каждую секунду времени скорость на 1 рад/с.
Учитывая выражение для ω, записанное выше, равенство можно представить в такой форме:
α = d2θ/dt2
В зависимости от особенностей движения по окружности величина α может быть постоянной, переменной или нулевой.
Равномерное движение
Когда на вращающееся тело не действует никакая внешняя сила, то угловая скорость будет оставаться постоянной сколь угодно длительное время. Такое движение получило название равномерного вращения. Оно описывается следующей формулой:
θ = ω*t
В этом выражении переменными являются всего две величины: t и θ. Скорость ω = const.
Следует отметить один важный момент: нулю равна лишь равнодействующая внешних сил на тело, внутренние же силы, действующие в системе, нулю не равны. Так, внутренняя сила заставляет вращающееся тело изменять свою прямолинейную траекторию на криволинейную (окружность). Эта сила приводит к появлению центростремительного ускорения. Последнее не изменяет ни скорость ω, ни линейную скорость v, оно лишь изменяет направление движения.
Равноускоренное движение по окружности
Формулы для этого типа перемещения можно получить непосредственно из приведенных математических выражений для величин ω и α. Равноускоренное движение предполагает, что за более-менее длительный промежуток времени модуль и направление ускорения α не изменяются. Благодаря этому можно проинтегрировать дифференциальное выражение для α и получить следующие две формулы:
ω = ω0 + α*t;
ω = ω0 — α*t
Очевидно, что в первом случае движение будет равноускоренным, во втором — равнозамедленным. Величина ω0 здесь — это некоторая начальная скорость, которой вращающееся тело обладало до появления ускорения.
Для равноускоренного движения не существует конечной скорости, поскольку она может возрастать сколь угодно долго. Для равнозамедленного движения конечным состоянием будет прекращение вращения, то есть ω = 0.
Теперь запишем формулы для определения угла θ при движении с постоянным ускорением. Эти формулы получаются, если произвести двойное интегрирование по времени для выражения α через θ. Получаются следующие выражения:
θ = ω0*t + α*t2/2;
θ = ω0*t — α*t2/2
То есть центральный угол θ, на который тело повернется за время t, будет равен сумме двух слагаемых. Первое слагаемое — это вклад в θ равномерного движения, второе — равноускоренного (равнозамедленного).
Связь между угловыми и линейными величинами
При рассмотрении понятия угла поворота θ уже была приведена формула, которая его связывает с линейным расстоянием L. Здесь же рассмотрим аналогичные выражения для скорости ω и ускорения α.
Линейная скорость v при равномерном движении определяется как расстояние L, пройденное за время t, то есть:
v = L/t
Подставляя сюда выражение для L через θ, получаем:
v = L/t = θ/t*r = ω*r
Мы получили связь между линейной и угловой скоростью. Важно отметить, что удобство использования угловой скорости связано с тем, что она не зависит от радиуса окружности. В свою очередь, линейная скорость v возрастает линейно с увеличением r.
Остается записать связь между линейным ускорением a и его угловым аналогом α. Чтобы это сделать, запишем выражение для скорости v при равноускоренном движении без начальной скорости v0. Получаем:
v = a*t
Подставляем сюда полученное выражение связи между v и ω:
ω*r = a*t =>
a = ω/t*r = α*r
Как и скорость, линейное ускорение, направленное по касательной к окружности, зависит от радиуса.
Ускорение центростремительное
Выше уже было сказано несколько слов об этой величине. Здесь приведем формулы, которые можно использовать для ее вычисления. Через скорость v выражение для центростремительного ускорения ac имеет вид:
ac = v2/r
Через угловую скорость его можно записать так:
ac = ω2*r2/r = ω2*r
Величина ac не имеет никакого отношения к тангенциальному ускорению a. Центростремительное ускорение обеспечивает поддержание вращающегося тела на одной окружности.
Задача на определение угловой скорости вращения планеты
Известно, что ближе всего к солнцу находится Меркурий. Полагая, что он вращается по окружности вокруг светила, мы можем определить его угловую скорость ω.
Для решения задачи следует обратиться к справочным данным. Из них известно, что планета делает полный оборот вокруг светила за 87 дней 23,23 часа земных. Это время называется периодом обращения. Учитывая, что движение происходит с постоянной угловой скоростью, запишем рабочую формулу:
θ = ω*t =>
ω = θ/t
Остается перевести время в секунды, подставить значение угла θ, соответствующее полному обороту (2*pi), и записать ответ: ω = 8,26*10-7 рад/c.
Центростремительное ускорение
Следующая: Закон всемирного тяготения Ньютона Up: Круговое движение и Пред .: Связь между линейным и
Рассмотрим объект, движущийся по окружности радиуса r с постоянным угловая скорость. Тангенциальная скорость постоянна, но направление тангенциального вектора скорости изменяется по мере того, как объект вращается.
Определение: Центростремительное ускорение
Центростремительное ускорение — скорость изменения тангенциальная скорость:
| = | (17) |
Примечание:
- Направление центростремительного ускорения всегда внутрь по радиус-вектор кругового движения.
- Величина центростремительного ускорения связана с
тангенциальная скорость и угловая скорость следующие:
a c = = r . (18) - В общем, частица, движущаяся по кругу, испытывает оба
угловатый
ускорение и центростремительное ускорение. Поскольку двое всегда
перпендикулярно, по определению, величине чистого ускорения a итого это:
a всего = =. (19)
Определение: Центростремительная сила
Центростремительная сила — чистая сила, вызывающая центростремительную ускорение объекта в круговом движении. К Второй закон Ньютона:
| = м . | (20) |
| F c = м c = м = м r . | (21) |
Следующая: Закон всемирного тяготения Ньютона Up: Круговое движение и Пред .: Связь между линейным и [email protected]
09.10.1997
Угловая скорость и ускорение — AP Physics 1
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или несколько ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Тангенциальная скорость: определение, формула и уравнение
Тангенциальная скорость — это составляющая движения вдоль края окружности, измеренная в любой произвольный момент времени.Тангенциальная скорость описывает движение объекта по краю этого круга, направление которого в любой заданной точке круга всегда вдоль касательной к этой точке.
Тангенциальная скорость измеряется в любой точке, касательной к вращающемуся колесу. Таким образом, угловая скорость ω связана с тангенциальной скоростью Vt формулой: Vt = ω r. Здесь r — радиус колеса. Тангенциальная скорость — это составляющая движения по краю круга, измеренная в любой произвольный момент времени.Как следует из названия, тангенциальная скорость описывает движение объекта по краю этого круга, направление которого в любой заданной точке круга всегда вдоль касательной к этой точке.
Спрыгивать с движущегося автобуса опасно, поэтому осознанное решение совершить прыжок вызывает чувство трепета. Прыжок с края крутящейся карусели — это ее 9-летняя версия, если только у вас нет брата или сестры, который добровольно дает вам пинок в стиле «Это спарта» и отправляет в небытие.
Помимо того, что я обычно отклоняюсь от того, что важно, и излишне делясь тем, что я считаю травмами, изменяющими мою жизнь, у меня было еще кое-что, известное как тангенциальная скорость . Ага! Вот о чем эта статья!
Что такое касательная?
Касательная — это линия, которая касается функции только в одной точке. Термин функция здесь используется для определения любой нелинейной кривой. Он представляет собой уравнение — взаимосвязь между координатами «x» и «y» на двухмерном графике.
Например, рассмотрим кривую, с которой мы больше всего знакомы — старый добрый круг. Круг определяется уравнением. Это означает, что для постоянного радиуса «r» конкретные значения «x» и «y» очерчивают великолепную дугу, которая, как конец игры Snake , встречает свой собственный конец.
Визуализация обведения круга с центром в исходной точке.
Однако для простоты я специально рассмотрел уравнение, описывающее ортодоксальную окружность, центр которой лежит в начале координат — опорной точке или координатах (0,0), а радиус r — это расстояние. от начала до края этого круга.
Как следует из названия, тангенциальная скорость описывает движение объекта по краю этой окружности, направление которого в любой заданной точке окружности всегда вдоль касательной к этой точке. Однако концепция не ограничивается только равномерным круговым движением; это также относится ко всем с нелинейным перемещением . Если объект движется из точки A в точку B по нелинейной кривой, то красные стрелки представляют тангенциальную скорость в различных точках этой траектории.
А пока остановимся на круге.
Формула для тангенциальной скорости
Сначала мы вычисляем угловое смещение «q», которое представляет собой отношение длины дуги «s», которую объект проводит по этой окружности, к ее радиусу «r». Это угловая часть под тенью дуги, между двумя линиями, исходящими из центра и соединенными с ее концами. Измеряется в радианах.
Скорость изменения углового смещения объекта называется его угловой скоростью.Он обозначается буквой «w», а его стандартная единица измерения — радианы в секунду (рад / с). Она отличается от линейной скорости, поскольку имеет дело только с объектами, движущимися по кругу. По сути, он измеряет скорость, с которой изменяется угловое смещение.
Вычисление линейной или тангенциальной скорости при равномерном круговом движении.
Линейная составляющая угловой скорости известна как линейная скорость, которая представляет собой скорость изменения линейного смещения объекта. Линейное смещение — это указанная выше дуга «s» — длина дуги.Скорость изменения произведения радиуса «r» и углового смещения «q» представляет собой линейную скорость объекта. Радиус исключается из операции, так как он постоянный. Мы понимаем, что скорость — это произведение угловой скорости объекта и радиуса круга, который он отслеживает.
Линейная скорость объекта , движущегося по кругу, измеренная в произвольный момент времени, и есть его тангенциальная скорость!
Другой способ определить линейную скорость — это период времени.Если период времени — это время, необходимое объекту для того, чтобы один раз обойти круг, то скорость, с которой он это делает, равна ‘s / t’ (расстояние / время).
Связь между линейной или тангенциальной скоростью «v» и периодом времени «T».
Величина, обратная «T», называется частотой и обозначается буквой «f». Это количество циклов, выполняемых за секунду. Произведение 2pf известно как угловая частота и обозначается буквой «w», что помогает нам прийти к ранее полученному результату.
Перекрестное произведение
Крайне важно знать, что тангенциальная скорость — это вектор, то есть у нее есть размер и направление.Векторы обозначены стрелкой над их стандартным символом. Хотя их направление постоянно меняется, их общая ценность остается неизменной. Каждый вектор представляет собой крест или векторное произведение двух векторов, которое является произведением их величин и синуса угла между ними. Результирующий вектор имеет направление, перпендикулярное обоим задействованным векторам.
Почему значение тангенциальной скорости безразлично к ее непрерывно меняющемуся направлению и тангенциальным скоростям с одинаковой величиной, но разными направлениями на произвольных краях окружности.
Два вектора, произведение которых нам требуется, — это радиус «r» и угловая скорость «w». Правило правой руки гласит, что если вы удерживаете ось правой рукой и вращаете пальцы в направлении движения вращающегося тела, то ваш большой палец будет указывать в направлении угловой скорости , явно подразумевает, что и перпендикулярны друг другу. И поскольку синус 90 равен единице, результирующий перпендикулярный вектор этих величин в любой точке на окружности всегда будет оставаться неизменным.
Интересно, что объекты внутри или на круге имеют одинаковую угловую скорость, но разные тангенциальные скорости. Это связано с его зависимостью от радиуса, как видно из его формулы. Следовательно, люди на краю карусели будут улетать с большей скоростью, чем те, кто сидит в ней глубже.
Почему объекты приобретают большую линейную скорость по мере удаления от центра круга.
Важность тангенциальной скорости
Касательная скорость может наблюдаться во многих случаях, включая любое нелинейное движение, такое как резкий скачок от качания или отклонение спутника или самой Земли от его круговой орбиты.Круговое движение спутника или нашей Земли происходит в оккультной зоне , где центростремительная сила, тянущая его внутрь, компенсируется линейной скоростью, толкающей его прямо вперед.
Земля перемещается в космос из-за своей линейной или тангенциальной скорости.
Статьи по теме
Статьи по теме
Однако, когда Земля или Солнце внезапно исчезают, мы прерываем наш цикл и мгновенно выбрасываемся в космос из-за нашей линейной скорости.Движение проводит прямую линию через точку в пространстве и времени, которая отмечает тот момент, когда сила тяжести исчезла — касательная.
Угловая скорость: определение, формула и примеры — стенограмма видео и урока
Радианы
Перед тем, как перейти к угловой скорости, нам нужно рассмотреть еще одну вещь, а именно радианы. Когда мы имеем дело с угловой скоростью, мы используем радианную меру угла, поэтому важно, чтобы мы были знакомы с радианной мерой.Техническое определение радиан. — это длина дуги, образуемой углом, деленная на радиус окружности, частью которой является угол, где подразумеваемый означает, что она должна быть противоположной углу и продолжаться от одной точки на круг к другому, оба отмечены углом. Это говорит нам, что угол theta = s / r радиан, где s = длина дуги, соответствующей тета, и r = радиус окружности, частью которой является тета.
Так как большинство из нас привыкли к градусному измерению углов, удобно, что мы можем легко преобразовать градус в радиан, умножив градус на пи / 180. Например, угол в 45 градусов имеет радиан. мера 45 (пи / 180), что равно пи / 4 радиана.
Угловая скорость
Угловая скорость встречается реже, чем линейная скорость, потому что она применяется только к объектам, движущимся по круговой траектории.Например, гоночная машина на круговой трассе, шар рулетки на колесе рулетки или колесо обозрения — все они имеют угловую скорость.
Угловая скорость объекта — это угловое смещение объекта относительно времени. Когда объект движется по круговой траектории, центральный угол, соответствующий положению объекта на круге, изменяется. Угловая скорость, представленная как w , представляет собой скорость изменения этого угла во времени.
Например, колесо обозрения может вращать пи / 6 радиан каждую минуту. Следовательно, угловая скорость колеса обозрения будет равна пи / 6 радиан в минуту.
Формулы угловой скорости
Существует трех формул , которые мы можем использовать для определения угловой скорости.
Вариант 1
Первое вытекает прямо из определения.Угловая скорость — это скорость изменения позиционного угла объекта относительно времени, поэтому w = theta / t , где w = угловая скорость, theta = позиционный угол и t = время.
Например, если гоночный автомобиль движется по круговой трассе и проходит 1 круг, или 2 радиана на дюйм за 4 минуты, то мы можем найти угловую скорость автомобиля, подставив theta = 2pi радиан и t = 4 минуты в наша формула, чтобы получить w = 2pi / 4 = pi / 2 радиан в минуту.Угловая скорость автомобиля составляет пи / 2 радиана в минуту.
Вариант 2
Чтобы получить нашу вторую формулу для угловой скорости, мы понимаем, что тета дана в радианах, а определение радианной меры дает theta = с / r . Таким образом, мы можем подставить theta = s / r в нашу первую формулу угловой скорости. Это дает w = ( s / r ) / t . Упрощение дает w = s / ( r t ), где s = длина дуги, r = радиус и t = время.
Например, если колесо рулетки имеет радиус 10 дюймов, а шарик проходит 7 дюймов по круговой траектории за 2 секунды, то мы можем определить угловую скорость шара, вставив s = 7 дюймов, r = 10 дюймов, и t = 2 секунды в w = s / ( r t ), чтобы получить w = 7 / (10 * 2) = 0,35 радиана в секунду. Угловая скорость мяча составляет 0,35 радиана в секунду.
Вариант 3
Последняя формула исходит из признания того, что мы можем переписать нашу вторую формулу угловой скорости как w = s / ( r t ) = ( s / t ) (1/ r ).Напомним, что с / t — это наша линейная скорость, поэтому мы можем переписать эту формулу как w = v (1/ r ) = v / r , где v = linear скорость и r = радиус круга.
Например, если гоночный автомобиль движется по круговой трассе со скоростью 110 миль в час, а радиус гоночной трассы составляет 0,2 мили, то мы можем найти угловую скорость автомобиля, подключив v = 110 миль в час и r = 0.2 мили в нашу формулу, чтобы получить w = 110 / 0,2 = 550 радиан в час.
Резюме урока
Мы рассмотрели линейной скорости, , скорость изменения положения объекта, движущегося по прямой, относительно времени и радиан, мера угла (тета = с / r , где s = длина дуги и r = радиус). Мы видели, что оба они играют важную роль в угловой скорости. Угловая скорость — это угловое смещение во времени объекта или частицы, которые движутся по круговой траектории.У нас есть три формулы, которые мы используем для определения угловой скорости, и они отображаются на экране.
Эти формулы и определения снабдили нас всем необходимым для эффективной и действенной работы с угловой скоростью.
Угловое смещение, скорость, ускорение
Мы живем в мире, который определяется тремя пространственными измерениями и одним измерение времени.Объекты перемещаются в этом домене двумя способами. Объект переводит, или меняет адрес , с одного указать на другое. И объект вращается , или меняет свою ориентацию . В общем, движение объекта включает в себя как перемещение во всех трех направлениях, так и вращение на вокруг три основных оси.
На этой странице мы будем рассматривать только вращение твердого объекта вокруг одна ось.Вращение объекта аналогично перемещению в номере переменных, которые мы должны учитывать, но обозначения очень сбивают с толку, потому что он традиционно описывался с использованием греческих символов. На слайде в вверху страницы мы использовали традиционные греческие обозначения. Чтобы упростить соблюдение статьи 508, мы просто укажем названия переменных. здесь в тексте, а не использовать символьный шрифт. Theta — это символ, который выглядит как 0 с горизонтальной линией, проходящей через него. Phi — это символ, который выглядит как 0 с вертикальной линией, проходящей через него. Омега — это символ, который выглядит как фигурный w . Альфа — это символ, похожий на перекрещенную ленту.
Поскольку объект вращается вокруг оси вращения самым простым способом для описания движения использовать полярные координаты. Мы можем указать угловую ориентацию объекта на в любой момент t , указав угол тета , на который объект повернулся от некоторой опорной линии.Изначально наш объект находится в ориентации «0», заданной углом тета 0 в момент времени t0 . Мы нарисовали красную линию на диске с указанием исходной ориентации. Объект вращается до тех пор, пока time t1 , а красная линия поворачивается на угол theta 1 . Мы можем определить угловое смещение — фи как разница угла между условием «0» и условием «1».
фи = тета 1 — тета 0
Угловое смещение — это векторная величина, означающая, что угловое смещение имеет размер и направление, связанные с ним.Направление важно для более поздних математических процессов, но определение немного сбивает с толку. Как объект вращается из точки «0» в точку «1», вращается вокруг оси, поэтому направление угловое смещение измеряется по оси. Положительное значение направления оси определяется правилом правой руки . Вытяните правую руку, как если бы пожать кому-нибудь руку. Согните пальцы с основанием в точке «0» и наконечниками, идущими в точку «1».Ваш большой палец указывает перпендикулярно плоскости вращения в положительном направлении вдоль оси вращения.Угловое смещение измеряется в единицах радиан . Два радиана пи равны 360 градусов. Угловое перемещение не является длиной (не измеряется в метрах или футах), поэтому угловое смещение отличается чем линейное перемещение. Поскольку твердый объект вращается вокруг оси вращения, все точек объекта испытывают такое же угловое смещение, но точки дальше от оси перемещаются дальше, чем точки ближе к оси.На слайде мы рассматриваем два очка; один расположен на радиусе ra на краю диска, и другой расположен в радиусе rb , что меньше ra . Как объект вращается за счет углового смещения фи , точка на краю диска перемещает расстояние sa по круговой траектории. Точка руб. также движется в круговой путь, но расстояние сб короче, чем расстояние сб .В основном, длина кругового пути с равна радиус r умноженный на угловое смещение phi , выраженное в радианах.
для углового перемещения фи ,
s = phi * r
ra> rb
sa> sb
Угловая скорость — омега объекта изменение угла во времени.Средняя угловая скорость — это угловое смещение, разделенное по временному интервалу:
омега = (тета 1 — тета 0) / (t1 — t0)
Это средняя угловая скорость за промежуток времени от t0 до t1 , но объект может ускоряться и замедляться в течение определенного промежутка времени. В любой момент объект может иметь угловую скорость, отличную от средней.Если мы сократим разница во времени вплоть до очень небольшого (дифференциального) размера, мы можем определить мгновенная угловая скорость — это дифференциальное изменение угла, деленное на дифференциальное изменение во времени;
омега = д тета / дт
где символ d / dt — это дифференциал от исчисления. Угловая скорость равна векторная величина и имеет как величину, так и направление. Направление совпадает с направлением углового смещения, от которого мы определили угловая скорость.
Угловая скорость измеряется в радианах в секунду , или оборотов в секунду или оборотов в минуту (об / мин). Угловая скорость разная чем линейная скорость, которая измеряется длиной за время (футы в секунду или метры в секунду). Все точки объекта вращаются с одинаковой угловой скоростью, но находятся дальше от ось вращения движется с тангенциальной скоростью , отличной от , чем точки ближе к оси вращения.Тангенциальная скорость измеряется по круговой траектории. с , что мы рассматривали ранее. Касательная скорость В равна угловой скорость омега в раз больше радиуса r :
для углового перемещения фи ,
V = омега * г
ra> rb
Va> Vb
Когда мы изначально укажите вращение нашего объекта с theta 0, и т0 , мы также должны указать начальную мгновенную угловую скорость omega 0 .Аналогично в конечной позиции theta 1, и t1 , угловая скорость меняется на угловую скорость omega 1 .
Среднее угловое ускорение — альфа объекта — это изменение угловой скорости во времени.
альфа = (омега 1 — омега 0) / (t1 — t0)
Как и угловая скорость, это только средняя угловая скорость. ускорение.В любой момент объект может иметь угловое ускорение, отличное от среднего. Если мы сократим разница во времени вплоть до очень небольшого (дифференциального) размера, мы можем определить мгновенное угловое ускорение должно быть изменением дифференциала в угловая скорость, деленная на дифференциальное изменение во времени:
альфа = d омега / dt
Точно так же, как силы производят линейные ускорения, a крутящий момент производит угловые ускорения.Если мы можем определить крутящие моменты на объекте и то, как крутящие моменты меняются со временем, мы можем использовать уравнения, представленные на этом слайде, для определения углового ускорения, угловая скорость и угловое смещение объекта как функция времени. Авиационные инженеры используют эту информацию для прогнозирования вращения самолета в полете, которые становятся важными для устойчивости и управление самолетом.
Действия:
Экскурсии с гидом
Навигация..
- Руководство для начинающих Домашняя страница
Круговое движение — центростремительная сила, центростремительное ускорение, угловая скорость, радианы, линейная скорость
Нажмите здесь, чтобы узнать о круговых движениях и домашнее задание
Click — ответы на вопрос о круговых движениях.
Круговое движение
Когда объект движется по кругу с постоянной скоростью, его скорость (которая является вектором) постоянно меняется.Его скорость меняется не потому, что меняется величина скорости, а потому, что меняется ее направление. Эта постоянно меняющаяся скорость означает, что объект ускоряется (центростремительное ускорение , ). Чтобы это ускорение произошло, должна быть равнодействующая сила, эта сила называется центростремительной силой .
Угловая скорость — нажмите, чтобы увидеть примеры вопросов.
Угловая скорость (w) объекта — это угол (q), через который он проходит, измеренный в радианах (рад), деленный на время (t), необходимое для прохождения этого угла.Это означает, что единицей измерения угловой скорости является радиан в секунду (рад с -1 ).
v — линейная скорость, измеренная в метрах в секунду (мс -1 ).
r — радиус круга в метрах (м).
f — частота вращения в герцах (Гц).
Центростремительное ускорение
Центростремительное ускорение (а) измеряется в метрах в секунду в секунду (мс -2 ). Он всегда направлен к центру круга.
Центростремительная сила
Когда объект движется по кругу, центростремительная сила (F) всегда действует по направлению к центру круга. Центростремительная сила, измеряемая в ньютонах (Н), может представлять собой разные силы в разных настройках, это может быть сила тяжести, трение, натяжение, подъемная сила, электростатическое притяжение и т. Д.
Ссылки на другие страницы;
Концепции Momentum
Простое гармоническое движение (SHM)
Принудительные колебания и резонанс
Постоянная угловая скорость — обзор
8.2.B Диамагнетизм Ландау
Теперь исследуем магнетизм, возникающий в результате квантования орбитального движения (заряженных) частиц в присутствии внешнего магнитного поля. В однородном поле напряженности B, направленном вдоль оси z, заряженная частица будет следовать по спиральной траектории, ось которой параллельна оси z, а проекция на плоскость ( x, y ) представляет собой круг. Движение в направлении z имеет постоянную линейную скорость u z , тогда как движение в плоскости ( x, y ) имеет постоянную угловую скорость eB / mc; последняя возникает из-за силы Лоренца, e ( u × B ) / c , испытываемой частицей.Квантово-механически энергия, связанная с круговым движением, равна квантованию в единицах eℏB / mc. Энергия, связанная с линейным движением вдоль оси z, также квантуется, но ввиду малости интервалов энергии ее можно принять как непрерывную переменную. Таким образом, для полной энергии частицы имеем 2
(28) ε = eћBmc (j + 12) + pz22m (j = 0,1,2,…).
Эти квантованные уровни энергии вырождены, потому что они являются результатом «слияния вместе» почти непрерывного набора уровней нулевого поля.Небольшое размышление показывает, что все те уровни, для которых значение количества (px2 + py2) / 2m лежит между eℏBj / mc и eℏB ( j + 1) / mc , теперь «сливаются» в единственный уровень, характеризуемый квантовым числом j. Количество этих уровней равно
(29) 1h3∫dxdydpxdpy = LxLyh3π [2meћBmc {(j + 1) -j}] = LxLyeBhc,
, которое не зависит от j. Коэффициент множественности (29) — это квантово-механическая мера свободы, доступной частице для того, чтобы центр ее орбиты «располагался» в любом месте общей площади L x L y физическое пространство.На рис. 8.3 показано, как уровни энергии в нулевом поле группы частиц сами превращаются в спектр уровней, подобных осциллятору, при приложении внешнего магнитного поля.
РИСУНОК 8.3. Одночастичные уровни энергии для двумерного движения в отсутствие внешнего магнитного поля ( B = 0) и в присутствии внешнего магнитного поля ( B & gt; 0).
Большая статистическая сумма газа задается стандартной формулой
(30) InQ = ∑εIn (1 + ze-βε),
, где суммирование должно проводиться по всем одночастичным состояниям в системе. .Подставляя (28) вместо ε, используя коэффициент кратности (29) и заменяя суммирование по p z на интегрирование, получаем
(31) InQ = ∫-∞∞Lzdpzh [∑j = 0 ∞ (LxLyeBhc) В {1 + ze-βeћB [j + (1/2)] / mc-βpz2 / 2m}].
При высоких температурах z ≪ 1; Итак, система эффективно Больцманова. Большая статистическая сумма затем уменьшается до
(32) InQ = zVeBh3c∫-∞∞e-βpz2 / 2mdpz∑j = 0∞e-βeћB [j + (1/2)] / mc = zVeBh3c (2πmβ) 1 / 2 {2sinh (βeћB2mc)} — 1.
Равновесное число частиц N¯ и магнитный момент M газа тогда даются как
(33) N¯ = (z∂∂zInQ) B, V, T,
и
(34 ) M = 〈- ∂H∂B〉 = 1β (∂∂BInQ) z, V, T,
, где H — гамильтониан системы; сравните с уравнением (3.9.4). Таким образом, получаем
(35) N¯ = zVλ3xsinhx,
и
(36) M = zVλ3μeff {1sinhx-xcoshxsinh3x},
, где λ {= h / (2πmk T ) 1/2 } — средняя длина тепловой волны частиц, а
(37) x = βμeffB (μeff = eh / 4πmc).
Ясно, что если e и m — это заряд электрона и его масса, то μ eff — это знакомый магнетон Бора μ B . Комбинируя (35) и (36), получаем
(38) M = -N¯μeffL (x),
, где L ( x ) — это функция Ланжевена :
(39) L (x) = cothx-1x.
Этот результат очень похож на результат, полученный в теории парамагнетизма Ланжевена; см. раздел 3.9. Однако наличие отрицательного знака означает, что эффект, полученный в данном случае, имеет характер диамагнетизма . Отметим также, что этот эффект является прямым следствием квантования; оно исчезает, если положить h → 0. Это полностью согласуется с теоремой Бора – ван Левена, , согласно которой явление диамагнетизма не возникает в классической физике; см. задачу 3.43.
Если напряженность поля B и температура T таковы, что μ eff B ≪ кТл , то вышеуказанные результаты станут
(40) N¯≃zVλ3
и
( 41) M≃-N¯μeff2B / 3kT.
Уравнение (40) согласуется с формулой нулевого поля z ≃ nλ 3 , а (41) приводит к диамагнитному аналогу закона Кюри:
(42) χ∞ = MVB = -n¯μeff2 / 3kT;
см. Уравнение (3.9.12). Здесь следует отметить, что диамагнитный характер этого явления не зависит от знака электрического заряда на частице. В частности, для электронного газа чистая восприимчивость при высоких температурах определяется суммой выражения (7) с заменой μ * на μ B , и выражением (42):
(43) χ∞ = n (μB2-13μ′B2) kT,
, где μ ′ B = eh / 4π m ′ c, m ′ — эффективная масса электрона в данной системе. .
Теперь посмотрим на эту проблему при при всех температурах , хотя мы продолжим предполагать, что магнитное поле слабое, так что μ eff B ≪ кТл . Ввиду последнего суммирование в (31) может производиться с помощью формулы суммирования Эйлера:
(44) ∑j = 0∞f (j + 12) ≃∫0∞f (x) dx + 124f ′ (0),
с результатом
(45) InQ≃VeBh3c [∫0∞dx∫-∞∞dpzIn {1 + ze-β (2μeffBx + pz2 / 2m)} — 112βμeffB∫-∞∞dpzz -1e-β (pz2 / 2m) +1].
Первая часть здесь не зависит от B, что можно увидеть, изменив переменную с x на x ′ = Bx. Вторая часть с заменой βpz2 / 2m = y становится
(46) -πV (2m) 3 / 26h4 (μeffB) 2β1 / 2∫0∞y-1 / 2dyz-1ey + 1.
Восприимчивость газа в слабом поле (на единицу объема) тогда определяется как
(47) χ = MVB = 1βVB (∂∂BInQ) z, V, T = — (2πm) 3 / 2μeff23h3β1 / 2f1 / 2 (z),
, что является желаемым результатом. Отметим, что, как и прежде, эффект носит диамагнитный характер — независимо от знака заряда на частице.
Затем для f1 / 2 (z) ≃z≃n¯λ3 мы восстанавливаем наш предыдущий результат (42).Для z ≫ 1 (что соответствует T≪TF), f1 / 2 (z) ≈ (2 / π1 / 2) (Inz) 1/2, тогда получаем
(48) χ0≈-2π (2m) 3 / 2μeff2εF1 / 23h4 = -12nμeff2 / εF;
здесь также использовался тот факт, что (β -1 ln z ) ≃ s F .