Уде́льное электри́ческое сопротивле́ние, или просто удельное сопротивление вещества — физическая величина, характеризующая способность вещества препятствовать прохождению электрического тока.
Удельное сопротивление обозначается греческой буквой ρ. Величина, обратная удельному сопротивлению, называется удельной проводимостью (удельной электропроводностью). В отличие от электрического сопротивления, являющегося свойством проводника и зависящего от его материала, формы и размеров, удельное электрическое сопротивление является свойством только вещества.
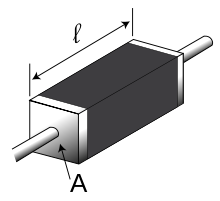
Электрическое сопротивление однородного проводника с удельным сопротивлением ρ, длиной l и площадью поперечного сечения S может быть рассчитано по формуле R = ρ ⋅ l S {\displaystyle R={\frac {\rho \cdot l}{S}}} (при этом предполагается, что ни площадь, ни форма поперечного сечения не меняются вдоль проводника). Соответственно, для ρ выполняется ρ = R ⋅ S l . {\displaystyle \rho ={\frac {R\cdot S}{l}}.}
Из последней формулы следует: физический смысл удельного сопротивления вещества заключается в том, что оно представляет собой сопротивление изготовленного из этого вещества однородного проводника единичной длины и с единичной площадью поперечного сечения.
Единицы измерения
Единица измерения удельного сопротивления в Международной системе единиц (СИ) — Ом·м
В технике также применяется устаревшая внесистемная единица Ом·мм²/м, равная 10−6 от 1 Ом·м[1]. Данная единица равна такому удельному сопротивлению вещества, при котором однородный проводник длиной 1 м с площадью поперечного сечения 1 мм², изготовленный из этого вещества, имеет сопротивление, равное 1 Ом[2]. Соответственно, удельное сопротивление какого-либо вещества, выраженное в этих единицах, численно равно сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 мм².
Обобщение понятия удельного сопротивления
Удельное сопротивление можно определить также для неоднородного материала, свойства которого меняются от точки к точке. В этом случае оно является не константой, а скалярной функцией координат — коэффициентом, связывающим напряжённость электрического поля E → ( r → ) {\displaystyle {\vec {E}}({\vec {r}})} и плотность тока J → ( r → ) {\displaystyle {\vec {J}}({\vec {r}})} в данной точке r → {\displaystyle {\vec {r}}} . Указанная связь выражается законом Ома в дифференциальной форме:
- E → ( r → ) = ρ ( r → ) J → ( r → ) . {\displaystyle {\vec {E}}({\vec {r}})=\rho ({\vec {r}}){\vec {J}}({\vec {r}}).}
Эта формула справедлива для неоднородного, но изотропного вещества. Вещество может быть и анизотропно (большинство кристаллов, намагниченная плазма и т. д.), то есть его свойства могут зависеть от направления. В этом случае удельное сопротивление является зависящим от координат тензором второго ранга, содержащим девять компонент ρ i j {\displaystyle \rho _{ij}} . В анизотропном веществе векторы плотности тока и напряжённости электрического поля в каждой данной точке вещества не сонаправлены; связь между ними выражается соотношением
- E i ( r → ) = ∑ j = 1 3 ρ i j ( r → ) J j ( r → ) . {\displaystyle E_{i}({\vec {r}})=\sum _{j=1}^{3}\rho _{ij}({\vec {r}})J_{j}({\vec {r}}).}
В анизотропном, но однородном веществе тензор ρ i j {\displaystyle \rho _{ij}} от координат не зависит.
Тензор ρ i j {\displaystyle \rho _{ij}} симметричен, то есть для любых i {\displaystyle i} и j {\displaystyle j} выполняется ρ i j = ρ j i {\displaystyle \rho _{ij}=\rho _{ji}} .
Как и для всякого симметричного тензора, для ρ i j {\displaystyle \rho _{ij}} можно выбрать ортогональную систему декартовых координат, в которых матрица ρ i j {\displaystyle \rho _{ij}} становится диагональной, то есть приобретает вид, при котором из девяти компонент ρ i j {\displaystyle \rho _{ij}} отличными от нуля являются лишь три: ρ 11 {\displaystyle \rho _{11}} , ρ 22 {\displaystyle \rho _{22}} и ρ 33 {\displaystyle \rho _{33}} . В этом случае, обозначив ρ i i {\displaystyle \rho _{ii}} как ρ i {\displaystyle \rho _{i}} , вместо предыдущей формулы получаем более простую
- E i = ρ i J i . {\displaystyle E_{i}=\rho _{i}J_{i}.}
Величины ρ i {\displaystyle \rho _{i}} называют главными значениями тензора удельного сопротивления.
Связь с удельной проводимостью
В изотропных материалах связь между удельным сопротивлением ρ {\displaystyle \rho } и удельной проводимостью σ {\displaystyle \sigma } выражается равенством
- ρ = 1 σ . {\displaystyle \rho ={\frac {1}{\sigma }}.}
В случае анизотропных материалов связь между компонентами тензора удельного сопротивления ρ i j {\displaystyle \rho _{ij}} и тензора удельной проводимости σ i j {\displaystyle \sigma _{ij}} имеет более сложный характер. Действительно, закон Ома в дифференциальной форме для анизотропных материалов имеет вид:
- J i ( r → ) = ∑ j = 1 3 σ i j ( r → ) E j ( r → ) . {\displaystyle J_{i}({\vec {r}})=\sum _{j=1}^{3}\sigma _{ij}({\vec {r}})E_{j}({\vec {r}}).}
Из этого равенства и приведённого ранее соотношения для E i ( r → ) {\displaystyle E_{i}({\vec {r}})} следует, что тензор удельного сопротивления является обратным тензору удельной проводимости. С учётом этого для компонент тензора удельного сопротивления выполняется:
- ρ 11 = 1 det ( σ ) [ σ 22 σ 33 − σ 23 σ 32 ] , {\displaystyle \rho _{11}={\frac {1}{\det(\sigma )}}[\sigma _{22}\sigma _{33}-\sigma _{23}\sigma _{32}],}
- ρ 12 = 1 det ( σ ) [ σ 33 σ 12 − σ 13 σ 32 ] , {\displaystyle \rho _{12}={\frac {1}{\det(\sigma )}}[\sigma _{33}\sigma _{12}-\sigma _{13}\sigma _{32}],}
где det ( σ ) {\displaystyle \det(\sigma )} — определитель матрицы, составленной из компонент тензора σ i j {\displaystyle \sigma _{ij}} . Остальные компоненты тензора удельного сопротивления получаются из приведённых уравнений в результате циклической перестановки индексов 1, 2 и 3[3].
Удельное электрическое сопротивление некоторых веществ
Металлические монокристаллы
В таблице приведены главные значения тензора удельного сопротивления монокристаллов при температуре 20 °C[4].
| Кристалл | ρ1=ρ2, 10−8 Ом·м | ρ3, 10−8 Ом·м |
|---|---|---|
| Олово | 9,9 | 14,3 |
| Висмут | 109 | 138 |
| Кадмий | 6,8 | 8,3 |
| Цинк | 5,91 | 6,13 |
| Теллур | 2,90·109 | 5,9·109 |
Металлы и сплавы, применяемые в электротехнике
Разброс значений обусловлен разной химической чистотой металлов, способов изготовления образцов, изученных разными учеными и непостоянством состава сплавов.
|
|
Значения даны при температуре t = 20 °C. Сопротивления сплавов зависят от их химического состава и могут варьироваться. Для чистых веществ колебания численных значений удельного сопротивления обусловлены различными методами механической и термической обработки, например, отжигом проволоки после волочения.
Другие вещества
Тонкие плёнки
Сопротивление тонких плоских плёнок (когда её толщина много меньше расстояния между контактами) принято называть «удельным сопротивлением на квадрат», R S q . {\displaystyle R_{\mathrm {Sq} }.} Этот параметр удобен тем, что сопротивление квадратного куска проводящей плёнки не зависит от размеров этого квадрата, при приложении напряжения по противоположным сторонам квадрата. При этом сопротивление куска плёнки, если он имеет форму прямоугольника, не зависит от его линейных размеров, а только от отношения длины (измеренной вдоль линий тока) к его ширине L/W: R S q = R W / L , {\displaystyle R_{\mathrm {Sq} }=RW/L,} где R — измеренное сопротивление. В общем случае, если форма образца отличается от прямоугольной, и поле в пленке неоднородное, используют метод ван дер Пау.
Примечания
- ↑ 1 2 Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М.: Издательство стандартов, 1990. — С. 93. — 240 с. — ISBN 5-7050-0118-5.
- ↑ 1 2 Чертов А. Г. Единицы физических величин. — М.: «Высшая школа», 1977. — 287 с.
- ↑ Давыдов А. С. Теория твёрдого тела. — М.: «Наука», 1976. — С. 191—192. — 646 с.
- ↑ Шувалов Л. А. и др. Физические свойства кристаллов // Современная кристаллография / Гл. ред. Б. К. Вайнштейн. — М.: «Наука», 1981. — Т. 4. — С. 317.
См. также
Уде́льное электри́ческое сопротивле́ние, или просто удельное сопротивление вещества — физическая величина, характеризующая способность вещества препятствовать прохождению электрического тока.
Удельное сопротивление обозначается греческой буквой ρ. Величина, обратная удельному сопротивлению, называется удельной проводимостью (удельной электропроводностью). В отличие от электрического сопротивления, являющегося свойством проводника и зависящего от его материала, формы и размеров, удельное электрическое сопротивление является свойством только вещества.
Электрическое сопротивление однородного проводника с удельным сопротивлением ρ, длиной l и площадью поперечного сечения S может быть рассчитано по формуле R = ρ ⋅ l S {\displaystyle R={\frac {\rho \cdot l}{S}}} (при этом предполагается, что ни площадь, ни форма поперечного сечения не меняются вдоль проводника). Соответственно, для ρ выполняется ρ = R ⋅ S l . {\displaystyle \rho ={\frac {R\cdot S}{l}}.}
Из последней формулы следует: физический смысл удельного сопротивления вещества заключается в том, что оно представляет собой сопротивление изготовленного из этого вещества однородного проводника единичной длины и с единичной площадью поперечного сечения.
Единицы измерения
Единица измерения удельного сопротивления в Международной системе единиц (СИ) — Ом·м[1]
В технике также применяется устаревшая внесистемная единица Ом·мм²/м, равная 10−6 от 1 Ом·м[1]. Данная единица равна такому удельному сопротивлению вещества, при котором однородный проводник длиной 1 м с площадью поперечного сечения 1 мм², изготовленный из этого вещества, имеет сопротивление, равное 1 Ом[2]. Соответственно, удельное сопротивление какого-либо вещества, выраженное в этих единицах, численно равно сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 мм².
Обобщение понятия удельного сопротивления

Удельное сопротивление можно определить также для неоднородного материала, свойства которого меняются от точки к точке. В этом случае оно является не константой, а скалярной функцией координат — коэффициентом, связывающим напряжённость электрического поля E → ( r → ) {\displaystyle {\vec {E}}({\vec {r}})} и плотность тока J → ( r → ) {\displaystyle {\vec {J}}({\vec {r}})} в данной точке r → {\displaystyle {\vec {r}}} . Указанная связь выражается законом Ома в дифференциальной форме:
- E → ( r → ) = ρ ( r → ) J → ( r → ) . {\displaystyle {\vec {E}}({\vec {r}})=\rho ({\vec {r}}){\vec {J}}({\vec {r}}).}
Эта формула справедлива для неоднородного, но изотропного вещества. Вещество может быть и анизотропно (большинство кристаллов, намагниченная плазма и т. д.), то есть его свойства могут зависеть от направления. В этом случае удельное сопротивление является зависящим от координат тензором второго ранга, содержащим девять компонент ρ i j {\displaystyle \rho _{ij}} . В анизотропном веществе векторы плотности тока и напряжённости электрического поля в каждой данной точке вещества не сонаправлены; связь между ними выражается соотношением
- E i ( r → ) = ∑ j = 1 3 ρ i j ( r → ) J j ( r → ) . {\displaystyle E_{i}({\vec {r}})=\sum _{j=1}^{3}\rho _{ij}({\vec {r}})J_{j}({\vec {r}}).}
В анизотропном, но однородном веществе тензор ρ i j {\displaystyle \rho _{ij}} от координат не зависит.
Тензор ρ i j {\displaystyle \rho _{ij}} симметричен, то есть для любых i {\displaystyle i} и j {\displaystyle j} выполняется ρ i j = ρ j i {\displaystyle \rho _{ij}=\rho _{ji}} .
Как и для всякого симметричного тензора, для ρ i j {\displaystyle \rho _{ij}} можно выбрать ортогональную систему декартовых координат, в которых матрица ρ i j {\displaystyle \rho _{ij}} становится диагональной, то есть приобретает вид, при котором из девяти компонент ρ i j {\displaystyle \rho _{ij}} отличными от нуля являются лишь три: ρ 11 {\displaystyle \rho _{11}} , ρ 22 {\displaystyle \rho _{22}} и ρ 33 {\displaystyle \rho _{33}} . В этом случае, обозначив ρ i i {\displaystyle \rho _{ii}} как ρ i {\displaystyle \rho _{i}} , вместо предыдущей формулы получаем более простую
- E i = ρ i J i . {\displaystyle E_{i}=\rho _{i}J_{i}.}
Величины ρ i {\displaystyle \rho _{i}} называют главными значениями тензора удельного сопротивления.
Связь с удельной проводимостью
В изотропных материалах связь между удельным сопротивлением ρ {\displaystyle \rho } и удельной проводимостью σ {\displaystyle \sigma } выражается равенством
- ρ = 1 σ . {\displaystyle \rho ={\frac {1}{\sigma }}.}
В случае анизотропных материалов связь между компонентами тензора удельного сопротивления ρ i j {\displaystyle \rho _{ij}} и тензора удельной проводимости σ i j {\displaystyle \sigma _{ij}} имеет более сложный характер. Действительно, закон Ома в дифференциальной форме для анизотропных материалов имеет вид:
- J i ( r → ) = ∑ j = 1 3 σ i j ( r → ) E j ( r → ) . {\displaystyle J_{i}({\vec {r}})=\sum _{j=1}^{3}\sigma _{ij}({\vec {r}})E_{j}({\vec {r}}).}
Из этого равенства и приведённого ранее соотношения для E i ( r → ) {\displaystyle E_{i}({\vec {r}})} следует, что тензор удельного сопротивления является обратным тензору удельной проводимости. С учётом этого для компонент тензора удельного сопротивления выполняется:
- ρ 11 = 1 det ( σ ) [ σ 22 σ 33 − σ 23 σ 32 ] , {\displaystyle \rho _{11}={\frac {1}{\det(\sigma )}}[\sigma _{22}\sigma _{33}-\sigma _{23}\sigma _{32}],}
- ρ 12 = 1 det ( σ ) [ σ 33 σ 12 − σ 13 σ 32 ] , {\displaystyle \rho _{12}={\frac {1}{\det(\sigma )}}[\sigma _{33}\sigma _{12}-\sigma _{13}\sigma _{32}],}
где det ( σ ) {\displaystyle \det(\sigma )} — определитель матрицы, составленной из компонент тензора σ i j {\displaystyle \sigma _{ij}} . Остальные компоненты тензора удельного сопротивления получаются из приведённых уравнений в результате циклической перестановки индексов 1, 2 и 3[3].
Удельное электрическое сопротивление некоторых веществ
Металлические монокристаллы
В таблице приведены главные значения тензора удельного сопротивления монокристаллов при температуре 20 °C[4].
| Кристалл | ρ1=ρ2, 10−8 Ом·м | ρ3, 10−8 Ом·м |
|---|---|---|
| Олово | 9,9 | 14,3 |
| Висмут | 109 | 138 |
| Кадмий | 6,8 | 8,3 |
| Цинк | 5,91 | 6,13 |
| Теллур | 2,90·109 | 5,9·109 |
Металлы и сплавы, применяемые в электротехнике
Разброс значений обусловлен разной химической чистотой металлов, способов изготовления образцов, изученных разными учеными и непостоянством состава сплавов.
|
|
Значения даны при температуре t = 20 °C. Сопротивления сплавов зависят от их химического состава и могут варьироваться. Для чистых веществ колебания численных значений удельного сопротивления обусловлены различными методами механической и термической обработки, например, отжигом проволоки после волочения.
Другие вещества
Тонкие плёнки
Сопротивление тонких плоских плёнок (когда её толщина много меньше расстояния между контактами) принято называть «удельным сопротивлением на квадрат», R S q . {\displaystyle R_{\mathrm {Sq} }.} Этот параметр удобен тем, что сопротивление квадратного куска проводящей плёнки не зависит от размеров этого квадрата, при приложении напряжения по противоположным сторонам квадрата. При этом сопротивление куска плёнки, если он имеет форму прямоугольника, не зависит от его линейных размеров, а только от отношения длины (измеренной вдоль линий тока) к его ширине L/W: R S q = R W / L , {\displaystyle R_{\mathrm {Sq} }=RW/L,} где R — измеренное сопротивление. В общем случае, если форма образца отличается от прямоугольной, и поле в пленке неоднородное, используют метод ван дер Пау.
Примечания
- ↑ 1 2 Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М.: Издательство стандартов, 1990. — С. 93. — 240 с. — ISBN 5-7050-0118-5.
- ↑ 1 2 Чертов А. Г. Единицы физических величин. — М.: «Высшая школа», 1977. — 287 с.
- ↑ Давыдов А. С. Теория твёрдого тела. — М.: «Наука», 1976. — С. 191—192. — 646 с.
- ↑ Шувалов Л. А. и др. Физические свойства кристаллов // Современная кристаллография / Гл. ред. Б. К. Вайнштейн. — М.: «Наука», 1981. — Т. 4. — С. 317.
См. также
r = R S/l.
В Си единицей удельного сопротивления является Ом.м.
Удельное сопротивление могут выражать также в Ом.см.
Удельное сопротивление является характеристикой материала, по которому протекает ток, и зависит от материала, из которого он изготовлен. Удельное сопротивление, равное r = 1 Ом.м означает, что цилиндрический проводник, изготовленный из данного материала, длиной l = 1м и с площадью поперечного сечения S = 1 м2 имеет сопротивление R = 1 Ом.м.
Величина удельного сопротивления металлов (см. МЕТАЛЛЫ), являющихся хорошими проводниками (см. ПРОВОДНИКИ), может иметь значения порядка 10-8 – 10-6Ом.м (например, медь, серебро, железо и т. д.). Удельное сопротивление некоторых твердых диэлектриков (см. ДИЭЛЕКТРИКИ) может достигать значения 1016-1018Ом.м (например, кварцевое стекло, полиэтилен, электрофарфор и др.). Величина удельного сопротивления многих материалов (особенного полупроводниковых материалов (см. ПОЛУПРОВОДНИКОВЫЕ МАТЕРИАЛЫ)) существенно зависит от степени их очистки, наличия легирующих добавок, термических и механических обработок и т. д.
Величина s, обратная удельному сопротивлению , называется удельной проводимостью:
s = 1/r
Удельная проводимость измеряется в сименсах (см. СИМЕНС (единица проводимости)) на метр См/м.
Удельное электрическое сопротивление (проводимость) является скалярной величиной для изотропного вещества; и тензорной — для анизотропного вещества.
В анизотропным монокристаллах анизотропия электропроводности является следствием анизотропии обратной эффективной массы (см. ЭФФЕКТИВНАЯ МАССА) электронов и дырок.
Удельное сопротивление металлов. Таблица | joyta.ru
Удельное сопротивление металлов является мерой их свойства противодействовать прохождению электрического тока. Эта величина выражается в Ом-метр (Ом⋅м). Символ, обозначающий удельное сопротивление, является греческая буква ρ (ро). Высокое удельное сопротивление означает, что материал плохо проводит электрический заряд.
Удельное сопротивление
Удельное электрическое сопротивление определяется как отношение между напряженностью электрического поля внутри металла к плотности тока в нем:
где:
ρ — удельное сопротивление металла (Ом⋅м),
Е — напряженность электрического поля (В/м),
J — величина плотности электрического тока в металле (А/м2)
Если напряженность электрического поля (Е) в металле очень большая, а плотность тока (J) очень маленькая, это означает, что металл имеет высокое удельное сопротивление.
Обратной величиной удельного сопротивления является удельная электропроводность, указывающая, насколько хорошо материал проводит электрический ток:
где:
Цифровой мультиметр AN8009Большой ЖК-дисплей с подсветкой, 9999 отсчетов, измерение TrueRMS…
Мультиметр — RICHMETERS RM101
Richmeters RM101 — удобный цифровой мультиметр с автоматическим изменен…
Мультиметр — MASTECH MY68
Измерение: напряжения, тока, сопротивления, емкости, частоты…
σ — проводимость материала, выраженная в сименс на метр (См/м).
Электрическое сопротивление
Электрическое сопротивление, одно из составляющих закона Ома, выражается в омах (Ом). Следует заметить, что электрическое сопротивление и удельное сопротивление — это не одно и то же. Удельное сопротивление является свойством материала, в то время как электрическое сопротивление — это свойство объекта.
Электрическое сопротивление резистора определяется сочетанием формы и удельным сопротивлением материала, из которого он сделан.
Например, проволочный резистор, изготовленный из длинной и тонкой проволоки имеет большее сопротивление, нежели резистор, сделанный из короткой и толстой проволоки того же металла.
В тоже время проволочный резистор, изготовленный из материала с высоким удельным сопротивлением, обладает большим электрическим сопротивлением, чем резистор, сделанный из материала с низким удельным сопротивлением. И все это не смотря на то, что оба резистора сделаны из проволоки одинаковой длины и диаметра.
В качестве наглядности можно провести аналогию с гидравлической системой, где вода прокачивается через трубы.
- Чем длиннее и тоньше труба, тем больше будет оказано сопротивление воде.
- Труба, заполненная песком, будет больше оказывать сопротивление воде, нежели труба без песка
Сопротивление провода
Величина сопротивления провода зависит от трех параметров: удельного сопротивления металла, длины и диаметра самого провода. Формула для расчета сопротивления провода:
где:
R — сопротивление провода (Ом)
ρ — удельное сопротивление металла (Ом.m)
L — длина провода (м)
А — площадь поперечного сечения провода (м2)
В качестве примера рассмотрим проволочный резистор из нихрома с удельным сопротивлением 1.10×10-6 Ом.м. Проволока имеет длину 1500 мм и диаметр 0,5 мм. На основе этих трех параметров рассчитаем сопротивление провода из нихрома:
R=1,1*10-6*(1,5/0,000000196) = 8,4 Ом
Нихром и константан часто используют в качестве материала для сопротивлений. Ниже в таблице вы можете посмотреть удельное сопротивление некоторых наиболее часто используемых металлов.
Поверхностное сопротивление
Величина поверхностного сопротивления рассчитывается таким же образом, как и сопротивление провода. В данном случае площадь сечения можно представить в виде произведения w и t:
Для некоторых материалов, таких как тонкие пленки, соотношение между удельным сопротивлением и толщиной пленки называется поверхностное сопротивление слоя RS:
где RS измеряется в омах. При данном расчете толщина пленки должна быть постоянной.
Часто производители резисторов для увеличения сопротивления вырезают в пленке дорожки, чтобы увеличить путь для электрического тока.
Свойства резистивных материалов
Удельное сопротивление металла зависит от температуры. Их значения приводится, как правило, для комнатной температуры (20°С). Изменение удельного сопротивления в результате изменения температуры характеризуется температурным коэффициентом.
Например, в термисторах (терморезисторах) это свойство используется для измерения температуры. С другой стороны, в точной электронике, это довольно нежелательный эффект.
Металлопленочные резисторы имеют отличные свойства температурной стабильности. Это достигается не только за счет низкого удельного сопротивления материала, но и за счет механической конструкции самого резистора.
Много различных материалов и сплавов используются в производстве резисторов. Нихром (сплав никеля и хрома), из-за его высокого удельного сопротивления и устойчивости к окислению при высоких температурах, часто используют в качестве материала для изготовления проволочных резисторов. Недостатком его является то, что его невозможно паять. Константан, еще один популярный материал, легко паяется и имеет более низкий температурный коэффициент.
Электрическое сопротивление. Удельное сопротивление
- Подробности
- Просмотров: 273
Электрическое сопротивление (R) — это физическая величина, численно равная отношению напряжения на концах проводника к силе тока, проходящего через проводник.
Величину сопротивления для участка цепи можно определить из формулы закона Ома для участка цепи.
Однако, сопротивление проводника не зависит от силы тока в цепи и напряжения, а определяется только формой, размерами и материалом проводника.
где l — длина проводника ( м ), S — площадь поперечного сечения (кв.м ), r ( ро) — удельное сопротивление (Ом м ).
Удельное сопротивление
— показывает, чему равно сопротивление проводника, выполненного из данного вещества, длиной в 1м и с поперечным сечением 1 м кв.
Единица измерения удельного сопротивления в системе СИ: 1 Ом м
Однако, на практике толщина проводов значительно меньше 1 м кв, поэтому чаще используют внесистемную единицу измерения удельного сопротивления:
Единица измерения сопротивления в системе в СИ:
[R] = 1 Ом
Сопротивление проводника равно 1 Ом, если при разности потенциалов на его концах в 1 В, по нему протекает ток силой 1 А.
___
Причиной наличия сопротивления у проводника является взаимодействие движущихся электронов с ионами кристалической решетки проводника. Из-за различия в строении криталической решетки у проводников, выполненных из различных веществ, сопротивления их отличаются друг от друга.
ЗАПОМНИ
Существует физическая величина обратная сопротивлению — электрическая проводимость.
R — это сопротивление проводника,
1/R — это электрическая проводимость проводника
___
Величины проводимости проводников и изоляторов различаются в большое число раз, измеряемое единицей с двадцатью двумя нулями!
ЗНАЕШЬ ЛИ ТЫ
… что сопротивления кожи человека обычно изменяется от 1 кОм ( для влажной кожи ) до 500 кОм ( для сухой кожи ). Сопротивление других тканей тела равно от 100 до 500 Ом.
___
… что соединительные провода, из которых собираются электрические цепи, обладают сопротивлением. Согласно закону Ома на проводах теряется часть напряжения, поэтому выгодно ставить провода с наименьшим удельным сопротивлением.
___
… что сопротивление проводника зависит от температуры.
ИНТЕРЕСНО
При повышении температуры металлического проводника его сопротивление увеличивается.
При увеличении температуры электролита (жидкого проводника) его сопротивление уменьшается.
Если взять в качестве проводника уголь (обычную таблетку активированногоугля из аптечки), то его сопротивление при надавливании на уголь уменьшается!
ДУМАЕМ НАД ЗАДАЧКАМИ
Если длину проволоки вытягиванием увеличить вдвое то, как изменится её сопротивление?
___
Две квадратные металлические пластины из одного металла разной толщины включены в электрическую цепь. Одинаковое ли сопротивление они оказывают току?
___
Какой проводник представляет большее сопротивление для постоянного тока: медный сплошной стержень или медная трубка, имеющая внешний диаметр, равный диаметру стержня? ( длину обоих проводников считать одинаковой)
Не сопротивляйся, иди скорее решать задачи!
Электрическое сопротивление, выражаемое в омах, отличается от понятия «удельное сопротивление». Чтобы понять, что такое удельное сопротивление, надо связать его с физическими свойствами материала.
Провода и кабели
Об удельной проводимости и удельном сопротивлении
Поток электронов не перемещается беспрепятственно через материал. При постоянной температуре элементарные частицы качаются вокруг состояния покоя. Кроме того, электроны в зоне проводимости мешают друг другу взаимным отталкиванием из-за аналогичного заряда. Таким образом возникает сопротивление.
Удельная проводимость является собственной характеристикой материалов и количественно определяет легкость, с которой заряды могут двигаться, когда вещество подвергается воздействию электрического поля. Удельное сопротивление является обратной величиной и характеризуется степенью трудности, которую электроны встречают при своих перемещениях внутри материала, давая представление о том, насколько хорош или плох проводник.
Важно! Удельное электрическое сопротивление с высоким значением указывает на то, что материал плохо проводящий, а с низким значением – определяет хорошее проводящее вещество.
Удельная проводимость обозначается буквой σ и рассчитывается по формуле:
σ = J/E.
Удельное сопротивление ρ, как обратный показатель, можно найти так:
ρ = E/J.
Удельная проводимость и удельное сопротивление
В этом выражении E является напряженностью создаваемого электрического поля (В/м), а J – плотностью электротока (А/м²). Тогда единица измерения ρ будет:
В/м х м²/А = ом м.
Для удельной проводимости σ единицей, в которой она измеряется, служит См/м или сименс на метр.
Типы материалов
В соответствии с удельным сопротивлением материалов, их можно классифицировать на несколько типов:
- Проводники. К ним относятся все металлы, сплавы, растворы, диссоциированные на ионы, а также термически возбужденные газы, включая плазму. Из неметаллов можно привести в пример графит;
- Полупроводники, фактически представляющие собой непроводящие материалы, кристаллические решетки которых целенаправленно легированы включением чужеродных атомов с большим или меньшим числом связанных электронов. В результате в структуре решетки образуются квазисвободные избыточные электроны или дырки, которые вносят вклад в проводимость тока;
- Диэлектрики или изоляторы диссоциированные – все материалы, которые в нормальных условиях не имеют свободных электронов.
Проводники и диэлектрики
Для транспортировки электрической энергии или в электроустановках бытового и промышленного назначения часто используемый материал – медь в виде одножильных или многожильных кабелей. Альтернативно применяется металл алюминий, хотя удельное сопротивление меди составляет 60% от такого же показателя для алюминия. Но он гораздо легче меди, что предопределило его использование в линиях электропередач сетей высокого напряжения. Золото в качестве проводника применяется в электроцепях специального назначения.
Интересно. Электропроводность чистой меди была принята Международной электротехнической комиссией в 1913 году в качестве стандарта по этой величине. Согласно определению, проводимость меди, измеренная при 20°, равна 0,58108 См/м. Это значение называется 100% LACS, а проводимость остальных материалов выражается как определенный процент LACS.
Большинство металлов имеют значение проводимости меньше 100% LACS. Однако есть исключения, такие как серебро или специальная медь с очень высокой проводимостью, обозначенные С-103 и С-110, соответственно.
Диэлектрики не проводят электричество и используются в качестве изоляторов. Примеры изоляторов:
- стекло,
- керамика,
- пластмасса,
- резина,
- слюда,
- воск,
- бумага,
- сухая древесина,
- фарфор,
- некоторые жиры для промышленного и электротехнического использования и бакелит.
Между тремя группами переходы являются текучими. Известно точно: абсолютно непроводящих сред и материалов нет. Например, воздух – изолятор при комнатной температуре, но в условиях мощного сигнала низкой частоты он может стать проводником.
Определение удельной проводимости
Если сравнивать удельное электрическое сопротивление различных веществ, требуются стандартизированные условия измерения:
- В случае жидкостей, плохих проводников и изоляторов, используют кубические образцы с длиной ребра 10 мм;
- Величины удельного сопротивления почв и геологических образований определяются на кубах с длиной каждого ребра 1 м;
- Проводимость раствора зависит от концентрации его ионов. Концентрированный раствор менее диссоциирован и имеет меньше носителей заряда, что снижает проводимость. По мере увеличения разведения увеличивается число ионных пар. Концентрация растворов устанавливается в 10%;
- Для определения удельного сопротивления металлических проводников используются провода метровой длины и сечения 1 мм².
Если материал, такой как металл, может обеспечить свободные электроны, то когда приложить разность потенциалов, по проводу потечет электрический ток. По мере увеличения напряжения большее количество электронов перемещается через вещество во временную единицу. Если все дополнительные параметры (температура, площадь поперечного сечения, длина и материал провода) неизменны, то отношение силы тока к приложенному напряжению тоже постоянно и именуется проводимостью:
G = I/U.
Соответственно, электросопротивление будет:
R = U/I.
Результат получается в ом.
В свою очередь, проводник может быть разных длины, размеров сечения и изготавливаться из различных материалов, от чего зависит значение R. Математически эта зависимость выглядит так:
R = ρ x l/S.
Фактор материала учитывает коэффициент ρ.
Удельное сопротивление проводника
Отсюда можно вывести формулу для удельного сопротивления:
ρ = R x S/l.
Если значения S и l соответствуют заданным условиям сравнительного расчета удельного сопротивления, т. е. 1 мм² и 1 м, то ρ = R. При изменении габаритов проводника количество омов тоже меняется.
Удельное сопротивление и температура
Удельное сопротивление проводника является величиной, которая меняется с температурой, поэтому ее точно рассчитывают для показателя 20°. Если температура отличается, значение ρ необходимо отрегулировать на основе другого коэффициента, называемого температурным и обозначаемым α (единица – 1/°С). Это тоже характерное значение для каждого материала.
Таблица удельных проводимостей и температурных коэффициентов
Модифицированный коэффициент рассчитывается на основе значений ρ, α и отклонения температуры от 20° – Δt:
ρ1 = ρ х (1 + α х Δt).
Если до этого сопротивление было известно, то можно напрямую произвести его расчет:
R1 = R x (1 + α х Δt).
Практическое использование различных материалов в электротехнике напрямую зависит от их удельного сопротивления.



