Треугольник сопротивлений

Дата публикации: 01 апреля 2015.
Категория: Электротехника.

Если стороны треугольника напряжений (рисунок 1, а) разделить на ток I (рисунок 1, б), то углы треугольника от этого не изменятся, и мы получим новый треугольник, подобный первому – треугольник сопротивлений (рисунок 1, в).

Рисунок 1. Получение треугольника сопротивлений

Рисунок 2. Треугольник сопротивлений

В треугольнике сопротивления, показанном отдельно на рисунке 2, все стороны обозначают сопротивления, причем гипотенуза его является полным или кажущимся сопротивлением цепи.

Из треугольника сопротивлений видно, что полное или кажущееся сопротивление z равно геометрической сумме активного

r и индуктивного x_L сопротивлений.

Применяя теорему Пифагора к треугольнику сопротивлений, получаем:

z² = r² + x_L² ,

откуда

Если одно из сопротивлений цепи (активное или реактивное), например, в 10 и более раз меньше другого, то меньшим можно пренебречь, в чем легко можно убедиться непосредственным расчетом.

Пример 1. Определить полное сопротивление цепи, в которой r = 9 Ом и x_L = 12 Ом.

Было бы совершенно неправильно, если бы для определенного полного сопротивления были арифметически сложены оба сопротивления r и x_L, так как

9 + 12 = 21 Ом.

Результат, как мы видим, в этом случае получается неверный.

Пример 2. Полное сопротивление обмотки электромагнита z = 25 Ом. Активное сопротивление обмотки r = 15 Ом. Определить индуктивное сопротивление.

Так как

z² = r² + x_L² ,

то

x_L² = z² – r² ,

откуда

Поэтому

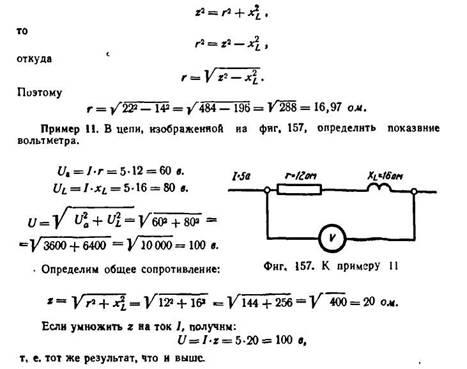
Пример 3. Индуктивное сопротивление обмотки электродвигателя переменного тока равно 14 Ом. Полное сопротивление ее равно 22 Ом. Найти активное сопротивление.

Так как

z² = r² + x_L² ,

то

r² = z² – x_L² ,

Поэтому

Пример 4. В цепи, изображенной на рисунке 3, определить показание вольтметра.

Рисунок 3. К примеру 4

U_а = I × r = 5 × 12 = 60 В.

U_L = I × x_L = 5 × 16 = 80 В.

Определим общее сопротивление:

Если умножить z на ток I, получим:

U = I × z = 5 × 20 = 100 В.

то есть тот же результат, что и выше.

Следовательно, если

U_а = I × r

и

U_L = I × x_L

то

U = I × z .

Источник: Кузнецов М. И., «Основы электротехники» — 9-е издание, исправленное — Москва: Высшая школа, 1964 — 560 с.

Треугольник сопротивлений

Если стороны треугольника напряжений (фиг. 155, а) разделить на ток I (фиг. 155, б), то углы треугольника от этого не из менятся, и мы получим новый треугольник, подобный первому — треугольник сопротивлений (фиг. 155, в).

В треугольнике сопротивления, показанном отдельно на фиг. 156, все стороны обозначают сопротивления, причем гипотенуза его является полным или кажущимся сопротивлением цепи.

Из треугольника сопротивлений видно, что полное или кажущееся сопротивление z равно геометрической сумме активного r и индуктивного x_Lсопротивлений.

Применяя теорему Пифагора к треугольнику сопротивлений, получаем:

Если одно из сопротивлений цепи — (активное или реактивное), например, в 10 и более раз меньше другого, то меньшим можно пренебречь, в чем легко убедиться непосредственным расчетом.

Пример 8. Определить полное сопротивление цепи, в которой r — 9 ом и х _L — 12 ом.

Было бы совершенно неправильно, если бы для определения полного сопротивления были арифметически сложены оба сопротивления r и х _L, так как

9+12=21 ом.

Результат, как видим, в этом случае получается неверный.

Пример 9. Полное сопротивление обмотки электромагнита z=25 ом. Активное сопротивление обмотки r=15 ом. Определить индуктивное сопротивление. Так как

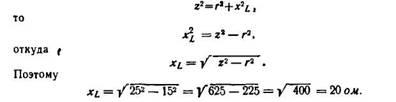
Пример 10. Индуктивное сопротивление обмотки электродвигателя переменного тока равно 14 ом. Полное сопротивление ее равно 22 ом. Найти активное сопротивление. Так как

Следовательно, если

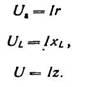
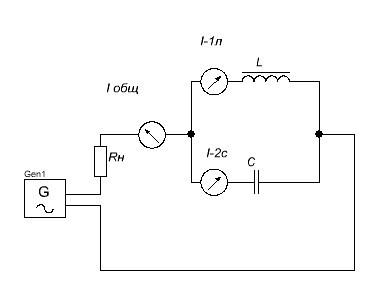
Измерение в омах.

10) Резонанс в электрических цепях – это увеличение токов и напряжений на отдельных

участках цепи при изменении частоты гармонического сигнала. Физической основой

резонанса в электрических цепях является обмен реактивной энергией между

емкостными и индуктивными элементами (конденсаторами и катушками

индуктивности), включенными в данную цепь.

Резонанс может быть двух видов резонанс токов и резонанс напряжений .  Опишу подробнее оба случая резонанса .  Параллельный колебательный контур – резонанс токов. 

В этом случае на катушке и на конденсаторе напряжение такое же, как у генератора. При резонансе, сопротивление контура между точками разветвления становится максимальным, а ток (I общ) через сопротивление нагрузки Rн будет минимальным (ток внутри контура I-1л и I-2с больше чем ток генератора).  В идеальном случае полное сопротивление контура равно бесконечности — схема не потребляет тока от источника. При изменение частоты генератора в любую сторону от резонансной частоты полное сопротивление контура уменьшается и линейный ток (I общ) возрастает.  Последовательный колебательный контур – резонанс напряжений. 

В этой схеме при резонансе полное сопротивление контура минимально, ток в контуре и через Rн возрастает до пиковой величины. Эта большая величина тока при ее умножении на индуктивное и емкостное сопротивление дает высокое падения напряжения на катушке индуктивности (U-1л) и на конденсаторе (U-2с) и в реальных условиях значительно превышают напряжение генератора.  Главной чертой последовательного резонансного контура является то, что его полное сопротивление минимально при резонансе. (ZL + ZC – минимум). При настройке частоты на величину, превышающую или лежащую ниже резонансной частоты, полное сопротивление возрастает.  Вывод:  В параллельном контуре при резонансе ток через выводы контура равен 0, а напряжение максимально.  В последовательном контуре наоборот — напряжение стремится к нулю, а ток максимален.  Добротность  Настроенный контур при резонансе характеризуется величиной добротности, которая обозначается Q. Добротность катушки индуктивности обычно выражается, как отношение её последовательного реактивного сопротивления к активному. Что это значит?  Добротность резонансного контура равна отношению увеличения напряжения на емкости и индуктивности по сравнению с напряжением, поданным на контур (для последовательного резонанса)  Также можно сказать, что отношение энергии, запасенной реактивными элементами контура, к энергии омических (резистивных) потерь за период принято называть добротностью контура Q. Величину, обратную добротности d=1/Q, называют затуханием контура.  Добротность зависит от качества элементов контура. Для ее увеличения необходимо минимальное активное сопротивление индуктивности (толстый провод) и минимальные утечки в ёмкости (хороший изолятор). Чем выше добротность, тем лучше (острее) резонансная кривая.  Говоря по-простому — чем выше добротность, тем дольше происходит затухание свободных колебаний в контуре после отключения поданного напряжения.  Добротность реальных колебательных контуров составляет от нескольких единиц до сотни и более.

11) РЕЗОНАНС НАПРЯЖЕНИЙ 

Имеются два случая резонанса в колебательных контурах: резонанс напряжений и резонанс токов. Резонанс напряжений, или последовательный резонанс, наблюдается в случае, когда генератор переменной эдс нагружен Рис.1 — Схема и резонансные кривые для резонанса напряжений на соединенные последовательно L и С контура (рис.1 а), т.е. включен внутри контура. В такой цепи имеется активное сопротивление г и общее реактивное сопротивление х, равное Разность хL, и xC берется потому, что индуктивное и емкостное сопротивления оказывают противоположные влияния на ток. Первое вызывает отставание по фазе тока от напряжения, а второе, наоборот, создает отставание напряжения от тока. Для собственных колебаний xL и хс равны друг другу. Если частота генератора равна частоте контура, то для тока, создаваемого генератором, xL и хC также одинаковы. Тогда общее реактивное сопротивление х станет равным нулю и полное сопротивление цепи для генератора равно только одному активному сопротивлению, которое в контурах имеет сравнительно небольшую величину. Благодаря этому ток значительно возрастает и устраняется сдвиг фаз между напряжением генератора и током. Резонанс напряжений выражается в том, что полное сопротивление контура становится наименьшим и равным активному сопротивлению, а ток становится максимальным. Условием резонанса напряжений является равенство частот генератора и контура f = fo, или равенство индуктивного и емкостного сопротивлений для тока генератора: xL = хC. Когда частота генератора больше частоты контура, индуктивное сопротивление преобладает над емкостным и контур представляет для генератора сопротивление индуктивного характера. Если частота генератора меньше частоты контура, то емкостное сопротивление больше индуктивного и контур для генератора является сопротивлением емкостного характера. В любом из этих случаев при отклонении от резонанса полное сопротивление контура возрастает по сравнению а его величиной при резонансе. На (рис.1 б) показаны графики изменения полного сопротивления контура z и тока I при изменении частоты генератора f. Для расчета сопротивления контура и тока при резонансе напряжений служат простые формулы: Таким образом, напряжение генератора U равно падению напряжения на активном сопротивлении (г). Большой ток в контуре при резонансе создает на индуктивном и емкостном сопротивлениях напряжения, значительно превышающие напряжение генератора. Они равны: Так как хL = хC = р, то эти напряжения равны, но они противоположны по фазе и взаимно компенсируют друг друга. Действительно, напряжение на катушке опережает ток на 90°, а напряжение на конденсаторе отстает от тока на 90°. Ясно, что между этими напряжениями сдвиг фаз равен 180°. Кривая резонанса для тока, приведенная на (рис.1 6), при небольшом Изменении частоты показывает также изменение напряжения UL и Uс (только в ином масштабе). Это следует из того, что при изменении частоты вблизи резонанса ток меняется сильно, а сопротивления xL и хC — сравнительно мало. Например, если fpeз — 1000 кгц и частота изменяется на 20 кгц, т.е. на 2%, то сопротивления xL и хС изменяются каждое также только на 2%. В результате напряжения UL = IxL и Uc = IxС изменяются почти точно пропорционально току. При резонансе напряжение на катушке или на конденсаторе в Q раз больше, чем напряжение генератора, равное U — Ir. Напряжение на L или С равно UL = Uc = р. Поэтому Чем выше добротность контура Q, тем больше увеличение напряжения при резонансе. Повышение напряжения на катушке и на конденсаторе характерно для резонанса напряжений, само название которого подчеркивает увеличение напряжения в момент резонанса. Большие напряжения на катушке и конденсаторе получаются за счет постепенного накопления энергии в контуре в процессе возникновения в нем колебаний. Эдс генератора возбуждает в контуре колебания, амплитуда которых нарастает до тех пор, пока энергия, даваемая генератором, не станет равна потерям энергии в активном сопротивлении контура. После этого в контуре происходят мощные колебания, характеризующиеся большой величиной тока и большими напряжениями, а генератор расходует небольшую мощность только для компенсации потерь энергии. Подобно этому можно, раскачивая тяжелый маятник легкими движениями руки с частотой, равной его собственной частоте, постепенно довести амплитуду колебаний маятника до значительной величины, во много раз превышающей амплитуду колебаний руки, играющей роль генератора. Резонанс напряжений применяется в радиотехнике для получения максимального тока и напряжения в контуре. Например, антенный контур радиопередатчика настраивают на резонанс напряжений для того, чтобы ток в антенне был максимальным. Тогда дальность действия передатчика будет наибольшей. Входной контур приемника также настраивают на резонанс напряжений для того, чтобы получить усиление напряжения сигналов той радиостанции, на частоту которой настроен контур. Напряжения сигналов других радиостанций, частоты которых отличаются от резонансной частоты приемного контура, усиливаются незначительно. При резонансе напряжений в величину активного сопротивления контура входит внутреннее сопротивление генератора. Если оно велико, то качество контура может стать низким и резонансные свойства его будут выражены слабо. Поэтому для резонанса напряжений генератор, питающий контур, должен иметь малое внутреннее сопротивление.

12) Добротность — характеристика колебательной системы, определяющая полосу резонанса и показывающая, во сколько раз запасы энергии в системе больше, чем потери энергии за один период колебаний.

13,16) Активная (мощность и проводимость)

Единица измерения — ватт (W, Вт).

Среднее за период T значение мгновенной мощности называется активной мощностью: В цепях однофазного синусоидального тока 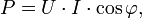где U и I — среднеквадратичные значения напряжения и тока, φ — угол сдвига фаз между ними. Для цепей несинусоидального тока электрическая мощность равна сумме соответствующих средних мощностей отдельных гармоник. Активная мощность характеризует скорость необратимого превращения электрической энергии в другие виды энергии (тепловую и электромагнитную). Активная мощность может быть также выражена через силу тока, напряжение и активную составляющую сопротивления цепи r или её проводимость g по формуле 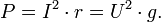В любой электрической цепи как синусоидального, так и несинусоидального тока активная мощность всей цепи равна сумме активных мощностей отдельных частей цепи, для трёхфазных цепей электрическая мощность определяется как сумма мощностей отдельных фаз. С полной мощностью S активная связана соотношением 

В теории длинных линий (анализ электромагнитных процессов в линии передачи, длина которой сравнима с длиной электромагнитной волны) полным аналогом активной мощности является проходящая мощность, которая определяется как разность между падающей мощностью и отраженной мощностью.

Реактивная

3.14. Треугольник сопротивлений и треугольник проводимостей.

Из (3.34) следует, что модуль комплексного сопротивления

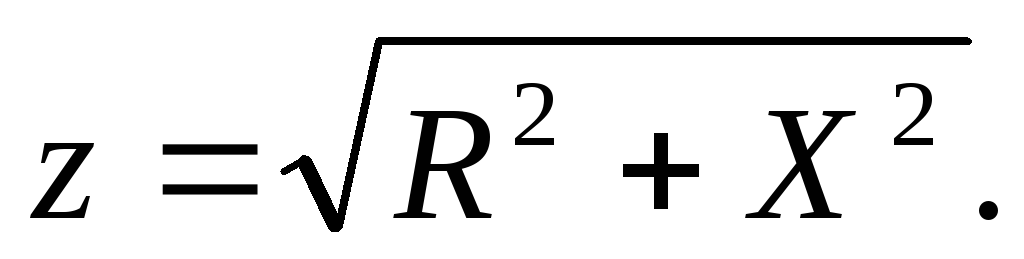(3.37)

Следовательно, z можно представить как гипотенузу прямоуголь­ного треугольника (рис. 3.10)-

треугольника сопротивлений, один катет которого равен R, другой X. При этом

tg =X/R. (3.38)

Аналогичным образом модуль комплексной проводимости в соот­ветствии с (3.36)

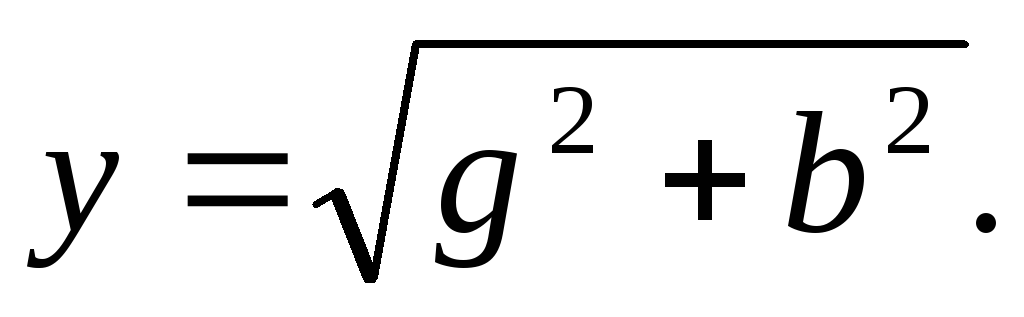Следовательно, y есть гипотенуза пря­моугольного треугольника (рис. 3.11), катетами которого являются активная g и реактивная b проводимости:

tg =b/g (3.39)

Треугольник сопротивлений дает графическую интерпретацию связи между модулем полного сопротивления z и активным и реактивным сопротивлениями цепи; треуголь­ник проводимостей —интерпретацию связи между модулем полной про­водимости y и ее Рис.3.10 Рис.3.11 активной и реак­тивной составляющими.

3.16. Законы Кирхгофа в символической форме записи. По первому закону Кирхгофа, алгебраическая сумма мгновенных значе­ний токов, сходящихся в любом узле схемы, равна нулю:

 i_k=0. (3.40′)

Подставив вместо i_k в (3.40′) I_k e ^jt и вынеся e ^jt за скобку, по­лучим e ^jt I_k = 0. Так как e ^jt не равно нулю при любом t, то

 İ_k = 0 (3.40)

Уравнение (3.40) представляет собой первый закон Кирхгофа в символической форме записи.

Для замкнутого контура сколь угодно сложной электрической цепи синусоидального тока можно составить уравнение по второму закону Кирхгофа для мгновенных значений токов, напряжений и

э. д. с.

Пусть замкнутый контур содержит п ветвей и каждая k-ветвь в общем случае включает в себя э. д. с. e_k , активное сопротивление R_k , индуктивность L_k и емкость C_k , по которым протекает ток i_k. Тогда по второму закону Кирхгофа

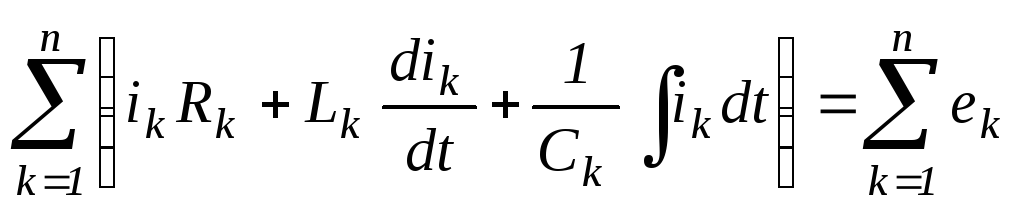(3.41a)

Но каждое слагаемое левой части уравнения в соответствии с § 3.12 можно заменить на I_kZ_k , а каждое слагаемое правой части на E_k . Поэтому уравнение (3.41) переходит в

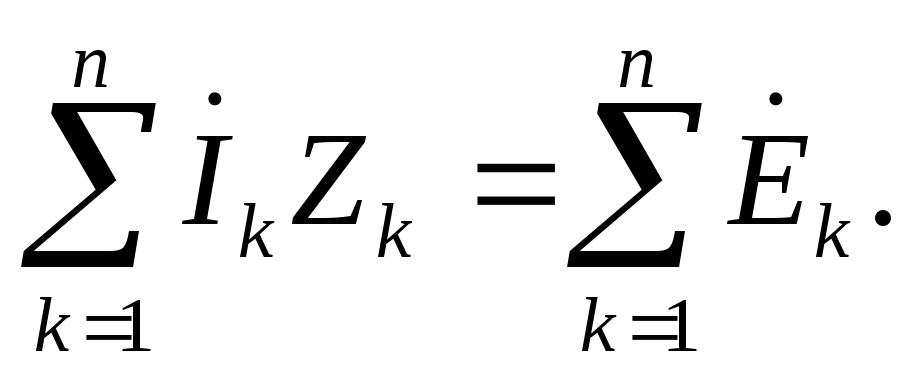(3.41a)

Уравнение (3.41a) представляет собой второй закон Кирхгофа в символической форме записи.

3.17. Применение к расчету цепей синусоидального тока мето­дов, рассмотренных в главе «Электрические цепи постоянного тока».

Для анализа и расчета электрических цепей постоянного тока разра­ботан ряд методов и приемов, облегчающих решение по сравнению с решением системы уравнений при непосредственном использовании законов Кирхгофа. Из гл. 1 известно, что к числу таких методов относятся метод контурных токов, метод узловых потенциалов, метод эквивалентного генератора и т. д. Известно также, что окончательные расчетные формулы этих методов получают в результате выводов, в основу которых положены первый и второй законы Кирхгофа.

Поскольку первый и второй законы Кирхгофа справедливы и для цепей синусоидального тока, то можно было бы записать уравнения для мгновенных значений величин цепей синусоидального тока, пе­рейти от них к уравнениям в комплексах и затем повторить вывод всех формул гл. 1 для цепей синусоидального тока. Понятно, что проделывать выводы заново нет необходимости.

В том случае, когда отдельные ветви электрической цепи синусо­идального тока не связаны между собой магнитно, все расчетные формулы гл. 1 пригодны и для расчета цепей синусоидального тока, если в этих формулах вместо постоянного тока I подставить комплекс тока I, вместо проводимости g — комплексную проводимость Y, вместо сопротивления R — комплексное сопротивление Z и вместо постоянной э. д. с. Е — комплексную э. д. с. Ё.

Если же отдельные ветви электрической цепи синусоидального тока связаны друг с другом магнитно (это имеет место при наличии взаимоиндукции), то падение напряжения на каком-либо участке, цепи зависит не только от тока данной ветви, но и от токов тех ветвей, с которыми данная ветвь связана магнитно. Расчет электрических цепей синусоидального то­ка при наличии в них магнитно-связанных ветвей приобретает ряд особенностей, которые не могут быть учтены, если в формулах гл. 1 непосредственно заменить Е на Ё, R на Z и g на Y. (Особенности расчета магнитносвязанных цепей рас­смотрены в § 3.36.)

Треугольник мощностей

Дата публикации: 17 апреля 2015.
Категория: Электротехника.

Если величины треугольника напряжений (рисунок 1, а) умножить на ток I (рисунок 1, б), то получим треугольник мощностей (рисунок 1, в). Все стороны треугольника мощностей, показанного отдельно на рисунке 2, представляют собой мощности.

Рисунок 1. Получение треугольника мощностей

Рисунок 2. Треугольник мощностей

Гипотенуза треугольника мощностей есть полная мощность S.

S = U × I .

Она измеряется в вольт-амперах (ВА) или киловольт-амперах (кВА) по показаниям вольтметра и амперметра. Величина полной мощности характеризует основные габариты (наибольшие размеры) генераторов и трансформаторов. В самом деле, изоляция обмоток генераторов и трансформаторов рассчитывается на определенное напряжение, а величина тока определяет нагрев их обмоток (I² × r).

Катет, прилегающий к углу φ, представляет собой известную нам активную мощность P.

P = U_а × I .

Так как U_а = I × r, то

P = I² × r .

Активная мощность в цепях переменного тока расходуется на нагрев. В двигателях переменного тока большая часть активной мощности превращается в механическую мощность.

Активная мощность измеряется ваттметром и выражается в ваттах (Вт) или киловаттах (кВт). Из треугольника мощностей имеем:

P = S × cos φ = U × I × cos φ .

Активная мощность характеризует степень нагрузки первичного двигателя, вращающего генератор.

Катет, лежащий против угла φ, есть реактивная мощность Q.

Q = U_r ×I .

Так как U_r = I × x (где x – реактивное сопротивление), то

Q = I² × x .

Реактивная мощность обусловлена наличием магнитных и электрических полей в индуктивностях и емкостях цепей. Из треугольника мощностей имеем:

Q = S × sin φ = U × I × sin φ .

Реактивная мощность измеряется в вольт-амперах реактивных (вар) или киловольт-амперах реактивных (квар). Применяя к треугольнику мощностей теорему Пифагора, получим:

S² = P² + Q²

или

Рисунок 3. Электрическая цепь с активным и индуктивным сопротивлениями и измерительными приборами

Рассмотрим электрическую цепь, показанную на рисунке 3, в которую входят индуктивное и активное сопротивления и измерительные приборы – амперметр, вольтметр и ваттметр.

1. Если подключить эту цепь к постоянному напряжению, то, поскольку индуктивное сопротивление xL при постоянном токе будет равно нулю, в цепи остается одно активное сопротивление r и тогда

Амперметр покажет ток 5 А.

Мощность

P = I × U = 5 × 120 = 600 Вт

или

P = I² × r = 25 × 24 = 600 Вт .

Следовательно, ваттметр покажет 600 Вт. Таким образом, ваттметр, включенный в цепь постоянного тока, показывает мощность в ваттах, потребляемую цепью. Показание ваттметра равно произведению показаний вольтметра и амперметра.

2. Подключим ту же цепь к переменному напряжению.

В этом случае:

Ток в цепи

Амперметр покажет ток 4 А.

Подсчитаем мощность, идущую на нагрев:

P = I² × r = 4² × 24 = 384 Вт .

Показание ваттметра в этом случае будет 384 Вт.

Полная мощность, забираемая цепью от источника переменного тока,

S = I × U = 4 × 120 = 480 Вт .

Следовательно, генератор, питающий эту цепь, отдает полную мощность S = 480 ВА. Но в самой цепи только активная мощность P = 384 Вт безвозвратно теряется в виде тепла.

Отсюда видно, что цепь переменного тока, содержащая наряду с активным сопротивлением индуктивное, из всей получаемой ею полной энергии только часть расходует на тепло. Остальная часть – реактивная энергия – то забирается цепью от генератора и запасается в магнитном поле катушки, то возвращается обратно генератору.

Источник: Кузнецов М. И., «Основы электротехники» — 9-е издание, исправленное — Москва: Высшая школа, 1964 — 560 с.

1.6.5 Преобразование «треугольника сопротивлений» в «звезду сопротивлений»

Впервые данное преобразование осуществлено итальянским ученым Кеннели.

Составляем расчетную схему.

Рисунок 1.22 — Преобразование «» сопротивлений в «»

Для треугольника сопротивлений дано: .

Найти: .

Уравнения перехода от треугольника к звезде сопротивлений запишутся:

; (1.26)

; (1.27)

. (1.28)

Решим полученную систему относительно неизвестных . Для этого сложим (1.26) и (1.28) и вычтем (1.27).

(1.29)

Откуда получаем

,

аналогично имеем:

; (1.30)

.

Выражения (1.30) позволяет определить сопротивления лучей звезды по заданным сопротивлениям сторон треугольника.

В частом случае, при симметричном треугольнике, когда все сопротивления сторон треугольника одинаковы, , сопротивления лучей звезды также будут одинаковы,.

Согласно выражений (1.30), получаем:

;

. (1.31)

Луч симметричной звезды всегда равен одной трети сопротивления стороны симметричного треугольника.

1.6.6 Преобразование «звезды сопротивлений» в «треугольник сопротивлений»

Рассмотрим, теперь обратное преобразование.

Рисунок 1.23 — Преобразование звезды в треугольник сопротивлений

Для звезды сопротивлений дано: .

Найти:..

Согласно схеме, на рисунке 1.23, будем иметь:

; (1.32)

; (1.33)

. (1.34)

Решаем полученную систему. Для этого сложим (1.33) с (1.34) и вычтем (1.32).

.

Откуда имеем

.

Аналогично получаем:

; (1.35)

.

Выразив из (1.35) сопротивления лучей звезды окончательно запишем:

;

; (1.36)

.

Эти же соотношения в проводимостях можно записать так

, откуда получим

.

Аналогично получаем остальные проводимости:

; (1.37)

.

Для симметричного случая, на основании выражения (1.31) имеем

. (1.38)

1.7 Методы расчета сложных цепей

В зависимости от конфигурации и условий заданной цепи применяются для расчета цепи различные методы. Однако все методы расчета основаны на законах Кирхгофа.

Искусство расчетчика состоит в том, что он находит наиболее рациональный метод решения к конкретно заданной цепи.

Рассмотрим наиболее употребительные методы расчета цепей.

1.7.1 Метод линейных преобразований

Данный метод основан на использовании закона Ома и формул последовательного, параллельного, смешанного соединения соп­ротивлений, а также перехода от соединения сопротивлений в треугольник к звезде.

Сначала сложная цепь свертывается до предельно простой и решается по закону Ома – прямой путь. Затем, полученное решение развертывается до заданной конфигурации цепи – обратный путь. Основное условие применимости метода – в цепи должен быть только один источник пи­тания.

Дано: цепь, показанная на рисунке 1.24; параметры Е, R₁, R₂, R₃, R₄, R₅, R₆.

Рисунок 1.24 – Исходная схема цепи

Найти

1. Эквивалентное сопротивление всей цепи относительно зажимов источника питания.

2. Все токи.

3. Проверить полученные результаты на: а) баланс токов, б) баланс мощности.

4. Напряжения на всех элементах цепи.

5. Проверить напряжения на баланс напряжений.

Порядок расчета

1. Расставляем на исходной схеме стрелки токов.

Поскольку в схеме только один источник энергии токи можно разметить сразу в правильном направлении. Токов будет столько, сколько ветвей в цепи. Стрелки токов размечают непосредственно на проводниках.

2. Размечаем стрелки напряжений. Напряжения расставляются на каждом элементе цепи. Направление стрелок напряжений всегда выбирается против токов текущих в ветви.

3. Определяем эквивалентное сопротивление всей цепи относительно зажимов источника питания.

Свертываем цепь (прямой путь). Первое преобразование (показано на рисунке 1.25).

Рисунок 1.25 – Расчетная схема после первого преобразования

. (1.39)

Проводим второе преобразование цепи (схема показана на рисунке 1.26).

Рисунок 1.26 – Расчетная схема после второго преобразования

. (1.40)

Третье преобразование (см. рисунок 1.27).

. (1.41)

Рисунок 1.27 – Расчетная схема после третьего преобразования

Четвертое преобразование (см. рисунок 1.28).

. (1.42)

Рисунок 1.29 – Расчетная схема после четвертого преобразования

Последнее, пятое преобразование (см. рисунок 1.30).

. (1.43)

Рисунок 1.30 – Расчетная схема после пятого преобразования

Определяем ток , в схеме на рисунке 1.30, по закону Ома.

. (1.44)

4. Развертываем решение (обратный путь) и находим токи в ветвях цепи. Воспользовавшись схемой изображенной на рисунке 1.27, найдем токи и:

;

. (1.45)

Переходя к рисунку 1.25, определяем токи и:

;

. (1.46)

Токи , иможно найти по-другому, например из рисунка 1.27:

; . (1.47)

Согласно второму закона Кирхгофа имеем

, откуда

, напряжение определится по закону Ома

.

5. Проверка полученных результатов.

а) Баланс токов.

Из рисунка 1.25 следует:

; (1.48)

,

б) Баланс мощности.

Мощность вырабатываемая генератором

. (1.49)

Мощность нагрузки

. (1.50)

6. Определяем напряжения на всех участках цепи. Делаем это по закону Ома:

;

;

;

; (1.52)

;

.

7. Проверяем напряжения на баланс напряжений. Для этого, составим урав­нения по второму закону Кирхгофа для цепи изображенной на рисунке 1.25.

Первое уравнение

. (1.53)

Второе уравнение

. (1.54)

Третье уравнение

или . (1.55)

Если балансы тока, напряжения и мощности сошлись с погрешностью не более 1%, то расчет считается выполненным правильно.

2.4.Преобразование звезды сопротивлений в эквивалентный треугольник

Иногда для упрощения схемы полезно  преобразовать звезду сопротивлений в эквивалентный треугольник.

Рассмотрим схему на рис. 2.5. Заменим звезду сопротивлений R₁-R₂-R₃эквивалентным треугольником сопротивлений R_Δ1-R_Δ2-R_Δ3, включенных между узлами 1-2-3.

Рис. 2.5.

Сопротивление стороны эквивалентного треугольника сопротивлений равно сумме сопротивлений двух прилегающих лучей звезды плюс произведение этих же сопротивлений, деленное на сопротивление оставшегося (противолежащего) луча. Сопротивления сторон треугольника определяются по формулам:

Эквивалентное сопротивление преобразованной схемы равно

3. Анализ электрических цепей постоянного тока с одним источником энергии

3.1. Расчет электрических цепей постоянного тока с одним источником методом свертывания

В соответствии с методом свертывания, отдельные участки схемы упрощают и постепенным преобразованием приводят схему к одному эквивалентному (входному) сопротивлению, включенному к зажимам источника. Схема упрощается с помощью замены группы последовательно или параллельно соединенных сопротивлений одним, эквивалентным по сопротивлению. Определяют ток в упрощенной схеме, затем возвращаются к исходной схеме и определяют в ней токи.

Рассмотрим  схему на  рис. 3.1. Пусть известны величины сопротивлений R₁, R₂, R₃, R₄, R₅, R₆, ЭДС Е. Необходимо определить токи в ветвях схемы.

Рис. 3.1                                                       Рис. 3.2

Сопротивления R₄и R₅соединены последовательно, а сопротивление R₆— параллельно с ними, поэтому их эквивалентное сопротивление

После проведенных преобразований схема принимает вид, показанный на рис. 3.2, а эквивалентное сопротивление всей цепи

Ток I₁в неразветвленной части схемы определяется по формуле:

Найдем токи I₂и I₃ в схеме на рис. 3.2 по формулам:

I₃= I₁— I₂— формула получается из уравнения, составленного по первому закону Кирхгофа:

I₁ — I₂ — I₃ = 0.

Переходим к исходной схеме на рис. 3.1 и определим токи в ней по формулам:

I₆= I₃— I₄(в соответствии с первым законом Кирхгофа I₃— I₄— I₆=0).

3.2. Расчет электрических цепей постоянного тока с одним источником методом подобия или методом пропорциональных величин

Возьмем электрическую схему на рис. 3.1, зададимся произвольным значением тока в сопротивлении R₆, наиболее удаленном от источника питания. По заданному току и сопротивлению R₆определим напряжение . Далее определим:

, ,

, ,

; .

Находим значение ЭДС

.

Найденное значение ЭДС отличается от заданной величины ЭДС   Е.

Вычислим коэффициент подобия . Умножим на него полученные при расчете значения токов и напряжений, находим действительные значения токов цепи.

4. Анализ сложных электрических цепей с несколькими источниками энергии

4.1. Метод непосредственного применения законов Кирхгофа

На рис. 4.1 изображена схема разветвленной электрической цепи. Известны величины сопротивлений и ЭДС, необходимо определить токи.

В схеме имеются четыре узла, можно составить четыре уравнения по первому закону Кирхгофа.

Укажем произвольно направления токов. Запишем уравнения:

Рис. 4.1

           (4.1)

Сложим эти уравнения. Получим тождество 0 = 0. Система уравнений (4.1) является зависимой.

Если в схеме имеется n узлов, количество независимых уравнений, которые можно составить по первому закону Кирхгофа, равно n — 1.

Для схемы на рис. 4.1 число независимых уравнений равно трем.

       (4.2)

Недостающее  количество  уравнений составляют по второму закону Кирхгофа. Уравнения по второму закону составляют для независимых контуров. Независимым является контур, в который входит хотя бы одна новая ветвь, не вошедшая в другие контуры.

Выберем три независимых контура и укажем направления обхода контуров. Запишем три уравнения по второму закону Кирхгофа.

       (4.3)

Решив совместно системы уравнений (4.2) и (4.3), определим токи в схеме.

Ток в ветви может иметь отрицательное значение. Это означает, что действительное направление тока противоположно выбранному нами.

Активное и реактивное сопротивление, треугольник сопротивлений. Е.Г.Воропаев Электротехника

7. Цепь переменного тока с активным и индуктивным сопротивлением.

Любая проволочная катушка, включенная в цепь переменного тока, обладает активным сопротивлением, зависящим от материала, Длины и сечения проволоки , и индуктивным сопротивлением, которое зависит от индуктивности катушки и частоты переменного тока, протекающего по ней (Х L =ωL=2π fL ). Такую катушку можно рассматривать как приемник энергии, в котором активное и индуктивное сопротивления соединены последовательно.

Рассмотрим цепь переменного тока, в которую включена катуш­ка индуктивности (рис. 56, а) с активным r и индуктивным Х L со­противлением. Падение напряжения на активном сопротивлении

Падение напряжения на индуктивном сопротивлении

общее напряжение на зажимах цепи

полное сопротивление цепи

Напряжение на индуктивности опережает ток на угол j = 90°. Поэтому век­тор UL откладываем вверх

под углом 90° к вектору тока.

В цепи с индуктивностью переменный ток отстает по фазе от напряжения на четверть периода

8.Цепь переменного тока с активным и ёмкостным сопротивлениями.

В цепи с емкостью, наоборот, напряжение отстает от тока на угол j = 90°. Поэтому вектор Uc откладываем на диаграмме вниз под углом 90° к вектору тока.

Сила тока, проходящего в цепи с емкостным сопротивлением, зависит от емкостного сопротивления конденсатора Хс и определяется по закону Ома

где U – напряжение источника эдс, В; Хс – емкостное сопротивление, Ом; / – сила тока, А.

Рис. 3. Цепь переменного тока с емкостным сопротивлением

Емкостное сопротивление в свою очередь определяется по формуле

где С – емкостное сопротивление конденсатора, Ф.

Z= корень(R 2 -Xc 2)

Ток опережает по фазе напряжение на четверть периода.

9.Цепь переменного тока с индуктивным и ёмкостным сопротивлением.

Для определения общего напряжения, приложенного к зажимам цепи, сложим векторы U L и U С. Для этого отнимем от большего вектора U L вектор U С и получим вектор U L -U C , выражающий вектор­ную сумму этих двух напряжений. Теперь сложим векторы (U L -U C) и U a . Суммой этих векторов будет диагональ параллелограмма – вектор U , изображающий общее напряжение на за­жимах цепи.

На основании теоремы Пифагора из треугольника напряжений АО Б следует, что

отсюда общее напряжение

Определим полное сопротивление цепи переменного тока, со­держащей активное, индуктивное и емкостное сопротивления. Для этого разделим стороны треугольника напряжений АОБ на число I выражающее силу тока в цепи, и получим подобный треугольник сопротивлений А»О»Б» (рис. 57, в). Его сторонами являются сопро­тивления r, (Х L — Хс) и полное сопротивление цепи Z.

10) Цепь переменного тока с активным, индуктивным и ёмкостным сопротивлением.

Определим полное сопротивление цепи переменного тока, со­держащей активное, индуктивное и емкостное сопротивления. Для этого разделим стороны треугольника напряжений АОБ на число I выражающее силу тока в цепи, и получим подобный треугольник сопротивлений А»О»Б» (рис. 57, в). Его сторонами являются сопро­тивления r, (Х L — Хс) и полное сопротивление цепиZ.

Пользуясь теоремой Пифагора, можно написать, что

Отсюда полное сопротивление цепи

Силу тока в цепи с активным, индуктивным и емкостным сопро­тивлениями определяют по закону Ома:

На векторной диаграмме (рис. 57, б) видно, что в рассматри­ваемой цепи ток и напряжение генератора не совпадают по фазе. Из треугольника напряжений следует, что

Из треугольника сопротивлений

Емкостное – ток опережает, напряжение отстает.

Индуктивное – ток отстает, напряжение опережает.

Опережает – против часовой.

Отстает – по часовой.

11)Цепь с параллельным соединением ветвей; преобразование схем замещения.

Соединение нескольких элементов называется параллельным, если их выводы объединены в два узла; на каждом элементе цепи имеет место одно и то же напряжение.

Узлом называют соединение трех и более элементов или ветвей. В узле ток разветвляется.

Рис. 1.3. Эквивалентное преобразование параллельного соединения элементов

На рис. 1.3,a показано параллельное соединение резистивных элементов. Его можно заменить эквивалентным, используя одну из формул:

где g k = 1/r k ; g э = 1/r э – проводимости элементов.

Для параллельного соединения элементов r 1 и r 2 имеем

Для параллельного соединения индуктивных элементов, емкостных элементов и источников тока на рис. 1.3,б,в,г формулы имеют вид

Электрические лампы накаливания, печи сопротивления, бытовые нагревательные приборы, реостаты и другие приемники, где электрическая энергия преобразуется в тепловую, на схемах замещения обычно представлены только сопротивлением R.
Для схемы, изображенной на рис. 13.1, а, заданы сопротивление R и напряжение, изменяющееся по закону

u = U m sinωt

Найдём ток и мощность в цепи.

Ток в цепи переменного тока с активным сопротивлением.

По закону Ома найдем выражение для мгновенного тока:

где I m = U m /R — амплитуда тока

Из уравнений напряжения и тока видно, что начальные фазы обеих кривых одинаковы, т. е. напряжение и ток в цепи с сопротивлением R совпадают по фазе. Это показано на графиках и векторной диаграмме (рис. 13.1, б, б).

Действующий ток найдем, разделив амплитуду на √ 2:

Формулы (13.1) выражают закон Ома для цепи переменного тока с сопротивлением R. Внешне они ничем не отличаются от формулы для цепи постоянного тока, если переменные напряжение и ток выражены действующими величинами.

Мгновенная мощность в цепи переменного тока с активным сопротивлением.

При переменных величинах напряжения и тока скорость преобразования электрической энергии в приемнике, т. е. его мощность, тоже изменяется. Мгновенная мощность равна произведению мгновенных величин напряжения и тока: p = U m sinωt * I m sinωt = U m I m sin 2 ωt

Из тригонометрии найдём

Более наглядное представление о характере изменения мощности в цепи дает график в прямоугольной системе координат, который строится после умножения ординат кривых напряжения и тока, соответствующих ряду значений их общего аргумента — времени t . Зависимость мощности от времени — периодическая кривая (рис. 13.2). Если ось времени t поднять по чертежу на величину р = P m √2 = U m I m √2, то относительно новой оси t’ график мощности является синусоидой с двойной частотой и начальной фазой 90°:

Таким образом, в первоначальной системе координат мгновенная, мощность равна сумме постоянной величины Р = UmIm√2 и перемен- ной р’:

р = Р + р’

Анализируя график мгновенной мощности, нетрудно заметить, что мощность в течение периода остается положительной, хотя ток и напряжение меняют свой знак. Это получается благодаря совпад