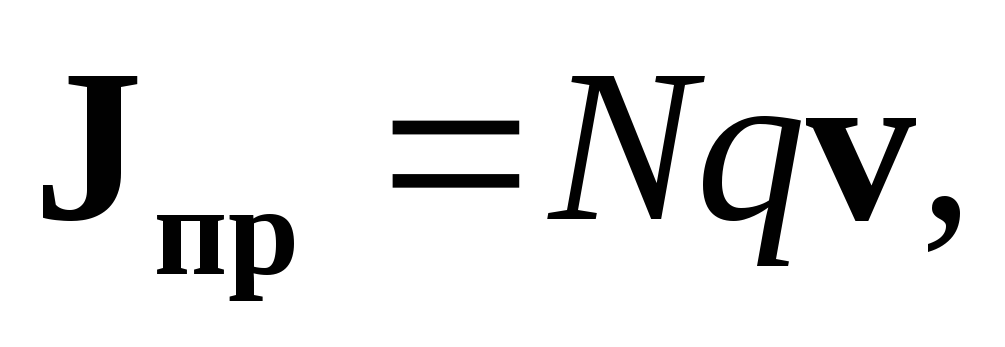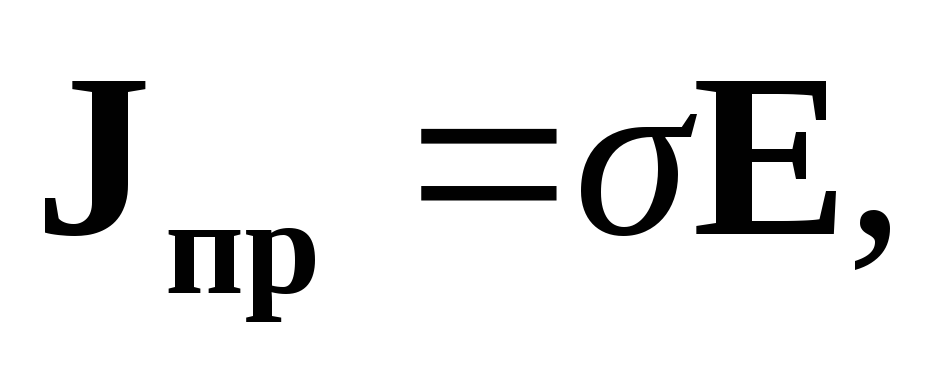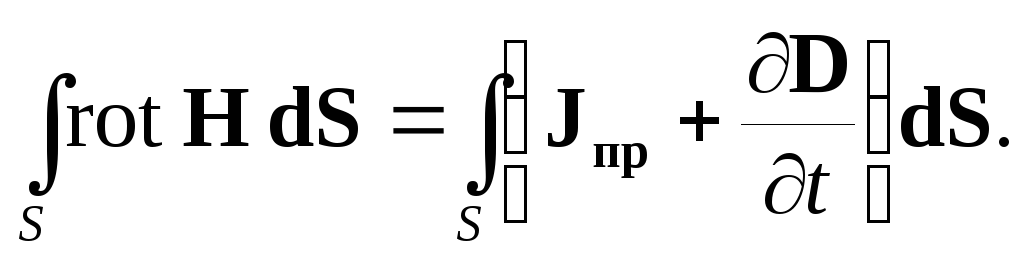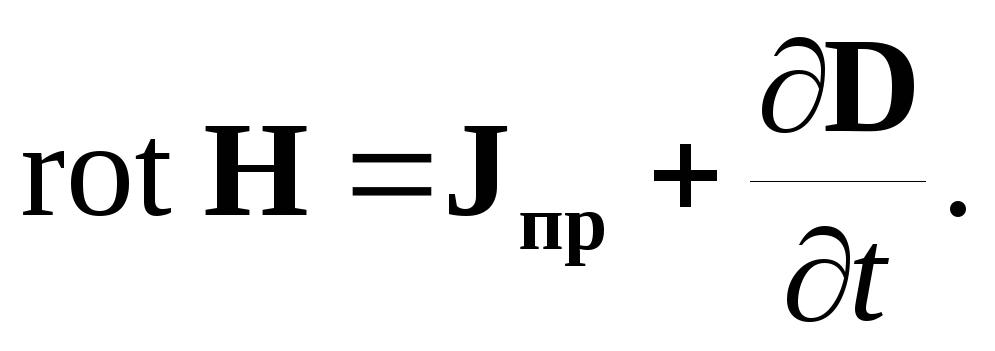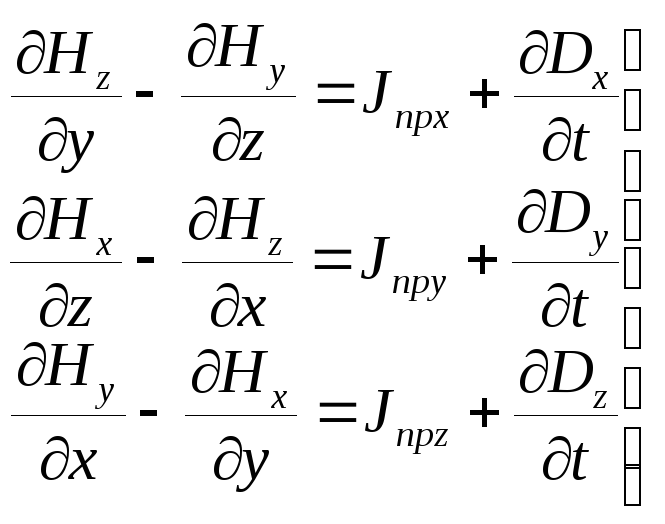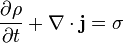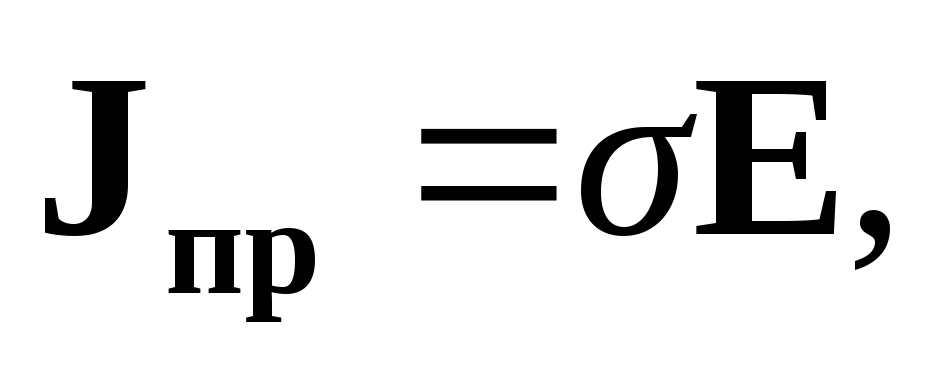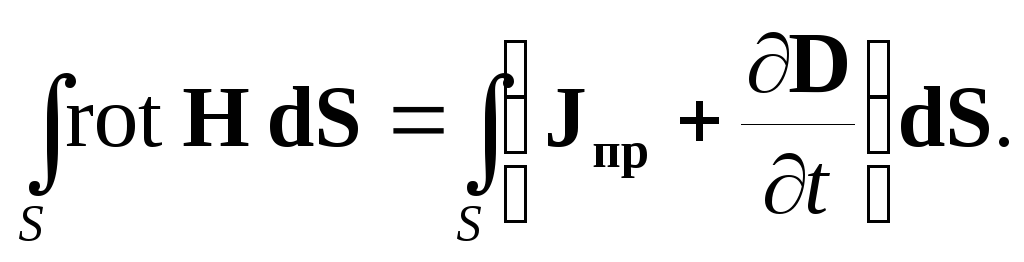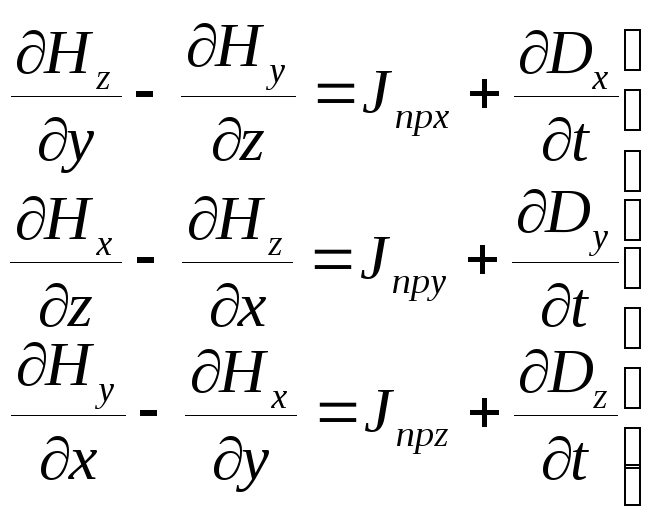Ток смещения (электродинамика) — Википедия
Ток смещения, или абсорбционный ток, — величина, прямо пропорциональная скорости изменения электрической индукции. Это понятие используется в классической электродинамике. Введено Дж. К. Максвеллом при построении теории электромагнитного поля.
Введение тока смещения позволило устранить противоречие[1] в формуле Ампера для циркуляции магнитного поля, которая после добавления туда тока смещения стала непротиворечивой и составила последнее уравнение, позволившее корректно замкнуть систему уравнений (классической) электродинамики.
Существование тока смещения также следует из закона сохранения электрического заряда[2].
Строго говоря, ток смещения не является[3]электрическим током, но измеряется в тех же единицах, что и электрический ток.
В вакууме, а также в любом веществе, в котором можно пренебречь поляризацией либо скоростью её изменения, током смещения JD{\displaystyle J_{D}} (с точностью до универсального постоянного коэффициента) называется
- JD=ε0∫s∂E∂t⋅ds{\displaystyle J_{D}=\varepsilon _{0}\int _{s}{\frac {\partial \mathbf {E} }{\partial t}}\cdot \mathbf {ds} } (СИ)
- JD=14π∫s∂E∂t⋅ds{\displaystyle J_{D}={\frac {1}{4\pi }}\int _{s}{\frac {\partial \mathbf {E} }{\partial t}}\cdot \mathbf {ds} } (СГС)
В диэлектриках (и во всех веществах, где нельзя пренебречь изменением поляризации) используется следующее определение:
- JD=∫s∂D∂t⋅ds{\displaystyle J_{D}=\int _{s}{\frac {\partial \mathbf {D} }{\partial t}}\cdot \mathbf {ds} } (СИ)
- JD=14π∫s∂D∂t⋅ds{\displaystyle J_{D}={\frac {1}{4\pi }}\int _{s}{\frac {\partial \mathbf {D} }{\partial t}}\cdot \mathbf {ds} } (СГС),
где D — вектор электрической индукции (исторически вектор D назывался электрическим смещением, отсюда и название «ток смещения»)
Соответственно, плотностью тока смещения в вакууме называется величина
- jD=ε0∂E∂t{\displaystyle \mathbf {j_{D}} =\varepsilon _{0}{\frac {\partial \mathbf {E} }{\partial t}}} (СИ)
- jD=14π∂E∂t{\displaystyle \mathbf {j_{D}} ={\frac {1}{4\pi }}{\frac {\partial \mathbf {E} }{\partial t}}} (СГС)
а в диэлектриках — величина
- jD=∂D∂t{\displaystyle \mathbf {j_{D}} ={\frac {\partial \mathbf {D} }{\partial t}}} (СИ)
- jD=14π∂D∂t{\displaystyle \mathbf {j_{D}} ={\frac {1}{4\pi }}{\frac {\partial \mathbf {D} }{\partial t}}} (СГС)
В некоторых книгах плотность тока смещения называется просто «током смещения».
В природе можно выделить два вида токов: ток связанных зарядов и ток проводимости.
Ток связанных зарядов — это перемещение средних положений связанных электронов и ядер, составляющих молекулу, относительно центра молекулы.
Ток проводимости — это направленное движение на большие расстояния свободных зарядов (например, ионов или свободных электронов). В случае, если этот ток идёт не в веществе, а в свободном пространстве, нередко вместо термина «ток проводимости» употребляют термин «ток переноса». Иначе говоря, ток переноса или ток конвекции обусловлен переносом электрических зарядов в свободном пространстве заряженными частицами или телами под действием электрического поля.
Во времена Максвелла ток проводимости мог быть экспериментально зарегистрирован и измерен (например, амперметром, индикаторной лампой), тогда как движение связанных зарядов внутри диэлектриков могло быть лишь косвенно оценено.
Сумма тока связанных зарядов и быстроты изменения потока электрического поля была названа током смещения в диэлектриках.
При разрыве цепи постоянного тока и включении в неё конденсатора ток в разомкнутом контуре отсутствует. При питании такого разомкнутого контура от источника переменного напряжения в нём регистрируется переменный ток (при достаточно высокой частоте и ёмкости конденсатора загорается лампа, включённая последовательно с конденсатором). Для описания «прохождения» переменного тока через конденсатор (разрыв по постоянному току) Максвелл ввёл понятие тока смещения.
Ток смещения существует и в проводниках, по которым течёт переменный ток проводимости, однако в данном случае он пренебрежимо мал по сравнению с током проводимости. Наличие токов смещения подтверждено экспериментально советским физиком А. А. Эйхенвальдом, изучившим магнитное поле тока поляризации, который является частью тока смещения. В общем случае, токи проводимости и смещения в пространстве не разделены, они находятся в одном и том же объеме. Поэтому Максвелл ввёл понятие полного тока, равного сумме токов проводимости (а также конвекционных токов) и смещения. Плотность полного тока:
- jΣ=j+jD=j+∂D∂t,{\displaystyle \mathbf {j} _{\Sigma }=\mathbf {j} +\mathbf {j} _{D}=\mathbf {j} +{\frac {\partial \mathbf {D} }{\partial t}},}
где j — плотность тока проводимости, jD — плотность тока смещения[6].
В диэлектрике (например, в диэлектрике конденсатора) и в вакууме нет токов проводимости. Поэтому в этом частном случае приведенная выше формула Максвелла сводится к:
- ↑ В магнитостатике этого противоречия не было, так как в ней на все токи наложено (искусственно) условие постоянства и замкнутости токов (соленоидальности поля плотности тока). В общем же случае переменных токов, с которым столкнулся Максвелл, ток может быть «незамкнутым», то есть например он может (некоторое время) течь в проводе, не выходя за его концы, на которых будут просто накапливаться заряды. Тогда, выбрав в теореме Ампера две различные поверхности, натянутые на один и тот же контур, но одну из которых провод будет пересекать, а другую (которую мы изогнём так, чтобы она проходила уже за концом провода) — нет, мы получим два разных выражения для тока, которые должны быть равны одному и тому же значению циркуляции магнитного поля. То есть приходим к явному противоречию, которое показывает необходимость исправления формулы, способ которого и нашел Максвелл, заменив ток в тех областях пространства, где он не течёт, током смещения.
- ↑ Я.Б.Зельдович, М.Ю.Хлопов. Ток смещения и сохранение заряда (неопр.) (1988).
- ↑ для случая вакуума; для случая же диэлектрика точнее было бы сказать, что ток смещения является электрическим током не весь, а только та его часть, что связана с поляризацией диэлектрика — то есть перемещением реальных
- ↑ При условии фиксированности (неподвижности) поверхности интегрирования или хотя бы постоянстве её края (или отсутствии края, то есть и для всех замкнутых поверхностей, производную в формулах ниже можно очевидно вынести оператор производной за знак интеграла, например: ∫s∂∂tE⋅ds=∂∂t∫sE⋅ds{\displaystyle \int _{s}{\frac {\partial }{\partial t}}\mathbf {E} \cdot \mathbf {ds} ={\frac {\partial }{\partial t}}\int _{s}\mathbf {E} \cdot \mathbf {ds} }, получив тождественную (при таком условии) формулировку: ток смещения (с точностью до универсального постоянного коэффициента) есть быстрота изменения потока электрического поля через поверхность
- ↑ Аналогично тому, как обычным током J{\displaystyle J} называется поток плотности тока через некоторую поверхность (например, через сечение проводника): J=∫sj⋅ds{\displaystyle J=\int _{s}\mathbf {j} \cdot \mathbf {ds} }
- ↑ Иногда для обозначения тока проводимости и тока смещения используют не индекс, а разные буквы: i и j соответственно.
Электрический ток
Полным электрическим токомназывают явление направленного движения зарядов и явление изменения электрического поля во времени, сопровождаемые магнитным полем.
Различают три основных вида электрического тока: ток проводимости, ток переноса, ток смещения.
Ток проводимости
Ток
проводимости может возникать в среде,
обладающей электропроводностью и
обусловлен движением свободных заряженных
частиц в проводнике. Количественная
сторона этого явления характеризуется
силой тока i ( [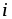 ] =
A).
Величина тока i определяется зарядом q, проходящим
через некоторую поверхность S в единицу времени
] =
A).
Величина тока i определяется зарядом q, проходящим
через некоторую поверхность S в единицу времени
Для
характеристики распределения в проводнике
заряженных частиц используется векторная
величина  ,
называемаяплотностью
тока. Направление
вектора
,
называемаяплотностью
тока. Направление
вектора  указывает направление движения
положительно заряженных частиц. Величина
указывает направление движения
положительно заряженных частиц. Величина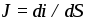 характеризует интенсивность их
прохождения через площадку
характеризует интенсивность их
прохождения через площадку ,
[
,
[
При
известной плотности тока 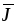 сила тока
сила тока ,
проходящего через некоторую поверхность
,
проходящего через некоторую поверхность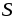 ,
может быть рассчитана по формуле
,
может быть рассчитана по формуле
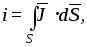
где
вектор 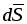 направлен по нормали к поверхности
направлен по нормали к поверхности .
.
Для
тока проводимости характерна зависимость 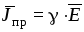 ,
где символом
,
где символом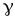 обозначена удельная электрическая
проводимость вещества проводника ([
обозначена удельная электрическая
проводимость вещества проводника ([ ]
= 1/Ом
]
= 1/Ом м).
м).
Типичным примером тока проводимости является электрический ток в металлах.
Ток переноса
Током
переноса называют явление перемещения
в свободном пространстве электрически
заряженных частиц. Принципиальное
отличие тока переноса от тока проводимости
заключается в том, что плотность тока
переноса 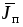 не пропорциональна напряженности
электрического поля, а определяется
объемной плотностью
не пропорциональна напряженности
электрического поля, а определяется
объемной плотностью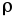 переносимого заряда и скоростью
переносимого заряда и скоростью движения частиц
движения частиц

Примером тока переноса может служить поток электронов в электронно-лучевой трубке.
Ток смещения
Ток смещения возникает в случае изменения электрического поля во времени, а под плотностью тока смещения понимают величину
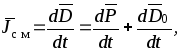
где 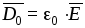 .
Первое слагаемое характеризует
перемещение связанных зарядов в процессе
поляризации диэлектрика. Второе
слагаемое, называемое током смещения
в пустоте, не имеет столь же наглядной
интерпретации и связано с появлением
магнитного поля, возникающего при
изменении напряженности электрического
поля в пустоте. Характерным примером
тока смещения является ток в конденсаторе.
.
Первое слагаемое характеризует
перемещение связанных зарядов в процессе
поляризации диэлектрика. Второе
слагаемое, называемое током смещения
в пустоте, не имеет столь же наглядной
интерпретации и связано с появлением
магнитного поля, возникающего при
изменении напряженности электрического
поля в пустоте. Характерным примером
тока смещения является ток в конденсаторе.
Таким образом, в зависимости от характера электрического тока его плотность может быть рассчитана по одному из следующих соотношений:

Принцип непрерывности электрического тока
Одним из основных принципов теории электромагнитного поля является принцип непрерывности электрического тока

В
этом соотношении символ 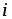 означает полный ток сквозь взятую в
любой среде замкнутую поверхность
означает полный ток сквозь взятую в
любой среде замкнутую поверхность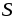 ,
то есть
,
то есть
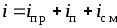 и
и 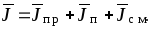 .
.
Из принципа непрерывности электрического тока следует, что линии тока не имеют ни начала, ни конца, то есть являются замкнутыми.
Электрическое напряжение. Разность электрических потенциалов
Электрическое
поле кроме векторов  и
и характеризуют скалярной величиной,
которая называется электрическим
напряжением
характеризуют скалярной величиной,
которая называется электрическим
напряжением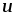 и измеряется в вольтах, [
и измеряется в вольтах, [ ]
= В .
]
= В .
Для
перемещения заряда 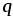 в электрическом поле из точки
в электрическом поле из точки в точку
в точку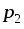 необходимо совершить работу
необходимо совершить работу
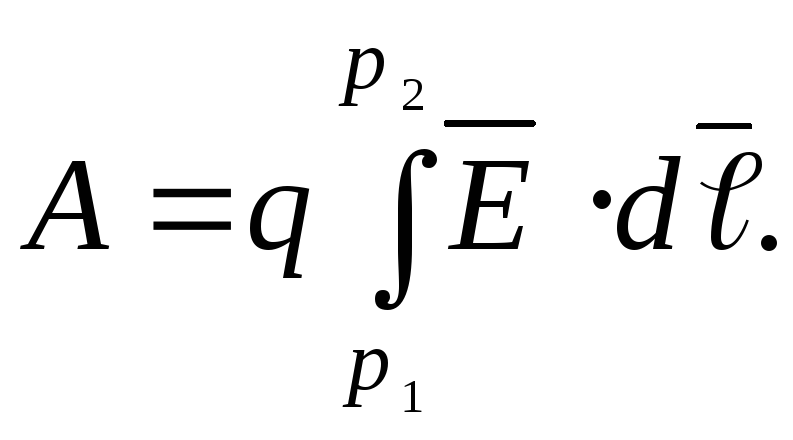
Электрическим
напряжением между точками 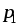 и
и называют величину, равную отношению
этой работы к перемещаемому заряду
называют величину, равную отношению
этой работы к перемещаемому заряду

где 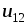 ‑ электрическое напряжение (или
падение напряжения) вдоль заданного
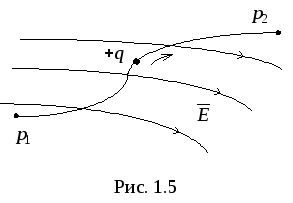
пути (рис.1.5).
‑ электрическое напряжение (или
падение напряжения) вдоль заданного
пути (рис.1.5).
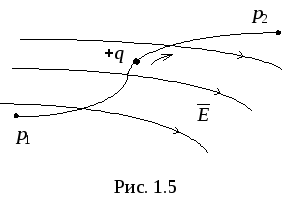
Для электрического поля неподвижных зарядов (электростатического поля) справедливо условие
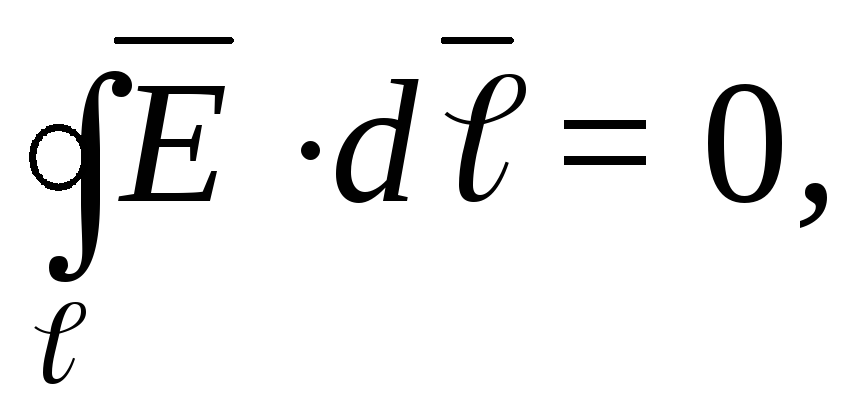
вытекающее из закона сохранения энергии в системе заряженных тел. Следовательно, (рис.1.6),

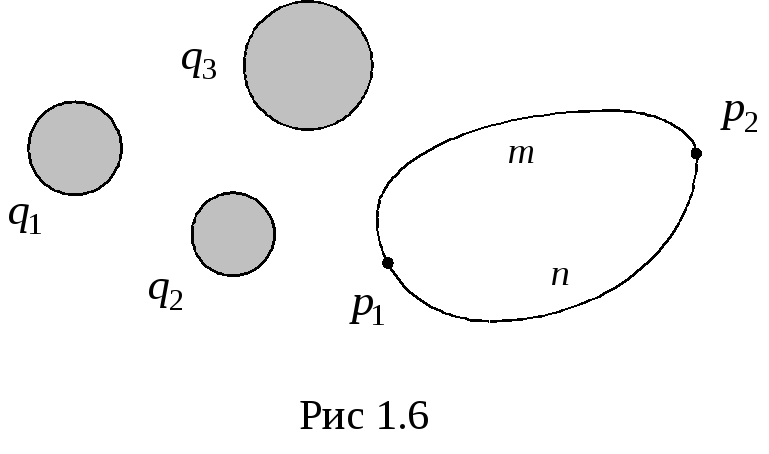
и
интеграл 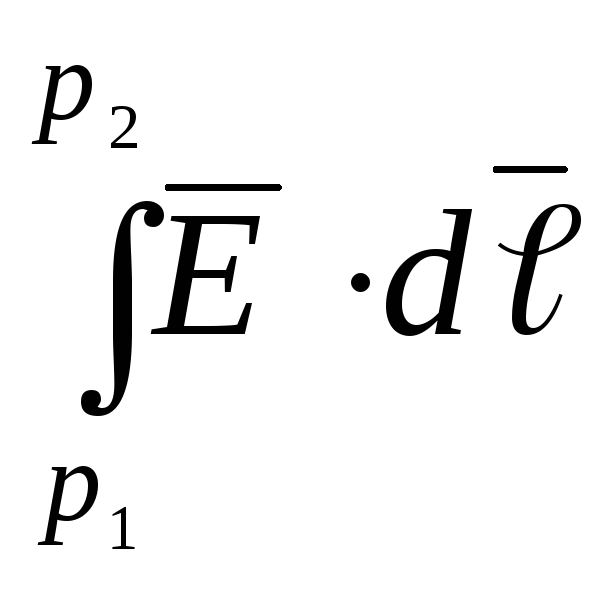 зависит
только от координат точек
зависит
только от координат точек  и
и  .
.
Это
обстоятельство позволяет ввести в
рассмотрение функцию  ,
зависящую от положения точки (
,
зависящую от положения точки ( )
в электростатическом поле:
)
в электростатическом поле:

где 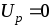 Потенциал точки определяется с точностью
до некоторой постоянной, зависящей от
того, где выбрана точка
Потенциал точки определяется с точностью
до некоторой постоянной, зависящей от
того, где выбрана точка нулевого потенциала.
нулевого потенциала.
В
электростатическом поле напряжение
между точками  и
и 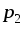 можетбыть вычислено как разность
потенциалов этих точек:
можетбыть вычислено как разность
потенциалов этих точек:

 Электрическое
поле, для которого справедливо условие
Электрическое
поле, для которого справедливо условие = 0, называется потенциальным электрическим
полем. При теоретическом исследовании
систем, в которых заряженные тела имеют
конечные размеры, точкаp,
выбирается, как правило, на бесконечности.
На практике часто U = 0 принимают на поверхности одного из
объектов рассматриваемой системы.
= 0, называется потенциальным электрическим
полем. При теоретическом исследовании
систем, в которых заряженные тела имеют
конечные размеры, точкаp,
выбирается, как правило, на бесконечности.
На практике часто U = 0 принимают на поверхности одного из
объектов рассматриваемой системы.
Введем понятие поверхности равного потенциала, как поверхности, во всех точках которой потенциал имеет одно и тоже значение. Силовые линии электрического поля перпендикулярны поверхностям равного потенциала. Действительно:
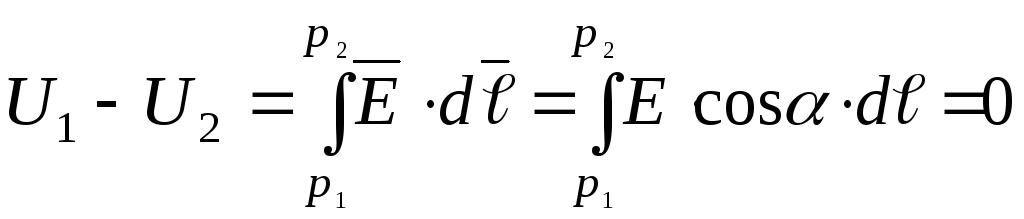
при 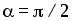 и, следовательно,
и, следовательно, (рис.1.7).
(рис.1.7).
Электрический ток
Полным электрическим токомназывают явление направленного движения зарядов и явление изменения электрического поля во времени, сопровождаемые магнитным полем.
Различают три основных вида электрического тока: ток проводимости, ток переноса, ток смещения.
Ток проводимости
Ток
проводимости может возникать в среде,
обладающей электропроводностью и
обусловлен движением свободных заряженных
частиц в проводнике. Количественная
сторона этого явления характеризуется
силой тока i ( [ ] =
A).
Величина тока i определяется зарядом q, проходящим
через некоторую поверхность S в единицу времени
] =
A).
Величина тока i определяется зарядом q, проходящим
через некоторую поверхность S в единицу времени
 .
.
Для
характеристики распределения в проводнике
заряженных частиц используется векторная
величина 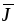 ,
называемаяплотностью
тока. Направление
вектора
,
называемаяплотностью
тока. Направление
вектора 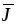 указывает направление движения
положительно заряженных частиц. Величина
указывает направление движения
положительно заряженных частиц. Величина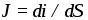 характеризует интенсивность их
прохождения через площадку
характеризует интенсивность их
прохождения через площадку ,
[
,
[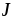 ]
= A/м2.
]
= A/м2.
При
известной плотности тока  сила тока
сила тока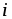 ,
проходящего через некоторую поверхность
,
проходящего через некоторую поверхность ,
может быть рассчитана по формуле
,
может быть рассчитана по формуле

где
вектор 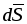 направлен по нормали к поверхности
направлен по нормали к поверхности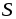 .
.
Для
тока проводимости характерна зависимость 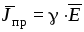 ,
где символом
,
где символом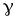 обозначена удельная электрическая
проводимость вещества проводника ([
обозначена удельная электрическая
проводимость вещества проводника ([ ]
= 1/Ом
]
= 1/Ом м).
м).
Типичным примером тока проводимости является электрический ток в металлах.
Ток переноса
Током
переноса называют явление перемещения
в свободном пространстве электрически
заряженных частиц. Принципиальное
отличие тока переноса от тока проводимости
заключается в том, что плотность тока
переноса  не пропорциональна напряженности
электрического поля, а определяется
объемной плотностью
не пропорциональна напряженности
электрического поля, а определяется
объемной плотностью переносимого заряда и скоростью
переносимого заряда и скоростью движения частиц
движения частиц

Примером тока переноса может служить поток электронов в электронно-лучевой трубке.
Ток смещения
Ток смещения возникает в случае изменения электрического поля во времени, а под плотностью тока смещения понимают величину

где  .
Первое слагаемое характеризует
перемещение связанных зарядов в процессе
поляризации диэлектрика. Второе
слагаемое, называемое током смещения
в пустоте, не имеет столь же наглядной
интерпретации и связано с появлением
магнитного поля, возникающего при
изменении напряженности электрического
поля в пустоте. Характерным примером
тока смещения является ток в конденсаторе.
.
Первое слагаемое характеризует
перемещение связанных зарядов в процессе
поляризации диэлектрика. Второе
слагаемое, называемое током смещения
в пустоте, не имеет столь же наглядной
интерпретации и связано с появлением
магнитного поля, возникающего при
изменении напряженности электрического
поля в пустоте. Характерным примером
тока смещения является ток в конденсаторе.
Таким образом, в зависимости от характера электрического тока его плотность может быть рассчитана по одному из следующих соотношений:
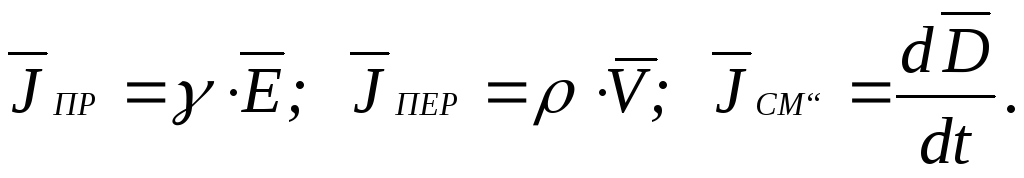
Принцип непрерывности электрического тока
Одним из основных принципов теории электромагнитного поля является принцип непрерывности электрического тока
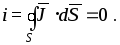
В
этом соотношении символ 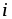 означает полный ток сквозь взятую в
любой среде замкнутую поверхность
означает полный ток сквозь взятую в
любой среде замкнутую поверхность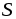 ,
то есть
,
то есть
 и
.
и
.
Из принципа непрерывности электрического тока следует, что линии тока не имеют ни начала, ни конца, то есть являются замкнутыми.
Электрическое напряжение. Разность электрических потенциалов
Электрическое
поле кроме векторов  и
и характеризуют скалярной величиной,
которая называется электрическим
напряжением
характеризуют скалярной величиной,
которая называется электрическим
напряжением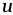 и измеряется в вольтах, [
и измеряется в вольтах, [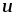 ]
= В .
]
= В .
Для
перемещения заряда 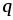 в электрическом поле из точки
в электрическом поле из точки в точку
в точку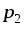 необходимо совершить работу
необходимо совершить работу

Электрическим
напряжением между точками  и
и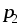 называют величину, равную отношению
этой работы к перемещаемому заряду
называют величину, равную отношению
этой работы к перемещаемому заряду
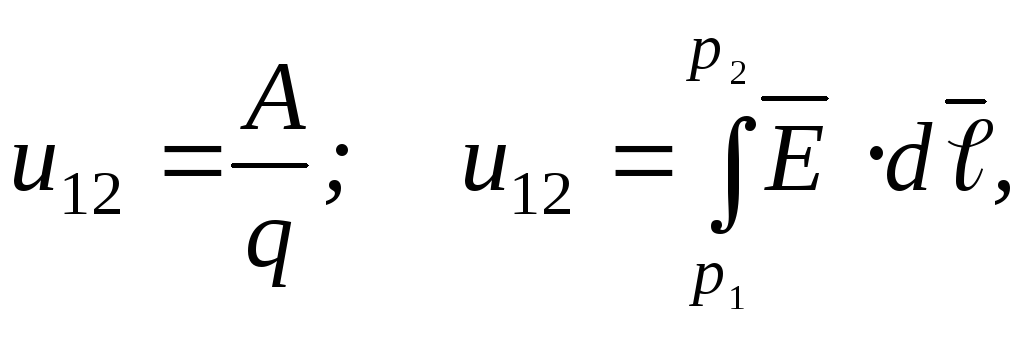
где 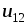 ‑ электрическое напряжение (или
падение напряжения) вдоль заданного
пути (рис.1.5).
‑ электрическое напряжение (или
падение напряжения) вдоль заданного
пути (рис.1.5).
Для электрического поля неподвижных зарядов (электростатического поля) справедливо условие

вытекающее из закона сохранения энергии в системе заряженных тел. Следовательно, (рис.1.6),
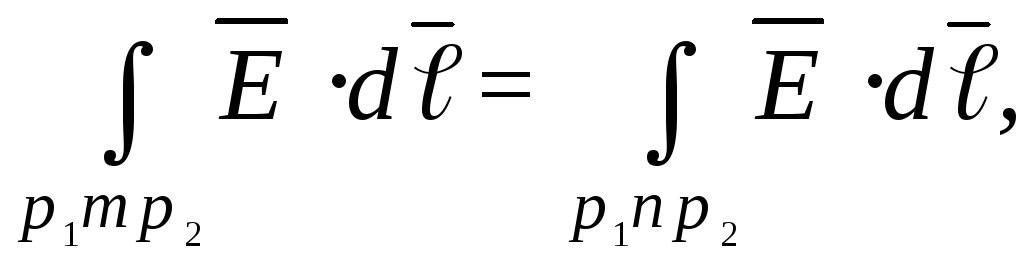

и
интеграл 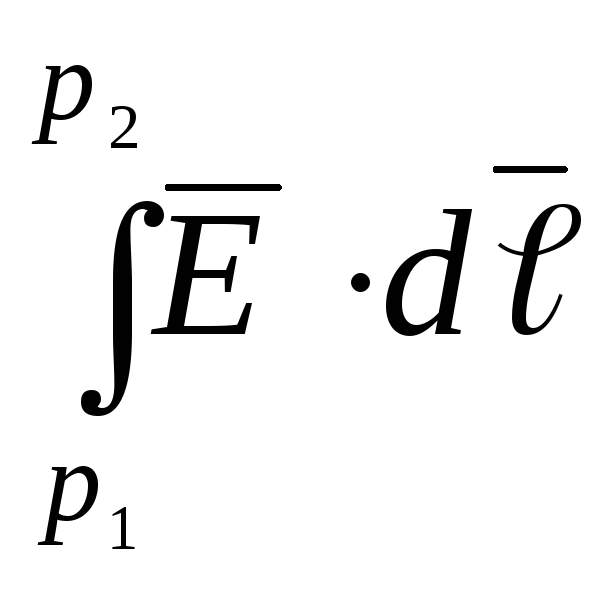 зависит
только от координат точек
зависит
только от координат точек  и
и 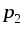 .
.
Это
обстоятельство позволяет ввести в
рассмотрение функцию  ,
зависящую от положения точки (
,
зависящую от положения точки (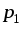 )
в электростатическом поле:
)
в электростатическом поле:
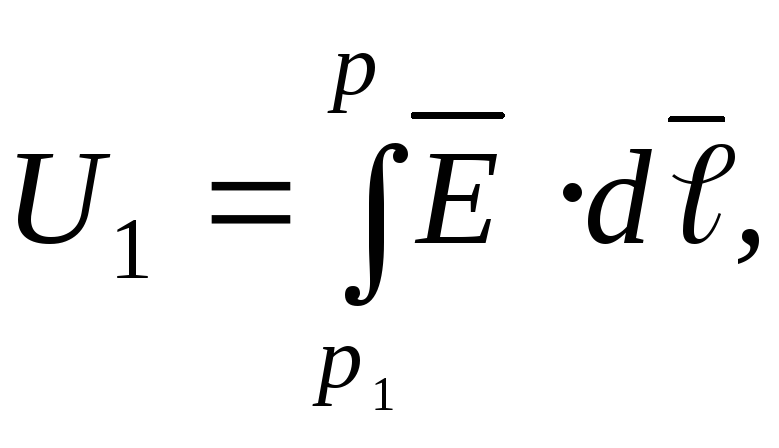
где 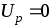 Потенциал точки определяется с точностью
до некоторой постоянной, зависящей от
того, где выбрана точка
Потенциал точки определяется с точностью
до некоторой постоянной, зависящей от
того, где выбрана точка нулевого потенциала.
нулевого потенциала.
В
электростатическом поле напряжение
между точками  и
и 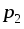 можетбыть вычислено как разность
потенциалов этих точек:
можетбыть вычислено как разность
потенциалов этих точек:

 Электрическое
поле, для которого справедливо условие
Электрическое
поле, для которого справедливо условие = 0, называется потенциальным электрическим
полем. При теоретическом исследовании
систем, в которых заряженные тела имеют
конечные размеры, точкаp,
выбирается, как правило, на бесконечности.
На практике часто U = 0 принимают на поверхности одного из
объектов рассматриваемой системы.
= 0, называется потенциальным электрическим
полем. При теоретическом исследовании
систем, в которых заряженные тела имеют
конечные размеры, точкаp,
выбирается, как правило, на бесконечности.
На практике часто U = 0 принимают на поверхности одного из
объектов рассматриваемой системы.
Введем понятие поверхности равного потенциала, как поверхности, во всех точках которой потенциал имеет одно и тоже значение. Силовые линии электрического поля перпендикулярны поверхностям равного потенциала. Действительно:

при 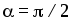 и, следовательно,
и, следовательно,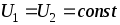 (рис.1.7).
(рис.1.7).
1.3. Ток проводимости и ток смещения
Током проводимости называется движение носителей электрических зарядов под действием электрического поля.
Для выяснения особенностей протекания тока проводимости в объемных телах рассмотрим проводящее тело в виде бесконечного слоя (рис. 1.5). К этому телу подведены два точечных электрода, соединенные с источником. Ток внутри вещества сконцентрируется вблизи кратчайшего расстояния между электродами, однако меньшая его часть ответвится в глубь тела.
Для описания состояния такой системы необходимо знать скорость и направление движения носителей заряда в каждой точке области протекания тока внутри тела. Для этого вводится понятие плотности тока проводимости. Вектор плотности тока проводимости описывается следующим образом:
| (1.18) |
где | | — количество носителей заряда в единице объема вещества; |
q | — заряд носителя, Кл; | |
v | — вектор скорости движения носителей заряда, м/с. |
Плотность тока проводимости является мерой тока, протекающего через единичную площадку, перпендикулярную вектору скорости движения носителей. Скорость носителей и плотность тока проводимости пропорциональны напряженности электрического поля:
| (1.19) |
где | σ | — электропроводность среды, См/м. |
Электропроводность является коэффициентом пропорциональности между векторами плотности тока проводимости и напряженности электрического поля.
Формула (1.19) также относится к материальным уравнениями называется закономОма в дифференциальной форме.
Лучшими проводниками являются металлы. Максимальную электропроводность имеет серебро — 6.1*107См/м. У меди она равна 5.7*107См/м, а у алюминия — 3.2*107См/м.
Если мы имеем дело с электрическим полем, постоянным во времени, тока проводимости достаточно. Однако в переменном поле только он не позволяет описать всю совокупность наблюдаемых явлений.
Рассмотрим цепь переменного тока с конденсатором. Переменный ток протекает между обкладками конденсатора и в том случае, когда между ними вакуум, то есть образование тока проводимости невозможно. Соединительный провод, по которому течет ток проводимости, окружен кольцевыми линиями магнитного поля, которые как бы образуют «оболочку» вокруг него. Максвелл предположил, что эта «оболочка» не обрывается у пластин конденсатора. Значит, переменное электрическое поле, так же как и ток проводимости, сопровождается появлением магнитного поля. Это дало Максвеллу основание для введения понятия тока смещения. Плотность тока смещения описывается формулой:
| (1.20) |
Природу тока смещения можно определить следующим образом. Всякое изменение электрического поля приводит к возникновению тока смещения.
Величина тока смещения прямо пропорциональна скорости изменения электрического поля.
2. Основные уравнения электродинамики
2.1. Первое уравнение Максвелла
Первое уравнение Максвелла является обобщением открытого Ампером закона полного тока. Ампер сформулировал этот закон следующим образом: циркуляция вектора напряженности магнитного поля по замкнутому контуру равна току, пронизывающему контур:
| (2.1) |
где | L – замкнутый контур, |
dl – векторный дифференциал длины контура: dl = l0dl, | |
l0 – орт дифференциала длины контура, | |
J – вектор плотности тока, пронизывающего контур, | |
S — произвольная поверхность, опирающаяся на контур L, | |
dS — векторный дифференциал поверхности: dS = n0dS, | |
n0 — орт нормали к поверхности S, образующий с направлением обхода контура правовинтовую систему. |
Форма замкнутого контура L может быть произвольной.
Под током, пронизывающим контур, Ампер понимал только ток проводимости, что справедливо для постоянного во времени поля. В переменном поле необходимо учесть введенный Максвеллом ток смещения. При этом формула (2.1) примет вид:
| (2.2) |
Уравнение (2.2) записано для контура конечных размеров и называется первым уравнением Максвелла в интегральной форме.
К дифференциальной форме первого уравнения перейдем с помощью теоремы Стокса (формула (1.34), [6]). Она позволяет заменить циркуляцию вектора Н по контуру L интегралом от rot Н по поверхности S, опирающейся на этот контур:
| (2.3) |
Так как поверхность S выбрана произвольно, то равенство (2.3) может быть удовлетворено только в случае равенства подынтегральных выражений:
| (2.4) |
Равенство (2.4) называется первым уравнением Максвелла в дифференциальной форме. Это векторное уравнение эквивалентно трем скалярным уравнениям. В декартовой системе координат х, у, z они примут следующий вид:
| (2.5) |
Аналогичные уравнения в других системах координат могут быть получены с помощью формул перехода (2.5) – (2.7) или (2.11) – (2.13) [6].
Ток проводимости. Условия возникновения тока проводимости. Сила и плотность тока.
Ток проводимости — это направленное движение на большие расстояния свободных зарядов (например, ионов или свободных электронов). В случае, если этот ток идёт не в веществе, а в свободном простанстве, нередко вместо термина «ток проводимости» употребляют термин «ток переноса». Иначе говоря, ток переноса или ток конвекции обусловлен переносом электрических зарядов в свободном пространстве заряженными частицами или телами под действием электрического поля.
ТОК
ПРОВОДИМОСТИ — физическая величина, характеризующая
движение свободных электр. зарядов и
зарядов, связанных с макромолекулами,
под действием электр. поля. Плотность
Т. п. 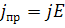 где
где  —
удельная электр. проводимость;
—
удельная электр. проводимость;  — напряженность электр. поля. В
соответствии с физической природой
носителей зарядов различают электронную,
ионную, молионную и полионную проводимости.
— напряженность электр. поля. В
соответствии с физической природой
носителей зарядов различают электронную,
ионную, молионную и полионную проводимости.
Т. п. связан с объемной и поверхностной электр. проводимостью полимеров, удельные значения которых для некоторых полимеров приведены в таблице.
Плотность тока— векторная физическая величина, имеющая смысл силы тока, протекающего через единицу площади. Например, при равномерном распределении плотности тока и всюду ортогональности ее плоскости сечения, через которое вычисляется или измеряется ток, величина вектора плотности тока:
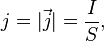
В общем случае:
 ,
,
Силой
тока называется физическая
величина 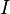 ,
равная отношению количества
заряда
,
равная отношению количества
заряда 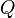 ,
прошедшего за некоторое время
,
прошедшего за некоторое время  через поперечное сечение проводника,
к величине этого промежутка времени[1]:
через поперечное сечение проводника,
к величине этого промежутка времени[1]:
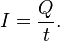
По
закону
Ома сила тока 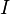 для участка цепи прямо пропорциональна
приложенному напряжению
для участка цепи прямо пропорциональна
приложенному напряжению  к участку цепи и обратно пропорциональна
сопротивлению
к участку цепи и обратно пропорциональна
сопротивлению 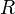 проводника
этого участка цепи :
проводника
этого участка цепи :
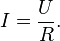
Уравнение непрерывности.
Уравнения непрерывности — (сильная) локальная форма законов сохранения. Дифференциальная форма общего уравнения непрерывности такова:
|
где
∇• — дивергенция,
t — время,
j — плотность потока (см. ниже),
σ — добавление q на единицу объёма в единицу времени. Члены, которые добавляют (σ > 0) или удаляют (σ < 0) q, называются «источниками» и «стоками» соответственно.
В электродинамике уравнение непрерывности выводится из уравнений Максвелла. Оно утверждает, что дивергенция плотности тока равна изменению плотности заряда со знаком минус,
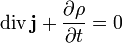 (
(  )
)
Сторонние силы. Электродвижущая сила. Электрическая цепь. Законы Ома и Джоуля – Ленца. Однородный и неоднородный участок цепи. Разность потенциалов и падение напряжения.
Сторонние силы, т. е. силы неэлектростатического происхождения. Они действуют лишь внутри источника тока. Разделяя заряды, эти силы создают разность потенциалов между концами остальной части цепи. В этой части движение зарядов обусловлено электрическим полем, возникающим в проводнике вследствие разности потенциалов между его концами.
Любые силы, действующие на заряд, за исключением потенциальных сил электростатического происхождения (т. е. кулоновских) называют сторонними силами. (Сторонние силы объясняются электромагнитным взаимодействием между электронами и ядрами).
Электродвижущая сила (ЭДС) — скалярная физическая величина, характеризующая работу сторонних (непотенциальных) сил в источниках постоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль контура.
ЭДС
можно выразить через напряжённость
электрического поля сторонних сил
( ).
В замкнутом контуре (
).
В замкнутом контуре ( )
тогда ЭДС будет равна:
)
тогда ЭДС будет равна:
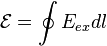 ,
где
,
где 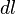 —
элемент длины контура.
—
элемент длины контура.
Причиной электродвижущей силы может стать изменение магнитного поля в окружающем пространстве. Это явление называется электромагнитной индукцией. Величина ЭДС индукции в контуре определяется выражением

где  —
поток
магнитного поля через замкнутую
поверхность
—
поток
магнитного поля через замкнутую
поверхность 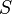 ,
ограниченную контуром. Знак «−» перед
выражением показывает, что индукционный
ток, созданный ЭДС индукции, препятствует
изменению магнитного потока в контуре.
,
ограниченную контуром. Знак «−» перед
выражением показывает, что индукционный
ток, созданный ЭДС индукции, препятствует
изменению магнитного потока в контуре.
Электрическая цепь — совокупность устройств, элементов, предназначенных для протекания электрического тока, электромагнитных процессов, в которых могут быть описаны с помощью понятий сила тока и напряжение.
Изображение электрической цепи с помощью условных знаков называют электрической схемой
Простейшая электрическая установка состоит из источника (гальванического элемента, аккумулятора, генератора и т. п.), потребителей или приемников электрической энергии (ламп накаливания, электронагревательных приборов, электродвигателей и т. п.) и соединительных проводов, соединяющих зажимы источника напряжения с зажимами потребителя. Т.е. электрическая цепь — совокупность соединенных между собой источников электрической энергии, приемников и соединяющих их проводов (линия передачи).
Закон Ома— физический закон, определяющий связь электродвижущей силы источника или электрического напряжения с силой тока и сопротивлением проводника. Экспериментально установлен в 1826 году, и назван в честь его первооткрывателя Георга Ома:
Закон Ома для полной цепи:
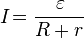 ,
(2)
,
(2)
где:
 —
ЭДС
источника
напряжения(В),
—
ЭДС
источника
напряжения(В),
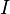 —
сила
тока в цепи (А),
—
сила
тока в цепи (А),
 —
сопротивление
всех внешних элементов цепи (Ом),
—
сопротивление
всех внешних элементов цепи (Ом),
 —
внутреннее
сопротивление источника
напряжения (Ом).
—
внутреннее
сопротивление источника
напряжения (Ом).
Из закона Ома для полной цепи вытекают следствия:
При r<<R сила тока в цепи обратно пропорциональна её сопротивлению. А сам источник в ряде случаев может быть назван источником напряжения
При r>>R сила тока от свойств внешней цепи (от величины нагрузки) не зависит. И источник может быть назван источником тока.
Часто[2] выражение:
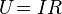 (3)
(3)
(где 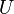 есть напряжение
или падение
напряжения, или, что то же, разность
потенциалов между началом и концом
участка проводника) тоже называют
«Законом Ома».
есть напряжение
или падение
напряжения, или, что то же, разность
потенциалов между началом и концом
участка проводника) тоже называют
«Законом Ома».
Таким образом, электродвижущая сила в замкнутой цепи, по которой течёт ток в соответствии с (2) и (3) равняется:
 (4)
(4)
То есть сумма падений напряжения на внутреннем сопротивлении источника тока и на внешней цепи равна ЭДС источника. Последний член в этом равенстве специалисты называют «напряжением на зажимах», поскольку именно его показывает вольтметр, измеряющий напряжение источника между началом и концом присоединённой к нему замкнутой цепи. В таком случае оно всегда меньше ЭДС.
К другой записи формулы (3), а именно:
 (5)
(5)
Закон Джоуля-Ленца— физический закон, дающий количественную оценку теплового действия электрического тока. Установлен в 1841 году Джеймсом Джоулем и независимо от него в 1842 году Эмилием Ленцем[1].
В словесной формулировке звучит следующим образом[2]
Мощность тепла, выделяемого в единице объёма среды при протекании электрического тока, пропорциональна произведению плотности электрического тока на величину напряженности электрического поля
Математически может быть выражен в следующей форме:
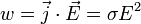
где 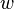 —
мощность выделения тепла в единице
объёма,
—
мощность выделения тепла в единице
объёма,  —
плотность электрического тока,
—
плотность электрического тока, 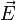 —
напряжённость
электрического поля, σ —
проводимость
среды.
—
напряжённость
электрического поля, σ —
проводимость
среды.
Закон также может быть сформулирован в интегральной форме для случая протекания токов в тонких проводах[3]:
Количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, пропорционально произведению квадрата силы тока на этом участке и сопротивления участка
В математической форме этот закон имеет вид


где dQ — количество теплоты, выделяемое за промежуток времени dt, I — сила тока, R — сопротивление, Q — полное количество теплоты, выделенное за промежуток времени от t1 до t2. В случае постоянных силы тока и сопротивления:

Участок
цепи, на котором не действуют сторонние
силы, приводящие к возникновению ЭДС
(рис. 1), называется однородным.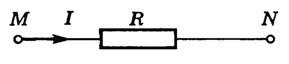
Закон
Ома для однородного участка цепи был
установлен экспериментально в 1826 г. Г.
Омом.
Согласно этому закону, сила тока I в однородном металлическом проводнике прямо пропорциональна напряжению U на концах этого проводника и обратно пропорциональна сопротивлению R этого проводника:
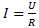
На некоторых участках этой цепи, кроме сил стационарного электрического поля, действуют и сторонние силы. Участок цепи, на котором действуют сторонние силы, называют неоднородным участком цепи.
Закон Ома для неоднородного участка цепи имеет вид:
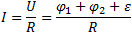
Электрический потенциал – это работа, которую необходимо совершить, чтобы увести заряд 1 Кл из данной точки в точку с нулевым потенциалом, то есть в точку, которая считается началом отсчёта. В электростатике за точку отсчёта обычно принимают бесконечно удалённую точку, в электронике – минусовой вывод источника питания, хотя в принципе точку отсчёта можно выбрать любую, исходя из соображений удобства.
Разность потенциалов – это разность между величинами электрических потенциалов в двух точках независимо от природы того явления, которое создаёт эту разность. Она равна работе по перемещению заряда 1 Кл из одной точки в другую.
Падение напряжения – это разность потенциалов, которая возникает на выводах сопротивления, когда через него течёт электрический ток.
Падение напряжения — постепенное уменьшение напряжения вдоль проводника, по которому течёт электрический ток, обусловленное тем, что проводник обладает активным сопротивлением. Под падением напряжения также понимают величину на которую меняется потенциал при переходе из одной точки цепи в другую.
По
закону
Ома на участке проводника, обладающем
активным сопротивлением 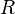 ,
ток
,
ток  создаёт падение напряжения
создаёт падение напряжения 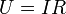 .
.
1.3. Ток проводимости и ток смещения
Током проводимости называется движение носителей электрических зарядов под действием электрического поля.
Для выяснения особенностей протекания тока проводимости в объемных телах рассмотрим проводящее тело в виде бесконечного слоя (рис. 1.5). К этому телу подведены два точечных электрода, соединенные с источником. Ток внутри вещества сконцентрируется вблизи кратчайшего расстояния между электродами, однако меньшая его часть ответвится в глубь тела.
Для описания состояния такой системы необходимо знать скорость и направление движения носителей заряда в каждой точке области протекания тока внутри тела. Для этого вводится понятие плотности тока проводимости. Вектор плотности тока проводимости описывается следующим образом:
| (1.18) |
где | | — количество носителей заряда в единице объема вещества; |
q | — заряд носителя, Кл; | |
v | — вектор скорости движения носителей заряда, м/с. |
Плотность тока проводимости является мерой тока, протекающего через единичную площадку, перпендикулярную вектору скорости движения носителей. Скорость носителей и плотность тока проводимости пропорциональны напряженности электрического поля:
| (1.19) |
где | σ | — электропроводность среды, См/м. |
Электропроводность является коэффициентом пропорциональности между векторами плотности тока проводимости и напряженности электрического поля.
Формула (1.19) также относится к материальным уравнениями называется закономОма в дифференциальной форме.
Лучшими проводниками являются металлы. Максимальную электропроводность имеет серебро — 6.1*107См/м. У меди она равна 5.7*107См/м, а у алюминия — 3.2*107См/м.
Если мы имеем дело с электрическим полем, постоянным во времени, тока проводимости достаточно. Однако в переменном поле только он не позволяет описать всю совокупность наблюдаемых явлений.
Рассмотрим цепь переменного тока с конденсатором. Переменный ток протекает между обкладками конденсатора и в том случае, когда между ними вакуум, то есть образование тока проводимости невозможно. Соединительный провод, по которому течет ток проводимости, окружен кольцевыми линиями магнитного поля, которые как бы образуют «оболочку» вокруг него. Максвелл предположил, что эта «оболочка» не обрывается у пластин конденсатора. Значит, переменное электрическое поле, так же как и ток проводимости, сопровождается появлением магнитного поля. Это дало Максвеллу основание для введения понятия тока смещения. Плотность тока смещения описывается формулой:
| (1.20) |
Природу тока смещения можно определить следующим образом. Всякое изменение электрического поля приводит к возникновению тока смещения.
Величина тока смещения прямо пропорциональна скорости изменения электрического поля.
2. Основные уравнения электродинамики
2.1. Первое уравнение Максвелла
Первое уравнение Максвелла является обобщением открытого Ампером закона полного тока. Ампер сформулировал этот закон следующим образом: циркуляция вектора напряженности магнитного поля по замкнутому контуру равна току, пронизывающему контур:
| (2.1) |
где | L – замкнутый контур, |
dl – векторный дифференциал длины контура: dl = l0dl, | |
l0 – орт дифференциала длины контура, | |
J – вектор плотности тока, пронизывающего контур, | |
S — произвольная поверхность, опирающаяся на контур L, | |
dS — векторный дифференциал поверхности: dS = n0dS, | |
n0 — орт нормали к поверхности S, образующий с направлением обхода контура правовинтовую систему. |
Форма замкнутого контура L может быть произвольной.
Под током, пронизывающим контур, Ампер понимал только ток проводимости, что справедливо для постоянного во времени поля. В переменном поле необходимо учесть введенный Максвеллом ток смещения. При этом формула (2.1) примет вид:
| (2.2) |
Уравнение (2.2) записано для контура конечных размеров и называется первым уравнением Максвелла в интегральной форме.
К дифференциальной форме первого уравнения перейдем с помощью теоремы Стокса (формула (1.34), [6]). Она позволяет заменить циркуляцию вектора Н по контуру L интегралом от rot Н по поверхности S, опирающейся на этот контур:
| (2.3) |
Так как поверхность S выбрана произвольно, то равенство (2.3) может быть удовлетворено только в случае равенства подынтегральных выражений:
| (2.4) |
Равенство (2.4) называется первым уравнением Максвелла в дифференциальной форме. Это векторное уравнение эквивалентно трем скалярным уравнениям. В декартовой системе координат х, у, z они примут следующий вид:
| (2.5) |
Аналогичные уравнения в других системах координат могут быть получены с помощью формул перехода (2.5) – (2.7) или (2.11) – (2.13) [6].
Ток смещения (электродинамика) — это… Что такое Ток смещения (электродинамика)?
Ток смещения или абсорбционный ток — величина, прямо пропорциональная быстроте изменения электрической индукции. Это понятие используется в классической электродинамике. Введено Дж. К. Максвеллом при построении теории электромагнитного поля.
Введение тока смещения позволило устранить противоречие[1] в формуле Ампера для циркуляции магнитного поля, которая после добавления туда тока смещения стала непротиворечивой и составила последнее уравнение, позволившее корректно замкнуть систему уравнений (классической) электродинамики.
Строго говоря, ток смещения не является[2]электрическим током, но измеряется в тех же единицах, что и электрический ток.
Точная формулировка
В вакууме, а также в любом веществе, в котором можно пренебречь поляризацией либо скоростью её изменения, током смещения (с точностью до универсального постоянного коэффициента) называется[3] поток вектора быстроты изменения электрического поля через некоторую поверхность[4]:
(СИ)
(СГС)
В диэлектриках (и во всех веществах, где нельзя пренебречь изменением поляризации) используется следующее определение:
(СИ)
(СГС),
где D — вектор электрической индукции (исторически вектор D назывался электрическим смещением, отсюда и название «ток смещения»)
Соответственно, плотностью тока смещения в вакууме называется величина
(СИ)
(СГС)
а в диэлектриках — величина
(СИ)
(СГС)
В некоторых книгах плотность тока смещения называется просто «током смещения».
Ток смещения и ток проводимости
В природе можно выделить два вида токов: ток связанных зарядов и ток проводимости.
Ток связанных зарядов — это перемещение средних положений связанных электронов и ядер, составляющих молекулу, относительно центра молекулы.
Ток проводимости — это направленное движение на большие расстояния свободных зарядов (например, ионов или свободных электронов). В случае, если этот ток идёт не в веществе, а в свободном простанстве, нередко вместо термина «ток проводимости» употребляют термин «ток переноса». Иначе говоря, ток переноса или ток конвекции обусловлен переносом электрических зарядов в свободном пространстве заряженными частицами или телами под действием электрического поля.
Во времена Максвелла ток проводимости мог быть экспериментально зарегистрирован и измерен (например, амперметром, индикаторной лампой), тогда как движение связанных зарядов внутри диэлектриков могло быть лишь косвенно оценено.
Сумма тока связанных зарядов и быстроты изменения потока электрического поля была названа током смещения в диэлектриках.
При разрыве цепи постоянного тока и включении в неё конденсатора ток в разомкнутом контуре отсутствует. При питании такого разомкнутого контура от источника переменного напряжения в нём регистрируется переменный ток (при достаточно высокой частоте и ёмкости конденсатора загорается лампа, включённая последовательно с конденсатором). Для описания и объяснения «прохождения» переменного тока через конденсатор (разрыв по постоянному току) Максвелл ввёл понятие тока смещения.
Ток смещения существует и в проводниках, по которым течёт переменный ток проводимости, однако в данном случае он пренебрежимо мал по сравнению с током проводимости. Наличие токов смещения подтверждено экспериментально советским физиком А. А. Эйхенвальдом, изучившим магнитное поле тока поляризации, который является частью тока смещения. В общем случае, токи проводимости и смещения в пространстве не разделены, они находятся в одном и том же объеме. Поэтому Максвелл ввёл понятие полного тока, равного сумме токов проводимости (а также конвекционных токов) и смещения. Плотность полного тока:
где j — плотность тока проводимости, jD — плотность тока смещения[5].
В диэлектрике (например, в диэлектрике конденсатора) и в вакууме нет токов проводимости. Поэтому приведенная выше формула Максвелла пишется так —
Примечания
- ↑ В магнитостатике этого противоречия не было, так как в ней на все токи наложено (искусственно) условие постоянства и замкнутости токов (соленоидальности поля плотности тока). В общем же случае переменных токов, с которым столкнулся Максвелл, ток может быть «незамкнутым», то есть например он может (некоторое время) течь в проводе, не выходя за его концы, на которых будут просто накапливаться заряды. Тогда, выбрав в теореме Ампера две различные поверхности, натянутые на один и тот же контур, но одну из которых провод будет пересекать, а другую (которую мы изогнем так, чтобы она проходила уже за концом провода) — нет, мы получим два разных выражения для тока, которые должны быть равны одному и тому же значению циркуляции магнитного поля. То есть приходим к явному противоречию, которое показывает необходимость исправления формулы, способ которого и нашел Максвелл, заменив ток в тех областях пространства, где он не течет, током смещения.
- ↑ для случая вакуума; для случая же диэлектрика точнее было бы сказать, что ток смещения является электрическим током не весь, а только та его часть, что связана с поляризацией диэлектрика — то есть перемещением реальных связанных зарядов в молекулах диэлектрика.
- ↑ При условии фиксированности (неподвижности) поверхности интегрирования или хотя бы постоянстве ее края (или отсутствии края, то есть и для всех замкнутых поверхностей, производную в формулах ниже можно очевидно вынести оператор производной за знак интеграла, например: , получив тождественную (при таком условии) формулировку: ток смещения (с точностью до универсального постоянного коэффициента) есть быстрота изменения потока электрического поля через поверхность — для вакуума, и аналогичные формулировки для всех случаев, описанных в статье.
- ↑ Аналогично тому, как обычным током называется поток плотности тока через некоторую поверхность (например, через сечение проводника):
- ↑ Иногда для обозначения тока проводимости и тока смещения используют не индекс, а разные буквы: i и j соответственно.