Бросок тока намагничивания трансформатора | Электротехнический журнал
Бросок тока намагничивания трансформатора — это кратковременный ток намагничивания трансформатора, превышающий номинальный ток нагрузки, возникающий при включении трансформатора (автотрансформатора) под напряжение или при его восстановлении. При этом, бросок тока намагничивания раз от раза может отличаться на одном и том же трансформаторе, так как имеет значение вектор и величина напряжения, подаваемая на обмотку трансформатора при включении коммутационного аппарата.
Причины возникновения броска тока намагничивания
Причиной возникновения БНТ в силовых трансформаторах является резкое изменение уровня напряжения намагничивания. Хотя обычно возникновение БНТ связывают с включением трансформатора под напряжение, он также может быть обусловлен:
- Возникновением внешнего КЗ,
- Восстановлением уровня напряжения после отключения внешнего КЗ,
- Переходом КЗ из одного вида в другой (к примеру, переход однофазного КЗ в двухфазное КЗ на землю),
- Несинхронным подключением генератора к системе.
Поскольку ветвь намагничивания схемы замещения трансформатора, может быть представлена как шунт при его насыщении, ток намагничивания нарушает баланс между токами на выводах трансформатора. Дифференциальная защита воспринимает ток БНТ как дифференциальный, однако должна устойчиво функционировать в таком случае. Отключение трансформатора при БНТ является нежелательным с точки зрения условий обеспечения длительного срока службы трансформатора (отключение тока индуктивного характера вызывает высокие перенапряжения, что может представлять угрозу для трансформатора и быть косвенной причиной возникновения внутреннего КЗ).
Описание процесса
Намагничивание трансформатора изза включения его под напряжение считается самым неблагоприятным случаем, вызывающим БНТ наибольшей амплитуды. Когда производится отключение трансформатора, напряжение намагничивания оказывается равным нулю, ток намагничивания снижается до нуля, в то время как магнитная индукция изменяется согласно характеристике намагничивания сердечника. Указанное обуславливает наличие остаточной индукции в сердечнике. Когда, по истечении некоторого времени, производится повторное включение трансформатора под напряжение, изменяющееся по синусоидальному закону, магнитная индукция начинает изменяться по тому же закону, однако со смещением на значение остаточной индукции. Остаточная индукция может составлять 80–90% номинальной индукции, и, таким образом, точка может переместиться за излом характеристики намагничивания, что, в свою очередь, обуславливает большую амплитуду и искажение формы кривой тока.

На рисунке представлена характерная форма БНТ. Данная осциллограмма отображает наличие длительно затухающей апериодической составляющей, может быть охарактеризована содержанием различных гармоник и большой амплитудой тока в начальный момент времени (до 30 раз превышающей значение номинального тока трансформатора). Кривая значительным образом затухает через десятые секунды, однако полное затухание характерно через несколько секунд. При определенных обстоятельствах БНТ затухает лишь спустя минуты после включения трансформатора под напряжение.
См. также
- Бросок зарядного тока конденсатора.
- Пусковой ток асинхронного электродвигателя.
Примечания
- Перевод статьи Богдана Каштенни и Ары Кулиджан из компании «General Electric» (английский), перевод был опубликован в журнале Релейщик №1 за 2009 год.
Для справки: http://www.ngpedia.ru/id270514p1.html
Просмотров всего: 6 075, Просмотров за день: 12
Расчет потери в стали и тока намагничивания трансформатора
Потери в стали сердечника трансформатора определяем по формуле:
Рст=руд.Gст=16,8.1,569=26,355,Вт;
руд=Кр.рi=1,4.12=16,8 Вт/кг;
где руд– удельные потери в сердечнике, Вт/кг;Gст– масса стали, кг; Кр– коэффициент увеличения потерь в сердечнике, равный 1,4; рi– удельные потери в материале, Вт/кг.
Величина удельных потерь в материале рiзависит от магнитной индукции Вст, марки стали, толщины листа, частоты сети и в данном случае равна 12 Вт/кг; откуда руд= 16,8 Вт/кг.
Масса стали трансформатора, определяется выражением:
Gст=YстVст=YстLстQстКст=0,0000078
где Yст= 7,8.10-6– удельный вес стали, кг/мм3;Lст– длина средней магнитной линии в сердечнике трансформатора (мм), определяемая по формуле:
Lст = 2.(h + c + a../2) = 2.(64,085 + 18,68 + 24,63./2) = 242,876 мм
Рст=Pуд.Gст= 16,8.1,569=26,355, Вт.
Активная составляющая тока холостого хода и намагничивающая мощность трансформатора определяется выражением:
Ioa= A.
A.
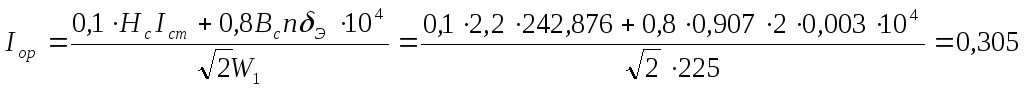 ,А
,А
где Нс– напряженность поля в стали, равная 4,2 А/см;э– величина эквивалентного воздушного зазора в стыках сердечника трансформатора, равная 0,002 см.
Ток в первичной обмотке трансформатора при номинальной нагрузке
I1=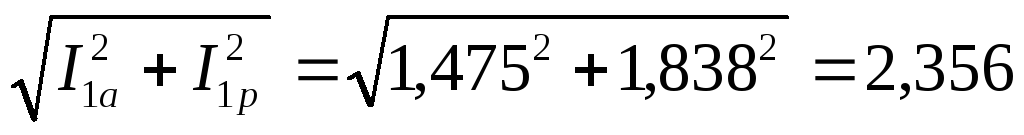 А,
А,
где I1аиI1р– активная и
реактивная составляющие тока первичной
обмотки трансформатора, которые
определяются выражениями:I
II2a=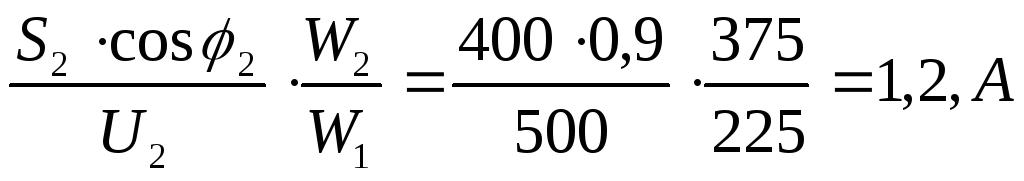
II3a=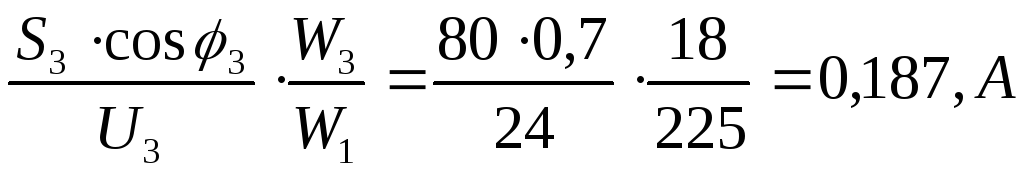
II2p=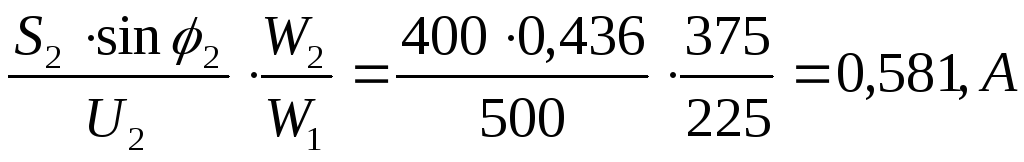
II3p=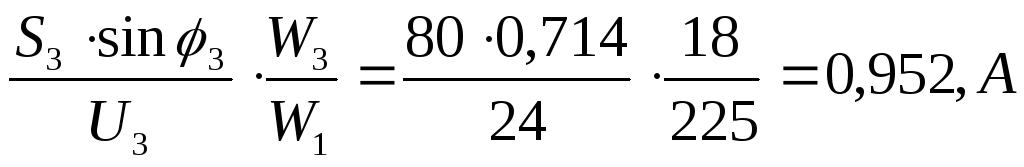
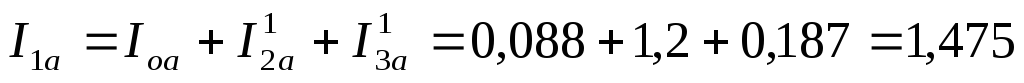 А;
А;
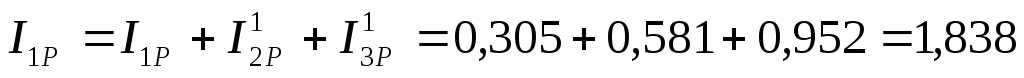 А;
А;
Ток холостого хода трансформатора
Io=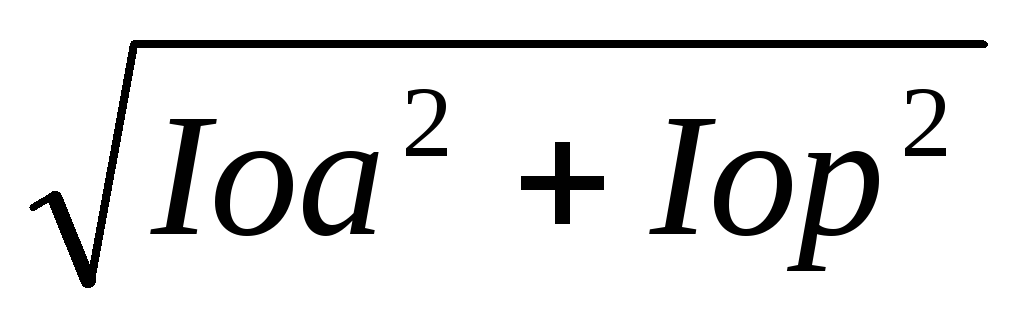
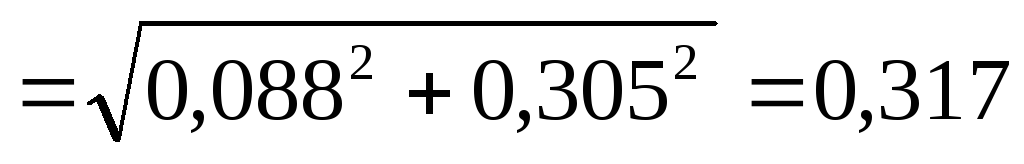
Так как величина относительного тока холостого хода Io/I1= 0,13 при частоте 400 Гц лежит в требуемых пределах (0,1-0,2), то выбор магнитопровода на этой стадии расчета окончен.
Коэффициент мощности трансформатора определяется выражением
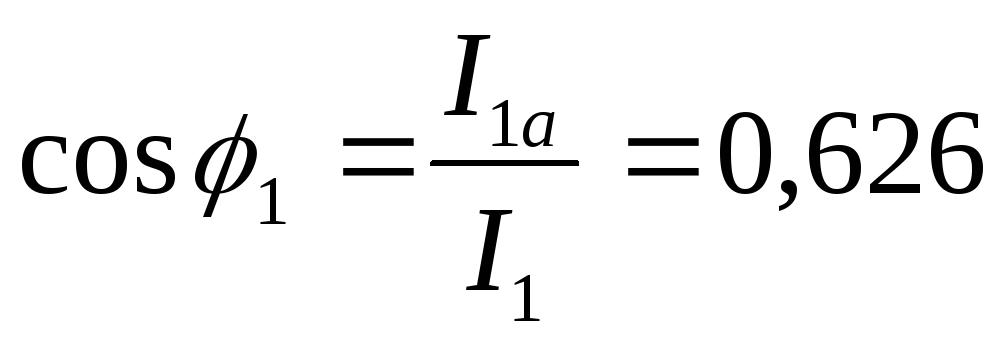
Расчет электрических и конструктивных параметров обмоток трансформатора
Плотность тока в обмотках оказывает существенное влияние на работу трансформатора. Выбор этого параметра при расположении 2-1-3 следующий:
J1=J3= 0,85.Jср=0,85.2,8=2,38А/мм2;
J
Определяем предварительные значения сечений проводов и обмоток и приводим к ближайшему стандартному значению:
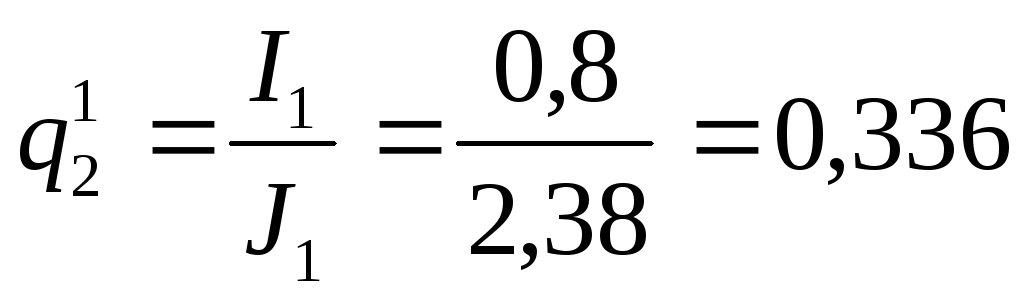 мм2;
мм2;
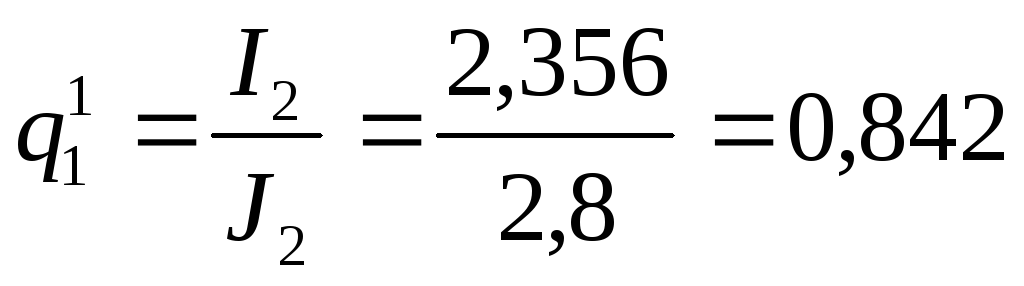 мм2;
мм2;
 мм2
мм2
q1 = 0,8495мм2; q2 =0,3217 мм2; q3 =1,4314 мм2.
По выбранным сечениям проводов уточняем плотности тока в обмотках
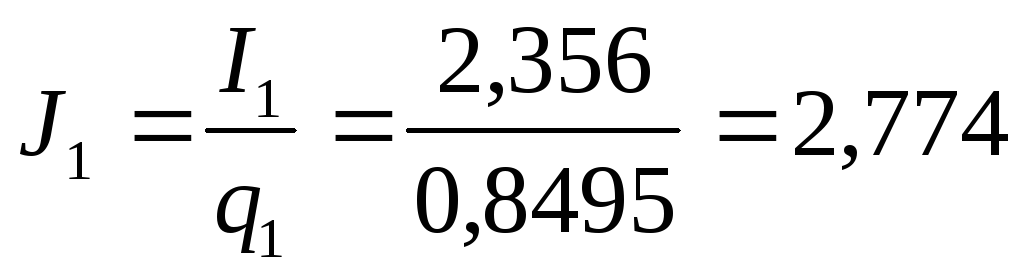
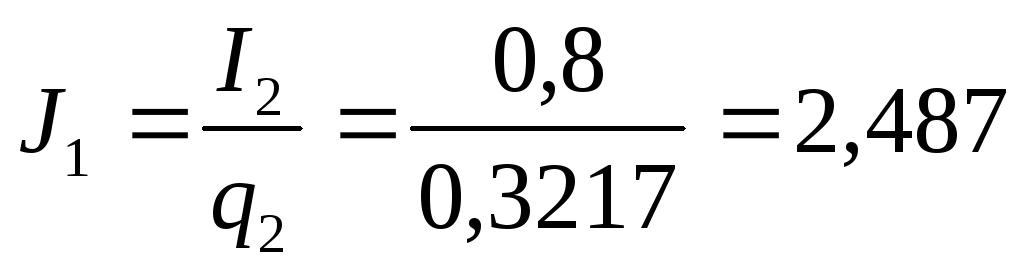 ,
A/мм2;
,
A/мм2;
 ,
A/мм2;
,
A/мм2;
и определяем диаметры проводов, диаметры проводов с изоляцией и массы 1 м провода:
d1= 0,64 мм;d1u= 0,69 мм;g1= 2,66 г;
d2= 1,04 мм;d2u= 1,12 мм;g2= 7,55 г;
d3= 1,35 мм;d3u= 1,43 мм;g3= 12,7 г;
Провода во всех обмотках будут марки ПЭЛ.
На следующем этапе проектирования определяем толщину обмоток трансформатора и размещение их в окне сердечника.
При намотке на каркасе высоту обмотки определяем по формуле:
ho= (h– 1) — 2=(64,085-1)-2.1,5=60,085,мм;
где hо– высота обмотки, мм;= 1,5–3,0 мм – толщина щечки каркаса. При= 1,5 мм,
Тогда число витков в одном слое для различных обмоток:
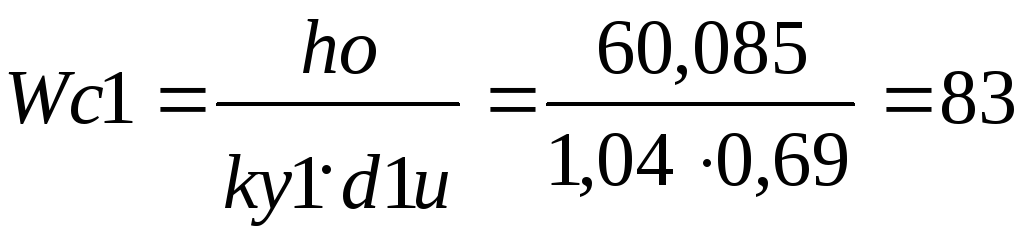 ;
;
 ;
;
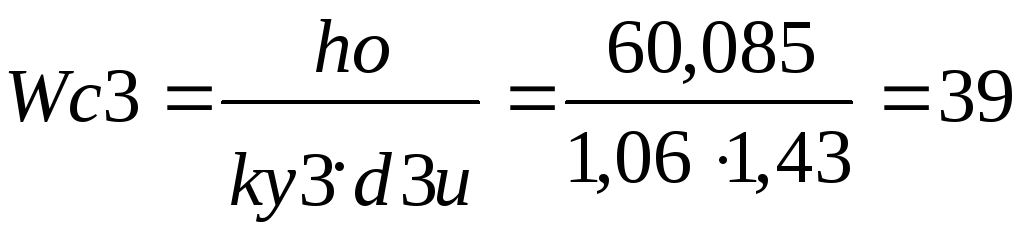
где ку1= 1,04, ку2= 1,045, ку3= 1,06 – коэффициенты укладки соответствующих обмоток в осевом направлении. Округлив число витков в меньшую сторону, получим, что:Wc1= 83;Wc2= 51;Wc3= 39.
Число слоев в обмотках трансформатора определим по формуле и округлим до ближайшего целого числа:
Nc1=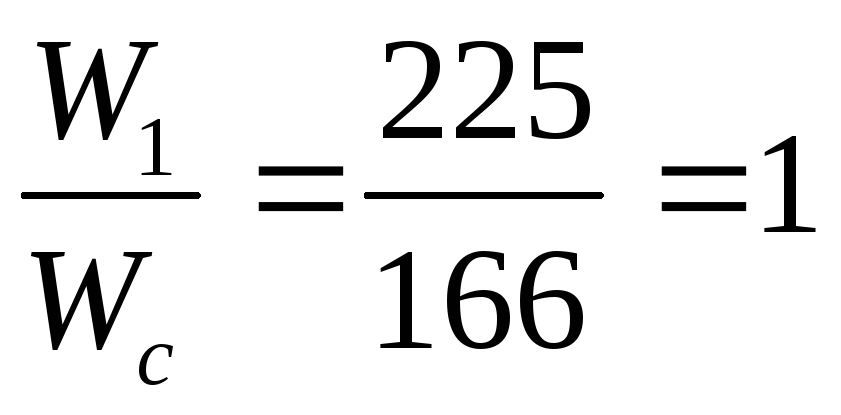 ;
;
Nc2= ;
;
N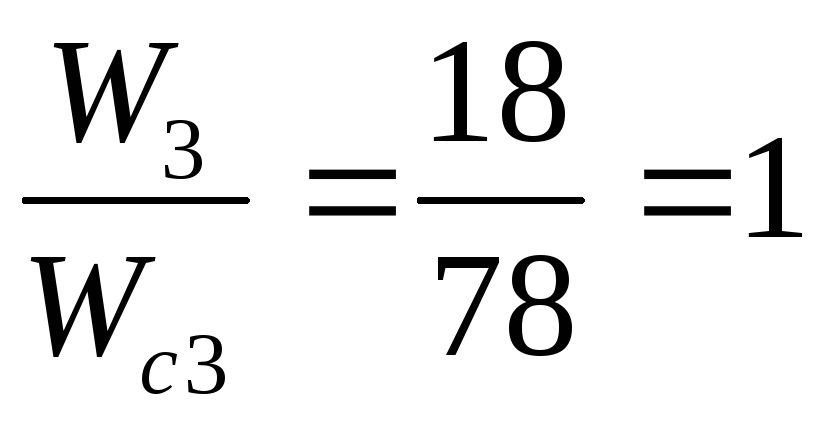 ;
;
Между слоями обмотки укладываем междуслоевую изоляцию, толщина которой зависит от диаметра провода с изоляцией и величины рабочего напряжения. Междуслоевая изоляция, укладываемая между слоями первых двух обмоток, будет выполнена из кабельной бумаги К-12 толщиной 0,11 мм.
Изоляцию между отдельными обмотками выбираем по наибольшему напряжению обмоток. Так как напряжение U2(большее) меньше 1000 В, междуобмоточную изоляцию принимаем за 0,3 мм, применяя в качестве такой изоляции 6 слоев телефонной бумаги КТН.
Толщину наружной
изоляции принимаем в зависимости от
рабочего напряжения последней обмотки
(U
Теперь рассчитаем радиальную толщину каждой из обмоток с учетом проводникового и междуосевого изоляционного материала:
i = Kpi. Nci. diu + (Nci – 1) . Yi
где: i– номер соответствующей обмотки;i– радиальная толщинаi-ой обмотки, ммNсi– число слоевi-ой обмотки;diu– диаметр провода с изоляциейi-ой обмотки, мм;Yi– толщина междуосевой изоляцииi-ой обмотки, мм.
1=1,05.1.0,69+(1-1).0,89=0,725мм;
2=1,055
3=1,06.1.1,43+(1-1).0,11=1,51мм.
Зная толщину обмоток, представим эскиз расположения этих обмоток на основе которого определим радиальные размеры катушки трансформатора. При чередовании обмоток 2-1-3 полный радиальный размер катушки трансформатора определяем по формуле
aг= (о+ 1+12+2+23+3+ Кни.ни).Кв,
где о=1,5мм – толщина,1,2,3– радиальные размеры обомоток, мм;12,23– толщина
изоляции между обмотками, мм; К
аг= (1,5+0,725+5,056+1,516+0,2+0,546+1,7.0,16).1=9,069 мм
Так как зазор между катушкой и сердечником с–2аг(для ленточных трансформаторов) лежит в пределах от 0,5 до 1 мм, то катушка нормально укладывается в окне выбранного сердечника.
Определим среднюю величину витка обмоток броневого трансформатора при расположении прямоугольных катушек в порядке 2-1-3:
Lw1=2(a+b+4(0+1+12)+21)=2(24,63+37+4(1,5+5,056+02)+2.0,725=180мм
Lw2=2(a+b+40+22)=2(24,63+37+4.1,5+2.5,056)=155,мм;
Lw3=2(a+b+4(0+2+12+1+13)+23=2(24,63+37+4(1,5+5,056+0,2+0,2)+2.1=191,мм;
Массу меди каждой из обмоток находим из выражения:
GМi=Lwi.Wi.gi.10-6, кг,
где Lwi, Wi, gi – соответственно средняя длина витка (мм), число витков и масса 1 м провода I-ой обмотки трансформатора.
GМ1=180.225.2,86.10-6=0,116,кг;
GМ2=155.375.7,55.10-6=0,439,кг;
GМ3=191.18.12,7.10-6=0,044,кг;
Общую массу меди обмоток трансформатора находим суммированием масс отдельных обмоток:
GМ=GМ1+GМ2+GМ3= 0,116+0,439+0,044=0,598,кг;
Так как отношение массы стали к массе меди, равное 2,622, лежит в рекомендуемых пределах (2-3 для минимума массы), то расчет можно продолжать дальше.
Находим потери в каждой из обмоток трансформатора по формуле:
Рмi=mj2iGMi,
где m – коэффициент, зависящий от температуры нагрева провода(m=2,65 при1050С).
Рм1=2,65.2,7742.0,116=2,362,Вт;
Рм2=2,65.2,4872.7,55=7,192,Вт;
Рм3= 2,65.2,3292.12,7=0,627,Вт;
Тогда потери в катушках трансформатора равны сумме потерь в отдельных обмотках:
РМ=Рм1+Рм2+Рм3=2,362+7,192+0,627=10,181,Вт;
Т. к. соотношение потерь в меди к потерям в стали, равное 0,386 лежит в рекомендуемых пределах (0,35 – 1,5 при частоте 400 Гц), то расчет продолжаем дальше.
Уравнение токов трансформатора. Формула.
Уравнение токов:
,
где Ix – ток холостого хода трансформатора.
18. Чем отличается приведенный трансформатор от реального?
Приведенный трансформатор отличается следующим: 1) число витков вторичной обмотки его равно числу витков первичной обмотки реального трансформатора; 2) активные, реактивные и полная мощности, а также потери вторичных обмоток приведенного и реального трансформаторов соответственно равны. 3) коэффициентом трансформации
k=El/E2=wl/w2=1
Так как число витков приведенной вторичной обмотки равно числу витков первичной, то индуктируемые потоком взаимоиндукции электродвижущие силы обеих обмоток равны, т. е.
Необходимо, чтобы приведенная обмотка была эквивалентна действительной вторичной обмотке. Поэтому потери должны сохраниться:
В приведенной обмотке должны сохраниться те же соотношения между активными и индуктивными падениями напряжений, которые существуют в действительной обмотке. Отсюда получим выражение для индуктивного сопротивления приведенной обмотки
Угол сдвига фаз между ЭДС и магнитным потоком. Число.
сдвиг фаз между E и Ф м = равен 90°
Что определяет намагничивающий ток?
величина намагничивающего тока и его форма в значительной степени определяются магнитными свойствами магнитопровода трансформатора, которые зависят от величины индукции в стали. При увеличении насыщения магнитопровода намагничивающий ток резко возрастает.
Намагничивающий ток-является главной составляющей тока Х.Х. Этот ток является Реактивным Iр .
Угол сдвига фаз между намагничивающим током и магнитным потоком. Число.
Намагничивающий ток , т.е. реактивная составляющая Iр, совпадает по фазе с магнитным потоком в сердечнике
сдвиг фаз между составляющими . активной Iа и Iр равен 90°.
Форма намагничивающего тока трансформатора в режиме насыщения. График.
Рис. 2.3. Построение кривой намагничивающего
тока трансформатора
Если магнитопровод трансформатора не насыщен, то намагничивающий ток −синусоидальный, если магнитопровод насыщен, то ток несинусоидальный. Но в любом случае намагничивающий ток совпадает по фазе с магнитным потоком . Внасыщенном трансформаторе ток определяется по кривой намагничивания представленной на рис.2.3 в первом квадранте.
Чем определяется активная составляющая тока холостого хода?
Активная составляющая тока холостого хода идет на покрытие потерь мощности
(14.4)
Активная составляющая тока холостого хода I0а = I0cosφ0 зависит от потерь холостого хода . Практически I0Ic. Активная составляющая Icа, как указывалось, определяется потерями .
Таким образом, активная составляющая тока холостого хода
,
где , и ток холостого хода
.
Чем отличаются постоянные потери в трансформаторе от переменных?
В работающем трансформаторевсегда имеются как магнитные, так и электрические потери. Магнитные потери в трансформаторе слагаются из потерь на вихревые токи и гистерезис:
Величина этих потерь зависит от напряжения U1 и магнитной индукции В. Можно считать, что при U1 = const, рон= В2. Они не зависят от нагрузки, то есть являются постоянными.
Электрические потери в обмотках, наоборот, переменные, то есть:
где ркн — соответствует потерям при коротком замыкании трансформатора.
Что делают, чтобы уменьшить потери на вихревые токи?
Для уменьшения потерь на вихревые токи
- магнитопроводы трансформаторов и других электромагнитных устройств изготавливают не из сплошных масс, а из отдельных пластин, изолированных друг от друга.
- магнитопроводы составляют из листов высоколегированной стали, удельное электрическое сопротивление которой значительно больше, чем обычной стали.
Таким образом, потери на вихревые токи зависят от материала магнитопровода, толщины стальных пластин и изоляции между ними. Кроме того, потери на вихревые токи пропорциональны квадратам частоты и магнитной индукции.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
1.5. Намагничивающий ток и ток холостого хода
Намагничивающий
ток. Величина и форма тока холостого
хода определяются магнитным потоком
трансформатора и свойствами его магнитной
системы. Выше показано, что магнитный
поток изменяется во времени синусоидально:  ,
а его амплитуда определяется ЭДС:
,
а его амплитуда определяется ЭДС:
(1.15)
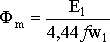 .
.
Так как при холостом ходе ЭДС практически равна напряжению, то значение магнитного потока определяется напряжением первичной обмотки, её числом витков и частотой.
Свойства магнитной системы трансформатора описываются в основном магнитной характеристикой, представляющей собой графическое изображение зависимости магнитного потока Ф от МДС трансформатора F или намагничивающего тока Iη, пропорционального МДС.
Активная
составляющая тока холостого хода.
Намагничивающий ток Iη является главной составляющей тока
холостого хода трансформатора I10.
Этот ток является реактивным, т.е.
Iη=I10p.
Однако реальный трансформатор в режиме
холостого хода потребляет от источника
переменного тока некоторую активную
мощность, так как при переменном магнитном
потоке в стальном магнитопроводе
возникают потери энергии от гистерезиса
и вихревых токов (магнитные потери ΔPc).
Поэтому ток холостого хода I10 должен иметь еще и активную составляющую 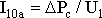 ,
которая обеспечивает поступление в
первичную обмотку мощности, компенсирующей
магнитные потери (электрическими
потерями в первичной обмотке в этом
режиме можно пренебречь из-за малости
тока холостого ход). Следовательно, ток
холостого хода
,
которая обеспечивает поступление в
первичную обмотку мощности, компенсирующей
магнитные потери (электрическими
потерями в первичной обмотке в этом
режиме можно пренебречь из-за малости
тока холостого ход). Следовательно, ток
холостого хода
(1.16)
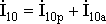 или
или 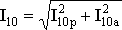 .
.
Обычно при выполнении магнитопровода трансформатора из листовой электротехнической стали толщиной 0,28-0,50 мм и частоте 50 Гц активная составляющая тока I10a не превышает 10% от тока I10, поэтому она оказывает весьма малое влияние на значение ток холостого хода (изменяет его не более чем на 1%). Форма кривой тока холостого хода определяется в основном кривой намагничивающего тока.
1.6. Комплексные уравнения и векторная диаграмма реального трансформатора
В
реальном трансформаторе помимо основного
магнитного потока Ф, замыкающегося по
магнитопроводу и сцепленного со всеми
обмотками трансформатора, имеются также
потоки рассеяния Фσ1 и Фσ2 (рис 1.7), которые сцеплены только с одной
из обмоток. Потоки рассеяния не участвуют
в передаче энергии, но создают в каждой
из обмоток соответствующие ЭДС
самоиндукции 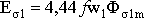 ;
;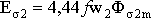 .
.
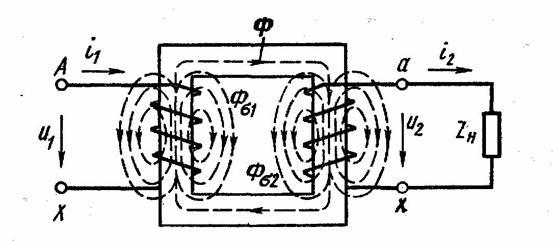 Рис.
1.7
Рис.
1.7
C учетом ЭДС самоиндукции и падений напряжения в активных сопротивлениях обмоток можно составить комплексные уравнения для первичной и вторичной обмоток трансформатора. С учетом (1.13) получим следующую систему уравнений:
(1.17)
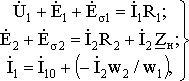
где:  —
сопротивление нагрузки, подключенной
к трансформатору.
—
сопротивление нагрузки, подключенной
к трансформатору.
Поскольку потоки рассеяния полностью или частично замыкаются по воздуху, они пропорциональны МДС соответствующих обмоток или соответствующим токам:
(1.18)
 ;
; 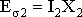 .
.
Величины X1 и X2 называют индуктивными сопротивлениями обмоток транс-форматора, обусловленными потоками рассеяния. Так как векторы ЭДС Еσ1 и Еσ2отстают от соответствующих потоков и токов на 90°, то
(1.19)
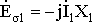 ;
;  .
.
При этом комплексные уравнения трансформатора примут вид
(1.20)
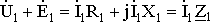 ;
;
(1.21)
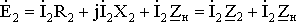 ;
;
(1.22)
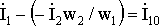 .
.
Замена
ЭДС 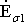 и
и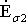 падениями
напряжений j Í1 X1 и j Í1 X2 наглядно показывает роль потоков
рассеяния: они создают индуктивные
падения напряжения в обмотках, не
участвуя в передаче энергии из одной
обмотки в другую. Проще становится и
построение векторной диаграммы,
соответствующей системе уравнений
(1.20) – (1.22), в которой целесообразно также
заменить падение напряжения в нагрузке
величиной
падениями
напряжений j Í1 X1 и j Í1 X2 наглядно показывает роль потоков
рассеяния: они создают индуктивные
падения напряжения в обмотках, не
участвуя в передаче энергии из одной
обмотки в другую. Проще становится и
построение векторной диаграммы,
соответствующей системе уравнений
(1.20) – (1.22), в которой целесообразно также
заменить падение напряжения в нагрузке
величиной 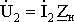 ,
т.е. вторичным напряжением трансформатора,
определяемым из (1.21):
,
т.е. вторичным напряжением трансформатора,
определяемым из (1.21):
(1.23)
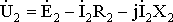 .
.
Векторную диаграмму вторичной обмотки трансформатора (рис. 1.8, а) строят согласно уравнению (1.23). Характер диаграммы определяется током нагрузки Í2, который принимается заданным по величине и фазе. Иными словами, задаваясь векторами вторичного тока Í2 и напряжения Ú2, можно построить вектор ЭДС
(1.24)
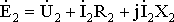 ,
,
если
известны параметры трансформатора.
Вектор Í2 R2 параллелен вектору тока Í2,
a вектор j Í2 X2 опережает вектор тока Í2 на угол 90°. На диаграмме изображен и
вектор магнитного потока 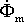 ,
который опережает вектор ЭДС É2 на 90°. Векторную диаграмму первичной
обмотки трансформатора (рис. 1.8, б) строят
в соответствии с уравнением
,
который опережает вектор ЭДС É2 на 90°. Векторную диаграмму первичной
обмотки трансформатора (рис. 1.8, б) строят
в соответствии с уравнением
(1.25)
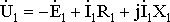 .
.
Построение
диаграммы начинают с вектора потока 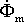 ,
который создается током холостого хода
Í10.
Этот ток опережает вектор потока
,
который создается током холостого хода
Í10.
Этот ток опережает вектор потока 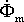 на
угол
на
угол .
Вектор ЭДС É1,
как и É2,
отстает от потока
.
Вектор ЭДС É1,
как и É2,
отстает от потока 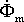 на
угол 90°.
на
угол 90°.
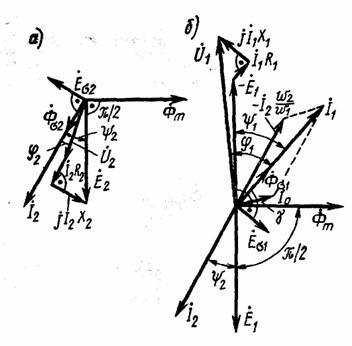 Рис.
1.8
Рис.
1.8
Ток
в первичной обмотке трансформатора 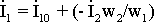 ,
поэтому на рис.1.8,б нужно показать и
вектор тока Í2,
сдвинутый на угол ψ2 относительно вектора É1 (векторы É1 и É2 совпадают по направлению). Зная Í2,
можно изобразить вектор
,
поэтому на рис.1.8,б нужно показать и
вектор тока Í2,
сдвинутый на угол ψ2 относительно вектора É1 (векторы É1 и É2 совпадают по направлению). Зная Í2,
можно изобразить вектор 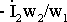 и
получить вектор Í1 как сумму векторов Í10 и
и
получить вектор Í1 как сумму векторов Í10 и 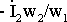 .
.
Найдя вектор тока Í1, можно определить значения векторов Í1 R1 и j Í1 X1 и построить искомый вектор напряжения Ú1 как сумму трех составляющих: векторов -É1 и падений напряжений в обмотках Í1 R1 и j Í1 X1.
Расчет магнитной цепи трансформатора
Дата публикации: .
Категория: Трансформаторы.
Расчет магнитной цепи производится с целью определения намагничивающего тока и магнитных потерь. Расчет реактивной составляющей намагничивающего тока можно выполнить двумя методами.
Первый метод
Первый метод аналогичен методу расчета магнитной цепи машины постоянного тока (смотрите статью «Метод расчета магнитной цепи машины постоянного тока»). При этом магнитная цепь вдоль средней магнитной линии (рисунок 1) разбивается на участки (стержни, ярма и воздушные зазоры или щели между ними), в пределах которых магнитные индукции Bст, Bя, Bδ можно считать постоянными. Задаваясь амплитудой потока стержня Фст, определяют амплитуды индукции Bст, Bя, Bδ = Bст и затем по кривым намагничивания стали находят Hст и Hя. Тогда намагничивающая сила однофазного трансформатора (рисунок 1, а)
 | (1) |
  |
| Рисунок 1. Магнитная цепь однофазного (а) и трехфазного стержневого (б) трансформатора |
где δ – величина зазора, которая для шихтованных магнитопроводов равна 0,003 – 0,005 см, а для стыковых магнитопроводов больше этого значения на толщину изоляционной прокладки в стыке.
Магнитная цепь трехстержневого трансформатора несколько несимметрична, и длины магнитных линий для крайних фаз несколько больше, чем для средней. Поэтому намагничивающая сила и намагничивающие токи крайних фаз также несколько больше. На практике этим различием пренебрегают и рассчитывают среднюю намагничивающую силу F для одной фазы. Тогда (рисунок 1, б)
  | (2) |
Здесь nф – среднее число стыков или зазоров на фазу. Для трехстержневого трансформатора с шихтованным магнитопроводом (смотрите рисунок 2, б) nф = 7/3 и со стыковым магнитопроводом nф = 2.
Действующее значение основной гармоники реактивной составляющей намагничивающего тока
  | (3) |
где w – число витков обмотки и k – коэффициент, учитывающий наличие в намагничивающем токе высших гармоник. При Bст = 1 Т и Bст = 1,4 Т соответственно k = 1,5 и k = 2,2.
Магнитная характеристика Фст = f(i0r) имеет вид, показанный на рисунке 1, в статье «Явления, возникающие при намагничивании магнитопроводов трансформаторов».
Второй метод
Второй метод основан на вычислении энергии магнитного поля магнитопровода или его намагничивающей (реактивной) мощности.
Допустим, что B и H представляют собой амплитуды индукции и напряженности магнитного поля, изменяющихся синусоидально во времени. Тогда максимум магнитной энергии в единице объема поля
W ’макс = BH / 2 ,
реактивная мощность на единицу объема
Q ’ = ωW ’макс = πfBH ,
а реактивная мощность магнитопровода с объемом V или массой G
  | (4) |
где γ – плотность стали магнитопровода, а
  | (5) |
  |
| Рисунок 2. Кривые удельной реактивной мощности магнитопровода и зазора |
представляет собой реактивную мощность на единицу массы стали магнитопровода.
Для воздушных зазоров выражение для Q можно представить в виде
Q = qnδSδ = nqδSδ ,
где Sδ – площадь зазора; n – число зазоров на весь магнитопровод; q – реактивная мощность на единицу объема зазора; qδ = qδ – реактивная мощность на единицу площади зазора.
Значение qс = f(B) в принципе можно вычислить, зная кривую B = f(H) для данного материала. Однако на практике пользуются данными, полученными непосредственно опытным путем. Кривые qδ = f(B) для шихтованных магнитопроводов также определяются опытным путем, так как в таких магнитопроводах зазоры одного слоя шунтируются листами другого слоя и индукция в зазорах уменьшается, а в листах стали по соседству с зазорами увеличивается, вследствие чего qδ зависит также от марки стали. Кривые qс = f(B) и qδ = f(B) представлены на рисунке 2
Так как реактивная намагничивающая мощность трансформатора
Q0 = mEI0r ,
где m – число фаз, то
  | (6) |
Здесь Gст и Gя – массы стержней и ярем трансформатора, а qс.ст и qс.я – удельные мощности qс для стержня и ярма.
Обычно пользуются вторым методом расчета.
Магнитные потери в магнитопроводе pмг легко вычислить, зная удельные потери p = f(B) для используемой марки стали:
| pмг = pстGст + pяGя . | (7) |
Активная составляющая намагничивающего тока
  | (8) |
а полный намагничивающий ток, или ток холостого хода,
  | (9) |
Ток I0 в силовых трансформаторах относительно мал и составляет при нормальном напряжении 0,5 – 4% от номинального тока, причем второе число относится к трансформаторам малой мощности (10 – 20 кВ×А). Малое значение тока I0 объясняется наличием замкнутого стального магнитопровода.
Источник: Вольдек А. И., «Электрические машины. Учебник для технических учебных заведений» – 3-е издание, переработанное – Ленинград: Энергия, 1978 – 832с.
Расчет бросков тока намагничивания трансформаторов (Страница 1) — Учимся делать расчёты — Советы бывалого релейщика
Добрый день уважаемые коллеги. Возникли вопросы про расчет отстройки ТО или ТНЗНП от бросков тока намагничивания:
1) Правильно ли я понимаю, что при расчете ТНЗНП согласно руководящим указаниям по релейной защите выпуск 12 для линий с односторонним питанием: «Условия “а” и “б” рассматриваются при расчете защит линий, оборудованных выключателями с пофазным приводом; указанные условия не учитываются, если первая ступень защиты отстроена по времени от одновременного включения фаз выключателя».
Из паспорта на выключатель ВГТ-110 кВ: разновременность работы полюсов, с, не более 0,002 с при включении в то время как время срабатывания реле тока ТНЗНП защит, выполненных на МП элементной базе, не превышает 0,025 с. Т.е. можно говорить, что время разновременности включения фаз выключателя практически не превышает собственного времени срабатывания защиты, поэтому условие отстройки от броска тока намагничивания трансформаторов можно не учитывать.
Или все-таки каким-то образом отстраиваются от бросков тока намагничивания трансформаторов в таких ситуациях?
2) Вопрос определения Сб. Каким образом его взять применительно для защит на МП элементной базе?
Ведь в «Руководящих указаниях по релейной защите. Вып.9. Дифференциально –фазная высокочастотная защита линий 110 – 330 кВ. М., “Энергия”, 1972. 114 с. с ил.» и в «Руководящих указаниях по релейной защите. Вып.12. Токовая защита нулевой последовательности от замыканий на землю линий 110 – 500 кВ. Расчеты. М., “Энергия”, 1980. 88 с. с ил.». таблицы П-6 и таблицы ПV-4 соответственно даны значения Сб для реле, выполненных на электромеханической элементной базе.
3) И еще такой вопрос касаемо параметрирования… У ЭКРы есть дополнительные ступени ТНЗНП V и VI, если мне не изменяет память, и там есть возможность завести разрешить работу ТНЗНП от устройства БТНТ (например в шкафе ШЭ2607 021_200), которое как я понимаю, блокирует действие ТНЗНП при бросках тока намагничивания, следовательно, это условие можно не учитывать получается?
Спасибо за ответы
Post’s attachmentsБТНТ.png 58.63 Кб, 1 скачиваний с 2016-08-29
You don’t have the permssions to download the attachments of this post.Токи намагничивания силовых трансформаторов и автотрансформаторов при включении их под напряжение
⇐ ПредыдущаяСтр 6 из 8Следующая ⇒
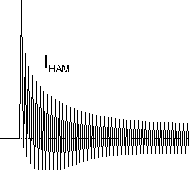 При включении силовых трансформаторов возникает резкий бросок тока намагничивания, имеющий затухающий характер (рис. 9.2.7.).
При включении силовых трансформаторов возникает резкий бросок тока намагничивания, имеющий затухающий характер (рис. 9.2.7.).
Изменение тока Iнам во времени характеризуется следующими особенностями:
1. Кривая тока носит асимметричный характер, пока ток Iнам не достигнет установившегося значения;
2.  кривая может быть разложена на апериодическую составляющую и синусоидальные токи различных гармоник. Апериодическая составляющая имеет весьма большое удельное значение в токе Iнам;
кривая может быть разложена на апериодическую составляющую и синусоидальные токи различных гармоник. Апериодическая составляющая имеет весьма большое удельное значение в токе Iнам;
3. Время затухания токов определяется постоянными времени трансформатора и сети, и может достигать 2-3 секунд. Чем мощнее трансформатор, тем дольше продолжается затухание;
4. Первоначальный бросок тока может достигать 5-10 кратного значения номинального тока трансформатора. У мощных трансформаторов кратность меньше, чем у маломощных.
Ток Iнам, появляется только в одной обмотке силового трансформатора (той, на которую подается напряжение при его включении (рис. 9.2.8.)). Для предотвращения ложных действий дифференциальной защиты, под влиянием Iнам принимают специальные меры:
1. Замедление защиты примерно на 1 секунду (широко применялся ранее). При этом теряется наиболее ценное свойство защиты – её быстродействие;
2. Блокировка при понижении напряжения;
3. Торможение от токов высших гармоник; (опыт эксплуатации отверг эти два способа, они были недостаточно надежны, приводили к чрезмерному усложнению защиты).
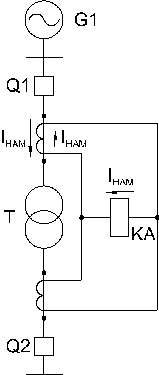 В настоящее время применяются следующие два способа:
В настоящее время применяются следующие два способа:
1. Использование БНТ (быстро насыщающегося трансформатора), через который включаются дифференциальные реле. БНТ не пропускает апериодический ток, который составляет значительную часть тока намагничивания;
2. Отстройка от тока намагничивания по величине Iнам<IС.З. На этом принципе работают дифференциальные отсечки.
Преимущество обоих способов:
1. простота;
2. надежность;
3. быстрота действия.
Рис. 9.2.8.
Схемы дифференциальных защит
Дифференциальная токовая отсечка
Схемы токовых цепей дифференциальной токовой отсечки (ДТО) могут выполняться в 2-х вариантах: по полной 3-х фазной схеме с тремя реле, и упрощенной схеме в 2-х фазном исполнении на стороне треугольника силового трансформатора с двумя реле (рис. 9.2.9.).
На трансформаторах большой и средней мощности следует применять 3-х фазную схему, как более совершенную.
Основным условием правильной работы ДТО является отстройка тока срабатывания от намагничивающего тока, возникающего при включении силового трансформатора. Для облегчения отстройки устанавливаются промежуточные реле с временем действия 0,04-0,06 с. (К этому моменту ток намагничивания спадает практически в два раза. (см. рис. 9.2.7.)):
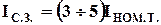 (9.12.)
(9.12.)
Из-за большой величины тока срабатывания, защита недостаточна чувствительна к витковым замыканиям.
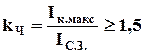 (9.13.)
(9.13.)
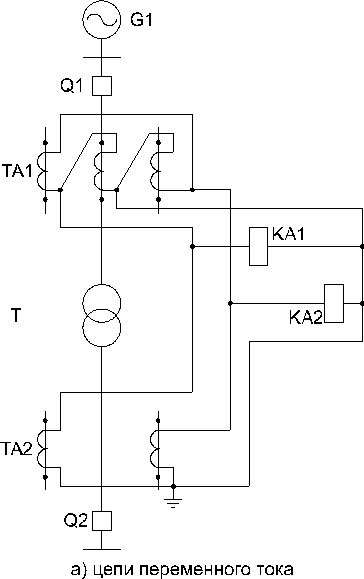

Рис. 9.2.9.
Достоинства ДТО:
1. Простота принципа действия;
2. Быстрота действия.
Недостатки ДТО:
Ограниченная чувствительность.
ДТО применяется на силовых трансформаторах малой мощности.
Дифференциальная защита с токовыми реле, включенными через БНТ
Общие сведенья
Схема дифференциальной защиты с реле тока РНТ-565 показана на рис. 9.2.10.

Рис. 9.2.10.
Применение БНТ позволяет выполнить простую и быстродействующую защиту, надежно отстроенную от токов небаланса и бросков намагничивания.
БНТ плохо трансформирует апериодические токи. В реле защиты попадает лишь переменная составляющая тока небаланса и броска намагничивающего тока силового трансформатора. (см. рис. 9.2.11. – осциллограммы токов в обмотках БНТ.) Временные зависимости наглядно показывают резкое снижение тока в реле и эффективность насыщающегося трансформатора.
За счет насыщения сердечника БНТ, обусловленного подмагничивающим действием апериодического тока, трансформация переменной составляющей также ухудшается, что ещё больше уменьшает ток в реле.
После затухания апериодической составляющей нормальные условия для трансформации периодического тока восстанавливаются.
Подмагничивающие действие апериодического тока, приводит к замедлению защиты при повреждении в её зоне. Трансформация уменьшается настолько, что ток в обмотке реле меньше тока срабатывания. Время замедления – 0,03 –0,01 секунды. Это является недостатком схемы дифференциальной защиты с БНТ.
Рис. 9.2.11.
Пояснения к рис.:
а) – при включении силового трансформатора под напряжение; б) – при сквозном КЗ. (Iнам — ток намагничивания в первичной обмотке; IP — ток намагничивания во вторичной обмотке; IK— ток сквозного КЗ на плече дифференциальной защиты; Iнб — ток небаланса в первичной обмотке; 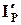 — ток небаланса во вторичной обмотке БНТ).
— ток небаланса во вторичной обмотке БНТ).
Ток срабатывания защиты должен отстраиваться от переменной составляющей переходных токов намагничивания и небаланса:
 (9.14.)
(9.14.)
Реле РНТ-565 совмещает в себе устройство выравнивания вторичных токов защиты и БНТ. На рис. 9.2.10.: wy1, wy2 – уравнительные обмотки, позволяют выровнять магнитный поток при неравенстве токов I1 и I2 при сквозных КЗ. w¶ — рабочая (дифференциальная) обмотка. В РНТ-565 используется токовое реле типа РТ-40.
Число витков уравнивающих обмоток регулируется отпайками и подбирается так, чтобы при внешних КЗ ток в обмотке реле КА был равен нулю. (См. формулу 9.4.)
Ток срабатывания защиты регулируется изменением числа витков обмотки w¶.
На магнитопроводе реле РНТ имеется короткозамкнутая обмотка wк. Она повышает степень отстройки реле от токов небаланса и бросков намагничивающих токов силового трансформатора особенно, когда эти токи имеют незначительную апериодическую составляющую, что понижает эффективность действия БНТ. Короткозамкнутая обмотка ограничивает периодический ток, возникающий во вторичной обмотке РНТ. Конструктивно размещение обмоток реле РНТ-565 показано на рис. 9.2.12.
Работа БНТ:
Ток I¶, поступающий в обмотку w¶ создает магнитодвижущую силу F¶ = I¶ w¶, которая образует в среднем стержне магнитный поток Ф¶, замыкающийся по крайним стержням магнитопровода.
В общем случае ток I¶ состоит из переменной I¶.п. и апериодической I¶.а. составляющих. Соответственно этому образуются два магнитных потока Ф¶.п. и Ф¶.а..
Переменный поток Ф¶.п., замыкаясь по стержню 2, наводит в обмотке w2, ЭДС Е2. Апериодический поток Ф¶.а.., медленно изменяющийся во времени, не создает ЭДС в w2 и полностью затрачивается на намагничивание магнитопровода.
Переменная составляющая потока Ф¶.п., наводит в витках короткозамкнутой обмотки wк ЭДС Ек и ток Iк. Короткозамкнутая обмотка создает потоки Фк и Ф’¶ направленные встречно потоку Ф¶.п. и заметно компенсируют его. В результате по магнитопроводу протекает остаточный поток Фп< Ф¶.п. (где Ф¶.п. – магнитный поток при отсутствии короткозамкнутой обмотки).
Таким образом короткозамкнутая обмотка уменьшает переменный магнитный поток, создаваемый периодическим током I¶.п., питающим обмотку w¶.
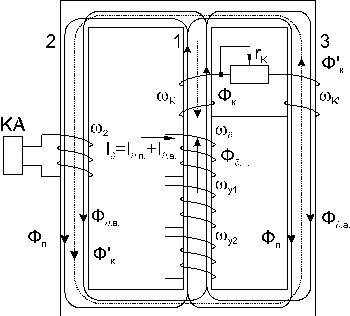
Рис. 9.2.12.
Варианты схем включения обмоток реле РНТ
Варианты схем включения обмоток реле РНТ-565 показаны на рис. 9.2.13.:
а) У 2-х обмоточных трансформаторов для компенсации неравенства токов в плечах защиты достаточно использовать только одну уравнительную обмотку (включается в плечо с меньшим током.
б) Для повышения точности компенсации применяются схемы с включением двух уравнительных обмоток.
в) Схема с использованием только уравнительных обмоток.
г) Защита 3-х обмоточных трансформаторов. Уравнительные обмотки включаются в плечи с меньшими токами. Плечо с большим током подсоединяется непосредственно к дифференциальной обмотке реле.
Рекомендуемые страницы:



