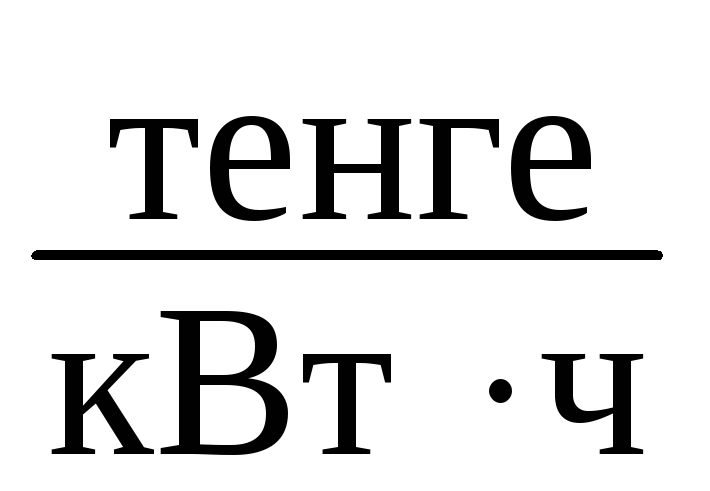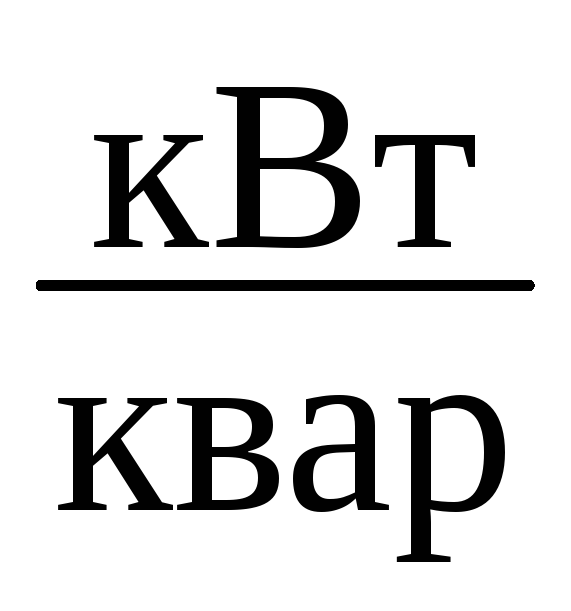3.6 Определение технико-экономических показателей системы внутризаводского электроснабжения

3.6.1 Определение капитальных затрат и расхода цветного металла на кабельные линии, выключатели и трансформаторы. Вес кабелей определяем по формуле (2.22).

Капитальные затраты на кабельные линии, выключатели и трансформаторы цеховых ТП вычисляются аналогично приведенной методике в разделе 2. Расчеты по определению капитальных затрат на систему внутризаводского электроснабжения приведены в таблице 3.7.

Капитальные затраты на строительную часть кабельных линий, т.е. на траншеи, определяются в зависимости от длины линии и стоимости одного километра траншеи с учетом количества кабелей в ней по формуле

К_транш.= С_транш.· ∑ℓ,

где С_транш.– стоимость 1 км траншеи, тыс. тенге;

∑ℓ − суммарная длина траншей с одинаковым количеством кабелей в ней, км.

Например, для рассматриваемого примера имеем

К_транш.= 0,54·(0,088+0,1+0,074+0,094) + 0,79·(0,05+0,172+0,05) =

= 0,40712·200 = 81,424 тыс.тенге.

3.6.2 Определение эксплуатационных расходов и потерь электроэнергии в линиях распределительной сети. Определение указанных параметров выполнено в соответствии с методикой, изложенной в разделе 2. Расчеты приведены в таблице 3.8. Определение эксплуатационных расходов и потерь электроэнергии в трансформаторах ЦТП выполнено в таблице 3.9.

Далее следует определить технико-экономические показатели по варианту системы внутризаводского электроснабжения предприятия.

Капитальные затраты на линию рассчитываются с учетом строительных работ по прокладке кабелей в траншеях.

Суммарные капитальные затраты составляют

К_внут.=К_Л+ К_В+ К_Т= 1470,249 + 8800 + 84916 = 95186,249 тыс.тенге.

Суммарные эксплуатационные затраты составляют

С_внут.= С_пл + С_пт+ С_ал + С_ав + С_ат = 169,2 + 2474,54 + 44,107 + 387,2 + 3736,304 =

= 6811,351 тыс.тенге/год.

Суммарные годовые расчетные затраты составляют

З_внутр.= 0,125К_внутр.+ С_внутр.=

= 0,125 95186,249 + 6811,351 = 18709,632 тыс.тенге/год.

Потери электроэнергии в сети и в трансформаторах внутризаводского электроснабжения составляют

∆Э_внутр.= ∆Э_Л+ ∆Э_Т= 84,6 + 1237,27 = 1321,87 тыс.кВт·ч.

Расход алюминия равен G_внутр.= 1,717 т.

3.6.3 Технико-экономические показатели системы электроснабжения предприятия. На основании технико-экономических расчетов, проведенных в разделах 2 и 3 курсовой работы, определяются технико-экономические показатели системы электроснабжения предприятия путем суммирования соответствующих показателей системы внешнего и внутризаводского электроснабжения.

Суммарные капитальные затраты составляют

К_сэс= К_внеш.+ К_внутр.= 45952 + 95186,249 = 141138,249 тыс.тенге.

Суммарные эксплуатационные затраты составляют

С_сэс= С_внеш. + С_внут.=4909,9 + 6811,351 = 11721,251тыс.тенге/год.

Суммарные годовые расчетные затраты составляют

З_сэс= 0,125К_сэс+ С_сэс=

= 0,125 141138,249 + 11721,251 = 29363,531 тыс.тенге/год.

Потери электроэнергии в сетях и в трансформаторах внешнего и внутризаводского электроснабжения составляют

∆Э_сэс= ∆Э_внеш.+ ∆Э_внут. = 1762 + 1321,87 = 3083,87 тыс.кВт·ч.

Расход алюминия равен

G_сэс =G_внеш.+G_внутр.= 46,26 + 1,717 = 47,977 т.

Таблица 3.7 –Определение капитальных затрат на линии, выключатели и трансформаторы

Ном. ли- нии	Спо- соб про- клад- ки	Линии						Выключатели				Трансформаторы
		Марка и сечение кабеля, мм2	Дли-на ℓ, км	Вес ка-беля, g, т/км	Расход цвет. мет., G, т	Стои-мость 1 км линии Сл,	Кап.затр. Кл, тыс.тенге	Тип	Кол., шт	Стоим. одной ячейки Св, тыс. тенге	Кв, тыс. тенге	Кол. и мощность n×SТ.ном, кВ·А	Кт, тыс. тенге
Ввод	—	—	—	—	—	—	—	ВВ/TЕL 10/1600 и ВВ/TЕL 10/630	3	550		—	—
Л1	транш.	2ААБ(3×95)	0,088	0,76	0,134	598	105,248		2			2×1600	13120
Л2	транш.	2ААБ(3×240)	0,172	1,92	0,66	1040	357,76		5			2×6300	2066
Л3	транш.	2ААБ(3×95)	0,05	0,76	0,076	598	59,8		2			2×1600	13120
Л4	констр.	2ААБГ(3×35)	0,08	0,28	0,045	414	66,24		—			2×1600
Л5	транш.	2ААБ(3×95)	0,124	0,76	0,188	598	148,304		2			2×1600
Л6	констр.	2ААБГ(3×35)	0,09	0,28	0,050	414	74,52		—			2×1600
Л7	транш.	2ААБ(3×35)	0,30	0,20	0,120	382	229,2		—			2×1000	5750
Л8	транш.	2ААБ(3×95)	0,266	0,76	0,404	598	318,136		2			2×1000
Л9	констр.	2ААБГ(3×35)	0,072	0,28	0,040	414	59,616		—			2×1000
Строительная часть		(траншеи)					81,424
Всего					1,717		1470,249		16		8800	—	84916

Таблица 3.8 – Определение эксплуатационных расходов и потерь электроэнергии в линиях сети

Ном. ли-нии	Марка и сечение кабеля, мм2	Исходные данные на линии						Расчетные данные на линии						Выключатели
		kз	k2з	ℓ, км	τ, ч	С0,	φЛ, %	∆Рном, кВт	∆РЛ, кВт	∆ЭЛ, кВт·ч в год	СпЛ, тыс. тенге	СаЛ, тыс. тенге	КЛ, тыс. тенге	КВ, тыс. тенге	φВ, %	СаВ
Л1	2ААБ(3×95)	0,5853	0,3426	0,088	2199	2	3	50	3,015						4,4
Л2	2ААБ(3×240)	0,6408	0,4106	0,127				58	8,192
Л3	2ААБ(3×95)	0,6363	0,4049	0,05				50	2,024
Л4	2ААБ(3×35)	0,6125	0,3751	0,08				42	2,52
Л5	2ААБ(3×95)	0,6363	0,4049	0,124				50	5,02
Л6	2ААБ(3×35)	0,6125	0,3751	0,09				42	2,836
Л7	2ААБ(3×35)	0,4568	0,2087	0,30				40	5,009
Л8	2ААБ(3×95)	0,5292	0,28	0,266				50	7,448
Л9	2ААБ(3×35)	0,5125	0,2626	0,072				42	2,406
Всего		—	—	—				—	38,47	84,6	169,2	44,107	1470,249	8800	—	387,2

Таблица 3.9 – Определение эксплуатационных расходов и потерь электроэнергии в трансформаторах цеховых подстанций

Ном. ТП	n×Sт.н, кВ·А	Исходные данные на один трансформатор							Расчетные данные на два трансформатора
		Iхх, %	Uкз, %	∆Рхх, кВт	∆Ркз, кВт	kип,	С0,	τ, ч	kз	k2з	∆Р´хх, кВт	∆Р´кз, кВт	∆Эт, тыс. кВт·ч	Сп.т, тыс. тенге	Кт, тыс. тенге	τт, %	Са.т, тыс. тенге
ТП1	2×1000	1,5	8,0	2,3	12,2	0,07	2	2199	0,62	0,384	3,35	17,8	88,78			4,4
ТП2	2×1000								0,68	0,462			94,89
ТП3	2×1000								0,68	0,462			94,89
ТП4	2×1600	1,3	5,5	3,3	18,0				0,62	0,384	4,76	24,16	124,24
ТП5	2×1600								0,64	0,409			126,92
ТП6	2×1600								0,64	0,409			126,92
ТП7	2×1600								0,64	0,409			126,92
ТП8	2×1600								0,64	0,409			126,92
ТП9*	2×6300	0,8	6,5	8,33	46,5				0,6	0,36	11,86	75,165	326,79
Всего		—	—	—	—	—	—	—	—	—	—	—	1237,27	2474,54	84916	—	3736,304

Онлайн калькулятор: Тригонометрические функции

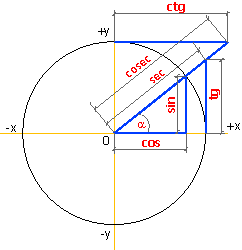Простейшие тригонометрические функции

Тригонометрические функции — вид элементарных функций, к которым относятся следующие функции:
sin — синус
cos — косинус
tg — тангенс
ctg — котангенс
sec — секанс
cosec — косеканс
versin — версинус (синус-верзус)
vercos — коверсинус (косинус-верзус)
haversin — гаверсинус (половина от синус-верзус)
exsec — экссеканс
excsc — экскосеканс

Для того чтобы вычислить все эти тригонометрические функции сразу для заданного угла, введите значение угла в поле Угол и получите результат в виде таблицы значений всех функций для этого угла. Угол можно задать в градусах, радианах, градах, минутах и секундах, для выбора единицы измерения — просто щелкните на ее название.

Тригонометрические функции

Единицы измерения Точность вычисления

Знаков после запятой: 10

save Сохранить share Поделиться extension Виджет

Как известно из школы, синус угла (sin) — это отношение длины противоположного этому углу катета к гипотенузе, а косинус (cos) — это отношение прилежащего этому углу катета к гипотенузе.

Остальные тригонометрические функции можно выразить через синус и косинус:
Тангенс: (отношение длины противоположного углу катета к прилежащему катету)
Котангенс: (отношение длины прилежащего к углу катета к противоположному катету)
Секанс: (отношение длины гипотенузы к прилежащему к углу катету)
Косеканс: (отношение длины гипотенузы к противоположному катету)

Редко используемые тригонометрические функции:

Версинус:

Коверсинус:

Гаверсинус:

Экссеканс:

Экскосеканс:

Ответы@Mail.Ru: Косинус и тангенс

Вот: cos^2 f=1/(1 + tg^2 f). tg f=0,4; 1+0,4*0,4=1,16; cos f=1/koren(1,16)=0,9284766…

tg(a)=sin(a)/cos(a) sin(a)^2+cos(a)^2=1 из второй находите синус, подставляете в первую, находите ваш косинус. Это аналитически. Ну если численными методами, то возьмите арктангенс, найдёте угол, и возьмите косинус этого угла. Калькулятор вам в руки.

Тангенс угла — это частное от деления значения синуса этого угла на значение косинуса того же угла (tg(x)= sin(x) / cos(x)). Арктангенс угла — величина. обратная тангенсу. Узнать значение самого угла и его косинуса можно по таблице: <a href=»/» rel=»nofollow» title=»17177736:##:s/c/planimetry/content/chapter5/section/paragraph5/theory.html» target=»_blank» >[ссылка заблокирована по решению администрации проекта]</a>

Теорема тангенсов — Википедия

Материал из Википедии — свободной энциклопедии

Теорема тангенсов^[1] — теорема, связывающая между собой тангенсы двух углов треугольника и длины сторон, противоположные этим углам.

Теорема тангенсов, хотя не настолько широко известна как теорема синусов или теорема косинусов, достаточна полезна, и может быть использована в тех случаях, когда известны две стороны и один угол, или, наоборот, два угла и одна сторона.

Теорема тангенсов для сферических углов была описана в XIII веке персидским математиком Насиром ад-Дином Ат-Туси (1201—1274), который также привёл теорему синусов для плоских треугольников в своей пятитомной работе Трактат о полном четырёхугольнике.^[2][3]

Теорему также называют формулой Региомонтана по имени немецкого астронома и математика Иоганна (или Йоганна) Мюллера (лат. Regiomontanus), установившего эту формулу. И. Мюллера называли «Кёнигсбержец»: по-немецки König — король, Berg — гора, а по-латински «король» и «гора» в родительном падеже — regis и montis. Отсюда «Региомонтан» — латинизированная фамилия И. Мюллера.^[4]

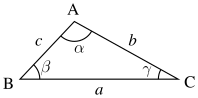Рис. 1. Треугольник

На рис. 1, a, b, и c — это длины трёх сторон треугольника, и α, β, и γ — это углы, лежащие соответственно напротив этих трёх сторон (противолежащие углы). Теорема тангенсов утверждает, что

a−ba+b=tgα−β2tgα+β2.{\displaystyle {\frac {a-b}{a+b}}={\frac {\mathrm {tg} {\frac {\alpha -\beta }{2}}}{\mathrm {tg} {\frac {\alpha +\beta }{2}}}}.}

Доказать теорему тангенсов можно с помощью теоремы синусов:

asin⁡α=bsin⁡β.{\displaystyle {\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}.}

Пусть

d=asin⁡α=bsin⁡β,{\displaystyle d={\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }},}

откуда

a=dsin⁡α{\displaystyle a=d\sin \alpha }

b=dsin⁡β.{\displaystyle b=d\sin \beta .}

Отсюда следует, что

a−ba+b=dsin⁡α−dsin⁡βdsin⁡α+dsin⁡β=sin⁡α−sin⁡βsin⁡α+sin⁡β.{\displaystyle {\frac {a-b}{a+b}}={\frac {d\sin \alpha -d\sin \beta }{d\sin \alpha +d\sin \beta }}={\frac {\sin \alpha -\sin \beta }{\sin \alpha +\sin \beta }}.}

Используя известное тригонометрическое тождество

sin⁡α±sin⁡β=2sin⁡α±β2cos⁡α∓β2,{\displaystyle \sin \alpha \pm \sin \beta =2\sin {\frac {\alpha \pm \beta }{2}}\cos {\frac {\alpha \mp \beta }{2}},\;}

получаем:

a−ba+b=sin⁡α−sin⁡βsin⁡α+sin⁡β=2sin⁡α−β2cos⁡α+β22sin⁡α+β2cos⁡α−β2=tgα−β2tgα+β2.◼{\displaystyle {\frac {a-b}{a+b}}={\frac {\sin \alpha -\sin \beta }{\sin \alpha +\sin \beta }}={\frac {2\sin {\frac {\alpha -\beta }{2}}\cos {\frac {\alpha +\beta }{2}}}{2\sin {\frac {\alpha +\beta }{2}}\cos {\frac {\alpha -\beta }{2}}}}={\frac {\mathrm {tg} {\frac {\alpha -\beta }{2}}}{\mathrm {tg} {\frac {\alpha +\beta }{2}}}}.\qquad \blacksquare }

Вместо формулы для суммы и разности синусов двух углов, в доказательстве можно использовать следующее известное тождество

tgα±β2=sin⁡α±sin⁡βcos⁡α+cos⁡β{\displaystyle \mathrm {tg} {\frac {\alpha \pm \beta }{2}}={\frac {\sin \alpha \pm \sin \beta }{\cos \alpha +\cos \beta }}}.

a+bc=cos⁡A−B2sin⁡C2;{\displaystyle {\frac {a+b}{c}}={\frac {\operatorname {cos} {\frac {A-B}{2}}}{\operatorname {sin} {\frac {C}{2}}}};}

a−bc=sin⁡A−B2cos⁡C2.{\displaystyle {\frac {a-b}{c}}={\frac {\operatorname {sin} {\frac {A-B}{2}}}{\operatorname {cos} {\frac {C}{2}}}}.}

где A,B,C{\displaystyle A,\;B,\;C} — значения углов при соответствующих вершинах треугольника и a,b,c{\displaystyle a,\;b,\;c} — длины сторон соответственно между вершинами B{\displaystyle B}и C{\displaystyle C}, C{\displaystyle C}и A{\displaystyle A}, A{\displaystyle A}и B{\displaystyle B}.

• Деля порознь правые и левые части двух последних равенств и приравнивая два полученных результата друг другу, имеем

a+ba−b=ctgC2tgA−B2.{\displaystyle {\frac {a+b}{a-b}}={\frac {\mathrm {ctg} {\frac {C}{2}}}{\mathrm {tg} {\frac {A-B}{2}}}}.}

• С учетом того, что ctgC2=ctgπ−A−B2=tgA+B2{\displaystyle \mathrm {ctg} {\frac {C}{2}}=\mathrm {ctg} {\frac {\pi -A-B}{2}}=\mathrm {tg} {\frac {A+B}{2}}}, окончательно имеем:

a+ba−b=tgA+B2tgA−B2,{\displaystyle {\frac {a+b}{a-b}}={\frac {\mathrm {tg} {\frac {A+B}{2}}}{\mathrm {tg} {\frac {A-B}{2}}}},}

что и требовалось доказать.