Металлы электропроводность — Справочник химика 21

    Электропроводность различных металлов различна. Наибольшей электропроводностью обладает серебро у других металлов электропроводность уменьшается в следующем порядке Ag, Си, Аи, Сг, А1, М , Ыа, 1г, Ве, КЬ, 2п. [c.219]

    Сопоставьте свойства п объясните различия разбавленной и концентрированной серной кислоты (действие на металлы, электропроводность, водоотнимающее действие). [c.230]

    Характерные свойства металлов — электропроводность и теплопроводность, в частности, зависят от передвижения электронов внутри решетки. Под воздействием внешнего электрического поля валентные электроны, число которых у атомов металлов невелико (1,2 или 3)-, перемещаются в направлении поля, создавая электрическую проводимость. [c.136]

    Подготовка поверхности неорганических диэлектриков К неорганическим диэлектрикам относятся керамика, стекло фарфор слюда ситаллы ферриты Металлизацию неорганических диэлектриков применяют для придания поверхности деталей свойств металла электропроводности способности к пайке, теплопроводности Металлизацию стекла используют для получения зеркал Силикатные материалы (стекло кварц ситаллы, слюда ИТ п ) подвергают сначала химическому обезжириванию а затем обработке в хромовой смеси и в растворе плавиковой кислоты  [c. 37]

    Физические свойства определяются видом щелочного металла. Электропроводность МСС выше, чем у применяемого для этого синтеза графита, по оси а в 10 раз, по оси с в 200 раз. Температурный коэффициент электросопротивления положительный, т. е. носит металлический характер. Аналогичные изменения наблюдаются у МСС щелочной металл (Аг)-графит. 

[c.273]

    Нитриды металлических элементов, как правило, тугоплавки и мало летучи. Расплавленные нитриды щелочных металлов электропроводны. Нитриды неметаллических элементов немногочисленны, и свойства их изучены еш,е недостаточно. [c.57]

    Важное свойство металлов — электропроводность, которое обусловлено наличием подвижных в кристаллической решетке металлов электронов. При обычных условиях наилучшей электрической проводимостью из всех металлов обладает серебро. Из элементов-металлов лишь германий является полупроводником (по электрической проводимости он занимает промежуточное место между проводниками и диэлектриками).

Возможностью перемещения электронов объясняется и высокая теплопроводность металлов. [c.196]

    Огромное большинство неорганических тел относится к категории полупроводников. Их удельная электропроводность меньше 10 Ом см В отличие от металлов электропроводность полупроводников растет с температурой. [c.516]

    В некоторых естественных в узком смысле слова подгруппах металлов электропроводность с возрастанием заряда ядра падает. Ниже приведены для некоторых металлов значения электропроводности в обратных омах, умноженные на 10  

[c.219]

    Графит хорошо проводит тепло (в 3 раза лучше ртути) и обладает близкой к металлам электропроводностью (0,1 от электропроводности ртути). И электро- и теплопроводность больше параллельно слоям, чем перпендикулярно им. Максимум теплопроводности графита наблюдается около 0°С, а электропроводности — около 600 °С. Механическая прочность графита при переходе от обычных температур к 2500 °С возрастает почти вдвое. Его сжимаемость примерно в 20 раз больше сжимаемости алмаза. Заметное окисление графита при нагревании на воздухе наступает лишь выше 700 С. 

[c.502]

    При Повышении температуры металла электропроводность его уменьшается. Причиной этого являются тепловые колебания положительных ионов металла. Амплитуда этих тепловых колебаний с повышением температуры увеличивается, что препятствует свободному перемещению электронов. [c.68]

    ПОЛУПРОВОДНИКИ — вещества с электронной проводимостью, величина электропроводности которых лежит между электропроводностью металлов и изоляторов. Характерной особенностью П. является положительный температурный коэффициент электропроводности (в отличие от металлов). Электропроводность П. зависит от температуры, количества и природы примесей, влияния электрического поля, света и других внешних факторов. К П. относятся простые вещества — бор, углерод (алмаз), кремний, германий, олово (серое), селен, теллур, а также соединения — карбид кремния, соединения типа filmen (инднй — сурьма, индий — мышьяк, галлий — сурьма, алюминий — сурьма), соединения двух или трех элементов, в состав которых входит хотя бы один элемент IV—VII групп периодической системы элементов Д.

И. Менделеева, некоторые органические вещества — полицены, азоаромати-ческие соединения, фталоцианин, некоторые свободные радикалы и др. К чистоте полупроводниковых материалов предъявляют повышенные требования, например, в германии контролируют примеси 40 элементов, в кремнии — 27 элементов и т. д. Тем не менее некоторые примеси придают П. определенные свойства и тип проводимости, а потому и являются необходимыми. Содержание примесей не должно превышать 10 —Ш %. П. применяются в приборах в виде монокристаллов с точно определенным содержанием примесей. Применение П. в различных отраслях техники, в радиотехнике, автоматике необычайно возросло в связи с большими преимуществами полупроводниковых приборов — они экономичны, надежны, имеют высокий КПД, малые размеры и др. 

[c.200]

    Атомы металлов в твердой и жидкой фазах образуют в основном плотноупакованные структуры. При плавлении металлов электропроводность а обычно падает примерно в 1,5—2 раза. При повышении температуры жидкого металла электропроводность уменьшается, но медленнее, чем у твердых металлов.

В жидких свинце и висмуте электропроводность почти не зависит от температуры, а у жидких цинка, кадмия и ртути она даже растет с увеличением температуры. Число электронов проводимости в единице объема жидких металлов часто почти совпадает с числом валентных электронов. Подвижность электронов в металлах, как было показано А. Р. Регелем [7], при плавлении меняется мало. Плотность жидких металлов меняется при их затвердевании незначительно. Сжимаемость жидких металлов, как и твердых, мала. Она примерно на порядок меньше сжимаемости жидких диэлектриков.  [c.169]

    Таким образом, при добавлении титранта (МОН) ионы Н+ заменяются ионами металла, а концентрация аниона остается неизменной. До точки эквивалентности число ионных частиц неизменно, только ионы водорода замещаются на ионы металла, и поскольку подвижность ионов водорода существенно вьппе подвижности ионов металла, электропроводность раствора падает, пока не достигается точка эквивалентности. После точки эквивалентности электропроводность определяется избытком гидроксид-ионов и возрастает с увеличением коицентрации титранта.

Кривая титрования сильной кислоты сильным основанием имеет У-образную форму. [c.379]

    Ковалентно-металлические связи. Полупроводники. В 6 мы уже упоминали, что наряду с металлами, обладающими большой электропроводностью, и изоляторами, которые практически ток не проводят, существует широкий класс кристаллических веществ, обладающих слабой (по сравнению с металлами) электропроводностью, причем температурная зависимость электропроводности таких кристаллов резко отлична от температурной зависимости электропроводности металлов (с повышением [c.214]

    Применение диэлектриков с металлическими покрытиями позволяет заменять легкие сплавы и цветные металлы (например, цинковые сплавы при изготовлении многих изделий сложной конфигурации), резко снижать массу и себестоимость конструкций, соединять детали пайкой, придавать их поверхности свойства металлов (электропроводность и магнитные свойства, экранирование от воздействий электрического и магнитного полей, газовых разрядов, дру- 

[c. 3]

    Исходя из этого представления о механизме собственно моющего действия присадок к моторным маслам, наибольшей собственно моющей эффективностью должны обладать присадки, которые при растворении в маслах образуют наибольшее количество частиц, несущих самый высокий электрический заряд, т. е. растворы таких присадок в маслах должны обладать наибольшей эквивалентной (по металлу) электропроводностью. 

[c.219]

    Металлы могут растворяться в расплавах солей и взаимодействовать, давая ионы металлов в неустойчивом валентном состоянии, что создает сложности при электролитическом получении металлов. Электропроводность таких растворов очень высока (ввиду избытка свободных электронов), и законы Фарадея неприменимы к подобным расплавам. [c.176]

    Легко понять, что величина электропроводности зависит от числа носителей тока и от их подвижности. Количество электронов, переносящих электричество в металле, от температуры не зависит. Однако при повышении температуры увеличивается взаимодействие электронов с ионами, и электропроводность падает.

В противоположность металлам электропроводность полупроводников при повышении температуры растет. Это может быть объяснено только тем, что возрастание температуры приводит к увеличению в них концентрации электронов, способных переносить ток. [c.265]

    Второе характерное свойство металлов — электропроводность. В отличие от большинства неметаллических сред металлы проводят электрический ток, не претерпевая при этом химических изменений. Поэтому без металлов немыслима была бы электротехника, в частности передача электроэнергии на большие расстояния от ее источника. [c.442]

    В более концентрированных растворах сольватированные ионы металла оказываются связанными в кластеры, а в области концентраций, больших 1 моль, растворы по свойствам приближаются к металлам. В последнем случае аммонизированные ионы металла удерживаются морем электронов , аналогично тому, что, имеет место в металле. Электропроводность растворов в аммиаке аномально большая при всех концентрациях, но особенно велика она в области больших концентраций и приближается к электропроводности металлического проводника. С позиций окислительно-510 [c.510]

    Марганец, обладая более устойчивым строением валентного слоя электронов (d s ), в меньшей степени склонен к образованию металлообразных соединений. Марганец и рений образуют только силиды, обладающие металлической электропроводностью, а карбиды, нитриды и бориды этих металлов электропроводностью такого типа не обладают. [c.123]

    Вначале оба металла получают в виде порошка грязно-серого цвета, но после переплавки они превращаются в блестящие, с серебристым оттенком плотные слитки по внешнему виду и свойствам это типичные металлы. Электропроводность их составляет приблизительно 30% электропроводности серебра. Они исключительно тугоплавки Мо плавится при 2610°, а W при 3380°. [c.359]

    Согласно электронной теории металлов электропроводность а=1/р и теплопроводности Я объясняют движением электронов, но физические сущности этих свойств-различны. Закон Виде-мана — Франца, связывающий эти свойства, имеет всеобщий характер. Анализ этого закона на основе представлений электроотрицательности металлов позволил выяснить, что значение Яр различно для электроположительных, электроотрицательных и переходных металлов. Кроме того, для электроотрицательных металлов (А1, Си, 2п, kg, 5п, 8Ь, Аи, Т1, РЬ и В1) произведение кр возрастает с увеличением Р = 1г.  [c.80]

    С повышением валентности металла электропроводность хлоридов уменьшается для повышения электропроводности таких расплавов к ним добавляют хлориды щелочных металлов. Данные по вязкости и плотности в системе NaF — AIF3 (гл. XI) говорят, например, о наличии криолита, как химического соединения не только в твердом (о чем говорит диаграмма плавкости), айв жидком состоянии. О наличии в расплаве магниевой ванны карналлита как химического соединения говорят кривые плотности, вязкости удельной электропроводности, (гл. XII). [c.409]

    Железо, кобальт и никель- серебристо-белые металлы, электропроводные, ковкие, обладающие магнитными свойствами.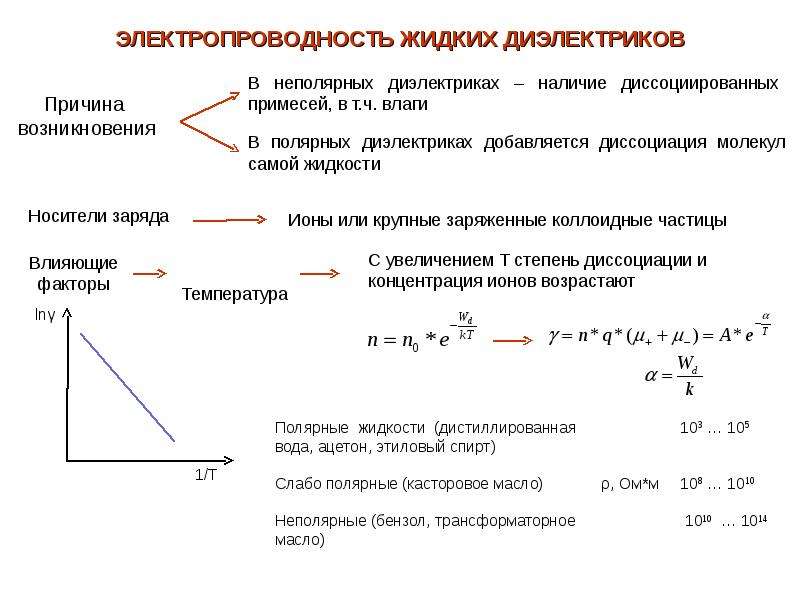  [c.211]

    При повышении температуры металла электропроводность его уменьшается. Причиной этого являются тепловые колебания положительных ионов металла. Амплитуда этих тепловых колебаний с повышением температуры увеличивается, что препятствует свободному перемещению электронов. При температуре, которая на 100° выше точки плавления металла, электропроводность понижается по линейному закону, делается исчезающе малой. При переходе в парообразное состояние следует ожидать еще более резкого падения электропроводности. При понижении температуры электропроводность металлов увеличивается вначале линейно, а при низких температурах необычайно быстро. Так, при температуре —260° С электропроводность серебра почти в 50 раз больше, чем при0°С. Камерлинг-Оннесом были проведены работы по измерению электропроводности металлов при очень низких [c.218]

    Несмотря на достигнутые успехи, вопрос об электронных полупроводниках остается и поныне одним из важнейших в тематике ЛФТИ. Однако в 40-е годы Абрам Федорович дал ему новое направление, связав электроппыс полупроводники не столько с типичными диэлектриками, в которые многие из них превраш аются при низких температурах, сколько с типичными металлами. Электропроводность металлов, как известно, не только не уменьшается, но, наоборот, увеличивается при понижении температуры. Опыты, проведенные Ю. П. Маслаковцем, Е. Д. Девятковой, Ю. А. Дунаевым и другими по указанию А. Ф. Иоффе, показали, во-первых, что многие полупроводники с проводимостью, обусловленной примесями (например, РЬЗд), при достаточно большом содержании последних или при достаточно низких температурах ведут себя фактически как металлы. При этом роль примесей в кристаллах типа СнзО играют избыточные (по отношению к химической формуле) атомы металла (Си) или металлоида (О). [c.19]

    Вследствие весьма прочной связи ионита с катионом образовавшаяся внутрикомплексная соль обладает очень низкой степенью диссоциации. Об этом свидетельствует низкая электропроводность порядка 10″ сим1см для солей формы того же ионита содержащей щелочные металлы, электропроводность составляет величину порядка 10″ сим1см.  [c.71]

    Таким образом, при Т 0 К могут существовать только два вида вещества — кепроводники (изоляторы) и проводники, Прн повышсини температуры вещества начинаются тепловые колебания атомов в решетке, тем большие, чем выше температура. Эти 1- олебания препятствуют движению электронов. Поэтому в проводника.х типа металла электропроводность с повышением температуры снижается. [c.282]

    Электрич. св-ва С.н. зависят от состава и т-ры среды-С.н. могут бьггь диэлектриками, полупроводниками или проводниками. Большая группа оксидных С.н. (силикатные, боратные, фосфатные) относится к классу изоляторов почти идеальный изолятор-кварцевое С.н. Поскольку носители тока в оксидных С.н.-катионы щелочных и щел.-зем. металлов, электропроводность, как правило, возрастает с увеличением их содержания в С. н. и повыщением т-ры. Стеклянные изоляторы используют для высоковольтных линий электропередач. Пригодность элежтротех-нических С.н. для работы в тех шш иных температурных условиях зависит от их состава и оценивается по т-ре (ТКюо), при к-рой С. н. имеет уд. электрич. проводимость [c.423]

    Одргако для металлов все же наиболее характерно, что электроны последней зоны можно рассматривать как почти свободные, вся совокупность этпх электронов участвует в образовании металлической связи, а та часть электронов, которая расположена в квантовых ячейках вблизи поверхности Ферми, ответственна за специфические физические свойства металлов (электропроводность, теплопроводность и т. п.). [c.203]

    Электропроводность ионных кристаллов очень различна у твердого тела и у расплава, поскольку она является следствием движения ионов, т. е. она является электролитической проводимостью в противоположность электронной проводимости в л еталлах. Электропроводность ионных кристаллов, зa eтнaя только при температурах, близких к точке плавления, составляет около 10 о.и см и быстро уменьшается с температурой. У расплавленных галогенидов характерная электропроводность находится в пределах от 0,1 до 10 о.и см (при температурах несколько выше точки плавления). С другой стороны, электрические и оптические свойства металлов (электропроводность. [c.138]

    Благодаря высокой электропроводности углеродных волокон карбоволокниты могут выполнять функции антистатических или радиопоглощающих материалов, применяться в качестве электропроводящих панелей радиационного отопления и антиобледенителей самолетов. Такая отопительная система, в которой конструкционный волокнит является одновременно тепловыделяющим материалом, экономична и ее можно полностью автоматизировать. В этом случае эффективность применения волокнита зависит от выбора связующего. Электрическое сопротивление последнего понижают введением порошка графита, саж, тонкодисперсных частиц металлов. Электропроводность углеродного наполнителя способствует сокращению продолжительности формования толстостенных изделий из карбоволокнита, обеспечивая равномерный и быстрый прогрев заготовки пропусканием электрического тока по наполнителю [61]- [c.230]

    Серебро обладает наивысшей среди металлов электропроводностью. Содержание металла в лакокрасочных материалах зависит от того, каким способом их наносят на отделываемую поверхность. При нанесении кистью оно не менее 50%, при распылении 35%, а при шелкографическом методе должно доходить до 60%, Токопроводящие лакокрасочные материалы приготовляют диспергированием порошка серебра в растворе связующего в органическом растворителе. Поверхность пластмассы покрывают лакокрасочными композициями, высыхающими на воздухе или отверждающимися на холоду. Покрытия горячего отверждения наносят [c.141]

---

Электропроводность металлов и полупроводников | Квантовая физика

Содержание работы

Электропроводность есть способность тела пропускать электрический ток под действием электрического поля. Для характеристики этого явления служит величина удельной электропроводности σ. Как показывает теория [1-3], величину σ можно выразить через концентрацию n свободных носителей заряда, их заряд е, массу m, время свободного пробега τ_e, длину свободного пробега λe и среднюю дрейфовую скорость носителей заряда. Для металлов в роли свободных носителей заряда выступают свободные электроны, так что:

σ = ne² · τе / m = (n · e² /  m) · (λe  / < v >) = e · n · u

(10.1)

где u — подвижность носителей, т.е. физическая величина, численно равная дрейфовой скорости, приобретенной носителями в поле единичной напряженности , а именно

u = < v > / E = (e · τ_е) / m

В зависимости от σ все вещества подразделяются; на проводники — с σ > 10⁶ (Ом · м)^-1, диэлектрики — с σ > 10^-8 (Ом · м)^-1 и полупроводники — с промежуточным значением σ.

С точки зрения зонной теории деление веществ на проводники, полупроводники и диэлектрики определяется тем, как заполнена электронами при 0 К валентная зона кристалла: частично или полностью.

Энергия, которая сообщается электронам даже слабым электрическим полем, сравнима с расстоянием между уровнями в энергетической зоне. Если в зоне есть свободные уровни, то электроны, возбужденные внешним электрическим полем, будут заполнять их. Квантовое состояние системы электронов будет изменяться, и в кристалле появится преимущественное (направленное) движение электронов против поля, т.е. электрический ток. Такие тела (рис.10.1,а) являются проводниками.

Если валентная зона заполнена целиком, то изменение состояния системы электронов может произойти только при переходе их через запрещенную зону. Энергия внешнего электрического поля такой переход осуществить не может. Перестановка электронов внутри полностью заполненной зоны не вызывает изменения квантового состояния системы, т.к. сами по себе электроны неразличимы.

В таких кристаллах (рис. 10.1,б) внешнее электрическое поле не вызовет появление электрического тока, и они будут непроводниками (диэлектриками). Из этой группы веществ выделены те у которых ширина запрещенной зоны ΔE ≤ 1 эВ (1эВ = 1,6 · 10^-19 Дж).

Переход электронов через запрещенную зону у таких тел можно осуществить, например, посредством теплового возбуждения. При этом освобождается часть уровней — валентной зоны и частично заполняются уровни следующей за ней свободной зоны (зоны проводимости). Эти вещества являются полупроводниками.

Согласно выражению (10.1) изменение электропроводности (электрического сопротивления) тел с температурой может быть вызвано изменением концентрации n носителей заряда или изменением их подвижности u .

Металлы

Квантово-механические расчеты показывают, что для металлов концентрация n свободных носителей заряда (электронов) равна:

n = (1 / 3π²) · (2mE_F / ђ²)^3/2

(10.2)

где ђ = h / 2π = 1,05 · 10^-34 Дж · с — нормированная постоянная Планка, E_F — энергия Ферми.

Так как E_F практически от температуры T не зависит, то и концентрация носителей заряда от температуры не зависит. Следовательно, температурная зависимость электропроводности металлов будет полностью определяться подвижностью u электронов, как и следует из формулы (10.1). Тогда в области высоких температур

u ~ λ_e / <v> ~ T^-1

(10. 3)

а в области низких температур

u ~ λ_e / <v> ~ const (T).

(10.4)

Степень подвижности носителей заряда будет определяться процессами рассеяния, т.е. взаимодействием электронов с периодическим полем решетки. Так как поле идеальной решетки строго периодическое, а состояние электронов — стационарное, то рассеяние (возникновение электрического сопротивления металла) может быть вызвано только дефектами (примесными атомами, искажениями структуры и т.д.) и тепловыми колебаниями решетки (фононами).

Вблизи 0 К , где интенсивность тепловых колебаний решетки и концентрация фононов близка к нулю, преобладает рассеяние на примесях (электрон-примесное рассеяние). Проводимость при этом практически не меняется, как следует из формулы (10.4), а удельное сопротивление

имеет постоянное значение, которое называется удельным остаточным сопротивлением ρ_ост или удельным примесным сопротивлением ρ_прим, т.е.

ρ_ост (или ρ_прим) = const (T)

(10. 5)

В области высоких температур у металлов становится преобладающим электрон-фононный механизм рассеяния. При таком механизме рассеяния электропроводность обратно пропорциональна температуре, как видно из формулы (10.3), а удельное сопротивление прямо пропорционально температуре:

График зависимости удельного сопротивления ρ от температуры приведен на рис. 10.2

При температурах отличных от 0 К и достаточно большом количестве примесей могут иметь место как электрон-фононное, так и электрон-примесное рассеяние; суммарное удельное сопротивление имеет вид

ρ = ρ_прим + ρ_ф

(10.6)

Выражение (10.6) представляет собой правило Матиссена об аддитивности сопротивления. Следует отметить, что как электрон-фононное, так и электрон-примесное рассеяние носит хаотический характер.

Полупроводники

Квантово-механические расчеты подвижности носителей в полупроводниках показали, что, во-первых, с повышением температуры подвижность носителей u убывает, и решающим в определении подвижности является тот механизм рассеяния, который обуславливает наиболее низкую подвижность.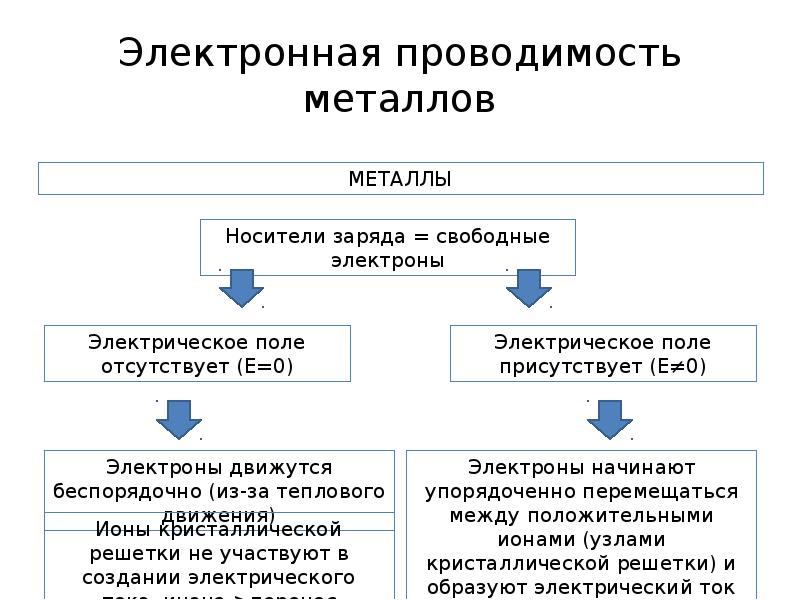 Во-вторых, зависимость подвижности носителей заряда от уровня легирования (концентрации примесей) показывает, что при малом уровне легирования подвижность будет определяться рассеянием на колебаниях решетки и, следовательно, не должна зависеть от концентрации примесей.

При высоких уровнях легирования она должна определяться рассеиванием на ионизированной легирующей примеси и уменьшаться с увеличением концентрации примеси. Таким образом, изменение подвижности носителей заряда не должно вносить заметного вклада в изменение электрического сопротивления полупроводника.

В соответствии с выражением (10.1) основной вклад в изменение электропроводности полупроводников должно вносить изменение концентрации п носителей заряда [1-3].

Главным признаком полупроводников является активационная природа проводимости, т.е. резко выраженная зависимость концентрации носителей от внешних воздействий, как-то температуры, облучения и т.д. Это объясняется узостью запрещенной зоны (ΔЕ < 1 эВ) у собственных полупроводников и наличием дополнительных уровней в запрещенной зоне у примесных полупроводников.

Электропроводность химически чистых полупроводников называется собственной проводимостью. Собственная проводимость полупроводников возникает в результате перехода электронов (n) с верхних уровней валентной зоны в зону проводимости и образованием дырок (p) в валентной зоне:

σ = σ_n + σ_ρ = e · n_n · u_n + e · n_ρ · u_ρ

(10.7)

где n_n и· n_ρ — концентрация электронов и дырок,
u_n и u_ρ — соответственно их подвижности,
e — заряд носителя.

С повышением температуры концентрация электронов в зоне проводимости и дырок в валентной зоне экспоненциально возрастает:

n_n = u_nо · exp(-ΔE / 2kT) = n_ρ = n_ρо· exp(-ΔE / 2kT)

(10.8)

где n_nо и n_pо — концентрации электронов и дырок при Т → ∞,
k = 1,38 · 10^–23 Дж/ К — постоянная Больцмана.

На рисунке 10.3,а приведен график зависимости логарифма электропровод-ности ln σ собственного полупроводника от обратной температуры 1 / Т : ln σ = = ƒ(1 / Т). График представляет собой прямую, по наклону которой можно опреде-лить ширину запрещенной зоны ∆Е.

Электропроводность легированных полупроводников обусловлена наличием в них примесных центров. Температурная зависимость таких полупроводников определяется не только концентрацией основных носителей, но и концентрацией носителей, поставляемых примесными центрами. На рис. 10.3,б приведены графики зависимости ln σ = ƒ (1 / Т) для полупроводников с различной степенью легирования (n1

Для слаболегированных полупроводников в области низких температур преобладают переходы с участием примесных уровней. С повышением температуры растет концентрация примесных носителей, значит растет и примесная проводимость. При достижении т. А (см. рис. 10.3,б; кривая 1) – температуры истощения примеси Т_S1 – все примесные носители будут переведены в зону проводимости.

Выше температуры Т_S1 и до температуры перехода к собственной проводимости Т_i1 (см. т. В, кривая 1, рис. 10.3,б) электропроводность падает, а сопротивление полупроводника растет. Выше температуры Т_i1 преобладает собственная электропроводность, т.е. в зону проводимости вследствие теплового возбуждения переходят собственные носители заряда. В области собственной проводимости σ растет, а ρ падает.

Для сильнолегированных полупроводников, у которых концентрация примеси n ~ 10²⁶ м^–3, т.е. соизмерима с концентрацией носителей заряда в металлах (см. кривая 3, рис. 10.3,б), зависимость σ от температуры наблюдается только в области собственной проводимости. С ростом концентрации примесей величина интервала АВ (АВ > A’B’ > A»B») уменьшается (см. рис. 10.3,б).

Как в области примесной проводимости, так и в области собственной проводимости преобладает электрон-фононный механизм рассеяния. В области истощения примеси (интервалы AB, A’B’, A»B») вблизи температуры Т_S преобладает электрон-примесное рассеяние. По мере увеличения температуры (перехода к Т_i) начинает преобладать электрон-фононное рассеяние. Таким образом, интервал АВ (A’B’ или A»B»), называемый областью истощения примеси, является также областью перехода от механизма примесной проводимости к механизму собственной проводимости.

Лабораторная работа №1 изучение зависимости сопротивления металлов и полупроводников от температуры

ПРЕДИСЛОВИЕ

Учебное пособие состоит из четырех глав и приложения. Пер-вая глава посвящена изучению влияния температуры на проводи-мость полупроводников и металлов. Опираясь на квантовую тео-рию электропроводности, показано, в результате каких явлений проводимость полупроводников и металлов по-разному меняется с ростом температуры. Для полупроводников рассчитывается энергия активации примесей – важнейшая характеристика при-месных полупроводников. Вторая и третья главы посвящены вза-имодействию света с полупроводниками. Представленные в этих главах теория и эксперимент позволяют получить очень важные характеристики полупроводников: ширину запрещенной зоны собственных полупроводников и рассчитать такие значимые ха-рактеристики как диффузионную длину и подвижность носителей заряда в p—n переходе под действием облучения. В четвертой гла-ве представлены физические основы работы транзистора, что позволяет глубже уяснить вопросы переноса зарядов в электри-ческом поле. В этой главе также представлен расчет внутренних параметров транзистора. В конце каждой лабораторной работы приведены по 30 контрольных вопросов для самостоятельного усвоения материала студентом.

В приложении приведены справочные данные: основные фи-зические постоянные, соотношение между внесистемными еди-ницами и единицами системы CИ, данные об удельных сопротив-лениях и температурных коэффициентах сопротивления метал-лов, приведены типичные зависимости коэффициентов поглоще-ния для полупроводников и спектральной чувствительности от длины волны.

Авторы выражают глубокую благодарность всем преподава-телям и сотрудникам кафедры «Физика», участвовавшим в об-суждении лабораторных работ.

Авторы благодарят студента МАТИ Никитина Игоря за по-мощь в создании настоящего учебного пособия.

Особую благодарность авторы выражают инженеру Борису Владимировичу Зверлову за работу по усовершенствованию экс-периментальных установок и созданию новых лабораторных ра-бот.

Лабораторная работа №1

Изучение зависимости сопротивления металлов и полупроводников от температуры

ЦЕЛЬ РАБОТЫ

Цель данной работы состоит в экспериментальном изу-чении зависимости сопротивления металлов и полупро-водников от температуры и в измерении температурных коэффициентов сопротивления.

ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ

С точки зрения способности проводить электрический ток все вещества делятся на три класса: проводники, полупро-водники и диэлектрики (изоляторы). Электрическое сопро-тивление полупроводников занимает промежуточное значе-ние между сопротивлением металлов и диэлектриков. Удель-ная электропроводность (или просто проводимость) метал-лов () имеет порядок (10⁸…10⁶) Ом^-1м^-1, диэлектриков (10¹⁵÷…10^-18) Ом^-1м^-1 полупроводников (10²…10^-11) Ом^-1м^-1. Удельное сопротивление проводников зависит от проводи-мости: . Для металлов удельные сопротивления имеют значения порядка 10⁷…10⁸ Омм.

Фундаментальным законом в этой области является за-кон Ома (в локальной форме), который можно записать в виде:

(1)

где – вектор плотности тока,

– вектор напряженности электрического поля внутри проводника.

Формула (1) называется законом Ома в дифференциаль-ной форме. Для вычисления силы тока, проходящего по проводнику, необходимо знать скорость, которую приоб-ретают электроны под действием электрического поля. Эта скорость () называется дрейфовой, и хотя она нам-ного меньше скорости теплового хаотического движения электронов, именно дрейфовая скорость определяет силу тока в проводнике. Дрейфовая скорость – это средняя ско-рость направленного движения носителей заряда. Если концентрация носителей тока равна , то плотность тока равна:

(2)

где е – элементарный электрический заряд.

Средняя дрейфовая скорость носителей тока прямо пропорциональна внешнему электрическому полю:

(3)

где – коэффициент пропорциональности, называемый «подвижность носителей тока». Из формулы (3) виден фи-зический смысл подвижности: подвижность носителей то-ка численно равна дрейфовой скорости носителей в элек-трическом поле единичной напряженности. Подвижность носителей является константой данного материала и зависит от температуры.

Согласно квантовой теории электропроводности прово-димость твердого тела определяется следующим соотно-шением:

. (4)

Подвижность носителей заряда определяется по этой теории следующим образом:

, (5)

где – средняя длина свободного пробега электрона;

– эффективная масса электрона в металле;

– средняя общая скорость движения электронов, равная сумме средней скорости теплового хаотического движения и дрейфовой скорости (), при этом обычно .

Физической причиной возникновения сопротивления электрическому току является взаимодействие электронов с реальной кристаллической средой, в которой движутся электроны. При этом согласно квантовой теории проводи-мости столкновения электронов (рассеяние электронных волн) происходят с какими-либо нарушениями периоди-ческой структуры кристалла: тепловыми колебаниями, примесными атомами, дислокациями, границами зёрен и другими дефектами. Поэтому в 100…1000 раз больше, чем расстояние между атомами металла.

Рассмотрим, какой характер температурной зависимос-ти проводимости вытекает из формул (4) и (5). Величина для металлов (в них электронный газ вырожден) имеет смысл скорости электронов, которые могут ускоряться под действием электрического поля. Это электроны, которые имеют энергию, близкую к энергии уровня Ферми , т.е. энер-гии, которой обладают электроны в металле при абсолют-ном нуле (V=V_ф). Так как концентрация электронов в ме-таллах практически не зависит от температуры, то темпе-ратурная зависимость проводимости в данном случае оп-ределяется температурной зависимостью подвижности но-сителей заряда (см. формулу (4)). Скорость электронов на уровне Ферми примерно на порядок больше, чем средняя скорость теплового движения, и очень слабо зависит от температуры, поэтому из всех величин, входящих в фор-мулу (5), в металлах только величина проявляет за-метную зависимость от температуры.

Зависимость от температуры объясняется тем, что чем интенсивнее тепловое движение, тем больше вероят-ность рассеивания электронов на кристаллической решет-ке и тем меньше длина свободного пробега электрона (). Отсюда следует: и .

Таким образом, сопротивление металлического провод-ника прямо пропорционально температуре:

(6)

где R₀ – сопротивление металлического проводника при 20 С;

t – температура, С;

 – температурный коэффициент сопротивления металла.

При низкой температуре, которая много меньше комнат-ной, в действие вступают другие механизмы рассеяния элек-тронов и функциональный характер зависимости изменя-ется, зависимость R(T) становится нелинейной ().

Напомним, что для невырожденного электронного газа , равная средней скорости теплового движения элект-ронов, вычисляется по известной формуле молекулярно-кинетической теории газов:

, (7)

где k – постоянная Больцмана.

В полупроводниках имеются носители тока двух видов: электроны и дырки – поэтому для полупроводников фор-мула (4) примет вид:

, (8)

где n_e, _e – концентрация и подвижность электронов;

n_p, _p – концентрация и подвижность дырок.

В полупроводниках, как и в металлах, подвижность но-сителей тока зависит от температуры, но характер темпе-ратурной зависимости проводимости определяется более сильной зависимостью концентрации носителей тока от температуры, в то время как у металлов концентрация сво-бодных электронов от температуры не зависит. При уве-личении температуры увеличивается вероятность теплового возбуждения электронов в зону проводимости и дырок в валентной зоне, то есть с ростом температуры сильно воз-растает концентрация носителей заряда. Из формулы (8) видно, что в полупроводниках температурная зависимость проводимости определяется зависимостью концентрации носителей зарядов от температуры.

В области собственной проводимости полупроводников температурная зависимость проводимости носит экспо-ненциальный характер:

(9)

где – ширина запрещенной зоны.

В области примесной проводимости полупроводников, когда носители заряда оказываются одного типа (т.е. име-ются примесные, либо акцепторные), эта зависимость име-ет аналогичный вид:

(10)

В случае частично скомпенсированных проводников, когда имеются примеси двух типов, температурная зави-симость проводимости принимает следующий вид:

, (11)

где – константа данного полупроводника;

– энергия активации примеси;

– константа Больцмана;

Т – температура, К.

Таким образом, при экспоненциальной зависимости кон-центрации носителей тока от температуры, именно эта за-висимость и будет определять характер температурной за-висимости проводимости полупроводника.

Если примесный полупроводник является полупровод-ником n-типа, то Е_акт определяет глубину расположения донорных уровней относительно дна зоны проводимости (Е_д=Е_акт), т. е. ту энергию, которая необходима для отры-ва электронов от атома примеси и перевода в зону прово-димости, где он может свободно перемещаться по крис-таллу.

Если полупроводник p-типа, то Е_акт определяет энер-гетическое положение акцепторных уровней относительно вершины валентной зоны (Е_а=Е_акт) (см. рис.1).

В настоящей работе измеряется зависимость R(T) тер-морезистора – полупроводникового прибора, в котором для практических целей используется сильная зависи-мость сопротивления полупроводникового материала от температуры. В том интервале температур, где имеет мес-то примесная проводимость, сопротивление полупровод-ника уменьшается с увеличением температуры по экс-поненциальному закону:

(12)

где R₀, A – константы для данного типа терморезистора, при этом константа А связана со свойствами полупро-водникового материала, из которого изготовлен терморе-зистор, соотношением:

(13)

Логарифмируя формулу (12), получим:

(14)

Зависимость (14), построенная в осях: x=1/T, y=lnR, является прямой линией, тангенс наклона которой к оси Х равен константе А. Получение из опытных данных прямой линии в зависимости lnR от 1/T является доказательством того, что сопротивление данного полупроводника зависит от температуры экспоненциально по формуле (12).

Температурный коэффициент сопротивления в общем случае определяется формулой:

(15)

Подставив в эту формулу R из (12), получим

(16)

ОПИСАНИЕ УСТАНОВКИ

Полупроводниковый резистор ММТ-4 и металлический резистор, представляющий собой катушку из медной прово-локи помещены в термостат. Температура в термостате изме-ряется с помощью ртутного термометра или термопары. Со-противление резисторов изменяется с помощью моста посто-янного тока Р-4833 или с помощью комбинированного при-бора Щ4313, работающего в режиме измерения сопротив-ления. На рис. 2 ИП – источник питания термостата.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТ

Измерения

1. Включить установку с соответствующим номером на стенде. Дать прогреться 5-10 минут.

2. Убедиться, что ручка «Установка температуры» на-ходится в положении min, а переключатель температуры – в положении «Текущая». В этом случае индикатор «Тем-пература» показывает значение комнатной температуры.

3. Измерить значение сопротивление полупроводника (R₁) и металла (R₂) при комнатной температуре. Для этого:

3.1. Поставить переключатель S₁ в положение «Полу-проводник» (вверх), снять показания с цифрового инди-катора «Сопротивление».

3.2. Поставить переключатель S₁ в положение «Ме-талл», снять показание с того же индикатора «Сопротив-ление».

Результаты измерений занести в табл. 1.

Таблица 1

№ п/п	1	2	3	…	12
t, оС
R1, Ом (П/п)
R2, Ом (металл)

4. Снять зависимость сопротивления полупроводника и метала от температуры:

– установить температуру нагрева образцов на С выше комнатной. Для этого:

– поставить переключатель температуры в положение «Заданная»;

– установить нужную температуру с помощью ручки «Установка температуры» по индикатору «Температура»;

– поставить переключатель температуры в положение «Текущая».

Когда температура достигнет заданной, измерить значения сопротивлений полупроводника и металла (см. пункт 3).

Результаты занести в Табл. 1.

– Последовательно увеличивая температуру нагрева на С снять зависимость сопротивления полупроводника и металла от температуры. Максимальная температура на-грева С.

5. После окончания работы выключите источник пита-ния термостата и всю установку.

Обработка результатов измерений

1. По данным табл. 1 построить на масштабной мил-лиметровой бумаге графики (но, возможно, в разном мас-штабе) зависимости сопротивления полупроводника и ме-талла от температуры.

2. Исходя из формулы (6) можно получить следующую формулу для вычисления – температурного коэффици-ента сопротивления металла:

(17)

Выбрать на прямой линии графика R(T) для металла две точки R₁(T₁) и R₂(T₂) в начале и в конце интервала температур измерений и вычислить по формуле (17). Если измерения проводились с начальной температуры, большей, чем 20^o С, то значение R₀ найти методом ин-терполяции.

Примечание: точки R₁(T₁) и R₂(T₂) не обязательно будут совпадать с экспериментально измеренными значениями. Сравнить полученное значение с табличным значением для меди.

3. Для вычисления температурного коэффициента со-противления полупроводника заполнить таблицу 2.

Таблица 2

№ п/п	1	2	3	…
T(K)
1/T
R, Ом
ln R


По значениям этой таблицы на миллиметровой масштабной бумаге построить график зависимости сопро-тивления полупроводника от температуры в координатах (1/T; lnR), проведя по экспериментальным точкам прямую линию. Для определения тангенса угла наклона прямой к оси 1/T, равной константе А в формуле (14), выбираются две произвольные точки на этой прямой (рис. 3).

Пусть координаты этих точек равны (1/T₁, lnR₁) и (1/T₂, lnR₂), тогда очевидно соотношение:

(18)

Затем исходя из формулы (13) необходимо вычислить энергию активации в электронвольтах:

(19)

Коэффициент сопротивления вычислить по формуле (16).

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Чем отличаются полупроводники от металлов и ди-электриков по своим электрическим свойствам?

2. Каков механизм сопротивления проводников элек-трическому току?

3. Чем объясняется температурная зависимость со-противления полупроводников?

4. Что такое собственная проводимость полупро-водника?

5. Что такое примесная проводимость полупровод-ника?

6. Что такое энергия активации примесного (локаль-ного) уровня?

7. В чем состоят явления термогенерации и ре-комбинации носителей заряда?

8. Что такое полупроводник p–типа и n–типа?

9. Какова будет проводимость металлов и полупро-водников при Т=0К?

10. Получите закон Ома в дифференциальной фор-ме, исходя из закона Ома в интегральной форме.

11. Как определяется физическая величина, называ-емая «подвижность носителей заряда»?

12. Как определяется температурный коэффициент сопротивления металлов?

13. Какой смысл имеет знак «минус» в формуле (16) для температурного коэффициента сопротивления по-лупроводника?

14. Что такое вырождение электронного газа?

15. Является ли совокупность электронов в метал-лах вырожденным электронным газом? Является ли совокупность электронов (дырок) в полупроводниках вырожденным газом электронов (дырок)?

16. Можно ли получить вырожденный газ элек-тронов (дырок) в полупроводниках?

17. Можно ли измерять сопротивление резистора с помощью омметра, если резистор находится в работа-ющей схеме, когда по нему течет ток?

18. Во время выполнения лабораторной работы вы-шел из строя комбинированный прибор Щ4313, ра-ботавший в режиме омметра, и его заменили новым прибором – тестером, установленным переключателем в режим измерения сопротивлений, однако тестер не давал никаких показаний. Каковы возможные причины «неисправности» нового тестера?

(В новом тестере нет обрывов проводов или на-рушения электрических контактов).

19. В зависимости от измеряемого сопротивления шкала омметра с помощью переключателя для измере-ния сопротивлений в следующих диапазонах: 0…1 Ом, 0…10 Ом, 0…100 Ом и т.д. Что меняется в схеме омметра при переключении диапазона измерения со-противлений?

20. Сопротивление 9 Ом можно измерить на двух из перечисленных в предыдущем вопросе диапазонах. На каком диапазоне измерение будет точнее?

21. Почему омметры со стрелочным указателем зна-чения сопротивления имеют неравномерную шкалу?

22. Почему для работы тестеров в режиме измере-ния сопротивления необходима батарея питания?

23. В данной работе температура измеряется с по-мощью ртутного термометра. Какие еще существуют датчики температуры?

24. Можно ли использовать термистор для измере-ния температуры?

25. Какие недостатки у ртутного термометра как датчика температуры?

26. Почему рекомендуется нагревать всю сборку со-противлений медленно, время от времени отключая нагреватель от сети?

27. Чем ограничено максимальное значение темпе-ратуры, достигаемое в данной работе?

28. Какие недостатки у термистора как датчика тем-пературы?

29. В лабораторной работе сопротивление измеря-лось тестером с батареей питания. Во время работы батарея совсем разрядилась и ее заменили новой бата-реей с более высоким значением ЭДС. Какую регу-лировку надо произвести, чтобы тестер с новой бата-реей давал правильные значения сопротивлений?

30. Одно из применений термисторов – измерение пониженного давления (измерение вакуума). Для этих целей используется термистор с принудительным наг-ревом (дополнительная обмотка, подогревающая термистор). При постоянном токе подогрева сопротив-ление резистора зависит от давления в откачиваемом объеме. Какова физическая причина этого явления?

Изучение влияния температуры на проводимость металлов и полупроводников

1. ЦЕЛЬ РАБОТЫ

1) Изучить квантовую теорию электропроводности твёрдых тел.

2) Исследовать температурную зависимость электропроводности металла и полупроводника.

3) Рассчитать энергию активации собственного полупроводника.

2. ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ

3.

РАБОЧЕЕ ЗАДАНИЕ

Таблица 1. Зависимость сопротивления металла и полупроводника от температуры.

T, C○	T, K	1/T, K-1	Rм, Ом	Rпп, Ом	Ln Rпп
20­○	293	0.00341	0.01	20.62	3.026
30­○	303	0.00330	0.02	19.95	2.944
40­○	313	0.00319	0.04	18	2.890
50­○	323	0.00309	0.06	16	2.773
60­○	333	0.00300	0.08	14.3	2.660
70­○	343	0.00291	0.10	12	2.484
80­○	353	0.00283	0.12	10.8	2.380
90­○	363	0.00275	0.14	8	2.080
100­○	373	0.00268	0.16	6	1.792

График зависимости R=R(T) для металла.

Значение температурного коэффициента α.

График зависимости Rпп=Rпп(T).

График зависимости ln Rпп= ln Rпп(T).

Значение энергии активации ΔЕ.

ВЫВОДЫ

Изучили квантовую теорию электропроводности твёрдых тел. Исследовали температурную зависимость электропроводности металла и полупроводника. Рассчитали энергию активации собственного полупроводника.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1) Как объясняет электропроводность твёрдых тел классическая теория? Недостатки этой теории.

Исходя из представлений о свободных электронах Друде создал классическую теорию металлов. Он предположил, что электроны проводимости в металле ведут себя подобно молекулам идеального газа. В промежутках между соударениями они движутся совершенно свободно, пробегая в среднем некоторый путь λ. Правда, в отличие от молекул газа, пробег которых определяется соударениями молекул друг с другом, электроны сталкиваются преимущественно не между собой, а с ионами, образующими кристаллическую решётку металла. Эти столкновения приводят к установлению теплового равновесия между электронным газом и кристаллической решёткой.

Полагая, что на электронный газ могут быть распространены результаты кинетической теории газов, оценку средней скорости теплового движения электронов можно произвести по формуле

При включении поля на хаотическое тепловое движение, происходящего со скоростью <v>, накладывается упорядоченное движение электронов с некоторой средней скоростью <u>, т. е. j=ne<u>.

Классическая теория смогла объяснить законы Ома и Джоуля-Ленца. Но она имеет два основных противоречия.

Из формулы δ=ne2λ/2mv, что сопротивление металлов должно возрастать как корень квадратный из Т. Действительно, скорость теплового движения пропорциональна корню из Т. Этот вывод теории противоречит опытным данным, согласно которым электрическое сопротивление металлов растёт пропорционально первой степени Т.

Второе затруднение классической теории заключается в том, что электронный газ должен обладать молярной теплоёмкостью, равной 3/2R. Добавив эту величину к теплоёмкости решётки, составляющей 3R, получим для молярной теплоёмкости металла значение 9/2R. Таким образом, согласно классической электронной теории молярная теплоёмкость металлов должна быть в 1.5 раза больше, чем у диэлектриков. В действительности же теплоёмкость металлов не отличается заметно от теплоёмкости неметаллических кристаллов.

Классическая теория не смогла объяснить самого главного – почему электроны в металлах оказываются свободными.

2) В чём отличие квантовой теории электропроводности твёрдых тел от классической теории?

При классическом рассмотрении предполагается, что все электроны возмущаются внешним электрическим полем. При квантовомеханической трактовке приходится принимать во внимание, что, хотя электрическим полем также возмущаются все электроны, однако их коллективное движение воспринимается в опыте как возмущение полем лишь электронов, занимающих состояния вблизи уровня Ферми. Кроме того, при классической трактовке в знаменателе формулы удельной электропроводности должна стоять обычная масса электрона M, при квантовомеханической трактовке вместо обычной массы должна быть взята эффективная масса электрона M*.

3) Основные положения зонной теории твёрдых тел.

Зонная теория – приближённая теория движения электронов в периодическом поле кристаллической решётки. С точки зрения зонной теории все физические свойства твёрдых тел определяются внешними (валентными) электронами, которые перемещаются по всему объёму кристалла от одного атома к другому и возможные уровни энергии которых образуют энергетические зоны.

4) Какие вещества называют проводниками, полупроводниками, диэлектриками.

Проводники – тела (вещества) , обладающие способностью хорошо проводить электрический ток.

Полупроводники – вещества, обладающие электронной проводимостью и по значению удельной электрической проводимости занимающие промежуточное положение между проводниками и изоляторами.

Диэлектрики – вещества, практически не проводящие электрический ток.

5) Как объясняются электрические свойства различных материалов зонной теорией?

Существование энергетических зон позволяет объяснить с единой точки зрения существование металлов, полупроводников и диэлектриков.

Разрешённую зону, возникшую из того уровня, на котором находятся валентные электроны в основном состоянии атома, называют валентной зоной. При абсолютном нуле валентные электроны заполняют попарно нижние уровни валентной зоны. Более высокие зоны будут от электронов свободны. В зависимости от степени заполнения валентной зоны электронами и ширины запрещённой зоны возможны три случая.

Записи по теме

Таблицы теплопроводимости материалов (металлы, бетон, гранит, дерево и др.)

Взято из: «Примеры и задачи по курсу процессов и аппаратов химической технологии» /под ред. Романкова. Приложение.
Н.И. Кошкин, М.Г. Ширкевич. Справочник по элементарной физике // Издание девятое, М.: «Наука», 1982 г.

Коэффициент теплопроводности металлов

Металл	Вт/(м•К)
Алюминий	209,3
Бронза	47-58
Железо	74,4
Золото	312,8
Латунь	85,5
Медь	389,6
Платина	70
Ртуть	29,1
Серебро	418,7
Сталь	45,4
Свинец	35
Серый чугун	50
Чугун	62,8

Коэффициент теплопроводности других материалов

Материал	Влажность массовая доля %	Вт/(м•К)
Бакелитовый лак	—	0,29
Бетон с каменным щебнем	8	1,28
Бумага обыкновенная	Воздушно-сухая	0,14
Винипласт	—	0,13
Гравий	Воздушно-сухая	0,36
Гранит	—	3,14
Глина	15-20	0,7-0,93
Дуб (вдоль волокон)	6-8	0,35-0,43
Дуб (поперек волокон)	6-8	0,2-0,21
Железобетон	8	1,55
Картон	Воздушно-сухая	0,14-0,35
Кирпичная кладка	Воздушно-сухая	0,67-0,87
Кожа	>>	0,14-0,16
Лед	—	2,21
Пробковые плиты	0	0,042-0,054
Снег свежевыпавший	—	0,105
Снег уплотненный	—	0,35
Снег начавший таять	—	0,64
Сосна (вдоль волокон)	8	0,35-0,41
Сосна (поперек волокон)	8	0,14-0,16
Стекло (обыкновенное)	—	0,74
Фторопласт-3	—	0,058
Фторопласт-4	—	0,233
Шлакобетон	13	0,698
Штукатурка	6-8	0,791

Коэффициент теплопроводности асбеста и пенобетона при различных температурах

(ρ_a=576кг/м³, ρ_п=400кг/м³,λ, Вт/(м•К))

Материал	-18oС	0oС	50oС	100oС	150oС
Асбест	—	0,15	0,18	0,195	0,20
Пенобетон	0,1	0,11	0,11	0,13	0,17

Коэффициент теплопроводности жидкости Вт/(м•К) при различных температурах

Материал	0oС	50oС	100oС
Анилин	0,19	0,177	0,167
Ацетон	0,17	0,16	0,15
Бензол	—	0,138	0,126
Вода	0,551	0,648	0,683
Масло вазелиновое	0,126	0,122	0,119
Масло касторовое	0,184	0,177	0,172
Спирт метиловый	0,214	0,207	—
Спирт этиловый	0,188	0,177	—
Толуол	0,142	0,129	0,119

Запись опубликована автором admin в рубрике Полезные материалы. Добавьте в закладки постоянную ссылку.

Удельное электрическое сопротивление металлов таблица. Зависимость удельного сопротивления от температуры

Содержание:

Удельным сопротивлением металлов считается их способность к противодействию электрическому току, проходящему через них. Единицей измерения данной величины служит Ом*м (Ом-метр). В качестве символа используется греческая буква ρ (ро). Высокие показатели удельного сопротивления означают плохую проводимость электрического заряда тем или иным материалом.

Технические характеристики стали

Прежде чем подробно рассматривать удельное сопротивление стали, следует ознакомиться с ее основными физико-механическими свойствами. Благодаря своим качествам, этот материал получил широкое распространение в производственной сфере и других областях жизни и деятельности людей.

Сталь представляет собой сплав железа и углерода, содержащегося в количестве, не превышающем 1,7%. Кроме углерода, сталь содержит определенное количество примесей — кремния, марганца, серы и фосфора. По своим качествам она значительно лучше чугуна, легко поддается закаливанию, ковке, прокату и другим видам обработки. Все виды сталей отличаются высокой прочностью и пластичностью.

По своему назначению сталь подразделяется на конструкционную, инструментальную, а также с особыми физическими свойствами. В каждой из них содержится различное количество углерода, благодаря которому материал приобретает те или иные специфические качества, например, жаропрочность, жаростойкость, устойчивость к действию ржавчины и коррозии.

Особое место занимают электротехнические стали, выпускаемые в листовом формате и применяющиеся в производстве электротехнических изделий. Для получения этого материала производится легирование кремнием, способным улучшить его магнитные и электрические свойства.

Для того чтобы электротехническая сталь приобрела необходимые характеристики, необходимо соблюдение определенных требований и условий. Материал должен легко намагничиваться и перемагничиваться, то есть, обладать высокой магнитной проницаемостью. Такие стали имеют хорошую , а их перемагничивание осуществляется с минимальными потерями.

От соблюдения этих требований зависят габариты и масса магнитных сердечников и обмоток, а также коэффициент полезного действия трансформаторов и величина их рабочей температуры. На выполнение условий оказывают влияние многие факторы, в том числе и удельное сопротивление стали.

Удельное сопротивление и другие показатели

Величина удельного электрического сопротивления представляет собой отношение напряженности электрического поля в металле и плотности тока, протекающего в нем. Для практических расчетов используется формула: в которой ρ является удельным сопротивлением металла (Ом*м), Е — напряженностью электрического поля (В/м), а J — плотностью электротока в металле (А/м 2). При очень большой напряженности электрического поля и низкой плотности тока, удельное сопротивление металла будет высоким.

Существует еще одна величина, называемая удельной электропроводностью, обратная удельному сопротивлению, указывающая на степень проводимости электрического тока тем или иным материалом. Она определяется по формуле и выражается в единицах См/м — сименс на метр.

Удельное сопротивление тесно связано с электрическим сопротивлением. Однако они имеют различия между собой. В первом случае — это свойство материала, в том числе и стали, а во втором случае определяется свойство всего объекта. На качество резистора влияет сочетание нескольких факторов, прежде всего, формы и удельного сопротивления материала, из которого он изготовлен. Например, если для изготовления проволочного резистора использовалась тонкая и длинная проволока, то его сопротивление будет больше, чем у резистора, изготовленного из толстой и короткой проволоки одинакового металла.

В качестве другого примера можно привести резисторы из проволоки с одинаковым диаметром и длиной. Однако, если в одном из них материал имеет высокое удельное сопротивление, а в другом низкое, то соответственно в первом резисторе электрическое сопротивление будет выше, чем во втором.

Зная основные свойства материала, можно использовать удельное сопротивление стали для определения величины сопротивления стального проводника. Для вычислений, кроме удельного электрического сопротивления потребуется диаметр и длина самого провода. Расчеты выполняются по следующей формуле: , в которой R является (Ом), ρ — удельным сопротивлением стали (Ом*м), L — соответствует длине провода, А — площади его поперечного сечения.

Существует зависимость удельного сопротивления стали и других металлов от температуры. В большинстве расчетов используется комнатная температура — 20 0 С. Все изменения под влиянием этого фактора учитываются с помощью температурного коэффициента.

Для каждого проводника существует понятие удельного сопротивления. Эта величина состоит из Омов, умножаемых на квадратный миллиметр, далее, делимое на один метр. Иными словами, это сопротивление проводника, длина которого составляет 1 метр, а сечение — 1 мм 2 . То же самое представляет собой и удельное сопротивление меди — уникального металла, получившего широкое распространение в электротехнике и энергетике.

Свойства меди

Благодаря своим свойствам этот металл одним из первых начал применяться в области электричества. Прежде всего, медь является ковким и пластичным материалом с отличными свойствами электропроводимости. До сих пор в энергетике нет равноценной замены этому проводнику.

Особенно ценятся свойства специальной электролитической меди, обладающей высокой чистотой. Этот материал позволил выпускать провода с минимальной толщиной в 10 микрон.

Кроме высокой электропроводности, медь очень хорошо поддается лужению и другим видам обработки.

Медь и ее удельное сопротивление

Любой проводник оказывает сопротивление, если через него пропустить электрический ток. Значение зависит от длины проводника и его сечения, а также от действия определенных температур. Поэтому, удельное сопротивление проводников зависит не только от самого материала, но и от его определенной длины и площади поперечного сечения. Чем легче материал пропускает через себя заряд, тем ниже его сопротивление. Для меди, показатель удельного сопротивления составляет 0,0171 Ом х 1 мм 2 /1 м и лишь немного уступает серебру. Однако, использование серебра в промышленных масштабах экономически невыгодно, поэтому, медь является лучшим проводником, используемым в энергетике.

Удельное сопротивление меди связано и с ее высокой проводимостью. Эти величины прямо противоположны между собой. Свойства меди, как проводника, зависят и от температурного коэффициента сопротивления. Особенно, это касается сопротивление, на которое оказывает влияние температура проводника.

Таким образом, благодаря своим свойствам, медь получила широкое распространение не только в качестве проводника . Этот металл используется в большинстве приборов, устройств и агрегатов, функционирование которых связано с электрическим током.

Одним из самых распространённых металлов для изготовления проводов является медь. Её электросопротивление минимальное из доступных по цене металлов. Оно меньше только у драгоценных металлов (серебра и золота) и зависит от разных факторов.

Что такое электрический ток

На разных полюсах аккумулятора или другого источника тока есть разноимённые носители электрического заряда. Если их соединить с проводником, носители заряда начинают движение от одного полюса источника напряжения к другому. Этими носителями в жидкости являются ионы, а в металлах – свободные электроны.

Определение. Электрический ток – это направленное движение заряженных частиц.

Удельное сопротивление

Удельное электрическое сопротивление – это величина, определяющая электросопротивление эталонного образца материала. Для обозначения этой величины используется греческая буква «р». Формула для расчета:

p=(R*S)/l .

Эта величина измеряется в Ом*м. Найти её можно в справочниках, в таблицах удельного сопротивления или в сети интернет.

Свободные электроны по металлу двигаются внутри кристаллической решётки. На сопротивление этому движению и удельное сопротивление проводника влияют три фактора:

• Материал. У разных металлов различная плотность атомов и количество свободных электронов;
• Примеси. В чистых металлах кристаллическая решётка более упорядоченная, поэтому сопротивление ниже, чем в сплавах;
• Температура. Атомы не находятся на своих местах неподвижно, а колеблются. Чем выше температура, тем больше амплитуда колебаний, создающая помехи движению электронов, и выше сопротивление.

На следующем рисунке можно увидеть таблицу удельного сопротивления металлов.

Интересно. Есть сплавы, электросопротивление которых падает при нагреве или не меняется.

Проводимость и электросопротивление

Так как размеры кабелей измеряются в метрах (длина) и мм² (сечение), то удельное электрическое сопротивление имеет размерность Ом·мм²/м. Зная размеры кабеля, его сопротивление рассчитывается по формуле:

R=(p*l )/S.

Кроме электросопротивления, в некоторых формулах используется понятие «проводимость». Это величина, обратная сопротивлению. Обозначается она «g» и рассчитывается по формуле:

Проводимость жидкостей

Проводимость жидкостей отличается от проводимости металлов. Носителями зарядов в них являются ионы. Их количество и электропроводность растут при нагревании, поэтому мощность электродного котла растёт при нагреве от 20 до 100 градусов в несколько раз.

Интересно. Дистиллированная вода является изолятором. Проводимость ей придают растворенные примеси.

Электросопротивление проводов

Самые распространенные металлы для изготовления проводов – медь и алюминий. Сопротивление алюминия выше, но он дешевле меди. Удельное сопротивление меди ниже, поэтому сечение проводов можно выбрать меньше. Кроме того, она прочнее, и из этого металла изготавливаются гибкие многожильные провода.

В следующей таблице показывается удельное электросопротивление металлов при 20 градусах. Для того чтобы определить его при других температурах, значение из таблицы необходимо умножить на поправочный коэффициент, различный для каждого металла. Узнать этот коэффициент можно из соответствующих справочников или при помощи онлайн-калькулятора.

Выбор сечения кабеля

Поскольку у провода есть сопротивление, при прохождении по нему электрического тока выделяется тепло, и происходит падение напряжения. Оба этих фактора необходимо учитывать при выборе сечения кабелей.

Выбор по допустимому нагреву

При протекании тока в проводе выделяется энергия. Её количество можно рассчитать по формуле электрической мощности:

В медном проводе сечением 2,5мм² и длиной 10 метров R=10*0.0074=0.074Ом. При токе 30А Р=30²*0,074=66Вт.

Эта мощность нагревает токопроводящую жилу и сам кабель. Температура, до которой он нагревается, зависит от условий прокладки, числа жил в кабеле и других факторов, а допустимая температура – от материала изоляции. Медь обладает большей проводимостью, поэтому меньше выделяемая мощность и необходимое сечение. Определяется оно по специальным таблицам или при помощи онлайн-калькулятора.

Допустимые потери напряжения

Кроме нагрева, при прохождении электрического тока по проводам происходит уменьшение напряжения возле нагрузки. Эту величину можно рассчитать по закону Ома:

Справка. По нормам ПУЭ оно должно составлять не более 5% или в сети 220В – не больше 11В.

Поэтому, чем длиннее кабель, тем больше должно быть его сечение. Определить его можно по таблицам или при помощи онлайн-калькулятора. В отличие от выбора сечения по допустимому нагреву, потери напряжения не зависят от условий прокладки и материала изоляции.

В сети 220В напряжение подаётся по двум проводам: фазному и нулевому, поэтому расчёт производится по двойной длине кабеля. В кабеле из предыдущего примера оно составит U=I*R=30A*2*0.074Ом=4,44В. Это немного, но при длине 25 метров получается 11,1В – предельно допустимая величина, придётся увеличивать сечение.

Электросопротивление других металлов

Кроме меди и алюминия, в электротехнике используются другие металлы и сплавы:

• Железо. Удельное сопротивление стали выше, но она прочнее, чем медь и алюминий. Стальные жилы вплетаются в кабеля, предназначенные для прокладки по воздуху. Сопротивление железа слишком велико для передачи электроэнергии, поэтому при расчёте сечения жилы не учитываются. Кроме того, оно более тугоплавкое, и из него изготавливаются вывода для подключения нагревателей в электропечах большой мощности;
• Нихром (сплав никеля и хрома) и фехраль (железо, хром и алюминий). Они обладают низкой проводимостью и тугоплавкостью. Из этих сплавов изготавливаются проволочные резисторы и нагреватели;
• Вольфрам. Его электросопротивление велико, но это тугоплавкий металл (3422 °C). Из него изготавливаются нити накала в электролампах и электроды для аргонно-дуговой сварки;
• Константан и манганин (медь, никель и марганец). Удельное сопротивление этих проводников не меняется при изменениях температуры. Применяются в претензионных приборах для изготовления резисторов;
• Драгоценные металлы – золото и серебро. Обладают самой высокой удельной проводимостью, но из-за большой цены их применение ограничено.

Индуктивное сопротивление

Формулы для расчёта проводимости проводов справедливы только в сети постоянного тока или в прямых проводниках при низкой частоте. В катушках и в высокочастотных сетях появляется индуктивное сопротивление, во много раз превышающее обычное. Кроме того, ток высокой частоты распространяется только по поверхности провода. Поэтому его иногда покрывают тонким слоем серебра или используют литцендрат.

Понятие об электрическом сопротивлении и проводимости

Любое тело, по которому протекает электрический ток, оказывает ему определенное сопротивление. Свойство материала проводника препятствовать прохождению через него электрического тока называется электрическим сопротивлением.

Электронная теория так объясняет сущность электрического сопротивления металлических проводников. Свободные электроны при движении по проводнику бесчисленное количество раз встречают на своем пути атомы и другие электроны и, взаимодействуя с ними, неизбежно теряют часть своей энергии. Электроны испытывают как бы сопротивление своему движению. Различные металлические проводники, имеющие различное атомное строение, оказывают различное сопротивление электрическому току.

Точно тем же объясняется сопротивление жидких проводников и газов прохождению электрического тока. Однако не следует забывать, что в этих веществах не электроны, а заряженные частицы молекул встречают сопротивление при своем движении.

Сопротивление обозначается латинскими буквами R или r .

За единицу электрического сопротивления принят ом.

Ом есть сопротивление столба ртути высотой 106,3 см с поперечным сечением 1 мм2 при температуре 0° С.

Если, например, электрическое сопротивление проводника составляет 4 ом, то записывается это так: R = 4 ом или r = 4ом.

Для измерения сопротивлений большой величины принята единица, называемая мегомом.

Один мегом равен одному миллиону ом.

Чем больше сопротивление проводника, тем хуже он проводит электрический ток, и, наоборот, чем меньше сопротивление проводника, тем легче электрическому току пройти через этот проводник.

Следовательно, для характеристики проводника (с точки зрения прохождения через него электрического тока) можно рассматривать не только его сопротивление, но и величину, обратную сопротивлению и называемую, проводимостью.

Электрической проводимостью называется способность материала пропускать через себя электрический ток.

Так как проводимость есть величина, обратная сопротивлению, то и выражается она как 1/R ,обозначается проводимость латинской буквой g.

Влияние материала проводника, его размеров и окружающей температуры на величину электрического сопротивления

Сопротивление различных проводников зависит от материала, из которого они изготовлены. Для характеристики электрического сопротивления различных материалов введено понятие так называемого удельного сопротивления.

Удельным сопротивлением называется сопротивление проводника длиной 1 м и площадью поперечного сечения 1 мм2. Удельное сопротивление обозначается буквой греческого алфавита р. Каждый материал, из которого изготовляется проводник, обладает своим удельным сопротивлением.

Например, удельное сопротивление меди равно 0,017, т. е. медный проводник длиной 1 м и сечением 1 мм2 обладает сопротивлением 0,017 ом. Удельное сопротивление алюминия равно 0,03, удельное сопротивление железа — 0,12, удельное сопротивление константана — 0,48, удельное сопротивление нихрома — 1-1,1.

Сопротивление проводника прямо пропорционально его длине, т. е. чем длиннее проводник, тем больше его электрическое сопротивление.

Сопротивление проводника обратно пропорционально площади его поперечного сечения, т. е. чем толще проводник, тем его сопротивление меньше, и, наоборот, чем тоньше проводник, тем его сопротивление больше.

Чтобы лучше понять эту зависимость, представьте себе две пары сообщающихся сосудов, причем у одной пары сосудов соединяющая трубка тонкая, а у другой — толстая. Ясно, что при заполнении водой одного из сосудов (каждой пары) переход ее в другой сосуд по толстой трубке произойдет гораздо быстрее, чем по тонкой, т. е. толстая трубка окажет меньшее сопротивление течению воды. Точно так же и электрическому току легче пройти по толстому проводнику, чем по тонкому, т. е. первый оказывает ему меньшее сопротивление, чем второй.

Электрическое сопротивление проводника равно удельному сопротивлению материала, из которого этот проводник сделан, умноженному на длину проводника и деленному на площадь площадь поперечного сечения проводника :

R = р l / S ,

Где — R — сопротивление проводника, ом, l — длина в проводника в м, S — площадь поперечного сечения проводника, мм 2 .

Площадь поперечного сечения круглого проводника вычисляется по формуле:

S = π d 2 / 4

Где π — постоянная величина, равная 3,14; d — диаметр проводника.

А так определяется длина проводника:

l = S R / p ,

Эта формула дает возможность определить длину проводника, его сечение и удельное сопротивление, если известны остальные величины, входящие в формулу.

Если же необходимо определить площадь поперечного сечения проводника, то формулу приводят к следующему виду:

S = р l / R

Преобразуя ту же формулу и решив равенство относительно р, найдем удельное сопротивление проводника:

р = R S / l

Последней формулой приходится пользоваться в тех случаях, когда известны сопротивление и размеры проводника, а его материал неизвестен и к тому же трудно определим по внешнему виду. Для этого надо определить удельное сопротивление проводника и, пользуясь таблицей, найти материал, обладающий таким удельным сопротивлением.

Еще одной причиной, влияющей на сопротивление проводников, является температура .

Установлено, что с повышением температуры сопротивление металлических проводников возрастает, а с понижением уменьшается. Это увеличение или уменьшение сопротивления для проводников из чистых металлов почти одинаково и в среднем равно 0,4% на 1°C . Сопротивление жидких проводников и угля с увеличением температуры уменьшается.

Электронная теория строения вещества дает следующее объяснение увеличению сопротивления металлических проводников с повышением температуры. При нагревании проводник получает тепловую энергию, которая неизбежно передается всем атомам вещества, в результате чего возрастает интенсивность их движения. Возросшее движение атомов создает большее сопротивление направленному движению свободных электронов, отчего и возрастает сопротивление проводника. С понижением же температуры создаются лучшие условия для направленного движения электронов, и сопротивление проводника уменьшается. Этим объясняется интересное явление — сверхпроводимость металлов .

Сверхпроводимость , т. е. уменьшение сопротивления металлов до нуля, наступает при огромной отрицательной температуре — 273° C , называемой абсолютным нулем. При температуре абсолютного нуля атомы металла как бы застывают на месте, совершенно не препятствуя движению электронов.

Каждое вещество способно проводить ток в разной степени, на эту величину влияет сопротивление материала. Обозначается удельное сопротивление меди, алюминия, стали и любого другого элемента буквой греческого алфавита ρ. Эта величина не зависит от таких характеристик проводника, как размеры, форма и физическое состояние, обычное же электросопротивление учитывает эти параметры. Измеряется удельное сопротивление в Омах, умноженных на мм² и разделенных на метр.

Категории и их описание

Любой материал способен проявлять два типа сопротивления в зависимости от подаваемого на него электричества. Ток бывает переменным или постоянным, что значительно влияет на технические показатели вещества. Так, существуют такие сопротивления:

1. Омическое. Проявляется под воздействием постоянного тока. Характеризует трение, которое создается движением электрически заряженных частиц в проводнике.
2. Активное. Определяется по такому же принципу, но создается уже под действием переменного тока.

В связи с этим определений удельной величины тоже два. Для постоянного тока она равна сопротивлению, которое оказывает единица длины проводящего материала единичной фиксированной площади сечения. Потенциальное электрополе воздействует на все проводники, а также полупроводники и растворы, способные проводить ионы. Эта величина определяет проводящие свойства самого материала. Форма проводника и его размеры не учитываются, поэтому ее можно назвать базовой в электротехнике и материаловедении.

При условии прохождения переменного тока удельная величина рассчитывается с учетом толщины проводящего материала. Здесь уже происходит воздействие не только потенциального, но и вихревого тока, кроме того, принимается во внимание частота электрических полей. Удельное сопротивление этого типа больше, чем при постоянном токе, поскольку здесь идет учет положительной величины сопротивления вихревому полю. Также эта величина зависит от формы и размеров самого проводника. Именно эти параметры и определяют характер вихревого движения заряженных частиц.

Переменный ток вызывает в проводниках определенные электромагнитные явления. Они очень важны для электротехнических характеристик проводящего материала:

1. Скин-эффект характеризуется ослаблением электромагнитного поля тем больше, чем дальше оно проникает в среду проводника. Это явление также носит название поверхностного эффекта.
2. Эффект близости снижает плотность тока благодаря близости соседних проводов и их влиянию.

Эти эффекты являются очень важными при расчете оптимальной толщины проводника, так как при использовании провода, у которого радиус больше глубины проникновения тока в материал, остальная его масса останется незадействованной, а следовательно, такой подход будет неэффективным. В соответствии с проведенными расчетами эффективный диаметр проводящего материала в некоторых ситуациях будет следующим:

• для тока в 50 Гц — 2,8 мм;
• 400 Гц — 1 мм;
• 40 кГц — 0,1 мм.

Ввиду этого для высокочастотных токов активно применяется использование плоских многожильных кабелей, состоящих из множества тонких проводов.

Характеристики металлов

Удельные показатели металлических проводников содержатся в специальных таблицах. По этим данным можно производить необходимые дальнейшие расчеты. Пример такой таблицы удельных сопротивлений можно увидеть на изображении.

На таблице видно, что наибольшей проводимостью обладает серебро — это идеальный проводник среди всех существующих металлов и сплавов. Если рассчитать, сколько потребуется провода из этого материала для получения сопротивления в 1 Ом, то выйдет 62,5 м. Проволоки из железа для такой же величины понадобится целых 7,7 м.

Какими бы замечательными свойствами ни обладало серебро, оно является слишком дорогим материалом для массового использования в электросетях, поэтому широкое применение в быту и промышленности нашла медь. По величине удельного показателя она стоит на втором месте после серебра, а по распространенности и простоте добычи намного лучше его. Медь обладает и другими преимуществами, позволившими ей стать самым распространенным проводником. К ним относятся:

Для применения в электротехнике используют рафинированную медь, которая после плавки из сульфидной руды проходит процессы обжигания и дутья, а далее обязательно подвергается электролитической очистке. После такой обработки можно получить материал очень высокого качества (марки М1 и М0), который будет содержать от 0,1 до 0,05% примесей. Важным нюансом является присутствие кислорода в крайне малых количествах, так как он негативно влияет на механические характеристики меди.

Часто этот металл заменяют более дешевыми материалами — алюминием и железом, а также различными бронзами (сплавами с кремнием, бериллием, магнием, оловом, кадмием, хромом и фосфором). Такие составы обладают более высокой прочностью по сравнению с чистой медью, хотя и меньшей проводимостью.

Преимущества алюминия

Хоть алюминий обладает большим сопротивлением и более хрупок, его широкое использование объясняется тем, что он не настолько дефицитен, как медь, а следовательно, стоит дешевле. Удельное сопротивление алюминия составляет 0,028, а его низкая плотность обеспечивает ему вес в 3,5 раза меньше, чем медь.

Для электрических работ применяют очищенный алюминий марки А1, содержащий не более 0,5% примесей. Более высокую марку АВ00 используют для изготовления электролитических конденсаторов, электродов и алюминиевой фольги. Содержание примесей в этом алюминии составляет не более 0,03%. Существует и чистый металл АВ0000 , включающий не более 0,004% добавок. Имеют значение и сами примеси: никель, кремний и цинк незначительно влияют на проводимость алюминия, а содержание в этом металле меди, серебра и магния дает ощутимый эффект. Наиболее сильно уменьшают проводимость таллий и марганец.

Алюминий отличается хорошими антикоррозийными свойствами. При контакте с воздухом он покрывается тонкой пленкой окиси, которая и защищает его от дальнейшего разрушения. Для улучшения механических характеристик металл сплавляют с другими элементами.

Показатели стали и железа

Удельное сопротивление железа по сравнению с медью и алюминием имеет очень высокие показатели, однако благодаря доступности, прочности и устойчивости к деформациям материал широко используют в электротехническом производстве.

Хоть железо и сталь, удельное сопротивление которой еще выше, имеют существенные недостатки, изготовители проводникового материала нашли методы их компенсирования. В частности, низкую стойкость к коррозии преодолевают путем покрытия стальной проволоки цинком или медью.

Свойства натрия

Металлический натрий также очень перспективен в проводниковом производстве. По показателям сопротивления он значительно превышает медь, однако имеет плотность в 9 раз меньше, чем у неё. Это позволяет использовать материал в изготовлении сверхлёгких проводов.

Металлический натрий очень мягкий и совершенно неустойчив к любого рода деформационным воздействиям, что делает его использование проблемным — провод из этого металла должен быть покрыт очень прочной оболочкой с крайне малой гибкостью. Оболочка должна быть герметичной, так как натрий проявляет сильную химическую активность в самых нейтральных условиях. Он моментально окисляется на воздухе и демонстрирует бурную реакцию с водой, в том числе и с содержащейся в воздухе.

Еще одним плюсом использования натрия является его доступность. Его можно получить в процессе электролиза расплавленного хлористого натрия, которого в мире существует неограниченное количество. Другие металлы в этом плане явно проигрывают.

Чтобы рассчитать показатели конкретного проводника, необходимо произведение удельного числа и длины проволоки разделить на площадь ее сечения. В результате получится значение сопротивления в Омах. Например, чтобы определить, чему равно сопротивление 200 м проволоки из железа с номинальным сечением 5 мм², нужно 0,13 умножить на 200 и разделить полученный результат на 5. Ответ — 5,2 Ом.

Правила и особенности вычисления

Для измерения сопротивления металлических сред пользуются микроомметрами. Сегодня их выпускают в цифровом варианте, поэтому проведенные с их помощью измерения отличаются точностью. Объяснить ее можно тем, что металлы обладают высоким уровнем проводимости и имеют крайне маленькое сопротивление. Для примера, нижний порог измерительных приборов имеет значение 10 -7 Ом.

С помощью микроомметров можно быстро определить, насколько качественен контакт и какое сопротивление проявляют обмотки генераторов, электродвигателей и трансформаторов, а также электрические шины. Можно вычислить присутствие включений другого металла в слитке. Например, вольфрамовый кусок, покрытый позолотой, показывает вдвое меньшую проводимость, чем полностью золотой. Тем же способом можно определить внутренние дефекты и полости в проводнике.

Формула удельного сопротивления выглядит следующим образом: ρ = Ом · мм 2 /м . Словами ее можно описать как сопротивление 1 метра проводника , имеющего площадь сечения 1 мм². Температура подразумевается стандартная — 20 °C.

Влияние температуры на измерение

Нагревание или охлаждение некоторых проводников оказывает значительное влияние на показатели измерительных приборов. В качестве примера можно привести следующий опыт: необходимо подключить к аккумулятору спирально намотанную проволоку и подключить в цепь амперметр.

Чем сильнее нагревается проводник, тем меньше становятся показания прибора. Сила тока имеет обратно пропорциональную зависимость от сопротивления. Следовательно, можно сделать вывод, что в результате нагрева проводимость металла уменьшается. В большей или меньшей степени так ведут себя все металлы, однако изменения проводимости у некоторых сплавов практически не наблюдается.

Примечательно, что жидкие проводники и некоторые твердые неметаллы имеют тенденцию уменьшать свое сопротивление с повышением температуры. Но и эту способность металлов ученые обратили себе на пользу. Зная температурный коэффициент сопротивления (α) при нагреве некоторых материалов, можно определять внешнюю температуру. Например, проволоку из платины, размещенную на каркасе из слюды, помещают в печь, после чего проводят измерение сопротивления. В зависимости от того, насколько оно изменилось, делают вывод о температуре в печи. Такая конструкция называется термометром сопротивления.

Если при температуре t 0 сопротивление проводника равно r 0, а при температуре t равно rt , то температурный коэффициент сопротивления равен

Расчет по этой формуле можно производить лишь в определенном интервале температур (примерно до 200 °C).

Проводящие металлы. Удельная электрическая проводимость

Длина и расстояние Масса Меры объема сыпучих продуктов и продуктов питания Площадь Объем и единицы измерения в кулинарных рецептах Температура Давление, механическое напряжение, модуль Юнга Энергия и работа Мощность Сила Время Линейная скорость Плоский угол Тепловая эффективность и топливная экономичность Числа Единицы измерения количества информации Курсы валют Размеры женской одежды и обуви Размеры мужской одежды и обуви Угловая скорость и частота вращения Ускорение Угловое ускорение Плотность Удельный объем Момент инерции Момент силы Вращающий момент Удельная теплота сгорания (по массе) Плотность энергии и удельная теплота сгорания топлива (по объему) Разность температур Коэффициент теплового расширения Термическое сопротивление Удельная теплопроводность Удельная теплоёмкость Энергетическая экспозиция, мощность теплового излучения Плотность теплового потока Коэффициент теплоотдачи Объёмный расход Массовый расход Молярный расход Плотность потока массы Молярная концентрация Массовая концентрация в растворе Динамическая (абсолютная) вязкость Кинематическая вязкость Поверхностное натяжение Паропроницаемость Паропроницаемость, скорость переноса пара Уровень звука Чувствительность микрофонов Уровень звукового давления (SPL) Яркость Сила света Освещённость Разрешение в компьютерной графике Частота и длина волны Оптическая сила в диоптриях и фокусное расстояние Оптическая сила в диоптриях и увеличение линзы (×) Электрический заряд Линейная плотность заряда Поверхностная плотность заряда Объемная плотность заряда Электрический ток Линейная плотность тока Поверхностная плотность тока Напряжённость электрического поля Электростатический потенциал и напряжение Электрическое сопротивление Удельное электрическое сопротивление Электрическая проводимость Удельная электрическая проводимость Электрическая емкость Индуктивность Американский калибр проводов Уровни в dBm (дБм или дБмВт), dBV (дБВ), ваттах и др. единицах Магнитодвижущая сила Напряженность магнитного поля Магнитный поток Магнитная индукция Мощность поглощенной дозы ионизирующего излучения Радиоактивность. Радиоактивный распад Радиация. Экспозиционная доза Радиация. Поглощённая доза Десятичные приставки Передача данных Типографика и обработка изображений Единицы измерения объема лесоматериалов Вычисление молярной массы Периодическая система химических элементов Д. И. Менделеева

Электрические поля регистрируются с использованием системы электрически чувствительных органов в коже. Каждый флакон содержит трубку, заполненную желатиновым веществом, которое контактирует с внешней средой через поры в коже животных. Внутренний конец трубки заканчивается в подвале, где размещаются клетки, которые несут электрические сигналы в нервную систему рыбы. До сих пор ученые не могли объяснить, как слабый электрический сигнал проходит через трубу снаружи в подвал.

Однако теперь физики и биофизика из Калифорнийского университета в Санта-Крус пришли вместе с другими коллегами, что желе является исключительно хорошим протонным проводником, что также объясняется передачей электрических сигналов. Команда попыталась проверить образцы акулы и редиса. Ученые из Розола помещают между двумя палладиевыми электродами, способными поглощать и излучать большое количество протонов. Напряжение, прикладываемое к электродам, заставляет протоны от положительного электрода поступать в желе и двигаться к отрицательному электроду.

Исходная величина

Преобразованная величина

сименс на метр пикосименс на метр мо на метр мо на сантиметр абмо на метр абмо на сантиметр статмо на метр статмо на сантиметр сименс на сантиметр миллисименс на метр миллисименс на сантиметр микросименс на метр микросименс на сантиметр условная единица электропроводности условный коэффициент электропроводности миллионных долей, коэф. пересчета 700 миллионных долей, коэф. пересчета 500 миллионных долей, коэф. пересчета 640 TDS, миллионных долей, коэф. пересчета 640 TDS, миллионных долей, коэф. пересчета 550 TDS, миллионных долей, коэф. пересчета 500 TDS, миллионных долей, коэф. пересчета 700

Протонный ток легко измеряется, потому что он такой же, как электрический ток, протекающий через приложенное напряжение. Хотя измерения показали, что желе является хорошим протонным проводником, он не обеспечивает точное значение проводимости. Протоны должны преодолевать контактное сопротивление, когда они входят и выходят из палладиевых электродов, а измерение проводимости влияет на них. Это было обойдено тем фактом, что измерение проводилось также на двух золотых электродах, помещенных в желе между палладиевыми электродами.

Измерение напряжения между золотыми электродами и током между палладиевыми электродами позволило вычислить точное значение проводимости. Ученые убеждены, что высокая протонная проводимость этого биологического материала связана с наличием цепной молекулы, называемой кератансульфатом. Это кислота, которая означает, что каждая молекула кератинового сульфата может обеспечить протон для повышения проводимости. Эти протоны затем могут перемещаться вдоль цепочек молекул воды, которые образуются вокруг кератансульфата.

Введение и определения

Удельная электрическая проводимость (или удельная электропроводность) является мерой способности вещества проводить электрический ток или перемещать электрические заряды в нем. Это отношение плотности тока к напряженности электрического поля. Если рассмотреть куб из проводящего материала со стороной 1 метр, то удельная проводимость будет равна электрической проводимости, измеренной между двумя противоположными сторонами этого куба.

Эксперты считают это открытие очень захватывающим и стимулирующим. Полученные данные должны вдохновлять на дальнейшие исследования функций электрической чувствительности не только ампулы Лоренцини, но и в целом различных органов. Такие данные обычно недоступны. Не только это открытие должно привести к разработке новых типов датчиков разных типов.

Вещества с одинаковой температурой кажутся по-разному теплыми. Если мы коснемся дерева и металла при той же температуре, металл будет выглядеть холодным, потому что это делает наше тепло более теплым и теплым, потому что наша поверхность нагревается нашей рукой.

Удельная проводимость связана с проводимостью следующей формулой:

G = σ(A/l)

где G — электрическая проводимость, σ — удельная электрическая проводимость, А — поперечное сечение проводника, перпендикулярное направлению электрического тока и l — длина проводника. Эту формулу можно использовать с любым проводником в форме цилиндра или призмы. Отметим, что эту формулу можно использовать и для прямоугольного параллелепипеда, потому что он является частным случаем призмы, основанием которой является прямоугольник. Напомним, что удельная электрическая проводимость — величина, обратная удельному электрическому сопротивлению.

Теплопроводность — это способность материала нагреваться. Фактически это скорость, с которой тепло распространяется от одной нагретой части ткани к другой, холоднее. Теплопроводность каждого вещества определяется коэффициентом теплопроводности. В зависимости от значения коэффициента теплопроводности мы различаем хорошие и плохие теплопроводности.

Все металлы обладают лучшей теплопроводностью. Лучшее тепловыделение приводит к чистым металлам, чем загрязненные металлом или сплавы. Металл, который является лучшим электрическим проводником, также является лучшим проводником тепла. Соотношение между коэффициентом теплопроводности и коэффициентом проводимости выражается в законе Лоренца-Лоренца. Тепловая и электропроводность металлов опосредованы свободными электронами. Хорошая теплопроводность металлов используется в технике, металлических радиаторах, стенках парового котла, охлаждающих телах и т.д. другими твердыми веществами являются плохие теплопроводники, за исключением твердых веществ.

Людям, далеким от физики и техники, бывает сложно понять разницу между проводимостью проводника и удельной проводимостью вещества. Между тем, конечно, это разные физические величины. Проводимость — это свойство данного проводника или устройства (например, резистора или гальванической ванны), в то время как удельная проводимость — это неотъемлемое свойство материала, из которого изготовлены этот проводник или устройство. Например, удельная проводимость меди всегда одинаковая, независимо от того как изменяется форма и размеры предмета из меди. В то же время, проводимость медного провода зависит от его длины, диаметра, массы, формы и некоторых других факторов. Конечно, похожие объекты из материалов с более высокой удельной проводимостью имеют более высокую проводимость (хотя и не всегда).

Опыт практики: очень плохие теплопроводники — это газы и жидкости, особенно вода. При нагревании воды в верхней части трубки мы можем довести ее до кипения, а на дне осталось холодно. Наименьшие коэффициенты теплопроводности имеют газы. Следовательно, также рыхлые пористые вещества, внутри которых находится воздух, являются плохими тепловыми проводниками. Проводимость таких веществ зависит от влажности, так что теплопроводность влажных веществ значительно больше. Вещества, которые являются плохими проводниками тепла, используются для теплоизоляции.

В Международной системе единиц (СИ) единицей удельной электрической проводимости является сименс на метр (См/м) . Входящая в нее единица проводимости названа в честь немецкого ученого, изобретателя, предпринимателя Вернера фон Сименса (1816–1892 гг.). Основанная им в 1847 г. компания Siemens AG (Сименс) является одной из самых больших компаний, выпускающих электротехническое, электронное, энергетическое, транспортное и медицинское оборудование.

Лучшим тепловым изолятором является вакуум. Теплокровные животные нагревают свое тело, чтобы изолировать свое тело, чтобы поддерживать его температуру с минимальной энергией. Хладнокровные животные, с другой стороны, исцеляют свои тела внешними источниками. Тепловая изоляция может помешать им. Утка или китообразные используют свой подкожный жир для теплоизоляции.

Интеллектуальные материалы для нового века. Общим знаменателем этой Нобелевской премии является работа трех ученых, ведущих к открытию и разработке нового класса веществ — проводящих полимеров. Проводящие полимеры сочетают электрическое поведение, типичное для полупроводников с свойствами материала, которые облегчают его обработку. Они могут изменять свою структуру, а потому — в зависимости от реакции на окружающую среду — их физические свойства. Вот почему они называются интеллектуальными материалами. «Умный» атрибут преувеличен, но поведение электропроводящих материалов делает его полезным.

Диапазон удельных электрических проводимостей очень широк: от материалов, обладающих высоким удельным сопротивлением, таких как стекло (которое, между прочим, хорошо проводит электрический ток, если его нагреть докрасна) или полиметилметакрилат (органическое стекло) до очень хороших проводников, таких как серебро, медь или золото. Удельная электрическая проводимость определяется количеством зарядов (электронов и ионов), скоростью их движения и количеством энергии, которое они могут переносить. Средними значениями удельной проводимости обладают водные растворы различных веществ, которые используются, например, в гальванических ваннах. Другим примером электролитов со средними значениями удельной проводимости является внутренняя среда организма (кровь, плазма, лимфа и другие жидкости).

Полимеры обычно известны как изоляторы. Они обладают хорошими механическими свойствами и легко обрабатываются. Они используются в качестве изолирующих электрических проводников, тепловых изоляторов или звукопоглощающих слоев. Их преимуществом является также их низкая плотность, и поэтому они все чаще используются в отраслях, где желателен малый вес материала, например, в авиационной технике или в производстве упаковочных материалов. Для многих применений функциональные свойства полимеров могут быть улучшены путем получения композитов, то есть полимеров, содержащих различные наполнители.

Проводимость металлов, полупроводников и диэлектриков подробно обсуждается в следующих статьях Конвертера физических величин сайт: , и Электрическая проводимость . В этой статье мы обсудим подробнее удельную проводимость электролитов, а также методы и простое оборудование для ее измерения.

Удельная электрическая проводимость электролитов и ее измерение

Так, например, сделаны фоточувствительные слои для ксерографий и лазерных принтеров, пьезоэлектрических и пироэлектрических детекторов или фотокопировальных аппаратов. В композитах, содержащих углеродную сажу или порошковый графит, электропроводность была значительно увеличена. Такие материалы подходят, например, для производства легких нефтяных канистр — проводящий композит обеспечивает электростатический заряд, поэтому нет риска воспламенения летучих паров.

В дополнение к проводящим композитам существуют также конъюгированные полимеры, которые могут проявлять свою высокую электропроводность. Это позволяет регулярно вращать одинарные и двойные связи в молекулярной структуре. В дополнение к системе этих связей предпосылкой является наличие подвижных носителей заряда, которые опосредуют конъюгированный транспорт цепи.

Удельная проводимость водных растворов, в которых электрический ток возникает в результате движения заряженных ионов, определяется количеством носителей заряда (концентрацией вещества в растворе), скоростью их движения (подвижность ионов зависит от температуры) и зарядом, которые они несут (определяемой валентностью ионов). Поэтому в большинстве водных растворов повышение концентрации приводит к увеличению числа ионов и, следовательно, к увеличению удельной проводимости. Однако после достижения определенного максимума удельная проводимость раствора может начать уменьшаться при дальнейшем увеличении концентрации раствора. Поэтому растворы с двумя различными концентрациями одной и той же соли могут иметь одинаковую удельную проводимость.

Структурно самым простым конъюгированным полимером является полиацетилен. Основополагающим открытием этих знатоков было выяснить, что когда тонкая полиацетиленовая пленка легирована парами иода, электропроводность пленки увеличивается примерно в миллион раз. Электрон удаляется из полимерной цепи. После переноса электрона из полиацетиленовой цепи в молекулу иода, которая заряжена отрицательно, молекула полиацетилена несет положительный заряд заряда. Существенное различие между легированием неорганических и органических полупроводников заключается в том, что мы можем существенно влиять на электрические свойства материала при следовых концентрациях легирующей примеси, для неорганических веществ нам нужна более высокая концентрация для полимеров.

Температура также влияет на проводимость, так как при повышении температуры ионы движутся быстрее, что приводит к увеличению удельной проводимости. Чистая вода — плохой проводник электричества. Обычная дистиллированная вода, в которой содержится в равновесном состоянии углекислый газ из воздуха и общая минерализация менее 10 мг/л, имеет удельную электрическую проводимость около 20 мСм/см. Удельная проводимость различных растворов приведена ниже в таблице.

Для переноса электрического заряда переполнение носителей между цепями является определяющим фактором. Этот транспорт менее эффективен, чем перенос заряда в металлах, поскольку он сильно зависит от порядка макромолекул. Доказательство состоит в том, что механически ориентированные пленки показывают более высокую электропроводность в направлении удлинения, чем исходные образцы.

Работа трех лауреатов по-прежнему остается вершиной исследований, начавшихся в 1950-х годах. Уже некоторые исследователи начали заниматься переносом электронов в низкомолекулярных веществах и образованием проводящих солей. В 1960-х годах Хидео Акамату и Хиро Инокучи писали монографию «Органический полупроводник», в которой реальные системы показали, что малые молекулы могут создавать проводники и даже сверхпроводники. В поисках подходящих веществ были синтезированы сотни органических материалов с повышенной электропроводностью, но до сих пор было невозможно приготовить подходящий полимер.

Для определения удельной проводимости раствора используется измеритель сопротивления (омметр) или проводимости. Это практически одинаковые устройства, отличающиеся только шкалой. Оба измеряют падение напряжения на участке цепи, по которому протекает электрический ток от батареи прибора. Измеренное значение проводимости вручную или автоматически пересчитывается в удельную проводимость. Это осуществляется с учетом физических характеристик измерительного устройства или датчика. Датчики удельной проводимости устроены просто: это пара (или две пары) электродов, погруженных в электролит. Датчики для измерения удельной проводимости характеризуются постоянной датчика удельной проводимости , которая в простейшем случае определяется как отношение расстояния между электродами D к площади (электрода), перпендикулярной течению тока А

Анилин черный известен с века. Из-за трудностей в синтезе внимание стало обращать на простейший модельный полимер — полиацетилен. Он имеет две конформации, транс и цис-форму. Синтез дает их смесь. С точки зрения электропроводности интересна только трансформация, полученная Хидеки Ширакавой в чистом виде полимерной пленки серебра. Это помогло ему по совпадению — он использовал катализатор различного типа для полимеризации, чем обычно, плюс тысячная концентрация.

На другом конце света МакДиармид и его коллега Хегер в то время рассматривали свойства неорганического полимера, состоящего из атомов серы и азота, которые они делали в виде пленки, подобной металлической пленке. О свойствах этого полимера было сообщено Макдиармидом на научной встрече в Токио, где он встретил Ширакаву. Они согласились начать совместную работу в Университете Пенсильвании. Транс-полиацетилен засевался иодом и изучал его электропроводность.

Эта формула хорошо работает, если площадь электродов значительно больше расстояния между ними, так как в этом случае большая часть электрического тока протекает между электродами. Пример: для 1 кубического сантиметра жидкости K = D/A = 1 см/1 см² = 1 см⁻¹. Отметим, что датчики удельной проводимости с маленькими электродами, раздвинутыми на относительно большое расстояние, характеризуются значениями постоянной датчика 1.0 cm⁻¹ и выше. В то же время, датчики с относительно большими электродами, расположенными близко друг к другу, имеют постоянную 0,1 cm⁻¹ или менее. Постоянная датчика для измерения удельной электрической проводимости различных устройств находится в пределах от 0,01 до 100 cm⁻¹.

Результатом стал ряд рабочих мест и компаний, которые затем улучшили химические процессы и повысили электропроводность. Хотя полиацетилен обладает высокой проводимостью, приближаясь к проводимости металлов, он не подходит для более широкого использования, он обладает низкой устойчивостью к атмосферным воздействиям. Поэтому интерес исследователей с середины 80-х годов был сфокусирован на других конъюгированных полимерах — полипирроле, политиофене, полианилина, полифенилена, поли.

Полянилин, вероятно, самый старый органический полимер, созданный человеком. Фриче, который вскоре после получения анилина стремился создать новые синтетические красители. Лэтби описал электрохимическое окисление анилина, которое после проталкивания щелочи изменило цвет на синий.

Теоретическая постоянная датчика: слева — K = 0,01 см⁻¹ , справа — K = 1 см⁻¹

Для получения удельной проводимости из измеренной проводимости используется следующая формула:

σ = K ∙ G

σ — удельная проводимость раствора в См/см;

K — постоянная датчика в см⁻¹;

G — проводимость датчика в сименсах.

Постоянную датчика обычно не рассчитывают по его геометрическим размерам, а измеряют в конкретном измерительном устройстве или в конкретной измерительной установке с использованием раствора с известной проводимостью. Эта измеренная величина и вводится в прибор для измерения удельной проводимости, который автоматически рассчитывает удельную проводимость по измеренным значениям проводимости или сопротивления раствора. В связи с тем, что удельная проводимость зависит от температуры раствора, устройства для ее измерения часто содержат датчик температуры, который измеряет температуру и обеспечивает автоматическую температурную компенсацию измерений, то есть, приведение результатов к стандартной температуре 25°C.

Самый простой способ измерения проводимости — приложить напряжение к двум плоским электродам, погруженным в раствор, и измерить протекающий ток. Этот метод называется потенциометрическим. По закону Ома, проводимость G является отношением тока I к напряжению U :

Однако не все так просто, как описано выше — при измерении проводимости имеется много проблем. Если используется постоянный ток, ионы собираются у поверхностей электродов. Также у поверхностей электродов может возникнуть химическая реакция. Это приводит к увеличению поляризационного сопротивления на поверхностях электродов, что, в свою очередь, приводит к получению ошибочных результатов. Если попробовать измерить обычным тестером сопротивление, например, раствора хлористого натрия, будет хорошо видно, как показания на дисплее цифрового прибора довольно быстро изменяются в сторону увеличения сопротивления. Чтобы исключить влияние поляризации, часто используют конструкцию датчика из четырех электродов.

Поляризацию также можно предотвратить или, во всяком случае, уменьшить, если использовать при измерении переменный ток вместо постоянного, да еще и подстраивать частоту в зависимости от проводимости. Низкие частоты используются для измерения низкой удельной проводимости, при которой влияние поляризации невелико. Более высокие частоты используются для измерения высоких проводимостей. Обычно частота подстраивается в процессе измерения автоматически, с учетом полученных значений проводимости раствора. Современные цифровые двухэлектродные измерители проводимости обычно используют переменный ток сложной формы и температурную компенсацию. Они откалиброваны на заводе-изготовителе, однако в процессе эксплуатации часто требуется повторная калибровка, так как постоянная измерительной ячейки (датчика) изменяется со временем. Например, она может измениться при загрязнении датчики или при физико-химических изменениях электродов.

В традиционном двухэлектродном измерителе удельной проводимости (именно такой мы будем использовать в нашем эксперименте) между двумя электродами приложено переменное напряжение и измеряется протекающий между электродами ток. Этот простой метод имеет один недостаток — измеряется не только сопротивление раствора, но и сопротивление, вызванное поляризацией электродов. Для сведения влияния поляризации к минимуму используют четырехэлектродную конструкцию датчика, а также покрытие электродов платиновой чернью.

Общая минерализация

Устройства для измерения удельной электрической проводимости часто используют для определения общей минерализации или содержания твёрдых веществ (англ. total dissolved solids, TDS). Это мера общего количества органических и неорганических веществ, содержащихся в жидкости в различных формах: ионизированной, молекулярной (растворенной), коллоидной и в виде суспензии (нерастворенной). К растворенным веществам относятся любые неорганические соли. Главным образом, это хлориды, бикарбонаты и сульфаты кальция, калия, магния, натрия, а также некоторые органические вещества, растворенные в воде. Чтобы относиться к общей минерализации, вещества должны быть или растворенными, или в форме очень мелких частиц, которые проходят сквозь фильтры с диаметром пор менее 2 микрометров. Вещества, которые постоянно находятся в растворе во взвешенном состоянии, но не могут пройти сквозь такой фильтр, называется взвешенными твердыми веществами (англ. total suspended solids, TSS). Общее количество взвешенных веществ обычно измеряется для определения качества воды.

Существует два метода измерения содержания твердых веществ: гравиметрический анализ , являющийся наиболее точным методом, и измерение удельной проводимости . Первый метод — самый точный, но требует больших затрат времени и наличия лабораторного оборудования, так как воду нужно выпарить до получения сухого остатка. Обычно это производится при температуре 180°C в лабораторных условиях. После полного испарения остаток взвешивается на точных весах.

Второй метод не такой точный, как гравиметрический анализ. Однако он очень удобен, широко распространен и является наиболее быстрым методом, так как представляет собой простое измерение проводимости и температуры, выполняемое за несколько секунд недорогим измерительным прибором. Метод измерения удельной электропроводности можно использовать в связи с тем, что удельная проводимость воды прямо зависит от количества растворенных в ней ионизированных веществ. Данный метод особенно удобен для контроля качества питьевой воды или оценки общего количества ионов в растворе.

Измеренная проводимость зависит от температуры раствора. То есть, чем выше температура, тем выше проводимость, так как ионы в растворе при повышении температуры движутся быстрее. Для получения измерений, независимых от температуры, используется концепция стандартной (опорной) температуры, к которой приводятся результаты измерения. Опорная температура позволяет сравнить результаты, полученные при разных температурах. Таким образом, измеритель удельной проводимости может измерять реальную проводимость, а затем использовать корректирующую функцию, которая автоматически приведет результат к опорной температуре 20 или 25°C. Если необходима очень высокая точность, образец можно поместить в термостат, затем откалибровать измерительный прибор при той же температуре, которая будет использоваться при измерениях.

Большинство современных измерителей удельной проводимости снабжены встроенным датчиком температуры, который используется как для температурной коррекции, так и для измерения температуры. Самые совершенные приборы способны измерять и отображать измеренные значения в единицах удельной проводимости, удельного сопротивления, солености, общей минерализации и концентрации. Однако еще раз отметим, что все эти приборы измеряют только проводимость (сопротивление) и температуру. Все физические величины, которые показывает дисплей, рассчитываются прибором с учетом измеренной температуры, которая используется для автоматической температурной компенсации и приведения измеренных значений к стандартной температуре.

Эксперимент: измерение общей минерализации и проводимости

В заключение мы выполним несколько экспериментов по измерению удельной проводимости с помощью недорогого измерителя общей минерализации (называемого также солемером, салинометром или кондуктомером) TDS-3. Цена «безымянного» прибора TDS-3 на eBay с учетом доставки на момент написания статьи менее US$3.00. Точно такой же прибор, но с названием изготовителя стоит уже в 10 раз дороже. Но это для любителей платить за брэнд, хотя очень высока вероятность того, что оба прибора будут выпущены на одном и том же заводе. TDS-3 осуществляет температурную компенсацию и для этого снабжен датчиком температуры, расположенным рядом с электродами. Поэтому его можно использовать и в качестве термометра. Следует еще раз отметить, что прибор реально измеряет не саму минерализацию, а сопротивление между двумя проволочными электродами и температуру раствора. Все остальное он автоматически рассчитывает с использованием калибровочных коэффициентов.

Измеритель общей минерализации поможет определить содержание твердых веществ, например, при контроле качества питьевой воды или определения солености воды в аквариуме или в пресноводном пруде. Его можно также использовать для контроля качества воды в системах фильтрации и очистки воды, чтобы узнать когда пришло время заменить фильтр или мембрану. Прибор откалиброван на заводе-изготовителе с помощью раствора хлорида натрия NaCl с концентрацией 342 ppm (частей на миллион или мг/л). Диапазон измерения прибора — 0–9990 ppm или мг/л. PPM — миллионная доля, безразмерная единица измерения относительных величин, равная 1 10⁻⁶ от базового показателя. Например, массовая концентрация 5 мг/кг = 5 мг в 1 000 000 мг = 5 частей на миллион или миллионных долей. Точно так же, как процент является одной сотой долей, миллионная доля является одной миллионной долей. Проценты и миллионные доли по смыслу очень похожи. Миллионные доли, в отличие от процентов, удобны для указания концентрации очень слабых растворов.

Прибор измеряет электрическую проводимость между двумя электродами (то есть величину, обратную сопротивлению), затем пересчитывает результат в удельную электрическую проводимость (в англоязычной литературе часто используют сокращение EC) по приведенной выше формуле проводимости с учетом постоянной датчика K, затем выполняет еще один пересчет, умножая полученную удельную проводимость на коэффициент пересчета 500. В результате получается значение общей минерализации в миллионных долях (ppm). Подробнее об этом — ниже.

Данный прибор для измерения общей минерализации нельзя использовать для проверки качества воды с высоким содержанием солей. Примерами веществ с высоким содержанием солей являются некоторые пищевые продукты (обычный суп с нормальным содержанием соли 10 г/л) и морская вода. Максимальная концентрация хлорида натрия, которую может измерить этот прибор — 9990 ppm или около 10 г/л. Это обычная концентрация соли в пищевых продуктах. Данным прибором также нельзя измерить соленость морской воды, так как она обычно равна 35 г/л или 35000 ppm, что намного выше, чем прибор способен измерить. При попытке измерить такую высокую концентрацию прибор выведет сообщение об ошибке Err.

Солемер TDS-3 измеряет удельную проводимость и для калибровки и пересчета в концентрацию использует так называемую «шкалу 500» (или «шкалу NaCl»). Это означает, что для получения концентрации в миллионных долях значение удельной проводимости в мСм/см умножается на 500. То есть, например, 1,0 мСм/см умножается на 500 и получается 500 ppm. В разных отраслях промышленности используют разные шкалы. Например, в гидропонике используют три шкалы: 500, 640 и 700. Разница между ними только в использовании. Шкала 700 основана на измерении концентрации хлорида калия в растворе и пересчет удельной проводимости в концентрацию выполняется так:

1,0 мСм/см x 700 дает 700 ppm

Шкала 640 использует коэффициент преобразования 640 для преобразования мСм в ppm:

1,0 мСм/см x 640 дает 640 ppm

В нашем эксперименте мы вначале измерим общую минерализацию дистиллированной воды. Солемер показывает 0 ppm. Мультиметр показывает сопротивление 1,21 МОм.

Для эксперимента приготовим раствор хлорида натрия NaCl с концентрацией 1000 ppm и измерим концентрацию с помощью TDS-3. Для приготовления 100 мл раствора нам нужно растворить 100 мг хлорида натрия и долить дистиллированной воды до 100 мл. Взвесим 100 мг хлорида натрия и поместим его в мерный цилиндр, добавим немного дистиллированной воды и размешаем до полного растворения соли. Затем дольем воду до метки 100 мл и еще раз как следует размешаем.

Для экспериментального определения проводимости мы использовали два электрода, изготовленные из того же материала и с теми же размерами, что и электроды TDS-3. Измеренное сопротивление составило 2,5 КОм.

Теперь, когда нам известно сопротивление и концентрация хлорида натрия в миллионных долях, мы можем приблизительно рассчитать постоянную измерительной ячейки солемера TDS-3 по приведенной выше формуле:

K = σ/G = 2 мСм/см x 2,5 кОм = 5 см⁻¹

Это значение 5 см⁻¹ близко к расчетной величине постоянной измерительной ячейки TDS-3 с указанными ниже размерами электродов (см. рисунок).

• D = 0,5 см — расстояние между электродами;
• W = 0,14 см — ширина электродов
• L = 1,1 см — длина электродов

Постоянная датчика TDS-3 равна K = D/A = 0,5/0,14×1,1 = 3,25 cm⁻¹. Это не сильно отличается от полученного выше значения. Напомним, что приведенная выше формула позволяет лишь приблизительно оценить постоянную датчика.

Вы затрудняетесь в переводе единицы измерения с одного языка на другой? Коллеги готовы вам помочь. Опубликуйте вопрос в TCTerms и в течение нескольких минут вы получите ответ.

Из курса физики Вы помните, что электрическое сопротивление любого проводника может быть рассчитано по формуле:

где R — сопротивление в Ом;

l — длина проводника, см;

S — площадь поперечного сечения, см 2 ;

r — удельное сопротивление, т.е. сопротивление проводника длиной 1 см с площадью поперечного сечения 1 см 2 .

В электрохимии принято пользоваться величинами, обратными указанным:

Величина L называется электрической проводимостью и измеряется в Сименсах (См) См = Ом -1 .

Величина À называется удельной электрической проводимостью. Нетрудно вывести, что величина À измеряется в См×см -1 . На рис.3.1. представлена кондуктометрическая ячейка, применяемая для измерения электрической проводимости. Она представляет собой сосуд 1, без дна, в который вставлены два платиновых электрода 2, помещаемые в исследуемый раствор 3.

Величину К определяют экспериментально. Для этого необходимо измерить электрическую проводимость L раствора, для которого À известна. Обычно для этого используют растворы хлорида калия известной концентрации (0,1; 0,05; 0,01 моль/дм 3), величины À которых имеются в таблицах.

Из уравнения (3.5.) следует, что

удельная проводимость — это электрическая проводимость раствора, помещенного между двумя электродами площадью 1 см 2 , находящимися на расстоянии 1 см.

À HCl KOH HF CH 3 COOH С Рис.3.2.Зависимость удельной прово-димости от концентрации

Удельная электрическая проводимость раствора зависит от природы растворителя и растворенного вещества, кон-центрации раствора и темпера-туры. На рис.3.2. приведены графики зависимости À от концентрации водных раство-ров некоторых электролитов при постоянной температу-ре.Из рисунка, прежде всего следует, что при равных концентрациях растворов про-водимость растворов сильных электролитов значительно выше, т.к. в них содержится

больше ионов-носителей электричества. В разбавленных растворах как сильных так и слабых электролитов увеличение концентрации приводит к повышению проводимости, что связано с увеличением количества ионов. В области высоких концентраций наблюдается уменьшение À. Для сильных электролитов это связано с увеличением вязкости растворов и усилением электростатического взаимодействия между ионами. Для слабых электролитов указанный эффект связан с уменьшением степени диссоциации и, следовательно, уменьшением количества ионов.

При повышении температуры удельная проводимость электролитов увеличивается:

À 2 = À 1 [ 1 + a(T 2 — T 1)] (3.7.)

В этом уравнении À 1 и À 2 – удельная проводимость при температурах Т 1 и Т 2 , а a – температурный коэффициент проводимости. Например, для солей a » 0,02. Это означает, что повышение температуры на один градус приводит к увеличению проводимости приблизительно на 2%. Связано это с тем, что при повышении температуры уменьшается степень гидратации и вязкость растворов.

Следует отметить, что в отличие от электролитов, электричес-кая проводимость металлов при повышении температуры уменьшается.

Молярная электрическая проводимость

Молярная проводимость l связана с удельной проводимостью формулой:

l = À×1000/с (3.8.)

В этом выражении с — молярная концентрация раствора, моль×дм -3 . Молярная проводимость выражена в См×см 2 ×моль -1 . Итак,

молярная проводимость — это проводимость раствора, содержащего 1 моль вещества при расстоянии между электродами, равном 1 см.

Молярная электрическая проводимость как сильных так и слабых электролитов с увеличением концентрации понижается. Характер зависимости l от с для сильных и слабых электролитов различен, т.к. влияние концентрации обусловлено различными причинами.

Сильные электролиты . При небольших концентрациях зависимость молярной проводимости от концентрации выражается эмпирическим уравнением Кольрауша:

l = l 0 –bÖс (3.9.)

где b – определяемая опытным путем постоянная,

а l 0 – молярная электрическая проводимость при бесконечном разбавлении или предельная молярная проводимость .

Таким образом,

liml C ® 0 = l 0 (3.10.)

Приготовить раствор, концентрация которого равна нулю, невозможно. Величину l 0 для сильных электролитов можно определить графически. Из уравнения (3.9.) следует, что график зависимости l = f(Öc) для сильных электролитов представляет собой прямую линию (рис.3.3.,линия 1).

Если приготовить ряд растворов различной концентрации, измерить их проводимость L,рассчитать и построить график l = f(Öс), то экстраполируя полученную прямую на ось ординат (с = 0), можно определить l 0 . Если учесть, что сильные электролиты, независимо от концентрации раствора полностью диссоциированы, то приходим к выводу, что количество ионов, образуемых из 1 моль вещества, всегда одно и то же. Значит, от концентрации раствора зависит скорость движения ионов, с увеличением концентрации усиливается торможение ионов . Это явление, связано с образованием вокруг каждого иона в растворе ионной атмосферы , состоящей преимущественно из ионов противоположного знака. С увеличением концентрации также увеличивается вязкость раствора. Существуют и другие причины замедления движения ионов в электрическом поле, на которых мы останавливаться не будем.

Если экспериментально определить величину l для раствора данной концентрации и графически найти l 0 можно рассчитать величину коэффициента электропроводности f :

f = l / l 0 (3.11.)

Коэффициент f характеризует степень торможения ионов и при разбавлении раствора стремится к единице.

Слабые электролиты . Молярная проводимость слабых электролитов значительно меньше, чем для растворов сильных электролитов (рис.3.3, линия 2). Это связано с тем, что даже при низких концентрациях степень диссоциации слабых электролитов мала. Повышение молярной проводимости слабых электролитов при разбавлении растворов связано с увеличением степени диссоциации в соответствии с законом разбавления Оствальда. С.Аррениус высказал предположение, что молярная проводимость слабого электролита связана с его степенью диссоциации выражением:

a = l / l 0 (3.12.)

Таким образом, степень диссоциации слабого электролита можно рассчитать, если известна его предельная молярная проводимость l 0 . Однако определить l 0 графически путем экстраполяции графика l= f(Öс) нельзя, т.к. кривая (рис.3.3., линия 2) при уменьшении концентрации асимптотически приближается к оси ординат.

Величину l 0 можно определить с помощью закона независимости движения ионов Кольрауша :

Молярная электрическая проводимость электролита при бесконечном разбавлении раствора равна сумме предельных подвижностей катионов и анионов.

l 0 =l 0,+ + l 0,– (3.13.)

Подвижности катиона и аниона пропорциональны абсолютным скоростям движения ионов (см.табл. 3.1.).

l 0,+ = F×U + ; l 0,– = F×U – (3.14.)

В этих формулах F — единица количества электричества, называемая Фарадеем, равная 96494 Кулонов (Кл). В табл.3.2. приведены предельные подвижности некоторых ионов.

Следует отметить, что закон независимости движения ионов справедлив как для слабых, так и для сильных электролитов.

Таблица 3.2.

Предельные подвижности ионов (см 2 ×См×моль -1) при 25 0 С

Катион	l 0,+	Анион	l 0,–
Н + К + Na + Li + Ag + Ba 2+ Ca 2+ Mg 2+	349,8 73,5 50,1 38,7 61,9 127,2 119,0 106,1	ОН — I — Br — Cl — NO 3 — CH 3 COO — SO 4 2-	76,8 78,4 76,3 71,4 40,9 160,0

Применение измерений проводимости

Метод исследования основанный на измерении электрической проводимости, называется кондуктометрией . Этот метод широко используется в лабораторной практике. Прибор для измерения электрической проводимости называется кондуктометром . В частности, кондуктометрический метод позволяет определять константы диссоциации слабых электролитов.

Пример. Определение константы диссоциации уксусной кислоты.

а)Для нахождения постоянной кондуктометрической ячейки приготовили растворы хлорида калия с молярными концентрациями 0,1 и 0,02 моль×дм -3 и измерили их проводимость.Она оказалась равной соответственно L 1 = 0,307 См и L 2 = 0,0645 См. По таблице находим значения удельной проводимости растворов хлорида калия указанных концентраций:

À 1 = 1,29×10 -1 См×см -1 ; À 2 = 2,58×10 -2 См×см -1

По уравнению 3.6. рассчитываем постоянную ячейки:

К 1 = À 1 /L 1 = 0,42 см -1

К 2 = À 2 /L 2 = 0,40 см -1

Среднее значение К = 0,41 см -1

б)Приготовили два раствора уксусной кислоты с концентрациями c 1 =0,02моль×дм -3 и c 2 = 1×10 -3 моль×дм -3 . С помощью кондуктометра измерили их электрическую проводимость:

L 1 = 5,8×10 -4 См; L 2 = 1,3×10 -4 См.

в) Рассчитываем удельную проводимость:

À 1 = L 1 ×K = 5,8×10 -4 ×0,41 = 2,378×10 -4 Cм×см -1

À 2 = L 2 ×К = 1,2×10 -4 ×0,41 = 0,492×10 -4 См×см -1

г) По формуле (3.8.) находим молярную электрическую проводимость l 1 =11,89См×см 2 ×моль -1 ; l 2 = 49,2 См×см 2 ×моль -1

д) Находим, пользуясь табл.3.2. величину предельной молярной прово-димости уксусной кислоты: l 0 = 349,8 +40,9 = 390,7 См×см 2 ×моль -1 .

е) Наконец, рассчитываем для каждого раствора степень диссоциации (уравнение 3.12.) и константу диссоциации

a 1 = 3,04×10 -2 ; a 2 = 1,26×10 -1

К 1 = 1,91×10 -5 ; К 2 = 1,82×10 -5

Среднее значение К = 1,86×10 -5

Теплопроводность металлов, металлических элементов и сплавов

Теплопроводность — k — это количество тепла, передаваемого за счет единичного температурного градиента в единицу времени в установившихся условиях в направлении, нормальном к поверхности единицы площади. Теплопроводность — k — используется в уравнении Фурье.

9 0038190 9003 8 0-25

Металл, металлический элемент или сплав	Температура — t — ( o C)	Теплопроводность — k — (Вт / м K)
Алюминий	-73	237
«	0	236
»	127	240
«	327	232
«	527	220
Алюминий — дюралюминий (94-96% Al, 3-5% Cu, следы Mg)	20	164
Алюминий — силумин (87% Al, 13% Si)	20	164
Алюминиевая бронза	0-25	70
Алюминиевый сплав 3003, прокат	0-25
Алюминиевый сплав 2014.отожженный	0-25	190
Алюминиевый сплав 360	0-25	150
Сурьма	-73	30,2
«	0	25,5
«	127	21,2
»	327	18,2
«	527	16,8
Бериллий	-73	301
»	0	218
«	127	161
»	327	126
«	527	107
»	727	89
«	927	73
Бериллиевая медь 25	80
Висмут	-73	9.7
«	0	8,2
Бор	-73	52,5
»	0	31,7
«	127	18,7
«	327	11,3
»	527	8,1
«	727	6,3
»	927	5.2
Кадмий	-73	99,3
«	0	97,5
»	127	94,7
Цезий	-73	36,8
«	0	36,1
Хром	-73	111
»	0	94,8
«	127	87.3
«	327	80,5
»	527	71,3
«	727	65,3
»	927	62,4
Кобальт	-73	122
«	0	104
»	127	84,8
Медь	-73	413
«	0	401
«	127	392
»	327	383
«	527	371
»	727	357
«	927	342
Медь электролитическая (ETP)	0-25	390
Медь — Адмиралтейская латунь	20	111
Медь — алюминиевая бронза (95% Cu, 5% Al)	20	83
Медь — Бронза (75% Cu, 25% Sn)	20	26
Медь — латунь (желтая латунь) (70% Cu, 30% Zn)	20	111
Медь — патронная латунь (UNS C26000)	20	120
Медь — константан (60% Cu, 40% Ni)	20	22.7
Медь — немецкое серебро (62% Cu, 15% Ni, 22% Zn)	20	24,9
Медь — фосфористая бронза (10% Sn, UNS C52400)	20	50
Медь — Красная латунь (85% Cu, 9% Sn, 6% Zn)	20	61
Мельхиор	20	29
Германий	-73	96,8
«	0	66.7
«	127	43,2
»	327	27,3
«	527	19,8
»	727	17,4
»	927	17,4
Золото	-73	327
«	0	318
»	127	312
«	327	304
«	527	292
»	727	278
«	927	262
Гафний	-73	24.4
«	0	23,3
»	127	22,3
«	327	21,3
»	527	20,8
»	727	20,7
«	927	20,9
Hastelloy C	0-25	12
Инконель	21-100	15
Инколой	0-100	12
Индий	-73	89.7
«	0	83,7
»	127	75,5
Иридий	-73	153
«	0	148
«	127	144
»	327	138
«	527	132
»	727	126
«	927	120
Железо	-73	94
«	0	83.5
«	127	69,4
»	327	54,7
«	527	43,3
»	727	32,6
»	927	28,2
Железо — литье	20	52
Железо — перлитное с шаровидным графитом	100	31
Кованое железо	20	59
Свинец	-73	36.6
«	0	35,5
»	127	33,8
«	327	31,2
Химический свинец	0-25	35
Сурьма свинец (твердый свинец)	0-25	30
Литий	-73	88,1
«	0	79.2
«	127	72,1
Магний	-73	159
»	0	157
«	127	153
«	327	149
»	527	146
Магниевый сплав AZ31B	0-25	100
Марганец	-73	7.17
«	0	7,68
Ртуть	-73	28,9
Молибден	-73	143
»	0	139
«	127	134
»	327	126
«	527	118
»	727	112
«	927	105
Монель	0-100	26
Никель	-73	106
«	0	94
»	127	80.1
«	327	65,5
»	527	67,4
«	727	71,8
»	927	76,1
Никель — Кованые	0-100	61-90
Мельхиор 50-45 (константан)	0-25	20
Ниобий (колумбий)	-73	52.6
«	0	53,3
»	127	55,2
«	327	58,2
»	527	61,3
»	727	64,4
«	927	67,5
Осмий	20	61
Палладий		75.5
Платина	-73	72,4
«	0	71,5
»	127	71,6
«	327	73,0
«	527	75,5
»	727	78,6
»	927	82,6
Плутоний	20	8.0
Калий	-73	104
«	0	104
»	127	52
Красная латунь	0-25	160
Рений	-73	51
«	0	48,6
»	127	46,1
«	327	44.2
«	527	44,1
»	727	44,6
«	927	45,7
Родий	-73	154
«	0	151
»	127	146
«	327	136
»	527	127
«	727	121
«	927	115
Рубидий	-73	58.9
«	0	58,3
Селен	20	0,52
Кремний	-73	264
»	0	168
«	127	98,9
»	327	61,9
«	527	42,2
»	727	31.2
«	927	25,7
Серебро	-73	403
»	0	428
«	127	420
«	327	405
»	527	389
«	727	374
»	927	358
Натрий	-73	138
«	0	135
Припой 50-50	0-25	50
Сталь — углерод, 0.5% C	20	54
Сталь — углеродистая, 1% C	20	43
Сталь — углеродистая, 1,5% C	20	36
«	400	36
«	122	33
Сталь — хром, 1% Cr	20	61
Сталь — хром, 5% Cr	20	40
Сталь — хром, 10% Cr	20	31
Сталь — хромоникель, 15% Cr, 10% Ni	20	19
Сталь — хромоникель, 20% Cr , 15% Ni	20	15.1
Сталь — Hastelloy B	20	10
Сталь — Hastelloy C	21	8,7
Сталь — никель, 10% Ni	20	26
Сталь — никель, 20% Ni	20	19
Сталь — никель, 40% Ni	20	10
Сталь — никель, 60% Ni	20	19
Сталь — хром никель, 80% никель, 15% никель	20	17
Сталь — хром никель, 40% никель, 15% никель	20	11.6
Сталь — марганец, 1% Mn	20	50
Сталь — нержавеющая, тип 304	20	14,4
Сталь — нержавеющая, тип 347	20	14,3
Сталь — вольфрам, 1% W	20	66
Сталь — деформируемый углерод	0	59
Тантал	-73	57.5
«	0	57,4
»	127	57,8
«	327	58,9
»	527	59,4
»	727	60,2
«	927	61
Торий	20	42
Олово	-73	73.3
«	0	68,2
»	127	62,2
Титан	-73	24,5
«	0	22,4
«	127	20,4
»	327	19,4
«	527	19,7
»	727	20.7
«	927	22
Вольфрам	-73	197
»	0	182
«	127	162
«	327	139
»	527	128
«	727	121
»	927	115
Уран	-73	25.1
«	0	27
»	127	29,6
«	327	34
»	527	38,8
»	727	43,9
«	927	49
Ванадий	-73	31,5
»	0	31.3
«	427	32,1
»	327	34,2
«	527	36,3
»	727	38,6
»	927	41,2
Цинк	-73	123
«	0	122
»	127	116
«	327	105
Цирконий	-73	25.2
«	0	23,2
»	127	21,6
«	327	20,7
»	527	21,6
»	727	23,7
«	927	25,7

Сплавы — температура и теплопроводность

Температура и теплопроводность для

• Hastelloy A
• Inconel
• Navarich
• Advance
• Монель

Сплавы:

Электропроводность металлов с сортировкой по удельному сопротивлению

 Исходный код:
 1 - CSNDT
 2 - Руководство по вихретоковым испытаниям методом вихретокового контроля
 3 - Журнал NDT, сентябрь / октябрь 1955 г., статья Косгроува

ОКАЗЫВАТЬ СОПРОТИВЛЕНИЕ.КОНД. ИСТОЧНИК
Ом-м SIEMENS / м% КОД IACS МАТЕРИАЛ
-------------------------------------------------- --------------------------------
1.591E-08 6.287E + 07 108.40 1 Серебро, чистое
1.642E-08 6.090E + 07 105.00 2 Серебро, чистое
1.664E-08 6.009E + 07103.60 1 Медь, чистая
1.707E-08 5.858E + 07 101.00 1 Медь, электролитический вязкий пек (отожженный)
1.724E-08 5.800E + 07 100.00 2 Медь, чистая
2.028E-08 4.930E + 07 85.00 1 Медь раскисленная (отожженная)
2.349E-08 4.257E + 07 73.40 1 Золото
2.463E-08 4.060E + 07 70.00 2 Золото, чистое
2.655E-08 3.767E + 07 64.94 1 Алюминий, 99,99%
2.826E-08 3.538E + 07 61.00 2 Алюминий чистый
2.871E-08 3.483E + 07 60.00 - 60.10 3 Алюминиевый сплав, 7072
2.903E-08 3.445E + 07 57.00 - 61.80 3 Алюминиевый сплав, 1100
2.922E-08 3.422E + 07 59.00 1 Алюминий, 2S Конд. «0»
3.025E-08 3.306E + 07 57.00 1 Алюминий, 2S Конд. h28
3.073E-08 3.254E + 07 55.70 - 56.50 3 Алюминиевый сплав, 6951-0
3.079E-08 3.248E + 07 56.00 1 Позолоченный металл (отожженный)
3.135E-08 3.190E + 07 55.00 1 Алюминий, A51S Cond. «0»
3.184E-08 3.141E + 07 53.30 - 55.00 3 Алюминиевый сплав, 6151-0
3.235E-08 3.091E + 07 52.30 - 54.30 3 Алюминиевый сплав, 4043-F
3.250E-08 3.077E + 07 53.00 - 53.10 3 Алюминиевый сплав, 6951-F
3.281E-08 3.048E + 07 52.30 - 52.80 3 Алюминиевый сплав, 5005
3.435E-08 2.912E + 07 50.10 - 50.30 3 Алюминиевый сплав, X3005-0
3.448E-08 2.900E + 07 50.00 1 Алюминий, 24S Конд. «0»
3.448E-08 2.900E + 07 50.00 1 Алюминий, 3S Cond. «0»
3.448E-08 2.900E + 07 50.00 1 Алюминий, 18S Конд. «0»
3.448E-08 2.900E + 07 50.00 1 Алюминий, 14S Конд. «0»
3.473E-08 2.880E + 07 48,60 - 50,70 3 Алюминиевый сплав, 2014-F и -0
3.490E-08 2.865E + 07 49.30 - 49.50 3 Алюминиевый сплав, 2017-F
3.515E-08 2.845E + 07 48.30 - 49.80 3 Алюминиевый сплав, 5050
3.519E-08 2.842E + 07 47.00 - 51.00 3 Алюминиевый сплав, 6062-F
3.540E-08 2.825E + 07 48.70 1 Кальций
3.592E-08 2.784E + 07 48.00 1 Bronze Phos., 1,25% Phos. Оценка E
3.592E-08 2.784E + 07 48.00 1 Phos.Бронза, 1,25% Phos. Оценка E
3.618E-08 2.764E + 07 46.80 - 48.50 3 Алюминиевый сплав, 2024-F
3.649E-08 2.741E + 07 44.70 - 49.80 3 Алюминиевый сплав, 3003-0
3.661E-08 2.732E + 07 44.70 - 49.50 3 Алюминиевый сплав, 6062-T6
3.736E-08 2.677E + 07 44.50 - 47.80 3 Алюминиевый сплав, 7075-F
3.769E-08 2.654E + 07 45.50 - 46.00 3 Алюминиевый сплав, X7178-F и -0
3.798E-08 2.633E + 07 42.30 - 48.50 3 Алюминиевый сплав, 6061-F и -0
3.831E-08 2.610E + 07 45.00 1 Алюминий, 17S Конд. «0»
3.831E-08 2.610E + 07 45.00 1 Алюминий, 53S Конд. «0»
3.831E-08 2.610E + 07 45.00 1 Алюминий, 61S Конд. «0»
3.831E-08 2.610E + 07 45.00 1 Алюминий, A51S Cond. Т4 и Т6
3.831E-08 2.610E + 07 45.00 1 Алюминиевый сплав, 750
3.861E-08 2.590E + 07 42.30 - 47.00 3 Алюминиевый сплав, 5357
3.861E-08 2.590E + 07 37.80 - 51.50 3 Алюминиевый сплав, 3003-h24 и -h22
3.879E-08 2.578E + 07 43.90 - 45.00 3 Алюминиевый сплав, 6151-T6
3.918E-08 2.552E + 07 44.00 1 бронза, коммерческая (отожженная)
3.918E-08 2.552E + 07 44.00 1 Алюминиевый сплав, 142 Sand Cond. T21
3.941E-08 2.538E + 07 43.50 - 44.00 3 Алюминиевый сплав, 6062-T4
3.950E-08 2.532E + 07 39.30 - 48.00 3 Алюминиевый сплав, 6053
4.000E-08 2.500E + 07 43.10 1 Бериллий
4.010E-08 2.494E + 07 43.00 1 Алюминиевый сплав, 355 Sand Cond.T51
4.010E-08 2.494E + 07 43.00 1 Алюминиевый сплав, 356 Sand Cond. T51
4.043E-08 2.474E + 07 37.80 - 47.50 3 Алюминиевый сплав, 3003-h34 и -h38
4.066E-08 2.459E + 07 40.00 - 44.80 3 Алюминиевый сплав, 6061-T6 и -T9
4.066E-08 2.459E + 07 41.50 - 43.30 3 Алюминиевый сплав, 6151-T4
4.081E-08 2.451E + 07 42.10 - 42.40 3 Алюминиевый сплав, 2127-T4
4.105E-08 2.436E + 07 42.00 1 Алюминиевый сплав, 355 Sand Cond.T7
4.105E-08 2.436E + 07 42.00 1 Алюминиевый сплав, 43 (отожженный)
4.105E-08 2.436E + 07 42.00 1 Алюминий, 3S Cond. H 12
4.105E-08 2.436E + 07 42.00 1 Бронза, коммерческий свинец
4.105E-08 2.436E + 07 42.00 1 Коммерческая бронза с содержанием свинца
4.160E-08 2.404E + 07 39.40 - 43.50 3 Алюминиевый сплав, 3004
4.205E-08 2.378E + 07 41.00 1 Алюминий, 3S Cond. H 14
4.205E-08 2.378E + 07 41.00 1 Алюминиевый сплав, 122 Sand Cond.Т2
4.289E-08 2.332E + 07 40.20 3 Алюминиевый сплав, 2618
4.310E-08 2.320E + 07 40.00 1 Алюминий, 24S Конд. T6
4.310E-08 2.320E + 07 40.00 1 Алюминий, 18S Конд. T61
4.310E-08 2.320E + 07 40.00 1 Алюминий, 11S Конд. Т3
4.310E-08 2.320E + 07 40.00 1 Алюминий, 14S Конд. T6
4.310E-08 2.320E + 07 40.00 1 Алюминий, 3S Cond. H 18
4.310E-08 2.320E + 07 40.00 1 Алюминий, 32S Конд. «0»
4.310E-08 2.320E + 07 40.00 1 Алюминий, 53S Конд. Т4 и Т6
4.310E-08 2.320E + 07 40.00 1 Алюминий, 61S Cond. Т4 и Т6
4.415E-08 2.265E + 07 37.60 - 40.50 3 Алюминиевый сплав, 6061-T4
4.421E-08 2.262E + 07 39.00 1 Алюминиевый сплав, 356 Sand Cond. T6
4.421E-08 2.262E + 07 39.00 1 Алюминиевый сплав, 355 Пермь. Mold Cond. T6
4.421E-08 2.262E + 07 39.00 1 Алюминиевый сплав, 13
4.432E-08 2.256E + 07 38.90 1 Бериллий
4.438E-08 2.253E + 07 38.00 - 39.70 3 Алюминиевый сплав, 2014-T6
4.467E-08 2.239E + 07 38.60 1 Магний, чистый
4.490E-08 2.227E + 07 38.40 1 Родий
4.610E-08 2.169E + 07 37.40 3 Алюминиевый сплав, 2218-T61
4.660E-08 2.146E + 07 37.00 1 Алюминиевый сплав, 142 Sand Cond. T77
4.660E-08 2.146E + 07 37.00 1 Алюминиевый сплав, 195 конд. T62
4.660E-08 2.146E + 07 37.00 2 Магний
4.660E-08 2.146E + 07 37.00 1 Алюминиевый сплав, 360
4.660E-08 2.146E + 07 37.00 1 Алюминиевый сплав, 355 Sand Cond. T61
4.660E-08 2.146E + 07 37.00 1 Алюминиевый сплав, 43 литой
4.660E-08 2.146E + 07 37.00 1 Алюминиевый сплав, A 108
4.660E-08 2.146E + 07 37.00 1 Латунь, красная (отожженная)
4.756E-08 2.103E + 07 36.00 - 36.50 3 Алюминиевый сплав, 2011-T3
4.789E-08 2.088E + 07 36.00 1 Алюминиевый сплав, B 195 Cond.T6
4.789E-08 2.088E + 07 36.00 1 Цельнолитой алюминий, конд. Sol. H.T. И стресс
4.789E-08 2.088E + 07 36.00 1 Алюминиевый сплав, 355 Sand Cond. T6
4.816E-08 2.076E + 07 35.30 - 36.30 3 Алюминиевый сплав, 4032-T6
4.843E-08 2.065E + 07 33.60 - 37.60 3 Алюминиевый сплав, 5052
4.926E-08 2.030E + 07 35.00 1 Алюминиевый сплав, 195 конд. Т4
4.926E-08 2.030E + 07 35.00 1 Алюминиевый сплав, 214
4.926E-08 2.030E + 07 35.00 1 Алюминиевый сплав, 40E
4.926E-08 2.030E + 07 35.00 1 Алюминий, 52S Конд. «0» и H 38
4.926E-08 2.030E + 07 35.00 1 Алюминий, 32S Конд. T6
4.926E-08 2.030E + 07 35.00 1 Алюминиевый сплав, B 195 Cond. Т4
4.998E-08 2.001E + 07 34.50 1 Магний (деформируемые сплавы)
5.071E-08 1.972E + 07 34.00 1 Алюминиевый сплав, 142 Sand Cond. T571
5.071E-08 1.972E + 07 34.00 1 Алюминиевый сплав, 122 Пермь.Форма как литая
5.124E-08 1.952E + 07 32.50 - 34.80 3 Алюминиевый сплав, 2014-T3 и -T4
5.209E-08 1.920E + 07 31.40 - 34.80 3 Алюминиевый сплав, 7075-T6
5.225E-08 1.914E + 07 33.00 1 Молибден
5.225E-08 1.914E + 07 33.00 1 Алюминиевый сплав, 122 Sand Cond. T61
5.225E-08 1.914E + 07 33.00 1 Алюминиевый сплав, A214
5.289E-08 1.891E + 07 32.60 1 Иридий
5.330E-08 1.876E + 07 28.60 - 36.10 3 Алюминиевый сплав, 2024-T3
5.388E-08 1.856E + 07 32.00 1 Латунь, низкая (отожженная)
5.388E-08 1.856E + 07 32.00 1 Алюминиевый сплав, 142 Пермь. Mold Cond. T61
5.388E-08 1.856E + 07 27.00 - 37.00 3 Алюминиевый сплав, 7075-W
5.388E-08 1.856E + 07 32.00 2 Алюминиевый сплав, 7075-T6
5.448E-08 1.836E + 07 30.50 - 32.80 3 Алюминиевый сплав, 5154
5.491E-08 1.821E + 07 31.40 1 Вольфрам
5.562E-08 1.798E + 07 31.00 1 Алюминиевый сплав, 108
5.747E-08 1.740E + 07 30.00 1 Алюминий, 24S Конд. Т4
5.747E-08 1.740E + 07 30.00 1 Алюминий Allcast, Sol H.T. и в возрасте
5.747E-08 1.740E + 07 30.00 1 Алюминий, 17S Конд. Т4
5.747E-08 1.740E + 07 30.00 1 Алюминиевый сплав, 113
5.747E-08 1.740E + 07 30.00 1 Алюминиевый сплав, R 317
5.747E-08 1.740E + 07 30.00 1 Алюминий, 75S Конд. T6
5.747E-08 1.740E + 07 30.00 1 Цельнолитой алюминий со снятым напряжением
5.766E-08 1.734E + 07 28.80 - 31.00 3 Алюминиевый сплав, 2024-T4
5.805E-08 1.723E + 07 26.80 - 32.60 3 Алюминиевый сплав, X7178-W и T6
5.884E-08 1.699E + 07 29.10 - 29.50 3 Алюминиевый сплав, 2024-T36
5.945E-08 1.682E + 07 29.00 1 Алюминиевый сплав, A 132 Cond. T551
5.945E-08 1.682E + 07 29.00 1 Алюминий, красный X-8 Cond. Снятие стресса
5.945E-08 1.682E + 07 29.00 1 Алюминий, 56S Конд. «0»
5.945E-08 1.682E + 07 29.00 2 Цинк
5.956E-08 1.679E + 07 28.10 - 29.80 3 Алюминиевый сплав, 5056
6.158E-08 1.624E + 07 28.00 1 Цинк, товарный прокат
6.158E-08 1.624E + 07 28.00 1 Алюминиевый сплав, 319 Пермь. Форма
6.158E-08 1.624E + 07 28.00 1 Патрон латунный (отожженный)
6.158E-08 1.624E + 07 28.00 1 Muntz Metal (отожженный)
6.158E-08 1.624E + 07 28.00 1 Алюминиевый сплав, 85
6.158E-08 1.624E + 07 28.00 1 Латунь, картридж (отожженный)
6.247E-08 1.601E + 07 27.60 1 Кобальт
6.386E-08 1.566E + 07 27.00 1 Алюминиевый сплав, C113
6.386E-08 1.566E + 07 27.00 1 Цинк, литье под давлением
6.386E-08 1.566E + 07 27.00 1 Алюминий, 56S Конд. H 38
6.386E-08 1.566E + 07 27.00 1 Алюминий Allcast, литой
6.386E-08 1.566E + 07 27.00 1 Алюминиевый сплав, 319 Песок
6.386E-08 1.566E + 07 27.00 1 Латунь, желтая (отожженная)
6.386E-08 1.566E + 07 27.00 1 Алюминиевый сплав, 380
6.631E-08 1.508E + 07 26.00 1 Латунь с низким содержанием свинца (отожженная)
6.631E-08 1.508E + 07 26.00 1 Латунь, свинцовая морская (отожженная)
6.631E-08 1.508E + 07 26.00 1 Латунь, военно-морская (отожженная)
6.631E-08 1.508E + 07 26.00 1 Алюминиевый сплав, красный X-8 в литом виде
6.842E-08 1.462E + 07 25.20 1 Кадмий
6.842E-08 1.462E + 07 25.20 1 Никель, чистый (электролитический)
6.897E-08 1.450E + 07 25.00 1 свинцовая желтая латунь
6.897E-08 1.450E + 07 25.00 1 Цинк, литье под давлением
6.897E-08 1.450E + 07 25.00 1 Латунь, желтый свинец
7.009E-08 1.427E + 07 24.60 1 Admiralty Metal (отожженный)
7.184E-08 1.392E + 07 24.00 2 Латунь, Адмиралтейство
7.184E-08 1.392E + 07 24.00 1 Алюминиевый сплав, 218
7.184E-08 1.392E + 07 24.00 1 Марганцевая бронза (отожженная)
7.184E-08 1.392E + 07 24.00 2 Адмиралтейство Латунь
7.184E-08 1.392E + 07 24.00 1 Марганцевая бронза (отожженная)
7.496E-08 1.334E + 07 23.00 1 Латунь, алюминий (отожженный)
7.496E-08 1.334E + 07 23.00 1 Алюминиевая латунь (отожженная)
7.595E-08 1.317E + 07 22.70 1 Рутений
8.210E-08 1.218E + 07 21.00 1 Алюминиевый сплав, 220
8.210E-08 1.218E + 07 21.00 1 Бериллиевая медь, конд. В
8.210E-08 1.218E + 07 21.00 1 Медь бериллий, конд. В
8.535E-08 1.172E + 07 20.20 1 Литий
9.473E-08 1.056E + 07 18.20 1 Осмий
9.579E-08 1.044E + 07 18.00 1 Никель "А"
9.579E-08 1.044E + 07 18.00 1 Phos. Бронза, 5% Phos. Оценка отлично
9.579E-08 1.044E + 07 18.00 2 Утюг
9.579E-08 1.044E + 07 18.00 1 латунь, полукрасный свинец
9.579E-08 1.044E + 07 18.00 1 Свинцовый полукрасный латунь
9.579E-08 1.044E + 07 18.00 1 Bronze Phos., 5% Phos.Оценка отлично
9.852E-08 1.015E + 07 17.50 1 бронзовый алюминий, 5% алюминия (отожженный)
9.852E-08 1.015E + 07 17.50 1 Алюминий - бронза, 5% алюминия (отожженный)
1.002E-07 9.976E + 06 17.20 1 Магний, A231
1.014E-07 9.860E + 06 17.00 1 Бериллиевая медь, конд. А
1.014E-07 9.860E + 06 17.00 1 Медь бериллий, конд. "А"
1.039E-07 9.628E + 06 16.60 1 Серебро, оловянный припой
1.039E-07 9.628E + 06 16.60 1 олово, серебряный припой
1.039E-07 9.628E + 06 16.60 1 Припой, олово серебро
1.059E-07 9.442E + 06 16.28 1 Платина
1.078E-07 9.280E + 06 16.00 1 Палладий
1.105E-07 9.048E + 06 15.60 1 Игнот железа (99,9% Fe)
1.105E-07 9.048E + 06 15.60 1 Слиток железа (99,9% Fe)
1.149E-07 8.700E + 06 15.00 1 Олово, чистое
1.149E-07 8.700E + 06 15.00 1 Магниевые сплавы (литые)
1.181E-07 8.468E + 06 14.60 1 Магний, A2 80
1.197E-07 8.352E + 06 14.40 1 Селен
1.232E-07 8.120E + 06 14.00 1 Бронза, свинцовое олово
1.232E-07 8.120E + 06 14.00 1 Оловянная бронза с содержанием свинца
1.232E-07 8.120E + 06 14.00 1 Олово (свинец), бронза
1.232E-07 8.120E + 06 14.00 1 Алюминий - бронза
1.232E-07 8.120E + 06 14.00 1 Бронза Алюминий
1.240E-07 8.062E + 06 13.90 1 Тантал
1.268E-07 7.888E + 06 13.60 1 Никель-платиновые сплавы
1.268E-07 7.888E + 06 13.60 1 Платина - никелевые сплавы
1.306E-07 7.656E + 06 13.20 1 Columbium
1.326E-07 7.540E + 06 13.00 1 Phos. Бронза, 8% Phos. Оценка C
1.326E-07 7.540E + 06 13.00 1 Bronze Phos., 8% Phos. Оценка C
1.347E-07 7.424E + 06 12.80 1 Магний, A251
1.368E-07 7.308E + 06 12.60 1 Алюминий - бронза, 10% алюминия (отожженный)
1.368E-07 7.308E + 06 12.60 1 бронзовый алюминий, 10% алюминия (отожженный)
1.379E-07 7.250E + 06 12.50 1 Магний, T454
1.402E-07 7.134E + 06 12.30 1 Магний, A261
1.437E-07 6.960E + 06 12.00 1 Бронза, кремний типа B (отожженный)
1.437E-07 6.960E + 06 12.00 1 Кремниевая бронза, тип B (отожженная)
1.437E-07 6.960E + 06 12.00 1 Латунь, высокопрочная желтая
1.449E-07 6.902E + 06 11.90 1 оловянный припой на основе сурьмы
1.449E-07 6.902E + 06 11.90 1 оловянный припой (сурьма)
1.449E-07 6.902E + 06 11.90 1 Припой, сурьмяное олово
1.486E-07 6.728E + 06 11.60 1 Платина, коммерческая
1.553E-07 6.438E + 06 11.10 1 Белый металл
1.567E-07 6.380E + 06 11.00 1 Phos. Бронза, 10% Phos. Оценка D
1.567E-07 6.380E + 06 11.00 1 Подшипник из олова из бронзы и свинца
1.567E-07 6.380E + 06 11.00 2 Бронза, Phos.
1.567E-07 6.380E + 06 11.00 1 Bronze Phos., 10% Phos. Оценка D
1.567E-07 6.380E + 06 11.00 2 Phos. Бронза
1.567E-07 6.380E + 06 11.00 1 Оловянный подшипник с свинцом, бронза
1.567E-07 6.380E + 06 11.00 1 припой, 50-50 мягкий
1.596E-07 6.264E + 06 10.80 1 Магний, AZ80BTA
1.611E-07 6.206E + 06 10.70 1 Сталь, литая
1.759E-07 5.684E + 06 9.80 1 припой, 20-80 мягкий
1.771E-07 5.647E + 06 9.74 4 Медь 90%, никель 10%
1.895E-07 5.278E + 06 9.10 1 Платино-иридиевые сплавы
1.895E-07 5.278E + 06 9.10 1 Иридий-платиновые сплавы
1.916E-07 5.220E + 06 9.00 1 Магниевые литейные сплавы
1.959E-07 5.104E + 06 8.80 1 припой, 5-95 мягкий
1.959E-07 5.104E + 06 8.80 1 Хром
2.053E-07 4.872E + 06 8.40 2 свинца
2.077E-07 4.814E + 06 8.30 1 Свинец, Корродин
2.077E-07 4.814E + 06 8.30 1 Корродин Свинец
2.188E-07 4.570E + 06 7.88 1 Свинец, 1% сурьмы (закаленная и выдержанная)
2.188E-07 4.570E + 06 7.88 1 Сурьма Свинец, 1% (закаленная и выдержанная)
2.239E-07 4.466E + 06 7.70 1 Свинец, твердый (закаленный и выдержанный)
2.330E-07 4.292E + 06 7.40 1 Никель-платиновые сплавы
2.330E-07 4.292E + 06 7.40 1 Платина - никелевые сплавы
2.463E-07 4.060E + 06 7.00 1 Кремниевая бронза, тип A (отожженная)
2.463E-07 4.060E + 06 7.00 1 Бронза, кремний типа A (отожженный)
2,612E-07 3,828E + 06 6,60 1 Ванадий
2.874E-07 3.480E + 06 6.00 1 Серебро, 18% никель, сплав A
2.874E-07 3.480E + 06 6.00 1 Уран
2.874E-07 3.480E + 06 6.00 1 Никель, 18% никель Sil
2.874E-07 3.480E + 06 6.00 1 Баббит, свинцовая база
3.135E-07 3.190E + 06 5.50 1 Платина - рутений (ювелирного качества)
3.135E-07 3.190E + 06 5.50 1 Рутений - Платина (ювелирного качества)
3.316E-07 3.016E + 06 5.20 1 Сплавы платины и иридия, 18% никеля
3.316E-07 3.016E + 06 5.20 1 Иридий-платиновые сплавы, 18% никелевого серебра
3,748E-07 2,668E + 06 4,60 1 Никель 30% - Купро
3,748E-07 2,668E + 06 4,60 1 Купро-никель 30%
3.831E-07 2.610E + 06 4.50 2 Никель 30%, медь 70%
3.831E-07 2.610E + 06 4.50 2 Медь 70%, никель 30%
3.918E-07 2.552E + 06 4.40 1 Сурьма
4.105E-07 2.436E + 06 4.20 1 Олово, фольга
4.105E-07 2.436E + 06 4.20 1 Цирконий
4.310E-07 2.320E + 06 4.00 1 Рутений-платина (контактный сорт)
4.310E-07 2.320E + 06 4.00 1 Платина - рутений (контактный сорт)
4.789E-07 2.088E + 06 3.60 2 Монель
4.816E-07 2.076E + 06 3.58 1 Монель
4.898E-07 2.042E + 06 3.52 1 Константан
5.071E-07 1.972E + 06 3.40 2 Цирконий
5.562E-07 1.798E + 06 3.10 2 Титан
5.945E-07 1.682E + 06 2.90 1 Сталь высоколегированная
6.897E-07 1.450E + 06 2.50 1 Сталь, нержавеющая сталь 304
6.897E-07 1.450E + 06 2.50 2 Сталь, нержавеющая сталь 304
7.184E-07 1.392E + 06 2.40 1 Сталь, 347 Нержавеющая сталь
7.184E-07 1.392E + 06 2.40 2 Циркалой - 2
7.496E-07 1.334E + 06 2.30 1 Сталь, нержавеющая сталь 316
7.837E-07 1.276E + 06 2.20 1 Титан
9.579E-07 1.044E + 06 1.80 1 Меркурий
9.796E-07 1.021E + 06 1.76 1 Инконель
1.014E-06 9.860E + 05 1.70 2 Инконель 600
1.149E-06 8.700E + 05 1.50 1 Хастеллой "D"
1.149E-06 8.700E + 05 1.50 2 Хастеллой "X"
1.232E-06 8.120E + 05 1.40 2 Васпалой
1.232E-06 8.120E + 05 1.40 1 Хастеллой "A"
1.326E-06 7.540E + 05 1.30 1 Хастеллой "B" и "C"
1.724E-06 5.800E + 05 1.00 2 Титан, 6АЛ-4В
7.837E-06 1.276E + 05 0.22 1 Графит 

Теплопроводность

Материал Теплопроводность (кал / сек) / (см 2 C / см) Теплопроводность (Вт / м · К) * Алмаз … 1000 Серебро 1,01 406,0 Медь 0.99 385,0 Золото … 314 Латунь … 109,0 Алюминий 0,50 205,0 Железо 0,163 79,5 Сталь … 50,2 Свинец 0,083 34,7 Меркурий … 8.3 Лед 0,005 1,6 Стекло обычное 0,0025 0,8 Бетон 0,002 0,8 Вода при 20 ° C 0,0014 0,6 Асбест 0,0004 0,08 Снег (сухой) 0,00026 … Стекловолокно 0.00015 0,04 Кирпич изоляционный … 0,15 Кирпич красный … 0,6 Пробковая плита 0,00011 0,04 Шерстяной войлок 0,0001 0,04 Минеральная вата … 0,04 Полистирол (пенополистирол) … 0,033 Полиуретан … 0,02 Дерево 0,0001 0,12-0,04 Воздух при 0 ° C 0,000057 0,024 Гелий (20 ° C) … 0,138 Водород (20 ° C) … 0,172 Азот (20 ° C) … 0,0234 Кислород (20 ° C) . .. 0,0238 Аэрогель кремнезема … 0,003 * Большая часть от Янга, Хью Д., Университетская физика, 7-е изд. Таблица 15-5. Значения для аэрогеля алмаза и диоксида кремния из Справочника по химии и физике CRC. Обратите внимание, что 1 (кал / сек) / (см 2 C / см) = 419 Вт / м K. Имея это в виду, два приведенных выше столбца не всегда совпадают. Все значения взяты из опубликованных таблиц, но не могут считаться достоверными. Значение 0,02 Вт / мК для полиуретана может быть принято как номинальное значение, которое определяет пенополиуретан как один из лучших изоляторов.NIST опубликовал процедуру численного приближения для расчета теплопроводности полиуретана на http://cryogenics.nist.gov/NewFiles/Polyurethane.html. Их расчет для полиуретана, наполненного фреоном, с плотностью 1,99 фунт / фут 3 при 20 ° C дает теплопроводность 0,022 Вт / мК. Расчет для полиуретана с наполнителем CO 2 с плотностью 2,00 фунт / фут 3 дает 0,035 Вт / мК.

Index Tables Reference Young Ch 15.

Коэффициент теплопроводности — обзор

2.5 Обнаружение и анализ тепловых свойств

Что касается тепловых свойств наноматериалов, физические величины, требующие определения характеристик, включают коэффициент теплопроводности, удельную теплоемкость, тепловое расширение, термостабильность и плавление точка.

Когда тонкопленочный слой материала достигает определенной толщины, эффект границ зерен будет оказывать все более значительное влияние на теплопроводность.Кроме того, коэффициент теплопроводности перпендикулярно пленке имеет тенденцию к уменьшению с уменьшением толщины пленки.

Теоретические предсказания и экспериментальные результаты подтвердили, что наноструктурированные материалы имеют значения удельной теплоемкости намного выше, чем у обычных объемных материалов. Наноматериалы имеют сравнительно хаотичное распределение атомов по структуре, которая имеет больший объем по сравнению с объемными аналогами. Таким образом, энтропийные вклады из-за этой некристаллической поверхности вносят гораздо больший вклад в удельную теплоемкость, чем средние крупнокристаллические материалы, что приводит к увеличению удельной теплоемкости.

Нанокристаллы почти в два раза больше средних кристаллов по коэффициенту теплового расширения, причем увеличение t в основном связано с составом кристаллических границ. Основной прибор для измерения коэффициента теплового расширения материалов известен как анализатор теплового расширения, но он также известен как термодилатометрический анализатор или термомеханический анализатор . Анализ коэффициента теплового расширения материалов может дать представление о молекулярном движении, структурных изменениях и поведении при тепловом расширении.Для решения таких проблем, как термическое соединение различных материалов при производстве полупроводниковых устройств, анализатор теплового расширения является лучшим инструментом для анализа.

Точка плавления — это температура, при которой материал переходит из твердого состояния в жидкость. Для кристаллических объектов существует четкая точка плавления; однако некристаллические объекты имеют плохо определенную температуру плавления. Температура может увеличиваться до значения, при котором небольшое количество атомов в общей структуре начинает двигаться одновременно с жидким поведением.Эта температура известна как температура стеклования ( T _g ). При температуре ниже Т _г стекломатериал находится в твердом состоянии; при температурах выше Т _г переохлажденная жидкость. Выражаясь в механических терминах, если температура ниже T _g , то произойдет упругая деформация; если температура выше Т _г , то начинается вязкостная (жидкая) деформация.

Температура термического разложения — это значение, при котором связи материала могут быть нагреты до разорванного состояния и диссоциированы на другие вещества.

Для пластифицированных некристаллических или аморфных наноматериалов температура стеклования и температура термической диссоциации, отличные от точки плавления, также являются очень важными тепловыми свойствами. Таблица 2.4 показывает температуру плавления нескольких видов материалов в разных масштабах.

Таблица 2.4. Точка плавления нескольких материалов в разных масштабах

Тип материала	Размер частиц: диаметр (нм) или общее количество атомов	Точка плавления (K)
Au	Обычные сыпучие материалы	1340
	300 нм	1336
	100 нм	1205
	20 нм	800
	2 нм	600
Sn	10–30	555
	500	480
Pb	Обычные сыпучие материалы	600
	30–45	583
CdS	Обычные сыпучие материалы	1678
	2 нм	≈910
	1.5 нм	≈600
Cu	Обычные насыпные материалы	1358
	20 нм	≈312

Термические свойства наноматериалов обычно обнаруживаются и анализируются с помощью термогравитационного анализа (TGA) и производная термогравиметрия (DTG).

ТГА может обеспечивать непрерывное измерение на основе изменения веса материалов в процессе нагрева во время измерения.В частности, изменения массы отслеживаются как функция температуры с заданной температурной скоростью и могут быть соотнесены с потерями массы и тепловыми переходами в материале. Одновременно можно проводить дифференцированное лечение. А именно, запись изменений качества составляет метод измерения DTG.

С помощью TGA (или DTG) можно определить ряд тепловых свойств материалов, например температуру старения во время пиролиза и динамику старения, поведение при старении при разных температурах и в различных газовых средах, упаковочные материалы IC, используемые в процесс изготовления исполняемых полупроводниковых устройств, гибких печатных плат и стеклянных подложек, керамических подложек и других компонентов анализа.

В коллоидной системе соответствующие термические свойства частиц также включают, среди прочего, броуновское движение, баланс диффузии и седиментации.

При броуновском движении среднее смещение частицы X¯ может быть выражено как:

X¯ = RTN0Z3πηr

где R — постоянная идеального газа, T — абсолютная температура, N ₀ — постоянная Авогадро, Z — интервал времени наблюдения, η — вязкость дисперсионной среды, r — радиус частицы.

Броуновское движение имеет большое значение для природы коллоидных частиц. Броуновское движение — важный фактор, который может повлиять на стабильность дисперсной системы коллоидных частиц. Из-за броуновского движения осаждение коллоидных частиц происходит не из-за гравиметрических сил, а из-за коллоидной агрегации, вызванной столкновениями между частицами, что приводит к осаждению.

Явление диффузии связано с переносом массы, который возникает из-за броуновского движения частиц (броуновского движения) при наличии градиента концентрации.Чем крупнее частицы и чем меньше тепловая скорость, тем менее заметной становится диффузия. Обычно коэффициент диффузии используется для измерения скорости диффузии. Это физическое количество материала, указывающее на диффузионную способность.

В коллоидной системе коэффициент диффузии D можно выразить как:

D = RTN0⋅16πηr

Здесь R — постоянная идеального газа, T — абсолютная температура, N ₀ — постоянная Авогадро, η — вязкость дисперсионной среды, r — радиус частицы.

Поскольку коэффициент диффузии коррелирует со средним смещением, полученный коэффициент диффузии D можно также выразить как:

D = X¯22Z

Здесь Z — это определенный интервал времени наблюдения, а X¯ — среднее смещение частицы при броуновском движении. В таблице 2.5 показан коэффициент диффузии золя, образующегося из наночастиц золота, при 291 К.

Таблица 2.5. Коэффициент диффузии золя, образующегося из частиц нано-Au при 291 K

Размер частиц нано-Au (нм)	Коэффициент диффузии (109 м 2 / с)
1	0 .213
10	0,0213
100	0,00213

Когда частицы, взвешенные в жидкости, показывают скорость осаждения, равную скорости диффузии, система достигает состояния равновесия, а именно равновесия седиментации. . В состоянии седиментационного равновесия концентрация коллоидных частиц подчиняется закону распределения Гаусса.

Закон распределения Гаусса для коллоидных частиц может быть выражен как:

n2 = n1e − N0RT⋅43r3 (ρp − ρ0) (x2 − x1) g

Здесь n ₁ и n ₂ — концентрация частиц в поперечном сечении на высоте x ₁ и x ₂ соответственно, R — идеальная газовая постоянная, T — абсолютная температура, A — Константа Авогадро, r — радиус частицы, ρ0 — плотность коллоидных частиц, ρp — плотность дисперсионной среды, г — ускорение свободного падения.

Физическое объяснение теплопроводности металлов

Известно, что металлы являются высокоэффективными проводниками тепла.

В этой статье будут изучены механизмы теплопередачи, что делает металлы идеальными проводниками тепла, а также способы использования обычных металлов и сплавов.

Важность теплопроводности в повседневной жизни

Изображение 1. A

Изображение 1. B

Изображение 1. A и B показывают визуальные иллюстрации людей на кухне, использующих кухонные принадлежности.

Кулинария — часть повседневной жизни большинства людей. Следовательно, кухонное оборудование разработано с целью обеспечения максимальной безопасности и эффективности. Это требует понимания теплофизики. Есть причина, по которой нагревательный элемент тостера обычно изготавливается из нихромовой проволоки, ложки для смешивания обычно бывают деревянными, а в конструкции рукавиц для духовки никогда не используется металлический состав.

Определение температуры и теплопроводности

Необходимо вспомнить определение температуры , чтобы понять теплопроводность математически.

Оперативное определение Т:

Оперативное определение температуры — это значение, измеренное термометром, который просто измеряет расширение объема ртути.

Изображение 2. Изображение двух термометров в единицах Цельсия и Фаренгейта

Физическое определение T:

В теплофизике температура и теплопроводность понимаются путем изучения движения молекул.

Шредер, автор « Introduction to Thermal Physics » математически описывает температуру как:

\ [\ frac {1} {T} = \ Bigg (\ frac {dS} {dU} \ Bigg) \ scriptscriptstyle N, V ​​\]

где:
S = энтропия,
U = энергия,
N = количество частиц,
V = объем системы (Schroeder, 2007).

Следовательно, температура системы зависит от энтропии и энергии , когда количество частиц и объем системы поддерживаются постоянными.

Шредер заявляет словами: «Температура — это мера тенденции объекта спонтанно отдавать энергию своему окружению. Когда два объекта находятся в тепловом контакте, тот, который имеет тенденцию спонтанно терять энергию, имеет более высокую температуру »(Schroeder, 2007). Это потому, что два соприкасающихся объекта будут пытаться достичь теплового равновесия ; становятся той же температуры.

Для визуализации температуры и теплопроводности на микроскопическом уровне Рисунки 1 A и B показаны ниже. Представьте, что неизвестные объекты A и B находятся в физическом контакте друг с другом. Объект A имеет более высокую температуру, чем объект B. Что произойдет с температурой с течением времени?

Рисунок 1. A

Рисунок 1.B

На рисунке 1.A показаны два неизвестных объекта, находящихся в физическом контакте друг с другом, а на рисунке 1.B отображает молекулы объектов.

При t _0, T _A > T _B

На t _1, T _A > T _B

.

.

При t _n, T _A = T _B

При t _0, ŝ _A > _B

На t _{1, A} > _B

.

.

При t _n, ŝ _A > ŝ _B

Учитывая, что t _n : момент времени, T _A : температура объекта A, T _B : температура объекта B, _A : средняя скорость частицы A, _B : средняя скорость частицы B.

В момент t ₀ атомы объекта A движутся с большей скоростью, а атомы объекта B движутся с меньшей скоростью (T _A > T _B ). Со временем объект A теряет энергию, а объект B получает энергию до тех пор, пока они не достигнут одинаковой температуры (T _A = T _B ) и не достигнут теплового равновесия. Это теплопроводности, описанное на молекулярном уровне. Ближайшие атомы объекта A сталкиваются с атомами объекта B. Атомы объекта B, которые первоначально взаимодействовали с атомами объекта A, сталкиваются с другими атомами объекта B, пока энергия не будет передана через все атомы объекта B.

Шредер определяет теплопроводность как «перенос тепла посредством молекулярного контакта: быстро движущиеся молекулы сталкиваются с медленно движущимися молекулами, отдавая при этом часть своей энергии» (Schroeder, 2007).

Режимы теплопередачи металлов

Полезно вспомнить три режима теплопередачи; конвекция для газов / жидкостей, излучение для объектов, разделенных пустым пространством и проводимость для объектов, находящихся в прямом контакте.

Теплопроводность также подразделяется на три категории: столкновения молекул, для форм газа / жидкости, колебаний решетки, для твердых тел и электронов проводимости, для металлов, как показано на рисунке 2 ниже.

Рисунок 2. Режимы теплопередачи.

Теплопроводность металлов будет включать столкновения молекул + электронов проводимости для металлов в газовом состоянии и колебания решетки + проводящие электроны для металлов в твердом состоянии. Электроны проводимости — это, по сути, то, что делает металл невероятным проводником . Прежде чем объяснять, что на самом деле представляет собой электрон проводимости, необходимо вспомнить определение металла.

Определение металлов

Все элементы могут быть найдены в периодической таблице, включая металлы, неметаллы и металлоиды. Металлы определяются как «элементы, которые образуют положительные ионы, теряя электроны во время химических реакций» (Blaber, 2015).

Рис. 3. Периодическая таблица, показывающая все элементы, разделенные на металлы, неметаллы и металлоиды.

Таблица 1. Список типичных физических свойств металлов.

Физические свойства большинства металлов
Твердое при комнатной температуре
Жесткий
Высокая плотность
Высокая температура плавления
Высокая температура кипения
Ковкий
Пластичный
Блестящий

Что делает металлы хорошими проводниками тепла?

Что делает металл хорошим проводником тепла, так это свободно текущих электронов проводимости .

Рис. 4. Металлический блок, который нагревается, показывая атомы и свободно текущие электроны.

Атомы металлов выделяют валентные электроны при химической реакции с атомами неметаллов, например образуя оксиды и соли. Таким образом, ионы металлов являются катионами в водном растворе. Что делает металлы и их сплавы хорошими проводниками, так это особая металлическая связь. В металлических твердых телах связанные атомы разделяют свои валентные электроны, образуя море свободно движущихся электронов проводимости, которые несут как тепло, так и электрический заряд.Итак, в отличие от, например, электронов в ковалентных связях, валентные электроны в металле могут свободно течь через металлические латексы, эффективно неся тепло, не будучи привязанными к отдельному атомному ядру.

Математическое моделирование значения теплопроводности (k)

Теплопроводность (k) измеряет способность объекта проводить тепло (Q).

Высокое значение k: высокая теплопроводность

Рис. 4. Лист материала с уравнением теплопроводности.

Данный:

k = теплопроводность (Вт / м • K),

ΔQ = передача энергии (Джоулей / сек),

Δt = изменение во времени (секунды),

ΔT = температурный градиент (K),

A = площадь теплопроводности (м ² ),

Δx = толщина материала.

Таблица 2. Список типичных физических свойств металлов.

Металлы	Теплопроводность при комнатной температуре (Вт / м • К)
Алюминий	226
Углеродистая сталь	71
Магний	151
Латунь (желтый)	117
Бронза (алюминий)	71
Медь	397
Утюг	72
Нержавеющая сталь (446)	23
Вольфрам	197
Свинец	34
Никель	88
Сталь углеродистая марки 1020 (0.2 — 0,6 в)	71
цинк	112
Титан	21
Олово	62

Примечание. Медь и алюминий имеют наивысшее значение теплопроводности (k). Проверьте нашу базу данных материалов.

Использование обычных металлов и сплавов в таблице выше

Металлы и сплавы (материалы, состоящие из комбинации металлов) используются в качестве строительных материалов в различных отраслях промышленности, таких как электроника, машиностроение, лабораторное оборудование, медицинские приборы, товары для дома и строительство.

Наивысшие значения теплопроводности металлов имеют серебро (-429 Вт / м • К), медь (-398 Вт / м • К) и золото (-315 Вт / м • К).

Металлы очень важны в производстве электроники, так как они хорошо проводят электричество. Медь, алюминий, олово, свинец, магний и пластик часто используются для изготовления деталей телефонов, ноутбуков, компьютеров и автомобильной электроники. Медь экономична и используется для электропроводки. Свинец используется для оболочки кабеля и изготовления аккумуляторов.Олово используется для изготовления припоев. Магниевые сплавы используются в производстве по новой технологии, так как они легкие. Пластик используется для изготовления деталей электроники, которые не должны проводить электричество, а титан используется для производства пластика.

Металлы также важны в машиностроении. Алюминий часто используется в производстве деталей автомобилей и самолетов, а также в качестве сплава, поскольку его чистая форма непрочна. Автомобильное литье изготавливается из цинка. Железо, сталь и никель — обычные металлы, используемые в строительстве и инфраструктуре.Сталь — это сплав железа и углерода (и часто других элементов). Увеличение содержания углерода в стали создает углеродистую сталь, которая делает материал более прочным, но менее пластичным. Углеродистая сталь часто используется в строительных материалах. Латунь и бронза (медь, легированная цинком и оловом, соответственно) обладают полезными свойствами поверхностного трения и используются для замков, петель и рам дверей и окон соответственно.

Наконец, традиционно нити накала ламп дневного света изготавливаются из вольфрама.Однако они постепенно сокращаются, поскольку только около 5% мощности преобразуется в свет в таком источнике света, а остальная часть энергии преобразуется в тепло. Современные источники света часто основаны на светодиодной технологии и полупроводниках.

В заключение, теплопроводность металлов очень важна для проектирования любой конструкции. Это неотъемлемая часть безопасности, эффективности и новых инноваций в отраслях. Электроны проводника являются механизмом высокой проводимости металлов по сравнению с неметаллическими материалами.Однако значение теплопроводности (k) также может сильно различаться для разных металлов.

Список литературы

Шредер, Д. В. (2018). Введение в теплофизику. Индия: Служба образования Pearson India.

База данных материалов — Термические свойства. (нет данных). Получено с https://thermtest.com/materials-database

.

Алюминиевые сплавы 101. (9 марта 2020 г.). Получено с https://www.aluminium.org/resources/industry-standards/aluminium-alloys-101

.

Элерт, Г.(нет данных). Проведение. Получено с https://physics.info/conduction/

.

Блабер, М. (3 июня 2019 г.). 9.2: Металлы и неметаллы и их ионы. Получено с https://chem.libretexts.org/Bookshelves/General_Chemistry/Map:_General_Chemistry_(Petrucci_et_al.)/09:_The_Periodic_Table_and_Some_Atomic_Properties/9.2:_Metals_and_Nonmetals_Ions_and_the

Теплопроводность. (нет данных). Получено с http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/thercond.html

.

Диоксид титана для пластмасс.(нет данных). Получено с https://polymer-additives.specialchem.com/centers/titanium-dioxide-for-plastics-center

.

Сандхана, Л., и Джозеф, А. (6 марта 2020 г.). Что такое углеродистая сталь? Получено с https://www.wisegeek.com/what-is-carbon-steel.html

.

(нет данных). Получено с http://www.elementalmatter.info/element-aluminium.html

.

Изображения

Изображение 1.A: Mohamed, M. (2019). Кулинария [Иллюстрация]. Получено с https://pxhere.com/en/photo/1584957.

Изображение 1.В: Мохамед, М. (2019). Шеф-повар Кулинария [Иллюстрация]. Получено с https://pxhere.com/en/photo/1587003.

Изображение 2: Википедия. Термометр [Иллюстрация]. Получено с https://upload.wikimedia.org/wikipedia/commons/7/70/Thermometer_CF.svg

.

Автор: Селен Йылдыр | Младший технический писатель | Thermtest

Теплопроводность металлов и сплавов

В этой статье представлены данные теплопроводности для ряда металлов и сплавов. Теплопроводность измеряет способность материала пропускать тепло через проводимость.

Теплопроводность измеряет способность материала пропускать тепло через проводимость. Теплопроводность материала сильно зависит от состава и структуры. Вообще говоря, плотные материалы, такие как металлы и камень, являются хорошими проводниками тепла, в то время как вещества с низкой плотностью, такие как газ и пористая изоляция, плохо проводят тепло.

Теплопроводность материалов требуется для анализа сетей теплового сопротивления при изучении теплопередачи в системе.

Дополнительную информацию см. В статье «Значения теплопроводности для других распространенных материалов».

В следующих таблицах показана теплопроводность некоторых металлов и сплавов при различных температурах.

938 Титан

Материал	Температура	Теплопроводность	Температура	Теплопроводность
Адмиралтейство Латунь	20	96.1	68	55,5
	100	103,55	212	59,8
	238	116,44	460	67,3
Алюминий	20	225		130
	100	218	212	126
	371	192	700	111
Сурьма	20	18.3	68	10,6
	100	16,8	212	9,69
Бериллий	20	139	68	80,1
	100	132	212	76,2
	371	109	700	63,0
Латунь	-165	106	-265	61,0
	20	144	68	83.0
	182	177	360	102
Бронза	20	189	68	109
Cadmiuim	20	92,8		53,69
	100	90,3	212	52,2
Медь	20	401	68	232
	100	377	212	218
	371	367	700	212
Золото	20	317	68	183
Германий	20	58.8	68	34,0
Инконель X	-3	13,2	27	7,62
	20	13,7	68	7,90
	577	25,5	1070	14,7
Железо	20	71,9	68	41,6
	100	65,7	212	38,0
	371	44.6	700	25,8
Чугун (кованый)	20	60,4	68	34,9
	100	59,9	212	34,6
Чугун (литье)	53	48,0	127	27,7
Свинец	0	35,1	32	20,3
	20	34,8	68	20.1
	260	30,3	500	17,5
Магний	20	170	68	98,5
	100	167	212	96,3
	188	163	370	93,9
Молибден	0	137	32	79,0
	20	136	68	78.4
	427	115	800	66,7
Монель	-250	20,73	-418	11,98
	20	27,5	68	15,86
	800	46,9	1472	27,1
Никель	20	62,4	68	36,0
	100	58.0	212	33,5
	293	47,5	560	27,4
Палладий	20	67,5	68	39,0
Платина	20	71,0	68	41,0
	100	70,6	212	40,8
	427	69,2	800	40,0
Плутоний	20	8.65	68	5,00
Родий	20	152	68	88,0
Серебро	20	419	68	242
	100	405	212	234
	316	366	600	211
Сталь, 1% углерода	20	45,3	68	26.2
	100	44,8	212	25,9
SS ANSI 301, 302, 303, 304	35	14,0	95	8,08
	100	15,0	212	8,69
	900	28,0	1652	16,2
SS ANSI 310	0	11,9	32	6,85
	20	12.3	68	7,11
	900	32,0	1652	18,5
SS ANSI 314	30	17,3	86	10,0
	100	17,6	212	10,2
	300	18,4	572	10,6
	900	22,6	1652	13,1
SS ANSI 316	-50	13.0	-58	7,51
	20	13,9	68	8,04
	950	26,1	1742	15,1
SS ANSI 321, 347, 348	— 70	14,3	-94	8,25
	20	15,7	68	9,06
	900	29,4	1652	17,0
SS ANSI 403, 410, 416 , 420	-70	26.0	-94	15,0
	20	26,0	68	15,0
	1000	26,0	1832	15,0
SS ANSI 430	50	21,8	122	12,6
	900	25,0	1652	14,4
SS ANSI 440	100	22,1	212	12.8
	500	27,5	932	15,9
SS ANSI 446	0	22,4	32	13,0
	20	22,7	68	13,1
	1000	38,0	1832	22,0
SS ANSI 501, 502	30	37,0	86	21,4
	100	36.2	212	20,9
	830	27,8	1526	16,0
Тантал	20	55,0	68	31,8
Таллий	0		32	29,0
Торий	20	29,4	68	17,0
	100	30,5	212	17.6
	299	33,3	570	19,3
Олово	20	62,1	68	35,9
	100	58,8	212	33,9
20	15,6	68	9,00
100	15,3	212	8,86
299	14.7	570	8,50
Вольфрам	20	159	68	92,0
	100	154	212	89,2
	299	142	5	82,0
Уран	20	24,2	68	14,0
	100	26,0	212	15,0
	770	40.6	1418	23,4
Ванадий	20	34,6	68	20,0
Цинк	20	112	68	64,9
	100	111	212	63,9
Цирконий	0	19,0	32	11,0

Статья создана: 5 ноября 2013 г.

---

Теги статьи

Теплопроводность жидких металлов

В этой колонке проводимость и температуры плавления жидких металлов.Думая о жидких металлах, многие люди связывают их с высокими температурами. Неизвестно, что некоторые металлические сплавы являются жидкими при температуре ниже 0 ° C, за исключением, конечно, ртути, которая была известна уже в древние времена. Говорят, что первый император Китая был похоронен в реках с текущей ртутью.

В области терморегулирования нас интересуют жидкие металлы при комнатной температуре или около нее для двух основных целей: для уменьшения сопротивления термоинтерфейса и для жидкостного охлаждения.Оба приложения приобретают все большее значение, поскольку они позволяют значительно снизить общее тепловое сопротивление. За исключением гораздо более высокой теплопроводности по сравнению со «стандартными» жидкими теплоносителями, жидкие металлы предлагают дополнительное преимущество, заключающееся в возможности более эффективной перекачивания из-за их низкого удельного электрического сопротивления. При более высоких температурах наиболее важным промышленным применением является пайка. Обзор тепловых характеристик см. В [1]. Другими важными приложениями при еще более высоких температурах являются использование Na в тепловых трубках и в атомной энергетике.

С точки зрения физики твердого тела, с жидкими металлами легче работать, чем с твердыми металлами, потому что тензоры преобразуются в скаляры из-за изотропии жидкого состояния. Это приводит к простой корреляции между электронным вкладом в теплопроводность kel, удельным электросопротивлением и температурой, так называемый закон Видемана-Франца (см. Также [2]). Поскольку решеточный вклад обычно на два порядка меньше электронного, можно с уверенностью заключить, что теплопроводность, рассчитанная с использованием закона W-F, является разумной оценкой k, причем преимущество заключается в том, что r намного легче измерить.

Если говорить о чистых металлах, то все щелочи имеют низкую температуру плавления. К сожалению, все они очень реактивны со многими жидкостями и большинством металлов, иногда бывают токсичными, поэтому керамическое покрытие часто является обязательным. Большинство сплавов с низкой температурой плавления состоят из смеси Ga, In, Sn, Pb и Bi, что приводит к целому ряду эвтектик. Особое значение имеет комбинация GaInSn, продаваемая как Galinstan, которая используется в качестве замены ртути.

Таблица 1. Теплопроводность и температуры плавления некоторых металлов и сплавов

В таблице указаны значения теплопроводности и температуры плавления для ряда чистых металлов и сплавов.Многие неэвтектические сплавы не имеют четко определенной точки плавления, а скорее имеют диапазон плавления, и, следовательно, данные о температурах плавления являются показательными. Наблюдайте за резким падением k от твердого тела к жидкости, вызванного тем, что кристаллический порядок исчезает во время фазового перехода, что приводит к большему количеству мод рассеяния. Практическое правило: k примерно вдвое.

Список литературы

1. Технические данные, охлаждение электроники, т.