Закон Ома | Мозган калькулятор онлайн
На данной странице калькулятор поможет рассчитать сопротивление, напряжение или силу тока по закону Ома онлайн.
Закон Ома — эмпирический физический закон, определяющий связь электродвижущей силы источника или электрического напряжения с силой тока и сопротивлением проводника установлен в 1826 году, и назван в честь его первооткрывателя Георга Ома.
Как найти сопротивление
Электрическое сопротивление определяет силу тока, текущего по цепи при заданном напряжении.
Под Электрическим сопротивлением R понимают отношение напряжения на концах проводника к силе тока, текущего по проводнику.
Формула для нахождения сопротивления по закону Ома:
U — напряжение; I — сила тока.Как найти силу тока
Сила тока в проводнике прямо пропорциональна напряжению и обратно пропорциональна сопротивлению.
Формула для нахождения силы тока по закону Ома:
U — напряжение; R — сопротивление.Как найти напряжение
Падение напряжения на участке проводника равно произведению силы тока в проводнике на сопротивление этого участка.
Формула для нахождения напряжения по закону Ома:
Закон Ома для участка цепи, пример расчета.
21 Января 2017
1950
Всем привет.
В предыдущей статье мы собрали простую замкнутую цепь, состоящий из источника питания, проводников по которым протекает ток и нагрузки. Выяснили, что такое сопротивление проводника и сопротивление нагрузки. Так же рассмотрели взаимосвязь между напряжением тока, силой тока и сопротивлением на разных участках цепи (проводника и нагрузки). Все эти отношения установлены в основном законе электротехники – в законе Ома.
Закон Ома для участка цепи
Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи.
Давайте рассмотрим этот закон на примере. Соберем следующую схему:
Так как сопротивление проводников близко к нулю, будем считать, что они равны нулю. В нашу электрическую цепь, кроме нагрузки, мы еще добавили два прибора.
Вольтметр – прибор для измерения напряжения тока, при подключении к нагрузке, показывает сколько падает напряжение на нагрузку. Соединятся параллельно с нагрузкой.
Давайте нагрузку поставим сопротивлением равной 100 Ом, с источника питания пустим напряжение 5 В (вольт). Снимем показания с приборов. Нас интересует показатель амперметра. Амперметр показывает — 0,05 А (ампер) для удобства можно перевести в миллиамперы – 50 мА (миллиампер).
наведите или кликните мышкой, для анимации
Теперь поменяем напряжение тока, вместо 5 В установим 10 В. Снимем показатель амперметра. Амперметр показывает — 0,1 А переводим в миллиамперы – 100 мА. Сразу отметим для себя — с увеличением напряжения увеличилась сила тока.
В законе ома: «сила тока в участке цепи прямо пропорциональна напряжению … ».
наведите или кликните мышкой, для анимации
Теперь вернемся к первому опыту, то есть установим напряжение обратно на значение 5 В. Попробуем изменить сопротивление нагрузки.
Поменяем нагрузку со значение сопротивления 200 Ом. Снимем показатели с амперметра и сравним с показателями первого опыта. Амперметр показывает — 0,025 А переводим в миллиамперы – 25 мА. Таким образом увеличение сопротивления нагрузки, уменьшило силу тока.
наведите или кликните мышкой, для анимации
Закон Ома для участка цепи записывается следующей формулой:
I = U/R
Как нам уже известно:
I = сила тока
U = напряжение тока
Так же эту формулу можно преобразовывать для определения напряжения тока или сопротивления нагрузки. Что бы легче запомнить формулы, надо запомнить треугольник Ома, который изображен выше. Закрывая искомую величину пальцем, можно увидеть формулу для нее.
Формула для определения напряжения:
Формула для определения сопротивления:
Рассмотрим простой пример расчета используя закон Ома для участка цепи. Если в примере выше, мы бы не использовали амперметр, зная напряжение тока 5 В (U) и сопротивление нагрузки 100 Ом (R). Использую следующую формулу I = U/R, мы бы получили результат: 5/100 = 0,05. Ответ 0,05 А = 50 мА.
Мы разобрали закон Ома для участка цепи, ознакомились с формулами для определения силы тока, напряжение тока и сопротивления. Так же хочу добавить, при расчетах, необходимо переводить единицы измерения в систему СИ. В примерах выше для демонстраций замкнутой цепи, я использовал программу — Electronics Workbench. Программа предназначена для моделирования и анализа электронных схем.
Простые примеры использования Закона Ома
Применение Закона Ома становится очевидным на простых электрических цепях, где имеется один источник тока (ЭДС).
Самый простая электрическая цепь — это такая цепь, которая содержит всего лишь два элемента, один из которых источник тока, а другой — резистивная нагрузка. В качестве источника может быть химический аккумулятор или гальваническая батарея. Для наглядности в качестве резистивной нагрузки может быть выбрана электрическая лампа накаливания, но вместо неё можно использовать любой нагревательный элемент, в том числе просто кусок провода.
Давайте посмотрим, как уравнения Закона Ома могут нам помочь анализировать простые схемы.
Рассмотрим схему нашей простейшей электрической цепи:
В приведённой выше схеме, есть только один источник напряжения (батареи, слева) и только одно сопротивление — резистивная нагрузка (лампы, справа). Для этой схемы достаточно легко применять Закон Ома. Если мы знаем значения любых двух из трёх величин (напряжение, ток и сопротивление) в этой схеме, тогда мы можем использовать Закон Ома для определения третьего.
В этом первом примере мы будем вычислять величину тока (I) в цепи, при заданных значениях напряжения ЭДС источника
Чему равна величина тока (I) в этой схеме?
Во втором примере мы рассчитаем величину сопротивления (R), при заданных значений напряжения (E) и тока (I):
Чему равна величина сопротивления (R) лампы?
В последнем примере мы рассчитаем величину напряжения, выдаваемое батареей, для известных значений тока (I) и сопротивление (R):
Какова величина напряжения, которое выдаёт аккумуляторная батарея?
Закон Ома очень простой и полезный инструмент для анализа электрических цепей. Он используется так часто при изучении электротехники и электроники, что должен быть хорошо отложен в памяти каждого серьёзного студента. При работе в качестве электротехнического персонала (электромонтёром), применение
Для тех, кто плохо знаком с алгеброй, есть хороший способ запомнить вариации применения Закона Ома. Для этого достаточно изобразить треугольник на листке бумаги, который будет разбит на три части. Вершина треугольника — это E, правый угол — это R, а левый угол — это I.
Для удобства полезно запомнить эту картинку:
Если вы знаете E и I, и желаете определить чему равно R, тогда нужно зачеркнуть на картинке неизвестное R, и наглядно будет видно, что нужно сделать:
Если вам известны E и R, и вы желаете отыскать значение тока I, тогда выполняем подобное действие, но зачёркиваем неизвестное I. В итоге наглядно видим, что для отыскания I нужно напряжение делить на сопротивление R:
Если вы знаете I и R, и желаете определить Е, тогда зачеркните E и посмотрите, что получилось. Вам нужно умножить величину тока I, протекающего в электрической цепи (ветви), на величину сопротивления участка цепи. В итоге вы получите значение падения напряжения E на этом участке:
В конце концов, вы придёте к тому, что знание алгебры необходимо для глубокого изучения электротехники и электроники. Приведённый выше способ позволит вам легко выполнять свои первые расчёты электрических цепей. Если же вы знакомы с алгеброй, то вам достаточно помнить формулировку Закона Ома с тем, чтобы составить необходимую пропорцию и из неё получить все остальные формулы для нахождения неизвестных величин.
Дата: 24.06.2015
© Valentin Grigoryev (Валентин Григорьев)
Возможно Вам будут интересны следующие статьи из этого раздела:
Если Вы не нашли ничего интересного в этом разделе, тогда Вам следует воспользоваться левым вертикальным меню, чтобы попасть в интересующий Вас раздел сайта.
Закон Ома
Доброго дня уважаемые радиолюбители!
Приветствую вас на сайте “Радиолюбитель“
Единицы измерения в электронике. Закон Ома.
Единицы измерения в электронике
Единицы измерения служат для количественного определения какой-либо физической величины. К примеру, покупая яблоки, вы измеряете их вес в килограммах. Аналогично мультиметр измеряет сопротивление элементов в омах, напряжение — в вольтах, а ток — в амперах. В табл. 1.1 показаны общепринятые единицы измерения и их аббревиатуры для физических величин, которые используются в электронике.
| Физическая величина | Аббревиатура | Единицы измерения | Символ единиц измерения |
| Сопротивление | R | ом | Ом, ? |
| Емкость | С | фарад | Ф |
| Индуктивность | L | генри | Гн |
| Напряжение | U (V или Е) | вольт | В |
| Ток | I | ампер | А |
| Мощность | Р | ватт | Вт |
| Частота | f | герц | Гц |
Таблица 1.1. Единицы измерения, используемые в электронике
Переход к большим или меньшим величинам. При измерении веса яблок очень даже можно столкнуться с малым количеством яблока (или его кусочка), а можно измерять и центнерами, не так ли? Диапазон измерения физических величин в электронике еще шире. В одной схеме вы можете иметь сопротивление в миллионы ом, тогда как в другой протекающий ток будет меньше одной тысячной ампера. Говоря о подобных величинах — как громадных, так и предельно малых, — приходится иметь дело со специальной терминологией. Чтобы показывать очень большие и очень малые числа, в электронике применяют специальные префиксы, или приставки, и экспоненциальное представление. В табл. 1.2 показаны самые широко используемые префиксы и тип записи числовых величин.
Тблица 1.2. Приставки, используемые в электронике
| Число | Название | Экспоненциальное представление | Префикс | Аббревиатура |
| 1000000000 | 1 миллиард | 109 | Гига | Г |
| 1000000 | 1 миллион | 106 | Мега | м |
| 1000 | 1 тысяча | 103 | кило | к |
| 100 | 1 сотня | 102 | ||
| 10 | 1 десяток | 101 | ||
| 1 | один | 100 | ||
| 0,1 | 1 десятая | 10-1 | ||
| 0,01 | 1 сотая | 10-2 | ||
| 0,001 | 1 тысячная | 10-3 | милли | м |
| 0,000001 | 1 миллионная | 10-6 | микро | мк |
| 0,000000001 | 1 миллиардная | 10-9 | нано | н |
| 0,000000000001 | 1триллионная | 10-12 | пико | п |
Как же правильно прочитать число, записанное как 106 или 10-6? Экспоненциальное представление представляет собой наиболее удобный способ указания того, сколько нулей нужно добавить к числу в десятичной системе счисления, т.е. основанной на степени числа 10. Например, верхний индекс “6” в записи 106 означает, что точка, разделяющая целую и дробную части числа, должна находиться на шесть разрядов правее, а в записи 10-6 — что эту точку нужно сдвинуть на шесть разрядов левее. Таким образом, в числе 1 х 106 разделитель разрядов сдвигается на шесть мест вправо, и мы получаем в результате число 1 000 000 (1 миллион). В числе же 1 х 10-6 разделитель разрядов сдвигается на столько же мест влево, и результатом является 0,000001, или одна миллионная. 3,21 х 104 можно записать, сдвинув запятую на 4 знака вправо: 32100.
Префиксы + единицы измерения = ?
В предыдущих абзацах вы увидели как для обозначения физических величин и единиц их измерения используются аббревиатуры. В этом разделе мы научимся объединять их и использовать очень краткую запись. Например, ток 5 миллиампер можно записать в виде 5 мА, а частоту 3 мегагерца — как 3 МГц.
Кроме того, так же, как при измерении яблок удобнее всего пользоваться килограммами, а при строительстве загородного офиса большой компании вес стальных конструкций определенно будут измерять не иначе как в тоннах, в электронике тоже существуют такие физические величины, для измерения которых пользуются большими числами, и такие, которые измеряются малыми. Это значит, что чаще всего вам придется иметь дело с одним и тем же набором приставок для каждой физической величины. Ниже приведены такие комбинации величин и единиц их измерения.
> Ток: пА, нА, мкА, мА, А.
> Индуктивность: нГн, мГн, мкГн, Гн.
> Емкость: пФ, нФ, мкФ, мФ, Ф.
> Напряжение: мкВ, мВ, В, кВ.
> Сопротивление: Ом, кОм, МОм.
> Частота: Гц, кГц, МГц, ГГц.
Использование некоторых новых терминов
Хотя ранее мы уже рассматривали такие понятия, как сопротивление, напряжение и ток, есть еще некоторые термины, которые могут оказаться для вас внове.
Емкость представляет собой способность накапливать заряд под воздействием электрического поля. Такой накопленный заряд может повышать или понижать напряжение более плавно, чем в отсутствие емкости. Для применения данного свойства на практике используется такой компонент, как конденсатор.
Частотой переменного тока называется мера повторяемости сигнала. Например, напряжение в настенной розетке совершает один полный цикл изменения 50 раз в секунду.
Индуктивность – это способность запасать энергию в магнитном поле; эта накопленная энергия препятствует изменению тока точно так же, как энергия, накопленная конденсатором, препятствует резким изменениям напряжения. Для использования данного свойства на практике в электронике применяются катушки индуктивности, или дроссели.
Мощность служит мерой количества работы, которую электрический ток совершает при протекании через элементы схемы. К примеру, если приложить к электрической лампе напряжение, подведя ток при помощи проводов, то на нагрев этих проводов будет затрачивться какая-то работа. В данном случае мощность можно вычислить, перемножив приложенное к лампе напряжение на ток, протекающий по проводам.
Используя информацию, приведенную в табл. 1.1 и 1.2, вы уже можете перевести экспоненциальную запись числа или аббревиатуру физической величины на человеческий язык. Ниже дано несколько примеров:
> мА: миллиампер, или 1 тысячная ампера;
> мкВ: микровольт, или 1 миллионная вольта;
> нФ: нанофарада, или 1 миллиардная фарады;
> кВ: киловольт, или 1 тысяча вольт;
> МОм: мегаом, или 1 миллион ом;
> ГГц: гигагерц, или 1 миллиард герц.
В аббревиатурах префиксов, которые представляют числа, превышающие 1, такие как М (для приставки Мега), используют прописные буквы. Аббревиатуры приставок, которые меньше 1, пишутся со строчной буквы — как, например, в слове милли. Единственным исключением из этого правила является приставка к для обозначения префикса кило-, которая также записывается с маленькой буквы.
Иногда все же для обозначения тысяч используют и прописную литеру К — а именно при записи килоом; если вы увидите запись вида 3,3 К, то это будет значить 3,3 килоома.
Вы должны научиться преобразовывать любое число к экспоненциальному виду, чтобы затем нормально проводить расчеты. Убедиться в этом вы сможете уже в следующем разделе.
Понятие о законе Ома
Итак, давайте предположим, что вы собрали свою первую схему. Вы знаете величину тока, которую компонент схемы может выдержать, не выходя из строя, и напряжение, выдаваемое источником питания. Следовательно, вам нужно рассчитать сопротивление, которое не позволит току в цепи превысить пороговое значение.
В начале 1800-х годов Георг Ом опубликовал уравнение, названное впоследствии законом Ома, которое позволяет выполнить такой расчет. Закон Ома гласит: напряжение равняется произведению тока на сопротивление, или (в стандартной математической записи):
U = I x R
Выводы из закона Ома
Помните ли вы из школы основы алгебры? Давайте еще раз вспомним вместе: если в уравнении с тремя величинами известны две, то достаточно легко рассчитать третью неизвестную величину. Закон Ома основывается именно на таком уравнении; члены уравнения можно переставлять как угодно, но зная любые два, всегда можно вычислить третий. Например, можно сказать, что ток является частным от деления напряжения на сопротивление:
I = U / R
Наконец, можно рассчитать сопротивление при известных токе и напряжении, переставив члены того же уравнения:
R = U / I
Итак, пока вроде бы все ясно. Теперь давайте попробуем проверить наши знания на практике: пусть есть схема, питающаяся от 12-вольтовой батареи, и электрическая лампа (скажем, большой фонарик). Перед установкой лампочки в фонарик вы измерили сопротивление схемы мультиметром и нашли, что оно равно 9 Ом. Вот формула для расчета электрического тока по закону Ома:
I = U / R = 12 вольт / 9 Ом = 1,3 A
Ну, а что, если вы обнаружили, что лампочка светит чересчур уж ярко? Яркость можно изменить, уменьшив ток, т.е. просто добавив в схему резистор. Изначально мы имели сопротивление схемы 9 Ом; добавив 5-омный резистор в схему, мы повысим ее сопротивление до 14 Ом. В этом случае ток будет равен:
I = U / R = 12 вольт / 14 Ом = 0,9 А
Расчеты с применением больших и малых величин
Предположим, что у вас есть схема с небольшой сиреной, которая имеет сопротивление 2 килоома, а также 12-вольтовая батарея. Для того чтобы рассчитать ток, вам нужно выразить сопротивление цепи не в килоомах, а в базовых единицах — омах, не используя приставку “кило”. В нашем случае это значит, что нужно разделить напряжение на 2000 Ом:
I = U / R = 12 вольт / 2000 Ом = 0,006 A
В результате мы получили ток, записанный как доля 1 А. После окончания расчета будет удобнее вновь использовать префикс, чтобы дать ответ в более лаконичном виде: 0,006 А = 6 мА
Подводя итоги, можно сказать: для проведения расчетов необходимо все исходные величины преобразовать к базовым единицам счисления.
Мощность и закон Ома
Георг Ом (вот уж поистине, наш пострел везде поспел!) также нашел выражение для мощности, вычисляемое при известных напряжении и токе:
Р = U х I; или Мощность = напряжение умноженное на силу тока.
Это уравнение можно использовать для расчета мощности, потребляемой сиреной из предыдущего примера:
Р = 12 В х 0,006 А = 0,072 Вт, или 72 мВт.
Ладно, а что же делать, если напряжение на сирене нам не известно? Вы можете заняться простейшим преобразованием формулы для мощности, используя школьные знания (а вы-то думали, что зря протираете штаны на уроках физики!). Поскольку U = I х R, можно подставить это выражение в формулу для мощности, получив
Р = I2 х R; или Мощность = сила тока в квадрате умноженная на сопротивление.
Вы также можете использовать алгебраические преобразования, чтобы самостоятельно прикинуть, как можно рассчитать сопротивление, напряжение или ток, зная мощность и любой другой из этих же параметров.
4. Закон ома
Между основными электрическими параметрами цепи, такими, как ток, сопротивление, эдс, напряжение, существует строго определенная связь (рис.13). Эта связь устанавливается законом Ома.
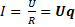(2-12)
т.е. сила тока на участке электрической цепи при постоянной проводимости пропорциональна напряжению.
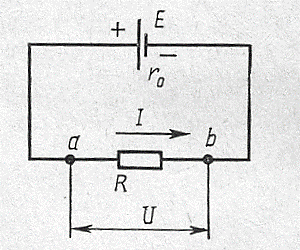
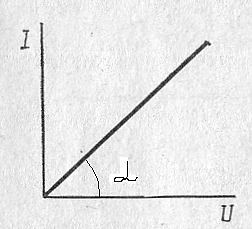
Рис.13 Рис. 14
Зависимость тока от напряжения называют вольтамперной характеристикой (ВАХ) (рис.14). Как следует из выражения(1-12), ВАХ участка цепи при его постоянной проводимости есть линейная функция, т.е. прямая линия, проходящая через начало координат. Причем, ctgα =R=U/I. Ранее приведенную формулу можно представить и так
U = IR,(2-13)
причем, величину равную произведению тока на сопротивление участка цепи, называют падением напряжения на этом участке.
При установлении связи между параметрами, относящимися ко всей цепи, необходимо учитывать сопротивление всей цепи, а также эдс источника, т.е. закон Ома для всей цепи
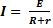, (2-14)
где R- сопротивление внешнего участка цепи,r-сопротивление внутреннего участка цепи. Произведение I r=ΔUназывают падением напряжения на внутреннем участке цепи.
5. Законы кирхгофа
Первый закон Кирхгофа — алгебраическая сумма токов, в узловой точке (а или б) (рис.15а) цепи равна нулю,
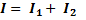или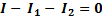 
(2-15)
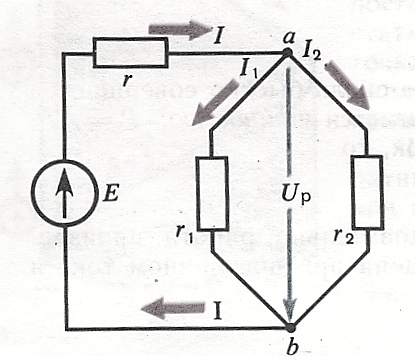
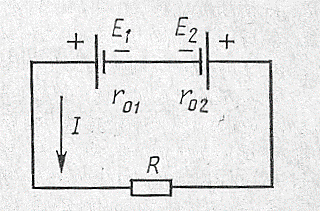
а б
Рис.15
Второй закон – алгебраическая сумма всех действующих эдс в любом контуре электрической цепи равна алгебраической сумме падений напряжений на резисторах, входящих в контур. Для замкнутого контура (рис.15б) второй закон Кирхгофа запишется в виде
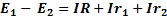(2-16)
Таким образом, закон Ома для всей цепи можно считать частным случаем второго закона Кирхгофа.
Знаки в алгебраической сумме для эдс и падений напряжений следует производить в соответствии со следующими правилами:
если направление эдс совпадает с условно выбранным направлением обхода по контуру, то эдс берут со знаком плюс и наоборот;
если направление тока на участке цепи совпадает с направлением выбранного обхода контура, то падение напряжения на этом участке берется со знаком плюс и наоборот.
6. Соединение резисторов
Последовательное соединение. Последовательным соединением резисторов называют такое соединение, при котором между ними не существует узловых точек и через все участки цепи проходит один и тот же ток.
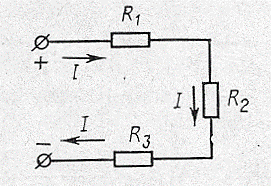
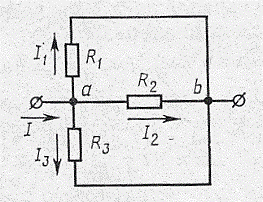
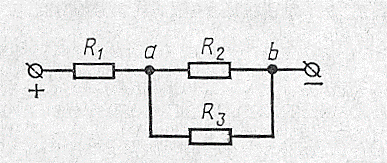
а б в
Рис.16
Электрическая цепь с последовательно соединенными резисторами (рис.16а)обладает следующими свойствами:
Сила тока на всех участках цепи одинакова:
I = const.(2-17)
Напряжение на зажимах цепи на отдельных ее участках равно арифметической сумме
U = U1 + U2 + U3. (2-18)
Напряжение на зажимах отдельных резисторов прямо пропорционально их сопротивлениям U~R
U1/U2 = R1/R2 или U2/U3 = R2/R3 (2-19)
Полное (эквивалентное) сопротивление цепи при последовательном сопротивлении равно сумме сопротивлений отдельных резисторов, включенных в цепь:
R = R1 + R2 + R3. (2-20)
Полная мощность цепи равна сумме мощностей, выделенных на каждом резисторе
Р = Р1+ Р2+ Р3.(2-21)
Параллельное соединение. Параллельным соединением резисторов называют такое соединение, при котором резисторы образуют две узловых точки и находятся под действием одного и того же напряжения (рис.16б)
Электрическая цепь с параллельно соединенными резисторами обладает следующими свойствами:
Ток в неразветвленной цепи равен сумме токов в ее отдельных ветвях
I = I1 + I2 + I3 + . . .(1-22)
Напряжение на всех ветвях одинаково:
U=U1=U2=U3 =const. (2-23)
Токи в отдельных ветвях обратно пропорциональны сопротивлениям этих ветвей:
I1/I2 = R2/R1 или I2/I3 =R3/R2. (2-24)
Полная проводимость цепи равна сумме проводимостей отдельных ветвей:
g=g1+g2+g3 + … или 1/R= 1/R1+ 1/R2+ 1/R3+ … (2-25)
Полная мощность цепи равна арифметической сумме мощностей, выделенных на каждом резисторе:
P= Р1+P2+P3+ … (2-26)
Параллельное соединение применяется в тех случаях, когда необходимо уменьшить полное сопротивление цепи.
Смешанное соединение. Смешанным соединением резисторов называют такое соединение, в котором сочетаются последовательное и параллельное соединение резисторов. На рис. 16 в представлена схема смешанного соединения резисторов. РезисторыR2иR3соединены параллельно, а резисторR1соединен с ними последовательно.
Методика расчета смешанных схем соединения резисторов состоит в том, чтобы путем замены отдельных видов соединений привести цепь к одному виду соединения – либо последовательному, либо параллельному.