Период колебаний Википедия

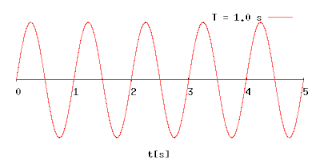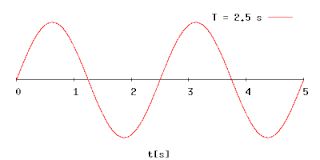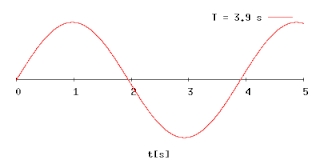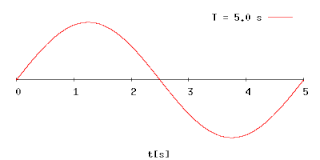
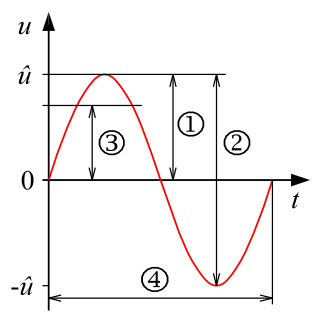
Период колеба́ний — наименьший промежуток времени, за который система совершает одно полное колебание (то есть возвращается в то же состояние^[1], в котором она находилась в первоначальный момент, выбранный произвольно).

В принципе совпадает с математическим понятием периода функции, но имея в виду под функцией зависимость физической величины, совершающей колебания, от времени.

Это понятие в таком виде применимо как к гармоническим, так и к ангармоническим строго периодическим колебаниям (а приближенно — с тем или иным успехом — и непериодическим колебаниям, по крайней мере к близким к периодичности).

В случае, когда речь идет о колебаниях гармонического осциллятора с затуханием, под периодом понимается период его осциллирующей составляющей (игнорируя затухание), который совпадает с удвоенным временным промежутком между ближайшими прохождениями колеблющейся величины через ноль. В принципе, это определение может быть с большей или меньшей точностью и пользой распространено в некотором обобщении и на затухающие колебания с другими свойствами.

Обозначения: обычное стандартное обозначение периода колебаний: T{\displaystyle T} (хотя могут применяться и другие, наиболее часто это τ{\displaystyle \tau }, иногда Θ{\displaystyle \Theta } и т. д.).

Единицы измерения: секунда и, в принципе, вообще единицы измерения времени.

Период колебаний связан соотношением взаимной обратности с частотой:

T=1ν,   ν=1T.{\displaystyle T={\frac {1}{\nu }},\ \ \ \nu ={\frac {1}{T}}.}

Для волновых процессов период связан кроме того очевидным образом с длиной волны λ{\displaystyle \lambda }

v=λν,   T=λv,{\displaystyle v=\lambda \nu ,\ \ \ T={\frac {\lambda }{v}},}

где v{\displaystyle v} — скорость распространения волны (точнее^[2] — фазовая скорость).

В квантовой физике период колебаний прямо связан с энергией

Период колебаний — это… Что такое Период колебаний?

Период колеба́ний — наименьший промежуток времени, за который осциллятор совершает одно полное колебание (то есть возвращается в то же состояние^[1], в котором он находился в первоначальный момент, выбранный произвольно).

В принципе совпадает с математическим понятием периода функции, но имея ввиду под функцией зависимость физической величины, совершающей колебания, от времени.

Это понятие в таком виде применимо как к гармоническим, так и к ангармоническим строго периодическими колебаниям (а приближенно — с тем или иным успехом — и непериодическим колебаниям, по крайней мере к близким к периодичности).

В случае, когда речь идет о колебаниях гармонического осциллятора с затуханием, под периодом понимается период его осциллирующей составляющей (игнорируя затухание), который совпадает с удвоенным временным промежутком между ближайшими прохождениями колеблющейся величины через ноль. В принципе, это определение может быть с большей или меньшей точностью и пользой распространено в некотором обобщении и на затухающие колебания с другими свойствами.

Обозначения: обычное стандартное обозначение периода колебаний: (хотя могут применяться и другие, наиболее часто это , иногда и т. д.).

Единицы измерения: секунда

Период колебаний связан соотношением взаимной обратности с частотой:

Для волновых процессов период связан кроме того очевидным образом с длиной волны

где — скорость распространения волны (точнее^[2] — фазовая скорость).

В квантовой физике период колебаний прямо связан с энергией (поскольку в квантовой физике энергия объекта — например, частицы — есть частота

[3] колебаний его волновой функции).

Теоретическое нахождение периода колебаний той или иной физической системы сводится, как правило, к нахождению решения динамических уравнений (уравнения), описывающего эту систему. Для категории линейных систем (а приближенно — и для линеаризуемых систем в линейном приближении, которое зачастую является очень хорошим) существуют стандартные сравнительно простые математические методы, позволяющие это сделать (если известны сами физические уравнения, описывающие систему).

Для экспериментального определения периода используются часы, секундомеры, частотомеры, стробоскопы, строботахометры, осциллографы. Также применяются биения, метод гетеродинирования в разных видах, используется принцип резонанса. Для волн можно померить период косвенно — через длину волны, для чего применяются интерферометры, дифракционные решетки итп. Иногда требуются и изощренные методы, специально разработанные для конкретного трудного случая (трудность могут представлять как само измерение времени, особенно если речь идет о предельно малых или наоборот очень больших временах, так и трудности наблюдения колеблющейся величины).

Периоды колебаний в природе

Представление о периодах колебаний различных физических процессов дает статья Частотные интервалы (учитывая то, что период в секундах есть обратная величина частоты в герцах).

Некоторое представление о величинах периодов различных физических процессов также может дать шкала частот элетромагнитных колебаний (см. Электромагнитный спектр) .

Периоды колебаний слышимого человеком звука находятся в диапазоне

от 5·10^-5с до 0,2с

(четкие границы его несколько условны).

Периоды электромагнитных колебаний, соответствующих разным цветам видимого света — в диапазоне

от 1,1·10^-15с до 2,3·10^-15с.

Поскольку при экстремально больших и экстремально маленьких периодах колебаний методы измерения имеют тенденцию становятся всё более косвенными (вплоть до плавного перетекая в теоретические экстраполяции), трудно назвать четкую верхнюю и нижнюю границы для периода колебаний, измеренного непосредственно. Какую-то оценку для верхней границы может дать время существования современной науки (сотни лет), а для нижней — период колебаний волновой функции самой тяжелой из известных сейчас частиц ().

В любом случае границей снизу может служить планковское время, которое столь мало, что по современным представлениям не только вряд ли может быть вообще как-то физически измерено^[4], но и вряд ли в более-менее обозримом будущем представляется возможность приблизиться к измерению величин даже на много порядков меньших. а границей сверху — время существования Вселенной — более десяти миллиардов лет.

Периоды колебаний простейших физических систем

Пружинный маятник

Период колебаний пружинного маятника может быть вычислен по следующей формуле:

,

где  — масса груза,  — жёсткость пружины.

Математический маятник

Период колебаний математического маятника:

где  — длина подвеса (к примеру нити),  — ускорение свободного падения.

Период колебаний (на Земле) математического маятника длиной 1 метр с хорошей точностью^[5] равен 2 секундам.

Физический маятник

Период колебаний физического маятника:

где — момент инерции маятника относительно оси вращения, — масса маятника, — расстояние от оси вращения до центра масс.

Крутильный маятник

Период колебаний крутильного маятника:

где  — момент инерции тела, а  — вращательный коэффициент жёсткости маятника.

Электрический колебательный (LC) контур

Период колебаний электрического колебательного контура:

,

где — индуктивность катушки, — ёмкость конденсатора.

Эту формулу вывел в 1853 году английский физик У. Томсон.

Примечания

1. ↑ Состояние механической системы характеризуется положениями и скоростями всех ее материальных точек (строже говоря — координатами и скоростями, соответствующими всем степеням свободы данной системы), для немеханической — их формальными аналогами (которые также можно назвать координатами и скоростями в смысле абстрактного описания динамической системы — в количестве, также равном количеству ее степеней свободы).
2. ↑ Для монохроматических волн это уточнение самоочевидно, для близких к монохроматическим — интуитивно очевидно по аналогии со строго монохроматическими, для существенно немонохроматических — наиболее ясный случай сводится к тому, что фазовые скорости всех монохроматических компонент совпадают друг с другом, поэтому комментируемое утверждение ьакже верно.
3. ↑ С точностью до единиц измерения: в традиционных (обычных) системах физических единиц частота и энергия измеряются в разных единицах (поскольку до появления квантовой теории совпадение энергии и частоты было неизвестно, и, естественно, для каждой из величин была выбрана своя независимая единица измерения), поэтому при измерении их в обычных (разных) единицах, например, джоулях и герцах требуется переводной коэффициент (так называемая константа Планка). Однако можно выбрать систему единиц измерения так, чтобы в ней константа Планка стала равной 1 и пропала из формул; в такой системе единиц энергия любой частицы просто равна частоте колебания ее волновой функции (а значит обрата периоду этого колебания).
4. ↑ Имеется в виду, конечно же, невозможность экспериментального измерения времен конкретных процессов или периодов колебаний такого порядка, а не просто вычисление некоторого числа.
5. ↑ Лучше, чем 0,5%, если взять метрологическое или принятое техническое значение ускорения свободного падения; И с разбросом ~0.53% для максимального и минимального значений ускорения свободного падения, наблюдаемых на земле.

Ссылки

Период колебаний — Википедия. Что такое Период колебаний

Период колеба́ний — наименьший промежуток времени, за который осциллятор совершает одно полное колебание (то есть возвращается в то же состояние^[1], в котором он находился в первоначальный момент, выбранный произвольно).

В принципе совпадает с математическим понятием периода функции, но имея в виду под функцией зависимость физической величины, совершающей колебания, от времени.

Это понятие в таком виде применимо как к гармоническим, так и к ангармоническим строго периодическими колебаниям (а приближенно — с тем или иным успехом — и непериодическим колебаниям, по крайней мере к близким к периодичности).

В случае, когда речь идет о колебаниях гармонического осциллятора с затуханием, под периодом понимается период его осциллирующей составляющей (игнорируя затухание), который совпадает с удвоенным временным промежутком между ближайшими прохождениями колеблющейся величины через ноль. В принципе, это определение может быть с большей или меньшей точностью и пользой распространено в некотором обобщении и на затухающие колебания с другими свойствами.

Обозначения: обычное стандартное обозначение периода колебаний: T{\displaystyle T} (хотя могут применяться и другие, наиболее часто это τ{\displaystyle \tau }, иногда Θ{\displaystyle \Theta } и т. д.).

Единицы измерения: секунда и, в принципе, вообще единицы измерения времени.

Период колебаний связан соотношением взаимной обратности с частотой:

T=1ν,   ν=1T.{\displaystyle T={\frac {1}{\nu }},\ \ \ \nu ={\frac {1}{T}}.}

Для волновых процессов период связан кроме того очевидным образом с длиной волны λ{\displaystyle \lambda }

v=λν,   T=λv,{\displaystyle v=\lambda \nu ,\ \ \ T={\frac {\lambda }{v}},}

где v{\displaystyle v} — скорость распространения волны (точнее^[2] — фазовая скорость).

В квантовой физике период колебаний прямо связан с энергией (поскольку в квантовой физике энергия объекта — например, частицы — есть частота^[3] колебаний его волновой функции).

Теоретическое нахождение периода колебаний той или иной физической системы сводится, как правило, к нахождению решения динамических уравнений (уравнения), описывающего эту систему. Для категории линейных систем (а приближенно — и для линеаризуемых систем в линейном приближении, которое зачастую является очень хорошим) существуют стандартные сравнительно простые математические методы, позволяющие это сделать (если известны сами физические уравнения, описывающие систему).

Для экспериментального определения периода используются часы, секундомеры, частотомеры, стробоскопы, строботахометры, осциллографы. Также применяются биения, метод гетеродинирования в разных видах, используется принцип резонанса. Для волн можно померить период косвенно — через длину волны, для чего применяются интерферометры, дифракционные решётки итп. Иногда требуются и изощренные методы, специально разработанные для конкретного трудного случая (трудность могут представлять как само измерение времени, особенно если речь идет о предельно малых или наоборот очень больших временах, так и трудности наблюдения колеблющейся величины).

Периоды колебаний в природе

Представление о периодах колебаний различных физических процессов дает статья Частотные интервалы (учитывая то, что период в секундах есть обратная величина частоты в герцах).

Некоторое представление о величинах периодов различных физических процессов также может дать шкала частот элетромагнитных колебаний (см. Электромагнитный спектр) .

Периоды колебаний слышимого человеком звука находятся в диапазоне

от 5·10⁻⁵с до 0,2с

(четкие границы его несколько условны).

Периоды электромагнитных колебаний, соответствующих разным цветам видимого света — в диапазоне

от 1,1·10⁻¹⁵с до 2,3·10⁻¹⁵с.

Поскольку при экстремально больших и экстремально маленьких периодах колебаний методы измерения имеют тенденцию становятся всё более косвенными (вплоть до плавного перетекания в теоретические экстраполяции), трудно назвать четкую верхнюю и нижнюю границы для периода колебаний, измеренного непосредственно. Какую-то оценку для верхней границы может дать время существования современной науки (сотни лет), а для нижней — период колебаний волновой функции самой тяжелой из известных сейчас частиц ().

В любом случае границей снизу может служить планковское время, которое столь мало, что по современным представлениям не только вряд ли может быть вообще как-то физически измерено^[4], но и вряд ли в более-менее обозримом будущем представляется возможность приблизиться к измерению величин даже намного порядков больших, а границей сверху — время существования Вселенной — более десяти миллиардов лет.

Периоды колебаний простейших физических систем

Пружинный маятник

Период колебаний пружинного маятника может быть вычислен по следующей формуле:

T=2πmk{\displaystyle T=2\pi {\sqrt {\frac {m}{k}}}},

где m{\displaystyle m} — масса груза, k{\displaystyle k} — жёсткость пружины.

Математический маятник

Период малых колебаний математического маятника:

T=2πlg{\displaystyle T=2\pi {\sqrt {\frac {l}{g}}}}

где l{\displaystyle l} — длина подвеса (к примеру, нити), g{\displaystyle g} — ускорение свободного падения.

Период малых колебаний (на Земле) математического маятника длиной 1 метр с хорошей точностью^[5] равен 2 секундам.

Физический маятник

Период малых колебаний физического маятника:

T=2πJmgl{\displaystyle T=2\pi {\sqrt {\frac {J}{mgl}}}}

где J{\displaystyle J} — момент инерции маятника относительно оси вращения, m{\displaystyle m} — масса маятника, l{\displaystyle l} — расстояние от оси вращения до центра масс.

Крутильный маятник

Период колебаний крутильного маятника:

T=2πIK{\displaystyle T=2\pi {\sqrt {\frac {I}{K}}}}

где I{\displaystyle I} — момент инерции маятника относительно оси кручения, а K{\displaystyle K} — вращательный коэффициент жёсткости маятника.

Электрический колебательный (LC) контур

Период колебаний электрического колебательного контура (формула Томсона):

T=2πLC{\displaystyle T=2\pi {\sqrt {LC}}},

где L{\displaystyle L} — индуктивность катушки, C{\displaystyle C} — ёмкость конденсатора.

Эту формулу вывел в 1853 году английский физик Уильям Томсон.

Примечания

1. ↑ Состояние механической системы характеризуется положениями и скоростями всех её материальных точек (строже говоря — координатами и скоростями, соответствующими всем степеням свободы данной системы), для немеханической — их формальными аналогами (которые также можно назвать координатами и скоростями в смысле абстрактного описания динамической системы — в количестве, также равном количеству её степеней свободы).
2. ↑ Для монохроматических волн это уточнение самоочевидно, для близких к монохроматическим — интуитивно очевидно по аналогии со строго монохроматическими, для существенно немонохроматических — наиболее ясный случай сводится к тому, что фазовые скорости всех монохроматических компонент совпадают друг с другом, поэтому комментируемое утверждение также верно.
3. ↑ С точностью до единиц измерения: в традиционных (обычных) системах физических единиц частота и энергия измеряются в разных единицах (поскольку до появления квантовой теории совпадение энергии и частоты было неизвестно, и, естественно, для каждой из величин была выбрана своя независимая единица измерения), поэтому при измерении их в обычных (разных) единицах, например, джоулях и герцах требуется переводной коэффициент (так называемая константа Планка). Однако можно выбрать систему единиц измерения так, чтобы в ней константа Планка стала равной 1 и пропала из формул; в такой системе единиц энергия любой частицы просто равна частоте колебания её волновой функции (а значит обратна периоду этого колебания).
4. ↑ Имеется в виду, конечно же, невозможность экспериментального измерения времен конкретных процессов или периодов колебаний такого порядка, а не просто вычисление некоторого числа.
5. ↑ Лучше, чем 0,5 %, если взять метрологическое или принятое техническое значение ускорения свободного падения; И с разбросом ~0.53 % для максимального и минимального значений ускорения свободного падения, наблюдаемых на земле.

Ссылки

опыты, формулы, задачи :: SYL.ru

Что такое период колебаний? Что это за величина, какой физический смысл она имеет и как ее рассчитать? В этой статье мы разберемся с этими вопросами, рассмотрим различные формулы, по которым можно рассчитать период колебаний, а также выясним, какая связь имеется между такими физическими величинами, как период и частота колебаний тела/системы.

Определение и физический смысл

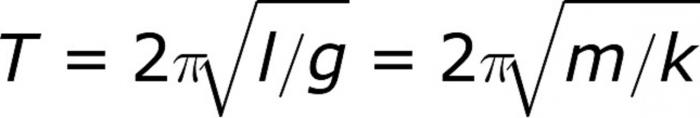
Периодом колебаний называется такой промежуток времени, при котором тело или система совершают одно колебание (обязательно полное). Параллельно можно отметить параметр, при выполнении которого колебание может считаться полным. В роли такого условия выступает возвращение тела в его первоначальное состояние (к первоначальной координате). Очень хорошо проводится аналогия с периодом функции. Ошибочно, кстати, думать, что она имеет место исключительно в обыкновенной и высшей математике. Как известно, эти две науки неразрывно связаны. И с периодом функций можно столкнуться не только при решении тригонометрических уравнений, но и в различных разделах физики, а именно речь идет о механике, оптике и прочих. При переносе периода колебаний из математики в физику под ним нужно понимать просто физическую величину (а не функцию), которая имеет прямую зависимость от проходящего времени.

Какие бывают колебания?

Колебания подразделяются на гармонические и ангармонические, а также на периодические и непериодические. Логично было бы предположить, что в случае гармонических колебаний они совершаются согласно некоторой гармонической функции. Это может быть как синус, так и косинус. При этом в деле могут оказаться и коэффициенты сжатия-растяжения и увеличения-уменьшения. Также колебания бывают затухающими. То есть, когда на систему действует определенная сила, которая постепенно “тормозит” сами колебания. При этом период становится меньше, в то время как частота колебаний неизменно увеличивается. Очень хорошо демонстрирует такую вот физическую аксиому простейший опыт с использованием маятника. Он может быть пружинного вида, а также математического. Это неважно. Кстати, период колебаний в таких системах будет определяться разными формулами. Но об этом чуточку позже. Сейчас же приведем примеры.

Опыт с маятниками

Взять первым можно любой маятник, разницы никакой не будет. Законы физики на то и законы физики, что они соблюдаются в любом случае. Но почему-то больше по душе математический маятник. Если кто-то не знает, что он собой представляет: это шарик на нерастяжимой нити, который крепится к горизонтальной планке, прикрепленной к ножкам (или элементам, которые играют их роль – держать систему в равновесном состоянии). Шарик лучше всего брать из металла, чтобы опыт был нагляднее.

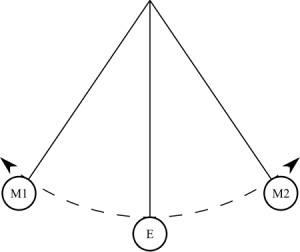
Итак, если вывести такую систему из равновесия, приложить к шару какую-то силу (проще говоря, толкнуть его), то шарик начнет раскачиваться на нити, следуя определенной траектории. Со временем можно заметить, что траектория, по которой проходит шар, сокращается. В то же время шарик начинает все быстрее сновать туда-сюда. Это говорит о том, что частота колебаний увеличивается. А вот время, за которое шарик возвращается в начальное положение, уменьшается. А ведь время одного полного колебания, как мы выяснили ранее, и называется периодом. Если одна величина уменьшается, а другая увеличивается, то говорят об обратной пропорциональности. Вот мы и добрались до первого момента, на основании которого строятся формулы для определения периода колебаний. Если же мы возьмем для проведения пружинный маятник, то там закон будет наблюдаться немного в другом виде. Для того чтобы он был наиболее наглядно представлен, приведем систему в движение в вертикальной плоскости. Чтобы было понятнее, сначала стоило сказать, что собой представляет пружинный маятник. Из названия понятно, что в его конструкции должна присутствовать пружина. И это действительно так. Опять же таки, у нас есть горизонтальная плоскость на опорах, к которой подвешивается пружина определенной длины и жесткости. К ней, в свою очередь, подвешивается грузик. Это может быть цилиндр, куб или другая фигурка. Это может быть даже какой-то сторонний предмет. В любом случае, при выведении системы из положения равновесия, она начнет совершать затухающие колебания. Наиболее четко просматривается увеличение частоты именно в вертикальной плоскости, без всякого отклонения. На этом с опытами можно закончить.

Итак, в их ходе мы выяснили, что период и частота колебаний это две физические величины, которые имеют обратную зависимость.

Обозначение величин и размерности

Обычно период колебаний обозначается латинской буквой T. Гораздо реже он может обозначаться по-другому. Частота же обозначается буквой µ (“Мю”). Как мы говорили в самом начале, период это не что иное, как время, за которое в системе происходит полное колебание. Тогда размерностью периода будет секунда. А так как период и частота обратно пропорциональны, то размерностью частоты будет единица, деленная на секунду. В записи задач все будет выглядеть таким образом: T (с), µ (1/с).

Формула для математического маятника. Задача №1

Как и в случае с опытами, я решил первым делом разобраться с маятником математическим. Подробно вдаваться в вывод формулы мы не будем, поскольку такая задача поставлена изначально не была. Да и вывод сам по себе громоздкий. Но вот с самими формулами ознакомимся, выясним, что за величины в них входят. Итак, формула периода колебаний для математического маятника имеет следующий вид:

Где l – длина нити, п = 3,14, а g – ускорение свободного падения (9,8 м/с^2). Никаких затруднений формула вызывать не должна. Поэтому без дополнительных вопросов перейдем сразу к решению задачи на определение периода колебания математического маятника. Металлический шар массой 10 грамм подвешен на нерастяжимой нити длиной 20 сантиметров. Рассчитайте период колебания системы, приняв ее за математический маятник. Решение очень простое. Как и во всех задачах по физике, необходимо максимально упростить ее за счет отброса ненужных слов. Они включаются в контекст для того чтобы запутать решающего, но на самом деле никакого веса абсолютно не имеют. В большинстве случаев, разумеется. Здесь можно исключить момент с “нерастяжимой нитью”. Это словосочетание не должно вводить в ступор. А так как маятник у нас математический, масса груза нас интересовать не должна. То есть слова о 10 граммах тоже просто призваны запутать ученика. Но мы ведь знаем, что в формуле масса отсутствует, поэтому со спокойной совестью можем приступать к решению. Итак, берем формулу и просто подставляем в нее величины, поскольку определить необходимо период системы. Поскольку дополнительных условий не было задано, округлять значения будем до 3-его знака после запятой, как и принято. Перемножив и поделив величины, получим, что период колебаний равен 0,886 секунд. Задача решена.

Формула для пружинного маятника. Задача №2

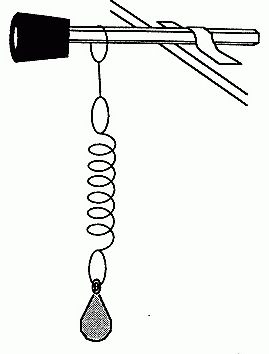
Формулы маятников имеют общую часть, а именно 2п. Эта величина присутствует сразу в двух формулах, но разнятся они подкоренным выражением. Если в задаче, касающейся периода пружинного маятника, указана масса груза, то избежать вычислений с ее применение невозможно, как это было в случае с математическим маятником. Но пугаться не стоит. Вот так выглядит формула периода для пружинного маятника:

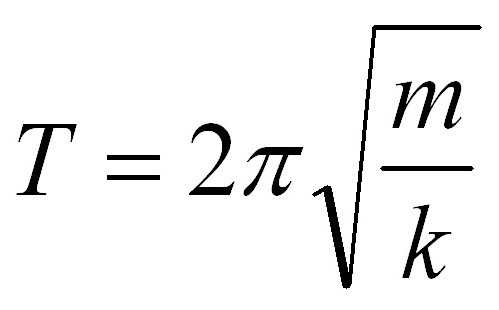
В ней m – масса подвешенного к пружине груза, k – коэффициент жесткости пружины. В задаче значение коэффициента может быть приведено. Но если в формуле математического маятника особо не разгуляешься – все-таки 2 величины из 4 являются константами – то тут добавляется 3 параметр, который может изменяться. И на выходе мы имеем 3 переменных: период (частота) колебаний, коэффициент жесткости пружины, масса подвешенного груза. Задача может быть сориентирована на нахождение любого из этих параметров. Вновь искать период было бы слишком легко, поэтому мы немного изменим условие. Найдите коэффициент жесткости пружины, если время полного колебания составляет 4 секунды, а масса груза пружинного маятника равна 200 граммам.

Для решения любой физической задачи хорошо бы сначала сделать рисунок и написать формулы. Они здесь – половина дела. Записав формулу, необходимо выразить коэффициент жесткости. Он у нас находится под корнем, поэтому обе части уравнения возведем в квадрат. Чтобы избавиться от дроби, умножим части на k. Теперь оставим в левой части уравнения только коэффициент, то есть разделим части на T^2. В принципе, задачку можно было бы еще немного усложнить, задав не период в числах, а частоту. В любом случае, при подсчетах и округлениях (мы условились округлять до 3-его знака после запятой), получится, что k = 0, 157 Н/м.

Период свободных колебаний. Формула периода свободных колебаний

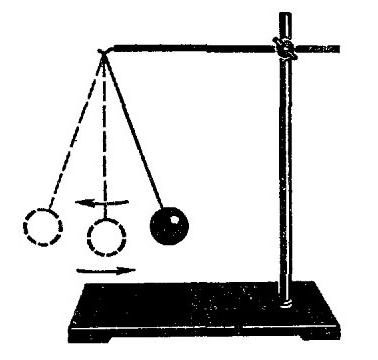
Под формулой периода свободных колебаний понимают те формулы, которые мы разобрали в двух ранее приведенных задачах. Составляют также уравнение свободных колебаний, но там речь идет уже о смещениях и координатах, а этот вопрос относится уже к другой статье.

Советы для решения задач, связанных с периодом

1) Прежде чем браться за задачу, запишите формулу, которая с ней связана.

2) Простейшие задачи не требуют рисунков, но в исключительных случаях их нужно будет сделать.

3) Старайтесь избавляться от корней и знаменателей, если это возможно. Записанное в строчку уравнение, не имеющее знаменателя, решать гораздо удобнее и проще.

Формула периода колебаний пружинного маятника в физике

Определение

Период — это минимальное время, за которое совершается одно полное колебательное движение.

Обозначают период буквой $T$.

\[T=\frac{\Delta t}{N}\left(1\right),\]

где $\Delta t$ — время колебаний; $N$ — число полных колебаний.

Уравнение колебаний пружинного маятника

Рассмотрим простейшую колебательную систему, в которой можно реализовать механические колебания. Это груз массы $m$, подвешенный на пружине, коэффициент упругости которой равен $k\ $(рис.1). Рассмотри вертикальное движение груза, которое обусловлено действием силы тяжести и силы упругости пружины. В состоянии равновесия такой системы, сила упругости равна по величине силе тяжести. Колебания пружинного маятника возникают, когда систему выводят из состояния равновесия, например, слегка дополнительно растянув пружину, после этого маятник предоставляют самому себе.

Допустим, что масса пружины мала в сравнении с массой груза, при описании колебаний ее учитывать не будем. Началом отсчета будем считать точку на оси координат (X), которая совпадает с положением равновесия груза. В этом положении пружина уже имеет удлинение, которое обозначим $b$. Растяжение пружины происходит из-за действия на груз силы тяжести, следовательно:

\[mg=kb\ \left(2\right).\]

Если груз смещают дополнительно, но закон Гука еще выполняется, то сила упругости пружины становится равна:

\[F_u=-k\left(x+b\right)\left(3\right).\]

Ускорение груза запишем, помня, что движение происходит по оси X, как:

\[a=\frac{d^2x}{dt^2}=\ddot{x\ }\left(4\right).\]

Второй закон Ньютона для груза принимает вид:

\[m\ddot{x}=-k\left(x+b\right)+mg\ \left(5\right).\]

Учтем равенство (2), формулу (5) преобразуем к виду:

\[m\ddot{x}=-kx-kb+mg=-kx-mg+mg=-kx\ \left(6\right).\]

Если ввести обозначение: ${\omega }^2_0=\frac{k}{m}$, то уравнение колебаний запишем как:

\[\ddot{x}+{\omega }^2_0x=0\left(7\right),\]

где ${\omega }^2_0=\frac{k}{m}$ — циклическая частота колебаний пружинного маятника. Решением уравнения (7) (это проверяется непосредственной подстановкой) является функция:

\[x=A{\cos \left({\omega }_0t+\varphi \right)=A{\sin \left({\omega }_0t+{\varphi }_1\right)\ }\ }\left(8\right),\]

где ${\omega }_0=\sqrt{\frac{k}{m}}>0$- циклическая частота колебаний маятника, $A$ — амплитуда колебаний; ${(\omega }_0t+\varphi )$ — фаза колебаний; $\varphi $ и ${\varphi }_1$ — начальные фазы колебаний.

Формулы периода колебаний пружинного маятника

Мы получили, что колебания пружинного маятника описывается функцией косинус или синус. Это периодические функции, значит, смещение $x$ будет принимать равные значения через определенные одинаковые про

Период колебаний — Википедия (с комментариями)

Материал из Википедии — свободной энциклопедии

Период колеба́ний — наименьший промежуток времени, за который осциллятор совершает одно полное колебание (то есть возвращается в то же состояние^[1], в котором он находился в первоначальный момент, выбранный произвольно).

В принципе совпадает с математическим понятием периода функции, но имея в виду под функцией зависимость физической величины, совершающей колебания, от времени.

Это понятие в таком виде применимо как к гармоническим, так и к ангармоническим строго периодическими колебаниям (а приближенно — с тем или иным успехом — и непериодическим колебаниям, по крайней мере к близким к периодичности).

В случае, когда речь идет о колебаниях гармонического осциллятора с затуханием, под периодом понимается период его осциллирующей составляющей (игнорируя затухание), который совпадает с удвоенным временным промежутком между ближайшими прохождениями колеблющейся величины через ноль. В принципе, это определение может быть с большей или меньшей точностью и пользой распространено в некотором обобщении и на затухающие колебания с другими свойствами.

Обозначения: обычное стандартное обозначение периода колебаний: <math>T</math> (хотя могут применяться и другие, наиболее часто это <math>\tau</math>, иногда <math>\Theta</math> и т. д.).

Единицы измерения: секунда и, в принципе, вообще единицы измерения времени.

Период колебаний связан соотношением взаимной обратности с частотой:

<math>T = \frac{1}{\nu},\ \ \ \nu = \frac{1}{T}.</math>

Для волновых процессов период связан кроме того очевидным образом с длиной волны <math>\lambda</math>

<math>v = \lambda \nu, \ \ \ T = \frac{\lambda}{v},</math>

где <math>v</math> — скорость распространения волны (точнее^[2] — фазовая скорость).

В квантовой физике период колебаний прямо связан с энергией (поскольку в квантовой физике энергия объекта — например, частицы — есть частота^[3] колебаний его волновой функции).

Теоретическое нахождение периода колебаний той или иной физической системы сводится, как правило, к нахождению решения динамических уравнений (уравнения), описывающего эту систему. Для категории линейных систем (а приближенно — и для линеаризуемых систем в линейном приближении, которое зачастую является очень хорошим) существуют стандартные сравнительно простые математические методы, позволяющие это сделать (если известны сами физические уравнения, описывающие систему).

Для экспериментального определения периода используются часы, секундомеры, частотомеры, стробоскопы, строботахометры, осциллографы. Также применяются биения, метод гетеродинирования в разных видах, используется принцип резонанса. Для волн можно померить период косвенно — через длину волны, для чего применяются интерферометры, дифракционные решетки итп. Иногда требуются и изощренные методы, специально разработанные для конкретного трудного случая (трудность могут представлять как само измерение времени, особенно если речь идет о предельно малых или наоборот очень больших временах, так и трудности наблюдения колеблющейся величины).

Периоды колебаний в природе

Представление о периодах колебаний различных физических процессов дает статья Частотные интервалы (учитывая то, что период в секундах есть обратная величина частоты в герцах).

Некоторое представление о величинах периодов различных физических процессов также может дать шкала частот элетромагнитных колебаний (см. Электромагнитный спектр) .

Периоды колебаний слышимого человеком звука находятся в диапазоне

от 5·10⁻⁵с до 0,2с

(четкие границы его несколько условны).

Периоды электромагнитных колебаний, соответствующих разным цветам видимого света — в диапазоне

от 1,1·10⁻¹⁵с до 2,3·10⁻¹⁵с.

Поскольку при экстремально больших и экстремально маленьких периодах колебаний методы измерения имеют тенденцию становятся всё более косвенными (вплоть до плавного перетекания в теоретические экстраполяции), трудно назвать четкую верхнюю и нижнюю границы для периода колебаний, измеренного непосредственно. Какую-то оценку для верхней границы может дать время существования современной науки (сотни лет), а для нижней — период колебаний волновой функции самой тяжелой из известных сейчас частиц ().

В любом случае границей снизу может служить планковское время, которое столь мало, что по современным представлениям не только вряд ли может быть вообще как-то физически измерено^[4], но и вряд ли в более-менее обозримом будущем представляется возможность приблизиться к измерению величин даже намного порядков больших, а границей сверху — время существования Вселенной — более десяти миллиардов лет.

Периоды колебаний простейших физических систем

Пружинный маятник

Период колебаний пружинного маятника может быть вычислен по следующей формуле:

<math>T=2\pi \sqrt{\frac{m}{k}}</math>,

где <math>m</math> — масса груза, <math>k</math> — жёсткость пружины.

Математический маятник

Период малых колебаний математического маятника:

<math>T=2\pi \sqrt{\frac{l}{g}}</math>

где <math>l</math> — длина подвеса (к примеру, нити), <math>g</math> — ускорение свободного падения.

Период малых колебаний (на Земле) математического маятника длиной 1 метр с хорошей точностью^[5] равен 2 секундам.

Физический маятник

Период малых колебаний физического маятника:

<math>T=2\pi \sqrt{\frac{J}{mgl}}</math>

где <math>J</math> — момент инерции маятника относительно оси вращения, <math>m</math> — масса маятника, <math>l</math> — расстояние от оси вращения до центра масс.

Крутильный маятник

Период колебаний крутильного маятника:

<math>T = 2 \pi \sqrt{\frac{I}{K}}</math>

где <math>I</math> — момент инерции маятника относительно оси кручения, а <math>K</math> — вращательный коэффициент жёсткости маятника.

Электрический колебательный (LC) контур

Период колебаний электрического колебательного контура (формула Томсона):

<math>T= 2\pi \sqrt{LC}</math>,

где <math>L</math> — индуктивность катушки, <math>C</math> — ёмкость конденсатора.

Эту формулу вывел в 1853 году английский физик У. Томсон.

Напишите отзыв о статье «Период колебаний»

Примечания

1. ↑ Состояние механической системы характеризуется положениями и скоростями всех её материальных точек (строже говоря — координатами и скоростями, соответствующими всем степеням свободы данной системы), для немеханической — их формальными аналогами (которые также можно назвать координатами и скоростями в смысле абстрактного описания динамической системы — в количестве, также равном количеству её степеней свободы).
2. ↑ Для монохроматических волн это уточнение самоочевидно, для близких к монохроматическим — интуитивно очевидно по аналогии со строго монохроматическими, для существенно немонохроматических — наиболее ясный случай сводится к тому, что фазовые скорости всех монохроматических компонент совпадают друг с другом, поэтому комментируемое утверждение также верно.
3. ↑ С точностью до единиц измерения: в традиционных (обычных) системах физических единиц частота и энергия измеряются в разных единицах (поскольку до появления квантовой теории совпадение энергии и частоты было неизвестно, и, естественно, для каждой из величин была выбрана своя независимая единица измерения), поэтому при измерении их в обычных (разных) единицах, например, джоулях и герцах требуется переводной коэффициент (так называемая константа Планка). Однако можно выбрать систему единиц измерения так, чтобы в ней константа Планка стала равной 1 и пропала из формул; в такой системе единиц энергия любой частицы просто равна частоте колебания её волновой функции (а значит обратна периоду этого колебания).
4. ↑ Имеется в виду, конечно же, невозможность экспериментального измерения времен конкретных процессов или периодов колебаний такого порядка, а не просто вычисление некоторого числа.
5. ↑ Лучше, чем 0,5 %, если взять метрологическое или принятое техническое значение ускорения свободного падения; И с разбросом ~0.53 % для максимального и минимального значений ускорения свободного падения, наблюдаемых на земле.

Ссылки

Отрывок, характеризующий Период колебаний

Ростов молчал.
– А вы что ж? тоже позавтракать? Порядочно кормят, – продолжал Телянин. – Давайте же.
Он протянул руку и взялся за кошелек. Ростов выпустил его. Телянин взял кошелек и стал опускать его в карман рейтуз, и брови его небрежно поднялись, а рот слегка раскрылся, как будто он говорил: «да, да, кладу в карман свой кошелек, и это очень просто, и никому до этого дела нет».
– Ну, что, юноша? – сказал он, вздохнув и из под приподнятых бровей взглянув в глаза Ростова. Какой то свет глаз с быстротою электрической искры перебежал из глаз Телянина в глаза Ростова и обратно, обратно и обратно, всё в одно мгновение.
– Подите сюда, – проговорил Ростов, хватая Телянина за руку. Он почти притащил его к окну. – Это деньги Денисова, вы их взяли… – прошептал он ему над ухом.
– Что?… Что?… Как вы смеете? Что?… – проговорил Телянин.
Но эти слова звучали жалобным, отчаянным криком и мольбой о прощении. Как только Ростов услыхал этот звук голоса, с души его свалился огромный камень сомнения. Он почувствовал радость и в то же мгновение ему стало жалко несчастного, стоявшего перед ним человека; но надо было до конца довести начатое дело.
– Здесь люди Бог знает что могут подумать, – бормотал Телянин, схватывая фуражку и направляясь в небольшую пустую комнату, – надо объясниться…
– Я это знаю, и я это докажу, – сказал Ростов.
– Я…
Испуганное, бледное лицо Телянина начало дрожать всеми мускулами; глаза всё так же бегали, но где то внизу, не поднимаясь до лица Ростова, и послышались всхлипыванья.
– Граф!… не губите молодого человека… вот эти несчастные деньги, возьмите их… – Он бросил их на стол. – У меня отец старик, мать!…
Ростов взял деньги, избегая взгляда Телянина, и, не говоря ни слова, пошел из комнаты. Но у двери он остановился и вернулся назад. – Боже мой, – сказал он со слезами на глазах, – как вы могли это сделать?
– Граф, – сказал Телянин, приближаясь к юнкеру.
– Не трогайте меня, – проговорил Ростов, отстраняясь. – Ежели вам нужда, возьмите эти деньги. – Он швырнул ему кошелек и выбежал из трактира.

Вечером того же дня на квартире Денисова шел оживленный разговор офицеров эскадрона.
– А я говорю вам, Ростов, что вам надо извиниться перед полковым командиром, – говорил, обращаясь к пунцово красному, взволнованному Ростову, высокий штаб ротмистр, с седеющими волосами, огромными усами и крупными чертами морщинистого лица.
Штаб ротмистр Кирстен был два раза разжалован в солдаты зa дела чести и два раза выслуживался.
– Я никому не позволю себе говорить, что я лгу! – вскрикнул Ростов. – Он сказал мне, что я лгу, а я сказал ему, что он лжет. Так с тем и останется. На дежурство может меня назначать хоть каждый день и под арест сажать, а извиняться меня никто не заставит, потому что ежели он, как полковой командир, считает недостойным себя дать мне удовлетворение, так…
– Да вы постойте, батюшка; вы послушайте меня, – перебил штаб ротмистр своим басистым голосом, спокойно разглаживая свои длинные усы. – Вы при других офицерах говорите полковому командиру, что офицер украл…
– Я не виноват, что разговор зашел при других офицерах. Может быть, не надо было говорить при них, да я не дипломат. Я затем в гусары и пошел, думал, что здесь не нужно тонкостей, а он мне говорит, что я лгу… так пусть даст мне удовлетворение…
– Это всё хорошо, никто не думает, что вы трус, да не в том дело. Спросите у Денисова, похоже это на что нибудь, чтобы юнкер требовал удовлетворения у полкового командира?
Денисов, закусив ус, с мрачным видом слушал разговор, видимо не желая вступаться в него. На вопрос штаб ротмистра он отрицательно покачал головой.
– Вы при офицерах говорите полковому командиру про эту пакость, – продолжал штаб ротмистр. – Богданыч (Богданычем называли полкового командира) вас осадил.
– Не осадил, а сказал, что я неправду говорю.
– Ну да, и вы наговорили ему глупостей, и надо извиниться.
– Ни за что! – крикнул Ростов.
– Не думал я этого от вас, – серьезно и строго сказал штаб ротмистр. – Вы не хотите извиниться, а вы, батюшка, не только перед ним, а перед всем полком, перед всеми нами, вы кругом виноваты. А вот как: кабы вы подумали да посоветовались, как обойтись с этим делом, а то вы прямо, да при офицерах, и бухнули. Что теперь делать полковому командиру? Надо отдать под суд офицера и замарать весь полк? Из за одного негодяя весь полк осрамить? Так, что ли, по вашему? А по нашему, не так. И Богданыч молодец, он вам сказал, что вы неправду говорите. Неприятно, да что делать, батюшка, сами наскочили. А теперь, как дело хотят замять, так вы из за фанаберии какой то не хотите извиниться, а хотите всё рассказать. Вам обидно, что вы подежурите, да что вам извиниться перед старым и честным офицером! Какой бы там ни был Богданыч, а всё честный и храбрый, старый полковник, так вам обидно; а замарать полк вам ничего? – Голос штаб ротмистра начинал дрожать. – Вы, батюшка, в полку без году неделя; нынче здесь, завтра перешли куда в адъютантики; вам наплевать, что говорить будут: «между павлоградскими офицерами воры!» А нам не всё равно. Так, что ли, Денисов? Не всё равно?
Денисов всё молчал и не шевелился, изредка взглядывая своими блестящими, черными глазами на Ростова.
– Вам своя фанаберия дорога, извиниться не хочется, – продолжал штаб ротмистр, – а нам, старикам, как мы выросли, да и умереть, Бог даст, приведется в полку, так нам честь полка дорога, и Богданыч это знает. Ох, как дорога, батюшка! А это нехорошо, нехорошо! Там обижайтесь или нет, а я всегда правду матку скажу. Нехорошо!
И штаб ротмистр встал и отвернулся от Ростова.
– Пг’авда, чог’т возьми! – закричал, вскакивая, Денисов. – Ну, Г’остов! Ну!
Ростов, краснея и бледнея, смотрел то на одного, то на другого офицера.
– Нет, господа, нет… вы не думайте… я очень понимаю, вы напрасно обо мне думаете так… я… для меня… я за честь полка.да что? это на деле я покажу, и для меня честь знамени…ну, всё равно, правда, я виноват!.. – Слезы стояли у него в глазах. – Я виноват, кругом виноват!… Ну, что вам еще?…
– Вот это так, граф, – поворачиваясь, крикнул штаб ротмистр, ударяя его большою рукою по плечу.
– Я тебе говог’ю, – закричал Денисов, – он малый славный.
– Так то лучше, граф, – повторил штаб ротмистр, как будто за его признание начиная величать его титулом. – Подите и извинитесь, ваше сиятельство, да с.
– Господа, всё сделаю, никто от меня слова не услышит, – умоляющим голосом проговорил Ростов, – но извиняться не могу, ей Богу, не могу, как хотите! Как я буду извиняться, точно маленький, прощенья просить?
Денисов засмеялся.
– Вам же хуже. Богданыч злопамятен, поплатитесь за упрямство, – сказал Кирстен.
– Ей Богу, не упрямство! Я не могу вам описать, какое чувство, не могу…
– Ну, ваша воля, – сказал штаб ротмистр. – Что ж, мерзавец то этот куда делся? – спросил он у Денисова.
– Сказался больным, завтг’а велено пг’иказом исключить, – проговорил Денисов.
– Это болезнь, иначе нельзя объяснить, – сказал штаб ротмистр.
– Уж там болезнь не болезнь, а не попадайся он мне на глаза – убью! – кровожадно прокричал Денисов.
В комнату вошел Жерков.
– Ты как? – обратились вдруг офицеры к вошедшему.
– Поход, господа. Мак в плен сдался и с армией, совсем.
– Врешь!
– Сам видел.
– Как? Мака живого видел? с руками, с ногами?
– Поход! Поход! Дать ему бутылку за такую новость. Ты как же сюда попал?
– Опять в полк выслали, за чорта, за Мака. Австрийской генерал пожаловался. Я его поздравил с приездом Мака…Ты что, Ростов, точно из бани?
– Тут, брат, у нас, такая каша второй день.
Вошел полковой адъютант и подтвердил известие, привезенное Жерковым. На завтра велено было выступать.
– Поход, господа!
– Ну, и слава Богу, засиделись.

Кутузов отступил к Вене, уничтожая за собой мосты на реках Инне (в Браунау) и Трауне (в Линце). 23 го октября .русские войска переходили реку Энс. Русские обозы, артиллерия и колонны войск в середине дня тянулись через город Энс, по сю и по ту сторону моста.

Математический маятник — Википедия

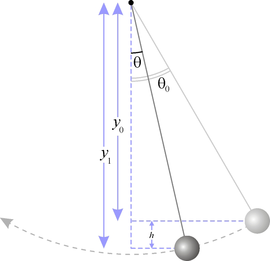
Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки на конце невесомой нерастяжимой нити или лёгкого стержня и находящуюся в однородном поле сил тяготения^[1]. Другой конец нити (стержня) обычно неподвижен. Период малых собственных колебаний маятника длины L, подвешенного в поле тяжести, равен

T=2πLg{\displaystyle T=2\pi {\sqrt {L \over g}}}

и не зависит, в первом приближении, от амплитуды колебаний и массы маятника. Здесь g — ускорение свободного падения.

Математический маятник служит простейшей моделью физического тела, совершающего колебания: она не учитывает распределение массы. Однако реальный физический маятник при малых амплитудах колеблется так же, как математический с приведённой длиной.

Математический маятник со стержнем способен колебаться только в какой-то одной плоскости (вдоль какого-то выделенного горизонтального направления) и, следовательно, является системой с одной степенью свободы. Если же стержень заменить на нерастяжимую нить, получится система с двумя степенями свободы (так как становятся возможными колебания по двум горизонтальным координатам).

При колебаниях в одной плоскости маятник движется по дуге окружности радиуса L{\displaystyle L}, а при наличии двух степеней свободы может описывать кривые на сфере того же радиуса^[1]. Нередко, в том числе в случае нити, ограничиваются анализом плоского движения; оно и рассматривается далее.

Колебания математического маятника описываются обыкновенным дифференциальным уравнением (ДУ) вида

x¨+ω2sin⁡x=0,{\displaystyle {\ddot {x}}+\omega ^{2}\sin x=0,}

где ω{\displaystyle \omega } ― положительная константа, определяемая исключительно из параметров маятника. Неизвестная функция x(t){\displaystyle x(t)} ― это угол отклонения маятника в момент t{\displaystyle t} от нижнего положения равновесия, выраженный в радианах; ω=g/L{\displaystyle \omega ={\sqrt {g/L}}}, где L{\displaystyle L} ― длина подвеса, g{\displaystyle g} ― ускорение свободного падения. Уравнение малых колебаний маятника около нижнего положения равновесия (т. н. гармоническое уравнение) имеет вид:

x¨+ω2x=0.{\displaystyle {\ddot {x}}+\omega ^{2}x=0.}

Приведённые уравнения предполагают, что потерь энергии в системе нет.

Гармонические колебания[править | править код]

Малые колебания маятника являются гармоническими. Это означает, что смещение маятника от положения равновесия изменяется во времени по синусоидальному закону^[2]. Поскольку уравнение движения является обыкновенным ДУ второго порядка, для определения закона движения маятника необходимо задать два начальных условия — координату и скорость, из которых определяются две независимые константы:

x=Asin⁡(θ0+ωt),{\displaystyle x=A\sin(\theta _{0}+\omega t),}

где A{\displaystyle A} — амплитуда колебаний маятника, θ0{\displaystyle \theta _{0}} — начальная фаза колебаний, ω{\displaystyle \omega } — циклическая частота, которая определяется из уравнения движения. Движение, совершаемое маятником, называется гармоническими колебаниями.

Нелинейный маятник[править | править код]

Для маятника, совершающего колебания с большой амплитудой, закон движения более сложен:

sin⁡x2=ϰ⋅sn⁡(ωt;ϰ),{\displaystyle \sin {\frac {x}{2}}=\varkappa \cdot \operatorname {sn} (\omega t;\varkappa ),}

где sn{\displaystyle \operatorname {sn} } — это синус Якоби. Для ϰ<1{\displaystyle \varkappa <1} он является периодической функцией, при малых ϰ{\displaystyle \varkappa } совпадает с обычным тригонометрическим синусом.

Параметр ϰ{\displaystyle \varkappa } определяется выражением

ϰ=ε+ω22ω2,{\displaystyle \varkappa ={\frac {\varepsilon +\omega ^{2}}{2\omega ^{2}}},}

где ε=EmL2{\displaystyle \varepsilon ={\frac {E}{mL^{2}}}} — энергия маятника в единицах t⁻².

Период колебаний нелинейного маятника составляет

T=2πΩ,Ω=π2ωK(ϰ),{\displaystyle T={\frac {2\pi }{\Omega }},\quad \Omega ={\frac {\pi }{2}}{\frac {\omega }{K(\varkappa )}},}

где K — эллиптический интеграл первого рода.

Для вычислений практически удобно разлагать эллиптический интеграл в ряд:

T=T0{1+(12)2sin2⁡(α2)+(1⋅32⋅4)2sin4⁡(α2)+⋯+[(2n−1)!!(2n)!!]2sin2n⁡(α2)+…}{\displaystyle T=T_{0}\left\{1+\left({\frac {1}{2}}\right)^{2}\sin ^{2}\left({\frac {\alpha }{2}}\right)+\left({\frac {1\cdot 3}{2\cdot 4}}\right)^{2}\sin ^{4}\left({\frac {\alpha }{2}}\right)+\dots +\left[{\frac {\left(2n-1\right)!!}{\left(2n\right)!!}}\right]^{2}\sin ^{2n}\left({\frac {\alpha }{2}}\right)+\dots \right\}},

где T0=2πLg{\displaystyle T_{0}=2\pi {\sqrt {\frac {L}{g}}}} — период малых колебаний, α{\displaystyle \alpha } — максимальный угол отклонения маятника от вертикали.

При углах до 1 радиана (≈60°) с приемлемой точностью (ошибка менее 1 %) можно ограничиться первым приближением:

T=T0(1+14sin2⁡(α2)).{\displaystyle T=T_{0}\left(1+{\frac {1}{4}}\sin ^{2}\left({\frac {\alpha }{2}}\right)\right).}

Точная формула периода, с квадратичной сходимостью для любого угла максимального отклонения, обсуждается на страницах сентябрьского выпуска журнала «Заметки американского математического общества» 2012 года^[3]:

T=2πM(cos⁡(θ0/2))Lg,{\displaystyle T={\frac {2\pi }{M{\big (}\cos(\theta _{0}/2){\big )}}}{\sqrt {\frac {L}{g}}},}

где M(x){\displaystyle M(x)} — арифметико-геометрическое среднее чисел 1 и x{\displaystyle x}.

Движение по сепаратрисе[править | править код]

Движение маятника по сепаратрисе является непериодическим. В бесконечно далёкий момент времени он начинает падать из крайнего верхнего положения в какую-то сторону с нулевой скоростью, постепенно набирает её, а затем останавливается, возвратившись в исходное положение.

Несмотря на свою простоту, математический маятник связан с рядом интересных явлений.

• Если амплитуда колебания маятника близка к π{\displaystyle \pi }, то есть движение маятника на фазовой плоскости близко к сепаратрисе, то под действием малой периодической вынуждающей силы система демонстрирует хаотическое поведение. Это одна из простейших механических систем, в которой хаос возникает под действием периодического возмущения^[4].
• Если точка подвеса не неподвижна, а совершает колебания, то у маятника может появиться новое положение равновесия. Если точка подвеса достаточно быстро колеблется вверх-вниз, то маятник приобретает устойчивое положение «вверх тормашками». Такая система называется маятником Капицы.
• В условиях вращения Земли при достаточно длинной нити подвеса плоскость, в которой маятник совершает колебания, будет медленно поворачиваться относительно земной поверхности в сторону, противоположную направлению вращения Земли (маятник Фуко).