Связь между угловой и линейной скоростями

Отсюда легко установить связь между линейной и угловой скоростями. Мы уже знаем, что угловая скорость связана с числом оборотов формулой: ω = 2πn; поэтому на основании формулы скорости движения по окружности получим:

v = ωR

Линейная скорость точки, движущейся равномерно по окружности, равна угловой скорости, умноженной на радиус окружности.

Известно, что вектор скорости точки, движущейся по окружности, направлен по касательной. Следовательно, линейная скорость направлена по касательной к окружности.

Из формулы видно, что линейная скорость измеряется в ^см/_сек , ^м/_сек и т.д.

 

14. Что называется линейным ускорением материальной точки, в каких единицах оно измеряется?

линейное ускорение — это производная от скорости по времени.

Формула линейного ускорения:

а = dv / dt = d²s/dt², где s – путь ,пройденный телом.

15. Закон равноускоренного движения по прямой

равноускоренным движением называют такое движение, при котором вектор ускорения остается неизменным по модулю и направлению.

Закон равноускоренного движения по прямой

Это выражение называют законом равноускоренного движения

Начальная скорость-υ0 , конечная скорость-υ, ускорения-a, время-t.

16. Что называется угловой скоростью, в каких единицах оно измеряется?

Угловая скорость — величина, характеризующая скорость вращения материальной точки вокруг центра вращения.

17. Что называется частотой вращения, в каких единицах оно измеряется?

Частота вращения — это физическая величина, равная числу полных оборотов за единицу времени

18. Что называется периодом вращения, в каких единицах он измеряется?

Период вращения (физический термин) — промежуток времени, в течение которого точка совершает полный оборот, двигаясь по окружности.

19. Связь между угловой скоростью вращения и его частотой.

Угловая скорость вращения ω это отношение угла, на которое тело повернется, к времени, за которое оно это сделает. Полному обороту

вокруг оси соответствует угол 2π или 360° в зависимости от единиц измерения угла. Число оборотов равно отношению пройденного угла к 2π или 360°. Частота вращения это число полных оборотов тела вокруг оси за единицу времени, таким образом она равна ω/(2π) или ω/360° для углов, измеряемых в градусах

20. Связь между угловой скоростью и периодом.

21. Связь между линейной и угловой скоростями

Связь между линейной и угловой скоростью. Скорость точки, движущейся по окружности, часто называют линейной скоростью, чтобы подчеркнуть ее отличие от угловой скорости. При вращении твердого тела разные его точки имеют разные

линейные скорости, но угловая скорость для всех точек одинакова. Междулинейной скоростью какой-либо точки вращающегося тела и угловой скоростьсуществует связь. Точка, лежащая на окружности радиуса R, за один оборот пройдет путь 2πR. А так как, время одного оборота тела есть период Т, то модуль линейнойскорости можно найти так: v=2πR/T=2πRν или v=ωR

22. Центростремительное ускорение

»

23. Что называется нормальным ускорением материальной точки, как его вычислить?

Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения .Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой

n. Вектор нормального ускорения направлен по радиусу кривизны траектории.

24. Что называется тангенциальным ускорением материальной точки, как его вычислить?

Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.

25. Напишите формулу для определения полного ускорения материальной точки

26. Какое падение тела называется свободным?

Свободным падением называется движение, которое совершило бы тело только под действием силы тяжести без учета сопротивления воздуха.

Читайте также:

Рекомендуемые страницы:

Поиск по сайту

Равномерное движение по прямой и вращение по окружности. Связь угловой и линейной скорости

Раздел физики, который изучает движение тел по различным траекториям, называется кинематикой. Практически полезными типами перемещения объектов являются движение по прямой и по окружности. Рассмотрим в статье, что представляют собой эти типы движения, какими формулами они описываются, а также приведем связь угловой и линейной скорости.

Движение по прямой

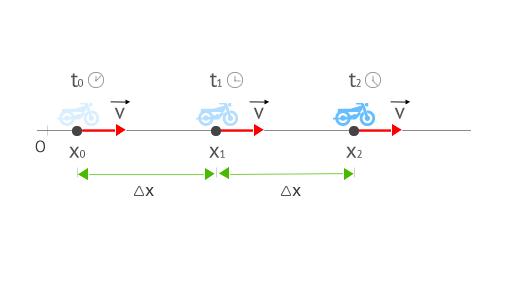
Связь угловой и линейной скорости можно определить, если знать, о каких величинах идет речь. Начнем со скорости линейной.

Со школьной скамьи каждый знает, что перемещение объектов в пространстве характеризуется тремя главными величинами:

• пройденный путь S;
• время движения t;
• скорость v.

Формула, связывающая в единое равенство названные величины, приведена ниже:

S = v * t.

Приведенное выражение описывает равномерное движение тела по прямой линии. В международной системе единиц СИ величина S измеряется в метрах (м), t — в секундах (с), v — в метрах в секунду (м/с). Помимо названных единиц, путь и время могут измеряться в километрах (км) и часах (ч), соответственно. Тогда скорость будет выражаться в километрах в час (км/ч).

Записанная формула может применяться для решения широкого круга практических задач, например, движение транспортных средств по дорогам, движение кораблей и лодок по рекам, полет птиц и так далее.

Движение по окружности

Перед тем как перейти к выводу формулы связи линейной и угловой скорости, следует рассмотреть последнюю с точки зрения физики.

Угловая скорость появляется в физике, когда речь идет о вращающихся объектах. Примерами могут быть вращение колеса велосипеда, маховика автомобиля или планеты вокруг своей звезды. Угловая скорость тела показывает, на какой угол в радианах оно поворачивается за единицу времени. Обычно эту величину обозначают греческой буквой ω (омега). Она измеряется в радианах в секунду (рад/с).

По аналогии с линейным случаем можно назвать три главных величины, которые описывают движение по окружности с постоянной скоростью угловой:

• угол поворота θ;
• время t;
• угловая скорость ω.

Соответствующая формула, которая связывает эти величины, выглядит так:

θ = ω * t.

Угол поворота тела θ вокруг оси вращения измеряется в радианах. Напомним, что окружность имеет 2 * pi радиан (около 6,28). Если полученное по формуле значение θ оказалось больше, чем 2 * pi, то это означает, что тело сделало больше одного оборота вокруг оси.

Таким образом, записанное выражение позволяет рассчитать число оборотов, совершаемых телом за известный промежуток времени t.

Связь угловой и линейной скорости

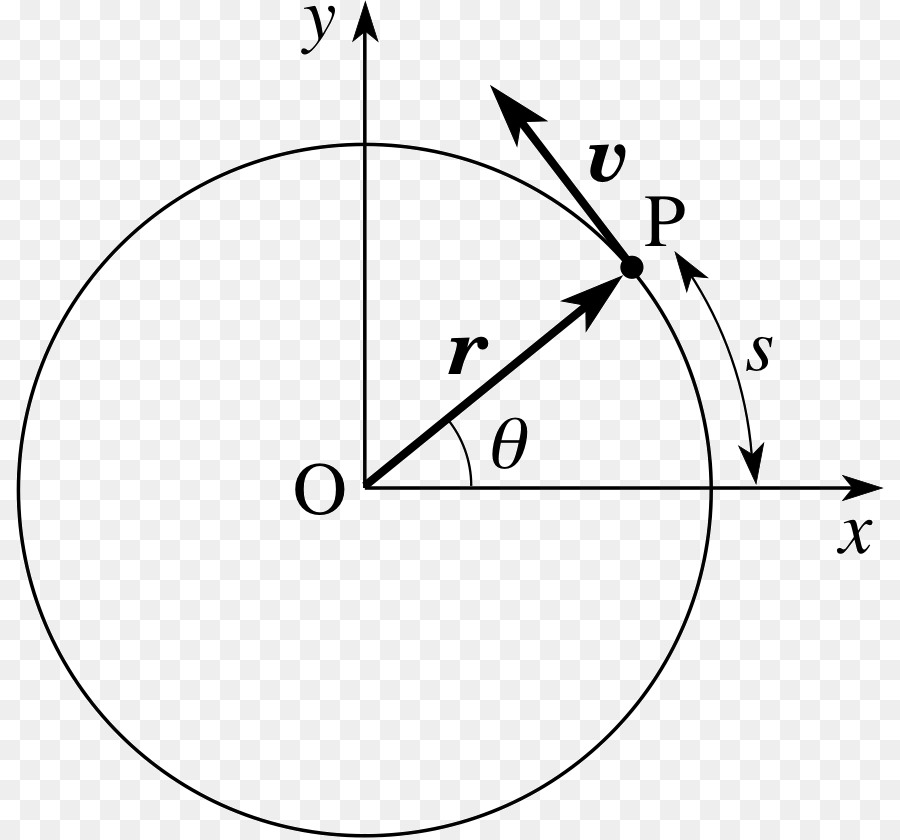
Теперь можно рассмотреть этот вопрос. Предположим, что тело, имеющее линейную скорость v, вращается по окружности радиусом R. Чтобы получить между линейной и угловой скоростью связь, рассмотрим, какое время понадобится телу, чтобы сделать полный один оборот. Поскольку пройденный путь будет равен длине окружности, то следующее выражение будет справедливым:

t = S/v = 2 * pi * R/v.

Теперь воспользуемся угловыми величинами. За найденное время одного оборота t, тело повернется точно на 2 * pi радиан. Последнее означает, что его угловая скорость будет равна:

ω = θ/t = 2 * pi/t.

Подставим рассчитанное выше время t и получим между угловой и линейной скоростью связь:

ω = 2 * pi/t = 2 * pi/(2 * pi * R/v) = v/R.

Полученную формулу можно записать в двух видах:

ω = v/R;

v = ω * R.

Каждое из выражений применяется в зависимости от того, какая величина в условии задачи известна. Формулы позволяют сделать важный вывод: чем больше радиус орбиты вращение, тем больше будет линейная скорость при постоянной угловой скорости.

Далее решим интересную задачу на применение полученных формул.

Что быстрее — Земля или Марс?

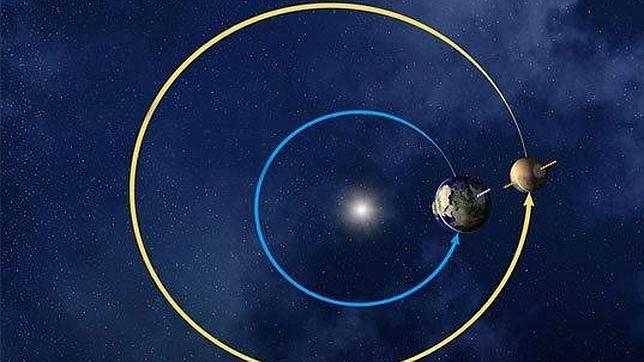
Известно, что Земля и Марс являются 3-й и 4-й планетами Солнечной системы, соответственно. Обе планеты движутся приблизительно по круглым орбитам. Расстояние от нашей звезды до Земли равно 149 597 870,691 км, а один оборот вокруг нее она делает за 365,256 дней. Марс расположен от Солнца на расстоянии 227 936 640 км, и один оборот вокруг него делает за 686,971 земных дня. Необходимо определить и сравнить линейные скорости планет.

Угловая скорость планеты может быть рассчитана по формуле:

ω = 2 * pi/T.

Где T — период (время совершения одного оборота вокруг звезды). Подставляя ω в формулу для v, получаем:

v = 2 * pi * R/T.

Переведем время оборота планет в часы и подставим данные в это равенство, получим:

• для Земли: v = 2 * 3,14 * 149597870,691/(365,256 * 24) ≈ 107,2 тыс. км/ч;
• для Марса: v = 2 * 3,14 * 227936640/(686,971 * 24) ≈ 86,8 тыс. км/ч.

Обе цифры являются огромными. Так, Земля за один час пролетает в космосе расстояние, практически равное трем ее окружностям по экватору. Полученные скорости свидетельствуют, что Земля движется быстрее Марса, и ее скорость на 24 % больше марсианской.

Связь линейных и угловых характеристик движения.

Если угловое перемещение всех точек абсолютно твёрдого тела одинаково, то все точки тела имеют одинаковую угловую скорость и одинаковое угловое ускорение в данный момент времени.

Линейные характеристики – перемещение, скорость, ускорение – различны для разных точек твёрдого тела. Связь между линейными и угловыми характеристиками движущейся точки можно получить, используя равенство d=ds/r.

Дифференцируя это равенство по времени, получаем: ds/dt=r(d/dt) или =r.

Дифференцируя это равенство по времени дважды, получаем соотношение между тангенциальным и угловым ускорением: d²s/dt²=r(d²/dt²) или a=r.

3. Инерциальные системы отсчёта.

Первый закон Ньютона (закон инерции). Всякое тело сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока внешнее воздействие не изменит это состояние.

Системы отсчёта, в которых выполняется первый закон Ньютона называют инерциальными.

К таким системам относится, например, гелиоцентрическая система отсчёта, в которой за начало координат принимают солнце, а оси проводят в направлении звёзд, которые считаются неподвижными.

Системы отсчета, движущиеся относительно инерциальной системы с ускорением, называются неинерциальными.

Понятие силы и инертной массы.

Сила – векторная физическая величина, являющаяся мерой механического воздействия на тело со стороны других тел.

Инертность – свойство тела сохранять состояние покоя или равномерного прямолинейного движения. Физическая величина, являющаяся мерой инертности тела при поступательном движении, называется массой. Масса тела равна сумме масс всех частиц (или материальных точек), из которых оно состоит.

Импульсом тела называют произведение массы тела на скорость его движения: p=mV.

Так как a=dV/dt, то формулу a=F/m можно записать в виде F=m(dV/dt)=(d/dt)mV=dp/dt.

Единица силы – ньютон(Н).

Ньютон – сила, которая телу массой 1 кг сообщает ускорение 1 м/с² в направлении действия силы.

4. Второй закон Ньютона. Этот закон устанавливает связь между динамическими и кинематическими величинами и является основным законом динамики.

Ускорение, приобретаемое материальной точкой (телом) в инерциальной системе отсчёта, пропорционально действующей на точку силе, обратно пропорционально массе материальной точки и по направлению совпадает с силой: a=F/m.

Ускорение центра масс системы определяется результирующей силой.

Ньютоном второй закон механики был сформулирован не через ускорение, а через импульс тела (количество движения).

Изменение количества движения (импульса тела) пропорционально приложенной движущей силе и происходит по направлению прямой, по которой эта сила действует.

Третий закон Ньютона. Силы с которыми два тела действуют друг на друга, равны по модулю и направлены в противоположные стороны прямой, соединяющей эти тела: F1=-F2.

Закон сохранения импульса системы материальных точек.

Силы взаимодействия между частицами (частями) некоторой рассматриваемой системы тел называют внутренними.

Силы, действующие на тела данной системы со стороны тел, не включённых в эту систему, называют внешними.

Если система состоит из n – материальных точек, то уравнение можно записать в виде 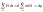. Перепишем это равенство в виде

В замкнутой системе внешние силы отсутствуют, т.е. sum(Fi)=0, следовательно dp/dt=0 или p=sum(miVi)=const.

Это равенство выражает закон сохранения импульса: полный вектор импульса замкнутой системы тел с течением времени не изменяется.

5.Поступательное движение твёрдого тела может быть охарактеризовано движением одной точки – центром масс (центром инерции).

Центр масс системы материальных точек – точка, координаты которой определяются следующими соотношениями:

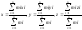
n – число материальных точек, mi – масса i-ой материальной точки, xi, yi, zi – координаты i-ой материальной точки.

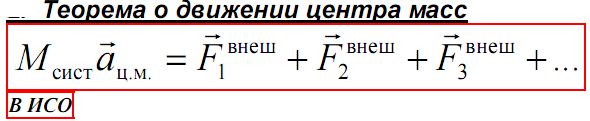
Элементы кинематики вращательного движения. Угловая скорость и угловое ускорение их связь с линейными скоростями и ускорениями точек вращающегося тела.

⇐ ПредыдущаяСтр 2 из 16Следующая ⇒

Рассмотрим твердое тело, которое вращается вокруг неподвижной оси. Тогда отдель­ные точки этого тела будут описывать окружности разных радиусов, центры которых лежат на оси вращения. Пусть некоторая точка движется по окружности радиуса R (рис. 6). Ее положение через промежуток времени Dt зададим углом D 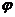. Элементар­ные (бесконечно малые) повороты можно рассматривать как векторы (они обозначают­ся 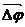или 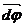). Модуль вектора 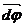равен углу поворота, а его направление совпадает с направлением поступательного движения острия винта, головка которого вращается в направлении движения точки по окружности, т.е. подчиняетсяправилу правого винта(рис.6). Векторы, направления которых связываются с направлением вращения, назы­ваютсяпсевдовекторами илиаксиальными векторами. Эти векторы не имеют опреде­ленных точек приложения: они могут откладываться из любой точки оси вращения.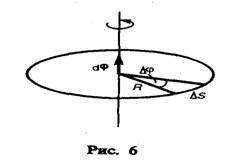

Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени: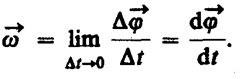

Вектор 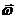направлен вдоль оси вращения по правилу правого винта, т.е. так же, как и вектор 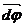(рис.7). Размерность угловой скорости dim w=T–1, а ее единица — ради­ан в секунду (рад/с).
Линейная скорость точки (см. рис. 6)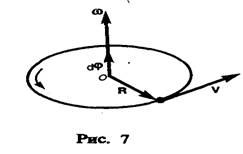


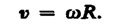
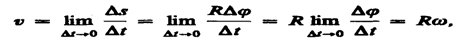
В векторном виде формулу для линейной скорости можно написать как векторное произведение: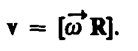

При этом модуль векторного произведения, по определению, равен 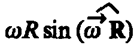, а направление совпадает с направлением поступательного движения правого винта при его вращении от 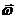к R.
Если ( = const, то вращение равномерное и его можно характеризовать периодом вращенияT — временем, за которое точка совершает один полный оборот, т.е. поворачивается на угол 2p. Так как промежутку времени Dt= T соответствует 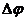= 2p, то = 2p/T, откуда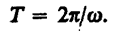

Число полных оборотов, совершаемых телом при равномерном его движении по окружности, в единицу времени называется частотой вращения: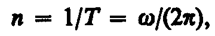

Откуда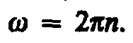

Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени: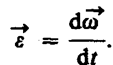

При вращении тела вокруг неподвижной оси вектор углового ускорения направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном движении вектор 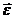сонаправлен вектору 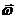(рис.8), при замедлен­ном — противонаправлен ему (рис.9).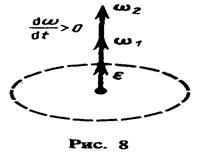

Тангенциальная составляющая ускорения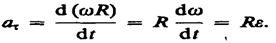

Нормальная составляющая ускорения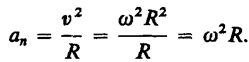

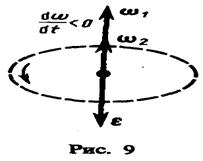
Таким образом, связь между линейными (длина пути s, пройденного точкой по дуге окружности радиуса R, линейная скорость v, тангенциальное ускорение 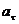, нормальное ускорение 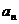) и угловыми величинами (угол поворота j, угловая скорость w, угловое ускорение e) выражается следующими формулами: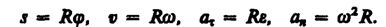

В случае равнопеременного движения точки по окружности (e=const)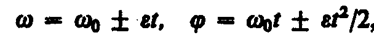

где w0 — начальная угловая скорость

5. Динамика материальной точки и поступательного движения твёрдого тела. Сила. Закон инерции и инерциальные системы отсчета. Закон динамики материальной точки (2 и 3 законы Ньютона)

Динамика рассматривает закон движения тел и причины, вызывающие или изменяющие это движение. Изменение движения тел или изменение их формы происходит в результате взаимодействия по меньшей мере двух тел.

Силой называется физическая величина, характеризующая взаимодействие тел; она определяет изменение движения тела или изменение формы тела, или то и другое вместе.

Сила – величина векторная. Две силы, действующие на тело, складываются по правилу параллелограмма.

Первый закон Ньютона (закон инерции).

Всякое тело находится в состоянии покоя или равномерного прямолинейного движения, пока приложенные к телу силы не вызовут изменения его состояния.

Свойство тел сохранять величину и направление скорости, когда на него не действуют силы или действие сил скомпенсировано, называется инерцией (или инертностью).

Инерциальная система отсчёта, система отсчёта, в которой справедлив закон инерции. Всякая система отсчёта, движущаяся по отношению к ИСО поступательно, равномерно и прямолинейно, есть также ИСО. Следовательно, теоретически может существовать сколько угодно равноправных ИСО, обладающих тем важным свойством, что во всех таких системах законы физики одинаковы (так называемый принцип относительности). Помимо закона инерции, в любой ИСО справедливы также 2-й закон Ньютона и законы сохранения количества движения, момента количества движения и движения для замкнутых, т. е. не подверженных внешним воздействиям, систем.

Второй закон Ньютона.

Ускорение тела в результате действия на него силы F пропорционально величине этой силы и обратно пропорционально массе тела m. Направление силы совпадает с направлением ускорения:

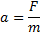
В системе СИ за единицу силы принимают силу, которая телу массой в 1 кг сообщает ускорение 1 м/c2. Эту единицу называют ньютоном (Н)

Третий закон Ньютона.

Силы, с которыми два тела действуют друг на друга, равны по модулю и противоположны по направлению.

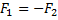
Закон сохранения импульса и его применение при воздействии на систему материальных точек только внутренних сил; только внешних сил. Центр масс механической системы. Координаты центра масс и закон его движения.

Закон сохранения импульса и его применение.

Если сумма внешних сил, действующих на систему, равна нулю, то равно нулю и изменение импульса системы: 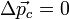. Это означает, что, какой бы интервал времени мы ни взяли, суммарный импульс в начале этого интервала 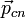и в его конце 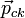один и тот же: 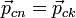. Импульс системы остается неизменным, или, как говорят, сохраняется:
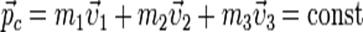. (10)
Закон сохранения импульсаформулируется так:
если сумма внешних сил, действующих на тела системы, равна нулю, то импульс системы сохраняется.
Тела могут только обмениваться импульсами, суммарное же значение импульса не изменяется. Надо только помнить, что сохраняется векторная сумма импульсов, а не сумма их модулей.
Как видно из проделанного нами вывода, закон сохранения импульса является следствием второго и третьего законов Ньютона. Система тел, на которую не действуют внешние силы, называется замкнутой или изолированной. В замкнутой системе тел импульс сохраняется. Но область применения закона сохранения импульса шире: если даже на тела системы действуют внешние силы, но их сумма равна нулю, импульс системы все равно сохраняется.
Полученный результат легко обобщается на случай системы, содержащей произвольное число N тел:
. (11)
Здесь 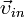— скорости тел в начальный момент времени, а 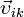— в конечный. Так как импульс — величина векторная, то уравнение (11) представляет собой компактную запись трех уравнений для проекций импульса системы на координатные оси.

Центр масс механической системы. Координаты центра масс и закон его движения.

Центр масс- геометрическая точка, положение которой характеризует распределение масс в телеили механической системе. Координаты Ц. м. определяются формулами

,

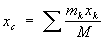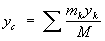
или для тела при непрерывном распределении масс

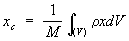
где m_к — массы материальных точек, образующих систему, x_k, у_к, z_k — координаты этих точек, М =Σm_к— масса системы, ρ — плотность, V — объём. Понятие о Ц. м. отличается от понятия о центре тяжести тем, что последнее имеет смысл только для твёрдого тела, находящегося в однородном полетяжести; понятие же о Ц. м. не связано ни с каким силовым полем и имеет смысл для любой механическойсистемы. Для твёрдого тела положения Ц. м. и центра тяжести совпадают.

При движении механической системы её Ц. м. движется так, как двигалась бы материальная точка,имеющая массу, равную массе системы, и находящаяся под действием всех внешних сил, приложенных ксистеме. Кроме того, некоторые уравнения движения механической системы (тела) по отношению к осям,имеющим начало в Ц. м. и движущимся вместе с Ц. м. поступательно, сохраняют тот же вид, что и длядвижения по отношению к инерциальной системе отсчёта .