Вопрос 2. Кинематика вращательного движения. Угловая скорость, угловое ускорение. Связь линейных и угловых величин. Псевдовекторы.
Вопрос 1. Механическое движение. Система отсчёта. Путь, перемещение, траектория. Расчёт пути при равноускоренном движении. Кинематика поступательного движения. Скорость мгновенная, средняя. Модуль скорости. Ускорение и его составляющие.
Механика – часть физики, которая изучает закономерности механического движения и причины, вызывающие или изменяющие это движение. Механическое движение – это изменение с течением времени взаимного расположения тел или их частей.
Механика Галилея-Ньютона называется классической механикой. В ней изучаются законы движения макроскопических тел, скорости которых малы по сравнению со скоростью света в вакууме. Законы движения тел со скоростями, сравнимыми со скоростью света, изучаются релятивистской механикой.
Движение тел происходит в пространстве и во времени. Положение материальной точки определяется по отношению к какому-либо другому телу, называемому телом отсчёта. С ним связана система отсчета – совокупность системы координат и часов, связанных с телом отсчета.
Траектория
движения материальной точки – линия,
описываемая этой точкой в пространстве.
В зависимости от формы траектории
движение может быть прямолинейным или
криволинейным. Длина участка АВ,
пройденного материальной точкой с
момента начала отсчета времени,
называется длиной пути 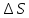 и является скалярной функцией времени:
и является скалярной функцией времени: 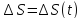 .
Вектор
.
Вектор
Равноускоренное
движение – движение точки с постоянным
ускорением. Ускорение – величина,
характеризующая быстроту изменения
скорости. В равноускоренном движении 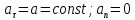 .
Формула расчета скорости при
равноускоренном движении в момент
времени:
.
Формула расчета скорости при
равноускоренном движении в момент
времени:
Проинтегрируем
эту формулу: 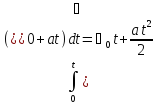 — путь при равноускоренном движении.
— путь при равноускоренном движении.
Мгновенная скорость (скорость) — предел отношения вектора перемещения к промежутку времени, за который это перемещение произошло, при стремлении длительности промежутка времени к нулю. Модуль мгновенной скорости равен первой производной пути по времени.
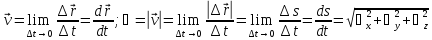
Средняя скорость (средняя путевая скорость) – отношение длины пути, пройденного телом, ко времени, за которое этот путь был пройден.

Средняя путевая скорость, в отличие от мгновенной скорости не является векторной величиной. Средняя скорость равна среднему арифметическому от скоростей тела во время движения только в том случае, когда тело двигалось с этими скоростями одинаковые промежутки времени.
В то же время если, например, половину пути автомобиль двигался со скоростью 180 км/ч, а вторую половину со скоростью 20 км/ч, то средняя скорость будет 36 км/ч. В примерах, подобных этому, средняя скорость равна среднему гармоническому всех скоростей на отдельных, равных между собой, участках пути.
Ускорение – величина, характеризующая быстроту изменения скорости по величине и направлению. Ускорение – векторная величина, состоит из двух составляющих – тангенциальной составляющей и нормальной.
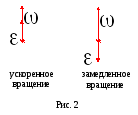
Тангенциальная составляющая характеризует изменение скорости по величине и направлена по направлению вектора скорости (если движение равноускоренное) или противоположно вектору скорости (равнозамедленное движение), равна:
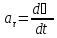
Вторая составляющая ускорения называется нормальной и направлена по нормали к траектории к центру ее кривизны (центростремительное ускорение):
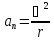
При вращательном движении точки тела описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Вращательное движение тела или точки характеризуется углом поворота, угловой скоростью и угловым ускорением.
Если
точка движется по окружности радиусом
R,
то через 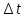
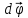 — элементарный угол поворота. Угол
поворота – координата точки при
вращательном движении; векторная
величина, модуль которой равен углу
поворота, а направление этого вектора
связано с направлением вращения (по
правилу правого винта). Сам вектор
находится на оси вращения.
— элементарный угол поворота. Угол
поворота – координата точки при
вращательном движении; векторная
величина, модуль которой равен углу
поворота, а направление этого вектора
связано с направлением вращения (по
правилу правого винта). Сам вектор
находится на оси вращения.Угловая
скорость 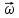 — векторная физическая величина,
показывающая, как изменяется угол
поворота в единицу времени и численно
равная первой производной от угла
поворота по времени. Направлен так же,
как и вектор
— векторная физическая величина,
показывающая, как изменяется угол
поворота в единицу времени и численно
равная первой производной от угла
поворота по времени. Направлен так же,
как и вектор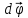
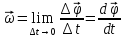
Если
угловая скорость остается постоянной,
то вращение будет равномерное, и оно
характеризуется периодом вращения
(время полного оборота на угол 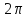 ).
).
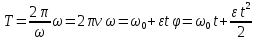
Угловым
ускорением 
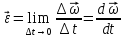
Векторы, направления которых связаны с направлением вращения, называются псевдовекторами.
Связь линейных и угловых величин:
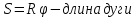
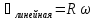
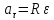
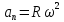
Вопрос3. Масса, свойство массы. Сила. Инерция. Первый закон Ньютона.
Динамика изучает движение тел, вскрывая причины, придающие движению тел тот или иной характер. Основы динамики составляют 3 закона Ньютона, которые представляют собой обобщение большого числа экспериментальных фактов.
Сила — векторная величина, которая является мерой механического воздействия одного тела на другое.
Вектор силы полностью задаётся точкой приложения, направлением, модулем (величиной).
Направление вектора силы совпадает с направлением ускорения сообщаемого телу данным воздействием. Под действием силы тела либо деформируются, либо изменяют скорость.
Инерция – свойство тела сохранять состояние покоя или равномерного прямолинейного движения называется инертностью
Первый закон Ньютона: всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит ее изменить это состояние.
Из этого закона следует:
— Тела обладают свойствами инертности (свойство состоит в стремлении тел сохранить состояние покоя или равномерного прямолинейного движение).
— Система отсчета, в которой материальная точка, свободная от внешних воздействий либо покоится, либо движется равномерно и прямолинейно, называется инерциальной системой отсчета.
Второй закон Ньютона
□
Если
рассматривать действие различных сил
на одно и то же тело, то оказывается,
что ускорение прямо пропорционально
равнодействующей приложенных сил: 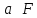 и
и  .
Можем записать, что
.
Можем записать, что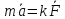 .
Это соотношение выражает второй закон
Ньютона.
■
.
Это соотношение выражает второй закон
Ньютона.
■
Ускорение, приобретаемое материальной точкой (телом), пропорционально вызывающей его силе, совпадает с нею по направлению и обратно пропорционально массе материальной точки (тела). В СИ коэффициент k=1.
Векторная величина, равная произведению массы тела на его скорость и имеющая направление скорости, называется импульсом:
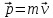
Выражение 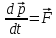 — второй закон Ньютона в общем виде:
скорость изменения импульса материальной
точки равна действующей на неё силе.
— второй закон Ньютона в общем виде:
скорость изменения импульса материальной
точки равна действующей на неё силе.
Принцип независимости сил: если на материальную точку действует одновременно несколько сил, то каждая из этих сил сообщает материальной точке ускорение, как если бы других сил не было вообще.
Взаимодействие между материальными точками (телами) определяется третьим законом Ньютона: всякое действие материальных точек (тел) друг на друга носит характер взаимодействия; силы, с которыми действуют тела друг на друга, всегда равны по модулю и противоположно направлены, действуют вдоль прямой, соединяющей эти точки.

В любой системе тел, силы действуют попарно и являются силами одной природы.
Таким
образом, 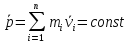 –закон
сохранения импульса:
импульс замкнутой системы сохраняется,
то есть не изменяется с течением времени.
Закон сохранения импульса выполняется
не только в классической физике. Закон
носит универсальный характер и является
фундаментальным законом природы.
–закон
сохранения импульса:
импульс замкнутой системы сохраняется,
то есть не изменяется с течением времени.
Закон сохранения импульса выполняется
не только в классической физике. Закон
носит универсальный характер и является
фундаментальным законом природы.
В классической механике из-за независимости массы от скорости импульс системы может быть выражен через скорость её центра масс. Центром масс системы материальных точек называется воображаемая точка С, положение которой характеризует распределение массы этой системы. Её радиус-вектор равен:

Если
мы найдём производную от радиус-вектора,
то мы найдём скорость, с которой движется
центр масс.  .
.
Центр масс системы движется так, как двигалась бы материальная точка с массой равной сумме масс системы тел под действием результирующей внешних сил. Для замкнутой системы сумма внешних сил равна 0, поэтому центр масс замкнутой системы движется равномерно и прямолинейно.
Вопрос 4. Динамика вращательного движения. Момент силы, момент импульса точки, твердого тела относительно оси вращения. Основной закон динамики вращательного движения. Понятие момента инерции точки, тв.тела относительно оси вращ-я.
Основное уравнение динамики вращательного движения:
Производная по времени от момента количества движения механической системы относительно неподвижной точки или центра инерции системы равна главному моменту относительно той же точки всех внешних сил, приложенных к системе: dL/dt=M.
Пример: Вращение системы вокруг неподвижной оси Oz: LX=LY=0, LZ=JZ, где –угловая скорость, JZ -момент инерции системы относительно оси Oz. Уравнение движения: (d/dt)(JZ)=MZ. Если система является абсолютно твёрдым телом, то JZ (d/dt)=MZ.
Момент импульса материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением:
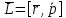
Модуль
вектора момента импульса: 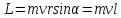
Моментом
импульса материальной точки относительно
неподвижной оси z
называется скалярная величина 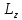 ,
равная проекции на эту ось вектора
момента импульса, определенного
относительно произвольной точки О
данной оси. Момент импульса
,
равная проекции на эту ось вектора
момента импульса, определенного
относительно произвольной точки О
данной оси. Момент импульса 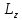 ,
не зависит от положения точки О на осиz.
,
не зависит от положения точки О на осиz.
При
вращении абсолютно твердого тела вокруг
неподвижной оси z
каждая отдельная точки тела движется
по окружности постоянного радиуса 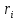 с некоторой скоростью
с некоторой скоростью  .
Скорость
.
Скорость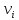 и импульс
и импульс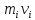 перпендикулярны этому радиусу, то есть
радиус является плечом вектора
перпендикулярны этому радиусу, то есть
радиус является плечом вектора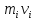 .
Поэтому можем записать, что момент
импульса отдельной частицы равен
.
Поэтому можем записать, что момент
импульса отдельной частицы равен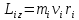 и направлен по оси в сторону, определяемую
правильном правого винта.
и направлен по оси в сторону, определяемую
правильном правого винта.
Момент инерции является мерой инертности при вращательном движении. Момент инерции материальной точки относительно оси – это произведение массы этой точки на квадрат расстояния до оси Z.

Моментом инерции тела относительно оси, проходящей через центр масс, называется сумма произведений масс материальных точек на квадрат расстояния их до оси вращения.

Если масса распределена неправильным образом, то тогда определить момент инерции в этом случае можно переходя к интегрированию.

Момент инерции — это величина аддитивная. Момент инерции системы материальных точек равен сумме моментов инерций этих точек, рассчитанных относительно одной и той же оси.
Момент инерции зависит от формы и размеров тела, от материалов, из которых сделано тело, а также от расположения тела относительно оси.
угловая скорость и угловое ускорение, их связь с линейной скоростью и ускорением
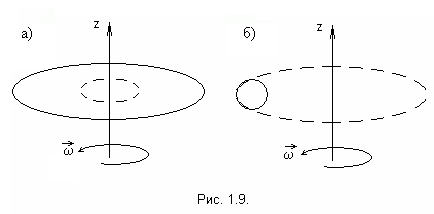 Вращательным
называют такое движение, при котором
все точки тела движутся по окружностям,
центры которых лежат на одной кривой,
называемой осью вращения (рис.1.9).Ось
вращения может находиться как внутри
(рис.1.9.а), так и вне тела (рис.1.9.б).
Вращательным
называют такое движение, при котором
все точки тела движутся по окружностям,
центры которых лежат на одной кривой,
называемой осью вращения (рис.1.9).Ось
вращения может находиться как внутри
(рис.1.9.а), так и вне тела (рис.1.9.б).
Поворот
тела на некоторый угол 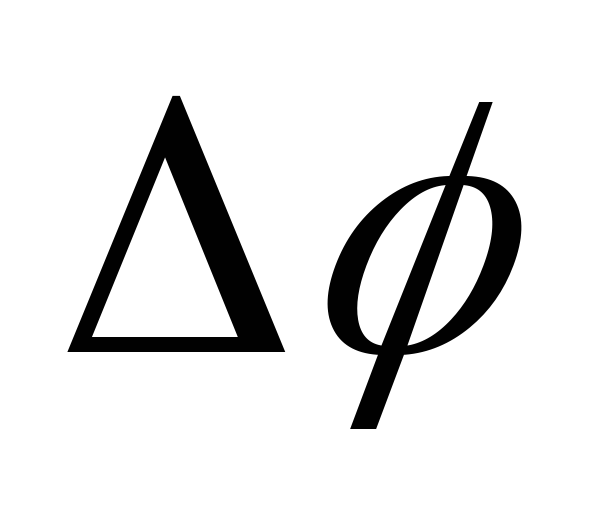 можно задать в виде отрезка, длина
которого
можно задать в виде отрезка, длина
которого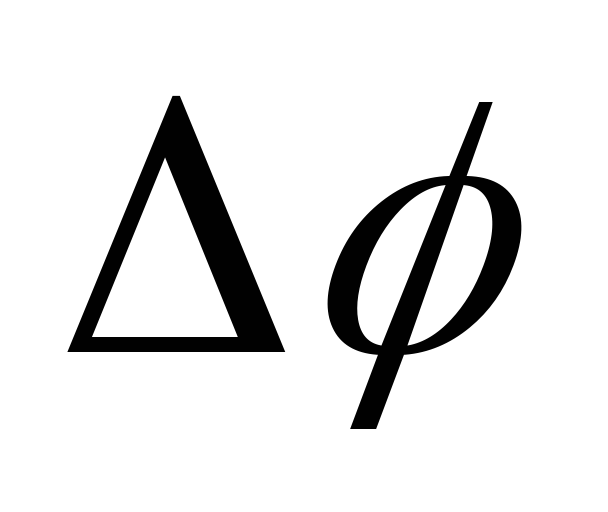 ,
а направление совпадает с осью вращения.
Для того, чтобы указать, в какую сторону
совершается поворот вокруг данной оси,
связывают направление поворота и
изображающего его отрезка правилом
правого винта: направление отрезка
должно быть таким, чтобы, глядя вдоль
него, мы видели поворот совершающимся
по часовой стрелке (рис.1.10). Вектор
поворота
,
а направление совпадает с осью вращения.
Для того, чтобы указать, в какую сторону
совершается поворот вокруг данной оси,
связывают направление поворота и
изображающего его отрезка правилом
правого винта: направление отрезка
должно быть таким, чтобы, глядя вдоль
него, мы видели поворот совершающимся
по часовой стрелке (рис.1.10). Вектор
поворота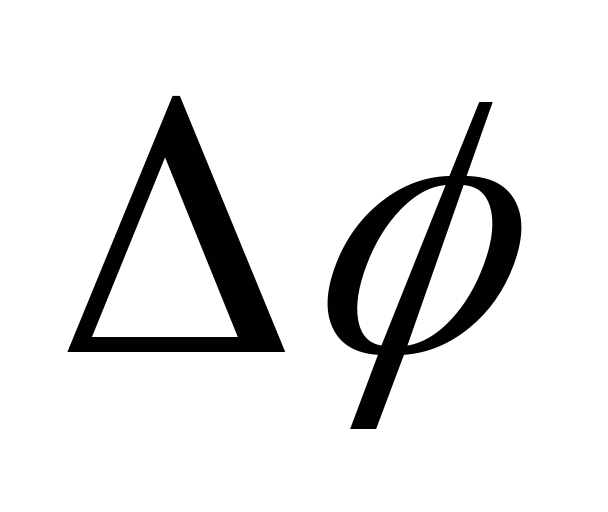 является не истинным вектором, а
псевдовектором.
является не истинным вектором, а
псевдовектором.
 Векторная
величина
Векторная
величина 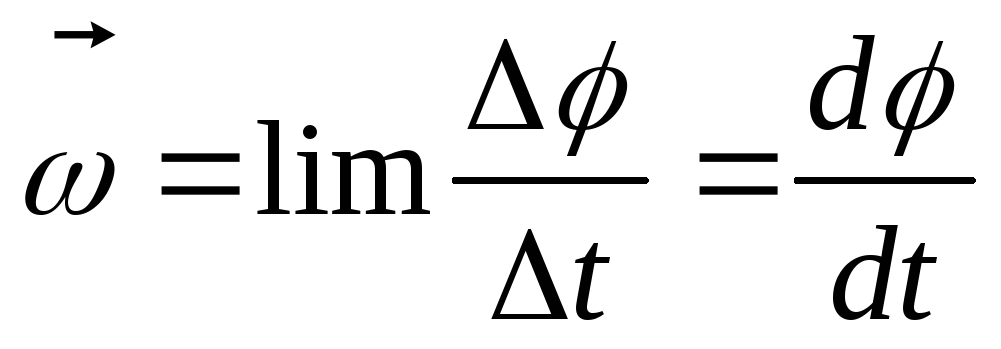 ,
,
где  –время, за которое совершается поворот
–время, за которое совершается поворот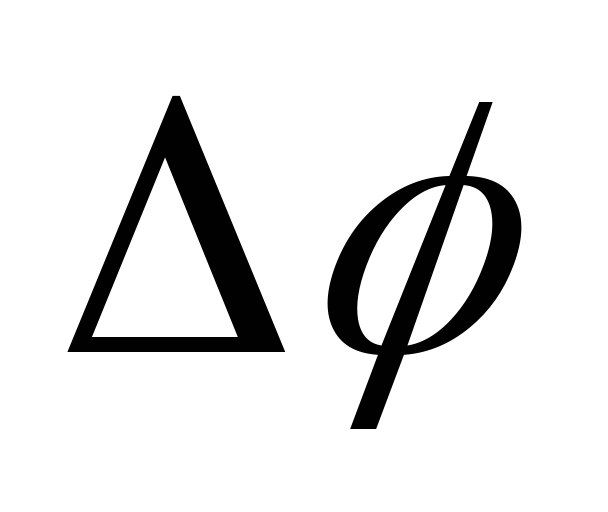 ,
называется угловой скоростью тела. Она
направлена по оси вращения в сторону,
определяемую правилом правого винта,
и представляет собой псевдовектор.
Модуль угловой скорости равен
,
называется угловой скоростью тела. Она
направлена по оси вращения в сторону,
определяемую правилом правого винта,
и представляет собой псевдовектор.
Модуль угловой скорости равен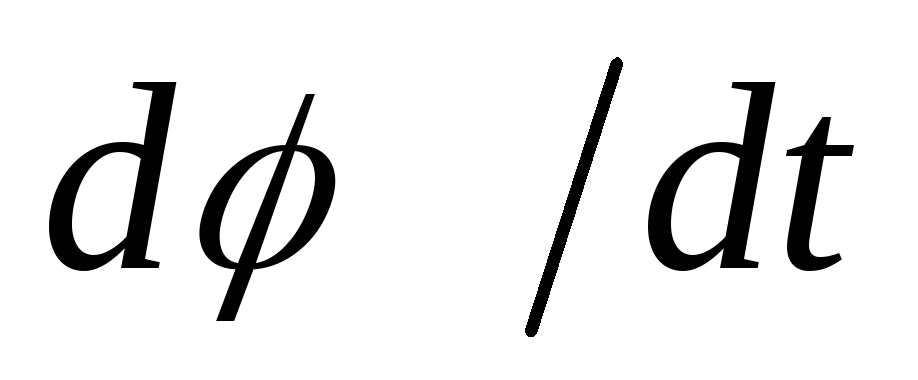 .
.
Вращение
с постоянной угловой скоростью называют
равномерным. Такое движение характеризуют
периодом  ,
под которым понимают время полного
оборота. При этом
,
под которым понимают время полного
оборота. При этом ,
тогда
,
тогда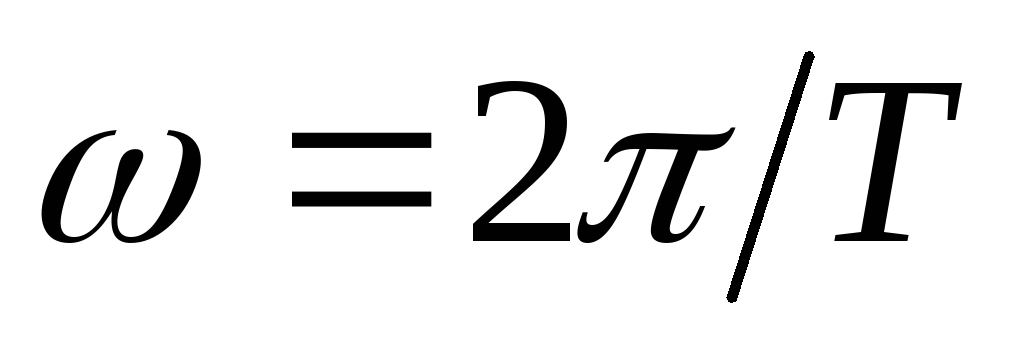 ,
и
,
и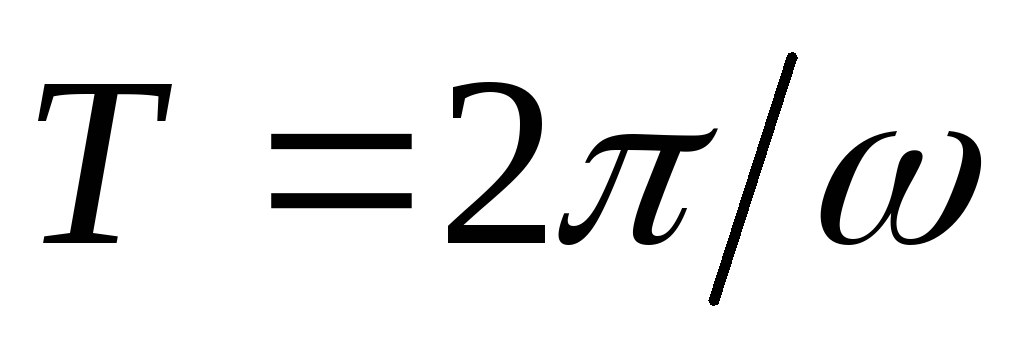 .
Число оборотов в единицу времени
( частота обращения) равно
.
Число оборотов в единицу времени
( частота обращения) равно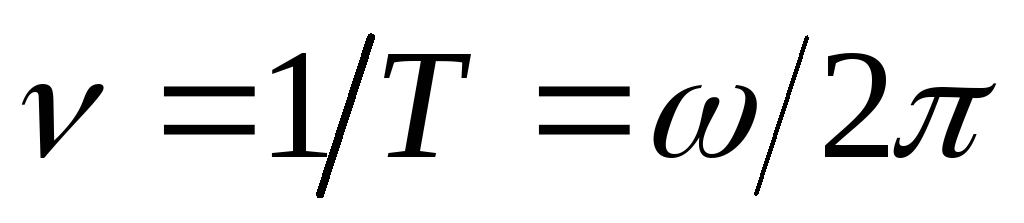 .
.
П одставив
одставив ,
получаем:
,
получаем: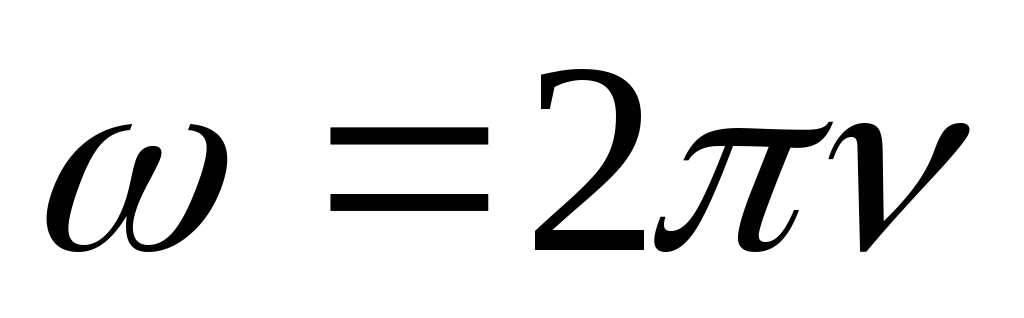 .
.
Вектор  может изменяться как при изменении
скорости вращения тела вокруг оси ( по
величине), так и при повороте оси вращения
в пространстве ( в этом случае
может изменяться как при изменении
скорости вращения тела вокруг оси ( по
величине), так и при повороте оси вращения
в пространстве ( в этом случае меняется по направлению). Изменение
вектора угловой скорости со временем
характеризуется угловым ускорением
меняется по направлению). Изменение
вектора угловой скорости со временем
характеризуется угловым ускорением .
Угловое ускорение, также как и угловая
скорость, является псевдовектором.
.
Угловое ускорение, также как и угловая
скорость, является псевдовектором.
Отдельные
точки вращающегося тела имеют различные
линейные скорости  .
Скорость каждой из точек непрерывно
изменяет свое направление. Величина
скорости
.
Скорость каждой из точек непрерывно
изменяет свое направление. Величина
скорости определяется угловой скоростью вращения
тела
определяется угловой скоростью вращения
тела и расстоянием
и расстоянием рассматриваемой
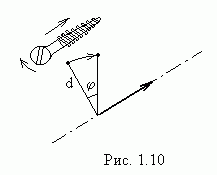
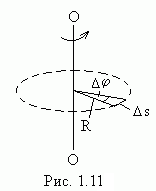
точки от оси вращения. Пусть за малый
промежуток времени тело повернулось
на угол
рассматриваемой
точки от оси вращения. Пусть за малый
промежуток времени тело повернулось
на угол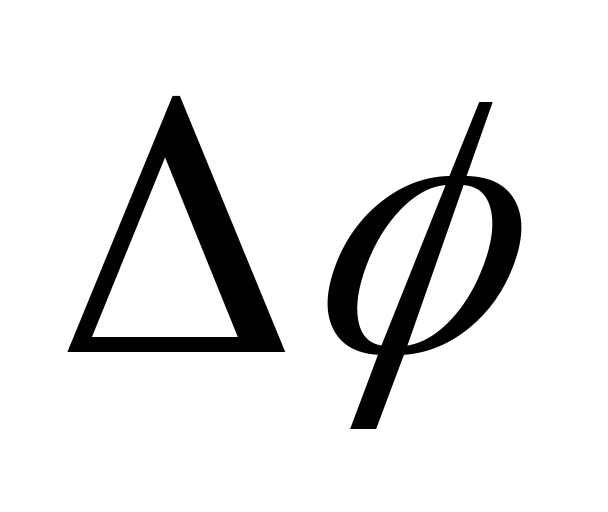 (рис.1.11). Точка, находящаяся на расстоянии
(рис.1.11). Точка, находящаяся на расстоянии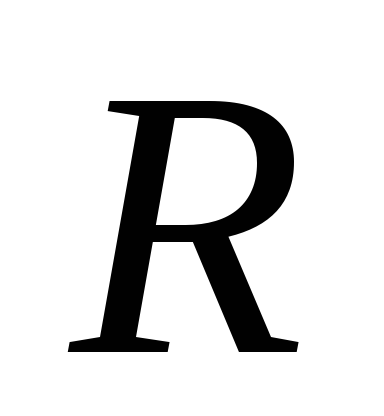 от оси, проходит при этом путь
от оси, проходит при этом путь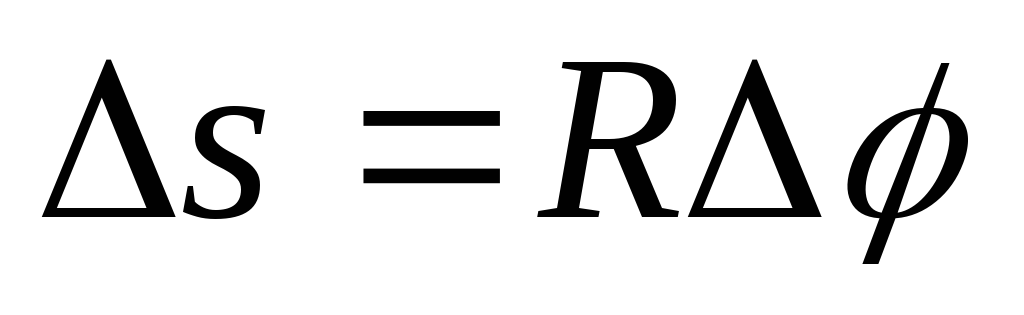 .
Линейная скорость точки равна
.
Линейная скорость точки равна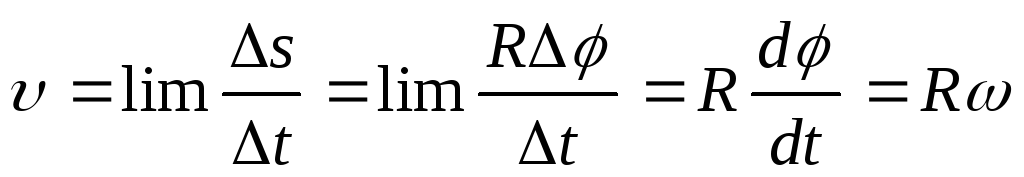 .
(1.9)
.
(1.9)
Эта
формула связывает модули линейной и
угловой скоростей. Найдем выражение,
связывающее векторы  и
и .
Положение рассматриваемой точки тела
будем определять радиус-вектором
.
Положение рассматриваемой точки тела
будем определять радиус-вектором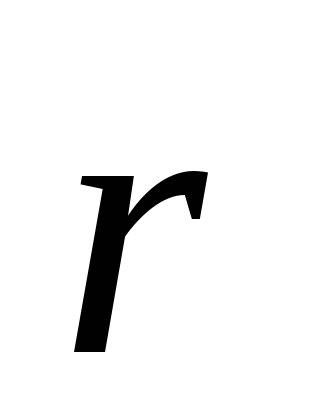 ,
проведенным из лежащего на оси вращения
начала координатО ( рис.1.12). Из рисунка видно, что векторное
произведение
,
проведенным из лежащего на оси вращения
начала координатО ( рис.1.12). Из рисунка видно, что векторное
произведение  совпадает по направлению с вектором
совпадает по направлению с вектором и имеет модуль, равный
и имеет модуль, равный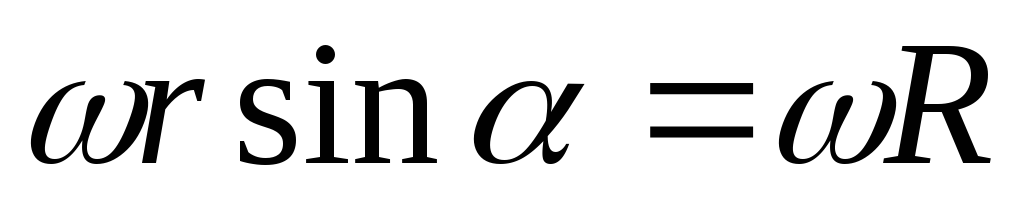 .
Следовательно,
.
Следовательно,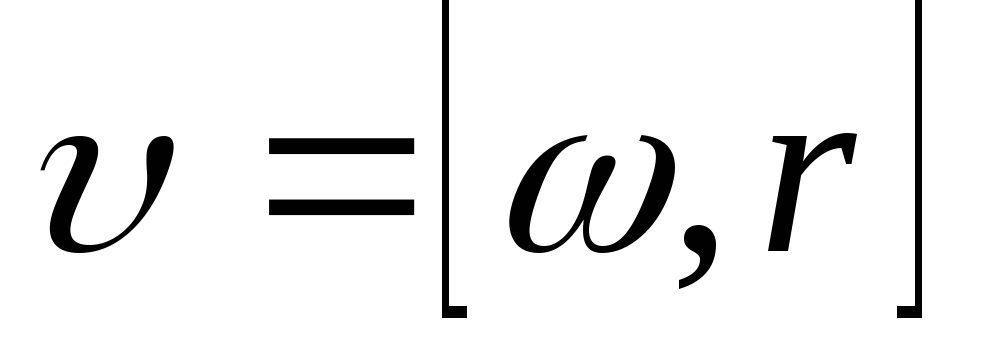 .
.
Нормальное
ускорение точек вращающегося тела равно  .
.
Если
ввести перпендикулярный к оси вращения
вектор  ,
проведенный в данную точку тела
(рис.1.12), это выражение можно записать
в векторной форме
,
проведенный в данную точку тела
(рис.1.12), это выражение можно записать
в векторной форме 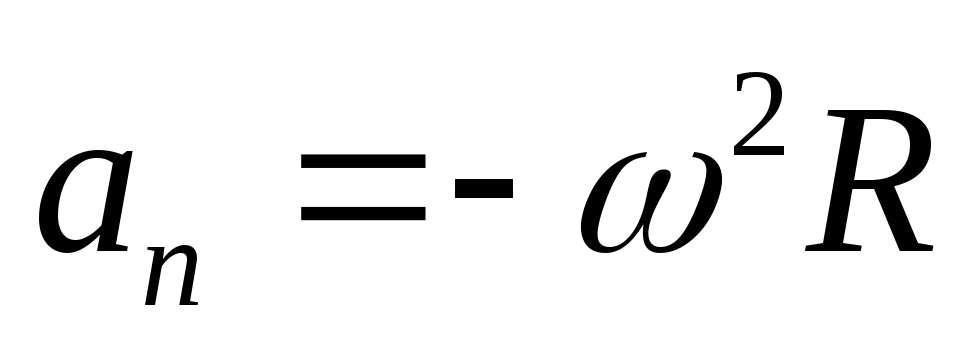 .
Знак минус поставлен, так как векторы
.
Знак минус поставлен, так как векторы 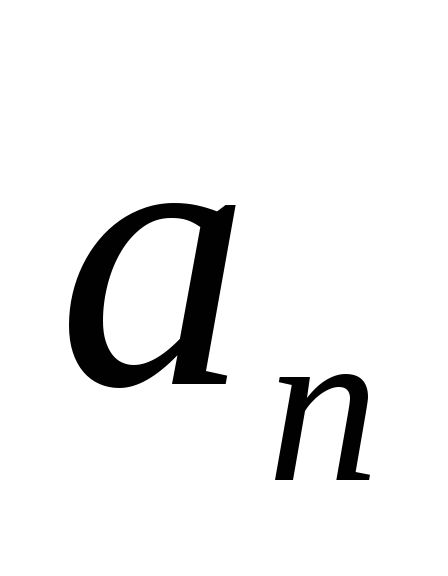 и
и  направлены противоположно.
направлены противоположно.
Будем
считать, что ось вращения не поворачивается
в пространстве. В этом случае расстояние
рассматриваемой точки до оси вращения
не меняется, 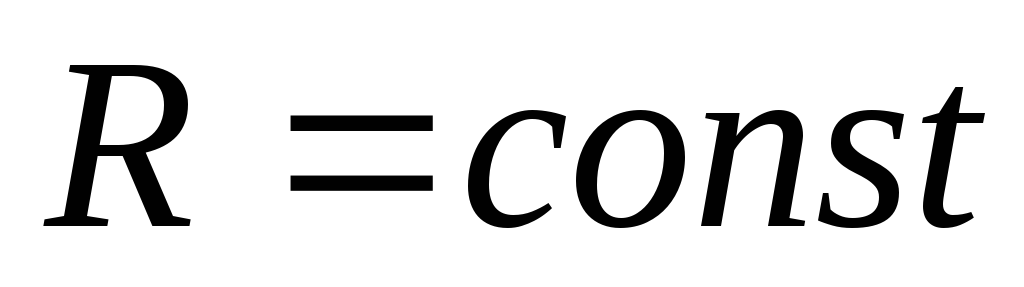 ,
и, взяв производную от выражения (1.9),
получаем
,
и, взяв производную от выражения (1.9),
получаем
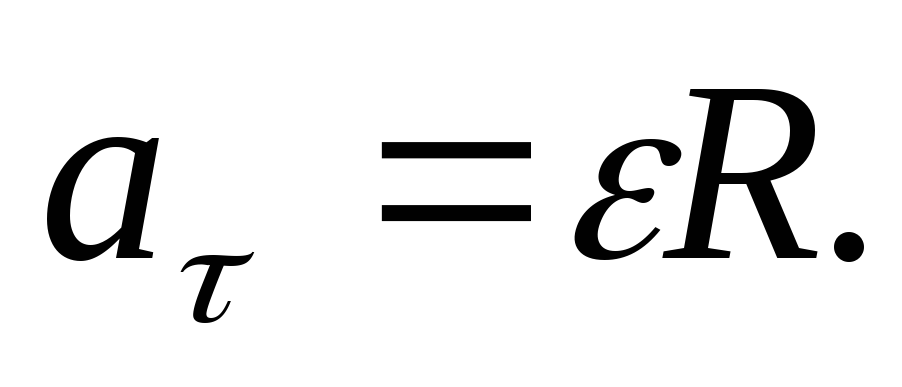 Таким образом,
нормальное и тангенциальное ускорения
растут линейно с увеличением расстояния
точки от оси вращения.
Таким образом,
нормальное и тангенциальное ускорения
растут линейно с увеличением расстояния
точки от оси вращения.
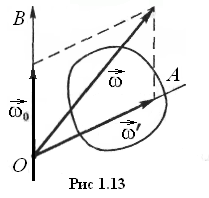 В
случае сложного вращения, когда тело
движется одновременно относительно
нескольких осей, необходимо производить
сложения угловых скоростей. Рассмотрим
движение твердого тела, вращающегося
одновременно вокруг двух пересекающихся
осей. Сообщим некоторому телу вращение
с угловой скоростью
В
случае сложного вращения, когда тело
движется одновременно относительно
нескольких осей, необходимо производить
сложения угловых скоростей. Рассмотрим
движение твердого тела, вращающегося
одновременно вокруг двух пересекающихся
осей. Сообщим некоторому телу вращение
с угловой скоростью 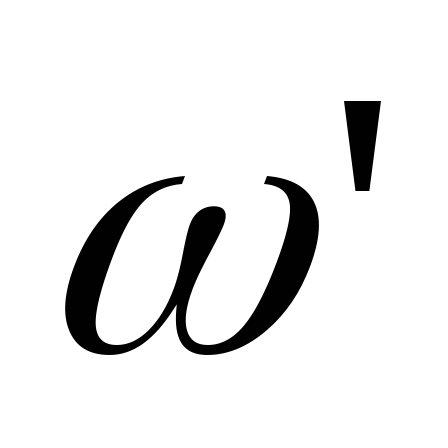 вокруг осиОА (рис.
1.13) и затем эту ось приведем во вращение
с угловой скоростью
вокруг осиОА (рис.
1.13) и затем эту ось приведем во вращение
с угловой скоростью  вокруг осиOB,
неподвижной
в К-системе
отсчета. Найдем результирующее
движение тела в К-системе.
вокруг осиOB,
неподвижной
в К-системе
отсчета. Найдем результирующее
движение тела в К-системе.
Введем
вспомогательную K‘-систему
отсчета, жестко связанную
с осями ОА и ОВ. Ясно,
что эта система вращается с угловой
скоростью  ,
и тело вращается относительно нее с
угловой скоростью
,
и тело вращается относительно нее с
угловой скоростью .
.
За
промежуток времени  тело совершит поворот
тело совершит поворот вокругоси АО в K‘—
системе и одновременно поворот
вокругоси АО в K‘—
системе и одновременно поворот 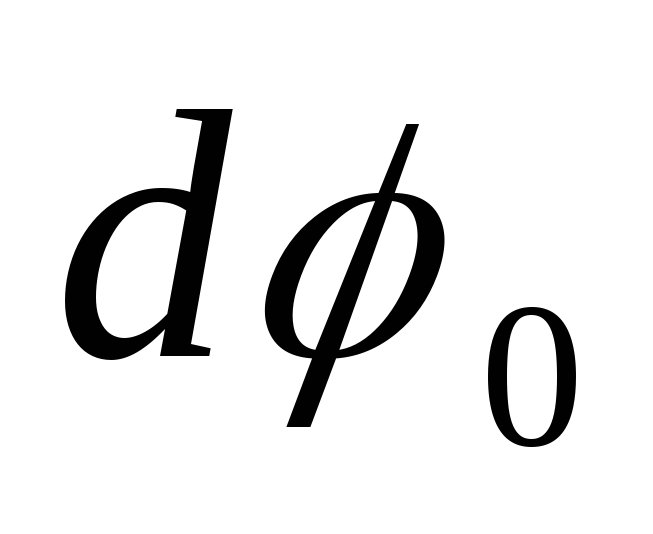 вокруг оси ОВ вместе
с K‘-
системой. Суммарный поворот есть
вокруг оси ОВ вместе
с K‘-
системой. Суммарный поворот есть 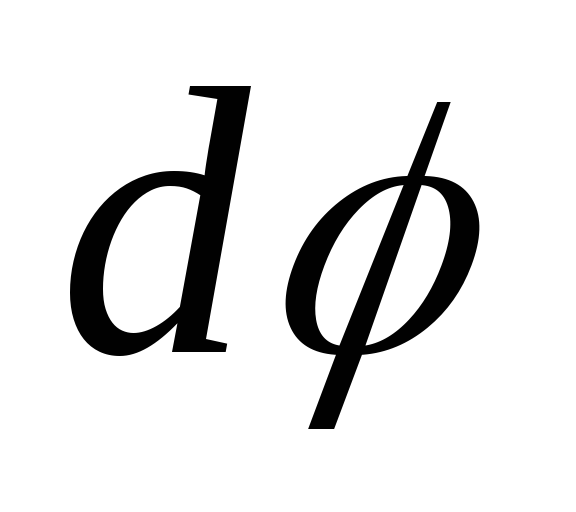 =
= 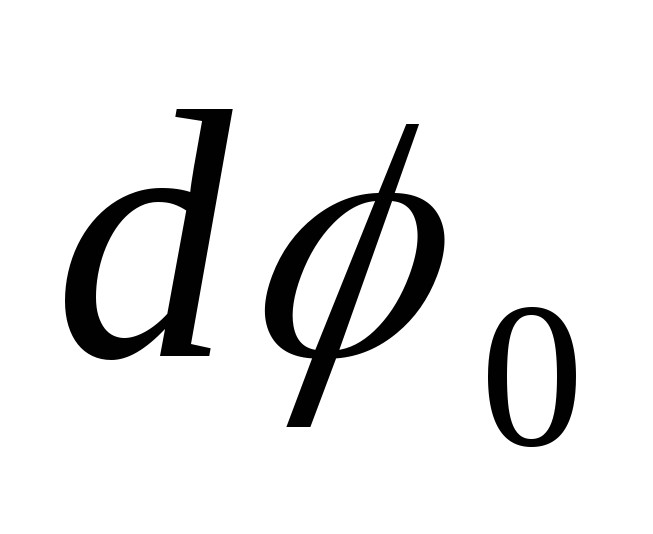 +
+ 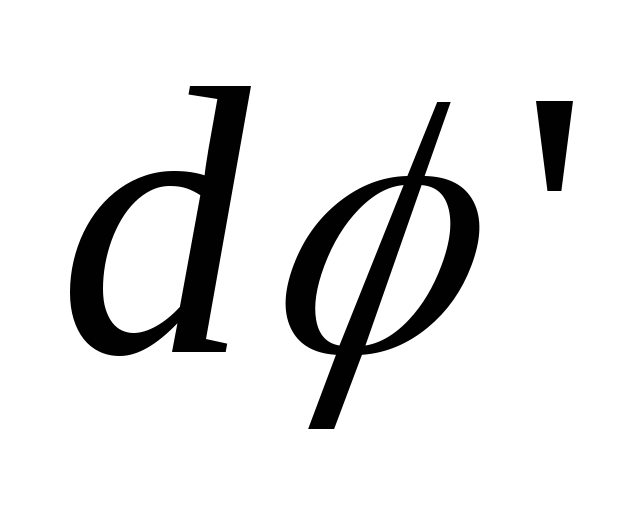 .
Разделив обе части этого равенства на
.
Разделив обе части этого равенства на 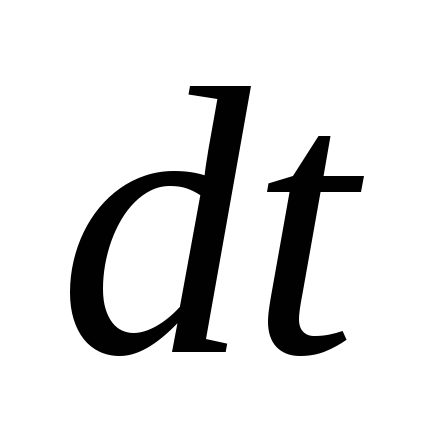 получим
получим
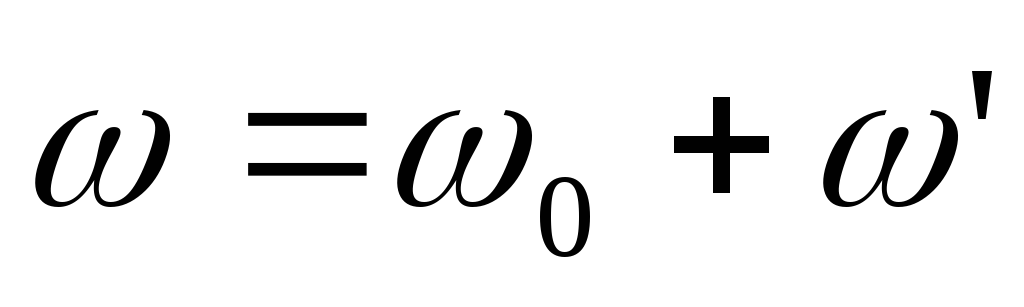 .
.
Таким
образом, результирующее движение
твердого тела в K—
системе представляет собой чистое
вращение с угловой скоростью  вокруг оси, совпадающей в каждый момент
с вектором
вокруг оси, совпадающей в каждый момент
с вектором 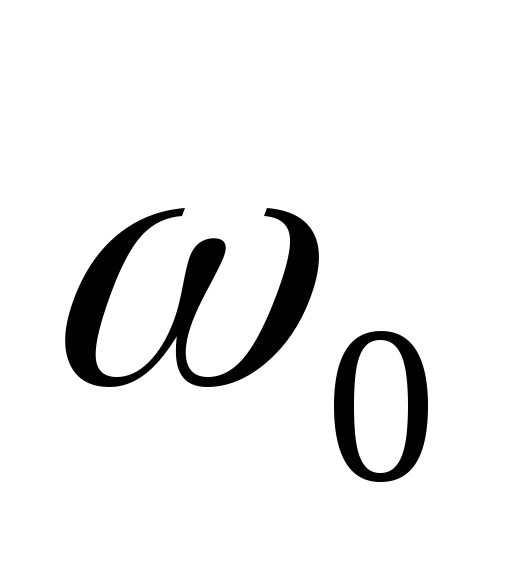 и проходящей через точкуO (рис. 1.13). Эта ось перемещается
относительно K—
системы — она поворачивается с угловой
скоростью
и проходящей через точкуO (рис. 1.13). Эта ось перемещается
относительно K—
системы — она поворачивается с угловой
скоростью  вместе с осью ОА вокруг
оси ОВ.
вместе с осью ОА вокруг
оси ОВ.
Нетрудно
сообразить, что даже в том случае, когда
угловые скорости 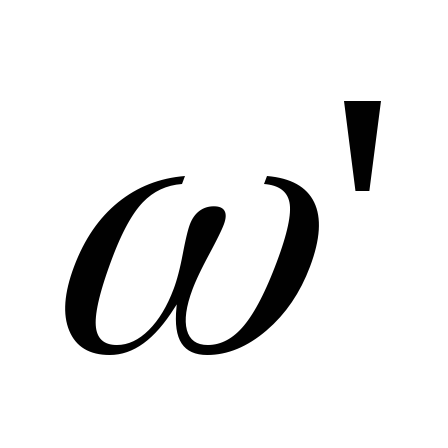 и
и 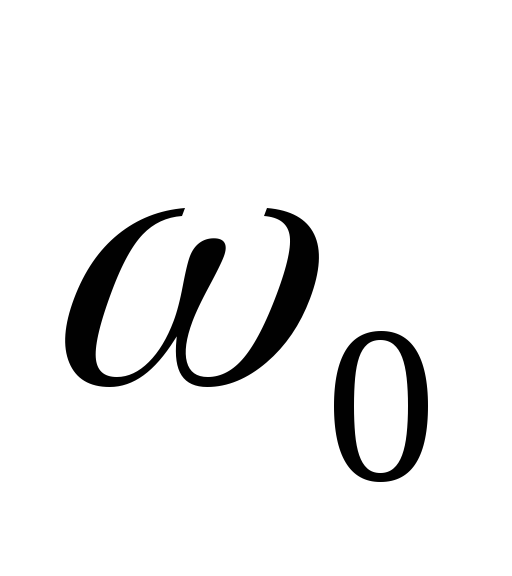 не
меняются по модулю, тело будет обладать
в K—
системе угловым ускорением
не
меняются по модулю, тело будет обладать
в K—
системе угловым ускорением 
 ,
направленным, согласно
,
направленным, согласно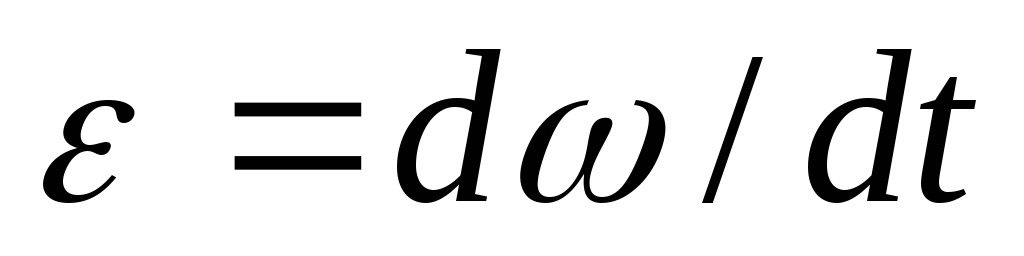 ,
за плоскость (рис. 1.13).
,
за плоскость (рис. 1.13).
И
последнее замечание. Поскольку вектор
угловой скорости  удовлетворяет основному свойству
векторов — векторному сложению,
удовлетворяет основному свойству
векторов — векторному сложению,  можно представить как векторную сумму
составляющих
на определенные направления, т. е.
можно представить как векторную сумму
составляющих
на определенные направления, т. е.  =
=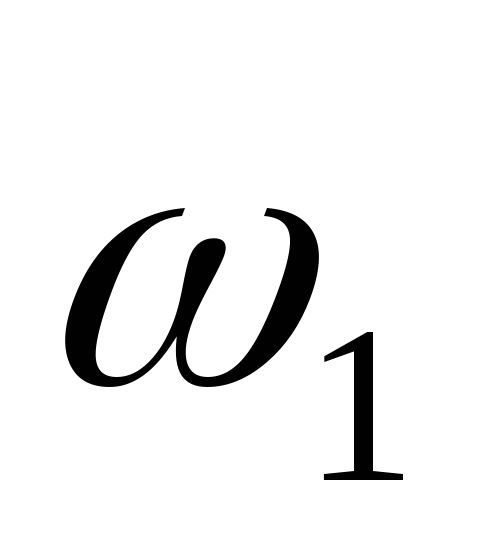 +
+ +…,
где
все векторы относятся к одной и той же
системе отсчета. Этим
удобным и полезным приемом часто
пользуются при анализе
сложного движения твердого тела.
+…,
где
все векторы относятся к одной и той же
системе отсчета. Этим
удобным и полезным приемом часто
пользуются при анализе
сложного движения твердого тела.
Движение точки по окружности. Угловые перемещение, скорость, ускорение. Связь между линейными и угловыми характеристиками.
Вращательным называется такое движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения.
Кинематические характеристики вращательного движения:
Угол поворота, угловая скорость, угловое ускорение.
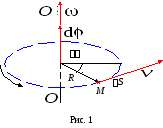
 ,
рад
вектор, численно равный
угловому пути, и направлен по оси вращения
так, что из его конца вращение видно
против часовой стрелки.
,
рад
вектор, численно равный
угловому пути, и направлен по оси вращения
так, что из его конца вращение видно
против часовой стрелки. Угловая
скорость  ,вектор,
характеризующий быстроту изменения
угла поворота,
и направлен по оси вращения так, что из
его конца вращение видно против часовой
стрелки.
,вектор,
характеризующий быстроту изменения
угла поворота,
и направлен по оси вращения так, что из
его конца вращение видно против часовой
стрелки.
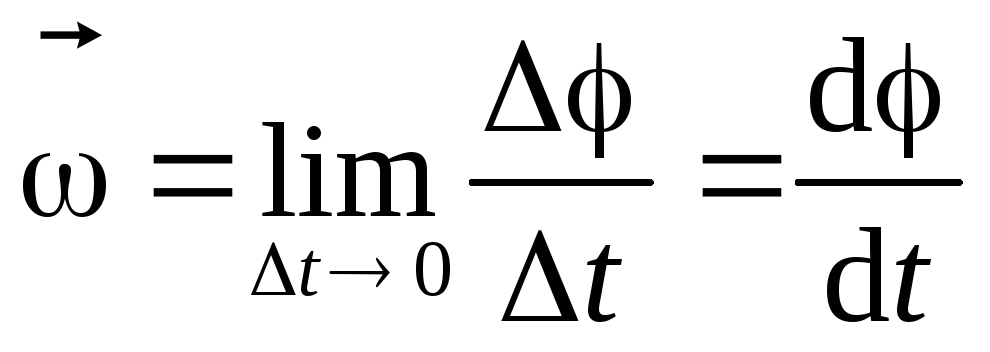 рад/c,
c-1 .(1)
рад/c,
c-1 .(1)
Характеристики равномерного вращения ( = const)
1. Период вращения Т это время, за которое тело совершает один полный оборот
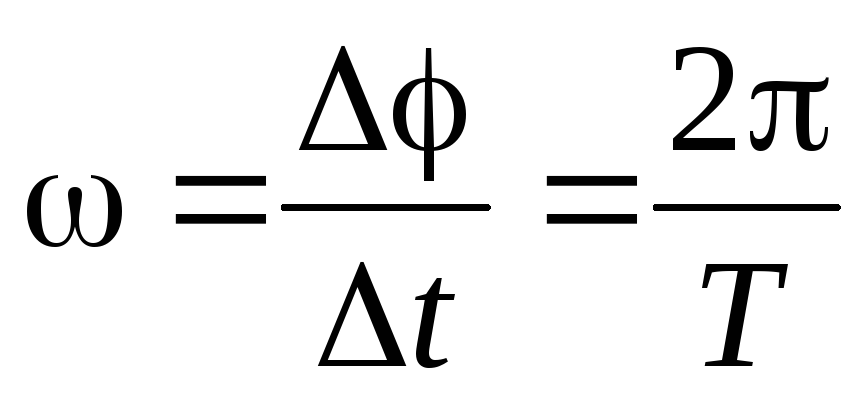

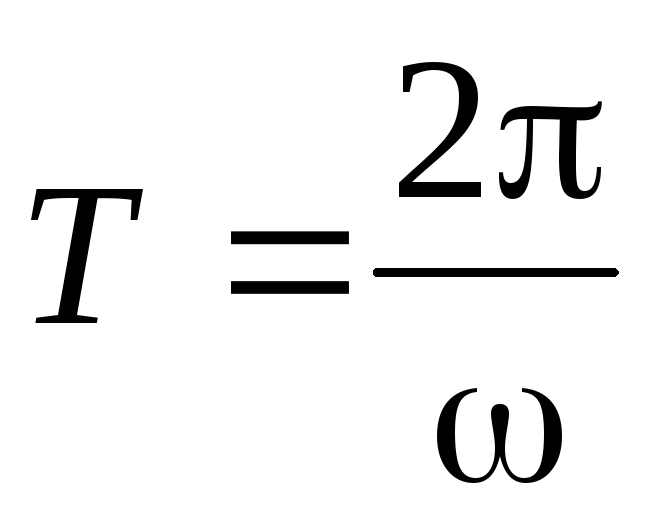 , с.(2)
, с.(2)
Частота вращения n это число полных оборотов, совершаемых телом за единицу времени
 , с1
Гц
, с1
Гц 
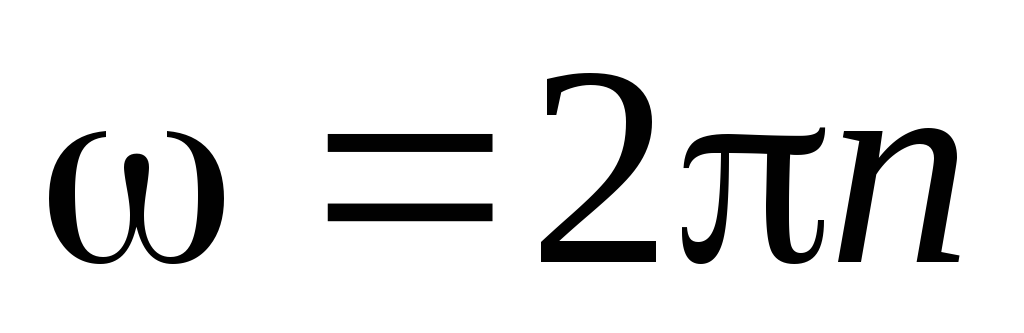 .
(3)
.
(3)
Угловое
ускорение  вектор,
характеризующий быстроту изменения
угловой скорости
вектор,
характеризующий быстроту изменения
угловой скорости
 , рад/c,
с1 (4)
, рад/c,
с1 (4)
Связь между линейными и угловыми характеристиками
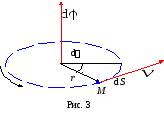
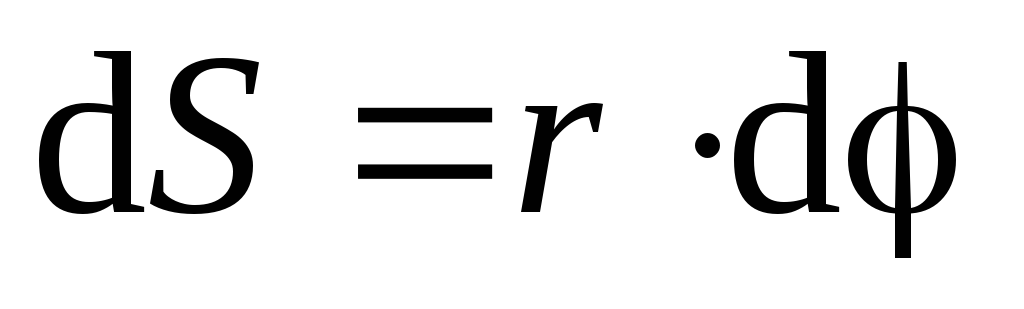 ;
;
;
; 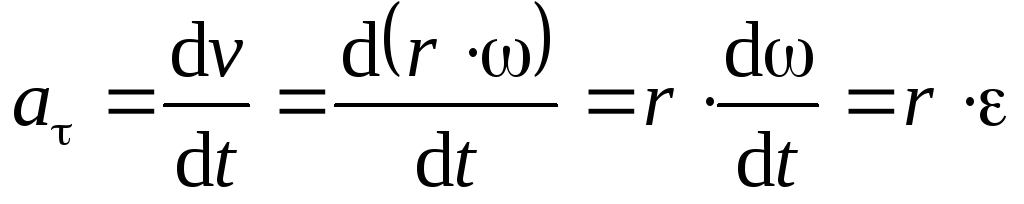 ;
;
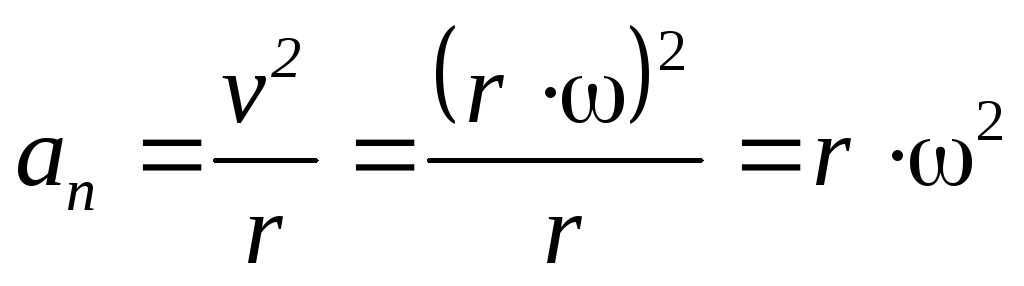 ;
;
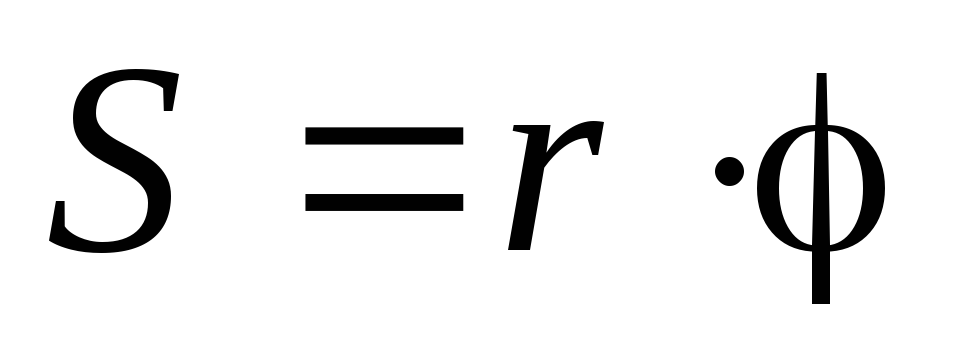 ;
; 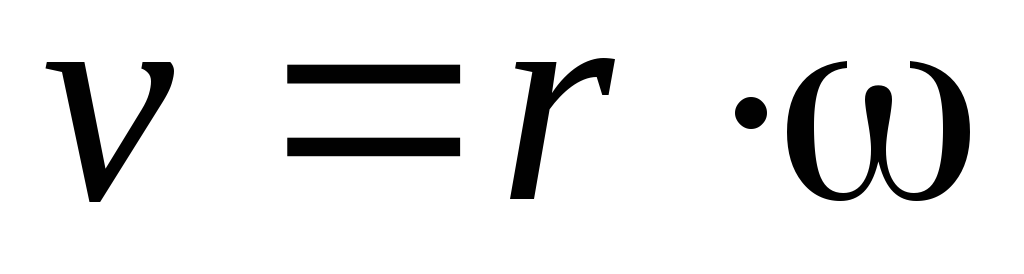 ;
; 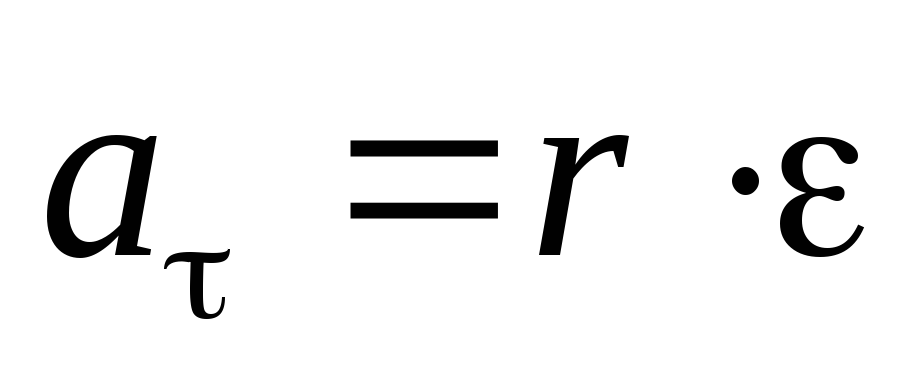 ;
; 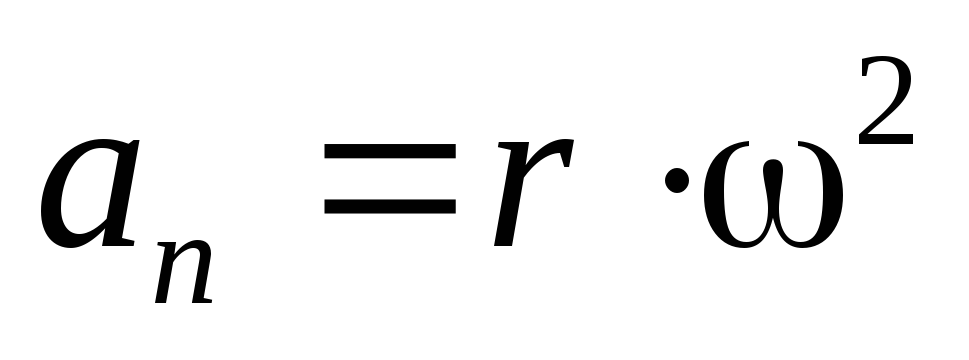
Динамика материальной точки. Инерциальные системы отсчета и первый закон Ньютона
Тело, не подверженное внешним воздействиям (в действительности можно говорить лишь о компенсации этих воздействий), называется свободным, а его движение –свободным движениемилидвижением по инерции.
Инерция – это способность тел сохранять состояние покоя или равномерного прямолинейного движения.
Первый закон Ньютона выполняется не во всякой системе отсчета, так как характер движения зависит от выбора системы отсчета.
Инерциальной называется любая система отсчета, которая находится в покое или движется равномерно и прямолинейно относительно гелиоцентрической системы (центр ее совпадает с Солнцем).
Первый закон Ньютона (закон инерции)
Всякое тело сохраняет состяние покоя или равномерного прямолинейного движения до тех пор, пока внешнее воздействие не заставит его изменить это состояние.
Фундаментальные взаимодействия. Силы различной природы (упругие, гравитационные, трения), второй закон Ньютона. Масса. Третий закон Ньютона.
В современной физике выделяют четыре вида фундаментальных, т.е. базовых, не сводящихся к каким-либо другим, взаимодействий:
сильное ядерное, обеспечивающее связь частиц в атомном ядре – самоеинтенсивное, нокороткодействующее: оно сказывается лишь на масштабах атомного ядра (порядка 10-15м).
слабое ядерное, ответственное за ряд процессов распада элементарных частиц – малоинтенсивное (порядка 10-13 от сильного ядерного) и также короткодействующее;
электромагнитное, обеспечивающее стабильность атомов и молекул. Электромагнитное взаимодействие является весьмаинтенсивным(порядка 10-2 от сильного ядерного) и одновременно –дальнодействующим. Оно могло бы доминировать при галактических масштабах, но редко проявляет себя явным образом в макромире, поскольку встречающиеся в нем объекты, как правило, электрически нейтральны (имеют нулевой суммарный заряд).
гравитационное, проявляющееся, например, как взаимодействие небесных тел и определяющее структуру Вселенной. Оно малоинтенсивное (порядка 10-38 от сильного ядерного), но дальнодействующее. Как и электромагнитное, гравитационное взаимодействие убывает обратно пропорционально квадрату расстояния между взаимодействующими телами.
Угловая скорость. Связь векторов линейной и угловой скоростей.
Стр 1 из 3Следующая ⇒Угловая скорость. Связь векторов линейной и угловой скоростей.
Угловая скорость — векторная физическая величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени:
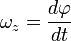
Легко найти связь между линейной скоростью точки v, ее угловой скоростью ω и радиусом r окружности, по которой она движется.
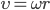
т. е. линейная скорость при движении по окружности равна угловой скорости, умноженной на радиус окружности.
При вращательном движении действуют: тангенциальное и центростремительное ускорения.
В любой точке вращательного движения шара вектор его линейной скорости направлен перпендикулярно радиусу. Нетрудно догадаться, что при таком вращении по окружности, вектор линейной скорости шара постоянно меняет свое направление. Ускорение, характеризующее такое изменение скорости, называется центробежным (центростремительным) ускорением.
Центробежное ускорение можно вычислить по формуле:
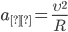
Угловое ускорение. Связь линейных и угловых величин.
Угловое ускорение — физическая величина, характеризующая быстроту изменения угловой скорости твёрдого тела.

Существует связь между тангенциальным и угловым ускорениями:
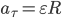
где R — радиус кривизны траектории точки в данный момент времени
Тангенциальное ускорение направлено по касательной в траектории движения тела, а нормальное — перпендикулярно ему.
13. Сформулируйте первый закон Ньютона.
Существуют такие системы отсчёта, относительно которых материальная точка, при отсутствии внешних воздействий, сохраняет состояние покоя или равномерного прямолинейного движения.
Что такое замкнутая механическая система.
Замкнутая механическая система, потенциальная энергия которой имеет минимальное значение и в которой отсутствуют движения тел, находится в состоянии равновесия. Примером может служить тяжелый шар, неподвижно; лежащий на дне ямы: его потенциальная энергия Ер имеет минимальное значение, и он находится в равновесии; без воздействия извне шар не может выкатиться из ямы.
20. Радиус-вектор, скорость, импульс, закон движения центра масс.
Радиус-вектор точки — это вектор, начало которого совпадает с началом системы координат, а конец — с данной точкой.
Таким образом, особенностью радиус-вектора, отличающего его от всех других векторов, является то, что его начало всегда находится в точке начала координат.
Скорость — физическая величина, характеризующая движение тела в пространстве. Физический смысл — Изменение координаты в единицу времени.
Импульс тела — это векторная величина, равная произведению массы тела на его скорость: . Специальных единиц измерения импульса нет. Размерность импульса — это просто произ- ведение размерности массы на размерность скорости: [p] = [m] · [v] = кг · м /с .
Воспользовавшись законом изменения импульса, получим закон движения центра масс:
dP/dt = M∙dVc/dt = ΣFi
Центр масс системы движется так же, как двигалась бы частица с массой, равной массе системы, под действием силы, равной векторной сумме всех внешних сил, действующих на входящие в систему частицы.
Энергия и работа. В чём разница?
Термин «работа» в механике имеет два смысла: работа как процесс, при котором сила перемещает тело, действуя под углом, отличном от 90°; работа — физическая величина, равная произведению силы, перемещения и косинуса угла между направлением действия силы и перемещением:
А = Fs cos a.
Работа равна нулю, когда тело движется по инерции (F = 0), когда нет перемещения (s = 0) или когда угол между перемещением и силой равен 90° (cos а = 0). Единицей работы в СИ служит джоуль (Дж).
1 джоуль — это такая работа, которая совершается силой 1 Н при перемещении тела на 1 м по линии действия силы. Для определения быстроты совершения работы вводят величину «мощность».
Мощность равняется отношению совершенной работы ко времени, за которое она выполнена:

Единицей мощности в СИ служит 1 ватт (Вт). 1 Вт — мощность, при которой совершается работа в 1 Дж за 1 секунду.
Сформулируйте закон Гука.
Закон Гука — утверждение, согласно которому деформация, возникающая в упругом теле (пружине, стержне, консоли, балке и т. п.), пропорциональна приложенной к этому телу силе. Открыт в 1660 году английским учёным Робертом Гуком.
Закон Гука выполняется только при малых деформациях. При превышении предела пропорциональности связь между напряжениями и деформациями становится нелинейной. Для многих сред закон Гука неприменим даже при малых деформациях.
Угловая скорость. Связь векторов линейной и угловой скоростей.
Угловая скорость — векторная физическая величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени:
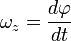
Легко найти связь между линейной скоростью точки v, ее угловой скоростью ω и радиусом r окружности, по которой она движется.
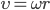
т. е. линейная скорость при движении по окружности равна угловой скорости, умноженной на радиус окружности.
При вращательном движении действуют: тангенциальное и центростремительное ускорения.
В любой точке вращательного движения шара вектор его линейной скорости направлен перпендикулярно радиусу. Нетрудно догадаться, что при таком вращении по окружности, вектор линейной скорости шара постоянно меняет свое направление. Ускорение, характеризующее такое изменение скорости, называется центробежным (центростремительным) ускорением.
Центробежное ускорение можно вычислить по формуле:
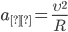
Кинематика вращательного движения
| При
вращении твердого тела вокруг
неподвижной оси OO’ точка M этого тела с радиус-вектором |
Для указания
направления вращения малым углам
поворота приписывают направление:  направлен по оси вращения так, чтобы
рассматриваемое с его конца вращение
происходило против часовой стрелки
(правило правого винта). Если тело сделалоN поворотов:
направлен по оси вращения так, чтобы
рассматриваемое с его конца вращение
происходило против часовой стрелки
(правило правого винта). Если тело сделалоN поворотов: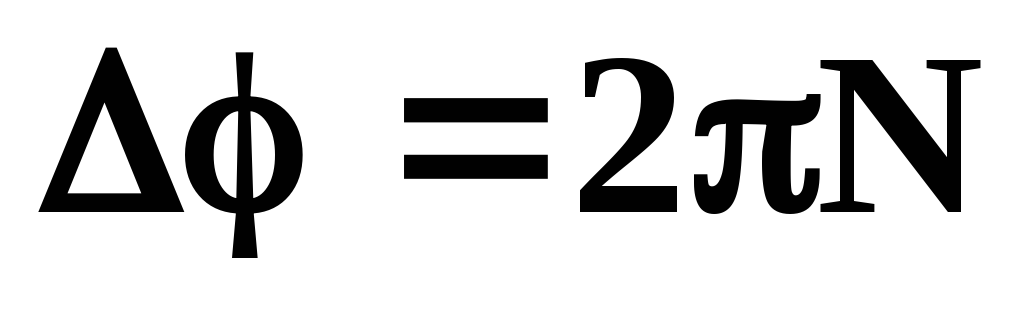 .
Средняя угловая скорость:
.
Средняя угловая скорость:
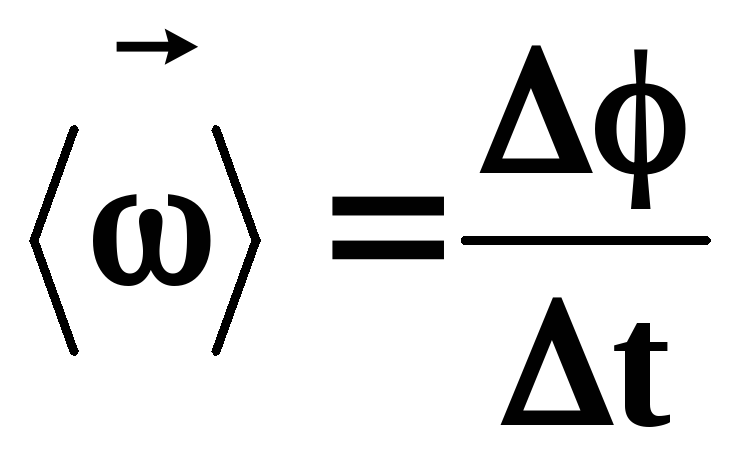 (11)
(11)
Мгновенная угловая скорость:
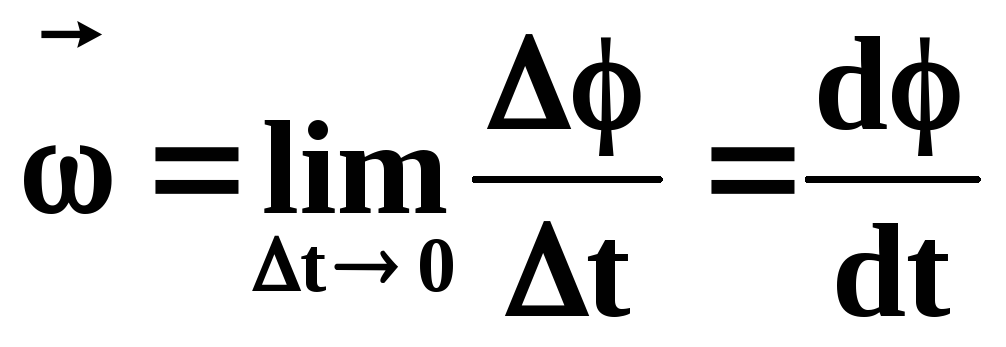 (12)
(12)
| Направление Если тело делает оборотов в сек, то его угловая скорость Связь линейной и угловой скоростей: |
или
 (13)
(13)
в векторной форме:
 (14)
(14)
Угловое ускорение вращающегося тела
Отношение  называетсясредним
угловым ускорением.
называетсясредним
угловым ускорением.
Связь углового и линейного ускорений
Продифференцируем (14) по времени:
 (16)
(16)
Первое слагаемое
– тангенциальное ускорение  ,
т.к. вектор
,
т.к. вектор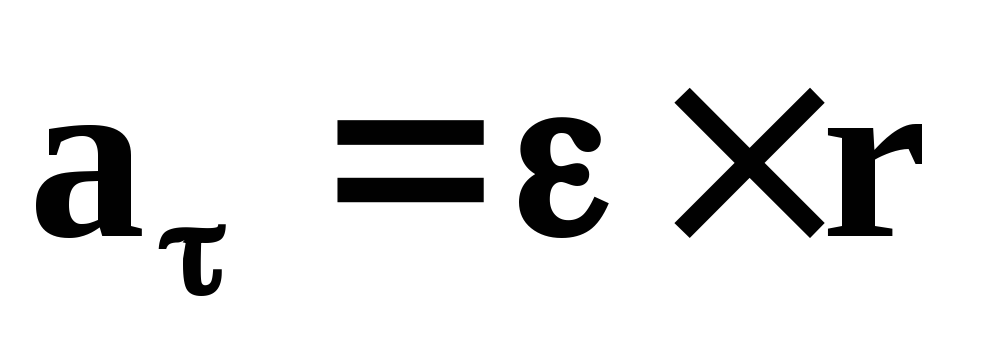 по правилу векторного произведения
направлен по касательной к траектории
и по модулю равен:
по правилу векторного произведения
направлен по касательной к траектории
и по модулю равен:
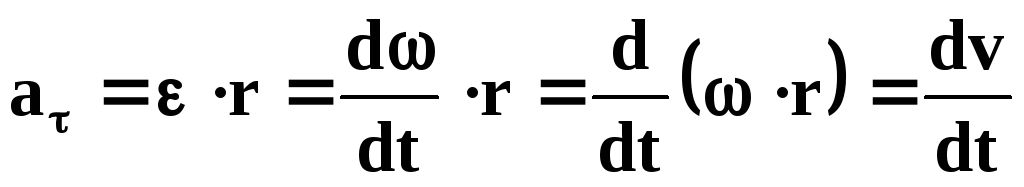
Основные уравнения кинематики
Поступательное движение | Вращательное движение |
Равномерное | |
|
|
|
|
|
|
| |
Равнопеременное | |
|
|
|
|
|
|
| |
Неравномерное | |
|
|
|
|
|
|
Связь линейных и угловых параметров | |
|
|
|
|
| |
Динамика частиц
Динамика рассматривает механическое движение с учетом причин, вызывающих это движение или изменение этого движения.
Основная задача динамики: для физической системы, находящейся в определенных внешних условиях, найти уравнение движения.
Уравнениями движения называются уравнения, описывающие изменение состояния системы во времени.
В классической
механике состояние частиц полностью
определяется заданием ее координат x, y, z и составляющих скорости vx, vy, vz,
т.е. заданием радиус-вектора  и скорости
и скорости .
.
Состояние системы
из N
нерелятивистских частиц определяется
заданием радиус-векторов 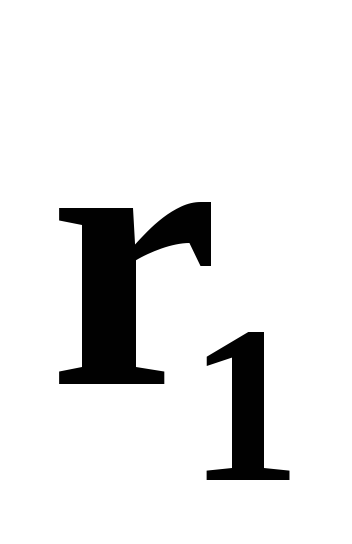 ,
,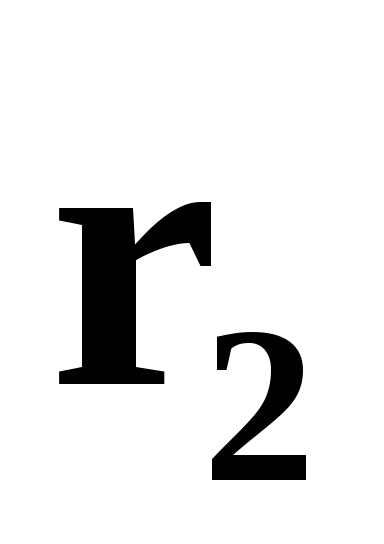 ,
…,
,
…,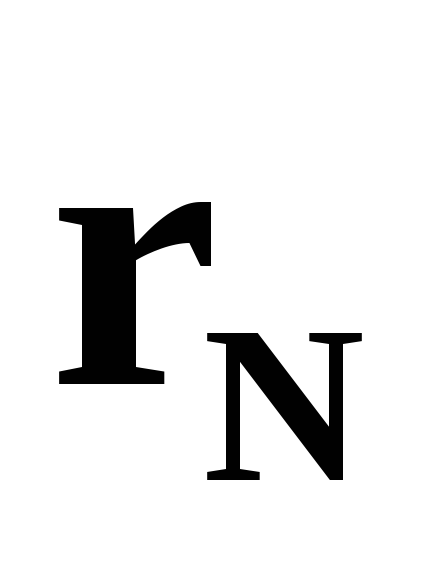 и скоростей
и скоростей ,
, ,
…,
,
…, всех частиц в данный момент времени.
всех частиц в данный момент времени.
В самом общем виде уравнения движения системы частиц может быть записано в виде

Вид функции  зависит от свойств частиц системы и
внешних условий, в которых они движутся
зависит от свойств частиц системы и
внешних условий, в которых они движутся
Общее решение уравнения может быть найдено, если известны:
вид функции
 и
иначальные условия, т.е. значения
 и
и в момент времениt=0/
в момент времениt=0/
Движение точки по окружности. Угловые перемещение, скорость, ускорение. Связь между линейными и угловыми характеристиками.
Вращательным называется такое движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения.
Кинематические характеристики вращательного движения:
Угол поворота, угловая скорость, угловое ускорение.
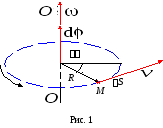
 ,
рад
вектор, численно равный
угловому пути, и направлен по оси вращения
так, что из его конца вращение видно
против часовой стрелки.
,
рад
вектор, численно равный
угловому пути, и направлен по оси вращения
так, что из его конца вращение видно
против часовой стрелки. Угловая
скорость  ,вектор,
характеризующий быстроту изменения
угла поворота,
и направлен по оси вращения так, что из
его конца вращение видно против часовой
стрелки.
,вектор,
характеризующий быстроту изменения
угла поворота,
и направлен по оси вращения так, что из
его конца вращение видно против часовой
стрелки.
 рад/c,
c-1 .(1)
рад/c,
c-1 .(1)
Характеристики равномерного вращения ( = const)
1. Период вращения Т это время, за которое тело совершает один полный оборот


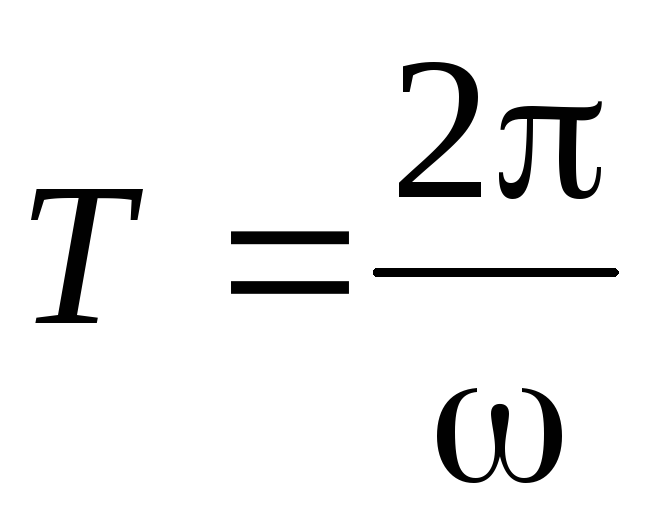 , с.(2)
, с.(2)
Частота вращения n это число полных оборотов, совершаемых телом за единицу времени
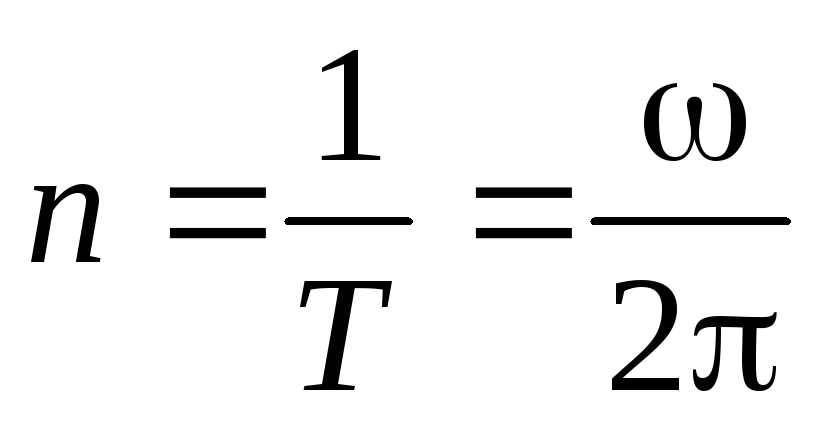 , с1
Гц
, с1
Гц 
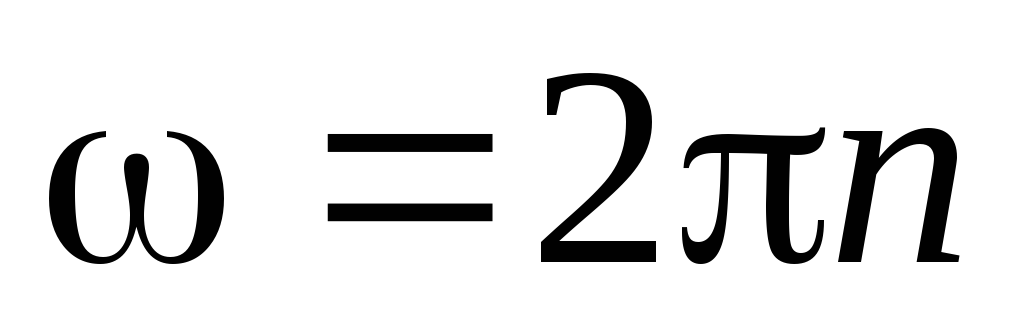 .
(3)
.
(3)
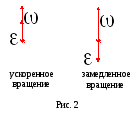
Угловое
ускорение  вектор,
характеризующий быстроту изменения
угловой скорости
вектор,
характеризующий быстроту изменения
угловой скорости
 , рад/c,
с1 (4)
, рад/c,
с1 (4)
Связь между линейными и угловыми характеристиками

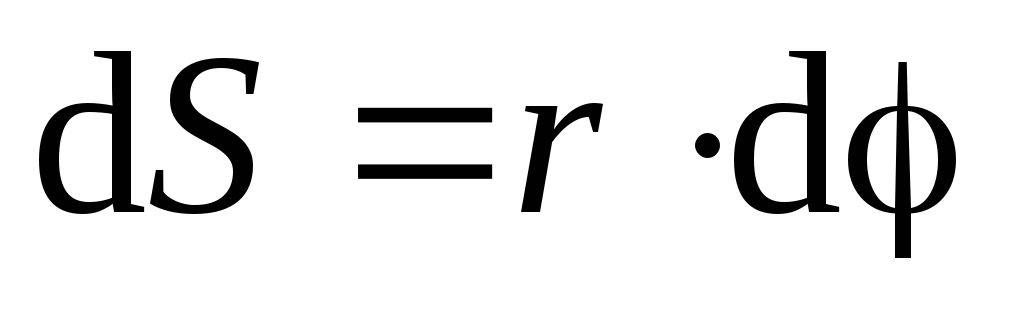 ;
; 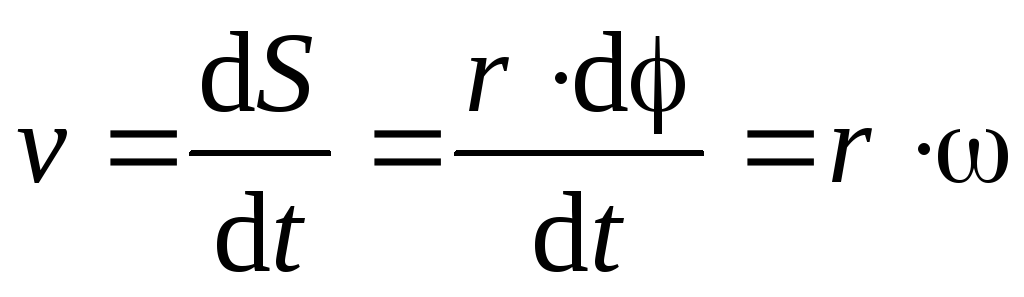 ;
; 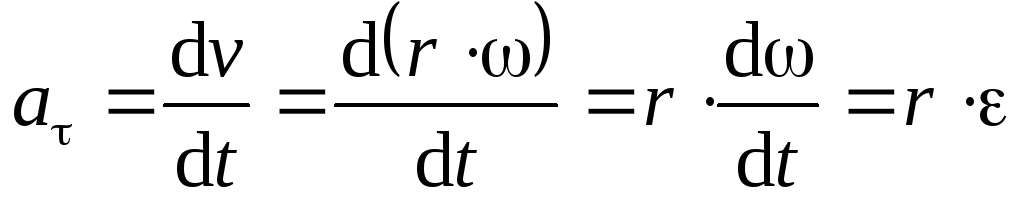 ;
;
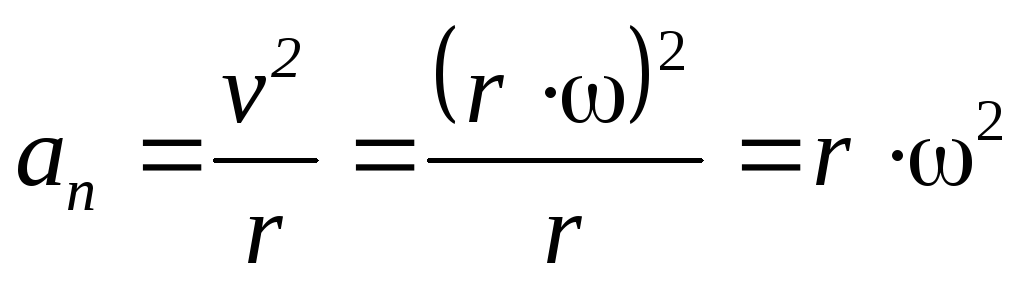 ;
;
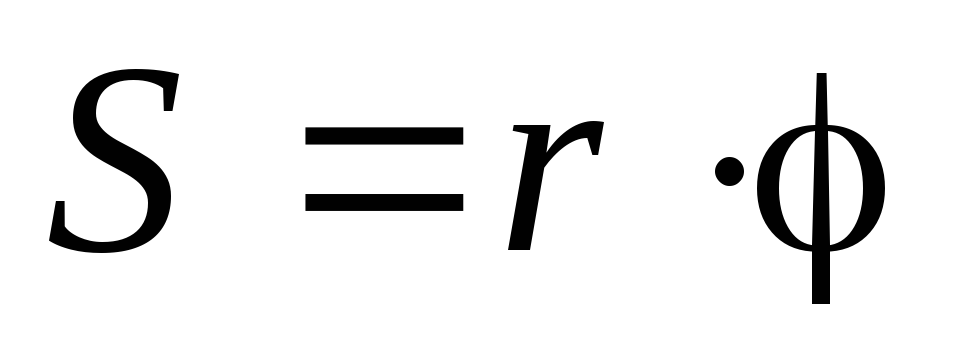 ;
; 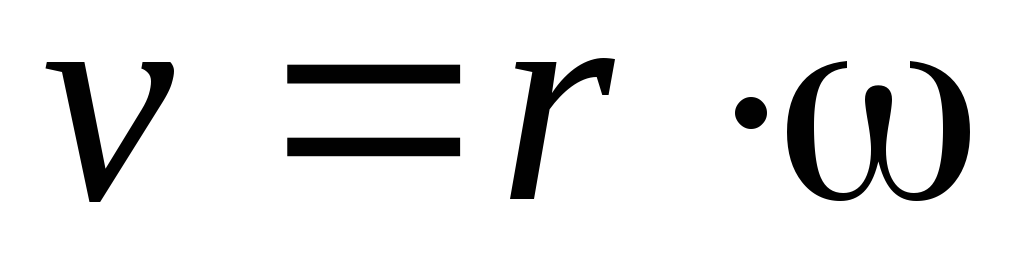 ;
; 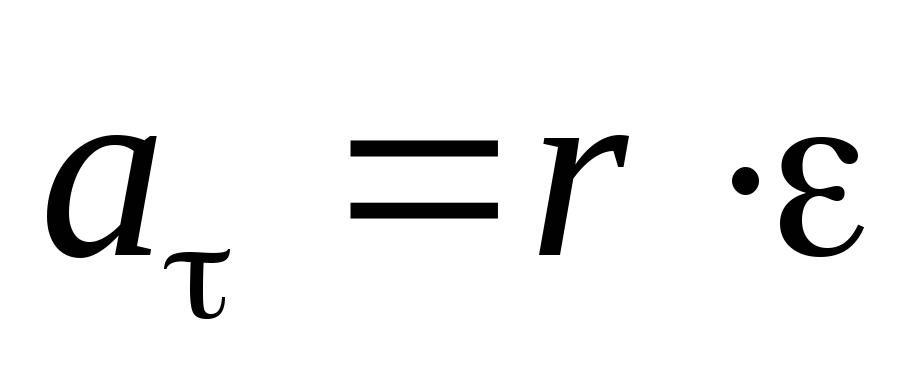 ;
; 
Динамика материальной точки. Инерциальные системы отсчета и первый закон Ньютона
Тело, не подверженное внешним воздействиям (в действительности можно говорить лишь о компенсации этих воздействий), называется свободным, а его движение –свободным движениемилидвижением по инерции.
Инерция – это способность тел сохранять состояние покоя или равномерного прямолинейного движения.
Первый закон Ньютона выполняется не во всякой системе отсчета, так как характер движения зависит от выбора системы отсчета.
Инерциальной называется любая система отсчета, которая находится в покое или движется равномерно и прямолинейно относительно гелиоцентрической системы (центр ее совпадает с Солнцем).
Первый закон Ньютона (закон инерции)
Всякое тело сохраняет состяние покоя или равномерного прямолинейного движения до тех пор, пока внешнее воздействие не заставит его изменить это состояние.
Фундаментальные взаимодействия. Силы различной природы (упругие, гравитационные, трения), второй закон Ньютона. Масса. Третий закон Ньютона.
В современной физике выделяют четыре вида фундаментальных, т.е. базовых, не сводящихся к каким-либо другим, взаимодействий:
сильное ядерное, обеспечивающее связь частиц в атомном ядре – самоеинтенсивное, нокороткодействующее: оно сказывается лишь на масштабах атомного ядра (порядка 10-15м).
слабое ядерное, ответственное за ряд процессов распада элементарных частиц – малоинтенсивное (порядка 10-13 от сильного ядерного) и также короткодействующее;
электромагнитное, обеспечивающее стабильность атомов и молекул. Электромагнитное взаимодействие является весьмаинтенсивным(порядка 10-2 от сильного ядерного) и одновременно –дальнодействующим. Оно могло бы доминировать при галактических масштабах, но редко проявляет себя явным образом в макромире, поскольку встречающиеся в нем объекты, как правило, электрически нейтральны (имеют нулевой суммарный заряд).
гравитационное, проявляющееся, например, как взаимодействие небесных тел и определяющее структуру Вселенной. Оно малоинтенсивное (порядка 10-38 от сильного ядерного), но дальнодействующее. Как и электромагнитное, гравитационное взаимодействие убывает обратно пропорционально квадрату расстояния между взаимодействующими телами.
Связь угловых и линейных величин
Рассмотрим движение тела по окружности. Скорость, с которой тело движется по окружности, называют линейной скоростью. Она находится по формуле
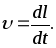 (7)
(7)
Выясним, какова связь между линейными и угловыми величинами при движении тела по окружности. Линейными величинами являются путь, скорость, касательное и нормальное ускорения, а угловыми угол поворота, угловая скорость и угловое ускорение.
Найдём связь между
угловой и линейной скоростью. Из геометрии
известно, что длина дуги lцентрального
угла равна произведению угла,
измеренного в радианах, на радиус
окружностиR, т.е.l = R.
Продифференцируем это выражение по
времени: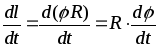 (Rвынесена за знак
производной, поскольку она постоянная).
Но
(Rвынесена за знак
производной, поскольку она постоянная).
Но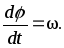 Тогда получаем, что
Тогда получаем, что
= R. (8)
Продифференцируем
выражение (8) по времени 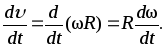 Но
Но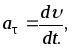 а
а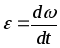 модуль углового
ускорения. Поэтому
модуль углового
ускорения. Поэтому
a = R. (9)
Подставляя выражение (7) в формулу (4), получаем для модуля нормального ускорения
an = R. (10)
Таким образом, при движении материальной точки по окружности для описания её движения можно пользоваться как линейными, так и угловыми величинами. Однако при вращении твёрдого тела удобно использовать угловые величины, а не линейные, поскольку уравнения движения разных точек, выраженные в угловых величинах, одинаковы для всех точек тела, в то время как при пользовании линейными величинами они различны.
Кинематика твёрдого тела
До сих пор изучалось движение тел, которые можно было рассматривать как материальные точки. Рассмотрим теперь движение протяжённых тел. При этом будем считать тела абсолютно твёрдыми (твёрдыми). Под твёрдым телом в механике понимается тело, взаимное расположение частей которого в условиях данной задачи считается неизменным.
Существует два вида движения твёрдого тела: поступательное и вращательное. Поступательным называется движение, при котором прямая, соединяющая любые две точки тела, движется в пространстве параллельно самой себе. Привращательном движениивсе точки тела движутся по окружностям, центры которых лежат на одной прямой, называемойосью вращения. Любое сложное движение можно представить как результат сложения поступательного и вращательного движений.
Рассмотрим поступательное движение. При этом движении все точки тела проходят одинаковые пути. Поэтому они имеют одинаковые скорости и ускорения. Отсюда следует, что для описания такого движения тела достаточно выбрать на нём произвольную точку и использовать формулы кинематики материальной точки. Обычно выбирают его центр тяжести.
При вращательном движении разные точки твёрдого тела проходят различные пути и, следовательно, обладают разными скоростями и ускорениями. Вследствие этого для характеристики такого движения надо выбирать такие величины, которые будут одинаковыми в данный момент времени для всех точек тела. Ими являются угол поворота, угловая скорость и угловое ускорение.
Динамика поступательного движения
Из первой лекции видно, что кинематика описывает движение и не рассматривает причины его вызывающие. Однако именно этот вопрос важен с практической точки зрения. Изучением взаимосвязи движения и сил, действующих в механической системе, и занимается динамика. Основу динамики составляют три закона Ньютона, являющиеся обобщением большого числа опытных данных. Прежде, чем перейти к их рассмотрению, введём понятия силы и массы тела.
СИЛА.
В повседневной жизни нам постоянно приходится сталкиваться с различными взаимодействиями. Например, с притяжением тел к Земле, отталкиванием и притяжением магнитов и токов, текущих по проводам, отклонением электронных пучков в электронно-лучевых трубках при действии на них электрических и магнитных полей и т.д. Для характеристики взаимодействия тел и вводится понятие силы. В механике сила, действующая на тело, является мерой его взаимодействия с окружающими телами. Действие силы проявляется в деформации тела или в приобретении им ускорения. Сила —это вектор. Поэтому она характеризуется модулем, направлением и точкой приложения.
МАССА
Как следует из опыта, тела обладают способностью противодействовать изменению скорости, которой они обладают, т.е. они противодействуют приобретению ускорения. Это свойство тел было названо инертностью. Для характеристики инертных свойств тел используют физическую величину, называемуюмассой. Чем больше масса тела, тем оно инертнее. Кроме того, вследствие гравитационных сил все тела притягиваются друг к другу. Модуль этих сил зависит от массы тел. Таким образом, масса характеризует и гравитационные свойства тел. Чем она больше, тем больше сила их гравитационного притяжения. Итак,масса — это мера инертности тел при поступательном движении и мера их гравитационного взаимодействия.
В системе единиц СИ масса измеряется в килограммах (кг).




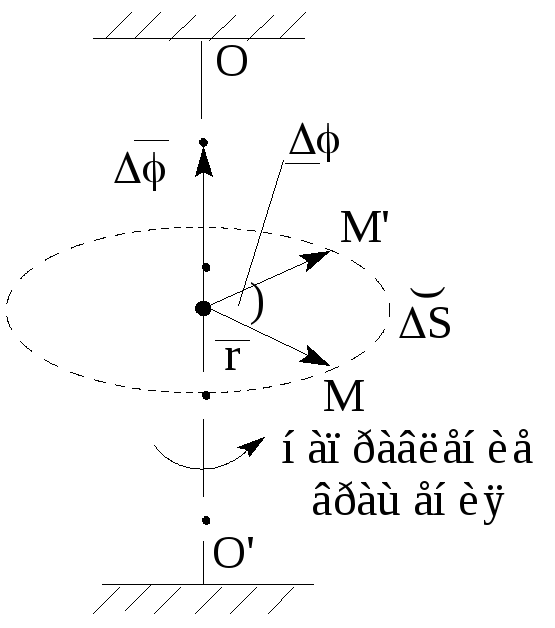
 за времяt пройдет путь равный длине дуги S,
а радиус вектор
за времяt пройдет путь равный длине дуги S,
а радиус вектор  повернется на угол.
Величина
повернется на угол.
Величина 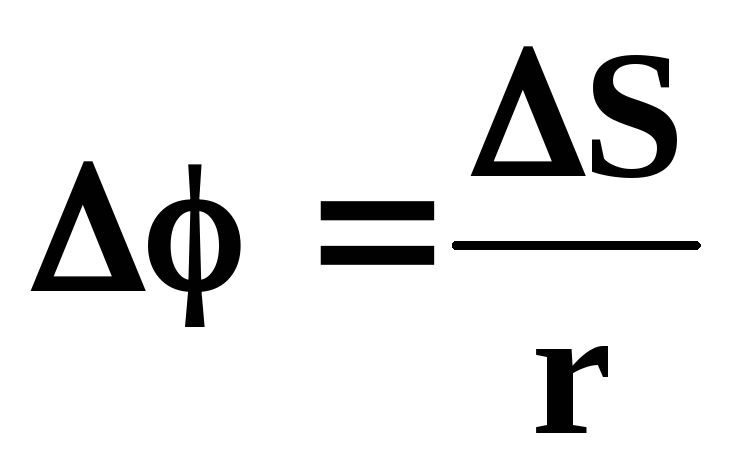 называетсяуглом
поворота радиус-вектора выбранной точки от
некоторого начального положения или
модулем углового перемещения.
называетсяуглом
поворота радиус-вектора выбранной точки от
некоторого начального положения или
модулем углового перемещения.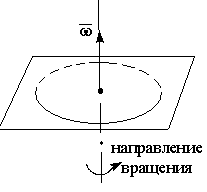
 связано с углом поворота правилом
правого винта. Размерность – рад/с.
связано с углом поворота правилом
правого винта. Размерность – рад/с. .
.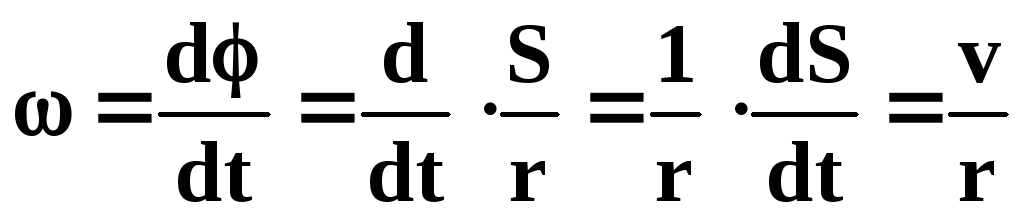 ;
;
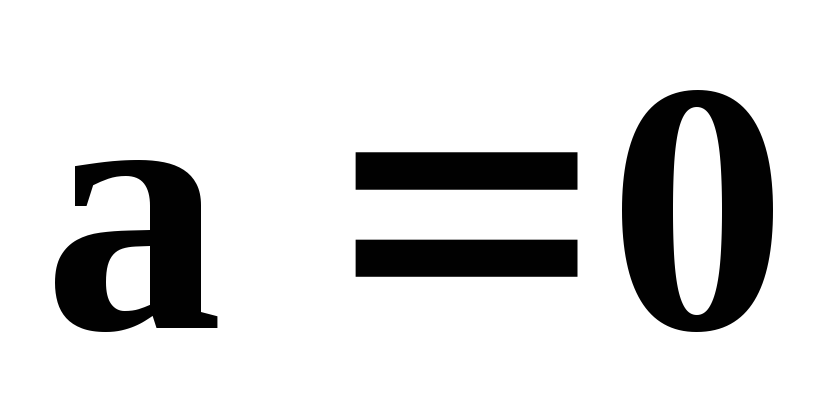
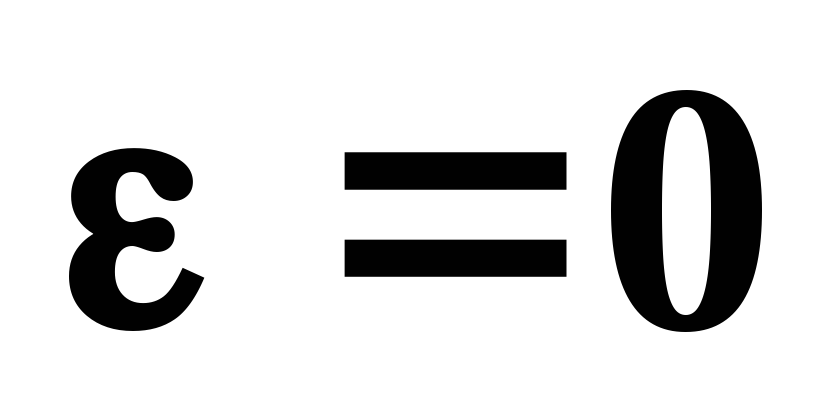


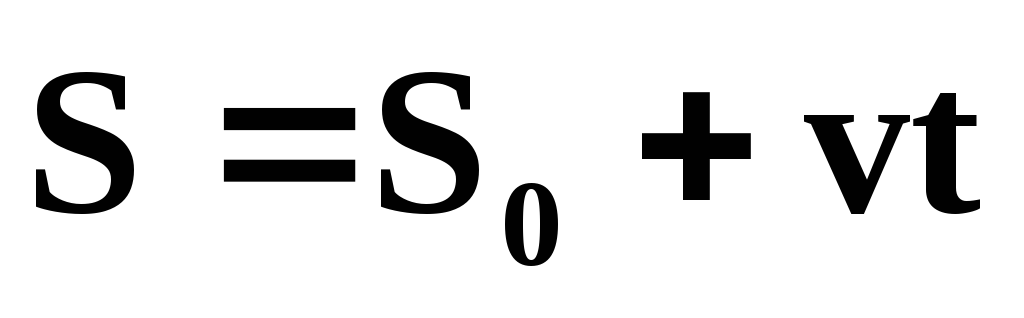
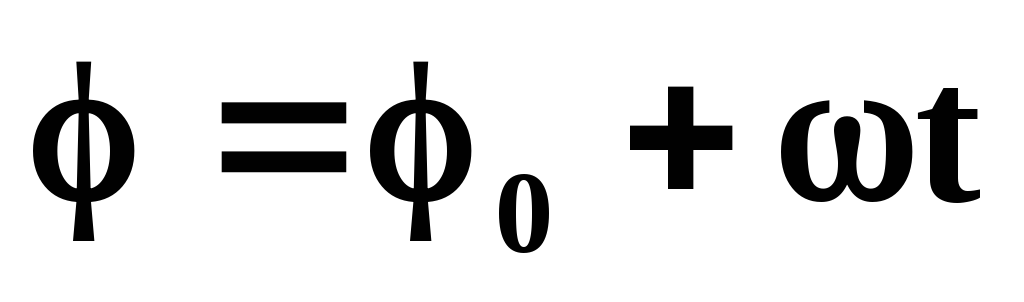
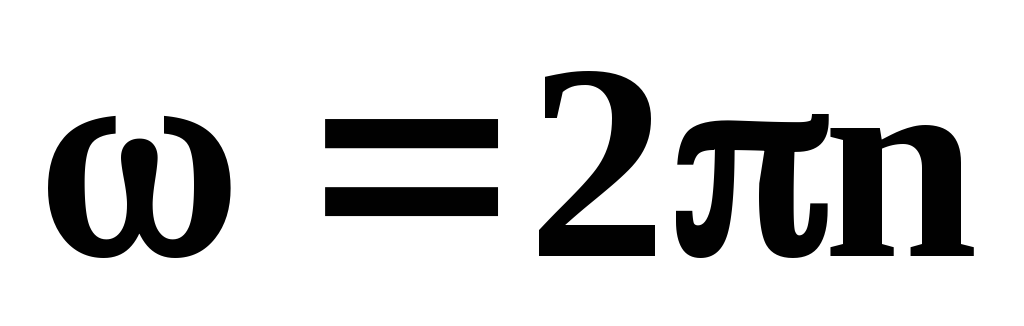 ;
; 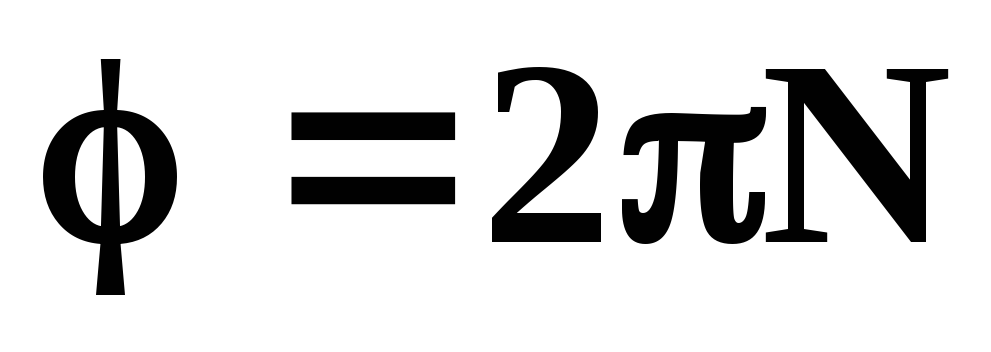
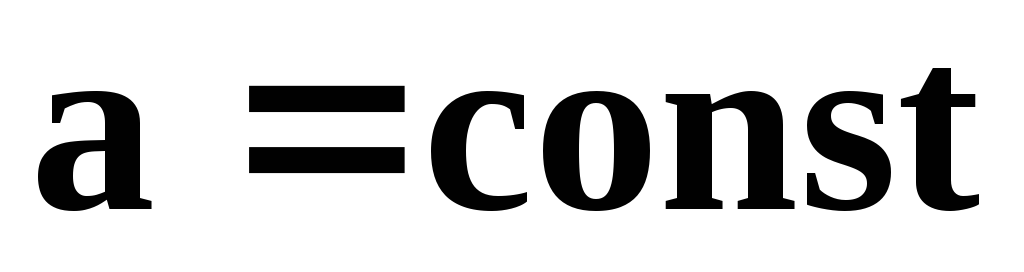

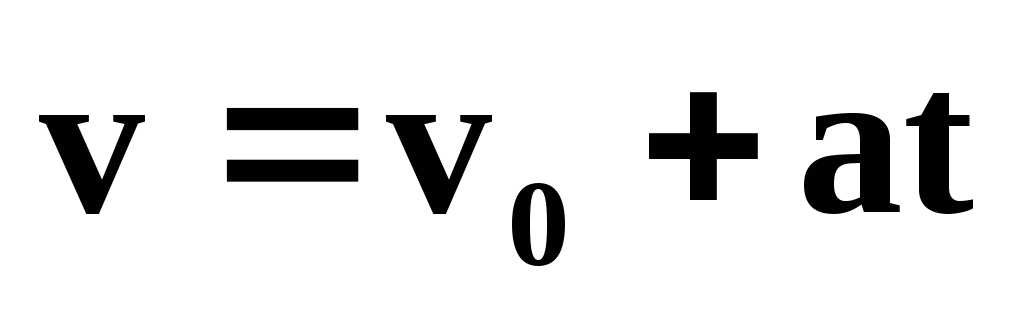
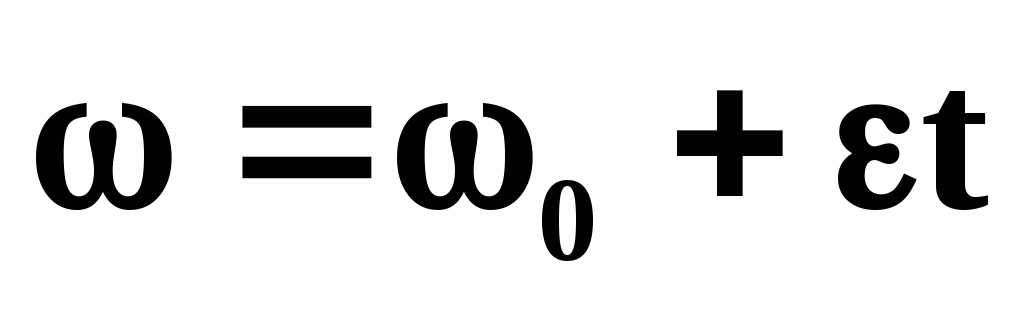
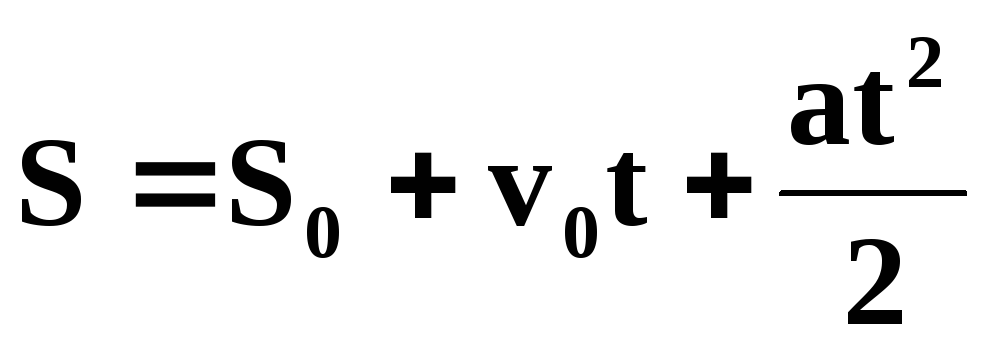
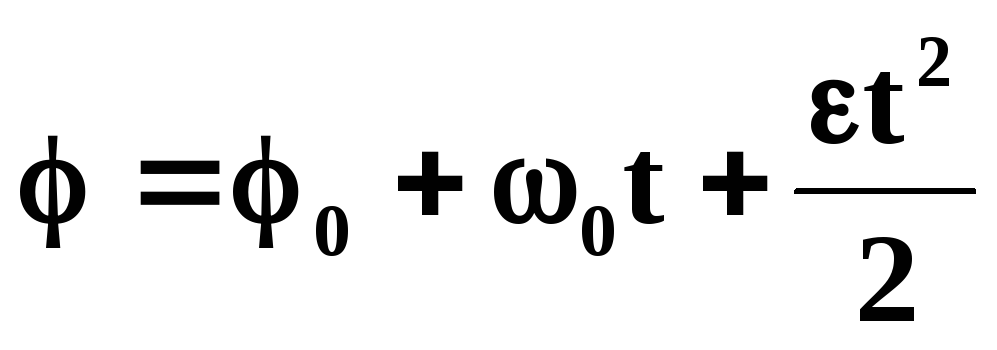
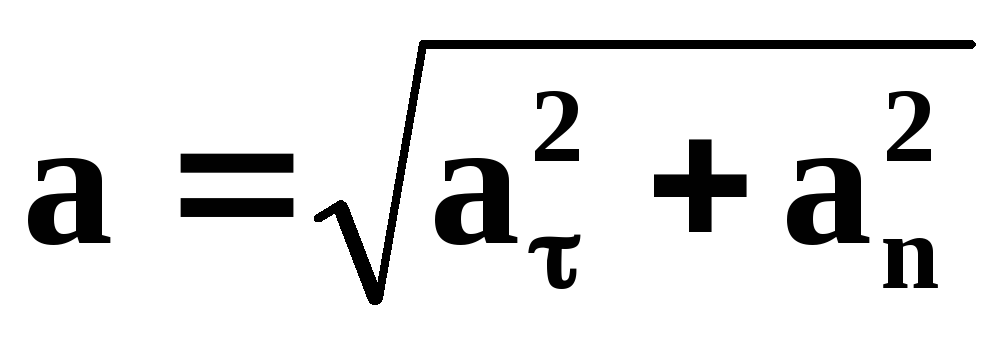
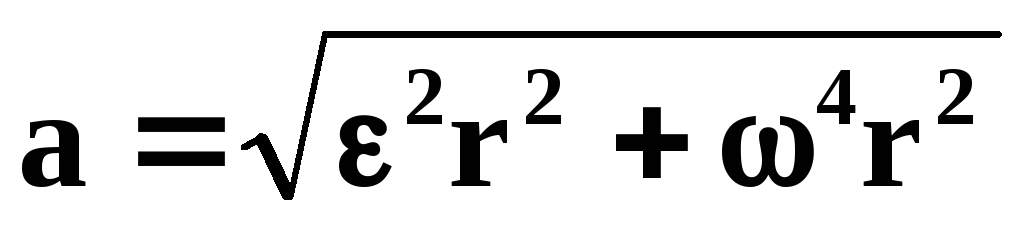
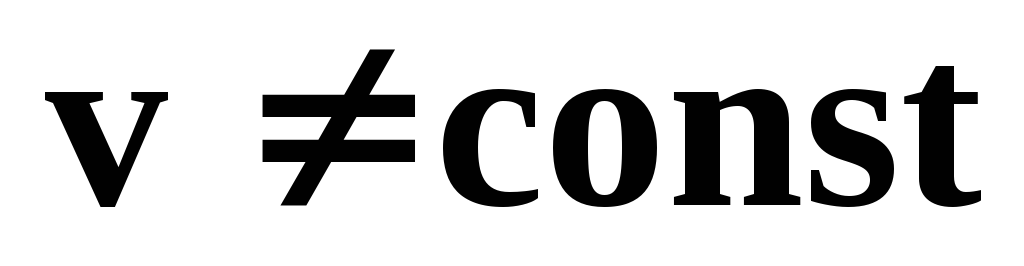 ;
; 
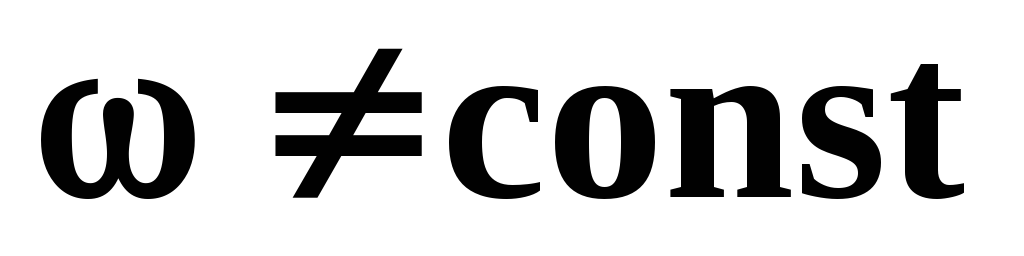 ;
; 
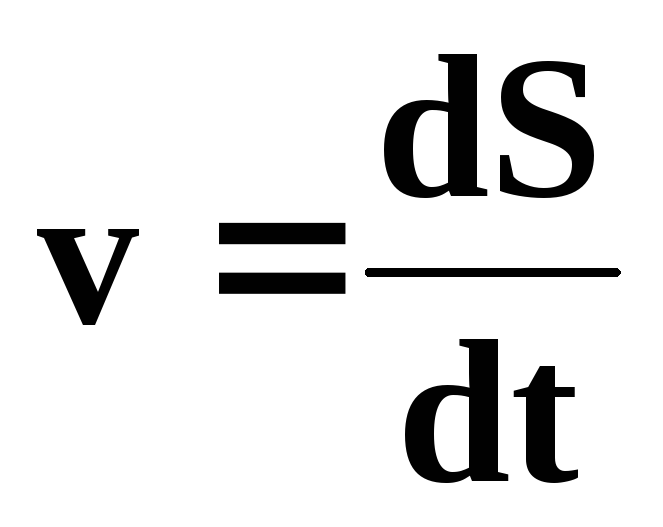
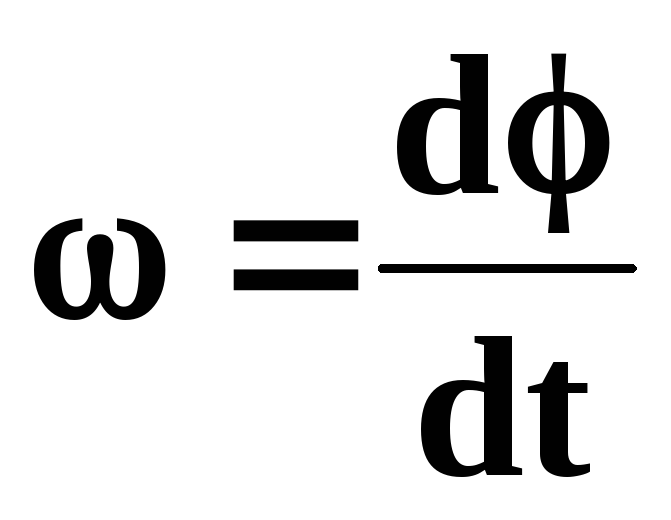
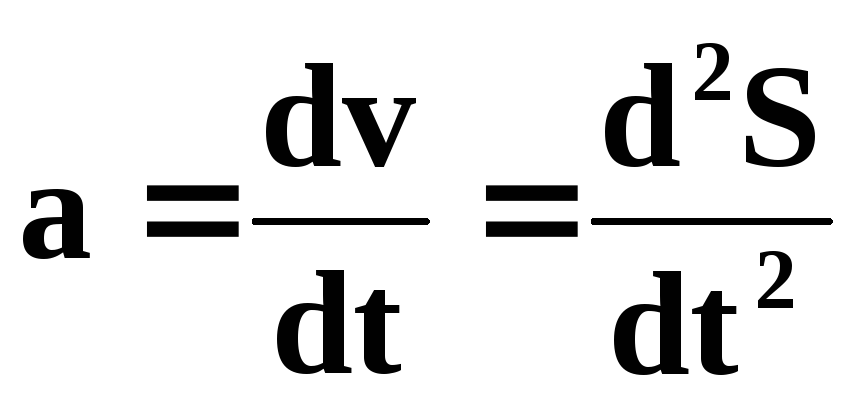
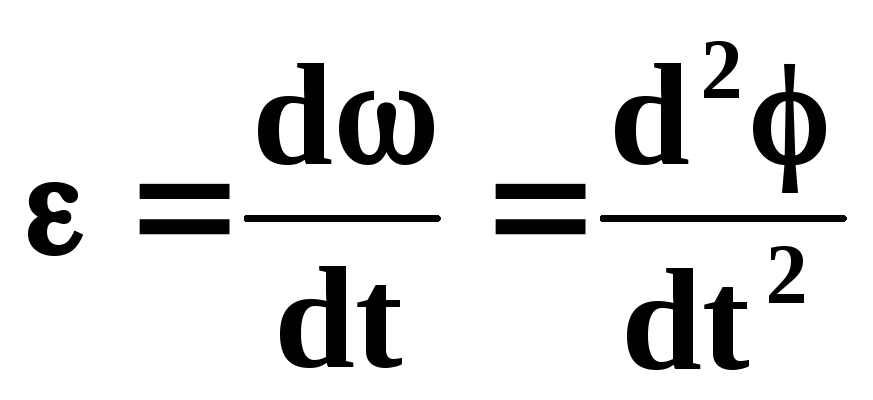


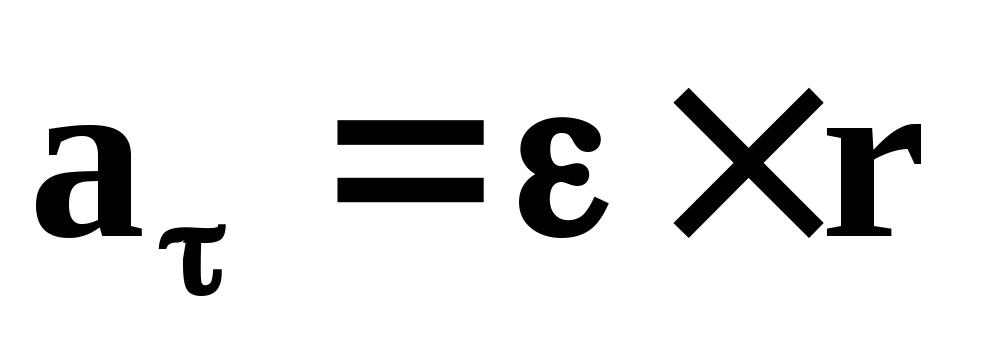
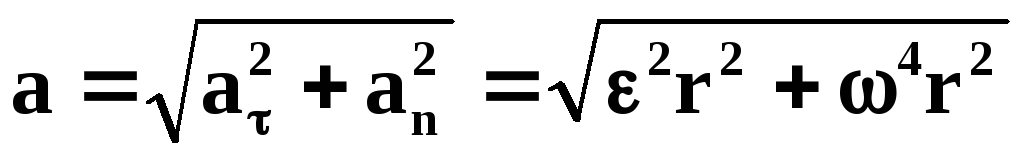
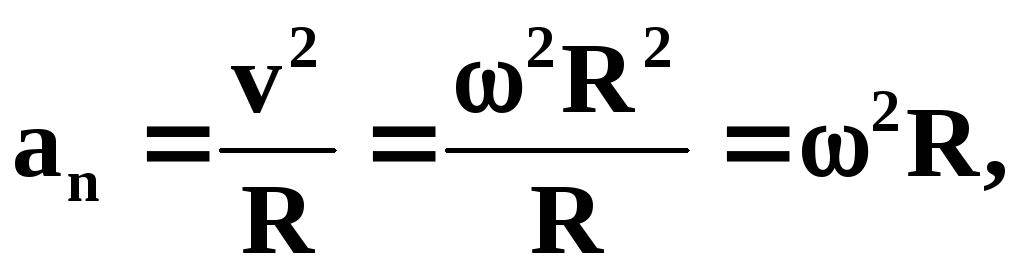
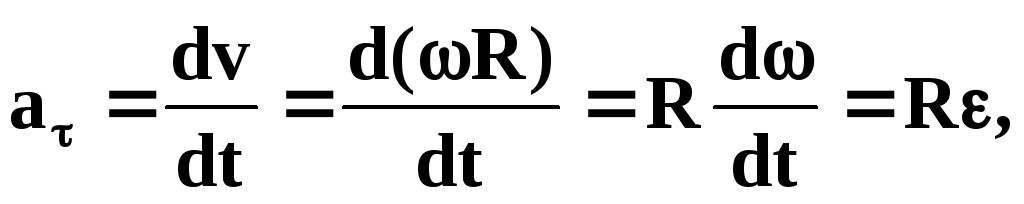

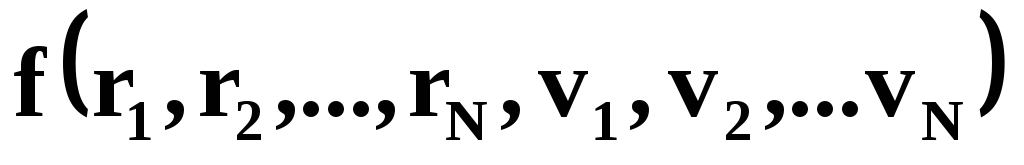 и
и и
и в момент времениt=0/
в момент времениt=0/