Угловые эффекты / Хабр
Добрый день, дорогой читатель! Это
втораяпереводная статья из цикла статей о создании физического движка авторства Chris Hecker. Если Вы ещё не ознакомились с
первой, то рекомендую это сделать, т. к. всё сразу станет понятнее. Большое спасибо за поддержку первого перевода: это очень стимулирует работать дальше и больше! Приятного чтения!
Только что я захотел подпереть дверь чем-нибудь тяжёлым, чтобы ко мне не вошёл злоумышленник. Неужели я многого прошу? Я хочу, чтобы его машина перевернулась и взорвалась в определенным месте. Я хочу, чтобы огромные шестерни заело перед тем, как меня расплющит. И я хочу наспех построить штуку, похожую на качели, для того, чтобы катапультировать милый пылающий подарок через крепостную стену замка. Кто же может мне помешать воплотить это всё в реальность? Вы предположите, что мой соперник в игровом мире, но в действительности – программист физического движка, потому что в основе всего вышеперечисленного лежит угловой эффект.
Основная причина, почему угловые (или иначе вращательные) эффекты не реализованы в играх на сегодняшний день – это то, что программисты считают, что физика, описывающая вращательное движение, слишком сложная для понимания и воплощения в реальность. На уроках физики в старшей школе (где мы все узнали второй закон Ньютона) обычно не рассказывают о вращательных эффектах, и это не совсем очевидно, как перейти от силы, приложенной к объекту, ко вращению этого объекта. Конечно, динамика вращательного движения немного труднее для понимания, чем динамика линейного движения, но она проще, чем кажется. Любой, кто может создать физический движок в соответствии с тем материалом, что представлен в первой статье цикла, справится и с тем, чтобы включить в него угловые эффекты, описанные в этой статье. Есть надежда, что после публикации данной статьи мир наполнится играми, которые используют все возможности и преимущества угловых эффектов, или, по меньшей мере, вы сможете создать игру, в которой вы, выгнувшись, выстрелите в ногу вашего друга в смертельном бою.
Краткое повторение
Несмотря на то, что каждая моя статья на какую-то единственную тему, я всегда перечитываю то, что написал ранее, для того, чтобы понять, где закончил. Я только что посмотрел свою первую статью о физике, и я в восторге: мы успели выучить так много, и притом, ни разу не писали программный код и не читали дополнительную литературу! Прежде, чем начнем, давайте освежим в памяти материал из последней статьи.
Таблица 1 содержит важнейшие выводы для динамики твердых тел. Из Уравнения 1 следует, что вектор коодинаты ( r ), вектор скорости (v), и вектор ускорения (a) связаны производными (и интегралами, если читать в обратном порядке). Как напоминание – мы отмечаем дифференцирование по времени штрихом (r’). r’ – это то же самое, что dr/dt, а r’’ – это то же, что и вторая производная по времени. Из Уравнения 2 следует, что сила связана с линейным импульсом (произведение массы на скорость), массой, и ускорением. Определение центра масс можно почерпнуть из Уравнения 3 (это точка, где все массы и расстояния уравновешивают друг друга).
Подведем итоги всему, что описано в первой статье: мы узнали, что общая сила, действующая на наш центр масс, равна сумме всех сил, приложенных к телу (включая силу гравитации, фуру злодея, взрыв неподалёку, импульс тяги нашего двигателя и т. д.). После мы разделили этот вектор суммы на массу тела для того, чтобы получить ускорение CM, и затем интегрировали ускорение по времени, чтобы получить скорость и координату тела.
Уравнение 5 – это просто шедевр! Вы увидите, что в нём нет понятия точек приложения сил к телу, а это является ключевым моментом для определения, как тело будет вращаться под их действием.
Каков твой угол?
В первой статье игнорировалось вращение, поэтому нам были необходимы лишь радиус-вектор и его производная для описания конфигурации нашего тела в 2D. Теперь добавим еще одну величину кинематики, ориентацию (обозначается заглавной буквой омега – Ω), для того, чтобы работать с угловыми эффектами. Для того, чтобы задать Ω, нам необходимо выбрать систему координат относительно твёрдого тела и систему координат игрового мира, и величина Ω будет равна разнице углов между ними в радианах, как показано на Рисунке 1.
Рисунок 1. Определение Ω
На рисунке оси xw, yw – оси координат игрового мира, а xb, yb – оси координат твердого тела. Ω больше 0, если считать против часовой стрелки. Здесь важно прояснить, почему мы изучаем динамику двумерного мира прежде, чем перейти в трёхмерный: ориентация в 2D – это скалярная величина (угол между системами координат в радианах), тогда как определение ориентации в трехмерном мире гораздо труднее.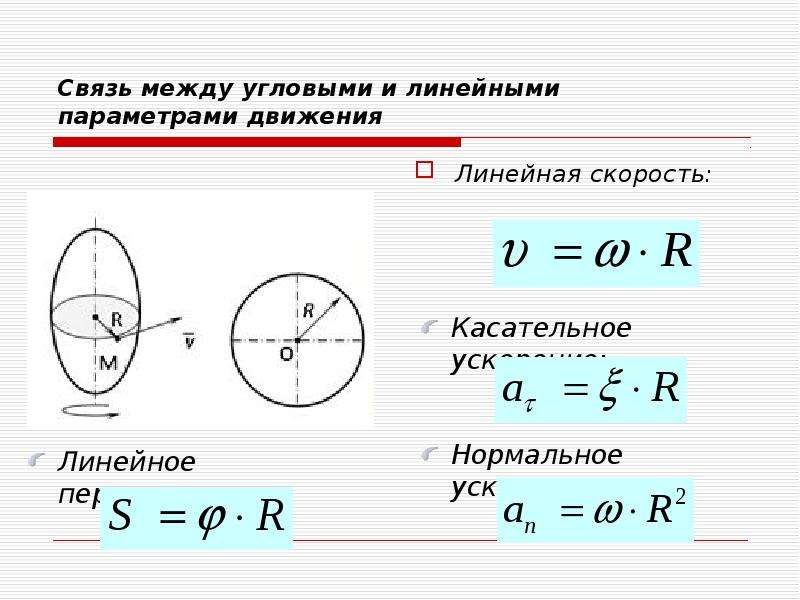
По ходу того, как тело вращается, величина Ω изменяется. Это изменение приводит нас к другой величине кинематики – угловой скорости (обозначается строчной буквой омега – ω). В отличие от координаты и линейной скорости тела, мы не обозначаем угловую скорость следующим образом – Ω’. Тем не менее, иногда мы обозначаем производную скорости по времени, или угловое ускорение, как ω’ (это еще одна величина кинематики) или как α (строчная альфа). Не вините меня: не я придумал все эти обозначения; и в каждой книге, что я прочел, имеются небольшие расхождения. Наш угловой аналог для Уравнения 1 – это:
Уравнение 6
Как и в Уравнении 1, мы дифференцируем ω по времени, чтобы получить α; и если мы интегрируем α по времени, получаем ω и т. д. Все по аналогии с предыдущей статьей: зная угловое ускорение α, мы можем дважды проинтегрировать его, чтобы получить новую ориентацию. Но ключевой момент здесь – надо знать величину α.
Как можно предположить, наша цель на эту статью – вывести угловой аналог для каждого из линейных уравнений в Таблице 1, и затем, учтя линейные и угловые уравнения и силу, приложенную к объекту, мы можем подсчитать его линейное ускорение a и угловое ускорение α. Наконец, мы можем численно проинтегрировать эти ускорения для нахождения новых позиции и ориентации нашего тел.
Наконец, мы можем численно проинтегрировать эти ускорения для нахождения новых позиции и ориентации нашего тел.
Для начала свяжем линейные и угловые величины вместе. А это довольно неочевидная проделка, в которой используется угловая скорость. При подсчетах в динамике нам нередко надо найти скорость произвольной точки объекта. Например, когда мы рассчитываем столкновения твердых тел, надо знать скорость столкнувшихся точек для того, чтобы понять, как сильно они ударили друг по другу. Если наши тела не вращаются, скорость каждой точки тела одинакова. Мы можем просто следить за скорость центра масс тела, и этого будет достаточно. Тогда как если наши тела вращаются, каждая точка этих тел может иметь разную скорость. Очевидно, что мы не можем просчитывать скорость бесконечного количества точек нашего твердого тела, поэтому нам необходимо иное, лучшее решение.
Один из простых способов, которые применяются для нахождения линейной скорости любой точки внутри объекта, использует угловую скорость объекта. B. Говоря русским языком, Уравнение 7 показывает, что Скорость точки вращающегося тела вычисляется умножением перпендикулярного вектора, проведённого из центра вращения, на угловую скорость. Как я это понял? Что ж, я прочел об этом в книге, но, очевидно, что такого объяснения недостаточно, поэтому докажем, что это истина.
B. Говоря русским языком, Уравнение 7 показывает, что Скорость точки вращающегося тела вычисляется умножением перпендикулярного вектора, проведённого из центра вращения, на угловую скорость. Как я это понял? Что ж, я прочел об этом в книге, но, очевидно, что такого объяснения недостаточно, поэтому докажем, что это истина.
Докажем истинность выводов из Уравнения 7 в два этапа. Сначала докажем, что величина результирующего вектора скорости правильная; затем – что его направление правильное. Для первой части доказательства рассмотрим Рисунок 2.
Рисунок 2. C = Ωr
Рисунок 2 демонстрирует вращение точки B на угол, равный Ω радиан по ходу вращения твердого тела с радиус-вектором длины r, направленным из центра вращения тела O в точку B. B прошла длину дуги C, где C = Ωr из определения радианов. (Радианная мера угла – это мера дуги, ограниченной радиусом окружности. Длина окружности C = 2πr, потому что радианная мера дуги окружности – это 2π [или 360 градусов]).
Скорость точки – это изменение ее координаты по времени. OB – это радиус-вектор, направленный из O к B. Фух, мы на полпути.
OB – это радиус-вектор, направленный из O к B. Фух, мы на полпути.
Для того, чтобы удостовериться в правильности направление вектора скорости в Уравнении 7, начнем того, что убедимся в том, что вектор скорости должен быть перпендикулярен к радиус-вектору. Это предположение понятно интуитивно, потому что точка, вращающаяся вокруг какой-либо другой заданной точки, может двигаться только перпендикулярно вектору между этими точками. Она не может приблизиться к центру вращения или отдалиться от него, или это движение попросту перестанет быть вращением. Можем подкрепить наше предположение расчетами для векторов, но я зажат в определенные рамки по объему статьи, поэтому будем считать, что наше предположение правильное. (Если вы горите желанием доказать это самостоятельно, продифференцируйте скалярное произведение вектора фиксированной длины на самого себя.)
Наконец, мы должны убедиться, что вектор обозначен правильно, т. к. на рисунке представлены два вектора, равной длины, перпендикулярных радиусу: v и -v. Т. к. величина Ω измеряется против часовой стрелки, ω > 0, когда точка вращается по часовой стрелке. Перпендикуляр указывает в направлении по часовой стрелке, как и радиус-вектор. На Рисунке 3 демонстрируются выводы из Уравнения 7:
Т. к. величина Ω измеряется против часовой стрелки, ω > 0, когда точка вращается по часовой стрелке. Перпендикуляр указывает в направлении по часовой стрелке, как и радиус-вектор. На Рисунке 3 демонстрируются выводы из Уравнения 7:
Рисунок 3. Связь линейной скорости и угловой
Дополним Уравнение 7, чтобы оно описывало вращение движущихся тел. Рассмотрим движение твердого тела, как простое перемещение центра вращения тела и простое вращение остальной части тела вокруг этой точки. Для тех, кому интересно, это Теорема Шаля о классификации движений.
Теорема Шаля разбивает наше движение на две составляющие – линейное и угловое. Пусть центр вращения тела O – это единственная перемещающаяся точка, затем используем ω, для вычисления вращения вокруг точки O, и это дает нам общую форму Уравнения 7:
Уравнение 9
Уравнение 9 гласит, что мы можем подсчитать скорость любой точки движущегося тела, используя линейную скорость центра вращения тела и, в дополнение к этому, скорость, приобретенную при вращении тела. B (синус – это еще один ключ к разгадке связи между векторным и скалярным произведением). Уравнение 10 даёт меру того, какая часть импульса точки B «смотрит» во «вращательном направлении» относительно точки A.
B (синус – это еще один ключ к разгадке связи между векторным и скалярным произведением). Уравнение 10 даёт меру того, какая часть импульса точки B «смотрит» во «вращательном направлении» относительно точки A.
Также, как мы использовали производную линейного импульса для определения силы, мы будем использовать производную момента импульса для определения углового близнеца силы – момента силы (обозначается строчной буквой тау – τ).
Уравнение 11
Для экономии места я немного смухлевал в Уравнении 11, пропустив пару трудных шагов, которые включают в себя нахождение производных. Из всего вышесказанного следует, что момент силы связан с силой в определенной точке посредством скалярного произведения.
Наконец, мы получили уравнение динамики, в котором используется точка приложения силы, которая ранее игнорировалась в уравнениях линейного импульса. В Уравнении 11 используется скалярное произведение с перпендикуляром как мера того, какая часть силы, приложенной к точке B, «вращает вокруг» точки A; эта «вращательная сила» называется моментом силы. i как произведение массы на скорость (mv). Это пригодится мне в будущем для того, чтобы сделать из Уравнения 12 что-то с более выраженным прикладным характером. Уравнение гласит, что для нахождения полного момента импульса для нашего объекта, необходимо просуммировать моменты импульса всех его точек. Для твердого тела, состоящего из граней (а не из отдельных точек), необходимо вычислить интеграл, на не дискретную сумму.
i как произведение массы на скорость (mv). Это пригодится мне в будущем для того, чтобы сделать из Уравнения 12 что-то с более выраженным прикладным характером. Уравнение гласит, что для нахождения полного момента импульса для нашего объекта, необходимо просуммировать моменты импульса всех его точек. Для твердого тела, состоящего из граней (а не из отдельных точек), необходимо вычислить интеграл, на не дискретную сумму.
К счастью, можно упростить наши вычисления, введя новую величину под названием «момент инерции», аналогично тому, как мы ввели центр масс для упрощения уравнения полного импульса. Вспомним о том, что благодаря Уравнению 7 мы можем найти скорость точки через угловую скорость. Пусть точка A в Уравнении 12 – это цент вращения из Уравнения 7, и индекс суммирования i в Уравнении 12 – это точка B из Уравнения 7, то возможно преобразовать Уравнение 7 в Уравнение 12. Получим:
Уравнение 13
Распишу Уравнение 13 подробнее, шаг за шагом. Сначала заменим Уравнение 7 на 12 для того, чтобы получить сумму в Уравнении 13.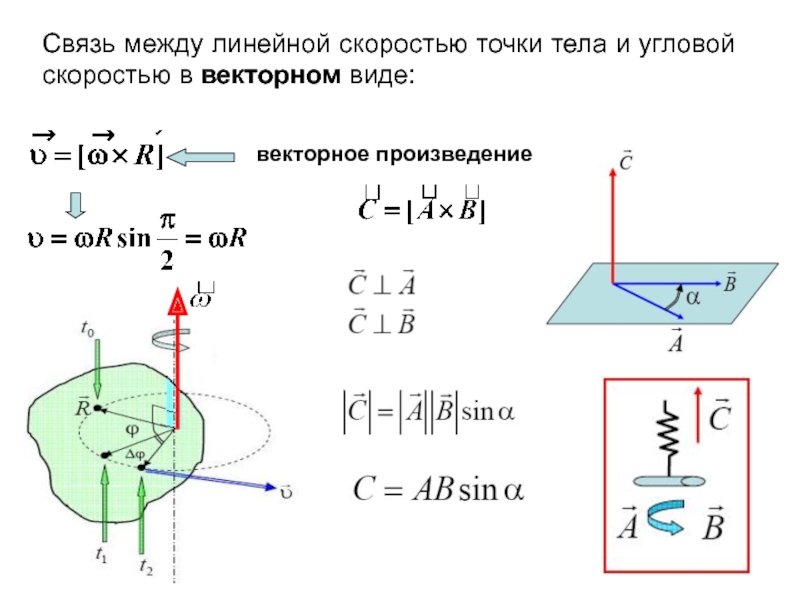 A – это константа, вынесем ее за знак дифференцирования):
A – это константа, вынесем ее за знак дифференцирования):
Уравнение 14
Это уравнение – угловой эквивалент Уравнения 5; по факту, это F = ma для угловой динамики. Это уравнение связи полного момента силы и угловое ускорение тела посредством скалярного момента инерции. Если мы знаем момент силы, оказываемой на наше тело, мы можем найти его угловое ускорение, а дальше – угловую скорость и ориентацию в пространстве посредством интегрирования – поделив момент силы на момент инерции.
Алгоритм динамики
Он с трудом видится нам через этот вихрь уравнений, но все они – его составная часть. Мы вывели достаточно уравнений для того, чтобы получить великолепную динамику двумерного мира с произвольно заданными силами и моментами сил, перемещающими и вращающими наши объекты. Как же использовать эти уравнения? Ниже представлен базовый алгоритм:
- Найти величину центра масс и момент инерции в центре масс.
- Задать начальные координаты тела, его ориентацию в пространстве, его линейную и угловую скорости.

- Учесть все силы, действующие на тело и точки их приложения.
- Найти равнодействующую всех сил и разделить ее на массу тела для того, чтобы найти линейное ускорение центра масс (Уравнение 5).
- Для каждой силы построить скалярное произведение с перпендикуляром между вектором, направленным из центра масс в точку приложения силы, и вектором приложенной силы, добавить эту величину в полный момент силы в уравнении центра масс (Уравнение 11).
- Найти частное для полного момента силы и момента инерции в центре масс для нахождения углового ускорения (Уравнение 14).
- Численно интегрировать линейное ускорение и угловое ускорение для обновления координаты, линейной скорости, ориентации в пространстве и угловой скорости (смотри последнюю статью).
- Отрисовать объект в полученной координате, и перейти к Шагу 3.
В алгоритме выше есть лишь два шага, которые я не объяснил. Во-первых, как подсчитать момент инерции в Шаге 1 для сплошного объекта? Во-вторых, как решить проблему с силами из Шага 3? Ответ на первый вопрос может быть найден в простом примере кода, который я оставлю в приложении в конце этой статьи (вы выполните интегрирование объекта по его площади). Множество книг по динамике содержат рассчитанный момент инерции для часто встречающихся форм объектов в приложении в самом конце, поэтому вам не придется каждый раз выводить их самостоятельно.
Множество книг по динамике содержат рассчитанный момент инерции для часто встречающихся форм объектов в приложении в самом конце, поэтому вам не придется каждый раз выводить их самостоятельно.
Ответ на вопрос, как подсчитать силы из Шага 3, зависит от приложения, но немного общих рекомендаций я дам. Во-первых, такие силы, как гравитация, всегда направленные в одну сторону (вниз, в случае с гравитацией), не создают момент силы, т. к. они тянут все точки в одно и то же время в одном направлении, хотя мы и прикладываем эти силы напрямую к центру масс. Силы, подобные силе упругости, приложены к определенной точке объекта, они создадут момент силы, поэтому рассматриваем их в общем случае. Как мы увидели в первой статье, сила трения – это та же сила, направленная в противоположную от скорости тела сторону.
Вы можете сделать простую физическую модель, демонстрирующую силу трения, и просто приложить силу к центру масс, или вы можете выбрать, к каким частям объекта будут приложены силы трения, и сделать это, что может создать момент силы, действующий на объект. Силы, которые тела испытывают при столкновениях, немного труднее, и мы познакомимся с ними в следующей статье. Силы, подобные тяге ракетного двигателя, нужно рассматривать, как силы с точкой приложения (вы этом случае, если один из двигателей откажет, вы начнете крутиться вокруг своей оси до тех пор, пока не отрегулируете руль, чтобы обеспечить уравновешивание момента силы!). Если вы хотите что-то, похожее на гравитационные лучи из НЛО, то эта сила должна рассчитываться, как сила гравитации и не создавать момент силы, или она должна быть приложена к определенной точке объекта, и он будет вращаться вокруг этой точки, пока поднимается ввысь? Выбор за вами. Ключевой момент – не бояться экспериментировать с различными силами, рассчитанными разными способами, ведь уже сейчас у вас есть настоящий симулятор двумерной графики, попробуйте разные виды сил!
Силы, которые тела испытывают при столкновениях, немного труднее, и мы познакомимся с ними в следующей статье. Силы, подобные тяге ракетного двигателя, нужно рассматривать, как силы с точкой приложения (вы этом случае, если один из двигателей откажет, вы начнете крутиться вокруг своей оси до тех пор, пока не отрегулируете руль, чтобы обеспечить уравновешивание момента силы!). Если вы хотите что-то, похожее на гравитационные лучи из НЛО, то эта сила должна рассчитываться, как сила гравитации и не создавать момент силы, или она должна быть приложена к определенной точке объекта, и он будет вращаться вокруг этой точки, пока поднимается ввысь? Выбор за вами. Ключевой момент – не бояться экспериментировать с различными силами, рассчитанными разными способами, ведь уже сейчас у вас есть настоящий симулятор двумерной графики, попробуйте разные виды сил!
Я оставил весь необходимый вам код и ссылки на своем веб-сайте, потому что здесь закончилось свободное место. В своем простом приложении я воплотил в жизнь алгоритм динамики двумерного мира, а также добавил объекты, скрепленные пружиной; они вращаются вокруг своей оси, и иногда даже сталкиваются со стенами, крутсясь. Но об этом я расскажу в другой раз. Перейдите по ссылке за дополнительной литературой и простым приложением для Windows 32 и Macintosh.
Но об этом я расскажу в другой раз. Перейдите по ссылке за дополнительной литературой и простым приложением для Windows 32 и Macintosh.
Очень редко Chris Hecker испытывает на себе действие момента инерции, но обычно это проходит и довольно быстро. Силы можно прикладывать к [email protected].
Примечания переводчика: здесь представлена игра слов, обыгрывается тема статьи и ее содержание.
P.S. Обратная связь приветствуется. Ваши комментарии позволяют повысить качество работ. Спасибо!
P.P.S. Автор перевода выражает отдельную благодарность пользователям berez и Василий Терешков за правки перевода. Спасибо!
Сопоставление формул кинематики и динамики поступательного и вращательного движений | Физика для студентов | Студенту | Статьи и обсуждение вопросов образования в Казахстане | Образовательный сайт Казахстана
Сопоставление формул кинематики и динамики поступательного и вращательного движений
На рис.4.5 представлены направления векторов линейной скорости v, угловой скорости ω и псевдовектора угла поворота Δφ при вращательном движении.
Рис.4.5. Связь между векторами v, ω и псевдовектором Δφ
На рис.4.6 представлены направления векторов линейной скорости v, тангенциального aτ, нормального an и полного aполн ускорений в случае равноускоренного (см. рис.4.6,а) и равнозамедленного (см. рис.4.6,б) вращательных движений.
Рис.4.6. Связь между векторами v, aτ, an и aполн
В табл.3 и 4 приведено сопоставление формул кинематики и динамики поступательного и вращательного движений.
Таблица 3
Сопоставление формул кинематики поступательного и вращательного движений
| Поступательное движение | Вращательное движение |
| Инертные свойства — масса m, [кг] F — сила, [кг•м/с2], [Н] Перемещение: r, Δr, dr, [м] Путь: S, ΔS, dS, [м] Линейная скорость: v, [м/с] v=lim(Δr/Δt)=dr/dt Ускорение: a=lim(Δv/Δt)=dv/dt, [м/с2] v=a•t равноускоренное (v0=0) равнопеременное (v0≠0) v=v0±at S=v0t±at2/2 | Инертные свойства – момент инерции I, [кг•м2] M = [r,F] — момент силы, [кг•м2/с2], [H•м] Угол поворота: φ, Δφ, dφ, [рад] Путь: φ, Δφ, dφ, [рад] Угловая скорость ω, [рад/с] ω=lim(Δω/ωt)=dω/dt Угловое ускорение: β=lim(Δω/Δt)=dω/dt, [рад/с2] ω=β•t равноускоренное (ω0=0) равнопеременное (ω0≠0) ω=ω0±βt φ=ω0t±βt2/2 |
| Связь линейной и угловой скорости v=ωR или v=[ω,R] Связь тангенциального и углового ускорений aτ=β•R aполн=√(aτ2+an2) aτ=dv/dt an=v2/R | |
Таблица 4
Сопоставление формул динамики поступательного и вращательного движений
| Вращательное движение | Поступательно движение |
| Основное уравнение динамики поступательного движения: F=ma, F ↑↑ a Импульс: Производная импульса определяет действующую силу: Кинетическая энергия при поступательном движении: Работа при поступательном движении: | Основное уравнение динамики вращательного движения: M=I • β, M ↑↑ β Момент импульса: Производная момента импульса определяет вращающий момент силы: Кинетическая энергия при вращательном движении: Работа при вращательном движении: |
3 Вращательное движение твёрдого тела
Лекция № 3
ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЁРДОГО ТЕЛА
План
1. Абсолютное твёрдое тело. Вращательное движение. Угловая скорость и угловое ускорение, их связь с линейными скоростями и ускорениями вращающегося твёрдого тела.
2. Момент инерции тела. Кинетическая энергия вращающегося твёрдого тела.
3. Вычисление моментов инерции. Теорема Штейнера. Свободные оси.
4. Момент силы. Момент импульса.
5. Уравнение моментов. Уравнение динамики вращательного движения твёрдого тела относительно неподвижной оси.
Рекомендуемые файлы
6. Гироскопы. Гироскопический эффект.
1. Абсолютно твёрдое тело. Абсолютно твёрдым телом называется такое тело, деформацией которого в условиях данной задачи можно пренебречь. Расстояние между любыми двумя точками тела остаётся неизменным.
Расстояние между любыми двумя точками тела остаётся неизменным.
Всякое движение твёрдого тела можно разложить на два основных вида движения – поступательное и вращательное.
Вращательным называется такое движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения.
Введём понятие угловой скорости и углового ускорения. Пусть твёрдое тело вращается вокруг неподвижной в данной системе отсчёта оси и за время совершает бесконечно малый поворот (рис. 3.1).
Соответствующий угол поворота будем характеризовать вектором , модуль которого равен углу поворота, а направление совпадает с осью , причём так, что направление поворота отвечает правилу правого винта по отношению к направлению вектора .
Рис. 3.1
Из рис. 3.1 следует, что . Вектор как бесконечно малую величину можно считать по модулю равным соответствующей дуге окружности , его направление соответствует правилу правого винта по отношению к векторам и
Разделим обе части на :
. (*)
(*)
Производная угла поворота по времени называется угловой скоростью.
Вектор совпадает по направлению с вектором . Изменение вектора со временем характеризуют вектором углового ускорения:
Из выражения * получаем связь линейной и угловой скоростей:
(**)
То есть скорость любой точки А твёрдого тела, вращающегося вокруг неподвижной оси с угловой скоростью , равна векторному произведению на радиус-вектор точки А относительно произвольной точки на оси вращения.
Если выбрать в качестве точки отсчёта для радиус-вектора центр окружности вращения (точка О), при неизменном радиусе окружности выражение (**) можно записать в скалярном виде:
Продифференцируем это выражение по времени: , отсюда получаем связь тангенциального и углового ускорений:
Нормальное ускорение можно представить как
Модуль полного ускорения:
2. Момент инерции тела. Определим кинетическую энергию вращения твёрдого тела (рис. 3.2). Разделим его мысленно на отдельные элементарные части, настолько малые, чтобы их можно было считать движущимися как материальные точки (). Обозначим массу i-го элемента , а скорость этого элемента .
Момент инерции тела. Определим кинетическую энергию вращения твёрдого тела (рис. 3.2). Разделим его мысленно на отдельные элементарные части, настолько малые, чтобы их можно было считать движущимися как материальные точки (). Обозначим массу i-го элемента , а скорость этого элемента .
Кинетическая энергия этого элемента
.
Просуммировав кинетическую энергию всех элементов, получим кинетическую энергию вращательного движения тела:
.
Линейная скорость связана с угловой скоростью вращения тела (постоянна для всех точек тела).
.
Определение. Моментом инерции материальной точки относительно оси z называется произведение массы этой точки на квадрат её расстояния от оси вращения:
Определение. Моментом инерции твёрдого тела относительно некоторой оси z называется сумма моментов инерций материальных точек относительно данной оси.
В соответствии с этими определениями:
(Сравните с выражением для кинетической энергии поступательного движения , очевидно соответствие ).
Физический смысл момента инерции. Момент инерции во вращательном движении играет такую же роль, как масса при поступательном движении, характеризует меру инертности тела при вращательном движении. Чем больше момент инерции тела, тем труднее при прочих равных условиях привести его во вращательное движение. Момент инерции определяется не только массой, но и тем, как эта масса распределена относительно оси вращения.
Соотношение является приближённым, причём тем более точным, чем меньше элементарные массы . Задача нахождения моментов инерции сводится к интегрированию.
(Интегрирование ведётся по всей массе тела ).
3. Вычисление моментов инерции. 1. Кольцо (полый цилиндр) (рис. 3.3). В случае достаточно тонких стенок вся масса сосредоточена на расстоянии от центра.
Кольцо (полый цилиндр) (рис. 3.3). В случае достаточно тонких стенок вся масса сосредоточена на расстоянии от центра.
Относительно оси, проходящей через центр кольца:
,
.
2. Однородный диск (сплошной цилиндр)
Дано: радиус диска, масса диска.
Найти: момент инерции диска относительно оси, проходящей через центр диска.
Разобьём диск (рис. 3.4) на кольца с радиусом , толщиной . По определению момента инерции . Пусть поверхностная плотность диска , тогда масса кольца , где площадь кольца, . Интегрируя по радиусу, находим момент инерции диска:
=,
3. Тонкий однородный стержень
Дано: масса стержня, длина стержня.
Найти: (момент инерции относительно оси ОО, проходящей через конец стержня перпендикулярно ему) (рис. 3.5).
Рис. 3.5
Ввиду одномерного характера задачи выражение можно заменить на , где , тогда .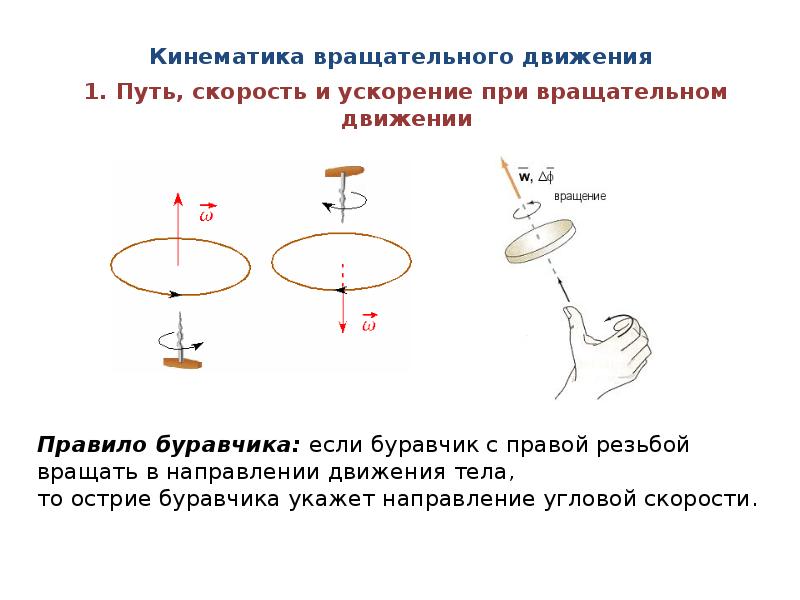
Теорема Штейнера (без вывода)
Постановка задачи. Известен момент инерции произвольного тела массой относительно оси, проходящей через его центр тяжести (рис. 3.6). Требуется найти, каков момент инерции относительно какой-либо оси , параллельной первой и находящейся на расстоянии от неё.
Теорема. Момент инерции тела относительно произвольной оси z равен сумме момента инерции относительно оси, проходящей через центр масс тела С и параллельной данной, и произведения массы тела на квадрат расстояния между осями a:
.
Пример применения теоремы Штейнера.
Требуется найти момент инерции тонкого однородного стержня массой и длиной относительно перпендикулярной к нему оси , проходящей через центр стержня (рис. 3.7).
Рис. 3.7
3.7
Решение:
Воспользуемся полученным ранее выражением для момента инерции стержня относительно оси, проходящей через его конец:
. Используя теорему Штейнера, получаем:
отсюда .
Свободные оси
Определение. Ось вращения тела, положение которой в пространстве остаётся неизменным без действия на неё внешних сил, называется свободной.
Можно доказать, что в любом теле существует три взаимно перпендикулярных оси, проходящие через центр масс тела, которые могут служить свободными осями. Они называются главными осями инерции тела. Например, главные оси инерции однородного прямоугольного параллелепипеда проходят через центры противоположных граней. Вращение вокруг главных осей с наибольшим и наименьшим (экстремальными) моментами инерции оказывается устойчивым, а вращение вокруг оси со средним моментом – неустойчивым. Этот факт является достаточно важным при проектировании конструкций с вращающимися частями.
4. Момент силы. Пусть О – какая-либо точка, относительно которой рассматривается момент вектора силы. Обозначим радиус-вектор, проведённый из этой точки к точке приложения силы (Рис. 3.8).
Рис. 3.8
Определение. Моментом силы относительно точки О называется векторное произведение радиуса-вектора на силу :
Раскрывая векторное произведение, получим где плечо силы (длина перпендикуляра, опущенного из точки О на линию действия силы).
В соответствии с определением векторного произведения вектор направлен перпендикулярно плоскости, в которой лежат векторы и в соответствии с правилом правого винта (буравчика).
Определение. Момент силы относительно оси , проходящей через точку О, есть проекция на эту ось вектора момента силы относительно точки, лежащей на этой же оси.
как проекция на ось является скалярной величиной.
Момент импульса
Пусть материальная точка массой движется со скоростью относительно точки О, а радиус-вектор этой материальной точки, проведённый из точки О (рис. 3.9).
Определение. Моментом импульса материальной точки относительно точки О называется векторное произведение радиуса-вектора на вектор импульса :
Направление перпендикулярно плоскости, в которой лежат векторы и , в соответствии с правилом правого винта, например момент импульса электрона, двигающегося по круговой орбите в боровской модели атома.
Свяжем момент импульса с моментом инерции и угловой скоростью. Пусть радиус-вектор некоторой частицы массой лежит в плоскости рис. 3.10, скорость перпендикулярна ей («от нас»), частица движется по окружности радиусом .
Модуль момента импульса . Линейную скорость можно связать с угловой относительно оси как , тогда . Проекция вектора на ось вращения равна
.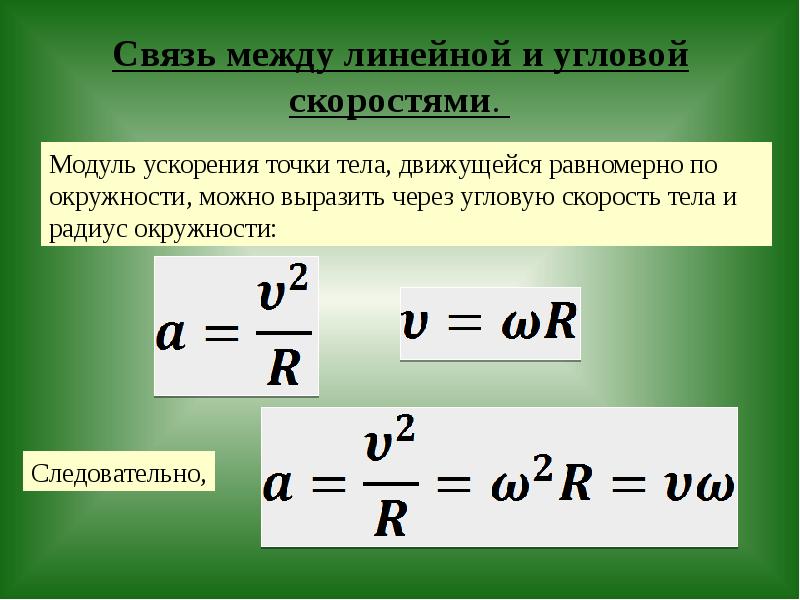 Как видно из рис. 3.10, , т.е.
Как видно из рис. 3.10, , т.е.
Для системы материальных точек (твёрдого тела) выражение связи , и формально такое, как и для материальной точки:
Но под здесь подразумевается сумма моментов инерции материальных точек системы:
Можно показать (см., например, в [1]), что для однородного тела, симметричного относительно оси вращения, суммарный момент импульса тела . Он направлен вдоль оси вращения в ту же сторону, что и , т.е.
(Для несимметричного тела в общем случае не совпадает по направлению с вектором ).
5. Уравнение моментов. В дальнейших преобразованиях условимся для упрощения записи индекс 0 у , и других величин не писать, но подразумевать, что он есть.
Продифференцируем выражение для момента импульса материальной точки: . .
Учтём, что , а .
Рассмотрим первое слагаемое (см.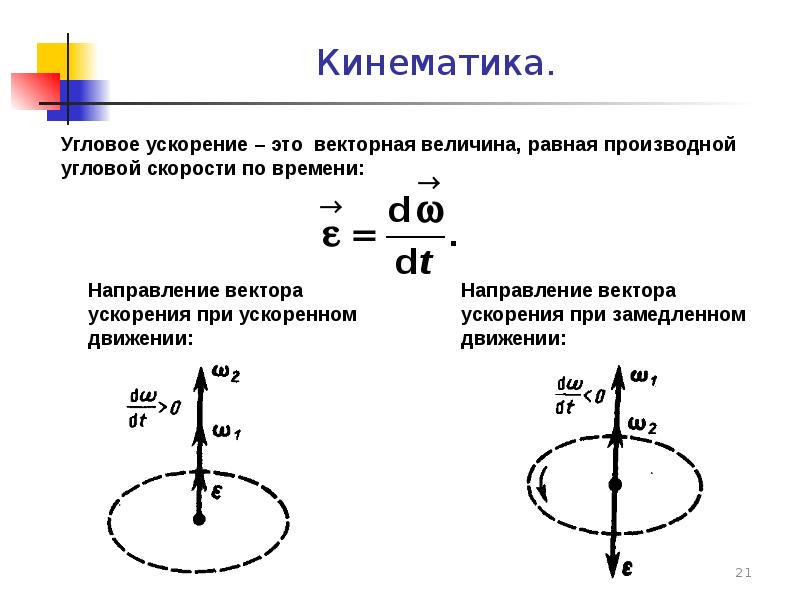 в лекции № 1 «Векторное произведение»).
в лекции № 1 «Векторное произведение»).
= (так как угол между и равен нулю).
Второе слагаемое в выражении для
(по определению момента силы).
В результате получаем:
Уравнение моментов (оно связывает момент импульса с моментом силы).
Производная по времени момента импульса материальной точки относительно точки О равна моменту действующей силы относительно точки О.
Уравнение моментов для твёрдого тела
Рассмотрим систему частиц, на которую действуют как внутренние, так внешние силы. Моментом импульса системы относительно точки О называется сумма моментов импульса отдельных частиц . Дифференцирование по времени даёт, что
.
Для каждой из частиц можно написать уравнение моментов
,
где момент внутренних сил, а момент внешних сил, действующих на -ю частицу. (по 3-му закону Ньютона, так как внутренние силы образуют пары, равные по величине, противоположные по направлению и действующие вдоль одной прямой, т.е. образуют равные по величине и противоположно направленные моменты сил).
(по 3-му закону Ньютона, так как внутренние силы образуют пары, равные по величине, противоположные по направлению и действующие вдоль одной прямой, т.е. образуют равные по величине и противоположно направленные моменты сил).
Получаем
Обозначим =, получаем окончательно
Производная по времени от момента импульса механической системы относительно некоторой точки О равна суммарному моменту относительно той же точки всех внешних сил, приложенных к системе (уравнение моментов).
Уравнение динамики вращательного движения твёрдого тела
относительно неподвижной оси
В проекции на ось предыдущее уравнение запишется:
а так как , то , если , то . Так как проекция углового ускорения на ось , то получим уравнение динамики вращательного движения относительно оси Z и сравним с уравнением динамики для поступательного движения (2-й закон Ньютона).
Соответствие очевидно:
Поступательное движение | Вращательное движение | ||
| |||
| |||
Замечание: если вокруг оси вращается однородное симметричное тело, то , и тогда очевидно:
(Угловое ускорение совпадает по направлению с вектором момента силы).
6. Гироскопы (от греч. круг, смотрю, наблюдаю).
Гироскопы (от греч. круг, смотрю, наблюдаю).
Гироскопом называется массивное симметричное тело, вращающееся с большой угловой скоростью вокруг своей оси симметрии.
Рассмотрим поведение гироскопа на примере волчка (рис. 3.11). Опыт показывает, что если ось вращающегося волчка наклонена к вертикали, то волчок не падает, а совершает так называемое прецессионное движение (прецессию) – т.е. его ось описывает конус вокруг вертикали с некоторой угловой скоростью , причём чем больше скорость вращения волчка, тем меньше угловая скорость прецессии ().
Из уравнения моментов следует:
Приращение совпадает по направлению с моментом внешних сил, относительно точки О. Момент силы тяжести , как видно из рис. 3.11, перпендикулярен моменту импульса, т.е. , следовательно, приращение момента импульса . В результате вектор (и ось волчка) будут поворачиваться вместе с вектором вокруг вертикали, описывая круговой конус с углом полураствора .
Найдём связь между , и :
или в векторном виде , сравнивая с , получаем уравнение для угловой скорости прецессии.
Из уравнения видно, что момент силы определяет угловую скорость прецессии, а не ускорение. Это означает, что мгновенное устранение момента приводит к мгновенному исчезновению и прецессии, т.е. прецессия не обладает инерцией.
Гироскопический эффект
Рассмотрим эффект, возникающий при вынужденном вращении оси гироскопа. Пусть ось гироскопа укреплена в -образной подставке, которую мы будем поворачивать вокруг оси (рис. 3.12).
Рис. 3.12
Если момент импульса гироскопа направлен вправо, то при таком повороте за время вектор получит приращение вектор, направленный перпендикулярно . Согласно уравнению это означает, что на гироскоп действует момент силы , совпадающий по направлению с вектором . Момент обусловлен возникновением пары сил , действующих на ось гироскопа со стороны подставки.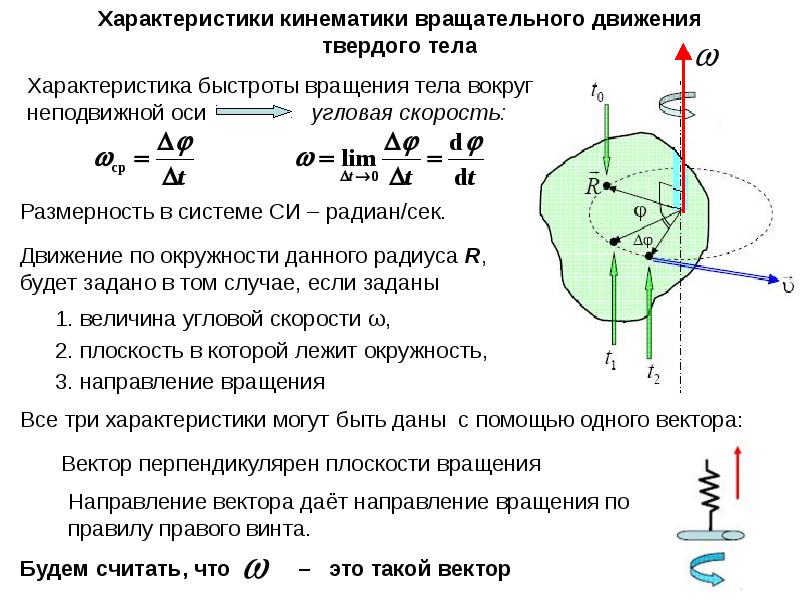 Ось гироскопа, в свою очередь, в соответствии с 3-им законом Ньютона будет действовать на подставку с силами . Эти силы называются гироскопическими. Они создают гироскопический момент . Появление гироскопических сил называют гироскопическим эффектом.
Ось гироскопа, в свою очередь, в соответствии с 3-им законом Ньютона будет действовать на подставку с силами . Эти силы называются гироскопическими. Они создают гироскопический момент . Появление гироскопических сил называют гироскопическим эффектом.
Замечание: в узком смысле гироскопическим эффектом иногда называют движение волчка не в сторону действия силы, а перпендикулярно к ней.
Примеры возникновения гироскопического эффекта: гироскопическое давление на подшипники у роторов турбин, компрессоров на кораблях, самолётах при поворотах, виражах.
Гироскопы являются основными узлами в гирокомпасах, в которых используется свойство гироскопов с тремя степенями свободы: его ось стремится устойчиво сохранить в мировом пространстве приданное ей первоначальное направление. Если ось направить на какую-либо звезду, то при любых перемещениях прибора и случайных толчках она будет указывать на эту звезду.
Вопросы для самоконтроля
1. Какое движение называется вращательным?
Какое движение называется вращательным?
2. Как определяют угловую скорость и угловое ускорение?
3. Что является мерой инертности при вращательном движении?
4. Дайте определение момента инерции материальной точки и момента инерции твёрдого тела.
5. Как вычисляют моменты инерции для сплошного цилиндра и тонкого стержня?
6. Сформулируйте теорему Штейнера.
7. Что называется свободной осью? Какие оси называют главными осями инерции?
8. Дайте определения момента силы и момента импульса материальной точки относительно некоторой точки.
9. Как связан момент импульса с моментом инерции и угловой скоростью?
Если Вам понравилась эта лекция, то понравится и эта — Специфические особенности личности учителя и воспитателя.
10. Выведите уравнение моментов.
11. Запишите уравнение динамики вращательного движения относительно оси .
12. Что называется гироскопом?
13. Что такое прецессия? От чего зависит скорость прецессии?
14. Что называется гироскопическим эффектом?
Что называется гироскопическим эффектом?
Связь между векторами угловой и линейной скоростей точки
Связь между векторами угловой и линейной скоростей точки [c.159]Связь между линейными и угловыми величинами. Найдем скорость v произвольной точки А твердого тела, вращающегося вокруг неподвижной оси 00 с угловой скоростью (О. Пусть положение точки А относительно некоторой точки О оси вращения характеризуется радиусом-вектором г (рис. 1.8). Воспользуемся формулой (1.11), поделив ее на соответствующий промежуток времени dif. Так как dr/d/ = v и d
[c.20]
Эта формула дает связь между сигналом s° датчика линейного ускорения точки А. и приведенным ускорением в° = в —g точки О, а также вектором и угловой скорости тела. [c.174]
Путь, пройденный точкой за один период по окружности радиуса Я, равен 2пЯ, а угол поворота радиус-вектора точки за тот же промежуток времени равен 2л рад, т. е. 2л/ =оГ и 2п (оТ. Отсюда находим связь между линейной и угловой скоростью
[c.32]
е. 2л/ =оГ и 2п (оТ. Отсюда находим связь между линейной и угловой скоростью
[c.32]
Для кинематического описания вращательного движения абсолютно твердого тела вокруг какой-то неподвижной оси используются те луравнения связи между ними), что и для описания движения точки по окружности угловая координата какой-либо точки тела (ф), угол поворота радиус-вектора г точки тела (Аф), средняя и мгновенная угловые скорости ( .р и со), линейные скорости различных точек тела (v). Промежуток времени Т, в течение которого тело совершает один полный оборот вокруг оси, называется периодом враш,ения, а величина V, обратная периоду,— частотой вращения. [c.35]
В заключение выпишем формулы, связывающие модули линейных и угловых скоростей и ускорений. Они вытекают из соотношения AS = RA
длиной дуги Д5, углом А(р и радиусом R окружности (модулем радиуса-вектора Л точки) (рис. 7 а). Разделив обе части равенства на At и переходя к пределу при At—>0, получим соотношение между модулями линейной и угловой скоростей v = Ra, а продифференцировав еще раз по времени, найдем связь между ускорениями а. = Л/3 (подчеркнем, что слева стоит не полное, а тангенциальное ускорение а. = dvjdt). Выразим также центростремительное ускорение через угловую скорость = v /R = a R в векторной форме
[c.25]
= Л/3 (подчеркнем, что слева стоит не полное, а тангенциальное ускорение а. = dvjdt). Выразим также центростремительное ускорение через угловую скорость = v /R = a R в векторной форме
[c.25]
Равномерное движение по прямой и вращение по окружности. Связь угловой и линейной скорости
Раздел физики, который изучает движение тел по различным траекториям, называется кинематикой. Практически полезными типами перемещения объектов являются движение по прямой и по окружности. Рассмотрим в статье, что представляют собой эти типы движения, какими формулами они описываются, а также приведем связь угловой и линейной скорости.
Движение по прямой
Связь угловой и линейной скорости можно определить, если знать, о каких величинах идет речь. Начнем со скорости линейной.
Со школьной скамьи каждый знает, что перемещение объектов в пространстве характеризуется тремя главными величинами:
- пройденный путь S;
- время движения t;
- скорость v.

Формула, связывающая в единое равенство названные величины, приведена ниже:
S = v * t.
Приведенное выражение описывает равномерное движение тела по прямой линии. В международной системе единиц СИ величина S измеряется в метрах (м), t — в секундах (с), v — в метрах в секунду (м/с). Помимо названных единиц, путь и время могут измеряться в километрах (км) и часах (ч), соответственно. Тогда скорость будет выражаться в километрах в час (км/ч).
Записанная формула может применяться для решения широкого круга практических задач, например, движение транспортных средств по дорогам, движение кораблей и лодок по рекам, полет птиц и так далее.
Движение по окружности
Перед тем как перейти к выводу формулы связи линейной и угловой скорости, следует рассмотреть последнюю с точки зрения физики.
Угловая скорость появляется в физике, когда речь идет о вращающихся объектах. Примерами могут быть вращение колеса велосипеда, маховика автомобиля или планеты вокруг своей звезды. Угловая скорость тела показывает, на какой угол в радианах оно поворачивается за единицу времени. Обычно эту величину обозначают греческой буквой ω (омега). Она измеряется в радианах в секунду (рад/с).
Угловая скорость тела показывает, на какой угол в радианах оно поворачивается за единицу времени. Обычно эту величину обозначают греческой буквой ω (омега). Она измеряется в радианах в секунду (рад/с).
По аналогии с линейным случаем можно назвать три главных величины, которые описывают движение по окружности с постоянной скоростью угловой:
- угол поворота θ;
- время t;
- угловая скорость ω.
Соответствующая формула, которая связывает эти величины, выглядит так:
θ = ω * t.
Угол поворота тела θ вокруг оси вращения измеряется в радианах. Напомним, что окружность имеет 2 * pi радиан (около 6,28). Если полученное по формуле значение θ оказалось больше, чем 2 * pi, то это означает, что тело сделало больше одного оборота вокруг оси.
Таким образом, записанное выражение позволяет рассчитать число оборотов, совершаемых телом за известный промежуток времени t.
Связь угловой и линейной скорости
Теперь можно рассмотреть этот вопрос.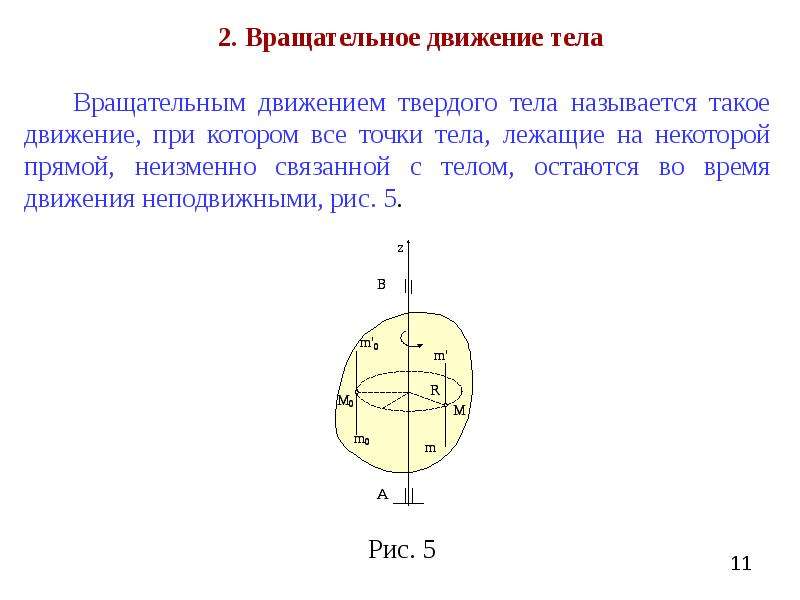 Предположим, что тело, имеющее линейную скорость v, вращается по окружности радиусом R. Чтобы получить между линейной и угловой скоростью связь, рассмотрим, какое время понадобится телу, чтобы сделать полный один оборот. Поскольку пройденный путь будет равен длине окружности, то следующее выражение будет справедливым:
Предположим, что тело, имеющее линейную скорость v, вращается по окружности радиусом R. Чтобы получить между линейной и угловой скоростью связь, рассмотрим, какое время понадобится телу, чтобы сделать полный один оборот. Поскольку пройденный путь будет равен длине окружности, то следующее выражение будет справедливым:
t = S/v = 2 * pi * R/v.
Теперь воспользуемся угловыми величинами. За найденное время одного оборота t, тело повернется точно на 2 * pi радиан. Последнее означает, что его угловая скорость будет равна:
ω = θ/t = 2 * pi/t.
Подставим рассчитанное выше время t и получим между угловой и линейной скоростью связь:
ω = 2 * pi/t = 2 * pi/(2 * pi * R/v) = v/R.
Полученную формулу можно записать в двух видах:
ω = v/R;
v = ω * R.
Каждое из выражений применяется в зависимости от того, какая величина в условии задачи известна. Формулы позволяют сделать важный вывод: чем больше радиус орбиты вращение, тем больше будет линейная скорость при постоянной угловой скорости.
Формулы позволяют сделать важный вывод: чем больше радиус орбиты вращение, тем больше будет линейная скорость при постоянной угловой скорости.
Далее решим интересную задачу на применение полученных формул.
Что быстрее — Земля или Марс?
Известно, что Земля и Марс являются 3-й и 4-й планетами Солнечной системы, соответственно. Обе планеты движутся приблизительно по круглым орбитам. Расстояние от нашей звезды до Земли равно 149 597 870,691 км, а один оборот вокруг нее она делает за 365,256 дней. Марс расположен от Солнца на расстоянии 227 936 640 км, и один оборот вокруг него делает за 686,971 земных дня. Необходимо определить и сравнить линейные скорости планет.
Угловая скорость планеты может быть рассчитана по формуле:
ω = 2 * pi/T.
Где T — период (время совершения одного оборота вокруг звезды). Подставляя ω в формулу для v, получаем:
v = 2 * pi * R/T.
Переведем время оборота планет в часы и подставим данные в это равенство, получим:
- для Земли: v = 2 * 3,14 * 149597870,691/(365,256 * 24) ≈ 107,2 тыс.
 км/ч;
км/ч; - для Марса: v = 2 * 3,14 * 227936640/(686,971 * 24) ≈ 86,8 тыс. км/ч.
Обе цифры являются огромными. Так, Земля за один час пролетает в космосе расстояние, практически равное трем ее окружностям по экватору. Полученные скорости свидетельствуют, что Земля движется быстрее Марса, и ее скорость на 24 % больше марсианской.
Вращательное движение твердых тел — Наука и образование
Простейшие движения твёрдого тела – поступательное и вращательное. С поступательным движением мы уже ознакомились в первой части курса.
Вращательное движение твёрдых тел весьма распространено в природе и технике. Например: движение Земли вокруг своей оси, движение шкивов, маховых колёс и обтачиваемых на токарных станках деталей, движение граммофонной пластинки и т. п.
На рисунке стрелками показано вращательное движение детали на токарном станке и поступательное движение резца.
Любое движение твёрдого тела может быть представлено как результат поступательного и вращательного движений. Особенно хорошо это видно на примере винтового движения. Болт, например, ввинчиваясь в гайку, движется поступательно и одновременно вращается. Сверло при работе также одновременно вращается и движется поступательно. Колесо повозки, вращаясь вокруг оси, одновременно вместе с повозкой движется поступательно. Таких примеров можно привести сколько угодно.
Особенно хорошо это видно на примере винтового движения. Болт, например, ввинчиваясь в гайку, движется поступательно и одновременно вращается. Сверло при работе также одновременно вращается и движется поступательно. Колесо повозки, вращаясь вокруг оси, одновременно вместе с повозкой движется поступательно. Таких примеров можно привести сколько угодно.
Возьмём картонный диск с нарисованными на нём кружочками на разных расстояниях от центра и приведём его в быстрое вращение – мы увидим ряд окружностей разных радиусов. Этот опыт показывает, что при вращательном движении тела различные его точки движутся по окружностям; центры этих окружностей лежат на прямой, называемой осью вращения. Угол поворота радиусов окружностей за данный промежуток времени для всех точек тела одинаков. Поэтому углом поворота радиуса окружности одной какой-нибудь точки тела за данный промежуток времени можно характеризовать движение всех точек тела, т. е. вращение тела в целом. Но угол поворота в 1 сек численно равен угловой скорости. Следовательно, угловая скорость у всех точек вращающегося тела одна и та же.
Следовательно, угловая скорость у всех точек вращающегося тела одна и та же.
При повороте колеса на угол ? разные точки колеса: А, А1, А2 – описывают разные по длине дуги: АВ, А1В1, А2В2; чем точка дальше от оси вращения, тем описываемая ею дуга больше, тем больше линейная скорость. Итак, при вращении тела разные его точки движутся с одинаковой угловой скоростью, но с разными линейными скоростями.
Формула, выражающая связь между угловой и линейной скоростями, дана в статье о линейной скорости.
Кинематика вращательного движения Характеристики кинематики вращательного движения
Кинематика вращательного движения
Характеристики кинематики вращательного движения твердого тела Точки тела находятся на разном расстоянии R от оси вращения их скорость разная. Рассмотрим вращательное движение абсолютно твердого тела относительно неподвижной оси вращения. Абсолютно твердое тело – тело, деформациями которого можно пренебречь в условиях данной задачи. Положение такого тела при вращении вокруг неподвижной оси можно охарактеризовать скалярной величиной – угловой координатой φ За время Δt = t 2 – t 1 угол поворота Δφ = φ2 – φ1 За время dt — dφ.
Абсолютно твердое тело – тело, деформациями которого можно пренебречь в условиях данной задачи. Положение такого тела при вращении вокруг неподвижной оси можно охарактеризовать скалярной величиной – угловой координатой φ За время Δt = t 2 – t 1 угол поворота Δφ = φ2 – φ1 За время dt — dφ.
Характеристики кинематики вращательного движения твердого тела Характеристика быстроты вращения тела вокруг неподвижной оси угловая скорость: Размерность в системе СИ – радиан/сек или 1/сек. Движение по окружности данного радиуса R, будет задано в том случае, если заданы 1. величина угловой скорости ω, 2. плоскость в которой лежит окружность, 3. направление вращения Все три характеристики могут быть даны с помощью одного вектора: Вектор перпендикулярен плоскости вращения Направление вектора даёт направление вращения по правилу правого винта. Будем считать, что – это такой вектор
Характеристики кинематики вращательного движения твердого тела При вращении с постоянной угловой скоростью полный оборот совершается за время Т – период обращения. Величина обратная периоду – число оборотов в единицу времени: Т и можно рассматривать и как характеристики движения с переменной угловой скоростью. Тогда они будут характеризовать вращение в данный момент времени. Пример: изменение скорости вращения ротора, двигателя и т. п. характеризуют изменением числа оборотов (а не изменением угловой скорости).
Величина обратная периоду – число оборотов в единицу времени: Т и можно рассматривать и как характеристики движения с переменной угловой скоростью. Тогда они будут характеризовать вращение в данный момент времени. Пример: изменение скорости вращения ротора, двигателя и т. п. характеризуют изменением числа оборотов (а не изменением угловой скорости).
Характеристики кинематики вращательного движения твердого тела Угловое ускорение — характеристика быстроты изменения угловой скорости При неподвижной оси вращения и совпадают по направлению в случае ускоренного вращательного движения. В случае замедленного вращательного движения и — противоположны.
Связь угловых и линейных величин Путь, пройденный точкой при движении по окружности: Связь между модулями линейной скорости точки тела и угловой скоростью: Связь между модулями тангенциального ускорения точки тела и углового ускорения: . Связь между модулем нормального ускорения точки тела и модулем угловой скорости:
Связь угловых и линейных величин Связь между линейной скоростью точки тела и угловой скоростью в векторном виде: векторное произведение . правило правой руки
правило правой руки
Связь угловых и линейных величин
Угловая скорость и линейная скорость — определение, взаимосвязь и часто задаваемые вопросы
Мы знаем, что угловое смещение — это угол, наблюдаемый частицей при круговом движении. Поскольку направление смещения — вдоль оси, угловое смещение — это осевой вектор.
Частица при круговом движении проявляет два типа смещения; это:
Если «r» — радиус окружности, то соотношение между угловым и линейным смещением будет:
S = Rθ или θ = \ [\ frac {S} {r} \]….. (1)
Линейная скорость определяется как скорость изменения линейного смещения. Для частицы P она определяется выражением:
v = \ [\ frac {\ Delta S} {\ Delta t} \]…. (2)
Угловая скорость частицы — это скорость изменения углового смещения.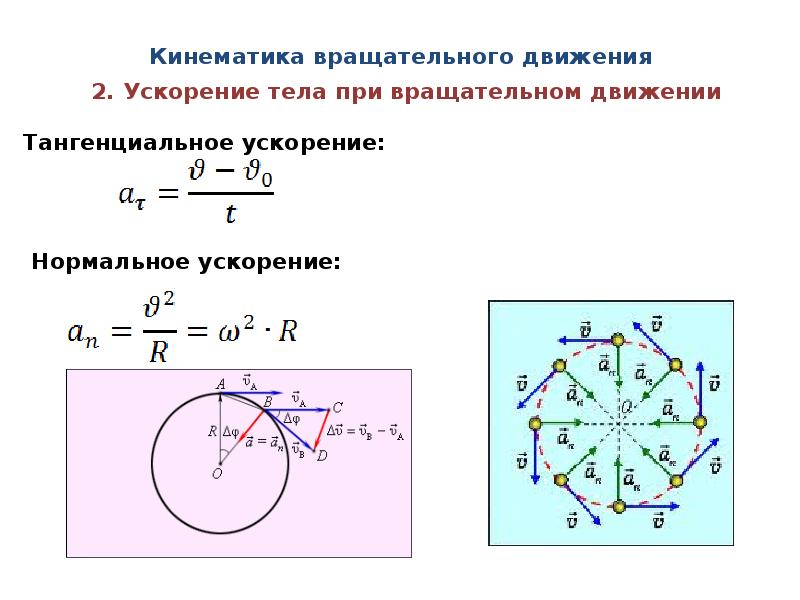 , т. е. как быстро меняется угол. Он определяется по формуле:
, т. е. как быстро меняется угол. Он определяется по формуле:
ω = \ [\ frac {\ Delta \ theta} {\ Delta t} \]… (3)
В этой статье мы выведем связь между линейной скоростью и угловой скоростью.Итак, приступим.
Связь между линейной скоростью и угловой скоростью
Мы знаем, что линейная скорость частицы P определяется выражением:
| v | = \ [\ frac {\ Delta (S)} {\ Delta t} \] и S = rθ
Теперь, подставив значение уравнения (1) в (3), мы получим:
v = \ [ \ frac {\ Delta r \ theta} {\ Delta t} \]
Мы знаем, что радиус ‘r’ является постоянным значением, поэтому получаем:
v = \ [\ frac {r \ Delta \ theta} {\ Delta t} \] (Как \ [\ frac {\ Delta \ theta} {\ Delta t} \] = ω)
⇒ | v | = rω, которое представляет собой «соотношение между линейной и угловой скоростью.
Здесь v зависит от r и ω следующим образом:
ω = скорость вращения объекта и
r = линейная скорость частицы в центре будет равна нулю. Когда частица начинает удаляться от центра, линейная скорость начинает увеличиваться. Максимум на окружности круга.
Когда частица начинает удаляться от центра, линейная скорость начинает увеличиваться. Максимум на окружности круга.
Касательная к окружности определяет направление линейной скорости.
Запомните
Согните пальцы против часовой стрелки, а большой палец, направленный наружу (вдоль оси), определяет направление угловой скорости.Точно так же, если вы согнете пальцы по часовой стрелке, большой палец, направленный внутрь, даст направление ω.
Соотношение угловой скорости и линейной скорости
Для тела, находящегося в равномерном круговом движении, соотношение между линейной и угловой скоростью составляет:
v = rω
Это уравнение утверждает, что линейная скорость (v) прямо пропорциональна расстояние частицы от центра кругового пути и ее угловая скорость.
В центре ноль.
Это минимум между центром и любой точкой на окружности.

Максимально на окружности круга. Однако угловая скорость остается неизменной во всех точках круговой траектории.
От угловой скорости к линейной
Исходя из наших знаний о круговом движении, мы можем сделать вывод, что величина линейной скорости частицы, движущейся по кругу, связана с угловой скоростью частицы следующим соотношением:
r = \ [\ frac {v} {\ omega} \]
В любой момент это соотношение применимо к каждой частице, имеющей твердое тело.
Разница между линейной скоростью и угловой скоростью
| | Линейная скорость | Угловая скорость |
Определение | Мы определяем линейную скорость как скорость изменения линейного перемещения. | Мы определяем угловую скорость как скорость изменения углового смещения. |
Ключевые различия |
| |
Символ | Символ для линейной скорости — v. | Символ угловой скорости — греческая буква, то есть ω (произносится как омега). |
Формула | v = \ [\ frac {\ Delta S} {\ Delta t} \] = \ [\ frac {2 \ pi r} {t} \] | ω = \ [\ frac {\ Delta \ theta} {\ Delta t} \] = \ [\ frac {2 \ pi r} {t} \] |
Количество | Это векторная величина это означает, что он имеет как величину, так и направление. | Это осевой вектор. Это потому, что направление смещения частицы находится вдоль оси круга. |
Измерительный блок | Мы измеряем линейную скорость в м / с. | Мы измеряем угловую скорость как в градусах, так и в радианах. Градус — безразмерная единица. Радиан — это единица СИ. |
Пример из реальной жизни | Если ваш офис находится на расстоянии 150 км от дома, ваша машина приобретет линейную скорость.{\правая стрелка }\]. Это потому, что v действует на окружность круга, а ω — вдоль оси. Чтобы векторы двух величин были равны, их направления должны быть одинаковыми. Здесь мы видим, что направления v и ω не равны; вот почему правильный способ записать соотношение: v = rω Угол поворота и угловая скорость — College PhysicsЦели обучения
В области кинематики мы изучали движение по прямой и ввели такие понятия, как смещение, скорость и ускорение. Двумерная кинематика имеет дело с движением в двух измерениях. Движение снаряда — это частный случай двумерной кинематики, в котором объект проецируется в воздух, находясь под действием силы тяжести, и приземляется на некотором расстоянии. В этой главе мы рассматриваем ситуации, когда объект не приземляется, а движется по кривой.Мы начинаем изучение равномерного кругового движения с определения двух угловых величин, необходимых для описания вращательного движения. Угловая скоростьНасколько быстро вращается объект? Мы определяем угловую скорость как скорость изменения угла. В символах это ., где угловое вращение происходит во времени. Чем больше угол поворота за заданный промежуток времени, тем больше угловая скорость. Единицы измерения угловой скорости — радианы в секунду (рад / с). Угловая скорость аналогична линейной скорости. Чтобы получить точное соотношение между угловой и линейной скоростью, мы снова рассмотрим ямку на вращающемся CD. Эта яма перемещается на длину дуги за время и поэтому имеет линейную скорость .Из этого мы видим. Подставляя это в выражение для дает Мы записываем эту взаимосвязь двумя разными способами и получаем два разных вывода: Первое соотношение в утверждает, что линейная скорость пропорциональна расстоянию от центра вращения, таким образом, она самая большая для точки на ободе (самая большая), как и следовало ожидать.Мы также можем назвать эту линейную скорость точки на ободе тангенциальной скоростью . Вторую взаимосвязь можно проиллюстрировать на примере шины движущегося автомобиля. Обратите внимание, что скорость точки на ободе шины такая же, как и скорость автомобиля. См. (Рисунок). Таким образом, чем быстрее движется машина, тем быстрее вращается шина — большой — значит большой, потому что. Точно так же шина большего радиуса, вращающаяся с той же угловой скоростью (), будет создавать для автомобиля большую линейную скорость (). Оба и имеют направления (следовательно, это угловые и линейные скорости , соответственно). Угловая скорость имеет только два направления относительно оси вращения — либо по часовой стрелке, либо против часовой стрелки. Линейная скорость касается пути, как показано на (Рисунок). Take-Home Experiment Привяжите какой-либо предмет к концу веревки и поверните его по горизонтальному кругу над головой (взмахнув запястьем). Поддерживайте постоянную скорость при качании объекта и измеряйте угловую скорость движения.Какая примерная скорость объекта? Определите точку рядом с вашей рукой и выполните соответствующие измерения, чтобы рассчитать линейную скорость в этой точке. Определите другие круговые движения и измерьте их угловые скорости. Когда объект движется по кругу, здесь муха на краю старомодной виниловой пластинки, его мгновенная скорость всегда касается круга. Направление угловой скорости в этом случае — по часовой стрелке. Исследования PhET: революция божьей коровки Присоединяйтесь к божьей коровке и исследуйте вращательное движение.Вращайте карусель, чтобы изменить ее угол, или выберите постоянную угловую скорость или угловое ускорение. Изучите, как круговое движение соотносится с координатами x, y, скоростью и ускорением жука, используя векторы или графики. Концептуальные вопросыСуществует аналогия между вращательными и линейными физическими величинами. Какие вращательные величины аналогичны расстоянию и скорости? Проблемные упражненияПолуприцепы имеют одометр на одной ступице колеса прицепа.Ступица утяжелена, поэтому она не вращается, но в ней есть шестерни для подсчета количества оборотов колеса — затем она вычисляет пройденное расстояние. Если колесо имеет диаметр 1,15 м и совершает 200 000 оборотов, сколько километров должен показывать одометр? Микроволновые печи вращаются со скоростью около 6 об / мин. Что это в оборотах в секунду? Какова угловая скорость в радианах в секунду? Автомобиль с шинами радиусом 0,260 м проезжает 80 000 км до износа.Сколько оборотов делают шины без учета поддержки и любого изменения радиуса из-за износа? а) Каков период вращения Земли в секундах? б) Какова угловая скорость Земли? (c) Учитывая, что Земля имеет радиус на экваторе, какова линейная скорость у поверхности Земли? Бейсбольный питчер вытягивает руку вперед во время подачи, поворачивая предплечье вокруг локтя. Если скорость мяча в руке питчера 35.0 м / с и мяч находится на расстоянии 0,300 м от локтевого сустава, какова угловая скорость предплечья? В лакроссе мяч выбрасывается из сетки на конец клюшки путем вращения клюшки и предплечья вокруг локтя. Если угловая скорость мяча относительно локтевого сустава составляет 30,0 рад / с, а мяч находится на 1,30 м от локтевого сустава, какова скорость мяча? Грузовик с шинами радиусом 0,420 м движется со скоростью 32,0 м / с. Какова угловая скорость вращающихся шин в радианах в секунду? Что это в об / мин? Integrated Concepts При ударе по футбольному мячу игрок, выполняющий удар, вращает ногой вокруг тазобедренного сустава. (a) Если скорость кончика ботинка кикера составляет 35,0 м / с, а тазобедренный сустав находится на расстоянии 1,05 м от кончика ботинка, какова угловая скорость кончика ботинка? (b) Башмак находится в контакте с первоначально неподвижным футбольным мячом весом 0,500 кг в течение 20,0 мс. Какая средняя сила прилагается к футбольному мячу, чтобы придать ему скорость 20,0 м / с? (c) Найдите максимальную дальность полета футбольного мяча, не обращая внимания на сопротивление воздуха. (а) 33,3 рад / с б 500 Н (в) 40.8 м Создайте свою проблему Рассмотрим аттракцион в парке развлечений, в котором участники вращаются вокруг вертикальной оси в цилиндре с вертикальными стенками. Как только угловая скорость достигает своего полного значения, пол опускается, и трение между стенами и пассажирами препятствует их скольжению. Постройте задачу, в которой вы вычисляете необходимую угловую скорость, которая гарантирует, что всадники не соскользнут со стены. Включите свободную диаграмму тела одного всадника.Среди переменных, которые следует учитывать, — радиус цилиндра и коэффициенты трения между одеждой гонщика и стеной. Глоссарий
6.1: Угол поворота и угловая скоростьЦели обучения К концу этого раздела вы сможете:
В области кинематики мы изучали движение по прямой и ввели такие понятия, как смещение, скорость и ускорение. Двумерная кинематика имеет дело с движением в двух измерениях.Движение снаряда — это частный случай двумерной кинематики, в котором объект проецируется в воздух, находясь под действием силы тяжести, и приземляется на некотором расстоянии. В этой главе мы рассматриваем ситуации, когда объект не приземляется, а движется по кривой. Мы начинаем изучение равномерного кругового движения с определения двух угловых величин, необходимых для описания вращательного движения. Угол поворотаКогда объекты вращаются вокруг некоторой оси — например, когда компакт-диск (компакт-диск) на рисунке вращается вокруг своего центра — каждая точка в объекте движется по дуге окружности.Рассмотрим линию от центра компакт-диска до его края. Каждая яма, используемая для записи звука вдоль этой линии, перемещается под одним и тем же углом за одно и то же время. Угол поворота — это величина поворота, аналогичная линейному расстоянию. Угол поворота \ (\ Delta \ theta \) определяется как отношение длины дуги к радиусу кривизны: \ [\ Delta \ theta = \ dfrac {\ Delta s} {r}. \] Рисунок \ (\ PageIndex {1} \): Все точки на компакт-диске движутся по дугам окружности. Ямы вдоль линии от центра к краю все перемещаются на один и тот же угол \ (\ Delta \ theta \) за время \ (\ Delta t \).Рисунок \ (\ PageIndex {2} \): Радиус круга повернут на угол \ (\ Delta \ theta \). Длина дуги \ (\ delta s \) описывается на окружности.Длина дуги \ (\ Delta s \) — это расстояние, пройденное по круговой траектории, как показано на рисунке. Обратите внимание, что это радиус кривизны круговой траектории. Мы знаем, что за один полный оборот длина дуги равна длине окружности радиуса \ (r \). Окружность круга равна \ (2 \ pi r \). Таким образом, за один полный оборот угол поворота равен \ [\ Delta \ theta = \ dfrac {2 \ pi r} {r} = 2 \ pi.\] Этот результат является основой для определения единиц, используемых для измерения углов поворота, \ (\ Delta \ theta \) равными радианам (рад), таким образом, что \ [2 \ pi \, радианы = 1 \ космический оборот. о \) | \ (\ dfrac {3 \ pi} {4} \) |
| \ (180 ° о \) | \ (\ pi \) |
Угловая скорость
Насколько быстро вращается объект? Мы определяем угловую скорость \ (\ omega \) как скорость изменения угла. В символах это
.\ [\ omega = \ dfrac {\ Delta \ theta} {\ Delta t}, \]
, где угловое вращение \ (\ Delta \ theta \) происходит за время \ (\ Delta t \). Чем больше угол поворота за заданный промежуток времени, тем больше угловая скорость. Единицы измерения угловой скорости — радианы в секунду (рад / с). Угловая скорость \ (\ omega \) аналогична линейной скорости \ (v \).Чтобы получить точное соотношение между угловой и линейной скоростью, мы снова рассмотрим ямку на вращающемся CD. Эта яма перемещается на длину дуги \ (\ Delta s \) за время \ (\ Delta t \), поэтому она имеет линейную скорость
.\ [v = \ dfrac {\ Delta s} {\ Delta t}. \]
Из \ (\ Delta \ theta = \ frac {\ Delta s} {r} \) мы видим, что \ (\ Delta s = r \ Delta \ theta \). Подставляя это в выражение для \ (v \), получаем
\ [v = \ dfrac {r \ Delta \ theta} {\ Delta t} = r \ omega. \]
Мы записываем эту взаимосвязь двумя разными способами и получаем два разных вывода:
\ [v = r \ omega, \ или \, \ omega = \ dfrac {v} {r}.\]
Первое соотношение в \ (v = r \ omega, \ или \, \ omega = \ dfrac {v} {r} \) утверждает, что линейная скорость \ (v \) пропорциональна расстоянию от центра вращение, таким образом, оно является наибольшим для точки на ободе (наибольшее значение \ (r \)), как и следовало ожидать. Мы также можем назвать эту линейную скорость \ (v \) точки на ободе тангенциальной скоростью . Второе соотношение в \ (v = r \ omega, \ или \, \ omega = \ dfrac {v} {r} \) можно проиллюстрировать на примере шины движущегося автомобиля.Обратите внимание, что скорость точки на ободе шины такая же, как скорость \ (v \) автомобиля. См. Рисунок. Таким образом, чем быстрее движется машина, тем быстрее вращается шина — большой \ (v \) означает большой \ (\ omega \), потому что \ (v = r \ omega \). Точно так же шина большего радиуса, вращающаяся с той же угловой скоростью \ ((\ omega) \), создаст большую линейную скорость \ ((v) \) для автомобиля.
Рисунок \ (\ PageIndex {4} \): Автомобиль, движущийся со скоростью \ (v \) вправо, имеет шину, вращающуюся с угловой скоростью \ (\ omega \).Скорость протектора шины относительно оси равна \ (v \), как если бы автомобиль был поднят домкратом. Таким образом, автомобиль движется вперед с линейной скоростью \ (v = r \ omega \), где \ (r \) — радиус шины. Чем больше угловая скорость шины, тем больше скорость автомобиля.Пример \ (\ PageIndex {1} \): Как быстро вращается автомобильная шина?
Рассчитайте угловую скорость автомобильной шины радиусом 0,300 м, когда автомобиль движется со скоростью \ (15,0 м / с \) (примерно \ (54 \, км / ч \)). См. Рисунок.
Стратегия
Поскольку линейная скорость обода шины такая же, как и скорость автомобиля, мы имеем \ (v = 15.0 м / с \). Радиус шины равен \ (r = 0,300 \, м \). Зная \ (v \) и \ (r \), мы можем использовать второе соотношение в \ (v = \ omega r \), \ (\ omega = \ frac {v} {r} \) для вычисления угловой скорости .
Решение
Для вычисления угловой скорости воспользуемся следующим соотношением:
\ [\ omega = \ dfrac {v} {r}. \]
Замена известных,
\ [\ omega = \ dfrac {15,0 \, м / с} {0,300 \, м} = 50,0 \, рад / с. \]
Обсуждение
Когда мы отменяем единицы в приведенном выше вычислении, мы получаем 50.0 / с. Но угловая скорость должна иметь единицы рад / с. Поскольку радианы на самом деле безразмерны (радианы определяются как отношение расстояний), мы можем просто вставить их в ответ для угловой скорости. Также обратите внимание, что если бы землерой с гораздо большими шинами, скажем, радиусом 1,20 м, двигался с той же скоростью 15,0 м / с, его шины вращались бы медленнее. У них была бы угловая скорость
.\ [\ omega = (15,0 \, м / с) / (1,20 \, м) = 12,5 \, рад / с. \]
И \ (\ omega \), и \ (v \) имеют направления (следовательно, это угловая и линейная скорости соответственно).Угловая скорость имеет только два направления относительно оси вращения — либо по часовой стрелке, либо против часовой стрелки. Линейная скорость касается пути, как показано на рисунке.
ЭКСПЕРИМЕНТ НА ДОМУ
Привяжите какой-либо предмет к концу веревки и поверните его по горизонтальному кругу над головой (взмахнув запястьем). Поддерживайте постоянную скорость при качании объекта и измеряйте угловую скорость движения. Какая примерная скорость объекта? Определите точку рядом с вашей рукой и выполните соответствующие измерения, чтобы рассчитать линейную скорость в этой точке.Определите другие круговые движения и измерьте их угловые скорости.
Рисунок \ (\ PageIndex {5} \): Когда объект движется по кругу, здесь муха на краю старомодной виниловой пластинки, его мгновенная скорость всегда касается круга. Направление угловой скорости в этом случае — по часовой стрелке.PHET EXPLORATIONS: LADYBUG REVOLUTION
Присоединяйтесь к божьей коровке и исследуйте вращательное движение. Вращайте карусель, чтобы изменить ее угол, или выберите постоянную угловую скорость или угловое ускорение.Изучите, как круговое движение связано с координатами x, y, скоростью и ускорением жука, используя векторы или графики.
Сводка раздела
- Равномерное круговое движение — это движение по окружности с постоянной скоростью. Угол поворота \ (\ delta \ theta \) определяется как отношение длины дуги к радиусу кривизны:
\ [\ Delta \ theta = \ dfrac {\ Delta s} {r} \]
, где длина дуги \ (\ delta s \) — это расстояние, пройденное по круговой траектории, а \ (r \) — радиус кривизны круговой траектории.о. \]
\ [\ omega = \ dfrac {\ Delta \ theta} {\ Delta t}, \]
, где вращение \ (\ Delta \ theta \) происходит за время \ (\ Delta t \). Единицы угловой скорости — радианы в секунду (рад / с). Линейная скорость \ (v \) и угловая скорость \ (\ omega \) связаны соотношением
\ [v = r \ omega, \ или \, \ omega = \ dfrac {v} {r}. \]
Глоссарий
- длина дуги
- Δs, расстояние, пройденное объектом по круговой траектории
- приямок
- крошечная выемка на спиральной дорожке, отформованной в верхней части слоя поликарбоната CD
- угол поворота
- отношение длины дуги к радиусу кривизны на круговой траектории: \ (Δθ = \ frac {Δs} {r} \)
- радиус кривизны
- радиус круговой траектории
- радиан
- единица измерения углов
- угловая скорость
- \ (ω \), скорость изменения угла, под которым объект движется по круговой траектории
Авторы и авторство
Пол Питер Урон (почетный профессор Калифорнийского государственного университета, Сакраменто) и Роджер Хинрикс (Государственный университет Нью-Йорка, колледж в Освего) с участвующими авторами: Ким Диркс (Оклендский университет) и Манджула Шарма (Сиднейский университет).Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
5.2 Угловая скорость — Биомеханика движения человека
Насколько быстро вращается объект? Определим угловую скорость ω как скорость изменения углового смещения. В символах это
.[латекс] \ boldsymbol {\ omega \: =} \ boldsymbol {\ frac {\ Delta \ theta} {\ Delta {t}}}, [/ latex]
, где угловой поворот Δ θ происходит за время Δ t .Чем больше угол поворота за заданный промежуток времени, тем больше угловая скорость. Единицы измерения угловой скорости — градусы в секунду (º / с), радианы в секунду (рад / с) или обороты в минуту (об / мин), если применимо.
Угловая скорость — это векторная величина. Угловая скорость имеет только два направления относительно оси вращения — либо по часовой стрелке, либо против часовой стрелки.
Угловая скорость используется в биомеханике двояко. Нас интересует либо средняя угловая скорость , либо мгновенная угловая скорость .Средняя угловая скорость говорит нам, сколько времени нужно, чтобы что-то повернулось через определенное угловое смещение. Мгновенная угловая скорость говорит нам, насколько быстро что-то вращается в определенный момент времени. Средняя угловая скорость удара теннисиста может определять, касается ли она мяча или нет, но именно мгновенная скорость ракетки при контакте с мячом определяет, насколько быстро и как далеко полетит мяч. В видах спорта, где важны повороты всего тела (прыжки в воду, гимнастика), угловая скорость является важным фактором, определяющим, выполнит ли спортсмен определенное количество поворотов или сальто перед приземлением.
В некоторых видах спорта, особенно в тех, где снаряжение используется как продолжение конечностей спортсмена (гольф, теннис, лакросс …), взаимосвязь между угловой и линейной скоростью становится важной. Преимущество использования орудий заключается в том, что они усиливают движение (смещение) наших конечностей. Возьмите теннисный мяч и бросьте его как можно дальше. Теперь ударьте по тому же мячу теннисной ракеткой. Что идет дальше всего? Ракетка обеспечивает более высокие линейные скорости, поскольку они увеличивают расстояние от точки контакта (ваша рука против теннисной ракетки) до оси вращения (плечевого сустава).Здесь также важна взаимосвязь между линейными переменными, угловыми переменными и радиусом, обсуждавшаяся в предыдущем разделе.
Первое соотношение в v = r ω или ω = v / r утверждает, что линейная скорость v пропорциональна расстоянию от центра вращения, таким образом, она является наибольшей для точка, наиболее удаленная от точки вращения. Второе соотношение утверждает, что чем быстрее объект вращается ( ω ), тем выше линейная скорость точки на объекте ( v ).Обратите внимание, что для использования этого уравнения угловая скорость должна быть выражена в рад / с.
Оба [latex] \ boldsymbol {\ omega} [/ latex] и [latex] \ boldsymbol {v} [/ latex] имеют направления (следовательно, они имеют угловую и линейную скорости соответственно). Угловая скорость имеет только два направления относительно оси вращения — либо по часовой стрелке, либо против часовой стрелки. Линейная скорость касается пути.
Рис. 4. Когда объект движется по кругу, здесь муха на краю старомодной виниловой пластинки, его мгновенная скорость всегда касается круга.Направление угловой скорости в этом случае — по часовой стрелке.Подумайте о своих любимых видах спорта и об оборудовании, необходимом для занятий. Если вид спорта, о котором вы думаете, включает использование клюшек, клюшек или ракеток, вы, вероятно, уже знакомы с соотношением между линейной и угловой скоростями. Линейная скорость точки, находящейся дальше от оси вращения, выше, если угловая скорость такая же. Эта линейная скорость передается шару (или снаряду) за счет сохранения количества движения, что будет обсуждаться позже.Например, в гольфе у нас есть два типа клюшек: клюшки и клюшки. Древесина — самые длинные клюшки, которые используются для придания мячу большей скорости, когда игрок ведёт мяч как можно дальше. Утюги — это более короткие дубинки, используемые для более близких ударов.
Вы не всегда можете переключаться между длинным и более коротким орудием, чтобы повлиять на линейную скорость снаряда, но вы также можете изменить ось вращения, чтобы уменьшить радиус. Скажем, взмах обычно начинается в плече.Вращаясь вокруг запястья, вы сокращаете радиус.
Возможно, вы также могли бы переместить рукоятку предмета, чтобы уменьшить или удлинить радиус. Это обычно наблюдается в бейсболе, когда игроки захлебываются битой.
Honors Rotational Kinematics
Радианы и градусы
Обычно люди обсуждают вращательное движение в градусах, где один полный оборот по окружности равен 360 °. Когда речь идет о вращательном движении с точки зрения физики, измерение вращательного движения в единицах, известных как радианы (рад), является гораздо более эффективным.Радиан измеряет расстояние вокруг дуги, равное длине радиуса дуги.
До этого момента вы описывали расстояния и смещения в терминах Δx и Δy. Обсуждая угловые смещения, вы должны перейти к описанию поступательного смещения вокруг дуги в терминах переменной s, продолжая использовать символ θ (тета) для обозначения углов и углового смещения.
Расстояние полностью по круговой траектории (360 °), известное как окружность, C, можно найти с помощью ∆s = C = 2𝜋r = 2𝜋 радиан.Следовательно, вы можете использовать это как коэффициент преобразования для перехода между градусами и радианами.
Вопрос: Преобразовать 90 ° в радианы.
Ответ:
Вопрос: Преобразуйте 6 радианов в градусы.
Ответ:
Углы также измеряются в оборотах (полные обходы по кругу). Полный единичный оборот равен 360 °, поэтому вы можете записать коэффициенты преобразования для углов поворота и смещений как 360 ° = 2𝜋 радиан = 1 оборот.
Вопрос: Преобразуйте 1,5 оборота в радианы и градусы.
Ответ:
Скорость и ускорение
Вращательная кинематика очень похожа на поступательную кинематику, все, что вам нужно сделать, это изучить вращательные версии кинематических переменных и уравнений. Когда вы изучали кинематику перевода, смещение обсуждалось в терминах Δx.При вращательной кинематике вместо этого вы будете использовать угловую координату θ. Когда в трансляционном мире была введена средняя скорость, вы использовали формулу:
При изучении вращательного движения вы будете говорить об угловой скорости ω (омега), выраженной в радианах в секунду (рад / с). Поскольку угловая (вращательная) скорость является вектором, определите положительное направление вращения как вращение против часовой стрелки по круговой траектории, а отрицательное направление как по часовой стрелке вокруг траектории.
ПРИМЕЧАНИЕ: Формально направление угловых векторов определяется правилом правой руки. Оберните пальцы правой руки в направлении вращения, скорости или ускорения, а большой палец будет указывать в направлении вектора.
Вопрос: Рекорд вращается на фонографе со скоростью 33 об / мин (оборотов в минуту) по часовой стрелке.Найдите угловую скорость записи.
Ответ:
Обратите внимание, что вектор угловой скорости отрицательный, потому что запись вращается по часовой стрелке.
Вопрос: Найдите величину угловой скорости Земли в радианах в секунду.
Ответ: Осознавая, что Земля совершает один полный оборот каждые 24 часа, мы можем оценить величину угловой скорости Земли как:
Аналогичным образом, когда вы узнали о поступательном ускорении, вы нашли ускорение как скорость изменения поступательной скорости объекта:
Угловое ускорение α (альфа), выраженное в радианах в секунду 2 , представляет собой скорость изменения угловой скорости объекта.Поскольку угловое ускорение также является вектором, вы можете определить его направление как положительное для увеличения угловой скорости в направлении против часовой стрелки и отрицательное для увеличения угловой скорости в направлении по часовой стрелке.
Вопрос: Лягушка едет на одноколесном велосипеде. Если колесо моноцикла начинается в состоянии покоя и равномерно ускоряется против часовой стрелки до угловой скорости 15 об / мин за 6 секунд, найдите угловое ускорение колеса моноцикла.
Ответ: Сначала преобразуйте 15 об / мин в рад / с.
Затем используйте определение углового ускорения.
Снова обратите внимание на положительное угловое ускорение, поскольку колесо велосипеда ускоряется против часовой стрелки.
Вращательные переменные
Объединяя эти определения, вы наблюдаете очень сильную параллель между поступательными кинематическими величинами и вращательными кинематическими величинами.
| Переменная | Трансляционный | Угловой |
|---|---|---|
| Рабочий объем | Δs | Δθ |
| Скорость | в | ω |
| Разгон | а | α |
| Время | т | т |
Также довольно просто выполнить перевод между поступательными и угловыми переменными, если вы знаете радиус (r) интересующей точки на вращающемся объекте.
Вопрос: Рыцарь взмахивает булавой радиусом 1 м за два полных оборота. Что такое поступательное смещение булавы?
Ответ:
Вопрос: Проигрыватель компакт-дисков предназначен для изменения скорости вращения диска, так что точка, считываемая лазером, перемещается с линейной скоростью, равной единице.25 м / с. Какова скорость вращения компакт-диска в оборотах / с, когда лазер считывает информацию с внутренней части диска на радиусе 0,03 м?
Ответ:
Вопрос: Какова скорость вращения компакт-диска в предыдущей задаче, когда лазер считывает крайнюю часть диска (радиус = 0,06 м)?
Ответ:
Вращательные кинематические уравнения
Параллели между поступательным и вращательным движением идут еще дальше.Вы разработали набор кинематических уравнений для поступательного движения, которые позволили вам исследовать взаимосвязь между смещением, скоростью и ускорением. Вы можете разработать соответствующий набор соотношений для углового смещения, угловой скорости и углового ускорения. Уравнения имеют ту же форму, что и трансляционные уравнения, все, что вам нужно сделать, это заменить трансляционные переменные на вращательные переменные, как показано в следующей таблице.
Уравнения вращательной кинематики можно использовать так же, как вы использовали уравнения поступательной кинематики для решения задач.Когда вы знаете три кинематические переменные, вы всегда можете использовать уравнения для решения двух других.
Вопрос: Плотник вырезает кусок дерева с помощью мощной циркулярной пилы. Пильный диск ускоряется из состояния покоя с угловым ускорением от 14 рад / с 2 до максимальной скорости 15 000 об / мин. Какова максимальная скорость пилы в радианах в секунду?
Ответ:
Вопрос: Сколько времени нужно пиле для достижения максимальной скорости?
Ответ: Для решения этой задачи можно использовать уравнения кинематики вращения:
Вопрос: Сколько полных оборотов делает пила при разгоне до максимальной скорости?
Ответ:
Вопрос: Предохранительный механизм остановит пильный диск в 0.3 секунды, если рука плотника оторвется от органов управления пилой. Какое угловое ускорение для этого требуется? Сколько полных оборотов пильное полотно сделает за это время?
Ответ: Начните с воссоздания таблицы кинематики вращения.
Сначала найдите угловое ускорение.
Затем найдите угловое смещение.
Наконец, преобразуйте угловое смещение в число оборотов.
Линейная скорость в зависимости от скорости вращения: определения и уравнения
Уравнения
Каждому из двух типов скорости соответствует уравнение. Обычная линейная скорость рассчитывается по следующему уравнению:
Скорость — это смещение (или изменение положения), деленное на время.Возьмите количество метров, которое переместился объект, и разделите его на время, которое потребовалось для перемещения.
Угловая скорость определяется следующим уравнением:
Угловая скорость — это угловое смещение (или изменение углового положения), деленное на время. Возьмите количество градусов, на которое повернулся объект, и разделите его на время, которое потребовалось для поворота.
Пример
Может быть, это было бы проще, если бы мы рассмотрели пример.Допустим, мяч летит по воздуху, но при этом вращается. Мяч перемещается на 20 метров за 4 секунды, при этом совершая за это время 5 оборотов. Каковы линейная и угловая скорости мяча?
Хорошо, прежде всего мы должны записать то, что мы знаем. Мы знаем, что смещение составляет 20 метров, и мы знаем, что время составляет 4 секунды. Мы также можем вычислить угловое смещение, потому что знаем, сколько раз оно повернулось. Каждое полное вращение составляет 2 пи радиана, и оно поворачивается 5 раз.2-пи умножить на 5 — это то же самое, что и 10-пи. Таким образом, угловое смещение составляет 10 пи. Подставьте эти числа в два уравнения, и мы получим ответы: линейная скорость составляет 5 метров в секунду, а угловая скорость составляет 7,9 радиан в секунду.
Резюме урока
Линейная скорость — это скорость и направление объекта, движущегося по прямой линии, измеряемая в метрах в секунду. Скорость вращения — это скорость вращения объекта, измеряемая в радианах в секунду. Радианы — альтернатива измерению углов в градусах. В круге 360 градусов; аналогично, в круге 2 пи радиана.
Вы можете рассчитать линейную скорость, разделив смещение (или изменение положения) на время, которое потребовалось для изменения положения. И вы можете рассчитать угловую скорость, разделив угловое смещение (или изменение углового положения) на время, которое потребовалось для изменения углового положения.
Практика:
Линейная скорость в сравнении с скоростью вращения: Викторина по определениям и уравнениям
Инструкции: Выберите ответ и нажмите «Далее». В конце вы получите свой счет и ответы.
Бейсбольный мяч проходит 150 метров за 4 секунды, при этом совершая 2-кратный оборот за это время. Какова линейная скорость мяча?
Создайте учетную запись, чтобы пройти этот тест
Как участник, вы также получите неограниченный доступ к более чем 84 000 уроков по математике, Английский язык, наука, история и многое другое.Кроме того, получайте практические тесты, викторины и индивидуальные тренировки, которые помогут вам добиться успеха.
Попробуй это сейчасНастройка займет всего несколько минут, и вы можете отменить ее в любой момент.
Уже зарегистрированы? Авторизуйтесь здесь для доступа
Связь между линейными величинами и величинами вращения
Определение кругового движения
Описание кругового движения лучше описывается с точки зрения угловой величины, чем его линейная противоположная часть.Причины понятны. Например, рассмотрим случай равномерного кругового движения. Здесь скорость частицы меняется — хотя движение «равномерное». Эти две концепции несовместимы. Общий смысл термина «равномерный» означает «постоянный», но скорость на самом деле все время меняется.
Вращающийся корпус
Каждая частица, составляющая тело, совершает равномерное круговое движение вокруг фиксированной оси. Для описания движения лучше всего подходят угловые величины.
Когда мы описываем равномерное круговое движение в терминах угловой скорости, нет противоречия. Скорость (то есть угловая скорость) действительно постоянна. Это первое преимущество описания равномерного кругового движения с точки зрения угловой скорости.
Второе преимущество состоит в том, что угловая скорость передает физический смысл вращения частицы по сравнению с линейной скоростью, которая указывает поступательное движение. В качестве альтернативы угловое описание подчеркивает различие между двумя типами движения (поступательным и вращательным).
Взаимосвязь между линейной и угловой скоростью
Для простоты рассмотрим равномерное круговое движение. Для длины дуги, проходящей под углом «в начале координат, а» r «- это радиус круга, содержащего положение частицы, мы имеем $ s = r \ theta $.
Дифференцируя по времени, получаем
$ \ frac {ds} {dt} = \ frac {dr} {dt} \ theta + r \ frac {d \ theta} {dt} $.
Поскольку $ \ frac {dr} {dt} = 0 $ для равномерного кругового движения получаем $ v = \ omega r $.Точно так же мы также получаем $ a = \ alpha r $, где $ a $ обозначает линейное ускорение, а $ \ alpha $ обозначает угловое ускорение (в более общем случае соотношение между угловыми и линейными величинами задается как $ \ bf {v = \ omega \ times r}, ~~ \ bf {a = \ alpha \ times r + \ omega \ times v} $.)
Кинематические уравнения вращения
С соотношением линейной и угловой скорости / ускорения , мы можем вывести следующие четыре кинематических уравнения вращения для постоянных $ a $ и $ \ alpha $:
$ \ omega = \ omega 0+ \ alpha t: v = v0 + при $
$ \ theta = \ omega 0t + (1/2) \ alpha t2: x = v0t + (1/2) at2 $
$ \ omega 2 = \ omega 02 + 2: v2 = v02 + 2ax $
Поскольку мы используем массу, линейный импульс, поступательную кинетическую энергию и 2-й закон Ньютона для описания линейного движения, мы можем описать общее вращательное движение, используя соответствующий скаляр / вектор / тензорные величины:
Например, так же, как мы используем уравнение движения $ F = ma $ для описания линейного движения, мы можем использовать его аналог $ \ bf {\ tau} = \ frac {d \ bf { L}} {dt} = \ bf {r} \ times \ bf {F} $ для описания углового движения.





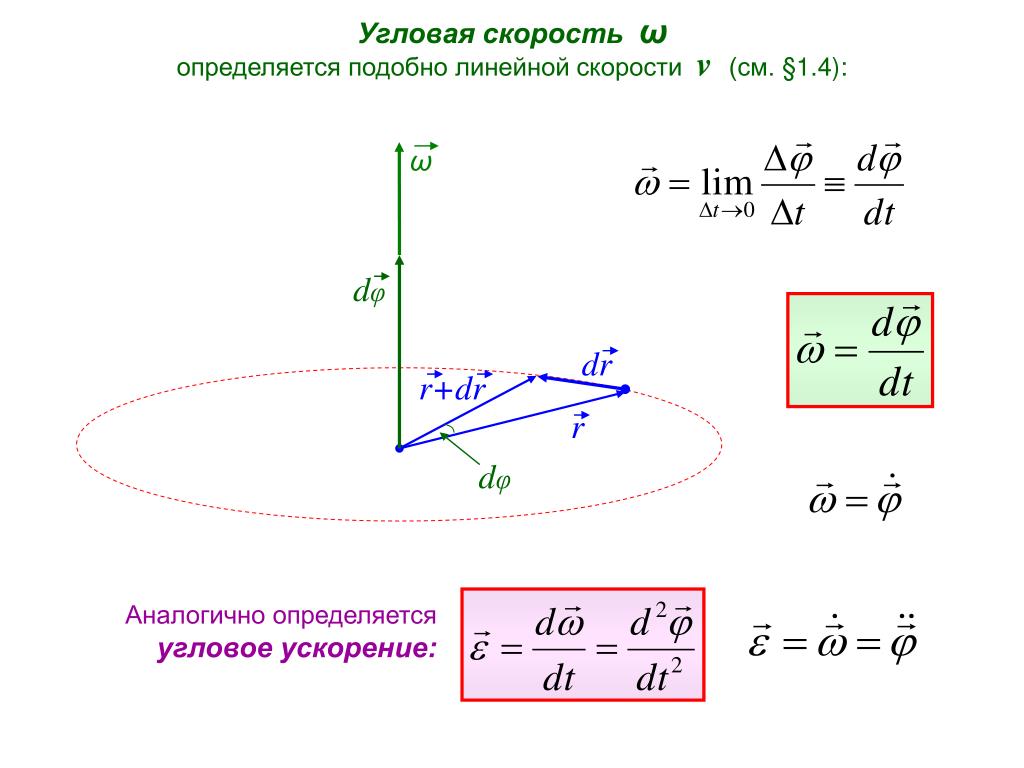 е. M=dL/dt или M=L
е. M=dL/dt или M=L
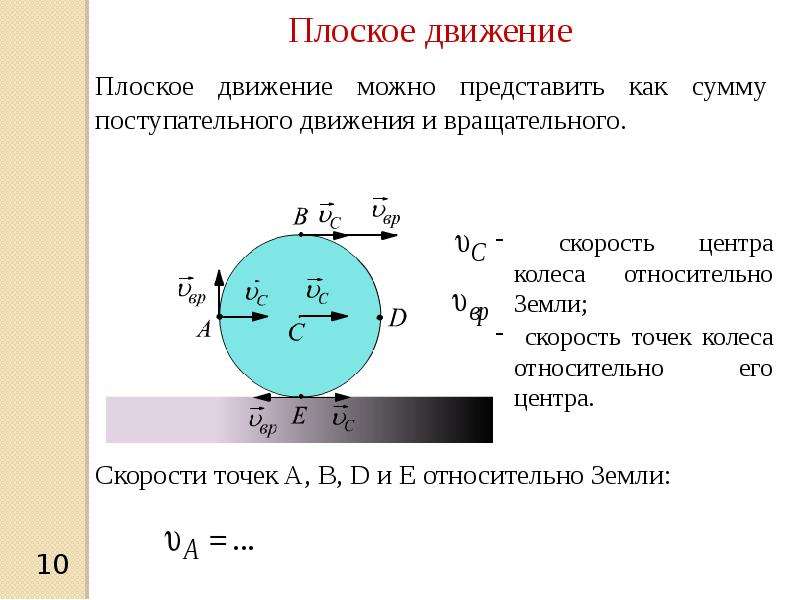 км/ч;
км/ч;
