Связь между напряжением и напряжённостью. Эквипотенциальные поверхности
В 1839 году немецкий учёный Карл Фридрих Гаусс предложил изображать электростатические поля с помощью эквипотенциальных поверхностей.
Эквипотенциальной называется воображаемая поверхность, в каждой точке которой потенциал одинаков.

Из определения эквипотенциальной поверхности следует, что разность потенциалов между двумя любыми её точками равна нулю.
Давайте с вами вспомним, что разностью потенциалов называют скалярную физическую величину, численно равную отношению работы сил поля по перемещению заряда между данными точками поля к величине этого заряда:

Из этого определения следует, что при переносе заряда вдоль эквипотенциальной поверхности работа полем не совершается (то есть она равна нулю).
Однако мы с вами знаем, что в общем случае работа сил электростатического поля пропорциональна переносимому заряду, модулю напряжённости поля, модулю перемещению и косинусу угла между направлением вектора электрической силы и вектора перемещения:

Но в записанной формуле значения заряда, модуля напряжённости
и модуля перемещения всегда отличны от нуля. Поэтому должно равняться нулю
значение косинуса угла альфа. А это значит, что угол альфа должен быть равен 90
Так, например, эквипотенциальные поверхности однородного электростатического поля представляют собой плоскости, перпендикулярные линиям напряжённости. А эквипотенциальные поверхности точечного заряда — это сферы, в центре которых расположен заряд.

Зная картину эквипотенциальных поверхностей, можно определить напряжённость поля в любой его точке. Например, пусть заряд перемещается с одной эквипотенциальной поверхности на другую, расстояние между которыми по нормали равно d.

Мы уже знаем, что в этом случае работа, совершаемая электростатическим полем по перемещению заряда прямо пропорциональна величине этого заряда, напряжённости поля и модулю перемещения заряда:

С другой стороны, работа поля по перемещению заряда из одной его точки в другую пропорциональна значению переносимого заряда и разности потенциалов начальной и конечной точек:

Давайте почленно разделим первое уравнение для работы на второе:

А из полученного выражения выразим модуль напряжённости поля:

Полученная нами формула выражает связь между напряжённостью и разностью потенциалов (или напряжением) однородного электростатического поля. На её основании и вводится единица напряжённости в СИ — вольт на метр (В/м).
1 В/м — это модуль напряжённости такого однородного электростатического поля, в котором напряжение между двумя точками, лежащими на одной силовой линии на расстоянии 1 м, составляет 1 В.
В заключении отметим, что при изучении электростатического поля мы очень часто сравнивали его с гравитационным полем Земли.

В таблице представлены соответствия между механическими и электрическими величинами этих полей. Обсудите их со своим соседом (или соседкой) по парте.
А теперь, для закрепления материала, решим с вами несколько несложных задач. Задача 1.

Задача 2. Между двумя разноимённо заряженными параллельными пластинами, находящимися на расстоянии 1 см друг от друга, покоится отрицательно заряженная капелька масла, плотность которого 900 кг/м3. Определите модуль заряда капельки, если её радиус равен 8 нм, а напряжение между пластинами составляет 650 В.

Работа сил электрического поля. Потенциал и разность потенциалов. Эквипотенциальные поверхности. Связь между напряжённостью и напряжением.
Потенциал электростатического поля — скалярная величина, равная отношению потенциальной энергии заряда в поле к этому заряду : 
— это энергетическая характеристика поля в данной точке.
Потенциал не зависит от величины заряда, помещенного в это поле.
Потенциал численно равен работе поля по перемещению единичного положительного заряда из данной точки электрического поля в бесконечность.
В СИ потенциал измеряется в вольтах: 
Напряжение — разность значений потенциала в начальной и конечной точках траектории.
Напряжение численно равно работе электростатического поля при перемещении единичного положительного заряда вдоль силовых линий этого поля. 
Разность потенциалов (напряжение) не зависит от выбора
 системы координат!
системы координат!
Единица разности потенциалов
Напряжение равно 1 В, если при перемещении положительного заряда в 1 Кл вдоль силовых линий поле совершает работу в 1 Дж.
 Связь между напряженностью и напряжением.
Связь между напряженностью и напряжением.
2. Модель строения атомного ядра. Ядерные силы. Энергия связи. Ядерные реакции.
В 1932г. после открытия протона и нейтрона учеными Д.Д. Иваненко (СССР) и В. Гейзенберг (Германия) была выдвинута протонно-нейтронная модель ядра атома
Согласно этой модели:
— ядра всех химических элементов состоят из нуклонов: протонов и нейтронов
— заряд ядра обусловлен только протонами
— число протонов в ядре равно порядковому номеру элемента
— число нейтронов равно разности между массовым числом и числом протонов (N=A-Z)
Условное обозначение ядра атома химического элемента: 
X – символ химического элемента
А – массовое число, которое показывает:
— массу ядра в целых атомных единицах массы (а.е.м.)
— число нуклонов в ядре (A = N + Z) , где N – число нейтронов в ядре атома
Z – зарядовое число, которое показывает:
— заряд ядра в элементарных электрических зарядах (э.э.з.)
( 1э.э.з. = заряду электрона = 1,6 х 10-19 Кл)
— число протонов
— число электронов в атоме
— порядковый номер в таблице Менделеева
Ядерные силы — силы притяжения, связывающие протоны и нейтроны в ядре.
Свойства:
1.На расстояниях порядка 10-13см сильные взаимодействия соответствуют притяжению, при уменьшении расстояния – отталкиванию.
2.Независимы от наличия электрического заряда (свойство зарядовой независимости).
Одинаковая сила действует и на протон и на нейтрон.
3.Взаимодействуют с ограниченным числом нуклонов (свойство насыщения).
4.Короткодействующие: быстро убывают, начиная с r ≈ 2,2.10-15 м.
Энергия, которая необходима для полного расщепления ядра на отдельные нуклоны, называется энергией связи. Энергия связи очень велика. При синтезе 4 г гелия выделяется такое же количество энергии, как при сжигании двух вагонов каменного угля.
Масса ядра всегда меньше суммы масс покоя свободных протонов и нейтронов, его составляющих.
Разность между массой ядра и суммой масс протонов и нейтронов называется дефектом масс.
Формула для вычисления энергии связи:

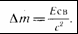 — дефект массы.
— дефект массы.
mp –масса покоя протона; mn – масса покоя нейтрона. Мя — масса ядра атома.
В атомной физике массу удобно выражать в атомных единицах массы:
1 а.е.м.=1,67·10-27 кг. Коэффициент связи энергии и массы (равный с2): с2= 931,5 МэВ/а·е·м.
Ядерные реакции — превращения атомных ядер, вызванные их взаимодействиями с различными частицами или друг с другом.
Символическая запись: А + а = В + b. При написании ядерных реакций используются законы сохранения заряда и массового числа (числа нуклонов).
Примеры:


Энергетический выход ядерной реакции — разность между суммарной энергией связи частиц, участвующих в реакции и продуктов реакции.
Реакции, происходящие с выделением энергии, наз. экзотермическими, с поглощением — эндотермическими.
Билет 23.
| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Физический справочник / / Физика для самых маленьких. Шпаргалки. Школа. / / Электростатика. Основные понятия. Электрический заряд. Закон сохранения электрического заряда. Закон Кулона. Принцип суперпозиции. Теория близкодействия. Потенциал электрического поля. Конденсатор. Поделиться:
| ||||||||||||||
Связь напряжённости и потенциала — Мегаобучалка
Электростатическое поле имеет две характеристики: силовую (напряжённость) и энергетическую (потенциал). Напряжённость и потенциал – различные характеристики одной и той же точки поля, следовательно, между ними должна быть связь.
Работа по перемещению единичного точечного положительного заряда из одной точки в другую вдоль оси х при условии, что точки расположены бесконечно близко друг к другу и х1– х2 = dx , равна qЕхdx. Та же работа равна q(φ1 — φ2 )= -dφq. Приравнивая оба выражения, можем записать
Ехdx = -dφ
Повторив аналогичные рассуждения для осей у и z, можем найти вектор :
где — единичные векторы координатных осей х, у, z.
Из определения градиента следует, что
или (12.31)
т.е. напряжённость поля Е равна градиенту потенциала со знаком минус. Знак минус определяется тем, что вектор напряжённости Е поля направлен в сторону убывания потенциала.
Установленная связь между напряжённостью и потенциалом позволяет по известной напряжённости поля найти разность потенциалов между двумя произвольными точками этого поля.
Ø Поле равномерно заряженной сферы радиусом R
Напряжённость поля вне сферы определяется по формуле
(r >R)
Разность потенциалов между точками r1 и r2 (r1>R; r2 >R ) определим, используя соотношение
Потенциал сферы получим, если r1= R, r2 → ∞:
Ø Поле равномерно заряженного бесконечно длинного цилиндра
Напряжённость поля вне цилиндра (r >R) определяется формулой
(τ – линейная плотность).
Разность потенциалов между двумя точками, лежащими на расстоянии r1 и r2 (r1>R; r2 >R ) от оси цилиндра, равна
(12.32)
Ø Поле равномерно заряженной бесконечной плоскости
Напряжённость поля этой плоскости определяется формулой
(σ — поверхностная плотность).
Разность потенциалов между точками, лежащими на расстоянии х1 и х2 от плоскости, равна
(12.33)
Ø Поле двух разноименно заряженных бесконечных параллельных плоскостей
Напряженность поля этих плоскостей определяется формулой
Разность потенциалов между плоскостями равна
(12.34)
(d – расстояние между плоскостями).
Примеры решения задач
Пример 12.1. Три точечных заряда Q1=2нКл, Q2 =3нКл и Q3=-4нКл расположены в вершинах равностороннего треугольника со стороной длиной a=10см. Определите потенциальную энергию этой системы.
Дано: Q1=2нКл=2∙10-9Кл; Q2 =3нКл=3∙10-9Кл; и Q3=-4нКл=4∙10-9Кл; a=10см=0,1м.
Найти: U.
Решение:Потенциальная энергия системы зарядов равна алгебраической сумме энергий взаимодействия каждой из взаимодействующих пар зарядов, т.е.
U=U12+U13+U23
где соответственно потенциальные энергии одного из зарядов, находящегося в поле другого заряда на расстоянии а от него, равны
; ; (2)
Подставим формулы (2) в выражение (1), найдём искомую потенциальную энергию системы зарядов
Ответ: U=-0,126мкДж.
Пример 12.2. Определите потенциал в центре кольца с внутренним радиусом R1=30см и внешним R2=60см, если на нём равномерно распределён заряд q=5нКл.
Дано: R1=30см=0,3м; R2=60см=0,6м; q=5нКл=5∙10-9Кл
Найти: φ.
Решение: Кольцо разобьём на концентрические бесконечно тонкие кольца внутренним радиусом r и внешним – (r+dr).
Площадь рассматриваемого тонкого кольца (см.рисунок) dS=2πrdr.
Потенциал в центре кольца, создаваемый бесконечно тонким кольцом,
где – поверхностная плотность заряда.
Для определения потенциала в центре кольца следует арифметически сложить dφ от всех бесконечно тонких колец. Тогда
Учитывая, что заряд кольца Q=σS, где S= π(R22-R12)- площадь кольца, получим искомый потенциал в центре кольца
Ответ: φ=25В
Пример 12.3. Два точечных одноименных заряда (q1=2нКл и q2=5нКл) находятся в вакууме на расстоянии r1= 20см. Определите работу А, которую надо совершить, чтобы сблизить их до расстояния r2=5см.
Дано: q1=2нКл=2∙10-9Кл; q 2=5нКл=5∙10-9Кл; r1= 20см=0,2м; r2=5см=0,05м.
Найти: А.
Решение: Работа, совершаемая силами электростатического поля при перемещении заряда Q из точки поля, имеющей потенциал φ1, в точку с потенциалом φ2.
A12= q(φ1— φ2)
При сближении одноимённых зарядов работу совершают внешние силы, поэтому работа этих сил равна по модулю, но противоположна по знаку работе кулоновских сил:
A= -q(φ1— φ2)= q(φ2— φ1). (1)
Потенциалы точек 1 и 2 электростатического поля
; (2)
Подставив формулы (2) в выражение (1), найдём искомую работу, которую надо совершить, чтобы сблизить заряды,
Ответ: А=1,35 мкДж.
Пример 12.4. Электростатическое поле создаётся положительно заряженной бесконечной нитью. Протон, двигаясь под действием электростатического поля вдоль линии напряжённости от нити с расстояния r1=2см до r2=10см, изменил свою скорость от υ1=1Мм/с до υ2=5Мм/с. Определите линейную плотность τ заряда нити..
Дано: q=1,6∙10-19 Кл; m=1,67∙10-27кг; r1=2см=2∙10-2м; r2= 10см=0,1м; r2=5см=0,05м; υ1=1Мм/с=1∙106м/с; до υ2=5Мм/с=5∙106м/с.
Найти:τ.
Решение: Работа, совершаемая силами электростатического поля при перемещении протона из точки поля с потенциалом φ1 в точку с потенциалом φ2 идёт на увеличение кинетической энергии протона
q(φ1— φ2)=ΔТ (1)
В случае нити электростатическое поле обладает осевой симметрией, поэтому
или dφ=-Edr,
тогда разность потенциалов между двумя точками, находящимися на расстоянии r1 и r2 от нити,
(учли, что напряжённость поля, создаваемого равномерно заряженной бесконечной нитью, ).
Подставив выражение (2) в формулу (1) и учитывая, что , получим
Откуда искомая линейная плотность заряда нити
Ответ: τ = 4,33 мкКл/м.
Пример 12.5. Электростатическое поле создаётся в вакууме шаром радиусом R=8см, равномерно заряженными с объёмной плотностью ρ=10нКл/м3. Определите разность потенциалов между двумя точками этого поля, лежащими от центра шара на расстояниях: 1) r1=10см и r2=15см; 2) r3= 2см и r4=5см..
Дано: R=8см=8∙10-2м; ρ=10нКл/м3=10∙10-9нКл/м3; r1=10см=10∙10-2м;
r2=15см=15∙10-2м; r3= 2см=2∙10-2м; r4=5см=5∙10-2м.
Найти:1) φ1— φ2; 2) φ3— φ4.
Решение: 1) Разность потенциалов между двумя точками, лежащими на расстоянии r1 и r2 от центра шара.
(1)
где — напряжённость поля, создаваемого равномерно заряженным с объёмной плотностью ρ шаром, в любой точке, лежащей вне шара на расстоянии r от его центра.
Подставив это выражение в формулу (1) и проинтегрировав, получим искомую разность потенциалов
2) Разность потенциалов между двумя точками, лежащими на расстоянии r3 и r4 от центра шара,
(2)
где — напряжённость поля, создаваемого равномерно заряженным с объёмной плотностью ρ шаром, в любой точке, лежащей внутри шара на расстоянии r от его центра.
Подставив это выражение в формулу (2) и проинтегрировав, получим искомую разность потенциалов
Ответ: 1) φ1— φ2=0,643 В; 2) φ3— φ4=0,395 В
какая связь между напряженностью электрического поля и потенциалом?
Напряженностью электрического поля называют физическую величину, равную отношению силы, с которой поле действует на положительный пробный заряд, помещенный в данную точку пространства, к величине этого заряда: <img src=»//content.foto.my.mail.ru/mail/dancevladka/_animated/i-2.gif» > Связь между напряженностью электрического поля и потенциалом Как известно, в потенциальном поле сила может быть получена из потенциальной энергии из соотношения <img src=»//content.foto.my.mail.ru/mail/dancevladka/_animated/i-3.gif» > Тогда для напряженности электрического поля из соотношений<img src=»//content.foto.my.mail.ru/mail/dancevladka/_animated/i-4.gif» > Получается<img src=»//content.foto.my.mail.ru/mail/dancevladka/_animated/i-5.gif» >
E-напряженность электрического поля ф-потенциал E = -grad ф как я понимаю потенциал можно определись в одной точке, а напряженность поля это совокупность этих потенциалов, лучше посмотри физический смысл градиента функции (ф1-ф2)=интерал от 1 до 2 E dl то есть разность потенциалов это напряжения, собственно напряжение это и есть напряженность электрического поля
Потенциал является важной характеристикой электрического поля, он определяет всевозможные энергетические характеристики процессов, проходящих в электрическом поле. Кроме того, расчет потенциала поля проще расчета напряженности, хотя бы потому, что является скалярной (а не векторной) величиной. Безусловно, что потенциал и напряженность поля связаны между собой достаточно сложными формулами. ПОПРОБУЕМ ВЫЯСНИТЬ СВЯЗЬ ПРОСТЫМИ СЛОВАМИ: . Eсли перемещать единичный заряд даже и в неоднородном эл. поле, то энергия на его перемещение и есть потенциал между точками, между которыми его перемещали. Напряженность — это силовая характеристика эл. поля, а разность потенциалов — энергетическая характеристика эл. поля, поэтому разность потенциалов равна произведению напряженности на перемещение заряда U=E*S Связь между напряженностью электростатического поля и потенциалом можно выразить с помощью понятия градиента потенциала: E = — grad Ф (далее математика).
что такое напряжение и напряжённость в физике?
Напряженность электрического поля. — количественная характеристика эл. поля. — это отношение силы, с которой поле действует на внесенный точечный заряд к величине этого заряда. — не зависит от величины внесенного заряда, а характеризует электрическое поле! <img src=»//otvet.imgsmail.ru/download/b95515d13e17a536045c1835890e32a8_i-479.jpg» > Напряжение характеризует электрическое поле, создаваемое током. <img src=»//otvet.imgsmail.ru/download/b95515d13e17a536045c1835890e32a8_i-480.jpg» > Напряжение ( U ) равно отношению работы электрического поля по перемещению заряда к величине перемещаемого заряда на участке цепи. <img src=»//otvet.imgsmail.ru/download/b95515d13e17a536045c1835890e32a8_i-481.jpg» > <a rel=»nofollow» href=»http://cla» target=»_blank»>http://cla</a>@ss-fizika.narod.ru/8_29.htm (Ccылка не проходит. Уберите «собаку» из нее и введите в поисковик. Это очень хороший сайт по физике с 7 по 11 класс, с видеороликами по многим темам. Эта <a rel=»nofollow» href=»http://cla» target=»_blank»>http://cla</a>@ss-fizika.narod.ru/mm10-11.htm> ссылка — иллюстративный материал по теме. Опять же нужно убрать собаку.
напряжение — это разность потенциалов. данная разность потенциалов создает вокруг проводника электрическое поле. Количественная мера электрического поля называется напряженностью электрического поля.
Напряжённость поля в данной точке равана отношению силы, с которой поле действует на точечный заряд, помещённый в эту точку, к этому заряду



