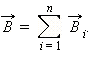Электромагнетизм
1. Вращающий момент, действующий на рамку с током со стороны магнитного поля. Магнитный момент рамки с током. Вращающий момент. Определение индукции магнитного поля. Единицы индукции и вращающего момента.
Поместив рамку в однородное магнитное поле, на нее действует пара сил, которая создает вращающий момент.
2. Напряженность магнитного поля и ее связь с индукцией. Единица напряженности.
Вектор магнитной индукции является общей характеристикой точек магнитного поля независимо от того, как создается магнитное поле: намагниченным телом или проводником с током находящимся в данной среде.
Однако можно ввести
некоторую характеристику магнитного
поля не зависящую от среды, а определяющуюся
токами и конфигурацией проводников — вектор
напряженности магнитного поля.
Эти две характеристики (одна общая, а
другая частная) связаны между собой: 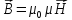
Напряженностью магнитного поля – отношение механической силы, действующей на положительный полюс пробного магнита, к величине его магнитной массы или механическая сила, действующая на положительный полюс пробного магнита единичной массы в данной точке поля.
Единица напряженности
магнитного поля — ампер на метр (А/м): 1 А/м — напряженность
такого поля, магнитная индукция которого
в вакууме равна 4π*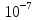 Тл.
Тл.
3. Изображение магнитных полей с помощью силовых линий индукции (напряженности). Вид линий магнитной индукции прямого и кругового токов, соленоида. Правила, но которым определяют направление линий магнитной индукции.
4. Магнитные поля проводников с токами. Закон Био-Савара-Лапласа.
Магнитное поле – это силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения.
Закон Био-Савара-Лапласа:
В векторной форме: 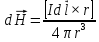
В скалярной форме: 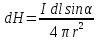
5. Применение закона Био-Савара-Лапласа для определения напряженности поля, создаваемого:
а) прямым проводником конечной длины (вывод формулы)
б) бесконечно длинным прямым проводником (вывод формулы)
в) круговым проводником в центре (вывод формулы)
г) соленоидом и тороидом
д) круговым проводником на оси (без вывода)
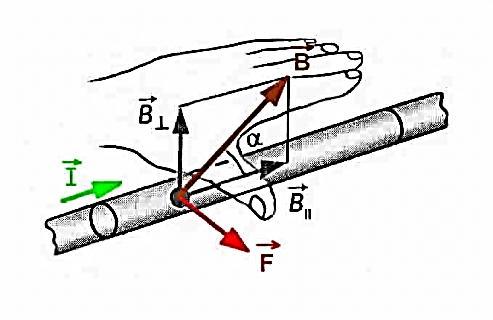
6. Сила Ампера. Правило для определения направления силы Ампера.
На проводник с током, находящийся в магнитном поле, действует сила, равная F = I·L·B·sina
I — сила тока в проводнике; B — модуль вектора индукции магнитного поля; L — длина проводника, находящегося в магнитном поле; a — угол между вектором магнитного поля инаправлением тока в проводнике.
Сила Ампера – Сила, действующую на проводник с током в магнитном поле.
Максимальная сила Ампера равна: F = I·L·B. Ей соответствует a = 90.
Направление силы Ампера определяется по правилу левой руки: если левую руку расположить так, чтобы перпендикулярная составляющая вектора магнитной индукции В входила в ладонь, а четыре вытянутых пальца были направлены по направлению тока, то отогнутый на 90 градусов большой палец покажет направление силы, действующей на отрезок проводника с током, то есть силы Ампера.
Магнитное поле в веществе. Часть 1
Всем доброго времени суток. В прошлой статье я рассказывал о основной характеристике магнитного поля – магнитной индукции, однако приведённые расчётные формулы соответствуют магнитному полю в вакууме. Что в практической деятельности встречается довольно редко. Когда проводники с током находятся в какой–либо среде, даже в воздухе, магнитное поле, которое они создают, претерпевает некоторые, а иногда и существенные изменения. Какие изменения происходят с магнитным полем, и от чего это зависит, я расскажу в данной статье.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Как связана индукция и напряженность магнитного поля?
Магнетиком называется вещество, которое под действием магнитного поля способно намагничиваться (или как говорят физики приобретать магнитный момент). Магнетиками являются практически все вещества. Намагничивание веществ объясняется тем, что в веществах присутствуют свои собственные микроскопические магнитные поля, которые создаются вращением электронов по своим орбитам. Когда внешнее магнитное поле отсутствует, то микроскопические поля расположены произвольным образом, а под воздействием внешнего магнитного поля соответствующим образом ориентируются.
Для характеристики намагничивания различных веществ используют так называемый вектор намагничивания J.
Таким образом, под действием внешнего магнитного поля с магнитной индукцией В0, магнетик намагничивается и создает свое магнитное поле с магнитной индукцией В’. В итоге общая индукция В будет состоять из двух слагаемых


Тут возникает проблема вычисления магнитной индукции намагниченного вещества В’, для решения которой необходимо считать электронные микротоки всего вещества, что практически нереально.
Альтернативой данного решения есть ввод вспомогательных параметров, а именно напряженность магнитного поля Н и магнитная восприимчивость χ. Напряженность связывает магнитную индукцию В и намагничивание вещества J следующим выражением
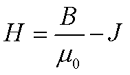
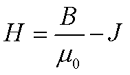
где В – магнитная индукция,
μ0 – магнитная постоянная, μ0 = 4π*10-7 Гн/м.
В то же время вектор намагничивания J связан с напряженность магнитного поля В параметром, характеризующим магнитные свойства вещества и называемым магнитной восприимчивостью χ


где J – вектор намагничивания вещества,
μr – относительная магнитная проницаемость вещества.
Однако наиболее часто для характеристики магнитных свойств веществ используют относительную магнитную проницаемость μr.
Таким образом, связь между напряженностью и магнитной индукцией будет иметь следующий вид
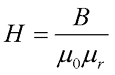
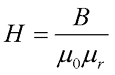
где μ0 – магнитная постоянная, μ0 = 4π*10-7 Гн/м,
μr – относительная магнитная проницаемость вещества.
Так как намагничивание вакуума равна нулю (J = 0), то напряженность магнитного поля в вакууме будет равна
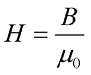
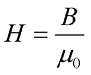
Отсюда можно вывести выражения напряженности для магнитного поля, создаваемого прямым проводом с током:
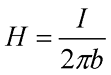
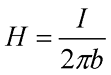
где I – ток протекающий по проводнику,
b – расстояние от центра провода до точки, в которой считается напряженность магнитного поля.
Как видно из данного выражения единицей измерения напряженности является ампер на метр (А/м) или эрстед (Э)
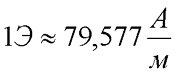
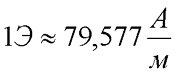
Таким образом, магнитная индукция В и напряженность Н являются основными характеристиками магнитного поля, а магнитная проницаемость μr – магнитной характеристикой вещества.
Намагничивание ферромагнетиков
В зависимости от магнитных свойств, то есть способности намагничиваться под действием внешнего магнитного поля, все вещества делятся на несколько классов. Которые характеризуются разной величиной относительной магнитной проницаемости μr и магнитной восприимчивости χ. Большинство веществ являются диамагнетиками (χ = -10-8 … -10-7 и μr < 1) и парамагнетиками (χ = 10-7 … 10-6 и μr > 1), несколько реже встречаются ферромагнетики (χ = 103 … 105 и μr >> 1). Кроме данных классов магнетиков существует ещё несколько классов магнетиков: антиферромагнетики, ферримагнетики и другие, однако их свойства проявляются только при определённых условиях.
Особый интерес в радиоэлектронике ферромагнитные вещества. Основным отличием данного класса веществ является нелинейная зависимость намагничивания, в отличие от пара- и диамагнетиков, имеющих линейную зависимость намагничивания J от напряженности Н магнитного поля.
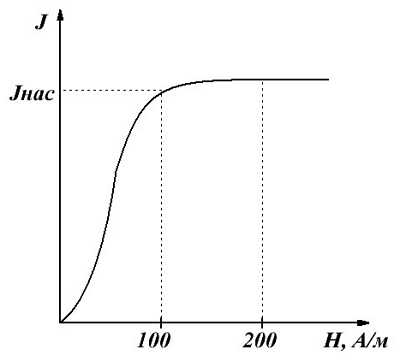

Зависимость намагничивания J ферромагнетика от напряженности Н магнитного поля.
На данном графике показана основная кривая намагничивания ферромагнетика. Изначально намагниченность J, в отсутствие магнитного поля (Н = 0), равна нулю. По мере возрастания напряженности намагничивание ферромагнетика проходит довольно интенсивно, вследствие того что его магнитная восприимчивость и проницаемость очень велика. Однако по достижении напряженности магнитного поля порядка H ≈ 100 А/м увеличение намагниченности прекращается, так как достигается точка насыщения JНАС. Данное явление называется магнитным насыщением. В данном режиме магнитная проницаемость ферромагнетиков сильно падает и при дальнейшем увеличении напряженности магнитного поля стремится к единице.
Гистерезис ферромагнетиков
Еще одной особенностью ферромагнетиков является наличие петли гистерезиса, которая является основополагающим свойством ферромагнетиков.
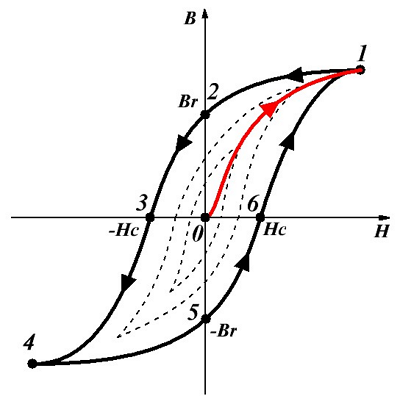

Петля гистерезиса ферромагнетика.
Для понимания процесса намагничивания ферромагнетика изобразим зависимость индукции В от напряженности Н магнитного поля, где красным цветом выделим основную кривую намагничивания. Данная зависимость довольно неопределенна, так как зависит от предыдущего намагничивания ферромагнетика.
Возьмём образец ферромагнитного вещества, которое не подвергалось намагничиванию (точка 0) и поместим его в магнитное поле, напряженность Н которого начнем увеличивать, то есть зависимость будет соответствовать кривой 0 – 1, пока не будет достигнуто магнитное насыщение (точка 1). Дальнейшее увеличение напряженности не имеет смысла, потому как намагниченность J практически не увеличивается, а магнитная индукция увеличивается пропорционально напряженности Н. Если же начинать уменьшать напряженность, то зависимость В(Н) будет соответствовать кривой 1 – 2 – 3, при этом когда напряженность магнитного поля упадёт до нуля (точка 2), то магнитная индукция не упадёт до нуля, а будет равна некоторому значению Br, которое называется остаточной индукцией, а намагничивание будет иметь значение Jr, называемое остаточным намагничиванием.
Для того чтобы снять остаточное намагничивание и уменьшить остаточную индукцию Br до нуля, необходимо создать магнитное поле, противоположное полю, вызвавшему намагничивание, причем напряженность размагничивающего поля должна составлять Нс, называемая коэрцитивной силой. При дальнейшем росте напряженности магнитного поля, которое противоположно первоначальному полю, происходит насыщение ферромагнетика (точка 4).
Таким образом, при действии на ферромагнетик переменного магнитного поля зависимость индукции от напряженности будет соответствовать кривой 1 – 2 – 3 – 4 – 5 – 6 – 1, которая называется петлёй гистерезиса. Таких петель для ферромагнетика может быть множество (пунктирные кривые), называемые частными циклами. Однако, если при максимальных значениях напряженности магнитного поля происходит насыщение, то получается максимальная петля гистерезиса (сплошная кривая).
Так как магнитная проницаемость μr ферромагнетиков имеет довольно сложную зависимость от напряженности магнитного поля, поэтому нормируются два параметра магнитной проницаемости:
μн – начальная магнитная проницаемость соответствует напряженности Н = 0;
μmax – максимальная магнитная проницаемость достигается в магнитном поле при приближении магнитного насыщения.
Таким образом, у ферромагнетиков величины Br, Нс и μн (μmax) являются основными характеристиками, влияющими на выбор вещества в конкретном случае.
Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.
Glava_18_Teoria_Maxvella
Электромагнитные волны.
§ 18.1 Теория Максвелла. Ток смещения. Уравнения Максвелла
Анализируя связь между величинами электрического и магнитного поля и обобщая результаты опытов Эрстеда и Фарадея, Максвелл создал теорию электромагнитного поля. Теория Максвелла с единой точки зрения позволяет объяснять свойства электрических и магнитных полей. Основные закономерности электромагнитных явлений описываются уравнениями Максвелла, и они составляют основу как электротехники и радиотехники, так и теории любых электромагнитных явлений.
В
каждой точке пространства и в каждый
момент времени состояние электромагнитного
поля характеризуется двумя векторами
– вектором
напряжённости электрического
поля  и вектором
магнитного поля -магнитной индукцией
и вектором
магнитного поля -магнитной индукцией  .
Вектора
.
Вектора  и
и 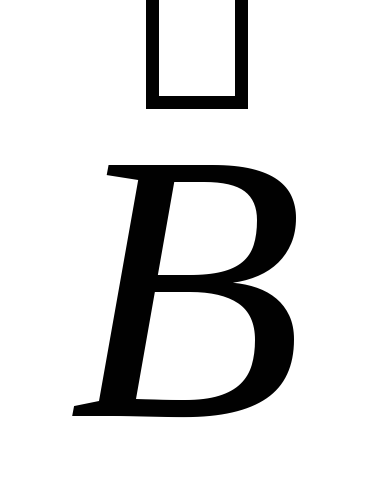 являются силовыми характеристиками
электромагнитного поля, т.е. такими
характеристиками, от которых зависит
сила, действующая со стороны этого поля
на любую находящуюся в нём заряженную
частицу.
являются силовыми характеристиками
электромагнитного поля, т.е. такими
характеристиками, от которых зависит
сила, действующая со стороны этого поля
на любую находящуюся в нём заряженную
частицу.
Электромагнитное поле по разному действует на заряженную частицу в том случае, когда эта частица покоится, и в том случае, когда она движется.
Сила, с которой электромагнитное поле действует на покоящийся в данной системе отсчёта заряд, называется электрической силой:
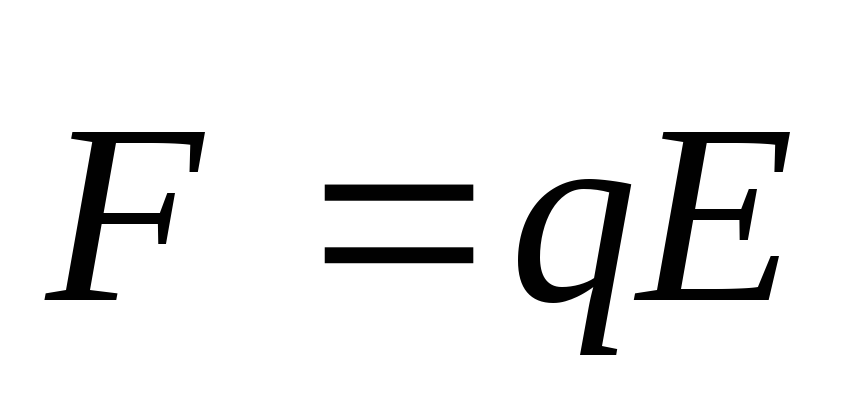
Сила, действующая в электромагнитном поле на движущийся заряд и дополнительная к электрической силе, называется магнитной силой или силой Лоренца:
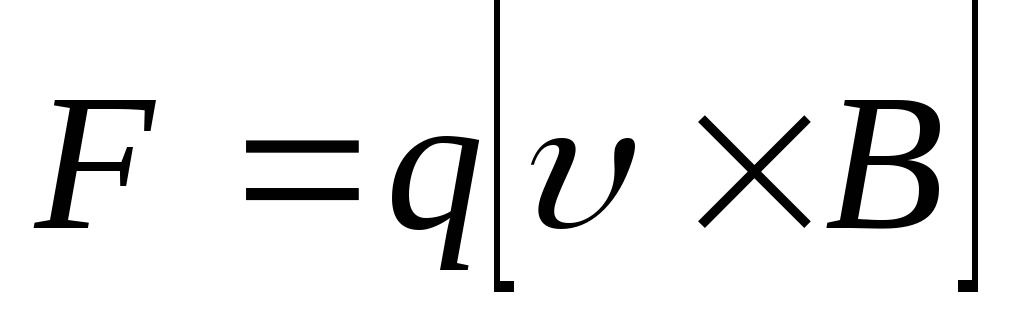
В 1892 г. Лоренц получает формулу силы, с которой электромагнитное поле действует на любую находящуюся в нём заряженную частицу:
 (18.1)
(18.1)
Эта сила называется электромагнитной силой Лоренца, а данное выражение является одним из основных законов классической электродинамики.
В теории решена основная задача электродинамики — по заданному распределению зарядов и токов определяются характеристики создаваемых ими электрических и магнитных полей. Уравнения Максвелла учитывают среду феноменологически, т. е. не раскрывают механизма взаимодействия среды и поля. Среда описывается с помощью трех величин: диэлектрической проницаемостью ε, магнитной проницаемостью μ и удельной электрической проводимостью γ.
Теория Максвелла – теория близкодействия, согласно которой электрические и магнитные взаимодействия распространяются с конечной скоростью, равной скорости света в данной среде.
В основе теории Максвелла лежат два положения.
1. Всякое переменное электрическое поле порождает вихревое магнитное.
2. Всякое переменное магнитное поле порождает вихревое электрическое.
При изучении явления электромагнитной индукции было показано, что переменное магнитное поле порождает вихревое электрическое поле, которое не связано с зарядами, как в случае электростатического поля; его силовые линии не начинаются и не заканчиваются на зарядах, а замкнуты сами на себя, подобно силовым линиям магнитного поля.
Сущность явления электромагнитной индукции заключается не столько в появлении индуцированного тока, сколько в возникновении вихревого электрического поля. Это фундаментальное положение электродинамики установлено Максвеллом как обобщение закона электромагнитной индукции Фарадея.
Направление вектора напряженности вихревого электрического поля устанавливается в соответствии с законом электромагнитной индукции Фарадея и правилом Ленца:
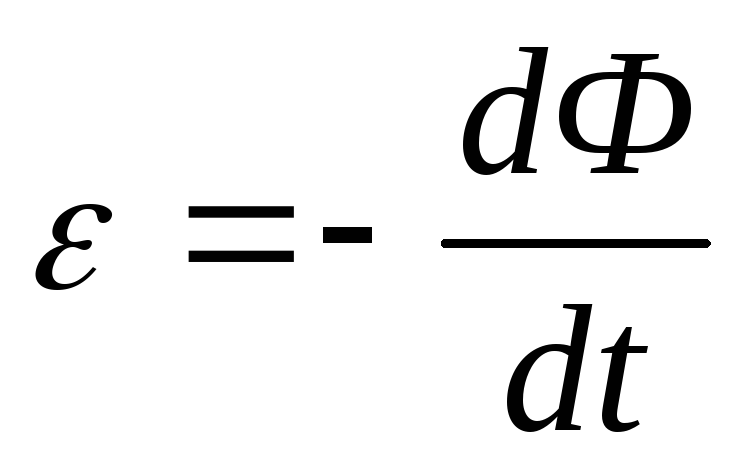
Согласно определению электродвижущей силы

EСТ -напряжённость поля сторонних сил.
В явлении электромагнитной индукции этой величиной является напряжённость вихревого электрического поля, поэтому
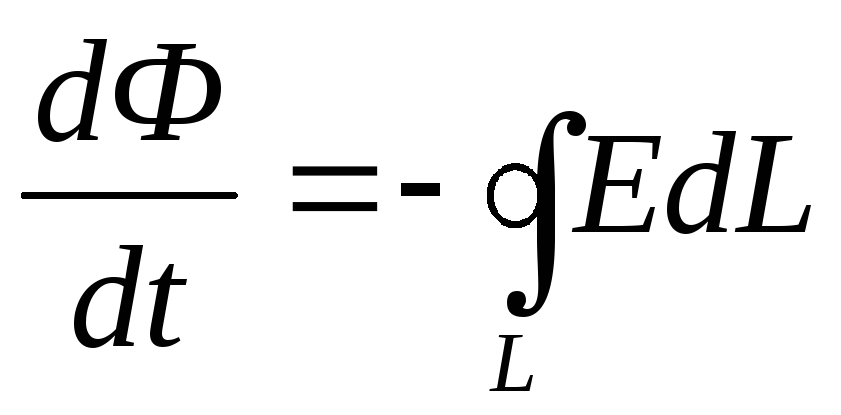 (18.2)
(18.2)
Уравнение (18.2) выражает количественную связь между изменяющимся магнитным полем В и вихревым электрическим полем Е:
 (18.3)
(18.3)
Циркуляция вектора напряженности электрического поля по любому замкнутому контуру пропорциональна скорости приращения магнитного потока сквозь любую поверхность, ограниченную данным контуром
При этом циркуляция электрического поля и скорость приращения магнитного потока имеют противоположные знаки.
Формула (18.3) выражает первое уравнение Максвелла в интегральной форме.
П ри
рассмотрении постоянного и переменного
токов в проводнике имеют место физические
эффекты, которые, как правило, отличаются
друг от друга. Например, когда по
проводнику проходит постоянный ток, то
линии тока всегда замкнуты. Обратимся
к процессу прохождения переменного
тока по цепи, содержащей конденсатор.
Между пластинами конденсатора заряды
не могут перемещаться. Это приводит к
тому, что линии тока обрываются у
поверхности пластины конденсатора,
в результате чего ток проводимости,
текущий по проводнику, соединяющему
обкладки конденсатора, оказывается
разомкнутым. До сих пор мы исходили из
представления, что электрические токи
представляют собой движение электрических
зарядов по проводникам и что плотность
их определяется электропроводимостью
проводника. В плоском конденсаторе одна
из обкладок его имеет положительный
заряд с поверхностной плотностью +σ,
другая — отрицательный с поверхностной
плотностью — σ (рис.18.1).
При разряде конденсатора через проводник,
соединяющий обкладки, ток течет от
обкладки М к N.
ри
рассмотрении постоянного и переменного
токов в проводнике имеют место физические
эффекты, которые, как правило, отличаются
друг от друга. Например, когда по
проводнику проходит постоянный ток, то
линии тока всегда замкнуты. Обратимся
к процессу прохождения переменного
тока по цепи, содержащей конденсатор.
Между пластинами конденсатора заряды
не могут перемещаться. Это приводит к
тому, что линии тока обрываются у
поверхности пластины конденсатора,
в результате чего ток проводимости,
текущий по проводнику, соединяющему
обкладки конденсатора, оказывается
разомкнутым. До сих пор мы исходили из
представления, что электрические токи
представляют собой движение электрических
зарядов по проводникам и что плотность
их определяется электропроводимостью
проводника. В плоском конденсаторе одна
из обкладок его имеет положительный
заряд с поверхностной плотностью +σ,
другая — отрицательный с поверхностной
плотностью — σ (рис.18.1).
При разряде конденсатора через проводник,
соединяющий обкладки, ток течет от
обкладки М к N.
Плотность тока j внутри обкладки конденсатора определяется производной по времени от плотности электрического заряда:
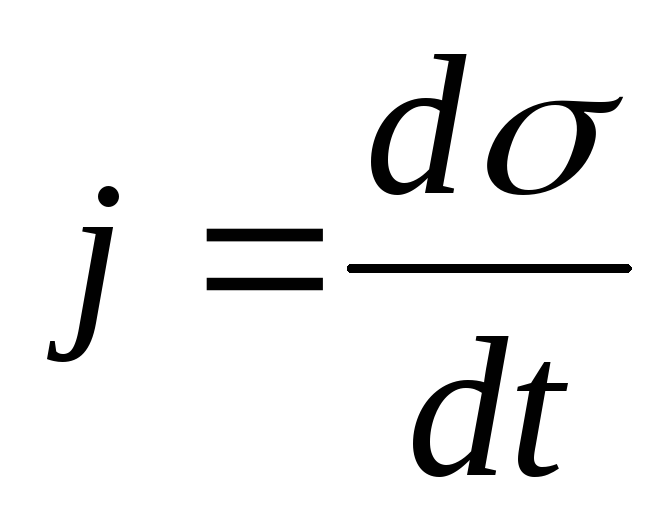 (18.4)
(18.4)
Ток такой плотности течет от обкладки М конденсатора.
Обратимся теперь к тому, что происходит в это время между обкладками конденсатора. Как известно, электрическое смещение поля связано с напряженностью соотношением
D=εε0Е (18.5)
а напряженность поля внутри конденсатора равна
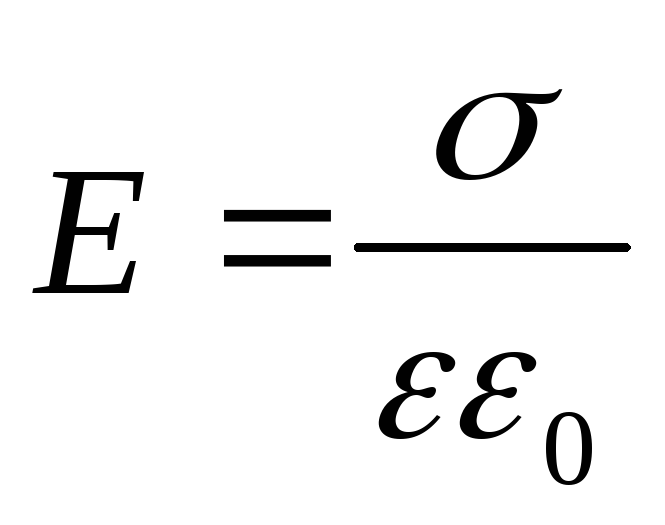 (18.6)
(18.6)
Объединяя формулы (18.5), (18.6), получаем, что электрическая индукция между обкладками конденсатора равна
D= σ (18.7)
При разряде конденсатора изменяется со временем поверхностная плотность σ заряда пластин конденсатора; следовательно, в соответствии с формулой (18.7) изменяется и электрическая индукция D:
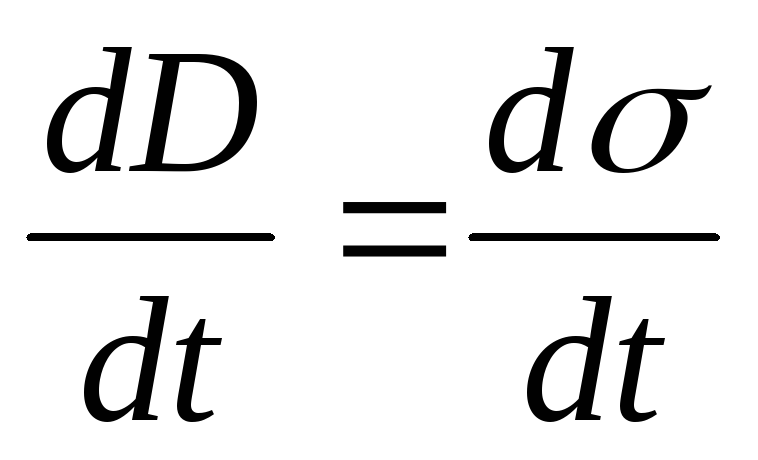 (18.8)
(18.8)
Так
как вектор электрического смещения
поля направлен от положительно заряженной
пластины N к отрицательно заряженной
пластине М, то при разряде конденсатора
скорость изменения электрической
индукции отрицательна и направлена в
сторону, противоположную вектору D.
Из сказанного следует, что направление
вектора 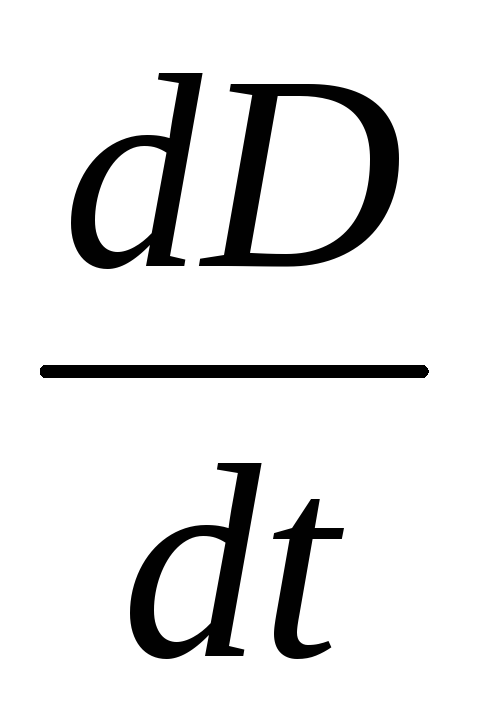 совпадает с направлением тока в цепи,
в которую включен конденсатор. Как видно
из уравнений (18.4) и (18.8), плотность
электрического тока j
и величина
совпадает с направлением тока в цепи,
в которую включен конденсатор. Как видно
из уравнений (18.4) и (18.8), плотность
электрического тока j
и величина 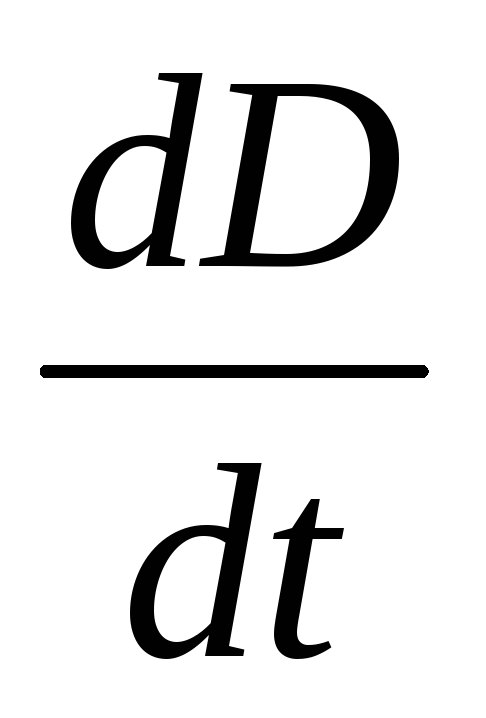 равны между собой.
равны между собой.
Максвелл
назвал величину  плотностью
тока смещения:
плотностью
тока смещения:
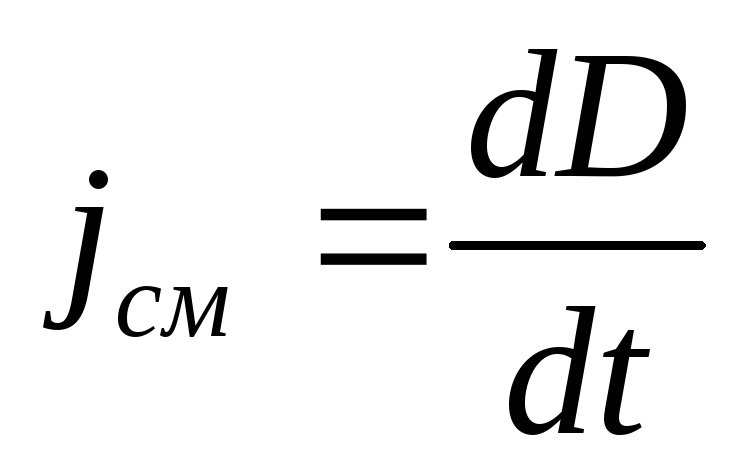 (18.9)
(18.9)
Таким образом, ток смещения — это скорость изменения электрического смещения, определяемого по формуле
D=ε0Е+P
[Е — напряженность электрического поля, Р — поляризованность].
Плотность тока смещения
 (18.10)
(18.10)
[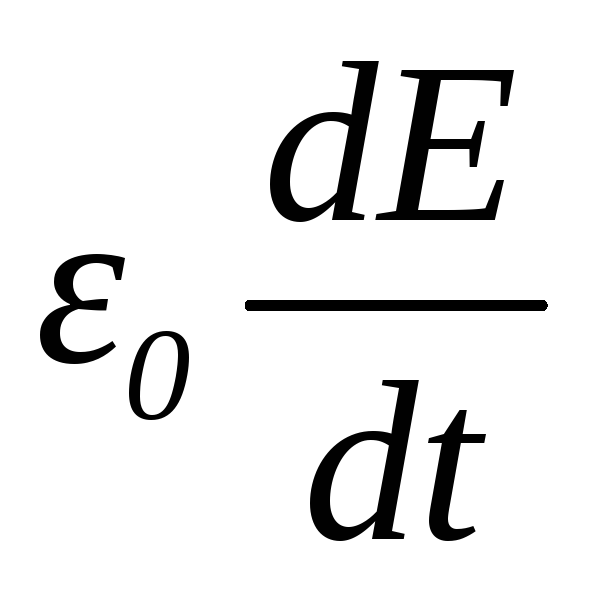 —
плотность тока смещения в вакууме:
—
плотность тока смещения в вакууме:  —
плотность тока поляризации, т. е.
упорядоченного движения электрических
зарядов в диэлектрике].
—
плотность тока поляризации, т. е.
упорядоченного движения электрических
зарядов в диэлектрике].
Так как числовые значения плотности тока смещения jсм и плотности тока проводимости j равны, то линии плотности тока проводимости внутри проводника (естественно, включая и пластины конденсатора) непрерывно переходят в линии плотности тока смещения между обкладками конденсатора. Для того чтобы ток был замкнут, вводится понятие полного тока, который включает в себя сумму тока проводимости и тока смещения; т. е. плотность полного тока равна
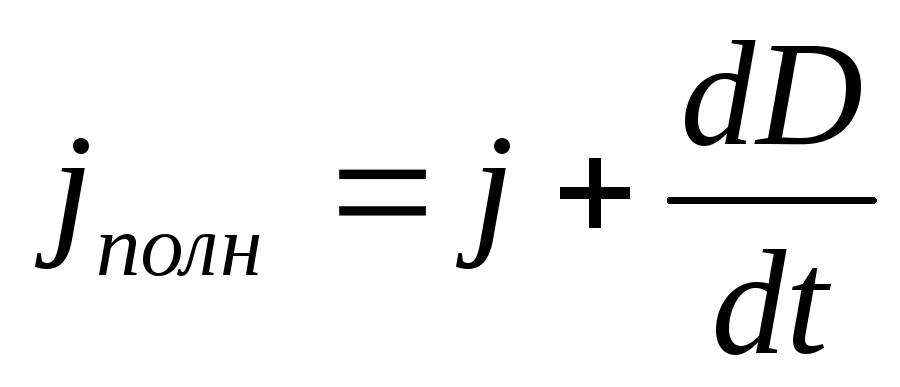 (18.11)
(18.11)
Таким образом, ток смещения – переменное электрическое поле; подобно току проводимости, порождает магнитное поле, силовые линии которого всегда замкнуты.
Максвелл, обобщая закон полного тока
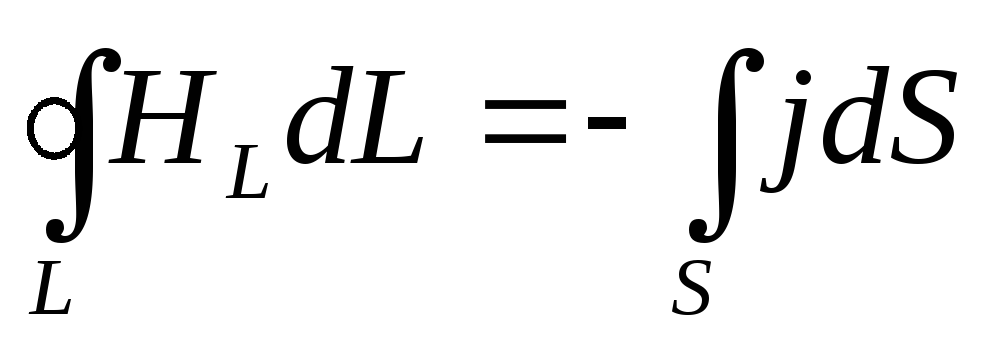 (18.12)
(18.12)
и вводя в правую часть тока проводимости также ток смещения, нашёл уравнение
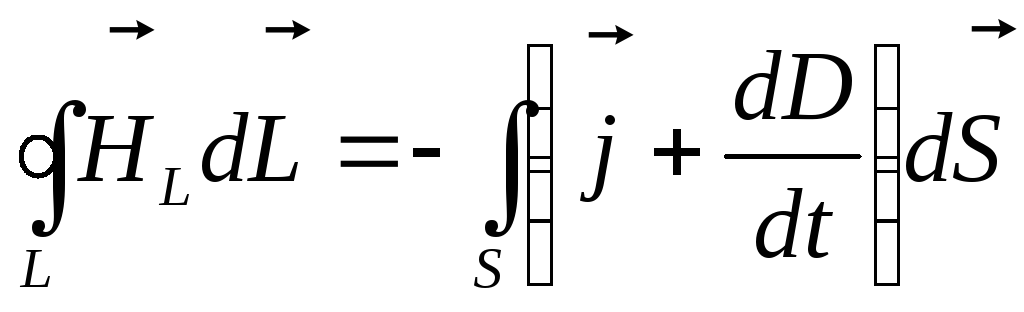 (18.13)
(18.13)
Получившее название второго уравнения Максвелла.
В систему уравнений Максвелла кроме двух описанных выше входят теорема Гаусса для электрического и магнитных полей:
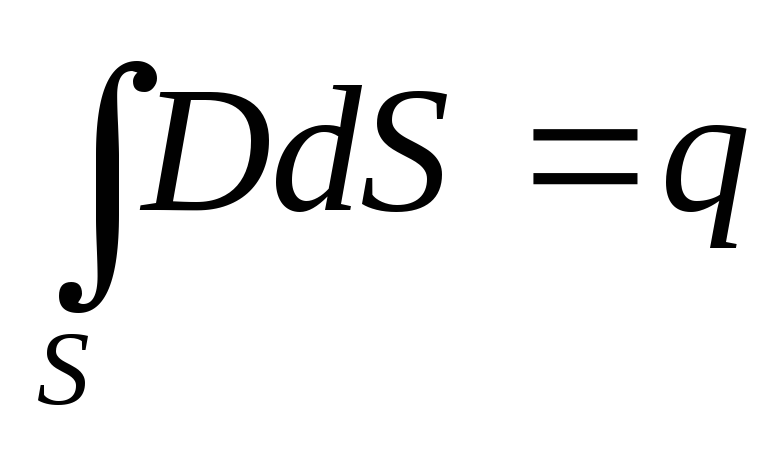
При непрерывном распределении заряда внутри замкнутой поверхности с объёмной плотностью выражение имеет вид
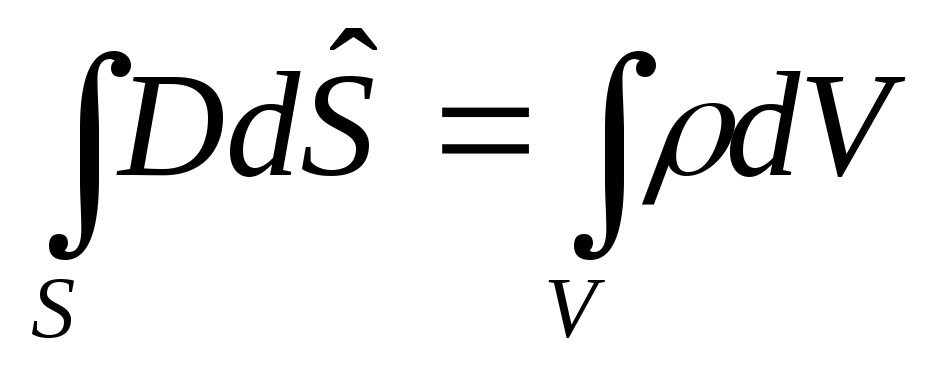

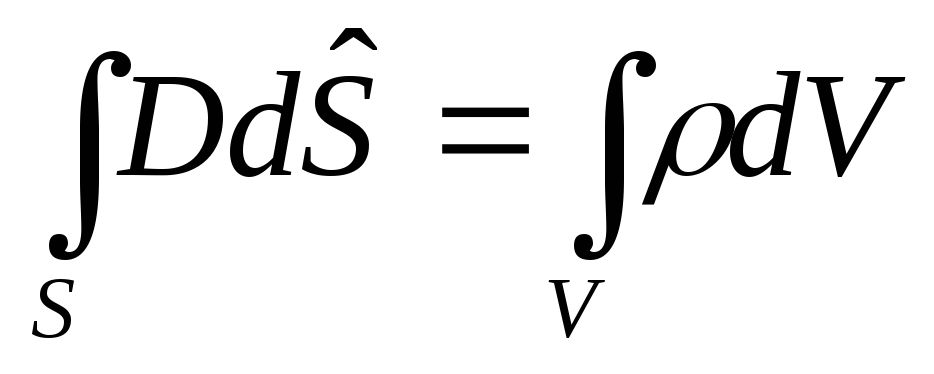
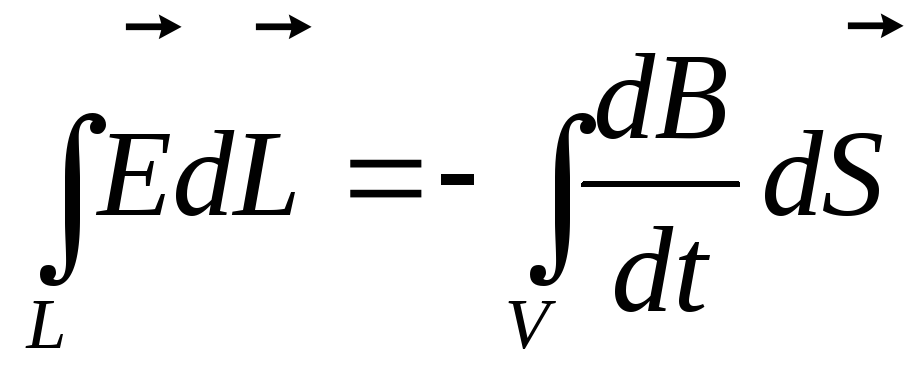

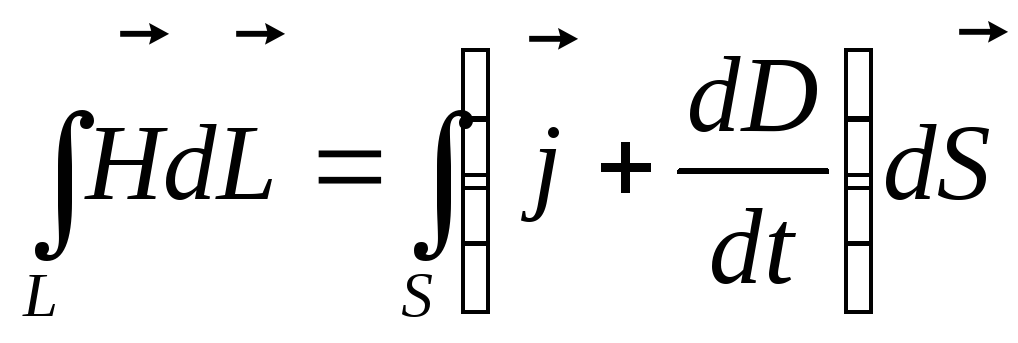
Первые два уравнения свидетельствуют о том, что электрическое поле возникает как вокруг неподвижных зарядов, так и в том случае, когда происходит изменение индукции магнитного поля во времени.
Вторые два уравнения показывают, что магнитное поле является вихревым и возникает лишь при наличии электрических токов или изменяющегося во времени электрического поля или того и другого одновременно, т.е. никаких магнитных зарядов не существует.
Из уравнений Максвелла следует, что электрические и магнитные поля являются проявлением единого электромагнитного поля.
Обычно
к системе уравнений максвелла присоединяют
формулы, выражающие связь между  и
и 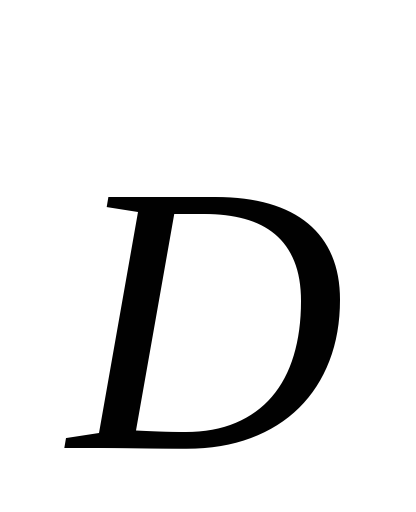 ,
,  и
и 

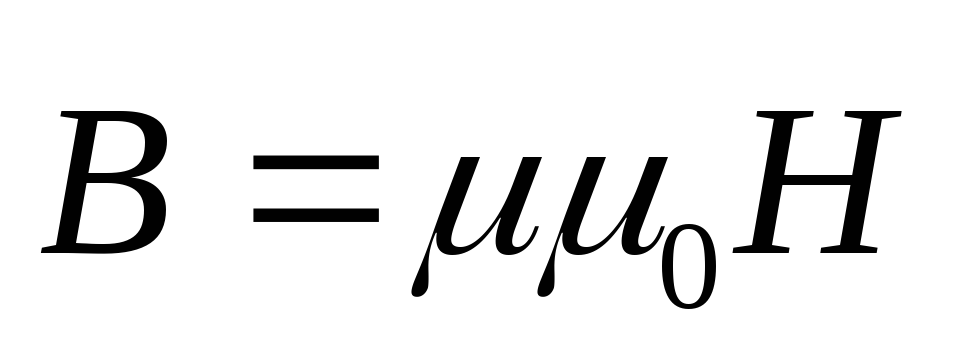
Физический смысл уравнений Максвелла:
1.Электромагнитное поле можно разделить на электрическое и магнитное лишь относительно;
2 .
Изменяющееся магнитное поле порождает
электрическое поле, и изменяющееся
электрическое поле порождает магнитное,
причём эти поля взаимосвязаны.
.
Изменяющееся магнитное поле порождает
электрическое поле, и изменяющееся
электрическое поле порождает магнитное,
причём эти поля взаимосвязаны.
Из уравнений Максвелла следует, что электромагнитное поле способно существовать в отсутствии электрических зарядов и токов.
При этом изменение его состояния имеет волновой характер, т.е. является электромагнитной волной. Электромагнитная волна в вакууме распространяется со скоростью света. Теоретические предсказания Максвелла подтвердили опыты Герца и изобретение радио Поповым
§ 18.2 Электромагнитные волны
Г ипотеза
Максвелла предполагает существование электромагнитной
волны, которая представляет собой
распространяющиеся в пространстве и
во времени электромагнитное поле.
Электромагнитные волны поперечны – векторы
ипотеза
Максвелла предполагает существование электромагнитной
волны, которая представляет собой
распространяющиеся в пространстве и
во времени электромагнитное поле.
Электромагнитные волны поперечны – векторы и
и  перпендикулярны
друг другу и лежат в плоскости,
перпендикулярной направлению
распространения волны (рис.18.3).
перпендикулярны
друг другу и лежат в плоскости,
перпендикулярной направлению
распространения волны (рис.18.3).
Электромагнитные волны распространяются в веществе с конечной скоростью
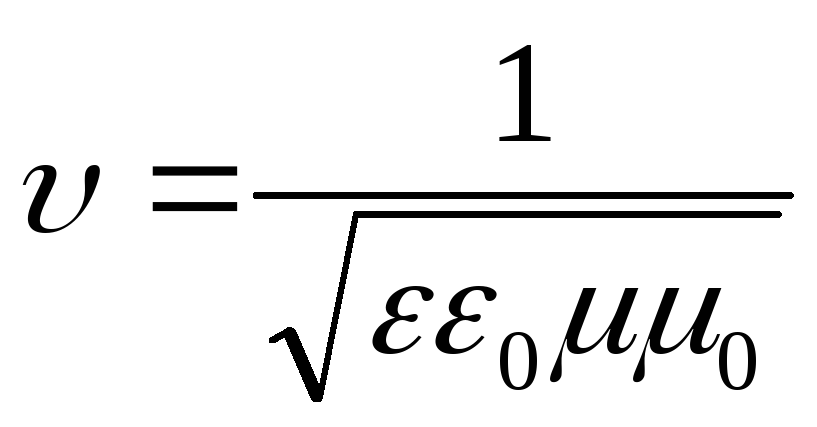 (18.14)
(18.14)
где ε и μ – диэлектрическая и магнитная проницаемости вещества, ε0 и μ0 – электрическая и магнитная постоянные: ε0 = 8,85419·10–12 Ф/м, μ0 = 1,25664·10–6 Гн/м.
Длина волны λ в синусоидальной волне связана со скоростью υ распространения волны соотношением λ = υT
Скорость электромагнитных волн в вакууме (ε = μ = 1):
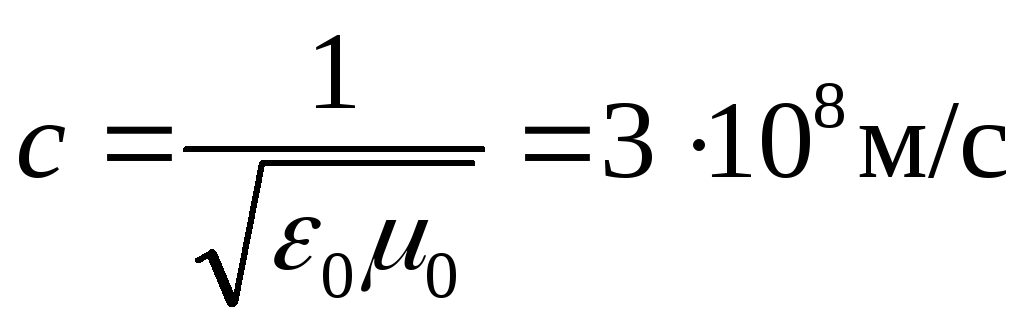 (18.15)
(18.15)
Скорость c распространения электромагнитных волн в вакууме является одной из фундаментальных физических постоянных.
Вывод Максвелла о конечной скорости распространения электромагнитных волн находился в противоречии с принятой в то время теорией дальнодействия, в которой скорость распространения электрического и магнитного полей принималась бесконечно большой. Поэтому теорию Максвелла называют теорией близкодействия.
В электромагнитной волне происходят взаимные превращения электрического и магнитного полей. Эти процессы идут одновременно, и электрическое и магнитное поля выступают как равноправные «партнеры». Поэтому объемные плотности электрической и магнитной энергии равны друг другу: ωЭ= ωм
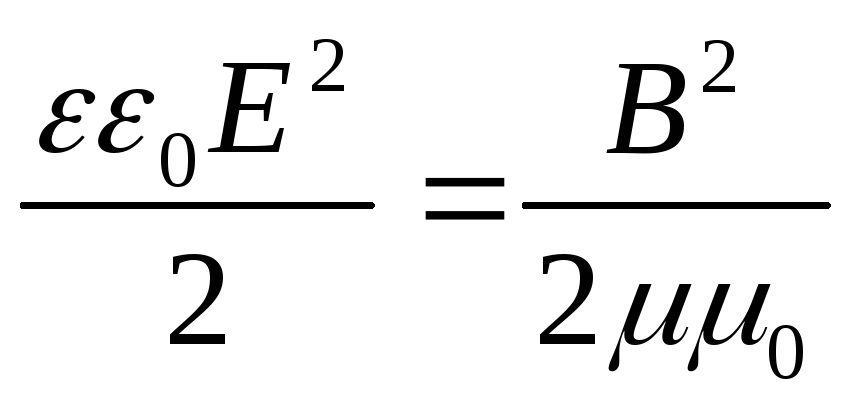 (18.16)
(18.16)
Отсюда
следует, что в электромагнитной волне
модули индукции магнитного поля  и
напряженности электрического поля
и
напряженности электрического поля  в каждой точке пространства связаны
соотношением
в каждой точке пространства связаны
соотношением
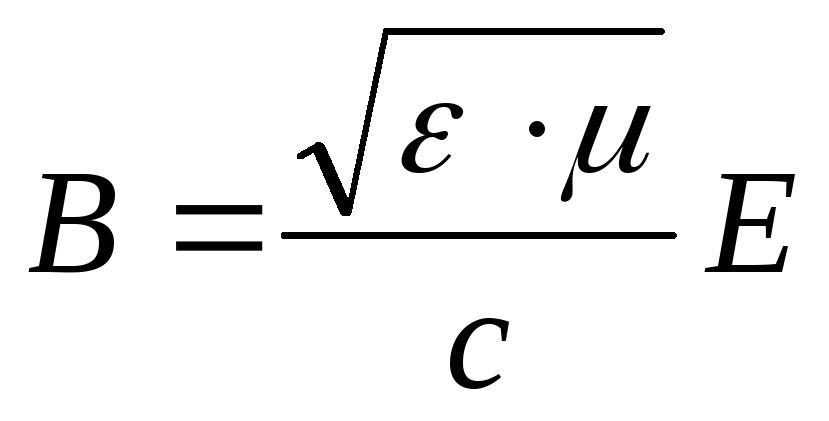 (18.17)
(18.17)
Электромагнитные волны переносят энергию. При распространении волн возникает поток электромагнитной энергии. Если выделить площадку S (рис. 2.6.3), ориентированную перпендикулярно направлению распространения волны, то за малое время Δt через площадку протечет энергия ΔWэм, равная
ΔWэм = (ωэ + ωм)υSΔt. |
Плотностью потока или интенсивностью I называют электромагнитную энергию, переносимую волной за единицу времени через поверхность единичной площади:
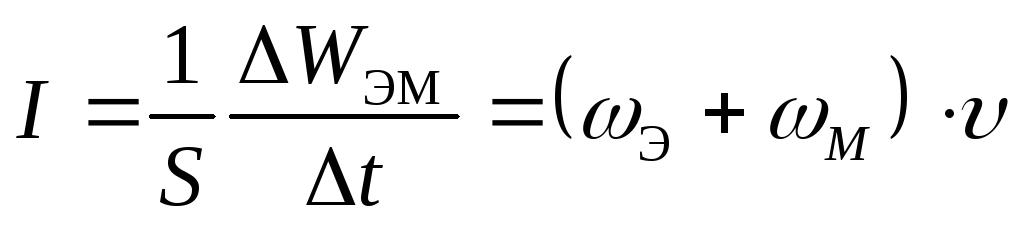
Подставляя сюда выражения для ωэ, ωм и υ, можно получить:
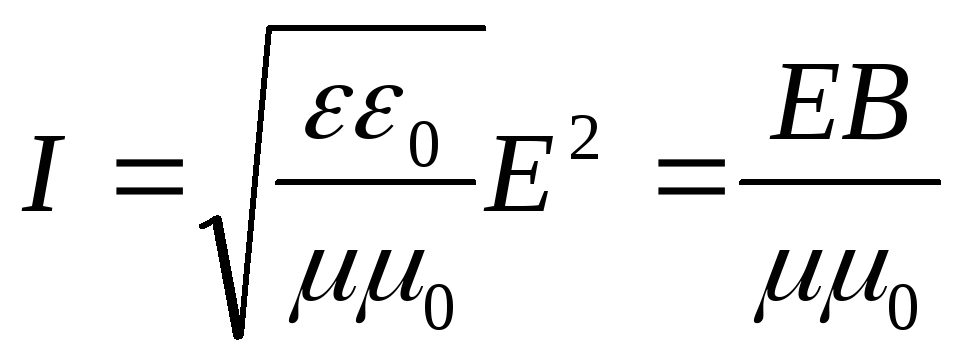 (18.18)
(18.18)
Поток
энергии в электромагнитной волне можно
задавать с помощью вектора  ,
направление
которого совпадает с направлением
распространения волны, а модуль равен
,
направление
которого совпадает с направлением
распространения волны, а модуль равен 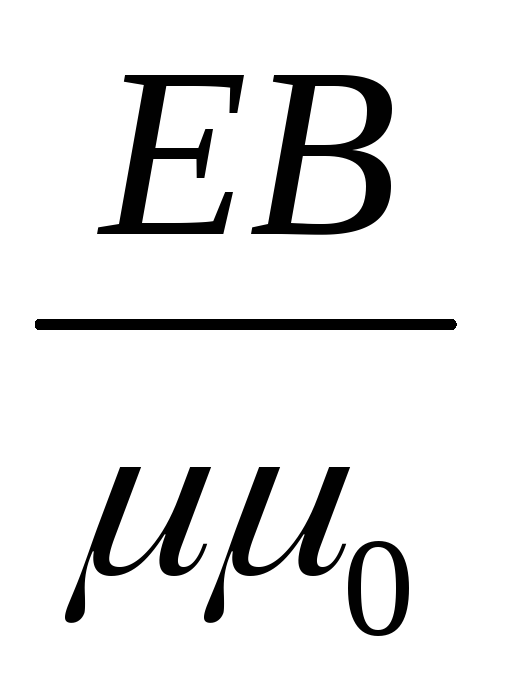 .
Этот вектор называют вектором
Умова-Пойнтинга.
.
Этот вектор называют вектором
Умова-Пойнтинга.
В синусоидальной (гармонической) волне в вакууме среднее значение Iср плотности потока электромагнитной энергии равно
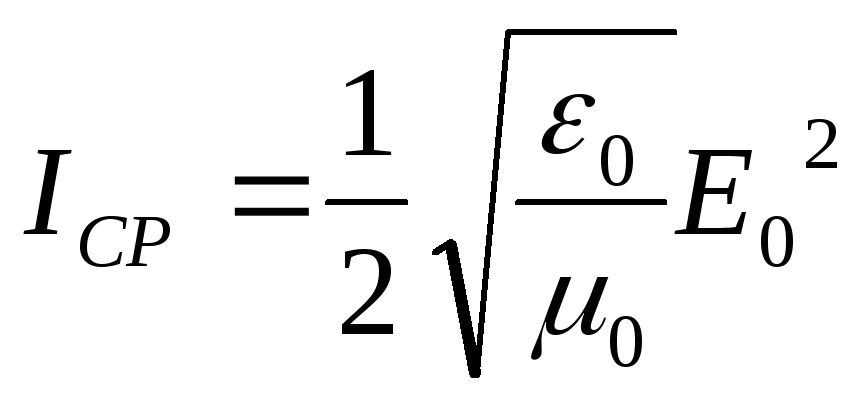 (18.19)
(18.19)
где E0 – амплитуда колебаний напряженности электрического поля.
Плотность потока энергии в СИ измеряется в ваттах на квадратный метр (Вт/м2).
Из теории Максвелла следует, что электромагнитные волны должны оказывать давление на поглощающее или отражающее тело. Давление электромагнитного излучения объясняется тем, что под действием электрического поля волны в веществе возникают слабые токи, то есть упорядоченное движение заряженных частиц. На эти токи действует сила Ампера со стороны магнитного поля волны, направленная в толщу вещества. Эта сила и создает результирующее давление. Обычно давление электромагнитного излучения ничтожно мало. Так, например, давление солнечного излучения, приходящего на Землю, на абсолютно поглощающую поверхность составляет примерно 5 мкПа. Первые эксперименты по определению давления излучения на отражающие и поглощающие тела, подтвердившие вывод теории Максвелла, были выполнены П. Н. Лебедевым в 1900 г. Опыты Лебедева имели огромное значение для утверждения электромагнитной теории Максвелла.
Существование давления электромагнитных волн позволяет сделать вывод о том, что электромагнитному полю присущ механический импульс. Импульс электромагнитного поля в единичном объеме выражается соотношением
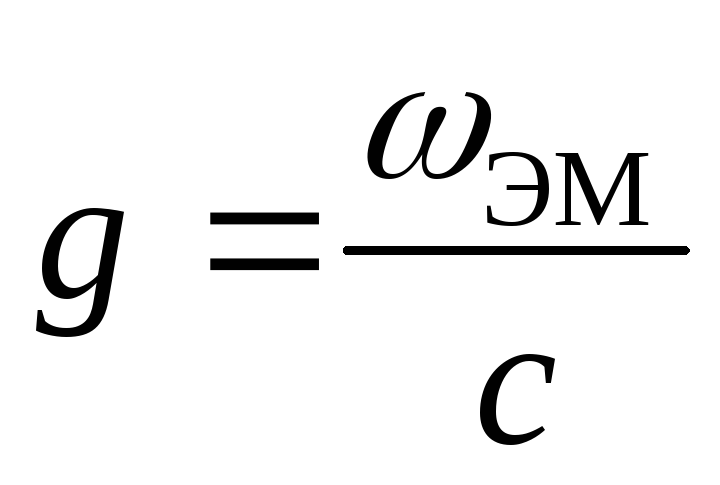
где ωэм – объемная плотность электромагнитной энергии, c – скорость распространения волн в вакууме. Наличие электромагнитного импульса позволяет ввести понятие электромагнитной массы.
Для поля в единичном объеме
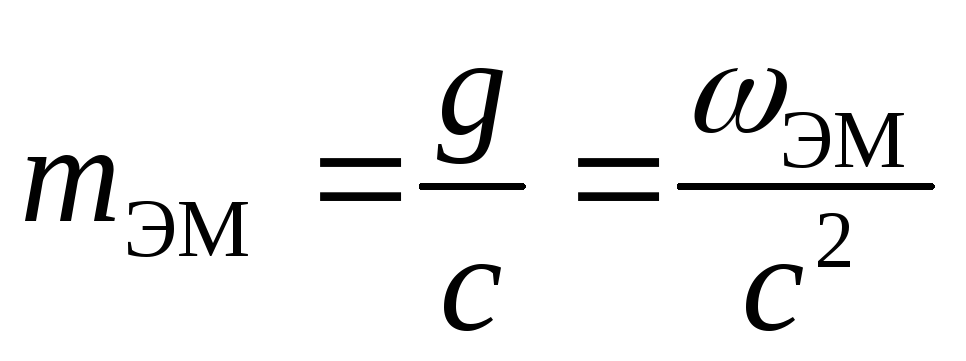
Отсюда следует:
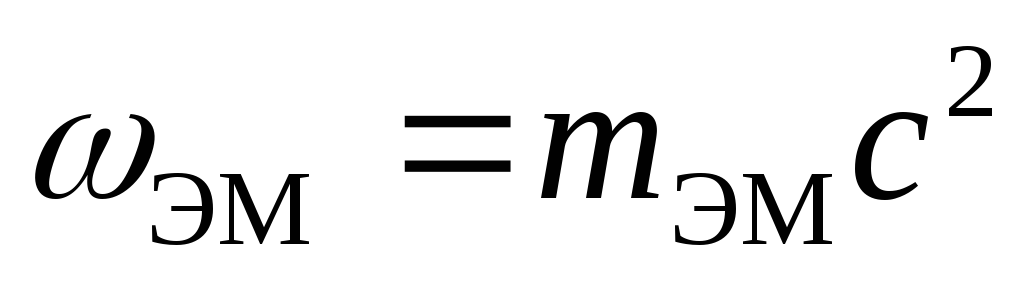
Это соотношение между массой и энергией электромагнитного поля в единичном объеме является универсальным законом природы. Согласно специальной теории относительности, оно справедливо для любых тел независимо от их природы и внутреннего строения.
Таким образом, электромагнитное поле обладает всеми признаками материальных тел – энергией, конечной скоростью распространения, импульсом, массой. Это говорит о том, что электромагнитное поле является одной из форм существования материи.
Первое экспериментальное подтверждение электромагнитной теории Максвелла было дано примерно через 15 лет после создания теории в опытах Г. Герца (1888 г.). Герц не только экспериментально доказал существование электромагнитных волн, но впервые начал изучать их свойства – поглощение и преломление в разных средах, отражение от металлических поверхностей и т. п. Ему удалось измерить на опыте длину волны и скорость распространения электромагнитных волн, которая оказалась равной скорости света.
Опыты Герца сыграли решающую роль для доказательства и признания электромагнитной теории Максвелла. Через семь лет после этих опытов электромагнитные волны нашли применение в беспроводной связи (А. С. Попов, 1895 г.).
Электромагнитные волны могут возбуждаться только ускоренно движущимися зарядами. Цепи постоянного тока, в которых носители заряда движутся с неизменной скоростью, не являются источником электромагнитных волн. В современной радиотехнике излучение электромагнитных волн производится с помощью антенн различных конструкций, в которых возбуждаются быстропеременные токи.
Простейшей системой, излучающей электромагнитные волны, является небольшой по размерам электрический диполь, дипольный момент которого быстро изменяется во времени: p=р0cosωt.
Т акой
элементарный диполь называют диполем
Герца.
В радиотехнике диполь Герца эквивалентен
небольшой антенне, размер которой много
меньше длины волны λ (рис. 18.4).
акой
элементарный диполь называют диполем
Герца.
В радиотехнике диполь Герца эквивалентен
небольшой антенне, размер которой много
меньше длины волны λ (рис. 18.4).
Рис. 18.5
дает представление о структуре
электромагнитной волны, излучаемой
таким диполем. С ледует
обратить внимание на то, что максимальный
поток электромагнитной энергии излучается
в плоскости, перпендикулярной оси
диполя. Вдоль своей оси диполь не излучает
энергии. Герц использовал элементарный
диполь в качестве излучающей и приемной
антенн при экспериментальном доказательстве
существования электромагнитных волн.
ледует
обратить внимание на то, что максимальный
поток электромагнитной энергии излучается
в плоскости, перпендикулярной оси
диполя. Вдоль своей оси диполь не излучает
энергии. Герц использовал элементарный
диполь в качестве излучающей и приемной
антенн при экспериментальном доказательстве
существования электромагнитных волн.
Из теории Максвелла следует, что различные электромагнитные волны имеют общую природу.
Опытами Герца была установлена идентичность природы электромагнитного излучения и света. Из этого следовал очень важный вывод, что видимый свет представляет электромагнитное излучение. Дальнейшие исследования подтвердили, что не только видимый свет, но и инфракрасное и ультрафиолетовое излучения, рентгеновское и гамма- излучение имеют электромагнитную природу, т. е. электромагнитные волны имеют очень широкий диапазон частот или длин волн.
Спектр электромагнитного излучения охватывает радиоволны, инфракрасное излучение, видимый свет, ультрафиолетовое, рентгеновское и гамма-излучение. Названия для лучей, лежащих в различных областях спектра, сложились исторически. Электромагнитные волны всех участков распространяются в пространстве с одной и той же скоростью. Отличаются они друг от друга только длиной волны:

[с — скорость света, ν— частота].
Радиоволны и УКВ имеют длину волны от нескольких километров до нескольких сантиметров. Генерируют их с помощью вибраторов различных конструкций. В лабораторных условиях получено с помощью радиотехнических устройств электромагнитное излучение, длина которого измеряется миллиметрами, т. е. находится в диапазоне инфракрасного излучения.
Инфракрасное излучение, видимый свет и ультрафиолетовые лучи испускают тела, нагретые до различных температур. Чем выше температура тела, тем короче длина волны испускаемых им электромагнитных волн. Рентгеновское излучение возникает при резком торможении заряженных частиц — электронов. Гамма-излучение испускается при радиоактивном распаде атомов.
19)Вектор индукции магнитного поля!! Связь между вектором магнитной индукции и напряженностью!!!
Магни́тная
инду́кция 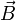 —векторнаявеличина,
являющаяся силовой характеристикоймагнитного
поля(его действия на заряженные
частицы) в данной точке пространства.
Определяет, с какойсилой
—векторнаявеличина,
являющаяся силовой характеристикоймагнитного
поля(его действия на заряженные
частицы) в данной точке пространства.
Определяет, с какойсилой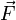 магнитное
поле действует назаряд
магнитное
поле действует назаряд ,
движущийся со скоростью
,
движущийся со скоростью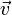 .
.
Более
конкретно, 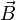 —
это такой вектор, чтосила
Лоренца
—
это такой вектор, чтосила
Лоренца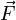 ,
действующая со стороны магнитного
поля[1] на
заряд
,
действующая со стороны магнитного
поля[1] на
заряд 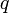 ,
движущийся со скоростью
,
движущийся со скоростью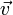 ,
равна
,
равна
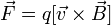

где
косым крестом обозначено векторное
произведение, α — угол между
векторами скорости и магнитной индукции
(направление вектора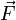 перпендикулярно
им обоим и направлено поправилу
правого винта).
перпендикулярно
им обоим и направлено поправилу
правого винта).
Также магнитная индукция может быть определена[2] как отношение максимального механического момента сил, действующих на рамку стоком, помещенную в однородное поле, к произведениюсилы токав рамке на еёплощадь.
Является основной фундаментальной характеристикой магнитного поля, аналогичной вектору напряжённости электрического поля.
В системе СГСмагнитная индукция поля измеряется вгауссах(Гс), в системеСИ— втеслах(Тл)
1 Тл = 104 Гс
20) Принцип суперпозиции для магнитных полей!! Закон Био-Савара-Лапласа!! Магнитное поле кругового тока и соленоида!!!
Принцип
суперпозиции магнитных полей:
если магнитное поле создано несколькими
проводниками с токами, то вектор
магнитной индукции в какой-либо точке
этого поля равен векторной сумме
магнитных индукций, созданных в этой
точке каждым током в отдельности: |
Компьютерная программа позволяет изменять величину и направление токов, текущих по параллельным проводникам, расстояние между ними. Положение точки, в которой производится измерение вектора магнитной индукции результирующего поля, изменяется с помощью курсора мыши.
Закон Био́—Савара—Лапла́са — физический закон для определения вектора индукции магнитного поля, порождаемого постоянным электрическим током.
Закон Био – Свара – Лапласа звучит так: если постоянный ток проходит по контуру, который находится в вакууме, rо – точка, в которой ищется поле, то индукция магнитного поля в этой точке будет выражено интегралом:
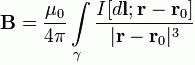
Где I –постоянный ток; γ – это контур; rо – произвольно взятая точка.
Направление dB перпендикулярно dI и r, что означает, что оно перпендикулярно плоскости, в которой лежат, и полностью совпадает с касательной к линии магнитной индукции. Данное направление можно без труда определить по правилу правой руки (по правилу буравчика): если поступательное движение буравчика совпадает с направление тока, то направление вращения руки будет совпадать с направлением dB. Модуль вектора dB выражается формулой:
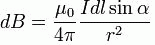
Векторный потенциал представляется следующим интегралом:
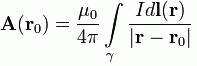
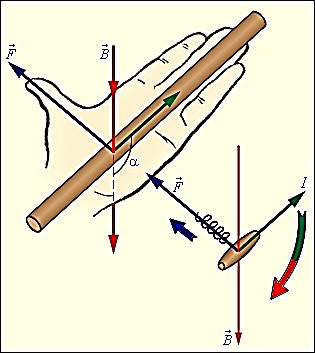
21) Закон Ампера!! Взаимодействие параллельных токов!!!
Как
нам уже известно, магнитное поле оказывает
на рамку с током ориентирующее действие.
Значит, вращающий момент, который
испытывает рамка, является результатом
действия сил на отдельные ее элементы.
Сравнивая и обобщая результаты
исследования действия магнитного поля
на различные проводники с током, Ампер
открыл, что сила dF,
с которой магнитное поле действует на
элемент проводника dl с
током, который находится в магнитном
поле, равна 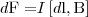 (1) где
dl —
вектор, по модулю равный dl и
совпадающий по направлению с током, В —
вектор магнитной индукции. Направление
вектора dF может
быть определено, используя (1), по правилу
векторного произведения, откуда
следует правило
левой руки:
если ладонь левой руки расположить так,
чтобы в нее входил вектор В,
а четыре вытянутых пальца расположить
по направлению тока в проводнике, то
отогнутый большой палец покажет
направление силы, которая действуюет
на ток. Модуль силы Ампера (см.
(1)) равен
(1) где
dl —
вектор, по модулю равный dl и
совпадающий по направлению с током, В —
вектор магнитной индукции. Направление
вектора dF может
быть определено, используя (1), по правилу
векторного произведения, откуда
следует правило
левой руки:
если ладонь левой руки расположить так,
чтобы в нее входил вектор В,
а четыре вытянутых пальца расположить
по направлению тока в проводнике, то
отогнутый большой палец покажет
направление силы, которая действуюет
на ток. Модуль силы Ампера (см.
(1)) равен  (2) где
α — угол между векторами dl и В. Закон
Ампера используется при нахождении
силы взаимодействия двух токов. Рассмотрим
два бесконечных прямолинейных параллельных
тока I1 и
I2;
(направления токов даны на рис. 1),
расстояние между которыми R. Каждый из
проводников создает вокруг себя магнитное
поле, которое действует по закону Ампера
на соседний проводник с током. Найдем,
с какой силой действует магнитное поле
тока I1 на
элемент dl второго
проводника с током I2.
Магнитное поле тока I1 есть
линии магнитной индукции, представляющие
собой концентрические окружности.
Направление вектора B1 задается
правилом правого винта, его модуль по
формуле (5) есть
(2) где
α — угол между векторами dl и В. Закон
Ампера используется при нахождении
силы взаимодействия двух токов. Рассмотрим
два бесконечных прямолинейных параллельных
тока I1 и
I2;
(направления токов даны на рис. 1),
расстояние между которыми R. Каждый из
проводников создает вокруг себя магнитное
поле, которое действует по закону Ампера
на соседний проводник с током. Найдем,
с какой силой действует магнитное поле
тока I1 на
элемент dl второго
проводника с током I2.
Магнитное поле тока I1 есть
линии магнитной индукции, представляющие
собой концентрические окружности.
Направление вектора B1 задается
правилом правого винта, его модуль по
формуле (5) есть 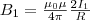 Направление
силы dF1,
с которой поле B1 действует
на участок dl второго
тока, находится по правилу левой руки
и указано на рисунке. Модуль силы,
используя (2), с учетом того, что угол α
между элементами тока I2 и
вектором B1 прямой,
будет равен
Направление
силы dF1,
с которой поле B1 действует
на участок dl второго
тока, находится по правилу левой руки
и указано на рисунке. Модуль силы,
используя (2), с учетом того, что угол α
между элементами тока I2 и
вектором B1 прямой,
будет равен  подставляя
значение дляВ1,
найдем
подставляя
значение дляВ1,
найдем 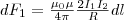 (3) Аналогично
рассуждая, можно показать, что сила
dF2 с
которой магнитное поле тока I2 действует
на элемент dl первого
проводника с током I1,
направлена в противоположную сторону
и по модулю равна
(3) Аналогично
рассуждая, можно показать, что сила
dF2 с
которой магнитное поле тока I2 действует
на элемент dl первого
проводника с током I1,
направлена в противоположную сторону
и по модулю равна  (4) Сопоставление
выражений (3) и (4) дает, что
(4) Сопоставление
выражений (3) и (4) дает, что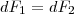 т.
е.два
параллельных тока одинакового направления
притягиваются друг к другу с
силой, равной
т.
е.два
параллельных тока одинакового направления
притягиваются друг к другу с
силой, равной 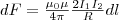 (5)
(5)
Связь между векторами индукции и напряжённости магнитного поля:

18) Элементарная теория диамагнетизма.
Вещества намагничивающиеся во внешнем магнитном поле против направления поля , называются диамагнетиками. ( Наведенные состовляющие магнитных полей атомов складываются и образуют собственное магнитное поле вещества ослабляющее внешнее магнитное поле. В отсутствие внешнего поля диамагнетик немагнитен.
Элементарная теория парамагнетизма.
Парамагнетики — вещества намагничивающиеся по направлению поля. Они всегда обладают магнитным моментом. Парамагнетик намагничивается создавая собственное магнитное поле совпадающее с внешним и усиливающем его.
19) Ферромагнетизм.
Ферромагнетики — вещества обладающие спонтанной намагниченостью. Ферромагнетики с узкой петлёй гистерезиса называются мягкими, с широкой жёсткими. Для каждого ферромагнетика существует определённая тем-ра ( точка Кюри ) при которой он теряет свои магнитные свойства.
Ферромагнетизм — магнитоупорядоченное состояние вещества, в котором большинство атомных магнитных моментов параллельны друг другу, так что вещество обладает самопроизвольной (спонтанной) намагниченностью.
При положительном значении интеграла обмена взаимодействие приводит к параллельной ориентации спинов, которая устанавливается при температурах ниже температуры Кюри Тс в отсутствие внешнего магнитного поля. Выше температуры Кюри ферромагнитные свойства ферромагнетика исчезают, вещество становится парамагнетиком.
В отсутствие внешнего магнитного поля ферромагнитный образец разбит в магнитном отношении на домены — области однородной спонтанной намагниченности. В пределах каждого домена ферромагнетик намагничен до насыщения и обладает определенным магнитным моментом. Направления этих моментов для разных доменов различны, так что в отсутствие внешнего поля суммарный момент всего тела равен нулю (см. рис.1).
Магнитный гистерезис — явление зависимости вектора намагничивания и вектора напряженности магнитного поля в веществе не только от приложенного внешнего поля, но и от предыстории данного образца. Магнитный гистерезис обычно проявляется в ферромагнетиках — Fe, Co, Ni и сплавах на их основе. Именно магнитным гистерезисом объясняется существование постоянных магнитов.
20) Электромагнитная индукция — явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через него.
Закон электромагнитной индукции(Фарадей):

где
— электродвижущая сила, действующая вдоль произвольно выбранного контура,
Правило Ленца:
Индукционный ток, возникающий в замкнутом проводящем контуре, имеет такое направление, что создаваемое им магнитное поле противодействует тому изменению магнитного потока, которым был вызван данный ток.
Магни́тный пото́к — поток как интеграл вектора магнитной индукции В через конечную поверхность .S Определяется через интеграл по поверхности:
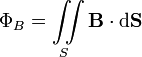
при этом векторный элемент площади поверхности определяется как
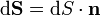
где 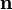 — единичный вектор, нормальный к
поверхности.
— единичный вектор, нормальный к
поверхности.
21) Самоиндукция — явление возникновения ЭДС индукции в проводящем контуре при изменении тока, протекающего через контур.
При изменении тока в контуре меняется магнитный поток через поверхность, ограниченную этим контуром, изменение потока магнитной индукции приводит к возбуждению ЭДС самоиндукции. Направление ЭДС оказывается таким, что при увеличении тока в цепи ЭДС препятствует возрастанию тока, а при уменьшении тока — убыванию.
Величина ЭДС самоиндукции пропорциональна скорости изменения силы тока I и индуктивности контура L:
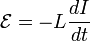
22)Индукти́вность (L)— коэффициент пропорциональности между магнитным потоком (создаваемым током какого-либо витка при отсутствии намагничивающих сред, например, в воздухе) и величиной этого тока
Если в проводящем контуре течёт ток, то ток создаёт магнитное поле. Величина магнитного потока, пронизывающего одновитковый контур, связана с величиной тока следующим образом:
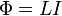
Пусть соленоид длиной l, во много раз превышающей его диаметр, имеет N витков, по которым течет ток силой I. Магнитная индукция поля в нем численно равна
B = μ(0)* μ* I*N / L = μ(0)* μ*I*n,
где n = N/l; I*n – число ампер-витков, приходящихся на единицу длины соленоида; μ(0) – магнитная постоянная, характеризующая магнитное поле в вакууме(μ0 = 4π · 10^(-7) {кг · м/(с^2 · А^2}.)
Энергию магнитного поля в катушке индуктивности можно найти по формуле:
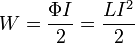 23) Причина возникновения электрического
тока в неподвижном проводнике —
электрическое поле.
23) Причина возникновения электрического
тока в неподвижном проводнике —
электрическое поле.
Всякое изменение магнитного поля порождает индукционное электрическое поле независимо от наличия или отсутствия замкнутого контура, при этом если проводник разомкнут, то на его концах возникает разность потенциалов; если проводник замкнут, то в нем наблюдается индукционный ток.
Индукционное электрическое поле является вихревым.
Направление силовых линий вихревого эл. поля совпадает с направлением индукционного тока
Индукционное электрическое поле имеет совершенно другие свойства в отличии от электростатического поля.
Ток смещения или абсорбционный ток — понятие из области теории классической электродинамики. Введено Дж. К. Максвеллом при построении теории электромагнитного поля для описания слабых токов, возникающих при смещении заряженных частиц в диэлектриках.
При разрыве цепи постоянного тока и включении в неё конденсатора ток в разомкнутом контуре отсутствует. При питании такого разомкнутого контура от источника переменного напряжения в нём регистрируется переменный ток (при достаточно высокой частоте и ёмкости конденсатора загорается лампа, включённая последовательно с конденсатором). Для описания и объяснения «прохождения» переменного тока через конденсатор (разрыв по постоянному току) Максвелл ввёл понятие тока смещения.
Ток смещения существует и в проводниках, по которым течёт переменный ток проводимости, однако в данном случае он пренебрежимо мал по сравнению с током проводимости. Наличие токов смещения подтверждено экспериментально советским физиком А. А. Эйхенвальдом, изучившим магнитное поле тока поляризации, который является частью тока смещения. В общем случае, токи проводимости и смещения в пространстве не разделены, они находятся в одном и том же объеме. Поэтому Максвелл ввёл понятие полного тока, равного сумме токов проводимости (а также конвекционных токов) и смещения. Плотность полного тока:
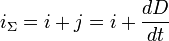

Опера́тор на́бла (оператор Гамильтона)
— векторный дифференциальный оператор,
обозначаемый символом  (набла) (в Юникоде U+2207, ∇).
Для трёхмерного евклидова пространства
в прямоугольных декартовых координатах[1]
оператор набла определяется следующим
образом:
(набла) (в Юникоде U+2207, ∇).
Для трёхмерного евклидова пространства
в прямоугольных декартовых координатах[1]
оператор набла определяется следующим
образом:
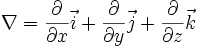
24) Диэлектри́ческая восприи́мчивость (или поляризуемость) вещества — физическая величина, мера способности вещества поляризоваться под действием электрического поля. Диэлектрическая восприимчивость χ(е) — коэффициент линейной связи между поляризацией диэлектрика P и внешним электрическим полем E в достаточно малых полях:
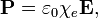
ДИЭЛЕКТРИЧЕСКАЯ ПРОНИЦАЕМОСТЬ — важнейшая электродинамическая характеристика среды (газа, жидкости, твёрдого тела, нейтронного вещества), частицы которой обладают зарядом или магнитным моментом; понятие Д. п. иногда распространяют и на непротяжённые системы (атом, ядро, нуклоны). Д. п. описывает как внутренние свойства среды (спектр возбуждений, взаимодействие частиц), так и результат воздействия на неё внеш. зарядов или токов (неупругое рассеяние заряженных частиц, прохождение электромагнитных волн). Д. п. содержится в материальных уравнениях, которые дополняют систему Максвелла уравнений, делая её замкнутой.
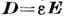
( электрическую индукцию D с напряжённостью E электрического поля в среде)
Электростатическая индукция — явление наведения собственного электростатического поля, при действии на тело внешнего электрического поля. Явление обусловлено перераспределением зарядов внутри проводящих тел, а также поляризацией внутренних микроструктур у непроводящих тел. Внешнее электрическое поле может значительно исказиться вблизи тела с индуцированным электрическим полем.
33 Намагниченность. Магнитное поле в веществе Связь между намагниченностью и напряженностью магнитного поля. Магнитная восприимчивость. Магнитная проницаемость вещества.
Для количественного описания намагниченности магнетиков вводят векторную величину – намагниченность – магнитный момент единицы объема магнетика:
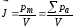 . (8)
. (8)
Магнитный момент магнетика – сумма магнитных моментов отдельных молекул:
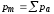 .
.
Связь между
векторами  и
и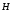 . Существует линейная зависимость между
намагниченностью и напряженностью
поля, вызывающего намагничевание
(соблюдается в случае несильных полей)
. Существует линейная зависимость между
намагниченностью и напряженностью
поля, вызывающего намагничевание
(соблюдается в случае несильных полей)
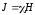 , (9)
, (9)
где
— магнитная
восприимчивость вещества. 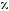 — безразмерная величина. Для диамагнетиков
— безразмерная величина. Для диамагнетиков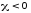 (поле молекулярных токов противоположно
внешнему), для пармагнетиков
(поле молекулярных токов противоположно
внешнему), для пармагнетиков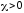 (поле молекулярных токов совпадает с
внешним).
(поле молекулярных токов совпадает с
внешним).
Для парамагнетиков:  (O2 (жидкий)
(O2 (жидкий) 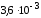 )
)
Для диамагнетиков: 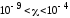 (N2 (газ)
)
(N2 (газ)
)
Магнитное поле
в веществе складывается из двух полей: внешнего
поля, создаваемого током и поля,
создаваемого намагниченным веществом. Вектор
магнитной индукции результирующего
поля в
магнетике равен векторной сумме магнитных
индукций внешнего поля 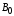 и поля
микротоков
и поля
микротоков 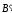 :
:
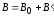 , (10)
, (10)
где  — вектор магнитной индукции, характеризующий
магнитное поле макротоков;
— вектор магнитной индукции, характеризующий
магнитное поле макротоков; — вектор магнитной индукции, характеризующий
магнитное поле микротоков.
— вектор магнитной индукции, характеризующий
магнитное поле микротоков.
Для описания поля
микротоков рассмотрим магнетик в виде
кругового цилиндра сечения S и длины l,
внесенного в однородное внешнее магнитное
поле с индукцией 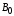 . Возникающее
в магнетике магнитное поле микротоков
будет направлено противоположно внешнему
полю для диамагнетиков и совпадать с
ним для парамагнетиков. Плоскости всех
микротоков расположатся перпендикулярно
вектору
. Возникающее
в магнетике магнитное поле микротоков
будет направлено противоположно внешнему
полю для диамагнетиков и совпадать с
ним для парамагнетиков. Плоскости всех
микротоков расположатся перпендикулярно
вектору 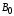 , т.к. векторы
их магнитных моментов
, т.к. векторы
их магнитных моментов 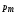 параллельны
параллельны (для
парамагнетиков) и антипараллельны
(для
парамагнетиков) и антипараллельны  (для
диамагнетиков).
(для
диамагнетиков).
Если рассмотреть любое сечение цилиндра, перпендикулярное его оси, то во внутренних участках сечения магнетика молекулярные токи соседних атомов направлены навстречу друг другу и взаимно компенсируются (рис. 11.2). Нескомпенсированными будут молекулярные токи, выходящие на боковую поверхность цилиндра.
Рис. 11.2
Ток, текущий по
боковой поверхности цилиндра, подобен
току соленоида и создает внутри него
магнитное поле, магнитную индукцию  которого можно вычислить по формуле
для магнитной индукции поля внутри
соленоида (в вакууме)
которого можно вычислить по формуле
для магнитной индукции поля внутри
соленоида (в вакууме)
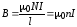 .
.
Для N = 1 (соленоид из одного витка):
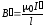 , (11)
, (11)
 — сила
молекулярного тока, l – длина рассматриваемого цилиндра,
μ0 = 1 – магнитная постоянная.
— сила
молекулярного тока, l – длина рассматриваемого цилиндра,
μ0 = 1 – магнитная постоянная.
С другой стороны, 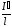
это линейная плотность тока (ток,
приходящийся на единицу длины цилиндра).
Магнитный момент такого тока
это линейная плотность тока (ток,
приходящийся на единицу длины цилиндра).
Магнитный момент такого тока
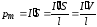 , (12)
, (12)
где V – объем магнетика.
Тогда, согласно
формуле (8) намагниченность 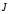 равна:
равна:
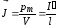 . (13)
. (13)
Сопоставляя формулы (11) и (13), получим выражение для магнитного поля микротоков:
 . (14)
. (14)
Таким образом, магнитное поле в веществе:
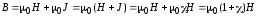 (15)
(15)
откуда видно, что
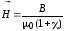 . (16)
. (16)
Безразмерная
величина  называется магнитной
проницаемостью вещества.
называется магнитной
проницаемостью вещества.
Для парамагнетиков μ > 1, для диамагнетиков μ < 1.
С учетом этого, магнитное поле макро- и микротоков:
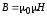 (17)
(17)
Связь между напряженностью магнитного поля, индукцией и намагниченностью
ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ В ДИЭЛЕКТРИКАХ
ЭЛЕКТРОСТАТИ́ЧЕСКОЕ ПО́ЛЕ, электрическое поле неподвижных и не меняющихся со временем электрических зарядов, осуществляющее взаимодействие между ними.
Электростатическое поле характеризуется напряженностью электрического поля Е, которая является его силовой характеристикой: Напряженность электростатического поля показывает, с какой силой электростатическое поле действует на единичный положительный электрический заряд, помещенный в данную точку поля.
- Диэлектрики – электрически нейтральные вещества, состоящие из атомов и молекул, которые можно представить в виде системы электрических зарядов, локализованных на атомах и молекулах. Если в молекуле заменить систему положительных зарядов суммарным зарядом, расположенным в центре тяжести положительных зарядов, а систему отрицательных зарядов суммарным зарядом, расположенным в центре тяжести отрицательных зарядов, то мы можем представить молекулу в виде диполя.
В отсутствие внешнего электрического поля все диэлектрики делятся на три группы:
неполярные диэлектрики – вещества с симметричным строением, у которых центры тяжести положительных и отрицательных зарядов совпадают. Дипольный момент таких диэлектриков равен нулю
полярные диэлектрики – вещества, в которых молекулы имеют асимметричное строение и центры тяжести положительных и отрицательных зарядов находятся на некотором расстоянии друг от друга. Молекулы таких веществ обладают дипольным моментом, но тепловое движение ориентирует дипольные моменты таких молекул в пространстве хаотично и результирующий момент равен нулю
ионные кристаллы – вещества с упорядоченным расположением ионов в пространстве в виде кристаллической решетки. В таких веществах положительные и отрицательные ионы чередуются и результирующий момент равен нулю.
Свободные и связанные заряды.
При рассмотрении электростатического поля, в случае наличия в нем диэлектриков, нужно различать два рода электрических зарядов: свободные и связанные. Под свободными зарядами мы будем понимать, во-первых, все электрические заряды, которые под влиянием электрического поля могут перемещаться на макроскопические расстояния (электроны в металлах и вакууме, ионы в газах и электролитах и т. п.), и, во-вторых, заряды, нанесенные извне на поверхность диэлектриков и нарушающие их нейтральность ). Заряды же, входящие в состав нейтральных молекул диэлектриков, равно как и ионы, закрепленные в твердых диэлектриках вблизи определенных положений равновесия, мы будем называть зарядами связанными.
Потенциал ф электростатического поля при наличии в нем диэлектриков равен, очевидно, сумме потенциала (фо, возбуждаемого свободными зарядами, и потенциала (р’, возбуждаемого связанными электрическими зарядами в диэлектриках:
Потенциал свободных зарядов определяется формулой (12.11):
Поляризованность.
Поляризованность J — определяет интенсивность поляризации диэлектрика и является количественной характеристикой диэлектрика. Средний электрический момент, приходящийся на одну молекулу диэлектрика, дипольныЙ момент молекулы p = q • l (1.1) где q — величина заряда, l — расстояние между центрами положительного и отрицательного заряда. Если существует n таких молекул (диполей) в 1 м3, то J = n • p. (1.2) Поляризованность J, Кл•м/м3 совпадает по зПоляризация диэлектриков — явление, связанное с ограниченным смещением связанных зарядов в диэлектрике или поворотом электрических диполей, обычно под воздействием внешнего электрического поля, иногда под действием других внешних сил или спонтанно.
Поляризацию диэлектриков характеризует вектор электрической поляризации. Физический смысл вектора электрической поляризации — это дипольный момент, отнесенный к единице объема диэлектрика. Иногда вектор поляризации коротко называют просто поляризацией.
§ Вектор поляризации применим для описания макроскопического состояния поляризации не только обычных диэлектриков, но и сегнетоэлектриков, и, в принципе, любых сред, обладающих сходными свойствами. Он применим не только для описания индуцированной поляризации, но и спонтанной поляризации (у сегнетоэлектриков).
Поляризация — состояние диэлектрика, которое характеризуется наличием электрического дипольного момента у любого (или почти любого) элемента его объема.
Различают поляризацию, наведенную в диэлектрике под действием внешнего электрического поля, и спонтанную (самопроизвольную) поляризацию, которая возникает всегнетоэлектриках в отсутствие внешнего поля. В некоторых случаях поляризация диэлектрика (сегнетоэлектрика) происходит под действием механических напряжений, сил трения или вследствие изменения температуры.
Поляризация не изменяет суммарного заряда в любом макроскопическом объеме внутри однородного диэлектрика. Однако она сопровождается появлением на его поверхности связанных электрических зарядов с некоторой поверхностной плотностью σ. Эти связанные заряды создают в диэлектрике дополнительное макроскопическое поле с напряженностью Е1, направленное против внешнего поля с напряженностью Е0. Результирующая напряженность поля Е внутри диэлектрика Е=Е0-Е1.
начению с поверхностной плотностью зарядов, возникающих на поверхности диэлектрика.
Типы поляризации
В зависимости от механизма поляризации, поляризацию диэлектриков можно подразделить на следующие типы:
§ Электронная — смещение электронных оболочек атомов под действием внешнего электрического поля. Самая быстрая поляризация (до 10−15 с). Не связана с потерями.
§ Ионная — смещение узлов кристаллической структуры под действием внешнего электрического поля, причем смещение на величину, меньшую, чем величина постоянной решетки. Время протекания 10−13 с, без потерь.
§ Дипольная (Ориентационная) — протекает с потерями на преодоление сил связи и внутреннего трения. Связана с ориентацией диполей во внешнем электрическом поле.
§ Электронно-релаксационная — ориентация дефектных электронов во внешнем электрическом поле.
§ Ионно-релаксационная — смещение ионов, слабо закрепленных в узлах кристаллической структуры, либо находящихся в междуузлие.
§ Структурная — ориентация примесей и неоднородных макроскопических включений в диэлектрике. Самый медленный тип.
§ Самопроизвольная (спонтанная) — благодаря этому типу поляризации у диэлектриков, у которых он наблюдается, поляризация проявляет существенно нелинейные свойства даже при малых значениях внешнего поля, наблюдается явление гистерезиса. Такие диэлектрики (сегнетоэлектрики) отличаются очень высокими значениями диэлектрической проницаемости (от 900 до 7500 у некоторых видов конденсаторной керамики). Введение спонтанной поляризации, как правило, увеличивает тангенс угла потерь материала (до 10−2)
§ Резонансная — ориентация частиц, собственные частоты которых совпадают с частотами внешнего электрического поля.
§ Миграционная поляризация обусловлена наличием в материале слоев с различной проводимостью, образованию объемных зарядов, особенно при высоких градиентах напряжения, имеет большие потери и является поляризацией замедленного действия.
- Помещение диэлектрика в электрическое поле вызывает его поляризацию – возникновение отличного от нуля результирующего дипольного момента pV.
где pi – дипольный момент одной молекулы. Для количественной оценки поляризации диэлектрика используют векторную величину – поляризованностьР
Поляризация диэлектрика приводит к тому, что в тонком поверхностном слое диэлектрика возникают некомпенсированные связанные зарядыqсвяз, называемые поверхностными поляризационными зарядами, величина которых может быть определена из значения индуцированного дипольного момента
которая для большинства веществ линейно зависит от напряженности внешнего электрического поля
где χ – диэлектрическая восприимчивость вещества. С увеличением напряженности внешнего поля и уменьшением температуры диэлектрическая восприимчивость возрастает.
ДИЭЛЕКТРИ́ЧЕСКАЯ ВОСПРИИ́МЧИВОСТЬ, коэффициент пропорциональности c междуполяризацией диэлектрика P (дипольным моментом единицы объема) и напряженностьюE внешнего электрического поля.
В диэлектрике, помещенном во внешнее электрическое поле, наблюдается процесс поляризации: диэлектрик приобретает определенный макроскопический дипольный момент. Для большинства диэлектриков в слабых электрических полях вектор поляризации пропорционален напряженности внешнего электрического поля, и эта связь выражается соотношением:
Р = ceоE,
где c — коэффициент пропорциональности, который и называют диэлектрической восприимчивостью; eо — электрическая постоянная, eо =8,854.10-12 Ф
5. теорема Остроградского –Гаусса в диэлектрической среде формулируется в следующем виде
Для произвольной замкнутой поверхности S поток вектора смещения электростатического поля D сквозь эту поверхность равен алгебраической сумме заключенных внутри этой поверхности свободных зарядов (вектором D описывается электростатическое поле, создаваемое свободными зарядами, но при таком их распределении, какое имеется при наличии диэлектрика).
Если электрическое поле имеет место в диэлектрике, то наблюдается поляризация вещества и появляются связанные электрические заряды.
Учитывают поляризацию с помощью вектора поляризации , который для анизотропных и однородных сред выражается через напряженность поля следующим образом: , где c – диэлектрическая восприимчивость вещества (диэлектрика). Вектор поляризации равен также поверхностной плотности связанных зарядов, возникающих в диэлектрике под воздействием внешнего электрического поля (Р = sсвяз ).
Кроме этого, при анализе электростатических полей используют вектор электрического смещения:
.
(1.8)
Единицей электрического смещения является кулон на метр квадратный (Кл/м2).
Величина e = e0 + c является основной характеристикой диэлектрика и называется абсолютной диэлектрической проницаемостью. Отношение er = e/e0 называют относительной диэлектрической проницаемостью.
Вопрос 16
- Магнитным полем называется одна из форм проявления электромагнитного поля.
Магнитное поле создается движущимися электрическими зарядами, частицами и телами, облалающими магнитным моментом, а также изменяющимся во времени электрическим полем.
Магнитное поле характеризуется вектором напряженности Н.
Магнитное поле действует только на движущиеся электрические заряды и на частицы и тела, облалающими магнитным моментом.
Силовой характеристикой магнитного поля является вектор магнитной индукции В (вектор индукции магнитного поля), который определяется:
по действию магнитного поля на движущуюся в нем заряженную частицу – точечный электрический заряд;
малый элемент проводника с током;
по действию магнитного поля на небольшую рамку с током.
НАПРЯЖЕННОСТЬ МАГНИТНОГО ПОЛЯ (Н), силовая характеристика магнитного поля, не зависящая от магнитных свойств среды. В вакууме H совпадает (в единицах СГС (сантиметр-грамм-секунда — система единиц)) с магнитной индукцией B. В среде Н определяет тот вклад в магнитную индукцию, который дают внешние источники поля.
Напряженностью магнитного поля называют векторную величину , характеризующую магнитное поле и определяемую следующим образом:
| , |
Напряженность магнитного поля заряда q, движущегося в вакууме равна:
| , |
Это выражение показывает закон Био–Савара–Лапласа для .
Напряженность магнитного поля является, как бы, аналогом вектора электрического смещения в электростатике.
Принцип суперпозиции
Магнитное поле, создаваемое несколькими движущимися зарядами или токами, равно векторной сумме магнитных полей, создаваемых каждым зарядом или током в отдельности.
Связь между напряженностью магнитного поля, индукцией и намагниченностью
В вакууме:
где H – напряженность магнитного поля, B – индукция магнитного поля, m0 = 4p10-7 В ∙ сек/А ∙ м = 4p10-7 Гн/м – магнитная постоянная.
Читайте также:
Рекомендуемые страницы: