Амплитуда колебаний ℹ️ определение, характеристика, обозначение и единицы измерения, формулы расчета периода и частоты, уравнения и графики

Амплитуда колебаний – это максимальное значение отклонения от нулевой точки. В физике данный процесс анализируется в разных разделах. 

Он изучается при механических, звуковых и электромагнитных колебаниях. В перечисленных случаях амплитуда измеряется по-разному и по своим законам.

Амплитуда колебаний

Амплитудой колебания называют максимальную отдаленную точку нахождения тела от положения равновесия. В физике она обозначается буквой А и измеряется в метрах. 

За амплитудой можно наблюдать на простом примере пружинного маятника.

 

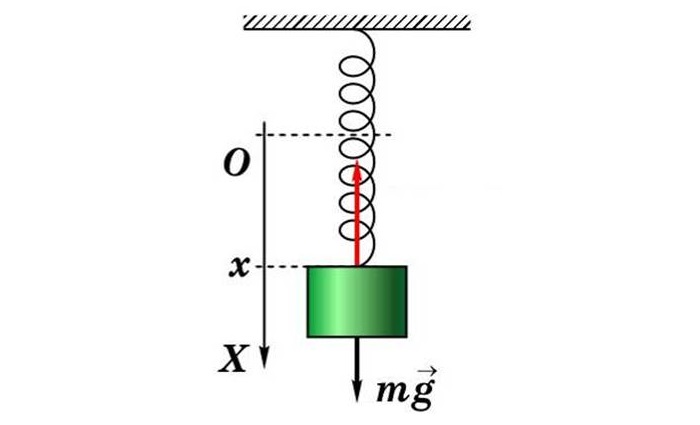
В идеальном случае, когда игнорируется сопротивление воздушного пространства и трение пружинного устройства, устройство будет колебаться бесконечно. Описание движения выполняется с помощью функций cos и sin:

x(t) = A * cos(ωt + φ0) или x(t) = A * sin(ωt + φ0),

где 

• величина А – это амплитуда свободных движений груза на пружине;

• (ωt + φ0) – это фаза свободных колебаний, где ω — это циклическая частота, а φ0 – это начальная фаза, когда t = 0. 

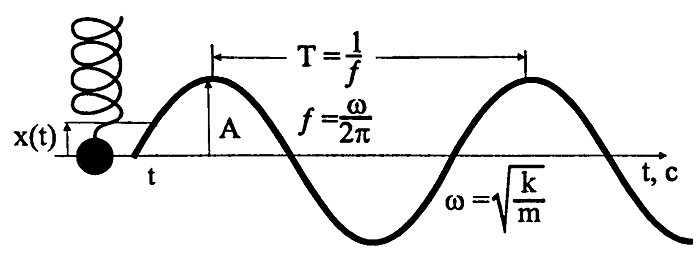
В физике указанную формулу называют уравнением гармонических колебаний. Данное уравнение полностью раскрывает процесс, где маятник движется с определенной амплитудой, периодом и частотой. 

Период колебаний

Результаты лабораторных опытов показывают, что циклический период движения груза на пружине напрямую зависит от массы маятника и жесткости пружины, но не зависит от амплитуды движения. 

В физике период обозначают буквой Т и описывают формулами:

Исходя из формул, период колебаний – это механические движения, повторяющиеся через определенный промежуток времени. Простыми словами периодом называют одно полное движение груза.

Частота колебаний

Под частотой колебаний следует понимать количество повторений движения маятника или прохождения волны. В разных разделах физики частота обозначается буквами ν, f или F. 

Данная величина описывается выражением:

v = n/t – количество колебаний за промежуток времени,

где 

В Международной системе измерений частоту измеряют в Гц (Герцах). Она относится к точным измеряемым составляющим колебательного процесса. 

Например, наукой установлена частота вращения Солнца вокруг центра Вселенной. Она равна -10

35 Гц при одинаковой скорости.

Циклическая частота

В физике циклическая и круговая частота имеют одинаковое значение. Данная величина еще называется угловой частотой. 

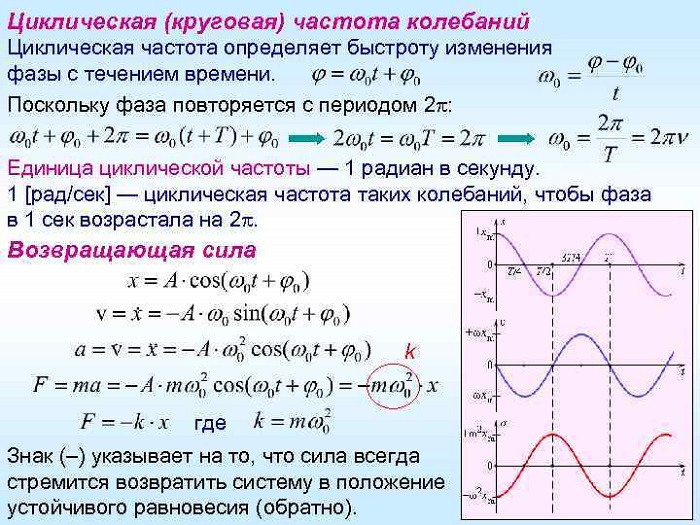
Обозначают ее буквой омега. Она равна числу собственных колебательных движений тела за 2π секунд времени:

ω = 2π/T = 2πν.

Данная величина нашла свое применение в радиотехнике и, исходя из математического расчета, имеет скалярную характеристику. Ее измерения проводят в радианах на секунду. С ее помощью значительно упрощаются расчеты процессов в радиотехнике. 

Например, резонансное значение угловой частоты колебательного контура рассчитывают по формуле:

WLC = 1/LC.

Тогда как обычная циклическая резонансная частота выражается:

VLC = 1/2π*√ LC.

 

В электрике под угловой частотой следует понимать число полных трансформаций ЭДС или число оборотов радиуса – вектора. Здесь ее обозначают буквой f.

Как определить амплитуду, период и частоту колебаний по графику

Для определения на графике составляющих колебательного механического процесса или, например, колебания температуры, нужно разобраться в терминах этого процесса. 

К ним относят:

• расстояние испытываемого объекта от исходной точки – называют смещением и обозначают х;

• наибольшее отклонение – амплитуда смещения А;

• фаза колебания – определяет состояние колебательной системы в любой момент времени;

• начальная фаза колебательного процесса – когда t = 0, то φ = φ₀.

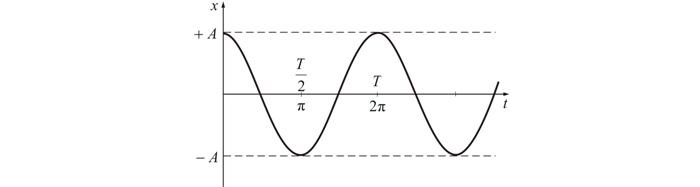
Из графика видно, что значение синуса и косинуса может меняться от -1 до +1. Значит, смещение х может быть равно –А и +А. Движение от –А до +А называют полным колебанием.

Построенный график четко показывает период и частоту колебаний. Стоить отметить, что фаза не воздействует на форму кривой, а только влияет на ее положение в заданный промежуток времени.

Гармонические колебания. Амплитуда, период и частота колебательного движения

В рамках прошлой темы говорилось о новом виде механического движения – колебательном движении.

Механическое колебательное движение —это движение, при котором состояния тела с течением времени повторяются, причем тело проходит через положение устойчивого равновесия поочередно в противоположных направлениях.

Если колебания происходят в системе только под действием внутренних сил, то такие колебания называют свободными.

Колебательной системой

называют такую физическую систему, в которой при отклонении от положения равновесия возникают и существуют колебания.

Маятник – это твердое тело, совершающее под действием приложенных сил колебания около неподвижной точки или вокруг оси.

В рамках данной темы будет рассмотрен простейший вид колебательного движения — гармонические колебания.

Гармонические колебания — это колебания, при которых смещение колеблющейся точки от положения равновесия изменяется с течением времени по закону синуса или косинуса.

Смещение от положения равновесия при гармонических колебаниях описывается уравнениями вида:

Эти уравнения называют кинематическим законом гармонического движения.

Покажем, что гармонические колебания действительно подчиняются закону синуса или косинуса. Для этого рассмотрим следующую установку.

Возьмем нитяной маятник, а в качестве груза к нему выберем небольшой массивный сосуд с маленьким отверстием снизу и насыплем в него песок.А под полученную систему положим длинную бумажную ленту.

Если ленту перемещать с постоянной скоростью в направлении, перпендикулярном плоскости колебаний, то на ней останется волнообразная дорожка из песка, каждая точка которой соответствует положению колеблющегося груза в тот момент, когда он проходил над ней. Из опыта видно, что след, который оставляет песок на листе бумаги, есть некая кривая.

Она называется синусоидой. Из курса математики старших классов вы узнаете о том, что аналогичные графики имеют функции типа

Значит, графически зависимость смещения колеблющейся точки от времени изображается синусоидой или косинусоидой.

Через точки, соответствующие положению равновесия маятника, проведена ось времени t, а перпендикулярно ей — ось смещения икс. График дает возможность приблизительно определить координату груза в любой момент времени.

Теперь разберемся с величинами, входящими в уравнение колебательного движения.

Смещение — величина, характеризующая положение колеблющейся точки в некоторый момент времени относительно положения равновесия и измеряемая расстоянием от положения равновесия до положения точки в данный момент времени.

Амплитуда колебаний — максимальное смещение тела от положения равновесия.

Циклическая, или круговая частота, показывающая, сколько колебаний совершает тело за 2p секунд.

j0 — это начальная фаза колебаний.

Фаза колебаний — это аргумент периодической функции, который при заданной амплитуде колебаний определяет состояние колебательной системы в любой момент времени.

Промежуток времени, в течение которого тело совершает одно полное колебание, называется периодом колебаний.

Период колебаний обычно обозначается буквой Т и в системе СИ измеряется в секундах.

Число колебаний в единицу времени называется частотой колебаний.  Обозначается частота буквой ν. За единицу частоты принято одно колебание в секунду. Эта единица названа в честь немецкого ученого Генриха Герца.

Период колебания и частота колебаний связаны следующей зависимостью:

Т.е. частота — это величина обратная периоду и равная числу полных колебаний, совершаемых за 1 секунду.

Циклическая частота также связана с периодом колебаний или частотой. Эту связь математически можно записать в следующем виде:

Таким образом, любое колебательное движение характеризуется амплитудой, частотой (или периодом) и фазой колебаний.

При совершении телом гармонических колебаний не только его координата, но и такие величины, как сила, ускорение, скорость, тоже изменяются по закону синуса или косинуса.

Это следует из известных вам законов и формул, в которых указанные величины попарно связаны прямо пропорциональной зависимостью, например законом Гука или вторым законом Ньютона. Из этих формул видно, что сила и ускорение достигают наибольших значений, когда колеблющееся тело находится в крайних положениях, где смещение наиболее велико, и равны нулю, когда тело проходит через положение равновесия.

Что же касается скорости, то она, наоборот, в крайних положениях равна нулю, а при прохождении телом положения равновесия достигает наибольшего значения.

Колебания, практически близкие к гармоническим, совершает тяжелый шарик, подвешенный на легкой и малорастяжимой нити, длина которой значительно больше диаметра шарика. Такую колебательную систему называют математическим маятником.

Математический маятник — это материальная точка, подвешенная на невесомой нерастяжимой нити, прикрепленной к подвесу и находящейся в поле силы тяжести.

Также гармонические колебания может совершать груз подвешенный на пружине, совершающий колебания в вертикальной плоскости. Такую колебательную систему называют пружинным маятником — это система, состоящая из материальной точки массой m и пружины.

Основные выводы:

– Гармонические колебания — это колебания, при которых смещение колеблющейся точки от положения равновесия изменяется с течением времени по закону синуса или косинуса.

– Любое колебательное движение характеризуется амплитудой, частотой (или периодом) и фазой колебаний.

– Амплитуда колебаний — максимальное смещение тела от положения равновесия.

– Промежуток времени, в течение которого тело совершает одно полное колебание, называется периодом колебаний.

– Число колебаний в единицу времени называется частотой колебаний.

– Фаза колебаний — это аргумент периодической функции, который при заданной амплитуде колебаний определяет состояние колебательной системы в любой момент времени.

– Математический и пружинный маятники — это простейшие идеализированные колебательные системы, подчиняющиеся закону синуса или косинуса.

– Математический маятник — это материальная точка, подвешенная на невесомой нерастяжимой нити, прикрепленной к подвесу и находящейся в поле силы тяжести.

– Пружинный маятник — это система, состоящая из материальной точки массой m и пружины, которая совершает колебания в вертикальной плоскости.

Механические, периодические колебания, характеристики: частота, период, фаза, амплитуда, Виды колебаний, резонанс, примеры

Тестирование онлайн

Колебательное движение

Особый вид неравномерного движения — колебательное. Это движение, которое повторяется с течением времени. Механические колебания — это движения, которые повторяются через определенные промежутки времени. Если промежутки времени одинаковые, то такие колебания называются периодическими.

Колебательная система

Это система взаимодействующих тел (минимум два тела), которые способны совершать колебания. Простейшими колебательными системами являются маятники.

Характеристика колебаний

Фаза определяет состояние системы, а именно координату, скорость, ускорение, энергию и др.

Циклическая частота характеризует скорость изменения фазы колебаний.

Начальное состояние колебательной системы характеризует начальная фаза

Амплитуда колебаний A — это наибольшее смещение из положения равновесия

Период T — это промежуток времени, в течение которого точка выполняет одно полное колебание.

Частота колебаний — это число полных колебаний в единицу времени t.

Частота, циклическая частота и период колебаний соотносятся как

Виды колебаний

Колебания, которые происходят в замкнутых системах называются свободными или собственными колебаниями. Колебания, которые происходят под действием внешних сил, называют вынужденными. Встречаются также автоколебания (вынуждаются автоматически).

Если рассматривать колебания согласно изменяющихся характеристик (амплитуда, частота, период и др.), то их можно разделить на гармонические, затухающие, нарастающие (а также пилообразные, прямоугольные, сложные).

При свободных колебаниях в реальных системах всегда происходят потери энергии. Механическая энергия расходуется, например, на совершение работы по преодолению сил сопротивления воздуха. Под влиянием силы трения происходит уменьшение амплитуды колебаний, и через некоторое время колебания прекращаются. Очевидно, что чем больше силы сопротивления движению, тем быстрее прекращаются колебания.

Вынужденные колебания. Резонанс

Вынужденные колебания являются незатухающими. Поэтому необходимо восполнять потери энергии за каждый период колебаний. Для этого необходимо воздействовать на колеблющееся тело периодически изменяющейся силой. Вынужденные колебания совершаются с частотой, равной частоте изменения внешней силы.

Вынужденные колебания

Амплитуда вынужденных механических колебаний достигает наибольшего значения в том случае, если частота вынуждающей силы совпадает с частотой колебательной системы. Это явление называется резонансом.

Например, если периодически дергать шнур в такт его собственным колебаниям, то мы заметим увеличение амплитуды его колебаний.

Если влажный палец двигать по краю бокала, то бокал будет издавать звенящие звуки. Хотя это и незаметно, палец движется прерывисто и передает стеклу энергию короткими порциями, заставляя бокал вибрировать

Стенки бокала также начинают вибрировать, если на него направить звуковую волну с частотой, равной его собственной. Если амплитуда станет очень большой, то бокал может даже разбиться. По причине резонанса при пении Ф.И.Шаляпина дрожали (резонировали) хрустальные подвески люстр. Возникновение резонанса можно проследить и в ванной комнате. Если вы будете негромко пропевать звуки разной частоты, то на одной из частот возникнет резонанс.

В музыкальных инструментах роль резонаторов выполняют части их корпусов. Человек также имеет собственный резонатор — это полость рта, усиливающая издаваемые звуки.

Явление резонанса необходимо учитывать на практике. В одних явлениях он может быть полезен, в других — вреден. Резонансные явления могут вызывать необратимые разрушения в различных механических системах, например, неправильно спроектированных мостах. Так, в 1905 году рухнул Египетский мост в Санкт-Петербурге, когда по нему проходил конный эскадрон, а в 1940 — разрушился Такомский мост в США.

Явление резонанса используется, когда с помощью небольшой силы необходимо получить большое увеличение амплитуды колебаний. Например, тяжелый язык большого колокола можно раскачать, действуя сравнительно небольшой силой с частотой, равной собственной частоте колебаний колокола.

Гармонические колебания

Определение 1

Техника и окружающий мир являются примерами того, что существуют такие процессы, которые повторяются через определенные промежутки времени, то есть периодически. Их называют колебательными.

Колебательные движения. Формулы

Такие движения относят к явлениям с разной физической природой с подчинением общим закономерностям. Запись колебания тока в электрической цепи и математического маятника производится одним и тем же уравнением. Различная природа колебательных движений позволяет рассматривать их с единой точки зрения, исходя из общности закономерностей.

Определение 2

Механические колебания – это периодические или непериодические изменения физической величины, описывающей механическое движение (скорость, перемещение и так далее).

Когда в заданной среде атомы располагаются очень близко или молекулы испытывают силовое воздействие, наблюдается возбуждение механических колебаний. Это говорит о том, что процесс будет иметь конечную скорость, зависящую от свойств среды, которая распространяется от точки к точке. Так возникают механические волны. Явный пример – звуковые волны в воздухе.

Волновые процессы и колебания разной природы имеют много общего, а их распространение может быть описано аналогичными математическими уравнениями. Это подтверждает единство материального мира.

Гармонические колебания. Определение

В механике предусмотрено движение поступательно, вращательно и с наличием колебаний.

Определение 3

Механические колебания – это движения тел, которые повторяются точно или приблизительно за определенные одинаковые временные промежутки.

Функция x=f(t) объясняет закон движения тела с наличием колебаний. При графическом изображении дается представление о протекании колебательного процесса во времени. Рисунок 2.1.1 наглядно показывает принцип простых колебательных систем груза на пружине или математического маятника.

Рисунок 2.1.1. Механические колебательные системы.

Механические колебания подразделяют на свободные и вынужденные.

Определение 4

Действия внутренних сил системы после выведения из равновесия порождают свободные колебания. Примером могут служить колебания груза на пружине или маятника. Если их действие происходит под воздействием внешних сил, тогда их называют вынужденными.

Простейшим видом колебаний являются гармонические колебания, которые описываются уравнением x=xmcos (ωt

Амплитудно-частотная характеристика — Википедия

Амплиту́дно-часто́тная характери́стика (АЧХ) — зависимость амплитуды выходного сигнала некоторой системы от частоты её входного гармонического сигнала^[1][2]. АЧХ — один из видов «частотного отклика» системы (англ. frequency response) наряду c ФЧХ и АФЧХ.

АЧХ в математической теории линейных стационарных систем описывает зависимость модуля комплексной передаточной функции линейной системы от частоты. Значение АЧХ на некоторой частоте указывает, во сколько раз амплитуда сигнала этой частоты на выходе системы отличается от амплитуды выходного сигнала на другой частоте. Обычно используют нормированные к максимуму значения АЧХ.

В математике АЧХ называют модулем комплексной функции. Для построения АЧХ обычно требуется 5-8 точек в рабочем диапазоне частот от ωmin до ωср. Эти характеристики так же, как и временные, содержат информацию о свойствах линейных динамических систем.^[3]

На графике АЧХ в декартовых координатах по оси абсцисс откладывается частота, а по оси ординат — отношение амплитуд выходного и входного сигналов системы.

Обычно для оси частоты используется логарифмический масштаб, так как отображаемый диапазон частот может изменяться в достаточно широких пределах (от единиц до миллионов герц или рад/с). В случае, когда логарифмический масштаб используется и на оси ординат, АЧХ принято называть логарифмической амплитудно-частотной характеристикой.

ЛАЧХ широкое применяется в теории автоматического управления в связи с простотой построения и наглядностью при исследовании поведения систем автоматического регулирования.

АЧХ в радиолокации, связи и других радиотехнических приложениях[править | править код]

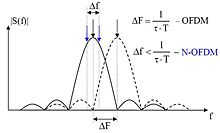
АЧХ приемных каналов средств радиолокации, связи и других радиотехнических систем характеризуют их помехозащищенность. Необходимо учесть, что при цифровой обработке сигналов АЧХ становится периодически повторяющейся, поэтому паразитные полосы приёма (так называемые боковые лепестки АЧХ (side lobe of frequency response) ^[4]) в цифровых средствах должны подавляться на этапе аналоговой обработки сигналов.

В многоканальных системах, например, в цифровых антенных решетках, важную роль имеет также межканальная идентичность АЧХ с коэффициентами межканальной корреляции до 0,999 и выше в области главной полосы пропускания. Чем выше этот показатель и чем шире полоса частот, в которой он соответствует требованиям, тем лучше удается минимизировать мультипликативные помехи, возникающие при межканальной обработке сигналов. Для повышения этой идентичности могут применяться специальные алгоритмы межканальной коррекции АЧХ приемных каналов.

Поскольку коэффициенты коррекции в общем случае зависят от уровня тестирующих сигналов, для многоканальных систем представляет интерес анализ зависимости АЧХ от уровня входного воздействия в пределах всего линейного динамического диапазона устройства. Соответствующий вариант АЧХ будет иметь трехмерную зависимость. Она должна формироваться после проведения коррекции АЧХ анализируемых устройств ^[5].

Классическим методом измерения АЧХ является подача на вход исследуемого объекта гармонического сигнала изменяемой частоты с постоянной или известной для каждой частоты сигнала амплитудой. В этом случае измеряется отношение модулей амплитуды выходного и входного сигналов (коэффициента передачи) исследуемой системы для разных частот .

Для сокращения времени, необходимого для формирования АЧХ, изменение частоты лучше производить с помощью генератора качающейся частоты — измерительного генератора, плавно перестраивающего частоту своего сигнала с неизменной амплитудой во времени. Обычно эти генераторы изменяют плавно свою частоту генерации от низких частот до высоких, затем быстро переключают частоту на низшую, периодически повторяя процесс. Такие генераторы называют генераторами качающейся частоты (ГКЧ) или «свип-генераторами» (от англ. sweep — мести метлой).

Указанные методы последовательной смены частот не пригодны для устройств с работающей автоматической регулировкой усиления (АРУ), выравнивающей различия в значениях АЧХ на разных частотах при времени перехода от одной частоты к другой, превышающем постоянную времени срабатывания АРУ. Они также не позволяют оценить интермодуляционные искажения между действующими одновременно сигналами разных частот. Метод измерения АЧХ с помощью линейно-частотно модулированных сигналов (ЛЧМ) не позволяет осуществлять когерентное накопление во времени напряжений сигнала для частотных компонент, поэтому его точность ограничена условием достаточно больших отношений сигнал-шум. По этой причине метод не пригоден для формирования трехмерных АЧХ, характеризующих зависимость линейного динамического диапазона от частоты, поскольку при слабых отношениях сигнал-шум дает большие погрешности.

Существуют измерители АЧХ, основанные на иных принципах, например, измерители, подающие на вход исследуемой системы широкополосный сигнал, широкополосный импульс с короткими фронтами или измерители с шумовым сигналом, имеющим в полосе частот, существенном для измерения, постоянную спектральную плотность мощности. Отклик системы анализируется с помощью анализатора спектра или фурье-измерителя АЧХ, выполняющего фурье-преобразование отклика системы из временно́й в частотную область для формирования полного вида АЧХ.

Любому методу измерения АЧХ присущи те или иные достоинства или недостатки. Приемлемый способ применения измерения зависит от конкретной задачи.

• Харкевич А.А. Спектры и анализ. — М.: Государственное издательство физико-математической литературы, 1962.
• Гоноровский И.С., Демин М.П. Радиотехнические цепи и сигналы. — М.: Радио и связь, 1994.
• Рабинер Л., Гоулд Б. Теория и применение цифровой обработки сигналов. — М.: Мир. — 1978. — С. 106. — 848 с.

Амплитудная модуляция — Википедия

Материал из Википедии — свободной энциклопедии

Амплиту́дная модуля́ция — вид модуляции, при которой изменяемым параметром несущего сигнала является его амплитуда^[1].

Первые опыты передачи речи и музыки с помощью радиоволн методом амплитудной модуляции произвёл в 1906 году американский инженер Р. Фессенден. В его опытах несущая частота 50 кГц радиопередатчика вырабатывалась электромашинным генератором (альтернатором), для её модуляции между генератором и антенной включался угольный микрофон, изменяющий затухание сигнала в цепи.

С 1920 года вместо электромашинных генераторов для генерации несущей частоты стали использоваться генераторы на электронных лампах. Во второй половине 1930-х годов, по мере освоения ультракоротких волн, амплитудная модуляция постепенно начала вытесняться из радиовещания и радиосвязи на УКВ частотной модуляцией.

С середины XX века в служебной и любительской радиосвязи на всех частотах начали применять модуляцию с одной боковой полосой (ОБП), которая имеет ряд важных преимуществ перед АМ, главное из которых — сужение в 2 раза полосы частот, занимаемой радиосигналом. В связи с этим предлагалось перевести на ОБП и массовое радиовещание, однако это потребовало бы замены всех радиовещательных приёмников на более сложные и дорогие, поэтому это не было осуществлено.

В конце XX века начался переход к цифровому радиовещанию с использованием сигналов с амплитудной манипуляцией^[2].

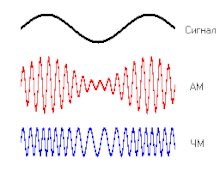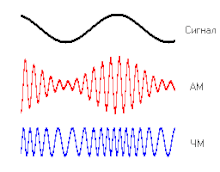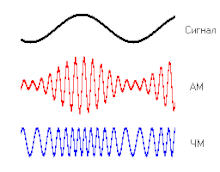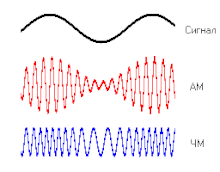Сигнал, например, аудиосигнал может модулировать амплитуду (AM) или частоту (ЧМ) несущей. Амплитудная модуляция с различным коэффициентом модуляции. На нижней осциллограмме — перемодуляция.

Пусть

• um(t){\displaystyle u_{m}(t)} — информационный (модулирующий) сигнал,
• uc(t){\displaystyle u_{c}(t)} — несущий (модулируемый) сигнал (несущее колебание).

Тогда амплитудно-модулированный сигнал uam(t){\displaystyle u_{\text{am}}(t)} имеет вид:

uam(t)=uc(t)[1+mum(t)|um(t)|max].(1){\displaystyle u_{\text{am}}(t)=u_{c}(t)\left[1+m{\frac {u_{m}(t)}{|u_{m}(t)|_{\max }}}\right].\qquad \qquad (1)}

Если uc(t)=Uccos⁡(ωct){\displaystyle u_{c}(t)=U_{c}\cos(\omega _{c}t)}, то (1) примет вид^[3]:

uam(t)=Uc[1+mum(t)|um(t)|max]cos⁡(ωct).{\displaystyle u_{\text{am}}(t)=U_{c}\left[1+m{\frac {u_{m}(t)}{|u_{m}(t)|_{\max }}}\right]\cos(\omega _{c}t).}

Здесь m{\displaystyle m} — некоторая неотрицательная константа, называемая коэффициентом модуляции. Формула (1) описывает несущий сигнал uc(t){\displaystyle u_{c}(t)}, модулированный по амплитуде сигналом um(t){\displaystyle u_{m}(t)} с коэффициентом модуляции m{\displaystyle m}.

Для неискаженной модуляции необходимо выполнение условия m≤1{\displaystyle m\leq 1}. Выполнение этого условия необходимо для того, чтобы выражение в квадратных скобках в (1) всегда было положительным. Если оно может принимать отрицательные значения в какой-то момент времени, то происходит так называемая перемодуляция (избыточная модуляция). Простые демодуляторы (типа квадратичного детектора) демодулируют такой сигнал с сильными искажениями.

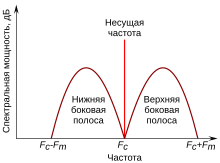Спектр АМ колебания.

Допустим, что мы хотим промодулировать несущее колебание моногармоническим сигналом. Выражение для несущего колебания с частотой ωc{\displaystyle \omega _{c}} имеет вид (начальную фазу положим равной нулю):

uc(t)=Uccos⁡(ωct),{\displaystyle u_{c}(t)=U_{c}\cos(\omega _{c}t),}

где Uc{\displaystyle U_{c}} — амплитуда несущего колебания.

Выражение для модулирующего синусоидального сигнала с частотой ωm{\displaystyle \omega _{m}} имеет вид:

um(t)=Umcos⁡(ωmt+φ),{\displaystyle u_{m}(t)=U_{m}\cos(\omega _{m}t+\varphi ),}

где φ{\displaystyle \varphi } — начальная фаза, |um(t)|max=Um{\displaystyle |u_{m}(t)|_{\max }=U_{m}} . Тогда, в соответствии с (1):

uam(t)=Uc[1+mcos⁡(ωmt+φ)]cos⁡(ωct).{\displaystyle u_{\mathrm {am} }(t)=U_{c}[1+m\cos(\omega _{m}t+\varphi )]\cos(\omega _{c}t).}

Приведённая выше формула для uam(t){\displaystyle u_{\mathrm {am} }(t)} может быть записана в следующем виде:

uam(t)=Uccos⁡(ωct)+{\displaystyle u_{\mathrm {am} }(t)=U_{c}\cos(\omega _{c}t)+}

+mUc2[cos⁡((ωc−ωm)t−φ)+cos⁡((ωc+ωm)t+φ)].{\displaystyle +{\frac {mU_{c}}{2}}[\cos((\omega _{c}-\omega _{m})t-\varphi )+\cos((\omega _{c}+\omega _{m})t+\varphi )].}

Радиосигнал состоит из несущего колебания и двух так называемых боковых полос, боковые полосы имеют частоту, отличную от ωc{\displaystyle \omega _{c}}. Для синусоидального сигнала, использованного в качестве примера здесь, боковые полосы представляют собой синусоидальные сигналы и их частоты равны ωc+ωm{\displaystyle \omega _{c}+\omega _{m}} и ωc−ωm{\displaystyle \omega _{c}-\omega _{m}}.

Пока несущие частоты соседних по частоте радиостанций достаточно разнесены по частоте, и боковые полосы в спектре сигналов соседних по частоте станций не перекрываются между собой, станции не будут создавать взаимных помех.

• Кулешов В. Н., Удалов Н. Н., Богачев В. М. и др. Генерирование колебаний и формирование радиосигналов. — М.: МЭИ, 2008. — 416 с. — ISBN 978-5-383-00224-7.

Формы световых волн и виды их колебаний. Длина волны. Амплитуда, период, частота и фаза колебаний. Связь длины волны с частотой.

⇐ ПредыдущаяСтр 3 из 17Следующая ⇒

Световая волна – электромагнитная волна видимого диапазона длин волн. Частота световой волны определяет цвет. Энергия, переносимая световой волной, пропорциональна квадрату ее амплитуды.

Световые волны охватывают на шкале электромагнитных волн огромный диапазон, лежащий за ультракороткими миллиметровыми радиоволнами и простирающийся до наиболее коротких гамма-лучей – электромагнитных волн с длиной волны ʎ меньшей, чем 0,1 нм (1 нм = 10^-9 м)

 

Всякая волна распространяется из одной точки в другую не мгновенно, а с определенной скоростью.

Скорость распространения световых и вообще электромагнитных волн в вакууме ( а практически и в воздухе) равна приблизительно 300 000 км\с

 

Вблизи предмета его тень имеет резкие края, однако очертания
тени размываются с увеличением расстояния между предметом
и тенью. Это нетрудно понять, если учесть, что свет распростра-
няется прямолинейно, а каждый источник света имеет конечные
размеры. Изучение распространения световых лучей показывает,
что на краю каждой тени существует частично освещенная об-
ласть. Эта так называемая полутень делает очертания тени раз-
мытыми. Наиболее темная часть тени (глубокая тень) полностью
отгорожена от источника света. Ширина полутени тем меньше,
чем ближе тень к объекту, который ее отбрасывает, поэтому
вблизи предмета тень выглядит более резкой.

Было установлено, что световая волна представляет собой колебания электрического и магнитного полей, распространяющиеся в пространстве; оба поля совершают колебания во взаимно перпендикулярных плоскостях, которые перпендикулярны также и направлению распространения волны. В действительности световые волны являются одним из типов электромагнитных волн, включающих также рентгеновское, ультрафиолетовое, инфракрасное излучения и радиоволны. Световые волны испускаются атомами, когда электроны в них переходят с одной орбиты на другую. Если атом получает энергию, например в форме тепла, света или электрической энергии, электроны удаляются от ядра на орбиты с большей энергией. Затем они вновь переходят на более близкие к ядру орбиты с меньшей энергией, излучая при этом энергию в виде электромагнитных волн. Так возникает свет.

Форма волны —  наглядное представление формы сигнала, такого как волна, распространяющегося в физической среде, или его абстрактное представление.

Во многих случаях среда, в которой распространяется волна, не позволяет наблюдать её форму визуально. В этом случае, термин «сигнал» относится к форме графика величины, изменяющейся по времени или зависящей от расстояния. Для наглядного представления формы волны может использоваться инструмент, называемый «осциллограф», отображающий на экране значение измеряемой величины и его изменение. В более широком смысле термин «сигнал» используется для обозначения формы графика значений любой величины, изменяющейся по времени.

 

Общими периодическими сигналами являются (t —  время):

· Синусоида: sin (2 π t). Амплитуда сигнала соответствует тригонометрической функции синуса (sin), изменяющейся по времени.

· Меандр: saw(t) − saw (t − duty). Этот сигнал как правило используется для представления и передачи цифровых данных. Прямоугольные импульсы с постоянным периодом содержат нечётные гармоники, которые попадают на −6дБ/октаву.

· Треугольная волна: (t − 2 floor ((t + 1) /2)) (−1)^{floor ((t + 1) /2)}. Включает в себя нечётные гармоники, которые попадают на −12дБ/октаву.

· Пилообразная волна: 2 (t − floor(t)) − 1. Выглядит как зубья пилы. Используется в качестве отправной точки cубтрактивного синтеза, так как пилообразная волна с постоянным периодом содержит чётные и нечётные гармоники, которые попадают на −6 дБ/октаву.

Другие формы сигналов часто называют композитными, так как в большинстве случаев они могут быть описаны как сочетание нескольких синусоидальных волн или суммой других базисных функций.

Ряд Фурье описывает разложение периодического сигнала на основе фундаментального принципа, гласящего, что любой периодический сигнал может быть представлен в виде суммы (возможно бесконечной) фундаментальных и гармонических составляющих. Энергетически-конечные непериодические сигналы могут быть проанализированы как синусоиды после преобразования Фурье.

Длина волны (λ) — кратчайшее расстояние между точками волны, колеблющимися в одинаковых фазах. Свет мы воспринимаем глазами. Он является электромагнитной волной с длиной волны (в вакууме) от 760 нм (красный) до 420 нм (фиолетовый). 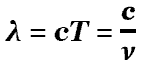— длина волны. Частота световых колебаний от 4.1014 Гц (фиолетовый) до 7.1014 Гц (красный). Это достаточно узкая полоска на шкале электромагнитных волн. Частота световой волны (длина волны в вакууме) определяет цвет видимого нами света: Синусоида символически показывает частоту (длину волны) соответствующего участка спектра (цвета). Основные спектральные цвета (имеющие собственное название), а также характеристики излучения этих цветов, представлены в таблице: Красный Оранжевый Жёлтый Зелёный Голубой Синий Фиолетовый Цвет 625—740 590—625 565—590 500—565 485—500 440—485 380—440 Диапазон длин волн, нм 480—400 510—480 530—510 600—530 620—600 680—620 790—680 Диапазон частот, ТГц 1,68—1,98 1,98—2,10 2,10—2,19 2,19—2,48 2,48—2,56 2,56—2,82 2,82—3,26 Диапазон энергии фотонов, эВ	λ — длина световой волны	м
с — скорость света	м/c
T — период ЭМ колебаний	с
ν — частота колебаний световой волны	Гц

Колеба́ния — повторяющийся в той или иной степени во времени процесс изменения состояний системы около точки равновесия. Например, при колебаниях маятника повторяются отклонения его в ту и другую сторону от вертикального положения; при колебаниях в электрическом колебательном контуре повторяются величина и направление тока, текущего через катушку.

Электромагнитными колебаниями называются периодические изменения напряженности Е и индукции В.

Электромагнитными колебаниями являются радиоволны, микроволны, инфракрасное излучение, видимый свет, ультрафиолетовое излучение, рентгеновские лучи, гамма-лучи.

 

Передача колебаний обусловлена тем, что смежные участки среды связаны между собой. Эта связь может осуществляться различно. Она может быть обусловлена, в частности, силами упругости, возникающими вследствие деформации среды при ее колебаниях. В результате колебание, вызванное каким-либо образом в одном месте, влечет за собой последовательное возникновение колебаний в других местах, все более и более удаленных от первоначального, и возникает так называемая волна.

Электромагнитные волны – эти волны представляют собой передачу из одних мест пространства в другие колебаний электрического и магнитного полей, создаваемых электрическими зарядами и токами. Всякое изменение электрического поля вызывает появление магнитного поля, и обратно, всякое изменение магнитного поля создаёт электрическое поле. Твердая, жидкая или газообразная среда может сильно влиять на распространение электромагнитных волн, но наличие такой среды для этих волн не необходимо. Электромагнитные волны могут распространяться всюду, где может существовать электромагнитное поле, а значит, и в вакууме, т.е. в пространстве, не содержащем атомов.

Всякая волна распространяется из одной точки в другую не мгновенно, а с определенной скоростью.

Электромагнитные колебания — взаимосвязанные колебания электрического и магнитного полей.

Электромагнитные колебания появляются в различных электрических цепях. При этом колеблются величина заряда, напряжение, сила тока, напряженность электрического поля, индукция магнитного поля и другие электродинамические величины.

Свободные электромагнитные колебания возникают в электромагнитной системе после выведения ее из состояния равновесия, например, сообщением конденсатору заряда или изменением тока в участке цепи.

Это затухающие колебания, так как сообщенная системе энергия расходуется на нагревание и другие процессы.

Вынужденные электромагнитные колебания — незатухающие колебания в цепи, вызванные внешней периодически изменяющейся синусоидальной ЭДС.

Электромагнитные колебания описываются теми же законами, что и механические, хотя физическая природа этих колебаний совершенно различна.

Электрические колебания — частный случай электромагнитных, когда рассматривают колебания только электрических величин. В этом случае говорят о переменных токе, напряжении, мощности и т.д.

КОЛЕБАТЕЛЬНЫЙ КОНТУР

Колебательный контур — электрическая цепь, состоящая из последовательно соединенных конденсатора емкостью C, катушки индуктивностью L и резистора сопротивлением R.

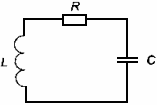
Состояние устойчивого равновесия колебательного контура характеризуется минимальной энергией электрического поля (конденсатор не заряжен) и магнитного поля (ток через катушку отсутствует).

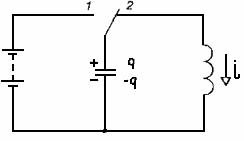
Величины, выражающие свойства самой системы (параметры системы): L и m, 1/C и k

величины, характеризующие состояние системы:

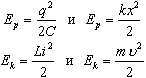
величины, выражающие скорость изменения состояния системы: u = x'(t) и i = q'(t) .