Условие статической прочности. Рациональные формы сечения балок. Потенциальная энергия.
Потенциальная энергия деформации при растяжении.
Внешние силы в процессе деформации тела производят работу. Часть затраченной на деформацию энергии поглощается телом и накапливается в нем в виде потенциальной энергии,называемой потенциальной энергией деформации. Остальная часть расходуется на необратимые процессы-нагрев тела,изменение его электромагнитных свойств и тд. Соотношение между двумя слагаемыми энергии внешних сил изменяется в процессе нагружения тела. В пределах упругих деформаций затрата энергии на необратимые процессы весьма незначительна, и поэтому можно считать,что в пределах упругости работа внешних сил полностью переходт в потенциальнуюэнергию деформации. Таким образом,упругое тело является как бы аккумулятором энергии. За пределами упругости большая часть работы внешних сил затрачивается на необратимые процессы, а при разгрузке выделяется лишь часть энергии,связанная с упругими деформациями тела. При разгрузке идеального упругого тела накопленная в нем потенциальная энергия полностью расходуется на восстановление его первоначальной формы и размеров, причем эту работу производят внутренние силы. Следовательно, потенциальная энергия деформации равна работе внутренних сил упругости на перемещениях точек их приложения, и поэтому всегда может быть выражена через эти силы. Формула (1) дает возможность определить удельную потенциальную энергию деформации в общем случае объемного напряженного состояния:
; ; .(2)
Потенциальная энергия деформации U определяется из уравнения (3) путем интегрирования по объему:
26.Дифференциальное уравнение упругой оси балки
Угол поворота сечения :
Прогиб (линейное перемещение) сечения балки:
C1 и C2 — постоянные интегрирования, определяемые из граничных условий
27.Интеграл Мора и правило Верещагина
Существует несколько основных метода определения перемещений припоперечном изгибе.Аналитический метод сводится к интегрированию дифференциальногоуравнения упругой линии балки. При этом записывается зависимостьизгибающего момента от текущей координаты и решается уравнение: где – вторая производная линейного перемещения по текущей координате;EI x – жесткость поперечного сечения при изгибе.Постоянные интегрирования, полученные при решении дифференциальногоуравнения, определяются из граничных условий (линейные перемещения в опорахравны нулю, угловые перемещения в заделке равны нулю).
Для определения угловых перемещений стоит учесть, что в зоне малых упругих деформаций
Другим способом является решение интеграла Мора: где Mx – зависимость
изгибающего момента от внешней нагрузки в зависимости от текущей координаты;
M‘x– зависимость изгибающего момента от единичной внешней нагрузки, приложенной в сечении, где необходимо определить перемещение; z – текущая координата. Графический метод сводится к раскрытию интеграла Мора способом Верещагина. Для этого строится эпюра изгибающих моментов от внешних нагрузок. После этого с балки снимаются все внешние нагрузки и в сечении, в котором определяется линейное перемещение, прикладывается сила, равная единице. Строится эпюра изгибающих моментов от единичной силы. Для определения перемещения эти две эпюры перемножаются между собой, при этом на одной из эпюр берется площадь фигуры и умножается на ординатувторой эпюры, лежащую под центром тяжести фигуры с первой эпюры.Суммируются все перемножения по длине эпюр.Для определения угловых перемещений, в рассматриваемом сечениивместо единичной силы прикладывается единичный момент.
28.Балка равного сопротивления
где MX – изгибающий момент в поперечном сечении, [Н·м]; WXмомент сопротивления поперечного сечения изгибу, [м3]. Условие равенства максимальных нормальных напряжений по всем поперечным сечениям можно записать в виде:
для балки с прямоугольным поперечным сечением, момент сопротивления определяется зависимостью:
Если предположить, что балка нагружена только сосредоточенной внешней силой F, то величина изгибающего момента будет зависеть от длины балки:
Читайте также:
Рекомендуемые страницы:
Поиск по сайту
Моделирование в электроэнергетике — Статическая устойчивость в электроэнергетической системе
Статическая устойчивость в электроэнергетической системе
Под понятием статической устойчивости понимают способность энергосистемы восстанавливать исходный или близкий к исходному режим работы энергосистемы после малого возмущения или медленных изменениях параметров режима.
Статическая устойчивость является необходимым условием существования установившегося режима работы системы, но не предопределяет способность системы продолжать работу при возникновении конечных возмущений, например, коротких замыканий, включения или отключения линий электропередачи.
Различают два вида нарушений статической устойчивости: апериодическое (сползание) и колебательное (самораскачивание).
Статическая апериодическая (сползание) устойчивость связана с изменением баланса активной мощности в энергосистеме (изменение разности между электрической и механической мощностями), что приводит к росту угла δ, в результате может произойти выпадение машины из синхронизма (нарушение устойчивости). Угол δ изменяется без колебаний (апериодически), сначала медленно, а затем всё быстрее, как бы сползая (см. рис. 1,а).
Статическая периодическая (колебательная) устойчивость связана с настройками автоматических регуляторов возбуждения (АРВ) генераторов. АРВ должны быть настроены таким образом, чтобы исключить возможность самораскачивания системы в широком диапазоне режимов работы. Однако, при некоторых сочетаниях ремонтов (схемно-режимной ситуации) и настройках регуляторов возбуждения могут возникнуть колебания в системе регулирования, вызывающие нарастающие колебания угла δ вплоть до выпадения машины из синхронизма. Это явление и называется самораскачиванием (см. рис. 1,б).
Рис.1. Характер изменения угла δ при нарушении статической устойчивости в виде сползания (а) и самораскачивания (б)
Статическая апериодическая (сползание) устойчивость
Первый этап исследования статической устойчивости – это исследование статической апериодической устойчивости. При исследовании статической апериодической устойчивости предполагается, что вероятность колебательного нарушения устойчивости при увеличении перетока по межсистемным связям очень мала и можно пренебречь самораскачиванием. Для определения области апериодической устойчивости энергосистемы производят утяжеление режима работы энергосистемы. Метод утяжеления заключается в последовательном изменении параметров узлов или ветвей, или их групп заданными шагами с последующим расчетом нового установившегося режима на каждом шаге изменения и выполняется до тех пор, пока обеспечивается возможность расчета.
Рассмотрим простейшую схему сети, которая состоит из генератора, силового трансформатора, линии электропередачи и шин бесконечной мощности (см. рис.2).
Рис.2. Схема замещения расчетной цепи
В рассматриваемом простейшем случае электромагнитная мощность, которую можно передать от генератора к шинам бесконечной мощности, описывается следующим выражением:
В записанном выражении переменная представляет собой модуль линейного напряжения на шинах станции, приведенный к стороне ВН, а переменная — модуль линейного напряжения в точке шин бесконечной мощности.
Рис.3. Векторная диаграмма напряжений
Взаимный угол между вектором напряжения и вектором напряжения обозначается через переменную — , для которого в качестве положительного направления принимается направление против часовой стрелки от вектора напряжения .
Следует отметить, что формула для электромагнитной мощности написана в предположении, что генератор снабжен автоматическим регулятором возбуждения, который контролирует напряжение на стороне генераторного напряжения (), а также для простоты выкладок пренебрегли активным сопротивлением в элементах расчетной схемы.
Анализируя формулу для электромагнитной мощности можно сделать вывод, что величина передаваемой мощности в энергосистему зависит от угла между напряжениями. Данная зависимость получила название угловой характеристикой мощности электропередачи (см. рис.4).
Рис.4. Угловая характеристика мощности
Установившийся (синхронный) режим работы генератора определяется равенством двух моментов, действующих на вал турбогенератора (считаем, что можно пренебречь моментом сопротивления, обусловленным трением в подшипниках и сопротивлением охлаждающей среды): момент турбины Мт, вращающий ротор генератора и стремящийся ускорить его вращение, и синхронный электромагнитный момент Мэм, противодействующий вращению ротора.
Допустим, что в турбину генератора поступает пар, который создает крутящий момент на валу турбины (при некотором приближении он равен внешнему моменту Мвн, передаваемому от первичного двигателя). Установившийся режим работы генератора может быть в двух точках: А и Б, так как в данных точках соблюдается баланс между моментом турбины и электромагнитным моментом с учетом потерь.
При работе синхронной машины в точке А увеличение/уменьшение мощности турбины на величину ΔP приведет к увеличению/уменьшению угла d, соответственно. Таким образом, сохраняется равновесие моментов, действующих на вал ротора (равенство момента турбины и электромагнитного момента с учетом потерь), и тем самым нарушение синхронной машины с сетью не происходит.
При работе синхронной машины в точке В увеличение/уменьшение мощности турбины на величину ΔP приведет к уменьшению/ увеличению угла d, соответственно. Таким образом, равновесие моментов, действующих на вал ротора, нарушается. В результате либо генератор выпадает из синхронизма (т. е. ротор начинает вращаться с частотой, отличающейся от частоты вращения магнитного поля статора), либо синхронная машина переходит в точку устойчивой работы (точка А).
Таким образом, из рассмотренного примера видно, что простейшим критерием сохранения статической устойчивости является положительный знак у выражения, которое определяет отношение приращения мощности к приращению угла:
Таким образом, область устойчивой работы определяется диапазоном углов от 0 до 90 градусов, а в области углов от 90 до 180 градусов, устойчивая параллельная работа невозможна.
Максимальное значение мощности, которая может быть передана в энергосистему, называется пределом статической устойчивости, и соответствует значению мощности при взаимном угле 90 градусов:
Работа на предельной мощности, соответствующей углу 90 градусов, не производится, так как малые возмущения, всегда имеющиеся в энергосистеме (например, колебания нагрузки), могут вызвать переход в неустойчивую область и нарушение синхронизма. Максимальное допустимое значение передаваемой мощности принимается меньшим предела статической устойчивости на величину коэффициента запаса статической апериодической устойчивости по активной мощности.
Запас статической устойчивости для электропередачи в нормальном режиме должен составлять не менее 20%. Значение допустимого перетока активной мощности в контролируемом сечении по данному критерию определяется по формуле:
Запас статической устойчивости для электропередачи в послеаварийном режиме должен составлять не менее 8%. Значение допустимого перетока активной мощности в контролируемом сечении по данному критерию определяется по формуле:
Статическая периодическая (колебательная) устойчивость
Неправильно выбранный закон управления или неправильная настройка параметров автоматического регулятора возбуждения (АРВ) может привести к нарушению колебательной устойчивости. При этом нарушение колебательной устойчивости может происходить в режимах не превышающих предельного режима по апериодической устойчивости, что неоднократно наблюдалось в действующих электроэнергетических системах.
Исследование колебательной статической устойчивости сводится к следующим этапам:
1. Составление системы дифференциальных уравнений, которая описывает рассматриваемую электроэнергетическую систему.
2. Выбор независимых переменных и выполнение линеаризации записанных уравнений с целью формирования системы линейных уравнений.
3. Составление характеристического уравнения и определение области статической устойчивости в пространстве регулируемых (независимых) параметров настройки АРВ.
Об устойчивости нелинейной системы судят по затуханию переходного процесса, который определяется корнями характеристического уравнения системы. Для обеспечения устойчивости необходимо и достаточно, чтобы корни характеристического уравнения имели отрицательные вещественные части.
Для оценки устойчивости применяют различные методы анализа характеристического уравнения:
1. алгебраические методы (метод Рауса, метод Гурвица), основанные на анализе коэффициентов характеристического уравнения.
2. частотные методы (метод Михайлова, Найквиста, D-разбиения), основанные на анализе частотных характеристик.
Мероприятия по повышению предела статической устойчивости
Мероприятия по повышению предела статической устойчивости определяются при анализе формулы для определения электромагнитной мощности (формула записана в предположении, что генератор снабжен автоматическим регулятором возбуждения):
1. Применение АРВ сильного действия на генерирующем оборудовании.
Одним из эффективных средств повышения статической устойчивости является применение АРВ генераторов сильного действия. При использовании устройств АРВ генераторов сильного действия угловая характеристика видоизменяется: максимум характеристики смещается в область значений углов больших 90° (с учетом относительного угла генератора).
2. Поддержание напряжения в точках сети с помощью устройств компенсации реактивной мощности.
Установка устройств компенсации реактивной мощности (СК, УШР, СТК и т.п.) для поддержания напряжения в точках сети (устройства поперечной компенсации). Устройства позволяют поддерживать напряжения в точках сети, что благоприятно сказывается на пределе статической устойчивости.
3. Установка устройств продольной компенсации (УПК).
При увеличении длины линии соответственно возрастает ее реактивное сопротивление и вследствие этого существенно ограничивается предел передаваемой мощности (ухудшается устойчивость параллельной работы). Уменьшение реактивного сопротивления длинной линии электропередачи повышает ее пропускную способность. Для уменьшения индуктивного сопротивления линии электропередачи в рассечку линии устанавливают устройство продольной компенсации (УПК), которое представляет собой батарею статических конденсаторов. Таким образом результирующее сопротивление линии уменьшается, тем самым увеличивается пропускная способность.
4. Повышения номинального класса напряжения.
В связи с тем, что величина напряжения прямо пропорциональна электромагнитной мощности, то увеличение класса напряжения позволит повысить предел передаваемой мощности от электростанции.
Энергетические методы расчета деформаций (Лекция №32)
Постановка задачи.
Кроме рассмотренных способов вычисления прогибов и углов поворота сечений балок существует более общий метод, пригодный для определения деформаций любых упругих конструкций. Он основан на применении закона сохранения энергии.
При статическом растяжении или сжатии упругого стержня происходит превращение потенциальной энергии из одного вида в другой; часть потенциальной энергии действующего на стержень груза полностью переходит в потенциальную энергию деформации стержня. Действительно, если мы будем нагружать стержень путем постепенного подвешивания к его нижнему концу очень малых грузов dP, то при добавлении каждого такого груза подвешенная уже часть нагрузки опустится и ее потенциальная энергия уменьшится, а потенциальная энергия деформации стержня соответственно увеличится.
Это явление имеет место при любом виде деформации всякой упругой конструкции при статической нагрузке; такую конструкцию можно рассматривать как своеобразную машину, преобразующую один вид потенциальной энергии в другой.
Мы условились называть «статической» такую нагрузку, которая возрастает постепенно и таким образом, что ускорениями элементов конструкции можно пренебречь; передача давлений (сил) от одной части конструкции на другую не меняет характера движения, этих частей, т. е. их скорость остается постоянной и ускорение отсутствует.
При этих условиях деформация конструкции не будет сопровождаться изменением кинетической энергии системы, и будет иметь место лишь преобразование потенциальной энергии из одного вида в другой. При этом мы пренебрегаем магнитными, электрическими и тепловыми явлениями, сопровождающими упругие статические деформации тела лишь в очень слабой мере.
Так как характер движения всех элементов конструкции с течением времени не меняется, то в каждый момент времени будет иметь место равновесие как для каждой части конструкции в целом под действием внешних сил и реакций, так и для каждого элемента этой части под действием внешних сил и напряжений, приложенных к этому элементу. Деформации конструкции, напряжения в ее частях и реакции, передающиеся от одной части на другую, успевают следовать за ростом нагрузки.
Таким образом, можно сказать, что полное преобразование одного вида потенциальной энергии в другой имеет место, если деформация происходит без нарушения равновесия системы. Мерой энергии, превратившейся в другой вид, является величина работы, произведенной силами, действующими на конструкцию.
Обозначим величину накопленной потенциальной энергии деформации через U, а уменьшение потенциальной энергии внешних нагрузок . Тогда величина измеряется положительной работой этих нагрузок , с другой стороны, накоплению потенциальной энергии деформации U соответствует отрицательная работа внутренних, междучастичных сил А, так как перемещения точек тела при деформации происходят в обратном по отношению к внутренним силам направлении.
Закон сохранения энергии при деформациях упругих систем принимает вид:
заменяя в этой формуле величины и U численно равными им значениями работ и А, получаем иную формулировку этого закона:
или
Эта формулировка закона сохранения энергии совпадает с так зазываемым «началом» возможных перемещений в применении к упругим системам. Последнее равенство выражает, что при перемещениях без нарушения равновесия сумма работ всех сил, приложенных к точкам тела, равна нулю.
Таким образом, начало возможных перемещений в применении к упругим системам является следствием закона сохранения энергии.
Таким образом, потенциальная энергия деформации численно равна работе внешних сил , проделанной ими этой деформации:
Вычисление потенциальной энергии.
При вычислении потенциальной энергии будем предполагать, что деформации не только материала, но и всей конструкции, следуя закону Гука, пропорциональны нагрузкам, т. е. линейно с ними связаны и растут постепенно вместе с ними.
Известно, что при статическом растяжении или сжатии стержня силами Р величина работы , а следовательно, и величина энергии U равняется:
В случае сдвига
При кручении
Так же как и при кручении, может быть вычислена потенциальная энергия при чистом изгибе.
Концевые сечения балки под действием изгибающих моментов(Рис.1) повернутся на угол , где центральный угол изогнувшейся по дуге радиусом р оси балки.
Рис.1. Модель расчета потенциальной энергии при чистом изгибе.
Тогда
так как из общей теории изгиба а
Из полученных выражений следует, что потенциальная энергия деформации равна половине произведения силы или пары сил на перемещение по ее направлению того сечения, где эта сила приложена. Условимся называть термином «обобщенная сила» всякую нагрузку, вызывающую соответствующее нагрузке перемещение, т. е. и сосредоточенную силу, и пару сил, и т. п.; перемещение же, соответствующее этой силе, будем называть «обобщенной координатой».
«Соответствие» заключается в том, что речь идет о перемещении того сечения, где приложена рассматриваемая сила, причем о таком перемещении, что произведение его на эту силу дает нам величину работы; для сосредоточенной силы это будет линейное перемещение по направлению действия силы прогиб, удлинение; для пары сил это угол поворота сечения по направлению действия пары.
Иначе: потенциальная энергия деформации численно равна половине произведения обобщенной силы на соответствующую ей координату.
,
где Робобщенная сила, обобщенная координата.
Полученные соотношения также показывают, что потенциальная энергия является функцией второй степени от независимых внешних сил, так как в эти формулы не входят реакции, зависящие от приложенных к элементу сил и связанные с ними уравнениями равновесия. Из тех же формул видно, что величина потенциальной энергии деформации является функцией второй степени от «обобщенных координат» системы и вполне ими определяется. Таким образом, порядок приложения нагрузок в этом отношении безразличен, важна лишь окончательная форма деформированного элемента. Поэтому, хотя результаты этого параграфа получены в предположении, что нагрузка возрастает статически, при сохранении равновесия в течение всего процесса нагружения, однако выведенные формулы сохраняют силу и при любом способе приложения нагрузок, лишь бы значения сил и деформаций были связаны линейной зависимостью и относились к тому моменту, когда установится равновесие конструкции.
Известно также, что в общем случае изгиба изгибающий момент М(х) является величиной переменной. В любом сечении ему будет сопутствовать поперечная сила Q(х). Поэтому рассматривать следует уже,не всю балку в целом, а лишь бесконечно малый элемент балки длиной dx.
Рис.2. Энергетическая модель поперечного изгиба
Под действием изгибающих усилий сечения элемента (рис.2, а) поворачиваются и образуют между собой угол (Рис.2, б). Касательные же усилия стремятся вызвать (Рис.2, в) перекос элемента; таким образом перемещения от нормальных напряжений идут перпендикулярно к направлению касательных напряжений, и наоборот.
Это позволяет независимо вычислять работу изгибающих и касательных усилий.
Обычно работа касательных усилий оказывается малой по сравнению с работой нормальных, поэтому мы пока ею будем пренебрегать. Элементарная работа нормальных усилий (как и в случае чистого изгиба) равна:
или
Рис.3. Расчетная схема примера расчета потенциальной энергии при поперечном изгибе.
Вся потенциальная энергия изгиба получится суммированием по длине балки
Знак предела интегрирования условно указывает, что интегрирование должно охватить всю балку; в тех случаях, когда для М(х) мы имеем несколько участков, то интеграл приходится разбивать на сумму интегралов.
Вычислим потенциальную энергию балки на двух опорах, нагруженной силой Р (Рис.3). Эпюра моментов имеет два участка; поэтому
Дальше…
Статическая устойчивость по активной мощности
Коэффициент запаса статической устойчивости по активной мощности в сечении (Кр) вычисляется по формуле:
Кр = (Рпр -Р- дР/ Р,
где Рпр – активная мощность, передаваемая через рассматриваемое сечение (переток в сечении) в режиме, предельном по статической устойчивости;
Р – переток в сечении в рассматриваемом режиме, Р > 0;
дР – расчетная амплитуда нерегулярных колебаний активной мощности в этом сечении в рассматриваемом режиме (принимается, что под действием нерегулярных колебаний переток Р изменяется в диапазоне (Р + дР)).
Определение предельного по статической устойчивости перетока в сечении осуществляется утяжелением режима (увеличением перетока). При этом рассматриваются траектории утяжеления режима, представляющие собой последовательности установившихся режимов, которые при изменении некоторого параметра или группы параметров позволяют достичь границы области статической устойчивости.
Следует рассматривать увеличение перетока в сечении для ряда траекторий утяжеления, которые характерны для данной ЭЭС и различаются перераспределением мощности между узлами, находящимися с каждой из сторон рассматриваемого сечения. Значение Р определяется по траектории, которой соответствует наименьшая предельная мощность.
Допускается рассматривать только сбалансированные по мощности способы утяжеления режима, т.е. такие, при которых частота остается практически неизменной. Если для конкретных условий увеличение перетока может вызываться или сопровождаться заметным изменением частоты, то такие способы утяжеления режима также должны быть рассмотрены.
Предельные по статической устойчивости перетоки определяются
с учетом перегрузки генераторов потоку ротора, допустимой в течение 20 мин.
Более высокую перегрузку разрешается учитывать (во всех режимах, кроме послеаварийного), если за допустимое время такая перегрузка автоматически ликвидируется без снижения запаса устойчивости в сечении (автоматический пуск гидрогенераторов, перевод их из компенсаторного режима в активный и т.п.).
Значение амплитуды нерегулярных колебаний активной мощности (АР) устанавливается для каждого сечения ЭЭС по данным измерений.
При отсутствии таких данных расчетная амплитуда нерегулярных колебаний активной мощности, МВт, может быть определена
по выражению:
где Рн1 , Рн2 – суммарные мощности нагрузки с каждой из сторон рассматриваемого сечения, МВт.
Коэффициент К принимается равным: 1,5 – при ручном регулировании и 0,75 – при автоматическом регулировании и ограничении перетоков мощности.
В эксплуатации для контроля за соблюдением нормативных запасов статической устойчивости следует, как правило, использовать значения перетоков активной мощности.
При необходимости максимально допустимые и аварийно допустимые перетоки задаются как функции перетоков в других сечениях и напряжении в узловых точках энергосистемы. Такие перетоки и напряжения следует включать в число контролируемых
параметров.
В зависимости от конкретных условий, в качестве контролируемых могут использоваться и другие параметры режима энергосистемы, в частности, значения углов между векторами напряжений по концам электропередачи. Допустимые значения контролируемых параметров, при которых обеспечивается нормативный коэффициент запаса статической устойчивости по активной мощности, устанавливаются на основе расчетов.
13. Удельная энергия сечения
Удельная энергия потока в каком — либо сечении выражается в виде
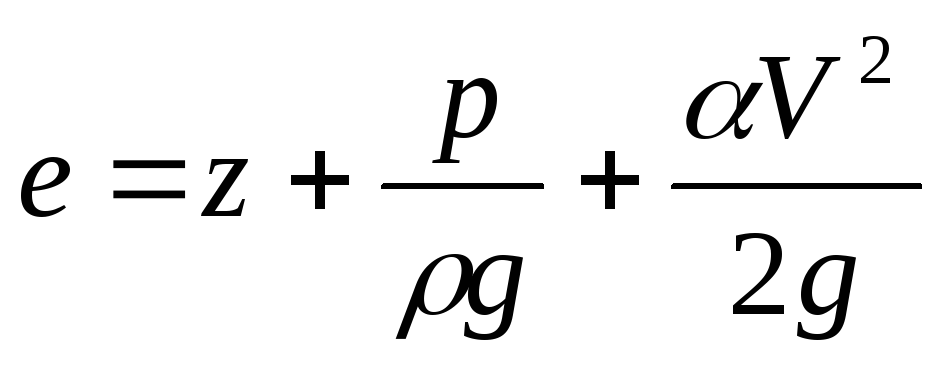
относительно произвольной плоскости сравнения, от которой отсчитывается высота положения точки z.
Для потоков со свободной поверхностью в дальнейшем не учитывается атмосферное давление, как постоянное во всех сечениях потока и в выражении для e принимается p, равное избыточному давлению. Кроме того, напомним, что при плавно изменяющемся движении гидродинамическое давление распределяется по закону изменения гидростатического давления. Поэтому, для любой точки М произвольного живого сечения (рис. 13.1)
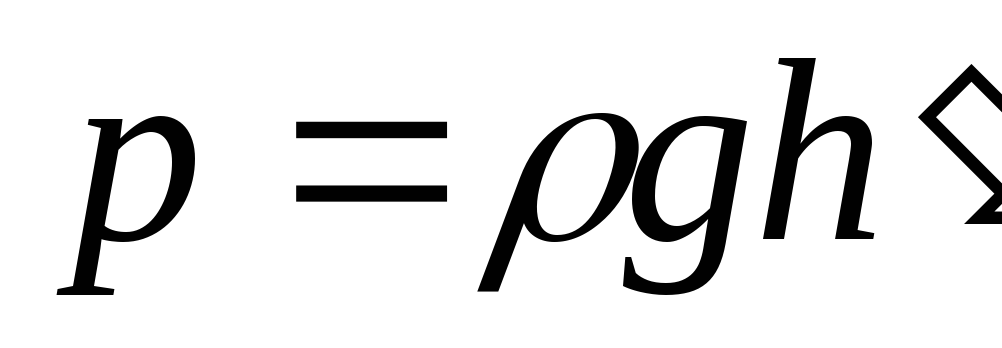
 или
или 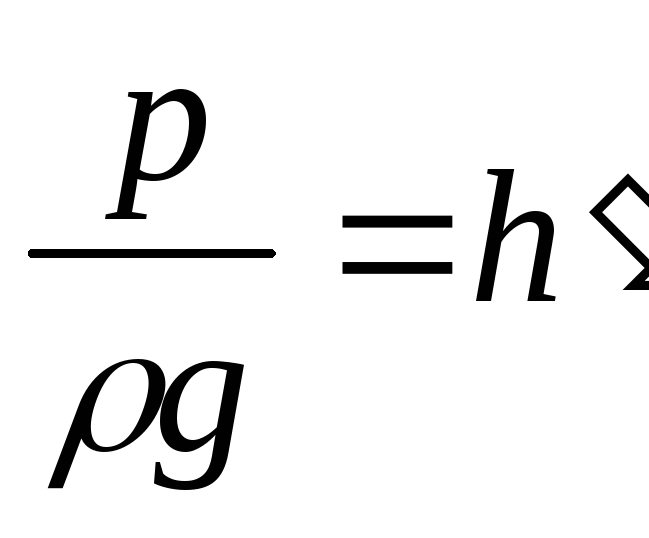 .
.
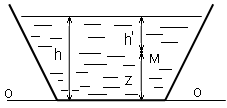
Рис.
13.1 Подставляя
в выражения для е вместо 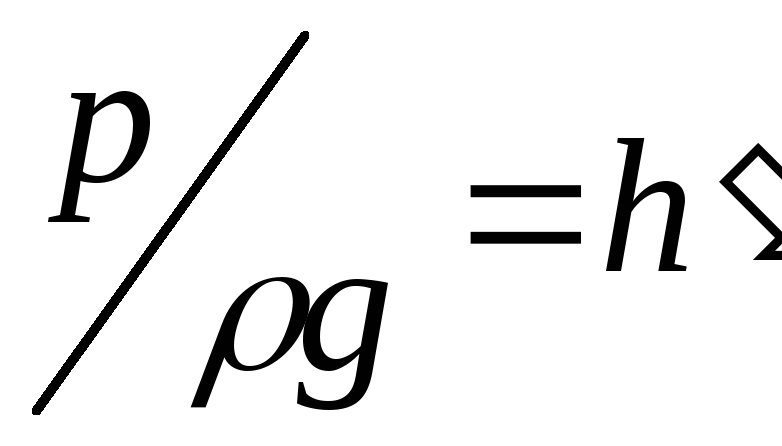 ,
получим
,
получим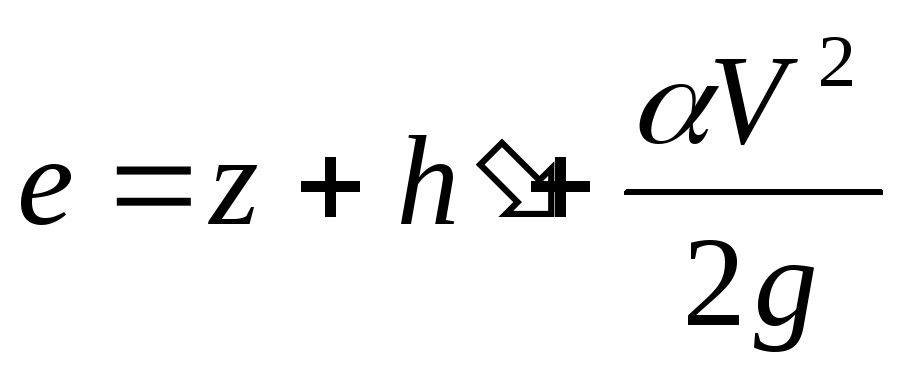 .
.
Если
плоскость сравнения провести через
самую нижнюю точку живого сечения, рис.
13.1, то 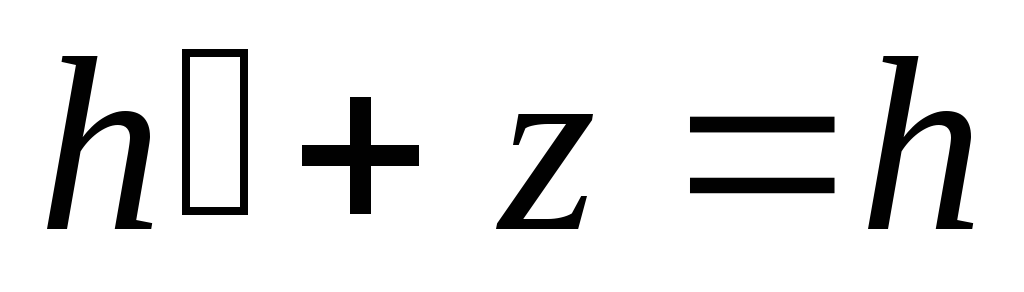 и выражение для удельной энергии будет
иметь вид
и выражение для удельной энергии будет
иметь вид
 ,
(13.1)
,
(13.1)
где h – глубина в данном сечении.
Удельная энергия потока Э относительно плоскости сравнения, проходящая через наинизшую точку сечения, называется удельной энергией сечения.
Понятие
удельной энергии сечения  не следует смешивать с понятием удельной
энергии потока Е. Удельная энергия
потока Е определяется для разных сечений
относительно одной и той же плоскости,
эта энергия уменьшается вниз по течению
потока. Удельная энергия сечения Э в
разных сечениях определяется относительно
разных плоскостей сравнения и может
как увеличиваться, так и уменьшаться.
не следует смешивать с понятием удельной
энергии потока Е. Удельная энергия
потока Е определяется для разных сечений
относительно одной и той же плоскости,
эта энергия уменьшается вниз по течению
потока. Удельная энергия сечения Э в
разных сечениях определяется относительно
разных плоскостей сравнения и может
как увеличиваться, так и уменьшаться.
14. Критическая глубина
Выражение для удельной энергии сечения в открытых руслах можно представить в следующем виде (учитывая, что V=Q/S)
Э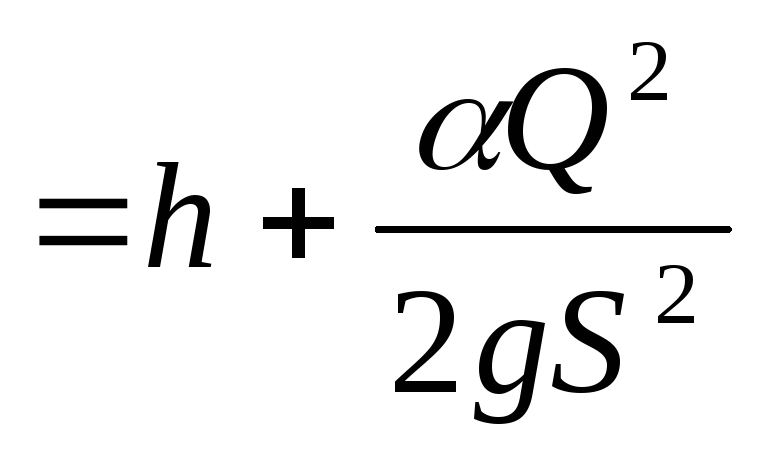 ,
(14.1)
,
(14.1)
г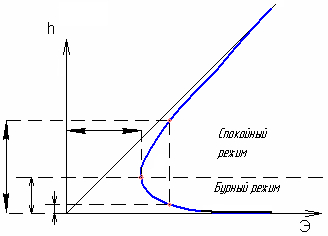
Э=f(h)
деh – глубина; Q – расход; S – площадь сечения при данной глубине; — коэффициент, учитывающий неравномерность
распределения скоростей.
— коэффициент, учитывающий неравномерность
распределения скоростей.И
А




П

Рис.14.1
ри этом: 1) еслиh 0, то
0, тоРис. 14.1


 и, следовательно, Э
и, следовательно, Э ,2) если
,2) если  ,
то
,
то и
и .
.Г
Рис. 14.1
рафик функции имеет вид, как на рис. 14.1; из графика
видно, что функциявыражается кривой, состоящей из двух
ветвей, разделяемых точкой А, соответствующей
минимуму
имеет вид, как на рис. 14.1; из графика
видно, что функциявыражается кривой, состоящей из двух
ветвей, разделяемых точкой А, соответствующей
минимуму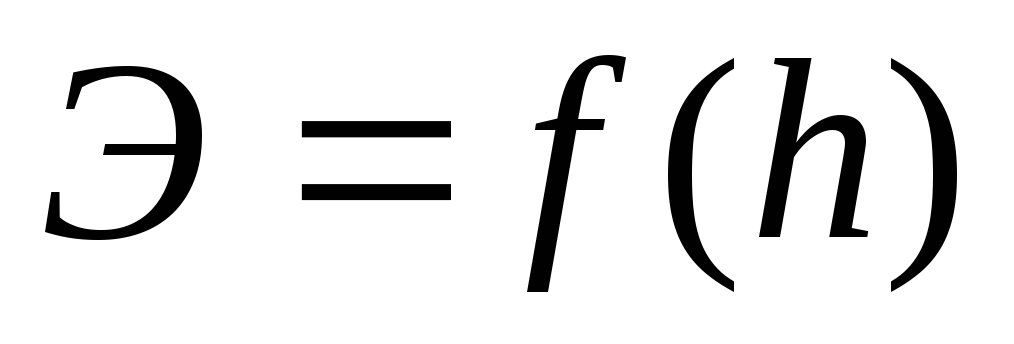 .
При этомнижняя ветвь
асимптотически приближается к оси
абсцисс, а верхняя ветвь —
к прямой, проходящей через начало
координат и составляющей с осью
абсцисс
угол 45о.
Так как кривая непрерывна, то при
некотором значении глубины h,
где-то удельная энергия будет иметь
наименьшее значение
.
При этомнижняя ветвь
асимптотически приближается к оси
абсцисс, а верхняя ветвь —
к прямой, проходящей через начало
координат и составляющей с осью
абсцисс
угол 45о.
Так как кривая непрерывна, то при
некотором значении глубины h,
где-то удельная энергия будет иметь
наименьшее значение 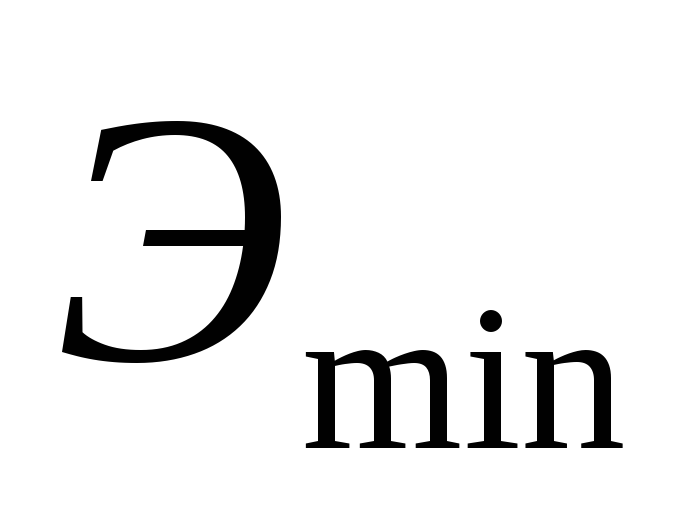 .
. Глубина
потока, при которой удельная энергия
сечения принимает минимальное значение,
называется критической глубиной  .
.
Для
нахождения величины 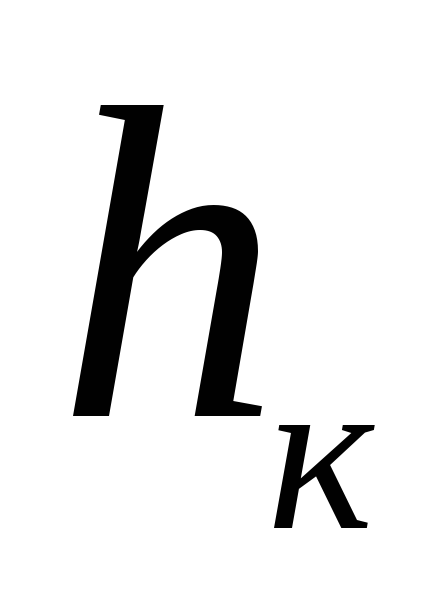 необходимо решить уравнение
необходимо решить уравнение
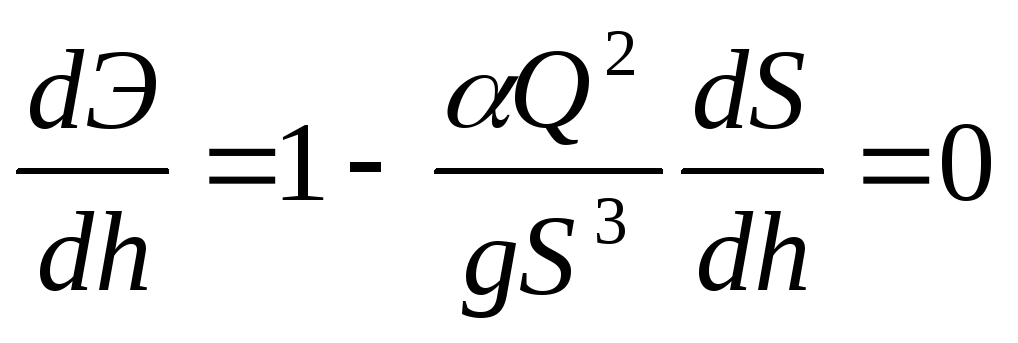 .
.
Так
как 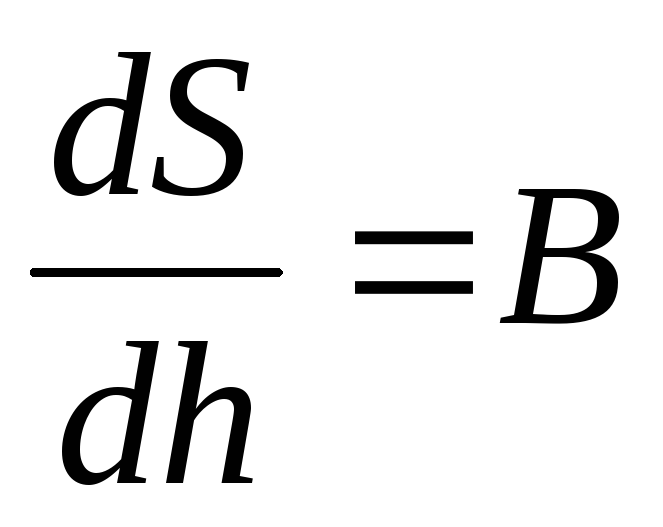 — ширина живого сечения, то уравнение
для определения критической глубины
будет таким
— ширина живого сечения, то уравнение
для определения критической глубины
будет таким
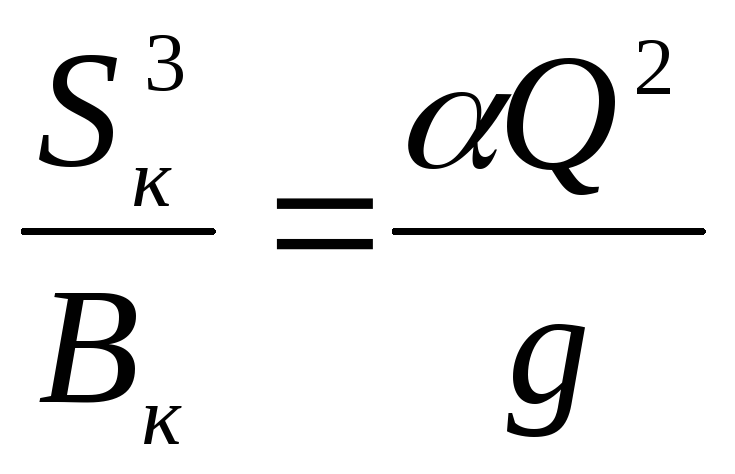 ,
(14.2)
,
(14.2)
где 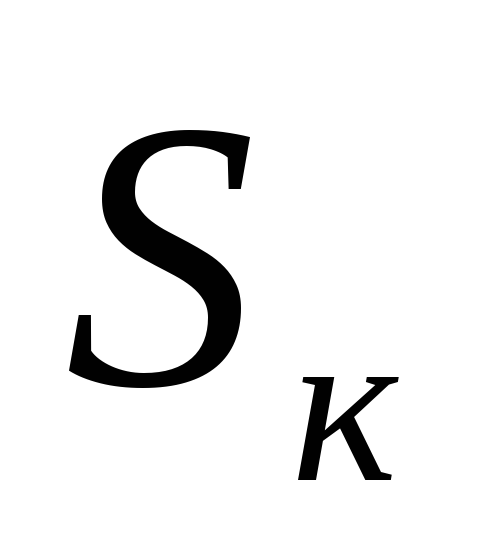 и
и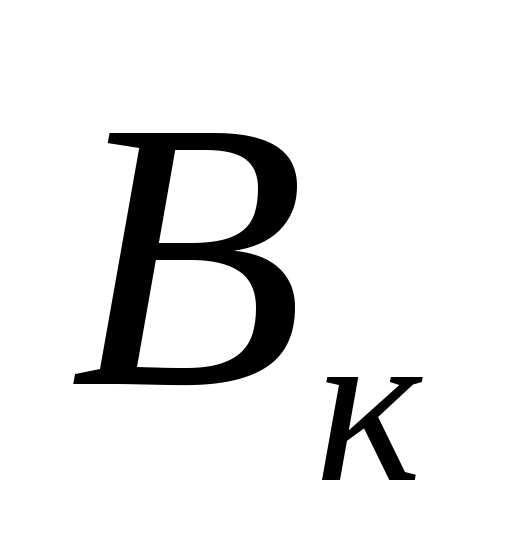 — площадь сечения и ширина русла по
верху, отвечающие критической глубинеhк.
— площадь сечения и ширина русла по
верху, отвечающие критической глубинеhк.
Уравнение
(14.2) является основной зависимостью для
определения критической глубины  при заданном расходе Q и любой заданной форме русла; из этого
уравнения следует, что при заданном
расходе критическая глубина зависит
только от размеров и формы живого
сечения. Критическая глубина не зависит
ни от уклона дна, ни от шероховатости.
при заданном расходе Q и любой заданной форме русла; из этого
уравнения следует, что при заданном
расходе критическая глубина зависит
только от размеров и формы живого
сечения. Критическая глубина не зависит
ни от уклона дна, ни от шероховатости.
Прямоугольное
русло. Для
прямоугольного русла шириной  =В критическую глубину возможно найти
аналитически. При критической глубине
=В критическую глубину возможно найти
аналитически. При критической глубине  площадь сечения
площадь сечения
 .
.
Подставляя  в (14.2), получим
в (14.2), получим
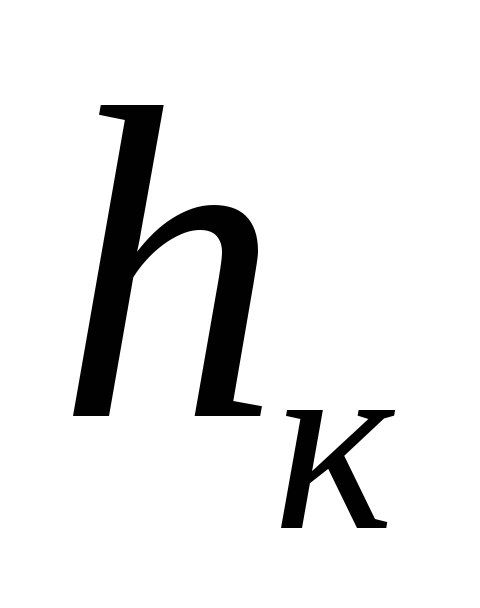 =
=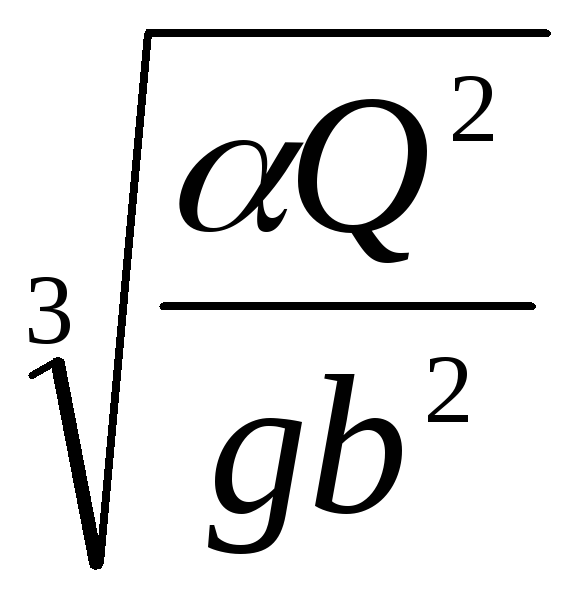 . (14.3)
. (14.3)
Задача
14.1. Определить
критическую глубину для трапецеидального
канала при следующих данных: 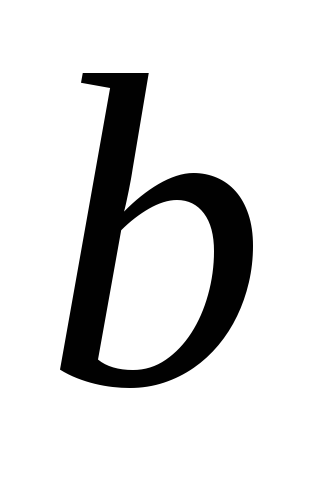 =5
м, т=1,5
м; расход воды в канале Q=6,6
м3/ч.
=5
м, т=1,5
м; расход воды в канале Q=6,6
м3/ч.
Решение. Вычисляем
значение правой части (14.2) при  ,
,
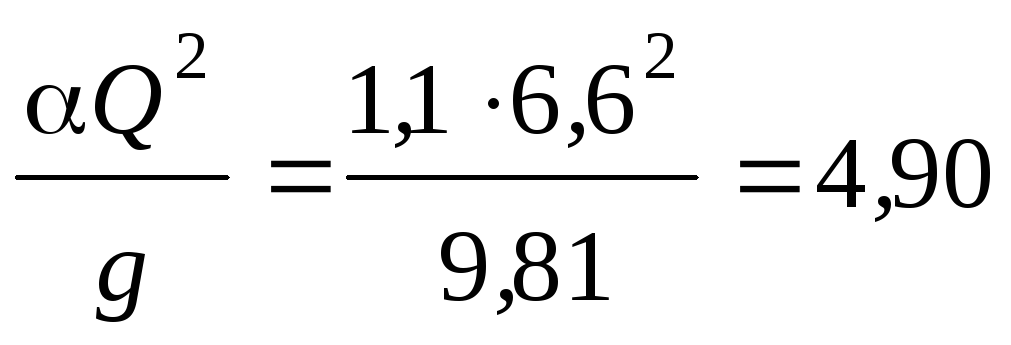 м5.
м5.
Задаваясь
затем различными глубинами h,
находим ширину по верху 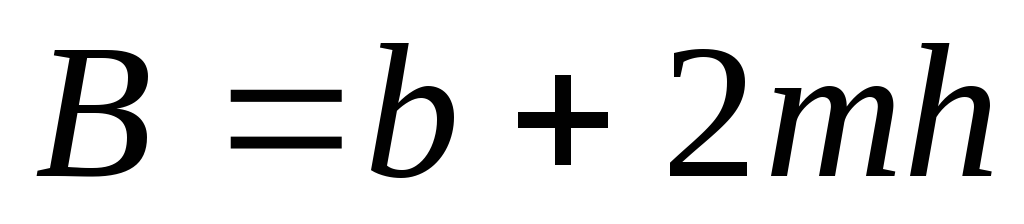 ,
площадь сечения
,
площадь сечения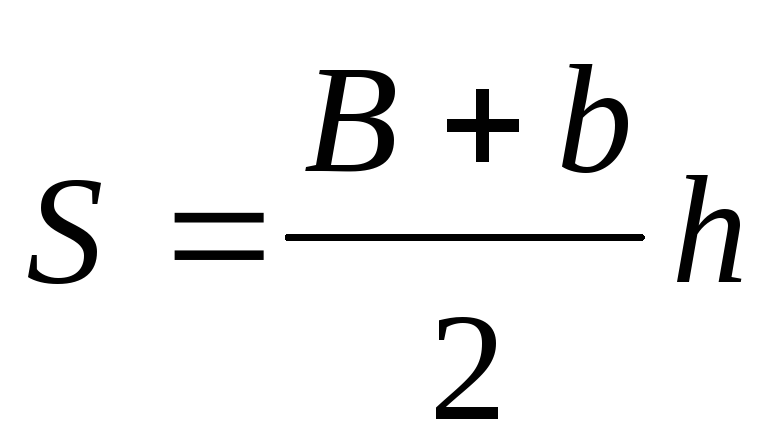 иS3.
Результаты этих подсчетов сводим в
табл. 14.1.
иS3.
Результаты этих подсчетов сводим в
табл. 14.1.
Таблица 14.1
h, м | B, м | S, м2 | S3 м6 |
|
0,50 | 6,5 | 2,81 | 3,68 | 3,68<4,9 |
0,60 | 6,8 | 3,54 | 6,52 | 6,52>4,9 |
0,55 | 6,65 | 3,20 | 4,94 | 4,94 |
4. Удельная энергия потока и удельная энергия сечения
4.1. Удельная энергия потока
П редставим,
что открытый поток движется по дну
произвольного очертания под действием
силы тяжести от точкиА до точки В,
рис. 4.1. При этом происходит преобразование
потенциальной энергии в кинетическую,
обусловленное превышением z начальной
точки А под конечной В.
Если жидкость идеальная, то на неё
действует только одна сила тяжести,
движение происходит с ускорением и
равномерного потока не может существовать.
Если жидкость не идеальная, то на неё
действует ещё и сила трения и в некоторых
случаях результирующая сила может быть
равной нулю – движения при этом может
быть равномерным. Напомним, что механическая
энергия жидкости, протекающей в единицу
времени через выбранное сечение потока,
отнесённая к весу и определяемая
относительно произвольной горизонтальной
плоскости, называется удельной энергией
потока Е. Горизонтальная плоскость отсчёта одна
и та же для всех рассматриваемых сечений
в потоке. Величина Е определяется из уравнения Бернулли и
при плавноизменяющемся движении для
любого сечения
редставим,
что открытый поток движется по дну
произвольного очертания под действием
силы тяжести от точкиА до точки В,
рис. 4.1. При этом происходит преобразование
потенциальной энергии в кинетическую,
обусловленное превышением z начальной
точки А под конечной В.
Если жидкость идеальная, то на неё
действует только одна сила тяжести,
движение происходит с ускорением и
равномерного потока не может существовать.
Если жидкость не идеальная, то на неё
действует ещё и сила трения и в некоторых
случаях результирующая сила может быть
равной нулю – движения при этом может
быть равномерным. Напомним, что механическая
энергия жидкости, протекающей в единицу
времени через выбранное сечение потока,
отнесённая к весу и определяемая
относительно произвольной горизонтальной
плоскости, называется удельной энергией
потока Е. Горизонтальная плоскость отсчёта одна
и та же для всех рассматриваемых сечений
в потоке. Величина Е определяется из уравнения Бернулли и
при плавноизменяющемся движении для
любого сечения
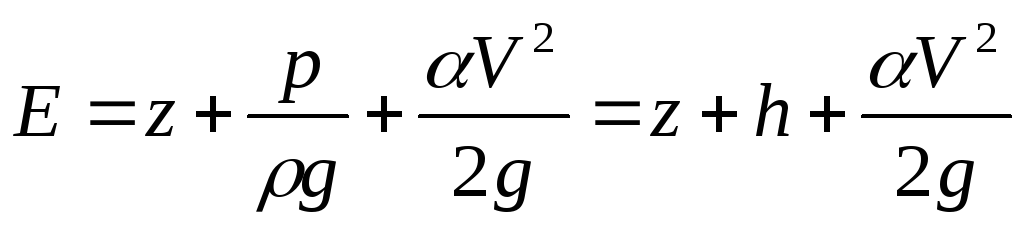 .
.
Если, имея ввиду рис.4.1 обозначить Е1 в сечении 1-1, а удельную энергию Е2 в сечении 2-2, то всегда по причине существования трения часть механической энергии при прохождении потока от сечения 1-1 до сечения 2-2 превращается в тепло и удельная энергия
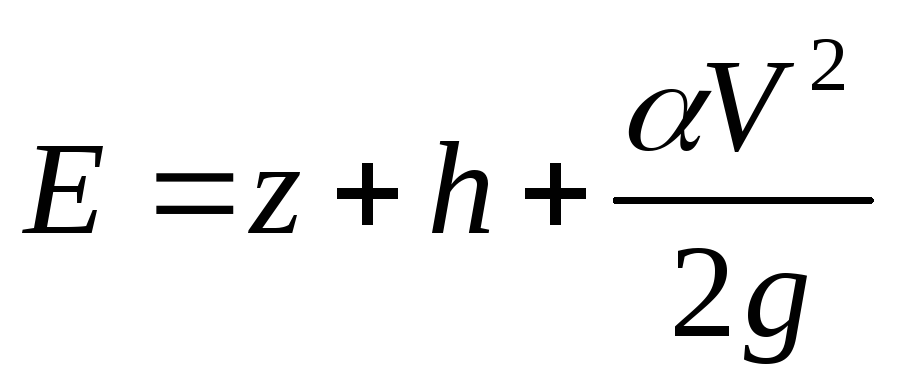 ,
,
непрерывно убывает вдоль потока. Если обозначить Е1 и Е2 (в первом и во втором сечениях соответственно), то всегда
Е1=Е2+hw,т.е. Е1>E2.
4.2. Удельная энергия сечения
Проведём в данном случае плоскость сравнения не произвольно, а через нижнюю точку рассматриваемого сечения, рис.4.2., в котором глубина равна h. Удельную энергию потока определяют по формуле
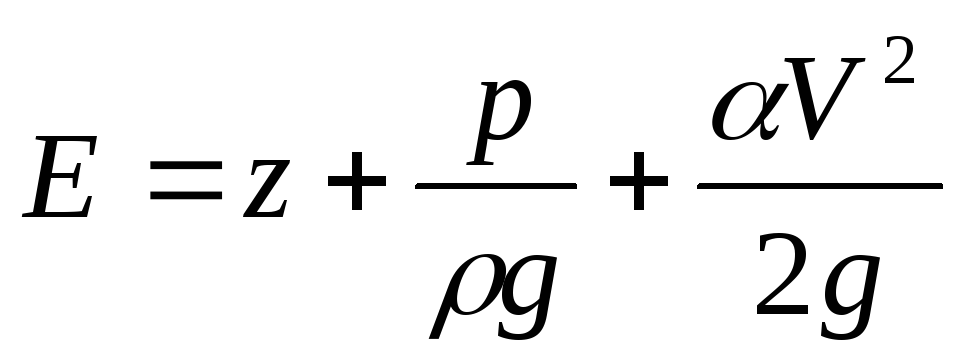 .
.
Для данного сечения при плавноизменяющемся движении в открытом русле
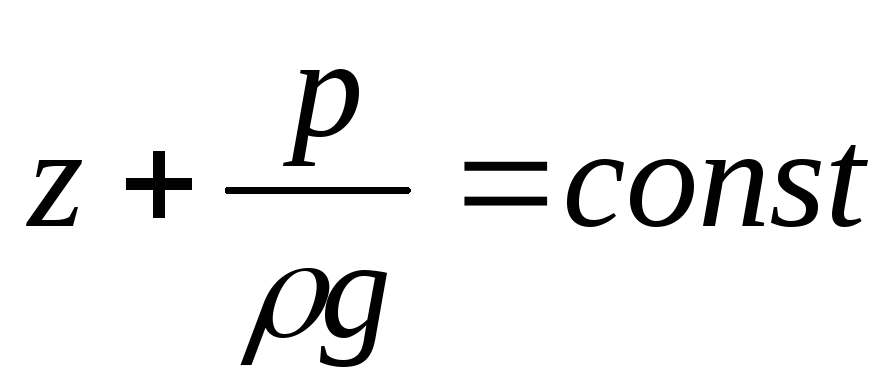 .
.
Если привести плоскость сравнения через наиболее низкую точку сечения, то
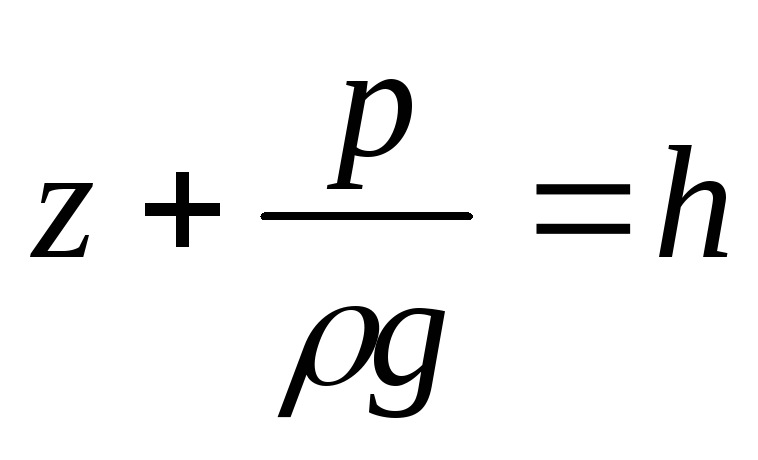
Тогда полная механическая энергия в данном сечении относительно этой плоскости равна
 =h+
=h+ =h+
=h+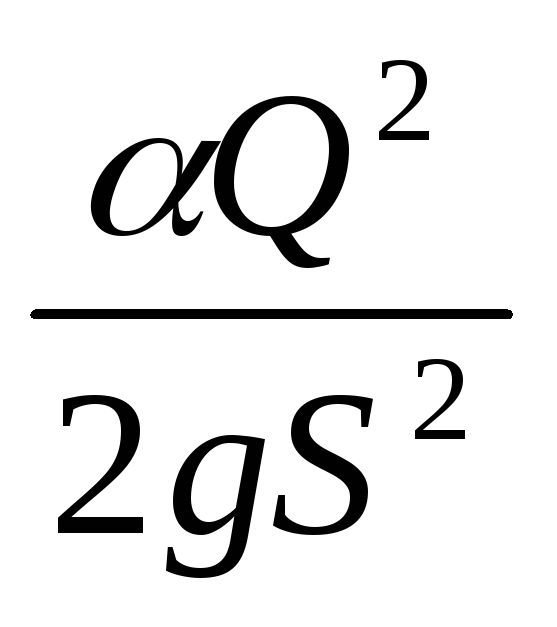 =(h). (4.1)
=(h). (4.1)
Удельной энергией
сечения (h) называется удельная энергия потока в
данном сечении, определённая относительно
горизонтальной плоскости, проходящей
через нижнюю точку этого сечения.
сечении, определённая относительно
горизонтальной плоскости, проходящей
через нижнюю точку этого сечения.
Как следует из (4.1) удельная энергия сечения (h) является функцией только глубины и всегда (h)>0 (Q=const, h и S всегда положительные величины).
Выясним связь
между величинами Е и с точки
зрения закона сохранения и превращения
энергии (в дальнейшем будем иметь в виду
удельную энергию). В точке А,
рис. 4.1 поток обладает некоторой
кинетической энергией 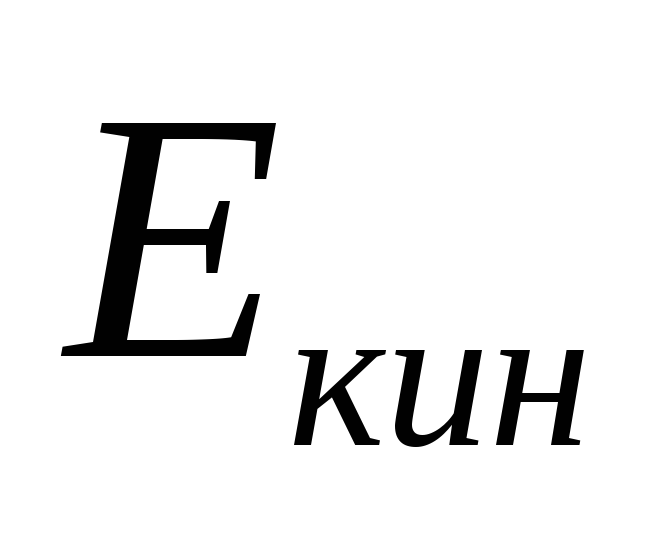 и потенциальной
(относительно оси О-О)
энергией
и потенциальной
(относительно оси О-О)
энергией 
 .
.
В дальнейшем, при движении жидкости до
точкиВ кинетическая и потенциальная энергия
могут преобразовываться одна в другую,
но сумма их непрерывно уменьшается по
причине потерь на трение hw.
На рис. 4.3 для двух сечений 1—1
и 2—2
запишем уравнение Бернулли (всё выводы
делаются нами при условии, что уравнение
Бернулли применимо к этим сечениям)-
рассматриваются не обязательно
призматические русла
дальнейшем, при движении жидкости до
точкиВ кинетическая и потенциальная энергия
могут преобразовываться одна в другую,
но сумма их непрерывно уменьшается по
причине потерь на трение hw.
На рис. 4.3 для двух сечений 1—1
и 2—2
запишем уравнение Бернулли (всё выводы
делаются нами при условии, что уравнение
Бернулли применимо к этим сечениям)-
рассматриваются не обязательно
призматические русла
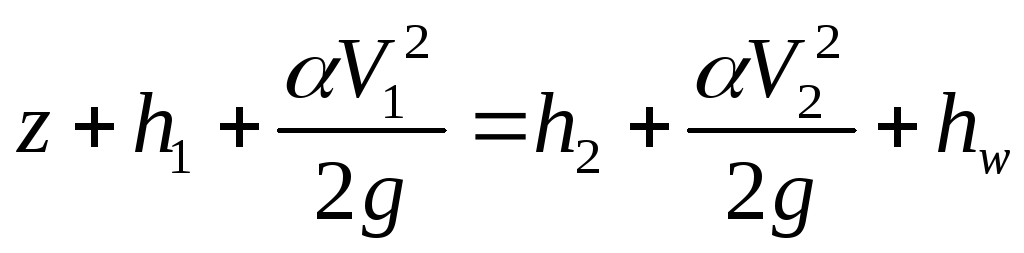 ,
,
откуда следует, что z+1=2+hw. (4.2)
Из последнего равенства (4.2) видно, что в зависимости от величин z и hw на участке потока между сечениями 1—1 и 2—2 удельная энергия может как убывать, так и возрастать, оставаясь неизменной лишь при равномерном движении, когда z=hw (Задача 1.2).
Статистический вес — Википедия
Материал из Википедии — свободной энциклопедии
Статисти́ческий вес — физическая величина, определяющая в квантовой механике и квантовой статистике количество различных квантовых состояний системы с одинаковой энергией (синоним: кратность вырождения энергетического уровня). В статистической физике и термодинамике статистическим весом называют количество способов (микросостояний системы), которыми может быть реализовано данное макроскопическое состояние статистической системы. Статистический вес обычно обозначается символами Γ, g, w, W или Ω.
По вышеприведённому определению, статистический вес является безразмерным целым числом, большим или равным единице, w⩾1{\displaystyle w\geqslant 1}. Иногда статвес называют термодинамической вероятностью, хотя необходимо отметить, что вероятность обычно определяется как действительное число в интервале от 0 до 1.
При рассмотрении квантовых систем с непрерывным спектром энергии под статистическим весом обычно понимают количество квантовых состояний, приходящихся на определённый энергетический интервал. В таком определении статвес имеет размерность обратной энергии.
В квазиклассическом приближении мерой статистического веса служит фазовый объём системы, приходящийся на определённый интервал энергии. Если система имеет n степеней свободы, то фазовый объём и соответствующий статистический вес выражается в единицах hn, где h — постоянная Планка.
Энтропия S системы и её статистический вес связаны соотношением Больцмана: S = k ln w (здесь k — постоянная Больцмана).
Статистический вес, определённый через фазовый объём или число микросостояний, является мультипликативной физической величиной: если система состоит из двух невзаимодействующих подсистем со статвесами w1 и w2, то общий статистический вес системы W = w1w2.
- Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
- Degeneracy. In: IUPAC. Compendium of Chemical Terminology, 2nd ed. (the «Gold Book»). Compiled by A. D. McNaught and A. Wilkinson. Blackwell Scientific Publications, Oxford (1997). XML on-line corrected version: http://goldbook.iupac.org (2006-) created by M. Nic, J. Jirat, B. Kosata; updates compiled by A. Jenkins. ISBN 0-9678550-9-8. doi:10.1351/goldbook.




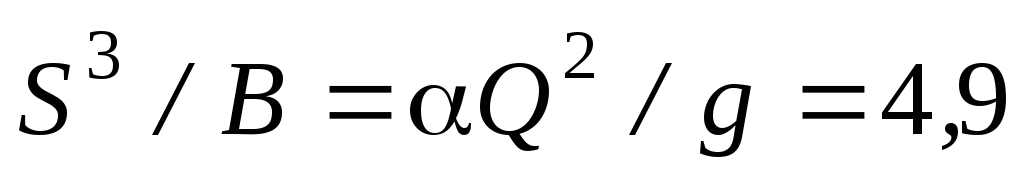 м5
м5 4,9
4,9