формулы, составляющие и особенности применения

В быту, как правило, применяются такие словосочетания, как потребляемая мощность или просто электрическая мощность. Всегда актуален вопрос о том, как много электроэнергии потребляет тот или другой прибор. Но в физике понятие мощности переменного тока трактуется несколько шире.

Особенности переменного тока

Формула мощности для тока, который меняется во времени по силе, напряжению и направлению, не совпадает с простой формулой для постоянного электротока. Она может примяться исключительно для вычисления мгновенного значения этой физической величины, но на практике для нахождения мощности меняющегося тока бесполезна. Рассчитывая её усреднённую величину напрямую, применяют интегрирование по такому параметру, как время. То есть интегрируется мгновенное значение на протяжении определённого периода.

Такой подход применяется для тех электрических цепей, в которых напряжение и сила электротока меняются циклически. В основном рассчитывается мощность в цепях с изменениями электрического напряжения и силы электротока по синусоиде.

В электродинамике различают связанные друг с другом понятия реактивной, активной и полной мощности.

Активная величина Real Power

Активная мощность Р измеряется в ваттах. Сокращённые варианты единицы измерения: Вт (русское обозначение) или W (международное). Само понятие этой мощностной величины означает среднее значение мгновенных показателей этой характеристики за промежуток времени Т (период).

Общая формула в этом случае выглядит следующим образом:

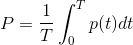
Для электрических цепей с одной фазой изменяющегося по синусоиде тока формула выглядит так:

.

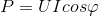В этом выражении Ι и U являются значениями силы электротока и напряжения в среднеквадратичном представлении. А угол φ показывает, на сколько сдвинуты фазы между этими физическими величинами.

Активная мощность указывает, как быстро превращается электрическая энергия в другие типы: тепловую или электромагнитную.

Она может выражаться как через силу тока и активное сопротивление цепи r, так и через напряжение и проводимость g по формуле:

.

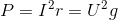В любых электрических цепях этот вид мощности равняется сумме значений на отдельных элементах. В трёхфазном варианте суммируются показатели для каждой отдельной фазы.

Реактивная характеристика

Реактивная мощность Q охарактеризовывает нагрузки, создаваемые в электроустройствах периодическими изменениями энергии электромагнитного поля в цепи с переменным током, который меняется во времени по синусоидальному принципу.

Численно она равняется умножению среднеквадратичных U (напряжения), I (силы) и синуса φ (угла сдвига фаз):

.

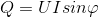Измеряется в вольт-амперах реактивных (русское сокращение: вар, а международное — var).

Реактивная Q даёт характеристику энергии, передающейся от источника питания к реактивным элементам и возвращающуюся обратно за временной промежуток, численно равный одному периоду колебаний. К элементам реактивного типа относят катушки индуктивности, конденсаторы, обмотки. Этот вид мощностной характеристики тока принимает:

• отрицательное значение, если нагрузка активно-ёмкостная;
• положительное — в случае активно-индуктивного характера нагрузочных элементов.

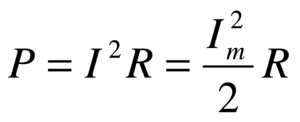Принято считать, что устройства с положительной Q потребляют энергию, а с отрицательной, наоборот, производят. Но это условные обозначения. Реактивная мощность по факту не принимает участия в работе электротока. Синхронные генераторы, которые функционируют на электростанциях, в зависимости от численного значения тока возбуждения в обмотке могут и вырабатывать, и потреблять эту реактивную характеристику тока.

Такую особенность синхронных электрических машин используют для регулирования определённого значения напряжения сети. Чтобы устранять перегрузки либо увеличение мощностного коэффициента, осуществляют компенсацию реактивной составляющей.

Полная мощность

Полная мощность S представляется в единицах измерения с названием вольт-амперы и вычисляется через умножение действующих значений I в цепи и напряжения U на её окончаниях:

.

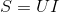
Этот вид электрической характеристики на практике описывает нагрузки, которые по факту налагаются потребителем на части электросети, обеспечивающей подвод электроэнергии (кабели разных видов, трансформирующие устройства и линии для передачи электрической энергии на большие расстояния).

Данные нагрузки находятся в зависимости исключительно от потребляемого тока, а не от энергии, которую по факту использует потребитель. Этот момент является причиной того, что полная мощность устройств, обеспечивающих трансформацию электрической энергии, а также распределительных щитов, измеряют в вольт-амперах, а не в ваттах.

Все виды мощностных характеристик переменного тока связываются между собой следующими математическими выражениями:

Эти формулы позволяют производить расчёты для цепей переменного тока любой конфигурации:

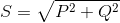
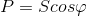
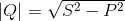
1. Полная, выраженная через активную и реактивную.
2. Активная — через полную и угол сдвига фаз.
3. Реактивная — через полную и активную.

Знания этих нюансов важны при подборе оборудования и построения систем энергообеспечения различных объектов. Учёт электрических параметров устройств даёт возможность сделать правильный выбор электрических устройств и построить экономически оптимальную схему энергетического обеспечения.

Мощность, выделяемая в цепи переменного тока

      Мгновенное значение мощности переменного тока равно произведению мгновенного значения напряжения на силу тока:

,

      где   и .

      Раскрыв , получим

.

      Практический интерес представляет не мгновенное значение мощности, а ее среднее значение за период колебания. Учитывая, что , , получим:

,

(4.5.1)

      где , поэтому среднее значение мощности будет равно:

.

(4.5.2)

      Такую же мощность развивает постоянный ток:  .

      Величины   и  называются

действующими (или эффективными) значениями тока и напряжения. Все амперметры и вольтметры градируются по действующим значениям тока и напряжения.

      Учитывая действующие значения тока и напряжения, выражение средней мощности (4.5.1) можно записать в виде:

,

(4.5.4)

      где множитель  называется коэффициентом мощности.

      Формула (4.5.4) показывает, что мощность, выделяемая в цепи переменного тока, в общем случае, зависит не только от силы тока и напряжения, но и от сдвига фаз между ними. Если в цепи отсутствует реактивное сопротивление

Х, то  и . Если цепь содержит только реактивное сопротивление (R = 0), то  и средняя мощность равна нулю, какими бы большими ни были ток и напряжение.

      Если  имеет значение существенно меньше единицы, то для передачи заданной мощности при данном напряжении генератора нужно увеличивать силу тока I, что приводит либо к выделению джоулевой теплоты, либо потребует увеличения сечения проводов, что повышает стоимость линий электропередачи. Поэтому на практике всегда стремятся увеличить . Наименьшее допустимое значение  для промышленных установок составляет примерно 0,85.

      В таблице 4.1 приведены сравнительные характеристики механических и электромагнитных колебаний.

Таблица 4.1

Колебания
механические		электромагнитные
Дифференциальное уравнение		Дифференциальное уравнение
Масса		Индуктивность катушки
Коэффициент жесткости		Обратная величина емкости
Смещение		Заряд
Скорость		Сила тока
Потенциальная энергия		Энергия электрич. поля
Кинетическая энергия		Энергия магнитного поля
Собств. частота пружинного маятника		Собств. частота колебательного контура
Период колебаний		Период колеб. Формула Томсона
Циклич. частота затухающих колебаний		Циклич. частота затухающих колебаний
Коэффициент затухания		Коэффициент затухания
Логарифмич. декремент затухания		Логарифмич. декремент затухания
Добротность пружинного маятника		Добротность колебательного контура
Резонансная частота		Резонансная частота

---

Переменный ток, мощность переменного тока

В свое время Эдисон и Тесла были противниками в вопросе использования электрического тока в энергетике. Тесла считал, что необходимо использовать переменный ток, а Эдисон – что нужно применять постоянный ток. У второго ученого было больше возможностей, так как он занимался бизнесом, однако Тесла в конечном итоге удалось победить, так как он был попросту прав.

Вступление

Переменный ток значительно эффективнее использовать для передачи энергии. Обсудим, как вычисляется мощность переменного тока, ведь переменный ток — это мощность, которая передается на расстоянии.

Вычисление мощности

Допустим, у нас имеется генератор переменного напряжения, который подключен к нагрузке. На выходе генератора, между двумя точками на клеммах, напряжение меняется по гармоническому закону, а нагрузка взята произвольная: катушки, активное сопротивление, конденсаторы, электромотор.

В цепи нагрузки течет ток, который меняется по гармоническому закону. Наша задача – установить, чему равна мощность потребляемой нагрузки от генератора. В распоряжении имеем генератор. В качестве исходных данных представлено направление на входе, которое будет меняться по гармоничному правилу:

(U(t) = U(m) cos w t)

Нагрузка – самое произвольное понятие.

Сила тока в нагрузке и, соответственно, в проводах, которые подводят мощность к нагрузке, будет меняться. Частота колебаний тока выйдет такая же, как частота колебаний напряжения, но существует также понятие сдвига фазы в промежутках колебаний тока и напряжения:

(I (t) = I (m) cos w t)

Дальнейшие вычисления

Показатели мощность будут равны произведению:

P (t) = I (t) U (t)

Этот закон остаётся справедливым как для переменного тока с мощностью, которую необходимо было вычислить, так и для постоянного.

(I (t) = I (m) cos (wt + J)

Мощность переменного тока при переменном токе вычисляется при помощи трех формул. Представленные выше расчеты относятся к основной формуле, которая вытекает из определения силы тока и напряжения.

Если участок цепи однородный и можно пользоваться законом Ома для этого участка цепи, здесь такие вычисления использовать нельзя, так как нам неизвестен характер нагрузки.

Определяем результат

Подставим показатели силы тока и напряжения в данную формулу, и тут нам на помощь придет знание тригонометрических формул:

cosa cosb = cos(a +b) + cos(a — b) / 2

Воспользуемся этой формулой и получим вычисления:

P(t) = I(m) U (m) cos (wt + J) cos wt

После упрощения результатов получим:

P(t) = I(m) U (m)/2 cos (wt + J) + I(m) U (m) cosJ

Посмотрим на эту формулу. Здесь первое слагаемое зависит от времени, меняясь по гармоническому закону, а второе является величиной постоянной. Мощность переменного тока при переменном токе складывается из постоянной и переменной составляющей.

Если мощность положительна, значит, нагрузка потребляет энергию от генератора. При отрицательной мощности, наоборот, нагрузка раскручивает генератор.

Найдем среднее значение мощности за период времени. Для этого работу, совершенную электрическим током, поделим на величину этого периода.

Мощность трехфазной цепи переменного тока– это сумма переменной и постоянной составляющих.

Активная и реактивная мощность

Многие физические процессы можно представить аналогиями друг друга. На этой базе постараемся раскрыть суть понятий активной мощности цепи переменного тока и реактивной мощности цепи переменного тока.

Стакан представляет собой электростанцию, вода – электроэнергию, трубочка – кабель или провод. Чем выше поднимается стакан, тем больше напряжение или давление.

Параметры мощности в сети переменного тока активного или реактивного типа зависят от тех элементов, которые потребляют такую энергию. Активная – энергия индуктивности и ёмкости.

Покажем это на конденсаторе, ёмкости и стакане. Активными называются те элементы, которые способны преобразовывать энергию в другой вид. К примеру, в тепло (утюг), свет (лампочка), движение (мотор).

Реактивная энергия

При имитации реактивной энергии напряжение увеличивается, и ёмкость заполняется. При уменьшении напряжения накопленная энергия возвращается по проводу обратно в электростанцию. Так повторяется циклически.

Сам смысл реактивных элементов заключается в накоплении энергии, которая потом обратно возвращается или используется для других функций. Но никуда не тратится. Основной минус этой производной в том, что виртуальный трубопровод, по которому как-бы идет энергия, имеет сопротивление, и на нем тратится процент экономии.

Полной мощности цепи переменного тока требуются затраты определенного процента усилий. По этой причине на крупных предприятиях идет борьба с реактивной составляющей полной мощности.

Активная мощность – это та энергия, которая потребляется или преобразуется в другие виды – свет, тепло, движение, то есть в какую-либо работу.

Опыт

Для опыта возьмем стакан, которые служит активной составляющей мощности. Он представляет часть энергии, которую необходимо потребить или преобразовать в другой вид.

Часть энергии воды можно выпить. Полная мощность переменного тока коэффициент мощности — это показатель, который складывается из реактивной и активной составляющих: энергии, текущей по водопроводу и той, которая преобразуется.

Как выглядит полная мощность в нашей аналогии? Часть воды выпиваем, а оставшаяся будет продолжать бежать по трубке. Так как у нас есть реактивный ёмкостной элемент – конденсатор или ёмкость, воду опускаем и начинаем имитировать увеличение и уменьшение напряжения. При этом видно, как вода перетекает в двух направлениях. Следовательно, в этом процессе применяется и активная, и реактивная составляющая. Вместе это – полная мощность.

Преобразование мощности

Активная мощность преобразовывается в другой вид энергии, к примеру, в механическое движение или нагрев. Реактивная мощность, которая накапливается в реактивном элементе, позднее возвращается назад.

Полная мощность – это геометрическая сумма активной и реактивной мощности.

Для произведения вычислений используем тригонометрические функции. Физический смысл расчетов такой. Возьмем прямоугольный треугольник, в котором одна из сторон равна 90 градусов. Одна из сторон – это его гипотенуза. Есть прилежащий и противолежащий относительно прямого угла катеты.

Косинус представлен отношением, которое предопределяет длина прилегающего катета относительно длины гипотенузы.

Синусом угла является вид отношения, которое составляет длина противолежащего катета относительно гипотенузы. Зная угол и длину любой из сторон, можно вычислить все остальные углы и длину.

В данном треугольнике можно взять длину гипотенузы и прилежащего катета и вычислить этот угол с помощью тригонометрической функции косинусов. Мощность постоянного и переменного тока вычисляется с применением таких знаний.

Для вычисления угла можно применять обратную функцию от косинуса. Получим необходимый результат вычислений. Чтобы вычислить длину противолежащего катета, можно вычислить синус и получить соотношение противолежащего катета к гипотенузе.

Вычисление мощности цепи переменного тока по формуле предложено в этом описании.

В цепях постоянного тока мощность равна произведению напряжения на ток. В цепях переменного тока также работает это правило, но его трактовка будет не совсем правильной.

Индуктивность

Помимо активных элементов, действуют реактивные элементы – индуктивность и ёмкость. В цепях постоянного тока, где амплитудное значение напряжения токов не меняется во времени, работа данного сопротивления будет происходить только во времени. Индуктивность и ёмкость могут негативным образом влиять на сеть.

Активная мощность, которую имеет трехфазная цепь переменного тока, может выполнять полезную работу, а реактивная не выполняет никакой полезной работы, а только расходуется на преодоление реактивных сопротивлений индуктивности и ёмкости.

Попытаемся выполнить опыт. Возьмем источник переменного напряжения на 220 Вт с частотой 50Гц, датчик напряжения и тока источника, нагрузка, которая составляет активное 1Ом и индуктивное 1ОМ сопротивление.

Также есть выключатель, который подключится в определенный момент, активно-ёмкостная нагрузка. Запустим такую систему. Для удобства рассмотрения введем коэффициенты поправки напряжения.

Запускаем устройство

При запуске устройства видно, что напряжение и ток сети не совпадают по фазе. Наблюдается переход через 0, при котором существует угол – коэффициент мощности сети. Чем меньше этот угол, тем выше коэффициент мощности, который указывается на всех устройствах переменного тока, к примеру, электрических машинах или сварочных трансформаторах.

Угол зависит от величины индуктивного сопротивления нагрузки. Когда сдвиг уменьшается, увеличивается ток сети. Представим, что сопротивление катушки уменьшить нельзя, но надо улучшить косинус сети. Для этого и нужны конденсаторы, которые, в отличие от индуктивности, опережают напряжение и могут взаимно компенсировать реактивную мощность.

В момент подключения конденсаторной батареи за 0,05 с происходит резкое снижение косинуса, практически до 0. Также идет резкое снижение тока, который без конденсаторной батареи имел амплитудное значение намного ниже, чем при включении конденсаторной батареи.

Фактически подключением конденсаторной батареи удалось снизить мощность тока, потребляемого из сети. Это является положительным моментом и позволяет снижать ток сети и экономить на сечение кабелей, трансформаторах, силовом оборудовании.

Если произойдет отключение индуктивной нагрузки и останется активное сопротивление, произойдет процесс, когда косинус сети после подключения конденсаторной батареи приведет к фазовому сдвигу и большому скачку тока, который идёт в сеть, а не потребляется из неё, что происходит в генераторном режиме реактивной мощности.

Итоги

Активная мощность опять остается постоянной и равна нулю, так как нет индуктивного сопротивления. Начался процесс генерации реактивной мощности в сеть.

Следовательно, компенсировать реактивную мощность на крупных предприятий, потребляемых колоссальные её объёмы из энергосистем, — это приоритетная задача, так как это позволяет экономить не только на электрооборудовании, но и на затратах по оплате самой реактивной мощности.

Такое понятие регламентируется, и предприятие оплачивает и потребляемую, и генерируемую мощность. Здесь устанавливаются автоматические компенсаторы, обеспечивающие поддержку баланса мощности на заданном уровне.

При отключении мощной нагрузки, если не выключить из сети компенсирующее устройство, будет происходить генерация реактивной мощности в сеть, что создаст проблемы в энергосистеме.

В быту компенсация реактивной мощности не имеет смысла, так как потребление мощности здесь значительно ниже.

Активная и реактивная мощность – понятия школьного курса физики.

Мощность переменного тока — fiziku5.ru

(1.18)

Энергия в катушке индуктивности не расходуется. В первую чет­верть периода она запасается в ее магнитном поле, а во вторую — отдается источнику тока. Произведение напряжения UL на величи­ну силы тока I в цепи называется реактивной мощностью.

В рассмотренной цепи активная мощность равна нулю, так как энергия в ней не расходуется, сдвиг по фазе между векторами тока I и напряжением U равен 90 ° и cos φ = 0.

Переменный ток в цепи с последовательными активным и индук­тивным сопротивлениями. Теперь рассмотрим цепь с реальной ка­тушкой, которую можно представить как цепь с последовательно включенными индуктивностью L и активным сопротивлением R (рис. 1.7). Если в цепи с последовательными активным и индуктив­ным сопротивлениями протекает переменный синусоидальный ток, то напряжение на индуктивности, как было установлено ранее, опережает ток на 90°, а напряжение на активном сопротивлении совпадает с ним по фазе.

Так как напряжения UL, UR по фазе не совпа­дают, то напряжение, приложенное ко всей цепи, равно их геомет­рической сумме. Сложив векторы UL и UR, нахо­дим величину вектора U, который сдвинут по фазе относительно вектора тока I на угол φ < 90°, опережая его. Таким об­разом, в цепи переменно­го тока с последователь­но соединенным активным сопротивлением и катушкой индуктивно­сти ток отстает по фазе от напряжения.

Построив векторную диаграмму, рассмотрим треугольник со сто­ронами UL, UR, U. Этот треугольник называется треугольником напря­жений. Так как он прямоугольный, то

(1.19)

Из треугольника напряжений можно получить подобный ему треугольник сопротивлений со сторонами R, XL и Z Из этого треу­гольника полное сопротивление цепи равно:

(1.20)

Так как сдвиг по фазе между током и напряжением меньше 90°, то энергия в такой цепи расходуется лишь на активном со­противлении R.

Активная мощность при этом равна:

(1.21)

Цепь переменного тока с емкостью. Если к источнику перемен­ного тока подключить конденсатор, то в цепи появится ток. Спо­собность конденсатора пропускать переменный ток объясняется тем, что под действием переменного синусоидального напряже­ния конденсатор периодически заряжается и разряжается, вслед­ствие чего происходит перемещение электрических зарядов в про­водниках, соединяющих конденсатор с источником тока. Соотно­шение фаз тока и напряжения представлено на рис. 1.8. В и, епи с емкостью ток опережает по фазе напряжение на 90°. Закон Ома для цепи переменного тока с емкостью определяет действующее зна­чение силы тока:

(1.22)

Величина называется емкостным сопротивлением. Она обратно пропорциональна частоте тока в цепи и емкости конден­сатора. Измеряется в омах (Ом).

1.9.  Мощность переменного тока

Для цепей переменного тока различают активную, полную и реактивную мощности.

Активная мощность представляет собой действительную мощ­ность переменного тока, аналогичную мощности, развиваемой постоянным током. Она производит полезную работу; может быть преобразована с помощью электродвигателей в механическую мощ­ность, механическую энергию; измеряется в ваттах (Вт) и опреде­ляется по формуле

(1.23)

Полной мощностью называют максимально возможную величи­ну активной мощности, развиваемую переменным током при за­данных значениях напряжения и силы тока и при наиболее благо­приятных условиях, а именно, когда cos φ = 1. Полная мощность обозначается латинской буквой S и измеряется в вольт-амперах (В-А). Из определения полной мощности следует выражение

(1.24)

Сравнивая между собой формулы (1.23) и (1.24), находим со­отношение между активной и полной мощностями:

(1.25)

(1.26)

Полной мощностью (кВ А) принято измерять мощность гене­раторов переменного тока, машин, производящих электроэнер­гию, и трансформаторов, аппаратов, предназначенных для преоб­разования электрической энергии одного напряжения в электри­ческую энергию другого напряжения. Полная мощность этих ма­шин определяется произведением номинальных (нормальных) ве­личин их напряжения и силы тока (т. е. величин этих параметров, на которые рассчитаны машины). А активная их мощность зависит от коэффициента мощности, при котором они работают (Р= Scosφ). В свою очередь этот коэффициент мощности зависит от соотноше­ния величин активного и реактивного сопротивления, включен­ных в цепь, иными словами, от характера электроприемников, питаемых данным генератором или трансформатором.

Реактивная мощность. Для рассмотрения реактивной мощнос­ти необходимо иметь представление об активной и реактивной со­ставляющих переменного тока. Сравнивая между собой формулы для определения мощности переменного и постоянного тока, мож­но видеть, что на месте полной величины силы тока I в формуле мощности стоит выражение I cos φ, где cos φ — величина, меньше единицы (и только в отдельных случаях равная ей). Отсюда следу­ет, что в цепях переменного тока не весь ток создает полезную, активную мощность, а только некоторая его часть, которая на­зывается активной составляющей тока.

Проекция вектора тока на горизонталь­ное направление, перпендикулярное вектору напряжения, равная /sin<p, называется ре­активной составляющей переменного тока. Реактивная составляющая тока не участвует в создании активной мощности.

Произведение действующего в цепи на­пряжения на реактивную составляющую тока носит название реактивной мощности и обо­значается латинской буквой Q. Реактивная мощность измеряется в единицах, называе­мых «вар». Из приведенного определения ре­активной мощности вытекает соотношение

(1.27)

где Q — реактивная мощность, вар; U — напряжение, В; I — сила тока, A; sin φ — числовой коэффициент, зависящий от угла сдвига фаз в данной цепи.

Реактивная мощность, так же как и реактивная составляющая тока, характеризует собой ту энергию, которая идет на создание магнит­ного поля индуктивности или электрического поля конденсатора (если последний включен в данную цепь). Эта энергия в процессе протека­ния переменного тока в цепях со сдвигом фаз совершает непрерыв­ные колебания между источником энергии и ее потребителем.

Активная, реактивная и полная мощности переменного тока связаны между собой соотношением

(1.28)

Это соотношение можно представить как векторную диаграм­му, получаемую на основании диаграммы напряжений или токов, носящую название «треугольника мощностей» (рис. 1.9). Два катета этого треугольника представляют собой в том или ином масштабе активную и реактивную мощности (соответственно в кВт и квар), а гипотенуза — полную мощность (в кВ-А). Угол ср численно равен углу сдвига фаз тока и напряжения в цепи. Значение косинуса это­го угла называют коэффициентом мощности.

1.10.  Понятие о трехфазном токе и его получении

Трехфазной системой называется совокупность трех однофаз­ных цепей, в которых действуют три ЭДС одинаковой частоты, сдвинутые по фазе одна относительно другой на 120°. Такая систе­ма получила наиболее широкое распространение, ибо она позво­ляет при передаче одной и той же мощности получить экономию металла в проводах, уменьшить потери энергии и создать простые и удобные в эксплуатации трехфазные двигатели переменного тока.

На рис. 1.10 показана система, состоящая из трех отдельных генераторов (рис. 1.10, б), и упрощенная схема генератора трех­фазного тока (рис. 1.10, а). Трехфазный генератор имеет три об­мотки, в которых индуктируются три ЭДС, сдвинутые по фазе на 120°. Каждая обмотка называется фазой, а напряжение на фазе — фазным напряжением (£/ф). Нагрузка подключается к обмоткам ге­нератора линейными проводами и нулевым проводом, который в некоторых случаях может отсутствовать.

Напряжение между линейными проводами называется линейным напряжением (Un). Ток в фазе генератора или нагрузки называется фазным током, а ток в линейном проводе — линейным током. Обмот­ки генератора и нагрузка могут включаться в «звезду» или в «треу­гольник». На рис. 1.11 показано соединение в «звезду»: начало или

концы обмоток генератора соединяют в одну точку. К оставшимся концам обмоток подключают линейные провода, а к общей точке — нулевой провод. Если нагрузка равномерная, то нулевой провод не нужен, ибо он обеспечивает независимость работы фаз при неравно­мерной нагрузке, когда по нему текут уравнительные токи.

Линейное напряжение при соединении в «звезду» в — Д раз боль­ше фазного, линейные и фазные токи одинаковы:

(1.29)

Чтобы соединить обмотки генератора в «треугольник», необхо­димо конец первой обмотки соединить с началом второй; конец второй — с началом третьей; конец третьей — с началом первой. Линейные провода подключают к точкам соединения фаз (рис. 1.12).

При соединении в «треугольник» линейные и фазные напряже­ния равны, а линейный ток в 7з раз больше фазного:

(1.30)

Мощность трехфазной системы складывается из мощностей каждой фазы. Чтобы найти общую мощность, надо по формуле Р=IФUФcosφ определить мощность в каждой фазе и все три мощ­ности сложить. Так поступают при любых нагрузках.

Общая мощность может быть определена по формуле

(1.31)

если нагрузка равномерная, т. е. если сопротивление и характер нагрузки всех трех фаз одинаковы.

1.11. Электроизмерительные приборы

Электроизмерительными приборами называются приборы, слу­жащие для измерения электрических величин. Они классифициру­ются по следующим признакам:

по роду измеряемой величины: амперметры, вольтметры, оммет­ры, ваттметры и комбинированные;

по роду тока: приборы постоянного тока, переменного тока и комбинированные;

по принципу действия: магнитоэлектрические, электромагнит­ные, электродинамические, индукционные, термоэлектрические, электростатические, электронные и др.;

по погрешностям измерений: на восемь классов — 0,05; 0,1; 0,2; 0,5; 1; 1,5; 2,5 и 4. Цифры показывают максимальную погрешность в процентах, которая возможна у прибора данного класса. Напри­мер, погрешность показаний амперметра класса 1,5 не превышает ±1,5%.

Существует два основных метода электрических измерений: метод непосредственной оценки; метод сравнения.

В методе непосредственной оценки измеряемая величина от­считывается непосредственно по шкале прибора. Достоинство ме­тода — удобство отсчета показаний прибора и малая затрата вре­мени на операцию измерения. Недостаток — сравнительно невы­сокая точность измерений.

В методе сравнения измеряемая величина сравнивается непос­редственно с эталоном. Метод сравнения используется в лабора­торных условиях.

Кроме обычных показывающих приборов, которые указывают то или иное измерение на данный момент времени (обычно стрелкой на шкале прибора) существуют самопишущие измерительные приборы, записывающие непрерывно на движущейся ленте свои показания.

Условные обозначения, определяющие основные характерис­тики прибора, выносятся на шкалу электроизмерительного при­бора (табл. 1.1).

Таблица 1.1

Основные условные обозначения, выносимые на шкалу электроизмерительного при­бора

1,5	Класс точности 1,5
	Постоянный ток
	Переменный (однофазный) ток
	Постоянный и переменный токи
	Трехфазный ток
	Прибор магнитоэлектрической системы
	Прибор электромагнитный системы
	Прибор электродинамической системы
	Прибор индукционной системы
	Прибор устанавливается горизонтально; вертикально; под углом 60“
	Изоляция прибора испытана при напряжении 2 кВ
А	Для закрытых отапливаемых помещений
Б	Для закрытых неотапливаемых помещений
В	Для полевых и морских условий

Пример. На шкале прибора имеются следующие условные обозначе­ния: 2,5; ;;;; Б. Это значит, что погрешность при из­ мерении — 2,5%; род тока — постоянный и переменный; электромагнит­ная измерительная система; вертикальная установка; изоляция испытана при напряжении 2 кВ; прибор предназначен для установки в закрытых неотапливаемых помещениях.

ГЛАВА 2. ЭЛЕКТРИЧЕСКИЕ МАШИНЫ

2.1.  Общие сведения

Электрические машины, действия которых основаны на элект­ромагнитных явлениях и которые служат для преобразования ме­ханической энергии в электрическую, называют электромашинными генераторами, а преобразующие электрическую энергию в механическую — электродвигателями. Применяют также электри­ческие машины для преобразования электрической энергии одних параметров в другие, которые называют преобразователями. Пре­образовываться могут: род тока, частота, напряжение, число фаз и другие параметры электроэнергии.

Электрические генераторы приводятся во вращение паровыми и водяными турбинами, двигателями внутреннего сгорания и др. Электродвигатели служат для приведения в действие станков, раз­личных машин, транспортного оборудования и др.

К электрическим машинам относят трансформаторы — стати­ческие аппараты, не имеющие движущихся частей, но по своему устройству и принципу действия имеющие много общего с элект­рическими машинами.

Электрические машины обладают свойством обратимости, т. е. могут работать генератором. Если их вращать каким-либо двигате­лем или подводить к ним электроэнергию, они могут использо­ваться как электродвигатели. Однако при проектировании элект­ромашин учитывают требования, предъявляемые особенностями их работы генератором или электродвигателем.

Электрические машины подразделяются на машины перемен­ного и постоянного тока.

Электрические машины переменного тока разделяют на синх­ронные, асинхронные, коллекторные.

Наибольшее применение имеют синхронные генераторы пере­менного трехфазного тока и трехфазные асинхронные электродви­гатели. Коллекторные электродвигатели переменного тока имеют ограниченное применение вследствие сложности устройства, об­служивания и более высокой стоимости. Основным их преимуще­ством является возможность регулирования скорости вращения в широких пределах, что затруднительно в асинхронных двигателях.

§52. Мощность, выделяемая в цепи переменного тока

Мгновенное значение мощности переменного тока равно произведению мгновенных значений напряжения и силы тока:

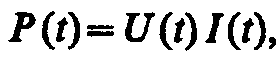
где U(t)=U_mcost, I(t)=I_mcos(t – ) (см. выражения (149.1) и (149.11)). Раскрыв cos(t – ), получим

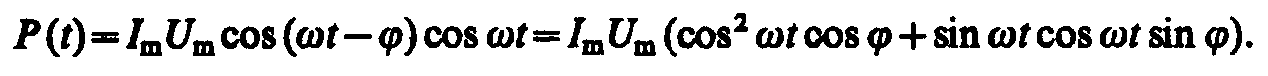
Практический интерес представляет не мгновенное значение мощности, а ее среднее значение за период колебания. Учитывая, что cos² t= ¹/₂, sin  t cos  t = 0, получим

(152.1)

Из векторной диаграммы (см. рис. 216) следует, что U_mсos  = RI_m. Поэтому

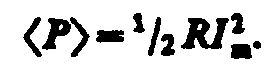
Такую же мощность развивает постоянный ток .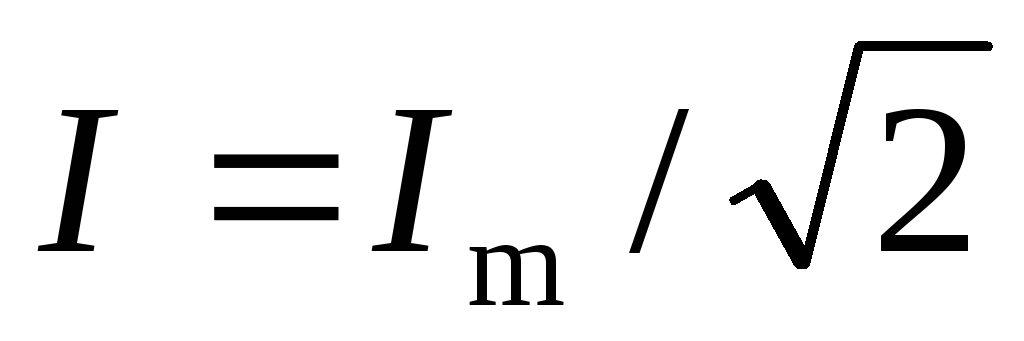

Величины

называются соответственно действующими (или эффективными) значениями тока и напряжения. Все амперметры и вольтметры градуируются по действующим значениям тока и напряжения.

Учитывая действующие значения тока и напряжения, выражение средней мощности (152.1) можно запасать в виде

(152.2)

где множитель соs  называется коэффициентом мощности.

Формула (152.2) показывает, что мощность, выделяемая в цепи переменного тока, в общем случае зависит не только от силы тока и напряжения, но и от сдвига фаз между ними. Если в цепи реактивное сопротивление отсутствует, то cos =1 и P=IU. Если цепь содержит только реактивное сопротивление (R=0), то cos=0 и средняя мощ­ность равна нулю, какими бы большими ни были ток и напряжение. Если cos имеет значения, существенно меньшие единицы, то для передачи заданной мощности при данном напряжении генератора нужно увеличивать силу тока I, что приведет либо к выделению джоулевой теплоты, либо потребует увеличения сечения проводов, что повышает стоимость линий электропередачи. Поэтому на практике всегда стремятся увеличить соs, наименьшее допустимое значение которого для промышленных уста­новок составляет примерно 0,85.

48. 49 Дифференциальное уравнение вынужденных колебаний (механических и электромагнитных) и его решение

Чтобы в реальной колебательной системе получить незатухающие колебания, надо компенсировать потери энергии. Такая компенсация возможна с помощью какого-либо периодически действующего фактора X(t), изменяющего по гармоническому закону:

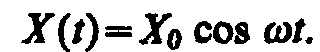
Если рассматривать механические колебания, то роль X(t) играет внешняя вынуж­дающая сила

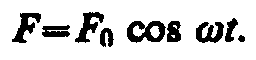(147.1)

С учетом (147.1) закон движения для пружинного маятника (146.9) запишется в виде

Используя (142.2) и (146.10), придем к уравнению

(147.2)

Если рассматривать электрический колебательный контур, то роль X(t) играет подводимая к контуру внешняя периодически изменяющаяся по гармоническому закону э.д.с. или переменное напряжение

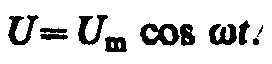(147.3)

Тогда уравнение (143.2) с учетом (147.3) можно записать в виде

Используя (143.4) и (146.11), придем к уравнению

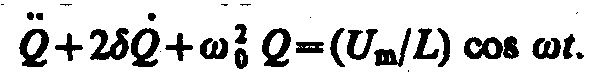(147.4)

Колебания, возникающие под действием внешней периодически изменяющейся силы или внешней периодически изменяющейся э.д.с., называются соответственно вынужденными механическими и вынужденными электромагнитными колебаниями.

Уравнения (147.2) и (147.4) можно свести к линейному неоднородному дифференци­альному уравнению

(147.5)

применяя впоследствии его решение для вынужденных колебаний конкретной физичес­кой природы (x₀ в случае механических колебаний равно F₀/m, в случае электромагнит­ных — U_m/L).

Решение уравнения (147.5) равно сумме общего решения (146.5) однородного урав­нения (146.1) и частного решения неоднородного уравнения. Частное решение найдем в комплексной форме (см. § 140). Заменим правую часть уравнения (147.5) на комплексную величину х₀: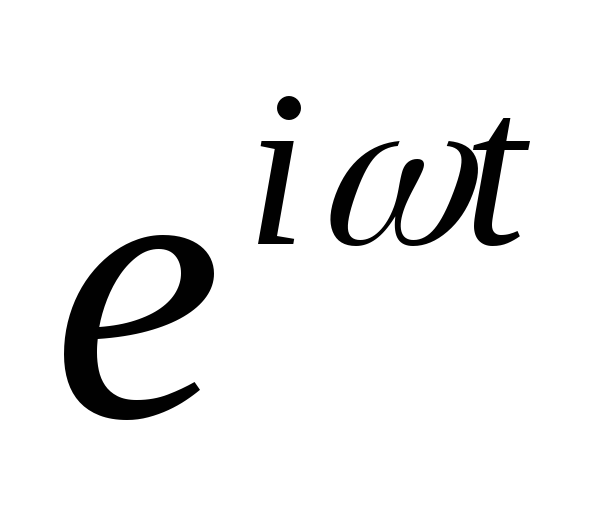

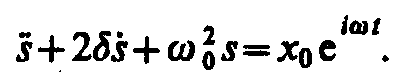(147.6)

Частное решение этого уравнения будем искать в виде

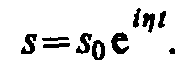
Подставляя выражение для s и его производных в уравнение (147.6), получаем

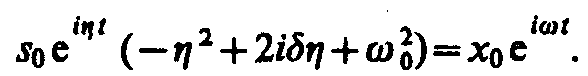(147.7)

Так как это равенство должно быть справедливым для всех моментов времени, то время t из него должно исключаться. Отсюда следует, что =. Учитывая это, из уравнения (147.7) найдем величину s₀ и умножим ее числитель и знаменатель на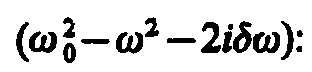

Это комплексное число удобно представить в экспоненциальной форме:

где

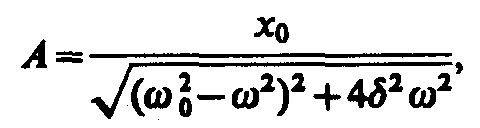(147.8)

(147.9)

Следовательно, решение уравнения (147.6) в комплексной форме примет вид

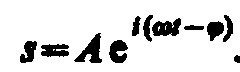
Его вещественная часть, являющаяся решением уравнения (147.5), равна

(147.10)

где А и  задаются соответственно формулами (147.8) и (147.9).

Таким образом, частное решение неоднородного уравнения (147.5) имеет вид

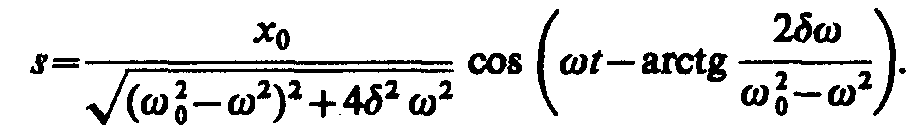(147.11)

Решение уравнения (147.5) равно сумме общего решения однородного уравнения

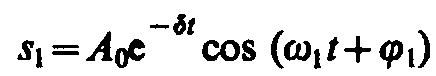(147.12)

(см. (146.5)) и частного решения (147.11). Слагаемое (147.12) играет существенную роль только в начальной стадии процесса (при установлении колебаний) до тех пор, пока амплитуда вынужденных колебаний не достигнет значения, определяемого равенством (147.8). Графически вынужденные колебания представлены на рис. 209. Следовательно, в установившемся режиме вынужденные колебания происходят с частотой  и являют­ся гармоническими; амплитуда и фаза колебаний, определяемые выражениями (147.8) и (147.9), также зависят от .

Запишем формулы (147.10), (147.8) и (147.9) для электромагнитных колебаний, учитывая, что (см. (143.4)) и (см. (146.11)):

(147.13)

Продифференцировав Q=Q_mcos(t–) по t, найдем силу тока в контуре при устано­вившихся колебаниях:

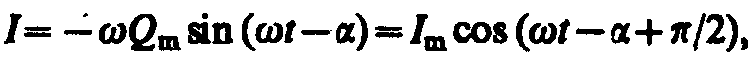(147.14)

где

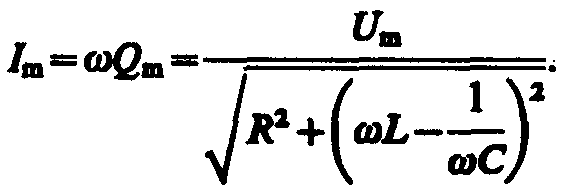(147.15)

Выражение (147.14) может быть записано в ввде

где = – /2 — сдвиг по фазе между током и приложенным напряжением (см. (147.3)). В соответствии с выражением (147.13)

(147.16)

Из формулы (147.16) вытекает, что ток отстает по фазе от напряжения (>0), если L>1/(С), и опережает напряжение (<0), если L<1/(С).

Формулы (147.15) и (147.16) можно также получить с помощью векторной диаграм­мы. Это сделано в §149 для переменных токов.

Мощность переменного тока — Основы электроники

Мы знаем, что в цепях переменного тока между током и напряжением может возникнуть разность фаз.

Как же вычислить мощность переменного тока в этом слу­чае, когда направления радиусов-векторов тока и напряжения не совпадают?

Представим себе, что мы тянем вагонетку с грузом, катя­щуюся по рельсам. Но наши усилия направлены не как обыч­но, вдоль рельсов, а под некоторым углом к ним. Угол между направлением движения вагонетки и направле­нием наших усилий обозначим буквой φ (фи).

Ясно, что при таком способе передвижения вагонетки часть наших сил будет затрачиваться бесполезно, не производя работы, то есть ра­бота не будет равна произведению приложен­ной силы на пройденный путь, как обычно (ра­бота = сила * путь),

а будет меньше этого про­изведения.

Для того чтобы вычислить количество про­изведенной работы, нужно силу, приложенную к вагонетке, разложить на две части или на две составляющие. Это разложение силы сде­лано на рисунке 1. Составляющая силы, направ­ленная вдоль движения, которая называется проекцией силы на направление движения, будет полезной силой, а, составляющая, на­правленная под прямым углом к направлению движения, будет силой бесполезной.

Если стрелка (вектор), изображающая си­лу, вычерчена в масштабе, то, измерив полез­ную составляющую силы, мы можем опреде­лить количество работы: работа = полезная сила * путь.

Теперь обратимся к радиусам-векторам тока и напряжения. Здесь полностью применим тот же самый метод. Мощность переменного тока при разности фаз φ = 0° будет равна половине произведения вектора напряжения Um и вектора тока Im.

Тогда мощность переменного тока, при разности фаз φ не равной нулю, будет равна половине произведения вектора напряжения Um и проекции вектора тока Imп, проецируемого на вектор напряжения (рисунок 2). Как нетрудно видеть, величина проекции зависит, во-первых, от длины проецируемого вектора, а во-вторых, от угла между ним и направлением, на которое он проецируется.

Если обо­значить этот угол буквой φ, то длина проекции будет равна длине проецируемого вектора, умноженной на особый коэф­фициент, характеризующий этот угол, называемый косинусом угла (cos φ ). Значения косинусов различных углов приве­дены в таблице.

Итак, проекция радиуса-вектора равна длине радиуса-вектора, умноженной на cos φ.

И, следовательно, мощность переменного тока равна:

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Похожие материалы:

Добавить комментарий

Ответы@Mail.Ru: Средняя мощность переменного тока

Понятие потенциала или разности потенциалов u позволяет определить работу, совершаемую электрическим полем при перемещении элементарного электрического заряда dq, как dA = udq. В то же время, электрический ток равен i = dq/dt. Отсюда dA = ui dt, следовательно, скорость совершения работы, т. е. мощность в данный момент времени или мгновенная мощность равна <img src=»//content.foto.my.mail.ru/bk/marusya_myr/_animated/i-4.gif» > (1) где u и i — мгновенные значения напряжения и тока. Величины тока и напряжения, входящие в выражение (1), являются синусоидальными функциями времени, поэтому и мгновенная мощность является переменной величиной и для ее оценки используется понятие средней мощности за период. Ее можно получить, интегрируя за период T работу, совершаемую электрическим полем, а затем соотнося ее с величиной периода, т. е. <img src=»//content.foto.my.mail.ru/bk/marusya_myr/_animated/i-5.gif» > (2) Пусть u=Umsinw t и Imsin(wt-j ), тогда средняя мощность будет равна <img src=»//content.foto.my.mail.ru/bk/marusya_myr/_animated/i-6.gif» > (3) т. к. интеграл второго слагаемого равен нулю. Величина cosj называется коэффициентом мощности. Из этого выражения следует, что средняя мощность в цепи переменного тока зависит не только от действующих значений тока I и напряжения U, но и от разности фаз j между ними. Максимальная мощность соответствует нулевому сдвигу фаз и равна произведению UI. При сдвиге фаз между током и напряжением в ± 90° средняя мощность равна нулю. Максимальные значения напряжения и тока любой электрической машины определяются ее конструкцией, а максимальная мощность, которую они могут развивать — произведением этих величин. Если электрическая цепь построена нерационально, т. е. сдвиг фаз j имеет значительную величину, то источник электрической энергии и нагрузка не могут работать на полную мощность. Поэтому в любой системе источник-нагрузка существует т. н. «проблема cosj «, которая заключается в требовании возможного приближения cosj к единице. Выражение (3) можно представить также с помощью понятий активных составляющих тока Iа и напряжения Uа в виде P = UI cosj = U(I cosj ) = UIа = I(U cosj ) = IUа . (4) Учитывая, что активные составляющие тока и напряжения можно выразить через резистивную состаляющую комплексного сопротивления цепи как Iа=U/R или Uа=IR, выражение (4) можно записать также в форме P = I2R = U2/R . (5) Среднюю мощность P называют также активной мощностью и измеряют в ваттах [Вт].

Мощность измеряется в ваттах, ток измеряется в амперах, напряжение измеряется в вольтах, сформулируйте вопрос корректно