Полное сопротивление электрической цепи

Понятие тока и напряжения

Закономерность учёного устанавливает зависимость между собой трёх электрических величин: тока, напряжения и сопротивления. Поэтому для того чтобы разобраться в сути закона Ома для полной электрической цепи, необходимо понимать, что же из себя они представляют.

В любом теле существуют свободные элементарные частички, обладающие определённым количеством энергии — зарядом. Если тело находится в спокойном состоянии, то есть на него не оказывается никакого воздействия, то происходит их хаотичное перемещение. Если же к телу приложено электрическое поле, то их перемещение становится упорядоченным, и они начинают передвигаться в одну сторону.

Такое направленное движение называют электрическим током. Мерой его служит сила тока, скалярная величина, определяемая отношением количества зарядов прошедших через поперечное сечение проводника за единицу времени: I = dq/dt. За единицу измерения силы тока принят ампер.

Если направление перемещения зарядов остаётся неизменным, то движение тока считается постоянным, а если изменяется — переменным. Возникновение тока возможно только в замкнутой цепи. Для того чтобы заряд переместился, приложенное поле должно выполнить работу. То есть затратить какую-то энергию для перемещения заряда с одной точки в другую. Если принять, что в начальном положении частичка обладает нулевым зарядом, то тогда переместившись, она уже будет иметь другое его значение. Разность между этими величинами называется разностью потенциалов или напряжением.

Для поддержания силы тока в полной цепи необходим источник, постоянно воздействующий на свободные заряды и поддерживающий разности потенциалов на различных участках цепи. Величина силы, которая действует на цепь, называется ЭДС. Физически она представляет собой отношение работы, затрачиваемой на передвижение заряда от одного своего полюса к другому, к значению заряда: E = A/q. Измеряется ЭДС, так же как и напряжение, в вольтах.

При перемещении заряд из-за особенностей строения кристаллической решётки вещества, он сталкивается с различными дефектами и примесями. В результате этого происходит частичное рассеивание его потенциала, а скорость движения замедляется. Потеря энергии характеризуется электрической величиной-сопротивлением. Другими словами, сопротивление — это величина, препятствующая прохождению тока.

Вычисление импеданса

Идеальные элементы

Для резистора импеданс всегда равен его сопротивлению R и не зависит от частоты:

zR=R{\displaystyle z_{R}=R}

(2)

Конденсатор

Ток и напряжение для конденсатора связаны соотношением:

i(t)=CdUdt. (jω) =R+1jωC+jωL=R−jωC+jωL=R+j(−1ωC+ωL).{\displaystyle {\hat {Z}}(j\omega )\ =R+{\frac {1}{j\omega C}}+j\omega L=R-{\frac {j}{\omega C}}+j\omega L=R+j\left(-{\frac {1}{\omega C}}+\omega L\right).}

(8)

Параллельное и последовательное соединение элементов

В разделе электротехники присутствует несколько вариантов того, как подключить детали в электрическую цепь. Есть параллельное и попеременное подсоединения. Их объединяет смешанная схема, которая представлена ниже.

Последовательное подключение — это когда все источники соединяются друг с другом последовательно. Получаемая цепь не обладает никакими разветвлениями. Сила тока в данном случае проходит через каждый источник. Она постоянная, общее напряжение одинаковое.

В случае препятствия резисторов заряду при последовательном подключении получится, что сопротивляемость будет равна сумме всех взаимозаменяемых пассивных элементов цепи. Рассчитывая параметры электротехнической схемы, не нужно применять частные параметры устройств. Их можно заменить одним значением, которое равно их суммарному показателю.

Обратите внимание! Польза взаимозаменяемости компонентов заключается в возможности замены нескольких пассивных элементов электрической сети одним. Соединение элементов

Соединение элементов

Параллельное подключение — это такое подсоединение источников, в котором входы всех устройств находятся в одних местах, а выходы — в других. Этими местами служат узлы.

В случае эквивалентного препятствия заряду при параллельном соединении определить его можно благодаря закону Ома с преобразованием формулировки подсчета. Так, сделать необходимый расчет можно, основываясь на следующей формуле: R · R / N·R = R / N.

Если это соединение нескольких индуктивных катушек, то их индуктивный показатель сопротивляемости будет рассчитываться по той же формуле, что для резисторных устройств.

Важно! В случае с параллельным подключением общий показатель будет меньше любого показателя резистора. При последовательном подсоединении все наоборот

Аналогия с электрическим сопротивлением проводника на примере резистора

Резистор — пассивный элемент, обладающий чисто активным сопротивлением. Реактивная составляющая комплексного сопротивления резистора равна нулю, так как соотношение между напряжением на резисторе и током через него не зависит от частоты тока/напряжения, а так же из-за того, что резистор является пассивным элементом (поскольку не содержит внутренних источников энергии). Если к его концам приложить некоторое напряжение U (подсоединить источник напряжения), то через резистор пойдёт электрический ток I. Если через резистор пропустить электрический ток I (подсоединить источник тока), то между концами резистора возникнет падение напряжения U. Резистор характеризуется электрическим сопротивлением, которое равно отношению напряжения U, к току I (см. закон Ома для участка цепи):

R=UI.{\displaystyle R={\frac {U}{I}}.}

Применение понятия «электрическое сопротивление» к реактивным элементам (катушка индуктивности и конденсатор) при постоянном токе приводит к тому, что:

сопротивление идеальной катушки индуктивности стремится к нулю:

если пропустить через идеальную катушку индуктивности некоторый постоянный ток I, то при любом значении I, падение напряжения на катушке будет нулевым:

U=;{\displaystyle U=0;}

R=UI=I=;{\displaystyle R={\frac {U}{I}}={\frac {0}{I}}=0;}

сопротивление идеального конденсатора стремится к бесконечности:

если приложить к конденсатору некоторое постоянное напряжение U, то при любом значении U, ток через конденсатор будет нулевым:

I=;{\displaystyle I=0;}

R=UI=U=∞. {\displaystyle R={\frac {U}{I}}={\frac {U}{0}}=\infty .}

Это справедливо лишь для постоянного тока и напряжения. В случае же приложения к реактивному элементу переменного тока и напряжения, свойства реактивных элементов существенно иные:

• напряжение между выводами катушки индуктивности не равно нулю;
• ток, протекающий через конденсатор, не будет равен нулю.

Такое поведение не может быть описано в терминах активного сопротивления для постоянного тока, поскольку активное сопротивление предполагает постоянное, не зависящее от времени соотношение тока и напряжения, то есть отсутствие фазовых сдвигов между током и напряжением.

Было бы удобно иметь некоторый параметр аналогичный активному сопротивлению и для реактивных элементов, который бы связывал ток и напряжение на них подобно активному сопротивлению в формуле закона Ома для постоянного тока.

Такую характеристику можно ввести, если рассмотреть свойства реактивных элементов при воздействиях на них гармонических сигналов. В этом случае ток и напряжение оказываются связаны некой константой (подобной в некотором смысле активному сопротивлению), которая и получила название «электрический импеданс» (или просто «импеданс»). При рассмотрении импеданса используется комплексное представление гармонических сигналов, поскольку именно в таком представлении одновременно учитывается и амплитудные, и фазовые характеристики гармонических сигналов и откликов систем на гармоническое воздействие.

Обобщенный импеданс в s-плоскости и преобразование Лапласа

Импедансы, определённые через комплексную частоту jω{\displaystyle j\omega }, позволяют вычислять частотный отклик некоторой линейной цепи, возбуждаемой гармоническим сигналом, причём только в установившемся режиме. Для расчёта отклика цепи на сигнал, произвольно изменяющийся во времени применяется обобщенный импеданс — функции комплексной переменной s=σ+jω{\displaystyle s=\sigma +j\omega } и отклик цепи во временно́й области вычисляется через обратное преобразование Лапласа, причем в таких вычислениях возбуждающий сигнал fin(t){\displaystyle f_{in}(t)} из временного представления должен быть предварительно преобразован в комплексное представление Ft(s){\displaystyle F_{t}(s)} через прямое преобразование Лапласа:

Ft(s)=∫∞fin(t)e−stdt. {-st}\,dt.}

Комплексный отклик системы выражается обычным способом через преобразованное комплексное представление возбуждающего сигнала и комплексную передаточную функцию системы H(s){\displaystyle H(s)}:

Ft,H(s)=H(s) Ft(s).{\displaystyle F_{t,H}(s)=H(s)\ F_{t}(s).}

Двухполюсник	Обобщённыйимпеданс
Резистор	R{\displaystyle R\,}
Катушкаиндуктивности	sL{\displaystyle sL\,}
Конденсатор	1sC{\displaystyle {\frac {1}{sC}}\,}

Комплексная передаточная функция вычисляется обычным методом расчёта электрических цепей, например, по правилам Кирхгофа, в формулы в качестве сопротивлений подставляются обобщённые импедансы. Обобщённые импедансы пассивных двухполюсников приведены в таблице. Например, обобщённый импеданс цепи, состоящей из последовательно включённых резистора и катушки индуктивности будет R+sL{\displaystyle R+sL}.

Отклик цепи во временно́й области вычисляется обратным преобразованием Лапласа:

fF,H(t)=L−1H(s) Ft(s)=12πi∫σ1−j⋅∞σ1+j⋅∞estH(s) Ft(s)ds,{\displaystyle f_{F,H}(t)={\mathcal {L}}^{-1}={\frac {1}{2\pi i}}\int \limits _{\sigma _{1}-j\cdot \infty }^{\sigma _{1}+j\cdot \infty }e^{st}H(s)\ F_{t}(s)\,ds,}

где σ1 {\displaystyle \sigma _{1}\ } — некоторое вещественное число, выбираемое из условий сходимости интеграла.

Пример вычисления временно́го отклика RC-фильтра нижних частот на ступенчатое возмущение

Пассивный RС-фильтр нижних частот 1-го порядка

Простейший фильтр нижних частот 1-го порядка изображён на рисунке и состоит из последовательно соединённых резистора и конденсатора, образующего делитель напряжения для входного сигнала где выходной сигнал снимается с конденсатора, обобщённый комплексный коэффициент передачи HRC(s){\displaystyle H_{RC}(s)} такого делителя:

HRC(s)=1sCR+1sC=1sRC+1=1sT+1,{\displaystyle H_{RC}(s)={\frac {1/sC}{R+1/sC}}={\frac {1}{sRC+1}}={\frac {1}{sT+1}},}

где обозначено T=RC{\displaystyle T=RC} — постоянная времени RС-цепи.

Ступенчатый входной сигнал можно выразить через функцию Хевисайда h(t){\displaystyle h(t)}:

Uin(t)=U h(t),{\displaystyle U_{in}(t)=U_{0}\ h(t),}

где U{\displaystyle U_{0}} — амплитуда ступеньки.

Преобразование Лапласа входного сигнала:

Fin(s)=LU h(t)=∫∞e−stUh(t)dt=Us. {-t/T}).}

Таким образом, получен отклик цепи при нулевом начальном условии (UC={\displaystyle U_{C}=0} при t={\displaystyle t=0}), такой же, как и при применении другого метода расчёта, например, из решения обыкновенного дифференциального уравнения.

Для практического применения расчета цепей (и других расчётов) составлены подробные таблицы прямого и обратного преобразования Лапласа многих часто встречающихся при расчётах функций.

Комбинируя преобразование Лапласа с использованием его свойств и интеграл Дюамеля обычно относительно легко найти отклики во временной области самых различных линейных электрических цепей.

Оцените статью:

Что такое активное реактивное и полное сопротивление. Реактивное сопротивление XL и XC. Полное сопротивление цепи при последовательном соединении активного и реактивного сопротивления

Итак, катушки индуктивности и конденсаторы препятствуют протеканию переменного тока. Такое сопротивление по переменному току носит название реактивного сопротивления Х и измеряется в омах. Реактивное сопротивление зависит как от величины индуктивности и емкости, так и от частоты сигнала.

Катушка индуктивности имеет индуктивное реактивное сопротивление VL равное

где f — частота в герцах, a L — индуктивность в генри.
Так как ω = 2πf, то можно записать XL = ωL. Например, реактивное сопротивление катушки с индуктивностью 10 мГн, на которую подается сигнал частотой 1 кГц, равно

XL = 2π*1*103*10 *10-3 = 62,8 Ом.

Реактивное сопротивление катушки индуктивности возрастает с увеличением частоты сигнала (рис. 4.26).
Конденсатор имеет емкостное сопротивление XC равное

где С — емкость в фарадах. Например, реактивное сопротивление конденсатора емкостью 1 мкФ, на который подается сигнал частотой 10 кГц, равно

Рис. 4.26. Зависимость индуктивного Рис. 4.27.
сопротивления от частоты.

Рис. 4.28. Векторная сумма емкостного (XC)

и индуктивного (XL) сопротивлений.

Рис. 4.29.
(а) Катушка индуктивности, соединенная последовательно с резистором R.
(б) Векторное представление R, XL и их векторной суммы Z

Реактивное сопротивление конденсатора уменьшается с увеличением частоты сигнала (рис. 4.27).
Результирующее сопротивление цепи, включающей в себя емкостное сопротивление XC и индуктивное сопротивление XL, равно векторной сумме XC и XL. Векторы XC и XL, как видно из рис. 4.28(б), находятся в противофазе, т. е. разность фаз между ними равна 1800. Поэтому результирующее сопротивление просто равно разности между XC и XL. Например, пусть XL = 100 Ом, а XC = 70 Ом. Тогда результирующее реактивное сопротивление Х = 100 – 70 = 30 Ом и является индуктивным так как XL больше, чем XС.

Импеданс
Результирующее сопротивление цепи, содержащей как активное, так и реактивное (индуктивное либо емкостное) сопротивление, носит название импеданса или полного сопротивления цепи.
Импеданс Z является векторной суммой реактивного сопротивления Х и активного сопротивления R.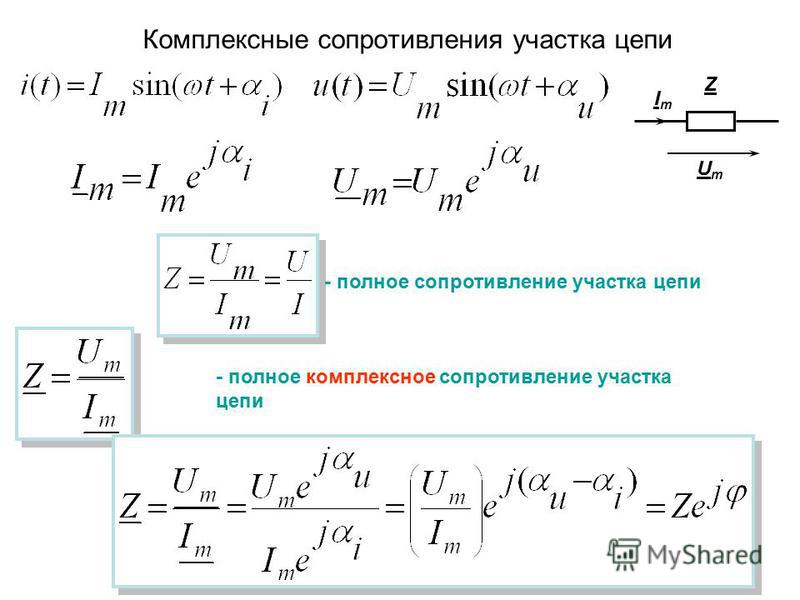

Рассмотрим, например, схему, изображенную на рис. 4.29. Она включает в себя индуктивное сопротивление XL соединенное последовательно с резистором R. Как видно из рис. 4.29(б), вектор XL опережает вектор R на 90°. Импеданс равен

Если XL = 400 Ом и R = 300 Ом, то Z = 500 Ом.

Реактивное сопротивление – электрическое сопротивление переменному току, обусловленное передачей энергии магнитным полем в индуктивностях или электрическим полем в конденсаторах.

Элементы, обладающие реактивным сопротивлением, называют реактивными.

Реактивное сопротивление катушки индуктивности.

При протекании переменного тока I в катушке, магнитное поле создаёт в её витках ЭДС, которая препятствует изменению тока.

При увеличении тока, ЭДС отрицательна и препятствует нарастанию тока, при уменьшении — положительна и препятствует его убыванию, оказывая таким образом сопротивление изменению тока на протяжении всего периода.

В результате созданного противодействия, на выводах катушки индуктивности в противофазе формируется напряжение U , подавляющее ЭДС, равное ей по амплитуде и противоположное по знаку.

При прохождении тока через нуль, амплитуда ЭДС достигает максимального значения, что образует расхождение во времени тока и напряжения в 1/4 периода.

Если приложить к выводам катушки индуктивности напряжение

U , ток не может начаться мгновенно по причине противодействия ЭДС, равного -U , поэтому ток в индуктивности всегда будет отставать от напряжения на угол 90°. Сдвиг при отстающем токе называют положительным.

Запишем выражение мгновенного значения напряжения u исходя из ЭДС (ε ), которая пропорциональна индуктивности L и скорости изменения тока: u = -ε = L(di/dt) .
Отсюда выразим синусоидальный ток .

Интегралом функции sin(t) будет -соs(t) , либо равная ей функция sin(t-π/2) .
Дифференциал dt функции sin(ωt) выйдет из под знака интеграла множителем 1/ω .
В результате получим выражение мгновенного значения тока со сдвигом от функции напряжения на угол

π/2 (90°).
Для среднеквадратичных значений U и I в таком случае можно записать .

В итоге имеем зависимость синусоидального тока от напряжения согласно Закону Ома, где в знаменателе вместо R выражение ωL , которое и является реактивным сопротивлением:

Реактивное сопротивлениие индуктивностей называют индуктивным.

Реактивное сопротивление конденсатора.

Электрический ток в конденсаторе представляет собой часть или совокупность процессов его заряда и разряда – накопления и отдачи энергии электрическим полем между его обкладками.

В цепи переменного тока, конденсатор будет заряжаться до определённого максимального значения, пока ток не сменит направление на противоположное. Следовательно, в моменты амплитудного значения напряжения на конденсаторе, ток в нём будет равен нулю. Таким образом, напряжение на конденсаторе и ток всегда будут иметь расхождение во времени в четверть периода.

В результате ток в цепи будет ограничен падением напряжения на конденсаторе, что создаёт реактивное сопротивление переменному току, обратно-пропорциональное скорости изменения тока (частоте) и ёмкости конденсатора.

Если приложить к конденсатору напряжение

U , мгновенно начнётся ток от максимального значения, далее уменьшаясь до нуля. В это время напряжение на его выводах будет расти от нуля до максимума. Следовательно, напряжение на обкладках конденсатора по фазе отстаёт от тока на угол 90 °. Такой сдвиг фаз называют отрицательным.

Ток в конденсаторе является производной функцией его заряда i = dQ/dt = C(du/dt) .
Производной от sin(t) будет cos(t) либо равная ей функция sin(t+π/2) .
Тогда для синусоидального напряжения u = U amp sin(ωt) запишем выражение мгновенного значения тока следующим образом:

i = U amp ωCsin(ωt+π/2) .

Отсюда выразим соотношение среднеквадратичных значений .

Закон Ома подсказывает, что 1/ωC есть не что иное, как реактивное сопротивление для синусоидального тока.

Сопротивление, оказываемое проводником проходящему на нему переменному току, называется активным сопротивлением .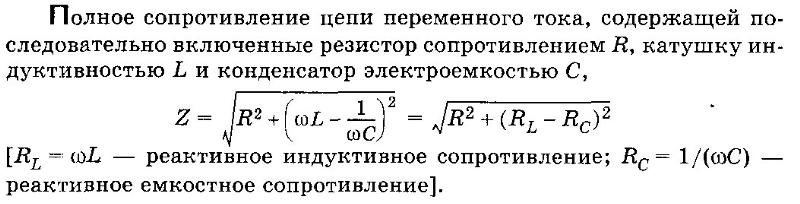

Если какой-либо потребитель не содержит в себе индуктивности и емкости (лампочка накаливания, нагревательный прибор), то он будет являться для переменного тока также активным сопротивлением.

Активное сопротивление зависит от частоты переменного тока, возрастая с ее увеличением.

Однако многие потребители обладают индуктивными и емкостными свойствами при прохождении через них переменного тока. К таким потребителям относятся трансформаторы, дроссели, электромагниты, конденсаторы, различного рода провода и многие другие.

При прохождении через них переменного тока необходимо учитывать не только активное, но и реактивное сопротивление , обусловленное наличием, в потребителе индуктивных и емкостных свойств его.

Активное сопротивление определяет действительную часть импеданса:

Где — импеданс, — величина активного сопротивления, — величина реактивного сопротивления, — мнимая единица.

Активное сопротивление — сопротивление электрической цепи или её участка, обусловленное необратимыми превращениями электрической энергии в другие виды энергии(в тепловую энергию)

Реакти́вное сопротивле́ние — электрическое сопротивление, обусловленное передачей энергии переменным током электрическому или магнитному полю (и обратно).

Величина реактивного сопротивления может быть выражена через величины индуктивного и ёмкостного сопротивлений:

Величина полного реактивного сопротивления

Индуктивное сопротивление () обусловлено возникновением ЭДС самоиндукции в элементе электрической цепи.

Ёмкостное сопротивление ().

Здесь — циклическая частота

Полное сопротивление цепи при переменном токе:

z =

√

r 2 + x 2

=

√

r 2 +(x L −x C) 2

Билет №12.

1. 1) Согласование генератора с нагрузкой — обеспечение требуемой величины активного эквивалентного сопротивления нагрузки генераторной лампы, R э, при всех возможных значениях входного сопротивления антенного фидера, которое зависит от его волнового сопротивления и коэффициента бегущей волны (КБВ)

Согласование (в электронике) сводится к правильному выбору сопротивлений генератора (источника), линии передачи и приёмника (нагрузки).

Идеального Согласование (в электронике) между линией и нагрузкой можно достичь при равенстве волнового сопротивления линии r полному сопротивлению нагрузки Zh = RH + j ХН, или при RH= r и XH= 0, где RH -активная часть полного сопротивления, XH — его реактивная часть. В этом случае в передающей линии устанавливается режим бегущих волн и характеризующий их коэффициент стоячей волны (КСВ) равен 1. Для линии с пренебрежимо малыми потерями электрической энергии Согласование и, благодаря ему, максимально эффективная передача энергии из генератора в нагрузку достигаются при условии, что полные сопротивления генератора Zr и нагрузки ZH являются комплексно-сопряжёнными, т. е. Zr = Z*H, или Rr = r = R Н =Xr- XH. В этом случае реактивное сопротивление цепи равно нулю, и соблюдаются условия резонанса, способствующие повышению эффективности работы радиотехнических систем (улучшается использование частотных диапазонов, повышается помехозащищенность, снижаются частотные искажения радиосигналов и т. п.). Оценку качества Согласование (в электронике) производят, измеряя коэффициент отражения и КСВ. Практически Согласование (в электронике) считают оптимальным, если в рабочей полосе частот КСВ не превышает 1,2-1,3 (в измерительных приборах 1,05). В отдельных случаях косвенными показателями Согласование (в электронике) могут служить реакции параметров генератора (частоты, мощности, уровня шумов) на изменение нагрузки, наличие электрических пробоев в линии, разогрев отдельных участков линии.

При таком режиме работы в приёмнике выделяется наибольшая мощность, равная половине мощности источника. В этом случае К.П.Д. =0,5. Такой режим используется в измерительных цепях, устройствах средств связи.

При передаче больших мощностей, например по высоковольтным линиям электропередач, работа в согласованном режиме, как правило, недопустима.

В цепь переменного электрического тока входят активные (содержащие внутренние источники энергии) и пассивные элементы (потребители энергии). К пассивным элементам относят резисторы и реактивные устройства.

Виды пассивных элементов

В электротехнике рассматривают два типа резисторов: активное и реактивное сопротивление. Активным – обладают приборы, в которых энергия электрического тока преобразуется в тепловую. В физике оно обозначается символом R. Единица измерения – Ом.

Этой формулой можно пользоваться для расчёта по мгновенным значениям тока и напряжения, максимальным или действующим.

Реактивные устройства энергию не рассеивают, а накапливают. К ним относятся:

• катушка индуктивности;
• конденсатор.

Реактивное сопротивление обозначается символом Х. Единица измерения – Ом.

Катушка индуктивности

Представляет собой проводник, выполненный в форме спирали, винта или винтоспирали. Благодаря высокой инерционности, прибор используют в схемах, которые применяются для уменьшения пульсаций в цепях переменного тока и колебательных контурах, для создания магнитного поля и т. д. Если она имеет большую длину при небольшом диаметре, то катушку называют соленоидом.

Для вычисления падения напряжения (U ) на концах катушки используют формулу:

U = –L·DI/Dt, где:

• L – индуктивность прибора, измеряется в Гн (генри),
• DI – изменение силы тока (измеряется в амперах) за промежуток времени Dt (измеряется в секундах).

Внимание! При любом изменении тока в проводнике возникает ЭДС самоиндукции, которая препятствует этому изменению.

Вследствие этого в катушке возникает сопротивление, которое называется индуктивным.

В электротехнике обозначается Х L и рассчитывается по формуле:

где w – угловая частота, измеряется в рад/с.

Угловая частота является характеристикой гармоничного колебания. Связана с частотой f (количество полных колебаний в секунду). Частота измеряется в колебаниях в секунду (1/с):

w = 2 · p · f.

Если в схеме используется несколько катушек, то при их последовательном соединении общее Х L для всей системы будет равно:

XL = XL1 + XL2 + …

В случае параллельного соединения:

1/XL = 1/XL1 + 1/XL2 + …

Закон Ома для такого соединения имеет вид:

где UL – падение напряжения.

Помимо индуктивного, устройство обладает и активным R.

Электрический импеданс в этом случае равен:

Емкостной элемент

В проводниках и обмотке катушки, кроме индуктивного и активного сопротивлений, присутствует и емкостное, которое обусловлено наличием ёмкости в этих приборах. Кроме резистора и катушки, в схему может быть включен конденсатор, который состоит из двух металлических пластин, между которыми размещён слой диэлектрика.

К сведению. Электрический ток протекает за счёт того, что в устройстве проходят процессы заряда и разряда пластин.

При максимальном заряде на пластинах прибора:

За счёт того, что резистивное устройство может накапливать энергию, его используют в приборах, которые стабилизируют напряжение в цепи.

Возможность накапливать заряд характеризуется ёмкостью.

Реактивное сопротивление конденсатора (ХС) можно рассчитать по формуле:

XC = 1/(w·C), где:

1. w – угловая частота,
2. С – ёмкость конденсатора.

Единица измерения ёмкости – Ф (фарада).

Учитывая, что угловая частота связана с циклической частотой, расчет значения реактивного сопротивления конденсатора можно выполнить по формуле:

XC=1/(2·p·f·C).

Если в цепи последовательно соединены несколько устройств, то общее X С системы будет равно:

XС = XС1 + XС2 + …

Если соединение объектов параллельное, то:

1/XC = 1/XC1 + 1/XC2+…

Закон Ома для этого случая записывается следующим образом:

где UС – падение напряжения на конденсаторе.

Расчёт цепи

При последовательном соединении I = const в любой точке и, согласно закону Ома, его можно рассчитать по формуле:

где Z – электрический импеданс.

Напряжение на устройствах рассчитывается следующим образом:

UR = I · R, UL = I · XL, UC = I · XC.

Вектор индуктивной составляющей напряжения направлен в противоположную сторону от вектора емкостной составляющей, поэтому:

следовательно, согласно расчётам:

Внимание! Для вычисления значения импеданса можно воспользоваться «треугольником сопротивлений», в котором гипотенузой является значение Z, а катетами – значения X и R.

Если в цепь подключены и конденсатор, и катушка индуктивности, то, согласно теореме Пифагора, гипотенуза (Z ) будет равна:

Так как X = XL – XC , то:

При решении электротехнических задач часто импеданс записывают в виде комплексного числа, в котором действительная часть соответствует значению активной составляющей, а мнимая – реактивной. Таким образом, выражение для импеданса в общем виде имеет вид:

где i – мнимая единица.

Для онлайн расчёта реактивного сопротивления можно использовать программу – калькулятор, которую можно найти в сети Интернет. Подобных сервисов достаточно много, поэтому вам не составит труда подобрать удобный для вас калькулятор.

Благодаря таким Интернет сервисам, можно быстро выполнить нужный расчёт.

Видео

Одной из основных проблем в сети переменного напряжения является наличие реактивной мощности. Она расходуется только на потери тепловые. Источником реактивной энергии есть накопители электрической энергии L и С. Я не буду очень глубоко рассматривать этот вопрос. Предлагаю рассмотреть этот вопрос на примере простых элементов цепи — индуктивности и емкости.

Индуктивный элемент L

Индуктивный элемент (рассмотрим на примере катушки индуктивности) представляют собой витки изолированного между собой провода. При протекании тока катушка намагничивается. Если изменить полярность источника, катушка начнет отдавать запасенную энергию обратно, стараясь поддержать величину тока в контуре. Поэтому при протекании через нее переменной составляющей, энергия запасенная при прохождении положительного полупериода, не успеет рассеяться и будет препятствовать прохождению отрицательного полупериода. В результате отрицательному полупериоду придется погасить энергию запасенную катушкой. В итоге напряжение(U), будет опережать ток (І) на какой-то угол φ. Ниже приведен результат моделирования работы на L-R нагрузку L=1*10 -3 Гн, R=0. 5 Ом. U ист = 250 В, частота f=50 Гц.

φ – это разница фаз между U и I.

Реактивное сопротивление обозначается буквой X, полное Z, активное R.

Для индуктивности:

Где ω – циклическая частота

L – индуктивность катушки;

Вывод: чем выше индуктивность L или частота, тем больше будет сопротивление катушки переменному току.

Емкостной элемент

Емкостной элемент (рассмотрим на примере конденсатора) представляет собой двухполюсник с переменным или постоянным значением емкости. Конденсатор — накопитель электрических зарядов. Если подключить его к источнику питания, он зарядится. Если к нему приложить источник с переменной составляющей, он будет заряжаться при прохождении через него положительного полупериода. Когда направление полупериода изменится на отрицательное значение, конденсатор начнет перезаряжаться, то есть энергия, которая накопилась в нем, начнет противодействовать перезарядке. В итоге мы получим напряжение на конденсаторе противоположное источнику. В результате І, будет опережать U на какой- то угол φ. Ниже приведен результат моделирования работы на С-R нагрузку С=900*10 — 6 Фа, R=0.5 Ом, U ист = 250 В, частота f=50 Гц.

Рисунок 2. Работа источника на R-C нагрузку

Для емкости:

Где ω – циклическая частота

— частота питающего напряжения, Гц;

С — емкость конденсатора;

Вывод: чем выше емкость С или частота, тем меньше будет сопротивление переменному току.

Сравнение влияния реактивного сопротивления на активную мощность сети

Из рисунков 1 и 2 видно, что сдвиг фаз на рисунках не одинаков. Вывод — чем больше в полном сопротивлении Z будет влияние X L или X C тем больше будет разница фаз U и I.

Угол сдвига между током и напряжением называется φ .

Реактивная мощность однофазная:

Трехфазная:

U ф, I ф — фазные ток и напряжение

Вывод: реактивная мощность – не выполняет полезного действия.

Она «перегоняется» по сети нагревая кабели и увеличивая потери. На крупных промышленных предприятиях это особо ощутимо в силу наличия электроприводов и других крупных потребителей. Этот вопрос очень актуален для энергосбережения и модернизации производства. Поэтому на пром. предприятиях устанавливаются компенсаторы реактивной мощности. Они могут быть разного типа и кроме компенсации выполнять еще и роль фильтров. С помощью компенсаторов стараются сохранить баланс реактивной мощности для минимизации ее влияния на сеть и подогнать угол φ к нулю.

Для необходимо максимально сбалансировать в сети количество (L, C) элементов.

Как найти полное сопротивление цепи

В любой цепи переменного тока наряду с чисто реактивным сопротивлением присутствует омическое (активное) сопротивление, которое нужно учитывать при определении полного сопротивления.

Z	полное сопротивление,	Ом
R	омическое (активное) сопротивление,	Ом
X	реактивное сопротивление,	Ом
Y = 1/Z	полная проводимость,	сименс
G	активная проводимость,	сименс
B	реактивная проводимость,	сименс
U	полное напряжение (эффективное значение),	Вольт
I	полный ток (эффективное значение),	Ампер

Полное сопротивление при последовательном соединении R и X

При последовательном соединении активное и реактивное сопротивления складываются геометрически

X определяется по формулам реактивного сопротивления и Величина U_x определяется, как произведение IX.

Сопротивление Z не зависит от времени. Вектор, изображающий сопротивление на векторной диаграмме, не вращается.

Полное сопротивление при параллельном соединение R и X

При параллельном соединении активная и реактивная проводимости складываются геометрически

Величина В = 1/Х определяется но формулам реактивного сопротивления. I_x определяется как произведение UB.

Величина Y не зависит от времени. Вектор, изображающий на векторной диаграмме проводимость, не вращается.

При последовательном соединении участков электрической цепи полное сопротивление всей цепи

(1.1)

и определяется из выражения (1.2)

где r — активное сопротивление всей цепи; x – реактивное сопротивление всей цепи.

Результаты измерений в неразветвленной цепи

№ п/п	Характер нагрузки	Измеренные величины	Примечание
U, B	I, A	P, Вт	Uk, B	Uc, B
Катушка индуктивности и конденсатор	xk xc(Cmax= )
Катушка индуктивности
Конденсатор	Cmin=
Ламповый реостат

Активное сопротивление катушки вычисляется по формуле:

(1. 3)

где Р_k — активная мощность, потребляемая катушкой индуктивности, в опытах 1, 2, 3 и 4 равная активной мощности всей цепи Р.

Реактивное (индуктивное) сопротивление катушки определяется следующим образом:

(1.4)

где – полное сопротивление катушки индуктивности.

Индуктивность катушки вычисляется по формуле:

(1.5)

где ω, с -1 — круговая частота напряжения питания; f = 50 Гц — циклическая частота напряжения питания.

Реактивное (емкостное) сопротивление конденсатора можно вычислить следующим образом:

(1.6)

Емкость конденсатора определяется по формуле:

. (1.7)

Коэффициенты мощности всей цепи cosφ и катушки индуктивности cosφ_к вычисляются по формулам:

(1.8)

(1.9)

Составляющие напряжения катушки U_ak — активная и реактивная U_pk — определяются по формулам:

(1.10)

Активное сопротивление лампового реостата определяется по данным опыта 6 как

(1. 11)

Реактивное сопротивление всей цепи при последовательном соединении катушки индуктивности и конденсатора можно определить по формуле:

. (1.12)

Рассчитанные значения параметров цепи записать в табл. 1.3.

По результатам измерений и расчетным данным строятся векторные диаграммы. На рис. 1.2 приведен пример построения векторной диаграммы.

Рис. 1.2. Пример построения векторной диаграммы для последовательного соединения катушки индуктивности и конденсатора

Параметры неразветвленной цепи

№ п/п

Ламповый реостат

Катушка индуктивности

Конденса-тор

Вся цепь

rr, Ом

rk, Ом

xk, Ом

zk, Ом

cosφk

L, мГн

Uak, B

Upk, B

xc,Ом

C, мкФ

r, Ом

x, Ом

z,Ом

cosφ

.

При построении векторных диаграмм для последовательного соединения элементов электрической цепи за исходный вектор принимается вектор тока. Векторы напряжений откладываются в масштабе, общем для всех напряжений. Вектор Ū_r совпадает по направлению с вектором тока, а вектор Ū_с отстает от вектора тока на угол π/2. Вектор напряжения Ū_k строится как векторная сумма вектора активной составляющей Ū_аk, совпадающего по фазе с вектором тока, и вектора индуктивной составляющей Ū_pk, опережающего вектор тока на угол π/2.

Вектор приложенного к схеме напряжения Ū равен векторной сумме векторов напряжений на отдельных элементах цепи.

При последовательном соединении катушки индуктивности и конденсатора и условии

наступает резонанс напряжений.

В этом режиме цепь ведет себя как активное сопротивление:

(1.14)

При резонансе напряжений, если реактивные сопротивления катушки индуктивности и конденсатора значительно больше активного сопротивления цепи, на катушке индуктивности и конденсаторе возникают перенапряжения, величина которых существенно больше напряжения питания, что может привести к пробою изоляции и выходу из строя этих элементов.

В отчете привести:

– принципиальные схемы с необходимыми пояснениями;

– паспортные данные приборов;

– таблицы и расчетные формулы;

– векторные диаграммы для режимов, указанных преподавателем.

Вопросы для самоконтроля

2. Как найти полное сопротивление последовательной цепи, если известно сопротивление отдельных элементов?

3. Что такое коэффициент мощности?

4. Как можно изменить коэффициент мощности всей цепи?

5. Вследствие чего ток в цепи при резонансе напряжений имеет наибольшее значение?

6. Что такое резонанс напряжений и каковы его характерные особенности?

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: При сдаче лабораторной работы, студент делает вид, что все знает; преподаватель делает вид, что верит ему. 9364 – | 7302 – или читать все.

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

При последовательном соединении приборов с активным и индуктивным сопротивлениями (рис. 1) полное сопротивление цепи нельзя находить арифметическим суммированием. Если обозначить полное сопротивление через z, то для его определения служит формула:

Как видно, полное сопротивление является геометрической суммой активного и реактивного сопротивлений. Так, например, если r = 30 Ом и XL = 40 Ом, то

т. е. z получилось меньше, чем r + XL = 30 + 40 = 70 Ом.

Для упрощения расчетов полезно знать, что если одно из сопротивлений (r или xL) превосходит другое в 10 или более раз, то можно пренебречь меньшим сопротивлением и считать, что z равно большему сопротивлению. Ошибка весьма невелика.

Например, если r = 1 Ом и xL = 10 Ом, то

Ошибка лишь 0,5 % вполне допустима, так как сами сопротивления r и х бывают известны с меньшей точностью.

При параллельном соединении ветвей, имеющих активные и реактивные сопротивления (рис. 2), расчет полного сопротивления удобнее делать с помощью активной проводимости

и реактивной проводимости

Полная проводимость цепи у равна геометрической сумме, активной и реактивной проводимостей:

А полное сопротивление цепи является величиной, обратной у,

Если выразить проводимость через сопротивления, то нетрудно получить следующую формулу:

Эта формула напоминает известную формулу

но только в знаменателе стоит не арифметическая, а геометрическая сумма сопротивлений ветвей.

Пример. Найти полное сопротивление, если параллельно соединены приборы, имеющие r = 30 Он и xL = 40 Ом.

При расчете z для параллельного соединения можно для упрощения пренебречь большим сопротивлением, если оно превосходит меньшее в 10 и более раз. Ошибка не будет превышать 0,5 %

Рис. 1. Последовательное соединение участков цепи с активным и индуктивным сопротивлением

Рис. 2. Параллельное соединение участков цепи с активным и индуктивным сопротивлением

Принцип геометрического сложения применяется для цепей переменного тока также в случаях, когда надо складывать активные и реактивные напряжения или токи. Для последовательной цепи по рис. 1 складываются напряжения:

При параллельном соединении (рис. 2) складываются токи:

Если же последовательно или параллельно соединены приборы, имеющие только одни активные или только одни индуктивные сопротивления, то сложение сопротивлений или проводимостей и соответствующих напряжений или токов, а также активных или реактивных мощностей производится арифметически.

При любой цепи переменного тока закон Ома можно писать в следующем виде:

где z — полное сопротивление, вычисляемое для каждого случая соединения так, как это было показано выше.

Коэффициент мощности cosφ для любой цепи равен отношению активной мощности Р к полной S. При последовательном соединении это отношение можно заменить отношением напряжений или сопротивлений:

При параллельном соединении получим:

Вывод основных расчетных формул для последовательной цепи переменного тока, имеющей активное и индуктивное сопротивления, можно сделать следующим образом.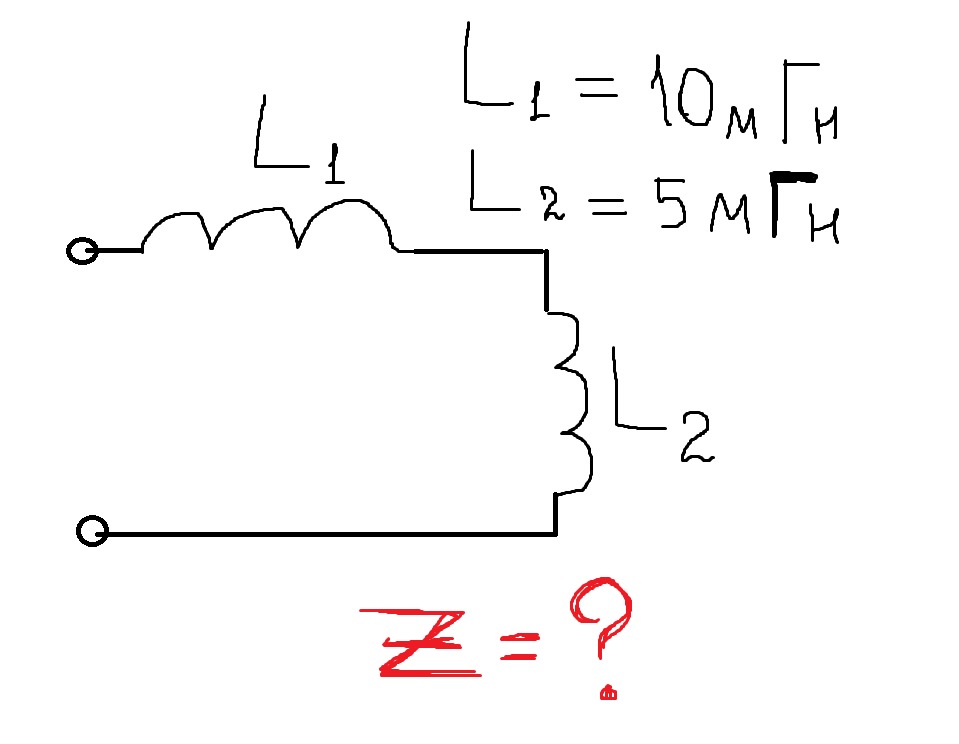

Проще всего построить векторную диаграмму для последовательной цепи (рис. 3).

Рис. 3. Векторная диаграмма для последовательной цепи с активным и индуктивным сопротивлением

На этой диаграмме показаны вектор тока I, вектор напряжения UA на активном участке, совпадающий по направлению с вектором I, и вектор напряжения UL на индуктивном сопротивлении. Это напряжение опережает ток на 90° (напомним, что векторы надо считать вращающимися против часовой стрелки). Полное напряжение U представляет собой суммарный вектор, т. е. диагональ прямоугольника со сторонами UA и UL. Иначе говоря, U есть гипотенуза, а UA и UL — катеты прямоугольного треугольника. Отсюда следует, что

Т. е. что напряжения на активном и реактивном участках складываются геометрически.

Разделив обе части равенства на I2, найдем формулу для сопротивлений:

6.4. Сопротивление в цепи синусоидального тока

      Если напряжение подключить к сопротивлению R, то через него протекает ток

     (6. 7)

     Анализ выражения (6.7) показывает, что напряжение на сопротивлении и ток, протекающий через него, совпадают по фазе.
        Формула (6.7) в комплексной форме записи имеет вид

     (6.8)

      где     и     — комплексные  амплитуды  тока и напряжения.
     Комплексному уравнению (6.8) соответствует векторная диаграмма (рис. 6.4).

     Из анализа диаграммы следует, что векторы напряжения и тока совпадают по направлению.

     Сопротивление участка цепи постоянному току называется омическим, а сопротивление того же участка переменному току — активным сопротивлением.

                               Рис.6.4
     Активное сопротивление больше омического из-за явления поверхностного эффекта.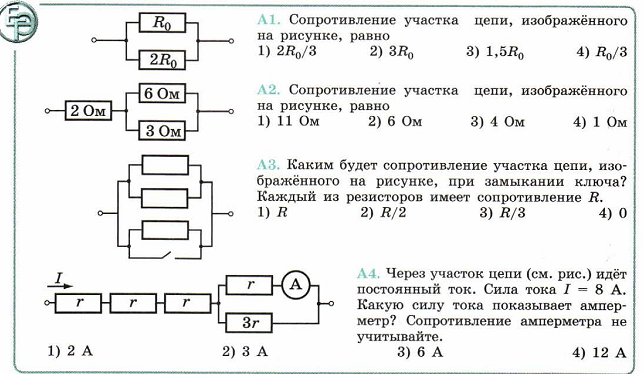 Поверхностный эффект заключается в том, что ток вытесняется из центральных частей к периферии сечения проводника.

6.5. Индуктивная катушка в цепи синусоидального тока

     Сначала рассмотрим идеальную индуктивную катушку, активное сопротивление которой равно нулю. Пусть по идеальной катушке с индуктивностью L протекает синусоидальный ток . Этот ток создает в индуктивной катушке переменное магнитное поле, изменение которого вызывает в катушке ЭДС самоиндукции

     (6.9)

     Эта ЭДС уравновешивается напряжением, подключенным к катушке: u = e_L = 0.

     (6.10)

     Таким образом, ток в индуктивности отстает по фазе от напряжения на 90^o из-за явления самоиндукции.
     Уравнение вида (6.10) для реальной катушки, имеющей активное сопротивление R, имеет следующий вид:

     (6.11)

     Анализ выражения (6.11) показывает, что ЭДС самоиндукции оказывает препятствие (сопротивление) протеканию переменного тока, из-за чего ток в реальной индуктивной катушке отстает по фазе от напряжения на некоторый угол φ (0^oo), величина которого зависит от соотношения R и L.      Выражение (6.11) в комплексной форме записи имеет вид:

     (6.12)

      где Z_L — полное комплексное сопротивление индуктивной катушки ;
            Z_L — модуль комплексного сопротивления;
            — начальная фаза комплексного сопротивления;
          — индуктивное сопротивление (фиктивная величина, характеризующая реакцию электрической цепи на переменное магнитное поле).
      Полное сопротивление индуктивной катушки или модуль комплексного сопротивления

.

       Комплексному уравнению (6.12) соответствует векторная диаграмма (рис.6.5).

Рис. 6.5

       Из анализа диаграммы видно, что вектор напряжения на индуктивности опережает вектор тока на 90^o.
    В цепи  переменного тока напряжения на  участках цепи складываются не арифметически, а геометрически.
       Если мы поделим стороны треугольника напряжений на величину тока I_m, то перейдем к подобному треугольнику сопротивлений (рис. 6.6).

     Из треугольника сопротивлений получим несколько формул:
                     ;                     ;
    Рис. 6.6

;

;           .

6.6. Емкость в цепи синусоидального тока

     Если к конденсатору емкостью C подключить синусоидальное напряжение, то в цепи протекает синусоидальный ток

;

.    (6.13)

      Из анализа выражений 6.13 следует, что ток опережает напряжение по фазе на 90^o.

      Выражение (6.13) в комплексной форме записи имеет вид:

,    (6.14)

       где — емкостное сопротивление, фиктивная расчетная величина, имеющая размерность сопротивления.

        Если комплексное сопротивление индуктивности положительно
       , то комплексное сопротивление емкости отрицательно

        .

       На рис. 6.7 изображена векторная диаграмма цепи с емкостью.
       Вектор тока опережает вектор напряжения на 90^o.

Рис. 6.7

6.7. Последовательно соединенные реальная индуктивная

катушка и конденсатор в цепи синусоидального тока

       Катушка с активным сопротивлением   R  и индуктивностью   L  и конденсатор емкостью  С  включены последовательно (рис.6.8). В схеме протекает синусоидальный ток

.

     Определим напряжение на входе схемы.
       В соответствии со вторым законом Кирхгофа,

               (6. 15)

       Подставим эти формулы в уравнение (6.15). Получим:

            (6.16)

     Из выражения (6.16) видно: напряжение в активном сопротивлении совпадает по фазе с током, напряжение на индуктивности опережает по фазе ток на 90^o, напряжение по емкости отстает по фазе от тока на 90^o.
     Запишем уравнение (6.16) в комплексной форме:

(6.17)

           Рис. 6.8

       Поделим левую и правую части уравнения (6.17) на √2.
       Получим уравнение для комплексов действующих значений токов и напряжений

       ,     (6.18)

       где — комплексное сопротивление цепи;
      — модуль комплексного сопротивления, или полное сопротивление цепи;
              — начальная фаза комплексного сопротивления.

       При построении векторных диаграмм цепи рассмотрим три случая.

1. X_L > X_C, цепь носит индуктивный характер. Векторы напряжений на индуктивности и емкости направлены в противоположные стороны, частично компенсируют друг друга. Вектор напряжения на входе схемы опережает вектор тока (рис.6.9).
2. Индуктивное сопротивление меньше емкостного. Вектор напряжения на входе схемы отстает от вектора тока. Цепь носит емкостный характер (рис.6.10).
3. Индуктивное и емкостное сопротивления одинаковы. Напряжения на индуктивности и емкости полностью компенсируют друг друга. Ток в цепи совпадает по фазе с входным напряжением. В электрической цепи наступает режим резонансного напряжения (рис.6.11).

       Ток в резонансном режиме достигает максимума, так как полное сопротивление (z) цепи имеет минимальное значение.

         Условие возникновения резонанса: , отсюда резонансная частота равна

      .

         Из формулы следует, что режима резонанса можно добиться следующими способами:

1. изменением частоты;
2. изменением индуктивности;
3. изменением емкости.

      В резонансном режиме входное напряжение равно падению напряжения в активном сопротивлении. На индуктивности и емкости схемы могут возникнуть напряжения, во много раз превышающие напряжение на входе цепи. Это объясняется тем, что каждое напряжение равно произведению тока I₀ (а он наибольший), на соответствующее индуктивное или емкостное сопротивление (а они могут быть большими).

.

Рис. 6.9                            Рис. 6.10                              Рис. 6.11

6.8. Параллельно соединенные индуктивность, емкость

и активное сопротивление в цепи синусоидального тока

       К схеме на рис. 6.12 подключено синусоидальное напряжение . Схема состоит из параллельно включенных индуктивности, емкости и активного сопротивления.
       Определим ток на входе схемы.

      В соответствии с первым законом Кирхгофа:
            ,     (6.19)
      где
            — активная проводимость.

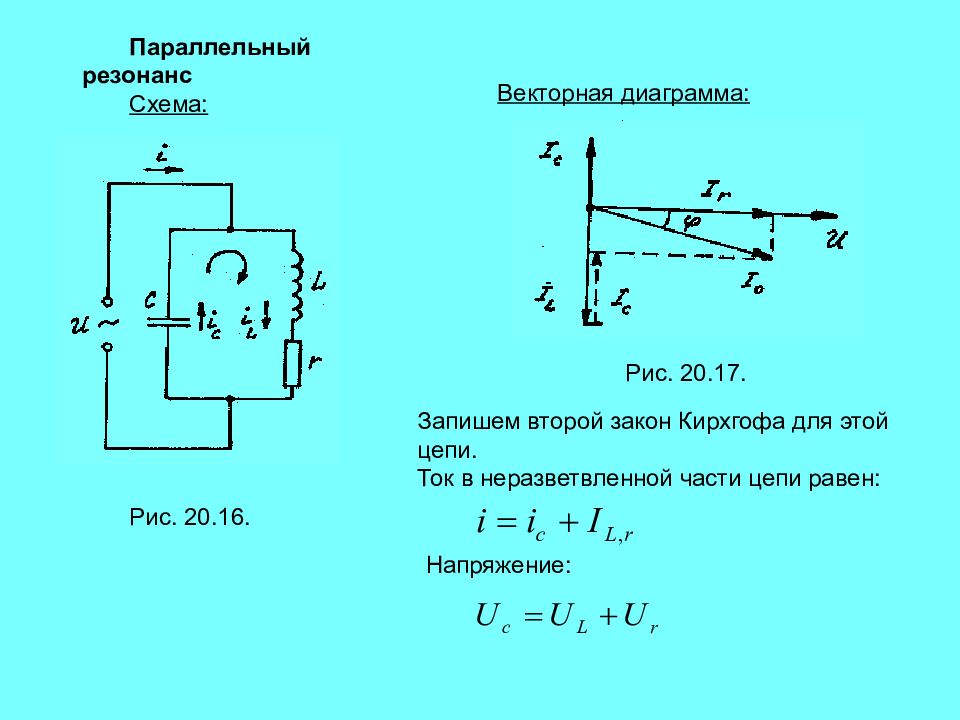                    Рис. 6.12                                            

        Подставим эти формулы в уравнение (6.19). Получим:

,     (6.20)

       где   — индуктивная проводимость;
                — емкостная проводимость.

      Из уравнения (6.20) видно, что ток в ветви с индуктивностью отстает по фазе от напряжения на 90^o, ток в ветви с активным сопротивлением совпадает по фазе с напряжением, ток в ветви с емкостью опережает по фазе напряжение на 90^o.
        Запишем уравнение (6.20) в комплексной форме.

,     (6.21)

        где   — комплексная проводимость;
              — полная проводимость;
              — начальная фаза комплексной проводимости.

        Построим векторные диаграммы, соответствующие комплексному уравнению (6.21).

Рис. 6.13                            Рис. 6.14                              Рис. 6.15

      В схеме на рис. 6.12 может возникнуть режим резонанса токов. Резонанс токов возникает тогда, когда индуктивная и емкостная проводимости одинаковы. При этом индуктивный и емкостный токи, направленные в противоположные стороны, полностью компенсируют друг друга. Ток в неразветвленной части схемы совпадает по фазе с напряжением.
      Из условия возникновения резонанса тока получим формулу для резонансной частоты тока

.

       В режиме резонанса тока полная проводимость цепи — минимальна, а полное сопротивление — максимально.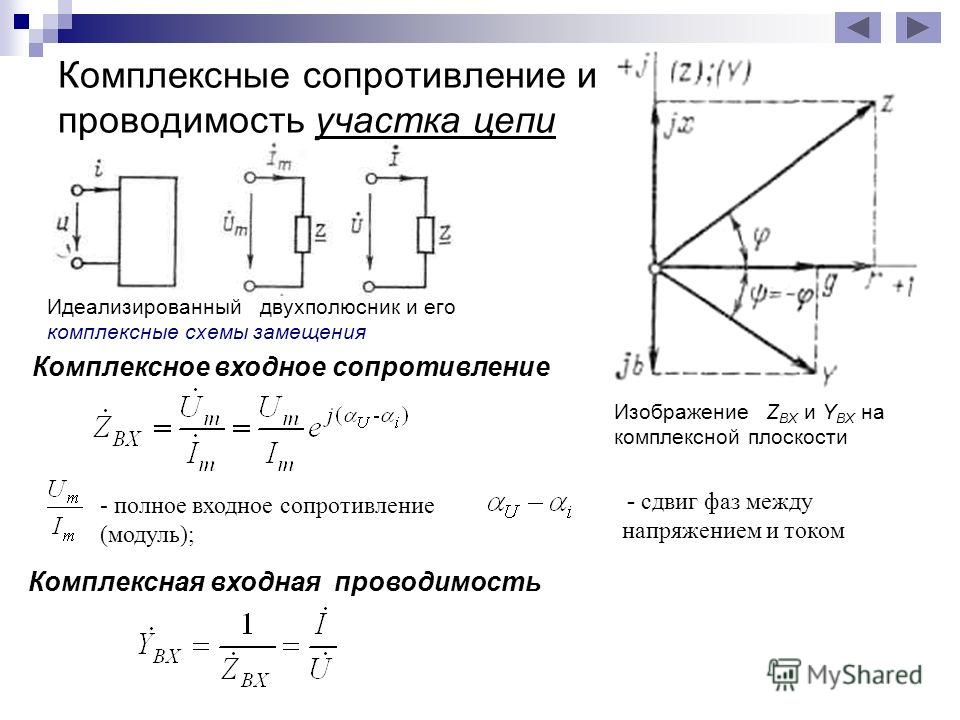 Ток в неразветвленной части схемы в резонансном режиме имеет минимальное значение. В идеализированном случае R = 0,

      и      .

        Ток в неразветвленной части цепи I = 0. Такая схема называется фильтр — пробкой.

6.9. Резонансный режим в цепи, состоящей

из параллельно включенных реальной индуктивной
катушки и конденсатора

           Комплексная проводимость индуктивной ветви

           где   — активная проводимость индуктивной катушки;
                   — полное сопротивление индуктивной катушки;
                   — индуктивная проводимость катушки;
                   — емкостная проводимость второй ветви.

           В режиме резонансов токов справедливо уравнение:

  или  

           Из этого уравнения получим формулу для резонанса частоты

     (6.22)

           На рисунке 6.16 изображена векторная диаграмма цепи в резонансном режиме.

     Вектор тока I₂ опережает вектор напряжения на 90^o. Вектор тока I₁ отстает от вектора напряжения на угол φ,

     где             .

     Разложим вектор тока I₁ на две взаимно перпендикулярные составляющих, одна из них, совпадающая с вектором напряжения, называется активной составляющей тока I_а1, другая — реактивной составляющей тока I_р1.

                  Рис. 6.16

     В режиме резонанса тока реактивная составляющая тока I_р1 и емкостный ток I₂ , направленные в противоположные стороны, полностью компенсируют друг друга, активная составляющая тока I_а1 совпадает по фазе с напряжением (рис. 6.17). Ток I в неразветвленной части схемы совпадает по фазе с напряжением.

                  Рис. 6.17

Однофазные цепи переменного тока (страница 2)

Решение:
Полное сопротивление схемы

Полная мощность на входе схемы

Потери мощности в обмотке катушки

Активная мощность схемы

Коэффициент мощности схемы

Из таблиц тригонометрических величин .
Активное сопротивление схемы

сопротивление дуги

Индуктивное сопротивление цепи представлено индуктивным сопротивлением катушки:

Эту же величину можно определить из треугольника сопротивлении (рис. 25, масштаб )

Искомая индуктивность катушки

Если бы вместо катушки был включен реостат, то сопротивление схемы имело бы ту же величину 6 Ом, но было бы чисто активным:

откуда

Потери мощности в катушке

Потери мощности в реостате

Отсюда ясно, что к. п. д. схемы выше при «погашении» избытка напряжения индуктивной катушкой. Действительно, к. п. д. при наличии катушки

к. п. д. при наличии реостата

Не следует забывать, что «погашение» избытка напряжения катушкой (или конденсатором) ухудшает коэффициент мощности (в данном примере при наличии катушки и при наличии реостата).

22. Последовательно с катушкой, параметры которой и L=15,92 мГн, включен реостат сопротивлением, . Цепь включена на напряжение U=130 В при частоте f=50 Гц.
Определить ток в цепи; напряжение на катушке и реостате; коэффициент мощности цепи и катушки.

Решение:
Индуктивное сопротивление катушки

Полное сопротивление катушки

Активное сопротивление цепи, состоящей из последовательно соединенных катушки и реостата,

Полное сопротивление цепи

На основании закона Ома ток в цепи

Напряжение на катушке

Напряжение на реостате

Арифметическая сумма много больше приложенного напряжения U=130 В. Коэффициент мощности цепи

Коэффициент мощности катушки

Следовательно, реостат увеличивает коэффициент мощности и сопротивление цепи, но уменьшает ток, увеличивает потребление энергии схемой.
Действительно, активная мощность катушки

активная мощность реостата

Так как цепь неразветвленная и ток один, то с него целесообразно начать построение векторной диаграммы (рис. 26).
Напряжение на реостате, представляющем собой чисто активное сопротивление, совпадает по фазе с током; на диаграмме вектор этого напряжения совпадает по направлению с вектором тока. Из конца вектора в сторону опережения вектора тока I, под углом в сторону, противоположную вращению стрелки часов, откладываем вектор напряжения на катушке . Векторы построены так с целью сложения по правилу многоугольника.

23. Неразветвленная цепь составлена из двух катушек: у первой катушки индуктивность и сопротивление , у второй катушки индуктивность и сопротивление .
Определить ток в цепи и напряжения на каждой катушке, а также построить в масштабе векторную диаграмму, если частота f=50 Гц и приложенное напряжение U=12,6 В.

Решение:
Индуктивное сопротивление первой катушки

т. е. оно численно равно активному сопротивлению , что обусловливает отставание тока по фазе от напряжения на 1/8 периода (на 45°).
Действительно, тангенс угла сдвига фаз

Индуктивное сопротивление второй катушки

Так как ее активное сопротивление то тангенс угла сдвига фаз

Построим в масштабе треугольник сопротивлений для рассматриваемой цепи. Для этого зададимся масштабом сопротивлений . Тогда на диаграмме сопротивление 1,57 Ом будет изображено отрезком 15,7 мм, сопротивление 2,7 Ом — отрезком 27 мм и т. д. На рис. 27 отрезок, изображающий активное сопротивление , отложен в горизонтальном направлении, а отрезок, изображающий индуктивное сопротивление , — в вертикальном направлении под прямым углом к .

Полное сопротивление первой катушки является гипотенузой прямоугольного треугольника. Из вершины с этого треугольника в горизонтальном направлении отложен отрезок, изображающий сопротивление , и под прямым углом к нему вверх — отрезок, изображающий сопротивление . Гипотенуза се прямоугольного треугольника означает полное сопротивление второй катушки.
Из рис. 27 видно, что отрезок ае, изображающий полное сопротивление z неразветвленной цепи из двух катушек, не равен сумме отрезков ас и се, т. е. . Чтобы определить полное сопротивление z рассматриваемой цепи, следует сложить отдельно активные (, отрезок аf) и индуктивные (, отрезок ef) сопротивления катушек.
Гипотенуза ае, означающая полное сопротивление z цепи, определяется по теореме Пифагора:

Ток в цепи определяется по закону Ома:

Напряжение на первой катушке

Напряжение на второй катушке

Строим векторную диаграмму (рис. 28), приняв масштабы:
а) для тока ; тогда вектор тока изобразится отрезком длиной 25 мм;
б) для напряжения ; при этом вектор напряжения будет иметь длину 55,2 мм, вектор напряжения — длину 71 мм, а вектор приложенного напряжения — длину 126 мм.
Начало вектора совмещено с концом вектора для возможности сложения векторов напряжений но правилу многоугольника (напряжение, приложенное к неразветвленной цепи катушек, равно геометрической сумме напряжений отдельных катушек).

 

Электрическое сопротивление ~ Электро мастер

Электрическое сопротивление

Любое тело, по которому протекает электрический ток, оказывает току  сопротивление – это явление называется электрическим сопротивлением.
Сопротивление обозначается латинскими буквами R, X, Z. Используются также прописные буквы r, x, z.
R – активное сопротивление (омическое)
X – реактивное сопротивление (индуктивное, емкостное)
Z – полное сопротивление (активное)
Размерность сопротивления Ом, размерность записывается так – Ом.
Сопротивление рассчитывается, в определённых пределах, постоянной величиной для данного проводника; её можно рассчитать по формуле:

R=U/I

где
R – сопротивление
U – разность электрических потенциалов на концах проводника (напряжение)
I – сила тока, протекающая между концами проводника под действием разности потенциалов (напряжения).
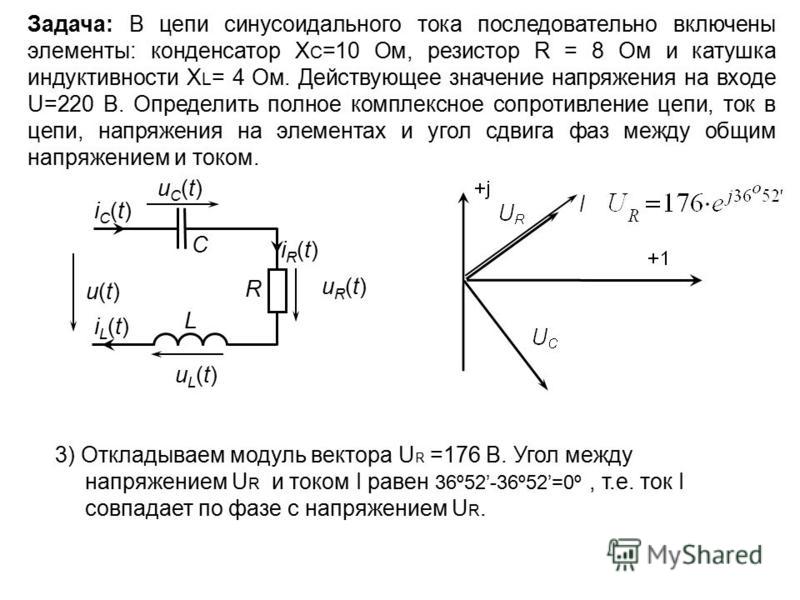
Сопротивление различных проводников зависит от материала и называется удельным сопротивление, единица измерения удельного сопротивления Ом*м, а величина удельного сопротивления обозначается символом ρ (ро).

Удельное сопротивление

Удельное сопротивление проводника может быть рассчитано по формуле:

R= (ρ *l)/S

где
ρ – удельное сопротивление проводника
l – длинна проводника
S – площадь сечения проводника

Удельное сопротивление некоторых веществ (при t 20° C)

Вещество	Удельное сопротивление,  ρ Ом*мм2/м
Алюминий	0,028
Вольфрам	0,055
Железо	0,098
Золото	0,023
Константан	0,44-0,52
Латунь	0,025-0,06
Манганин	0,42-0,48
Медь	0,0175
Молибден	0,057
Никелин	0,39-0,45
Никель	0,100
Олово	0,115
Ртуть	0,958
Свинец	0,221
Серебро	0,016
Тантал	0,155
Фехраль	1,1-1,3
Хром	0,027
Цинк	0,059

Чем больше сопротивление проводника, тем хуже он проводит электрический ток.
Удельное сопротивление обратно пропорционально электрической проводимости.
Электрическая проводимость – это способность материала пропускать через себя электрический ток.
Из выше изложенного следует – чем меньше сопротивление проводника, тем больше его электрическая проводимость, тем легче электрическому току пройти через этот проводник.

Виды электрического сопротивления:

Существует четыре вида электрического сопротивления:

1. Омическое сопротивление (активное сопротивление постоянному току)
2. Активное сопротивление (сопротивление переменному току)
3. Индуктивное сопротивление (реактивное сопротивление)
4. Емкостное сопротивление (реактивное сопротивление)

Рассмотрим каждое подробно:

Омическое сопротивление – сопротивление цепи постоянному току вызывающие безвозвратные потери энергии постоянного тока.
Величина омического сопротивления не зависит от величины  тока, это сопротивление материала (удельное сопротивление) и рассчитывается по формуле:

R=U/I

где
R – сопротивление
U – разность электрических потенциалов на концах проводника (напряжение)
I – сила тока, протекающая между концами проводника под действием разности потенциалов (напряжения).

Причиной потерь постоянного тока при омическом сопротивление является преодоление противодействия материала (его удельного сопротивления), энергия затраченная на преодоления противодействия материала превращается в тепловую.

Активное сопротивление – это сопротивление цепи переменному току вызывающие безвозвратные потери энергии переменного тока. Активное сопротивление обозначается латинской буквой Z и рассчитывается по формуле:

Z=R+jX

где
Z – импеданс
R — величина активного сопротивления
X — величина реактивного сопротивления
j — мнимая единица

Основной причиной вызывающей потери при активном сопротивление остается тоже, что и при омическом сопротивление – преодоление противодействия материала. Есть и другие причины, такие как
— поверхностный эффект
— вихревые токи
— потери за счет излучения электромагнитной энергии и др.

Абстрактно омическое и активное сопротивление можно представить как передвижение человека по узкому захламленному (препятствиями) коридору, который основную часть своей энергии будет безвозвратно тратить на преодоление этих препятствий, и чем больше удельное сопротивление проводника, тем захламленнее будет коридор.

Индуктивное сопротивление — обусловлено возникновением ЭДС самоиндукции в элементе электрической цепи. Изменение тока и, как следствие, изменение его магнитного поля вызывает препятствующее изменению этого тока ЭДС самоиндукции. Величина индуктивного сопротивления зависит от индуктивности  элемента и частоты  протекающего тока. Не вызывает безвозвратных потерь энергии.
Индуктивное сопротивление рассчитывается по формуле:

X_L=ωL=2πfL

где
X_L — индуктивное сопротивление проводника переменному току
ω — циклическая частота переменного тока
L — индуктивность проводника (катушки)
f- частота


На преодоление этого противодействия затрачивается часть энергии переменного тока генератора. Вся эта часть энергии полностью превращается в энергию магнитного поля катушки. Когда ток генератора будет убывать, магнитное поле катушки тоже будет убывать, пересекая витки катушки и индуктируя в цепи ток самоиндукции. Теперь ток самоиндукции будет идти в одном направлении с убывающим током генератора. Таким образом, вся энергия затраченная током генератора на преодоление противодействия тока самоиндукции катушки полностью вернулась в цепь в виде энергии электрического тока. Поэтому индуктивное сопротивление является реактивным, что значит не вызывающим безвозвратных потерь энергии.

Абстрактно индуктивное сопротивление можно представить как воду, текущую по трубе в которой установлена крыльчатка (водомер (счетчик воды) который установлен почти в каждой квартире), крыльчатка создает индуктивное сопротивление, чем больше ток (в нашем случае напор воды), тем больше сопротивление, при убывании напора воды крыльчатка пропустить всю оставшуюся воду, так как она крутиться в том же направлении, в которой течет вода. Из этого примера видно что такое индуктивное сопротивление и почему оно не вызывает безвозвратных потерь.

Индуктивную нагрузку (сопротивление) вызывают – индукционные печи и плиты, асинхронные двигатели (пылесосы, миксеры, фены) и т. д.
При индуктивной нагрузке в сеть генеруется реактивная мощность (ток по фазе отстает от напряжения), которая является паразитной и приводит к перегрузке электрический сетей и требует компенсации. Подробнее об этом будет написано в следующих статьях.

Емкостное сопротивление  — величина, характеризующая сопротивление, оказываемое переменному току электрической емкостью цепи (или ее участка).
Емкостное сопротивление рассчитывается по формуле:

Xc=1/ωC=1/2πfC

где
Xc  — емкостное сопротивление проводника переменному току
C — емкости элемента

Вся энергия затрачиваемая источником тока на преодоление емкостного сопротивления превращается в энергию электрического поля конденсатора. Когда конденсатор будет разряжаться вся энергия электрического поля вернется обратно в цепь в виде энергии электрического тока. Таким образом, емкостное сопротивление является реактивным.

 Абстрактно емкостное сопротивление можно представить как кастрюлю объемом 5 литров, в нашем случае объем кастрюли это не что иное, как ее емкость. При ее наполнении водой до краев, она будет переворачиваться, и вода из неё выливаться, после чего кастрюля будет снова наполняться (так же как и конденсатор при полном заряде будет разряжаться в сеть, после чего вновь заряжаться).

При емкостной нагрузке (конденсаторы) в сеть генерируется активная мощность (ток по фазе опережает напряжение). Активная мощность (конденсаторные батареи) используется для компенсации реактивной мощности.

II ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ОДНОФАЗНОГО СИНУСОИДАЛЬНОГО ТОКА Блок

II. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ОДНОФАЗНОГО СИНУСОИДАЛЬНОГО ТОКА

Блок заданий I уровня Тема: Способы представления и параметры синусоидальных величин.

Задание № 1. • Если частота синусоидального тока f=400 Гц, то его период Т равен _____мс. • • • Варианты ответа: 1) 2, 5 2) 3 3) 4 4) 15, 7

Задание № 2 • В выражении для тока i=Imsin(2πft+Ψ) в герцах измеряется… • Варианты ответа: • 1) начальная фаза ψ; • 2) фаза 2πft+Ψ; • 3) частота f ; • 4) угловая частота 2πf.

Задание № 3. • Начальная фаза заданного графически тока равна… • Варианты ответа: • 1) 1, 5 А • 2) 0 • 3) –π/2 рад • 4) π/2 рад

Задание № 4 • Частота синусоидального тока i=Imsin(ωt+Ψ) равна… • • • Варианты ответа: 1) 2πω 2) 2π/ω 3) ω /2π 4) 1/ω

• Задание № 5. • Действующее значение синусоидального тока i=2 sin(314 t+Ψ) А равно______ А. • • • Варианты ответа: 1) 2) 3) -1 4) 2

Задание № 6 • Мгновенное значение синусоидального напряжения u=141, 42 sin(ωt+π/6) В. Комплексное действующее значение этого напряжения равно_______В. • Варианты ответа: • 1) ; • 2) ; • 3) ; • 4) .

Ответы на вопросы • Задание • 1 • 2 • 3 • 4 • 5 • 6 • • Ответ 1 3 4 3 2 1

Тема: Электрические цепи переменного тока с резистивными, индуктивными и емкостными элементами.

Задание № 7. • В цепях синусоидального тока активными являются сопротивления ____ элементов. Варианты ответа: 1) резистивных 2) индуктивных 3) емкостных 4) индуктивно связанных

Задание № 8 На рисунке изображены идеальные элементы схем замещения цепей переменного тока. К пассивным не относится(-ятся) элементы… • Варианты ответа: • 1) R • 2) e, j • 3) L • 4) C

Задание № 9 • При f=400 Гц и С=5 мк. Ф комплексное сопротивление идеального конденсатора Zc равно____ Ом. • Варианты ответа: • 1) j 79, 58 • 2) 79, 58 • 3) –j 79, 58 • 4) -79, 58

Задание № 10. • При f=50 Гц и L=0, 1 Гн комплексное сопротивление идеального индуктивного элемента ZL равно_______ Ом. • Варианты ответа: • 1) j 31. 4 • 2) 31. 4 • 3) • 4) -31. 4

Задание № 11. Если действующее значение напряжения равно 220 В, то при i=10 sin(ωt+ψt) А сопротивление Xc равно_____ Ом. Варианты ответа: • 1) 22 • 2) 15, 6 • 3) 31 • 4) 14

Ответы на вопросы • Задание • 7 • 8 • 9 • 10 • 11 • • • Ответ 1 2 3 1 1

Тема: Сопротивления и фазовые соотношения между токами и напряжениями.

Задание № 12 В изображенной схеме угол сдвига фаз между током i и напряжением u ______ рад. Варианты ответа: 1) 0 2) π/2 3) π 4) –π/2

Задание № 13. 1 • При R=8 Ом, Xc=6 Ом комплексное сопротивление Z изображенного двухполюсника равно____ Ом. • • • Варианты ответа: 1) 8 -j 6 2) 6+j 8 3) 6 -j 8 4) 8+j 6

Задание № 13. 2 Изображенному • Варианты ответа: двухполюснику 1) 3) соответствует векторная диаграмма … 2) 4)

Задание № 14 При R=6 Ом, XL=8 Ом полное комплексное сопротивление изображенного двухполюсника равно_____ Ом. Варианты ответа: 1) 14 2) 10 3) 6 -j 8 4) 6+j 8

Задание № 15 • При XL=5 Ом, R=Xc=10 Ом входное комплексное сопротивление Z равно____ Ом. • • • Варианты ответа: 1) 5 2) 5 -j 5 3) 5 -j 10 4) 10

Задание № 16 • При U=100 В, I=10 А, φ=π/6 радиан полное и активное R сопротивления двухполюсника соответственно равно___ Ом, ____ Ом. • • • Варианты ответа: 1) 13, 7; 5 2) 10; 8, 66 3) 13, 7; 8, 66 4) 10; 5

Ответы на вопросы • Задание • 12 • 13. 1 • 13. 2 • 14 • 15 • 16 • • Ответ 4 1 1 4 1 2

Блок заданий II уровня МОДУЛЬ: ЦЕПИ ПЕРЕМЕННОГО ТОКА

Задание № 17. • В режиме резонанса равны между собой напряжения… • Варианты ответа: (не менее двух вариантов ответа): • 1) UL и UC • 2) U и UR • 3) UR и UC • 4) UR и UL

Задание № 18 • Катушка с сопротивлением R и индуктивностью L подключена к источнику синусоидального напряжения u, амплитуда которого Um неизменна, а частота может изменяться. К уменьшению тока приведет… • Варианты ответа: (не менее двух вариантов ответа): • 1) увеличение L • 2) уменьшение L • 3) увеличение R • 4) уменьшение R

Задание № 19 • На входе пассивного двухполюсника напряжение , ток . Верно определены мощности… • Варианты ответа: (не менее двух вариантов ответа): • • 1) полная S=500 ВА 2) реактивная Q=500 ВАр 3) активная Р=500 Вт 4) комплексная S=500 -j 500 ВА

Задание № 20 • Мгновенное значение тока i=4 sin(314 t-π) A. Верно, что его … • Варианты ответа(не менее двух вариантов ответа): : • 1) комплексная амплитуда • 2) период T=0, 02 c • 3) действующее значение • 4) частота f=60 Гц

Задание № 21 На рисунке приведена схема и векторная диаграмма цепи с параллельным соединением ветвей. Векторная диаграмма соответствует условиям … • Варианты ответа (не менее двух вариантов ответа): • 1) R

Ответы на вопросы • Задание • 17 • 18 • 19 • 20 • 21 • • • Ответы 1, 2 1, 3 2, 3 1, 2 2, 3, 4

Блок заданий III уровня. Кейс задания.

Задание № 22. На рисунке приведена схема лабораторной установки для исследования цепи с последовательным соединением катушки индуктивности с параметрами R и L и конденсатора C, ёмкость которого может изменяться. При постоянном входном напряжении для трех значений емкости С 1, С 2 и С 3 были приведены измерения тока I, угла сдвига фаз φ между входным напряжением и током и напряжения UC на конденсаторе (см. таблицу). Частота сети f=50 Гц. Uвх=50 В – const.

Задание № 22. 1 • Напряжение на входе приведенной цепи отстает от тока по фазе (при… • Варианты ответа: • 1) XC>R • 2) XLXC • 4) XL

Задание № 22. 2 а • В приведенной цепи при резонансе максимального значения достигают… • Варианты ответа (укажите не менее двух вариантов ответа): • • 1) ток I в цепи 2) напряжение Uк на зажимах катушки 3) полное сопротивление Z цепи 4) напряжение UC на зажимах конденсатора

Задание № 22. 2 б • В приведенной цепи при резонансе … • Варианты ответа (укажите не менее двух вариантов ответа): • 1) реактивное сопротивление X равно активному сопротивлению R • 2) полное сопротивление Z равно реактивному сопротивлению Х • 3) индуктивное сопротивление XL равно емкостному сопротивлению XC • 4) полное сопротивление Z равно активному сопротивлению R

Задание № 22. 2 в • В приведенной цепи при резонансе максимальны… • Варианты ответа (укажите не менее двух вариантов ответа): • • 1) реактивная мощность катушки QL 2) активная мощность цепи P 3) полное сопротивление цепи Z 4) реактивная мощность цепи Q

Задание № 22. 3 а • Значение емкости С при Введите ответ: резонансе равно_______ мк. Ф. (Результат вычислений округлить до целого числа).

Задание № 22. 3 б • Активное сопротивление R • Введите ответ: катушки равно __Ом. (Результат вычислений округлить до целого числа).

Задание № 22. 3 в • Максимальное из трёх • Введите ответ: значений емкости (С 1, С 2, С 3) равно_______ мк. Ф. (Результат вычислений округлить до целого числа).

Ответы на вопросы Задание • 22. 1 • 22. 2 а • 22. 2 б • 22. 2 в • 22. 3 а • 22. 3 б • 22. 3 в • • Ответ 2 1, 2 3, 4 1, 2 40 мк. Ф 40 Ом 80 мк. Ф

Импеданс (Z) = (Сопротивление + Реактивность)

Импеданс (Z) показывает сопротивление потоку постоянного или переменного тока. Импеданс — это векторное сложение сопротивления и реактивного сопротивления.

Сопротивление — это величина, противоположная протеканию электрического тока (постоянного или переменного тока).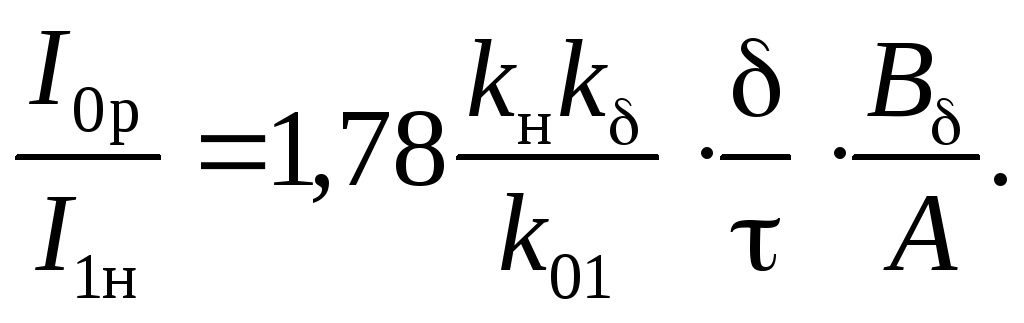 Реактивное сопротивление — это величина, противоположная протеканию переменного тока через конденсатор или катушку индуктивности.

Противодействие переменному току в конденсаторе называется емкостным реактивным сопротивлением, а сопротивление переменному току в катушке индуктивности называется индуктивным реактивным сопротивлением.

Импеданс (Z) = Сопротивление (R) + Реактивное сопротивление (X)

Когда эти элементы (резисторы, конденсаторы и катушки индуктивности) объединены в одну цепь и через них протекает переменный ток, сопротивление этого набора элементов поток переменного тока называется Импеданс .

Единицей измерения импеданса является Ом, и он равен векторному сложению значения сопротивления (сопротивления) и значения реактивной мощности, обусловленного реактивными компонентами (катушками индуктивности и конденсаторами): Z = R + jX

«j », Который стоит перед заглавной буквой X, говорит нам, что X — мнимое число. Это не обычное сложение, это поэтапное сложение (сумма фазоров).

Сдвиг фазы импеданса

Катушка индуктивности и конденсатор противодействуют протеканию переменного тока (плюс разность фаз), но в идеале они не вызывают какого-либо рассеивания мощности, как в резисторе (закон Джоуля).

Существует фазовый сдвиг между напряжением и током, протекающим через конденсатор и / или катушку индуктивности. Напряжение отстает от тока на конденсаторе.Ток отстает от напряжения на катушке индуктивности.

Этот фазовый сдвиг на катушке индуктивности и конденсаторе противоположен, и если они имеют одинаковую величину, они будут отменены, а полное сопротивление цепи будет равно сопротивлению резистора. (см. формулу выше).

Формула Z = R + jX представлена ​​на рисунке выше. Вы можете видеть, что:

• Реактивные сопротивления расположены по оси Y (мнимая ось), и они могут увеличиваться или уменьшаться, в зависимости от желаемого влияния выше, от конденсатора или индуктивности.
• Сопротивление всегда по оси X. (Это только с положительной стороны).

Формула сдвига фазы = φ = tan ^-1 ((wL — 1 / wC) / R) = φ = tan ^-1 ((XL — XC) / R)

Формула импеданса

Значение импеданса (диагональная линия) составляет: Z = (R ² + X ² ) ^1/2 .

Пример расчета импеданса в цепи последовательного RLC

Рассчитайте полное сопротивление цепи RLC последовательно с R = 10 Ом, C = 470 мкФ, L = 2 Генри и F = 1 кГц.

• Z = R + (XC + XL) = R + ((1 / jwC) + jwL), w = 2πf
• w = (2) (3,1416) (1000) = 6283,2
• XC = 1 / jwC = 1 / j (6283,2) (4700 x 10 ^-6 ) (Емкостное реактивное сопротивление)
• XL = wL = j (6283,2) (2) (Индуктивное реактивное сопротивление)
• Z = (R ² + (XC + XL) ² ) ^1/2 = 0,016 Ом

Сдвиг фазы импеданса

φ = tan ^-1 ((wL — 1 / wC) / R) = 51,41 °

Примечание. скобки в 1/2 степени равны квадратному корню.

Разница, объясненная между: импедансом (Z), сопротивлением (R), реактивным сопротивлением (X), индуктивным реактивным сопротивлением (XL), индуктивностью (L), емкостным реактивным сопротивлением (XC), c

Это часть первоначально опубликованного сообщения в блоге в нашем разделе бесплатных статей на www.electricalpereview.com

Вы можете прочитать всю статью здесь в исходном формате: Бесплатные статьи: Импеданс, Реактивность, Допуск, Подвеска — В чем разница?

Это будет отличный ресурс для всех, у кого есть какие-либо вопросы по любому из этих терминов.

Знайте, что чаще всего путают индуктивное реактивное сопротивление [[COLOR = rgb (51, 51, 51)] Ω] [/ COLOR] относительно индуктивности [L] и емкостное реактивное сопротивление [[COLOR = rgb (51, 51, 51)] Ω] [/ COLOR] в зависимости от емкости [F].

Не стесняйтесь распечатать это и добавить к своим рекомендациям для экзамена на электрооборудование PE.

Многочисленные термины «-tance» в электротехнике

Существует много различных типов компонентов полного сопротивления , и все они рифмуются, что затрудняет запоминание того, что есть что.

Многие даже имеют одинаковые блоки, что может привести к еще большей путанице.

Не позволяйте одному и тому же окончанию «-танс» ввести вас в заблуждение.

Если вы столкнетесь с вопросом на экзамене по электротехнике PE, который требует решения для одного из этих компонентов, и вы не знакомы с точными различиями, то вы можете в конечном итоге получить неправильный ответ , даже если ваши математические и расчеты надежны.

Скорее всего, вы уже сталкивались с подобной ошибкой или головной болью при работе с пробными практическими задачами на экзамене.

Чтобы этого не произошло в день экзамена , давайте взглянем на все различные компоненты и определим их, а также поймем, откуда они взялись.

Первый

Мы начнем с импеданса (Z) , комплексного числа, и более подробно рассмотрим его действительную и мнимую составляющие сопротивление (R), и реактивное сопротивление (X).

Второй

Мы немного углубимся в оба типа реактивных сопротивлений: индуктивное реактивное сопротивление , , (XL ), и емкостное сопротивление (XC).

Третий

Мы исследуем проводимость (Y) , другое комплексное число, и более подробно рассмотрим его действительную и мнимую составляющие проводимости (G) и проводимости (B) .

Импеданс (Z)

Импеданс лучше всего описать как полное противодействие протеканию тока через цепь при приложении напряжения. Импеданс — это комплексное число , с действительной и мнимой составляющими, оно представлено заглавной буквой Z и имеет единицу измерения Ом [Ом].

Записано в сложной прямоугольной форме , полное сопротивление выглядит следующим образом:

Импеданс — это сумма сопротивления (R) и реактивного сопротивления (X).

Сопротивление — это действительная составляющая импеданса , или Re {Z}, , а реактивное сопротивление — это мнимая составляющая импеданса , или Img {Z}.

Импеданс обычно представлен в схеме как блочный компонент:

Активный компонент с положительным индуктивным сопротивлением:

Или резистивный компонент с отрицательным емкостным сопротивлением:

Импеданс чаще всего рассчитывается по закону переписывания Ома для определения Z:

Дополнительная рекомендуемая литература: https: // en.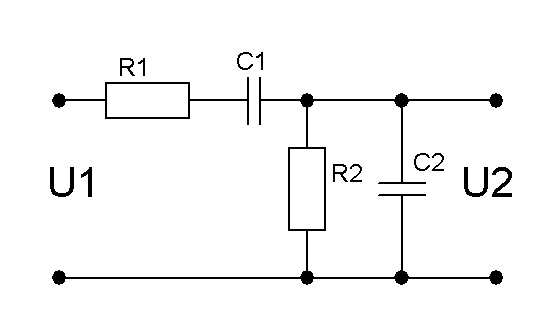 wikipedia.org/wiki/Electrical_impedance

Сопротивление (R)

Подобно импедансу, сопротивление также противодействует протеканию тока при приложении напряжения. В чисто резистивном импедансе отсутствует составляющая реактивного импеданса, такая как нагревательный элемент , радиатор или резистор.

Сопротивление обозначается заглавной буквой R , это действительная составляющая импеданса Re {Z} и, следовательно, не комплексное число, а единицей измерения является Ом [Ом].

Составляющая сопротивления и полного сопротивления представлена ​​в цепи как резистор:

Дополнительная рекомендуемая литература: https://en.wikipedia.org/wiki/Electrical_resistance_and_conductance

Реактивное сопротивление (X)

Существует два типа реактивного сопротивления. Реактивное сопротивление будет противодействовать изменению тока или напряжения в зависимости от того, к какому из двух типов оно относится.

Индуктивное реактивное сопротивление будет противодействовать изменению тока.

Емкостный реактивное сопротивление будет противодействовать изменению напряжения.

Реактивное сопротивление представлено заглавной буквой X , это мнимая составляющая импеданса Img {Z} , и, следовательно, не комплексное число, а единицей измерения является Ом [Ом].

Дополнительная рекомендуемая литература: https://en.wikipedia.org/wiki/Electrical_reactance

Индуктивное реактивное сопротивление (XL) и индуктивность (L)

Индуктивное реактивное сопротивление — это один из двух типов реактивного сопротивления и является мнимым. Составляющая полного сопротивления противодействует изменению тока .Он представлен заглавной буквой X с нижним индексом L , а также имеет единицу измерения Ом [Ом] .

Индуктивное реактивное сопротивление в омах получается из угловой частоты в радианах в секунду, умноженной на индуктивность на единицу длины, умноженную на общую длину компонента:

Где индуктивность измеряется в целом. Генри [H] :

И ω, угловая частота в радианах в секунду находится путем умножения частоты на 2π:

На принципиальной схеме индуктивное сопротивление обычно представляет собой , представленное катушкой , поскольку индукторы обычно изготавливаются путем наматывания проводника в форме соленоида.

Индуктивное реактивное сопротивление всегда будет составлять положительный мнимый импеданс , или + jX.

индуктивное реактивное сопротивление препятствует прохождению тока магнитным потоком , который создается вокруг него.

Примером индуктивного реактивного сопротивления . может быть идеальной идеальной катушкой, как обмотки в статоре двигателя или генератора .

Дополнительная рекомендуемая литература: https://en.wikipedia.org/wiki/Inductance

Дополнительная рекомендуемая литература: https: // en.wikipedia.org/wiki/Henry_(unit)

Емкостное реактивное сопротивление (XC) и емкость (C)

Емкостное реактивное сопротивление — это один из двух типов реактивного сопротивления и представляет собой мнимую составляющую импеданса, которая противодействует изменению напряжения. . Обозначается заглавной буквой X с нижним индексом C , а также имеет значение Ом [Ом].

Емкостное реактивное сопротивление в омах получается как величина, обратная угловой частоте в радианах в секунду, умноженной на емкость на единицу длины, умноженную на общую длину компонента:

Где емкость измеряется в фарадах [F] :

И ω, угловая частота в радианах в секунду находится путем умножения частоты на 2π:

На принципиальной схеме емкостное реактивное сопротивление обычно представлено символом конденсатора , поскольку конденсаторы обычно состоят из двух проводящих пластин, разделенных диэлектрической средой.

Емкостное реактивное сопротивление сопротивляется потоку напряжения за счет накопления заряда между двумя проводящими пластинами.

Емкостное реактивное сопротивление всегда будет отрицательным мнимая составляющая полного сопротивления или -jX.

Примером чисто емкостного реактивного сопротивления может быть идеальный конденсатор .

Дополнительная рекомендуемая литература: https://en.wikipedia.org/wiki/Capacitance

Дополнительная рекомендуемая литература: https: // en.Википедия. — это , допущенный через схему. Если сопротивление больше похоже на трение тока, чем полное сопротивление будет сопоставимо со льдом или скользкой поверхностью. Допуск представлен , заглавной буквой Y , и имеет единиц сименса (S), и — комплексное число.

Импеданс — это комплексное число , потому что оно имеет как действительное, так и мнимое значение.

Записано в сложной прямоугольной форме , пропускная способность выглядит так:

Это сумма проводимости (G) и проводимости (B).

Проводимость — это реальная составляющая проводимости Re {Y}, а проводимость — это мнимая составляющая проводимости Img {Y}.

Импеданс чаще всего рассчитывается как , обратная импедансу:

Закон Ома также можно переписать, чтобы использовать полную проводимость вместо импеданса, чтобы решить как для напряжения, так и для тока:

Импеданс

чаще всего представлен его антиномом проводимости, когда компонент импеданса помещается в цепь так, что он создает шунтирующий (параллельный) путь наименьшего сопротивления к земле, нейтрали или другой фазе.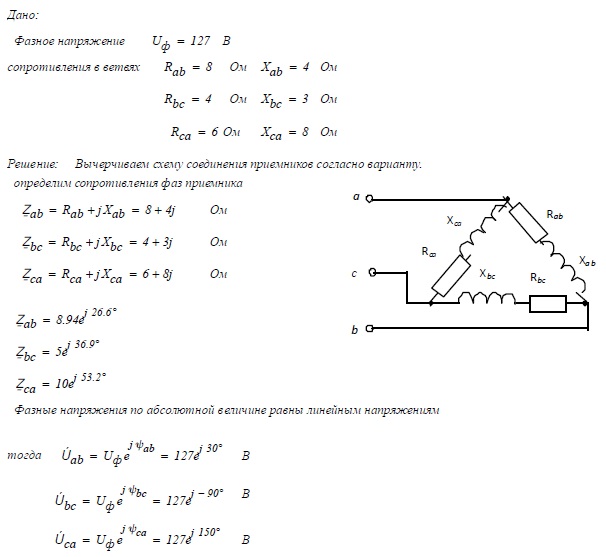

Поскольку больше тока будет проходить по пути наименьшего сопротивления (I = V / R), шунтирующее соединение с очень малым импедансом означает, что большая часть тока, входящего в общий узел, будет проходить через него , а не через какой-либо другой дорожка.

Дополнительная рекомендуемая литература: https://en.wikipedia.org/wiki/Admittance

Проводимость (G)

Проводимость противоположна сопротивлению , это реальный компонент проводимости Re {Y} и, следовательно, не комплексное число, оно представлено заглавной буквой G и имеет единиц сименса (S).

Электропроводность определяется как , обратная сопротивлению:

Если сопротивление является противодействием тока, то проводимость равна насколько легко может течь ток, аналогично нашей аналогии со льдом или скользкой поверхностью по сравнению с трением.

Самый простой способ запомнить определение проводимости — связать его с , насколько хорошо цепь будет проводить ток.

Дополнительная информация, рекомендуемая к прочтению: https: //en.wikipedia.org / wiki / Electrical_resistance_and_conductance

Susceptance (B)

Susceptance — это , противоположное реактивному сопротивлению, это мнимая составляющая полного сопротивления Img {Y} и, следовательно, не комплексное число, оно представлено заглавной буквой . буква B , и имеет единиц сименса (S).

Подвеска находится как , обратное реактивному сопротивлению:

Если реактивное сопротивление противодействует изменению тока или напряжения, то реактивное сопротивление — это качество того, насколько легко ток или напряжение могут изменяться в цепи.

Самый простой способ запомнить определение восприимчивости — связать его с , насколько схема восприимчива к изменению тока или напряжения.

Дополнительная рекомендуемая литература: https://en.wikipedia.org/wiki/Susceptance

Одноклеточные анализы выявляют повышенную внутриопухолевую гетерогенность после появления терапевтической резистентности при мелкоклеточном раке легкого

1.

Horn , L. et al. Атезолизумаб первой линии в сочетании с химиотерапией при обширной стадии мелкоклеточного рака легкого. N. Engl. J. Med. 379 , 2220–2229 (2018).

CAS PubMed Google Scholar

2.

H.R.733: Закон о восстановлении резервации оджибве в районе озера Пияк (Сенат и Палата представителей Соединенных Штатов Америки в Конгрессе, 2012 г.). https://www.congress.gov/bill/112th-congress/house-bill/733

3.

Hodgkinson, C. L. et al. Онкогенность и генетическое профилирование циркулирующих опухолевых клеток при мелкоклеточном раке легкого. Нат. Med. 20 , 897–903 (2014).

CAS PubMed Google Scholar

4.

Драпкин, Б. Дж. И др. Геномная и функциональная точность ксенотрансплантатов, полученных от пациентов с мелкоклеточным раком легкого. Рак Discov. 8 , 600–615 (2018).

CAS PubMed PubMed Central Google Scholar

5.

Халисхазар, М. Д.и другие. Мелкоклеточный рак легкого, управляемый MYC, метаболически отличается и уязвим для истощения аргинина. Clin. Cancer Res. 25 , 5107–5121 (2019).

PubMed PubMed Central Google Scholar

6.

Aggarwal, C. et al. Циркулирующие опухолевые клетки как прогностический биомаркер у пациентов с мелкоклеточным раком легкого, проходящих химиотерапию. Рак легких 112 , 118–125 (2017).

PubMed Google Scholar

7.

Farago, A. F. et al. Комбинация олапариба и темозоломида при рецидиве мелкоклеточного рака легкого. Рак Discov. 9 , 1372–1387 (2019).

PubMed Google Scholar

8.

Zhang, J. et al. Внутриопухолевая гетерогенность локализованных аденокарцином легких, выявленная с помощью мультирегионального секвенирования. Наука 346 , 256–259 (2014).

CAS PubMed PubMed Central Google Scholar

9.

Mollaoglu, G. et al. MYC вызывает прогрессирование мелкоклеточного рака легкого до варианта нейроэндокринного подтипа с уязвимостью к ингибированию киназы полярного сияния. Cancer Cell 31 , 270–285 (2017).

CAS PubMed PubMed Central Google Scholar

10.

Huang, Y.H. et al. POU2F3 является главным регулятором клеточно-пучкового варианта мелкоклеточного рака легкого. Genes Dev. 32 , 915–928 (2018).

CAS PubMed PubMed Central Google Scholar

11.

Cardnell, R.J. et al. Белковая экспрессия TTF1 и cMYC определяет различные молекулярные подгруппы мелкоклеточного рака легкого с уникальной уязвимостью к ингибированию киназы полярного сияния, нацеливанию на DLL3 и другим целевым методам лечения. Oncotarget 8 , 73419–73432 (2017).

PubMed PubMed Central Google Scholar

12.

Lim, J. S. et al. Внутриопухолевая гетерогенность, создаваемая передачей сигналов Notch, способствует мелкоклеточному раку легких. Nature 545 , 360–364 (2017).

CAS PubMed PubMed Central Google Scholar

13.

Шу, Ю. Т., Лим, Дж. С. и Сейдж, Дж. Гетерогенность опухоли при мелкоклеточном раке легкого определена и исследована на доклинических моделях на мышах. Пер. Lung Cancer Res. 7 , 21–31 (2018).

PubMed PubMed Central Google Scholar

14.

Tirosh, I. et al. Рассечение многоклеточной экосистемы метастатической меланомы с помощью одноклеточной RNA-Seq. Наука 352 , 189–196 (2016).

CAS PubMed PubMed Central Google Scholar

15.

Skoulidis, F. et al. Сопутствующие геномные изменения определяют основные подмножества KRAS-мутантной аденокарциномы легких с отличной биологией, иммунными профилями и терапевтической уязвимостью. Рак Discov. 5 , 860–877 (2015).

CAS PubMed PubMed Central Google Scholar

16.

Rudin, C.M. et al. Молекулярные подтипы мелкоклеточного рака легкого: синтез модельных данных человека и мыши. Нат. Rev. Cancer 19 , 289–297 (2019).

CAS PubMed Google Scholar

17.

Миш, Д.и другие. Значение фактора транскрипции щитовидной железы (TTF) -1 для диагностики и прогноза пациентов с местнораспространенным или метастатическим мелкоклеточным раком легкого. Диагн. Патол. 10 , 21 (2015).

PubMed PubMed Central Google Scholar

18.

Zhang, W. et al. Мелкоклеточные опухоли легкого и доклинические модели демонстрируют гетерогенность нейроэндокринных фенотипов. Пер. Lung Cancer Res. 7 , 32–49 (2018).

PubMed PubMed Central Google Scholar

19.

George, J. et al. Обширные геномные профили мелкоклеточного рака легкого. Nature 524 , 47–53 (2015).

CAS PubMed PubMed Central Google Scholar

20.

Jahchan, N. S. et al. Идентификация и нацеливание на клетки, которые долго размножаются в опухоли при мелкоклеточном раке легкого. Cell Rep. 16 , 644–656 (2016).

CAS PubMed PubMed Central Google Scholar

21.

Singhi, A. D. et al. Амплификация гена MYC часто происходит при летальных отдаленных метастазах рака молочной железы неамплифицированных первичных опухолей. Мод. Патол.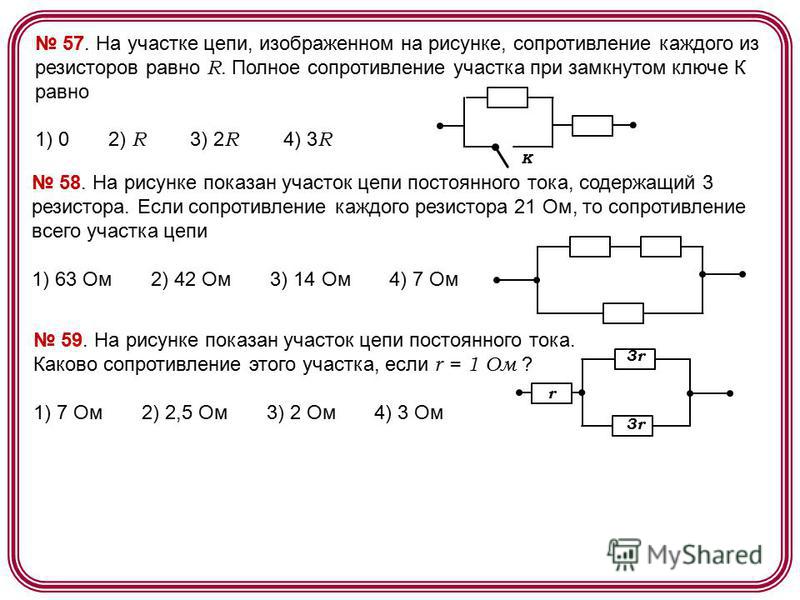 25 , 378–387 (2012).

CAS PubMed Google Scholar

22.

Lee, H.Y. et al. c-MYC вызывает метастазы рака молочной железы в мозг, но способствует синтетической летальности с помощью TRAIL. Мол. Cancer Res. 17 , 544–554 (2019).

CAS PubMed Google Scholar

23.

Stewart, C.A. et al. Динамические вариации эпителиально-мезенхимального перехода (EMT), ATM и SLFN11 регулируют ответ на ингибиторы PARP и цисплатин при мелкоклеточном раке легкого. Oncotarget 8 , 28575–28587 (2017).

PubMed Central Google Scholar

24.

Gardner, E. E. et al. Химиочувствительный рецидив мелкоклеточного рака легкого протекает по оси EZh3 – SLFN11. Cancer Cell 31 , 286–299 (2017).

CAS PubMed PubMed Central Google Scholar

25.

Wagner, A.H. et al. Рецидивирующие изменения пути WNT часто встречаются при рецидиве мелкоклеточного рака легкого. Нат. Commun. 9 , 3787 (2018).

PubMed PubMed Central Google Scholar

26.

Байерс, Л. А. и др. Протеомное профилирование выявляет дисрегулируемые пути мелкоклеточного рака легкого и новые терапевтические мишени, включая PARP1. Рак Discov. 2 , 798–811 (2012).

CAS PubMed PubMed Central Google Scholar

27.

Dammert, M.A. et al. MYC-паралог-зависимое апоптотическое праймирование управляет спектром уязвимостей при мелкоклеточном раке легкого. Нат. Commun. 10 , 3485 (2019).

PubMed PubMed Central Google Scholar

28.

Семенова Е.А. и др. Фактор транскрипции NFIB является движущей силой прогрессирования мелкоклеточного рака легкого у мышей и отмечает метастатическое заболевание у пациентов. Cell Rep. 16 , 631–643 (2016).

CAS PubMed PubMed Central Google Scholar

29.

Bottger, F. et al. Гетерогенность опухоли лежит в основе дифференциальной чувствительности к цисплатину на мышиных моделях мелкоклеточного рака легкого. Cell Rep. 27 , 3345–3358.e4 (2019).

CAS PubMed PubMed Central Google Scholar

30.

Wu, N. et al. Сверхэкспрессия NFIB взаимодействует с делецией Rb / p53 , способствуя развитию мелкоклеточного рака легких. Oncotarget 7 , 57514–57524 (2016).

PubMed PubMed Central Google Scholar

31.

Klameth, L. et al. Мелкоклеточный рак легкого: модель циркулирующих опухолевых клеток с химиорезистентностью. Sci. Отчет 7 , 5337 (2017).

PubMed PubMed Central Google Scholar

32.

Гамильтон, Г., Хохмайр, М., Rath, B., Klameth, L. & Zeillinger, R. Мелкоклеточный рак легкого: циркулирующие опухолевые клетки пациентов на расширенной стадии экспрессируют мезенхимно-эпителиальный переходный фенотип. Cell Adh. Мигр. 10 , 360–367 (2016).

CAS PubMed PubMed Central Google Scholar

33.

Ю., Н., Чжоу, Дж., Цуй, Ф. и Тан, X. Циркулирующие опухолевые клетки при раке легкого: методы обнаружения и клиническое применение. Легкое 193 , 157–171 (2015).

CAS PubMed Google Scholar

34.

Tanaka, F. et al. Циркулирующие опухолевые клетки как диагностический маркер первичного рака легкого. Clin. Cancer Res. 15 , 6980–6986 (2009).

CAS PubMed Google Scholar

35.

Rudin, C.M. et al. Ровальпитузумаб тезирин, конъюгат антитело-лекарство, нацеленный на DLL3, при рецидивирующем мелкоклеточном раке легкого: первое открытое исследование фазы 1 среди людей, первое в своем классе. Ланцет Онкол. 18 , 42–51 (2017).

CAS PubMed Google Scholar

36.

Giffin, M. et al. Нацеливание на DLL3 с помощью AMG 757, конструкции антитела BiTE®, и AMG 119, CAR-T, для лечения SCLC. J. Thorac. Онкол. 13 , abstr. П3.12-03 (2018).

Google Scholar

37.

Carbone, D. P. et al. Эффективность и безопасность тезирина ровалпитузумаба у пациентов с экспрессирующим DLL3 мелкоклеточным раком легкого ≥ 3-й линии: результаты исследования TRINITY фазы 2. J. Clin. Онкол. 36 (Дополнение), 8507 (2018).

Google Scholar

38.

Paz-Ares, L. et al. Общая выживаемость с дурвалумабом в сочетании с этопозидом платиной при экстенсивной стадии МРЛ первой линии: результаты исследования CASPIAN. J. Thorac. Онкол. 14 , S7 – S8 (2019).

Google Scholar

39.

Nugent, J. L. et al. Метастазы в ЦНС при мелкоклеточной бронхогенной карциноме: увеличение частоты и изменение картины с увеличением выживаемости. Рак 44 , 1885–1893 (1979).

CAS PubMed Google Scholar

40.

Батлер, А., Хоффман, П., Смиберт, П., Папалекси, Э. и Сатия, Р. Объединение транскриптомных данных отдельных клеток для различных условий, технологий и видов. Нат. Biotechnol. 36 , 411–420 (2018).

CAS PubMed PubMed Central Google Scholar

41.

Джеймисон, А. Р. и др. Изучение уменьшения размеров нелинейного пространства признаков и представления данных в CADx груди с помощью лапласовских собственных карт и t -SNE. Med. Phys. 37 , 339–351 (2010).

PubMed Google Scholar

42.

Subramanian, A. et al. Анализ обогащения набора генов: основанный на знаниях подход к интерпретации профилей экспрессии в масштабе всего генома. Proc. Natl Acad. Sci. США 102 , 15545–15550 (2005).

CAS Google Scholar

43.

Маккарти, Д. Дж., Чен, Ю. и Смит, Г. К. Анализ дифференциальной экспрессии многофакторных экспериментов с РНК-Seq в отношении биологической изменчивости. Nucleic Acids Res. 40 , 4288–4297 (2012).

CAS PubMed PubMed Central Google Scholar

44.

Робинсон, М. Д., Маккарти, Д. Дж. И Смит, Г.K. edgeR: пакет биопроводников для анализа дифференциальной экспрессии цифровых данных экспрессии генов. Биоинформатика 26 , 139–140 (2010).

CAS Google Scholar

45.

Тонг П., Чен Ю., Су, X. и Кумбс, К. Р. СИБЕР: систематическая идентификация бимодально экспрессируемых генов с использованием данных RNAseq. Биоинформатика 29 , 605–613 (2013).

CAS PubMed PubMed Central Google Scholar

46.

Wang, J., Wen, S., Symmans, W. F., Pusztai, L. & Coombes, K. R. Индекс бимодальности: критерий для обнаружения и ранжирования бимодальных сигнатур на основе данных профилирования экспрессии генов рака. Cancer Inform. 7 , 199–216 (2009).

PubMed PubMed Central Google Scholar

47.

Байерс, Л. А. и др. Сигнатура гена эпителиально-мезенхимального перехода предсказывает устойчивость к ингибиторам EGFR и PI3K и определяет Axl как терапевтическую мишень для преодоления устойчивости к ингибиторам EGFR. Clin. Cancer Res. 19 , 279–290 (2013).

CAS PubMed Google Scholar

48.

Группа разработки ядра R. R: язык и среда для статистических вычислений (Фонд R для статистических вычислений, 2015).

49.

Li, H. & Durbin, R. Быстрое и точное выравнивание в режиме длительного чтения с помощью преобразования Барроуза – Уиллера. Биоинформатика 26 , 589–595 (2010).

PubMed PubMed Central Google Scholar

50.

Koboldt, D. C. et al. VarScan: обнаружение вариантов при массовом параллельном секвенировании отдельных и объединенных образцов. Биоинформатика 25 , 2283–2285 (2009).

CAS PubMed PubMed Central Google Scholar

51.

Kim, D. et al. TopHat2: точное выравнивание транскриптомов при наличии вставок, делеций и слияний генов. Genome Biol. 14 , R36 (2013).

PubMed PubMed Central Google Scholar

52.

Андерс, С., Пил, П. Т. и Хубер, В. HTSeq — среда Python для работы с данными высокопроизводительного секвенирования. Биоинформатика 31 , 166–169 (2015).

CAS Google Scholar

53.

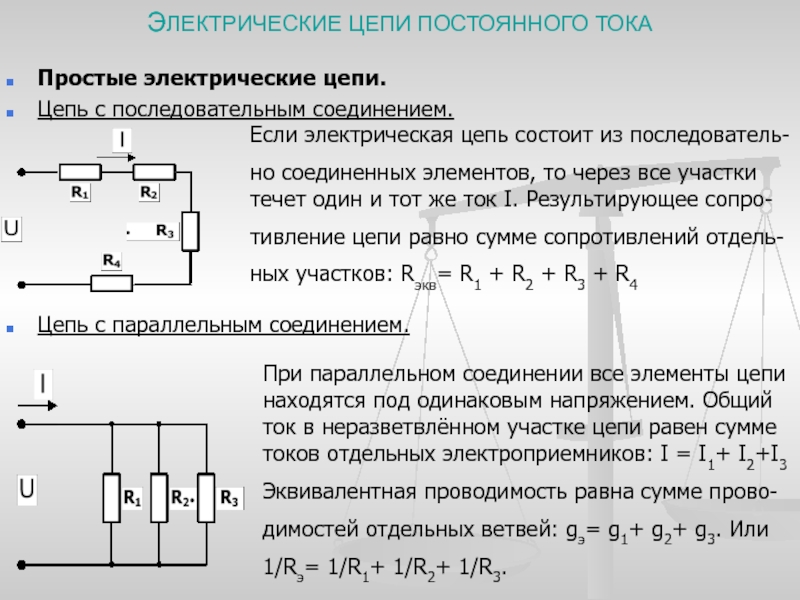
Dai, Z. et al. edgeR: универсальный инструмент для анализа генетических скринингов shRNA-Seq и CRISPR-Cas9. F1000Res 3 , 95 (2014).

PubMed PubMed Central Google Scholar

54.

Ван, К., Ли, М. и Хаконарсон, Х. ANNOVAR: функциональная аннотация генетических вариантов на основе данных высокопроизводительного секвенирования. Nucleic Acids Res. 38 , e164 (2010).

PubMed PubMed Central Google Scholar

55.

Стюарт, Т.и другие. Всесторонняя интеграция одноклеточных данных. Cell 177 , 1888–1902.e21 (2019).

CAS PubMed Google Scholar

Нейробиология устойчивой к лечению шизофрении: пути к устойчивости к антипсихотикам и план будущих исследований

1.

Howes, O. D. et al. Устойчивая к лечению шизофрения: реакция на лечение и сопротивление при психозе (TRRIP) согласованные руководящие принципы рабочей группы по диагностике и терминологии. Am. J. Psychiatry 174 , 216–229 (2017).

PubMed Google Scholar

2.

Lehman, A. F., et al. Практическое руководство по лечению больных шизофренией, второе издание. Am. J. Psychiatry 161 (2 доп.), 1–56 (2004).

3.

Demjaha, A. et al. Устойчивость к антипсихотическому лечению при первом эпизоде ​​психоза: распространенность, подтипы и предикторы. Psychol. Мед 47 , 1981–1989 (2017).

CAS PubMed Google Scholar

4.

Lally, J. et al. Две различные модели устойчивости к лечению: клинические предикторы устойчивости к лечению при первом эпизоде ​​психозов шизофренического спектра. Psychol. Мед 46 , 3231–3240 (2016).

CAS PubMed Google Scholar

5.

Meltzer, H.Y. et al. Возраст начала и пол больных шизофренией в зависимости от нейролептической резистентности. Am. J. Psychiatry 154 , 475–482 (1997).

CAS PubMed Google Scholar

6.

Фарук, С., Агид, О., Фуссиас, Г. и Ремингтон, Г. Использование терапевтического ответа на подтип шизофрении: предложение новой парадигмы в классификации. Schizophr. Бык. 39 , 1169–1172 (2013).

PubMed PubMed Central Google Scholar

7.

Робинсон, Д. Г. и др. Предикторы реакции на лечение от первого эпизода шизофрении или шизоаффективного расстройства. Am. J. Psychiatry 156 , 544–549 (1999).

CAS PubMed Google Scholar

8.

Альтамура, А. К., Бассетти, Р., Каттанео, Э. и Висмара, С. Некоторые биологические корреляты лекарственной устойчивости при шизофрении: многомерный подход. World J. Biol. Психиатрия 6 , 23–30 (2005).

PubMed Google Scholar

9.

Эмсли Р., Нуама И., Хаф Д. и Гопал С. Ответ на лечение после рецидива в плацебо-контролируемом исследовании поддерживающей терапии при шизофрении. Schizophr. Res 138 , 29–34 (2012).

PubMed Google Scholar

10.

Такеучи, Х.и другие. Способствует ли рецидив устойчивости к лечению? Антипсихотический ответ при первом и втором эпизодах шизофрении. Нейропсихофармакология 44 , 1036–1042 (2019).

CAS PubMed Google Scholar

11.

Долд М. и Лейхт С. Фармакотерапия устойчивой к лечению шизофрении: клиническая перспектива. Evid. На основе Ment. Здоровье 17 , 33–37 (2014).

PubMed Google Scholar

12.

Kane, J. et al. Клиническое руководство по выявлению и ведению устойчивой к лечению шизофрении. J. Clin. Психиатрия 80 , e1 – e9 (2019).

Google Scholar

13.

Карбон М. и Коррелл К. У. Клинические предикторы терапевтического ответа на антипсихотические препараты при шизофрении. Dialogues Clin. Neurosci. 16 , 505–524 (2014).

PubMed PubMed Central Google Scholar

14.

Yada, Y., Yoshimura, B. & Kishi, Y. Корреляция между задержкой начала приема клозапина и улучшением симптомов [письмо]. Schizophr. Res 168 , 585–586 (2015).

PubMed Google Scholar

15.

Клозапин (клозапин). Полная информация по назначению (HLS Therapeutics USA, Inc., Rosemont, PA, USA, 2017).

16.

Okhuijsen-Pfeifer, C. et al. Клозапин как средство первого или второго ряда при шизофрении: систематический обзор и метаанализ. Acta Psychiatr. Сканд. 138 , 281–288 (2018).

CAS PubMed PubMed Central Google Scholar

17.

Agid, O. et al. Алгоритмный подход к первому эпизоду шизофрении: частота ответа в 3 проспективных исследованиях нейролептиков с ретроспективным анализом данных. J. Clin. Психиатрия 72 , 1439–1444 (2011).

PubMed Google Scholar

18.

Kahn, R. S., et al. Амисульприд и оланзапин с последующим открытым лечением клозапином при первом эпизоде ​​шизофрении и шизофрениформном расстройстве (оптимизация): трехэтапное исследование переключения. Lancet Psychiatry 5 , 797–807 (2018).

19.

Siskind, D., Siskind, V. & Kisely, S. Частота ответа на клозапин среди людей с устойчивой к лечению шизофренией: данные систематического обзора и метаанализа. банка. J. Психиатрия 62 , 772–777 (2017).

PubMed PubMed Central Google Scholar

20.

Jeon, S. W., Kim, Y. K. Нерешенные вопросы использования атипичных нейролептиков при шизофрении: антипсихотическая полипрагмазия и метаболический синдром. Внутр. J. Mol. Sci. 18 , pii: E2174 (2017).

21.

Correll, C.U. et al. Эффективность 42 фармакологических стратегий совместного лечения, добавленных к монотерапии антипсихотиками при шизофрении: систематический обзор и оценка качества метааналитических данных. JAMA Psychiatry 74 , 675–684 (2017).

PubMed PubMed Central Google Scholar

22.

Wang, G. et al. Повышение эффективности клозапина при помощи ЭСТ при шизофрении, устойчивой к клозапину: метаанализ рандомизированных контролируемых исследований. J. Psychiatr. Res 105 , 23–32 (2018).

PubMed Google Scholar

23.

Петридес, Г.и другие. Повышение эффективности электросудорожной терапии при шизофрении, устойчивой к клозапину: проспективное рандомизированное исследование. Am. J. Psychiatry 172 , 52–58 (2015).

PubMed Google Scholar

24.

Demjaha, A. et al. Устойчивость к лечению антипсихотиками при шизофрении, связанная с повышенным уровнем глутамата, но нормальной функцией дофамина. Biol. Психиатрия 75 , e11 – e13 (2014).

CAS PubMed Google Scholar

25.

Howes, O. D. & Kapur, S. Нейробиологическая гипотеза для классификации шизофрении: тип A (гипердопаминергическая) и тип B (нормодопаминергическая). Br. J. Psychiatry 205 , 1–3 (2014).

PubMed Google Scholar

26.

Хоуз, О., Маккатчеон, Р. и Стоун, Дж. Глутамат и дофамин при шизофрении: обновление для 21 века. J. Psychopharmacol. 29 , 97–115 (2015).

PubMed PubMed Central Google Scholar

27.

Шуинар, Дж., Джонс, Б. Д. и Эннэйбл, Л. Психоз сверхчувствительности, вызванный нейролептиками. Am. J. Psychiatry 135 , 1409–1410 (1978).

CAS PubMed Google Scholar

28.

Chouinard, G. & Chouinard, V.A. Атипичные нейролептики: исследование CATIE, двигательное расстройство, вызванное лекарственными средствами, и возникающие в результате ятрогенные психиатрические симптомы, психоз с отскоком сверхчувствительности и синдромы отмены. Psychother. Психосом. 77 , 69–77 (2008).

PubMed Google Scholar

29.

Seeman, P., Lee, T., Chau-Wong, M. & Wong, K. Дозы антипсихотических препаратов и нейролептические / дофаминовые рецепторы. Nature 261 , 717–719 (1976).

CAS PubMed Google Scholar

30.

Капур, С. и Симан, П. Антипсихотические средства различаются по тому, насколько быстро они отрываются от дофаминовых рецепторов D2.Значение атипичного антипсихотического действия. J. Psychiatry Neurosci. 25 , 161–166 (2000).

CAS PubMed PubMed Central Google Scholar

31.

Meltzer, H.Y., Matsubara, S. & Lee, J.C. Классификация типичных и атипичных антипсихотических препаратов на основе значений pKi дофамина D-1, D-2 и серотонина 2. J. Pharm. Exp. Ther. 251 , 238–246 (1989).

CAS Google Scholar

32.

Suzuki, T. et al. Психоз сверхчувствительности к допамину как ключевой фактор резистентной к лечению шизофрении. Psychiatry Res. 227 , 278–282 (2015).

CAS PubMed Google Scholar

33.

Chouinard, G. et al. Психоз сверхчувствительности к допамину, вызванный антипсихотиками: фармакология, критерии и терапия. Psychother. Психосом. 86 , 189–219 (2017).

PubMed Google Scholar

34.

Chouinard, G. & Jones, B.D. Психоз сверхчувствительности, вызванный нейролептиками: клинические и фармакологические характеристики. Am. J. Psychiatry 137 , 16–21 (1980).

CAS PubMed Google Scholar

35.

Гилл, К. М., Кук, Дж. М., По, М. М. и Грейс, А. А. Предшествующее лечение антипсихотическими препаратами предотвращает ответ на новый антипсихотический агент в модели шизофрении с метилазоксиметанолацетатом. Schizophr. Бык. 40 , 341–350 (2014).

PubMed PubMed Central Google Scholar

36.

Ода, Ю., Канахара, Н. и Йо, М. Изменения рецепторов дофамина D2 и связанных с ними белков, взаимодействующих с рецепторами, при шизофрении: центральное место психоза сверхчувствительности дофамина при устойчивой к лечению шизофрении. Int J. Mol. Sci. 16 , 30144–30163 (2015).

CAS PubMed PubMed Central Google Scholar

37.

Iyo, M. et al. Оптимальная степень занятости рецептора дофамина D2 нейролептиками для лечения психоза сверхчувствительности дофамина и психоза с поздним началом. J. Clin. Psychopharmacol. 33 , 398–404 (2013).

CAS PubMed Google Scholar

38.

Schultz, S. K. et al. Жизненный цикл шизофрении: возраст и размеры симптомов. Schizophr. Res 23 , 15–23 (1997).

CAS PubMed Google Scholar

39.

Grunder, G. et al. Субхронический галоперидол подавляет способность синтеза дофамина в головном мозге больных шизофренией in vivo. Нейропсихофармакология 28 , 787–794 (2003).

PubMed Google Scholar

40.

Jauhar, S. et al. Влияние антипсихотического лечения на способность пресинаптического синтеза дофамина при первом эпизоде ​​психоза: исследование позитронно-эмиссионной томографии. Biol. Психиатрия 85 , 79–87 (2019).

CAS PubMed Google Scholar

41.

Kimura, H. et al. Проспективное сравнительное исследование инъекционного рисперидона длительного действия для лечения резистентной шизофрении с психозом сверхчувствительности к допамину. Schizophr. Res 155 , 52–58 (2014).

PubMed Google Scholar

42.

Ли, М. Сенсибилизация и толерантность, вызванная антипсихотиками: поведенческие характеристики, влияние на развитие и нейробиологические механизмы. J. Psychopharmacol. 30 , 749–770 (2016).

CAS PubMed PubMed Central Google Scholar

43.

Gitlin, M. et al. Клинический исход после отмены нейролептиков у пациентов с недавно начавшейся ремиссией шизофрении. Am. J. Psychiatry 158 , 1835–1842 (2001).

CAS PubMed Google Scholar

44.

Kishimoto, T. et al. Инъекционные и пероральные нейролептики пролонгированного действия для профилактики рецидивов шизофрении: метаанализ рандомизированных исследований. Schizophr. Бык. 40 , 192–213 (2014).

PubMed Google Scholar

45.

Эмсли, Р., Нуама, И., Гопал, С., Хью, Д., Флейшхакер, В.W. Рецидив после отмены антипсихотиков при шизофрении как феномен отмены по сравнению с рецидивом болезни: апостериорный анализ рандомизированного плацебо-контролируемого исследования. J. Clin. Психиатрия 79 , pii: 17m11874 (2018) [Epub].

46.

Alphs, L. et al. Факторы, связанные с рецидивом шизофрении, несмотря на соблюдение режима инъекционной антипсихотической терапии длительного действия. Внутр. Clin. Psychopharmacol. 31 , 202–209 (2016).

PubMed Google Scholar

47.

Leucht, S. et al. Антипсихотические препараты в сравнении с плацебо для профилактики рецидивов шизофрении: систематический обзор и метаанализ. Ланцет 379 , 2063–2071 (2012).

CAS PubMed Google Scholar

48.

Bowtell, M., McGorry, P. & O’Donoghue, B. Требуется ли более высокая доза антипсихотических препаратов для лечения рецидива после прекращения приема при первом эпизоде ​​психоза? Schizophr.Res. 204 , 407–408 (2019).

PubMed Google Scholar

49.

Гилл, К. М. и Грейс, А. А. Соответствующее снижение нейрональных маркеров сигнализирует о прогрессирующей потере нейронов парвальбумина в модели шизофрении MAM. Int J. Neuropsychopharmacol. 17 , 1609–1619 (2014).

CAS PubMed PubMed Central Google Scholar

50.

Гилл, К. М., Лодж, Д. Дж., Кук, Дж. М., Арас, С. и Грейс, А. А. Новый альфа5ГАМК (A) R-положительный аллостерический модулятор обращает вспять гиперактивацию дофаминовой системы в модели шизофрении МАМ. Нейропсихофармакология 36 , 1903–1911 (2011).

CAS PubMed PubMed Central Google Scholar

51.

Ларуэль, М. и Аби-Даргам, А. Дофамин как ветер психотического огня: новые данные исследований изображений мозга. J. Psychopharmacol. 13 , 358–371 (1999).

CAS PubMed Google Scholar

52.

Howes, O. D. et al. Способность к синтезу дофамина до начала психоза: проспективное исследование ПЭТ с [18F] -ДОФА. Am. J. Psychiatry 168 , 1311–1317 (2011).

PubMed PubMed Central Google Scholar

53.

Джаухар, С., и другие. Детерминанты терапевтического ответа при первом эпизоде ​​психоза: исследование (18) F-DOPA PET. Мол. Психиатрия 24 , 1502–1512 (2018).

54.

Howes, O. D. et al. Природа дисфункции дофамина при шизофрении и что это значит для лечения. Arch. Общая психиатрия 69 , 776–786 (2012).

CAS PubMed PubMed Central Google Scholar

55.

Демджаха, А., Мюррей, Р. М., Макгуайр, П. К., Капур, С. и Хоус, О. Д. Способность синтеза дофамина у пациентов с устойчивой к лечению шизофренией. Am. J. Psychiatry 169 , 1203–1210 (2012).

PubMed Google Scholar

56.

Kim, E. et al. Пресинаптическая дофаминовая способность у пациентов с устойчивой к лечению шизофренией, принимающих клозапин: исследование [(18) F] DOPA PET. Нейропсихофармакология 42 , 941–950 (2017).

CAS PubMed Google Scholar

57.

Билич, П., Юкич, В., Вилибич, М., Савич, А. и Бозина, Н. Лечебно-резистентная шизофрения и полиморфизмы DAT и SERT. Ген 543 , 125–132 (2014).

CAS PubMed Google Scholar

58.

Sagud, M. et al. Гаплотипическая и генотипическая ассоциация полиморфизмов катехол-о-метилтрансфераз rs4680 и rs4818 и устойчивость к лечению при шизофрении. Front Pharm. 9 , 705 (2018).

Google Scholar

59.

Schafer, M. et al. Связь краткосрочного ответа на лечение галоперидолом с полиморфизмом гена рецептора допамина D (2). Am. J. Psychiatry 158 , 802–804 (2001).

CAS PubMed Google Scholar

60.

Терзич, Т., Кастелич, М., Долзан, В.И Плесникар, Б. К. Генетические полиморфизмы в дофаминергической системе и резистентная к лечению шизофрения. Psychiatr. Дунай 28 , 127–131 (2016).

CAS PubMed Google Scholar

61.

Kushima, I. et al. Анализ вариаций числа копий шизофрении в Японии с высоким разрешением. Мол. Психиатрия 22 , 430–440 (2017).

CAS PubMed Google Scholar

62.

Ruderfer, D. M. et al. Полигенное совпадение между риском шизофрении и антипсихотическим ответом: подход геномной медицины. Lancet Psychiatry 3 , 350–357 (2016).

PubMed PubMed Central Google Scholar

63.

Moretti, P. N. et al. Доступ к экспрессии генов при устойчивой к лечению шизофрении. Мол. Neurobiol. 55 , 7000–7008 (2018).

CAS PubMed Google Scholar

64.

Шварц, Т. Л., Сачдева, С. и Шталь, С. М. Глутаматная нейросхема: теоретические основы в шизофрении. Front Pharm. 3 , 195 (2012).

Google Scholar

65.

Лодж, Д. Дж., Беренс, М. М. и Грейс, А. А. Потеря парвальбуминсодержащих интернейронов связана со сниженной осцилляторной активностью на животной модели шизофрении. J. Neurosci. 29 , 2344–2354 (2009).

CAS PubMed PubMed Central Google Scholar

66.

Лодж, Д. Дж. И Грейс, А. А. Аберрантная активность гиппокампа лежит в основе дисрегуляции дофамина в модели шизофрении на животных. J. Neurosci. 27 , 11424–11430 (2007).

CAS PubMed PubMed Central Google Scholar

67.

Розенбаум, Г., Коэн, Б.Д., Луби, Э. Д., Готтлиб, Дж. С. и Елен, Д. Сравнение сернила с другими лекарствами: моделирование шизофренической активности с помощью сернила, ЛСД-25 и амобарбитала (амитала) натрия; I. Внимание, двигательная функция и проприоцепция. AMA Arch. Gen. Psychiatry 1 , 651–656 (1959).

CAS PubMed Google Scholar

68.

Домино, Э. Ф. и Луби, Э. Д. Фенциклидин / шизофрения: один взгляд на прошлое, другой — на будущее. Schizophr. Бык. 38 , 914–919 (2012).

PubMed PubMed Central Google Scholar

69.

Гольдштейн, М. Э., Андерсон, В. М., Пиллаи, А., Кидд, Р. Р., Рассел, Б. Р. Глутаматергические нейрометаболиты при шизофрении, чувствительной и резистентной к клозапину. Внутр. J. Neuropsychopharmacol . 18 , pii: pyu117 (2015).

70.

Mouchlianitis, E. et al. Пациенты с устойчивой к лечению шизофренией демонстрируют повышенный уровень глутамата передней поясной коры головного мозга по сравнению с пациентами, реагирующими на лечение. Schizophr. Бык. 42 , 744–752 (2016).

PubMed Google Scholar

71.

Tanahashi, S., Yamamura, S., Nakagawa, M., Motomura, E. & Okada, M. Клозапин, но не галоперидол, усиливает высвобождение глиального D-серина и L-глутамата в лобной коре головного мозга крыс. и первичные культивированные астроциты. Br. J. Pharm. 165 , 1543–1555 (2012).

CAS Google Scholar

72.

Yuen, E. Y., Zhong, P. & Yan, Z. Гомеостатическая регуляция глутаматергической передачи с помощью дофаминовых рецепторов D4. Proc. Natl Acad. Sci. США 107 , 22308–22313 (2010).

CAS PubMed Google Scholar

73.

Веерман, С. Р., Шульте, П. Ф., Бегеманн, М. Дж., Энгельсбель, Ф. и де Хаан, Л. Клозапин с добавлением модуляторов глутамата при рефрактерной шизофрении: обзор и метаанализ. Фармакопсихиатрия 47 , 185–194 (2014).

CAS PubMed Google Scholar

74.

Yamamori, H. et al. Изменения уровней D-серина, L-серина и глицина в плазме при резистентной к лечению шизофрении до и после лечения клозапином. Neurosci. Lett. 582 , 93–98 (2014).

CAS PubMed Google Scholar

75.

Поткин С.Г., Джин Ю., Банни Б.Г., Коста Дж. И Гуласекарам Б. Эффект клозапина и дополнительных высоких доз глицина при резистентной к лечению шизофрении. Am. J. Psychiatry 156 , 145–147 (1999).

CAS PubMed Google Scholar

76.

Buchanan, R. W. et al. Когнитивные и негативные симптомы в исследовании шизофрении (CONSIST): эффективность глутаматергических агентов при негативных симптомах и когнитивных нарушениях. Am. J. Psychiatry 164 , 1593–1602 (2007).

PubMed Google Scholar

77.

Bugarski-Kirola, D. et al. Битопертин при негативных симптомах шизофрении — результаты исследований фазы III FlashLyte и DayLyte. Biol. Психиатрия 82 , 8–16 (2017).

CAS PubMed Google Scholar

78.

Бугарски-Кирола, Д.и другие. Эффективность и безопасность дополнительного битопертина по сравнению с плацебо у пациентов с субоптимально контролируемыми симптомами шизофрении, получавших антипсихотические препараты: результаты трех рандомизированных, двойных слепых, параллельных групп, плацебо-контролируемых многоцентровых исследований в программе клинических исследований SearchLyte 3 фазы. Lancet Psychiatry 3 , 1115–1128 (2016).

PubMed Google Scholar

79.

Zheng, W.и другие. Эффективность и безопасность дополнительного топирамата при шизофрении: метаанализ рандомизированных контролируемых исследований. Acta Psychiatr. Сканд. 134 , 385–398 (2016).

CAS PubMed Google Scholar

80.

Хоус, О. Д. и Маккатчеон, Р. Воспаление и гипотеза нервного диатеза-стресса шизофрении: реконцептуализация. Пер. Психиатрия 7 , e1024 (2017).

CAS PubMed PubMed Central Google Scholar

81.

Mondelli, V. et al. Кортизол и воспалительные биомаркеры предсказывают плохую реакцию на лечение при первом эпизоде ​​психоза. Schizophr. Бык. 41 , 1162–1170 (2015).

PubMed PubMed Central Google Scholar

82.

Noto, C. et al. Высокая прогностическая ценность иммуно-воспалительных биомаркеров для диагностики шизофрении и ассоциации с резистентностью к лечению. World J. Biol. Психиатрия 16 , 422–429 (2015).

PubMed Google Scholar

83.

Medina-Hernandez, V. et al. Повышенное перекисное окисление липидов и нейронспецифическая энолаза у резистентных к лечению шизофреников. J. Psychiatr. Res 41 , 652–658 (2007).

CAS PubMed Google Scholar

84.

Пиньейру, Д.S. et al. Генотип GSTM1 / GSTT1 с двойным нулем увеличивает риск резистентной к лечению шизофрении: исследование генетической ассоциации у бразильских пациентов. PLoS ONE 12 , e0183812 (2017).

PubMed PubMed Central Google Scholar

85.

Алекс, К. Д. и Пехек, Е. А. Фармакологические механизмы серотонинергической регуляции нейротрансмиссии дофамина. Pharm. Ther. 113 , 296–320 (2007).

CAS Google Scholar

86.

Степницки П., Кондей М., Качор А. А. Современные концепции и методы лечения шизофрении. Молекулы 23 , pii: E2087 (2018).

87.

Selvaraj, S., Arnone, D., Cappai, A. & Howes, O. Изменения в системе серотонина при шизофрении: систематический обзор и метаанализ исследований патологоанатомических исследований и молекулярной визуализации. Neurosci. Biobehav.Ред. 45 , 233–245 (2014).

CAS PubMed Google Scholar

88.

Bosia, M. et al. COMT Val158Met и 5-HT1A-R-1019 C / G-полиморфизмы: влияние на отрицательную симптоматическую реакцию на клозапин. Фармакогеномика 16 , 35–44 (2015).

CAS PubMed Google Scholar

89.

Galling, B. et al. Эффективность и безопасность усиления антидепрессивной терапии при продолжении антипсихотической терапии у пациентов с шизофренией. Acta Psychiatr. Сканд. 137 , 187–205 (2018).

CAS PubMed Google Scholar

90.

Брюггер, С. П. и Хоус, О. Д. Гетерогенность и однородность региональной структуры мозга при шизофрении: метаанализ. JAMA Psychiatry 74 , 1104–1111 (2017).

PubMed PubMed Central Google Scholar

91.

Миллер Б. Дж., Бакли П., Сиболт В., Меллор А. и Киркпатрик Б. Мета-анализ цитокиновых изменений при шизофрении: клинический статус и антипсихотические эффекты. Biol. Психиатрия 70 , 663–671 (2011).

CAS PubMed PubMed Central Google Scholar

92.

Maes, M. et al. Влияние атипичных нейролептиков на систему воспалительного ответа у больных шизофренией, резистентных к лечению типичными нейролептиками. Eur. Neuropsychopharmacol. 10 , 119–124 (2000).

CAS PubMed Google Scholar

93.

Sarpal, D. K. et al. Базовая функциональная связность полосатого тела как предиктор ответа на лечение антипсихотическими препаратами. Am. J. Psychiatry 173 , 69–77 (2016).

PubMed Google Scholar

94.

Сарпал, Д.K. et al. Антипсихотическое лечение и функциональная связность полосатого тела при первом эпизоде ​​шизофрении. JAMA Psychiatry 72 , 5–13 (2015).

PubMed PubMed Central Google Scholar

95.

Samanaite, R. et al. Биологические предикторы ответа клозапина: систематический обзор. Фронтальная психиатрия 9 , 327 (2018).

PubMed PubMed Central Google Scholar

96.

Судзуки Т., Учида Х., Ватанабе К. и Кашима Х. Факторы, связанные с ответом на клозапин при шизофрении: обзор. Psychopharmacol. Бык. 44 , 32–60 (2011).

PubMed PubMed Central Google Scholar

97.

Mouchlianitis, E., McCutcheon, R. & Howes, O.D. Исследования с помощью визуализации мозга устойчивой к лечению шизофрении: систематический обзор. Lancet Psychiatry 3 , 451–463 (2016).

PubMed PubMed Central Google Scholar

Поиск по чтению от А до Я Ресурсы для учителей

Искать термин

Тип ресурса Все анимационные алфавиты увеличиваются / Невероятные животные Бенчмарк Биографии / Биографии Canciones y rimas / Испанские песни и рифмы Комиксы декодируемые декодируемые отрывки Словарь ELL Книжная серия Художественная серия Тексты для успеваемости Графические книги Headsprout Раннее чтение Высокий Низкий Высокочастотный Слово Высокий / Низкий Графические книги Юмор идиома La vida en Latinoamerica y Espana / Жизнь в Латинской Америке и Испании Выровненная книга Leyendas y Mitos / Legends and Myths Los colores / Colours Los nmeros / Numbers Lugares de patrimonio en Latinoamrica / Объекты наследия в Латинской Америке. Основы чтения Документальная серия Карманная книга детских стишков Поэзия Чтение вслух Совместное чтение Совместное чтение Тексты для чтения Однокнижная классика Звук песни / символ Торговая книга Словарь Бессловесный алфавит Дополнительные ресурсы Оценка алфавита Алфавит Пение Алфавит Курсив Таблицы стиля Алфавит Фризы Буква алфавита Карточки Алфавит Изображение Карточки Алфавит Печать Таблицы стилей Упражнения по стилю Алфавит Наклонная печать Таблицы стилей Алфавит / Звук Наборы навыков Аргументация Аутентичные испанские контрольные отрывки Классика Закрыть Отрывки для чтения Закрыть Пакеты для чтения Пакеты навыков для понимания Связанный класс Страны по всему миру Ежедневная языковая практика Пакеты для декодируемых переходов Оценки ELL ELL Comic Conversations ELL Content Picture Packs ELL Grammar Resources ELL Language Skill Packs ELL Leveled Reader Packs ELL Vocabulary Games Guide ELL Vocabulary Power Packs Флорида Беглость речи Прохождение Оценка беглости Чтение предложений Беглость Практика Проходки Основные навыки Бесплатные PDF-файлы Гиганты высокого животного мира Ресурсы почерка Частота Оценка слов Высокочастотные карточки со словами Наборы текста с высоким / низким содержанием Графический органайзер среднего уровня (3-6) Учебные центры Приложение к уроку Литературный кружок Пользовательские журналы Литературный кружок Инструменты для Вы Литературный кружок Инструменты для ваших учеников Значимые беседы Основы чтения следующего поколения Основы чтения следующего поколения Не коллекционные фонограммы Оценка фонограмм Форма оценки фонологической осведомленности Книги по поэзии, детские стишки и песенники Обзор Программа сочинения стихов Таблицы советов дошкольного образования Первичный графический организатор ( K-2) Учебные пакеты на основе проектов Проецируемые макеты RAZ WOWzer Reader’s Theater Script Пересказ рубрики Текущая запись Испанский Пакет для прочтения Пакеты тем летней школы на испанском языке Руководство по выравниванию книг с переводом на испанский Зрелищные виды спорта Летние контракты и журналы Тематические пакеты летней школы Наборы текстов Ресурсы по теме Репетиторство и Наставник У.S. Правительство Визуальные устройства Словарный запас Графический органайзер Словарь Словарный запас Сортировка букв Словарь Открытая сортировка Словарный запас Сортировка звуков Словарный запас Сортировка по темам Мировые достопримечательности Мировые лидеры Тема ВсеПриключенияЖивотные и насекомыеИскусство и музыкаКлассикаСообщества и работаКультуры во всем миреЕдаДружбаГосударствоЗдоровье и человеческое телоИсторияПраздники и праздникиДом и семьяКак?

Художественная / Документальная ВсеФантастикаНеформальная Жанры Все Приключения Классическая концепция Описательная Басня Сказка Фэнтези Сказка Исторический Юмористический Информационный Информационный рассказ Легенда Тайна Миф Повествование Личное Личное повествование Личное повествование Убедительная Поэзия Сказка Пуркуа Реалистичная Научная фантастика Песня Рассказ Автобиография Концепция Биографии Творческое Описательное Фактическое Описание Историческое Как к Информационному Интервью Повествовательное Личное Повествование Личное Повествование Поэзия Pro / ConAllAdventureClassicConceptDescriptiveFableFairy TaleFantasyFolktaleHistoricalHumorousInformationalInformational NarrativeLegendMysteryMythNarrativePersonalPersonal NarrativePersonal RecountPersuasivePoetryPourquoi TaleRealisticScience FictionSongTall TaleAllAutobiographyBiographyConceptCreativeDescriptiveFactual DescriptionHistoricalHow toInformationalInterviewNarrativePersonal NarrativePersuasivePoetryPro / Con

Система выравнивания Выберите систему выравниванияLearning A-ZGradeLexileDRAFountas PinnellReading RecoveryRange

aaABCDEFGHIJKLMNOPQRSTUVWXYZZ1Z2 — aaABCDEFGHIJKLMNOPQRSTUVWXYZZ1Z2

ABCDEFGHIJKLMNOPQRSTU-VW-XY-Z до ABCDEFGHIJKLMNOPQRSTU-VW-XY-Z

A-123-468101214161820242830343840506070 + к A-123-468101214161820242830343840506070 +

123-45-67-89-1011-1213-1415-1617181^{30343840N / A до 123-45-67-89-1011-1213-1415-161718130343840N / A}

K123455 + к K123455 +

NPBR200LBR150LBR100LBR50L0L50L100L150L200L250L300L350L400L450L500L550L600L650L700L750L800L850L900L950L1000L1050L1100L1150L1200L1250L1300L1350L1400L к NPBR200LBR150LBR100LBR50L0L50L100L150L200L250L300L350L400L450L500L550L600L650L700L750L800L850L900L950L1000L1050L1100L1150L1200L1250L1300L1350L1400L

Языки ВсеанглийскийфранцузскийИспанскийбританский английскийПольскийукраинскийвьетнамскийавстралийский

Категория навыков ВсеСтратегия чтенияПониманиеФонологическая осведомленностьФоникаГрамматика и механикаСловесные работыОсобенности текстаЛитературный элемент Навыки урока ВсеЗадать вопрос и ответить на вопросыСвязаться с предыдущими знаниямиКонтекстные подсказкиОсновная идея и деталиСоздать соединения текста с собойСоздавать, проверять и подтверждать прогнозыРешение проблемРеласионарное совпадение с предыдущими сообщениямиРезумирРазвититьСамоконтрольСамостоятельный вопросПоследовательность событийSQA / Formular y Responder preguntasAuthentiznalyisVechnical Connections и отвечать на вопросы Точка зрения автораЦель автораКатегоризация информацииПричина и следствиеСвойства персонажаКлассификация информацииСравнение контрастаСравнить представление материала в графической книге с исходным материаломСравнить и противопоставить Рисование выводовЭлементы биографииФакт или мнениеФакты и подробностиВывод персонажей и обозначение точек зренияОпределить основные выводы характераОпределить характер и Настройка Идентифицировать Факты Идентифицировать Жанр Идентифицировать Настройки Интерпретировать ДиаграммыИнтерпретировать Диаграммы s и GraphsMain Идея и DetailsMake InferencesMake Умозаключения / Draw ConclusionsNarrative Точка ViewProblem и SolutionReality и FantasySequenceSequence EventsStory ElementsSummarizeAllAlliterationBlend Onset и RimeBlend PhonemesBlend SoundsBlend SyllablesBlendsCombinar fonemasCombinar slabasCombinar у segmentar уна Palabra ан slabasConsonant Digraph SoundsDiscriminate Начальный и конечный согласный DigraphsDiscriminate Начальная Согласные BlendDiscriminate Начальная DigraphDiscriminate медиальной SoundsDiscriminate R Контролируемые OrDiscriminate Variant Vowel SoundsEl sonido / __ / El sonido / __ / de la letra __El sonido de la letra / __ / El sonido final de una palabraEl sonido inicial de las palabras и финальные звуки Начальные сочетания Начальный согласный диграф Начальные согласные Начальный звук Длинный гласный диграф Длинные гласные звуки Длинные гласныеLos sonidos / b / y / v / Лос sonidos де ла Letra __Manipulate Final SoundsManipulate начальным и заключительным SoundsManipulate Initial SoundManipulate медиальной SoundsMedial SoundOmitir ла slaba inicialProducir rimasR-Controlled VowelsRhymeRimaSegment и Смешать PhonemesSegment Onset и RimeSegment PhonemesSegment SyllablesSegmentar oraciones ан palabrasSegmentar уна Palabra ан slabasSegmento де slabasShort Vowel SoundsShort VowelsSonido inicialSound DiscriminationSustituir slabasSyllable AwarenessVariant гласного SoundsVowelsWord AwarenessAllBlendsConsonant BlendsConsonant DigraphsConsonante finalConsonante inicialConsonantesConsonantsDiferenciar Entre consonantes у vocalesDiferenciar Entre эль Sonido де ла Letra __ у ла Letra __Diferentes patrones де slabasDgrafosDiphthongsDouble LettersEl Sonido / __ / де-ла-Letra __El Sonido де ла Letra __El Sonido-де-лас letrasGrupos consonnticos ан posicin inicialLa consonante окончательный _LA consonante Inicial _Длинные гласныеОткрытые гласные Патроны CV простые Патроны CVC Патроны VCPatrones VC y CVR VowelsRhymeShort VowelsSlabas контролируемая tnicas у slabas tonasSilent LettersSonido де ла Letra / __ / Sonido inicialSound Символ RelationshipVariant VowelsVCe Длинные гласные PatternsVCe PatternVowel DigraphsVowel орграфах Versus Vowel DipthongsVowel DiphthongVowel GeneralizationsVowel PatternsVowel YWord FamiliesAllAccentsAcentuacin де лас Palabras interrogativas у exclamativasAdjectivesAdjectives, глаголами и AdverbsAdjetivos comparativosAdjetivos superlativosAdverbsAgreement из AdjectivesAntonymsApostrophesArticlesArtculos definidosArtculos definidos е indefinidosBold PrintBulletsCapitalizationCapitalization и PunctuationColonColons и SemicolonsCombined SentencesCommandsCommasCommon NounsComparative AdjectivesComparative и Superlative AdjectivesComplete SentencesComplex SentencesCompound AdjectivesCompound PredicatesCompound SentencesCompound SubjectCompound WordsConcordancia де sujeto-verboConjuncionesConjunctionsConnecting WordsContext CluesContractionsCoordinate и накопительное Adje ctivesDashDeclarative SentencesDescribing WordsDialogueEllipsesEnding ErExclamation MarksExclamatory SentencesGender и NumberHyphenated Соединение AdjectivesIdentify HomophonesIdentify Prepostional PhrasesInflectional EndingsInterrogative SentencesIntroducing PhrasesIrregular VerbsMayscula inicialMayscula Inicial у Пунто окончательного де ла oracinMultiple Значение WordsNonfiction элементов в вымышленных TextNounsNouns Против ContractionsOraciones completasOraciones declarativasOraciones exclamativasOraciones interrogativasParagraph FormationParenthesesPast TensePast-Напряженная VerbsPeriodsPlural NounsPluralsPossessive NounsPossessivesPredicado simplePredicatesPrefixesPreposicionesPrepositional PhrasesPrepositionsPresent-Tense VerbsPronombres personalesPronounsProper СуществительныеПунктуацияPuntosВопросительные знакиЦифровые знакиЧтение символов с числамиПолуколонФрагменты предложенийТипы предложенийSignos de exclamacinSignos de interrogacinSimilesПростые и составные предметыПростые предикатыПростые предложенияSimple Su bjectSimple, соединение и комплекс SentencesSubjectSubject и PredicateSubject-Verb AgreementSuffixesSujeto simpleSuperlative AdjectivesSustantivosSustantivos pluralesSynonymsTime-Заказ WordsTypes из SentencesTypes предложений и PunctuationVerb EndingsVerb TenseVerbosVerbsVerbs и AdverbsVerbs и прямой ObjectsAllAbbreviationsAcrosticsAdjectivesAdverbsAffixesAlliterationAlphabetical OrderAlphabetizingAnimal NamesAntnimosAntonymsApostrophesBold PrintBoldface WordsCardinal и Порядковый NumbersCategorizar palabrasCategorize WordsColloquial phrasesColor WordsCommon PrefixesCommon SuffixesComparative и Superlative WordsCompound WordsConcept WordsConjunctionsContent VocabularyContext ПодсказкиСогласованияДни неделиОписательные словаДиалектСловарные навыкиИнформационный языкИностранный словарьВысокочастотные словаГомографыОмонимыГомофоныСоставные слова идиомыИдиомыИнфекционные окончанияСлова с нестандартным содержаниемLos nmeros en palabrasСлова для измеренийМетафоры sMultiple Syllable WordsNumber WordsNumbers и AbbreviationsNumbers в пределах TextOften Confused WordsOnomatopoeiaOrden alfabticoOrder WordsPalabras де coloresPalabras де medidasPalabras де posicinPalabras де УСО frecuentePalabras interrogativasPersonificationPlural EndingsPosition WordsPossessivesPrefixesPrepositional PhrasesPrepositionsPronounsPronunciationProper NounsQuestion WordsReading чисел в пределах TextReading символы, цифры и AbbreviationsRegional WordsRootsSensory WordsSimilesSimiles и MetaphorsSinnimosSpanish VocabularySuffixesSyllable PatternsSyllablesSymbolsSynonymsSynonyms и AntonymsTime и порядок WordsVerb TenseVerbsVocabulario-де-ла lectura Происхождение слов: Слова, префиксы, суффиксы и т. д.

Область содержимого ELL Все Искусство и музыка Искусство Цвета MusicELL Социальные и учебные программы Язык Сотрудничество Повседневные распорядки Чувства Следуя указаниям Дружба Хобби Решение проблем Обязанности Правила Безопасность Школа Спорт и игрыОсновные навыкиЯзыковые искусства Языковые навыки ELL Прилагательные Наречия Прилагательные слова Сочленения Существительные Детские стишки Поэзия Предлоги Местоимения Элементы текста Предложения Типы предложений Слова Жанр Коллекции Приключение Биография Басни Сказки Общие народные сказки Как и обработка Интервью Легенды Тайны Мифы Убедительные сказки Pourquoi Pro / Con Tall Tales Математика сложение и вычитание Диаграммы и графики Подсчет экономики и бизнеса Доли и проценты Измерение геометрии Число денег Шаблон смысла s Формы Сортировка и классификация Время Наука Животные Биология Земля и космос Электричество и магнетизм Энергия, силы и движение Среда обитания Здоровье и человеческое тело Земля и вода Свет и звук Машины имеют значение Люди Растения Камни и минералы Ученые и изобретатели Инструменты и технологии Вода Погода и времена годаСоциальные истории Запугивание Сотрудничество Чувства и эмоции Манеры дружбы Социальные исследования Искусство и музыка Праздники Сообщество и соседство Культура и религия Экономика и бизнес Исследователи Еда География и путешествия Дом и семья Работа Карты Деньги Люди Места Технологии Транспорт U.С. Правительство США История Всемирная история

Эквивалентный импеданс

— обзор

1

Импеданс верхней индуктивной ветви равен

Z ₁ = (8 + j10) ω = √ (8 ² + 10 ² ) ∠ tan ⁻¹ (10/8) ω

, поэтому

Z ₁ = 12,81∠51,34 ° ω

Импеданс нижней индуктивной ветви

Z ₂ = (7 + j9 ) ω = √ (7 ² + 9 ² ) ∠ tan ⁻¹ (9/7) ω

, поэтому

Z ₂ = 11.4∠52,13 ° ω

Сейчас

Z ₁ + Z ₂ = (8 + 7) + j (10 + 9) = (15 + j19) ω = √ (15 ² + 19 ² ) ∠ tan ⁻¹ (19/15) ω

so

Z ₁ + Z ₂ = 24,2∠51,7 ° ω

Эквивалентное сопротивление параллельной индуктивная ветвь

Z1Z2 / (Z1 + Z2) = [(12,81 × 11,4) /24,2] ∠ (51,34 + 52,13−51,7) = 6.03∠51.77 ° ω = 6.03 (Cos51.77 + j sin51.77) = (3.73 + j4.73) ω

Импеданс емкостной ветви

Z ₃ = (5 — j2) ω

Импеданс полной цепи,

Z _eq = Z ₃ + Z ₁ Z ₂ / ( Z ₂ ) = (5 + 3,73) + j (−2 + 4,73) ω

, поэтому

Z _eq = (8.73 + j2.73) = √ (8,73 ² + 2,73 ² ) ∠ tan ⁻¹ (2,73 / 8,73) = 9,15∠17,36 ° ω

2

Ток, потребляемый от источника питания, равен

V / Z _eq = (100 / 9,15) ∠0 — 17,36 = 10,92∠ − 17,36 ° A

Общая потребляемая мощность составляет

P = VI cos ϕ = 100 × 10,92 cos 17,36 = 1042 Вт

3

Реактивная мощность в емкостном реактивном сопротивлении составляет

Q = I ² X _C = 10.92 ² × 2 = 238 Var

4

Эквивалентное реактивное сопротивление всей цепи положительно, что указывает на эффективное индуктивное реактивное сопротивление, так что общий коэффициент мощности отстает и его значение определяется как cos ϕ = cos 17,36 = 0,9544.

PWHS — Z-Flex Z-Vent 2SVSRC05 Вентиляционное отверстие из нержавеющей стали 5 дюймов

Гарантия

ОГРАНИЧЕННАЯ ЖИЗНЕННАЯ ГАРАНТИЯ Z-FLEX®

Z-FLEX® («Продавец») расширяет следующую ОГРАНИЧЕННУЮ ГАРАНТИЮ на Z-VENT («Z-Vent»):

Продавец гарантирует, что во время покупки, Z-Vent не будет иметь дефектов материала и / или качества изготовления.Эта гарантия распространяется на первоначального покупателя Z-Vent или, если она приобретена подрядчиком, на конечного пользователя. Эта гарантия действительна в течение пятнадцати (15) лет с даты покупки при условии, что Z-Vent был установлен в соответствии с инструкциями по установке Z-Flex®. Отклонение от инструкций по установке и использованию, прилагаемых к Z-Vent, приведет к аннулированию гарантии.

В соответствии с настоящей Ограниченной гарантией единоличная ответственность Продавца заключается в замене Z-Vent и / или аксессуаров, если Продавец обнаружит дефект в соответствии с условиями гарантии, и не включает замену установки или другие расходы.

ВАЖНАЯ ИНФОРМАЦИЯ: Z-Vent разработан для использования с вентиляцией топки и котла категорий II, III и IV и не должен использоваться с каким-либо другим типом вентиляции топки и котла. Использование Z-образного вентиляционного отверстия с любыми другими типами вентиляции топки и котла, кроме рекомендованных Продавцом для использования с Z-образным вентиляционным отверстием, приведет к аннулированию гарантии. ВНИМАНИЕ: КОНДЕНСАЦИЯ С ВЫСОКИМ СОДЕРЖАНИЕМ КИСЛОТЫ МОЖЕТ ПРОИЗВОДИТЬСЯ ИЗ-ЗА НЕСОБХОДИМЫХ УСЛОВИЙ. ВАШ НАГРЕВАТЕЛЬ И СИСТЕМА ВЕНТИЛЯЦИИ ДОЛЖНЫ ЕЖЕГОДНО ПРОВЕРИТЬСЯ ЛИЦЕНЗИОННЫМ ПОДРЯДЧИКОМ на предмет ВОЗМОЖНЫХ ПРИЗНАКОВ ПОВРЕЖДЕНИЯ ИЗ-ЗА РОЖДЕНИЯ ИЛИ ОТВЕРСТИЙ ДЛЯ ПИН.КОНДЕНСАЦИЯ С ВЫСОКИМ СОДЕРЖАНИЕМ КИСЛОТЫ МОЖЕТ ВЫЗВАТЬ УТЕЧКУ ВРЕДНЫХ ГАЗОВ, ЧТО МОЖЕТ ПРИВЕСТИ К НАУЗЕ, ОБОЛАРЕНИЮ ИЛИ СМЕРТИ. ПРИ ОБНАРУЖЕНИИ ДЕФЕКТОВ ПРЕКРАТИТЕ ИСПОЛЬЗОВАНИЕ СИСТЕМЫ ОТОПЛЕНИЯ И ПОЗВОНИТЕ УСТАНОВЩИКУ ПЕЧИ / КОТЛА ДЛЯ РЕШЕНИЯ.

Для активации гарантии конечный пользователь должен заполнить и вернуть Карточку регистрации гарантии Z-Flex® в течение девяноста (90) дней с момента установки Z-Vent. После письменного уведомления о любых дефектах Z-Flex® оставляет за собой право проверить или предоставить разумные доказательства дефектного материала или изготовления, оправдывающие замену.

НИКАКИХ ДРУГИХ ЯВНЫХ ГАРАНТИЙ ОТ ИМЕНИ ПРОДАВЦА НЕ ПРЕДСТАВЛЯЕТСЯ И НЕ БУДУТ ПРЕДОСТАВЛЯТЬСЯ В ОТНОШЕНИИ Z-VENT ИЛИ УСТАНОВКИ ИЛИ ЗАМЕНЫ Z-VENT. ПРОДАВЕЦ НЕ НЕСЕТ ОТВЕТСТВЕННОСТИ ЗА КАКИЕ-ЛИБО СПЕЦИАЛЬНЫЕ, СЛУЧАЙНЫЕ, КОСВЕННЫЕ ИЛИ КОСВЕННЫЕ УБЫТКИ.

Поскольку некоторые юрисдикции не допускают исключения или ограничения случайных или косвенных убытков, вышеуказанные ограничения или исключения могут к вам не относиться.

ПОДРАЗУМЕВАЕМЫЕ ГАРАНТИИ, ВКЛЮЧАЯ ЛЮБЫЕ ГАРАНТИИ КОММЕРЧЕСКОЙ ЦЕННОСТИ ИЛИ ПРИГОДНОСТИ ДЛЯ КОНКРЕТНОЙ ЦЕЛИ, ПРЕДОСТАВЛЯЕМЫЕ ДЛЯ ДАННОЙ ПРОДАЖИ В соответствии с Государственным законодательством, ОГРАНИЧИВАЮТСЯ СРОКОМ, НА КОТОРЫЙ ДЕЙСТВУЕТ НАСТОЯЩАЯ ГАРАНТИЯ.