1. Обзор R, X, и Z | 5. Реактивное сопротивление и импеданс — R, L и C | Часть2

1. Обзор R, X, и Z

Обзор R, X, и Z

Прежде чем мы начнем исследовать цепи переменного тока, содержащие одновременно резисторы, катушки индуктивности и конденсаторы, давайте кратко рассмотрим некоторые основные термины и факты.

Сопротивление — это воздействие силы трения на электроны при их движении через проводник. Сопротивление в некоторой степени присутствует во всех проводниках (за исключением сверхпроводников). Особенно оно характерно для резисторов. Когда переменный ток проходит через сопротивление, произведенное им напряжение находится в фазе с этим током. Сопротивление обозначается буквой «R» и измеряется в Омах (Ом, Ω).

Реактивное сопротивление по существу — это инерция против движения электронов. Реактивное сопротивление существует там, где электрические или магнитные поля развиваются пропорционально приложенному напряжению или току. Прежде всего оно характерно для конденсаторов и катушек индуктивности. Когда переменный ток проходит через чисто реактивное сопротивление, производимое им напряжение не совпадает по фазе с током на 90

o. Реактивное сопротивление обозначается буквой «X» и измеряется тоже в Омах (Ом, Ω).

Импеданс является всеобъемлющим выражением всех видов сопротивлений потоку электронов (включая активное и реактивное сопротивления). Импеданс присутствует во всех схемах и во всех компонентах. Когда переменный ток проходит через импеданс, производимое им напряжение не совпадает по фазе с током от 0^o до 90^o. Импеданс обозначается буквой «Z» и измеряется так же в Омах (Ом, Ω).

Идеальные резисторы обладают обычным сопротивлением, но у них нет реактивного сопротивления. Идеальные катушки индуктивности и конденсаторы обладают реактивным сопротивлением, но у них нет обычного сопротивления. Все вышеперечисленные компоненты обладают импедансом. Исходя из этого, имеет смысл перевести все значения активных и реактивных сопротивлений в соответствующие импедансы. Это будет первым шагом в анализе цепей переменного тока.

 

 

Фазовый угол импеданса любого компонента представляет собой сдвиг фазы между напряжением на этом компоненте и током через него. У идеального резистора напряжение и ток всегда находятся в фазе друг с другом, а значит, угол его импеданса составляет 0^o

. У идеальной катушки индуктивности напряжение всегда опережает ток на 90^o, а значит, угол ее импеданса составляет +90^o. У идеального конденсатора напряжение всегда отстает от тока на 90^o, а значит, угол его импеданса составляет -90^o.

Импедансы в цепях переменного тока ведут себя аналогично сопротивлениям в цепях постоянного тока: в последовательных цепях их значение увеличивается, а в параллельных — уменьшается. Пересмотренный на основе импеданса Закон Ома выглядит следующим образом:

 

 

Законы Кирхгофа, все методы анализа цепей и теоремы, рассмотренные нами в предыдущем разделе, верны и для цепей переменного тока (при условии, что величины представляются в комплексной, а не скалярной форме). Несмотря на то, что эта эквивалентность может быть математически сложной, она концептуально проста и изящна. Единственное различие между расчетами постоянных и переменных цепей касается мощности. Поскольку реактивное сопротивление не рассеивает мощность (как это делает обычное сопротивление), понятие мощности в цепях переменного тока в корне отличается от понятия мощности в цепях постоянного тока. Подробнее об этом мы расскажем несколько позже.

Полное сопротивление | Формулы и расчеты онлайн

В любой цепи переменного тока наряду с чисто реактивным сопротивлением присутствует омическое (активное) сопротивление, которое нужно учитывать при определении полного сопротивления.

Если

Z	полное сопротивление,	Ом
R	омическое (активное) сопротивление,	Ом
X	реактивное сопротивление,	Ом
Y = 1/Z	полная проводимость,	сименс
G	активная проводимость,	сименс
B	реактивная проводимость,	сименс
U	полное напряжение (эффективное значение),	Вольт
I	полный ток (эффективное значение),	Ампер

то имеем:

Полное сопротивление при последовательном соединении R и X

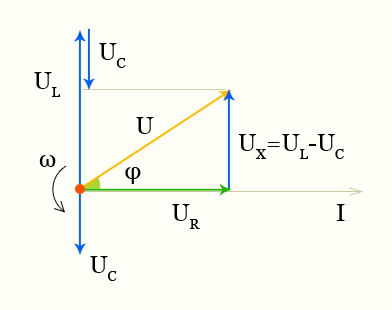
полное сопротивление векторная диаграмма тока и напряжений

При последовательном соединении активное и реактивное сопротивления складываются геометрически

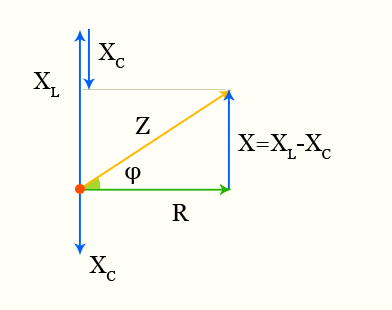
полное сопротивление векторная диаграмма

\[ Z = \sqrt{R^{2} + X^{2}} \]

и

\[ U = \sqrt{U^{2}_{R} + U^{2}_{X}} = IZ \]

Полное сопротивление при параллельном соединение R и X

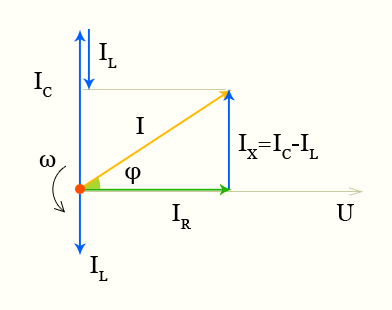
полное сопротивление векторная диаграмма тока и напряжений

При параллельном соединении активная и реактивная проводимости складываются геометрически

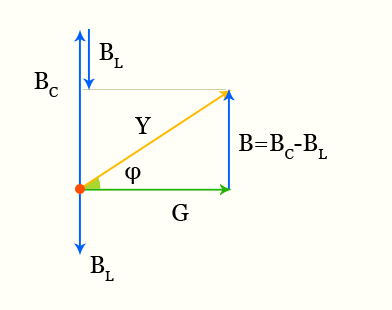
полное сопротивление векторная диаграмма

\[ Y = \sqrt{G^{2} + B^{2}} \]

и

\[ I = \sqrt{I^{2}_{R} + I^{2}_{X}} = UY \]

В помощь студенту

Полное сопротивление	стр. 689

Полное сопротивление цепи переменного тока

В предыдущих статьях мы узнали, что всякое сопротивление, поглощающее энергию, называется активным, а сопротивление, не поглощающее энергии, безваттным или реактивным. Кроме того, мы установили, что реактивные сопротивления делятся на два вида — индуктивные и емкостные.

Однако существуют цепи, где сопротивление не является чисто активным или чисто реактивным. То есть цепи, где вместе с активным сопротивлением включены в цепь, как емкости, так и индуктивности.

Введем понятие полного сопротивления цепи переменному току — Z, которое соответствует векторной сумме всех сопротивлений цепи (активных, емкостных и индуктивных). Понятие полного сопротивления цепи нам необходимо для более полного понимания закона Ома для переменного тока

На рисунке 1 представлены варианты электрических цепей и их классификация в зависимости от того какие элементы (активные или реактивные) включены в цепь.

Рисунок 1. Классификация цепей переменного тока.

Полное сопротивление цепи с чисто активными элементами соответствует сумме активных сопротивлений цепи и рассматривалось нами ранее. О чисто емкостном и индуктивном сопротивлении цепи мы тоже с вами говорили, и оно зависит соответственно от общей емкости и индуктивности цепи.

Рассмотрим более сложные варианты цепи, где последовательно с активным сопротивлением в цепь включено индуктивное и реактивное сопротивление.

Полное сопротивление цепи при последовательном соединении активного и реактивного сопротивления.

В любом сечении цепи, изображенной на рисунке 2,а, мгновенные значения тока должны быть одинаковыми, так как в противном случае наблюдались бы скопления и разрежения электронов в каких-либо точках цепи. Иными словами, фазы тока по всей длине цепи должны быть одинаковыми. Кроме того, мы знаем, что фаза напряжения на индуктивном сопротивлении опережает фазу тока на 90°, а фаза напряжения на активном сопротивлении совпадает с фазой тока (рисунок 2,б). Отсюда следует, что радиус-вектор напряжения U_L (напряжение на индуктивном сопротивлении) и напряжения U_R (напряжение на активном сопротивлении) сдвинуты друг относительно друга на угол в 90°.

Рисунок 2. Полное сопротивление цепи с активным сопротивлением и индуктивностью.        а) — схема цепи; б) — сдвиг фаз тока и напряжения; в) — треугольник напряжений; д) — треугольник сопротивлений.

Для получения радиуса-вектора результирующего напряжения на зажимах А и В (рис.2,а) мы произведем геометрическое сложение радиусов-векторов U_L и U_R. Такое сложение выполнено на рис. 2,в, из которого видно, что результирующий вектор U_AB является гипотенузой прямоугольного треугольника.

Из геометрии известно, что квадрат гипотенузы равен сумме квадратов катетов.

По закону Ома напряжение должно равняться силе тока, умноженной на сопротивление.

Так как сила тока во всех точках цепи одинакова, то квадрат полного сопротивления цепи (Z²) будет также равен сумме квадратов активного и индуктивного сопротивлений, т. е.

                                      (1)

 

Извлекая квадратный корень из обеих частей этого равенства, получим,

                                       (2)

 

 Таким образом, полное сопротивление цепи, изображенной на рис 2,а, равно корню квадратному из суммы квадратов активного и индуктивного сопротивлений

Полное сопротивление можно находить не только путем вычисления, но и путем построения треугольника сопротивлений, аналогичного треугольнику напряжений (рис 2,д), т. е. полное сопротивление цепи переменному току может быть получено путем измерения гипотенузы, прямоугольного треугольника, катетами которого являются активное и реактивное сопротивления. Разумеется, измерения катетов и гипотенузы должны производиться в одном и том же масштабе. Так, например, если мы условились, что 1 см длины катетов соответствует 1 ом, то число омов полного сопротивления будет равно числу сантиметров, укладывающихся на гипотенузе.

Полное сопротивление цепи, изображенной на рис.2,а, не является ни чисто активным, ни чисто реактивным; оно содержит в себе оба эти вида сопротивлений. Поэтому угол сдвига фаз тока и напряжения в этой цепи будет отличаться и от 0° и от 90°, то есть он будет больше 0°, но меньше 90°. К которому из этих двух значений он будет более близок, будет зависеть от того, какое из этих сопротивлений имеет преобладающее значение в цепи. Если индуктивное сопротивление будет больше активного, то угол сдвига фаз будет более близок к 90°, и наоборот, если преобладающим будет активное сопротивление, то угол сдвига фаз будет более близок к 0°.

В цепи, изображенной на рис 3,а, соединены последовательно активное и емкостное сопротивления. Полное сопротивление такой цепи можно определить при помощи треугольника сопротивлений так же, как мы определяли выше полное сопротивление активно-индуктивной цепи.

Рисунок 3. Полное сопротивление цепи с активным сопротивлением и емкостью.                                                а) — схема цепи; б) — треугольник сопротивлений.

Разница между обоими случаями состоит лишь в том, что треугольник сопротивлений для активно-емкостной цепи будет повернут в другую сторону (рис 3,б) вследствие того, что ток в емкостной цепи не отстает от напряжения, а опережает его.

Для данного случая:

(3)

 

 

 В общем случае, когда цепь содержит все три вида сопротивлений (рис. 4,а), сначала определяется реактивное сопротивление этой цепи, а затем уже полное сопротивление цепи.

Рисунок 4. Полное сопротивление цепи содержащей R, L и C. а) — схема цепи; б) — треугольник сопротивлений.

Реактивное сопротивление этой цепи состоит из индуктивного и емкостного сопротивлений. Так как эти два вида реактивного сопротивления противоположны друг другу по своему характеру, то общее реактивное сопротивление цепи будет равно их разности, т. е.

                           (4)

 

 

Общее реактивное сопротивление цепи может иметь индуктивный или емкостный характер, в зависимости от того, какое из этих двух сопротивлений (X_L или X_C преобладает).

После того как мы по формуле (4) определили общее реактивное сопротивление цепи, определение полного сопротивления не представит затруднений. Полное сопротивление будет равно корню квадратному из суммы квадратов активного и реактивного сопротивлений, т. е.

                                     (5)

 

 

Или

                         (6)

 

 

 

Способ построения треугольника сопротивлений для этого случая изображен на рис. 4 б.

Полное сопротивление цепи при параллельном соединении активного и реактивного сопротивления.

Полное сопротивление цепи при параллельном соединении активного и реактивного элемента.

Для того чтобы вычислить полное сопротивление цепи, составленной из активного и индуктивного сопротивлений, соединенных между собой параллельно(рис. 5,а), нужно сначала вычислить проводимость каждой из параллельных ветвей, потом определить полную проводимость всей цепи между точками А и В и затем вычислить полное сопротивление цепи между этими точками.

Рисунок 5. Полное сопротивление цепи при параллельном соединении активного и реактивных элементов. а) — параллельное соединение R и L; б) — параллельное соединение R и C

.

Проводимость активной ветви, как известно, равна 1/R, аналогично проводимость индуктивной ветви равна 1/ωL , а полная проводимость равна 1/Z

Полная проводимость равна корню квадратному из суммы квадратов активной и реактивной проводимости, т. е.

                       (7)

 

 

 

 

Приводя к общему знаменателю подкоренное выражение, получим:

  (8)

 

 

 

 

 откуда:

                              (9)

 

 

 

 

Формула (9) служит для вычисления полного сопротивления цепи, изображенной на рис. 5а.

Нахождение полного сопротивления для этого случая может быть произведено и геометрическим путем. Для этого нужно построить в соответствующем масштабе треугольник сопротивлений, и затем произведение длин катетов разделить на длину гипотенузы. Полученный результат и будет соответствовать полному сопротивлению.

Аналогично случаю, рассмотренному выше, полное сопротивление при параллельном соединении R и С (рис 5б) будет равно:

                             (10)

 

 

 

 

 

 Полное сопротивление может быть найдено также и в этом случае путем построения треугольника сопротивлений.

В радиотехнике наиболее часто встречается случай па¬раллельного соединения индуктивности и емкости, например колебательный контур для настройки приемников и передатчиков. Так как катушка индуктивности всегда обладает кроме индуктивного еще и активным сопротивлением, то эквивалентная (равноценная) схема колебательного контура будет содержать в индуктивной ветви активное сопротивление (рис 7).

Рисунок 6. Эквивалентная схема колебательного контура.

Формула полного сопротивления для этого случая будет:

                   (11)

 

 

 

 Так как обычно активное сопротивление катушки (R) бывает очень мало по сравнению с ее индуктивным сопротивлением (ωL), то мы имеем право формулу (11) переписать в следующем виде:

 (12)

 

 

 В колебательном контуре обычно подбирают величины L и С таким образом, чтобы индуктивное сопротивление равнялось емкостному, т. е. чтобы соблюдалось условие

                                     (13)

 

 

 При соблюдении этого условия полное сопротивление колебательного контура будет равно:

                                     (14)

 где L—индуктивность катушки в Гн;

С—емкость конденсатора в Ф;

R—активное сопротивление катушки в Ом.

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Похожие материалы:

Добавить комментарий

Расчет полного сопротивления в цепи переменного тока — импеданс

Понятие импеданса используется в разных сферах науки. Существуют разные его формы: гидродинамический, артериальный (медицинский термин, состоит из статического и кинетического компонентов), используемый при измерении гидростатического давления. Есть и электрический импеданс, описывающий полное сопротивление цепного фрагмента. Электрику необходимо знать, от чего зависит и как вычисляется эта величина в однофазных и трехфазных цепях с трансформаторами тока и иными компонентами.

Импеданс описывает сопротивление всей цепи

Что такое импеданс

Это понятие описывает комплексное сопротивление цепи или ее межузлового участка. Оно было введено лондонским инженером и физиком О. Хевисайдом в 1886 году. В состав полного сопротивления цепи входят активная и реактивная компоненты. Фазовый сдвиг и само значение импенданса при электротоке, чья кривая имеет форму синусоиды, могут быть рассчитаны с ориентиром на то, каким образом соединены входящие в цепь компоненты.

Аналогия с электрическим сопротивлением проводника на примере резистора

Чтобы суметь рассчитать импеданс цепи, нужно представлять, как себя ведут различные входящие в нее элементы: катушки индуктивности, резисторные и емкостные детали, с точки зрения вклада в составляющие общей резистивности цепи.

Активное сопротивление

Резистор относится к числу пассивных деталей цепи, не содержащих внутренних источников электроэнергии, при этом почти все создаваемое им противодействие приходится на активную компоненту. Реактивная составляющая если и присутствует, то настолько мала, что ею зачастую принято пренебрегать. Это связано с тем, что отношение напряжения на деталь и электротока, проходящего через нее, не зависит от их частоты. Когда к резисторной детали присоединяют источник напряжения (обозначим его U), через нее будет идти электроток значением I. Если к концам радиодетали подсоединяют источник тока, равного I, между ними будет иметь место падение напряжения U.

Важно! Выражение для сопротивления резистора можно записать так: R=U/I.

Резисторы – источники активного сопротивления

Реактивное сопротивление

К основным компонентам электроцепей, несущим такую нагрузку, относятся дроссели (и подобные им индуктивные элементы) и конденсаторы. При достижении резонанса наблюдается наименьшее значение общего противодействия подключенных последовательно конденсатора и дросселя и наибольшее – включенных параллельно.

Индуктивная нагрузка

Если индуктивный дроссель подключить к постоянному току, на нем будут наблюдаться следующие эффекты: резистивность будет приближаться к нулевому значению, а при пропускании электротока через катушечный элемент падение напряжения будет отсутствовать, независимо от токовой величины:

R=U/I=0/I=0.

Такие цифры справедливы для идеального дросселя, на практике они все же несколько отклоняются от нуля. Если к детали будет приложен переменный ток, напряжение между катушечными выводами будет отличным от нуля.

Катушка индуктивности

Емкостная нагрузка

При включении идеального конденсаторного элемента в сеть с постоянным напряжением его резистивность будет иметь очень большую величину, стремящуюся к бесконечной. Когда к радиодетали прикладывают такое напряжение, проходящий через нее ток будет равен нулю. Если к выводам конденсатора подсоединить источник переменного напряжения, ток будет ненулевым.

Детали, обладающие емкостью

Данные эффекты, наблюдаемые на емкостных радиодеталях и катушках, нельзя описывать в категориях активного противодействия в условиях константного электротока, так как последнее подразумевает стабильное, независимое от условий и не изменяющееся во времени отношение электротока и напряжения и исключает явление сдвига фаз между этими величинами. Таким образом, становится целесообразным введение для реактивных деталей характеристики, связывающей электроток и напряжение так, как это делает активное противодействие в омовском законе для константного тока.

Важно! При рассмотрении поведения катушек и конденсаторов под действием гармонических сигналов обнаруживается, что токовая сила и напряжение могут быть связаны константной величиной, которую также называют импедансом. При ее изучении применяется понятие о гармонических сигналах, учитывающее как их амплитудные характеристики, так и особенности, связанные с фазами.

Такое значение импеданса можно определить как частное комплексной амплитуды, которой обладает напряжение приложенного к двухполюсному элементу сигнала, и комплексной амплитуды идущего через элемент электротока. В отношении пассивных электроцепей со стабильными показателями в устоявшемся режиме стоит сказать, что импедансный показатель у них не будет привязанным к течению времени. Если временной параметр при формульной записи не сокращается, то категория импеданса для рассматриваемого двухполюсника окажется неприменимой.

Расчет эквивалентного сопротивления элементов цепи

Определение общего цепного сопротивления будет зависеть от того, какого типа конфигурацию составляют компоненты цепи. Для параллельного и последовательного подключений правила расчета будут неодинаковыми. Опираться при вычислениях нужно на закон Ома.

Согласно ему, у всех последовательно соединенных деталей, подключенных в цепь переменного тока, будет одно и то же значение электротока:

I=U/Z, где Z – общий импеданс цепи.

Напряжения будут различаться и окажутся привязанными к сопротивлениям деталей: на концах резистора его значение будет равно UR = IR (здесь R – активная резистивность элемента), для дросселя – UL = IXL, для емкостного элемента – UC = IXC (XL и XC – реактивные показатели соответствующих устройств). Так как векторы напряженности катушки и конденсатора имеют противоположные направления, суммарный показатель на реактивных деталях будет равен: UX = UL – UC . Противодействие будет равно: X = XL – XC.

Напряжения (общее, реактивное и активное) могут быть представлены в виде прямоугольного треугольника. Из него получается, что U² = UR² + UX². Поскольку противодействия входящих в цепь компонентов пропорциональны напряжениям, имеем Z2=R2+X2=R2+(XL – XC)2.

Для параллельного соединения принято выводить значения импеданса из проводимостей элементов, которые обратны их сопротивлениям. Отсюда 1/z2 = 1/R2 + 1/X2. Таким образом, выходит следующая формула:

Z2=1/(1/R2+(1/ XL – 1/ XC)2).

Общее сопротивление определяется компонентным составом цепи и характером соединения ее элементов. При расчетах показателей используется закон Ома.

Видео

2.5. Сопротивления в цепи переменного тока

В цепях переменного тока выделяют следующие виды сопротивлений.

Активное. Активным называют сопротивление резистора. Условное обозначение

Единицей измерения сопротивления является Ом. Сопротивление резистора не зависит от частоты.

Реактивное. В разделе реактивные выделяют три вида сопротивлений: индуктивное xL и емкостное хс и собственно реактивное. Для индуктивного сопротивления выше была получена формула X_L = ωL. Единицей измерения индуктивного сопротивления также является Ом. Величина xL линейно зависит от частоты.

Для емкостного сопротивления выше была получена формула X_C = 1 / ωC. Единицей измерения емкостного сопротивления является Ом. Величина хс зависит от частоты по обратно-пропорциональному закону. Просто реактивным сопротивлением цепи называют величину X = X_L — X_C.

Полное сопротивление. Полным сопротивлением цепи называют величину

(2.28)

.

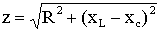Из этого соотношения следует, что сопротивления Z, R и X образуют треугольник: Z – гипотенуза, R и X – катеты. Для удобства в этом треугольнике рассматривают угол φ, который определяют уравнением

(2.29)

φ = arctg((X_L — X_C) / R),

и называют углом сдвига фаз. С учетом него можно дать дополнительные связи

(2.30)

R = Z cos φ,

(2.31)

X = Z sin φ.

2.6. Мощности в цепях переменного тока

По аналогии с мощностью в цепях постоянного тока P = U I, в цепях переменного тока рассматривают мгновенную мощность p = u i. Для упрощения рассмотрим мгновенную мощность в каждом из элементов R, L и С отдельно.

Элемент r (резистор)

Зададим напряжение и ток в виде соотношений

u(t) = U_m sin(ωt + ψ_u),

i(t) = I_m sin(ωt + ψ_i).

Известно, что для резистора ψ_u = ψ_i, тогда для р получим

(2.32)

p(t) = u(t) i(t) = U_m I_m sin²(ωt + ψ_i).

Из уравнения (2.32) видно, что мгновенная мощность всегда больше нуля и изменяется во времени. В таких случаях принять рассматривать среднюю за период Т мощность

(2.33)

.

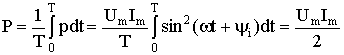Если записать U_m и I_m через действующие значения U и I: 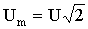,,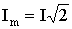 то получим

(2.34)

P = U I.

По форме уравнение (2.34) совпадает с мощностью на постоянном токе. Величину Р равную произведению действующих значений тока и напряжения называют активной мощностью. Единицей ее измерения является Ватт (Вт).

Элемент l (индуктивность)

Известно, что в индуктивности соотношение фаз ψ_u = ψ_i + 90°. Для мгновенной мощности имеет

(2.35)

.

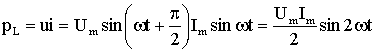Усредняя уравнение (2.35) по времени за период Т получим

.

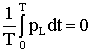Для количественной оценки мощности в индуктивности используют величину Q_L равную максимальному значению р_L

(2.36)

Q_L = (U_m I_m) / 2

и называют ее реактивной (индуктивной) мощностью. Единицей ее измерения выбрали ВАр (вольт-ампер реактивный). Уравнение (2.36) можно записать через действующие значения U и I и используя формулу U_L = I X_L получим

(2.37)

Q_L = I² X_L.

Элемент с (ёмкость)

Известно, что в емкости соотношение фаз ψ_u = ψ_i — 90°. Для мгновенной мощности получаем

p_C(t) = u(t) I(t) = (U_m I_m) / 2 · sin(2ωt).

Среднее значение за период здесь также равно нулю. По аналогии с уравнением (2.36) вводят величину Q_C = I² X_C, которую называют реактивной (емкостной) мощностью. Единицей ее измерения также является ВАр.

Если в цепи присутствуют элементы R, L и С, то активная и реактивная мощности определяются уравнениями

(2.37)

P = U I cos φ,

(2.38)

Q = Q_L — Q_C,

(2.39)

Q = U I sin φ,

где φ – угол сдвига фаз.

Вводят понятие полной мощности цепи

(2.40)

.

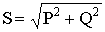С учетом уравнений (2.37) и (2.39), (2.40) можно записать в виде

(2.41)

S = U I.

Единицей измерения полной мощности является ВА – вольт-ампер.

Закон Ома. Онлайн расчёт для постоянного и переменного тока.

Онлайн расчёт электрических величин напряжения, тока и мощности для:
участка цепи, полной цепи с резистивными, ёмкостными и индуктивными
элементами.

— А любите ли Вы закон Ома так, как люблю его я? — спросил учитель физики стоящего рядом с щитком и разглядывающего свой обугленный палец электрика, — Всеми силами души Вашей, со всем энтузиазмом и исступлением, к которому только способна пылкая молодость, — никак не угомонялся он, сверкая из-под очков пытливым взглядом.
— Мужик, ты что, дурак? – вежливо поинтересовался обиженный противоестественным вопросом электрик и пошёл, насвистывая «Калинку-Малинку» в направлении ближайшего супермаркета — не ради пьянства окаянного, а дабы залечить свой увечный палец.

А тем временем, закон Ома является в электротехнике основным законом, который устанавливает связь силы электрического тока с сопротивлением и напряжением.

Формулировка закона Ома для участка цепи может быть представлена так: сила тока в проводнике прямо пропорциональна напряжению (разности потенциалов) на его концах и обратно пропорциональна сопротивлению этого проводника и записана в следующем виде:
I=U/R,

где
I – сила тока в проводнике, измеряемая в амперах [А];
U – электрическое напряжение (разность потенциалов), измеряемая в вольтах [В];
R – электрическое сопротивление проводника, измеряемое в омах [Ом].

Производные от этой формулы приобретают такой же незамысловатый вид: R=U/I и U=R×I.

Зная любые два из трёх приведённых параметров можно легко произвести расчёт и величины мощности, рассеиваемой на резисторе.
Мощность является функцией протекающего тока I(А) и приложенного напряжения U(В) и вычисляется по следующим формулам, также являющимся производными от основной формулы закона Ома:
P_(Вт) = U_(В)×I_(А) = I²_(А)×R_(Ом) = U²_(В)/R_(Ом)

Можно, конечно, описывая закон Ома обойтись и вообще без формул, а вместо них пользоваться словами или картинками:

С другой стороны, формулы настолько просты, что не стоят выеденного яйца и, возможно, вообще не заслуживают отдельной крупной статьи на страницах уважающего себя сайта.

Не заслуживают, так не заслуживают. Калькулятор Вам в помощь, дамы и рыцари!
Считайте, учитывайте размерность, не стирайте из памяти, что:
1В=1000мВ=1000000мкВ;
1А=1000мА=1000000мкА;
1Ом=0.001кОм=0.000001МОм;
1Вт=1000мВт=100000мкВт.

Ну и так, на всякий случай, чисто для проверки полученных результатов, приведём незамысловатую таблицу, позволяющую в онлайн режиме проверить расчёты, связанные со знанием формул закона Ома.

ТАБЛИЦА ДЛЯ ПРОВЕРКИ РЕЗУЛЬТАТОВ РАСЧЁТОВ ЗАКОНА ОМА.

Вводить в таблицу нужно только два имеющихся у Вас параметра, остальные посчитает таблица.

Все наши расчёты проводились при условии, что значение внешнего сопротивления R значительно превышает внутреннее сопротивление источника напряжения r_внутр.
Если это условие не соблюдается, то под величиной R следует принять сумму внешнего и внутреннего сопротивлений: R = R_внешн + r_внутр , после чего закон приобретает солидное название — закон Ома для полной цепи:
I=U/(R+r) .

Для многозвенных цепей возникает необходимость преобразования её к эквивалентному виду:

Значения последовательно соединённых резисторов просто суммируются, в то время как значения параллельно соединённых резисторов определяются исходя из формулы: 1/R_ll = 1/R₄+1/R₅.
А онлайн калькулятор для расчёта величин сопротивлений при параллельном соединении нескольких проводников можно найти на странице ссылка на страницу.

Теперь, что касается закона Ома для переменного тока.
Если внешнее сопротивление у нас чисто активное (не содержит ёмкостей и индуктивностей), то формула, приведённая выше, остаётся в силе.
Единственное, что надо иметь в виду для правильной интерпретации закона Ома для переменного тока — под значением U следует понимать действующее (эффективное) значение амплитуды переменного сигнала.

А что такое действующее значение и как оно связано с амплитудой сигнала переменного тока?
Приведём диаграммы для нескольких различных форм сигнала.

Слева направо нарисованы диаграммы синусоидального сигнала, меандра (прямоугольный сигнал со скважностью, равной 2), сигнала треугольной формы, сигнала пилообразной формы.
Глядя на рисунок можно осмыслить, что амплитудное значение приведённых сигналов — это максимальное значение, которого достигает амплитуда в пределах положительной, или отрицательной (в наших случаях они равны) полуволны.

Рассчитываем действующее значение напряжение интересующей нас формы:

Для синуса U = Uд = Uа/√2;
для треугольника и пилы U = Uд = Uа/√3;
для меандра U = Uд = Uа.

С этим разобрались!

Теперь посмотрим, как будет выглядеть формула закона Ома при наличии индуктивности или ёмкости в цепи переменного тока.
В общем случае смотреться это будет так:

А формула остаётся прежней, просто в качестве сопротивления R выступает полное сопротивление цепи Z, состоящее из активного, ёмкостного и индуктивного сопротивлений.
Поскольку фазы протекающего через эти элементы тока не одинаковы, то простым арифметическим сложением сопротивлений этих трёх элементов обойтись не удаётся, и формула приобретает вид:
Реактивные сопротивления конденсаторов и индуктивностей мы с Вами уже рассчитывали на странице ссылка на страницу и знаем, что величины эти зависят от частоты, протекающего через них тока и описываются формулами: X_C = 1/(2πƒС) ,   X_L = 2πƒL .

Нарисуем таблицу для расчёта полного сопротивления цепи для переменного тока.
Количество вводимых элементов должно быть не менее одного, при наличии индуктивного или емкостного элемента — необходимо указать значение частоты f !

КАЛЬКУЛЯТОР ДЛЯ ОНЛАЙН РАСЧЁТА ПОЛНОГО СОПРОТИВЛЕНИЯ ЦЕПИ.

Теперь давайте рассмотрим практический пример применения закона Ома в цепях переменного тока и рассчитаем простенький бестрансформаторный источник питания.

Токозадающими цепями в данной схеме являются элементы R1 и С1.

Допустим, нас интересует выходное напряжение Uвых = 12 вольт при токе нагрузки 100 мА.
Выбираем стабилитрон Д815Д с напряжением стабилизации 12В и максимально допустимым током стабилизации 1,4А.
Зададимся током через стабилитрон с некоторым запасом — 200мА.
С учётом падения напряжения на стабилитроне, напряжение на токозадающей цепи равно 220в — 12в = 208в.
Теперь рассчитаем сопротивление этой цепи Z для получения тока, равного 200мА: Z = 208в/200мА = 1,04кОм.
Резистор R1 является токоограничивающим и выбирается в пределах 10-100 Ом в зависимости от максимального тока нагрузки.
Зададимся номиналами R1 — 30 Ом, С1 — 1 Мкф, частотой сети f — 50 Гц и подставим всё это хозяйство в таблицу.
Получили полное сопротивление цепи, равное 3,183кОм. Многовато будет — надо увеличивать ёмкость С1.
Поигрались туда-сюда, нашли нужное значение ёмкости — 3,18 Мкф, при котором Z = 1,04кОм.

Всё — закон Ома выполнил свою функцию, расчёт закончен, всем спать полчаса!

 

Импеданс. Расчёт

Импеданс (impedance) – комплексное, полное сопротивление переменному току электрической цепи с активным и реактивным сопротивлением.

Импеданс и общий сдвиг фаз для синусоидального тока можно рассчитать исходя из последовательного или параллельного соединения элементов цепи.

Последовательное соединение

При последовательном соединении, согласно Закону Ома для переменного тока, во всех элементах цепи ток будет общим I = U/Z, а значения напряжений на каждом элементе определятся пропорционально его сопротивлению:
на выводах резистора U_R = IR; на выводах конденсатора U_C = IX_C; на выводах катушки U_L = IX_L.

Векторы индуктивной и ёмкостной составляющих напряжения направлены в противоположные стороны.
С учётом отрицательного ёмкостного сдвига, общее напряжение на реактивных элементах U_X = U_L — U_C .
Пропорционально напряжению, получим общее реактивное сопротивление X = X_L — X_C .
Векторы напряжений на активной и реактивной составляющей импеданса имеют угол сдвига фаз 90 градусов.
U , U_R и U_X представим в виде прямоугольного треугольника напряжений с углом сдвига фаз φ.

Тогда получим соотношение, согласно Теореме Пифагора, U ² = U_R² + U_X² .
Следовательно, с учётом пропорциональности элементов R, L, C значениям напряжений на их выводах, определим импеданс, который будет равен квадратному корню из суммы квадратов активного и реактивного сопротивлений цепи.

X_L = ωL = 2πfL — реактивное сопротивление индуктивности.
X_C = 1/(ωC) = 1/(2πfC) — реактивное сопротивление ёмкости.

Угол сдвига фаз φ и его дополнение до 90° δ определятся тригонометрическими функциями из треугольника сопротивлений с катетами R, X и гипотенузой Z, как показано на рисунке:

Обычно, для облегчения расчётов, импеданс представляют в виде комплексного числа, где действительной его частью является активное сопротивление, а мнимой — реактивное.
Для последовательного соединения импеданс можно записать в комплексном виде следующим образом:

Z = R + jX

Тогда в тригонометрической интерпретации модулем этого числа будет импеданс, а аргументом — угол φ.
В соответствии с формулой Эйлера, запишем показательную форму комплексного импеданса:

Z = |Z|e^jargZ = Ze^jφ

Отсюда активная составляющая импеданса R = Zcosφ
Реактивная составляющая X = Zsinφ.

---

Параллельное соединение

Для вычисления импеданса при параллельном соединении активных и реактивных сопротивлений будем исходить из суммы обратных им величин — проводимостей y = 1/Z, G = 1/R, b = 1/X.

y = 1/Z = √(G² + b²)

Сдвиг фаз в этом случае будет определён треугольником сопротивлений следующим образом:

Комплексную проводимость, как величину, обратную комплексному импедансу, запишем в алгебраической форме:

Y = G — jb

Либо в показательной форме:

Y = |Y|e ^-jφ = ye ^-jφ

Здесь:
Y — комплексная проводимость.
G — активная проводимость.
b — реактивная проводимость.
y — общая проводимость цепи, равная модулю комплексной проводимости.
e — константа, основание натурального логарифма.
j — мнимая единица.
φ — угол сдвига фаз.

---

Онлайн-калькулятор расчёта импеданса и угла сдвига фаз

Необходимо вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.

Последовательное соединение Z = √(R²+(XL-Xc)²)

Параллельное соединение Z = 1/√(1/R²+(1/XL-1/Xc)²)

---

Похожие страницы с расчётами:

Реактивное сопротивление. Расчёт.
Частота резонанса колебательного контура LC. Расчёт.
Реактивная мощность и компенсация. Расчёт.