Как посчитать сопротивление при последовательном соединении. Параллельное и последовательное соединение

На уроке рассматривается параллельное соединение проводников. Изображается схема такого соединения, показывается выражение для вычисления силы тока в такой цепи. Также вводится понятие эквивалентного сопротивления, находится его значение для случая параллельного соединения.

Соединения проводников бывают различные. Они могут быть параллельными, последовательными и смешанными. На данном уроке мы рассмотрим параллельное соединение проводников и понятие эквивалентного сопротивления.

Параллельным соединением проводников называется такое соединение, при котором начала и концы проводников соединяются вместе. На схеме такое соединение обозначается следующим образом (рис. 1):

Рис. 1. Параллельное соединение трех резисторов

На рисунке изображены три резистора (прибор, основанный на сопротивлении проводника) с сопротивлениями R1, R2, R3. Как видим, начала этих проводников соединены в точке А, концы — в точке Б, а расположены они параллельно друг другу.

Также в цепи может быть большее количество параллельно соединенных проводников.

Теперь рассмотрим следующую схему (рис. 2):

Рис. 2. Схема для исследования силы тока при параллельном соединении проводников

В качестве элементов цепи мы взяли две лампы (1а, 1б). Они также имеют свое сопротивление, поэтому мы их можем рассматривать наравне с резисторами. Эти две лампы соединены параллельно, соединяются они в точках А и Б. К каждой лампе подсоединен свой амперметр: соответственно, А 1 и А 2 . Также есть амперметр А 3 , который измеряет силу тока во всей цепи. В цепь еще входит источник питания (3) и ключ (4).

Замкнув ключ, мы будем следить за показаниями амперметров. Амперметр А 1 покажет силу тока, равную I 1 , в лампе 1а, амперметр А 2 — cилу тока, равную I 2 , в лампе 1б. Что же касается амперметра А 3 , то он покажет силу тока, равную сумме токов в каждой отдельной взятой цепи, соединенных параллельно: I = I 1 + I 2 . То есть, если сложить показания амперметров А 1 и А 2 , то получим показания амперметра А 3 .

Стоит обратить внимание, что если одна из ламп перегорит, то вторая будет продолжать работать. При этом весь ток будет проходить через эту вторую лампу. Это очень удобно. Так, например, электроприборы в наших домах включаются в цепь параллельно. И если один из них выходит из строя, то остальные остаются в рабочем состоянии.

Рис. 3. Схема для нахождения эквивалентного сопротивления при параллельном соединении

На схеме рис. 3 мы оставили один амперметр (2), но добавили в электрическую цепь вольтметр (5) для измерения напряжения. Точки А и Б являются общими и для первой (1а), и для второй лампы (1б), а значит, вольтметр измеряет напряжение на каждой из этих ламп (U 1 и U 2) и во всей цепи (U). Тогда U = U 1 = U 2 .

Эквивалентным сопротивлением называется сопротивление, которое может заменить все элементы, входящие в данную цепь. Посмотрим, чему же оно будет равно при параллельном соединении. Из закона Ома можно получить, что:

В данной формуле R — эквивалентное сопротивление, R 1 и R 2 — сопротивление каждой лампочки, U = U 1 = U 2 — напряжение, которое показывает вольтметр (5). При этом мы используем то, что сумма токов в каждой отдельной цепи равна общей силе тока (I = I 1 + I 2). Отсюда можно получить формулу для эквивалентного сопротивления:

Если в цепи будет больше элементов, соединенных параллельно, то и слагаемых будет больше. Тогда придется вспомнить, как работать с простыми дробями.

Стоить отметить, что при параллельном соединении эквивалентное сопротивление будет достаточно малым. Соответственно, сила тока будет достаточно большой. Это стоит учитывать при включении в розетки большого количества электрических приборов. Ведь тогда сила тока возрастет, что может привести к перегреванию проводов и пожарам.

На следующем уроке мы рассмотрим другой тип соединения проводников — последовательное.

Список литературы

1. Генденштейн Л.Э, Кайдалов А.Б., Кожевников В.Б. Физика 8 / Под ред. Орлова В.А., Ройзена И.И. — М.: Мнемозина.
2. Перышкин А.В. Физика 8. — М.: Дрофа, 2010.
3. Фадеева А.А., Засов А.В., Киселев Д. Ф. Физика 8. — М.: Просвещение.

1. Физика ().
2. Сверхзадача ().
3. Интернет-портал Nado5.ru ().

Домашнее задание

1. Стр. 114-117: вопросы № 1-6. Перышкин А.В. Физика 8. — М.: Дрофа, 2010.
2. Могут ли быть параллельно соединены более трех проводников?
3. Что случится, если одна из двух ламп, которые соединены параллельно, перегорит?
4. Если к любой цепи параллельно подключить еще один проводник, всегда ли её эквивалентное сопротивление будет уменьшаться?

Нужно вычислить сопротивление последовательной, параллельной или комбинированной цепей? Нужно, если вы не хотите сжечь плату! Эта статья расскажет вам, как это сделать. Перед чтением, пожалуйста, уясните, что у резисторов нет «начала» и нет «конца». Эти слова вводятся для облегчения понимания изложенного материала.

Шаги

Сопротивление последовательной цепи

Сопротивление параллельной цепи

Сопротивление комбинированной цепи

Некоторые факты

1. Каждый электропроводный материал имеет некоторое сопротивление, являющееся сопротивляемостью материала электрическому току.
2. Сопротивление измеряется в Омах. Символ единицы измерения Ом — Ω.
3. Разные материалы имеют разные значения сопротивления.
   • Например, сопротивление меди 0.0000017 Ом/см 3
   • Сопротивление керамики около 10 14 Ом/см 3
4. Чем больше значение сопротивления, тем выше сопротивляемость электрическому току. Медь, которая часто используется в электрических проводах, имеет очень малое сопротивление. С другой стороны, сопротивление керамики очень велико, что делает ее прекрасным изолятором.
5. Работа всей цепи зависит от того, какой тип соединения вы выберете для подключения резисторов в этой цепи.
6. U=IR. Это закон Ома, установленный Георгом Омом в начале 1800х. Если вам даны любые две из этих переменных, вы легко найдете третью.
   • U=IR: Напряжение (U) есть результат умножения силы тока (I) * на сопротивление (R).
   • I=U/R: Сила тока есть частное от напряжение (U) ÷ сопротивление (R).
   • R=U/I: Сопротивление есть частное от напряжение (U) ÷ сила тока (I).

• Запомните: при параллельном соединении существует несколько путей прохождения тока по цепи, поэтому в такой цепи общее сопротивление будет меньше сопротивления каждого отдельного резистора. При последовательном соединении ток проходит через каждый резистор в цепи, поэтому сопротивление каждого отдельного резистора добавляется к общему сопротивлению.
• Общее сопротивление в параллельной цепи всегда меньше сопротивления одного резистора с самым низким сопротивлением в этой цепи. Общее сопротивление в последовательной цепи всегда больше сопротивления одного резистора с самым высоким сопротивлением в этой цепи.

Темы кодификатора ЕГЭ : параллельное и последовательное соединение проводников, смешанное соединение проводников.

Есть два основных способа соединения проводников друг с другом — это последовательное и параллельное соединения. Различные комбинации последовательного и параллельного соединений приводят к смешанному соединению проводников.

Мы будем изучать свойства этих соединений, но сначала нам понадобится некоторая вводная информация.

Проводник, обладающий сопротивлением , мы называем резистором и изображаем следующим образом (рис. 1 ):

Рис. 1. Резистор

Напряжение на резисторе — это разность потенциалов стационарного электрического поля между концами резистора. Между какими именно концами? В общем-то, это неважно, но обычно удобно согласовывать разность потенциалов с направлением тока.

Ток в цепи течёт от «плюса» источника к «минусу». В этом направлении потенциал стационарного поля убывает. Напомним ещё раз, почему это так.

Пусть положительный заряд перемещается по цепи из точки в точку , проходя через резистор (рис. 2 ):

Рис. 2.

Стационарное поле совершает при этом положительную работу .

Так как alt=»q > 0″> и alt=»A > 0″> , то и alt=»\varphi_a — \varphi_b > 0″> , т. е. alt=»\varphi_a > \varphi_b»> .

Поэтому напряжение на резисторе мы вычисляем как разность потенциалов в направлении тока: .

Сопротивление подводящих проводов обычно пренебрежимо мало; на электрических схемах оно считается равным нулю. Из закона Ома следует тогда, что потенциал не меняется вдоль провода: ведь если и , то . (рис. 3 ):

Рис. 3.

Таким образом, при рассмотрении электрических цепей мы пользуемся идеализацией, которая сильно упрощает их изучение. А именно, мы считаем, что потенциал стационарного поля изменяется лишь при переходе через отдельные элементы цепи, а вдоль каждого соединительного провода остаётся неизменным . В реальных цепях потенциал монотонно убывает при движении от положительной клеммы источника к отрицательной.

Последовательное соединение

При последовательном соединении проводников конец каждого проводника соединяется с началом следующего за ним проводника.

Рассмотрим два резистора и , соединённых последовательно и подключённых к источнику постоянного напряжения (рис. 4 ). Напомним, что положительная клемма источника обозначается более длинной чертой, так что ток в данной схеме течёт по часовой стрелке.

Рис. 4. Последовательное соединение

Сформулируем основные свойства последовательного соединения и проиллюстрируем их на этом простом примере.

1. При последовательном соединении проводников сила тока в них одинакова.
В самом деле, через любое поперечное сечение любого проводника за одну секунду будет проходить один и тот же заряд. Ведь заряды нигде не накапливаются, из цепи наружу не уходят и не поступают в цепь извне.

2. Напряжение на участке, состоящем из последовательно соединённых проводников, равно сумме напряжений на каждом проводнике .

Действительно, напряжение на участке — это работа поля по переносу единичного заряда из точки в точку ; напряжение на участке — это работа поля по переносу единичного заряда из точки в точку . Складываясь, эти две работы дадут работу поля по переносу единичного заряда из точки в точку , то есть напряжение на всём участке:

Можно и более формально, без всяких словесных объяснений:

3. Сопротивление участка, состоящего из последовательно соединённых проводников, равно сумме сопротивлений каждого проводника.

Пусть — сопротивление участка . По закону Ома имеем:

что и требовалось.

Можно дать интуитивно понятное объяснение правила сложения сопротивлений на одном частном примере. Пусть последовательно соединены два проводника из одинакового вещества и с одинаковой площадью поперечного сечения , но с разными длинами и .

Сопротивления проводников равны:

Эти два проводника образуют единый проводник длиной и сопротивлением

Но это, повторяем, лишь частный пример. Сопротивления будут складываться и в самом общем случае — если различны также вещества проводников и их поперечные сечения.
Доказательство этого даётся с помощью закона Ома, как показано выше.
Наши доказательства свойств последовательного соединения, приведённые для двух проводников, переносятся без существенных изменений на случай произвольного числа проводников.

Параллельное соединение

При параллельном соединении проводников их начала подсоединяются к одной точке цепи, а концы — к другой точке.

Снова рассматриваем два резистора, на сей раз соединённые параллельно (рис. 5 ).

Рис. 5. Параллельное соединение

Резисторы подсоединены к двум точкам: и . Эти точки называются узлами или точками разветвления цепи. Параллельные участки называются также ветвями ; участок от к (по направлению тока) называется неразветвлённой частью цепи.

Теперь сформулируем свойства параллельного соединения и докажем их для изображённого выше случая двух резисторов.

1. Напряжение на каждой ветви одинаково и равно напряжению на неразветвлённой части цепи.
В самом деле, оба напряжения и на резисторах и равны разности потенциалов между точками подключения:

Этот факт служит наиболее отчётливым проявлением потенциальности стационарного электрического поля движущихся зарядов.

2. Сила тока в неразветвлённой части цепи равна сумме сил токов в каждой ветви.
Пусть, например, в точку за время из неразветвлённого участка поступает заряд . За это же время из точки к резистору уходит заряд , а к резистору — заряд .

Ясно, что . В противном случае в точке накапливался бы заряд, меняя потенциал данной точки, что невозможно (ведь ток постоянный, поле движущихся зарядов стационарно, и потенциал каждой точки цепи не меняется со временем). Тогда имеем:

что и требовалось.

3. Величина, обратная сопротивлению участка параллельного соединения, равна сумме величин, обратных сопротивлениям ветвей.
Пусть — сопротивление разветвлённого участка . Напряжение на участке равно ; ток, текущий через этот участок, равен . Поэтому:

Сокращая на , получим:

(1)

что и требовалось.

Как и в случае последовательного соединения, можно дать объяснение данного правила на частном примере, не обращаясь к закону Ома.
Пусть параллельно соединены проводники из одного вещества с одинаковыми длинами , но разными поперечными сечениями и . Тогда это соединение можно рассматривать как проводник той же длины , но с площадью сечения . Имеем:

Приведённые доказательства свойств параллельного соединения без существенных изменений переносятся на случай любого числа проводников.

Из соотношения (1) можно найти :

(2)

К сожалению, в общем случае параллельно соединённых проводников компактного аналога формулы (2) не получается, и приходится довольствоваться соотношением

(3)

Тем не менее, один полезный вывод из формулы (3) сделать можно. Именно, пусть сопротивления всех резисторов одинаковы и равны . Тогда:

Мы видим, что сопротивление участка из параллельно соединённых одинаковых проводников в раз меньше сопротивления одного проводника.

Смешанное соединение

Смешанное сединение проводников, как следует из названия, может являться совокупностью любых комбинаций последовательного и параллельного соединений, причём в состав этих соединений могут входить как отдельные резисторы, так и более сложные составные участки.

Расчёт смешанного соединения опирается на уже известные свойства последовательного и параллельного соединений. Ничего нового тут уже нет: нужно только аккуратно расчленить данную схему на более простые участки, соединённые последовательно или параллельно.

Рассмотрим пример смешанного соединения проводников (рис. 6 ).

Рис. 6. Смешанное соединение

Пусть В, Ом, Ом, Ом, Ом, Ом. Найдём силу тока в цепи и в каждом из резисторов.

Наша цепь состоит из двух последовательно соединённых участков и . Сопротивление участка :

Ом.

Участок является параллельным соединением: два последовательно включённых резистора и подключены параллельно к резистору . Тогда:

Ом.

Сопротивление цепи:

Ом.

Теперь находим силу тока в цепи:

Для нахождения тока в каждом резисторе вычислим напряжения на обоих участках:

(Заметим попутно, что сумма этих напряжений равна В, т. е. напряжению в цепи, как и должно быть при последовательном соединении. )

Оба резистора и находятся под напряжением , поэтому:

(В сумме имеем А, как и должно быть при параллельном соединении.)

Сила тока в резисторах и одинакова, так как они соединены последовательно:

Стало быть, через резистор течёт ток A.

Последовательным называется такое соединение резисторов, когда конец одного проводника соединяется с началом другого и т.д. (рис. 1). При последовательном соединении сила тока на любом участке электрической цепи одинакова. Это объясняется тем, что заряды не могут накапливаться в узлах цепи. Их накопление привело бы к изменению напряженности электрического поля, а следовательно, и к изменению силы тока. Поэтому

\(~I = I_1 = I_2 .\)

Амперметр А измеряет силу тока в цепи и обладает малым внутренним сопротивлением (R A → 0).

Включенные вольтметры V 1 и V 2 измеряют напряжение U 1 и U 2 на сопротивлениях R 1 и R 2 . Вольтметр V измеряет подведенное к клеммам Μ и N напряжение U . n R_i .\)

Если сопротивления отдельных резисторов равны между собой, т.е. R 1 = R 2 = … = R n , то общее сопротивление этих резисторов при последовательном соединении в n раз больше сопротивления одного резистора: R = nR 1 .

При последовательном соединении резисторов справедливо соотношение \(~\frac{U_1}{U_2} = \frac{R_1}{R_2}\), т.е. напряжения на резисторах прямо пропорциональны сопротивлениям.

Параллельным называется такое соединение резисторов, когда одни концы всех резисторов соединены в один узел, другие концы — в другой узел (рис. 2). Узлом называется точка разветвленной цепи, в которой сходятся более двух проводников. При параллельном соединении резисторов к точкам Μ и N подключен вольтметр. Он показывает, что напряжения на отдельных участках цепи с сопротивлениями R 1 и R 2 равны. Это объясняется тем, что работа сил стационарного электрического поля не зависит от формы траектории:

\(~U = U_1 = U_2 .n \frac{1}{R_i} .\)

Если сопротивления всех n параллельно соединенных резисторов одинаковы и равны R 1 то \(~\frac 1R = \frac{n}{R_1}\) . Откуда \(~R = \frac{R_1}{n}\) .

Сопротивление цепи, состоящей из n одинаковых параллельно соединенных резисторов, в n раз меньше сопротивления каждого из них.

При параллельном соединении резисторов справедливо соотношение \(~\frac{I_1}{I_2} = \frac{R_2}{R_1}\), т.е. силы токов в ветвях параллельно соединенной цепи обратно пропорциональны сопротивлениям ветвей.

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 257-259.

Последовательное соединение сопротивлений

Возьмем три неизменных сопротивления R1, R2 и R3 и включим их в цепь так, чтоб конец первого сопротивления R1 был соединен с началом второго сопротивления R 2, конец второго — с началом третьего R 3, а к началу первого сопротивления и к концу третьего подведем проводники от источника тока (рис. 1 ).

Такое соединение сопротивлений именуется поочередным. Разумеется, что ток в таковой цепи будет во всех ее точках один и тот же.

Рис 1 . Последовательное соединение сопротивлений

Как найти общее сопротивление цепи, если все включенные в нее поочередно сопротивления мы уже знаем? Используя положение, что напряжение U на зажимах источника тока равно сумме падений напряжений на участках цепи, мы можем написать:

U = U1 + U2 + U3

где

U1 = IR1 U2 = IR2 и U3 = IR3

либо

IR = IR1 + IR2 + IR3

Вынеся в правой части равенства I за скобки, получим IR = I(R1 + R2 + R3) .

Поделив сейчас обе части равенства на I , будем совсем иметь R = R1 + R2 + R3

Таким макаром, мы сделали вывод, что при поочередном соединении сопротивлений общее сопротивление всей цепи равно сумме сопротивлений отдельных участков.

Проверим этот вывод на последующем примере. Возьмем три неизменных сопротивления, величины которых известны (к примеру, R1 == 10 Ом, R 2 = 20 Ом и R 3 = 50 Ом). Соединим их поочередно (рис. 2 ) и подключим к источнику тока, ЭДС которого равна 60 В (внутренним сопротивлением источника тока пренебрегаем).

Рис. 2. Пример поочередного соединения 3-х сопротивлений

Подсчитаем, какие показания должны дать приборы, включенные, как показано на схеме, если замкнуть цепь. Определим наружное сопротивление цепи: R = 10 + 20 + 50 = 80 Ом.

Найдем ток в цепи по закону Ома: 60 / 80 = 0 ,75 А

Зная ток в цепи и сопротивления ее участков, определим падение напряжения на каждое участке цепи U 1 = 0,75х 10 = 7,5 В, U 2 = 0,75 х 20=15 В, U3 = 0,75 х 50 = 37,5 В.

Зная падение напряжений на участках, определим общее падение напряжения во наружной цепи, т. е. напряжение на зажимах источника тока U = 7,5+15 + 37,5 = 60 В.

Мы получили таким макаром, что U = 60 В, т. е. несуществующее равенство ЭДС источника тока и его напряжения. Разъясняется это тем, что мы пренебрегли внутренним сопротивлением источника тока.

Замкнув сейчас ключ выключатель К, можно убедиться по устройствам, что наши подсчеты приблизительно верны.

Возьмем два неизменных сопротивления R1 и R2 и соединим их так, чтоб начала этих сопротивлений были включены в одну общую точку а, а концы — в другую общую точку б. Соединив потом точки а и б с источником тока, получим замкнутую электронную цепь. Такое соединение сопротивлений именуется параллельным соединением.

Рис 3. Параллельное соединение сопротивлений

Проследим течение тока в этой цепи. От положительного полюса источника тока по соединительному проводнику ток дойдет до точки а. В точке а он разветвится, потому что тут сама цепь разветвляется на две отдельные ветки: первую ветвь с сопротивлением R1 и вторую — с сопротивлением R2. Обозначим токи в этих ветвях соответственно через I1 и I 2. Любой из этих токов пойдет по собственной ветки до точки б. В этой точке произойдет слияние токов в один общий ток, который и придет к отрицательному полюсу источника тока.

Таким макаром, при параллельном соединении сопротивлений выходит разветвленная цепь. Поглядим, какое же будет соотношение меж токами в составленной нами цепи.

Включим амперметр меж положительным полюсом источника тока (+) и точкой а и заметим его показания. Включив потом амперметр (показанный «а рисунке пунктиром) в провод, соединяющий точку б с отрицательным полюсом источника тока (-), заметим, что прибор покажет ту же величину силы тока.

Означает, сила тока в цепи до ее разветвления (до точки а) равна силе тока после разветвления цепи (после точки б).

Будем сейчас включать амперметр попеременно в каждую ветвь цепи, запоминая показания прибора. Пусть в первой ветки амперметр покажет силу тока I1 , а во 2-ой — I 2. Сложив эти два показания амперметра, мы получим суммарный ток, по величине равный току I до разветвления (до точки а).

Как следует, сила тока, протекающего до точки разветвления, равна сумме сил токов, утекающих от этой точки. I = I1 + I2 Выражая это формулой, получим

Это соотношение, имеющее огромное практическое значение, носит заглавие закона разветвленной цепи .

Разглядим сейчас, каково будет соотношение меж токами в ветвях.

Включим меж точками а и б вольтметр и поглядим, что он нам покажет. Во-1-х, вольтметр покажет напряжение источника тока, потому что он подключен, как это видно из рис. 3 , конкретно к зажимам источника тока. Во-2-х, вольтметр покажет падения напряжений U1 и U2 на сопротивлениях R1 и R2, потому что он соединен с началом и концом каждого сопротивления.

Как следует, при параллельном соединении сопротивлений напряжение на зажимах источника тока равно падению напряжения на каждом сопротивлении.

Это дает нам право написать, что U = U1 = U2 ,

где U — напряжение на зажимах источника тока; U1 — падение напряжения на сопротивлении R1 , U2 — падение напряжения на сопротивлении R2. Вспомним, что падение напряжения на участке цепи численно равно произведению силы тока, протекающего через этот участок, на сопротивление участка U = IR .

Потому для каждой ветки можно написать: U1 = I1R1 и U2 = I2R2 , но потому что U1 = U2, то и I1R1 = I2R2 .

Применяя к этому выражению правило пропорции, получим I1/ I2 = U2 / U1 т. е. ток в первой ветки будет во столько раз больше (либо меньше) тока во 2-ой ветки, во сколько раз сопротивление первой ветки меньше (либо больше) сопротивления 2-ой ветки.

Итак, мы пришли к принципиальному выводу, заключающемуся в том, что при параллельном соединении сопротивлений общий ток цепи разветвляется на токи, назад пропорциональные величинам сопротивлении параллельных веток. По другому говоря, чем больше сопротивление ветки, тем наименьший ток потечет через нее, и, напротив, чем меньше сопротивление ветки, тем больший ток потечет через эту ветвь.

Убедимся в корректности этой зависимости на последующем примере. Соберем схему, состоящую из 2-ух параллельно соединенных сопротивлений R1 и R 2, присоединенных к источнику тока. Пусть R1 = 10 Ом, R2 = 20 Ом и U = 3 В.

Подсчитаем поначалу, что покажет нам амперметр, включенный в каждую ветвь:

I1 = U / R1 = 3 / 10 = 0 ,3 А = 300 мА

I 2 = U / R 2 = 3 / 20 = 0,15 А = 150 мА

Общий ток в цепи I = I1 +I2 = 300 + 150 = 450 мА

Проделанный нами расчет подтверждает, что при параллельном соединении сопротивлений ток в цепи разветвляется назад пропорционально сопротивлениям.

Вправду, R1 == 10 Ом в два раза меньше R 2 = 20 Ом, при всем этом I1 = 300 мА в два раза больше I2 = 150 мА. Общий ток в цепи I = 450 мА разветвился на две части так, что большая его часть (I1 = 300 мА) пошла через наименьшее сопротивление (R1 = 10 Ом), а наименьшая часть (R2 = 150 мА) -через большее сопротивление (R 2 = 20 Ом).

Такое разветвление тока в параллельных ветвях сходно с течением воды по трубам. Представьте для себя трубу А, которая в каком-то месте разветвляется на две трубы Б и В различного поперечника (рис. 4). Потому что поперечник трубы Б больше поперечника трубок В, то через трубу Б в одно и то же время пройдет больше воды, чем через трубу В, которая оказывает сгустку воды большее сопротивление.

Рис. 4

Разглядим сейчас, чему будет равно общее сопротивление наружной цепи, состоящей из 2-ух параллельно соединенных сопротивлений.

Под этим общим сопротивлением наружной цепи нужно осознавать такое сопротивление, которым можно было бы поменять при данном напряжении цепи оба параллельно включенных сопротивления, не изменяя при всем этом тока до разветвления. Такое сопротивление именуется эквивалентным сопротивлением.

Вернемся к цепи, показанной на рис. 3, и поглядим, чему будет равно эквивалентное сопротивление 2-ух параллельно соединенных сопротивлений. Применяя к этой цепи закон Ома, мы можем написать: I = U/R , где I — ток во наружной цепи (до точки разветвления), U — напряжение наружной цепи, R — сопротивление наружной цепи, т. е. эквивалентное сопротивление.

Точно так же для каждой ветки I1 = U1 / R1 , I2 = U2 / R2 , где I1 и I 2 — токи в ветвях; U1 и U2 — напряжение на ветвях; R1 и R2 — сопротивления веток.

По закону разветвленной цепи: I = I1 + I2

Подставляя значения токов, получим U / R = U1 / R1 + U2 / R2

Потому что при параллельном соединении U = U1 = U2 , то можем написать U / R = U / R1 + U / R2

Вынеся U в правой части равенства за скобки, получим U / R = U (1 / R1 + 1 / R2 )

Разделив сейчас обе части равенства на U , будем совсем иметь 1 / R = 1 / R1 + 1 / R2

Помня, что проводимостью именуется величина, оборотная сопротивлению , мы можем сказать, что в приобретенной формуле 1 / R — проводимость наружной цепи; 1 / R1 проводимость первой ветки; 1 / R2- проводимость 2-ой ветки.

На основании этой формулы делаем вывод: при параллельном соединении проводимость наружной цепи равна сумме проводимостей отдельных веток.

Как следует, чтоб найти эквивалентное сопротивление включенных параллельно сопротивлений, нужно найти проводимость цепи и взять величину, ей оборотную.

Из формулы также следует, что проводимость цепи больше проводимости каждой ветки, а это означает, что эквивалентное сопротивление наружной цепи меньше меньшего из включенных параллельно сопротивлений.

Рассматривая случай параллельного соединения сопротивлений, мы взяли более ординарную цепь, состоящую из 2-ух веток. Но на практике могут повстречаться случаи, когда цепь состоит из 3-х и поболее параллельных веток. Как поступать в этих случаях?

Оказывается, все приобретенные нами соотношения остаются справедливыми и для цепи, состоящей из хоть какого числа параллельно соединенных сопротивлений.

Чтоб убедиться в этом, разглядим последующий пример.

Возьмем три сопротивления R1 = 10 Ом, R2 = 20 Ом и R3 = 60 Ом и соединим их параллельно. Определим эквивалентное сопротивление цепи (рис. 5 ). R = 1 / 6 Как следует, эквивалентное сопротивление R = 6 Ом.

Таким макаром, эквивалентное сопротивление меньше меньшего из включенных параллельно в цепь сопротивлений , т. е. меньше сопротивления R1.

Поглядим сейчас, вправду ли это сопротивление является эквивалентным, т. е. таким, которое могло бы поменять включенные параллельно сопротивления в 10, 20 и 60 Ом, не изменяя при всем этом силы тока до разветвления цепи.

Допустим, что напряжение наружной цепи, а как следует, и напряжение на сопротивлениях R1, R2, R3 равно 12 В. Тогда сила токов в ветвях будет: I1 = U/R1 = 12 / 10 = 1 ,2 А I 2 = U/R 2 = 12 / 20 = 1 ,6 А I 3 = U/R1 = 12 / 60 = 0,2 А

Общий ток в цепи получим, пользуясь формулой I = I1 + I2 + I3 =1,2 + 0,6 + 0,2 = 2 А.

Проверим по формуле закона Ома, получится ли в цепи ток силой 2 А, если заместо 3-х параллельно включенных узнаваемых нам сопротивлений включено одно эквивалентное им сопротивление 6 Ом.

I = U / R = 12 / 6 = 2 А

Как лицезреем, отысканное нами сопротивление R = 6 Ом вправду является для данной цепи эквивалентным.

В этом можно убедиться и на измерительных устройствах, если собрать схему с взятыми нами сопротивлениями, измерить ток во наружной цепи (до разветвления), потом поменять параллельно включенные сопротивления одним сопротивлением 6 Ом и опять измерить ток. Показания амперметра и в том и в другом случае будут приблизительно схожими.

На практике могут повстречаться также параллельные соединения, для которых высчитать эквивалентное сопротивление можно проще, т. е. не определяя за ранее проводимостей, сходу отыскать сопротивление.

К примеру, если соединены параллельно два сопротивления R1 и R2 , то формулу 1 / R = 1 / R1 + 1 / R2 можно конвертировать так: 1/R = (R2 + R1) / R1 R2 и, решая равенство относительно R, получить R = R1 х R2 / (R1 + R2 ), т. е. при параллельном соединении 2-ух сопротивлений эквивалентное сопротивление цепи равно произведению включенных параллельно сопротивлений, деленному на их сумму.

Последовательное и параллельное соединение проводников

Последовательное и параллельное соединение очень широко используется в электронике и электротехнике и порой даже необходимо для правильной работы того или иного узла электроники. И начнем, пожалуй, с самых простых компонентов радиоэлектронных цепей – проводников.

Для начала давайте вспомним, что такое проводник? Проводник – это вещество или какой-либо материал, который отлично проводит электрический ток. Если какой-либо проводник отлично проводит электрический ток, то он в любом случае обладает каким-либо сопротивлением. Сопротивление проводника мы находим по формуле:

формула сопротивление проводника

ρ – это удельное сопротивление, Ом × м

R – сопротивление проводника, Ом

S – площадь поперечного сечения, м2

l – длина проводника, м

Более подробно об этом я писал здесь.

Следовательно, любой проводник представляет из себя резистор с каким-либо сопротивлением. Значит, любой проводник можно нарисовать так.

обозначение резистора на схемах

Последовательное соединение проводников

Сопротивление при последовательном соединении проводников

Последовательное соединение проводников – это когда к одному проводнику мы соединяем другой проводник и так по цепочке. Это и есть последовательное соединение проводников. Их можно соединять с друг другом сколь угодно много.

последовательное соединение резисторов

Чему же будет равняться их общее сопротивление? Оказывается, все просто. Оно будет равняться сумме всех сопротивлений проводников в этой цепи.

Получается, можно записать, что

формула при последовательном соединении резисторов

Пример

У нас есть 3 проводника, которые соединены последовательно. Сопротивление первого 3 Ома, второго 5 Ом, третьего 2 Ома. Найти их общее сопротивление в цепи.

Решение

Rобщее =R1 + R2 + R3 = 3+5+2=10 Ом.

То есть, как вы видите, цепочку из 3 резисторов мы просто заменили на один резистор RAB .

показать на реальном примере с помощью мультиметра Видео где подробно расписывается про эти соединения:

Сила тока через последовательное соединение проводников

Что будет, если мы подадим напряжение на концы такого резистора? Через него сражу же побежит электрический ток, сила которого будет вычисляться по закону Ома I=U/R.

Получается, если через резистор RAB течет какой-то определенный ток, следовательно, если разложить наш резистор на составляющие R1 , R2 , R3 , то получится, что через них течет та же самая сила тока, которая текла через резистор RAB .

сила тока через последовательное соединение проводников

Получается, что при последовательном соединении проводников сила тока, которая течет через каждый проводник одинакова. То есть через резистор R1 течет такая же сила тока, как и через резистор R2 и такая же сила тока течет через резистор R3 .

Напряжение при последовательном соединении проводников

Давайте еще раз рассмотрим цепь с тремя резисторами

Как мы уже знаем, при последовательном соединении через каждый резистор проходит одна и та же сила тока. Но вот что будет с напряжением на каждом резисторе и как его найти?

Оказывается, все довольно таки просто. Для этого надо снова вспомнить закон дядюшки Ома и просто вычислить напряжение на любом резисторе. Давайте так и сделаем.

Пусть у нас будет цепь с такими параметрами.

Мы теперь знаем, что сила тока в такой цепи будет везде одинакова. Но какой ее номинал? Вот в чем загвоздка. Для начала нам надо привести эту цепь к такому виду.

Получается, что в данном случае RAB =R1 + R2 + R3 = 2+3+5=10 Ом. Отсюда уже находим силу тока по закону Ома I=U/R=10/10=1 Ампер.

Половина дела сделано. Теперь осталось узнать, какое напряжение падает на каждом резисторе. То есть нам надо найти значения UR1 , UR2 , UR3 . Но как это сделать?

Да все также, через закон Ома. Мы знаем, что через каждый резистор проходит сила тока 1 Ампер, мы уже вычислили это значение. Закон ома гласит I=U/R , отсюда получаем, что U=IR.

Следовательно,

UR1 = IR1 =1×2=2 Вольта

UR2 = IR2 = 1×3=3 Вольта

UR3 = IR3 =1×5=5 Вольт

Теперь начинается самое интересное. Если сложить все падения напряжений на резисторах, то можно получить… напряжение источника! Он у нас равен 10 Вольт.

Получается

U=UR1+UR2+UR3

Мы получили самый простой делитель напряжения.

Вывод: сумма падений напряжений при последовательном соединении равняется напряжению питания.

Методы соединения проводов

В соответствии с п.2.1.21. ПУЭ, соединение проводов можно осуществлять только методами сварки, пайки, опрессовки и сжимов. Как видим, излюбленный метод доморощенных электриков, скрутка, не входит в перечень разрешенных методов соединения.

А из всех представленных разрешенных методов наиболее оптимальным для использования в домашних условиях является сжим. Это может быть винтовое, болтовое или пружинное соединение.

Итак:

• Для монтажа болтовых и винтовых соединений промышленность сейчас выпускает большое количество самых разнообразных клеммных соединений. Их цена достаточно не велика, а удобство монтажа находится на высоком уровне.
• Отдельно хотелось бы сказать о пружинных клеммах. Я сам не являюсь сторонников пружинок, распорок и тому подобных соединений, но как-то раз довелось стать свидетелем испытаний одного из таких клеммников.
• Это были клеммы WAGO. На испытательной установке мы плавно поднимали ток, протекающий через клемму, пока наш медный провод в 4 мм2 не перегорел. При этом величина тока составляла 100А. После этого мы достали клеммник и не обнаружили на нем никаких дефектов. Это заставило изменить мое мнение о таких пружинных клеммниках, и поэтому вам я советую присмотреться к ним повнимательнее.
• Так же стоит отметить, что отдельным преимуществом таких клеммников является возможность соединения алюминиевых и медных проводов. В обычных же условиях это можно осуществлять только через латунную вставку.

Параллельное соединение проводников

Параллельное соединение проводников выглядит вот так.

параллельное соединение резисторов

Ну что, думаю, начнем с сопротивления.

Сопротивление при параллельном соединении проводников

Давайте пометим клеммы как А и В

В этом случае общее сопротивление RAB будет находиться по формуле

Если же мы имеем только два параллельно соединенных проводника

То в этом случае можно упростить длинную неудобную формулу и она примет вид такой вид.

Напряжение при параллельном соединении проводников

Здесь, думаю ничего гадать не надо. Так как все проводники соединяются параллельно, то и напряжение у всех будет одинаково.

Получается, что напряжение на R1 будет такое же как и на R2, как и на R3, так и на Rn

Как рассчитать сложные схемы соединения резисторов

Сложные схемы рассчитываются путем группировки по параллельному и последовательному способу соединения.

Перед нами сложная схема – задача рассчитать общее сопротивление:

1. R2, R3, R4 объединим в последовательную группу – применим формулу R2,3,4 = R2+R3+R4.
2. R5 и R2,3,4 – параллельно соединенные резисторы, рассчитаем R5,2,3,4 = 1/ (1/R5+1/R2,3,4).
3. R5,2,3,4, R1, R6 опять объединяем в последовательную группу – суммируя величины, получаем Rобщ = R5,2,3,4+R1+R6.

Варианты подключения электропроводки

Теперь давайте разберемся, какая должна быть электропроводка и как соединять провода. Для расключения однофазной сети необходимо применять трехжильный провод.

При этом следует применять нормы из п.1.1.29 ПУЭ для облегчения прокладки и снижения вероятности перепутывания проводов.

Цветовое обозначение проводов

Трехжильный провод следует применять со следующими проводами:

• Фазный провод – цветовое обозначение для однофазной сети не нормируется. Для трехфазной сети желтый, зеленый, красный – соответственно фазы А,В и С.

Обратите внимание! Для трехфазной цепи нормы ПУЭ нормируют не только цветовую гамму обозначения каждой фазы, но и их расположение в распределительных щитках разных конструкций.

• Нулевой провод – для любых сетей должен применяться проводник голубого цвета. При обозначении шин или клеммников применяется символ «N».
• Заземляющий провод – в любых сетях должен применяться провод с продольными желто-зелеными полосами. При обозначении шин и клеммников применяется знак заземления.

Подключение в распределительном щитке

Теперь давайте рассмотрим виды соединения электропроводки в разных участках нашей электрической сети.

Начнем с распределительного щитка:

• Сначала разберемся с фазным проводом. Он должен подключаться через защитное устройство. Это могут быть предохранители, пробки, но чаще всего используются автоматические выключатели. Питающий провод к автоматическим выключателям обычно подводится сверху, вы же подключаетесь снизу.
• Нулевой провод ,согласно норм ПУЭ, не должен иметь коммутационных устройств. Поэтому обычно для него организуют отдельный клеммник в боковой части щитка. К нему мы подключаем голубую жилу нашего провода.
• Это же правило относится и к заземляющему проводу. Только для него следует создать отдельный клеммник. К нему мы и подключаем наш желто-зеленый провод.

Подключение УЗО для всех групп потребителей

Отдельно остановимся на подключении УЗО. Для этого нам необходимо использовать не только фазный, но и нулевой провод. И схема во многом зависит от места установки УЗО.

Если вы устанавливаете УЗО на все группы вашей электрической сети:

• В этом случае фазный и нулевой провод с счетчика подключается к вводам УЗО. Тут важно не перепутать и нулевой провод подключить к клемме, обозначенной «N». Иначе УЗО не будет работать.
• Фазный провод на выходе УЗО подключаем ко всем автоматам, питающим отдельные группы.
• Нулевой провод на выходе УЗО подключаем к шине или клеммнику, от которого подключаются нулевые провода всех групп.

Если вы устанавливаете УЗО на отдельную группу:

• В этом случае фазный провод на ввод УЗО берется от автоматического выключателя группы.
• Нулевой провод на ввод УЗО берется с нулевой шины вашего распределительного щитка.
• С выводов УЗО нулевой и фазный провод идут непосредственно к потребителям.

Подключение в распределительной коробке

Соединение электропроводки на колодки при соблюдении указанных выше норм также не позволит вам запутаться. Отличается здесь только подключение светильников и розеток, но они незначительны.

При подключении розеток нам достаточно при помощи клемм сделать ответвление фазного, нулевого и заземляющего провода:

• Для этого приходящий провод разрезается и каждая жила подключается к отдельному клеммнику. Для подключения одной розетки необходимо три клеммы, двух розеток — четыре, трех — пять и так далее.
• Теперь подключаем к одной клемме фазный провод приходящего провода. Ко второй клемме подключается провод группы, идущий к другим присоединениям. К третьей клемме крепим фазный провод, идущий к нашей розетке.
• Идентично выполняем операции с нулевым и заземляющим проводом.

Подключение светильника

Подключение светильников несколько усложняется ввиду наличия включателя.

• Если вы вызвались подключать светильники своими руками, то на первом этапе делаем те же операции, что и при подключении розеток. То есть, разделываем кабель и каждую жилу подключаем к разным клеммникам. Так же можно сразу подключить провод, идущий к другим электроприемникам данной группы.
• Согласно норм ПУЭ, выключатель сети освещения должен отключать фазный провод. Поэтому от клеммника фазных проводов делаем подключение к выключателю.
• Если у вас однокнопочный выключатель, то на выходе с выключателя будет один провод. Если двух и более кнопочный, то два или более, соответственно. Мы рассмотрим однокнопочный выключатель для упрощения предоставления информации. Для двух, трех и более кнопочных выключателей схема подключения идентична.
• Провод, подключенный к выводу выключателя, отправляется обратно в распределительную коробку. Здесь мы устанавливаем еще один фазный клеммник, к которому и подключается наш провод.
• Теперь берется трехжильный провод, который подключен непосредственно к светильнику. Фазная жила этого провода подключается к фазному клеммнику провода, пришедшего от выключателя. Нулевая жила подключается к клеммнику нулевых жил, а заземляющая — к клеммнику заземляющих жил. Все, подключение нашего светильника выполнено. Если же посмотреть соответствующие видео, то данный процесс станет для вас еще более понятным.

Метод ключевых ситуаций на уроке физики «Параллельное и последовательное соединение проводников» в 8-м классе

Рассмотрены примеры использования метода ключевых ситуаций при изучении темы «Параллельное и последовательное соединение проводников» в 8 классе.

Ключевые моменты.

1. Расчет сопротивления цепи при параллельном и последовательном соединении проводников.
2. Распределение сил токов и напряжений при последовательном и параллельном соединении проводников.

Расчет сопротивления цепи при параллельном и последовательном соединении проводников

Первый уровень.

Имеется три проводника сопротивлением по 3 Ом каждый. Как надо соединить эти проводники, чтобы сопротивление цепи было максимальным? минимальным? Рассчитайте сопротивление для каждого случая.

Второй уровень.

Три одинаковых проводника соединены последовательно. Как изменится сила тока в цепи, если последовательно с ними подключить еще один проводник?

Как изменится сила тока, если к параллельно включенным проводникам добавить еще один?

Третий уровень.

Как получить сопротивления 16 Ом и 36 Ом, используя три одинаковых сопротивления по 24 Ом?

Или

Из одинаковых резисторов по 10 Ом требуется составить цепь сопротивлением 6 Ом. Какое наименьшее количество резисторов для этого потребуется?

Начертите схему цепи.

Методика решения задач

После рассмотрения закономерностей последовательного и параллельного соединения предлагается для устного решения ряд задач первого уровня.

Учитель: Рассчитайте сопротивление цепи, состоящей из двух проводников по 2 Ом, соединенных последовательно.

Ученики: При последовательном соединении проводников сопротивления складываются. Следовательно, ответ – 4 Ом.

Учитель: Каким станет сопротивление, если добавить еще один проводник 2 Ом? 10 Ом?

Ученики: 6 Ом, 14 Ом.

Если будем последовательно подключать еще проводники, как будет меняться общее сопротивление цепи?

Ученики: Увеличиваться.

Учитель: Попробуем обобщить результаты и сделать выводы. Если включаем последовательно n проводников сопротивлением R каждый, чему равно общее сопротивление цепи?

Ученики: R_общ = nR.

Учитель: Как изменяется общее сопротивление последовательно включенных проводников при подключении каждого последующего проводника?

Ученики. Увеличивается.

Учитель: Заметим также, что общее сопротивление цепи при последовательном включении проводников будет больше каждого, даже самого большого.

Рассмотрим аналогичную задачу, но проводники соединены параллельно. Итак, два проводника по 2 Ом соединены параллельно. Каково общее сопротивление цепи?

Ученики: при параллельном соединении складываются величины обратные сопротивлениям. Следовательно, воспользовавшись формулой 1/R = 1/R₁ + 1/R₂, получаем 1 Ом.

Учитель: А если величина сопротивлений по 4 Ом?

Ученики: Воспользуемся этой же формулой. Общее сопротивление цепи – 2 Ом.

Учитель: Посмотрите на результаты и скажите, как рассчитать без данной формулы общее сопротивление параллельно включенных резисторов, если их величины одинаковы?

Ученики: R_общ = R/n.

Учитель: А значит, если мы будем подключать параллельно еще резисторы, общее сопротивление будет…?

Ученики: Уменьшаться.

Учитель: Верно. А теперь добавим к нашим резисторам по 2 Ом параллельно в первом случае сопротивление 1/2 Ом, во втором — 1000 Ом. Что получим?

Ученики: Получаем в первом случае — 1/3 Ом, во втором — 1000/1001 Ом.

Учитель: Проанализируем результаты. При параллельном подключении маленького сопротивления общее сопротивление уменьшилось и стало меньше самого маленького. При подсоединении большого сопротивления общее все равно уменьшилось и его величина все равно меньше самого маленького.
Запомним наши выводы. Во-первых, при последовательном соединении одинаковых резисторов сопротивлением R общее сопротивление цепи nR, при параллельном включении — R/n. Во-вторых, при последовательном соединении общее сопротивление — больше самого большого, при параллельном – меньше самого маленького.

(В дальнейшем эти выводы пригодятся при рассмотрении причин короткого замыкания)

После этого можно предложить для устного или полу-устного решения задачи первого, второго и третьего уровней, помогая использовать при рассуждениях полученные знания.

Ученики: (Задача второго уровня) Если к последовательно подключить еще один проводник, то общее сопротивление увеличится: 4R → 5R.  I = U/R, следовательно, при неизменном напряжении сила тока уменьшится: I1 = U/4R → I2 = U/5R → сила тока уменьшится в 5/4 раз = 1,25 раз.  При параллельном соединении общее сопротивление уменьшиться: R/4 → R/5 → сила тока увеличится в 1,25 раз.

Задача третьего уровня.

Ученики: Максимальное и минимальное сопротивления, которые можно получить, используя данные резисторы – 72 Ом и 8 Ом соответственно. Значит, надо использовать оба вида соединений. Два параллельно включенных резистора дают 12 Ом + последовательно еще 24 Ом. (Рисуют схему). Два последовательно включенных дают сопротивление 48 Ом + параллельно с ними 24 Ом. Получаем 16 Ом (схема).

Учитель: В качестве домашнего задания подумайте, какие еще сопротивления можно получить. Используя данные резисторы.
Можно в качестве домашнего задания предложить вторую задачу.

Распределение сил токов и напряжений при последовательном и параллельном соединении проводников

Первый уровень.

Два резистора сопротивлением 3 Ом и 6 Ом соединены последовательно (параллельно). К концам цепи приложено напряжение 36 В. Найдите силу тока и напряжение на каждом резисторе.

Второй уровень.

Три резистора сопротивлением 3 Ом, 6 Ом и 18 Ом соединены последовательно (параллельно). К концам цепи приложено напряжение 36 В. Найдите силу тока и  напряжение на каждом резисторе.

Третий уровень.

К участку цепи приложено напряжение 6 В. Сопротивление каждого резистора 1 Ом. Сравните напряжения и силу тока в резисторах.

Методика разбора задач на уроке

1. Учитель, познакомив с закономерностями последовательного и параллельного соединения, предлагает решить задачу первого уровня. Сначала задача решается с помощью формул: R_общ = R₁+ R₂, I = U/ R_общ, I = I₁ = I₂, U₁ = IR₁, U₂ = IR₂ (или U₂ = U – U₁).
2. Затем учитель просит учеников предложить другой способ решения и подводит их к следующим рассуждениям: так как второе сопротивление в 2 раза больше, то напряжение на нем в два раза меньше, а их сумма известна и равна 36 В. Следовательно, если на первое сопротивление приходится одна часть напряжения, то на второе – две части, всего – три части. 36 В делим на три части. Получаем, что на каждую часть приходится 12 В. Следовательно, напряжение на первом резисторе равно 12 В, на втором – 24 В. То есть задача сводится к известной из курса математики «задаче на части».
3. Задачу второго уровня можно решить двумя способами для закрепления. Ученикам предложить высказаться в пользу одного или другого метода.
4. После предыдущих упражнений третью задачу можно решить устно: напряжение на резисторах 1 и 4 одинаково и равно 6 В. Следовательно, сила тока тоже одинакова и равна 6 А. Напряжение на среднем участке 6 В. Сопротивление среднего участка в два раза больше. Следовательно, сила тока в два раза меньше и равна 3 А. напряжения на резисторах 2 и 3 одинаковы и равны 3 В.
   Проверим: общее сопротивление резисторов 1 и 4 равно ½ Ом. Общее сопротивление резисторов 2 и 3 равно 2 Ом. Сопротивление всего участка 2/5 Ом. Сила тока на всем участке 15 А. Совпадает с полученным результатом 6А+6А+3А = 15 А.

Как изменяется сила тока при параллельном соединении. Последовательное и параллельное соединение проводников

Электрические цепи, с которыми приходится иметь дело на практике, обычно состоят не из одного приёмника электрического тока, а из нескольких различных, которые могут быть соединены между собой по-разному. Зная сопротивление каждого и способ их соединения, можно рассчитать общее сопротивление цепи.

На рисунке 78, а изображена цепь последовательного соединения двух электрических ламп, а на рисунке 78, б — схема такого соединения. Если выключать одну лампу, то цепь разомкнётся и другая лампа погаснет.

Рис. 78. Последовательное включение лампочек и источников питания

Последовательно соединены, например, аккумулятор, лампа, два амперметра и ключ в цепи, изображённой на рисунке 62 (см. § 38).

Мы уже знаем, что при последовательном соединении сила тока в любых частях цепи одна и та же , т. е.

А чему равно сопротивление последовательно соединённых проводников?

Соединяя проводники последовательно, мы как бы увеличиваем длину проводника. Поэтому сопротивление цепи становится больше сопротивления одного проводника.

Общее сопротивление цепи при последовательном соединении равно сумме сопротивлений отдельных проводников (или отдельных участков цепи):

Напряжение на концах отдельных участков цепи рассчитывается на основе закона Ома:

U 1 = IR 1 , U 2 = IR 2 .

Из приведённых равенств видно, что напряжение будет большим на проводнике с наибольшим сопротивлением, так как сила тока везде одинакова.

Полное напряжение в цепи при последовательном соединении, или напряжение на полюсах источника тока, равно сумме напряжений на отдельных участках цепи :

Это равенство вытекает из закона сохранения энергии. Электрическое напряжение на участке цепи измеряется работой электрического тока, совершающейся при прохождении по участку цепи электрического заряда в 1 Кл. Эта работа совершается за счёт энергии электрического поля, и энергия, израсходованная на всём участке цепи, равна сумме энергий, которые расходуются на отдельных проводниках, составляющих участок этой цепи.

Все приведённые закономерности справедливы для любого числа последовательно соединённых проводников.

Пример 1 . Два проводника сопротивлением R 1 = 2 Ом, R 2 = 3 Ом соединены последовательно. Сила тока в цепи I = 1 А. Определить сопротивление цепи, напряжение на каждом проводнике и полное напряжение всего участка цепи.

Запишем условие задачи и решим её.

Вопросы

1. Какое соединение проводников называют последовательным? Изобразите его на схеме.
2. Какая электрическая величина одинакова для всех проводников, соединённых последовательно?
3. Как найти общее сопротивление цепи, зная сопротивление отдельных проводников, при последовательном соединении?
4. Как найти напряжение участка цепи, состоящего из последовательно соединённых проводников, зная напряжение на каждом?

Упражнение

1. Цепь состоит из двух последовательно соединённых проводников, сопротивление которых 4 и 6 Ом. Сила тока в цепи 0,2 А. Найдите напряжение на каждом из проводников и общее напряжение.
2. Для электропоездов применяют напряжение 3000 В. Как можно использовать для освещения вагонов лампы, рассчитанные на напряжение 50 В каждая?
3. Две одинаковые лампы, рассчитанные на 220 В каждая, соединены последовательно и включены в сеть с напряжением 220 В. Под каким напряжением будет находиться каждая лампа?
4. Электрическая цепь состоит из источника тока — батареи аккумуляторов, создающей в цепи напряжение 6 В, лампочки от карманного фонаря сопротивлением 13,5 Ом, двух спиралей сопротивлением 3 и 2 Ом, ключа и соединительных проводов. Все детали цепи соединены последовательно. Начертите схему цепи. Определите силу тока в цепи, напряжение на концах каждого из потребителей тока.

1 Какое надо взять сопротивление R, чтобы можно было включить в сеть с напряжением V=220 В лампу, рассчитанную на напряжение Vо = 120 В и ток Iо = 4 А?

2 Две дуговые лампы и сопротивление R соединены последовательно и включены в сеть с напряжением V=110В. Найти сопротивление R, если каждая лампа рассчитана на напряжение Vо = 40 В, а ток в цепи I=12 А.

Напряжение на сопротивлении

По закону Ома

3 Для измерения напряжения на участке цепи последовательно включены два вольтметра (рис. 88). Первый вольтметр дал показание V1 = 20 В, второй- V2 = 80 В. Найти сопротивление второго вольтметра R2, если сопротивление первого вольтметра R1 = 5 кОм.

Через вольтметры протекает один и тот же ток I. Так как вольтметр показывает напряжение на собственном сопротивлении, то

и сопротивление второго вольтметра

4 Реостат из железной проволоки, миллиамперметр и источник тока включены последовательно. При температуре to = 0° С сопротивление реостата Ro = 200 Ом. Сопротивление миллиамперметра R = 20 Ом, его показание Iо = 30 мА. Какой ток It будет показывать миллиамперметр, если реостат нагреется до температуры t = 50° С? Температурный коэффициент сопротивления железа .

Последовательное и параллельное соединения проводников. Добавочные сопротивления и шунты

5 Проводник с сопротивлением R = 2000 Ом состоит из двух последовательно соединенных частей: угольного стержня и проволоки, имеющих температурные коэффициенты сопротивления . Какими следует выбрать сопротивления этих частей, чтобы общее сопротивление проводника R не зависело от температуры?

При температуре t общее сопротивление последовательно включенных частей проводника с сопротивлениями R1 и R2 будет

где R10 и R20 — сопротивления угольного стержня и проволоки при t0=0° С. Общее сопротивление проводника не зависит от температуры, если

В этом случае при любой температуре

Из последних двух уравнений найдем

6 Составить такую схему электропроводки для освещения одной лампочкой коридора, которая позволяет включать и выключать свет независимо в любом конце коридора.

Схемы электропроводки, позволяющие включать и выключать лампочку в любом конце коридора, показаны на рис. 347. У концов коридора устанавливаются два переключателя П1 и П2 каждый из которых имеет два положения. В зависимости от расположения выводов от сети может оказаться выгоднее с точки зрения экономии проводов вариант а) или б).

7 В сеть с напряжением V= 120 В включены две электрические лампочки с одинаковыми сопротивлениями R = 200 Ом. Какой ток пойдет через каждую лампочку при их параллельном и последовательном соединениях?

I1 = V/R=0,6 А при параллельном соединении; I2=V/2R=0,3 А при последовательном соединении.

8 Реостат со скользящим контактом, соединенный по схеме, приведенной на рис. 89, является потенциометром (делителем напряжения). При перемещении движка потенциометра снимаемое с него напряжение Vx изменяется от нуля до напряжения на клеммах источника тока V. Найти зависимость напряжения Vx от положения движка. Построить график этой зависимости для случая, когда полное сопротивление потенциометра Ro во много раз меньше сопротивления вольтметра r.

Пусть при данном положении движка сопротивление участка ах потенциометра равно rх (рис. 89). Тогда общее сопротивление этого участка и вольтметра (они соединены параллельно) а сопротивление остальной части потенциометра xb равно Таким образом, полное сопротивление между точками а и b будет

Ток в цепи I= V/R. Напряжение на участке ах

Так как по условию R0

т.е. напряжение Vх пропорционально сопротивлению rх. В свою очередь сопротивление rх пропорционально длине участка ах.

На рис. 348 сплошная прямая показывает зависимость Vx от rх, штрихпунктирная линия — зависимость Vx от rх, когда R0~r, т. е. когда в выражении для Vх нельзя пренебречь первым членом в знаменателе. Эта зависимость не является линейной, однако и в этом случае Vx изменяется в пределах от нуля до напряжения на клеммах источника V.

9 Найти сопротивление R биметаллического (железо- медь) провода длины l=100м. Диаметр внутренней (железной) части провода d=2 мм, общий диаметр провода D = 5 мм. Удельные сопротивления железа и меди . Для сравнения найти сопротивления железного и медного проводов Яж и Rм диаметра D и длины l.

Площади сечения железной и медной частей провода

(рис. 349). Их сопротивления

Сопротивление R биметаллического провода находится по формуле параллельного соединения проводников:

Сопротивления железного и медного проводов диаметра D и длины l

10 Найти общее сопротивление проводников, включенных в цепь по схеме, изображенной на рис. 90, если сопротивления R1= = R2 = R5 = Я6 = 1 Ом, R3 = 10 Ом, R4 = 8 Ом.

11 Общее сопротивление двух последовательно соединенных проводников R=5 Ом, а параллельно соединенных Rо=1,2 Ом. Найти сопротивление каждого проводника.

При последовательном соединении двух проводников с сопротивлениями R1 и R2 их общее сопротивление

а при параллельном соединении

Согласно известному свойству приведенного квадратного уравнения (теорема Виета) сумма корней этого уравнения равна второму его коэффициенту с обратным знаком, а произведение корней-свободному члену, т. е. R1 и R2 должны быть корнями квадратного уравнения

Подставив значения Rо и R, найдем R1 = З Ом и R2 = 2 0м (или R1 =2 Ом и R2 = 3 Ом).

12 К проволочному кольцу в двух точках присоединены подводящие ток провода. В каком отношении делят точки присоединения длину окружности кольца, если общее сопротивление получившейся цепи в n = 4,5 раза меньше сопротивления проволоки, из которой сделано кольцо?

Точки присоединения подводящих проводов делят длину окружности кольца в отношении 1:2, т. е. отстоят друг от друга по дуге на 120град.

13 В цепи, изображенной на рис. 91, амперметр показывает ток I=0,04 А, а вольтметр — напряжение V=20 В. Найти сопротивление вольтметра R2, если сопротивление проводника R1 = 1 кОм.

14 Найти сопротивление R1 лампочки по показаниям вольтметра (V=50 В) и амперметра (I=0,5 А), включенных по схеме, изображенной на рис. 92, если сопротивление вольтметра R2 = 40 кОм.

Ток в общей цепи I=I1+I2, где I1 и I2 — токи, текущие через лампочку и вольтметр. Так как

Пренебрегая током I2 = 1,25мА по сравнению с I=0,5 А получим по приближенной формуле

то же значение сопротивления лампочки: R1 = 100 Ом.

15 Найти сопротивление проводника R1 по показаниям амперметра (I=5 А) и вольтметра (V=100В), включенных по схеме, изображенной на рис. 93, если сопротивление вольтметра R2 = 2,5 кОм. Какова будет ошибка в определении R1, если, предположив, что , при расчетах пренебречь током, текущим через вольтметр?

Показание вольтметра

где I1 и I2-токи, текущие через сопротивление и вольтметр. Общий ток

Если пренебречь током I2 по сравнению с I, то искомое сопротивление

Ошибка в определении R`1 будет

Учитывая, что

найдем относительную ошибку:

16 К источнику тока с напряжением V присоединены последовательно два проводника с одинаковыми сопротивлениями R. Какова будет разница в показаниях вольтметров с сопротивлениями R и 10R, если их поочередно подключать к концам одного из проводников?

Вольтметры с сопротивлениями R и 10R показывают напряжения

поэтому разница в показаниях вольтметров

17 К источнику тока с напряжением V= 12 В присоединены две лампочки (рис. 94). Сопротивления участков цепи r1 = r2 = r3 = r4 = г = 1,5 Ом. Сопротивления лампочек R1 = R2 = R = 36 Ом. Найти напряжение на каждой лампочке.

18 В схеме, изображенной на рис. 95, напряжение источника тока V=200 В, а сопротивления проводников R1=60Ом, R2 = R3 = 30 Ом. Найти напряжение на сопротивлении R1.

19 Электрическая цепь состоит из источника тока с напряжением V=180В и потенциометра с полным сопротивлением R = 5 кОм. Найти показания вольтметров, присоединенных к потенциометру по схеме, изображенной на рис. 96. Сопротивления вольтметров R1=6 кОм и R2 = 4кОм. Движок x стоит посередине потенциометра.

20 Три резистора включены по схеме, изображенной на рис. 97. Если резисторы включены в цепь в точках а и b, то сопротивление цепи будет R = 20 Ом, а если в точках а и с, то сопротивление цепи будет Rо = 15 Oм. Найти сопротивления резисторов R1, R2, R3, если R1=2R2.

Эквивалентные схемы включения изображены на рис. 350. Сопротивления реостатов

21 На сколько равных частей нужно разрезать проводник, имеющий сопротивление R = 36 Ом, сопротивление его частей, соединенных параллельно, было Ro — 1 Ом?

Весь проводник имеет сопротивление R = nr, где r-сопротивление каждой из п равных частей проводника. При параллельном соединении п одинаковых проводников их общее сопротивление R0 = r/n. Исключая r, получим

n может быть лишь целым положительным числом, большим единицы. Поэтому решения возможны только в случаях, когда R/Rо = 4, 9, 16, 25, 36,… В нашем случае

22 Из проволоки сделан каркас в форме куба (рис. 98), каждое ребро которого имеет сопротивление r. Найти сопротивление R этого каркаса, если ток I в общей цепи идет от вершины А к вершине В.

На участках Аа и bВ (рис. 351), ввиду равенства сопротивлений ребер куба и их одинакового включения, ток I равномерно разветвляется по трем ветвям и поэтому в каждой из них равен I/3. На участках ab ток равен I/6, так как в каждой точке а ток вновь разветвляется по двум ребрам с равными сопротивлениями и все эти ребра включены одинаково.

Напряжение между точками А и В складывается из напряжения на участке Аа, напряжения на участке ab и напряжения на участке bВ:

23 Из проволоки, единица длины которой имеет сопротивление Rl, сделан каркас в форме окружности радиуса r, пересеченной двумя взаимно перпендикулярными диаметрами (рис. 99). Найти сопротивление Rx каркаса, если источник тока подключен к точкам c и d.

Если источник тока подключен к точкам с и d, то напряжения на участках da и ab равны, поскольку проволока

однородна. Следовательно, разность потенциалов между точками а и b равна нулю. Ток на этом участке отсутствует. Поэтому наличие или отсутствие контакта в точке пересечения проводников ab и cd безразлично. Сопротивление Rx, таким образом, представляет собой сопротивление трех параллельно включенных проводников: cd с сопротивлением 2rR1, cad и cbd с одинаковыми сопротивлениями prR1. Из соотношения

24 Провод длины L=1 м сплетен из трех жил, каждая из которых представляет собой кусок неизолированной проволоки с сопротивлением единицы длины Rl = 0,02 Ом/м. На концах провода создано напряжение V=0,01 В. На какую величину DI изменится ток в этом проводе, если от одной жилы удалить кусок длины l=20 см?

25 Источник тока первоначально присоединяют к двум соседним вершинам проволочной рамки в форме правильного выпуклого n-угольника. Затем источник тока присоединяют к вершинам, расположенным через одну. При этом ток уменьшается в 1,5 раза. Найти число сторон n-угольника.

26 Как надо соединить четыре проводника с сопротивлениями R1 = 10м, R2 = 2 0м, R3 = 3 Ом и R4 = 4 0м, чтобы получить сопротивление R = 2,5 Ом?

Сопротивление R = 2,5 Ом достигается, когда проводники включены по схеме сметанного соединения (рис. 352).

27 Найти проводимость k цепи, состоящей из двух последовательных групп параллельно включенных проводников. Проводимости каждого проводника первой и второй групп равны k1=0,5Cм и k2 = 0,25 См. Первая группа состоит из четырех проводников, вторая- из двух.

28 Вольтметр рассчитан на измерение напряжений до максимального значения Vо = 30 В. При этом через вольтметр идет ток I=10 мА. Какое добавочное сопротивление Rд нужно присоединить к вольтметру, чтобы им можно было измерять напряжения до V=150В?

Для измерения вольтметром более высоких напряжений, чем те, на которые рассчитана шкала, необходимо включить последовательно с вольтметром добавочное сопротивление Rд (рис. 353). Напряжение на этом сопротивлении Vд=V-Vо; поэтому сопротивление Rд=(V-Vо)/I=12 кОм.

29 Стрелка миллиамперметра отклоняется до конца шкалы, если через миллиамперметр идет ток I=0,01 А. Сопротивление прибора R = 5 0м. Какое добавочное сопротивление Rд нужно присоединить к прибору, чтобы его можно было использовать в качестве вольтметра с пределом измерения напряжений V= 300 В?

Для измерения прибором напряжений, не превышающих V, необходимо последовательно с ним включить такое добавочное сопротивление Rд, чтобы V=I(R + Rд), где I-максимальный ток через прибор; отсюда Rд= V/I-R30 кОм.

30 Вольтметр, соединенный последовательно с сопротивлением R1 = 10 кОм, при включении в сеть с напряжением V=220 В показывает напряжение V1 = 70 В, а соединенный последовательно с сопротивлением R2, показывает напряжение V2 = 20 В. Найти сопротивление R2.

31 Вольтметр с сопротивлением R = 3 кОм, включенный в городскую осветительную сеть, показал напряжение V=125В. При включении вольтметра в сеть через сопротивление Ro его показание уменьшилось до Vо = 115 В. Найти это сопротивление.

Городская осветительная сеть представляет собой источник тока, обладающий внутренним сопротивлением, намного меньшим сопротивления вольтметра R. Поэтому напряжение V=125 В, которое показывал вольтметр при непосредственном включении в сеть, равно напряжению источника тока. Это значит, что оно не изменяется и при включении вольтметра в сеть через сопротивление Rо. Поэтому V=I(R + Rо), где I=Vо/R — ток, текущий через вольтметр; отсюда Rо = (V-Vо)R/Vо = 261 Ом.

32 Вольтметр с сопротивлением R = 50 кОм, подключенный к источнику тока вместе с добавочным сопротивлением Rд = 120 кОм, показывает напряжение Vо =100 В. Найти напряжение V источника тока.

Ток, текущий через вольтметр и добавочное сопротивление, I=Vо/R. Напряжение источника тока V=I(R+Rд)= (R+Rд)Vо/R = 340 В.

33 Найти показание вольтметра V с сопротивлением R в цепи, изображенной на рис. 100. Ток до разветвления равен I, сопротивления проводников R1 и R2 известны.

34 Имеется прибор с ценой деления i0=1 мкА/дел и числом делений шкалы N= 100. Сопротивление прибора R = 50 Ом. Как этот прибор приспособить для измерения токов до значения I=10 мА или напряжений до значения V= 1 В?

Для измерения более высоких токов чем те, на которые рассчитана шкала, параллельно прибору включается шунт с сопротивлением

для измерения напряжений последовательно с прибором включается добавочное сопротивление — ток, текущий через прибор при максимальном отклонении стрелки,

Напряжение на его клеммах в этом случае.

35 Миллиамперметр с пределом измерения токов I0 = 25 мА необходимо использовать как амперметр с пределом измерения токов I=5 А. Какое сопротивление Rш должен иметь шунт? Во сколько раз уменьшается чувствительность прибора? Сопротивление прибора R=10 Oм.

При включении параллельно прибору шунта (рис. 354) ток I должен делиться так, чтобы через миллиамперметр протекал ток Iо. Через шунт при этом течет ток Iш, т.е. I=Iо + Iш. Напряжения на шунте и на миллиамперметре равны: IоR = IшRш; отсюда

Rш=IоR/(I-Iо)0,05 Ом. Чувствительность прибора уменьшается, а цена деления прибора увеличивается в n=I/Iо=200 раз.

36 Амперметр с сопротивлением R = 0,2 Ом, накоротко присоединенный к источнику тока с напряжением V=1,5B, показывает ток I=5А. Какой ток I0 покажет амперметр, если его зашунтировать сопротивлением Rш=0,1 Ом?

37 При шунтировании гальванометра сопротивлениями R1, R2 и R3 в них ответвляется 90%, 99% и 99,9% тока I общей цепи. Найти эти сопротивления, если сопротивление гальванометра R = 27 Ом.

Так как шунты присоединяются к гальванометру параллельно, то условие равенства напряжений на гальванометре и на шунтах дает

38 Миллиамперметр с числом делений шкалы N=50 имеет цену деления i0 = 0,5 мА/дел и сопротивление R = 200 Ом. Как этот прибор приспособить для измерения токов до значения I= 1 А?

Наибольший ток, протекающий через прибор, Iо = iоN. Для измерения токов, значительно превышающих ток Iо, необходимо параллельно прибору включить шунт, сопротивление которого Rш значительно меньше сопротивления миллиамперметра R:

39 К амперметру с сопротивлением R = 0,1 Ом подключен шунт с сопротивлением Rш= 11,1 мОм. Найти ток, текущий через амперметр, если ток в общей цепи I=27 А.

Ток, текущий через шунт, Iш = I-Iо. Падения напряжения на шунте и амперметре равны: IшRш = IоR; отсюда Iо=IRш/(R+Rш) =2,7 А.

Содержание:

Течение тока в электрической цепи осуществляется по проводникам, в направлении от источника к потребителям. В большинстве подобных схем используются медные провода и электрические приемники в заданном количестве, обладающие различным сопротивлением. В зависимости выполняемых задач, в электрических цепях используется последовательное и параллельное соединение проводников. В некоторых случаях могут быть применены оба типа соединений, тогда этот вариант будет называться смешанным. Каждая схема имеет свои особенности и отличия, поэтому их нужно обязательно заранее учитывать при проектировании цепей, ремонте и обслуживании электрооборудования.

Последовательное соединение проводников

В электротехнике большое значение имеет последовательное и параллельное соединение проводников в электрической цепи. Среди них часто используется схема последовательного соединения проводников предполагающая такое же соединение потребителей. В этом случае включение в цепь выполняется друг за другом в порядке очередности. То есть, начало одного потребителя соединяется с концом другого при помощи проводов, без каких-либо ответвлений.

Свойства такой электрической цепи можно рассмотреть на примере участков цепи с двумя нагрузками. Силу тока, напряжение и сопротивление на каждом из них следует обозначить соответственно, как I1, U1, R1 и I2, U2, R2. В результате, получились соотношения, выражающие зависимость между величинами следующим образом: I = I1 = I2, U = U1 + U2, R = R1 + R2. Полученные данные подтверждаются практическим путем с помощью проведения измерений амперметром и вольтметром соответствующих участков.

Таким образом, последовательное соединение проводников отличается следующими индивидуальными особенностями:

• Сила тока на всех участках цепи будет одинаковой.
• Общее напряжение цепи составляет сумму напряжений на каждом участке.
• Общее сопротивление включает в себя сопротивления каждого отдельного проводника.

Данные соотношения подходят для любого количества проводников, соединенных последовательно. Значение общего сопротивления всегда выше, чем сопротивление любого отдельно взятого проводника. Это связано с увеличением их общей длины при последовательном соединении, что приводит и к росту сопротивления.

Если соединить последовательно одинаковые элементы в количестве n, то получится R = n х R1, где R — общее сопротивление, R1 — сопротивление одного элемента, а n — количество элементов. Напряжение U, наоборот, делится на равные части, каждая из которых в n раз меньше общего значения. Например, если в сеть с напряжением 220 вольт последовательно включаются 10 ламп одинаковой мощности, то напряжение в любой из них составит: U1 = U/10 = 22 вольта.

Проводники, соединенные последовательно, имеют характерную отличительную особенность. Если во время работы отказал хотя-бы один из них, то течение тока прекращается во всей цепи. Наиболее ярким примером является , когда одна перегоревшая лампочка в последовательной цепи, приводит к выходу из строя всей системы. Для установления перегоревшей лампочки понадобится проверка всей гирлянды.

Параллельное соединение проводников

В электрических сетях проводники могут соединяться различными способами: последовательно, параллельно и комбинированно. Среди них параллельное соединение это такой вариант, когда проводники в начальных и конечных точках соединяются между собой. Таким образом, начала и концы нагрузок соединяются вместе, а сами нагрузки располагаются параллельно относительно друг друга. В электрической цепи могут содержаться два, три и более проводников, соединенных параллельно.

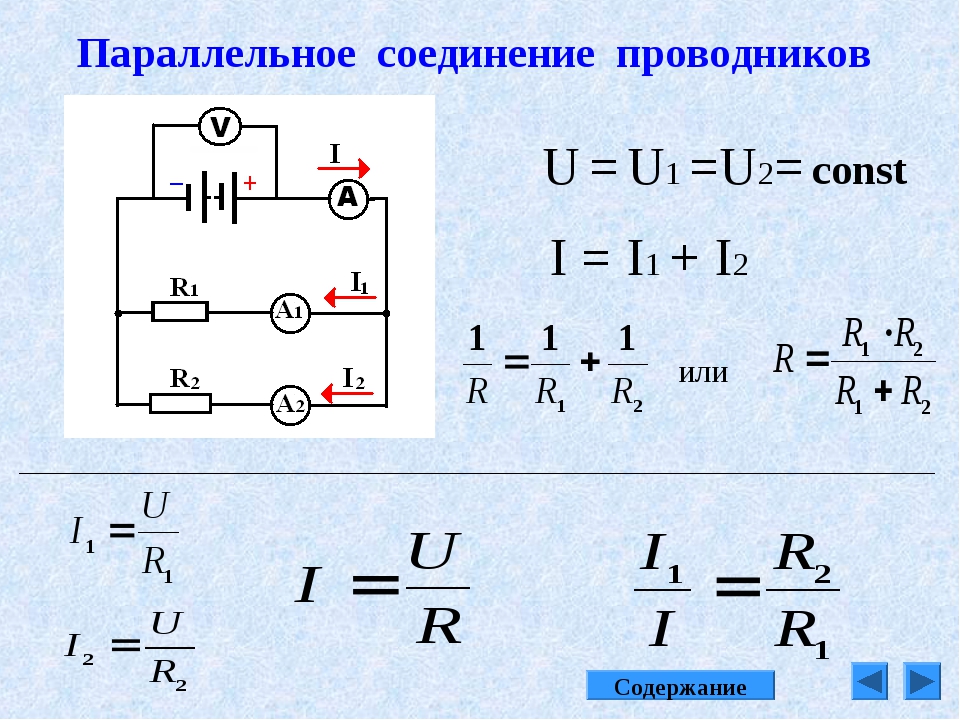
Если рассматривать последовательное и параллельное соединение, сила тока в последнем варианте может быть исследована с помощью следующей схемы. Берутся две лампы накаливания, обладающие одинаковым сопротивлением и соединенные параллельно. Для контроля к каждой лампочке подключается собственный . Кроме того, используется еще один амперметр, контролирующий общую силу тока в цепи. Проверочная схема дополняется источником питания и ключом.

После замыкания ключа нужно контролировать показания измерительных приборов. Амперметр на лампе № 1 покажет силу тока I1, а на лампе № 2 — силу тока I2. Общий амперметр показывает значение силы тока, равное сумме токов отдельно взятых, параллельно соединенных цепей: I = I1 + I2. В отличие от последовательного соединения, при перегорании одной из лампочек, другая будет нормально функционировать. Поэтому в домашних электрических сетях используется параллельное подключение приборов.

С помощью такой же схемы можно установить значение эквивалентного сопротивления. С этой целью в электрическую цепь добавляется вольтметр. Это позволяет измерить напряжение при параллельном соединении, сила тока при этом остается такой же. Здесь также имеются точки пересечения проводников, соединяющих обе лампы.

В результате измерений общее напряжение при параллельном соединении составит: U = U1 = U2. После этого можно рассчитать эквивалентное сопротивление, условно заменяющее все элементы, находящиеся в данной цепи. При параллельном соединении, в соответствии с законом Ома I = U/R, получается следующая формула: U/R = U1/R1 + U2/R2, в которой R является эквивалентным сопротивлением, R1 и R2 — сопротивления обеих лампочек, U = U1 = U2 — значение напряжения, показываемое вольтметром.

Следует учитывать и тот фактор, что токи в каждой цепи, в сумме составляют общую силу тока всей цепи. В окончательном виде формула, отражающая эквивалентное сопротивление будет выглядеть следующим образом: 1/R = 1/R1 + 1/R2. При увеличении количества элементов в таких цепях — увеличивается и число слагаемых в формуле. Различие в основных параметрах отличают друг от друга и источников тока, позволяя использовать их в различных электрических схемах.

Параллельное соединение проводников характеризуется достаточно малым значением эквивалентного сопротивления, поэтому сила тока будет сравнительно высокой. Данный фактор следует учитывать, когда в розетки включается большое количество электроприборов. В этом случае сила тока значительно возрастает, приводя к перегреву кабельных линий и последующим возгораниям.

Законы последовательного и параллельного соединения проводников

Данные законы, касающиеся обоих видов соединений проводников, частично уже были рассмотрены ранее.

Для более четкого их понимания и восприятия в практической плоскости, последовательное и параллельное соединение проводников, формулы следует рассматривать в определенной последовательности:

• Последовательное соединение предполагает одинаковую силу тока в каждом проводнике: I = I1 = I2.
• параллельное и последовательное соединение проводников объясняет в каждом случае по-своему. Например, при последовательном соединении, напряжения на всех проводниках будут равны между собой: U1 = IR1, U2 = IR2. Кроме того, при последовательном соединении напряжение составляет сумму напряжений каждого проводника: U = U1 + U2 = I(R1 + R2) = IR.
• Полное сопротивление цепи при последовательном соединении состоит из суммы сопротивлений всех отдельно взятых проводников, независимо от их количества.
• При параллельном соединении напряжение всей цепи равно напряжению на каждом из проводников: U1 = U2 = U.
• Общая сила тока, измеренная во всей цепи, равна сумме токов, протекающих по всем проводникам, соединенных параллельно между собой: I = I1 + I2.

Для того чтобы более эффективно проектировать электрические сети, нужно хорошо знать последовательное и параллельное соединение проводников и его законы, находя им наиболее рациональное практическое применение.

Смешанное соединение проводников

В электрических сетях как правило используется последовательное параллельное и смешанное соединение проводников, предназначенное для конкретных условий эксплуатации. Однако чаще всего предпочтение отдается третьему варианту, представляющему собой совокупность комбинаций, состоящих из различных типов соединений.

В таких смешанных схемах активно применяется последовательное и параллельное соединение проводников, плюсы и минусы которых обязательно учитываются при проектировании электрических сетей. Эти соединения состоят не только из отдельно взятых резисторов, но и довольно сложных участков, включающих в себя множество элементов.

Смешанное соединение рассчитывается в соответствии с известными свойствами последовательного и параллельного соединения. Метод расчета заключается в разбивке схемы на более простые составные части, которые считаются отдельно, а потом суммируются друг с другом.

Последовательным называют такое соединение элементов цепи, при котором во всех включенных в цепь элементах возникает один и тот же ток I (рис. 1.4).

На основании второго закона Кирхгофа (1.5) общее напряжение U всей цепи равно сумме напряжений на отдельных участках:

U = U 1 + U 2 + U 3 или IR экв = IR 1 + IR 2 + IR 3 ,

откуда следует

R экв = R 1 + R 2 + R 3 .

Таким образом, при последовательном соединении элементов цепи общее эквивалентное сопротивление цепи равно арифметической сумме сопротивлений отдельных участков. Следовательно, цепь с любым числом последовательно включенных сопротивлений можно заменить простой цепью с одним эквивалентным сопротивлением R экв (рис. 1.5). После этого расчет цепи сводится к определению тока I всей цепи по закону Ома

и по вышеприведенным формулам рассчитывают падение напряжений U 1 , U 2 , U 3 на соответствующих участках электрической цепи (рис. 1.4).

Недостаток последовательного включения элементов заключается в том, что при выходе из строя хотя бы одного элемента, прекращается работа всех остальных элементов цепи.

Электрическая цепь с параллельным соединением элементов

Параллельным называют такое соединение, при котором все включенные в цепь потребители электрической энергии, находятся под одним и тем же напряжением (рис. 1.6).

В этом случае они присоединены к двум узлам цепи а и b, и на основании первого закона Кирхгофа можно записать, что общий ток I всей цепи равен алгебраической сумме токов отдельных ветвей:

I = I 1 + I 2 + I 3 , т.е.

откуда следует, что

.

В том случае, когда параллельно включены два сопротивления R 1 и R 2 , они заменяются одним эквивалентным сопротивлением

.

Из соотношения (1.6), следует, что эквивалентная проводимость цепи равна арифметической сумме проводимостей отдельных ветвей:

g экв = g 1 + g 2 + g 3 .

По мере роста числа параллельно включенных потребителей проводимость цепи g экв возрастает, и наоборот, общее сопротивление R экв уменьшается.

Напряжения в электрической цепи с параллельно соединенными сопротивлениями (рис. 1.6)

U = IR экв = I 1 R 1 = I 2 R 2 = I 3 R 3 .

Отсюда следует, что

т.е. ток в цепи распределяется между параллельными ветвями обратно пропорционально их сопротивлениям.

По параллельно включенной схеме работают в номинальном режиме потребители любой мощности, рассчитанные на одно и то же напряжение. Причем включение или отключение одного или нескольких потребителей не отражается на работе остальных. Поэтому эта схема является основной схемой подключения потребителей к источнику электрической энергии.

Электрическая цепь со смешанным соединением элементов

Смешанным называется такое соединение, при котором в цепи имеются группы параллельно и последовательно включенных сопротивлений.

Для цепи, представленной на рис. 1.7, расчет эквивалентного сопротивления начинается с конца схемы. Для упрощения расчетов примем, что все сопротивления в этой схеме являются одинаковыми: R 1 =R 2 =R 3 =R 4 =R 5 =R. Сопротивления R 4 и R 5 включены параллельно, тогда сопротивление участка цепи cd равно:

.

В этом случае исходную схему (рис. 1.7) можно представить в следующем виде (рис. 1.8):

На схеме (рис. 1.8) сопротивление R 3 и R cd соединены последовательно, и тогда сопротивление участка цепи ad равно:

.

Тогда схему (рис. 1.8) можно представить в сокращенном варианте (рис. 1.9):

На схеме (рис. 1.9) сопротивление R 2 и R ad соединены параллельно, тогда сопротивление участка цепи аb равно

.

Схему (рис. 1.9) можно представить в упрощенном варианте (рис. 1.10), где сопротивления R 1 и R ab включены последовательно.

Тогда эквивалентное сопротивление исходной схемы (рис. 1.7) будет равно:

Рис. 1.10

Рис. 1.11

В результате преобразований исходная схема (рис. 1.7) представлена в виде схемы (рис. 1.11) с одним сопротивлением R экв. Расчет токов и напряжений для всех элементов схемы можно произвести по законам Ома и Кирхгофа.

ЛИНЕЙНЫЕ ЦЕПИ ОДНОФАЗНОГО СИНУСОИДАЛЬНОГО ТОКА.

Получение синусоидальной ЭДС. . Основные характеристики синусоидального тока

Основным преимуществом синусоидальных токов является то, что они позволяют наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Целесообразность их использования обусловлена тем, что коэффициент полезного действия генераторов, электрических двигателей, трансформаторов и линий электропередач в этом случае оказывается наивысшим.

Для получения в линейных цепях синусоидально изменяющихся токов необходимо, чтобы э. д. с. также изменялись по синусоидальному закону. Рассмотрим процесс возникновения синусоидальной ЭДС. Простейшим генератором синусоидальной ЭДС может служить прямоугольная катушка (рамка), равномерно вращающаяся в однородном магнитном поле с угловой скоростью ω (рис. 2.1, б ).

Пронизывающий катушку магнитный поток во время вращения катушки abcd наводит (индуцирует) в ней на основании закона электромагнитной индукции ЭДС е . Нагрузку подключают к генератору с помощью щеток 1 , прижимающихся к двум контактным кольцам 2 , которые, в свою очередь, соединены с катушкой. Значение наведенной в катушке abcd э. д. с. в каждый момент времени пропорционально магнитной индукции В , размеру активной части катушки l = ab + dc и нормальной составляющей скорости перемещения ее относительно поля v н :

e = Blv н (2.1)

где В и l — постоянные величины, a v н — переменная, зависящая от угла α. Выразив скорость v н через линейную скорость катушки v , получим

e = Blv·sinα (2.2)

В выражении (2.2) произведение Blv = const. Следовательно, э. д. с., индуцируемая в катушке, вращающейся в магнитном поле, является синусоидальной функцией угла α .

Если угол α = π/2 , то произведение Blv в формуле (2.2) есть максимальное (амплитудное) значение наведенной э. д. с. E m = Blv . Поэтому выражение (2.2) можно записать в виде

e = E m sinα (2.3)

Так как α есть угол поворота за время t , то, выразив его через угловую скорость ω , можно записать α = ωt , a формулу (2.3) переписать в виде

e = E m sinωt (2.4)

где е — мгновенное значение э. д. с. в катушке; α = ωt — фаза, характеризующая значение э. д. с. в данный момент времени.

Необходимо отметить, что мгновенную э. д. с. в течение бесконечно малого промежутка времени можно считать величиной постоянной, поэтому для мгновенных значений э. д. с. е , напряжений и и токов i справедливы законы постоянного тока.

Синусоидальные величины можно графически изображать синусоидами и вращающимися векторами. При изображении их синусоидами на ординате в определенном масштабе откладывают мгновенные значения величин, на абсциссе — время. Если синусоидальную величину изображают вращающимися векторами, то длина вектора в масштабе отражает амплитуду синусоиды, угол, образованный с положительным направлением оси абсцисс, в начальный момент времени равен начальной фазе, а скорость вращения вектора равна угловой частоте. Мгновенные значения синусоидальных величин есть проекции вращающегося вектора на ось ординат. Необходимо отметить, что за положительное направление вращения радиус-вектора принято считать направление вращения против часовой стрелки. На рис. 2.2 построены графики мгновенных значений э. д. с. е и е» .

Если число пар полюсов магнитов p ≠ 1 , то за один оборот катушки (см. рис. 2.1) происходит p полных циклов изменения э. д. с. Если угловая частота катушки (ротора) n оборотов в минуту, то период уменьшится в pn раз. Тогда частота э. д. с., т. е. число периодов в секунду,

f = Pn / 60

Из рис. 2.2 видно, что ωТ = 2π , откуда

ω = 2π / T = 2πf (2.5)

Величину ω , пропорциональную частоте f и равную угловой скорости вращения радиус-вектора, называют угловой частотой. Угловую частоту выражают в радианах в секунду (рад/с) или в 1 / с.

Графически изображенные на рис. 2.2 э. д. с. е и е» можно описать выражениями

e = E m sinωt; e» = E» m sin(ωt + ψ e» ) .

Здесь ωt и ωt + ψ e» — фазы, характеризующие значения э. д. с. e и e» в заданный момент времени; ψ e» — начальная фаза, определяющая значение э. д. с. е» при t = 0. Для э. д. с. е начальная фаза равна нулю (ψ e = 0 ). Угол ψ всегда отсчитывают от нулевого значения синусоидальной величины при переходе ее от отрицательных значений к положительным до начала координат (t = 0). При этом положительную начальную фазу ψ (рис. 2.2) откладывают влево от начала координат (в сторону отрицательных значений ωt ), а отрицательную фазу — вправо.

Если у двух или нескольких синусоидальных величин, изменяющихся с одинаковой частотой, начала синусоид не совпадают по времени, то они сдвинуты друг относительно друга по фазе, т. е. не совпадают по фазе.

Разность углов φ , равная разности начальных фаз, называют углом сдвига фаз. Сдвиг фаз между одноименными синусоидальными величинами, например между двумя э. д. с. или двумя токами, обозначают α . Угол сдвига фаз между синусоидами тока и напряжения или их максимальными векторами обозначают буквой φ (рис. 2.3).

Когда для синусоидальных величин разность фаз равна ±π , то они противоположны по фазе, если же разность фаз равна ±π/2 , то говорят, что они находятся в квадратуре. Если для синусоидальных величин одной частоты начальные фазы одинаковы, то это означает, что они совпадают по фазе.

Синусоидальные напряжение и ток, графики которых представлены на рис. 2.3, описываются следующим образом:

u = U m sin(ω t + ψ u ) ; i = I m sin(ω t + ψ i ) , (2.6)

причем угол сдвига фаз между током и напряжением (см. рис. 2.3) в этом случае φ = ψ u — ψ i .

Уравнения (2.6) можно записать иначе:

u = U m sin(ωt + ψ i + φ) ; i = I m sin(ωt + ψ u — φ) ,

поскольку ψ u = ψ i + φ и ψ i = ψ u — φ .

Из этих выражений следует, что напряжение опережает по фазе ток на угол φ (или ток отстает по фазе от напряжения на угол φ ).

Формы представления синусоидальных электрических величин.

Любая, синусоидально изменяющаяся, электрическая величина (ток, напряжение, ЭДС) может быть представлена в аналитическом, графическом и комплексном видах.

1). Аналитическая форма представления

I = I m ·sin(ω·t + ψ i ), u = U m ·sin(ω·t + ψ u ), e = E m ·sin(ω·t + ψ e ),

где I , u , e – мгновенное значение синусоидального тока, напряжения, ЭДС, т. е. Значения в рассматриваемый момент времени;

I m , U m , E m – амплитуды синусоидального тока, напряжения, ЭДС;

(ω·t + ψ ) – фазовый угол, фаза; ω = 2·π/Т – угловая частота, характеризующая скорость изменения фазы;

ψ i , ψ u , ψ e – начальные фазы тока, напряжения, ЭДС отсчитываются от точки перехода синусоидальной функции через нуль к положительному значению до начала отсчета времени (t = 0). Начальная фаза может иметь как положительное так и отрицательное значение.

Графики мгновенных значений тока и напряжения показаны на рис. 2.3

Начальная фаза напряжения сдвинута влево от начала отсчёта и является положительной ψ u > 0, начальная фаза тока сдвинута вправо от начала отсчёта и является отрицательной ψ i φ . Сдвиг фаз между напряжением и током

φ = ψ u – ψ i = ψ u – (- ψ i) = ψ u + ψ i .

Применение аналитической формы для расчёта цепей является громоздкой и неудобной.

На практике приходится иметь дело не с мгновенными значениями синусоидальных величин, а с действующими. Все расчёты проводят для действующих значений, в паспортных данных различных электротехнических устройств указаны действующие значения (тока, напряжения), большинство электроизмерительных приборов показывают действующие значения. Действующий ток является эквивалентом постоянного тока, который за одно и то же время выделяет в резисторе такое же количество тепла, как и переменный ток. Действующее значение связано с амплитудным простым соотношением

2). Векторная форма представления синусоидальной электрической величины – это вращающийся в декартовой системе координат вектор с началом в точке 0, длина которого равна амплитуде синусоидальной величины, угол относительно оси х – её начальной фазе, а частота вращения – ω = 2πf . Проекция данного вектора на ось у в любой момент времени определяет мгновенное значение рассматриваемой величины.

Рис. 2.4

Совокупность векторов, изображающих синусоидальные функции, называют векторной диаграммой, рис. 2.4

3). Комплексное представление синусоидальных электрических величин сочетает наглядность векторных диаграмм с проведением точных аналитических расчётов цепей.

Рис. 2.5

Ток и напряжение изобразим в виде векторов на комплексной плоскости, рис.2.5 Ось абсцисс называют осью действительных чисел и обозначают +1 , ось ординат называют осью мнимых чисел и обозначают +j . (В некоторых учебниках ось действительных чисел обозначают Re , а ось мнимых – Im ). Рассмотрим векторы U и I в момент времени t = 0. Каждому из этих векторов соответствует комплексное число, которое может быть представлено в трех формах:

а). Алгебраической

U = U ’+ jU «

I = I ’ – jI «,

где U «, U «, I «, I » – проекции векторов на оси действительных и мнимых чисел.

б). Показательной

где U , I – модули (длины) векторов; е – основание натурального логарифма; поворотные множители, т. к. умножение на них соответствует повороту векторов относительно положительного направления действительной оси на угол, равный начальной фазе.

в). Тригонометрической

U = U ·(cosψ u + j sinψ u)

I = I ·(cosψ i – j sinψ i).

При решении задач в основном применяют алгебраическую форму (для операций сложения и вычитания) и показательную форму (для операций умножения и деления). Связь между ними устанавливается формулой Эйлера

е j ·ψ = cosψ + j sinψ .

Неразветвлённые электрические цепи

Основы > Задачи и ответы > Постоянный электрический ток

Последовательное и параллельное соединения источников тока
Правило Кирхгофа

1 Найти разность потенциалов между точками а и b в схеме, изображенной на рис. 118. Э. д. с. источников тока e 1 = 1 В и e 2 =1,3 В, сопротивления резисторов R 1 = 10 Ом и R 2 = 5 Ом.
Решение:
Поскольку e 2 > e 1 то ток I будет идти в направлении, указанном на рис. 118, при этом разность потенциалов между точками а и b

2 Два элемента с э. д. с. e 1 = 1 ,5 B и e 2 r1 =0,6 Ом и r 2 = 0,4 Ом соединены по схеме, изображенной на рис. 119. Какую разность потенциалов между точками а и b покажет вольтметр, если сопротивление вольтметра велико по сравнению с внутренними сопротивлениями элементов?

Решение:
Поскольку e 2 > e 1 , то ток I будет идти в направлении, указанном на рис. 119. Током через вольтметр пренебрегаем ввиду
того, что его сопротивление велико по сравнению с внутренними сопротивлениями элементов. Падение напряжения на внутренних сопротивлениях элементов должно равняться разности э. д. с. элементов, так как они включены навстречу друг другу:
отсюда

Разность потенциалов между точками а и b (показание вольтметра)

3 Два элемента с э. д. с. e 1 =1.4B и e 2 = 1,1 В и внутренними сопротивлениями r =0,3 Ом и r 2 = 0,2 Ом замкнуты разноименными полюсами (рис. 120). Найти напряжение на зажимах элементов. При каких условиях разность потенциалов между точками а и b равна нулю?

Решение:

4 Два источника тока с одинаковыми э. д. с. e = 2 В и внутренними сопротивлениями r1 =0,4 Ом и r 2 = 0,2 Ом соединены последовательно. При каком внешнем сопротивлении цепи R напряжение на зажимах одного из источников будет равным нулю?

Решение:
Ток в цепи

(рис.361). Напряжения на зажимах источников тока

Решая первые два уравнения при условии V1=0, получим

Условие V2=0 неосуществимо, так как совместное решение первого и третьего уравнений приводит к значению R

5 Найти внутреннее сопротивление r1 первого элемента в схеме, изображенной на рис. 121, если напряжение на его зажимах равно нулю. Сопротивления резисторов R 1 = ЗОм, R 2 = 6 0м, внутреннее сопротивление второго элемента r 2 = 0,4 Ом, э. д. с. элементов одинаковы.

Решение:
Ток в общей цепи

По условию задачи напряжение на зажимах первого элемента

отсюда

6 При каком соотношении между сопротивлениями резисторов R 1 , R2, R3 и внутренними сопротивлениями элементов r1, r2 (рис. 122) напряжение на зажимах одного из элементов будет равно нулю? Э. д. с. элементов одинаковы.

Решение:

7 Два генератора с одинаковыми э. д. с. e = 6 В и внутренними сопротивлениями r1 =0,5 Ом и r2 = 0,38 Ом включены по схеме, изображенной на рис. 123. Сопротивления резисторов R 1 = 2 Ом, R2 = 4 Ом, R3 = 7 Ом. Найти напряжения V 1 и V2 на зажимах генераторов.

Решение:
Ток в общей цепи

где внешнее сопротивление цепи

Напряжения на зажимах первого и второго генератора
напряжение на зажимах второго генератора

8 Три элемента с э. д. с. e 1 = 2,2 В, e 2 = 1 ,1 В и e 3 = 0,9 В и внутренними сопротивлениями r 1 = 0,2 Ом, r 2 = 0,4 Ом и r з = 0,5 Ом включены в цепь последовательно. Внешнее сопротивление цепи R= 1 Ом. Найти напряжение на зажимах каждого элемента.

Решение:
По закону Ома для полной цепи ток

Напряжение на зажимах каждого элемента равно разности э. д. с. и падения напряжения на внутреннем сопротивлении элемента:


Напряжение на зажимах батареи элементов равно падению напряжения на внешнем сопротивлении цепи:

Напряжение на зажимах третьего элемента оказалось отрицательным, так как ток определяется всеми сопротивлениями цепи и суммарной э.д.с, а падение напряжения на внутреннем сопротивлении r3 больше, чем э.д.с. e 3 .

9 Батарея из четырех последовательно включенных в цепь элементов с э. д. с. e = 1,25 В и внутренним сопротивлением r = 0,1 Ом питает два параллельно соединенных проводника с сопротивлениями R1 = 50 Ом и R 2 = 200 Ом. Найти напряжение на зажимах батареи.

Решение:

10 Сколько одинаковых аккумуляторов с э. д. с. e = 1 ,25B и внутренним сопротивлением r = 0,004 Ом нужно взять, чтобы составить батарею, которая давала бы на зажимах напряжение V= 11 5 В при токе I =25 А?

Решение:
Напряжение на зажимах батареи

Следовательно,

11 Батарея из n = 40 последовательно включенных в цепь аккумуляторов с э. д. с. e = 2,5 В и внутренним сопротивлением r = 0,2 Ом заряжается от сети с напряжением V=121 В. Найти зарядный ток, если последовательно в цепь введен проводник с сопротивлением R = 2 Ом.

Решение:

12 Два элемента с э. д. с. e 1 = 1,25 В и e 2 = 1,5 В и одинаковыми внутренними сопротивлениями r = 0,4 Ом соединены параллельно (рис. 124). Сопротивление резистора R = 10 Ом. Найти токи, текущие через резистор и каждый элемент.

Решение:
Падение напряжения на резисторе, если токи текут в направлениях, указанных на рис. 124,

Учитывая, что I=I1+I2, находим

Заметим, что I1
13 Два элемента с э. д. с. e 1 =6 В и e 2 = 5 В и внутренними сопротивлениями r1 = 1 Ом и r2 = 20м соединены по схеме, изображенной на рис. 125. Найти ток, текущий через резистор с сопротивлением R = 10 Ом.

Решение:
Выбрав направления токов, указанные на рис. 362, составим уравнения Кирхгофа. Для узла b имеем I1+I2-I=0; для контура abef (обход по часовой стрелке)

и для контура bcde (обход против часовой стрелки)

Из этих уравнений найдем

14 Три одинаковых элемента с э. д. с. e = 1,6 В и внутренним сопротивлением r =0,8 Ом включены в цепь по схеме, изображенной на рис. 126. Миллиамперметр показывает ток I =100 мА. Сопротивления резисторов R 1 = 10Ом и R2 = 15 0м, сопротивление резистора R неизвестно. Какое напряжение V показывает вольтметр? Сопротивление вольтметра очень велико, сопротивление миллиамперметра пренебрежимо мало.

Решение:
Внутреннее сопротивление элементов

Сопротивление параллельно включенных резисторов

Общая э. д. с. элементов e 0 =2 e Согласно закону Ома для полной цепи

15 Сопротивления резисторов R 1 и R 2 и э. д. с. e 1 и e 2 источников тока в схеме, изображенной на рис. 127, известны. При какой э.д.с. e 3 третьего источника ток через резистор R3 не течет?

Решение:
Выберем направления токов I1, I2 и I3 через резисторы R1, R2 и R3, указанные на рис. 363. Тогда I3=I1+I2. Разность потенциалов между точками а и b будет равна

Если

Исключая I1 находим

16 Цепь из трех одинаковых последовательно соединенных элементов с э.д.с. e и внутренним сопротивлением r замкнута накоротко (рис. 128). Какое напряжение покажет вольтметр, подключенный к зажимам одного из элементов?

Решение:
Рассмотрим ту же схему без вольтметра (рис. 364). Из закона Ома для полной цепи находим

Из закона Ома для участка цепи между точками а и b получим

Подключение вольтметра к точкам, разность потенциалов между которыми равна нулю, ничего не может изменить в цепи. Поэтому вольтметр будет показывать напряжение, равное нулю.
17 Источник тока с э.д.с. e 0 включен в схему, параметры которой даны на рис. 129. Найти э.д.с. e источника тока и направление его подключения к выводам а и b , при которых ток через резистор с сопротивлением R2 не идет.

Решение:
Подключим источник тока к выводам а и b и выберем направления токов, указанные на рис. 365. Для узла е имеем I=I0+I2. При обходе контуров aefb и ecdf по часовой стрелке получим
Используя условие I2 = 0, находим

Знак минус показывает, что полюсы источника тока на рис. 365 нужно поменять местами.
18 Два элемента с одинаковыми э.д.с. e включены в цепь последовательно. Внешнее сопротивление цепи R = 5 Ом. Отношение напряжения на зажимах первого элемента к напряжению на зажимах второго элемента равно 2/3. Найти внутренние сопротивления элементов r1 и r 2, если r 1=2 r 2.

Решение:

19 Два одинаковых элемента с э.д.с. e = 1 ,5 В и внутренним сопротивлением r = 0,2 Ом замкнуты на резистор, сопротивление которого составляет в одном случае R1=0,2 Oм, В другом — R 2 = 20 Ом. Как нужно соединить элементы (последовательно или параллельно) в первом и во втором случаях, чтобы получить наибольший ток в цепи?

Решение:
При параллельном соединении двух элементов внутреннее сопротивление и э.д.с. равны r/2 и e при последовательном соединении они равны 2r и 2 e . Через резистор R при этом текут токи
Отсюда видно, что I2>I1, если R/2+rr. Поэтому ток больше при последовательном соединении.
20 Два элемента с э.д.с. e 1 =4В и e 2 = 2В и внутренними сопротивлениями r1 = 0,25 Ом и r 2 = 0,75 Ом включены в схему, изображенную на рис. 130. Сопротивления резисторов R1 = 1 Ом и R2 = 3 Ом, емкость конденсатора С=2 мкФ. Найти заряд на конденсаторе.

Решение:

21 К батарее из двух параллельно включенных элементов с э.д.с. e 1 и e 2 и внутренними сопротивлениями r1 и r 2 подключен резистор с сопротивлением R. Найти ток I , текущий через резистор R, и токи I1 и I 2 в первом и втором элементах. При каких условиях токи в отдельных цепях могут быть равными нулю или изменять свое направление на обратное?

Решение:
Выберем направления токов, указанные на рис. 366. Для узла b имеем I-I1-I2=0. При обходе контуров abef и bcde по часовой стрелке получим

Из этих уравнений находим

Ток I=0 тогда, когда изменена полярность включения одного из элементов и, кроме того, выполнено условие

Ток I1=0 при

а ток I2 = 0 при

Токи I1 и I2 имеют направления, указанные на рис.366, если

Они меняют свое направление при

22 Батарея из n одинаковых аккумуляторов, соединенных в одном случае последовательно, в другом- параллельно, замыкается на резистор с сопротивлением R. При каких условиях ток, текущий через резистор, в обоих случаях будет один и тот же?

Решение:
При n(R-r) = R-r. Если R=r, то число элементов произвольно; если R № r, задача не имеет решения ( n =1).
23 Батарея из n = 4 одинаковых элементов с внутренним сопротивлением r =2 Ом, соединенных в одном случае последовательно, в другом — параллельно, замыкается на резистор с сопротивлением R =10Ом. Во сколько раз показание вольтметра н одном случае отличается от показания вольтметра в другом случае? Сопротивление вольтметра велико по сравнению с R и r.

Решение:

где V1 — показание вольтметра при последовательном соединении элементов, V2-при параллельном.
24 Как изменится ток, текущий через резистор с сопротивлением R = 2 Ом, если n =10 одинаковых элементов, соединенных последовательно с этим резистором, включить параллельно ему? Э.д.с. элемента e = 2 В, его внутреннее сопротивление r = 0,2 Ом.

Решение:

25 Батарея составлена из N=600 одинаковых элементов так, что п групп соединены последовательно и в каждой из них содержится т элементов, соединенных параллельно. Э.д.с. каждого элемента e = 2 В, его внутреннее сопротивление r = 0,4 Ом. При каких значениях n и m батарея, будучи замкнута на внешнее сопротивление R = 0,6 Ом, отдаст во внешнюю цепь максимальную мощность? Найти при этом ток, текущий через сопротивление R.

Решение:
Общее число элементов N=nm (рис. 367). Ток во внешней цепи

где r/ m — внутреннее сопротивление группы из т параллельно соединенных элементов, а n r/ m — внутреннее сопротивление n групп, соединенных последовательно. Максимальная мощность (см. задачу 848) отдается во внешнюю цепь при равенстве сопротивления R внутреннему сопротивлению батареи элементов n r/ m , т. е.
При этом через сопротивление R течет точек I=46 А.

26 Емкость аккумулятора =80 А Ч ч. Найти емкость батареи из n = 3 таких аккумуляторов, включенных последовательно и параллельно.

Решение:
При последовательном соединении через все аккумуляторы батареи течет один и тот же ток, поэтому все они разрядятся в течение одного и того же времени. Следовательно, емкость батареи будет равна емкости каждого аккумулятора:
При параллельном соединении n аккумуляторов через каждый из них течет 1/n часть общего тока; поэтому при том же разрядном токе в общей цепи батареи будет разряжаться в n раз дольше, чем один аккумулятор, т. е. емкость батареи в п раз больше емкости отдельного аккумулятора:

Заметим, однако, что энергия

отдаваемая батареей в цепь, и при последовательном и при параллельном соединении n аккумуляторов в n раз больше энергии, отдаваемой одним аккумулятором. Это происходит потому, что при последовательном соединении э. д. с. батареи в n раз больше э. д. с. одного аккумулятора, а при параллельном соединении э.д.с. батареи остается той же, что и для каждого аккумулятора, но Q увеличивается в n раз.
27 Найти емкость батареи аккумуляторов, включенных по схеме, изображенной на рис.131. Емкость каждого аккумулятора Qo =64 А Ч ч .

Решение:
Каждая группа из пяти аккумуляторов, включенных последовательно, имеет емкость

Три параллельно включенные группы дают общую емкость батареи

28 Мост для измерения сопротивлений сбалансирован так, что ток через гальванометр не идет (рис. 132). Ток в правой ветви I =0,2 А. Найти напряжение V на зажимах источника тока. Сопротивления резисторов R1 = 2 Ом, R2 = 4 Ом, R3 = 1 Ом.

Решение:

29 Найти токи, протекающие в каждой ветви цепи, изображенной на рис. 133. Э.д.с. источников тока e 1 = 6,5 В и e 2 = 3,9 В. Сопротивления резисторов R1=R2=R3=R4=R5=R6=R=10 Ом.

Решение:
Составляем уравнения Кирхгофа в соответствии с направлениями токов, указанными на рис. 133: I1 + I2 — I3 = 0 для узла b;
I3 — I4 — I5 =0 для узла h; I5 — I1 — I6 = 0 для узла f: при этом

Для контура abfg (обход по часовой стрелке),

Для контура bcdh (обход против часовой стрелки) и

для контура hdef (обход по часовой
стрелке). Решая эту систему уравнений с учетом, что все сопротивления одинаковы и равны R=10 Ом, получим

Отрицательные значения токов I2, I4 и I6 показывают, что при данных э.д.с. источников и сопротивлениях резисторов эти токи текут в стороны, противоположные указанным на рис. 133.

Применение последовательного и параллельного соединения проводов. Последовательное и параллельное соединение сопротивления, соединения проводов

Содержание:

Во всех электрических цепях используются резисторы, которые представляют собой элементы с точно установленным значением сопротивления. Благодаря особым качествам этих устройств становится возможным регулировать напряжение и ток в любой части цепи. Эти свойства лежат в основе работы практически всех электронных устройств и оборудования. Итак, напряжение при параллельном и последовательном включении резисторов будет разным.Поэтому каждый вид подключения можно использовать только при определенных условиях, чтобы та или иная электрическая цепь могла полноценно выполнять свои функции.

Последовательное напряжение

При последовательном соединении два или более резистора включаются в общую цепь таким образом, что каждый из них контактирует с другим устройством только в одной точке. Другими словами, конец первого резистора соединен с началом второго, а конец второго соединен с началом третьего и т. Д.

Особенностью этой схемы является прохождение через все подключенные резисторы одинакового значения электрического тока. С увеличением количества элементов в рассматриваемом участке схемы протекание электрического тока становится все более затруднительным. Это связано с увеличением общего сопротивления резисторов при их последовательном включении. Это свойство отражается формулой: R total = R 1 + R 2.

Распределение напряжения, согласно закону Ома, осуществляется для каждого резистора по формуле: V Rn = I Rn x R n.Таким образом, с увеличением сопротивления резистора падает и напряжение на нем.

Параллельное напряжение

При параллельном включении резисторы включаются в электрическую цепь таким образом, что все элементы сопротивления соединяются между собой обоими контактами одновременно. Одна точка, представляющая собой электрическую сборку, может одновременно подключать несколько резисторов.

Это соединение предполагает отдельный ток в каждом резисторе.Сила этого тока обратно пропорциональна. В результате увеличивается общая проводимость этого участка цепи с общим уменьшением сопротивления. В случае параллельного соединения резисторов с разным сопротивлением значение общего сопротивления в этом участке всегда будет меньше наименьшего сопротивления одиночного резистора.

На показанной диаграмме напряжение между точками A и B представляет не только полное напряжение для всей секции, но также напряжение, подаваемое на каждый отдельный резистор.Таким образом, в случае параллельного подключения напряжение, подаваемое на все резисторы, будет одинаковым.

В результате напряжение при параллельном и последовательном подключении в каждом случае будет различным. Благодаря этому свойству есть реальная возможность корректировать это значение на любом участке цепочки.

Параллельное соединение резисторов, формула расчета которых получена из закона Ома и правил Кирхгофа, является наиболее распространенным типом включения элементов в электрическую цепь.При параллельном соединении проводов два или более элемента соединяются своими контактами с обеих сторон соответственно. Их подключение к общей схеме осуществляется именно этими узловыми точками.

Gif? X15027 «alt =» (! LANG: Общий вид «>!}

Общий вид

Особенности включения

Включенные таким образом проводники часто являются частью сложных цепей, которые, кроме того, содержат последовательное соединение отдельных участков .

Для такого включения типичны следующие характеристики:

• Общее напряжение в каждой из ветвей будет иметь одинаковое значение;
• Электрический ток, протекающий в любом из сопротивлений, всегда обратно пропорционален их сопротивлению. ценить.

В частном случае, когда все резисторы, соединенные параллельно, имеют одинаковые номиналы, «индивидуальные» токи, протекающие через них, также будут равны друг другу.

Плата

Сопротивления ряда проводящих элементов, соединенных параллельно, определяются в соответствии с хорошо известной формой расчета, которая включает в себя сложение их проводимостей (значений, обратных сопротивлению).

Ток, протекающий в каждом из отдельных проводников в соответствии с законом Ома, можно найти по формуле:

I = U / R (один из резисторов).

Ознакомившись с общими принципами расчета элементов сложных цепочек, можно переходить к конкретным примерам решения задач этого класса.

Типовые соединения

Пример № 1

Часто для решения проблемы, стоящей перед проектировщиком, требуется получить определенное сопротивление в результате объединения нескольких элементов. Рассматривая простейший вариант такого решения, предположим, что полное сопротивление цепи из нескольких элементов должно составлять 8 Ом.Этот пример требует отдельного рассмотрения по той простой причине, что в стандартной серии сопротивлений нет номинала 8 Ом (есть только 7,5 и 8,2 Ом).

Решение этой простейшей проблемы может быть получено путем соединения двух одинаковых элементов с сопротивлением по 16 Ом каждый (такие номиналы существуют в резистивной серии). По приведенной выше формуле общее сопротивление цепи в этом случае рассчитывается очень просто.

Отсюда следует:

16×16 / 32 = 8 (Ом), то есть ровно столько, сколько требовалось для получения.

Таким относительно простым способом можно решить задачу формирования общего сопротивления, равного 8 Ом.

Пример №2

В качестве еще одного типичного примера формирования необходимого сопротивления можно рассмотреть построение схемы, состоящей из 3х резисторов.

Суммарное значение R такого включения можно рассчитать по формуле для последовательного и параллельного соединения в проводниках.

Gif? X15027 «alt =» (! LANG: Example «>!}

В соответствии с обозначениями, указанными на картинке, общее сопротивление цепи будет равно:

1 / R = 1/200 + 1 / 220 + 1/470 = 0.0117;

R = 1 / 0,0117 = 85,67 Ом.

В результате находим полное сопротивление всей цепи, полученное при параллельном соединении трех элементов с номиналами 200, 240 и 470 Ом.

Важно! Указанный метод применим также при расчете произвольного количества параллельно включенных проводов или потребителей.

Также следует отметить, что при таком способе включения элементов разного размера общее сопротивление будет меньше, чем у самого маленького номинала.

Расчет комбинированных схем

Рассмотренный метод также может быть использован для расчета сопротивления более сложных или комбинированных схем, состоящих из целого набора компонентов. Иногда их называют смешанными, поскольку используются оба метода для формирования цепочек сразу. Смешанное подключение резисторов показано на рисунке ниже.

Gif? X15027 «alt =» (! LANG: Mixed schema «>!}

Mixed scheme

Для упрощения расчета сначала разделим все резисторы по типу включения на две независимые группы.Одно — последовательное соединение, другое — параллельное соединение.

Из вышеприведенной схемы видно, что элементы R2 и R3 соединены последовательно (они объединены в группу 2), который, в свою очередь, подключен параллельно резистору R1, принадлежащему группе 1.

В предыдущем синопсисе было обнаружено, что ток в проводнике зависит от напряжения на его концах. Если в эксперименте изменить проводники, оставив напряжение на них неизменным, то можно показать, что при постоянном напряжении на концах проводника сила тока обратно пропорциональна его сопротивлению.Комбинируя зависимость тока от напряжения и его зависимость от сопротивления проводника, можно записать: I = U / R … Этот закон, установленный экспериментально, называется законом Ома (для участка цепи).

Закон Ома для участка цепи : ток в проводнике прямо пропорционален напряжению, приложенному к его концам, и обратно пропорционален сопротивлению проводника. Прежде всего, закон всегда справедлив для твердых и жидких металлических проводников.А также для некоторых других веществ (обычно твердых или жидких).

Потребители электрической энергии (лампочки, резисторы и т. Д.) Могут быть соединены друг с другом в электрическую цепь различными способами. D ва основной тип подключения проводов : последовательный и параллельный. А также есть еще два редких соединения: смешанное и мостовое.

Последовательное соединение проводов

При последовательном соединении проводников конец одного проводника соединяется с началом другого проводника, а его конец — с началом третьего и т. Д.Например, подключение лампочек в елочную гирлянду. Когда проводники соединены последовательно, ток течет через все лампочки. В этом случае один и тот же заряд проходит через сечение каждого проводника за единицу времени. То есть заряд не накапливается ни в одной части проводника.

Следовательно, при последовательном соединении проводов сила тока в любой части цепи одинакова: I 1 = I 2 = I .

Общее сопротивление последовательно соединенных проводов равно сумме их сопротивлений : R 1 + R 2 = R … Потому что при последовательном соединении проводов их общая длина увеличивается. Он больше, чем длина каждого отдельного проводника, и соответственно увеличивается сопротивление проводников.

По закону Ома напряжение на каждом проводе составляет: U 1 = I * R 1 , U 2 = I * R 2 … В этом случае полное напряжение составляет U = I ( Р 1 + R 2) … Поскольку сила тока во всех проводниках одинакова, а общее сопротивление равно сумме сопротивлений проводников, то полное напряжение на последовательно соединенных проводниках равно сумме напряжений на каждый проводник : U = U 1 + U 2 .

Из приведенных равенств следует, что последовательное соединение проводников используется, если напряжение, на которое рассчитаны потребители электрической энергии, меньше полного напряжения в цепи.

Для последовательного соединения проводов действуют законы :

1) сила тока во всех проводниках одинакова; 2) напряжение во всем соединении равно сумме напряжений на отдельных проводниках; 3) сопротивление всего соединения равно сумме сопротивлений отдельных проводников.

Параллельное соединение проводов

Пример параллельное соединение жилы используются для подключения потребителей электрической энергии в квартире.Так, параллельно включаются электрические лампочки, чайник, утюг и т. Д.

При параллельном соединении проводов все проводники одним концом соединяются с одной точкой в ​​цепи. А другой конец — к другой точке цепочки. Вольтметр, подключенный к этим точкам, покажет напряжение как на проводе 1, так и на проводе 2. В этом случае напряжение на концах всех параллельно соединенных проводов одинаково: U 1 = U 2 = U .

При параллельном соединении проводов электрическая цепь разветвляется.Следовательно, часть общего заряда проходит по одному проводнику, а часть — по другому. Следовательно, при параллельном соединении проводов ток в неразветвленной части цепи равен сумме токов в отдельных проводниках: I = I 1 + I 2 .

По закону Ома I = U / R, I 1 = U 1 / R 1, I 2 = U 2 / R 2 … Это означает: U / R = U 1 / R 1 + U 2 / R 2, U = U 1 = U 2, 1 / R = 1 / R 1 + 1 / R 2 Сумма, обратная величине общего сопротивления параллельно соединенных проводников, является суммой обратных сопротивлений каждого проводника.

При параллельном соединении проводов их общее сопротивление меньше, чем сопротивление каждого проводника. Действительно, если два проводника соединены параллельно, имея одинаковое сопротивление G , то их общее сопротивление будет равно: R = r / 2 … Это связано с тем, что при параллельном соединении проводов , их площадь поперечного сечения, кажется, увеличивается. В результате сопротивление снижается.

Из приведенных формул понятно, почему потребители электроэнергии подключаются параллельно.Все они рассчитаны на определенное одинаковое напряжение, которое в квартирах составляет 220 В. Зная сопротивление каждого потребителя, можно рассчитать силу тока в каждом из них. А также соответствие общей силы тока максимально допустимой силе тока.

Для параллельного соединения проводов действуют законы:

1) напряжение на всех проводниках одинаковое; 2) сила тока на стыке проводов равна сумме токов в отдельных проводниках; 3) величина, обратная сопротивлению всего соединения, равна сумме значений, обратных сопротивлениям отдельных проводников.

Сопротивление проводов. Параллельное и последовательное соединение проводов.

Электрическое сопротивление — физическая величина, которая характеризует свойства проводника по предотвращению прохождения электрического тока и равна отношению напряжения на концах проводника к силе тока, протекающего по нему. Сопротивление цепей переменного тока и переменных электромагнитных полей описывается в терминах импеданса и характеристического импеданса.Сопротивление (резистор) также называют радиокомпонентом, предназначенным для введения активного сопротивления в электрические цепи.

Сопротивление (часто обозначается буквой R или r ) считается в определенных пределах постоянным значением для данного проводника; его можно рассчитать как

R — сопротивление;

У — разность электрических потенциалов (напряжений) на концах жилы;

I — сила тока, протекающего между концами проводника под действием разности потенциалов.

С последовательным подключением проводников (рис. 1.9.1) сила тока во всех проводниках одинакова:

Закон Ома, напряжения U 1 и U 2 на проводниках равны

При последовательном соединении общее сопротивление цепи равно сумме сопротивлений отдельных проводов.

Этот результат действителен для любого количества последовательно соединенных проводов.

Параллельное соединение (рис.1.9.2) напряжение U 1 и U 2 на обоих проводниках одинаковое:

Этот результат следует из того факта, что в точках разветвления токов (узлы A и B ) в цепи постоянного тока не могут накапливаться заряды. Например, к узлу A во времени Δ t утечки заряда I Δ t , и заряд утекает от узла одновременно I 1 Δ t + I 2 Δ т … Следовательно, I = I 1 + I 2.

Написание на основе закона Ома

Когда проводники соединены параллельно, величина, обратная общему сопротивлению цепи, равна сумме значений, обратных сопротивлениям параллельно соединенных проводов.

Этот результат действителен для любого количества параллельно соединенных проводов.

Формулы последовательного и параллельного соединения проводов позволяют во многих случаях рассчитать сопротивление сложной цепи, состоящей из множества резисторов.На рис. 1.9.3 показывает пример такой сложной цепочки и указывает последовательность вычислений.

Следует отметить, что не все сложные схемы, состоящие из проводов с разным сопротивлением, можно рассчитать по формулам для последовательного и параллельного соединения. На рис. 1.9.4 показывает пример электрической цепи, которую невозможно рассчитать указанным выше методом.

При решении задач принято преобразовывать схему, чтобы она была максимально простой.Для этого используются эквивалентные преобразования. Такие преобразования части электрической цепи называются эквивалентными, при которых токи и напряжения в ее непреобразованной части остаются неизменными.

Существует четыре основных типа подключения проводов: последовательный, параллельный, смешанный и мостовой.

Последовательное соединение

Последовательное соединение — это соединение, при котором сила тока одинакова по всей цепи. Яркий пример последовательного подключения — старая елочная гирлянда.Там лампочки включаются последовательно, одна за другой. А теперь представьте, перегорела одна лампочка, оборвалась электрическая цепь, а остальные лампочки погасли. Выход из строя одного элемента приводит к отключению всех остальных, это существенный недостаток последовательного подключения.

При последовательном соединении сопротивления элементов суммируются.

Параллельное соединение

Параллельное соединение — это соединение, при котором напряжение на концах участка цепи одинаковое.Параллельное соединение является наиболее распространенным, в основном потому, что все элементы находятся под одинаковым напряжением, ток распределяется по-разному, и когда один из элементов уходит, все остальные продолжают свою работу.

При параллельном подключении эквивалентное сопротивление находится как:

В случае двух параллельно включенных резисторов

В случае трех параллельно включенных резисторов:

Смешанное соединение

Смешанное соединение — соединение, представляющее собой совокупность последовательных и параллельных соединений.Чтобы найти эквивалентное сопротивление, вам нужно «свернуть» цепь, чередуя параллельные и последовательные участки цепи.

Сначала находим эквивалентное сопротивление для параллельного участка цепи, а затем добавляем к нему оставшееся сопротивление R 3. Следует понимать, что после преобразования эквивалентное сопротивление R 1 R 2 и резистор R 3 включены последовательно.

Итак, осталось самое интересное и сложное подключение проводов.

Мостовая схема

Схема подключения моста показана на рисунке ниже.

Чтобы свернуть мостовую схему, один из треугольников моста заменяется эквивалентной звездой.

И найдите сопротивления R 1, R 2 и R 3.

ЗАКОН О ТОКАХ И ОМС

ЗАКОН О ТОКАХ И ОМС

---

Рисунок 28.1. Электрическое поле в проводе. Когда провод подключен к клеммам аккумулятора, электрическое поле создается внутри провода (см. рисунок 28.1). Свобода электроны в проводе будут двигаться в направлении, противоположном направлению поля линии. Электрический заряд будет пытаться перераспределиться таким образом, чтобы чистое электрическое поле в проводе равно нулю. Однако положительный клемма батареи действует как сток для электронов, а отрицательная клемма действует как источник электронов, и непрерывный поток электронов будет созданный.Этот непрерывный поток электронов называется электрическим током . текущий . Символ тока — I, а его единица СИ — Ампер (А). Сила тока определена как

(28,1)

где dq — количество заряда, которое проходит через некоторую заданную точку на проводе. в течение периода времени dt. Ток 1 А равен 1 Кл / с. В плотность тока Дж определяется как

(28.2)

где I — ток, протекающий по проводнику, а A — площадь поперечного сечения проводника. Хотя электроны чувствуют электрическое поле внутри проводника, они не будут ускоряться. Электроны будет испытывать значительное трение в результате столкновений с положительные ионы в проводнике. В среднем электроны будут двигаться с постоянная скорость от отрицательной клеммы аккумулятора к положительной Терминал. Их средняя скорость, также называемая дрейфовой скоростью v _d , пропорционально электрическому полю E

(28.3)

При заданной плотности электронов в проводнике увеличение дрейфа скорость каждого из электронов увеличит количество проходящих электронов заданной точкой на проводнике в единицу времени. Это показано в Рисунок 28.2. За промежуток времени dt электроны пройдут в среднем около расстояние, равное dx, где

(28.4)

Рисунок 28.2. Движение среднего электрона в проводнике. Все электроны на расстоянии dx от точки P будут поэтому пройти эту точку в течение временного интервала dt.Предположим, что плотность электронов в проводнике n электронов / м ³ . Количество электронов dN, которые пройдут через P за промежуток времени dt, тогда будет равно

(28,5)

Поскольку каждый электрон несет заряд e, полный заряд dQ, который пройдет точка P на временном интервале dt равна

(28,6)

Следовательно, ток через проводник равен

. (28.7)

Уравнение (28.7) показывает, что ток в проводнике пропорционален силе тока. площадь поперечного сечения проводника и пропорциональна скорости дрейфа. Поскольку скорость дрейфа пропорциональна электрическому полю E, следующее соотношение выполняется для тока в проводнике:

(28,8)

Электрическое поле в проводнике определяется его длиной L и величиной разность потенциалов [Дельта] V между двумя его концами (E = [Дельта] V / L).Таким образом, уравнение (28.8) можно переписать как

(28,9)

Уравнение (28.9) можно переписать как

(28.10)

Константа пропорциональности [rho] называется удельным сопротивлением материал. Удельное сопротивление [rho] зависит от характеристик проводник ([rho] маленький для хорошего проводника, и [rho] очень большой для хорошего проводника изолятор). Сопротивление R проводника определяется как

. (28.11)

Единицей измерения сопротивления в системе СИ является ом ([Омега]). Используя сопротивление R, мы можем перепишите уравнение (28.10)

(28.12)

Уравнение (28.12) называется Закон Ома . Уравнение (28.12) показывает что ток через проводник пропорционален потенциалу разница между концами проводника и обратно пропорциональна его сопротивление. Уравнение (28.12) также показывает, что 1 [Омега] равно 1 В / А.

Пример: Задача 28,5

Алюминиевый провод имеет сопротивление 0,10 Ом. Если вы нарисуете это провод через матрицу, сделав ее тоньше и вдвое длиннее, что будет ее новым сопротивление ?

Начальное сопротивление R _и алюминиевой проволоки длиной L и площадь поперечного сечения A равна

(28,13)

Начальный объем проволоки — ^л. А.После прохождения провода через матрицу ее длина изменилась на L ‘, а площадь ее поперечного сечения равно A ‘. Таким образом, его конечный объем равен L ‘A’. Поскольку плотность алюминий не меняется, объем провода не меняется, и поэтому начальный и конечный размеры проволоки соотносятся:

(28,14)

или

(28.15)

Проблема заключается в том, что длина провода увеличена вдвое (L ‘= 2 L).В поэтому конечная площадь поперечного сечения A ‘связана с начальным площадь поперечного сечения A следующим образом:

(28.16)

Конечное сопротивление R _f провода равно

. (28,17)

Сопротивление провода увеличилось в четыре раза и теперь составляет 0,40. [Омега].

Удельное сопротивление [rho] выражается в единицах ом-метр ([Omega] ^. м). В удельное сопротивление большинства проводников находится между 10 ^-8 [Омега] ^. м и 10 ^-7 [Omega] ^. г. Удельное сопротивление проводник зависит не только от типа материала, но и от его температура. Удельное сопротивление изолятора колеблется в пределах 10 ¹¹ [Omega] ^. m и 10 ¹⁷ [Omega] ^. м. У всех материалов удельное сопротивление уменьшается с понижением температуры.В у некоторых материалов, таких как свинец, цинк, олово и ниобий, удельное сопротивление исчезает когда температура приближается к абсолютному нулю. При таких низких температурах эти материалы обладают сверхпроводимостью .

Пример: задача 28.17

Кондиционер в доме потребляет ток 12 А. Предположим, что пара проводов, соединяющих кондиционер с блоком предохранителей, №10 медные провода диаметром 0.259 см и длиной по 25 м.

а) Какое падение потенциала на каждом проводе? Предположим, что напряжение доставлено на дом ровно 110 В на блок предохранителей. Какое напряжение поставили кондиционер?

б) В некоторых старых домах используется медный провод № 12 диаметром 0,205. см. Повторите расчет части (а) для этого провода.

Рисунок 28.3. Электросхема кондиционера в проблеме 28.17.

а) Удельное сопротивление меди равно 1.7 x 10 ^-8 [Omega] ^. кв.м. (см. Таблицу 28.1). Сопротивление R _Cu каждого медного провода равно на номер

(28.18)

где L — длина проволоки, а d — ее диаметр. Ток I есть протекает по проводам и I = 12 A. Падение напряжения [Delta] V на каждом провод равен

(28,19)

На рисунке 28.3 схематично показана электрическая схема кондиционера. схема.Напряжение на блоке кондиционера 110-2 ^. [Дельта] V, где [Дельта] V определяется уравнением (28.19). Длина длина каждого медного кабеля составляет 25 м, а его диаметр равен 0,259 см. Напряжение падение на каждом проводе, таким образом, равно

(28.20)

Таким образом, напряжение на блоке переменного тока равно 108,1 В.

б) Проволока № 12 имеет диаметр 0,205 см. Падение напряжения на этот провод равен

(28.21)

а напряжение на блоке переменного тока равно 106,9 В.

Пример: Задача 28.12

ЛЭП высокого напряжения имеет алюминиевый кабель диаметром 3,0 мм. см, протяженностью 200 км. Какое сопротивление у этого кабеля?

Удельное сопротивление алюминия составляет 2,8 x 10 ^-8 Омега м. длина кабель 200 км или 2 х 10 ⁵ м. Диаметр кабеля 3 см. и его площадь поперечного сечения равна [пи] (d / 2) ² или 7.1 х 10 ^-4 м ² . Подставляя эти значения в уравнение (28.11), получаем сопротивление кабеля можно определить

(28.22)

Устройство, специально разработанное для обеспечения высокого сопротивления, называется резистор. Обозначение резистора на принципиальной схеме — зигзагообразная линия (см. Рисунок 28.4).

Рисунок 28.4. Символ резистора. На рисунке 28.5 показаны два резистора с сопротивлением R ₁ . и R ₂ , соединенные последовательно.Предположим, что ток, протекающий через цепь равна I. Падение напряжения [Дельта] В ₁ на резисторе R ₁ равно

(28,23)

и падение напряжения [Delta] V ₂ на резисторе R ₂ составляет равно

(28,24)

Разность потенциалов [Delta] V в последовательной цепи равна

. (28,25)

Уравнение (28.25) показывает, что два последовательно включенных резистора действуют как один резистор с сопротивлением, равным сумме сопротивлений резистора 1 и сопротивление резистора 2

(28.26)

Рисунок 28.5. Два резистора соединены последовательно. На рис. 28.6 показаны два резистора, включенных параллельно. В В этой схеме ток через каждый резистор будет разным, но падение напряжения [Delta] V на каждом резисторе будет одинаковым. Используя закон Ома ток I ₁ , протекающий через резистор R ₁ , может быть вычислено

(28.27)

и ток I ₂ , протекающий через резистор R ₂ , равен на номер

(28.28)

Полный ток, протекающий по цепи, равен сумме токи через каждый резистор

(28.29)

Таким образом, схема резисторов, показанная на рисунке 28.6, эквивалентна одиночной резистор R, где R можно получить из следующего соотношения

(28.30)

Уравнение (28.30) показывает, что сопротивление параллельной комбинации резисторов всегда меньше сопротивления каждого в отдельности резисторы.

Рисунок 28.6. Два резистора подключены параллельно.

Пример: задача 28.41

Промышленные сверхпроводящие кабели состоят из нитей сверхпроводящего провода, заключенного в матрицу из меди. Пока нити сверхпроводящие, в них течет весь ток, и нет тока течет в медь.Но если сверхпроводимость внезапно выйдет из строя из-за повышение температуры, ток может пролиться на медь; это предотвращает повреждение нитей сверхпроводника. Рассчитайте сопротивление на метр длины медной матрицы. Медная матрица имеет диаметр 0,7 мм, а каждая из 2100 нитей имеет диаметр 0,01 мм.

Считайте 1 метр кабеля. Площадь поперечного сечения каждой нити накала [пи] ^. (d / 2) ² = 7.9 x 10 ^-11 м ² . В площадь поперечного сечения 2100 нитей равна 1,65 x 10 ^-7 м ² . Диаметр медной матрицы равен 0,7 мм, а ее диаметр равен 0,7 мм. площадь поперечного сечения равна 1,54 х 10 ^-6 м ² . В площадь самой меди, таким образом, равна 1,37 x 10 ^-6 м ² . Сопротивление медной матрицы на единицу длины равно на номер

(28.31)

Предположим, что удельное сопротивление нити при комнатной температуре такое же, как у удельное сопротивление меди. Сопротивление каждой сверхпроводящей нити составляет равно

(28.32)

Провод можно рассматривать как параллельную цепь из одного резистора, представляющего сопротивление медной матрицы и 2100 резисторов, представляющих 2100 жилы сверхпроводящего провода. Доля тока, протекающего через медная матрица определяется легко.Предположим, что потенциал разность по проводнику равна [Delta] V. Электрический ток I _Cu , протекающая через медную матрицу, равна

(28,33)

Ток I _fil , протекающий через 2100 нитей, равен

. (28,34)

Доля F полного тока, протекающего через медную матрицу, равна на номер

(28.35)

Необходимо рассмотреть два особых случая.

1. Температура ниже критической. На уровне или ниже этого температура сопротивление нитей исчезает (R _fil = 0 [Омега]). Уравнение (28.35) показывает, что в этом случае ток не будет течь. через медную матрицу.

2. Если температура провода выше критической температуры, текущий поток резко изменится. В этом случае доля ток, протекающий через медь, равен

(28.36)

Медная матрица будет пропускать 90% общего тока.

Пример: задача 28.42

Какое сопротивление у комбинации из четырех резисторов, показанной на Рисунок 28.7. Каждый из резисторов имеет номинал R.

Рисунок 28.7. Проблема 28.42.

Чтобы найти сопротивление цепи, показанной на рисунке 28.7, мы начнем расчет чистого сопротивления R ₃₄ параллельной цепи резисторы R ₃ и R ₄ :

(28.37)

или

(28,38)

Таким образом, схема, показанная на рисунке 28.7, эквивалентна показанной схеме. на рисунке 28.8. Резисторы R ₂ и R ₃₄ образуют серию сети и может быть заменен одиночным резистором с сопротивлением R ₂₃₄ где

(28.39)

Рисунок 28.8. Проблема 28.42. Рисунок 28.9. Проблема 28.42. Схема показана на рисунке 28.8 теперь можно заменить на Эквивалентная схема показана на рисунке 28.9. Сопротивление R _до г. эта схема может быть получена из следующего соотношения

(28,40)

или

(28.41)

В рассматриваемом частном случае R ₁ = R ₂ = R ₃ = R ₄ = R. Таким образом,

(28,42)

(28.43)

(28,44)

Для R = 3 [Омега] полное сопротивление равно 1,8 [Омега].

---

Отправляйте комментарии, вопросы и / или предложения по электронной почте на адрес [email protected] и / или посетите домашнюю страницу Фрэнка Вольфса.

Рассчитайте сопротивление трех параллельных резисторов. Параллельное соединение сопротивлений в электрической цепи. Параллельное соединение конденсаторов и катушек

На практике часто встречается задача определения сопротивления проводников и резисторов при разных способах подключения.В статье обсуждается, как рассчитывается сопротивление, и некоторые другие технические вопросы.

Сопротивление проводника

Все проводники обладают способностью препятствовать прохождению электрического тока, это называется электрическим сопротивлением R, оно измеряется в омах. Это главное свойство проводниковых материалов.

Для проведения электрических расчетов применяется удельное сопротивление — ρ Ом · м / мм2. Все металлы являются хорошими проводниками, медь и алюминий используются чаще всего, а железо — гораздо реже.Лучший проводник — серебро, его используют в электротехнической и электронной промышленности. Широко распространены сплавы с высоким значением сопротивления.

При расчете сопротивления используется известная из школьного курса физики формула:

R = ρ · l / S, S — площадь сечения; l — длина.

Если взять два проводника, то их сопротивление при параллельном соединении станет меньше за счет увеличения общего сечения.

и нагревательный провод

Для практических расчетов режимов работы проводников используется понятие плотности тока — δ А / мм 2, она рассчитывается по формуле:

δ = I / S, I — ток , S — поперечное сечение.

Ток, протекающий по проводнику, нагревает его. Чем больше δ, тем сильнее нагревается проводник. Для проводов и кабелей разработаны нормы допустимой плотности, которые приведены в. Для токопроводящих жил нагревательных приборов существуют свои нормативы плотности тока.

Если плотность δ выше допустимой, проводник может разрушиться, например, если кабель перегреется, его изоляция разрушится.

Правила регулируют расчет кондукторов для отопления.

Способы подключения проводов

Любой проводник гораздо удобнее изобразить на схемах как электрическое сопротивление R, тогда их будет легче читать и анализировать. Подключить сопротивления можно всего тремя способами. Первый способ самый простой — последовательное подключение.

На фото видно, что импеданс равен: R = R 1 + R 2 + R 3.

Второй способ посложнее — параллельное подключение. Расчет сопротивлений при параллельном включении выполняется поэтапно.Вычислите общую проводимость G = 1 / R, а затем импеданс R = 1 / G.

Вы можете сделать иначе, сначала рассчитать общее сопротивление с R1 и R2, затем повторить операцию и найти R.

Третий способ подключения самый сложный — смешанный, то есть присутствуют все рассмотренные варианты. Схема представлена ​​на фото.

Для расчета этой схемы ее следует упростить; для этого резисторы R2 и R3 заменяются одним R2.3. Получается простая схема.

R2,3,4 = R2,3 · R4 / (R2,3 + R4).

Схема становится еще проще, остаются резисторы с последовательным включением. В более сложных ситуациях используется тот же метод преобразования.

Типы проводов

В электронной технике на производстве проводники представляют собой тонкие полоски медной фольги. Из-за небольшой длины сопротивления у них мало, им во многих случаях можно пренебречь. Для этих проводов сопротивление при параллельном подключении уменьшается из-за увеличения поперечного сечения.

Жилы большого сечения — это обмоточные провода. Доступны они разного диаметра — от 0,02 до 5,6 миллиметра. Для мощных трансформаторов и электродвигателей изготавливаются медные стержни прямоугольного сечения. Иногда при ремонте заменяют провод большого диаметра на несколько параллельных меньшего размера.

К особому сечению проводов относятся провода и кабели, промышленность предоставляет самый широкий выбор марок для самых разных нужд.Часто приходится заменять один кабель несколькими меньшими отрезками. Причины тому самые разные, например, кабель сечением 240 мм 2 очень сложно прокладывать на трассе с крутыми изгибами. Его заменяют на 2 × 120 мм 2, и проблема решается.

Расчет проводов на обогрев

Проводник нагревается протекающим током, если его температура превышает допустимую, происходит разрушение изоляции. ПУЭ предусматривает расчет токопроводов на обогрев, исходными данными для него являются сила тока и условия внешней среды, в которой проложен токопровод.Согласно этим данным, рекомендуемый проводник или кабель выбирается из таблиц в OLC).

На практике бывают ситуации, когда нагрузка на существующий кабель сильно увеличивается. Выхода два — заменить кабель на другой, может быть дорого, или проложить еще один параллельно ему, чтобы разгрузить основной кабель. В этом случае сопротивление проводника при параллельном включении уменьшается, следовательно, уменьшается тепловыделение.

Чтобы правильно подобрать сечение второго кабеля, воспользуйтесь таблицами PES, важно не ошибиться с определением его рабочего тока.В этой ситуации охлаждение кабелей будет даже лучше, чем у одного. Рекомендуется рассчитывать сопротивление при параллельном подключении двух кабелей, чтобы более точно определить их теплоотдачу.

Расчет проводов на потерю напряжения

При расположении потребителя R n на большом расстоянии L от источника энергии U 1 на проводах линии остается достаточно большое количество. К потребителю R n поступает напряжение U 2 значительно ниже начального U 1.Практически в качестве нагрузки выступает различное электрическое оборудование, подключенное к линии параллельно.

Чтобы решить эту проблему, рассчитайте сопротивление, когда все оборудование подключено параллельно, и сопротивление нагрузки R n. Далее определяем сопротивление проводов линии.

R l = ρ · 2L / S,

Здесь S — сечение провода, мм 2.

В этой теме можно привести множество примеров из нашей повседневной жизни, касающихся параллельного соединения сопротивлений.Параллельное соединение одинаковых сопротивлений — яркий пример подключения люстры с n-м числом ламп и с одинаковым сопротивлением для каждой лампы \ рис.1 \.

Если предположить, что в люстре, состоящей из нескольких ламп \ с одинаковым сопротивлением \ одна лампа перегорела, а другую мощность заменили лампой другой мощности — в этом случае подключение люстры будет иметь вид параллельное соединение с разным сопротивлением.

Какие еще примеры можно привести из практики — с параллельным соединением сопротивлений? Допустим, вы подключили в своей квартире через удлинитель три бытовых электроприбора:

• плита электрическая;
Стиральная машина
• ;
• телевидение.

Природа этого соединения будет иметь сопротивление параллельного соединения разного размера. То есть для каждого прибора сопротивление имеет свое значение.

Расчет сопротивления при параллельном включении

Как уже было сказано, при параллельном включении проводятся расчеты сопротивлений:

• с таким же сопротивлением;
• с разным сопротивлением
№

, а также выполнены расчеты сопротивлений для смешанного включения резисторов, при последовательном и параллельном включении \ для одной цепи \.Расчет сопротивления для смешанных подключений резисторов, больше подходит для различных блок-схем:

• аудиотехника;
• видеооборудование.

К этой теме расчеты для смешанных соединений отношения не имеют.

Параллельное соединение одинаковых сопротивлений

Представьте себе параллельное соединение, например, трех равных по величине сопротивлений \\ рис.2 \\, где R1 = R2 = R3 = 36 Ом \ сопротивление лампы накаливания мощностью 95 Вт. Напряжение 220 В подключается к двум узловым точкам \ A, B \.Необходимо рассчитать суммарное сопротивление всех трех ламп.

Для расчета общего сопротивления \ R total \ нам нужно 36 Ом разделить на количество сопротивлений. Решение простое, Rtotal = 12 Ом. То есть формула для расчета таких вычислений выглядит так:

R итого = R / n

Параллельное соединение разных сопротивлений

Допустим, мы берем выборочно три резистора, сопротивление:

• R1 = 20 Ом;
• R2 = 40 Ом;
• R3 = 10 Ом.

Необходимо определить полное сопротивление резисторов при параллельном включении. Для этого расчета мы используем формулу:

1 / R всего = 1 / R1 + 1 / R2 + 1 / R3.

Подставьте значения в формулу:

1 / R всего = 1/20 + 1/40 + 1/10 = 7/40 = 0,18

получаем: Rtotal = 1 / 0,18 = 5,5 Ом.

В каждой цепи есть резистор, имеющий сопротивление электрическому току. Резисторы бывают двух типов: фиксированные и переменные.При разработке любой электрической схемы и ремонте электронных изделий часто приходится использовать резистор, имеющий необходимый номинал.

Несмотря на то, что для резисторов существуют различные значения , может случиться так, что не удастся найти нужный или даже один элемент не сможет обеспечить требуемый показатель.

Решением этой проблемы может стать использование последовательного и параллельного подключения. Прочитав эту статью, вы узнаете об особенностях расчета и выбора различных значений сопротивления.

Часто при изготовлении любого устройства используют резисторы, которые подключаются по последовательной схеме. Эффект от использования такого варианта сборки сводится к увеличению общего сопротивления цепи. Для этого варианта соединения элементов создаваемое ими сопротивление рассчитывается как сумма номинальных значений. Если сборка деталей выполняется по параллельной схеме, здесь нужно рассчитать сопротивление по формулам ниже.

К схеме параллельного соединения прибегают в ситуации, когда стоит задача снизить общее сопротивление, и, кроме того, увеличить мощность для группы элементов, соединенных параллельно, которая должна быть больше, чем при их раздельном соединении.

Расчет сопротивления

В случае соединения частей между собой по параллельной схеме для расчета общего сопротивления будет использоваться следующая формула:

R (всего) = 1 / (1 / R1 + 1 / R2 + 1 / R3 + 1 / Rn).

• R1- R3 и Rn — резисторы, включенные параллельно.

Причем, если схема создана на основе всего двух элементов, то для определения общего номинального сопротивления используйте следующую формулу:

R (всего) = R1 * R2 / R1 + R2.

• R (total) — полное сопротивление;
• R1 и R2 — резисторы, включенные параллельно.

Универсальная схема расчета

Применительно к радиотехнике следует обратить внимание на одно важное правило: если элементы соединены между собой в параллельную цепь , имеют одинаковый показатель , то для расчета общего номинала общее значение следует разделить на количество подключаемых узлов:

• R (total) — суммарное значение сопротивления;
• R — номинал резистора, включенного параллельно;
• n — количество подключенных узлов.

Особое внимание следует обратить на то, что конечный показатель сопротивления в случае использования схемы параллельного подключения обязательно должен быть меньше по сравнению с номиналом любого элемента, подключенного к цепи.

Пример расчета

Для большей наглядности мы можем рассмотреть следующий пример: предположим, что у нас есть три резистора, номиналы которых составляют соответственно 100, 150 и 30 Ом. Если мы используем первую формулу для определения общей стоимости, мы получим следующее:

R (всего) = 1 / (1/100 + 1/150 + 1/30) = 1 / (0.01 + 0,007 + 0,03) = 1 / 0,047 = 21,28 Ом.

Если произвести несложные вычисления, можно получить следующее: для схемы, состоящей из трех частей, где наименьшее значение сопротивления составляет 30 Ом, результирующее значение номинала будет равно 21,28 Ом. Этот показатель будет меньше минимального номинала в цепочке почти на 30%.

Важные нюансы

Обычно для резисторов параллельное соединение применяется, когда стоит задача создать сопротивление большей мощности.Для ее решения потребуются резисторы, которые должны иметь одинаковое сопротивление и мощность. С помощью этой опции вы можете определить общую мощность следующим образом: : мощность одного элемента должна быть умножена на общее количество всех резисторов, которые составляют цепь, соединенную друг с другом в соответствии с параллельной цепью.

Допустим, если мы используем пять резисторов номиналом 100 Ом и мощностью каждого 1 Вт, которые соединены между собой по параллельной схеме, то общее сопротивление будет равно 20 Ом, а мощность будет 5 Вт.

Если взять те же резисторы, но подключить их по последовательной схеме, то конечная мощность будет 5 Вт, а общий номинал будет равен 500 Ом.

Заключение

Параллельная разводка резисторов очень востребована по той причине, что часто возникает задача создания такого номинала, которого нельзя достичь простым параллельным подключением. При этом в процедура вычисления этого параметра достаточно сложна, в необходимо учитывать разные параметры.

Здесь важную роль играет не только количество подключаемых элементов, но и рабочие параметры резисторов — в первую очередь сопротивление и мощность. Если один из подключаемых элементов будет иметь несоответствующий индикатор, то это не решит эффективно проблему создания необходимого номинала в цепи.

Параллельное соединение резисторов — один из двух типов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов.Часто или параллельно с целью создания более сложных электронных схем.

Схема параллельного подключения показана на рисунке ниже. При параллельном соединении резисторов напряжение на всех резисторах будет одинаковым, а ток, протекающий через них, будет пропорционален их сопротивлению:

Формула для параллельного включения резисторов

Суммарное сопротивление нескольких параллельно включенных резисторов определяется по следующей формуле:

Ток, протекающий через одиночный резистор, согласно, можно найти по формуле:

Параллельное соединение резисторов — расчет

Пример №1

При разработке устройства возникла необходимость в установке резистора сопротивлением 8 Ом.Если просмотреть весь номинальный ряд стандартных номиналов резисторов, то мы увидим, что в нем нет резистора с сопротивлением 8 Ом.

Выход из ситуации — использование двух параллельно включенных резисторов. Эквивалентное значение сопротивления для двух параллельно включенных резисторов рассчитывается следующим образом:

Это уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. Следовательно, когда R = 8 Ом, R1 и R2 должны иметь значение 2 × 8 = 16 Ом.
Теперь проверим, вычислив полное сопротивление двух резисторов:

Таким образом, мы получили необходимое сопротивление 8 Ом, подключив параллельно два резистора по 16 Ом.

Пример расчета № 2

Найдите полное сопротивление R трех параллельно соединенных резисторов:

Суммарное сопротивление R рассчитывается по формуле:

Этот метод расчета можно использовать для расчета любого количества отдельных сопротивлений, подключенных параллельно.

Один важный момент, который необходимо помнить при расчете параллельно соединенных резисторов, заключается в том, что полное сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.

Как рассчитать схемы подключения комплексных резисторов

Более сложные соединения резисторов можно рассчитать путем систематической группировки резисторов. На рисунке ниже нужно рассчитать полное сопротивление цепи, состоящей из трех резисторов:

Для упрощения расчетов сначала сгруппируем резисторы по параллельному и последовательному включению.
Резисторы R2 и R3 включены последовательно (группа 2). Они в свою очередь включены параллельно резистору R1 (группа 1).

Последовательное соединение резисторов группы 2 рассчитывается как сумма сопротивлений R2 и R3:

В результате упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей цепи можно рассчитать следующим образом:

Расчет более сложных соединений резисторов можно выполнить по законам Кирхгофа.

Ток, протекающий в цепи параллельно включенных резисторов

Полный ток I, протекающий в цепи параллельных резисторов, равен сумме отдельных токов, протекающих во всех параллельных ветвях, и ток в одной ветви не обязательно должен быть равен току в соседних ветвях.

Несмотря на параллельное соединение, на каждый резистор подается одинаковое напряжение. А поскольку значение сопротивления в параллельной цепи может быть разным, то величина тока, протекающего через каждый резистор, также будет отличаться (как определено законом Ома).

Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, протекающий через каждый из резисторов (I1 и I2), будет отличаться друг от друга, поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который входит в цепь в точке «A», должен выходить из цепи в точке «B».

Первое правило Кирхгофа гласит: «Полный ток, исходящий из цепи, равен току, входящему в цепь.«

Таким образом, протекающий полный ток в цепи можно определить как:

Затем, используя закон Ома, мы можем вычислить ток, протекающий через каждый резистор:

Ток протекающий через R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА

Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА

Таким образом, общий ток будет равен:

I = 0,545 мА + 0,255 мА = 0,8 мА

Это также можно проверить с помощью закона Ома:

I = U ÷ R = 12 В ÷ 15 кОм = 0.8 мА (то же)

, где 15 кОм — общее сопротивление двух параллельно включенных резисторов (22 кОм и 47 кОм)

И в заключение следует отметить, что на большинстве современных резисторов маркировка цветными полосами и их назначение можно встретить.

Параллельное соединение резисторов — онлайн калькулятор

Для быстрого расчета общего сопротивления двух или более резисторов, соединенных параллельно, вы можете использовать следующий онлайн-калькулятор:

Суммировать

Когда два или более резистора соединены так, что оба вывода одного резистора подключены к соответствующим выводам другого резистора или резисторов, они считаются подключенными параллельно друг другу.Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга в зависимости от сопротивления каждого резистора.

Эквивалент или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора, включенного в параллельное соединение.

Проверьте правильность приведенных здесь формул в простом эксперименте.

Берем два резистора МЛТ-2 на 3 и 47 Ом и соедините их последовательно.Затем измеряем полное сопротивление получившейся цепи цифровым мультиметром. Как видим, он равен сумме сопротивлений резисторов, входящих в эту цепочку.

Измерение полного сопротивления при последовательном включении

Теперь мы подключаем наши резисторы параллельно и измеряем их полное сопротивление.

Параллельное измерение сопротивления

Как видите, результирующее сопротивление (2,9 Ом) меньше наименьшего (3 Ом) входящего в цепь.Это приводит к другому хорошо известному правилу, которое можно применить на практике:

При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, включенного в эту цепь.

Что еще нужно учитывать при подключении резисторов?

В первую очередь учитывается обязательно их номинальная мощность. Например нам нужно подобрать на замену резистор 100 Ом и мощность 1 Вт .Возьмите два резистора по 50 Ом и соедините их последовательно. Какова рассеиваемая мощность этих двух резисторов?

Так как через последовательно соединенные резисторы протекают одни и те же резисторы. Округ Колумбия. (допустим 0,1 А ), а сопротивление каждого из них составляет 50 Ом , тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт . В результате каждый из них будет выделяться мощностью 0,5 Вт и единиц. В сумме это будет тот же 1 W .

Это довольно грубый пример. Поэтому в случае сомнений стоит брать резисторы с запасом мощности.

Подробнее о рассеиваемой мощности резистора.

Во-вторых, для подключения следует использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это всего лишь рекомендация.

Комбинация резисторов — последовательно и параллельно — Учебный материал для IIT JEE

Введение в сочетание резисторов — последовательных и параллельных

Электрический ток — это поток заряженных частиц.Поток зарядов будет постоянным в текущей электроэнергии. Электрический ток течет от более высокого электрического потенциала к более низкому электрическому потенциалу. Для протекания тока требуется замкнутый контур из проводящего материала. Схема состоит из проводов, соединенных встык, и электроны движутся в одном направлении.

Схема

А имеет жилы (провод), выключатель, нагрузку и источник питания. Схема начинается и останавливается в одной и той же точке. Обычно в качестве жил без изоляции используются медные провода.Именно по проводнику течет ток. Переключатель используется для размыкания или замыкания цепи. Когда переключатель замкнут, ток течет по цепи, а когда переключатель разомкнут, он размыкает цепь, и ток через нее не течет. Клетка может быть источником энергии. Если мы поместим более одной ячейки, она станет батареей.

Нагрузка, также известная как Резистор , использует электрическую энергию и преобразует ее в другую форму энергии. Это может быть лампочка или что-нибудь еще.Если в цепи нет нагрузки, произойдет короткое замыкание.

Схема А

Параметры цепи

Электрический ток измеряется в амперах с помощью амперметра, который будет последовательно соединен с другими компонентами в цепи. Ток, I = Q / t, где Q — заряд в кулонах, а t — время в секундах. Андре Мари Ампер обнаружил, что два параллельных провода притягиваются друг к другу, когда электрический ток течет в одном направлении.Кроме того, два параллельных провода отталкиваются друг от друга, когда электрический ток течет в противоположных направлениях. В результате его открытий в этой области единица измерения тока была получена от его имени, которое называется « amp ». Один ампер равен одному кулону заряда в секунду времени.

Напряжение определяется как разность электрических потенциалов между двумя точками в цепи. Единица измерения напряжения — вольты. Устройство происходит от имени Алессандро Вольта. Элементы или батареи обеспечивают необходимое напряжение или разность потенциалов.

Сопротивление препятствует прохождению тока. Это мера способности объекта сдерживать поток электронов. Сопротивление будет низким в проводнике и высоким в изоляторе. Измеряется в омах. Единица ома названа в честь ученого Георга Симона Ома, сформулировавшего закон Ома.

Резисторы используются для управления прохождением электрического тока в цепи. Он преобразует электрическую энергию в тепло и свет. Резистор является пассивным компонентом, поскольку он потребляет мощность, но не генерирует мощность.Обычно они состоят из металла, углерода или пленки оксида металла. Резисторы используются для ограничения тока и защиты полупроводниковых устройств, таких как светодиоды. Он также используется для ограничения частотной характеристики в цепи фильтра.

Закон Ома

Георг Симон Ом показал взаимосвязь между напряжением, током и сопротивлением и сформулировал закон Ома. Этот закон лежит в основе электричества.

Закон гласит, что V = I R, где напряжение V выражено в вольтах, ток I — в амперах, а сопротивление R — в омах.

Таким образом, I = V / R и R = V / I.

Для большей ясности электричество можно отнести к воде. Таким образом, напряжение в цепи, единицей измерения которой являются вольты, идентично давлению воды, текущей в трубе. Ток в цепи, где единица измерения равен амперам, эквивалентен току воды, протекающей по трубе. Сопротивление в контуре, измеряемое в омах, совпадает с сопротивлением трения и размером трубы, которая ограничивает поток воды.

Закон Ома

Последовательные и параллельные соединения

В основном есть два типа цепей: последовательные и параллельные.И последовательная, и параллельная цепи состоят из более чем одной нагрузки. Резисторы можно подключать последовательно, параллельно или их комбинацию.

В последовательной цепи электронов движутся только по одному пути. Здесь будет тот же ток, который проходит через каждый резистор. Напряжение на резисторе при последовательном включении будет другим. При последовательном соединении, если один резистор сломан или возникает какая-либо неисправность, вся цепь отключается. Последовательные цепи нелегко перегреть.Конструкция последовательной схемы проста по сравнению с параллельной схемой.

Некоторые огни рождественской елки могут быть включены в последовательные цепи. Если погаснет одна лампочка, погаснет вся струна. Предохранитель или автоматические выключатели будут подключены последовательно, чтобы защитить всю проводку от перегрузки по току. Его можно использовать как делитель напряжения. Батарейки в пульте подключены последовательно.

Последовательная цепь

В параллельной цепи электронов проходят через множество ветвей в ней.В этом случае напряжение на каждом резисторе в цепи остается неизменным. Здесь ток в цепи делится между каждой ветвью и, наконец, рекомбинирует, когда ветви встречаются в общей точке. Параллельная цепь может быть сформирована разными способами, что означает, что резисторы могут быть расположены в разных формах. Его можно использовать как делитель тока.

В большинстве случаев цепи подключаются параллельно. Это потому, что если один резистор сломан или поврежден, он не отключит всю систему.Но из-за этого эффекта трудно обнаружить отказ, если в цепи что-то пойдет не так, и поэтому в определенные моменты это может быть опасно. Легко подключить или отключить новый резистор или другой компонент, не затрагивая другие элементы в параллельной цепи. Но он использует много проводов и, следовательно, становится сложным. В основном в зданиях и домах мы используем параллельное подключение.

Параллельная цепь

Комбинация резисторов при последовательном включении

Рассмотрим три резистора R ₁ , R ₂ , R ₃ , которые включены последовательно.Здесь заряд сначала проходит через ₁ рандов, затем попадает в ₂ рандов и, наконец, достигает ₃ рандов.

Комбинация из трех последовательно соединенных резисторов

По закону Ома разность потенциалов на R ₁ = V ₁ = I R ₁

Разность потенциалов на R ₂ = V ₂ = I R ₂ .

Разность потенциалов на R ₃ = V ₃ = I R ₃ .

Таким образом, разность потенциалов V на этом последовательном соединении резисторов

В = В ₁ + В ₂ + В ₃

= I R ₁ + I R ₂ + I R ₃

= I (R ₁ + R ₂ + R ₃ )

Таким образом, в случае последовательного соединения эквивалентное сопротивление R _eq = V / I = (R ₁ + R ₂ + R ₃ ).

Для n числа резисторов, соединенных последовательно, эквивалентное сопротивление R _eq = R ₁ + R ₂ + R _{3 …………………} R _n .

Эквивалентное сопротивление — это полное сопротивление цепи. Это единственное значение сопротивления, которое может заменить количество резисторов в цепи без изменения тока и напряжения в сети. Таким образом, при последовательном соединении общее сопротивление цепи определяется путем сложения сопротивлений каждого отдельного резистора.

Для примера рассмотрим последовательную схему, которая состоит из трех резисторов с сопротивлением 5 Ом, 10 Ом, 5 Ом соответственно с батареей 15 В.

Итак, полное сопротивление R = R _{1 +} R _{2 +} R ₃ = 5 + 10 + 5 = 20 Ом

Мы знаем, что V = I R.

Ток I = V / R = 15/20 = 0,75 А. Хотя ток в последовательной сети одинаков, падение напряжения на каждом резисторе отличается. Каждый резистор с разным сопротивлением обеспечивает разное падение напряжения, и мы можем найти полное напряжение по закону Ома, V = I R. Давайте возьмем предыдущий пример. Упомянутое здесь напряжение составляет 15 В.Мы можем проверить это, рассчитав таким образом. V = I R ₁ + I R ₂ + I R ₃ = 0,75 (5 +10 + 5) = 15 В. Это точное измерение напряжения, которое мы предоставили в этом примере. Обнаружено, что резистор с большим сопротивлением имеет большее падение напряжения.

Комбинация резисторов при параллельном подключении

Рассмотрим три резистора R ₁ , R ₂ , R ₃ , включенных параллельно. Заряд делится на три части и проходит через ₁ рандов, 2 рандов и _{рандов 3.}

Комбинация из трех параллельно включенных резисторов

Ток I = I ₁ + I ₂ + I _3.

Разность потенциалов, приложенная к R1 = V = I ₁ R ₁

Разность потенциалов на R ₂ = V = I ₂ R ₂

Разность потенциалов на R ₃ = V = I ₃ R ₃

Таким образом, I = I ₁ + I ₂ + I ₃

= V / R ₁ + V / R ₂ + V / R ₃

= V (1 / R ₁ + 1 / R ₂ + 1 / R ₃ )

Если эту параллельную комбинацию заменить эквивалентным сопротивлением, R _eq

Тогда I = V / R _экв

1 / R _экв. = 1 / R ₁ + 1 / R ₂ + 1 / R ₃

Таким образом, для n количества резисторов, включенных параллельно, 1 / R _eq = 1 / R ₁ + 1 / R ₂ + 1 / R _{3 ……………………….} 1 / R _№ .

Итак, при параллельном соединении полное сопротивление цепи определяется путем сложения обратной величины сопротивления каждого отдельного резистора.

Для примера рассмотрим параллельную цепь, состоящую из трех резисторов с сопротивлением 5 Ом, 10 Ом, 5 Ом соответственно с батареей 15 В.

Таким образом, общее сопротивление, 1 / R = 1 / R ₁ + 1 / R ₂ + 1 / R ₃ = 1/5 + 1/10 + 1/5 = 5/10. Итак, R = 2Ω.

При параллельном подключении полное сопротивление или эквивалентное сопротивление всегда будет меньше наименьшего резистора, присутствующего в цепи. Значение эквивалентного сопротивления будет между наименьшим сопротивлением в цепи и наименьшим сопротивлением, деленным на количество резисторов, присутствующих в цепи. В этом примере наименьший резистор имеет сопротивление 5 Ом, а значение общего сопротивления составляет 2 Ом, что явно подтверждает вышеупомянутый факт.

Напряжение на каждом резисторе составляет 15 В.Теперь, чтобы найти ток через каждую ветвь, формула: I = V / R.

I ₁ = 15/5 = 3A

I ₂ = 15/10 = 1,5 A

I ₃ = 15/5 = 3A

Общий ток I = 3 + 1,5 + 3 = 7,5 A

Комбинация последовательных и параллельных резисторов

Рассмотрим схему, в которой R ₂ и R ₃ подключены параллельно, а R ₁ включены последовательно с R ₂ и R _3.

Комбинация резисторов последовательно и параллельно

Сначала рассмотрим R ₂ и R ₃ и, следовательно, 1 / R _23eq = 1 / R ₂ + 1 / R ₃

R _23eq = R ₂ R ₃ / R ₂ + R ₃

R _123eq = R _23eq + R ₁

Таким образом, ток I = V / R _123eq = V / [R ₁ + (R ₂ R ₃ / R ₂ + R ₃ )]

= V (R ₂ + R ₃ ) / R ₁ R ₂ + R ₁ R ₃ + R ₂ R _3.

Сводка

• Электрический ток — это поток заряженных частиц в цепи. Схема состоит из проводника, резистора, переключателя и источника питания.

• Ток, I = Q / t, где Q — заряд в кулонах, а t — время в секундах. Напряжение — это разность электрических потенциалов между двумя точками в цепи. Вольт — это единица измерения напряжения.

• Сопротивление — это способность управлять потоком электронов в цепи; единицей сопротивления является ом.

• Закон Ома гласит, что V = I R. Таким образом, I = V / R и R = V / I.

• Есть два типа цепей: последовательные и параллельные.

• При последовательном соединении ток, протекающий только по одному пути, будет одинаковым при прохождении через каждый резистор.

• При параллельном подключении напряжение на каждом резисторе в цепи остается неизменным, а ток распределяется между ветвями.

Посмотрите это видео, чтобы получить дополнительную информацию

Дополнительная информация

Комбинация резисторов — Series и Paralle

ПАРАЛЛЕЛЬНЫХ ЦЕПЕЙ

ПАРАЛЛЕЛЬНЫЕ ЦЕПИ ПАРАЛЛЕЛЬНЫЕ ЦЕПИ ПОСТОЯННОГО ТОКА

Цепь, в которой два или более электрических сопротивления или нагрузки подключен к одному источнику напряжения и представляет собой параллельную цепь.Параллель Схема отличается от последовательной схемы тем, что предусмотрено более одного пути для текущего потока — чем больше путей добавлено параллельно, тем меньше противодействия к потоку электронов от источника. В последовательной схеме сложение сопротивления увеличивает сопротивление току. Минимальные требования для параллельной цепи следующие:

(1) источник питания. (2) проводника. (3) сопротивление или нагрузка для каждого пути тока. (4) два или более путей для прохождения тока. На рисунке 8-62 показана параллельная цепь с тремя путями прохождения тока. Точки A, B, C и D подключены к одному и тому же проводнику и находятся на такой же электрический потенциал. Аналогичным образом точки E, F, G и H с таким же потенциалом. Поскольку приложенное напряжение появляется между точками A и E, одинаковое напряжение приложено между точками B и F, точками C и G, а между точками D и H. Таким образом, при параллельном включении резисторов на источнике напряжения каждый резистор имеет одинаковое приложенное напряжение, хотя токи через резисторы могут отличаться в зависимости от значений сопротивление.Напряжение в параллельной цепи может быть выражено следующим образом: Где ЕТ — приложенное напряжение, Е1 — напряжение на R1, Е2 — напряжение на R2, а E3 — это напряжение на R3 (рисунок 8-62).

Ток в параллельной цепи делится между различными ветвями. в зависимости от сопротивления каждой ветви (см. рисунок 8-63). Ветвь с малым сопротивлением будет иметь больший ток. поток, чем ветвь, содержащая высокое сопротивление.Действующий закон Кирхгофа утверждает, что ток, текущий к точке, равен току утекает из этой точки. Таким образом, ток в цепи может быть математически выражается следующим образом: где IT — общая ток, а I1, I2 и I3 — токи через R1, R2 и R3 соответственно. Закон Кирхгофа и Ома можно применить, чтобы найти полный ток в схеме, показанной на рисунке 8-63.

Ток через ветвь, содержащую сопротивление R1, составляет

Ток через R2 равен

Ток через R3 равен

Суммарный ток IT равен

В параллельной цепи IT = I1 + I2 + I3.По закону Ома следующее отношения можно получить:

Подставляя эти значения в уравнение для полного тока,

В параллельной цепи ET = E1 = E2 = E3. Следовательно,

Деление на E дает,

Это уравнение является обратной формулой для нахождения общей суммы или ее эквивалента. сопротивление параллельной цепи. Другая форма уравнения может быть получена решая для RT.

Анализ уравнения для полного сопротивления в параллельной цепи показывает, что RT всегда меньше наименьшего сопротивления в параллельном схема. Таким образом, резисторы на 10 Ом, 20 Ом и 40 Ом подключены параллельно. иметь общее сопротивление менее 10 Ом.

Если в параллельной цепи всего два резистора, обратная формула

В упрощенном виде это становится:

Эта упрощенная, более короткая формула может использоваться, когда два сопротивления в параллели.Другой метод можно использовать для любого количества резисторов в параллельны, если они имеют одинаковое сопротивление. Величина сопротивления одного резистора делится на количество параллельно включенных резисторов, чтобы определить общую сопротивление. Математически это выражается следующим образом:

Где RT — полное сопротивление, R — сопротивление одного резистора, N — количество резисторов.

Пример: батареи, включенные последовательно и параллельно

Понимание ситуации

В наших предыдущих двух примерах использования принципов Кирхгофа для анализа электрических сетей, последовательно включенных резисторов и параллельных резисторов анализ был довольно простым.

В последовательном случае два резистора действовали как один эффективный резистор с сопротивлением, равным сумме сопротивлений отдельных резисторов. В параллельном случае два резистора действовали как один эффективный резистор, равный, где сумма обратных сопротивлений давала эффективное обратное сопротивление.

Это связано с тем, что последовательно подключенные резисторы труднее протолкнуть ток — ток должен пройти через оба резистора — а резисторы, включенные параллельно, легче протолкнуть ток — ток может разделиться между двумя резисторами.Таким образом, как последовательные, так и параллельные резисторы в некотором смысле эквивалентны простейшему случаю подключения одного резистора к одной батарее.

Но многие важные электрические ситуации в биологии не могут быть смоделированы такими простыми системами. Например, то, что происходит в клеточной мембране (особенно в нервной клетке), является сильно электрическим явлением, зависящим от зарядов, протекающих через мембрану. Ионные насосы действуют как батареи, создавая разность потенциалов, и, поскольку существует несколько ионных насосов, которые могут перекачивать ионы внутрь или из ячеек, модели с одной батареей недостаточно.Кроме того, рассмотрение моделей с более чем одной батареей дает нам лучшее представление о том, как принципы Кирхгофа на самом деле работают в более реалистичных схемах, и показывает их ценность при интерпретации более сложных ситуаций.

Чтобы увидеть, как это работает, давайте решим задачу игрушечной модели с двумя идеальными батареями, включенными последовательно, и двумя идеальными батареями, включенными параллельно.

Представляем пример задачи

Рассмотрим три электрические сети, показанные справа. Идентичные батареи по-разному подключаются к одной и той же лампочке.Предположим, что батареи имеют незначительное внутреннее сопротивление. Положительный полюс каждой батареи отмечен плюсом. Расположите эти устройства в порядке убывания яркости лампы.

Решение этой проблемы

Яркость лампы пропорциональна мощности, которую она рассеивает (Мощность в ваттах). Если мы проведем небольшой заряд $ dq $ через резистор так, чтобы он испытал разницу напряжений $ ΔV $, мы действительно сработаем $ dq ΔV $. Если мы сделаем это за время $ dt $, скорость использования энергии составит $ dq / dt ΔV $ или

$$ P = I ΔV $$

произведение тока через резистор на падение напряжения на нем.2R $.

Это говорит нам о том, что если лампочка преобразует всю рассеиваемую ею электрическую энергию в свое сопротивление в виде света (что не совсем верно для лампы накаливания, которая нагревается, но лучше для светодиода), яркость лампы будет равна квадрату света. ток через него. Итак, давайте найдем ток в каждой из лампочек для трех случаев.

Давайте рассмотрим дела по очереди.

Корпус A: одна батарея

Случай А прост: всего одна батарея, подключенная к одному резистору.Текущее правило Кирхгофа гласит, что один и тот же ток должен проходить через все. Назовем это $ I $. Выберите нижнюю часть батареи в качестве нашего 0. Затем верхняя часть батареи находится на уровне $ V_0 $, и наша эвристика без сопротивления проводника позволяет нам отобразить потенциал повсюду, как показано. Мы видим, что падение напряжения на резисторе составляет $ V_0 $, а ток через него равен $ I $. Закон Ома связывает падение напряжения на резисторе с протекающим через него током. В этом случае мы можем предположить, что нам даны повышение напряжения батареи $ V_0 $ и сопротивление лампы $ R $.2} {R} $$

Вариант B: Батареи в серии

Теперь давайте рассмотрим случай B. У нас по-прежнему есть только один цикл, поэтому все, что проходит через один элемент, должно проходить через них все в соответствии с правилом цикла Кирхгофа.

Теперь давайте обозначим потенциал. Мы можем выбрать один 0 для потенциала, поэтому давайте выберем его как нижний предел правой батареи. Мы можем продолжить эти 0 вниз по правой стороне, как делали раньше, но по мере того, как мы идем влево, происходит что-то другое. Сторона высокого напряжения левой батареи подключена к стороне низкого напряжения правой батареи! Таким образом, мы не можем принять низкую сторону левой батареи как 0: она должна иметь потенциал В ₀ .Но мы знаем, что батарея повышает потенциал от своего низкого вывода до высокого на фиксированную величину, независимо от значения низкого напряжения. Таким образом, если мы поднимемся на В ₀ через левую батарею, мы должны получить потенциал 2 В ₀ ! По нашей эвристике без сопротивления проводника мы должны иметь это же значение по всей длине провода, пока мы не доберемся до резистора.

Таким образом, падение на резисторе в этом случае составляет $ ΔV = 2V_0 $. 2} {R} $$

Две батареи, соединенные последовательно, позволяют лампочке потреблять в четыре раза больше энергии, чем одна! Удвоение напряжения в такой схеме приводит к удвоению падения напряжения на резисторе и тока через него.Лампочка станет намного ярче.

Вариант C: Батареи, включенные параллельно

Теперь рассмотрим случай C. Это немного сложнее, поскольку существует два цикла. Нас интересует только ток через лампочку (резистор), поэтому давайте назовем ток через этот контур $ I $. После прохождения через резистор, когда он достигает первого разветвления, сумма выходящего тока с двух возможных путей должна быть добавлена ​​к I по правилу Кирхгофа. Поскольку два пути, по которым он может идти, идентичны, мы предполагаем, что он разделяется пополам, как показано.(Примечание: метки на токе в верхнем контуре означают «ток, деленный на 2», а не «половину».)

А теперь составим карту потенциала. Мы можем выбрать одну точку в сети как 0 нашего потенциала. Возьмем его за нижнюю часть нижней батареи. По принципу безопорного проводника любая часть провода, подключенная к этой точке без сопротивления между ними, также должна быть на 0. Это означает, что нижний конец второй батареи и правая сторона резистора. (Проследите за проводами от нижнего конца батареи и посмотрите все места, которые мы пометили как 0.)

Принцип, согласно которому батарея создает на своих выводах повышение потенциала до фиксированного значения, означает, что сторона высокого напряжения обеих батарей должна быть $ V_0 $. Используя принцип безопорного проводника, мы можем найти значения потенциала везде в цепи, в том числе на другом конце резистора. Это говорит нам о том, что падение потенциала на резисторе составляет $ V_0 $. По закону Ома (принципу сопротивления Кирхгофа) мы можем связать ток с падением на резисторе:

$$ I = \ frac {ΔV} {R} = \ frac {V_0} {R}.

$

Это тот же результат, что и в случае A, поэтому наш порядок яркости для трех случаев составляет

.

В> А = С.

Интерпретация результатов.

Две последовательно соединенные батареи обеспечивают вдвое больше «толчка» (электрического напряжения), чем одна, поэтому мы получаем больший ток и большую мощность, рассеиваемую в лампочке. Две параллельно включенные батареи обеспечивают одинаковое падение напряжения, поэтому наша лампочка не будет ярче, но поскольку ток через каждую батарею уменьшается вдвое, батареи прослужат дольше.

Хотя это решает нашу проблему, стоит еще немного рассмотреть случай C. Мы предположили, что батареи идентичны, но что, если это не так? Мы бы попали в беду! Мы бы запустили наши нулевые значения $ V $ вверх по правой стороне, а затем перепрыгнули через каждую батарею с их соответствующими подъемами и получили разные значения того, каким должен быть потенциал в левой части сети. Противоречие! Причина этого в том, что вначале мы исходили из предположения, что наши батареи были идеальными: они всегда поддерживали фиксированную разность напряжений на своих выводах и не имели внутреннего сопротивления.Мы также предположили, что наши провода были идеальными: имели нулевое сопротивление.

Эти предположения верны до тех пор, пока в цепях всегда есть резисторы, которые значительно больше, чем (обычно небольшие) сопротивления батарей и проводов. Но в верхнем шлейфе корпуса C мы соединили две батареи в шлейф без каких-либо резисторов. Это все равно, что соединить обе клеммы аккумулятора друг с другом просто проводом — короткое замыкание. Поскольку $ ΔV $ фиксировано и $ R ~ 0 $, получаем, что $ I = ΔV / R $ очень велико.Большой ток означает, что большая мощность рассеивается на очень маленьком сопротивлении провода. Он очень сильно нагревается и очень быстро разряжает батарею. Не пытайтесь повторить это дома! (Или в своей лаборатории!) Вы не можете разжечь огонь, но почти наверняка разрядите свои батареи.

Джо Редиш 15.03.16

МОЩНОСТЬ В КОМБИНИРОВАННЫХ ЦЕПЯХ

Как вы подсчитали ранее, общая мощность, потребляемая последовательной или параллельной цепью, равна сумме мощности, потребляемой каждым из компонентов цепи.То же самое и с комбинированной схемой. Часто предоставляется только один параметр (например, сопротивление, напряжение или ток). Ваша задача — уменьшить и объединить различные сопротивления, чтобы найти второй параметр.

Часто для этого требуется систематическое уменьшение цепи до единственного эквивалентного значения сопротивления. Затем вы работаете в обратном направлении, чтобы получить недостающие значения для различных компонентов, используя закон Ома. Помните, что вы не можете найти мощность, пока не получите два из трех параметров для каждого из компонентов.Общая мощность получается путем сложения всех индивидуальных мощностей каждого из компонентов.

Рассчитайте мощность, рассеиваемую каждым компонентом, и общую мощность комбинированной схемы, показанной на Рисунке 6–33. Первый шаг — просмотреть схему, проанализировать, что известно, а что неизвестно, и сравнить то, что вы видите, с тем, что вы решаете.

На рис. 6–33 нет компонентов с двумя значениями, с которыми можно работать.Это означает, что вам придется начать с объединения компонентов схемы, чтобы найти необходимую вторую переменную.

Вы можете использовать уравнение P _T = E _T × I _T для расчета полной мощности. Однако на рис. 6–33 нет значения для I _T . Поэтому первым делом нужно найти I _T . Чтобы рассчитать значение I _T , вам необходимо значение общего сопротивления (R _T ). Зная R _T , вы можете рассчитать I _T по следующей формуле:

Чтобы вычислить R _T в этой схеме, вы начнете с объединения резисторов R ₂ и R ₃ :

Просто для проверки мы могли бы использовать предполагаемое напряжение для резисторов 100 Ом и 200 Ом, включенных параллельно.В качестве примера возьмем параллельное напряжение 400 В.

Резистор 100 Ом допускает 4 А, а резистор 200 Ом допускает 2 А, всего 6 А. Эти 6 А будут общим током при приложенном 400 В. Таким образом,

Второй шаг — уменьшить последовательный резистор R ₁ и эквивалентный резистор R _2,3 до одного значения. Это дает R _T . Поскольку это последовательная схема, R _T вычисляется путем сложения последовательных элементов:

Теперь, когда у вас есть напряжение источника E _T 100 В и общее сопротивление R _T , вы можете вычислить общий ток (I _T ), используя следующую формулу:

Теперь у вас есть все три параметра эквивалентной схемы.Используя эти значения, вы можете найти общую мощность для цепи P _T и мощность, потребляемую каждым из компонентов схемы R ₁ , R ₂ и R ₃ . Сначала вы решите общую мощность цепи (P _T ), используя следующую формулу:

Теперь у вас есть необходимая информация для расчета индивидуальных потерь мощности, начиная с R ₁ . Поскольку в последовательной цепи ток одинаков во всей цепи, и поскольку вам известен общий ток I _T , ток в R ₁ и R _2,3 можно рассчитать как:

Теперь у вас есть ток и сопротивление для R ₁ , и, таким образом, вы можете рассчитать мощность, потребляемую R ₁ , используя следующую формулу:

Существует несколько способов расчета мощности, рассеиваемой R ₂ и R ₃ .Поскольку вам известен ток через параллельную ветвь R _2,3 и эквивалентное сопротивление R _2,3 (вычисленное ранее в задаче), вы можете рассчитать напряжение на этой ветви, используя закон Ома. Используйте следующую формулу:

Поскольку это параллельная ветвь, вы знаете, что напряжение одинаково как на R ₂ , так и на R ₃ :

Теперь у вас есть падение напряжения и сопротивление R ₂ и R ₃ , и вы можете рассчитать мощность, рассеиваемую каждым из этих компонентов, используя следующие формулы:

Вы выполнили все расчеты, необходимые для определения общей мощности и мощности, потребляемой отдельными компонентами, составляющими схему на Рисунке 6–33.Вы должны проверить свои расчеты, добавив отдельные рассеиваемые мощности и сравнив их с общей мощностью, рассчитанной ранее:

Ранее вы рассчитали P _T как 0,316 × 100 = 31,6 Вт. Небольшая ошибка вызвана округлением десятичных знаков во время вычислений.

ЦЕПИ

С ИЗВЕСТНЫМ ИСПОЛЬЗОВАНИЕМ ЭНЕРГИИ

Цепи, над которыми вы будете работать в своей работе, часто имеют известные значения мощности и напряжения. Один из аспектов, который вам необходимо принять во внимание, — это реальная потребляемая мощность для цепей с компонентами, которые уже рассчитаны.Например, посмотрите на рис. 6–34.

В этой схеме три лампы подключены к источнику питания с помощью медного провода №16 американского калибра (AWG) длиной 300 футов.

Из рисунка видно, что каждая лампа рассчитана на 25 Вт и что лампы подключаются параллельно. Когда вы смотрите на такую ​​схему, вы должны обязательно принять во внимание все параметры схемы. Электрик, установивший лампы, подсчитал, что лампы потребляют 0.5 А при приложенном 50 В, что делает общий ток цепи суммой тока в отдельных ветвях (т. Е. 1,5 А). Следующие формулы подтверждают расчеты электрика. Для расчета силы тока отдельных ламп (общий ток складывается из суммы всех трех ламп):

Кажется, все в порядке. Однако посмотрите на схему еще раз. Нагрузка, все три лампы, находится на расстоянии 300 футов от источника напряжения. Из предыдущих глав вы знаете, что все проводники, даже медные, обладают некоторым сопротивлением.Вы также знаете, что чем длиннее провод, тем выше сопротивление: медь # 16 AWG имеет сопротивление 4,99 Ом на 1000 футов. Эта информация взята из стандарта NEC ^® и применима к семжильному проводнику при температуре 75 ° C. Обратите внимание, что это значение немного отличается от значения, приведенного в предыдущей главе. Это связано с тем, что значение в этой таблице относится к одножильному, а не многожильному проводу. Просмотрите другие размеры проводников, чтобы узнать, какое сопротивление они имеют на тысячу футов проводника.Учтите, что чем крупнее проводник, тем меньше значение сопротивления. Тот факт, что нагрузка находится на расстоянии 300 футов от источника питания, означает, что при расчетах необходимо учитывать сопротивление медного проводника №16, идущего к лампам и возвращающегося от них. Поскольку в проводниках, питающих осветительную нагрузку, существует сопротивление, при расчетах для этой схемы необходимо учитывать и другие факторы.

Изучите рисунок 6–35. Эта схема была перерисована, чтобы представить все сопротивления, которые необходимо учитывать в схеме при выполнении расчетов.Номинальная мощность лампы — это количество энергии, которое лампа рассеивает при приложенном номинальном напряжении. Поскольку номинальное напряжение не будет применяться из-за падения напряжения на проводе, вам необходимо знать сопротивления ламп, чтобы вы могли решить эту схему как комбинированную схему, используя методы, которые вы изучили в этой и предыдущих главах. Поскольку лампы рассчитаны на 25 Вт при 50 В, вы можете рассчитать значение сопротивления лампы следующим образом:

Обратите внимание, что это сопротивление каждой лампы в отдельности.Чтобы полностью проанализировать эту схему, нужно также знать сопротивление провода, питающего лампы. Исходя из того, что сопротивление провода # 16 AWG составляет 4,99 Ом на 1000 футов провода, вы можете рассчитать общее сопротивление как:

Помните, в этой цепи 300 футов провода, идущего к лампам, и 300 футов провода, идущего от ламп. Необходимо учитывать оба расстояния. На Рис. 6–36 показана полная схема со всеми включенными сопротивлениями.

Это комбинированная схема, которую можно сократить с помощью методов, которые вы изучили.Начнем с расчета сопротивления трех параллельно включенных ламп, R _{Все лампы} :

Схема теперь сведена к простой последовательной схеме с двумя отрезками медного провода и параллельным комбинированным сопротивлением ламп. Общее сопротивление складывается из трех элементов серии:

Общий ток рассчитывается как:

Обратите внимание, что значение, рассчитанное электриком, устанавливающим данный проект (1.5 A) отличается от рассчитанного ранее значения. Уменьшение тока вызвано дополнительным сопротивлением провода. Теперь узнаем, какое напряжение на самом деле подается на лампы. Мы знаем, что полный ток для этой цепи на самом деле составляет 1,38 А, и мы знаем, что эквивалентное сопротивление для ламп, включенных последовательно с сопротивлением, равно 33,33. Используя закон Ома, мы можем легко рассчитать напряжение на лампах следующим образом:

Это означает, что мы потеряли (упали) на проводах 4 В.В процентах это:

Это большое падение является чрезмерным. Максимальные падения напряжения обычно не должны превышать 3%. Лампы не рассеивают мощность, на которую они рассчитаны. Другими словами, вместо ламп, фактически обеспечивающих свет в соответствии с их проектными параметрами, теперь огни будут работать в соответствии с фактическими параметрами установки. Посмотрим, как на самом деле влияют параметры установки на лампы. Поскольку теперь мы знаем, что установка питает лампы напряжением 46 В, мы можем пересчитать фактическую мощность ламп следующим образом:

Эта схема с учетом сопротивления проводников фактически потеряла примерно 15% мощности лампы.Это:

Как видите, при проектировании установки необходимо учитывать всю схему. Все компоненты сопротивления в комбинированной цепи потребляют мощность, и это необходимо учитывать. Посмотрите на сопротивление проводов и посмотрите, сколько энергии потребляет их сопротивление. Поскольку вы уже рассчитали ток и сопротивление проводников, вы можете легко рассчитать мощность, потребляемую проводниками, по следующей формуле:

Обратите внимание на множитель 2.Есть два проводника, и вы должны учитывать их обоих. Предыдущий расчет показывает, что из всей мощности, потребляемой установкой, часть этой мощности (5,69 Вт) потребляется проводниками и теряется в виде тепла. Не принимая во внимание потерю мощности в проводниках, фактическая схема не работала с оптимальной проектной эффективностью, фактическая мощность лампы была снижена, а проводники потребляли мощность, которая терялась в виде тепла. Всего этого можно было избежать или уменьшить, выбрав провод большего диаметра.

В последовательных и параллельных цепях, особенно в цепях с длинными проводниками или проводниками малого диаметра (например, пожарная сигнализация или акустические системы), вы должны учитывать падение напряжения и потери мощности из-за сопротивления проводника.

Другой пример проблемы обрыва линии и потери линии — использование цепей пожарной сигнализации. В схемах монитора, где в зоне защиты находится много тепловых датчиков или датчиков дыма, на двух проводниках, идущих от датчика к датчику, будет пропадание линии.В схемах уведомления (рис. 6–37) все чувствительные элементы включены параллельно через два параллельных проводника. Обычно датчики имеют разомкнутую связь с параллельной цепью.

Контроль цепи осуществляется путем размещения резистора между линейными проводниками в самом конце цепи. Этот резистор называется оконечным резистором. Его цель — позволить небольшому количеству тока течь по отрицательному проводнику до конца, через резистор и обратно к источнику.

При обрыве где-либо в цепи (обрыв) линейный ток становится равным нулю, и контрольная электроника указывает на проблему в цепи. Если какой-либо датчик обнаруживает тепло или дым, он создает замкнутую цепь (короткое замыкание) от одного проводника к другому. Электронная схема контроля обнаруживает большое увеличение тока, и срабатывает пожарная сигнализация.

.