Как я и обещал в статье про переменные резисторы (ссылка), сегодня речь пойдет о возможных способах соединения, в частности о последовательном соединении резисторов и о параллельном.
Последовательное соединение резисторов.
Давайте начнем с рассмотрения цепей, элементы которой соединены последовательно. И хоть мы и будем рассматривать только резисторы в качестве элементов цепи в данной статье, но правила, касающиеся напряжений и токов при разных соединениях будут справедливы и для других элементов. Итак, первая цепь, которую мы будем разбирать выглядит следующим образом:
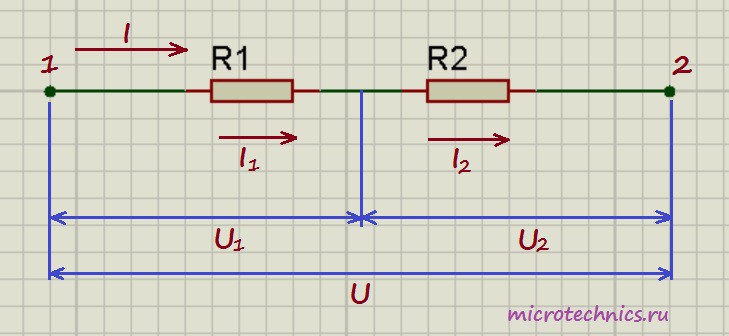
Здесь у нас классический случай последовательного соединения – два последовательно включенных резистора. Но не будем забегать вперед и рассчитывать общее сопротивление цепи, а для начала рассмотрим все напряжения и токи. Итак, первое правило заключается в том, что протекающие по всем проводникам токи при последовательном соединении равны между собой:
I = I_1 = I_2
А для определения общего напряжения при последовательном соединении, напряжения на отдельных элементах необходимо просуммировать:
U = U_1 + U_2
В то же время, по закону Ома для напряжений, сопротивлений и токов в данной цепи справедливы следующие соотношения:
U_1 = I_1R_1 = IR_1
U_2 = I_2R_2 = IR_2
Тогда для вычисления общего напряжения можно будет использовать следующее выражение:
U = U_1 + U_2 = IR_2 + IR_2 = I(R_1 + R_2)
Но для общего напряжение также справедлив закон Ома:
U = IR_0
Здесь R_0 – это общее сопротивление цепи, которое исходя из двух формул для общего напряжения равно:
R_0 = R_1 + R_2
Таким образом, при последовательном соединении резисторов общее сопротивление цепи будет равно сумме сопротивлений всех проводников.
Например для следующей цепи:
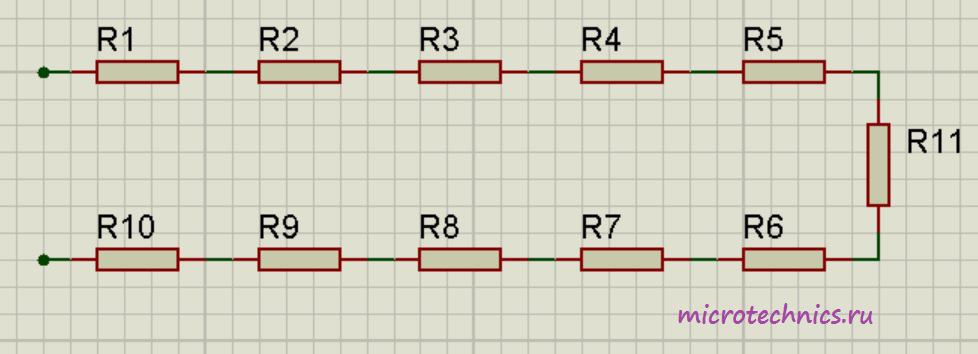
Общее сопротивление будет равно:
R_0 = R_1 + R_2 + R_3 + R_4 + R_5 + R_6 + R_7 + R_8 + R_9 + R_{10}
Количество элементов значения не имеет, правило, по которому мы определяем общее сопротивление будем работать в любом случае 🙂 А если при последовательном соединении все сопротивления равны (R_1 = R_2 = … = R), то общее сопротивление цепи составит:
R_0 = nR
В данной формуле n равно количеству элементов цепи. С последовательным соединением резисторов мы разобрались, давайте перейдем к параллельному.
Параллельное соединение резисторов.
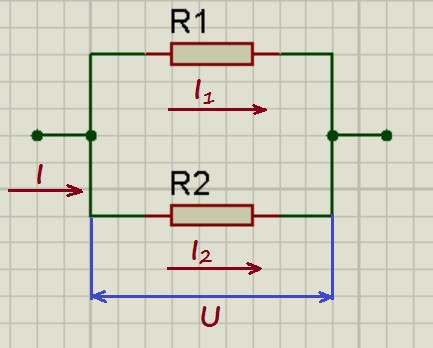
При параллельном соединении напряжения на проводниках равны:
U_1 = U_2 = U
А для токов справедливо следующее выражение:
I = I_1 + I_2
То есть общий ток разветвляется на две составляющие, а его значение равно сумме всех составляющих. По закону Ома:
I_1 = \frac{U_1}{R_1} = \frac{U}{R_1}
I_2 = \frac{U_2}{R_2} = \frac{U}{R_2}
Подставим эти выражения в формулу общего тока:
I = \frac{U}{R_1} + \frac{U}{R_2} = U\medspace (\frac{1}{R1} + \frac{1}{R2})
А по закону Ома ток:
I = \frac{U}{R_0}
Приравниваем эти выражения и получаем формулу для общего сопротивления цепи:
\frac{1}{R_0} = \frac{1}{R_1} + \frac{1}{R_2}
Данную формулу можно записать и несколько иначе:
R_0 = \frac{R_1R_2}{R_1 + R_2}
Таким образом, при параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Аналогичная ситуация будет наблюдаться и при большем количестве проводников, соединенных параллельно:
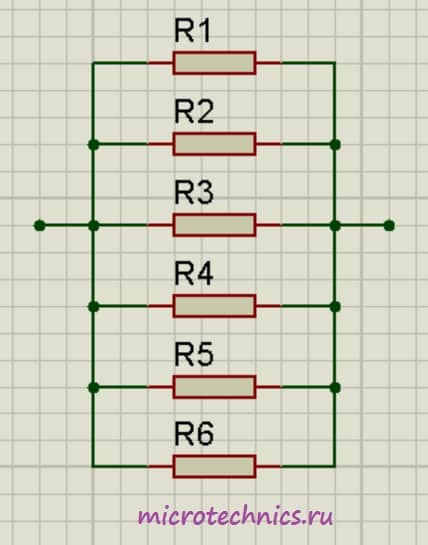
\frac{1}{R_0} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \frac{1}{R_4} + \frac{1}{R_5} + \frac{1}{R_6}
Смешанное соединение резисторов.
Помимо параллельного и последовательного соединений резисторов существует еще смешанное соединение. Из названия уже понятно, что при таком соединении в цепи присутствуют резисторы, соединенные как параллельно, так и последовательно. Вот пример такой цепи:
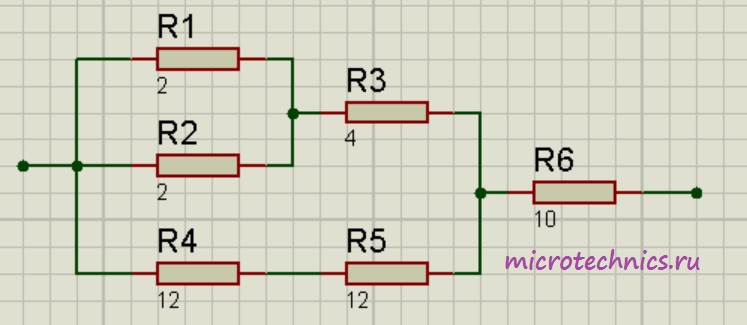
Давайте рассчитаем общее сопротивление цепи. Начнем с резисторов R_1 и R_2 – они соединены параллельно. Мы можем рассчитать общее сопротивление для этих резисторов и заменить их в схеме одним единственным резистором R_{1-2}:
R_{1-2} = \frac{R1\cdot R2}{R1 + R2} = 1
Теперь у нас образовались две группы последовательно соединенных резисторов:
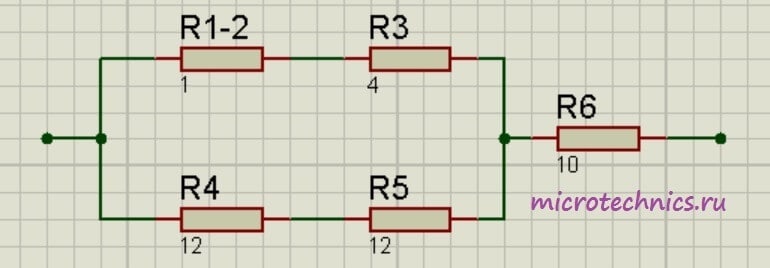
Заменим эти две группы двумя резисторами, сопротивление которых равно:
R_{1-2-3} = R_{1-2} + R_3 = 5
R_{4-5} = R_4 + R_5 = 24
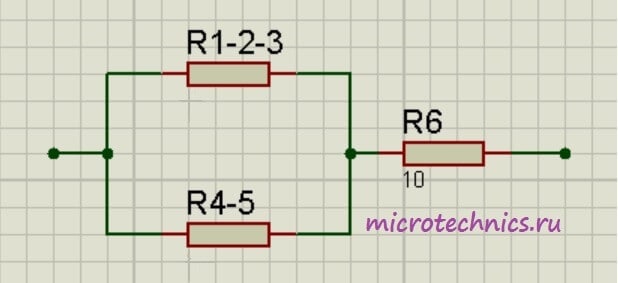
Как видите, схема стала уже совсем простой 🙂 Заменим группу параллельно соединенных резисторов R_{1-2-3} и R_{4-5} одним резистором R_{1-2-3-4-5}:
R_{1-2-3-4-5}\enspace = \frac{R_{1-2-3}\medspace\cdot R_{4-5}}{R_{1-2-3} + R_{4-5}} = \frac{5\cdot24}{5 + 24} = 4.14
И в итоге у нас на схеме осталось только два резистора соединенных последовательно:
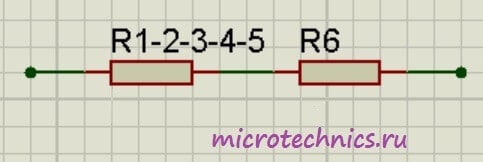
Общее сопротивление цепи получилось равным:
R_0 = R_{1-2-3-4-5}\medspace +\medspace R_6 = 4.14 + 10 = 14.14
Таким вот образом достаточно большая схема свелась к простейшему последовательному соединению двух резисторов!
Тут стоит отметить, что некоторые схемы невозможно так просто преобразовать и определить общее сопротивление – для таких схем нужно использовать правила Кирхгофа, о которых мы обязательно поговорим в будущих статьях. А сегодняшняя статья на этом подошла к концу, до скорых встреч на нашем сайте!
Последовательное и параллельное соединение очень широко используется в электронике и электротехнике и порой даже необходимо для правильной работы того или иного узла электроники. И начнем, пожалуй, с самых простых компонентов радиоэлектронных цепей – проводников.
Для начала давайте вспомним, что такое проводник? Проводник – это вещество или какой-либо материал, который отлично проводит электрический ток. Если какой-либо проводник отлично проводит электрический ток, то он в любом случае обладает каким-либо сопротивлением. Сопротивление проводника мы находим по формуле:
формула сопротивление проводникаρ – это удельное сопротивление, Ом × м
R – сопротивление проводника, Ом
S – площадь поперечного сечения, м2
l – длина проводника, м
Более подробно об этом я писал здесь.
Следовательно, любой проводник представляет из себя резистор с каким-либо сопротивлением. Значит, любой проводник можно нарисовать так.
 обозначение резистора на схемах
обозначение резистора на схемахПоследовательное соединение проводников
Сопротивление при последовательном соединении проводников
Последовательное соединение проводников – это когда к одному проводнику мы соединяем другой проводник и так по цепочке. Это и есть последовательное соединение проводников. Их можно соединять с друг другом сколь угодно много.
 последовательное соединение резисторов
последовательное соединение резисторов
Получается, можно записать, что
 формула при последовательном соединении резисторов
формула при последовательном соединении резисторовУ нас есть 3 проводника, которые соединены последовательно. Сопротивление первого 3 Ома, второго 5 Ом, третьего 2 Ома. Найти их общее сопротивление в цепи.
Решение
Rобщее =R1 + R2 + R3 = 3+5+2=10 Ом.
То есть, как вы видите, цепочку из 3 резисторов мы просто заменили на один резистор RAB .

показать на реальном примере с помощью мультиметра
Сила тока через последовательное соединение проводников
Что будет, если мы подадим напряжение на концы такого резистора? Через него сражу же побежит электрический ток, сила которого будет вычисляться по закону Ома

Получается, если через резистор RAB течет какой-то определенный ток, следовательно, если разложить наш резистор на составляющие R1 , R2 , R3 , то получится, что через них течет та же самая сила тока, которая текла через резистор RAB .
 сила тока через последовательное соединение проводников
сила тока через последовательное соединение проводниковПолучается, что при последовательном соединении проводников сила тока, которая течет через каждый проводник одинакова. То есть через резистор R1 течет такая же сила тока, как и через резистор R2 и такая же сила тока течет через резистор R3 .
Напряжение при последовательном соединении проводников
Давайте еще раз рассмотрим цепь с тремя резисторами

Как мы уже знаем, при последовательном соединении через каждый резистор проходит одна и та же сила тока. Но вот что будет с напряжением на каждом резисторе и как его найти?
Оказывается, все довольно таки просто. Для этого надо снова вспомнить закон дядюшки Ома и просто вычислить напряжение на любом резисторе. Давайте так и сделаем.
Пусть у нас будет цепь с такими параметрами.

Мы теперь знаем, что сила тока в такой цепи будет везде одинакова. Но какой ее номинал? Вот в чем загвоздка. Для начала нам надо привести эту цепь к такому виду.

Получается, что в данном случае RAB =R1 + R2 + R3 = 2+3+5=10 Ом. Отсюда уже находим силу тока по закону Ома I=U/R=10/10=1 Ампер.
Половина дела сделано. Теперь осталось узнать, какое напряжение падает на каждом резисторе. То есть нам надо найти значения UR1 , UR2 , UR3 . Но как это сделать?

Да все также, через закон Ома. Мы знаем, что через каждый резистор проходит сила тока 1 Ампер, мы уже вычислили это значение. Закон ома гласит I=U/R , отсюда получаем, что U=IR.
Следовательно,
UR1 = IR1 =1×2=2 Вольта
UR2 = IR2 = 1×3=3 Вольта
UR3 = IR3 =1×5=5 Вольт
Теперь начинается самое интересное. Если сложить все падения напряжений на резисторах, то можно получить… напряжение источника! Он у нас равен 10 Вольт.
Получается
U=UR1+UR2+UR3
Мы получили самый простой делитель напряжения.
Вывод: сумма падений напряжений при последовательном соединении равняется напряжению питания.
Параллельное соединение проводников
Параллельное соединение проводников выглядит вот так.
 параллельное соединение резисторов
параллельное соединение резисторовНу что, думаю, начнем с сопротивления.
Сопротивление при параллельном соединении проводников
Давайте пометим клеммы как А и В
В этом случае общее сопротивление RAB будет находиться по формуле
Если же мы имеем только два параллельно соединенных проводника

То в этом случае можно упростить длинную неудобную формулу и она примет вид такой вид.

Напряжение при параллельном соединении проводников
Здесь, думаю ничего гадать не надо. Так как все проводники соединяются параллельно, то и напряжение у всех будет одинаково.
Получается, что напряжение на R1 будет такое же как и на R2, как и на R3, так и на Rn

Сила тока при параллельном соединении проводников
Если с напряжением все понятно, то с силой тока могут быть небольшие затруднения. Как вы помните, при последовательном соединении сила тока через каждый проводник была одинакова. Здесь же совсем наоборот. Через каждый проводник будет течь своя сила тока. Как же ее вычислить? Придется опять прибегать к Закону Ома.
Чтобы опять же было нам проще, давайте рассмотрим все это дело на реальном примере. На рисунке ниже видим параллельное соединение трех резисторов, подключенных к источнику питания U.

Как мы уже знаем, на каждом резисторе одно и то же напряжение U. Но будет ли сила тока такая же, как и во всей цепи? Нет. Поэтому для каждого резистора мы должны вычислить свою силу тока по закону Ома I=U/R. В результате получаем, что
I1 = U/R1
I2 = U/R2
I3 = U/R3
Если бы у нас еще были резисторы, соединенные параллельно, то для них
In = U/Rn
В этом случае, сила тока в цепи будет равна:

Задача
Вычислить силу тока через каждый резистор и силу тока в цепи, если известно напряжение источника питания и номиналы резисторов.

Решение
Воспользуемся формулами, которые приводили выше.
I1 = U/R1
I2 = U/R2
I3 = U/R3
Если бы у нас еще были резисторы, соединенные параллельно, то для них
In = U/Rn
Следовательно,
I1 = U/R1 = 10/2=5 Ампер
I2 = U/R2 = 10/5=2 Ампера
I3 = U/R3 = 10/10=1 Ампер
Далее, воспользуемся формулой

чтобы найти силу тока, которая течет в цепи
I=I1 + I2 + I3 = 5+2+1=8 Ампер
2-ой способ найти I
I=U/Rобщее
Чтобы найти Rобщее мы должны воспользоваться формулой
Чтобы не париться с вычислениями, есть онлайн калькуляторы. Вот один из них. Я за вас уже все вычислил. Параллельное соединение 3-ех резисторов номиналом в 2, 5, и 10 Ом равняется 1,25 Ом, то есть Rобщее = 1,25 Ом.
I=U/Rобщее = 10/1,25=8 Ампер.
Параллельное соединение резисторов в электронике также называется делителем тока, так как резисторы делят ток между собой.
Ну а вот вам бонусом объяснение, что такое последовательное и параллельное соединение проводников от лучшего преподавателя России.
Похожие статьи по теме “последовательное и параллельное соединение”
Закон Ома
Проводник (электрический проводник)
Что такое резистор
Делитель напряжения
Делитель тока
Что такое напряжение
Что такое сила тока
Последовательное и параллельное соединение
В данной статье речь пойдет о последовательном и параллельном соединении проводников. На примерах будут рассмотрены данные соединения и как при таких соединениях будут изменяться такие величины как:
- ток;
- напряжение;
- сопротивление.
В таблице 1.8 [Л2, с.24] приведены схемы и формулы по определению сопротивлений, токов и напряжений при параллельном и последовательном соединении.
Последовательное соединение
Последовательным соединением называются те участки цепи, по которым всегда проходят одинаковые токи.
При последовательном соединении:
- сила тока во всех проводниках одинакова;
- напряжение на всём соединении равно сумме напряжений на отдельных проводниках;
- сопротивление всего соединения равно сумме сопротивлений отдельных проводников.
Пример 1
Последовательно подключены две лампы накаливания одинаковой мощности Рл1=Рл2=100 Вт к сети с напряжением Uн=220В. Сопротивление нити в лампах составляет Rл1=Rл2=122 Ом. Номинальное напряжение для ламп равно 220 B. На рис.1 показано последовательное включение ламп.
Решение
Составляем схему замещения, выражая каждую из входящих элементов цепи (в данном случае лампы накаливания) в виде сопротивлений.
1. Определяем ток протекающей по участкам цепи:
Iн = Uн/Rл1+ Rл2 = 220/122+122 = 0,9 A
2. Определяем напряжение на каждой из ламп накаливания, так как мощность ламп у нас одинаковая, то и напряжение для каждой из ламп будет одинаково:
Uл1=Uл2 = Iн*R = 0,9*122 = 110 B
Как мы видим напряжение источника (в данном примере 220 В) разделиться поровну, между обоими последовательно включенными лампами. При этом лампы будут ели светит, их накал будет неполным.
Для того чтобы лампы горели с полным накалом, нужно увеличить напряжение источника с 220В до 440В, при этом на каждой из ламп установиться номинальное (рабочее) напряжение равное 220В.
Пример 2
Последовательно подключены две лампы накаливания мощность Рл1 = 100 Вт и Рл2 = 75 Вт к сети с напряжением Uн=220В. Сопротивление нити в лампах составляют Rл1= 122 Ом для стоваттной лампы и Rл2= 153 Ом для семидесяти пяти ватной лампы.
Решение
1. Определяем ток протекающей по участкам цепи:
Iн = Uн/Rл1+ Rл2 = 220/100+75 = 0,8 A
2. Определяем напряжение на каждой из ламп накаливания:
Uл1= Iн*Rл1 = 0,8*122 = 98 B
Uл2= Iн*Rл2 = 0,8*153 = 122 B
Исходя из результатов расчетов, более мощная лампа 100 Вт получает при этом меньшее напряжение. Но ток в двух последовательно включенных даже разных лампах остается одинаковым. Например, если одна из ламп перегорит (порвется ее нить накаливания), погаснут обе лампы.
Данное соединение лампочек, например, используется в трамвайном вагоне для освещения салона.
Параллельное соединение
Параллельное соединение – это соединение, при котором начала всех проводников присоединяются к одной точке цепи, а их концы к другой.
Точки цепи, к которым сходится несколько проводов, называют узлами. Участки цепи, соединяющие между собой узлы, называют ветвями.
При параллельном соединении:
- напряжение на всех проводниках одинаково;
- сила тока в месте соединения проводников равна сумме токов в отдельных проводниках;
- величина, обратная сопротивлению всего соединения, равна сумме величин, обратных сопротивлениям отдельных проводников.
Пример 3
Определить токи и напряжения всех участков цепи (рис.5), если известно:
- Номинальное напряжение сети Uн = 220В;
- Сопротивление нити в лампах HL1 и HL2 составляют Rл1 = Rл2 = 122 Ом.
- Сопротивление нити в лампе HL3 составляют Rл3 = 153 Ом.
Решение
Составляем схему замещения для схемы, представленной на рис.5.
1. Определяем проводимость всей цепи [Л1, с.47] и согласно таблицы 1.8:
2. Определяем сопротивление всей цепи [Л1, с.47]:
3. Определяем силу тока цепи по закону Ома:
4. Определяем токи для каждой цепи [Л1, с.47]:
5. Выполним проверку, согласно которой, сила тока в месте соединения проводников равна сумме токов в отдельных проводниках:
Iл1+ Iл2+ Iл3=Iобщ.=1,8+1,8+1,44=5,04=5,04 (условие выполняется)
Смешанное соединение
Смешанным соединением – называется последовательно-параллельное соединение сопротивлений или участков цепи.
Пример 4
Определить токи и напряжения всех участков цепи (рис.7), если известно:
- Номинальное напряжение сети Uн = 220В;
- Сопротивление нити в лампах HL1, HL2, HL3 составляют Rл1 = Rл2 = Rл3 = 122 Ом.
- Сопротивление нити в лампе HL4 составляют Rл4 = 153 Ом.
- Результаты расчетов для участка цепи ВС (параллельное соединение проводников) применим из примера 3:
Сопротивление цепи ВС составляет Rвс = 43,668 Ом.
Решение
Составляем схему замещения для схемы, представленной на рис.7.
1. Определяем сопротивление всей цепи:
Rобщ = Rав+Rвс = Rл1+Rвс = 122+43,688 = 165,688 Ом
2. Определяем силу тока цепи, согласно закона Ома:
3. Определяем напряжение на первом сопротивлении:
Uав=Uл1= Iобщ*Rл1 = 1,33*122 = 162 B
4. Определяем напряжение на участке ВС:
Uвс= Iобщ*Rвс = 1,33*43,688 = 58,1 B
5. Определяем токи для каждой цепи участка ВС:
6. Выполним проверку для участка цепи ВС:
Iл2+ Iл3+ Iл4= Iобщ.=0,48+0,48+0,38=1,33=1,33 (условие выполняется)
Литература:
- Общая электротехника с основами электроники, В.С. Попов, 1972 г.
- Справочная книга электрика. В.И. Григорьева. 2004 г.
Автор Aluarius На чтение 7 мин. Просмотров 522 Опубликовано
Ни одна электрическая схема не обходится без резисторов. Что это такое, для чего он нужен и какими способами их подключают в электрическую цепь рассмотрим подробно.
Что такое резистор и для чего он нужен
Резистор – пассивный элемент электрической цепи, который поглощает энергию тока и преобразовывает её в тепло за счет сопротивления потоку электронов в цепи.
Зависимость тока от сопротивления описывается законом Ома и рассчитывается по формуле I = U/R.
Свойство резисторов ограничивать ток и снижать напряжение используется во многих электронных устройствах и бытовых приборах.
Справка: Резисторы бывают двух видов – постоянные и переменные, во втором случае сопротивление проводника изменяется механическим путем (вручную).
Последовательное и параллельное соединение резисторов – основные способы соединения резистивных элементов.
Внимание! Резистор не имеет полярности, длина выводов с обоих концов одинакова, поэтому для лучшего понимания сути соединения предлагается называть выводы:
- С правого края – правый.
- С левого края – левый.
Понятие параллельного подключения резисторов
При параллельном подключении правые выводы всех резисторов соединяются в один узел, левые – во второй узел.

При параллельном включении резисторов ток в цепь разветвляется по отдельным ветвям, протекая через каждый элемент – по закону Ома величина тока обратно пропорциональна сопротивлению, напряжение на всех элементах одинаковое.

Справка: Ветвь – фрагмент электрической цепи, содержащий один или несколько последовательно соединенных компонентов от узла до узла.
Последовательное подключение
При последовательном соединении резисторы нужно подключить в цепь друг за другом – правый вывод одного резистора к левому второго, правый второго – к левому третьего и так далее в зависимости от количества соединяемых элементов.

При последовательном соединении ток, не изменяя своей величины, течет через все резистивные элементы.

Смешанное подключение
При смешанном подключении в одной схеме сочетаются несколько видов соединений – последовательное, параллельное соединение резисторов и их комбинации. Самую сложную электрическую схему, состоящую из источников питания, диодов, транзисторов, конденсаторов и других радиоэлектронных элементов можно заменить резисторами и источниками напряжения, параметры которых изменяются в каждый момент времени. О параллельном соединении резистора и конденсатора читайте тут.
 Смешанная схема делится на фрагменты, ток и напряжение рассчитывается для каждого отдельно в зависимости от того, как они соединены на выбранном сегменте электрической схемы.
Смешанная схема делится на фрагменты, ток и напряжение рассчитывается для каждого отдельно в зависимости от того, как они соединены на выбранном сегменте электрической схемы.
Важно! Для расчета сопротивления резистора в схеме применяют отдельные формулы для каждого конкретного элемента в зависимости от вида соединения.
Что ещё нужно учитывать при подключении резисторов
Важный показатель в работе резистивного элемента мощность рассеивания – переход электрической энергии в тепловую, вызывающую нагрев элемента.
При превышении допустимой мощности рассеивания резисторы будут сильно греться и могут сгореть, поэтому при расчете схем соединения надо учитывать этот параметр – важно знать насколько изменится мощность резистивных элементов при включении в электрическую цепь.
Какая мощность тока при последовательном и параллельном соединении
Определение мощности отдельного резистивного элемента производится по формуле
P = U²/R или P = I²R , которую можно вывести из формулы расчета мощности электрической цепи P = UI по закону Ома.
Мощность при параллельном соединении
Рассчитав сопротивление каждого элемента в отдельности, считаем мощность каждого по формуле P = I²R, где
- R – не номинальное сопротивление резистивного элемента, а рассчитанное для данной цепи;
- I – сила тока в цепи.
При параллельном соединении через меньший резистор протекает больший ток – мощность рассеивания на этом резистивном элементе будет больше, чем на остальных.
Важно! При расчете параллельной цепи следует учитывать мощность сопротивления с самым маленьким номиналом.
Мощность при последовательном соединении
Вычислив сопротивление каждого резистивного элемента по отдельности, рассчитываем мощность каждого по формуле P = U²/R, где
- R – рассчитанное нами сопротивление для определенной схемы;
- U – падение напряжения на данном резистивном элементе.
Справка: Полную мощность цепи при последовательном и параллельном соединении можно найти, сложив вычисленные мощности отдельных элементов, входящих в цепь Pобщ = P1+P2+P3+…+Pn.
Как правильно рассчитать сопротивление
Применяется закон Ома для участка цепи – расчет сопротивления делается по формуле R = U/I, где
- U – падение напряжение на конкретном резистивном элементе;
- I – ток, протекающий через него.
При последовательном соединении
Для двух элементов считаем Rобщ = R1+R2.
Для нескольких сопротивлений разного номинала Rобщ = R1+R2+R3+…+Rn.
При параллельном соединении
Расчет для двух резисторов делаем по формуле Rобщ = (R1×R2)/(R1+R2).
Сопротивление параллельных резисторов с разным номиналом рассчитываем по формуле
Rобщ = 1/(1/R1+1/R2+1/R3+…+1/Rn).
Для элементов, соединенных в параллель, суммарное сопротивление всегда ниже наименьшего номинального.
Как рассчитать сложные схемы соединения резисторов
Сложные схемы рассчитываются путем группировки по параллельному и последовательному способу соединения.
 Перед нами сложная схема – задача рассчитать общее сопротивление:
Перед нами сложная схема – задача рассчитать общее сопротивление:
- R2, R3, R4 объединим в последовательную группу – применим формулу R2,3,4 = R2+R3+R4.
- R5 и R2,3,4 – параллельно соединенные резисторы, рассчитаем R5,2,3,4 = 1/ (1/R5+1/R2,3,4).
- R5,2,3,4, R1, R6 опять объединяем в последовательную группу – суммируя величины, получаем Rобщ = R5,2,3,4+R1+R6.
Для больших схем существуют специальные методы, облегчающие расчет. Один из таких методов – эквивалентное преобразование «треугольника» в «звезду». Такая система расчета применяется в том случае, когда невозможно по схеме определить последовательное или параллельное подключение резисторов.
Преобразование «звезда-треугольник»
Для соединения резистивных элементов, кроме вышеописанных способов, существует несколько других видов соединения:
- «звезда» – соединение трех ветвей с одним общим узлом;
- «треугольник» – соединение ветвей схемы в виде треугольника, сторонами которого служат ветви, вершины представляют узлы.
Справка: Узел – точка, в которой соединяются три и более проводника электрической цепи.
Эквивалентность замены предполагает стабильность токов, входящих в каждый узел, при одинаковых напряжения между одноименными узлами «треугольника» и «звезды».

Сопротивление резистора луча «звезды» равно произведению сопротивлений резисторов прилегающих сторон «треугольника», деленному на сумму сопротивлений резисторов трех сторон «треугольника».
RA = RAB RAC/(RAB+RAC+RDC).
Сопротивление резисторов сторон «треугольника» равно сумме произведения сопротивлений резисторов двух прилегающих лучей «звезды», деленного на сопротивление третьего луча.
RAB=(RARB+RARC+RBRС)/RC

О разнице подключения звезда и треугольник читайте здесь.
Чему равна сила тока в цепи при параллельном соединении резисторов
Согласно правилу Кирхгофа ток, поступающий в узел, равен току, выходящему из узла, – величина тока до группы параллельных резисторов и после нее должна быть неизменной.
Ток в группе параллельных резисторов распределяется по цепи в зависимости от их номинала, после прохождения через сопротивления суммируется в узле и выходит из него неизменным I = I1+I2+I3+…+In.
Как определить величину эквивалентного сопротивления при последовательном соединении резисторов
Справка: Эквивалентом сопротивления называется замена части схемы, состоящей из нескольких резистивных элементов, одним элементом.
Для последовательного соединения эквивалентное сопротивление равно сумме сопротивлений резисторов, включенных в группу, для расчета применяется формула Rэкв = R1+R2+…+Rn.
Например: Нужно посчитать эквивалентное сопротивление данной схемы.
 Решение задачи производится путем разделения резистивных элементов на системные группы.
Решение задачи производится путем разделения резистивных элементов на системные группы.
Выделяем первую группу из последовательно соединенных элементов – R2, R3, R4.
Считаем сопротивление Rобщ1 = R2+R3+R4.

Выделяем вторую группу из последовательных элементов R1, R5, R6.

Считаем сопротивление Rобщ2 = R1+R5+R6.
Получаем величину двух эквивалентных сопротивлений Rобщ1 и Rобщ2, соединенных параллельно.
Делаем расчет всей схемы Rэкв= Rобщ1× Rобш2/ (Rобщ1+ Rобщ2).
Зная способы соединения и формулы расчета можно рассчитать любую сложную схему соединения резистивных элементов, однако существует множество онлайн калькуляторов, которые сделают это быстрей человека, достаточно только ввести нужные параметры компонентов схемы.
Соединение резисторов ⋆ diodov.net

Соединение резисторов разными способами позволяет получить необходимую величину сопротивления и мощности рассеивания одного эквивалентного резистора. Всего существует три способы соединения резисторов – последовательное, параллельное и смешанное.
Последовательное соединение резисторов
Последовательное соединение резисторов предполагает использование двух и более радиоэлектронных элемента. Конец предыдущего элемента соединяется с началом последующего и так далее. При последовательном соединении сопротивления и мощности рассеивания всех резисторов складываются.
Рассмотрим следующий пример. Соединим последовательно четыре резистора, каждый имеет R = 1 кОм и мощность рассеивания P = 0,25 Вт.

Rобщ = R1 + R2 + R3 + R4 = 1кОм + 1кОм + 1кОм + 1кОм = 4 кОм.
Pобщ = P1 + P2 + P3 + P4 = 0,25 Вт + 0,25 Вт + 0,25 Вт + 0,25 Вт = 1 Вт.
Таким образом, получается один эквивалентный или общий резистор, имеющий следующие параметры:
Rобщ = 4 кОм; Pобщи = 1 Вт.

В последовательной цепи электрической ток протекает одной и той же величины, поэтому электроны на протяжении всего пути неизбежно наталкиваются на все препятствия в виде сопротивлений. С каждым препятствием уменьшается число свободных зарядов, что приводит к снижению силы электрического тока.
Параллельное соединение резисторов
При параллельном соединении резисторов увеличивается количество путей для перемещения свободных зарядов, то есть электронов, из одного участка пути к другому. Поэтому при параллельном соединении резисторов их суммарное (общее, эквивалентное) сопротивление всегда ниже наименьшего сопротивления из всех резисторов.


Величина, обратная сопротивлению называется проводимостью. Проводимость измеряется в сименсах [См] и обозначается большей латинской буквой G.
G = 1/R = 1/Ом = См
Поэтому при выполнении различных подсчетов в электрических цепях, имеющих параллельное соединение, пользуются проводимостью.
Если сопротивления всех параллельно соединенных резисторов равны, то для определения общего Rобщ достаточно R одного из них разделить на их общее количество:
Если R1 = R2 = R3 = R4 = R, то
Rобщ = R/4.
Например, каждый из четырех резисторов имеет R = 10 кОм, тогда
Rобщ = 10 кОм/4 = 2,5 кОм.
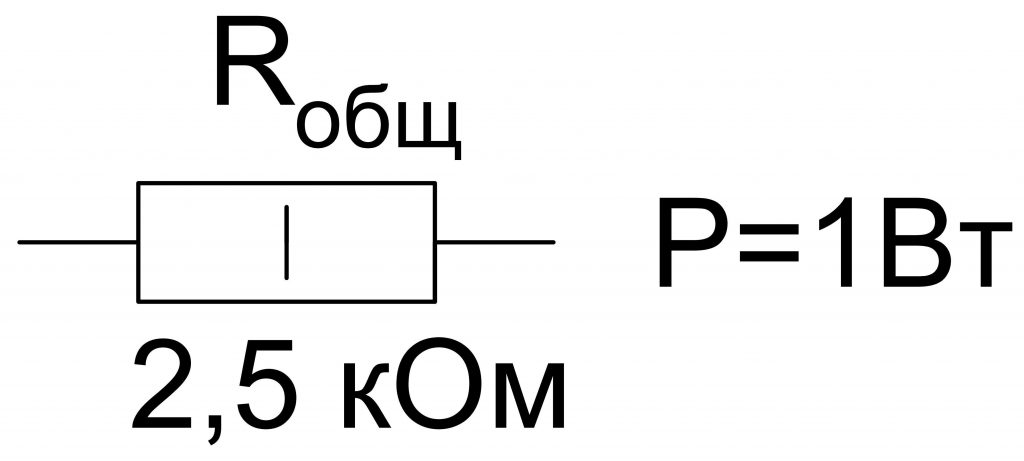
Мощности рассеивания суммируются также, как и при последовательном соединении.
Смешанное соединение резисторов
Смешанное соединение резисторов представляет собой комбинации последовательных и параллельных соединений. В принципе любую даже самую сложную электрическую цепь, состоящую из источников питания, конденсаторов, диодов, транзисторов и других радиоэлектронных элементов в конкретный момент времени можно заменить резисторами и источниками напряжения, параметры которых изменяются с каждым последующим моментом времени. Для примера изобразим схему, имеющую несколько соединений.

Общее (эквивалентное) сопротивление находится методом «сворачивания» схемы. Сначала определяется общее сопротивление одного отдельного соединения, затем последующего и так далее.

Теперь самостоятельно подсчитайте общее сопротивления схемы, приведенной ниже.

Правильный ответ: 2 ома.

Еще статьи по данной теме
Последовательное и параллельное соединение резисторов в схемах являются самыми распространенными, также – это база для расчета более сложных схем.
Последовательное подключение
Начнем с последовательного соединения. По этой схеме каждый резистор подключается с другим только в одной точке, их может быть в цепи 2, 3 и больше.
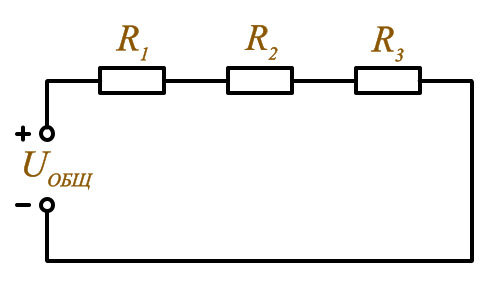
 Рис. Последовательное подключение.
Рис. Последовательное подключение.Обозначение:
Обозначим сопротивления: R1, R2, R3 и напряжение источника в цепи Uц. При подключении источника питания в ней начнет протекать ток Iц. В цепи с последовательным соединением ток протекает по всем резисторам один за другим. Поскольку ток течет через все резисторы их сопротивления и ток суммируется, Iц = I1+I2+I3, Rц = R1 +R2 + R3, чем больше отдельно взятое сопротивление, тем тяжелее электронам преодолевать участок цепи. Мощность резисторов при последовательном и параллельном соединении рассчитывается по разным формулам. В последовательных цепях – складываем, в параллельных – это обратно пропорциональная величина.
Параллельное соединение

 Рис. Параллельное подключение.
Рис. Параллельное подключение.Данный вид подключения характерен тем, что все элементы цепи соединяется выводами в одной точке друг другу, т.е. точка входа и выхода всех нагрузок сходятся в одну точку (или еще одно обозначение на схемах – //). Электроток, двигаясь по проводнику, дойдя до общего соединения делится на количество имеющихся веток. Если представить движение воды в трубе, то можно сказать, что вода двигающиеся по одной трубе, равномерно перетекает в несколько отводов, подсоединенных к ней. В нашем случае заряженные электроны, двигающиеся по проводнику, также растекаются на количества предложенных веток в узле.
Более наглядно это можно представить в виде формул:
1. Каждый вид соединения находится под одинаковым напряжением:
U = U1 = U2;
2. Суммарная сила тока равняется суммарному значению тока каждого участка
I = I1 + I2;
3. Сопротивление цепи равно сумме величина обратных сопротивлению участка:
1/R = 1/R1 + 17R2 + . . . + 1/Rn;
4. Сила тока пропорциональна сопротивлению каждого участка
I1/I2=R2/R1.
Далее рассмотрим схему как работает не только последовательное параллельное, но и смешанное соединение резисторов.
Смешанное подключение

 Рис. Смешанное подключение резисторов
Рис. Смешанное подключение резисторовВ электрических схемах используются не только типовые схемы, но и смешанное, созданное из критерий определенных требований. Чаще всего в схемах встречается третий вариант, представляющий набор из элементарных типов схем. В смешанных участках учитываются не только элементы, но и направления движения тока.
При вычислении мощности резисторов смешанного подключения используются формулы для параллельного и последовательного соединения резисторов, формула также является составной.
Основные законы электротехники, наиболее часто используемые для расчетов
Рассмотрим основные законы электротехники и свойства последовательного и параллельного соединения резисторов для участка цепи
Закон Ома
Напряжение находится по закону Ома по формуле I=U/R – чем больше сопротивление, тем меньше ток. Напряжение можно найти из этой же формулы. U=R*I, ток умножается на сопротивление. Запишем эту формулу для каждого участка U1=R1· I1, Un=Rn · In.
Законы Кирхгофа
Первый закон
Ещё один очень важный закон — это закон Кирхгофа. Для участка цепи постоянного тока их два.

 Рис. иллюстрация к пояснению действия первого закона Кирхгофа.
Рис. иллюстрация к пояснению действия первого закона Кирхгофа.Первый закон имеет формулировку: Сумма всех токов, входящих в узел и выходящих из него равна нулю.
Если посмотреть на схему, I1 – это ток, который заходит в узел, I2 и I3 – это электроны, которые вытекают из него.
Применяя формулировку первого закона можно записать формулу по-другому:
I1-I2+I3=0. В этой формуле знаки плюс имеют значения, которые прибывают в узел, минус, который отходит от него.
Второй закон Кирхгофа.

 Рис. иллюстрация к пояснению действия второго закона Кирхгофа.
Рис. иллюстрация к пояснению действия второго закона Кирхгофа.Если к цепи с включенными сопротивлениями подключен один источник ЭДС (батарея питания) тогда всё понятно, можно обойтись законом Ома. А, если, источников несколько и схема с различным схемным расположением элементов, тогда вступает в силу второй закон, который гласит: сумма токов всех источников питания для замкнутого контура, равна сумме падений напряжения на всех сопротивлениях участка в этом контуре.
E1- Е2 = – UR1 – UR2 или E1 = Е2 – UR1 – UR2.
Параллельное и последовательное соединение резисторов, решение задач
Алгоритм расчёта смешанных подключений находится в тех же правилах, что и в элементарных схемах расчета последовательного и параллельного соединения резисторов. Ничего нового нет: нужно правильно разбить предложенную схему на пригодные для расчета участки. Участки, с элементами, подключены поочередно либо параллельно.
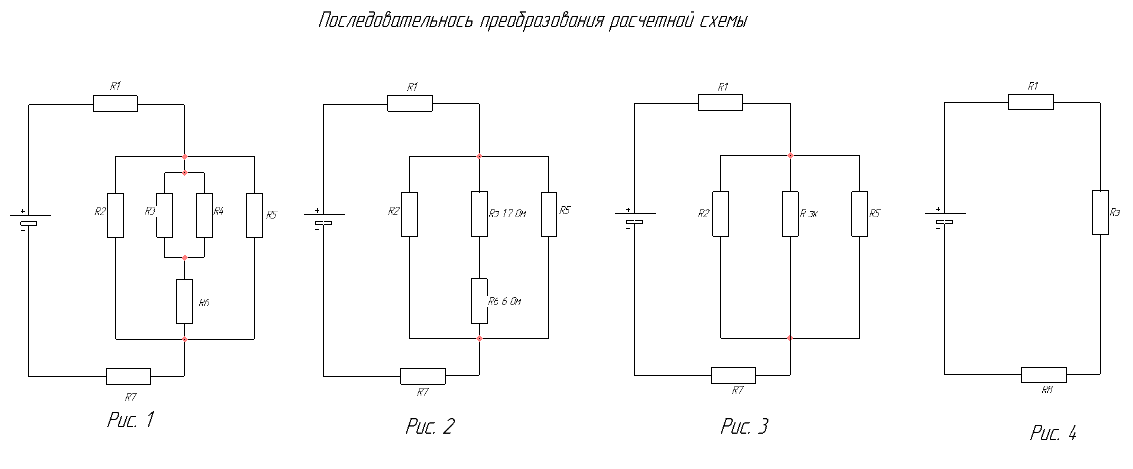
 Рис. Порядок замещения при расчете сложных позиций более простыми.
Рис. Порядок замещения при расчете сложных позиций более простыми.Для решения задачи на последовательное и параллельное соединение резисторов необходимо правильно оценить цепи элементов. Рассмотрим схему №1 на рис.
На схеме присутствует параллельная и последовательная часть соединения элементов. Для расчета очень важно аккуратно, шаг за шагом упрощать цепи и не брать сразу всю схему (рис.1). Как же правильно определить параллельное и последовательное соединение резисторов?
Для примера расчета возьмем резисторы R3, R4, которые подключены параллельно. Эквивалентный резистор этих элементов, будет равенRэ. = 1/R34 =1/R3 + 1/R4, после преобразования формулы и приведения к одному знаменателю получим R34 = R3 · R4 / (R3 + R4). Э. = 1/3+1/4 /(3+4) =1,7 Ом.
Далее видно, что приведённая эквивалентное R эк и R6 соединены последовательно, чтобы узнать сопротивление их необходимо сложить, тогда общее сопротивление будет равно R346 = R34 + R6, тогда Rэк346 = 1,7 + 6 = 7, 7 Ом.
Заменяем на схеме одним общим элементом, теперь, позиция упрощается еще больше (рис 3).
Теперь образовалась ситуация – включение трех элементов в //. Как вычисляется такое соединение нам уже известно, 1/ R23465 = 1/ R2 +1/R346 + 1/R5 после вычисления правой части получаем 0,82 Ом. После окончательного вычисления получаем R23465 = 2,1 Ом. Здесь следует обратить внимание, что общее сопротивление получилось меньше самого меньшего из трех.
Заменяем эти сопротивление одним эквивалентным R23465. В конечном итоге все выглядит уже намного проще. Rц = Rэк + R1+ R2. R об. = R ц = 1,21 +7+1 =9,21 Ом.
Из приведенного алгоритма расчёта видно, как из сложной схемы путем простого математического вычисления и применения правил сокращения резисторов участок становится простой и понятной.
Схема с подключением сопротивлений «треугольником»

 Рис. Расчетная схема соединения резисторов в треугольник.
Рис. Расчетная схема соединения резисторов в треугольник.Иногда некоторые затруднения возникают при разборе схемы соединения в треугольник.
Рассмотрим на примере рисунка расчет резисторов по этому подключению.
Из схемы видно, что R1 и R2 соединены последовательно Rэ12 будет соединяться R3 последовательно.
Затем Rэ123 соединяется с сопротивлением R4, R5 в последовательную цепь. Затем все это объединяется с Rэ в //.
Проведем несложные вычисления учитывая, что
R1, R2, R4, R5 равняется 1 Ом. R3, R7 – 2 Ом.
RЭ1,2 = R1+R2 = 1+1=2 Ом.
Вычисляем параллельное подключение: Rэ 12 с R3. Rэ1,3 = (Rэ12*R3) /(Rэ12+R3) = (2*2) /(2+2) = 1Ом.
Далее мы видим последовательное: RЭ123 + R4 + R5 = 1+1+1 = 3 Ом.
И последнее – Rэ123 4 5 с R6 – параллельное.
Общее сопротивление цепи Rц = Rоб = (RЭ1,2,3,4,5 *R6) /(RЭ1,2,3,4,5+R6) = (3 * 2) / (3+2) = 1,2 Ом. Как видно, что расчет подобного варианта также не сложный.
Расчет последовательного и параллельного подключения резисторов онлайн
Подсчитать значение мощность и сопротивлений подставляя их в формулы можно только в учебных целях, или, когда объемы не очень большие. Наиболее практичный вариант расчета является онлайн калькуляторы, которые расположены на многочисленных интернет ресурсах. Для расчёта любой сложности нужно правильно определить тип соединения резисторов последовательное или параллельное и внести данные для расчета в поля калькулятора.
Также такая форма расчета подойдет и для проверки результатов решения учебных задач.
Последовательное и параллельное соединение резисторов и конденсаторов
Электрические цепи состоят не только из резисторов, в них применяется большое количество различных деталей, например, конденсатор, которые подключаются в последовательное, // и смешанное соединение.

 Рис. Замещения последовательно включенных элементов.
Рис. Замещения последовательно включенных элементов.Определение этому элементу можно дать следующее: Конденсатор – это совокупность проводящих тел служащий для накопления электрического заряда.
Элементарный конденсатор имеет две пластины, форма этих пластин может быть различной: сферической, круглой, цилиндрической, прямоугольной – по форме пластин разделяется и тип конденсатора.
Важное свойство. Одно из важных свойств конденсатора: если заряжается одна пластина конденсатора, то благодаря явлению электростатической индукции заряжается и вторая половина, но с противоположным знаком.
Устройство конденсатора
Плоский конденсатор состоит из двух плоских пластин отстоящих друг от друга на маленькое расстояние. У конденсатора к двум пластинам припаивается вывод всего их получается два.
Типовые схемы подключения конденсаторов
Рассмотрим различные виды подключения конденсатора.
Последовательное
Первый вид — это последовательное соединение.
Предположим, что емкость этих конденсаторов будут равны. Тогда заряды также будут равны: q1=q2=q3, как и в примере с резисторами, сложный тип позиций с конденсатором можно упростить, заменив несколько элементов одним. У элементов соединенных друг за другом, общая емкость будет обратно пропорциональная всем имеющимся элементам. То есть: Rэк будет равняться 1/С1 + 1/С2 +…. 1/Сn/
Напряжение складывается, U эк = U1 + U2+ … Un.
Параллельное
Второй тип подключения конденсаторов – это соединение в паралель

 Рис. Схема замещения элементов, включенных в параллель.
Рис. Схема замещения элементов, включенных в параллель.Соответственно эти конденсаторов обозначены C1, C2, … Cn заряды: Q1, Q2, … Qn и напряжение: U1, U2, … Un.
У элементов в // емкость складывается Сэ = C1 + C2 + … C n.
Напряжение Un на каждом конденсаторе будет равно напряжению на эквивалентном
Uэ = U1 = U2 =… = Un – это особенность параллельного подсоединения всех элементов цепи.
Емкость будет складываться из суммы отдельных элементов Сэ =С1 + С2 + … Сп.

 Рис. Расчетные позиции элементов при различном включении.
Рис. Расчетные позиции элементов при различном включении.Простая позиция, которая не требует преобразования №1 – последовательное подключение. По известной формуле для этих поз. запишем 1/Сэ = 1/С1 +1/С2 +1/С3, подставив формулу значения, которые даны в условии задачи, получим 1/Сэ = 1/С1 +1/С2 +1/С3 = 59 мФ.
Не требует преобразования и 2 схема: емкость общего конденсатора будет равняться сумме конденсаторов которые включены в параллельной цепи: Сэ =С1 +С2 +С3
Сэ = 100 + 200 + 500 = 800 мФ.
Рассмотрев рис. №3 видно, что пара конденсаторов включена параллельно и один последовательно. Алгоритм преобразования таких цепей мы уже рассматривали, поэтому: сразу же находим емкость конденсатора Сэ соединения: Сэ = С1+С2 = 200+500 = 700 мФ.
Теперь находим общие эквивалентную емкость элементов с последовательным подключением 1/Сэ = 1/С2,3 +1/ С1 = 89 мф.
Практическая задача решена.
Вконтакте
Google+
Внимание покупателей подшипников
Уважаемые покупатели, отправляйте ваши вопросы и заявки по приобретению подшипников и комплектующих на почту или звоните сейчас: +7(499)403 39 91
Доставка подшипников по РФ и зарубежью. Каталог подшипников на сайте themechanic.ru
|


Внимание покупателей подшипников
Уважаемые покупатели, отправляйте ваши вопросы и заявки по приобретению подшипников и комплектующих на почту или звоните сейчас:
tel:+7 (495) 646 00 12
[email protected]
Доставка подшипников по РФ и зарубежью.
Каталог подшипников на сайте


Внимание покупателей подшипников
Уважаемые покупатели, отправляйте ваши вопросы и заявки по приобретению подшипников и комплектующих на почту или звоните сейчас:
tel:+7 (495) 646 00 12
[email protected]
Доставка подшипников по РФ и зарубежью.
Каталог подшипников на сайте

 90000 Introduction to Series, Parallel and Series-Parallel Connections 90001 90002 90003 Series, Parallel & Series-Parallel Circuits, their Comparison and Applications 90004 90005 90006 90003 Why Parallel Connection is Mostly Preferred over Series Connection? 90004 90009 90010 The use, application and importance of series and parallel circuit connection today can not be over emphasized. The application of series and parallel circuit connection can be evidently seen in our homes, school halls and in our street lights.With the press of a button, all the Bobs in our sitting rooms are turned on. some refer that the bobs in their homes should have different switches. 90011 90010 90013 90013 90011 90010 Well, it’s not a magic when more than three electric bobs or loads are controlled by one switch. A load is anything i.e. it could be an appliances, electric bobs or even ceiling fans that consumes electrical energy when connected to a power supply. The electric bobs, televisions, refrigerators etc can all be referred to as a load.The bobs convert electrical energy into light and heat form of energy. Fans convert the electrical energy into mechanical energy. 90011 90010 The type of connection done to our ceiling fans, electric bobs will determine if they will have a common switch or not. Series circuit connection gives us the opportunity to connect more than two loads to a common switch. Street lights are a very good example of this. Parallel circuit connection makes it possible for us to connect loads to their individual switch.Both series and parallel circuit connection are good but one is mostly preferred over the other for one reason or the other. Before we talk about the reason why parallel circuit connection is preferred over series connection, let’s recall what series and parallel connections are first. 90011 90006 90003 Series Circuit 90022 90004 90009 90010 A series circuit is a circuit in which resistors or loads are connected end to end so that the circuit will have only one path through which electric current flows.Thus, when a number of resistors are connected in series, the effective resistance (total resistance in the circuit) is gotten by adding the individual resistance algebraically. That is to say, if we have resistors with resistance R1, R2, R3 … Rn 90003 connected in series 90004, then; 90011 90010 90003 R 90031 eff 90032 = R 90031 T 90032 = R 90031 1 90032 + R 90031 2 90032 + R 90031 3 90032 + … R 90031 n 90032. 90004 90011 90010 In series connections, the same current flows across all the branches of the circuits, but different voltage across it thus making the resistors to have different voltage across them.Each resistor or load will experience a voltage drop. The applied voltage is equal to the sum of the voltage drop across the different parts of the circuit. Voltage drop is proportional to the resistance current being the same throughout the circuit. When loads are connected in series, the loads will tend to have a common switch. This kind of connection is employed in school halls, street lights. 90011 90047 90047 How To Wire Lights in Series? 90049 90003 Uses & Application of Series Connection 90004 90052 90010 Some people connect security lights in their homes in series which will make them to have common switch.The problem with this kind of connection is that when a load develops a problem, the other connected system will fail. It’s an all or none type of circuit connection. Till a load gets energy before it delivers it to the other and the one to deliver fails, there will be a black out. 90011 90010 Series circuit connections are common and greatly employed in electrical equipments. The tube filaments in small radios are usually in series. Current controlling devices are always connected in series with the device that they protect.Fuses are connected in series with the device they protect, Automatic house-heating equipment has a thermostat, electromagnetic coils, and safety cut-outs connected in series with a voltage source etc. 90011 90049 90058 Disadvantages of Series Circuit 90059 90052 90061 90062 The break in the wire, failure or removal of any single lamp will break the circuit and cause all of the others to stop working as there is only one single path of current to flow in the circuit. 90063 90062 If more lamps are added in series lighting circuit, they will all be reduced in brightness.because voltage are shared in series circuit. If we add more loads in series circuit, the over voltage drop is increases which is not a good sign for electrical appliances protection. 90063 90062 Series Wiring is «ALL or NONE» type wiring mean all the appliances will work at once or all of them will disconnect if fault occurs at any one of the connected device in series circuit. 90063 90062 High supply voltage are needed if we need to add more load (light bulbs, electric heaters, air conditioner etc) in the series circuit.For example, If five, 220V Lamps are to be connected in Series, Than Supply Voltage would have to be: 5 x 220V = 1.1kV. 90063 90062 The overall series circuit resistance increases (and current decreases) when more load added in the circuit. 90063 90062 According to future need, only those electrical appliances should be added in the current series circuit if they has the same current rating as current are same at each point in series circuit. However, we know that electrical appliances and devices i.e. light bulbs, fan, heater, air conditioner etc have different current rating, therefore, they can not be connected in series circuit for smooth and efficient operation. 90073 90073 Lights connected in Series 90063 90076 90049 90058 Advantages 90059 90058 of Series Connection 90059 90052 90061 90062 Less size of wire cable is required in series wiring. 90063 90062 We use to protect the circuit to connect fuse & circuit breakers in series with other appliances. 90063 90062 Series circuit do not get overhead easily due to high resistance when more load added in the circuit.90063 90062 The lifespan of battery in series circuit is more as compared to parallel. 90063 90062 It is most simple method of electrical wiring and fault can be easily detect and repair as compared to parallel or series-parallel wiring. 90063 90076 90006 90003 Parallel Circuit 90022 90004 90009 90010 Resistors, loads are said to be connected in parallel when the end of each of the resistors or loads have a common point or junction and the other ends are also connected to a common point or junction.Such circuits are known as parallel circuits. 90011 90102 90102 Light Bulbs Connected in Parallel 90010 Unlike the series circuit connection, when finding the total (effective) resistance in a parallel circuit, the reciprocal of the individual resistance is taken. Thus, when a number of resistances are connected in parallel, the reciprocal of the effective resistance is given by the arithmetic or algebraic sum of the reciprocal of the individual resistance. 90011 90010 90003 1 / R 90031 eff 90032 or 1 / R 90031 T 90032 = 1 / R 90031 1 90032 + 1 / R 90031 2 90032 + 1 / R 90031 3 90032 … 1 / R 90031 n 90032.90004 90011 90010 Parallel circuit connection have the same voltage flowing across all the branches of the circuits. Different resistors have their individual currents. 90011 90049 90003 Uses & Application of Parallel Connection 90004 90052 90010 Parallel circuit connection is very common in use. Various lamps and electrical appliances in our homes are connected in parallel so that each of the lamps or bobs and appliances can be operated independently. For us to have control over the individual lamps or loads, they have to be wired in parallel.90011 90049 90058 Advantages of Parallel Circuit 90059 90052 90061 90062 Each connected electrical device and appliance are independent from others. This way, switching ON / OFF a device will not affect the other appliances and their operation. 90063 90062 In case of break in the cable or removal of any lamp will not break the all circuits and connected loads, in other words, other lights / lamps and electrical appliances will still work smoothly. 90063 90062 If more lamps are added in the parallel lighting circuits, they will not be reduced in brightness (as it happens only in series lightning circuits).Because voltage is same at each point in a parallel circuit. In short, they get the same voltage as the source voltage. 90063 90062 It is possible to add more light fixture and load points in parallel circuits according to future need as far as the circuit is not overloaded. 90063 90062 Adding additional devices and components wont increase the resistance but will decrease the overall resistance of the circuit especially when high current rating devices are used such as air conditioner and electric heaters.90063 90062 parallel wiring is more reliable, safe and simple to use. 90146 90146 Faults in Parallel lighting circuits 90063 90076 90049 90058 Disadvantages of Parallel Connections 90059 90022 90052 90061 90062 More size of cable and wire is used in parallel lighting wiring circuit. 90063 90062 More current needed when additional light bulb added in the parallel circuit. 90063 90062 Battery runs out quicker for DC installation. 90063 90062 The parallel wiring design is more complex as compare to series wiring.90063 90076 90010 90166 90003 Related Post: Which Bulb Glows Brighter When Connected in Series and Parallel & Why? 90004 90169 90011 90006 90003 Series-Parallel Connections & Circuits 90004 90009 90010 The circuit is series nor parallel in the following fig i.e. it is series-parallel circuit. The first three lamps (B 90031 1 90032, B 90031 2 90032 & B 90031 3 90032) are connected in parallel while switches (S 90031 1 90032, S 90031 2 90032 & S 90031 3 90032) are wired in series accordingly.B 90031 7 90032, B 90031 8 90032, B 90031 9 90032 and B 90031 10 90032 are in series with each other while they are parallel with the first three bulbs (B 90031 1 90032, B 90031 2 90032 & B 90031 3 90032) while the switches (S5 & S6) are in parallel connected with Bulb (B 90031 10 90032). Also, bulbs (B 90031 4 90032, B 90031 5 90032 & B 90031 6 90032) and switch (S 90031 7 90032) are in series with each other while they are in parallel with (B 90031 1 90032, B 90031 2 90032 & B 90031 3 90032) and so on.90011 90010 As the circuit is combination of series and parallel, We can not simplify the current, voltage, resistance and power by simple ohm’s law. We have to apply different theorems like Norton’s, Thevenin’s, maximum power transfer theorem etc or will simplify the circuit in basic series and parallel circuits to find all those quantities. 90011 90010 Most common of household wiring installation nowadays using this wiring method. 90011 90223 90223 Series-Parallel Light Circuit & Connection 90006 90003 Comparison Between Series and Parallel Connection 90004 90009 90010 Below in the given table, the main differences between series and parallel connections are shown.90011 90231 90232 90233 90234 90003 S No 90004 90237 90234 90003 Series Circuit 90004 90237 90234 90003 Parallel Circuit 90004 90237 90246 90233 90234 90003 Current (I) 90004 90237 90234 Current are same in each point in series circuit: 90010 I 90031 1 90032 = I 90031 2 90032 = I 90031 3 90032 = …. I 90031 n 90032 90011 90237 90234 Current are additive in series circuit: 90010 I 90031 1 90032 + I 90031 2 90032 + I 90031 3 90032 + …. I 90031 n 90032 90011 90237 90246 90233 90234 90003 Voltage (V) 90004 90237 90234 Voltage are additive in series circuit: 90010 V 90031 1 90032 + V 90031 2 90032 + V 90031 3 90032 + ….V 90031 n 90032 90011 90237 90234 Voltages are same in each point in parallel circuit: 90010 V 90031 1 90032 = V 90031 2 90032 = V 90031 3 90032 = …. V 90031 n 90032 90011 90237 90246 90233 90234 90003 Resistance (R) & to Find (R) 90004 90237 90234 Resistance are additive in Series Circuit: 90010 R 90031 1 90032 + R 90031 2 90032 + R 90031 3 90032 + … R 90031 n = 90032 R 90031 eff 90032 = R 90031 T 90032 90011 90237 90234 Resistance are divided when more load added in the circuit.90010 1 / R 90031 T 90032 = 1 / R 90031 1 90032 + 1 / R 90031 2 90032 + 1 / R 90031 3 90032 … 1 / R 90031 n 90032 90011 90010 or 90011 90010 I = G 90031 1 90032 + G 90031 2 90032 + G 90031 3 90032 + … G 90031 n 90032 90011 90237 90246 90233 90234 90003 To Find Current (I) 90004 90237 90234 I = V 90031 1 90032 / R 90031 1 90032 = V 90031 2 90032 / R 90031 2 90032 = V 90031 3 90032 / R 90031 3 90032 = V 90031 n 90032 / R 90031 n 90032 90237 90234 I = V 90031 1 90032 / R 90031 1 90032 + V 90031 2 90032 / R 90031 2 90032 + V 90031 3 90032 / R 90031 3 90032 + V 90031 n 90032 / R 90031 n 90032 90237 90246 90233 90234 90003 To Find Voltage (V) 90004 90237 90234 V = I 90031 1 90032 R 90031 1 90032 + I 90031 2 90032 R 90031 2 90032 + I 90031 3 90032 R 90031 3 90032 + … I 90031 n 90032 R 90031 n 90032 90237 90234 V = I 90031 1 90032 R 90031 1 90032 = I 90031 2 90032 R 90031 2 90032 = I 90031 3 90032 R 90031 3 90032 = … I 90031 n 90032 R 90031 n 90032 90237 90246 90233 9 0234 90003 To Find Electric Power (P) 90004 90237 90234 90010 P = I 90446 2 90447 R 90031 1 90032 + I 90446 2 90447 R 90031 2 90032 + … I 90446 2 90447 R 90031 n 90032 90011 90010 or 90011 90010 P = V 90031 1 90032 90446 2 90447 / R 90031 1 90032 + V 90031 2 90032 90446 2 90447 / R 90031 2 90032 + … V 90031 n 90032 90446 2/90447 R 90031 n 90032 90011 90237 90234 90010 P = V 90446 2 90447 / R 90031 1 90032 + V 90446 2 90447 / R 90031 2 90032 + … V 90446 2/90447 R 90031 n 90032 90011 90010 or 90011 90010 P = I 90031 1 90032 90446 2 90447 R 90031 1 90032 + I 90031 2 90032 90446 2 90447 R 90031 2 90032 + … I 90031 n 90032 90446 2 90447 R 90031 n 90032 90011 90237 90246 90233 90234 90003 Current & Voltage Divider Rule 90004 90237 90234 V 90031 1 90032 = V 90031 T 90032 (R 90031 1 90032 / R 90031 T 90032 ), V 90031 2 90032 = V 90031 T 90032 (R 90031 2 90032 / R 90031 T 90032) 90237 90234 I 90031 1 90032 = I 90031 T 90032 (G 90031 1 90032 / G 90031 T 900 32), I 90031 2 90032 = I 90031 T 90032 (G 90031 2 90032 / G 90031 T 90032) 90237 90246 90233 90234 90003 Paths of flow of Electric Current 90004 90237 90234 Only one path 90237 90234 Two or more paths 90237 90246 90233 90234 90003 Brightness of Bulb 90004 90237 90234 Dimmer if added more bulbs (P = V x I) 90237 90234 Brighter due to same voltages 90237 90246 90233 90234 90003 If breaks occurs in the circuit 90004 90237 90234 Whole circuit is useless 90237 90234 The rest of the circuit will still work 90237 90246 90233 90234 90003 Battery Status 90004 90237 90234 Battery Discharge slowly (Ah Rating of Battery) 90237 90234 Battery Discharge Quickly (Battery Ah Time & Currents) 90237 90246 90233 90234 90003 Applications 90004 90237 90234 Used to protect the circuit while connecting fuses and circuit breakers in series with the connected appliances 90237 90234 Used in most of household electrical wiring installations 90237 90246 90613 90614 90006 90003 Advantages of Parallel Circuit Connection over Series Circuit Connection 90004 90009 90010 A series circuit connection is an all or none type of circuit connection.Meaning that if one of the appliances fails, all the other appliances will also fail which is why this type of connection is good only when we want to protect a device. 90620 90620 When a fuse gets burnt for instance due to high current, then the appliance it protects will not be damaged because current will no longer reach it. While series connection is an all or none, parallel circuit connection gives you the opportunity to give the loads and the appliances their individual switch. Parallel connection offers resistance to the flow of current compared to series connection.90011 90623 90623 Disadvantages of Series Lighting Circuit 90010 A 100 ohms and a 150 ohms resistors connected in parallel will have less effect on electric current compared to 50 ohms and 40 ohms resistors connected in series. In electronic devices, parallel connection is paramount. The cells in a power bank are all connected in parallel. Parallel connection makes electrical energy to last longer. The cells themselves have their internal resistance, so if they were connected in series, some of the energy will be lost overcoming the internal resistance since it’s effect is high when in series than when in parallel.90011 90010 Related Posts: 90022 90011.90000 Series and Parallel Circuits — learn.sparkfun.com 90001
Favorited
Favorite
48
90002 Series and Parallel Circuits 90003
90004 Simple circuits (ones with only a few components) are usually fairly straightforward for beginners to understand. But, things can get sticky when other components come to the party. Where’s the current going? What’s the voltage doing? Can this be simplified for easier understanding? Fear not, intrepid reader.Valuable information follows. 90005 90004 In this tutorial, we’ll first discuss the difference between series circuits and parallel circuits, using circuits containing the most basic of components — resistors and batteries — to show the difference between the two configurations. We’ll then explore what happens in series and parallel circuits when you combine different types of components, such as capacitors and inductors. 90005 90008 Covered in this Tutorial 90009 90010
90011 What series and parallel circuit configurations look like 90012
90011 How passive components act in these configurations 90012
90011 How a voltage source will act upon passive components in these configurations 90012
90017 90008 Suggested Reading 90009 90004 You may want to visit these tutorials on the basic components before diving into building the circuits in this tutorial.90005 90008 Video 90009 90004 90025 90026 90005
90002 Series Circuits 90003
90008 Nodes and Current Flow 90009 90004 Before we get too deep into this, we need to mention what a 90033 node 90034 is. It’s nothing fancy, just representation of an electrical junction between two or more components. When a circuit is modeled on a schematic, these nodes represent the wires between components. 90005 90004 90037 Example schematic with four uniquely colored nodes.90038 90005 90004 That’s half the battle towards understanding the difference between series and parallel. We also need to understand 90033 how current flows 90034 through a circuit. Current flows from a high voltage to a lower voltage in a circuit. Some amount of current will flow through every path it can take to get to the point of lowest voltage (usually called ground). Using the above circuit as an example, here’s how current would flow as it runs from the battery’s positive terminal to the negative: 90005 90004 90037 Current (indicated by the blue, orange, and pink lines) flowing through the same example circuit as above.Different currents are indicated by different colors. 90038 90005 90004 Notice that in some nodes (like between R 90049 1 90050 and R 90049 2 90050) the current is the same going in as at is coming out. At other nodes (specifically the three-way junction between R 90049 2 90050, R 90049 3 90050, and R 90049 4 90050) the main (blue) current splits into two different ones. 90037 That’s 90038 the key difference between series and parallel! 90005 90008 Series Circuits Defined 90009 90004 Two components are in series if they share a common node and if the 90033 same current 90034 flows through them.Here’s an example circuit with three series resistors: 90005 90004 There’s only one way for the current to flow in the above circuit. Starting from the positive terminal of the battery, current flow will first encounter R 90049 1 90050. From there the current will flow straight to R 90049 2 90050, then to R 90049 3 90050, and finally back to the negative terminal of the battery. Note that there is only one path for current to follow. These components are in series. 90005
90002 Parallel Circuits 90003
90008 Parallel Circuits Defined 90009 90004 If components share 90037 two 90038 common nodes, they are in parallel.Here’s an example schematic of three resistors in parallel with a battery: 90005 90004 From the positive battery terminal, current flows to R 90049 1 90050 … and R 90049 2 90050, and R 90049 3 90050. The node that connects the battery to R 90049 1 90050 is also connected to the other resistors. The other ends of these resistors are similarly tied together, and then tied back to the negative terminal of the battery. There are three distinct paths that current can take before returning to the battery, and the associated resistors are said to be in parallel.90005 90004 Where series components all have equal currents running through them, parallel components all have the same voltage drop across them — series: current :: parallel: voltage. 90005 90008 Series and Parallel Circuits Working Together 90009 90004 From there we can mix and match. In the next picture, we again see three resistors and a battery. From the positive battery terminal, current first encounters R 90049 1 90050. But, at the other side of R 90049 1 90050 the node splits, and current can go to both R 90049 2 90050 and R 90049 3 90050.The current paths through R 90049 2 90050 and R 90049 3 90050 are then tied together again, and current goes back to the negative terminal of the battery. 90005 90004 In this example, R 90049 2 90050 and R 90049 3 90050 are in parallel with each other, and R 90049 1 90050 is in series with the parallel combination of R 90049 2 90050 and R 90049 3 90050. 90005
90002 Calculating Equivalent Resistances in Series Circuits 90003
90004 Here’s some information that may be of some more practical use to you.When we put resistors together like this, in series and parallel, we change the way current flows through them. For example, if we have a 10V supply across a 10k & ohm; resistor, Ohm’s law says we’ve got 1mA of current flowing. 90005 90004 If we then put another 10k & ohm; resistor in series with the first and leave the supply unchanged, we’ve cut the current in half because the resistance is doubled. 90005 90004 In other words, there’s still only one path for current to take and we just made it even harder for current to flow.How much harder? 10k & ohm; + 10k & ohm; = 20k & ohm ;. And, that’s how we calculate resistors in series — just 90033 add their values 90034. 90005 90004 To put this equation more generally: the total resistance of 90037 N 90038 — some arbitrary number of — resistors is their total sum. 90005
90002 Calculating Equivalent Resistances in Parallel Circuits 90003
90004 What about parallel resistors? That’s a bit more complicated, but not by much.Consider the last example where we started with a 10V supply and a 10k & ohm; resistor, but this time we add another 10k & ohm; in parallel instead of series. Now there are two paths for current to take. Since the supply voltage did not change, Ohm’s Law says the first resistor is still going to draw 1mA. But, so is the second resistor, and we now have a total of 2mA coming from the supply, doubling the original 1mA. This implies that we’ve cut the total resistance in half. 90005 90004 While we can say that 10k & ohm; || 10k & ohm; = 5k & ohm; ( «||» roughly translates to «in parallel with»), we’re not always going to have 2 identical resistors.What then? 90005 90004 The equation for adding an arbitrary number of resistors in parallel is: 90005 90004 If reciprocals are not your thing, we can also use a method called «product over sum» when we have two resistors in parallel: 90005 90004 However, this method is only good for two resistors in one calculation. We can combine more than 2 resistors with this method by taking the result of R1 || R2 and calculating that value in parallel with a third resistor (again as product over sum), but the reciprocal method may be less work.90005
90002 Experiment Time — Part 1 90003
90004 What you’ll need: 90005 90004 Let’s try a simple experiment just to prove that these things work the way we’re saying they do. 90005 90004 First, we’re going to hook up some 10k & ohm; resistors in series and watch them add in a most un-mysterious way. Using a breadboard, place one 10k & ohm; resistor as indicated in the figure and measure with a multimeter. Yes, we already know it’s going to say it’s 10k & ohm ;, but this is what we in the biz call a «sanity check».Once we’ve convinced ourselves that the world has not changed significantly since we last looked at it, place another one in similar fashion but with a lead from each resistor connecting electrically through the breadboard and measure again. The meter should now say something close to 20k & ohm ;. 90005 90004 You may notice that the resistance you measure might not be exactly what the resistor says it should be. Resistors have a certain amount of 90033 tolerance 90034, which means they can be off by a certain percentage in either direction.Thus, you may read 9.99k & ohm; or 10.01k & ohm ;. As long as it’s close to the correct value, everything should work fine. 90005 90004 The reader should continue this exercise until convincing themselves that they know what the outcome will be before doing it again, or they run out of resistors to stick in the breadboard, whichever comes first. 90005
90002 Experiment Time — Part 2 90003
90004 Now let’s try it with resistors in a 90033 parallel 90034 configuration.Place one 10k & ohm; resistor in the breadboard as before (we’ll trust that the reader already believes that a single 10k & ohm; resistor is going to measure something close to 10k & ohm; on the multimeter). Now place a second 10k & ohm; resistor next to the first, taking care that the leads of each resistor are in electrically connected rows. But before measuring the combination, calculate by either product-over-sum or reciprocal methods what the new value should be (hint: it’s going to be 5k & ohm;).Then measure. Is it something close to 5k & ohm ;? If it’s not, double check the holes into which the resistors are plugged. 90005 90004 Repeat the exercise now with 3, 4 and 5 resistors. The calculated / measured values should be 3.33k & ohm ;, 2.5k & ohm; and 2k & ohm ;, respectively. Did everything come out as planned? If not, go back and check your connections. If it did, EXCELSIOR! Go have a milkshake before we continue. You’ve earned it. 90005
90002 Rules of Thumb for Series and Parallel Resistors 90003
90004 There are a few situations that may call for some creative resistor combinations.For example, if we’re trying to set up a very specific reference voltage you’ll almost always need a very specific ratio of resistors whose values are unlikely to be «standard» values. And while we can get a very high degree of precision in resistor values, we may not want to wait the X number of days it takes to ship something, or pay the price for non-stocked, non-standard values. So in a pinch, we can always build our own resistor values. 90005 90008 Tip # 1: Equal Resistors in Parallel 90009 90004 Adding 90037 N 90038 like-valued resistors 90037 R 90038 in parallel gives us 90037 R / N 90038 ohms.Let’s say we need a 2.5k & ohm; resistor, but all we’ve got is a drawer full of 10k & ohm; ‘s. Combining four of them in parallel gives us 10k & ohm; / 4 = 2.5k & ohm ;. 90005 90008 Tip # 2: Tolerance 90009 90004 Know what kind of tolerance you can tolerate. For example, if you needed a 3.2k & ohm; resistor, you could put 3 10k & ohm; resistors in parallel. That would give you 3.3k & ohm ;, which is about a 4% tolerance from the value you need. But, if the circuit you’re building needs to be closer than 4% tolerance, we can measure our stash of 10k & ohm; ‘s to see which are lowest values because they have a tolerance, too.In theory, if the stash of 10k & ohm; resistors are all 1% tolerance, we can only get to 3.3k & ohm ;. But part manufacturers are known to make just these sorts of mistakes, so it pays to poke around a bit. 90005 90008 Tip # 3: Power Ratings in Series / Parallel 90009 90004 This sort of series and parallel combination of resistors works for power ratings, too. Let’s say that we need a 100 & ohm; resistor rated for 2 watts (W), but all we’ve got is a bunch of 1k & ohm; quarter-watt (¼W) resistors (and it’s 3am, all the Mountain Dew is gone, and the coffee’s cold).You can combine 10 of the 1k & ohm; ‘s to get 100 & ohm; (1k & ohm; / 10 = 100 & ohm;), and the power rating will be 10×0.25W, or 2.5W. Not pretty, but it will get us through a final project, and might even get us extra points for being able to think on our feet. 90005 90004 We need to be a little more careful when we combine resistors of dissimilar values in parallel where total equivalent resistance and power ratings are concerned. It should be completely obvious to the reader, but … 90005 90008 Tip # 4: Different Resistors in Parallel 90009 90004 The combined resistance of two resistors of different values is always less than the smallest value resistor.The reader would be amazed at how many times someone combines values in their head and arrives at a value that’s halfway between the two resistors (1k & ohm; || 10k & ohm; does NOT equal anything around 5k & ohm ;!). The total parallel resistance will always be dragged closer to the lowest value resistor. Do yourself a favor and read tip # 4 10 times over. 90005 90008 Tip # 5: Power Dissipation in Parallel 90009 90004 The power dissipated in a parallel combination of dissimilar resistor values is not split evenly between the resistors because the currents are not equal.Using the previous example of (1k & ohm; || 10k & ohm;), we can see that the 1k & ohm; will be drawing 10X the current of the 10k & ohm ;. Since Ohm’s Law says power = voltage x current, it follows that the 1k & ohm; resistor will dissipate 10X the power of the 10k & ohm ;. 90005 90004 Ultimately, the lessons of tips 4 and 5 are that we have to pay closer attention to what we’re doing when combining resistors of dissimilar values in parallel. But tips 1 and 3 offer some handy shortcuts when the values are the same.90005
90002 Series and Parallel Capacitors 90003
90004 Combining capacitors is just like combining resistors … only the opposite. As odd as that sounds, it’s absolutely true. Why would this be? 90005 90004 A capacitor is just two plates spaced very close together, and it’s basic function is to hold a whole bunch of electrons. The greater the value of capacitance, the more electrons it can hold. If the size of the plates is increased, the capacitance goes up because there’s physically more space for electrons to hang out.And if the plates are moved farther apart, the capacitance goes down, because the electric field strength between them goes down as the distance goes up. 90005 90004 Now let’s say we’ve got two 10μF capacitors wired together in series, and let’s say they’re both charged up and ready discharge into the friend sitting next to you. 90005 90004 Remember that in a series circuit there’s only one path for current to flow. It follows that the number of electrons that are discharging from the cap on the bottom is going to be the same number of electrons coming out of the cap on the top.So the capacitance has not increased, has it? 90005 90004 In fact, it’s even worse than that. By placing the capacitors in series, we’ve effectively spaced the plates farther apart because the spacing between the plates of the two capacitors adds together. So we do not have 20μF, or even 10μF. We’ve got 5μF. The upshot of this is that we add series capacitor values the same way we add parallel resistor values. Both the product-over-sum and reciprocal methods are valid for adding capacitors in series.90005 90004 It may seem that there’s no point to adding capacitors in series. But it should be pointed out that one thing we did get is twice as much voltage (or voltage ratings). Just like batteries, when we put capacitors together in series the voltages add up. 90005 90004 Adding 90033 capacitors in parallel 90034 is like adding resistors in series: the values just add up, no tricks. Why is this? Putting them in parallel effectively increases the size of the plates without increasing the distance between them.More area equals more capacitance. Simple. 90005
90002 Experiment Time — Part 3 90003
90004 What you’ll need: 90005 90004 Let’s see some series and parallel connected capacitors in action. This will be a little trickier than the resistor examples, because it’s harder to measure capacitance directly with a multimeter. 90005 90004 Let’s first talk about what happens when a capacitor charges up from zero volts. When current starts to go in one of the leads, an equal amount of current comes out the other.And if there’s no resistance in series with the capacitor, it can be quite a lot of current. In any case, the current flows until the capacitor starts to charge up to the value of the applied voltage, more slowly trickling off until the voltages are equal, when the current flow stops entirely. 90005 90004 As stated above, the current draw can be quite large if there’s no resistance in series with the capacitor, and the time to charge can be very short (like milliseconds or less). For this experiment, we want to be able to watch a capacitor charge up, so we’re going to use a 10k & ohm; resistor in series to slow the action down to a point where we can see it easily.But first we need to talk about what an RC time constant is. 90005 90004 What the above equation says is that one time constant in seconds (called tau) is equal to the resistance in ohms times the capacitance in farads. Simple? No? We shall demonstrate on the next page. 90005
90002 Experiment Time — Part 3, Continued … 90003
90004 For the first part of this experiment, we’re going to use one 10K resistor and one 100μF (which equals 0.0001 farads). These two parts create a time constant of 1 second: 90005 90004 When charging our 100μF capacitor through a 10k & ohm; resistor, we can expect the voltage on the cap to rise to about 63% of the supply voltage in 1 time constant, which is 1 second.After 5 time constants (5 seconds in this case) the cap is about 99% charged up to the supply voltage, and it will follow a charge curve something like the plot below. 90005 90004 Now that we know that stuff, we’re going to connect the circuit in the diagram (make sure to get the polarity right on that capacitor!). 90005 90004 With our multimeter set to measure volts, check the output voltage of the pack with the switch turned on. That’s our supply voltage, and it should be something around 4.5V (it’ll be a bit more if the batteries are new). Now connect the circuit, taking care that the switch on the battery pack is in the «OFF» position before plugging it into the breadboard. Also, take care that the red and black leads are going to the right places. If it’s more convenient, you can use alligator clips to attach the meter probes to the legs of the capacitor for measurement (you can also spread those legs out a bit to make it easier). 90005 90004 Once we’re satisfied that the circuit looks right and our meter’s on and set to read volts, flip the switch on the battery pack to «ON».After about 5 seconds, the meter should read pretty close to the battery pack voltage, which demonstrates that the equation is right and we know what we’re doing. Now turn the switch off. It’s still holding that voltage pretty well, is not it? That’s because there’s no path for current to discharge the capacitor; we’ve got an open circuit. To discharge the cap, you can use another 10K resistor in parallel. After about 5 seconds, it will be back to pretty close to zero. 90005
90002 Experiment Time — Part 3, Even More… 90003
90004 Now we’re on to the interesting parts, starting with connecting two capacitors in series. Remember that we said the result of which would be similar to connecting two resistors in parallel. If this is true, we can expect (using product-over-sum) 90005 90004 What’s that going to do to our time constant? 90005 90004 With that in mind, plug in another capacitor in series with the first, make sure the meter is reading zero volts (or there-abouts) and flip the switch to «ON».Did it take about half as much time to charge up to the battery pack voltage? That’s because there’s half as much capacitance. The electron gas tank got smaller, so it takes less time to charge it up. A third capacitor is suggested for this experiment just to prove the point, but we’re betting the reader can see the writing on the wall. 90005 90004 Now we’ll try capacitors in parallel, remembering that we said earlier that this would be like adding resistors in series. If that’s true, then we can expect 200μF, right? Then our time constant becomes 90005 90004 This means that it will now take about 10 seconds to see the parallel capacitors charge up to the supply voltage of 4.5V. 90005 90004 For the proof, start with our original circuit of one 10k & ohm; resistor and one 100μF capacitor in series, as hooked up in the first diagram for this experiment. We already know that the capacitor is going to charge up in about 5 seconds. Now add a second capacitor in parallel. Make sure the meter is reading close to zero volts (discharge through a resistor if it is not reading zero), and flip the switch on the battery pack to «ON». Takes a long time, does not it? Sure enough, we made the electron gas tank bigger and now it takes longer to fill it up.To prove it to yourself, try adding the third 100μF capacitor, and watch it charge for a good, long time. 90005
90002 Series and Parallel Inductors 90003
90008 Series and Parallel Inductors 90009 90004 Cases where inductors need to be added either in series or in parallel are rather rare, but not unheard of. In any case, let’s address them just to be complete. 90005 90004 In a nutshell they add just like resistors do, which is to say they add with a plus sign when in series, and with product-over-sum when in parallel.The tricky part comes when they are placed close together so as to have interacting magnetic fields, whether intentionally or not. For this reason, it is preferable to have a single component rather than two or more, though most inductors are shielded to prevent interacting magnetic fields. 90005 90004 In any case, suffice it to say that they add like resistors do. More information than that regarding inductors is well beyond the scope of this tutorial. 90005
90002 Resources and Going Further 90003
90004 Now that you’re familiar with the basics of serial and parallel circuits, why not check out some of these tutorials? 90005 90010
90011 Voltage Dividers — One of the most basic, and recurring circuits is the voltage divider.This is a circuit which really builds upon the concepts explored in this tutorial. 90012
90011 What is an Arduino? — Now that you’ve got the basics of circuits under your belt, you could head directly to learning about microcontrollers with one of the most popular platforms out there: Arduino. 90012
90011 Switch Basics — We’ve talked about some of the more basic circuit elements in this tutorial, but this was not one of them. Switches are a critical component in just about every electronics project out there.Learn all about switches in this tutorial 90012
90011 Sewing with Conductive Thread — Circuits do not have to be all breadboards and wire. E-textiles uses conductive thread to sew lights and other electronics into clothing or other fabric. 90012
90017 .90000 What is a Resistance? Series and Parallel Resistance Circuit 90001
90002 90003 Resistance 90004 is the property of a material by virtue of which it opposes the flow of electrons through the material. It restricts the flow of the electron through the material. It is denoted by (R) and is measured in ohms (Ω). 90005 90002 When the voltage is applied across the resistor the free electrons start accelerating. These moving electrons collide with each other and hence opposes the flow of electrons.The opposition of electrons is known as the resistance. The heat is generated when the atom or molecules are colliding with each other. 90005
90002 90003 Contents: 90004 90005 90002 90013 90003 Explanation: 90004 90005
90002 The resistance of any material depends on two factors 90005
90019
90020 The shape of the material 90021
90020 Material type (what material it is made up of) 90021
90024
90002 Quantitatively it is obtained by Ohm’s Law, as the resistance offered by the material when a current of I ampere flows through it with a potential difference of (V) volts across the material.It is given by the equation shown below 90005
90002 90028 90005
90002 Where R is the resistance, V is the voltage, and I is the current in the circuit. 90005
90002 It is clear from the above equation (1) that resistance is directly proportional to the voltage and inversely proportional to the current of the circuit. It is also given as 90013 90034 90005
90002 Where, 90005 90019
90020 R is the resistance of any conductor or material measured in ohms 90021
90020 ρ is the resistivity of the material and is measured in ohms meter 90021
90020 90044 l 90045 is the length of the material or conductor in meters 90021
90020 A is the conductor’s cross-sectional area in meter square 90021
90024
90002 The resistance of any conducting material is directly proportional to the length of the conductor and inversely proportional to the conductor’s cross-sectional area.90013 90013 90003 Resistivity (90044 ρ 90045) 90004 is defined as the ability of the conductor or the material to oppose the electric current. The resistance of any conductor is measured by the instrument known as Ohmmeter. 90005
90002 The collision of atoms with the free electrons causes the heat to develop when an electric current flows through any conductor or material. If a current of I ampere is passing through the conductor and the potential difference is V volts across the conductor, then the power absorbed by the resistor is given by the equation (3) shown below 90005
90002 90061 90005
90002 As we know V = IR 90005
90002 90066 90005
90002 The energy lost in the resistance in the form of heat and is derived as 90013 90070 90005
90002 Putting the value of P from the equation (3) in equation (4) we will get 90005
90002 90075 90005
90002 As we know I = V / R, hence putting the value of I in equation (5) we will get 90005
90002 90080 90005
90002 The above equation (6) shows the equation for energy loss in the form of heat.90013 90005
90085 Types of Resistance 90086
90002 There are mainly two types of resistance 90005 90002 It is similar to the normal resistance of the circuit given as R = V / I. It determines the power dissipation in an electric circuit. It is also defined as the slope of the line from the origin through various points on the curve. 90005 90002 It is also known as the incremental or dynamic resistance of the circuit. It is the derivative of the ratio of voltage to the current. Differential resistance is given by the formula shown below 90005
90093 90094 90095 90085 Series and Parallel Resistance in the circuit 90086
90002 90003 Series Resistance Circuit 90004 90005
90002 If the various resistances suppose R 90103 1 90104, R 90103 2 90104, R 90103 3 90104 connected together in series as shown in the figure below is termed as a series resistance circuit 90013 90110 The equivalent or total resistance is given by the equation 90005
90002 90113 90005
90002 90003 Parallel Resistance Circuit 90004 90005
90002 The various resistances suppose R 90103 1 90104, R 90103 2 90104, R 90103 3 90104 are connected in parallel with each other as shown in the circuit below is known as Parallel Resistance Circuit.90013 90127 The equivalent or total resistance is given by the equation 90005
90002 90130 90013 This is all about resistance. 90005 .90000 Parallel Resistor Calculator R1 + R2 = equivalent resistor R resistance circuit equiv total resistor finder made easy piggyback = parallel 90001 Parallel Resistor Calculator R1 + R2 = equivalent resistor R resistance circuit equiv total resistor finder made easy piggyback = parallel — sengpielaudio Sengpiel Berlin 90002 90002 90002
90005
90006
90007 R 90008 total 90009 90010
90011 90010
90007 90014 Formula: 90015 90002
90014 R 90008 total 90009 = R1 × R2 / (R1 + R2) 90015 90002
90010
90023
90024
90002 Please enter 90014 two 90015 resistor values, the third value of the parallel circuit will be calculated.90002
You can even enter the total resistance 90029 R 90030 90008 total 90009 and one known resistance 90029 R 90030 90008 1 90009 or 90029 R 90030 90008 2 90009.
90002 90042 Formula (equation) for the calculation of two resistances 90029 R 90030 90008 1 90009 and 90029 R 90030 90008 2 90009 connected in parallel: 90051
90042 90051
90042 90051
90042 Calculation of the necessary parallel resistor 90029 R 90030 90008 2 90009, when 90029 R 90030 90008 1 90009 and the total resistance 90029 R 90030 90008 total 90009 is given: 90051
90042 90051
90005
90006
90011
Solving the formula 90029 R 90030 90008 total 90009 = (90029 R 90030 90008 1 90009 × 90029 R 90030 90008 2 90009) / (90029 R 90030 90008 1 90009 + 90029 R 90030 90008 2 90009) for 90029 R 90030 90008 1 90009: 90002
The first step is to clear all fractions by multiplying by the lowest 90002
common denominator, that is 90029 R 90030 90008 t 90009 × 90029 R 90030 90008 1 90009 × 90029 R 90030 90008 2 90009… so we get: 90002
1/90029 R 90030 90008 total 90009 = 1/90029 R 90030 90008 1 90009 + 1/90029 R 90030 90008 2 90009 90002
90029 R 90030 90008 total 90009 × 90029 R 90030 90008 1 90009 × 90029 R 90030 90008 2 90009 [1/90029 R 90030 90008 total 90009 = 1/90029 R 90030 90008 1 90009 + 1/90029 R 90030 90008 2 90009] 90002
90029 R 90030 90008 1 90009 × 90029 R 90030 90008 2 90009 = 90029 R 90030 90008 total 90009 × 90029 R 90030 90008 2 90009 + 90029 R 90030 90008 total 90009 × 90029 R 90030 90008 1 90009 then collect terms with 90029 R 90030 90008 1 90009 and solve 90002
90029 R 90030 90008 1 90009 × 90029 R 90030 90008 2 90009 — 90029 R 90030 90008 total 90009 × 90029 R 90030 90008 1 90009 = 90029 R 90030 90008 total 90009 × 90029 R 90030 90008 2 90009 90002
90029 R 90030 90008 1 90009 (90029 R 90030 90008 2 90009 — 90029 R 90030 90008 total 90009) = 90029 R 90030 90008 2 90009 × 90029 R 90030 90008 total 90009 90002
Last step: 90002
90029 90014 R 90015 90030 90014 90008 1 90009 = 90015 90014 90029 R 90030 90015 90014 90008 2 90009 90015 × 90014 90029 R 90030 90015 90014 90008 total 90009 / (90015 90014 90029 R 90030 90015 90014 90008 2 90009 — 90015 90014 90029 R 90030 90015 90014 90008 total 90009) 90015 90002
or: 90002
90029 90014 R 90015 90030 90014 90008 2 90009 = 90015 90014 90029 R 90030 90015 90014 90008 1 90009 90015 × 90014 90029 R 90030 90015 90014 90008 total 90009 / (90015 90014 90029 R 90030 90015 90014 90008 1 90009 — 90015 90014 90029 R 90030 90015 90014 90008 total 90009) 90015 90010
90023
90024
90042 90014 Notice: 90015 This calculator can also solve other math problems.Calculating resistors in parallel is 90002
precisely the same as the calculations required for inductors in parallel or for capacitors in series. 90051
90005
90006
90011 Two resistors in parallel and the resulting total resistance: Two of the same value, 90002
also show the equation that the results are always half. That makes it easier when 90002
designing circuits or prototyping. With caps it’s always double, then again caps just 90002
simply add up in parallel.90010
90023
90024
90042 90051
90042 90014 • Search resistances 90029 R 90030 90008 1 90009 and 90029 R 90030 90008 2 90009, when the target resistance (equivalent resistance) is known • 90015 90051
90042 90014 Calculation: Resistor pairs — reverse engineered calculator 90015 90002
90014 Search of 90029 R 90030 90008 1 90009 and 90029 R 90030 90008 2 90009 with known target resistance 90015 90051
90042 90051
90042 90014 ● Calculate many resistors in parallel ● 90015 90051
90005
90006
90011 This calculator determines the resistance of 90014 up to 10 resistors in parallel 90015.90002
Enter resistances into the boxes below and when all values have been input, 90002
click on the ‘calculate’ button and the result will appear in the box below that button. 90002
As a test, if we enter resistances of 4, 6, and 12 ohms, the answer should be 2 ohms. 90002
Notice: Manually clearing the boxes does not reset stored values. Use «reset». 90010
90023
90024
90002 90042 90014 Ohm’s law — calculator and formulas 90015 90051
90042 90014 Two resistors in parallel and the resulting total resistance 90015 90002
Resistance ranging from 1 ohm to 100 ohms 90051
90384
90006
90386 R2 90010
90388 R1 90010
90023
90006
90011 90014 1 90015 90010
90011 90014 1.5 90015 90010
90011 90014 2.2 90015 90010
90011 90014 3.3 90015 90010
90011 90014 4.7 90015 90010
90011 90014 6.8 90015 90010
90011 90014 10 90015 90010
90011 90014 15 90015 90010
90011 90014 22 90015 90010
90011 90014 33 90015 90010
90011 90014 47 90015 90010
90011 90014 68 90015 90010
90023
90006
90011 90014 1 90015 90010
90011 0.5 90010
90011 0.6 90010
90011 0.69 90010
90011 0.77 90010
90011 0.83 90010
90011 0.87 90010
90011 0.91 90010
90011 0.93 90010
90011 0.95 90010
90011 0.97 90010
90011 0.98 90010
90011 0.99 90010
90023
90006
90011 90014 1.5 90015 90010
90011 0.6 90010
90011 0.75 90010
90011 0.89 90010
90011 1.03 90010
90011 1.14 90010
90011 1.22 90010
90011 1.30 90010
90011 1.36 90010
90011 1.40 90010
90011 1.43 90010
90011 1.45 90010
90011 1.46 90010
90023
90006
90011 90014 2.2 90015 90010
90011 0.69 90010
90011 0.89 90010
90011 1.1 90010
90011 1.32 90010
90011 1.50 90010
90011 1.66 90010
90011 1.82 90010
90011 1.92 90010
90011 2.0 90010
90011 2.06 90010
90011 2.10 90010
90011 2.13 90010
90023
90006
90011 90014 3.3 90015 90010
90011 0.77 90010
90011 1.03 90010
90011 1.32 90010
90011 1.65 90010
90011 1.94 90010
90011 2.22 90010
90011 2.48 90010
90011 2.70 90010
90011 2.87 90010
90011 3.00 90010
90011 3.08 90010
90011 3.14 90010
90023
90006
90011 90014 4.7 90015 90010
90011 0.83 90010
90011 1.14 90010
90011 1.50 90010
90011 1.94 90010
90011 2.35 90010
90011 2.78 90010
90011 3.20 90010
90011 3.58 90010
90011 3.87 90010
90011 4.12 90010
90011 4.27 90010
90011 4.39 90010
90023
90006
90011 90014 6.8 90015 90010
90011 0.87 90010
90011 1.22 90010
90011 1.66 90010
90011 2.22 90010
90011 2.78 90010
90011 3.40 90010
90011 4.05 90010
90011 4.68 90010
90011 5.19 90010
90011 5.64 90010
90011 5.94 90010
90011 6.18 90010
90023
90006
90011 90014 10 90015 90010
90011 0.91 90010
90011 1.30 90010
90011 1.82 90010
90011 2.48 90010
90011 3.20 90010
90011 4.05 90010
90011 5.0 90010
90011 6.0 90010
90011 6.9 90010
90011 7.7 90010
90011 8.3 90010
90011 8.7 90010
90023
90006
90011 90014 15 90015 90010
90011 0.93 90010
90011 1.36 90010
90011 1.92 90010
90011 2.70 90010
90011 3.58 90010
90011 4.68 90010
90011 6.0 90010
90011 7.50 90010
90011 8.9 90010
90011 10.3 90010
90011 11.4 90010
90011 12.2 90010
90023
90006
90011 90014 22 90015 90010
90011 0.95 90010
90011 1.40 90010
90011 2.00 90010
90011 2.87 90010
90011 3.87 90010
90011 5.19 90010
90011 6.9 90010
90011 8.9 90010
90011 11.0 90010
90011 13.2 90010
90011 15.0 90010
90011 16.6 90010
90023
90006
90011 90014 33 90015 90010
90011 0.97 90010
90011 1.43 90010
90011 2.06 90010
90011 3.0 90010
90011 4.12 90010
90011 5.64 90010
90011 7.7 90010
90011 10.3 90010
90011 13.2 90010
90011 16.5 90010
90011 19.4 90010
90011 22.2 90010
90023
90006
90011 90014 47 90015 90010
90011 0.98 90010
90011 1.45 90010
90011 2.1 90010
90011 3.08 90010
90011 4.27 90010
90011 5.94 90010
90011 8.3 90010
90011 11.4 90010
90011 15,0 90010
90011 19.4 90010
90011 23.5 90010
90011 27.8 90010
90023
90006
90011 90014 68 90015 90010
90011 0.99 90010
90011 1.46 90010
90011 2.13 90010
90011 3.14 90010
90011 4.39 90010
90011 6.18 90010
90011 8.7 90010
90011 12.2 90010
90011 16.6 90010
90011 22.2 90010
90011 27.8 90010
90011 34.0 90010
90023
90024
90002
90042 90014 Notice: 90015 This calculator can also solve other math problems.Calculating resistors in parallel is 90002
precisely the same as the calculations required for inductors in parallel or for capacitors in series. 90051
90005
90006
90011 Power dissipated in resistor: 90029 P 90030 = 90029 V 90030 × 90029 I 90030, 90029 P 90030 = 90029 V 90030 90821 2 90822/90029 R 90030, 90029 P 90030 = 90029 I 90030 90821 2 90822 × 90029 R 90030. 90010
90023
90024
90002
90005
90006
90011 90014 Notice: 90015 For resistors in series, the 90014 current 90015 is the same for each resistor, 90002
and for resistors in parallel, the 90014 voltage 90015 is the same for each resistor.90010
90023
90024
90002 90002 .
90000 Introduction to Series, Parallel and Series-Parallel Connections 90001 90002 90003 Series, Parallel & Series-Parallel Circuits, their Comparison and Applications 90004 90005 90006 90003 Why Parallel Connection is Mostly Preferred over Series Connection? 90004 90009 90010 The use, application and importance of series and parallel circuit connection today can not be over emphasized. The application of series and parallel circuit connection can be evidently seen in our homes, school halls and in our street lights.With the press of a button, all the Bobs in our sitting rooms are turned on. some refer that the bobs in their homes should have different switches. 90011 90010 90013 90013 90011 90010 Well, it’s not a magic when more than three electric bobs or loads are controlled by one switch. A load is anything i.e. it could be an appliances, electric bobs or even ceiling fans that consumes electrical energy when connected to a power supply. The electric bobs, televisions, refrigerators etc can all be referred to as a load.The bobs convert electrical energy into light and heat form of energy. Fans convert the electrical energy into mechanical energy. 90011 90010 The type of connection done to our ceiling fans, electric bobs will determine if they will have a common switch or not. Series circuit connection gives us the opportunity to connect more than two loads to a common switch. Street lights are a very good example of this. Parallel circuit connection makes it possible for us to connect loads to their individual switch.Both series and parallel circuit connection are good but one is mostly preferred over the other for one reason or the other. Before we talk about the reason why parallel circuit connection is preferred over series connection, let’s recall what series and parallel connections are first. 90011 90006 90003 Series Circuit 90022 90004 90009 90010 A series circuit is a circuit in which resistors or loads are connected end to end so that the circuit will have only one path through which electric current flows.Thus, when a number of resistors are connected in series, the effective resistance (total resistance in the circuit) is gotten by adding the individual resistance algebraically. That is to say, if we have resistors with resistance R1, R2, R3 … Rn 90003 connected in series 90004, then; 90011 90010 90003 R 90031 eff 90032 = R 90031 T 90032 = R 90031 1 90032 + R 90031 2 90032 + R 90031 3 90032 + … R 90031 n 90032. 90004 90011 90010 In series connections, the same current flows across all the branches of the circuits, but different voltage across it thus making the resistors to have different voltage across them.Each resistor or load will experience a voltage drop. The applied voltage is equal to the sum of the voltage drop across the different parts of the circuit. Voltage drop is proportional to the resistance current being the same throughout the circuit. When loads are connected in series, the loads will tend to have a common switch. This kind of connection is employed in school halls, street lights. 90011 90047 90047 How To Wire Lights in Series? 90049 90003 Uses & Application of Series Connection 90004 90052 90010 Some people connect security lights in their homes in series which will make them to have common switch.The problem with this kind of connection is that when a load develops a problem, the other connected system will fail. It’s an all or none type of circuit connection. Till a load gets energy before it delivers it to the other and the one to deliver fails, there will be a black out. 90011 90010 Series circuit connections are common and greatly employed in electrical equipments. The tube filaments in small radios are usually in series. Current controlling devices are always connected in series with the device that they protect.Fuses are connected in series with the device they protect, Automatic house-heating equipment has a thermostat, electromagnetic coils, and safety cut-outs connected in series with a voltage source etc. 90011 90049 90058 Disadvantages of Series Circuit 90059 90052 90061 90062 The break in the wire, failure or removal of any single lamp will break the circuit and cause all of the others to stop working as there is only one single path of current to flow in the circuit. 90063 90062 If more lamps are added in series lighting circuit, they will all be reduced in brightness.because voltage are shared in series circuit. If we add more loads in series circuit, the over voltage drop is increases which is not a good sign for electrical appliances protection. 90063 90062 Series Wiring is «ALL or NONE» type wiring mean all the appliances will work at once or all of them will disconnect if fault occurs at any one of the connected device in series circuit. 90063 90062 High supply voltage are needed if we need to add more load (light bulbs, electric heaters, air conditioner etc) in the series circuit.For example, If five, 220V Lamps are to be connected in Series, Than Supply Voltage would have to be: 5 x 220V = 1.1kV. 90063 90062 The overall series circuit resistance increases (and current decreases) when more load added in the circuit. 90063 90062 According to future need, only those electrical appliances should be added in the current series circuit if they has the same current rating as current are same at each point in series circuit. However, we know that electrical appliances and devices i.e. light bulbs, fan, heater, air conditioner etc have different current rating, therefore, they can not be connected in series circuit for smooth and efficient operation. 90073 90073 Lights connected in Series 90063 90076 90049 90058 Advantages 90059 90058 of Series Connection 90059 90052 90061 90062 Less size of wire cable is required in series wiring. 90063 90062 We use to protect the circuit to connect fuse & circuit breakers in series with other appliances. 90063 90062 Series circuit do not get overhead easily due to high resistance when more load added in the circuit.90063 90062 The lifespan of battery in series circuit is more as compared to parallel. 90063 90062 It is most simple method of electrical wiring and fault can be easily detect and repair as compared to parallel or series-parallel wiring. 90063 90076 90006 90003 Parallel Circuit 90022 90004 90009 90010 Resistors, loads are said to be connected in parallel when the end of each of the resistors or loads have a common point or junction and the other ends are also connected to a common point or junction.Such circuits are known as parallel circuits. 90011 90102 90102 Light Bulbs Connected in Parallel 90010 Unlike the series circuit connection, when finding the total (effective) resistance in a parallel circuit, the reciprocal of the individual resistance is taken. Thus, when a number of resistances are connected in parallel, the reciprocal of the effective resistance is given by the arithmetic or algebraic sum of the reciprocal of the individual resistance. 90011 90010 90003 1 / R 90031 eff 90032 or 1 / R 90031 T 90032 = 1 / R 90031 1 90032 + 1 / R 90031 2 90032 + 1 / R 90031 3 90032 … 1 / R 90031 n 90032.90004 90011 90010 Parallel circuit connection have the same voltage flowing across all the branches of the circuits. Different resistors have their individual currents. 90011 90049 90003 Uses & Application of Parallel Connection 90004 90052 90010 Parallel circuit connection is very common in use. Various lamps and electrical appliances in our homes are connected in parallel so that each of the lamps or bobs and appliances can be operated independently. For us to have control over the individual lamps or loads, they have to be wired in parallel.90011 90049 90058 Advantages of Parallel Circuit 90059 90052 90061 90062 Each connected electrical device and appliance are independent from others. This way, switching ON / OFF a device will not affect the other appliances and their operation. 90063 90062 In case of break in the cable or removal of any lamp will not break the all circuits and connected loads, in other words, other lights / lamps and electrical appliances will still work smoothly. 90063 90062 If more lamps are added in the parallel lighting circuits, they will not be reduced in brightness (as it happens only in series lightning circuits).Because voltage is same at each point in a parallel circuit. In short, they get the same voltage as the source voltage. 90063 90062 It is possible to add more light fixture and load points in parallel circuits according to future need as far as the circuit is not overloaded. 90063 90062 Adding additional devices and components wont increase the resistance but will decrease the overall resistance of the circuit especially when high current rating devices are used such as air conditioner and electric heaters.90063 90062 parallel wiring is more reliable, safe and simple to use. 90146 90146 Faults in Parallel lighting circuits 90063 90076 90049 90058 Disadvantages of Parallel Connections 90059 90022 90052 90061 90062 More size of cable and wire is used in parallel lighting wiring circuit. 90063 90062 More current needed when additional light bulb added in the parallel circuit. 90063 90062 Battery runs out quicker for DC installation. 90063 90062 The parallel wiring design is more complex as compare to series wiring.90063 90076 90010 90166 90003 Related Post: Which Bulb Glows Brighter When Connected in Series and Parallel & Why? 90004 90169 90011 90006 90003 Series-Parallel Connections & Circuits 90004 90009 90010 The circuit is series nor parallel in the following fig i.e. it is series-parallel circuit. The first three lamps (B 90031 1 90032, B 90031 2 90032 & B 90031 3 90032) are connected in parallel while switches (S 90031 1 90032, S 90031 2 90032 & S 90031 3 90032) are wired in series accordingly.B 90031 7 90032, B 90031 8 90032, B 90031 9 90032 and B 90031 10 90032 are in series with each other while they are parallel with the first three bulbs (B 90031 1 90032, B 90031 2 90032 & B 90031 3 90032) while the switches (S5 & S6) are in parallel connected with Bulb (B 90031 10 90032). Also, bulbs (B 90031 4 90032, B 90031 5 90032 & B 90031 6 90032) and switch (S 90031 7 90032) are in series with each other while they are in parallel with (B 90031 1 90032, B 90031 2 90032 & B 90031 3 90032) and so on.90011 90010 As the circuit is combination of series and parallel, We can not simplify the current, voltage, resistance and power by simple ohm’s law. We have to apply different theorems like Norton’s, Thevenin’s, maximum power transfer theorem etc or will simplify the circuit in basic series and parallel circuits to find all those quantities. 90011 90010 Most common of household wiring installation nowadays using this wiring method. 90011 90223 90223 Series-Parallel Light Circuit & Connection 90006 90003 Comparison Between Series and Parallel Connection 90004 90009 90010 Below in the given table, the main differences between series and parallel connections are shown.90011 90231 90232 90233 90234 90003 S No 90004 90237 90234 90003 Series Circuit 90004 90237 90234 90003 Parallel Circuit 90004 90237 90246 90233 90234 90003 Current (I) 90004 90237 90234 Current are same in each point in series circuit: 90010 I 90031 1 90032 = I 90031 2 90032 = I 90031 3 90032 = …. I 90031 n 90032 90011 90237 90234 Current are additive in series circuit: 90010 I 90031 1 90032 + I 90031 2 90032 + I 90031 3 90032 + …. I 90031 n 90032 90011 90237 90246 90233 90234 90003 Voltage (V) 90004 90237 90234 Voltage are additive in series circuit: 90010 V 90031 1 90032 + V 90031 2 90032 + V 90031 3 90032 + ….V 90031 n 90032 90011 90237 90234 Voltages are same in each point in parallel circuit: 90010 V 90031 1 90032 = V 90031 2 90032 = V 90031 3 90032 = …. V 90031 n 90032 90011 90237 90246 90233 90234 90003 Resistance (R) & to Find (R) 90004 90237 90234 Resistance are additive in Series Circuit: 90010 R 90031 1 90032 + R 90031 2 90032 + R 90031 3 90032 + … R 90031 n = 90032 R 90031 eff 90032 = R 90031 T 90032 90011 90237 90234 Resistance are divided when more load added in the circuit.90010 1 / R 90031 T 90032 = 1 / R 90031 1 90032 + 1 / R 90031 2 90032 + 1 / R 90031 3 90032 … 1 / R 90031 n 90032 90011 90010 or 90011 90010 I = G 90031 1 90032 + G 90031 2 90032 + G 90031 3 90032 + … G 90031 n 90032 90011 90237 90246 90233 90234 90003 To Find Current (I) 90004 90237 90234 I = V 90031 1 90032 / R 90031 1 90032 = V 90031 2 90032 / R 90031 2 90032 = V 90031 3 90032 / R 90031 3 90032 = V 90031 n 90032 / R 90031 n 90032 90237 90234 I = V 90031 1 90032 / R 90031 1 90032 + V 90031 2 90032 / R 90031 2 90032 + V 90031 3 90032 / R 90031 3 90032 + V 90031 n 90032 / R 90031 n 90032 90237 90246 90233 90234 90003 To Find Voltage (V) 90004 90237 90234 V = I 90031 1 90032 R 90031 1 90032 + I 90031 2 90032 R 90031 2 90032 + I 90031 3 90032 R 90031 3 90032 + … I 90031 n 90032 R 90031 n 90032 90237 90234 V = I 90031 1 90032 R 90031 1 90032 = I 90031 2 90032 R 90031 2 90032 = I 90031 3 90032 R 90031 3 90032 = … I 90031 n 90032 R 90031 n 90032 90237 90246 90233 9 0234 90003 To Find Electric Power (P) 90004 90237 90234 90010 P = I 90446 2 90447 R 90031 1 90032 + I 90446 2 90447 R 90031 2 90032 + … I 90446 2 90447 R 90031 n 90032 90011 90010 or 90011 90010 P = V 90031 1 90032 90446 2 90447 / R 90031 1 90032 + V 90031 2 90032 90446 2 90447 / R 90031 2 90032 + … V 90031 n 90032 90446 2/90447 R 90031 n 90032 90011 90237 90234 90010 P = V 90446 2 90447 / R 90031 1 90032 + V 90446 2 90447 / R 90031 2 90032 + … V 90446 2/90447 R 90031 n 90032 90011 90010 or 90011 90010 P = I 90031 1 90032 90446 2 90447 R 90031 1 90032 + I 90031 2 90032 90446 2 90447 R 90031 2 90032 + … I 90031 n 90032 90446 2 90447 R 90031 n 90032 90011 90237 90246 90233 90234 90003 Current & Voltage Divider Rule 90004 90237 90234 V 90031 1 90032 = V 90031 T 90032 (R 90031 1 90032 / R 90031 T 90032 ), V 90031 2 90032 = V 90031 T 90032 (R 90031 2 90032 / R 90031 T 90032) 90237 90234 I 90031 1 90032 = I 90031 T 90032 (G 90031 1 90032 / G 90031 T 900 32), I 90031 2 90032 = I 90031 T 90032 (G 90031 2 90032 / G 90031 T 90032) 90237 90246 90233 90234 90003 Paths of flow of Electric Current 90004 90237 90234 Only one path 90237 90234 Two or more paths 90237 90246 90233 90234 90003 Brightness of Bulb 90004 90237 90234 Dimmer if added more bulbs (P = V x I) 90237 90234 Brighter due to same voltages 90237 90246 90233 90234 90003 If breaks occurs in the circuit 90004 90237 90234 Whole circuit is useless 90237 90234 The rest of the circuit will still work 90237 90246 90233 90234 90003 Battery Status 90004 90237 90234 Battery Discharge slowly (Ah Rating of Battery) 90237 90234 Battery Discharge Quickly (Battery Ah Time & Currents) 90237 90246 90233 90234 90003 Applications 90004 90237 90234 Used to protect the circuit while connecting fuses and circuit breakers in series with the connected appliances 90237 90234 Used in most of household electrical wiring installations 90237 90246 90613 90614 90006 90003 Advantages of Parallel Circuit Connection over Series Circuit Connection 90004 90009 90010 A series circuit connection is an all or none type of circuit connection.Meaning that if one of the appliances fails, all the other appliances will also fail which is why this type of connection is good only when we want to protect a device. 90620 90620 When a fuse gets burnt for instance due to high current, then the appliance it protects will not be damaged because current will no longer reach it. While series connection is an all or none, parallel circuit connection gives you the opportunity to give the loads and the appliances their individual switch. Parallel connection offers resistance to the flow of current compared to series connection.90011 90623 90623 Disadvantages of Series Lighting Circuit 90010 A 100 ohms and a 150 ohms resistors connected in parallel will have less effect on electric current compared to 50 ohms and 40 ohms resistors connected in series. In electronic devices, parallel connection is paramount. The cells in a power bank are all connected in parallel. Parallel connection makes electrical energy to last longer. The cells themselves have their internal resistance, so if they were connected in series, some of the energy will be lost overcoming the internal resistance since it’s effect is high when in series than when in parallel.90011 90010 Related Posts: 90022 90011.90000 Series and Parallel Circuits — learn.sparkfun.com 90001
Favorited
Favorite
48
90002 Series and Parallel Circuits 90003
90004 Simple circuits (ones with only a few components) are usually fairly straightforward for beginners to understand. But, things can get sticky when other components come to the party. Where’s the current going? What’s the voltage doing? Can this be simplified for easier understanding? Fear not, intrepid reader.Valuable information follows. 90005 90004 In this tutorial, we’ll first discuss the difference between series circuits and parallel circuits, using circuits containing the most basic of components — resistors and batteries — to show the difference between the two configurations. We’ll then explore what happens in series and parallel circuits when you combine different types of components, such as capacitors and inductors. 90005 90008 Covered in this Tutorial 90009 90010
90011 What series and parallel circuit configurations look like 90012
90011 How passive components act in these configurations 90012
90011 How a voltage source will act upon passive components in these configurations 90012
90017 90008 Suggested Reading 90009 90004 You may want to visit these tutorials on the basic components before diving into building the circuits in this tutorial.90005 90008 Video 90009 90004 90025 90026 90005
90002 Series Circuits 90003
90008 Nodes and Current Flow 90009 90004 Before we get too deep into this, we need to mention what a 90033 node 90034 is. It’s nothing fancy, just representation of an electrical junction between two or more components. When a circuit is modeled on a schematic, these nodes represent the wires between components. 90005 90004 90037 Example schematic with four uniquely colored nodes.90038 90005 90004 That’s half the battle towards understanding the difference between series and parallel. We also need to understand 90033 how current flows 90034 through a circuit. Current flows from a high voltage to a lower voltage in a circuit. Some amount of current will flow through every path it can take to get to the point of lowest voltage (usually called ground). Using the above circuit as an example, here’s how current would flow as it runs from the battery’s positive terminal to the negative: 90005 90004 90037 Current (indicated by the blue, orange, and pink lines) flowing through the same example circuit as above.Different currents are indicated by different colors. 90038 90005 90004 Notice that in some nodes (like between R 90049 1 90050 and R 90049 2 90050) the current is the same going in as at is coming out. At other nodes (specifically the three-way junction between R 90049 2 90050, R 90049 3 90050, and R 90049 4 90050) the main (blue) current splits into two different ones. 90037 That’s 90038 the key difference between series and parallel! 90005 90008 Series Circuits Defined 90009 90004 Two components are in series if they share a common node and if the 90033 same current 90034 flows through them.Here’s an example circuit with three series resistors: 90005 90004 There’s only one way for the current to flow in the above circuit. Starting from the positive terminal of the battery, current flow will first encounter R 90049 1 90050. From there the current will flow straight to R 90049 2 90050, then to R 90049 3 90050, and finally back to the negative terminal of the battery. Note that there is only one path for current to follow. These components are in series. 90005
90002 Parallel Circuits 90003
90008 Parallel Circuits Defined 90009 90004 If components share 90037 two 90038 common nodes, they are in parallel.Here’s an example schematic of three resistors in parallel with a battery: 90005 90004 From the positive battery terminal, current flows to R 90049 1 90050 … and R 90049 2 90050, and R 90049 3 90050. The node that connects the battery to R 90049 1 90050 is also connected to the other resistors. The other ends of these resistors are similarly tied together, and then tied back to the negative terminal of the battery. There are three distinct paths that current can take before returning to the battery, and the associated resistors are said to be in parallel.90005 90004 Where series components all have equal currents running through them, parallel components all have the same voltage drop across them — series: current :: parallel: voltage. 90005 90008 Series and Parallel Circuits Working Together 90009 90004 From there we can mix and match. In the next picture, we again see three resistors and a battery. From the positive battery terminal, current first encounters R 90049 1 90050. But, at the other side of R 90049 1 90050 the node splits, and current can go to both R 90049 2 90050 and R 90049 3 90050.The current paths through R 90049 2 90050 and R 90049 3 90050 are then tied together again, and current goes back to the negative terminal of the battery. 90005 90004 In this example, R 90049 2 90050 and R 90049 3 90050 are in parallel with each other, and R 90049 1 90050 is in series with the parallel combination of R 90049 2 90050 and R 90049 3 90050. 90005
90002 Calculating Equivalent Resistances in Series Circuits 90003
90004 Here’s some information that may be of some more practical use to you.When we put resistors together like this, in series and parallel, we change the way current flows through them. For example, if we have a 10V supply across a 10k & ohm; resistor, Ohm’s law says we’ve got 1mA of current flowing. 90005 90004 If we then put another 10k & ohm; resistor in series with the first and leave the supply unchanged, we’ve cut the current in half because the resistance is doubled. 90005 90004 In other words, there’s still only one path for current to take and we just made it even harder for current to flow.How much harder? 10k & ohm; + 10k & ohm; = 20k & ohm ;. And, that’s how we calculate resistors in series — just 90033 add their values 90034. 90005 90004 To put this equation more generally: the total resistance of 90037 N 90038 — some arbitrary number of — resistors is their total sum. 90005
90002 Calculating Equivalent Resistances in Parallel Circuits 90003
90004 What about parallel resistors? That’s a bit more complicated, but not by much.Consider the last example where we started with a 10V supply and a 10k & ohm; resistor, but this time we add another 10k & ohm; in parallel instead of series. Now there are two paths for current to take. Since the supply voltage did not change, Ohm’s Law says the first resistor is still going to draw 1mA. But, so is the second resistor, and we now have a total of 2mA coming from the supply, doubling the original 1mA. This implies that we’ve cut the total resistance in half. 90005 90004 While we can say that 10k & ohm; || 10k & ohm; = 5k & ohm; ( «||» roughly translates to «in parallel with»), we’re not always going to have 2 identical resistors.What then? 90005 90004 The equation for adding an arbitrary number of resistors in parallel is: 90005 90004 If reciprocals are not your thing, we can also use a method called «product over sum» when we have two resistors in parallel: 90005 90004 However, this method is only good for two resistors in one calculation. We can combine more than 2 resistors with this method by taking the result of R1 || R2 and calculating that value in parallel with a third resistor (again as product over sum), but the reciprocal method may be less work.90005
90002 Experiment Time — Part 1 90003
90004 What you’ll need: 90005 90004 Let’s try a simple experiment just to prove that these things work the way we’re saying they do. 90005 90004 First, we’re going to hook up some 10k & ohm; resistors in series and watch them add in a most un-mysterious way. Using a breadboard, place one 10k & ohm; resistor as indicated in the figure and measure with a multimeter. Yes, we already know it’s going to say it’s 10k & ohm ;, but this is what we in the biz call a «sanity check».Once we’ve convinced ourselves that the world has not changed significantly since we last looked at it, place another one in similar fashion but with a lead from each resistor connecting electrically through the breadboard and measure again. The meter should now say something close to 20k & ohm ;. 90005 90004 You may notice that the resistance you measure might not be exactly what the resistor says it should be. Resistors have a certain amount of 90033 tolerance 90034, which means they can be off by a certain percentage in either direction.Thus, you may read 9.99k & ohm; or 10.01k & ohm ;. As long as it’s close to the correct value, everything should work fine. 90005 90004 The reader should continue this exercise until convincing themselves that they know what the outcome will be before doing it again, or they run out of resistors to stick in the breadboard, whichever comes first. 90005
90002 Experiment Time — Part 2 90003
90004 Now let’s try it with resistors in a 90033 parallel 90034 configuration.Place one 10k & ohm; resistor in the breadboard as before (we’ll trust that the reader already believes that a single 10k & ohm; resistor is going to measure something close to 10k & ohm; on the multimeter). Now place a second 10k & ohm; resistor next to the first, taking care that the leads of each resistor are in electrically connected rows. But before measuring the combination, calculate by either product-over-sum or reciprocal methods what the new value should be (hint: it’s going to be 5k & ohm;).Then measure. Is it something close to 5k & ohm ;? If it’s not, double check the holes into which the resistors are plugged. 90005 90004 Repeat the exercise now with 3, 4 and 5 resistors. The calculated / measured values should be 3.33k & ohm ;, 2.5k & ohm; and 2k & ohm ;, respectively. Did everything come out as planned? If not, go back and check your connections. If it did, EXCELSIOR! Go have a milkshake before we continue. You’ve earned it. 90005
90002 Rules of Thumb for Series and Parallel Resistors 90003
90004 There are a few situations that may call for some creative resistor combinations.For example, if we’re trying to set up a very specific reference voltage you’ll almost always need a very specific ratio of resistors whose values are unlikely to be «standard» values. And while we can get a very high degree of precision in resistor values, we may not want to wait the X number of days it takes to ship something, or pay the price for non-stocked, non-standard values. So in a pinch, we can always build our own resistor values. 90005 90008 Tip # 1: Equal Resistors in Parallel 90009 90004 Adding 90037 N 90038 like-valued resistors 90037 R 90038 in parallel gives us 90037 R / N 90038 ohms.Let’s say we need a 2.5k & ohm; resistor, but all we’ve got is a drawer full of 10k & ohm; ‘s. Combining four of them in parallel gives us 10k & ohm; / 4 = 2.5k & ohm ;. 90005 90008 Tip # 2: Tolerance 90009 90004 Know what kind of tolerance you can tolerate. For example, if you needed a 3.2k & ohm; resistor, you could put 3 10k & ohm; resistors in parallel. That would give you 3.3k & ohm ;, which is about a 4% tolerance from the value you need. But, if the circuit you’re building needs to be closer than 4% tolerance, we can measure our stash of 10k & ohm; ‘s to see which are lowest values because they have a tolerance, too.In theory, if the stash of 10k & ohm; resistors are all 1% tolerance, we can only get to 3.3k & ohm ;. But part manufacturers are known to make just these sorts of mistakes, so it pays to poke around a bit. 90005 90008 Tip # 3: Power Ratings in Series / Parallel 90009 90004 This sort of series and parallel combination of resistors works for power ratings, too. Let’s say that we need a 100 & ohm; resistor rated for 2 watts (W), but all we’ve got is a bunch of 1k & ohm; quarter-watt (¼W) resistors (and it’s 3am, all the Mountain Dew is gone, and the coffee’s cold).You can combine 10 of the 1k & ohm; ‘s to get 100 & ohm; (1k & ohm; / 10 = 100 & ohm;), and the power rating will be 10×0.25W, or 2.5W. Not pretty, but it will get us through a final project, and might even get us extra points for being able to think on our feet. 90005 90004 We need to be a little more careful when we combine resistors of dissimilar values in parallel where total equivalent resistance and power ratings are concerned. It should be completely obvious to the reader, but … 90005 90008 Tip # 4: Different Resistors in Parallel 90009 90004 The combined resistance of two resistors of different values is always less than the smallest value resistor.The reader would be amazed at how many times someone combines values in their head and arrives at a value that’s halfway between the two resistors (1k & ohm; || 10k & ohm; does NOT equal anything around 5k & ohm ;!). The total parallel resistance will always be dragged closer to the lowest value resistor. Do yourself a favor and read tip # 4 10 times over. 90005 90008 Tip # 5: Power Dissipation in Parallel 90009 90004 The power dissipated in a parallel combination of dissimilar resistor values is not split evenly between the resistors because the currents are not equal.Using the previous example of (1k & ohm; || 10k & ohm;), we can see that the 1k & ohm; will be drawing 10X the current of the 10k & ohm ;. Since Ohm’s Law says power = voltage x current, it follows that the 1k & ohm; resistor will dissipate 10X the power of the 10k & ohm ;. 90005 90004 Ultimately, the lessons of tips 4 and 5 are that we have to pay closer attention to what we’re doing when combining resistors of dissimilar values in parallel. But tips 1 and 3 offer some handy shortcuts when the values are the same.90005
90002 Series and Parallel Capacitors 90003
90004 Combining capacitors is just like combining resistors … only the opposite. As odd as that sounds, it’s absolutely true. Why would this be? 90005 90004 A capacitor is just two plates spaced very close together, and it’s basic function is to hold a whole bunch of electrons. The greater the value of capacitance, the more electrons it can hold. If the size of the plates is increased, the capacitance goes up because there’s physically more space for electrons to hang out.And if the plates are moved farther apart, the capacitance goes down, because the electric field strength between them goes down as the distance goes up. 90005 90004 Now let’s say we’ve got two 10μF capacitors wired together in series, and let’s say they’re both charged up and ready discharge into the friend sitting next to you. 90005 90004 Remember that in a series circuit there’s only one path for current to flow. It follows that the number of electrons that are discharging from the cap on the bottom is going to be the same number of electrons coming out of the cap on the top.So the capacitance has not increased, has it? 90005 90004 In fact, it’s even worse than that. By placing the capacitors in series, we’ve effectively spaced the plates farther apart because the spacing between the plates of the two capacitors adds together. So we do not have 20μF, or even 10μF. We’ve got 5μF. The upshot of this is that we add series capacitor values the same way we add parallel resistor values. Both the product-over-sum and reciprocal methods are valid for adding capacitors in series.90005 90004 It may seem that there’s no point to adding capacitors in series. But it should be pointed out that one thing we did get is twice as much voltage (or voltage ratings). Just like batteries, when we put capacitors together in series the voltages add up. 90005 90004 Adding 90033 capacitors in parallel 90034 is like adding resistors in series: the values just add up, no tricks. Why is this? Putting them in parallel effectively increases the size of the plates without increasing the distance between them.More area equals more capacitance. Simple. 90005
90002 Experiment Time — Part 3 90003
90004 What you’ll need: 90005 90004 Let’s see some series and parallel connected capacitors in action. This will be a little trickier than the resistor examples, because it’s harder to measure capacitance directly with a multimeter. 90005 90004 Let’s first talk about what happens when a capacitor charges up from zero volts. When current starts to go in one of the leads, an equal amount of current comes out the other.And if there’s no resistance in series with the capacitor, it can be quite a lot of current. In any case, the current flows until the capacitor starts to charge up to the value of the applied voltage, more slowly trickling off until the voltages are equal, when the current flow stops entirely. 90005 90004 As stated above, the current draw can be quite large if there’s no resistance in series with the capacitor, and the time to charge can be very short (like milliseconds or less). For this experiment, we want to be able to watch a capacitor charge up, so we’re going to use a 10k & ohm; resistor in series to slow the action down to a point where we can see it easily.But first we need to talk about what an RC time constant is. 90005 90004 What the above equation says is that one time constant in seconds (called tau) is equal to the resistance in ohms times the capacitance in farads. Simple? No? We shall demonstrate on the next page. 90005
90002 Experiment Time — Part 3, Continued … 90003
90004 For the first part of this experiment, we’re going to use one 10K resistor and one 100μF (which equals 0.0001 farads). These two parts create a time constant of 1 second: 90005 90004 When charging our 100μF capacitor through a 10k & ohm; resistor, we can expect the voltage on the cap to rise to about 63% of the supply voltage in 1 time constant, which is 1 second.After 5 time constants (5 seconds in this case) the cap is about 99% charged up to the supply voltage, and it will follow a charge curve something like the plot below. 90005 90004 Now that we know that stuff, we’re going to connect the circuit in the diagram (make sure to get the polarity right on that capacitor!). 90005 90004 With our multimeter set to measure volts, check the output voltage of the pack with the switch turned on. That’s our supply voltage, and it should be something around 4.5V (it’ll be a bit more if the batteries are new). Now connect the circuit, taking care that the switch on the battery pack is in the «OFF» position before plugging it into the breadboard. Also, take care that the red and black leads are going to the right places. If it’s more convenient, you can use alligator clips to attach the meter probes to the legs of the capacitor for measurement (you can also spread those legs out a bit to make it easier). 90005 90004 Once we’re satisfied that the circuit looks right and our meter’s on and set to read volts, flip the switch on the battery pack to «ON».After about 5 seconds, the meter should read pretty close to the battery pack voltage, which demonstrates that the equation is right and we know what we’re doing. Now turn the switch off. It’s still holding that voltage pretty well, is not it? That’s because there’s no path for current to discharge the capacitor; we’ve got an open circuit. To discharge the cap, you can use another 10K resistor in parallel. After about 5 seconds, it will be back to pretty close to zero. 90005
90002 Experiment Time — Part 3, Even More… 90003
90004 Now we’re on to the interesting parts, starting with connecting two capacitors in series. Remember that we said the result of which would be similar to connecting two resistors in parallel. If this is true, we can expect (using product-over-sum) 90005 90004 What’s that going to do to our time constant? 90005 90004 With that in mind, plug in another capacitor in series with the first, make sure the meter is reading zero volts (or there-abouts) and flip the switch to «ON».Did it take about half as much time to charge up to the battery pack voltage? That’s because there’s half as much capacitance. The electron gas tank got smaller, so it takes less time to charge it up. A third capacitor is suggested for this experiment just to prove the point, but we’re betting the reader can see the writing on the wall. 90005 90004 Now we’ll try capacitors in parallel, remembering that we said earlier that this would be like adding resistors in series. If that’s true, then we can expect 200μF, right? Then our time constant becomes 90005 90004 This means that it will now take about 10 seconds to see the parallel capacitors charge up to the supply voltage of 4.5V. 90005 90004 For the proof, start with our original circuit of one 10k & ohm; resistor and one 100μF capacitor in series, as hooked up in the first diagram for this experiment. We already know that the capacitor is going to charge up in about 5 seconds. Now add a second capacitor in parallel. Make sure the meter is reading close to zero volts (discharge through a resistor if it is not reading zero), and flip the switch on the battery pack to «ON». Takes a long time, does not it? Sure enough, we made the electron gas tank bigger and now it takes longer to fill it up.To prove it to yourself, try adding the third 100μF capacitor, and watch it charge for a good, long time. 90005
90002 Series and Parallel Inductors 90003
90008 Series and Parallel Inductors 90009 90004 Cases where inductors need to be added either in series or in parallel are rather rare, but not unheard of. In any case, let’s address them just to be complete. 90005 90004 In a nutshell they add just like resistors do, which is to say they add with a plus sign when in series, and with product-over-sum when in parallel.The tricky part comes when they are placed close together so as to have interacting magnetic fields, whether intentionally or not. For this reason, it is preferable to have a single component rather than two or more, though most inductors are shielded to prevent interacting magnetic fields. 90005 90004 In any case, suffice it to say that they add like resistors do. More information than that regarding inductors is well beyond the scope of this tutorial. 90005
90002 Resources and Going Further 90003
90004 Now that you’re familiar with the basics of serial and parallel circuits, why not check out some of these tutorials? 90005 90010
90011 Voltage Dividers — One of the most basic, and recurring circuits is the voltage divider.This is a circuit which really builds upon the concepts explored in this tutorial. 90012
90011 What is an Arduino? — Now that you’ve got the basics of circuits under your belt, you could head directly to learning about microcontrollers with one of the most popular platforms out there: Arduino. 90012
90011 Switch Basics — We’ve talked about some of the more basic circuit elements in this tutorial, but this was not one of them. Switches are a critical component in just about every electronics project out there.Learn all about switches in this tutorial 90012
90011 Sewing with Conductive Thread — Circuits do not have to be all breadboards and wire. E-textiles uses conductive thread to sew lights and other electronics into clothing or other fabric. 90012
90017 .90000 What is a Resistance? Series and Parallel Resistance Circuit 90001
90002 90003 Resistance 90004 is the property of a material by virtue of which it opposes the flow of electrons through the material. It restricts the flow of the electron through the material. It is denoted by (R) and is measured in ohms (Ω). 90005 90002 When the voltage is applied across the resistor the free electrons start accelerating. These moving electrons collide with each other and hence opposes the flow of electrons.The opposition of electrons is known as the resistance. The heat is generated when the atom or molecules are colliding with each other. 90005
90002 90003 Contents: 90004 90005 90002 90013 90003 Explanation: 90004 90005
90002 The resistance of any material depends on two factors 90005
90019
90020 The shape of the material 90021
90020 Material type (what material it is made up of) 90021
90024
90002 Quantitatively it is obtained by Ohm’s Law, as the resistance offered by the material when a current of I ampere flows through it with a potential difference of (V) volts across the material.It is given by the equation shown below 90005
90002 90028 90005
90002 Where R is the resistance, V is the voltage, and I is the current in the circuit. 90005
90002 It is clear from the above equation (1) that resistance is directly proportional to the voltage and inversely proportional to the current of the circuit. It is also given as 90013 90034 90005
90002 Where, 90005 90019
90020 R is the resistance of any conductor or material measured in ohms 90021
90020 ρ is the resistivity of the material and is measured in ohms meter 90021
90020 90044 l 90045 is the length of the material or conductor in meters 90021
90020 A is the conductor’s cross-sectional area in meter square 90021
90024
90002 The resistance of any conducting material is directly proportional to the length of the conductor and inversely proportional to the conductor’s cross-sectional area.90013 90013 90003 Resistivity (90044 ρ 90045) 90004 is defined as the ability of the conductor or the material to oppose the electric current. The resistance of any conductor is measured by the instrument known as Ohmmeter. 90005
90002 The collision of atoms with the free electrons causes the heat to develop when an electric current flows through any conductor or material. If a current of I ampere is passing through the conductor and the potential difference is V volts across the conductor, then the power absorbed by the resistor is given by the equation (3) shown below 90005
90002 90061 90005
90002 As we know V = IR 90005
90002 90066 90005
90002 The energy lost in the resistance in the form of heat and is derived as 90013 90070 90005
90002 Putting the value of P from the equation (3) in equation (4) we will get 90005
90002 90075 90005
90002 As we know I = V / R, hence putting the value of I in equation (5) we will get 90005
90002 90080 90005
90002 The above equation (6) shows the equation for energy loss in the form of heat.90013 90005
90085 Types of Resistance 90086
90002 There are mainly two types of resistance 90005 90002 It is similar to the normal resistance of the circuit given as R = V / I. It determines the power dissipation in an electric circuit. It is also defined as the slope of the line from the origin through various points on the curve. 90005 90002 It is also known as the incremental or dynamic resistance of the circuit. It is the derivative of the ratio of voltage to the current. Differential resistance is given by the formula shown below 90005
90093 90094 90095 90085 Series and Parallel Resistance in the circuit 90086
90002 90003 Series Resistance Circuit 90004 90005
90002 If the various resistances suppose R 90103 1 90104, R 90103 2 90104, R 90103 3 90104 connected together in series as shown in the figure below is termed as a series resistance circuit 90013 90110 The equivalent or total resistance is given by the equation 90005
90002 90113 90005
90002 90003 Parallel Resistance Circuit 90004 90005
90002 The various resistances suppose R 90103 1 90104, R 90103 2 90104, R 90103 3 90104 are connected in parallel with each other as shown in the circuit below is known as Parallel Resistance Circuit.90013 90127 The equivalent or total resistance is given by the equation 90005
90002 90130 90013 This is all about resistance. 90005 .90000 Parallel Resistor Calculator R1 + R2 = equivalent resistor R resistance circuit equiv total resistor finder made easy piggyback = parallel 90001 Parallel Resistor Calculator R1 + R2 = equivalent resistor R resistance circuit equiv total resistor finder made easy piggyback = parallel — sengpielaudio Sengpiel Berlin 90002 90002 90002
90005
90006
90007 R 90008 total 90009 90010
90011 90010
90007 90014 Formula: 90015 90002
90014 R 90008 total 90009 = R1 × R2 / (R1 + R2) 90015 90002
90010
90023
90024
90002 Please enter 90014 two 90015 resistor values, the third value of the parallel circuit will be calculated.90002
You can even enter the total resistance 90029 R 90030 90008 total 90009 and one known resistance 90029 R 90030 90008 1 90009 or 90029 R 90030 90008 2 90009.
90002 90042 Formula (equation) for the calculation of two resistances 90029 R 90030 90008 1 90009 and 90029 R 90030 90008 2 90009 connected in parallel: 90051
90042 90051
90042 90051
90042 Calculation of the necessary parallel resistor 90029 R 90030 90008 2 90009, when 90029 R 90030 90008 1 90009 and the total resistance 90029 R 90030 90008 total 90009 is given: 90051
90042 90051
90005
90006
90011
Solving the formula 90029 R 90030 90008 total 90009 = (90029 R 90030 90008 1 90009 × 90029 R 90030 90008 2 90009) / (90029 R 90030 90008 1 90009 + 90029 R 90030 90008 2 90009) for 90029 R 90030 90008 1 90009: 90002
The first step is to clear all fractions by multiplying by the lowest 90002
common denominator, that is 90029 R 90030 90008 t 90009 × 90029 R 90030 90008 1 90009 × 90029 R 90030 90008 2 90009… so we get: 90002
1/90029 R 90030 90008 total 90009 = 1/90029 R 90030 90008 1 90009 + 1/90029 R 90030 90008 2 90009 90002
90029 R 90030 90008 total 90009 × 90029 R 90030 90008 1 90009 × 90029 R 90030 90008 2 90009 [1/90029 R 90030 90008 total 90009 = 1/90029 R 90030 90008 1 90009 + 1/90029 R 90030 90008 2 90009] 90002
90029 R 90030 90008 1 90009 × 90029 R 90030 90008 2 90009 = 90029 R 90030 90008 total 90009 × 90029 R 90030 90008 2 90009 + 90029 R 90030 90008 total 90009 × 90029 R 90030 90008 1 90009 then collect terms with 90029 R 90030 90008 1 90009 and solve 90002
90029 R 90030 90008 1 90009 × 90029 R 90030 90008 2 90009 — 90029 R 90030 90008 total 90009 × 90029 R 90030 90008 1 90009 = 90029 R 90030 90008 total 90009 × 90029 R 90030 90008 2 90009 90002
90029 R 90030 90008 1 90009 (90029 R 90030 90008 2 90009 — 90029 R 90030 90008 total 90009) = 90029 R 90030 90008 2 90009 × 90029 R 90030 90008 total 90009 90002
Last step: 90002
90029 90014 R 90015 90030 90014 90008 1 90009 = 90015 90014 90029 R 90030 90015 90014 90008 2 90009 90015 × 90014 90029 R 90030 90015 90014 90008 total 90009 / (90015 90014 90029 R 90030 90015 90014 90008 2 90009 — 90015 90014 90029 R 90030 90015 90014 90008 total 90009) 90015 90002
or: 90002
90029 90014 R 90015 90030 90014 90008 2 90009 = 90015 90014 90029 R 90030 90015 90014 90008 1 90009 90015 × 90014 90029 R 90030 90015 90014 90008 total 90009 / (90015 90014 90029 R 90030 90015 90014 90008 1 90009 — 90015 90014 90029 R 90030 90015 90014 90008 total 90009) 90015 90010
90023
90024
90042 90014 Notice: 90015 This calculator can also solve other math problems.Calculating resistors in parallel is 90002
precisely the same as the calculations required for inductors in parallel or for capacitors in series. 90051
90005
90006
90011 Two resistors in parallel and the resulting total resistance: Two of the same value, 90002
also show the equation that the results are always half. That makes it easier when 90002
designing circuits or prototyping. With caps it’s always double, then again caps just 90002
simply add up in parallel.90010
90023
90024
90042 90051
90042 90014 • Search resistances 90029 R 90030 90008 1 90009 and 90029 R 90030 90008 2 90009, when the target resistance (equivalent resistance) is known • 90015 90051
90042 90014 Calculation: Resistor pairs — reverse engineered calculator 90015 90002
90014 Search of 90029 R 90030 90008 1 90009 and 90029 R 90030 90008 2 90009 with known target resistance 90015 90051
90042 90051
90042 90014 ● Calculate many resistors in parallel ● 90015 90051
90005
90006
90011 This calculator determines the resistance of 90014 up to 10 resistors in parallel 90015.90002
Enter resistances into the boxes below and when all values have been input, 90002
click on the ‘calculate’ button and the result will appear in the box below that button. 90002
As a test, if we enter resistances of 4, 6, and 12 ohms, the answer should be 2 ohms. 90002
Notice: Manually clearing the boxes does not reset stored values. Use «reset». 90010
90023
90024
90002 90042 90014 Ohm’s law — calculator and formulas 90015 90051
90042 90014 Two resistors in parallel and the resulting total resistance 90015 90002
Resistance ranging from 1 ohm to 100 ohms 90051
90384
90006
90386 R2 90010
90388 R1 90010
90023
90006
90011 90014 1 90015 90010
90011 90014 1.5 90015 90010
90011 90014 2.2 90015 90010
90011 90014 3.3 90015 90010
90011 90014 4.7 90015 90010
90011 90014 6.8 90015 90010
90011 90014 10 90015 90010
90011 90014 15 90015 90010
90011 90014 22 90015 90010
90011 90014 33 90015 90010
90011 90014 47 90015 90010
90011 90014 68 90015 90010
90023
90006
90011 90014 1 90015 90010
90011 0.5 90010
90011 0.6 90010
90011 0.69 90010
90011 0.77 90010
90011 0.83 90010
90011 0.87 90010
90011 0.91 90010
90011 0.93 90010
90011 0.95 90010
90011 0.97 90010
90011 0.98 90010
90011 0.99 90010
90023
90006
90011 90014 1.5 90015 90010
90011 0.6 90010
90011 0.75 90010
90011 0.89 90010
90011 1.03 90010
90011 1.14 90010
90011 1.22 90010
90011 1.30 90010
90011 1.36 90010
90011 1.40 90010
90011 1.43 90010
90011 1.45 90010
90011 1.46 90010
90023
90006
90011 90014 2.2 90015 90010
90011 0.69 90010
90011 0.89 90010
90011 1.1 90010
90011 1.32 90010
90011 1.50 90010
90011 1.66 90010
90011 1.82 90010
90011 1.92 90010
90011 2.0 90010
90011 2.06 90010
90011 2.10 90010
90011 2.13 90010
90023
90006
90011 90014 3.3 90015 90010
90011 0.77 90010
90011 1.03 90010
90011 1.32 90010
90011 1.65 90010
90011 1.94 90010
90011 2.22 90010
90011 2.48 90010
90011 2.70 90010
90011 2.87 90010
90011 3.00 90010
90011 3.08 90010
90011 3.14 90010
90023
90006
90011 90014 4.7 90015 90010
90011 0.83 90010
90011 1.14 90010
90011 1.50 90010
90011 1.94 90010
90011 2.35 90010
90011 2.78 90010
90011 3.20 90010
90011 3.58 90010
90011 3.87 90010
90011 4.12 90010
90011 4.27 90010
90011 4.39 90010
90023
90006
90011 90014 6.8 90015 90010
90011 0.87 90010
90011 1.22 90010
90011 1.66 90010
90011 2.22 90010
90011 2.78 90010
90011 3.40 90010
90011 4.05 90010
90011 4.68 90010
90011 5.19 90010
90011 5.64 90010
90011 5.94 90010
90011 6.18 90010
90023
90006
90011 90014 10 90015 90010
90011 0.91 90010
90011 1.30 90010
90011 1.82 90010
90011 2.48 90010
90011 3.20 90010
90011 4.05 90010
90011 5.0 90010
90011 6.0 90010
90011 6.9 90010
90011 7.7 90010
90011 8.3 90010
90011 8.7 90010
90023
90006
90011 90014 15 90015 90010
90011 0.93 90010
90011 1.36 90010
90011 1.92 90010
90011 2.70 90010
90011 3.58 90010
90011 4.68 90010
90011 6.0 90010
90011 7.50 90010
90011 8.9 90010
90011 10.3 90010
90011 11.4 90010
90011 12.2 90010
90023
90006
90011 90014 22 90015 90010
90011 0.95 90010
90011 1.40 90010
90011 2.00 90010
90011 2.87 90010
90011 3.87 90010
90011 5.19 90010
90011 6.9 90010
90011 8.9 90010
90011 11.0 90010
90011 13.2 90010
90011 15.0 90010
90011 16.6 90010
90023
90006
90011 90014 33 90015 90010
90011 0.97 90010
90011 1.43 90010
90011 2.06 90010
90011 3.0 90010
90011 4.12 90010
90011 5.64 90010
90011 7.7 90010
90011 10.3 90010
90011 13.2 90010
90011 16.5 90010
90011 19.4 90010
90011 22.2 90010
90023
90006
90011 90014 47 90015 90010
90011 0.98 90010
90011 1.45 90010
90011 2.1 90010
90011 3.08 90010
90011 4.27 90010
90011 5.94 90010
90011 8.3 90010
90011 11.4 90010
90011 15,0 90010
90011 19.4 90010
90011 23.5 90010
90011 27.8 90010
90023
90006
90011 90014 68 90015 90010
90011 0.99 90010
90011 1.46 90010
90011 2.13 90010
90011 3.14 90010
90011 4.39 90010
90011 6.18 90010
90011 8.7 90010
90011 12.2 90010
90011 16.6 90010
90011 22.2 90010
90011 27.8 90010
90011 34.0 90010
90023
90024
90002
90042 90014 Notice: 90015 This calculator can also solve other math problems.Calculating resistors in parallel is 90002
precisely the same as the calculations required for inductors in parallel or for capacitors in series. 90051
90005
90006
90011 Power dissipated in resistor: 90029 P 90030 = 90029 V 90030 × 90029 I 90030, 90029 P 90030 = 90029 V 90030 90821 2 90822/90029 R 90030, 90029 P 90030 = 90029 I 90030 90821 2 90822 × 90029 R 90030. 90010
90023
90024
90002
90005
90006
90011 90014 Notice: 90015 For resistors in series, the 90014 current 90015 is the same for each resistor, 90002
and for resistors in parallel, the 90014 voltage 90015 is the same for each resistor.90010
90023
90024
90002 90002 .



