4. Основные формулы Электромагнетизм
Связь магнитной индукции
 с напряженностью
с напряженностью магнитного
поля.
магнитного
поля.
 ,
,
где — магнитная проницаемость однородной среды; 0 — магнитная постоянная. В вакууме = 1, и магнитная индукция в вакууме
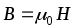 .
.
2. Закон Био-Савара-Лапласа
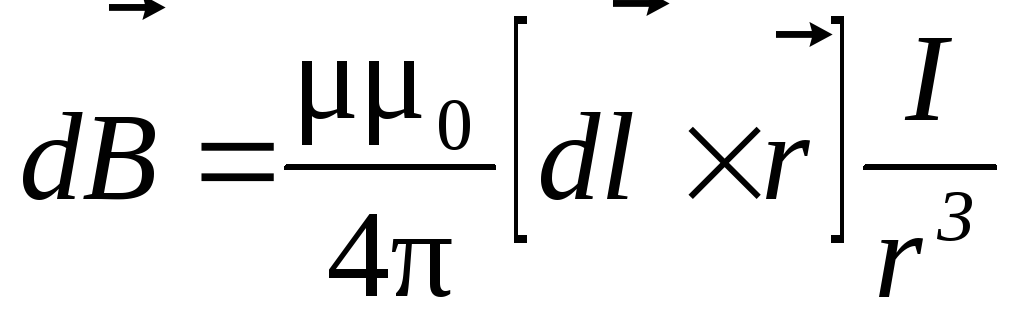 или
или 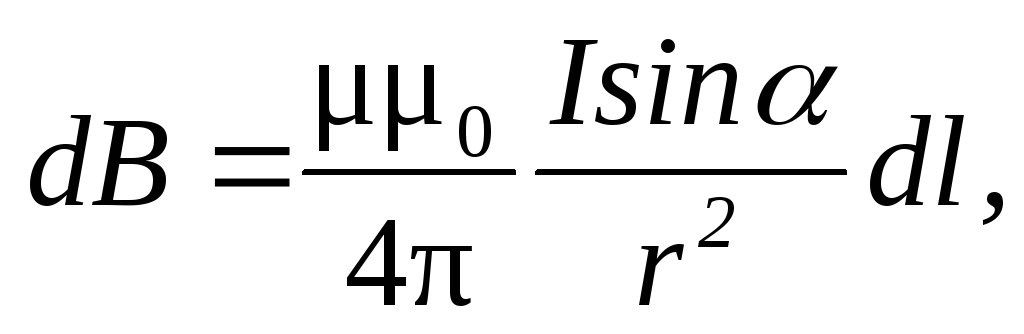
где 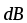 — магнитная индукция поля, создаваемого
элементом провода длиной
— магнитная индукция поля, создаваемого
элементом провода длиной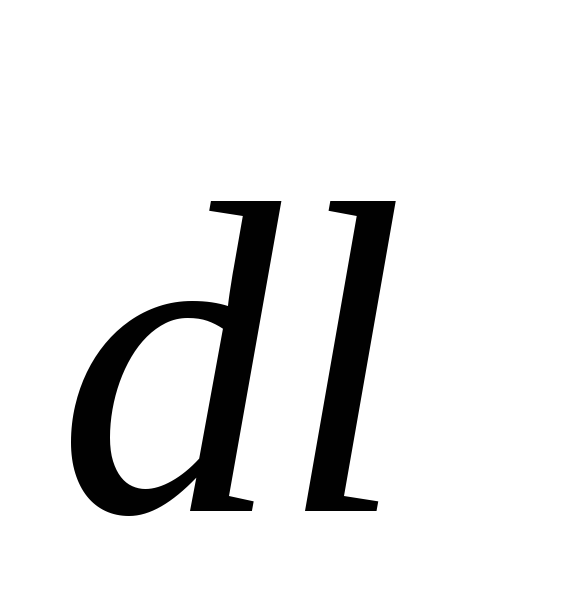 c
током I;
c
током I; 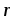 — радиус-вектор, направленный от элемента
проводника к точке, в которой определяется
магнитная индукция; — угол между радиус-вектором и направлением
тока в элементе провода.
— радиус-вектор, направленный от элемента
проводника к точке, в которой определяется
магнитная индукция; — угол между радиус-вектором и направлением
тока в элементе провода.
3. Принцип суперпозиции магнитных полей
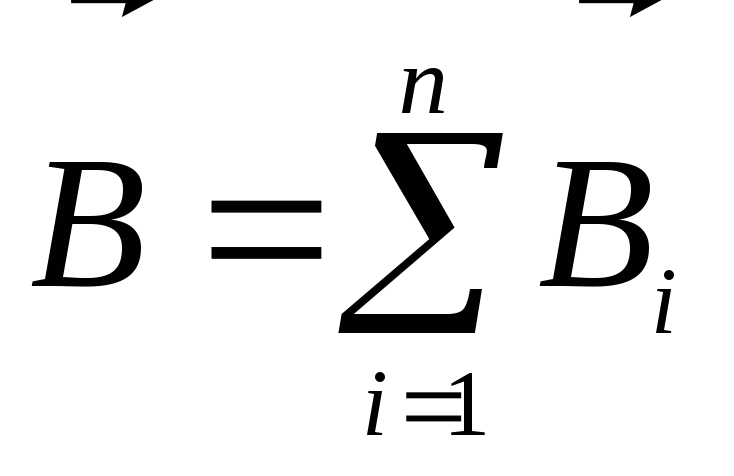 или
или 
 ,
созданных элементом тока
,
созданных элементом тока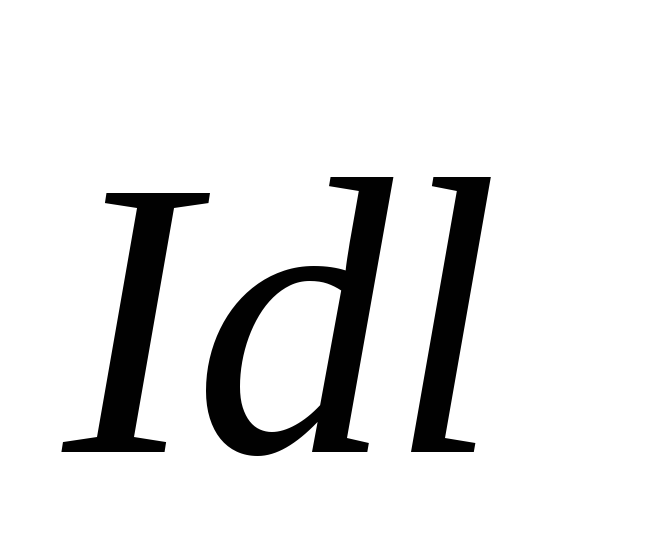 .
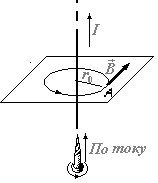
. Направление
вектора магнитной индукции 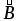 поля, создаваемого прямым током,
определяется по правилу буравчика
(правого винта). Для этого проводим
магнитную силовую линию (штриховая
линия на рис.) и по касательной к ней в
интересующей нас точке проводим вектор
поля, создаваемого прямым током,
определяется по правилу буравчика
(правого винта). Для этого проводим
магнитную силовую линию (штриховая
линия на рис.) и по касательной к ней в
интересующей нас точке проводим вектор
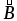 в точкеА направлен перпендикулярно плоскости
чертежа от нас.
в точкеА направлен перпендикулярно плоскости
чертежа от нас.Рис. 1
4. Магнитная индукция в центре кругового тока
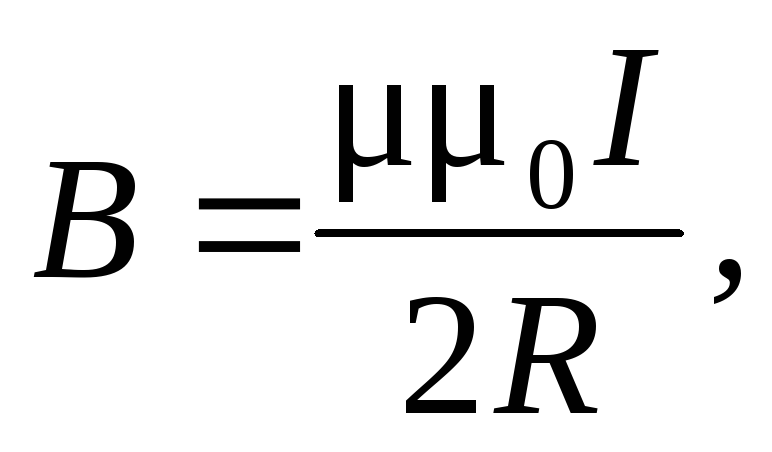
где R — радиус кругового витка.
Магнитная индукция на оси кругового тока
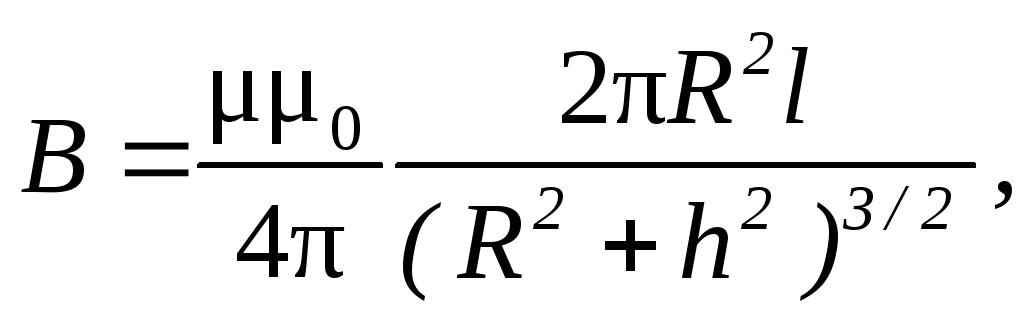
где h — расстояние от центра витка до точки, в которой определяется магнитная индукция.
Магнитная индукция поля, создаваемого отрезком провода с током (вывод этой формулы в примере № 1):
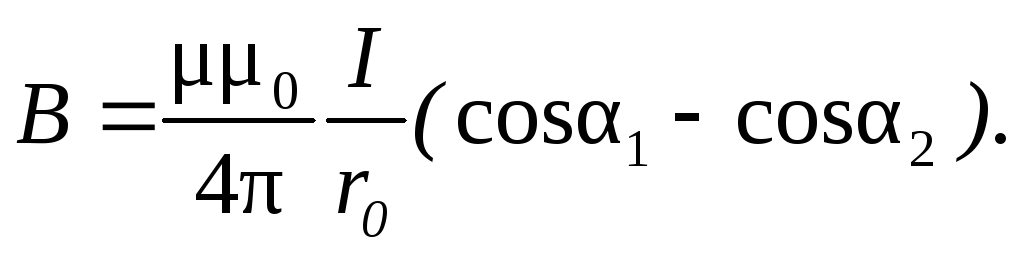
Магнитная индукция поля, создаваемого бесконечно длинным прямолинейным проводником с током:
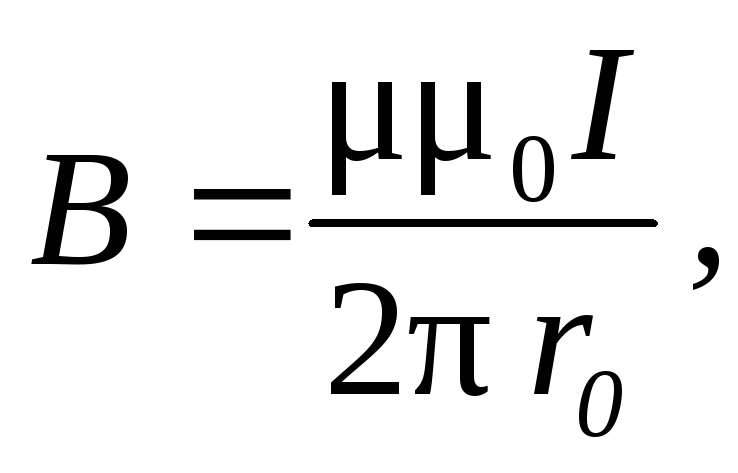
где r0 — расстояние от оси провода до точки, в которой определяется магнитная индукция.
Магнитная индукция поля бесконечно длинного соленоида
B = 0nI,
где n — отношение числа витков соленоида N к его длине l.
5. Сила, действующая на элемент провода с током в магнитном поле (закон Ампера):
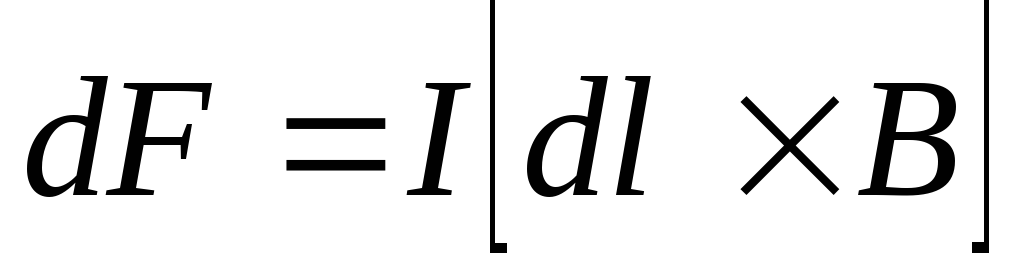 ,
,
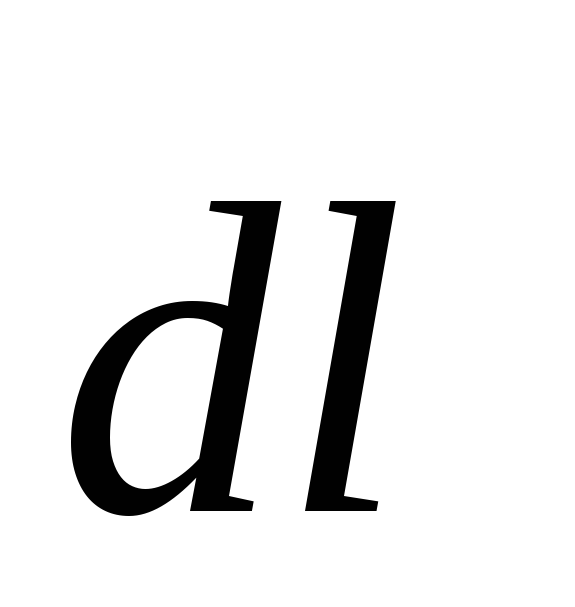 — вектор, равный по модулю длине участка
провода и совпадающий по направлению
с током; — угол между направлением тока в проводе
и вектором магнитной индукции
— вектор, равный по модулю длине участка
провода и совпадающий по направлению
с током; — угол между направлением тока в проводе
и вектором магнитной индукции  .
.Для однородного магнитного поля и прямого отрезка провода получим:
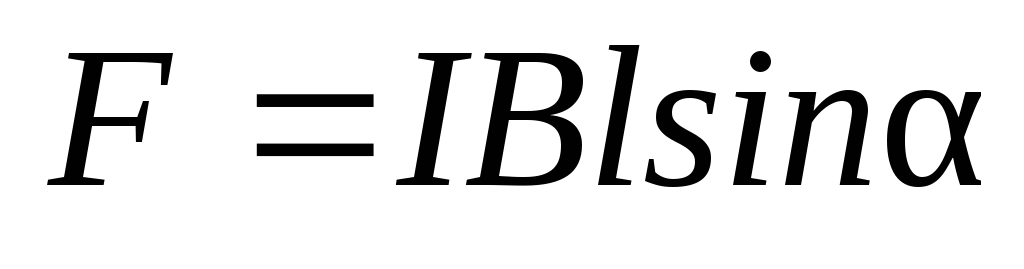 .
.
6. Магнитный момент плоского контура с током
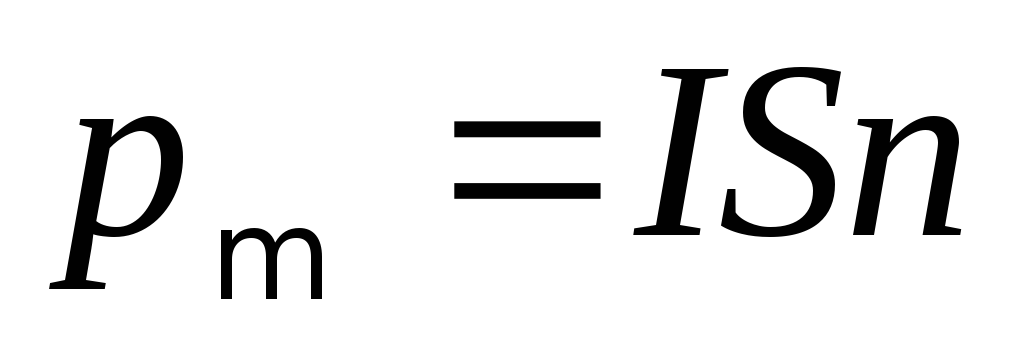 ,
,
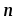 — единичный вектор нормали (положительной)
к плоскости контура;I — сила тока,
протекающего по контуру; S — площадь контура.
— единичный вектор нормали (положительной)
к плоскости контура;I — сила тока,
протекающего по контуру; S — площадь контура.7. Механический вращающий момент, действующий на контур с током, помещенный в однородное магнитное поле:
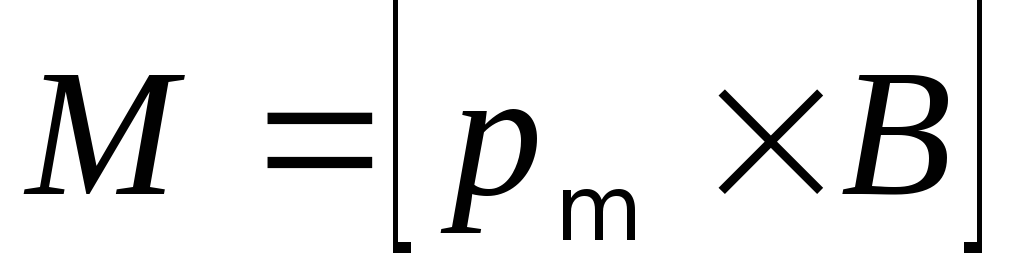 или
или 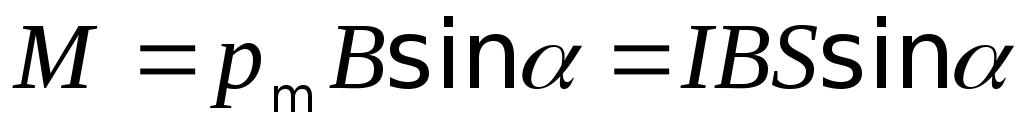 ,
,
где — угол между векторами 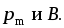
8. Сила Лоренца
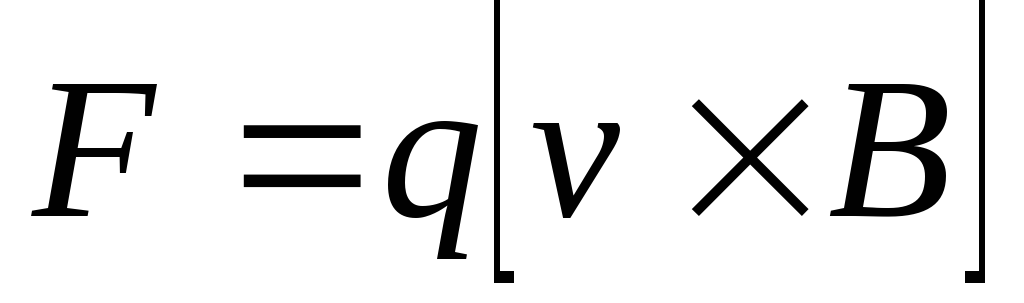 или
или 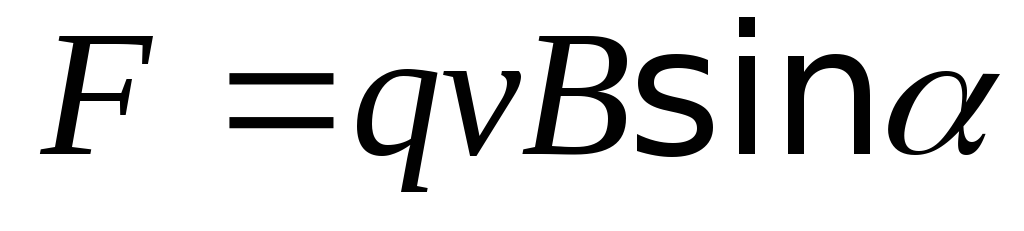 ,
,
где 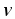 — скорость заряженной частицы; — угол между векторами
— скорость заряженной частицы; — угол между векторами 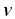 и
и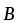 .
.
Если частица находится одновременно в электрическом и магнитном полях, то на нее действует сила
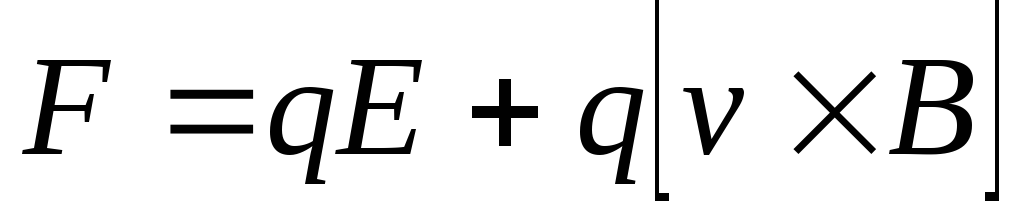 .
.
9. Магнитный поток (через поверхность S):
а) в случае однородного магнитного поля и плоской поверхности
Ф = BScos или Ф = BnS ,
где S — площадь контура; — угол между нормалью к плоскости контура и вектором магнитной индукции;
б) в случае неоднородного поля и произвольной поверхности
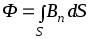
(интегрирование ведется по всей поверхности).
Потокосцепление (полный поток) – = NФ.
Эта формула верна для соленоида и тороида с равномерной намоткой плотно прилегающих друг к другу N витков.
10. Работа по перемещению замкнутого контура с током в магнитном поле dA=I dФилиА=IФ.
11. Основной закон электромагнитной
индукции (закон Фарадея-Максвелла): 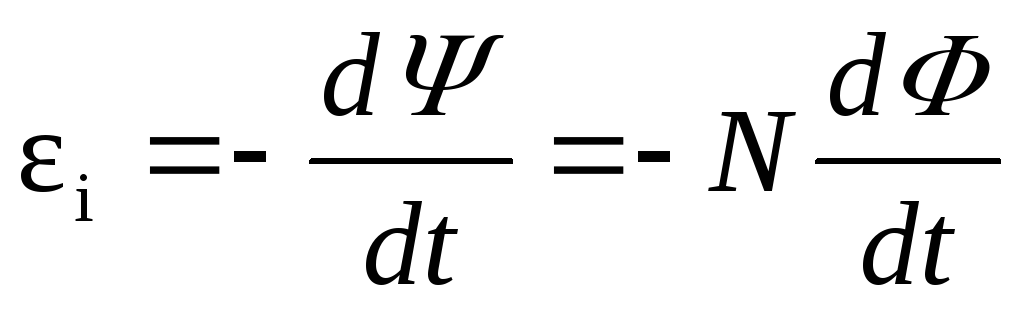 .
.
Разность
потенциалов на концах проводника,
движущегося со скоростью 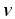
где l — длина провода; — угол между векторами 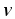 и
и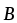 .
.
Заряд, протекающий по замкнутому контуру
при изменении магнитного потока,
пронизывающего этот контур: 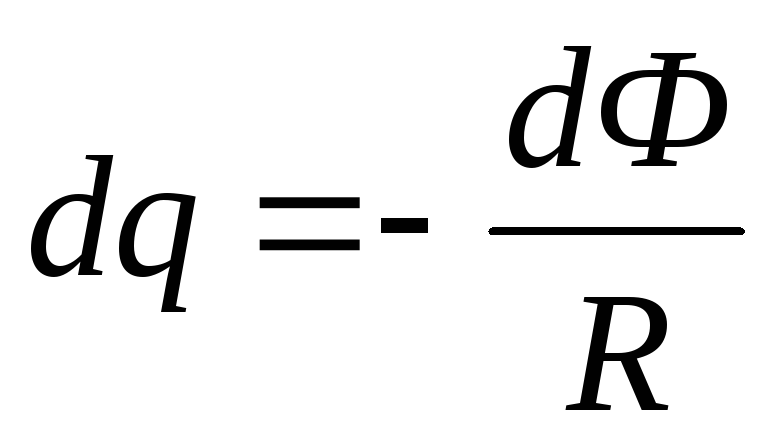 или
или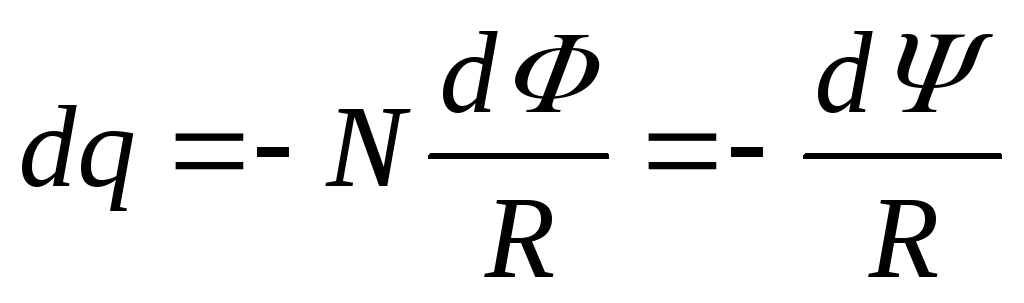 ,
гдеR
,
гдеR
12. Индуктивность контура L = Ф/I.
Индуктивность соленоида L = 0n2lS,
где n — отношение числа витков соленоида к его длине; l – длина соленоида, S – площадь его поперечного сечения.
13. Э.д.с. самоиндукции
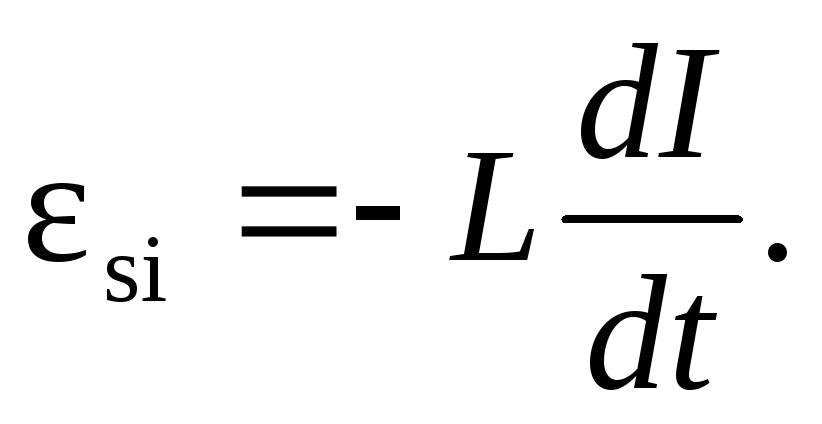
14. Мгновенное значение силы тока в цепи, обладающей сопротивлением R и индуктивностью L:
а) 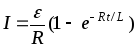
б) 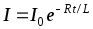 — при размыкании цепи, гдеI0 — сила тока в цепи при t = 0; t — время, прошедшее с момента размыкания
цепи.
— при размыкании цепи, гдеI0 — сила тока в цепи при t = 0; t — время, прошедшее с момента размыкания
цепи.
15.
Энергия магнитного поля соленоида W = 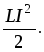
Объемная плотность энергии магнитного поля (отношение энергии поля к его объему)
w = BH/2 = B2/(20) = 0 H2/2.
Решебник по физике Чертова А.Г. 1987г
Решенные задачи из учебника ФИЗИКА. Методические указания и контрольные задания. Под редакцией А. Г. Чертова
Ниже приведены условия задач и отсканированные листы с решениями. Загрузка страницы может занять некоторое время.
403. По двум скрещенным под прямым углом бесконечно длинным проводам текут токи I и 2I (I= 100 А). Определить магнитную индукцию B в точке А (рис.). Расстояние d=10 см.
413. Квадратная проволочная рамка расположена в одной плоскости с длинным прямым проводом так, что две ее стороны параллельны проводу. По рамке и проводу текут одинаковые токи силой I=200 А. Определить силу, действующую на рамку, если ближайшая к проводу сторона рамки находится от него на расстоянии, равном ее длине.
423. Стержень длиной R=20 см заряжен равномерно распределенным зарядом с линейной плотностью τ = 0,2 мкКл/м. Стержень вращается с частотой ν= 10 с-1 относительно оси, перпендикулярной стержню и проходящей через его конец. Определить магнитный момент Рm, обусловленный вращением стержня.
433. Электрон прошел ускоряющую разность потенциалов U = 800 В и, влетев в однородное магнитное поле В = 47мТл, стал двигаться по винтовой линии с шагом h = 6 см. Определить радиус R винтовой линии.
443. Альфа-частица влетела в скрещенные под прямым углом магнитное (В = 5мТл) и электрическое (Е =30 кВ/м) поля. Определить ускорение а альфа-частицы, если ее скорость V (|V| = 2×106 м/с) перпендикулярна векторам В и Е, причем силы, действующие со стороны этих полей, противонаправлены.
453. В средней части соленоида, содержащего n = 8 витков/см, помещен круговой виток диаметром d=4 см. Плоскость витка расположена под углом φ = 60° к оси соленоида. Определить магнитный поток Ф, пронизывающий виток, если по обмотке соленоида течет ток I=1 А.
463. В проволочное кольцо, присоединенное к баллистическому гальванометру, вставили прямой магнит. При этом по цепи прошел заряд ΔQ=50 мкКл. Определить изменение магнитного потока ΔФ через кольцо, если сопротивление цепи гальванометра R=10 Ом.
473. Катушка, намотанная на немагнитный цилиндрический каркас, имеет N1=250 витков и индуктивность L1 = 36 мГн. Чтобы увеличить индуктивность катушки до L2=100 мГн, обмотку катушки сняли и заменили обмоткой из более тонкой проволоки с таким расчетом, чтобы длина катушки осталась прежней. Сколько витков оказалось в катушке после перемотки?
StudyPort.Ru — Электромагнитная индукция
Страница 1 из 2
175. Соленоид диаметром d = 4 см, имеющий N = 500 витков, помещен в магнитное поле, индукция которого изменяется со скоростью 1 мТл/с. Ось соленоида составляет с вектором магнитной индукции угол а = 45 градусов. Определите ЭДС индукции, возникающую в соленоиде.

176. В магнитное поле, изменяющееся по закону В = В0*cos(ω*t) (B0 = 0,1 Тл, w = 4 c-1), помещена квадратная рамка со стороной a = 50 см, причем нормаль к рамке образует с направлением поля угол α = 45 градусов. Определите ЭДС индукции, возникающую в рамке в момент времени t = 5 с.

177. Кольцо из алюминиевого провод (ρ = 26 нОм*м) помещено в магнитное поле перпендикулярно линиям магнитной индукции. Диаметр кольца D = 30 см, диаметр провода d = 2 мм. Определите скорость изменения магнитного поля, если ток в кольце I = 1 А.

178. Плоскость проволочного витка площадь S = 100 см2 и сопротивлением R = 5 Ом, находящего в однородном магнитном поле напряженность H = 10 кА/м, перпендикулярна линиям магнитной индукции. При повороте витка в магнитном поле отсчет гальванометра, замкнутого на виток, составляет 12,6 мкКл. Определите угол поворота витка.

179. В однородное магнитное поле с индукцией В = 0,3 Тл помещена прямоугольная рамка с подвижной стороной, длина которой l = 15 см. Определите ЭДС индукции, возникающей в рамке, если ее подвижная сторона перемещается перпендикулярно линиями магнитной индукции со скоростью v = 10 м/с.

180. Две гладкие замкнутые металлические шины, расстояние между которыми равно 30 см, со скользящей перемычкой, которая может двигаться без трения, находятся в однородном магнитном поле с индукцией В = 0,1 Тл, перпендикулярном плоскости контура. Перемычка массой m = 5 г скользит вниз с постоянной скоростью v = 0,5 м/с. Определите сопротивление перемычки, пренебрегая самоиндукцией контура и сопротивлением остальной части контура.

181. В катушке длиной l = 0,5 м, диаметром d = 5 см и числом витков N = 1500 ток равномерно увеличивается на 0,2 А за одну секунду. На катушку надето кольцо из медной проволоки (ρ = 17 нОм*м) площадью сечения Sк = 3 мм2. Определите силу тока в кольце.

182. Катушка диаметром d = 2 см, содержащая один слой плотно прилегающих друг к другу N =500 витков алюминиевого провода сечением S = 1 мм2, помещена в магнитное поле. Ось катушки параллельна линиям индукции. Магнитная индукция поля равномерно изменяется со скоростью 1 мТл/с. Определите тепловую мощность, выделяющуюся в катушке, если концы замкнуты накоротко. Удельное сопротивление алюминия ρ = 26 нОм/м.

183. В однородном магнитном поле (B = 0,1 Тл) вращается с постоянной угловой скоростью ω = 50 с-1 вокруг вертикальной оси стер длиной l = 0,4 м. Определите ЭДС индукции, возникающей в стержне, если ось вращения проходит через конец стержня параллельно линиям магнит индукции.

184. В однородном магнитном поле с индукцией В = 0,02 Тл равномерно вращается вокруг вертикальной оси горизонтальный стержень длиной l = 0,5 м. Ось вращения проходит через конец стержня параллельно линиям магнитной индукции. Определите число оборотов в секунду, при котором на концах стержня возникает разность потенциалов U = 0,1 В.

185. В однородном магнитном поле (В = 0,2 Тл) равномерно с частотой n = 600 мин-1 вращается рамка, содержащая N = 1200 витков, плотно прилегающих друг к другу. Площадь рамки S = 100 см2. Ось вращения лежит в плоскости рамки и перпендикулярна линиям магнитной индукции. Определите максимальную ЭДС, индуцируемую в рамке.

186. Магнитная индукция B поля между полюсами двухполюсного генератора равна 1 Тл. Ротор имеет 140 витков (площадь каждого витка S = 500 см2). Определите частоту вращения якоря, если максимальное значение ЭДС индукции равно 220 В.

187. В однородном магнитном поле (B = 0,2 Тл) равномерно вращается прямоугольная рамка, содержащая N = 200 витков, плотно прилегающих друг к другу. Площадь рамки S = 100 см2. Определите частоту вращения рамки, если максимальная ЭДС, индуцируемая в ней, εmax = 12,6 В

188. В однородном магнитном поле равномерно вращается прямоугольная рамка с частотой n = 600 мин-1. Амплитуда индуцируемой ЭДС ε0 = 3 В. Определите максимальный магнитный поток через рамку.

189. Катушка длиной l = 50 см и диаметром d = 5 см содержит N = 200 витков. По катушке течет ток I = 1 А. Определите: 1) индуктивность катушки; 2) магнитный поток, пронизывающий площадь ее поперечного сечения.

190. Длинный соленоид индуктивностью L = 4 мГн содержит N = 600 витков. Площадь поперечного сечения соленоида S = 20 см2. Определите магнитную индукцию поля внутри соленоида, если сила тока, протекающего по его обмотке, равна 6 А.

191. Две длинные катушки намотаны на общий сердечник, причем индуктивности этих катушек L1 = 0,64 Гн и L2 = 0,04 Гн. Определите, во сколько раз число витков первой катушки больше, чем второй.

192. Определите, сколько витков проволоки, вплотную прилегающих друг к другу, диаметром d = 0,5 мм с изоляцией ничтожной толщины надо намотать на картонный цилиндр диаметром D = 1,5 см, чтобы получить однослойную катушку индуктивностью L = 100 мкГн?

193. Определите индуктивность соленоида длиной l и сопротивлением R, если обмоткой соленоида является проволока массой m (принять плотность проволоки и ее удельное сопротивление соответственно за ρи ρ’).

194. Сверхпроводящий соленоид длиной l = 10 см и площадью поперечного сечения S = 3 см2, содержащий N = 1000 витков, может быть подключен к источнику ЭДС ε = 12 В. Определите силу тока через 0,01 с после замыкания ключа.

195. Через катушку, индуктивность L которой равна 200 мГн, проте ток, изменяющийся по закону I = 2cos(3*t). Определите: 1) за изменения ЭДС самоиндукции; 2) максимальное значение ЭДС самоин.

Задачи по физике и математике с решениями и ответами
Задача по физике — 7600
Имеется длинный прямой проводник с током $I_{0}$. На расстояниях $a$ и $b$ от него расположены два параллельных ему провода, замкнутых на одном конце сопротивлением $R$ (рис.). По проводам без трения перемещают с постоянной скоростью $v$ стержень-перемычку. Пренебрегая сопротивлением проводов, стержня и скользящих контактов, найти:а) значение и направление индукционного тока в стержне;
б) силу, необходимую для поддержания постоянства скорости стержня.
 Подробнее
Подробнее Задача по физике — 7601
Проводник АВ массы $m$ скользит без трения по двум длинным проводящим рельсам, расположенным на расстоянии $l$ друг от друга (рис.). На левом конце рельсы замкнуты сопротивлением $R$. Система находится в однородном магнитном поле, перпендикулярном к плоскости контура. В момент $t=0$ стержню АВ сообщили вправо начальную скорость $v_{0}$. Пренебрегая сопротивлением рельсов и стержня АВ, а также самоиндукцией, найти:а) расстояние, пройденное стержнем до остановки;
б) количество тепла, выделенное при этом на сопротивлении $R$.
 Подробнее
Подробнее Задача по физике — 7602
По П-образному проводнику, расположенному в горизонтальной плоскости, может скользить без трения перемычка АВ (рис.). Последняя имеет длину $l$, массу $m$ и сопротивление $R$. Вся система находится в однородном магнитном поле с индукцией $B$, направленном вертикально. В момент $t = 0$ на перемычку начали действовать постоянной горизонтальной силой $F$, и перемычка начала перемещаться поступательно вправо. Найти зависимость от времени $t$ скорости перемычки. Индуктивность контура и сопротивление П-образного проводника пренебрежимо малы. Подробнее
Подробнее Задача по физике — 7603
На рис. показаны плоские контуры из тонких проводов, находящиеся в однородном магнитном поле, которое направлено за плоскость рисунка. Индукцию поля начали уменьшать. Найти направление индукционных токов в этих контурах. Подробнее
Подробнее Задача по физике — 7604
Плоский контур (рис.), имеющий вид двух квадратов со сторонами $a = 20 см$ и $b = 10 см$, находится в однородном магнитном поле, перпендикулярном к его плоскости. Индукция поля меняется во времени по закону $B = B_{0} \sin \omega t$, где $B_{0} = 10 мТ$ и $\omega = 100 рад/с$. Найти амплитуду индукционного тока в контуре, если сопротивление единицы длины его $\rho = 50 мОм/м$. Индуктивностью контура пренебречь. Подробнее
Подробнее Задача по физике — 7605
Плоская спираль с очень большим числом витков $N$, плотно прилегающих друг к другу, находится в однородном магнитном поле, перпендикулярном к плоскости спирали. Наружный радиус витков спирали равен $a$. Индукция поля изменяется во времени по закону $B = B_{0} \sin \omega t$, где $B_{0}$ и $\omega$ — постоянные. Найти амплитудное значение э. д.с. индукции, наводимой в спирали. ПодробнееЗадача по физике — 7606
П-образный проводник находится в однородном магнитном поле, перпендикулярном к плоскости проводника и изменяющемся во времени со скоростью $\dot{B} = 0,10 Т/с$. Вдоль параллельных сторон этого проводника перемещают без начальной скорости проводник-перемычку с ускорением $w = 10 см/с^{2}$. Длина перемычки $l = 20 см$. Найти э. д. с. индукции в контуре через $t = 2,0 с$ после начала перемещения, если в момент $t = 0$ площадь контура и индукция магнитного поля равны нулю. Индуктивностью контура пренебречь. ПодробнееЗадача по физике — 7607
В длинном прямом соленоиде с радиусом сечения $a$ и числом витков на единицу длины $n$ изменяют ток с постоянной скоростью $f А/с$. Найти модуль вектора напряженности вихревого электрического поля как функцию расстояния $r$ от оси соленоида. Изобразить примерный график этой зависимости. ПодробнееЗадача по физике — 7608
На длинный прямой соленоид, имеющий диаметр сечения $d = 5 см$ и содержащий $n = 20$ витков на один сантиметр длины, плотно надет круговой виток из медного провода сечением $S = 1,0 мм^{3}$. Найти ток в витке, если ток в обмотке соленоида увеличивают с постоянной скоростью $I = 100 А/с$. Индуктивностью витка пренебречь. ПодробнееЗадача по физике — 7609
На длинный соленоид с радиусом сечения $a$ плотно надето тонкое проволочное кольцо в изоляции, причем одна половина кольца имеет сопротивление в $\eta$ раз больше, чем другая. Индукция магнитного поля соленоида меняется во времени по закону $B = bt$, где $b$ — постоянная. Найти модуль вектора напряженности электростатического поля в кольце. ПодробнееЗадача по физике — 7610
Непроводящее тонкое кольцо массы $m$, имеющее заряд $q$ может свободно вращаться вокруг своей оси. В начальный момент кольцо покоилось и магнитное поле отсутствовало. Затем включили практически однородное магнитное поле, перпендикулярное к плоскости кольца, которое начало нарастать во времени по некоторому закону $\vec{B} (t)$. Найти угловую скорость $\omega$ кольца в зависимости от индукции $\vec{B}(t)$. ПодробнееЗадача по физике — 7611
Тонкое проволочное кольцо, имеющее радиус $a$ и сопротивление $r$, расположено внутри длинного соленоида так, что их оси совпадают. Длина соленоида $l$, радиус сечения $b$. В некоторый момент соленоид подключили к источнику постоянного напряжения $U$. Полное сопротивление цепи равно $R$. Пренебрегая индуктивностью кольца, найти максимальное значение радиальной силы, действующей на единицу длины кольца. ПодробнееЗадача по физике — 7612
Магнитный поток через неподвижный контур с сопротивлением $R$ изменяется в течение времени $\tau$ по закону $\Phi = at ( \tau — t)$. Найти количество тепла, выделенное в контуре за это время. Индуктивностью контура пренебречь. ПодробнееЗадача по физике — 7613
В середине длинного соленоида находится коаксиальное кольцо прямоугольного сечения из проводящего материала с удельным сопротивлением $\rho$. Толщина кольца $h$, его внутренний и внешний радиусы $a$ и $b$. Найти индукционный ток в кольце, если индукция магнитного поля соленоида изменяется во времени по закону $B = \beta t$, где $\beta$ — постоянная. Индуктивностью кольца пренебречь. ПодробнееЗадача по физике — 7614
Сколько метров тонкого провода надо взять для изготовления соленоида длины $l_{0} = 100 см$ с индуктивностью $L = 1,0 мГ$, если диаметр сечения соленоида значительно меньше его длины? Подробнее4.4. Магнитное поле кругового тока
Рассмотрим проводник с током, имеющий форму окружности радиуса R (рис.4.5 ). Определим магнитную индукцию в его центре.
Каждый
элемент тока 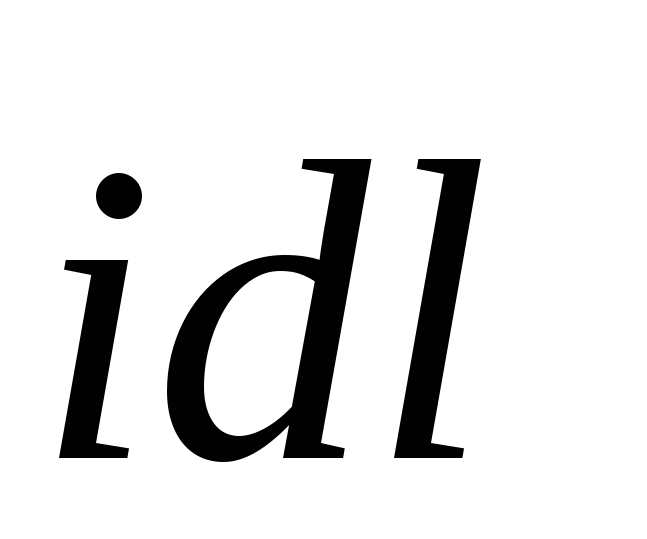 создает
магнитное поле индукцией
создает
магнитное поле индукцией ,
перпендикулярное к плоскости витка.
,
перпендикулярное к плоскости витка.
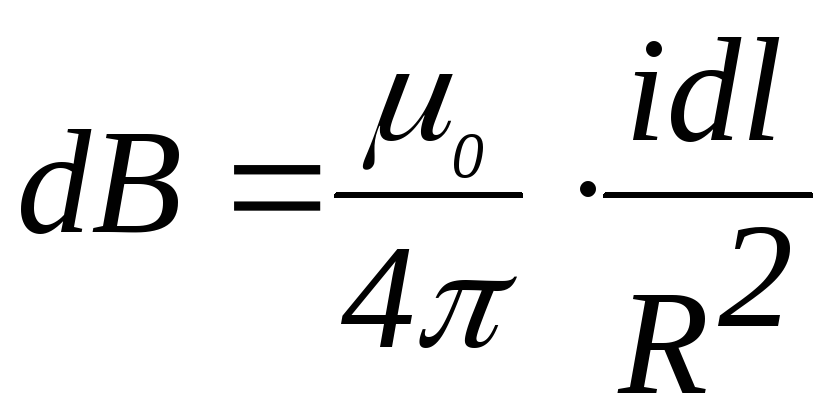 .
(4.19)
.
(4.19)
В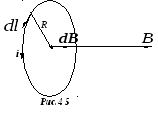 се
вектора
се
вектора направлены одинаково, поэтому их
векторное сложение сведется к сложению
их модулей. Тогда
направлены одинаково, поэтому их
векторное сложение сведется к сложению
их модулей. Тогда
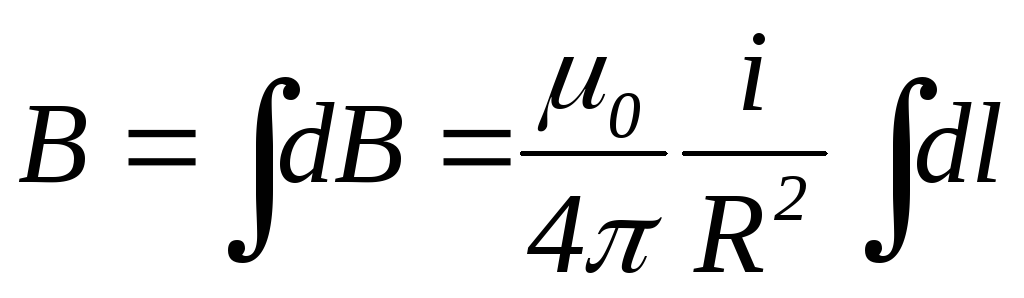 .
.
Так
как 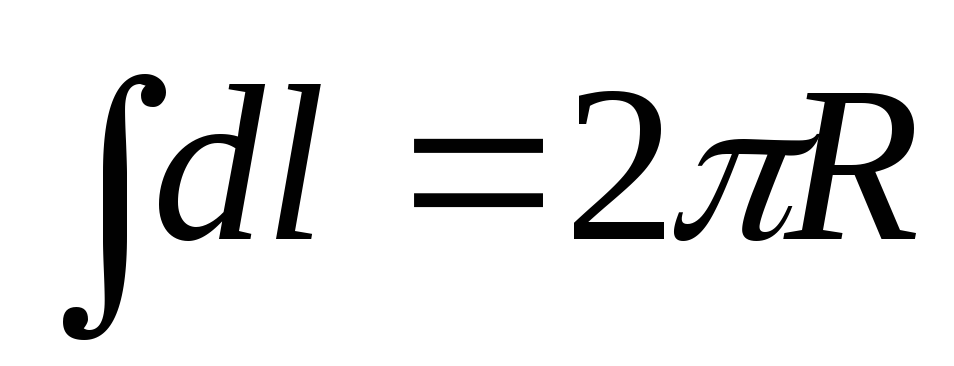 ,
то для магнитной индукции в центре
кругового тока получаем:
,
то для магнитной индукции в центре
кругового тока получаем:
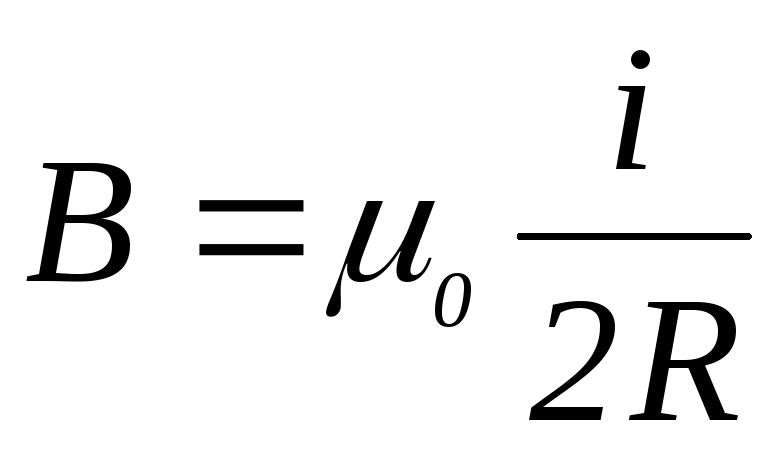 .
(4.20)
.
(4.20)
О пределим
магнитную индукцию в любой точке на оси
кругового тока. Обозначимx расстояние от плоскости контура до
некоторой точки на оси (рис.4.6).
пределим
магнитную индукцию в любой точке на оси
кругового тока. Обозначимx расстояние от плоскости контура до
некоторой точки на оси (рис.4.6).
Так
как вектор 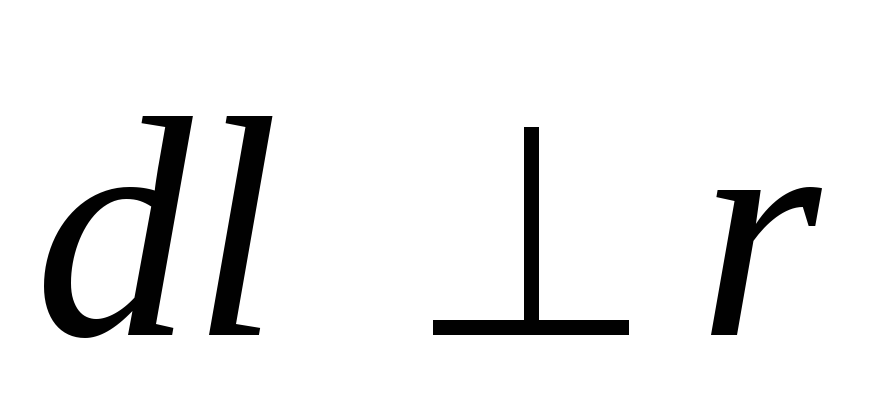 ,
то модуль вектора
,
то модуль вектора равен:
равен:
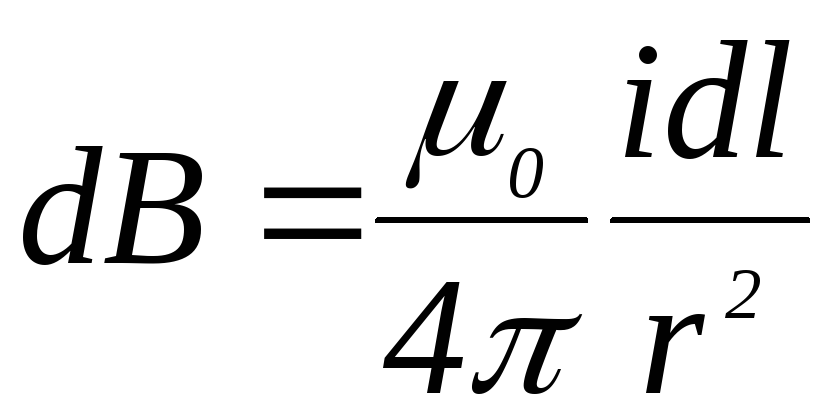 .
(4.21)
.
(4.21)
Вектор  перпендикулярен плоскостям, проходящим
через
перпендикулярен плоскостям, проходящим
через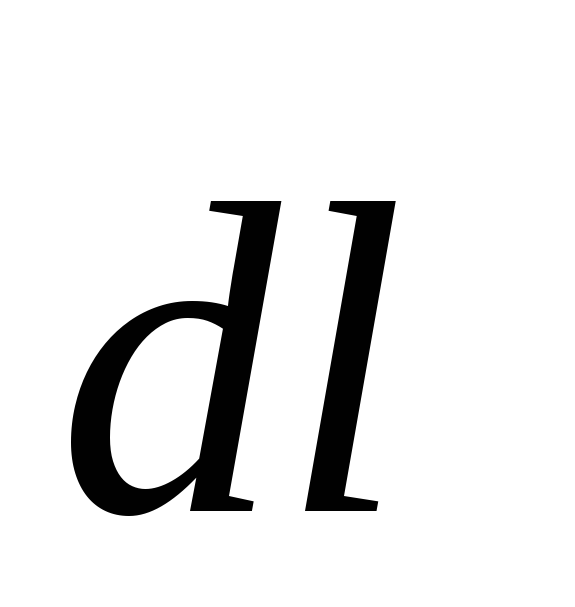 и
и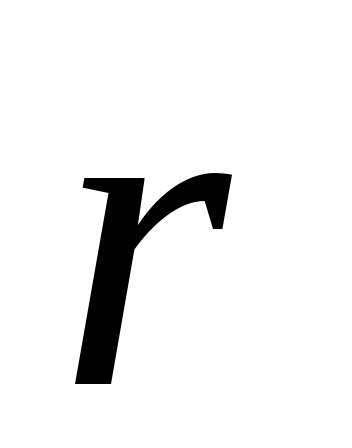 (рис.4.6). От всех элементов тока будет
образовываться «конус» векторов
(рис.4.6). От всех элементов тока будет
образовываться «конус» векторов .
.
Разложим
вектор  на две составляющие: перпендикулярную
и параллельную оси:
на две составляющие: перпендикулярную
и параллельную оси: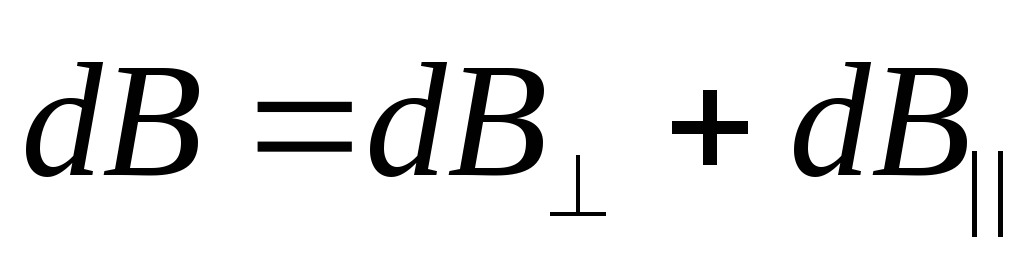 .
Применим принцип суперпозиции полей,
получим:
.
Применим принцип суперпозиции полей,
получим:
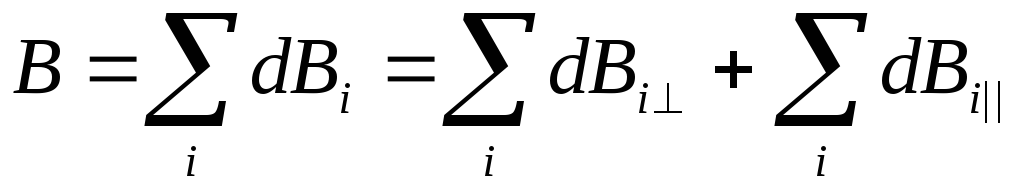
Нетрудно
убедиться, что векторная сумма всех
перпендикулярных составляющих равна
нулю, и результирующий вектор  будет направлен вдоль оси тока. Вклад
в него будут вносить только параллельные
оси составляющие векторов
будет направлен вдоль оси тока. Вклад
в него будут вносить только параллельные
оси составляющие векторов .
Тогда
.
Тогда
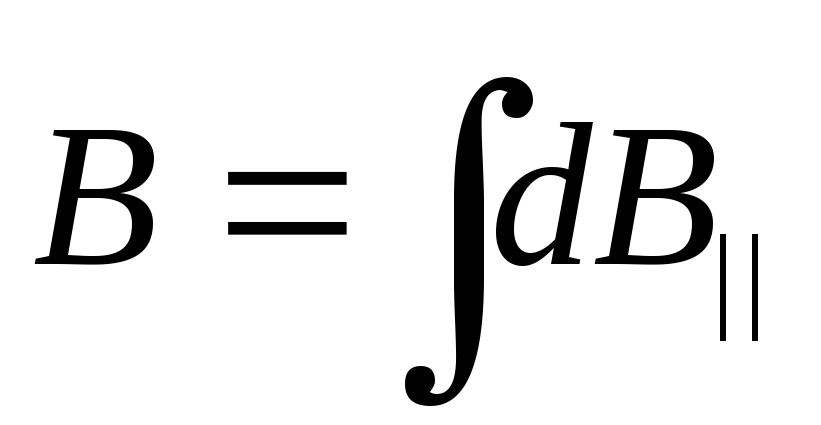 .
(4.22)
.
(4.22)
Из треугольника (см. рис.4.6) следует:
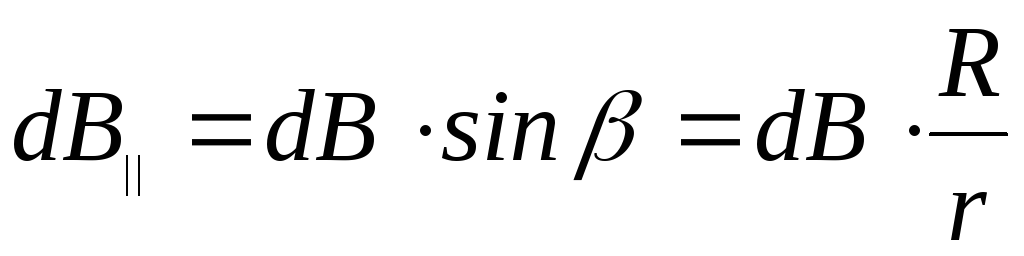 .
(4.23)
.
(4.23)
Подставим выражение (4.21) в формулу (4.23), получим:
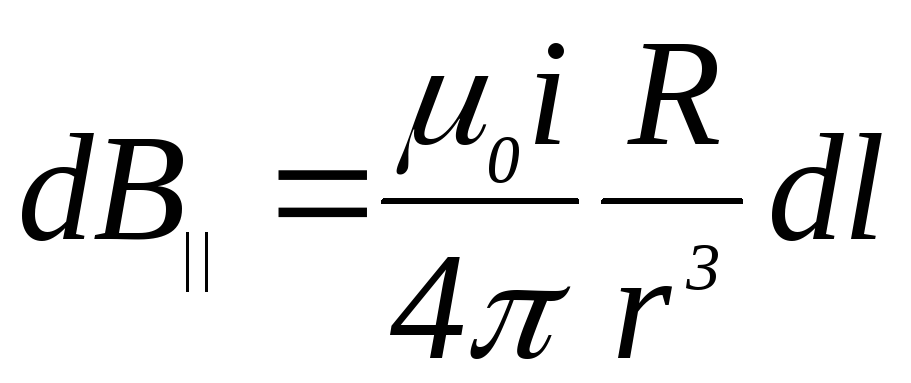 .
(4.24)
.
(4.24)
Возьмём
интеграл: 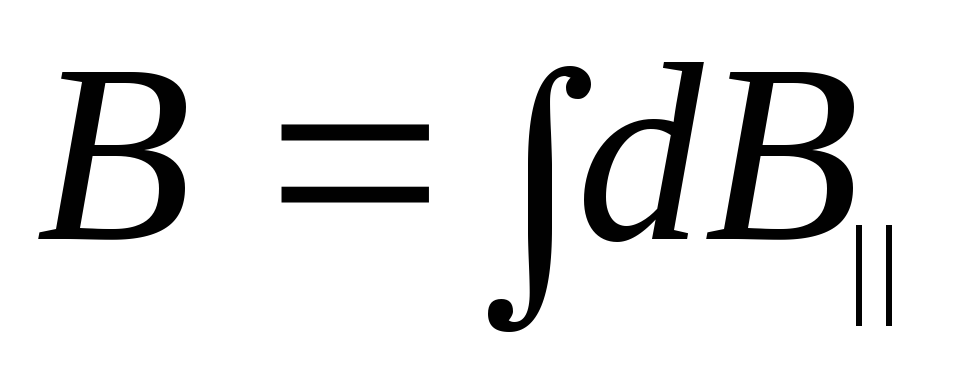 ,
получим:
,
получим:
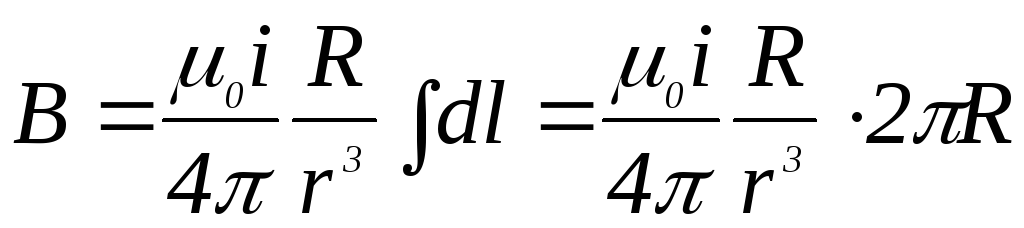 ,
,
или 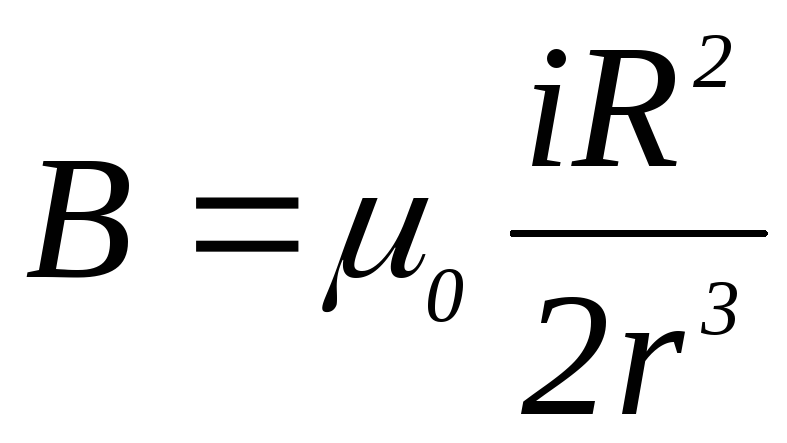 .
(4.25)
.
(4.25)
Так
как 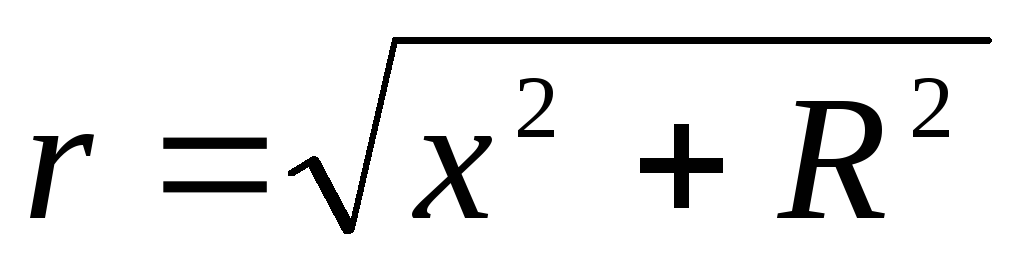 , то окончательно получим:
, то окончательно получим:
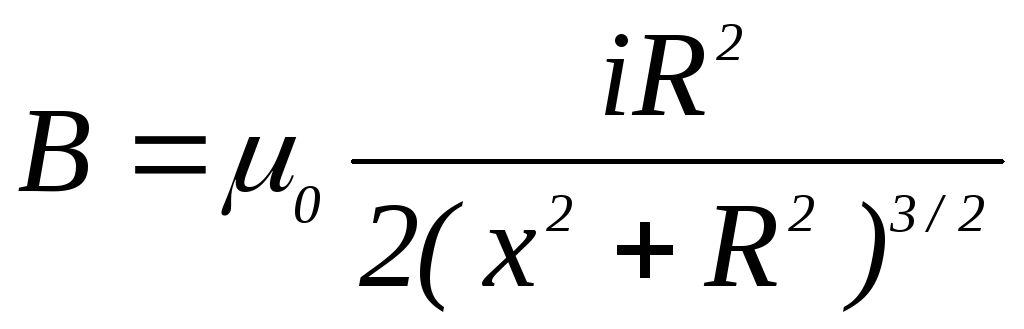 .
(4.26)
.
(4.26)
При x=0 формула (4.26) переходит в (4.20).
4.5. Магнитный момент витка с током
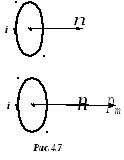
Рассмотрим
замкнутый контур с током (рис. 4.7).
Обозначим 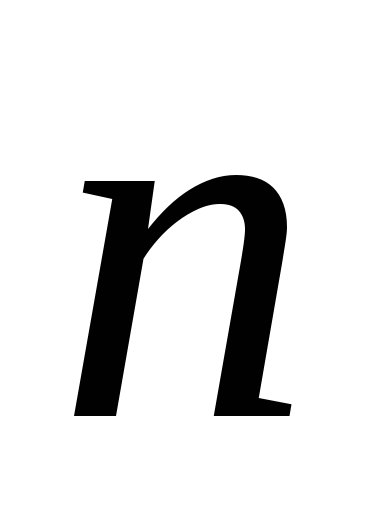 —
единичный вектор положительной
нормали к контуру. Этот вектор связан
с направлением тока правилом правого
винта.
—
единичный вектор положительной
нормали к контуру. Этот вектор связан
с направлением тока правилом правого
винта.
Магнитным
моментом контура с током называется
вектор 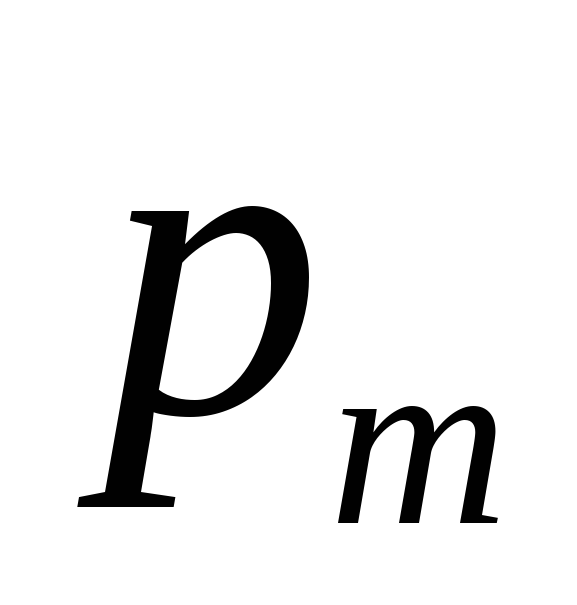 ,
равный
,
равный
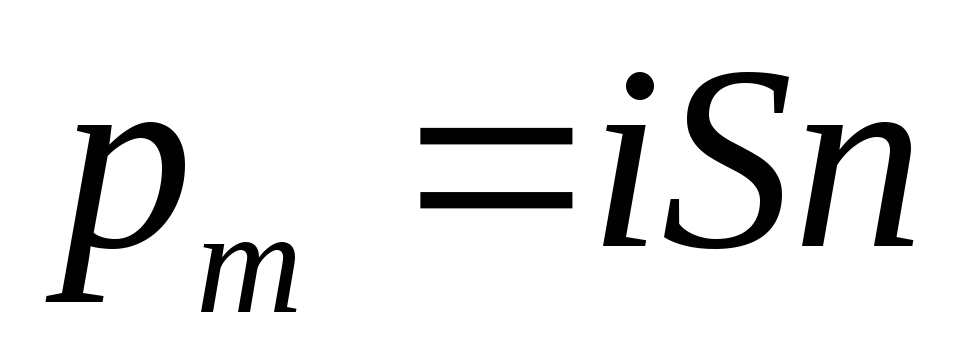 .
(4.27)
.
(4.27)
Здесь S — площадь,
охватываемая контуром. Если контур
круговой, то 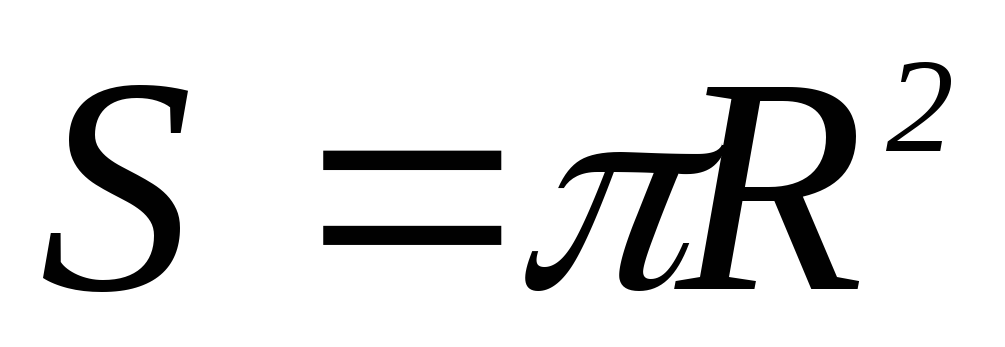 ,
тогда
,
тогда
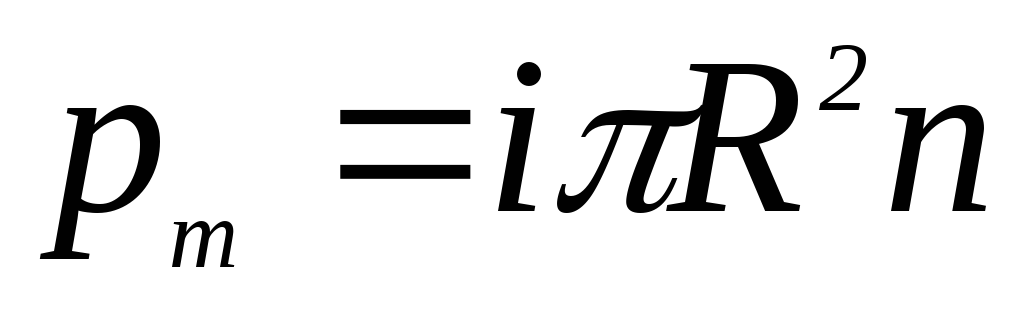
 .
(4.28)
.
(4.28)
Для магнитной индукции на оси кругового тока было получено выражение:
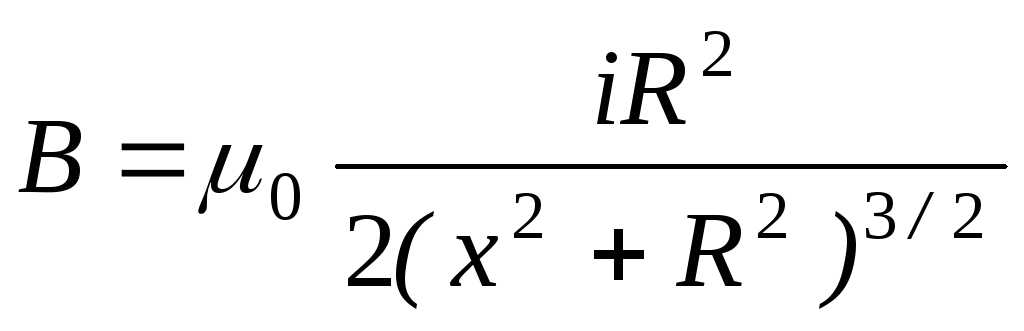 .
(4.29)
.
(4.29)
Во многих случаях приходиться иметь дело с замкнутыми токами, размеры которых малы по сравнению с расстояниями до точки наблюдения. Такие токи принято называть элементарными. (Пример: движущийся по замкнутой орбите электрон).
На больших расстояниях от контура x>>R и можно пренебречь вторым слагаемым в знаменателе, тогда
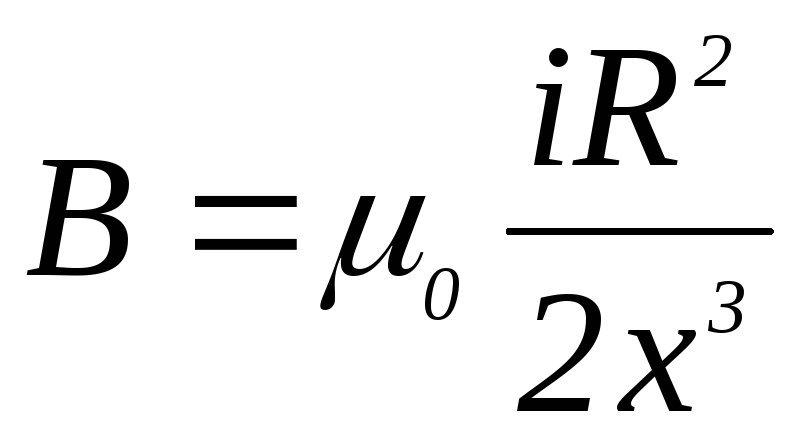 .
(4.30)
.
(4.30)
Умножим числитель и знаменатель этого выражения на π, получим:
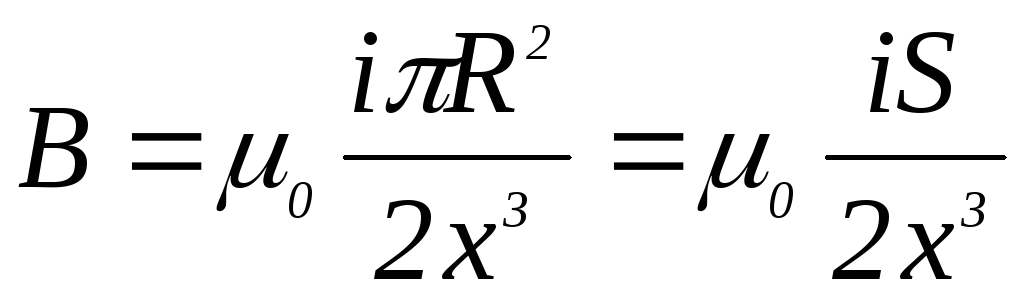 ,
(4.31)
,
(4.31)
где 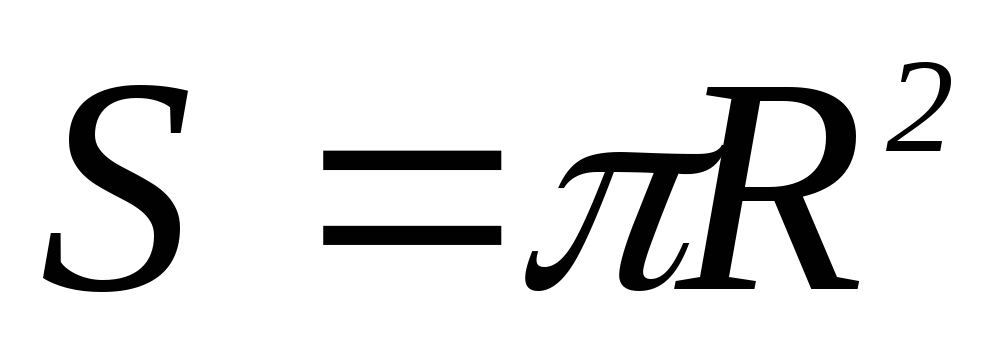 .
.
Произведение
силы тока на площадь контура равно по
величине магнитному моменту контура.
Так как векторы  и
и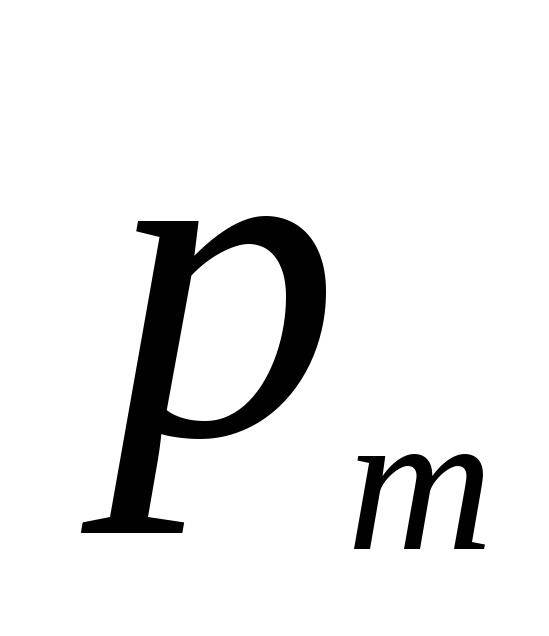 направлены
одинаково, то
направлены
одинаково, то
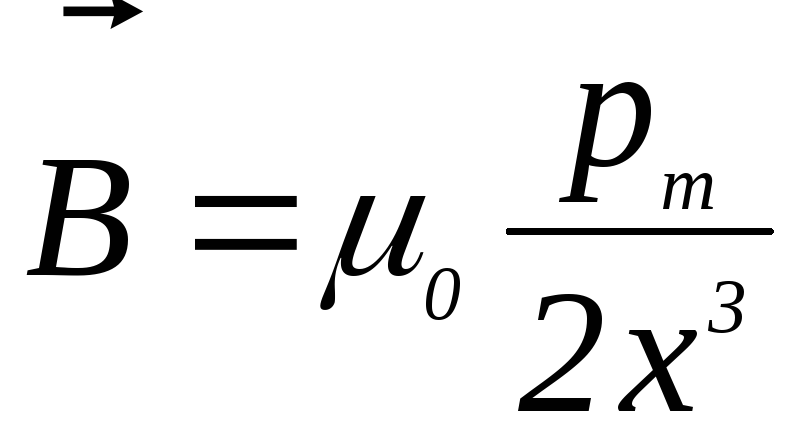 .
(4.32)
.
(4.32)
Индукция магнитного поля, созданного элементарным током, пропорциональна его магнитному моменту.
|
Рассмотрим поле, создаваемое током I, текущим по тонкому проводу, имеющему форму окружности радиуса R (рис. 1.7). Рис. 1.7 Определим магнитную индукцию на оси проводника с током на расстоянии х от плоскости кругового тока. Векторы перпендикулярны плоскостям, проходящим через соответствующие и . Следовательно, они образуют симметричный конический веер. Из соображения симметрии видно, что результирующий вектор направлен вдоль оси кругового тока. Каждый из векторов вносит вклад равный , а взаимно уничтожаются. Но , , а т.к. угол между и α – прямой, то тогда получим
Подставив в (1.6.1) и, проинтегрировав по всему контуру , получим выражение для нахождения магнитной индукции кругового тока:
При , получим магнитную индукцию в центре кругового тока:
Заметим, что в числителе (1.6.2) – магнитный момент контура. Тогда, на большом расстоянии от контура, при , магнитную индукцию можно рассчитать по формуле:
Силовые линии магнитного поля кругового тока хорошо видны в опыте с железными опилками (рис. 1.8).
Рис. 1.8 Другие аудио-видео демонстрации по теме или смежным темам:1. Силовые линии магнитов. 2. Линии магнитной индукции. 3. Намагниченность. 4. Электромагниты. 5. Компас. |




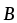 с напряженностью
с напряженностью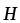 магнитного
поля.
магнитного
поля.