Катушка индуктивности в цепи постоянного тока
Катушка индуктивности – это элемент характеризующимся своим свойством накапливать энергию магнитной поля.
Первый закон коммутации гласит: ток, протекающий в катушке индуктивности, в момент коммутации не может измениться скачком.
Это понятно из формулы:

Предположим, что ток iL изменился скачком, то есть:

А значит, что и напряжение в данном случае будет бесконечно велико:

Чего в природе быть не может, так как, следуя закону сохранения энергии, для этого бы потребовался источник энергии бесконечной мощности.

На схеме представлена RL – цепь, запитанная от источника постоянного тока. При замыкании ключа в положение 1, ток протекает по цепи “плюс” источника – резистор R – катушка индуктивности — “минус” источника. Тем самым, происходит накопление энергии магнитного поля в катушке индуктивности.
Напряжение и ток, протекающие в данной цепи, изменяются по экспоненциальному закону. Причем, их изменения взаимообратные, т.е. с увеличением тока, падение напряжения на катушке уменьшается.

Если мы переведем ключ в положение 2, то ток, не изменив своего направления, начнет уменьшаться по экспоненте до нуля. С физической точки зрения, в данном случае катушка отдает накопленную энергию магнитного поля в цепь, где она расходуется на тепловые потери в резисторе.
Одной из характеристик данной цепи является постоянная времени τ. Она зависит от величины индуктивности и активного сопротивления. Примерно за 5 τ ток в цепи достигает своего минимума или максимума.

Реализуем эту схему в программной среде Multisim 13.0 , взяв значения R = 10 Ом, L = 0,1 Гн.

Скачать файл Multisim 13.0
Рассчитаем время, за которое ток в цепи достигает установившегося значения:

Собранная схема запитана от батареи 12 В. Для снятия значений тока, использовался инструмент “current probe”. Внутреннее активное сопротивление катушки индуктивности, принято равным нулю.
Катушка индуктивности в цепи постоянного тока. — Студопедия.Нет
Устройство и принцип работы катушки индуктивности.
Мы продолжаем изучать электронику с самого начала, то есть с самых основ и темой сегодняшней статьи будет принцип работы и основные характеристики катушек индуктивности. Забегая вперед скажу, что сначала мы обсудим теоретические аспекты, а несколько будущих статей посвятим целиком и полностью рассмотрению различных электрических схем, в которых используются катушки индуктивности, а также элементы, которые мы изучили ранее в рамках нашего курса — резисторы и конденсаторы.

Устройство и принцип работы катушки индуктивности.
Как уже понятно из названия элемента — катушка индуктивности, в первую очередь, представляет из себя именно катушку :), то есть большое количество витков изолированного проводника. Причем наличие изоляции является важнейшим условием — витки катушки не должны замыкаться друг с другом. Чаще всего витки наматываются на цилиндрический или тороидальный каркас:

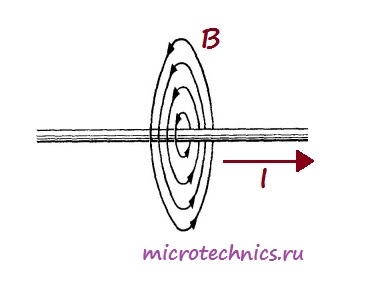
А вот как выглядит магнитное поле, возникающее при прохождении тока через катушку:
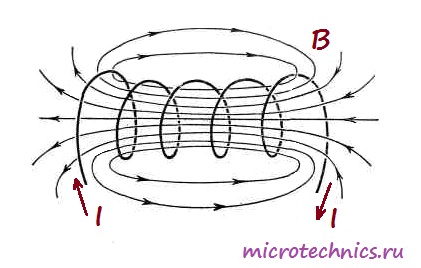
В общем то, строго говоря, любой элемент в электрической цепи имеет индуктивность, даже обычный кусок провода. Но дело в том, что величина такой индуктивности является очень незначительной, в отличие от индуктивности катушек. Собственно, для того, чтобы охарактеризовать эту величину используется единица измерения Генри (Гн). 1 Генри — это на самом деле очень большая величина, поэтому чаще всего используются мкГн (микрогенри) и мГн (милигенри). Величину
Давайте разберемся, что за величину входят в это выражение:
§ — магнитная проницаемость вакуума. Это табличная величина (константа) и равна она следующему значению:
§ — магнитная проницаемость магнитного материала сердечника. А что это за сердечник и для чего он нужен? Сейчас выясним. Дело все в том, что если катушку намотать не просто на каркас (внутри которого воздух), а на магнитный сердечник, то индуктивность возрастет многократно. Посудите сами — магнитная проницаемость воздуха равна 1, а для никеля она может достигать величины 1100. Вот мы и получаем увеличение индуктивности более чем в 1000 раз.
§ — площадь поперечного сечения катушки
§ — количество витков
§ — длина катушки
Из формулы следует, что при увеличении числа витков или, к примеру, диаметра (а соответственно и площади поперечного сечения) катушки, индуктивность будет увеличиваться. А при увеличении длины — уменьшаться. Таким образом, витки на катушке стоит располагать как можно ближе друг к другу, поскольку это приведет к уменьшению длины катушки.
С устройством катушки индуктивности мы разобрались, пришло время рассмотреть физические процессы, которые протекают в этом элементе при прохождении электрического тока. Для этого мы рассмотрим две схемы — в одной будем пропускать через катушку постоянный ток, а в другой -переменный
Катушка индуктивности в цепи постоянного тока.
Итак, в первую очередь, давайте разберемся, что же происходит в самой катушке при протекании тока. Если ток не изменяет своей величины, то катушка не оказывает на него никакого влияния. Значит ли это, что в случае постоянного тока использование катушек индуктивности и рассматривать не стоит? А вот и нет Ведь постоянный ток можно включать/выключать, и как раз в моменты переключения и происходит все самое интересное. Давайте рассмотрим цепь:
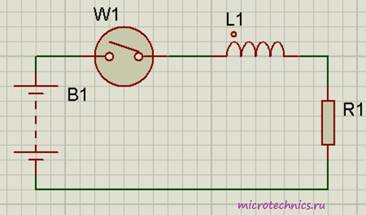
Резистор выполняет в данном случае роль нагрузки, на его месте могла бы быть, к примеру, лампа. Помимо резистора и индуктивности в цепь включены источник постоянного тока и переключатель, с помощью которого мы будем замыкать и размыкать цепь.
Что же произойдет в тот момент когда мы замкнем выключатель?
Возникновение ЭДС приведет к появлению индукционного тока в катушке, который будет протекать в направлении, противоположном направлению тока источника питания. Таким образом, ЭДС самоиндукции будет препятствовать протеканию тока через катушку (индукционный ток будет компенсировать ток цепи из-за того, что их направления противоположны). А это значит, что в начальный момент времени (непосредственно после замыкания выключателя) ток через катушку будет равен 0. В этот момент времени ЭДС самоиндукции максимальна. А что же произойдет дальше? Поскольку величина ЭДС прямо пропорциональна скорости изменения тока, то она будет постепенно ослабевать, а ток, соответственно, наоборот будет возрастать. Давайте посмотрим на графики, иллюстрирующие то, что мы обсудили:
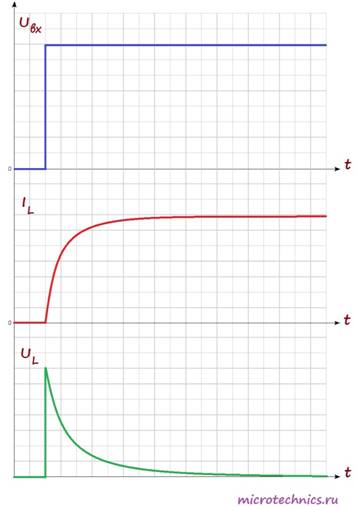
На первом графике мы видим входное напряжение цепи — изначально цепь разомкнута, а при замыкании переключателя появляется постоянное значение. На втором графике мы видим изменение величины тока через катушку индуктивности. Непосредственно после замыкания ключа ток отсутствует из-за возникновения ЭДС самоиндукции, а затем начинает плавно возрастать. Напряжения на катушке наоборот в начальный момент времени максимально, а затем уменьшается. График напряжения на нагрузке будет по форме (но не по величине) совпадать с графиком тока через катушку (поскольку при последовательном соединении ток, протекающий через разные элементы цепи одинаковый). Таким образом, если в качестве нагрузки мы будем использовать лампу, то они загорится не сразу после замыкания переключателя, а с небольшой задержкой (в соответствии с графиком тока).
Аналогичный переходный процесс в цепи будет наблюдаться и при размыкании ключа. В катушке индуктивности возникнет ЭДС самоиндукции, но индукционный ток в случае размыкания будет направлен в том же самом направлении, что и ток в цепи, а не в противоположном, поэтому запасенная энергия катушки индуктивности пойдет на поддержание тока в цепи:
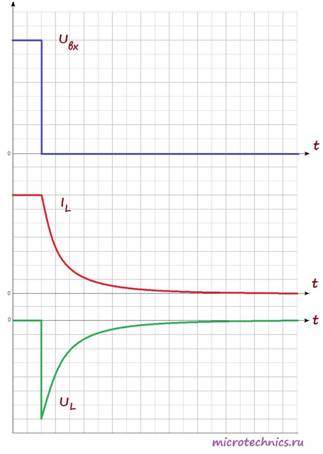
После размыкания ключа возникает ЭДС самоиндукции, которая препятствует уменьшению тока через катушку, поэтому ток достигает нулевого значения не сразу, а по истечении некоторого времени. Напряжение же в катушке по форме идентично случаю замыкания переключателя, но противоположно по знаку. Это связано с тем, что изменение тока, а соответственно и ЭДС самоиндукции в первом и втором случаях противоположны по знаку (в первом случае ток возрастает, а во втором убывает).
Кстати, я упомянул, что величина ЭДС самоиндукции прямо пропорциональна скорости изменения силы тока, так вот, коэффициентом пропорциональности является ни что иное как индуктивность катушки:
На этом мы заканчиваем с катушками индуктивности в цепях постоянного тока и переходим кцепям переменного тока.
Катушка индуктивности
Катушка индуктивности, как показано на рис. 4.11, представляет собой простомоток провода. Условное обозначение катушки индуктивности показано на рис. 4.12. В отличие от конденсатора, который препятствует изменению приложенного к нему напряжения, катушка индуктивности препятствует изменению протекающего через нее тока. Иными словами,

Рис. 4.12. Условное обозначение катушки индуктивности. Рис. 4.13
если ток, подаваемый в схему, которая содержит катушку, резко увеличить, то ток в схеме будет нарастать плавно до достижения своего максимального значения.
Способность катушки индуктивности препятствовать изменению силы тока, протекающего через нее, носит название индуктивности этой катушки. Индуктивность обозначается буквой L, единицей ее измерения является генри (Гн).
Постоянная времени RС-цепи
На рис. 4.13 последовательная цепочка из конденсатора и резистора соединяется через ключ с источником питания. Когда ключ находится в положении 1, конденсатор постепенно заряжается через сопротивление, пока напряжение на нем не достигнет уровня Е т. е. ЭДС или напряжения источника питания.
Процесс заряда конденсатора показан на рис. 4.14(а) экспоненциальной кривой. Время, за которое напряжение на конденсаторе достигает значения 0,63 от максимума, т. е. в данном случае 0,63Е, называется постоянной времени контура или цепи.
Вернемся к рис. 4.13. Если ключ установить в положение 2, конденсатор будет сохранять запасенную энергию. При переведении ключа в положение3 конденсатор начинает разряжаться на землю через резистор R, и напряжение на нем постепенно падает до нуля. Процесс разряда конденсаторапоказан на рис. 4.14(б). В этом случае постоянной времени цепи называется время, за которое напряжение на конденсаторе уменьшается 0,63 от своего максимального значения.

Рис. 4.14. Кривые заряда (а) и разряда (б) конденсатора, где t — постоянная времени.
Как для случая заряда, так и для случая разряда конденсатора через резистор R постоянная времени цепи выражается формулой
где t — постоянная времени в секундах, С — емкость в фарадах, R — сопротивление, выраженное в омах.
Например, для случая С = 10мкФ и R= 10 кОм постоянная времени цепи равна
На рис. 4.15 изображены графики процессов заряда для цепей с малой и с большой постоянной времени.

Рис. 4.15. Процессы заряда для цепей с малой и с большой постоянной времени.
Постоянная времени RL-цепи
Рассмотрим схему, изображенную на рис. 4.16. Катушка индуктивности L соединена последовательно с резистором R, имеющим сопротивление 1 кОм. В момент замыкания ключа S ток в цепи равен нулю, хотя под действиемЭДС источника он, казалось бы, должен резко увеличиться. Однако катушка индуктивности, как известно, препятствует всякому изменению силы тока, протекающего через нее, поэтому ток в цепи будет возрастать по экспоненциальному закону, как показано на рис. 4.17. Ток будет возрастать до тех пор, пока не достигнет своего максимального значения. После этого увеличение тока прекратится, а падение напряжения на резисторе R станет равным приложенному напряжению Е. Установившееся значение тока равно
E/R = 20 В/1 кОм = 20 мА.
Скорость изменения тока в цепи зависит от конкретных значений R и L. Время, необходимое для того, чтобы сила тока достигла значения, равного 0,63 от его максимальной величины, носит название постоянной времени цепи. Постоянная времени вычисляется по формуле L/R где L выражается в генри, а R — в омах. В этом случае постоянная времени получается в секундах. Используя значения L и R, указанные на рисунке, получаем
Следует заметить, что, чем больше R, тем меньше L/R и тем быстрее изменяется ток в цепи.

Рис. 4.16.

Рис. 4.17. Экспоненциальное увеличение тока, протекающего через катушку индуктивности.
Сопротивление по постоянному току
Катушка индуктивности, включенная в цепь, не препятствует протеканию постоянного тока, если, конечно, но принимать во внимание очень малое сопротивление провода, из которого она сделана. Следовательно, катушка индуктивности имеет нулевое или очень малое сопротивление и может рассматриваться в цепи постоянного тока как цепь короткого замыкания. Конденсатор же в связи с наличием в нем изолирующего диэлектрика имеет бесконечное или очень большое сопротивление и может рассматриваться в цепи постоянного тока как разрыв.
Векторное представление
Сигнал синусоидальной формы может быть представлен в виде вектора ОА, вращающегося против часовой стрелки с угловой скоростью ω= 2πf, где f – частота сигнала (рис. 4.18). По мере того как поворачивается вектор, ордината его конца характеризует показанный на рисунке синусоидальный сигнал. Один полный оборот вектора (360°, или 2π) соответствует одному полному периоду. Половина оборота (180°, или π) соответствует половине периода, и так далее. Таким образом, ось времени, как показано на рисунке, может использоваться для нанесения значений угла, на который повернулся вектор. Максимум сигнала достигается при 90° (1/4 периода), а минимум — при 270° (3/4 периода).
Теперь рассмотрим два синусоидальных сигнала, представленных на рис. 4.19(а) векторами ОА и ОВ соответственно. Если оба сигнала имеют одинаковые частоты, то векторы ОА и ОВ будут вращаться с одинаковой угловой скоростью ω= 2πf. Это означает, что угол между этими векторами

Рис. 4.18. Векторное представление синусоидального сигнала.

Рис. 4.19. Разность фаз. Вектор ОА опережает вектор ОВ
(или вектор ОВ отстает от вектора ОА) на угол θ.
изменяться не будет. Говорят, что вектор ОА опережает вектор ОВ на угол θ, а вектор ОВ отстает от вектора ОА на угол в. На рис. 4.19(б) эти сигналы развернуты во времени.
Если оба этих синусоидальных сигнала сложить, то в результате получим другой синусоидальный сигнал, имеющий ту же частоту f, но другую амплитуду. Результирующий сигнал может быть представлен вектором ОТ, который, как показано на рис. 4.19(в), является векторной суммой векторов ОА и ОВ. Вектор ОТ опережает вектор ОВ на угол α и отстает от вектора ОА на угол γ. Дальше вы увидите, что векторное представление является весьма удобным приемом при анализе и расчете цепей переменного тока.
В этом видео рассказывается о катушке индуктивности:
Добавить комментарий
2. Переходные процессы в цепях постоянного тока с катушкой индуктивности | 15. RC и L/R цепи | Часть1
2. Переходные процессы в цепях постоянного тока с катушкой индуктивности
Переходные процессы в цепях постоянного тока с катушкой индуктивности
Характеристики катушек индуктивности противоположны характеристикам конденсаторов. Если конденсаторы накапливают энергию в электрическом поле (создаваемом напряжением между двумя пластинами), то катушки индуктивности накапливают энергию в магнитном поле (создаваемом проходящим через провод током). Из этого можно сделать вывод, что энергия, запасенная в конденсаторе, пытается поддерживать на его выводах постоянное напряжение, а энергия, запасенная в катушке индуктивности, пытается поддерживать постоянный ток в ее обмотке. Таким образом, катушка индуктивности выступает против изменения тока и действует противоположно конденсатору, который выступает против изменения напряжения. Полностью разряженная катушка, ток через которую равен нулю, в момент подключения к источнику питания будет действовать как разомкнутая цепь (пытаясь поддерживать нулевой ток). Напряжение на ее выводах при этом будет максимальным. С течением времени, ток через катушку индуктивности будет возрастать до максимально допустимого значения, а напряжение — соответственно уменьшаться. Как только напряжение на выводах катушки снизится до минимума (ноль — для идеальной катушки), ток через нее достигнет максимального значения, и она будет действовать как короткозамкнутая перемычка.
В момент замыкания контактов выключателя напряжение на катушке индуктивности сразу возрастает до величины напряжения источника питания (действует в качестве обрыва цепи), а затем постепенно снижается до нуля (действует в качестве короткозамкнутой перемычки). Чтобы определить напряжение на катушке индуктивности, нужно рассчитать напряжение на резисторе (с учетом тока через катушку) и вычесть его из напряжения источника питания. Ток в момент замыкания контактов выключателя равен нулю. С течением времени он увеличивается, пока не достигнет величины напряжения источника питания поделенной на последовательное сопротивление 1 Ом. Такое поведение противоположно поведению RC цепи, в которой ток начинается с максимального значения, а напряжение — с нуля. Давайте посмотрим как все это работает, используя реальные значения:
-------------------------------------------------- | Время | Напряжение | Напряжение | Ток | |(секунды) | батареи | катушки | | |------------------------------------------------| | 0 | 15 В | 15 В | 0 | |------------------------------------------------| | 0.5 | 15 В | 9.098 В | 5.902 A | |------------------------------------------------| | 1 | 15 В | 5.518 В | 9.482 A | |------------------------------------------------| | 2 | 15 В | 2.030 В | 12.97 A | |------------------------------------------------| | 3 | 15 В | 0.747 В | 14.25 A | |------------------------------------------------| | 4 | 15 В | 0.275 В | 14.73 A | |------------------------------------------------| | 5 | 15 В | 0.101 В | 14.90 A | |------------------------------------------------| | 6 | 15 В | 37.181 мВ | 14.96 A | |------------------------------------------------| | 10 | 15 В | 0.681 мВ | 14.99 A | --------------------------------------------------
Так же как и для RC цепи, подход напряжения катушки к нулевому значению и подход тока через нее к 15 амперам носит асимптотический характер (обе эти величины с течением времени подходят к окончательным значениям все ближе и ближе, но никогда не достигают их). В практических целях мы можем сказать, что напряжение на катушке в конечном итоге достигнет нулевого значения, а ток в конечном счете будет равен 15 амперам.
Опять же, при помощи программы SPICE мы можем графически отобразить рассмотренное выше асимптотическое уменьшение напряжения и увеличение тока на катушке индуктивности (ток на графике показан с точки зрения напряжения на резисторе, который используется в качестве шунта для измерения данного тока):
inductor charging v1 1 0 dc 15 r1 1 2 1 l1 2 0 1 ic=0 .tran .5 10 uic .plot tran v(2,0) v(1,2) .end
legend: *: v(2) Inductor voltage +: v(1,2) Inductor current time v(2) (*+)------------ 0.000E+00 5.000E+00 1.000E+01 1.500E+01 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 0.000E+00 1.500E+01 + . . * 5.000E-01 9.119E+00 . . + * . . 1.000E+00 5.526E+00 . .* +. . 1.500E+00 3.343E+00 . * . . + . 2.000E+00 2.026E+00 . * . . + . 2.500E+00 1.226E+00 . * . . + . 3.000E+00 7.429E-01 . * . . + . 3.500E+00 4.495E-01 .* . . +. 4.000E+00 2.724E-01 .* . . +. 4.500E+00 1.648E-01 * . . + 5.000E+00 9.987E-02 * . . + 5.500E+00 6.042E-02 * . . + 6.000E+00 3.662E-02 * . . + 6.500E+00 2.215E-02 * . . + 7.000E+00 1.343E-02 * . . + 7.500E+00 8.123E-03 * . . + 8.000E+00 4.922E-03 * . . + 8.500E+00 2.978E-03 * . . + 9.000E+00 1.805E-03 * . . + 9.500E+00 1.092E-03 * . . + 1.000E+01 6.591E-04 * . . + - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Обратите внимание, как напряжение очень быстро уменьшается в начальный момент времени (с левой стороны графика), и практически не меняется в последующем. Аналогичная ситуация и с током: он очень быстро увеличивается в начальный момент времени (с правой стороны графика), и практически не растет в последующем.



