Сопротивление это в физике: Origin DNS error | www.fluke.com — groupnk.ru — Группа НК — комплексные поставки электрооборудования в Москве и регионах

Содержание

что это такое в физике, как найти трение в механике и динамике

Что такое сила сопротивления в физике

Сила сопротивления — сила, которая возникает во время движения тела в жидкой или газообразной среде и препятствует этому движению.

Важно уметь отличать силу сопротивления от силы трения. Во втором случае рассматривается характер взаимодействия твердых тел друг с другом. Таким образом, трение можно наблюдать, когда какой-либо предмет перемещается по поверхности другого. Вектор этой силы будет направлен в противоположную сторону направления движения.

Для того чтобы рассчитать силу сопротивления необходимо умножить коэффициент сопротивления материала на силу, провоцирующую перемещение этого предмета.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Примечание

В качестве примера силы сопротивления можно рассмотреть движение поезда.

Воздух, окружающий состав, замедляет скорость его перемещения, то есть возникает сила сопротивления.

От чего зависит в механике и динамике

Сила сопротивления зависит от нескольких факторов. На ее величину оказывают влияния следующие характеристики:

Особенности среды и показатели ее плотности, к примеру, жидкость обладает большей плотностью, чем газообразное вещество.
Форма тела, так как предметы, обладающие обтекаемыми вытянутыми вдоль направления движения формами подвержены меньшему сопротивлению, чем тела с множеством плоскостей, расположенных перпендикулярно движению.

Скорость перемещения тела.

Силу сопротивления можно наблюдать опытным путем. К примеру, если предмет переместился на величину пути l , когда на него воздействует сила сопротивления, обозначение которой представлено, как $$$F_{r}$$$, затрачивается работа, которую можно рассчитать по формуле:

$$$A=F_{r}\times l$$$

В случае, когда площадь поперечного сечения движущегося предмета равна S, он будет сталкиваться с частицами, объем которых составляет Sl. {2}}{2}$$\)

Разновидности сил сопротивления

Существует несколько типов силы сопротивления, отличающихся по характеру воздействия на движущиеся предметы.

Сила сопротивления качению

Сила сопротивления качению обозначается, как Pf. В данном случае сила определяется несколькими факторами:

разновидность и состояние опоры, по которой перемещается объект;
скорость движения тела;
давление воздуха и другие параметры окружающей среды.

Состояние и тип опорной поверхности определяет величину коэффициента сопротивления качению, который обозначается f. Если в среде повышается температура, и возрастает давление, то данный показатель будет уменьшаться.

Сила сопротивления воздуха

Сила сопротивления воздуха или величина лобового столкновения Pв образуется в результате различных показателей давления. Данная характеристика напрямую зависит от интенсивности вихреобразования спереди и сзади движущегося предмета. Указанные параметры определяются формой перемещающегося тела.

Примечание

Большее влияние на силу сопротивления будет оказывать вихреобразование в передней части объекта. Если плоскостенную фигуру закруглить спереди и сзади, то получится снизить сопротивление до 72%.

Рассчитать силу лобового сопротивления можно по формуле:

$$$P=cx\times p\times F_{b}$$$

сх — обтекаемость или коэффициент лобового сопротивления; p — плотность воздуха; Fв — площадь лобового сопротивления (миделевого сечения).

Во время поступательного движения масса объекта встречает сопротивление разгону, то есть ускорению. Найти данную силу можно с помощью второго закона Ньютона.

$$$Pj=m\times dVdt$$$

где m выражает массу движущегося объекта, а $dVdt$ обозначает ускорение центра масс.

Как найти трение

Определить силу сопротивления можно, если применить третий закон Ньютона. Для того чтобы предмет равномерно перемещался по опоре в горизонтальном направлении, к нему необходимо приложить силу, соизмеримой с силой сопротивления.

Корректно рассчитать данные величины можно с помощью динамометра. Сила сопротивления будет прямо пропорциональна массе объекта. Более точные расчеты производятся с учетом u коэффициента, который зависит от следующих факторов:

материал, из которого изготовлено опорное основание;
материал, из которого состоит перемещаемое тело.

Рассчитывая силу сопротивления, используют постоянную величину g, равную 9,8 метров на сантиметр в квадрате. При этом если движение тела происходит на определенной высоте, на него оказывает воздействие сила трения воздуха. Данная величина зависит от скорости, с которой движется предмет. Искомая величина определяется с помощью следующей формулы только при условии, что предмет перемещается на небольшой скорости:

$$$F=V\times a$$$

где V является скоростью перемещения тела, a — коэффициентом сопротивления среды.

Силы сопротивления при больших скоростях

Сила сопротивления, оказывающая воздействие на движущиеся предметы с малой скоростью, зависит от нескольких внешних факторов. К таким условиям относятся:

вязкость жидкости;

скорость перемещения тела;
линейные размеры движущегося предмета.

В условиях больших скоростей характер действия силы сопротивления несколько изменяется. Законы вязкого трения в этом случае не применяются для воздуха и воды. Если скорость предмета составляет 1 сантиметр в секунду, то данные факторы учитываются лишь тогда, когда тела обладают крошечными размерами, измеряемыми в миллиметрах.

Примечание

Если пловец ныряет в воду, то на него будет действовать сила сопротивления. Однако в данном случае закон вязкого трения не будет действовать.

Объект, двигаясь с малой скоростью в водной среде, плавно обтекается жидкостью. Сила сопротивления в данном случае будет рассчитываться, как

сила вязкого трения. Если скорость большая, то с задней части перемещающегося тела наблюдается более сложное движение жидкости с образованием необычных по форме фигур, вихрей, колец.

{2}$$\)

где V обозначает показатели скорости движения, L — соответствует линейным размерам тела, p — равна плотности среды.

Как найти внутреннее сопротивление формула в физике. Электродвижущая сила. Внутреннее сопротивление источника тока

Цель работы: изучить метод измерения ЭДС и внутреннего сопротивления источника тока с помощью амперметра и вольтметра.

Оборудование: металлический планшет, источник тока, амперметр, вольтметр, резистор, ключ, зажимы, соединительные провода.

Для измерения ЭДС и внутреннего сопротивления источника тока собирают электрическую цепь, схема которой показана на рисунке 1.

К источнику тока подключают амперметр, сопротивление и ключ, соединенные последовательно. Кроме того, непосредственно к выходным гнездам источника подключают еще и вольтметр.

ЭДС измеряют по показанию вольтметра при разомкнутом ключе. Этот прием определения ЭДС основан на следствии из закона Ома для полной цепи, согласно которому при бесконечно большом сопротивлении внешней цепи напряжение на зажимах источника равно его ЭДС.

(См. параграф «Закон Ома для полной цепи» учебника «Физика 10»).

Для определения внутреннего сопротивления источника замыкают ключ К. При этом в цепи можно условно выделить два участка: внешний (тот, который подключен к источнику) и внутренний (тот, который находится внутри источника тока). Поскольку ЭДС источника равна сумме падения напряжений на внутреннем и внешнем участках цепи:

ε = U r +U R , то U r = ε -U R (1)

По закону Ома для участка цепи U r = I

· r (2). Подставив равенство (2) в (1) получают:

I · r = ε — U r , откуда r = (ε — U R )/ J

Следовательно, чтобы узнать внутреннее сопротивление источника тока, необходимо предварительно определить его ЭДС, затем замкнуть ключ и измерить падение напряжения на внешнем сопротивлении, а также силу тока в нем.

Ход работы

1. Подготовьте таблицу для записи результатов измерений и вычислений:

ε ,в	U r , B	i,a	r , Ом

Начертите в тетради схему для измерения ЭДС и внутреннего сопротивления источника.

После проверки схемы соберите электрическую цепь. Ключ разомкните.

Измерьте величину ЭДС источника.

Замкните ключ и определите показания амперметра и вольтметра.

Вычислите внутреннее сопротивление источника.

Определение эдс и внутреннего сопротивления источника тока графическим методом

Цель работы: изучить измерения ЭДС, внутреннего сопротивления и тока короткого замыкания источника тока, основанный на анализе графика зависимости напряжения на выходе источника от силы тока в цепи.

Оборудование: гальванический элемент, амперметр, вольтметр, резистор R 1 , переменный резистор, ключ, зажимы, металлический планшет, соединительные провода.

Из закона Ома для полной цепи следует, что напряжение на выходе источника тока зависит прямо пропорционально от силы тока в цепи:

так как I =E/(R+r), то IR + Ir = Е, но IR = U, откуда U + Ir = Е или U = Е – Ir (1).

Если построить график зависимости U от I, то по его точкам пересечения с осями координат можно определить Е, I К.З. — силу тока короткого замыкания (ток, который потечет в цепи источника, когда внешнее сопротивление R станет равным нулю).

ЭДС определяют по точке пересечения графика с осью напряжений. Эта точка графика соответствует состоянию цепи, при котором ток в ней отсутствует и, следовательно, U = Е.

Силу тока короткого замыкания определяют по точке пересечения графика с осью токов. В этом случае внешнее сопротивление R = 0 и, следовательно, напряжение на выходе источника U = 0.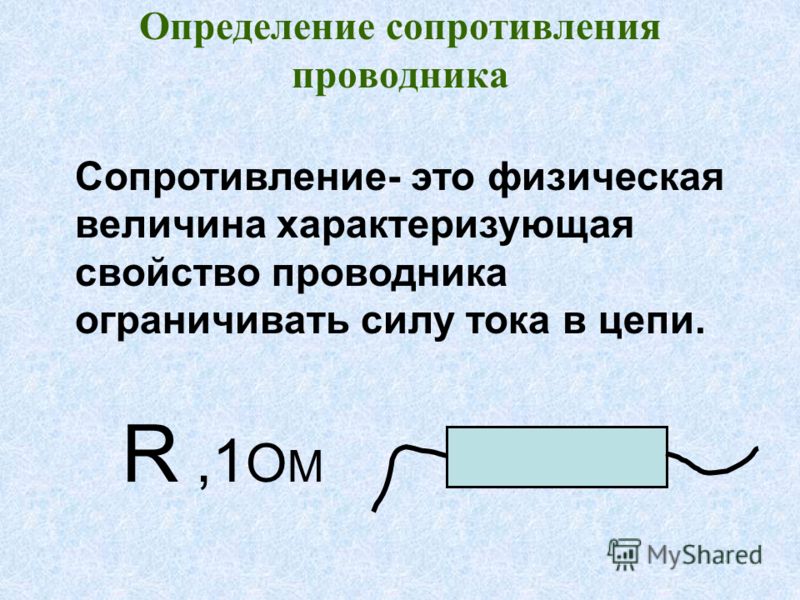

Внутреннее сопротивление источника находят по тангенсу угла наклона графика относительно оси токов. (Сравните формулу (1) с математической функцией вида У = АХ +В и вспомните смысл коэффициента при X).

Ход работы

Для записи результатов измерений подготовьте таблицу:

После проверки схемы преподавателем соберите электрическую цепь. Ползунок переменного резистора установите в положение, при котором сопротивление цепи, подключенной к источнику тока, будет максимальным.

Определите значение силы тока в цепи и напряжение на зажимах источника при максимальной величине сопротивления переменного резистора. Данные измерений занесите в таблицу.

Повторите несколько раз измерения силы тока и напряжения, уменьшая всякий раз величину переменного сопротивления так, чтобы напряжение на зажимах источника уменьшалось на 0,1В. Измерения прекратите, когда сила тока в цепи достигнет значения в 1А.

Нанесите полученные в эксперименте точки на график. Напряжение откладывайте по вертикальной оси, а силу тока — по горизонтальной. Проведите по точкам прямую линию.

Продолжите график до пересечения с осями координат и определите величины Е и, I К.З.

Измерьте ЭДС источника, подключив вольтметр к его выводам при разомкнутой внешней цепи. Сопоставьте значения ЭДС, полученные двумя способами, и укажите причину возможного расхождения результатов.

Определите внутреннее сопротивление источника тока. Для этого вычислите тангенс угла наклона построенного графика к оси токов. Так как тангенс угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему, то практически это можно сделать, найдя отношение Е / I К.З

На концах проводника, а значит, и тока необходимо наличие сторонних сил неэлектрической природы, с помощью которых происходит разделение электрических зарядов .

Сторонними силами называются любые силы, действующие на электрически заряженные частицы в цепи, за исключением электростатических (т. е. кулоновских).

Сторонние силы приводят в движение заряженные частицы внут-ри всех источников тока: в генераторах, на электростанциях, в гальванических элементах, аккумуляторах и т. д.

При замыкании цепи создается электрическое поле во всех про-водниках цепи. Внутри источника тока заряды движутся под действием сторонних сил против кулоновских сил (электроны движут-ся от положительно заряженного электрода к отрицательному), а во всей остальной цепи их приводит а движение электрическое поле (см. рис. выше).

В источниках тока в процессе работы по разделению заряженных частиц происходит превращение разных видов энергии в электричес-кую. По типу преобразованной энергии различают следующие виды электродвижущей силы:

— электростатическая — в электрофорной машине, в которой происходит превращение механической энергии при трении в электрическую;

— термоэлектрическая — в термоэлементе — внутренняя энергия нагретого спая двух проволок, изготовленных из разных металлов, превращается в электрическую;

— фотоэлектрическая — в фотоэлементе. Здесь происходит превращение энергии света в элек-трическую: при освещении некоторых веществ, например, селена, оксида меди (I) , кремния наблюдается потеря отрицательного электрического заряда;

— химическая — в гальванических элементах, аккумуляторах и др. источниках, в которых происходит превращение химической энергии в электрическую.

Электродвижущая сила (ЭДС) — характеристика источников тока. Понятие ЭДС было введено Г. Омом в 1827 г. для цепей постоянного тока. В 1857 г. Кирхгофф определил ЭДС как работу сторонних сил при переносе единичного электрического заряда вдоль замкнутого контура:

ɛ = A ст /q ,

где ɛ — ЭДС источника тока, А ст — работа сторонних сил , q — количество перемещенного заряда.

Электродвижущую силу выражают в вольтах.

Можно говорить об электродвижущей силе на любом участке цепи. Это удельная работа сторонних сил (работа по перемещению единичного заряда) не во всем контуре, а только на данном участке.

Внутреннее сопротивление источника тока.

Пусть имеется простая замкнутая цепь, состоящая из источника тока (например, гальванического элемента, аккумулятора или генератора) и резистора с сопротивлением R . Ток в замкну-той цепи не прерывается нигде, следовательно, oн существует и внутри источника тока. Любой источник представляет собой некоторое сопротивление дли тока. Оно называется внутренним сопротивлением источника тока и обозначается буквой r .

В генераторе r — это сопротивление обмотки, в гальваническом элементе — сопротивление раствора электролита и электродов.

Таким образом, источник тока характеризуется величинами ЭДС и внутреннего сопротивлении, которые определяют его качество. Например, электростатические машины имеют очень большую ЭДС (до десятков тысяч вольт), но при этом их внутреннее сопротивление огромно (до со-тни Мом). Поэтому они непригодны для получения сильных токов. У гальванических элементов ЭДС всего лишь приблизительно 1 В, но зато и внутреннее сопротивление мало (приблизительно 1 Ом и меньше). Это позволяет с их помощью получать токи, измеряемые амперами.

ЭДС и напряжение. Внутреннее сопротивление источников питания.
Ликбез так ликбез!
Закон Ома. Вот я о чем.
О законе Ома мы уже говорили. Поговорим еще раз — с несколько иной стороны. Не вдаваясь в физические подробности и выражаясь простым кошачьим языком, закон Ома гласит: чем больше э.д.с. (электродвижущая сила), тем больше ток, чем больше сопротивление, тем меньше ток.
Переведя сие заклинание на язык сухих формул получаем:

I=E/R

где:I — сила тока,E — Э.Д.С. — электродвижущая силаR — сопротивление
Ток измеряется в амперах, э.д.с. — в вольтах, а сопротивление носит гордое имя товарища Ома.Э.д.с. — это есть характеристика идеального генератора, внутренне сопротивление которого принято считать бесконечно малым. В реальной жизни такое бывает редко, поэтому в силу вступает закон Ома для последовательной цепи (более знакомый нам):

I=U/R

где:U — напряжение источника непосредственно на его клеммах.
Рассмотрим простой пример.
Представим себе обычную батарейку в виде источника э.д.с. и включенного последовательно с ним некоего резистора, который будет олицетворять собой внутреннее сопротивление батарейки. Подключим параллельно батарейке вольтметр. Его входное сопротивление значительно больше внутреннего сопротивления батарейки, но не бесконечно большое — то есть, через него потечет ток. Величина напряжения, которую покажет вольтметр будет меньше величины э.д.с. как раз на величину падения напряжения на внутреннем воображаемом резисторе при данном токе.Но, тем не менее именно эта величина и принимается за напряжение батарейки.
Формула конечного напряжения при этом будет иметь следующий вид:

U(бат)=E-U(внутр)

Так как со временем у всех элементов питания внутреннее сопротивление увеличивается, то и падение напряжения на внутреннем сопротивлении тоже увеличивается. При этом напряжение на клеммах батарейки уменьшается. Мяу!
Разобрались!
Что же происходит, если вместо вольтметра к батарейке подключить амперметр? Так как собственное сопротивление амперметра стремится к нулю, мы фактически будем измерять ток, протекающий через внутреннее сопротивление батарейки. Так как внутренне сопротивление источника очень небольшое, измеренный при этом ток может достигать н ескольких ампер.
Однако следует заметить, что внутреннее сопротивление источника является таким же элементом цепи, как и все остальные. Поэтому при увеличении тока нагрузки падение напряжения на внутреннем сопротивлении также увеличится, что приводит к уменьшению напряжения на нагрузке. Или как мы, радиокоты, любим выражаться — к просадке напруги.
Чтобы изменение нагрузки как можно меньше влияло на выходное напряжение источника его внутреннее сопротивление стараются свести к минимуму.
Можно так подобрать элементы последовательной цепи, чтобы на каком-нибудь из них получить напряжение, уменьшенное, по сравнению с исходным, во сколько угодно раз.

Допустим, есть простейшая электрическая замкнутая цепь, включающая в себя источник тока, например генератор, гальванический элемент или аккумулятор, и резистор, обладающий сопротивлением R. Поскольку ток в цепи нигде не прерывается, то и внутри источника он течет.

В такой ситуации можно сказать, что любой источник обладает некоторым внутренним сопротивлением, препятствующим току. Это внутреннее сопротивление характеризует источник тока и обозначается буквой r. Для или аккумулятора внутреннее сопротивление — это сопротивление раствора электролита и электродов, для генератора — сопротивление обмоток статора и т. д.

Таким образом, источник тока характеризуется как величиной ЭДС, так и величиной собственного внутреннего сопротивления r – обе эти характеристики свидетельствуют о качестве источника.

Электростатические высоковольтные генераторы (как генератор Ван де Граафа или генератор Уимшурста), к примеру, отличаются огромной ЭДС измеряемой миллионами вольт, при этом их внутреннее сопротивление измеряется сотнями мегаом, потому они и непригодны для получения больших токов.

Гальванические элементы (такие как батарейка) — напротив — имеют ЭДС порядка 1 вольта, хотя внутреннее сопротивление у них порядка долей или максимум — десятка Ом, и от гальванических элементов поэтому можно получать токи в единицы и десятки ампер.

На данной схеме показан реальный источник с присоединенной нагрузкой. Здесь обозначены , его внутреннее сопротивление, а также сопротивление нагрузки. Согласно , ток в данной цепи будет равен:

Поскольку участок внешней цепи однороден, то из закона Ома можно найти напряжение на нагрузке:

Выразив из первого уравнения сопротивление нагрузки, и подставив его значение во второе уравнение, получим зависимость напряжения на нагрузке от тока в замкнутой цепи:

В замкнутом контуре ЭДС равна сумме падений напряжений на элементах внешней цепи и на внутреннем сопротивлении самого источника. Зависимость напряжения на нагрузке от тока нагрузки в идеальном случае линейна.

График это показывает, но экспериментальные данные на реальном резисторе (крестики возле графика) всегда отличаются от идеала:

Эксперименты и логика показывают, что при нулевом токе нагрузки напряжение на внешней цепи равно ЭДС источника, а при нулевом напряжении на нагрузке ток в цепи равен .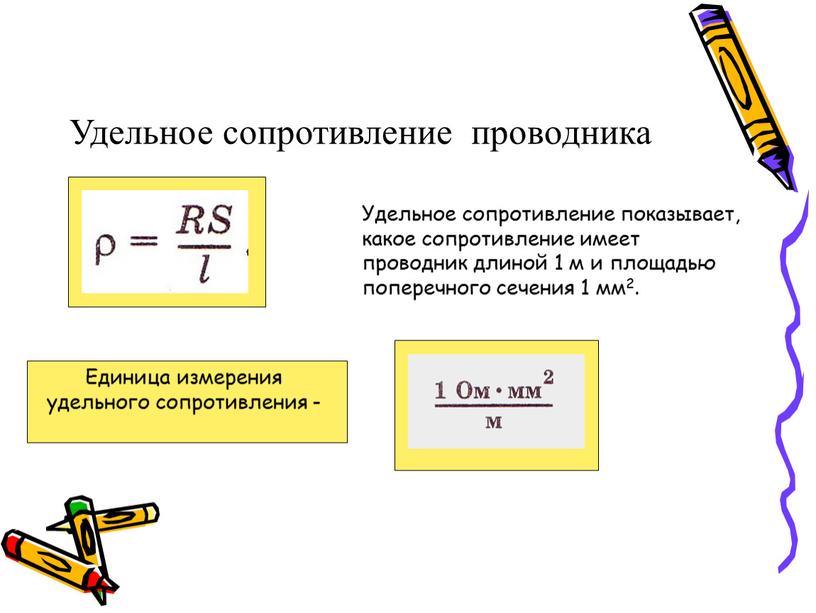 Это свойство реальных цепей помогает экспериментально находить ЭДС и внутреннее сопротивление реальных источников.

Экспериментальное нахождение внутреннего сопротивления

Чтобы экспериментально определить данные характеристики, строят график зависимости напряжения на нагрузке от величины тока, затем экстраполируют его до пересечения с осями.

В точке пересечения графика с остью напряжения находится значение ЭДС источника, а в точке пересечения с осью тока находится величина тока короткого замыкания. В итоге внутреннее сопротивление находится по формуле:

Развиваемая источником полезная мощность выделяется на нагрузке. График зависимости этой мощности от сопротивления нагрузки приведен на рисунке. Эта кривая начинается от пересечения осей координат в нулевой точке, затем возрастает до максимального значения мощности, после чего спадает до нуля при сопротивлении нагрузки равном бесконечности.

Чтобы найти максимальное сопротивление нагрузки, при котором теоретически разовьется максимальная мощность при данном источнике, берется производная от формулы мощности по R и приравнивается к нулю.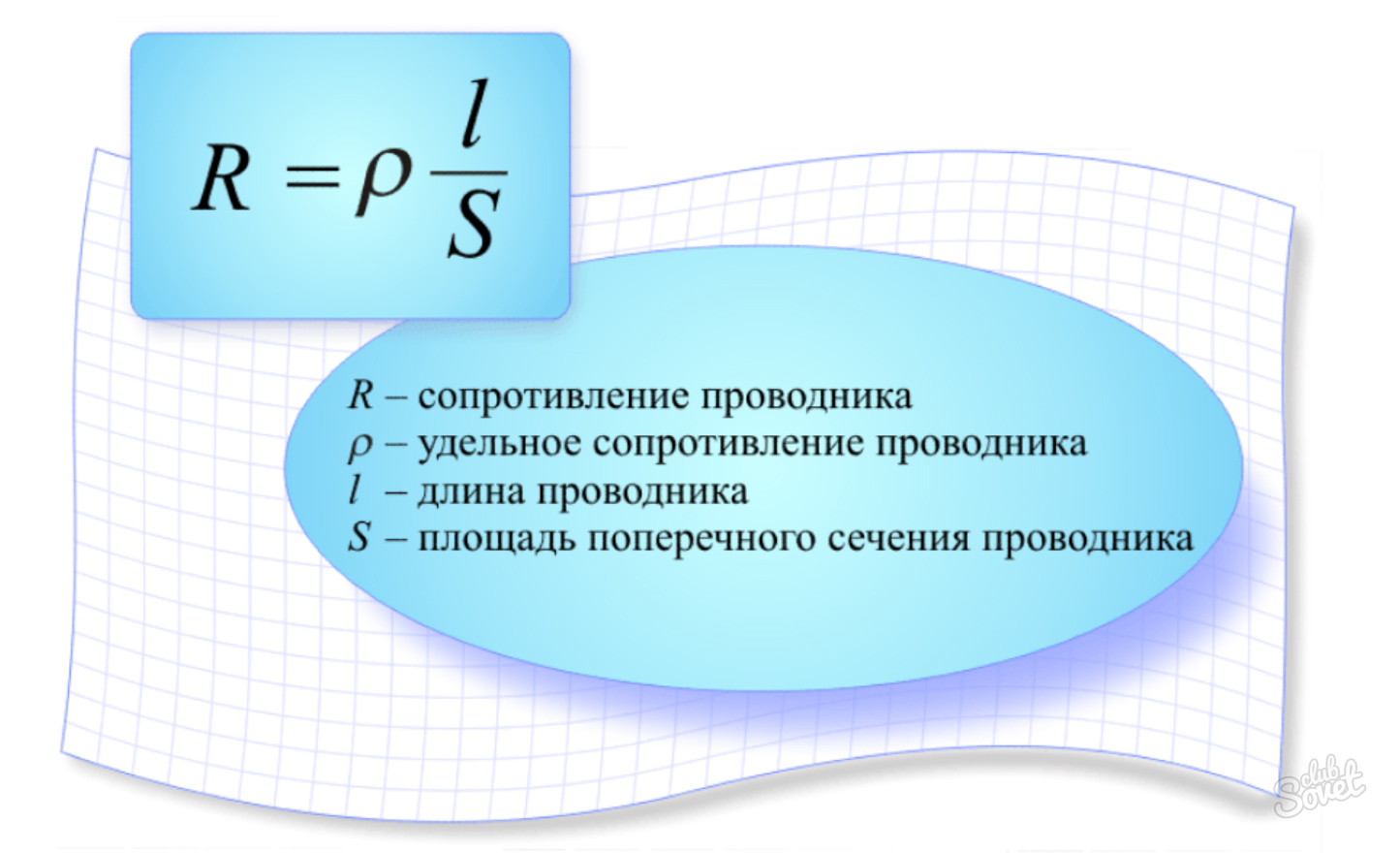 Максимальная мощность разовьется при сопротивлении внешней цепи, равном внутреннему сопротивлению источника:

Это положение о максимальной мощности при R = r, позволяет экспериментально найти внутреннее сопротивление источника, построив зависимость мощности, выделяемой на нагрузке, от величины сопротивления нагрузки. Найдя реальное, а не теоретическое, сопротивление нагрузки, обеспечивающее максимальную мощность, определяют реальное внутреннее сопротивление источника питания.

КПД источника тока показывает отношение максимальной выделяемой на нагрузке мощности к полной мощности, которую в данный момент развивает

Попробуем решить эту задачу на конкретном примере. Электродвижущая сила источника питания составляет 4,5 В. К нему подключили нагрузку, и через неё потёк ток, равный 0,26 А. Напряжение при этом стало равным 3,7 В. Первым делом, представим себе, что внутри источника спрятана последовательная цепь из идеального источника напряжения в 4,5 В, внутреннее сопротивление которого равно нулю, а также резистора, номинал которого и требуется найти. Понятно, что на самом деле это не так, но для расчётов аналогия вполне сойдёт.

2 шаг

Запомните, что буквой U обозначают только напряжение под нагрузкой. Для обозначения же электродвижущей силы зарезервирована другая буква – E. Абсолютно точно её измерить невозможно, потому что потребуется вольтметр с бесконечным входным сопротивлением. Даже у электростатического вольтметра (электрометра) оно огромно, но не бесконечно. Но одно дело – абсолютно точно, а другое – с точностью, приемлемой на практике. Второе вполне осуществимо: нужно лишь, чтобы внутреннее сопротивление источника было пренебрежимо мало по сравнению с внутренним сопротивлением вольтметра. А пока суть да дело, посчитаем разницу между ЭДС источника и его напряжением под нагрузкой, потребляющей ток в 260 мА. E-U = 4,5-3,7 = 0,8. Это и будет падение напряжения на том “виртуальном резисторе”.

3 шаг

Ну а дальше всё просто, ибо в дело вступает классический закон Ома. Помним, что ток через нагрузку и “виртуальный резистор” одинаков, ведь они соединены последовательно. Падение напряжения на последнем (0,8 В) делим на силу тока (0,26 А) и получаем 3,08 Ома. Вот и готов ответ! Можно ещё посчитать, какая мощность рассеивается на нагрузке, а какая – бесполезно на источнике. На нагрузке рассеивается: 3,7*0,26=0,962 Вт. На источнике: 0,8*0,26=0,208 Вт. Процентное соотношение между ними вычислите самостоятельно. Но эта не единственный вид задач на нахождение внутреннего сопротивления источника. Есть и такие, в которых вместо силы тока указано сопротивление нагрузки, а остальные исходные данные такие же. Тогда надо вначале проделать ещё одно вычисление. Приведённое в условии напряжение под нагрузкой (не ЭДС!) поделить на сопротивление нагрузки. И получится сила тока в цепи. После чего, как говорят физики, “задача сведена к предыдущей”! Попробуйте составить такую задачу и решить её.

Лекция 1. Сопротивление материалов. Основные понятия и определения

Основные определения

Сопротивление материалов — раздел физики, изучающий механические свойства различных материалов, используемых в строительстве и машиностроении

Сопротивление материалов позволяет определить прочность, жесткость и устойчивость элементов строительных конструкций и деталей машин, тем самым обеспечить долгую и надежную работу сооружений, машин и механизмов.

Объекты рассмотрения — твердые тела

Вещества и комбинации веществ, из которых состоят тела, и являются рассматриваемыми материалами. Все твердые тела по геометрической форме можно условно разделить на 3 группы:

1. Стержни — твердые тела, длина l которых значительно больше высоты h и ширины b.

Это можно выразить соотношением длины к высоте или ширине. Стержни можно условно разделить на 3 категории:

1.1. Стержни с соотношением l/h ≥ 10.

1.2. Стержни с соотношением 5 < l/h < 10.

1.3. Стержни с соотношением l/h ≤ 5. Чем меньше значение соотношения l/h или l/b, тем больше тело по своей геометрической форме приближается к пластине или массивному телу.

2. Пластины — тела, высота которых значительно меньше длины и ширины.

3. Массивные тела — тела, длина, ширина и высота которых сопоставимы.

Примечание: определение длины, ширины и высоты зависит от выбора системы координат. Например и балка перекрытия и колонна могут рассматриваться как стержни, а стена и плита перекрытия — как пластины.

Основной объект рассмотрения — стержень (балка, брус).

Так как высота и ширина стержня значительно меньше длины, то для решения множества задач на начальной стадии высотой и шириной стержня пренебрегают, а для расчетов используют только один параметр — длину стержня. Таким образом на чертежах стержень изображается как линия, имеющая некоторую длину l. Из курса геометрии нам известно, что линия может быть прямой, кривой, находящейся в одной плоскости, и кривой, для корректного описания которой нужно задавать координаты в трех плоскостях. То же можно сказать и о стержнях.

Ось стержня — линия, проходящая через центры тяжести поперечных сечений стержня.

Таким образом линия, изображающая стержень на чертежах, совпадает с осью стержня. Часто ось стержня называется упругой линией, нейтральной линией или нейтральной осью.

Поперечное сечение — сечение стержня в плоскости, перпендикулярной оси стержня.

Основными характеристиками поперечного сечения являются высота и ширина, а так как поперечное сечение перпендикулярно оси стержня, то высота и ширина поперечного сечения являются высотой и шириной стержня в рассматриваемом сечении. При решении некоторых строительных задач рассматриваются не только поперечные, но и наклонные сечения — сечения в плоскости, расположенной под некоторым углом к поперечному сечению или оси стержня. Для получения любого возможного сечения не нужна грубая физическая сила, а только сила мысли и немного пространственного воображения.

Расчет прочности — определение наименьших размеров поперечного сечения элементов конструкции

при которых исключается возможность разрушения конструкции при действии заданных нагрузок. Другими словами напряжения, возникающие в рассматриваемых поперечных сечениях, не должны превышать расчетного сопротивления материала.

Расчет жесткости — определение деформаций материала

возникающих под действием заданных нагрузок. Так как не существует материалов, имеющих бесконечно большую жесткость, то деформации материала конструкции приводят к изменению геометрической формы элементов конструкции, а значит и к перераспределению внутренних напряжений.

Устойчивость — состояние элементов конструкции

при котором изменение первоначальной геометрической формы под действием нагрузок и возникающего при этом перераспределения внутренних напряжений не приводит к разрушению конструкции.

Деформация — изменение геометрических размеров и первоначальной формы физического тела при действии сил.

Деформации рассматриваются как перемещение точек, линий и плоскостей.

Линейная деформация — перемещение рассматриваемой точки, линии или поперечного сечения относительно только одной из выбранных осей координат.

Линейная деформация измеряется в единицах длины.

Угловая деформация — перемещение, характеризуемое углом поворота рассматриваемой линии или поперечного сечения

относительно некоторой точки.

Абсолютная деформация — величина линейной деформации

на рассматриваемом участке длины элемента конструкции.

Относительная деформация — отношение абсолютной деформации к длине

рассматриваемого участка.

Пластические (остаточные) деформации — изменения геометрических размеров и формы тела

остающиеся после снятия нагрузки.

Упругие деформации — деформации тела под действием нагрузок, не приводящие к остаточным деформациям после снятия нагрузок

Другими словами остаточные деформации, при упругой деформации равны нулю.

Упругость — свойство материала полностью восстанавливать первоначальную геометрическую форму тела

после снятия нагрузок.

Пластичность — свойство материала накапливать остаточные деформации

Все материалы обладают определенными упругими и пластичными свойствами. Например изготовление профилированного листа из листа металлопроката происходит в результате накопления остаточных деформаций.

Сжатие или растяжение — такое воздействие на материал, при котором силы, действующие на стержень, направлены по оси или параллельно оси стержня.

Если силы направлены по оси, то такой элемент конструкции называют центрально сжатым или центрально растянутым. Если силы приложены на некотором расстоянии от оси, то такой элемент называют внецентренно сжатым или внецентренно растянутым, при этом расстояние от оси до точки приложения силы называется эксцентриситетом е.

Кручение — воздействие на материал пары сил, действующих в плоскости, перпендикулярной к оси стержня

т.е. в плоскости поперечного сечения

Изгиб — воздействие на материал пары сил, направленных в плоскости, проходящей через ось стержня.

т.е. в плоскости, перпендикулярной плоскости поперечного сечения.

Момент — создается любой парой сил, направленных не по одной прямой, а параллельно, а также любой силой, расположенной на некотором расстоянии от рассматриваемого сечения.

Моменты могут быть крутящими и изгибающими. Момент, возникающий при внецентренном растяжении или сжатии, является изгибающим.

Изотропный материал — материал, физико-механические свойства которого постоянны и одинаковы во всех направлениях

К изотропным материалам условно можно отнести металлы, камень, стекло.

Ортотропный материал — материал, физико-механические свойства которого постоянны, но не одинаковы в различных направлениях

Представителем такого материала является древесина.

Анизотропный материал — материал, не имеющий свойств изотропности или ортотропности

Свойства анизотропных материалов не являются предметом рассмотрения теории сопротивления материалов. Между тем не существует природных или искусственных материалов, имеющих идеальную упругость, изотропию или отротропию. Кроме того изготовить конструкцию идеальной геометрической формы практически невозможно. Это означает, что для точных расчетов необходимо учитывать все изменения геометрической формы, а также возможные отклонения от заданных физико-механических свойств. Однако в подавляющем большинстве случаев для обеспечения надежной работы строительной конструкции, машины или механизма достаточно выполнить приближенный (упрощенный) расчет. Выполняется такой расчет на основании следующих допущений.

Основные допущения, принимаемые в теории сопротивления материалов

1. Рассматриваемый материал является изотропным (или ортотропным) и идеально упругим.

2. Деформации материала пропорциональны приложенной нагрузке, не превышающей некоторой предельной величины, т.е рассматриваемые тела являются линейно-деформируемыми.

3. При составлении уравнений равновесия деформациями материала можно пренебречь, так как деформации рассматриваемых элементов значительно меньше геометрических размеров элементов. В данном случае не только значительно меньше длины, но также высоты и ширины.

4. При расчетах допускается использовать принцип независимости действия сил, т.е. упругую деформацию под действием нескольких сил можно рассматривать как сумму упругих деформаций от каждой отдельно взятой силы.

5. Предполагается, что сечения которые были плоскими до приложения нагрузок, остаются плоскими при деформациях материала.

Внешние и внутренние силы

Все силы, действующие на тело, можно условно разделить на внешние и внутренние. Условно потому, что силы тяжести, действующие на каждую частицу тела, находятся как бы внутри тела, а внутренние силы (силы взаимодействия между элементарными частицами вещества) действуют и до того, как к телу приложена какая-либо внешняя сила.

Потому внешние силы, вызывающие деформацию материала, чаще называют нагрузками, а разницу внутренних сил, возникающую при деформации — напряжениями или внутренними усилиями, подобно тому как в электротехнике напряжением называется разница потенциалов

Единицей измерения силы является Ньютон (Н) или килоНьютон (кН). Однако в технической литературе нередко встречается и другая единица — килограмм-сила (кгс) или тонно-сила (тс). Измерение силы в Ньютонах является более правильным.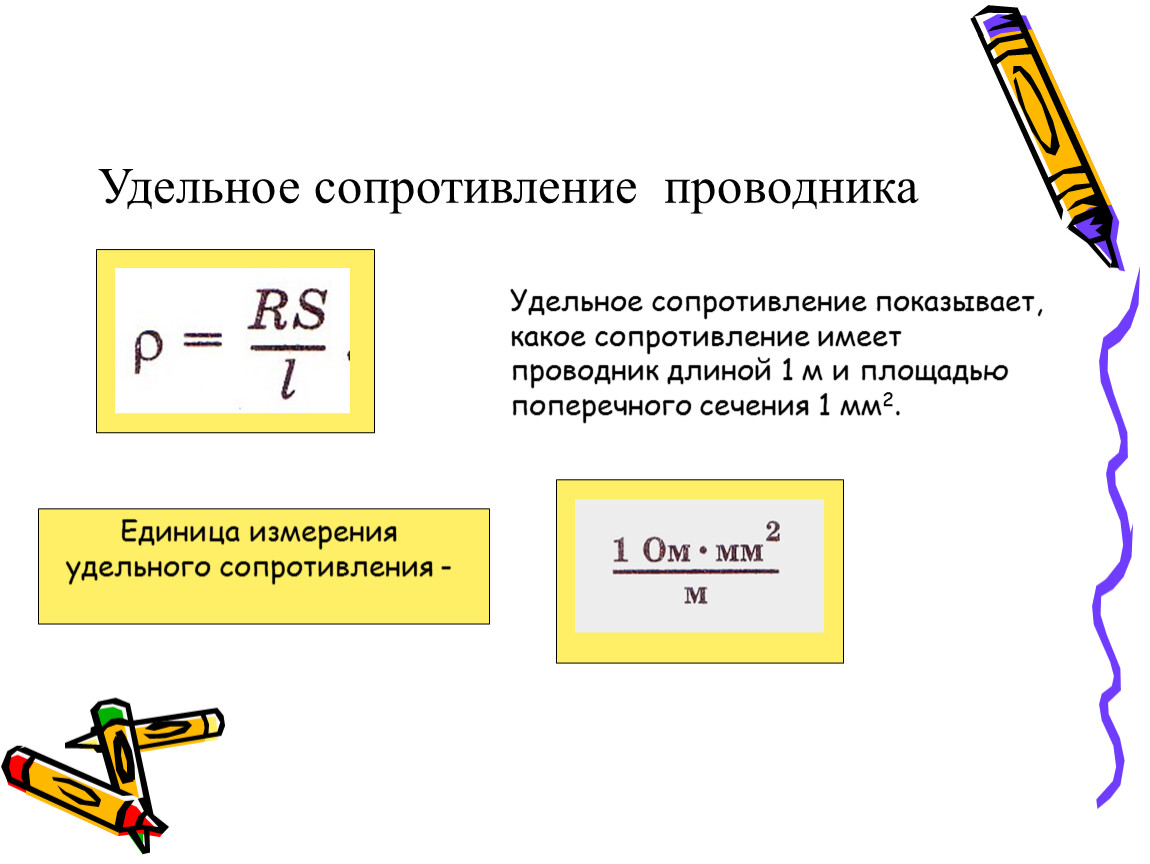 Так как сила есть произведение массы на ускорение, то тело массой в 1 кг создает нагрузку Q = mg = 1·9.81 м/с² = 9.81 кг·м/с² = 9.81 Н. Это означает, что при расчетах значения нагрузок вряд ли будут круглыми. И потому пользоваться при расчетах килограмм-силами или тонно-силами удобнее. Считается, что тело массой 1 кг создает нагрузку 1 кгс.

Внешние силы по характеру приложения можно разделить на четыре вида:

1. Объемные — действующие на все точки тела. Измеряются в Н/м³.

2. Плоские (поверхностные) — распределенные на некоторой площади поверхности тела. Измеряются в Н/м².

3. Линейные (распределенные) — распределенные непрерывно по некоторой длине. Измеряются в Н/м.

Интенсивность нагрузки — это величина распределенной нагрузки, приложенной к единице объема, площади или длины.

Так как при расчетах изначально рассматривается ось стержня, не имеющая высоты и ширины, то объемные и плоские нагрузки часто приводятся к линейной. Это допускается делать без каких-либо поправочных коэффициентов, если интенсивность объемной или плоской нагрузки является постоянной.

4. Точечные (сосредоточенные) — приложенные в одной точке.

В природе точечных нагрузок не существует. Любая нагрузка прикладывается к некоторой площади, но если площадь приложения нагрузки, точнее длина приложения нагрузки после приведения плоской нагрузки к линейной, значительно меньше длины тела, то такую нагрузку можно условно рассматривать, как сосредоточенную в одной точке. Переход от сосредоточенной нагрузки к равномерно распределенной и наоборот осуществляется только с помощью соответствующих коэффициентов.

По времени действия нагрузки делятся на постоянные и временные

Постоянные нагрузки, например, собственный вес конструкции, действуют в течение всего срока службы. Временные нагрузки ограничены по времени действия.

По характеру изменения во времени нагрузки делятся на статические и динамические

Статические нагрузки прикладываются как бы постепенно, поэтому инертные силы, возникающие при движении инертных масс, при расчетах не учитываются. Динамические нагрузки прикладываются очень быстро и потому при расчетах влияние инертных сил необходимо учитывать.

Все вышеприведенные нагрузки рассматриваются как активные.

Напряжение — величина внутренней силы, приложенной к единице площади рассматриваемого сечения

Равнодействующую внутренних сил, действующую на рассматриваемую площадь, называют внутренним усилием.

Примечание: распределенные нагрузки как правило обозначаются литерой «q» вне зависимости от того, объемная, плоская или линейная нагрузка имеется в виду. Сосредоточенная нагрузка часто обозначается литерой «P», однако я предпочитаю обозначать сосредоточенную нагрузку литерой «Q», а литерой «P» — реактивные внутренние усилия, соответственно литерой «p» — реактивные напряжения.

Уравнения равновесия. Метод сечений

Так как рассматриваемое тело должно быть неподвижным в заданной системе координат, то все опоры тела можно заменить на реактивные силы — опорные реакции. Опорные реакции также рассматриваются как внешние силы. При этом для соблюдения равновесия (неподвижности рассматриваемого тела) сумма активных и реактивных сил, действующих на тело относительно любой координатной оси, должна быть равна нулю. На основании этого предположения составляются уравнения равновесия системы.

Кроме того, если рассечь тело в любом месте, то чтобы тело по-прежнему оставалось в состоянии равновесия к полученному сечению нужно приложить некоторую внешнюю силу Q. Значение внешней силы определяется, исходя из условий равновесия. А так как сила действия равна силе противодействия, то считается, что внутренние усилия Р или напряжения р, возникающие в результате действия внешних сил (нагрузок) равны по значению нагрузкам, приложенным в рассматриваемом сечении и направлены в противоположную сторону. Такой метод расчета и называется методом сечений.

Примечание: Для решения статически неопределимых задач одних только уравнений равновесия и уравнения моментов недостаточно.

Рисунок 317.1

Так как напряжения, возникающие в рассматриваемых сечениях под действием внешних сил, редко бывают равномерно распределенными (не имеют постоянной интенсивности), то для решения задач сопротивления материалов важно знать не просто значение внутренних усилий, но также и значение напряжений в наиболее опасных точках сечения. Отношение внутреннего усилия ΔР, действующего на некоторой площади ΔF рассматриваемого сечения будет приближаться к некоторому пределу, если площадь ΔF будет стремиться к нулю (к точке А). Этот предел, как мы выяснили ранее, называется напряжением и определяет интенсивность внутренних усилий, действующих на рассматриваемую площадку в точке А. Напряжения могут быть различны не только в разных точках одного сечения, но и в одной и той же точке А, общей для различных сечений, т.е. сечений, рассекающих тело под различными углами.

Ось, перпендикулярная плоскости сечения, называется нормалью.

Полное напряжение в точке А, имеющей координаты (х, у, z) для сечения с нормалью n определяется по формуле:

(317.1)

где ΔР — элементарное внутреннее усилие, возникающее при отбрасывании части II тела и замене этой части элементарной внешней силой ΔQ, действующей на оставшуюся часть I для соблюдения условий равновесия.

Нормальное напряжение

σ_n действует в направлении нормали

Если усилие ΔР не перпендикулярно рассматриваемой плоскости сечения (как на рисунке 317.1), то значение нормального напряжения можно определить по формуле:

(317.2)

Касательное напряжение

т_n действует в плоскости сечения

Значение касательного напряжения можно определить по формуле:

(317.3)

Напряжения измеряются в Паскалях (Па) или МегаПаскалях (МПа), а также в кгс/см² или тс/см².

дальше

Конспект урока по физике на тему «Электрическое сопротивление проводников.

Единицы сопротивления». 8-й класс

Класс – 8.

Цель занятия: Экспериментальным путём познакомить учащихся с электрическим сопротивлением проводников как физической величиной, объяснить природу электрического сопротивления на основании электронной теории, ввести единицу измерения сопротивления.

Задачи занятия:

Образовательные:

Формирование понятия электрическое сопротивление проводника;
Закрепление умения учащихся работать с учебной литературой, таблицами;
Систематизация информации путем составления конспекта.

Развивающие:

Развитие познавательных умений: составлять план, наблюдать, прививать устойчивый интерес к предмету;
Развитие мышления учащихся в результате логических учебных действий;
Формирование умения анализировать новую информацию, видеть причинно-следственные связи в физических явлениях;
Развитие умения правильно высказывать мысли, опираясь на изученный материал.

Воспитательные:

Способствовать развитию умения анализировать свою деятельность и деятельность своих товарищей;
Воспитание потребности у учащихся применять знания, полученные на уроках, уважительного отношения друг к другу, инициативности, уверенности в своих силах, бережного отношения к школьному физическому оборудованию.

Тип урока: открытие новых знаний.

Форма урока: урок-исследование.

Оборудование: Компьютер, проектор, интерактивная доска, оборудование для проведения физического эксперимента (источник питания, амперметр, вольтметр, включатель, набор проводов), лампы на 15Вт и 100Вт, омметр, портреты учёных.

Используемые методы обучения:

проблемный,
исследовательский,
аналитический,
сравнительный.

Планируемые образовательные результаты:

Личностные: развитие самостоятельности в приобретении новых знаний и практических умений; развитие у обучающихся умения оценивать результаты своей собственной деятельности.
Предметные: формирование представлений у обучающихся о электрических свойствах проводников.

Основные термины, понятия: Электрическое сопротивление, единицы и причины сопротивления, омметр.

План проведения урока

Этапы урока	Временная реализация
Организационный момент	2 мин.
Актуализация знаний	6 мин.
Изучение нового материала	16 мин.
Первичная проверка понимания	5 мин
Первичное закрепление.	1 мин.
Информация о домашнем задании, инструктаж по его выполнению.	1 мин.
Домашнее задание	2 мин.

Этапы урока

1. Организационный момент

Проверка готовности к уроку. Вступительное слово учителя: «Тема нашего урока: «Электрическое сопротивление. Единицы сопротивления». Сегодня мы познакомимся с зависимостью силы тока от свойств проводника, узнаем в каких единицах измеряется сопротивление. Эта тема подготовит вас к изучению следующей важной темы: «Закон Ома для участка цепи».

II. Актуализация знаний

Повторение (фронтальный опрос). Этап подготовки к активной деятельности на основном этапе.

Фронтальная беседа по вопросам:

1. Дайте определение электрического тока.

2. Направление движения, каких частиц в проводнике принимают за направление тока?

3. Что представляет собой электрический ток в металлах? (упорядоченное движение свободных электронов)

4. Что такое напряжение? Как вычисляют напряжение? Каким прибором измеряют напряжение? Как включают вольтметр в электрическую цепь?

5. Чему равна сила тока? Что принимают за единицу силы тока? С помощью какого прибора измеряют силу тока? Как его включают в электрическую цепь? (1 ампер, последовательно)

6. От чего зависит сила тока? (прямо пропорциональна напряжению).

В целях подготовки обучающихся к восприятию нового учебного материала разбираем следующие вопросы:

7. Какое строение имеют металлы? (в узлах кристаллической решетки расположены положительные ионы, а в пространстве между ними движутся свободные электроны.)

8. Что происходит при движении свободных электронов?

(Они взаимодействуют с узлами (ионами) кристаллической решетки, то есть притягиваются к ним, вследствие чего некоторые электроны при движении тормозятся)

III. Изучение нового материала

Создание проблемной ситуации № 1.

Всегда ли сила тока будет зависить только от напряжения, и не будет зависить от других физических величин и свойств проводника? Для ответа на эти вопросы проведём следующие исследования:

1. В переносную лампу будем вкручивать поочерёдно две электрические лампы на 15 Вт и 100 Вт. Напряжение в сети в обоих случаях одно и тоже (220 В) Однако яркость ламп разная. Почему? (Ответы учащихся: Сила тока в цепи разная) Почему разная?

Создание проблемной ситуации № 2

2. Соберём электрическую цепь, состоящую из источника тока, вольтметра, амперметра, ключа, проводников из различных материалов.

— В первый раз используем в электрической цепи толстый и короткий медный провод (такой как в автомобилях, идущих от аккумуляторной батареи).

Записываем показания амперметра. (I = 4 A).

— Во второй раз вместо медного берём тонкий и длинный никелиновый провод. Снимаем показания амперметра (I = 2 A).

— И наконец, возьмём железный провод.

По результатам исследования составим таблицу:

№	Материал проводника	Сила тока (А)
1	Медь	4А
2	Железо	3А
3	Никелин	1А

Какой делаем вывод? Сила тока в электрической цепи при различных проводниках различна. Следовательно, сила тока зависит от свойств самого проводника, т.е. от рода вещества, из которого изготовлен проводник.

Способность проводника оказывать противодействие электрическому току и называют электрическим сопротивлением или просто сопротивлением. Запишем определение. Физическая величина, характеризующая противодействие проводника электрическому току называют сопротивлением и обозначают буквой R.

Таким образом, сопротивление характеризует сам проводник. В каких же единицах измеряют сопротивление? Единица измерения (СИ) — 1 Ом. В честь немецкого учёного Георга Ома, который впервые ввёл это понятие в физику.

За единицу сопротивления принимают 1 Ом — сопротивление такого проводника, в котором при напряжении на концах 1 вольт сила тока равна 1 амперу.

На практике часто используют и другие единицы: миллиом (мОм), килом (кОм), мегаом (МОм).

1 мОм=0,001 Ом;
1 кОм=1000 Ом;
1 Мом= 1 000 000 Ом.

Используемый на практике прибор для измерения сопротивления проводника называется омметром.

IV. Первичная проверка понимания

В чём причина электрического сопротивления, что же ограничивает силу тока в проводнике? Вспомним учебные вопросы начала урока?

Возникает дискуссия. Учащиеся выдвигают гипотезы, (например, движущиеся электроны испытывают помехи при своём движении) Правильные ответы заслуживают похвалу учителя.

В ходе обсуждения, учащиеся приходят к выводу, что причиной сопротивления является взаимодействие движущихся свободных электронов с ионами кристаллической решетки.

V. Первичное закрепление

Выполните Упр. 28 № 1,2 на стр.123 учебника.

VI. Информация о домашнем задании, инструктаж по его выполнению

Дома:

§ 43, Упр. 28 № 1-3; задачи № 1236,1251, 1269.
Подготовить сообщение по теме: «Омметры».

VII. Рефлексия

Подведение итогов

Какова была тема урока?
Какая проблема урока решена нами?
Что нового вы узнали на уроке?
Что вызвало затруднение? Что осталось непонятным? Что заинтересовало?
Анализ и оценка успешности достижения целей урока.
Выставление оценок за работу на уроке.

Мне урок понравился
Тема урока меня заинтересовала, и я постараюсь найти дополнительный материал
Урок был понятным
На уроке было скучно
На уроке я ничего не понял.

Список использованной литературы

1. Перышкин А.В. Физика. 8 класс: Учебник для образовательных учреждений. – 2-е изд. – М.: Дрофа, 2013.

2. Задачник «Сборник задач по физике для 7-9 классов» Лукашик В.И., Иванова Е.В., 17-е изд., М.: «Просвещение», 2011.

3. http://www.fizika.ru — электронные учебники по физике.

4. http://class-fizika.narod.ru- интересные материалы к урокам физики по темам; тесты по темам; наглядные м/м пособия к урокам.

Постоянный электрический ток

на главную

Официальный сайт АНО ДО Центра «Логос», г.Глазов

http://logos-glz.ucoz.net/

ГОТОВИМСЯ К УРОКУ

Кинематика

Динамика

МКТ

Термодинамика

Электростатика

Электрический ток

Электрический ток в средах

Магнитное поле Электромагнитная индукция

Оптика

Методы познания

постоянный электрический ток немного о физике:

Что называют электрическим током?

Электрический ток — упорядоченное движение заряженных частиц под действием сил электрического поля или сторонних сил.

За направление тока выбрано направление движения положительно заряженных частиц.

Электрический ток называют постоянным, если сила тока и его направление не меняются с течением времени.

Условия существования постоянного электрического тока.

Для существования постоянного электрического тока необходимо наличие свободных заряженных частиц и наличие источника тока. в котором осуществляется преобразование какого-либо вида энергии в энергию электрического поля.

Источник тока — устройство, в котором осуществляется преобразование какого-либо вида энергии в энергию электрического поля. В источнике тока на заряженные частицы в замкнутой цепи действуют сторонние силы. Причины возникновения сторонних сил в различных источниках тока различны. Например в аккумуляторах и гальванических элементах сторонние силы возникают благодаря протеканию химических реакций, в генераторах электростанций они возникают при движении проводника в магнитном поле, в фотоэлементах — при действия света на электроны в металлах и полупроводниках.

Электродвижущей силой источника тока называют отношение работы сторонних сил к величине положительного заряда, переносимого от отрицательного полюса источника тока к положительному.

Основные понятия.

Сила тока — скалярная физическая величина, равная отношению заряда, прошедшего через проводник, ко времени, за которое этот заряд прошел.

где I — сила тока, q — величина заряда (количество электричества), t — время прохождения заряда.

Плотность тока — векторная физическая величина, равная отношению силы тока к площади поперечного сечения проводника.

где j —плотность тока, S — площадь сечения проводника.

Направление вектора плотности тока совпадает с направлением движения положительно заряженных частиц.

Напряжение — скалярная физическая величина, равная отношению полной работе кулоновских и сторонних сил при перемещении положительного заряда на участке к значению этого заряда.

где A — полная работа сторонних и кулоновских сил, q — электрический заряд.

Электрическое сопротивление — физическая величина, характеризующая электрические свойства участка цепи.

где ρ — удельное сопротивление проводника, l — длина участка проводника, S — площадь поперечного сечения проводника.

Проводимостью называется величина, обратная сопротивлению

где G — проводимость.

Законы Ома.

Закон Ома для однородного участка цепи.

Сила тока в однородном участке цепи прямо пропорциональна напряжению при постоянном сопротивлении участка и обратно пропорциональна сопротивлению участка при постоянном напряжении.

где U — напряжение на участке, R — сопротивление участка.

Закон Ома для произвольного участка цепи, содержащего источник постоянного тока.

где φ₁_{— φ₂_{+ ε = U}} напряжение на заданном участке цепи, R — электрическое сопротивление заданного участка цепи.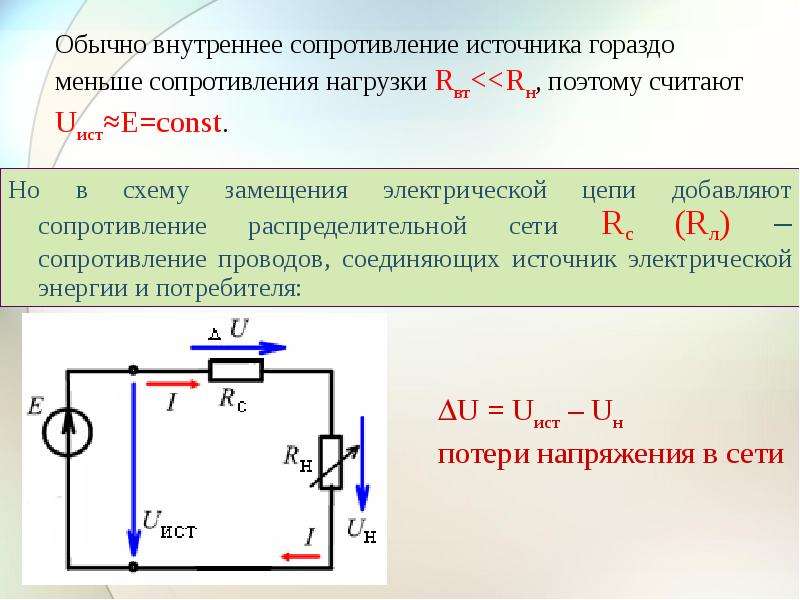

Закон Ома для полной цепи.

Сила тока в полной цепи равна отношению электродвижущей силы источника к сумме сопротивлений внешнего и внутреннего участка цепи.

где R — электрическое сопротивление внешнего участка цепи, r — электрическое сопротивление внутреннего участка цепи.

Короткое замыкание.

Из закона Ома для полной цепи следует, что сила тока в цепи с заданным источником тока зависит только от сопротивления внешней цепи R.

Если к полюсам источника тока подсоединить проводник с сопротивлением R<< r, то тогда только ЭДС источника тока и его сопротивление будут определять значение силы тока в цепи. Такое значение силы тока будет являться предельным для данного источника тока и называется током короткого замыкания.

Последовательное и параллельное

соединение проводников.

Электрическая цепь включает в себя источника тока и проводники (потребители, резисторы и др), которые могут соединятся последовательно или параллельно.

При последовательном соединении конец предыдущего проводника соединяется с началом следующего.

Во всех последовательно соединенных проводниках сила тока одинакова:

I₁= I₂=I

Сопротивление всего участка равно сумме сопротивлений всех отдельно взятых проводников:

R = R₁+ R₂

Падение напряжения на всем участке равно сумме паданий напряжений на всех отдельно взятых проводниках:

U= U₁ +U₂

Напряжения на последовательно соединенных проводниках пропорциональны их сопротивлениям.

При параллельном соединении проводники подсоединяются к одним и тем же точкам цепи.

Сила тока в неразветвленной части цепи равна сумме токов, текущих в каждом проводнике:

I = I₁+ I₂

Величина, обратная сопротивлению разветвленного участка, равна сумме обратных величин обратных сопротивлениям каждого отдельно взятого проводника:

Падение напряжения во всех проводниках одинаково:

U= U₁ = U₂

Силы тока в проводниках обратно пропорциональны их сопротивлениям

Смешанное соединение — комбинация параллельного и последовательного соединений.

Правила Кирхгофа.

Для расчета разветвленных цепей, содержащих неоднородные участки, используют правила Кирхгофа. Расчет сложных цепей состоит в отыскании токов в различных участках цепей.

Узел — точка разветвленной цепи, в которой сходится более двух проводников.

1 правило Кирхгофа: алгебраическая сумма сил токов, сходящихся в узле, равна нулю;

где n — число проводников, сходящихся в узле, I_i_{— сила тока в проводнике.}

токи, входящие в узел считают положительными, токи, отходящие из узла — отрицательными.

2 правило Кирхгофа: в любом произвольно выбранном замкнутом контуре разветвленной цепи алгебраическая сумма произведений сил токов и сопротивлений каждого из участков этого контура равна алгебраической сумме ЭДС в контуре.

Чтобы учесть знаки сил токов и ЭДС выбирается определенное направление обхода контура(по часовой стрелке или против нее). Положительными считают токи, направление которых совпадает с направлением обхода контура, отрицательными считают токи противоположного направления. ЭДС источников электрической энергии считают положительными если они создают токи, направление которых совпадает с направлением обхода контура, в противном случае — отрицательными.

Порядок расчета сложной цепи постоянного тока.

Произвольно выбирают направление токов во всех участках цепи.
Первое правило Кирхгофа записывают для (m-1) узла, где m — число узлов в цепи.
Выбирают произвольные замкнутые контуры, и после выбора направления обхода записывают второе правило Кирхгофа.
Система из составленных уравнений должна быть разрешимой: число уравнений должно соответствовать количеству неизвестных.

Шунты и добавочные сопротивления.

Шунт — сопротивление, подключаемое параллельно к амперметру (гальванометру), для расширения его шкалы при измерении силы тока.

Если амперметр рассчитан на силу тока I₀_{, а с помощью него необходимо измерить силу тока, превышающую в
n раз допустимое значение, то сопротивление,
подключаемого шунта должно удовлетворять следующему условию:}

Добавочное сопротивление — сопротивление, подключаемое последовательно с вольтметром (гальванометром), для расширения его шкалы при измерении напряжения.

Если вольтметр рассчитан на напряжение U₀_{, а с помощью него необходимо измерить напряжение, превышающее в
n раз допустимое значение, то добавочное сопротивление
должно удовлетворять следующему условию:}

9: Ток и сопротивление — Physics LibreTexts

Последнее обновление
Сохранить как PDF

Без заголовков

В этой главе мы изучаем электрический ток через материал, где электрический ток — это скорость протекания заряда.Мы также исследуем характеристику материалов, известную как сопротивление. Сопротивление — это мера того, насколько материал препятствует прохождению заряда, и будет показано, что сопротивление зависит от температуры. Как правило, хороший проводник, например медь, золото или серебро, имеет очень низкое сопротивление. Некоторые материалы, называемые сверхпроводниками, имеют нулевое сопротивление при очень низких температурах.

9.1: Prelude to Current and Resistance
Для работы электромагнитов требуются большие токи.Сверхпроводники могут быть использованы для изготовления электромагнитов, которые в 10 раз сильнее, чем самые сильные обычные электромагниты. Эти сверхпроводящие магниты используются при создании устройств магнитно-резонансной томографии (МРТ), которые можно использовать для получения изображений человеческого тела с высоким разрешением. У сверхпроводящих магнитов есть много других применений.
9.2: Электрический ток
Мгновенный электрический ток или просто ток I — это скорость, с которой протекает заряд.Направление обычного тока принимается за направление, в котором движется положительный заряд. В простой цепи постоянного тока (DC) это будет от положительной клеммы батареи к отрицательной. Единицей измерения тока в системе СИ является ампер (ампер). Ток состоит из потока свободных зарядов, таких как электроны, протоны и ионы.
9.3: Модель проводимости в металлах
Ток через проводник в основном зависит от движения свободных электронов.Когда к проводнику приложено электрическое поле, свободные электроны в проводнике не движутся через проводник с постоянной скоростью и направлением; вместо этого движение почти случайное из-за столкновений с атомами и другими свободными электронами. Хотя электроны движутся почти случайным образом, при приложении электрического поля общая скорость электронов может быть определена в терминах скорости дрейфа.
9.4: Удельное сопротивление и сопротивление
Когда источник напряжения подключен к проводнику, он прикладывает разность потенциалов V, которая создает электрическое поле.Электрическое поле, в свою очередь, воздействует на свободные заряды, вызывая ток. Величина тока зависит не только от величины напряжения, но и от характеристик материала, через который протекает ток. Материал может сопротивляться потоку зарядов, и мера того, насколько материал сопротивляется потоку зарядов, известна как удельное сопротивление.
9,5: Закон Ома
Многие материалы демонстрируют простую взаимосвязь между значениями этих свойств, известную как закон Ома.Многие другие материалы не демонстрируют эту взаимосвязь, поэтому, несмотря на то, что они называются законом Ома, они не считаются законом природы, как законы Ньютона или законы термодинамики. Но это очень полезно для расчетов с материалами, которые подчиняются закону Ома.
9.6: Электроэнергия и мощность
В электрической цепи электрическая энергия непрерывно преобразуется в другие формы энергии. Например, когда в проводнике течет ток, электрическая энергия преобразуется в тепловую энергию внутри проводника.Электрическое поле, создаваемое источником напряжения, ускоряет свободные электроны, увеличивая их кинетическую энергию на короткое время. Эта увеличенная кинетическая энергия преобразуется в тепловую энергию в результате столкновений с ионами решетчатой структуры проводника.
9.7: Сверхпроводники
Передача электроэнергии приводит к потерям в линии. Эти потери в линии существуют независимо от того, вырабатывается ли энергия на обычных электростанциях (использующих уголь, нефть или газ), атомных станциях, солнечных станциях, гидроэлектростанциях или ветряных электростанциях.Эти потери можно уменьшить, но не устранить, передавая с использованием более высокого напряжения. Было бы замечательно, если бы эти потери в линиях можно было устранить, но для этого потребовались бы линии передачи с нулевым сопротивлением.
9.A: ток и сопротивление (ответы)
9.E: ток и сопротивление (упражнения)
9.S: ток и сопротивление (сводка)

Что такое резисторы и сопротивление — AP Physics B

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

Сопротивление

Как мы узнали ранее, электрические заряды могут легко перемещаться в одних материалах (проводниках) и менее свободно в других (изоляторах).Мы описываем способность материала проводить электрический заряд как , проводимость . Хорошие проводники обладают высокой проводимостью. Электропроводность материала зависит от:

Плотность бесплатного перемещения
Подвижность этих бесплатных зарядов

Аналогичным образом мы описываем способность материала противостоять движению электрического заряда с помощью сопротивления , обозначенного греческой буквой ро (ρ). Удельное сопротивление измеряется в ом-метрах, которые представлены греческой буквой омега, умноженной на метры (Ом • м).И проводимость, и удельное сопротивление являются свойствами материала.

Когда объект создается из материала, тенденция материала проводить электричество или проводимость зависит от проводимости материала, а также от формы материала. Например, полая цилиндрическая труба имеет более высокую проводимость воды, чем цилиндрическая труба, заполненная ватой. Однако форма трубы также играет роль. Очень толстая, но короткая труба может пропускать много воды, но очень узкая и очень длинная труба не может проводить столько воды.И геометрия объекта, и состав объекта влияют на его проводимость .

Сосредоточившись на способности объекта противостоять потоку электрического заряда, мы обнаруживаем, что объекты, сделанные из материалов с высоким удельным сопротивлением, имеют тенденцию препятствовать прохождению электрического тока и имеют высокое сопротивление . Кроме того, материалы, имеющие форму длинных и тонких объектов, также увеличивают электрическое сопротивление объекта. Наконец, объекты обычно демонстрируют более высокое удельное сопротивление при более высоких температурах .Мы объединили все эти факторы, чтобы описать сопротивление объекта потоку электрического заряда. Сопротивление — это функциональное свойство объекта, которое описывает способность объекта препятствовать прохождению через него заряда. Единицы измерения сопротивления — Ом (Ом).

Для любой заданной температуры мы можем рассчитать электрическое сопротивление объекта в Ом по следующей формуле:

В этой формуле R — сопротивление объекта, в Ом (Ом), rho (ρ) — это сопротивление объекта. удельное сопротивление материала, из которого сделан объект, в Ом * метрах (Ом • м), L — длина объекта в метрах, а A — площадь поперечного сечения объекта в метрах в квадрате.Обратите внимание, что таблица удельного сопротивления материалов для постоянной температуры приведена справа.

Давайте попробуем на примере задачи вычислить электрическое сопротивление объекта:

Вопрос: Провод длиной 3,50 метра с площадью поперечного сечения
3,14 × 10 ^–6 м ² при 20 ° Цельсия имеет сопротивление 0,0625 Ом. Определите удельное сопротивление проволоки и материала, из которого она изготовлена.
Ответ:
Вопрос: При 20 ° C четыре проводящих провода из разных материалов имеют одинаковую длину и одинаковый диаметр.Какой провод имеет наименьшее сопротивление?
алюминий
золото
нихром
вольфрам
Ответ: (2) золото, потому что оно имеет самое низкое удельное сопротивление.

Mr Toogood Physics — Резисторы и сопротивление

Сопротивление

В большинстве цепей ток течет из-за движения свободных электронов по проводнику.SOme-проводники имеют больше свободных электронов, чем другие, и, следовательно, являются лучшими проводниками, чем проводники с меньшим количеством свободных электронов. Материалы без свободных электронов называются изоляторами и не пропускают через них ток. Есть также материалы, которые лежат где-то посередине и будут только высвобождать электроны или пропускать ток в ответ на внешний стимул, такой как свет, тепло или электрическое поле. Эти материалы называются полупроводниками и являются строительными блоками современной цифровой технологии.

В любом металле атомы выделяют электроны, образуя кристаллическую решетку, и эти свободные электроны беспорядочно перемещаются между ионными остовами атомов металла. Обычно, поскольку движение электронов является случайным, их чистая скорость равна нулю. Однако, когда ЭДС помещается поперек проводника, электроны будут двигаться от отрицательного вывода к положительному выводу.

Рисунок 1: Если бы мы могли видеть внутри провода …

Когда электроны начинают двигаться, их беспорядочное движение нарушается, но поскольку существует огромное количество ионных ядер, преграждающих путь между выводами, между ними происходит много столкновений. и электроны.Это приводит к тому, что траектория электронов не прямая, а общая скорость остается довольно низкой, однако теперь чистая скорость дрейфа меняется от отрицательной к положительной. Эта серия столкновений уменьшает количество энергии, которую имеют электроны, происходит передача электрической потенциальной энергии тепловой энергии. В более слабых проводниках больше столкновений и передается большее количество электрического потенциала. Это называется сопротивлением. Чем больше столкновений, тем большее количество энергии передается теплу, тем больше разность потенциалов и тем больше сопротивление компонента.

Резисторы — это компоненты, которые имеют фиксированное значение сопротивления в диапазоне разностей потенциалов. Ток через них прямо пропорционален разности потенциалов на них. Говорят, что они следуют закону Ома, который описан в:

$$ R = \ frac {V} {I} $$

Закон

Ома гласит, что ток через проводник прямо пропорционален разности потенциалов на нем для проводника при постоянной температуре. Проводники, такие как резисторы, ведут себя омически при фиксированных температурах, и график зависимости тока от разности потенциалов дает прямую линию, проходящую через начало координат.Сопротивление компонента обратно градиенту. Резистор с высоким сопротивлением будет иметь относительно неглубокую линию, тогда как компонент с низким сопротивлением будет иметь крутую линию. Глядя на графики ниже, мы видим, что при одинаковом увеличении p.d. синяя линия имеет меньшее увеличение тока, протекающего через нее, чем красная линия. Другие компоненты имеют отличительные формы для графиков IV , о которых вам необходимо знать.

Рисунок 2: I.V. Характеристики различных компонентов.

Лампа накаливания или старомодная лампочка работает, пропуская большой ток через тонкий кусок проволоки, который становится очень горячим и начинает раскаливаться докрасна. Это возбуждает инертный аргон внутри колбы, чтобы произвести свет. При низких значениях p.d. лампочка с проводом ведет себя омически и линия прямая, но когда p.d. увеличивается сопротивление лампы увеличивается, и линия сглаживается.

Диод является полупроводником и пропускает ток только при определенных условиях.В случае поляризованных диодов ток может течь только в одном направлении, поэтому при изменении разности потенциалов ток не может течь, что объясняет горизонтальную линию в отрицательном квадранте графика. Когда они размещаются в прямом направлении, они позволяют току легко течь, но только после достижения порогового напряжения, после этого их сопротивление падает почти до нуля, и линия поднимается почти вертикально.

Наверх

Сопротивление и температура

Когда проводник нагревается, энергия передается частицам внутри проводника, и они начинают двигаться быстрее.В твердом теле, поскольку частицы находятся в фиксированном положении, это означает, что они начинают вибрировать быстрее. Это приводит к увеличению количества столкновений между частицами твердого проводника и электронами. Фактически, длина свободного пробега электронов уменьшается, и количество заряда, протекающего в секунду, также уменьшается, что приводит к увеличению сопротивления.

Нагревание может вызвать увеличение количества столкновений между электронами и частицами, и обратное также верно.Увеличение тока через проводник увеличит количество столкновений между частицами и электронами. Это вызывает передачу энергии от электронов к частицам внутри проводника и генерирует тепло. Это, в свою очередь, увеличивает сопротивление проводника. Этот эффект можно отчетливо увидеть, когда лампа накаливания включена и ток, протекающий через нее, анализируется в течение первых нескольких секунд. График ниже был получен с использованием регистратора данных в классе.

Рисунок 3: Как изменяется ток через лампочку накаливания в первые 3 секунды после ее включения.
При включении лампы внезапное увеличение тока, протекающего через лампочку. Поскольку колба остыла перед включением, частицы в нити накала не очень быстро вибрируют, и колба имеет низкое сопротивление. Это означает, что через него может протекать большой ток. По мере протекания тока электроны сталкиваются с ионами в нити накала и заставляют ее нагреваться, увеличивая сопротивление колбы. Это более высокое сопротивление означает, что может протекать меньший ток, и мы видим, что ток снижается до более низкого постоянного значения, известного как рабочий ток.Это хороший пример отрицательной обратной связи , где выходной сигнал системы в момент времени a приводит к тому, что выходной сигнал в момент времени b становится ниже. Это объясняет форму ВАХ лампы накаливания и то, почему сопротивление увеличивается с увеличением силы тока.
По мере увеличения тока через колбу накаливания увеличивается и температура нити накала, и, следовательно, увеличивается сопротивление. Это дает отчетливую S-образную кривую.
Соотношение между сопротивлением и температурой можно использовать для создания точных термометров, которые можно использовать в широком диапазоне температур.Вы проведете в классе эксперимент по созданию простейшего термометра с проводом сопротивления.
Наверх
Резисторы вокруг цепи
Когда в цепи несколько резисторов, может потребоваться объединить их значения, чтобы вычислить общее сопротивление или ток, протекающий в цепи. Когда все резисторы включены последовательно, это довольно просто, поскольку значения резисторов можно просто сложить.В приведенном ниже примере есть три резистора, каждый с разным сопротивлением.
Рисунок 4: Добавление резисторов в последовательную цепь.
Суммарное сопротивление для этой цепи составляет:
$$ \ large R_ {Total} = R_ {1} + R_ {2} + R_ {3} + \ cdots $$ $$ \ amount {10} {Ω} + \ amount {5} {Ω} + \ amount {12} {Ω} = \ amount {27} {Ω}; $$
Несмотря на простую взаимосвязь, выражение для полного сопротивления в последовательной цепи может быть получено, если вспомнить, что сумма разностей потенциалов на каждом резисторе равна ЭДС, подаваемой в цепь (2-й закон Кирхгофа).
\ begin {align} ε & = V_ {1} + V_ {2} + V_ {3} + \ cdots \\ \\ IR_ {T} & = IR_ {1} + IR_ {2} + IR_ {3} + \ cdots \\ \\ IR_ {T} & = I \ left (R_ {1} + R_ {2} + R_ {3} + \ cdots \ right) \\ \\ R_ {T} & = R_ {1} + R_ {2} + R_ {3} + \ cdots \ end {align}
Наверх
Резисторы параллельно
С резисторами, включенными параллельно, ситуация несколько сложнее, и стоит подумать об этом простыми словами. Разница между последовательными и параллельными цепями заключается в том, что ток разделяется на соединениях в параллельной цепи.Каждая единица заряда получает от клетки определенное количество энергии. Он будет использовать эту энергию только при прохождении через сопротивление. На диаграмме ниже каждая оранжевая точка представляет $ \ amount {1} {C} $ заряда, несущего $ \ amount {1} {J} $ электрического потенциала. На перекрестке заряды либо повернут направо, либо продолжат движение прямо. Поскольку сопротивление каждой ветви одинаково, через каждую проходит одинаковое количество тока. Каждый заряд выполняет $ \ amount {1} {J} $ работы, когда проходит через сопротивление, а это означает, что разность потенциалов на каждой ветви равна $ \ amount {1} {V} $.
Рисунок 5: Разделение тока на стыке.
Мы также можем видеть, что ток на каждой ветви меньше, чем ток до соединения, но количество энергии, которое имеет каждый кулон заряда, одинаково до и после соединения. Мы также можем применить к этой схеме два закона Кирхгофа:
Ток в каждой ветви меньше, чем ток перед соединением, но их сумма равна току перед соединением. Это удовлетворяет первому закону.
Рассматривая каждую ветвь как отдельную петлю, мы можем видеть, что разность потенциалов на каждой ветке такая же, как энергия, удерживаемая каждым кулоновским зарядом (ЭДС) перед переходом, что, согласно второму закону, должно быть равным кейс.
Мы можем применить 1-й закон Кирхгофа, чтобы вывести уравнение для полного сопротивления в параллельной цепи. Сумма токов на каждой ветви будет равна общему току на выходе из ячейки:
\ begin {align} I_ {T} & = I_ {1} + I_ {2} + I_ {3} + \ cdots \\ \\ \ frac {V} {R_ {T}} & = \ frac {V} {R_ {1}} + \ frac {V} {R_ {2}} + \ frac {V} {R_ {3}} + \ cdots \\ \\ \ frac {1} {R_ {T}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + \ компакт-диски \ end {align}
Это уравнение заслуживает некоторого обсуждения, поскольку оно приводит к несколько нелогичному выводу, что если мы добавим больше параллельных резисторов, общее сопротивление цепи фактически уменьшится
Если мы посмотрим на схему ниже, то увидим, что с одним резистором $ \ amount {2} {Ω} $ разность потенциалов будет $ \ amount {6} {V} $, а ток будет $ \ amount {3} {A} $.
Рисунок 6: Ток, потребляемый одним резистором.
Если второй резистор более высокого номинала добавляется параллельно первому, открывается другой путь или путь, через который протекает ток. Даже из-за того, что сопротивление на этом пути выше, через него протекает меньше тока, теперь через цепь протекает больше тока в целом. Мы можем рассчитать ток в каждой ветви, используя закон Ома, помня, что каждая ветвь будет иметь одинаковую разность потенциалов.
Рисунок 7: Ток, потребляемый двумя параллельными резисторами.
Для резистора R ₁:
\ begin {align} I & = \ frac {V} {R} \\ \\ I & = \ frac {\ amount {6.0} {V}} {\ amount {2.0} {Ω}} \\ \\ I & = \ amount {3.0} {A} \ end {align}
Для резистора R ₂:
\ begin {align} I & = \ frac {V} {R} \\ \\ I & = \ frac {\ amount {6.0} {V}} {\ amount {20} {Ω}} \\ \\ I & = \ amount {0.30} {A} \ end {align}
Полный ток складывается из токов на ответвлениях:
$$ I_ {Итого} = \ количество {3.0} {A} + \ amount {0.30} {A} = \ amount {3.3} {A} $$
Когда добавляется третий резистор с еще более высоким значением, чем любой из первых двух, открывается еще один путь для протекания тока, и ток, выходящий из ячейки, снова увеличивается.
Рисунок 8: Ток, потребляемый тремя параллельными резисторами.
Поскольку каждый раз из ячейки выходит больше тока и ячейка имеет фиксированную ЭДС, следует сделать вывод, что поскольку $ R = \ frac {V} {I} $, поскольку I увеличивается каждый раз, когда добавляется резистор, то общее сопротивление цепи должно уменьшиться.
Мы можем рассчитать сопротивление конечной цепи, используя уравнение, которое мы вывели выше:
\ begin {align} \ frac {1} {R_ {T}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\ \\ \ frac {1} {R_ {T}} & = \ frac {1} {\ amount {2.0} {Ω}} + \ frac {1} {\ amount {20} {Ω}} + \ frac {1} {\ amount {200} {Ω}} \\ \\ \ frac {1} {R_ {T}} & = 0,555 \ end {align}
Мы должны быть очень осторожны, так как это значение, которое мы только что вычислили, это $ \ frac {1} {R} $, а не $ R $, поэтому мы должны найти обратное этому значению, чтобы найти сопротивление.
$$ R = \ frac {1} {0.555} = \ amount {1.8} {Ω} $$
Обратите внимание, что полное сопротивление цепи на самом деле ниже, чем у наименьшего резистора в цепи. Вы можете использовать это как хороший способ проверить свои расчеты, поскольку сопротивление параллельной сети всегда будет ниже, чем сопротивление любого из резисторов в этой сети.
Комбинированные резисторы последовательно и параллельно
Когда мы сталкиваемся с более сложными схемами, которые имеют комбинации последовательно включенных резисторов и , мы должны следовать следующим правилам, чтобы найти полное сопротивление схемы и, таким образом, произвести дальнейшие вычисления:
Работайте от самой дальней от ячейки ветви и выполняйте вычисления по направлению к ячейке.
Добавьте все последовательные резисторы, которые находятся на параллельных ветвях.
Рассчитайте сопротивление параллельных сетей.
Добавьте это сопротивление к любым другим резисторам серии.
В приведенном ниже примере ветвь, содержащая R ₄ и R ₅, должна обрабатываться первой, поскольку она наиболее удалена от ячейки.
Рисунок 9: Соединение резисторов последовательно и параллельно.
$$ R_ {4} + R_ {5} = \ amount {8.0} {Ω} + \ amount {6.0} {Ω} = \ amount {14} {Ω} $$
Таким образом, эта ветвь имеет сопротивление $ \ amount {14} {Ω} $, которое можно объединить с R ₃ со значением $ \ amount {12} {Ω} $, чтобы найти полное сопротивление параллельной сети. . Мы знаем, что полное сопротивление этой части схемы будет меньше $ \ amount {12} {Ω} $, так что это позволит нам проверить наш ответ на ошибки.
\ begin {align} \ frac {1} {R_ {T}} & = \ frac {1} {R_ {3}} + \ frac {1} {R_ {4 + 5}} \\ \\ \ frac {1} {R_ {T}} & = \ frac {1} {\ amount {12} {Ω}} + \ frac {1} {\ amount {14} {Ω}} \\ \\ \ frac {1} {R_ {T}} & = 0.1547619 \\ \\ R_ {T} & = \ amount {6.5} {Ω} \ end {align}
Наконец, теперь мы можем добавить это сопротивление к двум последовательным резисторам, R ₁ и R ₂, чтобы найти полное сопротивление цепи,
$$ \ amount {5.0} {Ω} + \ amount {2.0} {Ω} + \ amount {6.5} {Ω} = \ amount {13.5} {Ω} $$
Теперь мы знаем полное сопротивление цепи, учитывая, что ЭДС батареи равна $ \ amount {3} {V} $, мы можем вычислить ток как $ \ amount {0.22} {A}
долл. США
Наверх
Рабочий пример
В этом примере вопрос начинается с некоторых расчетов сопротивления, прежде чем вас попросят сравнить потенциалы между отмеченными точками.
На схеме ниже показана батарея $ \ amount {12} {V} $ с незначительным внутренним сопротивлением, подключенная к комбинации из трех резисторов и термистора.
Рисунок 10: Рабочий пример 1.
Когда сопротивление термистора равно $ \ amount {5.0} {kΩ}
долл. США
рассчитать полное сопротивление цепи,
Поскольку на обеих ветвях есть по два резистора, нам нужно сложить их вместе, чтобы найти общее сопротивление на каждой ветви, прежде чем мы найдем сопротивление параллельной сети.
Сопротивление между A-E
$$ \ amount {20} {kΩ} + \ amount {20} {kΩ} = \ amount {40} {kΩ} $$
Сопротивление между B-F
$$ \ amount {10} {kΩ} + \ amount {5.0} {kΩ} = \ amount {15} {kΩ} $$
Теперь, когда мы знаем полное сопротивление каждой ветви, мы можем использовать уравнение для параллельных резисторов, чтобы найти полное сопротивление цепи.
\ begin {align} \ frac {1} {R_ {T}} & = \ frac {1} {\ amount {40} {kΩ}} + \ frac {1} {\ amount {15} {kΩ}} \\ \ frac {1} {R_ {T}} & = 0,1916666 \\ \\ R_ {T} & = \ amount {10.9} {kΩ} = \ amount {11} {kΩ} \ end {align}
При выполнении подобного вычисления с промежуточным вычислением, в данном случае для $ \ frac {1} {R_ {T}} $, вы должны либо записать полный ответ, как показано на вашем калькуляторе, либо использовать память калькулятора. настройки, чтобы сохранить его для последнего шага.Для окончательного ответа я округлил результат до того же количества значащих цифр, что и данные в вопросе.

рассчитать ток в батарее (в $ \ units {mA} $).
С сопротивлением цепи, рассчитанным в части i. и ЭДС ячейки, указанной в вопросе, мы можем использовать закон Ома, чтобы найти полный ток, протекающий в цепи:
\ begin {align} I & = \ frac {V} {R} \\ \\ I & = \ frac {\ quantity {12} {V}} {\ amount {10.9} {кОм}} \\ \\ I & = \ amount {1.10} {mA} \ end {align}
Поскольку все сопротивления выражены в $ \ units {kΩ} $, а вопрос задает ток в $ \ units {mA} $, нет необходимости преобразовывать сопротивления в $ \ units {Ω} $.

Вольтметр с высоким сопротивлением используется для измерения разности потенциалов (pd) между точками A-C, D-F и C-D по очереди.
Заполните следующую таблицу, указав показания вольтметра в каждой из трех позиций.

вольтметр положение p.d. / V
A-C
D-F
C-D
Разности потенциалов между A-C и D-F легко вычислить без каких-либо дополнительных вычислений. Мы знаем, что п.д. на каждой ветви находится $ \ amount {12} {V} $, а на первой ветви два резистора имеют одинаковое значение, поэтому p.d. в каждом из них равны, в данном случае $ \ amount {6} {V} $.
Сопротивление резистора между ответвлением в два раза больше сопротивления термистора между D-F, поэтому p.d. на резисторе будет вдвое больше p.d. поперек термистора, поэтому p.d. поперек термистора находится $ \ amount {4} {V} $.
Наконец, между двумя ветвями подключается вольтметр, как показано на схеме ниже:
Рисунок 11: Рабочий пример 2.
Поначалу кажется, что решить эту проблему очень сложно, но, применив 2-й закон Кирхгофа к каждой ветви и сравнив величину электрического потенциала, удерживаемого током после прохождения через первый резистор, мы можем можно сравнить разность потенциалов в двух ветвях.
В верхней ветви ток содержит $ \ amount {12} {V} — \ amount {6} {V} = \ quantity {6} {V} $, а в нижней ветви мы уже сделали вывод, что ток имеет $ \ amount {4} {V} $. Разница в двух потенциалах будет показанием вольтметра и составит $ \ amount {6} {V} — \ amount {4} {V} = \ amount {2} {V} $
.
Термистор нагревается, поэтому его сопротивление уменьшается. Укажите и объясните, как это влияет на показания вольтметра в следующих положениях.

А-С
В этом вопросе мы должны дать объяснение наблюдаемого изменения на вольтметре. В этом случае показания вольтметра не изменяются. Причина в том, что сопротивление ветви цепи не изменяется, поэтому p.d. через эту ветку все то же самое.
D-F
В заключительной части вопроса отметим, что сопротивление термистора уменьшается, поэтому показания вольтметра также уменьшаются.Это потому, что p.d. прямо пропорциональна сопротивлению, и поэтому большая часть p.d. через эту ветвь будет над резистором $ \ amount {10} {kΩ} $.
Наверх
Что такое сопротивление в физике?
Какое определение сопротивления в физике?
Что такое сопротивление проводника
Движение электрона вызывает протекание тока через металлы.Движущиеся электроны сталкиваются друг с другом, а также с положительными ионами, присутствующими в металлическом проводнике. Эти столкновения замедляют скорость электронов и, следовательно, препятствуют прохождению электрического тока.
Свойство проводника, благодаря которому он препятствует прохождению электрического тока через него, называется его сопротивлением .
Мера сопротивления проводника потоку тока известна как сопротивление проводника .Разные проводники имеют разное сопротивление току.
Сопротивление обозначается буквой R.
Сопротивление R проводника определяется как отношение разности потенциалов V в проводнике к току I, протекающему по нему.
Таким образом:
Единица сопротивления в системе СИ — ом. Ом обозначается греческой буквой (Ω), которая называется омега.
Сопротивление — это скалярная величина.
Один Ом — это сопротивление проводника, когда разность потенциалов в 1 вольт, приложенная к его концам, вызывает протекание через него тока в 1 ампер.
Люди тоже спрашивают
Какие факторы влияют на сопротивление проводника?
В телекоммуникационной и энергетической отраслях очень важно выбрать подходящие электрические кабели для передачи электрического тока для различных целей.
Наиболее важным фактором, который следует учитывать при выборе кабелей, является сопротивление проводников в кабеле.
На сопротивление проводника влияет тип материала, из которого он сделан, а также его длина, толщина и температура.
Факторы, от которых зависит сопротивление проводника
Влияние длины на сопротивление проводника
Сопротивление проводника прямо пропорционально длине. Это сопротивление проводника ∝ длина проводника.
Влияние площади поперечного сечения на сопротивление проводника
Сопротивление проводника обратно пропорционально его площади поперечного сечения.
То есть сопротивление проводника;
\ (R \ propto \ frac {\ text {1}} {\ text {Area} \, \ text {of} \, \ text {cross-section} \, \ text {(a)} \, \ text {of} \, \ text {the} \, \ text {проводник}} \)
Если площадь поперечного сечения проводника увеличивается вдвое, его сопротивление уменьшается вдвое.
Влияние температуры на сопротивление проводника
Сопротивление всех чистых металлов увеличивается с повышением температуры. Сопротивление сплавов очень незначительно увеличивается с повышением температуры. Для металла при повышении температуры сопротивление увеличивается, а для полупроводников при повышении температуры сопротивление уменьшается.
Влияние природы материала на сопротивление проводника
Некоторые материалы имеют низкое сопротивление, тогда как другие имеют гораздо более высокое сопротивление.Как правило, сплав имеет более высокое сопротивление, чем чистые металлы, полученные из сплава.
* Медь, серебро, алюминий и т. Д. Имеют очень низкое сопротивление.
* Нихром, константан и др. Обладают более высокой стойкостью. Из нихрома изготавливают нагревательные элементы нагревателей, тостеров, утюга и т. Д.
Таким образом, сопротивление R данного проводника:
Прямо пропорциональна его длине, l (R∝ l)
обратно пропорционален его площади поперечного сечения, A (R ∝ 1 / A)
Зависит от типа материала или удельного сопротивления ρ
Влияет на температуру
В таблице приведены факторы, влияющие на сопротивление, и их взаимосвязь.

Факторы, влияющие на сопротивление проволоки Эксперимент
Цель: Исследовать факторы, влияющие на сопротивление.
Проблема: Какие факторы влияют на сопротивление проводящего провода?
Материалы: Эврика-проволока 50 см (SWG 24), 50-сантиметровая проволока из константана (SWG 24, SWG 30, SWG 34), медная проволока 50 см (SWG 24), константановая проволока 100 см (SWG 24)
Аппарат: Амперметр (0 — 1 А), вольтметр (0 — 5 В), держатель батареи, реостат (0 — 15 Ом), переключатель, соединительные провода, три 1.Сухие элементы 5 В
A. Как тип материала влияет на эксперимент на сопротивление
Гипотеза: При фиксированной длине и толщине используемого проводника его сопротивление зависит от типа материала.
Переменные:
(a) Управляемая переменная: Типы материала проволоки
(b) Реагирующая переменная: Сопротивление, R
(c) Фиксированная переменная: Толщина, длина и температура проволоки
Оперативное определение: Сопротивление , R токопроводящего провода определяется отношением показания вольтметра к показанию амперметра.
Метод:
Установлена электрическая схема, показанная на рисунке.
Провод P (эврика длиной 50 см с мерной массой 24) подключается к клеммам X и Y.
Переключатель замыкается, и реостат настраивается так, чтобы зафиксировать показания амперметра для тока I = 0,5 А. Показания вольтметра для разности потенциалов V записываются в таблицу.
Рассчитывается значение сопротивления R = V / I.
Шаги с 2 по 4 повторяются путем замены провода P на:
(a) Провод Q: провод из константана длиной 50 см на s.w.g. 24
(b) Провод 5: медный провод длиной 50 см с твердым покрытием. 24
Результатов:
Выводы:
Сопротивление R провода эврики самое высокое, тогда как сопротивление R медного провода самое низкое.
Мера способности материала противодействовать прохождению тока также известна как удельное сопротивление материала p. Таким образом, мы можем сделать вывод, что для фиксированной длины и толщины провода сопротивление зависит от типа материала, из которого изготовлена проволока.
B. Как длина провода влияет на сопротивление (эксперимент)
Гипотеза: Сопротивление проводящего провода увеличивается с увеличением его длины.
Переменные:
(a) Управляемая переменная: Длина провода, l
(b) Реагирующая переменная: Сопротивление, R
(c) Фиксированная переменная: Толщина, тип провода и температура провода
Оперативное определение: Сопротивление R проводника определяется отношением показания вольтметра к показанию амперметра.
Метод:
Используется та же электрическая схема, что и на рисунке.
Проволока из константана длиной 100 см из нерж. 24 подключен к клеммам X и Y.
Длину проволоки доводят до l = 20 см.
Переключатель замыкается, и реостат настраивается так, чтобы зафиксировать показания амперметра для тока I = 0,5 А. Показания вольтметра для разности потенциалов V записываются в таблицу.
Шаги с 3 по 4 повторяются для l = 40 см, 60 см, 80 см и 100 см.
Значение сопротивления R = V / I рассчитывается для каждого значения длины провода l.
Построен график зависимости R от l.
Результатов:
Табулирование результатов.
График зависимости R от l.
Вывод:
Сопротивление R токопроводящего провода прямо пропорционально длине провода l. Гипотеза принята. Сопротивление R провода увеличивается с увеличением его длины l.
C. Как площадь поперечного сечения (толщина проволоки) влияет на эксперимент по сопротивлению
Гипотеза: При фиксированной длине проводника, чем толще провод, тем меньше сопротивление.
Переменные:
(a) Управляемая переменная: Толщина проволоки
(b) Реагирующая переменная: Сопротивление, R
(c) Фиксированная переменная: Тип, длина и температура проволоки
Оперативное определение:
(a) Толщина проводника определяется величиной его s.w.g.
(b) Сопротивление R проводящего провода определяется отношением показания вольтметра к показанию амперметра.
Метод:
Используется та же электрическая схема, что и на рисунке выше.
Провод Q (константановый провод длиной 50 см с мерной массой 24) подключается к клеммам X и Y.
Переключатель замыкается, и реостат настраивается так, чтобы зафиксировать показания амперметра для тока I = 0,5 А. Показания вольтметра для разности потенциалов V записываются в таблицу.
Рассчитывается значение сопротивления R = V / I.
Шаги 2–4 повторяются с использованием проволоки из константана длиной 50 см с н.в.г. 30 и s.w.g. 34.
Результатов:
Обсуждение:
Стоимость s.w.g. проволоки соответствует ее диаметру. Проволока с большим с.в.г. имеет меньший диаметр.
Площадь поперечного сечения A провода можно определить по его диаметру D по уравнению:
Вывод:
Сопротивление R провода обратно пропорционально его площади поперечного сечения A.Чем толще провод, тем меньше сопротивление. Гипотеза принята. .
D. Как температура влияет на экспериментальное сопротивление
Гипотеза: Когда температура лампы накаливания увеличивается, ее сопротивление увеличивается.
Переменные:
(a) Управляемая переменная: температура нити
(b) Реагирующая переменная: сопротивление, R
(c) Фиксированная переменная: Тип используемой лампы
Оперативное определение:
(a) Температура нить накала определяется яркостью колбы.
(b) Сопротивление R нити накала определяется отношением показания вольтметра к показанию амперметра.
Метод:
Используется та же электрическая цепь, что и на рисунке выше, с заменой провода P лампой накаливания.
Переключатель замкнут и реостат выставлен на максимум, так что лампочка не загорается. Показания амперметра по току I и вольтметра по разности потенциалов V заносятся в таблицу.
Шаг 2 повторяется путем регулировки реостата до тех пор, пока лампочка не станет тускло, а затем немного ярче и очень яркой.
Рассчитывается значение сопротивления R = V / I.
Результатов:
Обсуждение:
Яркость лампочки соответствует температуре лампочки. Чем ярче колба, тем выше ее температура.
Заключение:
Сопротивление нити накала увеличивается с увеличением ее температуры.Гипотеза принята.
Сопротивление и класс сопротивления десять Наука Физика NCERT
Сопротивление
Сопротивление — это свойство проводника, благодаря которому он сопротивляется прохождению через него электрического тока. Компонент, который используется для сопротивления прохождению электрического тока в цепи, называется резистором.
На практике резисторы используются для увеличения или уменьшения электрического тока.
Переменное сопротивление: Компонент электрической цепи, который используется для регулирования тока без изменения напряжения от источника; называется переменным сопротивлением.
Реостат: Это устройство, которое используется в цепи для обеспечения переменного сопротивления.
Причина сопротивления в проводнике:
Поток электронов в проводнике — электрический ток. Частицы проводника создают препятствие потоку электронов; из-за притяжения между ними. Это препятствие является причиной сопротивления току электричества.
Сопротивление проводника зависит от типа, длины и площади поперечного сечения проводника.
Тип материала: Некоторые материалы создают наименьшие помехи и поэтому называются хорошими проводниками. Серебро — лучший проводник электричества. В то время как некоторые другие материалы создают больше препятствий для прохождения электрического тока, то есть прохождения через них электронов. Такие материалы называют плохими проводниками. Плохие проводники также известны как изоляторы. Жесткий пластик — один из лучших изоляторов электричества.
Длина проводника: Сопротивление R прямо пропорционально длине проводника.Это означает, что сопротивление увеличивается с увеличением длины проводника. Это причина того, что длинные электрические провода создают большее сопротивление электрическому току.
Таким образом, сопротивление (R) ∝ длина проводника (l)
Или `R ∝ l` ——— (i)
Площадь поперечного сечения: сопротивление R обратно пропорционально площади поперечного сечения (A) проводника. Это означает, что R будет уменьшаться с увеличением площади проводника и наоборот. Большая площадь проводника способствует прохождению электрического тока через большую площадь и, таким образом, снижает сопротивление.Это причина того, что толстый медный провод создает меньшее сопротивление электрическому току.
Таким образом, `текст (сопротивление) ∝ (1) / (текст (площадь))` поперечного сечения проводника (A)
Или, `R∝1 / A` ——— (ii)
Из уравнений (i) и (ii)
`R∝l / A`
Или, `R = ρ \ l / A` ———— (iii)
Где ρ (rho) — константа пропорциональности. Это называется удельным электрическим сопротивлением материала проводников.
Из уравнения (iii)
`RA = ρl`
Или, `ρ = (RA) / (l)` ———- (iv)
Единица измерения удельного сопротивления в системе СИ: Поскольку единицей измерения R в системе СИ является Ом, единицей измерения площади в системе СИ является м ², а единицей измерения длины в системе СИ является м.2) / (м) = & Ом; м`
Таким образом, единицей измерения удельного сопротивления (ρ) в системе СИ является Ом · м
Материалы с удельным сопротивлением в диапазоне от 10 ⁻⁸ Ом м до 10 ⁻⁶ Ом м считаются очень хорошими проводниками. Серебро имеет удельное сопротивление 1,60 X 10 ⁻⁸ Ом · м, а медь имеет удельное сопротивление 1,62 · 10 ⁻⁸ Ом · м.
Резина и стекло — очень хорошие изоляторы. Они имеют удельное сопротивление порядка от 10 ¹² Ом · м до 10 ¹⁷ Ом · м.
Удельное сопротивление материалов зависит от температуры.2) `
`= (10xx2 & ohm;) / (7.65xx10)`
`= (2 Ом;) / (7,65) = 0,26 Ом;`
Пример 4: Площадь поперечного сечения провода уменьшается вдвое, когда его длина увеличивается вдвое. Как изменится сопротивление провода в новом состоянии?
Решение: Пусть площадь сечения провода = А
Пусть длина проволоки перед растяжкой = L
Пусть Сопротивление провода = R
После натяжения проволоки пустить
Площадь поперечного сечения = A / 2
Длина = 2 л
Сопротивление = R1
Таким образом, отношение сопротивления перед растяжением к сопротивлению после растяжения можно представить следующим образом:
Или, `R: R_1 = (ρL) / (A): (ρ2L) / (A / 2)`
Или, `R: R_1 = (ρL) / (A): (4ρ L) / (A)`
Или, `R: R_1 = 1: 4`
Это означает R = 1 и R1 = 4
Таким образом, после растяжения проволоки сопротивление увеличивается в четыре раза.
SPM Physics Форма 4 / Форма 5 Примечания к редакции
Сопротивление
Сопротивление материала R определяется как отношение V: I, где V — это разность потенциалов в материале, а I — ток, протекающий в нем. VI = сопротивление (R)
В системе СИ единицей сопротивления является ом (Вт). Один Ом — это сопротивление материала, через который протекает ток в один ампер при сохранении разности потенциалов в один вольт.

Нахождение сопротивления по разнице потенциалов — график токов
На графике зависимости разности потенциалов от тока градиент графика равен сопротивлению резистора.
Сопротивление, R = Градиент графика
Пример :

На рисунке выше показан график зависимости разности потенциалов на проводе от его тока. Найдите сопротивление провода.
Ответ :
Сопротивление
R = VI = Градиент графика R = 153 = 5V
Омический проводник
(Примеры неомического проводника)

Проводники, подчиняющиеся закону Ома, называются омическими проводниками.
Примеры омического проводника: металл, раствор сульфата меди с медными электродами

Неомический проводник

Проводники, не подчиняющиеся закону Ома, называются неомическими проводниками.
Пример: полупроводниковый диод, ламповый диод
Факторы, влияющие на сопротивление 1
Сопротивление R данного проводника зависит от:
его длины l,
площадь его поперечного сечения А
его температура и
тип материала.

Длина

Сопротивление прямо пропорционально длине проводника.
Площадь поперечного сечения

Сопротивление обратно пропорционально площади поперечного сечения проводника.
Температура

Провод с более высокой температурой имеет более высокое сопротивление.
Материал

Разные материалы имеют разное удельное сопротивление. Сопротивление медной проволоки ниже, чем у железной.
Т.

Сопротивление это в физике: Origin DNS error | www.fluke.com

что это такое в физике, как найти трение в механике и динамике

Что такое сила сопротивления в физике

От чего зависит в механике и динамике

Разновидности сил сопротивления

Сила сопротивления качению

Сила сопротивления воздуха

Как найти трение

Силы сопротивления при больших скоростях

Как найти внутреннее сопротивление формула в физике. Электродвижущая сила. Внутреннее сопротивление источника тока

Ход работы

Определение эдс и внутреннего сопротивления источника тока графическим методом

Внутреннее сопротивление источника тока.

2 шаг

3 шаг

Лекция 1. Сопротивление материалов. Основные понятия и определения

Основные определения

Сопротивление материалов — раздел физики, изучающий механические свойства различных материалов, используемых в строительстве и машиностроении

Объекты рассмотрения — твердые тела

1. Стержни — твердые тела, длина l которых значительно больше высоты h и ширины b.

2. Пластины — тела, высота которых значительно меньше длины и ширины.

3. Массивные тела — тела, длина, ширина и высота которых сопоставимы.

Основной объект рассмотрения — стер­жень (балка, брус).

Ось стержня — линия, проходящая через центры тяжести поперечных сечений стержня.

Поперечное сечение — сечение стержня в плоскости, перпендикулярной оси стержня.

Расчет прочности — определение наименьших размеров поперечного сечения элементов конструкции

Расчет жесткости — определение деформаций материала

Устойчивость — состояние элементов конструкции

Деформация — изменение геометрических размеров и первоначальной формы физического тела при действии сил.

Линейная деформация — перемещение рассматриваемой точки, линии или поперечного сечения относительно только одной из выбранных осей координат.

Угловая деформация — перемещение, характеризуемое углом поворо­та рассматриваемой линии или поперечного сечения

Абсолютная деформация — величина линейной де­формации

Относительная деформация — отношение абсолютной деформации к длине

Пластические (остаточные) деформации — изменения геометрических размеров и формы тела

Упругие деформации — деформации тела под действием нагрузок, не приводящие к остаточным деформациям после снятия нагрузок

Упругость — свойство материала полностью восстанавливать первоначальную геометрическую форму тела

Пластичность — свойство материала накапливать остаточные деформации

Сжатие или растяжение — такое воздействие на материал, при котором силы, действующие на стержень, направлены по оси или параллельно оси стержня.

Кручение — воздействие на материал пары сил, действующих в плоскости, перпендикулярной к оси стержня

Изгиб — воздействие на материал пары сил, направленных в плоскости, проходящей через ось стержня.

Изотропный материал — материал, физико-механические свойства которого постоянны и одинаковы во всех направлениях

Ортотропный материал — материал, физико-механические свойства которого постоянны, но не одинаковы в различных направлениях

Анизотропный материал — материал, не имеющий свойств изотропности или ортотропности

Основные допущения, принимаемые в теории сопротивления материалов

Внешние и внутренние силы

Внешние силы по характеру приложения можно разделить на четыре вида:

Интенсивность нагрузки — это величина распределенной нагрузки, приложенной к единице объема, площади или длины.

По времени действия нагрузки делятся на постоянные и временные

По характеру изменения во времени нагрузки делятся на статические и динамические

Напряжение — величина внутренней силы, приложенной к единице площади рассматриваемого сечения

Уравнения равновесия. Метод сечений

Ось, перпендикулярная плоскости сечения, называется нормалью.

Нормальное напряжение

Касательное напряжение

дальше

Конспект урока по физике на тему «Электрическое сопротивление проводников.

Постоянный электрический ток

9: Ток и сопротивление — Physics LibreTexts

Что такое резисторы и сопротивление — AP Physics B

Сопротивление

Mr Toogood Physics — Резисторы и сопротивление

Сопротивление

Сопротивление и температура

Резисторы вокруг цепи

Резисторы параллельно

Комбинированные резисторы последовательно и параллельно

Рабочий пример

Что такое сопротивление в физике?

Какое определение сопротивления в физике?

Какие факторы влияют на сопротивление проводника?

B. Как длина провода влияет на сопротивление (эксперимент)

Сопротивление и класс сопротивления десять Наука Физика NCERT

Сопротивление

Причина сопротивления в проводнике:

SPM Physics Форма 4 / Форма 5 Примечания к редакции

Сопротивление

Нахождение сопротивления по разнице потенциалов — график токов

Омический проводник

Неомический проводник

Факторы, влияющие на сопротивление 1

Основной объект рассмотрения — стержень (балка, брус).

Угловая деформация — перемещение, характеризуемое углом поворота рассматриваемой линии или поперечного сечения

Абсолютная деформация — величина линейной деформации