Соотношение между фазными и линейными напряжениями
Напряжение фаз нагрузки отличны от значения ЭДС генератора из-за падения напряжения на линии от генератора к потребителю. Длина этих линий может составлять несколько метров, а может и пару сотен метров, также возможна длина и в тысячи километров. Вопросы о падении напряжений на линиях электрических передач ЛЭП, снабжающих потребителей энергией электрической от электрических станций будут рассматриваться чуть позже, в последующих статьях. Для упрощения расчетов указанным значением падений напряжений можно пренебречь.
Соединение звездой
При принятых допущениях для соединенных источников звездой:

применив второй закон Кирхгофа получим:

Из выражения (1) можно сделать вывод, что при симметричной системе ЭДС генератора его фазные напряжения также симметричны, и, соответственно, их векторная диаграмма:

не будет отличатся от векторной диаграммы ЭДС:

Исходя из уравнений, составленных по второму закону Кирхгофа для контуров (схема соединения в звезда указана выше):

Исходя из этих уравнений можно составить следующие уравнения, которые связывают линейные и фазные напряжения:

Использовав выражение (2) при наличии векторов фазных напряжений можно построить векторы линейных напряжений Uab, Ubc, Uca.
Исследовав векторную диаграмму при соединении звездой можно сделать вывод, что линейные напряжения будут равны и, как и фазные, сдвинуты друг относительно друга на угол 120

Из этого следует:

Соответственно такие же соотношение и между остальными фазными и линейными значениями:

Соединение треугольником
Выражения (1) будут правильны и при соединении в треугольник источника. Из формул (2) следует равенство фазных и линейных напряжений при соединении треугольником, и это можно представить в таком виде:

Или можно записать как Uл = Uф.
Векторная диаграмма при соединении треугольником для линейных и фазных напряжений:

Номинальные напряжения
Из выше перечисленного можно сделать такие выводы как – трехфазная сеть имеет два напряжения, а именно фазные и линейные. При соединении звездой линейные напряжения  больше фазных, а при соединении треугольником равны. Этот фактор необходимо учитывать при подключении нагрузки, чтоб не произошло аварийных ситуаций и выхода оборудования из строя.
больше фазных, а при соединении треугольником равны. Этот фактор необходимо учитывать при подключении нагрузки, чтоб не произошло аварийных ситуаций и выхода оборудования из строя.
Линейные напряжения тоже сдвинуты друг относительно друга на угол 1200 или 2π/3.
Номинальные напряжения – напряжения, на которые рассчитываются потребители электроэнергии, и которые соответствуют их нормальной работе.
Наиболее распространенными напряжениями в сетях до 1000 В являются 380В, 220В, 127В. 380 В и 220 В наиболее распространены в промышленности, а 220 В и 127 В в бытовых электросетях. Также при четырехпроводной электросети (соединения звезда с нулевым проводом) существует возможность получения фазного напряжения, которые при линейном 380 В будут равны 
 . Такое соединение дает плюс в виде возможности при наличии четырехпроводной сети производить подключение как трехфазных потребителей 380 В, так и однофазных с номиналом в 220 В.
. Такое соединение дает плюс в виде возможности при наличии четырехпроводной сети производить подключение как трехфазных потребителей 380 В, так и однофазных с номиналом в 220 В.Соотношение между линейными и фазными токами и напряжениями.
Силовое оборудование
Cиловое оборудование относится к категории электротехнических устройств, используемых для приема/подачи, учета, а так же распределения электроэнергии. Его основная задача — контроль над электричеством.
Существует множество методов учета и контроля. Они зависят от потребностей потребителя электроэнергии и требований, установленных на предприятии. Наиболее популярным методом остается установка электрического счетчика. В более сложных случаях монтируют интеллектуальные устройства, которые отслеживают поступление и распределение электричества.
Кроме этого, к группе силового оборудования относятся силовые разъемы, автоматические выключатели. Эти устройства используют на крупных объектах, где установлена техника высокой мощности. Это объясняется тем, что кроме контроля и учета, необходимо поддержание высокого уровня безопасности, бесперебойность работы, возможность работы в условиях большой нагрузки на электросеть.
Оборудование данной категории отвечает таким эксплуатационным требованиям:
Напряжение между линейным проводом и нейтралью (Ua, Ub, Uc) называется фазным. Напряжение между двумя линейными проводами(UAB, UBC, UCA) называется линейным. Для соединения обмоток звездой, при симметричной нагрузке, справедливо соотношение между линейными и фазными токами и напряжениями:
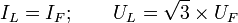
Двухпозиционное регулирование
Сущность двухпозиционного регулирования заключается в том, что регулирующий орган все время занимает одно из двух крайних положений — «включено» или «выключено»; причем включение или выключение форсунок в мазутных печах происходит в зависимости от того, в какую сторону отклонилась температура. Преимуществом двухпозиционного регулирования является возможность использования всех форсунок, дающих хорошее распыление, мазута, только на каком-нибудь одном режиме их работы; кроме того, схема автоматического регулирования достаточно проста.[399, С.174] Преимуществом двухпозиционного регулирования по сравнению с любым непрерывным является возможность использования на автоматизированных печах мазутных форсунок, обладающих узким диапазоном регулирования производительности, например форсунок низкого давления. При двухпозиционном регулировании форсунки работают всегда на одном режиме, а изменение нагрузки происходит при уменьшении или увеличении периодов выключения или включения форсунок.[400, С.277] Крупным недостатком двухпозиционного регулирования температуры является то, что вследствие периодичности подачи и сжигания мазута невозможно поддерживать оптимальное давление в печи, что периодически приводит к подсосу или выбиванию[
Гармонический
осциллятор (в классической
механике) —
это система,
которая при смещении из положения
равновесия испытывает действие возвращающей силы  ,
пропорциональной смещению
(согласно закону
Гука):
,
пропорциональной смещению
(согласно закону
Гука):
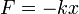
где k — положительная константа, описывающая жёсткость системы.
Если 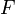 —
единственная сила, действующая на
систему, то систему называют простым или консервативным
гармоническим осциллятором.
Свободные колебания такой системы
представляют собой периодическое
движение около положения равновесия
(гармонические колебания). Частота и
амплитуда при этом постоянны, причём
частота не зависит от амплитуды.
—
единственная сила, действующая на
систему, то систему называют простым или консервативным
гармоническим осциллятором.
Свободные колебания такой системы
представляют собой периодическое
движение около положения равновесия
(гармонические колебания). Частота и
амплитуда при этом постоянны, причём
частота не зависит от амплитуды.
Если
имеется ещё и сила
трения (затухание),
пропорциональная скорости движения
(
Если осциллятор предоставлен сам себе, то говорят, что он совершает свободные колебания. Если же присутствует внешняя сила (зависящая от времени), то говорят, что осциллятор испытывает вынужденные колебания.
Механическими примерами гармонического осциллятора являются математический маятник (с малыми углами отклонения), груз на пружине, торсионный маятник и акустические системы. Среди других аналогов гармонического осциллятора стоит выделить электрический гармонический осциллятор (см. LC-цепь).
Жесткая сварка
Режимы разделяют на жесткие и мягкие. Жесткие режимы сварки характеризуются малой длительностью tсв протекания тока Iсв, а следовательно, и кратковременным нагревом свариваемого метала: мягкие режимы — сравнительно большой длительностью tсв. Жесткость режима зависит также от толщины и температуропроводности (и теплопроводности) свариваемого металла. При одинаковой tсв более жестким будет режим для сварки металла большей толщины или металла с меньшей температуропроводностью. Например, при одной и той же tсв режим сварки низкоуглеродистой стали будет более жестким, чем режим для алюминиевого сплава.
Достоинства электронно-лучевой сварки 1) Высокая концентрация ввода теплоты в изделие, которая выделяется не только на поверхности изделия, но и на некоторой глубине в объеме основного металла. Фокусировкой электронного луча можно получить пятно нагрева диаметром 0,0002-5 мм, что позволяет за один проход сваривать металлы толщиной от десятых долей миллиметра до 200 мм. В результате можно получить швы, в которых соотношение глубины провара к ширине до 20 : 1 и более. Появляется возможность сварки тугоплавких металлов (вольфрама, тантала и др.), керамики и т. д. Уменьшение протяженности зоны,»термического влияния снижает вероят-ность рекристаллизации основного металла в этой зоне. 2) Малое количество вводимой теплоты. Как правило, для получения равной глубины проплавления при электронно-лучевой сварке требуется вводить теплоты в 4-5 раз меньше, чем при дуговой. В результате резко снижаются коробления изделия. 3) Отсутствие насыщения расплавленного и нагретого металла газами. Наоборот, в целом ряде случаев наблюдается Дегазация металла шва и повышение его пластических свойств. В результате достигается высокое качество сварных соединений на химически активных металлах и сплавах, таких как ниобий, Цирконий, титан, молибден и др. Хорошее качество электроннолучевой сварки достигается также на низкоуглеродистых, коррозионно-стойких сталях, меди и медных никелевых, алюминиевых сплавах.
Электрохимическая обработка (ЭХО) — способ обработки электропроводящих материалов, основанный на анодном растворении материала при высоких плотностях электрического тока.
Электрохимическая обработка — обработка, заключающаяся в изменении формы, размеров и (или) шероховатости поверхности заготовки вследствие растворения ее материала в электролите под действием электрического тока.
Виды электрохимической обработки
Электрохимическое объемное копирование — Электрохимическая обработка, при которой форма электрода-инструмента отображается в заготовке
Электрохимическое прошивание — Электрохимическая обработка, при которой электрод-инструмент, углубляясь в заготовку, образует отверстие постоянного сечения
Струйное электрохимическое прошивание — Электрохимическое прошивание с использованием сформированной струи электролита
Электрохимическое калибрование — Электрохимическая обработка поверхности с целью повышения ее точности
Электрохимическое точение — Электрохимическая обработка, при вращении заготовки и поступательном перемещении электрода-инструмента
Электрохимическая отрезка — Электрохимическая обработка, при которой заготовка разделывается на части
Электрохимическое удаление заусенцев(ЭХУЗ, Electrochemical debuting) — Электрохимическая обработка, при которой удаляются заусенцы заготовки
Дроссель
Дроссель – катушка провода, намотанная на металлический сердечник или ферритовый сердечник, включенный в цепь последовательно, предназначенный для фильтрации или ограничения тока в цепи высоких частот.
Основное предназначение дросселя – защита от высокочастотных сигналов.
В широком смысле слова дросселем называют тот или иной ограничитель, регулятор.
Для дросселя характерно высокое сопротивление переменному току и малое сопротивление току постоянному.
В установках компенсации реактивной мощности дроссель используют как защитное, фильтрующее устройство от влияния высших гармоник на конденсатор.
При параллельной работе конденсаторных батарей с преобразователями частоты протекает ток повышенной частоты, который значительно увеличивает потери мощности, искажает напряжение питания, уменьшает полное сопротивлении конденсаторной батареи и может вызвать перегрузку конденсаторов, а также явление параллельного резонанса в системе.
Гармонически составляющие тока, напряжения создаваемые частотными преобразователями систем привода могут быть усилены в десятки раз в цепи параллельного резонанса в результате образовавшегося контура емкостного реактивного сопротивления конденсатора и индуктивного реактивного сопротивления сети. Для предотвращения данного явления используют LC фильтры, фильтры LC – компенсируют реактивную мощность и ограничивают влияние высших гармоник тока на конденсатор.
Дроссели для защиты конденсаторных батарей характеризуются коэффициентом успокоения р в процентах (%). Наиболее часто используемые дроссели с коэффициентом успокоения р=5% (частота резонанса fr =223 Гц) и р=7% (частота резонанса fr =189 Гц). В электрических сетях с преобладанием третей гармоники применяются дроссели с коэффициентом успокоением р=14% (частота резонанса fr =133 Гц).
Коэффициент р можно определить зная резонансную частоту fr и частоту сети fn к которой будет подключена установка компенсации реактивной мощности:
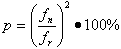
Значение высших гармоник в электросети зависит от нелинейных приемников и искажения синусоиды напряжения и тока, характеризуются коэффициентами THDU и THDI.
THD%- Total Harmonic Distortion – Суммарное Гармоническое Искажение:

где:
Данный параметр изменяется в процессе работы и для исключения проблем в эксплуатации установок компенсации реактивной мощности должны использоваться защитные дроссели.
Если Вы желаете подробнее ознакомиться с дросселями (фильтрами высших гармоник) предлагаемыми заводом Нюкон, перейдите по приведенной ссылке, если Вы желаете узнать цену или купить дроссели, позвоните по телефону указанному ниже или заполните приведенную форму
23. Симметричный режим трехфазной цепи при подключении нагрузки звездой. Соотношение между фазными и линейными напряжениями и токами.
При соединение фаз обмотки генератора (или трансформатора) звездой их концы X, Y и Z соединяют в одну общую точку N, называемую нейтральной точкой (или нейтралью) (рис. 3.6). Концы фаз приемников (Za, Zb, Zc) также соединяют в одну точку n. Такое соединение называется соединение звезда.
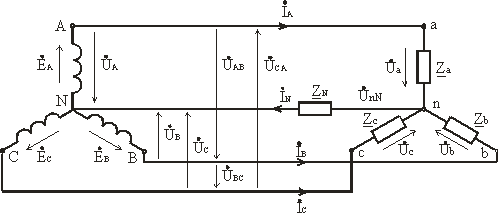
Провода A-a, B-b и C-c, соединяющие начала фаз генератора и приемника, называются линейными, провод N-n, соединяющий точку N генератора с точкой n приемника, – нейтральным.
Трехфазная цепь с нейтральным проводом будет четырехпроводной, без нейтрального провода – трехпроводной.
В трехфазных цепях различают фазные и линейные напряжения. Фазное напряжение UФ – напряжение между началом и концом фазы или между линейным проводом и нейтралью (UA, UB, UC у источника; Ua, Ub, Uc у приемника).Если сопротивлением проводов можно пренебречь, то фазное напряжение в приемнике считают таким же, как и в источнике. (UA = Ua, UB = Ub, UC = Uc). За условно положительные направления фазных напряжений принимают направления от начала к концу фаз.
Линейное напряжение (UЛ) – напряжение между линейными проводами или между одноименными выводами разных фаз (UAB, UBC, UCA). Условно положительные направления линейных напряжений приняты от точек, соответствующих первому индексу, к точкам соответствующим второму индексу (рис. 3.6).
По аналогии с фазными и линейными напряжениями различают также фазные и линейные токи:
При соединении в звезду фазные и линейные токи равны
Iф = IЛ
Ток, протекающий в нейтральном проводе, обозначают IN.
По первому закону Кирхгофа для нейтральной точки n(N) имеем в комплексной форме
İN = İA + İB + İC.
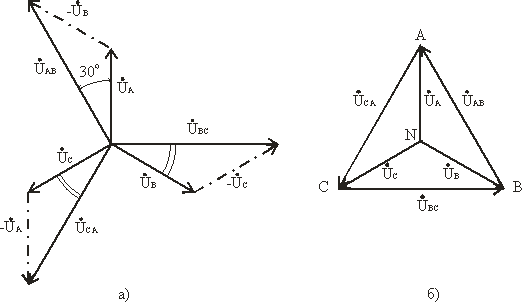
В соответствии с выбранными условными положительными направлениями фазных и линейных напряжений можно записать уравнения по второму закону Кирхгофа.
ÚAB = ÚA — ÚB; ÚBC = ÚB — ÚC; ÚCA = ÚC — ÚA.
Согласно этим выражениям на рис. 3.7а построена векторная диаграмма, из которой видно, что при симметричной системе фазных напряжений система линейных напряжений тоже симметрична: UAB,UBC,UCA равны по величине и сдвинуты по фазе относительно друг друга на 120° (общее обозначение UЛ), и опережают, соответственно, векторы фазных напряжений UA, UB, UC, (UФ) на угол 30°.
Действующие значения линейных напряжений можно определить графи-чески по векторной диаграмме или по формуле (3.8), которая следует из треугольника, образованного векторами двух фазных и одного линейного напряжений:
UЛ = 2 UФ cos 30° или UЛ = UФ.
Предусмотренные ГОСТом линейные и фазные напряжения для цепей низкого напряжения связаны между собой соотношениями:
UЛ = 660 В; UФ = 380 В;
UЛ = 380 В; UФ = 220 В;
UЛ = 220 В; UФ = 127 В.
Симметричная нагрузка приемника
При симметричной системе напряжений и симметричной нагрузке, когда Za = Zb = Zc, т.е. когда Ra = Rb = Rc = Rф и Xa = Xb = Xc = Xф, фазные токи равны по значению и углы сдвига фаз одинаковы
Ia = Ib = Ic = Iф = Uф / Zф,
φa = φb = φc = φ = arctg (Xф/Rф).
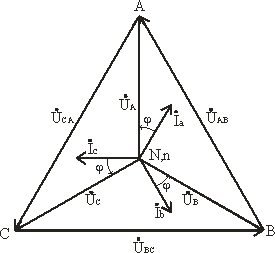
Построив векторную диаграмму токов для симметричного приемника (рис. 3.8), легко установить, что геометрическая сумма трех векторов тока равна нулю: İa + İb + İc = 0. Следовательно, в случае симметричной нагрузки ток в нейтральном проводе IN = 0, поэтому необходимость в нейтральном проводе отпадает.
Векторную диаграмму удобно выполнить топографической (рис. 3.7б), тогда каждой точке цепи соответствует определенная точка на диаграмме. Вектор, проведенный между двумя точками топографической диаграммы, выражает по величине и фазе напряжения между одноименными точками цепи.
§ 6.3. Cоотношения между фазными и линейными напряжениями и токами при симметричной нагрузке в трехфазной цепи, соединенной звездой
Чему равен ток в нулевом проводе при симметричной | Нулю |
| 55 |
трехфазной системе токов? |
|
|
|
| Значению, меньшему | суммы | 34 |
| действующих значений фазных |
| |
| токов |
|
|
|
|
|
|
Всегда ли векторная сумма токов фаз равняется нулю при | Всегда |
| 93 |
отсутствии нулевого провода? |
|
|
|
Не всегда |
| 20 | |
Может ли ток в нулевом проводе четырехпроводной цепи | Может |
| 66 |
быть равен нулю? |
|
|
|
Не может |
| 41 | |
|
|
|
|
| Всегда равен нулю |
| 91 |
Система ЭДС обмоток трехфазного генератора, работающего в энергосистеме, всегда симметрична: ЭДС поддерживаются строго постоянными по амплитуде и сдвинутыми по фазе на
120°.
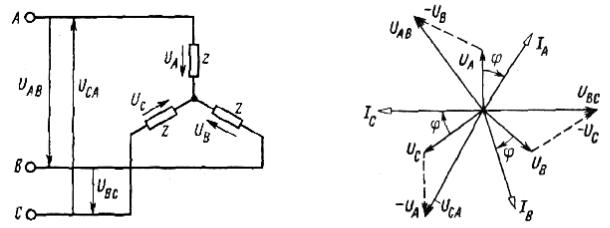
Рассмотрим симметричную нагрузку (рис. 6.10), для которой
ZA=ZB=ZC=Z,ϕA=ϕB=ϕC=ϕ.
К зажимам А, В, С подходят провода линии электропередачи — линейные провода.
Введем обозначения: Iл— линейный ток в проводах линии электропередачи; Iф—ток в сопротивлениях (фазах) нагрузки; Uл—линейное напряжение между линейными проводами; Uф— фазное напряжение на фазах нагрузки.
Врассматриваемой схеме фазные и линейные токи совпадают: Iл=Iф, напряжения UAB, UBC
иUCA являются линейными, а напряжения UA, UB, UС — фазными. Складывая напряжения, находим (рис. 6.10):
UAB=UA-UB; | UBC=UB-UC; | UCA=UС-UA. |
Векторную диаграмму, удовлетворяющую этим уравнениям (рис. 6.11), начинаем строить с | ||
изображения звезды фазных напряжений UA, UB, | UC. Затем строим вектор UAB— как | |
геометрическую сумму векторов UA и —UB, вектор UBC — как геометрическую сумму векторов UB и —UC, вектор UCA — как геометрическую сумму векторов UC и — UA
Рис. 6.10. Соединение нагрузки звездой | Рис. 6.11. Полярная векторная диаграмма напряжений |
Для полноты картины на векторной | диаграмме изображены также векторы токов, |
отстающих на угол ϕ от векторов соответствующих фазных напряжений (нагрузку считаем индуктивной).
На построенной векторной диаграмме начала всех векторов совмещены в одной точке (полюсе), поэтому ее называют полярной. Основное достоинство полярной векторной диаграммы
— ее наглядность.

Рис. 6.12. Топографическая векторная диаграмма | Рис. 6.13. Векторная диаграмма фазных и линейных |
напряжений | напряжений при симметричной нагрузке |
Уравнениям, связывающим векторы линейных и фазных напряжений, удовлетворяет также векторная диаграмма рис. 6.12, которую называют топографической. Она позволяет графически найти напряжение между любыми точками схемы, изображенной на рис. 6.10. Например, для определения напряжения между точкой С и точкой, которая делит пополам сопротивление, включенное в фазу В, достаточно соединить на векторной диаграмме точку С с серединой вектора UB. На диаграмме вектор искомого напряжения показан пунктиром.
При симметричной нагрузке модули векторов фазных (и линейных) напряжений равны между собой. Тогда топографическую диаграмму можно изобразить так, как показано на рис. 6.13.
|
|
| Опустив |
| перпендикуляр | ОМ, | из | прямоугольного | треугольника | находим | ||||||||
|
|
|
|
|
| U | ф2 |
|
|
|
| Uф |
|
|
|
|
|
|
U | л | = | U | ф2 − | = |
| 3 | . |
|
|
|
|
| |||||
2 | 4 |
| 2 |
|
|
|
|
| ||||||||||
|
|
|
|
|
|
|
|
|
|
|
| |||||||
В симметричной звезде фазные и линейные токи и напряжения связаны соотношениями
Iл=Iф; Uл = 
 3 UФ.
3 UФ.
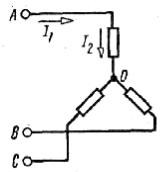
Карточка № 6.3 (189).
Соотношения между фазными и линейными напряжениями и токами при симметричной нагрузке в трехфазной цепи, соединенной звездой
Какой из токов в схеме линейный, какой — фазный? | Оба тока линейные |
| 6 | |||||
|
|
| Оба тока фазные |
|
| 64 | ||
|
|
| Ток I1 — линейный, ток I2 — | 29 | ||||
|
|
| фазный |
|
|
|
|
|
|
|
| Ток I2 — линейный, ток I1 — | 105 | ||||
|
|
| фазный |
|
|
|
|
|
|
|
|
|
|
| |||
Между различными точками схемы, изображенной выше, | Напряжение |
| UAО | — | 15 | |||
включены вольтметры. Какой из них показывает линейное | линейное, | напряжение | UВО |
| ||||
напряжение, какой — фазное? |
|
| — фазное |
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
| Напряжение |
| UAB | — | 78 | |
|
|
| линейное, напряжение UBC |
| ||||
|
|
| — фазное |
|
|
|
|
|
|
|
| Напряжение |
| UCA | — | 51 | |
|
|
| линейное, напряжение UCО |
| ||||
|
|
| — фазное |
|
|
|
|
|
|
|
|
|
|
|
| ||
Чему равен вектор UAC, если UСА=UC-UА? |
| UAC=-UC-UА. |
|
|
| 89 | ||
|
|
| UAC=UА-UC |
|
|
| 2 | |
|
|
| UAC=UC+UА |
|
|
| 62 | |
Укажите причину того, что полярная и | топографическая | Уравнения имеют векторную | 36 | |||||
векторные диаграммы трехфазной | цепи | удовлетворяют | форму |
|
|
|
|
|
одной и той же системе векторных уравнений. |
|
|
|
|
|
| ||
|
|
| Уравнения | написаны | для | 101 | ||
|
|
| симметричной нагрузки |
|
| |||
|
|
|
|
|
|
| ||
|
|
| Векторы | можно | переносить | 22 | ||
|
|
| параллельно | их | начальному |
| ||
|
|
| положению |
|
|
|
| |
|
|
|
|
|
|
|
| |
Симметричная нагрузка соединена | звездой. Линейное | 380 В |
|
|
|
| 74 | |
напряжение 380 В. Определить фазное напряжение. |
|
|
|
|
|
| ||
250 В |
|
|
|
| 44 | |||
|
|
| 220 В |
|
|
|
| 85 |
|
|
| 127 В |
|
|
|
| 9 |
§6.4. Назначение нулевого провода в четырехпроводной цепи
Ток в нулевом проводе равен нулю при строго симметричной нагрузке. Если нагрузка несимметричная, т. е. ZA¹ZB¹ZС, то неравными будут и токи: IA¹IB¹IС Тогда на основе построения, аналогичного приведенному на рис. 6.8, нетрудно убедиться, что при симметрии фазных напряжений ток в нулевом проводе не равен нулю: I0¹0 (за исключением некоторых частных случаев). Таким образом, при Симметрии фазных напряжений и несимметрии нагрузки в нулевом проводе есть ток. Представим себе, что нулевой провод оборвался: I0=0. При этом токи IA, IB, IС должны измениться так, чтобы их векторная сумма оказалась равной нулю: IA+IB+IС= 0.
Но при заданных сопротивлениях нагрузки ZA, ZB, ZС токи могут измениться только за счет изменения фазных напряжений. Следовательно, обрыв нулевого провода в общем случае приводит к изменению фазных напряжений; симметричные фазные напряжения становятся несимметричными.
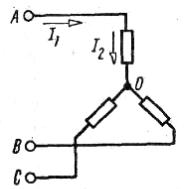
Рассмотрим топографическую векторную диаграмму, представленную на рис. 6.14.
Для простоты пренебрежем падением напряжений внутри обмоток генератора и проводах линии и будем считать, что напряжения на нагрузке равны ЭДС генератора.
При несимметрии нагрузки и отсутствии нулевого провода фазные напряжения UA, UB, UС будут различными и точка О’ займет на векторной диаграмме положение, отличное от точки О.
Введем нулевой провод с пренебрежимо малым сопротивлением, как показано на рис. 6.7. При этом потенциалы точек О и О’ окажутся одинаковыми. Это означает, что точки О и О’ на топографической диаграмме рис. 6.14 должны быть совмещены.
Рис. 6.14. Топографическая векторная диаграмма ЭДС и
напряжений трехфазной цепи при отсутствии нулевого провода
Точка О на топографической диаграмме не может изменить своего положения, так как симметрия ЭДС ЕА, ЕВ, ЕС обеспечивается конструкцией генератора. Следовательно, точка О’ перейдет в точку О, т. е. фазные напряжения на нагрузке станут симметричными.
Таким образом, нулевой провод в четырехпроводной цепи предназначен для обеспечения симметрии фазных напряжений при несимметричной нагрузке.
Несимметрия фазных напряжений недопустима, так как приводит к нарушению нормальной работы потребителей, рассчитанных на определенное рабочее напряжение.
Карточка № 6.4 (233).
Назначение нулевого провода в четырехпроводной цепи
Может ли геометрическая сумма линейных токов быть отличной | Может |
|
| 60 |
от нуля при отсутствии нулевого провода? |
|
|
|
|
Не может |
|
| 32 | |
|
|
|
| |
Будут ли меняться линейные токи при обрыве нулевого провода | а) Будут; б) не будут |
| 99 | |
в случае: а) симметричной нагрузки; б) несимметричной |
|
|
|
|
Будут |
|
| 18 | |
нагрузки? |
|
|
|
|
а) Не будут; б) будут |
| 53 | ||
|
| |||
| Не будут |
|
| 71 |
|
|
|
| |
За счет чего могут измениться линейные токи при постоянной | Изменения | линейных | 82 | |
ЭДС генератора и неизменных сопротивлениях нагрузки? | напряжений |
|
|
|
|
|
|
| |
| Изменения | фазных | 4 | |
| напряжений |
|
|
|
| Изменения | фазных | и | 57 |
| линейных напряжений |
|
| |
|
|
|
|
|
Чему равна разность потенциалов точек О и О’ при наличии | 0 |
|
| 39 |
нулевого провода с активным сопротивлением R0? |
|
|
|
|
I0R0 |
|
| 96 | |
|
|
| ||
| Uл |
|
| 26 |
Может ли нулевой провод, обладающий большим активным | Может |
|
| 69 |
сопротивлением, обеспечить симметрию фазных напряжений |
|
|
|
|
Не может |
|
| 48 | |
при несимметричной нагрузке? |
|
|
|
|
|
|
|
|
|
3.2. Соединение источников и потребителей электрической энергии звездой. Соотношения между фазными и линейными напряжениями и токами при симметричной и несимметричной нагрузках
3.2.1. Наличие нулевого провода
Пусть
трёхфазная система представлена в виде
трёхфазного генератора
и
активной трёхфазной нагрузки  ,
которые звездой. На рис. 3.5 указаны:
фазные ЭДС генератора
,
которые звездой. На рис. 3.5 указаны:
фазные ЭДС генератора 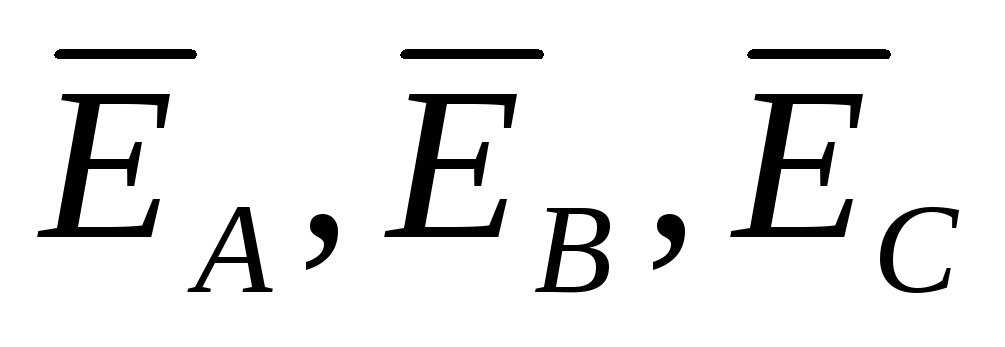 ,
фазные напряжения нагрузки
,
фазные напряжения нагрузки  ,
, 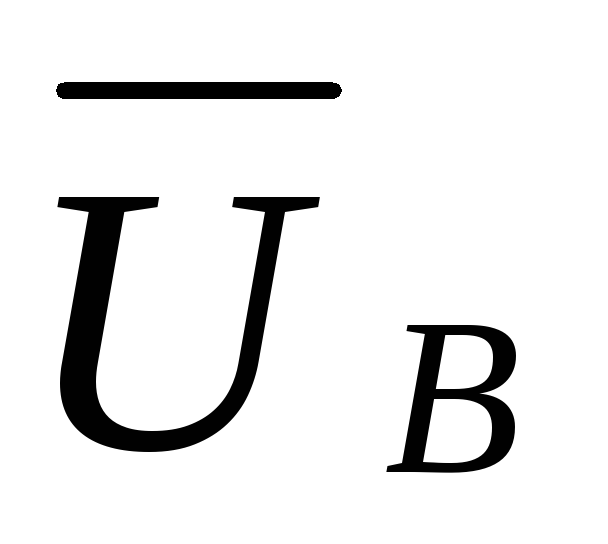 ,
, 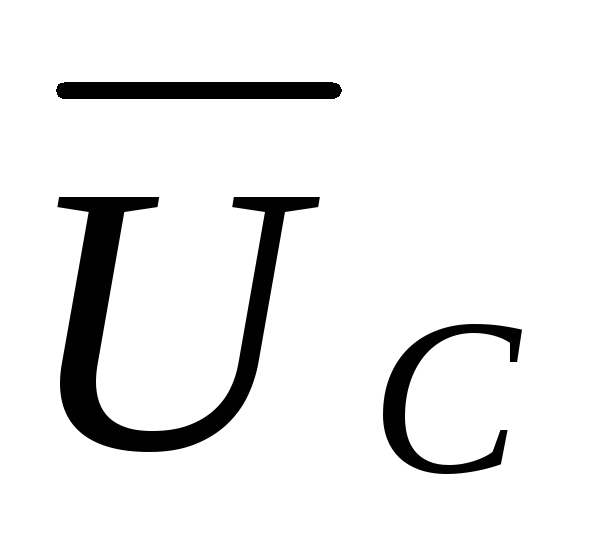 ,
линейные напряжения
,
линейные напряжения 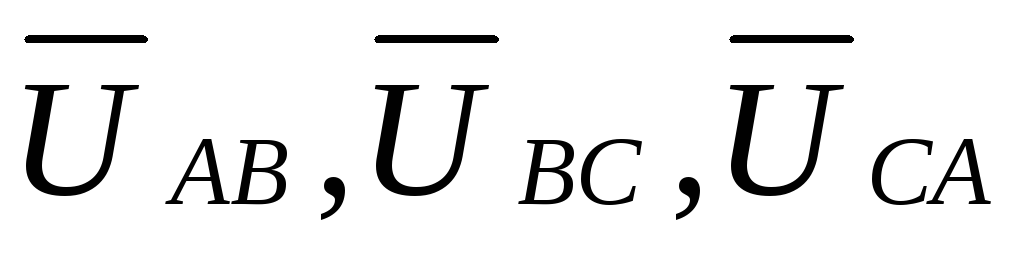 между линейными проводами Аа, Bb, Cc;
линейные токи
между линейными проводами Аа, Bb, Cc;
линейные токи 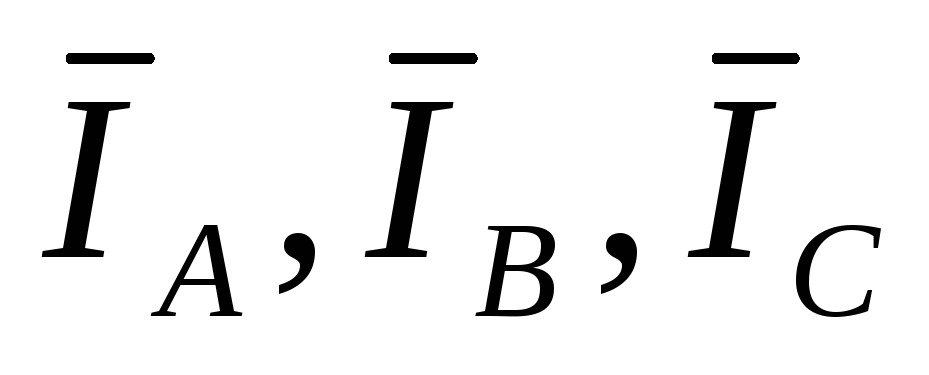 ,
равные фазным токам;
,
равные фазным токам; 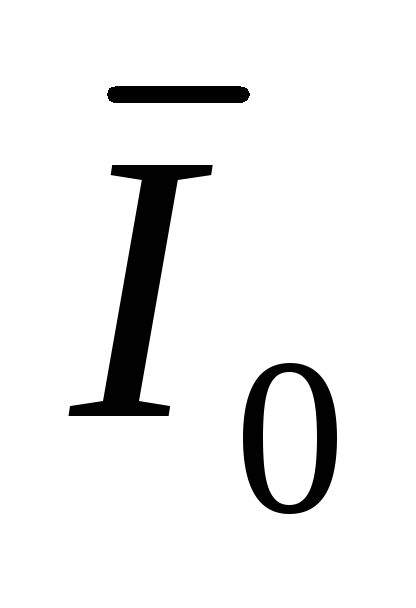 —
ток в нулевом проводе.
—
ток в нулевом проводе.
При
симметричной нагрузке 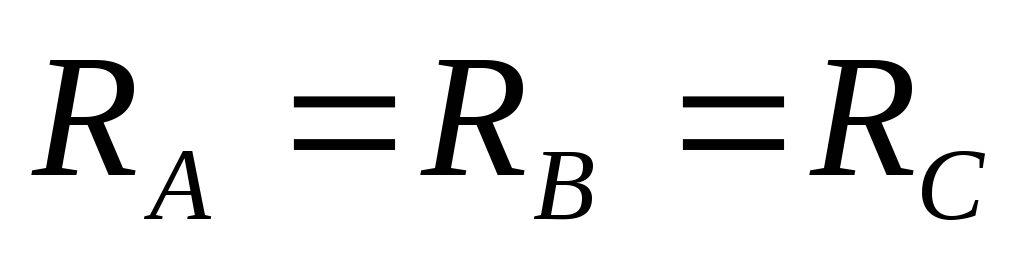 ,
, 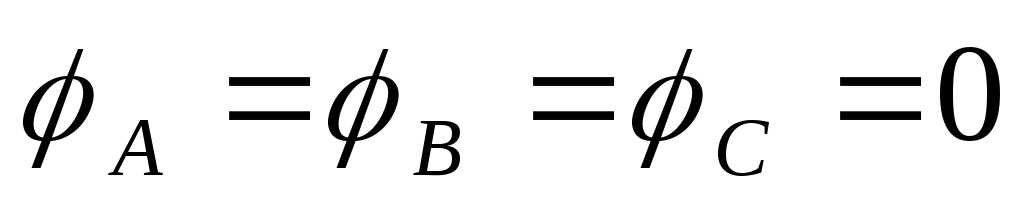 .
По первому закону Кирхгофа ток в нулевом
проводе равен геометрической сумме
токов фаз:
.
По первому закону Кирхгофа ток в нулевом
проводе равен геометрической сумме
токов фаз:
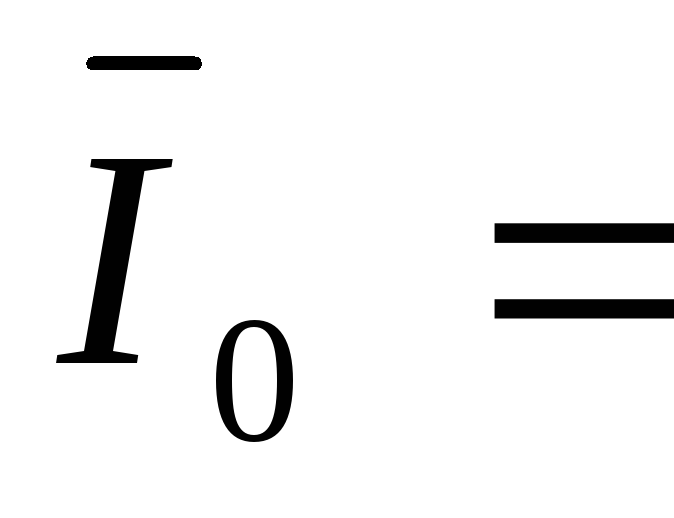
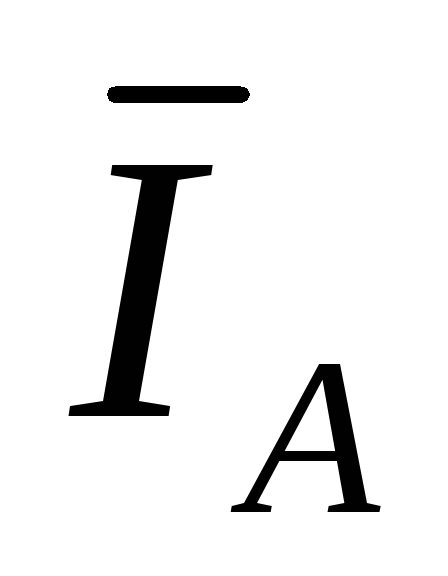 +
+ +
+ .
(3.1)
.
(3.1)
Если
принять нулевую точку генератора за
условную точку нулевого потенциала, то
потенциалы точек A,B,C
будут равны фазным напряжением 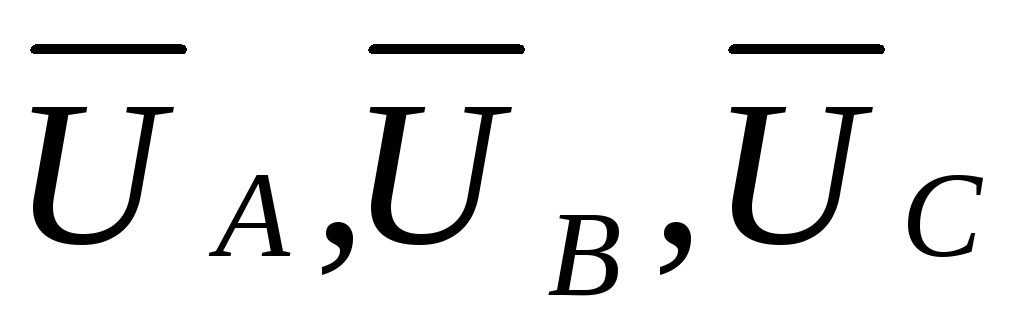 ,
а линейные напряжения являются разностями
потенциалов фазных напряжений:
,
а линейные напряжения являются разностями
потенциалов фазных напряжений:
 ;
; 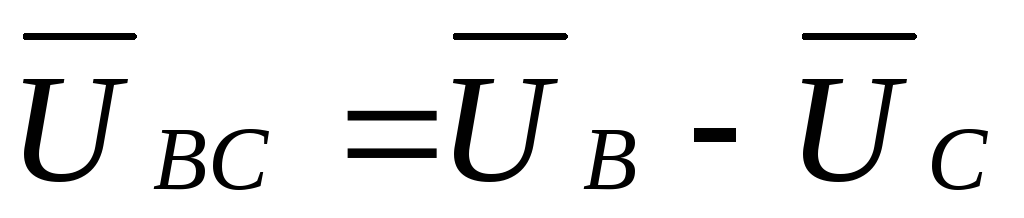 ;
; 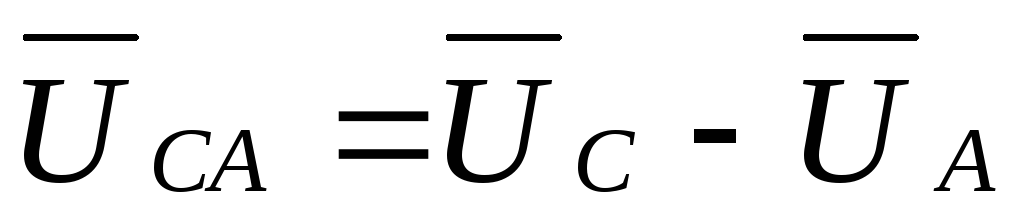 .
(3.2)
.
(3.2)
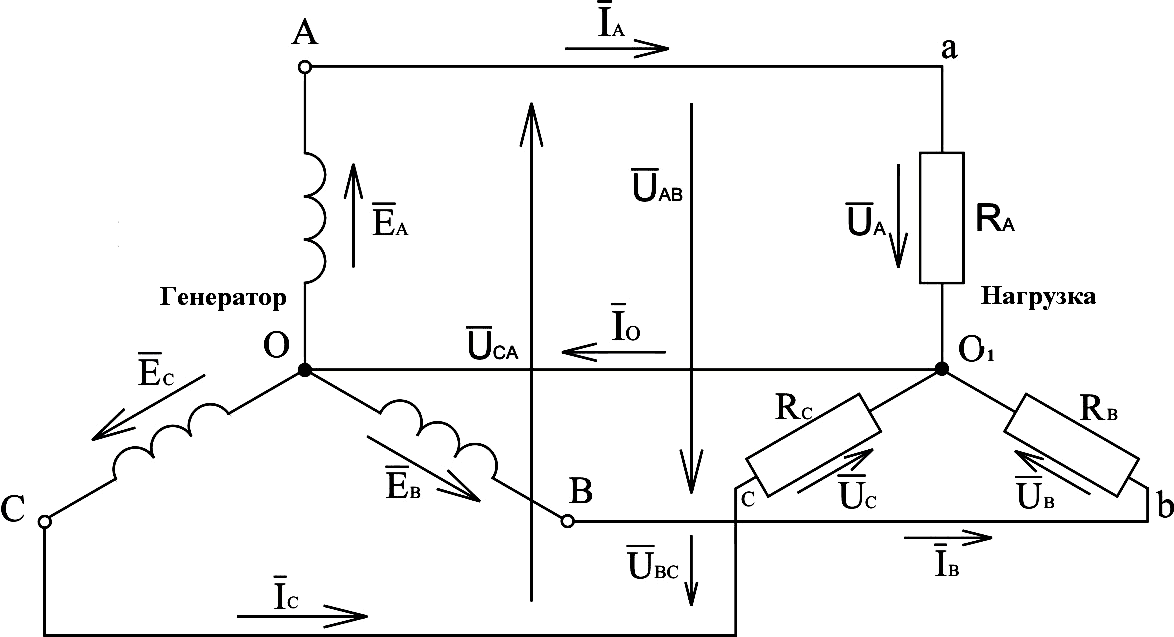
Рис.3.5. Электрическая схема трёхфазной системы с нулевым проводом, представленной в виде трёхфазного генератора и активной трёхфазной нагрузки, соединённых звездой
Используя
рис.3.5, геометрические выражения (3.2)
можно получить по второму закону
Кирхгофа. Так, если 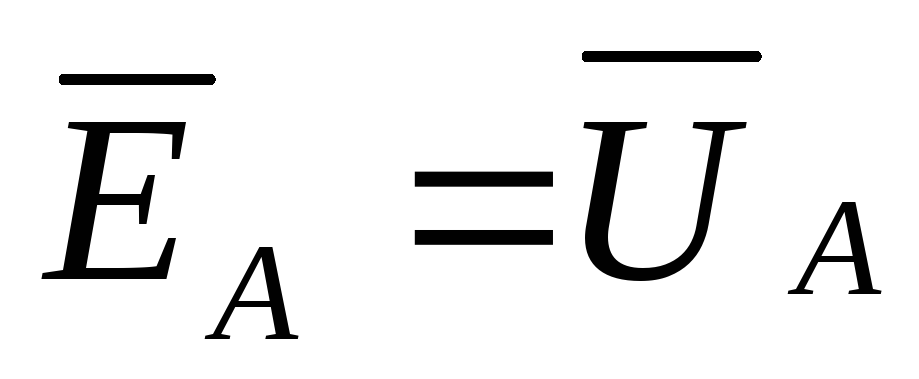 ,
, 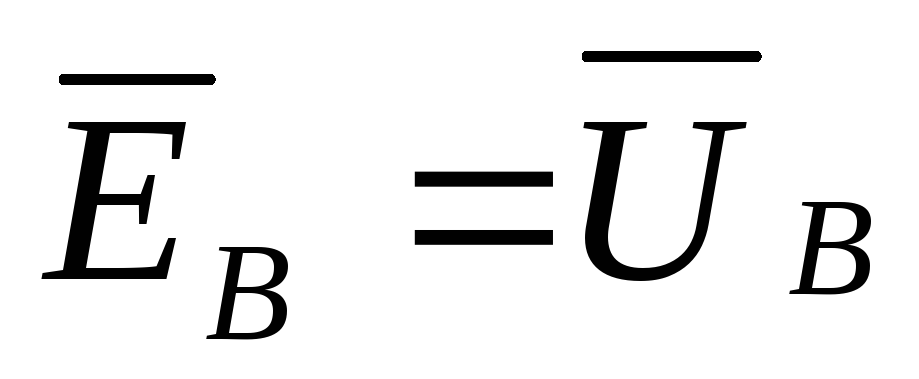 ,
, 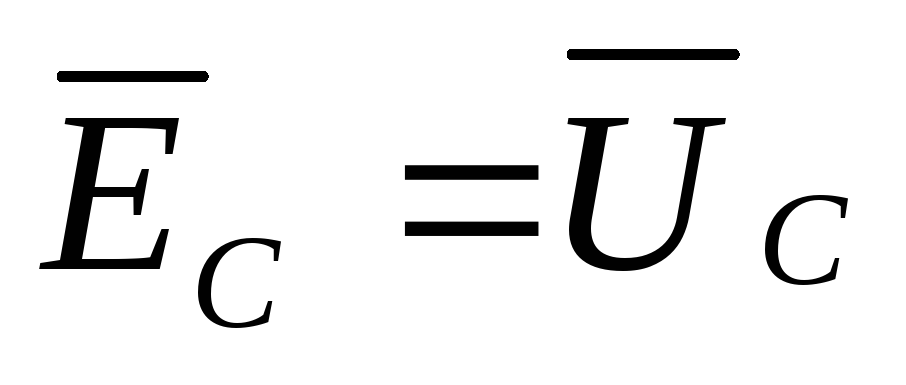 , то
, то 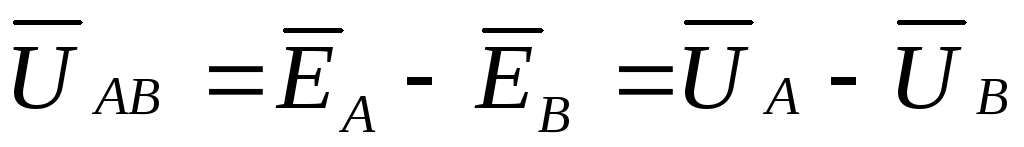 ,
,
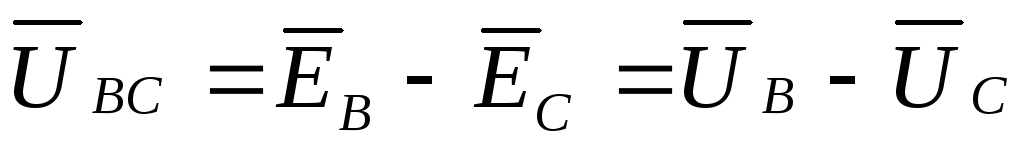 ,
,  .
.
На рис.3.6 изображена векторная диаграмма напряжений и токов при симметричной нагрузке.
Из
диаграммы следует: .
.
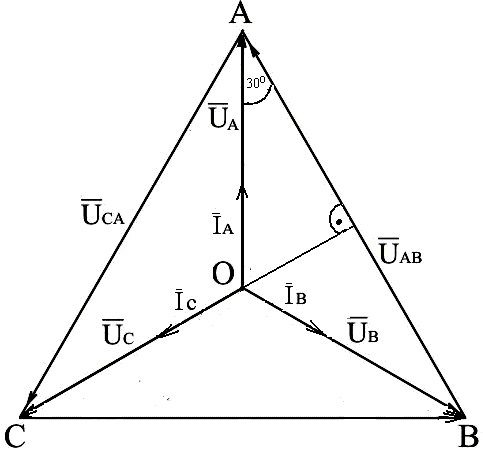
Рис.3.6. Векторная диаграмма напряжений и токов при симметричной нагрузке
Соотношения между линейными и фазными напряжениями и токами при симметричной нагрузке:
 ,
, 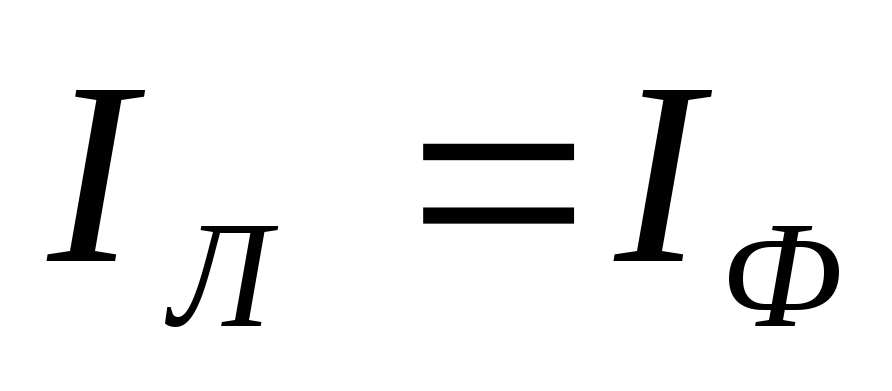 .
(3.3)
.
(3.3)
Если
активная нагрузка несимметрична, то  .
В нулевом проводе появится нулевой ток:
.
В нулевом проводе появится нулевой ток:
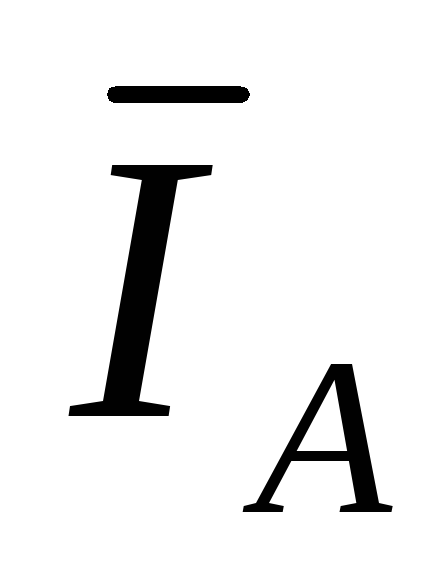 +
+ +
+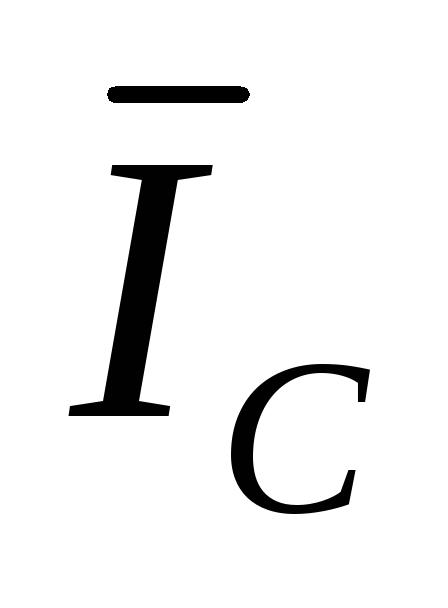
 .
(3.4)
.
(3.4)
Векторная диаграмма будет иметь вид:
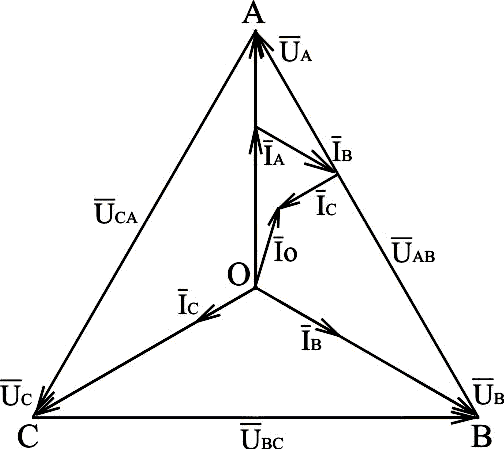
Рис.3.7. Векторная диаграмма напряжений и токов при несимметричной нагрузке
На рис.3.8 приведена схема обрыва фазы А при симметричной нагрузке.

Рис.3.8. Электрическая схема трёхфазной системы с нулевым проводом с выключенной фазой
На
схеме указаны генераторные напряжения 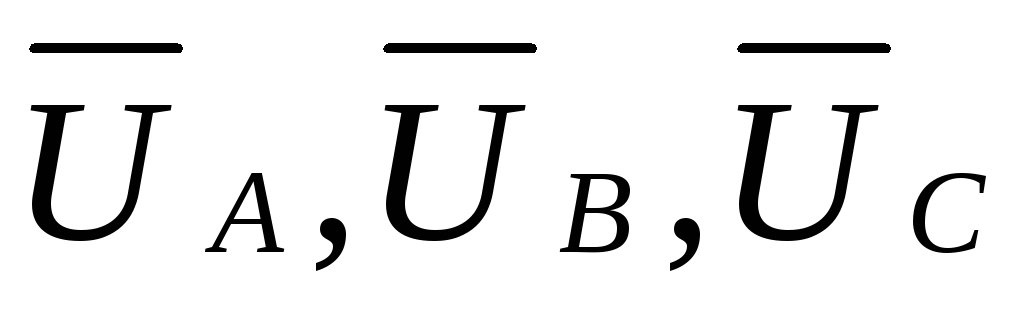 равные фазным напряжениям. Так как при
обрыве фазы А ток
равные фазным напряжениям. Так как при
обрыве фазы А ток  ,
то ток в нулевом проводе
,
то ток в нулевом проводе 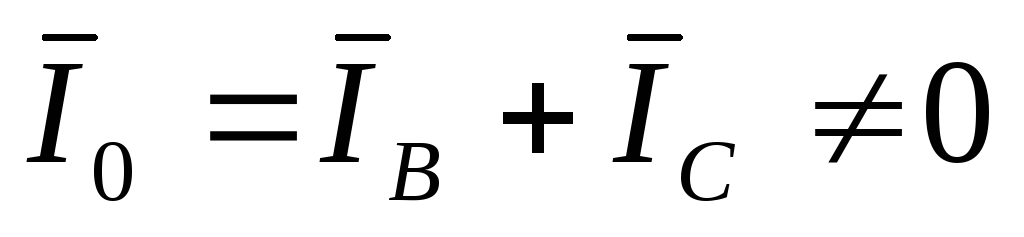 .
.
Векторная диаграмма будет иметь вид:
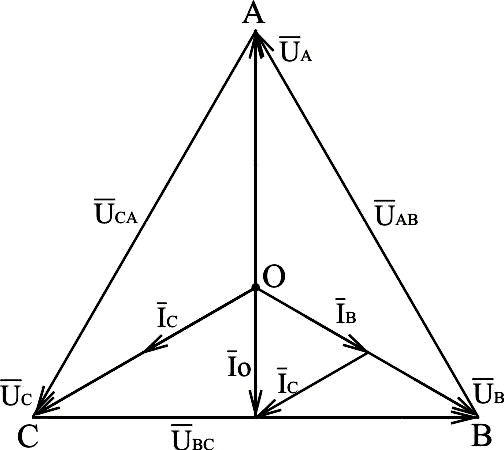
Рис.3.9. Векторная диаграмма напряжений и токов при обрыве фазы
3.2.2. Отсутствие нулевого провода
При
симметричной нагрузке 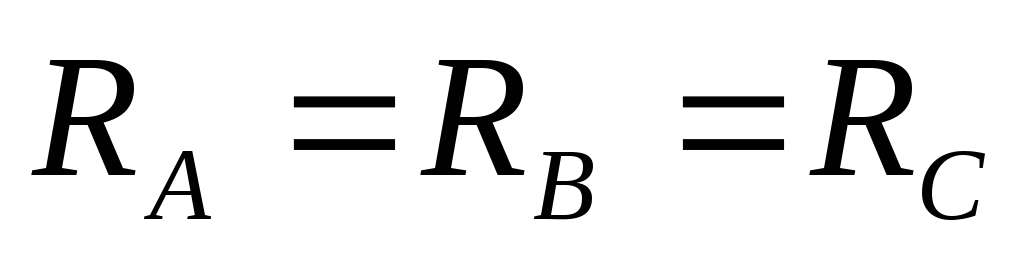 ,
, 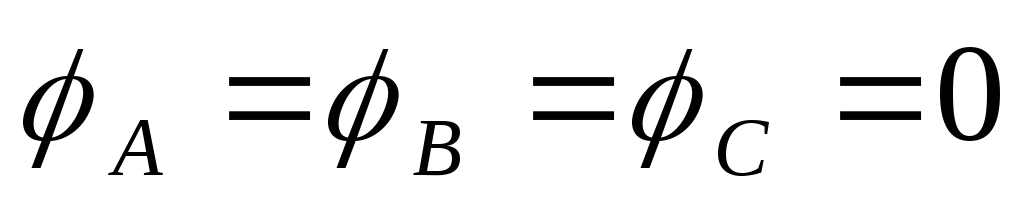 .
Векторная диаграмма аналогична рис.3.6.
.
Векторная диаграмма аналогична рис.3.6.
Электрическая
схема несимметричной нагрузки 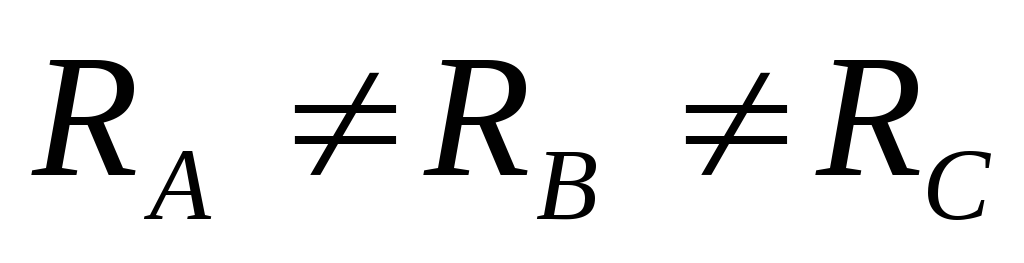 приведена на рис.3.10.
приведена на рис.3.10.
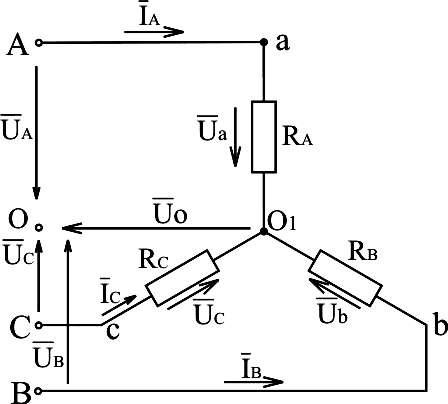
Рис.3.10. Электрическая схема трёхфазной системы без нулевого провода при несимметричной нагрузке
На
схеме указаны фазные генераторные
напряжения  ,
фазные напряжения нагрузки
,
фазные напряжения нагрузки 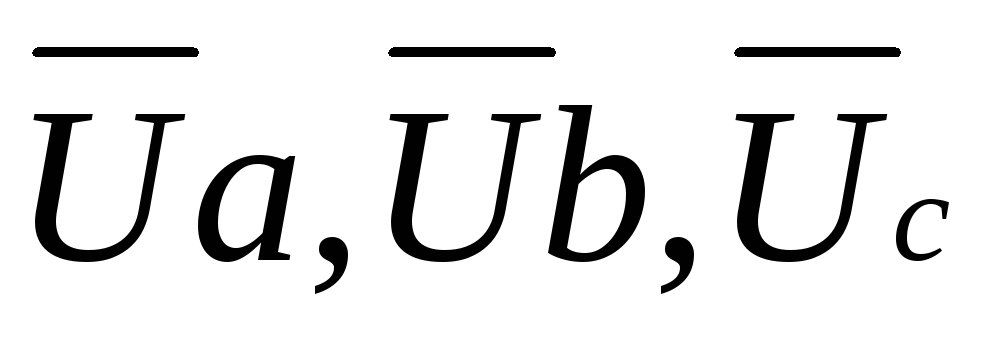 ,
напряжение между нулевыми точками
генератора и нагрузки
,
напряжение между нулевыми точками
генератора и нагрузки 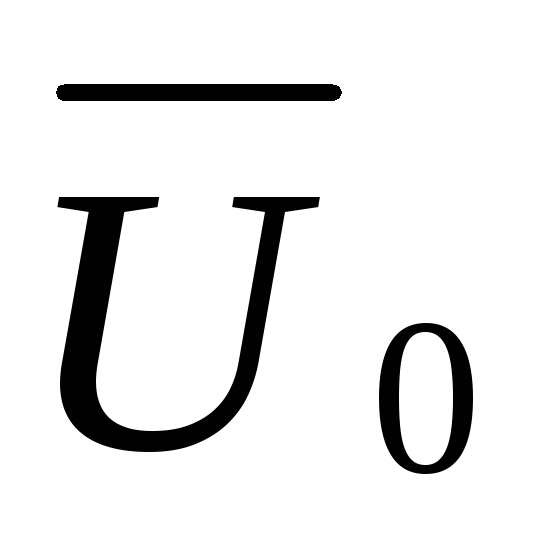 .
По первому закону Кирхгофа:
.
По первому закону Кирхгофа:
 .
(3.5)
.
(3.5)
По второму закону Кирхгофа:
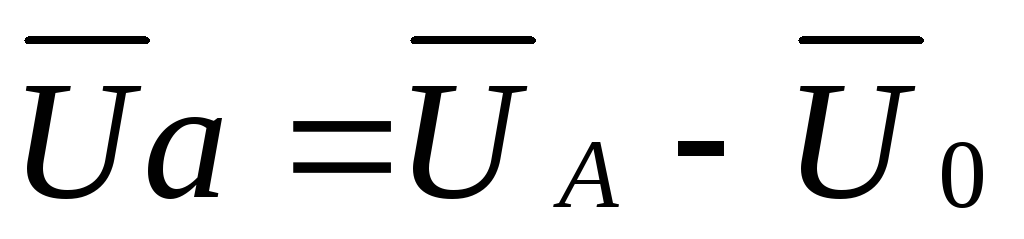 ;
;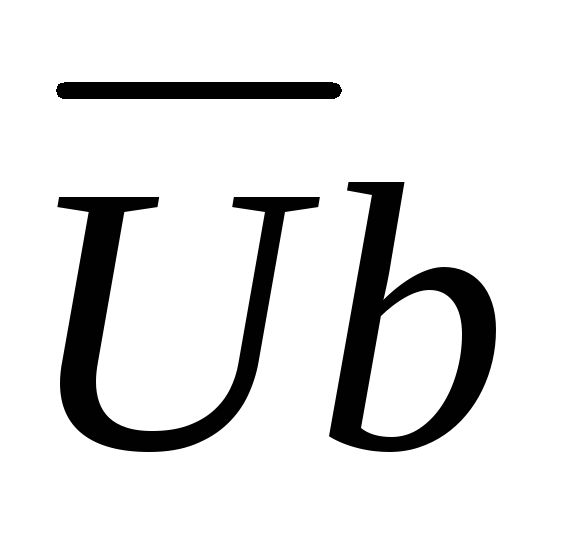
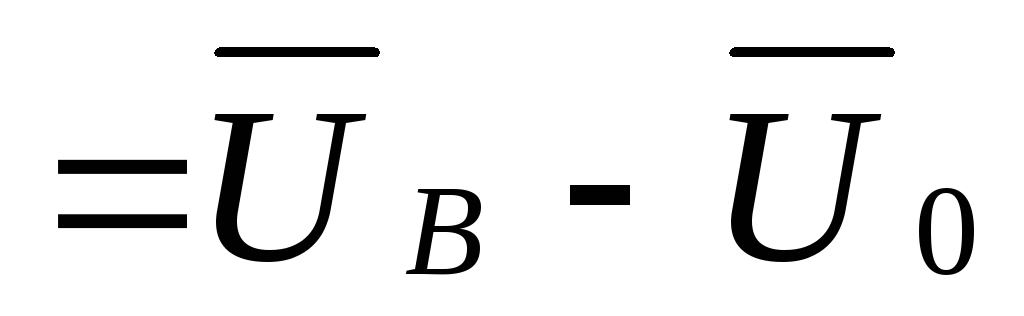 ;
;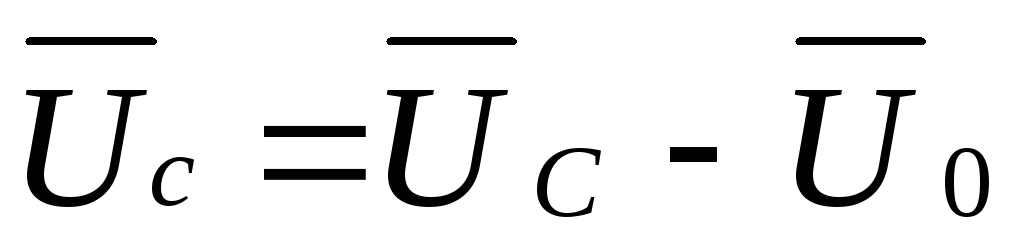 .
(3.6) Используя
формулы (3.5) и (3.6), построим векторную
диаграмму:
.
(3.6) Используя
формулы (3.5) и (3.6), построим векторную
диаграмму:
Рис.3.11. Векторная диаграмма напряжений и токов трёхфазной системы без нулевого провода при несимметричной нагрузке
12. Элементы трехфазной электрической цепи. Фазные, линейные токи, напряжения.
Трехфазная цепь состоит из трех основных элементов: трехфазного генератора, линии передачи со всем необходимым оборудованием, приемников (потребителей). Напряжение между линейным проводом и нейтралью (Ua, Ub, Uc) называется фазным. Напряжение между двумя линейными проводами (UAB, UBC, UCA) называется линейным. Для соединения обмоток звездой, при симметричной нагрузке, справедливо соотношение между линейными и фазными токами и напряжениями:
. 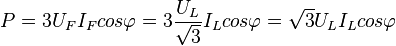
13. Симметричный и несимметричный приемники в трехфазных цепях, векторные диаграммы.
Векторная диаграмма при соединении приемника звездой в случае симметричной нагрузки.
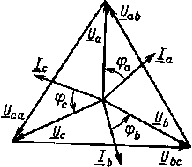
Векторная диаграмма при соединении приемника звездой в случае симметричной нагрузки.

14. Ток в нейтральном проводе в трехфазных цепях. Нейтральный (нулевой рабочий) провод — провод, соединяющий между собой нейтрали электроустановок в трёхфазных электрических сетях. При соединении обмоток генератора и приёмника электроэнергии по схеме «звезда» фазное напряжение зависит от подключаемой к каждой фазе нагрузки. В случае подключения, например, трёхфазного двигателя, нагрузка будет симметричной, и напряжение между нейтральными точками генератора и двигателя будет равно нулю. Однако, в случае, если к каждой фазе подключается разная нагрузка, в системе возникнет так называемое напряжение смещения нейтрали, которое вызовет несимметрию напряжений нагрузки. На практике это может привести к тому, что часть потребителей будет иметь пониженное напряжение, а часть повышенное. Пониженное напряжение приводит к некорректной работе подключённых электроустановок, а повышенное может, кроме этого, привести к повреждению электрооборудования или возникновению пожара. Соединение нейтральных точек генератора и приёмника электроэнергии нейтральным проводом позволяет снизить напряжение смещения нейтрали практически до нуля и выровнять фазные напряжения на приёмнике электроэнергии. Небольшое напряжение будет обусловлено только сопротивлением нулевого провода.
Трехфазные цепи с нейтральным проводе называют четерехпроводными цепями.
Обычно
сопротивлением проводов не учитывается 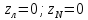 /
/
Тогда
фазные напр. приемника будут равны
фазн. напряжением генератора.  .
.
При
том что комплексные сопротивления
равны 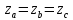 ,
то токи определяются
,
то токи определяются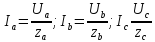
В
соответствии с 1 зак. Киргофа ток в
нейтр. проводе 
При
симмет. напр. 
При
несим. напр. 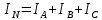
Нейтр провод выравнивает фазные напряжения.
15И16 Режимы работы трехфазного премника.
Различают два вида соединений: в звезду и в треугольник. В свою очередь при соединении в звезду система может быть трех- и четырехпроводной.
Соединение в звезду
На рис. 6 приведена трехфазная система при соединении фаз генератора и нагрузки в звезду. Здесь провода АА’, ВВ’ и СС’ – линейные провода.
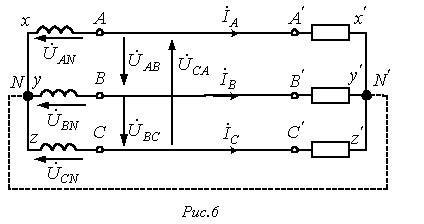
Линейным называется провод, соединяющий начала фаз обмотки генератора и приемника. Точка, в которой концы фаз соединяются в общий узел, называется нейтральной (на рис. 6 N и N’ – соответственно нейтральные точки генератора и нагрузки).
Провод, соединяющий нейтральные точки генератора и приемника, называется нейтральным (на рис. 6 показан пунктиром). Трехфазная система при соединении в звезду без нейтрального провода называется трехпроводной, с нейтральным проводом – четырехпроводной.
Все
величины, относящиеся к фазам, носят
название фазных
переменных, к
линии — линейных. Как
видно из схемы на рис. 6, при соединении
в звезду линейные токи  и
и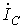 равны
соответствующим фазным токам. При
наличии нейтрального провода ток в
нейтральном проводе
равны
соответствующим фазным токам. При
наличии нейтрального провода ток в
нейтральном проводе .
Если система фазных токов симметрична,
то
.
Если система фазных токов симметрична,
то .
Следовательно, если бы симметрия токов
была гарантирована, то нейтральный
провод был бы не нужен. Как будет показано
далее, нейтральный провод обеспечивает
поддержание симметрии напряжений на
нагрузке при несимметрии самой нагрузки.
.
Следовательно, если бы симметрия токов
была гарантирована, то нейтральный
провод был бы не нужен. Как будет показано
далее, нейтральный провод обеспечивает
поддержание симметрии напряжений на
нагрузке при несимметрии самой нагрузки.
Поскольку
напряжение на источнике противоположно
направлению его ЭДС, фазные напряжения
генератора (см. рис. 6) действуют от точек
А, В и С к нейтральной точке N; 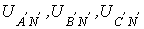 —
фазные напряжения нагрузки.
—
фазные напряжения нагрузки.
Линейные
напряжения действуют между линейными
проводами. В соответствии со вторым
законом Кирхгофа для линейных напряжений
можно записать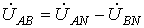
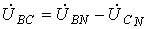

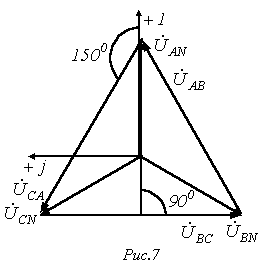
Отметим,
что всегда 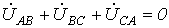 —
как сумма напряжений по замкнутому
контуру.
—
как сумма напряжений по замкнутому
контуру.
На рис. 7 представлена векторная диаграмма для симметричной системы напряжений. Как показывает ее анализ (лучи фазных напряжений образуют стороны равнобедренных треугольников с углами при осно. вании, равными 300), в этом случае
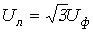
Обычно
при расчетах принимается 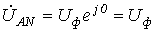 .
Тогда для случаяпрямого
чередования фаз
.
Тогда для случаяпрямого
чередования фаз 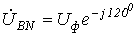 ,
,  (приобратном
чередовании фаз фазовые
сдвиги у
(приобратном
чередовании фаз фазовые
сдвиги у  и
и меняются
местами). С учетом этого на основании
соотношений (1) …(3) могут быть определены
комплексы линейных напряжений. Однако
при симметрии напряжений эти величины
легко определяются непосредственно
из векторной диаграммы на рис. 7. Направляя
вещественную ось системы координат по
вектору
меняются
местами). С учетом этого на основании
соотношений (1) …(3) могут быть определены
комплексы линейных напряжений. Однако
при симметрии напряжений эти величины
легко определяются непосредственно
из векторной диаграммы на рис. 7. Направляя
вещественную ось системы координат по
вектору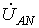 (его
начальная фаза равна нулю), отсчитываем
фазовые сдвиги линейных напряжений по
отношению к этой оси, а их модули
определяем в соответствии с (4). Так для
линейных напряжений
(его
начальная фаза равна нулю), отсчитываем
фазовые сдвиги линейных напряжений по
отношению к этой оси, а их модули
определяем в соответствии с (4). Так для
линейных напряжений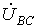 и
и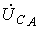 получаем:
получаем: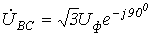 ;
;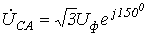 .
.
Соединение в треугольник
В связи с тем, что значительная часть приемников, включаемых в трехфазные цепи, бывает несимметричной, очень важно на практике, например, в схемах с осветительными приборами, обеспечивать независимость режимов работы отдельных фаз. Кроме четырехпроводной, подобными свойствами обладают и трехпроводные цепи при соединении фаз приемника в треугольник. Но в треугольник также можно соединить и фазы генератора (см. рис. 8).
Для симметричной системы ЭДС имеем
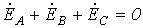 .
.
Таким
образом, при отсутствии нагрузки в
фазах генератора в схеме на рис. 8 токи
будут равны нулю. Однако, если поменять
местами начало и конец любой из фаз,
то 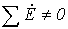 и
в треугольнике будет протекать ток
короткого замыкания. Следовательно,
для треугольника нужно строго соблюдать
порядок соединения фаз: начало одной
фазы соединяется с концом другой.
и
в треугольнике будет протекать ток
короткого замыкания. Следовательно,
для треугольника нужно строго соблюдать
порядок соединения фаз: начало одной
фазы соединяется с концом другой.
Схема соединения фаз генератора и приемника в треугольник представлена на рис. 9.
Очевидно, что при соединении в треугольник линейные напряжения равны соответствующим фазным. По первому закону Кирхгофа связь между линейными и фазными токами приемника определяется соотношениями
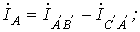


Аналогично можно выразить линейные токи через фазные токи генератора.
На рис. 10 представлена векторная диаграмма симметричной системы линейных и фазных токов. Ее анализ показывает, что при симметрии токов

В заключение отметим, что помимо рассмотренных соединений «звезда — звезда» и «треугольник — треугольник» на практике также применяются схемы «звезда — треугольник» и «треугольник — звезда».
Контрольные вопросы
Какое соединение фаз называется соединением в треугольник?
Каково соотношение между фазным и линейным напряжениями при соединении приемников в треугольник?
Каковы соотношения между фазными и линейными токами для любой нагрузки и для симметричной нагрузки при соединении приемников в треугольник?
Каковы особенности соединения фаз приемников треугольником?
В каком случае следует применять соединение фаз приемников в треугольник?
В чем достоинства схемы соединения в треугольник по сравнению со схемой соединения в звезду?
Изменяются ли линейные токи при изменении сопротивления одной из фаз приемников?
Изменяются ли линейные токи при обрыве одной из фаз приемников?
Как влияет на режим работы цепи обрыв одного из линейных проводов?
Как изменяются линейный ток и мощность, если соединенные в звезду одинаковые однофазные приемники переключить на треугольник (линейные напряжения в обоих случаях одинаковы)?
Объяснить построение векторных диаграмм.
Ответы:
Соединением в треугольник называется соединение, когда конец одной фазы соединяется с началом другой, образуя замкнутый контур. Полученные узлы присоединяют к соответствующим началам фаз генератора линейными проводами
При соединении фаз приемников с сопротивлениями в треугольник каждая фаза включается на линейное напряжение источника. Поэтому фазные напряжения равны линейным напряжениям.
Фазные токи
 определяются по формулам
определяются по формулам
 ;
;  ;
; .
.
Линейные
токи  определяются по фазным токам из уравнений,
составленных по первому закону Кирхгофа
для узлова,
в, с (см. рис. 19).
определяются по фазным токам из уравнений,
составленных по первому закону Кирхгофа
для узлова,
в, с (см. рис. 19).
 ,
, 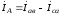 ;
;
ж ,
, ;
;
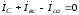 ,
, 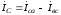 .
.

Рис. 19. Схема трехпроводной трехфазной цепи при соединении приемников в треугольник
При симметричной нагрузке
При несимметричной нагрузке в результате изменении сопротивления одной из фаз, режим работы других фаз останется неизменным, так как сохраняется постоянство напряжений на фазах нагрузки, что является важной особенностью соединения фаз приемника треугольником.
В случае, когда необходимо сохранить режим работы других фаз неизменным, то есть сохранить постоянство напряжений на фазах нагрузки. Схему соединения треугольником используют для включения несимметричных однофазных приемников, например, осветительных приборов в трехпроводную осветительную сеть.
В зависимости от условий работы нагрузки целесообразно изменять способ соединения фаз – переключать со звезды на треугольник и обратно, при этом линейный ток нагрузки изменяется в три раза, а следовательно и мощность.
При изменении сопротивления одной из фаз, режим работы других фаз останется неизменным, так как сохраняется постоянство напряжений на фазах нагрузки
Не изменятся, так как любой из линейных токов равен геометрической разности токов тех двух фаз нагрузки, которые соединяются с данным линейным проводом.
Изменений наблюдаться не будет
В зависимости от условий работы нагрузки целесообразно изменять способ соединения фаз – переключать со звезды на треугольник и обратно, при этом линейный ток нагрузки изменяется в три раза.
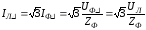 ;
;
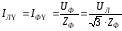 ,
тогда отношение
,
тогда отношение 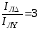 ,
т. е.
,
т. е.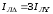 .
.
Активную мощность каждой фазы можно определить по формуле
 ,
,
а
всей цепи – как 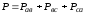 .
.
Активная
мощность симметричного трехфазного
приемника, как и при соединении фаз
звездой:  .
.
Реактивная мощность каждой фазы определяется по формуле
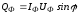 .
.
11. Построение векторной диаграммы
1.
Выбрать масштаб для тока  и для напряжения
и для напряжения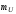 .
.
2. Построить равносторонний треугольник фазных (линейных) напряжений приемника Uав, Uвс, Uса (см. рис. 20).
3.
С учетом характера нагрузки (активная,
индуктивная, емкостная) строятся векторы
фазных токов. При индуктивной нагрузке
вектор фазного тока отстает от своего
напряжения на 90о,
при емкостной – вектор фазного тока
опережает напряжение на 90о,
при чисто активной нагрузке фазный ток
совпадает по направлению со своим
напряжением  .
.
4. На основании уравнений (21) построить векторы линейных токов.




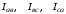 определяются по формулам
определяются по формулам