Kvant. Сила Ампера — PhysBook
Лузин А. Сила Ампера в однородном магнитном поле //Квант. — 1991. — № 5. — С. 39,42-43.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Согласно закону Ампера, выражение для модуля силы \(~\vec F\), действующей на малый отрезок проводника Δl, по которому течет ток I, в магнитном поле с индукцией \(~\vec B\), имеет вид
\(~F = BI \Delta l \sin \alpha\) .Здесь α — угол между направлением магнитной индукции и направлением тока. Можно сказать также, что это угол между вектором \(~\vec B\) и вектором \(~\vec {\Delta l}\), направленным по току. Сила \(~\vec F\) направлена перпендикулярно векторам \(~\vec B\) и \(~\vec {\Delta l}\) — по известному правилу левой руки.
Чтобы найти силу, действующую на криволинейный участок проводника в произвольном магнитном поле, нужно:
- а) разбить его на отрезки, настолько малые, что их можно считать прямолинейными, а поле в этой области однородным;
- б) определить силы Ампера, действующие на каждый такой отрезок;
- в) вычислить векторную сумму полученных сил.
Разумеется этот «рецепт» известен каждому, кто изучал закон Ампера по школьному учебнику физики. Наша же задача — познакомить вас с весьма полезными свойствами силы Ампера, действующей на криволинейный участок проводника с током в простейшем магнитном поле — однородном.
Пусть проводник представляет собой пространственную (в частном случае плоскую) ломаную линию, состоящую из N прямолинейных отрезков (Δl)1, (Δl)2, …, (Δl)3. Просуммируем сначала силы \(~\vec F_1\) и \(~\vec F_2\), действующие на отрезки проводника (Δ
Рис. 1
Предположим, что вектор \(~\vec B\) перпендикулярен плоскости выбранных отрезков (рис. 1). Сила \(~\vec F_1\) перпендикулярна вектору \(~(\vec {\Delta l})_1\), а ее направление определяется правилом левой руки. Точно так же сила \(~\vec F_2\) перпендикулярна вектору \(~(\vec {\Delta l})_2\). Модули этих сил равны соответственно
\(~F_1 = BI (\Delta l)_1\) и \(~F_2 = BI (\Delta l)_2\) .Сложим попарно силы \(~\vec F_1\) и \(~\vec F_2\) и отрезки \(~(\vec {\Delta l})_1\) и \(~(\vec {\Delta l})_2\). Поскольку ∠LMN = ∠ADC, как углы со взаимно перпендикулярными сторонами, треугольники LMN и ADC подобны, а вектор \(~\vec F_{12} = \vec F_1 + \vec F_2\) перпендикулярен вектору \(~(\vec {\Delta l})_{12}\), причем \(~F_{12} = BI (\Delta l)_{12}\). Следовательно, сила Ампера, действующая на участок проводника
Рис. 2
Рассмотрим теперь другой, тоже простой случай, когда вектор \(~\vec B\) лежит в плоскости отрезков проводника (Δl)1 и (Δl)2 (рис. 2). Направим ось координат X вдоль вектора \(~\vec B\), а ось
Здесь мы воспользовались тем, что сумма проекций на ось Y векторов \(~(\vec {\Delta l})_1\) и \(~(\vec {\Delta l})_2\) равна проекции суммарного вектора \(~(\vec {\Delta l})_{12}\).
Таким образом, в обоих рассмотренных нами случаях при вычислении силы Ампера два соседних прямолинейных отрезка проводника можно заменить одним, начало которого находится в начале первого отрезка, а конец — в конце второго.
Когда вектор \(~\vec B\) направлен под произвольным углом к плоскости отрезков проводника (Δl)1 и (Δl)2, его можно разложить на два взаимно перпендикулярных вектора, один из которых перпендикулярен упомянутой плоскости, а другой лежит в ней. Отсюда, а также из принципа суперпозиции магнитных полей следует, что и при вычислении силы Ампера, действующей на проводник в произвольно ориентированном магнитном поле, два соседних прямолинейных отрезка проводника (Δl)1 и (Δl)2 можно заменить одним (Δl)12, соединяющим начало первого и конец второго. Точно так же два прямолинейных отрезка (Δ
А теперь — об обещанных свойствах силы Ампера. Из всего сказанного следует, что сила Ампера, действующая на криволинейный участок проводника с током в однородном магнитном поле, не зависит от формы проводника, а зависит только от координат начала и конца этого участка. Следует также и то, что сила Ампера, действующая на замкнутый проводник с током в однородном магнитном поле, равна нулю. Эти два свойства силы Ампера взаимосвязаны — из первого следует второе и наоборот.
Урок физики: Решение задач. Сила Ампера.
Урок 4. Решение задач. Сила Ампера
Цель: отработка практических навыков при решении задач.
Ход урока
I. Организационный момент
II. Повторение материала
— Что устанавливает закон Ампера?
— Чему равен модуль силы Ампера?
— Сформулируйте правило, позволяющее определить направление силы Ампера.
— Приведите примеры использования силы Ампера.
III. Решение задач
1. В однородное магнитное поле внесены проводники с силами тока, направления которых указаны на рис. 2. Определите направления силы, действующей на каждый проводник со стороны магнитного поля.
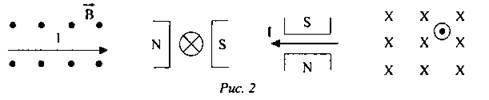
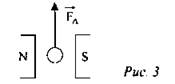
2. Определить направление тока в проводнике, находящемся в магнитном поле, если действующая на проводник сила имеет направление:
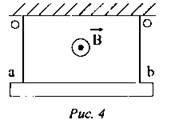
3. Прямой проводник ab длиной l = 0,5 м, массой m = 0,5 г подвешен горизонтально на двух невесомых нитях оа и оb в однородном магнитном поле (см. рис. 4). В = 24,5 мТл и перпендикулярно к проводнику. Какой ток надо пропустить через проводник, чтобы одна из нитей разорвалась, если нить разрывается при нагрузке, равной силе, превышающей Mg — 39,2 мН.
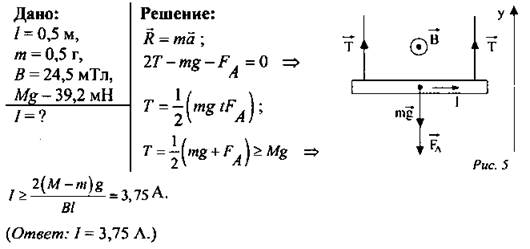
4. Проводник с током I = 1 А, массой m = 20 г и длиной l = 20 м подвешен на двух тонких проволоках и помещен в однородное магнитное иоле с вектором 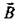 , направленным вертикально (см. рис. 6). Величина индукции тока В = 0,5 Тл. На какой угол от вертикали отклонится проволока, поддерживающая проводник?
, направленным вертикально (см. рис. 6). Величина индукции тока В = 0,5 Тл. На какой угол от вертикали отклонится проволока, поддерживающая проводник?

5. Рамка площадью S = 25 см2, содержащая N = 100 витков провода, помещена в однородное магнитное поле так, что индукция 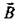
6. Прямолинейный проводник с током помещен в однородное магнитное поле с индукцией В = 0,2 Тл. Найдите величину силы, действующую на проводник, если его длина l = 10 см, величина тока I = 3 А, а направление тока составляет с направлением вектора индукции магнитного поля угол α = 45° (4,2 · 10-2 Н).
7. Жесткая проводящая квадратная рамка лежит на горизонтальной непроводящей поверхности и находится в магнитном поле, линии индукции которого параллельны двум сторонам рамки. Масса рамки m = 20 г, длина ее стороны а = 4 см, величина магнитной индукции В = 0,5 Тл. Какой величины ток следует пропустить по рамке, чтобы одна из ее сторон начала подниматься (I = 5 А)?
IV. Подведение итогов урока
Домашнее задание
Упражнение № 1 (1:2).
Р — 829; Р — 830.
Общая физика. Оптика / Шпоргалки / 17-19
17. Действие магнитного поля на проводник и контур с током.
Закон Ампера
Рассмотрим
проводник с током, помещенный в магнитное
поле. Поскольку электрический ток –
это направленное движение заряженных
частиц в одну сторону, то на каждую из
них будет действовать магнитная
составляющая силы Лоренца, причем все
эти силы будут сонаправлены. Следовательно,
результирующая сила, действующая со
стороны магнитного поля на элемент
проводника с током, может быть найдена
так:
,
где dN – количество свободных электронов в
элементе проводника. Сила  определяется выражением (5.29). Если длина
элемента dl,
площадь поперечного сечения S,
а концентрация свободных электронов в
металле п,
то
определяется выражением (5.29). Если длина
элемента dl,
площадь поперечного сечения S,
а концентрация свободных электронов в
металле п,
то
 .
.
Таким образом, сила, действующая со стороны магнитного поля на бесконечно малый элемент проводника с током, помещенный в магнитное поле, определяется как
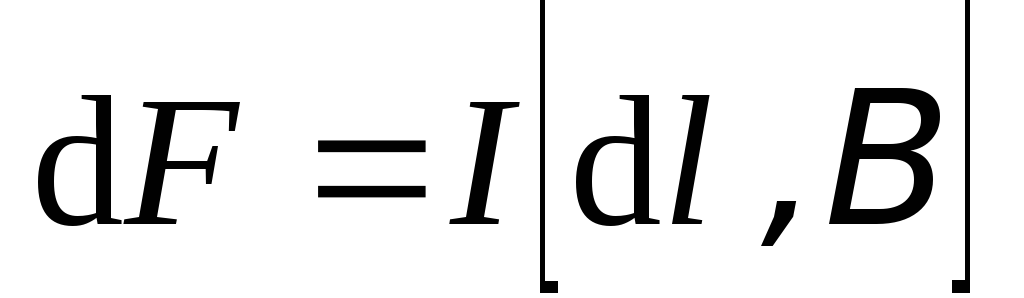 .
(5.32)
.
(5.32)
Полученное
соотношение выражает закон
Ампера,
а сила, определяемая по (5.32), называется силой
Ампера.
Направление силы Ампера можно определить
по правилу
“левой руки”: если
расположить ладонь левой руки так, чтобы
четыре пальца показывали направление
тока в проводнике, а линии магнитной
индукции входили в раскрытую ладонь,
то отогнутый под прямым углом большой
палец покажет направление силы,
действующей на элемент проводника с
током. Опишем взаимодействие двух параллельных
бесконечно длинных проводников с токами
(рис. 5.22). Каждый из проводников создает
магнитное поле, индукция которого
определяется по (5.12). Рассмотрим левый
проводник с током 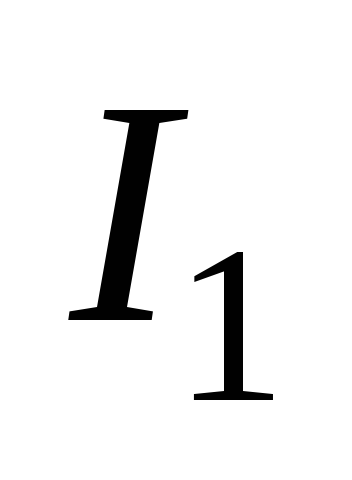 ,
находящийся в поле правого проводника.
Во всех точках первого проводника
магнитная индукция поля второго
проводника
,
находящийся в поле правого проводника.
Во всех точках первого проводника
магнитная индукция поля второго
проводника  ,
где а – расстояние между проводниками. Учтем,
что вектор
,
где а – расстояние между проводниками. Учтем,
что вектор  направлен перпендикулярно плоскости
рисунка “на нас”. Если выделить в
проводнике элемент с током
направлен перпендикулярно плоскости
рисунка “на нас”. Если выделить в
проводнике элемент с током  ,
то, по правилу левой руки, сила
,
то, по правилу левой руки, сила 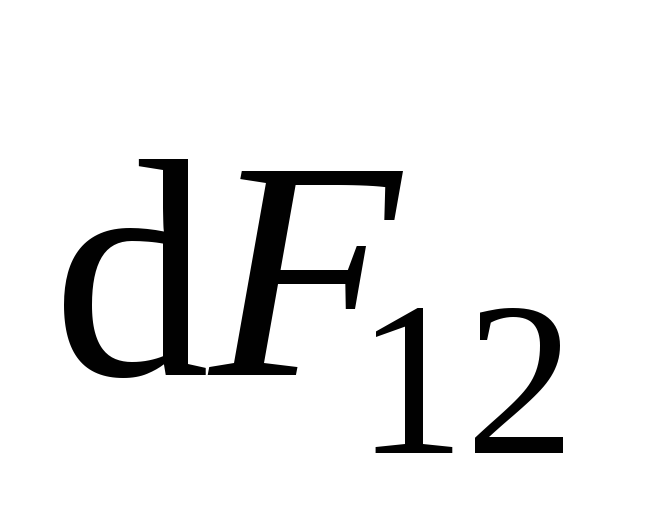 ,
действующая на него, будет направлена
вправо. Это означает, что левый проводник
притягивается к правому. Модуль силы
определяется таким образом:
,
действующая на него, будет направлена
вправо. Это означает, что левый проводник
притягивается к правому. Модуль силы
определяется таким образом:
 .
.
Если
теперь рассмотреть правый проводник с
током 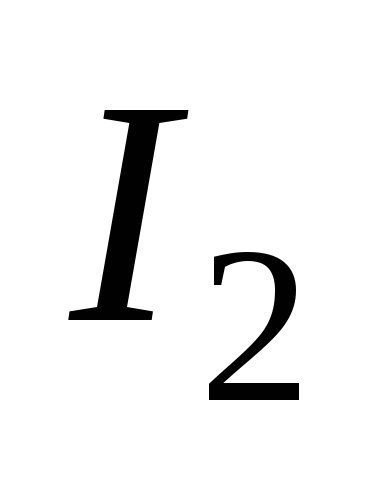 ,
находящийся в поле левого проводника,
то выводы будут аналогичными. Во всех
точках второго проводника магнитная
индукция поля первого проводника
,
находящийся в поле левого проводника,
то выводы будут аналогичными. Во всех
точках второго проводника магнитная
индукция поля первого проводника 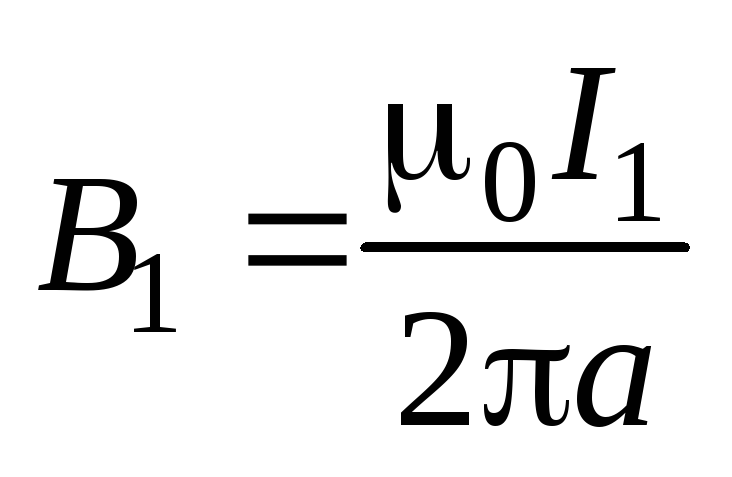 .
Вектор
.
Вектор 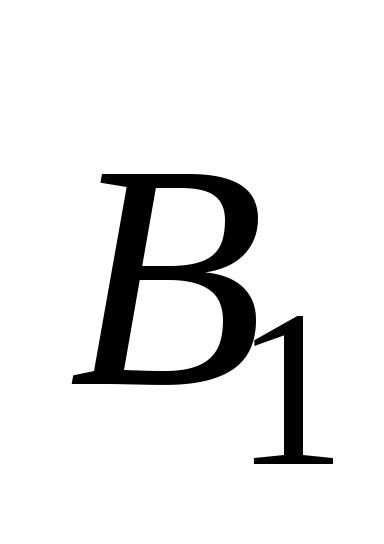 направлен перпендикулярно плоскости
рисунка “к нам”. Если выделить в
проводнике элемент с током
направлен перпендикулярно плоскости
рисунка “к нам”. Если выделить в
проводнике элемент с током 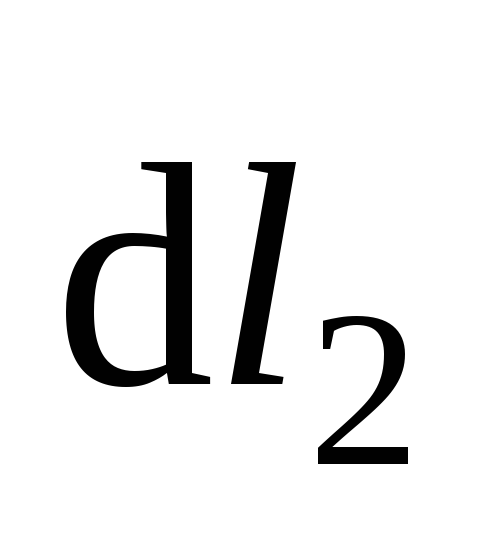 ,
то, по правилу левой руки, сила
,
то, по правилу левой руки, сила 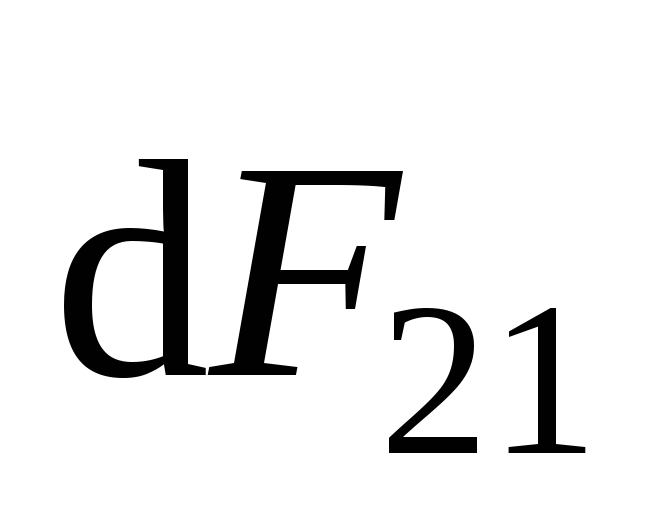 ,
действующая на него, будет направлена
влево. Это означает, что правый проводник
притягивается к левому. Модуль силы
определяется таким образом:
,
действующая на него, будет направлена
влево. Это означает, что правый проводник
притягивается к левому. Модуль силы
определяется таким образом:
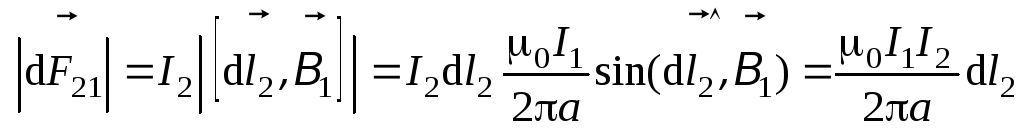 .
.
Нетрудно
видеть, что выполняется третий закон
Ньютона: силы, с которыми взаимодействуют
равные отрезки проводников  одинаковы:
одинаковы:

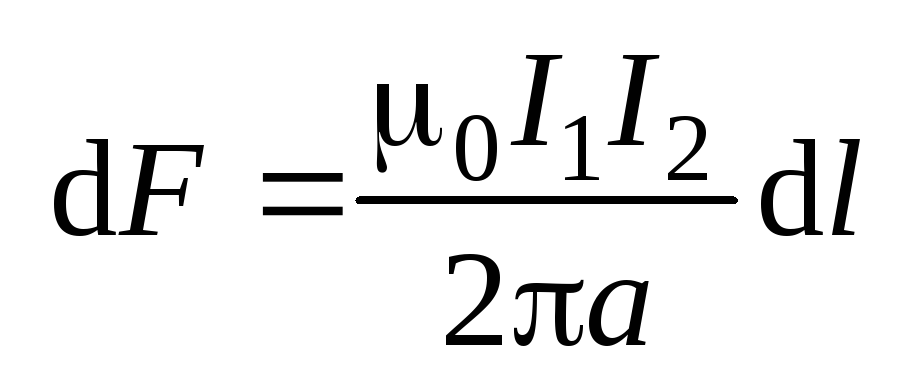 .
(5.33)
.
(5.33)Таким образом, параллельные проводники с сонаправленными токами притягиваются друг к другу. Если направления тока в проводниках противоположны, то направления действующих между проводниками сил изменятся на противоположное, и проводники будут отталкиваться.
Из (5.33) следует определение основой единицы измерения электрических величин в СИ – ампера. 1 ампер – сила неизменяющегося тока, который, протекая по двум параллельным бесконечно длинным проводникам ничтожно малого кругового сечения, расположенным в вакууме на расстоянии 1 м друг от друга, вызывает между ними силу взаимодействия 210–7 Н на каждый метр длины проводников.
Рассмотрим
теперь поведение контура с током в
магнитном поле. Пусть прямоугольная
рамка с током находится в однородном
магнитном поле, причем направления
магнитного момента рамки и индукции
поля совпадают (рис.5.23). Со стороны
магнитного поля на каждую сторону рамки
будет действовать сила, направления
всех сил указаны на рисунке. Действие
сил приводит к растяжению рамки. Если
изменить направление тока (или направление  ),
то действие сил будет приводить к сжатию
рамки. Однако в любом случае, поскольку
),
то действие сил будет приводить к сжатию
рамки. Однако в любом случае, поскольку  ,
то
,
то
 ,
, 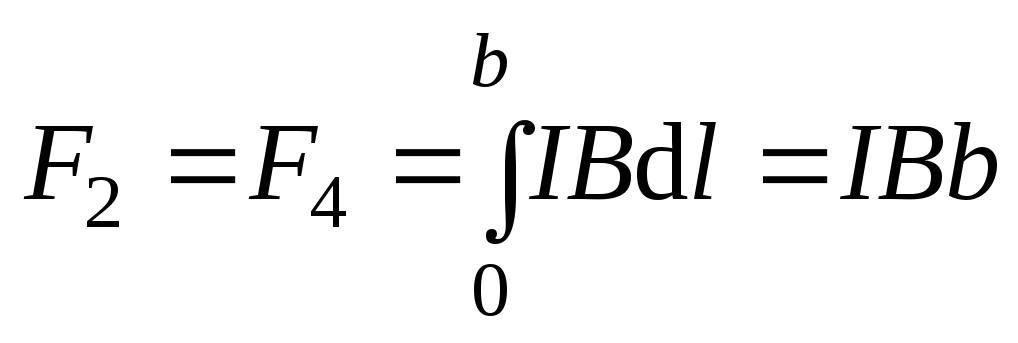 .
.
Н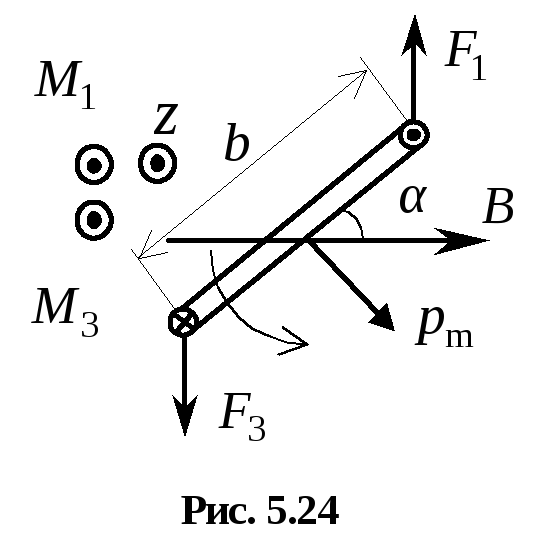 етрудно
увидеть, что
етрудно
увидеть, что 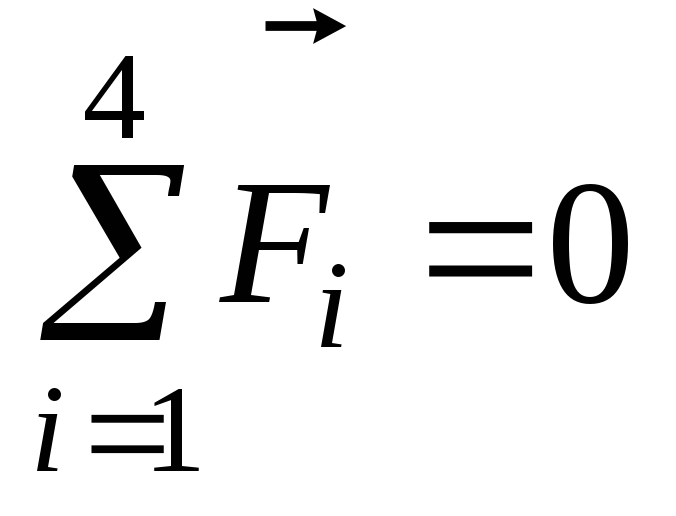 ,
т.е. первоначально покоившаяся рамка в
целом будет сохранять состояние покоя
в однородном магнитном поле. Таким
образом, действие магнитного поля на
рамку сводится в данном случае только
к ее деформации.
,
т.е. первоначально покоившаяся рамка в
целом будет сохранять состояние покоя
в однородном магнитном поле. Таким
образом, действие магнитного поля на
рамку сводится в данном случае только
к ее деформации.
Повернем
плоскость рамки на угол
относительно положения, указанного на
рис. 5.23. На такой же угол повернется
вектор  относительно вектора магнитной индукции.
На рис. 5.24 показан вид сверху на рамку.
Видно, что векторы сил
относительно вектора магнитной индукции.
На рис. 5.24 показан вид сверху на рамку.
Видно, что векторы сил 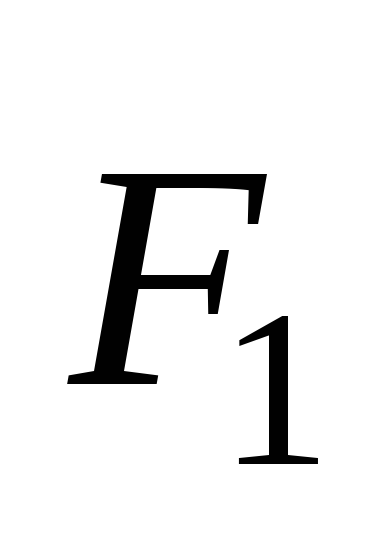 и
и  изменили свои направления (мы предлагаем
вам самостоятельно убедиться в том, что
направления
изменили свои направления (мы предлагаем
вам самостоятельно убедиться в том, что
направления  и
и  остались прежними). Несмотря на то, что
в таком положении рамки по-прежнему
остались прежними). Несмотря на то, что
в таком положении рамки по-прежнему 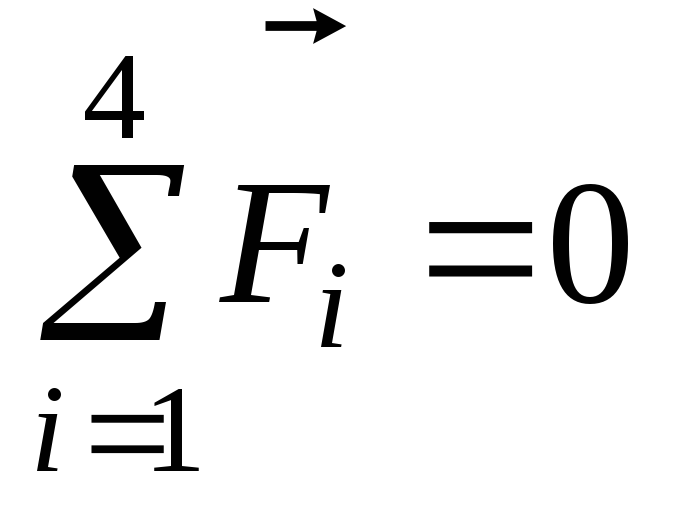 ,
рамка не будет сохранять положение
покоя. Если предоставить рамке возможность
вращения, то она будет вращаться под
действием моментов сил
,
рамка не будет сохранять положение
покоя. Если предоставить рамке возможность
вращения, то она будет вращаться под
действием моментов сил 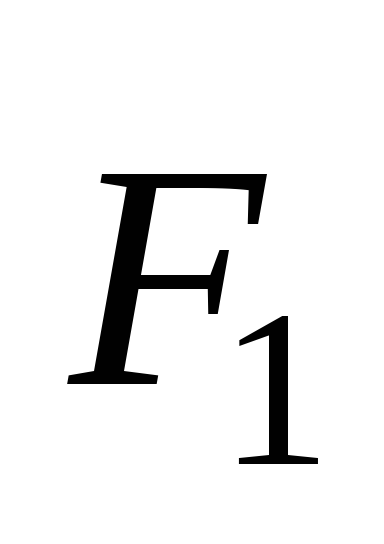 и
и  вокруг оси z,
перпендикулярной плоскости рис. 5.24,
против часовой стрелки. Определим эти
моменты:
вокруг оси z,
перпендикулярной плоскости рис. 5.24,
против часовой стрелки. Определим эти
моменты:
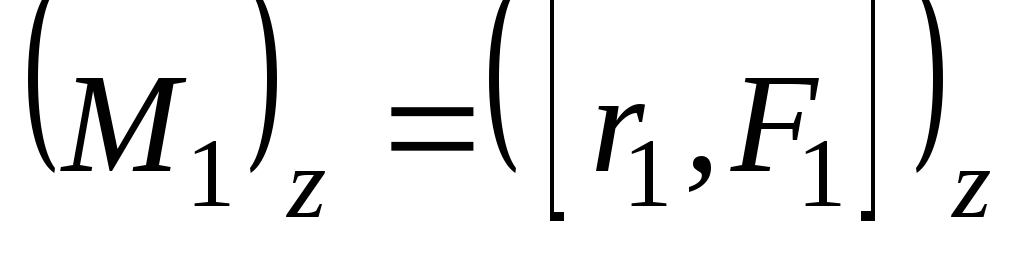 ;
; 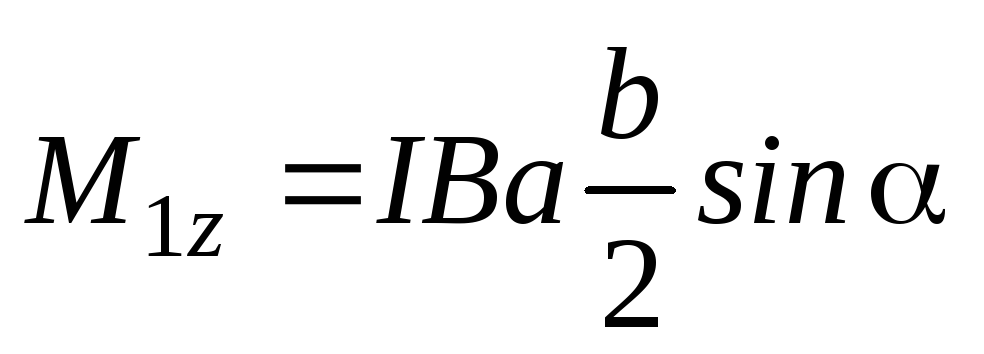 ;
;
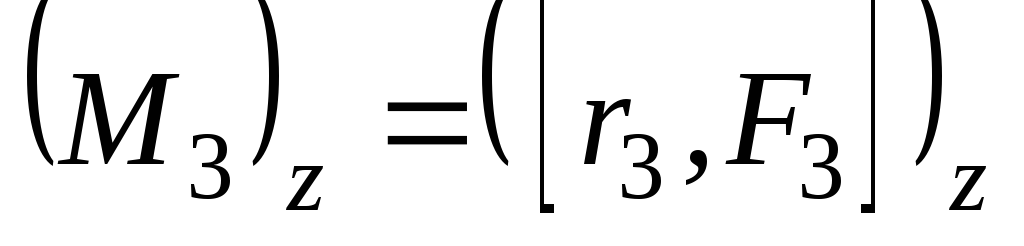 ;
;  ,
,
где 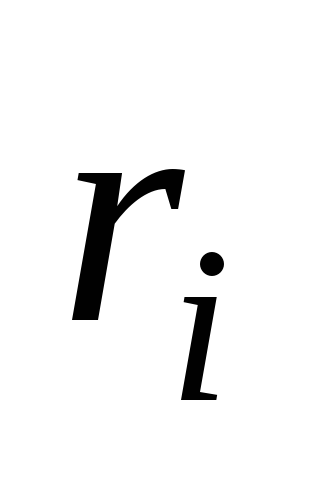 – радиусы-векторы, проведенные от оси
вращения в точки приложения соответствующих
сил.
– радиусы-векторы, проведенные от оси
вращения в точки приложения соответствующих
сил.
Направления векторов моментов указаны на рисунке. Ясно, что суммарный момент сил, действующих на рамку, определится как
 .
.
Поскольку  (площадь рамки), то, воспользовавшись
(5.16), получим
(площадь рамки), то, воспользовавшись
(5.16), получим
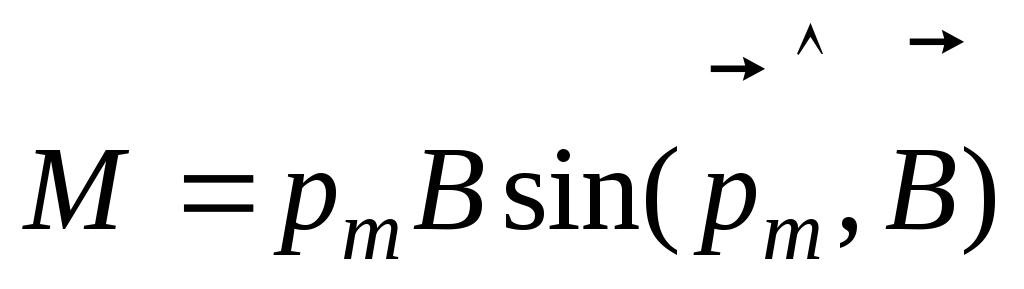 ,
, 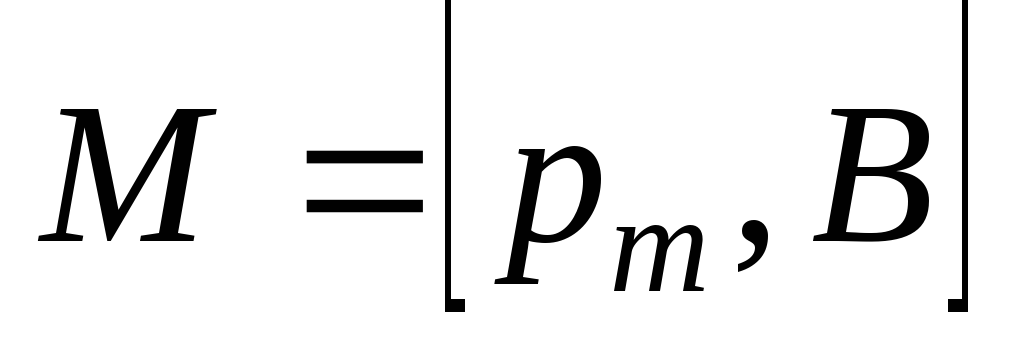 .
(5.34)
.
(5.34)
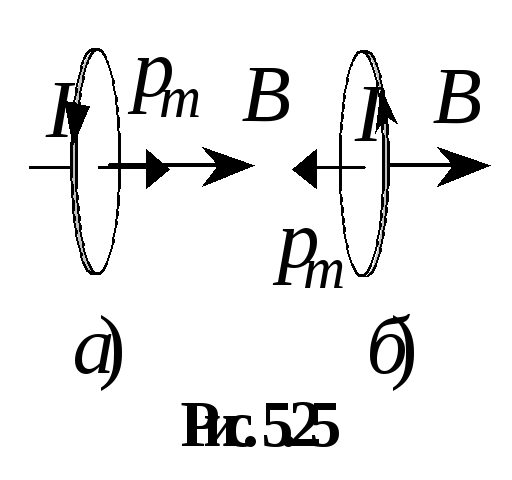
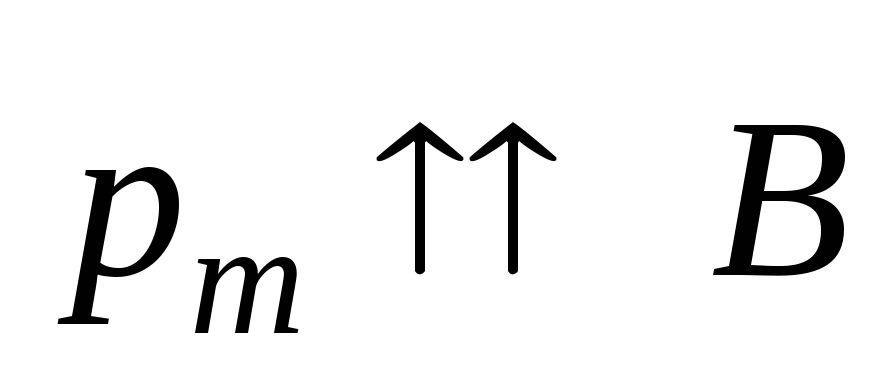 или
или 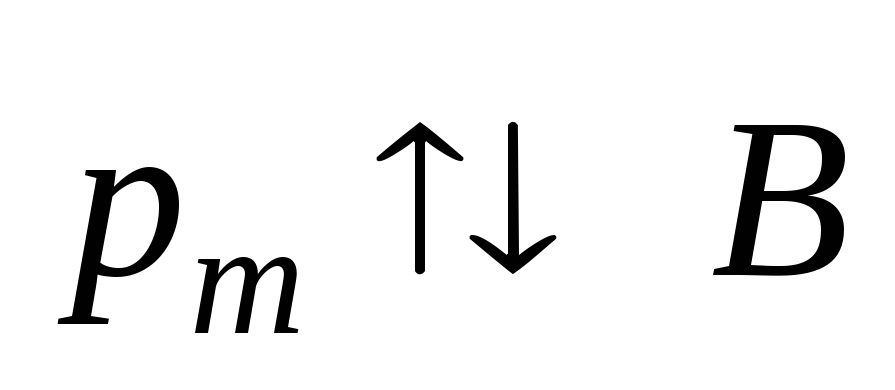 вращающий момент станет равным нулю,
то поворот рамки будет продолжаться до
достижения рамкой положений, указанных
на рис. 5.25. Однако нетрудно видеть, что
положение, указанное на рис. 5.25, а – это положение устойчивого равновесия.
При выведении рамки из этого положения
действие момента сил возвращает рамку
обратно (рис. 5.26, а).
Положение рамки на рис. 5.25, б – это положение неустойчивого равновесия.
При выведении рамки из этого положения
действие момента сил разворачивает
рамку еще больше (рис. 5.26, б).
вращающий момент станет равным нулю,
то поворот рамки будет продолжаться до
достижения рамкой положений, указанных
на рис. 5.25. Однако нетрудно видеть, что
положение, указанное на рис. 5.25, а – это положение устойчивого равновесия.
При выведении рамки из этого положения
действие момента сил возвращает рамку
обратно (рис. 5.26, а).
Положение рамки на рис. 5.25, б – это положение неустойчивого равновесия.
При выведении рамки из этого положения
действие момента сил разворачивает
рамку еще больше (рис. 5.26, б). 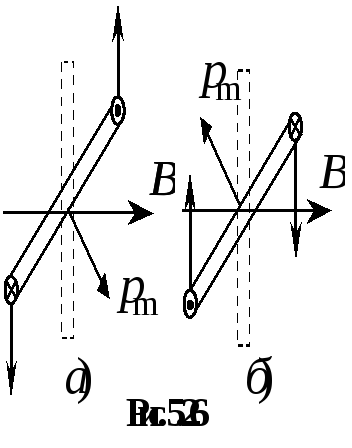
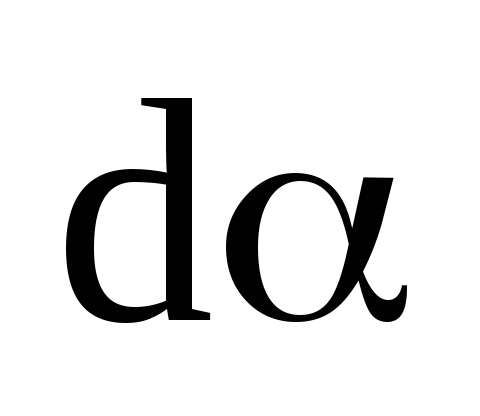 .
Воспользуемся выводом п.4.7 первой части
курса:
.
Воспользуемся выводом п.4.7 первой части
курса: 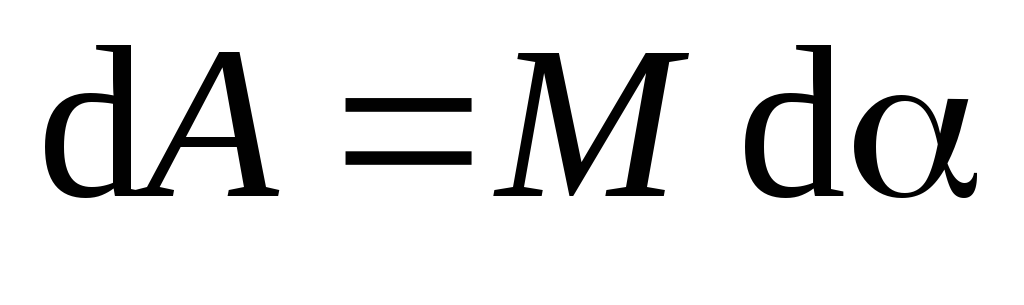 .
Тогда
.
Тогда 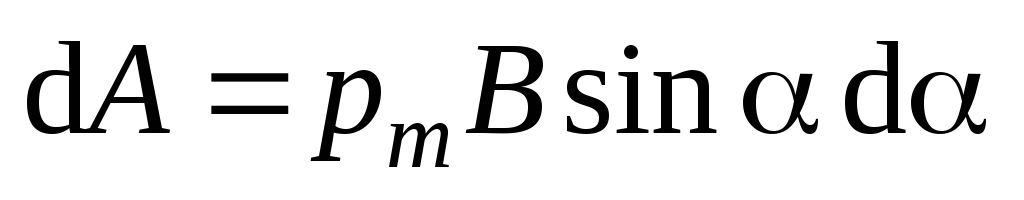 .
С точки зрения закона сохранения энергии
положительная работа внешних сил
увеличивает энергию рамки с током в
магнитном поле:
.
С точки зрения закона сохранения энергии
положительная работа внешних сил
увеличивает энергию рамки с током в
магнитном поле:  .
Поэтому энергия рамки с током в поле
выразится так:
.
Поэтому энергия рамки с током в поле
выразится так: 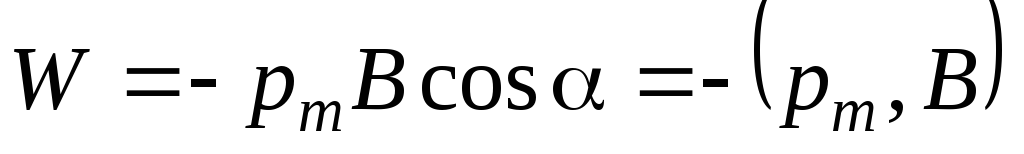 .
(5.35)
.
(5.35)
Если
теперь рассмотреть поведение рамки с
током в неоднородном поле, то необходимо
учесть, что на различные элементы рамки
будут действовать силы, направленные
по-разному (рис.5.27). В результате
суммирования элементарных сил 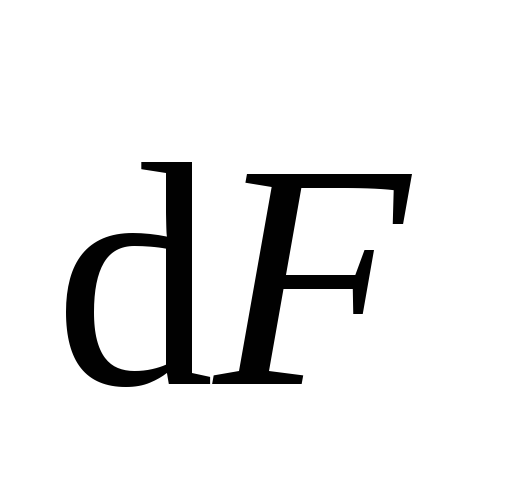 можно получить результирующую силу,
действующую на рамку в неоднородном
поле. Поскольку далее будет показано,
что силы Ампера потенциальны, то
справедливо соотношение (3.12) из первой
части курса:
можно получить результирующую силу,
действующую на рамку в неоднородном
поле. Поскольку далее будет показано,
что силы Ампера потенциальны, то
справедливо соотношение (3.12) из первой
части курса: 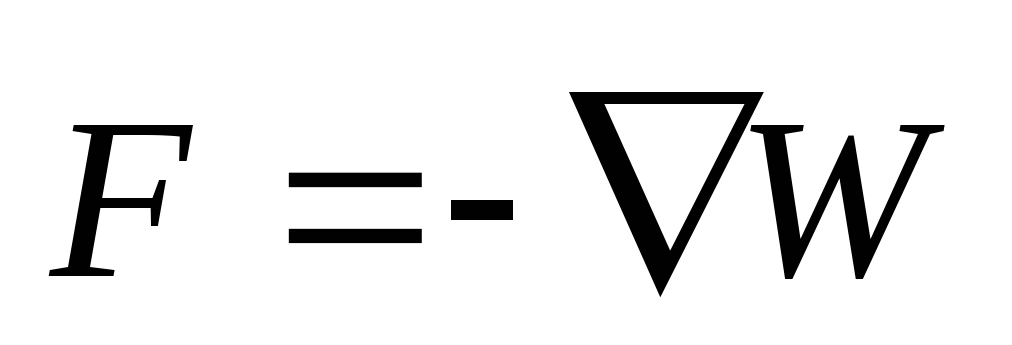 .
Тогда, если неоднородность магнитного
поля проявляется вдоль какой-нибудь
оси Ох,
то
.
Тогда, если неоднородность магнитного
поля проявляется вдоль какой-нибудь
оси Ох,
то
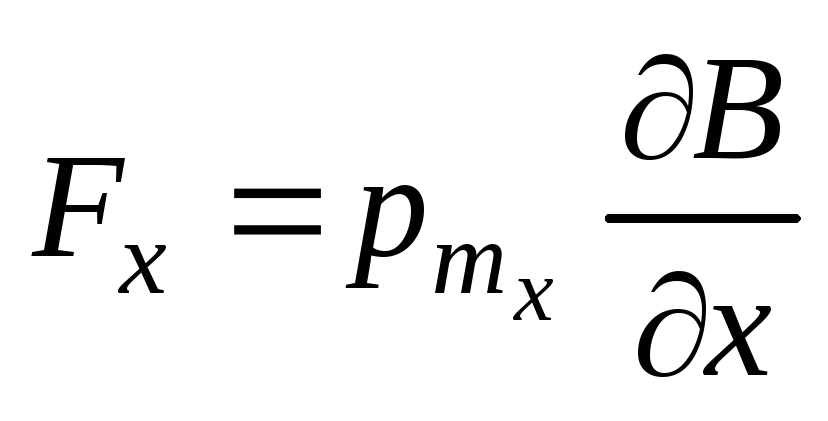 ,
,
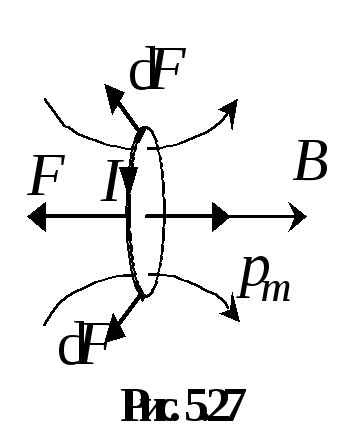
 больше,
т.е. влево на рис. 5.27). Если направления
магнитного момента рамки и индукции
поля противоположны, то рамка выталкивается
в область слабого поля.
больше,
т.е. влево на рис. 5.27). Если направления
магнитного момента рамки и индукции
поля противоположны, то рамка выталкивается
в область слабого поля.Суммируя все сделанные выводы, резюмируем: в наиболее общем случае поведение контура с током во внешнем магнитном поле описывается его поступательным движением, вращением и деформацией.
18. Работа сил магнитного поля
по перемещению проводника и контура с током
Рассмотрим
движение элемента  проводника с током в магнитном поле под
действием силы Ампера, действующей на
этот элемент со стороны поля (рис. 5.28).
Для простоты изображения сначала
допустим, что линии магнитной индукции
перпендикулярны проводнику, а поле
однородное. Если перемещение элемента
проводника равно
проводника с током в магнитном поле под
действием силы Ампера, действующей на
этот элемент со стороны поля (рис. 5.28).
Для простоты изображения сначала
допустим, что линии магнитной индукции
перпендикулярны проводнику, а поле
однородное. Если перемещение элемента
проводника равно 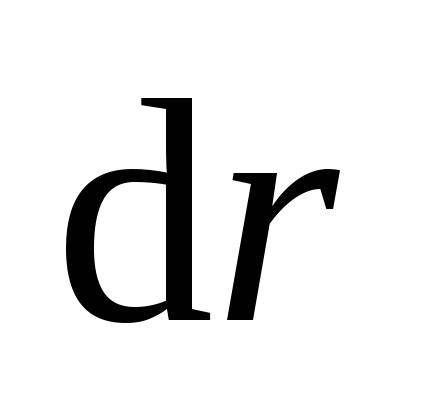 ,
то элементарная работа силы Ампера
будет равна
,
то элементарная работа силы Ампера
будет равна
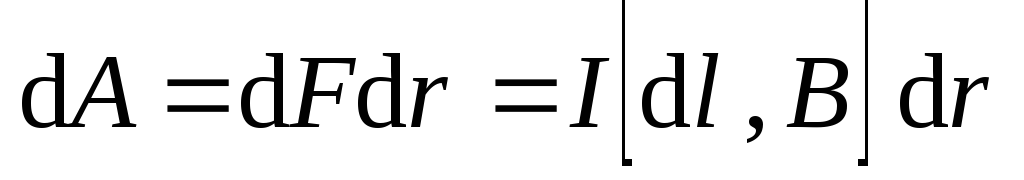 .
.
Поскольку в смешанном произведении векторов допустима циклическая перестановка сомножителей, то
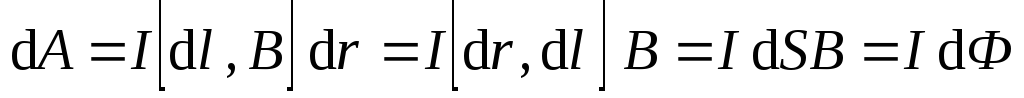 ,
,
где  – вектор площади элемента поверхности,
очерчиваемой при движении элемента
проводника (она заштрихована на рис.
5.28), а dФ – элементарный магнитный поток чрез
заштрихованную поверхность.
– вектор площади элемента поверхности,
очерчиваемой при движении элемента
проводника (она заштрихована на рис.
5.28), а dФ – элементарный магнитный поток чрез
заштрихованную поверхность.
Полная работа по перемещению всего проводника может быть найдена так:
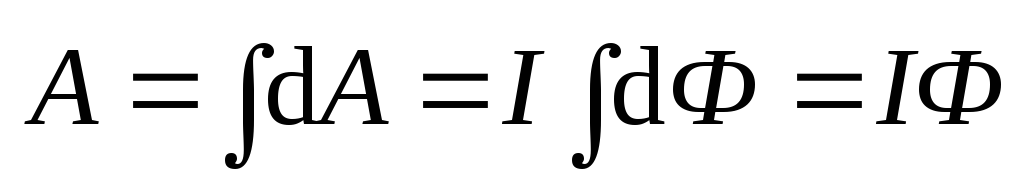 .
(5.36)
.
(5.36)
Работа сил магнитного поля по перемещению проводника с током равна произведению силы тока в проводнике и магнитного потока через поверхность, очерчиваемую проводником при своем движении.
Рассмотрим
теперь перемещение замкнутого контура
с током (рис. 5.29). Пусть контур произвольной
формы перемещается из положения abcda в положение 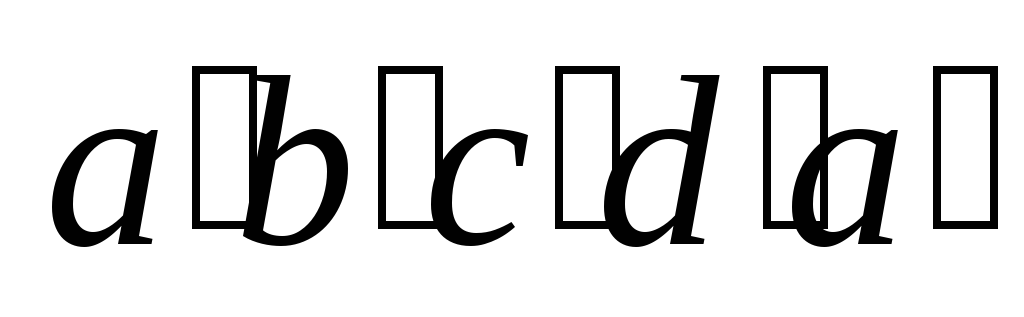 .
Разделим контур abcda на две части abc и cda.
Найдем работы по перемещению каждой
части.
.
Разделим контур abcda на две части abc и cda.
Найдем работы по перемещению каждой
части.
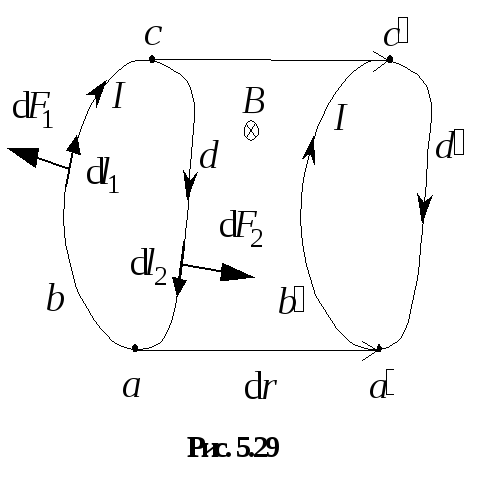
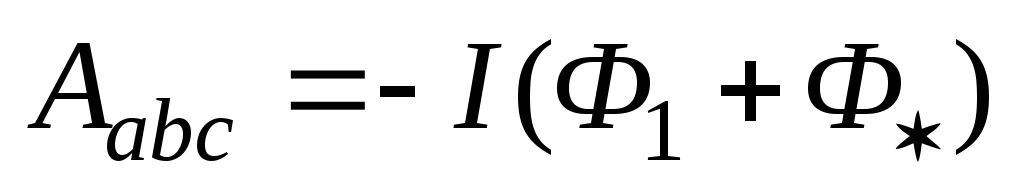
 ,
где Ф1 – магнитный поток через поверхность,
ограниченную контуром в его начальном
положении,
,
где Ф1 – магнитный поток через поверхность,
ограниченную контуром в его начальном
положении,  – магнитный поток через поверхность,
ограниченную контуром
– магнитный поток через поверхность,
ограниченную контуром 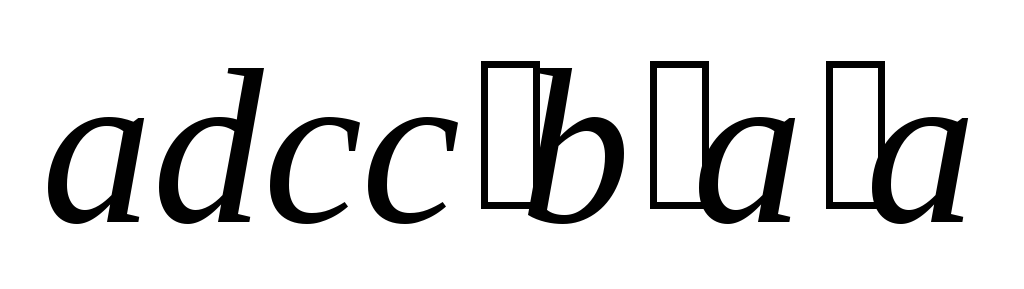 .
Знак “–” в этой формуле вызван тем,
что векторы перемещения
.
Знак “–” в этой формуле вызван тем,
что векторы перемещения 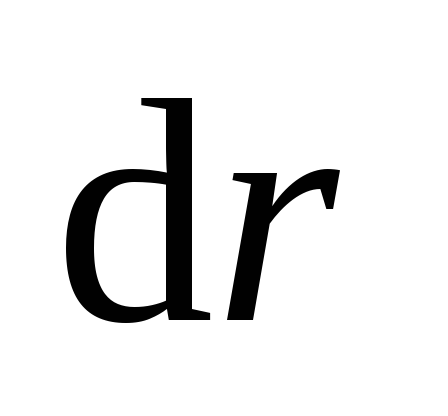 и силы Ампера
и силы Ампера  образуют друг с другом тупые углы для
всех элементов
образуют друг с другом тупые углы для
всех элементов 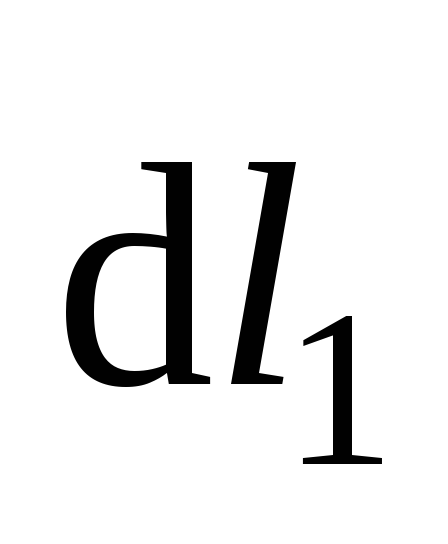 проводника abc.
проводника abc. 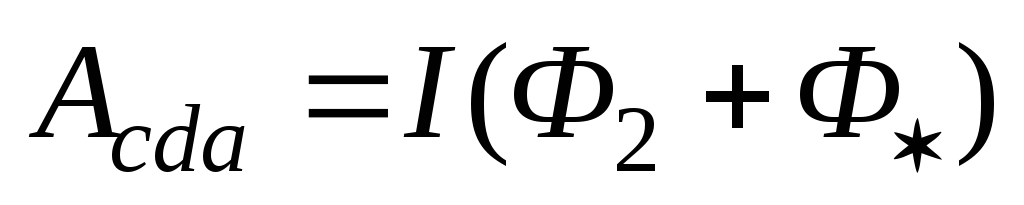 ,
где Ф2 – магнитный поток через поверхность,
ограниченную контуром в его конечном
положении.
,
где Ф2 – магнитный поток через поверхность,
ограниченную контуром в его конечном
положении.
Работа
по перемещению всего замкнутого контура
найдется так: 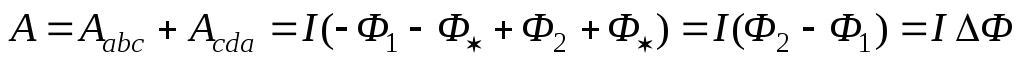 . Работа
сил магнитного поля по перемещению
контура с током равна произведению силы
тока в контуре и изменения магнитного
потока через площадь, ограниченную
контуром:
. Работа
сил магнитного поля по перемещению
контура с током равна произведению силы
тока в контуре и изменения магнитного
потока через площадь, ограниченную
контуром:
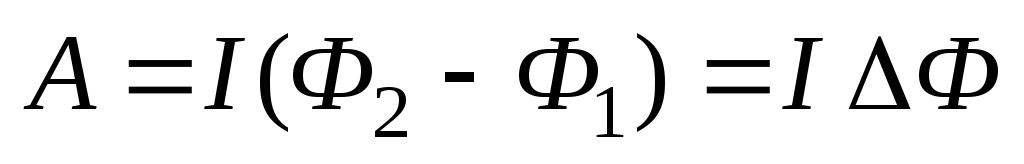 .
(5.37)
.
(5.37)

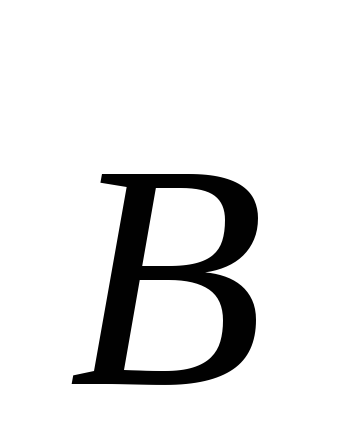 всегда можно разложить по трем взаимно
перпендикулярным направлениям (рис.
5.30) так, что
всегда можно разложить по трем взаимно
перпендикулярным направлениям (рис.
5.30) так, что 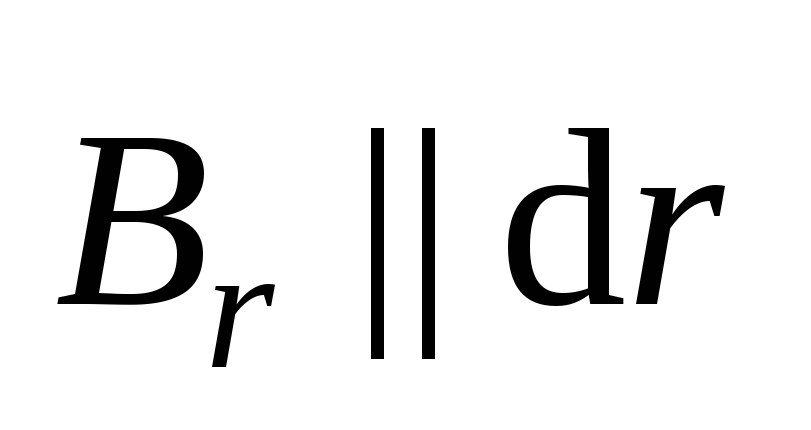 ,
, 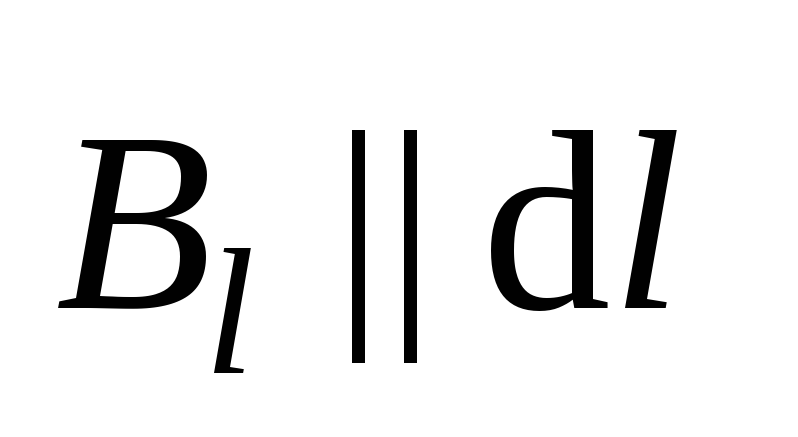 ,
,  .
Эти три составляющие магнитной индукции
определяют выражения для трех составляющих
силы Ампера
.
Эти три составляющие магнитной индукции
определяют выражения для трех составляющих
силы Ампера 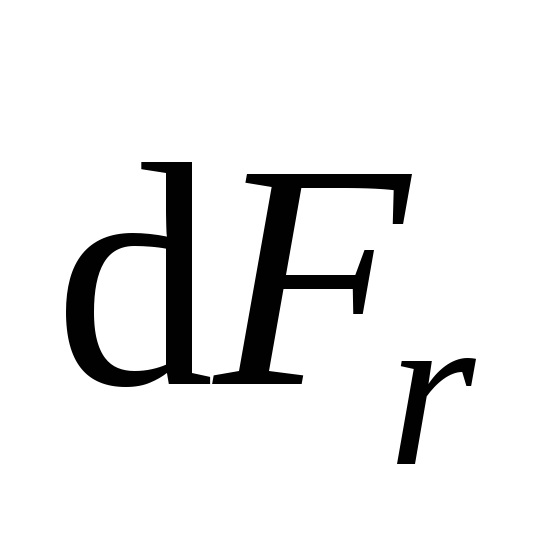 ,
, 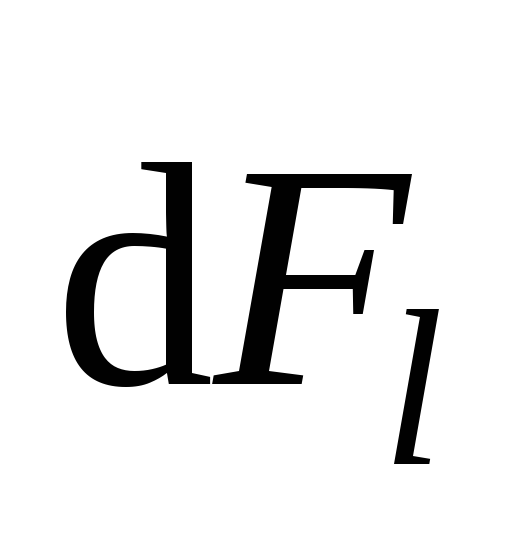 ,
, 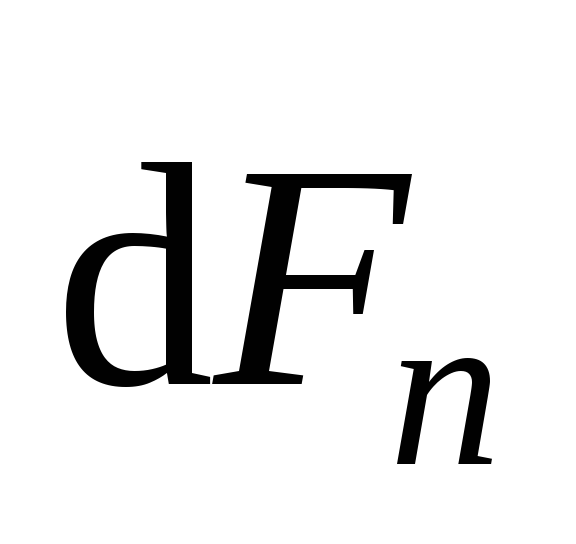 .
Однако, согласно (5.32),
.
Однако, согласно (5.32), 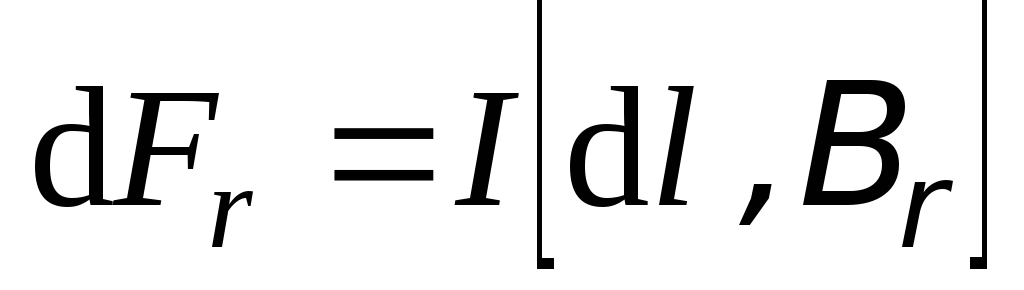 ,
причем
,
причем 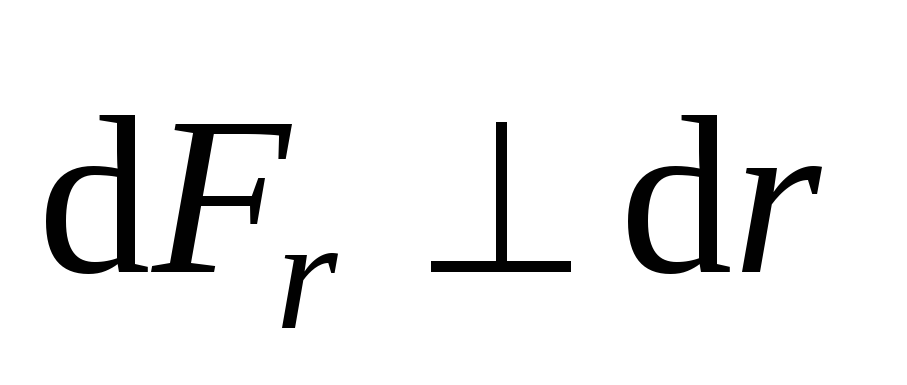 ,
а поэтому работа данной составляющей
силы Ампера по перемещению проводника
будет равна нулю. Кроме того,
,
а поэтому работа данной составляющей
силы Ампера по перемещению проводника
будет равна нулю. Кроме того,  .
Поэтому работу по перемещению проводника
будет совершать только сила
.
Поэтому работу по перемещению проводника
будет совершать только сила 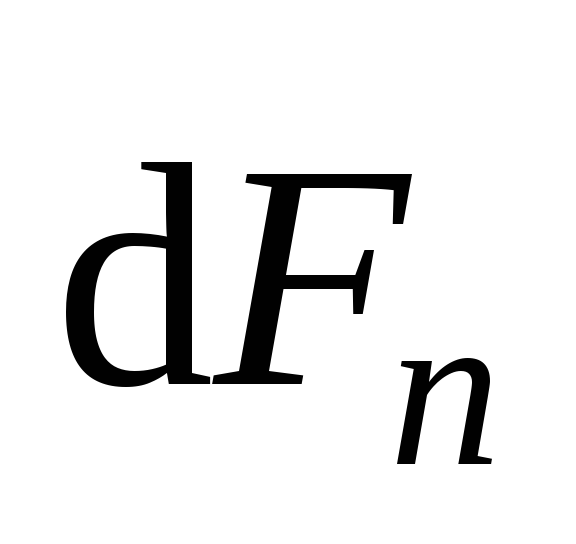 ,
а именно этот случай мы и рассматривали
раньше.
,
а именно этот случай мы и рассматривали
раньше.Заметим, что при перемещении контура с током в магнитном поле работа сил Ампера определяется магнитными потоками через контур только в начальном и конечном его положениях. Поэтому силы Ампера можно отнести к потенциальным.
19. Явление электромагнитной индукции.
Закон Фарадея–Максвелла
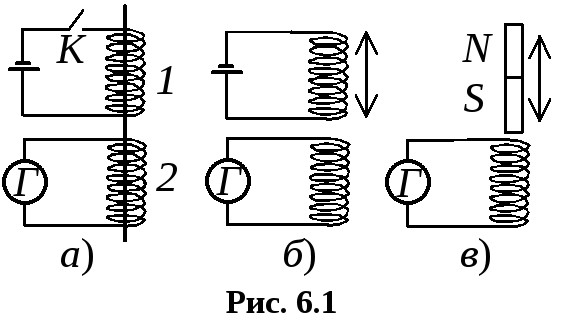
Для ответа на этот вопрос поставим второй опыт (рис. 6.1, б). Теперь катушка 1 постоянно подключена к источнику, а поэтому ток в ней неизменен. Однако в процессе смещения катушек друг относительно друга гальванометр дает показания, т.е. причиной появления тока в катушке 2 является изменение магнитного поля, в котором она находилась.
Чтобы подтвердить этот вывод, Фарадей проводит третий опыт (рис.6.1, в), в котором первая катушка заменяется постоянным магнитом. Результаты опыта при смещении магнита относительно катушки 2 полностью аналогичны предыдущим. Однако в этом случае видно, что причиной всех электрических явлений в катушке 2 является исключительно поведение магнитного поля, в которое она помещена, а источник создания магнитного поля никак не влияет на результат наблюдений.
Общим для всех трех опытов было то, что при осуществлении действий, описанных выше, изменялся магнитный поток через вторую катушку, в которой создавался (индуцировался) электрический ток. Важно также и то, что появление тока наблюдалось только в процессе изменения магнитного потока. Как только изменение магнитного потока прекращалось (полностью замыкался ключ, прекращалось относительное смещение катушек или останавливался магнит), стрелка гальванометра занимала нулевое положение. Если гальванометр заменить вольтметром, то он аналогично будет показывать появление разности потенциалов на концах катушки 2.
Наблюдаемое явление Фарадей назвал электромагнитной индукцией, т.е. явлением возникновения ЭДС индукции (а также индукционного тока в замкнутом контуре) при любом изменении магнитного потока через площадь, ограниченную контуром.
Экспериментально обнаружено, что величина возбуждаемой ЭДС определяется только скоростью изменения магнитного потока через контур и не зависит от способа его изменения. Напомним, что, согласно определению магнитного потока (5.18), его величина может изменяться при изменении модуля индукции в точках поверхности, ограниченной контуром, при изменении ориентации контура относительно линий магнитной индукции поля, при изменении площади контура.
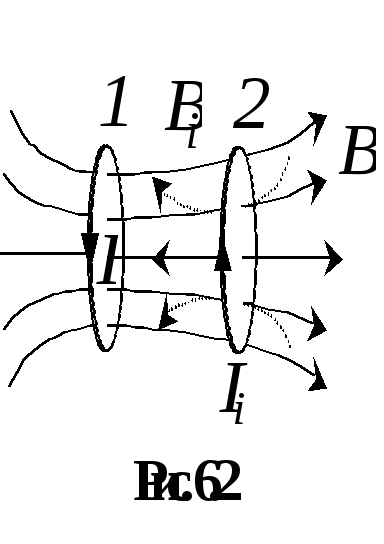
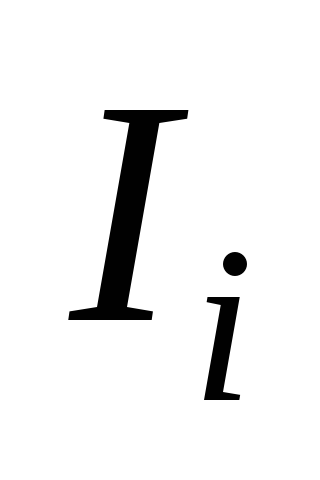 .
Его направление таково, что линии
индукции создаваемого им магнитного
поля (
.
Его направление таково, что линии
индукции создаваемого им магнитного
поля (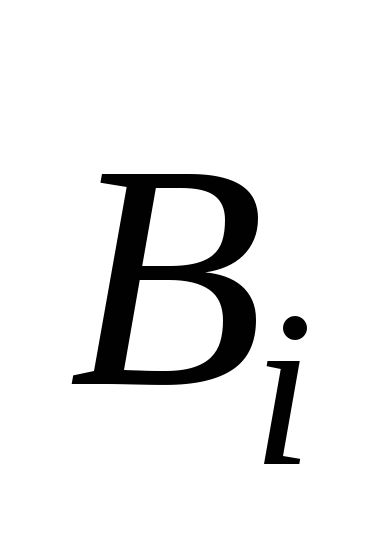 )
направлены противоположно внешнему.
Тогда суммарный магнитный поток через
контур 2 определяется разностью потоков внешнего
и индуцированного полей. Поэтому величина
магнитного потока через контур 2 увеличивается слабее. Если же ток в
контуре 1 будет уменьшаться, то явление
электромагнитной индукции создаст ток
в контуре 2,
направленный в противоположную сторону.
)
направлены противоположно внешнему.
Тогда суммарный магнитный поток через
контур 2 определяется разностью потоков внешнего
и индуцированного полей. Поэтому величина
магнитного потока через контур 2 увеличивается слабее. Если же ток в
контуре 1 будет уменьшаться, то явление
электромагнитной индукции создаст ток
в контуре 2,
направленный в противоположную сторону.Таким образом, процессы, происходящие при электромагнитной индукции, приводят к тому, что магнитный поток через исследуемый контур стремится остаться неизменным. Можно показать, что это – следствие закона сохранения энергии. Итак, правило Ленца показывает, что следствие процесса (появляющийся индукционный ток) всегда препятствует причине, его вызывающей (изменению магнитного потока).
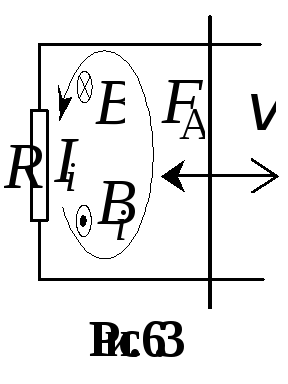
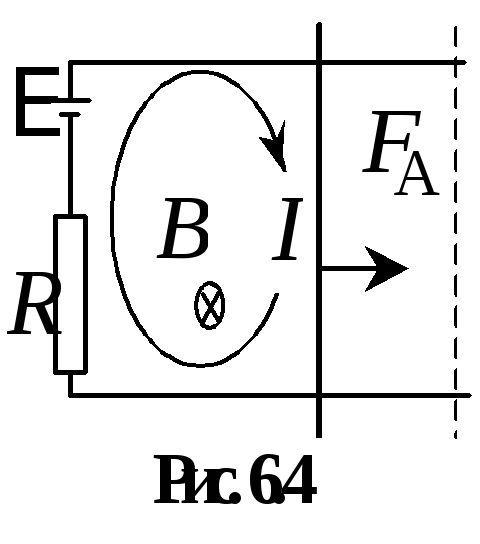
 систему двух параллельных проводников,
замкнутых на резистор сопротивлением R.
Пусть между проводниками располагается
перемычка, способная перемещаться по
ним без нарушения электрического
контакта. Тогда при ее движении вправо
со скоростью
систему двух параллельных проводников,
замкнутых на резистор сопротивлением R.
Пусть между проводниками располагается
перемычка, способная перемещаться по
ним без нарушения электрического
контакта. Тогда при ее движении вправо
со скоростью  будет увеличиваться площадь проводящего
контура, образованного проводниками,
резистором и перемычкой. Соответственно,
будет увеличиваться и магнитный поток
через этот контур, что приведет к
появлению индукционного тока. Индукционный
ток в контуре будет иметь такое направление
(против часовой стрелки), что вектор его
магнитной индукции
будет увеличиваться площадь проводящего
контура, образованного проводниками,
резистором и перемычкой. Соответственно,
будет увеличиваться и магнитный поток
через этот контур, что приведет к
появлению индукционного тока. Индукционный
ток в контуре будет иметь такое направление
(против часовой стрелки), что вектор его
магнитной индукции 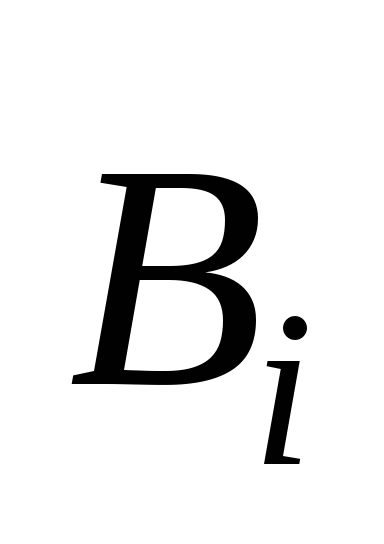 будет противоположен вектору индукции
внешнего магнитного поля. В магнитном
поле с индукцией
будет противоположен вектору индукции
внешнего магнитного поля. В магнитном
поле с индукцией 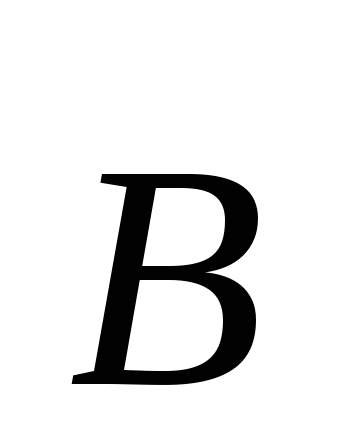 на перемычку с индукционным током будет
действовать сила Ампера, направление
которой определим по правилу левой руки
(см. рис. 6.3). Появившаяся сила стремится
замедлить движение перемычки, т.е.
препятствует ее движению. Поскольку
причиной электромагнитной индукции в
контуре было движение перемычки, то
следствие явления – появившаяся сила
Ампера – препятствует причине своего
появления.
на перемычку с индукционным током будет
действовать сила Ампера, направление
которой определим по правилу левой руки
(см. рис. 6.3). Появившаяся сила стремится
замедлить движение перемычки, т.е.
препятствует ее движению. Поскольку
причиной электромагнитной индукции в
контуре было движение перемычки, то
следствие явления – появившаяся сила
Ампера – препятствует причине своего
появления.Выведем количественные соотношения, описывающие содержание явления электромагнитной индукции.
1
способ (на
основе закона сохранения энергии). Рассмотрим схему, аналогичную предыдущей.
На рис.6.4 показан проводящий контур,
образованный двумя параллельными
проводниками, замкнутыми свободно
двигающейся по ним перемычкой. В контур
включен источник тока с ЭДС E и резистор
сопротивлением R.
Поместим контур в однородное магнитное
поле с индукцией 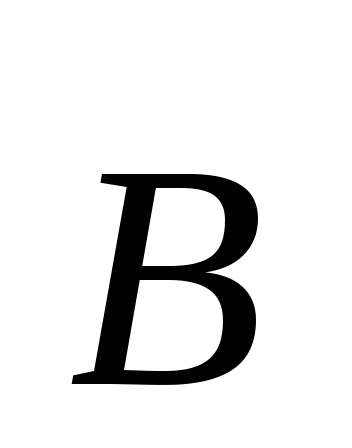 .
Поскольку в контуре существует
электрический ток, то на перемычку будет
действовать сила Ампера, что вызовет
движение перемычки вправо. Поэтому
площадь контура будет возрастать, а,
следовательно, магнитный поток через
площадь, ограниченную контуром, также
будет увеличиваться. Это будет причиной
появления электромагнитной индукции.
.
Поскольку в контуре существует
электрический ток, то на перемычку будет
действовать сила Ампера, что вызовет
движение перемычки вправо. Поэтому
площадь контура будет возрастать, а,
следовательно, магнитный поток через
площадь, ограниченную контуром, также
будет увеличиваться. Это будет причиной
появления электромагнитной индукции.
Согласно
закону сохранения энергии работа,
совершенная источником тока за время 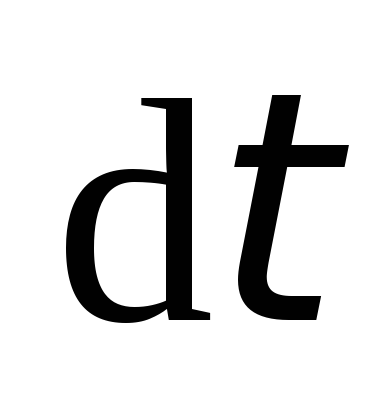 ,
равна работе сил магнитного поля по
перемещению перемычки и выделившемуся
в контуре за это время количеству
теплоты:
,
равна работе сил магнитного поля по
перемещению перемычки и выделившемуся
в контуре за это время количеству
теплоты: 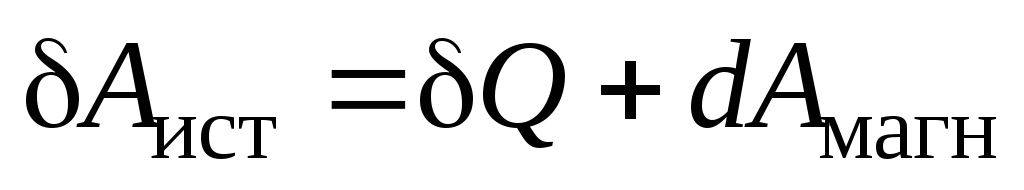 ,
т.е.
,
т.е.
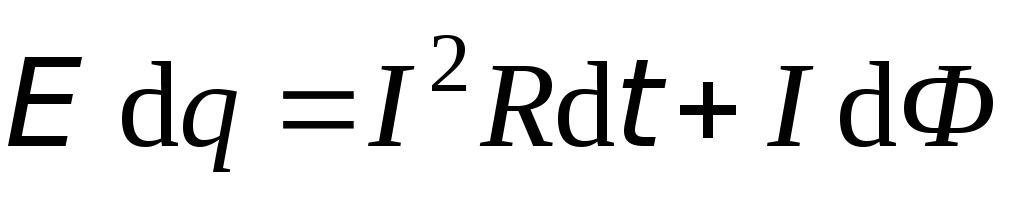 ,
,
где 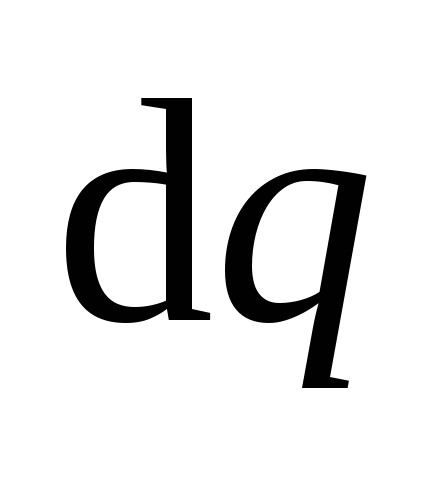 – заряд, перенесенный источником за
время
– заряд, перенесенный источником за
время  .
Поскольку
.
Поскольку 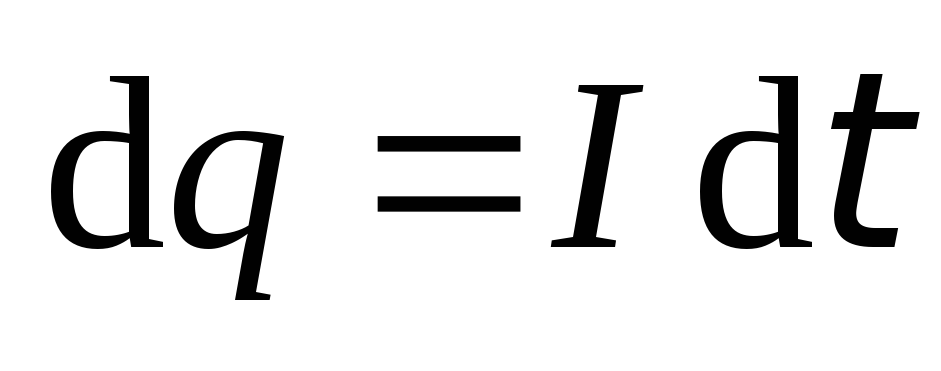 ,
то
,
то
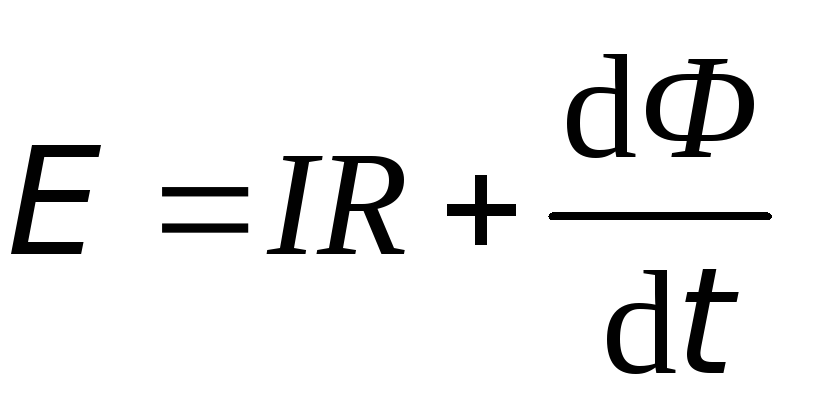 ,
,
откуда сила тока в контуре
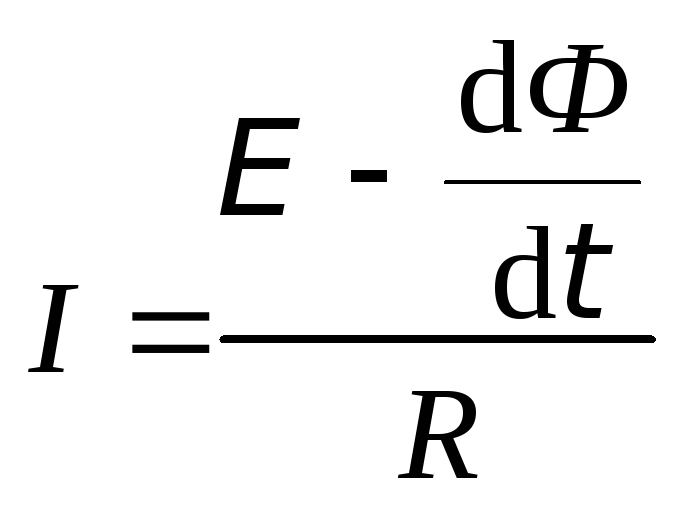 .
.
Поскольку, согласно закону Ома, числитель последнего выражения должен определять суммарную ЭДС в контуре, то, следовательно, второе слагаемое выражает ЭДС индукции, возникшую в нем:
 .
(6.1)
.
(6.1)
2
способ (на
основе электронных представлений). Рассмотрим процессы, происходящие
внутри перемычки (рис.6.5, а).
Поскольку все свободные электроны
двигаются вместе с ней вправо, то со
стороны магнитного поля на них действует
магнитная составляющая силы Лоренца  (5.29). Ее действие приводит к смещению
электронов к нижнему краю перемычки, в
результате чего происходит разделение
зарядов внутри нее. Между разделенными
зарядами возникает электрическое поле
напряженностью
(5.29). Ее действие приводит к смещению
электронов к нижнему краю перемычки, в
результате чего происходит разделение
зарядов внутри нее. Между разделенными
зарядами возникает электрическое поле
напряженностью  ,
которое действует на электроны с силой
,
которое действует на электроны с силой 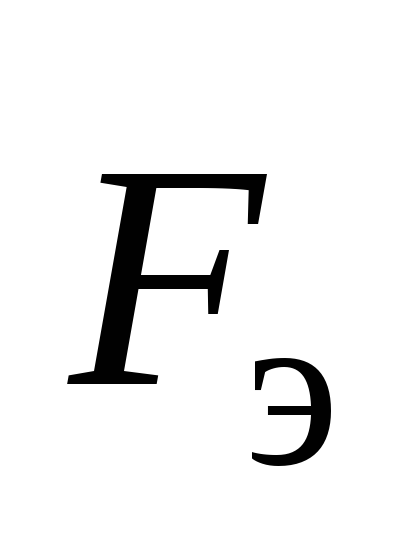 (рис.6.5, б).
В стационарном режиме
(рис.6.5, б).
В стационарном режиме 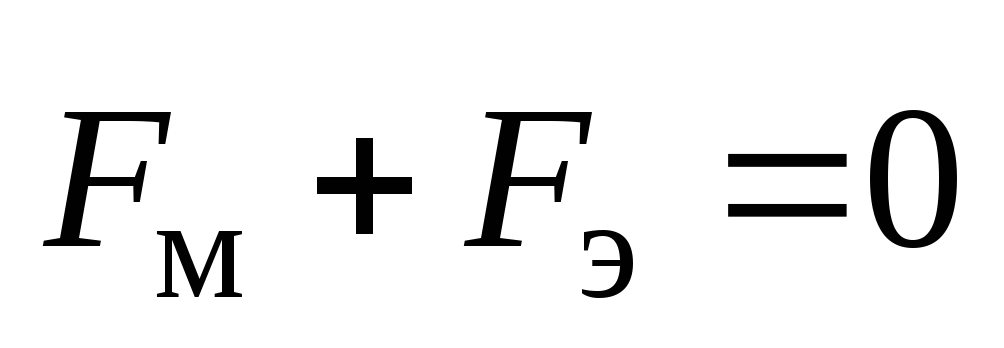 .
Следовательно,
.
Следовательно, 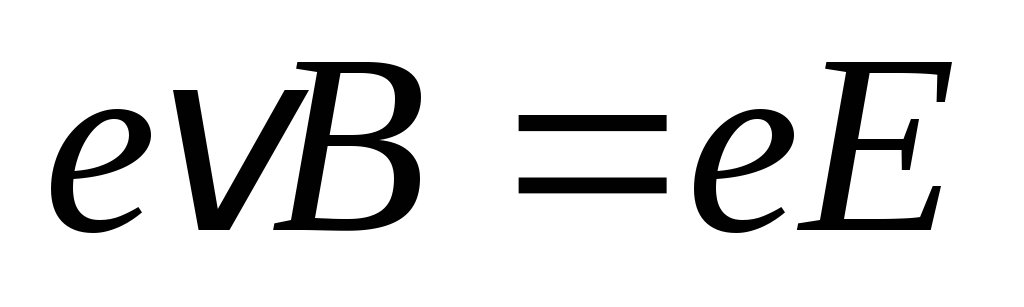 ,
т.е.
,
т.е. 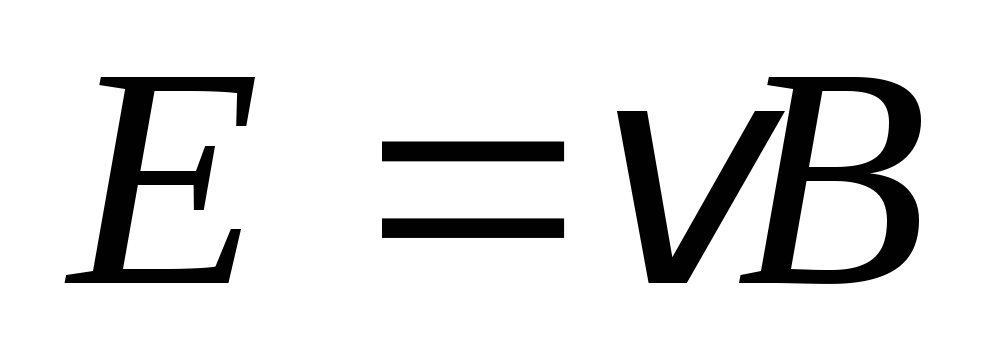 .
Найдем разность потенциалов между
концами перемычки:
.
Найдем разность потенциалов между
концами перемычки:
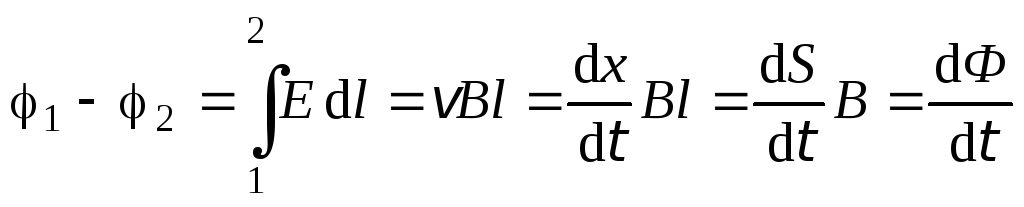 ,
,
поскольку 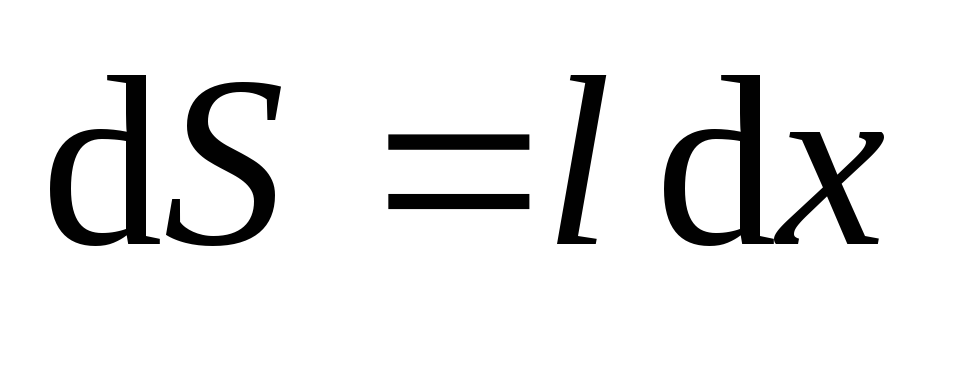 –
площадь, очерчиваемая проводником за
время
–
площадь, очерчиваемая проводником за
время 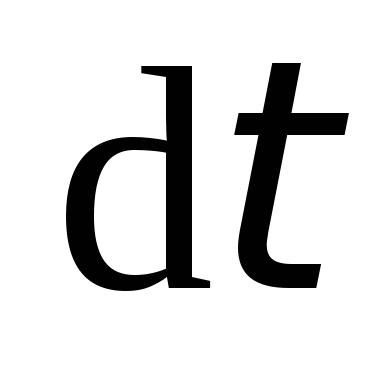 при движении (рис.6.5, в).
Перемычка играет роль источника
индукционного тока, а положительным
направлением тока внутри источника
считается направление от “–” к “+”.
Поэтому ЭДС индукции, возникшая при
движении перемычки, определится как
при движении (рис.6.5, в).
Перемычка играет роль источника
индукционного тока, а положительным
направлением тока внутри источника
считается направление от “–” к “+”.
Поэтому ЭДС индукции, возникшая при
движении перемычки, определится как
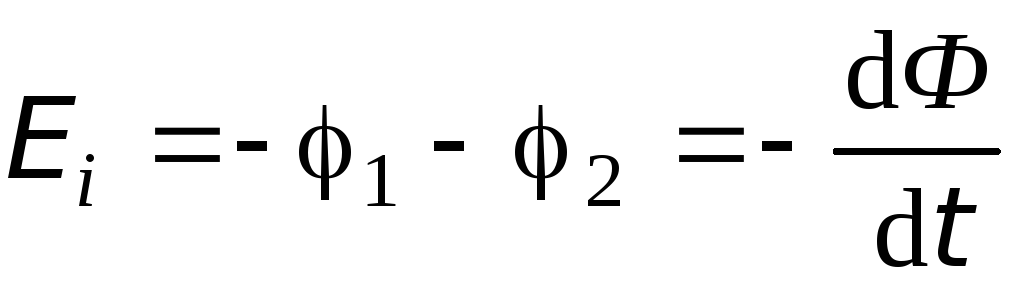 .
(6.2)
.
(6.2)
Сборник задач абитуриенту. МАГНЕТИЗМ. Сила Ампера. Индукция магнитного поля. Тема 22-1
МАГНЕТИЗМ. Сила Ампера. Индукция магнитного поля. Тема 22-1
22.1. На проводник длиной 0,5 м с током силой 20 A в однородном магнитном поле с индукцией 0,1 Тл действует сила 0,5 H. Какой угол (в градусах) составляет направление тока в проводнике с вектором магнитной индукции?
Ответ22.2. Прямой проводник с током помещен в однородное магнитное поле перпендикулярно линиям индукции. Во сколько раз уменьшится сила, действующая на проводник со стороны магнитного поля, если его повернуть так, чтобы направление тока в проводнике составляло угол 30° с вектором индукции поля?
Ответ22.3. Проводник с током помещен в однородное магнитное поле с индукцией B = 20 мТл. Определить силу, действующую на этот проводник, если его длина l = 0,1 м, сила тока I = 3,А, а угол между направлением тока и вектором B равен α = 45°.
Ответ22.4. Проводник длиной 140 см согнули под прямым углом так, что одна из сторон угла равна 60 см, и поместили в однородное магнитное поле с индукцией 2 мТл обеими сторонами перпендикулярно линиям индукции. Какая сила (в мН) будет действовать на этот проводник, если по нему пропустить ток силой 10 A?
Ответ22.5. Проводник длиной 110 см согнули под утлом 60° так, что одна из сторон угла равна 30 см, и поместили в однородное магнитное поле с индукцией 2 мТл обеими сторонами перпендикулярно линиям индукции. Какая сила (в мН) будет действовать на этот проводник, если по нему пропустить ток силой 10 A
Ответ22.6. Определить направление силы взаимодействия тока с магнитным полем для каждого из случаев показанных на рисунке.
Ответ22.7. Определить направление магнитного поля для каждого из случаев, показанных на рисунке. Проводник помещают перпендикулярно магнитному полю.
Ответ22.8. По очень длинному вертикальному проводнику снизу вверх проходит ток силой 4 A. Определить положение точки вблизи проводника, в которой результирующий вектор магнитной индукции полей Земли и проводника имеет вертикальное направление. Горизонтальная составляющая индукции магнитного поля Земли 20 мкТл, провод расположен в северном полушарии.
Ответ22.9. Два прямолинейных параллельных проводника с одинаковыми токами находятся на расстоянии 8 см друг от друга и притягиваются с силой 2,5 мН. Определить силу тока в проводниках, если их длина 250 см, а токи идут в одну сторону.
Ответ


