Преобразование треугольник-звезда — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 8 декабря 2014; проверки требуют 9 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 8 декабря 2014; проверки требуют 9 правок.

Преобразование треугольник-звезда — способ эквивалентного преобразования пассивного участка линейной электрической цепи — «треугольника» (соединения трёх ветвей, которое имеет вид треугольника, сторонами которого являются ветви, а вершинами — узлы), в «звезду» (соединение трёх ветвей, которые имеют один общий узел). Эквивалентность «треугольника» и «звезды» обусловлена тем, что при одинаковых напряжениях между одноименными выводами электрической цепи токи, которые втекают в одноименные выводы, а следовательно и мощности также будут одинаковыми^[1].

Дальнейшие рассуждения проводятся для резисторов, но фактически применимы к произвольным импедансам.

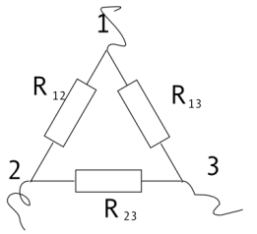
Рассмотрим приведенные выше схемы относительно выводов 1 и 2.

В схеме «треугольник» резистор R12{\displaystyle R_{12}} соединён параллельно с последовательно соединёнными резисторами R13{\displaystyle R_{13}} и R23{\displaystyle R_{23}}, что соответствует последовательно соединенным сопротивлениям R1{\displaystyle R_{1}} и R2{\displaystyle R_{2}} в схеме «звезда». Отсюда следует, что:

R1+R2=R12⋅(R23+R13)R12+R23+R13{\displaystyle R_{1}+R_{2}={\frac {R_{12}\cdot (R_{23}+R_{13})}{R_{12}+R_{23}+R_{13}}}}

Аналогично для других пар выводов:

R1+R3=R13⋅(R12+R23)R12+R23+R13{\displaystyle R_{1}+R_{3}={\frac {R_{13}\cdot (R_{12}+R_{23})}{R_{12}+R_{23}+R_{13}}}}

R2+R3=R23⋅(R12+R13)R12+R23+R13{\displaystyle R_{2}+R_{3}={\frac {R_{23}\cdot (R_{12}+R_{13})}{R_{12}+R_{23}+R_{13}}}}

Решая данную систему уравнений относительно сопротивлений R1{\displaystyle R_{1}}, R2{\displaystyle R_{2}} и R3{\displaystyle R_{3}} , получаем:

R1=R12⋅R13R12+R23+R13{\displaystyle R_{1}={\frac {R_{12}\cdot R_{13}}{R_{12}+R_{23}+R_{13}}}}

R2=R12⋅R23R12+R23+R13{\displaystyle R_{2}={\frac {R_{12}\cdot R_{23}}{R_{12}+R_{23}+R_{13}}}}

R3=R23⋅R13R12+R23+R13{\displaystyle R_{3}={\frac {R_{23}\cdot R_{13}}{R_{12}+R_{23}+R_{13}}}}

Решив исходную систему уравнений относительно сопротивлений R12{\displaystyle R_{12}}, R13{\displaystyle R_{13}} и R23{\displaystyle R_{23}} получим формулы для обратного преобразования, из «звезды» в «треугольник»:

R12=R1+R2+R1⋅R2R3{\displaystyle R_{12}=R_{1}+R_{2}+{\frac {R_{1}\cdot R_{2}}{R_{3}}}}

R13=R1+R3+R1⋅R3R2{\displaystyle R_{13}=R_{1}+R_{3}+{\frac {R_{1}\cdot R_{3}}{R_{2}}}}

R23=R2+R3+R2⋅R3R1{\displaystyle R_{23}=R_{2}+R_{3}+{\frac {R_{2}\cdot R_{3}}{R_{1}}}}

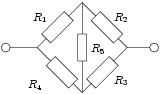
Преобразование треугольник-звезда может быть полезным для расчёта сопротивления несбалансированного моста при R1R2≠R4R3{\displaystyle {\frac {R_{1}}{R_{2}}}\neq {\frac {R_{4}}{R_{3}}}}.

1. ↑ Бессонов Л.А. Теоретические основы электротехники: Электрические цепи: Учебник для Вузов. — 8. — М.: Высшая школа, 1984. — 559 с.

Вопрос 18. Соединение резисторов треугольником и звездой. Мостовые схемы. Преобразование треугольников сопротивлений в эквивалентную звезду и наоборот.

Если имеется 3 сопротивления, образующих 3 узла, то такое сопротивление составляет

пассивный треугольник, а если имеется только один узел, то сопротивления составляютпассивную звезду.

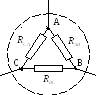
пассивный треугольник

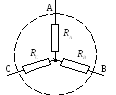
пассивная звезда

Эти схемы можно эквивалентно заменить одна другой, если все токи в ветвях не подвергнутся преобразованию (то есть то, что за пределами штриховой линии не изменится). Из этих предпосылок получим следующие

формулы преобразования:

(преобразование треугольника в звезду):

Сопротивление луча эквивалентной звезды равно произведению сопротивлений сторон треугольника, примыкающих к той же вершине, что и луч звезды, делённое на сумму всех сопротивлений сторон треугольника:

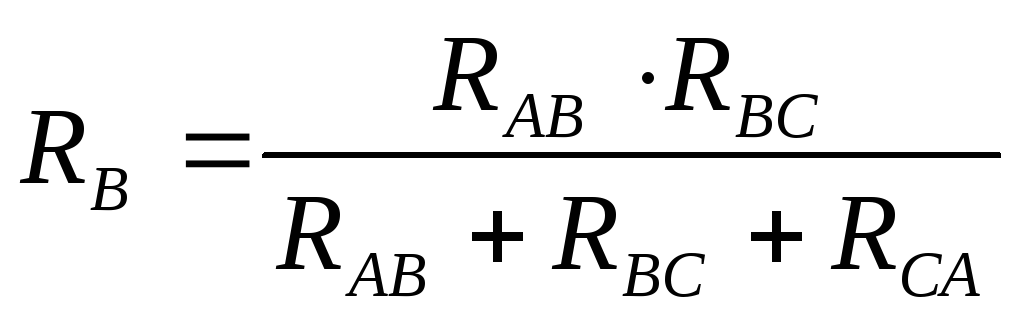
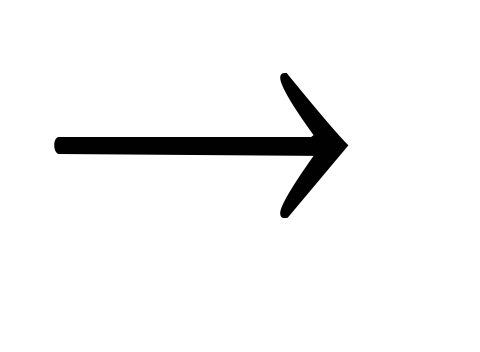
(преобразование звезды в треугольник):

Сопротивление стороны треугольника равно сумме сопротивлений лучей звезды, примыкающих к тем же вершинам, что и сторона треугольника, плюс произведение этих сопротивлений, делённое на сопротивление третьего луча звезды:

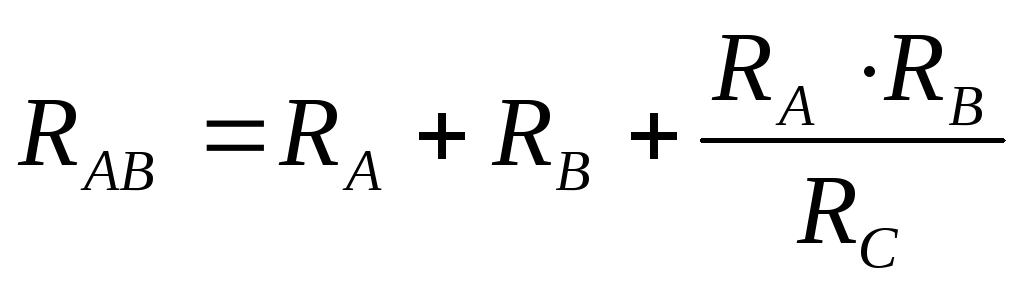
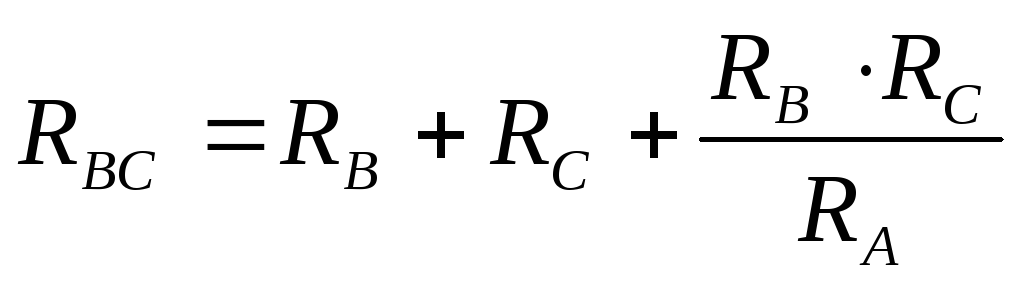
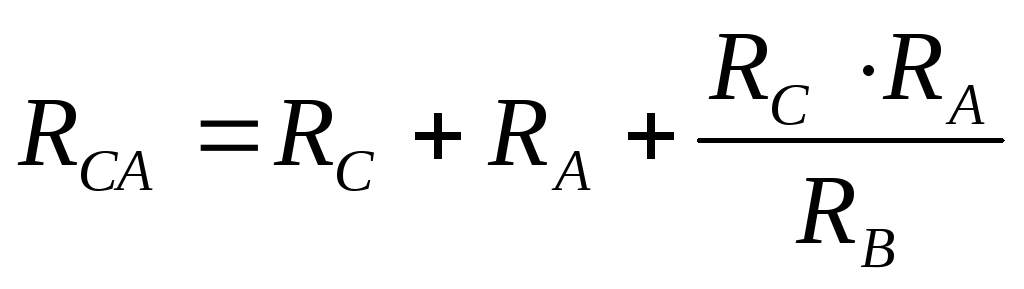
Преобразование треугольника в звезду применяется в мостовых схемах, которые представляют собой 4 резистора, соединённых четырёхугольником, в одну диагональ которого ставится источник, во вторую — измерительные приборы. Найти входное сопротивление таких схем без предварительного преобразования невозможно.

Задача

Д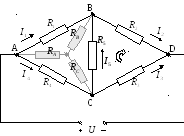ано:

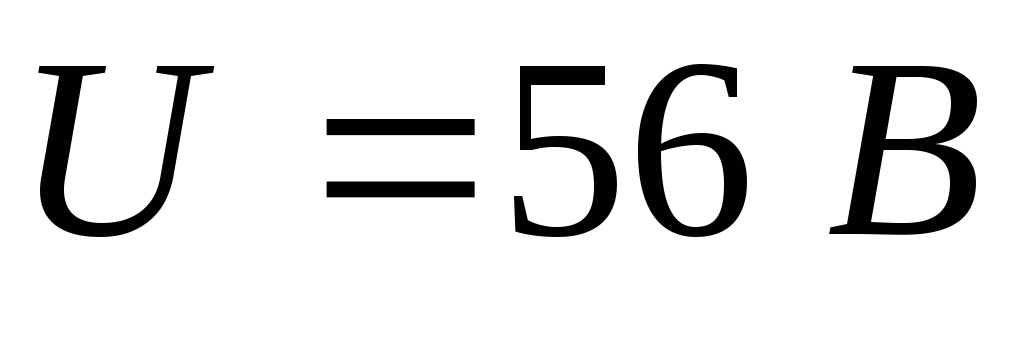
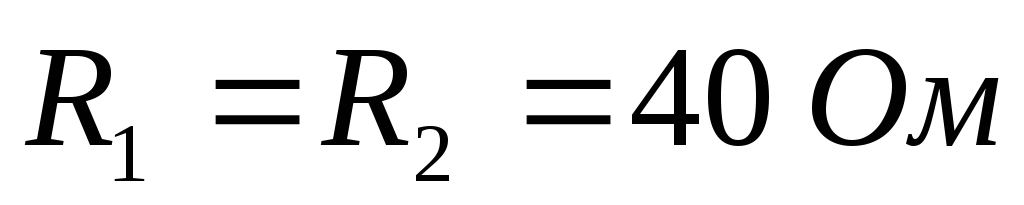
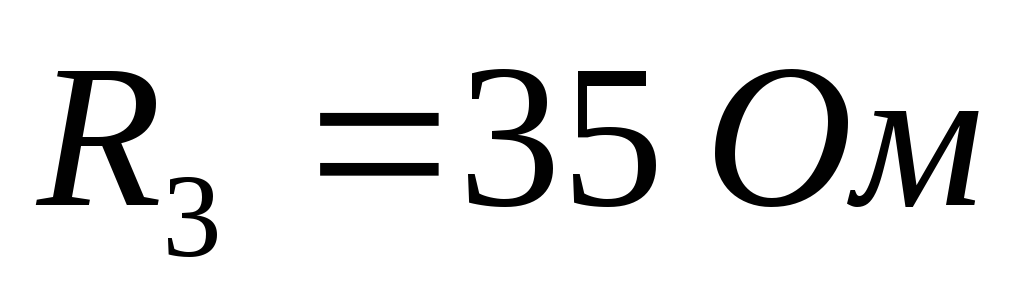
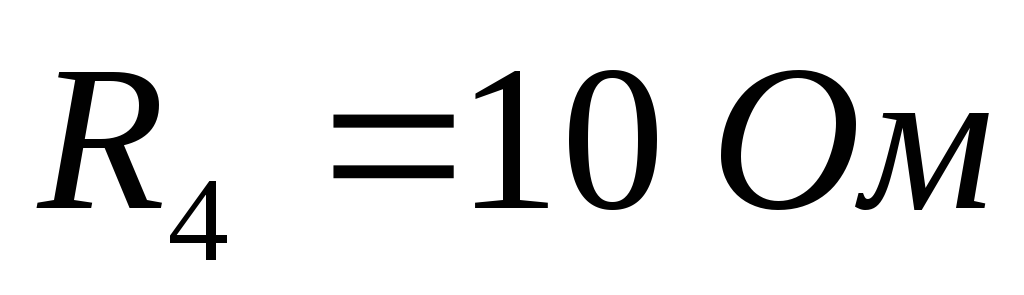
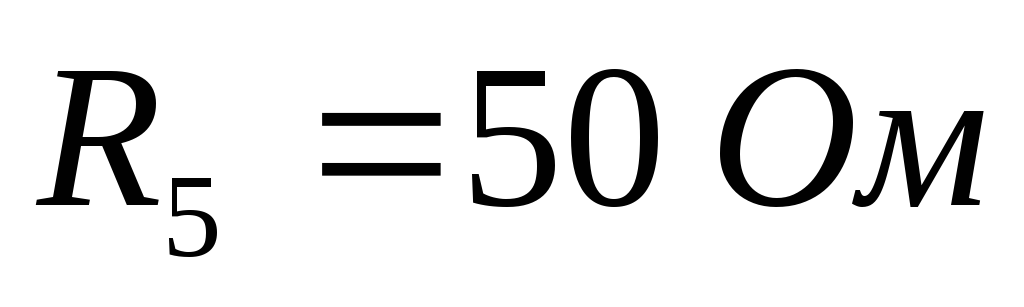
Найти все токи и направить их.

В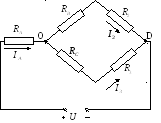ыполним преобразование треугольника ABC в эквивалентную звезду:

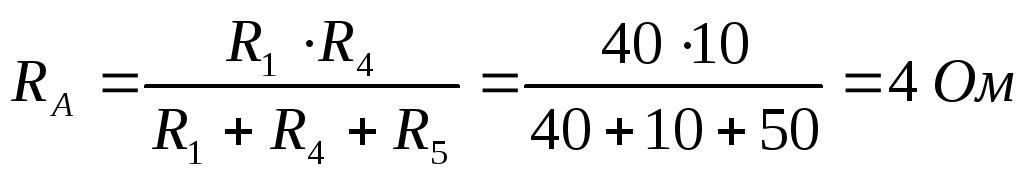
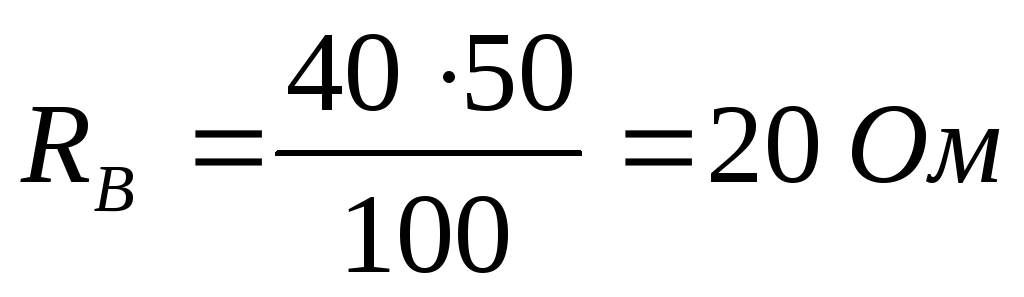
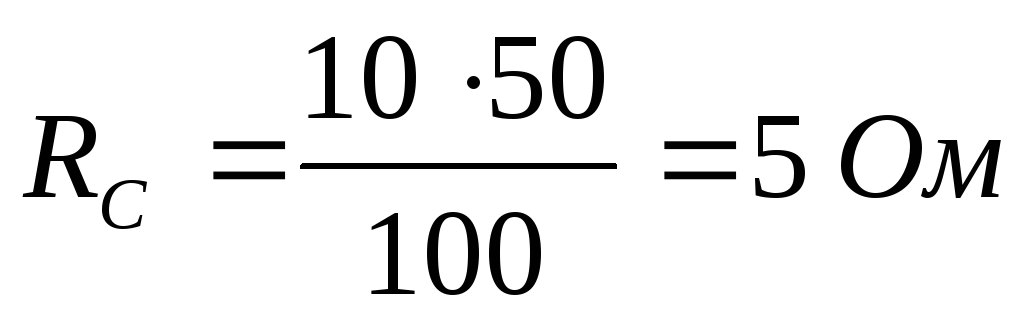
Рассчитаем входное сопротивление и ток:

Найдём напряжение на разветвлённом участке OD и токи в его ветвях:

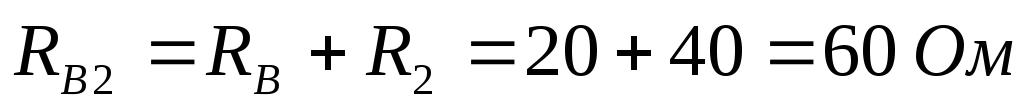
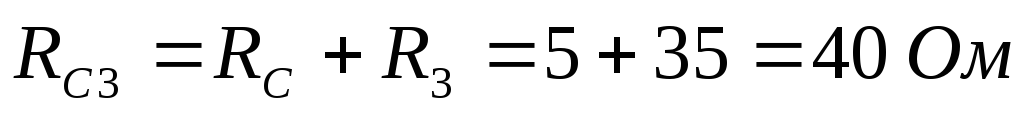
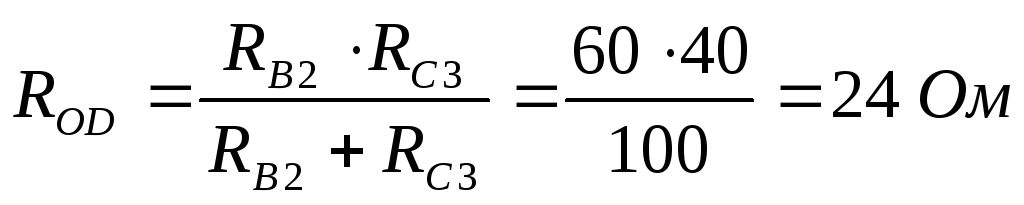
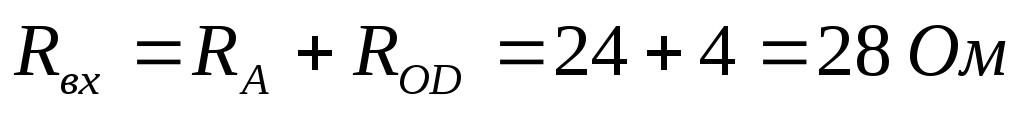
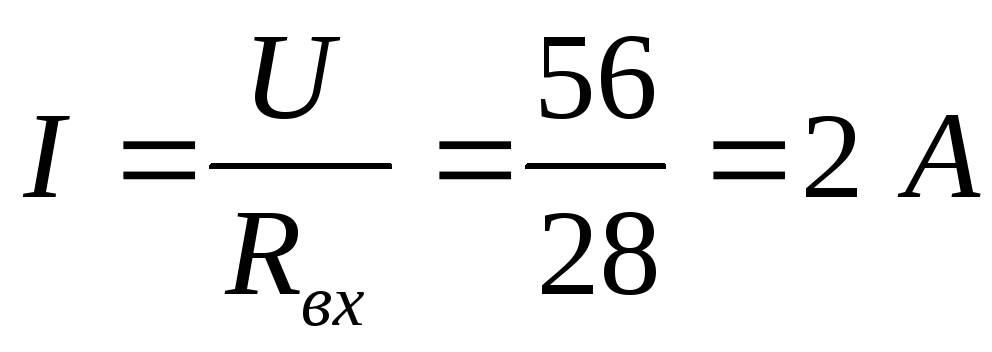
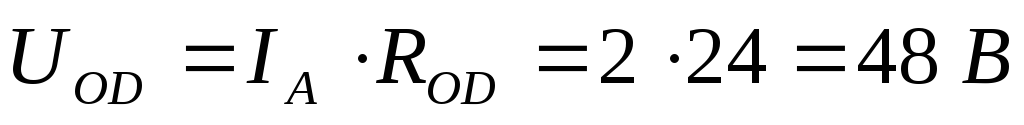
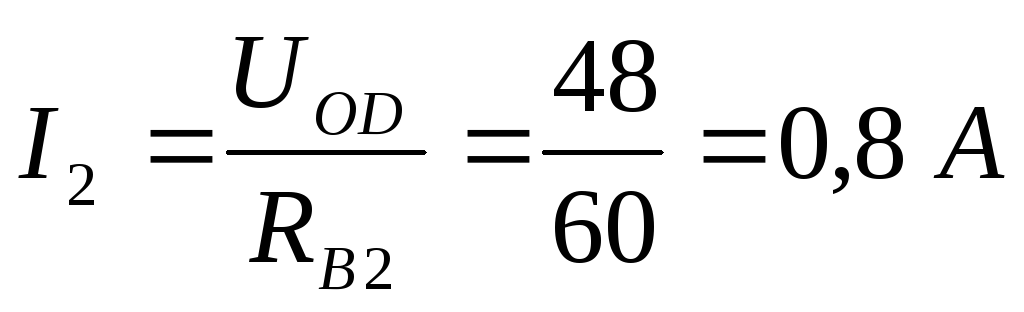
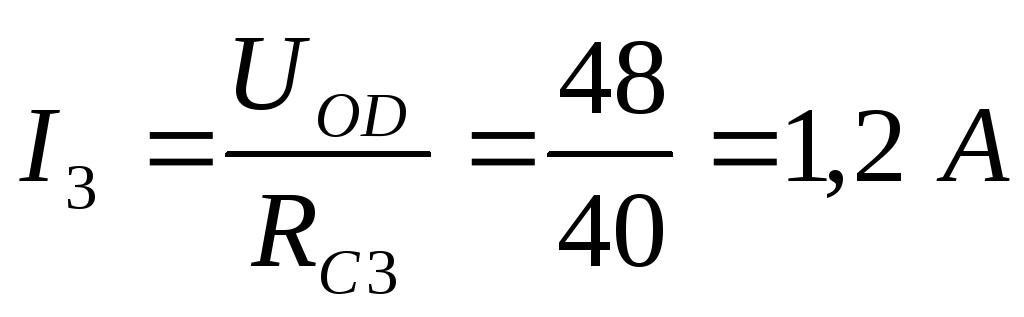
В первоначальной схеме направим токи, ток 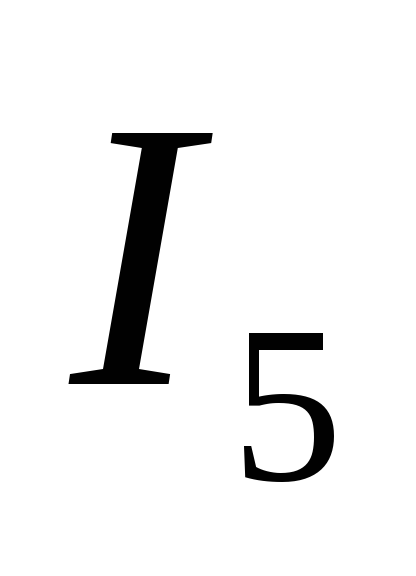направим произвольно.

Для треугольника, который не заменяли, составляем уравнение по второму закону Кирхгофа: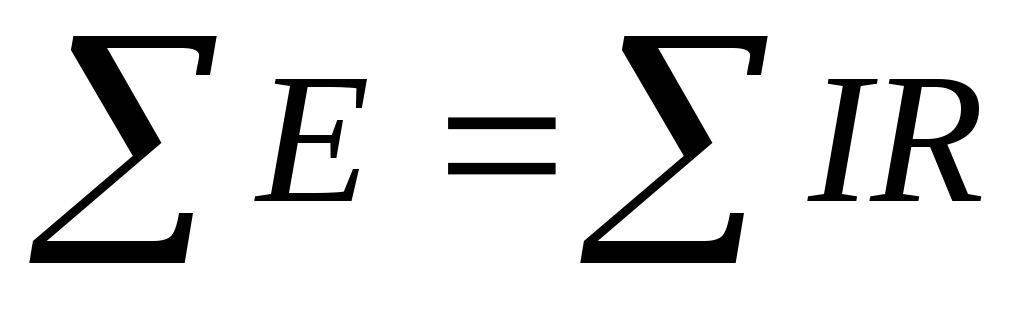

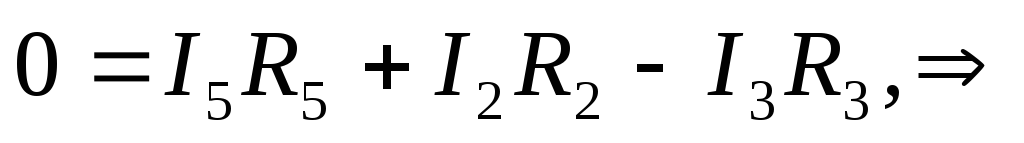
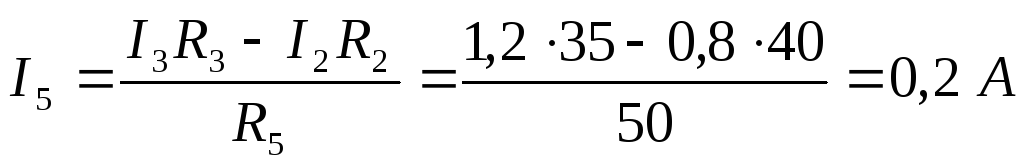
Чтобы найти ток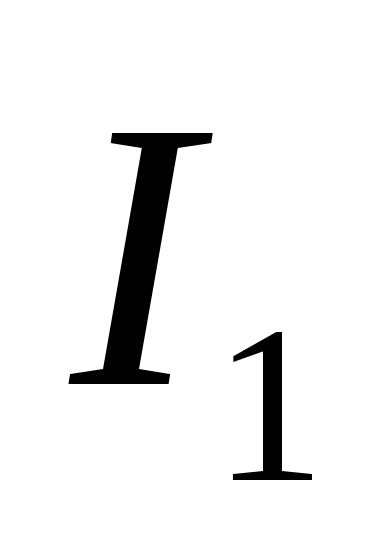и и 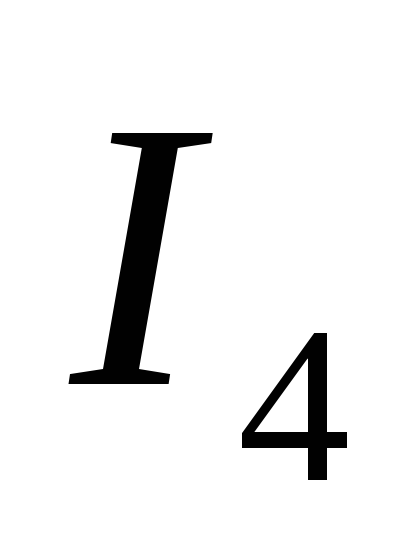, составляем уравнения по первому закону Кирхгофа для узлов B и C: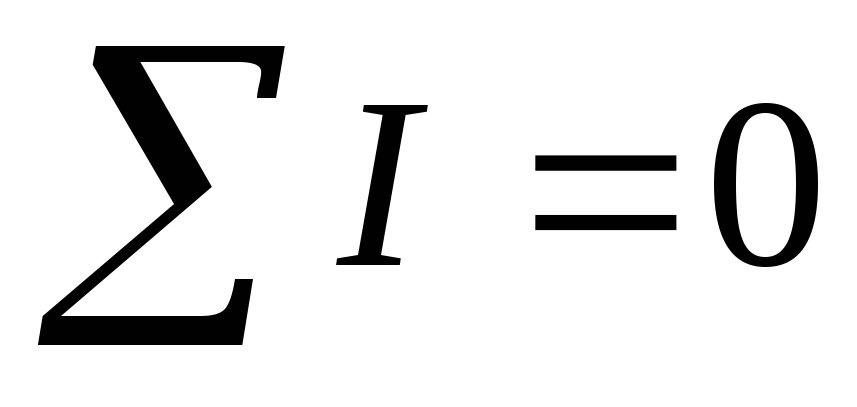

B: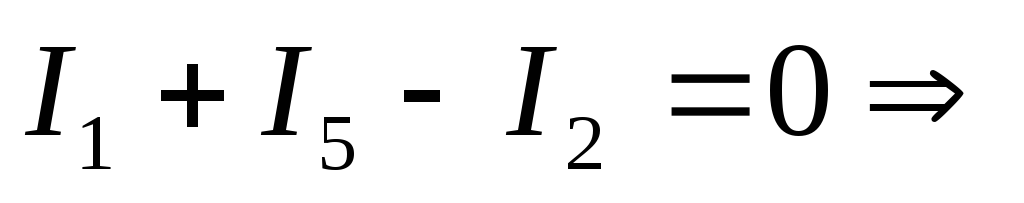

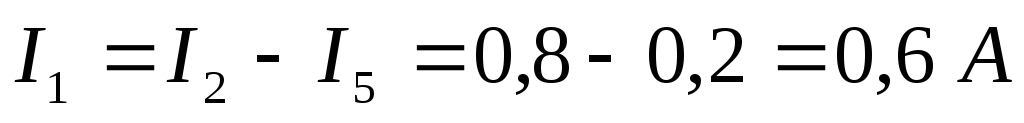
С: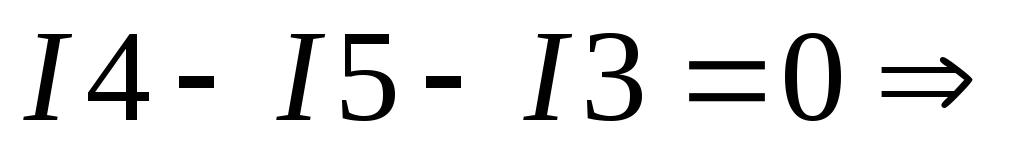

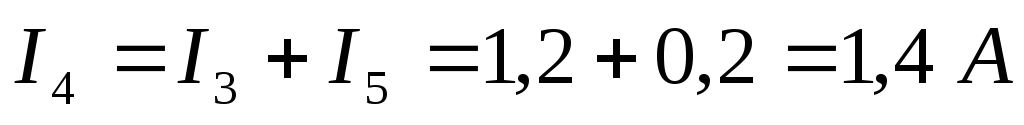
Вопрос 19. Первый закон Кирхгофа, узловые уравнения. Второй закон Кирхгофа, контурные уравнения.

Узел— точка, в которой сходятся не менее 3-х токов.

Ветвь— участок цепи, по которому течёт один и тот же ток.

Контур— любой замкнутый путь в схеме.

Первый закон Кирхгофа

Для любого узла сумма токов, приходящих к узлу, равна сумме токов, отходящих от узла.

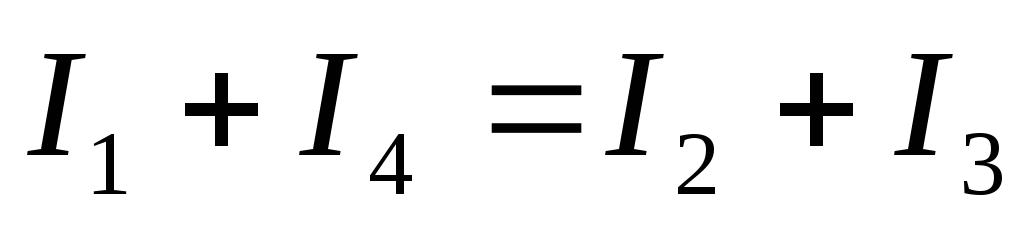
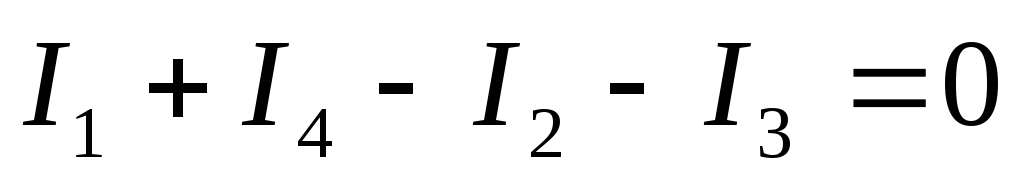
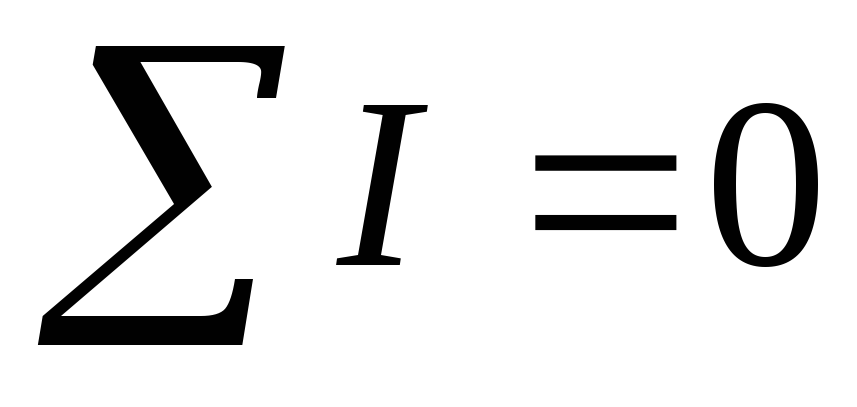
Для любого узла электрической цепи алгебраическая сумма токов равна нулю. Ток, который притекает к узлу, берётся со знаком “+”, который оттекает — со знаком “–”.

Второй закон Кирхгофа

Для любого замкнутого контура алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений на участках этого контура.

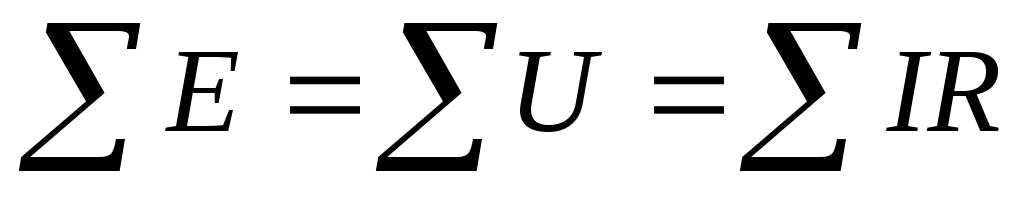
Порядок составления контурных уравнений:

1. Выбираем произвольное направление тока ветвей.

2. Если в схеме n узлов, то составляем n – 1 уравнение по первому закону Кирхгофа.

3. Выбираем произвольное направление обхода контура.

4. Если направление обхода и ЭДС совпадают, то она входит в уравнение со знаком “+”, если нет — со знаком “–”.

5. Если ток ветви и направление обхода совпадают, то падение напряжения входит в уравнение со знаком “+”, если нет — со знаком “–”.

6. Если при расчёте получился отрицательный ток, значит его направление противоположно выбранному.

Задача

С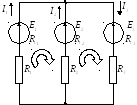оставить контурные уравнения для решения сложной электрической цепи.

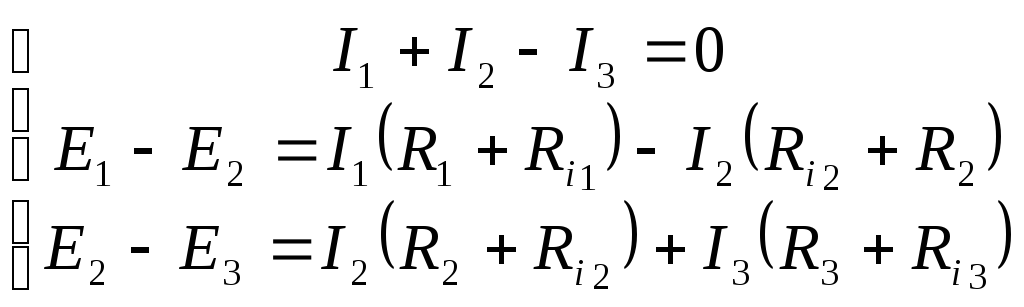
14. Преобразования треугольник-звезда и звезда-треугольник | 9. Анализ цепей постоянного тока | Часть1

14. Преобразования треугольник-звезда и звезда-треугольник

Преобразования треугольник-звезда и звезда-треугольник

Во многих схемах можно встретить такие конфигурации компонентов, в которых невозможно выделить последовательные или параллельные цепи. К этим конфигурациям относятся соединения компонентов в виде звезды (Y)  и треугольника (Δ):

 

 

Очень часто, в ходе анализа электрических цепей, оказывается полезным преобразовать треугольник в звезду или, наоборот, звезду в треугольник. Практически, чаще возникает необходимость преобразования треугольника в звезду. Если при замене одной из этих схем другой не изменяются потенциалы одноименных точек и подтекающие к ним токи, то во внешней цепи также не произойдет никаких изменений. Иными словами, эквивалентные Δ и Y цепи ведут себя одинаково.

Существует несколько уравнений, используемых для преобразования одной цепи в другую:

 

 

Δ и Y цепи очень часто встречаются в 3-фазных сетях переменного тока, но там они, как правило, сбалансированы (все резисторы равны по значению) и преобразование одной цепи в другую не требует таких сложных расчетов. Тогда возникает вопрос: где мы сможем использовать эти уравнения?

Использовать их можно в несбалансированных мостовых схемах:

 

 

Анализ данной схемы при помощи Метода Токов Ветвей или Метода Контурных Токов довольно сложен. Теорема Миллмана и Теорема Наложения здесь тоже не помощники, так как в схеме имеется только один источник питания. Можно было бы использовать теорему Тевенина или Нортона, выбрав в качестве нагрузки резистор R₃, но и здесь у нас вряд ли что-нибудь получится.

Помочь в этой ситуации нам сможет преобразование треугольник — звезда.  Итак, давайте выберем конфигурацию резисторов R₁, R₂ и R₃, представляющих собой треугольник (R_ab, R_ac и R_bc соответственно), и преобразуем ее в звезду:

 

 

После преобразования схема примет следующий вид:

 

 

В результате преобразования у нас получилась простая последовательно-параллельная цепь. Если мы правильно выполним расчеты, то напряжения между точками А, В и С преобразованной схемы будут аналогичны напряжениям между этими же точками исходной схемы, и мы сможем вернуть их обратно.

 

 

 

Сопротивления резисторов R₄ и R₅ остаются неизменными: 18 и 12 Ом соответственно. Применив к схеме последовательно-параллельный анализ, мы получим следующие значения:

 

 

Теперь, используя значения напряжений из приведенной выше таблицы, нам нужно рассчитать напряжения между точками А, В и С. Для этого мы применим обычную математическую операцию сложения (или вычитания для напряжения между точками В и С):

 

 

 

 

Переносим эти напряжения в исходную схему (между точками А, В и С):

 

Напряжение на резисторах R₄ и R₅ останется таким же, каким оно было в преобразованной схеме.

К данному моменту у нас есть все необходимые данные для определения токов через резисторы (используем для этой цели Закон Ома I = U / R):

 

 

Моделирование при помощи программы PSPICE подтвердит наши расчеты:

 

 

 

 

2.5 Соединение резисторов треугольником и звездой

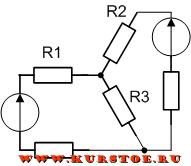
Под соединением резисторов треугольником (рис. 2.7, а) понимают такое соединение, при котором конец (х) одного из резисторов соединяется с началом (в) второго, конец (у) второго – с началом (с) третьего, конец (z) третьего – с началом (а) первого, а полученные точки а, в, с подключаются к остальной части цепи.

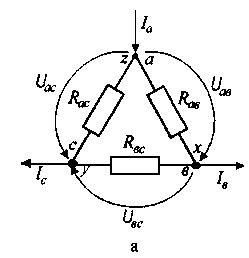
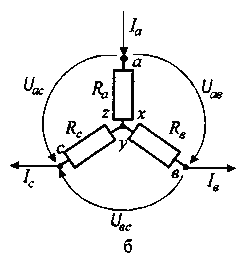
Рис. 2.7. Схемы соединений резисторов треугольником (а) и звездой (б)

Для упрощения анализа и расчета некоторых электрических цепей, содержащих соединения резисторов треугольником, целесообразно заменить эти резисторы эквивалентными резисторамиR_а, R_в, R_с, соединенными звездой (рис. 2.7, б).

Замена треугольника резисторов эквивалентной звездой должна быть произведена таким образом, чтобы после нее токи I_а, I_в, I_с и напряжения U_ав, U_вс, U_ас в незатронутой части электрической цепи остались без изменения.

Значения сопротивленийR_а, R_в, R_с эквивалентной звезды находятся по формулам

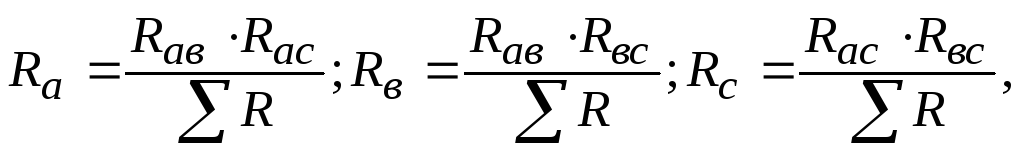(2.11)

где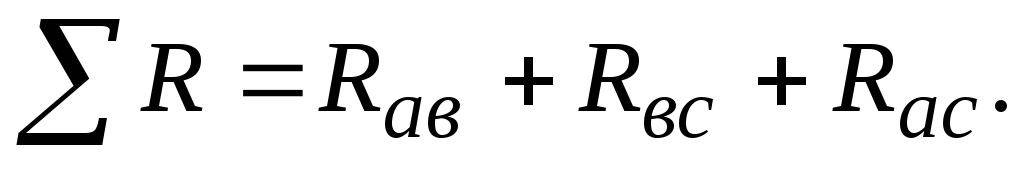

Иногда может возникнуть обратная задача – преобразование звезды резисторов в треугольник резисторов. В этом случае используют формулы:

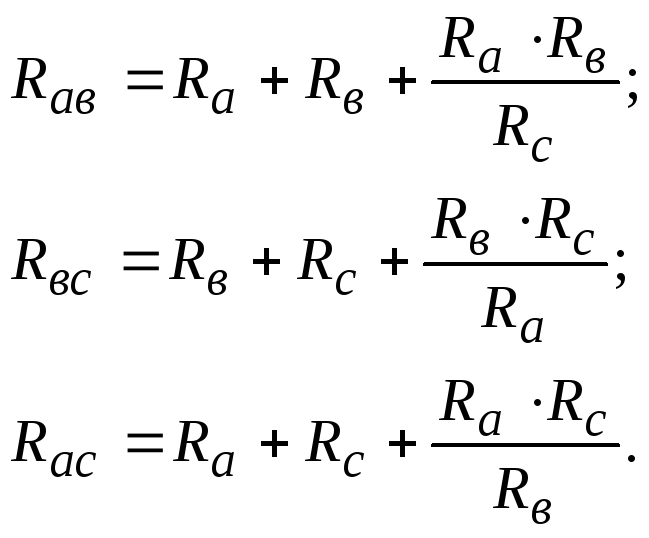(2.12)

2.6 Электрическая энергия и мощность

В любой электрической цепи электрическая энергия (а также мощность) вырабатываемая источниками, равна энергии (мощности), потребляемой приемниками.

Согласно закону Джоуля-Ленца энергия, потребляемая резистивным элементом (резистором) с сопротивлением R, определяется по формулам:

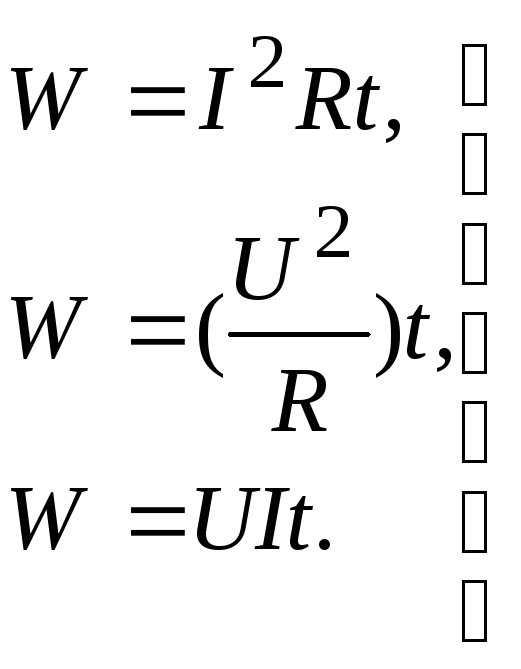(2.13)

В электрической цепи постоянного тока мощность Р равна отношению энергии W к промежутку времени t, в течение которого энергия была выработана источником или преобразована приемником электрической энергии.

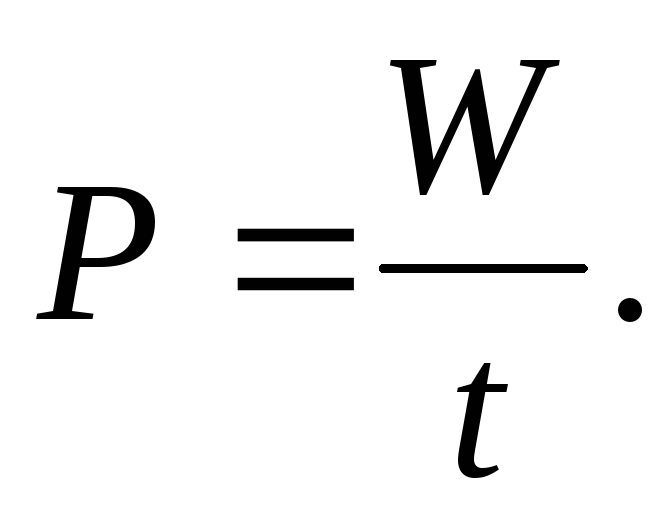(2.14)

Мощность численно равна энергии W, если промежуток времени t равен единице.

Из (2.13) и (2.14) получаем выражения для расчета мощности резистивного приемника:

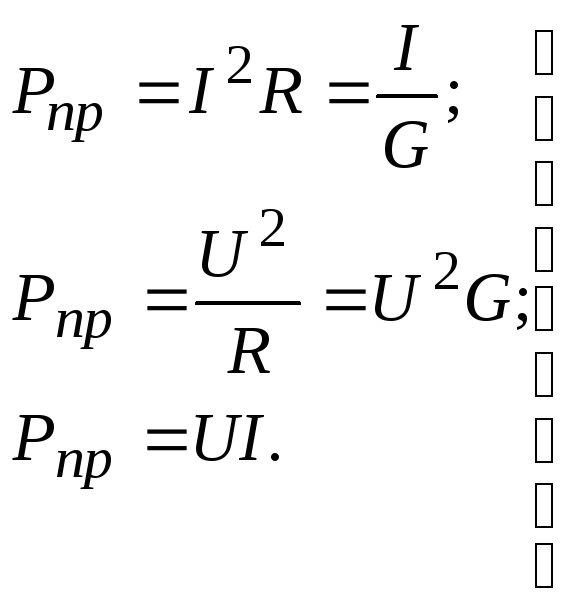(2.15)

Если направление ЭДС и тока через источник совпадают, то мощность, вырабатываемая источником с ЭДС Е, равна:

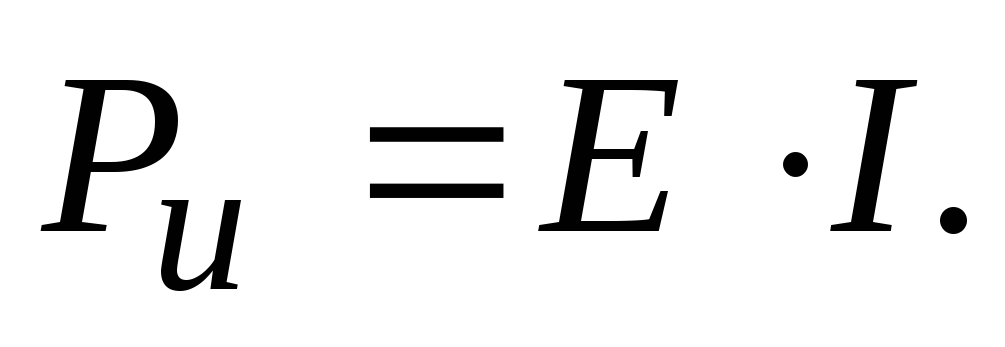
В противном случае мощность источника отрицательна и ее относят к мощности приемника.

Для любой электрической цепи можно записать уравнение баланса мощностей,

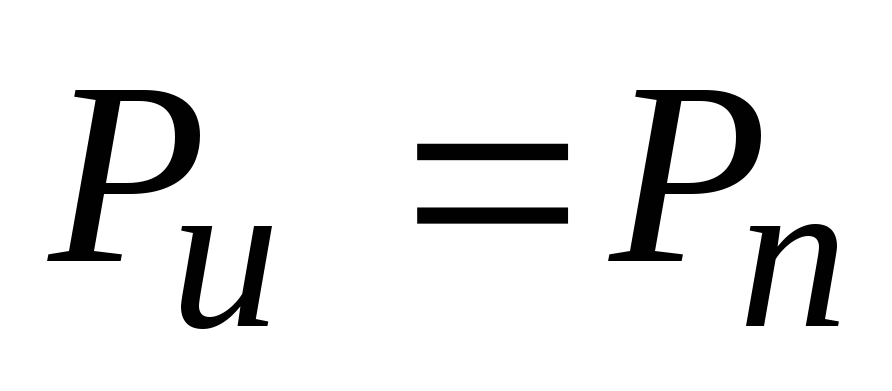или (2.16)

В левой части уравнения (2.16) находятся мощности, вырабатываемые всеми источниками электрической энергии, в правой – мощности, преобразуемые (потребляемые) всеми приемниками электрической энергии.

Основными единицами электрической энергии (ЭЭ) и мощности являются 1 джоуль (1 Дж = 1 В·А·с) и 1 ватт (1 Вт = 1 Дж/с=1 В·А). Для мощности и энергии промышленных установок часто используются более крупные единицы: 1 киловатт (1 кВт = 10³Вт), 1 мегаватт (1 МВт = 10⁶ Вт), 1 киловатт-час (1 кВтч = 3,6·10⁶Втс).

2.7 Номинальные величины источников и приемников.

Режимы работы электрических цепей

Каждый приемник электрической энергии характеризуется номинальными величинами, которые приводятся в справочной литературе, на щитке, прикрепленном к корпусу, и др.

К номинальным величинам приемников относят номинальное напряжение_Uн, мощность _Рн и ток _Iн (например, на лампах накаливания имеется штамп, в котором указываются номинальное напряжение и мощность).

В качестве номинальных величин аккумуляторов указываются напряжение и емкость (в ампер-часах), которая показывает, какое количество электричества может пройти через аккумулятор, пока его напряжение не снизится до некоторого минимального значения.

Электрические цепи могут работать в различных режимах.

Номинальным режимом работы какого-либо элемента электрической цепи (источника, приемника) считается такой режим, в котором данный элемент работает при номинальных величинах.

Согласованным называется режим, при котором мощность, отдаваемая источником или потребляемая приемником, имеет максимальное значение. Максимальные значения мощностей получаются при определенном соотношении (согласовании) параметров ЭЦ.

Под режимом холостого хода ХХ понимается такой режим, при котором через источник или приемник не протекает ток. При этом источник не отдает энергию во внешнюю цепь, а приемник не потребляет ее.

Режимом короткого замыкания (КЗ) называется режим, возникающий при соединении между собой без какого-либо сопротивления (накоротко) зажимов источника или иных элементов электрической цепи, между которыми имеется напряжение.

Режим короткого замыкания может быть следствием нарушения изоляции, обрыва проводов, ошибки оператора при сборке электрической цепи и др.

При коротком замыкании могут возникнуть недопустимо большие токи, электрическая дуга, что может привести к тяжелым последствиям, поэтому режим короткого замыкания является аварийным.

Эквивалентное преобразование треугольника в звезду

Расчет и исследование сложных электрических цепей во многих случаях можно значительно облегчить и сделать более наглядным путем преобразования электрических схем одного вида в схемы другого вида. Одним из способов является эквивалентное преобразование треугольника в звезду. В этом методе выполняется преобразование пассивной части электрической цепи, т.е. приемников электрической энергии.

Определение соединения сопротивлений треугольником

Если три сопротивления соединены так, что образуют собою стороны треугольника, то такое соединение сопротивлений называют треугольником сопротивлений.

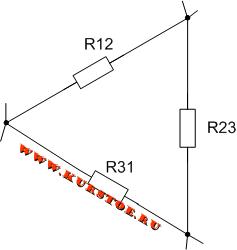
Соединение, при котором три сопротивления, находящиеся в пассивных ветвях, соединены между собою попарно и образуют замкнутый контур — называется треугольником.

Обычно в курсе электротехники принято элементы рисовать только горизонтально и вертикально. На следующем рисунке так же представлено соединение треугольником.

Определение соединения сопротивлений звездой

Если соединение трех сопротивлений имеет общий узел и имеет внешний вид трехлучевой звезды, то такое соединение сопротивлений называется звездой.

Причина преобразования треугольника в звезду

При расчете электрической цепи бывают случаи, когда нет ни последовательных, ни параллельных соединений сопротивлений. В этом случае можно попробовать отыскать соединение сопротивлений треугольником и выполнить экивалентное преобразование треугольника в звезду.

Если в электрической цепи нашли соединение сопротивлений треугольником, то в узлы соединения сопротивлений подставляем концы лучей соединения сопротивлений в виде звезды.

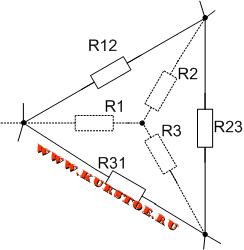
 Далее убираем (удаляем первоначальное) соединение треугольником. В результате получается эквивалентное соединение звездой.

Формулы для расчета  преобразования треугольника в звезду

           

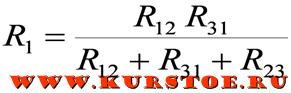
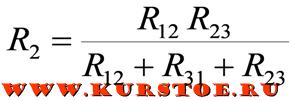
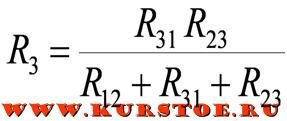
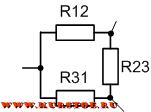
Пример преобразования

Для электрической цепи необходимо выполнить преобразование треуголькника R12 — R23 — R31 в звезду. 

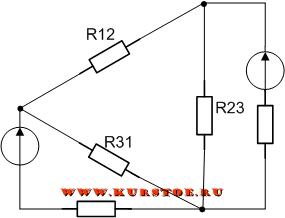
Добавляем к узлам подключения сопротивлений треугольником концы лучей подключения сопротивлений звездой.

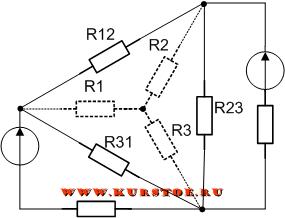
Удаляем соединение сопротивлений треугольником. В результате остается подключение сопротивлений звездой. По формулам рассчитываются значения сопротивлений R1, R2, R3.

2.5 Соединение резисторов треугольником и звездой

2.7 Номинальные величины источников и приемников. Режимы работы электрических цепей

Каждый приемник электрической энергии характеризуется номинальными величинами, которые приводятся в справочной литературе, на щитке, прикрепленном к корпусу и др.

К номинальным величинам приемников относят номинальное напряжение Uн, мощность Pн и ток Iн (например, на лампах накаливания

имеется штамп, в котором указывается номинальное напряжение и мощность).

В качестве номинальных величин аккумуляторов указываются напряжение и емкость (в ампер-часах), которая показывает, какое количество электричества может пройти через аккумулятор, пока его напряжение не снизится до некоторого минимального значения.

Электрические цепи могут работать в различных режимах. Номинальный режим работы какого-либо элемента электрической

цепи (источника, приемника) считается такой режим, в котором данный элемент работает при номинальных величинах.

Согласованным называется режим, при котором мощность, отдаваемая источником или потребляемая приемником, имеет максимальное значение. Максимальные значения мощностей получаются при определенном соотношении (согласовании) параметров ЭЦ.

Под режимом холостого хода (ХХ) понимается такой режим, при котором через источник или приемник не протекает ток. При этом источник не отдает энергию во внешнюю цепь, а приемник не потребляет ее.

Режимом короткого замыкания (КЗ) называется режим, возни-

кающий при соединении между собой без какого-либо сопротивления (накоротко) зажимов источника или иных элементов электрической цепи, между которыми имеется напряжение.

Режим короткого замыкания может быть следствием нарушения изоляции, обрыва проводов, ошибки оператора при сборке электрической цепи и др. При коротком замыкании могут возникнуть недопустимо большие токи, электрическая дуга, что может привести к тяжелым последствиям, поэтому режим короткого замыкания является аварийным.

3 Линейные однофазные электрические цепи синусоидального тока

3.1 Основные величины, характеризующие синусоидальные ток, напряжение и ЭДС

Этими основными величинами являются:

-мгновенное значение;

-амплитудное значение;

2.5 Соединение резисторов треугольником и звездой

Под соединением резисторов треугольником, (рис. 2.7, а) понимают такое соединение, при котором конец (х) одного из резисторов соединяется с началом (в) второго, конец (у) второго – с началом (с) третьего, конец (z) третьего с началом (а) первого, а полученные точки а, в, с подключаются к остальной части цепи.

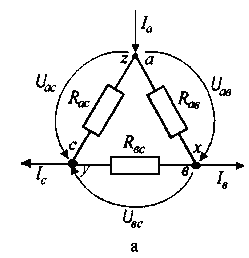
Рисунок 2.7. – Схемы соединений резисторов треугольником (а) и звездой (б)

Для упрощения анализа и расчета некоторых электрических цепей, содержащих соединения резисторов треугольником, целесообразно заменить эти резисторы эквивалентными резисторамиR_а, R_в, R_с, соединенными звездой (рис. 2.7, б).

Замена треугольника резисторов эквивалентной звездой должна быть произведена таким образом, чтобы после нее токи I_а, I_в, I_с и напряжения U_ав, U_вс, U_ас в незатронутой части электрической цепи остались без изменения.

Значения сопротивленийR_а, R_в, R_с эквивалентной звезды находятся по формулам

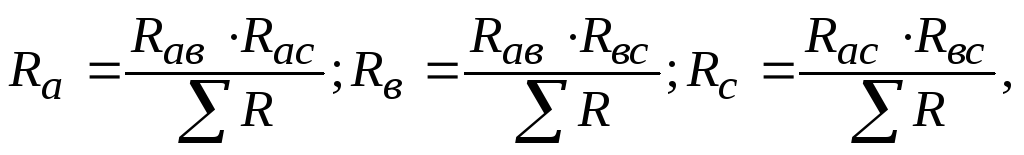(2.11)

где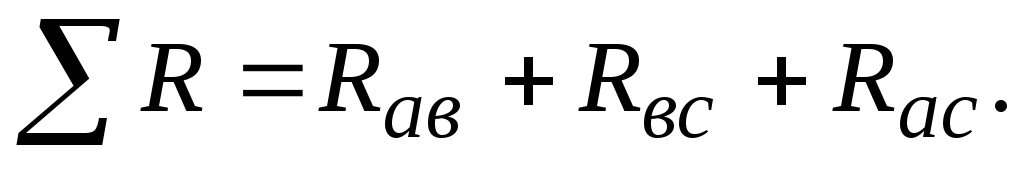

Иногда может возникнуть обратная задача – преобразование звезды резисторов в треугольник резисторов. В этом случае используют формулы:

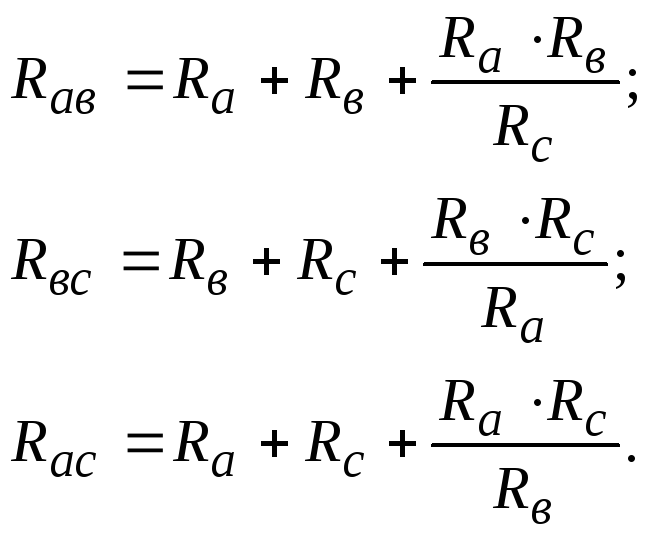(2.12)

2.6 Электрическая энергия и мощность

В любой электрической цепи электрическая энергия (а также мощность) вырабатываемая источниками, равна энергии (мощности), потребляемой приемниками.

Согласно закону Джоуля-Ленца энергия, потребляемая резистивным элементом (резистором) с сопротивлением R, определяется по формулам:

(2.13)

В электрической цепи постоянного тока мощность Р равна отношению энергии W к промежутку времени t, в течение которого энергия была выработана источником или преобразована приемником электрической энергии.

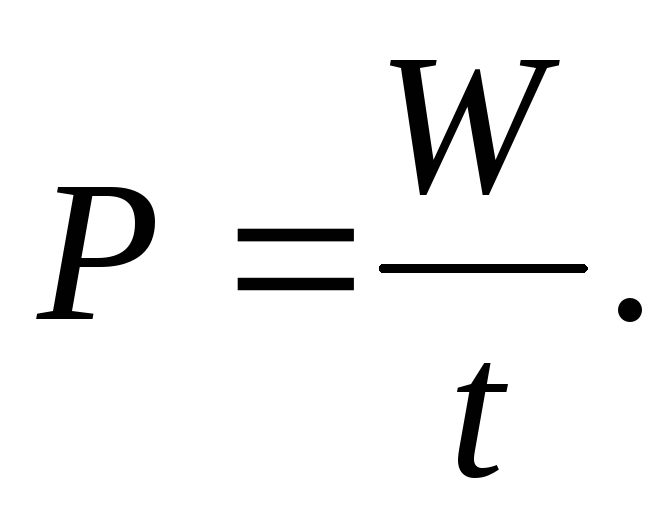(2.14)

Мощность численно равна энергии W, если промежуток времени t равен единице.

Из (2.13) и (2.14) получаем выражения для расчета мощности рези-стивного приемника:

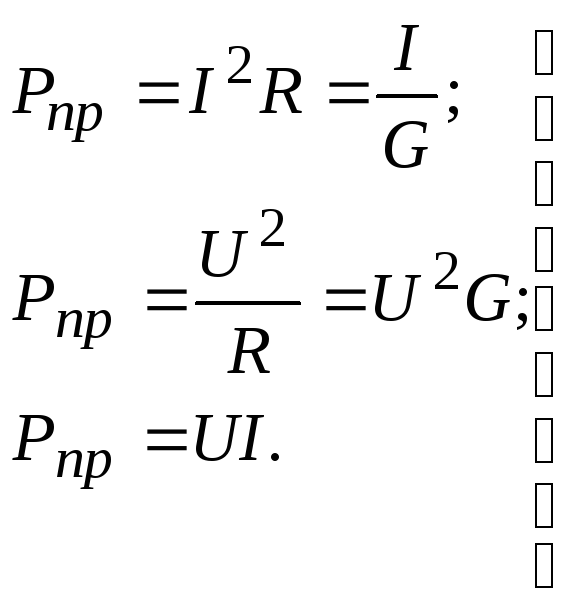(2.15)

Если направление ЭДС и тока через источник совпадают, то мощность, вырабатываемая источником с ЭДС Е равна:

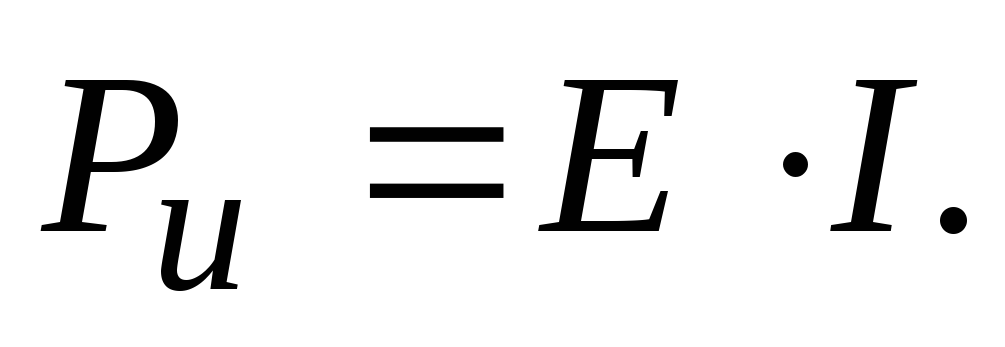
В противном случае мощность источника отрицательна и ее относят к мощности приемника.

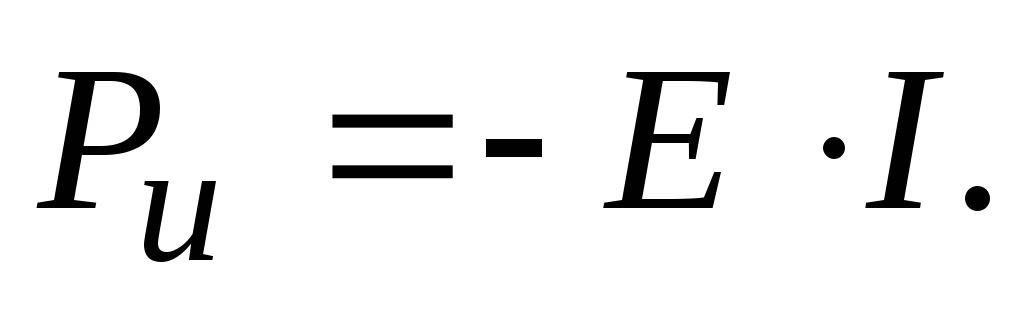
Для любой электрической цепи можно записать уравнение баланса мощностей,

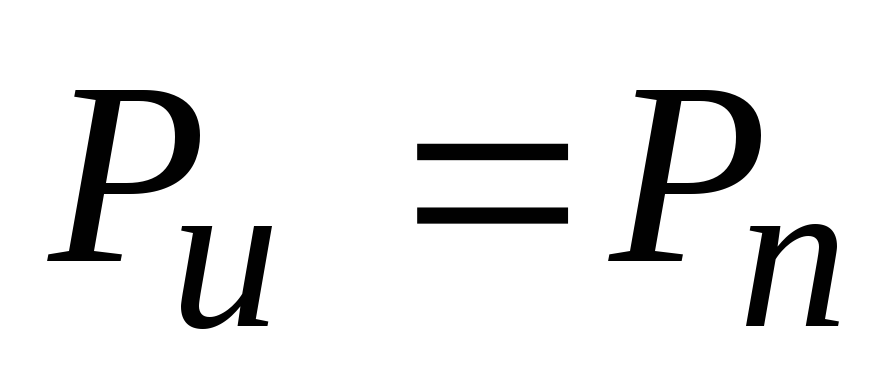или 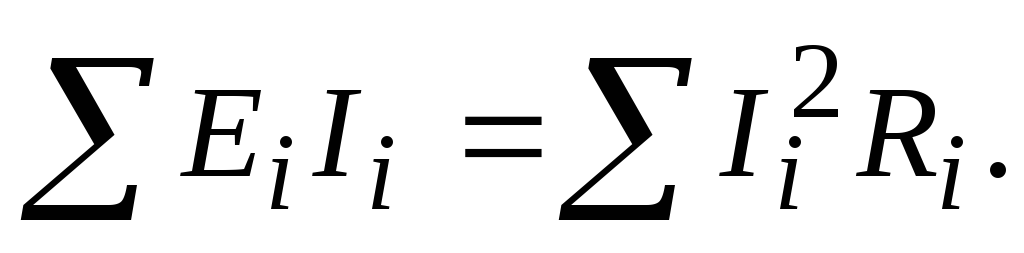(2.16)

В левой части уравнения (2.16) находятся мощности, вырабатываемые всеми источниками электрической энергии, в правой – мощности, преобразуемые (потребляемые) всеми приемниками электрической энергии.

Основными единицами электрической энергии (ЭЭ) и мощности являются 1 джоуль (1 Дж=1 ВАс) и 1 ватт (1 Вт=1 Дж/с=1 ВА). Для мощности и энергии промышленных установок часто используются более крупные единицы: 1 киловатт (1 кВт=10³Вт), 1 мегаватт (1 МВт=10⁶ Вт), 1 киловатт-час (1 кВтч=3,6 10⁶Втс).

2.7 Номинальные величины источников и приемников. Режимы работы электрических цепей

Каждый приемник электрической энергии характеризуется номинальными величинами, которые приводятся в справочной литературе, на щитке, прикрепленном к корпусу и др.

К номинальным величинам приемников относят номинальное напряжение_Uн, мощность _Рн и ток _Iн (например, на лампах накаливания имеется штамп, в котором указывается номинальное напряжение и мощность).

В качестве номинальных величин аккумуляторов указываются напряжение и емкость (в ампер-часах), которая показывает, какое количество электричества может пройти через аккумулятор, пока его напряжение не снизится до некоторого минимального значения.

Электрические цепи могут работать в различных режимах.

Номинальный режим работы какого-либо элемента электрической цепи (источника, приемника) считается такой режим, в котором данный элемент работает при номинальных величинах.

Согласованным называется режим, при котором мощность, отдаваемая источником или потребляемая приемником, имеет максимальное значение. Максимальные значения мощностей получаются при определенном соотношении (согласовании) параметров ЭЦ.

Под режимом холостого хода ХХ понимается такой режим, при котором через источник или приемник не протекает ток. При этом источник не отдает энергию во внешнюю цепь, а приемник не потребляет ее.

Режимом короткого замыкания (КЗ) называется режим, возникающий при соединении между собой без какого-либо сопротивления (накоротко) зажимов источника или иных элементов электрической цепи, между которыми имеется напряжение.

Режим короткого замыкания может быть следствием нарушения изоляции, обрыва проводов, ошибки оператора при сборке электрической цепи и др.

При коротком замыкании могут возникнуть недопустимо большие токи, электрическая дуга, что может привести к тяжелым последствиям, поэтому режим короткого замыкания является аварийным.