14. Преобразования треугольник-звезда и звезда-треугольник | 9. Анализ цепей постоянного тока | Часть1
14. Преобразования треугольник-звезда и звезда-треугольник
Преобразования треугольник-звезда и звезда-треугольник
Во многих схемах можно встретить такие конфигурации компонентов, в которых невозможно выделить последовательные или параллельные цепи. К этим конфигурациям относятся соединения компонентов в виде звезды (Y) и треугольника (Δ):
Очень часто, в ходе анализа электрических цепей, оказывается полезным преобразовать треугольник в звезду или, наоборот, звезду в треугольник. Практически, чаще возникает необходимость преобразования треугольника в звезду. Если при замене одной из этих схем другой не изменяются потенциалы одноименных точек и подтекающие к ним токи, то во внешней цепи также не произойдет никаких изменений. Иными словами, эквивалентные Δ и Y цепи ведут себя одинаково.
Существует несколько уравнений, используемых для преобразования одной цепи в другую:
Δ и Y цепи очень часто встречаются в 3-фазных сетях переменного тока, но там они, как правило, сбалансированы (все резисторы равны по значению) и преобразование одной цепи в другую не требует таких сложных расчетов. Тогда возникает вопрос: где мы сможем использовать эти уравнения?
Использовать их можно в несбалансированных мостовых схемах:
Анализ данной схемы при помощи Метода Токов Ветвей или Метода Контурных Токов довольно сложен. Теорема Миллмана и Теорема Наложения здесь тоже не помощники, так как в схеме имеется только один источник питания. Можно было бы использовать теорему Тевенина или Нортона, выбрав в качестве нагрузки резистор R
Помочь в этой ситуации нам сможет преобразование треугольник — звезда. Итак, давайте выберем конфигурацию резисторов R1, R2 и R3, представляющих собой треугольник (Rab, Rac и Rbc соответственно), и преобразуем ее в звезду:
После преобразования схема примет следующий вид:
В результате преобразования у нас получилась простая последовательно-параллельная цепь.
Сопротивления резисторов R4 и R5 остаются неизменными: 18 и 12 Ом соответственно. Применив к схеме последовательно-параллельный анализ, мы получим следующие значения:
Теперь, используя значения напряжений из приведенной выше таблицы, нам нужно рассчитать напряжения между точками А, В и С. Для этого мы применим обычную математическую операцию сложения (или вычитания для напряжения между точками В и С):
Переносим эти напряжения в исходную схему (между точками А, В и С):
Напряжение на резисторах R4 и R5 останется таким же, каким оно было в преобразованной схеме.
К данному моменту у нас есть все необходимые данные для определения токов через резисторы (используем для этой цели Закон Ома I = U / R):
Моделирование при помощи программы PSPICE подтвердит наши расчеты:
Сопротивления звезда — Энциклопедия по машиностроению XXL
Преобразование соединения сопротивлений звездой в эквивалентное соединение треугольником (рис.

Суш,ествуют различные приборы для измерения температуры нагретых тел (термометры расширения, электрические термометры сопротивления, термопары и т. д.). Однако для сильно нагретых тел (свыше 2000 С) эти методы измерения температуры непригодны. Кроме того, эти методы совершенно неприменимы, если раскаленные тела, температуру которых необходимо определить, чрезвычайно удалены от наблюдателя (например. Солнце, звезды). В этом, а также и в других случаях в качестве термометрического фактора можно использовать тепловое излучение.
Аналитический расчет МЭС указанного типа производится по формулам (2.2) — (2.5), в которых величины Рд/п, Ркт заменяются соответственно величинами рд + г внешн. т+г внутр. ml РКт + г внешн, т + внутр, m J РАп » внешн. п внутр, пвнутреннее сопротивление в луче «звезды», соединяющемся с т -ья электродом г внешн, т — сопротивление растекания т-го электрода, / внутр. я. г внешн, я — то же для п-го электрода. При этом значения г внешн, т определяются по материалам разд. 2.1, а значения г внутр, т являются заданными параметрами.
я. г внешн, я — то же для п-го электрода. При этом значения г внешн, т определяются по материалам разд. 2.1, а значения г внутр, т являются заданными параметрами.
Если отвлечься не только от движения Земли (относительно неподвижных звезд), но также и от сопротивления воздуха, то останется только рассмотреть движение в пустоте под действием силы тяжести, которую в достаточно ограниченном пространстве можно рассматривать как постоянную по величине и направлению. [c.96]
Число включений г не должно превышать [4] 60 в час — при-регулировании переводом на холостой ход 30 в час —при автоматическом пуске электродвигателя и переключением со звезды на треугольник 15 в час — при автоматическом пуске электродвигателя с реостатом сопротивления.
В асинхронных двигателях с кольцами номинальное сопротивление для ротора при соединении его обмоток звездой [c.6]
Требования к пуску двигателей исполнения HY такие же, как для исполнения Н, но необходимо уменьшить момент сопротивления, так как при некоторых нагрузках пусковой момент при соединении в звезду может быть недостаточен для разгона двигателя до приемлемой частоты вращения.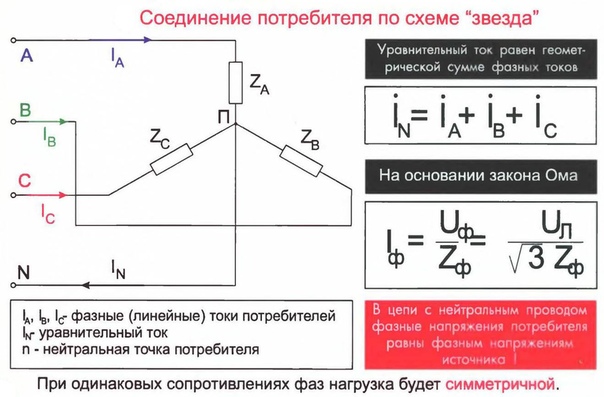 [c.783]
[c.783]
Движущаяся между плоскими электродами вода нагревается при протекании через нее электрического тока. Объемы воды в межэлектродных пространствах представляют активные сопротивления, включенные под нагрузку по схеме треугольник . При работе котла имеется незначительное протекание тока между фазными электродами и корпусом, определяющее частичную нагрузку, включенную по схеме звезда . Диапазон регулирования мощности в рассматриваемых котлах 100-ь 25% номинальной мощности.
Температуру в электропечах сопротивления регулируют большей частью наиболее простым методом ступенчатого (позиционного) изменения мощности. При этом. мощность печи изменяют переключением нагревателей. Например, в трехфазных печах сопротивления при переключении соединения нагревателей с треугольника на звезду мощность печи снижается в 3 раза.
Предположим, что мы имеем систему, состоящую из четырех электродов (рис. 27), соединенных звездой . Пусть начальные потенциалы электродов равны ф > ф > ф > ф°. Сопротивление между электродом и общей точкой О, соединяющей все электроды, R, R2, R3, 4-Значение потенциала в точке О в зависимости от силы тока, сопротивления в каждой ветви и потенциала электродов определяется соотношением
[c.73]
27), соединенных звездой . Пусть начальные потенциалы электродов равны ф > ф > ф > ф°. Сопротивление между электродом и общей точкой О, соединяющей все электроды, R, R2, R3, 4-Значение потенциала в точке О в зависимости от силы тока, сопротивления в каждой ветви и потенциала электродов определяется соотношением
[c.73]
Проиллюстрируем возможности этого метода на примере реальной многоэлектродной системы [32]. На рис. 30 представлена поляризационная диаграмма для систем из четырех электродов (медь, железо, платина, цинк), соединенных звездой при различных сопротивлениях
В тех случаях, когда электроды системы столь сильно удалены друг от друга, что взаимное влияние их можно не учитывать, величина сопротивления в каждом луче для электродов, соединенных звездой, равняется величине сопротивления растекания соответствующего электрода. [c.84]
При нагревателе трехфазного тока общую длину ленты делят при помощи мостика иа три равные по сопротивлению секции.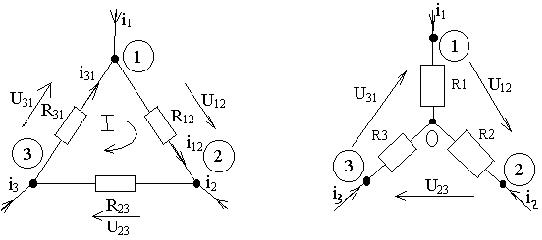
Для включения в цепь ротора дополнительного реостата используют выключатель В13 с ножным приводом и контактор К1. Если педаль выключателя не нажата, то контактор К1 включен, а его контакты закорачивают дополнительные сопротивления н включают в звезду все три фазы ротора [c.146]
Из наблюдений за сгорающими в атмосфере метеорами ( падающие звезды ) известно, что их траектории мало отличаются от прямых линий и, следовательно, влияние силы тяжести на закон движения метеора пренебрежимо мало по сравнению с силой аэродинамического сопротивления. При такой схематизации мы приходим к простой задаче динамики точки. Если принять экспоненциальный закон изменения плотности атмосферы и постоянство аэродинамического коэффициента сопротивления, то мы получаем простую, решаемую Б квадратурах задачу, исследование которой позволяет разъяснять любознательным студентам многие вопросы входа объектов в
 29]
29]
Небесный корабль должен быть подобен ракете, говорил Циолковский. В самом деле, основа действия каждого экипажа и корабля одна и та же они отталкивают какую-либо массу в одну сторону, а сами от этого двигаются в противоположную. Пароход отталкивает воду, дирижабль и аэроплан — воздух, человек и лошадь —- земной шар. Ракета заключает в самой себе вещества для отброса. Это компоненты топлива горючее плюс окислитель. Для создания движения ракете не нужна внешняя среда (внешняя опора) . В пустоте увеличение скорости ракеты происходит быстрее, так как не нужно преодолевать силу сопротивления воздуха. Очевидно, прибор для движения в пустоте должен быть подобен ракете, т. е. содержать не только энергию, но и опорную массу в самом себе . Реактивная сила, развивающаяся при работе реактивного двигателя, может быть использована для любых перемещений в пространстве. Снаряд-ракета в состоянии удаляться от Земли, блуждать между планетами, между звездами, посещать планеты, их спутники и другие небесные тела, возвращаться на Землю. Лишь бы было довольно содержащего энергию взрывчатого материала .
[c.95]
Лишь бы было довольно содержащего энергию взрывчатого материала .
[c.95]
Сопротивление измеряется между каждой фазой и наконечником центра звезды с помощью вольтметра и амперметра отношение между указанным напряжением в вольтах, измеренным с большой точностью, и силой тока, потребляемой обмоткой, в амперах, дает [c.250]
Для включения в цепь ротора дополнительного сопротивления спользуют выключатель управления В2с ножным приводом и контактор К1- Если педаль выключателя не нажата, то контактор К1 вклю—чен, а его контакты закорачивают дополнительное сопротивление и включают в звезду все три фазы ротора. В этом случае работа схемы аналогична рассмотренной выше и двигатель работает на одной из характеристик П при подъеме или С при спуске. [c.160]
Ввиду того что свободные границы криволинейны, приближенное удовлетворение условия = О вблизи границ с помощью электрических сеток сопротивлений также нецелесообразно.
 Эту же задачу при решении ее методом релаксации в связи с применением так называемых нерегулярных звезд трудно запрограммировать для быстродействующей вычислительной машины, хотя она не представляет серьезных затруднений для опытного вычислителя 2°).
[c.283]
Эту же задачу при решении ее методом релаксации в связи с применением так называемых нерегулярных звезд трудно запрограммировать для быстродействующей вычислительной машины, хотя она не представляет серьезных затруднений для опытного вычислителя 2°).
[c.283]Из наблюдений за сгорающими в атмосфере метеорами ( падающие звезды ) известно, что их траектории мало отличаются от прямых линий и, следовательно, влияние силы тяжести на закон движения метеора пренебрежимо мало по сравнению с силой аэродинамического сопротивления. Мы приходим при такой схематизации к простой задаче динамики точки. Если допустить экспоненциальный закон изменения плотности атмосферы и постоянство аэродинамического коэффициента сопротивления, то мы получаем простую, решаемую е квадратурах задачу, исследование которой позволяет разъяснить любознательным студентам многие вопросы входа объектов в атмосферу Земли (в частности, рассчитать максимальную перегрузку и определить законы изменения высоты и скорости объекта). [c.11]
[c.11]
В Началах (стр. 659—661) мы читаем Такое изящнейшее соединение Солнца, планет и комет не могло произойти иначе, как по намерению и по власти могущественного и премудрого существа. Если и неподвижные звезды представляют центры подобных же систем, то все они, будучи построены по одинаковому намерению, подчинены и власти единого… Чтобы системы неподвижных звезд от своего тяготения не падали друг на друга, он их расположил в таких громадных расстояниях друг от друга . Ньютон даже рассматривает вопрос о том, как влияет присутствие бога на движения тел Бог не испытывает воздействия от движущихся тел, движущиеся тела не испытывают сопротивления от вездесущия божия . [c.27]
Решение А. Л. Гонора строится следующим образом. Выбирается число лучей звезды в поперечном сечении и задается угол наклона к направлению набегающего потока ребра, идущего от конца луча к вершине конического тела. Выбирается интенсивность плоского скачка, присоединенного к ребру этим определяется угол поперечного сечения тела у конца луча. Скачки, идущие от двух смежных ребер, пересекаются отраженные от линии пересечения скачки доходят до поверхности тела. При соответствующем изломе контура сечения в этом месте дальнейшее отражение не происходит. Пример тела, построенного Гонором, приведен на рис. 3, б. Такое тело может иметь сопротивление, значительно меньшее сопротивления круглого конуса того же поперечного сечения.
[c.164]
Скачки, идущие от двух смежных ребер, пересекаются отраженные от линии пересечения скачки доходят до поверхности тела. При соответствующем изломе контура сечения в этом месте дальнейшее отражение не происходит. Пример тела, построенного Гонором, приведен на рис. 3, б. Такое тело может иметь сопротивление, значительно меньшее сопротивления круглого конуса того же поперечного сечения.
[c.164]
Проверить принцип инерции прямым и непосредственным экспериментом вряд ли можно. Для такого эксперимента понадобилось бы тело, на которое не действуют никакие силы это тело должно быть полностью изолировано от всех других тел. Никакое тело, никакая материальная система во Вселенной не являются полностью нзолмрованнымп. Но ввиду громадности расстояний до звезд можно допустить, что звезды не оказывают заметного действия на солнечную систему, т. е. на систему, состоящую из Солнца, планет и их спутников. Полагают, кроме того, что эта система не подвержена никаким другим посторонним воздействиям, как, например, сопротивление среды, заполняющей мировое пространство.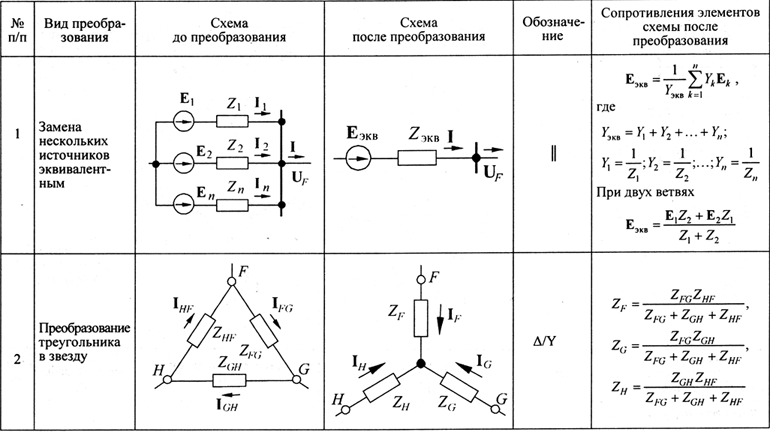 Тогда можно считать, что центр масс (центр тяжести) солнечной системы в данное время находится в состоянии равномерного прямолинейного движения. Центр масс солнечной системы почти совпадает с центром Солнца, и в дальнейшем мы будем называть его центром Солнца.
[c.247]
Тогда можно считать, что центр масс (центр тяжести) солнечной системы в данное время находится в состоянии равномерного прямолинейного движения. Центр масс солнечной системы почти совпадает с центром Солнца, и в дальнейшем мы будем называть его центром Солнца.
[c.247]
Строятся суммарные анодная и катодная вольт-амперные характеристики (ВАХ) цепи всех электродов, кроме электродов с крайними (наиболее положительным и отрицательным) значениями стационарных потенциалов (для электрода с наиболее отрицательным значением стационарного потенциала строится только анодная ВАХ, а для электрода с наиболее положительным потенциалом — только катодная ВАХ). Для этого производится суммирование по потенциалу катодной кривой полной поляризации с вольт- амперными характеристиками внешнего и внутреннего сопротивлений (т.е. с прямыми, проведенными через начало координат под углами, для которых tg = Гвнешн, 1/М) = «= внутр, л(Е/ 1/М), где Гвнутр, я — внутреннее сопротивление в луче «звезды», соединяющемся с л-м электродом г — сопротивление растекания / гo электрода [а] и [/ ] — принятые на графике масштабы потенциала и тока), а анодной кривой полной поляризации — с теми же
[c.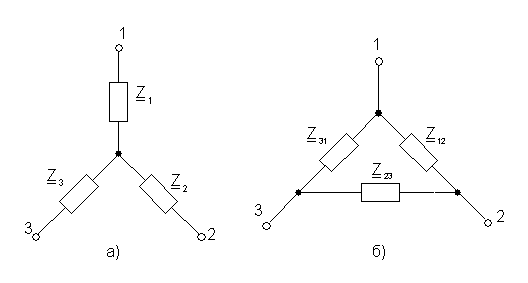 91]
91]
N, но необходимо уменьшить момент сопротивления, так как при некоторых нагрузках пусковой момент при соединении в звезду может бьпъ недостаточен для разгона двигателя до приемлемой частоты вращения. [c.782]
Аналогичным образом устроен электродный водогрейный котел КЭВ-9/04, имеющий идентичные технические характеристики. В котлах этого типа электри-ческйй ток проходит через воду, заполняющую меж-электродные пространства, от электрода одной фазы к расположенным рядом электродам других фаз. Объемы воды в межэлектродных пространствах образуют сопротивления, собранные по схеме треугольник , а неэк-ранированные от корпуса токоведущие части электродной системы обусловливают протекание тока между электродами и корпусом котла, т. е. работу по схеме звезда . Включение котлов для работы на воде с различными величинами удельного электрического сопротивления производится выбором схемы соединения электродных пластин. [c.97]
Графический расчет такого случая для многоэлектродных э. те-> ентов, соед шенных звездой , был дап Г. В. Акимовым совмест по с И. А. Левиным и Г. Б. Кларк. В основу графического расчета была положена эквивалентность поляризации и омического сопро-гпв.тения, что позволило путем суммирования определить сумма.р-.ную анодную и катоднук ) кривую каждого электрода, учитывающую как поляризацию, так и омическое сопротивление (фиг. 14).
[c.48]
те-> ентов, соед шенных звездой , был дап Г. В. Акимовым совмест по с И. А. Левиным и Г. Б. Кларк. В основу графического расчета была положена эквивалентность поляризации и омического сопро-гпв.тения, что позволило путем суммирования определить сумма.р-.ную анодную и катоднук ) кривую каждого электрода, учитывающую как поляризацию, так и омическое сопротивление (фиг. 14).
[c.48]
Скорость опускания можно. регулировать, изменяя контроллером сопротивление пускорегулирующего реостата. Так, во вто ром положении контроллера будут закорочены две ступени реостата, а все три фазы ротора соединятся в звезду, и скорость опускания уменьшится. В третьем положении будет закорочена еще часть сопротивления реостата и т. д. [c.146]
Мост уравновешивается при двух положениях переключателя П. В положении 1 испытуемый образец (Сг, Rx) подключается на-раллетьно конденсатору Сз и производится уравновешивание моста по емкостной составляющей при помощи конденсатора Сз, а по активной— при помощи резистора Ru который в сочетании с резисторами и Ri образует звезду, позволяющую имитировать высокое сопротивление.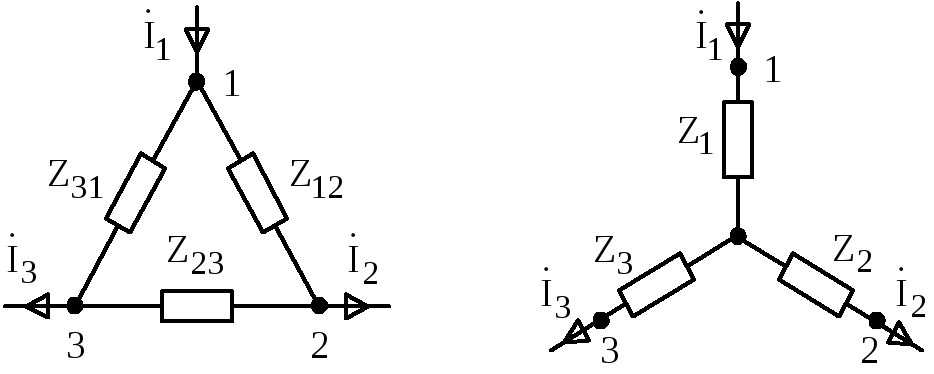 Затем переключатель устанавливается в положение 2, при этом образец включается параллельно резистору и конденсатору С% и производится вторичное уравновешивание моста. Значения С и R рассчитывают по формулам
[c.373]
Затем переключатель устанавливается в положение 2, при этом образец включается параллельно резистору и конденсатору С% и производится вторичное уравновешивание моста. Значения С и R рассчитывают по формулам
[c.373]
Для солнечной системы, состоящей из Солнца, плапет и их спутников, силы всемирного тяготения между членами этой системы являются внутренними силами силы тяготения членов солнечной системы к звездам, не принадлежащим к этой системе, являются силами внешними. Для движущегося поезда, рассматриваемого как одна система, его вес, нормальная реакция рельсов, трение колес о рельсы, сопротивление воздуха — все это силы внешние давление пара в котле, давление вагонных буферов друг на друга, трение в нодпшнниках — эти силы являются внутренними. Силы, с которыми действуют друг на друга мате- [c.460]
Относительное сопротивление материала обычно определялось по наклону приблизительно линейного участка кривой, обычно следующему за первым плохо воспроизводимым участком, для которого интенсивность разрушения гораздо меньше ( инкубационный период).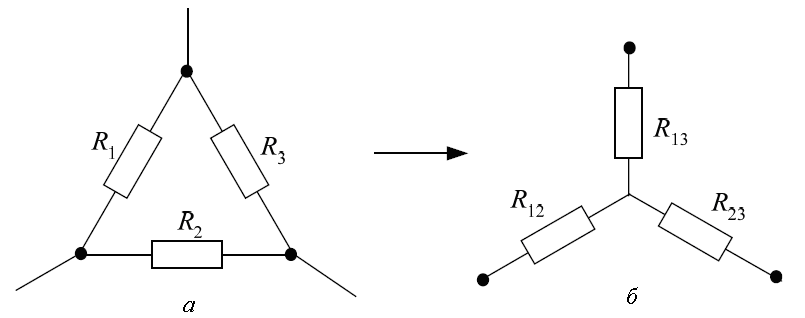 Однако в настоящее время нет четкого представления о форме, которую должна иметь кривая уменьшения веса в зависимости от времени. Согласно имеющимся данным, она, по-видимому, может сильно изменяться в зависимости от многих факторов, таких, как сочетание жидкости, материала и температуры, частота, амплитуда, п ерохо-ватость поверхности образца, его форма и статическое давление в жидкости. Ясно также, что часть поверхности, подверженная воздействию схлопывающихся пузырьков, зависит (не совсем понятным образом) от тех же параметров, что и форма кавитационной области. Эта область часто имеет форму звезды с произвольным ЧИСЛОМ лучей (фнг. 9.14), однако она может быть и более симметричной (фиг. 9.15). В некоторых случаях остается неповрежденной внешняя область, а в других — централь-
[c.458]
Однако в настоящее время нет четкого представления о форме, которую должна иметь кривая уменьшения веса в зависимости от времени. Согласно имеющимся данным, она, по-видимому, может сильно изменяться в зависимости от многих факторов, таких, как сочетание жидкости, материала и температуры, частота, амплитуда, п ерохо-ватость поверхности образца, его форма и статическое давление в жидкости. Ясно также, что часть поверхности, подверженная воздействию схлопывающихся пузырьков, зависит (не совсем понятным образом) от тех же параметров, что и форма кавитационной области. Эта область часто имеет форму звезды с произвольным ЧИСЛОМ лучей (фнг. 9.14), однако она может быть и более симметричной (фиг. 9.15). В некоторых случаях остается неповрежденной внешняя область, а в других — централь-
[c.458]
В цепь ротора двигателя М включено пускорегулирующее сопротивление R, соединенное звездой. Выводы каждой ступени и нулевая точка звезды присоединены к контактам контроллера. Позиции контроллера показаны на рисунке вертикальными пунктирными линиями. Точки на линиях возле контактов означают, что в данной позиции контакт замкнут.
[c.157]
Точки на линиях возле контактов означают, что в данной позиции контакт замкнут.
[c.157]
В цепь ротора двигателя М5 включено пускорегулирующее сопротивление R5, соединенное в звезду. Сопротивление разбито на пять частей (ступеней). Контакты каждой ступени и общая точка соединены с клеммами роторных контактов контроллера двигателя грузовой тележки. По такой же схеме включены пускорегулирующие сопротивления R1 и R2, R3 двигателя поворота MI и двигателей передвижения М2 и М3. [c.169]
Во втором положении контроллера замыкаются контакты ВЗ—8 и ВЗ—9, которые закорачивают три ступени пускорегулирующего сопротивления и включают в звезду все три фазы ротора. В третьем положении замыкается контакт ВЗ—10, который закорачивает еще одну ступень сопротивления, и т, д. [c.175]
Питание плазмотрона (рис. 2) осуществляется от трех включенных в звезду однофа(зных тращсфар,матор в СТШ-500, вторичные обмотки которых соединены последовательно это обеспечивает напряжение холостого хода выпрямителя ТЛх. х — ЗОО в. Зажигание дуги, ток которой ограничен двумя сопротивлениями и Яд, осу-щест1вляется пробоем промежутка электрод— сапло. с помощью ос-
[c.4]
х — ЗОО в. Зажигание дуги, ток которой ограничен двумя сопротивлениями и Яд, осу-щест1вляется пробоем промежутка электрод— сапло. с помощью ос-
[c.4]
Лекция по теме «СОЕДИНЕНИЕ «ЗВЕЗДА» И «ТРЕУГОЛЬНИК». ПРИНЦИП ПОДКЛЮЧЕНИЯ. ОСОБЕННОСТИ И РАБОТА»
СОЕДИНЕНИЕ «ЗВЕЗДА» И «ТРЕУГОЛЬНИК».
ПРИНЦИП ПОДКЛЮЧЕНИЯ. ОСОБЕННОСТИ И РАБОТА.
До сих пор мы изучали переменный ток, который создавался одной э. д. с. Такой ток называется однофазным переменным током. Система из трех однофазных токов, создаваемых тремя э. д. с. одной частоты, но сдвинутых один относительно другого на одну треть периода (120°), называется трехфазным током.
Нагрузка в трехфазной электрической цепи подразделяется на симметричную и несимметричную.
При симметричной нагрузке сопротивления фаз совпадают как по величине, так и по характеру.
Нагрузка считается несимметричной, когда сопротивление хотя бы одной из фаз не равно сопротивлениям других фаз.
Для увеличения мощности передачи без увеличения напряжения сети, снижения пульсаций напряжения в блоках питания, для уменьшения числа проводов при подключении нагрузки к питанию, применяют различные схемы соединения обмоток источников питания и потребителей («звезда» и «треугольник»).
Схемы.
Обмотки генераторов и приемников при работе с 3-фазными сетями могут соединяться с помощью двух схем: звезды и треугольника. Такие схемы имеют между собой несколько отличий, различаются также нагрузкой по току. Поэтому, перед подключением электрических машин необходимо выяснить разницу в этих двух схемах — «звезда» и «треугольник».
Схема «звезда».
Соединение различных обмоток по схеме «звезда» предполагает их подключение в одной точке, которая называется нулевой (нейтральной), и имеет обозначение на схемах «О», либо х, у, z. Нулевая точка может иметь соединение с нулевой точкой источника питания, но не во всех случаях такое соединение имеется. Если такое соединение есть, то такая система считается 4-проводной, а если нет такого соединения, то 3-проводной.
Если такое соединение есть, то такая система считается 4-проводной, а если нет такого соединения, то 3-проводной.
Схема «треугольника».
При такой схеме концы обмоток не объединяются в одну точку, а соединяются с другой обмоткой. То есть, получается схема, похожая по виду на «треугольник», и соединение обмоток в ней идет последовательно друг с другом.
Нужно отметить отличие от схемы «звезда» в том, что в схеме «треугольник» система бывает только 3-проводной, так как общая точка отсутствует.
В схеме треугольника при отключенной нагрузке и симметричной ЭДС равно 0.
Фазные и линейные величины.
В 3-фазных сетях питания имеется два вида тока и напряжения – это фазные и линейные.
Фазное напряжение – это его величина между концом и началом фазы приемника.
Фазный ток протекает в одной фазе приемника.
При применении схемы «звезда» фазными напряжениями являются Ua, Ub, Uc,
а фазными токами являются I a, I b, I c.
При применении схемы «треугольник» для обмоток нагрузки или генератора фазные напряжения — Uaв, Ubс, Ucа, фазные токи – I ac, I bс, I cа.
Линейные значения напряжения измеряются между началами фаз или между линейных проводников. Линейный ток протекает в проводниках между источником питания и нагрузкой.
В случае схемы «звезда» линейные токи равны фазным, а линейные напряжения равны U ab, Ubc, U ca.
В схеме «треугольник» получается все наоборот – фазные и линейные напряжения равны, а линейные токи равны I a, I b, I c.
Большое значение уделяется направлению ЭДС напряжений и токов при анализе и расчете 3-фазных цепей, так как его направление влияет на соотношение между векторами на диаграмме.
Особенности схем.
Между этими схемами есть существенная разница. Давайте разберемся, для чего в различных электроустановках используют разные схемы, и в чем их особенности.
Во время пуска электрического мотора ток запуска имеет повышенную величину, которая больше его номинального значения в несколько раз. Если это механизм с низкой мощностью, то защита может и не сработать. При включении мощного электромотора защита обязательно сработает, отключит питание, что обусловит на некоторое время падение напряжения и перегорание предохранителей, или отключение электрических автоматов. Электродвигатель будет работать с малой скоростью, которая меньше номинальной.
Видно, что имеется немало проблем, возникающих из-за большого пускового тока. Необходимо каким-либо образом снижать его величину.
Для этого можно применить некоторые методы:
Подключить на запуск электродвигателя реостат, дроссель, либо трансформатор.
Изменить вид соединения обмоток ротора электродвигателя.

В промышленности в основном применяют второй способ, так как он наиболее простой и дает высокую эффективность. Здесь работает принцип переключения обмоток электромотора на такие схемы, как звезда и треугольник. То есть, при запуске мотора его обмотки имеют соединение «звезда», после набора эксплуатационных оборотов, схема соединения изменяется на «треугольник». Этот процесс переключения в промышленных условиях научились автоматизировать.
В электромоторах целесообразно применение сразу двух схем — «звезда» и «треугольник». К нулевой точке необходимо подключить нейтраль источника питания, так как во время использования таких схем возникает повышенная вероятность перекоса фазных амплитуд. Нейтраль источника компенсирует эту асимметрию, которая возникает вследствие разных индуктивных сопротивлений обмоток статора.
Построение векторных диаграмм ( см. видео по ссылке:
https://www.youtube.com/ ›watch?v=wcyQvK84lsU
youtube.com›watch?v=XBoF0gFU_FI)
Достоинства схем.
Соединение по схеме звезды имеются важные преимущества:
Плавный пуск электрического мотора.
Позволяет функционировать электродвигателю с заявленной номинальной мощностью, соответствующей паспорту.
Электродвигатель будет иметь нормальный рабочий режим при различных ситуациях: при высоких кратковременных перегрузках, при длительных незначительных перегрузках.
При эксплуатации корпус электродвигателя не перегреется.
Основным достоинством схемы треугольника является получение от электродвигателя наибольшей возможной мощности работы. Целесообразно поддерживать режимы эксплуатации по паспорту двигателя. При исследовании электромоторов со схемой треугольника выяснилось, что его мощность повышается в 3 раза, по сравнению со схемой звезды.
При рассмотрении генераторов, схемы – звезда и треугольник по параметрам аналогичны при функционировании электродвигателей. Выходное напряжение генератора будет больше в схеме треугольника, чем в схеме звезды. Однако, при повышении напряжения снижается сила тока, так как по закону Ома эти параметры обратно пропорциональны друг другу.
Однако, при повышении напряжения снижается сила тока, так как по закону Ома эти параметры обратно пропорциональны друг другу.
Поэтому можно сделать вывод, что при разных соединениях концов обмоток генератора можно получить два разных номинала напряжения. В современных мощных электромоторах при запуске схемы – звезда и треугольник переключаются автоматически, так как это позволяет снизить нагрузку по току, возникающей при пуске мотора.
Процессы, происходящие при изменении схемы «звезда» и «треугольник» в разных случаях.
Здесь, изменение схемы — имеется ввиду переключение на щитах и в клеммных коробках электрических устройств, при условии, что имеются выводы обмоток.
Обмотки генератора и трансформатора.
При переходе со звезды в треугольник напряжение уменьшается с 380 до 220 вольт, мощность остается прежней, так как фазное напряжение не изменяется, хотя линейный ток увеличивается в 1,73 раза.
При обратном переключении возникают обратные явления: линейное напряжение увеличивается с 220 до 380 вольт, а фазные токи не изменяются, однако линейные токи снижаются в 1,73 раза. Поэтому можно сделать вывод, что если есть вывод всех концов обмоток, то вторичные обмотки трансформатора и генераторы можно применять на два типа напряжения, которые отличаются в 1,73 раза.
Поэтому можно сделать вывод, что если есть вывод всех концов обмоток, то вторичные обмотки трансформатора и генераторы можно применять на два типа напряжения, которые отличаются в 1,73 раза.
Лампы освещения.
При переходе со «звезда» в «треугольник» лампы сгорят. Если переключение сделать обратное, при условии, что лампы при треугольнике горели нормально, то лампы будут гореть тусклым светом. Без нулевого провода лампы можно соединять звездой при условии, что их мощность одинакова, и распределяется равномерно между фазами. Такое подключение применяется в театральных люстрах.
Рассмотрим примеры решения задач.
Задача 1.
Освещение здания питается от четырехпроводной трехфазной сети с линейным напряжением UЛ = 380 В. Первый этаж питается от фазы «А» и потребляет мощность 1760 Вт, второй – от фазы «В» и потребляет мощность 2200 Вт, третий – от фазы «С», его мощность 2640 Вт. Составить электрическую схему цепи, рассчитать токи, потребляемые каждой фазой, и ток в нейтральном проводе, вычислить активную мощность всей нагрузки.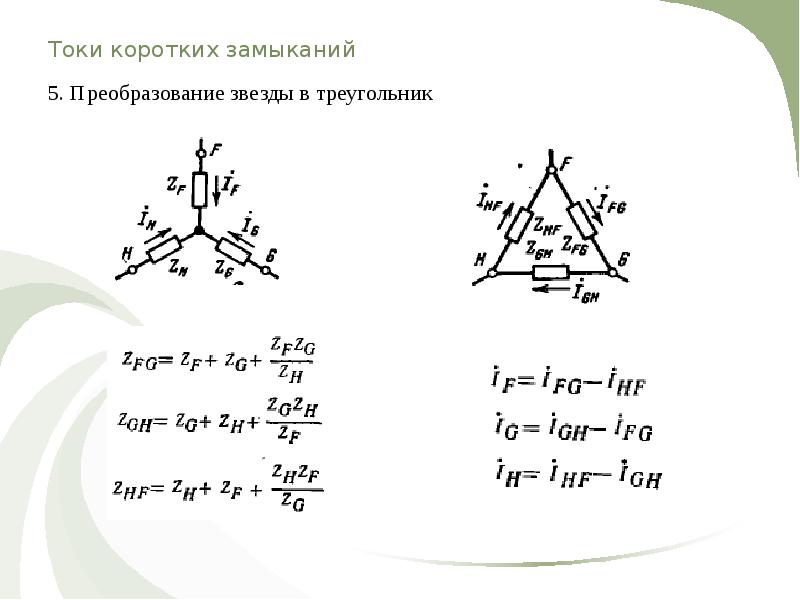 Построить векторную диаграмму.
Построить векторную диаграмму.
Анализ и решение задачи 1
Схема цепи показана на рис. 1
Лампы освещения соединяются по схеме звезда с нейтральным проводом.
Рис. 1
Расчет фазных напряжений и токов. При соединении звездой UЛ = UФ, отсюда UФ = UЛ / = 380 / = 220 В. Осветительная нагрузка имеет коэффициент мощности cos φ = 1, поэтому PФ = UФ · IФ и фазные токи будут равны:
IА = PА / UФ = 1760 / 220 = 8 А; IB = PB / UФ = 2200 / 220 = 10 А; IC = PC / UФ = 2640 / 220 = 12 А.
Построение векторной диаграммы и определение тока в нейтральном проводе.
Векторная диаграмма показана на рис. 6.27. Ее построение начинаем с равностороннего треугольника линейных напряжений ÚAB, ÚBC, ÚCA, и симметричной звезды фазных напряжений Úa, Úb, Úc. При таком построении напряжение между любыми точками схемы можно найти как вектор, соединяющий соответствующие точки диаграммы, поэтому диаграмму называют топографической.
При таком построении напряжение между любыми точками схемы можно найти как вектор, соединяющий соответствующие точки диаграммы, поэтому диаграмму называют топографической.
Токи фаз ÍA, ÍB, ÍC связаны каждый со своим напряжением; в нашем случае по условию φ = 0, и токи совпадают по фазе с напряжениями. Ток в нейтральном проводе ÍN = ÍA + ÍB + ÍC. По построению (в масштабе) по величине ÍN = 2,5 А.
Вычисление активной мощности в цепи.
Активная мощность цепи равна сумме мощностей ее фаз:
P = PA + PB + PC = 1760 + 2200 + 2640 = 6600 Вт.
Домашнее задание:
1.Выучить лекцию.
2. Ответьте на вопросы для самоконтроля:
Вопросы для самоконтроля:
1. Что такое симметричная трехфазная система напряжений? Чем отличаются друг от друга системы с прямым и обратным следованием (чередованием) фаз? Показать на векторных диаграммах.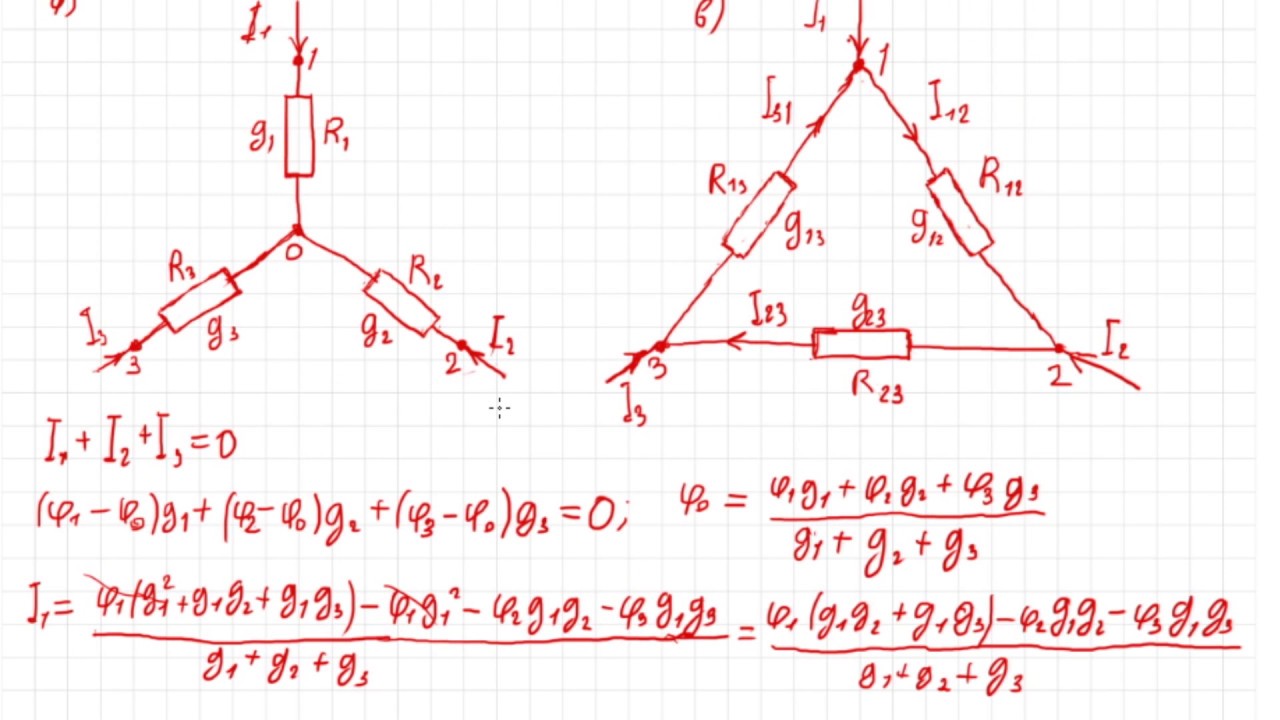
2. Как обозначаются (маркируются) начала и концы фаз трехфазных источников и потребителей? Как осуществить их соединение звездой и треугольником?
3. Дать определение фазных и линейных напряжений. Каково соотношение между линейными и фазными напряжениями на зажимах генератора, соединенного по схеме звезда?
4. Дать определение фазных и линейных токов. Каково соотношение между этими токами при соединении приемника по схеме звезда?
5. Какая нагрузка называется симметричной?
6. Как вычислить фазные токи приемника, соединенного звездой, если известны линейные напряжения источника и сопротивления фаз приемника?
7. В каких случаях применяется четырехпроводная система электроснабжения? Каково значение нейтрального провода?
8. Как вычислить ток в нейтральном проводе?
9. Каково соотношение между линейными и фазными напряжениями при соединении фаз источника или приемника треугольником?
10. Как вычислить фазные и линейные токи приемника, соединенного треугольником, если известно линейное напряжение источника и сопротивление фаз приемника?
11. Каково соотношение между линейными и фазными токами симметричного приемника, соединенного треугольником?
Каково соотношение между линейными и фазными токами симметричного приемника, соединенного треугольником?
12. Может ли ток в нейтральном проводе быть равным нулю?
13. Как изменится режим работы цепи, если в одну из фаз вместо освещения включить двигатель?
14. Какие токи изменятся, если в одной из фаз произойдет обрыв?
15. Как изменится режим работы цепи при обрыве нейтрального провода?
На рис. 2.1 изображена электрическая цепь с последовательно соединенными сопротивлениями.
Рис. 2.1
Напряжение на зажимах источника ЭДС равно величине
электродвижущей силы. Поэтому часто источник на схеме не изображают.
Падения напряжений на сопротивлениях определяются по формулам

где — эквивалентное сопротивление.
Эквивалентное сопротивление электрической цепи, состоящей из n последовательно включенных элементов, равно сумме сопротивлений этих элементов.2.2. Параллельное соединение элементов
электрических цепей
На рис. 2.2 показана электрическая цепь с параллельным соединением сопротивлений.
Рис. 2.2
Токи в параллельных ветвях определяются по формулам:
В соответствии с первым законом Кирхгофа, ток в неразветвленной части схемы равен сумме токов в параллельных ветвях.
где Эквивалентная проводимость электрической цепи, состоящей из n параллельно включенных элементов, равна сумме проводимостей параллельно включенных элементов.
Эквивалентным сопротивлением цепи называется величина, обратная эквивалентной проводимости Пусть электрическая схема содержит три параллельно включенных сопротивления.
Эквивалентная проводимость Эквивалентное сопротивление схемы, состоящей из n одинаковых элементов, в n раз меньше сопротивлений R одного элемента Возьмем схему, состоящую из двух параллельно включенных сопротивлений (рис. 2.3). Известны величины сопротивлений и ток в неразветвленной части схемы. Необходимо определить токи в параллельных ветвях.
Рис. 2.3 Эквивалентная проводимость схемы
,
а эквивалентное сопротивлениеНапряжение на входе схемы
Токи в параллельных ветвях
Аналогично
Ток в параллельной ветви равен току в неразветвленной части схемы, умноженному
на сопротивление противолежащей, чужой параллельной ветви и деленному
на сумму сопротивлений чужой и своей параллельно включенных ветвей.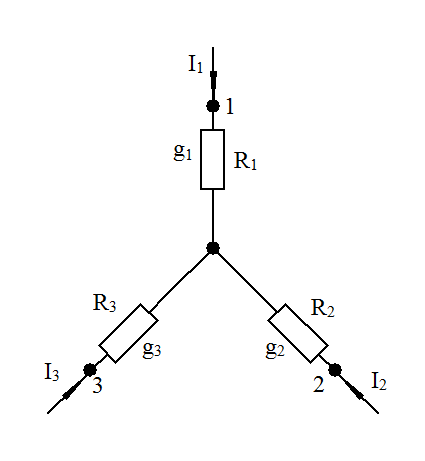
2.3.Преобразование треугольника сопротивлений
в эквивалентную звезду
Встречаются схемы, в которых отсутствуют сопротивления,
включенные последовательно или параллельно, например, мостовая схема,
изображенная на рис. 2.4. Определить эквивалентное сопротивление этой
схемы относительно ветви с источником ЭДС описанными выше методами нельзя.
Если же заменить треугольник сопротивлений
R1-R2-R3, включенных между узлами 1-2-3, трехлучевой звездой сопротивлений,
лучи которой расходятся из точки 0 в те же узлы 1-2-3, эквивалентное
сопротивление полученной схемы легко определяется.
Рис. 2.4 Сопротивление луча эквивалентной звезды сопротивлений равно
произведению сопротивлений прилегающих сторон треугольника, деленному
на сумму сопротивлений всех сторон треугольника.
В соответствии с указанным правилом, сопротивления лучей звезды определяются
по формулам:
Эквивалентное
соединение полученной схемы определяется по формуле
Сопротивления R0 и R?1 включены последовательно, а ветви с сопротивлениями R?1 + R4 и R?3 + R5 соединены параллельно.
2.4.Преобразование звезды сопротивлений
в эквивалентный треугольник
Иногда для упрощения схемы полезно преобразовать звезду
сопротивлений в эквивалентный треугольник.
Рассмотрим схему на рис. 2.5. Заменим звезду сопротивлений R1-R2-R3
эквивалентным треугольником сопротивлений R?1-R?2-R?3, включенных между
узлами 1-2-3.
2.5. Преобразование звезды сопротивлений
в эквивалентный треугольник
Сопротивление стороны эквивалентного треугольника сопротивлений равно
сумме сопротивлений двух прилегающих лучей звезды плюс произведение
этих же сопротивлений, деленное на сопротивление оставшегося (противолежащего)
луча. Сопротивления сторон треугольника определяются по формулам:
Сопротивления сторон треугольника определяются по формулам:
Преобразование сопротивлений (звезда в дельту и дельта в звезду)
В этом разделе мы преобразуем сопротивление звездообразования в сопротивления образования дельты.
Мы сделаем это, найдя эквивалентные сопротивления вместо сопротивлений, указанных в задаче.
Например,
Чтобы заменить R1R_1R1 и R2R_2R2 (см. Формирование звезды) на данной диаграмме, мы будем там эквивалентными, то есть R12R_ {12} R12 (см. Формирование дельты).
Вот формула преобразования —
R12 = R1 + R2 + R1.R2R3R_ {12} = R_1 + R_2 + \ frac {R_1.R_2} {R_3} R12 = R1 + R2 + R3 R1 .R2
Обратите внимание, что приведенная выше формула является циклической по своей природе, поэтому она работает одинаково для R23R_ {23} R23 и R31R_ {31} R31.
Докажите, что R12 = R1 + R2 + R1.R2R3R_ {12} = R_1 + R_2 + \ frac {R_1.R_2} {R_3} R12 = R1 + R2 + R3 R1 .
R2
Это та же установка, что и в предыдущей установке, с резисторами, переименованными следующим образом:
- R1 → R23R_1 \ вправо R_ {23} R1 → R23
- R2 → R13R_2 \ стрелка вправо R_ {13} R2 → R13
- R3 → R12R_3 \ стрелка вправо R_ {12} R3 → R12
- R23 → R1R_ {23} \ rightarrow R_1R23 → R1
- R13 → R2R_ {13} \ вправо R_2R13 → R2
- R12 → R3R_ {12} \ вправо R_3R12 → R3
Итак, общие результаты приведенного выше доказательства становятся:
R3 = R23R13R1 + R13 + R12R_ {3} = \ frac {R_ {23} R_ {13}} {R_1 + R_ {13} + R_ {12}} R3 = R1 + R13 + R12 R23 R13
И аналогично:
R1 = R13R12R1 + R12 + R23R_ {1} = \ frac {R_ {13} R_ {12}} {R_1 + R_ {12} + R_ {23}} R1 = R1 + R12 + R23 R13 R12 R2 = R12R23R1 + R23 + R13R_ {2} = \ frac {R_ {12} R_ {23}} {R_1 + R_ {23} + R_ {13}} R2 = R1 + R23 + R13 R12 R23
Итак,
R1 + R2 + R1R2R12 = R12 (R23 + R13) R23 + R13 + R12 + R13R12R23R12R23R13R_1 + R_2 + \ frac {R_1R_2} {R_ {12}} = \ frac {R_ {12} (R_ {23} + R_ { 13})} {R_ {23} + R_ {13} + R_ {12}} + \ frac {R_ {13} R_ {12} R_ {23} R_ {12}} {R_ {23} R_ {13} } R1 + R2 + R12 R1 R2 = R23 + R13 + R12 R12 (R23 + R13) + R23 R13 R13 R12 R23 R12
R1 + R2 + R1R2R12 = R12 (R23 + R13 + R12) R23 + R13 + R12R_1 + R_2 + \ frac {R_1R_2} {R_ {12}} = \ frac {R_ {12} (R_ {23} + R_ { 13} + R_ {12})} {R_ {23} + R_ {13} + R_ {12}} R1 + R2 + R12 R1 R2 = R23 + R13 + R12 R12 ( R23 + R13 + R12)
R1 + R2 + R1R2R12 = R12R_1 + R_2 + \ frac {R_1R_2} {R_ {12}} = R_ {12} R1 + R2 + R12 R1 R2 = R12
QED
Найдите эквивалентное сопротивление в данной принципиальной схеме (в единицах RRR) —
Чтобы решить этот вопрос, мы преобразуем схему и применим формулу рядом —
Обратите внимание на выделенную область в цепи, а затем обратите внимание на изменение.
Можете ли вы определить это преобразование («звезда-треугольник» или «дельта-звезда»)?
Затем мы проделаем то же самое с другой стороной цепи. Это будет выглядеть так —
Теперь наблюдайте —
Поздравляем! Мы превратили сложную схему в простую схему, которую мы можем легко решить.
Разве это не было просто? Обратите внимание, что метод, показанный в этом примере, — не единственный способ решить вопрос.Попробуйте трансформировать другие точки, проложите свой путь.
Общий ответ на вопрос: 2R3 \ boxed {\ frac {2R} {3}} 32R.
Теперь мы можем решать вопросы, связанные с преобразованием сопротивлений.
Разница между соединением звездой и соединением треугольником (с таблицей)
Трехфазные цепи используются в трансформаторах, генераторах, распределителях для выработки электроэнергии. Он имеет три напряжения, которые соединяются между собой с использованием соединения звездой или звездой, треугольником или сеткой для экономии меди и удешевления системы. Угол между линейными токами резисторов составляет 120 градусов.
Угол между линейными токами резисторов составляет 120 градусов.
Разница между соединением звездой и соединением треугольником заключается в том, что соединение звездой используется в линиях передачи на большие расстояния, а соединение треугольником используется в распределенных сетях на короткие расстояния. В звездообразном соединении используются 4 провода: три для подключения к внешней цепи и один для нейтральной точки. Дельта-соединение использует три провода для формирования петли сетки.
В системе подключения «звезда» начальный или конечный концы соединены с нейтральной точкой. Он использует четыре провода для подключения к внешней цепи нагрузки, из которых три провода для внешней цепи и четвертый огонь предназначены для подключения нейтрали, образуя трехфазное соединение звездой. Напряжение между каждой линией и нейтральной точкой — это фазное напряжение, а напряжение между двумя выводами соединения — это линейное напряжение.
Delta Connection — это система, в которой начальный конец соединяется с конечным концом фазы, образуя петлю сетки.Система с соединением по схеме треугольника не имеет нейтральной точки. Таким образом, для соединения треугольником используются только три провода. Соединения треугольником используются в том случае, если сумма напряжений на любых замкнутых путях равна нулю.
Таблица сравнения между соединением звездой и соединением треугольником| Параметры сравнения | Соединение звездой | Соединение треугольником |
| Определение | четырехфазное соединение система start connected обычно используется для передачи электроэнергии на большие расстояния в распределенной сети. | Это трехфазная трехпроводная система с подключением по схеме «треугольник», обычно используемая для передачи электроэнергии на короткие расстояния в распределенной сети. |
| Нейтральная точка | Он имеет нейтральную точку, где встречаются все начальные и конечные точки каждого резистора. | В треугольнике нет нейтральной точки; вместо этого начальная точка одного резистора соединена с конечной точкой другого резистора, образуя петлю сетки. |
| Напряжение сети | Напряжение сети = √3 * Фазное напряжение | Напряжение сети равно фазному напряжению. |
| Линейный ток | Линейный ток равен фазному току. | Линейный ток = √3 * фазный ток |
| Истинная мощность | √3 * Линейное напряжение * Линейный ток * CosΘ Где Θ — разница между фазным напряжением и фазным током | √3 * Линейное напряжение * Линейный ток * CosΘ Где Θ — разница между фазным напряжением и фазным током |
Соединение звездой — одна из форм соединения трехфазной цепи.Он имеет нейтральную точку N, в которой соединяются все аналогичные концы резисторов либо в начале, либо в конце.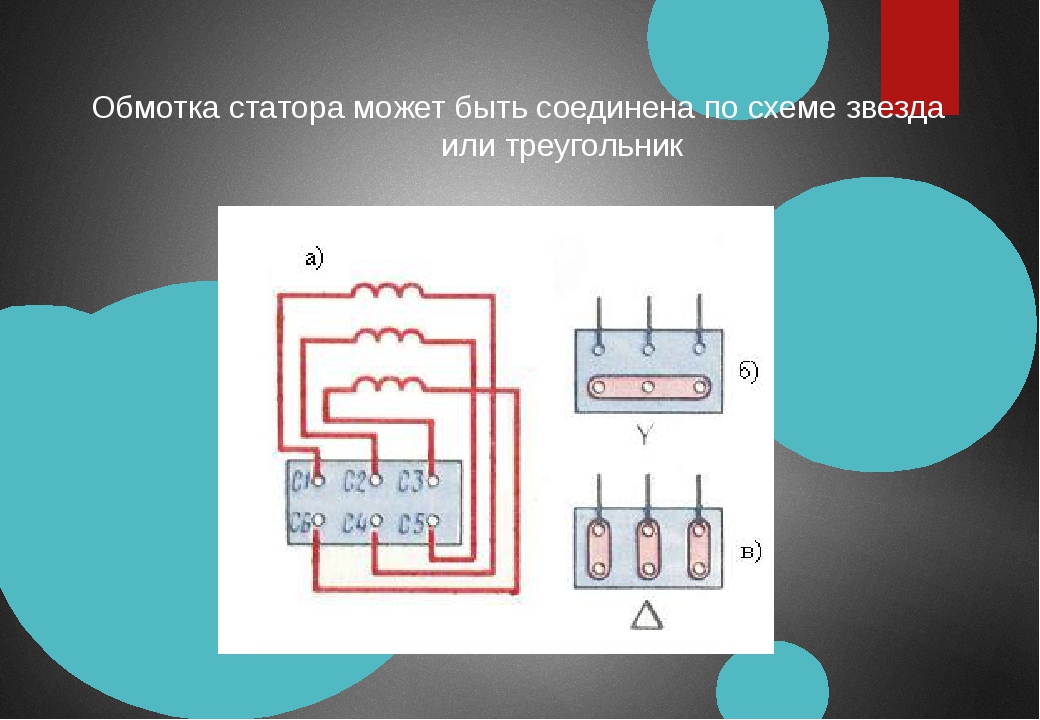 Система, соединенная звездой, образует Y- или T-образную форму или меняет Y-образную форму, используя четыре провода, три для трех фаз, а последний — для нейтральной точки. Фазное напряжение — это напряжение между фазными обмотками, а линейное напряжение — это напряжение между двумя выводами обмотки. Каждая пара клемм имеет двухфазную обмотку, противоположную друг другу, так как у них одинаковые концы.
Система, соединенная звездой, образует Y- или T-образную форму или меняет Y-образную форму, используя четыре провода, три для трех фаз, а последний — для нейтральной точки. Фазное напряжение — это напряжение между фазными обмотками, а линейное напряжение — это напряжение между двумя выводами обмотки. Каждая пара клемм имеет двухфазную обмотку, противоположную друг другу, так как у них одинаковые концы.
Сбалансированная система с соединением звездой имеет одинаковое напряжение во всех фазах с углом 120 градусов между каждым линейным напряжением, и она имеет равный ток во всех фазах с углом между фазными напряжениями 30 градусов.В этой системе линейный ток и линейный ток равны. Потенциальная энергия в нейтральной точке равна нулю.
Формулы
E L (линейное напряжение) = √3 * E ф. (фазное напряжение) или E ф. = E L
Фактическая мощность (p) = √3 * E L * I L * CosΘ здесь Θ — угол между фазным напряжением и фазным током.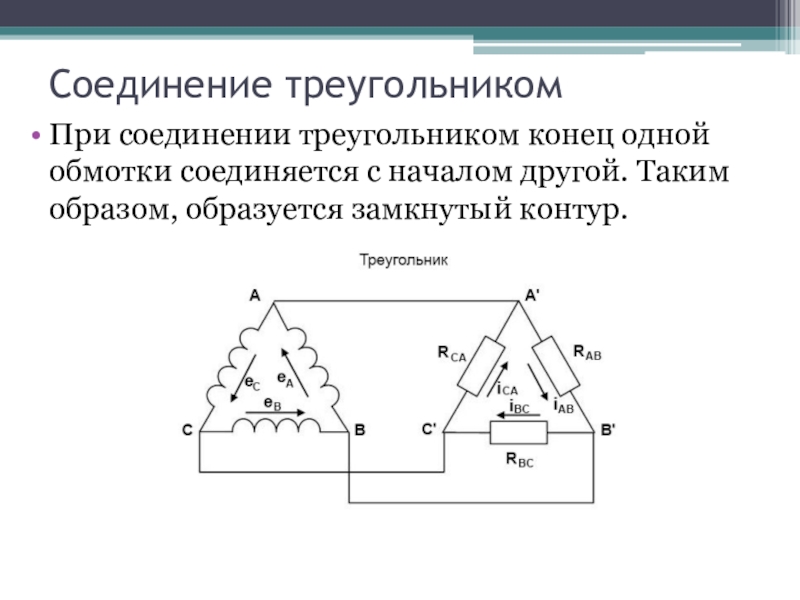
Полная мощность = √3 * E L * I L
Что такое соединение треугольником?Соединение в треугольник — это еще одна форма соединения трехфазной цепи.В этой схеме фазы имеют разные концы, где начальная точка резистора соединена с конечной точкой другого резистора, образуя петлю сетки. Системы, соединенные треугольником, имеют более высокий пусковой момент, чем системы, соединенные звездой. Следовательно, они используются в распределенной сети кратчайшего расстояния. В системе с соединением по схеме «треугольник» фазы соединены последовательно.
В сбалансированной системе, соединенной треугольником, линейное и фазное напряжения равны. Эта система не имеет нейтральной точки.Поэтому в системе используется всего три провода. Линейные токи разделены на 120 градусов, и каждый линейный ток на 30 градусов меньше его фазного тока. Если нагрузка не подключена к системе, то в сетке не будет проходить ток.
Формулы
I L (линейный ток) = √3 * I ф. (фазный ток) или I ф. = I L
(фазный ток) или I ф. = I L
Фактическая мощность (p) = √3 * E L * I L * CosΘ здесь Θ — угол между фазным током и фазным напряжением.
Полная мощность = √3 * E L * I L
Основные различия между соединением звездой и соединением треугольником- Система соединения звездой представляет собой трехфазную четырехпроводную систему с нейтральной точкой, тогда как Система соединения треугольником представляет собой трехфазную трехпроводную систему без нейтральной точки.
- Системы соединения звездой используются как для малых, так и для больших нагрузок при передаче электроэнергии на большие расстояния, тогда как системы соединения Delta используются для передачи больших нагрузок на более короткие расстояния.
- В системе соединения звездой линейное напряжение и фазное напряжение одинаковы, тогда как в системе соединения треугольником фазное напряжение и линейное напряжение одинаковы.
- Трехфазная цепь соединения звездой образует Y-образную форму, а трехфазная цепь соединения треугольником образует петлю сетки.
- Системы соединения звездой имеют меньший пусковой момент, тогда как система соединения треугольником имеет высокий пусковой момент.
Трехфазная цепь используется в трансформаторах, генераторах, распределителях для преобразования мощности.Чтобы уменьшить сложность схемы и снизить цену продукта, фазы в трехфазной цепи соединяются между собой посредством соединения звезды или треугольника. Эти системы сокращают использование меди и, следовательно, удешевляют распределение электроэнергии.
Системы звездообразного соединения используются в генераторах и генераторах переменного тока для передачи энергии. Системы подключения Delta используются в распределенных сетях малой протяженности. Система с соединением звездой требует меньшей изоляции, чем соединение треугольником, поэтому предпочтительнее для систем передачи электроэнергии на большие расстояния.
Ссылки- https://www.google.co.in/books/edition/Basic_Electrical_Engineering/e-ZbzLvhKzAC?hl=en&gbpv=1&dq=basic+electrical+engineering+by+uma+rao+and+ jayalakshmi & pg = PA3 & printsec = frontcover
4.12: Преобразование Delta-Star — Physics LibreTexts
Рассмотрим две схемы (каждая заключена в черный ящик) на рисунке IV.10.
\ (\ text {РИСУНОК IV.10} \)
Конфигурация в левом поле называется «дельта» (\ (\ Delta \)), а конфигурация в правом поле называется «Звезда» или «Y».Я отметил на каждом резисторе его сопротивление и проводимость, причем проводимость, конечно, просто обратна сопротивлению. Я собираюсь предположить, что сопротивление между клеммами X и Y одинаково для каждой коробки. В этом случае:
\ [\ label {4.12.1} r_1 + r_2 = \ frac {R_3 (R_1 + R_2)} {R_1 + R_2 + R_3}. \]
Мы можем получить аналогичные уравнения для терминальных пар Y, Z и Z, X. Решая три уравнения для r 1 , r 2 и r 3 , получаем
\ [\ begin {align} r_1 & = \ frac {R_2R_3} {R_1 + R_2 + R_3 }, \ label {4.12.2} \\ r_2 & = \ frac {R_3R_1} {R_1 + R_2 + R_3}, \ label {4.12.3} \\ r_3 & = \ frac {R_1R_2} {R_1 + R_2 + R_3}, \ label {4.12.4} \\ \ end {align} \]
С точки зрения проводимости это
\ [\ begin {align} g_1 & = \ frac {G_2G_3 + G_3G_1 + G_1G_2} {G_1}, \ label {4.12.5} \\ g_2 & = \ frac {G_2G_3 + G_3G_1 + G_1G_2} {G_2}, \ label {4.12.6} \\ g_3 & = \ frac {G_2G_3 + G_3G_1 + G_1G_2} {G_3}, \ label {4.12.7} \\ \ end {align} \]
Эти уравнения обратные:
\ [\ begin {align} R_1 & = \ frac {r_2r_3 + r_3r_1 + r_1r_2} {r_1}, \ label {4.12.8} \\ R_2 & = \ frac {r_2r_3 + r_3r_1 + r_1r_2} {r_2}, \ label {4.12.9} \\ R_3 & = \ frac {r_2r_3 + r_3r_1 + r_1r_2} {r_3}, \ label {4.12.10} \\ G_1 & = \ frac {g_2g_3} {g_1 + g_2 + g_3}, \ label {4.12.11} \\ G_2 & = \ frac {g_3g_1} {g_1 + g_2 + g_3}, \ label {4.12.12} \\ G_3 & = \ frac {g_1g_2} {g_1 + g_2 + g_3}, \ label {4.12.13} \\ \ end {align} \]
Это означает, что если сопротивления и проводимости в одной ячейке связаны к сопротивлениям и проводимости в другом по этим уравнениям, то вы не сможете сказать, если бы у вас были амперметр, вольтметр и омметр, какая цепь была в какой коробке.Эти две коробки неотличимы от их электрических характеристик.
Эти уравнения нелегко запомнить, если вы не используете их каждый день, и они достаточно неудобны, поэтому при их численной оценке возможны ошибки. Поэтому, чтобы формулы были полезными, вы должны запрограммировать свой калькулятор или компьютер так, чтобы они мгновенно переводили между дельтой и звездочкой, даже не задумываясь об этом. В следующем примере показаны используемые формулы.Это будет тяжелая работа, если вы не запрограммировали свой компьютер заранее, но если у вас есть , вы увидите, насколько полезны преобразования.
Пример . Рассчитайте сопротивление между точками A и B на рисунке ниже. Отдельные сопротивления даны в омах.
Сначала не знаешь, с чего начать. Но обратите внимание, что резисторы на 1, 3 и 4 Ом соединены треугольником, и поэтому схема эквивалентна
После этого это легко, и вскоре вы обнаружите, что сопротивление между A и B равно 2.85 \ (\ Омега \).
Соединение конденсаторов звездой и треугольником — нарушение напряжения
Силовые конденсаторы в 3-фазных соединениях конденсаторных батарей соединяются треугольником или звездой (звезда). Между этими двумя типами соединений существуют различия в их применениях, номинальном значении кВАр, обнаружении неисправных конденсаторов и т. Д. В этой статье обсуждается разница между конденсаторами, соединенными звездой и треугольником, а также преимущества конденсаторных батарей, соединенных звездой и треугольником.
Калькулятор, представленный ниже, может использоваться для расчета эффективных кВАр, произведенных для конденсатора при соединении треугольником или звездой.
Конденсаторы высокого напряжения
Блок конденсаторов с подключением по схеме Delta Конденсаторы, соединенные треугольником, чаще всего используются при низком напряжении, хотя их можно применять и при более высоких напряжениях. Каждый конденсатор будет иметь полное фазное напряжение, приложенное к его клемме. Почему низковольтные конденсаторные батареи соединены треугольником? Помните, что генерируемая кВАр изменяется как квадрат приложенного напряжения.Формула для VAR, генерируемого в конденсаторной батарее, имеет следующий вид:
Подключение конденсаторной батареи по схеме треугольника дает больше VAR по сравнению с подключением по схеме звезды. Это связано с тем, что при соединении звездой на конденсатор подается только напряжение фаза-нейтраль, а в случае соединения треугольником — полное фазное напряжение.
Соединение конденсаторов треугольником
Соединение конденсаторов треугольником требует двух вводов. Поскольку нет соединения с землей, конденсаторная батарея не может быть «стоком» для любых токов заземления или токов нулевой последовательности. .Отдельную ветвь конденсатора, соединенного треугольником, необходимо защитить от межфазного короткого замыкания с помощью токоограничивающего предохранителя.
Блок конденсаторов со звездообразным подключениемПри соединении звездой напряжение на каждом конденсаторе в 1 / sqrt (3) раз больше напряжения фаза-фаза. Следовательно, полученный VAR также будет соответственно меньше по сравнению с соединением треугольником . Соединение звездой в основном используется в системах среднего напряжения (> 1 кВ). Одним из основных преимуществ использования соединения звездой является то, что конденсатор должен быть рассчитан только на напряжение фаза-нейтраль системы по сравнению с номиналом фаза-фаза в системе треугольником.Следовательно, отдельные конденсаторы среднего напряжения будут подвергаться нагрузке только при более низком уровне напряжения, что увеличивает срок их службы. Есть и другие преимущества использования звездообразного соединения на конденсаторах среднего напряжения. Существует два основных типа соединения звездой:
Заземленная звезда (звезда)
При соединении «звезда» или «звезда» нейтральная точка батареи надежно заземлена. Это означает, что нейтраль не нужно изолировать до уровня BIL всей системы.Следовательно, при использовании этого соединения может быть достигнута некоторая экономия средств. Кроме того, в этой связи переходное восстанавливающееся напряжение (TRV) может быть менее серьезным. Неисправность одной фазы конденсаторной батареи не приведет к повышению напряжения на других исправных ветвях батареи. Как показано ниже, неисправность конденсатора фазы B не приведет к повышению напряжения на других исправных фазах.
Подключение конденсатора звездой с заземлением
Недостатком заземленного соединения звездой является то, что заземленная нейтраль может пропускать токи земли и гармонические токи нулевой последовательности. .Это может вызвать помехи от телефона. Кроме того, заземленная звездочка также вносит ток короткого замыкания в систему во время замыкания фазы на землю. Из-за заземленного соединения может протекать высокий ток между фазой и землей, когда конденсатор не замыкается на землю. Это требует использования токоограничивающих предохранителей для этого приложения.
Незаземленная звезда (звезда)
При подключении незаземленной звездой нейтраль конденсаторной батареи , а не , подключенная к земле.Следовательно, это соединение не допускает протекания токов заземления и гармонических токов нулевой последовательности. При замыкании фазы на землю в системе незаземленная звездочка не вносит тока замыкания.
Недостатком этого подключения является то, что нейтраль батареи должна быть полностью изолирована от фазного напряжения системы. Нейтральная точка может находиться под потенциалом фаза-фаза во время переключения или во время неисправности. Для банков выше 15 кВ это может стать дорогим.
Еще одним недостатком этого подключения является то, что при выходе из строя конденсатора на одной фазе нейтральная точка смещается.Напряжение на исправных фазах возрастет до полного фазо-фазного потенциала. Ток через неисправные конденсаторы достигает 1,732 о.е., а максимальный ток на поврежденной фазе составит 3 о.е. Такое увеличение напряжения и тока в банке могло привести к дополнительным сбоям.
Как показано ниже, неисправность конденсатора фазы B приведет к повышению напряжения в 1,732 (квадрат 3) раз от номинального напряжения между фазой и нейтралью, которое является полным фазным напряжением на других исправных фазах.Следовательно, исправные конденсаторы будут перенапряжены, и защитное реле должно будет быстро устранить неисправность, чтобы предотвратить повреждение исправных конденсаторов.
Звезда незаземленного подключения конденсатора
Существуют и другие варианты этого соединения, например, незаземленная звездочка и заземленная звездочка .
Дополнительное чтение:
кВАр в амперах Расчет
Калькулятор преобразования дельта-звезда
Векторная диаграмма соединений звезды и треугольника
Преобразование звезды в треугольник и из треугольника в звезду — Анализ несимметричной нагрузки, подключенной по схеме треугольник
Преобразование или преобразование или замена сети нагрузки, соединенной звездой, в сеть, соединенную треугольником, и аналогично, сеть, соединенная треугольником, в сеть звездой выполняется с помощью Преобразование звезды в треугольник или преобразование из треугольника в звезду.
Состав:
Звезда в дельта-преобразование
При преобразовании звезды в треугольник нагрузку, подключенную звездой, необходимо преобразовать в подключение по схеме треугольник. Предположим, что у нас есть нагрузка, подключенная по схеме звезды, как показано на рисунке выше, и ее необходимо преобразовать в подключение по схеме треугольник, как показано на рисунке B.
Следующие значения дельты следующие:
Следовательно, если значения Z A , Z B и Z C известны, следовательно, зная эти значения и поместив их в приведенные выше уравнения, вы можете преобразовать соединение звезды в соединение треугольником.
Преобразование дельты в звезду
Аналогично, сеть соединения треугольником дана, как показано выше, на рисунке B, и она должна быть преобразована в соединение звездой, как показано выше, на рисунке A. Для преобразования используются следующие формулы, приведенные ниже:
Если заданы значения Z 1 , Z 2 и Z 3 , то, подставив эти значения импедансов в приведенные выше уравнения, можно выполнить преобразование соединения треугольником в соединение звездой.
Поскольку импеданс (Z) является векторной величиной, поэтому все вычисления выполняются в полярной и прямоугольной форме.
Этапы анализа трехфазной несимметричной нагрузки, подключенной по схеме треугольника
Давайте возьмем пример несимметричной нагрузки, подключенной треугольником, подключенной к трехфазному источнику питания 400 В, как показано на рисунке ниже:
Следующие шаги приведены ниже для решения проблемы трехфазных несимметричных нагрузок, подключенных по схеме треугольник.
Шаг 1 — Решите, ток каждой фазы I 1 , I 2 и I 3 как в однофазной цепи.
Как
Шаг 2 — Вычислите линейные токи I L1 , I L2 и I L3 в прямоугольной форме.
Шаг 3 — Теперь вычислим мощность разных фаз.
Шаг 4 — Рассчитайте полную мощность по приведенному ниже уравнению.
Аналогичная процедура будет применяться для решения проблемы несбалансированной нагрузки, подключенной звездой. Во-первых, импеданс звезды будет преобразован в соответствующий дельта-импеданс.Остальные расчеты будут выполнены для нагрузки, подключенной по схеме треугольника, как показано выше.
Что такое преобразование звезда-дельта
Здравствуйте, друзья, надеюсь, у вас все отлично. В сегодняшнем руководстве мы обсудим Что такое преобразование звезды в треугольник . Мы также рассмотрим его инверсию, то есть преобразование дельты в звезду . В электрических системах нам приходится иметь дело с сопротивлениями, расположенными по разным схемам, то есть параллельным, последовательным, сетчатым и т. Д.Простые однофазные резистивные цепи, в которых сопротивления присутствуют в параллельной или последовательной комбинации, могут быть решены с помощью последовательной или параллельной формулы сопротивлений, есть также несколько других методов, например, законы Кирхгофа, узловой анализ и т. Д. Для решения таких схем. Но в случае сложных трехфазных резистивных цепей мы не можем использовать эти основные формулы, и поэтому нам нужны более совершенные методы. Один из них — метод преобразования звезды в дельту.
Преобразование звезды в треугольник также можно выразить как Преобразование Y-Δ , это математический метод, используемый для решения сложных резистивных цепей в трехфазных электрических системах.Свое название он получил из-за конструкции. Как показано на рисунке, звезда (звезда) выглядит как Y, а Дельта выглядит как Δ . Эту технику преобразования из одной формы в другую дал Эдвин Кеннелли в 1899 году , инженер-электрик из США. Помимо использования в электрических схемах преобразование звезда-треугольник также может использоваться в математике для решения различных плоских графиков. В сегодняшнем посте мы рассмотрим его работу, формулу, уравнение и использование.Итак, давайте начнем с , что такое преобразование звезда-дельта?
Что такое преобразование звезда-треугольник?
- Преобразование звезда-треугольник (Y-∆) — это математический метод, предложенный Эдвином Кеннелли в 1899 г. и используемый для решения сложных трехфазных резистивных электрических цепей путем преобразования конструкции звезды ( Y ) в конструкцию. Дельта ( ∆ ) рассчитывается по формулам.
Прежде чем идти дальше, давайте сначала разберемся, зачем нам нужно преобразование звезды в дельту?
Почему трансформация звезда-дельта?
- Мы используем преобразование звезда-треугольник для упрощения сложных трехфазных цепей.
- Эти упрощенные версии решить намного проще, чем исходные сложные.
- Таким образом, такие преобразования фактически избавляют нас от сложных вычислений, тем самым уменьшая количество ошибок и экономя время.
Теперь давайте посмотрим на схемы Star & Delta, один за другим:
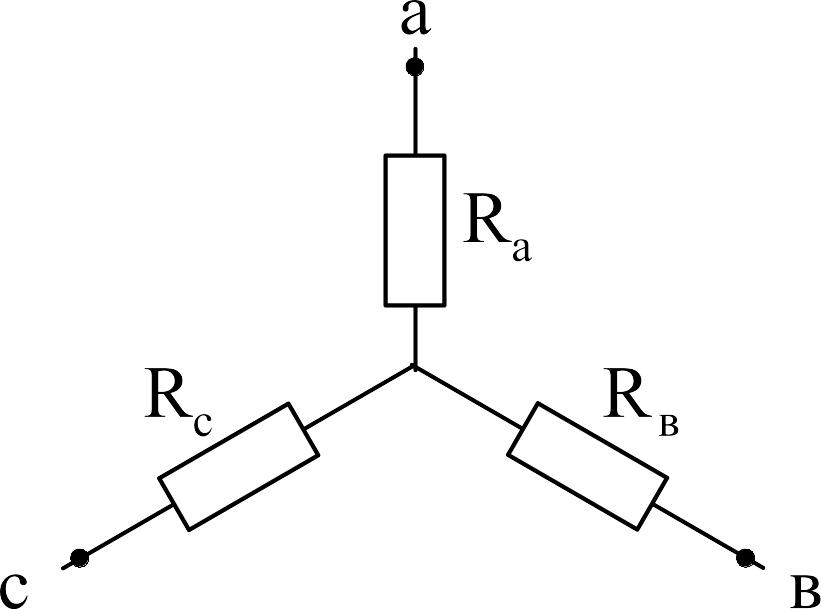
Что такое Star (Y) Network?
- Если все сопротивления подключены к общей точке (также называемой соединением) с одного конца, в то время как другой конец (сопротивлений) открыт, этот стиль соединения обозначается как Star Network или Y-соединение (также называемое звездой). схема).
- Star Connection также обозначается как без обратной связи , поскольку в нем нет петли.
- На рисунке ниже показана Т-образная нормальная цепь и ее эквивалентное Y-образное соединение:
- Мы не выполняли никаких преобразований на приведенном выше рисунке, вместо этого мы просто нарисовали одну цепь в двух разных стилях, один называется Т-образный , а второй — Y-образный .
- В обеих этих формах сопротивления соединены в одной общей точке, называемой соединением / соединением, обозначенной буквой J на приведенном выше рисунке.
Теперь давайте посмотрим, как выглядит Delta Network?
Что такое сеть Delta (
∆ )?- Если сопротивления образуют петлю, то есть каждый конец сопротивления соединен с другим сопротивлением, такая схема называется Дельта-схема , Дельта-сеть или Дельта-соединение , обозначенная как ∆ . Дельта-соединение
- также называется замкнутым контуром , поскольку оно включает контур.
- На рисунке ниже показана нормальная контурная схема и ее эквивалентная дельта-схема:
- Опять же, мы не выполняем никаких преобразований, вместо этого мы просто отображаем одну схему в ее двух эквивалентных формах.
- В обоих форматах сопротивления образовали петлю и соединены друг с другом.
К настоящему времени вы, должно быть, поняли разницу между соединением «звезда» и «треугольник», и если вам представлена схема, вы легко сможете определить, является ли она звездой или треугольником.Теперь давайте посмотрим, как преобразовать одну форму в другую (например, звезду в дельту и дельту в звезду).
Преобразование звезды в треугольник
- Преобразование цепи из звезды в треугольник называется Преобразование звезды в треугольник .
- Как показано на рисунке ниже, оба соединения имеют одинаковое количество сопротивлений, но их значения различаются.
- Итак, если мы хотим преобразовать соединение звездой в соединение треугольником, то нам нужно найти значения всех сопротивлений треугольника i.е. R A , R B и R C .
Итак, давайте посмотрим, как управлять уравнениями для преобразования звезда-треугольник.
Уравнение преобразования звезда-треугольник
- Как показано на рисунке выше, нам нужно найти значения сопротивлений треугольника.
- Для этого давайте выясним сопротивление между узлами.
Между N1 и N2:
- При соединении звездой сопротивление между N1 и N2 равно R 1 + R 2 .
- При соединении треугольником сопротивление R A параллельно с R B и R C , поэтому сопротивление между N1 и N2 будет равно R A (R B + R C ) / (R A + R B + R C ). (с использованием формулы параллельного сопротивления)
- Поскольку обе цепи эквивалентны, сопротивление между одинаковыми узлами должно быть одинаковым и даст нам уравнение A, показанное ниже:
Между N2 и N3:
- Сопротивление между узлами N2 и N3 даст us уравнение B:
Между N3 и N1:
- Сопротивление между узлами N3 и N1 даст нам уравнение C:
- Теперь давайте добавим уравнения A, B и C, и мы будем получите уравнение D, как показано на рисунке ниже:
- Теперь вычтем уравнения A, B и C из уравнения D, и мы получим значения R 1 , R 2 и R 3 , как показано на рисунке ниже:
- Теперь, используя эти значения R 1 , R 2 и R 3 , мы можем получить значение R A , R B & R C , как показано на рисунке ниже:
- Итак, используя эти шесть уравнений, мы можем легко преобразовать звезду в дельту и дельту в звезду, это станет более понятным, когда мы решим примеры в следующем разделе.
Пример преобразования звезды в треугольник
- Усложнения изменения звезды-∆ — лучшие образцы для понимания идеи схем.
- Сопротивление в звездной системе представлено с помощью (X, Y, Z), что можно увидеть на приведенной выше диаграмме, и значения этих сопротивлений: (X = 80 Ом), (Y = 120 Ом) и (Z = 40 Ом. ).
A = (XY / Z) + Y + X)
X = 80 Ом, Y = 120 Ом и Z = 40 Ом
- Подставляя эти параметры в приведенную выше формулу, мы вычисляем значение A.
A = (80 X 120/40) + 120 + 80) = (240 + 120 + 80) = (440 Ω)
- Как мы нашли значение сопротивления (B), которое равно ((ZX / Y ) + X + Z).
- Теперь мы подставляем значения в это уравнение, чтобы найти значение B.
B = ((40X80 / 120) + 80 + 40) = (27 + 120) = (147 Ом).
- Теперь мы можем вычислить значение сопротивления C по этому уравнению
C = ((YZ / X) + Z + Y)
- Подставив значение в это уравнение, мы получим C.
((120 x 40/80) + 40 + 120) = (60 + 160) = (220 Ом)
Преобразование из треугольника в звезду
- Теперь мы увидим, как можно преобразовать схему из треугольника обратно в звезду.
- Давайте решим схему, которая соединена в форме треугольника и имеет 3 точки a, b, c. Значение сопротивления между соединениями a и b равно (R1), сопротивление между соединениями b и c равно (R2), а c и d равно (R3).
- Здесь указано значение сопротивления между точками и b.
(Rab) = (R1) ΙΙ (R1 + R2)
= [(R1). (R2 + R3)] / [(R1 + R2 + R3)]
- Вы можете видеть, что есть еще одна схема который подключен в соединении Y, он имеет три ветви a, a, c, которые имеют сопротивление (Ra, Rb, Rc).
- Если мы находим сопротивление между точками a и b, то мы имеем.
(Rab) = (Ra + Rb)
- Поскольку обе эти схемы эквивалентны, значение сопротивления измеряется между точками a и b.
(Ra + Rb) = [(R1). (R2 + R3)] / (R1 + R2 + R3) —- (x)
- Таким образом, значения сопротивления также будут одинаковыми в точках b и c.
(Rb + Rc) = [(R2). (R3 + R1)] / (R1 + R2 + R3) — (y)
- И значение сопротивления между c и a также будет одинаковым.
(Rc + Ra) = [(R3) x (R1 + R2)] / (R1 + R2 + R3) — (z)
- Если сложить выражения (x), (y), (z) тогда у нас есть.
(2) (R1 + R2 + R3) = 2 [(R1.R2) + (R2.R3) + (R3.R1)]
(R1 + R2 + R3) = [(R1.R2) + (R2.R3) + (R3.R1)] / [(R1 + R2 + R3)] —- (d)
- Если мы вычтем уравнение (x), (y), (z) из уравнения ( г) тогда имеем.
Ra = (R3.R1) / (R1 + R2 + R3) — (e)
Rb = (R1.R2) / (R1 + R2 + R3) — (f)
Rc = (R2. R3) / (R1 + R2 + R3) — (g)
- Выражение преобразования Y-Δ можно определить как.
- Из уравнений e, f, g можно сделать вывод, что сопротивление в звездообразной конфигурации эквивалентно кратному из двух резисторов, соединенных в одной точке, деленному на сумму всех резисторов в схеме Δ.
- Если в схеме треугольника значения всех резисторов идентичны, то соответствующее значение сопротивления (r) в схеме звезды будет равным.
r = (R.R) / (R + R + R)
r = R / 3
Преимущество преобразования звезда-треугольник
- Здесь описаны некоторые преимущества этого преобразования.
- Звездообразное преобразование хорошо подходит для передачи напряжений на большие расстояния, а также имеет нейтральную точку, которая может использоваться для несимметричного переходного тока схемы на землю. Преобразование
- Дельта может передавать сбалансированное трехфазное напряжение (В) без нейтрального (n) провода, что соответствует ∆ наилучшим образом для сети передачи.
Это была подробная статья о преобразовании звезда-дельта, если у вас есть какие-либо вопросы по этому поводу, задавайте в комментариях.Будьте осторожны до следующего урока.
Автор: Захид Али
Я профессиональный писатель технического контента, мое хобби — узнавать новые вещи и делиться ими с новыми учениками. Также имею опыт работы в различных отраслях в качестве инженера. Теперь я делюсь своими техническими знаниями со студентами инженерных специальностей.
Вопросы и ответы о трансформации звездообразной дельты
Этот набор вопросов и ответов с множественным выбором (MCQ) по базовой электротехнике посвящен «преобразованию в треугольную звезду».
1. Значение трех сопротивлений при соединении звездой составляет _________
a) 2,32 Ом, 1,22 Ом, 4,54 Ом
b) 3,55 Ом, 4,33 Ом, 5,67 Ом
c) 2,78 Ом, 1,67 Ом, 0,83 Ом
г) 4,53 Ом, 6,66 Ом, 1,23 Ом
Просмотреть ответ
Ответ: c
Пояснение: После преобразования треугольника в звезду:
R1 = 10 * 5 / (10 + 5 + 3) = 2,78 Ом
R2 = 10 * 3 / (10 + 5 + 3) = 1,67 Ом
R3 = 5 * 3 / (10 + 5 + 3) = 0,83 Ом.
2. Какое из следующих выражений является правильным для преобразования дельты в звезду?
а) R1 = Ra * Rb / (Ra + Rb + Rc), R2 = Rb * Rc / (Ra + Rb + Rc), R3 = Rc * Ra / (Ra + Rb + Rc)
б) R1 = Ra / (Ra + Rb + Rc), R2 = Rb / (Ra + Rb + Rc), Rc = / (Ra + Rb + Rc)
c) R1 = Ra * Rb * Rc / (Ra + Rb + Rc), R2 = Ra * Rb / (Ra + Rb + Rc), R3 = Ra / (Ra + Rb + Rc)
d) R1 = Ra * Rb * Rc / (Ra + Rb + Rc), R2 = Ra * Rb * Rc / (Ra + Rb + Rc), R3 = Ra * Rb * Rc / (Ra + Rb + Rc)
Просмотреть ответ
Ответ: a
Пояснение: После преобразования в звезду сопротивление каждой звезды, подключенное к ней, равно отношению произведения сопротивлений, к которым он подключен, и общей суммы сопротивлений.Следовательно, R1 = Ra * Rb / (Ra + Rb + Rc), R2 = Rb * Rc / (Ra + Rb + Rc), R3 = Rc * Ra / (Ra + Rb + Rc).
3. Найдите эквивалентную звездообразную сеть.
a) 2,3 Ом, 2,3 Ом, 2,3 Ом
b) 1,2 Ом, 1,2 Ом, 1,2 Ом
c) 3,3 Ом, 3,3 Ом, 3,3 Ом
d) 4,5 Ом, 4,5 Ом, 4,5 Ом
Посмотреть ответ
Ответ: b
Пояснение: Сопротивления 6 Ом и 9 Ом подключены параллельно. Их эквивалентные сопротивления: 6 * 9 / (9 + 6) = 3,6 Ом.
3 резистора 3,6 Ом подключены по схеме треугольник. Преобразование в звезду:
R1 = R2 = R3 = 3.6 * 3,6 / (3,6 + 3,6 + 3,6) = 1,2 Ом.
4. Звездообразное соединение также известно как __________
a) Y-соединение
b) Сетчатое соединение
c) Y-соединение или сетчатое соединение
d) Ни Y-соединение, ни сетчатое соединение
Посмотреть ответ
Ответ: a
Объяснение : Соединение звездой также известно как соединение Y, потому что оно образовано буквой Y.
5. Rab — это сопротивление между выводами A и B, Rbc между B и C и Rca между C и A.Эти 3 резистора соединены треугольником. После преобразования в звезду сопротивление в точке A будет?
a) Rab * Rac / (Rab + Rbc + Rca)
b) Rab / (Rab + Rbc + Rca)
c) Rbc * Rac / (Rab + Rbc + Rca)
d) Rac / (Rab + Rbc + Rca)
Посмотреть ответ
Ответ: a
Объяснение: При преобразовании из треугольника в звезду сопротивление в звездном соединении равно произведению сопротивлений, к которым он подключен, деленному на общую сумму сопротивлений.
Следовательно, Rab * Rac / (Rab + Rbc + Rca).
6.Rab — это сопротивление между клеммами A и B, Rbc между B и C и Rca между C и A. Эти 3 резистора соединены треугольником. После преобразования в звезду сопротивление в точке B будет?
a) Rac / (Rab + Rbc + Rca)
b) Rab / (Rab + Rbc + Rca)
c) Rbc * Rab / (Rab + Rbc + Rca)
d) Rab / (Rab + Rbc + Rca)
Посмотреть ответ
Ответ: c
Объяснение: При преобразовании из треугольника в звезду сопротивление в соединении звездой равно произведению сопротивлений, к которым он подключен, деленному на общую сумму сопротивлений.
Следовательно, Rab * Rbc / (Rab + Rbc + Rca).
7. Rab — это сопротивление между клеммами A и B, Rbc между B и C и Rca между C и A. Эти 3 резистора соединены треугольником. После преобразования в звезду сопротивление в точке C будет?
a) Rac / (Rab + Rbc + Rca)
b) Rab / (Rab + Rbc + Rca)
c) Rbc * Rac / (Rab + Rbc + Rca)
d) Rab / (Rab + Rbc + Rca)
Посмотреть ответ
Ответ: c
Объяснение: При преобразовании из треугольника в звезду сопротивление в соединении звездой равно произведению сопротивлений, к которым он подключен, деленному на общую сумму сопротивлений.
Следовательно, Rac * Rbc / (Rab + Rbc + Rca).
8. Найдите ток в цепи.
a) 0,54A
b) 0,65A
c) 0,67A
d) 0,87A
Посмотреть ответ
Ответ: a
Пояснение: Резисторы на 3 5 Ом соединены треугольником. Меняя его на звезду:
R1 = R2 = R3 = 1,67 Ом.
Один из резисторов 1,67 Ом соединен последовательно с резистором 2 Ом, а другой резистор 1,67 Ом подключен последовательно к резистору 3 Ом.
Полученная сеть имеет 1.Резистор 67 Ом, включенный последовательно с параллельным включением резисторов 3,67 и 4,67.
Эквивалентное сопротивление 3,725 А.
I = 2 / 3,725 = 0,54 А.
9. Если резистор 6 Ом, 2 Ом и 4 Ом подключен по схеме треугольника, найдите эквивалентное соединение звездой.
a) 1 Ом, 2 Ом, 3 Ом
b) 2 Ом, 4 Ом, 7 Ом
c) 5 Ом, 4 Ом, 2 Ом
d) 1 Ом, 2 Ом, 2/3 Ом
Посмотреть ответ
Ответ: d
Объяснение: Использование дельты для звезды Формула преобразования:
R1 = 2 * 6 / (2 + 6 + 4)
R2 = 2 * 4 / (2 + 6 + 4)
R3 = 4 * 6 / (2 + 6 + 4).
10. Если резистор 4 Ом, 3 Ом и 2 Ом подключен по схеме треугольника, найдите эквивалентное соединение звездой.
a) 8/9 Ом, 4/3 Ом, 2/3 Ом
b) 8/9 Ом, 4/3 Ом, 7/3 Ом
c) 7/9 Ом, 4/3 Ом, 2/3 Ом
d) 8/9 Ом, 5 / 3ohm, 2 / 3ohm
Посмотреть ответ
Ответ: a
Объяснение: Используя формулу преобразования треугольник-звезда:
R1 = 4 * 3 / (2 + 3 + 4)
R2 = 2 * 3 / (2 + 3 +4)
R3 = 2 * 4 / (2 + 3 + 4).




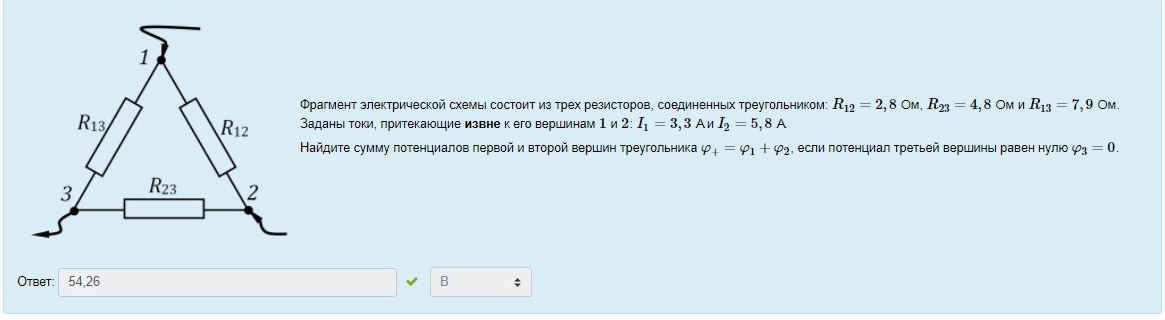
 R2
R2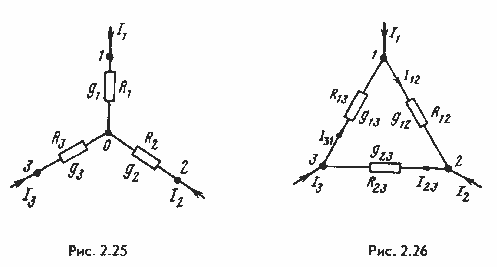 Можете ли вы определить это преобразование («звезда-треугольник» или «дельта-звезда»)?
Можете ли вы определить это преобразование («звезда-треугольник» или «дельта-звезда»)?