Колебания и волны — основные формулы по физике

При изучении этого раздела следует иметь в виду, что колебания различной физической природы описываются с единых математических позиций. Здесь надо четко уяснить такие понятия, как гармоническое колебание, фаза, разность фаз, амплитуда, частота, период колебания.

Надо иметь в виду, что во всякой реальной колебательной системе есть сопротивления среды, т.е. колебания будут затухающими. Для характеристики затухания колебаний вводится коэффициент затухания и логарифмический декремент затухания.

Если колебания совершаются под действием внешней, периодически изменяющейся силы, то такие колебания называют вынужденными. Они будут незатухающими. Амплитуда вынужденных колебаний зависит от частоты вынуждающей силы. При приближении частоты вынужденных колебаний к частоте собственных колебаний амплитуда вынужденных колебаний резко возрастает. Это явление называется резонансом.

Переходя к изучению электромагнитных волн нужно четко представлять, что электромагнитная волна — это распространяющееся в пространстве электромагнитное поле. Простейшей системой, излучающей электромагнитные волны, является электрический диполь. Если диполь совершает гармонические колебания, то он излучает монохроматическую волну.

Смотрите также основные формулы квантовой физики

Таблица формул: колебания и волны

Физические законы, формулы, переменные	Формулы колебания и волны
Уравнение гармонических колебаний: где х — смещение (отклонение) колеблющейся величины от положения равновесия; А — амплитуда; ω — круговая (циклическая) частота; t — время; α — начальная фаза; (ωt+α ) — фаза.
Связь между периодом и круговой частотой:
Частота:
Связь круговой частоты с частотой:
Периоды собственных колебаний 1) пружинного маятника: где k — жесткость пружины; 2) математического маятника: где l — длина маятника, g — ускорение свободного падения; 3) колебательного контура: где L — индуктивность контура, С — емкость конденсатора.
Частота собственных колебаний:
Сложение колебаний одинаковой частоты и направления: 1) амплитуда результирующего колебания где А1 и А2 — амплитуды составляющих колебаний, α1 и α2 — начальные фазы составляющих колебаний; 2) начальная фаза результирующего колебания	1) 2)
Уравнение затухающих колебаний: е = 2,71… — основание натуральных логарифмов.
Амплитуда затухающих колебаний: где А0 — амплитуда в начальный момент времени; β — коэффициент затухания; t — время.
Коэффициент затухания: колеблющегося тела где r — коэффициент сопротивления среды, m — масса тела; колебательного контура где R — активное сопротивление, L — индуктивность контура.
Частота затухающих колебаний ω:
Период затухающих колебаний Т:
Логарифмический декремент затухания:
Связь логарифмического декремента χ и коэффициента затухания β:
Амплитуда вынужденных колебаний где ω — частота вынужденных колебаний, fо — приведенная амплитуда вынуждающей силы, при механических колебаниях: при электромагнитных колебаниях:
Резонансная частота
Резонансная амплитуда
Полная энергия колебаний:
Уравнение плоской волны: где ξ — смещение точек среды с координатой х в момент времени t; k — волновое число:
Длина волны: где v скорость распространения колебаний в среде, Т — период колебаний.
Связь разности фаз Δφ колебаний двух точек среды с расстоянием Δх между точками среды:

§ 1.6. Механические колебания

Колебательные процессы весьма часто встречаются в окружающей нас природе и технике. Значительная часть механических движений – движение машин, работающих циклически; почти все акустические явления; переменный ток, применяющийся в быту и в разнообразных технических устройствах; радиотехника и часть электроники; вся волновая оптика; волновые свойства частиц – вот далеко не полный перечень явлений и технических приложений, описываемых на языке колебательных и волновых процессов. В конце концов, наши сердца бьются; наши легкие колеблются при дыхании; мы дрожим, когда нам холодно; мы можем слышать и разговаривать благодаря колебаниям барабанных перепонок и голосовых связок. Световые волны, которые позволяют нам видеть, имеют колебательную природу. Когда мы ходим, наши ноги совершают колебания. Колеблются даже атомы, из которых мы состоим. Если расширенно толковать термин «колебания», то сразу становится очевидным, что многие события повседневной жизни обладают необычайной цикличностью. Мир, в котором мы живем, удивительно склонен к колебаниям. Именно поэтому колебательному движению уделяется особое внимание в физике и технике.

Кроме того, периодическое негармоническое движение можно свести к сумме гармонических движений, причем эти составные движения доступны непосредственному наблюдению при помощи современной аппаратуры. Более того, существует аппаратура, позволяющая складывать заданные гармонические движения и получать, таким образом, периодические движения сложного характера.

В процессе развития науки создан мощный и удобный математический аппарат для описания и исследования периодических движений различной физической природы.

Колебаниями называются движения, процессы, изменения состояния, которые характеризуются определенной повторяемостью во времени значений физических величин, определяющих это движение, процесс или состояние.

Колебание называют периодическим, если значения величин, изменяющихся в процессе колебаний, повторяются через равные промежутки времени. Период колебания Т – это минимальный промежуток времени через который повторяются определенные состояния системы (время, за которое совершается одно полное колебание). Период измеряется в секундах.

Частота колебаний (линейная частота) – это скалярная физическая величина равная числу колебаний, совершаемых системой за единицу времени. Частота колебаний измеряется в Герцах (Гц).

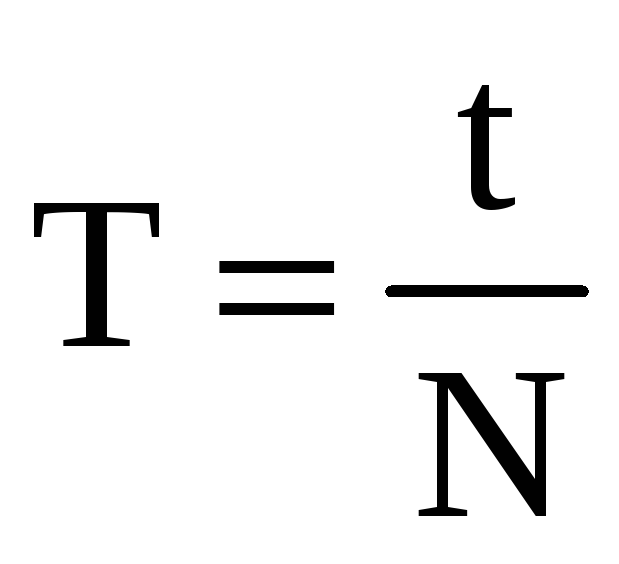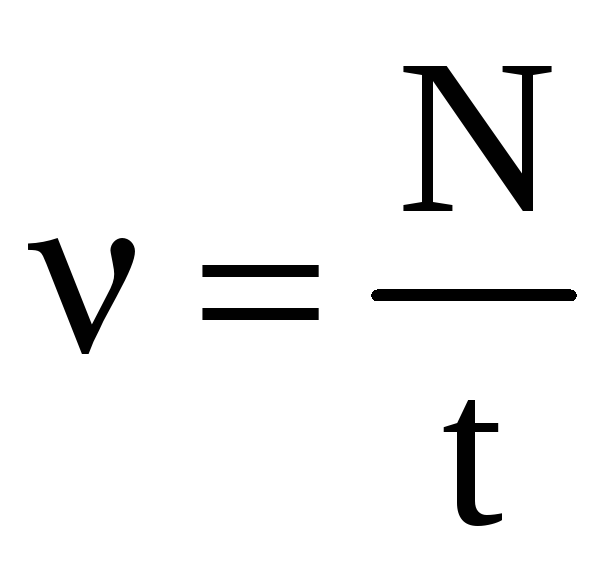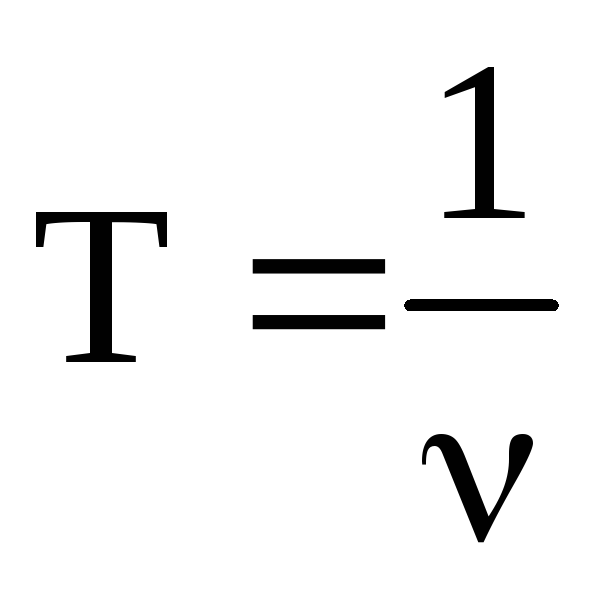Если за какое-то время t система совершает N колебаний, то и . Отсюда следует, что и .

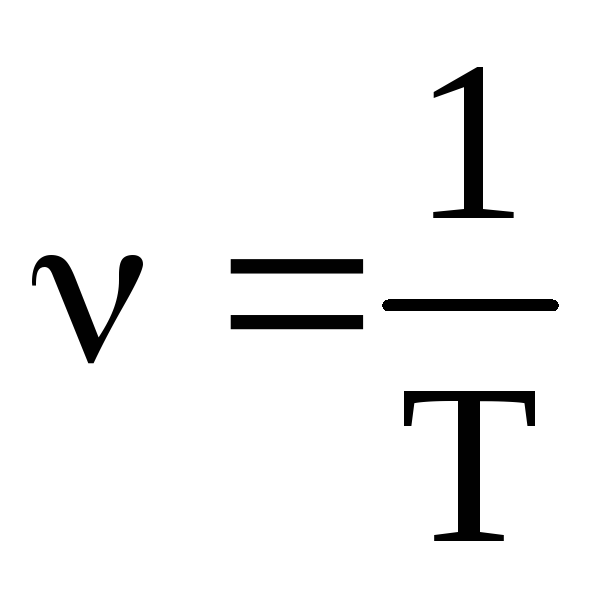Гармонические колебания

Среди разнообразных периодических движений особое место занимает гармоническое колебательное движение. Гармоническими называют колебания, в которых интересующая нас величина х (например, линейное или угловое смещение из положения равновесия, скорость, ускорение, заряд, напряжение и т.д.) изменяется со временем t по закону косинуса или синуса, то есть

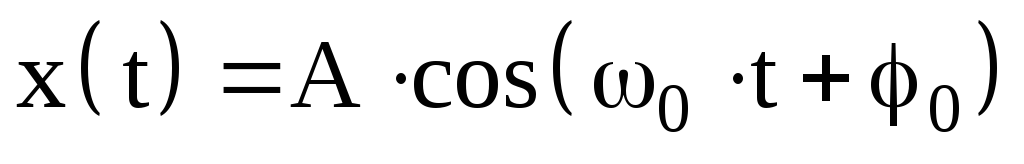, (1)

или

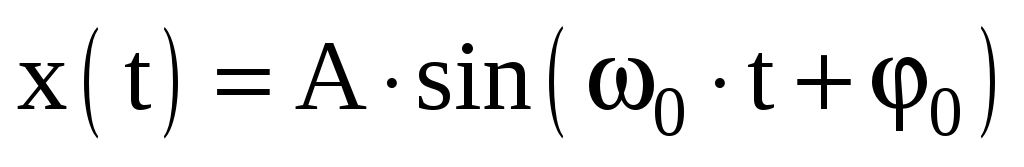
Здесь:

Циклическая частота связана с линейной частотой и периодом следующими соотношениями .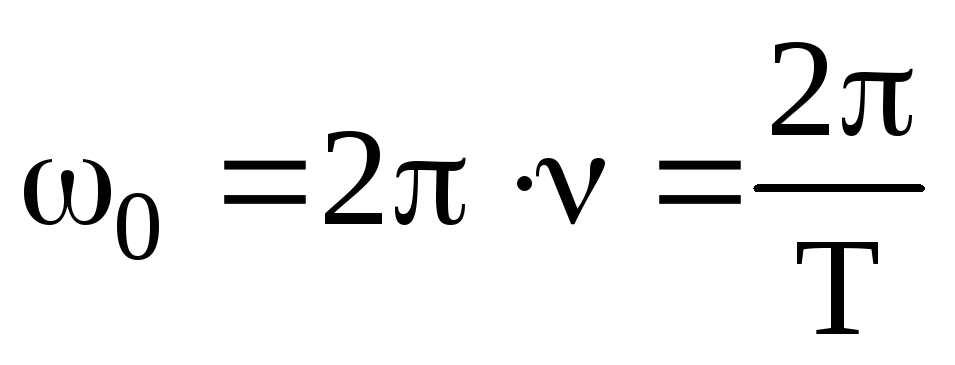

С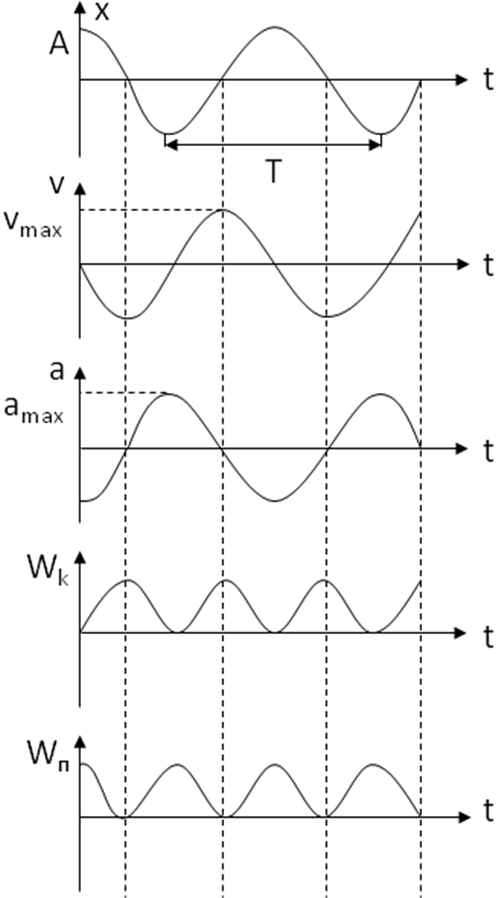корость и ускорение тела также изменяются по гармоническому закону. Продифференцировав по времени уравнение (1) найдем скорость изменения величины х — 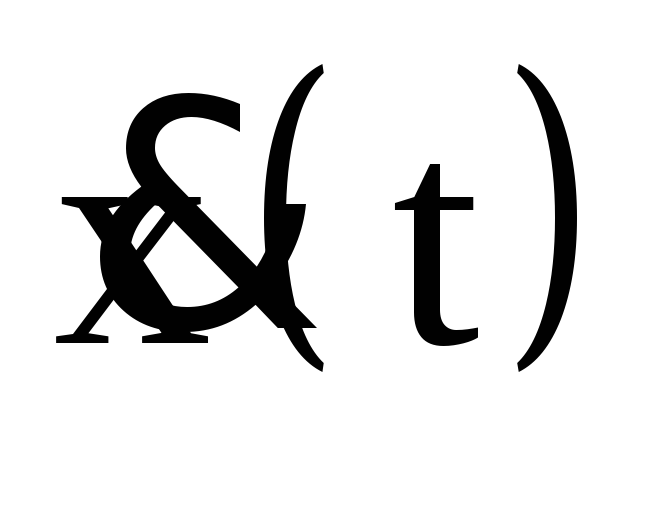и ускорение :

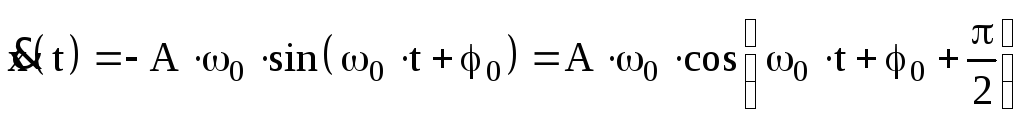
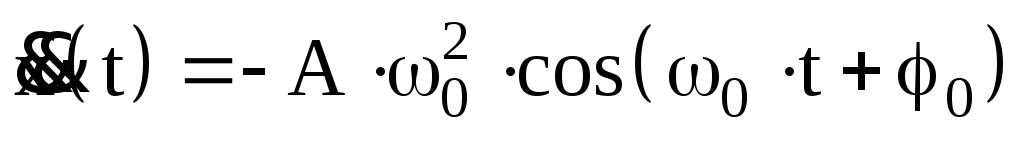. (2)

При этом максимальное значение скорости колеблющегося тела V_max = Aω₀, максимальное значение модуля ускорения a_{max =} Aω₀².

Кинетическая энергия колеблющегося тела W_k = ½mv² = ½mA²ω₀² sin² (ω₀t+φ).

Потенциальная энергия (учитывая, что сила квазиупругая) W_п = ½ kx² = ½ kA² cos² (ω₀t+φ).

Полная энергия системы при гармонических колебаниях W= W_k+ W_п =½ kA² = ½ mω₀² A².

На рисунке приведены графики зависимости от времени смещения х, скорости V, ускорения а, кинетической W_k и потенциальной W_п энергии гармонических колебаний при начальной фазе φ = 0. Из рисунка видно, частота изменения кинетической W_k и потенциальной W_п энергии при гармонических колебаниях вдвое больше частоты изменения смещения, скорости и ускорения.

Сопоставив уравнения (1) и (2), видим, что 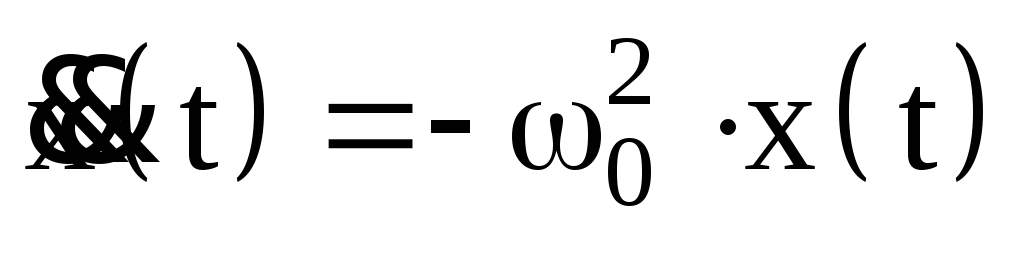, или

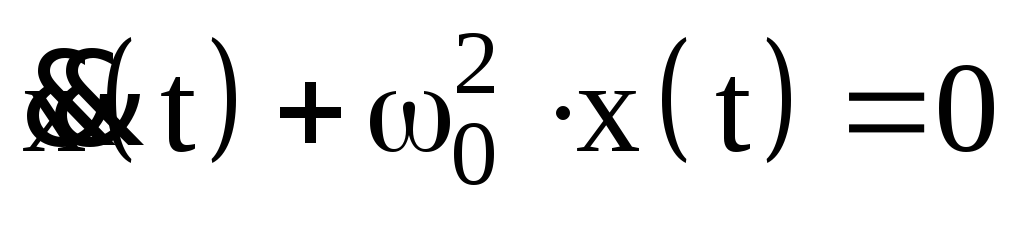. (3)

Это линейное однородное дифференциальное уравнение второго порядка называют уравнением гармонических колебаний.

Колебательная система, совершающая гармонические колебания, называется гармоническим осциллятором. Если колебательная система, совершающая гармонические колебания, обладает одной степенью свободы (для характеристики положения достаточно одной координаты), то такая система называется линейным гармоническим осциллятором.

Для определения характера движения механической системы составляют уравнение движения системы (исходя из законов динамики или закона сохранения энергии). Если уравнение при этом приводится к виду (3), то можно однозначно утверждать, что данная система совершает гармоническое колебание, собственная частота которого равна корню квадратному из коэффициента при х(t). Воспользуемся этим методом для определения циклических частот и периодов колебаний пружинного и математического маятников.

Рассмотрим сначала пружинный маятник (рис 1 б). Пусть подвешенное к пружине тело оттянуто от положения равновесия на расстояние х (рис.1.в), а затем предоставлено самому себе. На тело действуют сила тяжести и сила упругости. Под действием этих сил тело движется с ускорением. Запишем уравнение второго закона Ньютона для этого случая (рис.1.в)

.

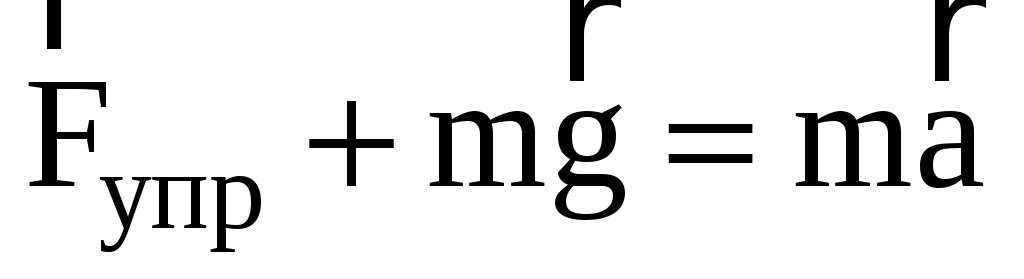Это уравнение в проекции на ось ОХ и с учетом того, что для одномерного движения ускорение – это вторая производная от координаты по времени, то есть 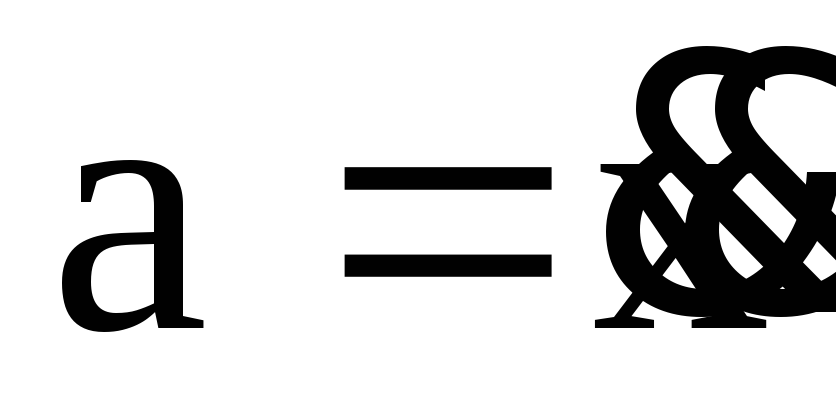, запишется

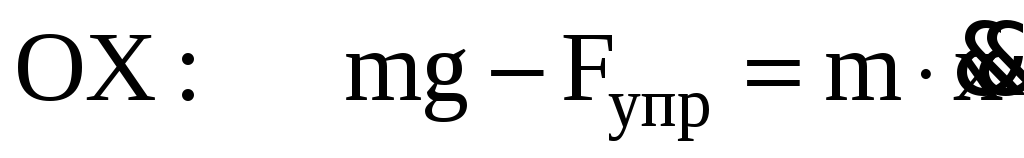. (4)

Величину силы упругости 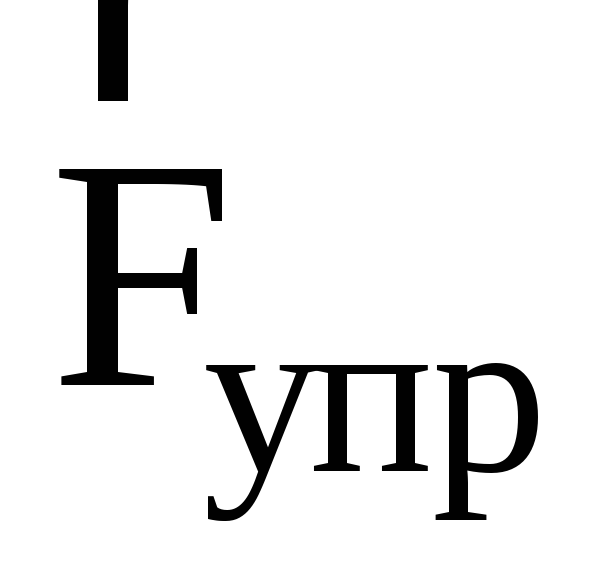, действующей на тело массой m, найдем по формуле закона Гука

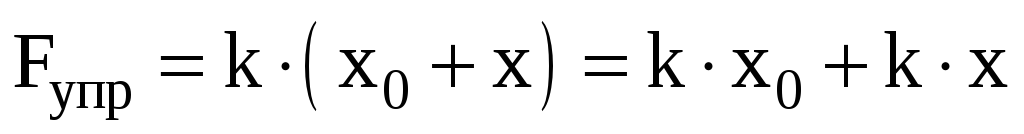. (5)

После подстановки (5) в (4) получим

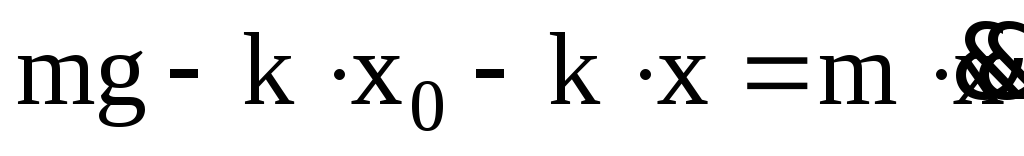(6)

Величину растяжения пружины в положении равновесия 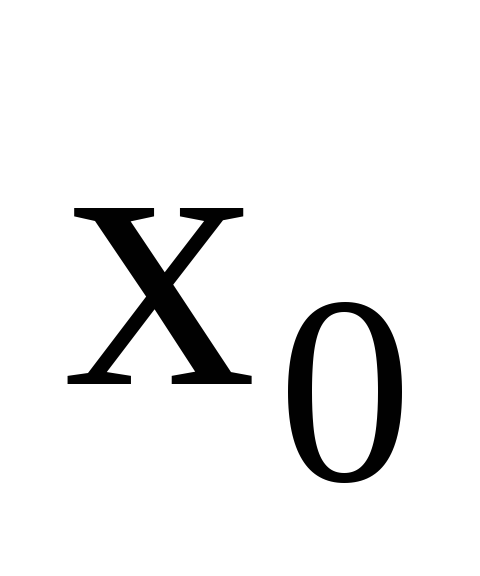(рис.1.а и 1.б) найдем из уравнения второго закона Ньютона для неподвижного тела, подвешенного к пружине ,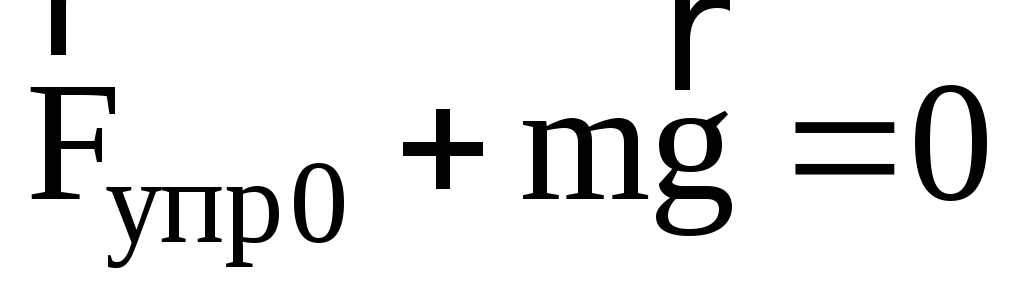

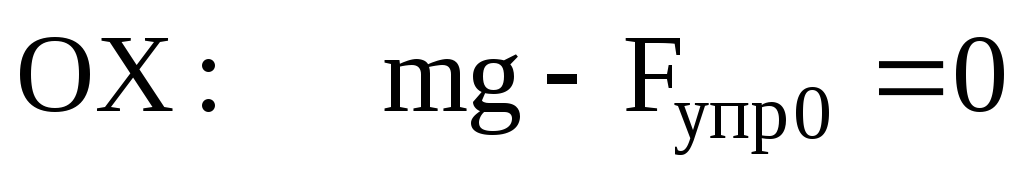, (7)

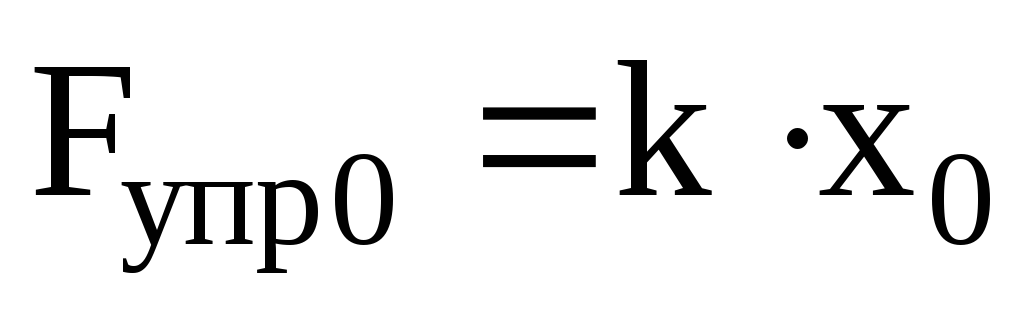, (8)

Из (7) и (8) следует, что

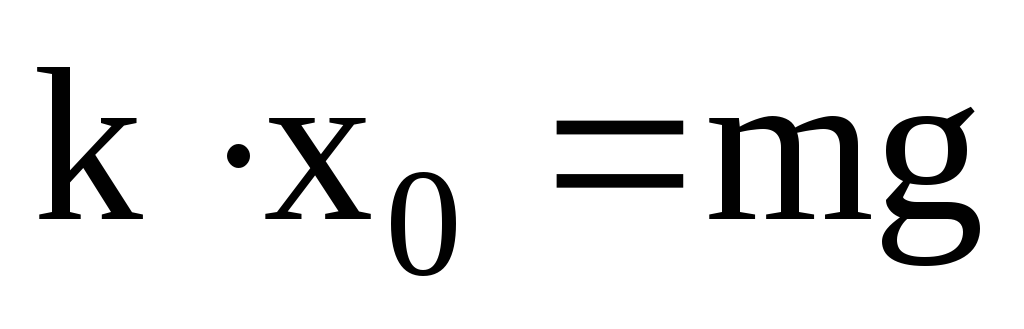. (9)

После подстановки (9) в (6) и приведения подобных слагаемых получаем: 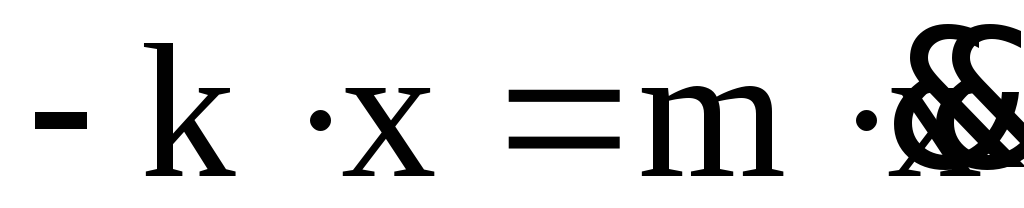, или

(10)

Сравнив уравнения (3) и (10), получим, что для пружинного маятника . .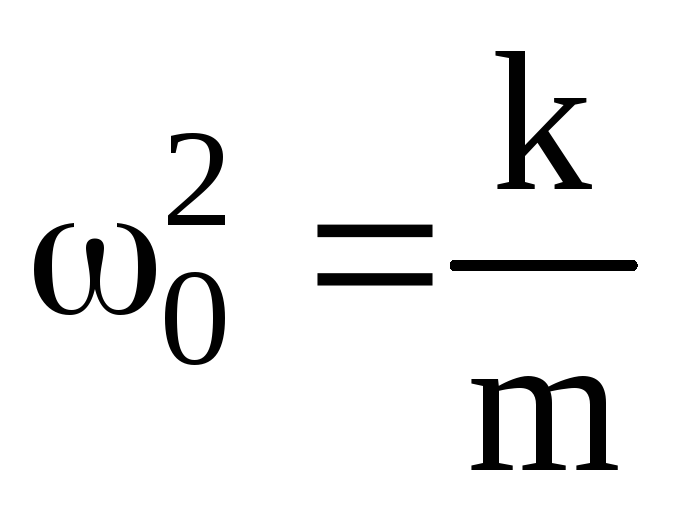

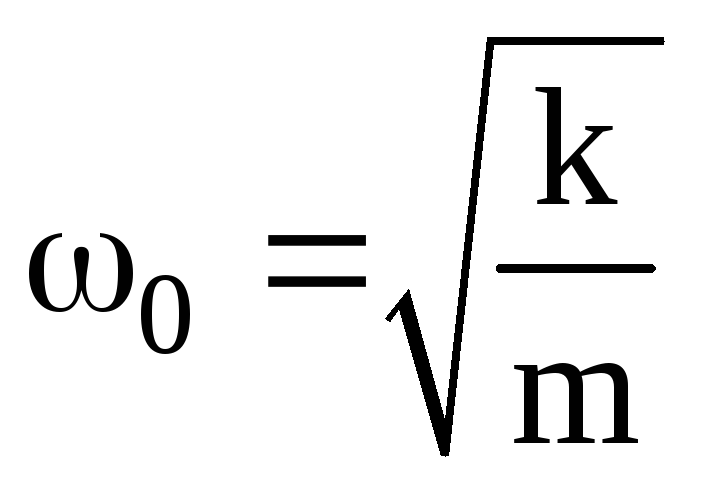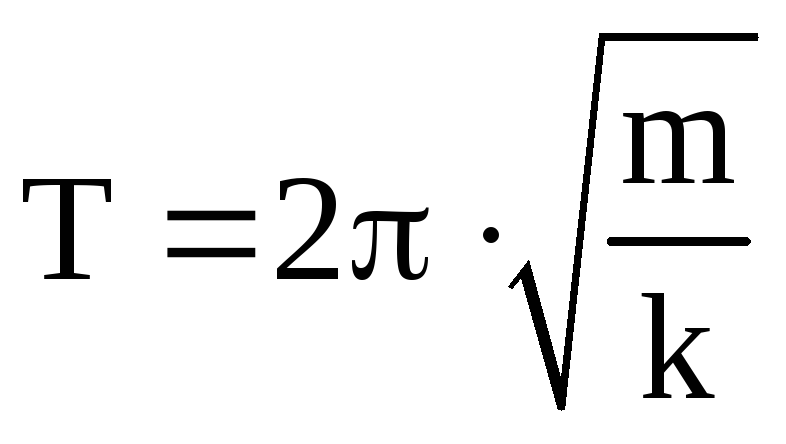(11)

Похожие рассуждения можно провести для математического маятника (рис.2) и показать, что . .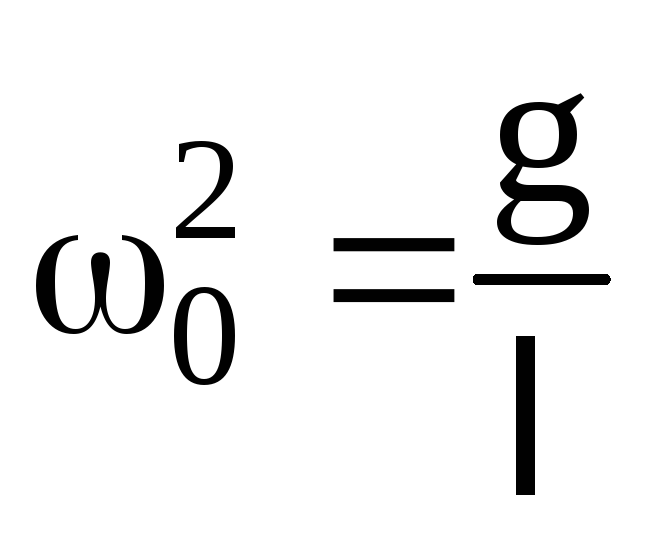

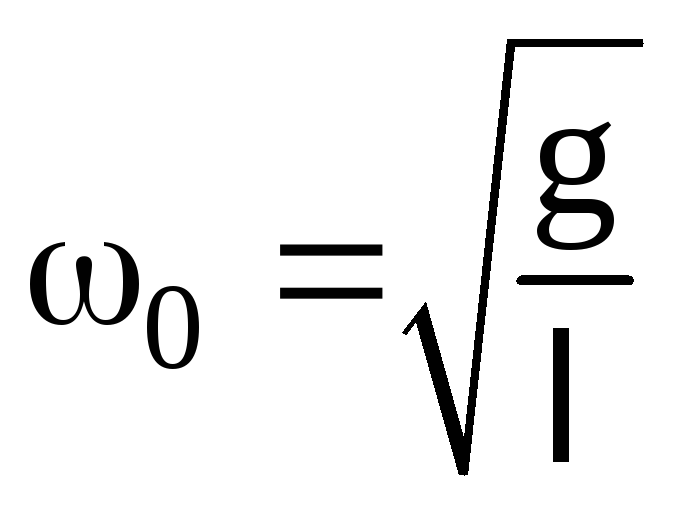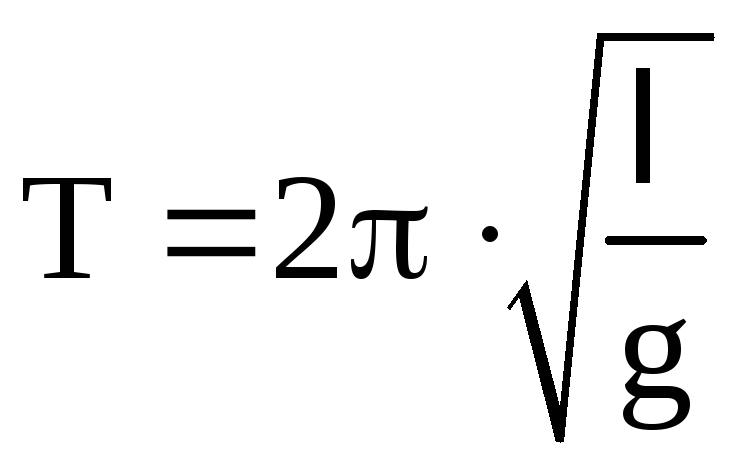(12)

Математический маятник – это материальная точка на невесомой и нерастяжимой нити длиной. При гармонических колебаниях смещение маятника от положения равновесия х много меньше длины нити х << 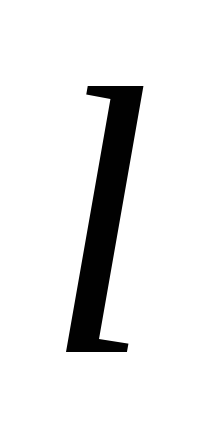, поэтому для угла отклонения нити от вертикали имеет место соотношение

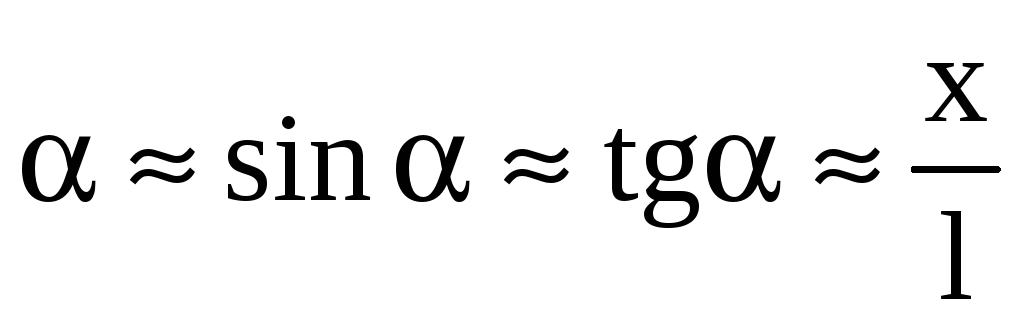
Следовательно, второй закон Ньютона для материальной точки массы m: ma = F можно записать в виде , где — ускорение точки, F = mg sin=mg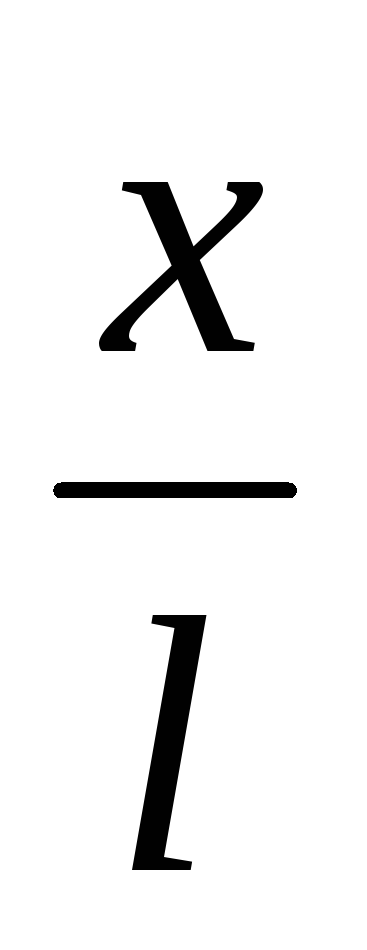 — возвращающая сила. Знак минус в правой части означает, что возвращающая сила направлена противоположно смещению х.

Таким образом, дифференциальное уравнение гармонических колебаний математического маятника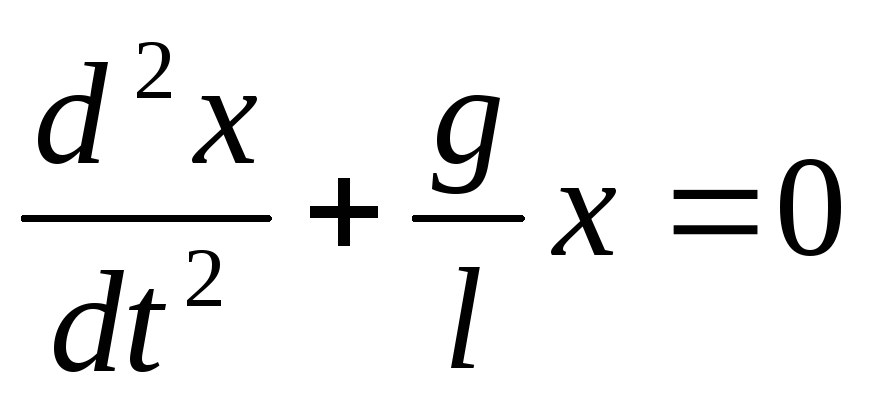

Сравнивая это уравнение с уравнением (3), получаем формулы для собственной частоты и периода колебаний математического маятника 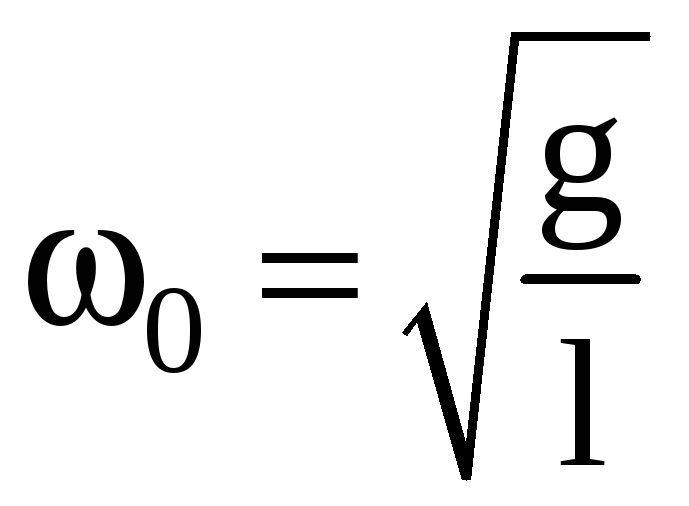и .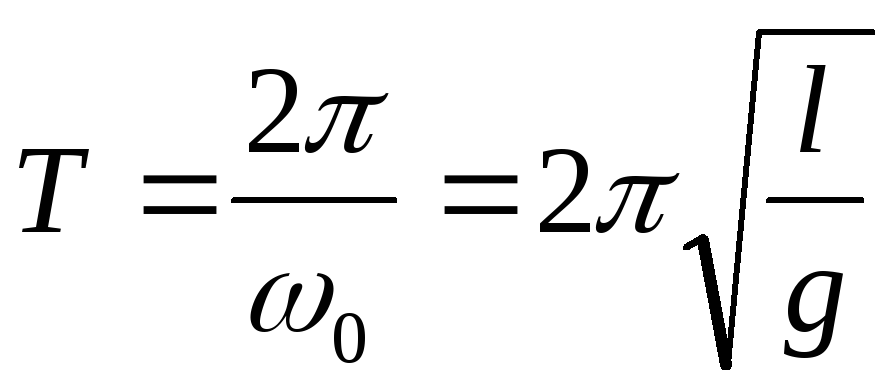

Физический маятник – это абсолютно твёрдое тело, совершающее колебания относительно горизонтальной оси О, не проходящей через центр масс маятника С. Основное уравнение динамики вращательного движения для маятника Jε = M, где J – момент инерции маятника относительно горизонтальной оси проходящей через точку О. Угловое ускорение маятника ε 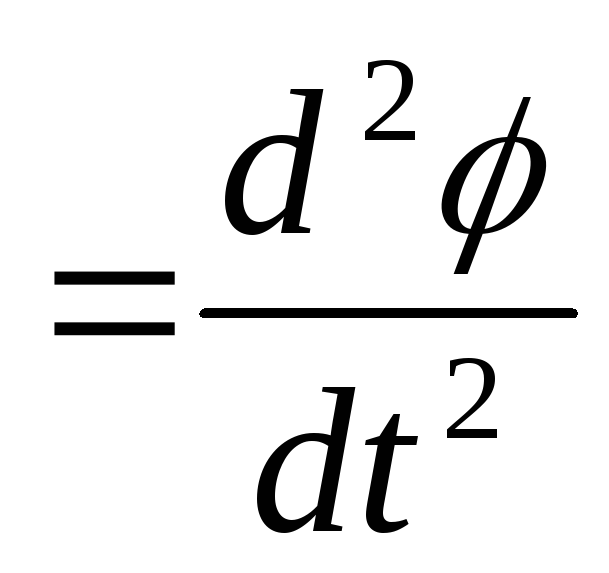. Момент силы тяжести маятника относительно горизонтальной оси, проходящей через точку О M = mgd sinφ, где m – масса маятника, d = CO – расстояние от оси до центра масс маятника С. При малых углах отклонения маятника от вертикали можно считать, что

Подставляя всё в уравнение второго закона Ньютона, получаем .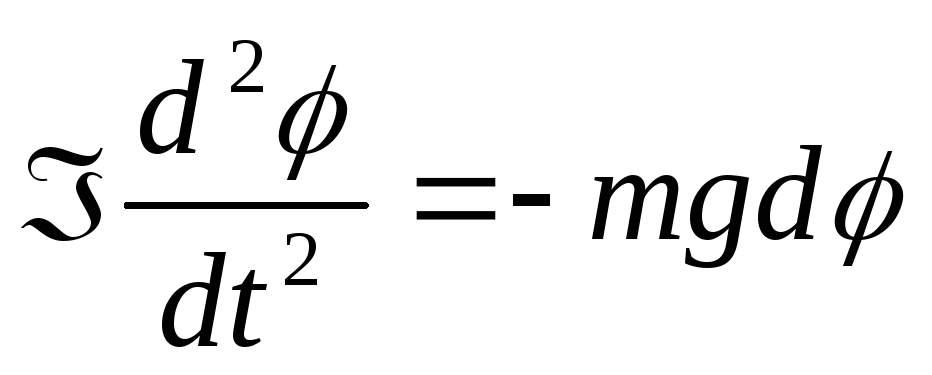

Минус означает, что момент возвращающей силы противоположен угловому перемещению. Отсюда получаем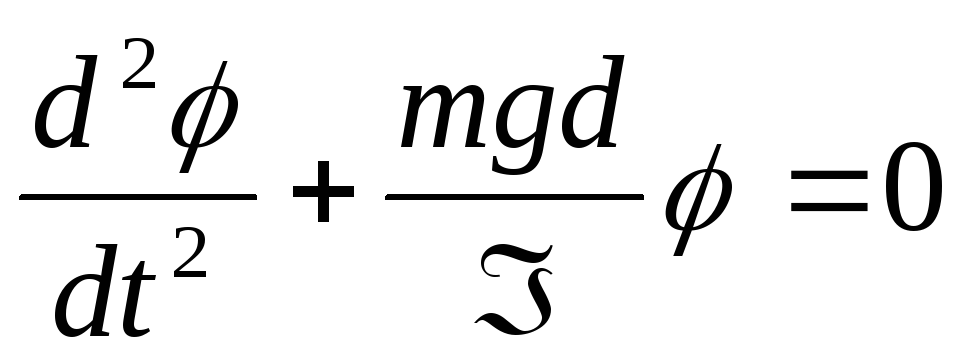

Это дифференциальное уравнение гармонических колебаний физического маятника. Из сравнения этого уравнения с уравнением (3), находим период колебаний физического маятника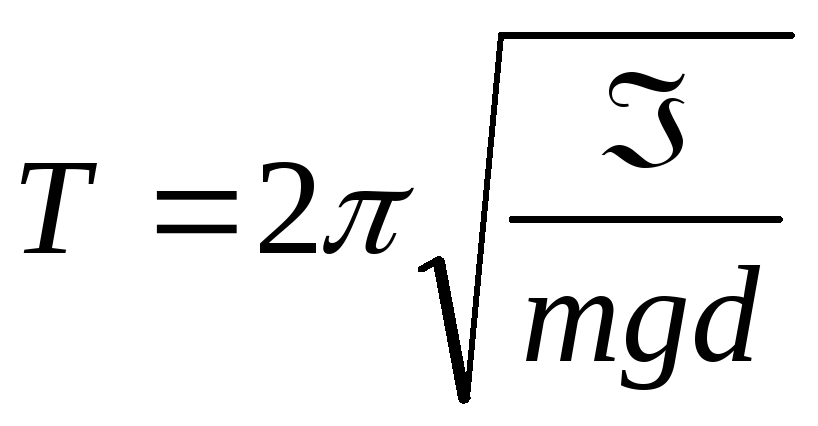

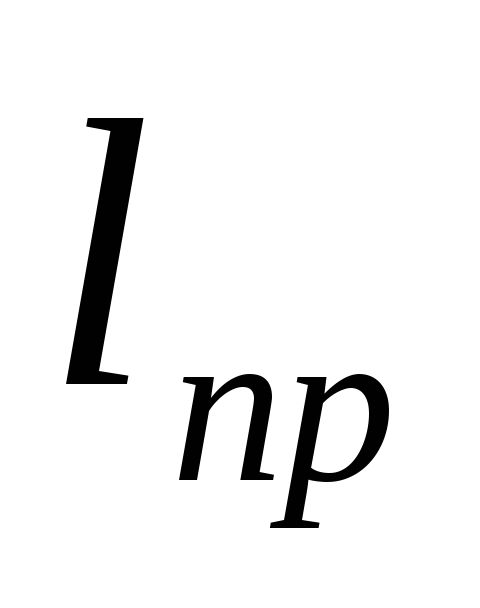Приведенная длина физического маятника — это длина нити математического маятника, у которого период колебаний совпадает с периодом данного физического маятника.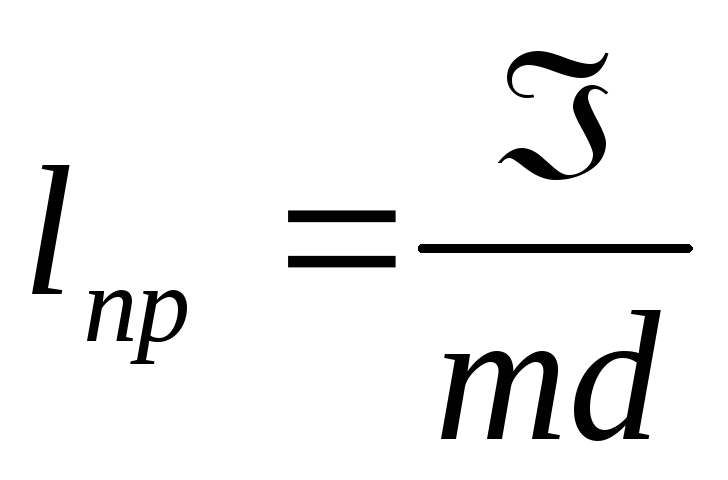

Колебания называются собственными, если они совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий на колебательную систему.

Как определить собственную частоту колебаний

Собственные колебания

Определение 1

Собственные или свободные колебания – это колебания, происходящие в системе при отсутствии переменных внешних воздействий. Такие колебания возникают по причине начального отклонения одного из параметров от состояния равновесия.

В целом колебания представляют собой повторяющийся во времени процесс изменения состояния системы около точки равновесия (при колебании маятника все углы его отклонения от вертикали повторяются с определенной периодичностью.

В реальных макроскопических системах собственные колебания затухают по причине потерь энергии. Любой колебательный процесс связан с переходом энергии из одной формы в другую.

Следует заметить, что колебания различной физической природы имеют ряд общих закономерностей и тесно связаны с волнами. В этой связи исследованием таких закономерностей занимается теория колебаний и волн. Принципиальное отличие колебаний от волн заключается в том, что распространение последних сопровождается переносом, а не переходом энергии.

По характеру взаимодействия с окружающей средой колебания разделяют на:

• вынужденные;
• автоколебания;
• параметрические;
• собственные.

В настоящей статье речь пойдет о собственных колебаниях, т.е. о колебаниях системы под действием внутренних сил после выведения системы из равновесия.

При небольших отклонениях от состояния равновесия движение любой системы будет удовлетворять принципу суперпозиции. Согласно данному принципу сумма произвольных движений составляет допустимое движение системы. Подобные движения описываются линейными (дифференциальными) уравнениями.

В случае, если в системе нет потерь энергии (она консервативна), а ее параметры не изменяются во времени, то любое собственное колебание может быть представлено, как совокупность нормальных колебаний, изменяющихся во времени по закону синуса с определенными частотами собственных колебаний.

Если положение системы в любой момент времени описывается единственным параметром, то такая система имеет одну степень свободы. Идеальным примером такой системы является маятник, колеблющийся в плоскости. И действительно, положение маятника в любой момент может определяться лишь углом его отклонения от вертикали.

В природе существует большое количество весьма интересных систем, имеющих две степени свободы. Например, молекулы и элементарные частицы (наиболее примечательны нейтральные К-мезоны). Более простым и понятным примером является двойной маятник (один маятник подвешивается к опоре, второй – к гире первого маятника; два маятника, объединенные пружиной).

Чтобы описать состояние системы с двумя степенями свободы необходимо уже две переменные. Например, в случае со сферическим маятником роль таких переменных будут выполнять положения маятника в двух взаимно перпендикулярных плоскостях. В случае объединенных маятников эти переменные соответствуют положению каждого из маятников.

В общем виде движение системы, имеющей две степени свободы, может иметь весьма сложный вид, не напоминающий простое гармоническое движение.

Для двух степеней свободы, а также при линейных уравнениях движения общий вид движения представляет собой суперпозицию двух простейших гармонических зависимостей, происходящих в один момент. Эти два элементарных движения называют нормальными (собственными) колебаниями или гармониками.

Колебательные системы с сосредоточенными параметрами, состоящими из N связанных осцилляторов (например, цепочка из связанных между собой пружинками шариков), число гармоник будет равно N. В системах с распределенными параметрами (мембрана или резонатор) таких колебаний существует бесчисленное множество. Например, для закрепленной струны длиной L гармоники будут отличаться количеством полуволн, которые возможно уложить по всей длине струны. Если скорость распространения волн струны равна v, то спектр собственных частот определяется по формуле:

Рисунок 1. Формула 1. Автор24 — интернет-биржа студенческих работ

Наличие дисперсии волн искажает данное простое распределение частот, спектр которых определяется уже из дисперсионных уравнений.

Что касается реальных систем, то в них собственные колебания затухают из-за потерь энергии, поэтому их следует считать лишь приближенно гармоническими в интервале времени, меньшем $1/δ$. Затухающие колебания могут быть представлены в виде нескольких гармонических колебаний, непрерывно заполняющих определенный интервал частот, тем меньшим, чем меньше $δ$. В таком случае следует говорить о расширении спектральной линии, характеризуемой добротностью $Q$ и равной отношению запасенной энергии $W$ к потерям $P$. Отсюда следует, что отношение сгущение спектра из-за потерь энергии может повлечь за собой превращение дискретного спектра в сплошной при приближении ширины линий к интервалу между ними.

Колебания в нелинейных системах

Собственные колебания нелинейных систем не поддаются простой классификации. Нелинейность систем с дискретным спектром частот собственных колебаний приводят к переходу энергии по спектральным компонентам. При этом возникает явление конкуренции гармоник – выживание одних и подавление других.

Подобный процесс может стабилизировать дисперсия. Она может привести к появлению устойчивых пространственно-временных образований (например, солитоны).

Большое значение при возбуждении колебаний может иметь явление резонанса, которое заключается в резком увеличении амплитуды колебаний (отклика). Данное явление наблюдается при приближении частоты внешних воздействий на систему к некоторой резонансной частоте, которая характеризует настоящую систему.

Если система линейна и ее параметры находятся вне зависимости от времени, то резонансные частоты совпадают с частотой собственных ее колебаний. Отклик системы в данном случае будет усиливаться с увеличением добротности колебательной системы $Q$.

Раскачка будет происходить до тех пор, пока энергия, поступающая извне (например, полученная при отклонении маятника от положения равновесия) будет превышать потери за время осцилляции. Что касается линейных колебаний, то энергия, вносимая извне будет пропорциональна амплитуде, а потери будут расти пропорционально ее квадрату. Отсюда следует, что баланс энергии достижим во всех случаях.

Нормальные колебания — Википедия

Различные нормальные моды в 1D решётке.

Норма́льные колеба́ния, со́бственные колебания или мо́ды — набор характерных для колебательной системы типов гармонических колебаний. Каждое из нормальных колебаний физической системы, например, колебаний атомов в молекулах, характеризуется своей частотой. Такая частота называется нормальной частотой, или собственной частотой^[1] (по аналогии с линейной алгеброй: собственное число и собственный вектор). Набор частот нормальных колебаний составляет колебательный спектр. Произвольное колебание физической системы можно представить в виде суперпозиции различных нормальных колебаний. Вынужденные колебания физической системы испытывают резонанс на частотах, которые совпадают с частотами нормальных колебаний этой системы.

Общая теория[править | править код]

Потенциальная энергия взаимодействия атомов в молекулах является определённой функцией их обобщённых координат U(r1,…,ri,…,rN){\displaystyle U(\mathbf {r} _{1},\ldots ,\mathbf {r} _{i},\ldots ,\mathbf {r} _{N})}. Эта функция теоретически рассчитывается методами квантовой механики в адиабатическом приближении или задаётся определёнными модельными эмпирическими потенциалами. Равновесные положения атомов в молекулах ri0{\displaystyle \mathbf {r} _{i0}} задаются условием минимума этой функции:

∂U∂ri=0.{\displaystyle {\frac {\partial U}{\partial \mathbf {r} _{i}}}=0.}

При выводе конфигурации молекулы из равновесия так, что каждый атом сместится на некую величину δri{\displaystyle \delta \mathbf {r} _{i}}, в молекуле возникнут силы, которые стремятся вернуть атомы в положение равновесия, отвечающего минимуму потенциальной энергии, а потенциальная энергия возрастёт и станет равной:

U(r1,…,ri,…,rN)=U0+12∑i,j=1N∑α,β=13aijαβδriαδrjβ+o(‖r‖2),{\displaystyle U(\mathbf {r} _{1},\ldots ,\mathbf {r} _{i},\ldots ,\mathbf {r} _{N})=U_{0}+{\frac {1}{2}}\sum _{i,j=1}^{N}\sum _{\alpha ,\beta =1}^{3}a_{ij}^{\alpha \beta }\delta r_{i}^{\alpha }\delta r_{j}^{\beta }+o(\left\|\mathbf {r} \right\|^{2}),},

где i{\displaystyle i} и j{\displaystyle j} — индексы атомов,

α{\displaystyle \alpha } и β{\displaystyle \beta } — индексы осей координат,

U0{\displaystyle U_{0}} — потенциальная энергия молекулы в положении равновесия,

а коэффициенты aijαβ{\displaystyle a_{ij}^{\alpha \beta }} определяются разложением потенциальной энергии в ряд Тейлора в окрестности положения равновесия.

Коэффициенты в разложении в ряд, соответствующие первым производным равны нулю, так как в положение равновесия — минимум потенциальной энергии, то есть «дно» потенциальной ямы и поэтому первые производные по координатам обращаются в нуль.

aijαβ=∂2U∂riα∂rjβ|ri=ri0+∂2U∂riα∂riβ|rj=rj0.{\displaystyle a_{ij}^{\alpha \beta }={\frac {\partial ^{2}U}{\partial r_{i}^{\alpha }\partial r_{j}^{\beta }}}{\bigg |}_{\mathbf {r} _{i}=\mathbf {r} _{i0}}+{\frac {\partial ^{2}U}{\partial r_{i}^{\alpha }\partial r_{i}^{\beta }}}{\bigg |}_{\mathbf {r} _{j}=\mathbf {r} _{j0}}.}

Уравнения движения для смещённых из положения равновесия атомов имеют следующий вид:

mid2dt2δriα=−∑j=1N∑β=13aijαβδrjβ{\displaystyle m_{i}{\frac {d^{2}}{dt^{2}}}\delta r_{i}^{\alpha }=-\sum _{j=1}^{N}\sum _{\beta =1}^{3}a_{ij}^{\alpha \beta }\delta r_{j}^{\beta }},

где mi{\displaystyle m_{i}} — масса i-го атома.

Если искать решения системы дифференциальных уравнений в виде

δriα=biαeiωt.{\displaystyle \delta r_{i}^{\alpha }=b_{i}^{\alpha }e^{i\omega t}.}

то получим систему линейных уравнений:

miω2biα−∑j=1N∑β=13aijαβbjβ=0.(A){\displaystyle m_{i}\omega ^{2}b_{i}^{\alpha }-\sum _{j=1}^{N}\sum _{\beta =1}^{3}a_{ij}^{\alpha \beta }b_{j}^{\beta }=0.\qquad ({\text{A}})}

Всего таких уравнений 3N−6{\displaystyle 3N-6} (3N−5{\displaystyle 3N-5} в случае линейных молекул), где N{\displaystyle N} — число атомов.

3 других уравнений описывают движение центра массы молекулы, а ещё три (два в случае линейных молекул) — вращения молекулы как целого^[2]. Система этих дифференциальных уравнений однородная, а следовательно, имеет нетривиальное решение лишь при наборе определённых частот, называемых собственными частотами, которые находятся из решения уравнения равенства нулю детерминанта этой системы:

|miω2δijδαβ−aijαβ|=0{\displaystyle \left|m_{i}\omega ^{2}\delta _{ij}\delta _{\alpha \beta }-a_{ij}^{\alpha \beta }\right|=0},

где δij{\displaystyle \delta _{ij}} — символ Кронекера.

Данный детерминант является уравнением 3N−6{\displaystyle 3N-6}-ой степени относительно ω2{\displaystyle \omega ^{2}}, которое называется вековым или секулярным уравнением. Его корни определяют спектр собственных частот колебаний молекулы.

Собственные векторы bi{\displaystyle \mathbf {b} _{i}} уравнения (A) определяют 3N−6{\displaystyle 3N-6} нормальных мод колебаний молекулы.

Нормальные моды взаимно линейно независимы и взаимно ортогональны:

∑i=1Nbim⋅bin=0{\displaystyle \sum _{i=1}^{N}\mathbf {b} _{i}^{m}\cdot \mathbf {b} _{i}^{n}=0},

если m≠n{\displaystyle m\neq n}, где m{\displaystyle m} и n{\displaystyle n} — индексы, которыми обозначены различные собственные векторы. Именно этой особенности нормальные моды обязаны своим названием.

Собственные векторы матрицы вторых производных потенциальной энергии по масс-взвешенным декартовым координатам пропорциональны малым смещениям таких координат атомов относительно положения равновесия. Эти смещения должны быть достаточно малыми, чтобы соответствующие члены в разложении Тейлора потенциальной энергии по координатам были пренебрежимо малы. Поэтому нормальные колебания есть малые колебания, при нарастании амплитуды колебаний увеличивается ангармонизм колебаний, то есть при разложении колебаний в ряд Фурье в спектре появляются высшие гармоники, что делает теорию колебаний молекулы очень сложной.

Произведение вектора нормальной моды на вектор взвешенных по массе декартовых координат является т. н. нормальной координатой. Базис нормальных координат представляет собой направления колебательных движений молекулы.

В теории механизма химических реакций элементарный акт химической перестройки молекулы представляется как движение по одной из нормальных координат (она называется в таком случае естественной координатой реакции, англ. intrinsic reaction coordinate). При этом система преодолевает «горб» потенциальной энергии и колебательное движение перестаёт быть колебательным, а становится поступательным. В более сложных случаях акт перестройки молекулярной структуры описывается изменением не одной, а двух или более нормальных координат, в этом случае говорят о сильном взаимодействии колебательных мод и большой кривизне реакционного пути в поперечном направлении.

Дипольный момент[править | править код]

Если известны нормальные моды, которые задаются векторами bin{\displaystyle \mathbf {b} _{i}^{n}}, где индекс n — номер моды, а также частичные заряды атомов в молекулах, то можно образовать векторы:

dn=∑iqibin,{\displaystyle \mathbf {d} ^{n}=\sum _{i}q_{i}\mathbf {b} _{i}^{n},}

которые называются дипольными моментами нормальных мод.

Во внешнем электрическом поле, например, в поле электромагнитной волны, энергия диполя определяется формулой:

E⋅d.{\displaystyle \mathbf {E} \cdot \mathbf {d} .}

Поэтому те нормальные моды, которые имеют значительный дипольный момент сильно взаимодействуют с электромагнитными волнами (обычно их частоты лежат в инфракрасном диапазоне). Те нормальные моды, для которых дипольный момент пренебрежимо мал, не поглощают и не излучают инфракрасные волны.

Например, симметричная молекула O₂ имеет равный электрический симметричный заряд на своих атомах, следовательно, нулевой дипольный момент и поэтому кислород в атмосфере не поглощает инфракрасное излучение и не является «парниковым» газом.

В молекуле углекислого газа CO₂ атомы кислорода несколько подтягивают электроны общего электронного облака к себе от центрального атома углерода, поэтому все три атома имеют небольшой частичный заряд. В линейной молекуле углекислого газа присутствуют четыре (3N−5{\displaystyle 3N-5}) нормальные моды. Одна из них — это симметричные колебания атомов кислорода вдоль оси молекулы. Эта мода не имеет дипольного момента. Другая мода колебаний — асимметричные колебания атомов кислорода вдоль оси молекулы и изгибные колебания имеют ненулевой дипольный момент, — третья и четвёртая вырожденные моды, описывающие угловые колебания молекулы во взаимно перпендикулярных направлениях.

• Федорченко, А. М. Теоретическая механика. — Киев : Высшая школа, 1975. — 516 с.