«Смешанное соединение проводников». Видеоурок. Физика 8 Класс
На уроке приведены формулы для расчета цепей при последовательном и параллельном соединениях. Решены задачи на смешанное соединение проводников, то есть на такие цепи, в которых присутствует и параллельное, и последовательное соединения проводников.
Под соединением проводников подразумевается соединение резисторов – приборов, сделанных на основе сопротивления проводников. На предыдущих уроках были рассмотрены параллельное и последовательное соединения. На данном уроке будут рассмотрены задачи на смешанное соединение проводников, то есть когда в цепи присутствует и последовательное, и параллельное соединение.
Для решения задач сначала рассмотрим формулы для связи различных величин при параллельном и последовательном соединениях:

Если проводники соединены последовательно, то сила тока в них одинакова и равна силе тока в цепи. При этом общее напряжение в цепи будет состоять из суммы напряжений на каждом проводнике. А если говорить о сопротивлении этого участка цепи, в котором проводники соединены последовательно, то оно равно сумме сопротивлений проводников.
В параллельном соединении все по-другому. Сила тока в каждой ветке этой цепи будет различной, при этом общая сила тока в цепи будет вычисляться как сумма сил токов в проводниках. Напряжение на проводниках, соединенных последовательно, будет одинаковым. Общее сопротивление этого участка цепи, так называемое «эквивалентное сопротивление» R, будет вычисляться по следующей формуле:  .
.
Также стоит отметить, что параллельное соединение обычно применяется при включении бытовых приборов, а последовательное – для того, чтобы создать длинную неразветвленную цепь.
Рассмотрим следующую задачу. Участок цепи состоит из двух последовательно соединенных сопротивлений, каждое из которых равно 1 Ом. К этим двум резисторам параллельно подключают еще одно сопротивление, значение которого составляет 2 Ом. Всю эту цепь подключают к источнику тока, который создает на концах данного соединения напряжение 2,4 В. Необходимо определить силу тока во всей электрической цепи (рис. 1).

Рис. 1. Условия и рисунок задачи № 1
Как видим, резисторы R1 и R2 соединены последовательно, резистор R3 – параллельно к ним. Источник дает напряжение 2,4 В, соответственно, на участке АВ напряжение будет также 2,4 В. Сила тока, которую требуется найти, – это сила тока, протекающая через амперметр А.
Такое соединение проводников называется неразветвленным. В промышленности обычно изготавливается набор резисторов с четко определенными сопротивлениями, но для экспериментов могут понадобиться любые различные сопротивления. Тогда с помощью таких схем можно создавать нужное сопротивление для эксперимента или прибора.
Далее требуется определить эквивалентное сопротивление неразветвленной части. Сначала посмотрим, чему равно сопротивление R’ участка цепи АВ, который содержит только резисторы R1 и R2. Они соединены последовательно, тогда R′=R1+R2=2 [Ом]. Теперь можно перерисовать электрическую цепь, заменив сопротивления R1 и R2 эквивалентным им сопротивлением R’ (рис. 2).

Рис. 2. Первая замена эквивалентным сопротивлением
Теперь можно сказать, что участок АВ включает в себя не три, а два сопротивления: R3 и R’. Эти два сопротивления соединены параллельно, соответственно, можно найти общее сопротивление электрической цепи по формуле  . Выразив R и подставив значения
. Выразив R и подставив значения 

Стоит отметить, что сопротивления были соединены, но общее сопротивление получилось все равно равным 1 Ом. Теперь электрическую цепь можно заменить следующей (рис. 3):

Рис. 3. Вторая замена эквивалентным сопротивлением
На рис. 3 сопротивление R=1 Ом называется эквивалентным сопротивлением, поскольку три сопротивления были заменены на одно. Чтобы рассчитать силу тока в цепи, надо использовать закон Ома для участка цепи: 
 . Это и будет значение силы тока в электрической цепи, которое покажет амперметр.
. Это и будет значение силы тока в электрической цепи, которое покажет амперметр.Теперь рассмотрим задачу, в которой также будет три сопротивления, но соединены они будут по-другому (рис. 4):

Рис. 4. Условие задачи № 2
Два сопротивления R1 и R2 соединены параллельно (R1=R2=2 Ом), к ним еще последовательно присоединено сопротивление R3=1 Ом. Амперметр показывает силу тока в цепи, равную I=0,5 А. Требуется определить напряжение на концах участка этой цепи, то есть на участке АВ.
Для начала определим сопротивление участка цепи, содержащего сопротивления R1 и R2. Эти два сопротивления соединены параллельно, значит, их эквивалентное сопротивление R’ можно найти из формулы 

Теперь можно сказать, что цепь включает в себя только два сопротивления: R’и R3, которые соединены последовательно.

Рис. 5. Замена параллельного соединения эквивалентным сопротивлением
В задаче требуется определить напряжение. Для этого используется прибор, который называется вольтметр. В цепь он включается параллельно. И рассмотрим участок цепи, в котором все три сопротивления уже заменены эквивалентным.
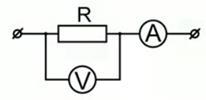
Рис. 6. Включение вольтметра в цепь
Вольтметр включен в месте, соответствующем участку АВ на рис. 4. Соответственно, он измеряет напряжение на это участке цепи. Чтобы найти значения этого напряжения, требуется сначала найти эквивалентное сопротивление. Сопротивления R’ и R3 соединены последовательно (рис. 5), значит, эквивалентное сопротивление определяется по формуле:

Теперь из закона Ома для участка цепи можно найти напряжение:

Значит, вольтметр должен будет показать значения напряжения в 1 В.
На уроке были рассмотрены соединения только трех сопротивлений, когда они были последовательные, к ним параллельно подключается третий, или когда два соединены параллельно, а к ним последовательно подключают третье сопротивление. Но реальные схемы значительно сложнее. Они содержат огромное количество различных элементов, сопротивлений, поэтому имеются достаточно сложные методы расчетов электрических цепей.
Впервые расчетами таких сложных электрических цепей озадачились ученые приблизительно в XIX веке, и появились новые правила, которые используются и по сей день. Немецкий ученый Кирхгоф разработал возможность расчета электрических сложных цепей, поэтому правила, которые используют для сложных цепей, называются «правилами Кирхгофа».
На следующих уроках будет рассмотрено понятие мощности и работы силы тока.
Список литературы
- Генденштейн Л.Э, Кайдалов А.Б., Кожевников В.Б. / Под ред. Орлова В.А., Ройзена И.И. Физика 8. – М.: Мнемозина.
- Перышкин А.В. Физика 8. – М.: Дрофа, 2010.
- Фадеева А.А., Засов А.В., Киселев Д.Ф. Физика 8. – М.: Просвещение.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Festival.1september.ru (Источник).
- Electroandi.ru (Источник).
- Bocharova.ucoz.ru (Источник).
Домашнее задание
- Стр. 117: задачи № 4, 5. Перышкин А.В. Физика 8. – М.: Дрофа, 2010.
- В каком случае эквивалентное сопротивление будет больше: если три проводника с сопротивлениями 1 Ом каждый соединить параллельно или последовательно?
- Два сопротивления R1=1 Ом и R2= 2 Ом соединены последовательно, к ним параллельно присоединено сопротивление 3 Ом. Чему равно эквивалентное сопротивление?
- Сколько различных цепей можно составить из трех резисторов с сопротивлениями 1 Ом каждый так, чтоб их эквивалентные сопротивления была различными?
Смешанное соединение сопротивлений — Мегаобучалка
Эквивалентное сопротивление цепи.
| R12 = R1 + R2 | R = R1 + R23 |
| U = U3 = I·R = I3·R3 | U = I· R; U1 = I1·R1 |
| U2 = U3 = I2·R2 = I3·R3 | |
| U1 = I1·R1 U2 = I2·R2 |
Баланс мощностей.
Пример 1.1. Цепь постоянного тока со смешанным соединением состоит из четырёх резисторов. Мощность электрической цепи Р = 750 Вт. Определить эквивалентное сопротивление цепи, токи и напряжения на всех резисторах и для всей цепи. Решение проверить, используя баланс мощностей.
(Указание: номера токов, напряжений и мощностей должны совпадать номерами сопротивлений.)
Дано: R1=10 Ом; R2 = 50 Ом; R3 = 40 Ом; R4= 6 Ом; Р = 750 Вт.
Определить: R -? U-? U1-? U2 -? U3 -? U4 -? I1 -? I2 -? I3 -? I4 -?
Решение:
Определим эквивалентное сопротивление цепи методом свёртывания.
Если между сопротивлениями нет узла, то они соединены последовательно, а между двумя узлами имеется параллельное соединение сопротивлений.
R1 и R2 соединены последовательно, R12 и R3 параллельно, а R123 и R4 последовательно.
R12 = R1 + R2 = 10 + 50 = 60 Ом.
R = R123 + R4 = 24 + 6 = 30 Ом.
Определим токи и напряжения на всех резисторах.
Ток и напряжение для всей цепи:
Рис. 1.9. получается свёртыванием рис. 1.8. На рисунке 1.10 покажем токи и напряжения на резисторах R123 и R4:
U3 = I·R123 = 5 · 24 = 120 В. U4 = I4·R4 = 5 · 6 = 30 В.
Решение проверим, используя 2-ой закон Кирхгофа.
U = U3 + U4 = 120 + 30 = 150 В.
Резистор R123 получается от параллельного соединения резисторов R12 и R3.
Из рис. 1.11. имеем:
Решение проверим, используя 1-ый закон Кирхгофа.
I = I1 + I2 = 2 + 3 = 5 A.
Резистор R12 получается от последовательного соединения резисторов
R1 и R2. Из рис. 1.12. имеем:
U1 = I1·R1 = 2 · 10 = 20 В. U2 = I2·R2 = 2 · 50 = 100 В.
Решение проверим, используя 2 — ой закон Кирхгофа.
U3 = U1 + U2 ; 120 = 20 + 100 = 120;
Баланс мощностей: Р = Р1 + Р2 + Р3 + Р4 ; Р = U· I;
150 · 5 =20 · 2 + 100 · 2 + 120 · 3 + 30 · 5 = 40 + 200 + 360 + 150 = 750;
750 = 750;
Ответ представим в виде таблицы:
| R1 | R2 | R3 | R4 | вся цепь | |
| R (Ом) | |||||
| U (В) | |||||
| I (А) | |||||
| Р (Вт) |
Задача 1.1. Цепь постоянного тока со смешанным соединением состоит из четырёх резисторов. Дана одна из величин U,I или Р. Определить эквивалент- ное сопротивление цепи, токи и напряжения на всех резисторах и для всей цепи. Решение проверить, используя баланс мощностей.
(Указание: номера токов, напряжений и мощностей должны совпадать номерами сопротивлений.) Данные выбрать из таблицы 1.1.
Таблица 1.1.
| № варианта | № рис. | R1 Ом | R2 Ом | R3 Ом | R4 Ом | U, I, P | |
| 1.13 1.14 1.15 | U =120 В I = 5 A P = 1152 Вт | ||||||
| 1.16 1.17 1.18 | U =160 В I = 10 A P = 576 Вт | ||||||
| 1.19 1.20 1.21 | U =12 В I = 6 A P = 450 Вт | ||||||
| 1.22 1.13 1.14 | U =96 В I = 15 A P = 250 Вт | ||||||
| 1.15 1.16 1.17 | U =48 В I = 15 A P = 375 Вт | ||||||
| 1.18 1.19 1.20 | U =60 В I = 6 A P = 720 Вт | ||||||
| 1.21 1.22 1.13 | U =60 В I = 3 A P = 937,5 Вт | ||||||
| 1.14 1.15 1.16 | U =60 В I = 12 A P = 1440 Вт | ||||||
| 1.17 1.18 1.19 | U =90 В I = 24A P = 1440 Вт | ||||||
| 1.20 1.21 1.22 | U =100 В I = 5 A P = 320 Вт | ||||||
| 1.13 1.14 1.15 | U = 48 В I = 9 A P = 172 Вт | ||||||
| 1.16 1.17 1.18 | U = 120B I = 10A U = 96 B | ||||||
| 1.19 1.20 1.21 | U = 90 B I = 9 A U = 90 B | ||||||
| 1.22 1.13 1.14 | U = 78 B Р = 720 Вт U = 144 Вт | ||||||
| 1.15 1.16 1.17 | U = 72 Вт I = 12 А U = 90 B | ||||||
| 1.18 1.19 1.20 | I = 48 A I = 9 A U = 117В | ||||||
| 1.21 1.22 | I = 15A I = 9A | ||||||
Пример 1.2.Дана электрическая цепь со смешанным соединением резисторов. Номера токов, напряжений и мощностей совпадают с номером резистора.
Определить:
1.эквивалентное сопротивление электрической цепи;
2.используя известную величину тока, напряжения или мощности вычис-
лить токи и напряжения, по закону Ома для участка цепи, на всех резис-
торах и для всей цепи; законы Кирхгофа использовать для проверки;
3.проверить решение методом баланса мощностей.
| Рис. | R1 Ом | R2 Ом | R3 Ом | R4 Ом | R5 Ом | R6 Ом | Дополнительный параметр |
| 1.23 | Р = 250 Вт |
Решение:
Для определения эквивалентного сопротивления используем метод свёртывания.
R5 и R6 cоединены параллельно, а R4 и R56 последовательно.
R3 и R456 cоединены параллельно, R1 и R2 c R3456 последовательно.
Определим ток и напряжение всей цепи:
Из рис. 1.26 видим, что резисторы R1, R3456, R2 соединены последовательно,
определим напряжения и токи на R1, R3456, R2. На рис.1.27 покажем токи и напряжения.
I = I1 = I2 = I3456 = 5 А.
U1 = I1· R1= 5 · 1 = 5 В. U2 = I2· R2= 5 · 3 = 15 В. U3 = I·R3456 = 5 ·6 = 30 B.
Проверим используя 2-ой закон Кирхгофа.
U = U1 + U3 + U2 ; 50 = 5 + 30 + 15 = 50
Рассмотрим резистор R3456. Выделим из рис. 1.25. часть с резисторами R3 и R456, получим рис.1.28. Ток I456 равен I4 т.е. I456 = I4. Определим токи I4 и I1. Из рис. 1.28 видно: напряжение U456 = U3 т.к. R3 и R456 соединены параллельно. Токи в ветвях:
Проверим, используя 1-ый закон Кирхгофа.
I1 = I3 + I4; 5 = 2 + 3 = 5.
Отделим из рис.1.24 резисторы R4 и R56. Эти резисторы соединены последовательно. На рис. 1.29 покажем напряжения U4 и U56 = U5 = U6.
Ток I56 = I4 = 3А.
U4 = I4· R4 = 3 · 6 = 18 В. U5 = U6 = U56 = I4· R56 = 3 · 4 = 12 В.
Проверим используя 2-ой закон Кирхгофа.
U456 = U3 = U4 + U56 ; 30 = 18 + 12 = 30.
Из рис.1.23 видим, что резисторы R5 = R6 соединены параллельно. На рис.1.30 покажем токи I5 и I6. Определим токи на резисторах R5 и R6 .
Проверим используя 1-ый закон Кирхгофа: I4= I5 + I6; 3 = 2 + 1.
Из рис.1.30 определим напряжения на R1 и R2: I = I1 = I2 = I3456 = 5 А.
U1 = I1· R1= 5 · 1 = 5 В. U2 = I2· R2= 5 · 3 = 15 В.
Решение проверим используя баланс мощностей:
P·I = Ʃ U·I; U·I = U1·I1 + U2·I2 + U3·I3 + U4·I4 + U5·I5 + U6·I6;
50·5 = 5·5 + 15·5 + 30·2 + 18·3 + 12·2 + 12·2 = 250.
250 = 250
Таблица ответов:
| R1 Ом | R2 Ом | R3 Ом | R4 Ом | R5 Ом | R6 Ом | Вся Цепь | |
| R Ом | |||||||
| U В | |||||||
| I А | |||||||
| P Вт |
Задача 1.2.Дана электрическая цепь со смешанным соединением резисто- ров. Номера токов, напряжений и мощностей совпадают с номером резистора. Данные выбрать из таблицы 1.2.
Определить используя заданную величину U,I, или Р:
1.Эквивалентное сопротивление электрической цепи.
2.Используя известную величину тока, напряжения или мощности вычислить токи и напряжения, по закону Ома для участка цепи, на всех резисторах и для всей цепи. Законы Кирхгофа использовать для проверки.
3. Решение проверить методом баланса мощностей.
Таблица 1.2.
| № варианта | № рис. | R1 Ом | R2 Ом | R3 Ом | R4 Ом | R5 Ом | U, I, P | |
| 1.31 1.32 1.33 | U = 24 В. U = 60 В. U = 24 В. | |||||||
| 1.34 1.35 1.36 | U = 24 В. U = 40 В. U = 90 В. | |||||||
| 1.37 1.38 1.39 | U = 20 В. U = 50 В. U = 40 В. | |||||||
| 1.40 1.31 1.32 | U = 40 В. I = 9 А. I = 12 А. | |||||||
| 1.33 1.34 1.35 | I = 12 А. I = 6 А. I = 15 А. | |||||||
| 1.36 1.37 1.38 | I = 20 А. I = 18 А. I = 8 А. | |||||||
| 1.39 1.40 1.31 | I = 15 А. I = 12 A. P = 288 Вт. | |||||||
| 1.32 1.33 1.34 | P = 320 Вт. P = 108 Вт. P = 1200 Вт. | |||||||
| 1.35 1.36 1.37 | P = 864 Вт. P = 324 Вт. P = 364 Вт. | |||||||
| 1.38 1.39 1.40 | P = 648 Вт. P = 150 Вт. P = 2400 Вт. | |||||||
| 1.31 1.32 1.33 | U = 48 В. U = 48 В. U = 45 B. | |||||||
| 1.34 1.35 1.36 | U = 60 B. U = 56 B. I = 4 A. | |||||||
| 1.37 1.38 1.39 | Р = 108 Вт U = 48 B. U = 60 B. | |||||||
| 1.40 1.31 1.32 | U = 40 B. I = 18 А I = 10 А | |||||||
| 1.33 1.34 1.35 | I = 8 A. U = 60 B. I = 30 A. | |||||||
| 1.36 1.37 1.38 | I = 4 A. U = 54 B. I = 18 A. | |||||||
| 1.39 1.40 | I = 6 A. I = 10 A. | |||||||
Методика расчета смешанного соединения резисторов
R1 = 0ОмR2 = 120Oм
R3 =120Oм
R4 = 10 Oм
R5 =150Oм
R6 =130Oм
R7 =170Oм
R0 =1,3Ом
Е =68В
I1-7 = ?, Rэкв =?
U1-7 = ?Pmax=?
Определить потенциал точки С.
Схема цепи.
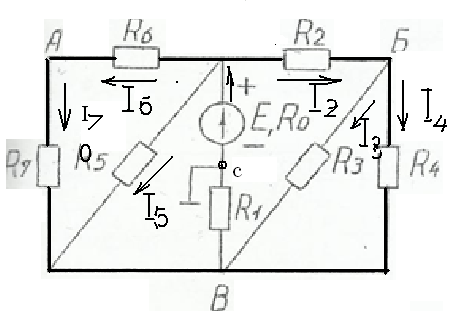
Решение
Эквивалентное сопротивление цепи определяется методом «свертывания» схемы.
При последовательном сопротивлении общее сопротивление равно сумме сопротивлений:
R6-7 = R6+ R7 = 130 + 170 =300 Ом.
При параллельном соединении резисторов общее определится:
При параллельном соединении резисторов общее определится:
При последовательном сопротивлении общее сопротивление равно сумме сопротивлений:
R2-4= R2+ R3-4 = 140 + 60 =200 Ом.
После этих преобразований схема соединения резисторов примет вид:
Эквивалентное сопротивление определится:
Rэкв=
Ток цепи или ток источника определится по закону Ома:
I = 1 А
Падение напряжения на внешнем участке цепи:
U= I * Rэкв = 1 * 66,7 = 66,7 В
U = U 5=U 5-7= U 6-7= U 2-4 = 66,7 В
Ток в резисторах:
I5 =0,45А
I6-7 =I6= I7 = 0,22А
I2-4 =I2= I3-4 = 0,33А
Падение напряжения на участках цепи:
U6 = I6 * R6 = 0,22 * 130 = 28,6 В
U7 = U6-7 — U6 = 66,7 – 28,6=38,1В
U2 = I2 * R2 = 0,33 * 120 = 39,6 В
U3-4= U3= U4= U2-4 — U2= 66,7 – 39,6=27,1В
Мощность на резисторе с большим сопротивлением определится:
Р7 = I2 * R7 =
Потенциал точки А:
φА больше φс =0 на падение напряжения на резисторе R6так как ток течет от большего потенциала к меньшему:
φА=φс +U6 =0 +28,6 = 28,6В
1.4. Эквивалентное преобразование схемы при смешанном соединении резисторов
Смешанным соединением называют сочетание последовательного и параллельного соединений резисторов. Большое разнообразие этих соединений не позволяет вывести общую формулу для определения эквивалентного сопротивления цепи. Поэтому в каждом конкретном случае правило расчета свое.
При смешанном соединении элементов для эквивалентного преобразования пользуются методом последовательных эквивалентных преобразований, т.е. последовательно преобразуются участки цепи, имеющие простое (только последовательное, или только параллельное) соединение элементов.
Поясним это на конкретном примере расчета электрической цепи (рис.1.3).
В схеме на рис.1.3а простое соединение имеют резисторы только резисторы R3 и R4 — они соединены последовательно.
На первом этапе – преобразуем участок цепи с резисторами R3 и R4. Поскольку они соединены последовательно, то их эквивалентное сопротивление R34определяется из соотношения R34=R3+R4. В результате эквивалентного преобразования этих резисторов получаем схему см. рис.1.3б.
Рис. 1.3. Эквивалентные преобразования при смешанном соединении
На втором этапе, из анализа схемы на рис.1.3б следует, что простое соединение имеют резисторы R2 и R34— они соединены параллельно. Их заменяем одним эквивалентным резистором R234= R34R2/(R2+R34). В результате преобразования исходной схемы на втором этапе получаем схему см. рис.1.3в.
На третьем этапе, из анализа схемы на рис.1.3в, следует, что простое соединение имеют резисторы R1 и R234—они соединены последовательно. Их заменяем одним эквивалентным резистором R1234=R1+R234=R1+ R2(R3+R4)/(R2+R3+R4) = Rэкв.
В результате преобразования исходной схемы на третьем этапе получаем схему см. рис.1.3г. Она явна проще исходной схемы, поскольку состоит из одного элемента.
1.4. Эквивалентное преобразование резисторов, соединенных треугольником в звезду (и наоборот)
В сложных электрических цепях часто встречаются ветви, соединенные треугольником (рис.1.4а) или звездой (рис.1.4б).
Соединения такого вида очень распространены в трехфазных цепях, при этом часто возникает необходимость перехода от одного вида соединения к другому, но эквивалентному. Кроме того, такое преобразование часто применяется для упрощения схемы.

Рис.1.4. Схемное соединение резисторов треугольником (а) и звездой (б)
Практический интерес представляют соотношения сопротивлений резисторов этих цепей при их эквивалентных преобразованиях. Условие эквивалентности преобразования этих цепей заключается в том, что при одинаковых напряжениях между узлами 1, 2 и 3 , втекающие (вытекающие) извне токи I1, I2, I3в этих узлах также одинаковы, т.е. должны быть одинаковыми сопротивления между этими узлами.
Рассмотрим эквивалентное преобразование звезды в треугольник и треугольника в звезду на схемах приведенных на рис.1.5.

а) б)
Рис. 1.5. Схема для расчета правила эквивалентного преобразование звезды в треугольник и треугольника в звезду
Для того чтобы преобразование было эквивалентным, достаточно равенства сопротивлений между точками 1 – 2, 2 – 3 и 3 – 1 в обеих схемах. Запишем систему уравнений для сопротивлений между указанными точками для обеих схем.
Для точек 1 – 2:
| (1.17) |
Для точек 2 – 3:
| (1.18) |
Для точек 3 – 1:
| (1.19) |
Если решить эту систему относительно сопротивлений R12, R23 и R31 получим формулы преобразования звезды в треугольник:
| (1.20) |
| (1.21) |
| (1.22) |
Если решить систему исходных уравнений относительно сопротивлений R1, R2 и R3 получим формулы преобразования треугольника в звезду:
| (1.23) |
| (1.24) |
. | (1.25) |
Содержание:
Широкое распространение в радиоэлектронных и электрических цепях получили резисторы, представляющие собой элементы с переменным или постоянным сопротивлением. С их помощью осуществляются различные действия, связанные с преобразованиями силы тока и напряжения, влияющих на работу всей схемы. Поэтому в большинстве случаев резисторы выполняют регулировочные функции. В большинстве цепей применяется последовательное и параллельное соединение резисторов. При необходимости они используются в комбинированном виде. Каждый вид того или иного соединения дает различные показатели сопротивления, в связи с чем для каждого из них разработана собственная методика расчетов. Благодаря стабильным и точным параметрам резисторов, обеспечивается устойчивая и надежная эксплуатация схем с различными типами соединений. Последовательное соединениеПоследовательным называется соединение двух и более резисторов, при котором конец первого элемента соединяется с началом второго и так далее. В результате получается последовательная цепочка, где по всем ее составляющим проходит одинаковый ток. В качестве примера можно взять последовательную цепь, состоящую из трех резисторов R1, R2 и R3. Сопротивление в источнике тока принимается с нулевым значением. В соответствии со вторым законом Кирхгофа получается следующая формула: E = IR1 + IR2 + IR3 = I(R1 + R2 + R3) = IRэк.
В этой формуле значение эквивалентного сопротивления последовательной цепи составит сумму сопротивлений всех резисторов, имеющихся в данной цепи: Rэк = R1 + R2 + R3. По закону Ома напряжение при последовательном соединении на отдельных участках будет иметь следующее значение, поскольку E = U: U1=IR1; U2 = IR2, U3 = IRз, то есть U = U1 + U2 +U3. Данные формулы показывают, что в резисторах, последовательно соединенных между собой, напряжения распределяются пропорционально их сопротивлениям. То есть, чем выше сопротивление любого из резисторов, тем больше напряжение, приложенное к нему. В виде формулы — это утверждение будет выглядеть следующим образом: U1 : U2 : U3 = R1 : R2 : R3. При последовательном соединении сопротивление R1 нескольких резисторов в количестве n, будет одинаковым. Следовательно, значение эквивалентного сопротивления цепи будет в n раз превышать сопротивление каждого из них: Rэк = nR1. Следовательно напряжение на каждом отдельном резисторе будет в n раз меньше, чем общее напряжение цепи: U1 = U/n. Таким образом, изменение сопротивления любого из резисторов при последовательном соединении, приводит к изменению напряжения на других резисторах, находящихся с ним в одной цепи. Поэтому, если электрическая цепь обрывается или выключается в одной из нагрузок, в других нагрузках также прекращается течение тока. Из-за этого последовательное соединение в электрических схемах используется довольно редко. Параллельное соединениеГораздо чаще в электрических цепях применяется параллельное соединение резисторов, отличающихся наличием общих точек, где соединяются начала и концы каждого элемента. Данный вид соединения характеризуется собственными физическими свойствами.
Основными из них являются следующие:
Смешанное соединениеВ радиоэлектронных и электрических схемах широко применяется последовательное, параллельное и смешанное соединение резисторов, наиболее подходящее на том или ином конкретном участке. Первые два соединения были рассмотрены выше, осталось лишь отметить характерные особенности комбинированного варианта.
В смешанных схемах нашли отражение свойства, присущие последовательному и параллельному соединениям. Частично выполняется последовательное подключение резисторов, а другая группа элементов подключается параллельно. Резисторы R1 и R2, изображенные на схеме, включаются последовательно, а резисторы R1, R2 и R3 соединены параллельно. Существуют определенные трудности при расчетах сопротивления для таких цепей. Для получения правильных результатов используется специальная методика, основой которой является преобразование сложных цепей в более простые в течение нескольких этапов. Например, для одной группы резисторов применяется формула последовательного соединения, позволяющая получить предварительный результат. Точно также для другой группы элементов используется формула параллельного соединения. Постепенно складывая полученные данные можно получить точное общее значение сопротивления смешанной цепи. |




 .
. .
. .
. .
. .
. .
. .
. .
.

