явление электромагнитной индукции, магнитный поток, закон электромагнитной индукции Фарадея, правило Ленца

9.5. Индукционный ток

9.5.1. Тепловое действие индукционного тока

Возникновение ЭДС приводит к появлению в проводящем контуре индукционного тока , сила которого определяется по формуле

I i = | ℰ i | R ,

где ℰ i — ЭДС индукции, возникающая в контуре; R — сопротивление контура.

При протекании индукционного тока в контуре выделяется теплота , количество которой определяется одним из выражений:

Q i = I i 2 R t , Q i = ℰ i 2 t R , Q i = I i | ℰ i | t ,

где I i — сила индукционного тока в контуре; R — сопротивление контура; t — время; ℰ i — ЭДС индукции, возникающая в контуре.

Мощность индукционного тока вычисляется по одной из формул:

P i = I i 2 R , P i = ℰ i 2 R , P i = I i | ℰ i | ,

где I i — сила индукционного тока в контуре; R — сопротивление контура; ℰ i — ЭДС индукции, возникающая в контуре.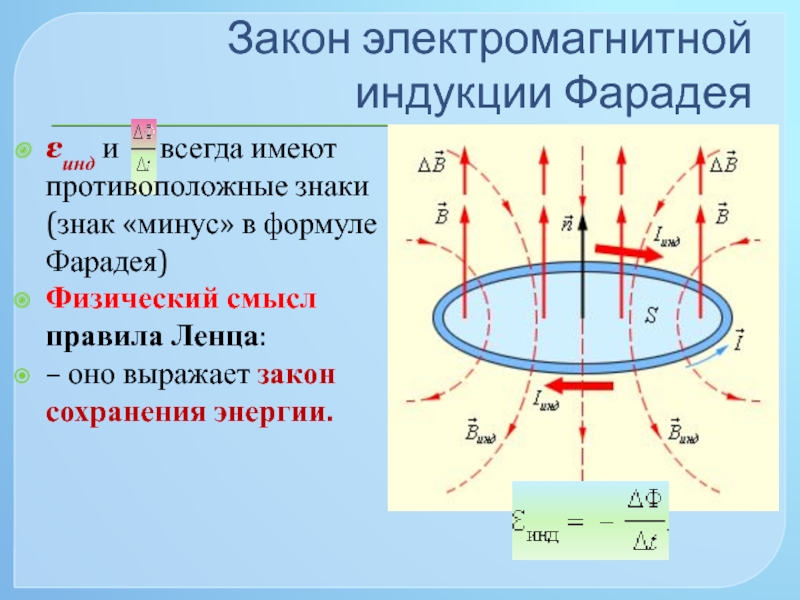

При протекании индукционного тока в проводящем контуре через площадь поперечного сечения проводника переносится заряд , величина которого вычисляется по формуле

q i = I i ∆t ,

где I i — сила индукционного тока в контуре; Δt — интервал времени, в течение которого по контуру течет индукционный ток.

Пример 21. Кольцо, изготовленное из проволоки с удельным сопротивлением 50,0 ⋅ 10 −10 Ом ⋅ м, находится в однородном магнитном поле с индукцией 250 мТл. Длина проволоки равна 1,57 м, а площадь ее поперечного сечения составляет 0,100 мм 2 . Какой максимальный заряд пройдет по кольцу при выключении поля?

Решение . Появление ЭДС индукции в кольце вызвано изменением потока вектора индукции, пронизывающего плоскость кольца, при выключении магнитного поля.

Поток индукции магнитного поля через площадь кольца определяется формулами:

• до выключения магнитного поля

Ф 1 = B 1 S  cos α,

где B 1 — первоначальное значение модуля индукции магнитного поля, B 1 = 250 мТл; S — площадь кольца; α — угол между направлениями вектора магнитной индукции и вектора нормали (перпендикуляра) к плоскости кольца;

• после выключения магнитного поля

Ф 2 = B 2 S  cos α = 0,

где B 2 — значение модуля индукции после выключения магнитного поля, B 2 = 0.

∆Ф = Ф 2 − Ф 1 = −Ф 1 ,

или, с учетом явного вида Ф 1 ,

∆Ф = −B 1 S  cos α.

Среднее значение ЭДС индукции, возникающей в кольце при выключении поля,

| ℰ i | = | Δ Ф Δ t | = | − B 1 S cos α Δ t | = B 1 S | cos α | Δ t ,

где ∆t — интервал времени, за который происходит выключение поля.

Наличие ЭДС индукции приводит к появлению индукционного тока; сила индукционного тока определяется законом Ома:

I i = | ℰ i | R = B 1 S | cos α | R Δ t ,

где R — сопротивление кольца.

При протекании индукционного тока по кольцу переносится индукционный заряд

q i = I i Δ t = B 1 S | cos α | R .

Максимальному значению заряда соответствует максимальное значение функции косинус (cos α = 1):

q i max = I i Δ t = B 1 S R .

Полученная формула определяет максимальное значение заряда, который пройдет по кольцу при выключении поля.

Однако для расчета заряда необходимо получить выражения, которые позволят найти площадь кольца и его сопротивление.

Площадь кольца — площадь круга радиусом r , периметр которого определяется формулой длины окружности и совпадает с длиной проволоки, из которой изготовлено кольцо:

l = 2πr ,

где l — длина проволоки, l = 1,57 м.

Отсюда следует, что радиус кольца определяется отношением

r = l 2 π ,

а его площадь —

S = π r 2 = π l 2 4 π 2 = l 2 4 π .

Сопротивление кольца задается формулой

R = ρ l S 0 ,

где ρ — удельное сопротивление материала проволоки, ρ = 50,0 × × 10 −10 Ом ⋅ м; S 0 — площадь поперечного сечения проволоки, S 0 = = 0,100 мм 2 .

Подставим полученные выражения для площади кольца и его сопротивления в формулу, определяющую искомый заряд:

q i max = B 1 l 2 S 0 4 π ρ l = B 1 l S 0 4 π ρ .

Вычислим:

q i max = 250 ⋅ 10 − 3 ⋅ 1,57 ⋅ 0,100 ⋅ 10 − 6 4 ⋅ 3,14 ⋅ 50,0 ⋅ 10 − 10 = 0,625 Кл = 625 мКл.

При выключении поля по кольцу проходит заряд, равный 625 мКл.

Пример 22. Контур площадью 2,0 м 2 и сопротивлением 15 мОм находится в однородном магнитном поле, индукция которого возрастает на 0,30 мТл в секунду. Найти максимально возможную мощность индукционного тока в контуре.

Решение . Появление ЭДС индукции в контуре вызвано изменением потока вектора индукции, пронизывающего плоскость контура, при изменении индукции магнитного поля с течением времени.

Изменение потока вектора индукции магнитного поля определяется разностью

∆Ф = ∆BS  cos α,

где ∆B — изменение модуля индукции магнитного поля за выбранный интервал времени; S — площадь, ограниченная контуром, S = 2,0 м 2 ; α — угол между направлениями вектора магнитной индукции и вектора нормали (перпендикуляра) к плоскости контура.

Среднее значение ЭДС индукции, возникающей в контуре, при изменении индукции магнитного поля:

| ℰ i | = | Δ Ф Δ t | = | Δ B S cos α Δ t | = Δ B S | cos α | Δ t ,

где ∆B /∆t — скорость изменения модуля вектора индукции магнитного поля с течением времени, ∆B /∆t = 0,30 мТл/с.

Появление ЭДС индукции приводит к появлению индукционного тока; сила индукционного тока определяется законом Ома:

I i = | ℰ i | R = Δ B S | cos α | R Δ t ,

где R — сопротивление контура.

Мощность индукционного тока

P i = I i 2 R = (Δ B Δ t) 2 S 2 R cos 2 α R 2 = (Δ B Δ t) 2 S 2 cos 2 α R .

Максимальному значению мощности индукционного тока соответствует максимальное значение функции косинус (cos α = 1):

P i max = (Δ B Δ t) 2 S 2 R .

Вычислим:

P i max = (0,30 ⋅ 10 − 3) 2 (2,0) 2 15 ⋅ 10 − 3 = 24 ⋅ 10 − 6 Вт = 24 мкВт.

Максимальная мощность индукционного тока в данном контуре равна 24 мкВт.

Взаимосвязь электрических и магнитных полей замечена очень давно. Данную связь еще в 19 веке обнаружил английский ученый-физик Фарадей и дал ему название . Она появляется в тот момент, когда магнитный поток пронизывает поверхность замкнутого контура. После того как происходит изменение магнитного потока в течение определенного времени, в этом контуре наблюдается появление электрического тока.

Взаимосвязь электромагнитной индукции и магнитного потока

Суть магнитного потока отображается известной формулой: Ф = BS cos α. В ней Ф является магнитным потоком, S — поверхность контура (площадь), В — вектор магнитной индукции. Угол α образуется за счет направления вектора магнитной индукции и нормали к поверхности контура. Отсюда следует, что максимального порога магнитный поток достигнет при cos α = 1, а минимального — при cos α = 0.

Во втором варианте вектор В будет перпендикулярен к нормали. Получается, что линии потока не пересекают контур, а лишь скользят по его плоскости. Следовательно, определять характеристики будут линии вектора В, пересекающие поверхность контура. Для расчета в качестве единицы измерения используется вебер: 1 вб = 1в х 1с (вольт-секунда). Еще одной, более мелкой единицей измерения служит максвелл (мкс).

Он составляет: 1 вб = 108 мкс, то есть 1 мкс = 10-8 вб.

Для исследования Фарадеем были использованы две проволочные спирали, изолированные между собой и размещенные на катушке из дерева. Одна из них соединялась с источником энергии, а другая — с гальванометром, предназначенным для регистрации малых токов. В тот момент, когда цепь первоначальной спирали замыкалась и размыкалась, в другой цепи стрелка измерительного устройства отклонялась.

Проведение исследований явления индукции

В первой серии опытов Майкл Фарадей вставлял намагниченный металлический брусок в катушку, подключенную к току, а затем вынимал его наружу (рис. 1, 2).

1 2

В случае помещения магнита в катушку, подключенную к измерительному прибору, в цепи начинает протекать индукционный ток. Если магнитный брусок удаляется из катушки, индукционный ток все равно появляется, но его направление становится уже противоположным. Следовательно, параметры индукционного тока будут изменены по направлению движения бруска и в зависимости от полюса, которым он помещается в катушку.

На силу тока оказывает влияние быстрота перемещения магнита.

Во второй серии опытов подтверждается явление, при котором изменяющийся ток в одной катушке, вызывает индукционный ток в другой катушке (рис. 3, 4, 5). Это происходит в моменты замыкания и размыкания цепи. От того, замыкается или размыкается электрическая цепь, будет зависеть и направление тока. Кроме того, эти действия есть ни что иное, как способы изменения магнитного потока. При замыкании цепи он будет увеличиваться, а при размыкании — уменьшаться, одновременно пронизывая первую катушку.

3 4

5

В результате опытов было установлено, что возникновение электрического тока внутри замкнутого проводящего контура возможно лишь в том случае, когда они помещаются в переменное магнитное поле. При этом, поток может изменяться во времени любыми способами.

Электрический ток, появляющийся под действием электромагнитной индукции, получил название индукционного, хотя это и не будет током в общепринятом понимании. Когда замкнутый контур оказывается в магнитном поле, происходит генерация ЭДС с точным значением, а не тока, зависящего от разных сопротивлений.

Данное явление получило название ЭДС индукции, которую отражает формула: Еинд = — ∆Ф/∆t. Ее значение совпадает с быстротой изменений магнитного потока, пронизывающего поверхность замкнутого контура, взятого с отрицательным значением. Минус, присутствующий в данном выражении, является отражением правила Ленца.

Правило Ленца в отношении магнитного потока

Известное правило было выведено после проведения цикла исследований в 30-х годах 19 века. Оно сформулировано в следующем виде:

Направление индукционного тока, возбуждаемого в замкнутом контуре изменяющимся магнитным потоком, оказывает влияние на создаваемое им магнитное поле таким образом, что оно в свою очередь создает препятствие магнитному потоку, вызывающему появление индукционного тока.

Когда магнитный поток увеличивается, то есть становится Ф > 0, а ЭДС индукции снижается и становится Еинд

Если поток снижается, то наступает обратный процесс, когда Ф 0, то есть действие магнитного поля индукционного тока, происходит увеличение магнитного потока, проходящего через контур.

Физический смысл правила Ленца заключается в отражении закона сохранения энергии, когда при уменьшении одной величины, другая увеличивается, и, наоборот, при увеличении одной величины другая будет уменьшаться. Различные факторы влияют и на ЭДС индукции. При вводе в катушку поочередно сильного и слабого магнита, прибор соответственно будет показывать в первом случае более высокое, а во втором — более низкое значение. То же самое происходит, когда изменяется скорость движения магнита.

На представленном рисунке видно, как определяется направление индукционного тока с применением правила Ленца. Синий цвет соответствует силовым линиям магнитных полей индукционного тока и постоянного магнита. Они расположены в направлении полюсов от севера к югу, которые имеются в каждом магните.

Изменяющийся магнитный поток приводит к возникновению индукционного электрического тока, направление которого вызывает противодействие со стороны его магнитного поля, препятствующее изменениям магнитного потока. В связи с этим, силовые линии магнитного поля катушки направлены в сторону, противоположную силовым линиям постоянного магнита, поскольку его движение происходит в сторону этой катушки.

Для определения направления тока используется с правой резьбой. Он должен ввинчиваться таким образом, чтобы направление его поступательного движения совпадало с направлением индукционных линий катушки. В этом случае направления индукционного тока и вращения рукоятки буравчика будут совпадать.

На рисунке показано направление индукционного тока,возникающего в короткозамкнутой проволочной катушке,когда относительно нее перемещают

магнит.Отметьте,какие из следующих утверждений правильные,а какие- неправильные.
А.Магнит и катушка притягиваются друг к другу.
Б. Внутри катушки магнитное поле индукционного тока направленно вверх.
В. Внутри катушки линии магнитной индукции поля магнита направлены вверх.
Г. Магнит удаляют от катушки.

1. Первый закон Ньютона?

2. Какие системы отсчета являются инерциальными и неинерциальными? Приведите примеры.
3. В чем состоит свойство тел, называемое инертностью? Какой величиной характеризуется инертность?
4. Какова связь между массами тел и модулями ускорений, которые они получают при взаимодействии?
5. Что такое сила и чем она характеризуется?
6. Формулировка 2 закона Ньютона? Какова его математическая запись?
7. Как формулируется 2 закон Ньютона в импульсной форме? Его математическая запись?
8. Что такое 1 Ньютон?
9. Как движется тело, если к нему приложена сила постоянная по модулю и направлению? Как направлено ускорение, вызванное действующей на него силой?
10. Как определяется равнодействующая сил?
11. Как формулируется и записывается 3 закон Ньютона?
12. Как направлены ускорения, взаимодействующих между собой тел?
13. Приведите примеры проявления 3 закона Ньютона.
14. Каковы границы применимости всех законов Ньютона?
15. Почему мы можем считать Землю инерциальной системой отсчета, если она двигается с центростремительным ускорением?
16. Что такое деформация, какие виды деформации вы знаете?
17. Какая сила называется силой упругости? Какова природа этой силы?
18. Каковы особенности силы упругости?
19. Как направлена сила упругости (сила реакции опоры, сила натяжения нити?)
20. Как формулируется и записывается закон Гука? Каковы его границы применимости? Постройте график, иллюстрирующий закон Гука.
21. Как формулируется и записывается закон Всемирного тяготения, когда он применим?
22. Опишите опыты, по определению значения гравитационной постоянной?
23. Чему равна гравитационная постоянная, каков ее физический смысл?
24. Зависит ли работа силы тяготения от формы траектории? Чему равна работа силы тяжести по замкнутому контуру?
25. Зависит ли работа силы упругости от формы траектории?
26. Что вы знаете о силе тяжести?
27. Как вычисляется ускорение свободного падения на Земле и других планетах?
28. Что такое первая космическая скорость? Как ее вычисляют?
29. Что называют свободным падением? Зависит ли ускорение свободного падения от массы тела?
30. Опишите опыт Галилео Галилея, доказывающий, что все тела в вакууме падают с одинаковым ускорением.
31. Какая сила называется силой трения? Виды сил трения?
32. Как вычисляют силу трения скольжения и качения?
33. Когда возникает сила трения покоя? Чему она равна?
34. Зависит ли сила трения скольжения от площади соприкасающихся поверхностей?
35. От каких параметров зависит сила трения скольжения?
36. От чего зависит сила сопротивления движению тела в жидкостях и газах?
37. Что называют весом тела? В чем заключается различие между весом тела и силой тяжести, действующей на тело?
38. В каком случае вес тела численно равен модулю силы тяжести?
39. Что такое невесомость? Что такое перегрузка?
40. Как вычислить вес тела при его ускоренном движении? Изменяется ли вес тела, если оно движется по неподвижной горизонтальной плоскости с ускорением?
41. как изменяется вес тела при его движении по выпуклой и вогнутой части окружности?
42. Каков алгоритм решения задач при движении тела под действием нескольких сил?
43. Какая сила называется Силой Архимеда или выталкивающей силой? От каких параметров зависит эта сила?
44. По каким формулам можно вычислить силу Архимеда?
45. При каких условиях тело, находящееся в жидкости плавает, тонет, всплывает?
46. Как зависит глубина погружения в жидкость плавающего тела от его плотности?
47. Почему воздушные шары наполняют водородом, гелием или горячим воздухом?
48. Объясните влияние вращения Земли вокруг своей оси на значение ускорения свободного падения.
49. Как изменяется значение силы тяжести при: а) удалении тела от поверхности Земли, Б) при движении тела вдоль меридиана, параллели

электрической цепи?

3. Каков физический смысл ЭДС? Дать определение вольту.

4. Соединить на короткое время вольтметри источником электрической энергии, соблюдая полярность. Сравнить его показания с вычислением по результатам опыта.

5. От чего зависит напряжение на зажимах источников тока?

6. Пользуясь результатами измерений, определить напряжение на внешней цепи (если работа выполнена I методом), сопротивление внешней цепи (если работа выполнена II методом). Свитый в катушку проводник замыкается на гальванометре (рис. 3.19). Если вдвигать в катушку постоянный магнит, то гальванометр покажет наличие тока в течение всего промежутка времени, пока магнит перемещается относительно катушки. При выдергивании магнита из катушки гальванометр показывает наличие тока противоположного направления. Изменения направления тока происходит при изменении вдвигаемого или выдвигаемого полюса магнита.

Аналогичные результаты наблюдались при замене постоянного магнита электромагнитом (катушкой с током). Если обе катушки закрепить неподвижно, но в одной из них менять значение тока, то в этот момент в другой катушке наблюдается индукционный ток.

ЯВЛЕНИЕ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ состоит в возникновении электродвижущей силы (э.д.с.) индукции в проводящем контуре, через который меняется поток вектора магнитной индукции. Если контур является замкнутым, то в нем возникает индукционный ток.

Открытие явления электромагнитной индукции:

1) показало взаимосвязь между электрическим и магнитным полем ;

2) предложило способ получения электрического тока с помощью магнитного поля.

Основные свойства индукционного тока :

1. Индукционный ток возникает всегда, когда происходит изменение сцепленного с контуром потока магнитной индукции.

2. Сила индукционного тока не зависит от способа изменения потока магнитной индукции, а определяется лишь скоростью его изменения.

Опытами Фарадея было установлено, что величина электродвижущей силы индукции пропорциональна скорости изменения магнитного потока, пронизывающего контур проводника (закон электромагнитной индукции Фарадея)

Или , (3.46)

где (dF) – изменение потока в течении времени (dt).МАГНИТНЫМ ПОТОКОМ или ПОТОКОМ МАГНИТНОЙ ИНДУКЦИИ называется величина, которая определяется на основе следующего соотношения: (магнитный поток через поверхность площадью S ): Ф=ВScosα, (3.45), угол a – угол между нормалью к рассматриваемой поверхности и направлением вектора индукции магнитного поля

единица магнитного потока в системе СИ носит название вебер – [Вб=Тл×м 2 ].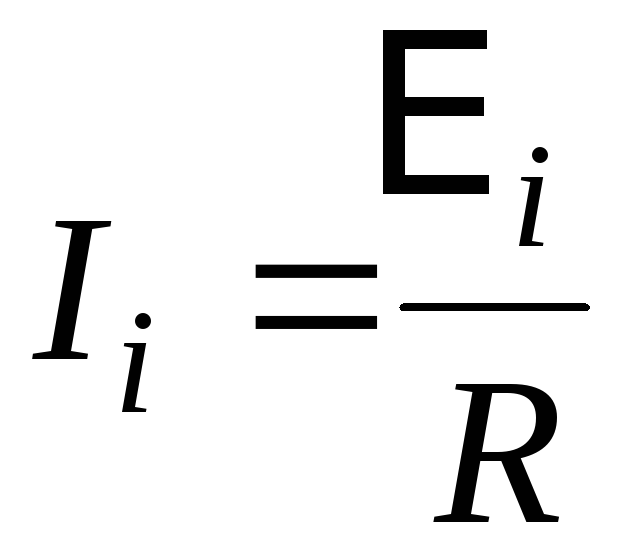

Знак «–» в формуле означает, что э.д.с. индукции вызывает индукционный ток, магнитное поле которого противодействует всякому изменению магнитного потока, т.е. при >0 э.д.с. индукции e И

э.д.с. индукции измеряется в вольтах

Для нахождения направления индукционного тока существует правило Ленца (правило установлено в 1833 г.): индукционный ток имеет такое направление, что создаваемое им магнитное поле стремится компенсировать изменение магнитного потока, вызвавшее этот индукционный ток.

Например, если вдвигать северный полюс магнита в катушку, т. е. увеличивать магнитный поток через его витки, в катушке возникает индукционный ток такого направления, что на ближайшем к магниту конце катушки возникает северный полюс (рис.3.20). Итак, магнитное поле индукционного тока стремится нейтрализовать вызвавшее его изменение магнитного потока.

Не только переменное магнитное поле порождает индукционный ток в замкнутом проводнике, но и при движении замкнутого проводника длиной l в постоянном магнитном поле (В) со скоростью v в проводнике возникает эдс:

a (B Ùv) (3.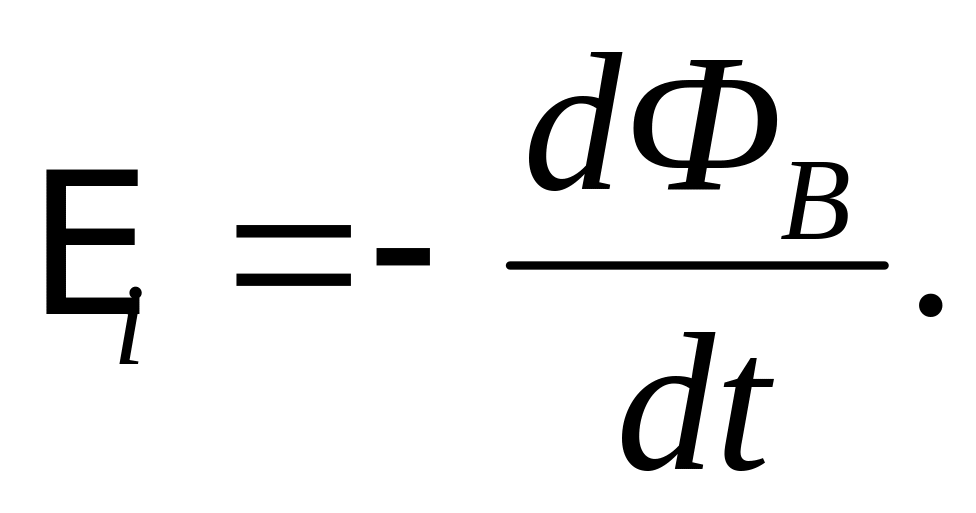 47)

Как вы уже знаете, электродвижущая сила в цепи– это результат действия сторонних сил. При движении проводника в магнитном поле роль сторонних сил выполняет сила Лоренца (которая действует со стороны магнитного поля на движущийся электрический заряд). Под действием этой силы происходит разделение зарядов и на концах проводника возникает разность потенциалов. Э.д.с. индукции в проводнике является работой по перемещению единичных зарядов вдоль проводника.

Направление индукционного тока можно определитьпо правилу правой руки: Вектор В входит в ладонь, отведенный большой палец совпадает с направлением скорости проводника, а 4 пальца укажут направление индукционного тока.

Таким образом переменное магнитное поле вызывает появление индуцированного электрического поля. Оно не потенциально (в отличие от электростатического), т.к. работа по перемещению единичного положительного заряда равна э.д.с. индукции , а не нулю.

Такие поля называются вихревыми. Силовые линии вихревого электрического поля – замкнуты сами на себя, в отличие от линий напряженности электростатического поля.

Э.д.с. индукции возникает не только в соседних проводниках, но и в самом проводнике при изменении магнитного поля тока, идущего по проводнику. Возникновение э.д.с. в каком-либо проводнике при изменении в нем самом силы тока (следовательно, магнитного потока в проводнике) называется самоиндукцией, а ток, индуцируемый в этом проводнике, – током самоиндукции.

Ток в замкнутом контуре создает в окружающем пространстве магнитное поле, напряженность которого пропорциональна силе тока I. Поэтому магнитный поток Ф, пронизывающий контур, пропорционален силе тока в контуре

Ф=L×I, (3.48).

L – коэффициент пропорциональности, который носит название коэффициента самоиндукции, или, просто, индуктивности. Индуктивность зависит от размеров и формы контура, а также от магнитной проницаемости среды, окружающей контур.

В этом смысле индуктивность контура — аналог электрической емкости уединенного проводника, которая также зависит только от формы проводника, его размеров и диэлектрической проницаемости среды.

Единица индуктивности — генри (Гн) : 1Гн — индуктивность такого контура, магнитный поток самоиндукции которого при токе в 1А равен 1Вб (1Гн=1Вб/А=1В·с/А).

Если L=const, то э.д.с. самоиндукции можно представить в следующем виде:

, или , (3.49)

где DI (dI) – изменение тока в цепи, содержащей катушку индуктивности (или контур) L, за время Dt (dt). Знак «–» в этом выражении означает, что э.д.с. самоиндукции препятствует изменению тока (т. е. если ток в замкнутом контуре уменьшается, то э.д.с. самоиндукции приводит к возникновению тока того же направления и наоборот).

Одним из проявлений электромагнитной индукции является возникновение замкнутых индукционных токов в сплошных проводящих средах: металлических телах, растворах электролитов, биологических органах и т. д. Такие токи носят название вихревых токов или токов Фуко. Эти токи возникают при перемещении проводящего тела в магнитном поле и/или при изменении со временем индукции поля, в которое помещены тела. Сила токов Фуко зависит от электрического сопротивления тел, а также от скорости изменения магнитного поля.

Токи Фуко также подчиняются правилу Ленца : их магнитное поле направлено так, чтобы противодействовать изменению магнитного потока, индуцирующему вихревые токи.

Поэтому массивные проводники тормозятся в магнитном поле. В электрических машинах, для того чтобы минимизировать влияние токов Фуко, сердечники трансформаторов и магнитные цепи электрических машин собирают из тонких пластин, изолированных друг от друга специальным лаком или окалиной.

Вихревые токи вызывают сильное нагревание проводников. Джоулево тепло, выделяемое токами Фуко , используется в индукционных металлургических печах для плавки металлов, согласно закону Джоуля-Ленца .

Величина равная скорости изменения магнитного потока. Изменение магнитного потока создает электрическое поле

Электрические и магнитные поля порождаются одними и теми же источниками – электрическими зарядами, поэтому можно предположить, что между этими полями существует определенная связь. Это предположение нашло экспериментальное подтверждение в 1831 г. в опытах выдающегося английского физика М.Фарадея. Он открыл явление электромагнитной индукции.

Явление электромагнитной индукции лежит в основе работы индукционных генераторов электрического тока, на которые приходится вся вырабатываемая в мире электроэнергия.

• Магнитный поток

Замкнутый контур, помещенный в однородное магнитное поле

Количественной характеристикой процесса изменения магнитного поля через замкнутый контур является физическая величина называемая магнитным потоком . Магнитным потоком (Ф) через замкнутый контур площадью (S) называют физическую величину, равную произведению модуля вектора магнитной индукции (В) на площадь контура (S) и на косинус угла между вектором В и нормалью к поверхности : Φ = BS cos α. Единица магнитного потока Ф — вебер (Вб): 1 Вб = 1 Тл · 1 м 2 .

перпендикулярен максимальный.

Если вектор магнитной индукции параллелен площади контура, то магнитный поток равен нулю.

• Закон электромагнитной индукции

Опытным путем был установлен закон электромагнитной индукции: ЭДС индукции в замкнутом контуре равна по модулю скорости изменения магнитного потока через поверхность, ограниченную контуром: Эта формула носит название закона Фарадея .

Классической демонстрацией основного закона электромагнитной индукции является первый опыт Фарадея. В нем, чем быстрее перемещать магнит через витки катушки, тем больше возникает индукционный ток в ней, а значит, и ЭДС индукции.

• Правило Ленца

Зависимость направления индукционного тока от характера изменения магнитного поля через замкнутый контур в 1833 г. опытным путем установил русский физик Э. Х.Ленц. Согласно правилу Ленца , возникающий в замкнутом контуре индукционный ток своим магнитным полем противодействует тому изменению магнитного потока, которым он вызван. Более кратко это правило можно сформулировать следующим образом: индукционный ток направлен так, чтобы препятствовать причине, его вызывающей. Правило Ленца отражает тот экспериментальный факт, что всегда имеют противоположные знаки (знак «минус» в формуле Фарадея ).

Ленцем был сконструирован прибор, представляющий собой два алюминиевых кольца, сплошное и разрезанное, укрепленные на алюминиевой перекладине. Они могли вращаться вокруг оси, как коромысло. При внесении магнита в сплошное кольцо оно начинало «убегать» от магнита, поворачивая соответственно коромысло. При вынесении магнита из кольца оно стремилось «догнать» магнит. При движении же магнита внутри разрезанного кольца никакого движения не происходило. Ленц объяснял опыт тем, что магнитное поле индукционного тока стремилось компенсировать изменение внешнего магнитного потока.

Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.

> Изменение магнитного потока создает электрическое поле

Рассмотрите возникновение электрического поля при изменении магнитного потока : закон электромагнитной индукции Фарадея, уравнение Максвелла, теорема Стокса.

При перемене магнитного потока создается электрическое поле. Это утверждает закон индукции Фарадея:

Задача обучения

• Охарактеризовать связь меняющегося магнитного поля и электрического.

Основные пункты

Термины

• Уравнение Максвелла – набор формул, характеризующих электрические и магнитные поля и их взаимодействие.
• Область вектора – величина рассматриваемого вектора, расположенная перпендикулярно плоскости.
• Теорема Стокса – интегрирование дифференциальных форм на многообразие, упрощающее и обобщающее несколько теорем из векторных вычислений.

Закон индукции Фарадея говорит о том, что при перемене магнитного поля создается электрическое: (ε индуцируется ЭДС, а Φ B – магнитный поток).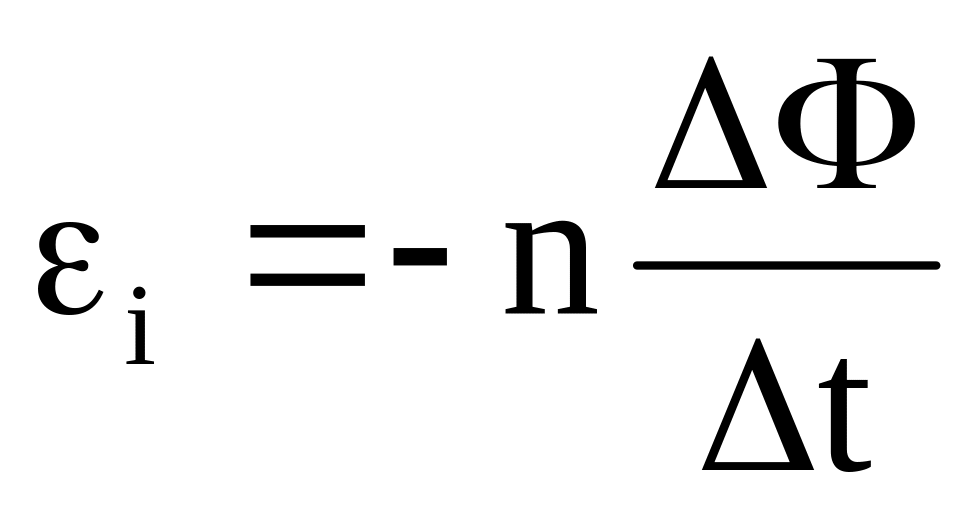 Это главный закон в электромагнетизме, предсказывающий принципы взаимодействия магнитного поля с электрической цепью, что приведет к ЭДС.

В этом эксперименте демонстрируется индукция между катушками провода: жидкая батарея (справа) создает ток, протекающий сквозь небольшую катушку (А), формируя магнитное поле. Если катушки лишены движения, ток не индуцируется. Если же катушка смещается из/в более крупную (B ), то магнитный поток изменится и создаст ток, который проявит себя в гальванометре

Дифференциальная форма закона Фарадея

Магнитный поток , где – векторная площадь над замкнутой поверхностью S. Устройство, способное поддерживать разность потенциалов, несмотря на токовые потоки, выступает источником ЭДС. В математическом виде: , где интеграл характеризуется по замкнутой петле C.

Закон Фарадея теперь можно переписать: . Используя теорему Стокса в векторном исчислении, левая часть приравнивается к

В правой части . Поэтому мы получаем альтернативную форму закона индукции Фарадея: .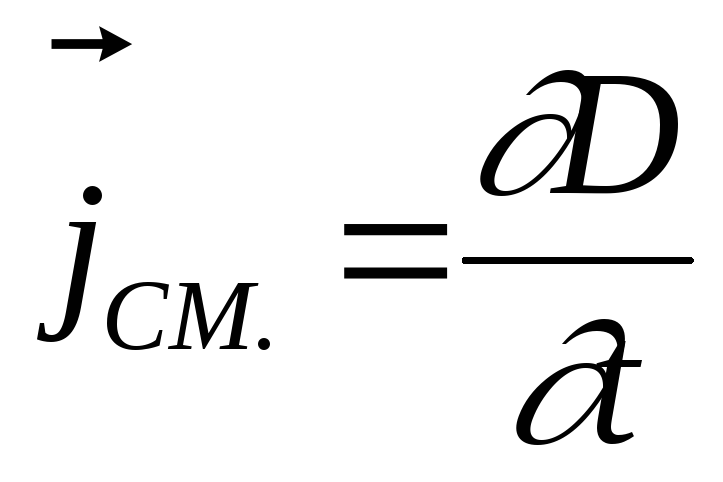 Ее также именуют дифференциальной формой закона Фарадея. Это одно из четырех уравнений Максвелла, контролирующих все электромагнитные явления.

Если в магнитном поле находится замкнутый проводящий контур, не содержащий источников тока, то при изменении магнитного поля в контуре возникает электрический ток. Это явление называется электромагнитной индукцией. Появление тока свидетельствует о возникновении в контуре электрического поля, которое может обеспечить замкнутое движение электрических зарядов или, другими словами, о возникновении ЭДС. Электрическое поле, которое возникает при изменении поля магнитного и работа которого при перемещении зарядов по замкнутому контуру не равна нулю, имеет замкнутые силовые линии и называется вихревым.

Для количественного описания электромагнитной индукции вводится понятие магнитного потока (или потока вектора магнитной индукции) через замкнутый контур. Для плоского контура, расположенного в однородном магнитном поле (а только такие ситуации и могут встретиться школьникам на едином государственном экзамене), магнитный поток определяется как

где — индукция поля, — площадь контура, — угол между вектором индукции и нормалью (перпендикуляром) к плоскости контура (см. рисунок; перпендикуляр к плоскости контура показан пунктиром). Единицей магнитного потока в международной системе единиц измерений СИ является Вебер (Вб), который определяется как магнитный поток через контур площади 1 м 2 однородного магнитного поля с индукцией 1 Тл, перпендикулярной плоскости контура.

Величина ЭДС индукции , возникающая в контуре при изменении магнитного потока через этот контур, равна скорости изменения магнитного потока

Здесь — изменение магнитного потока через контур за малый интервал времени . Важным свойством закона электромагнитной индукции (23.2) является его универсальность по отношению к причинам изменения магнитного потока: магнитный поток через контур может меняться из-за изменения индукции магнитного поля, изменения площади контура или изменения угла между вектором индукции и нормалью, что происходит при вращении контура в поле. Во всех этих случаях по закону (23.2) в контуре будет возникать ЭДС индукции и индукционный ток.

Знак минус в формуле (23.2) «отвечает» за направление тока, возникающего в результате электромагнитной индукции (правило Ленца). Однако понять на языке закона (23.2), к какому направлению индукционного тока приведет этот знак при том или ином изменении магнитного потока через контур, не так-то просто. Но достаточно легко запомнить результат: индукционный ток будет направлен таким образом, что созданное им магнитное поле будет «стремиться» компенсировать то изменение внешнего магнитного поля, которое этот ток и породило. Например, при увеличении потока внешнего магнитного поля через контур в нем возникнет индукционный ток, магнитное поле которого будет направлено противоположно внешнему магнитному полю так, чтобы уменьшить внешнее поле и сохранить, таким образом, первоначальную величину магнитного поля. При уменьшении потока поля через контур поле индукционного тока будет направлено так же, как и внешнее магнитное поле.

Если в контуре с током ток в силу каких-то причин изменяется, то изменяется и магнитный поток через контур того магнитного поля, которое создано самим этим током. Тогда по закону (23.2) в контуре должна возникать ЭДС индукции. Явление возникновения ЭДС индукции в некоторой электрической цепи в результате изменения тока в самой этой цепи называется самоиндукцией. Для нахождения ЭДС самоиндукции в некоторой электрической цепи необходимо вычислить поток магнитного поля, создаваемого этой цепью через нее саму. Такое вычисление представляет собой сложную проблему из-за неоднородности магнитного поля. Однако одно свойство этого потока является очевидным. Поскольку магнитное поле, создаваемого током в цепи, пропорционально величине тока, то и магнитный поток собственного поля через цепь пропорционален току в этой цепи

где — сила тока в цепи, — коэффициент пропорциональности, который характеризует «геометрию» цепи, но не зависит от тока в ней и называется индуктивностью этой цепи. Единицей индуктивности в международной системе единиц СИ является Генри (Гн). 1 Гн определяется как индуктивность такого контура, поток индукции собственного магнитного поля через который равен 1 Вб при силе тока в нем 1 А. С учетом определения индуктивности (23.3) из закона электромагнитной индукции (23.2) получаем для ЭДС самоиндукции

Благодаря явлению самоиндукции ток в любой электрической цепи обладает определенной «инерционностью» и, следовательно, энергией. Действительно, для создания тока в контуре необходимо совершить работу по преодолению ЭДС самоиндукции. Энергия контура с током и равна этой работе. Необходимо запомнить формулу для энергии контура с током

где — индуктивность контура, — сила тока в нем.

Явление электромагнитной индукции широко применяется в технике. На нем основано создание электрического тока в электрических генераторах и электростанциях. Благодаря закону электромагнитной индукции происходит преобразование механических колебаний в электрические в микрофонах. На основе закона электромагнитной индукции работает, в частности, электрическая цепь, которая называется колебательным контуром (см.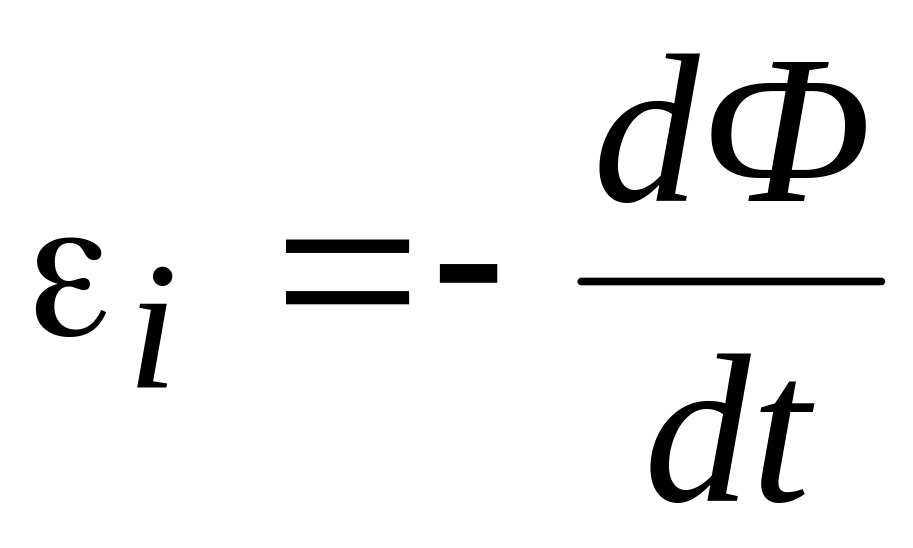 следующую главу), и которая является основой любой радиопередающей или радиопринимающей техники.

Рассмотрим теперь задачи.

Из перечисленных в задаче 23.1.1 явлений только одно есть следствие закона электромагнитной индукции — появление тока в кольце при проведении сквозь него постоянного магнита (ответ 3 ). Все остальное — результат магнитного взаимодействия токов.

Как указывалось во введении к настоящей главе, явление электромагнитной индукции лежит в основе работы генератора переменного тока (задача 23.1.2 ), т.е. прибора, создающего переменный ток, заданной частоты (ответ 2 ).

Индукция магнитного поля, создаваемого постоянным магнитом, уменьшается с увеличением расстояния до него. Поэтому при приближении магнита к кольцу (задача 23.1.3 ) поток индукции магнитного поля магнита через кольцо изменяется, и в кольце возникает индукционный ток. Очевидно, это будет происходить при приближении магнита к кольцу и северным, и южным полюсом. А вот направление индукционного тока в этих случаях будет различным. Это связано с тем, что при приближении магнита к кольцу разными полюсами, поле в плоскости кольца в одном случае будет направлено противоположно полю в другом. Поэтому для компенсации этих изменений внешнего поля магнитное поле индукционного тока должно быть в этих случаях направлено по-разному. Поэтому и направления индукционных токов в кольце будут противоположными (ответ 4 ).

Для возникновения ЭДС индукции в кольце необходимо, чтобы менялся магнитный поток через кольцо. А поскольку магнитная индукция поля магнита зависит от расстояния до него, то в рассматриваемом в задаче 23.1.4 случае поток через кольцо будет меняться, в кольце возникнет индукционный ток (ответ 1 ).

При вращении рамки 1 (задача 23.1.5 ) угол между линиями магнитной индукции (а, значит, и вектором индукции) и плоскостью рамки в любой момент времени равен нулю. Следовательно, магнитный поток через рамку 1 не изменяется (см. формулу (23.1)), и индукционный ток в ней не возникает. В рамке 2 индукционный ток возникнет: в положении показанном на рисунке, магнитный поток через нее равен нулю, когда рамка повернется на четверть оборота — будет равен , где — индукция, — площадь рамки. Еще через четверть оборота поток снова будет равен нулю и т.д. Поэтому поток магнитной индукции через рамку 2 изменяется в процессе ее вращения, следовательно, в ней возникает индукционный ток (ответ 2 ).

В задаче 23.1.6 индукционный ток возникает только в случае 2 (ответ 2 ). Действительно, в случае 1 рамка при движении остается на одном и том же расстоянии от проводника, и, следовательно, магнитное поле, созданное этим проводником в плоскости рамки, не изменяется. При удалении рамки от проводника магнитная индукция поля проводника в области рамки изменяется, меняется магнитный поток через рамку, и возникает индукционный ток

В законе электромагнитной индукции утверждается, что индукционный ток в кольце будет течь в такие моменты времени, когда изменяется магнитный поток через это кольцо. Поэтому пока магнит покоится около кольца (задача 23.1.7 ) индукционный ток в кольце течь не будет. Поэтому правильный ответ в этой задаче — 2 .

Согласно закону электромагнитной индукции (23.2) ЭДС индукции в рамке определяется скоростью изменения магнитного потока через нее. А поскольку по условию задачи 23.1.8 индукция магнитного поля в области рамки изменяется равномерно, скорость ее изменения постоянна, величина ЭДС индукции не изменяется в процессе проведения опыта (ответ 3 ).

В задаче 23.1.9 ЭДС индукции, возникающая в рамке во втором случае, вчетверо больше ЭДС индукции, возникающей в первом (ответ 4 ). Это связано с четырехкратным увеличением площади рамки и, соответственно, магнитного потока через нее во втором случае.

В задаче 23.1.10 во втором случае в два раза увеличивается скорость изменения магнитного потока (индукция поля меняется на ту же величину, но за вдвое меньшее время). Поэтому ЭДС электромагнитной индукции, возникающая в рамке во втором случае, в два раза больше, чем в первом (ответ 1 ).

При увеличении тока в замкнутом проводнике в два раза (задача 23.2.1 ), величина индукции магнитного поля возрастет в каждой точке пространства в два раза, не изменившись по направлению. Поэтому ровно в два раза изменится магнитный поток через любую малую площадку и, соответственно, и весь проводник (ответ 1 ). А вот отношение магнитного потока через проводник к току в этом проводнике, которое и представляет собой индуктивность проводника , при этом не изменится (задача 23.2.2 — ответ 3 ).

Используя формулу (23.3) находим в задаче 32.2.3 Гн (ответ 4 ).

Связь между единицами измерений магнитного потока, магнитной индукции и индуктивности (задача 23.2.4 ) следует из определения индуктивности (23.3): единица магнитного потока (Вб) равна произведению единицы тока (А) на единицу индуктивности (Гн) — ответ 3 .

Согласно формуле (23.5) при двукратном увеличении индуктивности катушки и двукратном уменьшении тока в ней (задача 23.2.5 ) энергия магнитного поля катушки уменьшится в 2 раза (ответ 2 ).

Когда рамка вращается в однородном магнитном поле, магнитный поток через рамку меняется из-за изменения угла между перпендикуляром к плоскости рамки и вектором индукции магнитного поля. А поскольку и в первом и втором случае в задаче 23.2.6 этот угол меняется по одному и тому же закону (по условию частота вращения рамок одинакова), то ЭДС индукции меняются по одному и тому же закону, и, следовательно, отношение амплитудных значений ЭДС индукции в рамках равно единице (ответ 2 ).

Магнитное поле, создаваемое проводником с током в области рамки (задача 23.2.7 ), направлено «от нас» (см. решение задач главы 22). Величина индукции поля провода в области рамки при ее удалении от провода будет уменьшаться. Поэтому индукционный ток в рамке должен создать магнитное поле, направленное внутри рамки «от нас». Используя теперь правило буравчика для нахождения направления магнитной индукции, заключаем, что индукционный ток в рамке будет направлен по часовой стрелке (ответ 1 ).

При увеличении тока в проводе будет возрастать созданное им магнитное поле и в рамке возникнет индукционный ток (задача 23.2.8 ). В результате возникнет взаимодействие индукционного тока в рамке и тока в проводнике. Чтобы найти направление этого взаимодействия (притяжение или отталкивание) можно найти направление индукционного тока, а затем по формуле Ампера силу взаимодействия рамки с проводом. Но можно поступить и по-другому, используя правило Ленца. Все индукционные явления должны иметь такое направление, чтобы компенсировать вызывающую их причину. А поскольку причина — увеличение тока в рамке, сила взаимодействия индукционного тока и провода должна стремиться уменьшить магнитный поток поля провода через рамку. А поскольку магнитная индукция поля провода убывает с увеличением расстояния до него, то эта сила будет отталкивать рамку от провода (ответ 2 ). Если бы ток в проводе убывал, то рамка притягивалась бы к проводу.

Задача 23.2.9 также связана с направлением индукционных явлений и правилом Ленца. При приближении магнита к проводящему кольцу в нем возникнет индукционный ток, причем направление его будет таким, чтобы компенсировать вызывающую его причину. А поскольку эта причина — приближение магнита, кольцо будет отталкиваться от него (ответ 2 ). Если магнит отодвигать от кольца, то по тем же причинам возникло бы притяжение кольца к магниту.

Задача 23.2.10 — единственная вычислительная задача в этой главе. Для нахождения ЭДС индукции нужно найти изменение магнитного потока через контур . Это можно сделать так. Пусть в некоторый момент времени перемычка находилась в положении, показанном на рисунке, и пусть прошел малый интервал времени . За этот интервал времени перемычка переместится на величину . Это приведет к увеличению площади контура на величину . Поэтому изменение магнитного потока через контур будет равно , а величина ЭДС индукции (ответ 4 ).

На картинке показано однородное магнитное поле. Однородное означает одинаковое во всех точках в данном объеме. В поле помещена поверхность с площадью S. Линии поля пересекают поверхность.

Определение магнитного потока :

Магнитным потоком Ф через поверхность S называют количество линий вектора магнитной индукции B, проходящих через поверхность S.

Формула магнитного потока:

здесь α — угол между направлением вектора магнитной индукции B и нормалью к поверхности S.

Из формулы магнитного потока видно, что максимальным магнитный поток будет при cos α = 1, а это случится, когда вектор B параллелен нормали к поверхности S. Минимальным магнитный поток будет при cos α = 0, это будет, когда вектор B перпендикулярен нормали к поверхности S, ведь в этом случае линии вектора B будут скользить по поверхности S, не пересекая её.

А по определению магнитного потока учитываются только те линии вектора магнитной индукции, которые пересекают данную поверхность.

Измеряется магнитный поток в веберах (вольт-секундах): 1 вб = 1 в * с. Кроме того, для измерения магнитного потока применяют максвелл: 1 вб = 10 8 мкс. Соответственно 1 мкс = 10 -8 вб.

Магнитный поток является скалярной величиной.

ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ ТОКА

Вокруг проводника с током существует магнитное поле, которое обладает энергией. Откуда она берется? Источник тока, включенный в эл.цепь, обладает запасом энергии. В момент замыкания эл.цепи источник тока расходует часть своей энергии на преодоление действия возникающей ЭДС самоиндукции. Эта часть энергии, называемая собственной энергией тока, и идет на образование магнитного поля. Энергия магнитного поля равна собственной энергии тока. Собственная энергия тока численно равна работе, которую должен совершить источник тока для преодоления ЭДС самоиндукции, чтобы создать ток в цепи.

Энергия магнитного поля, созданного током, прямо пропорциональна квадрату силы тока. Куда пропадает энергия магнитного поля после прекращения тока? — выделяется (при размыкании цепи с достаточно большой силой тока возможно возникновение искры или дуги)

4.1. Закон электромагнитной индукции. Самоиндукция. Индуктивность

Основные формулы

· Закон электромагнитной индукции (закон Фарадея):

, (39)

где – эдс индукции;– полный магнитный поток (потокосцепление).

· Магнитный поток, создаваемый током в контуре,

где – индуктивность контура;– сила тока.

· Закон Фарадея применительно к самоиндукции

· Эдс индукции, возникающая при вращении рамки с током в магнитном поле,

где – индукция магнитного поля;– площадь рамки;– угловая скорость вращения.

· Индуктивность соленоида

, (43)

где – магнитная постоянная;– магнитная проницаемость вещества;– число витков соленоида;– площадь сечения витка;– длина соленоида.

· Сила тока при размыкании цепи

где – установившаяся в цепи сила тока;– индуктивность контура,– сопротивление контура;– время размыкания.

· Сила тока при замыкании цепи

. (45)

· Время релаксации

Примеры решения задач

Пример 1.

Магнитное поле изменяется по закону , где= 15 мТл,. В магнитное поле помещен круговой проводящий виток радиусом = 20 см под угломк направлению поля (в начальный момент времени). Найти эдс индукции, возникающую в витке в момент времени= 5 с.

Решение

По закону электромагнитной индукции возникающая в витке эдс индукции , где– магнитный поток, сцепленный в витке.

где – площадь витка,;– угол между направлением вектора магнитной индукциии нормалью к контуру:.

Подставим числовые значения: = 15 мТл,,= 20 см = = 0,2 м,.

Вычисления дают .

Пример 2 В однородном магнитном поле с индукцией = 0,2 Тл расположена прямоугольная рамка, подвижная сторона которой длиной= 0,2 м перемещается со скоростью= 25 м/с перпендикулярно линиям индукции поля (рис. 42). Определить эдс индукции, возникающую в контуре. Решение При движении проводника АВ в магнитном поле площадь рамки увеличивается, следовательно, возрастает магнитный поток сквозь рамку и возникает эдс индукции.

По закону Фарадея , где, тогда, но, поэтому.

Знак «–» показывает, что эдс индукции и индукционный ток направлены против часовой стрелки.

САМОИНДУКЦИЯ

Каждый проводник, по которому протекает эл.ток, находится в собственном магнитном поле.

При изменении силы тока в проводнике меняется м.поле, т.е. изменяется магнитный поток, создаваемый этим током. Изменение магнитного потока ведет в возникновению вихревого эл.поля и в цепи появляется ЭДС индукции. Это явление называется самоиндукцией.Самоиндукция — явление возникновения ЭДС индукции в эл.цепи в результате изменения силы тока. Возникающая при этом ЭДС называется ЭДС самоиндукции

Проявление явления самоиндукции

Замыкание цепи При замыкании в эл.цепи нарастает ток, что вызывает в катушке увеличение магнитного потока, возникает вихревое эл.поле, направленное против тока, т.е. в катушке возникает ЭДС самоиндукции, препятствующая нарастанию тока в цепи (вихревое поле тормозит электроны). В результатеЛ1 загорается позже, чем Л2.

Размыкание цепи При размыкании эл.цепи ток убывает, возникает уменьшение м.потока в катушке, возникает вихревое эл.поле, направленное как ток (стремящееся сохранить прежнюю силу тока) , т.е. в катушке возникает ЭДС самоиндукции, поддерживающая ток в цепи. В результате Л при выключении ярко вспыхивает. Вывод в электротехнике явление самоиндукции проявляется при замыкании цепи (эл.ток нарастает постепенно) и при размыкании цепи (эл.ток пропадает не сразу).

ИНДУКТИВНОСТЬ

От чего зависит ЭДС самоиндукции? Эл.ток создает собственное магнитное поле. Магнитный поток через контур пропорционален индукции магнитного поля (Ф ~ B), индукция пропорциональна силе тока в проводнике (B ~ I), следовательно магнитный поток пропорционален силе тока (Ф ~ I). ЭДС самоиндукции зависит от скорости изменения силы тока в эл.цепи, от свойств проводника (размеров и формы) и от относительной магнитной проницаемости среды, в которой находится проводник. Физическая величина, показывающая зависимость ЭДС самоиндукции от размеров и формы проводника и от среды, в которой находится проводник, называется коэффициентом самоиндукции или индуктивностью. Индуктивность — физ. величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1Ампер за 1 секунду. Также индуктивность можно рассчитать по формуле:

где Ф — магнитный поток через контур, I — сила тока в контуре.

Единицы измерения индуктивности в системе СИ:

Индуктивность катушки зависит от: числа витков, размеров и формы катушки и от относительной магнитной проницаемости среды (возможен сердечник).

ЭДС САМОИНДУКЦИИ

ЭДС самоиндукции препятствует нарастанию силы тока при включении цепи и убыванию силы тока при размыкании цепи.

Для характеристики намагниченности вещества в магнитном поле используетсямагнитный момент (Р м ). Он численно равен механическому моменту, испытываемому веществом в магнитном поле с индукцией в 1 Тл.

Магнитный момент единицы объема вещества характеризует его намагниченность — I , определяется по формуле:

I = Р м /V , (2.4)

где V — объем вещества.

Намагниченность в системе СИ измеряется, как и напряженность, в А/м , величина векторная.

Магнитные свойства веществ характеризуются объемной магнитной восприимчивостью — c о , величина безразмерная.

Если какое-либо тело поместить в магнитное поле с индукцией В 0 , то происходит его намагничивание. Вследствие этого тело создает свое собственное магнитное поле с индукцией В » , которое взаимодействует с намагничивающим полем.

В этом случае вектор индукции в среде (В) будет слагаться из векторов:

В = В 0 + В » (знак вектора опущен), (2.5)

где В » — индукция собственного магнитного поля намагнитившегося вещества.

Индукция собственного поля определяется магнитными свойствами вещества, которые характеризуются объемной магнитной восприимчивостью — c о , справедливо выражение:В » = c о В 0 (2.6)

Разделим на m 0 выражение (2.6):

В » / m о = c о В 0 /m 0

Получим: Н » = c о Н 0 , (2.7)

но Н » определяет намагниченность вещества I , т.е. Н » = I , тогда из (2.7):

I = c о Н 0 . (2.8)

Таким образом, если вещество находится во внешнем магнитном поле с напряженностьюН 0 , то внутри него индукция определяется выражением:

В=В 0 + В » = m 0 Н 0 +m 0 Н » = m 0 (Н 0 + I) (2.9)

Последнее выражение строго справедливо, когда сердечник (вещество) находится полностью во внешнем однородном магнитном поле (замкнутый тор, бесконечно длинный соленоид и т.д.).

МАГНИТНОЕ ПОЛЕ

Магнитное взаимодействие движущихся электрических зарядов согласно представлениям теории поля объясняется следующим образом: всякий движущийся электрический заряд создает в окружающем пространстве магнитное поле, способное действовать на другие движущиеся электрические заряды.

В — физическая величина, являющаяся силовой характеристикой магнитного поля. Она называется магнитной индукцией (или индукцией магнитного поля).

Магнитная индукция — векторная величина. Модуль вектора магнитной индукции равен отношению максимального значения силы Ампера, действующей на прямой проводник с током, к силе тока в проводнике и его длине:

Единица магнитной индукции . В Международной системе единиц за единицу магнитной индукции принята индукция такого магнитного поля, в котором на каждый метр длины проводника при силе тока 1 А действует максимальная сила Ампера 1 Н. Эта единица называется тесла (сокращенно: Тл), в честь выдающегося югославского физика Н. Тесла:

СИЛА ЛОРЕНЦА

Движение проводника с током в магнитном поле показывает, что магнитное поле действует на движущиеся электрические заряды. На проводник действует сила Ампера F А = IBlsin a , а сила Лоренца действует на движущийся заряд:

где a — угол между векторами B и v .

Движение заряженных частиц в магнитном поле. В однородном магнитном поле на заряженную частицу, движущуюся со скоростью перпендикулярно линиям индукции магнитного поля, действует сила м, постоянная по модулю и направленная перпендикулярно вектору скорости.Под действием магнитной силы частица приобретает ускорение, модуль которого равен:

В однородном магнитном поле эта частица движется по окружности. Радиус кривизны траектории, по которой движется частица, определяется из условияоткуда следует,

Радиус кривизны траектории является величиной постоянной, поскольку сила, перпендикулярная вектору скорости, меняется только ее направление, но не модуль. А это и означает, что данная траектория является окружностью.

Период обращения частицы в однородном магнитном поле равен:

Последнее выражение показывает, что период обращения частицы в однородном магнитном поле не зависит от скорости и радиуса траектории ее движения.

Если напряженность электрического поля равна нулю, то сила Лоренца л равна магнитной силе м:

ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ

Явление электромагнитной индукции открыл Фарадей, который установил, что в замкнутом проводящем контуре возникает электрический ток при любом изменении магнитного поля, пронизывающего контур.

МАГНИТНЫЙ ПОТОК

Магнитный поток Ф (поток магнитной индукции) через поверхность площадью S — величина, равная произведению модуля вектора магнитной индукции на площадь S и косинус угла а между вектором и нормалью к поверхности:

Ф=BScos

В СИ единица магнитного потока 1 Вебер (Вб) — магнитный поток через поверхность площадью 1 м 2 , расположенную перпендикулярно направлению однородного магнитного поля, индукция которого равна 1 Тл:

Электромагнитная индукция -явление возникновения электрического тока в замкнутом проводящем контуре при любом изменении магнитного потока, пронизывающего контур.

Возникающий в замкнутом контуре, индукционный ток имеет такое направление, что своим магнитным полем противодействует тому изменению магнитного потока, которым он вызван (правило Ленца).

ЗАКОН ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ

Опыты Фарадея показали, что сила индукционного тока I i в проводящем контуре прямо пропорциональна скорости изменения числа линий магнитной индукции, пронизывающих поверхность, ограниченную этим контуром.

Поэтому сила индукционного тока пропорциональна скорости изменения магнитного потока через поверхность, ограниченную контуром:

Известно, что если в цепи появился ток, это значит, что на свободные заряды проводника действуют сторонние силы. Работа этих сил по перемещению единичного заряда вдоль замкнутого контура называется электродвижущей силой (ЭДС). Найдем ЭДС индукции ε i .

По закону Ома для замкнутой цепи

Так как R не зависит от , то

ЭДС индукции совпадает по направлению с индукционным током, а этот ток в соответствии с правилом Ленца направлен так, что созданный им магнитный поток противодействует изменению внешнего магнитного потока.

Закон электромагнитной индукции

ЭДС индукции в замкнутом контуре равна взятой с противоположным знаком скорости изменения магнитного потока, пронизывающего контур:

САМОИНДУКЦИЯ. ИНДУКТИВНОСТЬ

Опыт показывает, что магнитный поток Ф , связанный с контуром, прямо пропорционален силе тока в этом контуре:

Ф = L*I .

Индуктивность контура L — коэффициент пропорциональности между проходящим по контуру током и созданным им магнитным потоком.

Индуктивность проводника зависит от его формы, размеров и свойств окружающей среды.

Самоиндукция — явление возникновения ЭДС индукции в контуре при изменении магнитного потока, вызванном изменением тока, проходящего через сам контур.

Самоиндукция — частный случай электромагнитной индукции.

Индуктивность — величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока в нем на единицу за единицу времени. В СИ за единицу индуктивности принимают индуктивность такого проводника, в котором при изменении силы тока на 1 А за 1 с возникает ЭДС самоиндукции 1 В. Эта единица называется генри (Гн):

ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ

Явление самоиндукции аналогично явлению инерции. Индуктивность при изменении тока играет ту же роль, что и масса при изменении скорости тела. Аналогом скорости является сила тока.

Значит энергию магнитного поля тока можно считать величиной, подобной кинетической энергии тела :

Предположим, что после отключения катушки от источника,ток в цепи убывает со временем по линейному закону.

ЭДС самоиндукции имеет в этом случае постоянное значение:

где I — начальное значение тока, t — промежуток времени, за который сила тока убывает от I до 0.

За время t в цепи проходит электрический заряд q = I cp t . Так как I cp = (I + 0)/2 = I/2 , то q=It/2 . Поэтому работа электрического тока:

Эта работа совершается за счет энергии магнитного поля катушки. Таким образом, снова получаем:

Пример. Определите энергию магнитного поля катушки, в которой при токе 7,5 А магнитный поток равен 2,3*10 -3 Вб. Как изменится энергия поля, если сила тока уменьшиться вдвое?

Энергия магнитного поля катушки W 1 = LI 1 2 /2. По определению, индуктивность катушки L = Ф/I 1 . Следовательно,

Ответ: энергия поля равна 8,6 Дж; при уменьшении тока вдвое она уменьшится в 4 раза.

Физика — 11

Из вышесказанного становится ясно, что возникающий в контуре собственный магнитный поток прямо пропорционален силе проходящего через контур тока — Ф~I или:

Ф = LI. (1)

Здесь L является коэффициентом пропорциональности (между Ф и I) и называется индуктивностью контура (катушки).

Индуктивность зависит от геометрических размеров контура (катушки), от магнитной проницаемости среды внутри него, от числа витков. Она не зависит от силы тока в контуре и магнитного потока.

Индуктивность — скалярная величина, единица ее измерения в СИ названа генри (1 Гн), в честь американского ученого Джозефа Генри:

[L] = [Ф]I 
[  ] = 1 Вб
A = 1 Гн.

• 1 Гн — индуктивность такого контура (катушки), в которой при силе тока 1А через контур проходит собственный магнитный поток 1 Вб.

Если учесть выражение (1) в законе электромагнитной индукции, то получим, что ЭДС самоиндукции прямо пропорциональна скорости изменения силы тока, проходящего через контур:

ε_is = — ΔФt
  Δ      = — Δ(LI)
Δt = —L ΔI
Δt. (2)

Здесь ε_is — ЭДС самоиндукции, ΔI
Δt — скорость изменения силы тока в контуре.

Энергия магнитного поля. Согласно закону сохранения энергии, работа, совершенная при создании ЭДС индукции, будет равна энергии магнитного поля, создавшего его. Для определения этой энергии удобно воспользоваться схожестью явления самоиндукции с явлением инерции. Так, индуктивность L играет такую же роль при изменениях силы тока I в электромагнитных процессах, какую играет масса m — при изменениях скорости υ в механических процессах. Тогда для энергии магнитного поля, создаваемого контуром в электромагнитных явлениях, можно принять выражение, аналогичное выражению кинетической энергии тела в механических явлениях:

W_m = LI²
2. (3)

Если в этом выражении учесть формулу (1), получим ещё две формулы для энергии магнитного поля:

W_m = Ф²L
2     = ФI
2. (4)

Из теоретических вычислений получено, что плотность энергии магнитного поля прямо пропорциональна квадрату магнитной индукции и обратно пропорциональна магнитным свойствам среды:

W_m = B² μ₀ μ
2        . (5)

Здесь μ₀ — магнитная постоянная: μ₀ = 4π • 10^-7Гн
м.

Закон Фарадея

Концепция закона Фарадея состоит в том, что любое изменение магнитной среды катушки с проволокой вызывает в катушке «индуцированное» напряжение (ЭДС). Независимо от того, как производится изменение, напряжение будет генерироваться. Изменение может быть произведено изменением напряженности магнитного поля, перемещением магнита по направлению к катушке или от нее, перемещением катушки в магнитное поле или из него, вращением катушки относительно магнита и т. Д.

Слева вверху на иллюстрации две катушки пронизаны изменяющимся магнитным полем.Магнитный поток F определяется как F = BA, где B — магнитное поле или среднее магнитное поле, а A — площадь, перпендикулярная магнитному полю. Обратите внимание, что для данной скорости изменения потока через катушку генерируемое напряжение пропорционально количеству витков N, через которые проходит поток. Этот пример относится к работе трансформаторов, где магнитный поток обычно следует за железным сердечником от первичной катушки ко вторичной катушке и генерирует вторичное напряжение, пропорциональное количеству витков во вторичной катушке.

По часовой стрелке второй пример показывает напряжение, генерируемое при перемещении катушки в магнитное поле. Иногда это называют «ЭДС движения», и она пропорциональна скорости, с которой катушка перемещается в магнитное поле. Эта скорость может быть выражена через скорость изменения области, находящейся в магнитном поле.

Следующий пример — это стандартная геометрия генератора переменного тока, в которой катушка с проволокой вращается в магнитном поле. Вращение изменяет перпендикулярную площадь катушки по отношению к магнитному полю и генерирует напряжение, пропорциональное мгновенной скорости изменения магнитного потока.При постоянной скорости вращения генерируемое напряжение является синусоидальным.

Последний пример показывает, что напряжение можно генерировать, перемещая магнит по направлению к катушке с проволокой или от нее. При постоянной площади изменяющееся магнитное поле вызывает генерируемое напряжение. Направление или «чувство» генерируемого напряжения таково, что любой результирующий ток создает магнитное поле, противодействующее изменению магнитного поля, которое его создало. Это значение знака минус в законе Фарадея, и это называется законом Ленца.

Закон индукции Фарадея | физика

Закон индукции Фарадея в физике количественная связь между изменяющимся магнитным полем и электрическим полем, создаваемым этим изменением, разработанный на основе экспериментальных наблюдений, сделанных в 1831 году английским ученым Майклом Фарадеем.

Явление, называемое электромагнитной индукцией, было впервые замечено и исследовано Фарадеем; закон индукции — это его количественное выражение.Фарадей обнаружил, что всякий раз, когда магнитное поле вокруг электромагнита возрастает и схлопывается за счет замыкания и размыкания электрической цепи, частью которой он является, электрический ток может быть обнаружен в отдельном проводнике поблизости. Перемещение постоянного магнита в катушку с проволокой и из нее также индуцировало ток в проволоке, пока магнит находился в движении. При перемещении проводника рядом с неподвижным постоянным магнитом в проводе также протекал ток, пока он двигался.

Подробнее по этой теме

Электромагнетизм: закон индукции Фарадея

Открытие Фарадеем в 1831 году явления магнитной индукции — одна из важнейших вех на пути к пониманию и…

Фарадей визуализировал магнитное поле как состоящее из множества линий индукции, вдоль которых будет указывать небольшой магнитный компас. Совокупность линий, пересекающих данную область, называется магнитным потоком. Таким образом, электрические эффекты были объяснены Фарадеем изменяющимся магнитным потоком. Несколькими годами позже шотландский физик Джеймс Клерк Максвелл предположил, что фундаментальным эффектом изменения магнитного потока является создание электрического поля не только в проводнике (где он может приводить в движение электрический заряд), но и в космосе даже при отсутствии электрического поля. обвинения.Максвелл сформулировал математическое выражение, связывающее изменение магнитного потока с наведенной электродвижущей силой ( E, или ЭДС ). Это соотношение, известное как закон индукции Фарадея (чтобы отличить его от его законов электролиза), гласит, что величина ЭДС , индуцированная в цепи, пропорциональна скорости изменения магнитного потока, проходящего через цепь. Если скорость изменения магнитного потока выражается в единицах Веберов в секунду, наведенная ЭДС имеет единицы вольт.Закон Фарадея — одно из четырех уравнений Максвелла, определяющих теорию электромагнетизма.

Последней редакцией и обновлением этой статьи был Уильям Л. Хош.

Электромагнитная индукция — Обучение — ScienceFlip

Электромагнитная индукция — Learn

---

Электромагнитная индукция используется в двигателях и трансформаторах, которые будут изучены позже. В этом разделе рассматриваются как закон индукции Фарадея, так и закон Ленца.Эти законы важны для понимания электромагнитной индукции.

---

Фарадей провел множество исследований с магнитными полями и катушками из проволоки. В ходе одного расследования он обнаружил следующее:

• , если бы он переместил магнит в катушку, это вызвало бы ЭДС, что привело к возникновению тока в катушке
• , когда магнит был удален, можно было наблюдать тот же ток, но в противоположном направлении
• чем быстрее движется магнит в катушку, тем больше ток
• , если магнит удерживался неподвижно, а катушка двигалась, создавая такое же относительное движение, все наблюдения, приведенные выше, все еще наблюдались

Фарадей пришел к выводу, что неважно, двигается ли это магнит или катушка, именно изменение потока на индуцировало ЭДС, приводящую к любому наблюдаемому току.В дополнение к этому он обнаружил, что именно скорость изменения потока определяет величину любой ЭДС или тока.

---

Закон индукции Фарадея

Закон индукции Фарадея гласит: Индуцированная ЭДС в цепи равна по величине скорости, с которой магнитный поток, проходящий через цепь, изменяется со временем.

Закон Фарадея можно записать в виде уравнения:

где:

— наведенная ЭДС (в В)

— количество витков в катушке

— магнитный поток (в Вб)

— изменение во времени (с)

* примечание: отрицательный знак в уравнении сообщает нам направление наведенной ЭДС, которое будет обсуждаться позже.

---

Закон Ленца

Закон Ленца используется для определения направления индуцированного тока в результате наведенной ЭДС. Это также демонстрирует, как электромагнитная индукция подчиняется закону сохранения энергии.

Ленц открыл способ предсказать направление, в котором будет течь ток, в результате изменения магнитного поля вокруг проводника (провода, катушки, соленоида).

Закон Ленца можно сформулировать так: Индуцированная ЭДС всегда вызывает ток, который создает магнитное поле, которое противодействует первоначальному изменению потока через цепь.

Вспомните отрицательный знак в уравнении. Это отсылка к идее, что индуцированный ток создает поле, которое на противоположно к исходному полю.

При применении закона Ленца есть три шага, которые можно использовать для определения направления индуцированного тока:

1. В каком направлении изменяется магнитное поле?
2. В каком направлении магнитное поле будет противодействовать этому полю?
3. В каком направлении должен течь индуцированный ток, чтобы создать это поле?

---

Соленоиды и электромагнитная индукция

Напомним, что соленоид — это катушка из проводящего провода, которая создает магнитное поле, когда через него проходит ток.Соленоиды также могут использоваться для наведения токов в других соленоидах. У них также есть то преимущество, что они не требуют движущихся частей. Скорее они используют изменения тока для создания изменяющегося магнитного потока. На схеме ниже показана типичная установка, которая может использоваться для демонстрации электромагнитной индукции с помощью соленоидов:

---

Следующая анимация может использоваться для демонстрации электромагнитной индукции. Обратите внимание на разницу в наведенном токе при перемещении магнита с разной скоростью, изменении полярности магнитов, а также при использовании разных катушек.

---

Пример 1:

Используйте закон Ленца для определения направления индуцированного тока в каждом из приведенных ниже примеров:

Ответы: (следуя 3 шагам, описанным выше)

а) Направление магнитного поля через катушку увеличивается вниз. Магнитное поле, направленное вверх через катушку, будет противодействовать этому изменению. Используя правую ручку для захвата, пальцы, проходящие сквозь катушку вверх, показывают, что ток течет против часовой стрелки, если смотреть сверху.

б) Направление магнитного поля через катушку уменьшается и вверх. Магнитное поле, направленное вверх через катушку, будет противодействовать этому изменению. Используя правую ручку для захвата, пальцы, проходящие сквозь катушку вверх, показывают, что ток течет против часовой стрелки, если смотреть сверху.

c) Направление магнитного поля увеличивается в катушке / странице. Магнитное поле, направленное наружу через катушку / страницу, будет противодействовать этому изменению. Используя правую ручку для захвата, пальцы проходят сквозь катушку, показывая, что ток течет против часовой стрелки.

г) Направление магнитного поля убывает из катушки / страницы. Магнитное поле, направленное наружу через катушку / страницу, будет противодействовать этому изменению. Используя правую ручку для захвата, пальцы проходят сквозь катушку, показывая, что ток течет против часовой стрелки.

---

Пример 2:

На схеме ниже показана прямоугольная петля, движущаяся в магнитное поле силой 0,5 Тл внутрь страницы за интервал времени 0,1 с. Определите следующее:

а) Величина наведенной ЭДС в контуре?

б) В каком направлении ток течет по петле?

Ответы:

a) используя:

где:

*

* примечание: и поле параллельно нормали к площади катушки.

б) Направление магнитного поля увеличивается за пределы катушки / страницы. Магнитное поле, направленное внутрь через катушку / страницу, будет противодействовать этому изменению. Используя правую ручку для захвата пальцами через катушку, показывает, что ток течет по часовой стрелке.

Закон Фарадея — обзор

Пример 12.7

Прямоугольная петля, протянутая через поле B →

В предыдущем примере рассматривалась ситуация, когда изменение потока происходит из-за изменения поля во времени.Здесь мы рассматриваем ситуацию, когда поле постоянно во времени, но поток изменяется, потому что контур перемещается в область поля, так что площадь в поле изменяется. Таким образом, как на рисунке 12.13 (a), рассмотрим прямоугольную петлю (наша вторичная обмотка) с сопротивлением R , длиной a вдоль x и длиной l вдоль y . Он движется вдоль + x с постоянной скоростью v в области нулевого магнитного поля, пока не достигнет области однородного поля B , которая указывает на бумагу (-z∩).См. Рисунок 12.13 (а). Для конкретности возьмем B = 0,005 T, v = 2 м / с, l = 0,1 м и R = 0,1 Ом. (Если бы петлю просто бросили в поле, по закону Ленца петля замедлилась бы, поэтому необходима сила, чтобы петля двигалась с постоянной скоростью.) Найдите (а) магнитный поток, (б) ЭДС, (c) магнитная сила, действующая на петлю, и (d) мощность, необходимая для того, чтобы тянуть петлю с постоянной скоростью.

Рисунок 12.13. (а) Та же ситуация, что и на рисунке 12.11, но поподробнее. (b) Отношение цепи-нормальности для части (a).

Решение: Чтобы найти магнитную силу, мы должны решить одновременно и для тока, и для скорости. (a) Возьмите d A → = n∩d A из бумаги (чтобы ds → вращался против часовой стрелки, чтобы согласоваться с анализом ЭДС движения, показанным ранее), как на рисунке 12.13 (b). Тогда

(12,5) ΦB = ∫B → ⋅n∩dA = ∫ B → ⋅z∩dA = −B∫dA = −BA = −Blx

, когда петля входит в область поля. (b) Пусть v = dx / dt .Из-за движения скорость изменения потока определяется как

(12,6) dΦBdt = −Blv,

, где v = dx / dt . Это приводит к ЭДС

(12.7) ε− = dΦBdt = Blv

, которая циркулирует вдоль ds → :: против часовой стрелки, что согласуется с качественным анализом примера 12.4. Аналогичный анализ проводится при выходе петли из поля. В то время как в поле поток остается на постоянном значении Bla , поэтому наведенная ЭДС отсутствует.

Для наших значений B, l и v , (12.7) дает ε = (0,005 Тл) (0,1 м) (2 м / с) = 1,0 × 10 ⁻³ В. Принимая (12,7) за единственную действующую ЭДС, это вызывает ток

(12,8 ) I = εR = BlvR.

Для R = 0,1 Ом, (12,8) дает I = 1,0 × 10 ⁻³ В / 0,1 Ом = 0,01 А. (c) Соответствующая магнитная сила F → на правом плече получается из

(12,9) F → = I ∫ ds → × B →.

(Напомним, что I — индуцированный ток, а B → — приложенное поле.) Из (12.9), F → указывает налево, и из (12.9) и (12.7) он имеет звездную величину

(12.10) F = IlB = v (Bl) 2R.

В нашем случае F = (0,01 A) (0,1 м) (. 006 T ) = 6,0 × 10 ⁻⁶ Н. (d) Чтобы петля двигалась с постоянной скоростью v , внешняя сила (например, от нашей руки) величиной F должна быть приложена в противоположном направлении. Используя (12.10), эта внешняя сила обеспечивает мощность

(12.11) P = Fv = (vBl) 2R = (IR) 2R = I2R.

Это точно соответствует скорости джоулева нагрева.В нашем случае P = (0,01 A) ² (0,1 Ом) = 1,0 × 10 ⁻⁵ Вт. Таким образом, вся мощность, обеспечиваемая рукой ( Fv ), идет на нагрев ( I ² R ) проволоки. Это генерирование электрического тока за счет механической энергии означает, что контур представляет собой электрический генератор . Наконец, обратите внимание, что на верхние и нижние рычаги также действуют равные и противоположные силы, которые стремятся сжимать петлю, что согласуется с анализом закона Ленца в Примере 12.4. См. Рисунок 12.13 (а).

Формула магнитной индукции — CoolGyan.Org

Магнитная индукция была открыта Майклом Фарадеем в 1831 году. Позже Максвелл описал ее математически, и она стала известна как закон индукции Фарадея. Фарадей провел три эксперимента, чтобы понять электромагнитную индукцию. Затем закон Фарадея стал решающим для понимания индукции, которая теперь имеет несколько практических применений, например, в генераторах, трансформаторах и т. Д.

Закон магнитной индукции

Магнитная индукция, также называемая электромагнитной индукцией, относится к созданию напряжения (или ЭДС) на электрическом проводнике, помещенном в изменяющееся магнитное поле.Согласно закону Фарадея, для замкнутой цепи индуцированная электродвижущая сила равна скорости изменения магнитного потока, заключенного в цепи. Чтобы узнать больше о магнитной индукции, посетите страницу «Электромагнитная индукция».

Формула для магнитной индукции

Согласно закону Фарадея, ЭДС, индуцированная в замкнутой цепи, равна —

Здесь

— магнитный поток, t — время, — наведенная ЭДС.

Примечание:

Где B = магнитное поле, а ds — очень маленькая площадь.

В катушке с N витками ЭДС будет —

.

Позже, согласно закону Ленца, уравнение Фарадея было изменено соответствующим образом, которое теперь имеет вид —

Теперь это уравнение определяет направление индуцированного тока и подчиняется закону сохранения энергии.

Для подвижного проводника ЭДС определяется по формуле:

Где l = длина проводника, v = скорость проводника и θ — угол между магнитным полем и направлением движения.

Пример, связанный с магнитной индукцией, приведен ниже для лучшего понимания.

Решенных примеров

Пример 1:

Рассчитайте наведенную ЭДС, если магнитный поток, связанный с катушкой, изменяется с 12 x 10-3 Вт до 6 x 10-3 Вт за 0,01 секунды.

Решение:

Пример 2:

Длинный соленоид, имеющий 15 витков на см и небольшую площадь петли 2 см2, помещается в соленоид относительно его оси.Найдите наведенную ЭДС в контуре, когда ток, переносимый соленоидом, постоянно изменяется от 2,0 А до 4,0 А за 0,1 с.

Следите за обновлениями CoolGyan’S, чтобы увидеть больше таких интересных статей. Кроме того, зарегистрируйтесь в CoolGyan’S — Learning App, чтобы получать множество интерактивных увлекательных видеороликов по физике и неограниченную помощь в учебе.

Закон Фарадея | S-cool, сайт доработки

Для проводника в изменяющемся магнитном поле факторы, влияющие на размер наведенной ЭДС:

• Как быстро меняется магнитное поле;
• Количество витков или витков проводника в поле.

Это приводит к закону Фарадея, , который таков:

Индуцированная ЭДС равна скорости изменения магнитной индукционной связи или скорости сокращения магнитного потока

Самолет с размахом крыла 30 м летит через вертикальное поле напряженностью 5 x 10 ^-4 T. Рассчитайте ЭДС, наводимую на концах крыла, если его скорость = 150 мс ^-1 .

Ответ:

Вычислите площадь, которую каждую секунду выметают крылья.Умножьте это на напряженность поля B, и вы получите поток, исчезнувший за секунду.

Таким образом, каждую секунду выметается 2,25 Вт потока.

Этот метод приводит нас к более простому уравнению для ЭДС, индуцированной резкой флюса:

E = Blv

Где:

B = плотность магнитного потока, Тл

l = длина проводника, прорезающего поле, м

v = скорость, с которой проводник рассекает поле, м / с

Помните: ЭДС индуцирует только движение, перпендикулярное полю.

Катушка провода площадью 2 см ² , с 20 витками находится в магнитном поле. Магнитное поле изменяется от 20 Тл до 10 Тл за 2 секунды.

Какая ЭДС индуцируется в катушке с проволокой?

Ответ:

= 0,02 В

Что произойдет, если катушка вращается в магнитном поле?

Если катушка вращается в магнитном поле, поток через катушку изменяется, как на этом графике.

Поток через катушку наибольший, когда катушка перпендикулярна полю, и равна нулю, когда катушка параллельна полю. Если катушка продолжает вращаться, поток изменяется как синусоида.

Примечание: Магнитное поле должно быть , изменяя , чтобы вызвать ЭДС. Когда градиент графика магнитного поля равен нулю (например, вверху пиков и внизу впадин) магнитное поле не изменяется, поэтому ЭДС не индуцируется — проверьте график.

Магнитное поле изменяется наиболее быстро на крутых участках графика, когда оно пересекает ось x. Они производят максимальные значения ЭДС.

Итак, магнитное поле и наведенная ЭДС сдвинуты по фазе на 90 ° или π / 2 радиан (не в шаге). Этот принцип используется в генераторе переменного тока — генераторе переменного тока.

Если вы проведете проводник через магнитное поле, вы всегда индуцируете ЭДС!

Если имеется цепь , ЭДС проталкивает через нее ток.

Если нет цепи , вы все равно получите ЭДС, но не получите тока.

(PDF) О методе связи ЭДС и скорости изменения магнитного потока

Биография

Доктор Виджаякумар Х. Доддамани

Профессор

Кафедра физики

Бангалорский университет

Джнанабхаратхи

Кампус Майнкрафт

-56

Штат Карнатака

Индия

Д-р В.Х. Доддамани обучал аспирантов и докторантов последние 20 лет.Его исследования

областей включают активные галактические ядра, радиоастрономию, физику плазмы и т. Д. Под его руководством на докторскую степень работают несколько ученых

человек. Он опубликовал исследовательские работы в известных журналах и представил статьи на

национальных и международных конференциях. Он является членом нескольких ассоциаций и академических комитетов

, внося свой вклад в разработку лучших методик обучения и учебных программ. В настоящее время он участвует в разработке

экспериментов, связанных с радиоастрономией.

Равиша К.Х.

Факультет

Физический факультет

Технологический институт CMR

IT Park Road

Кундалахалли

Бангалор-37

Штат Карнатака

Индия

студентов инженерного факультета Равеисха Кундалахалли, штат Карнатака. последние 18 лет. В настоящее время он

занимается разработкой лабораторных экспериментов для студентов бакалавриата.Он проводит исследования в области радиоастрономии

в Бангалорском университете и Индийском институте астрофизики в Бангалоре. Его интересы

включают разработку экспериментов, связанных с электромагнетизмом.

Ссылки

[1] Майкл Фарадей, Фил. Пер. R. Soc. Лондон. 1832, 122, 125-162

[2] Оливер Хевисайд, Электромагнитная теория, Лондон, Челси, 1897

[3] Дэвид Дж. Гриффитс, Введение в электродинамику (3-е издание), Нью-Дели, Прентис

Зал Индии , 2004

[4] D.Ченг, Полевая и волновая электромагнетизм (2-е издание), Нью-Дели, Пирсон

Education (Индия), 2002

[5] Натан Ида, Engineering Electromagnetics (2-е издание), Нью-Дели, Спрингер (Индия),

1998

[6] D. Chattopadyay et al., Electricity and Magnetism, Calcutta, Central, 2006,

[7] Джон Д. Краус, Electromagnetics (3-е издание), Нью-Йорк, McGraw-Hill, 2001

[8] Дж. Д. Джексон, Классическая электродинамика (3-е издание), Нью-Дели, издание Wiley India,

2000

International Letters of Chemistry, Physics and Astronomy Vol.